| << Предыдущий параграф | Следующий параграф >> |
Пред.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
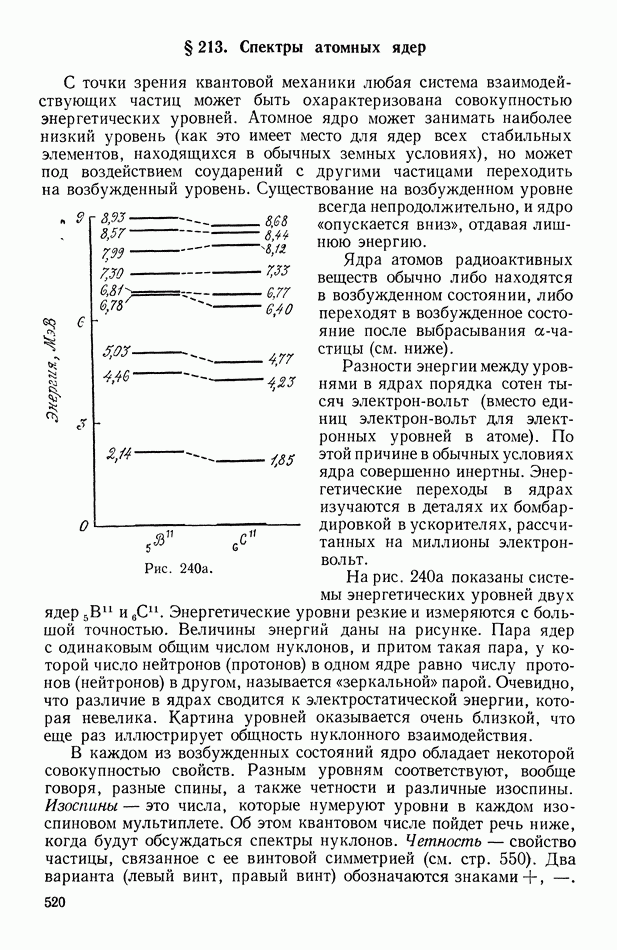
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
333
334
335
336
337
338
339
340
341
342
343
344
345
346
347
348
349
350
351
352
353
354
355
356
357
358
359
360
361
362
363
364
365
366
367
368
369
370
371
372
373
374
375
376
377
378
379
380
381
382
383
384
385
386
387
388
389
390
391
392
393
394
395
396
397
398
399
400
401
402
403
404
405
406
407
408
409
410
411
412
413
414
415
416
417
418
419
420
421
422
423
424
425
426
427
428
429
430
431
432
433
434
435
436
437
438
439
440
441
442
443
444
445
446
447
448
449
450
451
452
453
454
455
456
457
458
459
460
461
462
463
464
465
466
467
468
469
470
471
472
473
474
475
476
477
478
479
480
481
482
483
484
485
486
487
488
489
490
491
492
493
494
495
496
497
498
499
500
501
502
503
504
505
506
507
508
509
510
511
512
513
514
515
516
517
518
519
520
521
522
523
524
525
526
527
528
529
530
531
532
533
534
535
536
537
538
539
540
541
542
543
544
545
546
547
548
549
550
551
552
553
554
555
556
557
558
559
560
561
562
563
564
565
566
567
568
569
570
571
572
573
574
575
576
577
578
579
580
581
582
583
584
585
586
587
588
589
590
591
592
593
594
595
596
597
598
599
600
601
602
603
604
605
606
607
608
609
610
611
612
613
614
615
616
617
618
619
620
621
622
623
624
625
626
627
628
629
630
631
632
633
634
635
636
637
638
639
640
641
642
643
644
645
646
647
648
649
650
651
652
653
654
655
656
657
658
659
660
661
662
663
664
665
666
667
668
669
670
671
672
673
674
675
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 187. Электронное облако для s- и p-состояний
Состояние, характеризуемое тройкой чисел  описывается волновой функцией Этому состоянию соответствует характерная форма электронного облака, определяемая функцией
описывается волновой функцией Этому состоянию соответствует характерная форма электронного облака, определяемая функцией  Остановимся на виде
Остановимся на виде  -функций водородного атома, характеризующих различные возбужденные состояния этого атома.
-функций водородного атома, характеризующих различные возбужденные состояния этого атома.
Рассмотрим  -состояния. Так как
-состояния. Так как  то и
то и  значит, для каждого
значит, для каждого  имеется лишь одна
имеется лишь одна  -функция. Равенство
-функция. Равенство  говорит об отсутствии у электрона вращательного импульса. Естественно, это требует отсутствия предпочтительных направлений движения, т. е. сферической симметрии электронного облака. Уравнение Шредингера и дает такой результат: функции
говорит об отсутствии у электрона вращательного импульса. Естественно, это требует отсутствия предпочтительных направлений движения, т. е. сферической симметрии электронного облака. Уравнение Шредингера и дает такой результат: функции  сферически симметричны.
сферически симметричны.
На рис. 216 построены кривые радиального распределения плотности электронного облака (или, что то же самое, плотности вероятности пребывания электрона в данном месте). По оси ординат отложена величина  называемая радиальной плотностью; очевидно,
называемая радиальной плотностью; очевидно,  есть число электронов, заключенных в шаровом слое между радиусами
есть число электронов, заключенных в шаровом слое между радиусами  Кривые радиальной плотности
Кривые радиальной плотности
показывают, что в состоянии  имеется один максимум электронной плотности, у атома водорода он находится на расстоянии 0,53 А от ядра. В состоянии
имеется один максимум электронной плотности, у атома водорода он находится на расстоянии 0,53 А от ядра. В состоянии  имеются два максимума плотности; правда, в основном электрон будет внутри второго максимума.
имеются два максимума плотности; правда, в основном электрон будет внутри второго максимума.

Рис. 216.
Наконец, в состоянии  имеются три максимума плотности, из которых наиболее «посещаемым» является дальний.
имеются три максимума плотности, из которых наиболее «посещаемым» является дальний.
С возрастанием главного числа  электронное облако расплывается.
электронное облако расплывается.

Рис. 217.
Совершенно иначе выглядят функции  -состояний. Значению
-состояний. Значению  могут соответствовать три значения
могут соответствовать три значения  Представление о конфигурациях электронного облака дает рис. 217. При
Представление о конфигурациях электронного облака дает рис. 217. При  длинная ось «восьмерки» располагается вдоль выделенного направления, при
длинная ось «восьмерки» располагается вдоль выделенного направления, при  перпендикулярно к нему. Очевидно, состояния с
перпендикулярно к нему. Очевидно, состояния с  имеет смысл различать лишь тогда, когда они присутствуют оба. Рисунок дает некоторое представление о
имеет смысл различать лишь тогда, когда они присутствуют оба. Рисунок дает некоторое представление о
симметрии электронного облака. Она одинакова для всех  -состояний. Различие в главном квантовом числе сводится лишь к изменению характера радиального спада плотности: чем больше
-состояний. Различие в главном квантовом числе сводится лишь к изменению характера радиального спада плотности: чем больше  тем больше растянется картина.
тем больше растянется картина.
Мы не будем обсуждать состояний с большими значениями  их электронные облака более сложны.
их электронные облака более сложны.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ
- ЧАСТЬ I. МЕХАНИЧЕСКОЕ И ТЕПЛОВОЕ ДВИЖЕНИЕ
- Уравнения движения материальной точки.
- Средняя скорость.
- Истинная скорость.
- Векторное ускорение.
- § 2. Силы
- Гравитационные силы.
- Электромагнитные силы.
- Ядерные силы.
- Силы «слабого» взаимодействия.
- Поле сил.
- § 3. Основной закон механики
- Законы Ньютона.
- Относительность движения.
- Законы механики в неинерциальной системе координат.
- § 4. Приложение основного закона механики к ускоренному прямолинейному движению
- Горизонтальное движение под действием постоянной силы.
- Вертикально движущийся лифт.
- Тяга свободно подвешенного груза.
- § 5. Приложение основного закона механики к движению по окружности
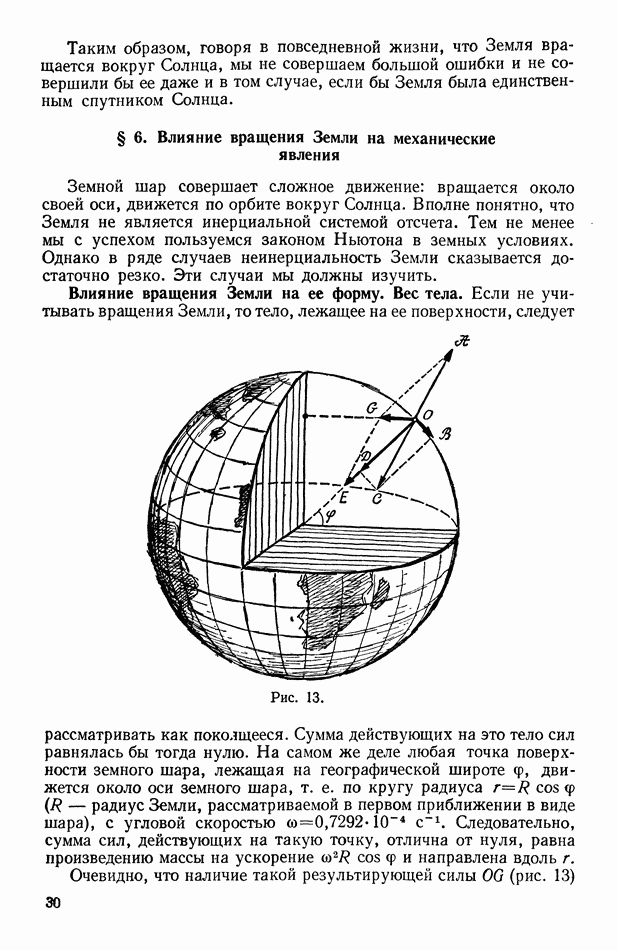
- § 6. Влияние вращения Земли на механические явления
- Влияние вращения Земли на ее форму. Вес тела.
- Влияние вращения Земли на движение тел по земной поверхности.
- § 7. Какие данные необходимы для решения механической задачи?
- § 8. Коэффициенты пропорциональности в формулах физики и размерности физических величин
- ГЛАВА 2. МЕХАНИЧЕСКАЯ ЭНЕРГИЯ
- § 9. Работа
- § 10. Кинетическая энергия
- § 11. Потенциальная энергия
- § 12. Закон сохранения механической энергии
- § 13. Потенциальные кривые. Равновесие
- ГЛАВА 3. ИМПУЛЬС
- § 14. Сохранение импульса
- § 15. Центр инерции
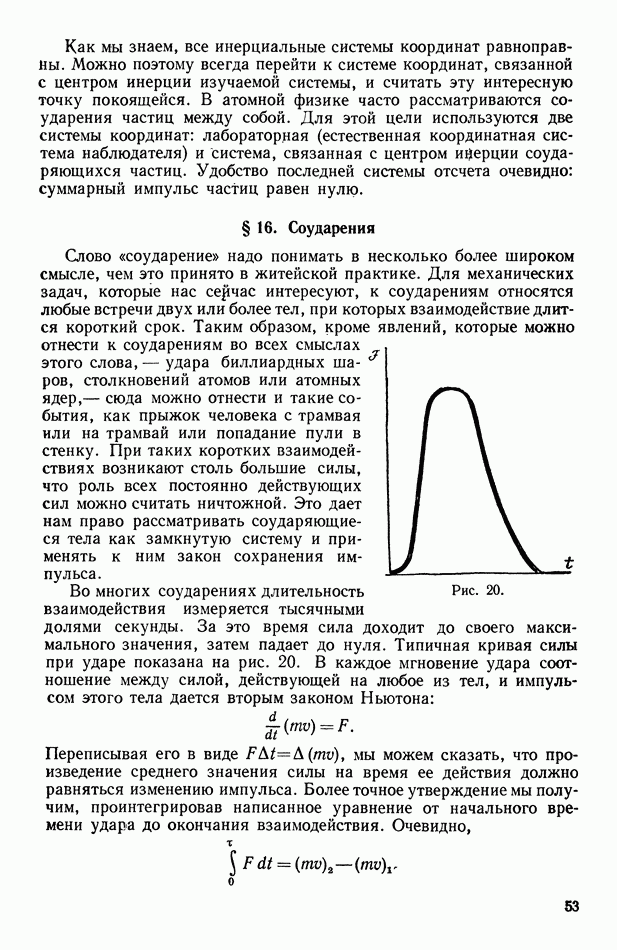
- § 16. Соударения
- § 17. Явления отдачи
- ГЛАВА 4. ВРАЩЕНИЕ ТВЕРДОГО ТЕЛА
- § 18. Кинетическая энергия вращения
- § 19. Момент инерции
- § 20. Работа вращения и основное уравнение вращения
- § 21. Момент импульса
- § 22. Свободные оси вращения
- § 23. Гироскопы
- ГЛАВА 5. КОЛЕБАНИЯ
- § 24. Малые отклонения от равновесия
- § 25. Частные случаи колебаний
- § 26. Превращения энергии. Затухающие колебания
- § 27. Вынужденные колебания
- § 28. Автоколебания
- § 29. Сложение колебаний одного направления
- § 30. Спектр колебания
- § 31. Сложение взаимно перпендикулярных колебаний
- ГЛАВА 6. БЕГУЩИЕ ВОЛНЫ
- § 32. Распространение деформации
- § 33. Возникновение волнового движения
- § 34. Волны давления и скорости колебания
- § 35. Поток энергии
- § 36. Затухание упругих волн
- § 37. Интерференция волн
- § 38. Принцип Гюйгенса — Френеля. Отражение и преломление волн
- § 39. Коэффициент отражения
- § 40. Явление Доплера
- ГЛАВА 7. СТОЯЧИЕ ВОЛНЫ
- § 41. Наложение двух волн, бегущих в противоположные стороны
- § 42. Собственные колебания стержней
- § 43. Собственные колебания двумерных и трехмерных систем
- § 44. Вынужденные колебания стержней и пластинок
- § 45. Колебания пьезоэлектриков
- ГЛАВА 8. ВОПРОСЫ АКУСТИКИ
- § 46. Объективная и субъективная характеристики звука
- § 47. Сила и громкость звука
- § 48. Архитектурная акустика
- § 49. Атмосферная акустика
- § 50. Действие ультразвука
- ГЛАВА 9. ТЕМПЕРАТУРА И ТЕПЛОТА
- § 51. Тепловое равновесие
- § 52. Внутренняя энергия
- § 53. Первое начало термодинамики
- § 54. Энергия микроскопических систем
- § 55. Уравнение состояния
- § 56. Уравнение газового состояния
- § 57. Уравнения состояния реальных газов
- ГЛАВА 10. ТЕРМОДИНАМИЧЕСКИЕ ПРОЦЕССЫ
- § 58. Графическое изображение процессов
- § 59. Работа. Циклы
- § 60. Процессы изменения состояния газов
- Изобарический процесс.
- Изотермический процесс.
- Адиабатический процесс.
- Измерение теплоемкостей газов.
- § 61. Процесс Джоуля — Томсона
- ГЛАВА 11. ЭНТРОПИЯ
- § 62. Принцип существования энтропии
- § 63. Принцип возрастания энтропии
- § 64. Принцип действия тепловой машины
- § 65. Цикл Карно. Максимальный к. п. д.
- § 66. Второе начало термодинамики
- ГЛАВА 12. КИНЕТИЧЕСКАЯ ТЕОРИЯ ГАЗОВ
- § 68. Длина свободного пробега
- § 69. Давление газа. Средняя квадратичная скорость молекул
- § 70. Внутренняя энергия газа
- § 71. Статистическое распределение
- § 72. Закон Больцмана
- § 73. Распределение частиц по высоте в поле тяжести
- § 74. Распределение молекул по скоростям
- § 75. Измерение скоростей молекул газа
- § 76. Вероятность состояния
- § 77. Необратимые процессы с молекулярной точки зрения
- § 78. Флуктуации. Границы применения второго начала
- ГЛАВА 13. ПРОЦЕССЫ ПЕРЕХОДА К РАВНОВЕСИЮ
- § 79. Диффузия
- § 80. Теплопроводность и вязкость
- § 81. Быстрота выравнивания
- § 82. Стационарные процессы
- § 83. Движение в вязкой среде
- § 84. Коэффициенты диффузии, вязкости и теплопроводности для газов
- § 85. Ультраразреженные газы
- ЧАСТЬ II. ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ
- § 86. Векторные характеристики электрического поля: напряженность и смещение
- § 87. Диэлектрическая проницаемость
- § 88. Законы электрического поля
- § 89. Вычисление полей простейших систем
- Система точечных зарядов.
- Универсальные формулы потенциала.
- Поле сферического конденсатора.
- Поле равномерно заряженной сферы.
- Поле с цилиндрической симметрией.
- Однородные поля.
- Поле на поверхности металла.
- Электрическое изображение.
- § 90. Электрическая энергия
- Энергия конденсатора.
- Энергия поля
- Энергия взаимодействия.
- § 91. Радиус электрона и границы классической электродинамики
- § 92. Электрические силы
- § 93. Дипольный момент системы зарядов
- § 94. Поляризация изотропного диэлектрика
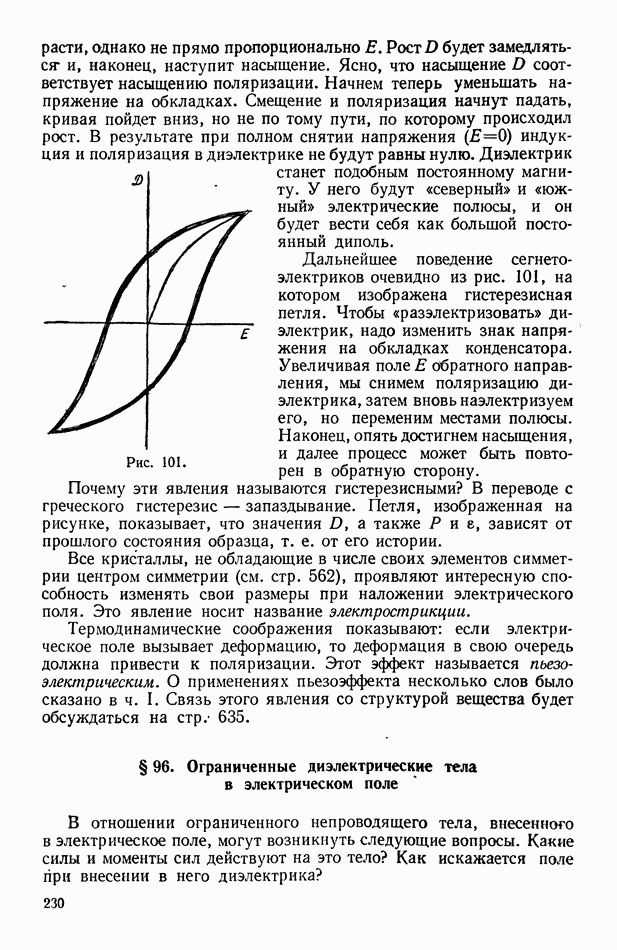
- § 95. Поляризация кристаллических веществ
- § 96. Ограниченные диэлектрические тела в электрическом поле
- ГЛАВА 15. МАГНИТНОЕ ПОЛЕ
- § 97. Магнитный момент
- § 98. Сила Ампера
- § 99. Сила, действующая на движущийся заряд
- § 100. Магнитное поле, создаваемое постоянными магнитами
- § 101. Напряженность магнитного поля
- § 102. Взаимодействия токов и магнитов
- § 103. Эквивалентность токов и магнитов
- § 104. Вихревой характер магнитного поля
- § 105. Закон электромагнитной индукции и сила Лоренца
- § 106. Измерения магнитного поля методом индукционного толчка
- § 107. Ограниченные тела в магнитном поле
- § 108. Связь между магнитной проницаемостью и восприимчивостью
- § 109. Искажение магнитного поля при внесении в него магнетика
- § 110. Магнитный гистерезис
- ГЛАВА 16. ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ. УРАВНЕНИЯ МАКСВЕЛЛА
- § 111. Обобщение закона электромагнитной индукции
- § 112. Ток смещения
- § 113. Картина электромагнитного поля
- ГЛАВА 17. ЭНЕРГЕТИЧЕСКИЕ ПРЕВРАЩЕНИЯ В ЭЛЕКТРОМАГНИТНОМ ПОЛЕ
- § 114. Превращения в цепи постоянного тока
- § 115. Превращения в замкнутой цепи переменного тока
- § 116. Магнитная энергия поля
- § 117. Электрические колебания
- § 118. Электромагнитная энергия
- § 119. Импульс и давление электромагнитного поля
- ГЛАВА 18. ЭЛЕКТРОМАГНИТНОЕ ИЗЛУЧЕНИЕ
- § 120. Элементарный диполь
- § 121. Антенна как электрический диполь
- § 122. Излучение диполя
- § 123. Электромагнитный спектр
- § 124. Квантовая природа излучения
- ГЛАВА 19. РАСПРОСТРАНЕНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН
- § 126. Поведение электромагнитной волны на границе двух сред
- § 127. Естественный и поляризованный свет. Поляризация при отражении
- § 128. Распространение световых волн в среде с градиентом показателя преломления
- § 129. Распространение радиоволн
- § 130. Радиолокация
- ГЛАВА 20. ИНТЕРФЕРЕНЦИОННЫЕ ЯВЛЕНИЯ
- § 131. Сложение волн от двух источников
- § 132. Когерентность
- § 133. Интерференция в пластинке
- § 134. Полосы равной толщины и полосы равного наклона
- § 135. Практические применения интерференции
- ГЛАВА 21. РАССЕЯНИЕ
- § 136. Вторичное излучение
- § 137. Дифракция волн на отверстиях
- § 138. Система беспорядочно расположенных рассеивателей
- § 139. Поведение сплошной однородной среды
- § 140. Рассеяние в неоднородной среде
- § 141. Дифракционная решетка
- § 142. Направленные излучатели радиоволн
- § 142а. Голография
- ГЛАВА 22. ДИФРАКЦИЯ РЕНТГЕНОВСКИХ ЛУЧЕЙ НА КРИСТАЛЛЕ
- § 143. Кристалл как дифракционная решетка
- § 144. Определение параметров элементарной ячейки кристалла
- § 145. Интенсивность дифракционных лучей
- § 146. Методы рентгеновского анализа
- ГЛАВА 23. ДВОЙНОЕ ЛУЧЕПРЕЛОМЛЕНИЕ
- § 147. Анизотропия поляризуемости
- § 148. Раснространение света в одноосных кристаллах
- § 149. Поляризаторы. Исследование поляризационного состояния света
- § 150. Кристаллическая пластинка между «скрещенными» николями
- § 151. Двойное лучепреломление, вызванное внешним воздействием
- § 152. Оптическая активность
- § 153. Принципы теории оптической активности
- ГЛАВА 24. ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ
- § 155. Опытные подтверждения принципа постоянства скорости света
- § 156. Время в теории относительности
- § 157. Масса
- § 158. Энергия
- § 159. Дефект массы
- § 160. Принцип эквивалентности и понятие об общей теории относительности
- ГЛАВА 25. КВАНТОВАЯ ПРИРОДА ПОЛЯ
- § 161. Фотон
- § 162. Фотоэлектрический эффект
- § 163. Флуктуации светового потока
- § 164. Закон Кирхгофа
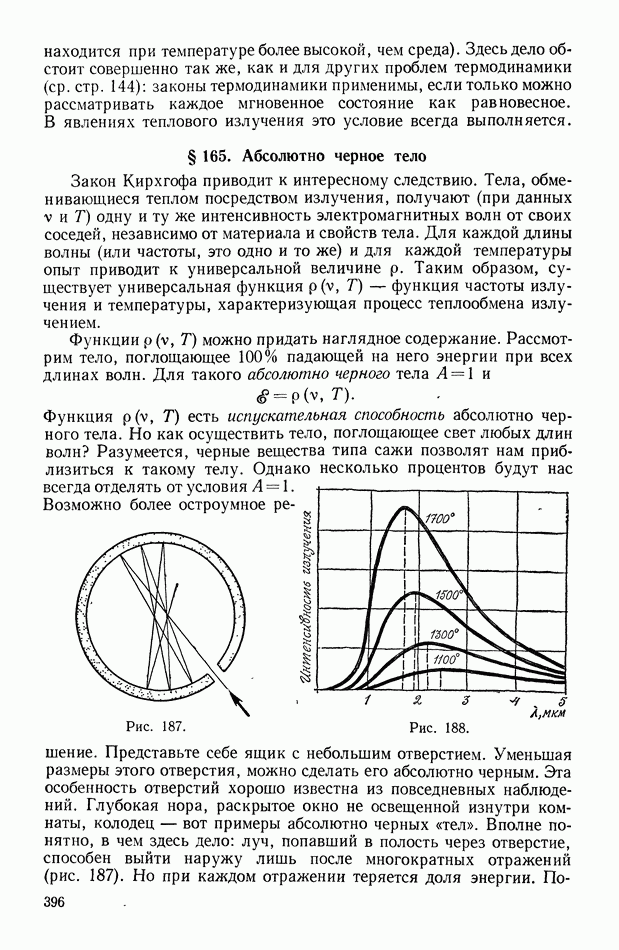
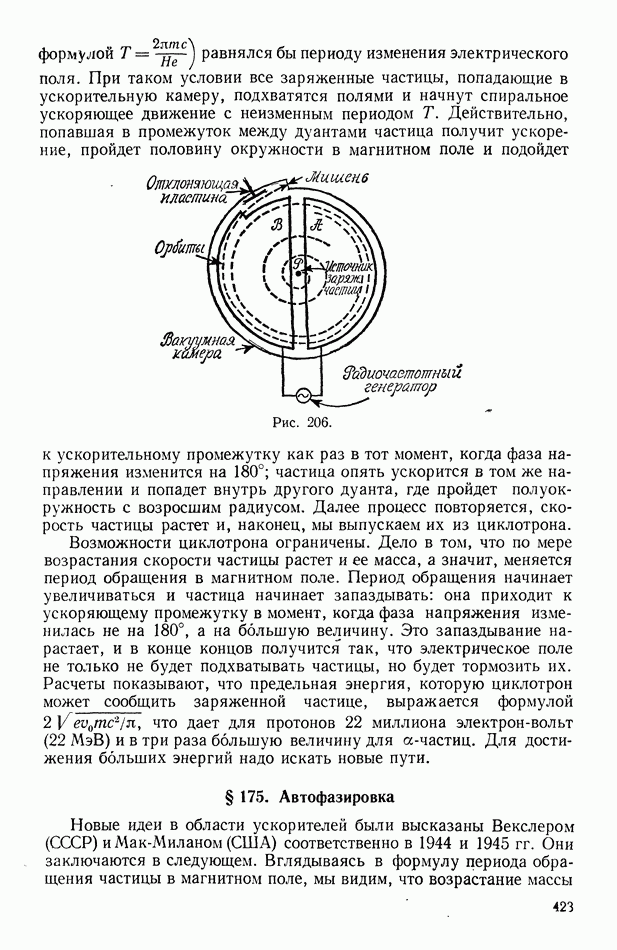
- § 165. Абсолютно черное тело
- § 166. Теория теплового излучения
- § 166а. Стимулированное излучение
- § 166б, Люминесценция
- ЧАСТЬ III. СТРОЕНИЕ И СВОЙСТВА ВЕЩЕСТВА
- § 167. Движение заряженной частицы в электрическом и магнитном полях
- § 168. Получение пучков заряженных частиц
- § 169. Электронные линзы
- § 170. Электронный микроскоп
- § 171. Электронные и ионные проекторы
- § 172. Электронно-лучевая трубка
- § 173. Масс-спектрограф
- § 174. Ускорители заряженных частиц
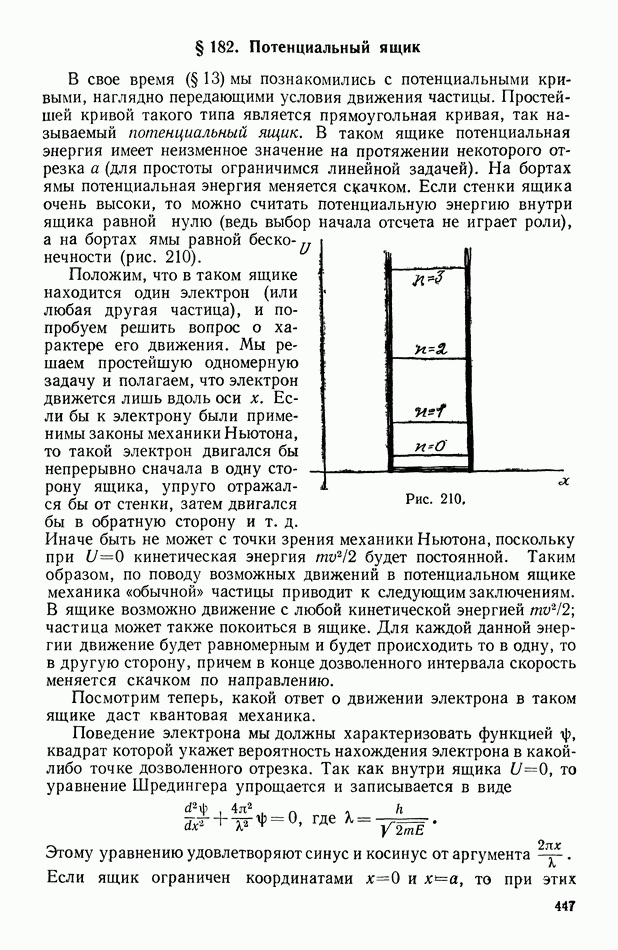
- § 175. Автофазировка
- § 176. Синхрофазотрон. Синхротрон
- § 177. Ионизованный газ
- § 178. Электрический разряд в газе
- § 178а. Плазма
- Вещество в состоянии плазмы.
- Плазма в магнитном поле.
- Проблемы устойчивости.
- ГЛАВА 27. ВОЛНОВЫЕ СВОЙСТВА МИКРОЧАСТИЦ
- § 179. Дифракция электронов
- § 180. Основные идеи квантовой механики
- § 181. Принцип неопределенности
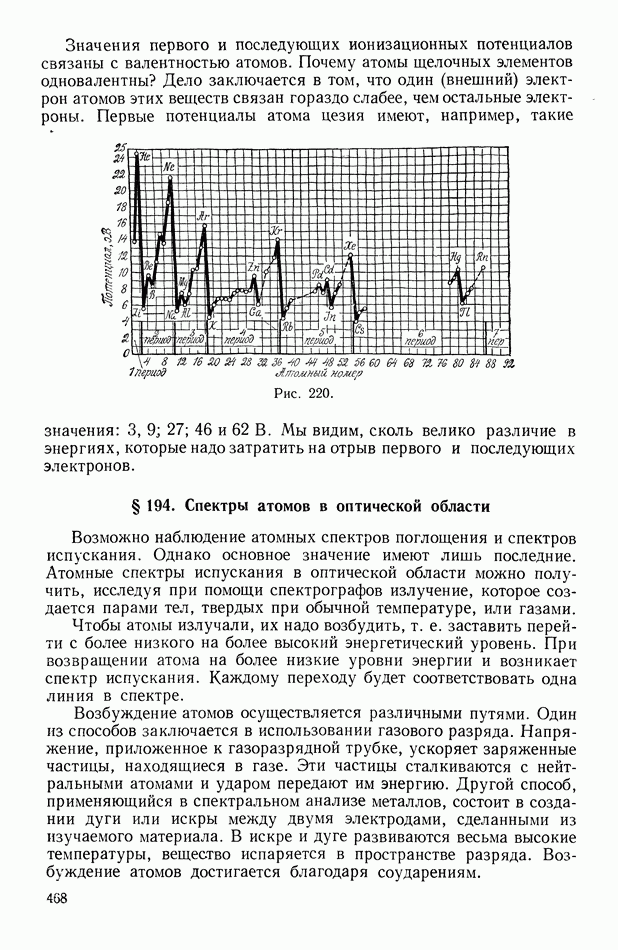
- § 182. Потенциальный ящик
- § 183. Что дает решение уравнения Шредингера
- § 184. Туннельный переход
- ГЛАВА 28. СТРОЕНИЕ АТОМА
- § 185. Энергетические уровни атома водорода
- § 186. Квантовые числа
- § 187. Электронное облако для s- и p-состояний
- § 188. Принцип Паули
- § 189. Отклонение атомного пучка в магнитном поле
- § 190. Спин электрона
- § 191. Магнитные моменты атомов
- § 192. Периодический закон Менделеева
- § 193. Ионизационные потенциалы
- § 194. Спектры атомов в оптической области
- § 195. Атомные рентгеновские спектры
- ГЛАВА 29. МОЛЕКУЛА
- § 196. Химическая связь
- § 197. Геометрия молекул
- § 198. Электронная оболочка молекулы
- § 199. Энергетические уровни молекул
- § 200. Вращательный спектр молекул
- § 201. Инфракрасный колебательно-вращательный спектр
- Колебания многоатомной молекулы.
- § 202. Комбинационное рассеяние света
- § 203. Электронный спектр поглощения
- § 204. Магнитный резонанс
- § 205. Квадрупольный резонанс
- § 206. Газовые лазеры
- ГЛАВА 30. АТОМНОЕ ЯДРО
- § 207. Экспериментальные методы ядерной физики
- § 208. Частицы, входящие в состав ядра
- § 209. Масса и энергия атомного ядра
- § 210. Спин и магнитный момент ядра
- § 211. Силы взаимодействия нуклонов
- § 212. Нуклоны в ядре
- § 213. Спектры атомных ядер
- § 214. Нейтрино бета-распада
- § 215. Общие закономерности химических и ядерных превращений
- § 216. Радиоактивность
- § 217. Ядерные реакции
- § 217а. Реакции деления тяжелых ядер
- § 217б. Цепная реакция
- § 217в. Принципы действия ядерного реактора
- § 217г. Искусственные радиоактивные продукты
- § 218. Термоядерные реакции
- ГЛАВА 31. ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ
- § 219. Термин «элементарная» частица
- § 220. Взаимодействие быстродвижущихся электронов
- § 221. Мезонная теория взаимодействия нуклонов
- § 222. Мезоны
- § 223. Релятивистская теория электрона
- § 224. Рождение и аннигиляция пар частиц
- § 225. Частицы и античастицы
- § 226. Асимметрия элементарных частиц
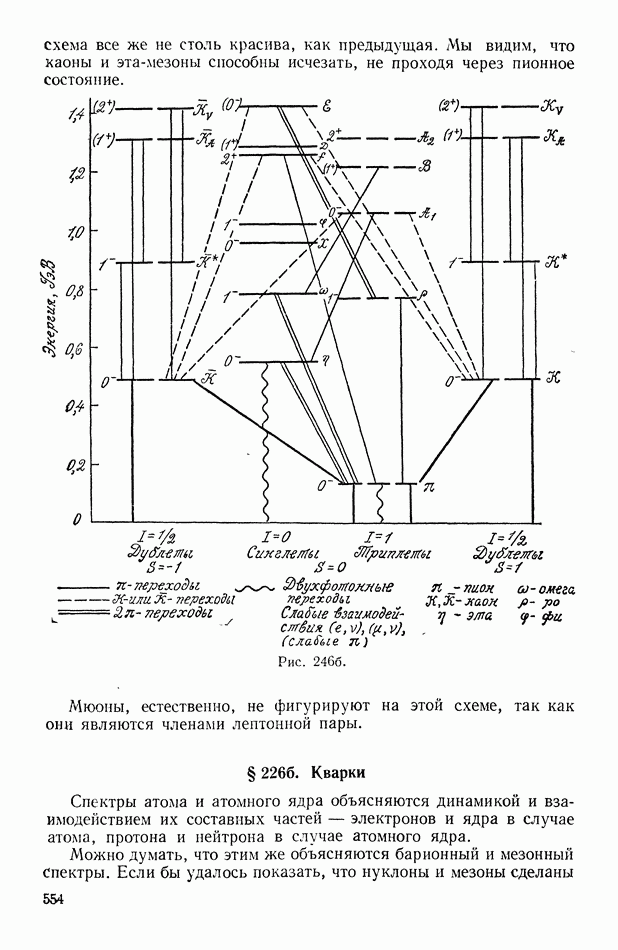
- § 226а. Барионный спектр
- § 2266. Кварки
- ГЛАВА 32. АТОМНОЕ СТРОЕНИЕ ТЕЛ
- § 227. Поликристаллическое вещество и монокристаллы
- § 228. Пространственная решетка
- § 229. Выбор ячейки. Симметрия кристалла
- § 230. Упаковка частиц в кристалле
- § 231. Молекулярный кристалл
- § 232. Плотные упаковки шаров
- § 233. Примеры кристаллических структур
- § 234. Тепловые колебания в кристалле
- § 235. Тепловые волны
- § 236. Тепловое расширение
- § 237. Дефекты кристалла
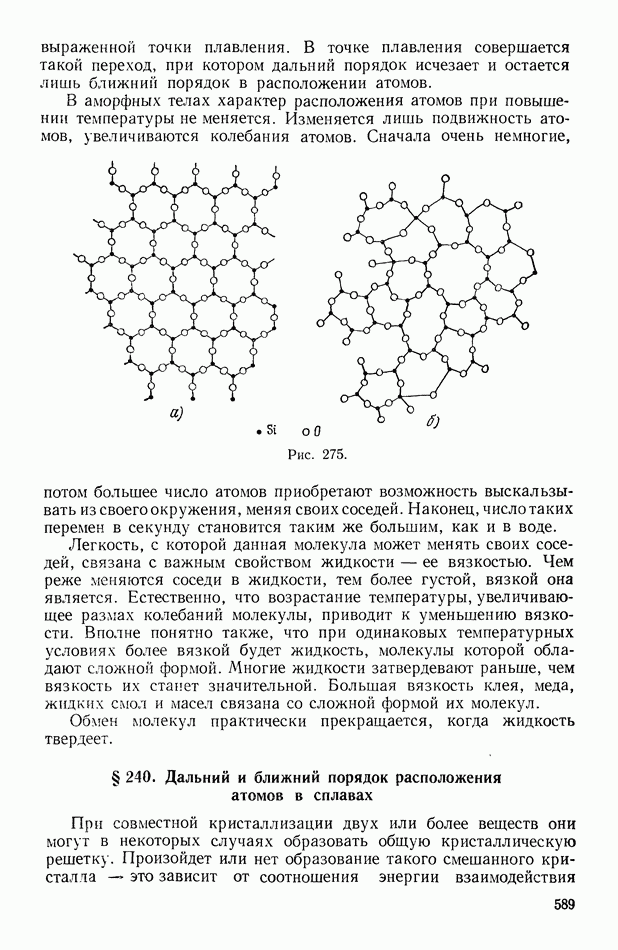
- § 238. Ближний порядок. Жидкости
- § 239. Аморфные тела
- § 240. Дальний и ближний порядок расположения атомов в сплавах
- § 241. Жидкие кристаллы
- § 242. Полимерные вещества
- § 242а. Биологические макромолекулы
- ГЛАВА 33. ФАЗОВЫЕ ПРЕВРАЩЕНИЯ
- § 244. Фазовые превращения
- § 244а. Диаграмма состояния и свойства гелия
- § 245. Условия устойчивого состояния фазы
- § 246. Метастабильные состояния
- § 247. Превращения газ жидкость
- § 248. Сжижение газов
- § 249. Превращения газ кристалл
- § 250. Превращения жидкость кристалл
- § 251. Превращения кристалл-кристалл
- § 252. Диффузия в твердых телах
- ГЛАВА 34. ДЕФОРМАЦИЯ ТЕЛ
- § 254. Пластические свойства
- § 255. Предел прочности
- § 256. Механические свойства поликристаллического материала
- § 257. Влияние поверхностно-активных веществ на деформацию
- § 258. Разрушение материалов под действием потока частиц
- ГЛАВА 35. ДИЭЛЕКТРИКИ
- § 259. Связь между диэлектрической проницаемостью и поляризуемостью молекулы
- § 260. Поляризация полярных и неполярных молекул
- § 261. Аддитивность молекулярной рефракции
- § 262. Пиро- и пьезоэлектрики
- § 262а. Сегнетоэлектрики
- ГЛАВА 36. МАГНЕТИКИ
- § 263. Три класса магнетиков
- § 264. Диамагнетизм
- § 265. Парамагнетизм
- § 266. Ферромагнетизм
- ГЛАВА 37. ЭЛЕКТРОННОЕ СТРОЕНИЕ И СВОЙСТВА ТЕЛ
- § 267. Свободные электроны
- § 268. Энергетические уровни в твердом теле
- § 269. Электронный газ
- § 270. Проводимость
- § 271. Сверхпроводимость
- § 272. Полупроводники
- § 273. Эмиссия электронов
- § 274. Фотоэлектрический эффект
- § 275. Запирающие слои
- § 276. Контактная разность потенциалов
- § 276a. Электролюминесценция полупроводников
- § 277. Распределение зарядов в неравномерно нагретом теле
- § 278. Термоэлектродвижущая сила
- § 279. Выделение тепла в электрических цепях
- § 280. Применения термоэлектрического эффекта