| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 7. Какие данные необходимы для решения механической задачи?
Основной задачей механики является нахождение движения по заданным силам. Найти движение — это значит суметь указать, в каком месте пространства и в какой момент времени находится любая из материальных точек. Если же нас интересует сложная механическая система, то такие сведения нужны по отношению к каждой из материальных точек, на которые эта система мысленно разделена.
Для того чтобы справиться с такой задачей, мы прежде всего должны располагать исчерпывающими сведениями о действующих силах. Силы должны быть известны для любой точки и любого места нахождения этой точки. Если силы известны, то при помощи
уравнения Ньютона мы можем определить ускорение материальной точки. Однако сведения о траектории, скорости, знание момента времени, которому соответствует прохождение через данную точку пространства, — все эти сведения при помощи одних только уравнений движения Ньютона не могут быть получены. Чтобы описать движение, надо для любого момента времени знать место, где находилась материальная точка, а также знать ее скорость как по величине, так и по направлению. Всего требуется задать шесть чисел: три координаты и три проекции скорости по осям. Эти данные однозначно характеризуют «механическое состояние» точки; их можно назвать параметрами состояния.
Итак, задача сводится к нахождению параметров состояния, а уравнения Ньютона дают лишь ускорения.
Чтобы решить задачу, нужно знать начальные условия, т. е. значения параметров состояния для какого-либо момента времени (обычно этот момент обозначают  отсюда и название: начальные условия). Если начальные значения параметров состояния известны, то дальнейшее является уже делом математика. Уравнения движения Ньютона плюс начальные данные однозначно решают механическую задачу. Дальнейшая судьба точки, а также ее прошлое могут быть прослежены в принципе на сколь угодно большие сроки вперед и назад. Эта идея в свое время поражала ученых. Великий французский ученый и мыслитель Лаплас говорил: если бы знать начальные координаты и скорости всех частиц, из которых состоит мир, то можно было бы предсказать судьбу мира. Эта несколько наивная точка зрения, сводящая все сущее к чисто механическим явлениям, несправедлива в принципе, и не только потому, что практически невозможно располагать требуемыми сведениями. Дело в том, что механика, основывающаяся на законах Ньютона, имеет ограниченное применение и выводы ее не могут применяться столь широко.
отсюда и название: начальные условия). Если начальные значения параметров состояния известны, то дальнейшее является уже делом математика. Уравнения движения Ньютона плюс начальные данные однозначно решают механическую задачу. Дальнейшая судьба точки, а также ее прошлое могут быть прослежены в принципе на сколь угодно большие сроки вперед и назад. Эта идея в свое время поражала ученых. Великий французский ученый и мыслитель Лаплас говорил: если бы знать начальные координаты и скорости всех частиц, из которых состоит мир, то можно было бы предсказать судьбу мира. Эта несколько наивная точка зрения, сводящая все сущее к чисто механическим явлениям, несправедлива в принципе, и не только потому, что практически невозможно располагать требуемыми сведениями. Дело в том, что механика, основывающаяся на законах Ньютона, имеет ограниченное применение и выводы ее не могут применяться столь широко.
Вернемся, однако, к шести начальным условиям. Необходимость задания для материальной точки именно шести цифр отчетливо видна из самих уравнений Ньютона.
Векторное уравнение можно разложить по трем осям и написать его в виде трех равенств:  Определить движение — это значит найти, как меняются со временем все три координаты точки:
Определить движение — это значит найти, как меняются со временем все три координаты точки:  Нахождение зависимости координатах от времени производится интегрированием уравнения
Нахождение зависимости координатах от времени производится интегрированием уравнения

Первое интегрирование позволяет найти х-компоненту скорости. При интегрировании появляется первая постоянная интегрирования. Второе интегрирование позволяет найти координату х в функции времени. При втором интегрировании, появляется вторая произвольная постоянная. То же самое относится и к уравнениям изменения со временем других двух координат. Всего появятся шесть
произвольных постоянных, которые могут быть найдены лишь в том случае, если известны какие-либо шесть независимых данных о координатах и скоростях частицы.
Начальные условия — это, как мы говорили, три начальные координаты и три начальные проекции скорости. Однако задача может быть решена, если известны и другие шесть чисел. Например, можно задать три координаты начальной точки, числовое значение начальной скорости и две координаты конечной точки. Траектория точки однозначно определится и этими шестью условиями.
Параметры точки могут быть заданы различным способом. Положение точки в пространстве можно задать тремя декартовыми координатами, можно задать расстояние от начала координат и два угла, образованных радиусом-вектором с осями. То же самое относится и к скорости.
Характерным примером зависимости движения тела от начальных условий является поведение ракеты, выброшенной с поверхности Земли. Траектория ракеты и ее судьба определяются направлением выброса, географическим расположением места запуска и величиной начальной скорости. При небольших скоростях брошенное с Земли тело описывает, как хорошо известно, параболическую кривую. При скорости около  обеспечивается равенство центробежной силы и силы притяжения и брошенное тело может быть положено на круговую орбиту. При скоростях между
обеспечивается равенство центробежной силы и силы притяжения и брошенное тело может быть положено на круговую орбиту. При скоростях между  брошенное тело описывает около Земли эллиптическую траекторию. При начальной скорости около
брошенное тело описывает около Земли эллиптическую траекторию. При начальной скорости около  кинетическая энергия тела становится достаточной для полного преодоления притяжения Земли. Ракета, брошенная с такой скоростью, будет двигаться по гиперболе.
кинетическая энергия тела становится достаточной для полного преодоления притяжения Земли. Ракета, брошенная с такой скоростью, будет двигаться по гиперболе.
Если механическая система состоит из  независимых точек, то число параметров системы будет равно
независимых точек, то число параметров системы будет равно 
Однако в ряде случаев на механическую систему могут накладываться связи, уменьшающие это число. Простым примером является центробежный регулятор, который можно представить себе как систему из двух связанных шариков, которые могут раздвигаться и крутиться около общей оси. Ясно, что заданием расстояния точки от оси вращения и азимутального угла по отношению к произвольной линии мы однозначно определяем механическое состояние системы. Две «координаты» и две скорости изменения этих координат являются параметрами этого состояния.
Рассмотрим теперь произвольно вращающееся твердое тело и подумаем, какими данными надо располагать, чтобы фиксировать его расположение по отношению к неподвижной системе координат. Ясно, что тремя данными мы определим расположение центра тяжести тела. Для описания же поворота тела достаточно знания трех углов. Можно не останавливаться на этом положении, так как очевидно, что тремя поворотами около взаимно перпендикулярных осей всегда можно придать телу любую ориентировку.
Итак, твердое тело надо характеризовать шестью координатами и шестью скоростями изменения этих координат, всего двенадцатью параметрами.
В качестве еще одного примера рассмотрим две жестко связанные точки. Если бы они были свободны, то для их характеристики требовалось бы знание шести координат. Так как они жестко связаны, то имеется дополнительное условие, связывающее координаты этих точек:

Таким образом, независимых величин, характеризующих указанную систему, имеется пять. Пять координат и пять скоростей изменения этих координат дают для этой системы десять параметров.
Так как параметры состояния разбиваются всегда пополам на «координаты» и скорости изменения «координат», то принято говорить о степенях свободы системы, подразумевая под этим число независимых координат, нужных для описания системы. Таким образом, одна точка имеет три степени свободы, две жестко скрепленные точки — пять степеней свободы, твердое тело — шесть степеней свободы, система из  независимых точек —
независимых точек —  степеней свободы и т. д. Теперь нам будет ясен смысл утверждения: механическое состояние системы определяется заданием ее параметров по числу степеней свободы.
степеней свободы и т. д. Теперь нам будет ясен смысл утверждения: механическое состояние системы определяется заданием ее параметров по числу степеней свободы.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ
- ЧАСТЬ I. МЕХАНИЧЕСКОЕ И ТЕПЛОВОЕ ДВИЖЕНИЕ
- Уравнения движения материальной точки.
- Средняя скорость.
- Истинная скорость.
- Векторное ускорение.
- § 2. Силы
- Гравитационные силы.
- Электромагнитные силы.
- Ядерные силы.
- Силы «слабого» взаимодействия.
- Поле сил.
- § 3. Основной закон механики
- Законы Ньютона.
- Относительность движения.
- Законы механики в неинерциальной системе координат.
- § 4. Приложение основного закона механики к ускоренному прямолинейному движению
- Горизонтальное движение под действием постоянной силы.
- Вертикально движущийся лифт.
- Тяга свободно подвешенного груза.
- § 5. Приложение основного закона механики к движению по окружности
- § 6. Влияние вращения Земли на механические явления
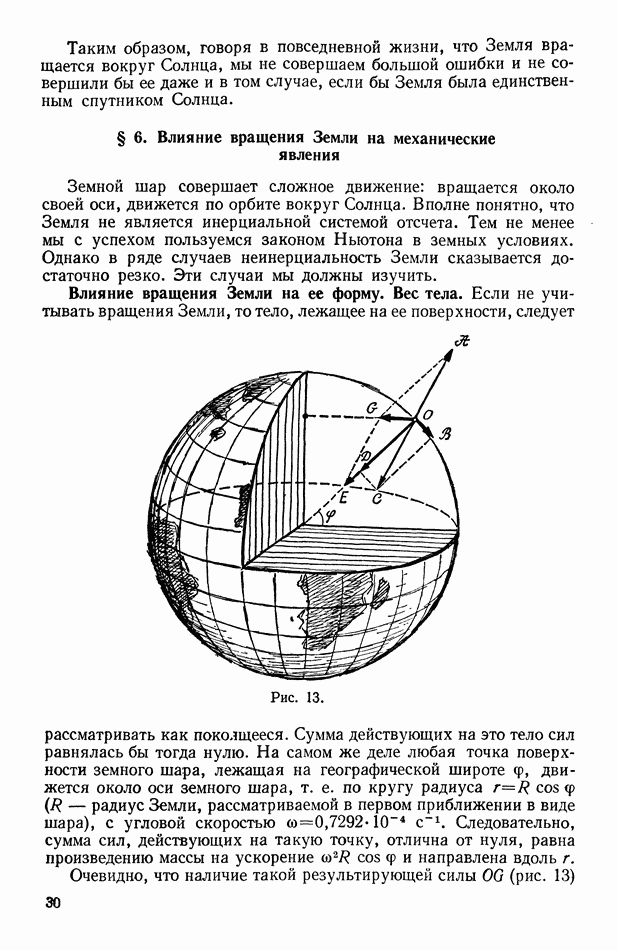
- Влияние вращения Земли на ее форму. Вес тела.
- Влияние вращения Земли на движение тел по земной поверхности.
- § 7. Какие данные необходимы для решения механической задачи?
- § 8. Коэффициенты пропорциональности в формулах физики и размерности физических величин
- ГЛАВА 2. МЕХАНИЧЕСКАЯ ЭНЕРГИЯ
- § 9. Работа
- § 10. Кинетическая энергия
- § 11. Потенциальная энергия
- § 12. Закон сохранения механической энергии
- § 13. Потенциальные кривые. Равновесие
- ГЛАВА 3. ИМПУЛЬС
- § 14. Сохранение импульса
- § 15. Центр инерции
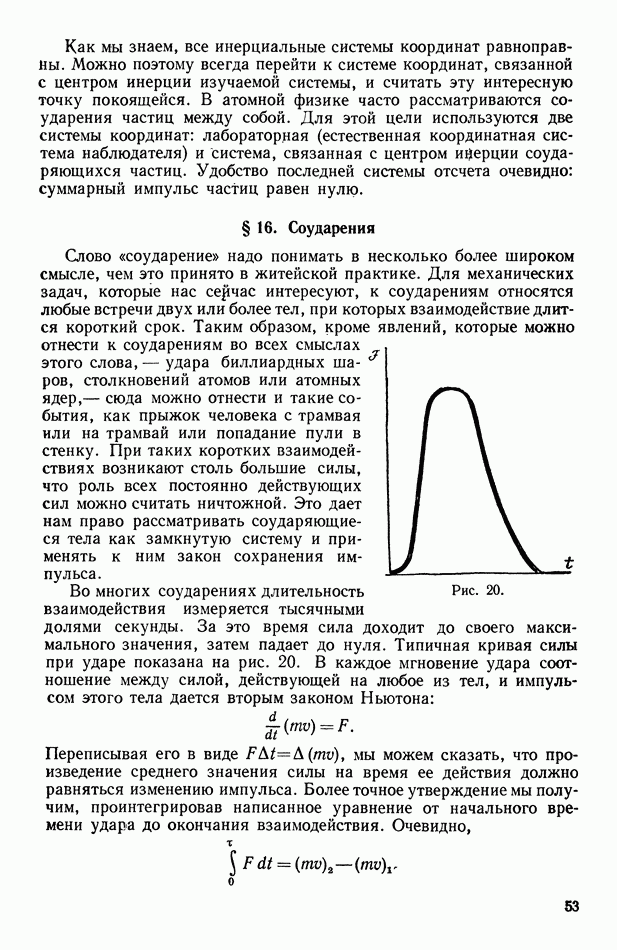
- § 16. Соударения
- § 17. Явления отдачи
- ГЛАВА 4. ВРАЩЕНИЕ ТВЕРДОГО ТЕЛА
- § 18. Кинетическая энергия вращения
- § 19. Момент инерции
- § 20. Работа вращения и основное уравнение вращения
- § 21. Момент импульса
- § 22. Свободные оси вращения
- § 23. Гироскопы
- ГЛАВА 5. КОЛЕБАНИЯ
- § 24. Малые отклонения от равновесия
- § 25. Частные случаи колебаний
- § 26. Превращения энергии. Затухающие колебания
- § 27. Вынужденные колебания
- § 28. Автоколебания
- § 29. Сложение колебаний одного направления
- § 30. Спектр колебания
- § 31. Сложение взаимно перпендикулярных колебаний
- ГЛАВА 6. БЕГУЩИЕ ВОЛНЫ
- § 32. Распространение деформации
- § 33. Возникновение волнового движения
- § 34. Волны давления и скорости колебания
- § 35. Поток энергии
- § 36. Затухание упругих волн
- § 37. Интерференция волн
- § 38. Принцип Гюйгенса — Френеля. Отражение и преломление волн
- § 39. Коэффициент отражения
- § 40. Явление Доплера
- ГЛАВА 7. СТОЯЧИЕ ВОЛНЫ
- § 41. Наложение двух волн, бегущих в противоположные стороны
- § 42. Собственные колебания стержней
- § 43. Собственные колебания двумерных и трехмерных систем
- § 44. Вынужденные колебания стержней и пластинок
- § 45. Колебания пьезоэлектриков
- ГЛАВА 8. ВОПРОСЫ АКУСТИКИ
- § 46. Объективная и субъективная характеристики звука
- § 47. Сила и громкость звука
- § 48. Архитектурная акустика
- § 49. Атмосферная акустика
- § 50. Действие ультразвука
- ГЛАВА 9. ТЕМПЕРАТУРА И ТЕПЛОТА
- § 51. Тепловое равновесие
- § 52. Внутренняя энергия
- § 53. Первое начало термодинамики
- § 54. Энергия микроскопических систем
- § 55. Уравнение состояния
- § 56. Уравнение газового состояния
- § 57. Уравнения состояния реальных газов
- ГЛАВА 10. ТЕРМОДИНАМИЧЕСКИЕ ПРОЦЕССЫ
- § 58. Графическое изображение процессов
- § 59. Работа. Циклы
- § 60. Процессы изменения состояния газов
- Изобарический процесс.
- Изотермический процесс.
- Адиабатический процесс.
- Измерение теплоемкостей газов.
- § 61. Процесс Джоуля — Томсона
- ГЛАВА 11. ЭНТРОПИЯ
- § 62. Принцип существования энтропии
- § 63. Принцип возрастания энтропии
- § 64. Принцип действия тепловой машины
- § 65. Цикл Карно. Максимальный к. п. д.
- § 66. Второе начало термодинамики
- ГЛАВА 12. КИНЕТИЧЕСКАЯ ТЕОРИЯ ГАЗОВ
- § 68. Длина свободного пробега
- § 69. Давление газа. Средняя квадратичная скорость молекул
- § 70. Внутренняя энергия газа
- § 71. Статистическое распределение
- § 72. Закон Больцмана
- § 73. Распределение частиц по высоте в поле тяжести
- § 74. Распределение молекул по скоростям
- § 75. Измерение скоростей молекул газа
- § 76. Вероятность состояния
- § 77. Необратимые процессы с молекулярной точки зрения
- § 78. Флуктуации. Границы применения второго начала
- ГЛАВА 13. ПРОЦЕССЫ ПЕРЕХОДА К РАВНОВЕСИЮ
- § 79. Диффузия
- § 80. Теплопроводность и вязкость
- § 81. Быстрота выравнивания
- § 82. Стационарные процессы
- § 83. Движение в вязкой среде
- § 84. Коэффициенты диффузии, вязкости и теплопроводности для газов
- § 85. Ультраразреженные газы
- ЧАСТЬ II. ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ
- § 86. Векторные характеристики электрического поля: напряженность и смещение
- § 87. Диэлектрическая проницаемость
- § 88. Законы электрического поля
- § 89. Вычисление полей простейших систем
- Система точечных зарядов.
- Универсальные формулы потенциала.
- Поле сферического конденсатора.
- Поле равномерно заряженной сферы.
- Поле с цилиндрической симметрией.
- Однородные поля.
- Поле на поверхности металла.
- Электрическое изображение.
- § 90. Электрическая энергия
- Энергия конденсатора.
- Энергия поля
- Энергия взаимодействия.
- § 91. Радиус электрона и границы классической электродинамики
- § 92. Электрические силы
- § 93. Дипольный момент системы зарядов
- § 94. Поляризация изотропного диэлектрика
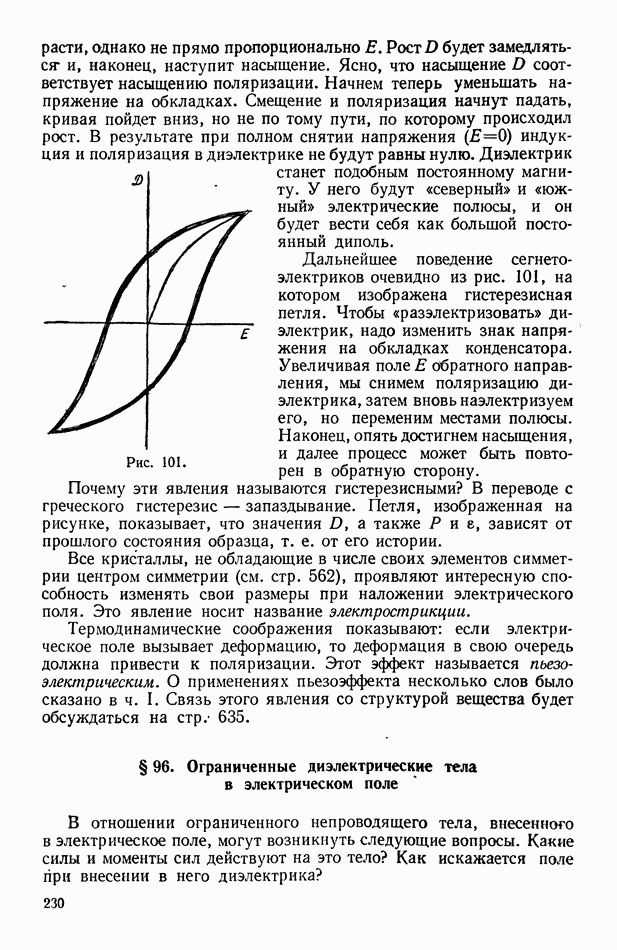
- § 95. Поляризация кристаллических веществ
- § 96. Ограниченные диэлектрические тела в электрическом поле
- ГЛАВА 15. МАГНИТНОЕ ПОЛЕ
- § 97. Магнитный момент
- § 98. Сила Ампера
- § 99. Сила, действующая на движущийся заряд
- § 100. Магнитное поле, создаваемое постоянными магнитами
- § 101. Напряженность магнитного поля
- § 102. Взаимодействия токов и магнитов
- § 103. Эквивалентность токов и магнитов
- § 104. Вихревой характер магнитного поля
- § 105. Закон электромагнитной индукции и сила Лоренца
- § 106. Измерения магнитного поля методом индукционного толчка
- § 107. Ограниченные тела в магнитном поле
- § 108. Связь между магнитной проницаемостью и восприимчивостью
- § 109. Искажение магнитного поля при внесении в него магнетика
- § 110. Магнитный гистерезис
- ГЛАВА 16. ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ. УРАВНЕНИЯ МАКСВЕЛЛА
- § 111. Обобщение закона электромагнитной индукции
- § 112. Ток смещения
- § 113. Картина электромагнитного поля
- ГЛАВА 17. ЭНЕРГЕТИЧЕСКИЕ ПРЕВРАЩЕНИЯ В ЭЛЕКТРОМАГНИТНОМ ПОЛЕ
- § 114. Превращения в цепи постоянного тока
- § 115. Превращения в замкнутой цепи переменного тока
- § 116. Магнитная энергия поля
- § 117. Электрические колебания
- § 118. Электромагнитная энергия
- § 119. Импульс и давление электромагнитного поля
- ГЛАВА 18. ЭЛЕКТРОМАГНИТНОЕ ИЗЛУЧЕНИЕ
- § 120. Элементарный диполь
- § 121. Антенна как электрический диполь
- § 122. Излучение диполя
- § 123. Электромагнитный спектр
- § 124. Квантовая природа излучения
- ГЛАВА 19. РАСПРОСТРАНЕНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН
- § 126. Поведение электромагнитной волны на границе двух сред
- § 127. Естественный и поляризованный свет. Поляризация при отражении
- § 128. Распространение световых волн в среде с градиентом показателя преломления
- § 129. Распространение радиоволн
- § 130. Радиолокация
- ГЛАВА 20. ИНТЕРФЕРЕНЦИОННЫЕ ЯВЛЕНИЯ
- § 131. Сложение волн от двух источников
- § 132. Когерентность
- § 133. Интерференция в пластинке
- § 134. Полосы равной толщины и полосы равного наклона
- § 135. Практические применения интерференции
- ГЛАВА 21. РАССЕЯНИЕ
- § 136. Вторичное излучение
- § 137. Дифракция волн на отверстиях
- § 138. Система беспорядочно расположенных рассеивателей
- § 139. Поведение сплошной однородной среды
- § 140. Рассеяние в неоднородной среде
- § 141. Дифракционная решетка
- § 142. Направленные излучатели радиоволн
- § 142а. Голография
- ГЛАВА 22. ДИФРАКЦИЯ РЕНТГЕНОВСКИХ ЛУЧЕЙ НА КРИСТАЛЛЕ
- § 143. Кристалл как дифракционная решетка
- § 144. Определение параметров элементарной ячейки кристалла
- § 145. Интенсивность дифракционных лучей
- § 146. Методы рентгеновского анализа
- ГЛАВА 23. ДВОЙНОЕ ЛУЧЕПРЕЛОМЛЕНИЕ
- § 147. Анизотропия поляризуемости
- § 148. Раснространение света в одноосных кристаллах
- § 149. Поляризаторы. Исследование поляризационного состояния света
- § 150. Кристаллическая пластинка между «скрещенными» николями
- § 151. Двойное лучепреломление, вызванное внешним воздействием
- § 152. Оптическая активность
- § 153. Принципы теории оптической активности
- ГЛАВА 24. ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ
- § 155. Опытные подтверждения принципа постоянства скорости света
- § 156. Время в теории относительности
- § 157. Масса
- § 158. Энергия
- § 159. Дефект массы
- § 160. Принцип эквивалентности и понятие об общей теории относительности
- ГЛАВА 25. КВАНТОВАЯ ПРИРОДА ПОЛЯ
- § 161. Фотон
- § 162. Фотоэлектрический эффект
- § 163. Флуктуации светового потока
- § 164. Закон Кирхгофа
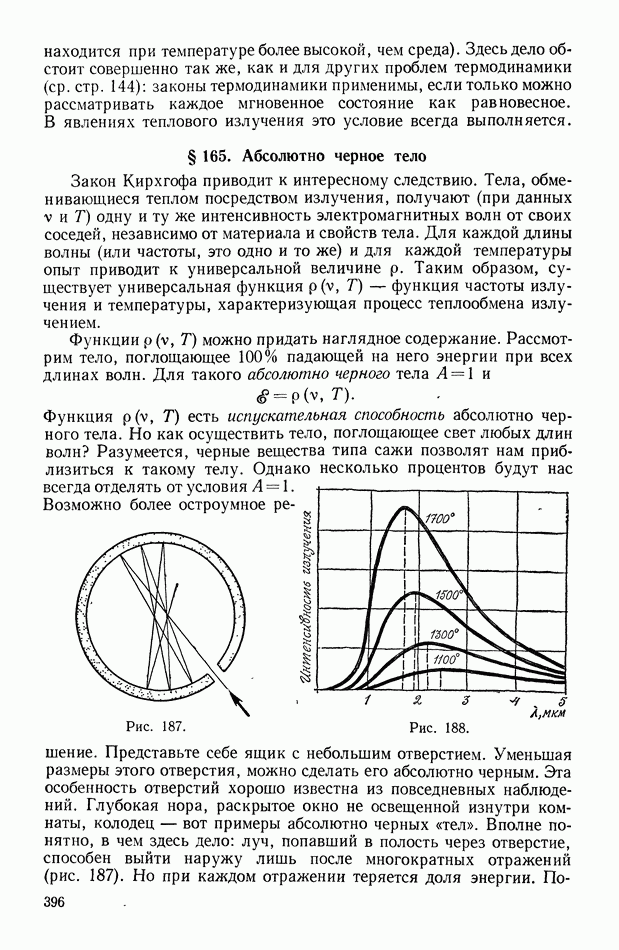
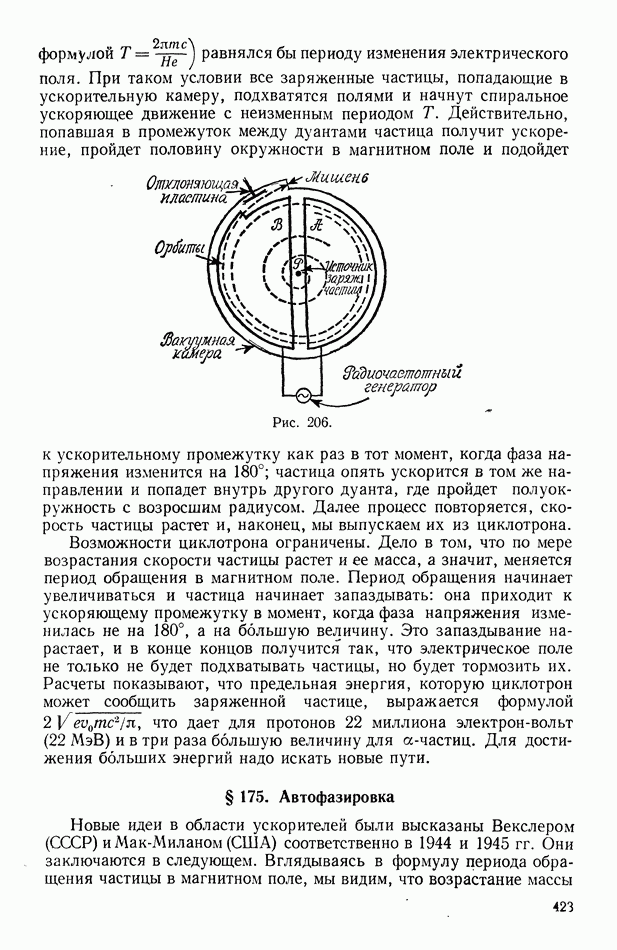
- § 165. Абсолютно черное тело
- § 166. Теория теплового излучения
- § 166а. Стимулированное излучение
- § 166б, Люминесценция
- ЧАСТЬ III. СТРОЕНИЕ И СВОЙСТВА ВЕЩЕСТВА
- § 167. Движение заряженной частицы в электрическом и магнитном полях
- § 168. Получение пучков заряженных частиц
- § 169. Электронные линзы
- § 170. Электронный микроскоп
- § 171. Электронные и ионные проекторы
- § 172. Электронно-лучевая трубка
- § 173. Масс-спектрограф
- § 174. Ускорители заряженных частиц
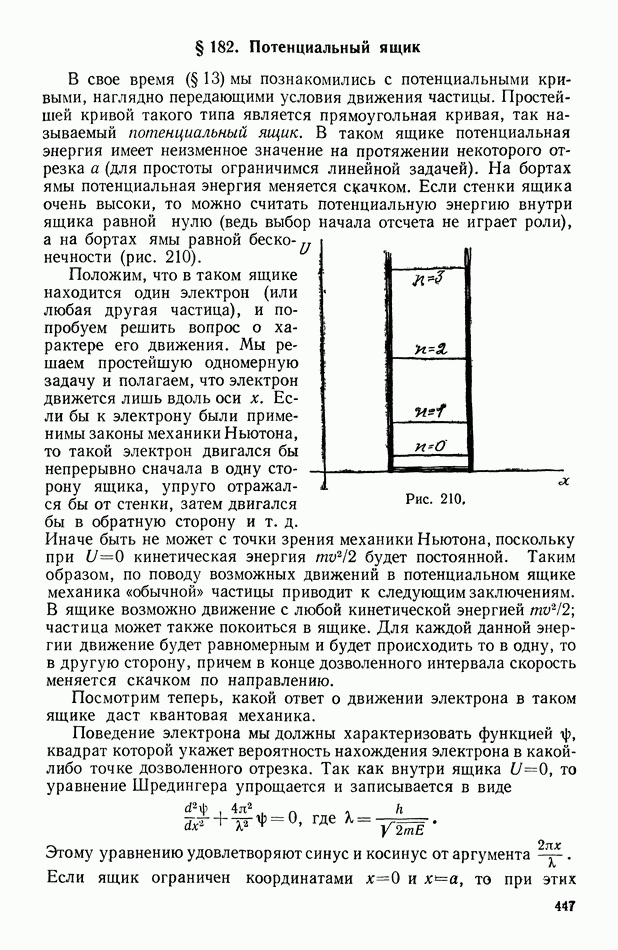
- § 175. Автофазировка
- § 176. Синхрофазотрон. Синхротрон
- § 177. Ионизованный газ
- § 178. Электрический разряд в газе
- § 178а. Плазма
- Вещество в состоянии плазмы.
- Плазма в магнитном поле.
- Проблемы устойчивости.
- ГЛАВА 27. ВОЛНОВЫЕ СВОЙСТВА МИКРОЧАСТИЦ
- § 179. Дифракция электронов
- § 180. Основные идеи квантовой механики
- § 181. Принцип неопределенности
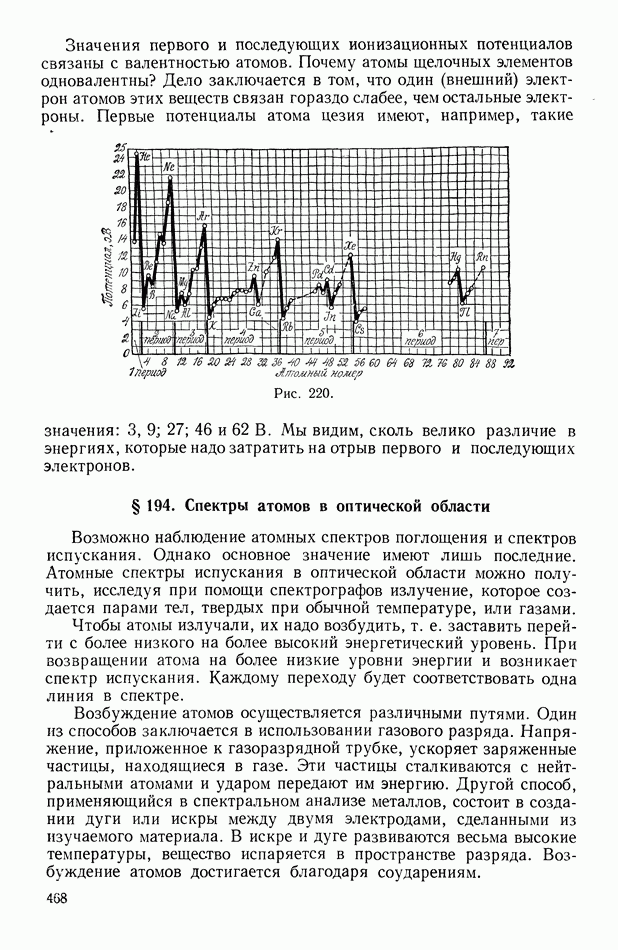
- § 182. Потенциальный ящик
- § 183. Что дает решение уравнения Шредингера
- § 184. Туннельный переход
- ГЛАВА 28. СТРОЕНИЕ АТОМА
- § 185. Энергетические уровни атома водорода
- § 186. Квантовые числа
- § 187. Электронное облако для s- и p-состояний
- § 188. Принцип Паули
- § 189. Отклонение атомного пучка в магнитном поле
- § 190. Спин электрона
- § 191. Магнитные моменты атомов
- § 192. Периодический закон Менделеева
- § 193. Ионизационные потенциалы
- § 194. Спектры атомов в оптической области
- § 195. Атомные рентгеновские спектры
- ГЛАВА 29. МОЛЕКУЛА
- § 196. Химическая связь
- § 197. Геометрия молекул
- § 198. Электронная оболочка молекулы
- § 199. Энергетические уровни молекул
- § 200. Вращательный спектр молекул
- § 201. Инфракрасный колебательно-вращательный спектр
- Колебания многоатомной молекулы.
- § 202. Комбинационное рассеяние света
- § 203. Электронный спектр поглощения
- § 204. Магнитный резонанс
- § 205. Квадрупольный резонанс
- § 206. Газовые лазеры
- ГЛАВА 30. АТОМНОЕ ЯДРО
- § 207. Экспериментальные методы ядерной физики
- § 208. Частицы, входящие в состав ядра
- § 209. Масса и энергия атомного ядра
- § 210. Спин и магнитный момент ядра
- § 211. Силы взаимодействия нуклонов
- § 212. Нуклоны в ядре
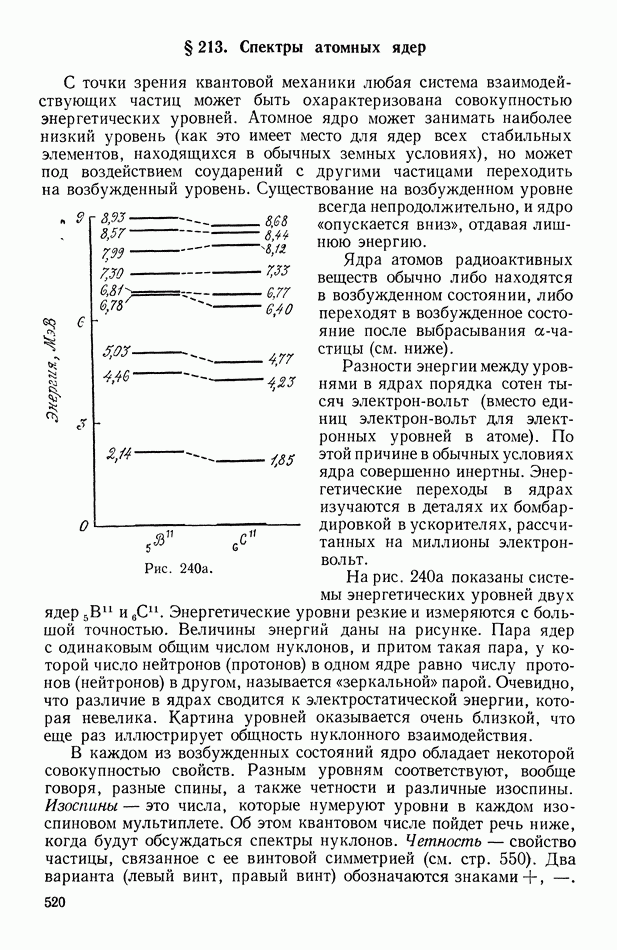
- § 213. Спектры атомных ядер
- § 214. Нейтрино бета-распада
- § 215. Общие закономерности химических и ядерных превращений
- § 216. Радиоактивность
- § 217. Ядерные реакции
- § 217а. Реакции деления тяжелых ядер
- § 217б. Цепная реакция
- § 217в. Принципы действия ядерного реактора
- § 217г. Искусственные радиоактивные продукты
- § 218. Термоядерные реакции
- ГЛАВА 31. ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ
- § 219. Термин «элементарная» частица
- § 220. Взаимодействие быстродвижущихся электронов
- § 221. Мезонная теория взаимодействия нуклонов
- § 222. Мезоны
- § 223. Релятивистская теория электрона
- § 224. Рождение и аннигиляция пар частиц
- § 225. Частицы и античастицы
- § 226. Асимметрия элементарных частиц
- § 226а. Барионный спектр
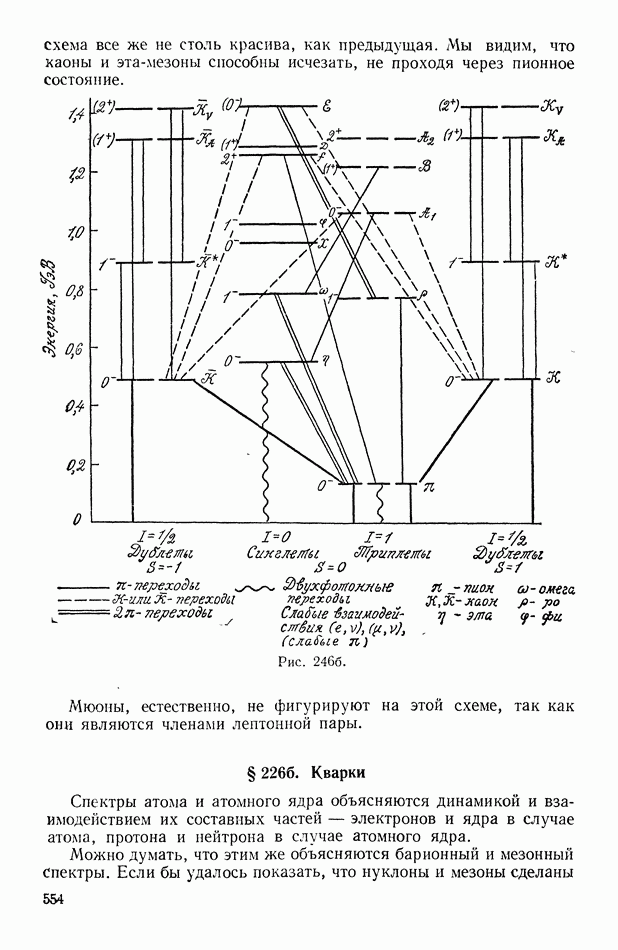
- § 2266. Кварки
- ГЛАВА 32. АТОМНОЕ СТРОЕНИЕ ТЕЛ
- § 227. Поликристаллическое вещество и монокристаллы
- § 228. Пространственная решетка
- § 229. Выбор ячейки. Симметрия кристалла
- § 230. Упаковка частиц в кристалле
- § 231. Молекулярный кристалл
- § 232. Плотные упаковки шаров
- § 233. Примеры кристаллических структур
- § 234. Тепловые колебания в кристалле
- § 235. Тепловые волны
- § 236. Тепловое расширение
- § 237. Дефекты кристалла
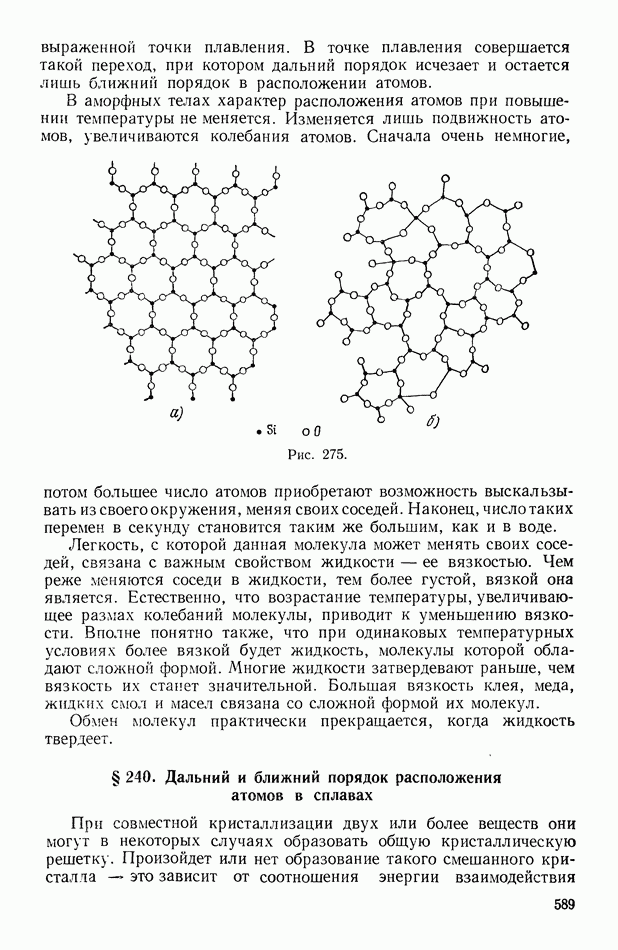
- § 238. Ближний порядок. Жидкости
- § 239. Аморфные тела
- § 240. Дальний и ближний порядок расположения атомов в сплавах
- § 241. Жидкие кристаллы
- § 242. Полимерные вещества
- § 242а. Биологические макромолекулы
- ГЛАВА 33. ФАЗОВЫЕ ПРЕВРАЩЕНИЯ
- § 244. Фазовые превращения
- § 244а. Диаграмма состояния и свойства гелия
- § 245. Условия устойчивого состояния фазы
- § 246. Метастабильные состояния
- § 247. Превращения газ жидкость
- § 248. Сжижение газов
- § 249. Превращения газ кристалл
- § 250. Превращения жидкость кристалл
- § 251. Превращения кристалл-кристалл
- § 252. Диффузия в твердых телах
- ГЛАВА 34. ДЕФОРМАЦИЯ ТЕЛ
- § 254. Пластические свойства
- § 255. Предел прочности
- § 256. Механические свойства поликристаллического материала
- § 257. Влияние поверхностно-активных веществ на деформацию
- § 258. Разрушение материалов под действием потока частиц
- ГЛАВА 35. ДИЭЛЕКТРИКИ
- § 259. Связь между диэлектрической проницаемостью и поляризуемостью молекулы
- § 260. Поляризация полярных и неполярных молекул
- § 261. Аддитивность молекулярной рефракции
- § 262. Пиро- и пьезоэлектрики
- § 262а. Сегнетоэлектрики
- ГЛАВА 36. МАГНЕТИКИ
- § 263. Три класса магнетиков
- § 264. Диамагнетизм
- § 265. Парамагнетизм
- § 266. Ферромагнетизм
- ГЛАВА 37. ЭЛЕКТРОННОЕ СТРОЕНИЕ И СВОЙСТВА ТЕЛ
- § 267. Свободные электроны
- § 268. Энергетические уровни в твердом теле
- § 269. Электронный газ
- § 270. Проводимость
- § 271. Сверхпроводимость
- § 272. Полупроводники
- § 273. Эмиссия электронов
- § 274. Фотоэлектрический эффект
- § 275. Запирающие слои
- § 276. Контактная разность потенциалов
- § 276a. Электролюминесценция полупроводников
- § 277. Распределение зарядов в неравномерно нагретом теле
- § 278. Термоэлектродвижущая сила
- § 279. Выделение тепла в электрических цепях
- § 280. Применения термоэлектрического эффекта