| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 16. Соударения
Слово «соударение» надо понимать в несколько более широком смысле, чем это принято в житейской практике. Для механических задач, которые нас серчас интересуют, к соударениям относятся любые встречи двух или более тел, при которых взаимодействие длится короткий срок. Таким образом, кроме явлений, которые можно отнести к соударениям во всех смыслах этого слова, — удара биллиардных шаров, столкновений атомов или атомных ядер, — сюда можно отнести и такие события, как прыжок человека с трамвая или на трамвай или попадание пули в стенку. При таких коротких взаимодействиях возникают столь большие силы, что роль всех постоянно действующих сил можно считать ничтожной. Это дает нам право рассматривать соударяющиеся тела как замкнутую систему и применять к ним закон сохранения импульса.

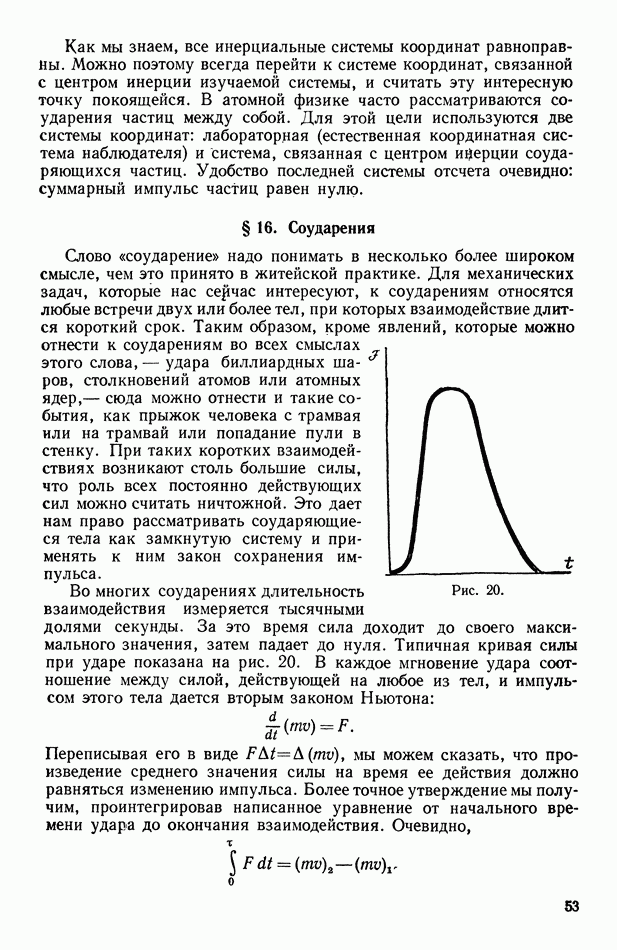
Рис. 20.
Во многих соударениях длительность взаимодействия измеряется тысячными долями секунды. За это время сила доходит до своего максимального значения, затем падает до нуля. Типичная кривая силы при ударе показана на рис. 20. В каждое мгновение удара соотношение между силой, действующей на любое из тел, и импульсом этого тела дается вторым законом Ньютона:

Переписывая его в виде  мы можем сказать, что произведение среднего значения силы на время ее действия должно равняться изменению импульса. Более точное утверждение мы получим, проинтегрировав написанное уравнение от начального времени удара до окончания взаимодействия. Очевидно,
мы можем сказать, что произведение среднего значения силы на время ее действия должно равняться изменению импульса. Более точное утверждение мы получим, проинтегрировав написанное уравнение от начального времени удара до окончания взаимодействия. Очевидно,

Интеграл в левой части называют иногда импульсом силы. Геометрический смысл этой величины на графике — площадь под кривой удара (см. рис. 20).
В зависимости от упругих свойств тел соударения могут протекать весьма различно. Принято выделять два крайних случая: идеально упругий и абсолютно неупругий удары.
Остановимся сначала на втором из них. Под неупругим ударом понимают такую встречу двух тел, в результате которой эти тела объединяются. К неупругим ударам относятся столкновение глиняных шаров, прыжок человека на движущуюся вагонетку, столкновение двух разноименных ионов с образованием молекулы, захват электрона положительным ионом и т. д.
Пусть до встречи тела двигались со скоростями и  суммарный импульс равнялся
суммарный импульс равнялся  После встречи тела имеют общую массу, равную
После встречи тела имеют общую массу, равную  и движутся с какой-то скоростью К. Импульс системы после встречи равен
и движутся с какой-то скоростью К. Импульс системы после встречи равен  Закон сохранения импульса требует равенства
Закон сохранения импульса требует равенства

откуда скорость тел после неупругого удара представится формулой

Вектор имйульса после встречи тел должен равняться сумме векторов импульса тел до удара.
Если встречное движение происходит вдоль одной прямой, то после удара тела будут двигаться в том направлении, куда ранее шло тело с большим импульсом. Если импульсы тел равняются по величине, то  значит, V равно нулю — столкнувшиеся тела остановятся.
значит, V равно нулю — столкнувшиеся тела остановятся.
Неупругий удар сопровождается энергетическим превращением. Из только что приведенного примера видно, что кинетическая энергия может даже обратиться в нуль. Нетрудно подсчитать величину, на которую возрастает внутренняя энергия встретившихся тел в том или ином случае; для этого лишь надо составить разность

Рассмотрим теперь идеально упругие столкновения, т. е. такие, при которых тела полностью восстанавливают свою форму. Это значит, что в состоянии этих тел не происходят какие-либо изменения, их потенциальная и внутренняя энергия до и после удара неизменна и, следовательно, кинетическая энергия должна сохраняться. Для двух тел, соударяющихся таким образом, можно составить два уравнения: закон охранения импульса и закон сохранения кинетической энергии. Обозначим массы тел через  и
и  Всегда можцо выбрать начало координат совпадающим с одним из тел. Это упрощает задачу, нисколько не уменьшая общности
Всегда можцо выбрать начало координат совпадающим с одним из тел. Это упрощает задачу, нисколько не уменьшая общности
рассмотрения. Мы положим поэтому тело с массой  покоящимся до удара. Указанные два закона сохранения дадут тогда такие равенства:
покоящимся до удара. Указанные два закона сохранения дадут тогда такие равенства:

здесь и  скорости шара
скорости шара  до и после удара, V — скорость шара
до и после удара, V — скорость шара  после удара.
после удара.
Рассмотрим несколько примеров применения этих уравнений. Прежде всего, изучим нецентральное соударение двух шаров равной массы (рис. 21). Тогда массы сокращаются в обоих уравнениях и мы получим

Из векторного равенства ясно, что вектор и является замыкающей треугольника, построенного на векторах  и
и  Из правого уравнения следует, что треугольник, в котором и — гипотенуза, должен быть прямоугольным; отсюда следует, что скорости после столкновения двух частиц равной массы должны быть направлены под прямым углом друг к другу. Этот интересный вывод легко проследить для биллиардной игры: направления движений шара, который подвергся удару, и «своего» шара образуют угол в 90°. В остальном характер изменения вектора скорости не определяется нашими уравнениями, в которых не учитывается отклонение линии удара от линии, проходящей через центры шаров.
Из правого уравнения следует, что треугольник, в котором и — гипотенуза, должен быть прямоугольным; отсюда следует, что скорости после столкновения двух частиц равной массы должны быть направлены под прямым углом друг к другу. Этот интересный вывод легко проследить для биллиардной игры: направления движений шара, который подвергся удару, и «своего» шара образуют угол в 90°. В остальном характер изменения вектора скорости не определяется нашими уравнениями, в которых не учитывается отклонение линии удара от линии, проходящей через центры шаров.

Рис. 21.
Полные сведения о движении шаров после удара мы получим, если ограничим себя случаем центрального удара. Движение столкнувшихся шаров будет тогда и после удара происходить вдоль той же прямой. Поэтому можно не пользоваться векторными символами, помня, однако, что изменение знака скорости будет означать изменение направления движения. В этом случае нам нет зато нужды рассматривать упрощенный случай равных масс. Уравнения центрального соударения имеют вид

Преобразовывая эти уравнения к виду

и деля их друг на друга, найдем:  или
или  Мы замечаем, что относительная скорость движения шара
Мы замечаем, что относительная скорость движения шара  по
по
отношению к шару  до удара (мы ее обозначили через
до удара (мы ее обозначили через  ) равна с обратным знаком той же относительной скорости после удара.
) равна с обратным знаком той же относительной скорости после удара.
Интересная формула возникает при подстановке  в формулу закона сохранения импульса. Находим выражение скорости шара
в формулу закона сохранения импульса. Находим выражение скорости шара  после удара через скорость этого же шара до удара:
после удара через скорость этого же шара до удара:


Рис. 22.
Если массы шаров равны, то скорость  обращается в нуль. Это явление можно очень эффектно демонстрировать на стальных или костяных шариках. Шары как бы обмениваются скоростями при таком ударе (рис. 22). В остальных случаях шар
обращается в нуль. Это явление можно очень эффектно демонстрировать на стальных или костяных шариках. Шары как бы обмениваются скоростями при таком ударе (рис. 22). В остальных случаях шар  замедляется. Чем ближе массы соударяющихся шаров, тем эффектнее замедление. Нетрудно прикинуть, что нейтрон (масса 1) отскочит от ядра атома углерода (масса 12), потеряв
замедляется. Чем ближе массы соударяющихся шаров, тем эффектнее замедление. Нетрудно прикинуть, что нейтрон (масса 1) отскочит от ядра атома углерода (масса 12), потеряв  своей скорости, а от ядра атома урана (масса 235) — потеряв всего лишь 2/23в своей скорости.
своей скорости, а от ядра атома урана (масса 235) — потеряв всего лишь 2/23в своей скорости.

Рис. 23.
Для макроскопических тел законы упругого удара неплохо выполняются для таких материалов как слоновая кость, сталь, резина и т. д. Эти материалы обладают способностью превосходно восстанавливать свою форму, что видно из интересной фотографии, приводимой на рис. 23, где при помощи так называемой «лупы времени» снят момент удара хоккейного мяча о препятствие. За  секунды мяч сжимается почти на один сантиметр, такое же время затрачивается на восстановительную фазу удара. В первой фазе кинетическая энергия удара превращается в потенциальную энергию упругого сжатия. Во второй фазе потенциальная энергия переходит в кинетическую. При идеально упругом ударе этот обратный переход должен был бы полностью восстановить значение кинетической энергии, затраченной в первой фазе удара.
секунды мяч сжимается почти на один сантиметр, такое же время затрачивается на восстановительную фазу удара. В первой фазе кинетическая энергия удара превращается в потенциальную энергию упругого сжатия. Во второй фазе потенциальная энергия переходит в кинетическую. При идеально упругом ударе этот обратный переход должен был бы полностью восстановить значение кинетической энергии, затраченной в первой фазе удара.
Нашими формулами не охватывается важный случай упругого удара шара о стенку (рис. 24). Так как кинетическая энергия должна сохраняться, то скорость шара не может измениться по величине. Что же касается направления движения шара после удара, то оно должно образовывать тот же угол  с нормалью, что и вектор скорости до удара. Действительно, в случае удара о гладкую
с нормалью, что и вектор скорости до удара. Действительно, в случае удара о гладкую
стенку тангенциальная (касательная) составляющая скорости остается неизменной, так как отсутствуют тангенциальные силы сцепления со стенкой. Как видно из рисунка, приращение импульса численно равно  и направлено вдоль нормали к стенке. Согласно основному закону механики, в момент удара сила, действующая на шар со стороны стенки, должна быть направлена туда же, куда направлен вектор изменения импульса. Поэтому-то и угол падения шара равен углу отражения.
и направлено вдоль нормали к стенке. Согласно основному закону механики, в момент удара сила, действующая на шар со стороны стенки, должна быть направлена туда же, куда направлен вектор изменения импульса. Поэтому-то и угол падения шара равен углу отражения.

Рис. 24.
Рассмотрим неупругий удар на примере баллистического маятника (прибор для измерения скорости пули). Ящик с песком массой  подвешен на тросе. Пуля влетает в ящик и застревает в песке. Импульс пули до удара та, импульс системы после удара
подвешен на тросе. Пуля влетает в ящик и застревает в песке. Импульс пули до удара та, импульс системы после удара  Имеем
Имеем

Приобретя кинетическую энергию  ящик израсходует ее, поднявшись на высоту
ящик израсходует ее, поднявшись на высоту  удовлетворяющую условию
удовлетворяющую условию

Пусть  тогда
тогда  см.
см.
Если бы мы не пользовались законом сохранения импульса, а определили бы  основываясь на полном переходе кинетической энергии пули в потенциальную энергию маятника, то получили бы
основываясь на полном переходе кинетической энергии пули в потенциальную энергию маятника, то получили бы  Это означает, что в нашем примере
Это означает, что в нашем примере  механической энергии (99,9% общего запаса) «исчезло» (пошло на нагревание системы). Так как абсолютно упругих тел не существует, то при каждом «упругом» ударе механическая энергия не сохраняется, часть ее переходит в энергию теплового движения молекул и рассеивается. Мы еще вернемся к этому в гл. 11 (стр. 159).
механической энергии (99,9% общего запаса) «исчезло» (пошло на нагревание системы). Так как абсолютно упругих тел не существует, то при каждом «упругом» ударе механическая энергия не сохраняется, часть ее переходит в энергию теплового движения молекул и рассеивается. Мы еще вернемся к этому в гл. 11 (стр. 159).
Теперь на примере соударений мы проиллюстрируем достоинства системы координат, связанной с центром инерции.
Пусть на шарик с массой  покоящийся в лабораторной системе координат, налетает другой такой же шарик со скоростью
покоящийся в лабораторной системе координат, налетает другой такой же шарик со скоростью  Если удар неупругий, то какая-то часть кинетической энергии системы
Если удар неупругий, то какая-то часть кинетической энергии системы  перейдет в тепло. В иных системах координат кинетическая энергия этой пары шариков выразится другими числами. Что же касается выделяемого тепла, то оно будет одним и тем же для данной пары шариков и будет определяться скоростью их относительного движения. Поэтому, вместо того чтобы с помощью закона сохранения импульса искать переходящую в тепло долю кинетической энергии, вычисленной для лабораторной системы координат, достаточно рассчитать кинетическую энергию для системы, связанной с центром инерции. Так как в этой системе координат суммарный импульс тел равен нулю, то после неупругого соударения шары останавливаются: вся кинетическая энергия переходит в тепло. Кинетическая энергия для системы, связанной с центром инерции, будет иметь минимальное значение.
перейдет в тепло. В иных системах координат кинетическая энергия этой пары шариков выразится другими числами. Что же касается выделяемого тепла, то оно будет одним и тем же для данной пары шариков и будет определяться скоростью их относительного движения. Поэтому, вместо того чтобы с помощью закона сохранения импульса искать переходящую в тепло долю кинетической энергии, вычисленной для лабораторной системы координат, достаточно рассчитать кинетическую энергию для системы, связанной с центром инерции. Так как в этой системе координат суммарный импульс тел равен нулю, то после неупругого соударения шары останавливаются: вся кинетическая энергия переходит в тепло. Кинетическая энергия для системы, связанной с центром инерции, будет иметь минимальное значение.
В системе координат, связанной с центром инерции, шары движутся навстречу друг другу со скоростями  Кинетическая энергия каждого шарика равна
Кинетическая энергия каждого шарика равна  а полная энергия системы
а полная энергия системы 
Таково будет количество тепла, выделяемое при неупругом соударении. Какой бы ни был удар, выделение тепла (или другой формы энергии) за счет кинетической энергии тел может произойти в количестве, не превышающем кинетическую энергию, подсчитанную для системы, связанной с центром инерции. И наоборот, для выделения заданного количества тепла нужно эквивалентное количество кинетической энергии, подсчитанное для системы центра инерции.
Пример. Ядерная реакция бомбардировки азота  -частицами протекает согласно уравнению
-частицами протекает согласно уравнению

и идет с поглощением энергии  Какой кинетической энергией в лабораторной системе координат должна обладать
Какой кинетической энергией в лабораторной системе координат должна обладать  -частица, чтобы реакция пошла? На первый взгляд кажется, что для этого достаточно энергии
-частица, чтобы реакция пошла? На первый взгляд кажется, что для этого достаточно энергии  Номы
Номы  знаем, что это не так. В системе координат, связанной с центром инерции, нужна энергия
знаем, что это не так. В системе координат, связанной с центром инерции, нужна энергия  однако в лабораторной системе координат нужна большая энергия.
однако в лабораторной системе координат нужна большая энергия.
Действительно, скорость центра инерции  где
где  импульс первой частицы,
импульс первой частицы,  второй. Скорость первой частицы в системе координат центра инерции
второй. Скорость первой частицы в системе координат центра инерции

Отсюда кинетическая энергия системы  в системе координат центра инерции будет
в системе координат центра инерции будет

— так называемая приведенная масса обеих частиц. Будем считать ядра  неподвижными
неподвижными  Это предположение справедливо, так как всегда можно пренебречь медленным тепловым движением ядер-мишеней по сравнению с огромными скоростями налетающих частиц. Тогда кинетическая энергия в лабораторной системе координат
Это предположение справедливо, так как всегда можно пренебречь медленным тепловым движением ядер-мишеней по сравнению с огромными скоростями налетающих частиц. Тогда кинетическая энергия в лабораторной системе координат  следовательно,
следовательно,

Реакция идет, если  Учитывая, что
Учитывая, что  получим
получим

| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ
- ЧАСТЬ I. МЕХАНИЧЕСКОЕ И ТЕПЛОВОЕ ДВИЖЕНИЕ
- Уравнения движения материальной точки.
- Средняя скорость.
- Истинная скорость.
- Векторное ускорение.
- § 2. Силы
- Гравитационные силы.
- Электромагнитные силы.
- Ядерные силы.
- Силы «слабого» взаимодействия.
- Поле сил.
- § 3. Основной закон механики
- Законы Ньютона.
- Относительность движения.
- Законы механики в неинерциальной системе координат.
- § 4. Приложение основного закона механики к ускоренному прямолинейному движению
- Горизонтальное движение под действием постоянной силы.
- Вертикально движущийся лифт.
- Тяга свободно подвешенного груза.
- § 5. Приложение основного закона механики к движению по окружности
- § 6. Влияние вращения Земли на механические явления
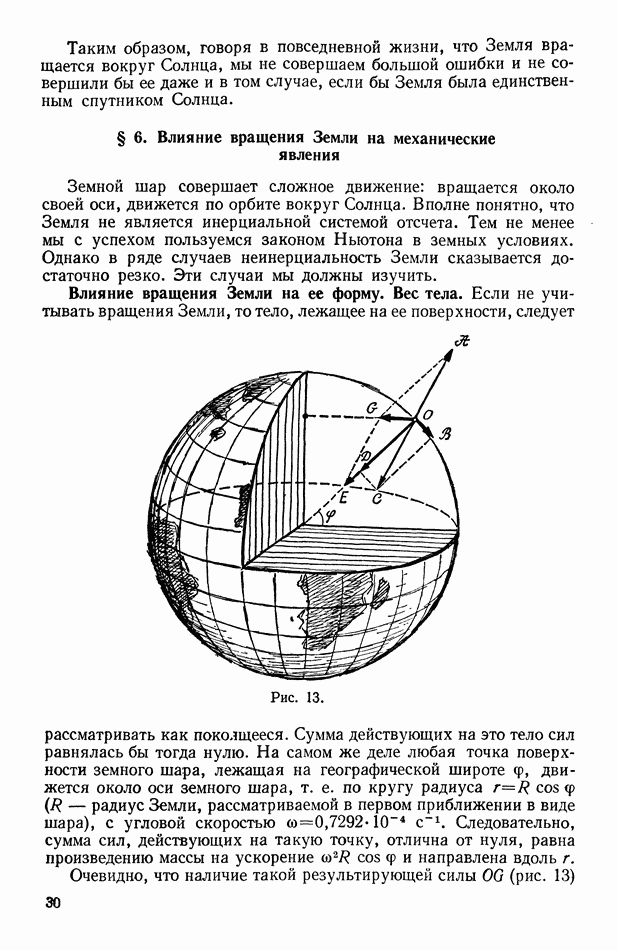
- Влияние вращения Земли на ее форму. Вес тела.
- Влияние вращения Земли на движение тел по земной поверхности.
- § 7. Какие данные необходимы для решения механической задачи?
- § 8. Коэффициенты пропорциональности в формулах физики и размерности физических величин
- ГЛАВА 2. МЕХАНИЧЕСКАЯ ЭНЕРГИЯ
- § 9. Работа
- § 10. Кинетическая энергия
- § 11. Потенциальная энергия
- § 12. Закон сохранения механической энергии
- § 13. Потенциальные кривые. Равновесие
- ГЛАВА 3. ИМПУЛЬС
- § 14. Сохранение импульса
- § 15. Центр инерции
- § 16. Соударения
- § 17. Явления отдачи
- ГЛАВА 4. ВРАЩЕНИЕ ТВЕРДОГО ТЕЛА
- § 18. Кинетическая энергия вращения
- § 19. Момент инерции
- § 20. Работа вращения и основное уравнение вращения
- § 21. Момент импульса
- § 22. Свободные оси вращения
- § 23. Гироскопы
- ГЛАВА 5. КОЛЕБАНИЯ
- § 24. Малые отклонения от равновесия
- § 25. Частные случаи колебаний
- § 26. Превращения энергии. Затухающие колебания
- § 27. Вынужденные колебания
- § 28. Автоколебания
- § 29. Сложение колебаний одного направления
- § 30. Спектр колебания
- § 31. Сложение взаимно перпендикулярных колебаний
- ГЛАВА 6. БЕГУЩИЕ ВОЛНЫ
- § 32. Распространение деформации
- § 33. Возникновение волнового движения
- § 34. Волны давления и скорости колебания
- § 35. Поток энергии
- § 36. Затухание упругих волн
- § 37. Интерференция волн
- § 38. Принцип Гюйгенса — Френеля. Отражение и преломление волн
- § 39. Коэффициент отражения
- § 40. Явление Доплера
- ГЛАВА 7. СТОЯЧИЕ ВОЛНЫ
- § 41. Наложение двух волн, бегущих в противоположные стороны
- § 42. Собственные колебания стержней
- § 43. Собственные колебания двумерных и трехмерных систем
- § 44. Вынужденные колебания стержней и пластинок
- § 45. Колебания пьезоэлектриков
- ГЛАВА 8. ВОПРОСЫ АКУСТИКИ
- § 46. Объективная и субъективная характеристики звука
- § 47. Сила и громкость звука
- § 48. Архитектурная акустика
- § 49. Атмосферная акустика
- § 50. Действие ультразвука
- ГЛАВА 9. ТЕМПЕРАТУРА И ТЕПЛОТА
- § 51. Тепловое равновесие
- § 52. Внутренняя энергия
- § 53. Первое начало термодинамики
- § 54. Энергия микроскопических систем
- § 55. Уравнение состояния
- § 56. Уравнение газового состояния
- § 57. Уравнения состояния реальных газов
- ГЛАВА 10. ТЕРМОДИНАМИЧЕСКИЕ ПРОЦЕССЫ
- § 58. Графическое изображение процессов
- § 59. Работа. Циклы
- § 60. Процессы изменения состояния газов
- Изобарический процесс.
- Изотермический процесс.
- Адиабатический процесс.
- Измерение теплоемкостей газов.
- § 61. Процесс Джоуля — Томсона
- ГЛАВА 11. ЭНТРОПИЯ
- § 62. Принцип существования энтропии
- § 63. Принцип возрастания энтропии
- § 64. Принцип действия тепловой машины
- § 65. Цикл Карно. Максимальный к. п. д.
- § 66. Второе начало термодинамики
- ГЛАВА 12. КИНЕТИЧЕСКАЯ ТЕОРИЯ ГАЗОВ
- § 68. Длина свободного пробега
- § 69. Давление газа. Средняя квадратичная скорость молекул
- § 70. Внутренняя энергия газа
- § 71. Статистическое распределение
- § 72. Закон Больцмана
- § 73. Распределение частиц по высоте в поле тяжести
- § 74. Распределение молекул по скоростям
- § 75. Измерение скоростей молекул газа
- § 76. Вероятность состояния
- § 77. Необратимые процессы с молекулярной точки зрения
- § 78. Флуктуации. Границы применения второго начала
- ГЛАВА 13. ПРОЦЕССЫ ПЕРЕХОДА К РАВНОВЕСИЮ
- § 79. Диффузия
- § 80. Теплопроводность и вязкость
- § 81. Быстрота выравнивания
- § 82. Стационарные процессы
- § 83. Движение в вязкой среде
- § 84. Коэффициенты диффузии, вязкости и теплопроводности для газов
- § 85. Ультраразреженные газы
- ЧАСТЬ II. ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ
- § 86. Векторные характеристики электрического поля: напряженность и смещение
- § 87. Диэлектрическая проницаемость
- § 88. Законы электрического поля
- § 89. Вычисление полей простейших систем
- Система точечных зарядов.
- Универсальные формулы потенциала.
- Поле сферического конденсатора.
- Поле равномерно заряженной сферы.
- Поле с цилиндрической симметрией.
- Однородные поля.
- Поле на поверхности металла.
- Электрическое изображение.
- § 90. Электрическая энергия
- Энергия конденсатора.
- Энергия поля
- Энергия взаимодействия.
- § 91. Радиус электрона и границы классической электродинамики
- § 92. Электрические силы
- § 93. Дипольный момент системы зарядов
- § 94. Поляризация изотропного диэлектрика
- § 95. Поляризация кристаллических веществ
- § 96. Ограниченные диэлектрические тела в электрическом поле
- ГЛАВА 15. МАГНИТНОЕ ПОЛЕ
- § 97. Магнитный момент
- § 98. Сила Ампера
- § 99. Сила, действующая на движущийся заряд
- § 100. Магнитное поле, создаваемое постоянными магнитами
- § 101. Напряженность магнитного поля
- § 102. Взаимодействия токов и магнитов
- § 103. Эквивалентность токов и магнитов
- § 104. Вихревой характер магнитного поля
- § 105. Закон электромагнитной индукции и сила Лоренца
- § 106. Измерения магнитного поля методом индукционного толчка
- § 107. Ограниченные тела в магнитном поле
- § 108. Связь между магнитной проницаемостью и восприимчивостью
- § 109. Искажение магнитного поля при внесении в него магнетика
- § 110. Магнитный гистерезис
- ГЛАВА 16. ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ. УРАВНЕНИЯ МАКСВЕЛЛА
- § 111. Обобщение закона электромагнитной индукции
- § 112. Ток смещения
- § 113. Картина электромагнитного поля
- ГЛАВА 17. ЭНЕРГЕТИЧЕСКИЕ ПРЕВРАЩЕНИЯ В ЭЛЕКТРОМАГНИТНОМ ПОЛЕ
- § 114. Превращения в цепи постоянного тока
- § 115. Превращения в замкнутой цепи переменного тока
- § 116. Магнитная энергия поля
- § 117. Электрические колебания
- § 118. Электромагнитная энергия
- § 119. Импульс и давление электромагнитного поля
- ГЛАВА 18. ЭЛЕКТРОМАГНИТНОЕ ИЗЛУЧЕНИЕ
- § 120. Элементарный диполь
- § 121. Антенна как электрический диполь
- § 122. Излучение диполя
- § 123. Электромагнитный спектр
- § 124. Квантовая природа излучения
- ГЛАВА 19. РАСПРОСТРАНЕНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН
- § 126. Поведение электромагнитной волны на границе двух сред
- § 127. Естественный и поляризованный свет. Поляризация при отражении
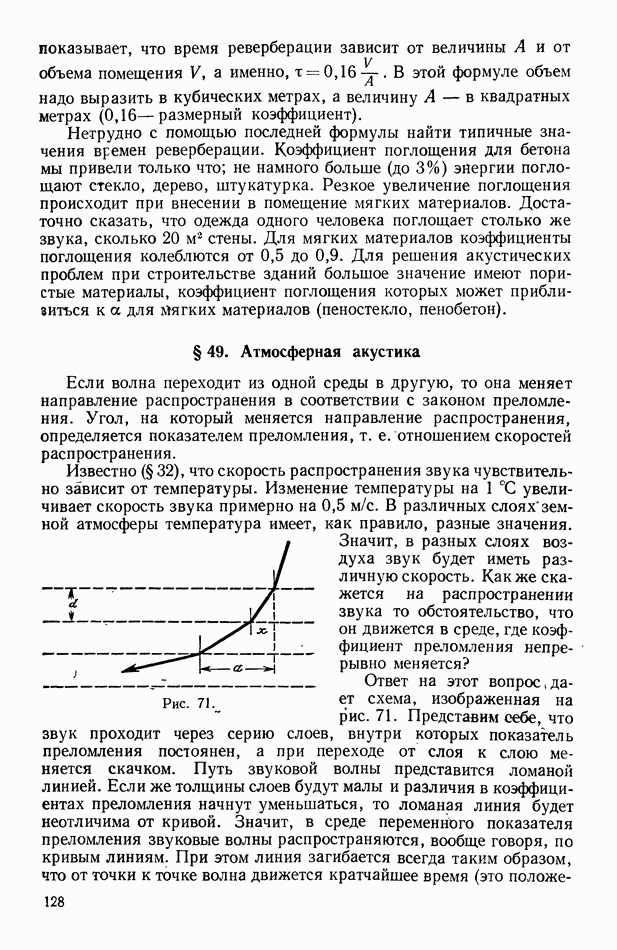
- § 128. Распространение световых волн в среде с градиентом показателя преломления
- § 129. Распространение радиоволн
- § 130. Радиолокация
- ГЛАВА 20. ИНТЕРФЕРЕНЦИОННЫЕ ЯВЛЕНИЯ
- § 131. Сложение волн от двух источников
- § 132. Когерентность
- § 133. Интерференция в пластинке
- § 134. Полосы равной толщины и полосы равного наклона
- § 135. Практические применения интерференции
- ГЛАВА 21. РАССЕЯНИЕ
- § 136. Вторичное излучение
- § 137. Дифракция волн на отверстиях
- § 138. Система беспорядочно расположенных рассеивателей
- § 139. Поведение сплошной однородной среды
- § 140. Рассеяние в неоднородной среде
- § 141. Дифракционная решетка
- § 142. Направленные излучатели радиоволн
- § 142а. Голография
- ГЛАВА 22. ДИФРАКЦИЯ РЕНТГЕНОВСКИХ ЛУЧЕЙ НА КРИСТАЛЛЕ
- § 143. Кристалл как дифракционная решетка
- § 144. Определение параметров элементарной ячейки кристалла
- § 145. Интенсивность дифракционных лучей
- § 146. Методы рентгеновского анализа
- ГЛАВА 23. ДВОЙНОЕ ЛУЧЕПРЕЛОМЛЕНИЕ
- § 147. Анизотропия поляризуемости
- § 148. Раснространение света в одноосных кристаллах
- § 149. Поляризаторы. Исследование поляризационного состояния света
- § 150. Кристаллическая пластинка между «скрещенными» николями
- § 151. Двойное лучепреломление, вызванное внешним воздействием
- § 152. Оптическая активность
- § 153. Принципы теории оптической активности
- ГЛАВА 24. ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ
- § 155. Опытные подтверждения принципа постоянства скорости света
- § 156. Время в теории относительности
- § 157. Масса
- § 158. Энергия
- § 159. Дефект массы
- § 160. Принцип эквивалентности и понятие об общей теории относительности
- ГЛАВА 25. КВАНТОВАЯ ПРИРОДА ПОЛЯ
- § 161. Фотон
- § 162. Фотоэлектрический эффект
- § 163. Флуктуации светового потока
- § 164. Закон Кирхгофа
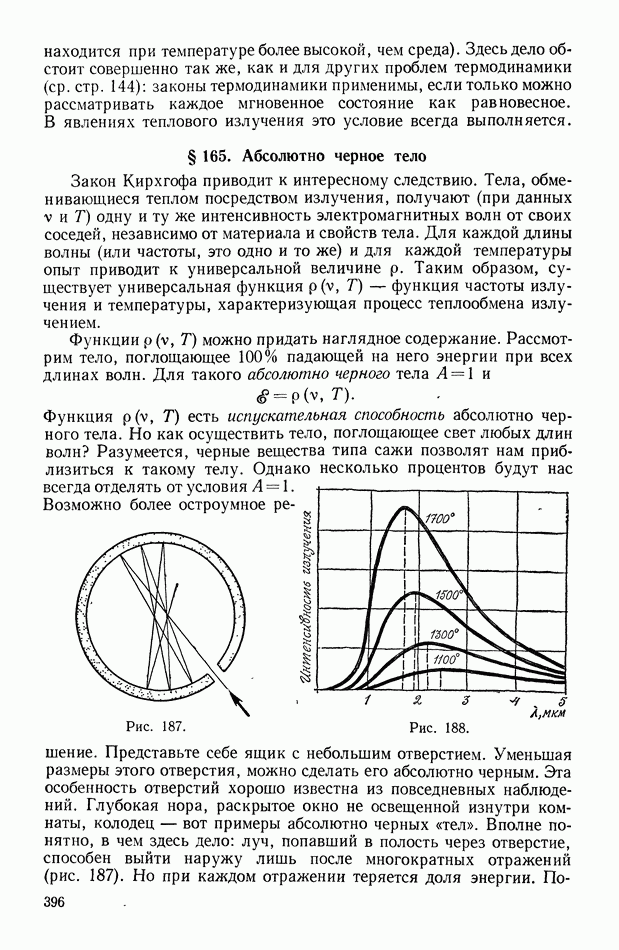
- § 165. Абсолютно черное тело
- § 166. Теория теплового излучения
- § 166а. Стимулированное излучение
- § 166б, Люминесценция
- ЧАСТЬ III. СТРОЕНИЕ И СВОЙСТВА ВЕЩЕСТВА
- § 167. Движение заряженной частицы в электрическом и магнитном полях
- § 168. Получение пучков заряженных частиц
- § 169. Электронные линзы
- § 170. Электронный микроскоп
- § 171. Электронные и ионные проекторы
- § 172. Электронно-лучевая трубка
- § 173. Масс-спектрограф
- § 174. Ускорители заряженных частиц
- § 175. Автофазировка
- § 176. Синхрофазотрон. Синхротрон
- § 177. Ионизованный газ
- § 178. Электрический разряд в газе
- § 178а. Плазма
- Вещество в состоянии плазмы.
- Плазма в магнитном поле.
- Проблемы устойчивости.
- ГЛАВА 27. ВОЛНОВЫЕ СВОЙСТВА МИКРОЧАСТИЦ
- § 179. Дифракция электронов
- § 180. Основные идеи квантовой механики
- § 181. Принцип неопределенности
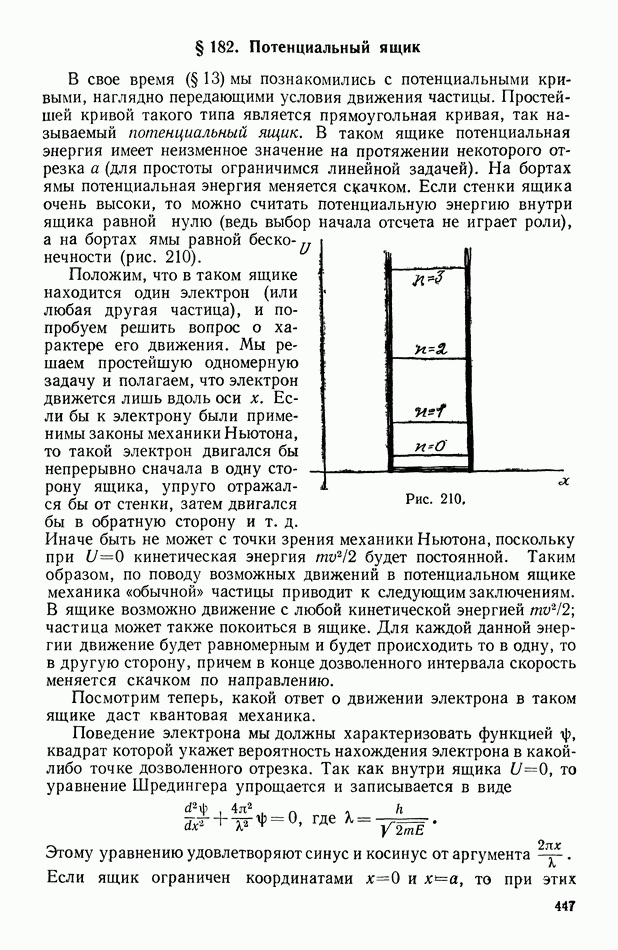
- § 182. Потенциальный ящик
- § 183. Что дает решение уравнения Шредингера
- § 184. Туннельный переход
- ГЛАВА 28. СТРОЕНИЕ АТОМА
- § 185. Энергетические уровни атома водорода
- § 186. Квантовые числа
- § 187. Электронное облако для s- и p-состояний
- § 188. Принцип Паули
- § 189. Отклонение атомного пучка в магнитном поле
- § 190. Спин электрона
- § 191. Магнитные моменты атомов
- § 192. Периодический закон Менделеева
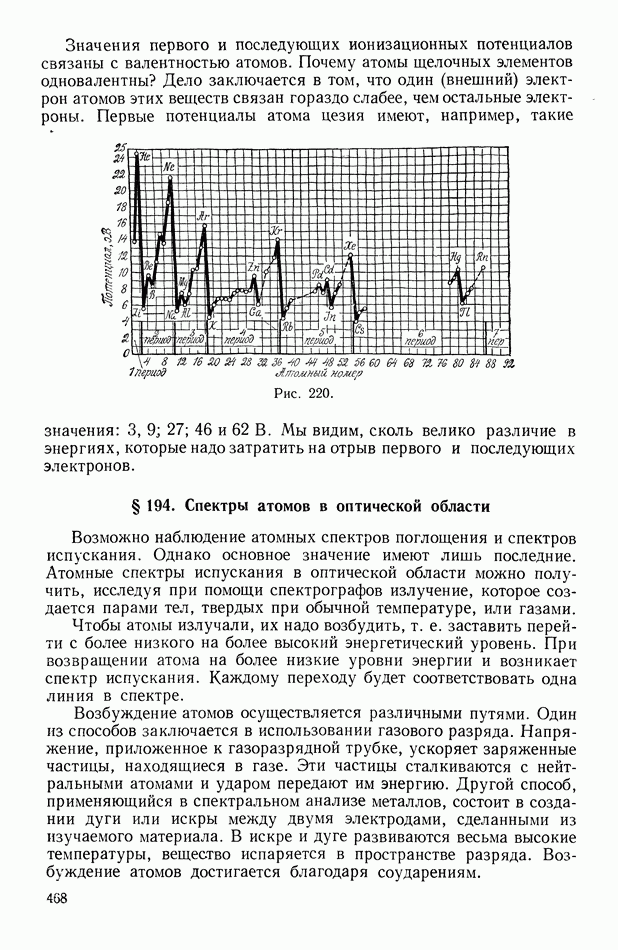
- § 193. Ионизационные потенциалы
- § 194. Спектры атомов в оптической области
- § 195. Атомные рентгеновские спектры
- ГЛАВА 29. МОЛЕКУЛА
- § 196. Химическая связь
- § 197. Геометрия молекул
- § 198. Электронная оболочка молекулы
- § 199. Энергетические уровни молекул
- § 200. Вращательный спектр молекул
- § 201. Инфракрасный колебательно-вращательный спектр
- Колебания многоатомной молекулы.
- § 202. Комбинационное рассеяние света
- § 203. Электронный спектр поглощения
- § 204. Магнитный резонанс
- § 205. Квадрупольный резонанс
- § 206. Газовые лазеры
- ГЛАВА 30. АТОМНОЕ ЯДРО
- § 207. Экспериментальные методы ядерной физики
- § 208. Частицы, входящие в состав ядра
- § 209. Масса и энергия атомного ядра
- § 210. Спин и магнитный момент ядра
- § 211. Силы взаимодействия нуклонов
- § 212. Нуклоны в ядре
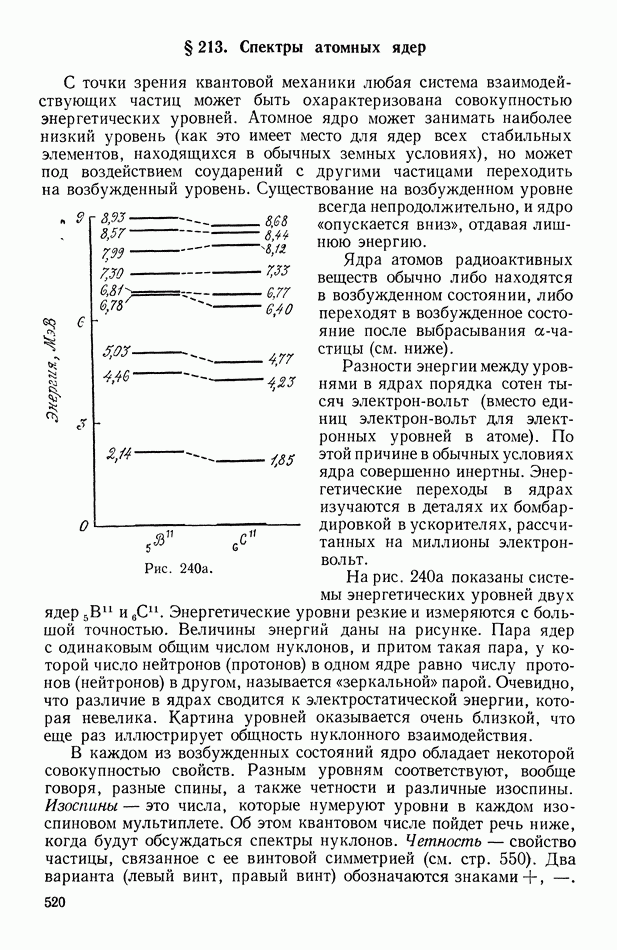
- § 213. Спектры атомных ядер
- § 214. Нейтрино бета-распада
- § 215. Общие закономерности химических и ядерных превращений
- § 216. Радиоактивность
- § 217. Ядерные реакции
- § 217а. Реакции деления тяжелых ядер
- § 217б. Цепная реакция
- § 217в. Принципы действия ядерного реактора
- § 217г. Искусственные радиоактивные продукты
- § 218. Термоядерные реакции
- ГЛАВА 31. ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ
- § 219. Термин «элементарная» частица
- § 220. Взаимодействие быстродвижущихся электронов
- § 221. Мезонная теория взаимодействия нуклонов
- § 222. Мезоны
- § 223. Релятивистская теория электрона
- § 224. Рождение и аннигиляция пар частиц
- § 225. Частицы и античастицы
- § 226. Асимметрия элементарных частиц
- § 226а. Барионный спектр
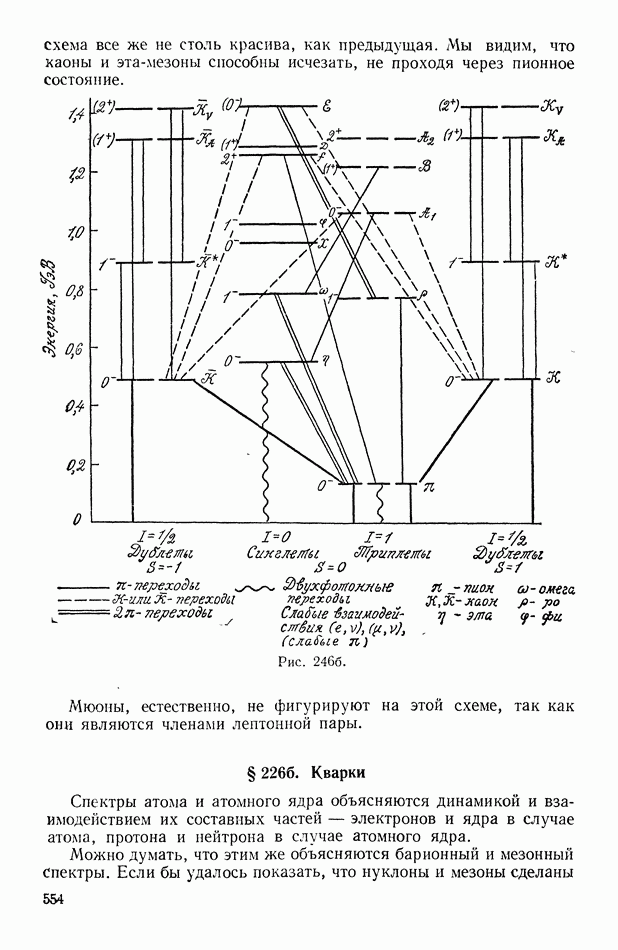
- § 2266. Кварки
- ГЛАВА 32. АТОМНОЕ СТРОЕНИЕ ТЕЛ
- § 227. Поликристаллическое вещество и монокристаллы
- § 228. Пространственная решетка
- § 229. Выбор ячейки. Симметрия кристалла
- § 230. Упаковка частиц в кристалле
- § 231. Молекулярный кристалл
- § 232. Плотные упаковки шаров
- § 233. Примеры кристаллических структур
- § 234. Тепловые колебания в кристалле
- § 235. Тепловые волны
- § 236. Тепловое расширение
- § 237. Дефекты кристалла
- § 238. Ближний порядок. Жидкости
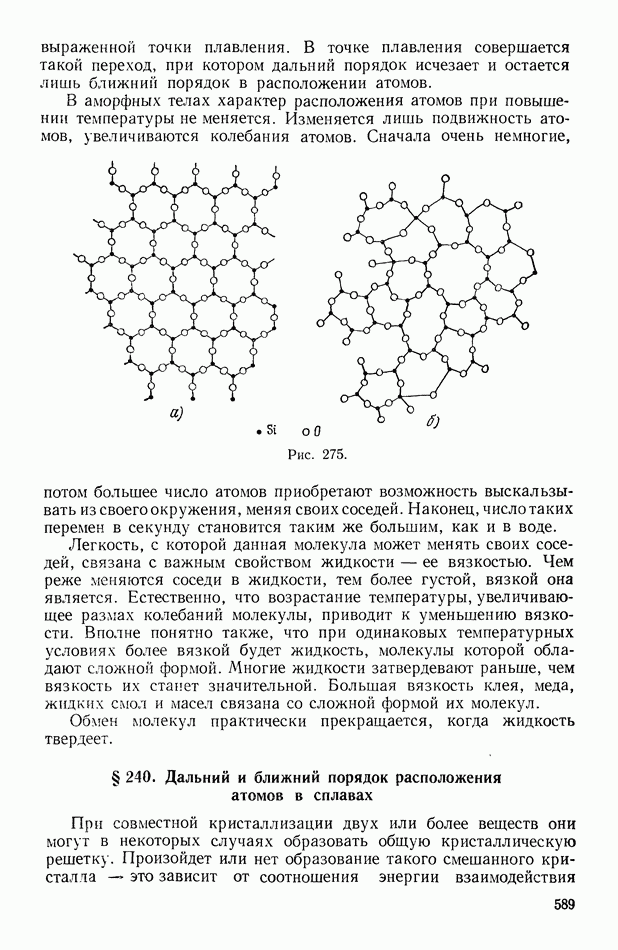
- § 239. Аморфные тела
- § 240. Дальний и ближний порядок расположения атомов в сплавах
- § 241. Жидкие кристаллы
- § 242. Полимерные вещества
- § 242а. Биологические макромолекулы
- ГЛАВА 33. ФАЗОВЫЕ ПРЕВРАЩЕНИЯ
- § 244. Фазовые превращения
- § 244а. Диаграмма состояния и свойства гелия
- § 245. Условия устойчивого состояния фазы
- § 246. Метастабильные состояния
- § 247. Превращения газ жидкость
- § 248. Сжижение газов
- § 249. Превращения газ кристалл
- § 250. Превращения жидкость кристалл
- § 251. Превращения кристалл-кристалл
- § 252. Диффузия в твердых телах
- ГЛАВА 34. ДЕФОРМАЦИЯ ТЕЛ
- § 254. Пластические свойства
- § 255. Предел прочности
- § 256. Механические свойства поликристаллического материала
- § 257. Влияние поверхностно-активных веществ на деформацию
- § 258. Разрушение материалов под действием потока частиц
- ГЛАВА 35. ДИЭЛЕКТРИКИ
- § 259. Связь между диэлектрической проницаемостью и поляризуемостью молекулы
- § 260. Поляризация полярных и неполярных молекул
- § 261. Аддитивность молекулярной рефракции
- § 262. Пиро- и пьезоэлектрики
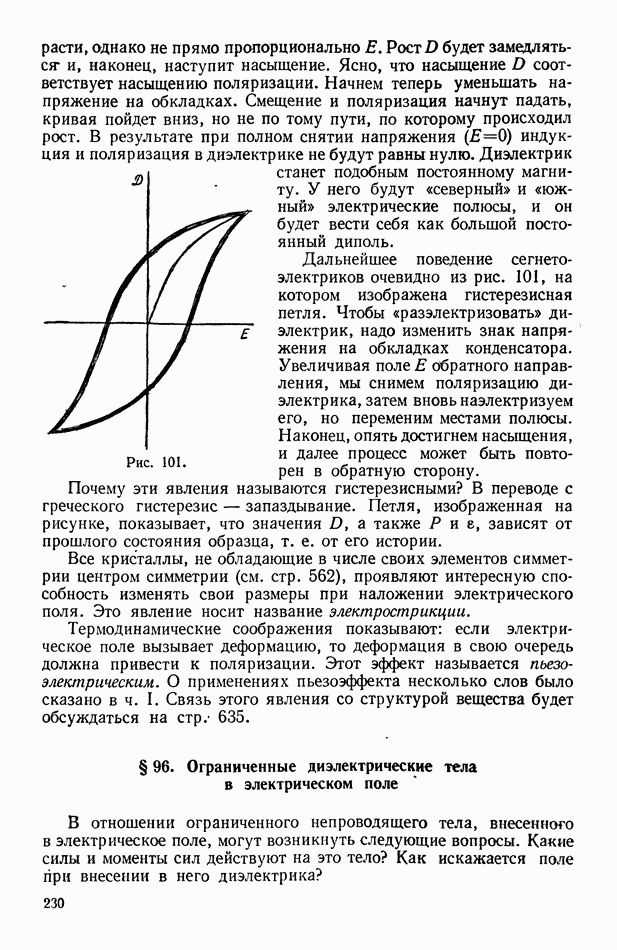
- § 262а. Сегнетоэлектрики
- ГЛАВА 36. МАГНЕТИКИ
- § 263. Три класса магнетиков
- § 264. Диамагнетизм
- § 265. Парамагнетизм
- § 266. Ферромагнетизм
- ГЛАВА 37. ЭЛЕКТРОННОЕ СТРОЕНИЕ И СВОЙСТВА ТЕЛ
- § 267. Свободные электроны
- § 268. Энергетические уровни в твердом теле
- § 269. Электронный газ
- § 270. Проводимость
- § 271. Сверхпроводимость
- § 272. Полупроводники
- § 273. Эмиссия электронов
- § 274. Фотоэлектрический эффект
- § 275. Запирающие слои
- § 276. Контактная разность потенциалов
- § 276a. Электролюминесценция полупроводников
- § 277. Распределение зарядов в неравномерно нагретом теле
- § 278. Термоэлектродвижущая сила
- § 279. Выделение тепла в электрических цепях
- § 280. Применения термоэлектрического эффекта