| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
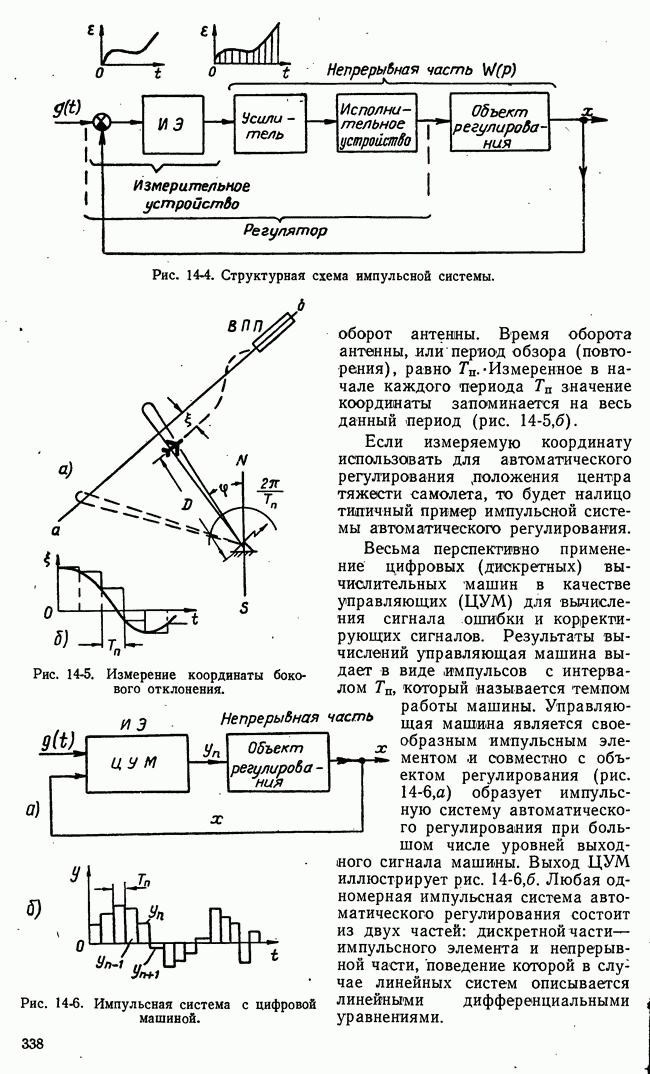
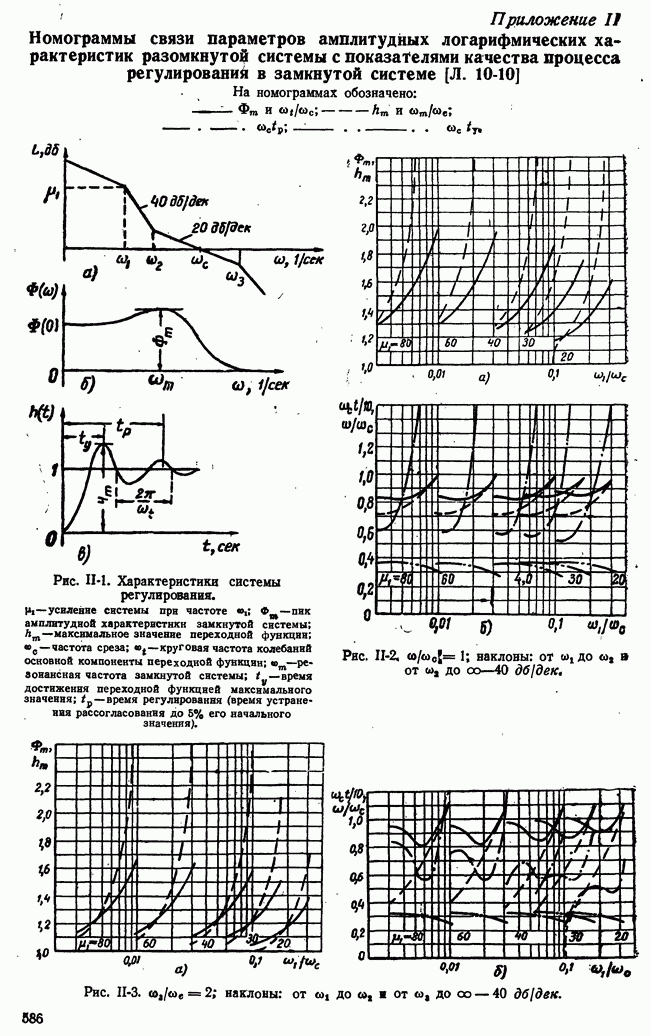
б) Значение выходной величины непрерывной системы внутри интервалов повторения
Определение непрерывной выходной величины  только в дискретных точках в виде функции
только в дискретных точках в виде функции  может оказаться недостаточным. Могут потребоваться сведения о поведении
может оказаться недостаточным. Могут потребоваться сведения о поведении  внутри интервалов повторения
внутри интервалов повторения  Для получения таких сведений введем в рассмотрение дискретную функцию
Для получения таких сведений введем в рассмотрение дискретную функцию  или, кратко,
или, кратко,  Параметр
Параметр  лежит в пределах от
лежит в пределах от  до 1. При фиксированном значении параметра
до 1. При фиксированном значении параметра  получается дискретная функция
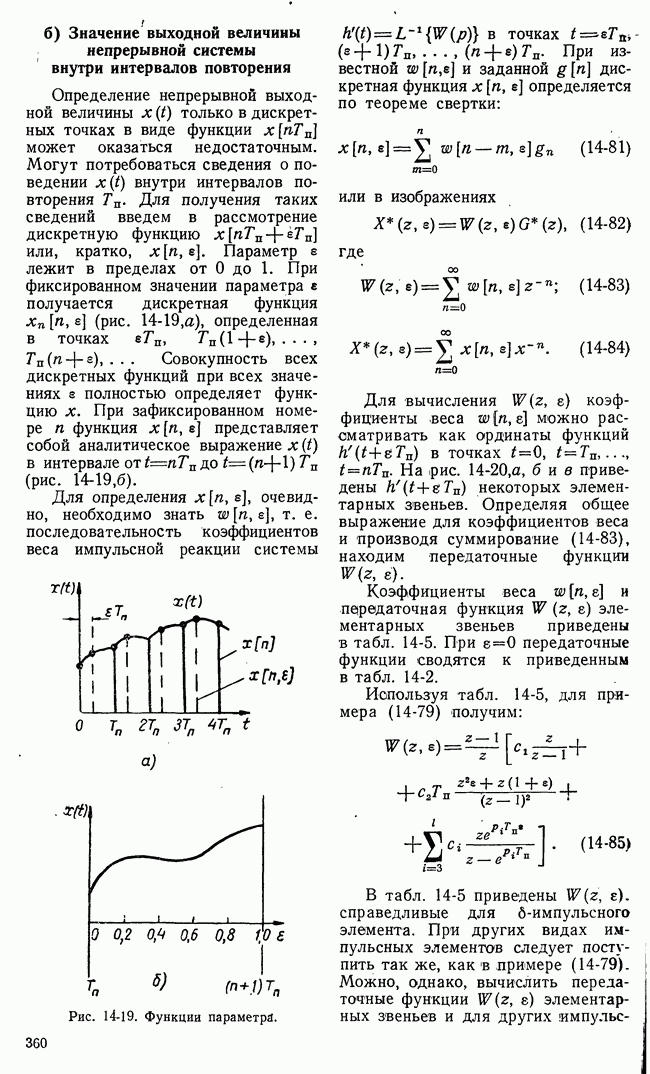
получается дискретная функция  (рис. 14-19,а), определенная в точках
(рис. 14-19,а), определенная в точках  Совокупность всех дискретных функций при всех значениях
Совокупность всех дискретных функций при всех значениях  полностью определяет функцию х. При зафиксированном номере
полностью определяет функцию х. При зафиксированном номере  функция
функция  представляет собой аналитическое выражение
представляет собой аналитическое выражение  в интервале от
в интервале от  до
до  (рис. 14-19,б).
(рис. 14-19,б).
Для определения  очевидно, необходимо знать
очевидно, необходимо знать  т. е. последовательность коэффициентов веса импульсной реакции системы
т. е. последовательность коэффициентов веса импульсной реакции системы  в точках
в точках 

Рис. 14-19. Функции параметра.
При известной  и заданной
и заданной  дискретная функция
дискретная функция  определяется по теореме свертки:
определяется по теореме свертки:

или в изображениях

где

Для вычисления  коэффициенты веса
коэффициенты веса  можно рассматривать как ординаты функций
можно рассматривать как ординаты функций  в точках
в точках  На рис.
На рис.  приведены
приведены  некоторых элементарных звеньев. Определяя общее выражение для коэффициентов веса и производя суммирование (14-83), находим передаточные функции
некоторых элементарных звеньев. Определяя общее выражение для коэффициентов веса и производя суммирование (14-83), находим передаточные функции 
Коэффициенты веса  и передаточная функция
и передаточная функция  элементарных звеньев приведены в табл. 14-5. При
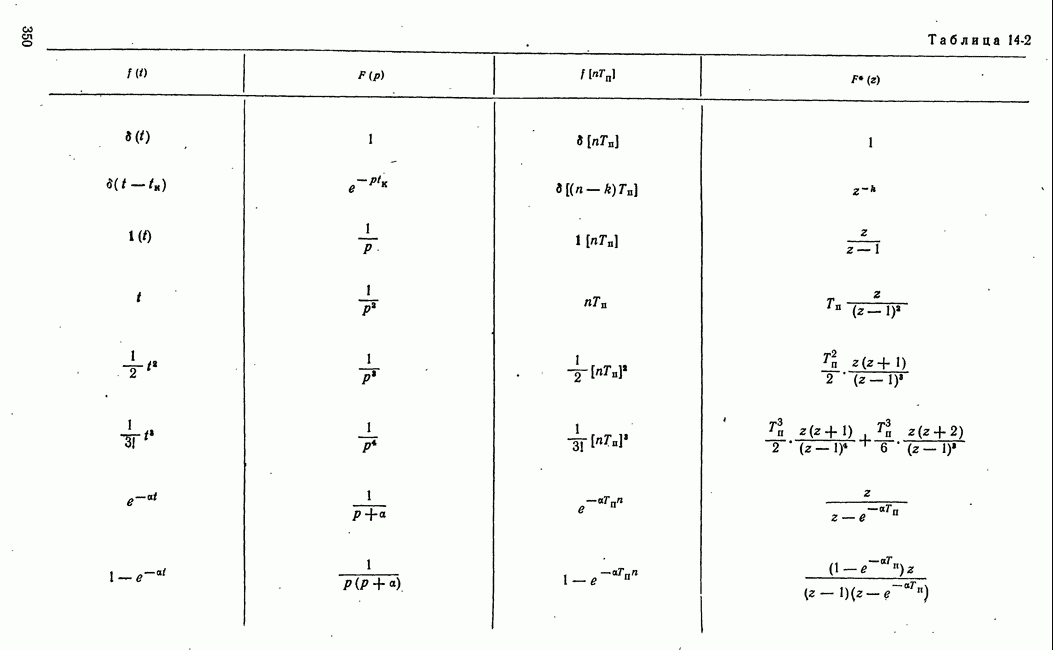
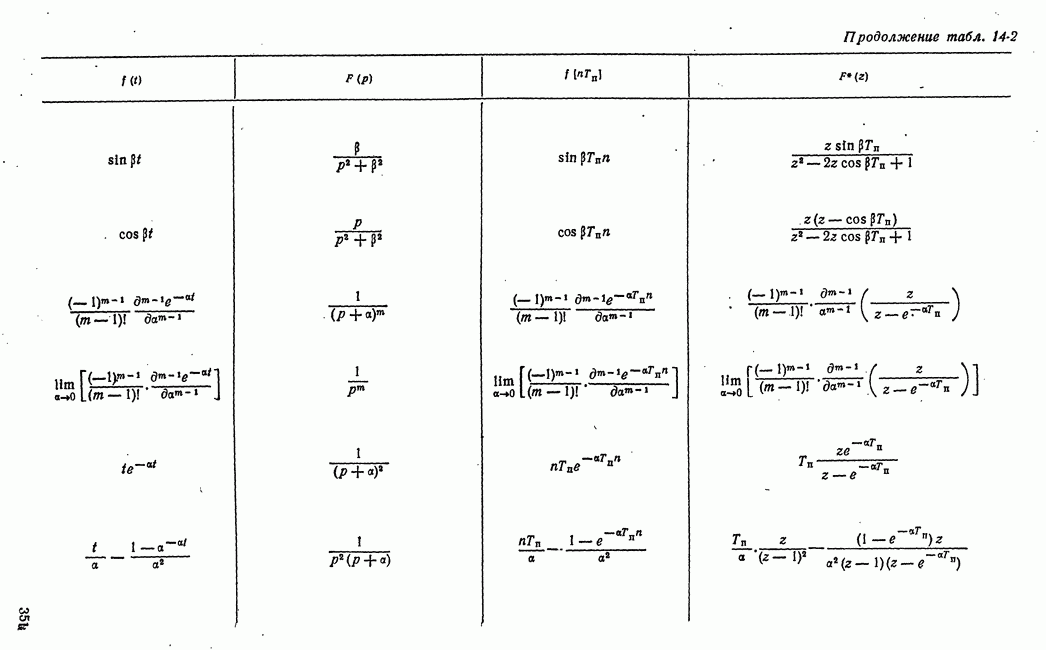
элементарных звеньев приведены в табл. 14-5. При  передаточные функции сводятся к приведенным в табл. 14-2.
передаточные функции сводятся к приведенным в табл. 14-2.
Используя табл. 14-5, для примера (14-79) получим:

В табл. 14-5 приведены  справедливые для
справедливые для  -импульсного элемента. При других видах импульсных элементов следует поступить так же, как в примере (14-79). Можно, однако, вычислить передаточные функции
-импульсного элемента. При других видах импульсных элементов следует поступить так же, как в примере (14-79). Можно, однако, вычислить передаточные функции  элементарных звеньев и для других
элементарных звеньев и для других

Рис. 14-20. К вычислению 
Таблица 14-5 (см. скан)  -импульсный элемент
-импульсный элемент
импульсных элементов. В табл. 14-6 приведены  для «прямоугольного» импульсного элемента.
для «прямоугольного» импульсного элемента.
Заметим, что дискретное преобразование Лапласа для функции  в
в  и обратно иногда называют [Л. 14-4] модифицированным
и обратно иногда называют [Л. 14-4] модифицированным  -преобразованием.
-преобразованием.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ГЛАВА ПЕРВАЯ. ВВОДНАЯ
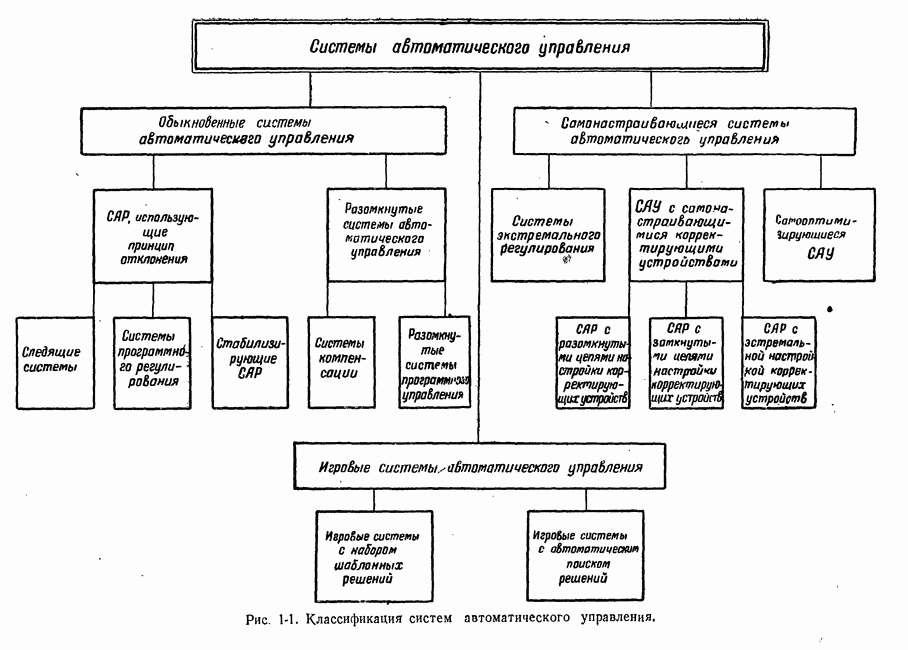
- 1-1. О КЛАССИФИКАЦИИ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- 1-2. ОБЫКНОВЕННЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- 1-3. САМОНАСТРАИВАЮЩИЕСЯ СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- 1-4. ИГРОВЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- 1-5. КЛАССИФИКАЦИЯ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ ПО ДРУГИМ ПРИЗНАКАМ
- ГЛАВА ВТОРАЯ. ОБЩИЕ ПЕРЕДАТОЧНЫЕ СВОЙСТВА ЭЛЕМЕНТОВ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- 2-1. УРАВНЕНИЯ ЭЛЕМЕНТОВ. СТАТИЧЕСКИЕ И ДИНАМИЧЕСКИЕ СВОЙСТВА ЭЛЕМЕНТОВ
- б) Центробежный измеритель скорости вращения
- в) Электромагнитный измеритель напряжения
- 2-2. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ
- 2-3. ЭЛЕМЕНТАРНЫЕ ДИНАМИЧЕСКИЕ ЗВЕНЬЯ, ИХ УРАВНЕНИЯ И ПЕРЕДАТОЧНЫЕ ФУНКЦИИ
- 2-4. ТИПОВЫЕ ВХОДНЫЕ СИГНАЛЫ. ВОЗМУЩАЮЩИЕ ФУНКЦИИ
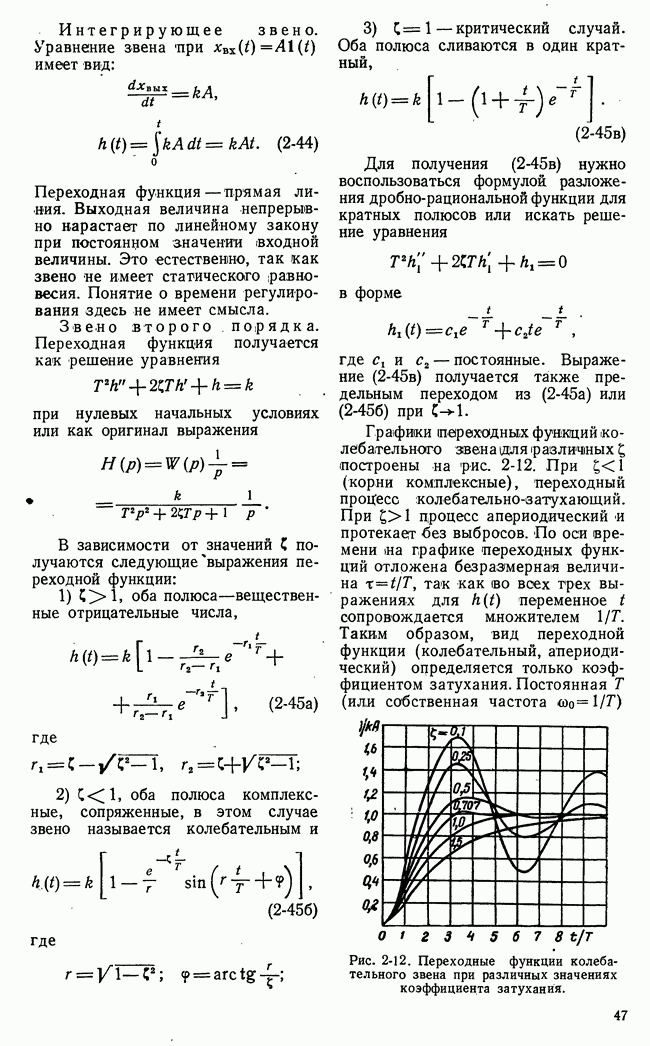
- 2-5. ПЕРЕХОДНЫЕ ФУНКЦИИ ЭЛЕМЕНТАРНЫХ ЗВЕНЬЕВ
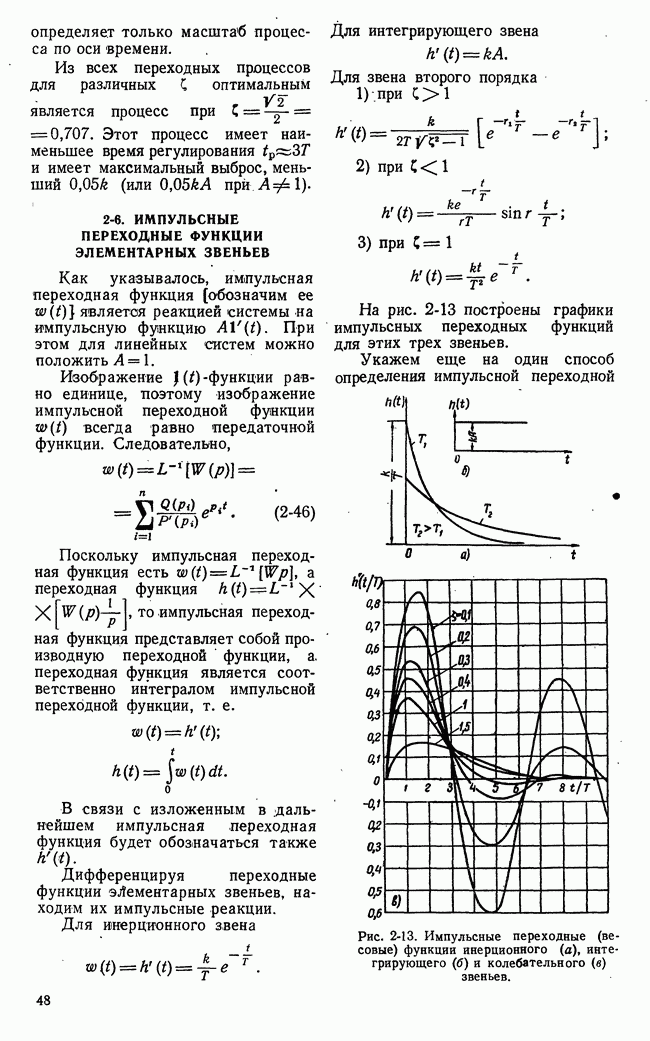
- 2-6. ИМПУЛЬСНЫЕ ПЕРЕХОДНЫЕ ФУНКЦИИ ЭЛЕМЕНТАРНЫХ ЗВЕНЬЕВ
- 2-7. РЕАКЦИЯ ЗВЕНЬЕВ НА ПРОИЗВОЛЬНЫЕ ИЗВЕСТНЫЕ ФУНКЦИИ ВРЕМЕНИ
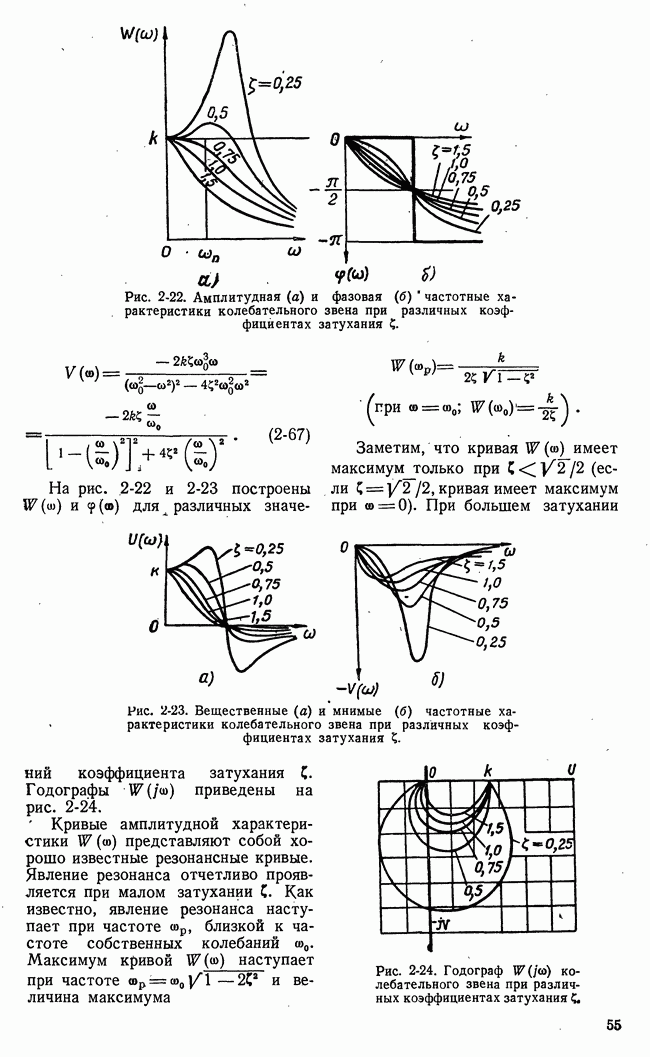
- 2-8. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ
- б) Частотные характеристики элементарных звеньев
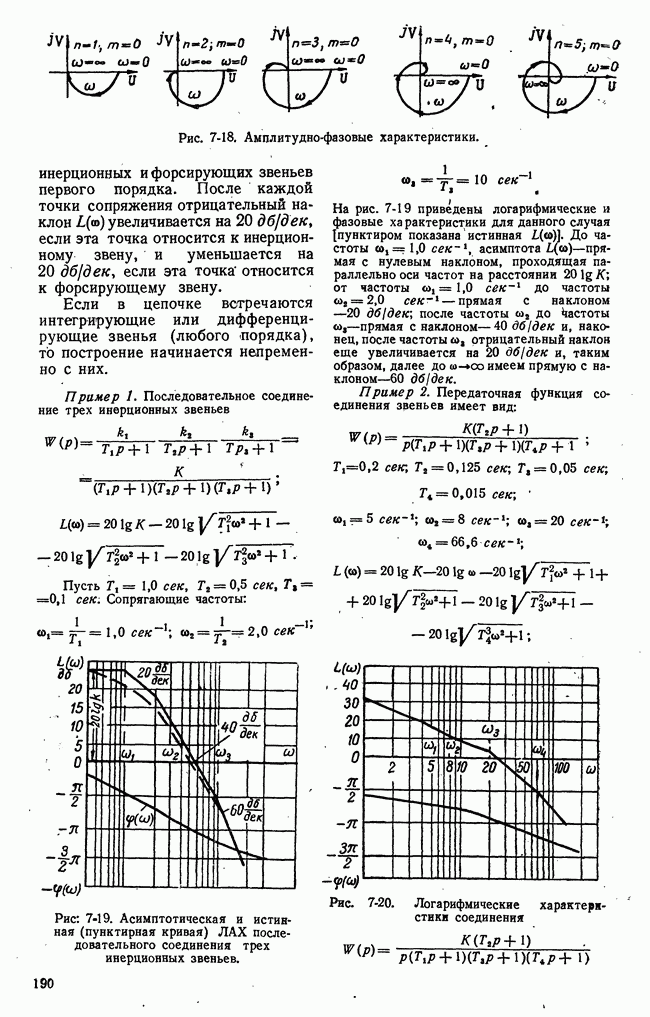
- в) Логарифмические характеристики элементарных звеньев
- 2-9. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ОБ ЭЛЕМЕНТАРНЫХ ЗВЕНЬЯХ
- 2-10. СОЕДИНЕНИЯ ЗВЕНЬЕВ. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ СОЕДИНЕНИИ
- 2-11. ЭЛЕМЕНТЫ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ КАК ЧЕТЫРЕХПОЛЮСНИКИ. ПЕРЕДАТОЧНЫЕ УРАВНЕНИЯ
- ГЛАВА ТРЕТЬЯ. ДАТЧИКИ СИГНАЛОВ
- 3-1. ОБЩИЕ СВОЙСТВА ДАТЧИКОВ
- 3-2. ПОТЕНЦИОМЕТРИЧЕСКИЕ ДАТЧИКИ
- б) Выходная мощность потенциометрических датчиков и условия согласования
- в) Динамические свойства
- г) Ошибка ступенчатости. Параметры потенциометрических датчиков
- 3-3. ИНДУКТИВНЫЕ ДАТЧИКИ
- б) Двухтактные индуктивные датчики
- в) Характеристики двухтактных индуктивных датчиков
- г) Трансформаторные индуктивные датчики
- д) Динамические свойства индуктивных датчиков
- е) Шумы индуктивных датчиков
- ж) Общие свойства индуктивных датчиков
- 3-4. СЕЛЬСИНЫ В ТРАНСФОРМАТОРНОМ РЕЖИМЕ
- б) Характеристики сельсинного датчика
- в) Динамические свойства сельсинных датчиков
- г) Шумы и ошибки датчика
- д) Устанавливающий момент
- е) Дифференциальные сельсины
- ж) Сельсины точного и грубого каналов
- ГЛАВА ЧЕТВЕРТАЯ. УСИЛИТЕЛИ СИГНАЛОВ
- 4-2. МАГНИТНЫЕ УСИЛИТЕЛИ
- а) Рабочий процесс и статическая характеристика магнитного усилителя с прямоугольной кривой намагничивания сердечников
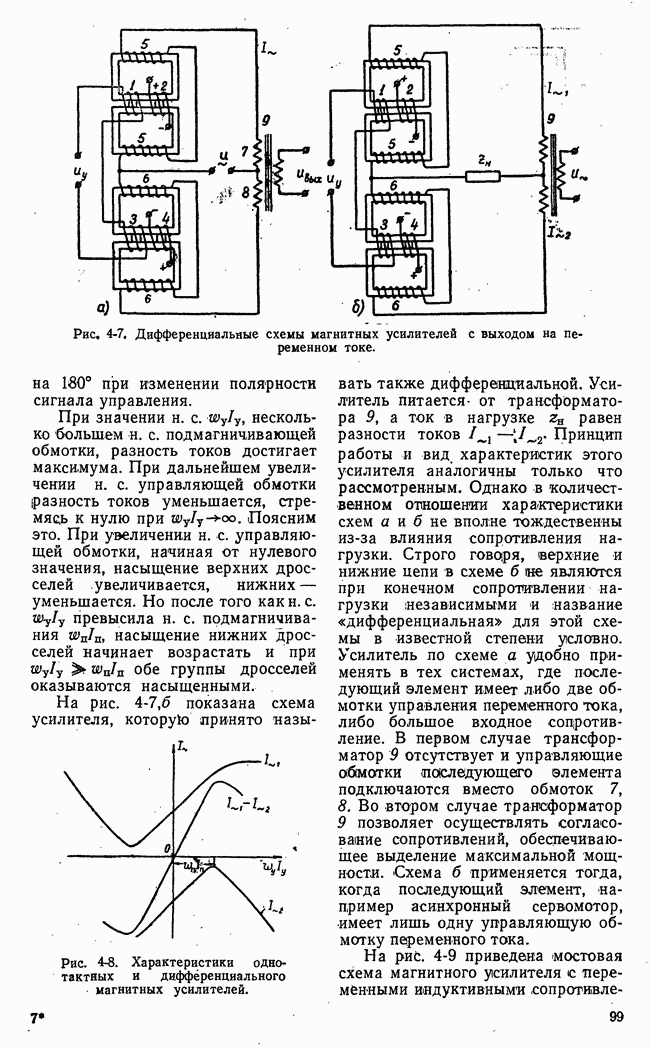
- б) Двухтактные магнитные усилители с выходом на переменном токе
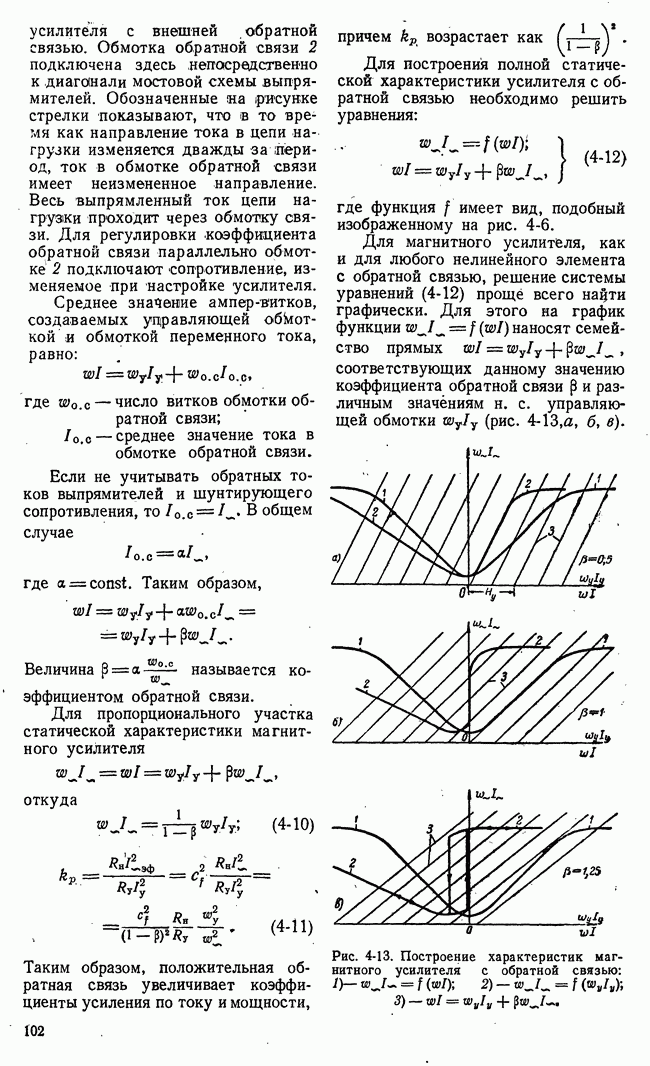
- в) Магнитные усилители с обратной связью
- г) Динамические свойства магнитных усилителей
- д) Шумы магнитных усилителей. Общие свойства магнитных усилителей
- 4-3. ЭЛЕКТРОМАШИННЫЕ УСИЛИТЕЛИ
- б) Однокаскадный электромашицный усилитель как четырехполюсник
- в) Двухкаскадный электромашинный усилитель с поперечным полем
- г) Шумы электромашинных усилителей
- 4-4. РЕЛЕ
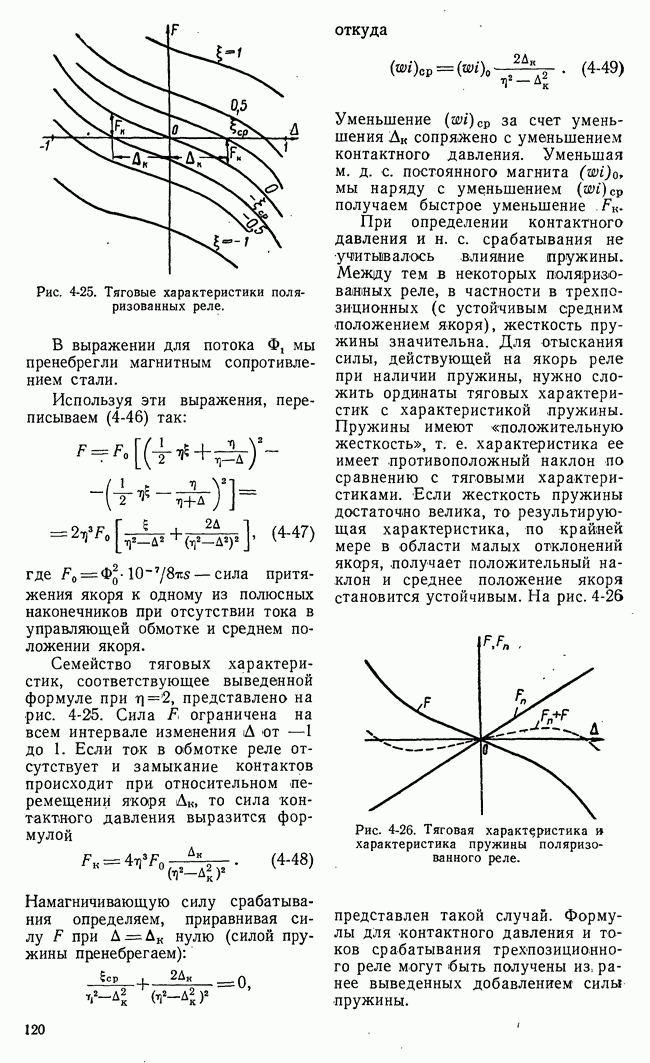
- б) Поляризованные реле
- в) Магнитоэлектрическое реле
- 4-5. РЕЛЕЙНЫЕ УСИЛИТЕЛИ
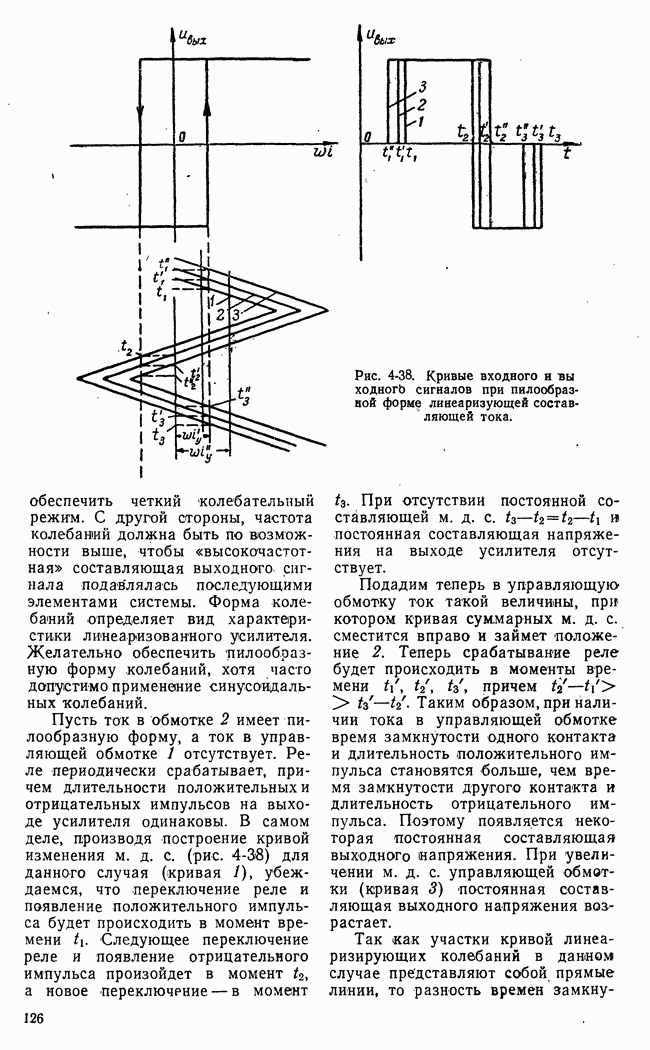
- б) Вибрационная линеаризация релейных усилителей
- в) Релейный усилитель как четырехполюсник
- 4-6. ЭЛЕКТРОННЫЕ УСИЛИТЕЛИ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- б) Фазочувствительные усилители и синхронные детекторы
- в) Электронные усилители постоянного тока
- г) Шумы электронных усилителей
- 4-7. ПОЛУПРОВОДНИКОВЫЕ УСИЛИТЕЛИ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- ГЛАВА ПЯТАЯ. ИСПОЛНИТЕЛЬНЫЕ УСТРОЙСТВА СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- 5-2. СЕРВОДВИГАТЕЛИ ПОЧТОЯННОГО ТОКА
- 5-3. СЕРВОДВИГАТЕЛИ ПЕРЕМЕННОГО ТОКА
- 5-4. СЕРВОДВИГАТЕЛИ С ЭЛЕКТРОМАГНИТНЫМИ И ПОРОШКОВЫМИ МУФТАМИ
- б) Характеристики серводвигателей с электромагнитными муфтами
- в) Порошковые муфты
- г) Характеристики серводвигателей с порошковыми муфтами
- 5-5. ГИДРАВЛИЧЕСКИЕ И ПНЕВМАТИЧЕСКИЕ СЕРВОДВИГАТЕЛИ
- б) Обратные связи в гидравлических серводвигателях
- в) Свойства гидравлических серводвигателей
- г) Электрогидравлические серводвигатели
- д) Пневматические серводвигатели
- ГЛАВА ШЕСТАЯ. СТАБИЛИЗИРУЮЩИЕ УСТРОЙСТВА СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- 6-1. ПАССИВНЫЕ КОРРЕКТИРУЮЩИЕ ЦЕПИ СИСТЕМ ПОСТОЯННОГО ТОКА
- б) Интегрирующие и интегродифференцирующие цепи
- 6-2. АКТИВНЫЕ КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА СИСТЕМ ПОСТОЯННОГО ТОКА
- 6-3. КОРРЕКТИРУЮЩИЕ ЦЕПИ СИСТЕМ ПЕРЕМЕННОГО ТОКА
- 6-4. ФИЛЬТРЫ В ЦЕПЯХ ОБРАТНЫХ СВЯЗЕЙ. МЕХАНИЧЕСКИЕ СТАБИЛИЗИРУЮЩИЕ УСТРОЙСТВА
- ГЛАВА СЕДЬМАЯ. СТРУКТУРНЫЕ СХЕМЫ И ХАРАКТЕРИСТИКИ ЛИНЕЙНЫХ СТАЦИОНАРНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
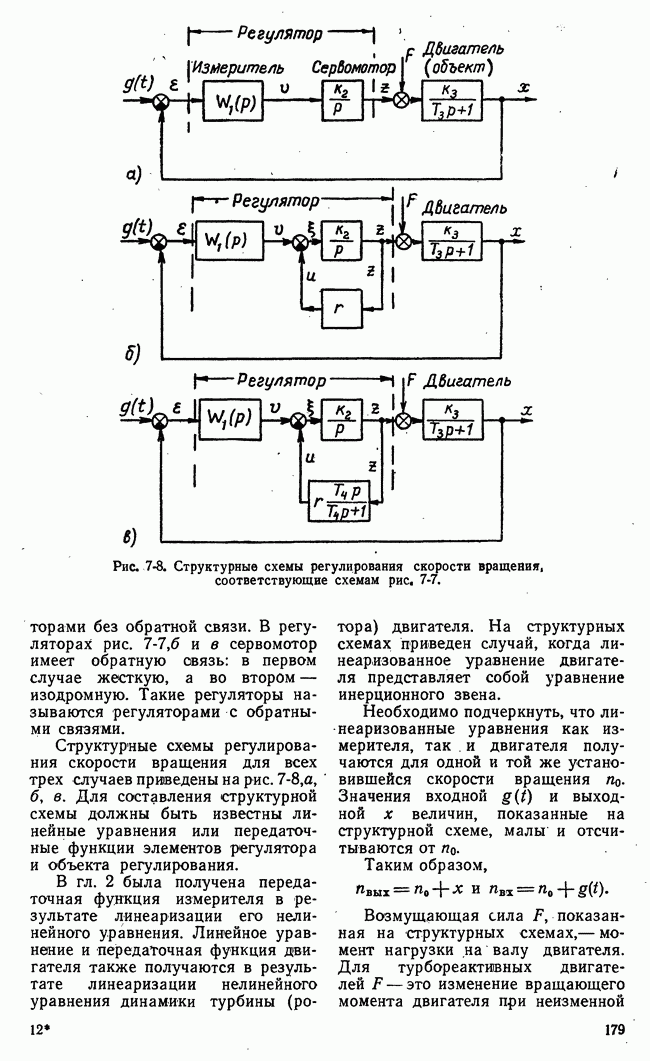
- 7-1. СТРУКТУРНЫЕ СХЕМЫ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 7-2. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ ДЛЯ ВХОДНОЙ ВЕЛИЧИНЫ
- 7-3. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ ДЛЯ ВОЗМУЩЕНИЯ
- 7-4. ПРИМЕРЫ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ И ИХ СТРУКТУРНЫЕ СХЕМЫ
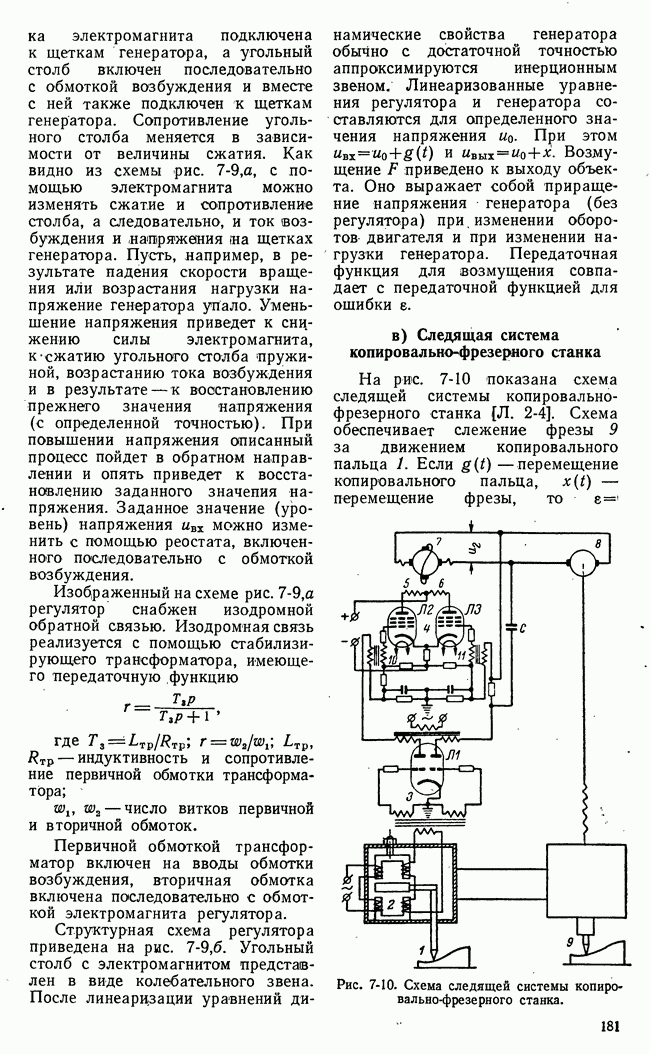
- б) Стабилизация напряжения самолетных генераторов
- в) Следящая система копировально-фрезерного станка
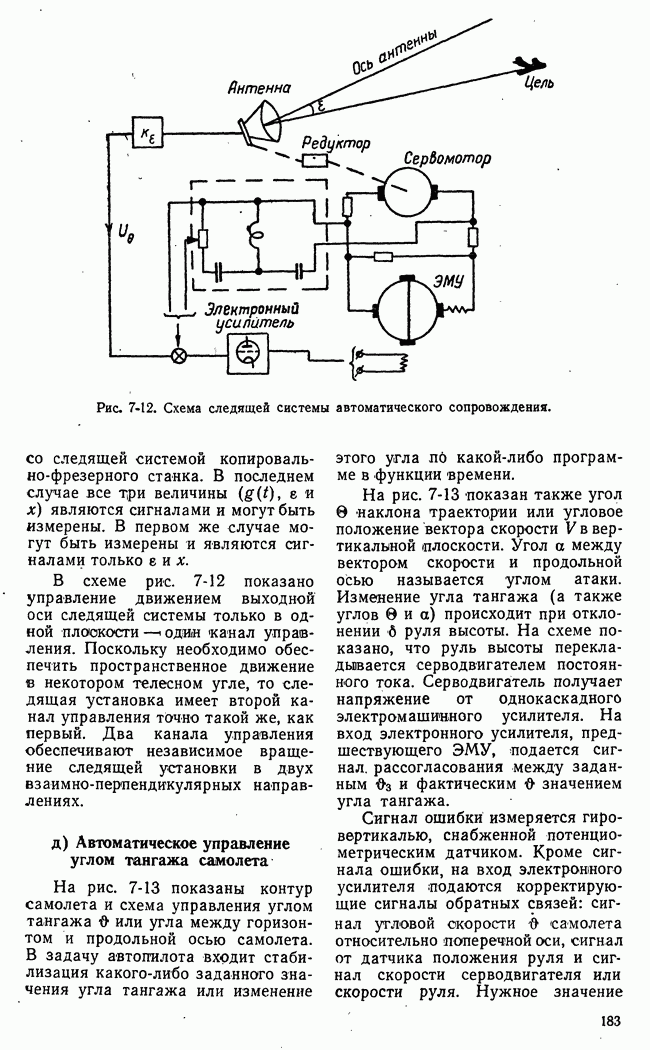
- г) Следящая система автосопровождения
- д) Автоматическое управление углом тангажа самолета
- 7-5. ВРЕМЕННЫЕ ХАРАКТЕРИСТИКИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 7-6. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
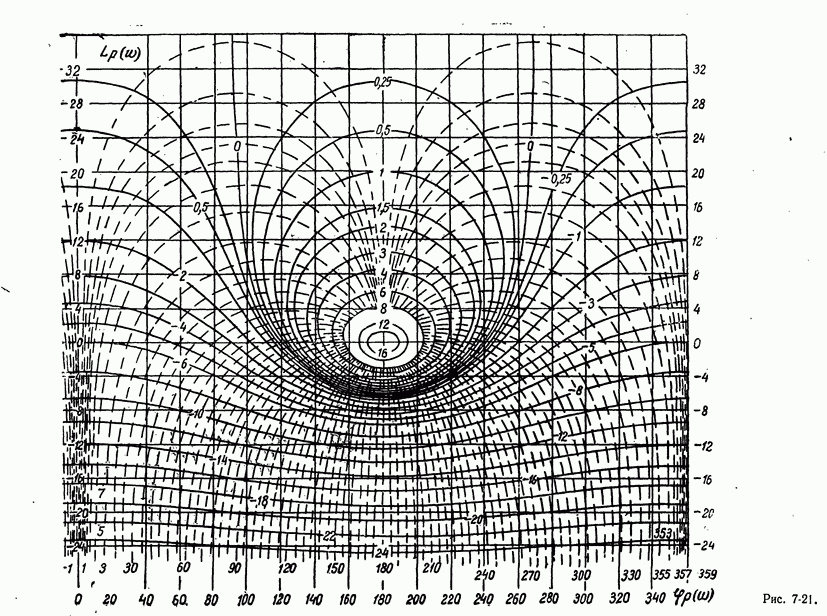
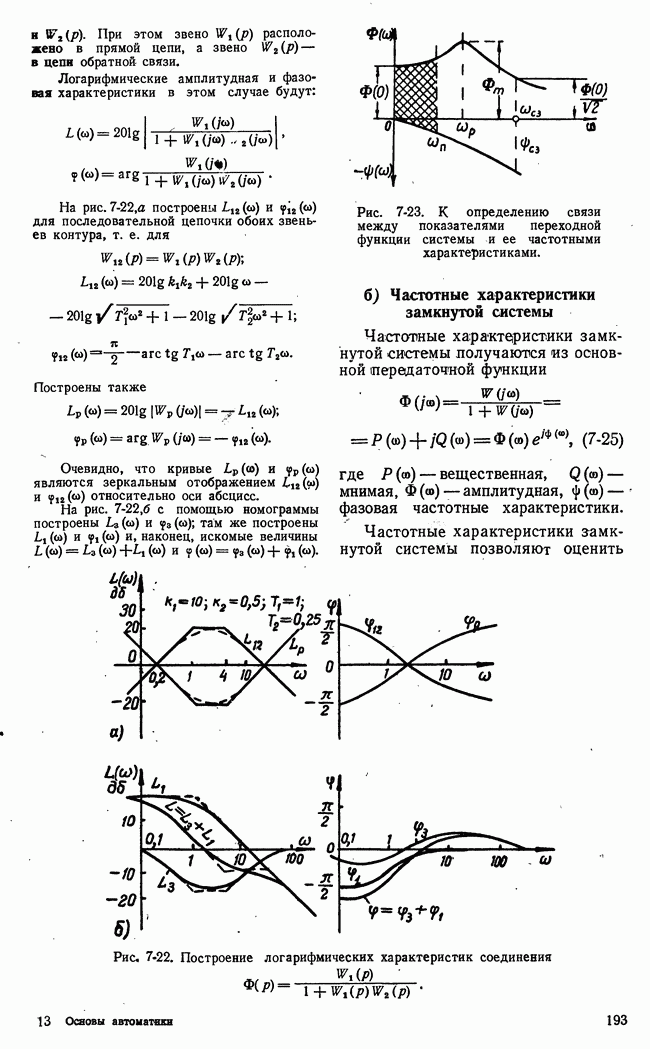
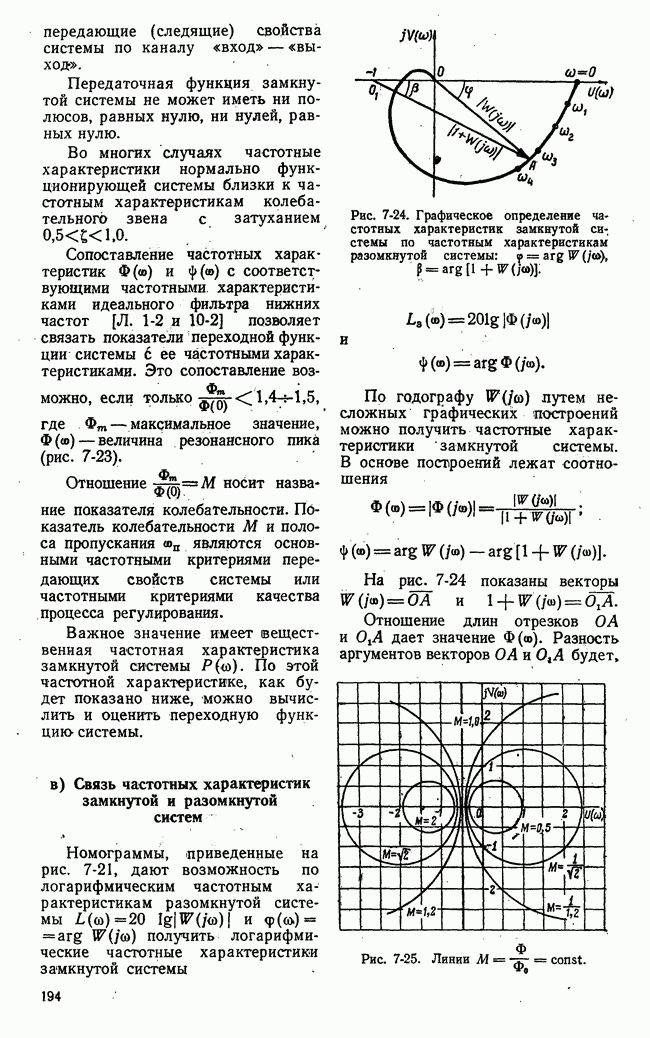
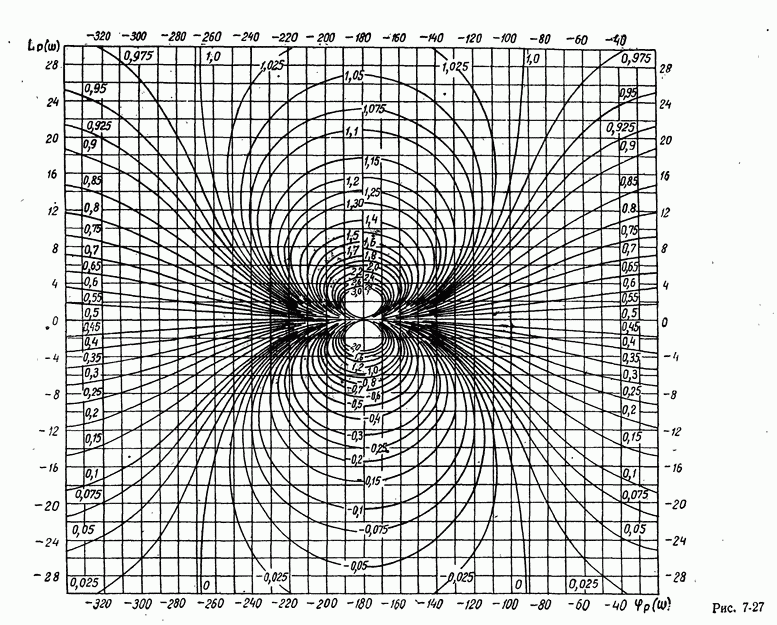
- б) Частотные характеристики замкнутой системы
- в) Связь частотных характеристик замкнутой и разомкнутой систем
- ГЛАВА ВОСЬМАЯ. ЭНЕРГЕТИЧЕСКИЙ РАСЧЕТ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ И СОГЛАСОВАНИЕ ХАРАКТЕРИСТИК ЭЛЕМЕНТОВ
- 8-1. ВЫБОР МОЩНОСТИ ИСПОЛНИТЕЛЬНЫХ УСТРОЙСТВ И УСЛОВИЯ СОГЛАСОВАНИЯ С НАГРУЗКОЙ
- а) Определение необходимой мощности по переходным процессам при типовых воздействиях
- б) Мгновенная мощность при гармонических колебаниях
- в) Необходимая мощность при случайных колебаниях регулирующего органа
- г) Выбор мощности сервомотора
- д) Условия согласования с нагрузкой сервомотора без обратной связи
- е) Согласование с нагрузкой сервомотора с жесткой обратной связью
- 8-2. СОГЛАСОВАНИЕ ДАТЧИКОВ, УСИЛИТЕЛЬНЫХ И КОРРЕКТИРУЮЩИХ УСТРОЙСТВ. РАСПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТОВ УСИЛЕНИЯ
- б) Передаточные функции последовательных соединений элементов
- в) Согласование пропорциональных участков характеристик
- г) Распределение коэффициентов усиления
- ГЛАВА ДЕВЯТАЯ. УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ СТАЦИОНАРНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 9-2. КРИТЕРИЙ УСТОЙЧИВОСТИ РАУСА—ГУРВИЦА
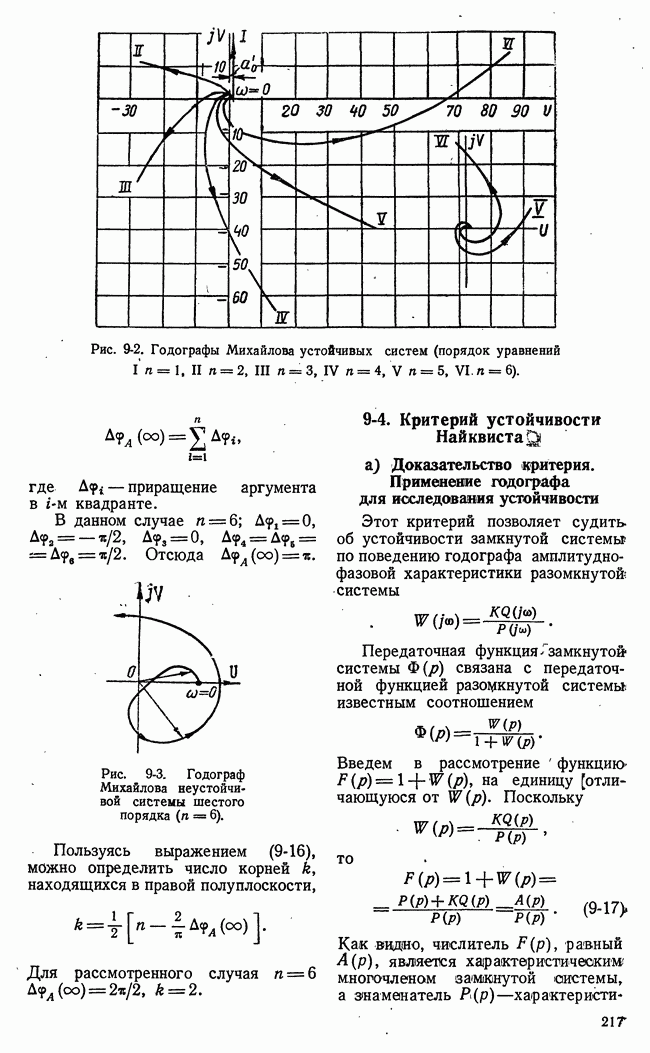
- 9-3. КРИТЕРИЙ УСТОЙЧИВОСТИ МИХАЙЛОВА
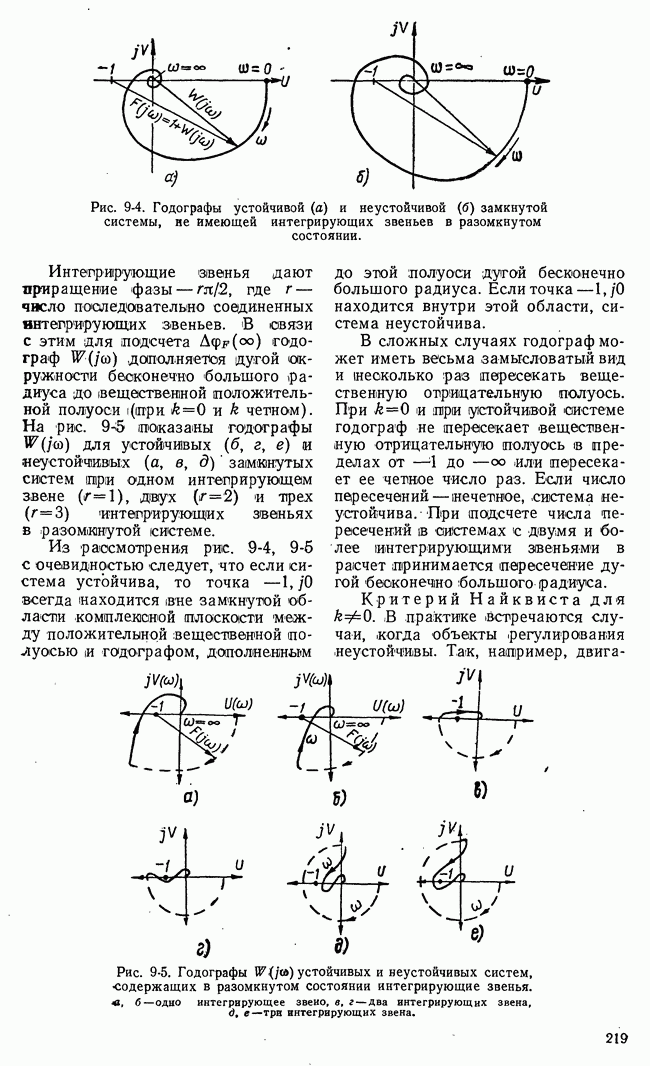
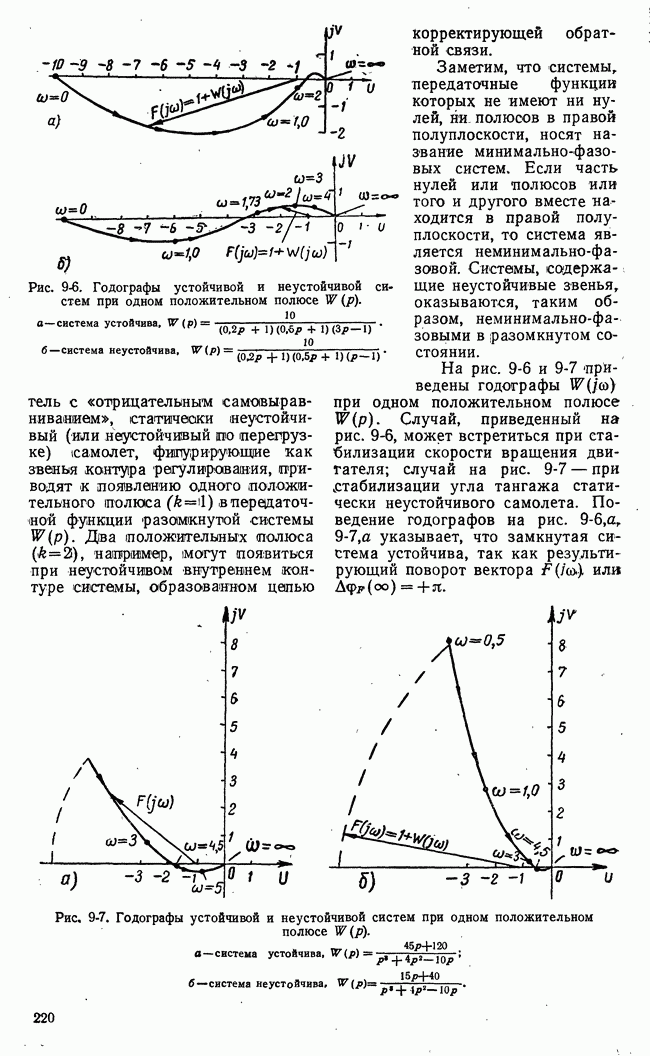
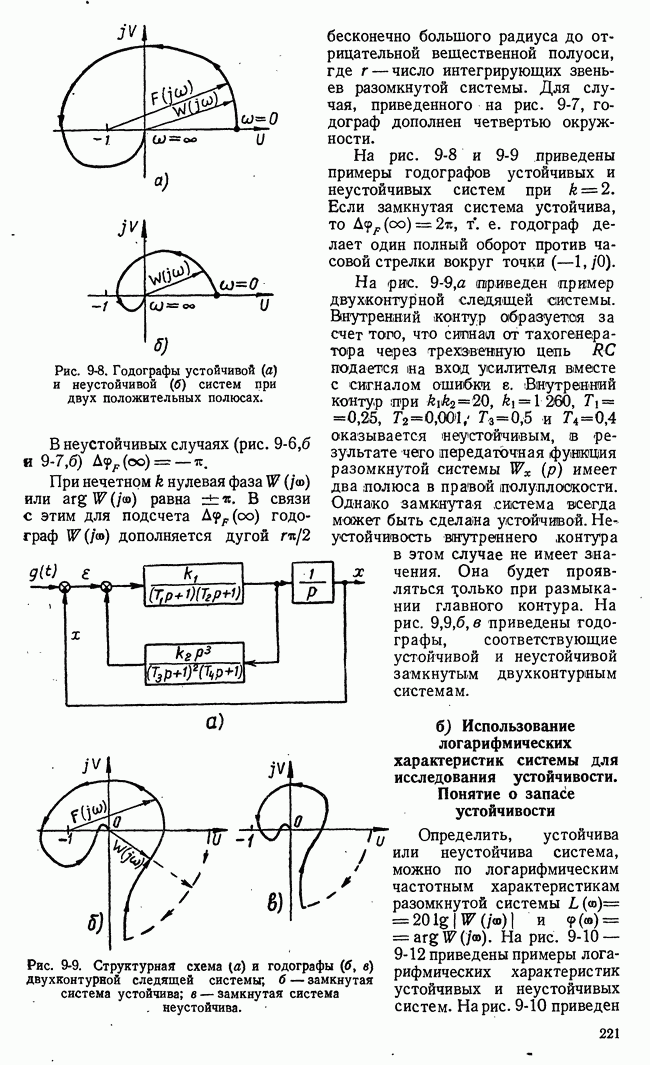
- 9-4. КРИТЕРИЙ УСТОЙЧИВОСТИ НАЙКВИСТА
- б) Использование логарифмических характеристик системы для исследования устойчивости. Понятие о запасе устойчивости
- 9-5. КОЭФФИЦИЕНТ УСИЛЕНИЯ И УСТОЙЧИВОСТЬ. ВЛИЯНИЕ КОРРЕКТИРУЮЩИХ ЦЕПЕЙ НА УСТОЙЧИВОСТЬ
- 9-6. ВЫДЕЛЕНИЕ ОБЛАСТЕЙ УСТОЙЧИВОСТИ В ПРОСТРАНСТВЕ ПАРАМЕТРОВ СИСТЕМЫ ДИАГРАММЫ ВЫШНЕГРАДСКОГО
- б) Общий метод D-разбиения в плоскости двух параметров. Линейная задача
- в) Выделение области устойчивости в плоскости двух параметров. Нелинейная задача
- г) Выделение области устойчивости в плоскости одного комплексного параметра
- ГЛАВА ДЕСЯТАЯ. КАЧЕСТВО ПРОЦЕССОВ РЕГУЛИРОВАНИЯ В ЛИНЕЙНЫХ СИСТЕМАХ
- 10-1. КРИТЕРИИ КАЧЕСТВА ПРОЦЕССА РЕГУЛИРОВАНИЯ
- 10-2. ТОЧНОСТЬ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ В УСТАНОВИВШИХСЯ РЕЖИМАХ. СТАТИЧЕСКИЕ И АСТАТИЧЕСКИЕ СИСТЕМЫ
- б) Точность при медленно меняющихся воздействиях. Коэффициенты ошибок. Астатические системы высших порядков
- в) Общие условия неискаженного воспроизведения входных сигналов в вынужденном режиме
- г) Повышение точности системы коррекцией входного сигнала
- д) Повышение точности системы путем компенсации возмущения F(t)
- 10-18. ПЕРЕХОДНЫЕ ФУНКЦИИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- б) Некоторые особенности вычисления переходных функций
- 10-4. РАСПРЕДЕЛЕНИЕ НУЛЕЙ И ПОЛЮСОВ ПЕРЕДАТОЧНОЙ ФУНКЦИИ И ПЕРЕХОДНЫЕ ПРОЦЕССЫ
- б) Оценки распределения корней. Степень устойчивости. Коэффициент затухания колебаний
- в) Влияние параметров на распределение корней. Метод Эванса
- г) Оценка переходных функций по распределению полюсов передаточной функции или корней характеристического уравнения
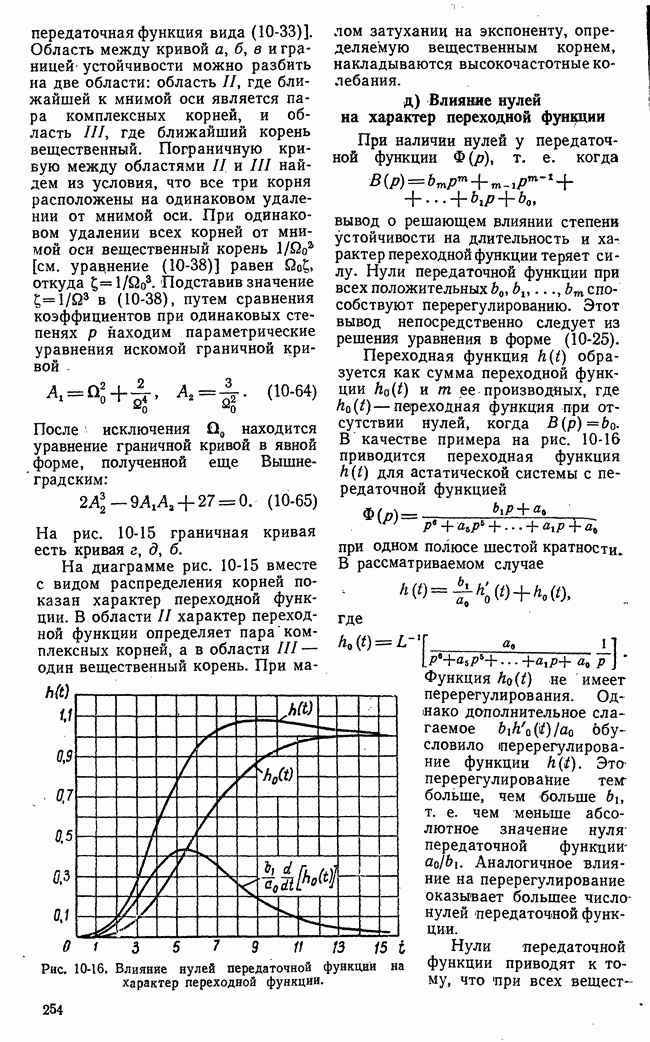
- д) Влияние нулей на характер переходной функции
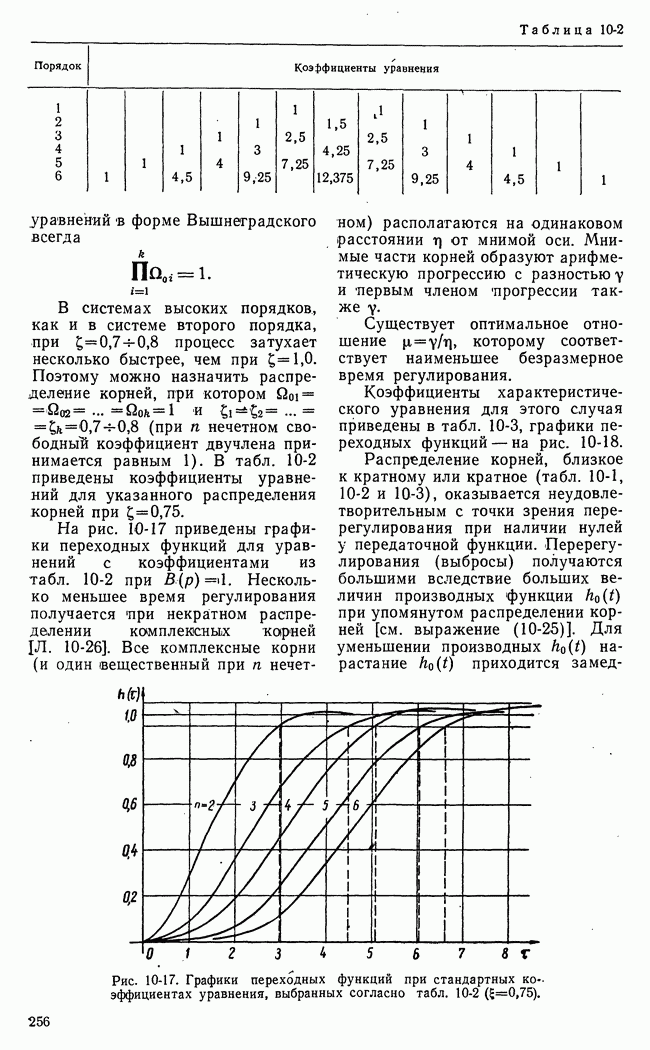
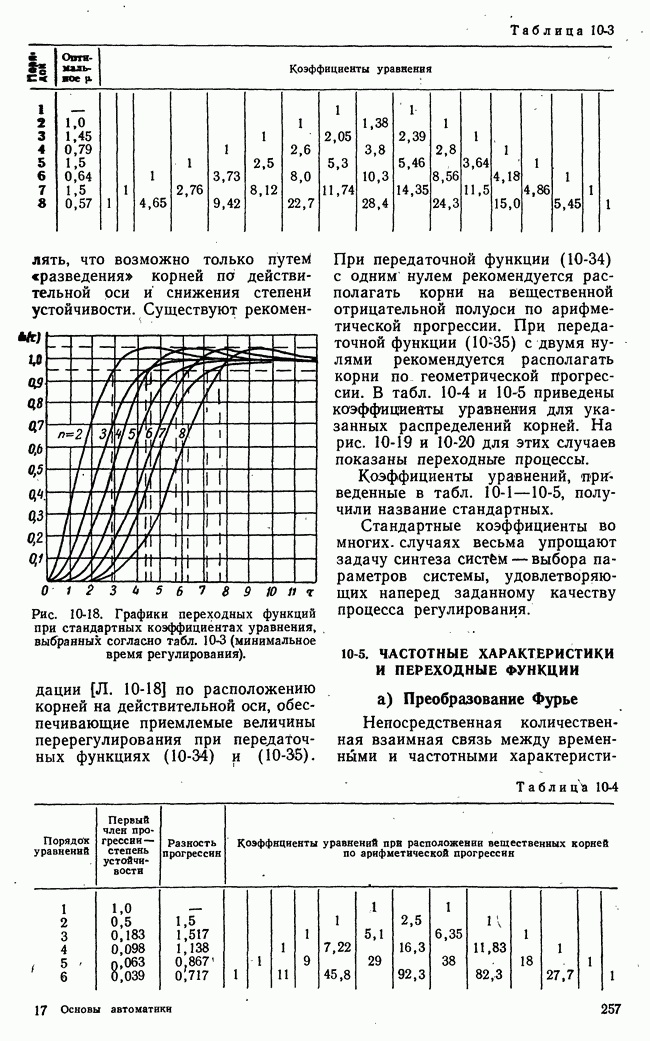
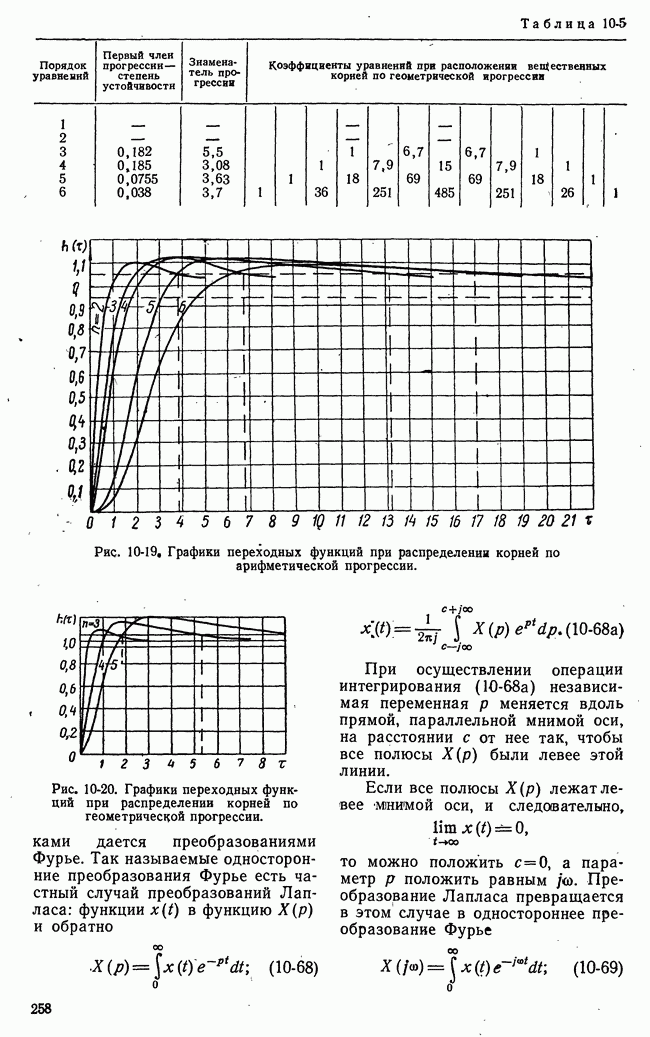
- е) Определение коэффициентов уравнений по заданному распределению корней. Стандартные коэффициенты характеристических уравнений
- 10-5. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ И ПЕРЕХОДНЫЕ ФУНКЦИИ
- б) Приближенное вычисление переходных функций и переходных процессов
- в) Оценка качества процесса регулирования по характеристикам замкнутой системы Ф(w) и ф(w) и характеристике разомкнутой системы W(jw)
- г) Оценка качества по амплитудным логарифмическим характеристикам. Минимально-фазовые системы
- д) Связь между логарифмическими амплитудными характеристиками разомкнутой системы и полюсами передаточной функции замкнутой системы
- 10-6. ИНТЕГРАЛЬНЫЕ ОЦЕНКИ ПЕРЕХОДНЫХ ПРОЦЕССОВ
- г) Приближение кривых x(t) к эталонной кривой хэ(t) по критерию …
- ГЛАВА ОДИННАДЦАТАЯ. НЕСТАЦИОНАРНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 11-1. ОБЩИЕ СВЕДЕНИЯ О НЕСТАЦИОНАРНЫХ СИСТЕМАХ
- 11-2. ПРИМЕРЫ СУЩЕСТВЕННО НЕСТАЦИОНАРНЫХ СИСТЕМ
- 11-3. ДИНАМИЧЕСКИЕ ХАРАКТЕРИСТИКИ НЕСТАЦИОНАРНЫХ СИСТЕМ АВТОМАТИЧ ЕСКОГО РЕГУЛИРОВАНИЯ
- 11-4. ОСОБЕННОСТИ СОСТАВЛЕНИЯ УРАВНЕНИЙ И СТРУКТУРНЫХ СХЕМ НЕСТАЦИОНАРНЫХ СИСТЕМ
- 11-5. МЕТОДЫ ОПРЕДЕЛЕНИЯ ЧАСТОТНОЙ ХАРАКТЕРИСТИКИ И ИМПУЛЬСНОЙ РЕАКЦИИ НЕСТАЦИОНАРНЫХ СИСТЕМ
- ГЛАВА ДВЕНАДЦАТАЯ. СТАТИСТИЧЕСКАЯ ДИНАМИКА ЛИНЕЙНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 12-1. СТАЦИОНАРНЫЕ И НЕСТАЦИОНАРНЫЕ СЛУЧАЙНЫЕ ПРОЦЕССЫ
- б) Стационарные и нестационарные случайные функций
- в) Свойства корреляционной функции
- г) Свойство эргодичности
- д) Гауссовы случайные процессы
- 12-2. ПРЕОБРАЗОВАНИЕ СТАЦИОНАРНЫХ СЛУЧАЙНЫХ ФУНКЦИЙ СТАЦИОНАРНЫМИ ЛИНЕЙНЫМИ СИСТЕМАМИ
- б) Преобразование корреляционных функций при прохождении случайного сигнала через линейную систему
- в) Интегральная квадратичная оценка импульсной переходной функции и дисперсия реакции системы на белый шум
- г) Преобразование спектральных плотностей при прохождении случайного сигнала через линейную систему
- 12-3. ОПТИМАЛЬНЫЕ ЛИНЕЙНЫЕ СТАЦИОНАРНЫЕ СИСТЕМЫ
- б) Условия оптимальности при свободном выборе передаточной функции
- ГЛАВА ТРИНАДЦАТАЯ. О СИНТЕЗЕ ЛИНЕЙНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 13-2. МЕТОД ЛОГАРИФМИЧЕСКИХ ЧАСТОТНЫХ ХАРАКТЕРИСТИК
- б) Синтез корректирующих цепей
- в) О синтезе на основе требований к реакции системы на возмущение F(t)
- 13-3. ВЫБОР ПАРАМЕТРОВ НА ОСНОВЕ АНАЛИЗА РАСПРЕДЕЛЕНИЯ НУЛЕЙ И ПОЛЮСОВ ПЕРЕДАТОЧНОЙ ФУНКЦИИ
- 13-4. ВЫБОР ПАРАМЕТРОВ НА ОСНОВЕ ИНТЕГРАЛЬНЫХ КВАДРАТИЧНЫХ ОЦЕНОК
- 13-5. СПЕЦИАЛЬНЫЕ ПРИЕМЫ УЛУЧШЕНИЯ КАЧЕСТВА ПРОЦЕССА РЕГУЛИРОВАНИЯ
- б) Подавление помех во входном сигнале при инерционном объекте управления
- в) Использование двух источников информации для выделения истинного сигнала
- г) Компенсация влияния запаздывания измерителей на динамические свойства системы
- д) Исключение перерегулирования в системах, передаточные функции которых имеют только вещественные полюсы
- ГЛАВА ЧЕТЫРНАДЦАТАЯ. ИМПУЛЬСНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 14-2. ИМПУЛЬСЫ И ИМПУЛЬСНЫЕ ЭЛЕМЕНТЫ
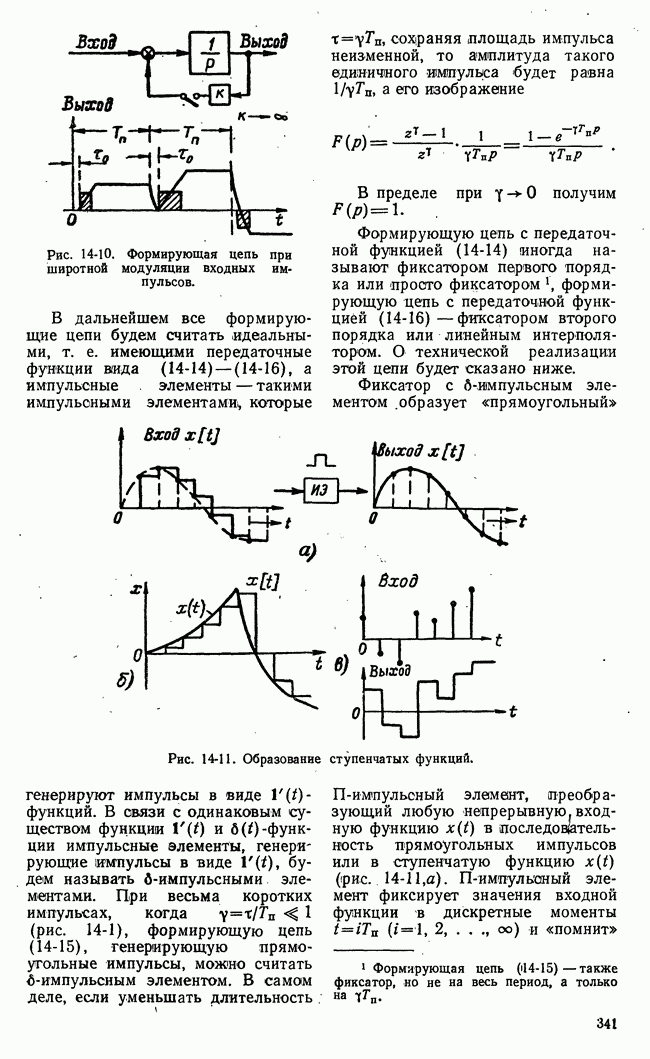
- б) Формирующие цепи и импульсные элементы
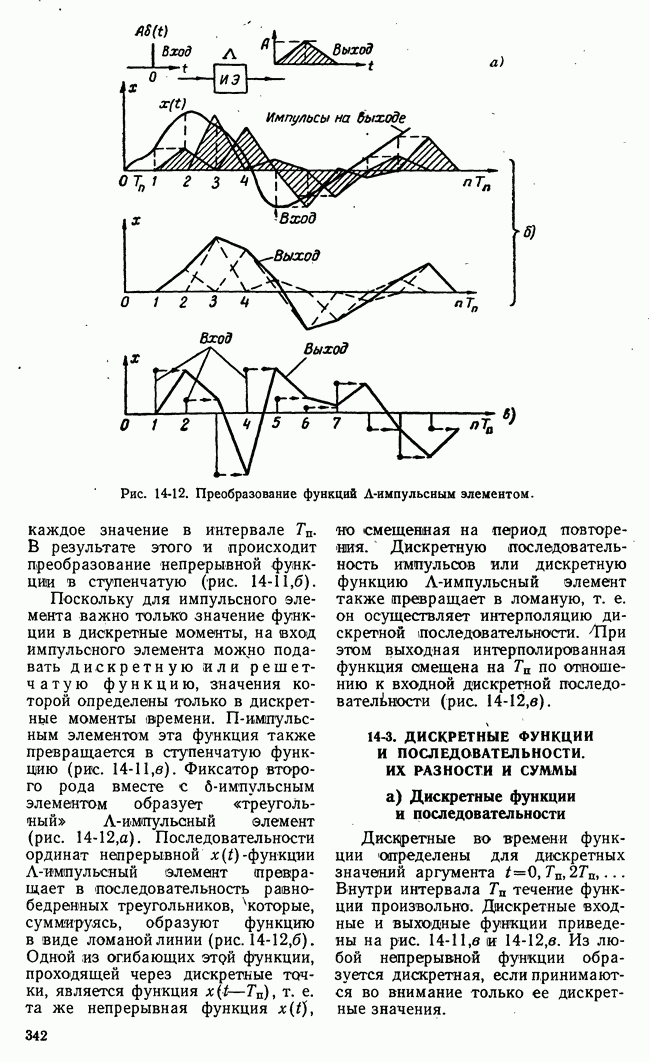
- 14-3. ДИСКРЕТНЫЕ ФУНКЦИИ И ПОСЛЕДОВАТЕЛЬНОСТИ. ИХ РАЗНОСТИ И СУММЫ
- 14-4. РЕАКЦИЯ ЛИНЕЙНЫХ НЕПРЕРЫВНЫХ СИСТЕМ НА ПОСЛЕДОВАТЕЛЬНОСТИ ИЛИ ДЕЛЬТА-ИМПУЛЬСОВ
- б) Свертка двух дискретных функций
- в) Уравнения в конечных разностях непрерывных звеньев первого и второго порядков
- г) Символические изображения дискретных функций и их использование для решения уравнений в конечных разностях
- 14-5. ДИСКРЕТНОЕ ПРЕОБРАЗОВАНИЕ ЛАПЛАСА ИЛИ z-ПРЕОБРАЗОВАНИЕ. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ КОМПЛЕКСНОГО АРГУМЕНТА
- 14-6. ДИНАМИКА РАЗОМКНУТЫХ ИМПУЛЬСНЫХ СИСТЕМ
- б) Значение выходной величины непрерывной системы внутри интервалов повторения
- в) Передаточные функции, систем с запаздыванием
- г) Свободные и вынужденные движения
- д) Полюсы. Устойчивость разомкнутых систем
- е) Переходные функции
- ж) Частотные характеристики
- 14-7. СВЯЗЬ МЕЖДУ ЧАСТОТНЫМИ И ПЕРЕХОДНЫМИ ФУНКЦИЯМИ. ДИСКРЕТНОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ
- 14-8. ИНТЕГРАЛЬНАЯ КВАДРАТИЧНАЯ ОЦЕНКА
- 14-9. ДИСКРЕТНЫЕ СЛУЧАЙНЫЕ ФУНКЦИИ (СЛУЧАЙНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ)
- ГЛАВА ПЯТНАДЦАТАЯ. ДИНАМИКА ИМПУЛЬСНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 15-1. УРАВНЕНИЯ И ПЕРЕДАТОЧНЫЕ ФУНКЦИИ СИСТЕМ С ОДНИМ ИМПУЛЬСНЫМ ЭЛЕМЕНТОМ
- 15-2. УСТОЙЧИВОСТЬ ЗАМКНУТЫХ СИСТЕМ
- 15-3. КАЧЕСТВО ПРОЦЕССА РЕГУЛИРОВАНИЯ
- 15-4. ПРИМЕРЫ ИМПУЛЬСНЫХ СИСТЕМ
- 15-5. ИМПУЛЬСНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ С ДИСКРЕТНЫМИ КОРРЕКТИРУЮЩИМИ ЦЕПЯМИ
- ГЛАВА ШЕСТНАДЦАТАЯ. СТРУКТУРНЫЕ СХЕМЫ, ХАРАКТЕРИСТИКИ И УРАВНЕНИЯ НЕЛИНЕЙНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- б) Уравнения продольного движения самолета
- в) Уравнения продольного движения ракеты
- 16-2. НЕЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ СИГНАЛА ОШИБКИ
- б) Структурные схемы с нелинейными элементами
- в) Релейные системы. Релейные элементы
- 16-3. НЕЛИНЕЙНЫЙ ОБЪЕКТ РЕГУЛИРОВАНИЯ И НЕЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ СИГНАЛА ОШИБКИ
- ГЛАВА СЕМНАДЦАТАЯ. СВОЙСТВА НЕЛИНЕЙНЫХ СИСТЕМ И (МЕТОДЫ ИССЛЕДОВАНИЯ
- б) Суждение об устойчивости по уравнениям первого приближения. Теоремы Ляпунова
- в) Суждение о качестве процессов регулирования по уравнениям первого приближения
- г) Прямой метод Ляпунова
- д) Техническая устойчивость
- 17-2. АВТОКОЛЕБАНИЯ НЕЛИНЕЙНЫХ СИСТЕМ
- б) Автоколебания релейных систем
- в) Метод точечных преобразований
- г) Описание процесса в релейной системе разностным уравнением. Устойчивость автоколебаний
- д) Примера исследования автоколебаний релейных систем второго порядка
- 17-3. ВЛИЯНИЕ КОРРЕКТИРУЮЩИХ ЦЕПЕЙ НА АВТОКОЛЕБАНИЯ И НА ПЕРЕХОДНЫЕ ПРОЦЕССЫ НЕЛИНЕЙНЫХ СИСТЕМ
- б) Влияние корректирующих цепей на переходные процессы. Скользящие режимы. Оптимальные переходные процессы
- 17-4. ГАРМОНИЧЕСКАЯ ЛИНЕАРИЗАЦИЯ ПРОЦЕССОВ В НЕЛИНЕЙНЫХ СИСТЕМАХ
- б) Исследование автоколебаний при помощи гармонической линеаризации
- в) Гармоническая линеаризация и критерии устойчивости линейных систем
- 17-5. ТЕОРИЯ РЕЛЕЙНЫХ СИСТЕМ
- в) Частотные характеристики релейных систем
- г) Оценка устойчивости релейных систем
- д) Вынужденные колебания релейных систем. Захватывание (синхронизация или подавление) автоколебаний
- е) Вибрационная линеаризация релейных систем, Реакция релейных систем на медленно меняющиеся возмущения
- 17-6. ОПТИМАЛЬНЫЕ ПРОЦЕССЫ РЕГУЛИРОВАНИЯ
- б) Системы, оптимальные по быстродействию. Принцип максимума
- в) Системы, близкие к оптимальным по быстродействию
- ГЛАВА ВОСЕМНАДЦАТАЯ. ЭНТРОПИЯ, ИНФОРМАЦИЯ, АЛГОРИТМ В СИСТЕМАХ АВТОМАТИЧЕОКОГО УПРАВЛЕНИЯ
- 18-1. ЭНТРОПИЯ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ УПРАВЛЯЕМОГО ПРОЦЕССА
- 18-2. КОЛИЧЕСТВО ИНФОРМАЦИИ В ПРОЦЕССАХ УПРАВЛЕНИЯ
- 18-3. ЭНТРОПИЯ И ИНФОРМАЦИЯ В ЗАМКНУТЫХ СИСТЕМАХ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- 18-4. АЛГОРИТМЫ ПРОЦЕССОВ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- ГЛАВА ДЕВЯТНАДЦАТАЯ. СИСТЕМЫ ЭКСТРЕМАЛЬНОГО РЕГУЛИРОВАНИЯ
- 19-1. ПРИМЕРЫ СИСТЕМ ЭКСТРЕМАЛЬНОГО РЕГУЛИРОВАНИЯ
- 19-2. СПОСОБЫ ПОИСКА ЭКСТРЕМУМА
- б) Методы организации процесса поиска
- 19-3. СТРУКТУРНЫЕ СХЕМЫ СИСТЕМ ЭКСТРЕМАЛЬНОГО РЕГУЛИРОВАНИЯ
- 19-4. ДИНАМИКА НЕПРЕРЫВНЫХ СИСТЕМ ЭКСТРЕМАЛЬНОГО РЕГУЛИРОВАНИЯ В КВАЗИСТАЦИОНАРНОМ РЕЖИМЕ
- б) Динамика квазистационарного режима систем экстремального регулирования, основанных на методе градиента
- 19-5. ДИНАМИКА НЕПРЕРЫВНЫХ СИСТЕМ ЭКСТРЕМАЛЬНОГО РЕГУЛИРОВАНИЯ ПРИ СЛУЧАЙНЫХ СИГНАЛАХ ПОИСКА
- б) Уравнения замкнутой системы экстремального регулирования
- в) Точность экстремального регулирования
- 19-6. ФОРСИРОВАННЫЕ ПРОЦЕССЫ ЭКСТРЕМАЛЬНОГО РЕГУЛИРОВАНИЯ ОДНОМЕРНОГО БЕЗЫНЕРЦИОННОГО ОБЪЕКТА
- ГЛАВА ДВАДЦАТАЯ. СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ С САМОНАСТРАИВАЮЩИМИСЯ КОРРЕКТИРУЮЩИМИ УСТРОЙСТВАМИ
- 20-1. СИСТЕМЫ С РАЗОМКНУТЫМИ ЦЕПЯМИ НАСТРОЙКИ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ
- 20-2. СИСТЕМЫ С ЗАМКНУТЫМИ ЦЕПЯМИ НАСТРОЙКИ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ
- 20-3. СИСТЕМЫ С ЭКСТРЕМАЛЬНОЙ НАСТРОЙКОЙ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ
- 20-4. СТАТИСТИЧЕСКАЯ ДИНАМИКА НЕПРЕРЫВНЫХ СИСТЕМ С ЭКСТРЕМАЛЬНОЙ НАСТРОЙКОЙ ПОСЛЕДОВАТЕЛЬНЫХ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ
- б) Уравнения замкнутой самонастраивающейся системы
- в) Случай сильной фильтрации. Квазистационарный режим
- г) Общий случай квазистационарного режима
- ГЛАВА ДВАДЦАТЬ ПЕРВАЯ. ИГРОВЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- 21-1. НАЗНАЧЕНИЕ И ПРИНЦИПЫ ДЕЙСТВИЯ ИГРОВЫХ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- 21-2. НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ ИГР
- 21-3. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ. ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
- 21-4. ОБ АЛГОРИТМАХ ИГРОВЫХ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- ПРИЛОЖЕНИЯ