| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
20-2. СИСТЕМЫ С ЗАМКНУТЫМИ ЦЕПЯМИ НАСТРОЙКИ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ
В системах данного типа определяются фактические характеристики замкнутой системы, сопоставляются с эталонными, заранее установленными характеристиками и в соответствии с измеренными отклонениями осуществляется такое воздействие на корректирующее устройство, при котором фактическая характеристика замкнутой системы приближается к эталонной.
Рассмотрим два принципа построения систем с замкнутыми цепями настройки. Пусть заданная оптимальная передаточная функция  замкнутой системы получается при передаточных функциях
замкнутой системы получается при передаточных функциях  двух основных звеньев:
двух основных звеньев:

Изменение внешних условий вызывает изменение  и через цепи самонастройки изменение
и через цепи самонастройки изменение  Обозначаем:
Обозначаем:

Из формулы

следует:

и

Приращения  по самому назначению рассматриваемых систем должны быть малыми. Поэтому
по самому назначению рассматриваемых систем должны быть малыми. Поэтому

Вычитая из этого равенства соотношение

получаем:

Задача сводится к установлению такой связи между  и
и  которая, во-первых, обеспечивала бы достаточную малость отклонений
которая, во-первых, обеспечивала бы достаточную малость отклонений  при имеющихся отклонениях Лги, во-вторых, могла бы быть практически реализована.
при имеющихся отклонениях Лги, во-вторых, могла бы быть практически реализована.
Наиболее простой в отношении реализации является, как видно из
дальнейшего, следующая пропорциональная зависимость между приращением передаточной функции  и изменением передаточной функции замкнутой системы:
и изменением передаточной функции замкнутой системы:

где  Выражение (20-10) при этом принимает вид:
Выражение (20-10) при этом принимает вид:

Если коэффициент  достаточно велик, то изменения
достаточно велик, то изменения  вызванные изменением
вызванные изменением  малы. Изменение передаточной функции корректирующего устройства
малы. Изменение передаточной функции корректирующего устройства  очевидно, эквивалентно введению дополнительного сигнала:
очевидно, эквивалентно введению дополнительного сигнала:

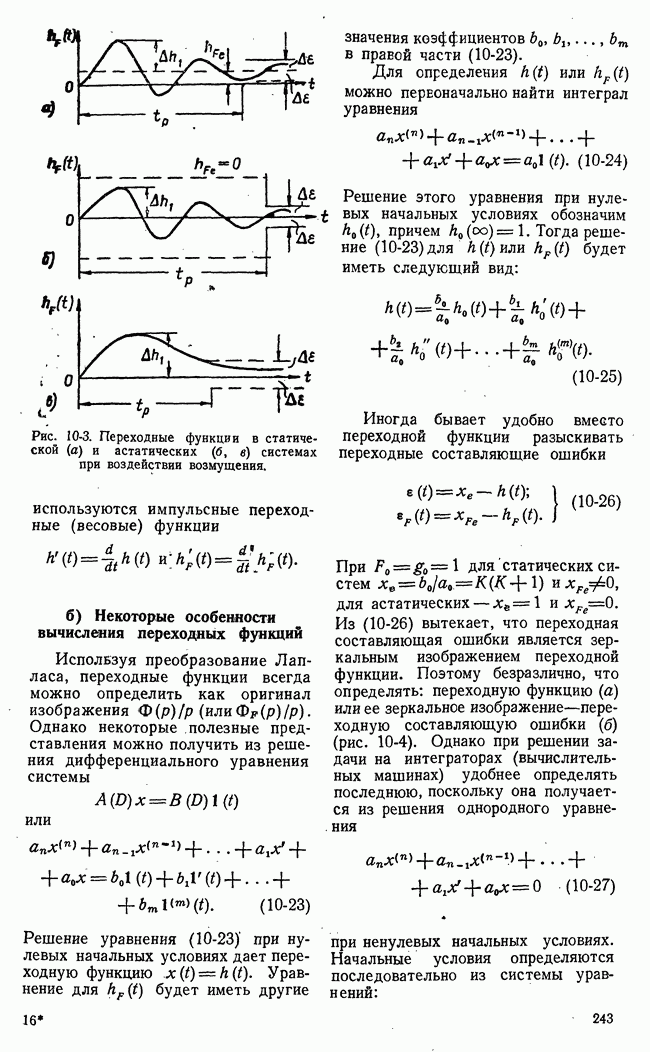
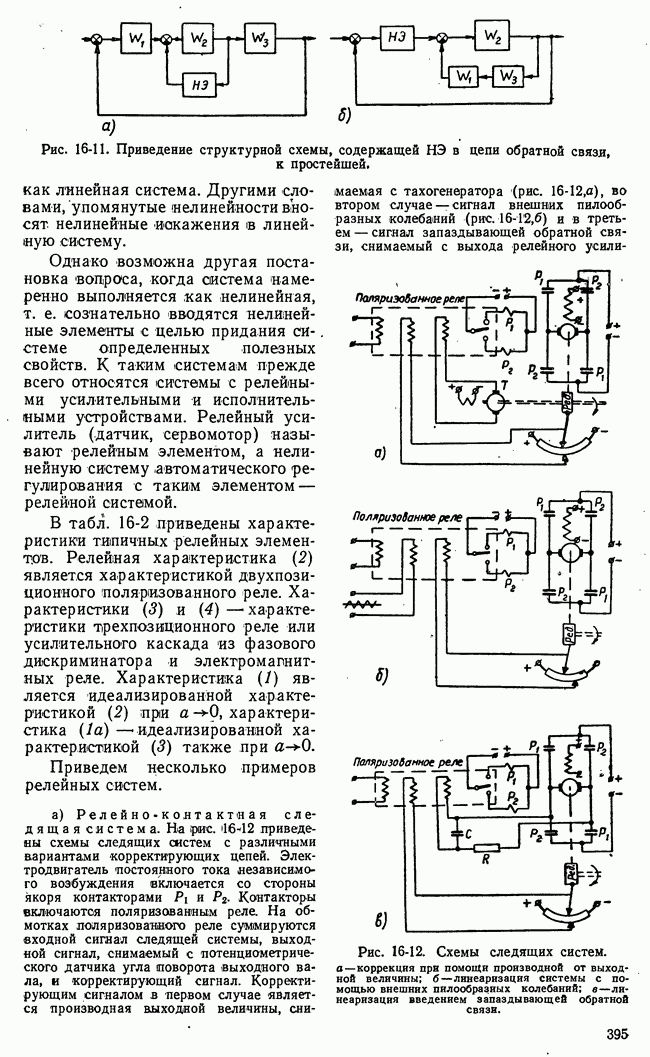
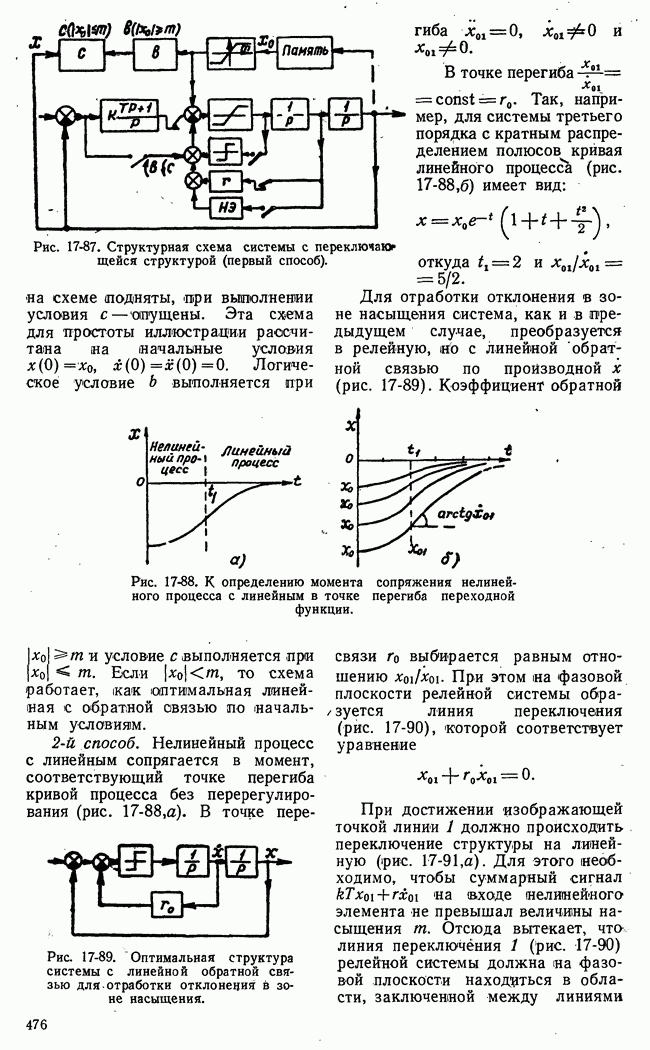
приложенного к выходу корректирующего устройства  (рис. 20-5,а).
(рис. 20-5,а).
Но

и


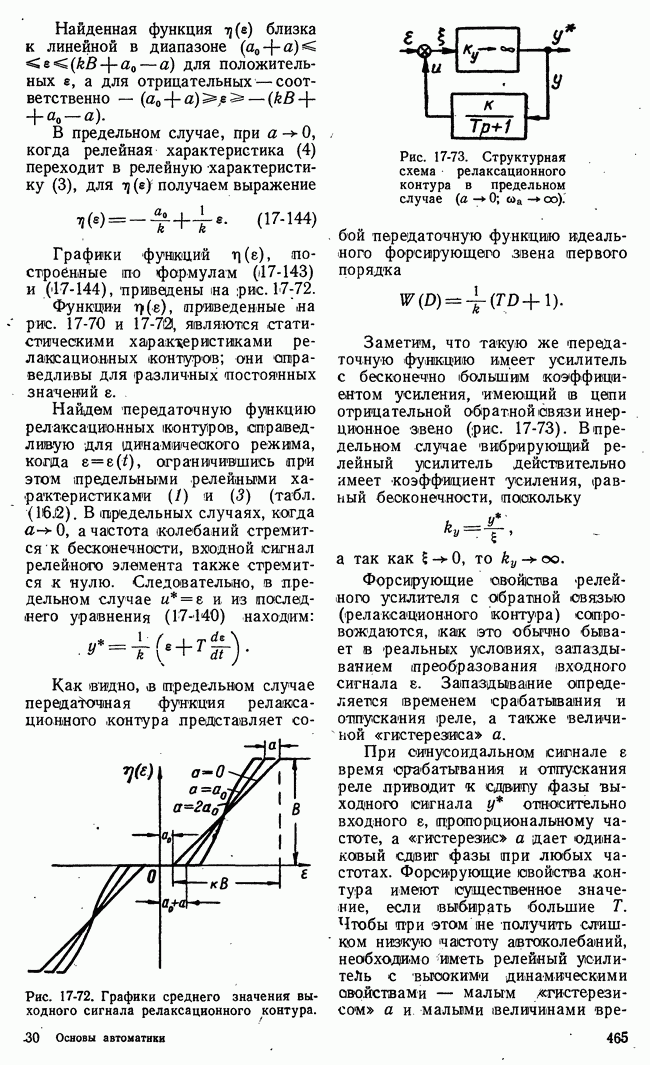
Рис. 20-5. а — структурная схема с обозначением сигнала, эквивалентного стабилизирующему изменению передаточной функции;  структурная схема системы с эталоном передаточных свойств.
структурная схема системы с эталоном передаточных свойств.
Итак, мы показали, что изменение передаточной функции корректирующего устройства  (см. (20-11)] эквивалентно введению на выходе корректирующего устройства с неизменными параметрами дополнительного сигнала
(см. (20-11)] эквивалентно введению на выходе корректирующего устройства с неизменными параметрами дополнительного сигнала  . Последний может быть сравнительно легко сформирован посредством дополнительных связей в системе и фильтра с передаточной функцией
. Последний может быть сравнительно легко сформирован посредством дополнительных связей в системе и фильтра с передаточной функцией  Соответствующая структурная схема представлена на рис. 20-5,6.
Соответствующая структурная схема представлена на рис. 20-5,6.
Входной сигнал  помимо корректирующего устройства
помимо корректирующего устройства  с неизменными параметрами, поступает на фильтр со стабильной передаточной функцией
с неизменными параметрами, поступает на фильтр со стабильной передаточной функцией  Выходной сигнал этого фильтра вычитается из сигнала всей замкнутой системы
Выходной сигнал этого фильтра вычитается из сигнала всей замкнутой системы  Сигнал разности через передаточное звено с коэффициентом усиления
Сигнал разности через передаточное звено с коэффициентом усиления  поступает на выход корректирующего устройства.
поступает на выход корректирующего устройства.
Легко показать, что уравнение замкнутой системы с дополнительными связями имеет вид:

Если  достаточно велико (но устойчивость замкнутой системы обеспечивается), то приближенно
достаточно велико (но устойчивость замкнутой системы обеспечивается), то приближенно

Тем самым подтверждено, что в системе обеспечивается стабильность передаточных свойств, несмотря на изменение передаточной функции объекта.
Необходимо подчеркнуть, что в рассмотренной системе стабилизация динамических свойств  достигается введением прямой и обратной дополнительных связей с эталонным фильтром в цепи прямой связи. Однако эффект от указанных связей согласно (20-11) эквивалентен частному случаю самонастройки
достигается введением прямой и обратной дополнительных связей с эталонным фильтром в цепи прямой связи. Однако эффект от указанных связей согласно (20-11) эквивалентен частному случаю самонастройки

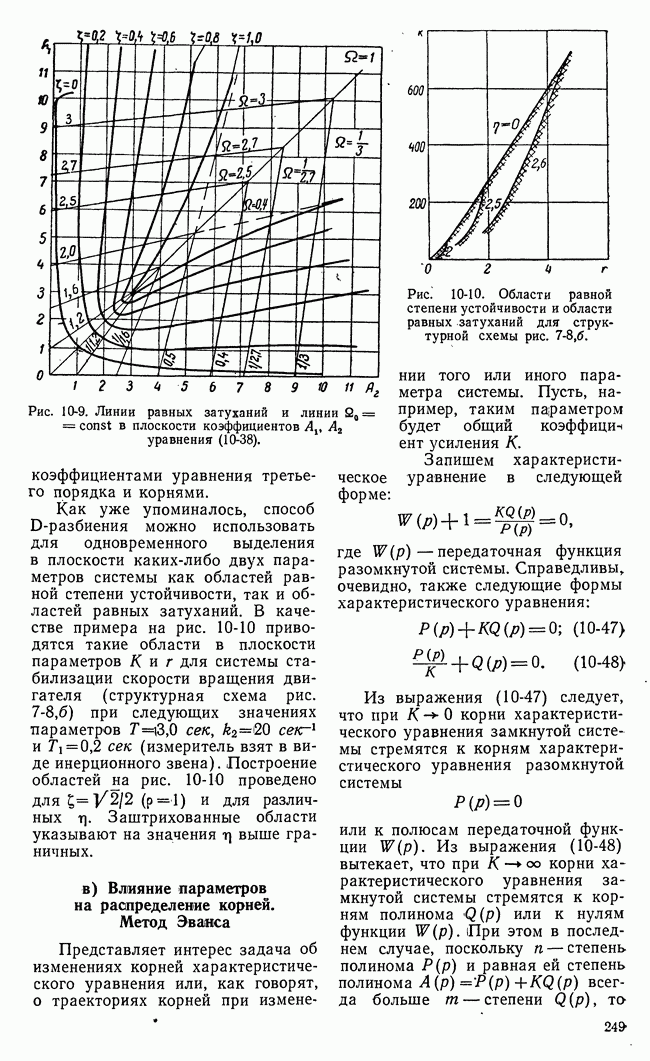
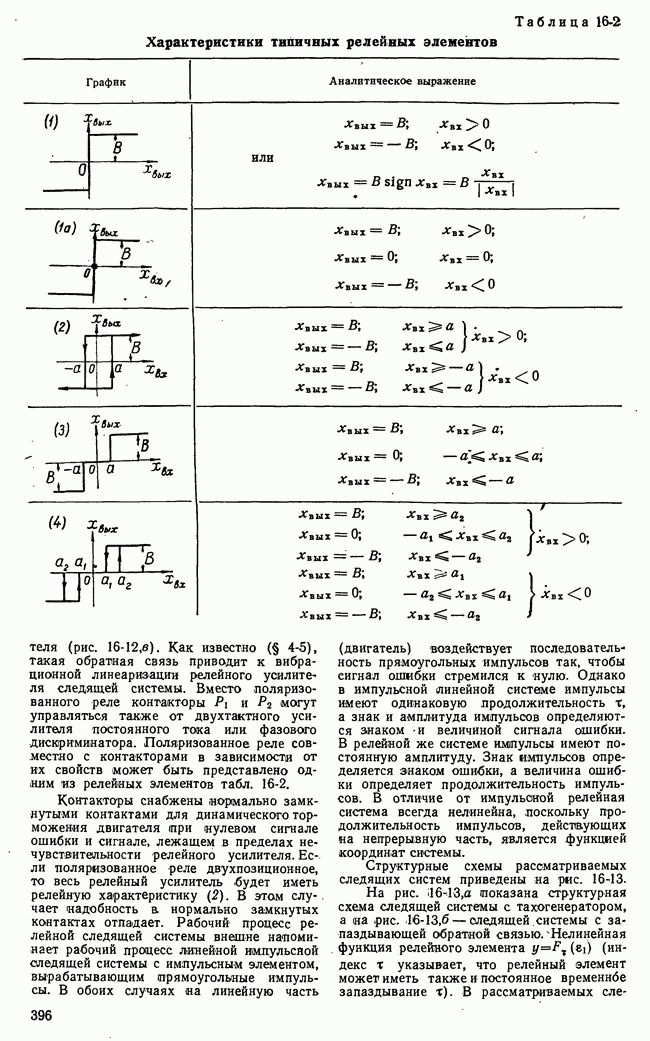
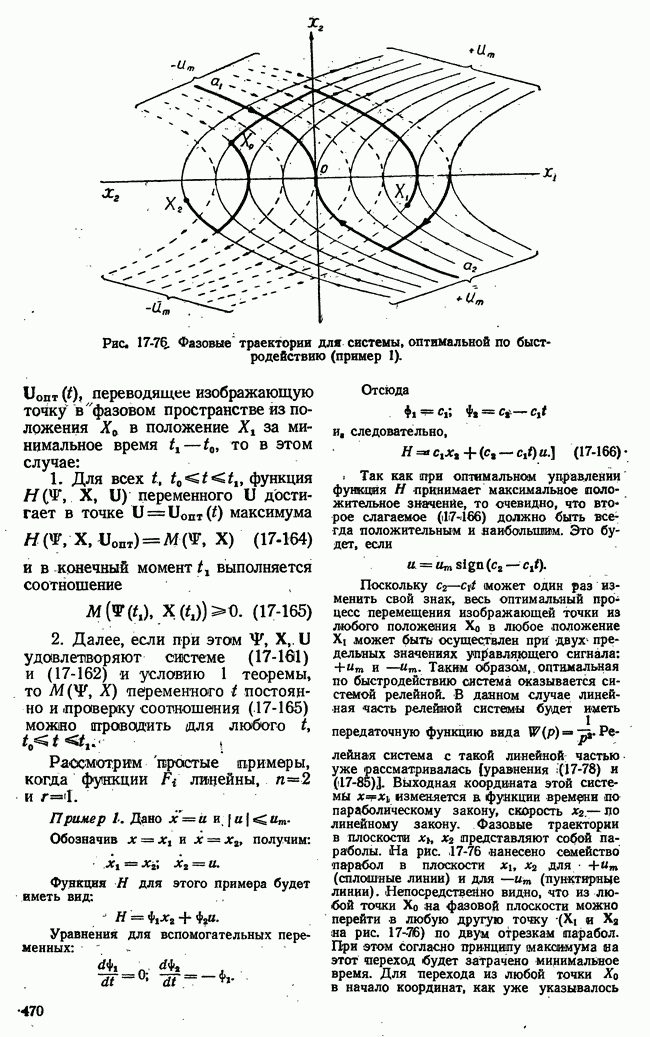
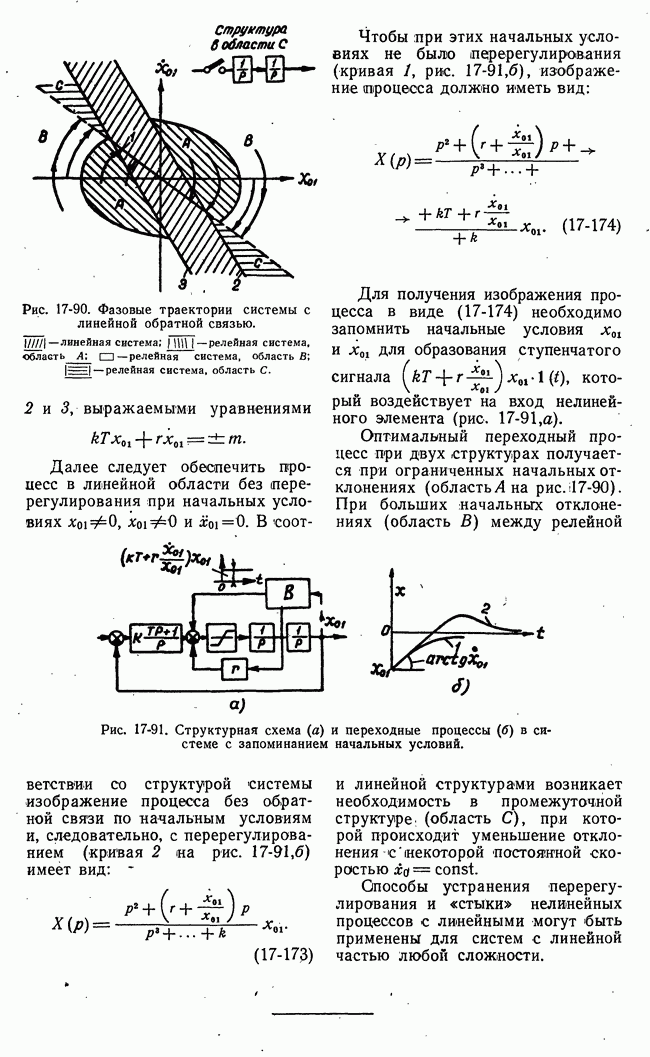
Рис. 20-6, Общая схема системы с замкнутыми цепями настройки параметра последовательного корректирующего устройства.
корректирующего устройства. Поэтому мы рассмотрели системы данного тцпа в числе самонастраивающихся систем. Во избежание путаницы для данной системы введем специальное название: система со стабилизацией качества процессов регулирования посредством глубоких связей.
Возможности систем со стабилизацией качества процессов посредством глубоких связей ограничены. Увеличение  [формулы
[формулы  и (20-13)] в реальных системах неизбежно ограничивается устойчивостью, причем чем шире диапазон изменений
и (20-13)] в реальных системах неизбежно ограничивается устойчивостью, причем чем шире диапазон изменений  тем меньше допустимые значения
тем меньше допустимые значения  Это затруднение частично преодолевается введением релейнрго элемента вместо усилительного звена
Это затруднение частично преодолевается введением релейнрго элемента вместо усилительного звена  (рис. 20-6). Такие релейные контуры работают в автоколебательном режиме, причем чем меньше амплитуда (выше частота) автоколебаний, тем больше эффективный коэффициент усиления линеаризованного автоколебаниями релейного элемента. Однако малая амплитуда автоколебаний возможна лишь при определенной структуре звена
(рис. 20-6). Такие релейные контуры работают в автоколебательном режиме, причем чем меньше амплитуда (выше частота) автоколебаний, тем больше эффективный коэффициент усиления линеаризованного автоколебаниями релейного элемента. Однако малая амплитуда автоколебаний возможна лишь при определенной структуре звена  и в определенном диапазоне изменений его параметров.
и в определенном диапазоне изменений его параметров.
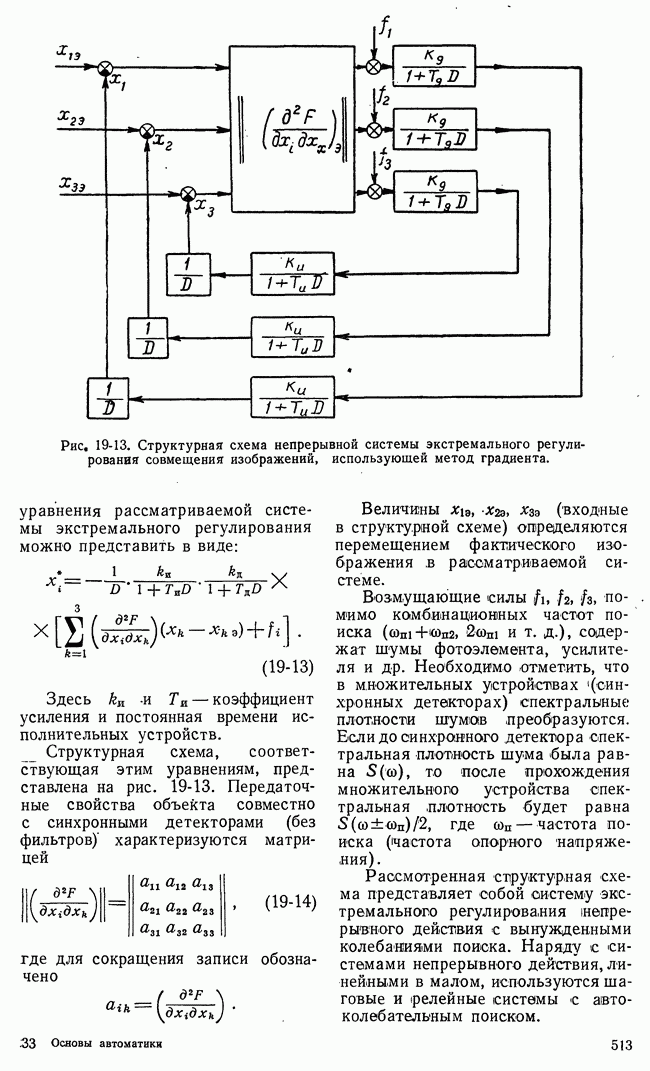
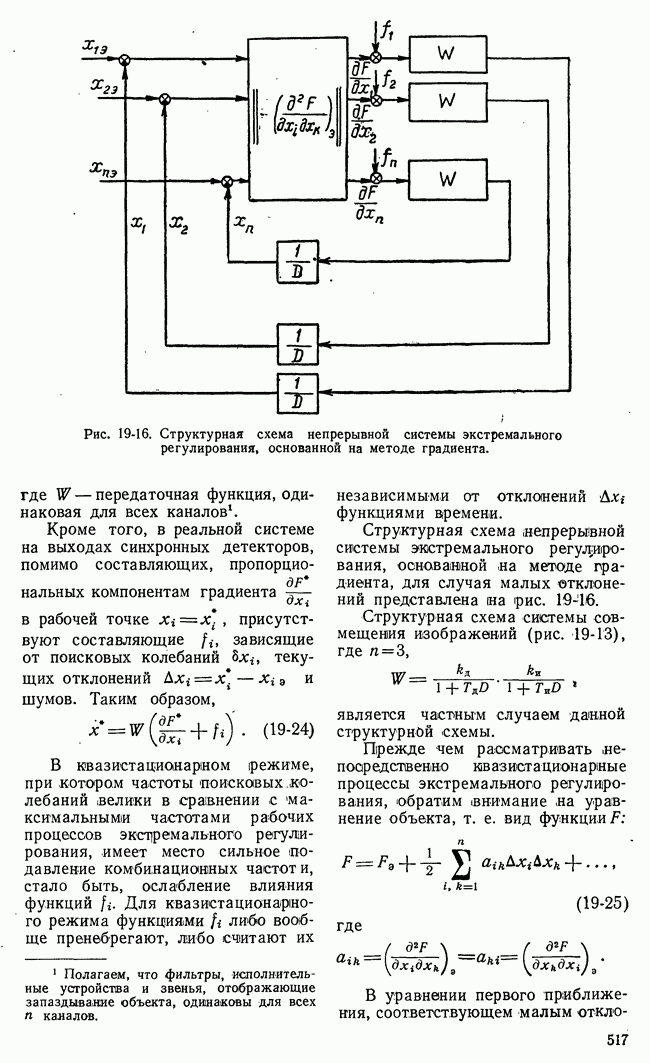
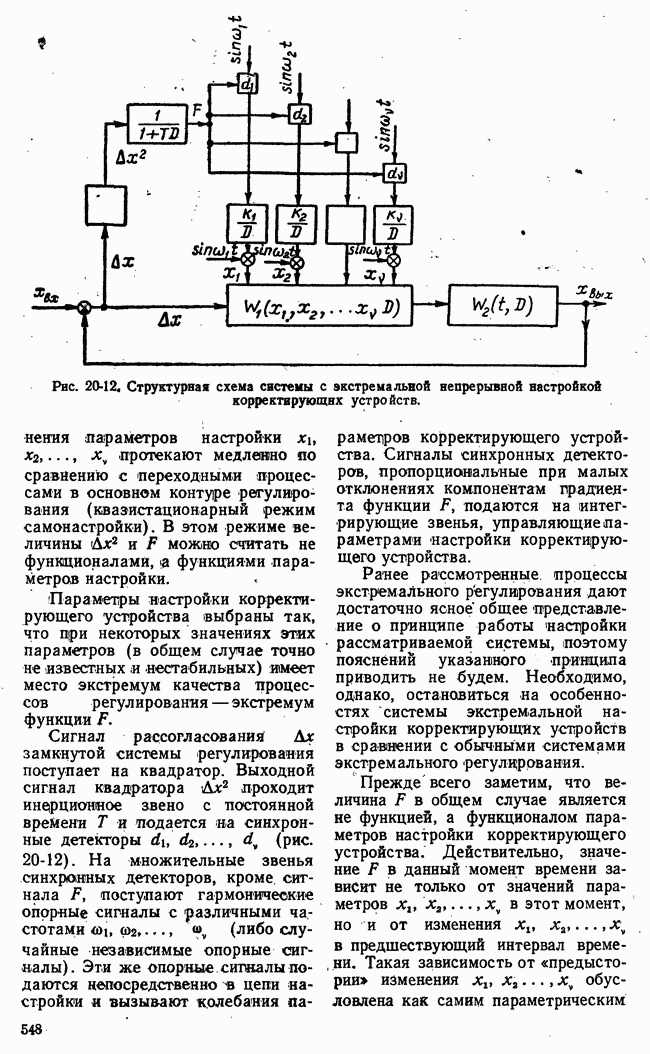
Перейдем к рассмотрению систем с замкнутыми цепями настройки параметров корректирующих устройств. Общая схема таких систем при последовательном корректирующем устройстве представлена на рис. 20-6.
Специальным устройством осуществляется контроль характеристик замкнутой системы. Для контроля можно использовать колебания системы, создаваемые различными возмущающими силами или специальными пробными сигналами.
Разумеется, возможно одновременное использование обоих видов колебаний. Характеристики замкнутой системы сопоставляются с эталонными. Определяются отклонения фактических характеристик замкнутой системы от эталонных и в соответствии с отклонениями осуществляется воздействие на параметры корректирующего устройства. В результате устанавливаются такие значения параметров корректирующего устройства, при которых характеристики замкнутой системы близки к эталонным. Контроль свойств замкнутой системы может осуществляться путем определения временных или частотных характеристик системы.
Ввиду того что эти системы основаны на измерении и вычислении характеристик объектов в процессе их работы, они часто именуются аналитическими.
Для определения временных или частотных характеристик в самонастраивающихся системах, аналитического типа в принципе могут использоваться те же способы, что и при испытаниях объектов с целью определения их динамических свойств. А именно возможна регистрация реакции системы на импульсные или ступенчатые пробные воздействия, поступающие периодически, но с интервалами, большими времени переходных процессов. В этом случае контролируются переходные функции. Основная трудность, возникающая при использовании подобного способа, заключается в том, что применение больших пробных воздействий обычно оказывается недопустимым, а реакцию на малые воздействия трудно
выделить на фоне шумов. Для выделения реакции системы на малые пробные воздействия необходимо использовать накопление сигналов в течение нескольких циклов, что увеличивает общее время контроля характеристик и поэтому ограничивает допустимые скорости их изменения.
Можно применить другой распространенный способ контроля динамических характеристик — статистический  ]. Если на вход системы с импульсной переходной функцией
]. Если на вход системы с импульсной переходной функцией  воздействует стационарная случайная функция
воздействует стационарная случайная функция  вызывающая реакцию
вызывающая реакцию  то взаимная корреляционная функция
то взаимная корреляционная функция  равна:
равна:

Взаимная корреляционая функция входной и выходной величин  и автокорреляционная функция входной величины
и автокорреляционная функция входной величины  можно определять с помощью корреляторов
можно определять с помощью корреляторов  Для этого временному сдвигу
Для этого временному сдвигу  задаются значения в пределах интервалов существенных значений корреляционных функций.
задаются значения в пределах интервалов существенных значений корреляционных функций.
После определения  импульсная переходная (весовая) функция системы находится как решение интегрального уравнения
импульсная переходная (весовая) функция системы находится как решение интегрального уравнения

В общем случае для этого (необходимо вычислительное устройство непрерывного или цифрового типа. Особо простое решение получается в случае, когда спектральная плотность входной величины постоянна в пределах полосы пропускания системы, т. е.  эквивалентна белому шуму. В этом случае можно принять
эквивалентна белому шуму. В этом случае можно принять  Таким образом, в данном случае взаимная корреляционная функция непосредственно дает искомую весовую функцию системы.
Таким образом, в данном случае взаимная корреляционная функция непосредственно дает искомую весовую функцию системы.
К числу достоинств статистического метода контроля динамических характеристик объектов следует отнести возможность использования естественных флюктуаций входных, величин в качестве пробных сигналов, а также слабое влияние некоррелированных с входными величинами шумов объекта и измерителей.
Самыми важными показателями самонастраивающихся систем являются время и точность самонастройки. Эти показатели в рассматриваемых системах определяются прежде всего временем и точностью контроля динамических характеристик объекта. Чем больше время контроля, тем, вообще/говоря, выше точность, но больше время самонастройки.
При статистическом способе контроля временных характеристик и использовании белого шума в качестве пробного воздействия минимальное допустимое время накопления при определении корреляционной функции значительно превышает предельное время корреляции. Предельное время корреляции выражает интервал, при котором практически исчезает корреляционная связь. Оно равно времени переходных процессов  в контролируемой системе. Время самонастройки должно в несколько раз превышать время накопления при контроле. Таким образом, минимальное время самонастройки при статистическом способе контроля временных характеристик грубо можно оценить по формуле
в контролируемой системе. Время самонастройки должно в несколько раз превышать время накопления при контроле. Таким образом, минимальное время самонастройки при статистическом способе контроля временных характеристик грубо можно оценить по формуле

где а обычно имеет порядок нескольких десятков.
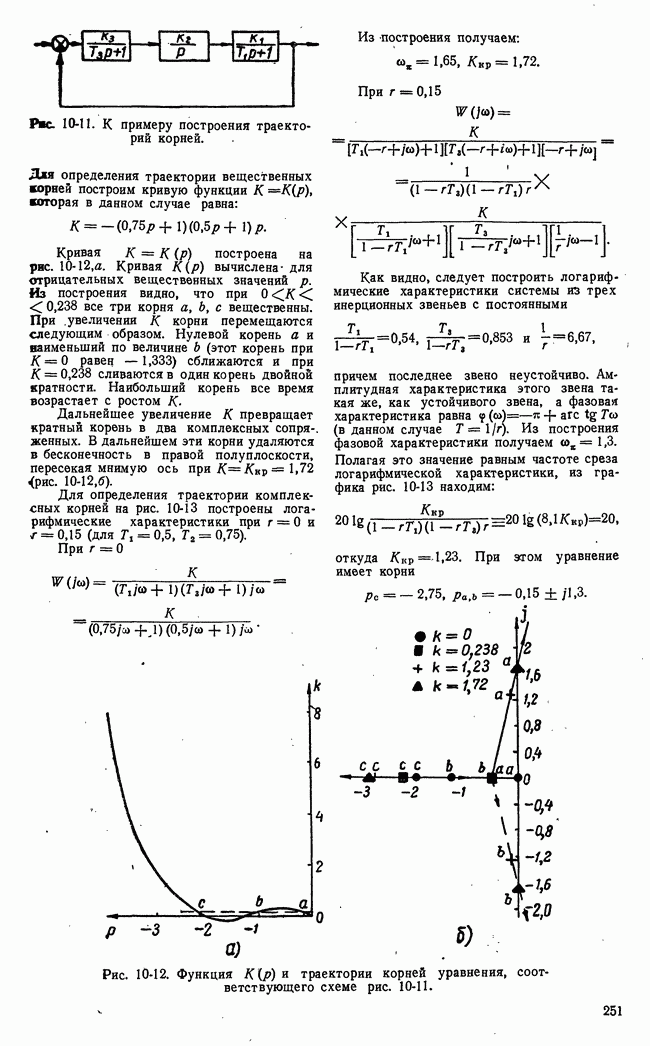
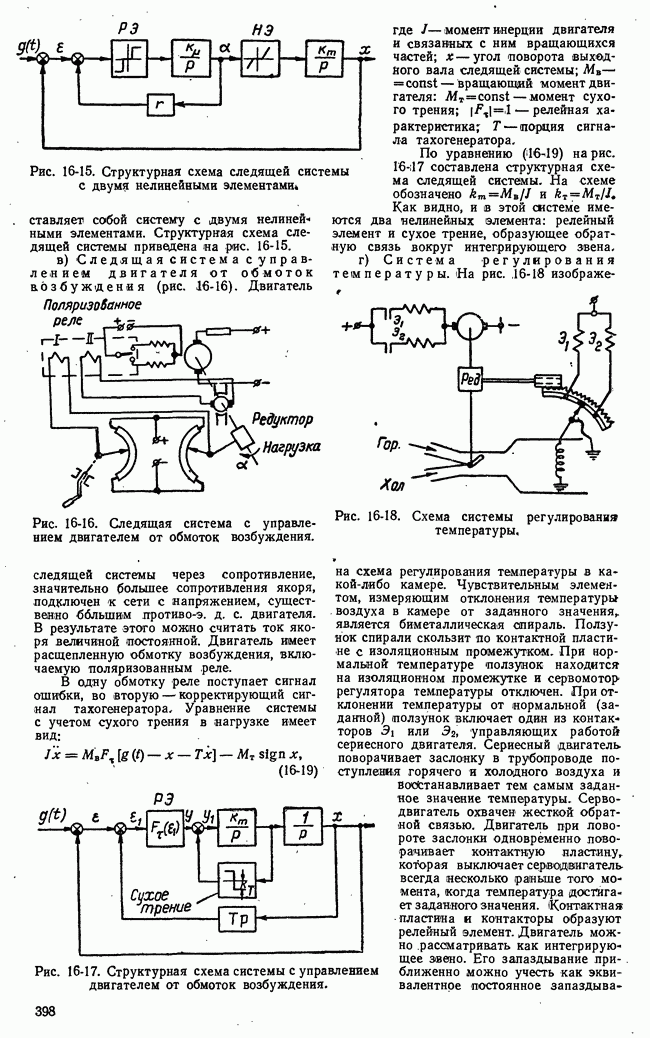
Рассмотрим один из возможных способов контроля частотных характеристик замкнутой системы. Как и ранее, везде будем предполагать, что изменения параметров линейной системы и ее звеньев

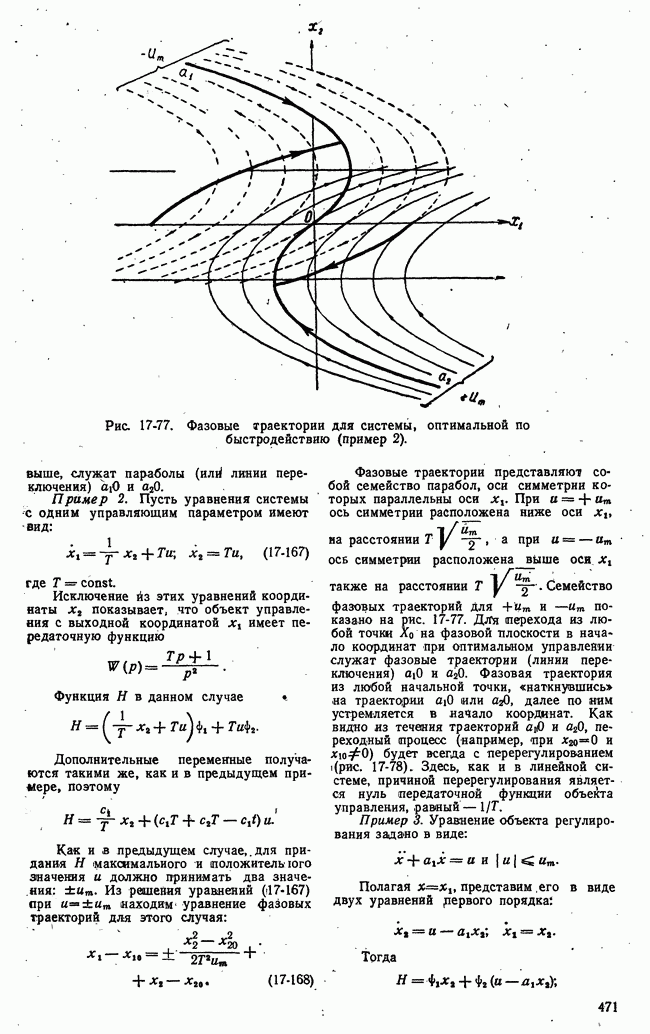
Рис. 20-7. Схема измерителя значений частотной характеристики системы.
протекают настолько медленно, что динамические свойства системы в каждый данный момент времени достаточно точно характеризуются частотными характеристиками системы с фиксированными параметрами, равными мгновенным значениям соответствующих переменных параметров. Это основное предположение сводится к тому, что описание системы с медленно меняющимися параметрами производится посредством семейства характеристик систем с постоянными параметрами.
Амплитудно-фазовая характеристика системы может быть представлена в виде вещественной и мнимой частотных характеристик:

Для определения значений  достаточно иметь гармоническую составляющую с частотой со на входе системы, измерить амплитуду этой составляющей и измерить две компоненты гармонической составляющей с частотой со на выходе системы.
достаточно иметь гармоническую составляющую с частотой со на входе системы, измерить амплитуду этой составляющей и измерить две компоненты гармонической составляющей с частотой со на выходе системы.
В соответствии с этим схема измерителя значений  может иметь вид, представленный на рис. 20-7.
может иметь вид, представленный на рис. 20-7.
Узкополосные фильтры 1 и 2, настроенные на частоту  выделяют гармонические составляющие входного и выходного сигналов, которые поступают на устройство 3. В 3 определяется отношение амплитуд и сопоставляются фазы гармонических составляющих; тем самым» определяются значения
выделяют гармонические составляющие входного и выходного сигналов, которые поступают на устройство 3. В 3 определяется отношение амплитуд и сопоставляются фазы гармонических составляющих; тем самым» определяются значения  Если вероятность присутствия во входном сигнале заметной составляющей с частотой со недостаточно велика, то на вход подается специальный сигнал с частотой
Если вероятность присутствия во входном сигнале заметной составляющей с частотой со недостаточно велика, то на вход подается специальный сигнал с частотой  .
.
В качестве узкополосных фильтров удобно применять синхронные детекторы с гармоническим опорным напряжением частоты  Полоса пропускания такого фильтра определяется полосой пропускания фильтра низших частот на выходе синхронного детектора и может быть сделана очень узкой (десятые, сотые и даже тысячные доли герца). Минимальные допустимые полосы пропускания определяются требованиями к необходимому быстродействию цепей самонастройки.
Полоса пропускания такого фильтра определяется полосой пропускания фильтра низших частот на выходе синхронного детектора и может быть сделана очень узкой (десятые, сотые и даже тысячные доли герца). Минимальные допустимые полосы пропускания определяются требованиями к необходимому быстродействию цепей самонастройки.
При использовании синхронных детекторов в качестве выделителей гармонических составляющих вещественная и мнимая частотные характеристики выделяются очень, просто: значение  получается на синхронном детекторе, где опорное напряжение совпадает по фазе с входным сигналом, а значение
получается на синхронном детекторе, где опорное напряжение совпадает по фазе с входным сигналом, а значение  на детекторе, где фаза, опорного напряжения отличается на 90°.
на детекторе, где фаза, опорного напряжения отличается на 90°.
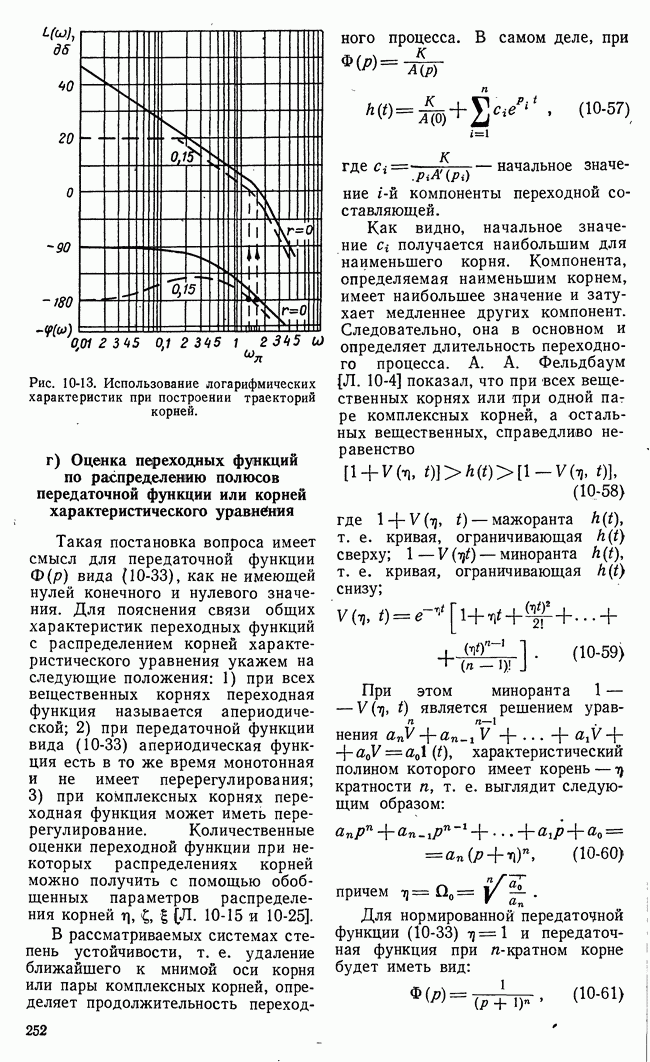
Схема измерителя частотных характеристик, построенного на синхронных детекторах, представлена на рис. 20-8. В этой схеме для увеличения надежности измерений к «естественному» входному сигналу  добавляется опорное напряжение
добавляется опорное напряжение  вызывающее дополнительные малые колебания всей системы с частотой
вызывающее дополнительные малые колебания всей системы с частотой  Эти колебания в дальнейшем будут именоваться
Эти колебания в дальнейшем будут именоваться

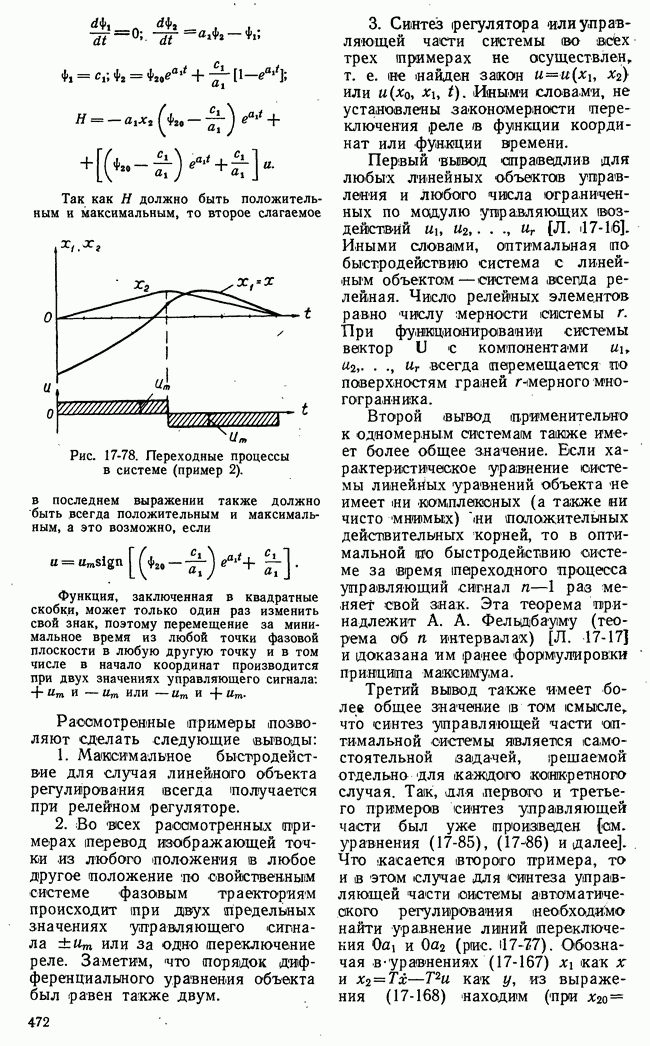
Рис. 20-8. Структурная схема измерителя значений частотных характеристик замкнутой системы, использующего синхронные детекторы.
пробными колебаниями. Входной сигнал вместе с функцией  имеет гармоническую составляющую Лвхто
имеет гармоническую составляющую Лвхто  Амплитуда это? составляющей измеряется синхронным детектором, подключенным ко входу системы. Синхронный детектор состоит из множительного звена и фильтра низших частот
Амплитуда это? составляющей измеряется синхронным детектором, подключенным ко входу системы. Синхронный детектор состоит из множительного звена и фильтра низших частот  Выходная величина указанного синхронного детектора, пропорциональная
Выходная величина указанного синхронного детектора, пропорциональная  , подается на делительные звенья. На эти же звенья поступают сигналы от основных синхронных детекторов, подключенных к выходу системы. На один из этих синхронных детекторов в качестве опорного сигнала подается величина
, подается на делительные звенья. На эти же звенья поступают сигналы от основных синхронных детекторов, подключенных к выходу системы. На один из этих синхронных детекторов в качестве опорного сигнала подается величина  а на второй — величина
а на второй — величина  Вследствие этого в установившемся режиме выходные сигналы основных синхронных детекторов пропорциональны Хвхт
Вследствие этого в установившемся режиме выходные сигналы основных синхронных детекторов пропорциональны Хвхт  После прохождения делительных звеньев эти сигналы с точностью до постоянного коэффициента становятся равными
После прохождения делительных звеньев эти сигналы с точностью до постоянного коэффициента становятся равными  и
и 
Такое строение имеет схема измерения значений вещественной и мнимой частотных характеристик при одном значении  . Часто необходимо контролировать
. Часто необходимо контролировать  при нескольких значениях
при нескольких значениях  . Для этого можно применить несколько каналов измерения, аналогичных изображенному на рис. 20-8, но имеющих различные частоты опорных напряжений. Можно также использовать переключение значений частоты
. Для этого можно применить несколько каналов измерения, аналогичных изображенному на рис. 20-8, но имеющих различные частоты опорных напряжений. Можно также использовать переключение значений частоты  . В последнем случае система самонастройки уже не будет непрерывной.
. В последнем случае система самонастройки уже не будет непрерывной.
Одновременный контроль вещественной  и мнимой
и мнимой  частотных характеристик или амплитудной
частотных характеристик или амплитудной  и фазовой
и фазовой  частотных характеристик необходим только в неминимальнофазовых системах. В минимальнофазовых системах
частотных характеристик необходим только в неминимальнофазовых системах. В минимальнофазовых системах  однозначно связана с
однозначно связана с  Поэтому в минимальнофазовой системе достаточно контролировать и регулировать одну частотную характеристику, например амплитудную частотную характеристику Схема самонастраивающейся системы с управлением корректирующим устройством посредством контроля амплитудных частотных характеристик разомкнутого контура представлена
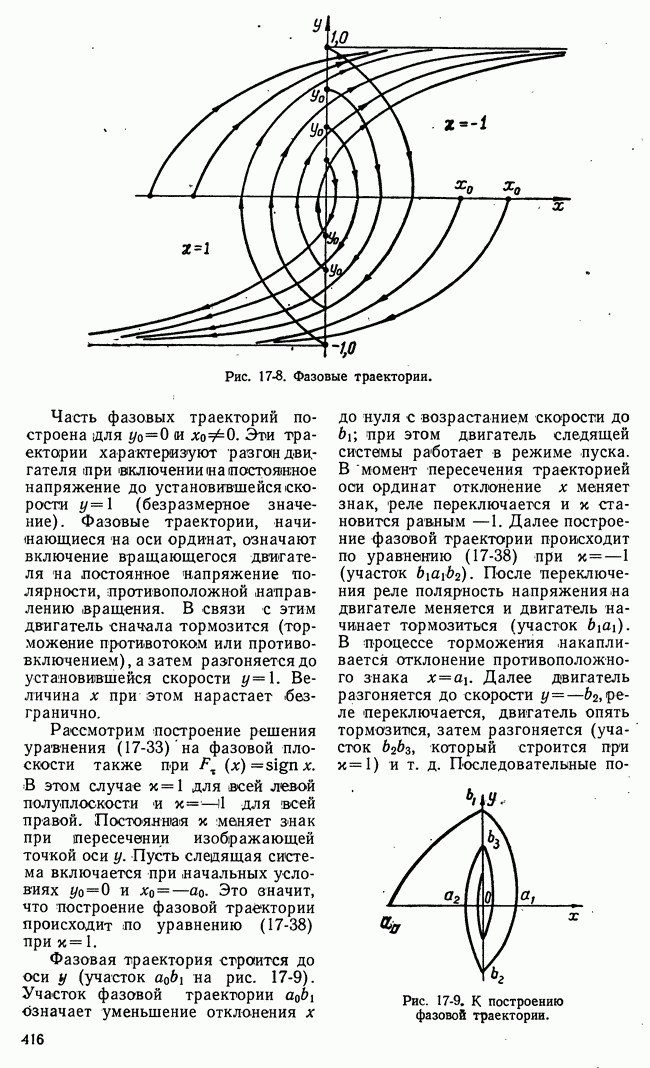
Поэтому в минимальнофазовой системе достаточно контролировать и регулировать одну частотную характеристику, например амплитудную частотную характеристику Схема самонастраивающейся системы с управлением корректирующим устройством посредством контроля амплитудных частотных характеристик разомкнутого контура представлена  рис. 20-9. Гармоники с частотами
рис. 20-9. Гармоники с частотами  сигнала ошибки выделяются достаточно узкополосными резонансными фильтрами
сигнала ошибки выделяются достаточно узкополосными резонансными фильтрами  Гармоники с теми же частотами на выходе объекта выделяются аналогичными фильтрами
Гармоники с теми же частотами на выходе объекта выделяются аналогичными фильтрами  После фильтров следуют детекторы, выходные напряжения
После фильтров следуют детекторы, выходные напряжения  которых пропорциональны амплитудам гармоник.
которых пропорциональны амплитудам гармоник.
Для детекторов  на выходе все коэффициенты пропорциональности одинаковы, так что
на выходе все коэффициенты пропорциональности одинаковы, так что

Рис. 20-9. Схема самонастраивающейся системы с контролем амплитудных частотных характеристик разомкнутого контура.
напряжения и просто соответствуют амплитудам гармоник на выходе контура:

где  амплитудная частотная характеристика разомкнутого контура;
амплитудная частотная характеристика разомкнутого контура;  амплитуда гармоники сигнала рассогласования.
амплитуда гармоники сигнала рассогласования.
Для детекторов  на входе коэффициенты пропорциональности (коэффициенты усиления) подобраны так, что соответствуют ординатам желаемой амплитудной частотной характеристики разомкнутого контура
на входе коэффициенты пропорциональности (коэффициенты усиления) подобраны так, что соответствуют ординатам желаемой амплитудной частотной характеристики разомкнутого контура  Поэтому
Поэтому

Выходные сигналы детекторов  вычитаются и поступают на усилительные, точнее делительные, звенья с коэффициентами усиления
вычитаются и поступают на усилительные, точнее делительные, звенья с коэффициентами усиления

Таким образом, на выходах звеньев формируются сигналы вида:

Эти сигналы интегрируются и воздействуют на корректирующее устройство  Выходные величины интегрирующих звеньев
Выходные величины интегрирующих звеньев  будем называть параметрами настройки. При определенной структуре корректирующего устройства ордината его амплитудной характеристики в точке
будем называть параметрами настройки. При определенной структуре корректирующего устройства ордината его амплитудной характеристики в точке  пропорциональна
пропорциональна 

Учитывая, что

и вводя обозначение

записываем:

или

где 
В этих уравнениях не учитывается запаздывание в системе контроля частотных характеристик и прежде всего в узкополосных резонансных фильтрах. Таким образом, уравнение (20-20) справедливо для столь медленных процессов самонастройки, при которых инерционность системы контроля не играет заметной роли и ею можно пренебречь.
Из (20-20) следует, что такие процессы самонастройки всегда устойчивы, коль скоро

Последнее неравенство всегда можно обеспечить, так как  Постоянные времени медленных процессов самонастройки
Постоянные времени медленных процессов самонастройки  определяют и «скоростные» ошибки настройки, вызванные дрейфом характеристик объекта. Эти ошибки при
определяют и «скоростные» ошибки настройки, вызванные дрейфом характеристик объекта. Эти ошибки при

равны:

Величину  можно интерпретировать как приращение амплитудной характеристики ненастраиваемого разомкнутого контура за время Таким образом, основная ошибка (20-21) медленно действующей системы самонастройки рассматриваемого типа равна приращению характеристики ненастраиваемого контура за время, равное постоянной времени
можно интерпретировать как приращение амплитудной характеристики ненастраиваемого разомкнутого контура за время Таким образом, основная ошибка (20-21) медленно действующей системы самонастройки рассматриваемого типа равна приращению характеристики ненастраиваемого контура за время, равное постоянной времени  процессов самонастройки. При сокращении
процессов самонастройки. При сокращении  (увеличении
(увеличении  проявляется инерционность системы контроля. Наибольшая допустимая полоса пропускания резонансных фильтров должна быть меньше полосы пропускания настраиваемого разомкнутого контура. Отсюда следует, что минимальное время запаздывания при контроле превышает время переходного процесса
проявляется инерционность системы контроля. Наибольшая допустимая полоса пропускания резонансных фильтров должна быть меньше полосы пропускания настраиваемого разомкнутого контура. Отсюда следует, что минимальное время запаздывания при контроле превышает время переходного процесса  в контролируемом контуре. Для обеспечения устойчивости самонастройки время переходных процессов самонастройки Т [в случае (20-20) 737] должно по крайней мере в несколько раз превышать запаздывание в системе контролй. Поэтому минимальное время самонастройки может быть оценено по формуле
в контролируемом контуре. Для обеспечения устойчивости самонастройки время переходных процессов самонастройки Т [в случае (20-20) 737] должно по крайней мере в несколько раз превышать запаздывание в системе контролй. Поэтому минимальное время самонастройки может быть оценено по формуле

где а имеет порядок десятков. Это соотношение аналогично тому, которое имеет место при статистическом контроле временных характеристик настраиваемой системы.
Сопоставляя системы с разомкнутыми и замкнутыми цепями автоматической настройки корректирующих устройств, можно констатировать, что последний тип самонастраивающихся систем более совершенен. Основным достоинством систем с замкнутыми цепями самонастройки является возможность стабилизации качества процессов регулирования в условиях влияния на характеристики объекта самых разнообразных неконтролируемых факторов.
Однако системы с замкнутыми цепями настройки корректирующих устройств требуют все же значительного объема начальной информации о свойствах управляемого объекта. Системы с экстремальной застройкой требуют меньшей начальной информации.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ГЛАВА ПЕРВАЯ. ВВОДНАЯ
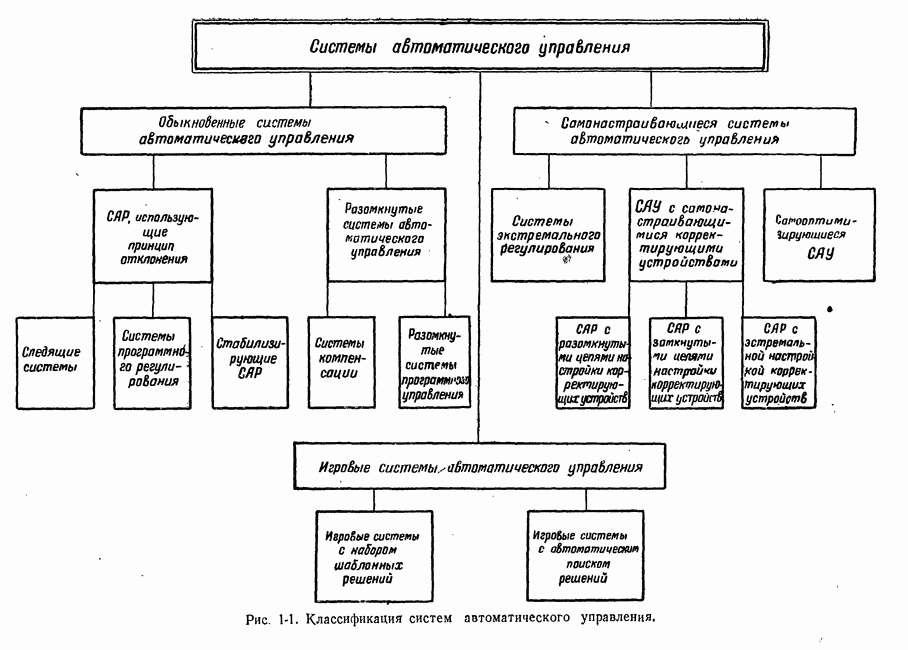
- 1-1. О КЛАССИФИКАЦИИ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- 1-2. ОБЫКНОВЕННЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- 1-3. САМОНАСТРАИВАЮЩИЕСЯ СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- 1-4. ИГРОВЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- 1-5. КЛАССИФИКАЦИЯ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ ПО ДРУГИМ ПРИЗНАКАМ
- ГЛАВА ВТОРАЯ. ОБЩИЕ ПЕРЕДАТОЧНЫЕ СВОЙСТВА ЭЛЕМЕНТОВ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- 2-1. УРАВНЕНИЯ ЭЛЕМЕНТОВ. СТАТИЧЕСКИЕ И ДИНАМИЧЕСКИЕ СВОЙСТВА ЭЛЕМЕНТОВ
- б) Центробежный измеритель скорости вращения
- в) Электромагнитный измеритель напряжения
- 2-2. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ
- 2-3. ЭЛЕМЕНТАРНЫЕ ДИНАМИЧЕСКИЕ ЗВЕНЬЯ, ИХ УРАВНЕНИЯ И ПЕРЕДАТОЧНЫЕ ФУНКЦИИ
- 2-4. ТИПОВЫЕ ВХОДНЫЕ СИГНАЛЫ. ВОЗМУЩАЮЩИЕ ФУНКЦИИ
- 2-5. ПЕРЕХОДНЫЕ ФУНКЦИИ ЭЛЕМЕНТАРНЫХ ЗВЕНЬЕВ
- 2-6. ИМПУЛЬСНЫЕ ПЕРЕХОДНЫЕ ФУНКЦИИ ЭЛЕМЕНТАРНЫХ ЗВЕНЬЕВ
- 2-7. РЕАКЦИЯ ЗВЕНЬЕВ НА ПРОИЗВОЛЬНЫЕ ИЗВЕСТНЫЕ ФУНКЦИИ ВРЕМЕНИ
- 2-8. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ
- б) Частотные характеристики элементарных звеньев
- в) Логарифмические характеристики элементарных звеньев
- 2-9. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ОБ ЭЛЕМЕНТАРНЫХ ЗВЕНЬЯХ
- 2-10. СОЕДИНЕНИЯ ЗВЕНЬЕВ. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ СОЕДИНЕНИИ
- 2-11. ЭЛЕМЕНТЫ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ КАК ЧЕТЫРЕХПОЛЮСНИКИ. ПЕРЕДАТОЧНЫЕ УРАВНЕНИЯ
- ГЛАВА ТРЕТЬЯ. ДАТЧИКИ СИГНАЛОВ
- 3-1. ОБЩИЕ СВОЙСТВА ДАТЧИКОВ
- 3-2. ПОТЕНЦИОМЕТРИЧЕСКИЕ ДАТЧИКИ
- б) Выходная мощность потенциометрических датчиков и условия согласования
- в) Динамические свойства
- г) Ошибка ступенчатости. Параметры потенциометрических датчиков
- 3-3. ИНДУКТИВНЫЕ ДАТЧИКИ
- б) Двухтактные индуктивные датчики
- в) Характеристики двухтактных индуктивных датчиков
- г) Трансформаторные индуктивные датчики
- д) Динамические свойства индуктивных датчиков
- е) Шумы индуктивных датчиков
- ж) Общие свойства индуктивных датчиков
- 3-4. СЕЛЬСИНЫ В ТРАНСФОРМАТОРНОМ РЕЖИМЕ
- б) Характеристики сельсинного датчика
- в) Динамические свойства сельсинных датчиков
- г) Шумы и ошибки датчика
- д) Устанавливающий момент
- е) Дифференциальные сельсины
- ж) Сельсины точного и грубого каналов
- ГЛАВА ЧЕТВЕРТАЯ. УСИЛИТЕЛИ СИГНАЛОВ
- 4-2. МАГНИТНЫЕ УСИЛИТЕЛИ
- а) Рабочий процесс и статическая характеристика магнитного усилителя с прямоугольной кривой намагничивания сердечников
- б) Двухтактные магнитные усилители с выходом на переменном токе
- в) Магнитные усилители с обратной связью
- г) Динамические свойства магнитных усилителей
- д) Шумы магнитных усилителей. Общие свойства магнитных усилителей
- 4-3. ЭЛЕКТРОМАШИННЫЕ УСИЛИТЕЛИ
- б) Однокаскадный электромашицный усилитель как четырехполюсник
- в) Двухкаскадный электромашинный усилитель с поперечным полем
- г) Шумы электромашинных усилителей
- 4-4. РЕЛЕ
- б) Поляризованные реле
- в) Магнитоэлектрическое реле
- 4-5. РЕЛЕЙНЫЕ УСИЛИТЕЛИ
- б) Вибрационная линеаризация релейных усилителей
- в) Релейный усилитель как четырехполюсник
- 4-6. ЭЛЕКТРОННЫЕ УСИЛИТЕЛИ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- б) Фазочувствительные усилители и синхронные детекторы
- в) Электронные усилители постоянного тока
- г) Шумы электронных усилителей
- 4-7. ПОЛУПРОВОДНИКОВЫЕ УСИЛИТЕЛИ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- ГЛАВА ПЯТАЯ. ИСПОЛНИТЕЛЬНЫЕ УСТРОЙСТВА СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- 5-2. СЕРВОДВИГАТЕЛИ ПОЧТОЯННОГО ТОКА
- 5-3. СЕРВОДВИГАТЕЛИ ПЕРЕМЕННОГО ТОКА
- 5-4. СЕРВОДВИГАТЕЛИ С ЭЛЕКТРОМАГНИТНЫМИ И ПОРОШКОВЫМИ МУФТАМИ
- б) Характеристики серводвигателей с электромагнитными муфтами
- в) Порошковые муфты
- г) Характеристики серводвигателей с порошковыми муфтами
- 5-5. ГИДРАВЛИЧЕСКИЕ И ПНЕВМАТИЧЕСКИЕ СЕРВОДВИГАТЕЛИ
- б) Обратные связи в гидравлических серводвигателях
- в) Свойства гидравлических серводвигателей
- г) Электрогидравлические серводвигатели
- д) Пневматические серводвигатели
- ГЛАВА ШЕСТАЯ. СТАБИЛИЗИРУЮЩИЕ УСТРОЙСТВА СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- 6-1. ПАССИВНЫЕ КОРРЕКТИРУЮЩИЕ ЦЕПИ СИСТЕМ ПОСТОЯННОГО ТОКА
- б) Интегрирующие и интегродифференцирующие цепи
- 6-2. АКТИВНЫЕ КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА СИСТЕМ ПОСТОЯННОГО ТОКА
- 6-3. КОРРЕКТИРУЮЩИЕ ЦЕПИ СИСТЕМ ПЕРЕМЕННОГО ТОКА
- 6-4. ФИЛЬТРЫ В ЦЕПЯХ ОБРАТНЫХ СВЯЗЕЙ. МЕХАНИЧЕСКИЕ СТАБИЛИЗИРУЮЩИЕ УСТРОЙСТВА
- ГЛАВА СЕДЬМАЯ. СТРУКТУРНЫЕ СХЕМЫ И ХАРАКТЕРИСТИКИ ЛИНЕЙНЫХ СТАЦИОНАРНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 7-1. СТРУКТУРНЫЕ СХЕМЫ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 7-2. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ ДЛЯ ВХОДНОЙ ВЕЛИЧИНЫ
- 7-3. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ ДЛЯ ВОЗМУЩЕНИЯ
- 7-4. ПРИМЕРЫ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ И ИХ СТРУКТУРНЫЕ СХЕМЫ
- б) Стабилизация напряжения самолетных генераторов
- в) Следящая система копировально-фрезерного станка
- г) Следящая система автосопровождения
- д) Автоматическое управление углом тангажа самолета
- 7-5. ВРЕМЕННЫЕ ХАРАКТЕРИСТИКИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 7-6. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- б) Частотные характеристики замкнутой системы
- в) Связь частотных характеристик замкнутой и разомкнутой систем
- ГЛАВА ВОСЬМАЯ. ЭНЕРГЕТИЧЕСКИЙ РАСЧЕТ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ И СОГЛАСОВАНИЕ ХАРАКТЕРИСТИК ЭЛЕМЕНТОВ
- 8-1. ВЫБОР МОЩНОСТИ ИСПОЛНИТЕЛЬНЫХ УСТРОЙСТВ И УСЛОВИЯ СОГЛАСОВАНИЯ С НАГРУЗКОЙ
- а) Определение необходимой мощности по переходным процессам при типовых воздействиях
- б) Мгновенная мощность при гармонических колебаниях
- в) Необходимая мощность при случайных колебаниях регулирующего органа
- г) Выбор мощности сервомотора
- д) Условия согласования с нагрузкой сервомотора без обратной связи
- е) Согласование с нагрузкой сервомотора с жесткой обратной связью
- 8-2. СОГЛАСОВАНИЕ ДАТЧИКОВ, УСИЛИТЕЛЬНЫХ И КОРРЕКТИРУЮЩИХ УСТРОЙСТВ. РАСПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТОВ УСИЛЕНИЯ
- б) Передаточные функции последовательных соединений элементов
- в) Согласование пропорциональных участков характеристик
- г) Распределение коэффициентов усиления
- ГЛАВА ДЕВЯТАЯ. УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ СТАЦИОНАРНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 9-2. КРИТЕРИЙ УСТОЙЧИВОСТИ РАУСА—ГУРВИЦА
- 9-3. КРИТЕРИЙ УСТОЙЧИВОСТИ МИХАЙЛОВА
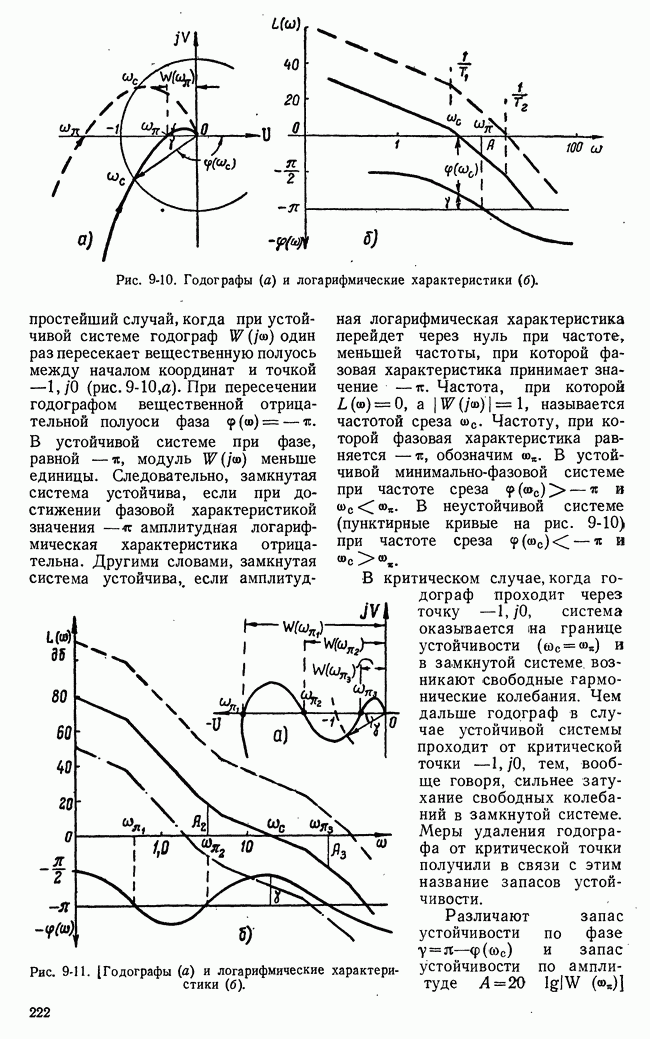
- 9-4. КРИТЕРИЙ УСТОЙЧИВОСТИ НАЙКВИСТА
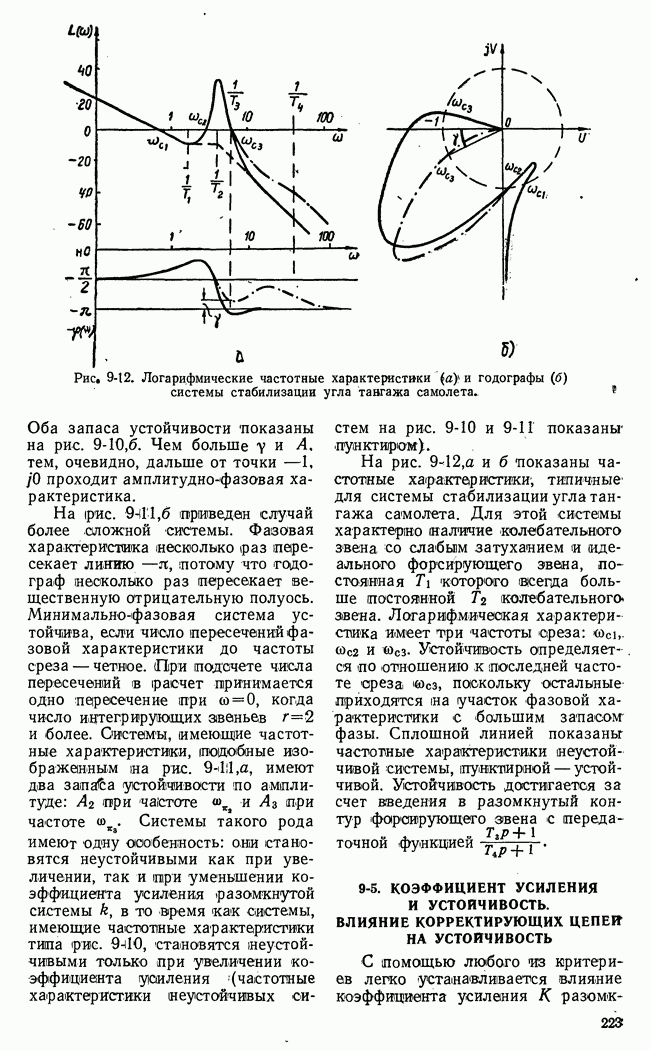
- б) Использование логарифмических характеристик системы для исследования устойчивости. Понятие о запасе устойчивости
- 9-5. КОЭФФИЦИЕНТ УСИЛЕНИЯ И УСТОЙЧИВОСТЬ. ВЛИЯНИЕ КОРРЕКТИРУЮЩИХ ЦЕПЕЙ НА УСТОЙЧИВОСТЬ
- 9-6. ВЫДЕЛЕНИЕ ОБЛАСТЕЙ УСТОЙЧИВОСТИ В ПРОСТРАНСТВЕ ПАРАМЕТРОВ СИСТЕМЫ ДИАГРАММЫ ВЫШНЕГРАДСКОГО
- б) Общий метод D-разбиения в плоскости двух параметров. Линейная задача
- в) Выделение области устойчивости в плоскости двух параметров. Нелинейная задача
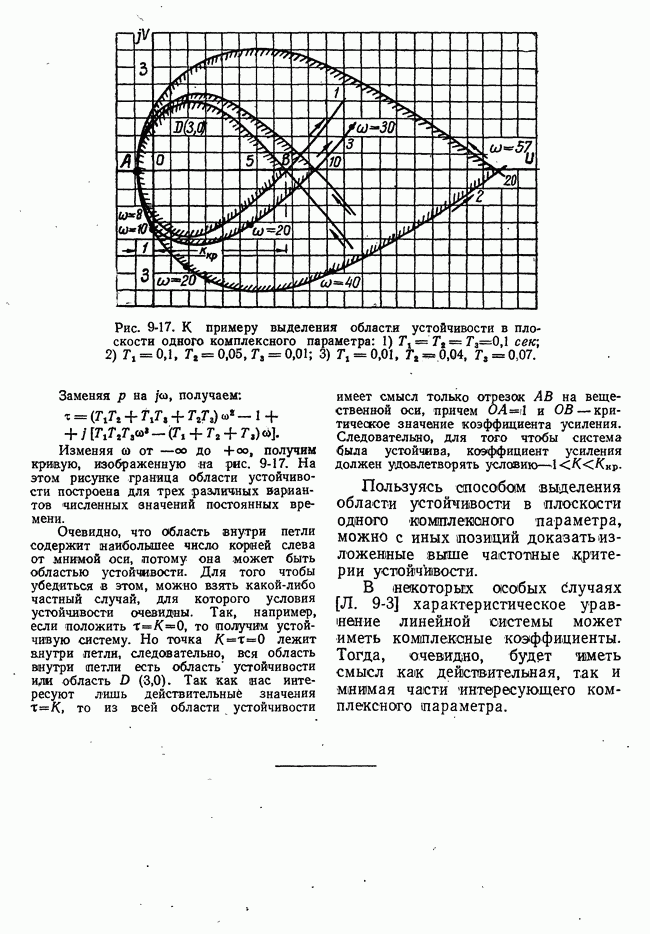
- г) Выделение области устойчивости в плоскости одного комплексного параметра
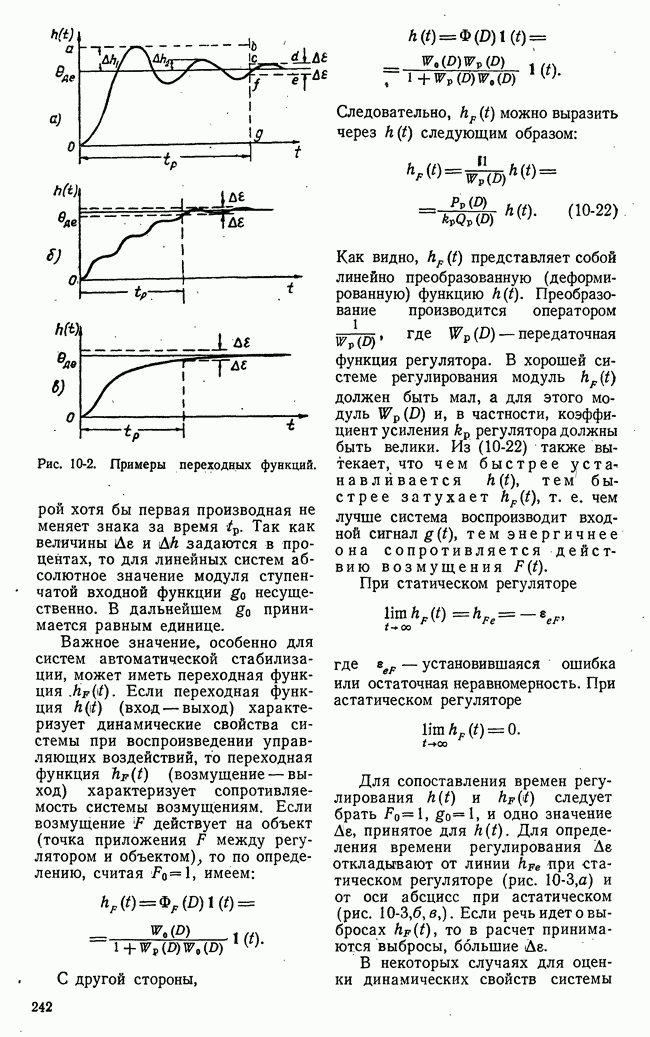
- ГЛАВА ДЕСЯТАЯ. КАЧЕСТВО ПРОЦЕССОВ РЕГУЛИРОВАНИЯ В ЛИНЕЙНЫХ СИСТЕМАХ
- 10-1. КРИТЕРИИ КАЧЕСТВА ПРОЦЕССА РЕГУЛИРОВАНИЯ
- 10-2. ТОЧНОСТЬ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ В УСТАНОВИВШИХСЯ РЕЖИМАХ. СТАТИЧЕСКИЕ И АСТАТИЧЕСКИЕ СИСТЕМЫ
- б) Точность при медленно меняющихся воздействиях. Коэффициенты ошибок. Астатические системы высших порядков
- в) Общие условия неискаженного воспроизведения входных сигналов в вынужденном режиме
- г) Повышение точности системы коррекцией входного сигнала
- д) Повышение точности системы путем компенсации возмущения F(t)
- 10-18. ПЕРЕХОДНЫЕ ФУНКЦИИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- б) Некоторые особенности вычисления переходных функций
- 10-4. РАСПРЕДЕЛЕНИЕ НУЛЕЙ И ПОЛЮСОВ ПЕРЕДАТОЧНОЙ ФУНКЦИИ И ПЕРЕХОДНЫЕ ПРОЦЕССЫ
- б) Оценки распределения корней. Степень устойчивости. Коэффициент затухания колебаний
- в) Влияние параметров на распределение корней. Метод Эванса
- г) Оценка переходных функций по распределению полюсов передаточной функции или корней характеристического уравнения
- д) Влияние нулей на характер переходной функции
- е) Определение коэффициентов уравнений по заданному распределению корней. Стандартные коэффициенты характеристических уравнений
- 10-5. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ И ПЕРЕХОДНЫЕ ФУНКЦИИ
- б) Приближенное вычисление переходных функций и переходных процессов
- в) Оценка качества процесса регулирования по характеристикам замкнутой системы Ф(w) и ф(w) и характеристике разомкнутой системы W(jw)
- г) Оценка качества по амплитудным логарифмическим характеристикам. Минимально-фазовые системы
- д) Связь между логарифмическими амплитудными характеристиками разомкнутой системы и полюсами передаточной функции замкнутой системы
- 10-6. ИНТЕГРАЛЬНЫЕ ОЦЕНКИ ПЕРЕХОДНЫХ ПРОЦЕССОВ
- г) Приближение кривых x(t) к эталонной кривой хэ(t) по критерию …
- ГЛАВА ОДИННАДЦАТАЯ. НЕСТАЦИОНАРНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 11-1. ОБЩИЕ СВЕДЕНИЯ О НЕСТАЦИОНАРНЫХ СИСТЕМАХ
- 11-2. ПРИМЕРЫ СУЩЕСТВЕННО НЕСТАЦИОНАРНЫХ СИСТЕМ
- 11-3. ДИНАМИЧЕСКИЕ ХАРАКТЕРИСТИКИ НЕСТАЦИОНАРНЫХ СИСТЕМ АВТОМАТИЧ ЕСКОГО РЕГУЛИРОВАНИЯ
- 11-4. ОСОБЕННОСТИ СОСТАВЛЕНИЯ УРАВНЕНИЙ И СТРУКТУРНЫХ СХЕМ НЕСТАЦИОНАРНЫХ СИСТЕМ
- 11-5. МЕТОДЫ ОПРЕДЕЛЕНИЯ ЧАСТОТНОЙ ХАРАКТЕРИСТИКИ И ИМПУЛЬСНОЙ РЕАКЦИИ НЕСТАЦИОНАРНЫХ СИСТЕМ
- ГЛАВА ДВЕНАДЦАТАЯ. СТАТИСТИЧЕСКАЯ ДИНАМИКА ЛИНЕЙНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 12-1. СТАЦИОНАРНЫЕ И НЕСТАЦИОНАРНЫЕ СЛУЧАЙНЫЕ ПРОЦЕССЫ
- б) Стационарные и нестационарные случайные функций
- в) Свойства корреляционной функции
- г) Свойство эргодичности
- д) Гауссовы случайные процессы
- 12-2. ПРЕОБРАЗОВАНИЕ СТАЦИОНАРНЫХ СЛУЧАЙНЫХ ФУНКЦИЙ СТАЦИОНАРНЫМИ ЛИНЕЙНЫМИ СИСТЕМАМИ
- б) Преобразование корреляционных функций при прохождении случайного сигнала через линейную систему
- в) Интегральная квадратичная оценка импульсной переходной функции и дисперсия реакции системы на белый шум
- г) Преобразование спектральных плотностей при прохождении случайного сигнала через линейную систему
- 12-3. ОПТИМАЛЬНЫЕ ЛИНЕЙНЫЕ СТАЦИОНАРНЫЕ СИСТЕМЫ
- б) Условия оптимальности при свободном выборе передаточной функции
- ГЛАВА ТРИНАДЦАТАЯ. О СИНТЕЗЕ ЛИНЕЙНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
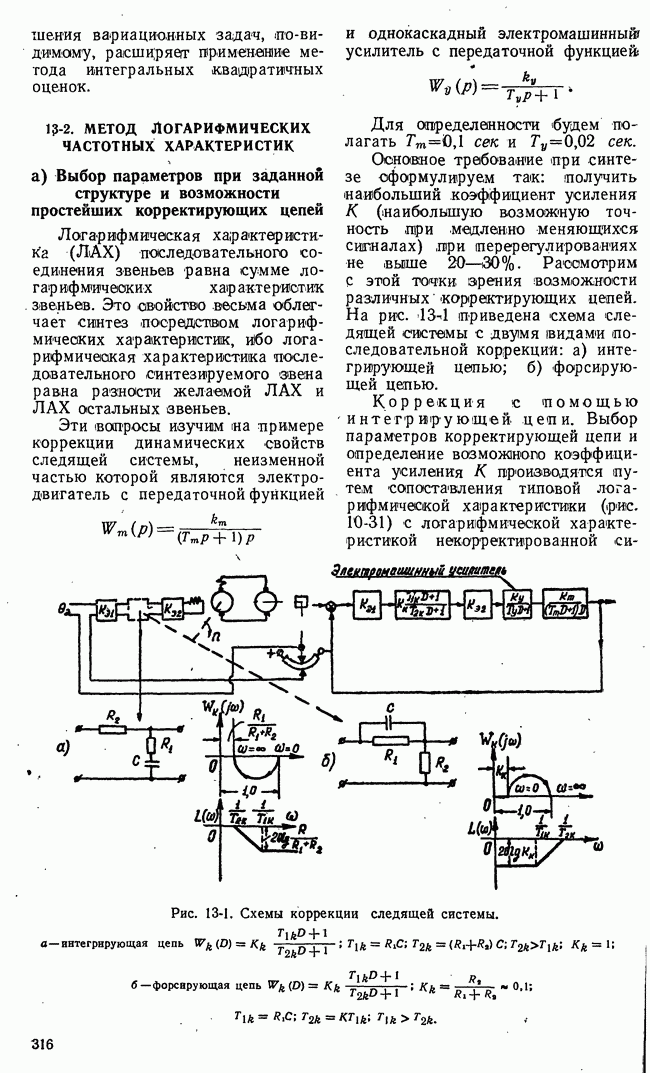
- 13-2. МЕТОД ЛОГАРИФМИЧЕСКИХ ЧАСТОТНЫХ ХАРАКТЕРИСТИК
- б) Синтез корректирующих цепей
- в) О синтезе на основе требований к реакции системы на возмущение F(t)
- 13-3. ВЫБОР ПАРАМЕТРОВ НА ОСНОВЕ АНАЛИЗА РАСПРЕДЕЛЕНИЯ НУЛЕЙ И ПОЛЮСОВ ПЕРЕДАТОЧНОЙ ФУНКЦИИ
- 13-4. ВЫБОР ПАРАМЕТРОВ НА ОСНОВЕ ИНТЕГРАЛЬНЫХ КВАДРАТИЧНЫХ ОЦЕНОК
- 13-5. СПЕЦИАЛЬНЫЕ ПРИЕМЫ УЛУЧШЕНИЯ КАЧЕСТВА ПРОЦЕССА РЕГУЛИРОВАНИЯ
- б) Подавление помех во входном сигнале при инерционном объекте управления
- в) Использование двух источников информации для выделения истинного сигнала
- г) Компенсация влияния запаздывания измерителей на динамические свойства системы
- д) Исключение перерегулирования в системах, передаточные функции которых имеют только вещественные полюсы
- ГЛАВА ЧЕТЫРНАДЦАТАЯ. ИМПУЛЬСНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 14-2. ИМПУЛЬСЫ И ИМПУЛЬСНЫЕ ЭЛЕМЕНТЫ
- б) Формирующие цепи и импульсные элементы
- 14-3. ДИСКРЕТНЫЕ ФУНКЦИИ И ПОСЛЕДОВАТЕЛЬНОСТИ. ИХ РАЗНОСТИ И СУММЫ
- 14-4. РЕАКЦИЯ ЛИНЕЙНЫХ НЕПРЕРЫВНЫХ СИСТЕМ НА ПОСЛЕДОВАТЕЛЬНОСТИ ИЛИ ДЕЛЬТА-ИМПУЛЬСОВ
- б) Свертка двух дискретных функций
- в) Уравнения в конечных разностях непрерывных звеньев первого и второго порядков
- г) Символические изображения дискретных функций и их использование для решения уравнений в конечных разностях
- 14-5. ДИСКРЕТНОЕ ПРЕОБРАЗОВАНИЕ ЛАПЛАСА ИЛИ z-ПРЕОБРАЗОВАНИЕ. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ КОМПЛЕКСНОГО АРГУМЕНТА
- 14-6. ДИНАМИКА РАЗОМКНУТЫХ ИМПУЛЬСНЫХ СИСТЕМ
- б) Значение выходной величины непрерывной системы внутри интервалов повторения
- в) Передаточные функции, систем с запаздыванием
- г) Свободные и вынужденные движения
- д) Полюсы. Устойчивость разомкнутых систем
- е) Переходные функции
- ж) Частотные характеристики
- 14-7. СВЯЗЬ МЕЖДУ ЧАСТОТНЫМИ И ПЕРЕХОДНЫМИ ФУНКЦИЯМИ. ДИСКРЕТНОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ
- 14-8. ИНТЕГРАЛЬНАЯ КВАДРАТИЧНАЯ ОЦЕНКА
- 14-9. ДИСКРЕТНЫЕ СЛУЧАЙНЫЕ ФУНКЦИИ (СЛУЧАЙНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ)
- ГЛАВА ПЯТНАДЦАТАЯ. ДИНАМИКА ИМПУЛЬСНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 15-1. УРАВНЕНИЯ И ПЕРЕДАТОЧНЫЕ ФУНКЦИИ СИСТЕМ С ОДНИМ ИМПУЛЬСНЫМ ЭЛЕМЕНТОМ
- 15-2. УСТОЙЧИВОСТЬ ЗАМКНУТЫХ СИСТЕМ
- 15-3. КАЧЕСТВО ПРОЦЕССА РЕГУЛИРОВАНИЯ
- 15-4. ПРИМЕРЫ ИМПУЛЬСНЫХ СИСТЕМ
- 15-5. ИМПУЛЬСНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ С ДИСКРЕТНЫМИ КОРРЕКТИРУЮЩИМИ ЦЕПЯМИ
- ГЛАВА ШЕСТНАДЦАТАЯ. СТРУКТУРНЫЕ СХЕМЫ, ХАРАКТЕРИСТИКИ И УРАВНЕНИЯ НЕЛИНЕЙНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- б) Уравнения продольного движения самолета
- в) Уравнения продольного движения ракеты
- 16-2. НЕЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ СИГНАЛА ОШИБКИ
- б) Структурные схемы с нелинейными элементами
- в) Релейные системы. Релейные элементы
- 16-3. НЕЛИНЕЙНЫЙ ОБЪЕКТ РЕГУЛИРОВАНИЯ И НЕЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ СИГНАЛА ОШИБКИ
- ГЛАВА СЕМНАДЦАТАЯ. СВОЙСТВА НЕЛИНЕЙНЫХ СИСТЕМ И (МЕТОДЫ ИССЛЕДОВАНИЯ
- б) Суждение об устойчивости по уравнениям первого приближения. Теоремы Ляпунова
- в) Суждение о качестве процессов регулирования по уравнениям первого приближения
- г) Прямой метод Ляпунова
- д) Техническая устойчивость
- 17-2. АВТОКОЛЕБАНИЯ НЕЛИНЕЙНЫХ СИСТЕМ
- б) Автоколебания релейных систем
- в) Метод точечных преобразований
- г) Описание процесса в релейной системе разностным уравнением. Устойчивость автоколебаний
- д) Примера исследования автоколебаний релейных систем второго порядка
- 17-3. ВЛИЯНИЕ КОРРЕКТИРУЮЩИХ ЦЕПЕЙ НА АВТОКОЛЕБАНИЯ И НА ПЕРЕХОДНЫЕ ПРОЦЕССЫ НЕЛИНЕЙНЫХ СИСТЕМ
- б) Влияние корректирующих цепей на переходные процессы. Скользящие режимы. Оптимальные переходные процессы
- 17-4. ГАРМОНИЧЕСКАЯ ЛИНЕАРИЗАЦИЯ ПРОЦЕССОВ В НЕЛИНЕЙНЫХ СИСТЕМАХ
- б) Исследование автоколебаний при помощи гармонической линеаризации
- в) Гармоническая линеаризация и критерии устойчивости линейных систем
- 17-5. ТЕОРИЯ РЕЛЕЙНЫХ СИСТЕМ
- в) Частотные характеристики релейных систем
- г) Оценка устойчивости релейных систем
- д) Вынужденные колебания релейных систем. Захватывание (синхронизация или подавление) автоколебаний
- е) Вибрационная линеаризация релейных систем, Реакция релейных систем на медленно меняющиеся возмущения
- 17-6. ОПТИМАЛЬНЫЕ ПРОЦЕССЫ РЕГУЛИРОВАНИЯ
- б) Системы, оптимальные по быстродействию. Принцип максимума
- в) Системы, близкие к оптимальным по быстродействию
- ГЛАВА ВОСЕМНАДЦАТАЯ. ЭНТРОПИЯ, ИНФОРМАЦИЯ, АЛГОРИТМ В СИСТЕМАХ АВТОМАТИЧЕОКОГО УПРАВЛЕНИЯ
- 18-1. ЭНТРОПИЯ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ УПРАВЛЯЕМОГО ПРОЦЕССА
- 18-2. КОЛИЧЕСТВО ИНФОРМАЦИИ В ПРОЦЕССАХ УПРАВЛЕНИЯ
- 18-3. ЭНТРОПИЯ И ИНФОРМАЦИЯ В ЗАМКНУТЫХ СИСТЕМАХ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- 18-4. АЛГОРИТМЫ ПРОЦЕССОВ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- ГЛАВА ДЕВЯТНАДЦАТАЯ. СИСТЕМЫ ЭКСТРЕМАЛЬНОГО РЕГУЛИРОВАНИЯ
- 19-1. ПРИМЕРЫ СИСТЕМ ЭКСТРЕМАЛЬНОГО РЕГУЛИРОВАНИЯ
- 19-2. СПОСОБЫ ПОИСКА ЭКСТРЕМУМА
- б) Методы организации процесса поиска
- 19-3. СТРУКТУРНЫЕ СХЕМЫ СИСТЕМ ЭКСТРЕМАЛЬНОГО РЕГУЛИРОВАНИЯ
- 19-4. ДИНАМИКА НЕПРЕРЫВНЫХ СИСТЕМ ЭКСТРЕМАЛЬНОГО РЕГУЛИРОВАНИЯ В КВАЗИСТАЦИОНАРНОМ РЕЖИМЕ
- б) Динамика квазистационарного режима систем экстремального регулирования, основанных на методе градиента
- 19-5. ДИНАМИКА НЕПРЕРЫВНЫХ СИСТЕМ ЭКСТРЕМАЛЬНОГО РЕГУЛИРОВАНИЯ ПРИ СЛУЧАЙНЫХ СИГНАЛАХ ПОИСКА
- б) Уравнения замкнутой системы экстремального регулирования
- в) Точность экстремального регулирования
- 19-6. ФОРСИРОВАННЫЕ ПРОЦЕССЫ ЭКСТРЕМАЛЬНОГО РЕГУЛИРОВАНИЯ ОДНОМЕРНОГО БЕЗЫНЕРЦИОННОГО ОБЪЕКТА
- ГЛАВА ДВАДЦАТАЯ. СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ С САМОНАСТРАИВАЮЩИМИСЯ КОРРЕКТИРУЮЩИМИ УСТРОЙСТВАМИ
- 20-1. СИСТЕМЫ С РАЗОМКНУТЫМИ ЦЕПЯМИ НАСТРОЙКИ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ
- 20-2. СИСТЕМЫ С ЗАМКНУТЫМИ ЦЕПЯМИ НАСТРОЙКИ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ
- 20-3. СИСТЕМЫ С ЭКСТРЕМАЛЬНОЙ НАСТРОЙКОЙ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ
- 20-4. СТАТИСТИЧЕСКАЯ ДИНАМИКА НЕПРЕРЫВНЫХ СИСТЕМ С ЭКСТРЕМАЛЬНОЙ НАСТРОЙКОЙ ПОСЛЕДОВАТЕЛЬНЫХ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ
- б) Уравнения замкнутой самонастраивающейся системы
- в) Случай сильной фильтрации. Квазистационарный режим
- г) Общий случай квазистационарного режима
- ГЛАВА ДВАДЦАТЬ ПЕРВАЯ. ИГРОВЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- 21-1. НАЗНАЧЕНИЕ И ПРИНЦИПЫ ДЕЙСТВИЯ ИГРОВЫХ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- 21-2. НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ ИГР
- 21-3. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ. ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
- 21-4. ОБ АЛГОРИТМАХ ИГРОВЫХ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- ПРИЛОЖЕНИЯ