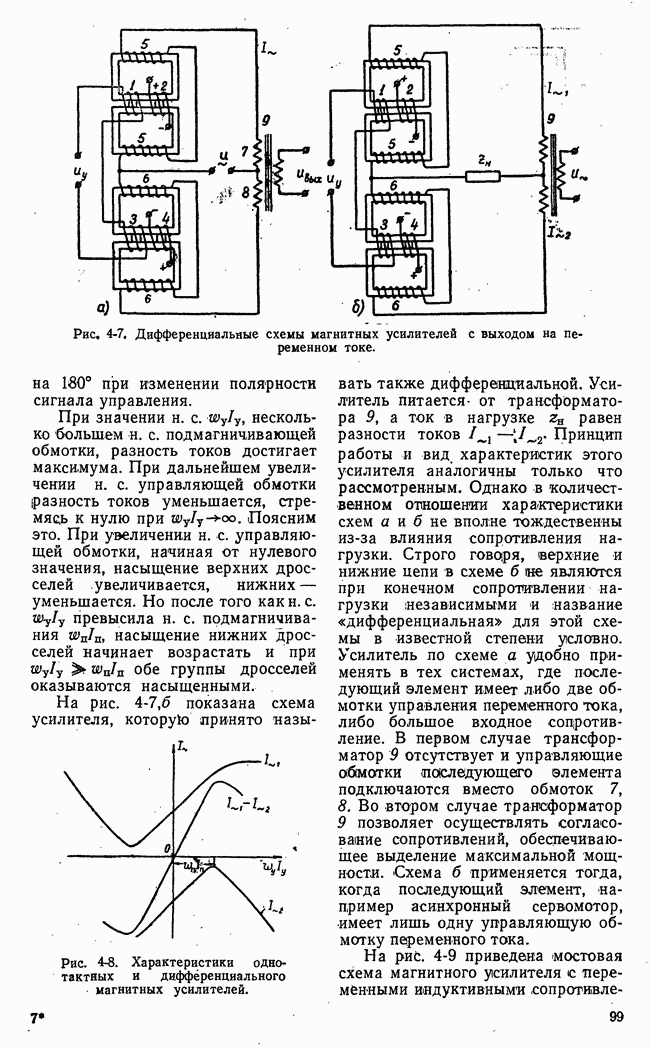
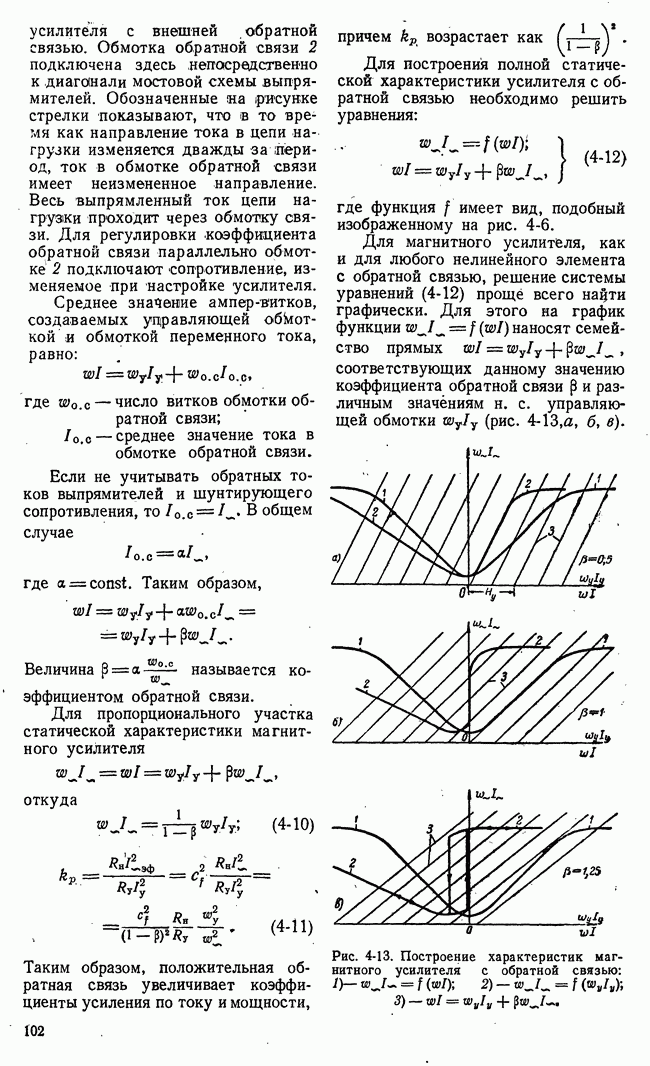
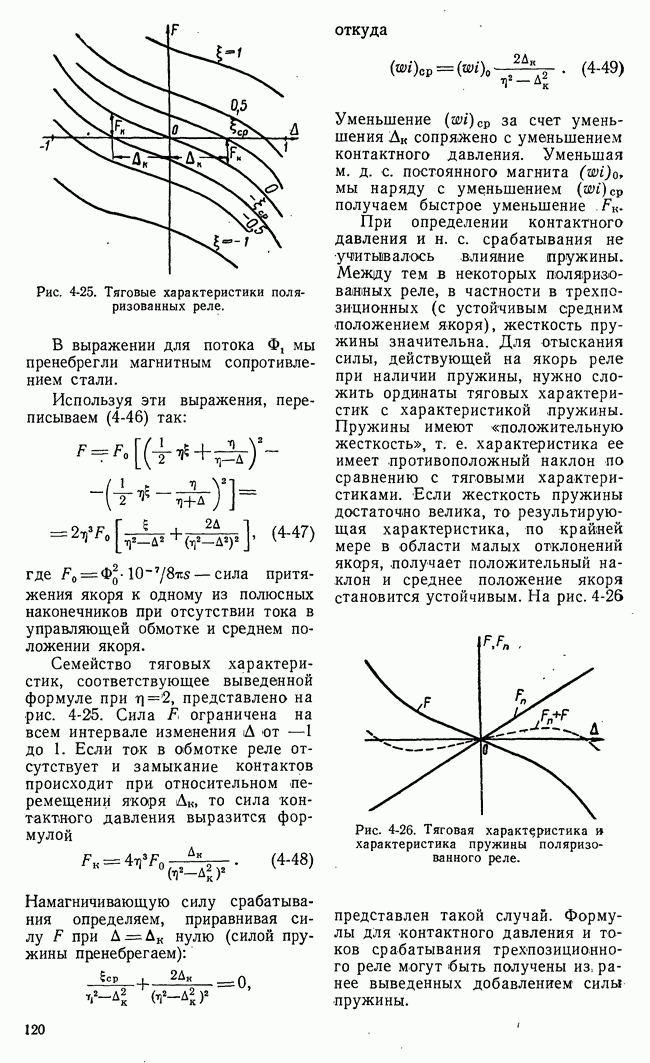
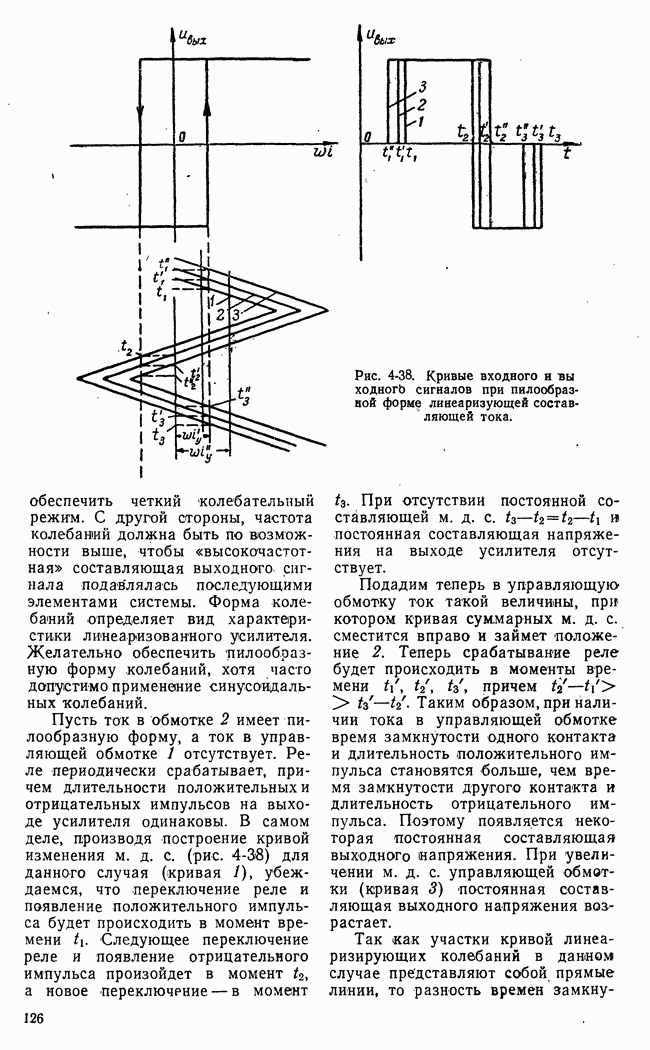
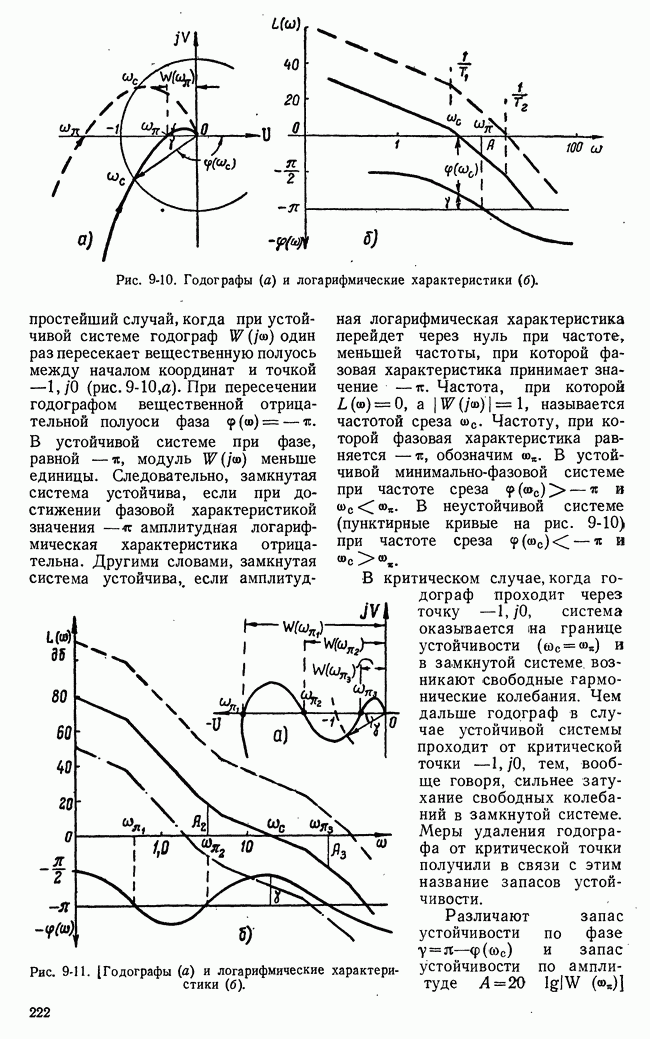
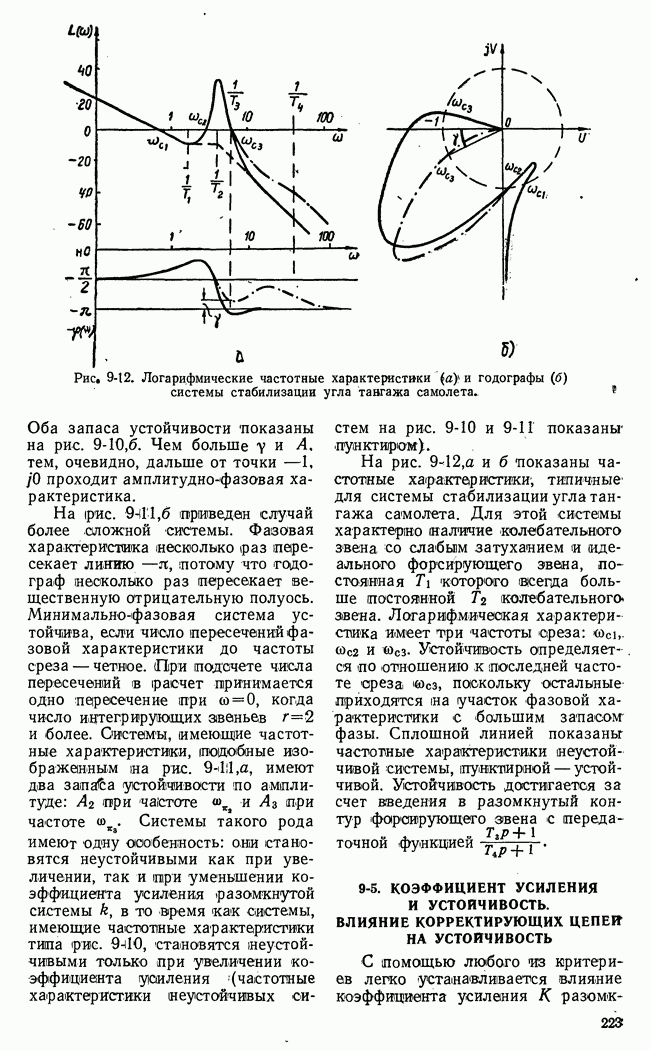
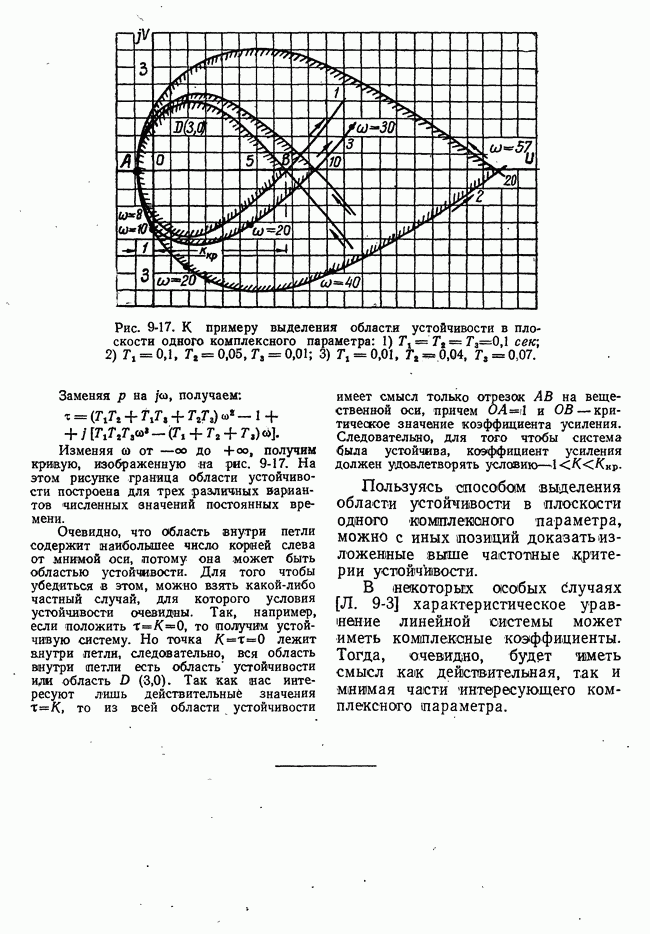
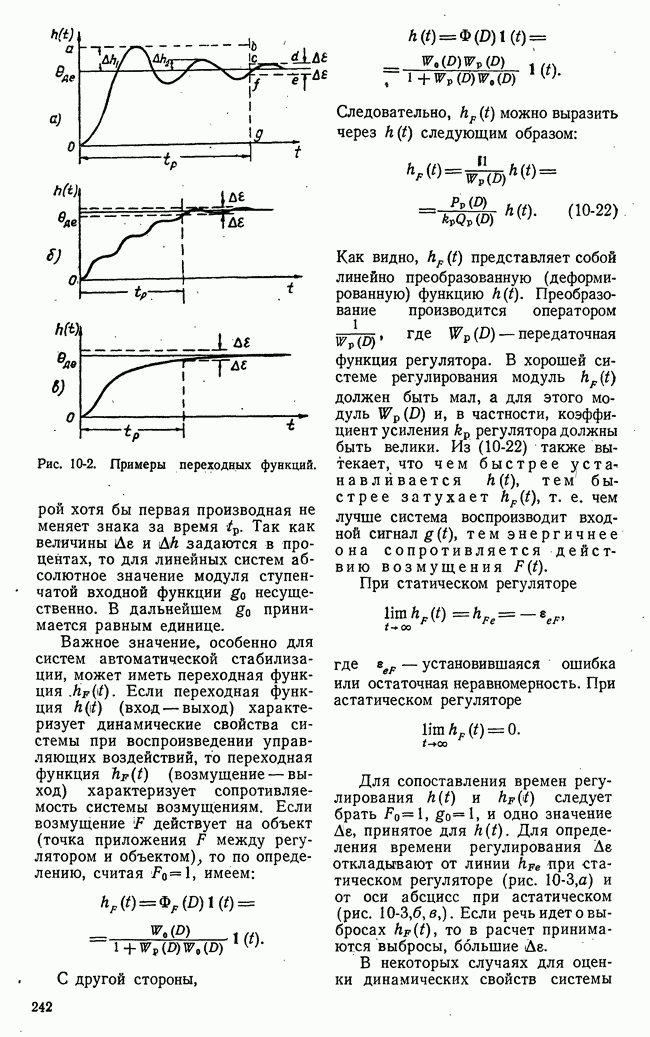
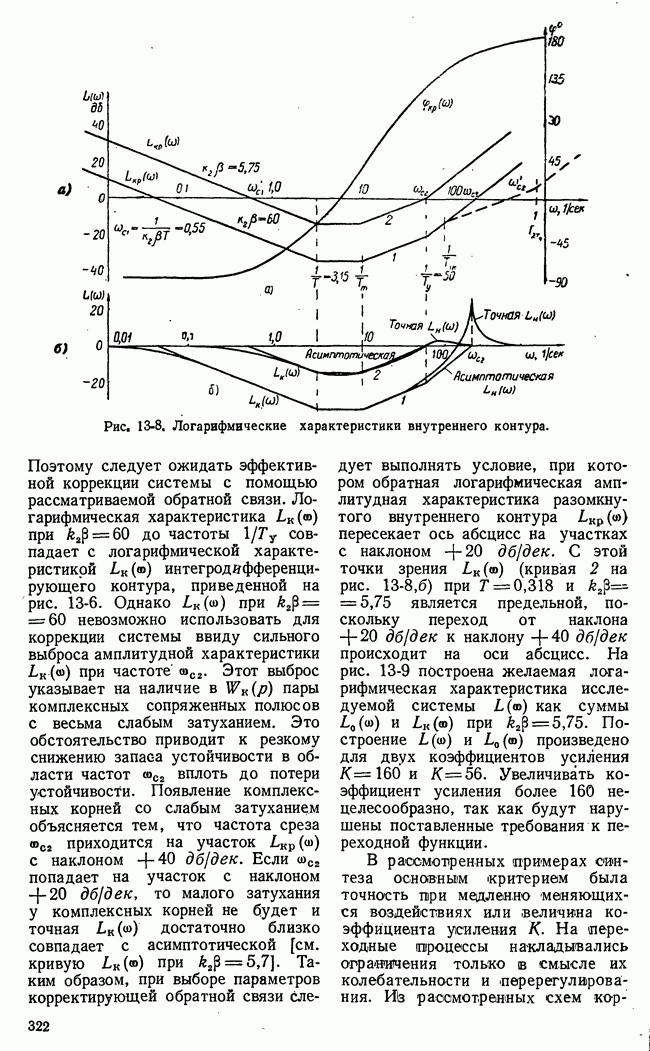
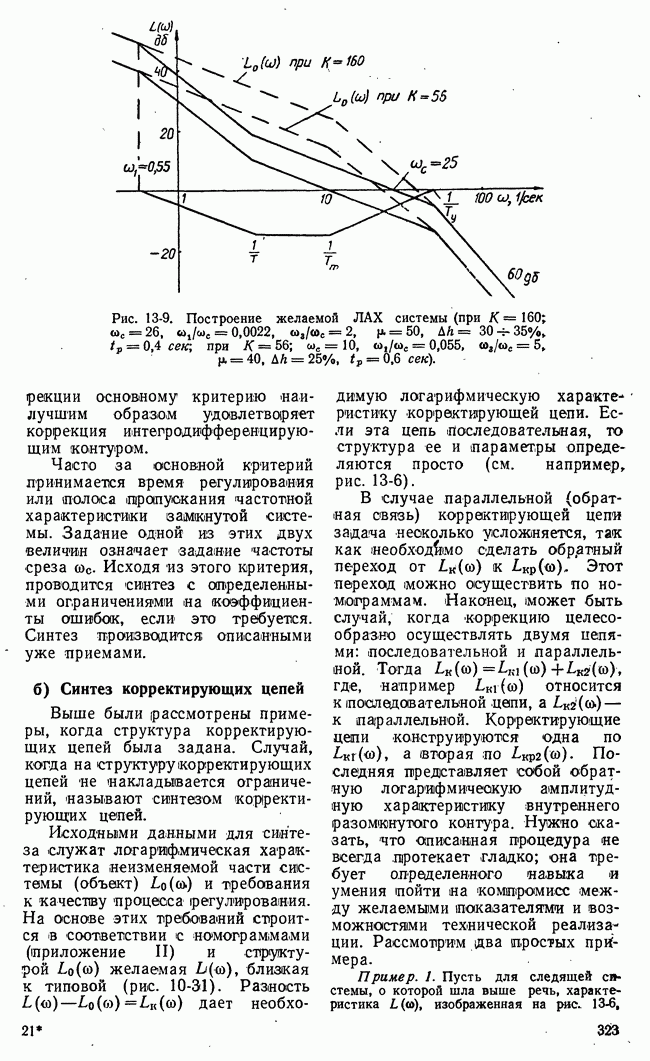
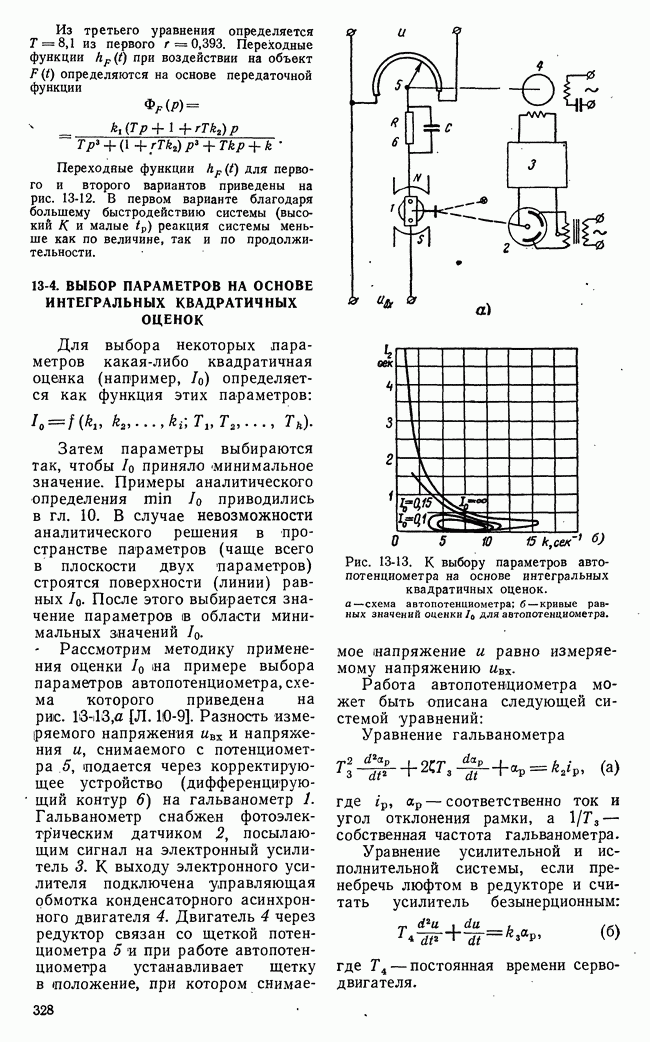
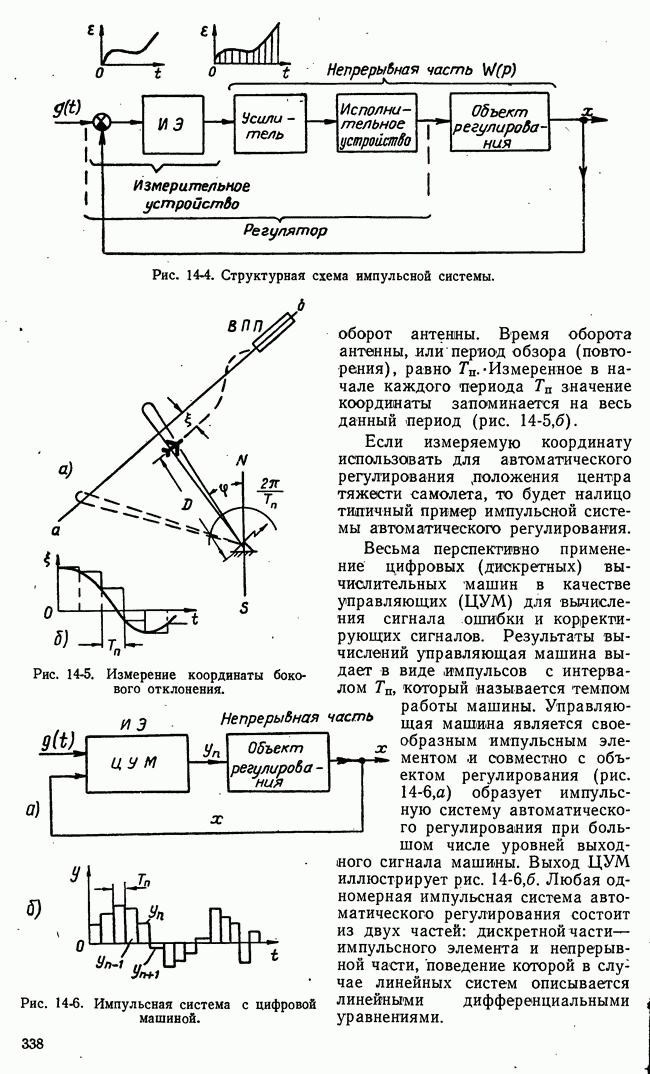
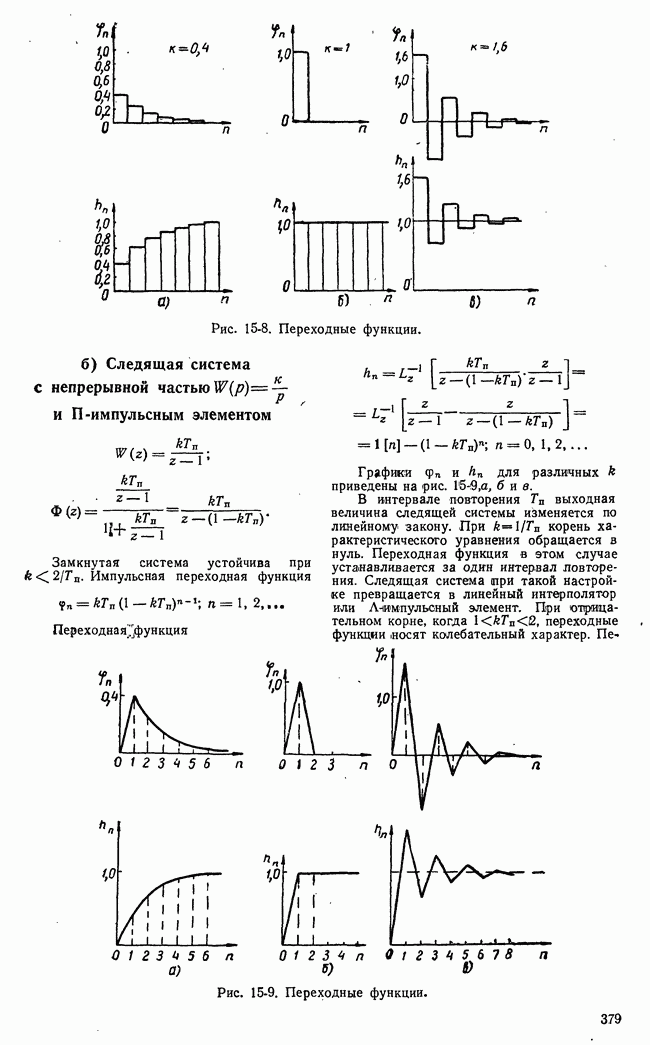
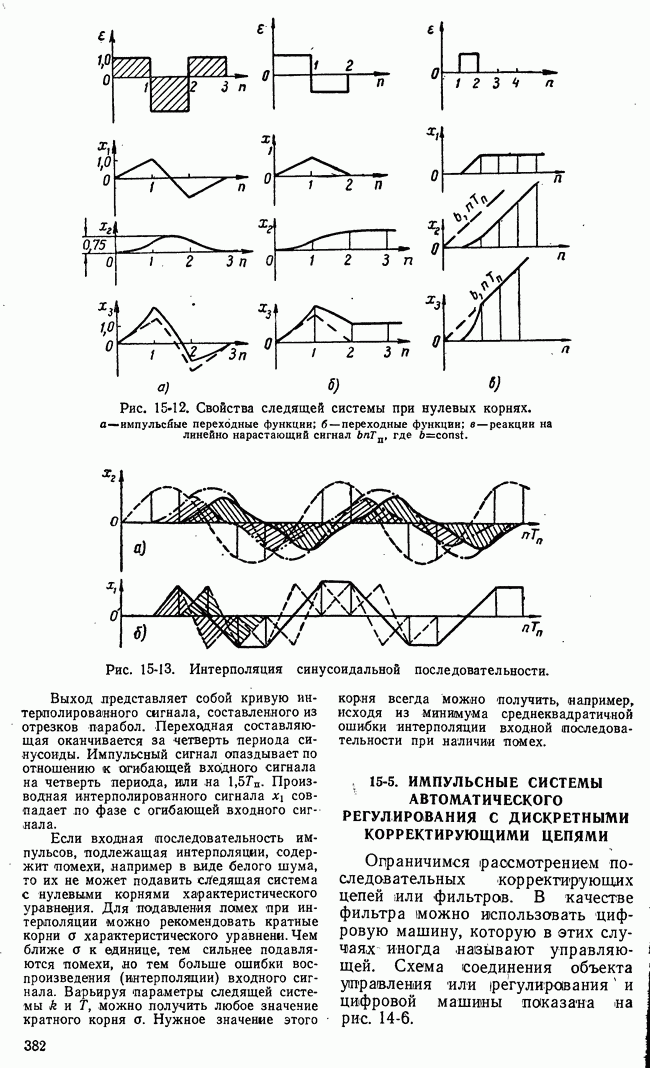
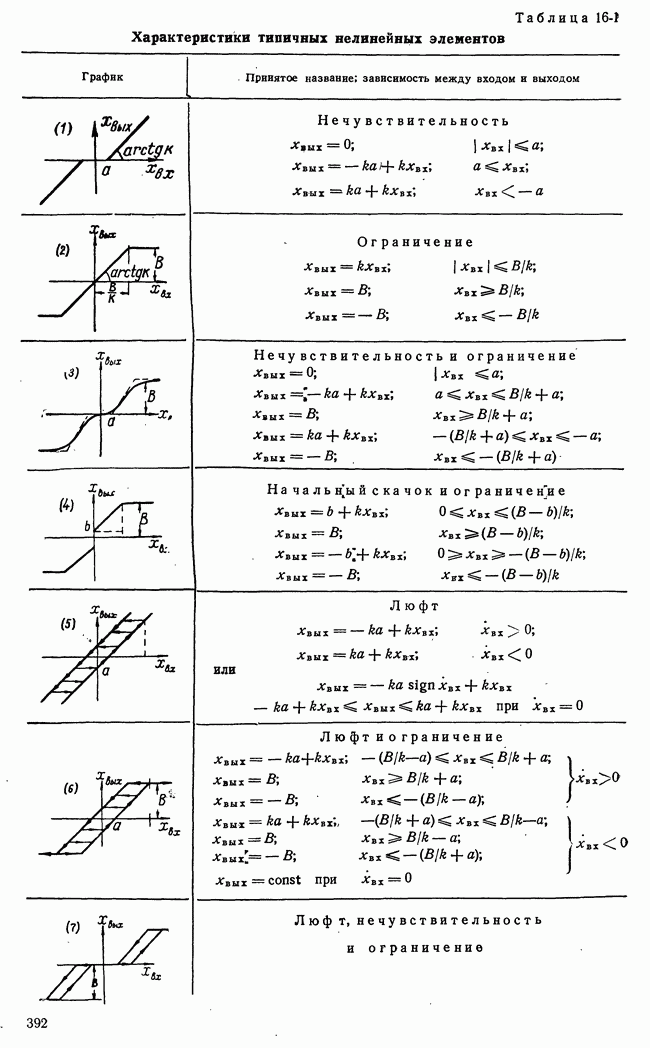
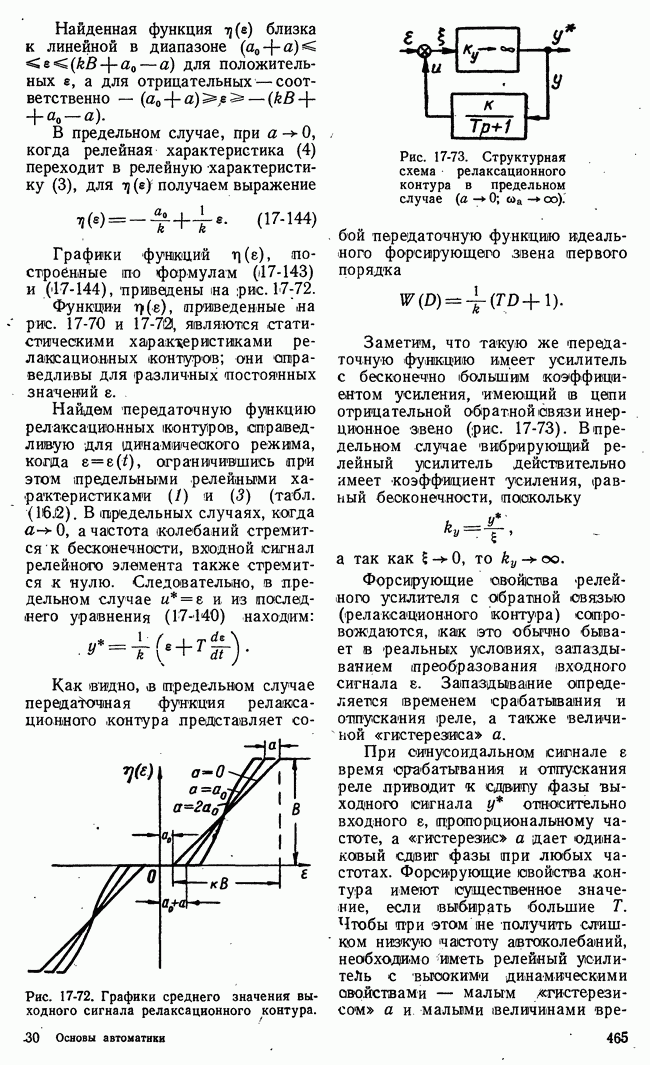
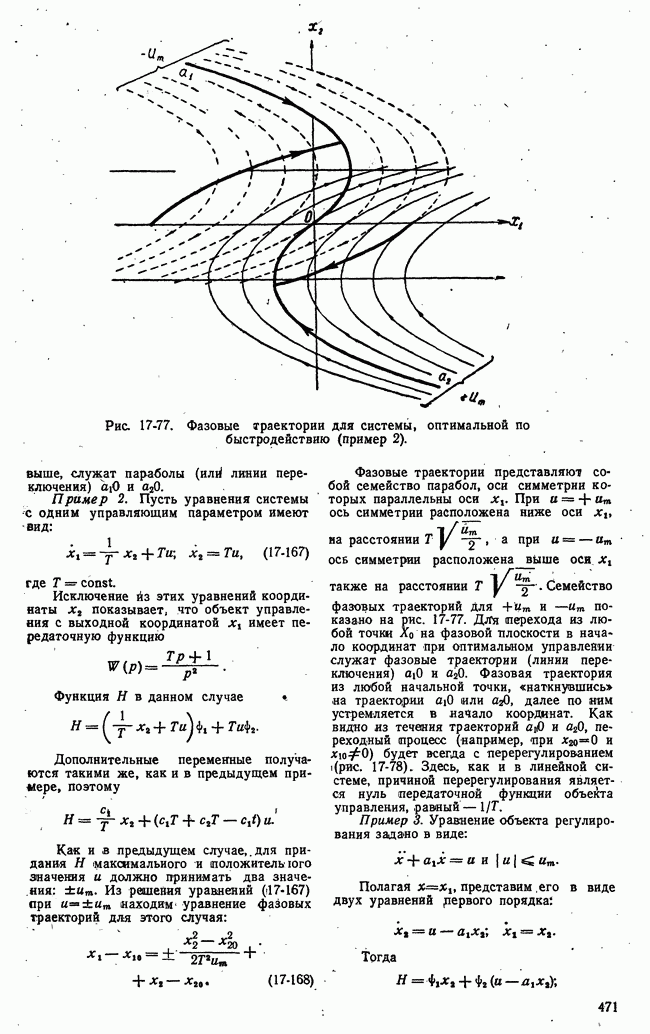
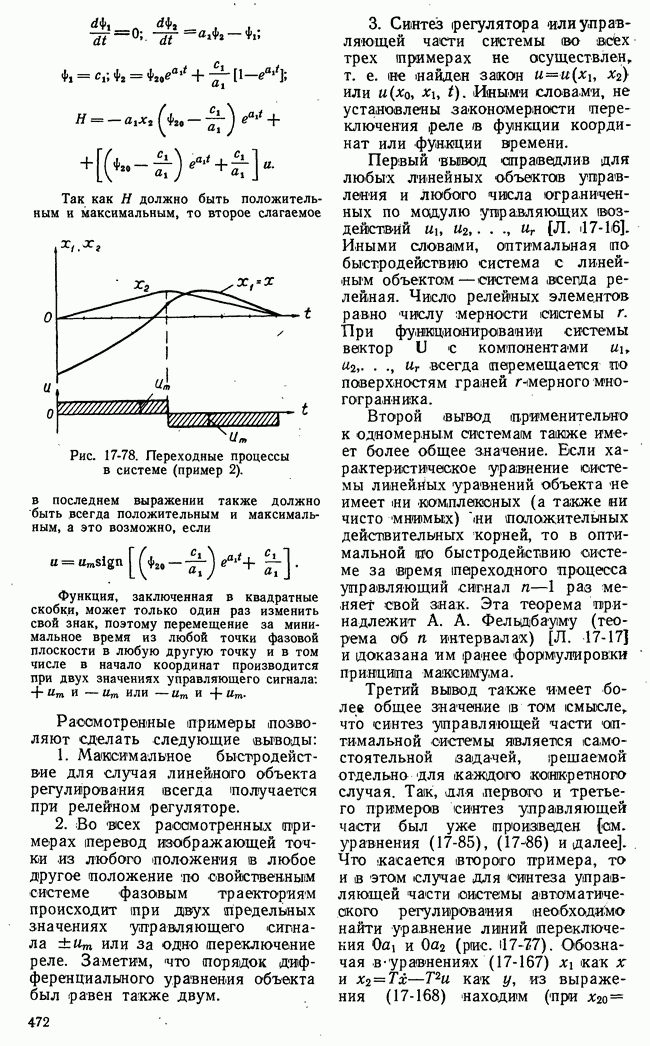
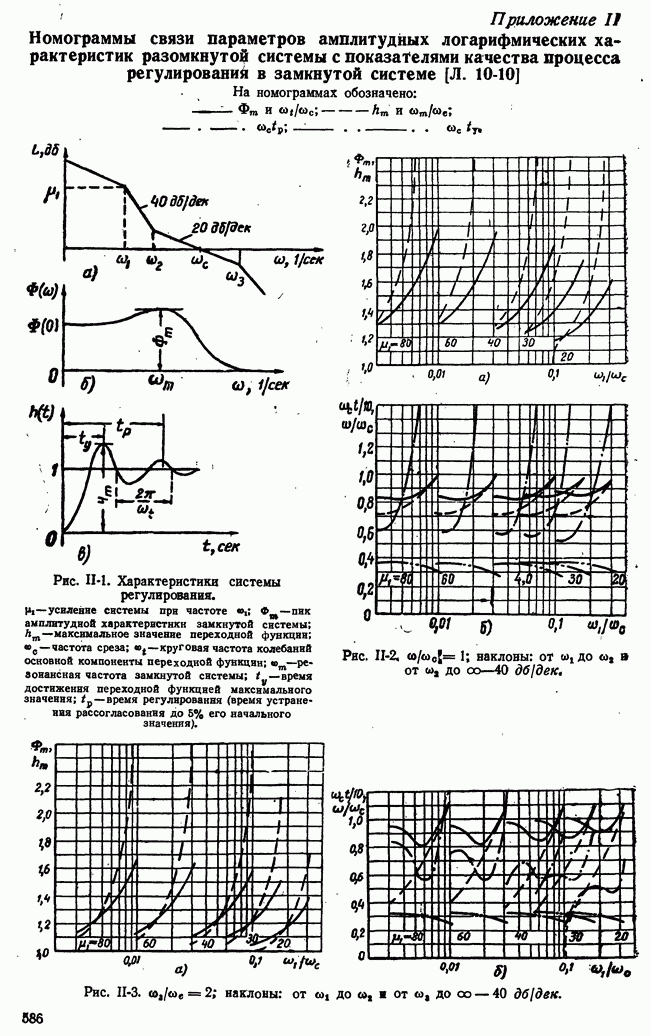
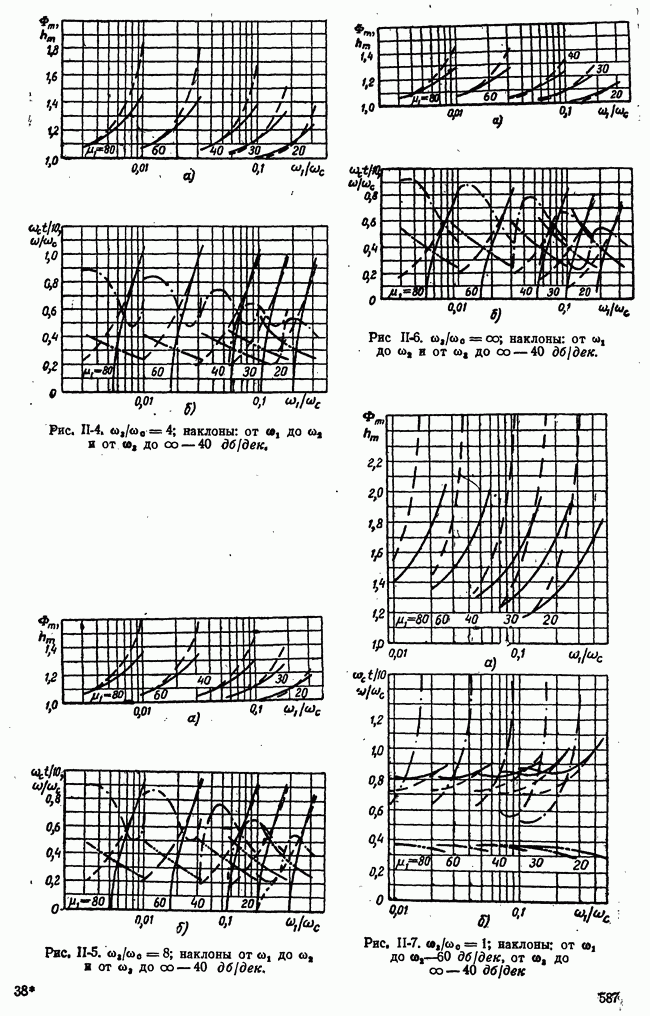
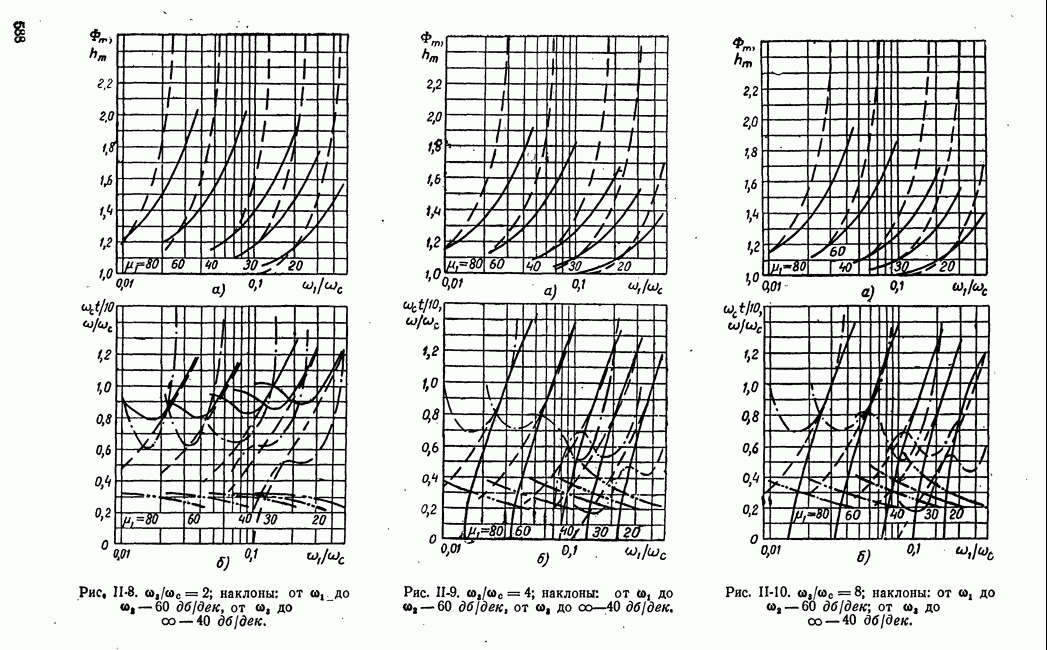
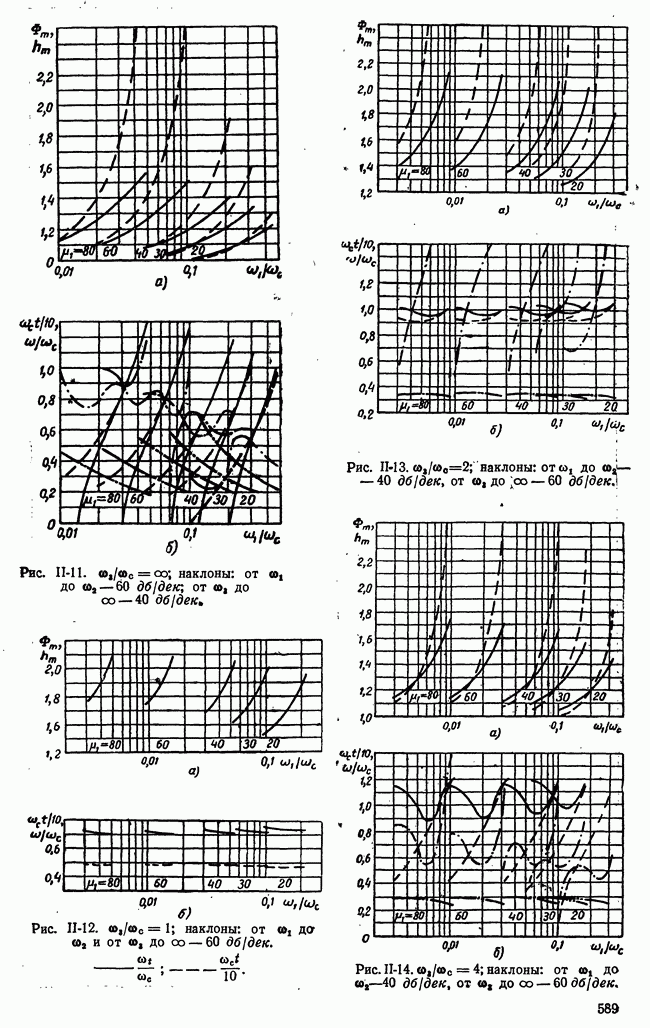
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
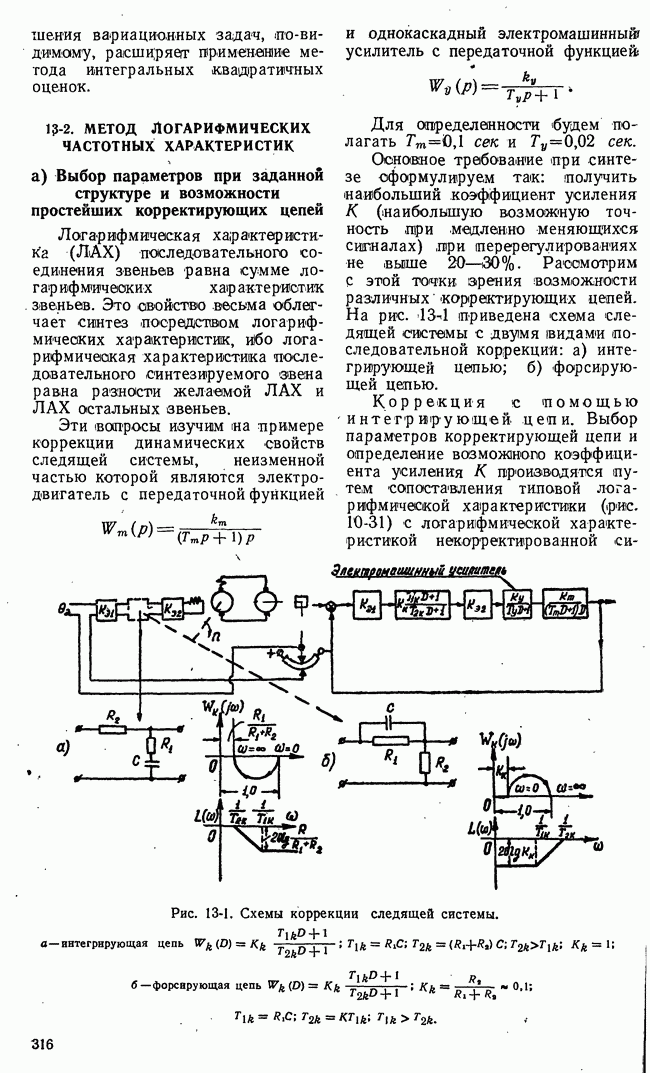
17-2. АВТОКОЛЕБАНИЯ НЕЛИНЕЙНЫХ СИСТЕМ
а) Основные понятия теории колебаний
Автоколебания — явление, свойственное только нелинейным "системам, и сам термин «автоколебания» относится к теории нелинейных колебаний. Теория нелинейных колебаний создана в основном трудами советских ученых. В основе этой науки лежат работы ученых школы академиков Мандельштама и Папалекси. Теория колебаний изложена в монографиях А. А. Андронова, А. А. Витта, С. Э. Хайкина [Л.16-2], Н. М. Крылова и Н. Н. Боголюбова [Л. 17-12], В. Б. Булгакова [Л. 16-1], И. Г. Малкина [Л. 17-11].
Задачи, рассматриваемые в теории линейных колебаний, сводятся в частном случае к изучению, процессов в колебательном звене

Соответственно в теории нелинейных колебаний исследуются интегралы уравнения

или в более общем виде

В (17-27) сила сопротивления  является нелинейной функцией скорости. На наличие такой силы указывает аргумент х функции
является нелинейной функцией скорости. На наличие такой силы указывает аргумент х функции  в уравнении (17-28). Упругая сила
в уравнении (17-28). Упругая сила  нелинейная функция отклонения или перемещения х.
нелинейная функция отклонения или перемещения х.
Уравнения (17-27) и (17-28) описывают колебания в самых различных физических системах (ламповый генератор, релейные и другие виды нелинейных систем автоматического регулирования, большие колебания. маятника и т. п.).
Если  или зависимость от
или зависимость от  функции
функции  отсутствует, то система называется автономной. В автономной системе колебания, возникшие в результате ненулевых начальных условий, называются свободными колебаниями. В такой системе
отсутствует, то система называется автономной. В автономной системе колебания, возникшие в результате ненулевых начальных условий, называются свободными колебаниями. В такой системе  для линейной системы и
для линейной системы и  для нелинейной характеризуют мгновенный запас потенциальной энергии. Величина
для нелинейной характеризуют мгновенный запас потенциальной энергии. Величина  является кинетической энергией.
является кинетической энергией.
Члены  если они положительны, указывают на рассеяние начального запаса энергии системы во внешнюю среду. Напротив, если члены
если они положительны, указывают на рассеяние начального запаса энергии системы во внешнюю среду. Напротив, если члены  отрицательны, то это указывает на пополнение энергии системы извне. Если члены
отрицательны, то это указывает на пополнение энергии системы извне. Если члены  равны нулю, то система называется консервативной, так как ее общее количество энергии, полученное при начальном возмущении, в процессе колебаний остается неизменным. При
равны нулю, то система называется консервативной, так как ее общее количество энергии, полученное при начальном возмущении, в процессе колебаний остается неизменным. При  происходит пополнение или убыль энергии системы (диссипация энергии) и система называется диссипативной.
происходит пополнение или убыль энергии системы (диссипация энергии) и система называется диссипативной.
Если одним из решений (17-26), (17-27), (17-28) является периодическая функция

где  период колебаний, то говорят, что уравнение имеет периодическое решение. Периодические колебания [колебания, удовлетворяющие условию (17-29)
период колебаний, то говорят, что уравнение имеет периодическое решение. Периодические колебания [колебания, удовлетворяющие условию (17-29)  бывают вынужденными и собственными. Собственные колебания — это колебания автономных систем. Вынужденные колебания происходят под действием пёриодической возмущающей силы
бывают вынужденными и собственными. Собственные колебания — это колебания автономных систем. Вынужденные колебания происходят под действием пёриодической возмущающей силы 
В линейной системе собственные (или свободные) периодические колебания могут быть, если только система консервативна. В диссипативных линейных автономных системах второго порядка колебания описываются функциями

которые не являются периодическими [не удовлетворяют условию (17-29)].
В отличие от линейных систем в нелинейных диссипативных системах возможны собственные периодические колебания, которые акад. А. А. Андронов назвал автоколебаниями.
Андронов ввел также в теорию "колебаний представления о фазовом пространстве, об особых точках решения дифференциальных уравнений — понйтия, широко применяющиеся в качественной теории дифференциальных уравнений. Наполнение этих абстрактных математических понятий физическим содержанием было большой заслугой А. А. Андронова и его школы.
Далее (§ 17-2 и 17-3) будем иметь в виду нелинейные системы, описываемые уравнением второго порядка (17-28), когда динамические процессы в стстеме могут быть отображены на фазовой плоскости. Для автономной системы, обозначив скорость  запишем (17-28) в виде двух уравнений первого порядка:
запишем (17-28) в виде двух уравнений первого порядка:

или в более общем виде:

где  нелинейные функции скорости у и отклонения х.
нелинейные функции скорости у и отклонения х.
Уравнение фазовых траекторий в плоскости х, у получается из (17-30) делением первого уравнения на второе:

Положение изображающей точки на фазовой плоскости можно определить радиусом-вектором  Соответственно скорость движения изображающей точки или фазовая скорость будет равна:
Соответственно скорость движения изображающей точки или фазовая скорость будет равна:

Когда фазовая скорость  система оказывается в положении равновесия, так как и скорость,
система оказывается в положении равновесия, так как и скорость,  и ускорение
и ускорение  равны нулю.
равны нулю.
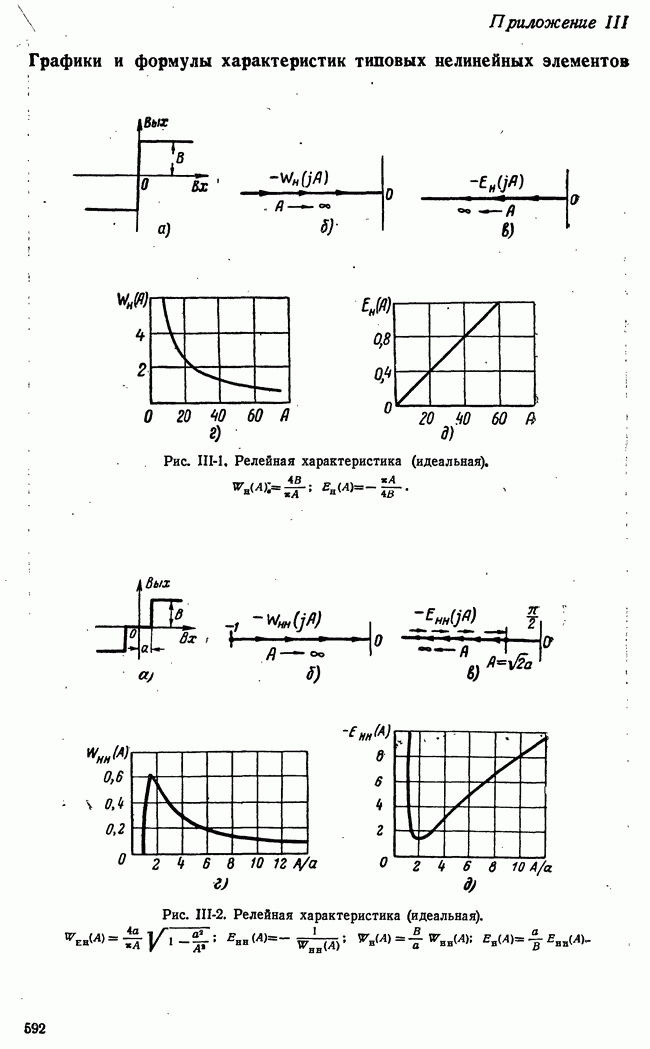
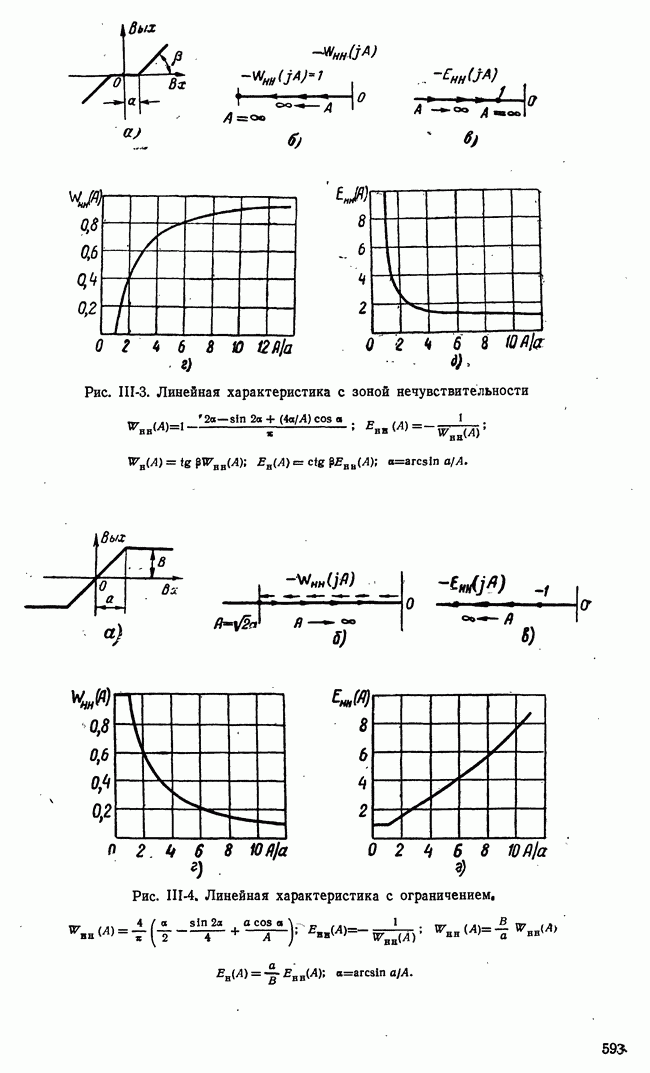
В состоянии равновесия  или в более общем случае
или в более общем случае  где а — зона нечувствительности (табл. 16-1 и 16-2). Поскольку в состоянии равновесия и
где а — зона нечувствительности (табл. 16-1 и 16-2). Поскольку в состоянии равновесия и  там выполняются условия:
там выполняются условия:

Из решения уравнений (17-31) получаем значения точек с координатами х, у, которые называются особыми точками дифференциального уравнения (17-30а). Как уже указывалось, физически особая точка означает состояние равновесия системы. Для выяснения устойчивости состояния равновесия и поведения фазовых траекторий в окрестности особой точки (можно воспользоваться (уравнениями первого приближения

где

Уравнения (17-32) справедливы в случае функций 
представляемых в виде рядов, и положения равновесия в начале координат, когда  Они огут быть записаны в виде одного уравнения второго порядка
Они огут быть записаны в виде одного уравнения второго порядка

Корни характеристического уравнения

определяют все виды фазовых траекторий около особой точки и позволяют произвести классификацию этих точек. х
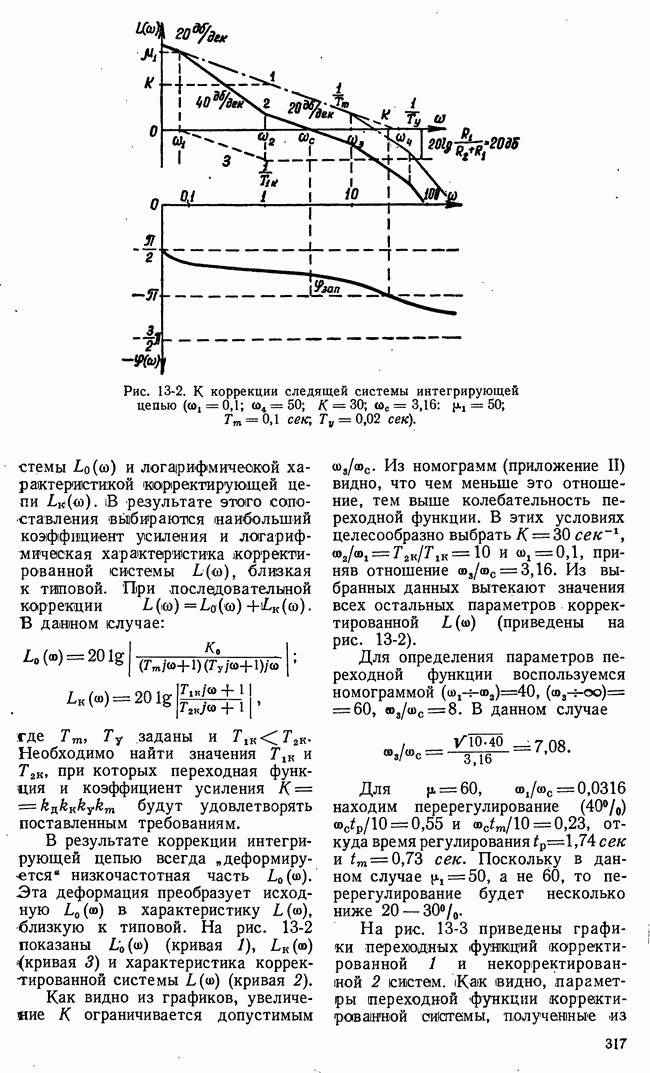
Возьмем случай консервативной системы, когда  В этом случае
В этом случае

При начальных условиях  решение уравнения (17-32а) имеет вид:
решение уравнения (17-32а) имеет вид:

что указывает на гармонические изменения отклонения и скорости.
В то же время (17-326) можно рассматривать как параметрические уравнения фазовой траектории. Исключая  получаем уравнение эллипса:
получаем уравнение эллипса:

Это же уравнение эллипса получается из решения дифференциального уравнения фазовых траекторий

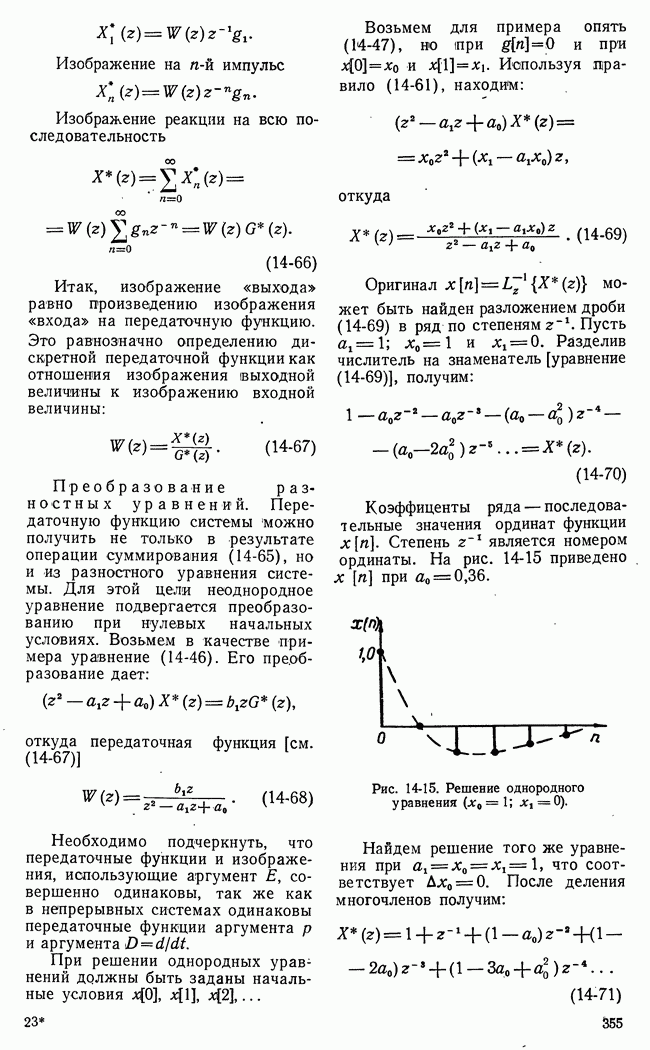
при тех же начальных условиях.
Изображающая точка на фазовой плоскости будет все время перемещаться по одному и тому же эллипсу с полуосями  Как известно, по гармоническому закону, колеблется груз между пружинами без трения и — ток в колебательном контуре без сопротивления.
Как известно, по гармоническому закону, колеблется груз между пружинами без трения и — ток в колебательном контуре без сопротивления.
На рис. 17-5 показаны состоянии механической и электрической цепей и соответствующие положения изображающей точки на эллипсе. Координата х обозначает перемещение груза и напряжение на конденсаторе или его заряд, координата у — скорость перемещения груза и ток в колебательном контуре.
При периодических колебаниях изображающая точка всегда описывает на фазовой плоскости замкнутую кривую. При синусоидальных колебаниях такой кривой будет эллипс. Период обращения изображающей точки по замкнутой кривой, очевидно, равен периоду колебаний системы.
В консервативной системе размеры замкнутой кривой, в данном случае эллипса, определяются начальными условиями. Множество эллипсов на фазовой плоскости, соответствующее множеству начальных условий, образует фазовую картину или фазовый портрет движения системы. Начало координат  является вырожденным эллипсом. Эта особая точка дифференциального уравнения (17-32а)
является вырожденным эллипсом. Эта особая точка дифференциального уравнения (17-32а)

Рис. 17-5. Фазовые траектории и схемы реализации консервативной системы по уравнению 
есть положение равновесия системы. Запас энергии в системе при  отсутствует. Особая точка в начале координат, окруженная множеством замкнутых циклов, определяемых начальными условиями, называется особой точкой типа центра.
отсутствует. Особая точка в начале координат, окруженная множеством замкнутых циклов, определяемых начальными условиями, называется особой точкой типа центра.
Если взять устойчивую (неконсервативную) колебательную систему, когда  то решения уравнений (17-32) будут иметь вид затухающих синусоидальных колебаний. Поскольку амплитуды отклонения х и скорости у будут убывать
то решения уравнений (17-32) будут иметь вид затухающих синусоидальных колебаний. Поскольку амплитуды отклонения х и скорости у будут убывать  экспоненциальному закону, фазовый траектории будут представлять собой семейство логарифмических спиралей, стягивающихся к началу координат. Изображающая точка, приближаясь к началу координат, будет замедлять свою фазовую скорость. Так как колебания затухают при
экспоненциальному закону, фазовый траектории будут представлять собой семейство логарифмических спиралей, стягивающихся к началу координат. Изображающая точка, приближаясь к началу координат, будет замедлять свою фазовую скорость. Так как колебания затухают при  то Изображающая точка лопадет в начало координат через бесконечно большой промежуток времени. Начало координат есть положение равновесия и особая точка уравнения. Очевидно, что положение равновесия асимптотически устойчиво. Все фазовые траектории при всех начальных условиях сходятся к особой точке. Такая особая точка называется устойчивым фокусом. Если же взять
то Изображающая точка лопадет в начало координат через бесконечно большой промежуток времени. Начало координат есть положение равновесия и особая точка уравнения. Очевидно, что положение равновесия асимптотически устойчиво. Все фазовые траектории при всех начальных условиях сходятся к особой точке. Такая особая точка называется устойчивым фокусом. Если же взять  то амплитуды колебаний отклонения и скорости будут нарастать. Фазовые траектории будут теми же спиралями, но по ним изображающая точка будет удаляться от начала координат. Положение равновесия системы
то амплитуды колебаний отклонения и скорости будут нарастать. Фазовые траектории будут теми же спиралями, но по ним изображающая точка будет удаляться от начала координат. Положение равновесия системы  будет неустойчивым. Достаточно бесконечно малого начального отклонения, чтобы началось безграничное нарастание отклонения и скорости. Особая точка в этом случае
будет неустойчивым. Достаточно бесконечно малого начального отклонения, чтобы началось безграничное нарастание отклонения и скорости. Особая точка в этом случае  носит название неустойчивого фокуса. Другие комбинации коэффициентов уравнений
носит название неустойчивого фокуса. Другие комбинации коэффициентов уравнений  а следовательно, и другие виды корней характеристического уравнения приводят к еще нескольким типам фазовых картин и особых точек
а следовательно, и другие виды корней характеристического уравнения приводят к еще нескольким типам фазовых картин и особых точек  ], которые здесь не рассмотрены.
], которые здесь не рассмотрены.
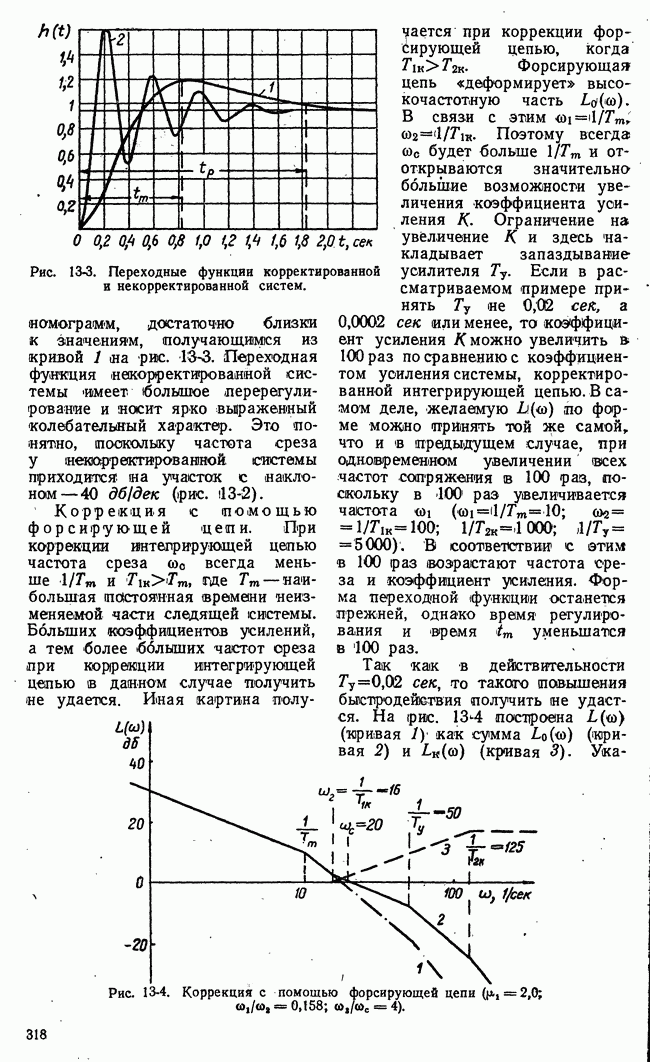
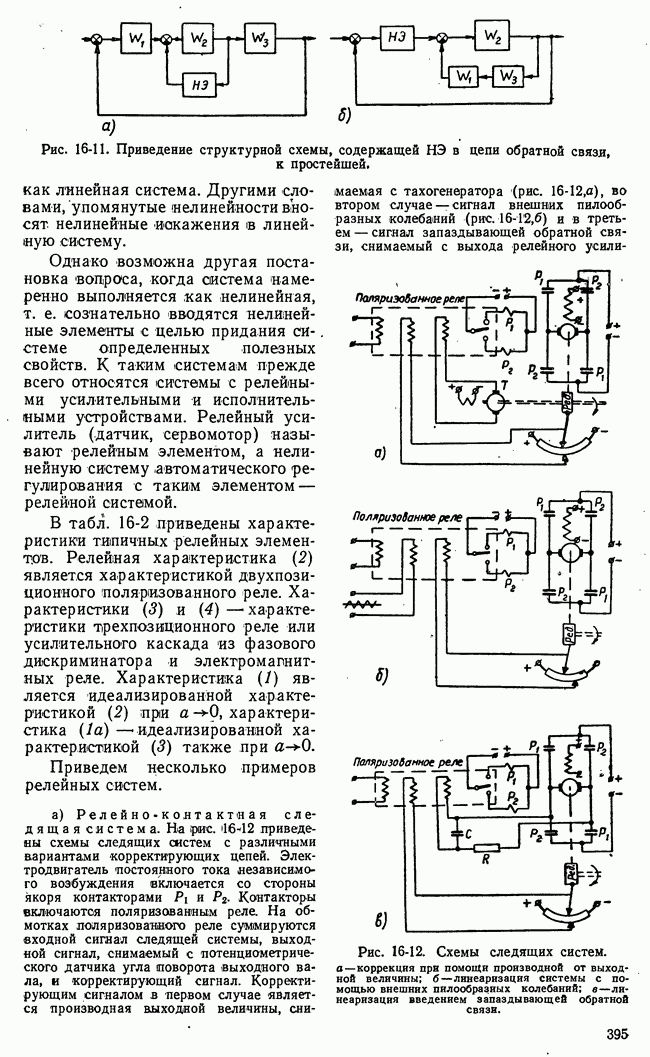
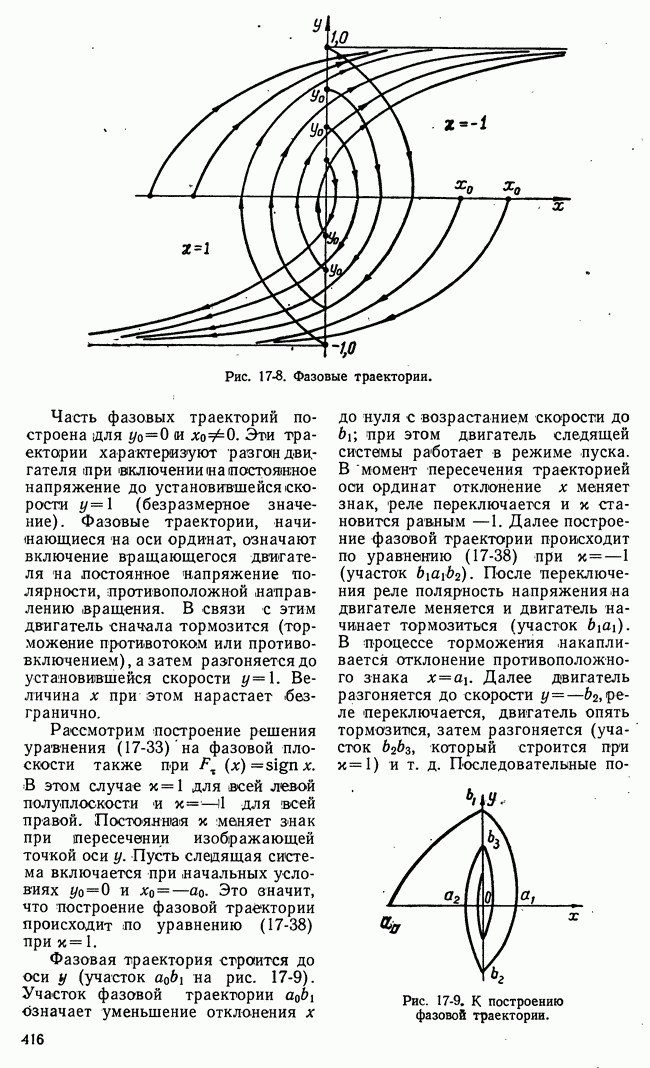
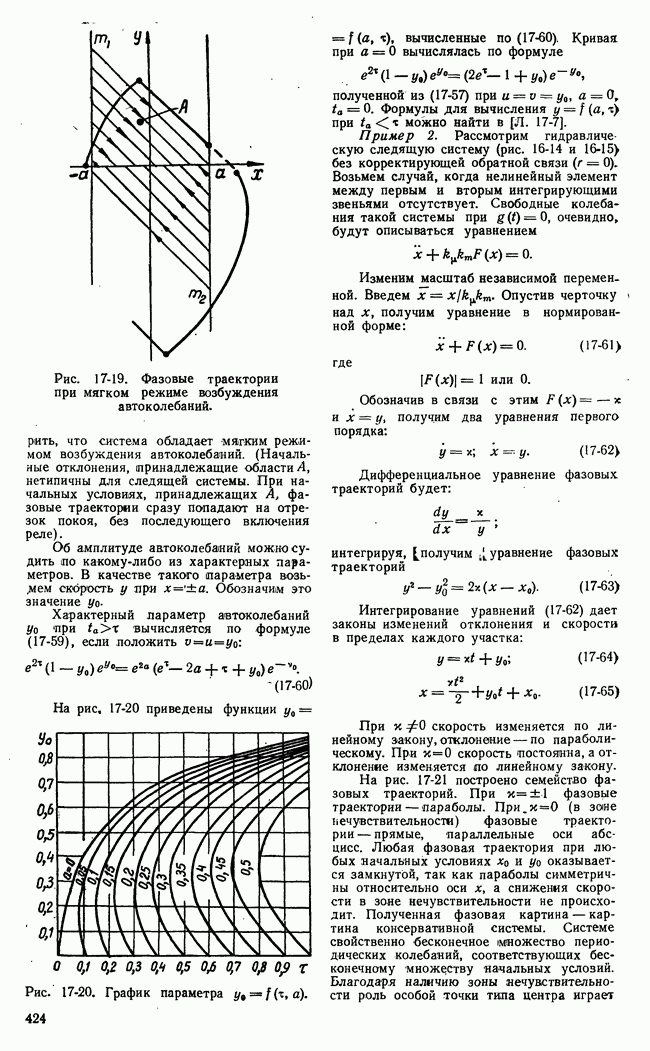
Характер движения и виды фазовых картин нелинейных систем гораздо разнообразнее, чем линейных. Здесь возможны автоколебания. Существование автоколебаний означает наличие в фазовом пространстве замкнутых кривых или циклов. В нелинейной системе может быть один или несколько автоколебательных режимов. Следовательно, в фазовой плоскости может быть несколько замкнутых кривых или циклов. Какой именно автоколебательный режим устанавливается в системе, зависит от начальных условий (т. е. от энергии, сообщенной системе в начальный момент). Автоколебания есть периодические колебания и они устанавливаются не сразу. Процесс установления автоколебаний можно сравнить с переходным процессом в линейной системе. Свободные колебания или переходный процесс в линейной устойчивой системе характеризуются семейством спиралей в фазовой плоскости, стремящихся к началу координат. В нелинейной системе процесс установления автоколебаний характеризуется семейством фазовых траекторий, стремящихся (или навивающихся) к замкнутой кривой или циклу. Эти замкнутые кривые или циклы называются предельными. Как точки равновесия линейной системы, так и предельные циклы нелинейной системы могут быть устойчивыми и неустойчивыми. В первом случае фазовые траектории навиваются на предельный цикл, во втором — свиваются с предельного цикла. Неустойчивый предельный цикл означает неустойчивые автоколебания. Они физически неосуществимы и являются просто одним из решений нелинейного уравнения системы. Устойчивый предельный цикл соответствует устойчивым, реально осуществимым автоколебаниям. Если имеется несколько предельных циклов, то неустойчивые и устойчивые циклы, как правило, чередуются. На рис. 17-6,а приведен пример неустойчивого положения равновесия, которое окружено устойчивым циклом 1, неустойчивым 2 и устойчивым 3.
На рис. 17-6, б устойчивое положение равновесия окружено неустойчивым циклом 1 и устойчивым 2.

Рис. 17-6. Чередование устойчивы и неустойчивых  циклов.
циклов.
В первом случае положение равновесия системы неустойчиво. При включении в ней устанавливается  один из режимов автоколебаний. Другого установившегося состояния у системы быть не может, и она называется системой с мягким режимом возбуждения колебаний. К таким системам относятся некоторые виды ламповых генераторов и релейных систем автоматического регулирования.
один из режимов автоколебаний. Другого установившегося состояния у системы быть не может, и она называется системой с мягким режимом возбуждения колебаний. К таким системам относятся некоторые виды ламповых генераторов и релейных систем автоматического регулирования.
Во втором случае, поскольку состояние равновесия устойчиво и окружено неустойчивым циклом, автоколебания установятся, если в результате начальных условий изображающая точка окажется вне неустойчивого цикла. В этом случае колебания в системе раскачаются до автоколебаний. Если изображающая точка в начальный момент окажется внутри неустойчивого цикла, то колебания затухнут, так как положение равновесия устойчиво. Система с такими свойствами называется системой с жестким режимом возбуждения. Типичным примером системы с жестким режимом возбуждения являются стенные часы (ходики). Часы «не пойдут», будучи заведенными, если отклонить маятник на недостаточный для возбуждения колебаний угол.
Многие виды ламповых генераторов и релейных систем автоматического регулирования имеют жесткий, режим возбуждения автоколебаний.
Отметим энергетическую сторону автоколебательных режимов. Устойчивая линейная система рассеивает всю свою начальную энергию и успокаивается в начале координат. Неустойчивая (при  ) линейная система раскачивается и непрерывно потребляет энергию от какого-либо источника, причем, поскольку колебания увеличиваются, потребление энергии в единицу времени нарастает. Автоколебательная система в установившемся периодическом режиме всю энергию, полученную от источника за одну часть периода (илицикла), полностью рассеивает во внешнюю среду за другую
) линейная система раскачивается и непрерывно потребляет энергию от какого-либо источника, причем, поскольку колебания увеличиваются, потребление энергии в единицу времени нарастает. Автоколебательная система в установившемся периодическом режиме всю энергию, полученную от источника за одну часть периода (илицикла), полностью рассеивает во внешнюю среду за другую  часть цикла. Таким образом, потребление энергии от источника за период остается постоянным. Источником энергии для таких автоколебательных систем, как ламповые генераторы или релейные следящие системы, является соответствующий источник электрической энергии. Источником энергии для таких автоколебательных систем, как часы, служит закрученная пружина или поднятая на некоторую высоту гиря.
часть цикла. Таким образом, потребление энергии от источника за период остается постоянным. Источником энергии для таких автоколебательных систем, как ламповые генераторы или релейные следящие системы, является соответствующий источник электрической энергии. Источником энергии для таких автоколебательных систем, как часы, служит закрученная пружина или поднятая на некоторую высоту гиря.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ГЛАВА ПЕРВАЯ. ВВОДНАЯ
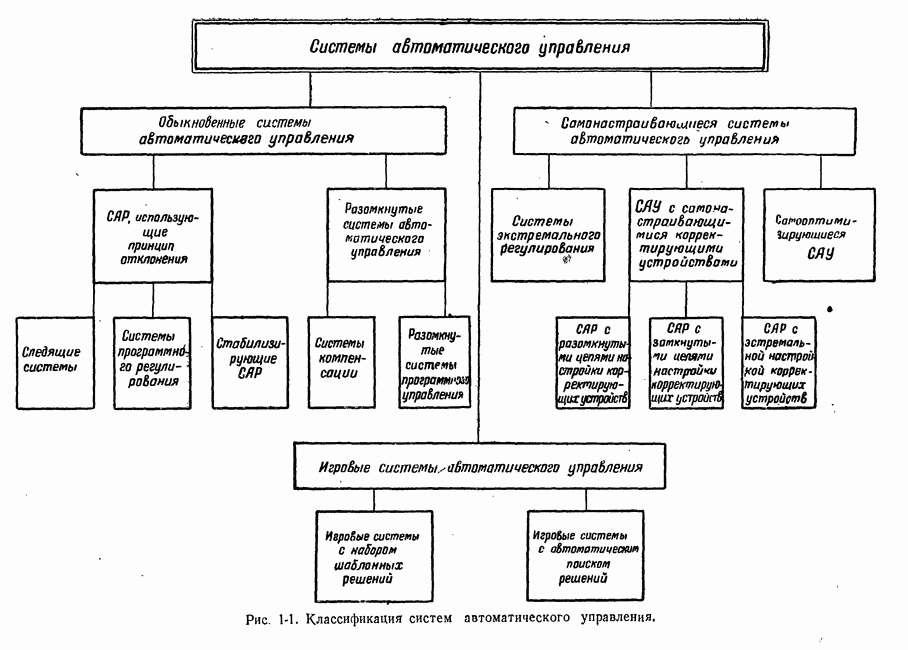
- 1-1. О КЛАССИФИКАЦИИ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- 1-2. ОБЫКНОВЕННЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- 1-3. САМОНАСТРАИВАЮЩИЕСЯ СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- 1-4. ИГРОВЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- 1-5. КЛАССИФИКАЦИЯ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ ПО ДРУГИМ ПРИЗНАКАМ
- ГЛАВА ВТОРАЯ. ОБЩИЕ ПЕРЕДАТОЧНЫЕ СВОЙСТВА ЭЛЕМЕНТОВ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- 2-1. УРАВНЕНИЯ ЭЛЕМЕНТОВ. СТАТИЧЕСКИЕ И ДИНАМИЧЕСКИЕ СВОЙСТВА ЭЛЕМЕНТОВ
- б) Центробежный измеритель скорости вращения
- в) Электромагнитный измеритель напряжения
- 2-2. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ
- 2-3. ЭЛЕМЕНТАРНЫЕ ДИНАМИЧЕСКИЕ ЗВЕНЬЯ, ИХ УРАВНЕНИЯ И ПЕРЕДАТОЧНЫЕ ФУНКЦИИ
- 2-4. ТИПОВЫЕ ВХОДНЫЕ СИГНАЛЫ. ВОЗМУЩАЮЩИЕ ФУНКЦИИ
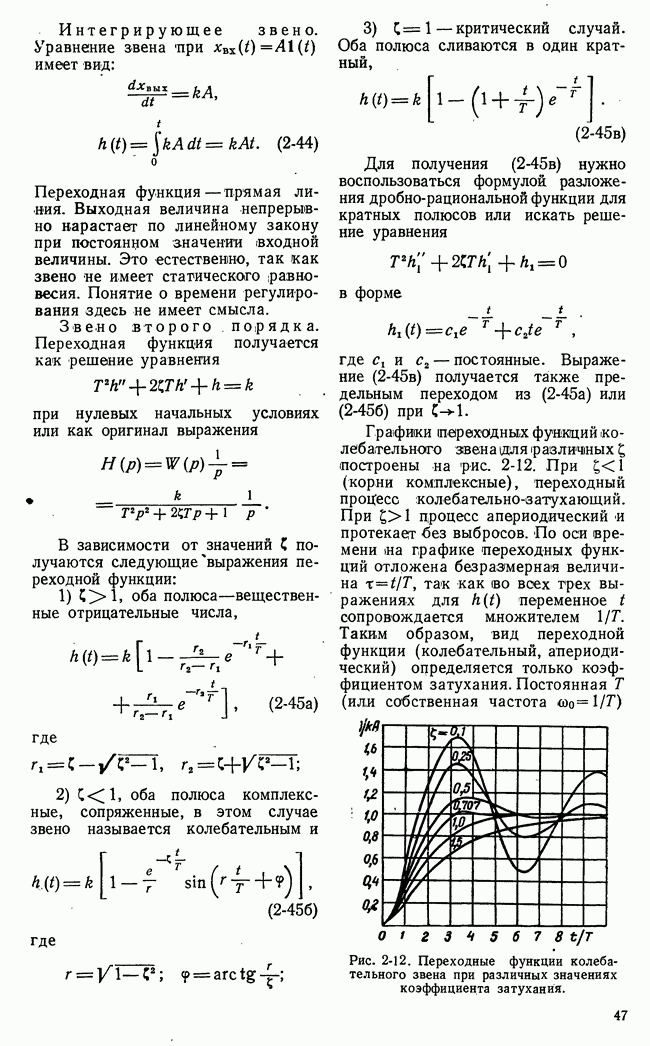
- 2-5. ПЕРЕХОДНЫЕ ФУНКЦИИ ЭЛЕМЕНТАРНЫХ ЗВЕНЬЕВ
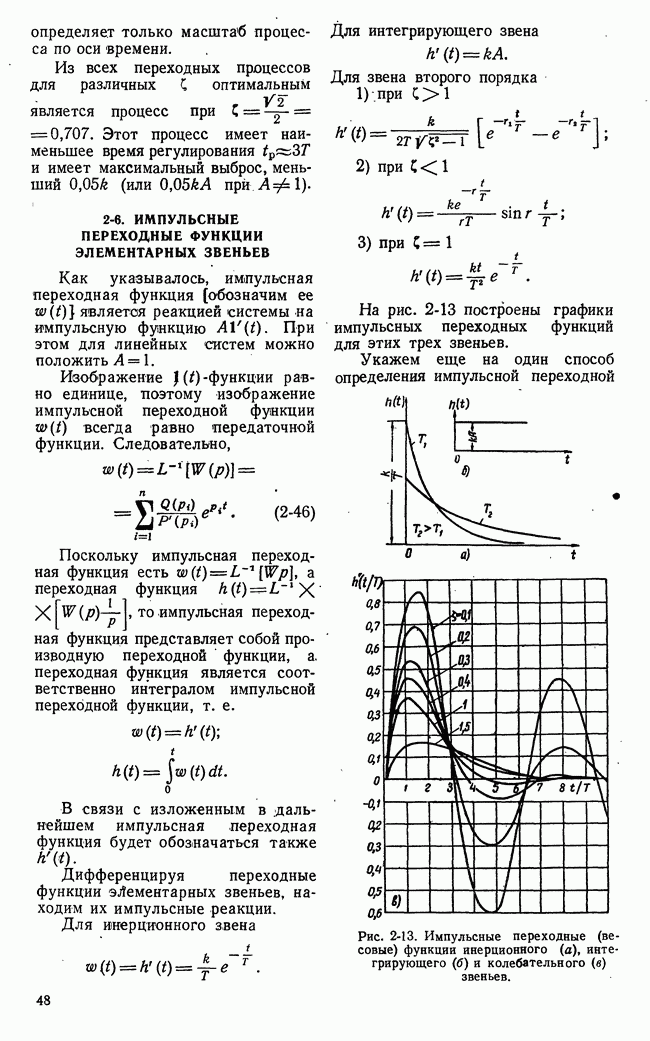
- 2-6. ИМПУЛЬСНЫЕ ПЕРЕХОДНЫЕ ФУНКЦИИ ЭЛЕМЕНТАРНЫХ ЗВЕНЬЕВ
- 2-7. РЕАКЦИЯ ЗВЕНЬЕВ НА ПРОИЗВОЛЬНЫЕ ИЗВЕСТНЫЕ ФУНКЦИИ ВРЕМЕНИ
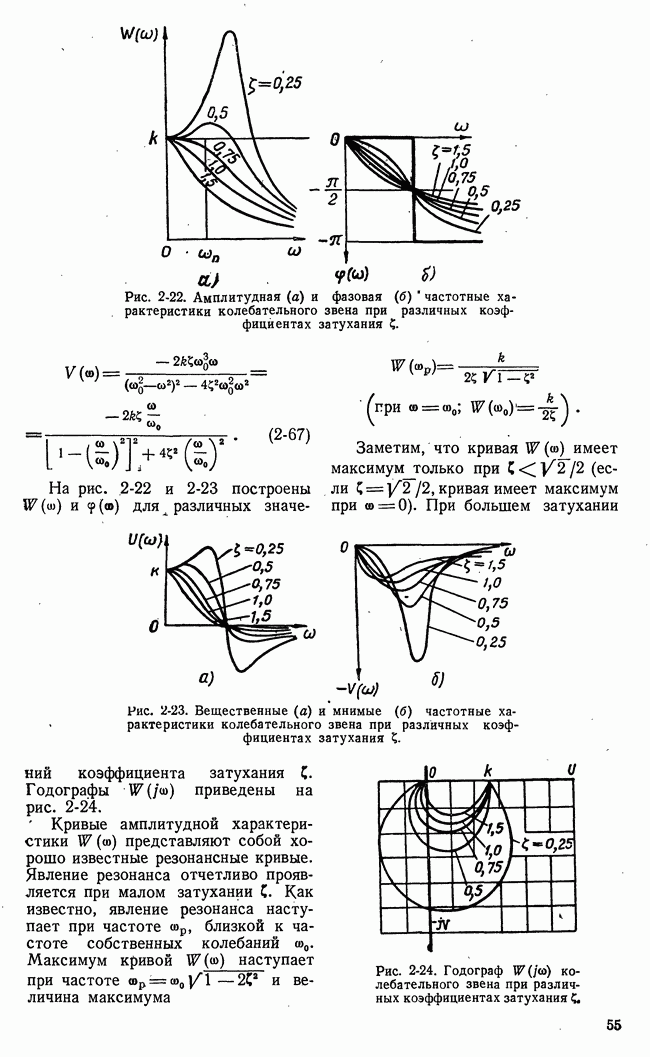
- 2-8. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ
- б) Частотные характеристики элементарных звеньев
- в) Логарифмические характеристики элементарных звеньев
- 2-9. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ОБ ЭЛЕМЕНТАРНЫХ ЗВЕНЬЯХ
- 2-10. СОЕДИНЕНИЯ ЗВЕНЬЕВ. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ СОЕДИНЕНИИ
- 2-11. ЭЛЕМЕНТЫ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ КАК ЧЕТЫРЕХПОЛЮСНИКИ. ПЕРЕДАТОЧНЫЕ УРАВНЕНИЯ
- ГЛАВА ТРЕТЬЯ. ДАТЧИКИ СИГНАЛОВ
- 3-1. ОБЩИЕ СВОЙСТВА ДАТЧИКОВ
- 3-2. ПОТЕНЦИОМЕТРИЧЕСКИЕ ДАТЧИКИ
- б) Выходная мощность потенциометрических датчиков и условия согласования
- в) Динамические свойства
- г) Ошибка ступенчатости. Параметры потенциометрических датчиков
- 3-3. ИНДУКТИВНЫЕ ДАТЧИКИ
- б) Двухтактные индуктивные датчики
- в) Характеристики двухтактных индуктивных датчиков
- г) Трансформаторные индуктивные датчики
- д) Динамические свойства индуктивных датчиков
- е) Шумы индуктивных датчиков
- ж) Общие свойства индуктивных датчиков
- 3-4. СЕЛЬСИНЫ В ТРАНСФОРМАТОРНОМ РЕЖИМЕ
- б) Характеристики сельсинного датчика
- в) Динамические свойства сельсинных датчиков
- г) Шумы и ошибки датчика
- д) Устанавливающий момент
- е) Дифференциальные сельсины
- ж) Сельсины точного и грубого каналов
- ГЛАВА ЧЕТВЕРТАЯ. УСИЛИТЕЛИ СИГНАЛОВ
- 4-2. МАГНИТНЫЕ УСИЛИТЕЛИ
- а) Рабочий процесс и статическая характеристика магнитного усилителя с прямоугольной кривой намагничивания сердечников
- б) Двухтактные магнитные усилители с выходом на переменном токе
- в) Магнитные усилители с обратной связью
- г) Динамические свойства магнитных усилителей
- д) Шумы магнитных усилителей. Общие свойства магнитных усилителей
- 4-3. ЭЛЕКТРОМАШИННЫЕ УСИЛИТЕЛИ
- б) Однокаскадный электромашицный усилитель как четырехполюсник
- в) Двухкаскадный электромашинный усилитель с поперечным полем
- г) Шумы электромашинных усилителей
- 4-4. РЕЛЕ
- б) Поляризованные реле
- в) Магнитоэлектрическое реле
- 4-5. РЕЛЕЙНЫЕ УСИЛИТЕЛИ
- б) Вибрационная линеаризация релейных усилителей
- в) Релейный усилитель как четырехполюсник
- 4-6. ЭЛЕКТРОННЫЕ УСИЛИТЕЛИ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- б) Фазочувствительные усилители и синхронные детекторы
- в) Электронные усилители постоянного тока
- г) Шумы электронных усилителей
- 4-7. ПОЛУПРОВОДНИКОВЫЕ УСИЛИТЕЛИ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- ГЛАВА ПЯТАЯ. ИСПОЛНИТЕЛЬНЫЕ УСТРОЙСТВА СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- 5-2. СЕРВОДВИГАТЕЛИ ПОЧТОЯННОГО ТОКА
- 5-3. СЕРВОДВИГАТЕЛИ ПЕРЕМЕННОГО ТОКА
- 5-4. СЕРВОДВИГАТЕЛИ С ЭЛЕКТРОМАГНИТНЫМИ И ПОРОШКОВЫМИ МУФТАМИ
- б) Характеристики серводвигателей с электромагнитными муфтами
- в) Порошковые муфты
- г) Характеристики серводвигателей с порошковыми муфтами
- 5-5. ГИДРАВЛИЧЕСКИЕ И ПНЕВМАТИЧЕСКИЕ СЕРВОДВИГАТЕЛИ
- б) Обратные связи в гидравлических серводвигателях
- в) Свойства гидравлических серводвигателей
- г) Электрогидравлические серводвигатели
- д) Пневматические серводвигатели
- ГЛАВА ШЕСТАЯ. СТАБИЛИЗИРУЮЩИЕ УСТРОЙСТВА СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- 6-1. ПАССИВНЫЕ КОРРЕКТИРУЮЩИЕ ЦЕПИ СИСТЕМ ПОСТОЯННОГО ТОКА
- б) Интегрирующие и интегродифференцирующие цепи
- 6-2. АКТИВНЫЕ КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА СИСТЕМ ПОСТОЯННОГО ТОКА
- 6-3. КОРРЕКТИРУЮЩИЕ ЦЕПИ СИСТЕМ ПЕРЕМЕННОГО ТОКА
- 6-4. ФИЛЬТРЫ В ЦЕПЯХ ОБРАТНЫХ СВЯЗЕЙ. МЕХАНИЧЕСКИЕ СТАБИЛИЗИРУЮЩИЕ УСТРОЙСТВА
- ГЛАВА СЕДЬМАЯ. СТРУКТУРНЫЕ СХЕМЫ И ХАРАКТЕРИСТИКИ ЛИНЕЙНЫХ СТАЦИОНАРНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 7-1. СТРУКТУРНЫЕ СХЕМЫ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 7-2. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ ДЛЯ ВХОДНОЙ ВЕЛИЧИНЫ
- 7-3. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ ДЛЯ ВОЗМУЩЕНИЯ
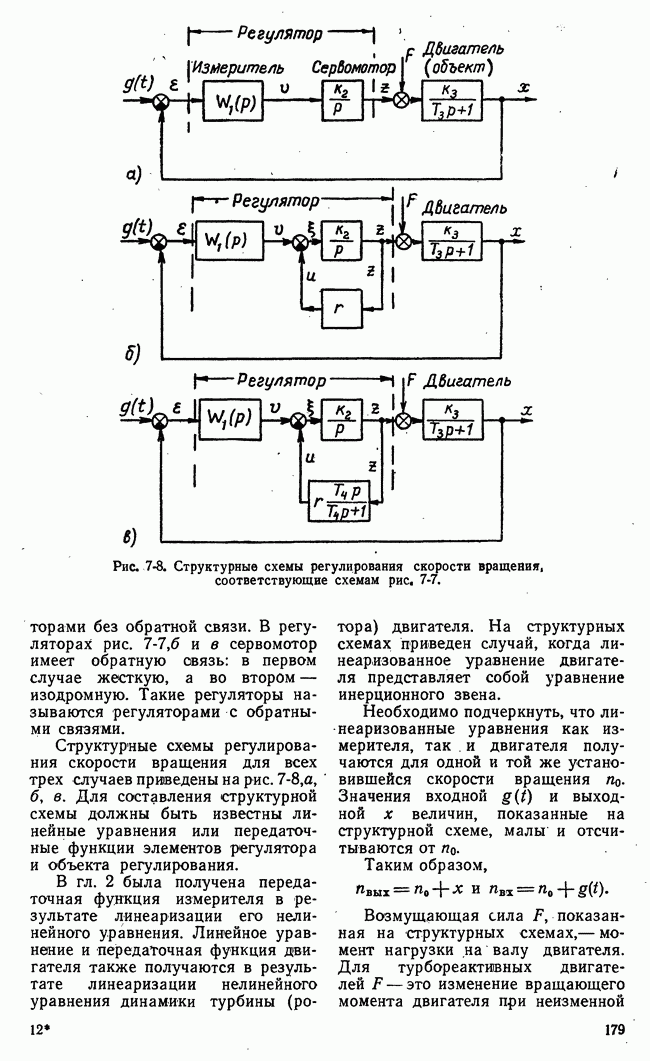
- 7-4. ПРИМЕРЫ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ И ИХ СТРУКТУРНЫЕ СХЕМЫ
- б) Стабилизация напряжения самолетных генераторов
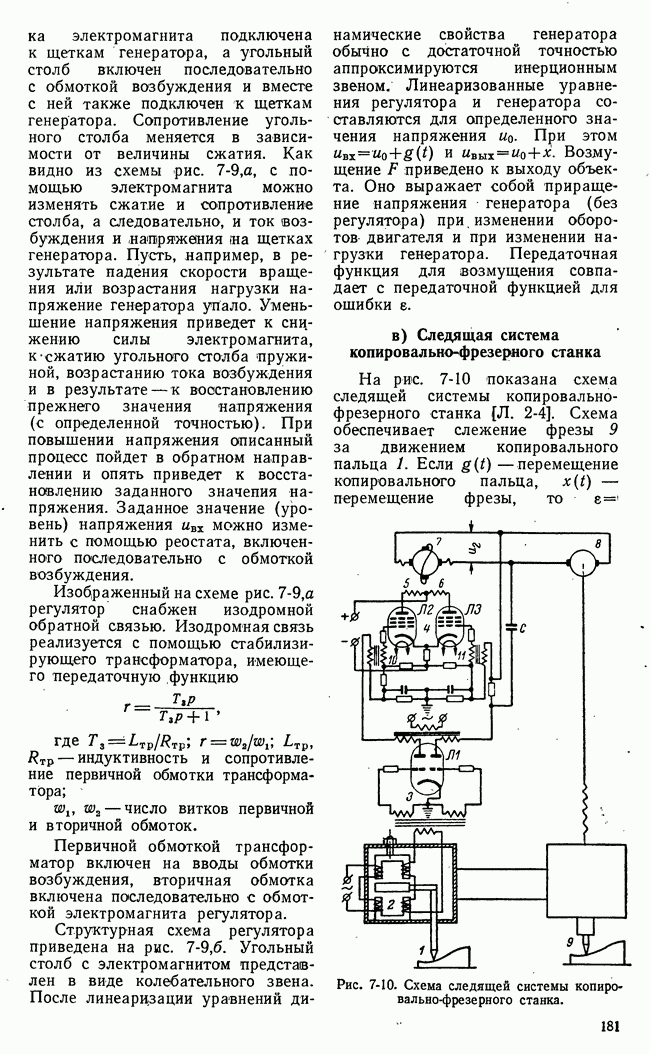
- в) Следящая система копировально-фрезерного станка
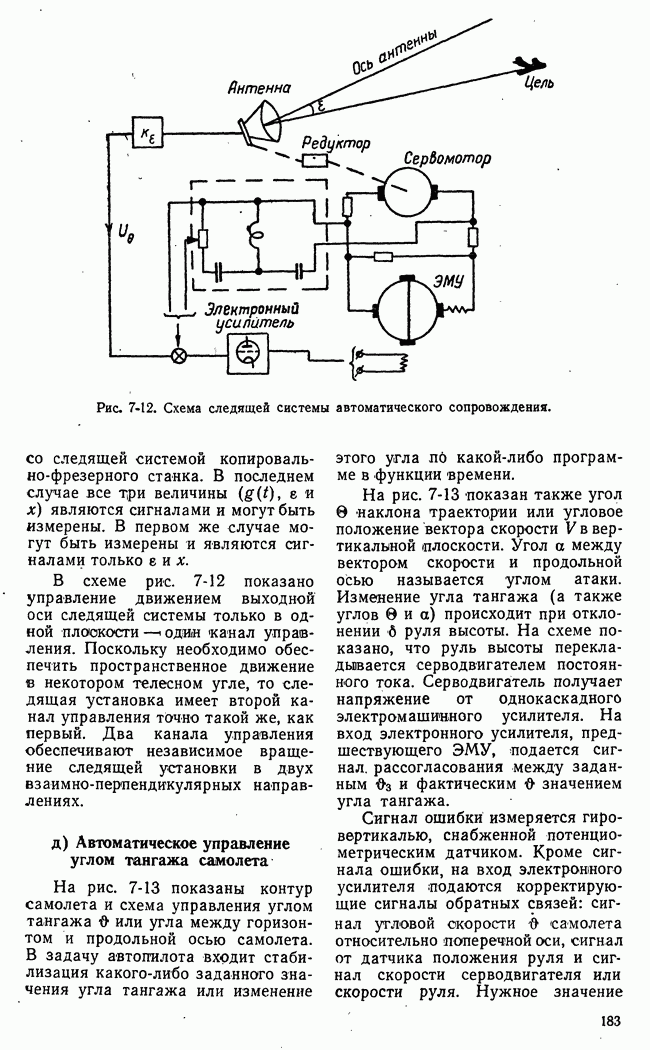
- г) Следящая система автосопровождения
- д) Автоматическое управление углом тангажа самолета
- 7-5. ВРЕМЕННЫЕ ХАРАКТЕРИСТИКИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
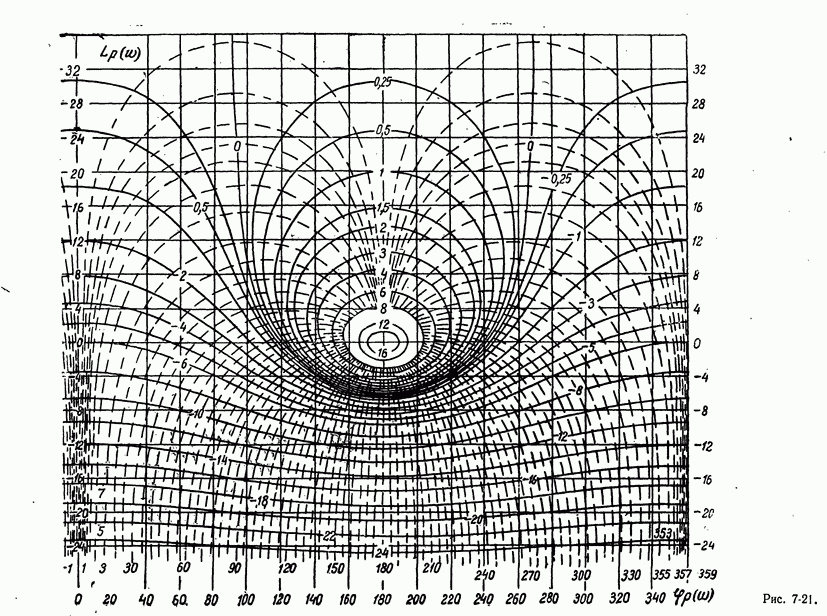
- 7-6. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
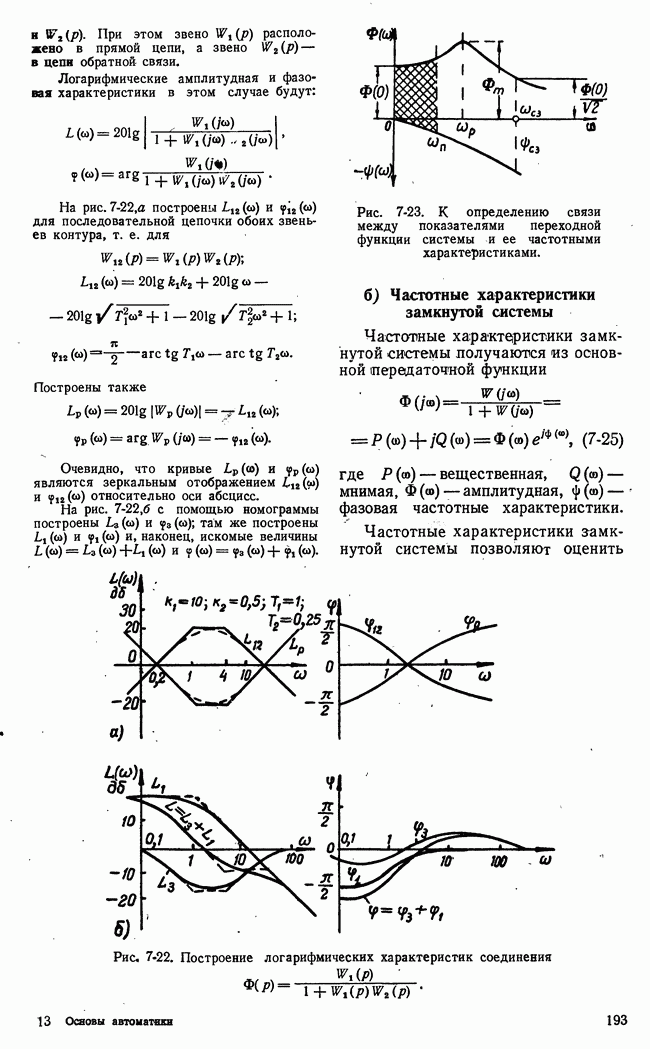
- б) Частотные характеристики замкнутой системы
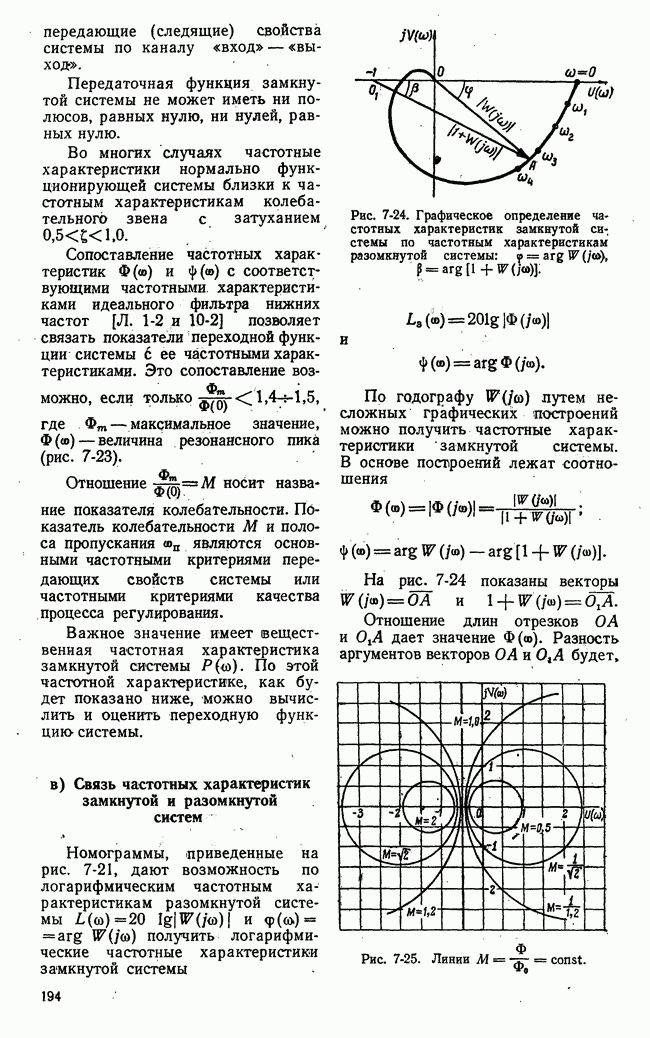
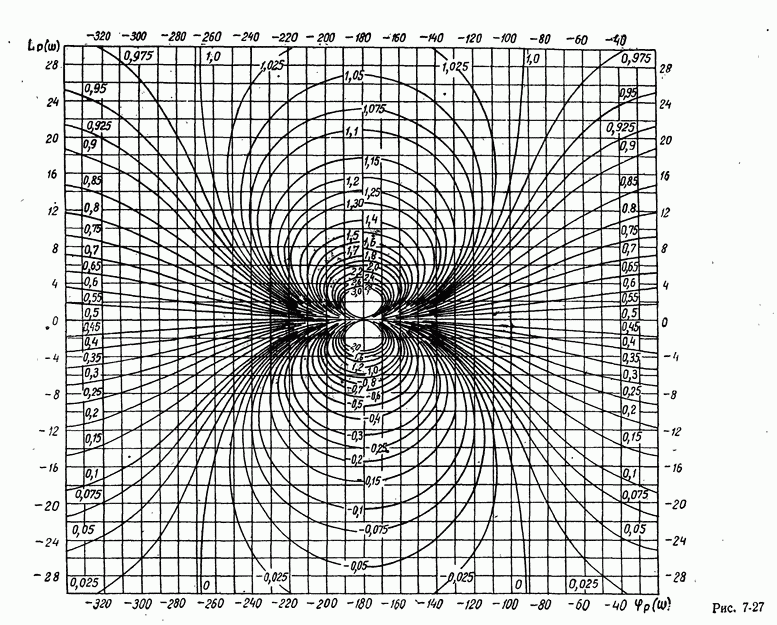
- в) Связь частотных характеристик замкнутой и разомкнутой систем
- ГЛАВА ВОСЬМАЯ. ЭНЕРГЕТИЧЕСКИЙ РАСЧЕТ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ И СОГЛАСОВАНИЕ ХАРАКТЕРИСТИК ЭЛЕМЕНТОВ
- 8-1. ВЫБОР МОЩНОСТИ ИСПОЛНИТЕЛЬНЫХ УСТРОЙСТВ И УСЛОВИЯ СОГЛАСОВАНИЯ С НАГРУЗКОЙ
- а) Определение необходимой мощности по переходным процессам при типовых воздействиях
- б) Мгновенная мощность при гармонических колебаниях
- в) Необходимая мощность при случайных колебаниях регулирующего органа
- г) Выбор мощности сервомотора
- д) Условия согласования с нагрузкой сервомотора без обратной связи
- е) Согласование с нагрузкой сервомотора с жесткой обратной связью
- 8-2. СОГЛАСОВАНИЕ ДАТЧИКОВ, УСИЛИТЕЛЬНЫХ И КОРРЕКТИРУЮЩИХ УСТРОЙСТВ. РАСПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТОВ УСИЛЕНИЯ
- б) Передаточные функции последовательных соединений элементов
- в) Согласование пропорциональных участков характеристик
- г) Распределение коэффициентов усиления
- ГЛАВА ДЕВЯТАЯ. УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ СТАЦИОНАРНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 9-2. КРИТЕРИЙ УСТОЙЧИВОСТИ РАУСА—ГУРВИЦА
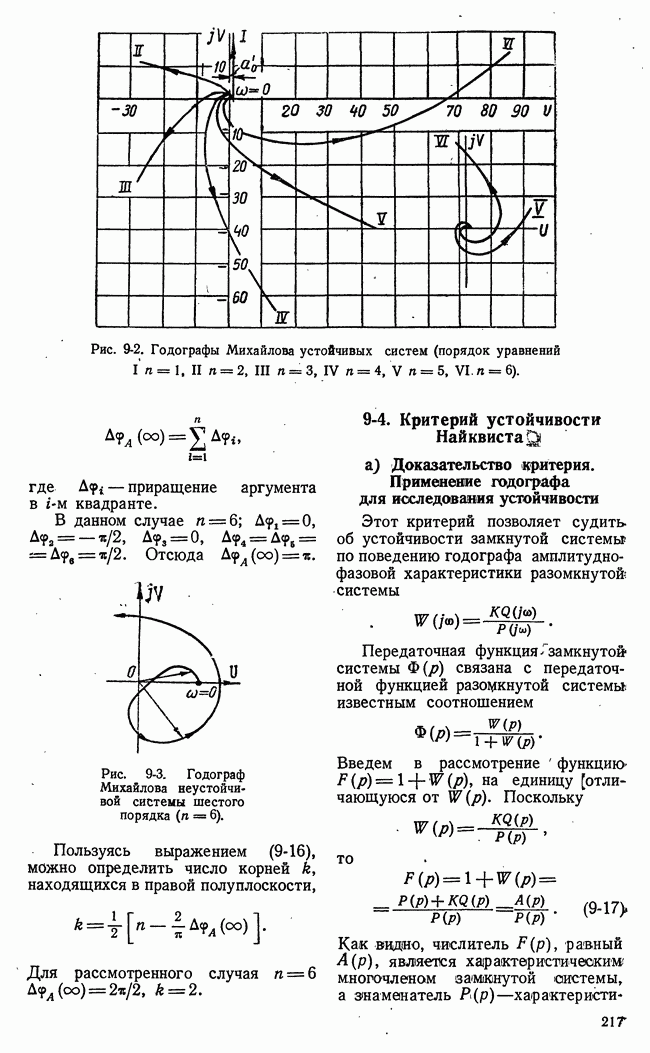
- 9-3. КРИТЕРИЙ УСТОЙЧИВОСТИ МИХАЙЛОВА
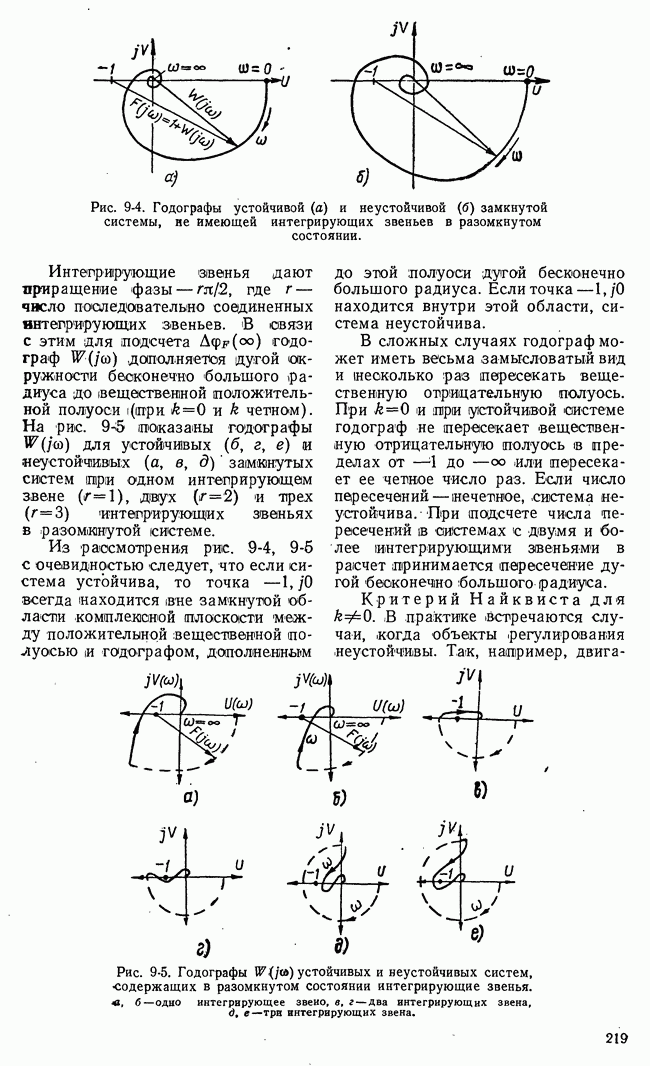
- 9-4. КРИТЕРИЙ УСТОЙЧИВОСТИ НАЙКВИСТА
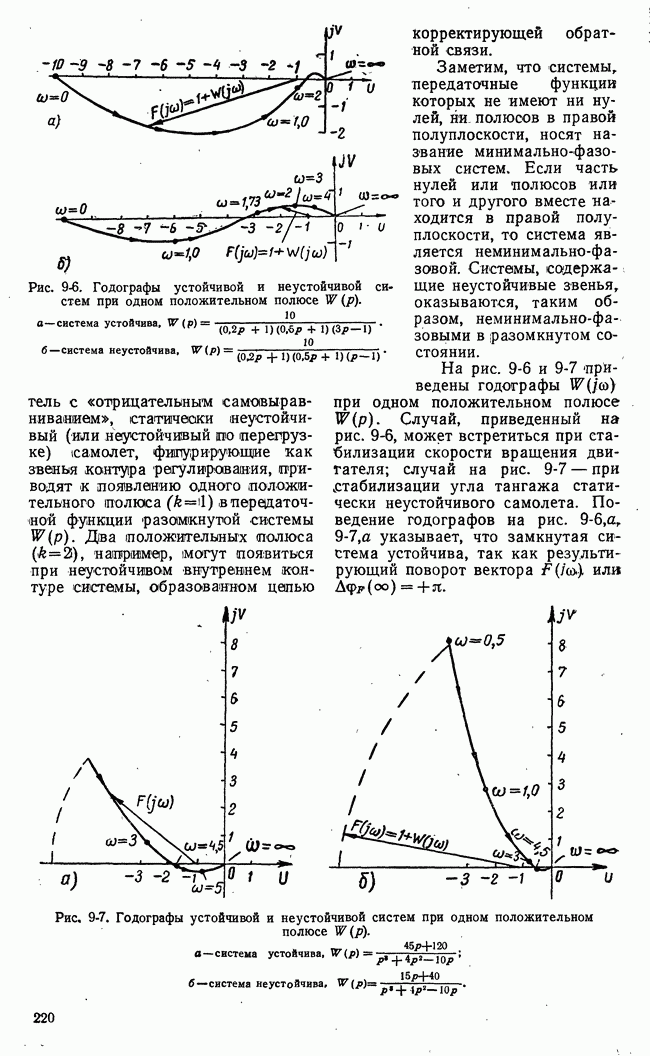
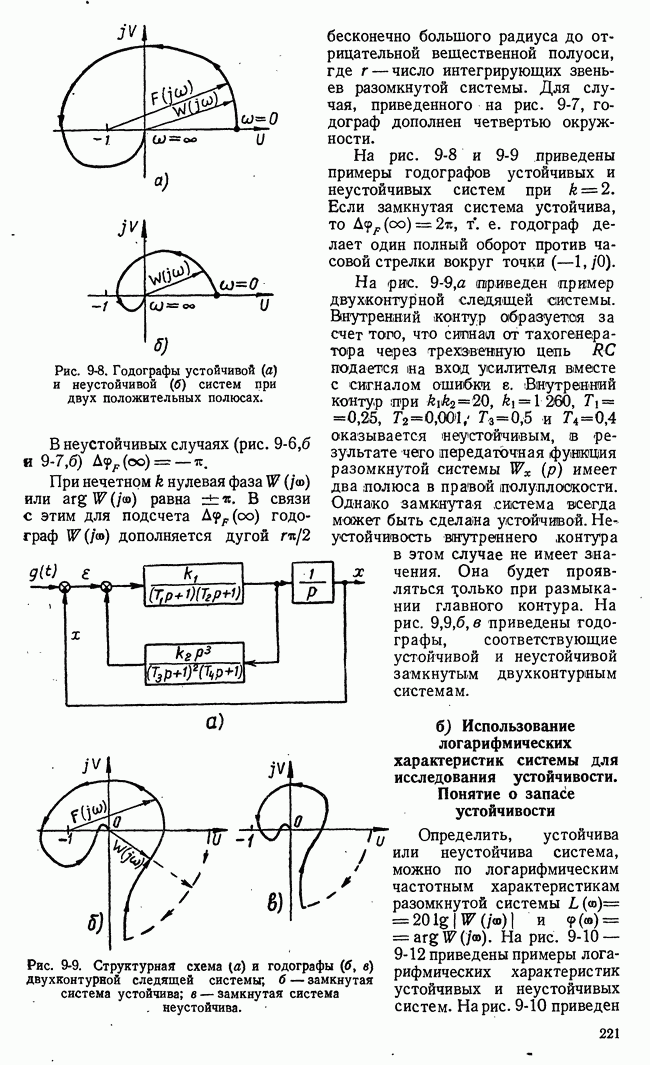
- б) Использование логарифмических характеристик системы для исследования устойчивости. Понятие о запасе устойчивости
- 9-5. КОЭФФИЦИЕНТ УСИЛЕНИЯ И УСТОЙЧИВОСТЬ. ВЛИЯНИЕ КОРРЕКТИРУЮЩИХ ЦЕПЕЙ НА УСТОЙЧИВОСТЬ
- 9-6. ВЫДЕЛЕНИЕ ОБЛАСТЕЙ УСТОЙЧИВОСТИ В ПРОСТРАНСТВЕ ПАРАМЕТРОВ СИСТЕМЫ ДИАГРАММЫ ВЫШНЕГРАДСКОГО
- б) Общий метод D-разбиения в плоскости двух параметров. Линейная задача
- в) Выделение области устойчивости в плоскости двух параметров. Нелинейная задача
- г) Выделение области устойчивости в плоскости одного комплексного параметра
- ГЛАВА ДЕСЯТАЯ. КАЧЕСТВО ПРОЦЕССОВ РЕГУЛИРОВАНИЯ В ЛИНЕЙНЫХ СИСТЕМАХ
- 10-1. КРИТЕРИИ КАЧЕСТВА ПРОЦЕССА РЕГУЛИРОВАНИЯ
- 10-2. ТОЧНОСТЬ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ В УСТАНОВИВШИХСЯ РЕЖИМАХ. СТАТИЧЕСКИЕ И АСТАТИЧЕСКИЕ СИСТЕМЫ
- б) Точность при медленно меняющихся воздействиях. Коэффициенты ошибок. Астатические системы высших порядков
- в) Общие условия неискаженного воспроизведения входных сигналов в вынужденном режиме
- г) Повышение точности системы коррекцией входного сигнала
- д) Повышение точности системы путем компенсации возмущения F(t)
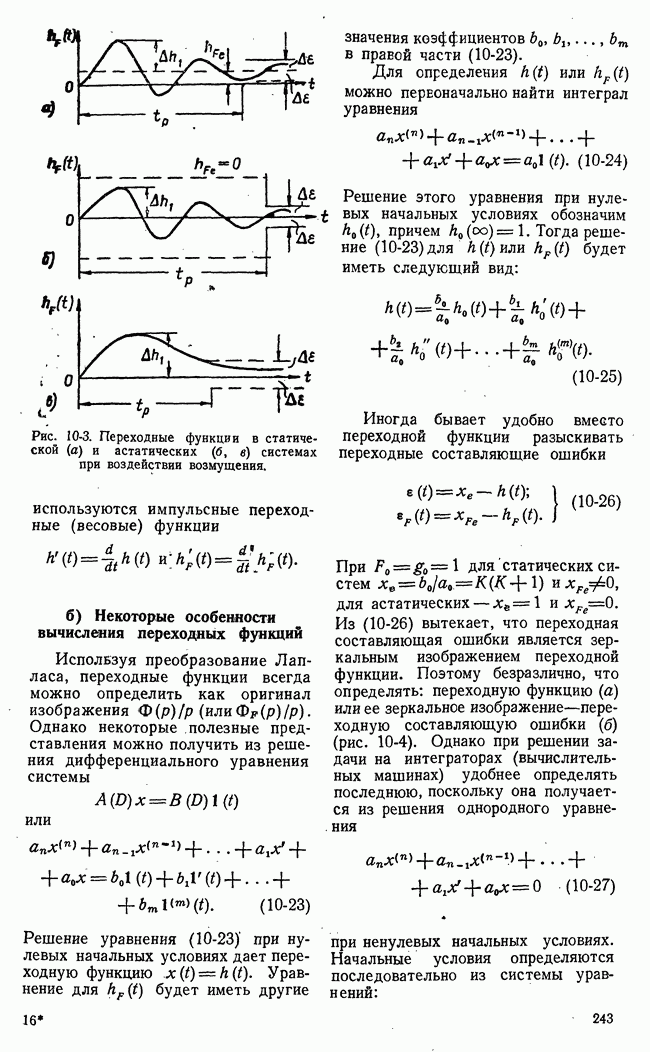
- 10-18. ПЕРЕХОДНЫЕ ФУНКЦИИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- б) Некоторые особенности вычисления переходных функций
- 10-4. РАСПРЕДЕЛЕНИЕ НУЛЕЙ И ПОЛЮСОВ ПЕРЕДАТОЧНОЙ ФУНКЦИИ И ПЕРЕХОДНЫЕ ПРОЦЕССЫ
- б) Оценки распределения корней. Степень устойчивости. Коэффициент затухания колебаний
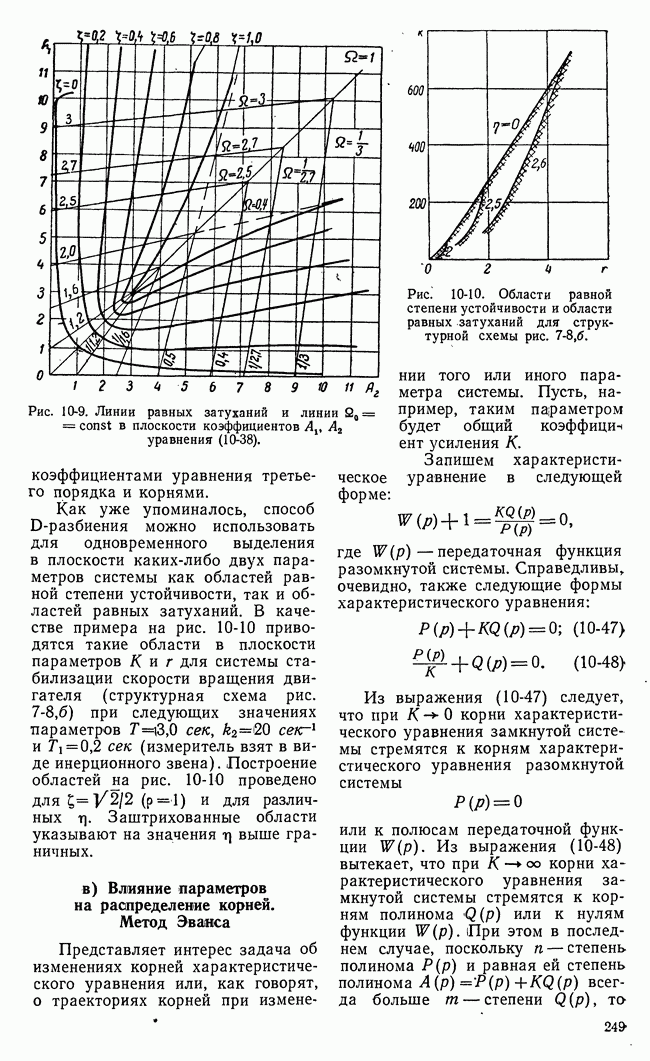
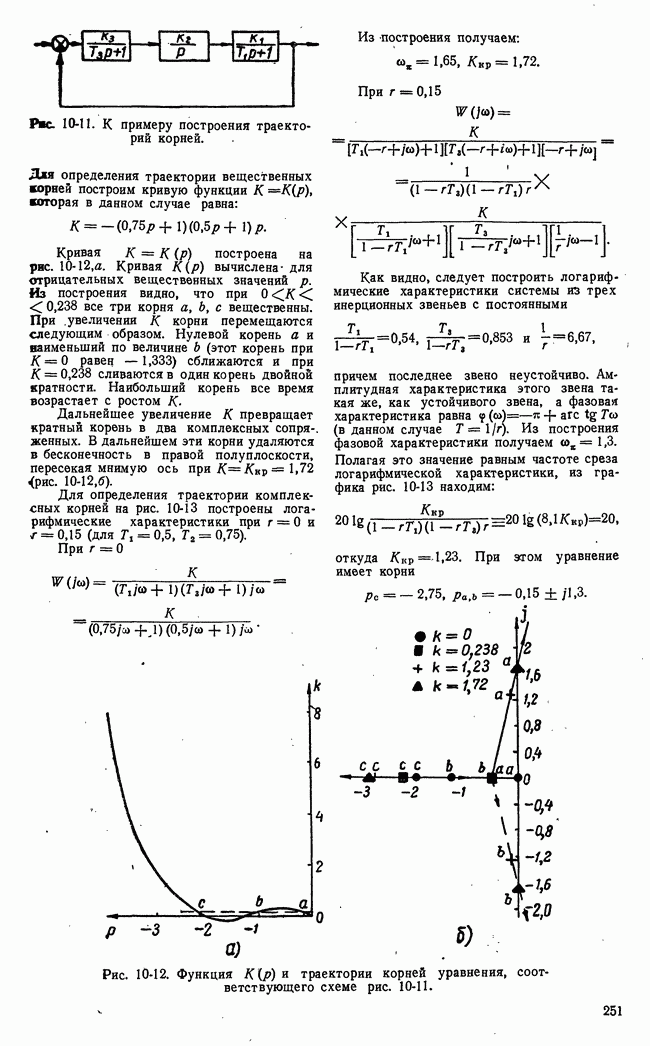
- в) Влияние параметров на распределение корней. Метод Эванса
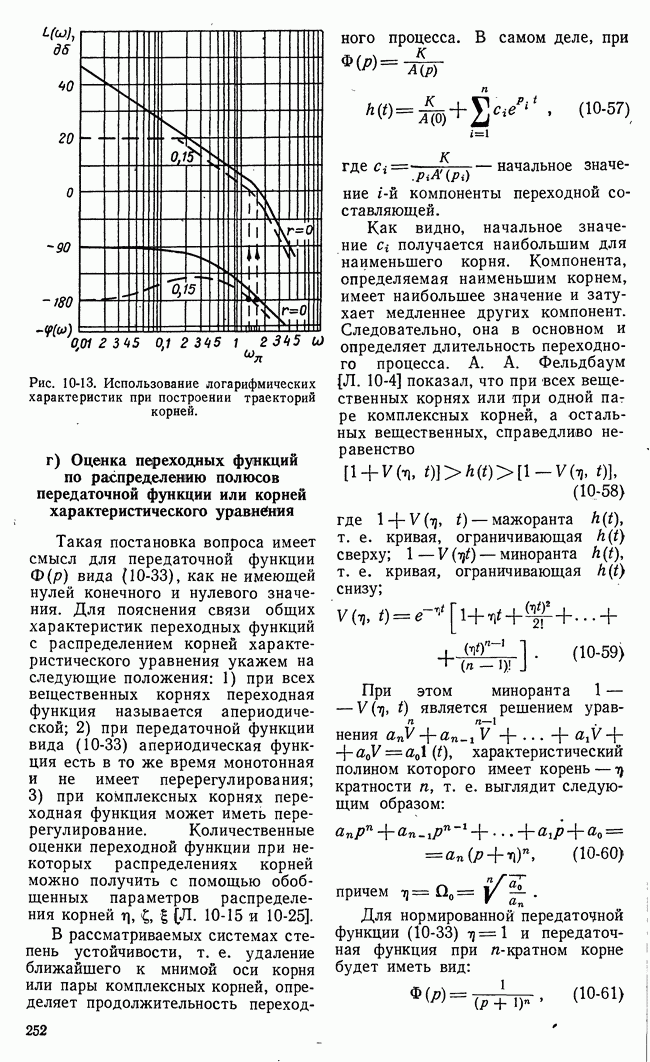
- г) Оценка переходных функций по распределению полюсов передаточной функции или корней характеристического уравнения
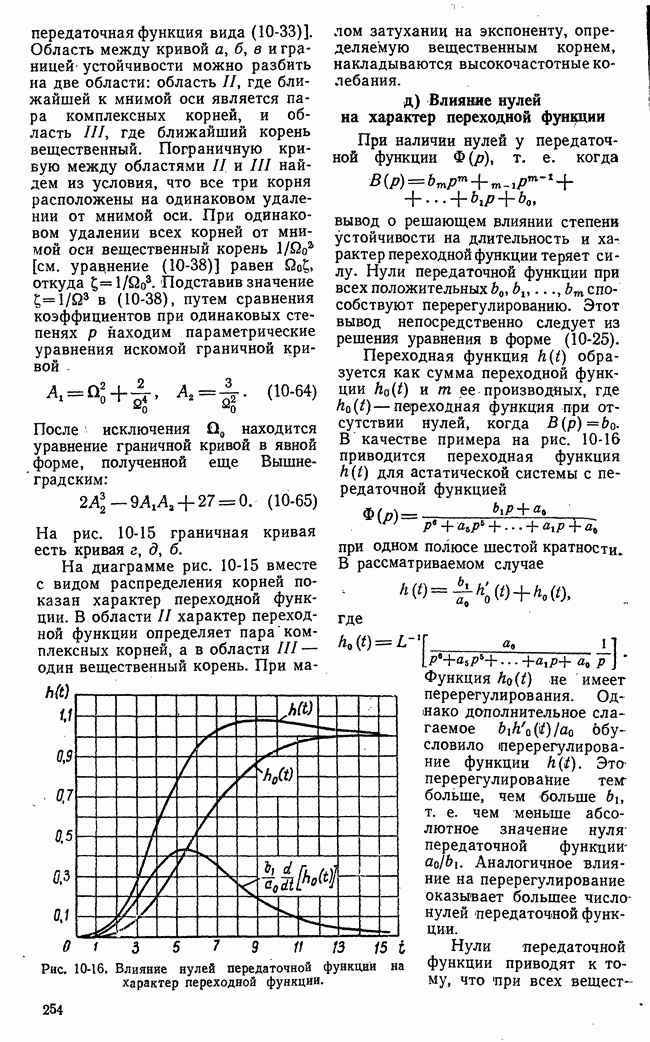
- д) Влияние нулей на характер переходной функции
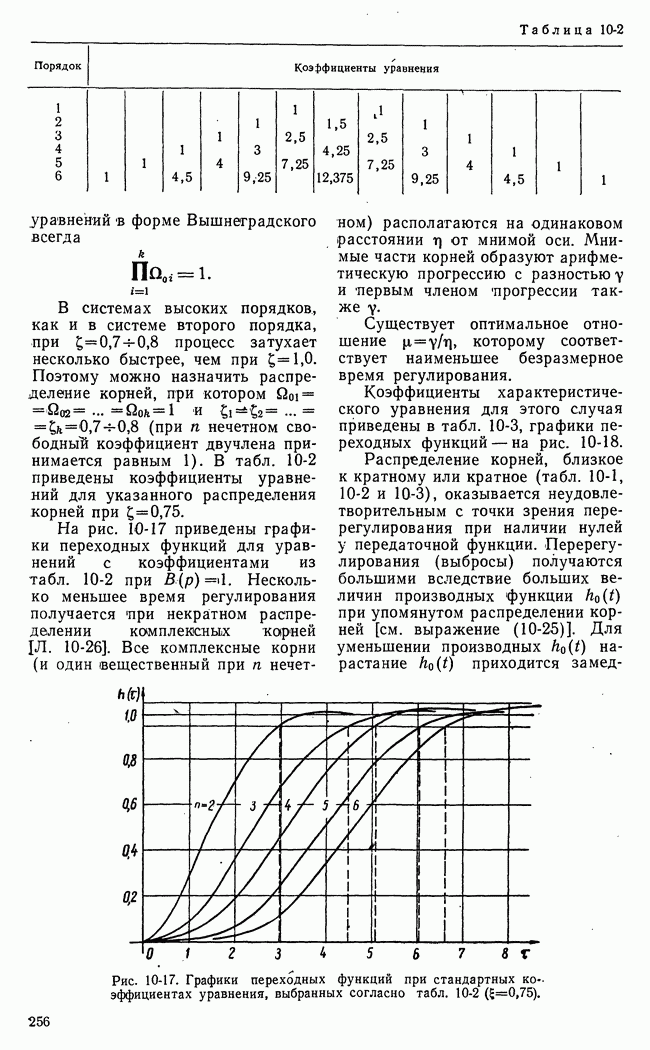
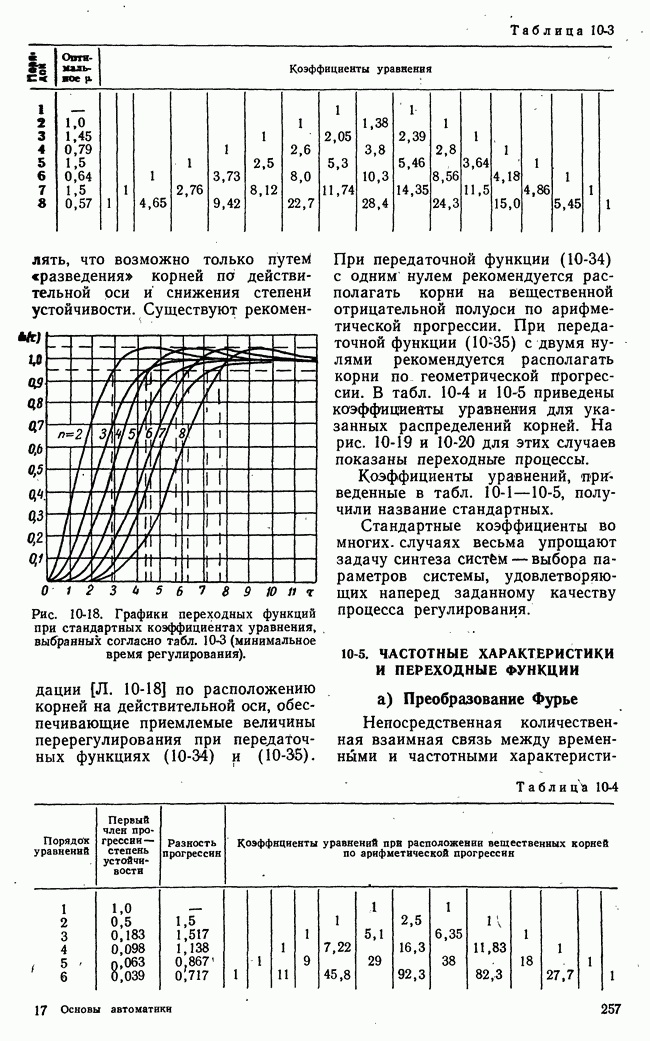
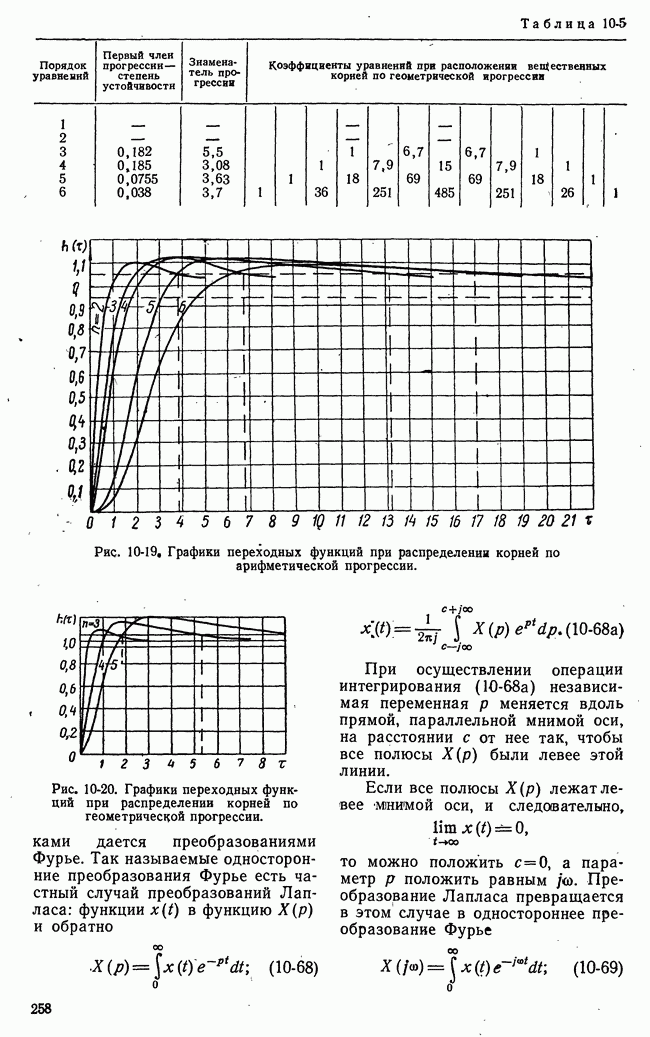
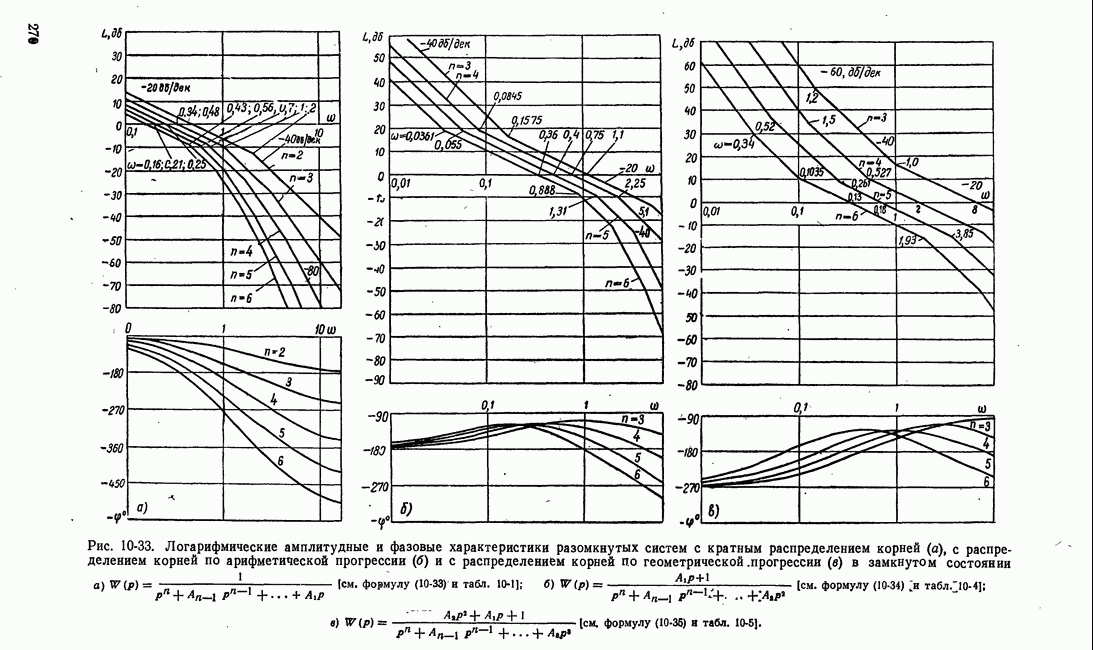
- е) Определение коэффициентов уравнений по заданному распределению корней. Стандартные коэффициенты характеристических уравнений
- 10-5. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ И ПЕРЕХОДНЫЕ ФУНКЦИИ
- б) Приближенное вычисление переходных функций и переходных процессов
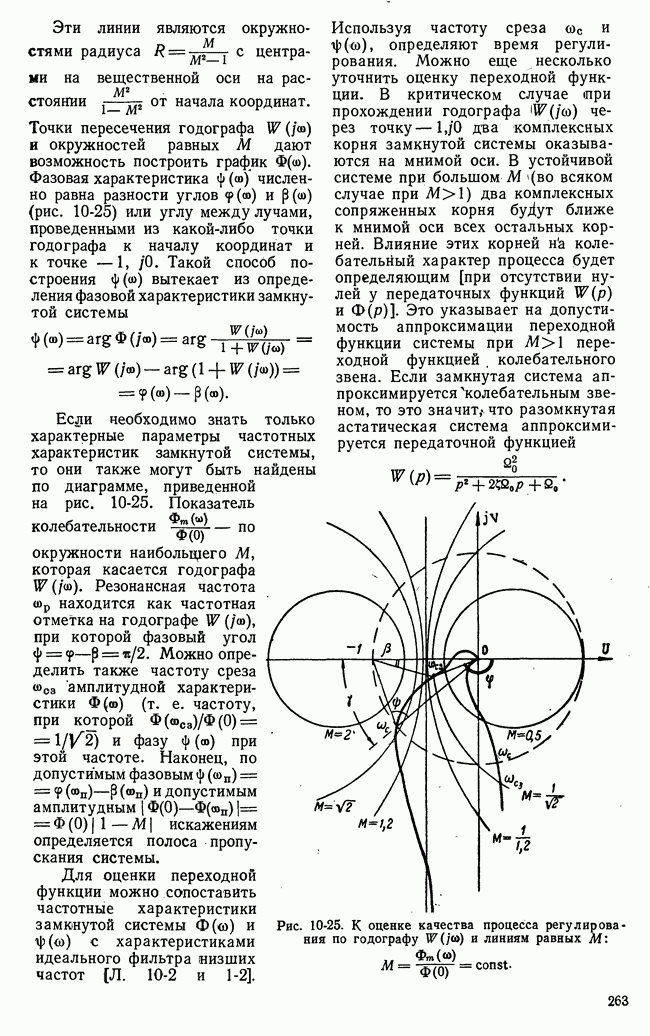
- в) Оценка качества процесса регулирования по характеристикам замкнутой системы Ф(w) и ф(w) и характеристике разомкнутой системы W(jw)
- г) Оценка качества по амплитудным логарифмическим характеристикам. Минимально-фазовые системы
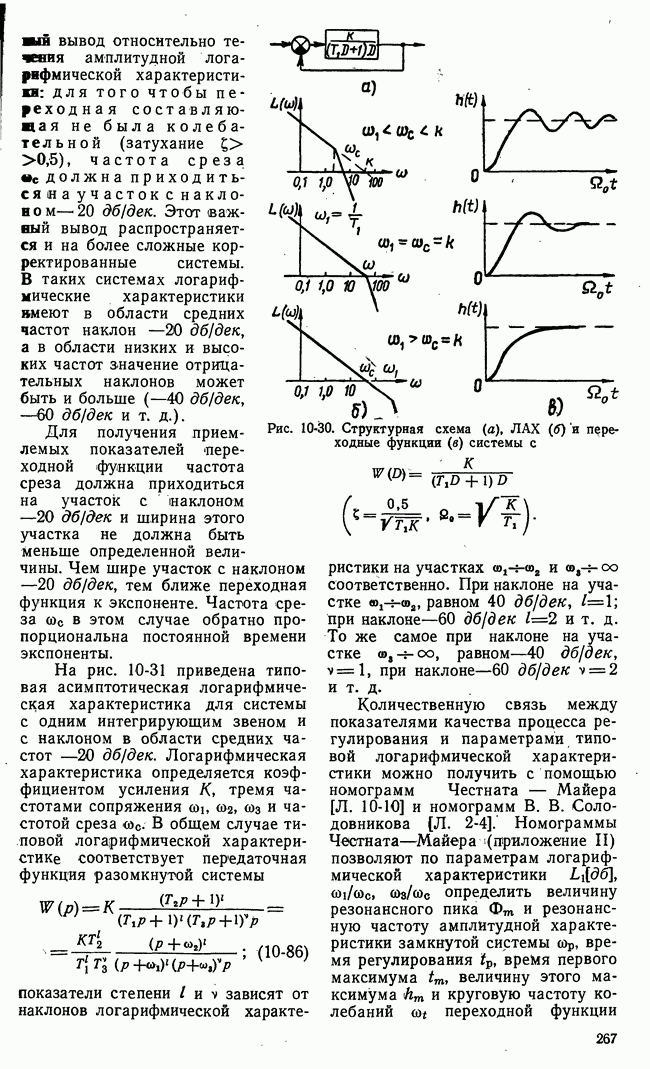
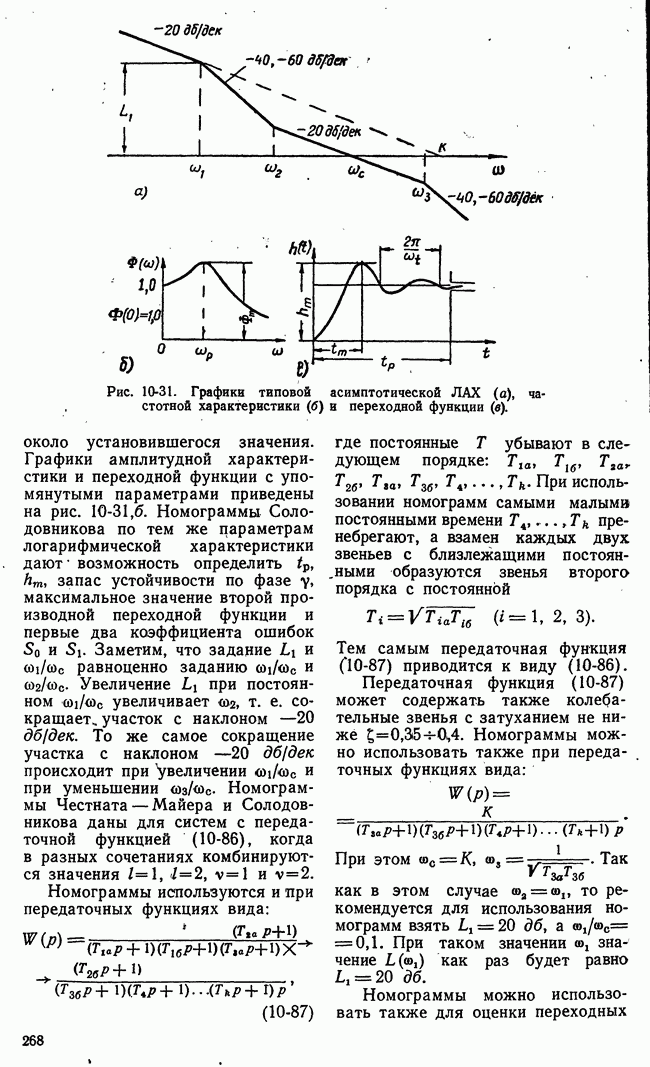
- д) Связь между логарифмическими амплитудными характеристиками разомкнутой системы и полюсами передаточной функции замкнутой системы
- 10-6. ИНТЕГРАЛЬНЫЕ ОЦЕНКИ ПЕРЕХОДНЫХ ПРОЦЕССОВ
- г) Приближение кривых x(t) к эталонной кривой хэ(t) по критерию …
- ГЛАВА ОДИННАДЦАТАЯ. НЕСТАЦИОНАРНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 11-1. ОБЩИЕ СВЕДЕНИЯ О НЕСТАЦИОНАРНЫХ СИСТЕМАХ
- 11-2. ПРИМЕРЫ СУЩЕСТВЕННО НЕСТАЦИОНАРНЫХ СИСТЕМ
- 11-3. ДИНАМИЧЕСКИЕ ХАРАКТЕРИСТИКИ НЕСТАЦИОНАРНЫХ СИСТЕМ АВТОМАТИЧ ЕСКОГО РЕГУЛИРОВАНИЯ
- 11-4. ОСОБЕННОСТИ СОСТАВЛЕНИЯ УРАВНЕНИЙ И СТРУКТУРНЫХ СХЕМ НЕСТАЦИОНАРНЫХ СИСТЕМ
- 11-5. МЕТОДЫ ОПРЕДЕЛЕНИЯ ЧАСТОТНОЙ ХАРАКТЕРИСТИКИ И ИМПУЛЬСНОЙ РЕАКЦИИ НЕСТАЦИОНАРНЫХ СИСТЕМ
- ГЛАВА ДВЕНАДЦАТАЯ. СТАТИСТИЧЕСКАЯ ДИНАМИКА ЛИНЕЙНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 12-1. СТАЦИОНАРНЫЕ И НЕСТАЦИОНАРНЫЕ СЛУЧАЙНЫЕ ПРОЦЕССЫ
- б) Стационарные и нестационарные случайные функций
- в) Свойства корреляционной функции
- г) Свойство эргодичности
- д) Гауссовы случайные процессы
- 12-2. ПРЕОБРАЗОВАНИЕ СТАЦИОНАРНЫХ СЛУЧАЙНЫХ ФУНКЦИЙ СТАЦИОНАРНЫМИ ЛИНЕЙНЫМИ СИСТЕМАМИ
- б) Преобразование корреляционных функций при прохождении случайного сигнала через линейную систему
- в) Интегральная квадратичная оценка импульсной переходной функции и дисперсия реакции системы на белый шум
- г) Преобразование спектральных плотностей при прохождении случайного сигнала через линейную систему
- 12-3. ОПТИМАЛЬНЫЕ ЛИНЕЙНЫЕ СТАЦИОНАРНЫЕ СИСТЕМЫ
- б) Условия оптимальности при свободном выборе передаточной функции
- ГЛАВА ТРИНАДЦАТАЯ. О СИНТЕЗЕ ЛИНЕЙНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 13-2. МЕТОД ЛОГАРИФМИЧЕСКИХ ЧАСТОТНЫХ ХАРАКТЕРИСТИК
- б) Синтез корректирующих цепей
- в) О синтезе на основе требований к реакции системы на возмущение F(t)
- 13-3. ВЫБОР ПАРАМЕТРОВ НА ОСНОВЕ АНАЛИЗА РАСПРЕДЕЛЕНИЯ НУЛЕЙ И ПОЛЮСОВ ПЕРЕДАТОЧНОЙ ФУНКЦИИ
- 13-4. ВЫБОР ПАРАМЕТРОВ НА ОСНОВЕ ИНТЕГРАЛЬНЫХ КВАДРАТИЧНЫХ ОЦЕНОК
- 13-5. СПЕЦИАЛЬНЫЕ ПРИЕМЫ УЛУЧШЕНИЯ КАЧЕСТВА ПРОЦЕССА РЕГУЛИРОВАНИЯ
- б) Подавление помех во входном сигнале при инерционном объекте управления
- в) Использование двух источников информации для выделения истинного сигнала
- г) Компенсация влияния запаздывания измерителей на динамические свойства системы
- д) Исключение перерегулирования в системах, передаточные функции которых имеют только вещественные полюсы
- ГЛАВА ЧЕТЫРНАДЦАТАЯ. ИМПУЛЬСНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 14-2. ИМПУЛЬСЫ И ИМПУЛЬСНЫЕ ЭЛЕМЕНТЫ
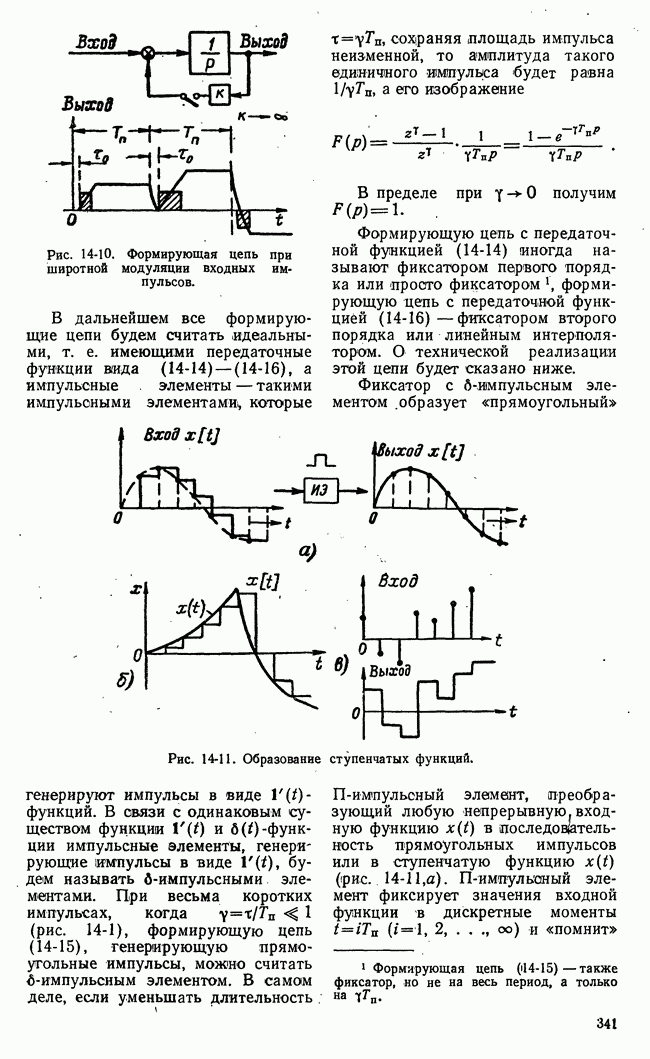
- б) Формирующие цепи и импульсные элементы
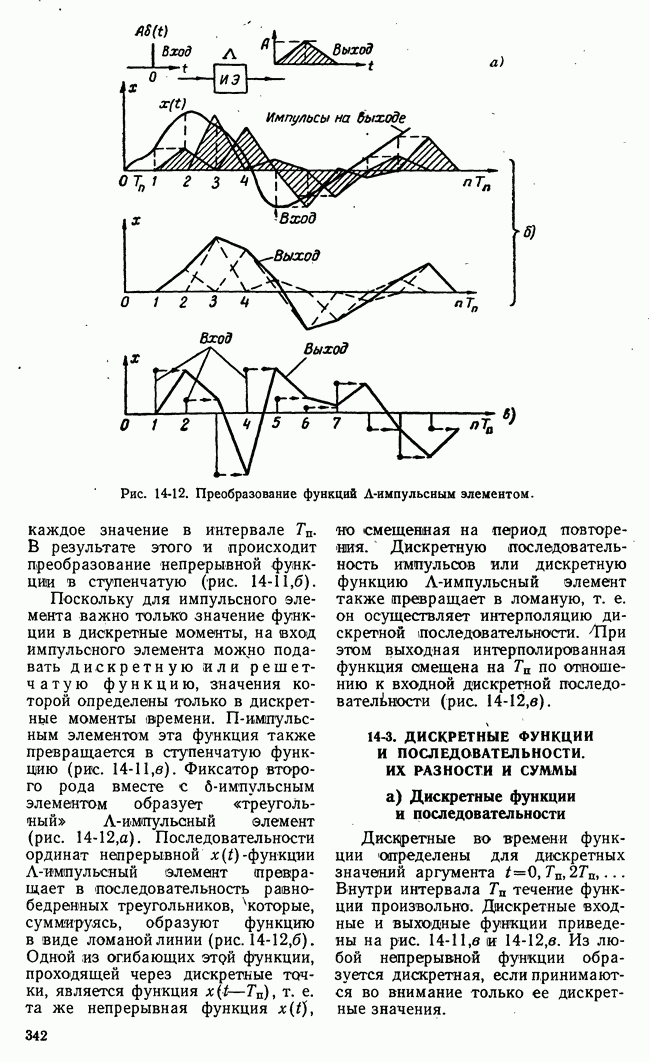
- 14-3. ДИСКРЕТНЫЕ ФУНКЦИИ И ПОСЛЕДОВАТЕЛЬНОСТИ. ИХ РАЗНОСТИ И СУММЫ
- 14-4. РЕАКЦИЯ ЛИНЕЙНЫХ НЕПРЕРЫВНЫХ СИСТЕМ НА ПОСЛЕДОВАТЕЛЬНОСТИ ИЛИ ДЕЛЬТА-ИМПУЛЬСОВ
- б) Свертка двух дискретных функций
- в) Уравнения в конечных разностях непрерывных звеньев первого и второго порядков
- г) Символические изображения дискретных функций и их использование для решения уравнений в конечных разностях
- 14-5. ДИСКРЕТНОЕ ПРЕОБРАЗОВАНИЕ ЛАПЛАСА ИЛИ z-ПРЕОБРАЗОВАНИЕ. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ КОМПЛЕКСНОГО АРГУМЕНТА
- 14-6. ДИНАМИКА РАЗОМКНУТЫХ ИМПУЛЬСНЫХ СИСТЕМ
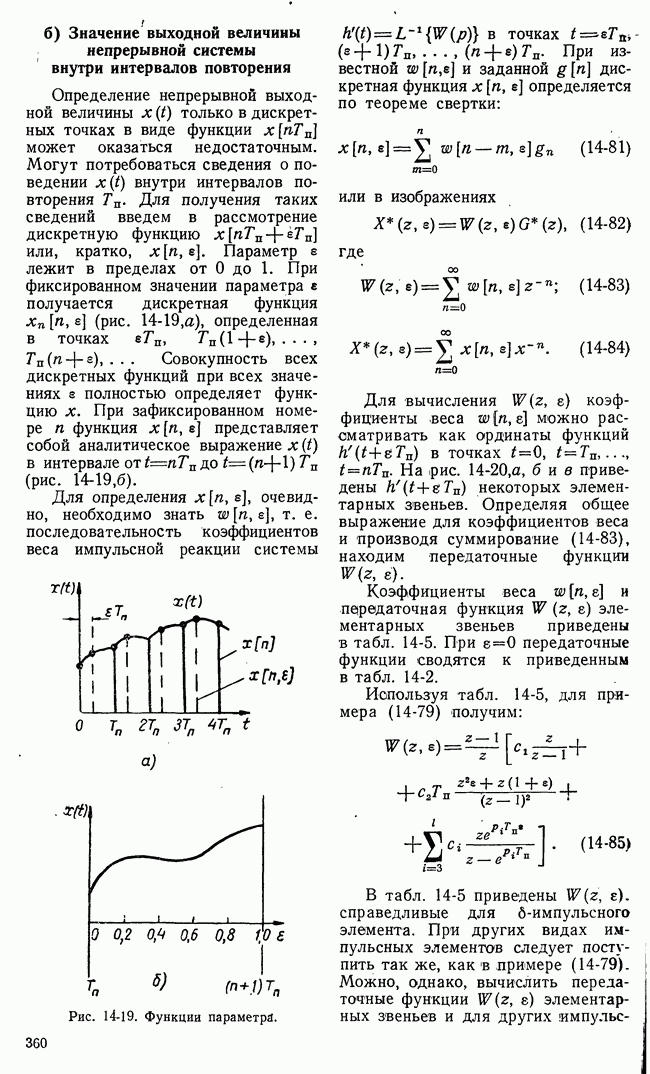
- б) Значение выходной величины непрерывной системы внутри интервалов повторения
- в) Передаточные функции, систем с запаздыванием
- г) Свободные и вынужденные движения
- д) Полюсы. Устойчивость разомкнутых систем
- е) Переходные функции
- ж) Частотные характеристики
- 14-7. СВЯЗЬ МЕЖДУ ЧАСТОТНЫМИ И ПЕРЕХОДНЫМИ ФУНКЦИЯМИ. ДИСКРЕТНОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ
- 14-8. ИНТЕГРАЛЬНАЯ КВАДРАТИЧНАЯ ОЦЕНКА
- 14-9. ДИСКРЕТНЫЕ СЛУЧАЙНЫЕ ФУНКЦИИ (СЛУЧАЙНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ)
- ГЛАВА ПЯТНАДЦАТАЯ. ДИНАМИКА ИМПУЛЬСНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 15-1. УРАВНЕНИЯ И ПЕРЕДАТОЧНЫЕ ФУНКЦИИ СИСТЕМ С ОДНИМ ИМПУЛЬСНЫМ ЭЛЕМЕНТОМ
- 15-2. УСТОЙЧИВОСТЬ ЗАМКНУТЫХ СИСТЕМ
- 15-3. КАЧЕСТВО ПРОЦЕССА РЕГУЛИРОВАНИЯ
- 15-4. ПРИМЕРЫ ИМПУЛЬСНЫХ СИСТЕМ
- 15-5. ИМПУЛЬСНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ С ДИСКРЕТНЫМИ КОРРЕКТИРУЮЩИМИ ЦЕПЯМИ
- ГЛАВА ШЕСТНАДЦАТАЯ. СТРУКТУРНЫЕ СХЕМЫ, ХАРАКТЕРИСТИКИ И УРАВНЕНИЯ НЕЛИНЕЙНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- б) Уравнения продольного движения самолета
- в) Уравнения продольного движения ракеты
- 16-2. НЕЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ СИГНАЛА ОШИБКИ
- б) Структурные схемы с нелинейными элементами
- в) Релейные системы. Релейные элементы
- 16-3. НЕЛИНЕЙНЫЙ ОБЪЕКТ РЕГУЛИРОВАНИЯ И НЕЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ СИГНАЛА ОШИБКИ
- ГЛАВА СЕМНАДЦАТАЯ. СВОЙСТВА НЕЛИНЕЙНЫХ СИСТЕМ И (МЕТОДЫ ИССЛЕДОВАНИЯ
- б) Суждение об устойчивости по уравнениям первого приближения. Теоремы Ляпунова
- в) Суждение о качестве процессов регулирования по уравнениям первого приближения
- г) Прямой метод Ляпунова
- д) Техническая устойчивость
- 17-2. АВТОКОЛЕБАНИЯ НЕЛИНЕЙНЫХ СИСТЕМ
- б) Автоколебания релейных систем
- в) Метод точечных преобразований
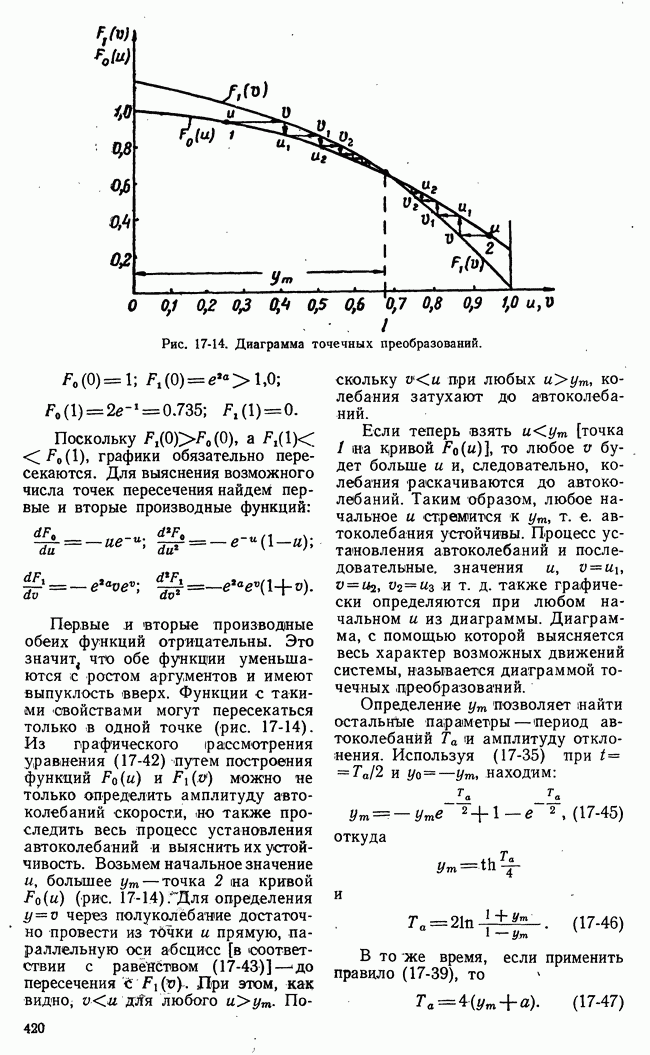
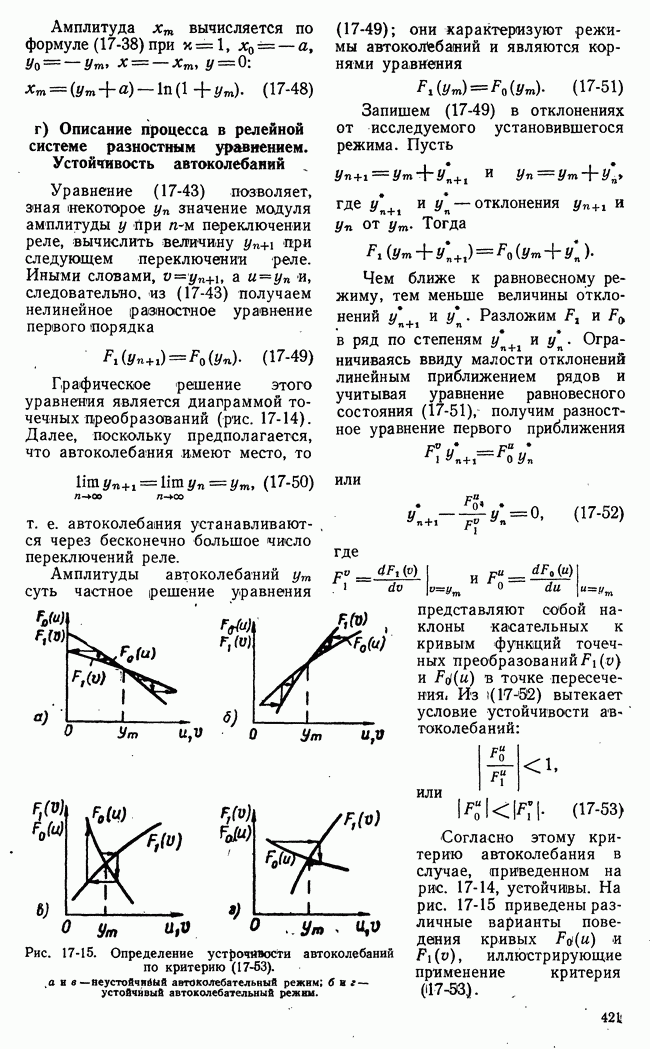
- г) Описание процесса в релейной системе разностным уравнением. Устойчивость автоколебаний
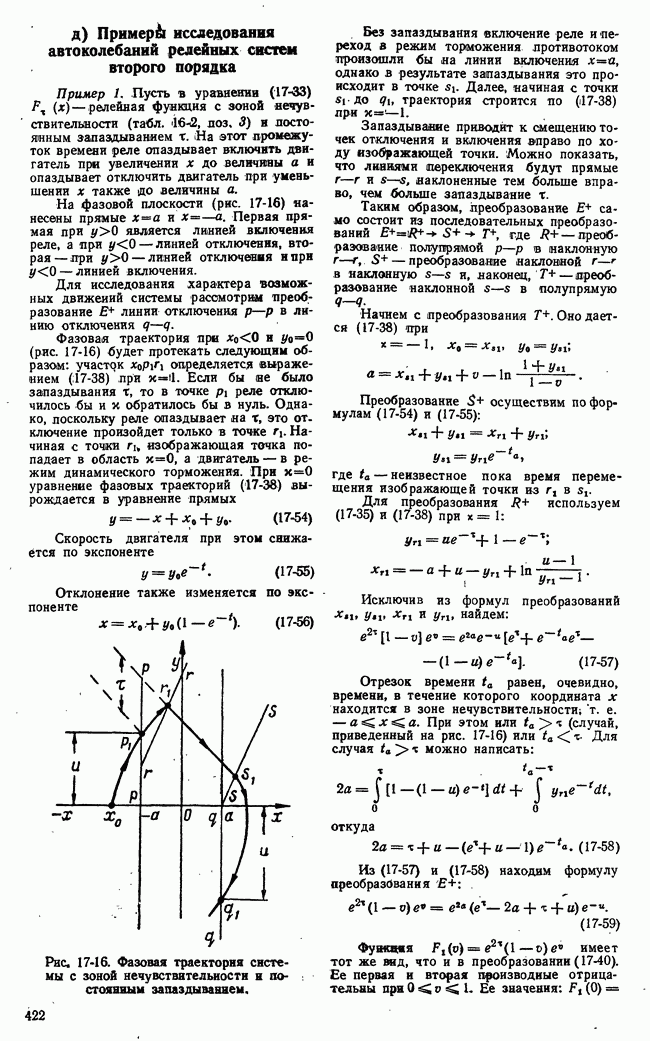
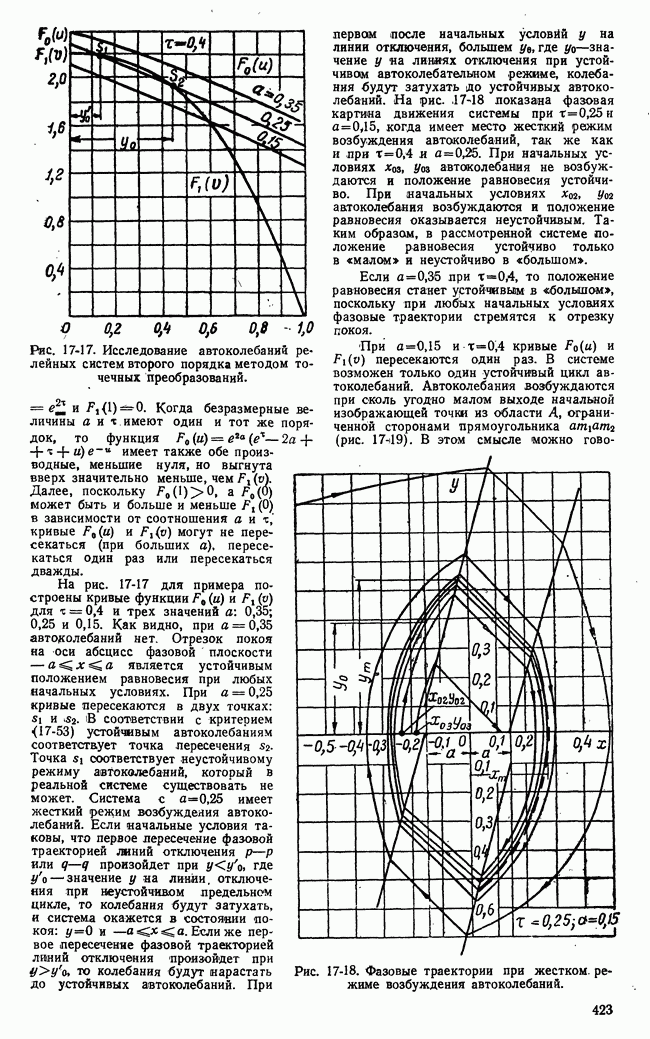
- д) Примера исследования автоколебаний релейных систем второго порядка
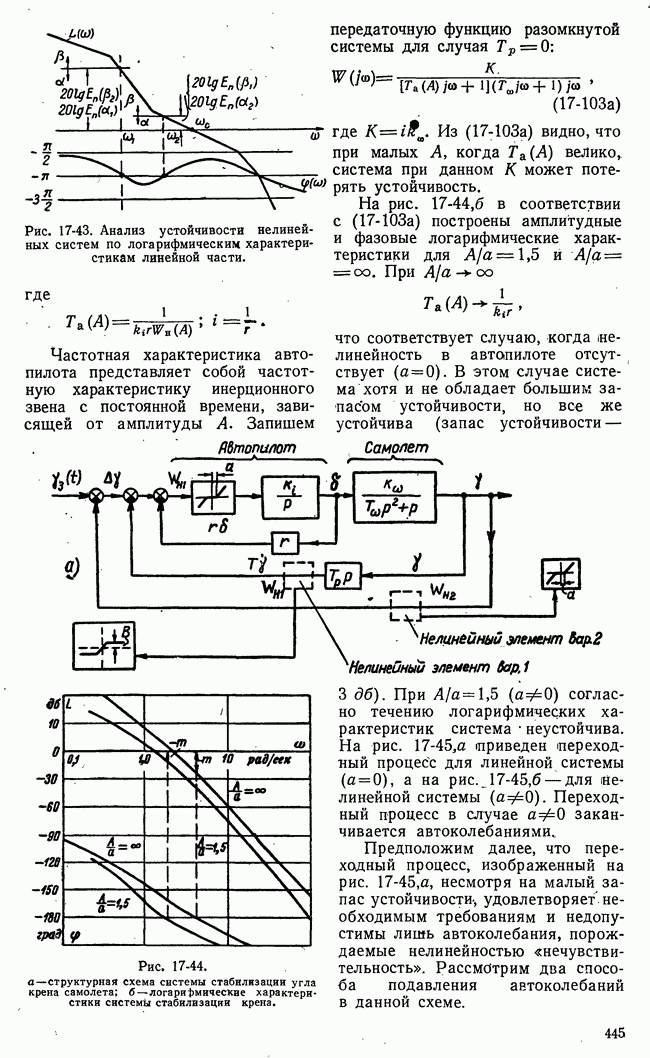
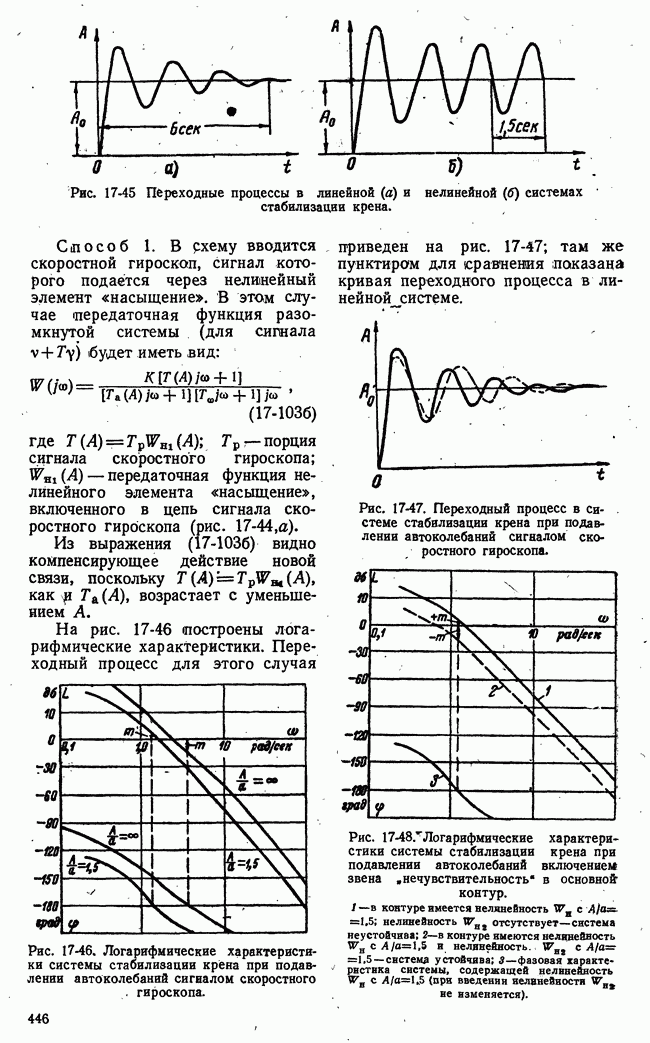
- 17-3. ВЛИЯНИЕ КОРРЕКТИРУЮЩИХ ЦЕПЕЙ НА АВТОКОЛЕБАНИЯ И НА ПЕРЕХОДНЫЕ ПРОЦЕССЫ НЕЛИНЕЙНЫХ СИСТЕМ
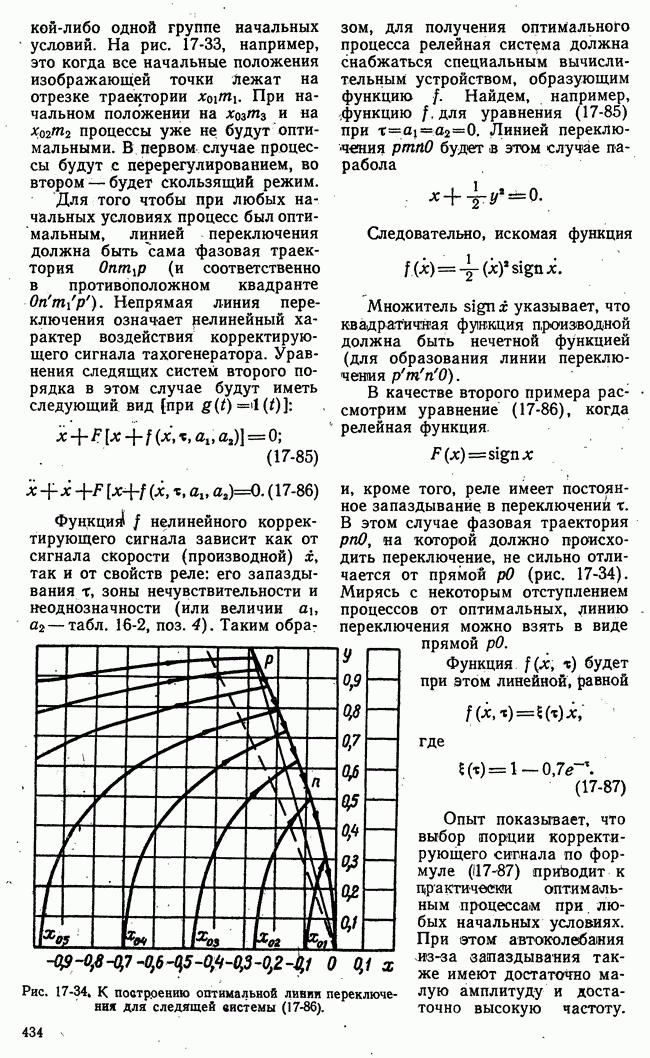
- б) Влияние корректирующих цепей на переходные процессы. Скользящие режимы. Оптимальные переходные процессы
- 17-4. ГАРМОНИЧЕСКАЯ ЛИНЕАРИЗАЦИЯ ПРОЦЕССОВ В НЕЛИНЕЙНЫХ СИСТЕМАХ
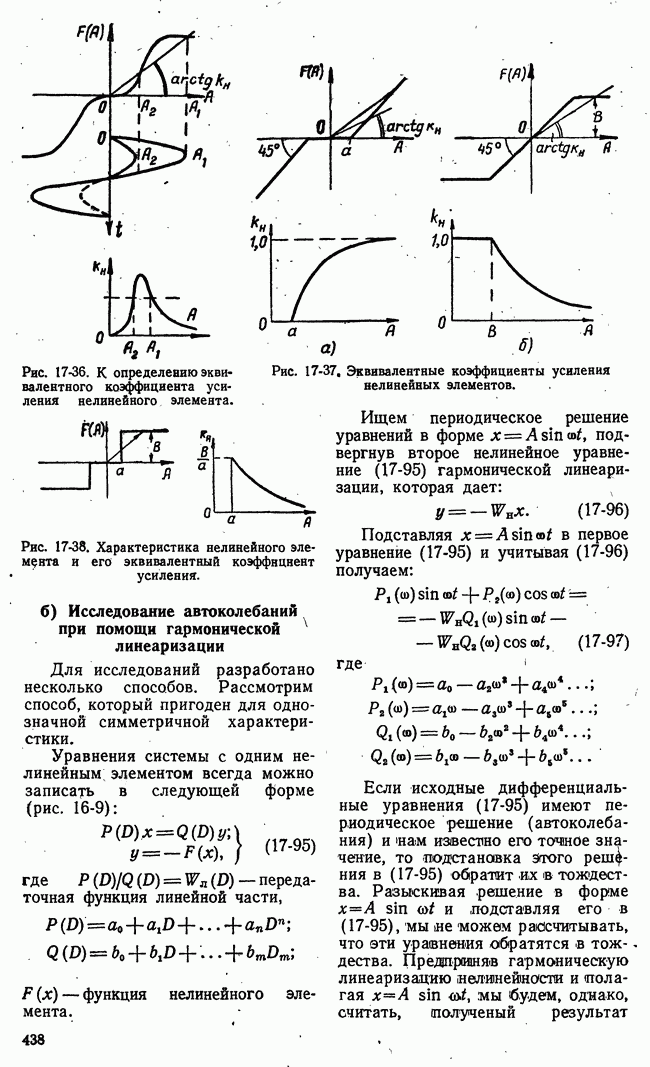
- б) Исследование автоколебаний при помощи гармонической линеаризации
- в) Гармоническая линеаризация и критерии устойчивости линейных систем
- 17-5. ТЕОРИЯ РЕЛЕЙНЫХ СИСТЕМ
- в) Частотные характеристики релейных систем
- г) Оценка устойчивости релейных систем
- д) Вынужденные колебания релейных систем. Захватывание (синхронизация или подавление) автоколебаний
- е) Вибрационная линеаризация релейных систем, Реакция релейных систем на медленно меняющиеся возмущения
- 17-6. ОПТИМАЛЬНЫЕ ПРОЦЕССЫ РЕГУЛИРОВАНИЯ
- б) Системы, оптимальные по быстродействию. Принцип максимума
- в) Системы, близкие к оптимальным по быстродействию
- ГЛАВА ВОСЕМНАДЦАТАЯ. ЭНТРОПИЯ, ИНФОРМАЦИЯ, АЛГОРИТМ В СИСТЕМАХ АВТОМАТИЧЕОКОГО УПРАВЛЕНИЯ
- 18-1. ЭНТРОПИЯ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ УПРАВЛЯЕМОГО ПРОЦЕССА
- 18-2. КОЛИЧЕСТВО ИНФОРМАЦИИ В ПРОЦЕССАХ УПРАВЛЕНИЯ
- 18-3. ЭНТРОПИЯ И ИНФОРМАЦИЯ В ЗАМКНУТЫХ СИСТЕМАХ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- 18-4. АЛГОРИТМЫ ПРОЦЕССОВ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- ГЛАВА ДЕВЯТНАДЦАТАЯ. СИСТЕМЫ ЭКСТРЕМАЛЬНОГО РЕГУЛИРОВАНИЯ
- 19-1. ПРИМЕРЫ СИСТЕМ ЭКСТРЕМАЛЬНОГО РЕГУЛИРОВАНИЯ
- 19-2. СПОСОБЫ ПОИСКА ЭКСТРЕМУМА
- б) Методы организации процесса поиска
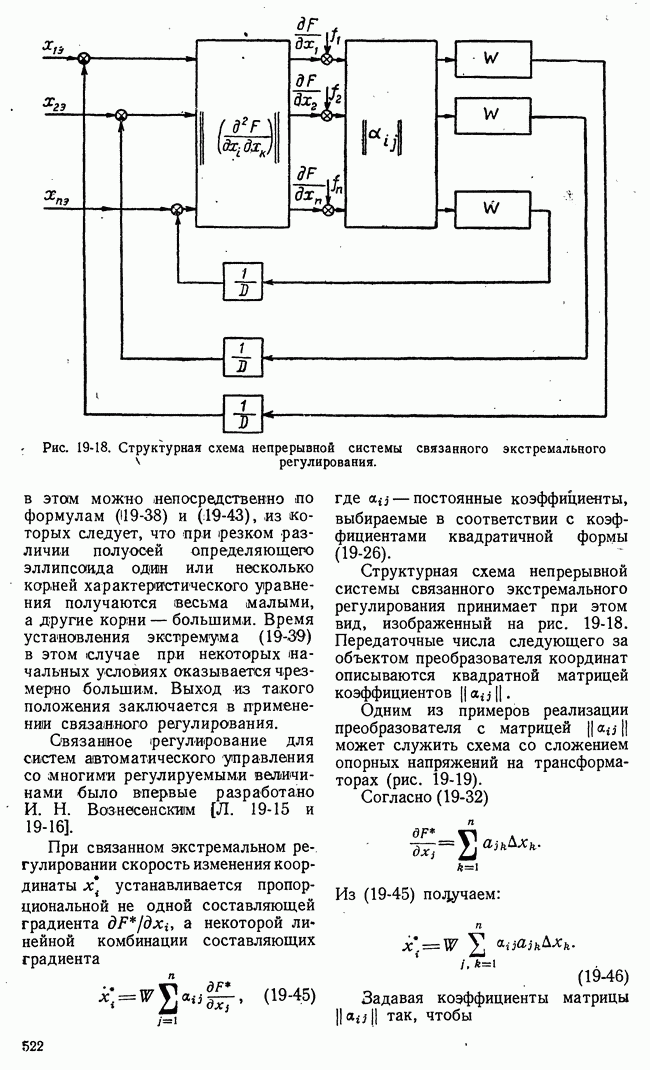
- 19-3. СТРУКТУРНЫЕ СХЕМЫ СИСТЕМ ЭКСТРЕМАЛЬНОГО РЕГУЛИРОВАНИЯ
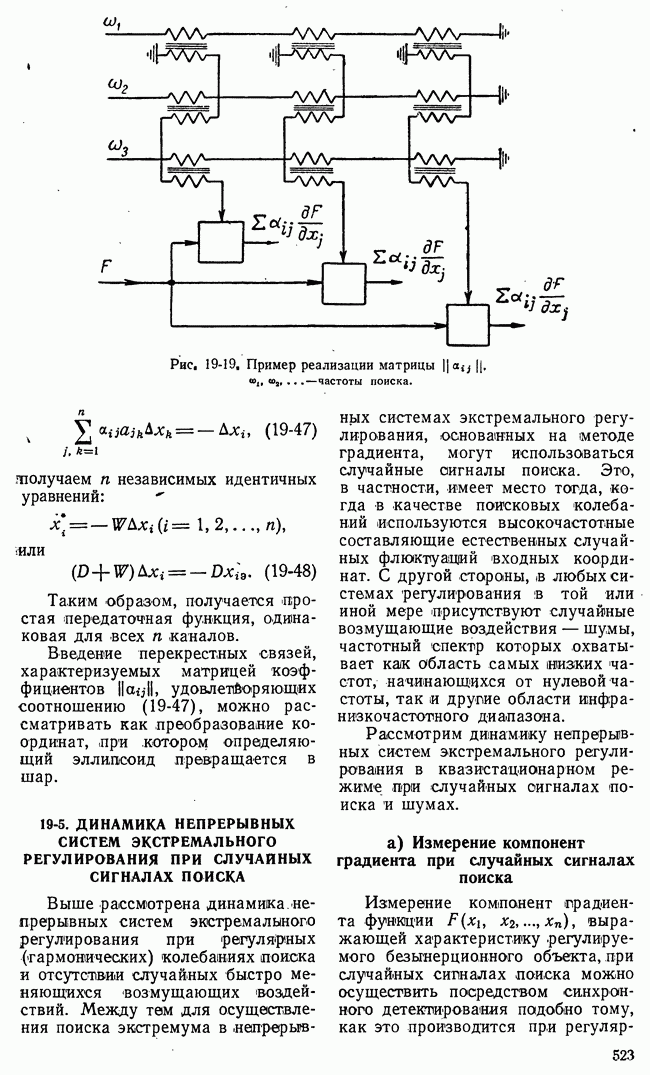
- 19-4. ДИНАМИКА НЕПРЕРЫВНЫХ СИСТЕМ ЭКСТРЕМАЛЬНОГО РЕГУЛИРОВАНИЯ В КВАЗИСТАЦИОНАРНОМ РЕЖИМЕ
- б) Динамика квазистационарного режима систем экстремального регулирования, основанных на методе градиента
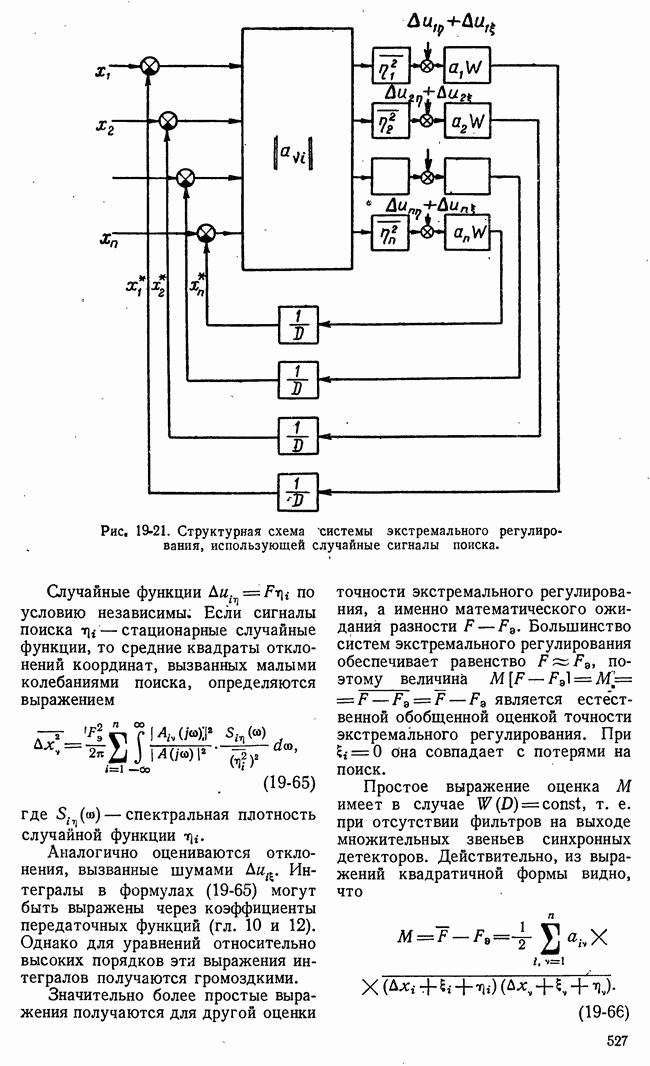
- 19-5. ДИНАМИКА НЕПРЕРЫВНЫХ СИСТЕМ ЭКСТРЕМАЛЬНОГО РЕГУЛИРОВАНИЯ ПРИ СЛУЧАЙНЫХ СИГНАЛАХ ПОИСКА
- б) Уравнения замкнутой системы экстремального регулирования
- в) Точность экстремального регулирования
- 19-6. ФОРСИРОВАННЫЕ ПРОЦЕССЫ ЭКСТРЕМАЛЬНОГО РЕГУЛИРОВАНИЯ ОДНОМЕРНОГО БЕЗЫНЕРЦИОННОГО ОБЪЕКТА
- ГЛАВА ДВАДЦАТАЯ. СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ С САМОНАСТРАИВАЮЩИМИСЯ КОРРЕКТИРУЮЩИМИ УСТРОЙСТВАМИ
- 20-1. СИСТЕМЫ С РАЗОМКНУТЫМИ ЦЕПЯМИ НАСТРОЙКИ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ
- 20-2. СИСТЕМЫ С ЗАМКНУТЫМИ ЦЕПЯМИ НАСТРОЙКИ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ
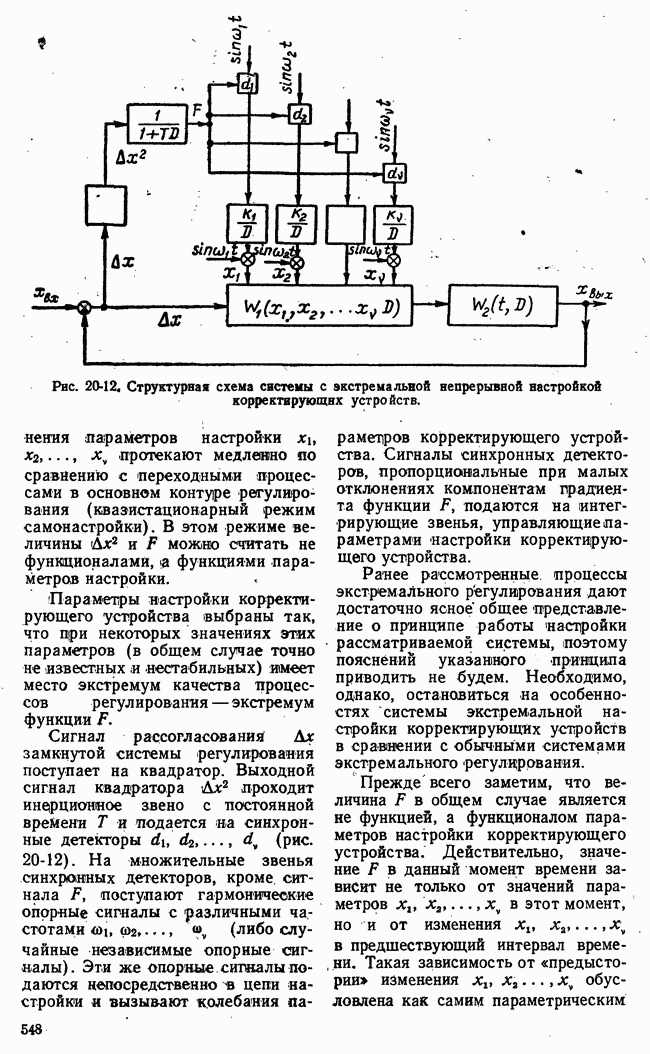
- 20-3. СИСТЕМЫ С ЭКСТРЕМАЛЬНОЙ НАСТРОЙКОЙ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ
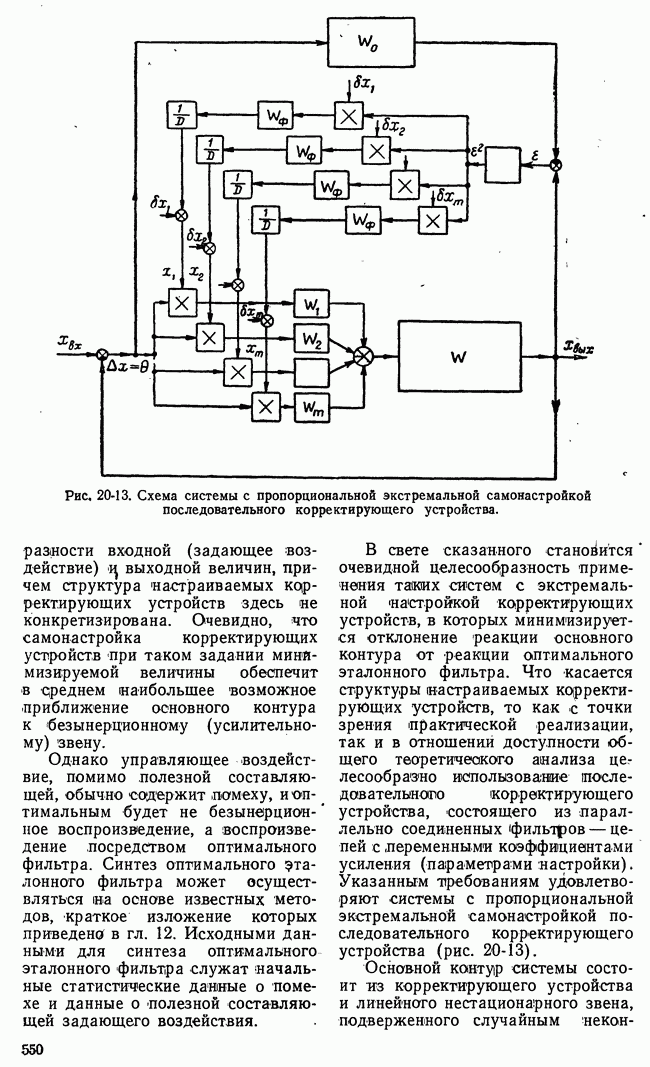
- 20-4. СТАТИСТИЧЕСКАЯ ДИНАМИКА НЕПРЕРЫВНЫХ СИСТЕМ С ЭКСТРЕМАЛЬНОЙ НАСТРОЙКОЙ ПОСЛЕДОВАТЕЛЬНЫХ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ
- б) Уравнения замкнутой самонастраивающейся системы
- в) Случай сильной фильтрации. Квазистационарный режим
- г) Общий случай квазистационарного режима
- ГЛАВА ДВАДЦАТЬ ПЕРВАЯ. ИГРОВЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
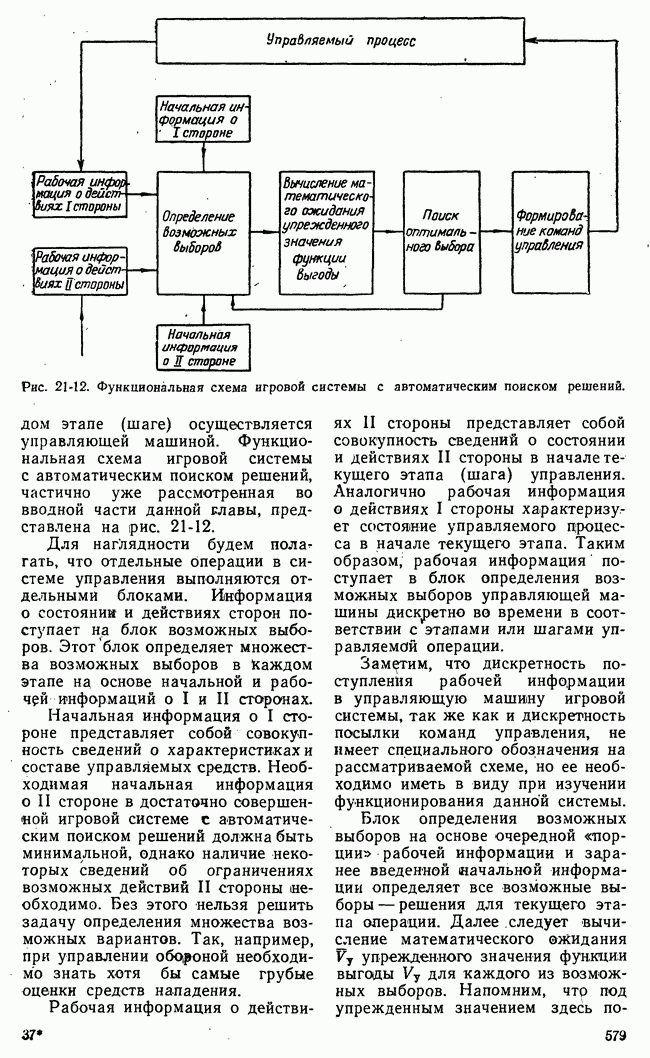
- 21-1. НАЗНАЧЕНИЕ И ПРИНЦИПЫ ДЕЙСТВИЯ ИГРОВЫХ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- 21-2. НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ ИГР
- 21-3. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ. ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
- 21-4. ОБ АЛГОРИТМАХ ИГРОВЫХ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- ПРИЛОЖЕНИЯ