| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
21-3. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ. ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
Современная наука и техника все чаще сталкиваются с задачами отыскания оптимальных процессов
и решений. В одних областях, как-то: планирование производства, планирование перевозок и др., прежде всего выступают проблемы нахождения оптимальных решений и процессов. В других областях, к которым относятся и области применения игровых систем, требуется автоматическое оптимальное управление.
Математика давно располагает методами нахождения значений переменных или функций, соответствующих экстремуму функции или функционала (оператора). Это прежде всего способ отыскания экстремума функции одной или нескольких переменных при дополнительных условиях (ограничениях) в виде произвольного числа алгебраических или трансцендентных уравнений и классический метод вариационного исчисления.
Одной из типичных классических задач вариационного исчисления является нахождение функции (процесса)  максимизирующей (обеспечивающей максимум) определенный интеграл (функционал) вида
максимизирующей (обеспечивающей максимум) определенный интеграл (функционал) вида 

где  некоторая функция x и ее производных, и заданы граничные условия в виде значений
некоторая функция x и ее производных, и заданы граничные условия в виде значений

при  (начало процесса) и
(начало процесса) и  (конец процесса). Заменой переменных
(конец процесса). Заменой переменных

задача приводится к отысканию функции, соответствующей максимуму (экстремаль) функционала: 

при заданных граничных значениях

Решение задачи дается вариационным исчислением в виде решения соответствующего дифференциального уравнения Эйлера порядка  при заданных граничных условиях.
при заданных граничных условиях.

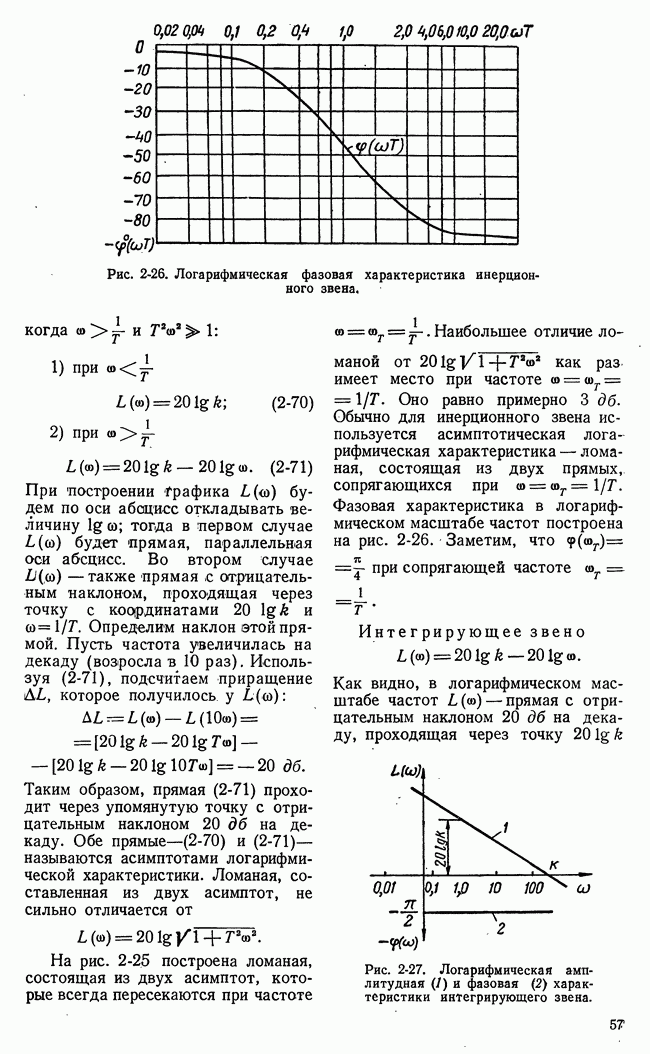
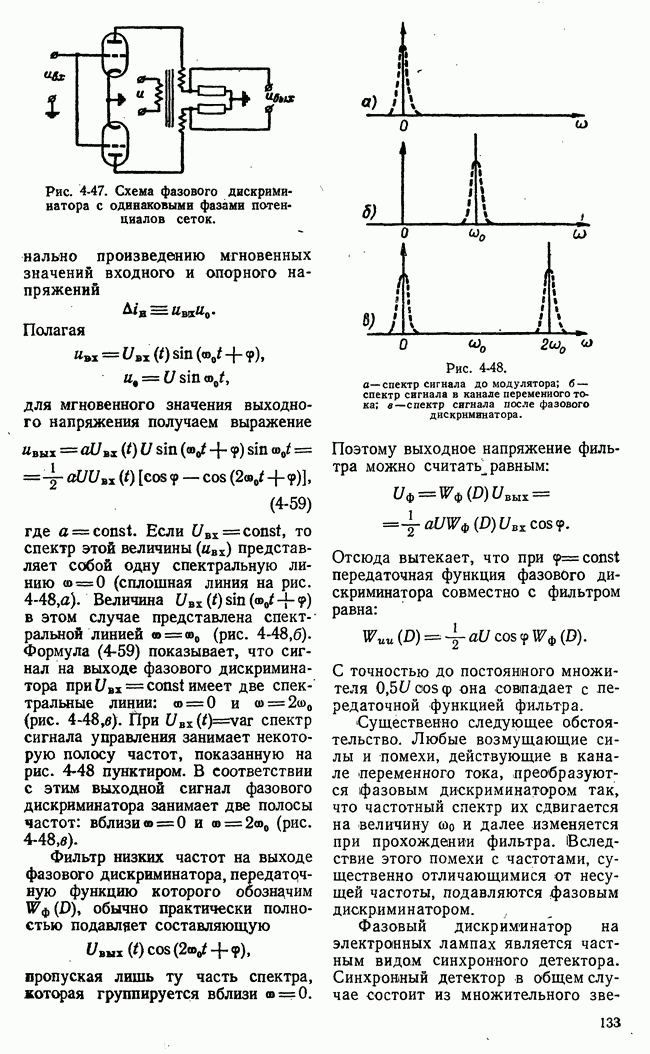
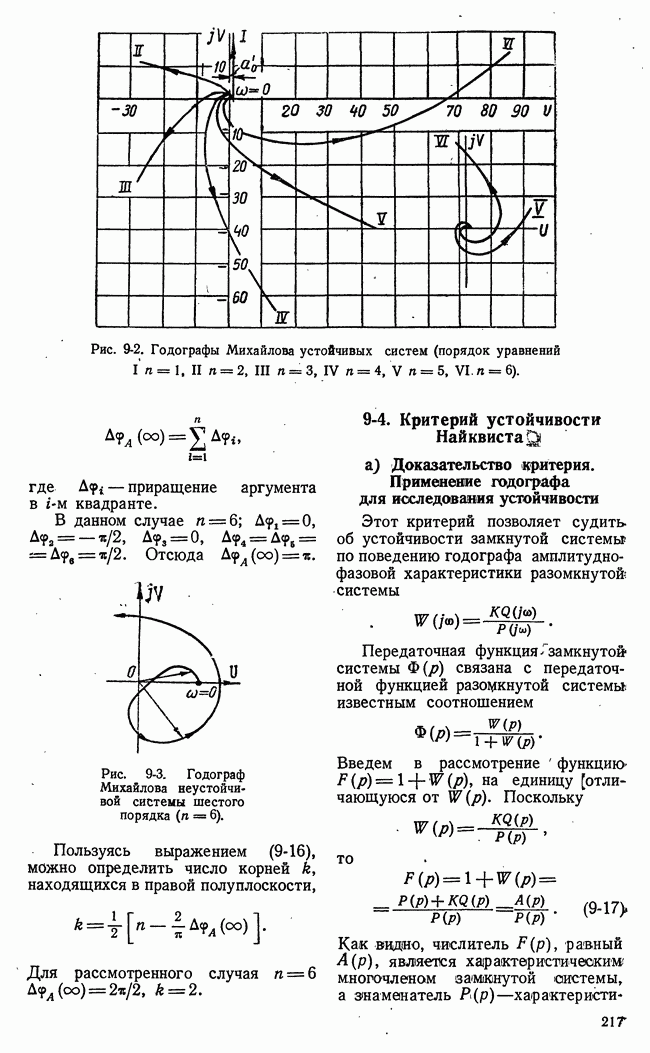
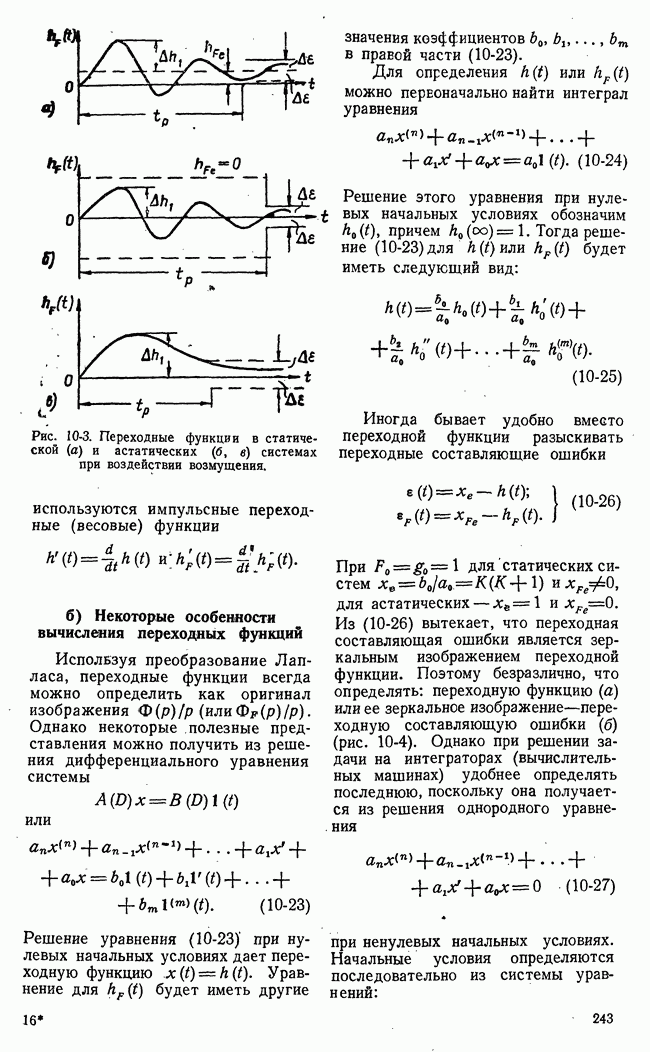
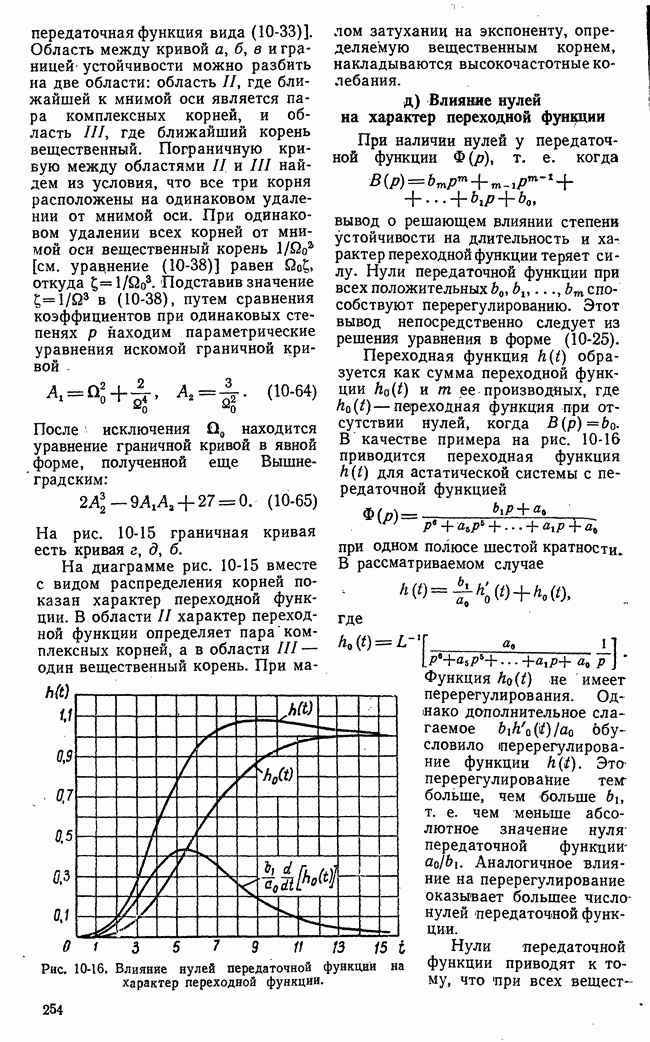
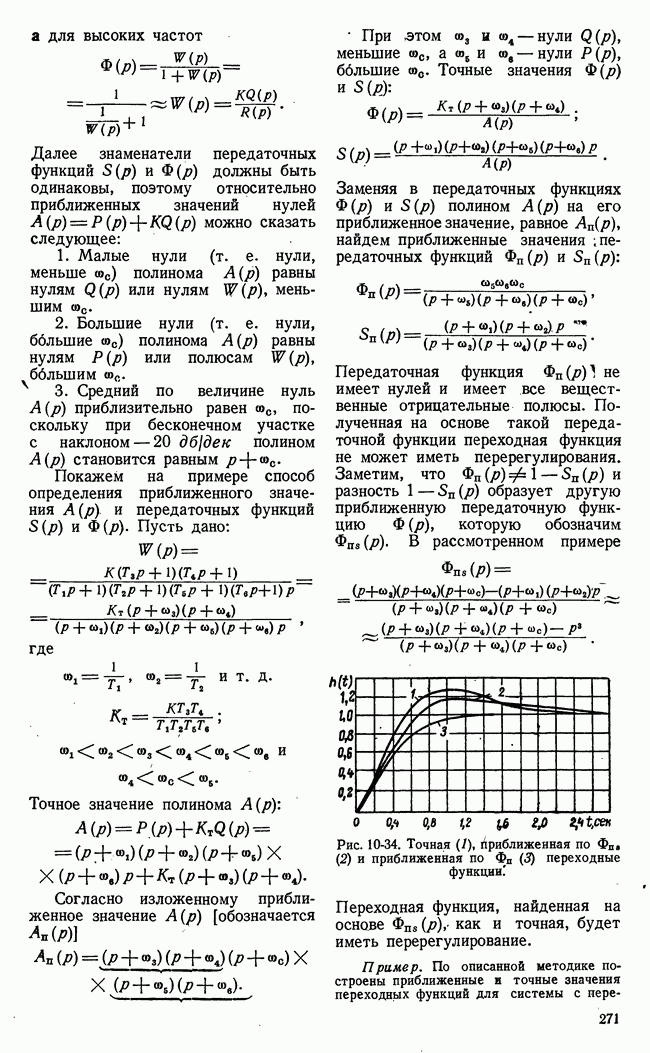
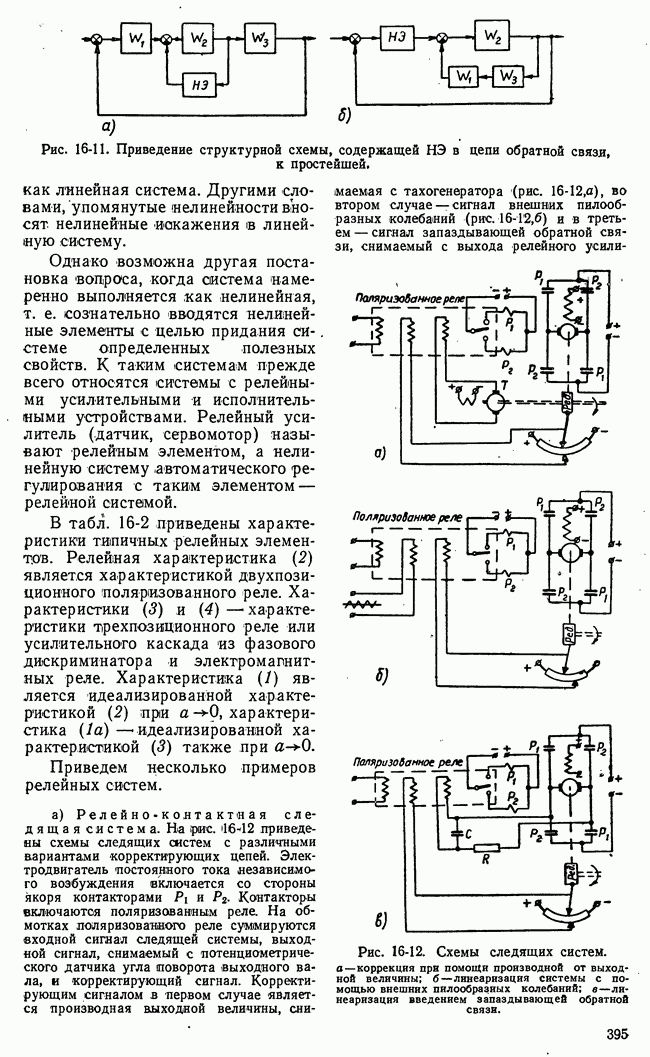
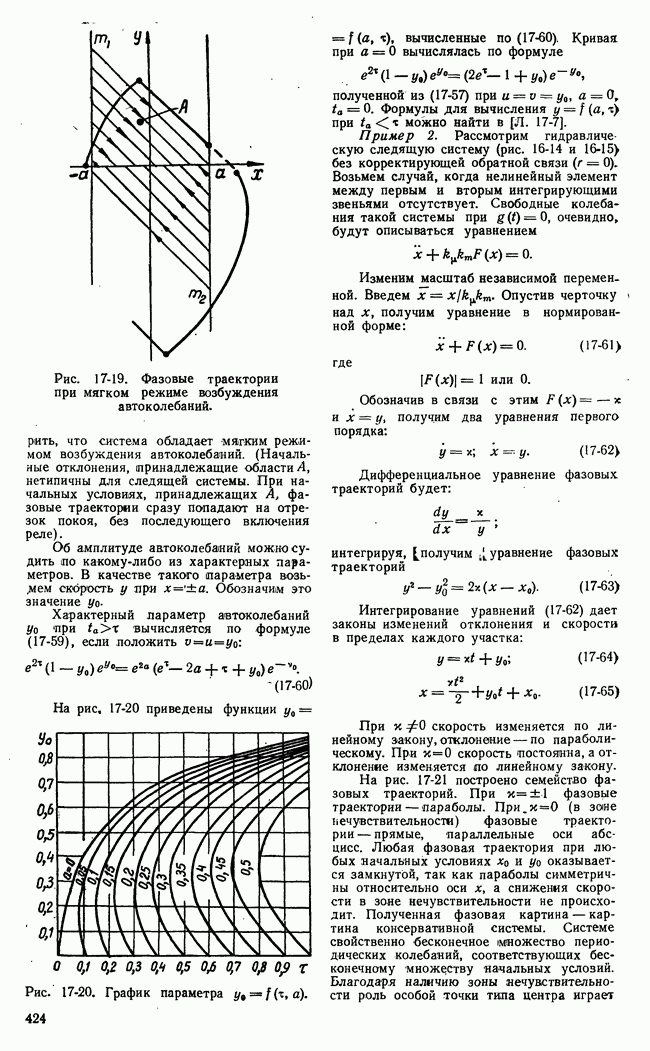
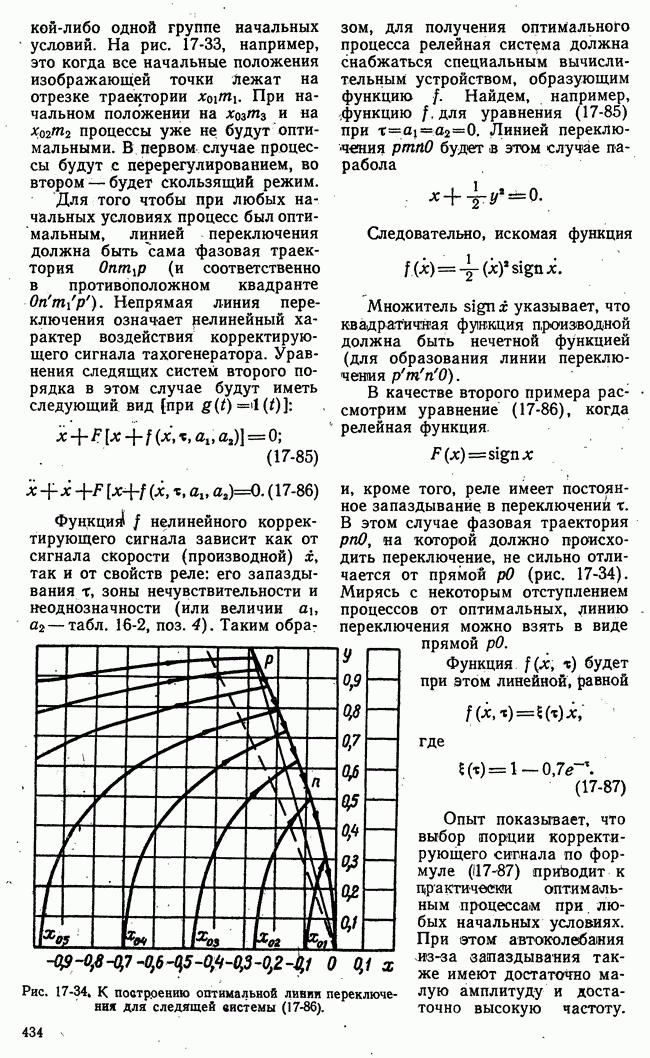
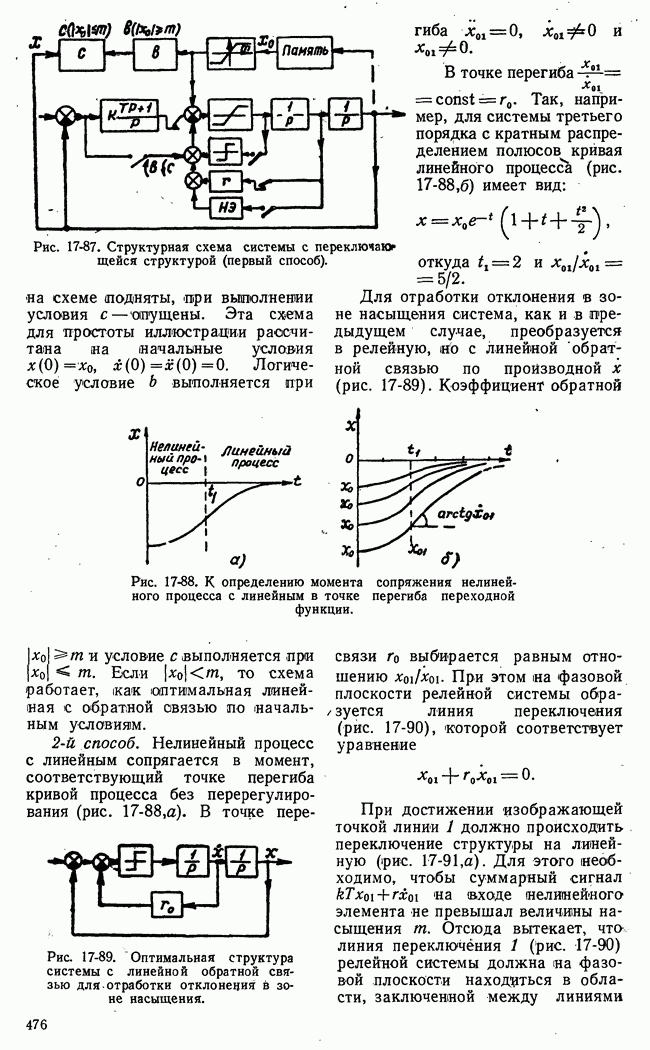
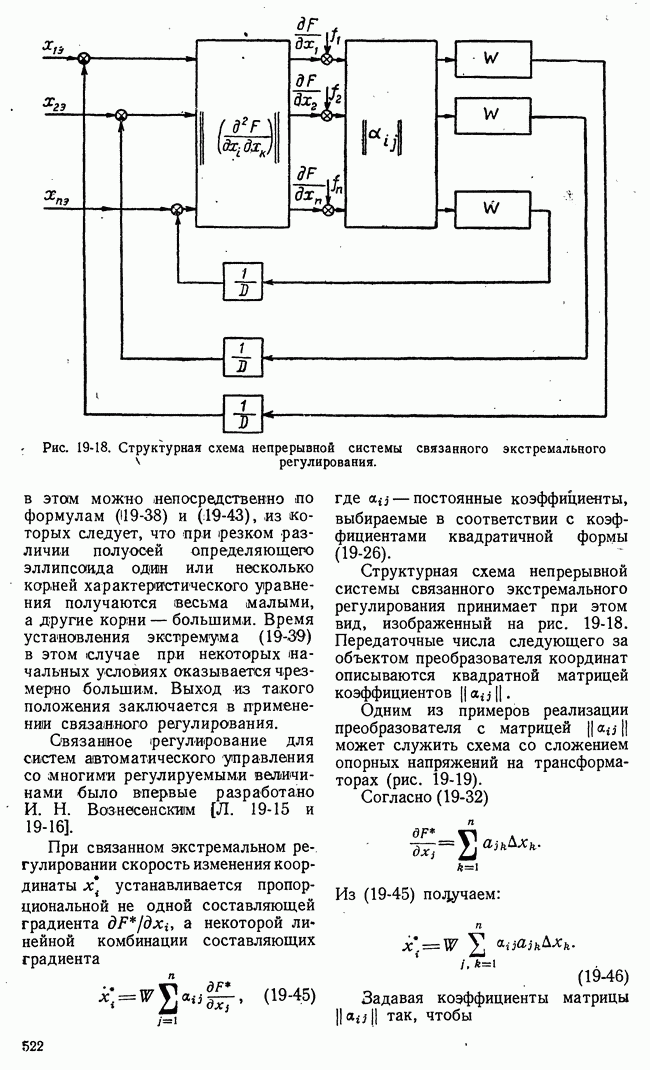
Рис. 21-7. Пример функции одной переменной, иллюстрирующий недостаточность классических методов для решения проблем оптимальности.
Аналогично решается задача определения экстремума функционала

при более общих условиях типа системы дифференциальных уравнений

Классические методы вариационного исчисления и методы определения экстремума функции недостаточны для эффективного решения задач оптимальности в проблемах автоматического управления, рационального планирования и других проблемах.
Применение классических методов вариационного исчисления наталкивается на большие трудности при ограничениях переменных в виде неравенств. Число элементарных арифметических операций, необходимых для достаточно точного численного решения уравнения Эйлера с заданными условиями частично в начале и частично в конце (граничные условия), во многих практических задачах чрезмерно велико. Классический методы позволяют определить лишь те значения (рис. 21-7) функционала или функции, которым соответствует двусторонний
экстремум 2, 5 (вариации первого порядка малости обращаются в нуль). В практических задачах часто необходимо найти просто положение наибольшего 1 или наименьшего 4 значения функции или функционала на границе области переменных, определяемой ограничениями типа неравенств.
Кроме того, могут встретиться двусторонние экстремумы неаналитического типа 3 (рис. 21-7), отыскание которых требует в лучшем случае видоизменения классических приемов.
Все это вызвало в последнее время, с одной стороны, развитие вариационного исчисления в направлении решения неклассических задач, а с другой — разработку приближенного общего метода, называемого динамическим программированием. Понтрягиным и его учениками создан важный метод решения задач оптимального управления, получивший название принципа максимума [Л. 21-6]. Метод динамического программирования развит Беллманом [Л. 21-5]. Что касается определения экстремума функции многих переменных три ограничении типа неравенств, то для решения частного вида этой задачи широко попользуется способ линейного программирования. Хотя оба последних метода разработаны как чисто вычислительные, мы изложим основные идеи этих методов для выяснения целесообразного вида алгоритмов игровых систем автоматического управления.

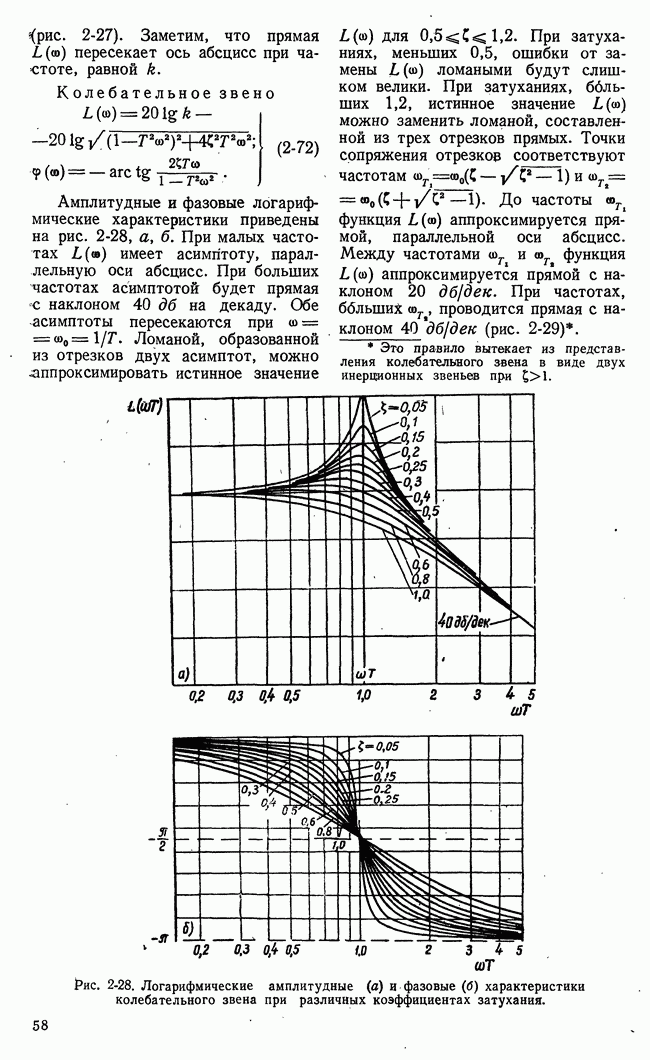
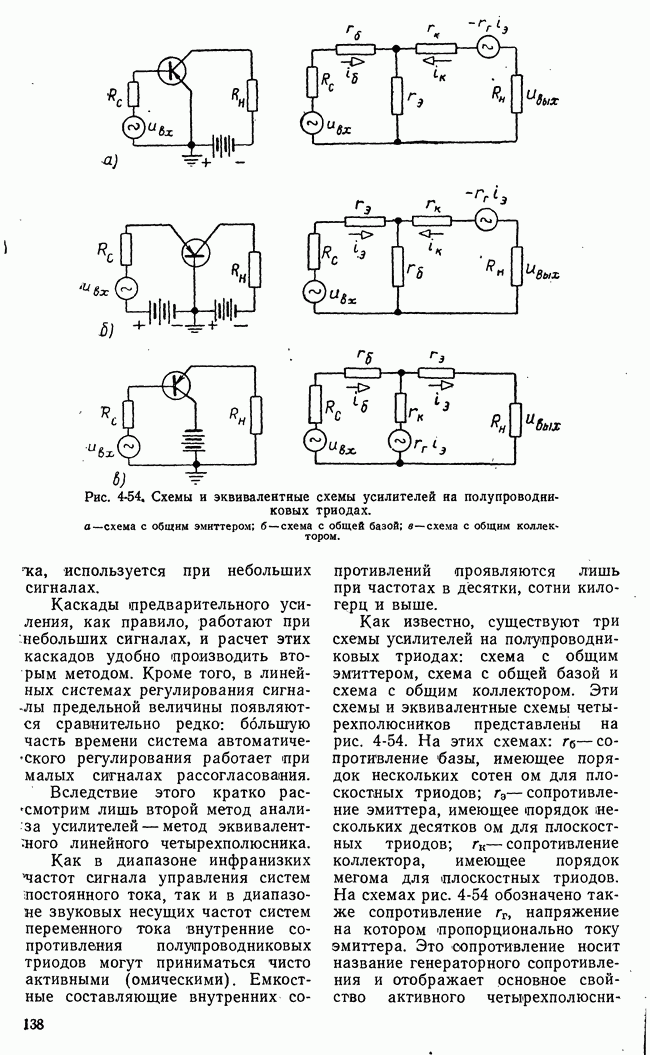
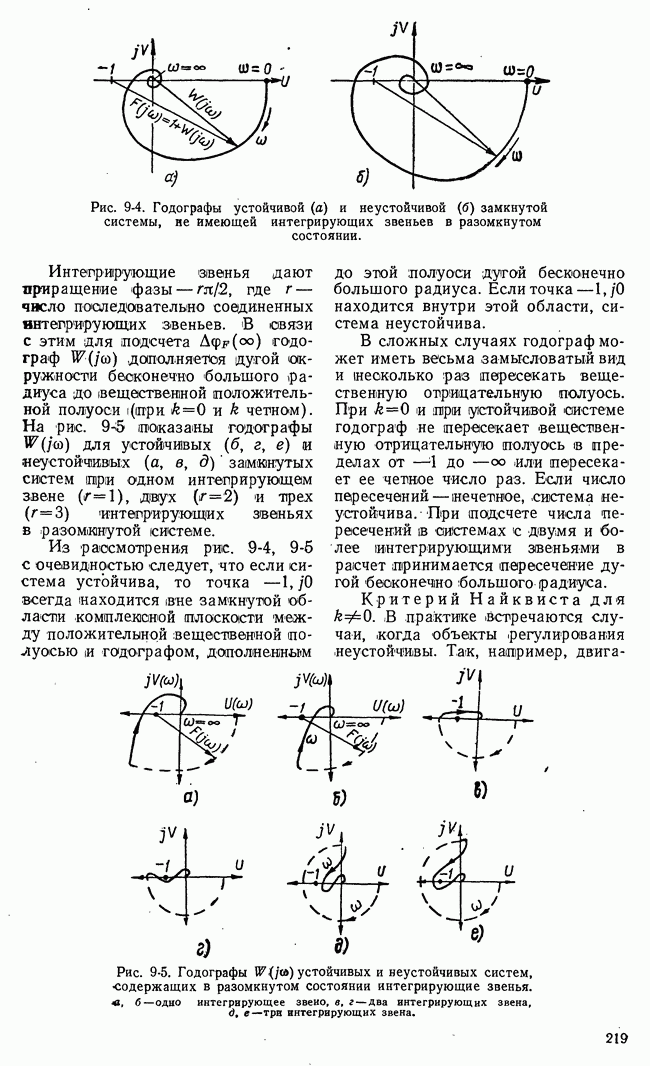
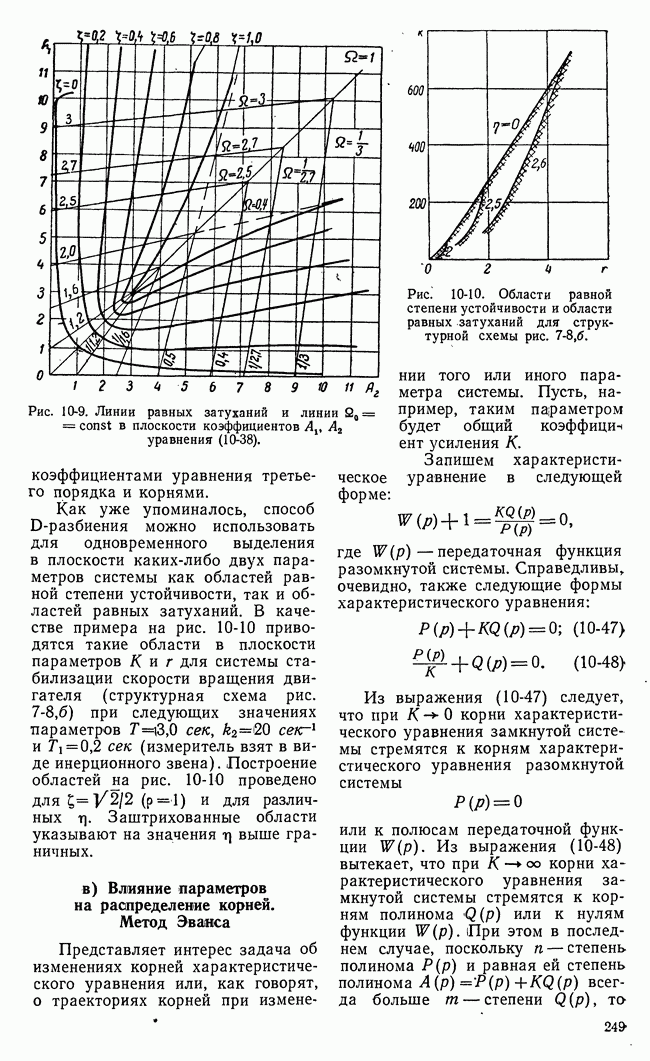
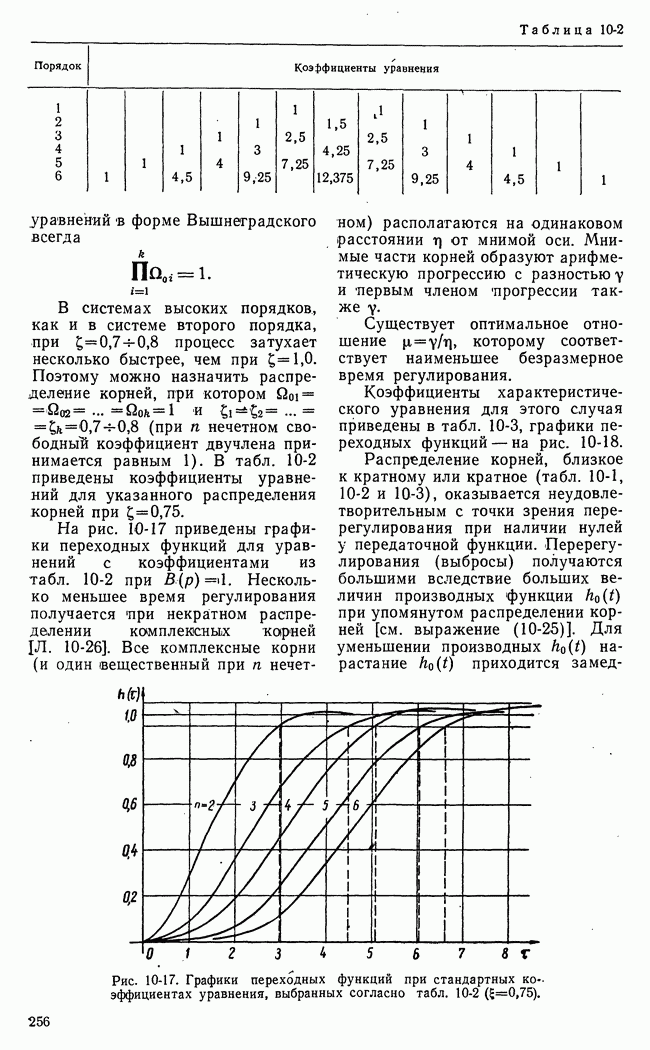
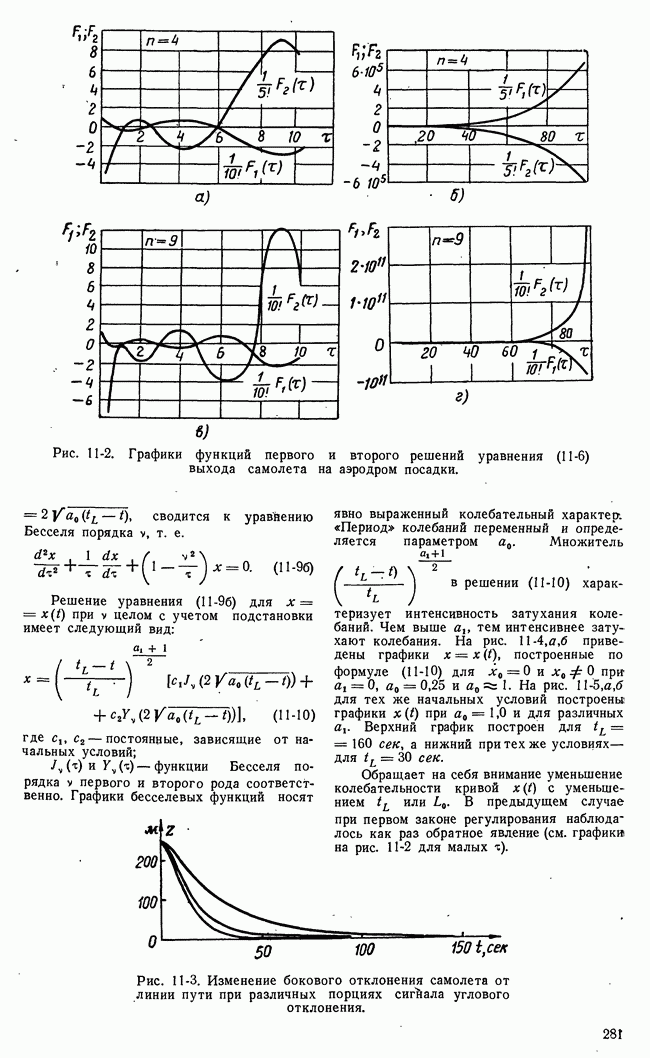
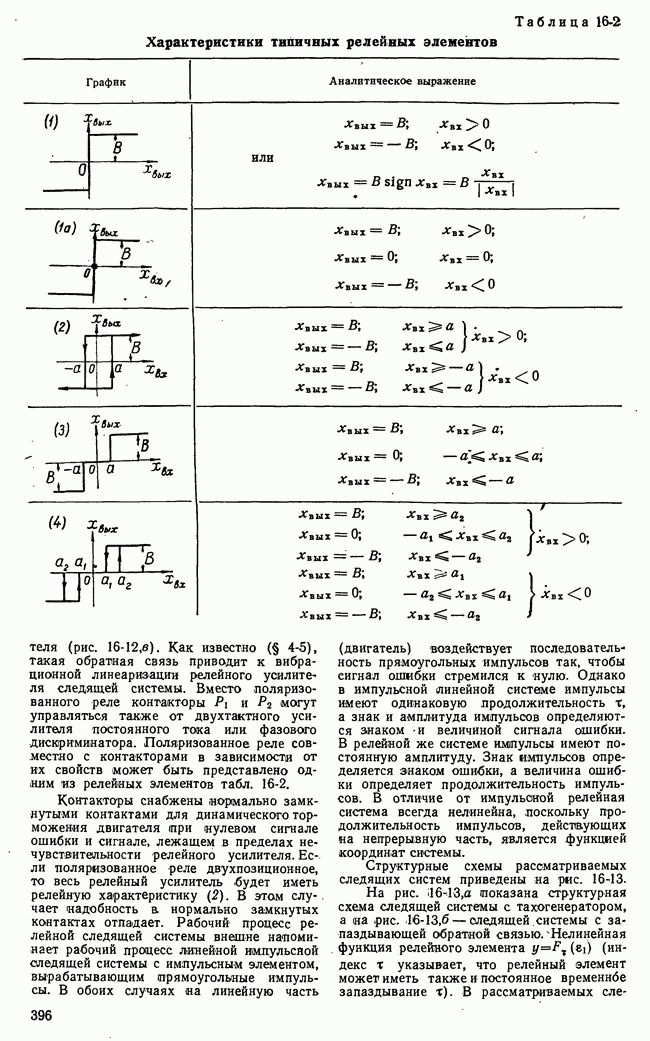
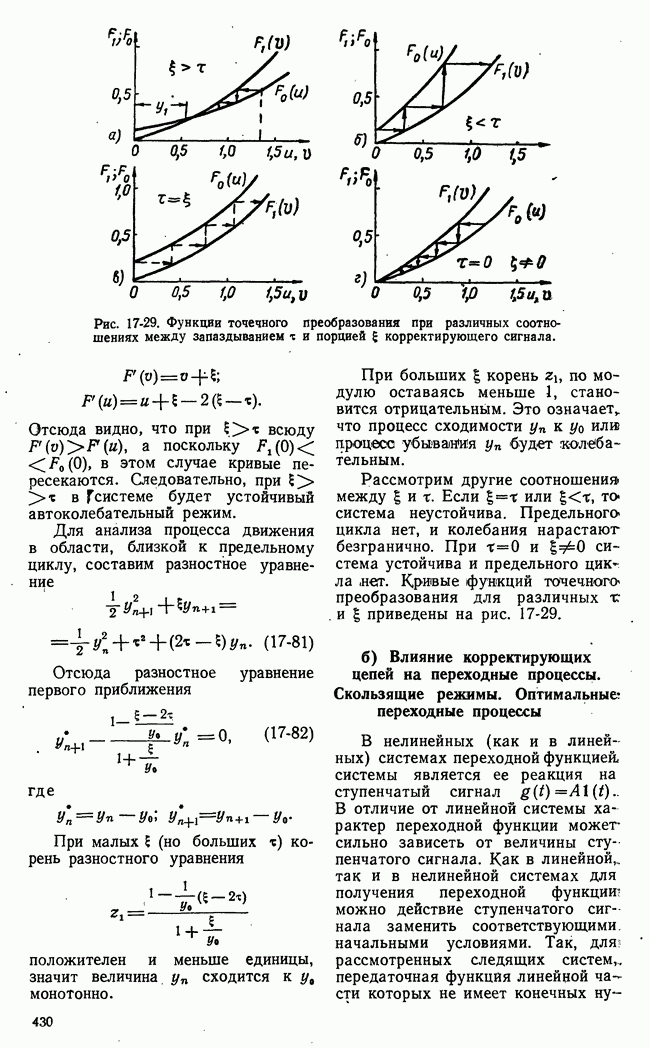
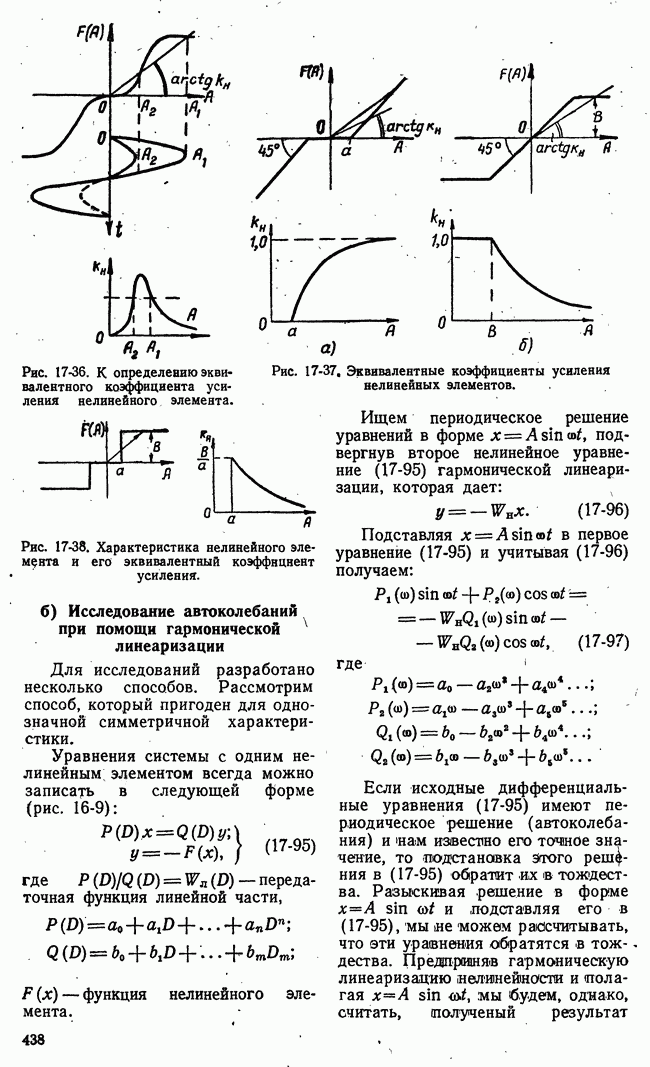
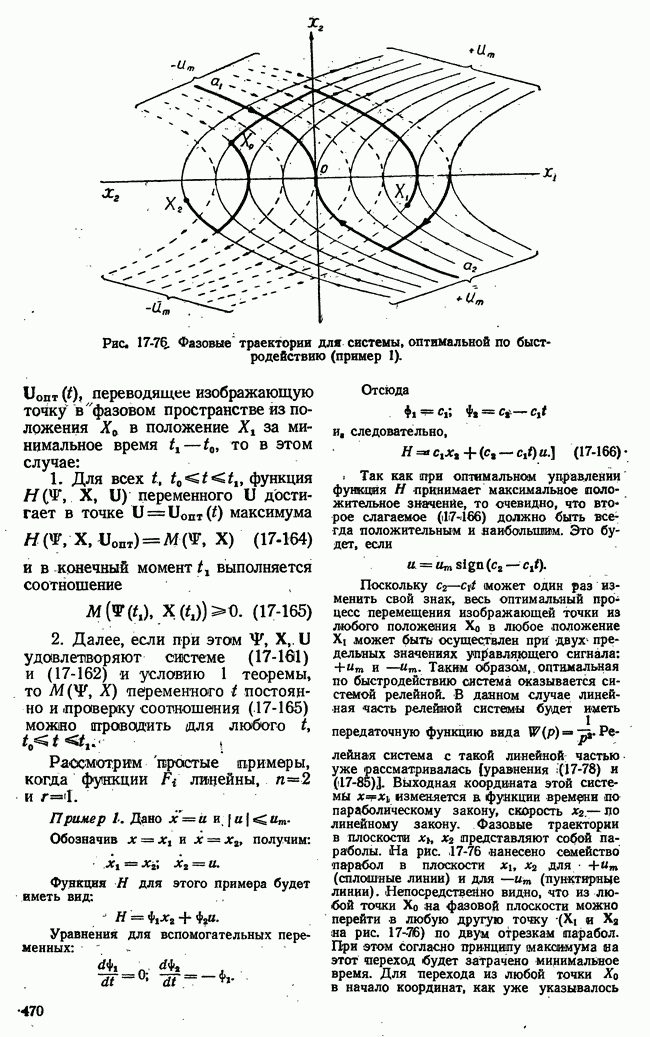
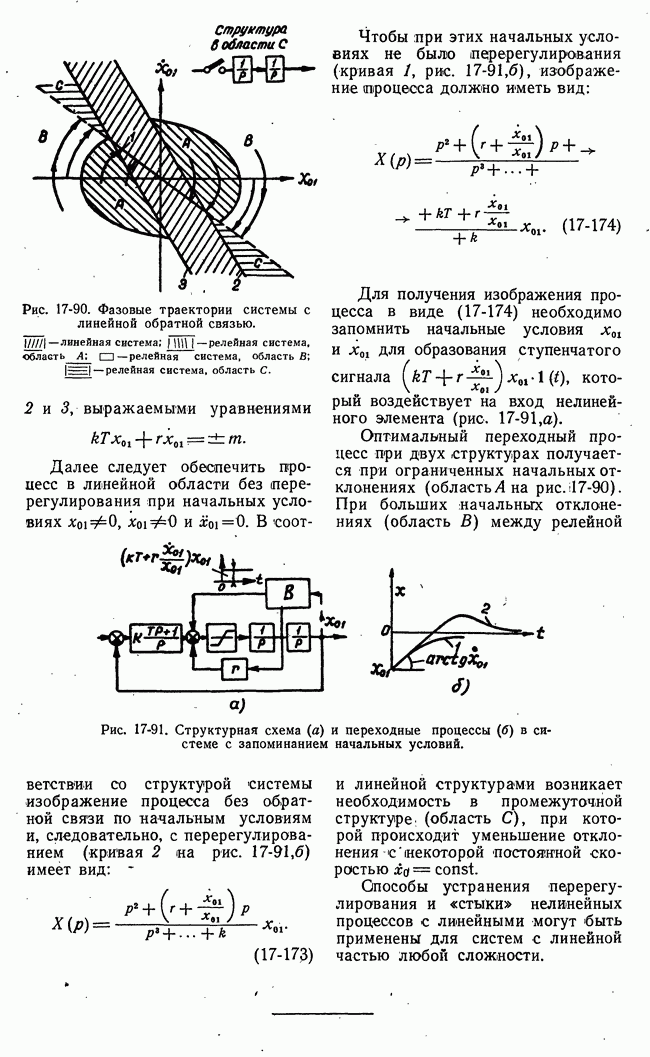
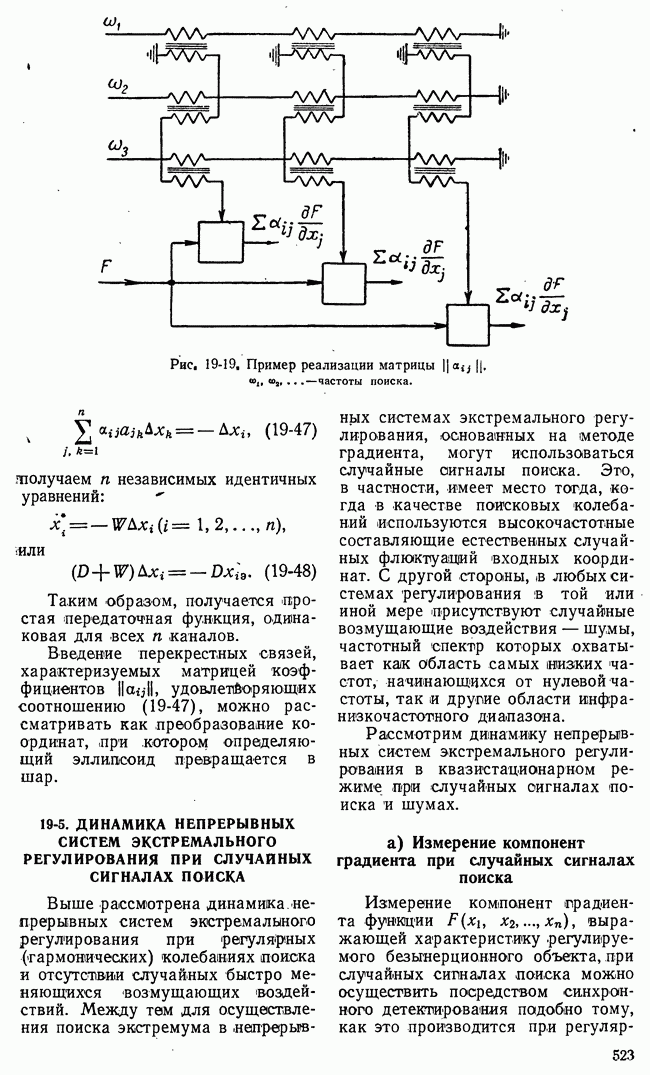
Рис. 21-8. К пояснению основной идеи метода динамического программирования.
а) Динамическое программирование
Весьма часто процессы и решения по своей природе являются многоэтапными или многошаговыми. Оптимизация многоэтапных в том или ином смысле процессов и решений и составляет предмет динамического программирования.
Для пояснения основной идеи динамического программирования рассмотрим одну простую иллюстрацию. Пусть состояние некоторой системы характеризуется координатами х, у, принимающими  дискретных значений
дискретных значений  Требуется перевести систему из состояния
Требуется перевести систему из состояния  в состояние
в состояние  На плоскости существует множество процессов или траекторий перевода системы из
На плоскости существует множество процессов или траекторий перевода системы из  (рис. 21-8,а). Все множество траекторий образуется путем перехода изображающей точки из какого-либо квадрата в квадрат, лежащий справа, или в квадрат, лежащий сверху. Всего изображающая точка при любой траектории пройдет через
(рис. 21-8,а). Все множество траекторий образуется путем перехода изображающей точки из какого-либо квадрата в квадрат, лежащий справа, или в квадрат, лежащий сверху. Всего изображающая точка при любой траектории пройдет через  этапов или сделает
этапов или сделает  переходов. Пусть далее для каждой траектории перехода из состояния
переходов. Пусть далее для каждой траектории перехода из состояния  в состояние
в состояние  определена функция выгоды
определена функция выгоды  Функция выгоды
Функция выгоды  образуется как сумма приращений
образуется как сумма приращений
функций выгоды  во всех квадратах, через которые пройдет изображающая точка.
во всех квадратах, через которые пройдет изображающая точка.
Требуется перевести систему из положения  в положение
в положение  по такой траектории, чтобы суммарная функция выгоды
по такой траектории, чтобы суммарная функция выгоды  была наибольшей. Итак, весь процесс перевода системы из начального состояния в конечное представляет собой
была наибольшей. Итак, весь процесс перевода системы из начального состояния в конечное представляет собой  -этапный процесс. При этом на каждом этапе следует принять такое решение о направлении движения (вверх или вправо), чтобы получить наибольшее значение суммарной функции выгоды
-этапный процесс. При этом на каждом этапе следует принять такое решение о направлении движения (вверх или вправо), чтобы получить наибольшее значение суммарной функции выгоды 
Решение поставленной задачи можно, конечно, попытаться получить методом слепого поиска или перебором всех возможных траекторий. Однако такой подход возможен только в очень простых случаях. В более или менее сложных случаях, для которых и разработан собственно метод динамического программирования, слепой поиск оптимальных решений требует непомерной вычислительной работы.
В основе метода динамического программирования лежит интуитивный принцип оптимальности, который позволяет решать задачи оптимизации многоэтапных процессов последовательно путем построения рекуррентных соотношений. Для применения принципа оптимальности в рассматриваемом примере разделим траекторию изображающей точки на два участка: от начала до некоторого промежуточного этапа  и от этого промежуточного этапа до конца
и от этого промежуточного этапа до конца  (рис. 21-8,6).
(рис. 21-8,6).
В соответствии с принципом оптимальности каков бы ни был начальный участок траектории и какое бы значение функции выгоды ни накопилось к этапу  для того чтобы в сложившейся ситуации все-таки получить наивысший эффект, последний участок траектории от
для того чтобы в сложившейся ситуации все-таки получить наивысший эффект, последний участок траектории от  до
до  должен быть оптимальным. Очевидно, чем ближе промежуточный этап
должен быть оптимальным. Очевидно, чем ближе промежуточный этап  к конечному, тем проще определить оптимальную траекторию. Так, для промежуточного этапа
к конечному, тем проще определить оптимальную траекторию. Так, для промежуточного этапа  наибольшее значение функции выгоды
наибольшее значение функции выгоды  будет равно наибольшей из двух сумм:
будет равно наибольшей из двух сумм:

где

Вместе с определением определяется и траектория, от  т. е. движение вверх—направо или направо—вверх. После определения
т. е. движение вверх—направо или направо—вверх. После определения  можно» найти:
можно» найти:

и

где

Поступая далее аналогичным образом, можно шаг за шагом для любого промежуточного этапа  определить наибольшее значение функции выгоды
определить наибольшее значение функции выгоды  которая накопится при перемещении от этого промежуточного этапа до конца. Одновременно с определением
которая накопится при перемещении от этого промежуточного этапа до конца. Одновременно с определением  определяется и траектория перемещения от
определяется и траектория перемещения от  до
до  вдоль которой накапливается наибольшее значение функции выгоды
вдоль которой накапливается наибольшее значение функции выгоды  Траектория эта оптимальна. Последней из всех
Траектория эта оптимальна. Последней из всех  определяется
определяется  и соответствующая ей оптимальная траектория перемещения из
и соответствующая ей оптимальная траектория перемещения из  что и является решением поставленной задачи.
что и является решением поставленной задачи.
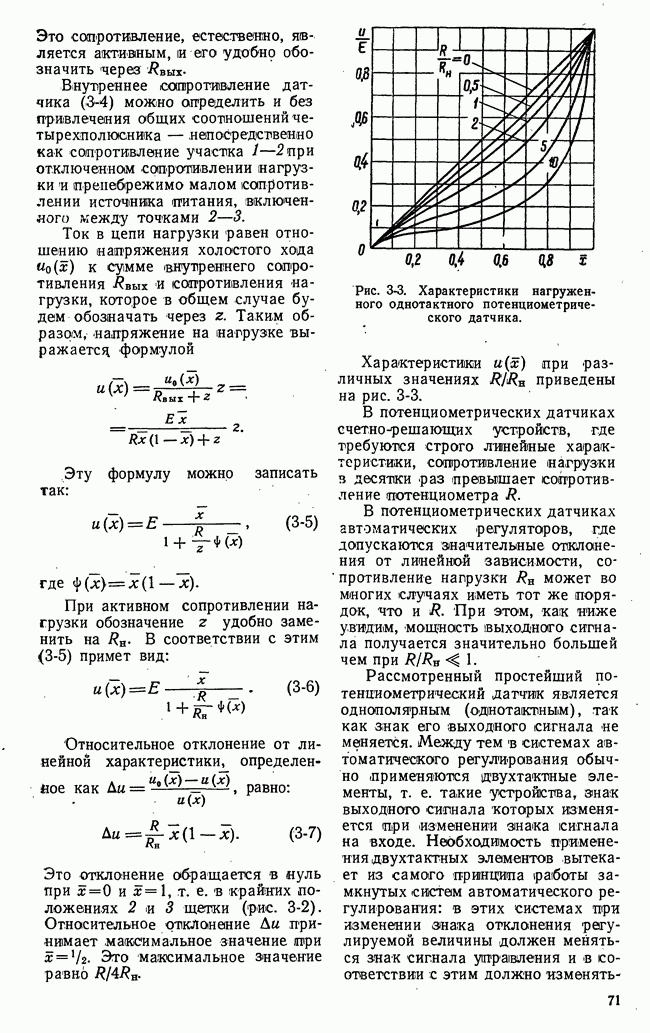
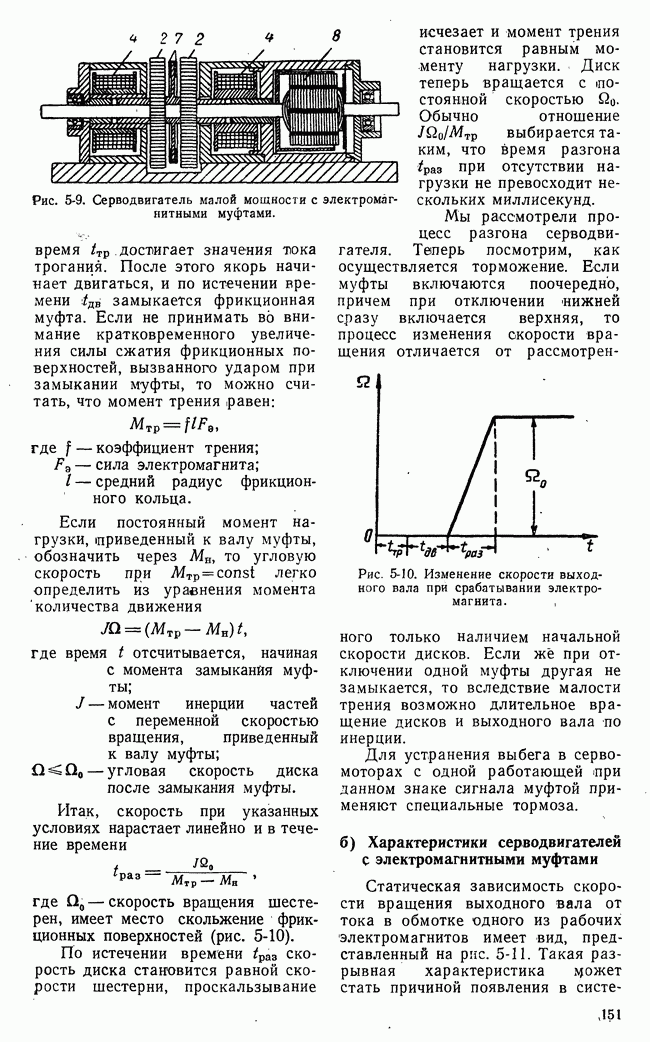
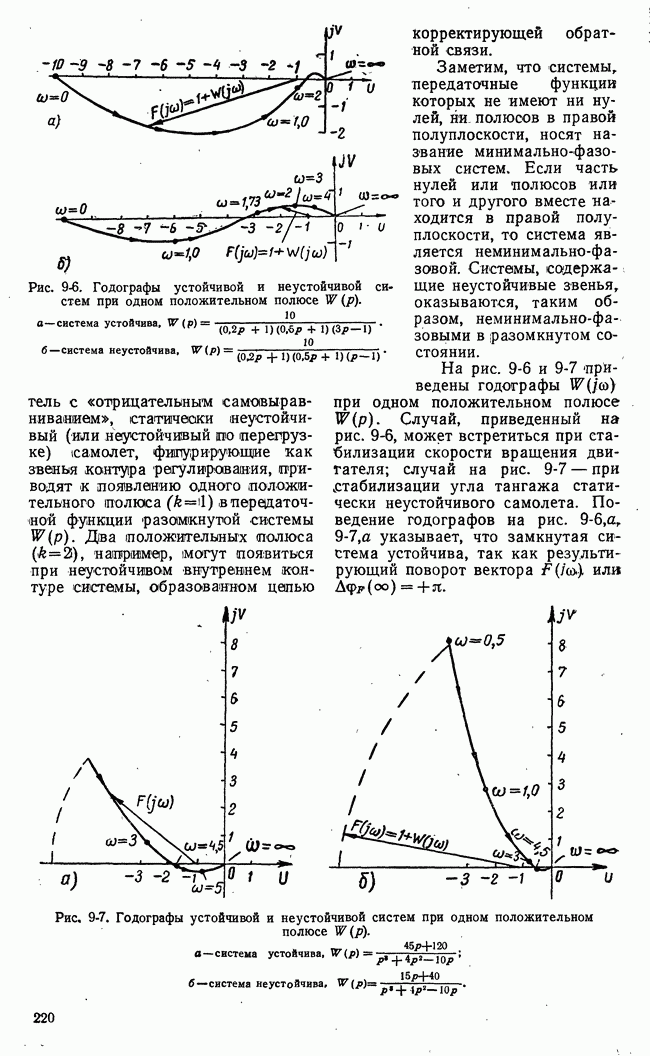
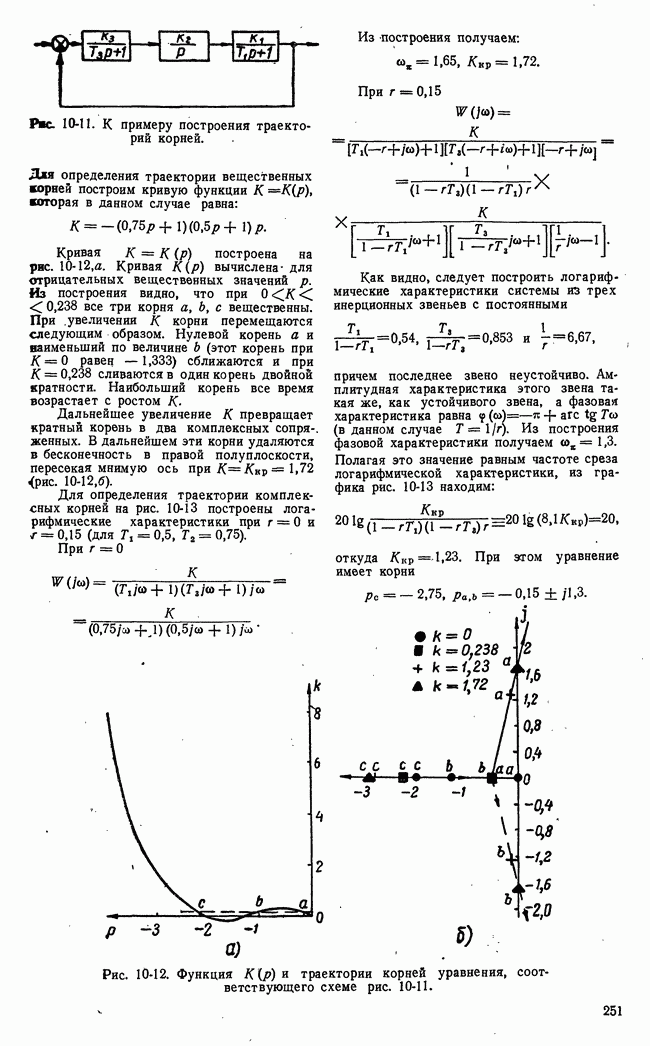
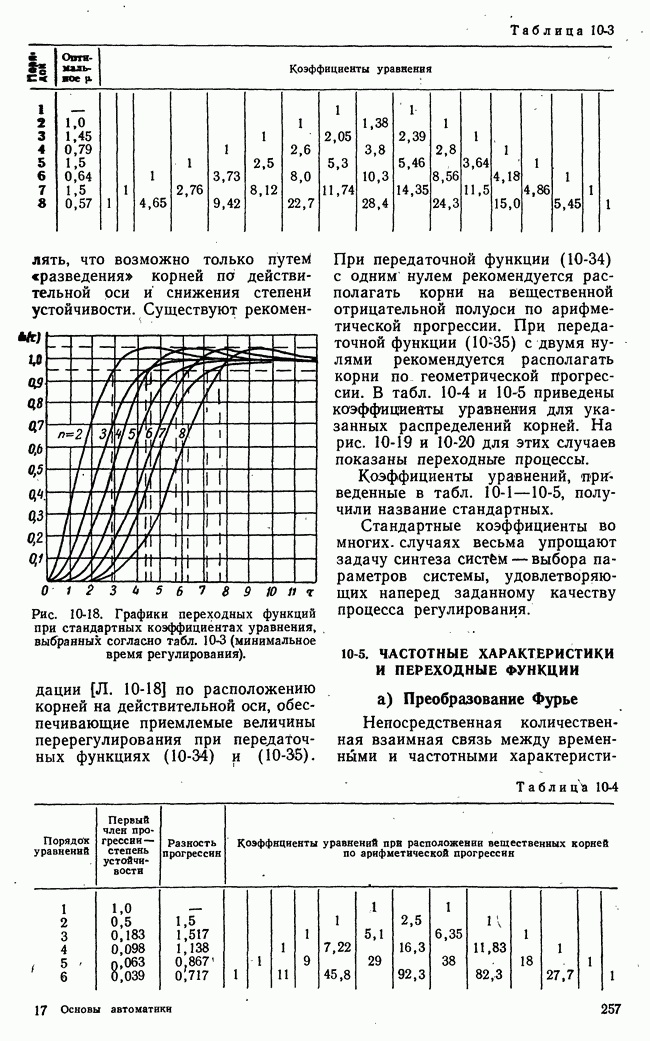
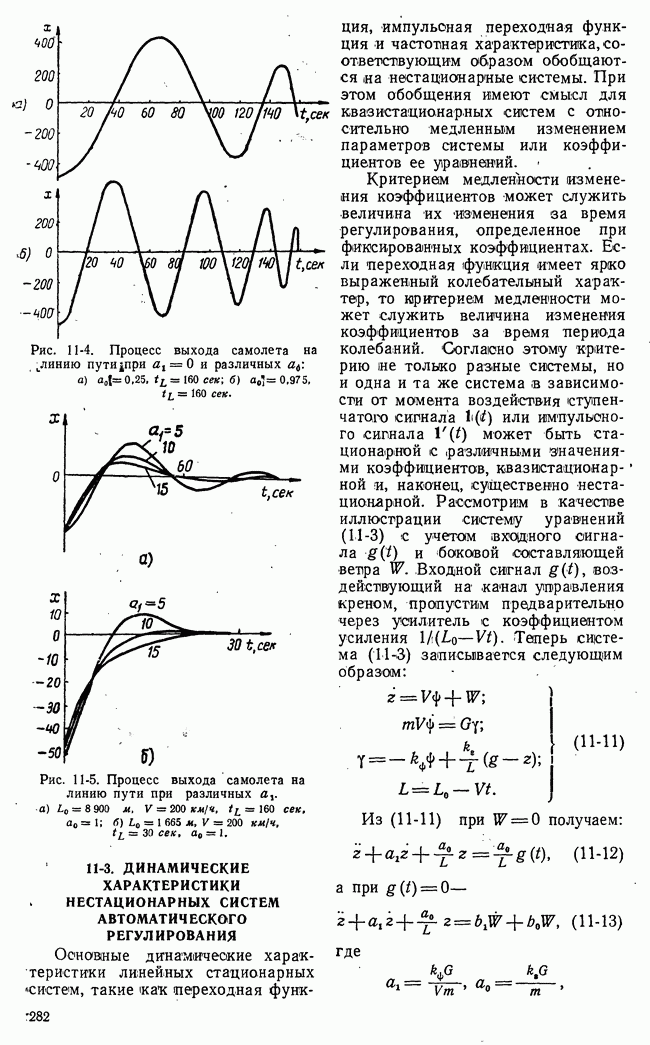
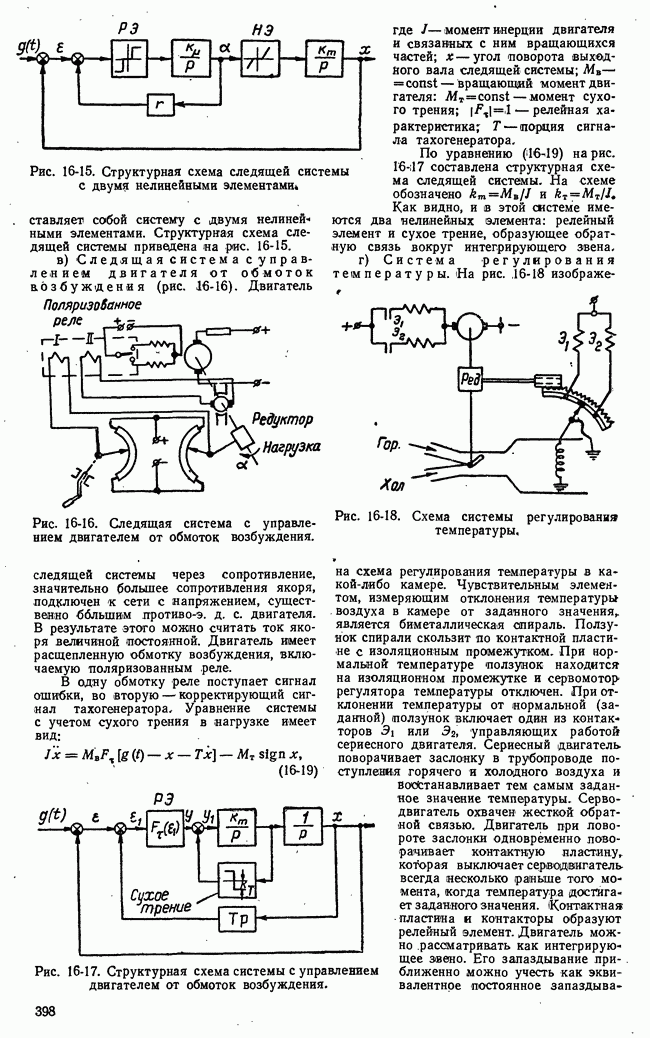
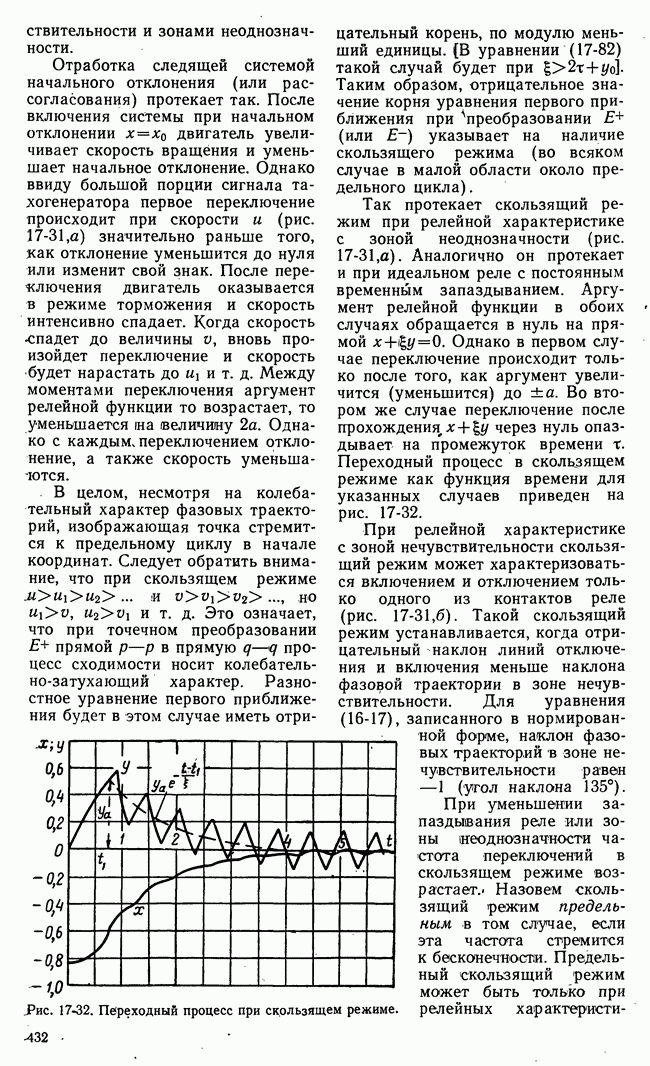
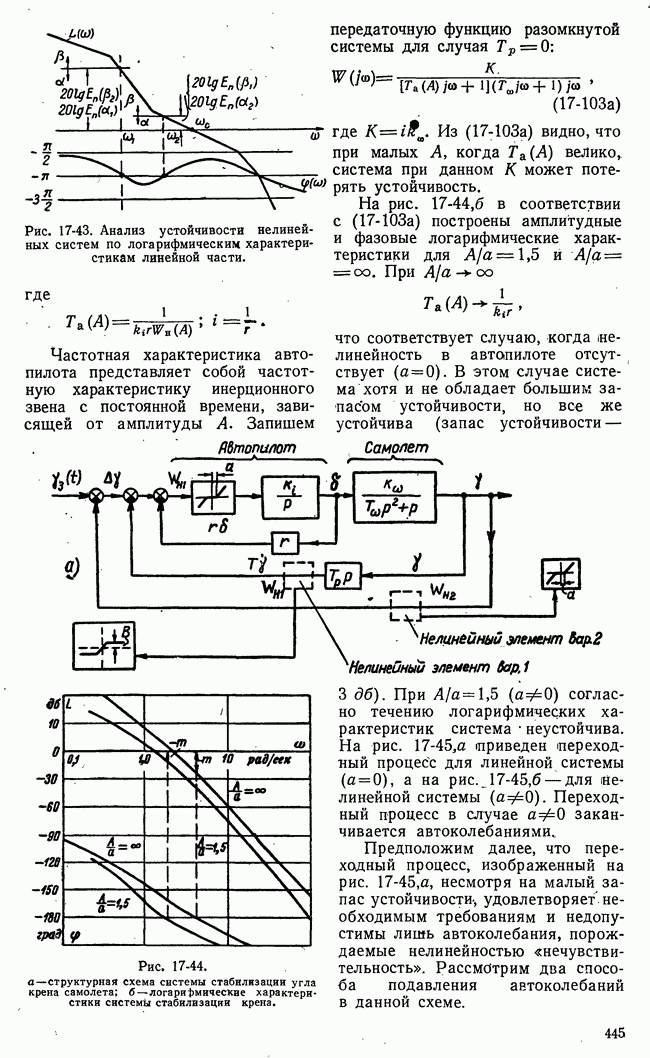
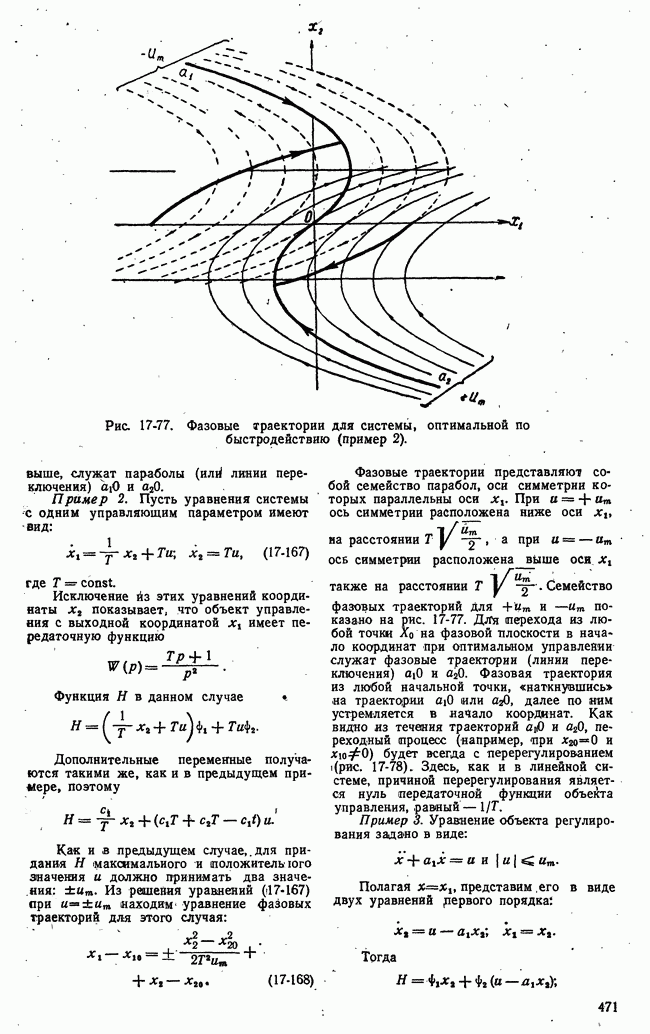
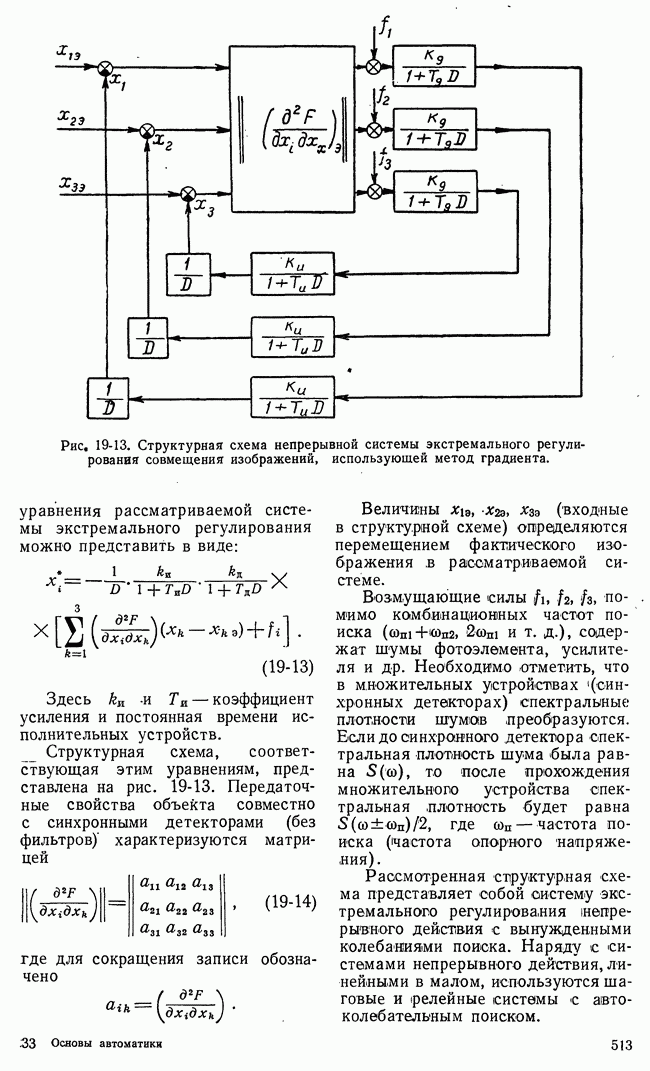
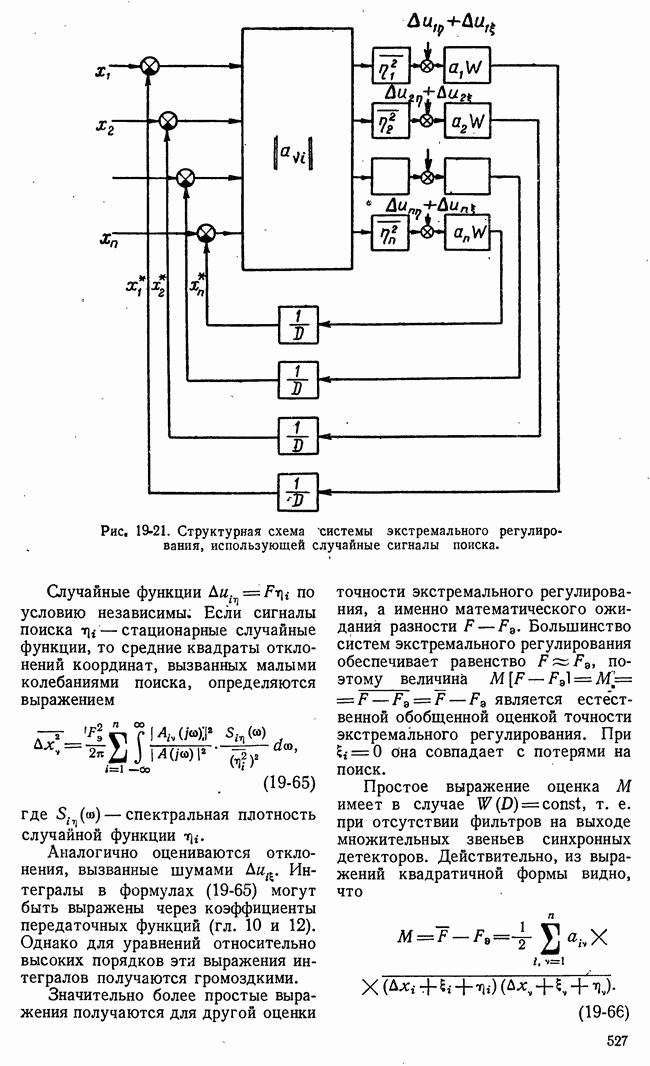
В табл. рис. 21-9 приведен числовой пример для  В табл. а приведены числовые значения
В табл. а приведены числовые значения  а в табл.
а в табл.  числовые значения
числовые значения  и оптимальная траектория от
и оптимальная траектория от 
до  Пример не претендует на строгость и общность выявления методики динамического программирования, однако он достаточно ясно иллюстрирует основную идею метода.
Пример не претендует на строгость и общность выявления методики динамического программирования, однако он достаточно ясно иллюстрирует основную идею метода.
Перейдем к более общей математической формулировке метода, динамического программирования.
Пусть имеется система, состояние которой характеризуется вектором  координатами в
координатами в  -мерном пространстве. С какой-либо целью в течение
-мерном пространстве. С какой-либо целью в течение  этапов происходит преобразование системы так, что вектор х, начиная со своего начального значения
этапов происходит преобразование системы так, что вектор х, начиная со своего начального значения  принимает еще
принимает еще  значений
значений  Будем полагать, что переход системы из одного состояния в другое на каждом этапе происходит в соответствии с зависимостью достаточно общего вида
Будем полагать, что переход системы из одного состояния в другое на каждом этапе происходит в соответствии с зависимостью достаточно общего вида

где  векторная величина, состоящая на каждом этапе из определенного числа скалярных компонент
векторная величина, состоящая на каждом этапе из определенного числа скалярных компонент  представляет собой параметр преобразования.
представляет собой параметр преобразования.
При заданном векторе состояния системы  в начале какого-либо этапа состояние системы в конце этого этапа или в начале следующего этапа зависит от выбора параметра преобразования
в начале какого-либо этапа состояние системы в конце этого этапа или в начале следующего этапа зависит от выбора параметра преобразования  Задавая все возможные значения параметру преобразования на каждом этапе, получаем все возможные течения многоэтапного процесса или все возможные способы преобразования системы из начального состояния
Задавая все возможные значения параметру преобразования на каждом этапе, получаем все возможные течения многоэтапного процесса или все возможные способы преобразования системы из начального состояния  в конечное
в конечное  Выбор параметра преобразования
Выбор параметра преобразования  на каждом этапе соответствует принятию решения о способе перехода или преобразования системы из состояния
на каждом этапе соответствует принятию решения о способе перехода или преобразования системы из состояния  в состояние
в состояние  Выбранная последовательность параметров преобразования
Выбранная последовательность параметров преобразования  называется программой. Пусть целью многоэтапного процесса преобразования является достижение оптимума некоторой скалярной величины
называется программой. Пусть целью многоэтапного процесса преобразования является достижение оптимума некоторой скалярной величины  характеризующей результат, эффект или выход многоэтапного процесса. Таким эффектом или выходом может быть функция выгоды, стоимость или выход готового продукта многоэтапного процесса производства, максимальное или минимальное значение какого-либо дискретного функционала и т. п. Для определенности будем полагать
характеризующей результат, эффект или выход многоэтапного процесса. Таким эффектом или выходом может быть функция выгоды, стоимость или выход готового продукта многоэтапного процесса производства, максимальное или минимальное значение какого-либо дискретного функционала и т. п. Для определенности будем полагать  функцией выгоды и требовать такого течения многоэтапного процесса, чтобы функция выгоды была максимальной. На каждом этапе функция выгоды будет зависеть от начального состояния системы
функцией выгоды и требовать такого течения многоэтапного процесса, чтобы функция выгоды была максимальной. На каждом этапе функция выгоды будет зависеть от начального состояния системы  и выбранной программы
и выбранной программы  т. е.
т. е. 

При оптимальной программе  Функция выгоды примет максимальное значение и будет зависеть только от начального состояния системы. Обозначив максимумы функций выгоды как
Функция выгоды примет максимальное значение и будет зависеть только от начального состояния системы. Обозначив максимумы функций выгоды как  будем иметь:
будем иметь:

Индексы  обозначают, что наибольшее значение
обозначают, что наибольшее значение  ищется по всему множеству программ или по всему множеству последовательностей
ищется по всему множеству программ или по всему множеству последовательностей  Непосредственное определение максимума выражений (21-10) путем слепого поиска часто оказывается практически невыполнимой задачей. Применение метода динамического программирования, основанного на принципе оптимальности, упрощает во многих случаях определение максимальной функции выгоды
Непосредственное определение максимума выражений (21-10) путем слепого поиска часто оказывается практически невыполнимой задачей. Применение метода динамического программирования, основанного на принципе оптимальности, упрощает во многих случаях определение максимальной функции выгоды  и
и
оптимальной программы  обеспечивающей эту максимальную функцию выгоды.
обеспечивающей эту максимальную функцию выгоды.
В соответствии с принципом оптимальности, каково бы ни было начальное состояние  и начальное решение
и начальное решение  оставшаяся программа
оставшаяся программа  должна быть оптимальной и функция выгоды на оставшихся
должна быть оптимальной и функция выгоды на оставшихся  этапах должна быть максимальной. Применим этот принцип последовательно к двух-, трех-, и
этапах должна быть максимальной. Применим этот принцип последовательно к двух-, трех-, и  -этапным процессам.
-этапным процессам.
Для одного этапа, как уже указывалось, имеем:

Согласно (21-9) состояние системы на втором этапе двухэтапного процесса равно:

По условию каковы бы ни были  второй этап должен быть оптимальным, т. е.
второй этап должен быть оптимальным, т. е.

Суммарная функция выгоды двухэтапного процесса

Соответственно максимальное значение функции, выгоды для двухэтапного процесса

Рассуждая аналогичным образом, для трехэтапного процесса будем  иметь:
иметь:

и, наконец, для  этапов
этапов


Рис. 21-9. Иллюстрация задачи, решаемой методом динамического программирования.
Рекуррентное сотношение (21-13) позволяет последовательно вычислить искомое значение  и оптимальное решение
и оптимальное решение  на первом этапе для
на первом этапе для  -этапного процесса, которое будет некоторой функцией начального состояния системы, т. е.
-этапного процесса, которое будет некоторой функцией начального состояния системы, т. е.

Поскольку после определения  определяется окончательно и
определяется окончательно и  для определения
для определения  следует откинуть начальный этап и обратиться к
следует откинуть начальный этап и обратиться к  -этапному процессу с начальный состоянием
-этапному процессу с начальный состоянием  т. е. определить
т. е. определить  как функцию
как функцию 

Таким же образом определяются остальные члены оптимальной программы:

Метод динамического программирования разработан не только для дискретных, но и для непрерывных процессов или задач [Л. 21-5]. С другой стороны, непрерывные задачи оптимизации путем разбиения на этапы могут быть приблйженно решены методом динамического программирования в дискретной форме.
Пусть, например, требуется найти функцию  соответствующую максимуму функционала
соответствующую максимуму функционала 

при условии

Для приближенного решения задачи разбиваем интервал  на
на  этапов длиной
этапов длиной  Интеграл заменяем суммой, а дифференциальное уравнение — уравнением в конечных разностях:
Интеграл заменяем суммой, а дифференциальное уравнение — уравнением в конечных разностях:

В рассматриваемой задаче  характеризует состояние системы,
характеризует состояние системы,  функцию выгоды, выражение
функцию выгоды, выражение

играет роль функции преобразования  является параметром преобразования. На основании общего уравнения динамического программирования (21-13) записываем:
является параметром преобразования. На основании общего уравнения динамического программирования (21-13) записываем:

Отыскивая последовательно максимумы функций

 находим приближенное значение максимума функционала
находим приближенное значение максимума функционала  и начальную ординату
и начальную ординату  функции
функции  Вторую ординату находим из рассмотрения всех этапов без первого:
Вторую ординату находим из рассмотрения всех этапов без первого:

и соответственно далее:

Итак, задача нахождения экстремума функционала при динамическом программировании свелась к задаче последовательного определения экстремумов функций. Это, естественно, упрощает [решение задачи, особенно при использовании цифровой вычислительной машины. Наличие ограничений, выраженных в виде неравенств, не только не усложняет, а, напротив, упрощает решение задачи методом динамического программирования, так как сужает область изменения переменных, в которой отыскивается максимум.
Максимум функции в каждом этапе при небольшом числе аргументов — компонент вектора параметра — можно находить по способу «слепого» поиска.
Так, например, в приведенной одномерной задаче поиск по у в каждом этапе может осуществляться путем придания у дискретных значений и сравнения соответствующих значений функции выгоды. При большом числе измерений этот способ, однако, оказывается неприменимым.
В этих задачах необходимо применять методы поиска, основанные на использовании той или иной начальной информации об экстремальной функции.
Например, если  известно, что функция выгоды в каждом этапе имеет лишь один максимум «двустороннего» типа, расположенный внутри области допустимых изменений параметра
известно, что функция выгоды в каждом этапе имеет лишь один максимум «двустороннего» типа, расположенный внутри области допустимых изменений параметра  то поиск может осуществляться на основе метода наискорейшего спуска или метода Гаусса-Зайделя, или метода градиента
то поиск может осуществляться на основе метода наискорейшего спуска или метода Гаусса-Зайделя, или метода градиента  Для случая, когда функция выгоды линейна и ограничения изменения аргументов представляют собой линейные неравенства, применяются специальные методы поиска наибольшего значения, получившие название методов линейного программирования. Линейное программирование может использоваться как способ отыскания максимума функции выгоды в каждом этапе динамического программирования и как самостоятельный способ решения линейных задач на оптимум, часто возникающих в различных областях планирования.
Для случая, когда функция выгоды линейна и ограничения изменения аргументов представляют собой линейные неравенства, применяются специальные методы поиска наибольшего значения, получившие название методов линейного программирования. Линейное программирование может использоваться как способ отыскания максимума функции выгоды в каждом этапе динамического программирования и как самостоятельный способ решения линейных задач на оптимум, часто возникающих в различных областях планирования.

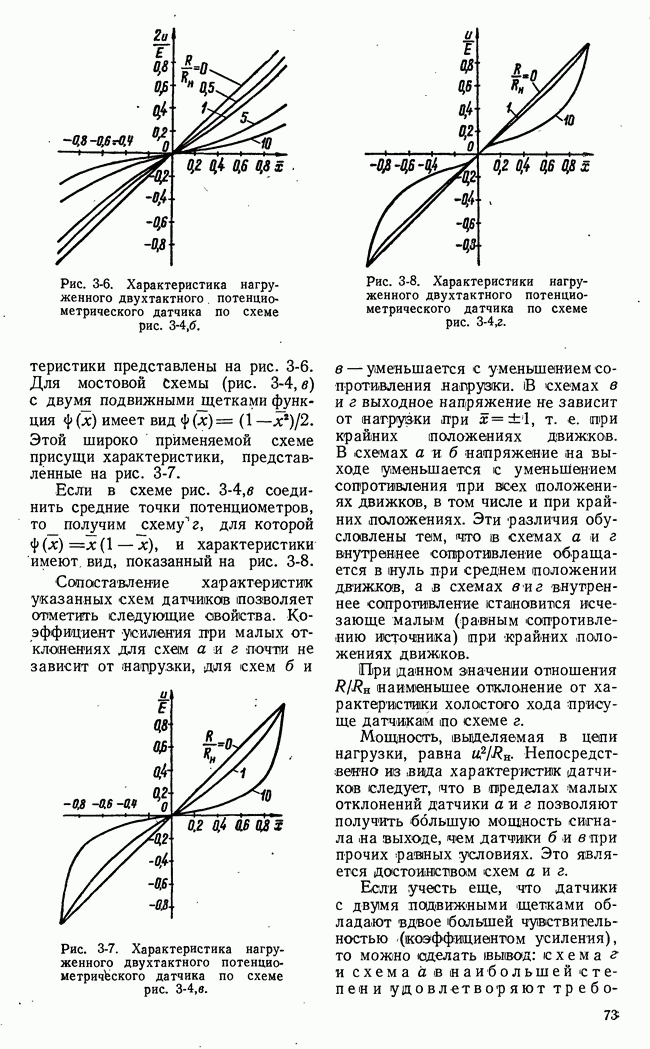
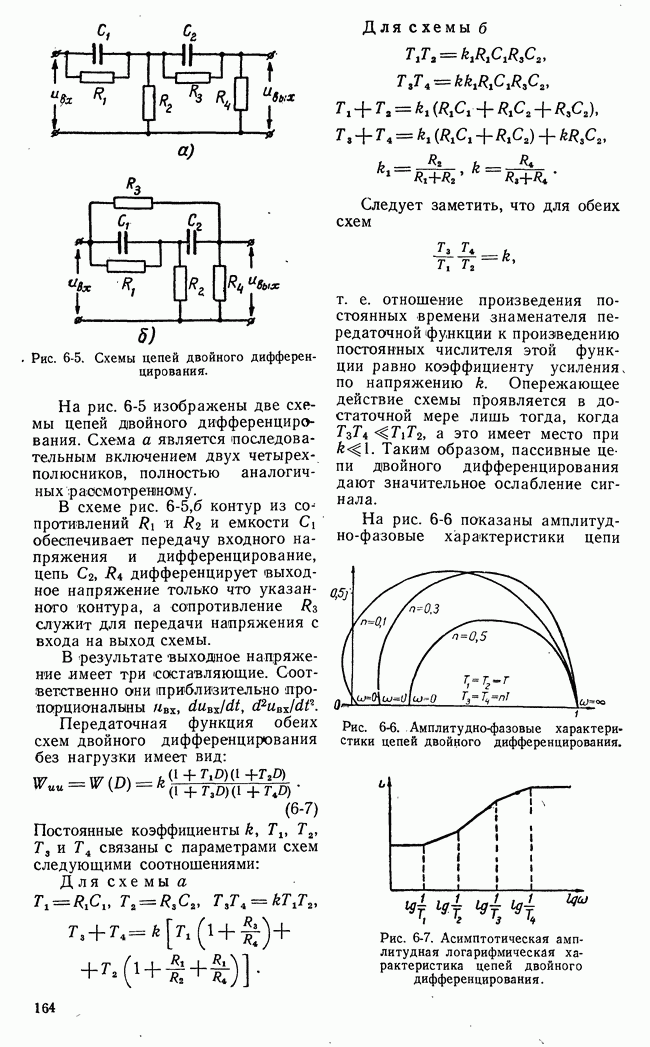
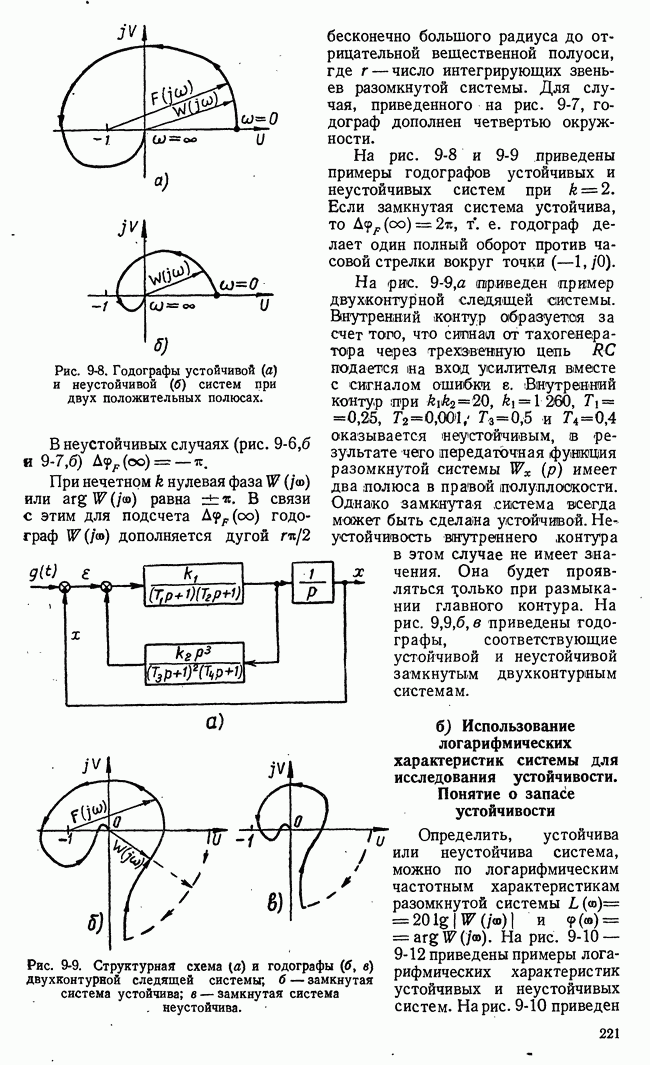
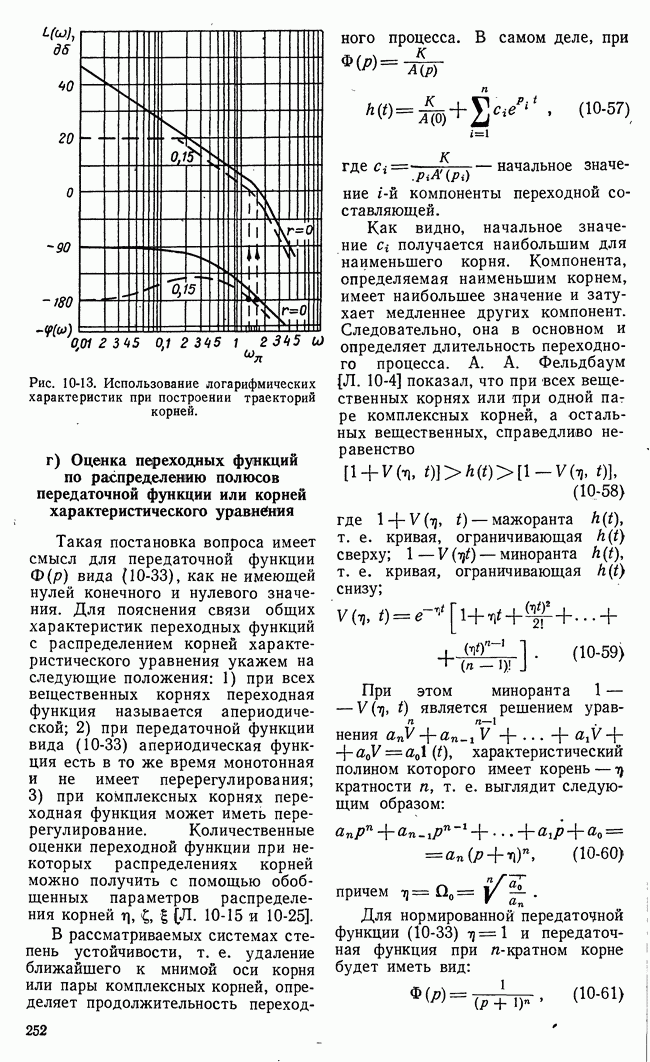
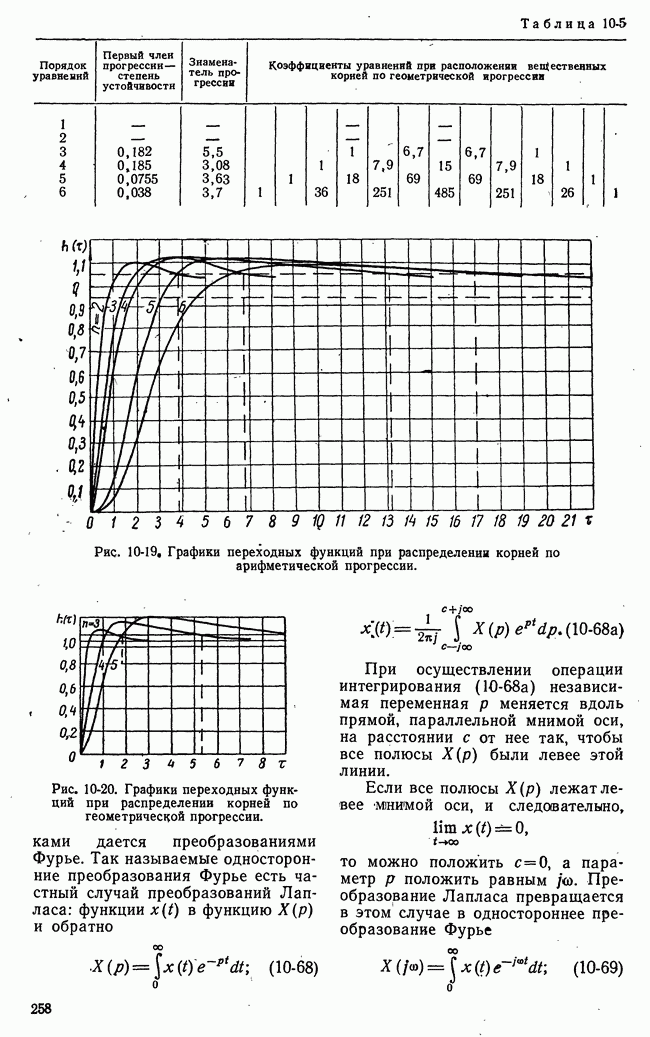
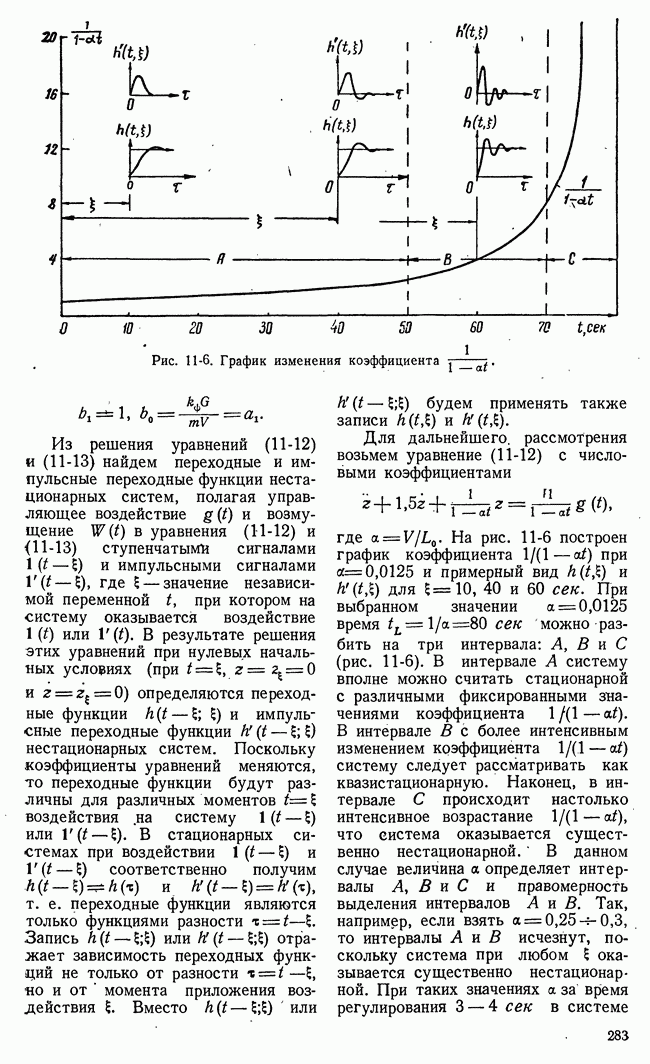
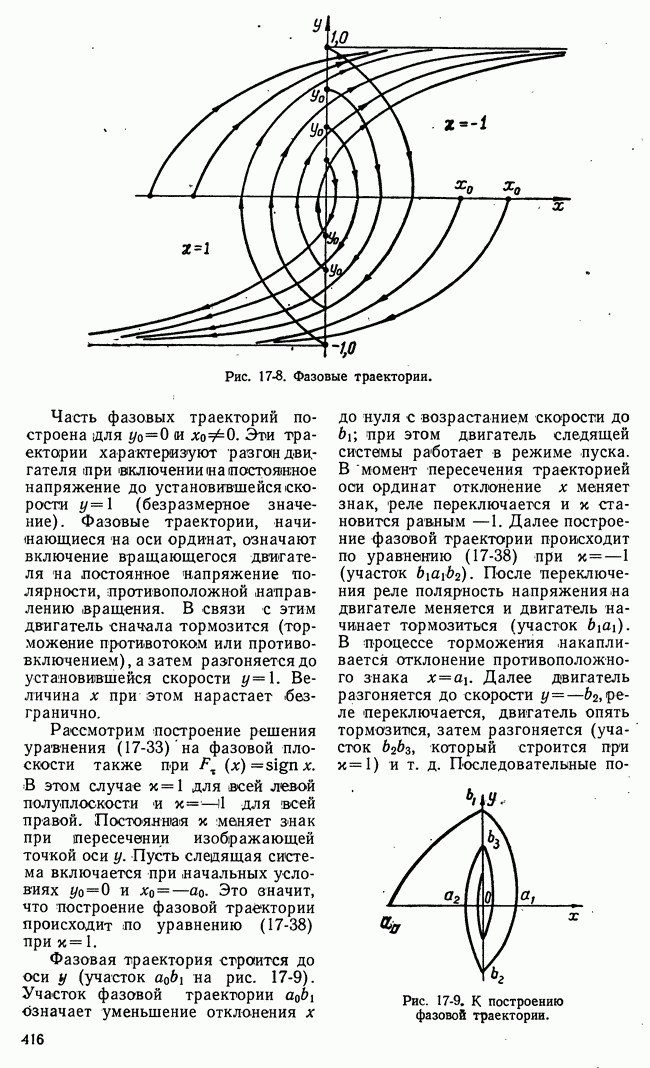
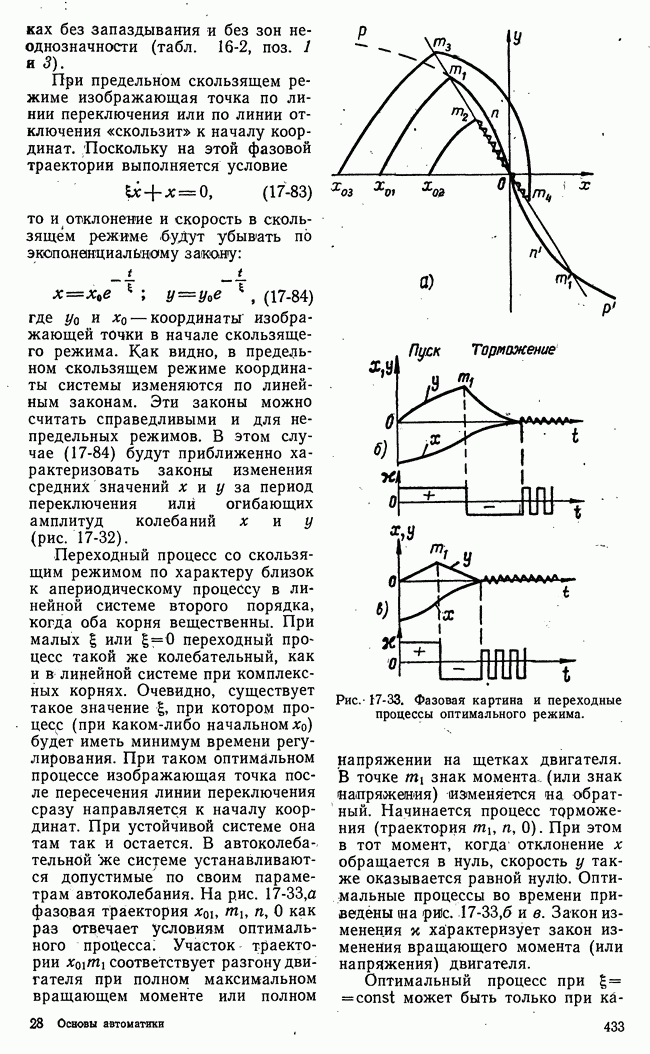
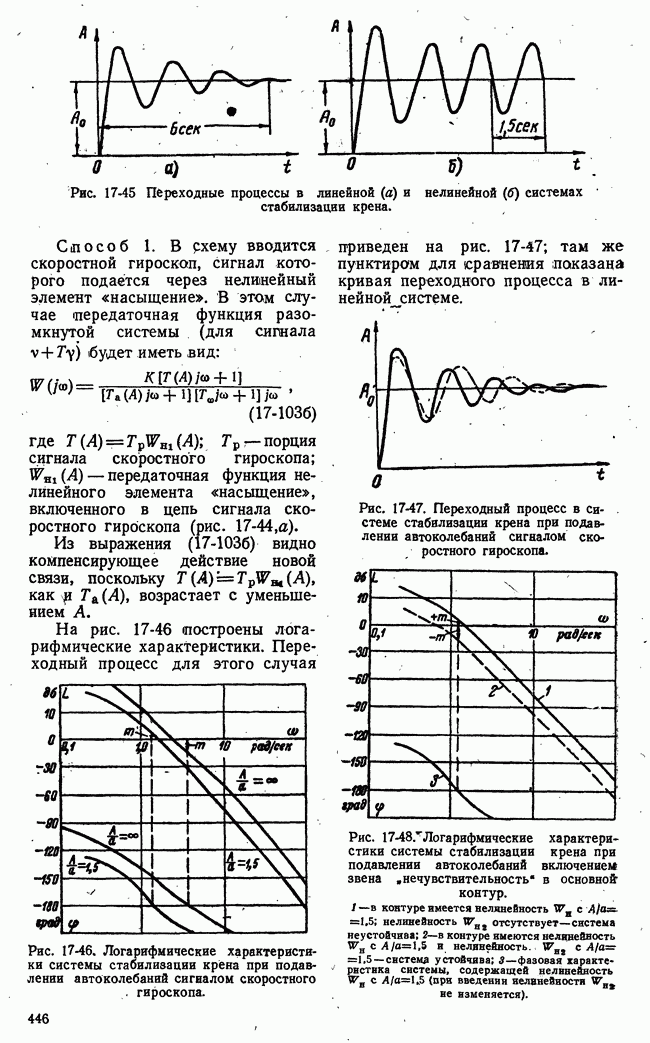
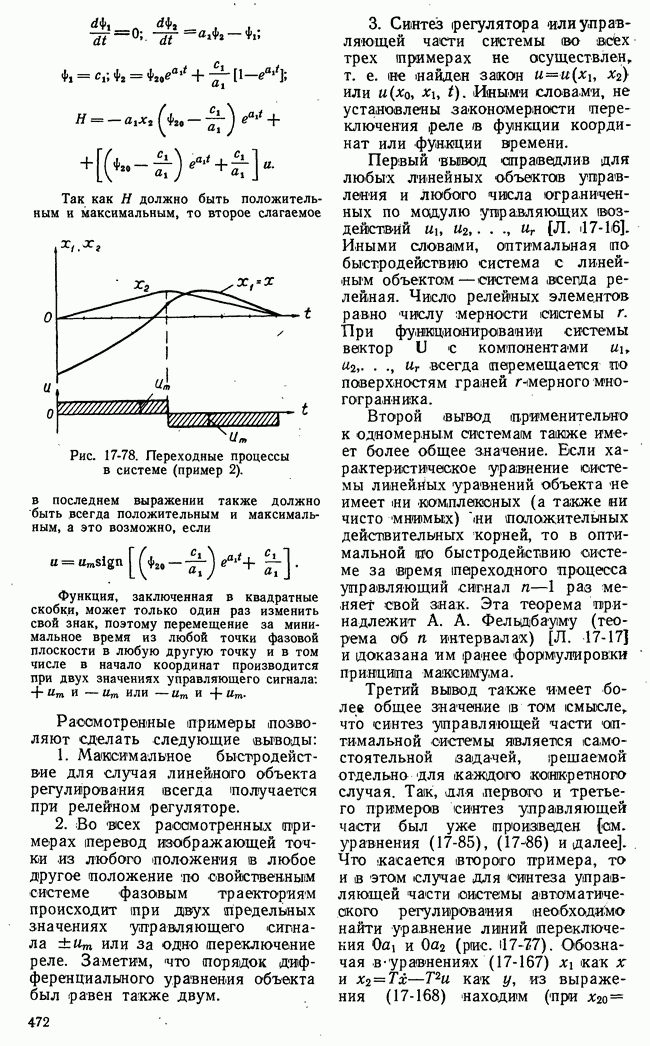
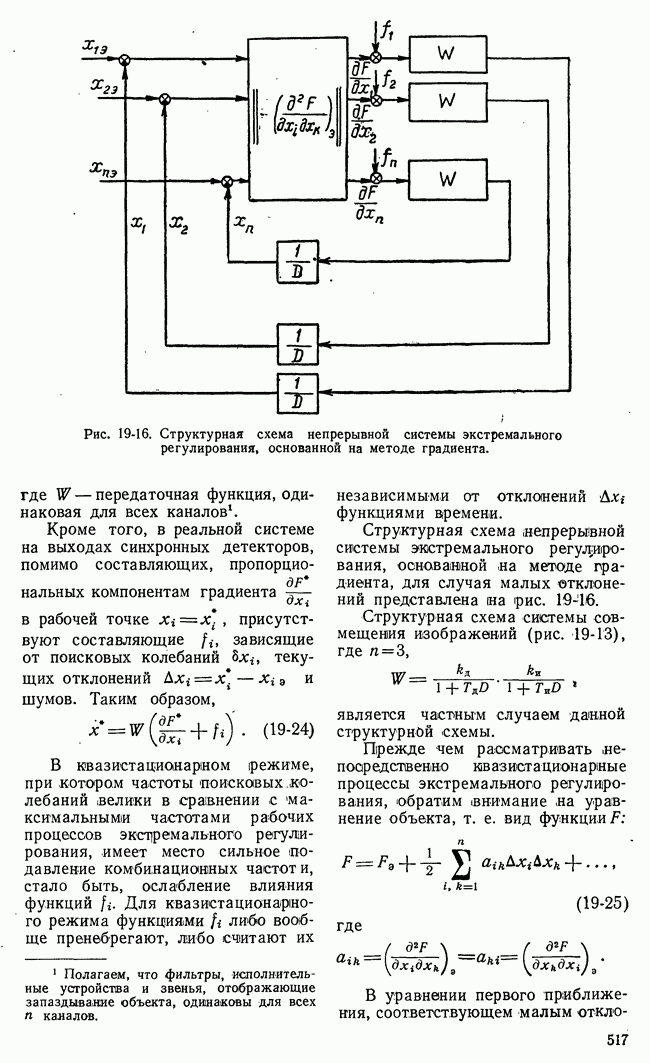
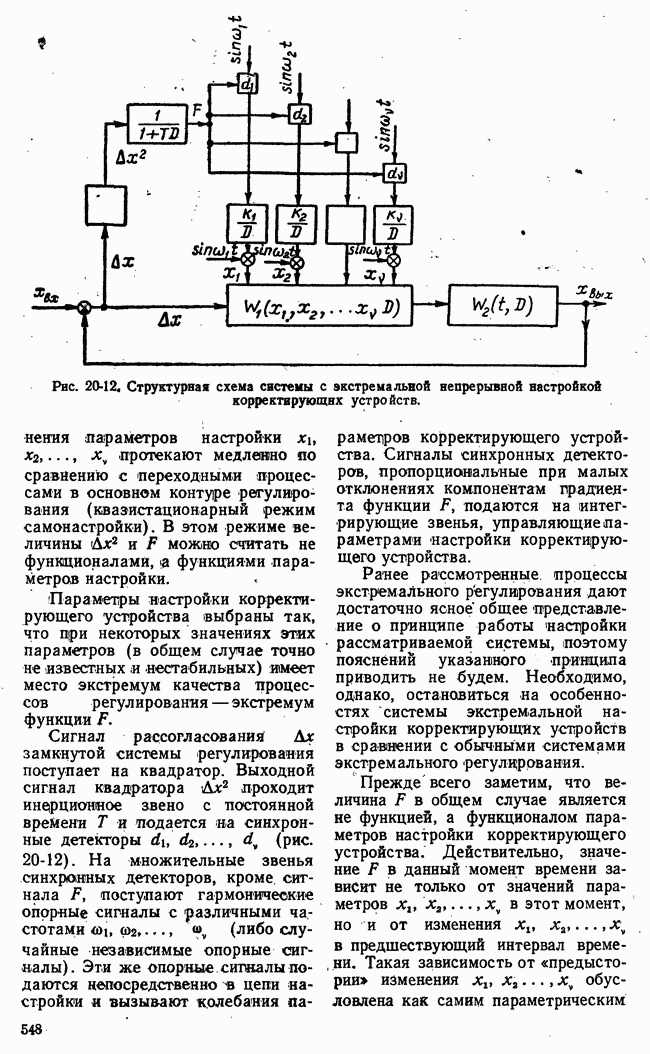
Рис. 21-10. Геометрическая интерпретация задач линейного программирования.
б) Линейное программирование
Прежде чем формулировать задачу линейного программирования в общем виде, рассмотрим простой пример. Пусть требуется найти наибольшее значение линейной функции двух переменных

при ограничениях в виде неравенств

Здесь  заданные постоянные коэффициенты.
заданные постоянные коэффициенты.
Легко указать геометрическую интерпретацию сформулированной задачи. Ограничения (21-16) определяют область на плоскости переменных  Границами этой области возможных значений являются, с одной стороны, оси
Границами этой области возможных значений являются, с одной стороны, оси  с другой — прямые
с другой — прямые

Таким образом, область возможных значений в данном случае представляет собой четырехугольник на плоскости  Эта область на рис. 21-10,а имеет внутреннюю штриховку. В особых случаях, когда одно из неравенств (21-16) есть следствие других, четырехугольная область возможных решений уступает место треугольной области.
Эта область на рис. 21-10,а имеет внутреннюю штриховку. В особых случаях, когда одно из неравенств (21-16) есть следствие других, четырехугольная область возможных решений уступает место треугольной области.
Требуется найти наибольшее значение функции выгоды  в пределах (включая границы) указанной области и соответствующие этому максимуму значения
в пределах (включая границы) указанной области и соответствующие этому максимуму значения 
Очевидно, что обычный способ отыскания экстремума функции двух переменных здесь неприменим. Действительно, частные производные линейной функции есть постоянные  не обращающиеся в нуль, так как функция
не обращающиеся в нуль, так как функция  в каждом своем сечении является линейной, т. е. монотонной функцией.
в каждом своем сечении является линейной, т. е. монотонной функцией.
Функция  достигает своего наибольшего значения на границе области возможных решений
достигает своего наибольшего значения на границе области возможных решений  На рис. 21-10,а функция
На рис. 21-10,а функция  представлена прямыми равных значений
представлена прямыми равных значений  а на рис. 21-10,б - плоскостью в трехмерном пространстве.
а на рис. 21-10,б - плоскостью в трехмерном пространстве.
Очевидно, что в рассматриваемом частном случае наибольшее значение функции выгоды  получается в угловой точке
получается в угловой точке  области возможных значений и координаты этой точки являются, решением данной задачи линейного программирования. Найти координаты точки А очень легко. Столь простое решение задачи линейного программирования имеет место, однако, лишь для двух независимых переменных. Для большого числа переменных и ограничений отыскание наибольшего значения линейной функции выгоды не имеет столь наглядного и простого геометрического изобра-, жения и требует обычно значительного объема вычислений. Сокращение этих вычислений и их систематизация достигаются применением
области возможных значений и координаты этой точки являются, решением данной задачи линейного программирования. Найти координаты точки А очень легко. Столь простое решение задачи линейного программирования имеет место, однако, лишь для двух независимых переменных. Для большого числа переменных и ограничений отыскание наибольшего значения линейной функции выгоды не имеет столь наглядного и простого геометрического изобра-, жения и требует обычно значительного объема вычислений. Сокращение этих вычислений и их систематизация достигаются применением
того или иного способа линейного программирования.
Сформулируем задачу линейного программирования 1 в общем виде. Линейное программирование заключается в отыскании наибольшего значения линейной функции

при ограничениях в виде системы линейных неравенств

Следует заметить, что если первые  неравенств даны не в виде
неравенств даны не в виде  а в виде положительности некоторых линейных функций, то линейным преобразованием переменных ограничения можно (за исключением особых случаев) привести к виду (21-18).
а в виде положительности некоторых линейных функций, то линейным преобразованием переменных ограничения можно (за исключением особых случаев) привести к виду (21-18).
Необходимо также отметить, что на число  второй группы неравенств никаких ограничений не накладывается, кроме
второй группы неравенств никаких ограничений не накладывается, кроме  При
При  т. е. при отсутствии дополнительных ограничений (кроме положительности
т. е. при отсутствии дополнительных ограничений (кроме положительности  задача не имеет решения (наибольшее значение
задача не имеет решения (наибольшее значение  здесь равно
здесь равно  При
При  задача имеет решение.
задача имеет решение.
Можно дать формальную интерпретацию многомерной задачи линейного программирования, подобную рассмотренной геометрической интерпретации двухмерной задачи. А именно: задача линейного программирования заключается в отыскании наибольшего значения линейной функции переменных  область возможных изменений которых задана в виде многогранника (21-18) в
область возможных изменений которых задана в виде многогранника (21-18) в  -мерном пространстве. Однако подобная геометрическая интерпретация, как и любая интерпретация в
-мерном пространстве. Однако подобная геометрическая интерпретация, как и любая интерпретация в  -мерном пространстве при
-мерном пространстве при  не дает непосредственно способа числового решения задачи.
не дает непосредственно способа числового решения задачи.
Для решения задач линейного программирования разработано несколько методов. Давно применяется метод транспортирования, получивший свое название в задачах оптимального планирования перевозок. Более общим является симплексный метод. Мы не будем здесь останавливаться на этих вычислительных методах, довольно громоздкое описание которых можно найти. в специальной литературе [Л. 21-3 и 21-4].
Кратко остановимся на специальной форме метода градиента, применимой для решения задач линейного программирования. Достоинство этого способа — его прозрачное геометрическое содержание.
Как указывалось, мтод градиента в обычной форме неприменим для линейного программирования, так как, двигаясь вдоль вектора градиента линейной функции, мы выходим за пределы области ограничения аргументов. Однако видоизменение метода градиента с учетом ограничений позволяет решать задачи линейного программирования. Метод заключается в следующем.
Первое перемещение точки  начинается от начала координат
начинается от начала координат  в направлении вектора градиента функции выгоды
в направлении вектора градиента функции выгоды

т. е. по прямой

Увеличивая т. е. двигаясь вдоль указанного первого вектора градиента, следим одновременно за условиями (21-18) нахождения в многограннике ограничений

которые в данном случае принимают вид:

Пусть при достижении некоторого значения  одно из неравенств (21-19) первым обратилось в равенство
одно из неравенств (21-19) первым обратилось в равенство

Следует заметить, что одновременное обращение в равенства двух или большего числа неравенств (21-19) является особым случаем, благоприятным, кстати сказать, для решения задачи линейного программирования. Излагаемая методика легко обобщается на этот особый случай, но для краткости мы не будем на нем останавливаться.
Выполнение равенства (21-20) при некотором означает, что мы, двигаясь вдоль первого вектора градиента, достигли  грани многогранника ограничений в точке
грани многогранника ограничений в точке

Дальнейшее движение для отыскания наибольшего значения функции выгоды  должно, очевидно, осуществляться вдоль
должно, очевидно, осуществляться вдоль  грани многогранника ограничений в направлении градиента функции выгоды вдоль этой грани.
грани многогранника ограничений в направлении градиента функции выгоды вдоль этой грани.
Для того чтобы получить вектор градиента функции  при движении вдоль
при движении вдоль  грани (этот вектор будем для краткости называть вторым вектором градиента), можно поступить следующим образом. Из уравнений
грани (этот вектор будем для краткости называть вторым вектором градиента), можно поступить следующим образом. Из уравнений

можно исключить один из аргументов, напимер  Тогда
Тогда


В соответствии с этим компоненты второго вектора градиента равны:

Движение вдоль второго вектор» градиента начинается от точки  где
где

Поэтому координаты на втором участке поиска максимума  можно выразить в виде:
можно выразить в виде:

Здесь  — положительная переменная. Движению вдоль второго вектора градиента соответствует увеличение
— положительная переменная. Движению вдоль второго вектора градиента соответствует увеличение  начиная с
начиная с 
При некотором значении  нарушается еще одно из неравенств (21-18). Особый случай одновременного нарушения нескольких неравенств не рассматривается. Тогда
нарушается еще одно из неравенств (21-18). Особый случай одновременного нарушения нескольких неравенств не рассматривается. Тогда

Отсюда определяется значение  и по формулам (21-22) координаты конца второго участка поиска. Далее находится третий вектор градиента функции выгоды
и по формулам (21-22) координаты конца второго участка поиска. Далее находится третий вектор градиента функции выгоды

при условии

и аналогично предыдущему определяется третий участок поиска и т. д.
Процесс поиска заканчивается тогда, когда движение по вектору градиента в следующем этапе приводит в начальной точке к нарушению ограничений (21-18). Для двухмерной задачи линейного программирования (рис. 21-10) изложенная методика сводится к движению по первому вектору градиента  (рис. 21-10,б) и далее по второму участку поиска
(рис. 21-10,б) и далее по второму участку поиска  до точки А.
до точки А.
Пример. Требуется решить задачу линейного программирования функции

для условий

Координаты первого участка поиска равны:

Подставляя эти выражения в неравенства ограничений

убеждаемся, что при возрастании  первым нарушается верхнее неравенство при
первым нарушается верхнее неравенство при  Координаты конца первого участка поиска здесь равны:
Координаты конца первого участка поиска здесь равны:

Для второго участка поиска исключаем переменную  из выражений
из выражений

Тогда

Таким образом, на втором участке поиска

Подставляя эти выражения во второе неравенство, находим  . Таким образом,
. Таким образом,  и координаты конца второго участка поиска равны:
и координаты конца второго участка поиска равны:

Получанные координаты конца второго участка поиска являются решением задачи линейного программирования, т. е. соответствуют наибольшему  оределах области ограничений значению функции выгоды
оределах области ограничений значению функции выгоды 
Для того чтобы убедиться в этом, согласно общей методике определим направление третьего участка поиска. Исключая  из выражений
из выражений

получаем:

Таким образом, координаты третьего участка будут равны:

Подставляя это выражение в неравенство находим  и убеждаемся, что оно выполняется только при
и убеждаемся, что оно выполняется только при  т. е. в точке конца второго участка поиска. Это и указывает на то, что 22 являются решениями задачи.
т. е. в точке конца второго участка поиска. Это и указывает на то, что 22 являются решениями задачи.
Алгоритм рассмотренного метода линейного программирования может быть достаточно просто реализован в любой цифровой вычислительной машине. Из существа рассмотренного метода поиска наибольшего значения линейной функции можно установить, что при некоторых видоизменениях процесс поиска может выполняться и машинами непрерывного действия (электронными интеграторами).
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ГЛАВА ПЕРВАЯ. ВВОДНАЯ
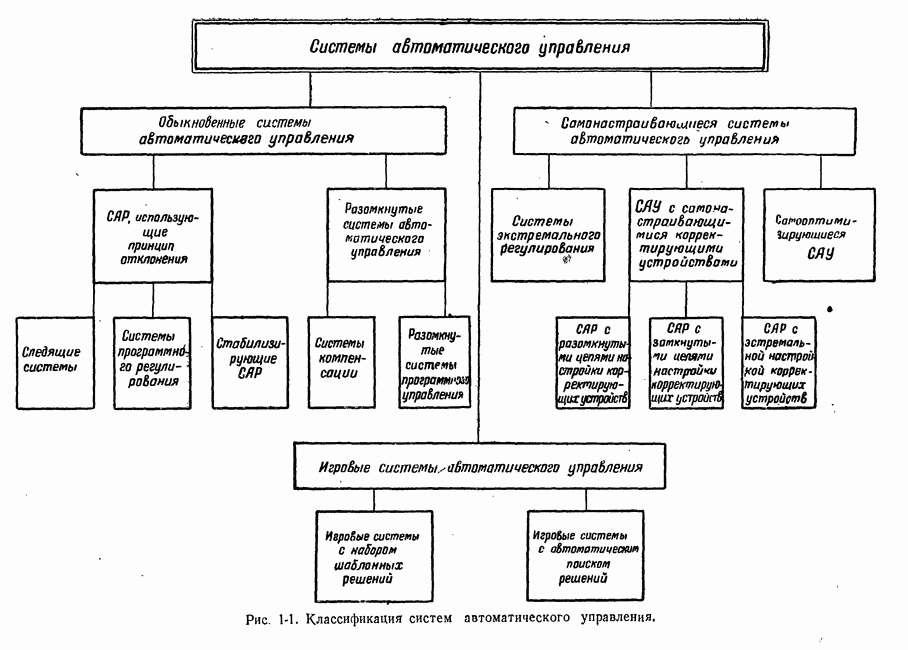
- 1-1. О КЛАССИФИКАЦИИ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- 1-2. ОБЫКНОВЕННЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- 1-3. САМОНАСТРАИВАЮЩИЕСЯ СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- 1-4. ИГРОВЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- 1-5. КЛАССИФИКАЦИЯ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ ПО ДРУГИМ ПРИЗНАКАМ
- ГЛАВА ВТОРАЯ. ОБЩИЕ ПЕРЕДАТОЧНЫЕ СВОЙСТВА ЭЛЕМЕНТОВ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- 2-1. УРАВНЕНИЯ ЭЛЕМЕНТОВ. СТАТИЧЕСКИЕ И ДИНАМИЧЕСКИЕ СВОЙСТВА ЭЛЕМЕНТОВ
- б) Центробежный измеритель скорости вращения
- в) Электромагнитный измеритель напряжения
- 2-2. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ
- 2-3. ЭЛЕМЕНТАРНЫЕ ДИНАМИЧЕСКИЕ ЗВЕНЬЯ, ИХ УРАВНЕНИЯ И ПЕРЕДАТОЧНЫЕ ФУНКЦИИ
- 2-4. ТИПОВЫЕ ВХОДНЫЕ СИГНАЛЫ. ВОЗМУЩАЮЩИЕ ФУНКЦИИ
- 2-5. ПЕРЕХОДНЫЕ ФУНКЦИИ ЭЛЕМЕНТАРНЫХ ЗВЕНЬЕВ
- 2-6. ИМПУЛЬСНЫЕ ПЕРЕХОДНЫЕ ФУНКЦИИ ЭЛЕМЕНТАРНЫХ ЗВЕНЬЕВ
- 2-7. РЕАКЦИЯ ЗВЕНЬЕВ НА ПРОИЗВОЛЬНЫЕ ИЗВЕСТНЫЕ ФУНКЦИИ ВРЕМЕНИ
- 2-8. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ
- б) Частотные характеристики элементарных звеньев
- в) Логарифмические характеристики элементарных звеньев
- 2-9. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ОБ ЭЛЕМЕНТАРНЫХ ЗВЕНЬЯХ
- 2-10. СОЕДИНЕНИЯ ЗВЕНЬЕВ. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ СОЕДИНЕНИИ
- 2-11. ЭЛЕМЕНТЫ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ КАК ЧЕТЫРЕХПОЛЮСНИКИ. ПЕРЕДАТОЧНЫЕ УРАВНЕНИЯ
- ГЛАВА ТРЕТЬЯ. ДАТЧИКИ СИГНАЛОВ
- 3-1. ОБЩИЕ СВОЙСТВА ДАТЧИКОВ
- 3-2. ПОТЕНЦИОМЕТРИЧЕСКИЕ ДАТЧИКИ
- б) Выходная мощность потенциометрических датчиков и условия согласования
- в) Динамические свойства
- г) Ошибка ступенчатости. Параметры потенциометрических датчиков
- 3-3. ИНДУКТИВНЫЕ ДАТЧИКИ
- б) Двухтактные индуктивные датчики
- в) Характеристики двухтактных индуктивных датчиков
- г) Трансформаторные индуктивные датчики
- д) Динамические свойства индуктивных датчиков
- е) Шумы индуктивных датчиков
- ж) Общие свойства индуктивных датчиков
- 3-4. СЕЛЬСИНЫ В ТРАНСФОРМАТОРНОМ РЕЖИМЕ
- б) Характеристики сельсинного датчика
- в) Динамические свойства сельсинных датчиков
- г) Шумы и ошибки датчика
- д) Устанавливающий момент
- е) Дифференциальные сельсины
- ж) Сельсины точного и грубого каналов
- ГЛАВА ЧЕТВЕРТАЯ. УСИЛИТЕЛИ СИГНАЛОВ
- 4-2. МАГНИТНЫЕ УСИЛИТЕЛИ
- а) Рабочий процесс и статическая характеристика магнитного усилителя с прямоугольной кривой намагничивания сердечников
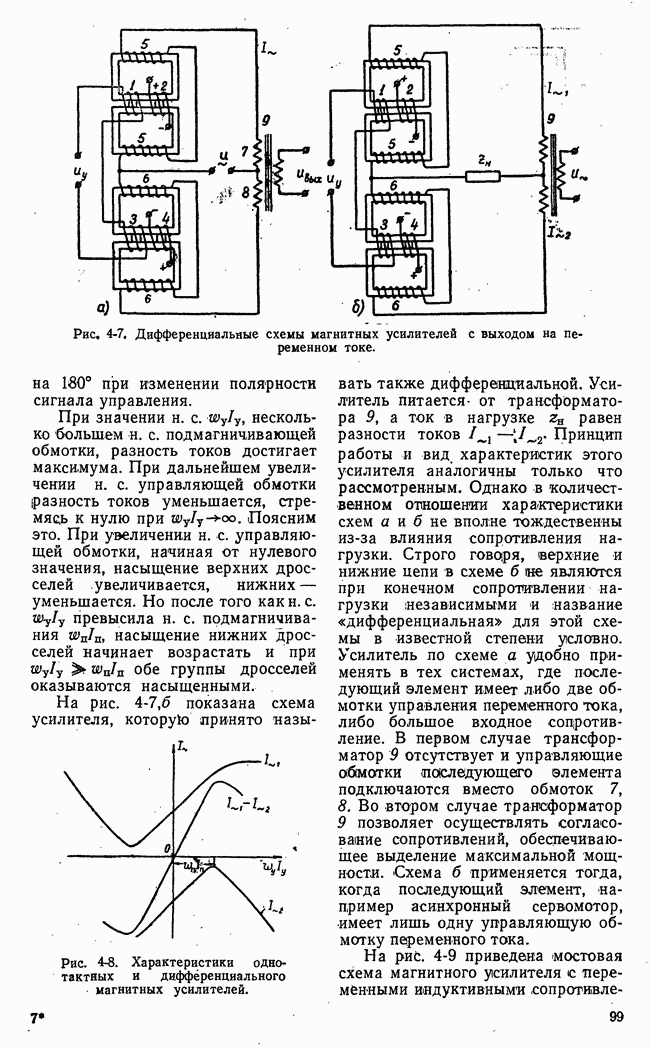
- б) Двухтактные магнитные усилители с выходом на переменном токе
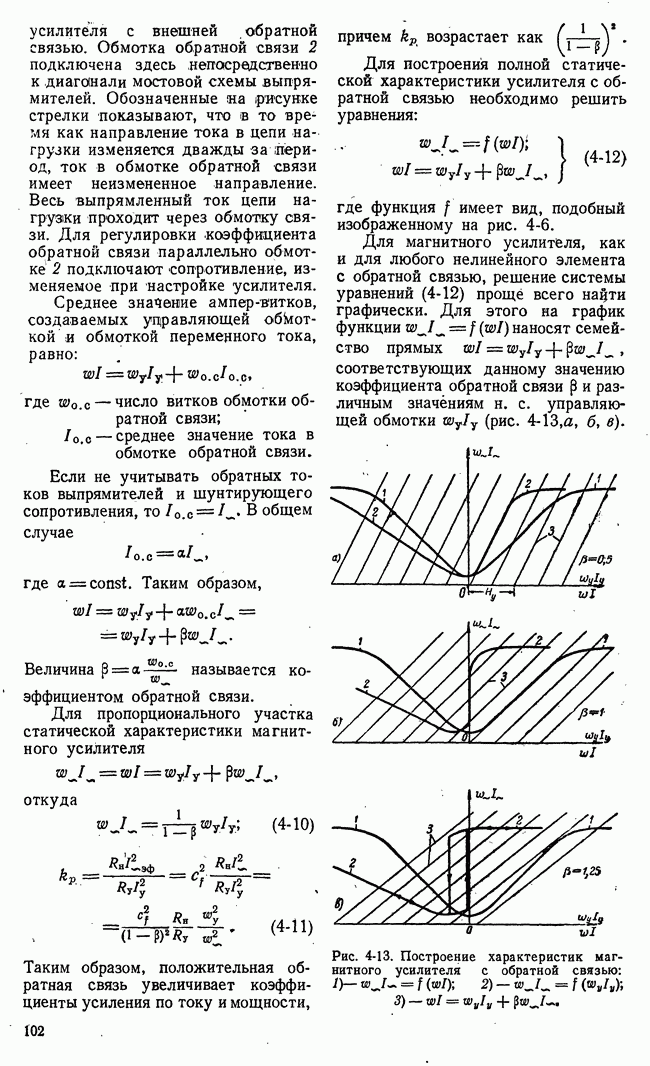
- в) Магнитные усилители с обратной связью
- г) Динамические свойства магнитных усилителей
- д) Шумы магнитных усилителей. Общие свойства магнитных усилителей
- 4-3. ЭЛЕКТРОМАШИННЫЕ УСИЛИТЕЛИ
- б) Однокаскадный электромашицный усилитель как четырехполюсник
- в) Двухкаскадный электромашинный усилитель с поперечным полем
- г) Шумы электромашинных усилителей
- 4-4. РЕЛЕ
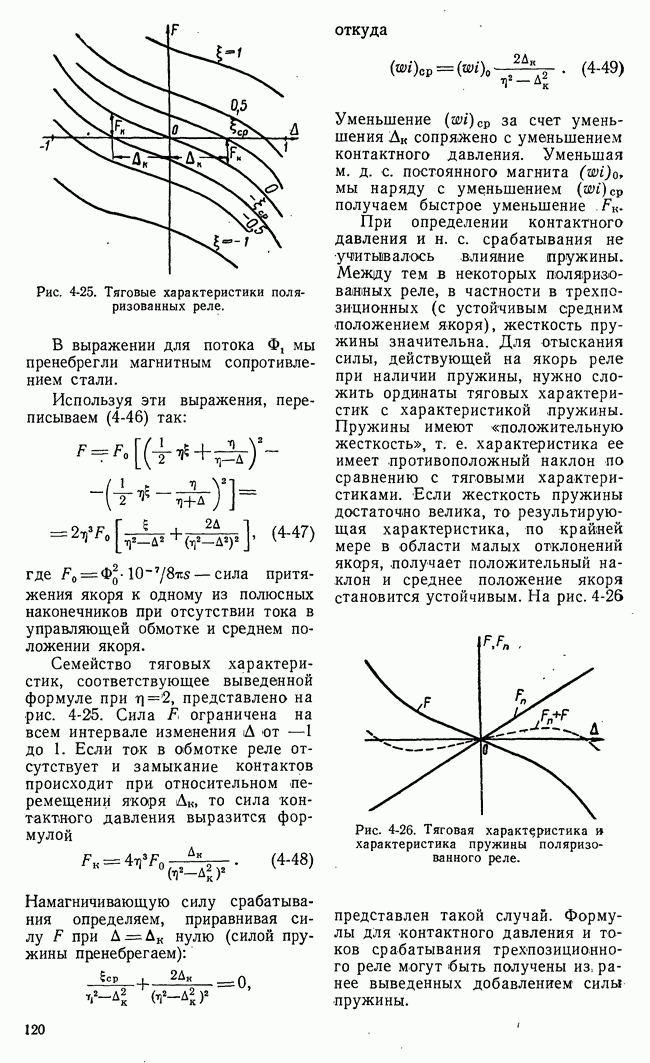
- б) Поляризованные реле
- в) Магнитоэлектрическое реле
- 4-5. РЕЛЕЙНЫЕ УСИЛИТЕЛИ
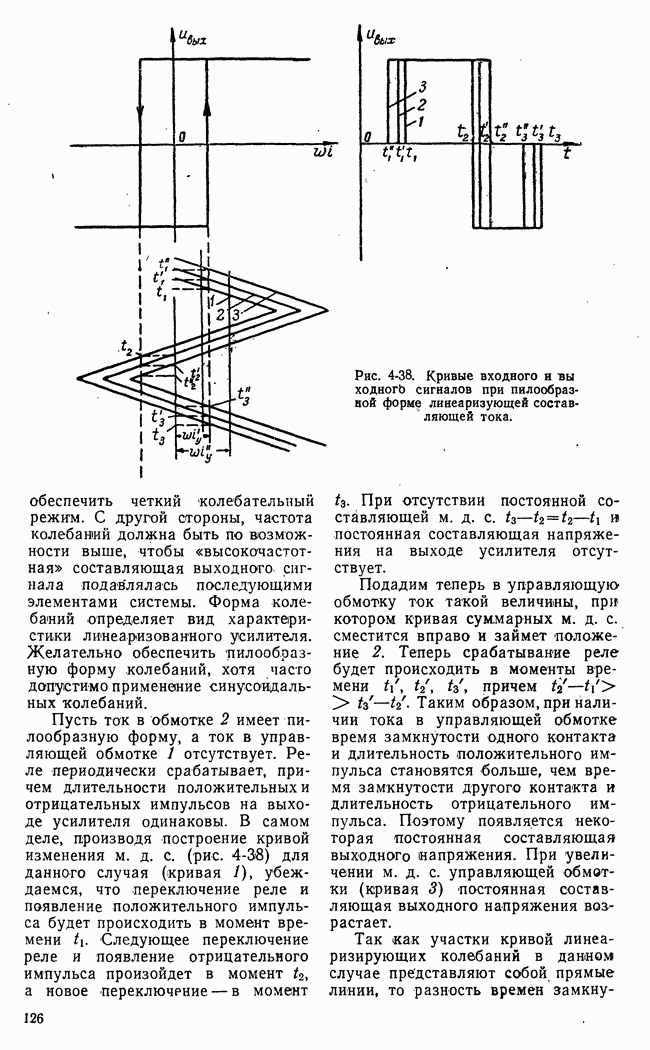
- б) Вибрационная линеаризация релейных усилителей
- в) Релейный усилитель как четырехполюсник
- 4-6. ЭЛЕКТРОННЫЕ УСИЛИТЕЛИ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- б) Фазочувствительные усилители и синхронные детекторы
- в) Электронные усилители постоянного тока
- г) Шумы электронных усилителей
- 4-7. ПОЛУПРОВОДНИКОВЫЕ УСИЛИТЕЛИ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- ГЛАВА ПЯТАЯ. ИСПОЛНИТЕЛЬНЫЕ УСТРОЙСТВА СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- 5-2. СЕРВОДВИГАТЕЛИ ПОЧТОЯННОГО ТОКА
- 5-3. СЕРВОДВИГАТЕЛИ ПЕРЕМЕННОГО ТОКА
- 5-4. СЕРВОДВИГАТЕЛИ С ЭЛЕКТРОМАГНИТНЫМИ И ПОРОШКОВЫМИ МУФТАМИ
- б) Характеристики серводвигателей с электромагнитными муфтами
- в) Порошковые муфты
- г) Характеристики серводвигателей с порошковыми муфтами
- 5-5. ГИДРАВЛИЧЕСКИЕ И ПНЕВМАТИЧЕСКИЕ СЕРВОДВИГАТЕЛИ
- б) Обратные связи в гидравлических серводвигателях
- в) Свойства гидравлических серводвигателей
- г) Электрогидравлические серводвигатели
- д) Пневматические серводвигатели
- ГЛАВА ШЕСТАЯ. СТАБИЛИЗИРУЮЩИЕ УСТРОЙСТВА СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- 6-1. ПАССИВНЫЕ КОРРЕКТИРУЮЩИЕ ЦЕПИ СИСТЕМ ПОСТОЯННОГО ТОКА
- б) Интегрирующие и интегродифференцирующие цепи
- 6-2. АКТИВНЫЕ КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА СИСТЕМ ПОСТОЯННОГО ТОКА
- 6-3. КОРРЕКТИРУЮЩИЕ ЦЕПИ СИСТЕМ ПЕРЕМЕННОГО ТОКА
- 6-4. ФИЛЬТРЫ В ЦЕПЯХ ОБРАТНЫХ СВЯЗЕЙ. МЕХАНИЧЕСКИЕ СТАБИЛИЗИРУЮЩИЕ УСТРОЙСТВА
- ГЛАВА СЕДЬМАЯ. СТРУКТУРНЫЕ СХЕМЫ И ХАРАКТЕРИСТИКИ ЛИНЕЙНЫХ СТАЦИОНАРНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 7-1. СТРУКТУРНЫЕ СХЕМЫ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 7-2. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ ДЛЯ ВХОДНОЙ ВЕЛИЧИНЫ
- 7-3. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ ДЛЯ ВОЗМУЩЕНИЯ
- 7-4. ПРИМЕРЫ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ И ИХ СТРУКТУРНЫЕ СХЕМЫ
- б) Стабилизация напряжения самолетных генераторов
- в) Следящая система копировально-фрезерного станка
- г) Следящая система автосопровождения
- д) Автоматическое управление углом тангажа самолета
- 7-5. ВРЕМЕННЫЕ ХАРАКТЕРИСТИКИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 7-6. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- б) Частотные характеристики замкнутой системы
- в) Связь частотных характеристик замкнутой и разомкнутой систем
- ГЛАВА ВОСЬМАЯ. ЭНЕРГЕТИЧЕСКИЙ РАСЧЕТ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ И СОГЛАСОВАНИЕ ХАРАКТЕРИСТИК ЭЛЕМЕНТОВ
- 8-1. ВЫБОР МОЩНОСТИ ИСПОЛНИТЕЛЬНЫХ УСТРОЙСТВ И УСЛОВИЯ СОГЛАСОВАНИЯ С НАГРУЗКОЙ
- а) Определение необходимой мощности по переходным процессам при типовых воздействиях
- б) Мгновенная мощность при гармонических колебаниях
- в) Необходимая мощность при случайных колебаниях регулирующего органа
- г) Выбор мощности сервомотора
- д) Условия согласования с нагрузкой сервомотора без обратной связи
- е) Согласование с нагрузкой сервомотора с жесткой обратной связью
- 8-2. СОГЛАСОВАНИЕ ДАТЧИКОВ, УСИЛИТЕЛЬНЫХ И КОРРЕКТИРУЮЩИХ УСТРОЙСТВ. РАСПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТОВ УСИЛЕНИЯ
- б) Передаточные функции последовательных соединений элементов
- в) Согласование пропорциональных участков характеристик
- г) Распределение коэффициентов усиления
- ГЛАВА ДЕВЯТАЯ. УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ СТАЦИОНАРНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 9-2. КРИТЕРИЙ УСТОЙЧИВОСТИ РАУСА—ГУРВИЦА
- 9-3. КРИТЕРИЙ УСТОЙЧИВОСТИ МИХАЙЛОВА
- 9-4. КРИТЕРИЙ УСТОЙЧИВОСТИ НАЙКВИСТА
- б) Использование логарифмических характеристик системы для исследования устойчивости. Понятие о запасе устойчивости
- 9-5. КОЭФФИЦИЕНТ УСИЛЕНИЯ И УСТОЙЧИВОСТЬ. ВЛИЯНИЕ КОРРЕКТИРУЮЩИХ ЦЕПЕЙ НА УСТОЙЧИВОСТЬ
- 9-6. ВЫДЕЛЕНИЕ ОБЛАСТЕЙ УСТОЙЧИВОСТИ В ПРОСТРАНСТВЕ ПАРАМЕТРОВ СИСТЕМЫ ДИАГРАММЫ ВЫШНЕГРАДСКОГО
- б) Общий метод D-разбиения в плоскости двух параметров. Линейная задача
- в) Выделение области устойчивости в плоскости двух параметров. Нелинейная задача
- г) Выделение области устойчивости в плоскости одного комплексного параметра
- ГЛАВА ДЕСЯТАЯ. КАЧЕСТВО ПРОЦЕССОВ РЕГУЛИРОВАНИЯ В ЛИНЕЙНЫХ СИСТЕМАХ
- 10-1. КРИТЕРИИ КАЧЕСТВА ПРОЦЕССА РЕГУЛИРОВАНИЯ
- 10-2. ТОЧНОСТЬ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ В УСТАНОВИВШИХСЯ РЕЖИМАХ. СТАТИЧЕСКИЕ И АСТАТИЧЕСКИЕ СИСТЕМЫ
- б) Точность при медленно меняющихся воздействиях. Коэффициенты ошибок. Астатические системы высших порядков
- в) Общие условия неискаженного воспроизведения входных сигналов в вынужденном режиме
- г) Повышение точности системы коррекцией входного сигнала
- д) Повышение точности системы путем компенсации возмущения F(t)
- 10-18. ПЕРЕХОДНЫЕ ФУНКЦИИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- б) Некоторые особенности вычисления переходных функций
- 10-4. РАСПРЕДЕЛЕНИЕ НУЛЕЙ И ПОЛЮСОВ ПЕРЕДАТОЧНОЙ ФУНКЦИИ И ПЕРЕХОДНЫЕ ПРОЦЕССЫ
- б) Оценки распределения корней. Степень устойчивости. Коэффициент затухания колебаний
- в) Влияние параметров на распределение корней. Метод Эванса
- г) Оценка переходных функций по распределению полюсов передаточной функции или корней характеристического уравнения
- д) Влияние нулей на характер переходной функции
- е) Определение коэффициентов уравнений по заданному распределению корней. Стандартные коэффициенты характеристических уравнений
- 10-5. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ И ПЕРЕХОДНЫЕ ФУНКЦИИ
- б) Приближенное вычисление переходных функций и переходных процессов
- в) Оценка качества процесса регулирования по характеристикам замкнутой системы Ф(w) и ф(w) и характеристике разомкнутой системы W(jw)
- г) Оценка качества по амплитудным логарифмическим характеристикам. Минимально-фазовые системы
- д) Связь между логарифмическими амплитудными характеристиками разомкнутой системы и полюсами передаточной функции замкнутой системы
- 10-6. ИНТЕГРАЛЬНЫЕ ОЦЕНКИ ПЕРЕХОДНЫХ ПРОЦЕССОВ
- г) Приближение кривых x(t) к эталонной кривой хэ(t) по критерию …
- ГЛАВА ОДИННАДЦАТАЯ. НЕСТАЦИОНАРНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 11-1. ОБЩИЕ СВЕДЕНИЯ О НЕСТАЦИОНАРНЫХ СИСТЕМАХ
- 11-2. ПРИМЕРЫ СУЩЕСТВЕННО НЕСТАЦИОНАРНЫХ СИСТЕМ
- 11-3. ДИНАМИЧЕСКИЕ ХАРАКТЕРИСТИКИ НЕСТАЦИОНАРНЫХ СИСТЕМ АВТОМАТИЧ ЕСКОГО РЕГУЛИРОВАНИЯ
- 11-4. ОСОБЕННОСТИ СОСТАВЛЕНИЯ УРАВНЕНИЙ И СТРУКТУРНЫХ СХЕМ НЕСТАЦИОНАРНЫХ СИСТЕМ
- 11-5. МЕТОДЫ ОПРЕДЕЛЕНИЯ ЧАСТОТНОЙ ХАРАКТЕРИСТИКИ И ИМПУЛЬСНОЙ РЕАКЦИИ НЕСТАЦИОНАРНЫХ СИСТЕМ
- ГЛАВА ДВЕНАДЦАТАЯ. СТАТИСТИЧЕСКАЯ ДИНАМИКА ЛИНЕЙНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 12-1. СТАЦИОНАРНЫЕ И НЕСТАЦИОНАРНЫЕ СЛУЧАЙНЫЕ ПРОЦЕССЫ
- б) Стационарные и нестационарные случайные функций
- в) Свойства корреляционной функции
- г) Свойство эргодичности
- д) Гауссовы случайные процессы
- 12-2. ПРЕОБРАЗОВАНИЕ СТАЦИОНАРНЫХ СЛУЧАЙНЫХ ФУНКЦИЙ СТАЦИОНАРНЫМИ ЛИНЕЙНЫМИ СИСТЕМАМИ
- б) Преобразование корреляционных функций при прохождении случайного сигнала через линейную систему
- в) Интегральная квадратичная оценка импульсной переходной функции и дисперсия реакции системы на белый шум
- г) Преобразование спектральных плотностей при прохождении случайного сигнала через линейную систему
- 12-3. ОПТИМАЛЬНЫЕ ЛИНЕЙНЫЕ СТАЦИОНАРНЫЕ СИСТЕМЫ
- б) Условия оптимальности при свободном выборе передаточной функции
- ГЛАВА ТРИНАДЦАТАЯ. О СИНТЕЗЕ ЛИНЕЙНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 13-2. МЕТОД ЛОГАРИФМИЧЕСКИХ ЧАСТОТНЫХ ХАРАКТЕРИСТИК
- б) Синтез корректирующих цепей
- в) О синтезе на основе требований к реакции системы на возмущение F(t)
- 13-3. ВЫБОР ПАРАМЕТРОВ НА ОСНОВЕ АНАЛИЗА РАСПРЕДЕЛЕНИЯ НУЛЕЙ И ПОЛЮСОВ ПЕРЕДАТОЧНОЙ ФУНКЦИИ
- 13-4. ВЫБОР ПАРАМЕТРОВ НА ОСНОВЕ ИНТЕГРАЛЬНЫХ КВАДРАТИЧНЫХ ОЦЕНОК
- 13-5. СПЕЦИАЛЬНЫЕ ПРИЕМЫ УЛУЧШЕНИЯ КАЧЕСТВА ПРОЦЕССА РЕГУЛИРОВАНИЯ
- б) Подавление помех во входном сигнале при инерционном объекте управления
- в) Использование двух источников информации для выделения истинного сигнала
- г) Компенсация влияния запаздывания измерителей на динамические свойства системы
- д) Исключение перерегулирования в системах, передаточные функции которых имеют только вещественные полюсы
- ГЛАВА ЧЕТЫРНАДЦАТАЯ. ИМПУЛЬСНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 14-2. ИМПУЛЬСЫ И ИМПУЛЬСНЫЕ ЭЛЕМЕНТЫ
- б) Формирующие цепи и импульсные элементы
- 14-3. ДИСКРЕТНЫЕ ФУНКЦИИ И ПОСЛЕДОВАТЕЛЬНОСТИ. ИХ РАЗНОСТИ И СУММЫ
- 14-4. РЕАКЦИЯ ЛИНЕЙНЫХ НЕПРЕРЫВНЫХ СИСТЕМ НА ПОСЛЕДОВАТЕЛЬНОСТИ ИЛИ ДЕЛЬТА-ИМПУЛЬСОВ
- б) Свертка двух дискретных функций
- в) Уравнения в конечных разностях непрерывных звеньев первого и второго порядков
- г) Символические изображения дискретных функций и их использование для решения уравнений в конечных разностях
- 14-5. ДИСКРЕТНОЕ ПРЕОБРАЗОВАНИЕ ЛАПЛАСА ИЛИ z-ПРЕОБРАЗОВАНИЕ. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ КОМПЛЕКСНОГО АРГУМЕНТА
- 14-6. ДИНАМИКА РАЗОМКНУТЫХ ИМПУЛЬСНЫХ СИСТЕМ
- б) Значение выходной величины непрерывной системы внутри интервалов повторения
- в) Передаточные функции, систем с запаздыванием
- г) Свободные и вынужденные движения
- д) Полюсы. Устойчивость разомкнутых систем
- е) Переходные функции
- ж) Частотные характеристики
- 14-7. СВЯЗЬ МЕЖДУ ЧАСТОТНЫМИ И ПЕРЕХОДНЫМИ ФУНКЦИЯМИ. ДИСКРЕТНОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ
- 14-8. ИНТЕГРАЛЬНАЯ КВАДРАТИЧНАЯ ОЦЕНКА
- 14-9. ДИСКРЕТНЫЕ СЛУЧАЙНЫЕ ФУНКЦИИ (СЛУЧАЙНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ)
- ГЛАВА ПЯТНАДЦАТАЯ. ДИНАМИКА ИМПУЛЬСНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 15-1. УРАВНЕНИЯ И ПЕРЕДАТОЧНЫЕ ФУНКЦИИ СИСТЕМ С ОДНИМ ИМПУЛЬСНЫМ ЭЛЕМЕНТОМ
- 15-2. УСТОЙЧИВОСТЬ ЗАМКНУТЫХ СИСТЕМ
- 15-3. КАЧЕСТВО ПРОЦЕССА РЕГУЛИРОВАНИЯ
- 15-4. ПРИМЕРЫ ИМПУЛЬСНЫХ СИСТЕМ
- 15-5. ИМПУЛЬСНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ С ДИСКРЕТНЫМИ КОРРЕКТИРУЮЩИМИ ЦЕПЯМИ
- ГЛАВА ШЕСТНАДЦАТАЯ. СТРУКТУРНЫЕ СХЕМЫ, ХАРАКТЕРИСТИКИ И УРАВНЕНИЯ НЕЛИНЕЙНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- б) Уравнения продольного движения самолета
- в) Уравнения продольного движения ракеты
- 16-2. НЕЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ СИГНАЛА ОШИБКИ
- б) Структурные схемы с нелинейными элементами
- в) Релейные системы. Релейные элементы
- 16-3. НЕЛИНЕЙНЫЙ ОБЪЕКТ РЕГУЛИРОВАНИЯ И НЕЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ СИГНАЛА ОШИБКИ
- ГЛАВА СЕМНАДЦАТАЯ. СВОЙСТВА НЕЛИНЕЙНЫХ СИСТЕМ И (МЕТОДЫ ИССЛЕДОВАНИЯ
- б) Суждение об устойчивости по уравнениям первого приближения. Теоремы Ляпунова
- в) Суждение о качестве процессов регулирования по уравнениям первого приближения
- г) Прямой метод Ляпунова
- д) Техническая устойчивость
- 17-2. АВТОКОЛЕБАНИЯ НЕЛИНЕЙНЫХ СИСТЕМ
- б) Автоколебания релейных систем
- в) Метод точечных преобразований
- г) Описание процесса в релейной системе разностным уравнением. Устойчивость автоколебаний
- д) Примера исследования автоколебаний релейных систем второго порядка
- 17-3. ВЛИЯНИЕ КОРРЕКТИРУЮЩИХ ЦЕПЕЙ НА АВТОКОЛЕБАНИЯ И НА ПЕРЕХОДНЫЕ ПРОЦЕССЫ НЕЛИНЕЙНЫХ СИСТЕМ
- б) Влияние корректирующих цепей на переходные процессы. Скользящие режимы. Оптимальные переходные процессы
- 17-4. ГАРМОНИЧЕСКАЯ ЛИНЕАРИЗАЦИЯ ПРОЦЕССОВ В НЕЛИНЕЙНЫХ СИСТЕМАХ
- б) Исследование автоколебаний при помощи гармонической линеаризации
- в) Гармоническая линеаризация и критерии устойчивости линейных систем
- 17-5. ТЕОРИЯ РЕЛЕЙНЫХ СИСТЕМ
- в) Частотные характеристики релейных систем
- г) Оценка устойчивости релейных систем
- д) Вынужденные колебания релейных систем. Захватывание (синхронизация или подавление) автоколебаний
- е) Вибрационная линеаризация релейных систем, Реакция релейных систем на медленно меняющиеся возмущения
- 17-6. ОПТИМАЛЬНЫЕ ПРОЦЕССЫ РЕГУЛИРОВАНИЯ
- б) Системы, оптимальные по быстродействию. Принцип максимума
- в) Системы, близкие к оптимальным по быстродействию
- ГЛАВА ВОСЕМНАДЦАТАЯ. ЭНТРОПИЯ, ИНФОРМАЦИЯ, АЛГОРИТМ В СИСТЕМАХ АВТОМАТИЧЕОКОГО УПРАВЛЕНИЯ
- 18-1. ЭНТРОПИЯ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ УПРАВЛЯЕМОГО ПРОЦЕССА
- 18-2. КОЛИЧЕСТВО ИНФОРМАЦИИ В ПРОЦЕССАХ УПРАВЛЕНИЯ
- 18-3. ЭНТРОПИЯ И ИНФОРМАЦИЯ В ЗАМКНУТЫХ СИСТЕМАХ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- 18-4. АЛГОРИТМЫ ПРОЦЕССОВ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- ГЛАВА ДЕВЯТНАДЦАТАЯ. СИСТЕМЫ ЭКСТРЕМАЛЬНОГО РЕГУЛИРОВАНИЯ
- 19-1. ПРИМЕРЫ СИСТЕМ ЭКСТРЕМАЛЬНОГО РЕГУЛИРОВАНИЯ
- 19-2. СПОСОБЫ ПОИСКА ЭКСТРЕМУМА
- б) Методы организации процесса поиска
- 19-3. СТРУКТУРНЫЕ СХЕМЫ СИСТЕМ ЭКСТРЕМАЛЬНОГО РЕГУЛИРОВАНИЯ
- 19-4. ДИНАМИКА НЕПРЕРЫВНЫХ СИСТЕМ ЭКСТРЕМАЛЬНОГО РЕГУЛИРОВАНИЯ В КВАЗИСТАЦИОНАРНОМ РЕЖИМЕ
- б) Динамика квазистационарного режима систем экстремального регулирования, основанных на методе градиента
- 19-5. ДИНАМИКА НЕПРЕРЫВНЫХ СИСТЕМ ЭКСТРЕМАЛЬНОГО РЕГУЛИРОВАНИЯ ПРИ СЛУЧАЙНЫХ СИГНАЛАХ ПОИСКА
- б) Уравнения замкнутой системы экстремального регулирования
- в) Точность экстремального регулирования
- 19-6. ФОРСИРОВАННЫЕ ПРОЦЕССЫ ЭКСТРЕМАЛЬНОГО РЕГУЛИРОВАНИЯ ОДНОМЕРНОГО БЕЗЫНЕРЦИОННОГО ОБЪЕКТА
- ГЛАВА ДВАДЦАТАЯ. СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ С САМОНАСТРАИВАЮЩИМИСЯ КОРРЕКТИРУЮЩИМИ УСТРОЙСТВАМИ
- 20-1. СИСТЕМЫ С РАЗОМКНУТЫМИ ЦЕПЯМИ НАСТРОЙКИ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ
- 20-2. СИСТЕМЫ С ЗАМКНУТЫМИ ЦЕПЯМИ НАСТРОЙКИ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ
- 20-3. СИСТЕМЫ С ЭКСТРЕМАЛЬНОЙ НАСТРОЙКОЙ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ
- 20-4. СТАТИСТИЧЕСКАЯ ДИНАМИКА НЕПРЕРЫВНЫХ СИСТЕМ С ЭКСТРЕМАЛЬНОЙ НАСТРОЙКОЙ ПОСЛЕДОВАТЕЛЬНЫХ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ
- б) Уравнения замкнутой самонастраивающейся системы
- в) Случай сильной фильтрации. Квазистационарный режим
- г) Общий случай квазистационарного режима
- ГЛАВА ДВАДЦАТЬ ПЕРВАЯ. ИГРОВЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- 21-1. НАЗНАЧЕНИЕ И ПРИНЦИПЫ ДЕЙСТВИЯ ИГРОВЫХ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- 21-2. НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ ИГР
- 21-3. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ. ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
- 21-4. ОБ АЛГОРИТМАХ ИГРОВЫХ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- ПРИЛОЖЕНИЯ