| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
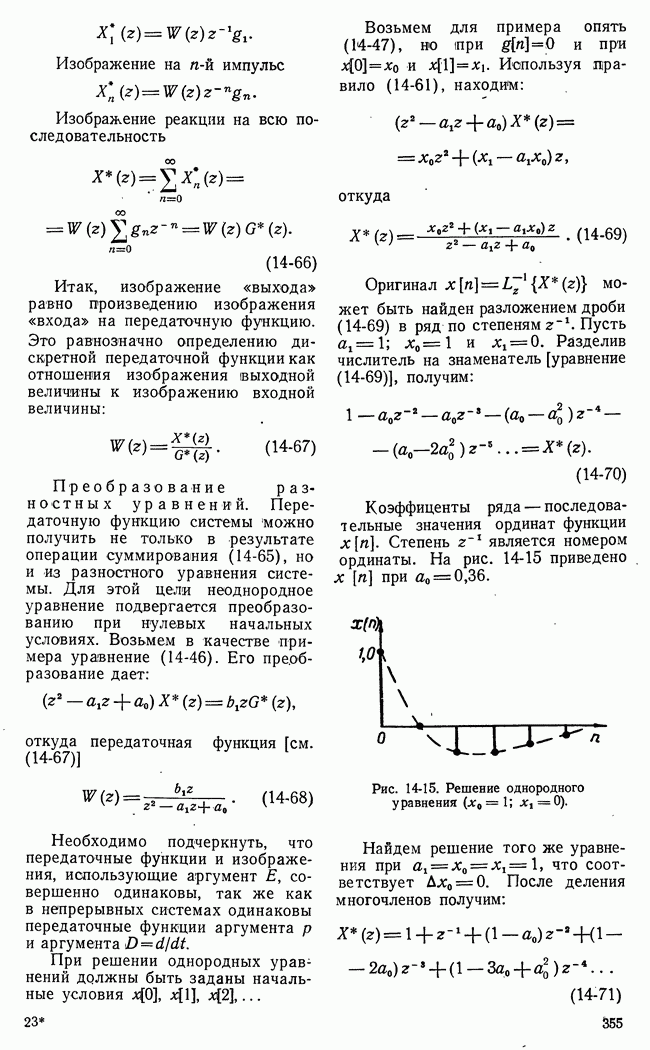
21-4. ОБ АЛГОРИТМАХ ИГРОВЫХ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
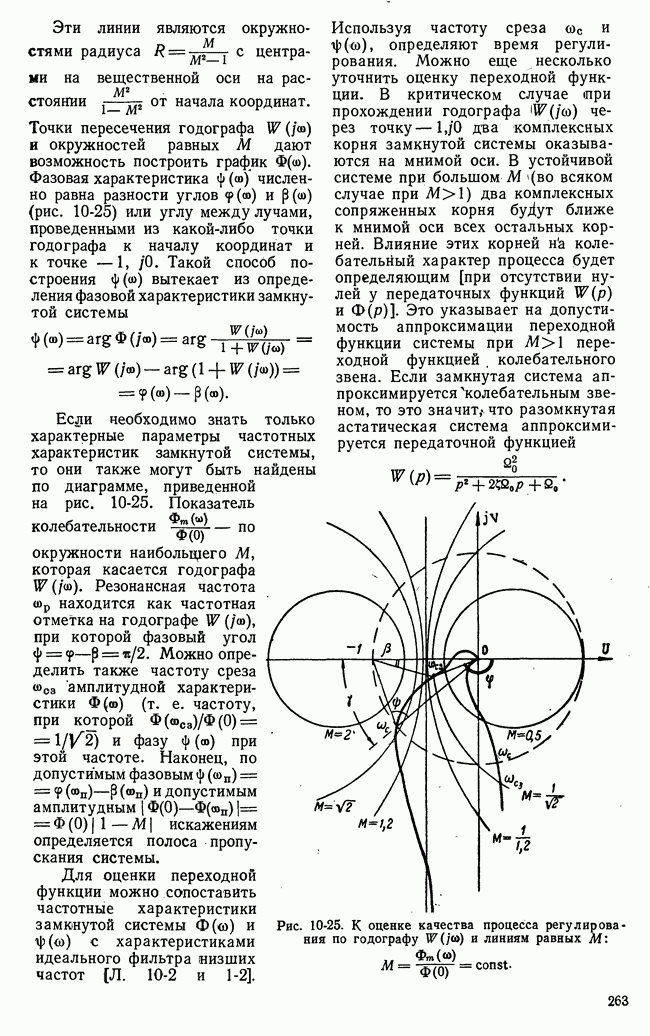
Как указывалось ранее, характерная особенность игровых систем автоматического управления состоит в формировании команд управления путем сопоставления возможных выборов и решений. Критерием сопоставления служит функция

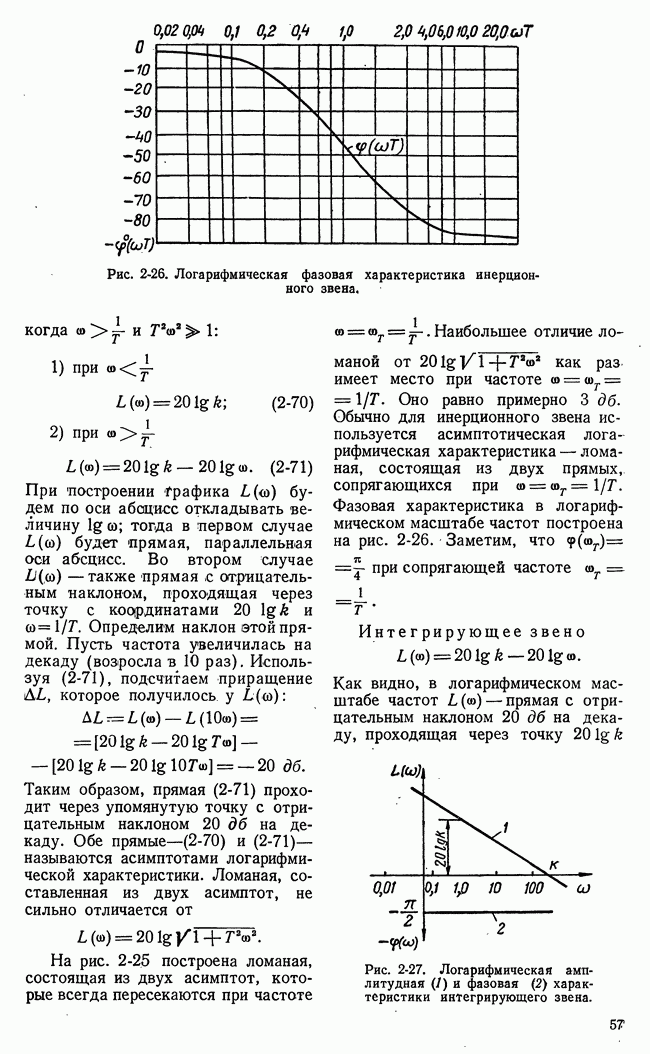
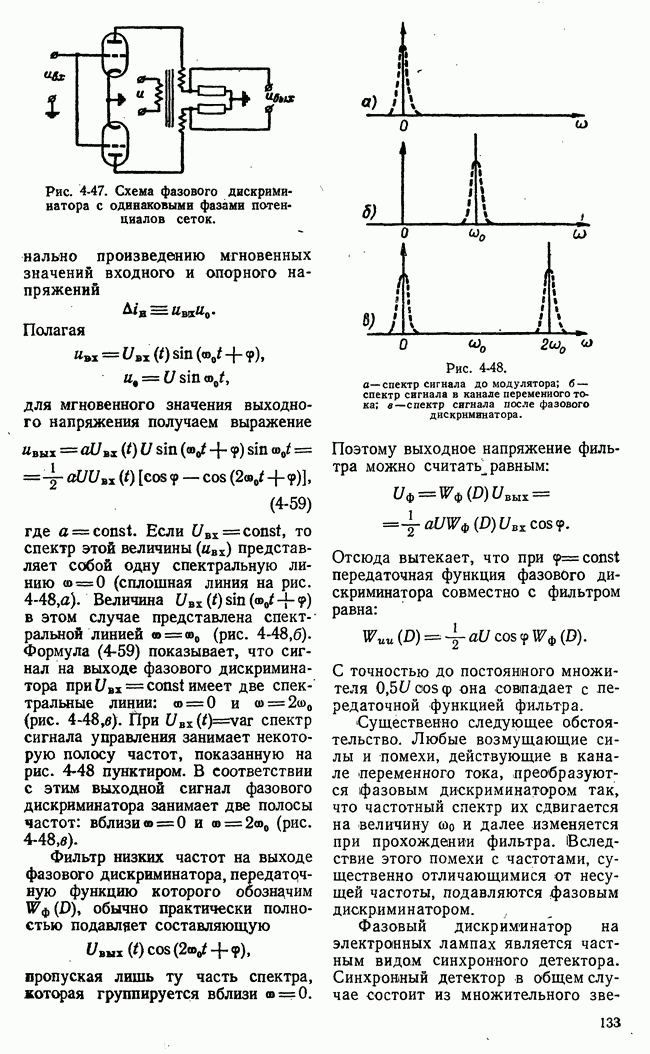
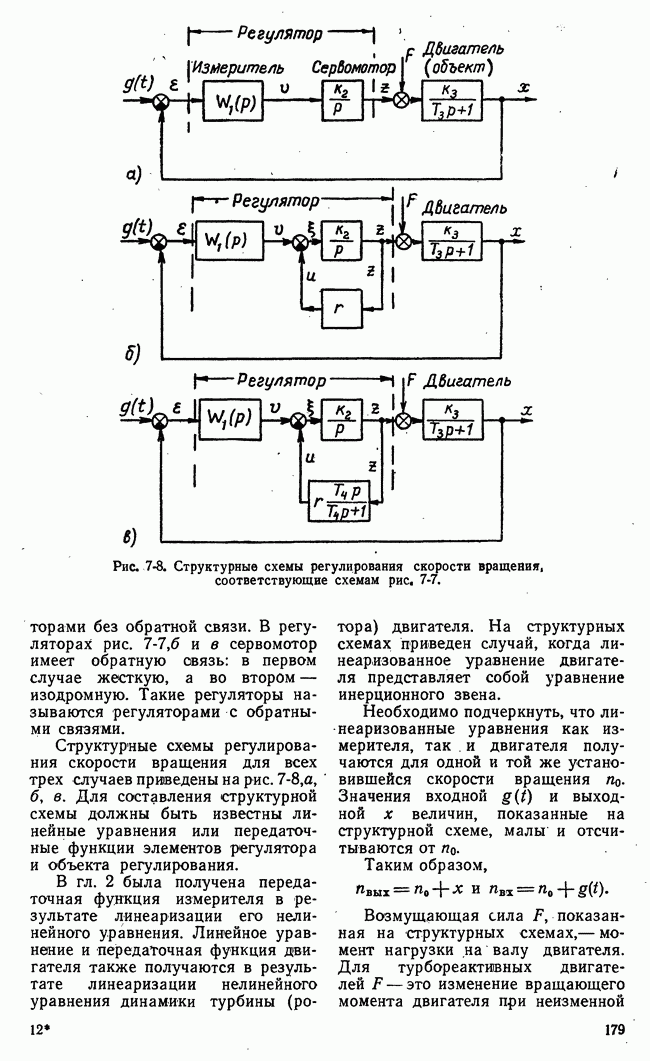
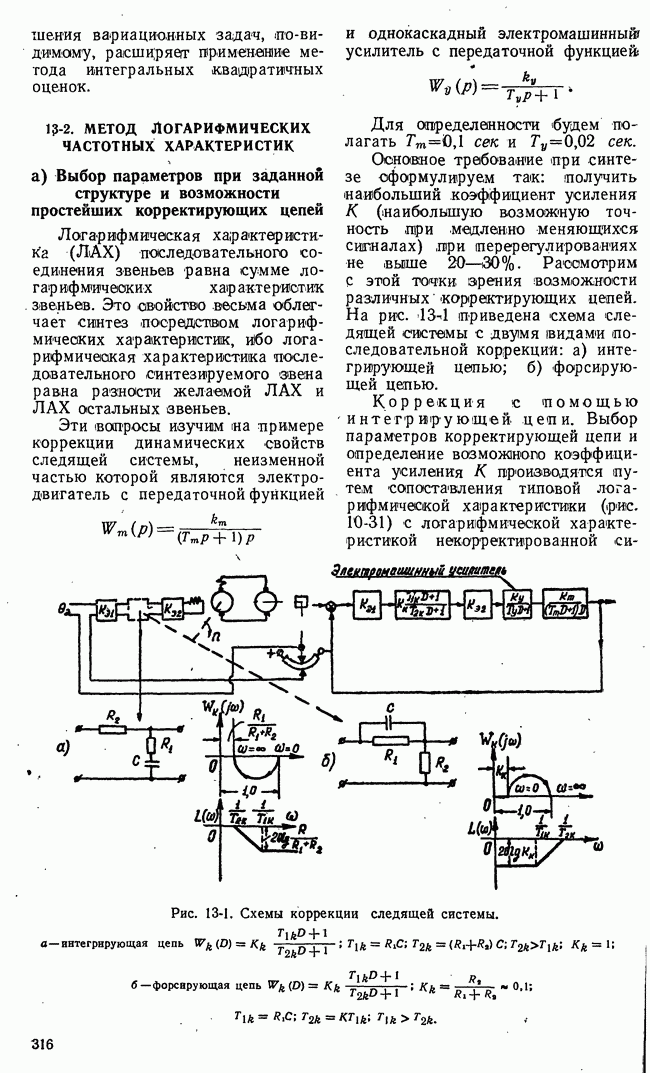
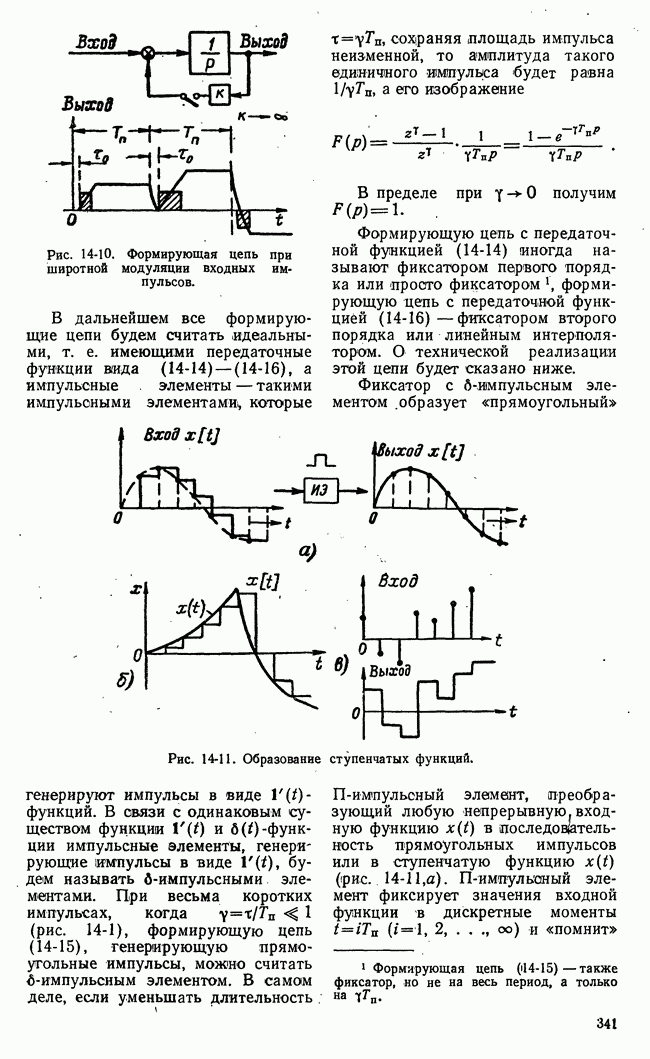
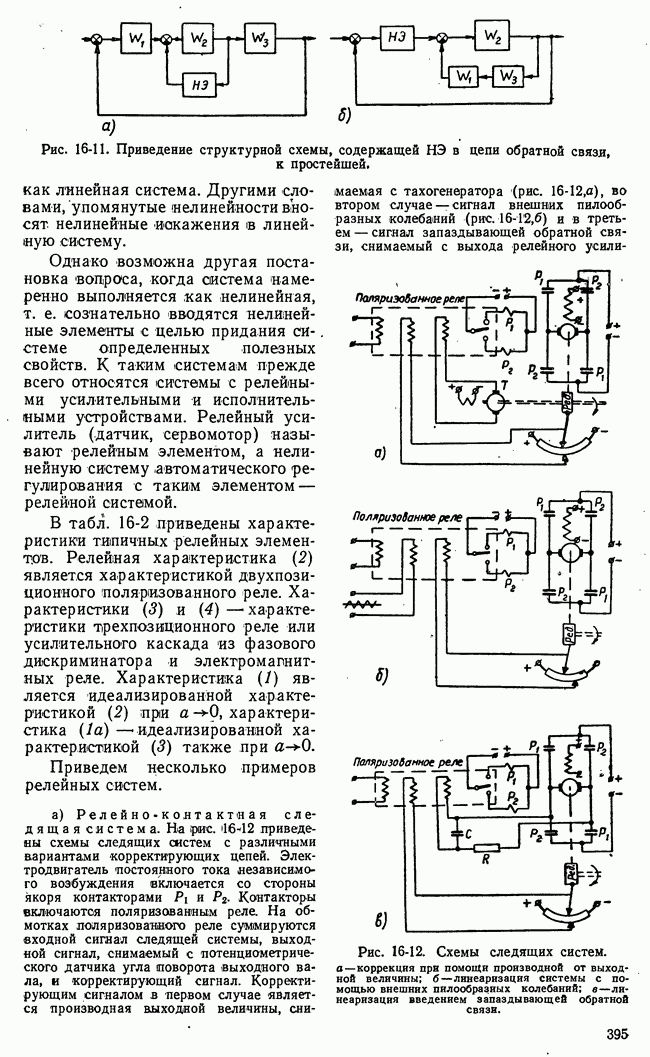
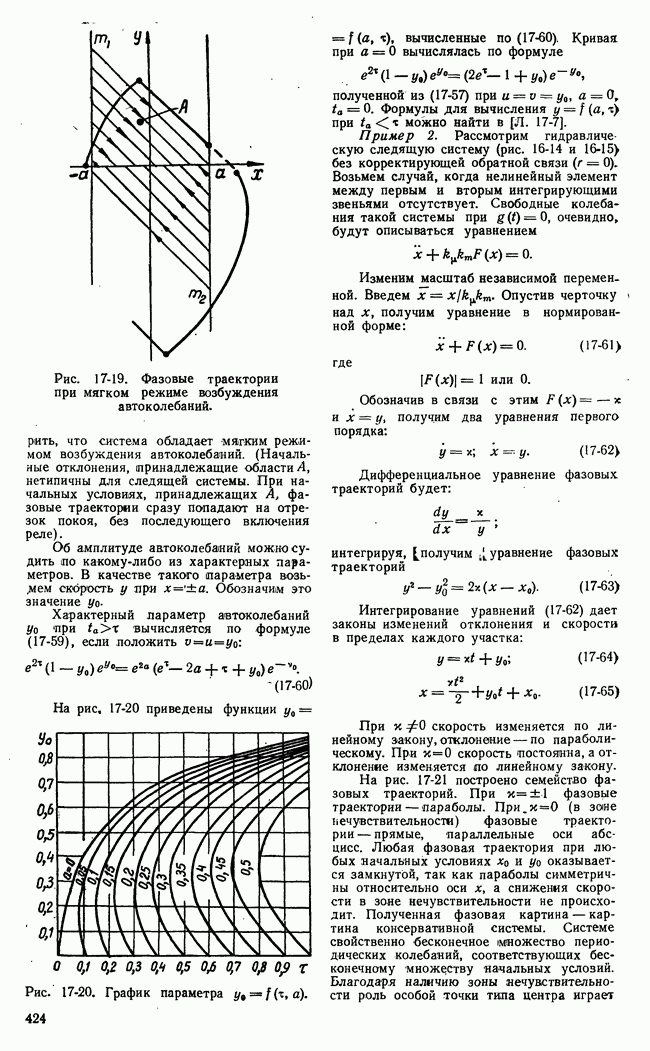
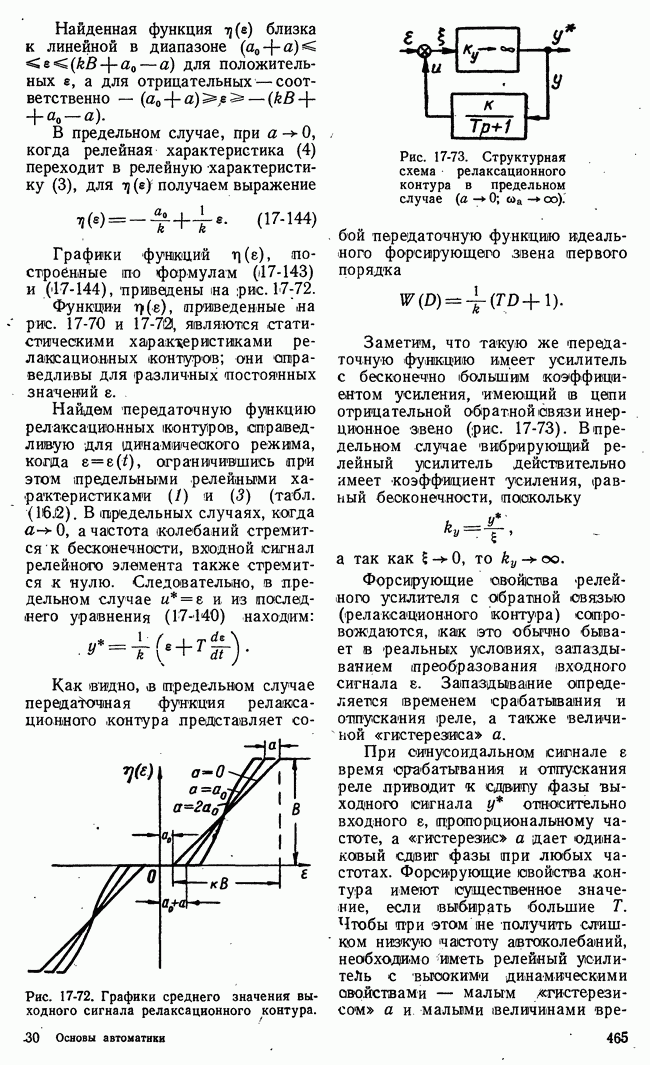
Рис. 21-11. Функциональная схема игровой системы с набором шаблонных решений.
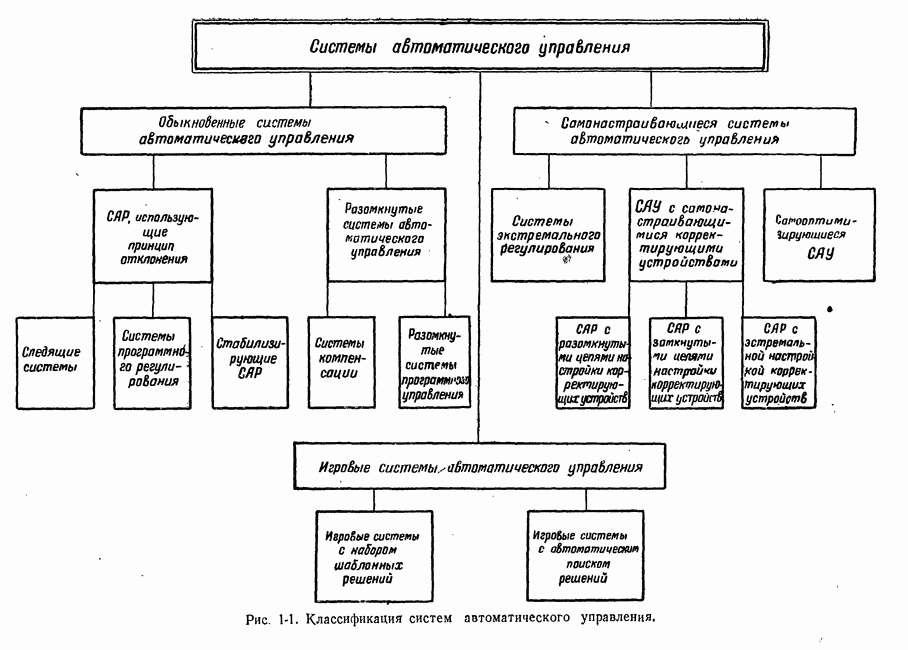
выгоды, точнее ее математическое ожидание вконце данного хода или в конце всей последовательности ходов. Целесообразный алгоритм игровой системы автоматического управления определяется множествами возможных выборов сторон, принятой функцией выгоды, располагаемой информацией и другими факторами. По-видимому, возможно большее число классов алгоритмов игровых систем автоматического управления. В настоящее время с достаточной отчетливостью можно выделить два принципиально различных класса. Соответствующие этим классам алгоритмов типы игровых систем автоматического управления обозначены на рис. 1-1.
Первый (наименее совершенный) тип назван системами с набором шаблонных решений. Пользуясь приведенным выше термином, системы этого типа можно также назвать системами с исчерпывающим алгоритмом.
Сущность алгоритма подобных систем весьма проста. Она заключается в том, что возможные действия I стороны, управляемой данной системой, и II стороны, не управляемой данной системой, разбиваются на конечное число определенных вариантов. Эти варианты нумеруются. Следует сказать, что под действием здесь понимается не один ход, а вся последовательность ходов в течение игры (операции).
Далее производится предварительное теоретическое или экспериментальное исследование рационального соответствия действий I и II сторон. Это исследование имеет целью указать такое соответствие между элементами множеств возможных действий сторон, при котором гарантированное значение функции выгоды I стороны было бы наибольшим. В понятиях теории игр (§ 21-2) это означает, что отыскивается оптимальная стратегия 1-го игрока. Все это делается до проведения игры и даже до построения управляющей части системы.
Полученное соответствие действий — оптимальная стратегия — есть алгоритм рассматриваемого типа систем. Для реализации этого алгоритма в запоминающем устройстве управляющей машины записывают выбранное соответствие пронумерованных действий I и II сторон. Например (в десятичном коде):

Эта запись означает, что при первом варианте действий II стороны выбирается 278-й вариант действий I стороны. При втором варианте действий II стороны выбирается 43-й вариант действий I стороны и т. д. Помимо записи стратегии в запоминающем устройстве, реализация рассматриваемых систем с набором шаблонных решений требует осуществления преобразования номера действия I стороны в последовательность соответствующих команд и преобразования получаемой информации о II стороне в номер наиболее вероятного варианта действия этой стороны.
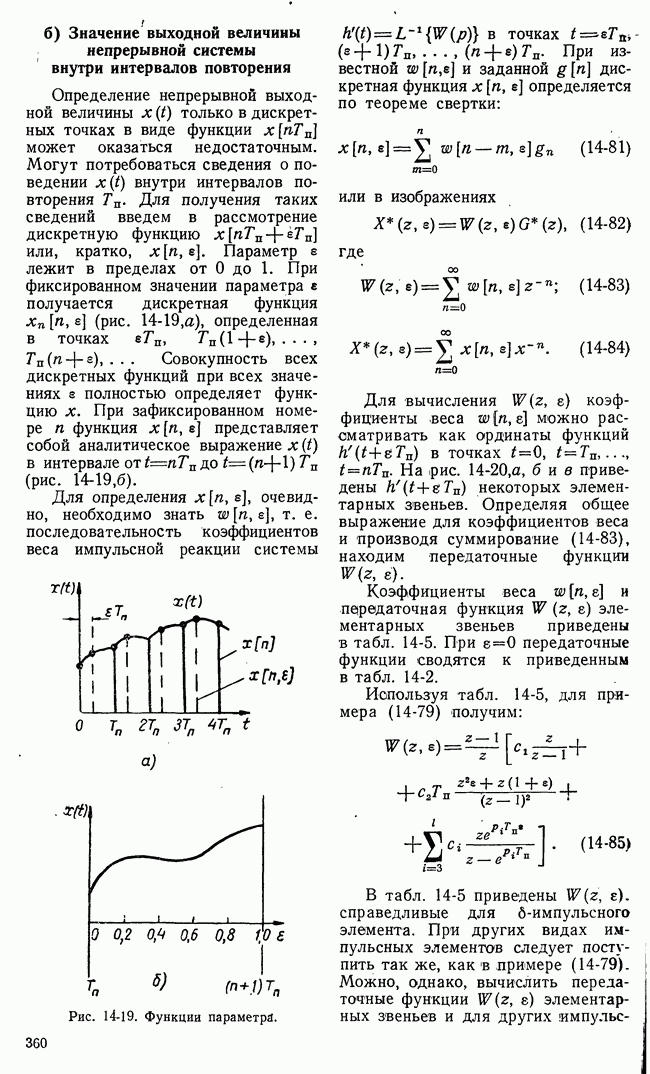
Работа игровой системы автоматического управления с набором шаблонных решений заключается в следующем (рис. 21-11). По полученной информации о действиях
II стороны управляющая машина определяет «а основе некоторых показателей номер  подходящего варианта действий II стороны из числа предусмотренных в машине. Определенный номер подается в блок соответствия, в котором записана стратегия в виде соответствия
подходящего варианта действий II стороны из числа предусмотренных в машине. Определенный номер подается в блок соответствия, в котором записана стратегия в виде соответствия  номеров вариантов действия I и II сторон. Номер
номеров вариантов действия I и II сторон. Номер  варианта действия управляемой системы (I сторона) поступает в блок формирования команд, где этот номер преобразуется в последовательность команд. Команды воздействуют на управляемый процесс. Контроль выполнения команд может составлять дополнительный контур передачи информации (обратную связь), воздействующий на блок формирования команд.
варианта действия управляемой системы (I сторона) поступает в блок формирования команд, где этот номер преобразуется в последовательность команд. Команды воздействуют на управляемый процесс. Контроль выполнения команд может составлять дополнительный контур передачи информации (обратную связь), воздействующий на блок формирования команд.
Рассматривая функциональную схему и принцип действия игровой системы автоматического управления с набором шаблонных решений, замечаем, что системы этого типа сами по себе не выполняют никаких логических действий, заменяющих в той или иной мере мыслительную деятельность. Все здесь подчинено заранее составленной подробной «инструкции», рассчитанной на строго определенные варианты действий II стороны. Управляющая машина выполняет здесь весьма элементарную операцию соответствия номеров вариантов 
Действия системы шаблонны, что можно считать основным недостатком рассматриваемого типа игровых систем автоматического управления.
Действительно, лишь в отдельных случаях можно указать строго ограниченное число вариантов возможных действий II стороны. В большинстве практических применений игровых систем управления число возможных вариантов обстановки и действий II стороны весьма велико или неограниченно велико. Между тем всякое действие II стороны, не предусмотренное заранее в наборе номеров  управляющей машины, делает систему неработоспособной. Далее, количество рабочей информации о действиях II стороны, как правило, ограниченно, неполно.
управляющей машины, делает систему неработоспособной. Далее, количество рабочей информации о действиях II стороны, как правило, ограниченно, неполно.
Поэтому во многих случаях очень трудно правильно решить задачу подбора номера варианта, наиболее точно соответствующего фактическим действиям II стороны. Работа блока определения номера подходящего варианта (рис. 21-11) затруднена из-за недостатка информации. К этому следует добавить, что составление инструкции в виде соответствия номеров вариантов  т. е. определение оптимальной стратегии, основывается на вполне определенных правилах игры — определенных условиях, накладываемых на действия сторон и их взаимодействие. В практических применениях часто нельзя указать строго определенные правила «игры» — строго определенные ограничения, накладываемые на действия сторон. Все эти обстоятельства указывают на то, что игровые системы автоматического управления с набором шаблонных решений могут применяться лишь в специальных простейших случаях, когда разнообразие возможных действий сторон огракиченно и располагаемая рабочая информация достаточно полна.
т. е. определение оптимальной стратегии, основывается на вполне определенных правилах игры — определенных условиях, накладываемых на действия сторон и их взаимодействие. В практических применениях часто нельзя указать строго определенные правила «игры» — строго определенные ограничения, накладываемые на действия сторон. Все эти обстоятельства указывают на то, что игровые системы автоматического управления с набором шаблонных решений могут применяться лишь в специальных простейших случаях, когда разнообразие возможных действий сторон огракиченно и располагаемая рабочая информация достаточно полна.
Во всех других случаях необходимы игровые системы, обеспечивающие большую «гибкость» управления. К числу таких систем относятся игровые системы автоматичекого управления, названные нами игровыми системами с автоматическим поиском решений (рис. 1-1).
Напомним, что существо метода динамического программирования заключается в поэтапном решении задачи оптимальности. Разработанный как метод вычислений оптимальных процессов (§ 21-3), он является также естественным методом управления. Действительно, если обратиться к аналогиям из области управления человеком различными операциями и сложными процессами, то можно убедиться, что это управление часто состоит в поэтапном принятии решений на основе поэтапной оценки обстановки и контроля результатов выполнения предыдущих решений.
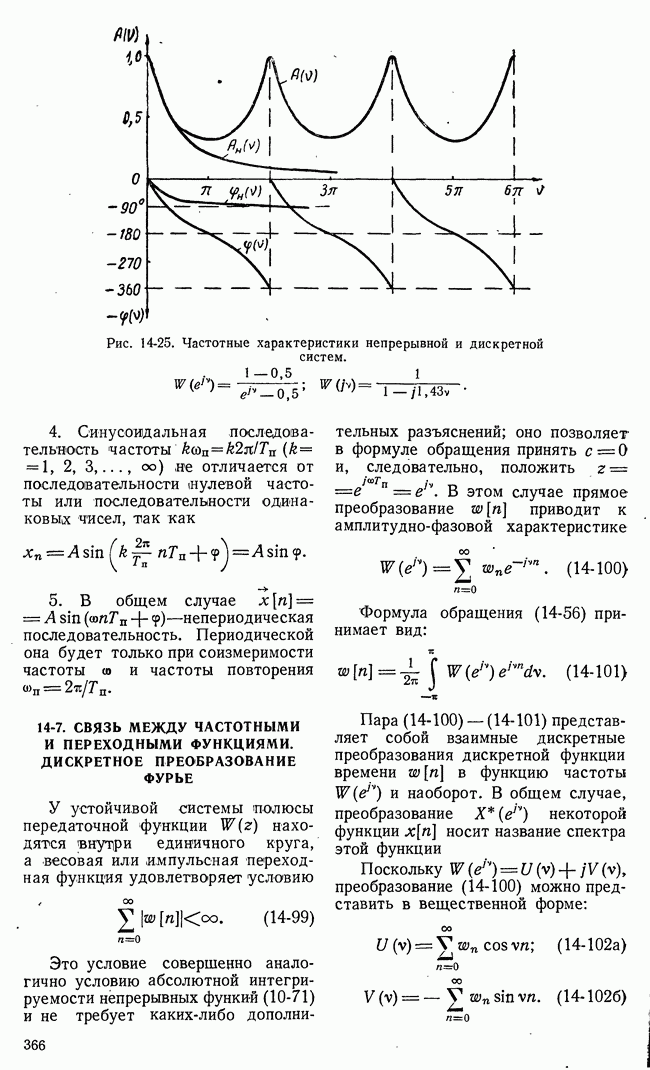
В рассматриваемой игровой системе автоматического управления поиск оптимального выбора в

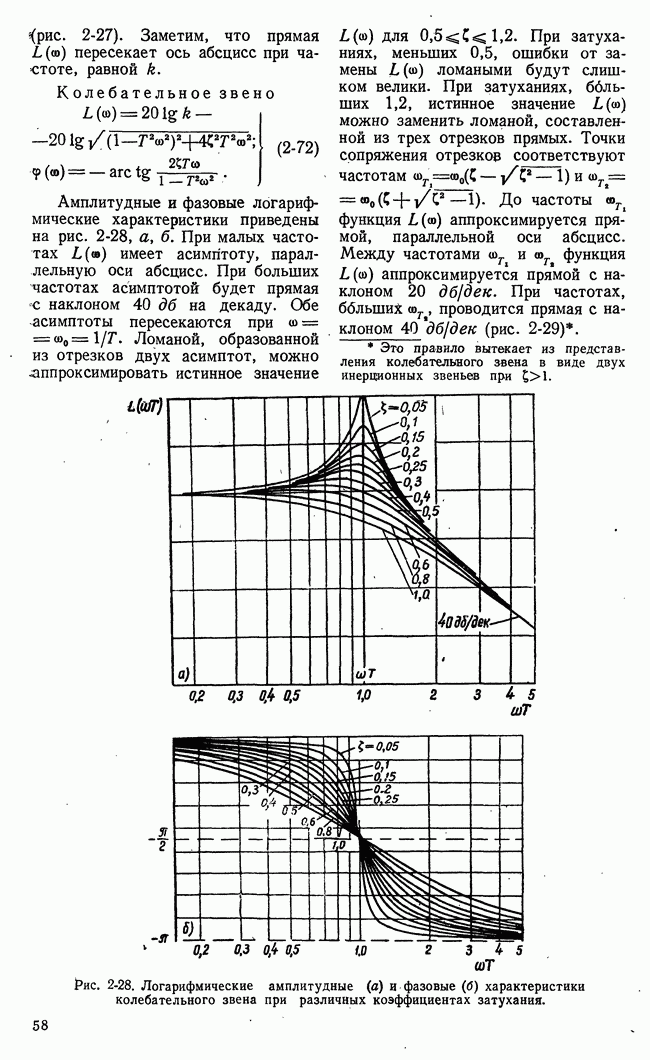
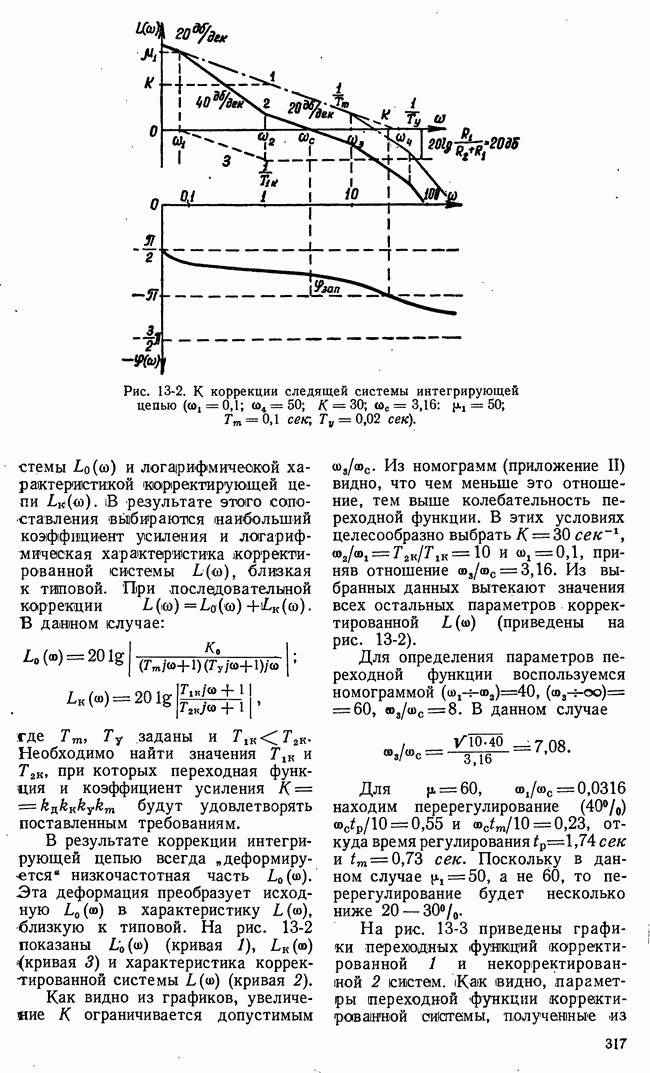
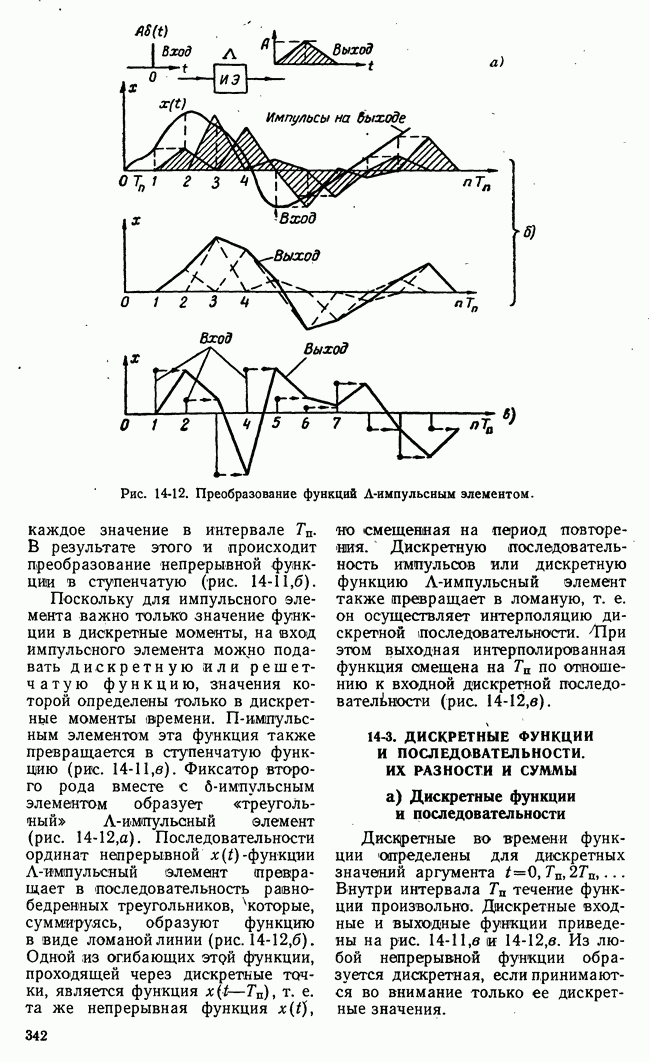
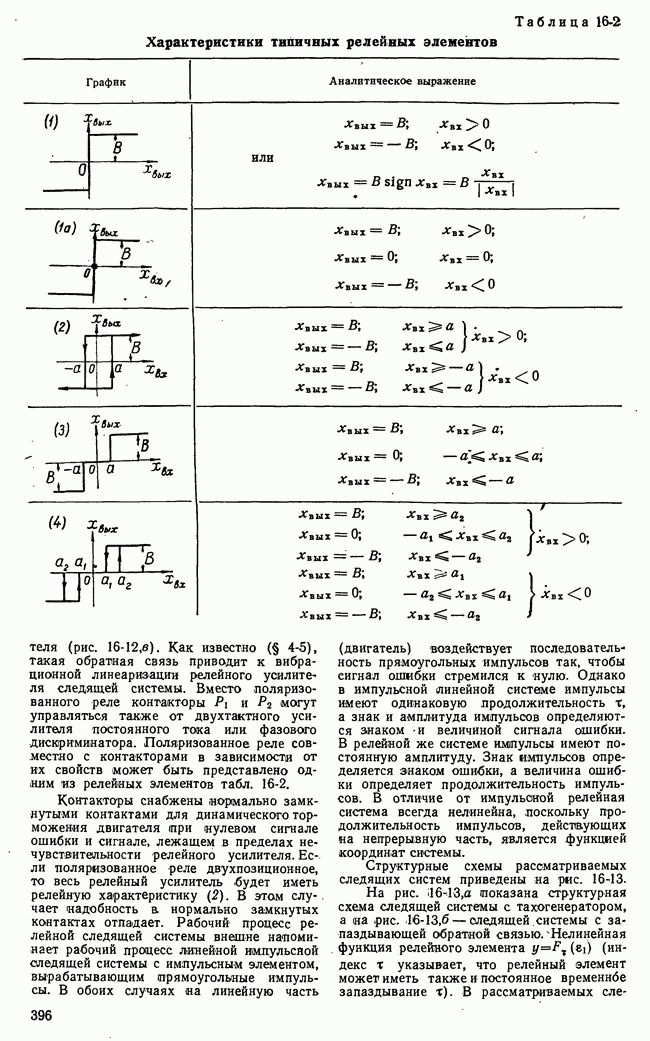
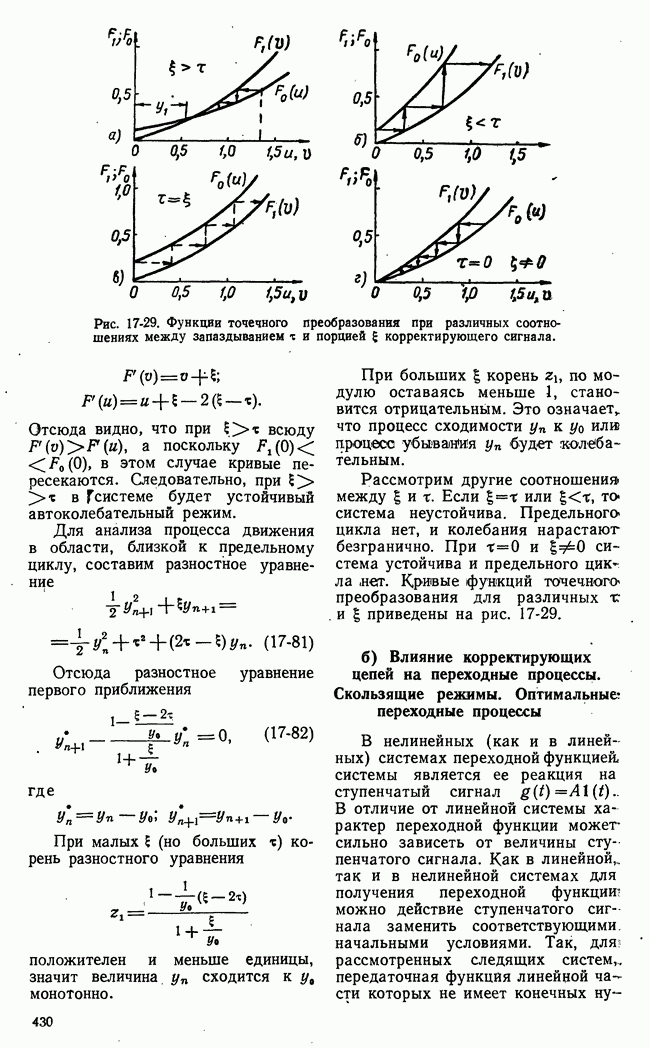
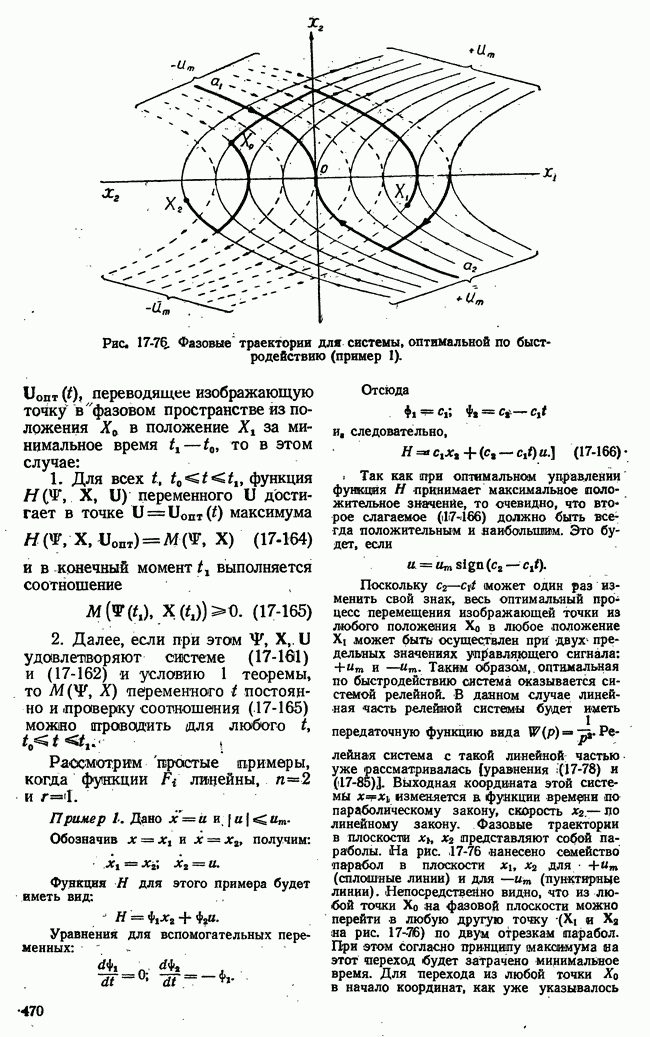
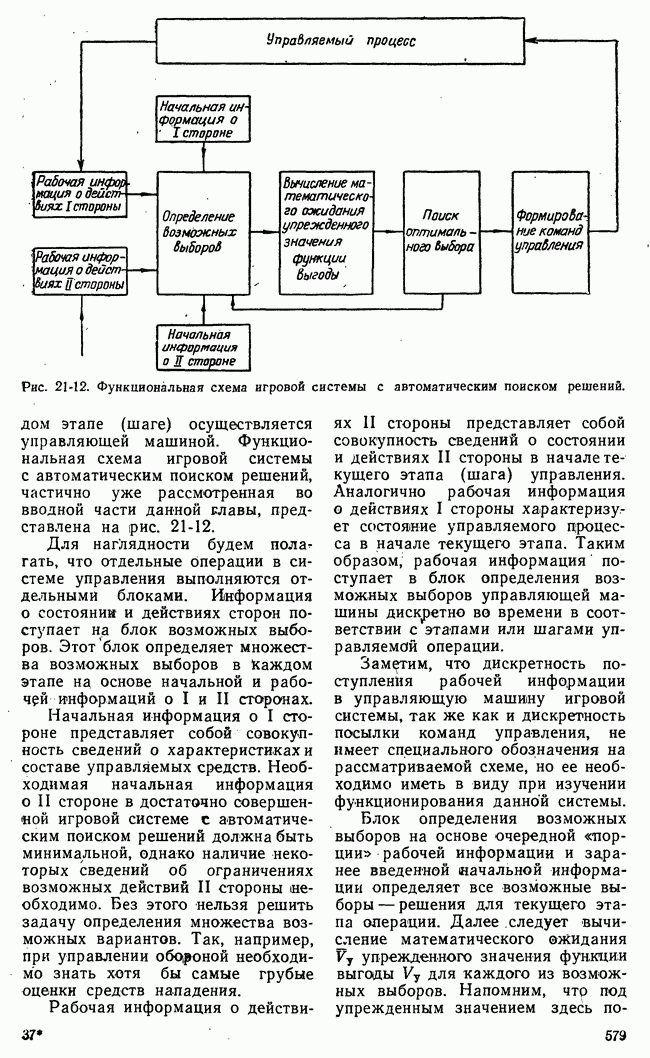
Рис. 21-12. Функциональная схема игровой системы с автоматическим поиском решений.
каждом этапе (шаге) осуществляется управляющей машиной. Функциональная схема игровой системы с автоматическим поиском решений, частично уже рассмотренная во вводной части данной славы, представлена на рис. 21-12.
Для наглядности будем полагать, что отдельные операции в системе управления выполняются отдельными блоками. Информация о состоянии и действиях сторон поступает на блок возможных выборов. Этот блок определяет множества возможных выборов в каждом этапе на основе начальной и рабочей информаций о I и II сторонах.
Начальная информация о I стороне представляет собой совокупность сведений о характеристиках и составе управляемых средств. Необходимая начальная информация о II стороне в достаточно совершенной игровой системе с автоматическим поиском решений должна быть минимальной, однако наличие некоторых сведений об ограничениях возможных действий II стороны необходимо. Без этого нельзя решить задачу определения множества возможных вариантов. Так, например, при управлении обороной необходимо знать хотя бы самые грубые оценки средств нападения.
Рабочая информация о действиях II стороны представляет собой совокупность сведений о состоянии и действиях II стороны в начале текущего этапа (шага) управления. Аналогично рабочая информация о действиях I стороны характеризует состояние управляемого процесса в начале текущего этапа. Таким образом, рабочая информация поступает в блок определения возможных выборов управляющей машины дискретно во времени в соответствии с этапами или шагами управляемой операции.
Заметим, что дискретность поступления рабочей информации в управляющую машину игровой системы, так же как и дискретность посылки команд управления, не имеет специального обозначения на рассматриваемой схеме, но ее необходимо иметь в виду при изучении функционирования данной системы.
Блок определения возможных выборов на основе очередной «порции» рабочей информации и заранее введенной начальной информации определяет все возможные выборы — решения для текущего этапа операции. Далее следует вычисление математического ожидания  упрежденного значения функции выгоды
упрежденного значения функции выгоды  для каждого из возможных выборов. Напомним, что под упрежденным значением здесь
для каждого из возможных выборов. Напомним, что под упрежденным значением здесь

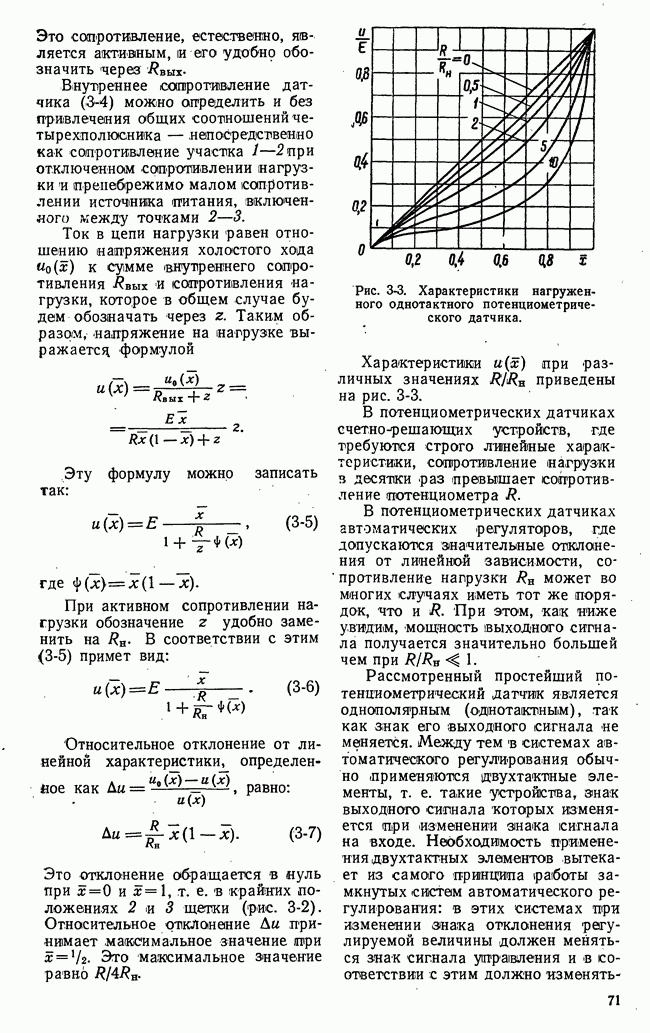
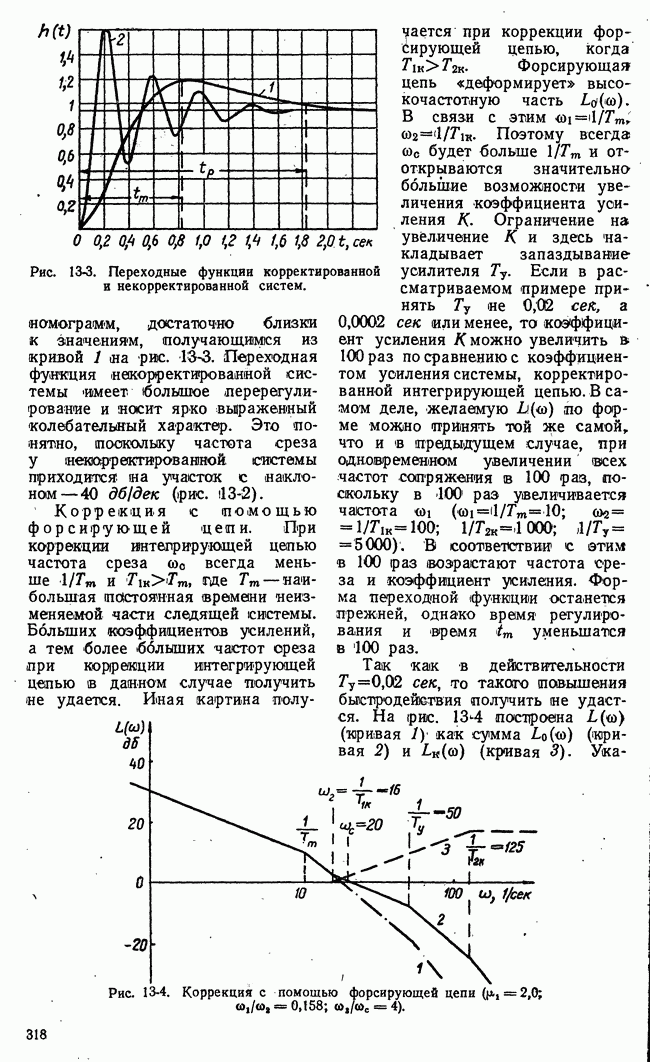
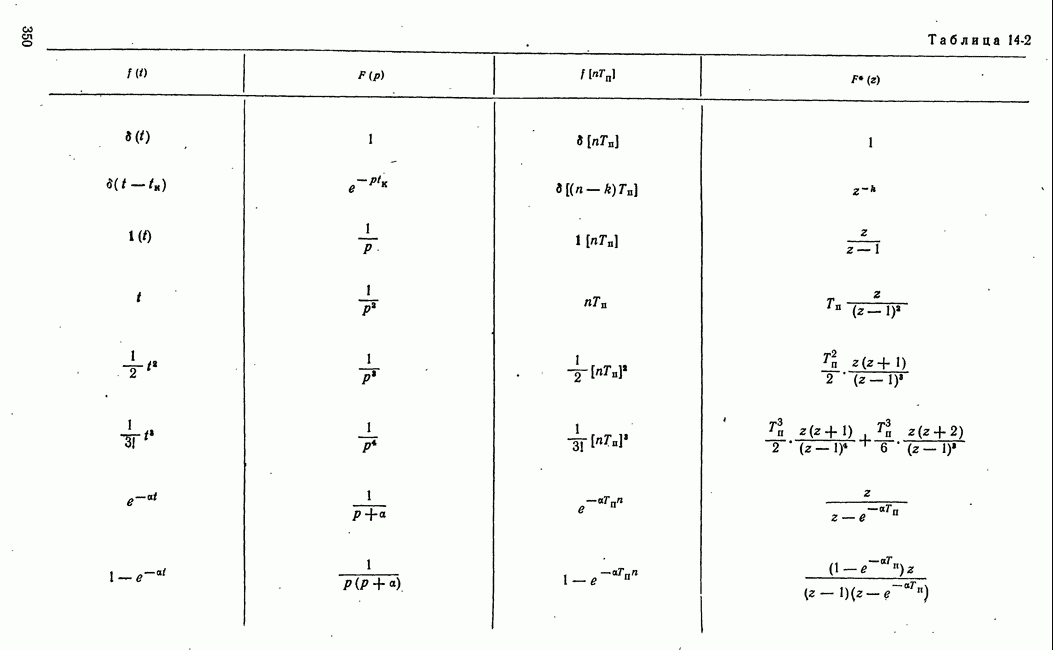
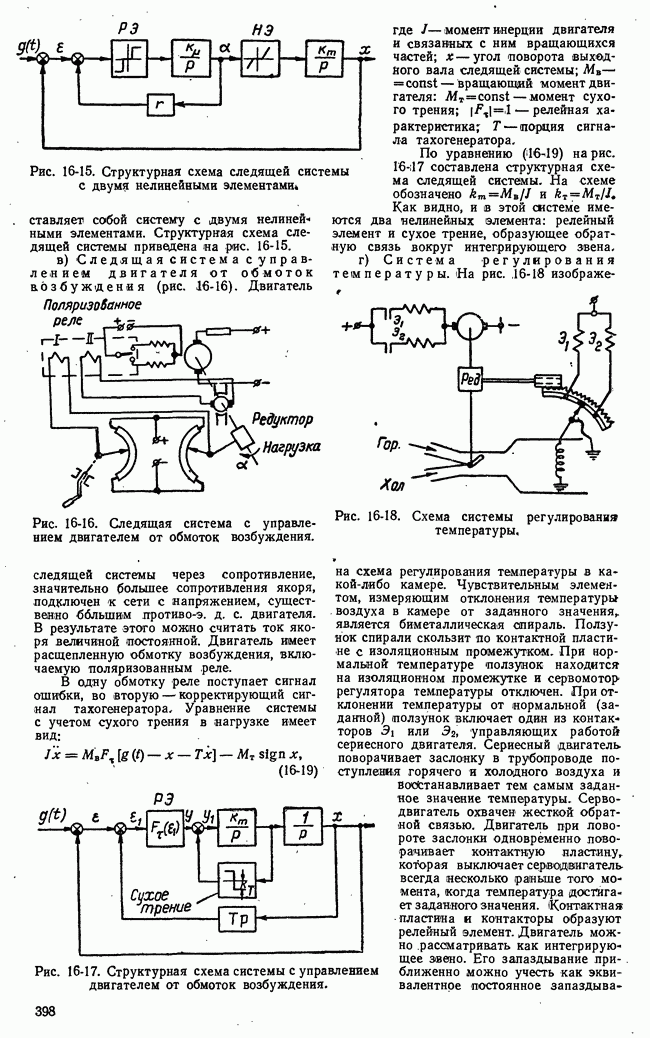
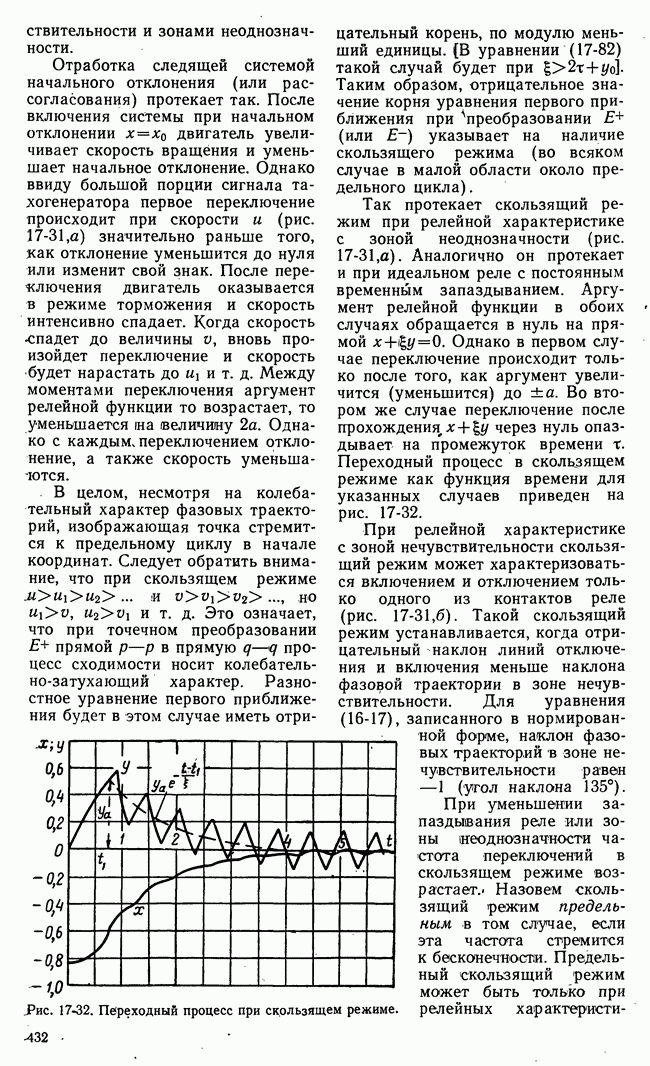
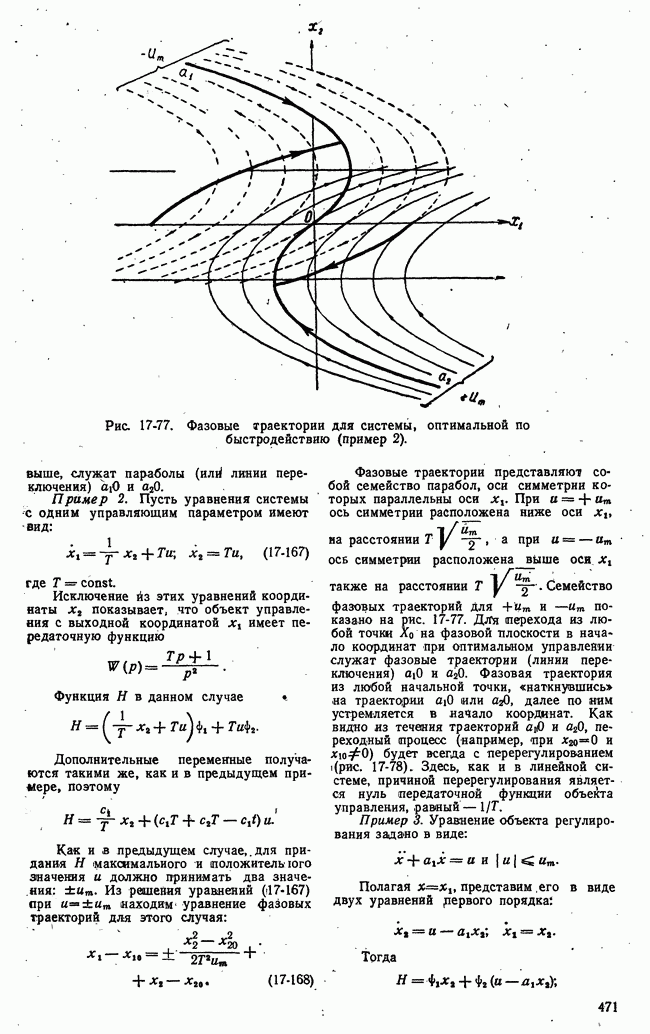
Рис. 21-13. Изменение во времени математического ожидания функции выгоды.
понимается значение в конце текущего этапа операции. Далее следует поиск того выбора, которому соответствует наибольшее значение  т. е. поиск оптимального выбора в данном этапе операции (рис. 21-12). Организация поиска оптимального выбора может быть различной.
т. е. поиск оптимального выбора в данном этапе операции (рис. 21-12). Организация поиска оптимального выбора может быть различной.
Если структура функции выгоды  на множестве выборов совершенно неизвестна, то приходится применять «слепой» поиск, т. е. перебирать все возможные выборы и соответствующие им значения
на множестве выборов совершенно неизвестна, то приходится применять «слепой» поиск, т. е. перебирать все возможные выборы и соответствующие им значения  и путем сравнения находить выбор или выборы, дающие наибольшее математическое ожидание упрежденного значения функции выгоды. Если же структура функции
и путем сравнения находить выбор или выборы, дающие наибольшее математическое ожидание упрежденного значения функции выгоды. Если же структура функции  на множестве выборов в какой-то мере известна, то возможны более экономные методы поиска. При этом может быть также сокращен объем вычислений возможных выборов и значений
на множестве выборов в какой-то мере известна, то возможны более экономные методы поиска. При этом может быть также сокращен объем вычислений возможных выборов и значений  т. е. «облегчена» работа двух предыдущих блоков (несколько подробнее это пояснено ниже). После оптимального выбора в текущем этапе операции формируются команды управления, предназначенные Для реализации этого выбора, т. е. изменения течения управляемого процесса в соответствии с оптимальным выбором (рис. 21-12). Эти команды воздействуют на управляемый процесс в течение текущего этапа операции.
т. е. «облегчена» работа двух предыдущих блоков (несколько подробнее это пояснено ниже). После оптимального выбора в текущем этапе операции формируются команды управления, предназначенные Для реализации этого выбора, т. е. изменения течения управляемого процесса в соответствии с оптимальным выбором (рис. 21-12). Эти команды воздействуют на управляемый процесс в течение текущего этапа операции.
По окончании данного этапа операции весь цикл управления повторяется; вновь поступает рабочая информация в управляющую машину, вновь определяются возможные выборы и соответствующие им значения  делается оптимальный выбор, формируются новые команды управления и т. д. Процесс может быть конечным, т. е. может заканчиваться после некоторого конечного числа этапов, и может быть бесконечным, т. е. содержать неограниченное число этапов, каждый из которых занимает конечный интервал времени. В первом случае окончание операции обусловливается определенными ограничениями, например израсходованием всех управляемых средств.
делается оптимальный выбор, формируются новые команды управления и т. д. Процесс может быть конечным, т. е. может заканчиваться после некоторого конечного числа этапов, и может быть бесконечным, т. е. содержать неограниченное число этапов, каждый из которых занимает конечный интервал времени. В первом случае окончание операции обусловливается определенными ограничениями, например израсходованием всех управляемых средств.
Из приведенного описания очевидно, что многоэтапный процесс управления в игровой системе с автоматическим поиском решений является замкнутым дискретным процессом: результат выполнения команд предыдущего этапа служит исходным для формирования и отработки команд следующего этапа. Полное описание динамики замкнутого процесса управления в игровой системе зависит от изменения во времени всех координат этого процесса.
Однако важнейшие показатели динамики процессов управления в игровых системах могут быть определены при (рассмотрении двух основных характеристик: изменения во времени математического ожидания функции выгоды  разброса функции выгоды, характеризуемого энтропией этой функции.
разброса функции выгоды, характеризуемого энтропией этой функции.
Последовательность значений математического ожидания  функции выгоды в этапах операции характеризует основной ожидаемый эффект управления и изменение его во времени. Эта последовательность — дискретная функция времени
функции выгоды в этапах операции характеризует основной ожидаемый эффект управления и изменение его во времени. Эта последовательность — дискретная функция времени

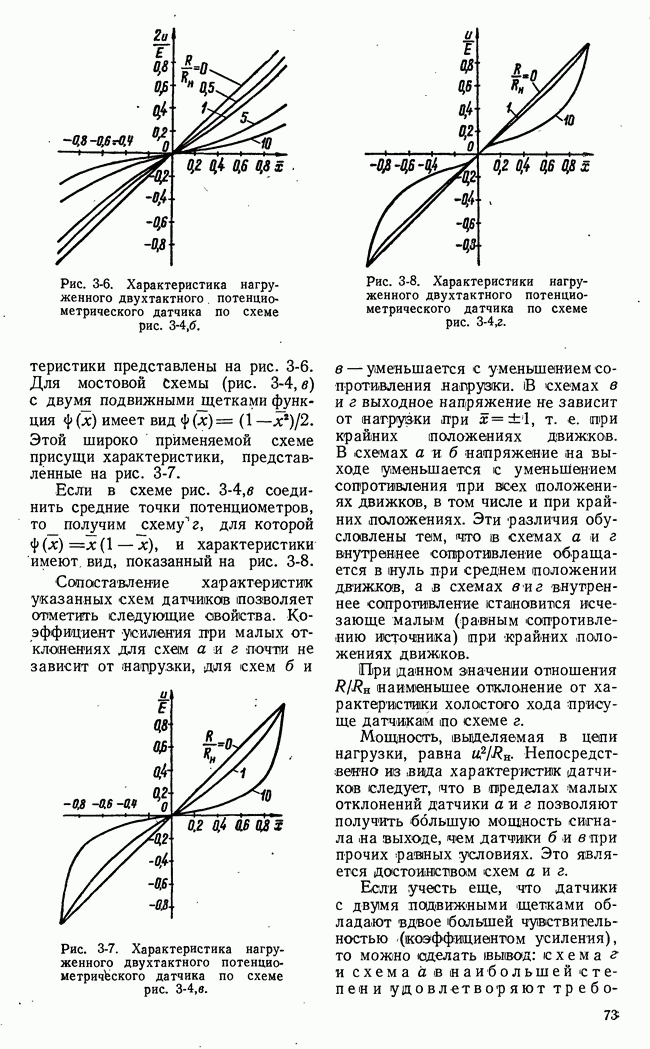
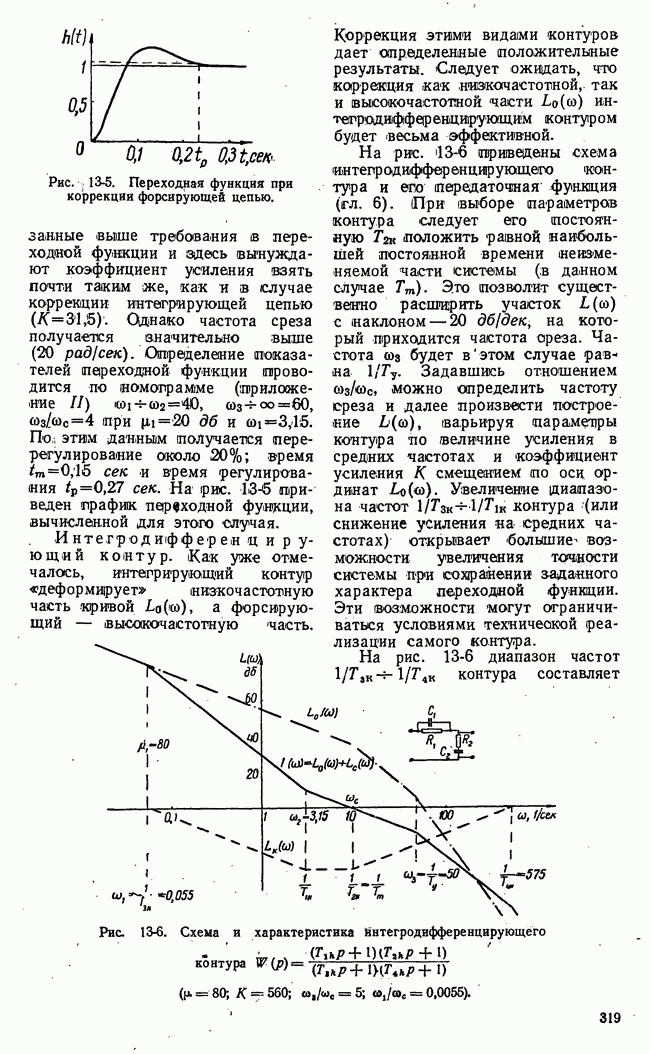
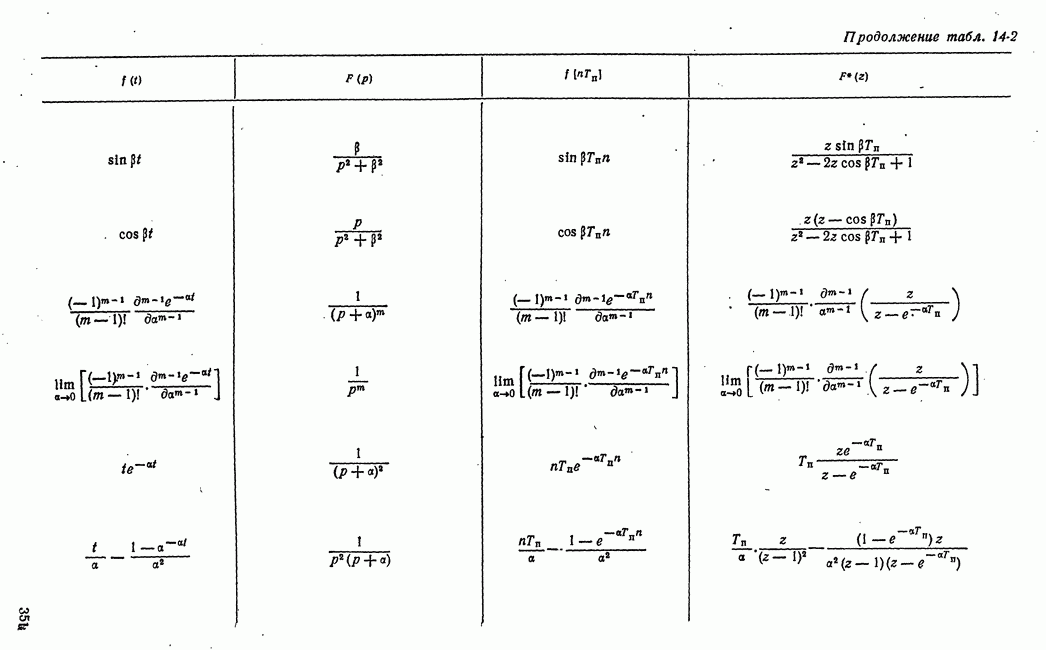
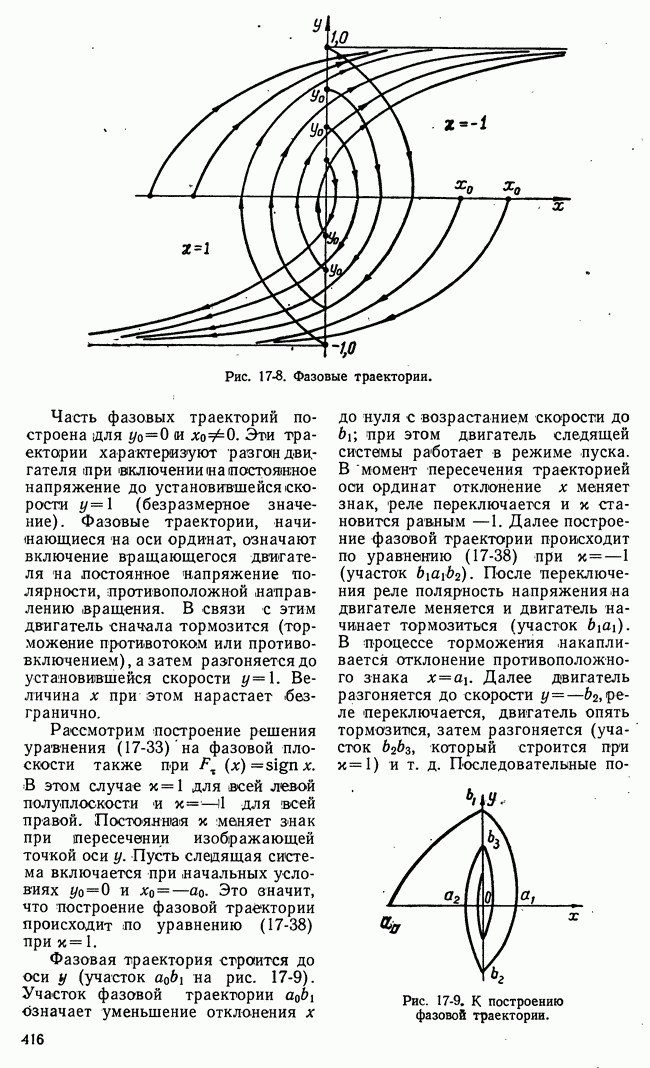
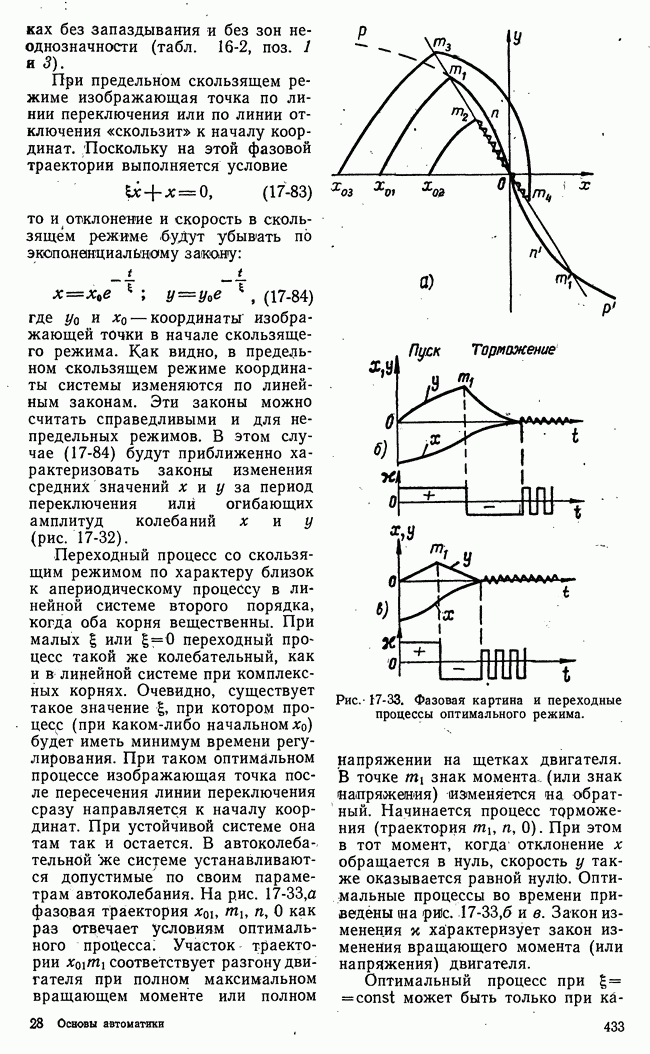
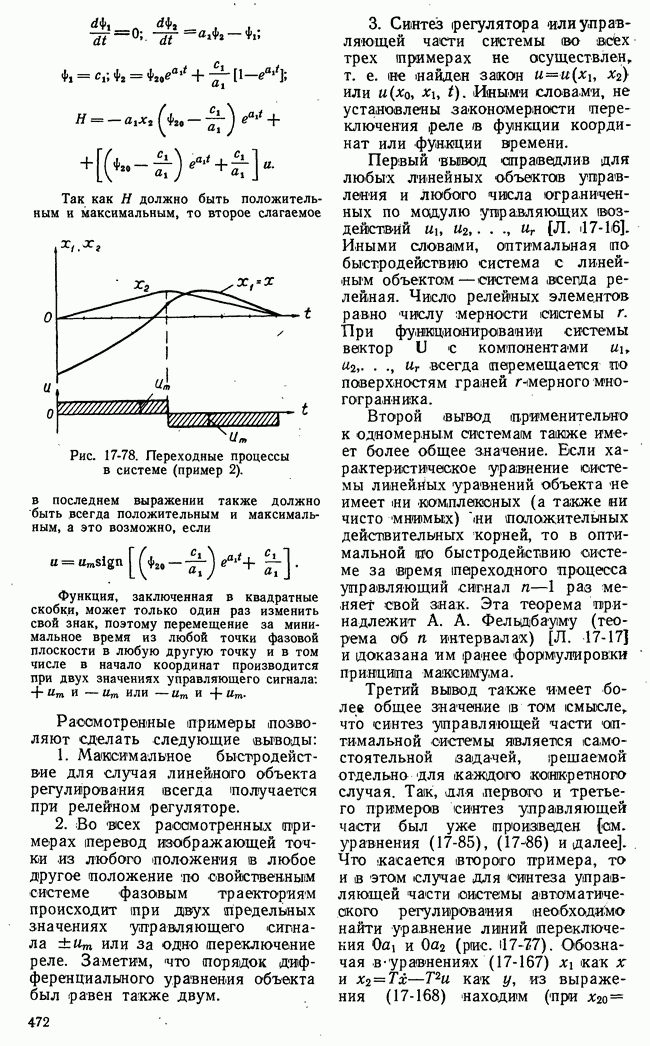
Рис. 21-14. Изменение разброса функции выгоды во времени.
(рис. 21-13) - определяет математическое ожидание выгоды по истечении  этапов управляемой операции
этапов управляемой операции  Однако знания математического ожидания функции выгоды еще недостаточно. Как рабочая, так и начальная информация в игровых системах никогда не бывают полными в том смысле, что действительные свойства и действия сторон отличаются от тех действий и свойств, которые выдаются источниками информации. Поэтому процесс управления в игровой системе — всегда случайный процесс. В соответствии с этим и функция выгоды является дискретной случайной функцией времени.
Однако знания математического ожидания функции выгоды еще недостаточно. Как рабочая, так и начальная информация в игровых системах никогда не бывают полными в том смысле, что действительные свойства и действия сторон отличаются от тех действий и свойств, которые выдаются источниками информации. Поэтому процесс управления в игровой системе — всегда случайный процесс. В соответствии с этим и функция выгоды является дискретной случайной функцией времени.
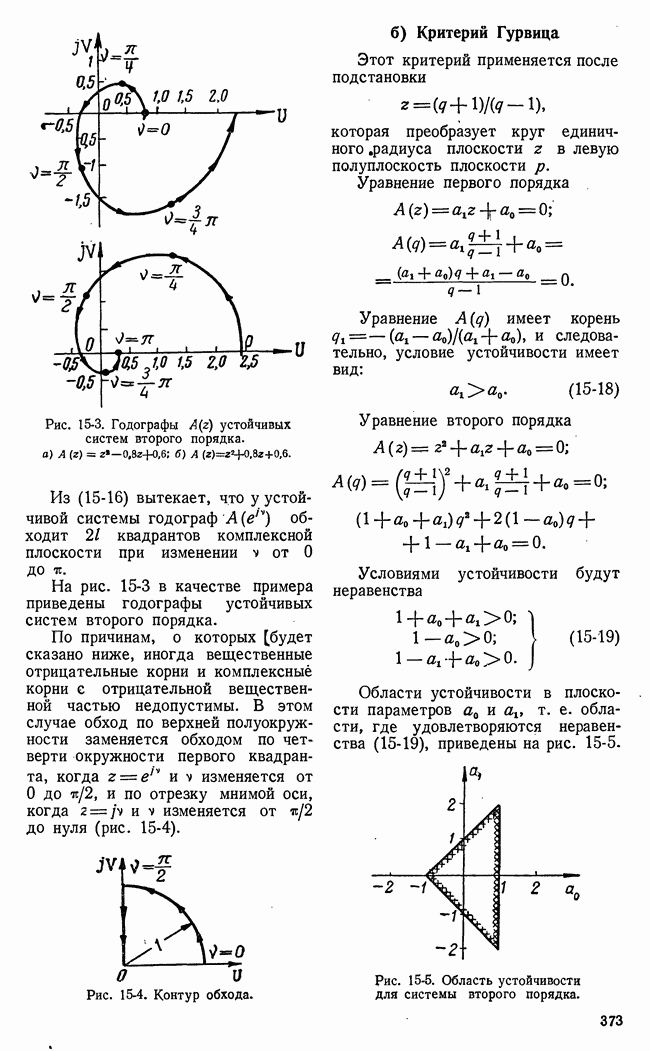
Второй основной характеристикой динамики процесса управления в игровой системе является изменение разброса функции выгоды во. времени. Это изменение условно показано на рис. 21-14 в виде заштрихованной полосы. Разброс функции выгоды удобно характеризовать энтропией этой функции или дисперсией. Таким образом, кривая изменения энтропии или дисперсии функции выгоды во времени представляет вторую основную характеристику динамики процесса управления в игровой системе.
Изменение во времени математического ожидания и дисперсии функции выгоды — наиболее важные показатели динамики процессов управления в игровых системах.
Игровые системы автоматического управления с автоматическим поиском решений имеют широкую перспективу применения и совершенствования. Укажем два пути развития и усовершенствования этих систем. Первый путь заключается в придании игровым системам свойств систем с накоплением опыта. Второй путь заключается в усовершенствовании способа поиска оптимальных выборов.
Системами с накоплением опыта называются системы, способные изменять характеристики и алгоритм действия в соответствии с опытом предшествующей работы. В игровых системах это касается прежде всего накопления опыта корректировки функции выгоды.
Действительно, из самого принципа работы игровой системы следует, что вид функции выгоды имеет фундаментальное значение для процесса управления. Между тем ввиду принципиальной неполноты априорной информации, имеющейся при построении игровой системы, первоначальная функция выгоды всегда строится на основе более или менее оправданных гипотез. Это относится не только к структуре функции выгоды, но и к числовым значениям параметров, входящих в эту функцию. Например, расчетная эффективность различных средств обороны может существенно отличаться от фактической эффективности в каждой данной операции из-за помех или других непредвиденных обстоятельств. При  этом система, отыскивающая максимум расчетной функции выгоды, уже не будет в состоянии обеспечить максимум фактической выгоды. Путь совершенствования системы заключается в корректировке значений параметров и структуры функции выгоды в каждом данном этапе операции по результатам предшествующих этапов управления операцией. Так, например, если частоты поражения средств нападения средствами обороны в первом этапе операции не соответствуют принятым начальным вероятностям поражения, то во втором этапе функция выгоды должна быть скорректирована. Вследствие ограниченного объема опыта и ограниченной информации о результатах этого опыта в одном этапе операции точное определение действительных вероятностей невозможно. Поэтому для уменьшения влияния случайных ошибок в определении вероятностей необходима постепенная корректировка принятых значений путем накопления результатов предшествующих этапов операции. Эта корректировка должна осуществляться автоматически с помощью специальной программы управляющей машины. Так в общих чертах выглядит путь усовершенствования игровых систем автоматического управления при помощи накопления опыта.
этом система, отыскивающая максимум расчетной функции выгоды, уже не будет в состоянии обеспечить максимум фактической выгоды. Путь совершенствования системы заключается в корректировке значений параметров и структуры функции выгоды в каждом данном этапе операции по результатам предшествующих этапов управления операцией. Так, например, если частоты поражения средств нападения средствами обороны в первом этапе операции не соответствуют принятым начальным вероятностям поражения, то во втором этапе функция выгоды должна быть скорректирована. Вследствие ограниченного объема опыта и ограниченной информации о результатах этого опыта в одном этапе операции точное определение действительных вероятностей невозможно. Поэтому для уменьшения влияния случайных ошибок в определении вероятностей необходима постепенная корректировка принятых значений путем накопления результатов предшествующих этапов операции. Эта корректировка должна осуществляться автоматически с помощью специальной программы управляющей машины. Так в общих чертах выглядит путь усовершенствования игровых систем автоматического управления при помощи накопления опыта.
Что касается усовершенствования способов поиска оптимальных выборов, то здесь основой служит информация о структуре функции выгоды на множестве возможных выборов в каждом этапе.
Несмотря на то, что многоэтапный процесс управления в игровых системах с автоматическим поиском решений резко сокращает число возможных решений по сравнению с одноэтапным процессом, во многих практических применениях число возможных выборов в каждом этапе все же весьма велико. Слепой поиск оптимального выбора здесь может оказаться технически неосуществимым или затрудненным. Между тем если структура функции выгоды на множестве выборов известна, то возможны весьма экономные методы поиска. Так, например, если возможный выборы удается пронумеровать так, что каждому выбору соответствует условный номер.

где  целые положительные числа, удовлетворяющие неравенствам
целые положительные числа, удовлетворяющие неравенствам

и функция выгоды есть линейная функция чисел х,

то для поиска наибольшего значения  и соответствующего оптимального выбора следует использовать способ линейного программирования (§ 21-3). Оптимальный выбор определяется при этом весьма быстро.
и соответствующего оптимального выбора следует использовать способ линейного программирования (§ 21-3). Оптимальный выбор определяется при этом весьма быстро.
В заключение следует сказать, что игровые системы автоматического управления относятся к высшим формам автоматических систем, имеющим огромные перспективы развития и применения.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ГЛАВА ПЕРВАЯ. ВВОДНАЯ
- 1-1. О КЛАССИФИКАЦИИ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- 1-2. ОБЫКНОВЕННЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- 1-3. САМОНАСТРАИВАЮЩИЕСЯ СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- 1-4. ИГРОВЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- 1-5. КЛАССИФИКАЦИЯ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ ПО ДРУГИМ ПРИЗНАКАМ
- ГЛАВА ВТОРАЯ. ОБЩИЕ ПЕРЕДАТОЧНЫЕ СВОЙСТВА ЭЛЕМЕНТОВ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- 2-1. УРАВНЕНИЯ ЭЛЕМЕНТОВ. СТАТИЧЕСКИЕ И ДИНАМИЧЕСКИЕ СВОЙСТВА ЭЛЕМЕНТОВ
- б) Центробежный измеритель скорости вращения
- в) Электромагнитный измеритель напряжения
- 2-2. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ
- 2-3. ЭЛЕМЕНТАРНЫЕ ДИНАМИЧЕСКИЕ ЗВЕНЬЯ, ИХ УРАВНЕНИЯ И ПЕРЕДАТОЧНЫЕ ФУНКЦИИ
- 2-4. ТИПОВЫЕ ВХОДНЫЕ СИГНАЛЫ. ВОЗМУЩАЮЩИЕ ФУНКЦИИ
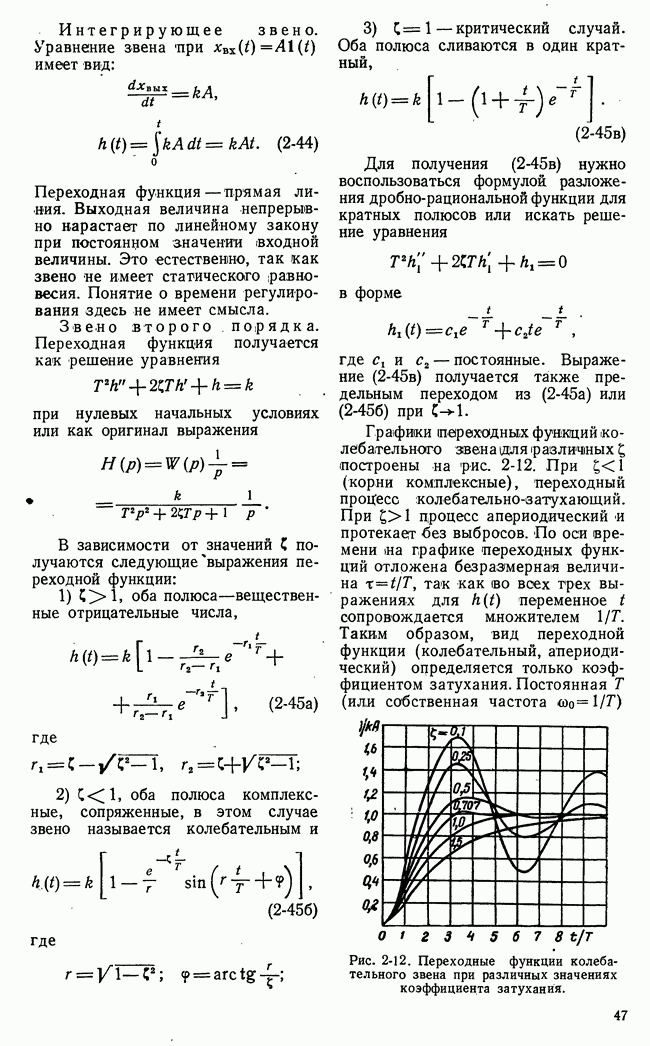
- 2-5. ПЕРЕХОДНЫЕ ФУНКЦИИ ЭЛЕМЕНТАРНЫХ ЗВЕНЬЕВ
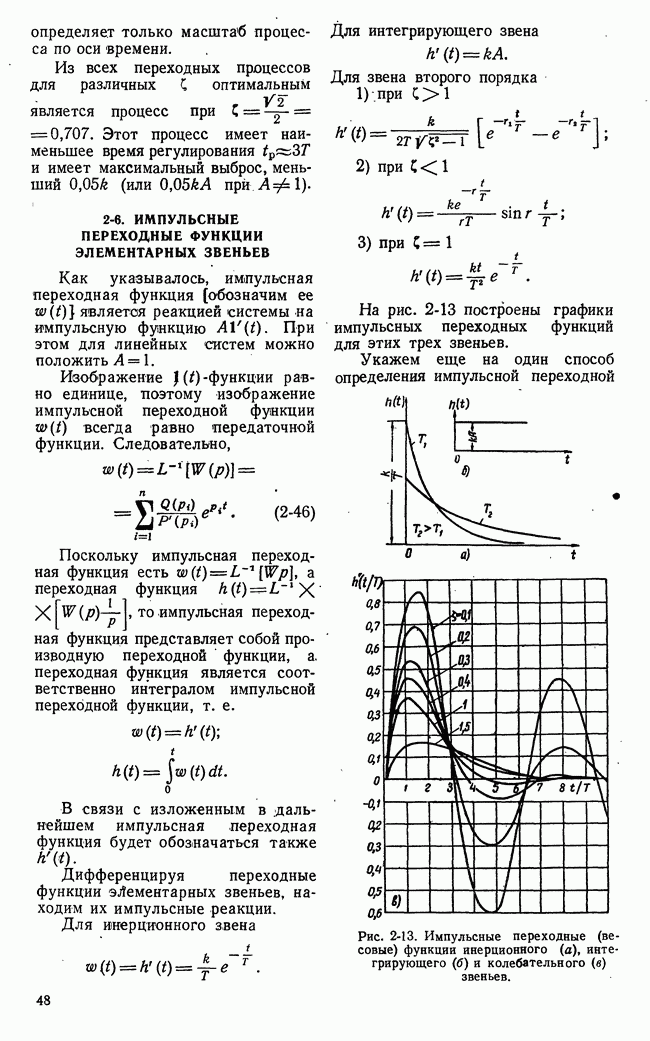
- 2-6. ИМПУЛЬСНЫЕ ПЕРЕХОДНЫЕ ФУНКЦИИ ЭЛЕМЕНТАРНЫХ ЗВЕНЬЕВ
- 2-7. РЕАКЦИЯ ЗВЕНЬЕВ НА ПРОИЗВОЛЬНЫЕ ИЗВЕСТНЫЕ ФУНКЦИИ ВРЕМЕНИ
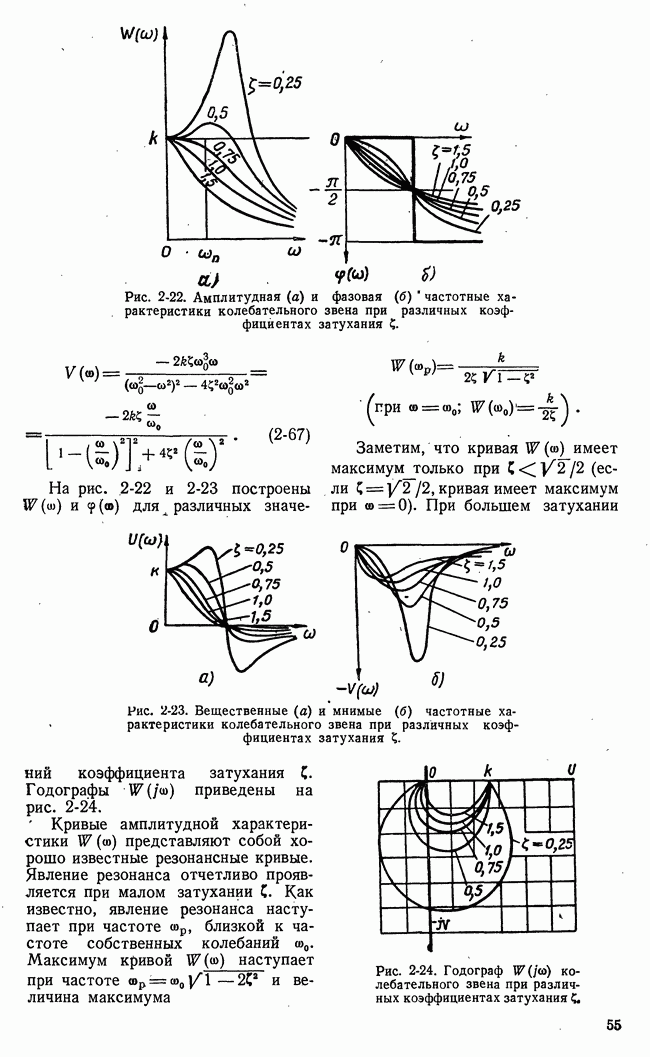
- 2-8. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ
- б) Частотные характеристики элементарных звеньев
- в) Логарифмические характеристики элементарных звеньев
- 2-9. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ОБ ЭЛЕМЕНТАРНЫХ ЗВЕНЬЯХ
- 2-10. СОЕДИНЕНИЯ ЗВЕНЬЕВ. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ СОЕДИНЕНИИ
- 2-11. ЭЛЕМЕНТЫ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ КАК ЧЕТЫРЕХПОЛЮСНИКИ. ПЕРЕДАТОЧНЫЕ УРАВНЕНИЯ
- ГЛАВА ТРЕТЬЯ. ДАТЧИКИ СИГНАЛОВ
- 3-1. ОБЩИЕ СВОЙСТВА ДАТЧИКОВ
- 3-2. ПОТЕНЦИОМЕТРИЧЕСКИЕ ДАТЧИКИ
- б) Выходная мощность потенциометрических датчиков и условия согласования
- в) Динамические свойства
- г) Ошибка ступенчатости. Параметры потенциометрических датчиков
- 3-3. ИНДУКТИВНЫЕ ДАТЧИКИ
- б) Двухтактные индуктивные датчики
- в) Характеристики двухтактных индуктивных датчиков
- г) Трансформаторные индуктивные датчики
- д) Динамические свойства индуктивных датчиков
- е) Шумы индуктивных датчиков
- ж) Общие свойства индуктивных датчиков
- 3-4. СЕЛЬСИНЫ В ТРАНСФОРМАТОРНОМ РЕЖИМЕ
- б) Характеристики сельсинного датчика
- в) Динамические свойства сельсинных датчиков
- г) Шумы и ошибки датчика
- д) Устанавливающий момент
- е) Дифференциальные сельсины
- ж) Сельсины точного и грубого каналов
- ГЛАВА ЧЕТВЕРТАЯ. УСИЛИТЕЛИ СИГНАЛОВ
- 4-2. МАГНИТНЫЕ УСИЛИТЕЛИ
- а) Рабочий процесс и статическая характеристика магнитного усилителя с прямоугольной кривой намагничивания сердечников
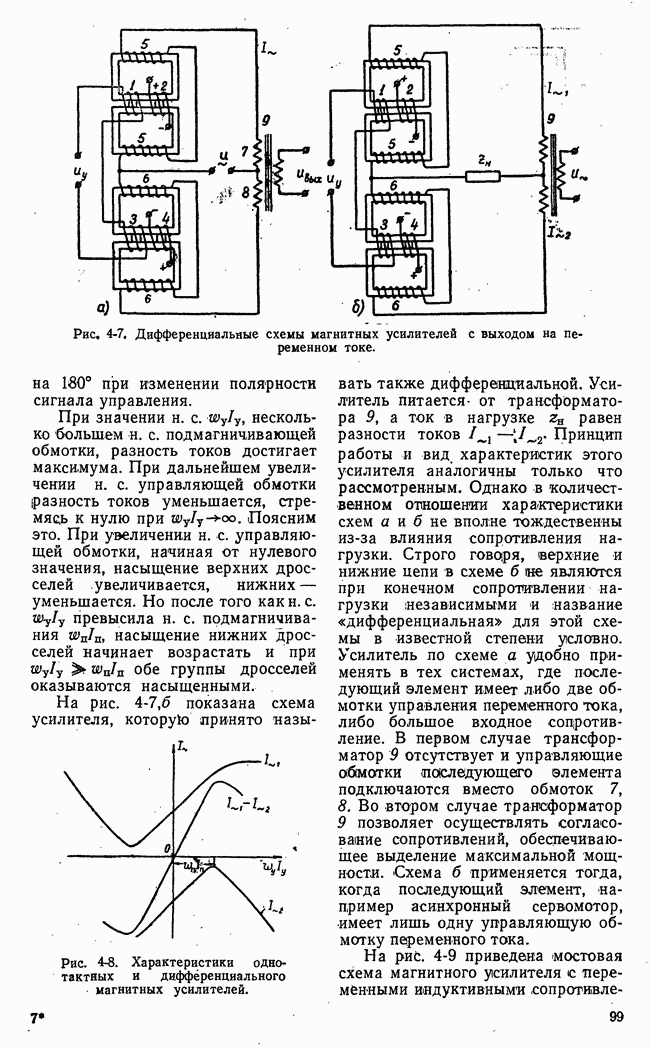
- б) Двухтактные магнитные усилители с выходом на переменном токе
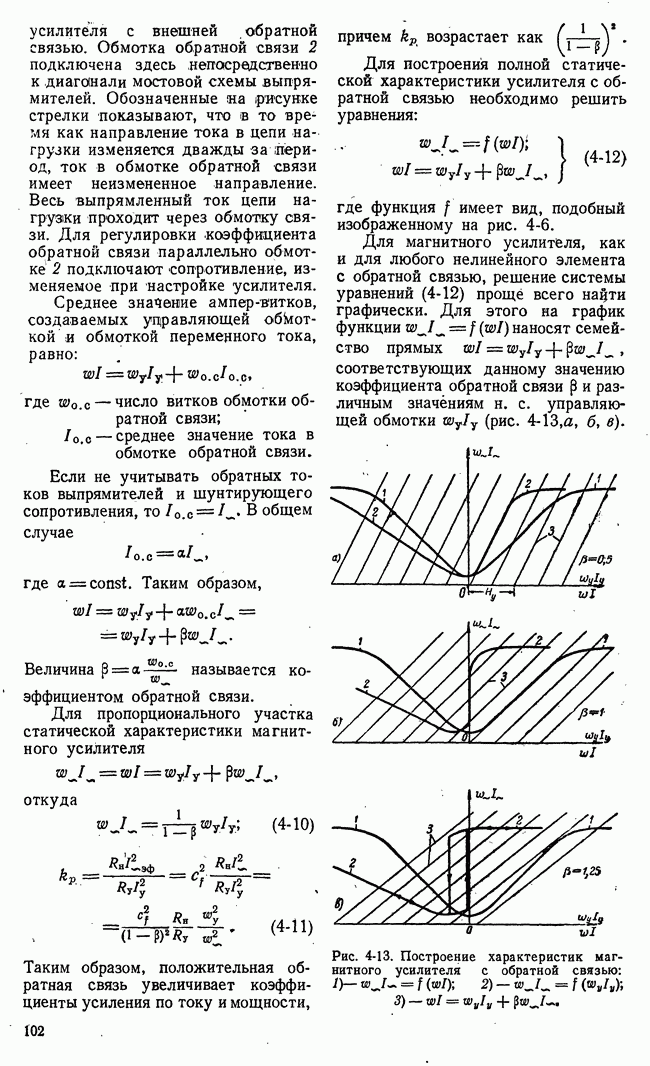
- в) Магнитные усилители с обратной связью
- г) Динамические свойства магнитных усилителей
- д) Шумы магнитных усилителей. Общие свойства магнитных усилителей
- 4-3. ЭЛЕКТРОМАШИННЫЕ УСИЛИТЕЛИ
- б) Однокаскадный электромашицный усилитель как четырехполюсник
- в) Двухкаскадный электромашинный усилитель с поперечным полем
- г) Шумы электромашинных усилителей
- 4-4. РЕЛЕ
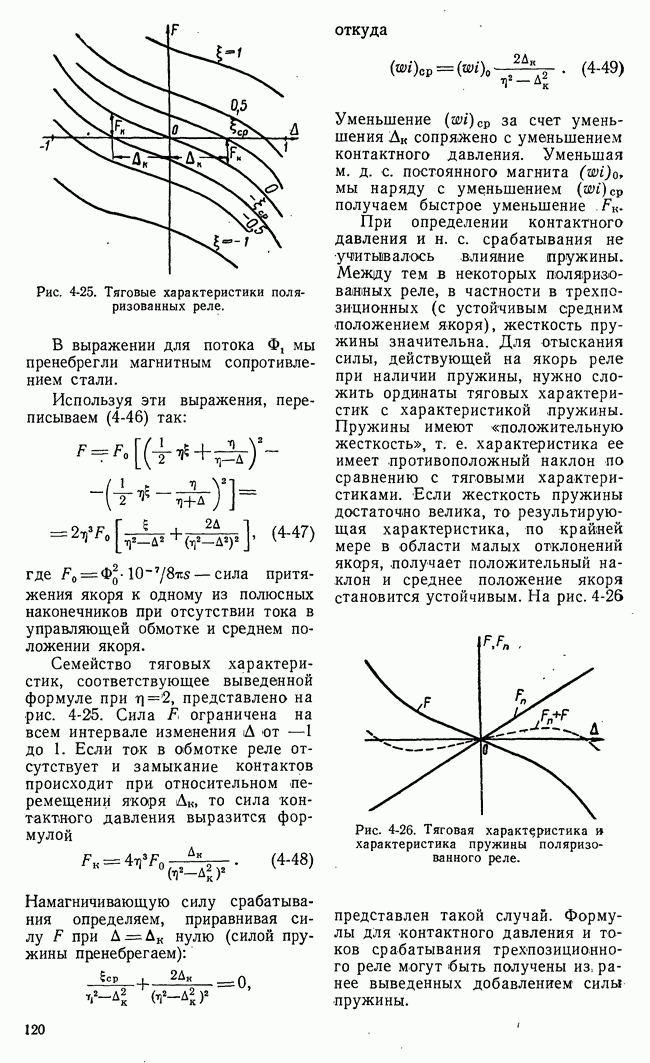
- б) Поляризованные реле
- в) Магнитоэлектрическое реле
- 4-5. РЕЛЕЙНЫЕ УСИЛИТЕЛИ
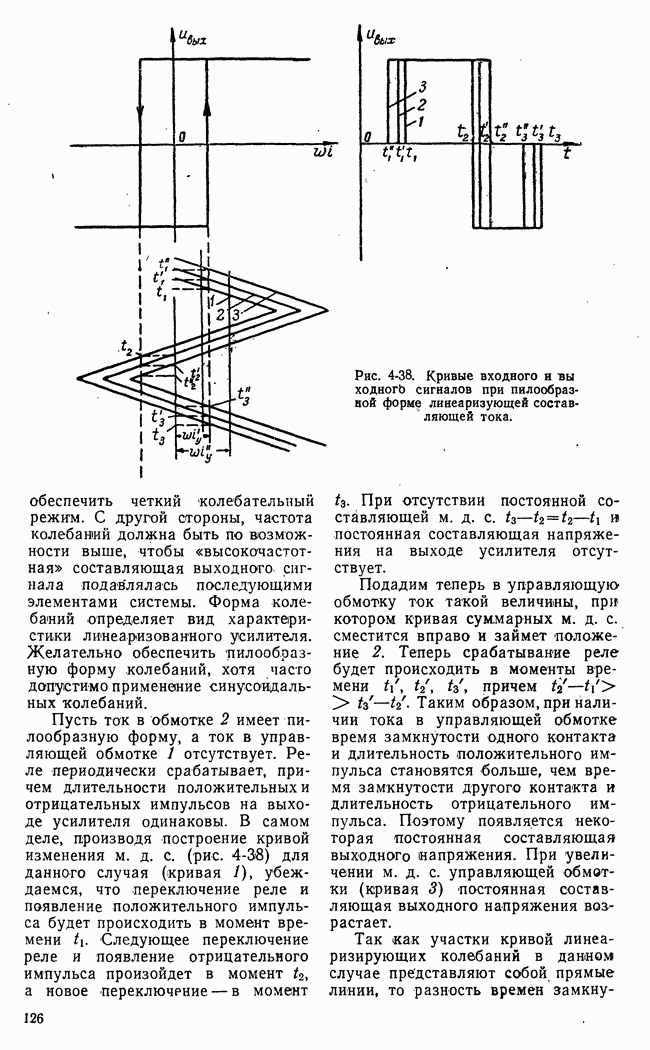
- б) Вибрационная линеаризация релейных усилителей
- в) Релейный усилитель как четырехполюсник
- 4-6. ЭЛЕКТРОННЫЕ УСИЛИТЕЛИ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- б) Фазочувствительные усилители и синхронные детекторы
- в) Электронные усилители постоянного тока
- г) Шумы электронных усилителей
- 4-7. ПОЛУПРОВОДНИКОВЫЕ УСИЛИТЕЛИ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- ГЛАВА ПЯТАЯ. ИСПОЛНИТЕЛЬНЫЕ УСТРОЙСТВА СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- 5-2. СЕРВОДВИГАТЕЛИ ПОЧТОЯННОГО ТОКА
- 5-3. СЕРВОДВИГАТЕЛИ ПЕРЕМЕННОГО ТОКА
- 5-4. СЕРВОДВИГАТЕЛИ С ЭЛЕКТРОМАГНИТНЫМИ И ПОРОШКОВЫМИ МУФТАМИ
- б) Характеристики серводвигателей с электромагнитными муфтами
- в) Порошковые муфты
- г) Характеристики серводвигателей с порошковыми муфтами
- 5-5. ГИДРАВЛИЧЕСКИЕ И ПНЕВМАТИЧЕСКИЕ СЕРВОДВИГАТЕЛИ
- б) Обратные связи в гидравлических серводвигателях
- в) Свойства гидравлических серводвигателей
- г) Электрогидравлические серводвигатели
- д) Пневматические серводвигатели
- ГЛАВА ШЕСТАЯ. СТАБИЛИЗИРУЮЩИЕ УСТРОЙСТВА СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- 6-1. ПАССИВНЫЕ КОРРЕКТИРУЮЩИЕ ЦЕПИ СИСТЕМ ПОСТОЯННОГО ТОКА
- б) Интегрирующие и интегродифференцирующие цепи
- 6-2. АКТИВНЫЕ КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА СИСТЕМ ПОСТОЯННОГО ТОКА
- 6-3. КОРРЕКТИРУЮЩИЕ ЦЕПИ СИСТЕМ ПЕРЕМЕННОГО ТОКА
- 6-4. ФИЛЬТРЫ В ЦЕПЯХ ОБРАТНЫХ СВЯЗЕЙ. МЕХАНИЧЕСКИЕ СТАБИЛИЗИРУЮЩИЕ УСТРОЙСТВА
- ГЛАВА СЕДЬМАЯ. СТРУКТУРНЫЕ СХЕМЫ И ХАРАКТЕРИСТИКИ ЛИНЕЙНЫХ СТАЦИОНАРНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 7-1. СТРУКТУРНЫЕ СХЕМЫ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 7-2. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ ДЛЯ ВХОДНОЙ ВЕЛИЧИНЫ
- 7-3. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ ДЛЯ ВОЗМУЩЕНИЯ
- 7-4. ПРИМЕРЫ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ И ИХ СТРУКТУРНЫЕ СХЕМЫ
- б) Стабилизация напряжения самолетных генераторов
- в) Следящая система копировально-фрезерного станка
- г) Следящая система автосопровождения
- д) Автоматическое управление углом тангажа самолета
- 7-5. ВРЕМЕННЫЕ ХАРАКТЕРИСТИКИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 7-6. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- б) Частотные характеристики замкнутой системы
- в) Связь частотных характеристик замкнутой и разомкнутой систем
- ГЛАВА ВОСЬМАЯ. ЭНЕРГЕТИЧЕСКИЙ РАСЧЕТ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ И СОГЛАСОВАНИЕ ХАРАКТЕРИСТИК ЭЛЕМЕНТОВ
- 8-1. ВЫБОР МОЩНОСТИ ИСПОЛНИТЕЛЬНЫХ УСТРОЙСТВ И УСЛОВИЯ СОГЛАСОВАНИЯ С НАГРУЗКОЙ
- а) Определение необходимой мощности по переходным процессам при типовых воздействиях
- б) Мгновенная мощность при гармонических колебаниях
- в) Необходимая мощность при случайных колебаниях регулирующего органа
- г) Выбор мощности сервомотора
- д) Условия согласования с нагрузкой сервомотора без обратной связи
- е) Согласование с нагрузкой сервомотора с жесткой обратной связью
- 8-2. СОГЛАСОВАНИЕ ДАТЧИКОВ, УСИЛИТЕЛЬНЫХ И КОРРЕКТИРУЮЩИХ УСТРОЙСТВ. РАСПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТОВ УСИЛЕНИЯ
- б) Передаточные функции последовательных соединений элементов
- в) Согласование пропорциональных участков характеристик
- г) Распределение коэффициентов усиления
- ГЛАВА ДЕВЯТАЯ. УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ СТАЦИОНАРНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 9-2. КРИТЕРИЙ УСТОЙЧИВОСТИ РАУСА—ГУРВИЦА
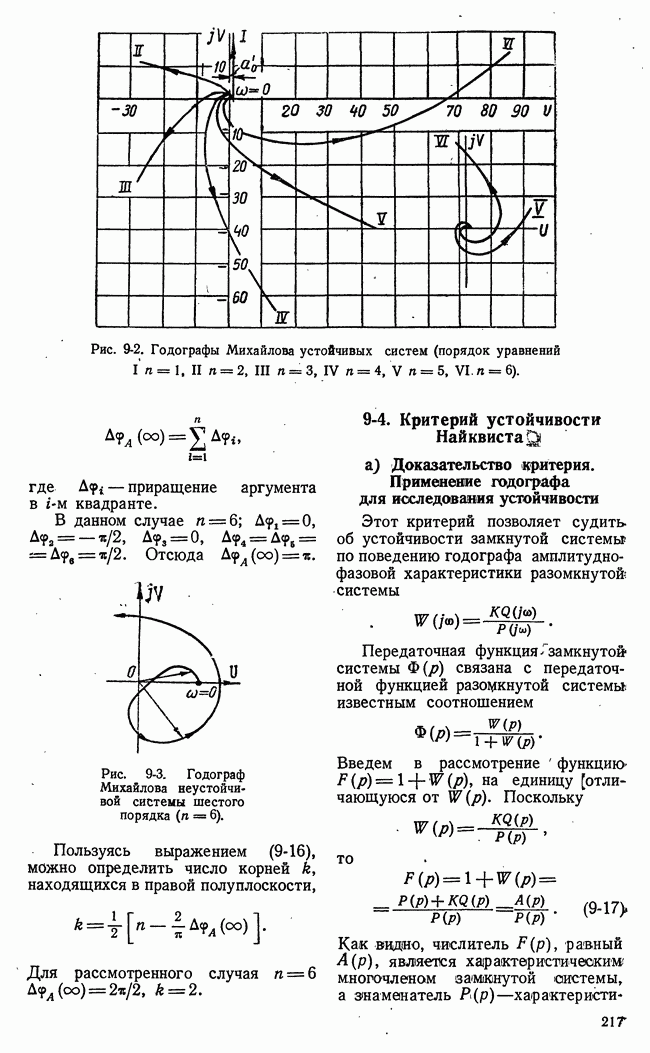
- 9-3. КРИТЕРИЙ УСТОЙЧИВОСТИ МИХАЙЛОВА
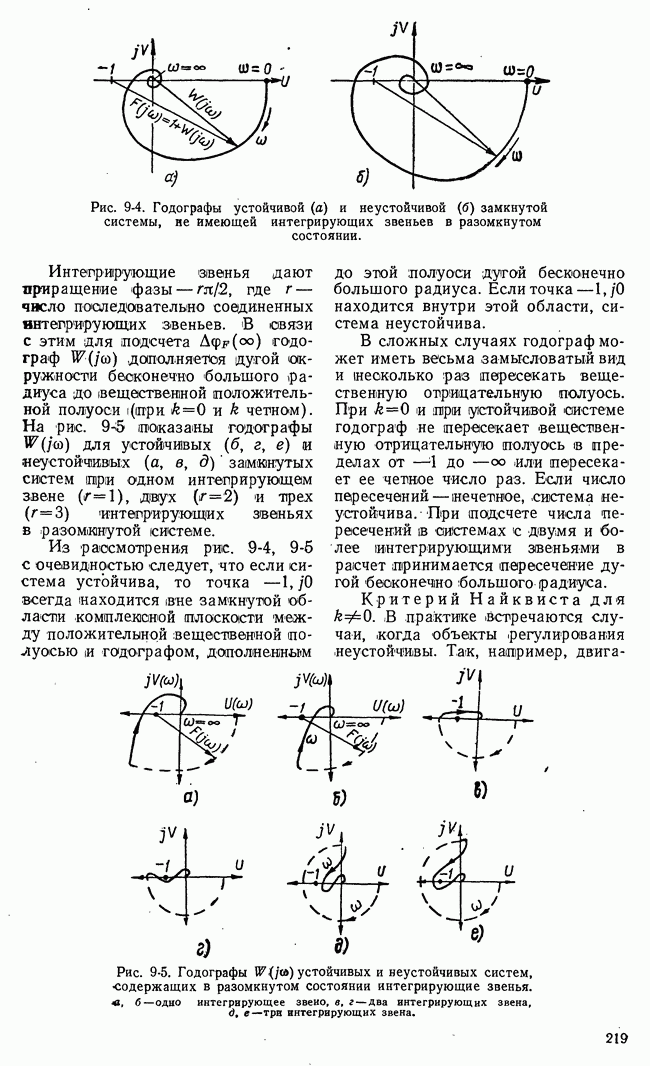
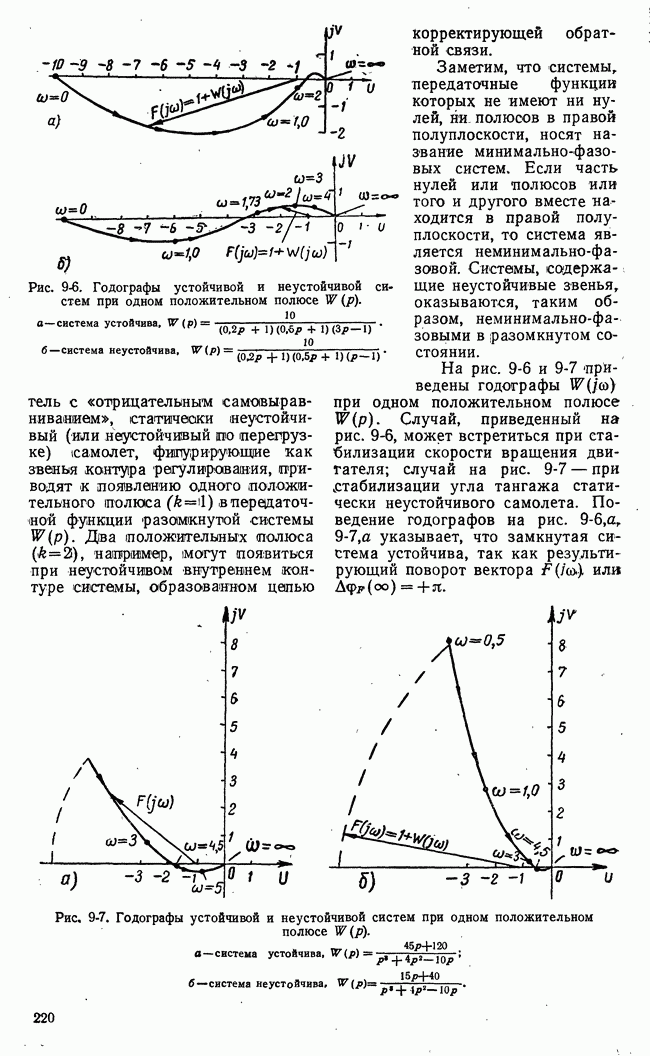
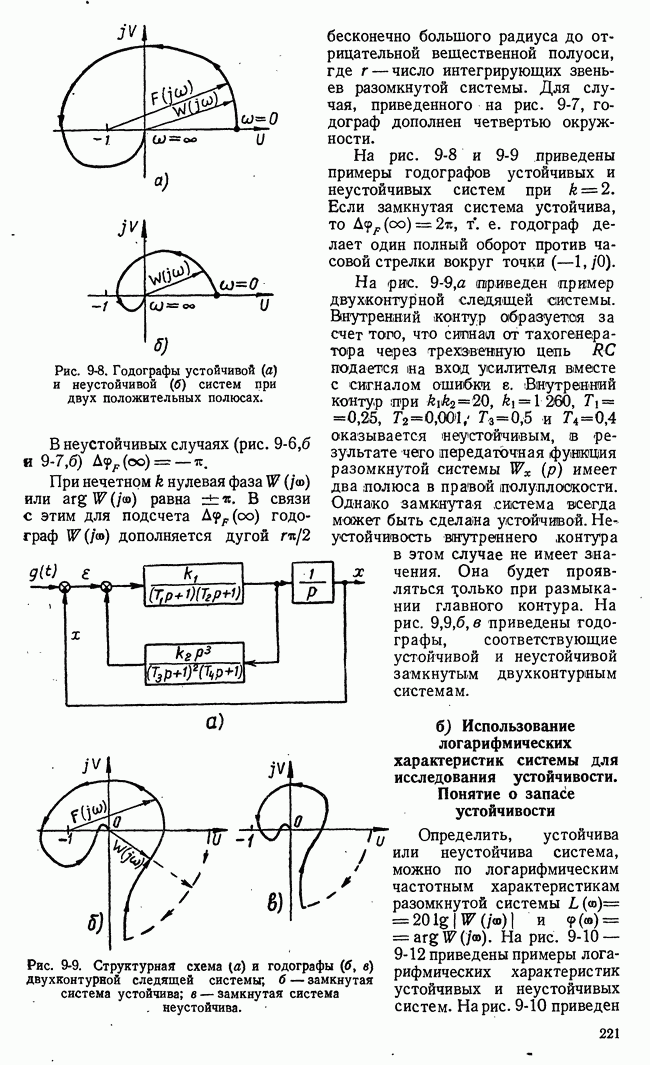
- 9-4. КРИТЕРИЙ УСТОЙЧИВОСТИ НАЙКВИСТА
- б) Использование логарифмических характеристик системы для исследования устойчивости. Понятие о запасе устойчивости
- 9-5. КОЭФФИЦИЕНТ УСИЛЕНИЯ И УСТОЙЧИВОСТЬ. ВЛИЯНИЕ КОРРЕКТИРУЮЩИХ ЦЕПЕЙ НА УСТОЙЧИВОСТЬ
- 9-6. ВЫДЕЛЕНИЕ ОБЛАСТЕЙ УСТОЙЧИВОСТИ В ПРОСТРАНСТВЕ ПАРАМЕТРОВ СИСТЕМЫ ДИАГРАММЫ ВЫШНЕГРАДСКОГО
- б) Общий метод D-разбиения в плоскости двух параметров. Линейная задача
- в) Выделение области устойчивости в плоскости двух параметров. Нелинейная задача
- г) Выделение области устойчивости в плоскости одного комплексного параметра
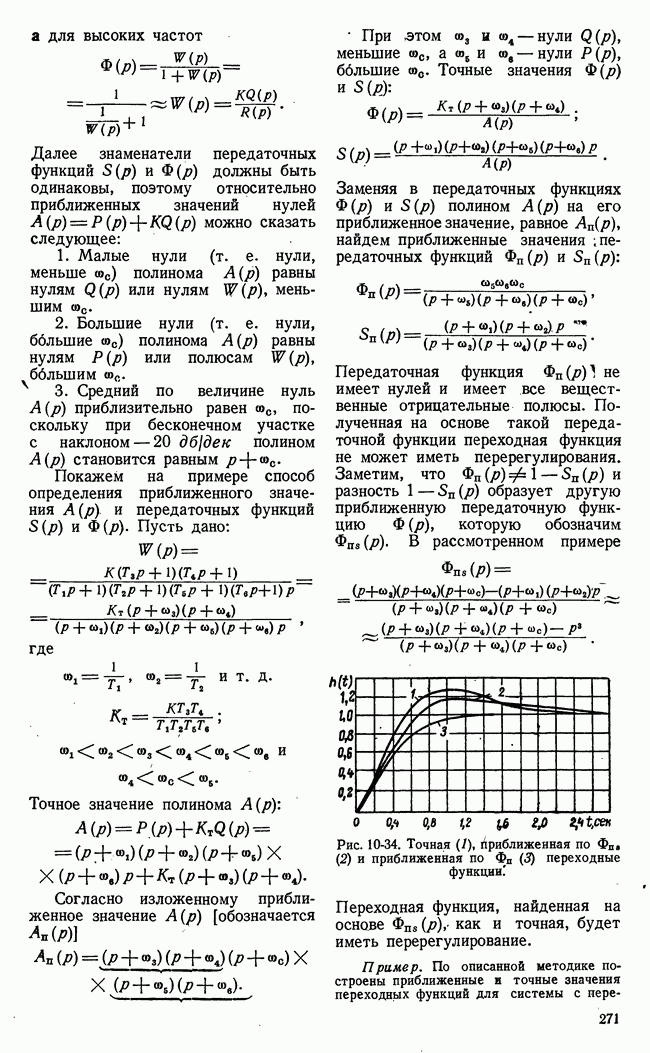
- ГЛАВА ДЕСЯТАЯ. КАЧЕСТВО ПРОЦЕССОВ РЕГУЛИРОВАНИЯ В ЛИНЕЙНЫХ СИСТЕМАХ
- 10-1. КРИТЕРИИ КАЧЕСТВА ПРОЦЕССА РЕГУЛИРОВАНИЯ
- 10-2. ТОЧНОСТЬ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ В УСТАНОВИВШИХСЯ РЕЖИМАХ. СТАТИЧЕСКИЕ И АСТАТИЧЕСКИЕ СИСТЕМЫ
- б) Точность при медленно меняющихся воздействиях. Коэффициенты ошибок. Астатические системы высших порядков
- в) Общие условия неискаженного воспроизведения входных сигналов в вынужденном режиме
- г) Повышение точности системы коррекцией входного сигнала
- д) Повышение точности системы путем компенсации возмущения F(t)
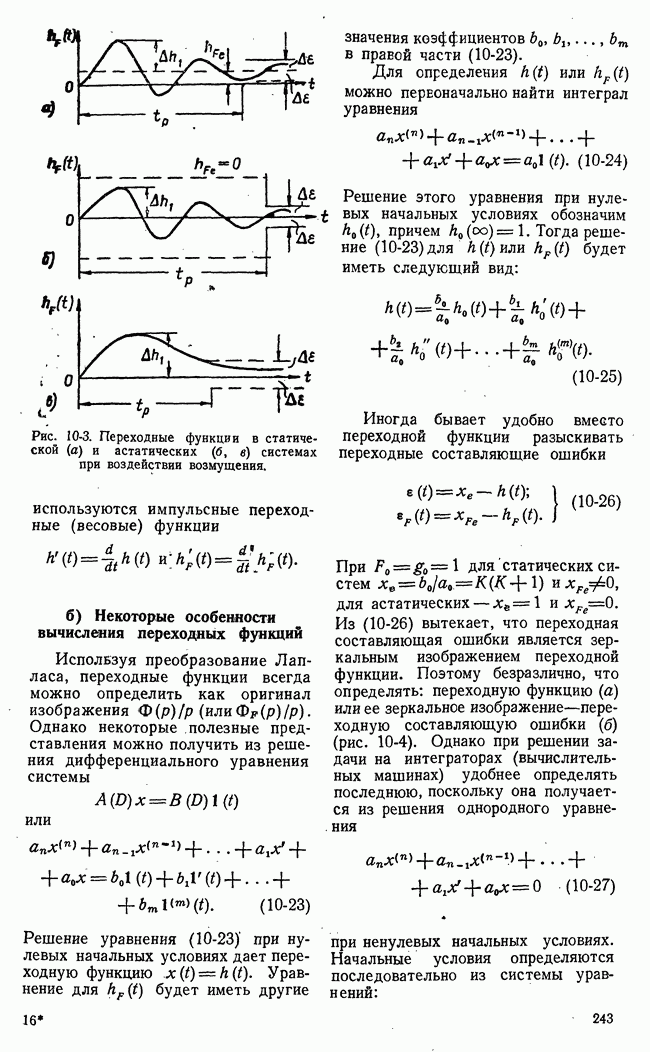
- 10-18. ПЕРЕХОДНЫЕ ФУНКЦИИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- б) Некоторые особенности вычисления переходных функций
- 10-4. РАСПРЕДЕЛЕНИЕ НУЛЕЙ И ПОЛЮСОВ ПЕРЕДАТОЧНОЙ ФУНКЦИИ И ПЕРЕХОДНЫЕ ПРОЦЕССЫ
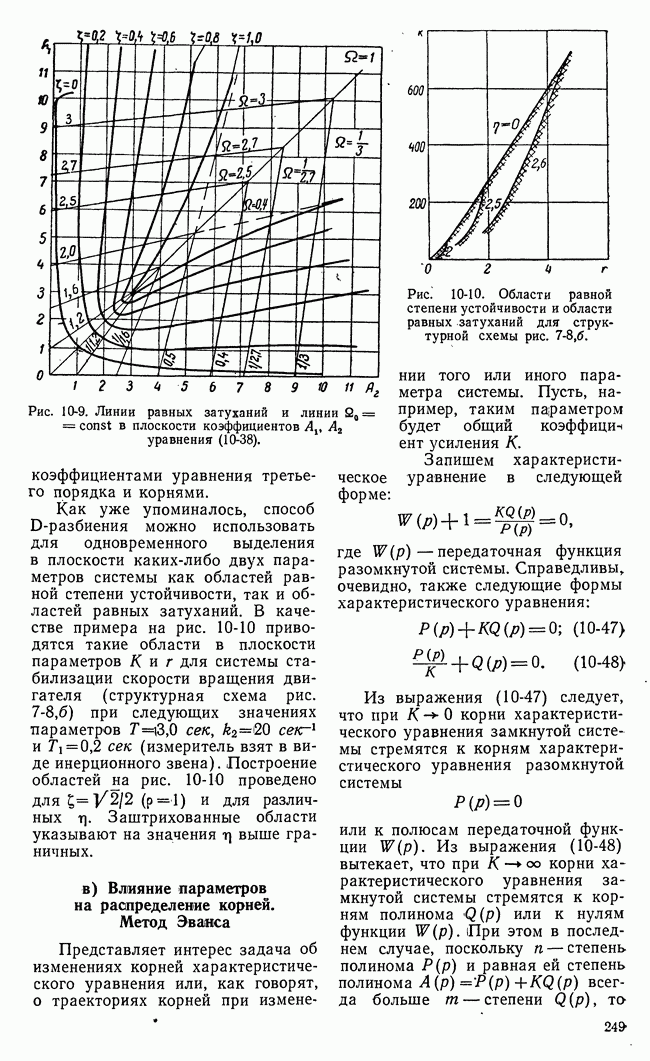
- б) Оценки распределения корней. Степень устойчивости. Коэффициент затухания колебаний
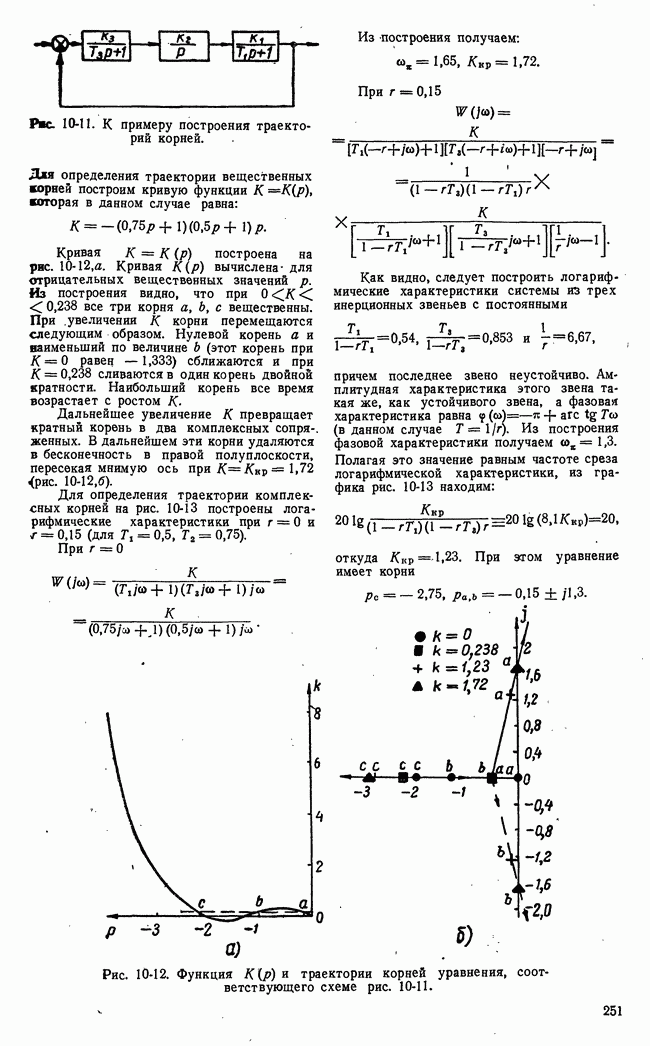
- в) Влияние параметров на распределение корней. Метод Эванса
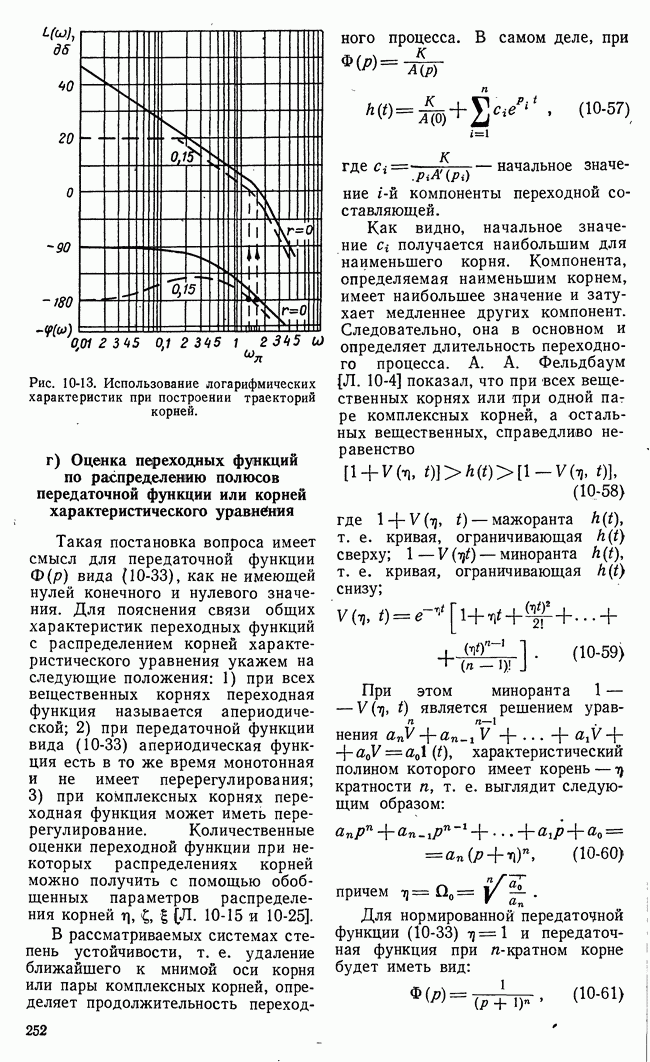
- г) Оценка переходных функций по распределению полюсов передаточной функции или корней характеристического уравнения
- д) Влияние нулей на характер переходной функции
- е) Определение коэффициентов уравнений по заданному распределению корней. Стандартные коэффициенты характеристических уравнений
- 10-5. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ И ПЕРЕХОДНЫЕ ФУНКЦИИ
- б) Приближенное вычисление переходных функций и переходных процессов
- в) Оценка качества процесса регулирования по характеристикам замкнутой системы Ф(w) и ф(w) и характеристике разомкнутой системы W(jw)
- г) Оценка качества по амплитудным логарифмическим характеристикам. Минимально-фазовые системы
- д) Связь между логарифмическими амплитудными характеристиками разомкнутой системы и полюсами передаточной функции замкнутой системы
- 10-6. ИНТЕГРАЛЬНЫЕ ОЦЕНКИ ПЕРЕХОДНЫХ ПРОЦЕССОВ
- г) Приближение кривых x(t) к эталонной кривой хэ(t) по критерию …
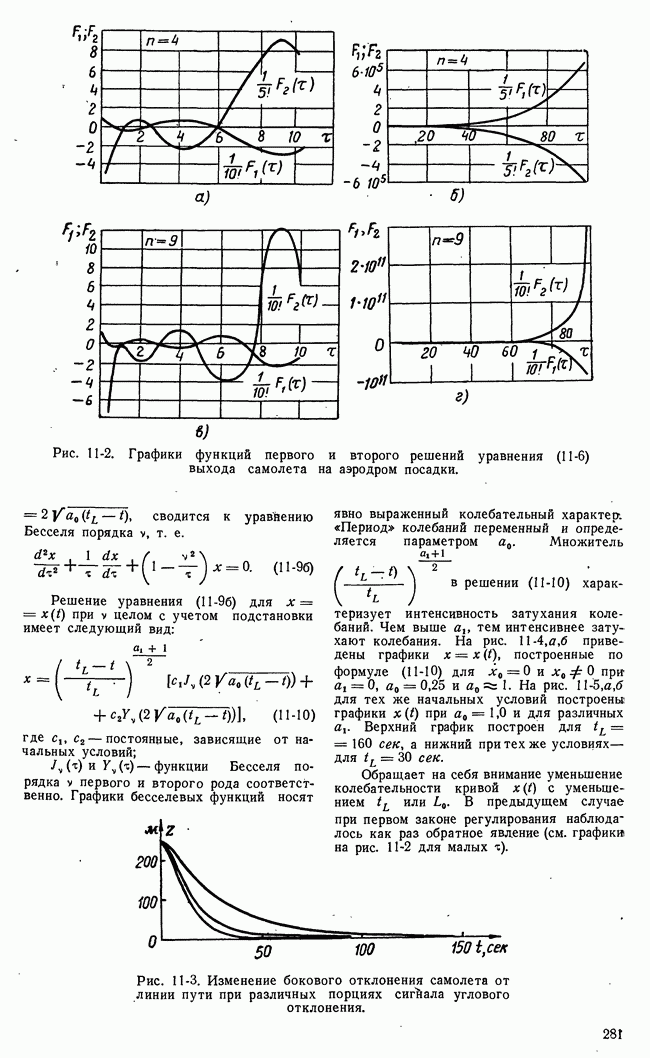
- ГЛАВА ОДИННАДЦАТАЯ. НЕСТАЦИОНАРНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 11-1. ОБЩИЕ СВЕДЕНИЯ О НЕСТАЦИОНАРНЫХ СИСТЕМАХ
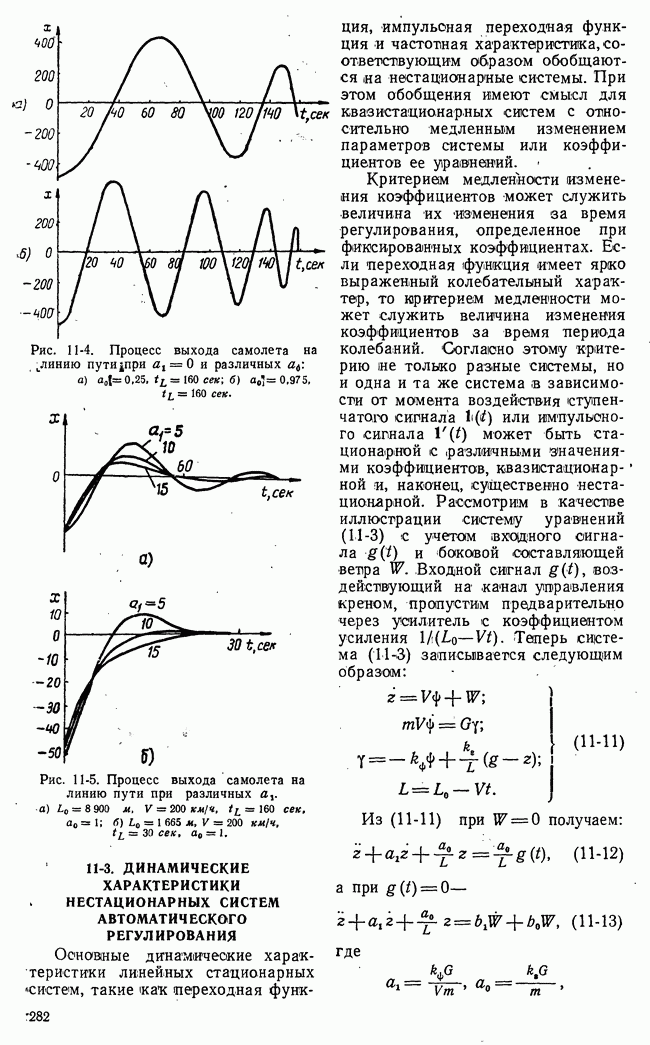
- 11-2. ПРИМЕРЫ СУЩЕСТВЕННО НЕСТАЦИОНАРНЫХ СИСТЕМ
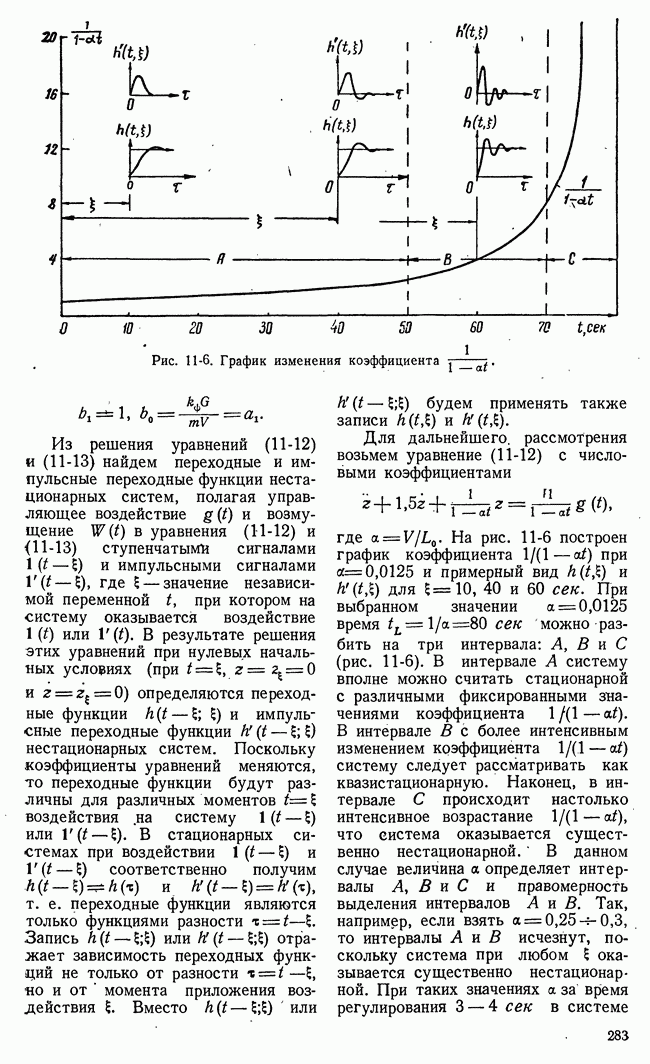
- 11-3. ДИНАМИЧЕСКИЕ ХАРАКТЕРИСТИКИ НЕСТАЦИОНАРНЫХ СИСТЕМ АВТОМАТИЧ ЕСКОГО РЕГУЛИРОВАНИЯ
- 11-4. ОСОБЕННОСТИ СОСТАВЛЕНИЯ УРАВНЕНИЙ И СТРУКТУРНЫХ СХЕМ НЕСТАЦИОНАРНЫХ СИСТЕМ
- 11-5. МЕТОДЫ ОПРЕДЕЛЕНИЯ ЧАСТОТНОЙ ХАРАКТЕРИСТИКИ И ИМПУЛЬСНОЙ РЕАКЦИИ НЕСТАЦИОНАРНЫХ СИСТЕМ
- ГЛАВА ДВЕНАДЦАТАЯ. СТАТИСТИЧЕСКАЯ ДИНАМИКА ЛИНЕЙНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 12-1. СТАЦИОНАРНЫЕ И НЕСТАЦИОНАРНЫЕ СЛУЧАЙНЫЕ ПРОЦЕССЫ
- б) Стационарные и нестационарные случайные функций
- в) Свойства корреляционной функции
- г) Свойство эргодичности
- д) Гауссовы случайные процессы
- 12-2. ПРЕОБРАЗОВАНИЕ СТАЦИОНАРНЫХ СЛУЧАЙНЫХ ФУНКЦИЙ СТАЦИОНАРНЫМИ ЛИНЕЙНЫМИ СИСТЕМАМИ
- б) Преобразование корреляционных функций при прохождении случайного сигнала через линейную систему
- в) Интегральная квадратичная оценка импульсной переходной функции и дисперсия реакции системы на белый шум
- г) Преобразование спектральных плотностей при прохождении случайного сигнала через линейную систему
- 12-3. ОПТИМАЛЬНЫЕ ЛИНЕЙНЫЕ СТАЦИОНАРНЫЕ СИСТЕМЫ
- б) Условия оптимальности при свободном выборе передаточной функции
- ГЛАВА ТРИНАДЦАТАЯ. О СИНТЕЗЕ ЛИНЕЙНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 13-2. МЕТОД ЛОГАРИФМИЧЕСКИХ ЧАСТОТНЫХ ХАРАКТЕРИСТИК
- б) Синтез корректирующих цепей
- в) О синтезе на основе требований к реакции системы на возмущение F(t)
- 13-3. ВЫБОР ПАРАМЕТРОВ НА ОСНОВЕ АНАЛИЗА РАСПРЕДЕЛЕНИЯ НУЛЕЙ И ПОЛЮСОВ ПЕРЕДАТОЧНОЙ ФУНКЦИИ
- 13-4. ВЫБОР ПАРАМЕТРОВ НА ОСНОВЕ ИНТЕГРАЛЬНЫХ КВАДРАТИЧНЫХ ОЦЕНОК
- 13-5. СПЕЦИАЛЬНЫЕ ПРИЕМЫ УЛУЧШЕНИЯ КАЧЕСТВА ПРОЦЕССА РЕГУЛИРОВАНИЯ
- б) Подавление помех во входном сигнале при инерционном объекте управления
- в) Использование двух источников информации для выделения истинного сигнала
- г) Компенсация влияния запаздывания измерителей на динамические свойства системы
- д) Исключение перерегулирования в системах, передаточные функции которых имеют только вещественные полюсы
- ГЛАВА ЧЕТЫРНАДЦАТАЯ. ИМПУЛЬСНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 14-2. ИМПУЛЬСЫ И ИМПУЛЬСНЫЕ ЭЛЕМЕНТЫ
- б) Формирующие цепи и импульсные элементы
- 14-3. ДИСКРЕТНЫЕ ФУНКЦИИ И ПОСЛЕДОВАТЕЛЬНОСТИ. ИХ РАЗНОСТИ И СУММЫ
- 14-4. РЕАКЦИЯ ЛИНЕЙНЫХ НЕПРЕРЫВНЫХ СИСТЕМ НА ПОСЛЕДОВАТЕЛЬНОСТИ ИЛИ ДЕЛЬТА-ИМПУЛЬСОВ
- б) Свертка двух дискретных функций
- в) Уравнения в конечных разностях непрерывных звеньев первого и второго порядков
- г) Символические изображения дискретных функций и их использование для решения уравнений в конечных разностях
- 14-5. ДИСКРЕТНОЕ ПРЕОБРАЗОВАНИЕ ЛАПЛАСА ИЛИ z-ПРЕОБРАЗОВАНИЕ. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ КОМПЛЕКСНОГО АРГУМЕНТА
- 14-6. ДИНАМИКА РАЗОМКНУТЫХ ИМПУЛЬСНЫХ СИСТЕМ
- б) Значение выходной величины непрерывной системы внутри интервалов повторения
- в) Передаточные функции, систем с запаздыванием
- г) Свободные и вынужденные движения
- д) Полюсы. Устойчивость разомкнутых систем
- е) Переходные функции
- ж) Частотные характеристики
- 14-7. СВЯЗЬ МЕЖДУ ЧАСТОТНЫМИ И ПЕРЕХОДНЫМИ ФУНКЦИЯМИ. ДИСКРЕТНОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ
- 14-8. ИНТЕГРАЛЬНАЯ КВАДРАТИЧНАЯ ОЦЕНКА
- 14-9. ДИСКРЕТНЫЕ СЛУЧАЙНЫЕ ФУНКЦИИ (СЛУЧАЙНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ)
- ГЛАВА ПЯТНАДЦАТАЯ. ДИНАМИКА ИМПУЛЬСНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 15-1. УРАВНЕНИЯ И ПЕРЕДАТОЧНЫЕ ФУНКЦИИ СИСТЕМ С ОДНИМ ИМПУЛЬСНЫМ ЭЛЕМЕНТОМ
- 15-2. УСТОЙЧИВОСТЬ ЗАМКНУТЫХ СИСТЕМ
- 15-3. КАЧЕСТВО ПРОЦЕССА РЕГУЛИРОВАНИЯ
- 15-4. ПРИМЕРЫ ИМПУЛЬСНЫХ СИСТЕМ
- 15-5. ИМПУЛЬСНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ С ДИСКРЕТНЫМИ КОРРЕКТИРУЮЩИМИ ЦЕПЯМИ
- ГЛАВА ШЕСТНАДЦАТАЯ. СТРУКТУРНЫЕ СХЕМЫ, ХАРАКТЕРИСТИКИ И УРАВНЕНИЯ НЕЛИНЕЙНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- б) Уравнения продольного движения самолета
- в) Уравнения продольного движения ракеты
- 16-2. НЕЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ СИГНАЛА ОШИБКИ
- б) Структурные схемы с нелинейными элементами
- в) Релейные системы. Релейные элементы
- 16-3. НЕЛИНЕЙНЫЙ ОБЪЕКТ РЕГУЛИРОВАНИЯ И НЕЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ СИГНАЛА ОШИБКИ
- ГЛАВА СЕМНАДЦАТАЯ. СВОЙСТВА НЕЛИНЕЙНЫХ СИСТЕМ И (МЕТОДЫ ИССЛЕДОВАНИЯ
- б) Суждение об устойчивости по уравнениям первого приближения. Теоремы Ляпунова
- в) Суждение о качестве процессов регулирования по уравнениям первого приближения
- г) Прямой метод Ляпунова
- д) Техническая устойчивость
- 17-2. АВТОКОЛЕБАНИЯ НЕЛИНЕЙНЫХ СИСТЕМ
- б) Автоколебания релейных систем
- в) Метод точечных преобразований
- г) Описание процесса в релейной системе разностным уравнением. Устойчивость автоколебаний
- д) Примера исследования автоколебаний релейных систем второго порядка
- 17-3. ВЛИЯНИЕ КОРРЕКТИРУЮЩИХ ЦЕПЕЙ НА АВТОКОЛЕБАНИЯ И НА ПЕРЕХОДНЫЕ ПРОЦЕССЫ НЕЛИНЕЙНЫХ СИСТЕМ
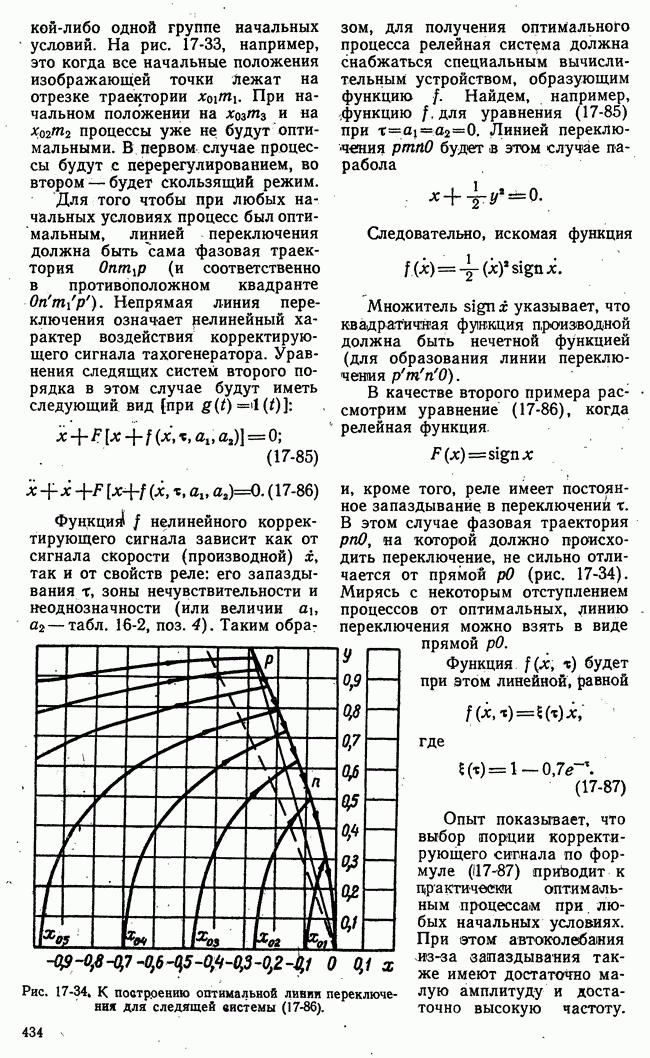
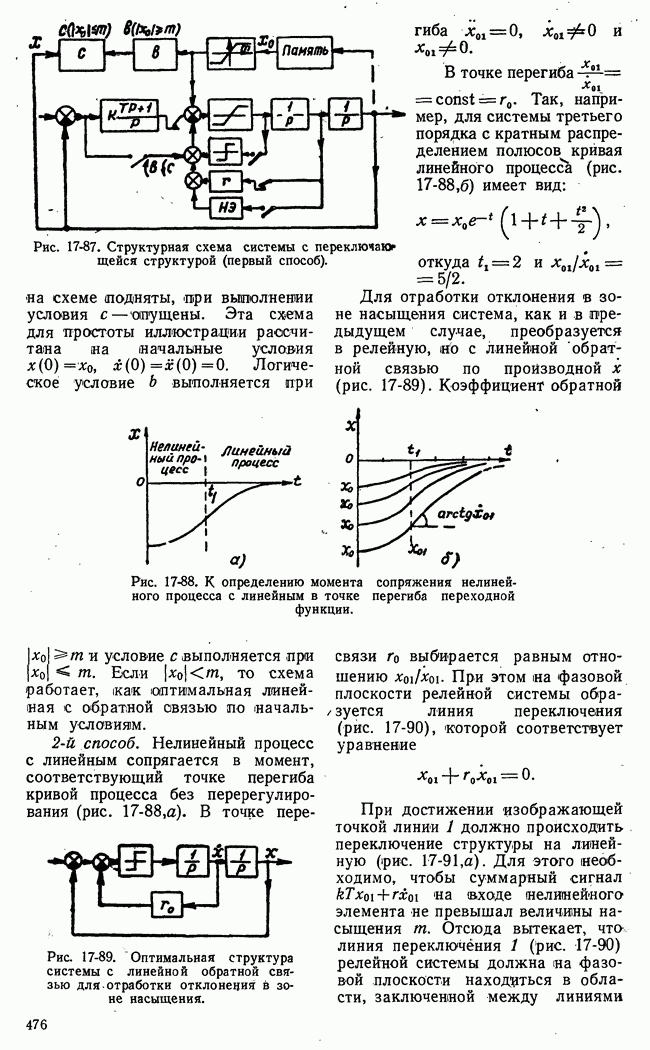
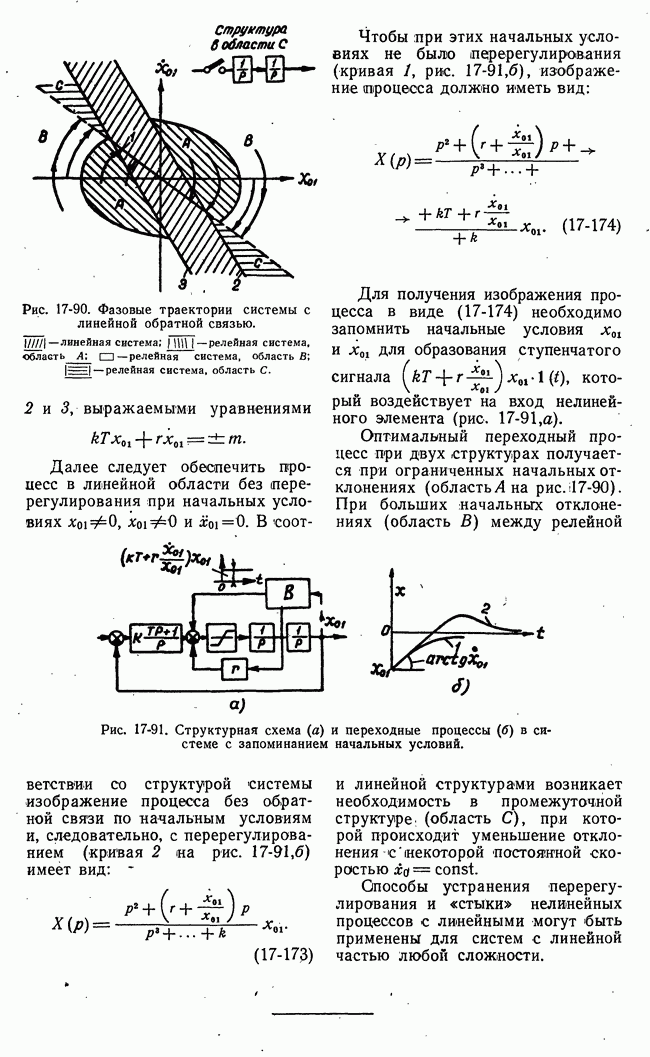
- б) Влияние корректирующих цепей на переходные процессы. Скользящие режимы. Оптимальные переходные процессы
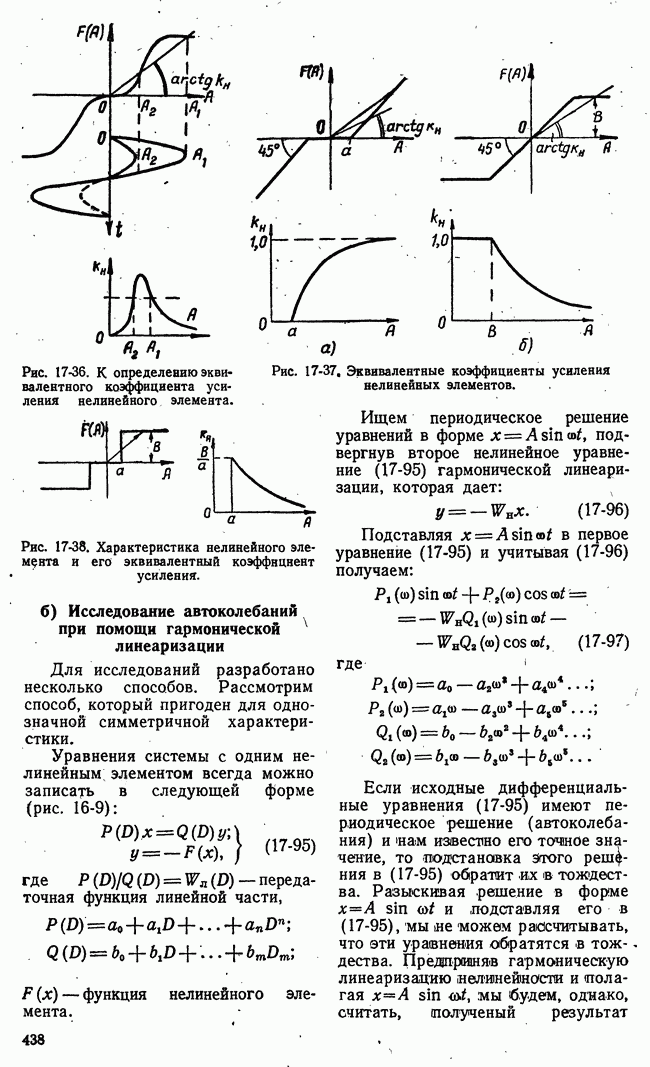
- 17-4. ГАРМОНИЧЕСКАЯ ЛИНЕАРИЗАЦИЯ ПРОЦЕССОВ В НЕЛИНЕЙНЫХ СИСТЕМАХ
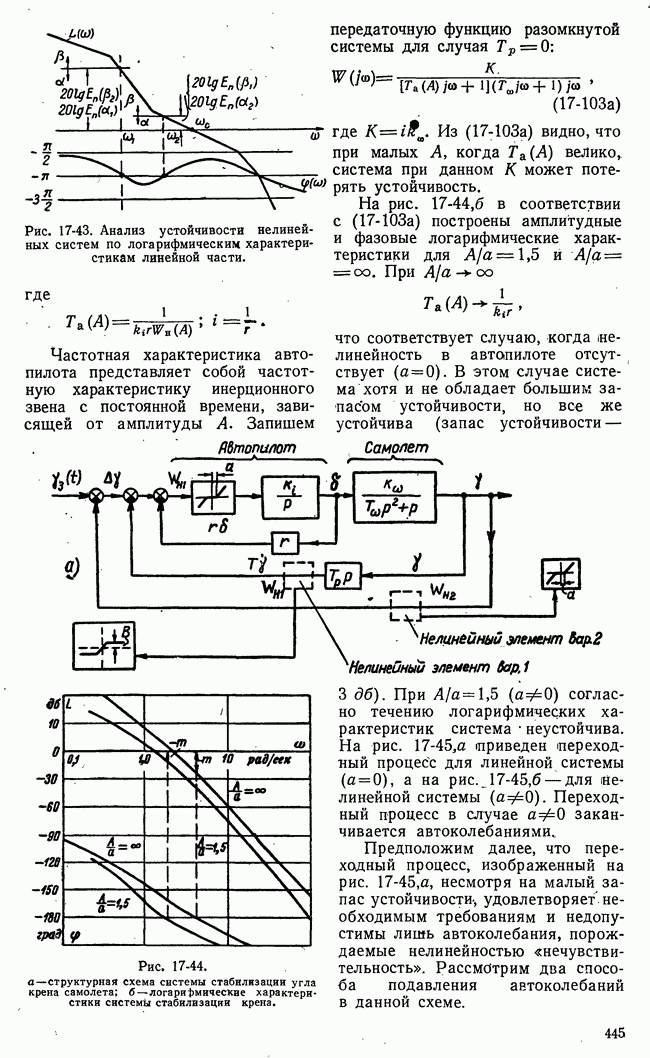
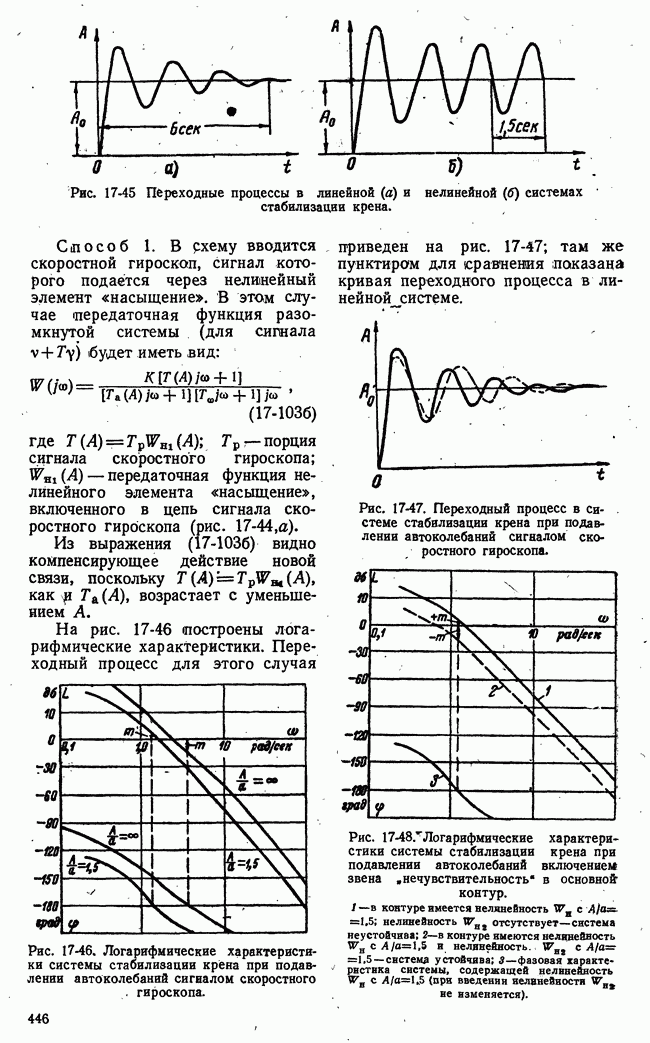
- б) Исследование автоколебаний при помощи гармонической линеаризации
- в) Гармоническая линеаризация и критерии устойчивости линейных систем
- 17-5. ТЕОРИЯ РЕЛЕЙНЫХ СИСТЕМ
- в) Частотные характеристики релейных систем
- г) Оценка устойчивости релейных систем
- д) Вынужденные колебания релейных систем. Захватывание (синхронизация или подавление) автоколебаний
- е) Вибрационная линеаризация релейных систем, Реакция релейных систем на медленно меняющиеся возмущения
- 17-6. ОПТИМАЛЬНЫЕ ПРОЦЕССЫ РЕГУЛИРОВАНИЯ
- б) Системы, оптимальные по быстродействию. Принцип максимума
- в) Системы, близкие к оптимальным по быстродействию
- ГЛАВА ВОСЕМНАДЦАТАЯ. ЭНТРОПИЯ, ИНФОРМАЦИЯ, АЛГОРИТМ В СИСТЕМАХ АВТОМАТИЧЕОКОГО УПРАВЛЕНИЯ
- 18-1. ЭНТРОПИЯ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ УПРАВЛЯЕМОГО ПРОЦЕССА
- 18-2. КОЛИЧЕСТВО ИНФОРМАЦИИ В ПРОЦЕССАХ УПРАВЛЕНИЯ
- 18-3. ЭНТРОПИЯ И ИНФОРМАЦИЯ В ЗАМКНУТЫХ СИСТЕМАХ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- 18-4. АЛГОРИТМЫ ПРОЦЕССОВ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- ГЛАВА ДЕВЯТНАДЦАТАЯ. СИСТЕМЫ ЭКСТРЕМАЛЬНОГО РЕГУЛИРОВАНИЯ
- 19-1. ПРИМЕРЫ СИСТЕМ ЭКСТРЕМАЛЬНОГО РЕГУЛИРОВАНИЯ
- 19-2. СПОСОБЫ ПОИСКА ЭКСТРЕМУМА
- б) Методы организации процесса поиска
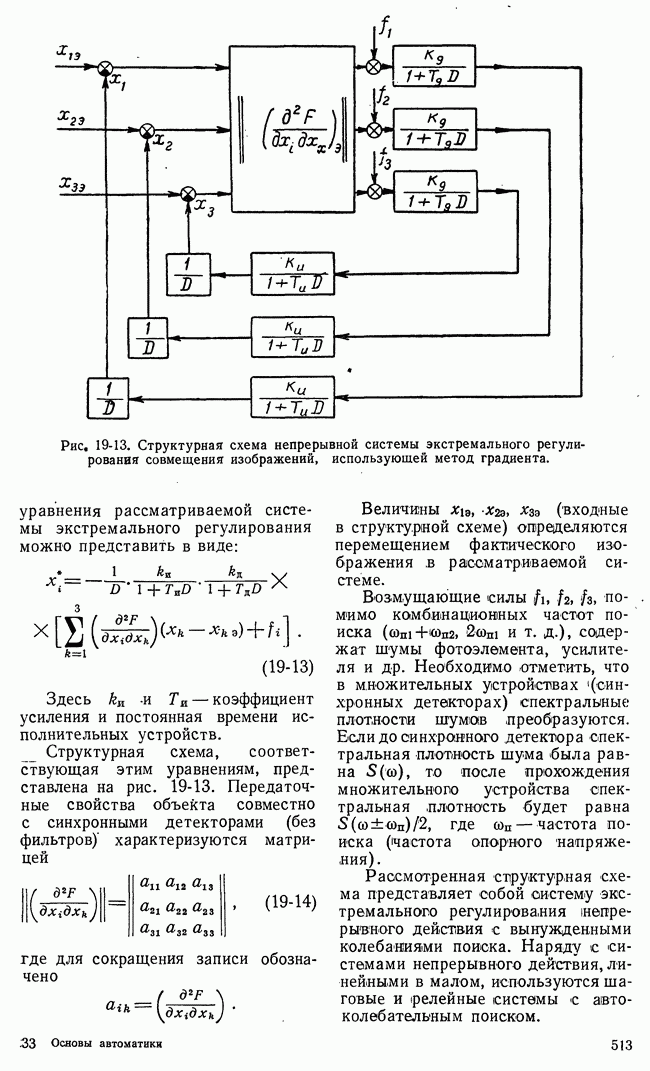
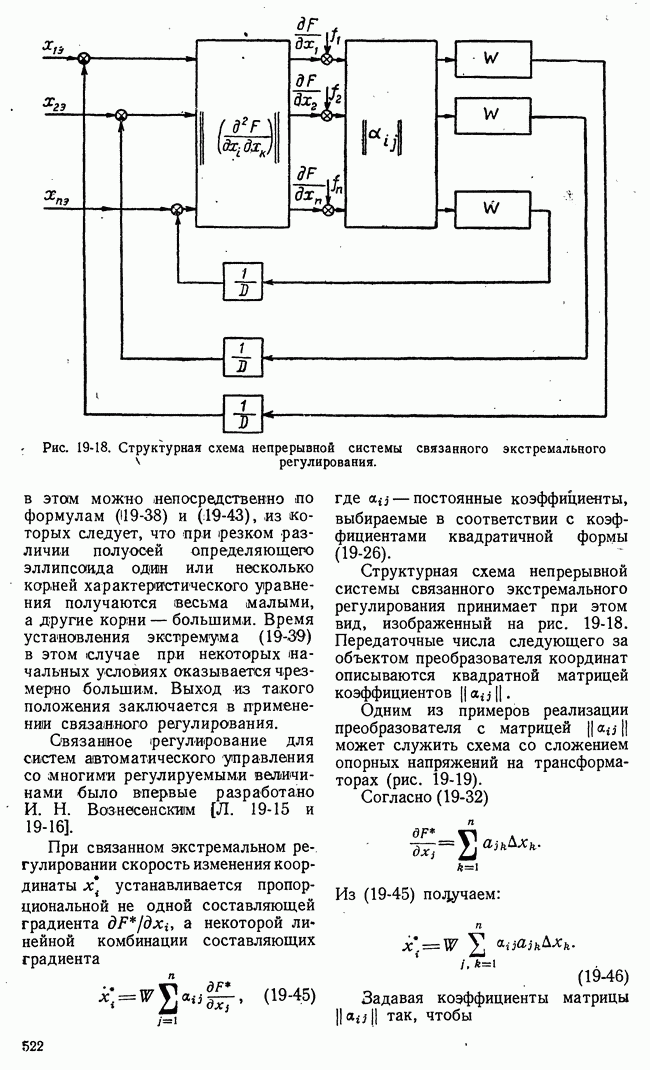
- 19-3. СТРУКТУРНЫЕ СХЕМЫ СИСТЕМ ЭКСТРЕМАЛЬНОГО РЕГУЛИРОВАНИЯ
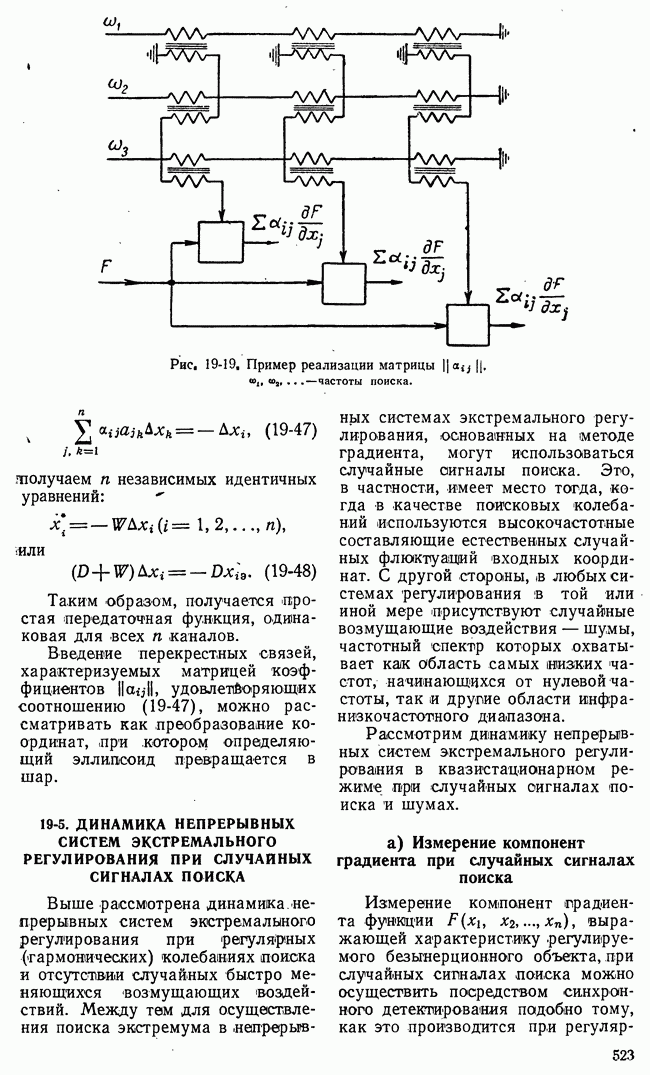
- 19-4. ДИНАМИКА НЕПРЕРЫВНЫХ СИСТЕМ ЭКСТРЕМАЛЬНОГО РЕГУЛИРОВАНИЯ В КВАЗИСТАЦИОНАРНОМ РЕЖИМЕ
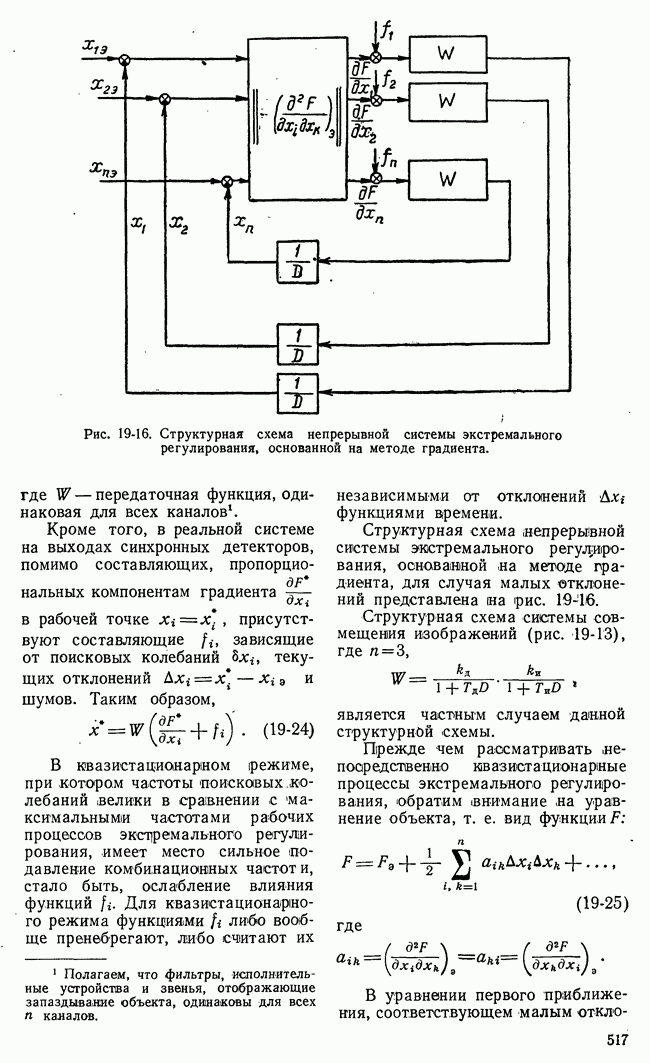
- б) Динамика квазистационарного режима систем экстремального регулирования, основанных на методе градиента
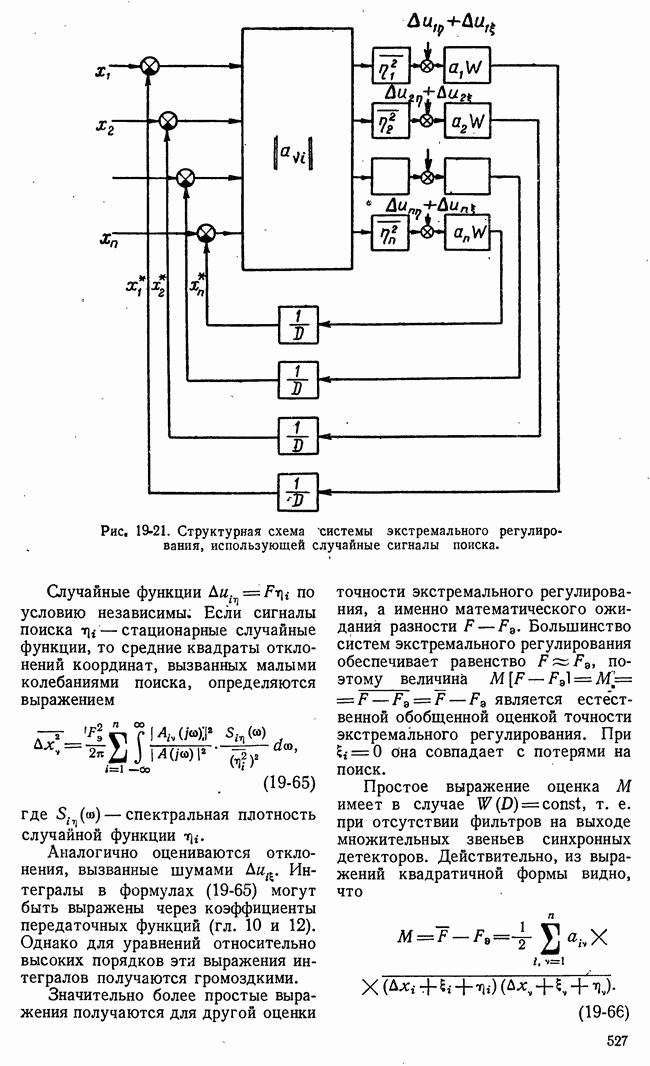
- 19-5. ДИНАМИКА НЕПРЕРЫВНЫХ СИСТЕМ ЭКСТРЕМАЛЬНОГО РЕГУЛИРОВАНИЯ ПРИ СЛУЧАЙНЫХ СИГНАЛАХ ПОИСКА
- б) Уравнения замкнутой системы экстремального регулирования
- в) Точность экстремального регулирования
- 19-6. ФОРСИРОВАННЫЕ ПРОЦЕССЫ ЭКСТРЕМАЛЬНОГО РЕГУЛИРОВАНИЯ ОДНОМЕРНОГО БЕЗЫНЕРЦИОННОГО ОБЪЕКТА
- ГЛАВА ДВАДЦАТАЯ. СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ С САМОНАСТРАИВАЮЩИМИСЯ КОРРЕКТИРУЮЩИМИ УСТРОЙСТВАМИ
- 20-1. СИСТЕМЫ С РАЗОМКНУТЫМИ ЦЕПЯМИ НАСТРОЙКИ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ
- 20-2. СИСТЕМЫ С ЗАМКНУТЫМИ ЦЕПЯМИ НАСТРОЙКИ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ
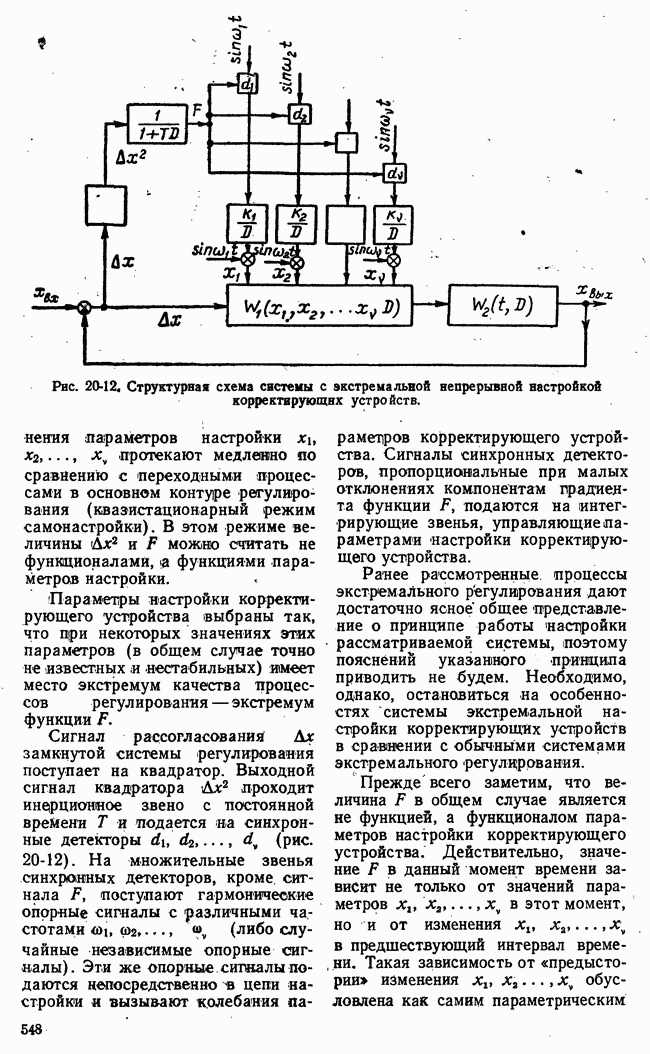
- 20-3. СИСТЕМЫ С ЭКСТРЕМАЛЬНОЙ НАСТРОЙКОЙ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ
- 20-4. СТАТИСТИЧЕСКАЯ ДИНАМИКА НЕПРЕРЫВНЫХ СИСТЕМ С ЭКСТРЕМАЛЬНОЙ НАСТРОЙКОЙ ПОСЛЕДОВАТЕЛЬНЫХ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ
- б) Уравнения замкнутой самонастраивающейся системы
- в) Случай сильной фильтрации. Квазистационарный режим
- г) Общий случай квазистационарного режима
- ГЛАВА ДВАДЦАТЬ ПЕРВАЯ. ИГРОВЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- 21-1. НАЗНАЧЕНИЕ И ПРИНЦИПЫ ДЕЙСТВИЯ ИГРОВЫХ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- 21-2. НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ ИГР
- 21-3. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ. ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
- 21-4. ОБ АЛГОРИТМАХ ИГРОВЫХ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- ПРИЛОЖЕНИЯ