| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ГЛАВА ВОСЕМНАДЦАТАЯ. ЭНТРОПИЯ, ИНФОРМАЦИЯ, АЛГОРИТМ В СИСТЕМАХ АВТОМАТИЧЕОКОГО УПРАВЛЕНИЯ
Предыдущие разделы курса основ автоматики посвящены рассмотрению весьма важных, но частных систем автоматического управления. Между тем, помимо нарастающего разнообразия возможных частных видов автоматических устройств, в современной технике ясно выражена тенденция комплексного использования этих устройств — объединение автоматических устройств в единые системы. Понятие системы автоматического управления охватывает как простейшие автоматические устройства, так и сложнейшие комплексы автоматических систем. Такие системы комплексной автоматизации, как системы управления технологическими процессами целых предприятий и групп предприятий, системы автоматического управления боевыми действиями и т. п., могут включать множество источников информации, систем регулирования, вычислительных и управляющих машин, каналов передачи информации и других устройств.
Кроме того, комплексные системы автоматизации на всех этапах развития техники будут в той или иной мере использовать участие человека в процессах управления. Человек будет контролировать и утверждать наиболее важные решения управляющих машин» выполнять операции, не поддающиеся автоматизации при данном уровне техники. Оптимальное рзаимодействие человека с системой относится к чжцу важнейших вопросов построения комплексных автоматизированных систем.
Для качественного описания и исследования процессов в комплексных автоматических системах необт ходимы соответствующие определения и понятия.
Основные определения и понятия, используемые при анализе систем регулирования, как-то: передаточные функции, законы регулирования, частотные характеристики и т. д., недостаточны для анализа и бписания сложных систем автоматического управления. Необходимы более общие определения и понятия. Такие определения и понятия формируются в общей науке об управлении — кибернетике.
18-1. ЭНТРОПИЯ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ УПРАВЛЯЕМОГО ПРОЦЕССА
Пусть имеется некоторый процесс, управление которым подлежит автоматизации. Состояние процесса в каждый данный момент времени характеризуется совокупностью величин  которые будем называть координатами процесса.
которые будем называть координатами процесса.
Координаты процесса всегда имеют разброс относительно желаемых значений, т. е. содержат случайные составляющие. Одним из основных назначений автоматизации управления процессом являются уменьшение неопределенности протекания процесса, уменьшение отклонений процесса от желаемого его течения. При этом требование
увеличения точности управления часто сочетается с требованием увеличения скорости протекания процесса.
Для иллюстрации тезиса о разбросе координат процесса, подлежащего автоматизации, приведем несколько примеров.
При пусках неуправляемых ракет наблюдается большое рассеивание как координат точек падений, так и координат в процессе полета. Назначение автоматического управления ракетой прежде всего заключается в уменьшении указанного рассеивания.
При работе генератора без регулятора напряжения имеют место большие колебания напряжения, вызванные случайными изменениями нагрузки и скорости вращения. Назначение регулятора заключается в уменьшении этих колебаний до допустимых пределов.
При. работе автоматического станка без контроля размеров обрабатываемой детали разброс конечных размеров деталей в некоторых случаях превосходит установленные допуски. Система автоматического контроля, воздействующая на настройку станка, увеличивает точность обработки.
Командир или штаб соединения, осуществляя управление боевой операцией, может допускать значительные отклонения от оптимальных решений. Автоматизация управления операцией уменьшит отклонения от оптимальных решений при одновременном увеличении скорости операции.
Число подобных примеров беспредельно велико.
Исчерпывающей характеристикой координат процесса в каждый заданный момент времени является распределение вероятностей этих величин.
Для непрерывных координат, принимающих произвольные значения в некоторых интервалах, будем рассматривать плотность вероятностей

Функция

выражает вероятность одновременного нахождения координат в интервалах

Если распределение дискретно, т. е. координаты могут иметь лишь дискретные значения, то функция плотности вероятности вырождается в сумму  -функций.
-функций.
Отметим, что координаты процесса, протекающего во времени, являются случайными функциями времени и выражение (18-1) (Следует рассматривать как плотность вероятности сечения случайных функций при заданном 
Распределение вероятностей требует при эмпирическом определении большого числа экспериментов. В теории информации была введена интегральная характеристика неопределенности, названная энтропией. Эта характеристика имеет близкое родство с понятием энтропии в статистической физике и термодинамике.
В термодинамике, рассматривающей макроскопические тепловые процессы, энтропия определяется как функция теплового состояния тела, зависящая от таких макроскопических характеристик, как температура и приращение  количества тепла. Статистическая физика, рассматривающая тела как системы частиц — атомов и молекул, вскрыла другое значение термодинамической или физической энтропии. Эта статистическая сущность физической энтропии состоит в следующем.
количества тепла. Статистическая физика, рассматривающая тела как системы частиц — атомов и молекул, вскрыла другое значение термодинамической или физической энтропии. Эта статистическая сущность физической энтропии состоит в следующем.
Молекулы, образующие тело, могут иметь различные скорости и координаты. Каждую совокупность значений скоростей и координат молекул данного тела можно рассматривать как определенное состояние тела.
Физическая энтропия есть характеристика распределения вероятностей состояний тела как системы молекул. Следует подчеркнуть» что физическая энтропия есть объективная характеристика макроскопического состояния тела, объективная в той же мере, как температура, количество тепла и т. п.
В теории вероятностей и теории информации понятие энтропии было распространено на распределения вероятностей любых переменных. Энтропией непрерывного распределения вероятностей переменных  называется величина
называется величина

Энтропия зависит только от распределения вероятностей — однозначно определяется плотностью вероятности  Однако, для того чтобы указать величины, к распределению которых относится энтропия, мы будем часто обозначать
Однако, для того чтобы указать величины, к распределению которых относится энтропия, мы будем часто обозначать 
Теория информации рассматривает энтропию распределения вероятностей в системах получения и передачи информации. При этом считается, что после получения информации о какой-либо величине распределение вероятности этой величины и, стало быть, энтропия могут существенным образом измениться. Тем самым энтропии в теории информации приписывается смысл «субъективной» или относительной характеристики. Подобную энтропию будем называть информационной энтропией там, где это необходимо в интересах ясности изложения.
Информационная энтропия для данного наблюдателя изменяется всякий раз, когда этот наблюдатель получает информацию о рассматриваемых величинах. Информационной энтропии в наибольшей мере соответствует формулировка Больцмана, согласно которой энтропия есть мера недостающей информации.
Связь информационной энтропии с количеством информации подробно рассматривается далее. Здесь уместно отметить, что основание логарифма в выражении энтропии в принципе может быть произвольным положительным числом. Однако для удобства сопоставления с количеством информации это основание выбирают равным 2 (двоичный логарифм).
Помимо информационной энтропии, в теории автоматического управления целесообразно использовать другое понятие энтропии, которое является как бы приложением понятия физической энтропии к управляемым процесса  характеризуемым не координатами множества молекул, а ограниченным числом различных величин — координат.
характеризуемым не координатами множества молекул, а ограниченным числом различных величин — координат.
Этот вид энтропии будем называть энтропией распределения вероятностей координат управляемого процесса (объекта) или просто энтропией процесса. Указанные понятия энтропии имеют одинаковые математические выражения. Энтропия распределения вероятностей координат управляемого процесса выражается той же формулой, что и информационная энтропия:

Различие же имеет место в существе указанных понятий и заключается в следующем. Информационная. энтропия, как выше указывалось, существенным образом зависит от информации, получаемой данным наблюдателем, и является вследствие этого относительной «субъективной» характеристикой. Энтропия процесса и распределение вероятностей координат этого процесса — объективные характеристики, не зависящие от информации, полученной отдельным наблюдателем.
Иными словами, считается, что энтропию распределения вероятностей координат какого-либо процесса нельзя изменить, только измерив с той или иной точностью эти координаты. Для изменения энтропии процесса необходимо вмешательство в этот процесс, т. е. управление или «естественное» воздействие. Физическая энтропия есть частный случай энтропии процесса, а именно тот случай, когда координатами процесса являются координаты и скорости большого числа молекул.
Таким образом, есть два общих понятия энтропии, имеющие одинаковое математическое выражение: энтропия процесса и информационная энтропия.
Рассмотрим некоторые свойства энтропии. Поскольку математические определения информационной энтропии и энтропии процесса одинаковы, все соотношения в равной мере справедливы для обоих видов энтропии и в формулировках вид энтропии можно не указывать.
Если координаты  независимы, то
независимы, то

и

где  плотности распределения вероятностей величин
плотности распределения вероятностей величин 
Таким образом, для независимых величин

Но по определению плотностей вероятности

Поэтому

где  энтропия
энтропия  из независимых величин.
из независимых величин.
Итак, энтропия независимых координат процесса равна сумме энтропии, каждой координаты.
Если процесс характеризуется лишь одной координатой х, то энтропия равна:

Если координата х может принимать лишь дискретные значения, вероятности которых равны  то энтропия такой координаты выражается формулой
то энтропия такой координаты выражается формулой

Эта формула не может быть получена простым предельным переходом из (18-4).
Если дискретная величина не имеет разброса, т. е. значение ее строго фиксировано, то все вероятности  кроме одной, равны нулю, а эта единственная вероятность равна единице. Таким образом, энтропия дискретной величины при отсутствии разброса равна нулю 1. Энтропия дискретной величины всегда положительна или равна нулю. Это непосредственно вытекает из выражения (18-5), где
кроме одной, равны нулю, а эта единственная вероятность равна единице. Таким образом, энтропия дискретной величины при отсутствии разброса равна нулю 1. Энтропия дискретной величины всегда положительна или равна нулю. Это непосредственно вытекает из выражения (18-5), где 
Энтропия величины, могущей принимать  значений, максимальна в том случае, когда все эти значения равновероятны,
значений, максимальна в том случае, когда все эти значения равновероятны,  Для доказательства этого положения найдем условие максимума энтропии
Для доказательства этого положения найдем условие максимума энтропии  из (18-5) при учете очевидного соотношения
из (18-5) при учете очевидного соотношения

Согласно известному правилу отыскания эстремума функции, аргументы которой удовлетворяют определенным уравнениям (условный экстремум), значения  определяются из уравнения
определяются из уравнения

где  множитель Лангранжа.
множитель Лангранжа.
Производя дифференцирование, находим

Из этого равенства следует, что все вероятности  соответствующие экстремуму, одинаковы:
соответствующие экстремуму, одинаковы:

и в силу (118-6) равны  Легко проверить, что найденные значения соответствуют экстремуму максимуму.
Легко проверить, что найденные значения соответствуют экстремуму максимуму.
Энтропия непрерывной величины, заданной абсолютно точно, равна отрицательной бесконечности. Это положение легко доказать, осуществляя предельный переход от распределения вероятностей с конечной дисперсией к случаю, когда дисперсия равна нулю. Плотность вероятности  при таком переходе обращается в
при таком переходе обращается в  -функцию и энтропия стремится
-функцию и энтропия стремится 

Следует заметить, что возрастание абсолютной величины энтропии по мере уменьшения дисперсии (увеличения точности) происходит в логарифмической пропорции, т. е. «медленно». Обращение в бесконечность  при точном задании непрерывной величины х нельзя считать недостатком понятия энтропии как характеристики неопределенности. Отмеченное положение указывает лишь на бесплодность использования понятия энтропии в тех случаях, когда применяется идеализация (модель) процесса с точным заданием непрерывных величин.
при точном задании непрерывной величины х нельзя считать недостатком понятия энтропии как характеристики неопределенности. Отмеченное положение указывает лишь на бесплодность использования понятия энтропии в тех случаях, когда применяется идеализация (модель) процесса с точным заданием непрерывных величин.
В реальных процессах физические величины никогда не могут быть измерены и заданы абсолютно точно, и энтропия никогда не обращается в бесконечность. Кроме того, предел непрерывности физических величин кладется квантовой структурой процессов.
Энтропия непрерывной величины, имеющей заданный средний квадрат, максимальна при нормальном законе распределения вероятностей. Для подтверждения этого положения найдем экстремум энтропии

при условиях

Условие экстремума функционала

заключается в равенстве

откуда

где 
Определяя  из условий (18-7), получаем формулу нормального распределения вероятностей
из условий (18-7), получаем формулу нормального распределения вероятностей

(распределение Гаусса). Легко проверить, что нормальное
распределение при заданных условиях соответствует именно максимуму энтропии и этот максимум равен:

Таким образом, при заданном среднем квадрате нормальное распределение соответствует наибольшей неопределенности величины х из всех возможных распределений.
Здесь необходимо указать на важное положение: практическое значение имеет не абсолютная величина энтропии, а ее приращение. Это положение справедливо, пожалуй, в той же мере, как утверждение, что значение имеет не абсолютная величина потенциала, а разность потенциалов. Оно снимает затруднение, связанное с размерностями величин. Действительно, если  размерная физическая величина, то плотность вероятностей
размерная физическая величина, то плотность вероятностей  имеет размерность, обратную размерности х. Таким образом, под знаком логарифма появляется размерная величина. Однако в выражении разности энтропий всегда фигурирует логарифм отношения и физические размерности сокращаются. Это наглядно демонстрирует формула (188). Разность энтропий двух состояний, имеющих нормальные распределения и средние квадраты
имеет размерность, обратную размерности х. Таким образом, под знаком логарифма появляется размерная величина. Однако в выражении разности энтропий всегда фигурирует логарифм отношения и физические размерности сокращаются. Это наглядно демонстрирует формула (188). Разность энтропий двух состояний, имеющих нормальные распределения и средние квадраты  равна:
равна:

Для иллюстрации понятия энтропии состояния процесса, подлежащего управлению, приведем примеры.
Пример 1. Генератор переменного тока без регулятора напряжения  и частоты
и частоты  имеет при некоторых условиях разброс напряжения
имеет при некоторых условиях разброс напряжения  в и частоты
в и частоты  При включенной сфтеме регулирования напряжения и частоты и тех же условиях неопределенность координат характеризуется величинами
При включенной сфтеме регулирования напряжения и частоты и тех же условиях неопределенность координат характеризуется величинами  Считая распределения вероятностей нормальными и координаты
Считая распределения вероятностей нормальными и координаты  независимыми (что в данном случае неточно), найдем уменьшение энтропии при переходе от неуправляемого к управляемому процессу.
независимыми (что в данном случае неточно), найдем уменьшение энтропии при переходе от неуправляемого к управляемому процессу.
Поскольку величины  приняты независимыми, общее приращение энтропии будет равно сумме приращений энтропий:
приняты независимыми, общее приращение энтропии будет равно сумме приращений энтропий:

Пример 2. В результате полной дезорганизации управления  самолетов движутся с произвольными случайными курсами. После восстановления управления все самолеты взчли общий курс сточностью
самолетов движутся с произвольными случайными курсами. После восстановления управления все самолеты взчли общий курс сточностью  Найдем уменьшение энтропии.
Найдем уменьшение энтропии.
Считая в первом случае распределение вероятностей равномерным, а во втором случае — нормальным, находим: 130

Использование понятия энтропии, разумеется, не заменяет детального изучения управляемого процесса, так же как использование понятия общей энергии системы не заменяет определения каждой из координат системы. Однако рассмотрение энтропии позволяет установить некоторые общие условия организации управления процессами.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ГЛАВА ПЕРВАЯ. ВВОДНАЯ
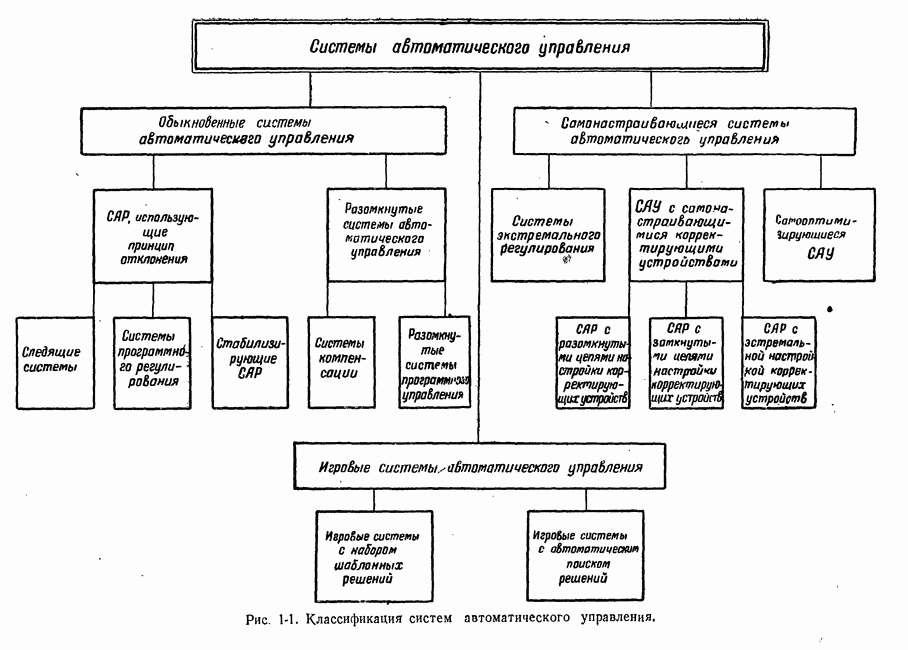
- 1-1. О КЛАССИФИКАЦИИ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- 1-2. ОБЫКНОВЕННЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- 1-3. САМОНАСТРАИВАЮЩИЕСЯ СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- 1-4. ИГРОВЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- 1-5. КЛАССИФИКАЦИЯ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ ПО ДРУГИМ ПРИЗНАКАМ
- ГЛАВА ВТОРАЯ. ОБЩИЕ ПЕРЕДАТОЧНЫЕ СВОЙСТВА ЭЛЕМЕНТОВ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- 2-1. УРАВНЕНИЯ ЭЛЕМЕНТОВ. СТАТИЧЕСКИЕ И ДИНАМИЧЕСКИЕ СВОЙСТВА ЭЛЕМЕНТОВ
- б) Центробежный измеритель скорости вращения
- в) Электромагнитный измеритель напряжения
- 2-2. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ
- 2-3. ЭЛЕМЕНТАРНЫЕ ДИНАМИЧЕСКИЕ ЗВЕНЬЯ, ИХ УРАВНЕНИЯ И ПЕРЕДАТОЧНЫЕ ФУНКЦИИ
- 2-4. ТИПОВЫЕ ВХОДНЫЕ СИГНАЛЫ. ВОЗМУЩАЮЩИЕ ФУНКЦИИ
- 2-5. ПЕРЕХОДНЫЕ ФУНКЦИИ ЭЛЕМЕНТАРНЫХ ЗВЕНЬЕВ
- 2-6. ИМПУЛЬСНЫЕ ПЕРЕХОДНЫЕ ФУНКЦИИ ЭЛЕМЕНТАРНЫХ ЗВЕНЬЕВ
- 2-7. РЕАКЦИЯ ЗВЕНЬЕВ НА ПРОИЗВОЛЬНЫЕ ИЗВЕСТНЫЕ ФУНКЦИИ ВРЕМЕНИ
- 2-8. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ
- б) Частотные характеристики элементарных звеньев
- в) Логарифмические характеристики элементарных звеньев
- 2-9. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ОБ ЭЛЕМЕНТАРНЫХ ЗВЕНЬЯХ
- 2-10. СОЕДИНЕНИЯ ЗВЕНЬЕВ. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ СОЕДИНЕНИИ
- 2-11. ЭЛЕМЕНТЫ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ КАК ЧЕТЫРЕХПОЛЮСНИКИ. ПЕРЕДАТОЧНЫЕ УРАВНЕНИЯ
- ГЛАВА ТРЕТЬЯ. ДАТЧИКИ СИГНАЛОВ
- 3-1. ОБЩИЕ СВОЙСТВА ДАТЧИКОВ
- 3-2. ПОТЕНЦИОМЕТРИЧЕСКИЕ ДАТЧИКИ
- б) Выходная мощность потенциометрических датчиков и условия согласования
- в) Динамические свойства
- г) Ошибка ступенчатости. Параметры потенциометрических датчиков
- 3-3. ИНДУКТИВНЫЕ ДАТЧИКИ
- б) Двухтактные индуктивные датчики
- в) Характеристики двухтактных индуктивных датчиков
- г) Трансформаторные индуктивные датчики
- д) Динамические свойства индуктивных датчиков
- е) Шумы индуктивных датчиков
- ж) Общие свойства индуктивных датчиков
- 3-4. СЕЛЬСИНЫ В ТРАНСФОРМАТОРНОМ РЕЖИМЕ
- б) Характеристики сельсинного датчика
- в) Динамические свойства сельсинных датчиков
- г) Шумы и ошибки датчика
- д) Устанавливающий момент
- е) Дифференциальные сельсины
- ж) Сельсины точного и грубого каналов
- ГЛАВА ЧЕТВЕРТАЯ. УСИЛИТЕЛИ СИГНАЛОВ
- 4-2. МАГНИТНЫЕ УСИЛИТЕЛИ
- а) Рабочий процесс и статическая характеристика магнитного усилителя с прямоугольной кривой намагничивания сердечников
- б) Двухтактные магнитные усилители с выходом на переменном токе
- в) Магнитные усилители с обратной связью
- г) Динамические свойства магнитных усилителей
- д) Шумы магнитных усилителей. Общие свойства магнитных усилителей
- 4-3. ЭЛЕКТРОМАШИННЫЕ УСИЛИТЕЛИ
- б) Однокаскадный электромашицный усилитель как четырехполюсник
- в) Двухкаскадный электромашинный усилитель с поперечным полем
- г) Шумы электромашинных усилителей
- 4-4. РЕЛЕ
- б) Поляризованные реле
- в) Магнитоэлектрическое реле
- 4-5. РЕЛЕЙНЫЕ УСИЛИТЕЛИ
- б) Вибрационная линеаризация релейных усилителей
- в) Релейный усилитель как четырехполюсник
- 4-6. ЭЛЕКТРОННЫЕ УСИЛИТЕЛИ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- б) Фазочувствительные усилители и синхронные детекторы
- в) Электронные усилители постоянного тока
- г) Шумы электронных усилителей
- 4-7. ПОЛУПРОВОДНИКОВЫЕ УСИЛИТЕЛИ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- ГЛАВА ПЯТАЯ. ИСПОЛНИТЕЛЬНЫЕ УСТРОЙСТВА СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- 5-2. СЕРВОДВИГАТЕЛИ ПОЧТОЯННОГО ТОКА
- 5-3. СЕРВОДВИГАТЕЛИ ПЕРЕМЕННОГО ТОКА
- 5-4. СЕРВОДВИГАТЕЛИ С ЭЛЕКТРОМАГНИТНЫМИ И ПОРОШКОВЫМИ МУФТАМИ
- б) Характеристики серводвигателей с электромагнитными муфтами
- в) Порошковые муфты
- г) Характеристики серводвигателей с порошковыми муфтами
- 5-5. ГИДРАВЛИЧЕСКИЕ И ПНЕВМАТИЧЕСКИЕ СЕРВОДВИГАТЕЛИ
- б) Обратные связи в гидравлических серводвигателях
- в) Свойства гидравлических серводвигателей
- г) Электрогидравлические серводвигатели
- д) Пневматические серводвигатели
- ГЛАВА ШЕСТАЯ. СТАБИЛИЗИРУЮЩИЕ УСТРОЙСТВА СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- 6-1. ПАССИВНЫЕ КОРРЕКТИРУЮЩИЕ ЦЕПИ СИСТЕМ ПОСТОЯННОГО ТОКА
- б) Интегрирующие и интегродифференцирующие цепи
- 6-2. АКТИВНЫЕ КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА СИСТЕМ ПОСТОЯННОГО ТОКА
- 6-3. КОРРЕКТИРУЮЩИЕ ЦЕПИ СИСТЕМ ПЕРЕМЕННОГО ТОКА
- 6-4. ФИЛЬТРЫ В ЦЕПЯХ ОБРАТНЫХ СВЯЗЕЙ. МЕХАНИЧЕСКИЕ СТАБИЛИЗИРУЮЩИЕ УСТРОЙСТВА
- ГЛАВА СЕДЬМАЯ. СТРУКТУРНЫЕ СХЕМЫ И ХАРАКТЕРИСТИКИ ЛИНЕЙНЫХ СТАЦИОНАРНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 7-1. СТРУКТУРНЫЕ СХЕМЫ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 7-2. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ ДЛЯ ВХОДНОЙ ВЕЛИЧИНЫ
- 7-3. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ ДЛЯ ВОЗМУЩЕНИЯ
- 7-4. ПРИМЕРЫ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ И ИХ СТРУКТУРНЫЕ СХЕМЫ
- б) Стабилизация напряжения самолетных генераторов
- в) Следящая система копировально-фрезерного станка
- г) Следящая система автосопровождения
- д) Автоматическое управление углом тангажа самолета
- 7-5. ВРЕМЕННЫЕ ХАРАКТЕРИСТИКИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 7-6. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- б) Частотные характеристики замкнутой системы
- в) Связь частотных характеристик замкнутой и разомкнутой систем
- ГЛАВА ВОСЬМАЯ. ЭНЕРГЕТИЧЕСКИЙ РАСЧЕТ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ И СОГЛАСОВАНИЕ ХАРАКТЕРИСТИК ЭЛЕМЕНТОВ
- 8-1. ВЫБОР МОЩНОСТИ ИСПОЛНИТЕЛЬНЫХ УСТРОЙСТВ И УСЛОВИЯ СОГЛАСОВАНИЯ С НАГРУЗКОЙ
- а) Определение необходимой мощности по переходным процессам при типовых воздействиях
- б) Мгновенная мощность при гармонических колебаниях
- в) Необходимая мощность при случайных колебаниях регулирующего органа
- г) Выбор мощности сервомотора
- д) Условия согласования с нагрузкой сервомотора без обратной связи
- е) Согласование с нагрузкой сервомотора с жесткой обратной связью
- 8-2. СОГЛАСОВАНИЕ ДАТЧИКОВ, УСИЛИТЕЛЬНЫХ И КОРРЕКТИРУЮЩИХ УСТРОЙСТВ. РАСПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТОВ УСИЛЕНИЯ
- б) Передаточные функции последовательных соединений элементов
- в) Согласование пропорциональных участков характеристик
- г) Распределение коэффициентов усиления
- ГЛАВА ДЕВЯТАЯ. УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ СТАЦИОНАРНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 9-2. КРИТЕРИЙ УСТОЙЧИВОСТИ РАУСА—ГУРВИЦА
- 9-3. КРИТЕРИЙ УСТОЙЧИВОСТИ МИХАЙЛОВА
- 9-4. КРИТЕРИЙ УСТОЙЧИВОСТИ НАЙКВИСТА
- б) Использование логарифмических характеристик системы для исследования устойчивости. Понятие о запасе устойчивости
- 9-5. КОЭФФИЦИЕНТ УСИЛЕНИЯ И УСТОЙЧИВОСТЬ. ВЛИЯНИЕ КОРРЕКТИРУЮЩИХ ЦЕПЕЙ НА УСТОЙЧИВОСТЬ
- 9-6. ВЫДЕЛЕНИЕ ОБЛАСТЕЙ УСТОЙЧИВОСТИ В ПРОСТРАНСТВЕ ПАРАМЕТРОВ СИСТЕМЫ ДИАГРАММЫ ВЫШНЕГРАДСКОГО
- б) Общий метод D-разбиения в плоскости двух параметров. Линейная задача
- в) Выделение области устойчивости в плоскости двух параметров. Нелинейная задача
- г) Выделение области устойчивости в плоскости одного комплексного параметра
- ГЛАВА ДЕСЯТАЯ. КАЧЕСТВО ПРОЦЕССОВ РЕГУЛИРОВАНИЯ В ЛИНЕЙНЫХ СИСТЕМАХ
- 10-1. КРИТЕРИИ КАЧЕСТВА ПРОЦЕССА РЕГУЛИРОВАНИЯ
- 10-2. ТОЧНОСТЬ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ В УСТАНОВИВШИХСЯ РЕЖИМАХ. СТАТИЧЕСКИЕ И АСТАТИЧЕСКИЕ СИСТЕМЫ
- б) Точность при медленно меняющихся воздействиях. Коэффициенты ошибок. Астатические системы высших порядков
- в) Общие условия неискаженного воспроизведения входных сигналов в вынужденном режиме
- г) Повышение точности системы коррекцией входного сигнала
- д) Повышение точности системы путем компенсации возмущения F(t)
- 10-18. ПЕРЕХОДНЫЕ ФУНКЦИИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- б) Некоторые особенности вычисления переходных функций
- 10-4. РАСПРЕДЕЛЕНИЕ НУЛЕЙ И ПОЛЮСОВ ПЕРЕДАТОЧНОЙ ФУНКЦИИ И ПЕРЕХОДНЫЕ ПРОЦЕССЫ
- б) Оценки распределения корней. Степень устойчивости. Коэффициент затухания колебаний
- в) Влияние параметров на распределение корней. Метод Эванса
- г) Оценка переходных функций по распределению полюсов передаточной функции или корней характеристического уравнения
- д) Влияние нулей на характер переходной функции
- е) Определение коэффициентов уравнений по заданному распределению корней. Стандартные коэффициенты характеристических уравнений
- 10-5. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ И ПЕРЕХОДНЫЕ ФУНКЦИИ
- б) Приближенное вычисление переходных функций и переходных процессов
- в) Оценка качества процесса регулирования по характеристикам замкнутой системы Ф(w) и ф(w) и характеристике разомкнутой системы W(jw)
- г) Оценка качества по амплитудным логарифмическим характеристикам. Минимально-фазовые системы
- д) Связь между логарифмическими амплитудными характеристиками разомкнутой системы и полюсами передаточной функции замкнутой системы
- 10-6. ИНТЕГРАЛЬНЫЕ ОЦЕНКИ ПЕРЕХОДНЫХ ПРОЦЕССОВ
- г) Приближение кривых x(t) к эталонной кривой хэ(t) по критерию …
- ГЛАВА ОДИННАДЦАТАЯ. НЕСТАЦИОНАРНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 11-1. ОБЩИЕ СВЕДЕНИЯ О НЕСТАЦИОНАРНЫХ СИСТЕМАХ
- 11-2. ПРИМЕРЫ СУЩЕСТВЕННО НЕСТАЦИОНАРНЫХ СИСТЕМ
- 11-3. ДИНАМИЧЕСКИЕ ХАРАКТЕРИСТИКИ НЕСТАЦИОНАРНЫХ СИСТЕМ АВТОМАТИЧ ЕСКОГО РЕГУЛИРОВАНИЯ
- 11-4. ОСОБЕННОСТИ СОСТАВЛЕНИЯ УРАВНЕНИЙ И СТРУКТУРНЫХ СХЕМ НЕСТАЦИОНАРНЫХ СИСТЕМ
- 11-5. МЕТОДЫ ОПРЕДЕЛЕНИЯ ЧАСТОТНОЙ ХАРАКТЕРИСТИКИ И ИМПУЛЬСНОЙ РЕАКЦИИ НЕСТАЦИОНАРНЫХ СИСТЕМ
- ГЛАВА ДВЕНАДЦАТАЯ. СТАТИСТИЧЕСКАЯ ДИНАМИКА ЛИНЕЙНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 12-1. СТАЦИОНАРНЫЕ И НЕСТАЦИОНАРНЫЕ СЛУЧАЙНЫЕ ПРОЦЕССЫ
- б) Стационарные и нестационарные случайные функций
- в) Свойства корреляционной функции
- г) Свойство эргодичности
- д) Гауссовы случайные процессы
- 12-2. ПРЕОБРАЗОВАНИЕ СТАЦИОНАРНЫХ СЛУЧАЙНЫХ ФУНКЦИЙ СТАЦИОНАРНЫМИ ЛИНЕЙНЫМИ СИСТЕМАМИ
- б) Преобразование корреляционных функций при прохождении случайного сигнала через линейную систему
- в) Интегральная квадратичная оценка импульсной переходной функции и дисперсия реакции системы на белый шум
- г) Преобразование спектральных плотностей при прохождении случайного сигнала через линейную систему
- 12-3. ОПТИМАЛЬНЫЕ ЛИНЕЙНЫЕ СТАЦИОНАРНЫЕ СИСТЕМЫ
- б) Условия оптимальности при свободном выборе передаточной функции
- ГЛАВА ТРИНАДЦАТАЯ. О СИНТЕЗЕ ЛИНЕЙНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 13-2. МЕТОД ЛОГАРИФМИЧЕСКИХ ЧАСТОТНЫХ ХАРАКТЕРИСТИК
- б) Синтез корректирующих цепей
- в) О синтезе на основе требований к реакции системы на возмущение F(t)
- 13-3. ВЫБОР ПАРАМЕТРОВ НА ОСНОВЕ АНАЛИЗА РАСПРЕДЕЛЕНИЯ НУЛЕЙ И ПОЛЮСОВ ПЕРЕДАТОЧНОЙ ФУНКЦИИ
- 13-4. ВЫБОР ПАРАМЕТРОВ НА ОСНОВЕ ИНТЕГРАЛЬНЫХ КВАДРАТИЧНЫХ ОЦЕНОК
- 13-5. СПЕЦИАЛЬНЫЕ ПРИЕМЫ УЛУЧШЕНИЯ КАЧЕСТВА ПРОЦЕССА РЕГУЛИРОВАНИЯ
- б) Подавление помех во входном сигнале при инерционном объекте управления
- в) Использование двух источников информации для выделения истинного сигнала
- г) Компенсация влияния запаздывания измерителей на динамические свойства системы
- д) Исключение перерегулирования в системах, передаточные функции которых имеют только вещественные полюсы
- ГЛАВА ЧЕТЫРНАДЦАТАЯ. ИМПУЛЬСНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 14-2. ИМПУЛЬСЫ И ИМПУЛЬСНЫЕ ЭЛЕМЕНТЫ
- б) Формирующие цепи и импульсные элементы
- 14-3. ДИСКРЕТНЫЕ ФУНКЦИИ И ПОСЛЕДОВАТЕЛЬНОСТИ. ИХ РАЗНОСТИ И СУММЫ
- 14-4. РЕАКЦИЯ ЛИНЕЙНЫХ НЕПРЕРЫВНЫХ СИСТЕМ НА ПОСЛЕДОВАТЕЛЬНОСТИ ИЛИ ДЕЛЬТА-ИМПУЛЬСОВ
- б) Свертка двух дискретных функций
- в) Уравнения в конечных разностях непрерывных звеньев первого и второго порядков
- г) Символические изображения дискретных функций и их использование для решения уравнений в конечных разностях
- 14-5. ДИСКРЕТНОЕ ПРЕОБРАЗОВАНИЕ ЛАПЛАСА ИЛИ z-ПРЕОБРАЗОВАНИЕ. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ КОМПЛЕКСНОГО АРГУМЕНТА
- 14-6. ДИНАМИКА РАЗОМКНУТЫХ ИМПУЛЬСНЫХ СИСТЕМ
- б) Значение выходной величины непрерывной системы внутри интервалов повторения
- в) Передаточные функции, систем с запаздыванием
- г) Свободные и вынужденные движения
- д) Полюсы. Устойчивость разомкнутых систем
- е) Переходные функции
- ж) Частотные характеристики
- 14-7. СВЯЗЬ МЕЖДУ ЧАСТОТНЫМИ И ПЕРЕХОДНЫМИ ФУНКЦИЯМИ. ДИСКРЕТНОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ
- 14-8. ИНТЕГРАЛЬНАЯ КВАДРАТИЧНАЯ ОЦЕНКА
- 14-9. ДИСКРЕТНЫЕ СЛУЧАЙНЫЕ ФУНКЦИИ (СЛУЧАЙНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ)
- ГЛАВА ПЯТНАДЦАТАЯ. ДИНАМИКА ИМПУЛЬСНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 15-1. УРАВНЕНИЯ И ПЕРЕДАТОЧНЫЕ ФУНКЦИИ СИСТЕМ С ОДНИМ ИМПУЛЬСНЫМ ЭЛЕМЕНТОМ
- 15-2. УСТОЙЧИВОСТЬ ЗАМКНУТЫХ СИСТЕМ
- 15-3. КАЧЕСТВО ПРОЦЕССА РЕГУЛИРОВАНИЯ
- 15-4. ПРИМЕРЫ ИМПУЛЬСНЫХ СИСТЕМ
- 15-5. ИМПУЛЬСНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ С ДИСКРЕТНЫМИ КОРРЕКТИРУЮЩИМИ ЦЕПЯМИ
- ГЛАВА ШЕСТНАДЦАТАЯ. СТРУКТУРНЫЕ СХЕМЫ, ХАРАКТЕРИСТИКИ И УРАВНЕНИЯ НЕЛИНЕЙНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- б) Уравнения продольного движения самолета
- в) Уравнения продольного движения ракеты
- 16-2. НЕЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ СИГНАЛА ОШИБКИ
- б) Структурные схемы с нелинейными элементами
- в) Релейные системы. Релейные элементы
- 16-3. НЕЛИНЕЙНЫЙ ОБЪЕКТ РЕГУЛИРОВАНИЯ И НЕЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ СИГНАЛА ОШИБКИ
- ГЛАВА СЕМНАДЦАТАЯ. СВОЙСТВА НЕЛИНЕЙНЫХ СИСТЕМ И (МЕТОДЫ ИССЛЕДОВАНИЯ
- б) Суждение об устойчивости по уравнениям первого приближения. Теоремы Ляпунова
- в) Суждение о качестве процессов регулирования по уравнениям первого приближения
- г) Прямой метод Ляпунова
- д) Техническая устойчивость
- 17-2. АВТОКОЛЕБАНИЯ НЕЛИНЕЙНЫХ СИСТЕМ
- б) Автоколебания релейных систем
- в) Метод точечных преобразований
- г) Описание процесса в релейной системе разностным уравнением. Устойчивость автоколебаний
- д) Примера исследования автоколебаний релейных систем второго порядка
- 17-3. ВЛИЯНИЕ КОРРЕКТИРУЮЩИХ ЦЕПЕЙ НА АВТОКОЛЕБАНИЯ И НА ПЕРЕХОДНЫЕ ПРОЦЕССЫ НЕЛИНЕЙНЫХ СИСТЕМ
- б) Влияние корректирующих цепей на переходные процессы. Скользящие режимы. Оптимальные переходные процессы
- 17-4. ГАРМОНИЧЕСКАЯ ЛИНЕАРИЗАЦИЯ ПРОЦЕССОВ В НЕЛИНЕЙНЫХ СИСТЕМАХ
- б) Исследование автоколебаний при помощи гармонической линеаризации
- в) Гармоническая линеаризация и критерии устойчивости линейных систем
- 17-5. ТЕОРИЯ РЕЛЕЙНЫХ СИСТЕМ
- в) Частотные характеристики релейных систем
- г) Оценка устойчивости релейных систем
- д) Вынужденные колебания релейных систем. Захватывание (синхронизация или подавление) автоколебаний
- е) Вибрационная линеаризация релейных систем, Реакция релейных систем на медленно меняющиеся возмущения
- 17-6. ОПТИМАЛЬНЫЕ ПРОЦЕССЫ РЕГУЛИРОВАНИЯ
- б) Системы, оптимальные по быстродействию. Принцип максимума
- в) Системы, близкие к оптимальным по быстродействию
- ГЛАВА ВОСЕМНАДЦАТАЯ. ЭНТРОПИЯ, ИНФОРМАЦИЯ, АЛГОРИТМ В СИСТЕМАХ АВТОМАТИЧЕОКОГО УПРАВЛЕНИЯ
- 18-1. ЭНТРОПИЯ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ УПРАВЛЯЕМОГО ПРОЦЕССА
- 18-2. КОЛИЧЕСТВО ИНФОРМАЦИИ В ПРОЦЕССАХ УПРАВЛЕНИЯ
- 18-3. ЭНТРОПИЯ И ИНФОРМАЦИЯ В ЗАМКНУТЫХ СИСТЕМАХ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- 18-4. АЛГОРИТМЫ ПРОЦЕССОВ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- ГЛАВА ДЕВЯТНАДЦАТАЯ. СИСТЕМЫ ЭКСТРЕМАЛЬНОГО РЕГУЛИРОВАНИЯ
- 19-1. ПРИМЕРЫ СИСТЕМ ЭКСТРЕМАЛЬНОГО РЕГУЛИРОВАНИЯ
- 19-2. СПОСОБЫ ПОИСКА ЭКСТРЕМУМА
- б) Методы организации процесса поиска
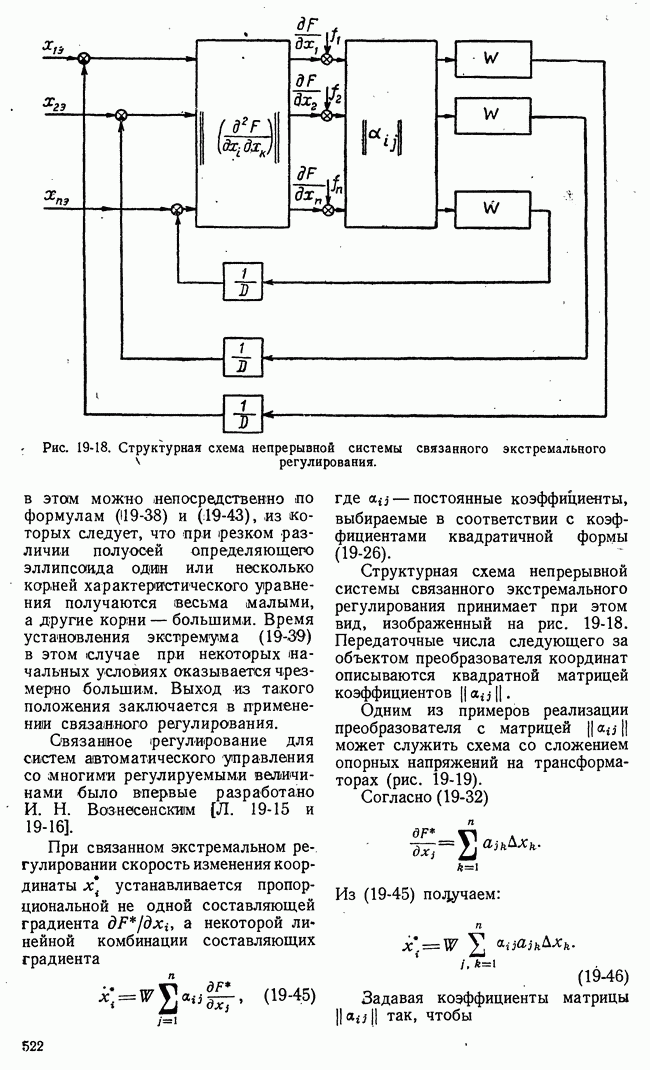
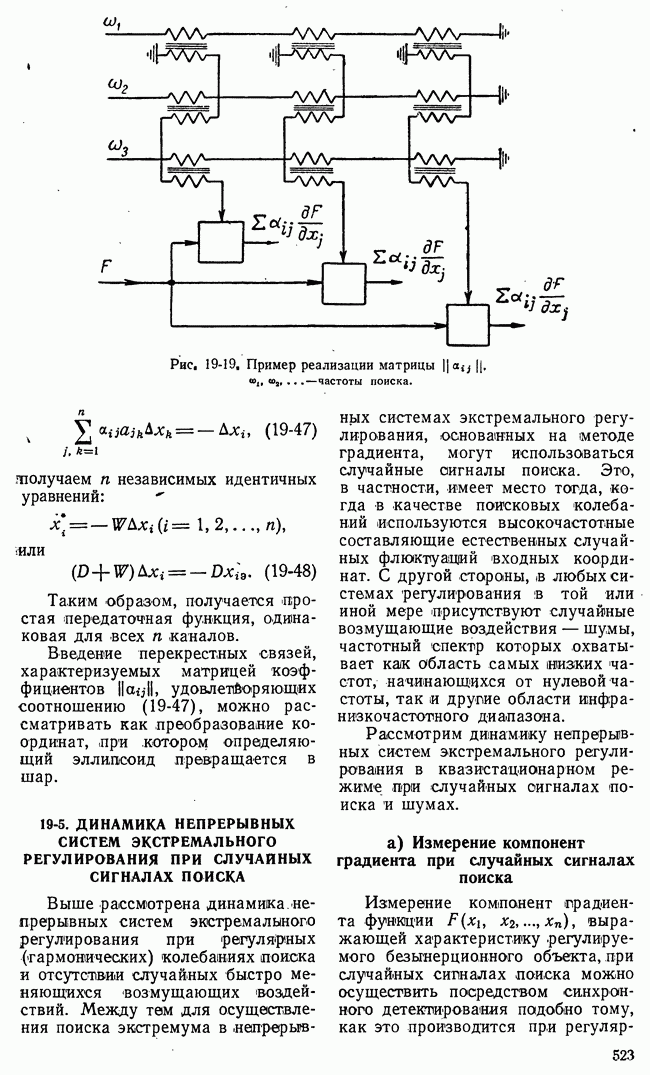
- 19-3. СТРУКТУРНЫЕ СХЕМЫ СИСТЕМ ЭКСТРЕМАЛЬНОГО РЕГУЛИРОВАНИЯ
- 19-4. ДИНАМИКА НЕПРЕРЫВНЫХ СИСТЕМ ЭКСТРЕМАЛЬНОГО РЕГУЛИРОВАНИЯ В КВАЗИСТАЦИОНАРНОМ РЕЖИМЕ
- б) Динамика квазистационарного режима систем экстремального регулирования, основанных на методе градиента
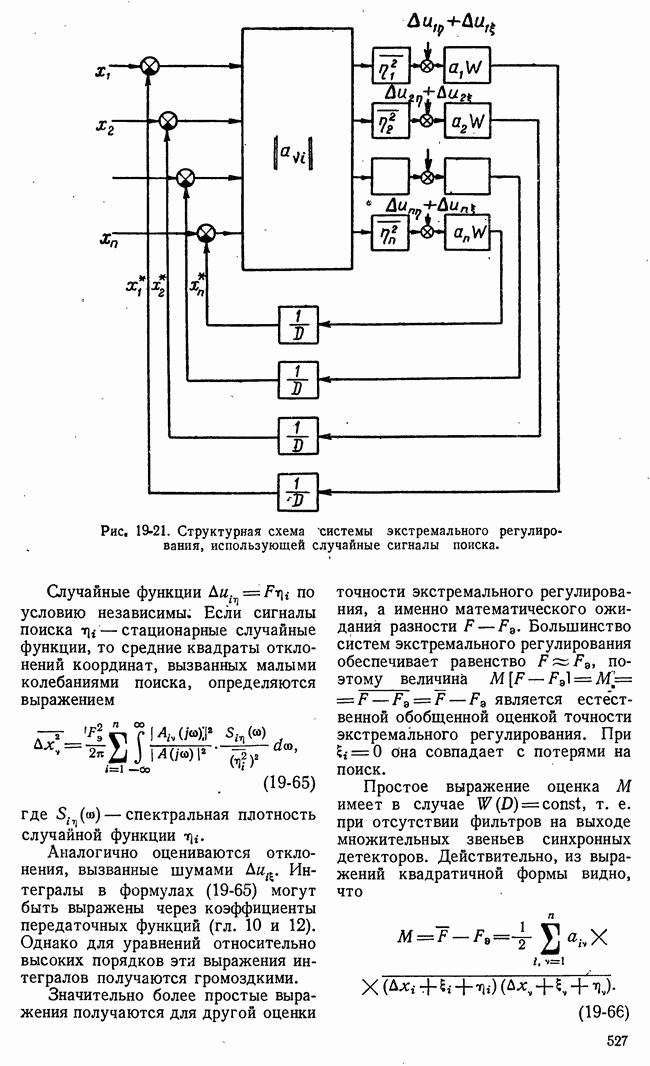
- 19-5. ДИНАМИКА НЕПРЕРЫВНЫХ СИСТЕМ ЭКСТРЕМАЛЬНОГО РЕГУЛИРОВАНИЯ ПРИ СЛУЧАЙНЫХ СИГНАЛАХ ПОИСКА
- б) Уравнения замкнутой системы экстремального регулирования
- в) Точность экстремального регулирования
- 19-6. ФОРСИРОВАННЫЕ ПРОЦЕССЫ ЭКСТРЕМАЛЬНОГО РЕГУЛИРОВАНИЯ ОДНОМЕРНОГО БЕЗЫНЕРЦИОННОГО ОБЪЕКТА
- ГЛАВА ДВАДЦАТАЯ. СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ С САМОНАСТРАИВАЮЩИМИСЯ КОРРЕКТИРУЮЩИМИ УСТРОЙСТВАМИ
- 20-1. СИСТЕМЫ С РАЗОМКНУТЫМИ ЦЕПЯМИ НАСТРОЙКИ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ
- 20-2. СИСТЕМЫ С ЗАМКНУТЫМИ ЦЕПЯМИ НАСТРОЙКИ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ
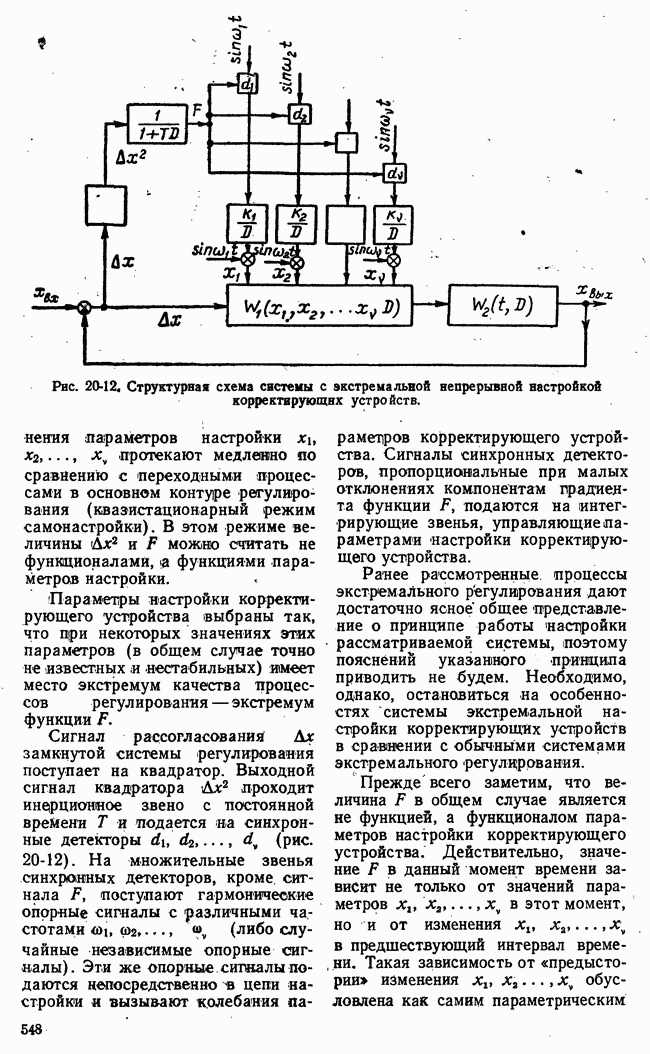
- 20-3. СИСТЕМЫ С ЭКСТРЕМАЛЬНОЙ НАСТРОЙКОЙ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ
- 20-4. СТАТИСТИЧЕСКАЯ ДИНАМИКА НЕПРЕРЫВНЫХ СИСТЕМ С ЭКСТРЕМАЛЬНОЙ НАСТРОЙКОЙ ПОСЛЕДОВАТЕЛЬНЫХ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ
- б) Уравнения замкнутой самонастраивающейся системы
- в) Случай сильной фильтрации. Квазистационарный режим
- г) Общий случай квазистационарного режима
- ГЛАВА ДВАДЦАТЬ ПЕРВАЯ. ИГРОВЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- 21-1. НАЗНАЧЕНИЕ И ПРИНЦИПЫ ДЕЙСТВИЯ ИГРОВЫХ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- 21-2. НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ ИГР
- 21-3. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ. ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
- 21-4. ОБ АЛГОРИТМАХ ИГРОВЫХ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- ПРИЛОЖЕНИЯ