| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
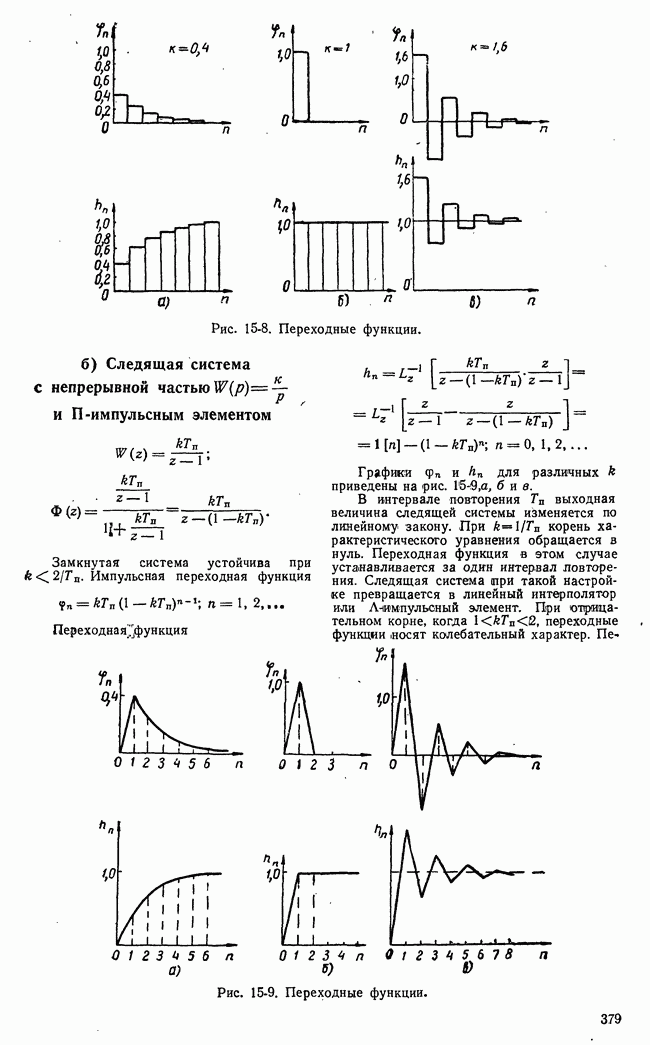
21-2. НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ ИГР
Последние 10—15 лет быстро развивается специальная математическая дисциплина, получившая название теории игр [Л. 21-1]. В этой теории рассматриваются игры в широком смысле слова как последовательности подчиненных определенным правилам и статистическим зависимостям шагов сторон-игроков.
Основное содержание теории игр при современном ее состоянии состоит в строгом математическом обосновании существования оптимальных стратегий в определенных классах игр. Хотя прикладное значение теории игр применительно к игровым системам автоматического управления еще невелико, мы приведем некоторые понятия и положения этой теории, как имеющей непосредственное отношение к обоснованию существования оптимальных алгоритмов управляющих машин.
Ходы в теории игр делятся на личные и случайные. Личные ходы производятся на основе определенных алгоритмов — стратегий игроков, случайные ходы подчиняются лишь определенным распределениям вероятностей. Так, при карточной игре сдача карт является случайным ходом, а все другие ходы игроков — личными ходами. При игре в шахматы все ходы личные. Как личные, так и случайные ходы подчинены определенным правилам игры. Каждый ход представляет собой выбор одного решения из заданного множества вариантов. Решение, принятое при личном ходе, называется выбором.
Стратегией игрока называется инструкция, однозначно определяющая каждый личный его ход (выбор) в любой ситуации, возможной в рамках правил игры. Стратегию игрока часто называют алгоритмом игрока.
В играх, где число возможных ходов и выборов велико, стратегии игроков и тем более какая-либо инструментальная реализация исчерпывающих алгоритмов крайне затруднены или неосуществимы, так как они требуют колоссального объема памяти запоминающих устройств.
Так, например, для записи стратегии игрока в шахматы

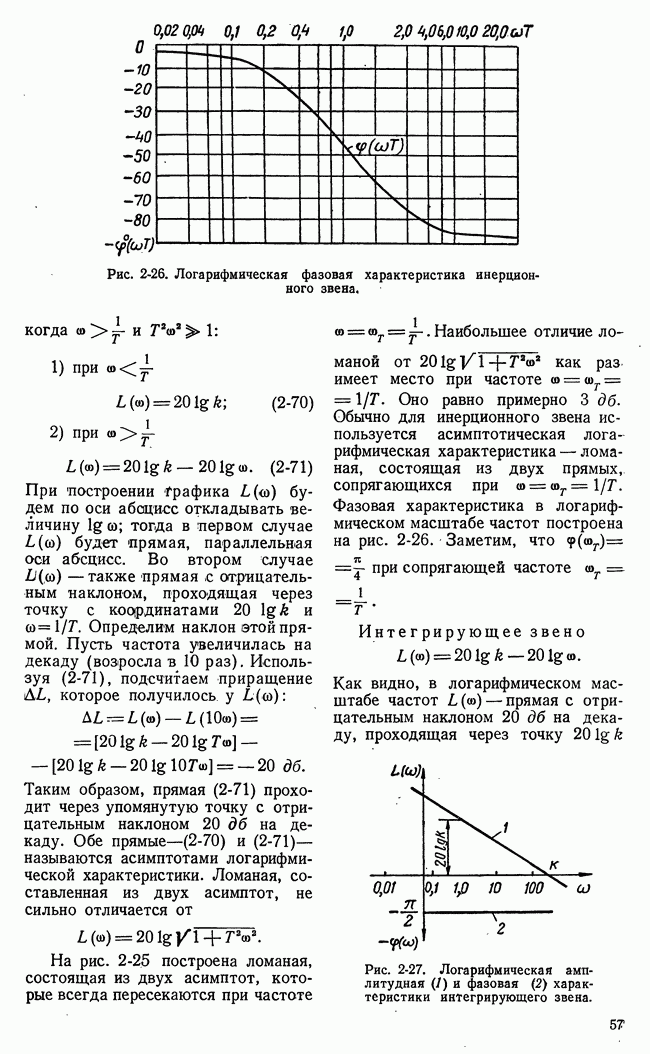
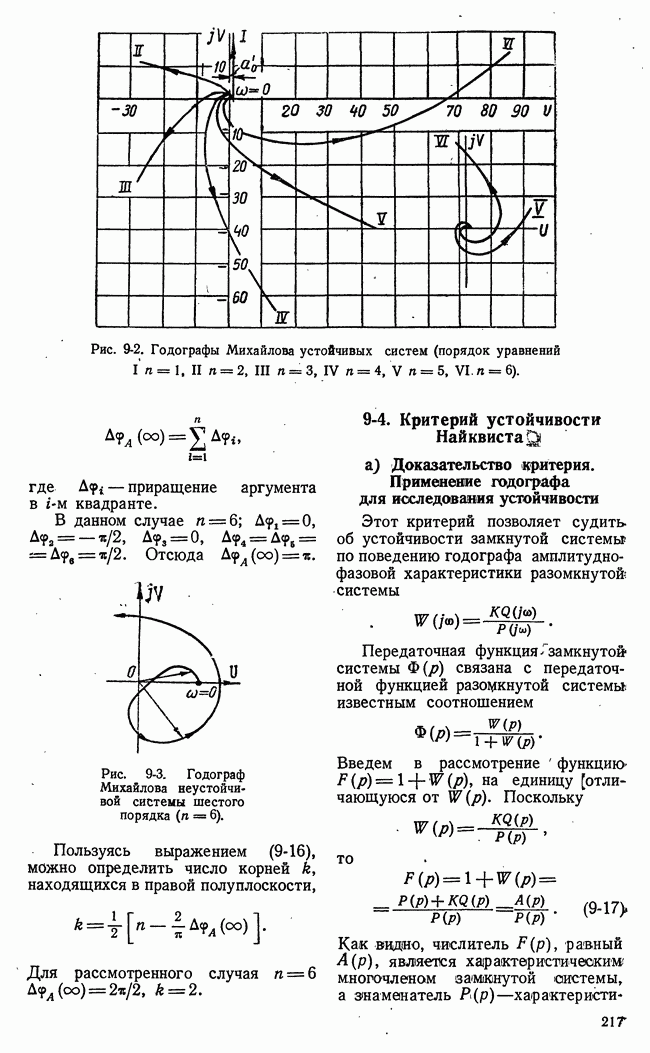
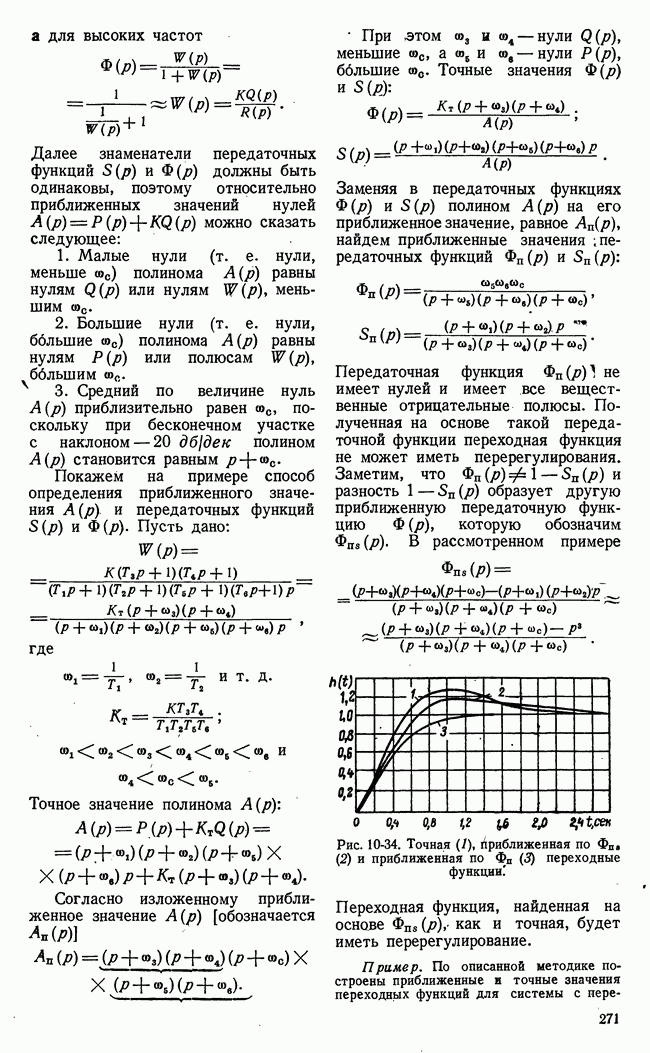
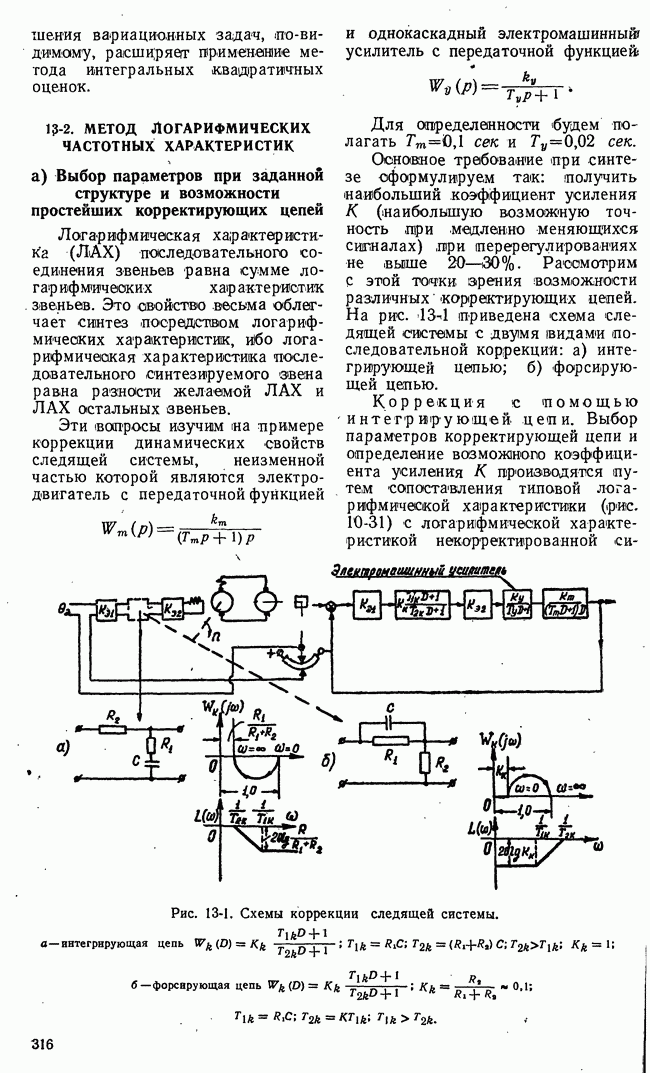
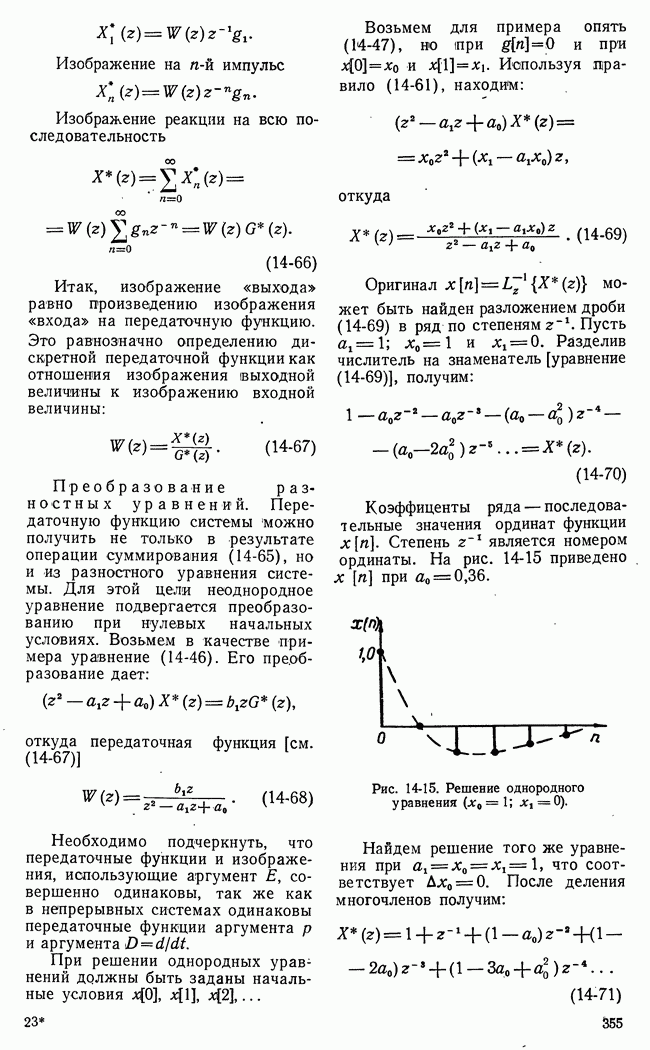
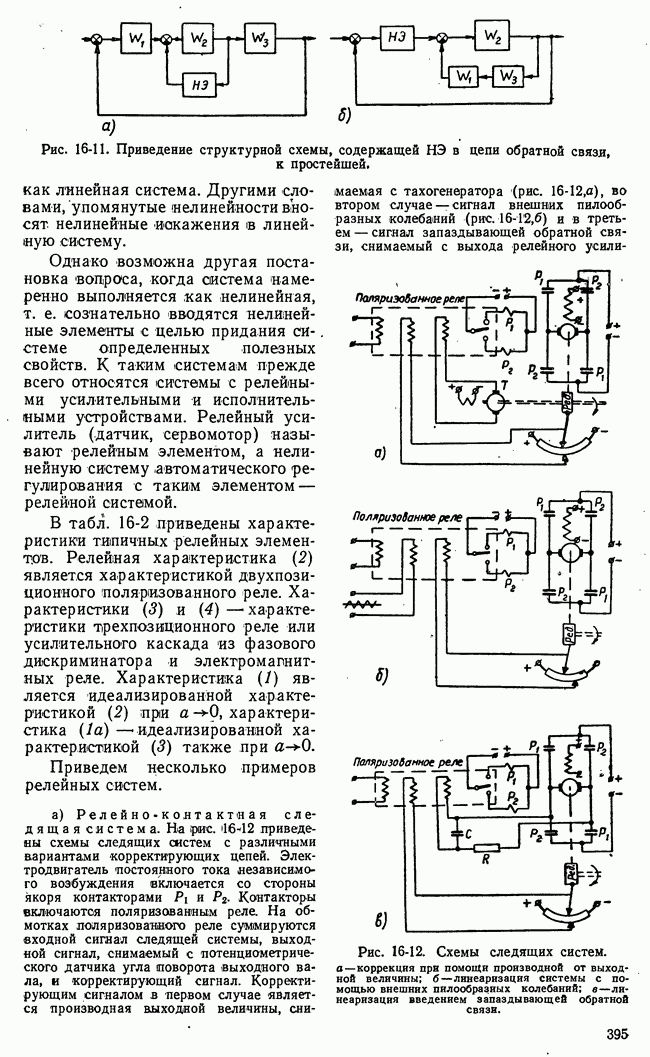
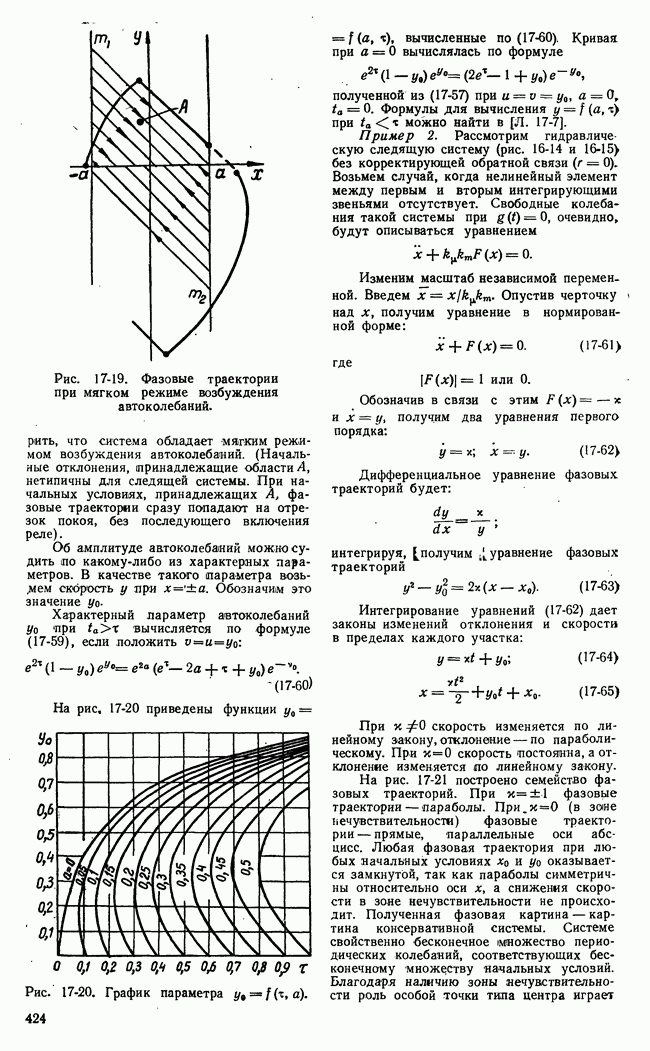
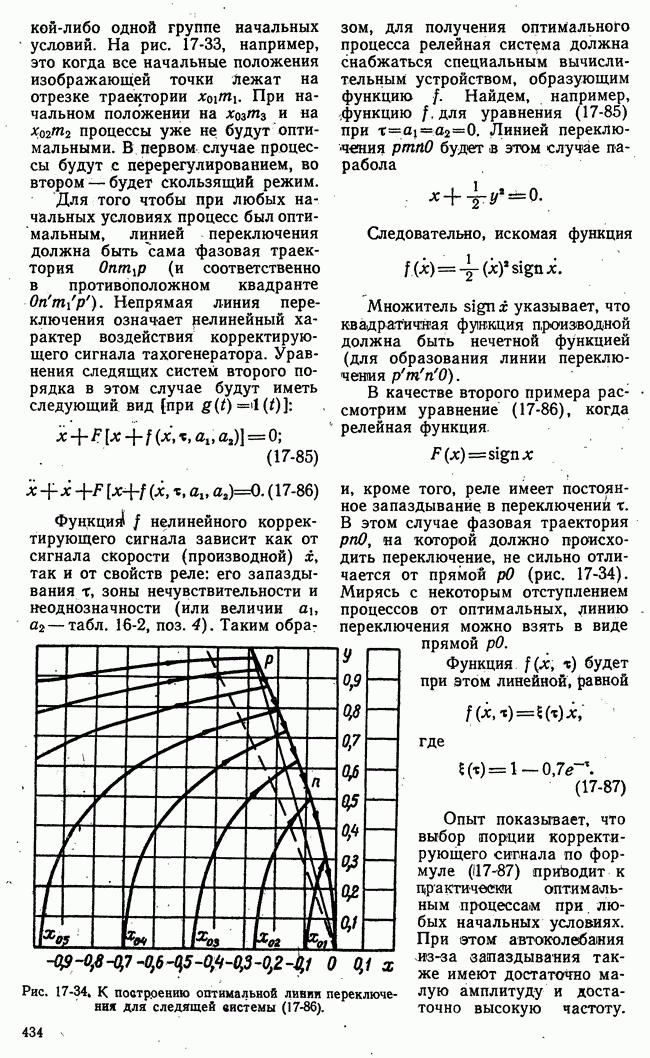
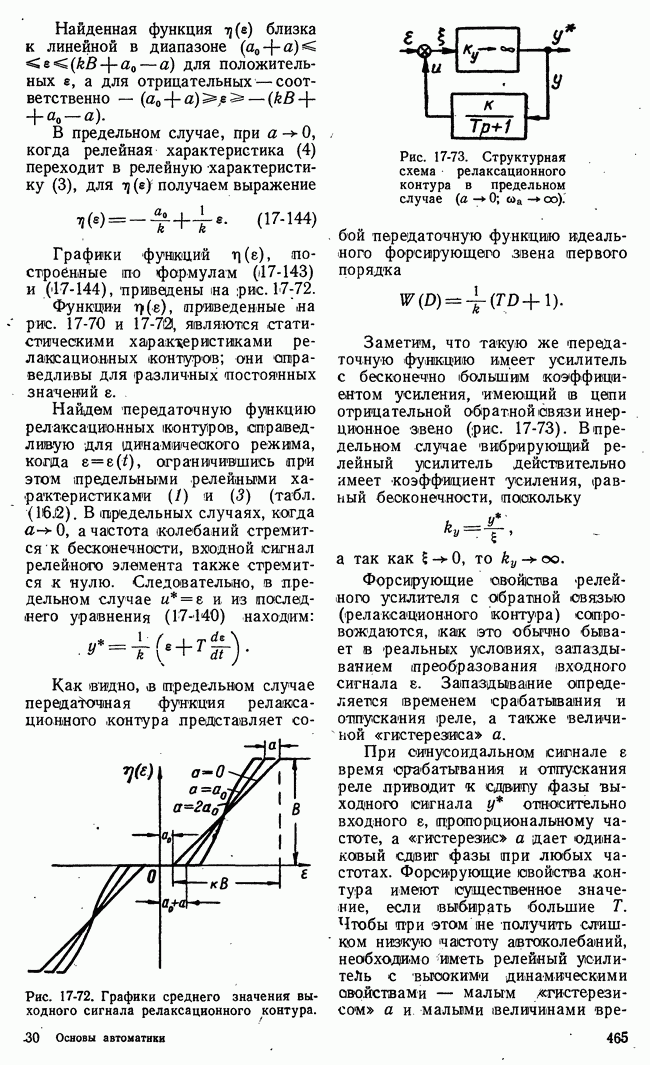
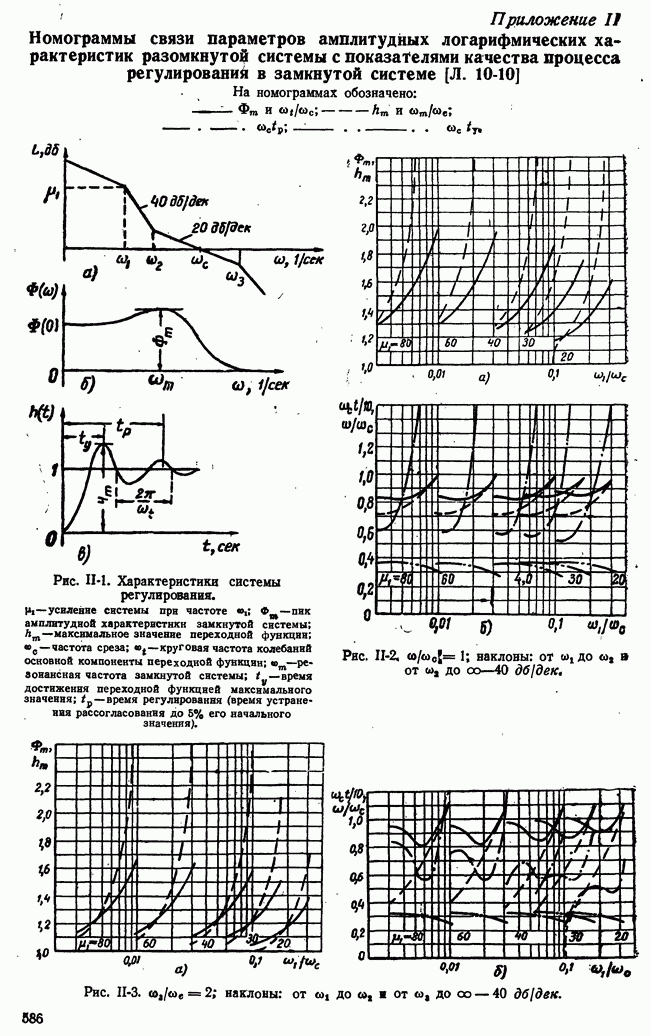
Рис. 21-2. Множества стратегий игроков конечной игры с двумя сторонами.
потребовалось бы описать огромное количество вариантов, подавляющее большинство которых не встретится в каждой данной конкретной игре. Столь же велико и число возможных стратегий. Это обстоятельство, весьма существенное при построении Алгоритмов игровых управляющих машин (§ 21-4), не может, однако, служить препятствием успешному применению понятия стратегии или исчерпывающего алгоритма в общей математической теории игр.
Если число возможных ходов и выборов в каждом ходе конечно, то игра называется конечной. Теория конечных игр разработана наиболее полно. Если игра конечна, то число возможных стратегий каждого из игроков также конечно, хотя, быть может, и весьма велико.
Множество возможных стратегий игрока I обозначим  игрока
игрока  Если число сторон-игроков равно
Если число сторон-игроков равно  то всего будем иметь
то всего будем иметь  множеств возможных стратегий
множеств возможных стратегий 
Для игр с двумя сторонами, которые главным образом рассматриваются в современной теории игр, множества возможных стратегий  будем обозначать соответственно
будем обозначать соответственно  Для конечных игр каждое из множеств стратегий
Для конечных игр каждое из множеств стратегий  конечно. Элементы этих множеств стратегии можно пронумеровать и представить в виде точек некоторых пространств, в частности числовых осей. Таким образом, для конечной игры с двумя сторонами множества возможных стратегий каждого из игроков можно представить в виде дискретной последовательности
конечно. Элементы этих множеств стратегии можно пронумеровать и представить в виде точек некоторых пространств, в частности числовых осей. Таким образом, для конечной игры с двумя сторонами множества возможных стратегий каждого из игроков можно представить в виде дискретной последовательности  точек осей прямоугольной системы координат, а совокупность множеств стратегий обоих игроков (обозначается
точек осей прямоугольной системы координат, а совокупность множеств стратегий обоих игроков (обозначается  виде точек плоскости
виде точек плоскости  (рис. 21-2), имеющих соответствующие координаты.
(рис. 21-2), имеющих соответствующие координаты.
Если игра содержит лишь личные ходы (т. е. не имеет случайных хрдов), то задание стратегий игроков полностью определяет исход игры. Таким образом, если выбраны стратегии  принадлежащие множествам
принадлежащие множествам  то исход игры, не имеющей случайных ходов, полностью предрешен. Для игры с двумя сторонами без случайных ходов выбор точки на плоскости стратегий
то исход игры, не имеющей случайных ходов, полностью предрешен. Для игры с двумя сторонами без случайных ходов выбор точки на плоскости стратегий  однозначно определяет исход игры.
однозначно определяет исход игры.
Для игр, содержащих как личные, так и случайные ходы, выбор стратегий игроков определит распределение вероятностей  исхода игры. Множество возможных исходов игры обозначим через
исхода игры. Множество возможных исходов игры обозначим через  Тогда результатом любых возможных стратегий
Тогда результатом любых возможных стратегий  является распределение (вероятностей
является распределение (вероятностей  на множестве
на множестве  Последнее утверждение можно обобщить и на игры без случайных ходов, если принять во внимание, что распределение плотности вероятности в виде одной
Последнее утверждение можно обобщить и на игры без случайных ходов, если принять во внимание, что распределение плотности вероятности в виде одной  -функции соответствует достоверному событию.
-функции соответствует достоверному событию.
Различные исходы игры для игроков неравноценны. Для описания

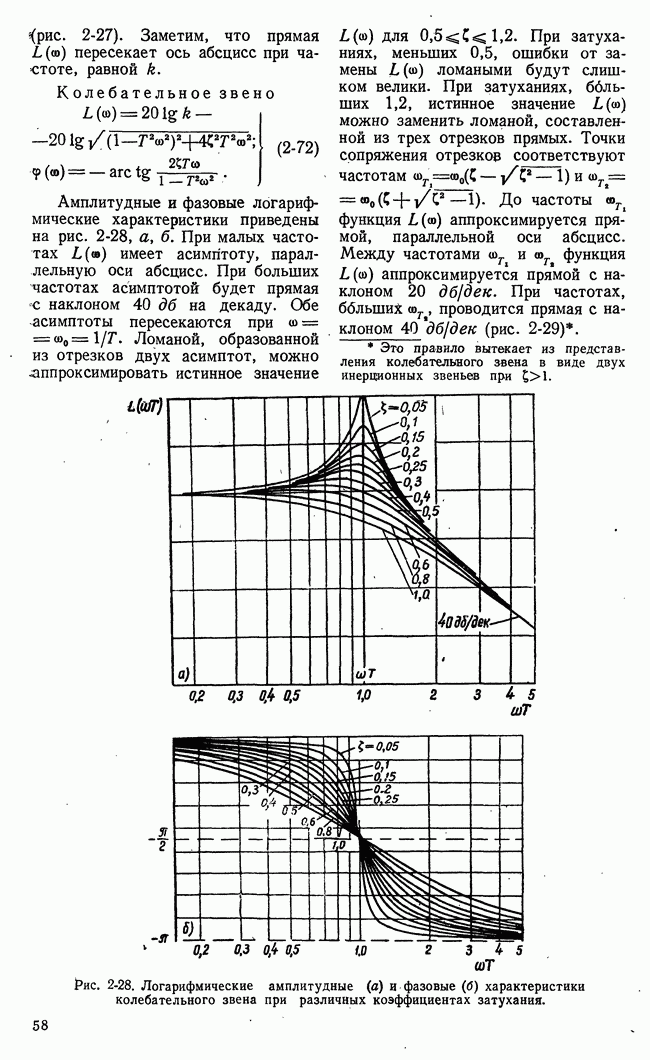
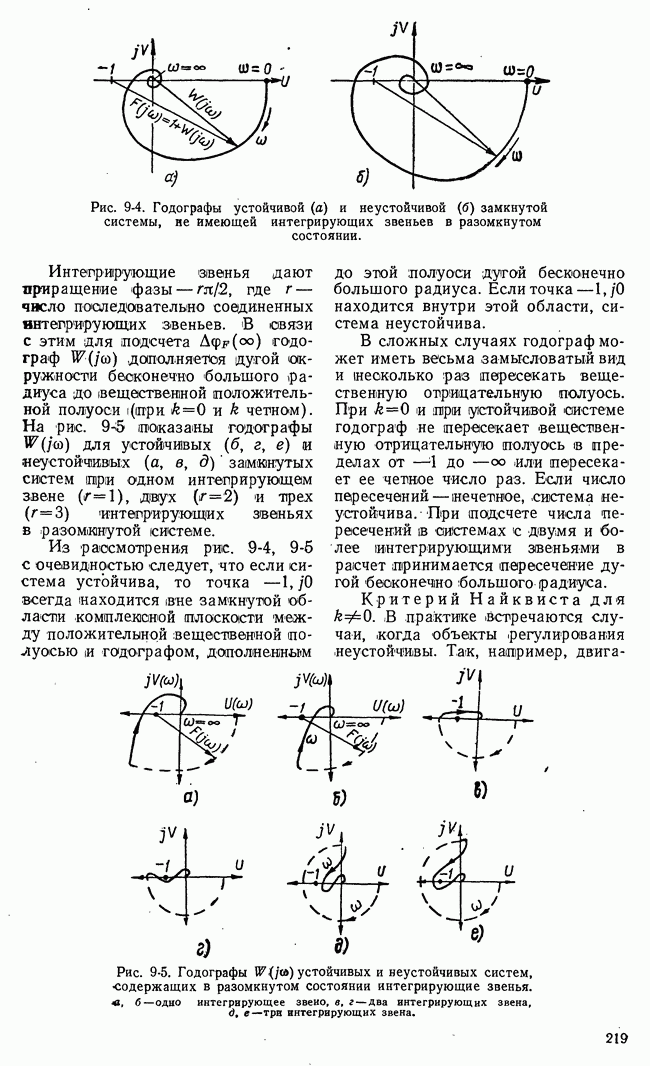
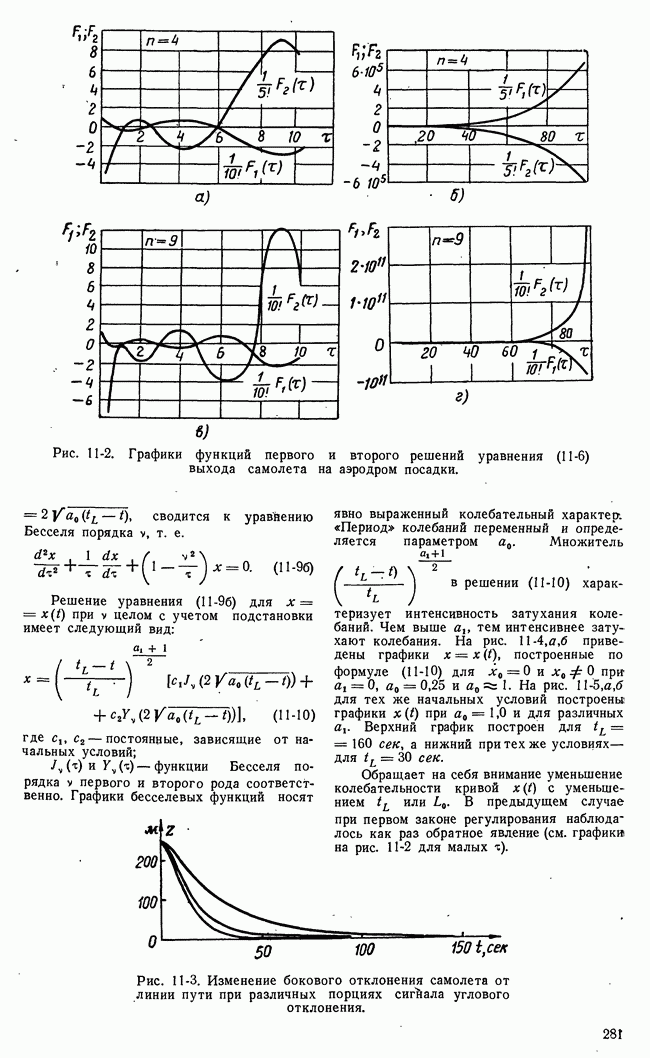
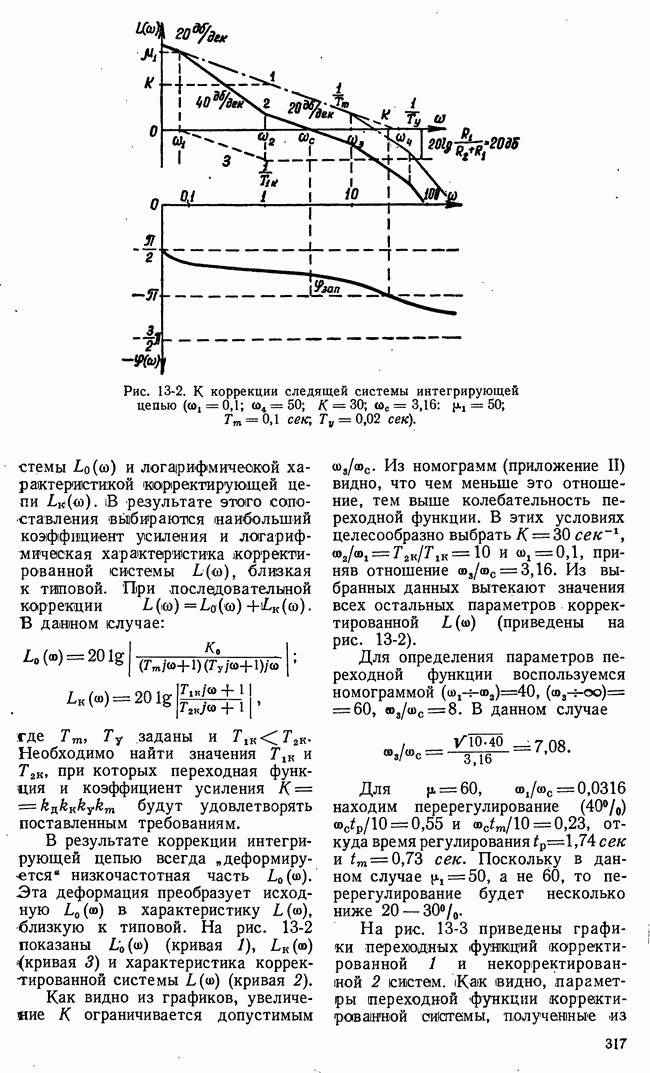
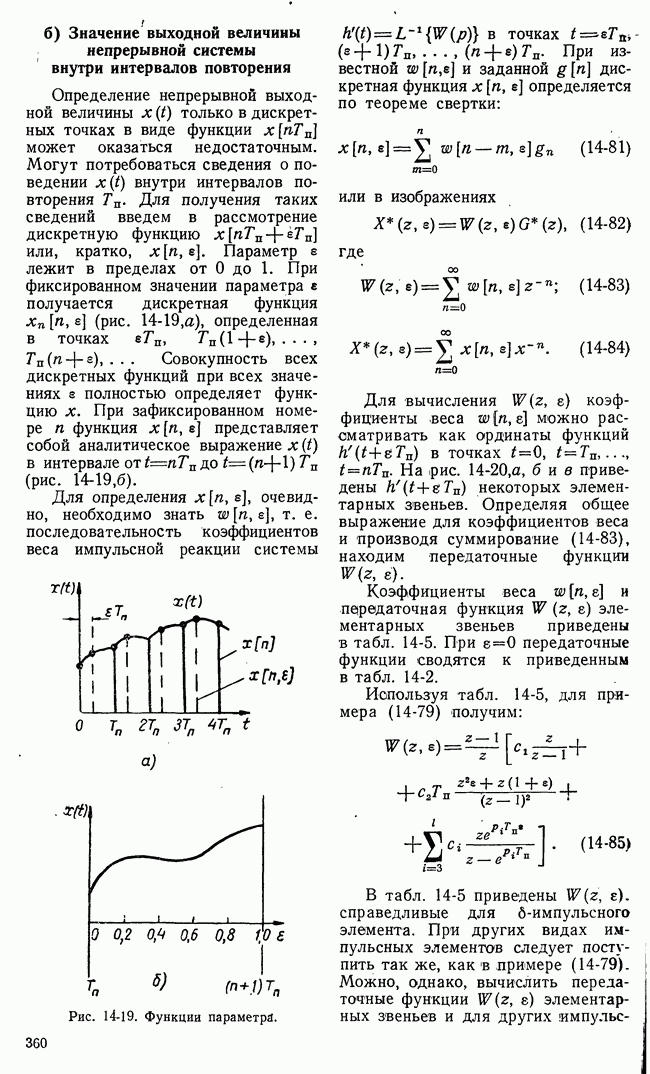
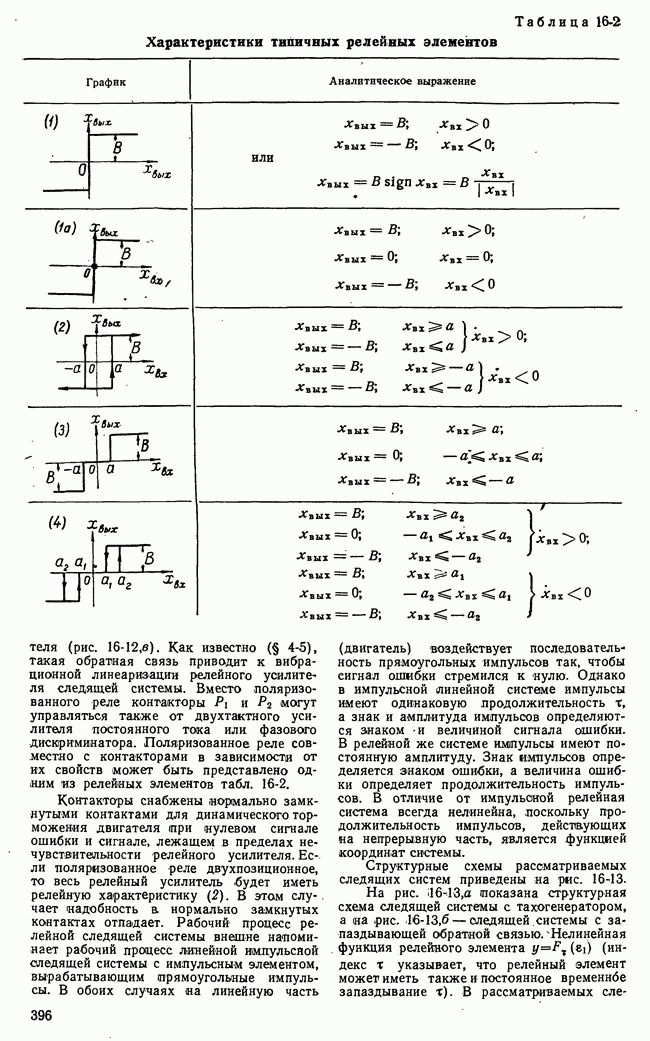
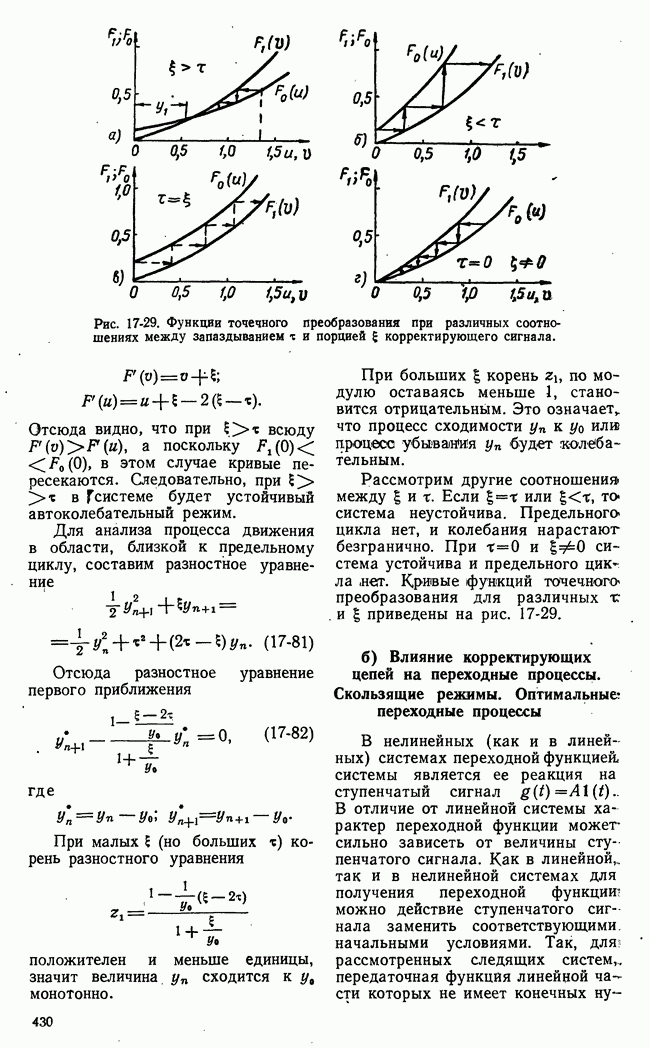
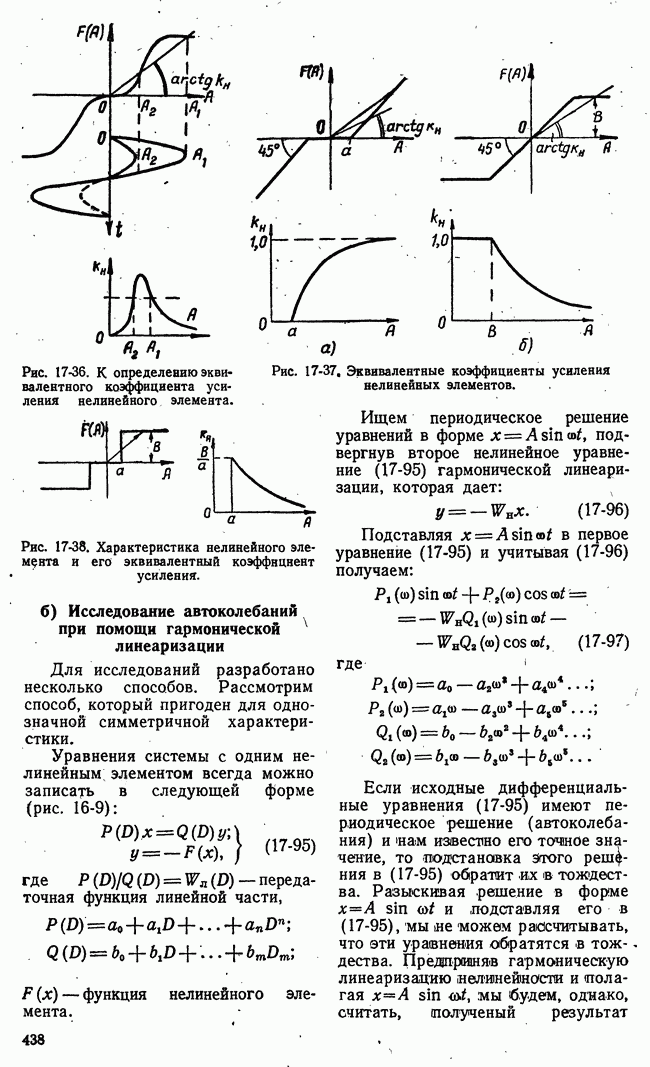
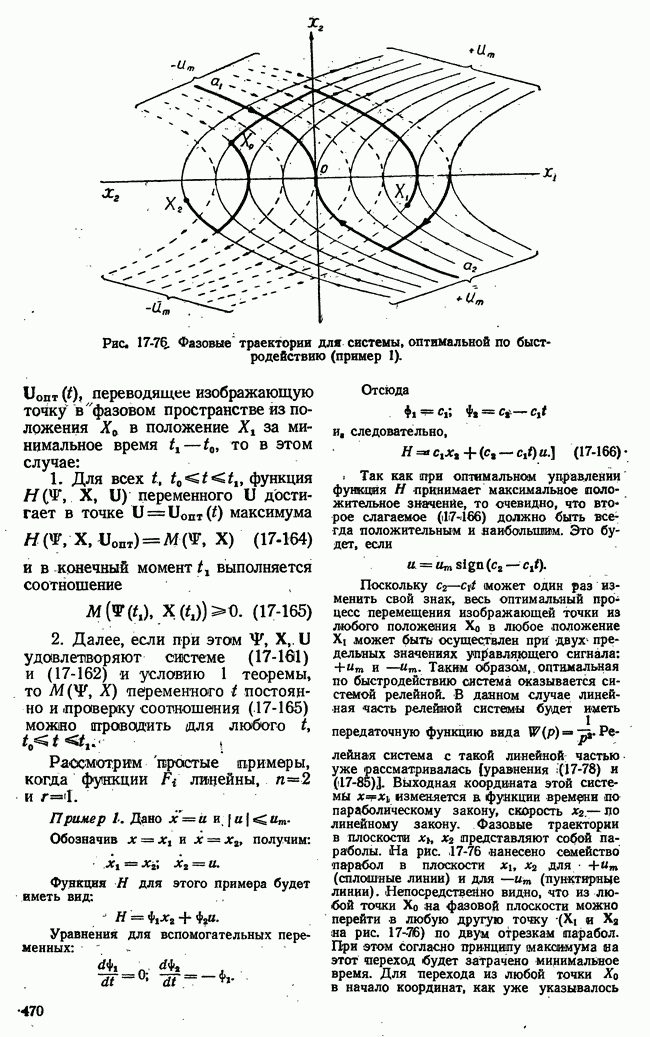
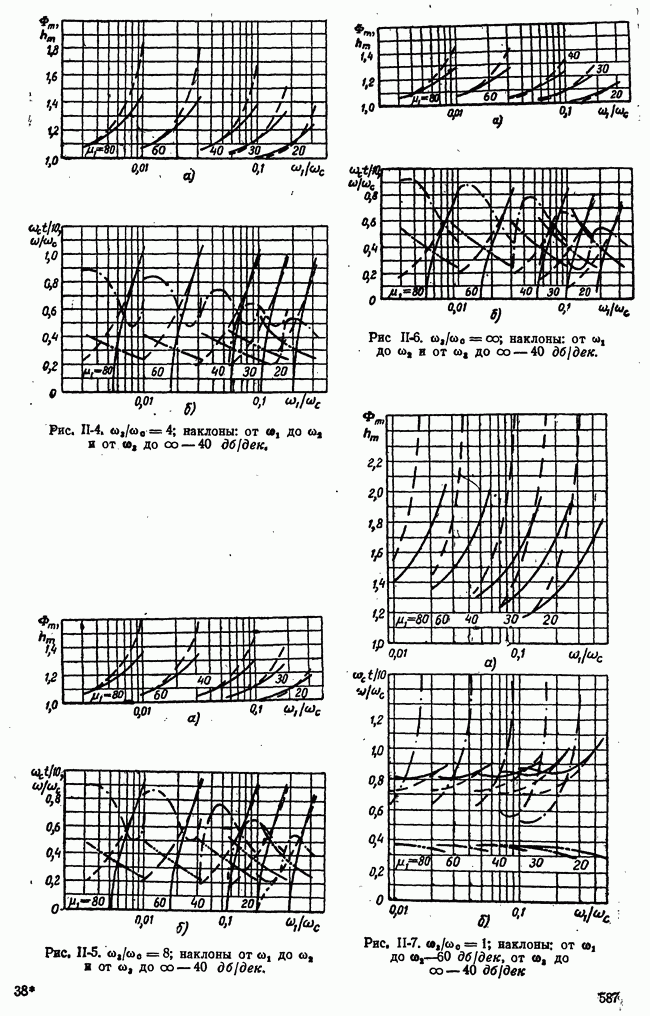
Рис. 21-3. Возможные стратегии игроков и значения функции выигрыша нормальной формы игры.
интересов игроков в множестве возможных исходов игры вводится функция выгоды. Понятие функции выгоды для игровых систем автоматического управления в некоторой мере уже было пояснено. В теории игр понятие функции выгоды имеет сходное, но не тождественное указанному значение.
Под функцией выгоды  игрока понимается числовая функция
игрока понимается числовая функция  зависящая от распределения вероятностей
зависящая от распределения вероятностей  стало быть, от выбранных стратегий
стало быть, от выбранных стратегий  возрастанию которой соответствует увеличение выигрыша
возрастанию которой соответствует увеличение выигрыша  игрока. Таким образом, функция
игрока. Таким образом, функция  соответствует математическому ожиданию выигрыша по окончании игры. Основное отличие этого понятия от математического ожидания упрежденного значения функции выгоды
соответствует математическому ожиданию выигрыша по окончании игры. Основное отличие этого понятия от математического ожидания упрежденного значения функции выгоды  в игровых системах управления заключается в том, что здесь рассматривается математическое ожидание выигрыша в конце игры, в то время как
в игровых системах управления заключается в том, что здесь рассматривается математическое ожидание выигрыша в конце игры, в то время как  представляет собой математическое ожидание выигрыша в конце очередного хода.
представляет собой математическое ожидание выигрыша в конце очередного хода.
Если сумма функций выгоды игроков согласно правилам игры постоянна: 

то игра называется игрой с постоянной суммой. Заменой

игра с постоянной суммой преобразуется в игру с нулевой суммой:

Для игры с двумя сторонами условие нулевой суммы имеет вид:

Функция

в играх с нулевой суммой называется функцией выигрыша. Эта функция совпадает с функцией выгоды I игрока и противоположна по знаку функции выгоды II игрока.
Все дальнейшие положения относятся к играм с двумя сторонами и нулевой суммой [см. 21-1]. Приведенные понятия и определения позволяют рассматривать в теории игр весьма простую и единую форму игры — так называемую нормальную форму игры.
Игра в нормальной форме состоит из пространства (множеств) возможных стратегий  и функции выигрыша
и функции выигрыша  где
где  Рис. 21-3 поясняет нормальную форму игры. Пронумерованные возможные стратегии I и II игроков
Рис. 21-3 поясняет нормальную форму игры. Пронумерованные возможные стратегии I и II игроков

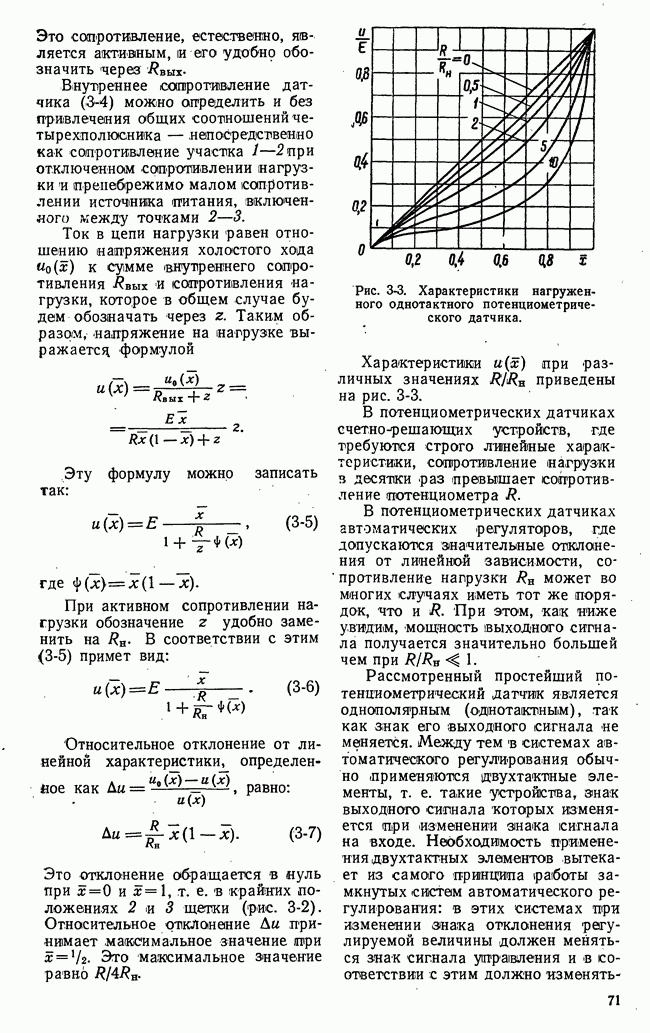
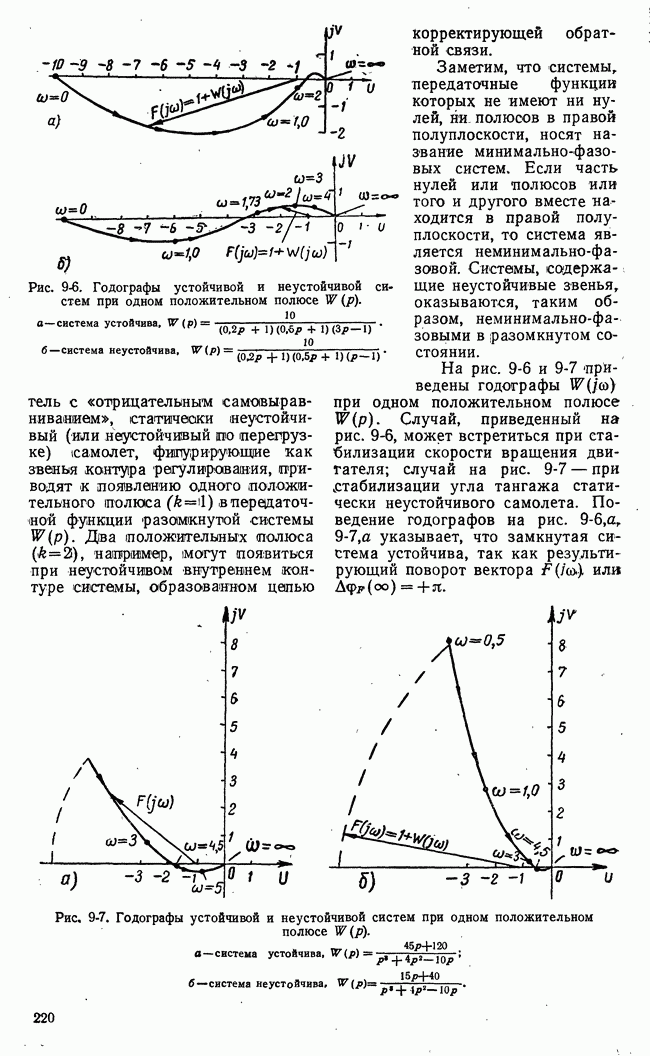
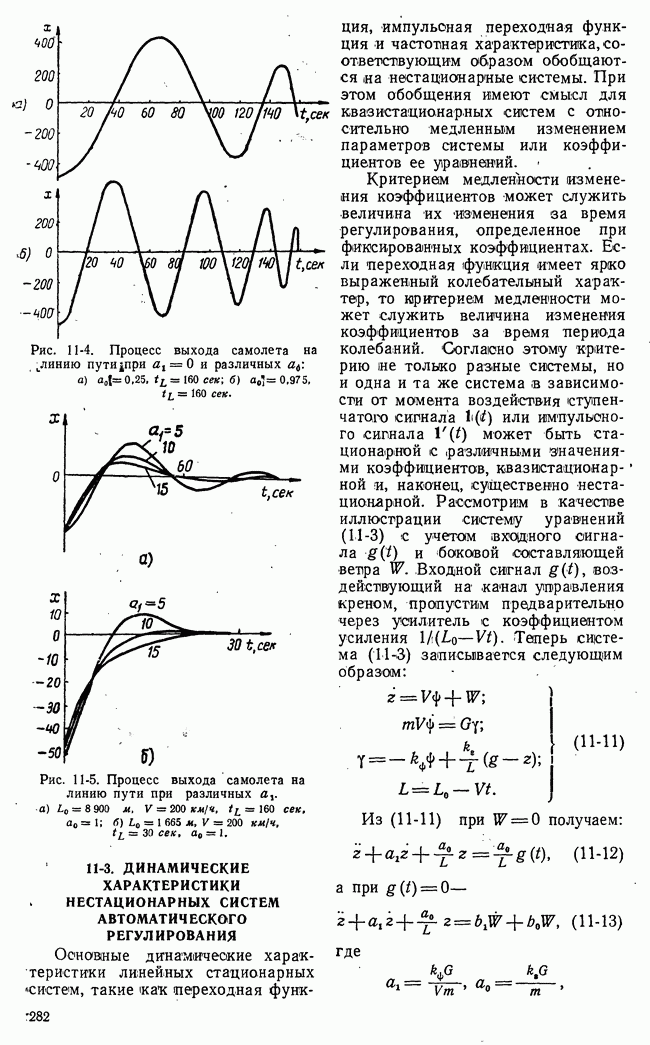
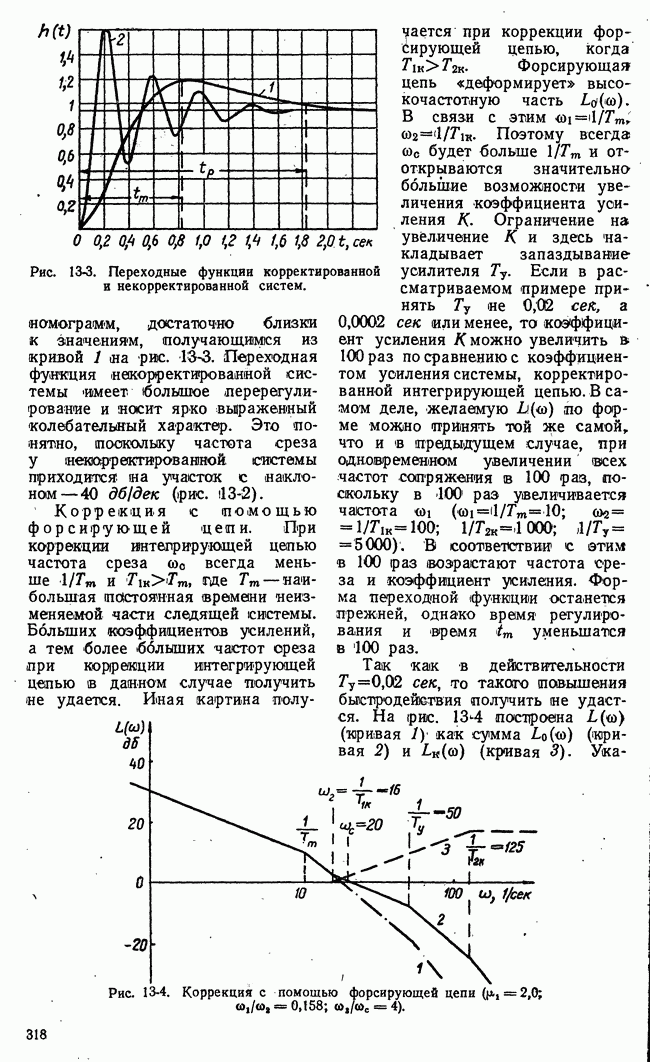
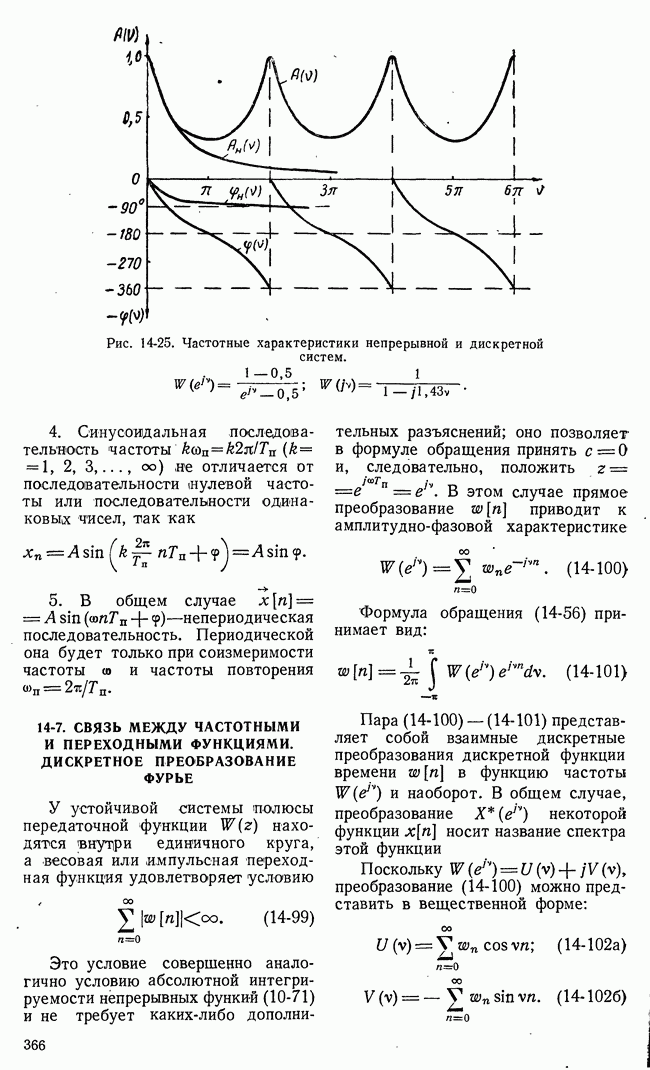
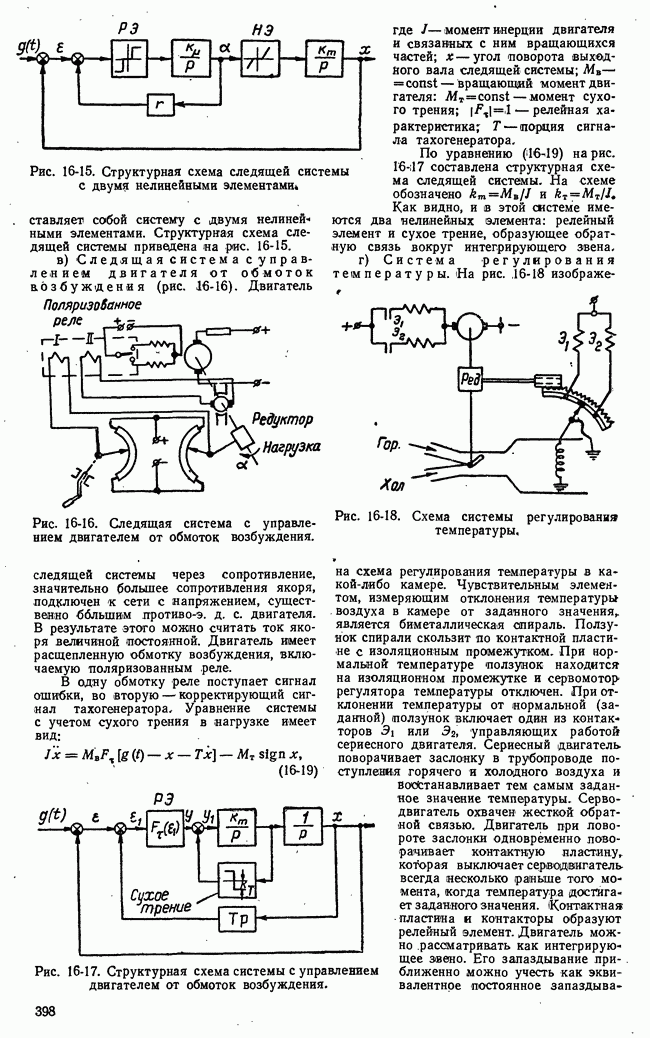
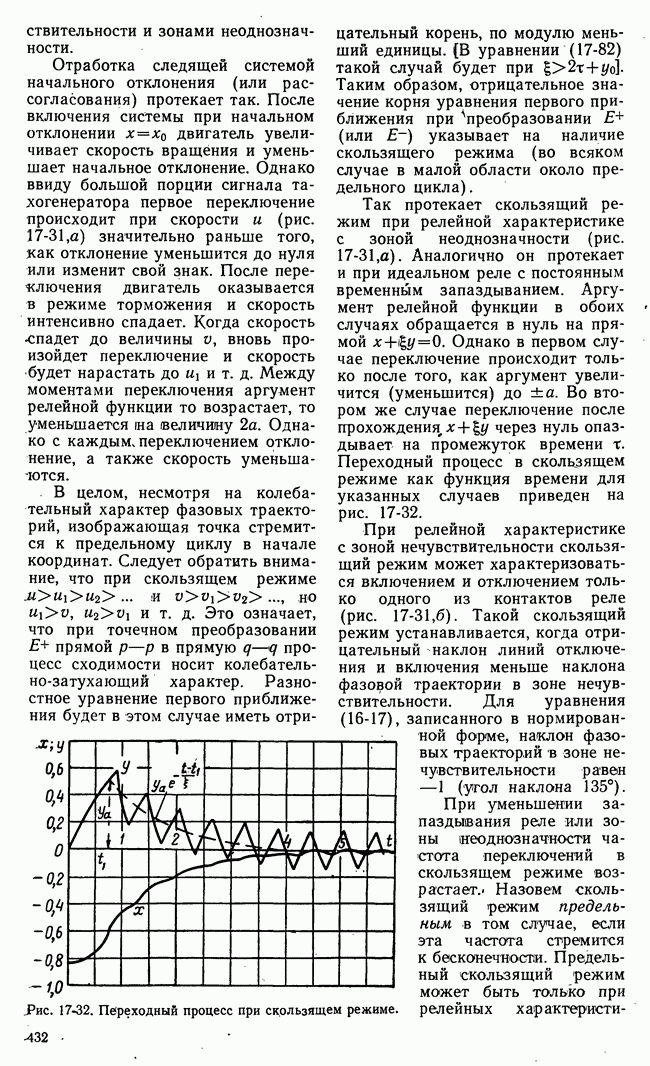
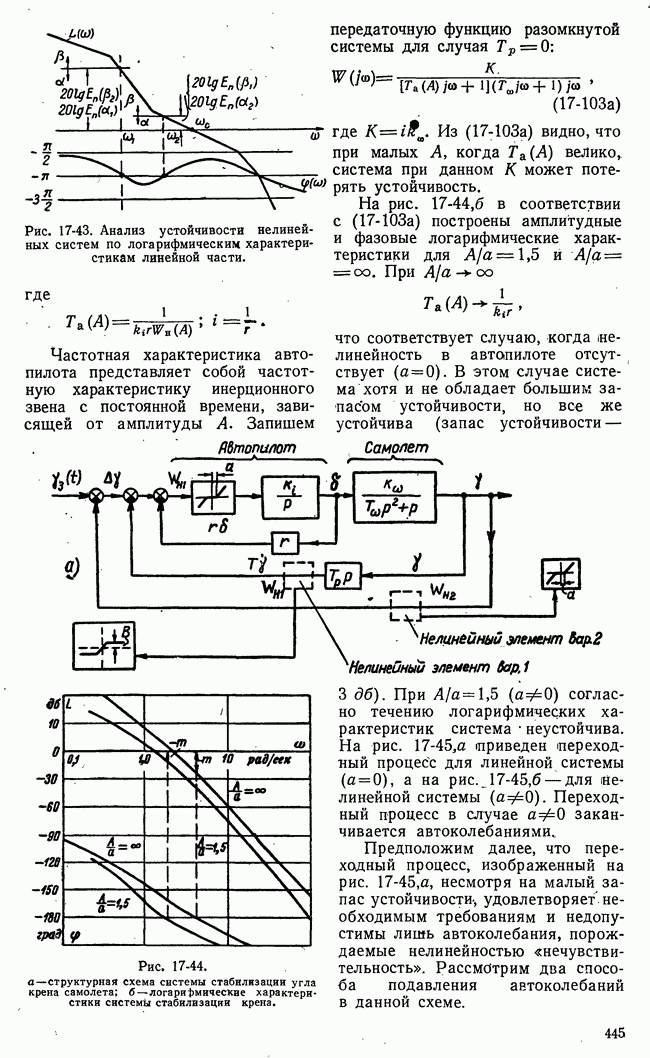
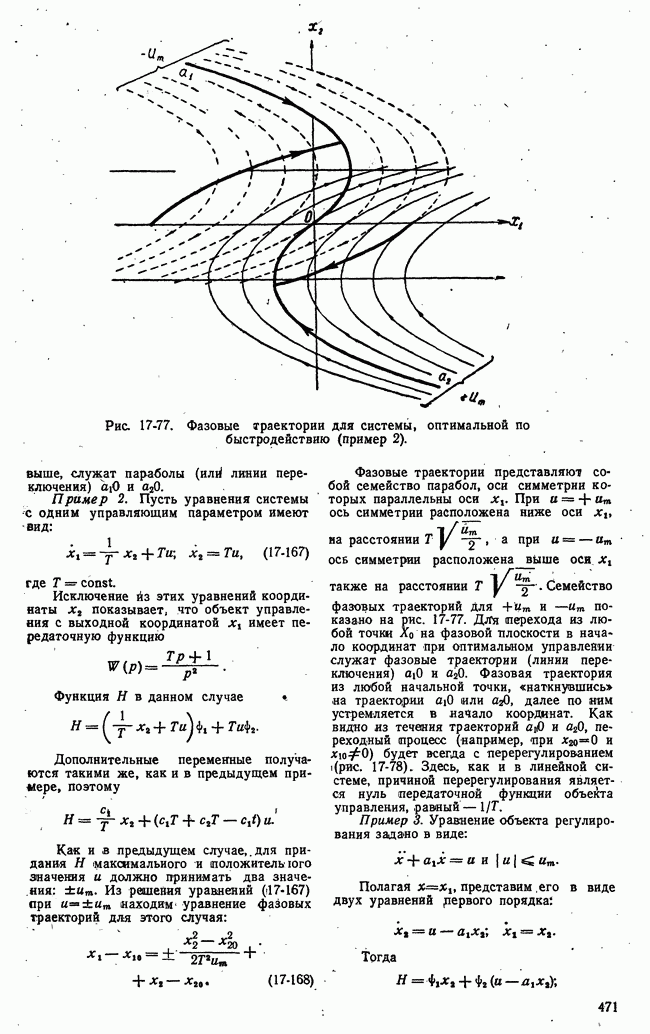
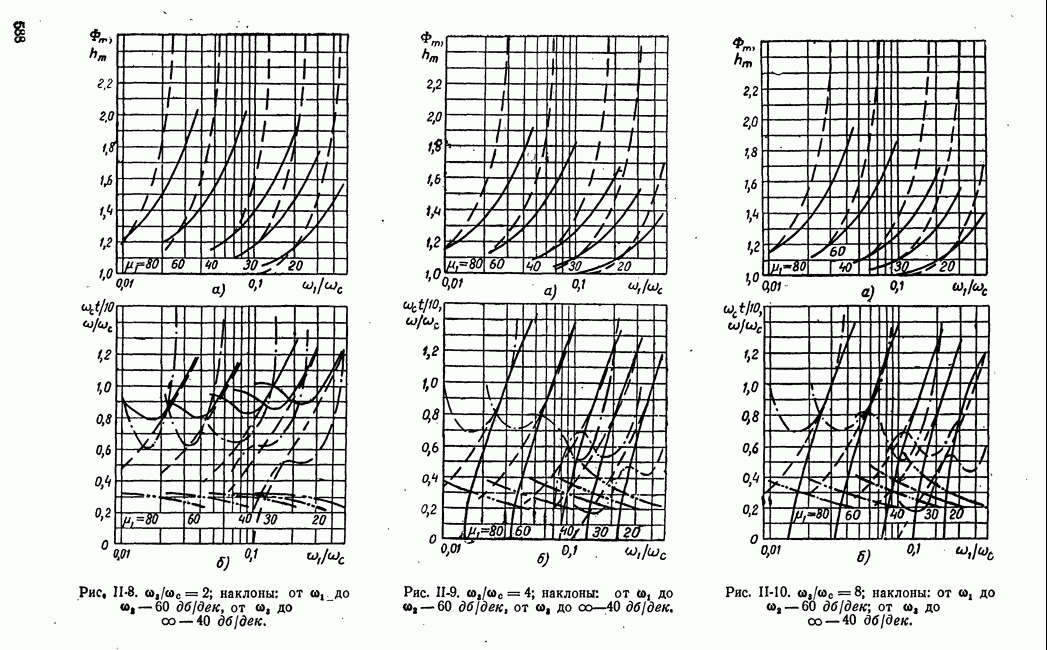
Рис. 21-4. К определению точной нижней и точной верхней цен игры.
представлены здесь точками осей  а функция выигрыша
а функция выигрыша  поверхностью в трехмерном пространстве.
поверхностью в трехмерном пространстве.
Если игра конечна, то множество значений функции выигрыша  также конечно, и удобно вместо этой функции рассматривать матрицу игры:
также конечно, и удобно вместо этой функции рассматривать матрицу игры:

Элементы этой матрицы равны значениям функции выигрыша в точках, соответствующих номерам строк и столбцов:

Еще одним фундаментальным понятием теории игр является оптимальная стратегия. Чтобы дать строгое определение оптимальной стратегии, необходимо ввести определения так называемых верхней и нижней цен игры. Точной нижней границей  какого-либо множества
какого-либо множества  чисел 5 называется такое наибольшее число
чисел 5 называется такое наибольшее число  , что все числа множества больше или равны
, что все числа множества больше или равны  при всех
при всех  Точной верхней границей
Точной верхней границей  множества
множества  называется наименьшее число
называется наименьшее число  для которого
для которого  при
при 
Если представить множество чисел точками на числовой оси, то точной нижней границе множества  будет соответствовать крайняя левая точка множества, а точной (верхней границе
будет соответствовать крайняя левая точка множества, а точной (верхней границе  -крайняя правая точка множества (рис. 21-4).
-крайняя правая точка множества (рис. 21-4).
Каждая функция имеет некоторое множество значений, и понятия точных верхней и нижней границ непосредственно распространяются на функции.
Обратимся теперь к рис. 21-3, поясняющему нормальную форму игры. Первой игрок распоряжается лишь смещением вдоль оси  т. е. заданием стратегии
т. е. заданием стратегии  Второй игрок распоряжается координатой по оси
Второй игрок распоряжается координатой по оси  т. е. заданием стратегии У.
т. е. заданием стратегии У.
Первый игрок, задавая х, стремится сделать функцию выигрыша  как можно большей. Второй игрок заданием стратегии У стремится сделать функцию
как можно большей. Второй игрок заданием стратегии У стремится сделать функцию  возможно меньшей.
возможно меньшей.
Вместо пространственной картины и поверхностиможно рассматривать семейство сечений этой поверхности плоскостями  или
или  Соответствующие семейства сечений представлены на рис. 21-5 и 21-6.
Соответствующие семейства сечений представлены на рис. 21-5 и 21-6.
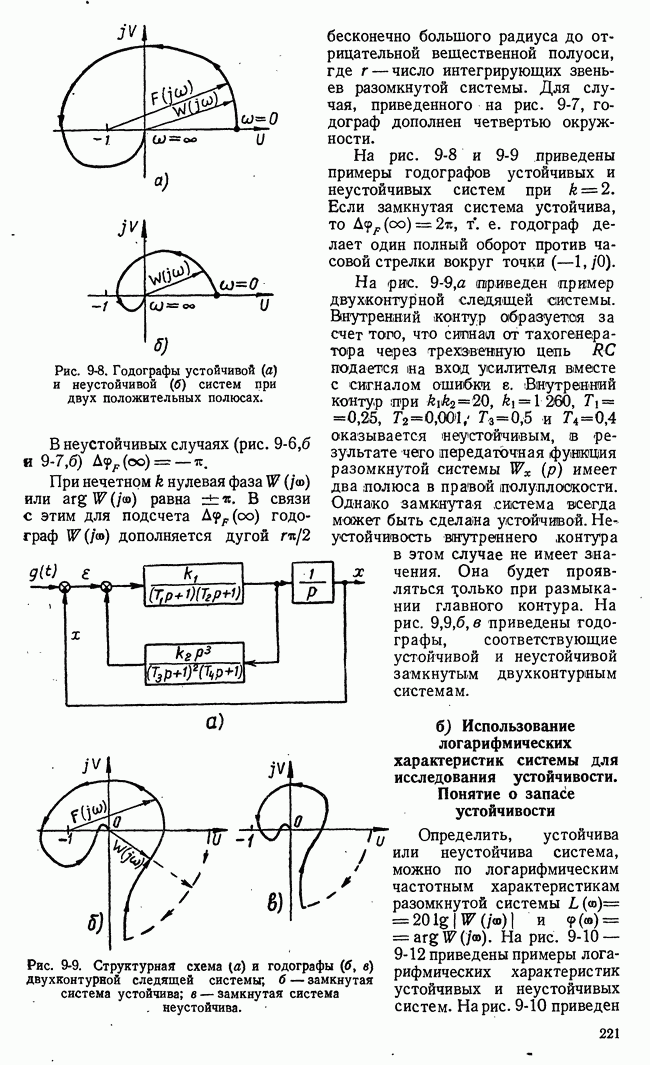
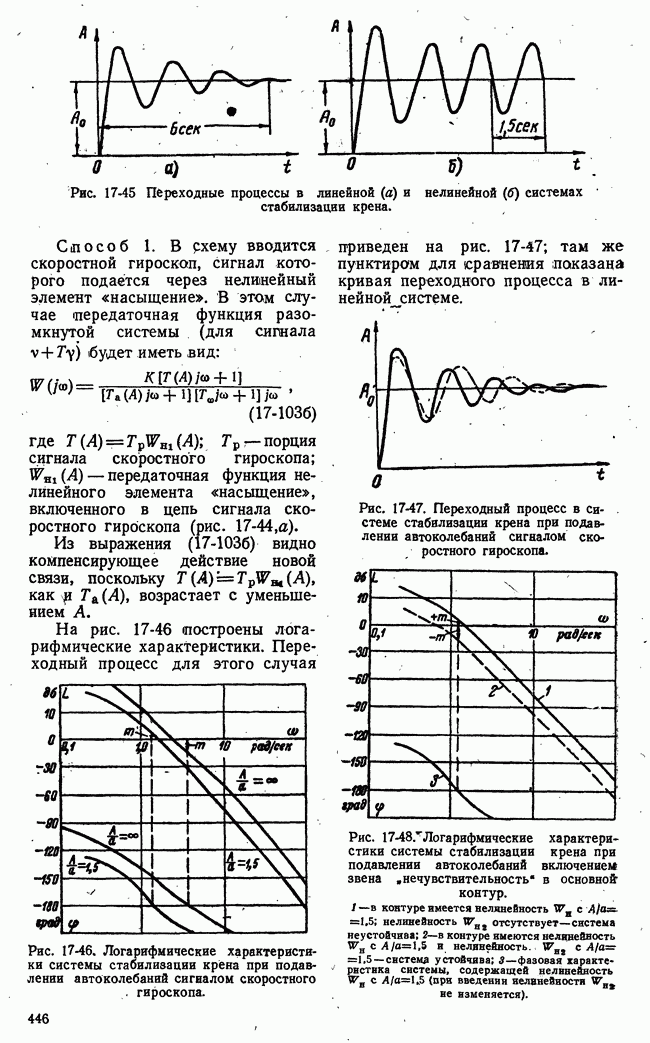
На рис. 21-5 представлены сечения плоскостями  Выбрав стратегию, первый игрок определяет тем самым график этого семейства. Там же указаны точные нижние границы
Выбрав стратегию, первый игрок определяет тем самым график этого семейства. Там же указаны точные нижние границы  при
при 
Точная верхняя граница множества значений точных нижних границ функции выигрыша при  называется нижней чистой ценой игры
называется нижней чистой ценой игры  :
:


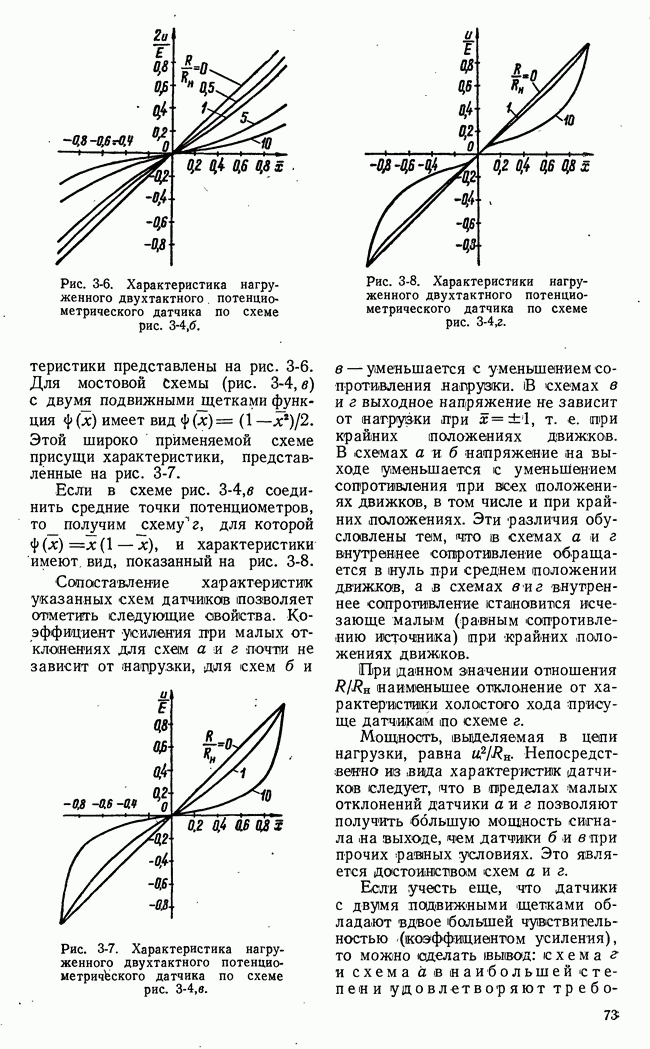
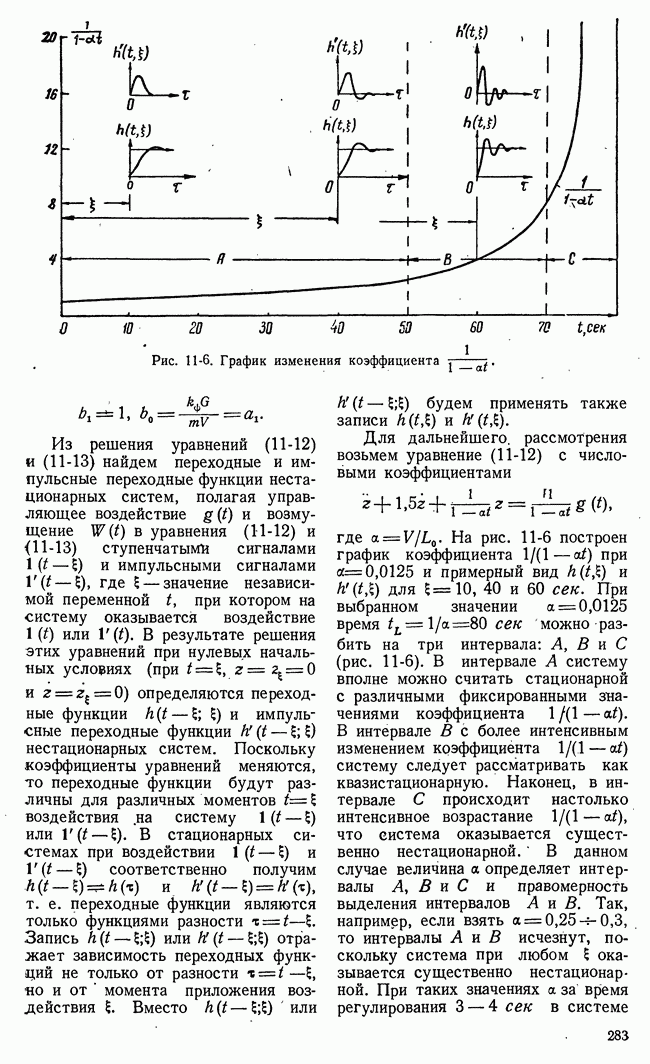
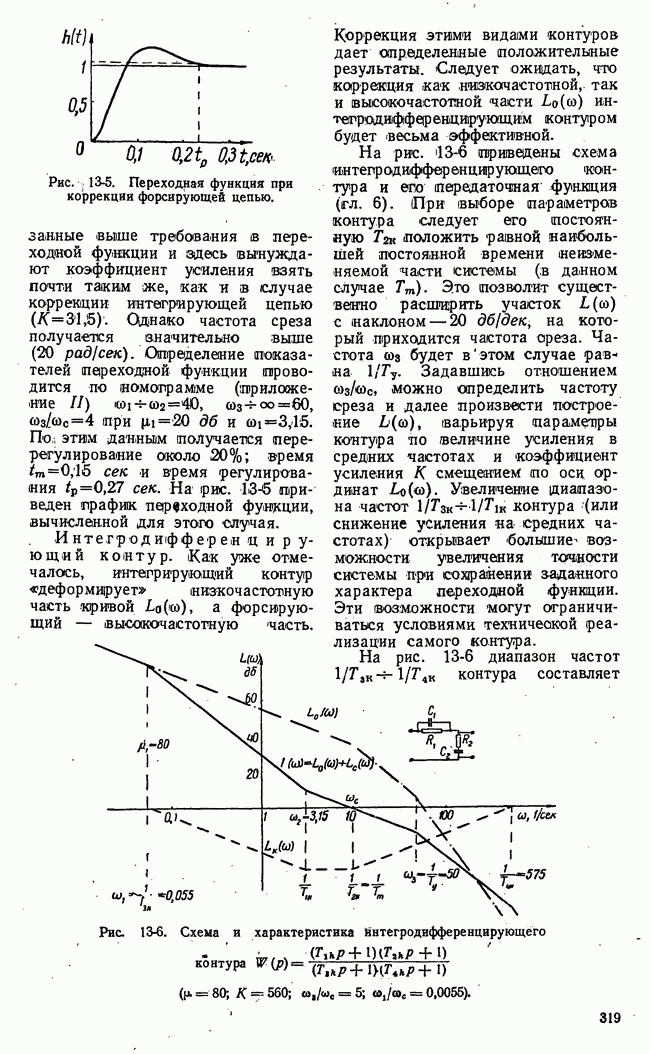
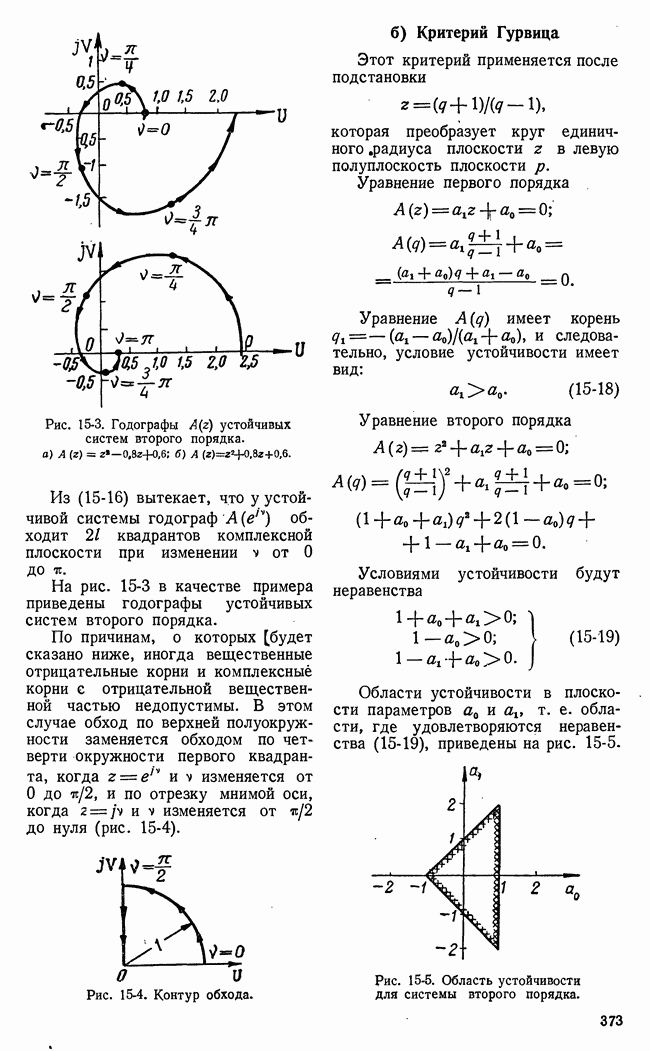
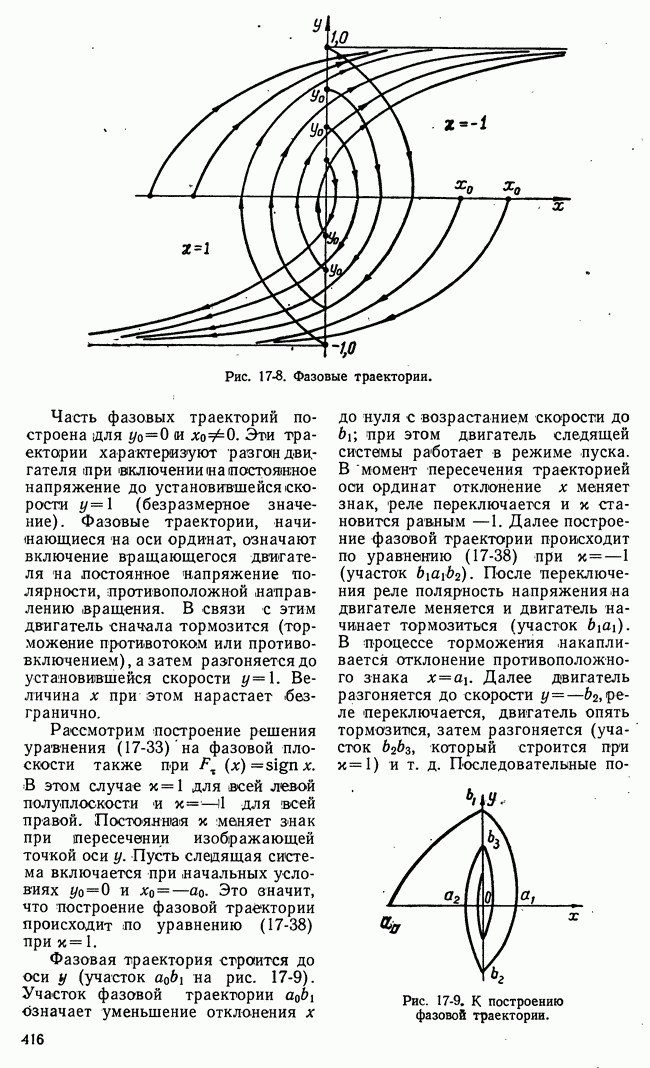
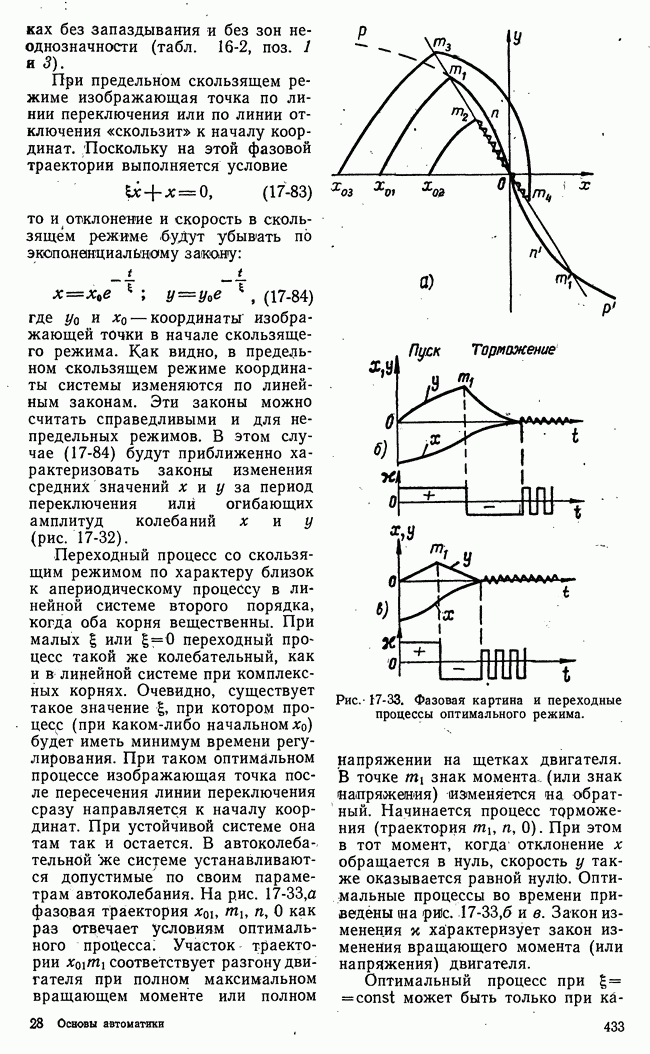
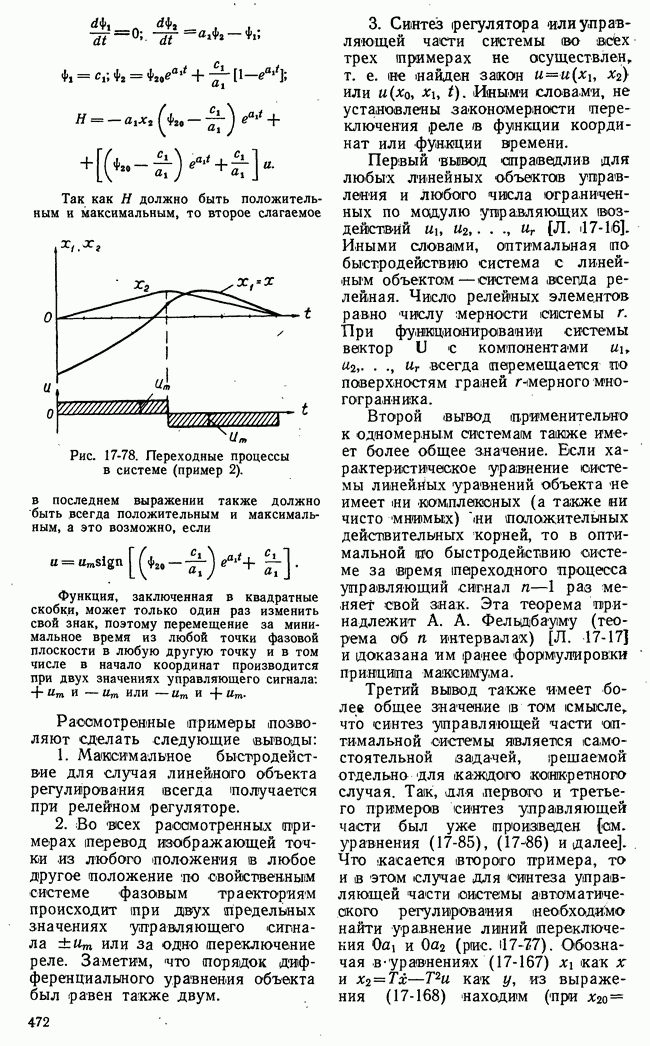
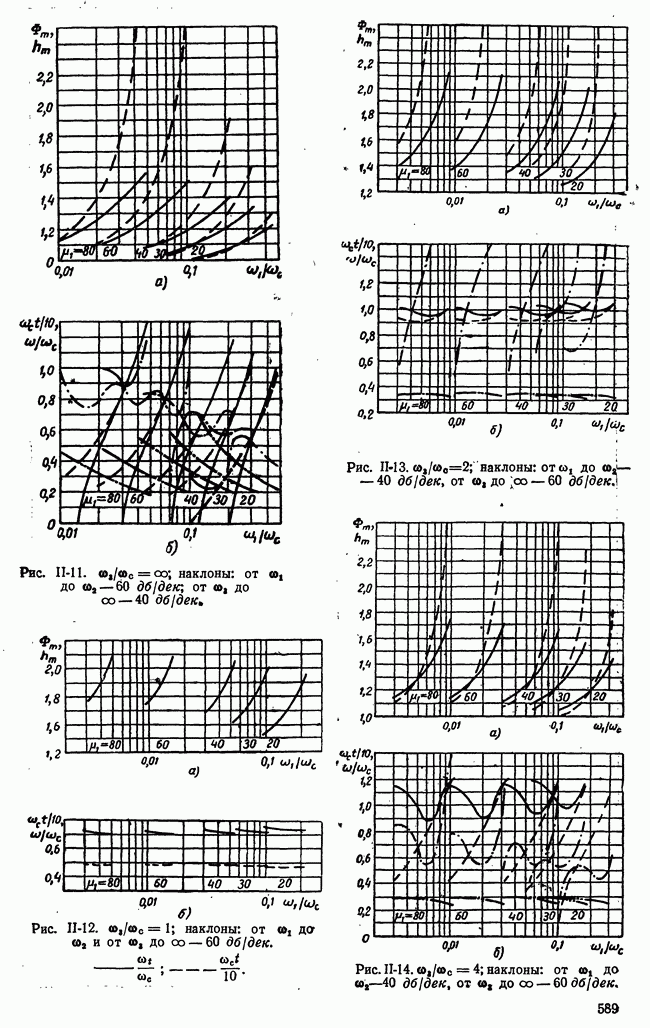
Рис. 21-5. Семейство сечений поверхности  плоскостями
плоскостями  и определение нижней чистой цены игры.
и определение нижней чистой цены игры.
Для случая, представленного на рис. 21-5, нижняя чистая цена игры совпадает с  т. е. с точной нижней границей при
т. е. с точной нижней границей при 
Нижняя чистая цена игры имеет следующий смысл. Первый игрок правильным выбором своей стратегии всегда может обеспечить значение функции выигрыша не ниже нижней чистой цены игры X при любой возможной стратегии второго игрока. Таким образом, нижняя чистая цена игры является верхней гранью выигрыша, который первый игрок может себе гарантировать.
На рис. 21-6 представлено семейство сечений поверхности  плоскостями
плоскостями  Второй игрок, выбирая свою стратегию, определяет выбор одного из графиков семейства. Там же обозначены точные верхние границы сечений функции выигрыша при
Второй игрок, выбирая свою стратегию, определяет выбор одного из графиков семейства. Там же обозначены точные верхние границы сечений функции выигрыша при 
Второй игрок соответствующим выбором своей стратегии всегда может сделать значение функции выигрыша первого игрока  не большим нижней границы множества значений
не большим нижней границы множества значений  при
при 
Точная нижняя граница множества значений точных верхних границ функции выигрыша при  называется верхней чистой ценой игры Я:
называется верхней чистой ценой игры Я:

Таким образом, второй игрок может лимитировать выигрыш первого игрока значением Я. Для указанного на рис. 21-6 случая верхняя чистая цена игры  совпадает с
совпадает с 
Нижняя и верхняя чистые цены игры обозначены также на рис. 21-3. Легко видеть, что в рассматриваемой игре они совпадают:

Величина  носит название чистой цены игры.
носит название чистой цены игры.

Рис. 21-6. Семейство сечений поверхности  плоскостями
плоскостями  и определение верхней чистой цены игры.
и определение верхней чистой цены игры.
Равенство (21-4) справедливо для широкого класса игр, именуемых играми, имеющими чистую цену.
Оптимальной стратегией первого игрока в игре, имеющей чистую цену  , называется такая стратегия лгош при которой
, называется такая стратегия лгош при которой 
Оптимальной стратегией второго игрока в игре, имеющей чистую цену  , называется такая стратегия
, называется такая стратегия  при которой
при которой  Для случая, представленного на рис. 21-3, оптимальная стратегия первого игрока есть
Для случая, представленного на рис. 21-3, оптимальная стратегия первого игрока есть  а оптимальная стратегия второго игрока
а оптимальная стратегия второго игрока 
Ввиду важности понятия оптимальных стратегий целесообразно дать дополнительные пояснения.
Оптимальной стратегией первого игрока (в играх, имеющих чистую цену) называется такая стратегия этого игрока, которая при любой возможной стратегии второго игрока гарантирует первому игроку выигрыш не ниже чистой цены.
Оптимальной стратегией второго игрока (в играх, имеющих чистую цену) называется такая стратегия этого игрока, которая при любой возможной стратегии первого игрока дает значение функции выигрыша (выигрыш первого игрока), не большее чистой цены 
Если для наглядности принять, что значение функции выигрыша  равное чистой цене X, соответствует ничейному результату (исходу) игры, то можно также формулировать: оптимальная стратегия
равное чистой цене X, соответствует ничейному результату (исходу) игры, то можно также формулировать: оптимальная стратегия
первого игрока  это такая стратегия, которая в наихудшем для первого игрока случае гарантирует ничейный результат. Аналогично оптимальная стратегия второго игрока — это такая стратегия
это такая стратегия, которая в наихудшем для первого игрока случае гарантирует ничейный результат. Аналогично оптимальная стратегия второго игрока — это такая стратегия  которая в наихудшем для второго игрока случае гарантирует ничейный результат. Если оба игрока выбрали оптимальные стратегии:
которая в наихудшем для второго игрока случае гарантирует ничейный результат. Если оба игрока выбрали оптимальные стратегии:

то согласно принятому условию всегда будет иметь место ничейный исход игры.
Выше было указано, что для конечных игр, в которых число возможных стратегий первого и второго игроков конечно, функция выиг рыша  может быть заменена матрицей игры
может быть заменена матрицей игры

где элементы матрицы равны:

Элемент расположен в  строке и
строке и  столбце.
столбце.
Элемент, минимальный (наименьший) в своей строке и максимальный (наибольший) в своем столбце называется седловым элементом матрицы.
Матрица конечной игры, имеющей чистую цену и имеющей, стало быть, оптимальные стратегии, всегда содержит седловой элемент. Седловой элемент матрицы конечной игры, имеющей чистую цену, равен этой чистой цене Я:

и индексы этого элемента  соответствуют оптимальным стратегиям игроков.
соответствуют оптимальным стратегиям игроков.
Значительная часть теории игр посвящена математическому определению классов игр, имеющих оптимальные стратегии. В частности, вводится понятие игр с полной информацией. В играх с полной информацией игрок при каждом личном ходе знает выборы и исходы всех предыдущих личных и случайных ходов. Доказано [Л. 21-1], что всякая игра с полной информацией имеет чистую цену; матрица конечной игры с полной информацией всегда имеет седловой элемент.
Наряду с нормальной формой игры и понятием стратегии в теории игр вводится понятие усреднения игры  смешанных стратегий. Ранее рассмотренные стратегии в отличие от смешанных называются чистыми стратегиями.
смешанных стратегий. Ранее рассмотренные стратегии в отличие от смешанных называются чистыми стратегиями.
Мы рассмотрели лишь некоторые понятия и положения современной теории игр, составляющие небольшую часть этой теории. Однако приведенные понятия и положения в достаточной мере характеризуют эту математическую дисциплину. Теория игр занимается вопросами существования оптимальных стратегий, т. е. оптимальных исчерпывающих алгоритмов, и методами нахождения этих стратегий в условиях, когда правила игры строго  ределены, а множество возможных стратегий обозримо, т. е. доступно для рассмотрения.
ределены, а множество возможных стратегий обозримо, т. е. доступно для рассмотрения.
Как отчасти вытекает из предыдущего изложения и будет дополнительно пояснено, во многих случаях применения игровых систем автоматического управления указанные условия не выполняются. Правила игры не определены строго, а множества возможных стратегий практически необозримы. Поэтому для решения практических задач синтеза алгоритмов многих игровых систем управления необходимо видоизменение подхода и специальное развитие теории игр. Наиболее перспективен с практической точки зрения метод поэтапного оптимального выбора, т. е. оптимального выбора в каждом шаге. В связи с этим уместно привести сведения о динамическом программировании и линейном программировании.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ГЛАВА ПЕРВАЯ. ВВОДНАЯ
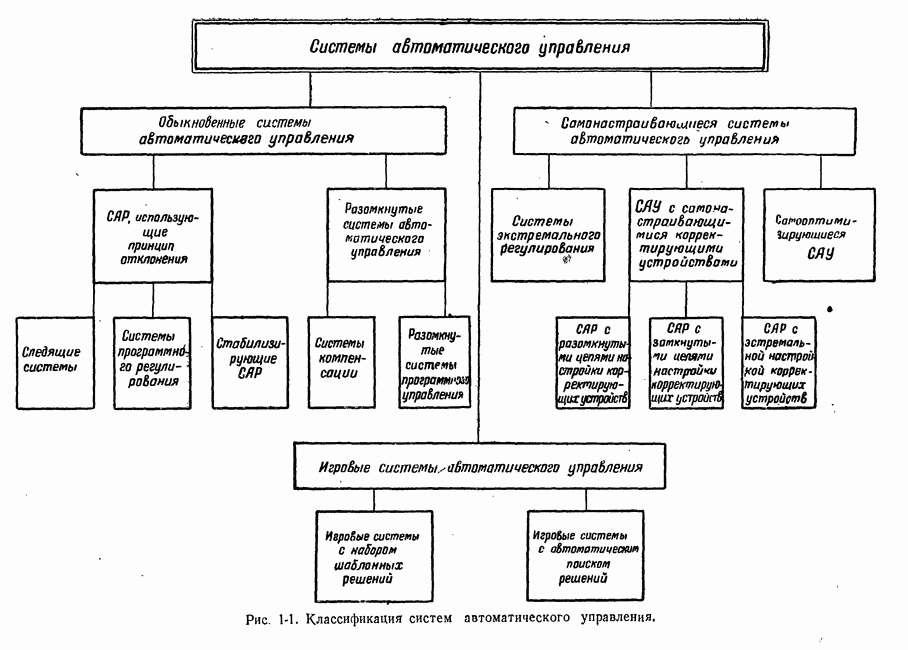
- 1-1. О КЛАССИФИКАЦИИ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- 1-2. ОБЫКНОВЕННЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- 1-3. САМОНАСТРАИВАЮЩИЕСЯ СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- 1-4. ИГРОВЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- 1-5. КЛАССИФИКАЦИЯ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ ПО ДРУГИМ ПРИЗНАКАМ
- ГЛАВА ВТОРАЯ. ОБЩИЕ ПЕРЕДАТОЧНЫЕ СВОЙСТВА ЭЛЕМЕНТОВ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- 2-1. УРАВНЕНИЯ ЭЛЕМЕНТОВ. СТАТИЧЕСКИЕ И ДИНАМИЧЕСКИЕ СВОЙСТВА ЭЛЕМЕНТОВ
- б) Центробежный измеритель скорости вращения
- в) Электромагнитный измеритель напряжения
- 2-2. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ
- 2-3. ЭЛЕМЕНТАРНЫЕ ДИНАМИЧЕСКИЕ ЗВЕНЬЯ, ИХ УРАВНЕНИЯ И ПЕРЕДАТОЧНЫЕ ФУНКЦИИ
- 2-4. ТИПОВЫЕ ВХОДНЫЕ СИГНАЛЫ. ВОЗМУЩАЮЩИЕ ФУНКЦИИ
- 2-5. ПЕРЕХОДНЫЕ ФУНКЦИИ ЭЛЕМЕНТАРНЫХ ЗВЕНЬЕВ
- 2-6. ИМПУЛЬСНЫЕ ПЕРЕХОДНЫЕ ФУНКЦИИ ЭЛЕМЕНТАРНЫХ ЗВЕНЬЕВ
- 2-7. РЕАКЦИЯ ЗВЕНЬЕВ НА ПРОИЗВОЛЬНЫЕ ИЗВЕСТНЫЕ ФУНКЦИИ ВРЕМЕНИ
- 2-8. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ
- б) Частотные характеристики элементарных звеньев
- в) Логарифмические характеристики элементарных звеньев
- 2-9. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ОБ ЭЛЕМЕНТАРНЫХ ЗВЕНЬЯХ
- 2-10. СОЕДИНЕНИЯ ЗВЕНЬЕВ. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ СОЕДИНЕНИИ
- 2-11. ЭЛЕМЕНТЫ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ КАК ЧЕТЫРЕХПОЛЮСНИКИ. ПЕРЕДАТОЧНЫЕ УРАВНЕНИЯ
- ГЛАВА ТРЕТЬЯ. ДАТЧИКИ СИГНАЛОВ
- 3-1. ОБЩИЕ СВОЙСТВА ДАТЧИКОВ
- 3-2. ПОТЕНЦИОМЕТРИЧЕСКИЕ ДАТЧИКИ
- б) Выходная мощность потенциометрических датчиков и условия согласования
- в) Динамические свойства
- г) Ошибка ступенчатости. Параметры потенциометрических датчиков
- 3-3. ИНДУКТИВНЫЕ ДАТЧИКИ
- б) Двухтактные индуктивные датчики
- в) Характеристики двухтактных индуктивных датчиков
- г) Трансформаторные индуктивные датчики
- д) Динамические свойства индуктивных датчиков
- е) Шумы индуктивных датчиков
- ж) Общие свойства индуктивных датчиков
- 3-4. СЕЛЬСИНЫ В ТРАНСФОРМАТОРНОМ РЕЖИМЕ
- б) Характеристики сельсинного датчика
- в) Динамические свойства сельсинных датчиков
- г) Шумы и ошибки датчика
- д) Устанавливающий момент
- е) Дифференциальные сельсины
- ж) Сельсины точного и грубого каналов
- ГЛАВА ЧЕТВЕРТАЯ. УСИЛИТЕЛИ СИГНАЛОВ
- 4-2. МАГНИТНЫЕ УСИЛИТЕЛИ
- а) Рабочий процесс и статическая характеристика магнитного усилителя с прямоугольной кривой намагничивания сердечников
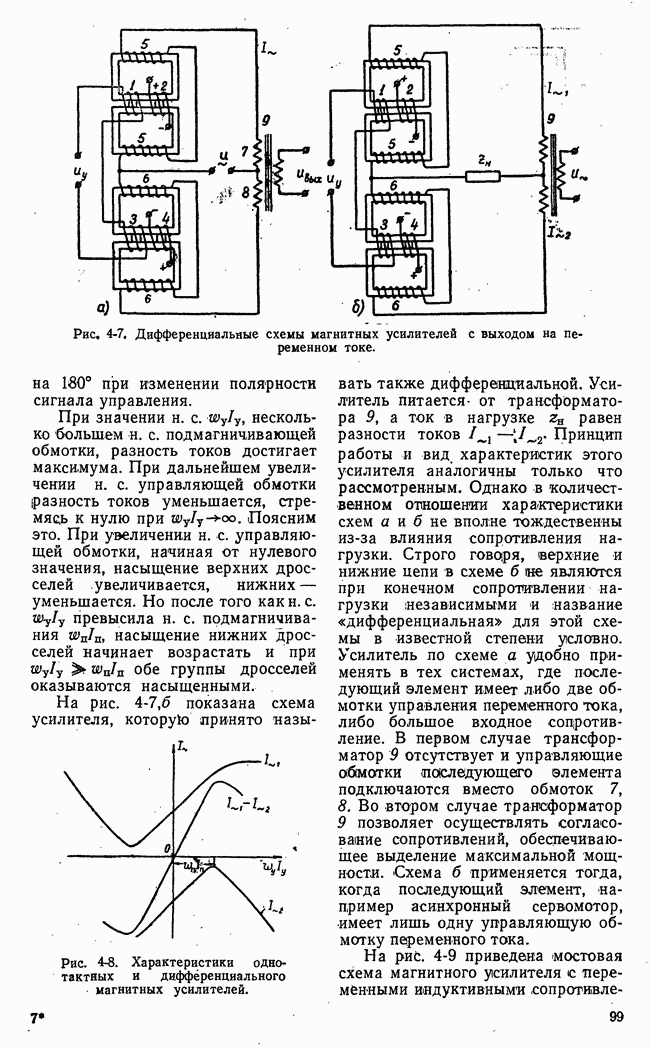
- б) Двухтактные магнитные усилители с выходом на переменном токе
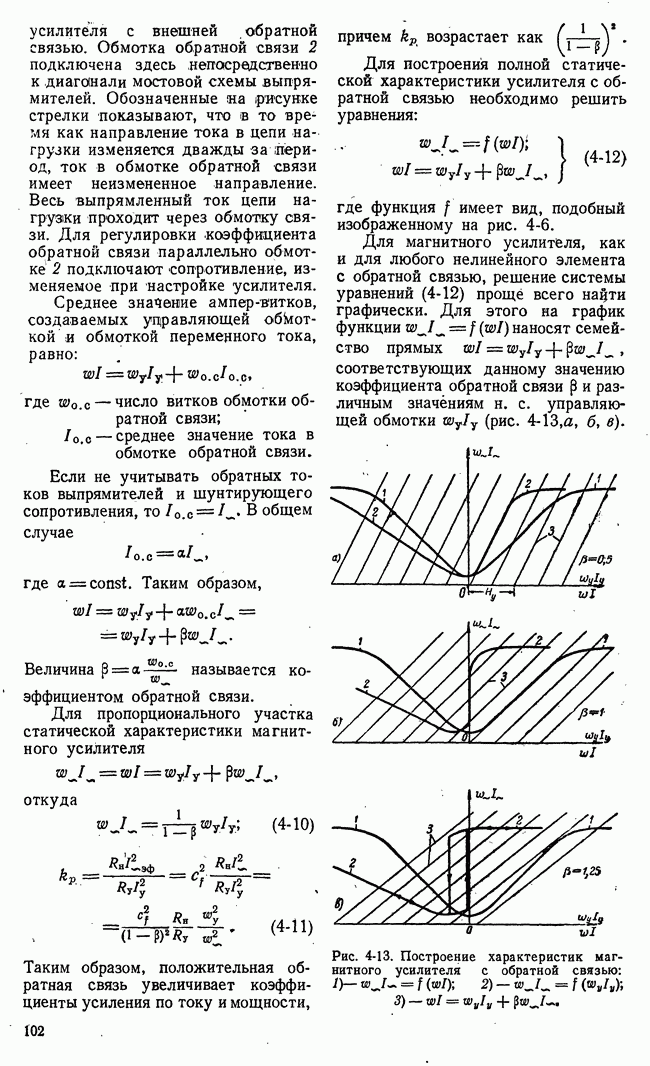
- в) Магнитные усилители с обратной связью
- г) Динамические свойства магнитных усилителей
- д) Шумы магнитных усилителей. Общие свойства магнитных усилителей
- 4-3. ЭЛЕКТРОМАШИННЫЕ УСИЛИТЕЛИ
- б) Однокаскадный электромашицный усилитель как четырехполюсник
- в) Двухкаскадный электромашинный усилитель с поперечным полем
- г) Шумы электромашинных усилителей
- 4-4. РЕЛЕ
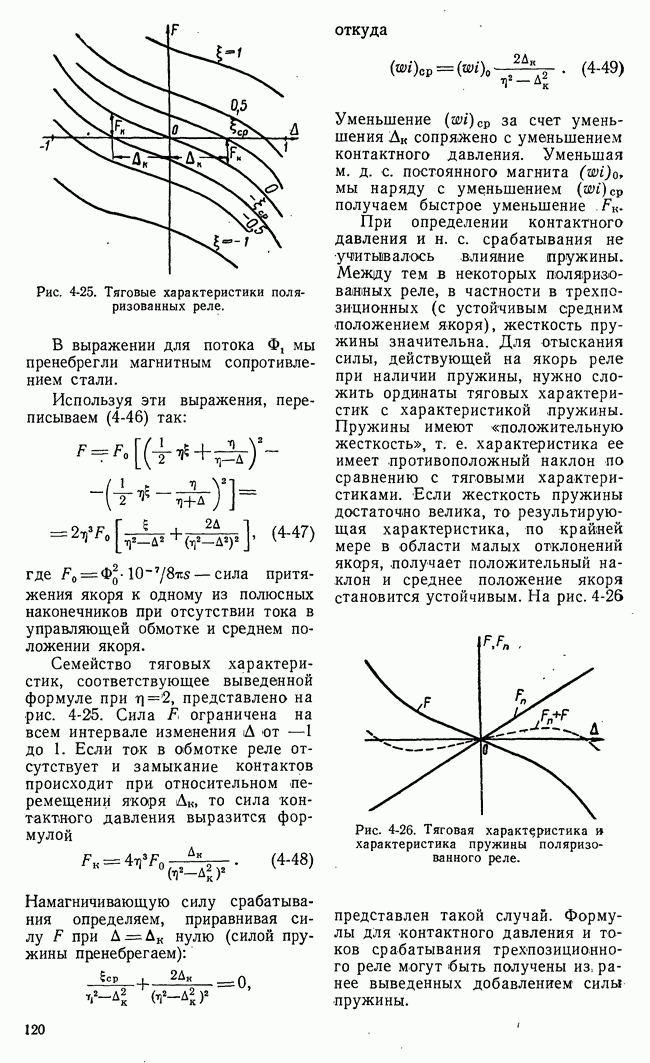
- б) Поляризованные реле
- в) Магнитоэлектрическое реле
- 4-5. РЕЛЕЙНЫЕ УСИЛИТЕЛИ
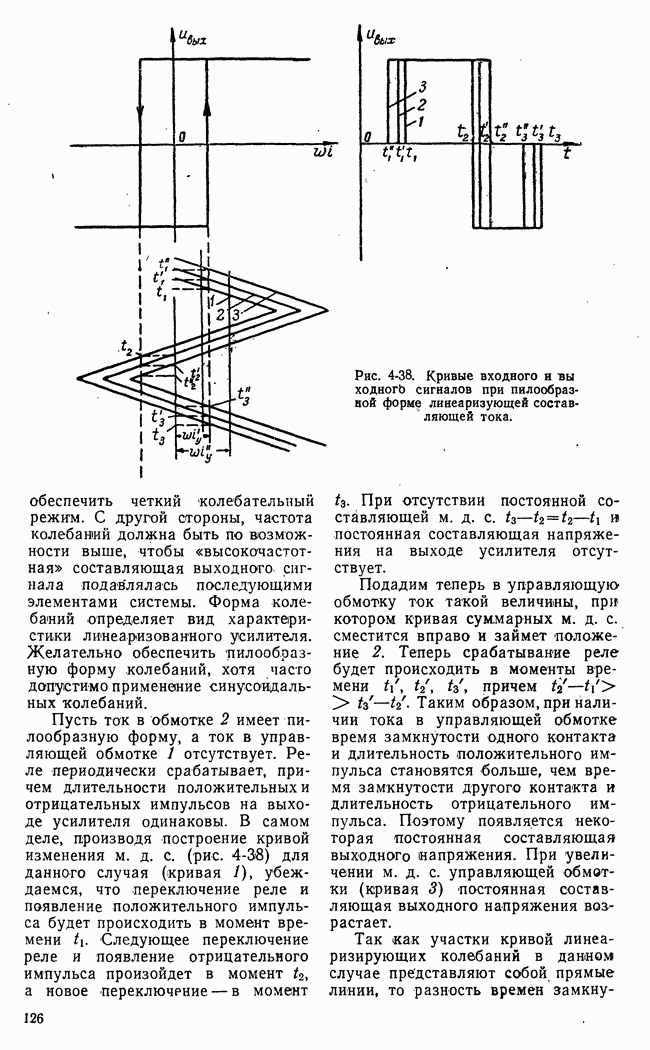
- б) Вибрационная линеаризация релейных усилителей
- в) Релейный усилитель как четырехполюсник
- 4-6. ЭЛЕКТРОННЫЕ УСИЛИТЕЛИ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- б) Фазочувствительные усилители и синхронные детекторы
- в) Электронные усилители постоянного тока
- г) Шумы электронных усилителей
- 4-7. ПОЛУПРОВОДНИКОВЫЕ УСИЛИТЕЛИ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- ГЛАВА ПЯТАЯ. ИСПОЛНИТЕЛЬНЫЕ УСТРОЙСТВА СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- 5-2. СЕРВОДВИГАТЕЛИ ПОЧТОЯННОГО ТОКА
- 5-3. СЕРВОДВИГАТЕЛИ ПЕРЕМЕННОГО ТОКА
- 5-4. СЕРВОДВИГАТЕЛИ С ЭЛЕКТРОМАГНИТНЫМИ И ПОРОШКОВЫМИ МУФТАМИ
- б) Характеристики серводвигателей с электромагнитными муфтами
- в) Порошковые муфты
- г) Характеристики серводвигателей с порошковыми муфтами
- 5-5. ГИДРАВЛИЧЕСКИЕ И ПНЕВМАТИЧЕСКИЕ СЕРВОДВИГАТЕЛИ
- б) Обратные связи в гидравлических серводвигателях
- в) Свойства гидравлических серводвигателей
- г) Электрогидравлические серводвигатели
- д) Пневматические серводвигатели
- ГЛАВА ШЕСТАЯ. СТАБИЛИЗИРУЮЩИЕ УСТРОЙСТВА СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- 6-1. ПАССИВНЫЕ КОРРЕКТИРУЮЩИЕ ЦЕПИ СИСТЕМ ПОСТОЯННОГО ТОКА
- б) Интегрирующие и интегродифференцирующие цепи
- 6-2. АКТИВНЫЕ КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА СИСТЕМ ПОСТОЯННОГО ТОКА
- 6-3. КОРРЕКТИРУЮЩИЕ ЦЕПИ СИСТЕМ ПЕРЕМЕННОГО ТОКА
- 6-4. ФИЛЬТРЫ В ЦЕПЯХ ОБРАТНЫХ СВЯЗЕЙ. МЕХАНИЧЕСКИЕ СТАБИЛИЗИРУЮЩИЕ УСТРОЙСТВА
- ГЛАВА СЕДЬМАЯ. СТРУКТУРНЫЕ СХЕМЫ И ХАРАКТЕРИСТИКИ ЛИНЕЙНЫХ СТАЦИОНАРНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 7-1. СТРУКТУРНЫЕ СХЕМЫ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 7-2. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ ДЛЯ ВХОДНОЙ ВЕЛИЧИНЫ
- 7-3. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ ДЛЯ ВОЗМУЩЕНИЯ
- 7-4. ПРИМЕРЫ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ И ИХ СТРУКТУРНЫЕ СХЕМЫ
- б) Стабилизация напряжения самолетных генераторов
- в) Следящая система копировально-фрезерного станка
- г) Следящая система автосопровождения
- д) Автоматическое управление углом тангажа самолета
- 7-5. ВРЕМЕННЫЕ ХАРАКТЕРИСТИКИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 7-6. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- б) Частотные характеристики замкнутой системы
- в) Связь частотных характеристик замкнутой и разомкнутой систем
- ГЛАВА ВОСЬМАЯ. ЭНЕРГЕТИЧЕСКИЙ РАСЧЕТ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ И СОГЛАСОВАНИЕ ХАРАКТЕРИСТИК ЭЛЕМЕНТОВ
- 8-1. ВЫБОР МОЩНОСТИ ИСПОЛНИТЕЛЬНЫХ УСТРОЙСТВ И УСЛОВИЯ СОГЛАСОВАНИЯ С НАГРУЗКОЙ
- а) Определение необходимой мощности по переходным процессам при типовых воздействиях
- б) Мгновенная мощность при гармонических колебаниях
- в) Необходимая мощность при случайных колебаниях регулирующего органа
- г) Выбор мощности сервомотора
- д) Условия согласования с нагрузкой сервомотора без обратной связи
- е) Согласование с нагрузкой сервомотора с жесткой обратной связью
- 8-2. СОГЛАСОВАНИЕ ДАТЧИКОВ, УСИЛИТЕЛЬНЫХ И КОРРЕКТИРУЮЩИХ УСТРОЙСТВ. РАСПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТОВ УСИЛЕНИЯ
- б) Передаточные функции последовательных соединений элементов
- в) Согласование пропорциональных участков характеристик
- г) Распределение коэффициентов усиления
- ГЛАВА ДЕВЯТАЯ. УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ СТАЦИОНАРНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 9-2. КРИТЕРИЙ УСТОЙЧИВОСТИ РАУСА—ГУРВИЦА
- 9-3. КРИТЕРИЙ УСТОЙЧИВОСТИ МИХАЙЛОВА
- 9-4. КРИТЕРИЙ УСТОЙЧИВОСТИ НАЙКВИСТА
- б) Использование логарифмических характеристик системы для исследования устойчивости. Понятие о запасе устойчивости
- 9-5. КОЭФФИЦИЕНТ УСИЛЕНИЯ И УСТОЙЧИВОСТЬ. ВЛИЯНИЕ КОРРЕКТИРУЮЩИХ ЦЕПЕЙ НА УСТОЙЧИВОСТЬ
- 9-6. ВЫДЕЛЕНИЕ ОБЛАСТЕЙ УСТОЙЧИВОСТИ В ПРОСТРАНСТВЕ ПАРАМЕТРОВ СИСТЕМЫ ДИАГРАММЫ ВЫШНЕГРАДСКОГО
- б) Общий метод D-разбиения в плоскости двух параметров. Линейная задача
- в) Выделение области устойчивости в плоскости двух параметров. Нелинейная задача
- г) Выделение области устойчивости в плоскости одного комплексного параметра
- ГЛАВА ДЕСЯТАЯ. КАЧЕСТВО ПРОЦЕССОВ РЕГУЛИРОВАНИЯ В ЛИНЕЙНЫХ СИСТЕМАХ
- 10-1. КРИТЕРИИ КАЧЕСТВА ПРОЦЕССА РЕГУЛИРОВАНИЯ
- 10-2. ТОЧНОСТЬ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ В УСТАНОВИВШИХСЯ РЕЖИМАХ. СТАТИЧЕСКИЕ И АСТАТИЧЕСКИЕ СИСТЕМЫ
- б) Точность при медленно меняющихся воздействиях. Коэффициенты ошибок. Астатические системы высших порядков
- в) Общие условия неискаженного воспроизведения входных сигналов в вынужденном режиме
- г) Повышение точности системы коррекцией входного сигнала
- д) Повышение точности системы путем компенсации возмущения F(t)
- 10-18. ПЕРЕХОДНЫЕ ФУНКЦИИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- б) Некоторые особенности вычисления переходных функций
- 10-4. РАСПРЕДЕЛЕНИЕ НУЛЕЙ И ПОЛЮСОВ ПЕРЕДАТОЧНОЙ ФУНКЦИИ И ПЕРЕХОДНЫЕ ПРОЦЕССЫ
- б) Оценки распределения корней. Степень устойчивости. Коэффициент затухания колебаний
- в) Влияние параметров на распределение корней. Метод Эванса
- г) Оценка переходных функций по распределению полюсов передаточной функции или корней характеристического уравнения
- д) Влияние нулей на характер переходной функции
- е) Определение коэффициентов уравнений по заданному распределению корней. Стандартные коэффициенты характеристических уравнений
- 10-5. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ И ПЕРЕХОДНЫЕ ФУНКЦИИ
- б) Приближенное вычисление переходных функций и переходных процессов
- в) Оценка качества процесса регулирования по характеристикам замкнутой системы Ф(w) и ф(w) и характеристике разомкнутой системы W(jw)
- г) Оценка качества по амплитудным логарифмическим характеристикам. Минимально-фазовые системы
- д) Связь между логарифмическими амплитудными характеристиками разомкнутой системы и полюсами передаточной функции замкнутой системы
- 10-6. ИНТЕГРАЛЬНЫЕ ОЦЕНКИ ПЕРЕХОДНЫХ ПРОЦЕССОВ
- г) Приближение кривых x(t) к эталонной кривой хэ(t) по критерию …
- ГЛАВА ОДИННАДЦАТАЯ. НЕСТАЦИОНАРНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 11-1. ОБЩИЕ СВЕДЕНИЯ О НЕСТАЦИОНАРНЫХ СИСТЕМАХ
- 11-2. ПРИМЕРЫ СУЩЕСТВЕННО НЕСТАЦИОНАРНЫХ СИСТЕМ
- 11-3. ДИНАМИЧЕСКИЕ ХАРАКТЕРИСТИКИ НЕСТАЦИОНАРНЫХ СИСТЕМ АВТОМАТИЧ ЕСКОГО РЕГУЛИРОВАНИЯ
- 11-4. ОСОБЕННОСТИ СОСТАВЛЕНИЯ УРАВНЕНИЙ И СТРУКТУРНЫХ СХЕМ НЕСТАЦИОНАРНЫХ СИСТЕМ
- 11-5. МЕТОДЫ ОПРЕДЕЛЕНИЯ ЧАСТОТНОЙ ХАРАКТЕРИСТИКИ И ИМПУЛЬСНОЙ РЕАКЦИИ НЕСТАЦИОНАРНЫХ СИСТЕМ
- ГЛАВА ДВЕНАДЦАТАЯ. СТАТИСТИЧЕСКАЯ ДИНАМИКА ЛИНЕЙНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 12-1. СТАЦИОНАРНЫЕ И НЕСТАЦИОНАРНЫЕ СЛУЧАЙНЫЕ ПРОЦЕССЫ
- б) Стационарные и нестационарные случайные функций
- в) Свойства корреляционной функции
- г) Свойство эргодичности
- д) Гауссовы случайные процессы
- 12-2. ПРЕОБРАЗОВАНИЕ СТАЦИОНАРНЫХ СЛУЧАЙНЫХ ФУНКЦИЙ СТАЦИОНАРНЫМИ ЛИНЕЙНЫМИ СИСТЕМАМИ
- б) Преобразование корреляционных функций при прохождении случайного сигнала через линейную систему
- в) Интегральная квадратичная оценка импульсной переходной функции и дисперсия реакции системы на белый шум
- г) Преобразование спектральных плотностей при прохождении случайного сигнала через линейную систему
- 12-3. ОПТИМАЛЬНЫЕ ЛИНЕЙНЫЕ СТАЦИОНАРНЫЕ СИСТЕМЫ
- б) Условия оптимальности при свободном выборе передаточной функции
- ГЛАВА ТРИНАДЦАТАЯ. О СИНТЕЗЕ ЛИНЕЙНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 13-2. МЕТОД ЛОГАРИФМИЧЕСКИХ ЧАСТОТНЫХ ХАРАКТЕРИСТИК
- б) Синтез корректирующих цепей
- в) О синтезе на основе требований к реакции системы на возмущение F(t)
- 13-3. ВЫБОР ПАРАМЕТРОВ НА ОСНОВЕ АНАЛИЗА РАСПРЕДЕЛЕНИЯ НУЛЕЙ И ПОЛЮСОВ ПЕРЕДАТОЧНОЙ ФУНКЦИИ
- 13-4. ВЫБОР ПАРАМЕТРОВ НА ОСНОВЕ ИНТЕГРАЛЬНЫХ КВАДРАТИЧНЫХ ОЦЕНОК
- 13-5. СПЕЦИАЛЬНЫЕ ПРИЕМЫ УЛУЧШЕНИЯ КАЧЕСТВА ПРОЦЕССА РЕГУЛИРОВАНИЯ
- б) Подавление помех во входном сигнале при инерционном объекте управления
- в) Использование двух источников информации для выделения истинного сигнала
- г) Компенсация влияния запаздывания измерителей на динамические свойства системы
- д) Исключение перерегулирования в системах, передаточные функции которых имеют только вещественные полюсы
- ГЛАВА ЧЕТЫРНАДЦАТАЯ. ИМПУЛЬСНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 14-2. ИМПУЛЬСЫ И ИМПУЛЬСНЫЕ ЭЛЕМЕНТЫ
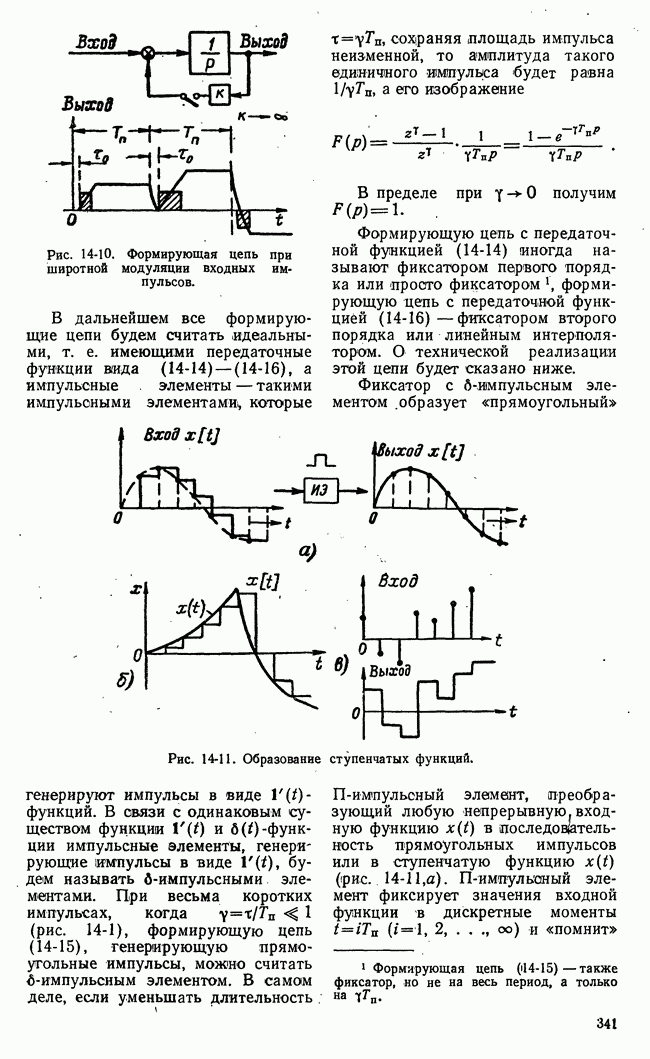
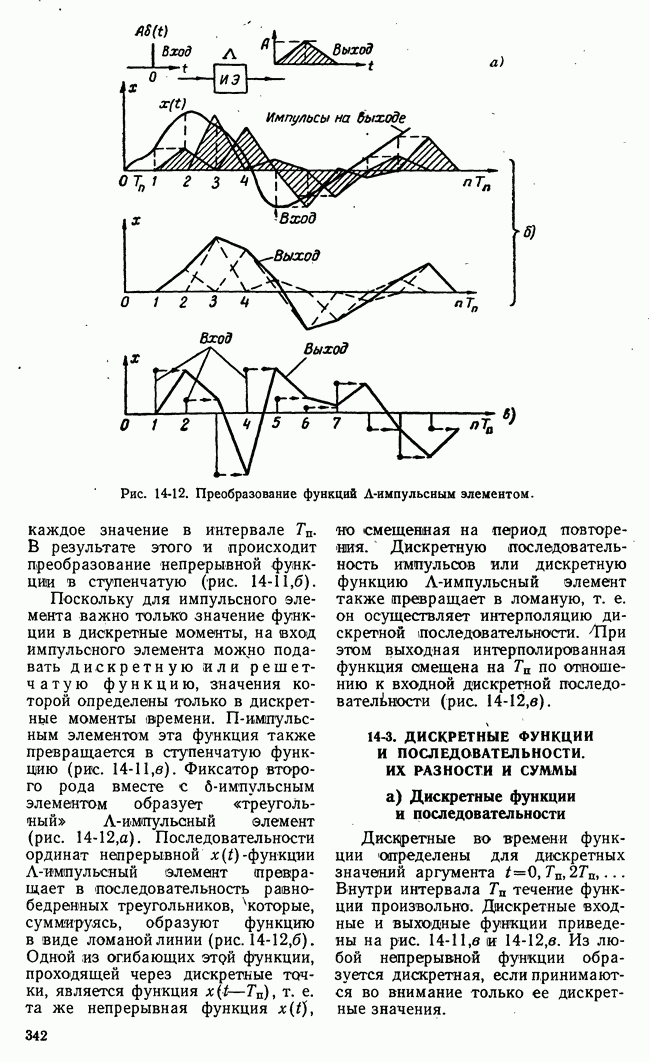
- б) Формирующие цепи и импульсные элементы
- 14-3. ДИСКРЕТНЫЕ ФУНКЦИИ И ПОСЛЕДОВАТЕЛЬНОСТИ. ИХ РАЗНОСТИ И СУММЫ
- 14-4. РЕАКЦИЯ ЛИНЕЙНЫХ НЕПРЕРЫВНЫХ СИСТЕМ НА ПОСЛЕДОВАТЕЛЬНОСТИ ИЛИ ДЕЛЬТА-ИМПУЛЬСОВ
- б) Свертка двух дискретных функций
- в) Уравнения в конечных разностях непрерывных звеньев первого и второго порядков
- г) Символические изображения дискретных функций и их использование для решения уравнений в конечных разностях
- 14-5. ДИСКРЕТНОЕ ПРЕОБРАЗОВАНИЕ ЛАПЛАСА ИЛИ z-ПРЕОБРАЗОВАНИЕ. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ КОМПЛЕКСНОГО АРГУМЕНТА
- 14-6. ДИНАМИКА РАЗОМКНУТЫХ ИМПУЛЬСНЫХ СИСТЕМ
- б) Значение выходной величины непрерывной системы внутри интервалов повторения
- в) Передаточные функции, систем с запаздыванием
- г) Свободные и вынужденные движения
- д) Полюсы. Устойчивость разомкнутых систем
- е) Переходные функции
- ж) Частотные характеристики
- 14-7. СВЯЗЬ МЕЖДУ ЧАСТОТНЫМИ И ПЕРЕХОДНЫМИ ФУНКЦИЯМИ. ДИСКРЕТНОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ
- 14-8. ИНТЕГРАЛЬНАЯ КВАДРАТИЧНАЯ ОЦЕНКА
- 14-9. ДИСКРЕТНЫЕ СЛУЧАЙНЫЕ ФУНКЦИИ (СЛУЧАЙНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ)
- ГЛАВА ПЯТНАДЦАТАЯ. ДИНАМИКА ИМПУЛЬСНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 15-1. УРАВНЕНИЯ И ПЕРЕДАТОЧНЫЕ ФУНКЦИИ СИСТЕМ С ОДНИМ ИМПУЛЬСНЫМ ЭЛЕМЕНТОМ
- 15-2. УСТОЙЧИВОСТЬ ЗАМКНУТЫХ СИСТЕМ
- 15-3. КАЧЕСТВО ПРОЦЕССА РЕГУЛИРОВАНИЯ
- 15-4. ПРИМЕРЫ ИМПУЛЬСНЫХ СИСТЕМ
- 15-5. ИМПУЛЬСНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ С ДИСКРЕТНЫМИ КОРРЕКТИРУЮЩИМИ ЦЕПЯМИ
- ГЛАВА ШЕСТНАДЦАТАЯ. СТРУКТУРНЫЕ СХЕМЫ, ХАРАКТЕРИСТИКИ И УРАВНЕНИЯ НЕЛИНЕЙНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- б) Уравнения продольного движения самолета
- в) Уравнения продольного движения ракеты
- 16-2. НЕЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ СИГНАЛА ОШИБКИ
- б) Структурные схемы с нелинейными элементами
- в) Релейные системы. Релейные элементы
- 16-3. НЕЛИНЕЙНЫЙ ОБЪЕКТ РЕГУЛИРОВАНИЯ И НЕЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ СИГНАЛА ОШИБКИ
- ГЛАВА СЕМНАДЦАТАЯ. СВОЙСТВА НЕЛИНЕЙНЫХ СИСТЕМ И (МЕТОДЫ ИССЛЕДОВАНИЯ
- б) Суждение об устойчивости по уравнениям первого приближения. Теоремы Ляпунова
- в) Суждение о качестве процессов регулирования по уравнениям первого приближения
- г) Прямой метод Ляпунова
- д) Техническая устойчивость
- 17-2. АВТОКОЛЕБАНИЯ НЕЛИНЕЙНЫХ СИСТЕМ
- б) Автоколебания релейных систем
- в) Метод точечных преобразований
- г) Описание процесса в релейной системе разностным уравнением. Устойчивость автоколебаний
- д) Примера исследования автоколебаний релейных систем второго порядка
- 17-3. ВЛИЯНИЕ КОРРЕКТИРУЮЩИХ ЦЕПЕЙ НА АВТОКОЛЕБАНИЯ И НА ПЕРЕХОДНЫЕ ПРОЦЕССЫ НЕЛИНЕЙНЫХ СИСТЕМ
- б) Влияние корректирующих цепей на переходные процессы. Скользящие режимы. Оптимальные переходные процессы
- 17-4. ГАРМОНИЧЕСКАЯ ЛИНЕАРИЗАЦИЯ ПРОЦЕССОВ В НЕЛИНЕЙНЫХ СИСТЕМАХ
- б) Исследование автоколебаний при помощи гармонической линеаризации
- в) Гармоническая линеаризация и критерии устойчивости линейных систем
- 17-5. ТЕОРИЯ РЕЛЕЙНЫХ СИСТЕМ
- в) Частотные характеристики релейных систем
- г) Оценка устойчивости релейных систем
- д) Вынужденные колебания релейных систем. Захватывание (синхронизация или подавление) автоколебаний
- е) Вибрационная линеаризация релейных систем, Реакция релейных систем на медленно меняющиеся возмущения
- 17-6. ОПТИМАЛЬНЫЕ ПРОЦЕССЫ РЕГУЛИРОВАНИЯ
- б) Системы, оптимальные по быстродействию. Принцип максимума
- в) Системы, близкие к оптимальным по быстродействию
- ГЛАВА ВОСЕМНАДЦАТАЯ. ЭНТРОПИЯ, ИНФОРМАЦИЯ, АЛГОРИТМ В СИСТЕМАХ АВТОМАТИЧЕОКОГО УПРАВЛЕНИЯ
- 18-1. ЭНТРОПИЯ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ УПРАВЛЯЕМОГО ПРОЦЕССА
- 18-2. КОЛИЧЕСТВО ИНФОРМАЦИИ В ПРОЦЕССАХ УПРАВЛЕНИЯ
- 18-3. ЭНТРОПИЯ И ИНФОРМАЦИЯ В ЗАМКНУТЫХ СИСТЕМАХ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- 18-4. АЛГОРИТМЫ ПРОЦЕССОВ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- ГЛАВА ДЕВЯТНАДЦАТАЯ. СИСТЕМЫ ЭКСТРЕМАЛЬНОГО РЕГУЛИРОВАНИЯ
- 19-1. ПРИМЕРЫ СИСТЕМ ЭКСТРЕМАЛЬНОГО РЕГУЛИРОВАНИЯ
- 19-2. СПОСОБЫ ПОИСКА ЭКСТРЕМУМА
- б) Методы организации процесса поиска
- 19-3. СТРУКТУРНЫЕ СХЕМЫ СИСТЕМ ЭКСТРЕМАЛЬНОГО РЕГУЛИРОВАНИЯ
- 19-4. ДИНАМИКА НЕПРЕРЫВНЫХ СИСТЕМ ЭКСТРЕМАЛЬНОГО РЕГУЛИРОВАНИЯ В КВАЗИСТАЦИОНАРНОМ РЕЖИМЕ
- б) Динамика квазистационарного режима систем экстремального регулирования, основанных на методе градиента
- 19-5. ДИНАМИКА НЕПРЕРЫВНЫХ СИСТЕМ ЭКСТРЕМАЛЬНОГО РЕГУЛИРОВАНИЯ ПРИ СЛУЧАЙНЫХ СИГНАЛАХ ПОИСКА
- б) Уравнения замкнутой системы экстремального регулирования
- в) Точность экстремального регулирования
- 19-6. ФОРСИРОВАННЫЕ ПРОЦЕССЫ ЭКСТРЕМАЛЬНОГО РЕГУЛИРОВАНИЯ ОДНОМЕРНОГО БЕЗЫНЕРЦИОННОГО ОБЪЕКТА
- ГЛАВА ДВАДЦАТАЯ. СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ С САМОНАСТРАИВАЮЩИМИСЯ КОРРЕКТИРУЮЩИМИ УСТРОЙСТВАМИ
- 20-1. СИСТЕМЫ С РАЗОМКНУТЫМИ ЦЕПЯМИ НАСТРОЙКИ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ
- 20-2. СИСТЕМЫ С ЗАМКНУТЫМИ ЦЕПЯМИ НАСТРОЙКИ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ
- 20-3. СИСТЕМЫ С ЭКСТРЕМАЛЬНОЙ НАСТРОЙКОЙ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ
- 20-4. СТАТИСТИЧЕСКАЯ ДИНАМИКА НЕПРЕРЫВНЫХ СИСТЕМ С ЭКСТРЕМАЛЬНОЙ НАСТРОЙКОЙ ПОСЛЕДОВАТЕЛЬНЫХ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ
- б) Уравнения замкнутой самонастраивающейся системы
- в) Случай сильной фильтрации. Квазистационарный режим
- г) Общий случай квазистационарного режима
- ГЛАВА ДВАДЦАТЬ ПЕРВАЯ. ИГРОВЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- 21-1. НАЗНАЧЕНИЕ И ПРИНЦИПЫ ДЕЙСТВИЯ ИГРОВЫХ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- 21-2. НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ ИГР
- 21-3. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ. ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
- 21-4. ОБ АЛГОРИТМАХ ИГРОВЫХ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- ПРИЛОЖЕНИЯ