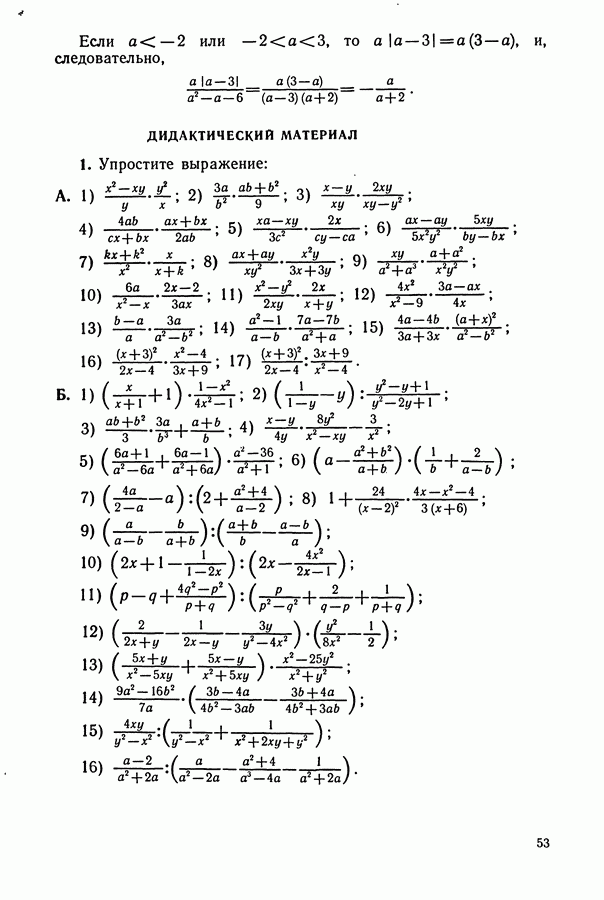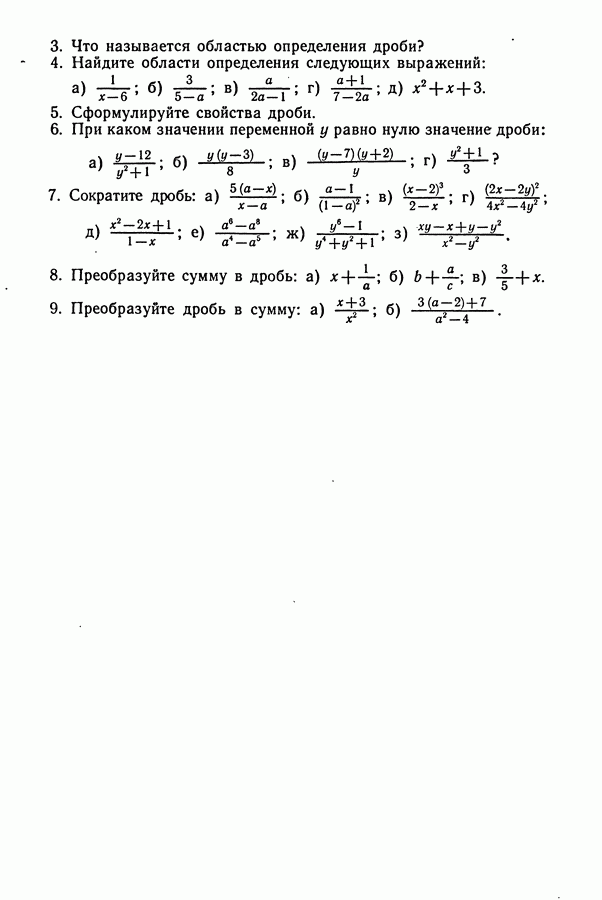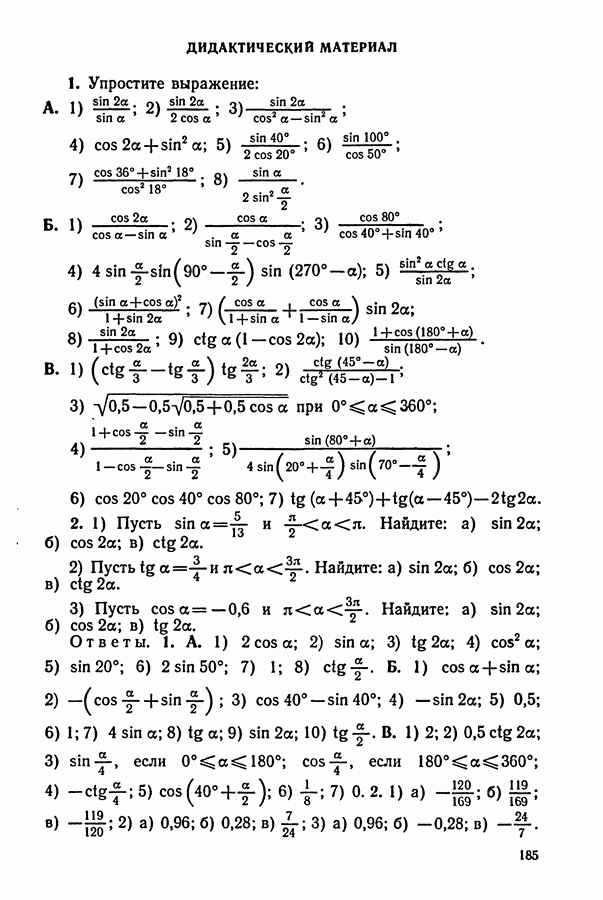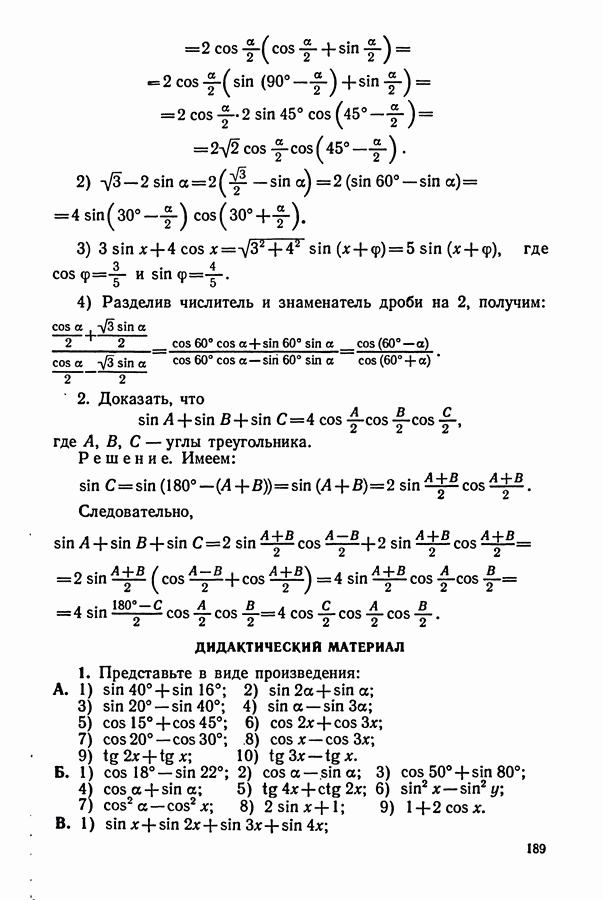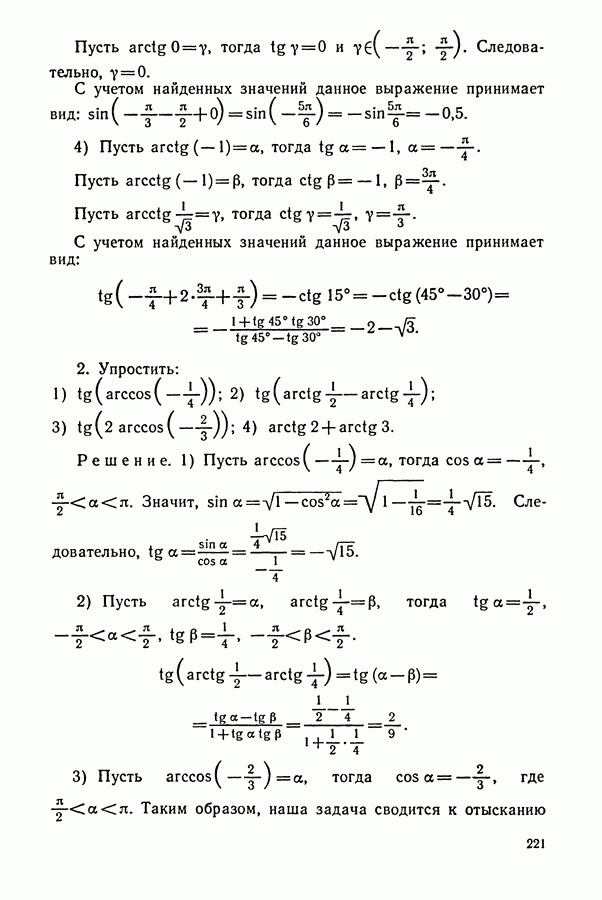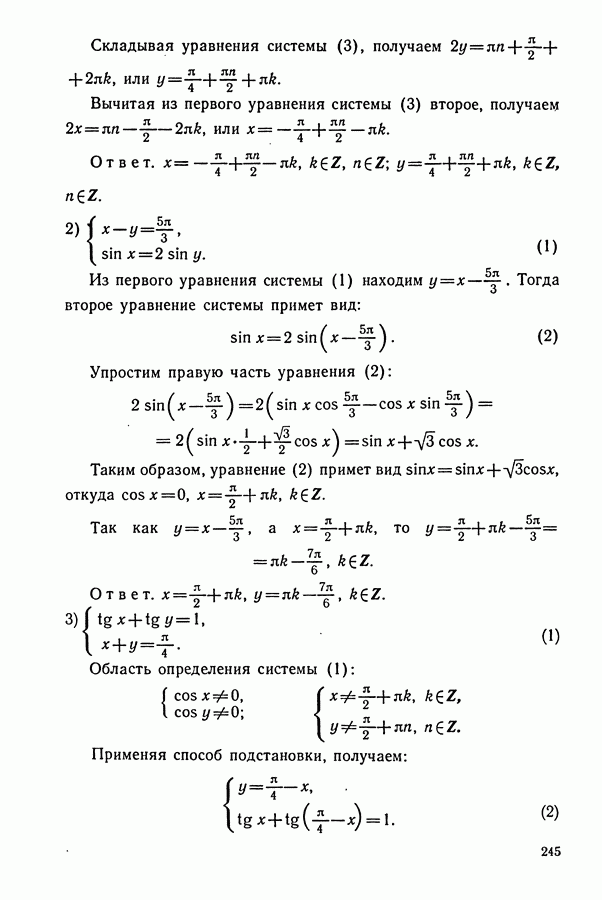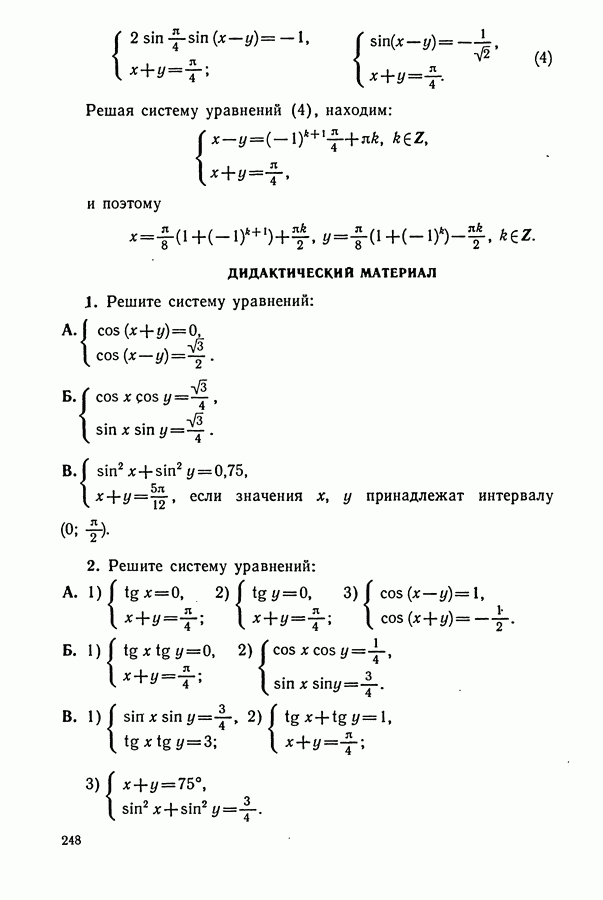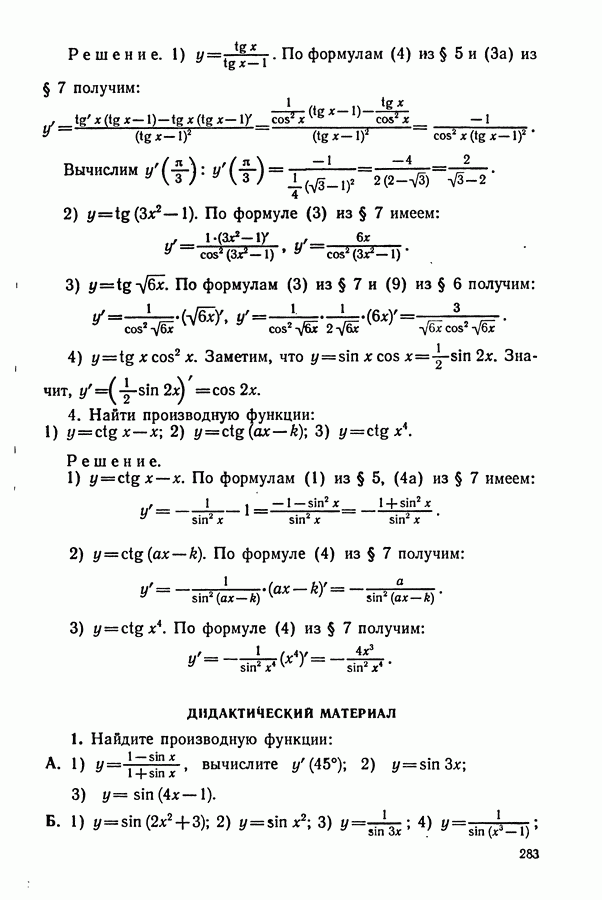| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 4. ПРЕОБРАЗОВАНИЕ ПРОИЗВЕДЕНИЯ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ В СУММУ
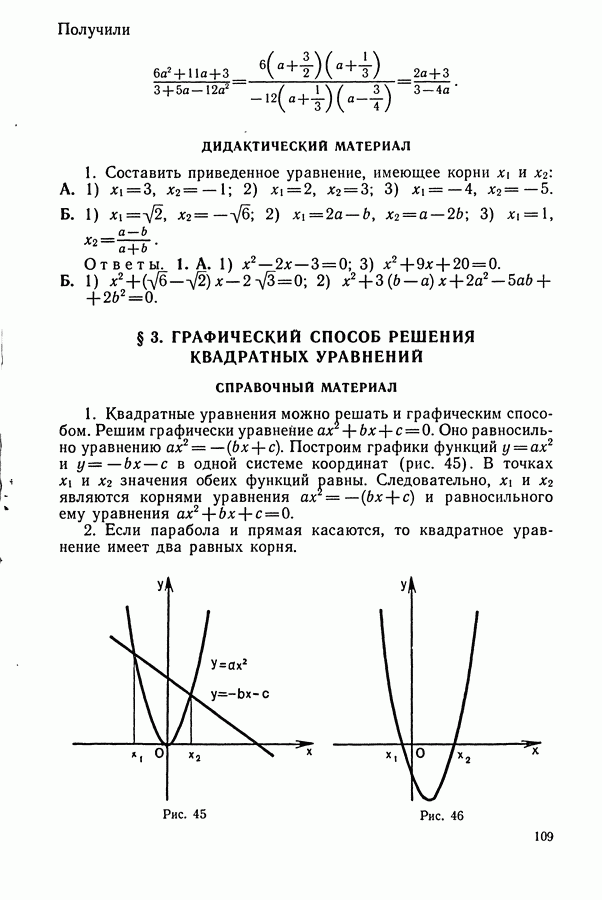
СПРАВОЧНЫЙ МАТЕРИАЛ
1. Формулы для преобразования произведения синуса и косинуса в сумму получаются из формул сложения для синуса и косинуса. Запишем формулы для синуса суммы и синуса разности углов 

Сложив почленно эти равенства и разделив результат на 2, получим:

2. Запишем формулы для косинуса суммы и косинуса разности углов 

Сложив почленно эти равенства и разделив результат на 2, получим:

3. Аналогично, вычитая из второго равенства первое, в результате получаем:

4. Полезно также знать формулы преобразования произведения тангенсов и котангенсов в сумму:

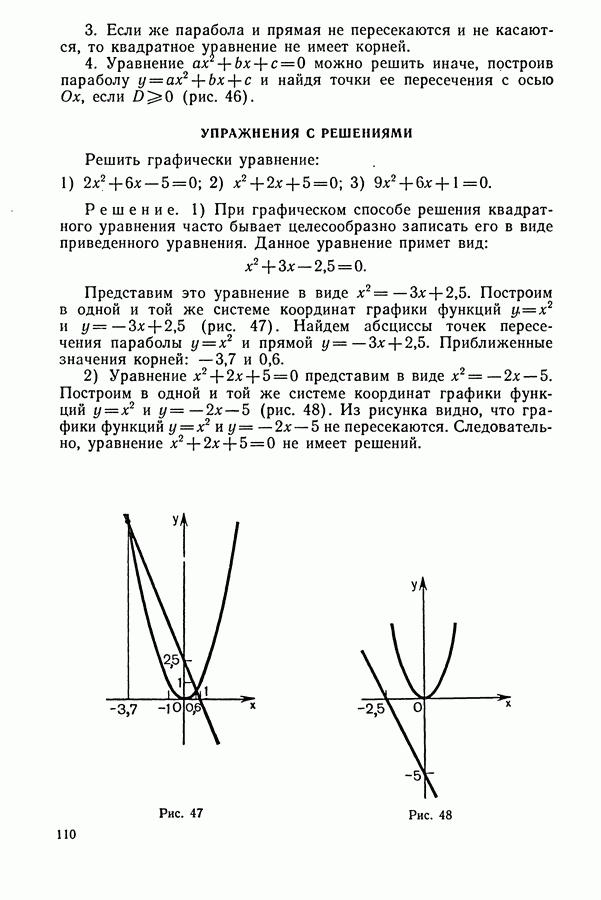
УПРАЖНЕНИЯ С РЕШЕНИЯМИ
1. Представить  в виде суммы тригонометрических функций.
в виде суммы тригонометрических функций.
Решение. Заменив  выражением
выражением  получим:
получим:

Теперь применим формулу (2):

Итак,

2. Упростить:  .
.
Решение. Заменим  на
на  (по формуле
(по формуле  ). Тогда
). Тогда  . По формуле синуса двойного угла имеем
. По формуле синуса двойного угла имеем 
Произведение синуса на косинус преобразуем в сумму:  данное выражение примет вид:
данное выражение примет вид:

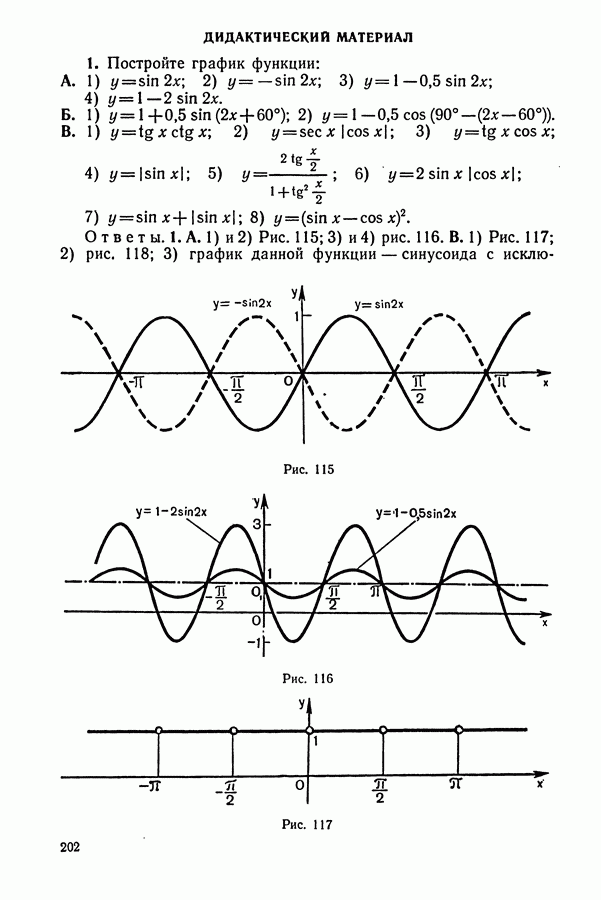
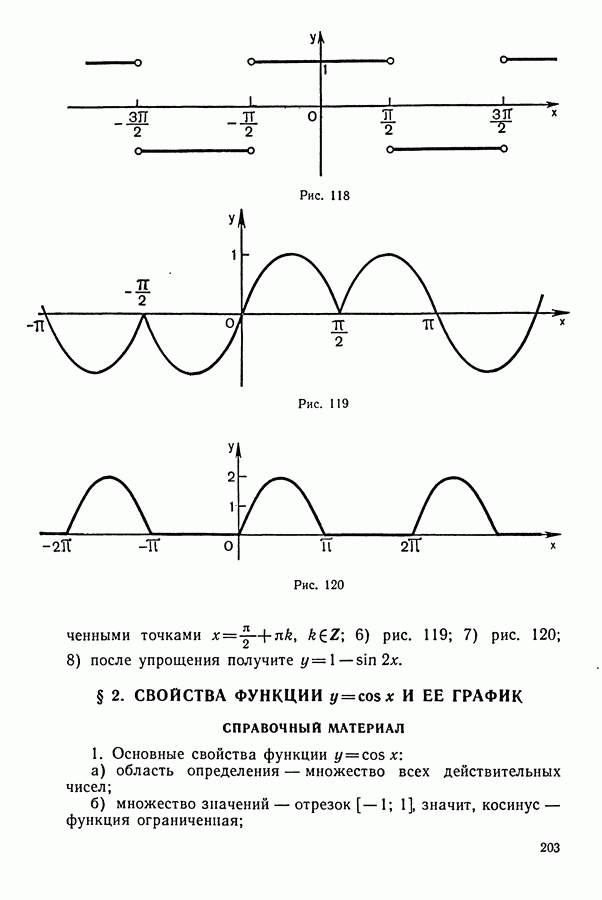
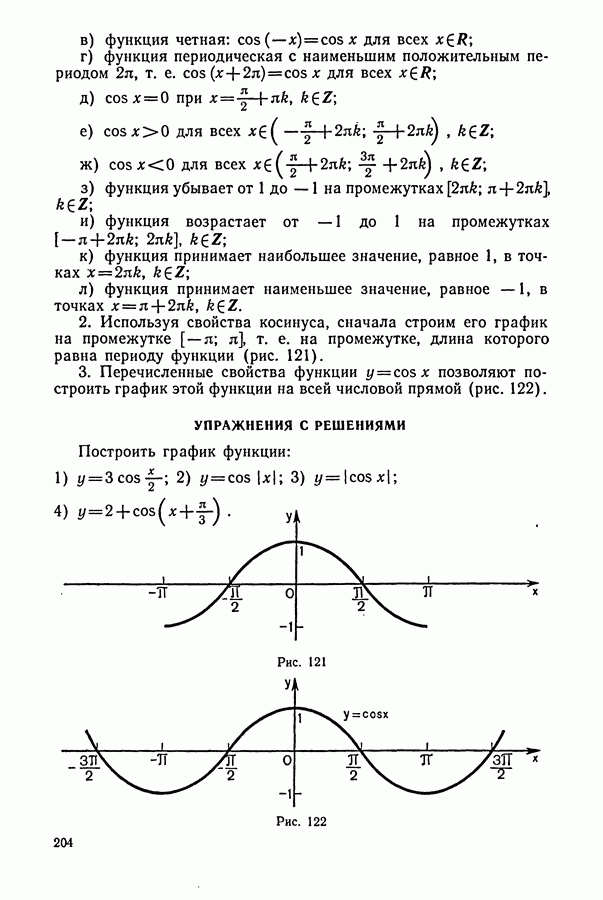
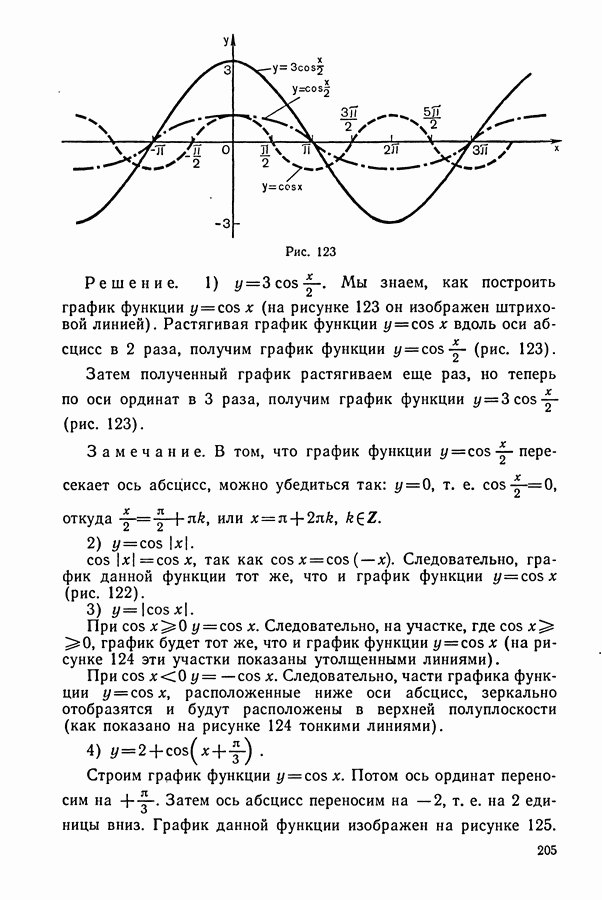
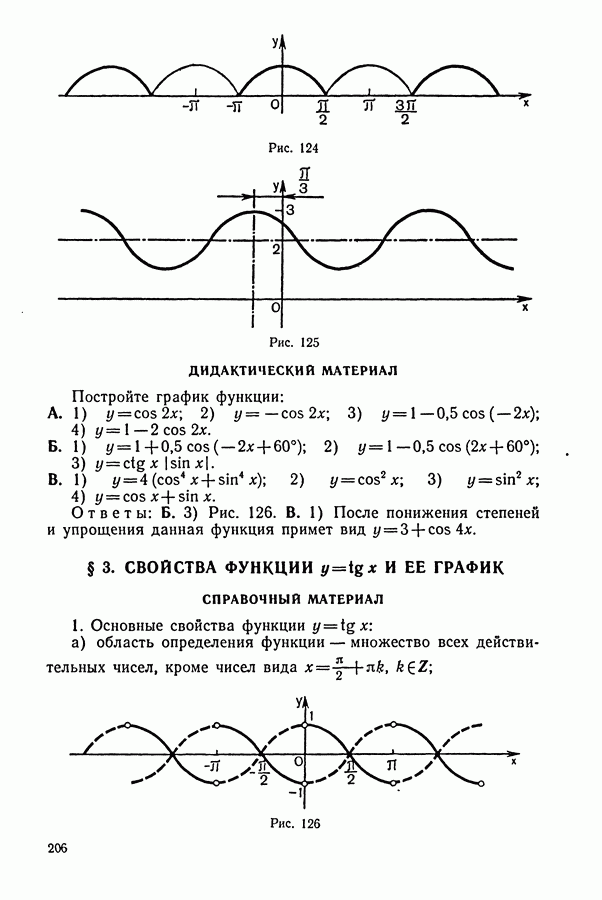
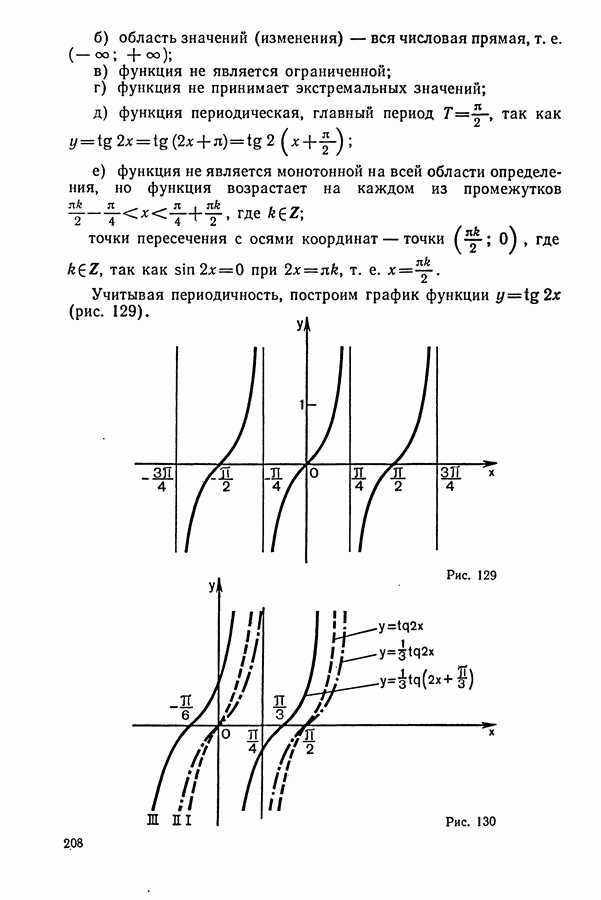
ДИДАКТИЧЕСКИЙ МАТЕРИАЛ
(см. скан)
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ГЛАВА I.
- § 1. НАТУРАЛЬНЫЕ ЧИСЛА И ДЕЙСТВИЯ НАД НИМИ
- § 2. СЛОЖЕНИЕ И ЗАКОНЫ СЛОЖЕНИЯ
- § 3. ВЫЧИТАНИЕ
- § 4. УМНОЖЕНИЕ И ЗАКОНЫ УМНОЖЕНИЯ
- § 5. ДЕЛЕНИЕ
- § 6. ПРИЗНАКИ ДЕЛИМОСТИ ЧИСЕЛ
- § 7. ПОНЯТИЕ МНОЖЕСТВА
- § 8. ОПЕРАЦИИ НАД МНОЖЕСТВАМИ
- § 9. ВЗАИМНО ОДНОЗНАЧНОЕ СООТВЕТСТВИЕ
- § 10. ПРОСТЫЕ И СОСТАВНЫЕ ЧИСЛА
- § 11. НАИБОЛЬШИЙ ОБЩИЙ ДЕЛИТЕЛЬ
- § 12. НАИМЕНЬШЕЕ ОБЩЕЕ КРАТНОЕ
- Контрольные вопросы
- ГЛАВА II
- § 1. ОБЫКНОВЕННЫЕ ДРОБИ
- § 2. ПРАВИЛЬНЫЕ И НЕПРАВИЛЬНЫЕ ДРОБИ
- § 3. ОСНОВНОЕ СВОЙСТВО ДРОБИ
- § 4. СЛОЖЕНИЕ И ВЫЧИТАНИЕ ДРОБЕЙ
- § 5. УМНОЖЕНИЕ ДРОБЕЙ
- § 6. ДЕЛЕНИЕ ДРОБЕЙ
- § 7. ДЕСЯТИЧНЫЕ ДРОБИ
- § 8. ОБРАЩЕНИЕ ДЕСЯТИЧНОЙ ДРОБИ В ОБЫКНОВЕННУЮ И ОБЫКНОВЕННОЙ В ДЕСЯТИЧНУЮ. ПЕРИОДИЧЕСКИЕ ДРОБИ
- § 9. ОТНОШЕНИЕ. ПРОПОРЦИЯ
- § 10. СВОЙСТВА ПРОПОРЦИИ
- § 11. ПРОЦЕНТ. ОСНОВНЫЕ ЗАДАЧИ НА ПРОЦЕНТЫ
- § 12. ДЕЛЕНИЕ ЧИСЛА НА ЧАСТИ, ПРЯМО И ОБРАТНО ПРОПОРЦИОНАЛЬНЫЕ ДАННЫМ ЧИСЛАМ
- Контрольные вопросы
- ГЛАВА III
- § 1. КООРДИНАТНАЯ ПРЯМАЯ
- § 2. МНОЖЕСТВО ЦЕЛЫХ ЧИСЕЛ
- § 3. МНОЖЕСТВО РАЦИОНАЛЬНЫХ ЧИСЕЛ
- § 4. МОДУЛЬ ЧИСЛА
- § 5. СРАВНЕНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ
- § 6. СЛОЖЕНИЕ И ВЫЧИТАНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ
- § 7. УМНОЖЕНИЕ И ДЕЛЕНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ
- § 8. ВОЗВЕДЕНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ В СТЕПЕНЬ С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ
- Контрольные вопросы
- ГЛАВА IV
- § 1. СВОЙСТВА СТЕПЕНИ С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ
- § 2. ЧИСЛОВЫЕ ВЫРАЖЕНИЯ
- § 3. ВЫРАЖЕНИЯ С ПЕРЕМЕННЫМИ
- § 4. ТОЖДЕСТВЕННО РАВНЫЕ ВЫРАЖЕНИЯ
- § 5. ОДНОЧЛЕНЫ
- § 6. МНОГОЧЛЕНЫ
- § 7. ПРЕОБРАЗОВАНИЕ СУММЫ И РАЗНОСТИ МНОГОЧЛЕНОВ
- § 8. УМНОЖЕНИЕ МНОГОЧЛЕНА НА ОДНОЧЛЕН И МНОГОЧЛЕНА НА МНОГОЧЛЕН
- § 9. РАЗЛОЖЕНИЕ МНОГОЧЛЕНА НА МНОЖИТЕЛИ СПОСОБОМ ВЫНЕСЕНИЯ ОБЩЕГО МНОЖИТЕЛЯ ЗА СКОБКИ
- § 10. РАЗЛОЖЕНИЕ МНОГОЧЛЕНА НА МНОЖИТЕЛИ СПОСОБОМ ГРУППИРОВКИ
- § 11. ФОРМУЛЫ СОКРАЩЕННОГО УМНОЖЕНИЯ
- Контрольные вопросы
- ГЛАВА V
- § 1. ДРОБЬ
- § 2. ЦЕЛЫЕ И ДРОБНЫЕ ВЫРАЖЕНИЯ
- § 3. ТОЖДЕСТВЕННОЕ ПРЕОБРАЗОВАНИЕ СУММЫ И РАЗНОСТИ ДВУХ ДРОБЕЙ
- § 4. ТОЖДЕСТВЕННОЕ ПРЕОБРАЗОВАНИЕ ПРОИЗВЕДЕНИЯ И ЧАСТНОГО ДВУХ ДРОБЕЙ
- § 5. СТЕПЕНЬ ДРОБИ
- Контрольные вопросы
- ГЛАВА VI
- § 1. ПОНЯТИЕ ОБ ИРРАЦИОНАЛЬНОМ ЧИСЛЕ
- § 2. РАЗВИТИЕ ПОНЯТИЯ О ЧИСЛЕ. МНОЖЕСТВО ДЕЙСТВИТЕЛЬНЫХ ЧИСЕЛ
- § 3. КОРЕНЬ СТЕПЕНИ ИЗ ДЕЙСТВИТЕЛЬНОГО ЧИСЛА
- § 4. АЛГОРИТМ ИЗВЛЕЧЕНИЯ КВАДРАТНОГО КОРНЯ ИЗ ЧИСЛА
- § 5. АРИФМЕТИЧЕСКИЕ ДЕЙСТВИЯ С ДЕЙСТВИТЕЛЬНЫМИ ЧИСЛАМИ
- § 6. ПРЕОБРАЗОВАНИЯ АРИФМЕТИЧЕСКИХ КОРНЕЙ
- § 7. СТЕПЕНЬ С ЦЕЛЫМ И ДРОБНЫМ ПОКАЗАТЕЛЕМ
- Контрольные вопросы
- ГЛАВА VII
- § 1. УРАВНЕНИЯ С ОДНОЙ ПЕРЕМЕННОЙ
- § 2. ПОНЯТИЕ О РАВНОСИЛЬНОСТИ УРАВНЕНИЙ
- § 3. СВОЙСТВА ЧИСЛОВЫХ РАВЕНСТВ И ТЕОРЕМЫ О РАВНОСИЛЬНОСТИ УРАВНЕНИЙ
- § 4. ЛИНЕЙНОЕ УРАВНЕНИЕ С ОДНОЙ ПЕРЕМЕННОЙ, СОДЕРЖАЩЕЕ ПАРАМЕТР
- Контрольные вопросы
- ГЛАВА VIII
- § 1. ПОНЯТИЕ ФУНКЦИИ
- § 2. СПОСОБЫ ЗАДАНИЯ ФУНКЦИИ
- § 3. МОНОТОННОСТЬ ФУНКЦИИ
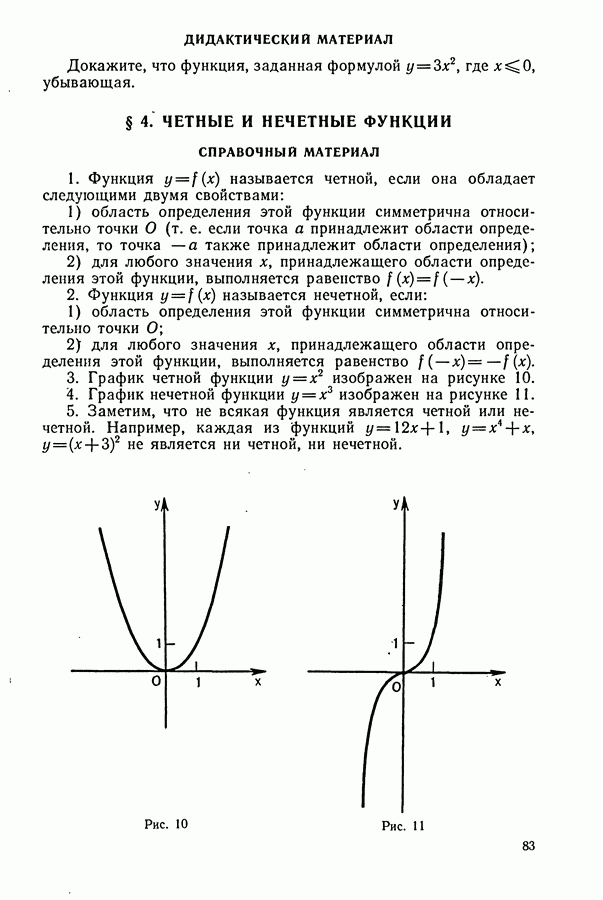
- § 4. ЧЕТНЫЕ И НЕЧЕТНЫЕ ФУНКЦИИ СПРАВОЧНЫЙ МАТЕРИАЛ
- § 5. ПЕРИОДИЧЕСКИЕ ФУНКЦИИ
- § 6. ПРОМЕЖУТКИ ЗНАКОПОСТОЯНСТВА И КОРНИ ФУНКЦИИ
- Контрольные вопросы
- ГЛАВА IX
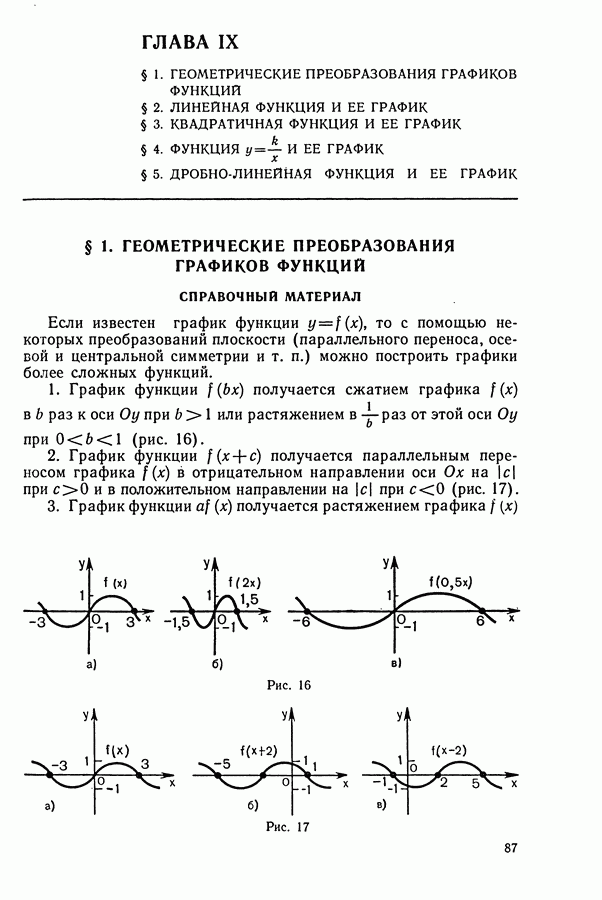
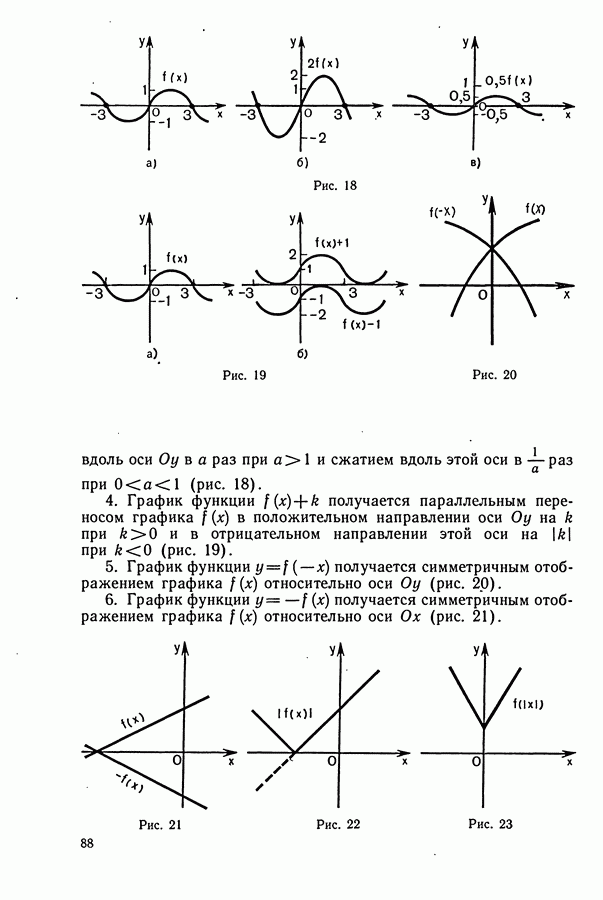
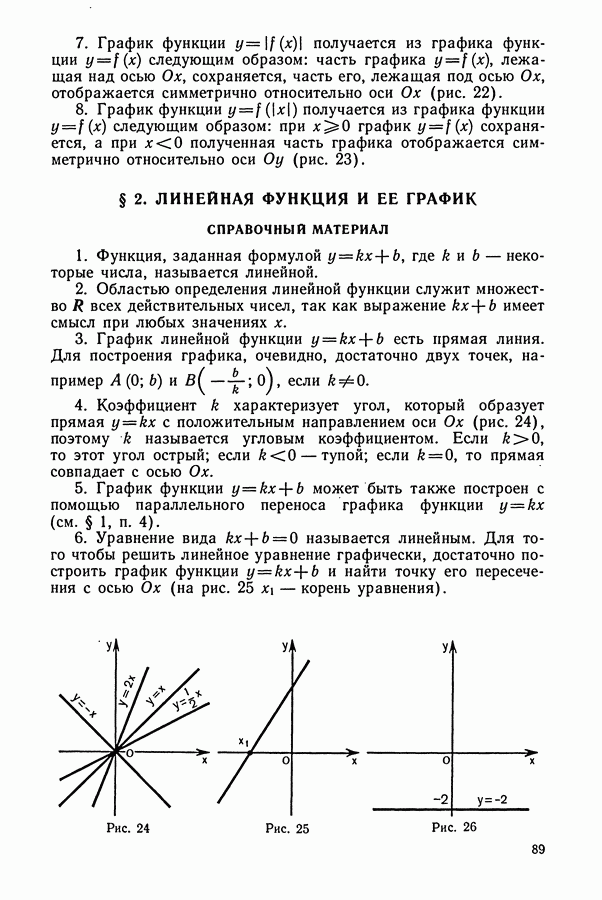
- § 1. ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ ГРАФИКОВ ФУНКЦИЙ
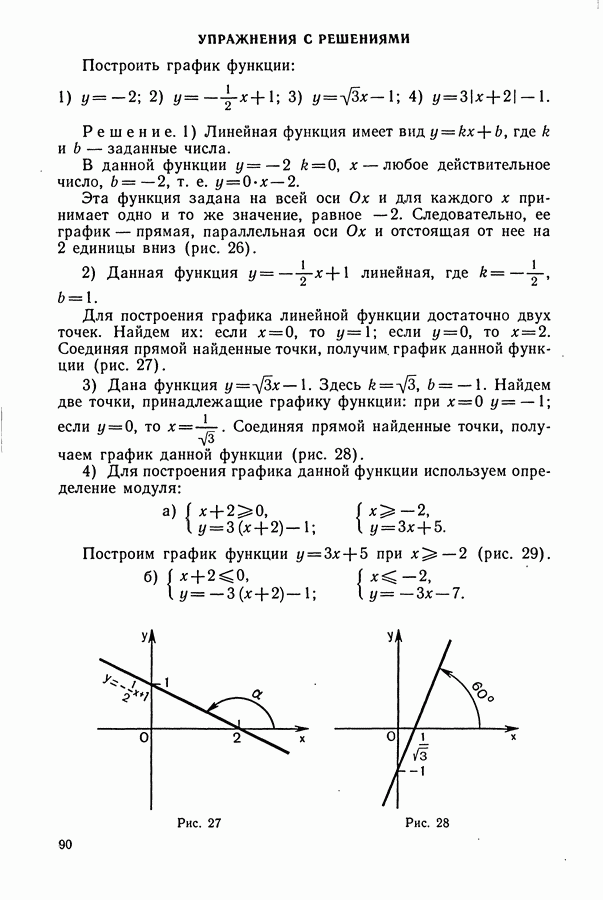
- § 2. ЛИНЕЙНАЯ ФУНКЦИЯ И ЕЕ ГРАФИК
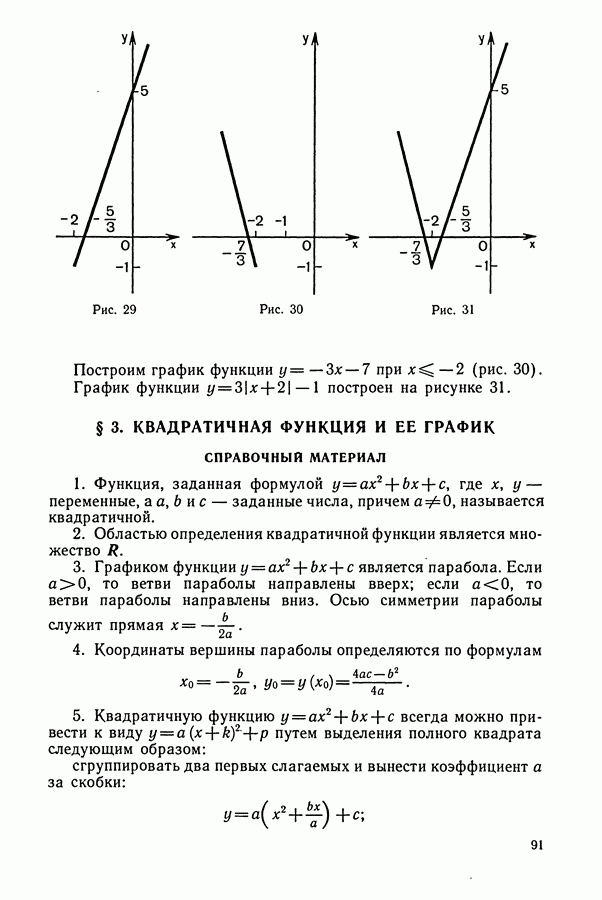
- § 3. КВАДРАТИЧНАЯ ФУНКЦИЯ И ЕЕ ГРАФИК
- § 4. ФУНКЦИЯ y=k/x И ЕЕ ГРАФИК
- § 5. ДРОБНО-ЛИНЕЙНАЯ ФУНКЦИЯ И ЕЕ ГРАФИК
- Контрольные вопросы
- ГЛАВА X
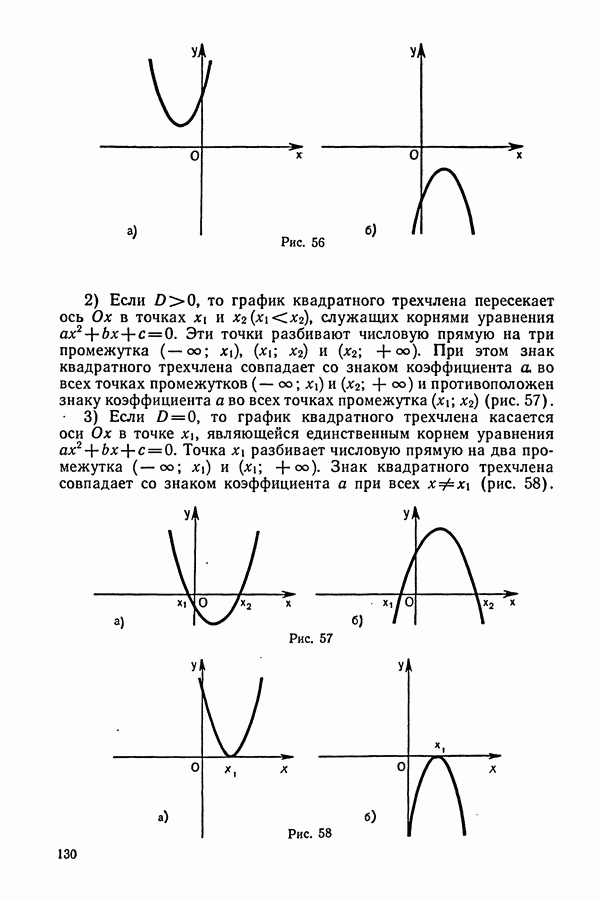
- § 1. КВАДРАТНЫЕ УРАВНЕНИЯ
- § 2. ТЕОРЕМА ВИЕТА
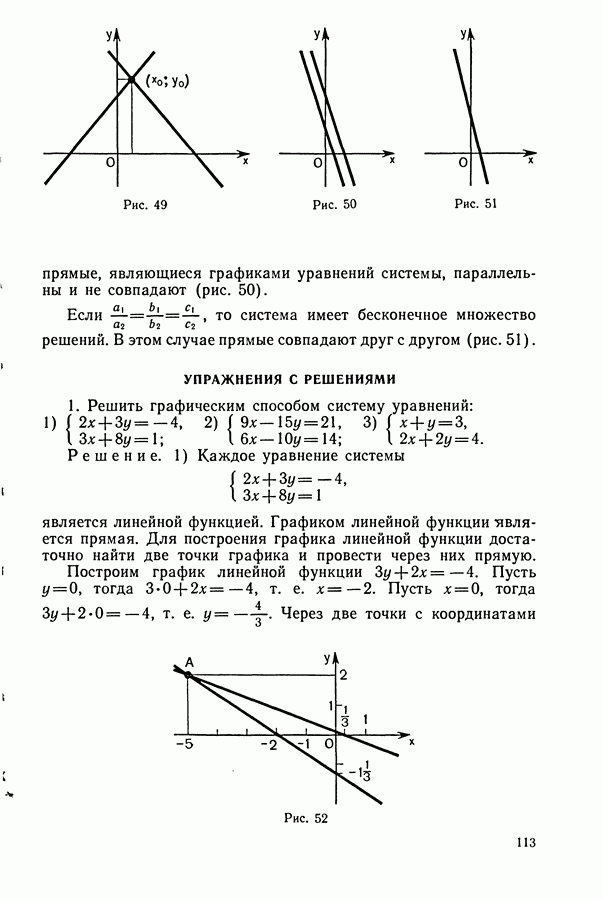
- § 3. ГРАФИЧЕСКИЙ СПОСОБ РЕШЕНИЯ КВАДРАТНЫХ УРАВНЕНИЙ
- § 4. УРАВНЕНИЕ СО МНОГИМИ ПЕРЕМЕННЫМИ
- § 5. СИСТЕМЫ УРАВНЕНИЙ
- Контрольные вопросы
- ГЛАВА XI
- § 1. НЕРАВЕНСТВА
- § 2. ОСНОВНЫЕ СВОЙСТВА НЕРАВЕНСТВ
- § 3. ДЕЙСТВИЯ С НЕРАВЕНСТВАМИ
- § 4. ДОКАЗАТЕЛЬСТВА НЕРАВЕНСТВ
- § 5. НЕРАВЕНСТВА, СОДЕРЖАЩИЕ ПЕРЕМЕННУЮ
- § 6. РЕШЕНИЕ ЛИНЕЙНЫХ И КВАДРАТНЫХ НЕРАВЕНСТВ
- Контрольные вопросы
- ГЛАВА XII
- § 1. СИСТЕМЫ И СОВОКУПНОСТИ НЕРАВЕНСТВ
- § 2. НЕРАВЕНСТВА И СИСТЕМЫ НЕРАВЕНСТВ С ДВУМЯ ПЕРЕМЕННЫМИ
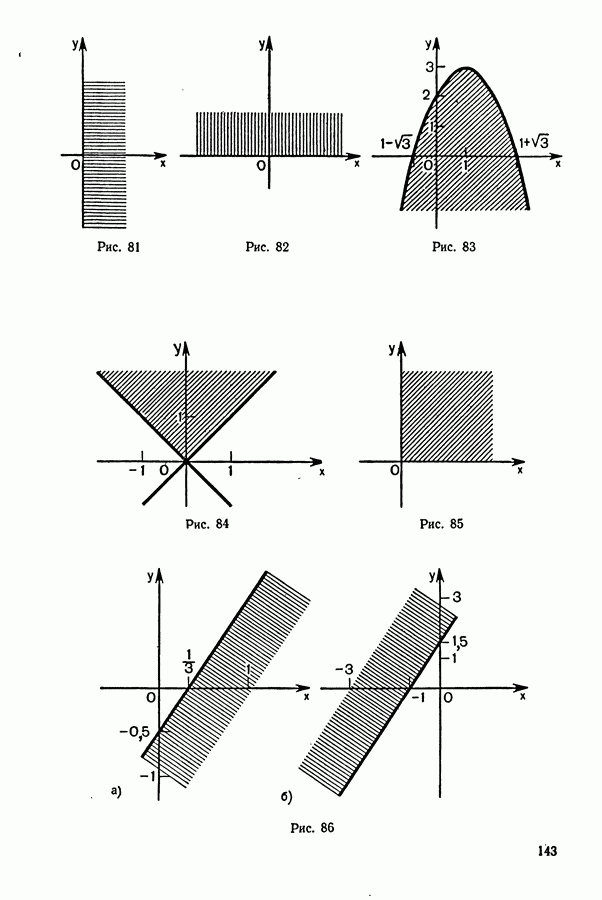
- § 3. РЕШЕНИЕ НЕРАВЕНСТВ, СОДЕРЖАЩИХ ПЕРЕМЕННУЮ ПОД ЗНАКОМ МОДУЛЯ
- § 4. РЕШЕНИЕ РАЦИОНАЛЬНЫХ НЕРАВЕНСТВ МЕТОДОМ ПРОМЕЖУТКОВ
- Контрольные вопросы
- ГЛАВА XIII
- § 1. ЧИСЛОВАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ
- § 2. АРИФМЕТИЧЕСКАЯ ПРОГРЕССИЯ
- § 3. ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИЯ
- § 4. СУММА БЕСКОНЕЧНОЙ ГЕОМЕТРИЧЕСКОЙ ПРОГРЕССИИ ПРИ |q|<1
- Контрольные вопросы
- ГЛАВА XIV
- § 1. ГРАДУСНОЕ ИЗМЕРЕНИЕ УГЛОВЫХ ВЕЛИЧИН
- § 2. РАДИАННОЕ ИЗМЕРЕНИЕ УГЛОВЫХ ВЕЛИЧИН
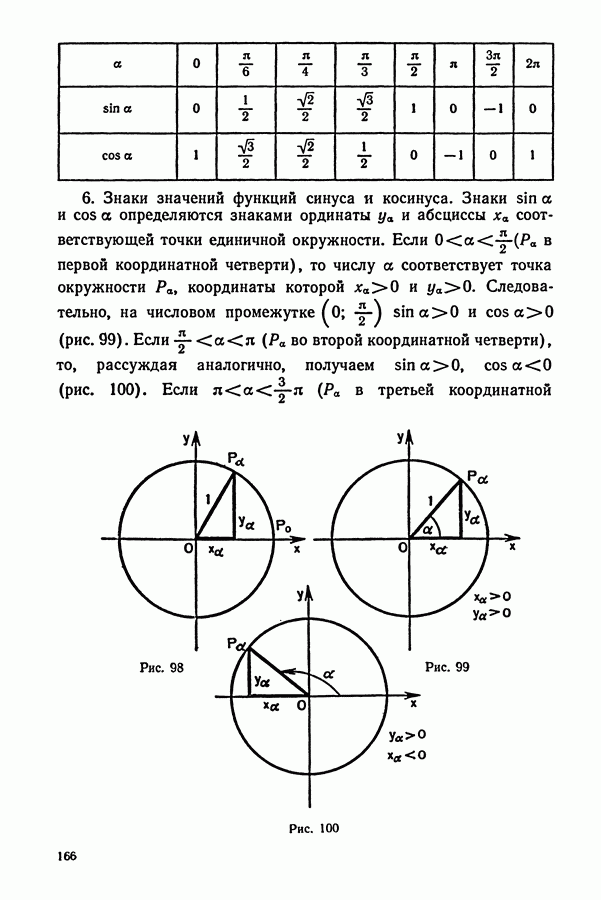
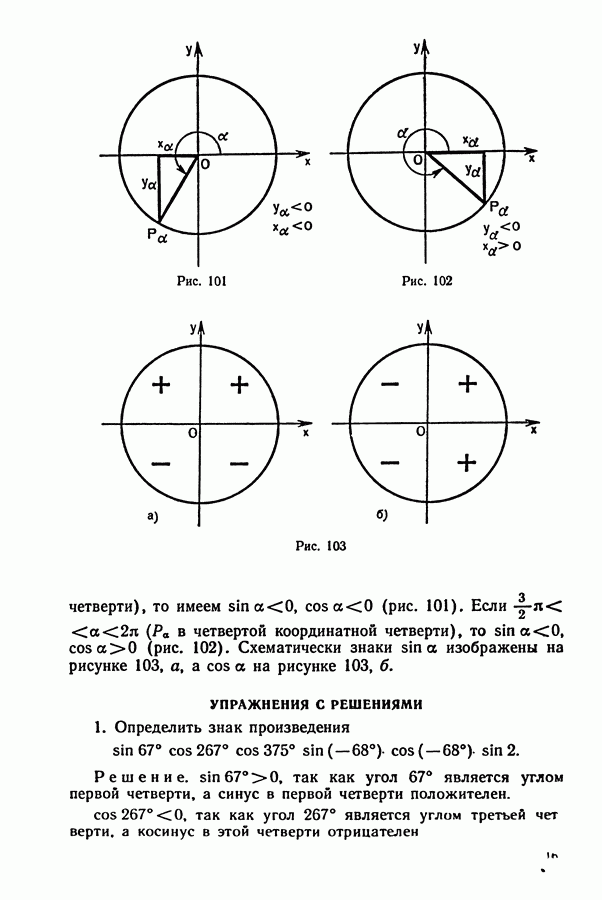
- § 3. СИНУС И КОСИНУС ЧИСЛОВОГО АРГУМЕНТА
- § 4. ТАНГЕНС И КОТАНГЕНС ЧИСЛОВОГО АРГУМЕНТА. СЕКАНС И КОСЕКАНС ЧИСЛА а
- § 5. ОСНОВНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ТОЖДЕСТВА
- § 6. ДОПОЛНИТЕЛЬНЫЕ СВОЙСТВА ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ
- Контрольные вопросы
- ГЛАВА XV
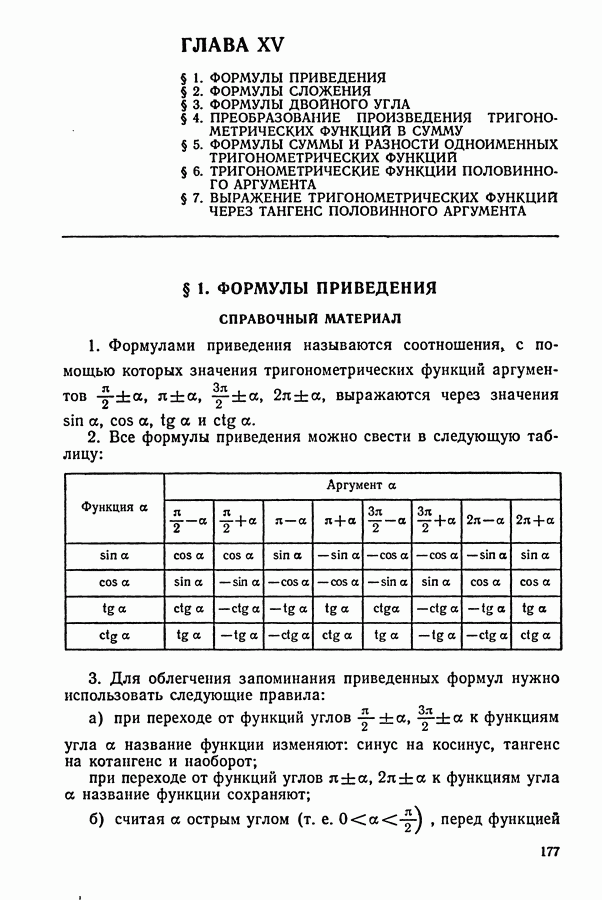
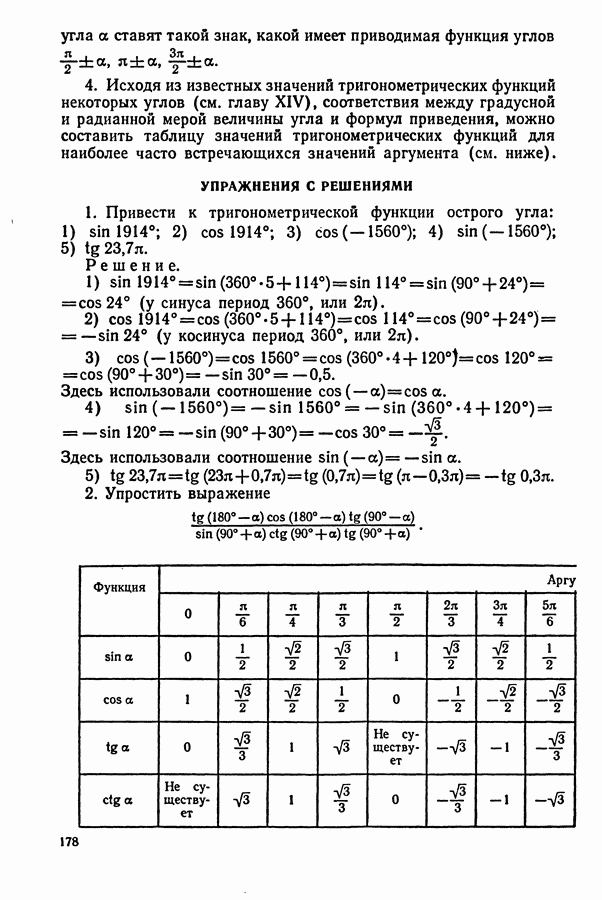
- § 1. ФОРМУЛЫ ПРИВЕДЕНИЯ
- § 2. ФОРМУЛЫ СЛОЖЕНИЯ
- § 3. ФОРМУЛЫ ДВОЙНОГО УГЛА СПРАВОЧНЫЙ МАТЕРИАЛ
- § 4. ПРЕОБРАЗОВАНИЕ ПРОИЗВЕДЕНИЯ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ В СУММУ
- § 5. ФОРМУЛЫ СУММЫ И РАЗНОСТИ ОДНОИМЕННЫХ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ
- § 6. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ ПОЛОВИННОГО АРГУМЕНТА
- § 7. ВЫРАЖЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ ЧЕРЕЗ ТАНГЕНС ПОЛОВИННОГО АРГУМЕНТА
- Контрольные вопросы
- ГЛАВА XVI
- § 1. СВОЙСТВА ФУНКЦИИ y = sin(x) И ЕЕ ГРАФИК
- § 2. СВОЙСТВА ФУНКЦИ И у = cos(x) И ЕЕ ГРАФИК
- § 3. СВОЙСТВА ФУНКЦИ И у=tg(x) И ЕЕ ГРАФИК
- § 4. СВОЙСТВА ФУНКЦИ И y=ctg(x) И ЕЕ ГРАФИК
- § 5. НАХОЖДЕНИЕ ПЕРИОДОВ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ
- Контрольные вопросы
- ГЛАВА XVII
- § 1. АРКСИНУС И АРККОСИНУС
- § 2. АРКТАНГЕНС И АРККОТАНГЕНС
- Контрольные вопросы
- ГЛАВА XVIII
- § 1. РЕШЕНИЕ УРАВНЕНИЙ ВИДА cos(x)=а
- § 2. РЕШЕНИЕ УРАВНЕНИЙ ВИДА sin(x)=a
- § 3. РЕШЕНИЕ УРАВНЕНИЙ ВИДА tg(х)=а
- § 4. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ, ПРИВОДИМЫХ К КВАДРАТНОМУ
- § 5. РЕШЕНИЕ ОДНОРОДНЫХ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ
- § 6. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ, РЕШАЕМЫЕ С ПОМОЩЬЮ ФОРМУЛ СЛОЖЕНИЯ, ПОНИЖЕНИЯ СТЕПЕНИ
- § 7. РЕШЕНИЕ СИСТЕМ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ
- Контрольные вопросы
- ГЛАВА XIX
- § 1. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ ВИДА sin(х) > а, sin(х) < а
- § 2. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ ВИДА cos(x) > a, cos(x) < a
- § 3. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ ВИДА tg(х) > a, tg(х) < a
- § 4. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ
- ГЛАВА XX
- § 1. ПРИРАЩЕНИЕ АРГУМЕНТА И ПРИРАЩЕНИЕ ФУНКЦИИ
- § 2. ПРЕДЕЛ ФУНКЦИИ
- § 3. НЕПРЕРЫВНОСТЬ ФУНКЦИИ
- § 4. ОПРЕДЕЛЕНИЕ ПРОИЗВОДНОЙ
- § 5. ПРОИЗВОДНАЯ СУММЫ, ПРОИЗВЕДЕНИЯ, ЧАСТНОГО
- § 6. ПРОИЗВОДНАЯ СТЕПЕННОЙ И СЛОЖНОЙ ФУНКЦИИ
- § 7. ПРОИЗВОДНЫЕ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ
- Контрольные вопросы
- ГЛАВА XXI
- § 1. ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ К НАХОЖДЕНИЮ ПРОМЕЖУТКОВ МОНОТОННОСТИ ФУНКЦИИ
- § 2. КРИТИЧЕСКИЕ ТОЧКИ ФУНКЦИИ, ЕЕ МАКСИМУМЫ И МИНИМУМЫ
- § 3. ОБЩАЯ СХЕМА ИССЛЕДОВАНИЯ ФУНКЦИИ
- § 4. ЗАДАЧИ НА НАХОЖДЕНИЕ НАИМЕНЬШЕГО И НАИБОЛЬШЕГО ЗНАЧЕНИЯ ФУНКЦИИ
- Контрольные вопросы
- ГЛАВА XXII
- § 1. ФОРМУЛЫ ПРИБЛИЖЕННЫХ ВЫЧИСЛЕНИЙ СПРАВОЧНЫЙ МАТЕРИАЛ
- § 2. КАСАТЕЛЬНАЯ К ГРАФИКУ ФУНКЦИИ
- § 3. СКОРОСТЬ И УСКОРЕНИЕ В ДАННЫЙ МОМЕНТ ВРЕМЕНИ
- § 4. ГРАФИКИ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ
- Контрольные вопросы
- ГЛАВА XXIII
- § 1. ПОТЕРЯННЫЕ И ПОСТОРОННИЕ КОРНИ ПРИ РЕШЕНИИ УРАВНЕНИЙ (НА ПРИМЕРАХ)
- § 2. ПОСТОРОННИЕ КОРНИ ИРРАЦИОНАЛЬНОГО УРАВНЕНИЯ (НА ПРИМЕРАХ)
- § 3. РЕШЕНИЕ ИРРАЦИОНАЛЬНЫХ УРАВНЕНИЙ
- § 4. РЕШЕНИЕ ИРРАЦИОНАЛЬНЫХ НЕРАВЕНСТВ СПРАВОЧНЫЙ МАТЕРИАЛ
- Контрольные вопросы
- ГЛАВА XXIV
- § 1. ПОКАЗАТЕЛЬНАЯ ФУНКЦИЯ, ЕЕ СВОЙСТВА И ГРАФИК
- § 2. ПОКАЗАТЕЛЬНЫЕ УРАВНЕНИЯ
- § 3. ПОКАЗАТЕЛЬНЫЕ НЕРАВЕНСТВА
- § 4. СИСТЕМЫ ПОКАЗАТЕЛЬНЫХ УРАВНЕНИЙ И НЕРАВЕНСТВ
- Контрольные вопросы
- ГЛАВА XXV
- § 1. ОБРАТНАЯ ФУНКЦИЯ
- § 2. ПОНЯТИЕ ЛОГАРИФМА
- § 3. СВОЙСТВА ЛОГАРИФМОВ
- § 4. ЛОГАРИФМИЧЕСКАЯ ФУНКЦИЯ, ЕЕ СВОЙСТВА И ГРАФИК
- § 5. ТЕОРЕМЫ О ЛОГАРИФМЕ ПРОИЗВЕДЕНИЯ, ЧАСТНОГО И СТЕПЕНИ. ФОРМУЛА ПЕРЕХОДА К НОВОМУ ОСНОВАНИЮ
- § 6. ДЕСЯТИЧНЫЕ ЛОГАРИФМЫ И ИХ СВОЙСТВА
- § 7. ЛОГАРИФМИРОВАНИЕ И ПОТЕНЦИРОВАНИЕ
- Контрольные вопросы
- ГЛАВА XXVI
- § 1. ЛОГАРИФМИЧЕСКИЕ УРАВНЕНИЯ
- § 2. ЛОГАРИФМИЧЕСКИЕ НЕРАВЕНСТВА
- § 3. СИСТЕМЫ ЛОГАРИФМИЧЕСКИХ УРАВНЕНИЙ И НЕРАВЕНСТВ
- § 4. ПРОИЗВОДНЫЕ ЛОГАРИФМИЧЕСКОЙ И ПОКАЗАТЕЛЬНОЙ ФУНКЦИЙ. ЧИСЛО e
- Контрольные вопросы
- ГЛАВА XXVII
- § 1. ПОНЯТИЕ ПЕРВООБРАЗНОЙ ФУНКЦИИ
- § 2. ОСНОВНОЕ СВОЙСТВО ПЕРВООБРАЗНОЙ ФУНКЦИИ
- § 3. ТРИ ПРАВИЛА НАХОЖДЕНИЯ ПЕРВООБРАЗНЫХ
- § 4. КРИВОЛИНЕЙНАЯ ТРАПЕЦИЯ И ЕЕ ПЛОЩАДЬ
- Контрольные вопросы
- ГЛАВА XXVIII
- § 1. ФОРМУЛА НЬЮТОНА—ЛЕЙБНИЦА
- § 2. ОСНОВНЫЕ ПРАВИЛА ИНТЕГРИРОВАНИЯ
- § 3. ВЫЧИСЛЕНИЕ ПЛОЩАДЕЙ С ПОМОЩЬЮ ИНТЕГРАЛА
- § 4. МЕХАНИЧЕСКИЕ И ФИЗИЧЕСКИЕ ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
- ПРИЛОЖЕНИЕ
- Введение
- 1. Задачи на движение
- 2. Задачи на совместную работу
- 3. Задачи на планирование
- 4. Задачи на зависимость между компонентами арифметических действий
- 5. Задачи на проценты
- 6. Задачи на смеси (сплавы)
- 7. Задачи на разбавление