| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
4. Задачи на зависимость между компонентами арифметических действий
Составление уравнений в задачах данного раздела вытекает непосредственно из условия задачи.
Задачи, в которых требуется найти сумму слагаемых, каждое из которых составляет ту или иную часть искомой суммы
Задача (№ 13.040). Трое изобретателей получили за свое изобретение премию в размере  причем второй получил того, что получил первый, и еще
причем второй получил того, что получил первый, и еще  , а третий получил
, а третий получил  денег второго и еще
денег второго и еще  Какую премию получил каждый? Решение.
Какую премию получил каждый? Решение.
1. Пусть первый изобретатель получил х рублей.
2. Тогда второй получил  рублей, третий получил
рублей, третий получил  рублей.
рублей.
3. Из условия следует  откуда
откуда 
Ответ. 
Решите задачи:
1. Задача (№ 13.015). Турист проехал расстояние между двумя городами за 3 дня. В первый день он проехал всего пути и еще 60 км, во второй всего пути и еще 20 км и в третий день  всего пути и оставшиеся 25 км. Найти расстояние между городами.
всего пути и оставшиеся 25 км. Найти расстояние между городами.
2. Задача (№ 13.018). Вкладчик взял из сберкассы сначала
 своих денег, потом оставшихся и еще
своих денег, потом оставшихся и еще  После этого у него осталось на сберкнижке — всех его денег. Как велик был вклад?
После этого у него осталось на сберкнижке — всех его денег. Как велик был вклад?
3. Задача (№ 13.092). Денежная премия была распределена между тремя изобретателями: первый получил половину всей премии без части того, что получили двое других вместе; второй получил  часть всей премии и часть денег, полученных вместе с остальными двумя; третий получил
часть всей премии и часть денег, полученных вместе с остальными двумя; третий получил  Как велика была премия и сколько денег получил каждый изобретатель?
Как велика была премия и сколько денег получил каждый изобретатель?
Ответ. 1. 400 км. 2. 240 р. 3. 950 р., 400 р., 250 р., 300 р.
Задачи, в которых используется формула двузначного числа
Задача (13.027). Сумма квадратов цифр двузначного числа равна 13. Если от этого числа отнять 9, то получим число, записанное теми же цифрами, но в обратном порядке. Найти число.
Решение.
1. Пусть х — цифра десятков,
у — цифра единиц,
 — искомое двузначное число.
— искомое двузначное число.
2. Из условия задачи следует:

 — не подходит, так как х — цифра).
— не подходит, так как х — цифра).
Ответ. 32.
Решите задачи:
1. Задача (№ 13.119). Произведение цифр двузначного числа в 3 раза меньше самого числа. Если к искомому числу прибавить 18, то получится число, написанное теми же цифрами, но в обратном порядке. Найти это число.
2. Задача (№ 13.160). Если двузначное число разделить на сумму его цифр, то получится в частном 4 и в остатке 3. Если же это число разделить на произведение его цифр, то получится в частном 3 и в остатке 5. Найти это число.
Ответы. 1. 24. 2. 23.
Задачи, в которых слагаемые пропорциональны некоторым числам (или дано их отношение)
Задача (№ 13.028). Числители трех дробей пропорциональны числам 1, 2, 5, а знаменатели соответственно пропорциональны
числам 1, 3, 7. Среднее арифметическое этих дробей равно 222. Найти эти дроби.
Решение.
1. Числители дробей:  (по условию задачи).
(по условию задачи).
2. Знаменатели дробей:  (по условию задачи).
(по условию задачи).
3. Дроби: 
4. Из условия задачи следует:

 первая дробь;
первая дробь;
 вторая дробь;
вторая дробь;
 третья дробь.
третья дробь.
Ответ. 
Решите задачи:
1. Задача (№ 13.042). Площади трех участков земли находятся в отношении Известно, что с первого участка собрано зерна на  больше, чем со второго. Найти площадь всех трех участков, если средняя урожайность составляет
больше, чем со второго. Найти площадь всех трех участков, если средняя урожайность составляет 
2. Задача (№ 13.048). Длина Дуная относится к длине Днепра как 6-5-: 5, а длина Дона относится к длине Дуная как  Найти протяженность каждой из рек, если Днепр длиннее Дона на 300 км.
Найти протяженность каждой из рек, если Днепр длиннее Дона на 300 км.
Ответы. 1. 26 га. 2. 2850 км, 2250 км, 1950 км.
Задачи, где неизвестные являются членами прогрессии (или пропорции)
Задача (№ 13.061). Для оплаты пересылки четырех бандеролей понадобились 4 различные почтовые марки на общую сумму  . Определить стоимость марок, приобретенных отправителем, если эти стоимости составляют арифметическую прогрессию, а самая дорогая марка в 2,5 раза дороже самой дешевой.
. Определить стоимость марок, приобретенных отправителем, если эти стоимости составляют арифметическую прогрессию, а самая дорогая марка в 2,5 раза дороже самой дешевой.
Решение.
1. Пусть х рублей — стоимость самой дешевой марки.
2. Тогда 2,5 рублей — стоимость самой дорогой марки.
3. Стоимость всех четырех марок по условию есть сумма членов арифметической прогрессии, т. е. 
4. Из формулы общего члена прогрессии имеем: 

Ответ. 0,4; 0,6; 0,8; 1.
Решите задачи:
1. Задача (№ 13.144). Сумму всех четных двузначных чисел разделили на одно из них. Остатка не было. Получившееся частное только порядком цифр отличается от делителя, а сумма его цифр равна девяти. Какое двузначное число являлось делителем?
2. Задача (№ 13.211). Цифры некоторого трехзначного числа составляют геометрическую прогрессию. Если в этом числе поменять местами цифры сотен и единиц, то новое трехзначное число будет на 594 меньше искомого. Если же в искомом числе зачеркнуть цифру сотен и в полученном двузначном числе переставить его цифры, то новое двузначное число будет на 18 меньше числа, выраженного двумя последними цифрами искомого числа. Найти это число.
3. Задача (№ 13.299). Найти четыре числа, образующих пропорцию, если известно, что сумма крайних членов равна 14, сумма средних членов равна 11, а сумма квадратов таких четырех чисел равна 221.
Ответы. 1. 54. 2. 842. 3. 12; 8; 3; 2.
Задачи, компонентами которых являются геометрические величины
Задача (№ 13.057). Две силы приложены к одной точке и направлены под прямым углом. Величина одной из них на 4 Н больше величины другой, а величина равнодействующей на 8 Н меньше суммы величин данных сил. Найти величины данных сил и их равнодействующей (рис. 257).
Решение.
1. I сила —  .
.
2. II сила —  .
.
3. Равнодействующая сил:


Рис. 257
4. Из прямоугольного треугольника  следует
следует

 — не удовлетворяет условию задачи.
— не удовлетворяет условию задачи.
5. Следовательно, 12 Н - I сила,
 - II сила,
- II сила,
 — равнодействующая сила.
— равнодействующая сила.
Ответ. 12 Н; 16 Н; 20 Н.
Решите задачи:
1. Задача (№ 13.059). По обе стороны улицы длиной  во вновь разбиваемом поселке лежат прямоугольные полосы земли, отведенные на участки: одна шириной
во вновь разбиваемом поселке лежат прямоугольные полосы земли, отведенные на участки: одна шириной  а другая —
а другая —  На сколько участков разбит весь поселок, если более узкая полоса содержит на 5 участков больше, чем широкая, при условии, что на узкой полосе каждый участок на
На сколько участков разбит весь поселок, если более узкая полоса содержит на 5 участков больше, чем широкая, при условии, что на узкой полосе каждый участок на  меньше, чем каждый участок на широкой полосе?
меньше, чем каждый участок на широкой полосе?
2. Задача (№ 13.147). Имеется лист жести в форме прямоугольника, у которого отношение длины к ширине равно  Из этого листа изготовлена открытая сверху коробка таким образом, что по углам листа вырезано по квадрату со стороной 3 см и получившиеся края загнуты. Определить размеры листа жести, если объем коробки оказался равным
Из этого листа изготовлена открытая сверху коробка таким образом, что по углам листа вырезано по квадрату со стороной 3 см и получившиеся края загнуты. Определить размеры листа жести, если объем коробки оказался равным 
3. Задача (№ 13.191). К материальной точке приложены две силы, угол между которыми равен 30°. Величина одной из приложенных сил в  раза больше величины другой, а величина равнодействующей силы на 24 Н больше, чем величина меньшей силы. Определить величину меньшей силы и равнодействующей силы.
раза больше величины другой, а величина равнодействующей силы на 24 Н больше, чем величина меньшей силы. Определить величину меньшей силы и равнодействующей силы.
4. Задача  Величины двух сил, действующих на материальную точку под прямым углом, и величина их равнодействующей составляют арифметическую прогрессию. Определить, в каком отношении находятся величины сил.
Величины двух сил, действующих на материальную точку под прямым углом, и величина их равнодействующей составляют арифметическую прогрессию. Определить, в каком отношении находятся величины сил.
Ответы. 1. На 45. 2. 
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ГЛАВА I.
- § 1. НАТУРАЛЬНЫЕ ЧИСЛА И ДЕЙСТВИЯ НАД НИМИ
- § 2. СЛОЖЕНИЕ И ЗАКОНЫ СЛОЖЕНИЯ
- § 3. ВЫЧИТАНИЕ
- § 4. УМНОЖЕНИЕ И ЗАКОНЫ УМНОЖЕНИЯ
- § 5. ДЕЛЕНИЕ
- § 6. ПРИЗНАКИ ДЕЛИМОСТИ ЧИСЕЛ
- § 7. ПОНЯТИЕ МНОЖЕСТВА
- § 8. ОПЕРАЦИИ НАД МНОЖЕСТВАМИ
- § 9. ВЗАИМНО ОДНОЗНАЧНОЕ СООТВЕТСТВИЕ
- § 10. ПРОСТЫЕ И СОСТАВНЫЕ ЧИСЛА
- § 11. НАИБОЛЬШИЙ ОБЩИЙ ДЕЛИТЕЛЬ
- § 12. НАИМЕНЬШЕЕ ОБЩЕЕ КРАТНОЕ
- Контрольные вопросы
- ГЛАВА II
- § 1. ОБЫКНОВЕННЫЕ ДРОБИ
- § 2. ПРАВИЛЬНЫЕ И НЕПРАВИЛЬНЫЕ ДРОБИ
- § 3. ОСНОВНОЕ СВОЙСТВО ДРОБИ
- § 4. СЛОЖЕНИЕ И ВЫЧИТАНИЕ ДРОБЕЙ
- § 5. УМНОЖЕНИЕ ДРОБЕЙ
- § 6. ДЕЛЕНИЕ ДРОБЕЙ
- § 7. ДЕСЯТИЧНЫЕ ДРОБИ
- § 8. ОБРАЩЕНИЕ ДЕСЯТИЧНОЙ ДРОБИ В ОБЫКНОВЕННУЮ И ОБЫКНОВЕННОЙ В ДЕСЯТИЧНУЮ. ПЕРИОДИЧЕСКИЕ ДРОБИ
- § 9. ОТНОШЕНИЕ. ПРОПОРЦИЯ
- § 10. СВОЙСТВА ПРОПОРЦИИ
- § 11. ПРОЦЕНТ. ОСНОВНЫЕ ЗАДАЧИ НА ПРОЦЕНТЫ
- § 12. ДЕЛЕНИЕ ЧИСЛА НА ЧАСТИ, ПРЯМО И ОБРАТНО ПРОПОРЦИОНАЛЬНЫЕ ДАННЫМ ЧИСЛАМ
- Контрольные вопросы
- ГЛАВА III
- § 1. КООРДИНАТНАЯ ПРЯМАЯ
- § 2. МНОЖЕСТВО ЦЕЛЫХ ЧИСЕЛ
- § 3. МНОЖЕСТВО РАЦИОНАЛЬНЫХ ЧИСЕЛ
- § 4. МОДУЛЬ ЧИСЛА
- § 5. СРАВНЕНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ
- § 6. СЛОЖЕНИЕ И ВЫЧИТАНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ
- § 7. УМНОЖЕНИЕ И ДЕЛЕНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ
- § 8. ВОЗВЕДЕНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ В СТЕПЕНЬ С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ
- Контрольные вопросы
- ГЛАВА IV
- § 1. СВОЙСТВА СТЕПЕНИ С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ
- § 2. ЧИСЛОВЫЕ ВЫРАЖЕНИЯ
- § 3. ВЫРАЖЕНИЯ С ПЕРЕМЕННЫМИ
- § 4. ТОЖДЕСТВЕННО РАВНЫЕ ВЫРАЖЕНИЯ
- § 5. ОДНОЧЛЕНЫ
- § 6. МНОГОЧЛЕНЫ
- § 7. ПРЕОБРАЗОВАНИЕ СУММЫ И РАЗНОСТИ МНОГОЧЛЕНОВ
- § 8. УМНОЖЕНИЕ МНОГОЧЛЕНА НА ОДНОЧЛЕН И МНОГОЧЛЕНА НА МНОГОЧЛЕН
- § 9. РАЗЛОЖЕНИЕ МНОГОЧЛЕНА НА МНОЖИТЕЛИ СПОСОБОМ ВЫНЕСЕНИЯ ОБЩЕГО МНОЖИТЕЛЯ ЗА СКОБКИ
- § 10. РАЗЛОЖЕНИЕ МНОГОЧЛЕНА НА МНОЖИТЕЛИ СПОСОБОМ ГРУППИРОВКИ
- § 11. ФОРМУЛЫ СОКРАЩЕННОГО УМНОЖЕНИЯ
- Контрольные вопросы
- ГЛАВА V
- § 1. ДРОБЬ
- § 2. ЦЕЛЫЕ И ДРОБНЫЕ ВЫРАЖЕНИЯ
- § 3. ТОЖДЕСТВЕННОЕ ПРЕОБРАЗОВАНИЕ СУММЫ И РАЗНОСТИ ДВУХ ДРОБЕЙ
- § 4. ТОЖДЕСТВЕННОЕ ПРЕОБРАЗОВАНИЕ ПРОИЗВЕДЕНИЯ И ЧАСТНОГО ДВУХ ДРОБЕЙ
- § 5. СТЕПЕНЬ ДРОБИ
- Контрольные вопросы
- ГЛАВА VI
- § 1. ПОНЯТИЕ ОБ ИРРАЦИОНАЛЬНОМ ЧИСЛЕ
- § 2. РАЗВИТИЕ ПОНЯТИЯ О ЧИСЛЕ. МНОЖЕСТВО ДЕЙСТВИТЕЛЬНЫХ ЧИСЕЛ
- § 3. КОРЕНЬ СТЕПЕНИ ИЗ ДЕЙСТВИТЕЛЬНОГО ЧИСЛА
- § 4. АЛГОРИТМ ИЗВЛЕЧЕНИЯ КВАДРАТНОГО КОРНЯ ИЗ ЧИСЛА
- § 5. АРИФМЕТИЧЕСКИЕ ДЕЙСТВИЯ С ДЕЙСТВИТЕЛЬНЫМИ ЧИСЛАМИ
- § 6. ПРЕОБРАЗОВАНИЯ АРИФМЕТИЧЕСКИХ КОРНЕЙ
- § 7. СТЕПЕНЬ С ЦЕЛЫМ И ДРОБНЫМ ПОКАЗАТЕЛЕМ
- Контрольные вопросы
- ГЛАВА VII
- § 1. УРАВНЕНИЯ С ОДНОЙ ПЕРЕМЕННОЙ
- § 2. ПОНЯТИЕ О РАВНОСИЛЬНОСТИ УРАВНЕНИЙ
- § 3. СВОЙСТВА ЧИСЛОВЫХ РАВЕНСТВ И ТЕОРЕМЫ О РАВНОСИЛЬНОСТИ УРАВНЕНИЙ
- § 4. ЛИНЕЙНОЕ УРАВНЕНИЕ С ОДНОЙ ПЕРЕМЕННОЙ, СОДЕРЖАЩЕЕ ПАРАМЕТР
- Контрольные вопросы
- ГЛАВА VIII
- § 1. ПОНЯТИЕ ФУНКЦИИ
- § 2. СПОСОБЫ ЗАДАНИЯ ФУНКЦИИ
- § 3. МОНОТОННОСТЬ ФУНКЦИИ
- § 4. ЧЕТНЫЕ И НЕЧЕТНЫЕ ФУНКЦИИ СПРАВОЧНЫЙ МАТЕРИАЛ
- § 5. ПЕРИОДИЧЕСКИЕ ФУНКЦИИ
- § 6. ПРОМЕЖУТКИ ЗНАКОПОСТОЯНСТВА И КОРНИ ФУНКЦИИ
- Контрольные вопросы
- ГЛАВА IX
- § 1. ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ ГРАФИКОВ ФУНКЦИЙ
- § 2. ЛИНЕЙНАЯ ФУНКЦИЯ И ЕЕ ГРАФИК
- § 3. КВАДРАТИЧНАЯ ФУНКЦИЯ И ЕЕ ГРАФИК
- § 4. ФУНКЦИЯ y=k/x И ЕЕ ГРАФИК
- § 5. ДРОБНО-ЛИНЕЙНАЯ ФУНКЦИЯ И ЕЕ ГРАФИК
- Контрольные вопросы
- ГЛАВА X
- § 1. КВАДРАТНЫЕ УРАВНЕНИЯ
- § 2. ТЕОРЕМА ВИЕТА
- § 3. ГРАФИЧЕСКИЙ СПОСОБ РЕШЕНИЯ КВАДРАТНЫХ УРАВНЕНИЙ
- § 4. УРАВНЕНИЕ СО МНОГИМИ ПЕРЕМЕННЫМИ
- § 5. СИСТЕМЫ УРАВНЕНИЙ
- Контрольные вопросы
- ГЛАВА XI
- § 1. НЕРАВЕНСТВА
- § 2. ОСНОВНЫЕ СВОЙСТВА НЕРАВЕНСТВ
- § 3. ДЕЙСТВИЯ С НЕРАВЕНСТВАМИ
- § 4. ДОКАЗАТЕЛЬСТВА НЕРАВЕНСТВ
- § 5. НЕРАВЕНСТВА, СОДЕРЖАЩИЕ ПЕРЕМЕННУЮ
- § 6. РЕШЕНИЕ ЛИНЕЙНЫХ И КВАДРАТНЫХ НЕРАВЕНСТВ
- Контрольные вопросы
- ГЛАВА XII
- § 1. СИСТЕМЫ И СОВОКУПНОСТИ НЕРАВЕНСТВ
- § 2. НЕРАВЕНСТВА И СИСТЕМЫ НЕРАВЕНСТВ С ДВУМЯ ПЕРЕМЕННЫМИ
- § 3. РЕШЕНИЕ НЕРАВЕНСТВ, СОДЕРЖАЩИХ ПЕРЕМЕННУЮ ПОД ЗНАКОМ МОДУЛЯ
- § 4. РЕШЕНИЕ РАЦИОНАЛЬНЫХ НЕРАВЕНСТВ МЕТОДОМ ПРОМЕЖУТКОВ
- Контрольные вопросы
- ГЛАВА XIII
- § 1. ЧИСЛОВАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ
- § 2. АРИФМЕТИЧЕСКАЯ ПРОГРЕССИЯ
- § 3. ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИЯ
- § 4. СУММА БЕСКОНЕЧНОЙ ГЕОМЕТРИЧЕСКОЙ ПРОГРЕССИИ ПРИ |q|<1
- Контрольные вопросы
- ГЛАВА XIV
- § 1. ГРАДУСНОЕ ИЗМЕРЕНИЕ УГЛОВЫХ ВЕЛИЧИН
- § 2. РАДИАННОЕ ИЗМЕРЕНИЕ УГЛОВЫХ ВЕЛИЧИН
- § 3. СИНУС И КОСИНУС ЧИСЛОВОГО АРГУМЕНТА
- § 4. ТАНГЕНС И КОТАНГЕНС ЧИСЛОВОГО АРГУМЕНТА. СЕКАНС И КОСЕКАНС ЧИСЛА а
- § 5. ОСНОВНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ТОЖДЕСТВА
- § 6. ДОПОЛНИТЕЛЬНЫЕ СВОЙСТВА ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ
- Контрольные вопросы
- ГЛАВА XV
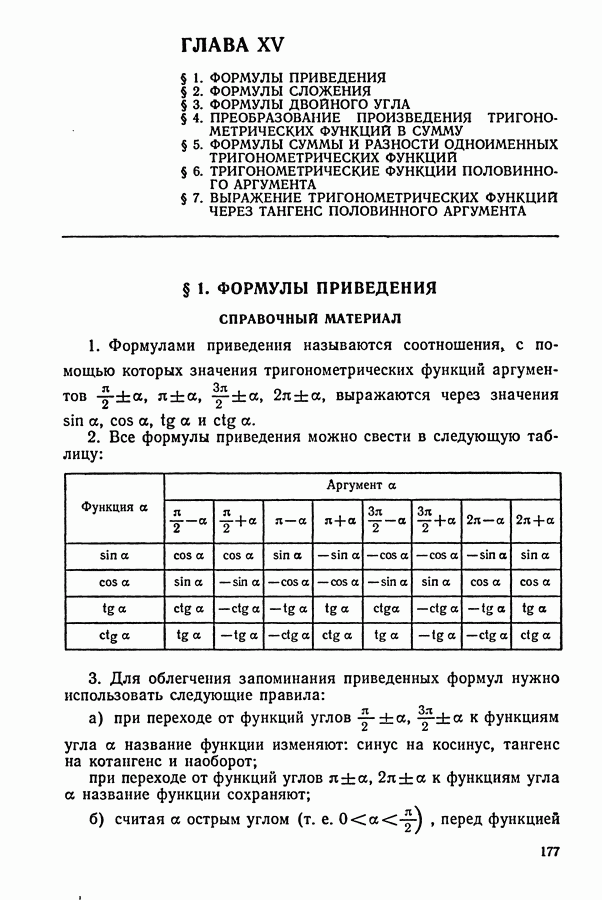
- § 1. ФОРМУЛЫ ПРИВЕДЕНИЯ
- § 2. ФОРМУЛЫ СЛОЖЕНИЯ
- § 3. ФОРМУЛЫ ДВОЙНОГО УГЛА СПРАВОЧНЫЙ МАТЕРИАЛ
- § 4. ПРЕОБРАЗОВАНИЕ ПРОИЗВЕДЕНИЯ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ В СУММУ
- § 5. ФОРМУЛЫ СУММЫ И РАЗНОСТИ ОДНОИМЕННЫХ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ
- § 6. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ ПОЛОВИННОГО АРГУМЕНТА
- § 7. ВЫРАЖЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ ЧЕРЕЗ ТАНГЕНС ПОЛОВИННОГО АРГУМЕНТА
- Контрольные вопросы
- ГЛАВА XVI
- § 1. СВОЙСТВА ФУНКЦИИ y = sin(x) И ЕЕ ГРАФИК
- § 2. СВОЙСТВА ФУНКЦИ И у = cos(x) И ЕЕ ГРАФИК
- § 3. СВОЙСТВА ФУНКЦИ И у=tg(x) И ЕЕ ГРАФИК
- § 4. СВОЙСТВА ФУНКЦИ И y=ctg(x) И ЕЕ ГРАФИК
- § 5. НАХОЖДЕНИЕ ПЕРИОДОВ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ
- Контрольные вопросы
- ГЛАВА XVII
- § 1. АРКСИНУС И АРККОСИНУС
- § 2. АРКТАНГЕНС И АРККОТАНГЕНС
- Контрольные вопросы
- ГЛАВА XVIII
- § 1. РЕШЕНИЕ УРАВНЕНИЙ ВИДА cos(x)=а
- § 2. РЕШЕНИЕ УРАВНЕНИЙ ВИДА sin(x)=a
- § 3. РЕШЕНИЕ УРАВНЕНИЙ ВИДА tg(х)=а
- § 4. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ, ПРИВОДИМЫХ К КВАДРАТНОМУ
- § 5. РЕШЕНИЕ ОДНОРОДНЫХ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ
- § 6. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ, РЕШАЕМЫЕ С ПОМОЩЬЮ ФОРМУЛ СЛОЖЕНИЯ, ПОНИЖЕНИЯ СТЕПЕНИ
- § 7. РЕШЕНИЕ СИСТЕМ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ
- Контрольные вопросы
- ГЛАВА XIX
- § 1. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ ВИДА sin(х) > а, sin(х) < а
- § 2. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ ВИДА cos(x) > a, cos(x) < a
- § 3. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ ВИДА tg(х) > a, tg(х) < a
- § 4. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ
- ГЛАВА XX
- § 1. ПРИРАЩЕНИЕ АРГУМЕНТА И ПРИРАЩЕНИЕ ФУНКЦИИ
- § 2. ПРЕДЕЛ ФУНКЦИИ
- § 3. НЕПРЕРЫВНОСТЬ ФУНКЦИИ
- § 4. ОПРЕДЕЛЕНИЕ ПРОИЗВОДНОЙ
- § 5. ПРОИЗВОДНАЯ СУММЫ, ПРОИЗВЕДЕНИЯ, ЧАСТНОГО
- § 6. ПРОИЗВОДНАЯ СТЕПЕННОЙ И СЛОЖНОЙ ФУНКЦИИ
- § 7. ПРОИЗВОДНЫЕ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ
- Контрольные вопросы
- ГЛАВА XXI
- § 1. ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ К НАХОЖДЕНИЮ ПРОМЕЖУТКОВ МОНОТОННОСТИ ФУНКЦИИ
- § 2. КРИТИЧЕСКИЕ ТОЧКИ ФУНКЦИИ, ЕЕ МАКСИМУМЫ И МИНИМУМЫ
- § 3. ОБЩАЯ СХЕМА ИССЛЕДОВАНИЯ ФУНКЦИИ
- § 4. ЗАДАЧИ НА НАХОЖДЕНИЕ НАИМЕНЬШЕГО И НАИБОЛЬШЕГО ЗНАЧЕНИЯ ФУНКЦИИ
- Контрольные вопросы
- ГЛАВА XXII
- § 1. ФОРМУЛЫ ПРИБЛИЖЕННЫХ ВЫЧИСЛЕНИЙ СПРАВОЧНЫЙ МАТЕРИАЛ
- § 2. КАСАТЕЛЬНАЯ К ГРАФИКУ ФУНКЦИИ
- § 3. СКОРОСТЬ И УСКОРЕНИЕ В ДАННЫЙ МОМЕНТ ВРЕМЕНИ
- § 4. ГРАФИКИ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ
- Контрольные вопросы
- ГЛАВА XXIII
- § 1. ПОТЕРЯННЫЕ И ПОСТОРОННИЕ КОРНИ ПРИ РЕШЕНИИ УРАВНЕНИЙ (НА ПРИМЕРАХ)
- § 2. ПОСТОРОННИЕ КОРНИ ИРРАЦИОНАЛЬНОГО УРАВНЕНИЯ (НА ПРИМЕРАХ)
- § 3. РЕШЕНИЕ ИРРАЦИОНАЛЬНЫХ УРАВНЕНИЙ
- § 4. РЕШЕНИЕ ИРРАЦИОНАЛЬНЫХ НЕРАВЕНСТВ СПРАВОЧНЫЙ МАТЕРИАЛ
- Контрольные вопросы
- ГЛАВА XXIV
- § 1. ПОКАЗАТЕЛЬНАЯ ФУНКЦИЯ, ЕЕ СВОЙСТВА И ГРАФИК
- § 2. ПОКАЗАТЕЛЬНЫЕ УРАВНЕНИЯ
- § 3. ПОКАЗАТЕЛЬНЫЕ НЕРАВЕНСТВА
- § 4. СИСТЕМЫ ПОКАЗАТЕЛЬНЫХ УРАВНЕНИЙ И НЕРАВЕНСТВ
- Контрольные вопросы
- ГЛАВА XXV
- § 1. ОБРАТНАЯ ФУНКЦИЯ
- § 2. ПОНЯТИЕ ЛОГАРИФМА
- § 3. СВОЙСТВА ЛОГАРИФМОВ
- § 4. ЛОГАРИФМИЧЕСКАЯ ФУНКЦИЯ, ЕЕ СВОЙСТВА И ГРАФИК
- § 5. ТЕОРЕМЫ О ЛОГАРИФМЕ ПРОИЗВЕДЕНИЯ, ЧАСТНОГО И СТЕПЕНИ. ФОРМУЛА ПЕРЕХОДА К НОВОМУ ОСНОВАНИЮ
- § 6. ДЕСЯТИЧНЫЕ ЛОГАРИФМЫ И ИХ СВОЙСТВА
- § 7. ЛОГАРИФМИРОВАНИЕ И ПОТЕНЦИРОВАНИЕ
- Контрольные вопросы
- ГЛАВА XXVI
- § 1. ЛОГАРИФМИЧЕСКИЕ УРАВНЕНИЯ
- § 2. ЛОГАРИФМИЧЕСКИЕ НЕРАВЕНСТВА
- § 3. СИСТЕМЫ ЛОГАРИФМИЧЕСКИХ УРАВНЕНИЙ И НЕРАВЕНСТВ
- § 4. ПРОИЗВОДНЫЕ ЛОГАРИФМИЧЕСКОЙ И ПОКАЗАТЕЛЬНОЙ ФУНКЦИЙ. ЧИСЛО e
- Контрольные вопросы
- ГЛАВА XXVII
- § 1. ПОНЯТИЕ ПЕРВООБРАЗНОЙ ФУНКЦИИ
- § 2. ОСНОВНОЕ СВОЙСТВО ПЕРВООБРАЗНОЙ ФУНКЦИИ
- § 3. ТРИ ПРАВИЛА НАХОЖДЕНИЯ ПЕРВООБРАЗНЫХ
- § 4. КРИВОЛИНЕЙНАЯ ТРАПЕЦИЯ И ЕЕ ПЛОЩАДЬ
- Контрольные вопросы
- ГЛАВА XXVIII
- § 1. ФОРМУЛА НЬЮТОНА—ЛЕЙБНИЦА
- § 2. ОСНОВНЫЕ ПРАВИЛА ИНТЕГРИРОВАНИЯ
- § 3. ВЫЧИСЛЕНИЕ ПЛОЩАДЕЙ С ПОМОЩЬЮ ИНТЕГРАЛА
- § 4. МЕХАНИЧЕСКИЕ И ФИЗИЧЕСКИЕ ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
- ПРИЛОЖЕНИЕ
- Введение
- 1. Задачи на движение
- 2. Задачи на совместную работу
- 3. Задачи на планирование
- 4. Задачи на зависимость между компонентами арифметических действий
- 5. Задачи на проценты
- 6. Задачи на смеси (сплавы)
- 7. Задачи на разбавление