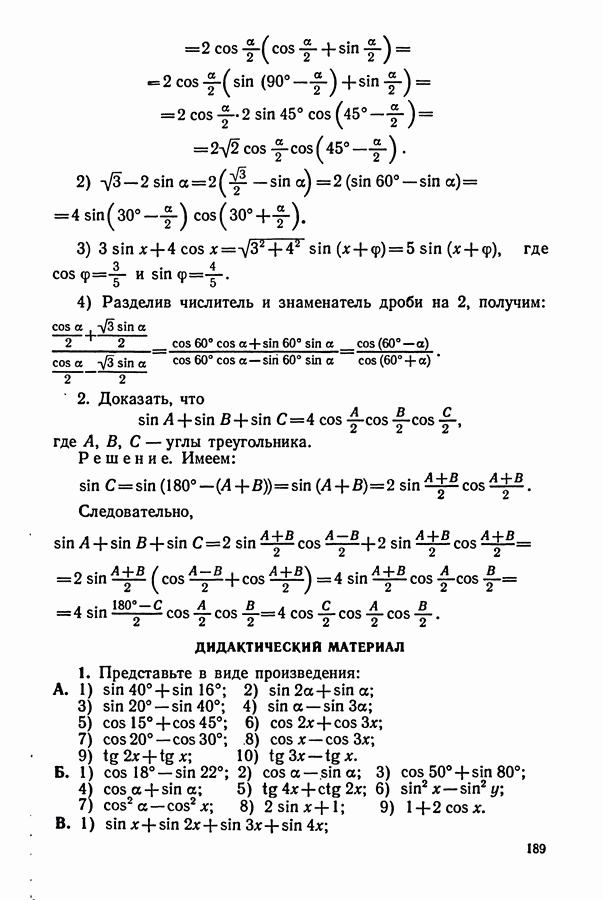| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2. Задачи на совместную работу
Некоторые указания к задачам на совместную работу:
1. Основными компонентами этого типа задач являются: а) работа; б) время; в) производительность труда (работа, выполненная в единицу времени).
2. План решения задачи обычно сводится к следующему:
а) Принимаем всю работу, которую необходимо выполнить, за 1.
б) Находим производительность труда каждого рабочего в отдельности, т. е.  где
где  — время, за которое указанный рабочий может выполнить всю работу, работая отдельно.
— время, за которое указанный рабочий может выполнить всю работу, работая отдельно.
в) Находим ту часть всей работы, которую выполняет каждый рабочий отдельно, за то время, которое он работал.
г) Составляем уравнение, приравнивая объем всей работы (т. е. 1) к сумме слагаемых, каждое из которых есть часть всей работы, выполненная отдельно каждым из рабочих (если, разумеется, в условии сказано, что при совместной работе всех рабочих выполнен весь объем работы).
3. Следует заметить, что в указанных задачах не всегда сравнивается выполненная работа. Основанием для составления уравнения может служить также указанное в условии соотношение затраченного времени или производительности труда.
Рассмотрим решение некоторых задач.
Вычисление неизвестного времени работы
Задача (№ 13.107). Две бригады, работая вместе, должны отремонтировать заданный участок шоссейной дороги за 18 дней. В действительности же получилось так, что сначала работала только одна первая бригада, а заканчивала ремонт участка дороги одна вторая бригада, производительность труда которой более высокая, чем первой бригады. В результате ремонт заданного участка дороги продолжался 40 дней, причем первая бригада в свое рабочее время выполнила  всей работы. За сколько дней был бы отремонтирован участок дороги каждой бригадой отдельно?
всей работы. За сколько дней был бы отремонтирован участок дороги каждой бригадой отдельно?
Решение.
1. Пусть вся работа может быть выполнена первой бригадой за х дней, а второй — за у дней.
2. Принимая всю работу за 1, имеем:
 — производительность первой бригады,
— производительность первой бригады,
 — производительность второй бригады,
— производительность второй бригады,
 — часть работы, которую могла выполнить первая бригада за 18 дней,
— часть работы, которую могла выполнить первая бригада за 18 дней,  — часть работы, которую могла выполнить вторая бригада за 18 дней.
— часть работы, которую могла выполнить вторая бригада за 18 дней.
3. Составление уравнения.
Так как обе бригады, работая совместно, могли выполнить всю работу за 18 дней, то на основании этого имеем

4. Далее из условия задачи следует, что первая бригада выполнила  всей работы, следовательно, она затратила на это
всей работы, следовательно, она затратила на это
 дней, а вторая бригада выполнила — всей работы, следовательно, она затратила на это
дней, а вторая бригада выполнила — всей работы, следовательно, она затратила на это  дней.
дней.
5. Так как всего было затрачено 40 дней, то можно составить второе уравнение: 
6. Составим систему уравнений и решим ее:

Имеем 
7. Так как производительность второй бригады была выше, чем первой, то условию задачи удовлетворяют 
Проверка.
Пусть известно, что первая бригада может выполнить всю работу за 45 дней, а вторая бригада — за 30 дней, тогда первая бригада за 1 день выполнит часть всей работы, а вторая бригада —  всей работы, и, следовательно, вместе за 1 день они выполнят
всей работы, и, следовательно, вместе за 1 день они выполнят  всей
всей  Значит, им понадобится на выполнение всей работы 18 дней, что соответствует условию задачи. Рассуждая аналогично, получим, что первая бригада выполнит — всей работы за
Значит, им понадобится на выполнение всей работы 18 дней, что соответствует условию задачи. Рассуждая аналогично, получим, что первая бригада выполнит — всей работы за  дней, а вторая бригада выполнит
дней, а вторая бригада выполнит  всей работы за
всей работы за  дней, т. е. всего будет затрачено
дней, т. е. всего будет затрачено  дней, что соответствует условию.
дней, что соответствует условию.
Ответ. 45 дней, 30 дней.
Решите задачи:
1. Задача (№ 13.135). Бригада слесарей может выполнить некоторое задание по обработке деталей на  скорее, чем бригада учеников. Если бригада учеников отработает
скорее, чем бригада учеников. Если бригада учеников отработает  выполняя это задание, а потом бригада слесарей продолжит выполнение задания в течение
выполняя это задание, а потом бригада слесарей продолжит выполнение задания в течение  то и тогда будет выполнено только
то и тогда будет выполнено только  всего задания. Сколько времени требуется бригаде учеников для самостоятельного выполнения данного задания?
всего задания. Сколько времени требуется бригаде учеников для самостоятельного выполнения данного задания?
2. Задача (№ 13.138). Два рабочих, из которых второй начал работать полутора днями позже первого, работая независимо один от другого, оклеили обоями несколько комнат за 7 дней, считая с момента выхода на работу первого рабочего. Если бы эта работа была поручена каждому отдельно, то первому
для ее выполнения понадобилось бы тремя днями больше, чем второму. За сколько дней каждый из них отдельно выполнил бы эту же работу?
Ответы. 1. 45 ч. 2. За 14 и 11 дней.
Путь, пройденный движущимися телами, рассматривается как совместная работа
Задача (№ 13.110). Два поезда отправляются из пунктов  навстречу друг другу. Они встретятся на половине пути, если поезд из А выйдет на
навстречу друг другу. Они встретятся на половине пути, если поезд из А выйдет на  раньше, чем поезд из В. Если же оба поезда выйдут одновременно, то через
раньше, чем поезд из В. Если же оба поезда выйдут одновременно, то через  расстояние между ними составит расстояния между пунктами А и
расстояние между ними составит расстояния между пунктами А и  За какие промежутки времени каждый поезд проходит весь путь?
За какие промежутки времени каждый поезд проходит весь путь?
Решение.
1. На первый взгляд эта задача кажется типичной задачей на движение. Однако следует обратить внимание на то, что в ней нет никаких данных о пройденном пути. Поэтому будем рассматривать эту задачу как задачу на совместную работу, где всю работу (пройденный путь) примем за 1.
2. Полагая, что первый поезд пройдет весь путь за х часов, а второй — за у часов, и учитывая, что первый вышел на  раньше, составим уравнение
раньше, составим уравнение 
3. Скорость каждого поезда будет соответственно и  следовательно,
следовательно, 
4. Составим систему уравнений и решим ее:

Получим 
Ответ. 
Решите задачу:
Задача (№ 13.330). Два грузовых автомобиля должны были перевезти некоторый груз в течение  Второй автомобиль задержался в гараже, и, когда он прибыл на место погрузки, первый перевез уже
Второй автомобиль задержался в гараже, и, когда он прибыл на место погрузки, первый перевез уже  всего груза; остальную часть груза перевез второй автомобиль, и весь груз был перевезен, таким образом, за
всего груза; остальную часть груза перевез второй автомобиль, и весь груз был перевезен, таким образом, за  Сколько времени нужно было каждому автомобилю в отдельности для перевозки груза?
Сколько времени нужно было каждому автомобилю в отдельности для перевозки груза?
Ответ.  или по
или по 
Задачи на «бассейн», который одновременно наполняется разными трубами
Задача (№ 13.290). Если две трубы открыть одновременно, то бассейн наполнится за  мин. В действительности же сначала была открыта только первая труба в течение одной четверти времени, которое необходимо второй трубе, чтобы наполнить бассейн, действуя отдельно. Затем действовала вторая труба также в течение одной четверти времени, которое необходимо первой, чтобы одной наполнить бассейн, после чего оказалось, что остается наполнить полной вместимости бассейна. Сколько времени необходимо для наполнения бассейна каждой трубой в отдельности?
мин. В действительности же сначала была открыта только первая труба в течение одной четверти времени, которое необходимо второй трубе, чтобы наполнить бассейн, действуя отдельно. Затем действовала вторая труба также в течение одной четверти времени, которое необходимо первой, чтобы одной наполнить бассейн, после чего оказалось, что остается наполнить полной вместимости бассейна. Сколько времени необходимо для наполнения бассейна каждой трубой в отдельности?
Решение.
1. Пусть первая труба наполняет бассейн за х часов, а вторая наполняет бассейн за у часов, тогда производительность каждой трубы будет соответственно — и — в час (примем объем воды в бассейне за 1).
2. Из условия следует, что первая труба наполнила часть бассейна, вторая труба часть бассейна, а вместе они наполнили  части бассейна. Отсюда
части бассейна. Отсюда 
3. Так как обе трубы при одновременной работе наполняют весь бассейн за  мин,
мин, 
4. Составим систему и решим ее:

5. Полагая  имеем:
имеем:

Очевидно, результаты однозначны. Будем полагать, что первая труба работала быстрее.
Ответ. 
Решите задачи:
1. Задача (№ 13.142). Чан наполняется двумя кранами А и В. Наполнение чана только через кран А длится на 22 мин дольше, чем через кран В. Если же открыть оба крана, то чан наполнится за  За какой промежуток времени каждый кран отдельно может наполнить чан?
За какой промежуток времени каждый кран отдельно может наполнить чан?
2. Задача (№ 13.289). Из автоцистерны сливали бензин в подземное хранилище по двум шлангам разного сечения. Первоначально а мин бензин поступал через оба шланга, затем первый шланг был отключен, и весь оставшийся бензин прошел через второй шланг за  мин. Но если бы после первоначальных а мин был отключен не первый, а второй шланг, то весь оставшийся бензин прошел бы через первый шланг за с мин. Сколько времени продолжалось бы переливание всего бензина из автоцистерны в хранилище только через один первый шланг?
мин. Но если бы после первоначальных а мин был отключен не первый, а второй шланг, то весь оставшийся бензин прошел бы через первый шланг за с мин. Сколько времени продолжалось бы переливание всего бензина из автоцистерны в хранилище только через один первый шланг?
3. Задача (№ 13.132). В лабораторной установке некоторая жидкость поступает в сосуд через три входных крана. Если открыть все краны одновременно, то сосуд наполнится за 6 мин. Если же наполнять сосуд только через второй кран, то на это потребуется  того времени, за которое может наполнится сосуд только через один первый кран. Через один третий кран этот сосуд наполняется на 10 мин дольше, чем через один второй кран. На какое время надо открывать каждый кран в отдельности для наполнения сосуда?
того времени, за которое может наполнится сосуд только через один первый кран. Через один третий кран этот сосуд наполняется на 10 мин дольше, чем через один второй кран. На какое время надо открывать каждый кран в отдельности для наполнения сосуда?
Ответы.  .
.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ГЛАВА I.
- § 1. НАТУРАЛЬНЫЕ ЧИСЛА И ДЕЙСТВИЯ НАД НИМИ
- § 2. СЛОЖЕНИЕ И ЗАКОНЫ СЛОЖЕНИЯ
- § 3. ВЫЧИТАНИЕ
- § 4. УМНОЖЕНИЕ И ЗАКОНЫ УМНОЖЕНИЯ
- § 5. ДЕЛЕНИЕ
- § 6. ПРИЗНАКИ ДЕЛИМОСТИ ЧИСЕЛ
- § 7. ПОНЯТИЕ МНОЖЕСТВА
- § 8. ОПЕРАЦИИ НАД МНОЖЕСТВАМИ
- § 9. ВЗАИМНО ОДНОЗНАЧНОЕ СООТВЕТСТВИЕ
- § 10. ПРОСТЫЕ И СОСТАВНЫЕ ЧИСЛА
- § 11. НАИБОЛЬШИЙ ОБЩИЙ ДЕЛИТЕЛЬ
- § 12. НАИМЕНЬШЕЕ ОБЩЕЕ КРАТНОЕ
- Контрольные вопросы
- ГЛАВА II
- § 1. ОБЫКНОВЕННЫЕ ДРОБИ
- § 2. ПРАВИЛЬНЫЕ И НЕПРАВИЛЬНЫЕ ДРОБИ
- § 3. ОСНОВНОЕ СВОЙСТВО ДРОБИ
- § 4. СЛОЖЕНИЕ И ВЫЧИТАНИЕ ДРОБЕЙ
- § 5. УМНОЖЕНИЕ ДРОБЕЙ
- § 6. ДЕЛЕНИЕ ДРОБЕЙ
- § 7. ДЕСЯТИЧНЫЕ ДРОБИ
- § 8. ОБРАЩЕНИЕ ДЕСЯТИЧНОЙ ДРОБИ В ОБЫКНОВЕННУЮ И ОБЫКНОВЕННОЙ В ДЕСЯТИЧНУЮ. ПЕРИОДИЧЕСКИЕ ДРОБИ
- § 9. ОТНОШЕНИЕ. ПРОПОРЦИЯ
- § 10. СВОЙСТВА ПРОПОРЦИИ
- § 11. ПРОЦЕНТ. ОСНОВНЫЕ ЗАДАЧИ НА ПРОЦЕНТЫ
- § 12. ДЕЛЕНИЕ ЧИСЛА НА ЧАСТИ, ПРЯМО И ОБРАТНО ПРОПОРЦИОНАЛЬНЫЕ ДАННЫМ ЧИСЛАМ
- Контрольные вопросы
- ГЛАВА III
- § 1. КООРДИНАТНАЯ ПРЯМАЯ
- § 2. МНОЖЕСТВО ЦЕЛЫХ ЧИСЕЛ
- § 3. МНОЖЕСТВО РАЦИОНАЛЬНЫХ ЧИСЕЛ
- § 4. МОДУЛЬ ЧИСЛА
- § 5. СРАВНЕНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ
- § 6. СЛОЖЕНИЕ И ВЫЧИТАНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ
- § 7. УМНОЖЕНИЕ И ДЕЛЕНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ
- § 8. ВОЗВЕДЕНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ В СТЕПЕНЬ С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ
- Контрольные вопросы
- ГЛАВА IV
- § 1. СВОЙСТВА СТЕПЕНИ С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ
- § 2. ЧИСЛОВЫЕ ВЫРАЖЕНИЯ
- § 3. ВЫРАЖЕНИЯ С ПЕРЕМЕННЫМИ
- § 4. ТОЖДЕСТВЕННО РАВНЫЕ ВЫРАЖЕНИЯ
- § 5. ОДНОЧЛЕНЫ
- § 6. МНОГОЧЛЕНЫ
- § 7. ПРЕОБРАЗОВАНИЕ СУММЫ И РАЗНОСТИ МНОГОЧЛЕНОВ
- § 8. УМНОЖЕНИЕ МНОГОЧЛЕНА НА ОДНОЧЛЕН И МНОГОЧЛЕНА НА МНОГОЧЛЕН
- § 9. РАЗЛОЖЕНИЕ МНОГОЧЛЕНА НА МНОЖИТЕЛИ СПОСОБОМ ВЫНЕСЕНИЯ ОБЩЕГО МНОЖИТЕЛЯ ЗА СКОБКИ
- § 10. РАЗЛОЖЕНИЕ МНОГОЧЛЕНА НА МНОЖИТЕЛИ СПОСОБОМ ГРУППИРОВКИ
- § 11. ФОРМУЛЫ СОКРАЩЕННОГО УМНОЖЕНИЯ
- Контрольные вопросы
- ГЛАВА V
- § 1. ДРОБЬ
- § 2. ЦЕЛЫЕ И ДРОБНЫЕ ВЫРАЖЕНИЯ
- § 3. ТОЖДЕСТВЕННОЕ ПРЕОБРАЗОВАНИЕ СУММЫ И РАЗНОСТИ ДВУХ ДРОБЕЙ
- § 4. ТОЖДЕСТВЕННОЕ ПРЕОБРАЗОВАНИЕ ПРОИЗВЕДЕНИЯ И ЧАСТНОГО ДВУХ ДРОБЕЙ
- § 5. СТЕПЕНЬ ДРОБИ
- Контрольные вопросы
- ГЛАВА VI
- § 1. ПОНЯТИЕ ОБ ИРРАЦИОНАЛЬНОМ ЧИСЛЕ
- § 2. РАЗВИТИЕ ПОНЯТИЯ О ЧИСЛЕ. МНОЖЕСТВО ДЕЙСТВИТЕЛЬНЫХ ЧИСЕЛ
- § 3. КОРЕНЬ СТЕПЕНИ ИЗ ДЕЙСТВИТЕЛЬНОГО ЧИСЛА
- § 4. АЛГОРИТМ ИЗВЛЕЧЕНИЯ КВАДРАТНОГО КОРНЯ ИЗ ЧИСЛА
- § 5. АРИФМЕТИЧЕСКИЕ ДЕЙСТВИЯ С ДЕЙСТВИТЕЛЬНЫМИ ЧИСЛАМИ
- § 6. ПРЕОБРАЗОВАНИЯ АРИФМЕТИЧЕСКИХ КОРНЕЙ
- § 7. СТЕПЕНЬ С ЦЕЛЫМ И ДРОБНЫМ ПОКАЗАТЕЛЕМ
- Контрольные вопросы
- ГЛАВА VII
- § 1. УРАВНЕНИЯ С ОДНОЙ ПЕРЕМЕННОЙ
- § 2. ПОНЯТИЕ О РАВНОСИЛЬНОСТИ УРАВНЕНИЙ
- § 3. СВОЙСТВА ЧИСЛОВЫХ РАВЕНСТВ И ТЕОРЕМЫ О РАВНОСИЛЬНОСТИ УРАВНЕНИЙ
- § 4. ЛИНЕЙНОЕ УРАВНЕНИЕ С ОДНОЙ ПЕРЕМЕННОЙ, СОДЕРЖАЩЕЕ ПАРАМЕТР
- Контрольные вопросы
- ГЛАВА VIII
- § 1. ПОНЯТИЕ ФУНКЦИИ
- § 2. СПОСОБЫ ЗАДАНИЯ ФУНКЦИИ
- § 3. МОНОТОННОСТЬ ФУНКЦИИ
- § 4. ЧЕТНЫЕ И НЕЧЕТНЫЕ ФУНКЦИИ СПРАВОЧНЫЙ МАТЕРИАЛ
- § 5. ПЕРИОДИЧЕСКИЕ ФУНКЦИИ
- § 6. ПРОМЕЖУТКИ ЗНАКОПОСТОЯНСТВА И КОРНИ ФУНКЦИИ
- Контрольные вопросы
- ГЛАВА IX
- § 1. ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ ГРАФИКОВ ФУНКЦИЙ
- § 2. ЛИНЕЙНАЯ ФУНКЦИЯ И ЕЕ ГРАФИК
- § 3. КВАДРАТИЧНАЯ ФУНКЦИЯ И ЕЕ ГРАФИК
- § 4. ФУНКЦИЯ y=k/x И ЕЕ ГРАФИК
- § 5. ДРОБНО-ЛИНЕЙНАЯ ФУНКЦИЯ И ЕЕ ГРАФИК
- Контрольные вопросы
- ГЛАВА X
- § 1. КВАДРАТНЫЕ УРАВНЕНИЯ
- § 2. ТЕОРЕМА ВИЕТА
- § 3. ГРАФИЧЕСКИЙ СПОСОБ РЕШЕНИЯ КВАДРАТНЫХ УРАВНЕНИЙ
- § 4. УРАВНЕНИЕ СО МНОГИМИ ПЕРЕМЕННЫМИ
- § 5. СИСТЕМЫ УРАВНЕНИЙ
- Контрольные вопросы
- ГЛАВА XI
- § 1. НЕРАВЕНСТВА
- § 2. ОСНОВНЫЕ СВОЙСТВА НЕРАВЕНСТВ
- § 3. ДЕЙСТВИЯ С НЕРАВЕНСТВАМИ
- § 4. ДОКАЗАТЕЛЬСТВА НЕРАВЕНСТВ
- § 5. НЕРАВЕНСТВА, СОДЕРЖАЩИЕ ПЕРЕМЕННУЮ
- § 6. РЕШЕНИЕ ЛИНЕЙНЫХ И КВАДРАТНЫХ НЕРАВЕНСТВ
- Контрольные вопросы
- ГЛАВА XII
- § 1. СИСТЕМЫ И СОВОКУПНОСТИ НЕРАВЕНСТВ
- § 2. НЕРАВЕНСТВА И СИСТЕМЫ НЕРАВЕНСТВ С ДВУМЯ ПЕРЕМЕННЫМИ
- § 3. РЕШЕНИЕ НЕРАВЕНСТВ, СОДЕРЖАЩИХ ПЕРЕМЕННУЮ ПОД ЗНАКОМ МОДУЛЯ
- § 4. РЕШЕНИЕ РАЦИОНАЛЬНЫХ НЕРАВЕНСТВ МЕТОДОМ ПРОМЕЖУТКОВ
- Контрольные вопросы
- ГЛАВА XIII
- § 1. ЧИСЛОВАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ
- § 2. АРИФМЕТИЧЕСКАЯ ПРОГРЕССИЯ
- § 3. ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИЯ
- § 4. СУММА БЕСКОНЕЧНОЙ ГЕОМЕТРИЧЕСКОЙ ПРОГРЕССИИ ПРИ |q|<1
- Контрольные вопросы
- ГЛАВА XIV
- § 1. ГРАДУСНОЕ ИЗМЕРЕНИЕ УГЛОВЫХ ВЕЛИЧИН
- § 2. РАДИАННОЕ ИЗМЕРЕНИЕ УГЛОВЫХ ВЕЛИЧИН
- § 3. СИНУС И КОСИНУС ЧИСЛОВОГО АРГУМЕНТА
- § 4. ТАНГЕНС И КОТАНГЕНС ЧИСЛОВОГО АРГУМЕНТА. СЕКАНС И КОСЕКАНС ЧИСЛА а
- § 5. ОСНОВНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ТОЖДЕСТВА
- § 6. ДОПОЛНИТЕЛЬНЫЕ СВОЙСТВА ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ
- Контрольные вопросы
- ГЛАВА XV
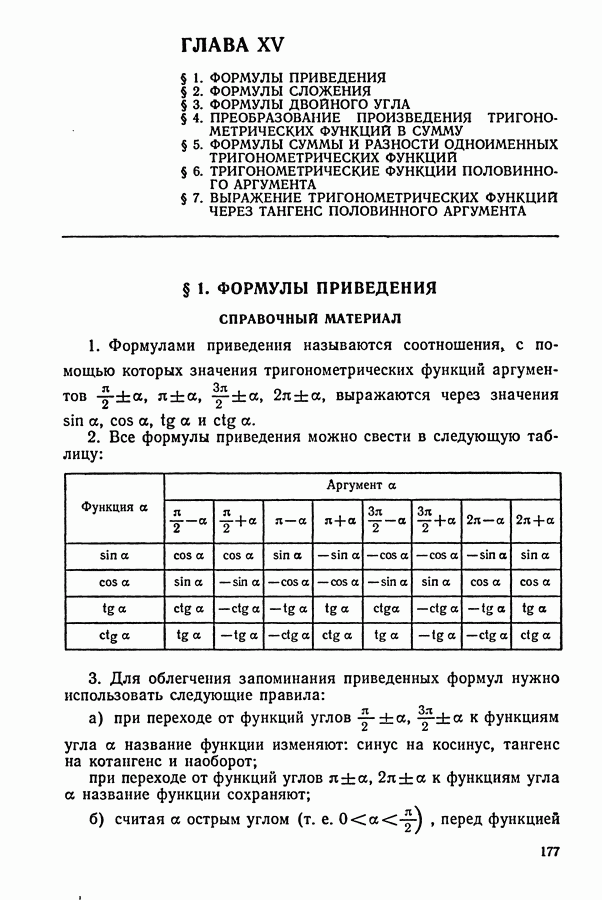
- § 1. ФОРМУЛЫ ПРИВЕДЕНИЯ
- § 2. ФОРМУЛЫ СЛОЖЕНИЯ
- § 3. ФОРМУЛЫ ДВОЙНОГО УГЛА СПРАВОЧНЫЙ МАТЕРИАЛ
- § 4. ПРЕОБРАЗОВАНИЕ ПРОИЗВЕДЕНИЯ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ В СУММУ
- § 5. ФОРМУЛЫ СУММЫ И РАЗНОСТИ ОДНОИМЕННЫХ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ
- § 6. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ ПОЛОВИННОГО АРГУМЕНТА
- § 7. ВЫРАЖЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ ЧЕРЕЗ ТАНГЕНС ПОЛОВИННОГО АРГУМЕНТА
- Контрольные вопросы
- ГЛАВА XVI
- § 1. СВОЙСТВА ФУНКЦИИ y = sin(x) И ЕЕ ГРАФИК
- § 2. СВОЙСТВА ФУНКЦИ И у = cos(x) И ЕЕ ГРАФИК
- § 3. СВОЙСТВА ФУНКЦИ И у=tg(x) И ЕЕ ГРАФИК
- § 4. СВОЙСТВА ФУНКЦИ И y=ctg(x) И ЕЕ ГРАФИК
- § 5. НАХОЖДЕНИЕ ПЕРИОДОВ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ
- Контрольные вопросы
- ГЛАВА XVII
- § 1. АРКСИНУС И АРККОСИНУС
- § 2. АРКТАНГЕНС И АРККОТАНГЕНС
- Контрольные вопросы
- ГЛАВА XVIII
- § 1. РЕШЕНИЕ УРАВНЕНИЙ ВИДА cos(x)=а
- § 2. РЕШЕНИЕ УРАВНЕНИЙ ВИДА sin(x)=a
- § 3. РЕШЕНИЕ УРАВНЕНИЙ ВИДА tg(х)=а
- § 4. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ, ПРИВОДИМЫХ К КВАДРАТНОМУ
- § 5. РЕШЕНИЕ ОДНОРОДНЫХ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ
- § 6. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ, РЕШАЕМЫЕ С ПОМОЩЬЮ ФОРМУЛ СЛОЖЕНИЯ, ПОНИЖЕНИЯ СТЕПЕНИ
- § 7. РЕШЕНИЕ СИСТЕМ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ
- Контрольные вопросы
- ГЛАВА XIX
- § 1. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ ВИДА sin(х) > а, sin(х) < а
- § 2. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ ВИДА cos(x) > a, cos(x) < a
- § 3. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ ВИДА tg(х) > a, tg(х) < a
- § 4. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ
- ГЛАВА XX
- § 1. ПРИРАЩЕНИЕ АРГУМЕНТА И ПРИРАЩЕНИЕ ФУНКЦИИ
- § 2. ПРЕДЕЛ ФУНКЦИИ
- § 3. НЕПРЕРЫВНОСТЬ ФУНКЦИИ
- § 4. ОПРЕДЕЛЕНИЕ ПРОИЗВОДНОЙ
- § 5. ПРОИЗВОДНАЯ СУММЫ, ПРОИЗВЕДЕНИЯ, ЧАСТНОГО
- § 6. ПРОИЗВОДНАЯ СТЕПЕННОЙ И СЛОЖНОЙ ФУНКЦИИ
- § 7. ПРОИЗВОДНЫЕ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ
- Контрольные вопросы
- ГЛАВА XXI
- § 1. ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ К НАХОЖДЕНИЮ ПРОМЕЖУТКОВ МОНОТОННОСТИ ФУНКЦИИ
- § 2. КРИТИЧЕСКИЕ ТОЧКИ ФУНКЦИИ, ЕЕ МАКСИМУМЫ И МИНИМУМЫ
- § 3. ОБЩАЯ СХЕМА ИССЛЕДОВАНИЯ ФУНКЦИИ
- § 4. ЗАДАЧИ НА НАХОЖДЕНИЕ НАИМЕНЬШЕГО И НАИБОЛЬШЕГО ЗНАЧЕНИЯ ФУНКЦИИ
- Контрольные вопросы
- ГЛАВА XXII
- § 1. ФОРМУЛЫ ПРИБЛИЖЕННЫХ ВЫЧИСЛЕНИЙ СПРАВОЧНЫЙ МАТЕРИАЛ
- § 2. КАСАТЕЛЬНАЯ К ГРАФИКУ ФУНКЦИИ
- § 3. СКОРОСТЬ И УСКОРЕНИЕ В ДАННЫЙ МОМЕНТ ВРЕМЕНИ
- § 4. ГРАФИКИ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ
- Контрольные вопросы
- ГЛАВА XXIII
- § 1. ПОТЕРЯННЫЕ И ПОСТОРОННИЕ КОРНИ ПРИ РЕШЕНИИ УРАВНЕНИЙ (НА ПРИМЕРАХ)
- § 2. ПОСТОРОННИЕ КОРНИ ИРРАЦИОНАЛЬНОГО УРАВНЕНИЯ (НА ПРИМЕРАХ)
- § 3. РЕШЕНИЕ ИРРАЦИОНАЛЬНЫХ УРАВНЕНИЙ
- § 4. РЕШЕНИЕ ИРРАЦИОНАЛЬНЫХ НЕРАВЕНСТВ СПРАВОЧНЫЙ МАТЕРИАЛ
- Контрольные вопросы
- ГЛАВА XXIV
- § 1. ПОКАЗАТЕЛЬНАЯ ФУНКЦИЯ, ЕЕ СВОЙСТВА И ГРАФИК
- § 2. ПОКАЗАТЕЛЬНЫЕ УРАВНЕНИЯ
- § 3. ПОКАЗАТЕЛЬНЫЕ НЕРАВЕНСТВА
- § 4. СИСТЕМЫ ПОКАЗАТЕЛЬНЫХ УРАВНЕНИЙ И НЕРАВЕНСТВ
- Контрольные вопросы
- ГЛАВА XXV
- § 1. ОБРАТНАЯ ФУНКЦИЯ
- § 2. ПОНЯТИЕ ЛОГАРИФМА
- § 3. СВОЙСТВА ЛОГАРИФМОВ
- § 4. ЛОГАРИФМИЧЕСКАЯ ФУНКЦИЯ, ЕЕ СВОЙСТВА И ГРАФИК
- § 5. ТЕОРЕМЫ О ЛОГАРИФМЕ ПРОИЗВЕДЕНИЯ, ЧАСТНОГО И СТЕПЕНИ. ФОРМУЛА ПЕРЕХОДА К НОВОМУ ОСНОВАНИЮ
- § 6. ДЕСЯТИЧНЫЕ ЛОГАРИФМЫ И ИХ СВОЙСТВА
- § 7. ЛОГАРИФМИРОВАНИЕ И ПОТЕНЦИРОВАНИЕ
- Контрольные вопросы
- ГЛАВА XXVI
- § 1. ЛОГАРИФМИЧЕСКИЕ УРАВНЕНИЯ
- § 2. ЛОГАРИФМИЧЕСКИЕ НЕРАВЕНСТВА
- § 3. СИСТЕМЫ ЛОГАРИФМИЧЕСКИХ УРАВНЕНИЙ И НЕРАВЕНСТВ
- § 4. ПРОИЗВОДНЫЕ ЛОГАРИФМИЧЕСКОЙ И ПОКАЗАТЕЛЬНОЙ ФУНКЦИЙ. ЧИСЛО e
- Контрольные вопросы
- ГЛАВА XXVII
- § 1. ПОНЯТИЕ ПЕРВООБРАЗНОЙ ФУНКЦИИ
- § 2. ОСНОВНОЕ СВОЙСТВО ПЕРВООБРАЗНОЙ ФУНКЦИИ
- § 3. ТРИ ПРАВИЛА НАХОЖДЕНИЯ ПЕРВООБРАЗНЫХ
- § 4. КРИВОЛИНЕЙНАЯ ТРАПЕЦИЯ И ЕЕ ПЛОЩАДЬ
- Контрольные вопросы
- ГЛАВА XXVIII
- § 1. ФОРМУЛА НЬЮТОНА—ЛЕЙБНИЦА
- § 2. ОСНОВНЫЕ ПРАВИЛА ИНТЕГРИРОВАНИЯ
- § 3. ВЫЧИСЛЕНИЕ ПЛОЩАДЕЙ С ПОМОЩЬЮ ИНТЕГРАЛА
- § 4. МЕХАНИЧЕСКИЕ И ФИЗИЧЕСКИЕ ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
- ПРИЛОЖЕНИЕ
- Введение
- 1. Задачи на движение
- 2. Задачи на совместную работу
- 3. Задачи на планирование
- 4. Задачи на зависимость между компонентами арифметических действий
- 5. Задачи на проценты
- 6. Задачи на смеси (сплавы)
- 7. Задачи на разбавление