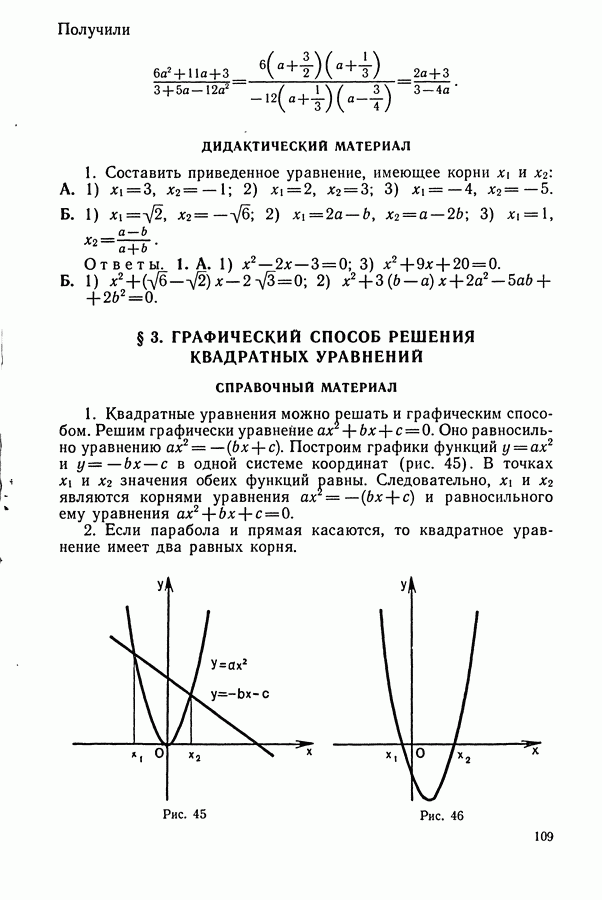
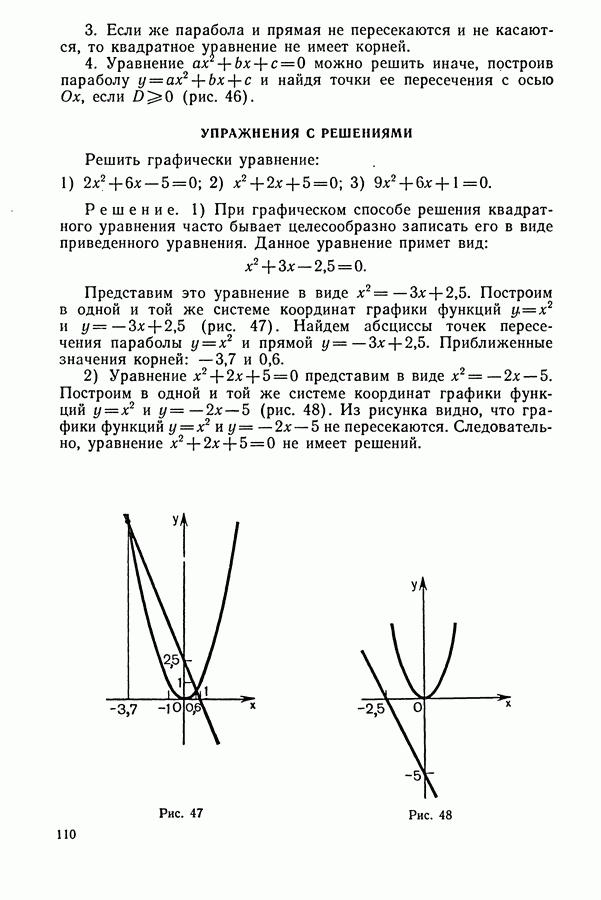
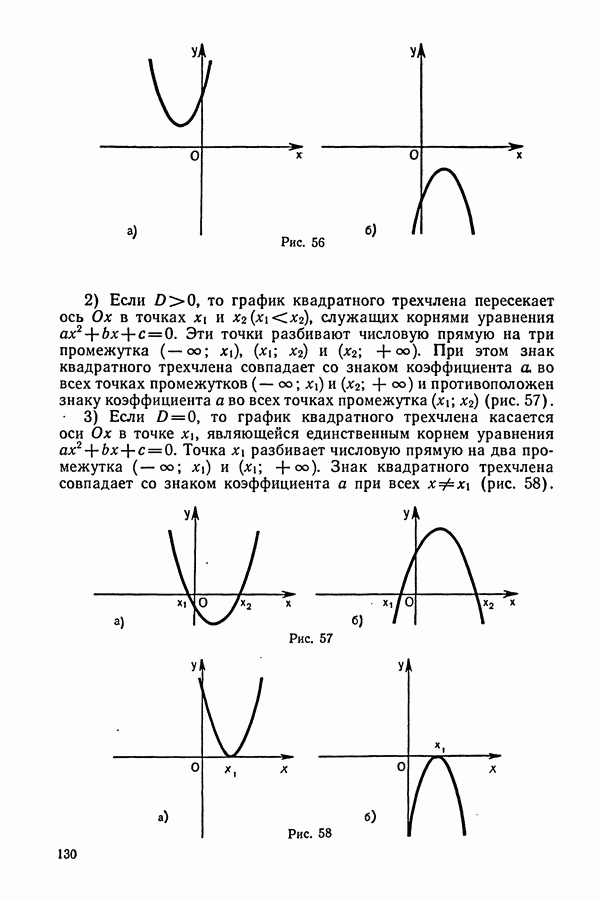
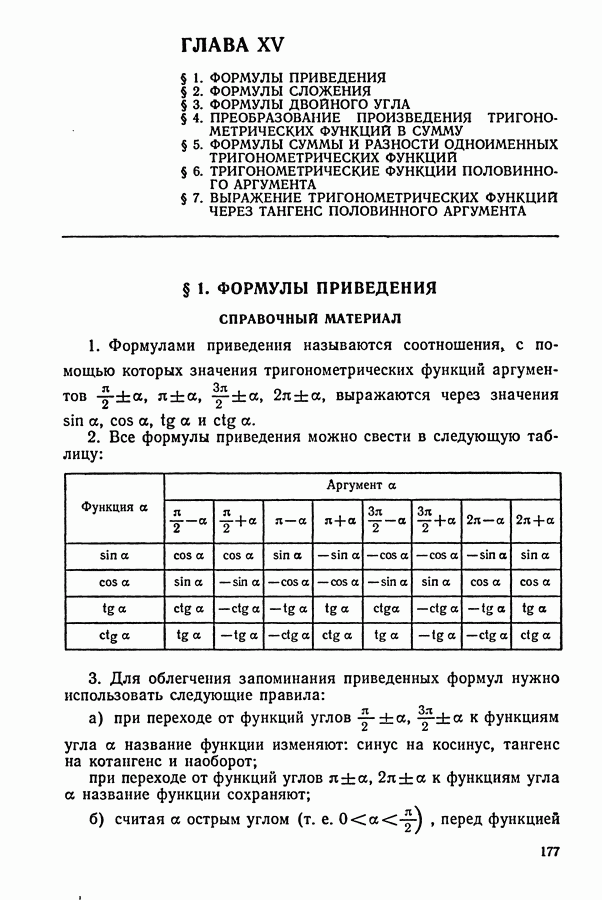
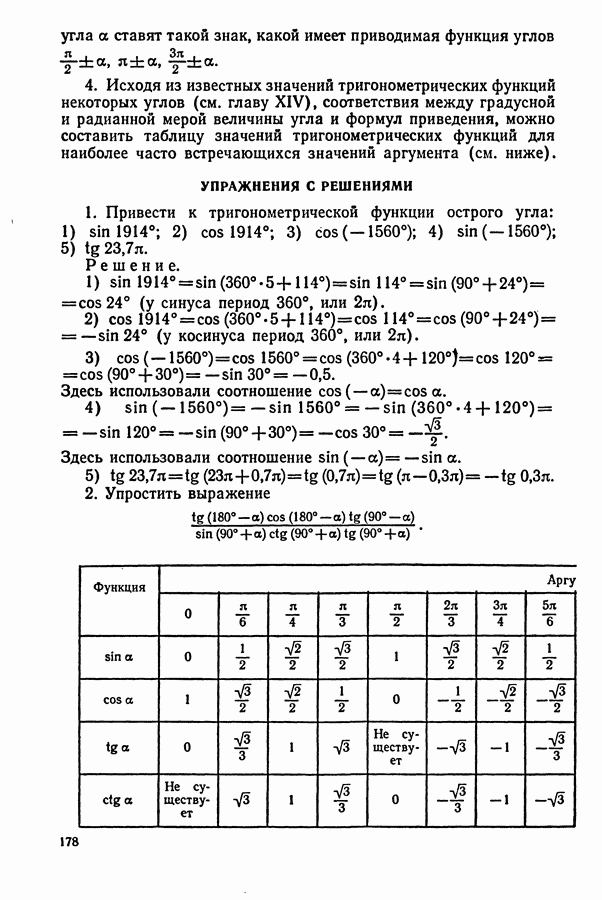
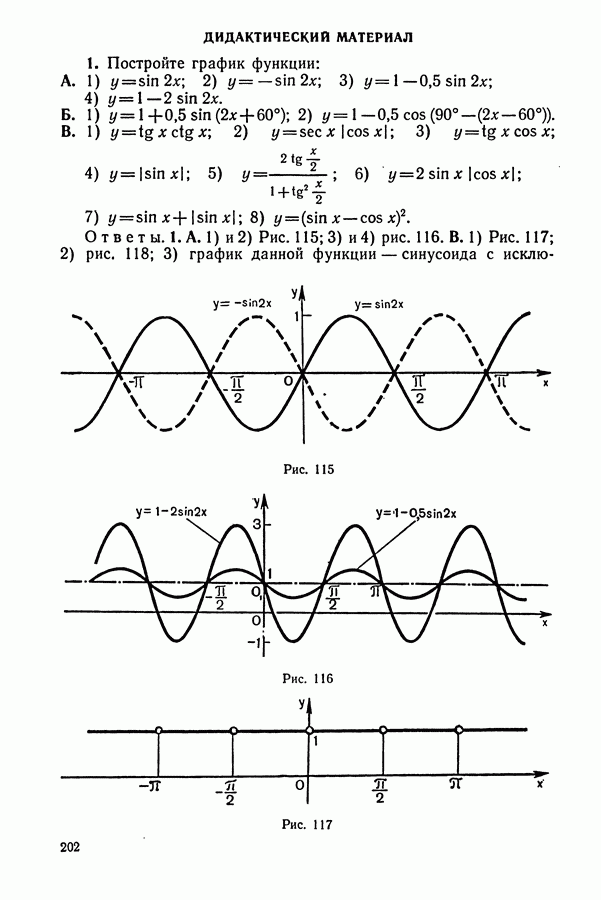
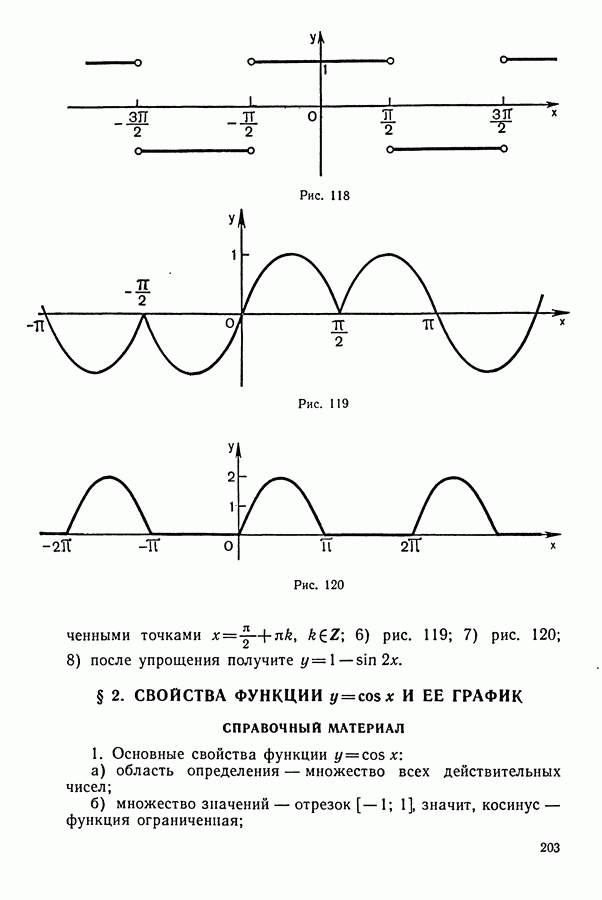
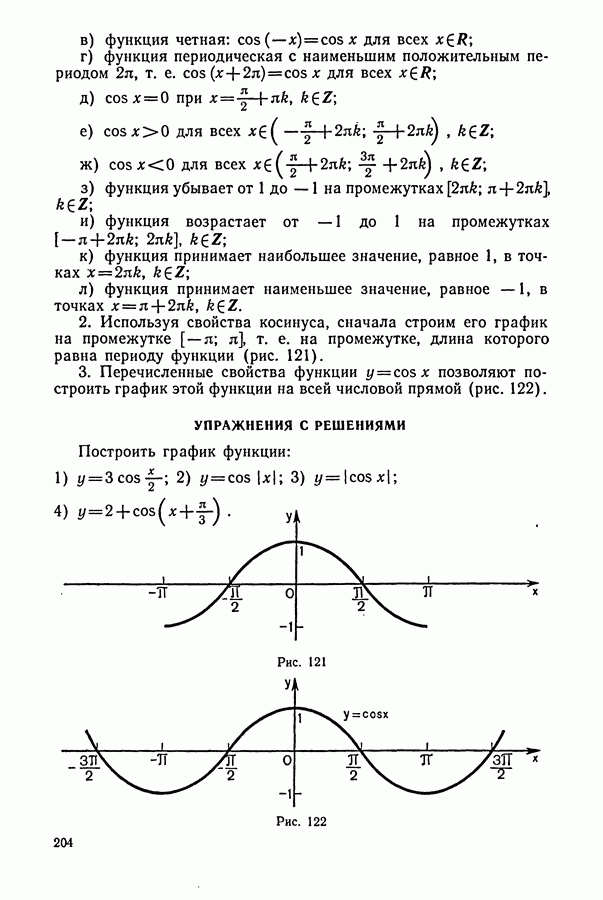
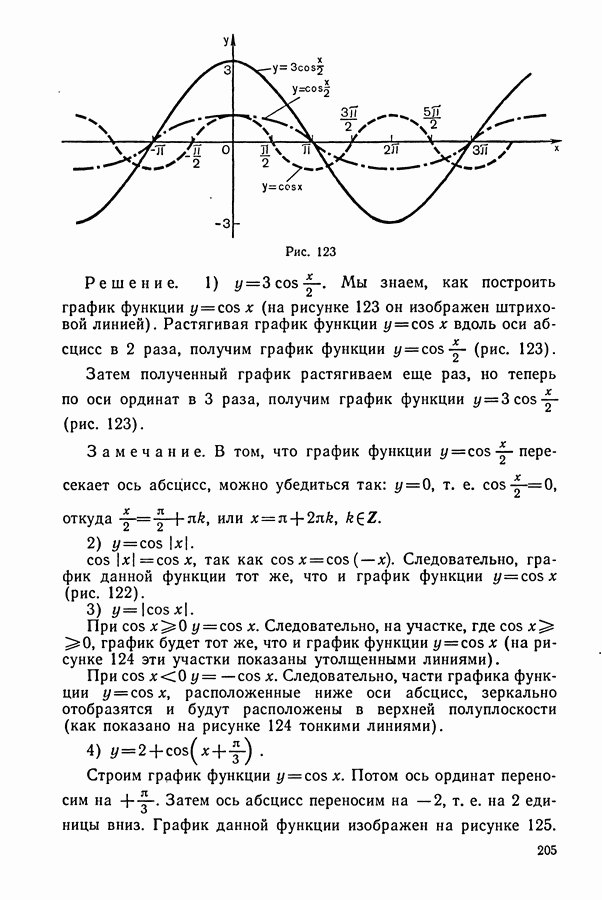
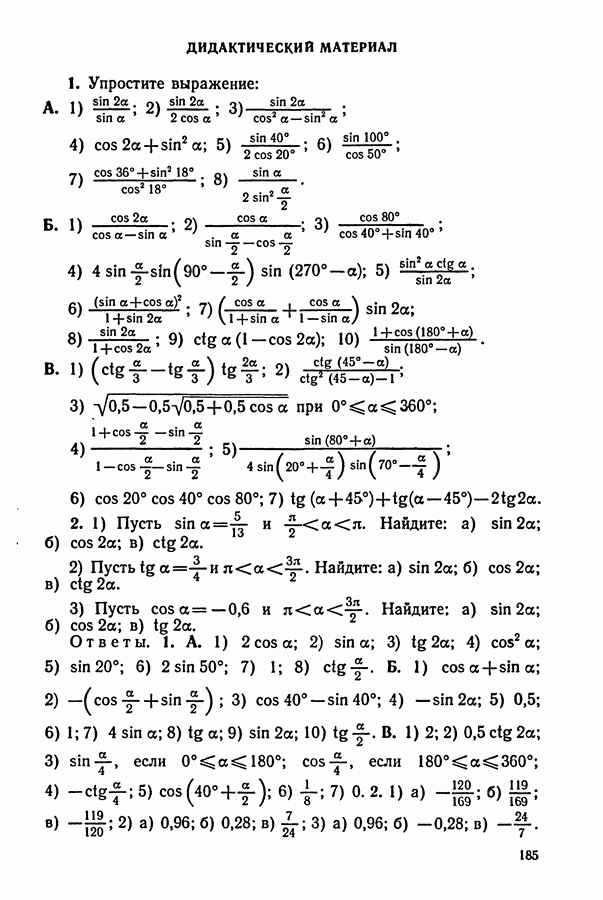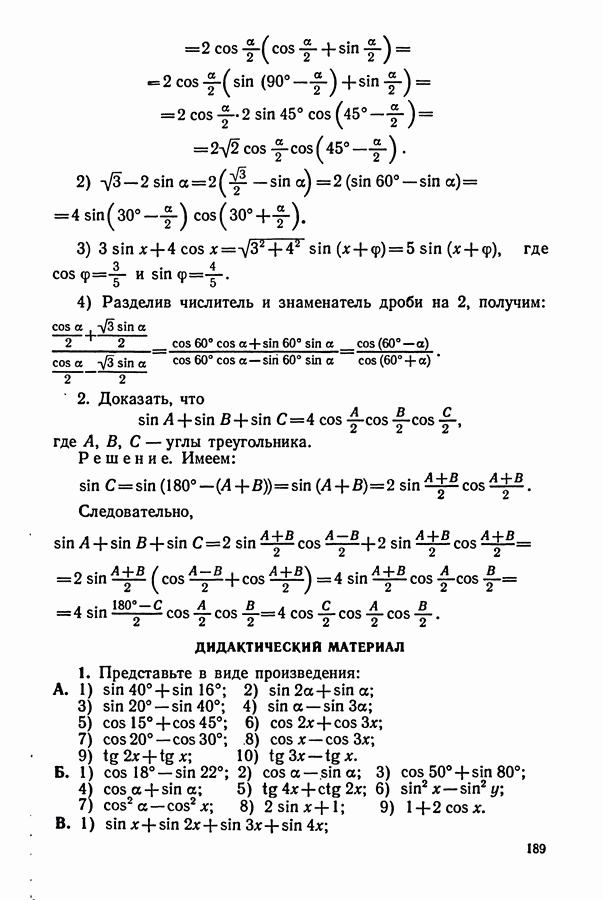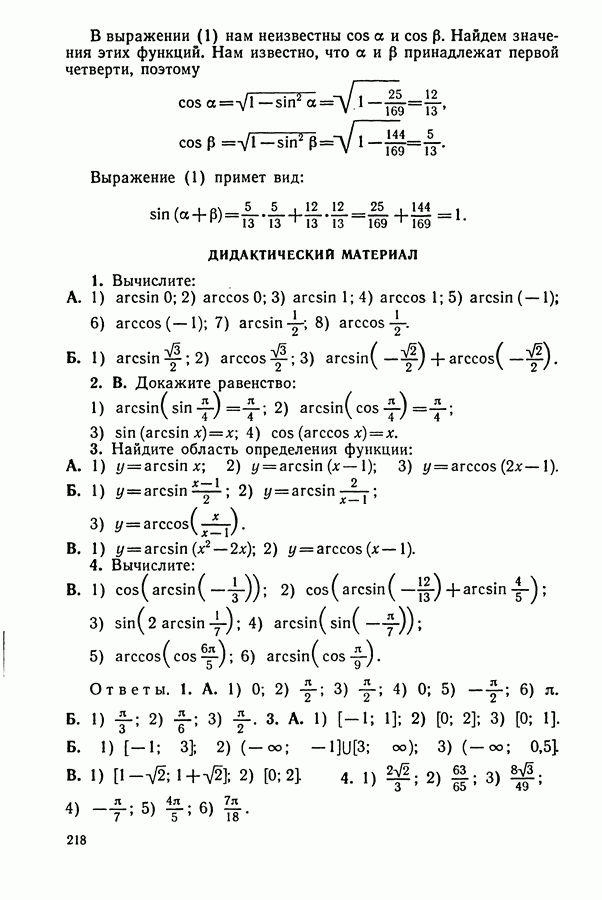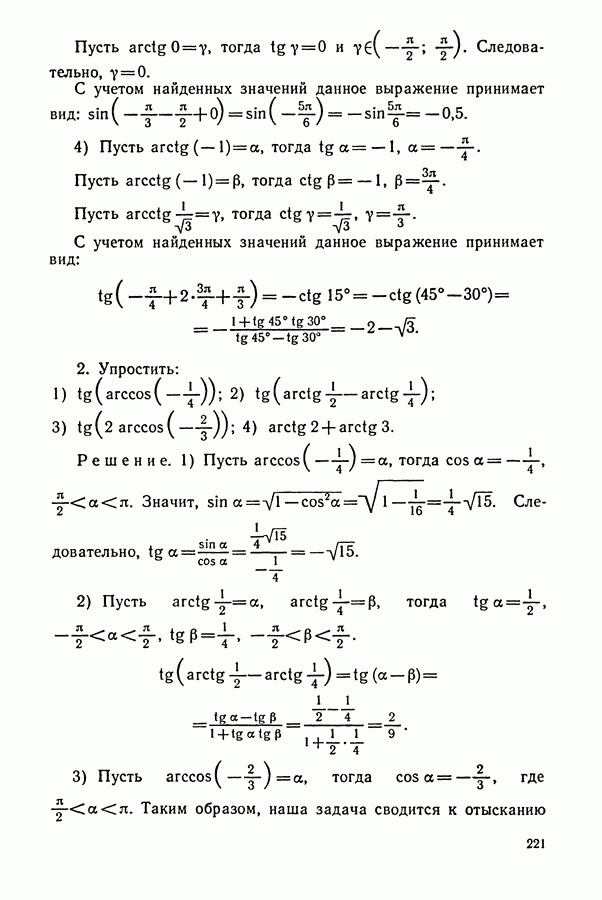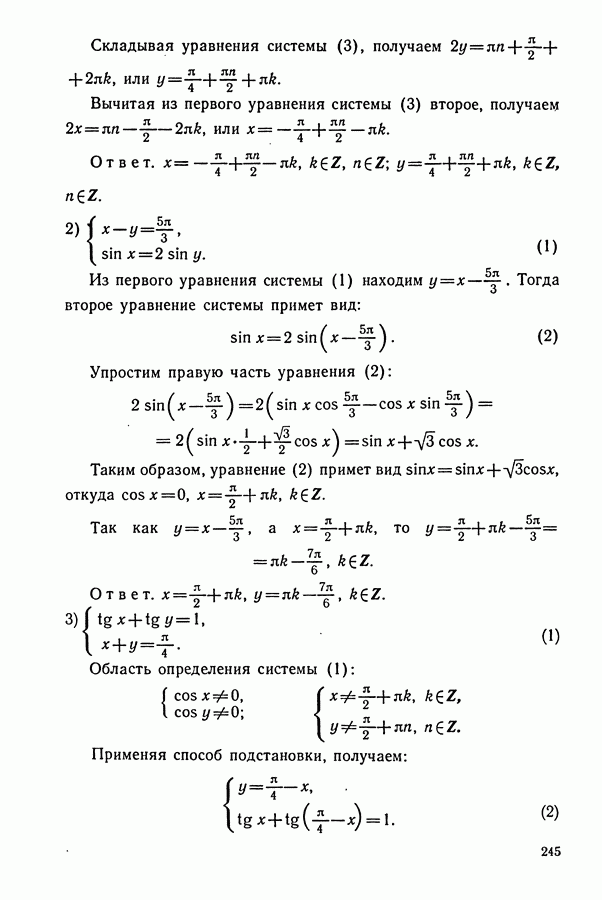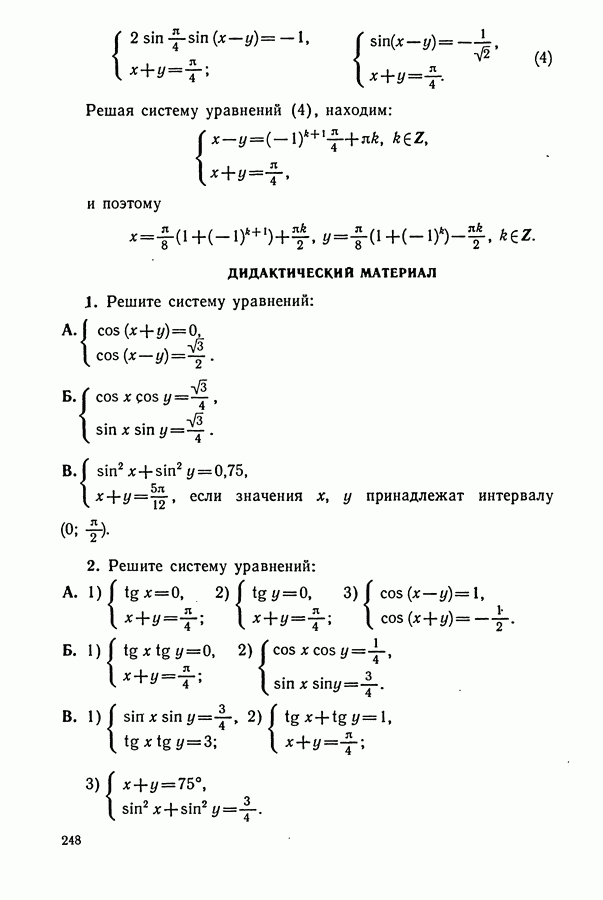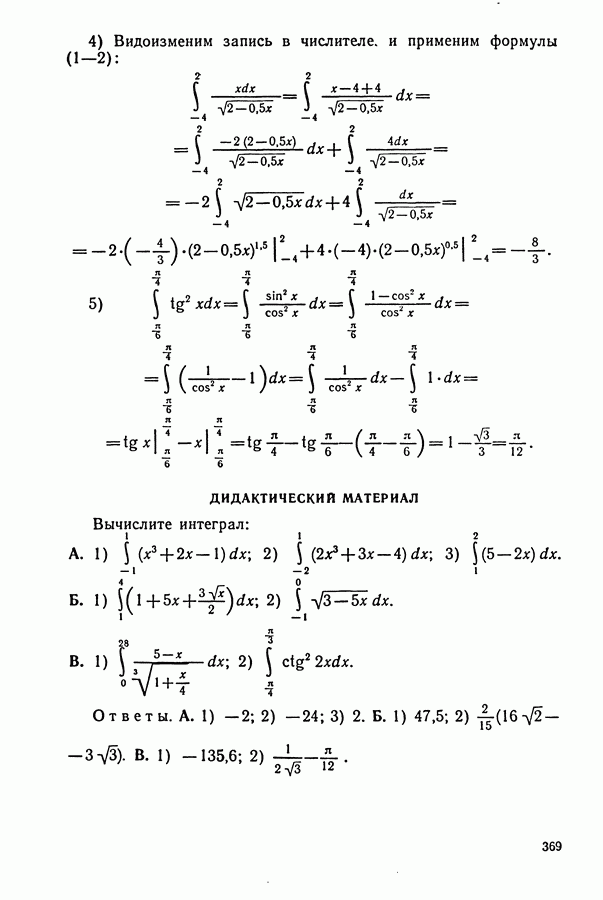| << Предыдущий параграф | Следующий параграф >> |
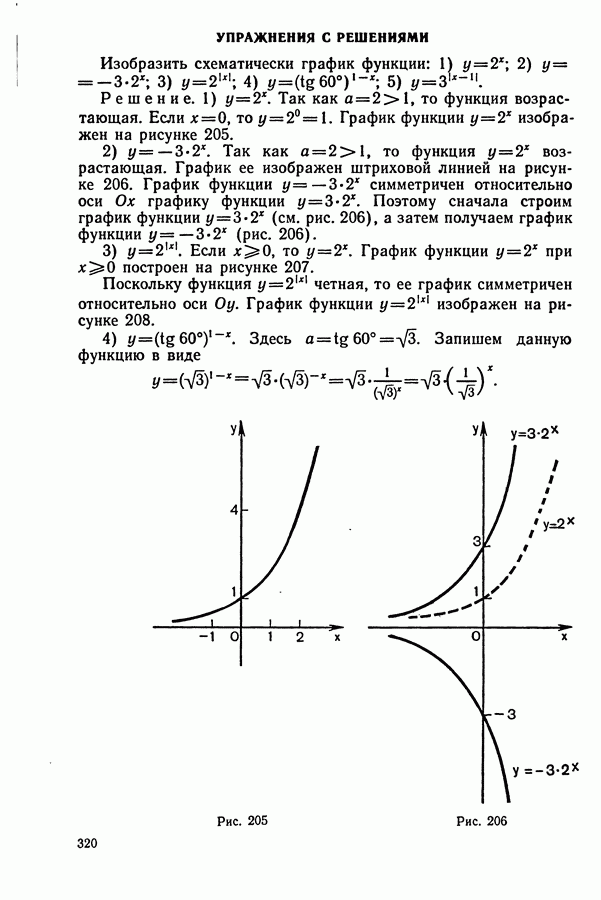
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
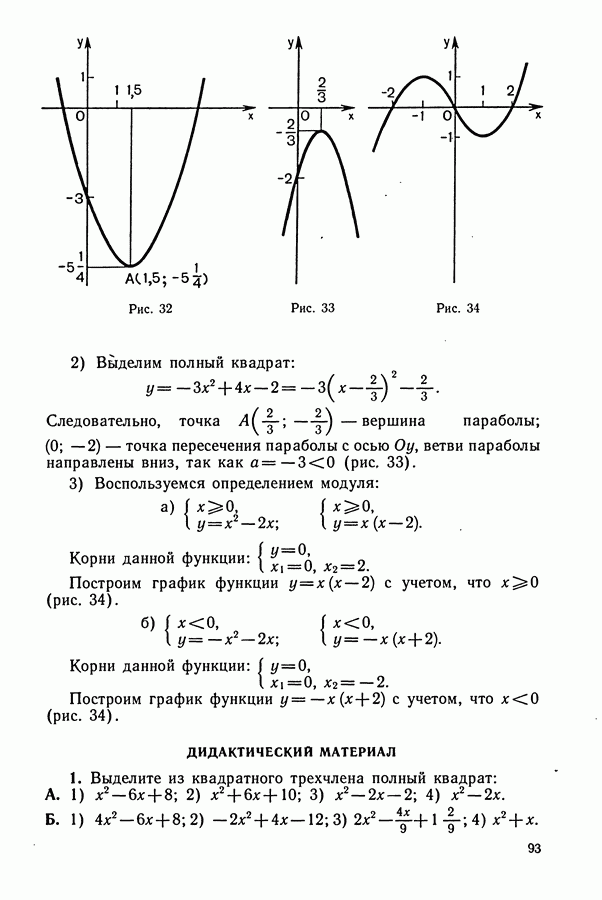
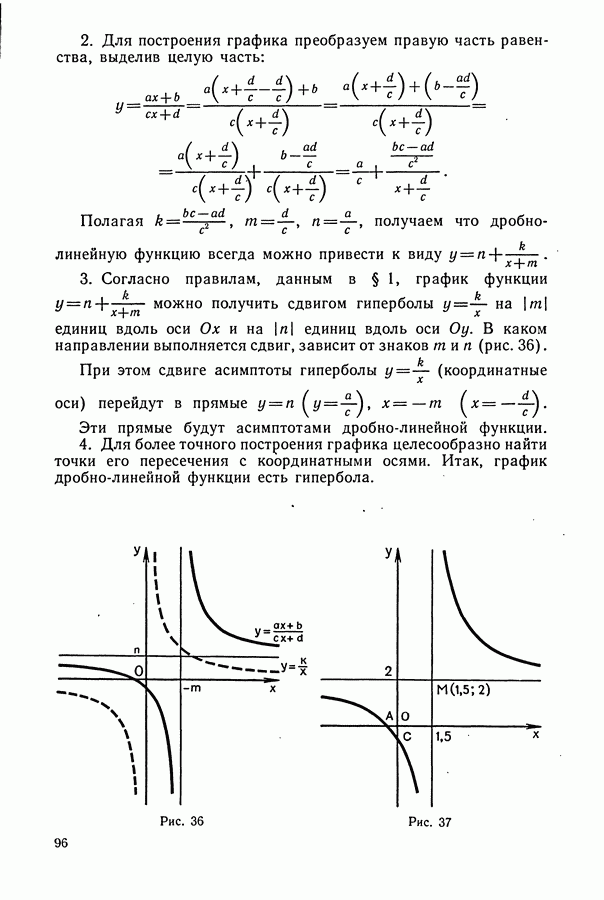
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
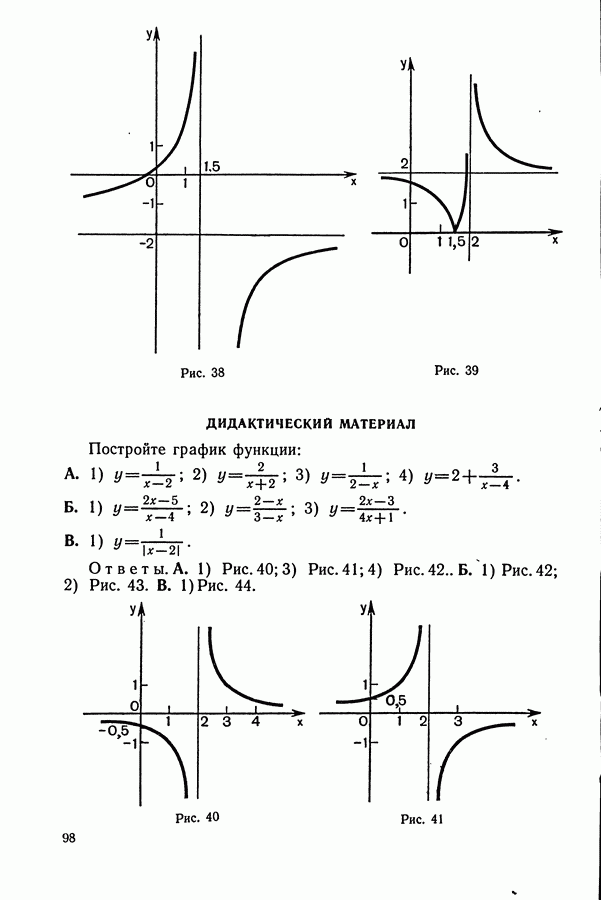
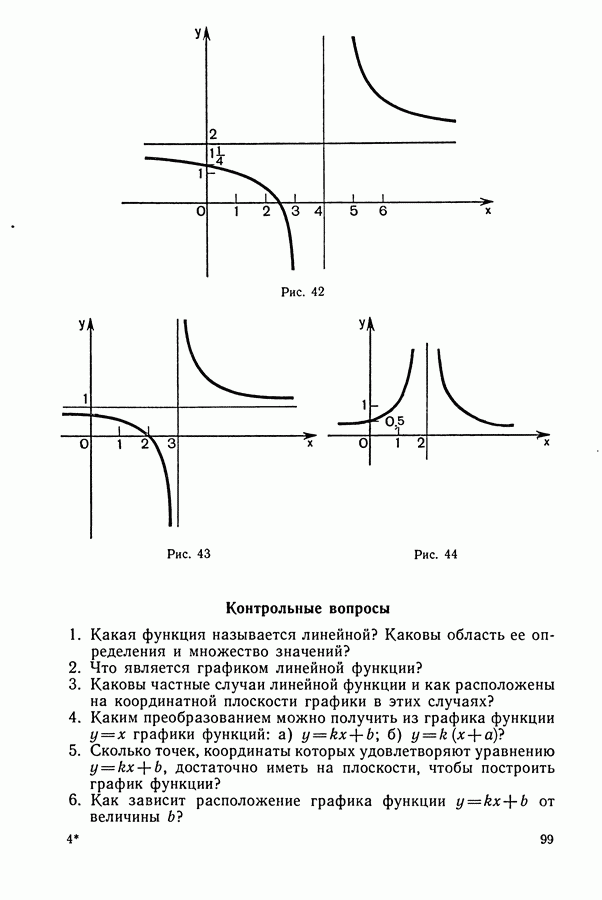
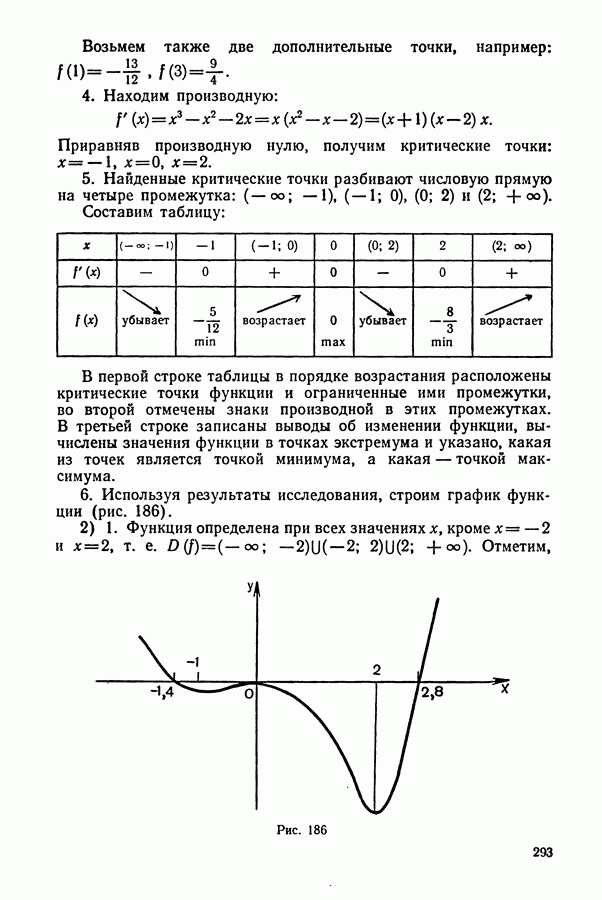
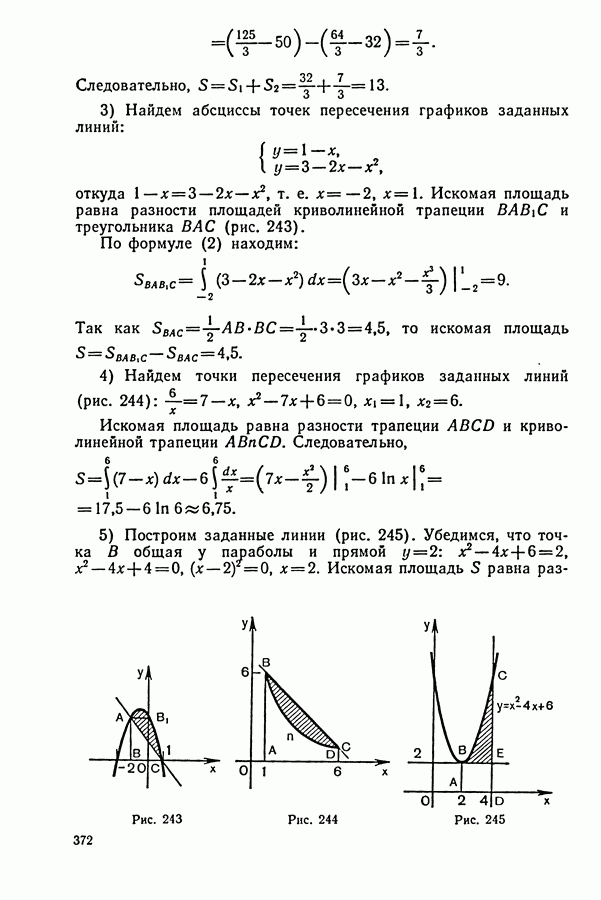
1. Задачи на движение
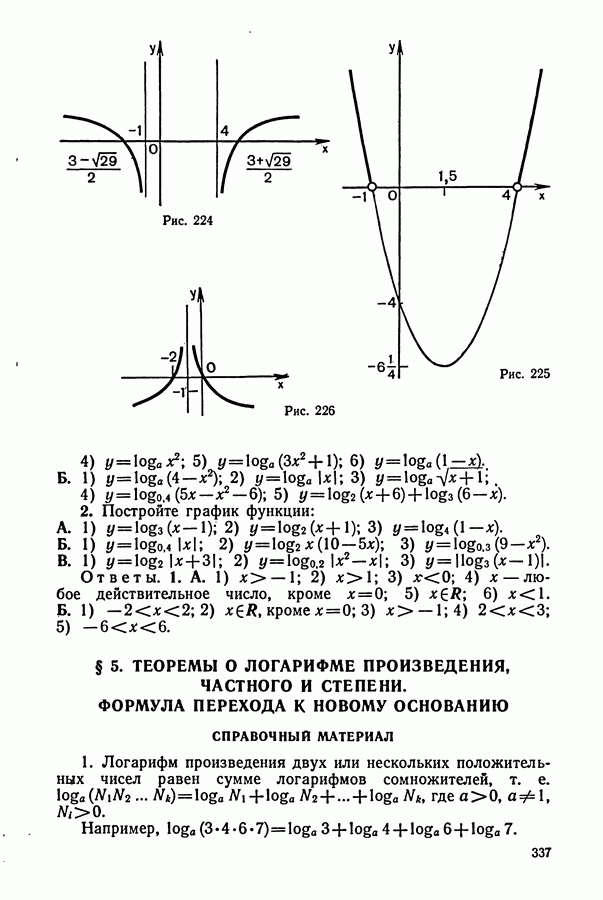
Некоторые указания к задачам на «движение»:
1. Основными компонентами этого типа задач являются: а) пройденный путь  скорость (у); в) время
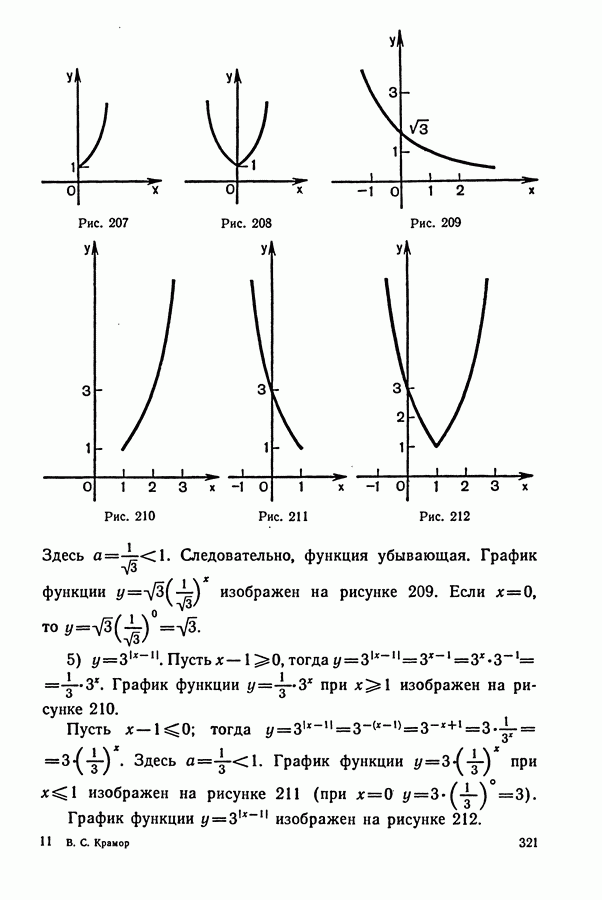
скорость (у); в) время  Зависимость между указанными величинами выражается известными формулами:
Зависимость между указанными величинами выражается известными формулами:

(указанные величины должны быть в одной системе единиц, например: если путь в километрах, а время в часах, то скорость в километрах в час).
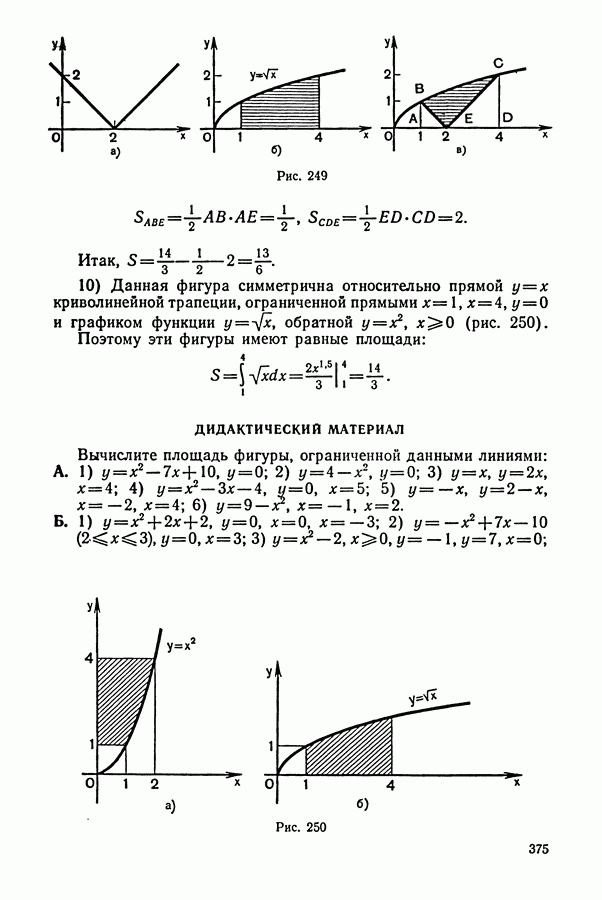
2. План решения обычно сводится к следующему:
а) Выбираем одну из величин, которая по условию задачи является неизвестной, и обозначаем ее через  или
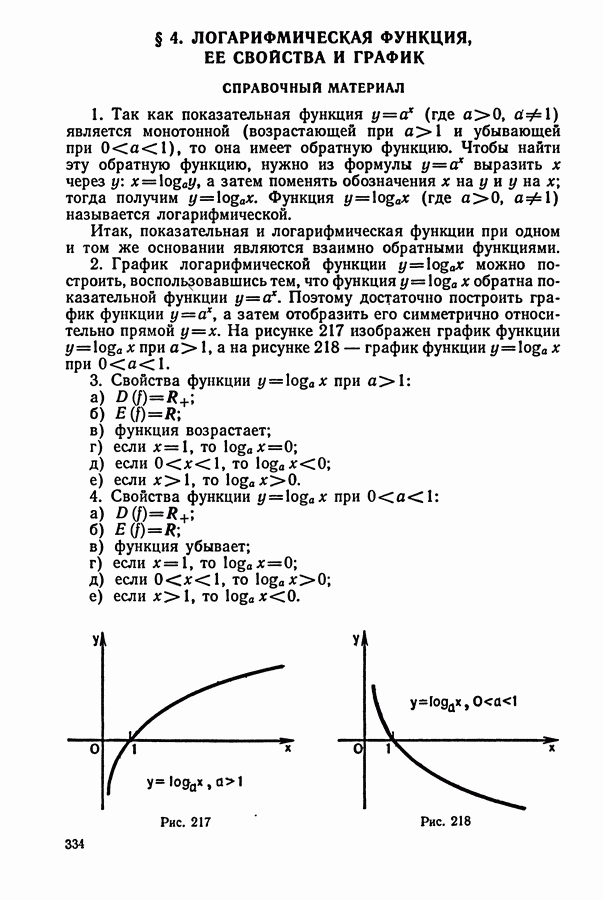
или 
б) Устанавливаем, какая из величин является по условию задачи известной.
в) Третью (из оставшихся) величину выражаем через неизвестную  и известную с помощью одной из формул (1).
и известную с помощью одной из формул (1).
г) Составляем уравнение на основании условия задачи, в котором указано, как именно изменилась (уменьшилась, увеличилась и т. д.) третья величина.
3. Заметим, что если два каких-либо тела начинают движение одновременно, то в случае, если они встречаются, каждое с момента выхода и до встречи затрачивает, очевидно, одинаковое время. Аналогично обстоит дело и в случае, если одно тело догоняет другое.
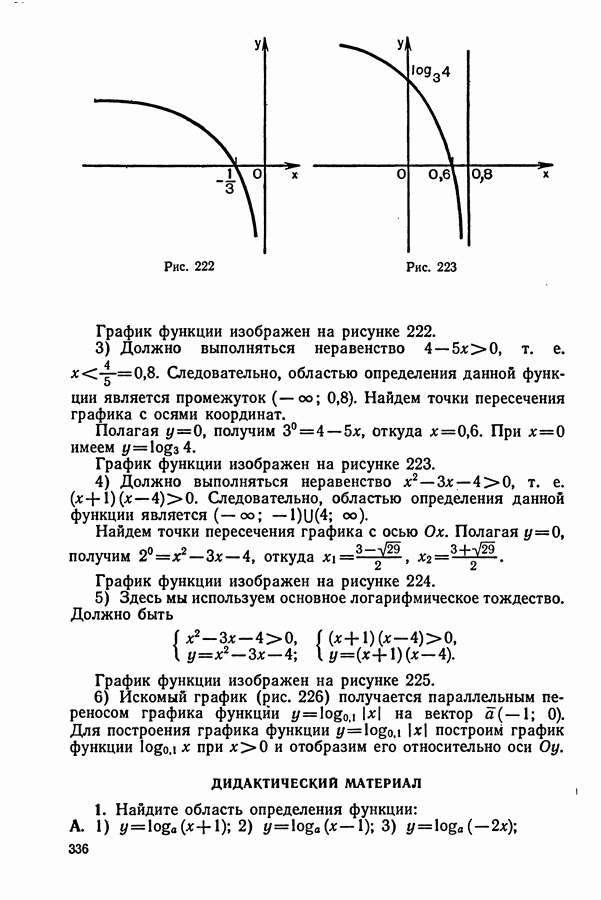
4. Если же тела выходят в разное время, то до момента встречи из них затрачивает времени больше то, которое выходит раньше.
5. В задачах на движение по реке необходимо помнить следующие формулы:

Рассмотрим теперь примерное решение некоторых задач.
Движение из одного пункта в другой в одном направлении
Задача (№ 13.079. Первый турист, проехав  на велосипеде со скоростью
на велосипеде со скоростью  делает остановку на
делает остановку на  а затем продолжает путь с первоначальной скоростью. Четыре часа спустя после отправки в дорогу первого туриста вдогонку ему выезжает на мотоцикле второй турист со скоростью
а затем продолжает путь с первоначальной скоростью. Четыре часа спустя после отправки в дорогу первого туриста вдогонку ему выезжает на мотоцикле второй турист со скоростью  Какое расстояние они проедут, прежде чем второй турист догонит первого?
Какое расстояние они проедут, прежде чем второй турист догонит первого?
Решение.
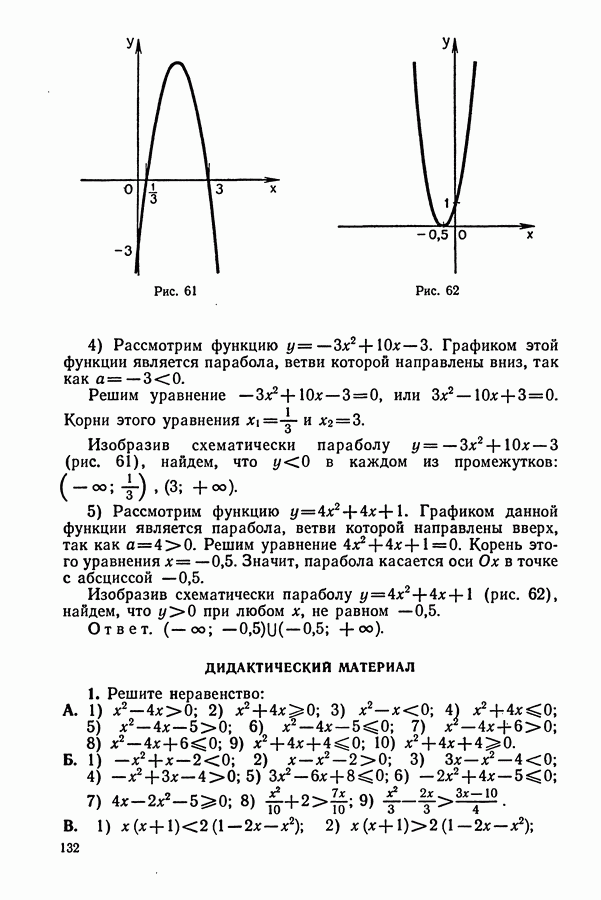
1. Из условия задачи ясно, что первый турист вышел в путь на  раньше второго. В точке В (рис. 253) он сделал остановку на
раньше второго. В точке В (рис. 253) он сделал остановку на  Второй турист догнал первого в точке
Второй турист догнал первого в точке  Чтобы проехать
Чтобы проехать

Рис. 253
это расстояние  первый турист затратил больше времени, чем второй, на
первый турист затратил больше времени, чем второй, на 
2. Пусть х — расстояние (в км) от точки А до точки  Тогда
Тогда  — время, за которое первый турист проезжает расстояние
— время, за которое первый турист проезжает расстояние  — время, за которое второй турист проезжает расстояние
— время, за которое второй турист проезжает расстояние 

Составим и решим уравнение:

Ответ. 56 км.
Решите задачи:
1. Задача (№ 13.077). Старший брат на мотоцикле, а младший на велосипеде совершили двухчасовую безостановочную поездку в лес и обратно. При этом мотоциклист проезжал каждый километр на 4 мин быстрее, чем велосипедист. Сколько километров проехал каждый из братьев за  если известно, что путь, проделанный старшим братом за это время, на 40 км больше?
если известно, что путь, проделанный старшим братом за это время, на 40 км больше?
2. Задача (№ 13.078). Турист ехал на автомобиле - -всего пути, а остальную часть — на катере. Скорость катера на
-всего пути, а остальную часть — на катере. Скорость катера на  меньше скорости автомобиля. На автомобиле турист ехал на 15 мин дольше, чем на катере. Чему равны скорость автомобиля и скорость катера, если весь путь туриста равен 160 км?
меньше скорости автомобиля. На автомобиле турист ехал на 15 мин дольше, чем на катере. Чему равны скорость автомобиля и скорость катера, если весь путь туриста равен 160 км?
Ответы. 1.20 км, 60 км. 2. Скорость автомобиля  или
или  скорость катера
скорость катера  или
или 
Движение из одного пункта в другой с остановкой в пути
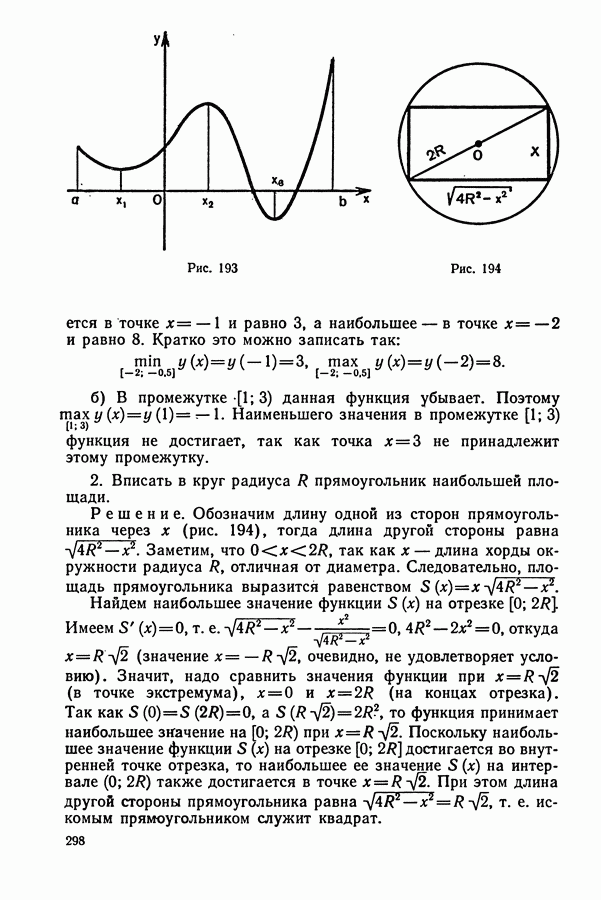
Задача (№ 13.083). Товарный поезд был задержан в пути на 12 мин, а затем на расстоянии 60 км наверстал потерянное время, увеличив скорость на  Найти первоначальную скорость поезда.
Найти первоначальную скорость поезда.
Решение.
1. Из условия задачи следует, что если бы поезд после остановки в пункте В (рис. 254) продолжал двигаться с прежней скоростью, то затратил бы на 12 мин  больше, чем предусмотрено расписанием.
больше, чем предусмотрено расписанием.

Рис. 254
2. Пусть  первоначальная скорость поезда
первоначальная скорость поезда  Тогда
Тогда 
3. Составим и решим уравнение:  — не удовлетворяет условию задачи, так как скорость — величина неотрицательная.
— не удовлетворяет условию задачи, так как скорость — величина неотрицательная.
Ответ. 
Решите задачи:
1. Задача (№ 13.081). Мотоциклист отправился из пункта А в пункт В, отстоящий от А на 120 км. Обратно он выехал с той же скоростью, но через час после выезда должен был остановиться на 10 мин. После этой остановки он продолжал путь до А, увеличив скорость на  Какова была первоначальная скорость мотоциклиста, если известно, что на обратный путь он затратил столько же времени, сколько на путь от А до В?
Какова была первоначальная скорость мотоциклиста, если известно, что на обратный путь он затратил столько же времени, сколько на путь от А до В?
2. Задача (№ 13.222), Расстояние между станциями  равно 103 км. Из Л в В вышел поезд и, пройдя некоторое расстояние, был задержан, а потому оставшийся путь до В проходил со скоростью, на
равно 103 км. Из Л в В вышел поезд и, пройдя некоторое расстояние, был задержан, а потому оставшийся путь до В проходил со скоростью, на  большей прежней. Найти первоначальную скорость поезда, если известно, что оставшийся путь до В был на 23 км длиннее пути, пройденного до задержки, и на прохождение пути после задержки было затрачено на 15 мин больше, чем на прохождение пути до задержки.
большей прежней. Найти первоначальную скорость поезда, если известно, что оставшийся путь до В был на 23 км длиннее пути, пройденного до задержки, и на прохождение пути после задержки было затрачено на 15 мин больше, чем на прохождение пути до задержки.
Ответы. 
Движение из разных пунктов навстречу друг другу
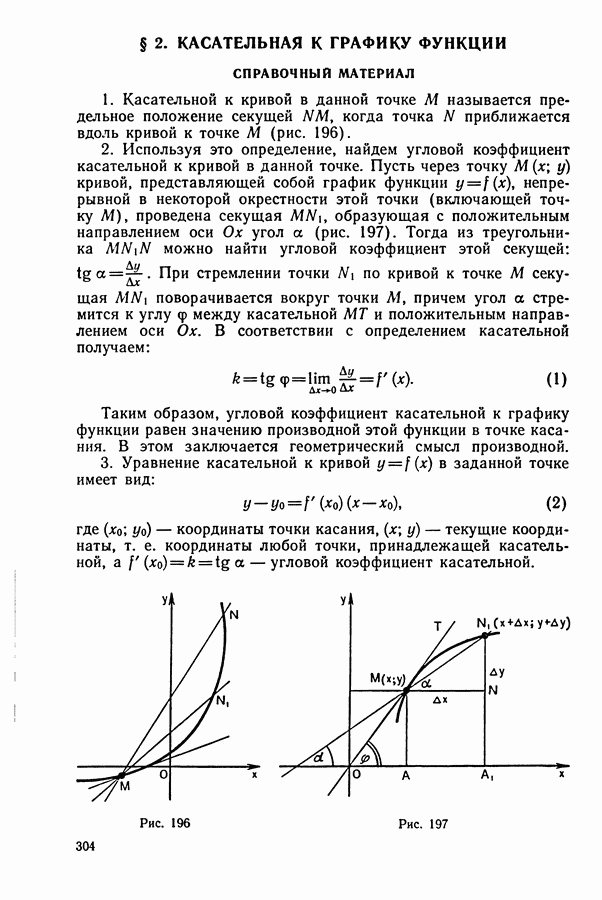
Задача (№ 13.101). В один и тот же час навстречу друг другу должны были выйти А из поселка М и В из поселка К. Но А задержался и вышел позже на  При встрече выяснилось, что А прошел на 12 км меньше, чем В. Отдохнув, они одновременно покинули место встречи и продолжили путь с прежней скоростью. В результате А пришел в К через
При встрече выяснилось, что А прошел на 12 км меньше, чем В. Отдохнув, они одновременно покинули место встречи и продолжили путь с прежней скоростью. В результате А пришел в К через  , а В пришел в М через
, а В пришел в М через  после встречи. Определить расстояние
после встречи. Определить расстояние  и скорости пешеходов.
и скорости пешеходов.
Решение.
1. Пусть  (рис. 255).
(рис. 255).
Тогда  — время, которое затратит А на путь из М в
— время, которое затратит А на путь из М в 

Рис. 255
 — время, которое затратит В на путь из К в
— время, которое затратит В на путь из К в  (см. рис. 255).
(см. рис. 255).
2. Из условия задачи следует, что  Так как пешеход В вышел раньше, чем А, на
Так как пешеход В вышел раньше, чем А, на  то на основании этого составим второе уравнение:
то на основании этого составим второе уравнение: 
3. Составим систему уравнений и решим ее:

Расстояние  км.
км.
Ответ. 84 км; 
Решите задачи:
11 Задача (№ 13.098). Пешеход и велосипедист отправляются одновременно навстречу друг другу из городов А и В, расстояние между которыми 40 км, и встречаются спустя  после отправления. Затем они продолжают путь, причем велосипедист прибывает в А на
после отправления. Затем они продолжают путь, причем велосипедист прибывает в А на  мин раньше, чем пешеход в В. Найти скорости пешехода и велосипедиста, полагая, что оба все время двигались с неизменными скоростями.
мин раньше, чем пешеход в В. Найти скорости пешехода и велосипедиста, полагая, что оба все время двигались с неизменными скоростями.
2. Задача (№ 13.112). Два тела движутся навстречу друг другу из двух мест, расстояние между которыми  Первое тело прошло в первую секунду
Первое тело прошло в первую секунду  а в каждую следующую проходило на
а в каждую следующую проходило на  больше, чем в предыдущую. Второе тело двигалось равномерно со скоростью
больше, чем в предыдущую. Второе тело двигалось равномерно со скоростью  и начало движение спустя 5 с после первого. Через сколько секунд после того, как начало двигаться первое тело, они встретятся?
и начало движение спустя 5 с после первого. Через сколько секунд после того, как начало двигаться первое тело, они встретятся?
Ответы.  Через 10 с.
Через 10 с.
Основные компоненты движения заданы в общем виде (задачи с параметрами)
Задача (№ 13.111). Поезд был задержан на  Увеличив скорость на а
Увеличив скорость на а  машинист на перегоне в
машинист на перегоне в  км ликвидировал опоздание. Определить, какую скорость должен был иметь поезд на этом перегоне, если бы не было задержки.
км ликвидировал опоздание. Определить, какую скорость должен был иметь поезд на этом перегоне, если бы не было задержки.
Решение.
1. Полагая, что скорость поезда по расписанию  имеем:
имеем:

2. Теперь следует выяснить, оба ли корня уравнения удовлетворяют условию задачи:

Ответ. 
Решите задачи:
1. Задача (№ 13.099). Расстояние между поселками А и В равно  км. Из А отправились в В одновременно и по одной и той же дороге два автотуриста, которые должны были прибыть в В в одно и то же время. В действительности первый турист прибыл в В на
км. Из А отправились в В одновременно и по одной и той же дороге два автотуриста, которые должны были прибыть в В в одно и то же время. В действительности первый турист прибыл в В на  часов раньше срока, а второй на 36 часов опоздал, так как последний проезжал за каждый час в среднем на а км меньше первого. Определить среднюю часовую скорость каждого автотуриста.
часов раньше срока, а второй на 36 часов опоздал, так как последний проезжал за каждый час в среднем на а км меньше первого. Определить среднюю часовую скорость каждого автотуриста.
2. Задача (№ 13.217). Дорога между поселками A и В сначала имеет подъем, а потом спуск. Велосипедист, двигаясь на спуске со скоростью на а  больше, чем на подъеме, затрачивает на путь от А до В ровно
больше, чем на подъеме, затрачивает на путь от А до В ровно  часов, а на обратный путь от В до А половину этого времени. Найти скорость велосипедиста на подъеме и на спуске, если расстояние между поселками
часов, а на обратный путь от В до А половину этого времени. Найти скорость велосипедиста на подъеме и на спуске, если расстояние между поселками  км.
км.
Ответы. 
Движение по водному пути
Задача (№ 13.129). В 9 ч самоходная баржа вышла из А вверх по реке и прибыла в пункт  спустя после прибытия в В эта баржа отправилась в обратный путь и прибыла в А в
спустя после прибытия в В эта баржа отправилась в обратный путь и прибыла в А в  мин того же дня. Предполагая, что средняя скорость течения реки
мин того же дня. Предполагая, что средняя скорость течения реки  и собственная скорость баржи все время постоянна, определить, в котором часу баржа прибыла в пункт В. Расстояние между A и В равно 60 км.
и собственная скорость баржи все время постоянна, определить, в котором часу баржа прибыла в пункт В. Расстояние между A и В равно 60 км.
Решение.
1. Для решения этого типа задач следует использовать указание 5.
2. Обозначим собственную скорость баржи через х км/ч. Тогда время, затраченное на движение по течению реки, составляет  часов, а против течения реки
часов, а против течения реки  часов.
часов.
3. Всего было затрачено времени  На основании этого составим уравнение и решим его:
На основании этого составим уравнение и решим его:

 (не удовлетворяет условию).
(не удовлетворяет условию).
4. Время, затраченное на движение против течения реки,  Следовательно, баржа прибыла в пункт В в
Следовательно, баржа прибыла в пункт В в  Решите задачи:
Решите задачи:
1. Задача (№ 13.130). Два приятеля в одной лодке прокатились по реке вдоль берега и вернулись по той же речной трассе через  с момента отплытия. Весь рейс составил 10 км. По их подсчетам получилось, что на каждые 2 км против течения в среднем требовалось им столько же времени, сколько требовалось на каждые 3 км по течению. Найти скорость течения и время проезда туда и обратно.
с момента отплытия. Весь рейс составил 10 км. По их подсчетам получилось, что на каждые 2 км против течения в среднем требовалось им столько же времени, сколько требовалось на каждые 3 км по течению. Найти скорость течения и время проезда туда и обратно.
2. Задача (№ 13.145). Сначала катер шел а км по течению реки, а затем вдвое большее расстояние по озеру, в которое река впадала. Весь рейс продолжался  Найти собственную скорость катера, если скорость течения реки с
Найти собственную скорость катера, если скорость течения реки с 
Ответы. 
Определение скорости при встречном прямолинейном движении тел
Задача  Пассажир поезда знает, что на данном участке пути скорость этого поезда
Пассажир поезда знает, что на данном участке пути скорость этого поезда  Как только мимо окна начал проходить встречный поезд, пассажир пустил секундомер и заметил, что встречный поезд проходил мимо окна в течение 3 с. Определить скорость встречного поезда, если известно, что его длина
Как только мимо окна начал проходить встречный поезд, пассажир пустил секундомер и заметил, что встречный поезд проходил мимо окна в течение 3 с. Определить скорость встречного поезда, если известно, что его длина 
Решение.
1. Пусть скорость встречного поезда  Скорость поезда, в котором ехал пассажир,
Скорость поезда, в котором ехал пассажир, 
2. Встречный поезд за 3 с прошел  а поезд с пассажиром
а поезд с пассажиром 
3. Всего оба поезда прошли по условию  следовательно,
следовательно, 
Ответ. 
Решите задачи:
1. Задача (№ 13.284). Найти скорость и длину поезда, зная, что он проходил с постоянной скоростью мимо неподвижного
ного наблюдателя в течение 7 с и затратил 25 с на то, чтобы проехать с той же скоростью вдоль платформы длиной 
2. Задача (№ 13.370). На расстоянии  от окна будки параллельно плоскости окна проходит горизонтальный железнодорожный путь. Обходчик, находясь в будке на расстоянии
от окна будки параллельно плоскости окна проходит горизонтальный железнодорожный путь. Обходчик, находясь в будке на расстоянии  от окна, видит в течение 20 с, как проходит весь поезд (от локомотива до последнего вагона). Длина поезда
от окна, видит в течение 20 с, как проходит весь поезд (от локомотива до последнего вагона). Длина поезда  и идет он с постоянной скоростью. Вычислить скорость поезда.
и идет он с постоянной скоростью. Вычислить скорость поезда.
Ответы. 
Составление неравенств
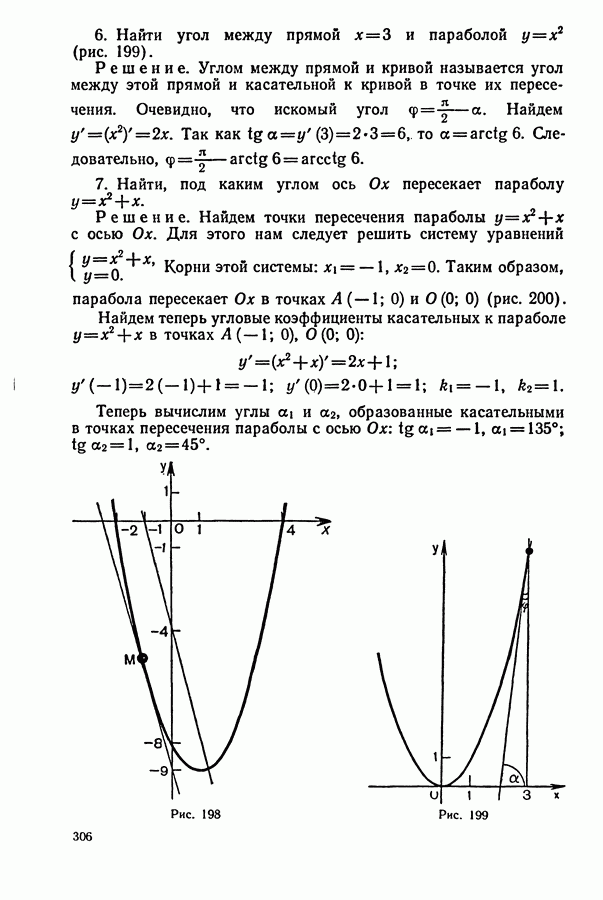
Задача (№ 13.360). Велосипедист отправляется из А в В. Расстояние от Л до В равно 60 км; скорость велосипедиста постоянна. Не задерживаясь в В, он едет обратно с той же скоростью, но через час после выезда из В делает остановку на 20 мин. После этого он продолжает путь, увеличив скорость на  . В каких границах заключена скорость
. В каких границах заключена скорость  велосипедиста, если известно, что на обратный путь от В до А он потратил времени не более, чем на путь от А до В?
велосипедиста, если известно, что на обратный путь от В до А он потратил времени не более, чем на путь от А до В?
Решение.
1. Пусть  — первоначальная скорость велосипедиста.
— первоначальная скорость велосипедиста.
Из условия задачи следует, что  (рис. 256).
(рис. 256).
2. Особенность задачи в том, что для решения требуется составить неравенство.
Так как  то Решая это неравенство, получим
то Решая это неравенство, получим

Следовательно, 
Ответ. 
Решите задачи:
1. Задача (№ 13.367). В заезде на одну и ту же дистанцию участвовали два автомобиля и мотоцикл. Второму автомобилю

Рис. 256
на всю дистанцию потребовалось минутой больше, чем первому  автомобилю. Первый автомобиль двигался в 4 раза быстрее мотоцикла. Какую часть дистанции в минуту проходил второй автомобиль, если он проходил в минуту на часть дистанции больше, чем мотоцикл, а мотоцикл прошел дистанцию быстрее чем за 10 мин?
автомобилю. Первый автомобиль двигался в 4 раза быстрее мотоцикла. Какую часть дистанции в минуту проходил второй автомобиль, если он проходил в минуту на часть дистанции больше, чем мотоцикл, а мотоцикл прошел дистанцию быстрее чем за 10 мин?
2. Задача (№ 13.369). Расстояние между станциями А и В равно 360 км. В одно и то же время из А и из В навстречу друг другу выходят два поезда. Поезд, вышедший из А, прибывает на станцию В не ранее чем через  Если бы его скорость была в 1,5 раза больше, чем на самом деле, то он встретил бы второй поезд раньше чем через
Если бы его скорость была в 1,5 раза больше, чем на самом деле, то он встретил бы второй поезд раньше чем через  после своего выхода из Л. Скорость какого поезда больше?
после своего выхода из Л. Скорость какого поезда больше?
Ответы.  Вышедшего из В.
Вышедшего из В.
Пройденный путь принимается за 1, а единственной данной величиной является время
Задача. Два пешехода вышли одновременно навстречу друг другу и встретились через  мин. Сколько времени понадобится каждому из них, чтобы пройти все расстояние, если первый пришел в то место, из которого вышел второй, на
мин. Сколько времени понадобится каждому из них, чтобы пройти все расстояние, если первый пришел в то место, из которого вышел второй, на  позже, чем второй пришел в то место, откуда вышел первый?
позже, чем второй пришел в то место, откуда вышел первый?
Решение.
1. Особенностью этой задачи является то, что в ней нет никаких данных о пройденном расстоянии. В таких случаях удобно все расстояние принять за 1, тогда скорость а  часов — время в пути первого пешехода, а у часов — время второго пешехода).
часов — время в пути первого пешехода, а у часов — время второго пешехода).
2. Из условия задачи составим систему уравнений:

3. Решая эту систему, получим 
Ответ. 
Решите задачу:
Задача (№ 13.317). Один турист вышел в  а второй навстречу ему в
а второй навстречу ему в  Встретились они в
Встретились они в  , не останавливаясь, продолжили путь. Сколько времени затратил каждый из них на весь путь, если первый пришел в то место, из которого вышел второй, на 28 мин позже, чем второй пришел в то место, откуда вышел первый? Считается, что каждый шел без остановок с постоянной скоростью.
, не останавливаясь, продолжили путь. Сколько времени затратил каждый из них на весь путь, если первый пришел в то место, из которого вышел второй, на 28 мин позже, чем второй пришел в то место, откуда вышел первый? Считается, что каждый шел без остановок с постоянной скоростью.
Ответ.  мин и
мин и  мин.
мин.
Скорость выражена косвенно через время
Задача. Два велосипедиста выехали одновременно из двух пунктов в третий, куда они договорились прибыть одновременно. Первый прибыл на место встречи через  а второму, чтобы прибыть вовремя, надо было проезжать каждый километр на 1 мин быстрее первого, так как его путь был длиннее на
а второму, чтобы прибыть вовремя, надо было проезжать каждый километр на 1 мин быстрее первого, так как его путь был длиннее на  км. Какова скорость каждого велосипедиста?
км. Какова скорость каждого велосипедиста?
Решение.
1. Особенностью этой задачи является не прямое, а косвенное указание скорости велосипедистов.
2. Пусть первый велосипедист проезжал каждый километр за х мин, т. е. его скорость была  Тогда скорость второго
Тогда скорость второго 
3. Составим уравнение и решим его: 

4. Следовательно, 
Ответ. 
Решите задачи:
1. Задача (№ 13.096). Велосипедист каждую минуту проезжает на  меньше, чем мотоциклист, поэтому на путь в 120 км он затрачивает времени на
меньше, чем мотоциклист, поэтому на путь в 120 км он затрачивает времени на  больше, чем мотоциклист. Вычислить скорость каждого из них.
больше, чем мотоциклист. Вычислить скорость каждого из них.
2. Задача (№ 13.221). Из пунктов А и С в пункт В выехали одновременно два всадника и, несмотря на то что пункт С отстоял от пункта В на 20 км дальше, чем пункт А от пункта В, прибыли в пункт В одновременно. Найти расстояние от пункта С до пункта В, если всадник, выехавший из С, проезжал каждый километр на 1 мин скорее, чем всадник, выехавший из пункта А, и всадник, выехавший из А, приехал в пункт В через 
Ответы.  км.
км.
Тела движутся по окружности
Задача (№ 13.302). По окружности длиной  равномерно и в одном направлении движутся две точки. Одна из них делает полный оборот на 5 с скорее другой. При этом совпадения точек происходят каждый раз через 1 мин. Определить скорости точек.
равномерно и в одном направлении движутся две точки. Одна из них делает полный оборот на 5 с скорее другой. При этом совпадения точек происходят каждый раз через 1 мин. Определить скорости точек.
Решение.
1. Пусть первая точка проходит полный оборот за  , а вторая точка — за у с. Тогда
, а вторая точка — за у с. Тогда 
2. Будем полагать, что  тогда из условия задачи следует уравнение
тогда из условия задачи следует уравнение 
3. Так как точки встречаются каждую минуту и первая движется быстрее, то она должна за 1 мин пройти полный круг  и еще столько, сколько успеет пройти за 1 мин вторая точка, т. е.
и еще столько, сколько успеет пройти за 1 мин вторая точка, т. е. 
4. Отсюда имеем второе уравнение:  .
.
5. Составим систему и решим ее:

Тогда 
Ответ. 
Решите задачи:
1. Задача (№ 13.298). Два спортсмена бегают по одной замкнутой дорожке стадиона. Скорость каждого постоянна, но на пробег всей дорожки первый тратит на 10 с меньше, чем второй. Если начнут они пробег с общего старта в одном направлении, то еще раз сойдутся через 720 с. Какую часть длины всей дорожки пробегает в секунду каждый бегун?
2. Задача (№ 13.126). По двум концентрическим окружностям равномерно вращаются две точки. Одна из них совершает полный оборот на 5 с быстрее, чем другая, и поэтому успевает сделать в 1 мин на два оборота больше. Сколько оборотов в минуту совершает каждая точка?
3. Задача (№ 13.251). Часовая и минутная стрелки совпадают в полночь, и начинается новый день. В котором часу этого нового дня впервые вновь совпадут часовая и минутная стрелки, если допустить, что стрелки часов движутся без скачков?
Ответы.  и 5 мин.
и 5 мин.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ГЛАВА I.
- § 1. НАТУРАЛЬНЫЕ ЧИСЛА И ДЕЙСТВИЯ НАД НИМИ
- § 2. СЛОЖЕНИЕ И ЗАКОНЫ СЛОЖЕНИЯ
- § 3. ВЫЧИТАНИЕ
- § 4. УМНОЖЕНИЕ И ЗАКОНЫ УМНОЖЕНИЯ
- § 5. ДЕЛЕНИЕ
- § 6. ПРИЗНАКИ ДЕЛИМОСТИ ЧИСЕЛ
- § 7. ПОНЯТИЕ МНОЖЕСТВА
- § 8. ОПЕРАЦИИ НАД МНОЖЕСТВАМИ
- § 9. ВЗАИМНО ОДНОЗНАЧНОЕ СООТВЕТСТВИЕ
- § 10. ПРОСТЫЕ И СОСТАВНЫЕ ЧИСЛА
- § 11. НАИБОЛЬШИЙ ОБЩИЙ ДЕЛИТЕЛЬ
- § 12. НАИМЕНЬШЕЕ ОБЩЕЕ КРАТНОЕ
- Контрольные вопросы
- ГЛАВА II
- § 1. ОБЫКНОВЕННЫЕ ДРОБИ
- § 2. ПРАВИЛЬНЫЕ И НЕПРАВИЛЬНЫЕ ДРОБИ
- § 3. ОСНОВНОЕ СВОЙСТВО ДРОБИ
- § 4. СЛОЖЕНИЕ И ВЫЧИТАНИЕ ДРОБЕЙ
- § 5. УМНОЖЕНИЕ ДРОБЕЙ
- § 6. ДЕЛЕНИЕ ДРОБЕЙ
- § 7. ДЕСЯТИЧНЫЕ ДРОБИ
- § 8. ОБРАЩЕНИЕ ДЕСЯТИЧНОЙ ДРОБИ В ОБЫКНОВЕННУЮ И ОБЫКНОВЕННОЙ В ДЕСЯТИЧНУЮ. ПЕРИОДИЧЕСКИЕ ДРОБИ
- § 9. ОТНОШЕНИЕ. ПРОПОРЦИЯ
- § 10. СВОЙСТВА ПРОПОРЦИИ
- § 11. ПРОЦЕНТ. ОСНОВНЫЕ ЗАДАЧИ НА ПРОЦЕНТЫ
- § 12. ДЕЛЕНИЕ ЧИСЛА НА ЧАСТИ, ПРЯМО И ОБРАТНО ПРОПОРЦИОНАЛЬНЫЕ ДАННЫМ ЧИСЛАМ
- Контрольные вопросы
- ГЛАВА III
- § 1. КООРДИНАТНАЯ ПРЯМАЯ
- § 2. МНОЖЕСТВО ЦЕЛЫХ ЧИСЕЛ
- § 3. МНОЖЕСТВО РАЦИОНАЛЬНЫХ ЧИСЕЛ
- § 4. МОДУЛЬ ЧИСЛА
- § 5. СРАВНЕНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ
- § 6. СЛОЖЕНИЕ И ВЫЧИТАНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ
- § 7. УМНОЖЕНИЕ И ДЕЛЕНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ
- § 8. ВОЗВЕДЕНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ В СТЕПЕНЬ С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ
- Контрольные вопросы
- ГЛАВА IV
- § 1. СВОЙСТВА СТЕПЕНИ С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ
- § 2. ЧИСЛОВЫЕ ВЫРАЖЕНИЯ
- § 3. ВЫРАЖЕНИЯ С ПЕРЕМЕННЫМИ
- § 4. ТОЖДЕСТВЕННО РАВНЫЕ ВЫРАЖЕНИЯ
- § 5. ОДНОЧЛЕНЫ
- § 6. МНОГОЧЛЕНЫ
- § 7. ПРЕОБРАЗОВАНИЕ СУММЫ И РАЗНОСТИ МНОГОЧЛЕНОВ
- § 8. УМНОЖЕНИЕ МНОГОЧЛЕНА НА ОДНОЧЛЕН И МНОГОЧЛЕНА НА МНОГОЧЛЕН
- § 9. РАЗЛОЖЕНИЕ МНОГОЧЛЕНА НА МНОЖИТЕЛИ СПОСОБОМ ВЫНЕСЕНИЯ ОБЩЕГО МНОЖИТЕЛЯ ЗА СКОБКИ
- § 10. РАЗЛОЖЕНИЕ МНОГОЧЛЕНА НА МНОЖИТЕЛИ СПОСОБОМ ГРУППИРОВКИ
- § 11. ФОРМУЛЫ СОКРАЩЕННОГО УМНОЖЕНИЯ
- Контрольные вопросы
- ГЛАВА V
- § 1. ДРОБЬ
- § 2. ЦЕЛЫЕ И ДРОБНЫЕ ВЫРАЖЕНИЯ
- § 3. ТОЖДЕСТВЕННОЕ ПРЕОБРАЗОВАНИЕ СУММЫ И РАЗНОСТИ ДВУХ ДРОБЕЙ
- § 4. ТОЖДЕСТВЕННОЕ ПРЕОБРАЗОВАНИЕ ПРОИЗВЕДЕНИЯ И ЧАСТНОГО ДВУХ ДРОБЕЙ
- § 5. СТЕПЕНЬ ДРОБИ
- Контрольные вопросы
- ГЛАВА VI
- § 1. ПОНЯТИЕ ОБ ИРРАЦИОНАЛЬНОМ ЧИСЛЕ
- § 2. РАЗВИТИЕ ПОНЯТИЯ О ЧИСЛЕ. МНОЖЕСТВО ДЕЙСТВИТЕЛЬНЫХ ЧИСЕЛ
- § 3. КОРЕНЬ СТЕПЕНИ ИЗ ДЕЙСТВИТЕЛЬНОГО ЧИСЛА
- § 4. АЛГОРИТМ ИЗВЛЕЧЕНИЯ КВАДРАТНОГО КОРНЯ ИЗ ЧИСЛА
- § 5. АРИФМЕТИЧЕСКИЕ ДЕЙСТВИЯ С ДЕЙСТВИТЕЛЬНЫМИ ЧИСЛАМИ
- § 6. ПРЕОБРАЗОВАНИЯ АРИФМЕТИЧЕСКИХ КОРНЕЙ
- § 7. СТЕПЕНЬ С ЦЕЛЫМ И ДРОБНЫМ ПОКАЗАТЕЛЕМ
- Контрольные вопросы
- ГЛАВА VII
- § 1. УРАВНЕНИЯ С ОДНОЙ ПЕРЕМЕННОЙ
- § 2. ПОНЯТИЕ О РАВНОСИЛЬНОСТИ УРАВНЕНИЙ
- § 3. СВОЙСТВА ЧИСЛОВЫХ РАВЕНСТВ И ТЕОРЕМЫ О РАВНОСИЛЬНОСТИ УРАВНЕНИЙ
- § 4. ЛИНЕЙНОЕ УРАВНЕНИЕ С ОДНОЙ ПЕРЕМЕННОЙ, СОДЕРЖАЩЕЕ ПАРАМЕТР
- Контрольные вопросы
- ГЛАВА VIII
- § 1. ПОНЯТИЕ ФУНКЦИИ
- § 2. СПОСОБЫ ЗАДАНИЯ ФУНКЦИИ
- § 3. МОНОТОННОСТЬ ФУНКЦИИ
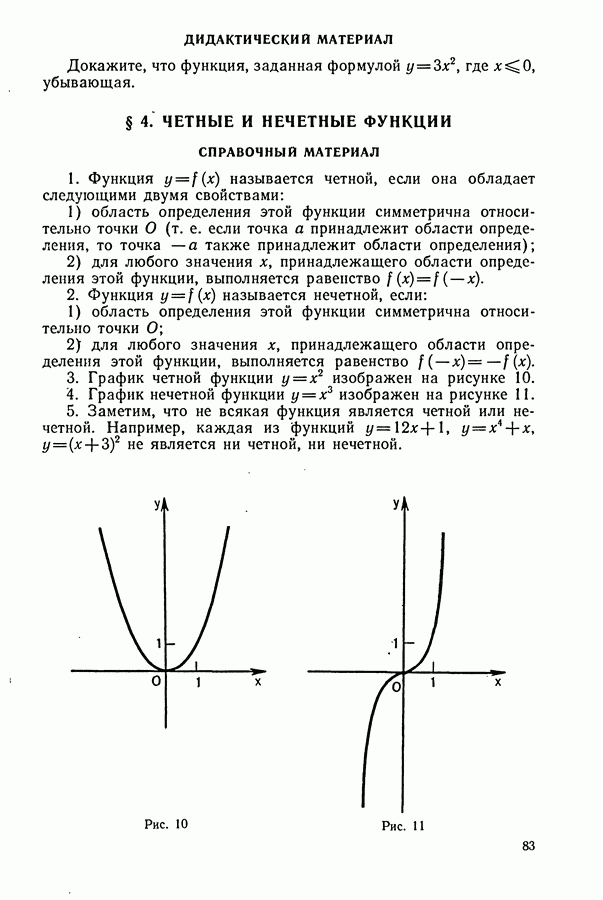
- § 4. ЧЕТНЫЕ И НЕЧЕТНЫЕ ФУНКЦИИ СПРАВОЧНЫЙ МАТЕРИАЛ
- § 5. ПЕРИОДИЧЕСКИЕ ФУНКЦИИ
- § 6. ПРОМЕЖУТКИ ЗНАКОПОСТОЯНСТВА И КОРНИ ФУНКЦИИ
- Контрольные вопросы
- ГЛАВА IX
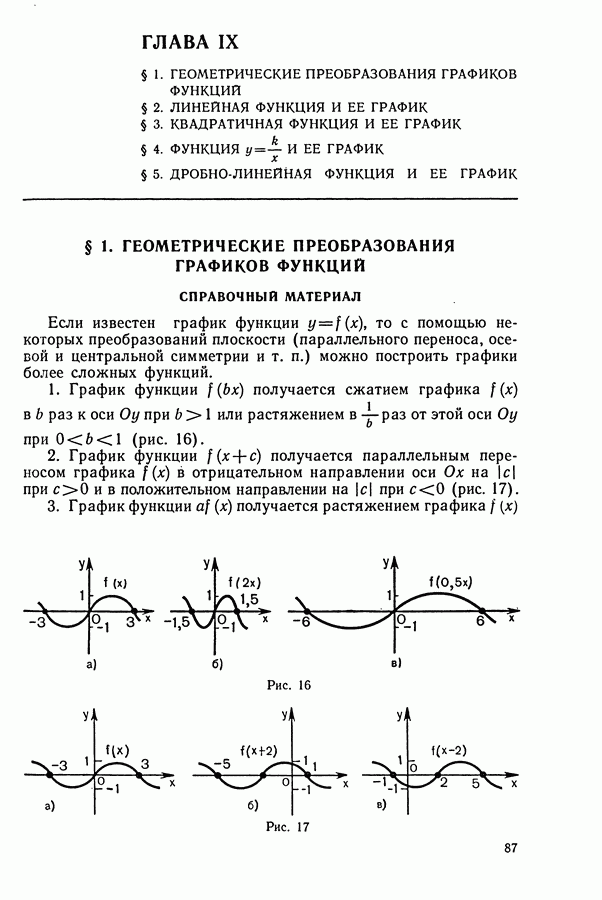
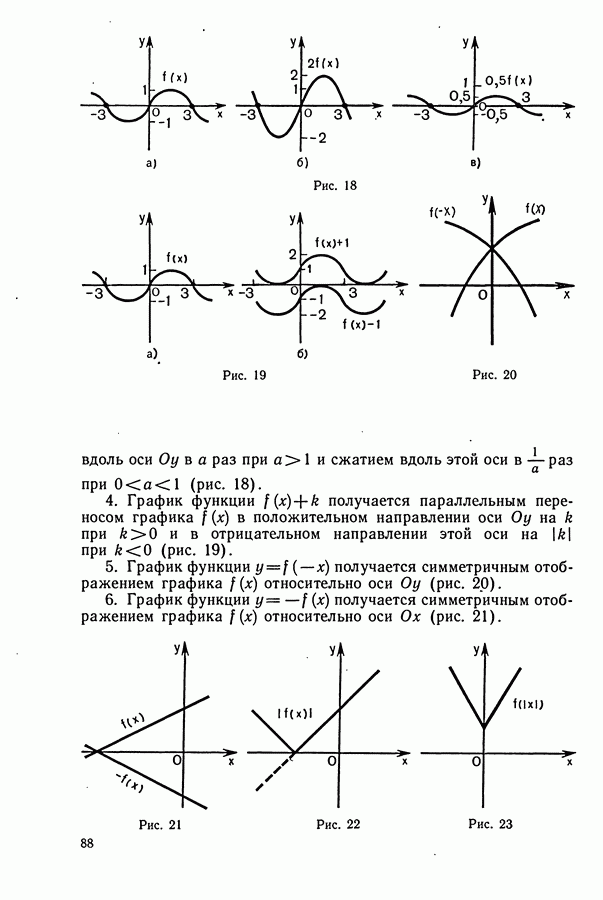
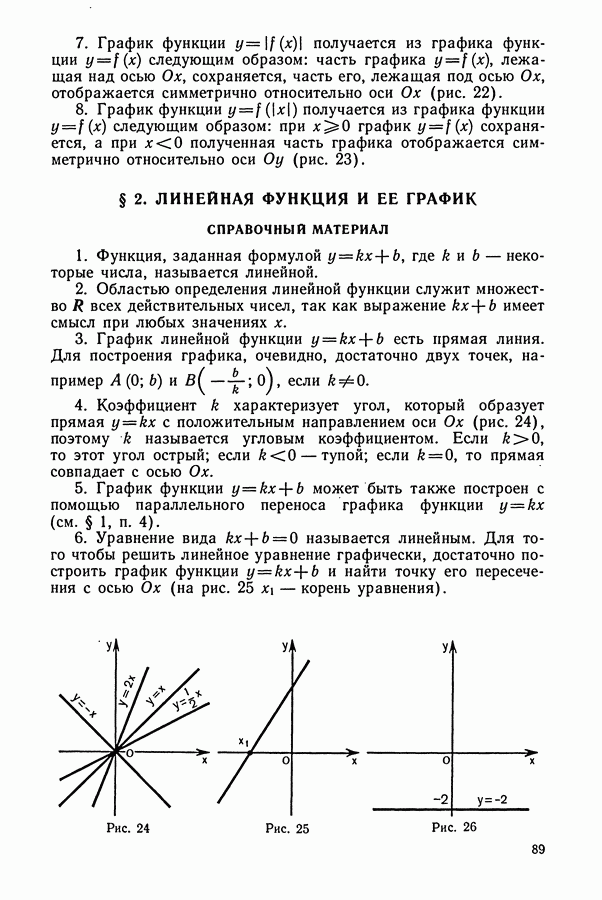
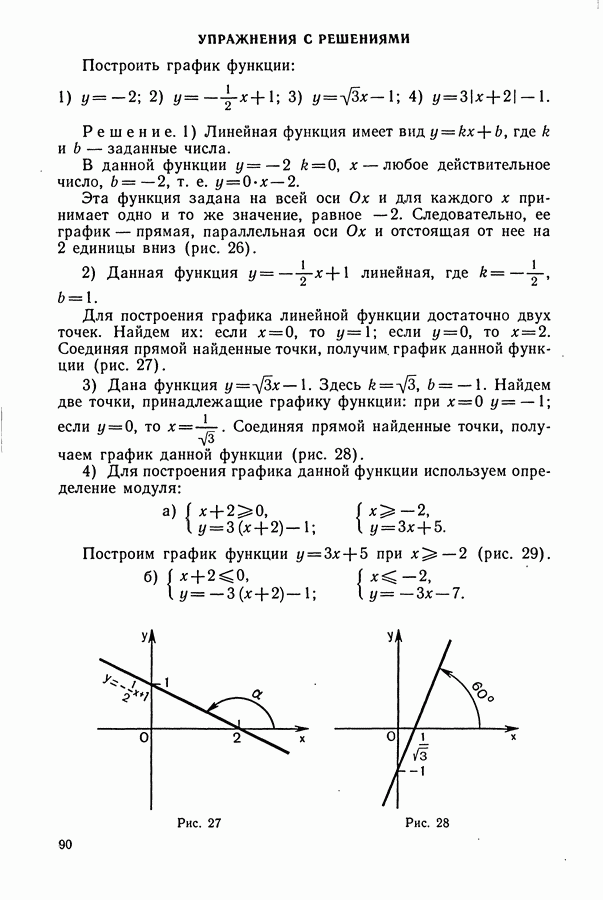
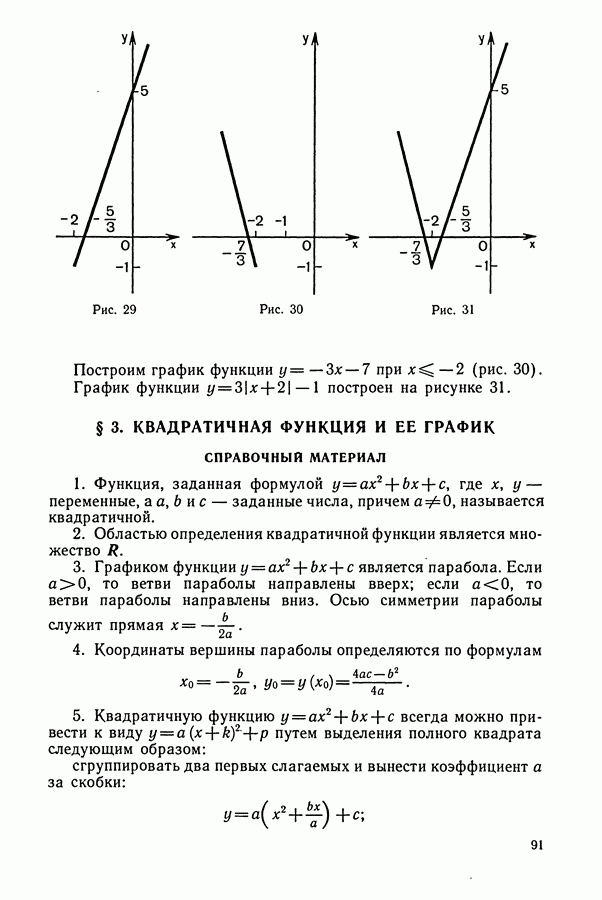
- § 1. ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ ГРАФИКОВ ФУНКЦИЙ
- § 2. ЛИНЕЙНАЯ ФУНКЦИЯ И ЕЕ ГРАФИК
- § 3. КВАДРАТИЧНАЯ ФУНКЦИЯ И ЕЕ ГРАФИК
- § 4. ФУНКЦИЯ y=k/x И ЕЕ ГРАФИК
- § 5. ДРОБНО-ЛИНЕЙНАЯ ФУНКЦИЯ И ЕЕ ГРАФИК
- Контрольные вопросы
- ГЛАВА X
- § 1. КВАДРАТНЫЕ УРАВНЕНИЯ
- § 2. ТЕОРЕМА ВИЕТА
- § 3. ГРАФИЧЕСКИЙ СПОСОБ РЕШЕНИЯ КВАДРАТНЫХ УРАВНЕНИЙ
- § 4. УРАВНЕНИЕ СО МНОГИМИ ПЕРЕМЕННЫМИ
- § 5. СИСТЕМЫ УРАВНЕНИЙ
- Контрольные вопросы
- ГЛАВА XI
- § 1. НЕРАВЕНСТВА
- § 2. ОСНОВНЫЕ СВОЙСТВА НЕРАВЕНСТВ
- § 3. ДЕЙСТВИЯ С НЕРАВЕНСТВАМИ
- § 4. ДОКАЗАТЕЛЬСТВА НЕРАВЕНСТВ
- § 5. НЕРАВЕНСТВА, СОДЕРЖАЩИЕ ПЕРЕМЕННУЮ
- § 6. РЕШЕНИЕ ЛИНЕЙНЫХ И КВАДРАТНЫХ НЕРАВЕНСТВ
- Контрольные вопросы
- ГЛАВА XII
- § 1. СИСТЕМЫ И СОВОКУПНОСТИ НЕРАВЕНСТВ
- § 2. НЕРАВЕНСТВА И СИСТЕМЫ НЕРАВЕНСТВ С ДВУМЯ ПЕРЕМЕННЫМИ
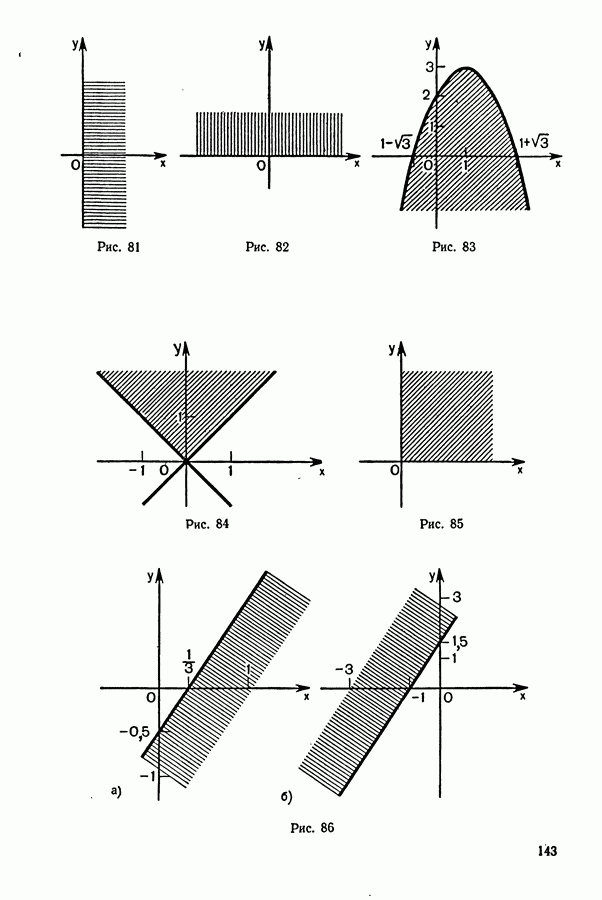
- § 3. РЕШЕНИЕ НЕРАВЕНСТВ, СОДЕРЖАЩИХ ПЕРЕМЕННУЮ ПОД ЗНАКОМ МОДУЛЯ
- § 4. РЕШЕНИЕ РАЦИОНАЛЬНЫХ НЕРАВЕНСТВ МЕТОДОМ ПРОМЕЖУТКОВ
- Контрольные вопросы
- ГЛАВА XIII
- § 1. ЧИСЛОВАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ
- § 2. АРИФМЕТИЧЕСКАЯ ПРОГРЕССИЯ
- § 3. ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИЯ
- § 4. СУММА БЕСКОНЕЧНОЙ ГЕОМЕТРИЧЕСКОЙ ПРОГРЕССИИ ПРИ |q|<1
- Контрольные вопросы
- ГЛАВА XIV
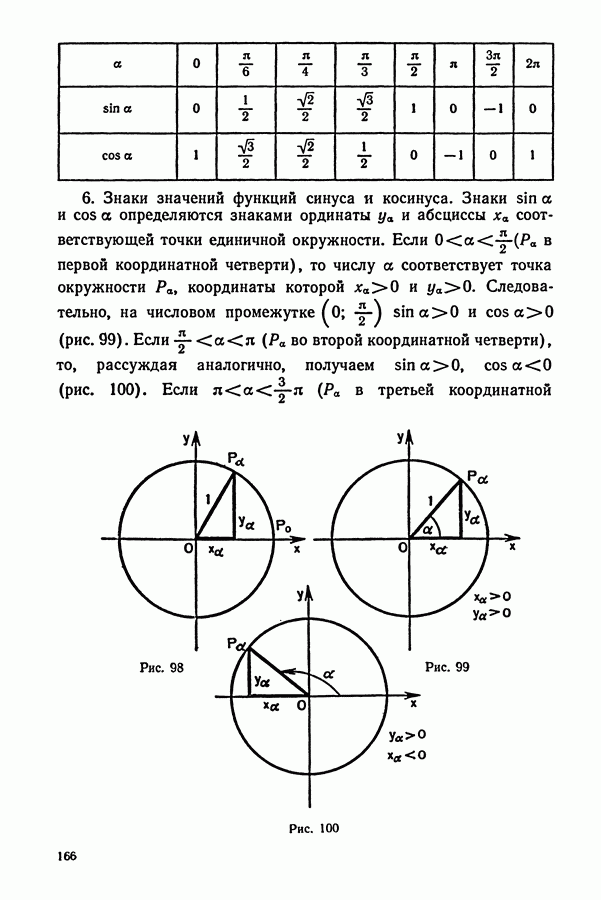
- § 1. ГРАДУСНОЕ ИЗМЕРЕНИЕ УГЛОВЫХ ВЕЛИЧИН
- § 2. РАДИАННОЕ ИЗМЕРЕНИЕ УГЛОВЫХ ВЕЛИЧИН
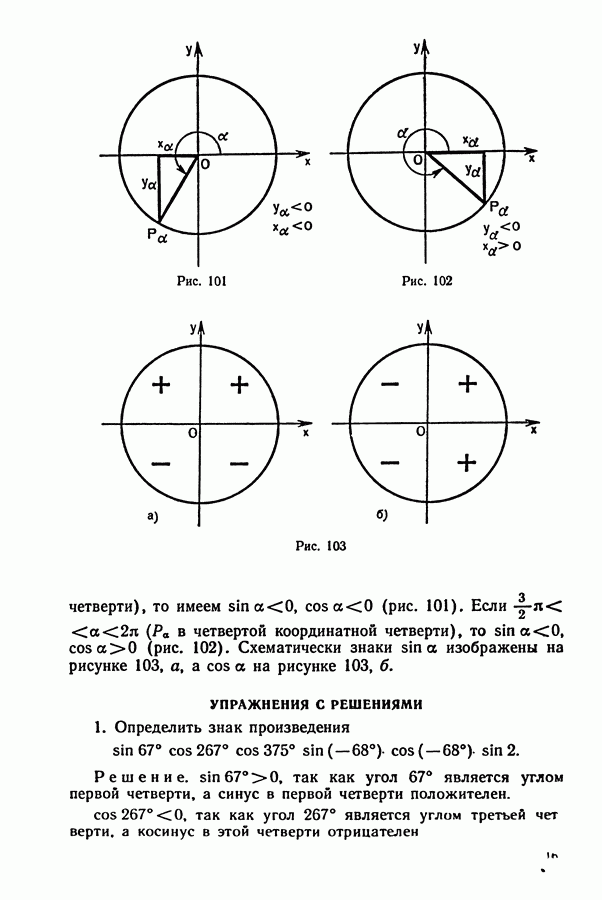
- § 3. СИНУС И КОСИНУС ЧИСЛОВОГО АРГУМЕНТА
- § 4. ТАНГЕНС И КОТАНГЕНС ЧИСЛОВОГО АРГУМЕНТА. СЕКАНС И КОСЕКАНС ЧИСЛА а
- § 5. ОСНОВНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ТОЖДЕСТВА
- § 6. ДОПОЛНИТЕЛЬНЫЕ СВОЙСТВА ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ
- Контрольные вопросы
- ГЛАВА XV
- § 1. ФОРМУЛЫ ПРИВЕДЕНИЯ
- § 2. ФОРМУЛЫ СЛОЖЕНИЯ
- § 3. ФОРМУЛЫ ДВОЙНОГО УГЛА СПРАВОЧНЫЙ МАТЕРИАЛ
- § 4. ПРЕОБРАЗОВАНИЕ ПРОИЗВЕДЕНИЯ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ В СУММУ
- § 5. ФОРМУЛЫ СУММЫ И РАЗНОСТИ ОДНОИМЕННЫХ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ
- § 6. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ ПОЛОВИННОГО АРГУМЕНТА
- § 7. ВЫРАЖЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ ЧЕРЕЗ ТАНГЕНС ПОЛОВИННОГО АРГУМЕНТА
- Контрольные вопросы
- ГЛАВА XVI
- § 1. СВОЙСТВА ФУНКЦИИ y = sin(x) И ЕЕ ГРАФИК
- § 2. СВОЙСТВА ФУНКЦИ И у = cos(x) И ЕЕ ГРАФИК
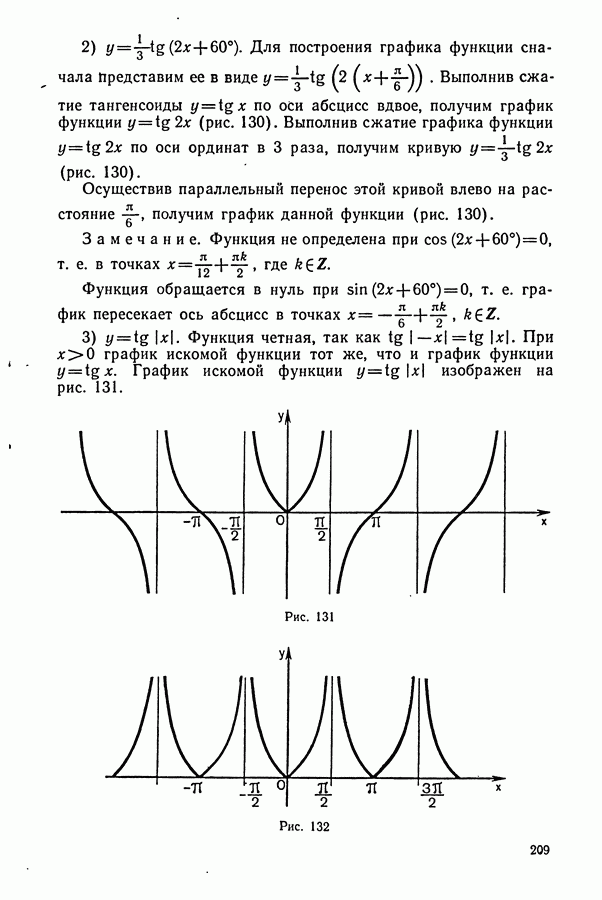
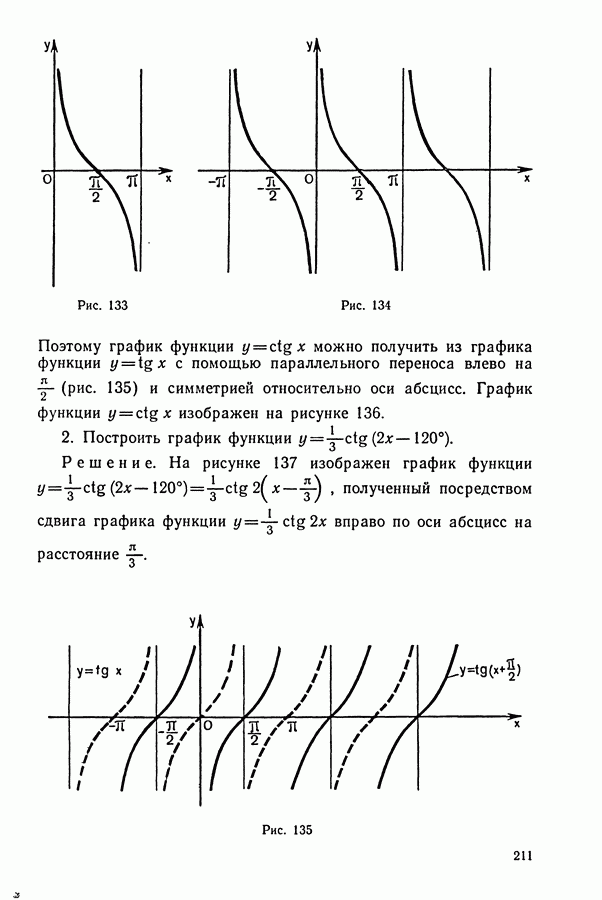
- § 3. СВОЙСТВА ФУНКЦИ И у=tg(x) И ЕЕ ГРАФИК
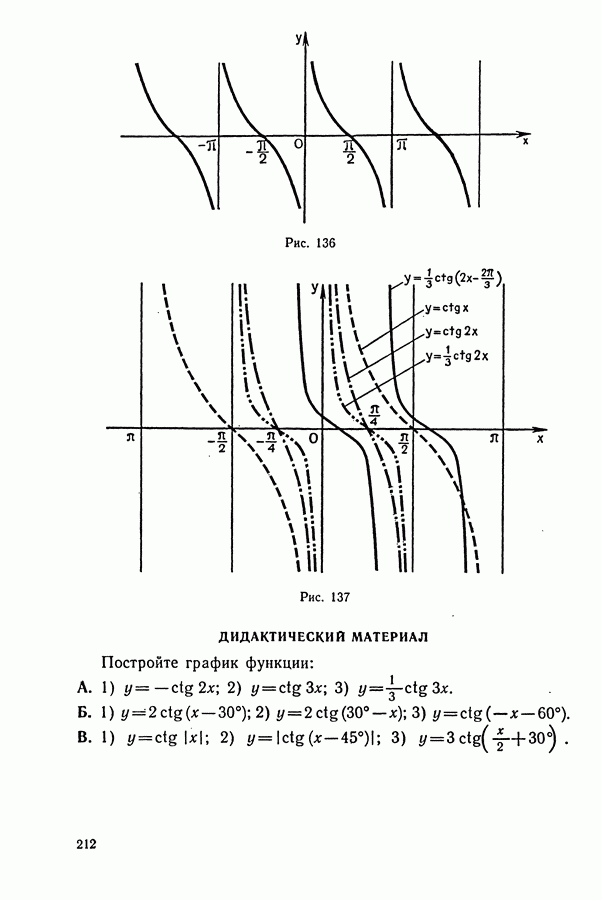
- § 4. СВОЙСТВА ФУНКЦИ И y=ctg(x) И ЕЕ ГРАФИК
- § 5. НАХОЖДЕНИЕ ПЕРИОДОВ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ
- Контрольные вопросы
- ГЛАВА XVII
- § 1. АРКСИНУС И АРККОСИНУС
- § 2. АРКТАНГЕНС И АРККОТАНГЕНС
- Контрольные вопросы
- ГЛАВА XVIII
- § 1. РЕШЕНИЕ УРАВНЕНИЙ ВИДА cos(x)=а
- § 2. РЕШЕНИЕ УРАВНЕНИЙ ВИДА sin(x)=a
- § 3. РЕШЕНИЕ УРАВНЕНИЙ ВИДА tg(х)=а
- § 4. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ, ПРИВОДИМЫХ К КВАДРАТНОМУ
- § 5. РЕШЕНИЕ ОДНОРОДНЫХ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ
- § 6. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ, РЕШАЕМЫЕ С ПОМОЩЬЮ ФОРМУЛ СЛОЖЕНИЯ, ПОНИЖЕНИЯ СТЕПЕНИ
- § 7. РЕШЕНИЕ СИСТЕМ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ
- Контрольные вопросы
- ГЛАВА XIX
- § 1. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ ВИДА sin(х) > а, sin(х) < а
- § 2. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ ВИДА cos(x) > a, cos(x) < a
- § 3. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ ВИДА tg(х) > a, tg(х) < a
- § 4. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ
- ГЛАВА XX
- § 1. ПРИРАЩЕНИЕ АРГУМЕНТА И ПРИРАЩЕНИЕ ФУНКЦИИ
- § 2. ПРЕДЕЛ ФУНКЦИИ
- § 3. НЕПРЕРЫВНОСТЬ ФУНКЦИИ
- § 4. ОПРЕДЕЛЕНИЕ ПРОИЗВОДНОЙ
- § 5. ПРОИЗВОДНАЯ СУММЫ, ПРОИЗВЕДЕНИЯ, ЧАСТНОГО
- § 6. ПРОИЗВОДНАЯ СТЕПЕННОЙ И СЛОЖНОЙ ФУНКЦИИ
- § 7. ПРОИЗВОДНЫЕ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ
- Контрольные вопросы
- ГЛАВА XXI
- § 1. ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ К НАХОЖДЕНИЮ ПРОМЕЖУТКОВ МОНОТОННОСТИ ФУНКЦИИ
- § 2. КРИТИЧЕСКИЕ ТОЧКИ ФУНКЦИИ, ЕЕ МАКСИМУМЫ И МИНИМУМЫ
- § 3. ОБЩАЯ СХЕМА ИССЛЕДОВАНИЯ ФУНКЦИИ
- § 4. ЗАДАЧИ НА НАХОЖДЕНИЕ НАИМЕНЬШЕГО И НАИБОЛЬШЕГО ЗНАЧЕНИЯ ФУНКЦИИ
- Контрольные вопросы
- ГЛАВА XXII
- § 1. ФОРМУЛЫ ПРИБЛИЖЕННЫХ ВЫЧИСЛЕНИЙ СПРАВОЧНЫЙ МАТЕРИАЛ
- § 2. КАСАТЕЛЬНАЯ К ГРАФИКУ ФУНКЦИИ
- § 3. СКОРОСТЬ И УСКОРЕНИЕ В ДАННЫЙ МОМЕНТ ВРЕМЕНИ
- § 4. ГРАФИКИ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ
- Контрольные вопросы
- ГЛАВА XXIII
- § 1. ПОТЕРЯННЫЕ И ПОСТОРОННИЕ КОРНИ ПРИ РЕШЕНИИ УРАВНЕНИЙ (НА ПРИМЕРАХ)
- § 2. ПОСТОРОННИЕ КОРНИ ИРРАЦИОНАЛЬНОГО УРАВНЕНИЯ (НА ПРИМЕРАХ)
- § 3. РЕШЕНИЕ ИРРАЦИОНАЛЬНЫХ УРАВНЕНИЙ
- § 4. РЕШЕНИЕ ИРРАЦИОНАЛЬНЫХ НЕРАВЕНСТВ СПРАВОЧНЫЙ МАТЕРИАЛ
- Контрольные вопросы
- ГЛАВА XXIV
- § 1. ПОКАЗАТЕЛЬНАЯ ФУНКЦИЯ, ЕЕ СВОЙСТВА И ГРАФИК
- § 2. ПОКАЗАТЕЛЬНЫЕ УРАВНЕНИЯ
- § 3. ПОКАЗАТЕЛЬНЫЕ НЕРАВЕНСТВА
- § 4. СИСТЕМЫ ПОКАЗАТЕЛЬНЫХ УРАВНЕНИЙ И НЕРАВЕНСТВ
- Контрольные вопросы
- ГЛАВА XXV
- § 1. ОБРАТНАЯ ФУНКЦИЯ
- § 2. ПОНЯТИЕ ЛОГАРИФМА
- § 3. СВОЙСТВА ЛОГАРИФМОВ
- § 4. ЛОГАРИФМИЧЕСКАЯ ФУНКЦИЯ, ЕЕ СВОЙСТВА И ГРАФИК
- § 5. ТЕОРЕМЫ О ЛОГАРИФМЕ ПРОИЗВЕДЕНИЯ, ЧАСТНОГО И СТЕПЕНИ. ФОРМУЛА ПЕРЕХОДА К НОВОМУ ОСНОВАНИЮ
- § 6. ДЕСЯТИЧНЫЕ ЛОГАРИФМЫ И ИХ СВОЙСТВА
- § 7. ЛОГАРИФМИРОВАНИЕ И ПОТЕНЦИРОВАНИЕ
- Контрольные вопросы
- ГЛАВА XXVI
- § 1. ЛОГАРИФМИЧЕСКИЕ УРАВНЕНИЯ
- § 2. ЛОГАРИФМИЧЕСКИЕ НЕРАВЕНСТВА
- § 3. СИСТЕМЫ ЛОГАРИФМИЧЕСКИХ УРАВНЕНИЙ И НЕРАВЕНСТВ
- § 4. ПРОИЗВОДНЫЕ ЛОГАРИФМИЧЕСКОЙ И ПОКАЗАТЕЛЬНОЙ ФУНКЦИЙ. ЧИСЛО e
- Контрольные вопросы
- ГЛАВА XXVII
- § 1. ПОНЯТИЕ ПЕРВООБРАЗНОЙ ФУНКЦИИ
- § 2. ОСНОВНОЕ СВОЙСТВО ПЕРВООБРАЗНОЙ ФУНКЦИИ
- § 3. ТРИ ПРАВИЛА НАХОЖДЕНИЯ ПЕРВООБРАЗНЫХ
- § 4. КРИВОЛИНЕЙНАЯ ТРАПЕЦИЯ И ЕЕ ПЛОЩАДЬ
- Контрольные вопросы
- ГЛАВА XXVIII
- § 1. ФОРМУЛА НЬЮТОНА—ЛЕЙБНИЦА
- § 2. ОСНОВНЫЕ ПРАВИЛА ИНТЕГРИРОВАНИЯ
- § 3. ВЫЧИСЛЕНИЕ ПЛОЩАДЕЙ С ПОМОЩЬЮ ИНТЕГРАЛА
- § 4. МЕХАНИЧЕСКИЕ И ФИЗИЧЕСКИЕ ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
- ПРИЛОЖЕНИЕ
- Введение
- 1. Задачи на движение
- 2. Задачи на совместную работу
- 3. Задачи на планирование
- 4. Задачи на зависимость между компонентами арифметических действий
- 5. Задачи на проценты
- 6. Задачи на смеси (сплавы)
- 7. Задачи на разбавление