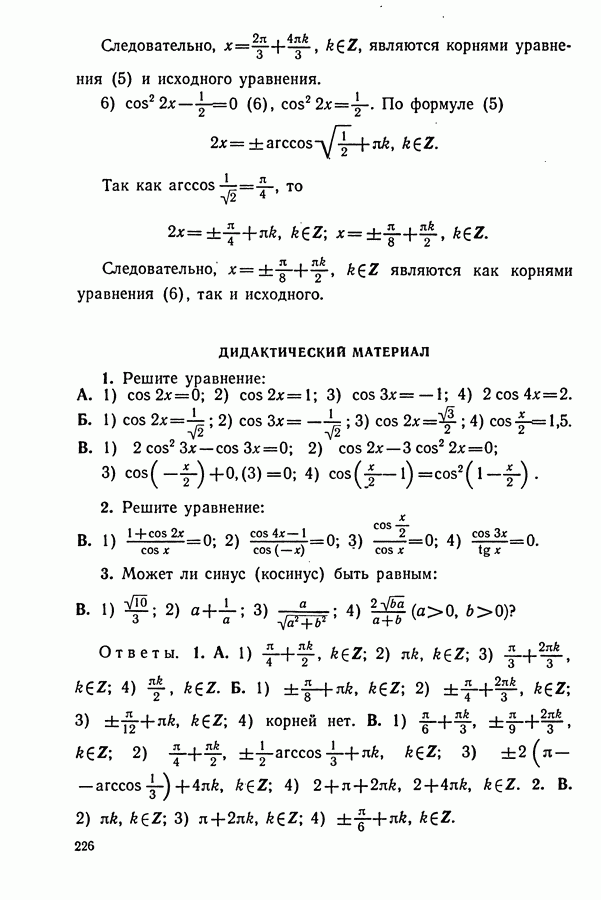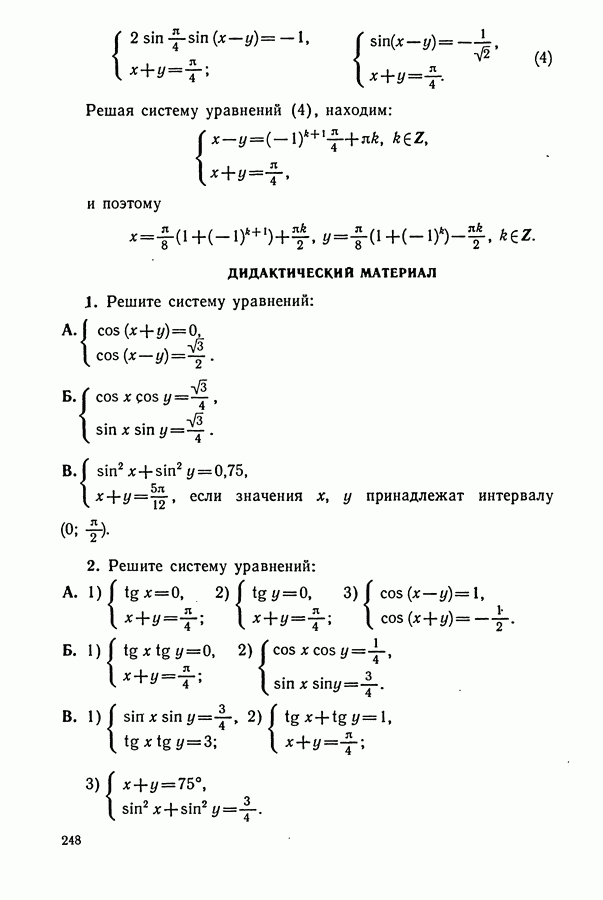| << Предыдущий параграф | Следующий параграф >> |
Пред.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
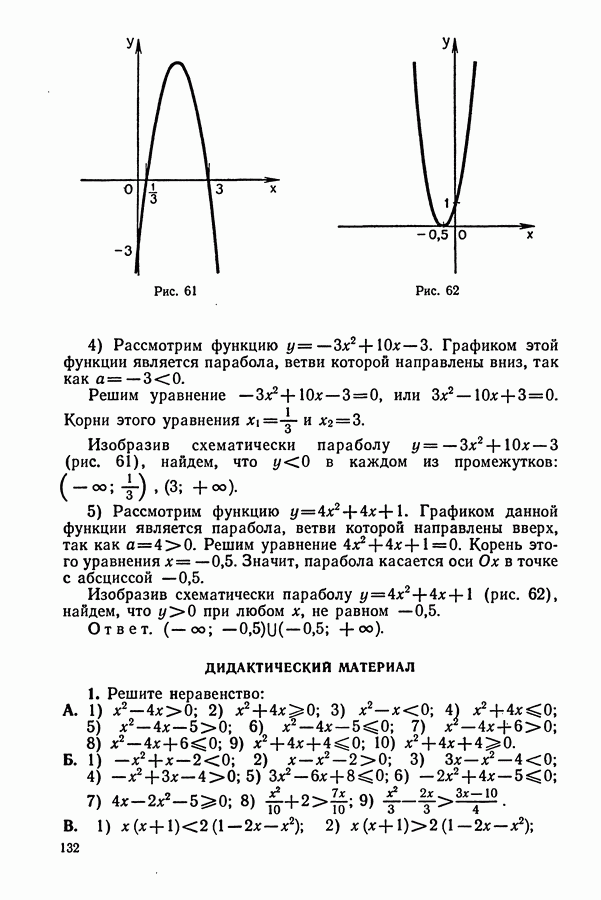
61
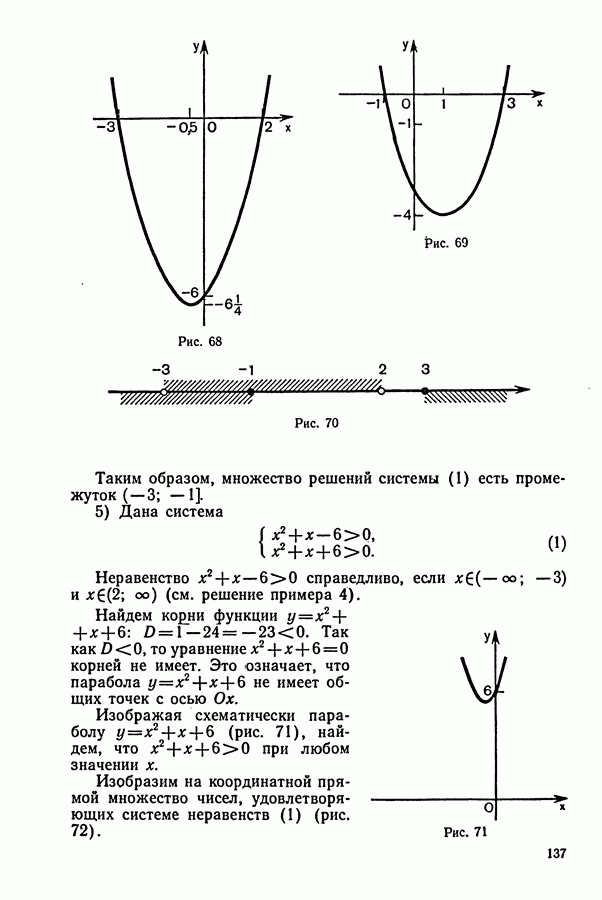
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
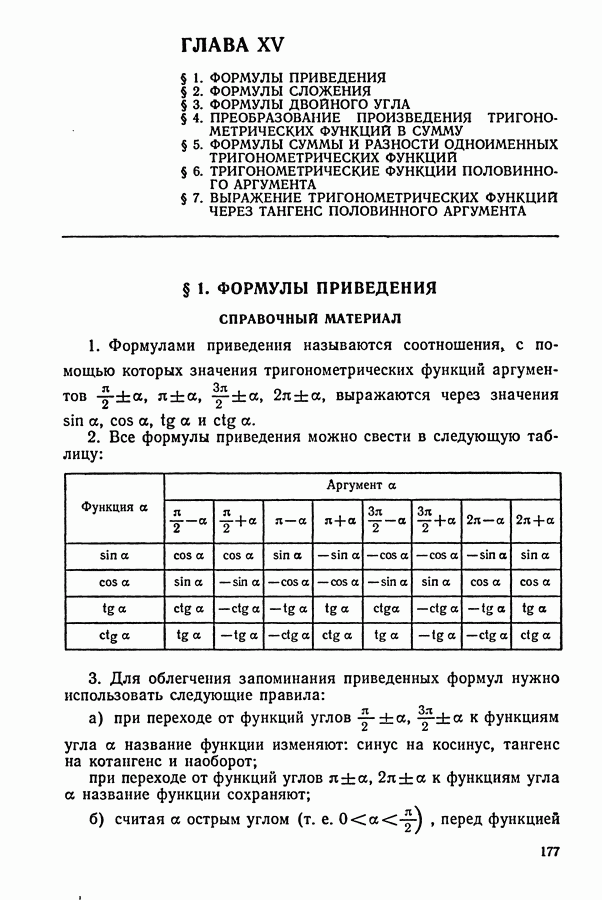
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
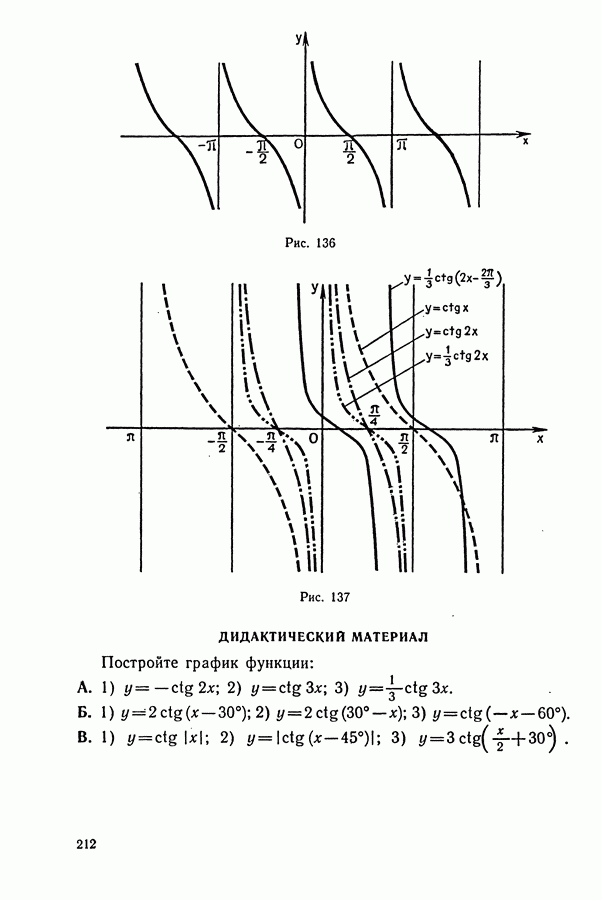
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
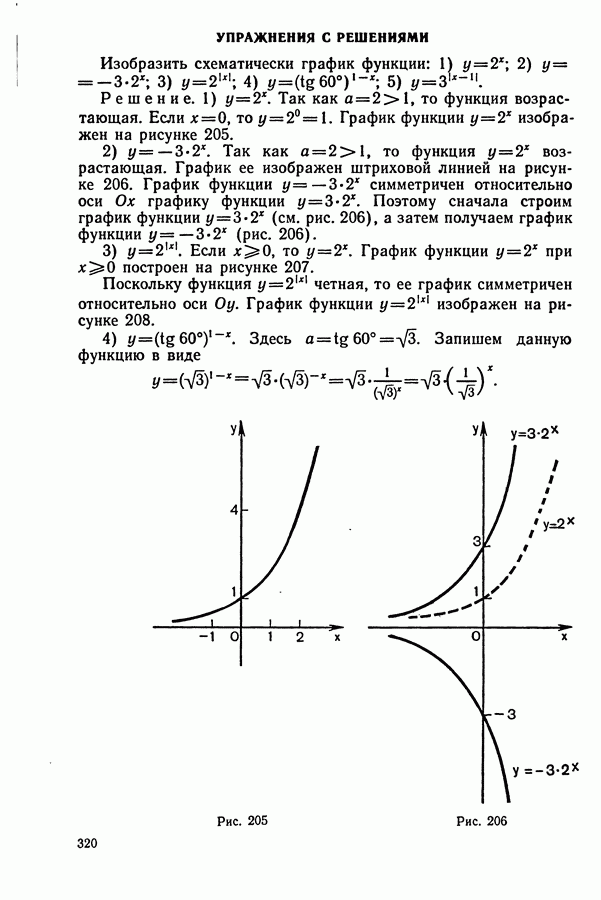
320
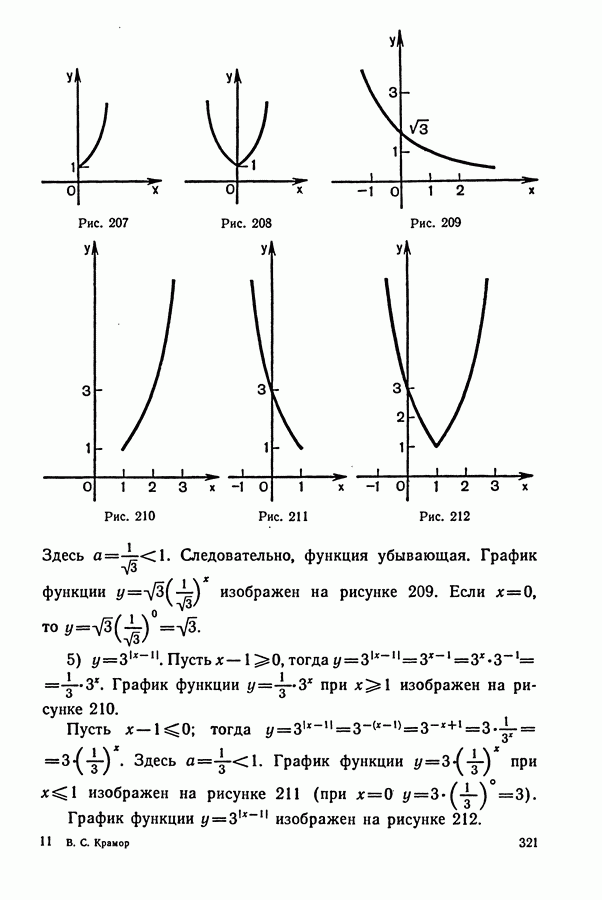
321
322
323
324
325
326
327
328
329
330
331
332
333
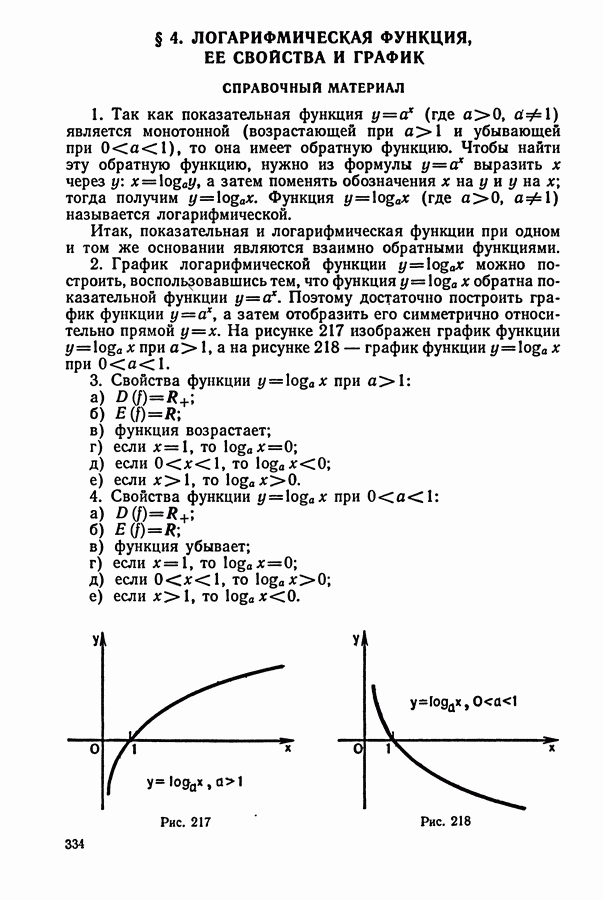
334
335
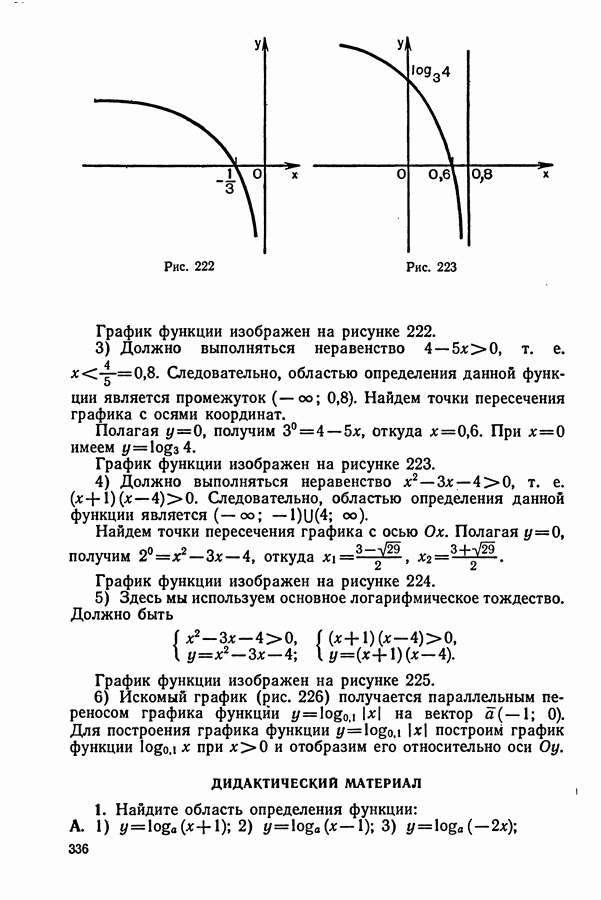
336
337
338
339
340
341
342
343
344
345
346
347
348
349
350
351
352
353
354
355
356
357
358
359
360
361
362
363
364
365
366
367
368
369
370
371
372
373
374
375
376
377
378
379
380
381
382
383
384
385
386
387
388
389
390
391
392
393
394
395
396
397
398
399
400
401
402
403
404
405
406
407
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 3. СИНУС И КОСИНУС ЧИСЛОВОГО АРГУМЕНТА
СПРАВОЧНЫЙ МАТЕРИАЛ
1. Рассмотрим единичную окружность, т. е. окружность с центром в начале координат и радиусом, равным 1 (рис. 98). На единичной окружности отметим точку  . При повороте начального радиуса около центра О на угол а радиан точка
. При повороте начального радиуса около центра О на угол а радиан точка  перейдет в некоторую точку
перейдет в некоторую точку  Обозначим координаты этой точки
Обозначим координаты этой точки  (Заметим, что поворот можно осуществить как в положительном, так и в отрицательном направлении.)
(Заметим, что поворот можно осуществить как в положительном, так и в отрицательном направлении.)
2. Определения:
а) Синусом угла а называется отношение ординаты точки  к радиусу. Таким образом,
к радиусу. Таким образом, 
б) Косинусом угла а называется отношение абсциссы точки  к радиусу. Таким образом,
к радиусу. Таким образом, 
3. Каждому углу а соответствует единственная точка  , следовательно, единственное значение синуса и косинуса этого числа. Таким образом,
, следовательно, единственное значение синуса и косинуса этого числа. Таким образом,  а являются функциями числового аргумента. (Заметим, что в курсе геометрии мы рассматривали
а являются функциями числового аргумента. (Заметим, что в курсе геометрии мы рассматривали  а как функции угловой величины а, а не числа а.)
а как функции угловой величины а, а не числа а.)
4. Основное соотношение между  а. Координаты любой точки
а. Координаты любой точки  единичной окружности удовлетворяют уравнению:
единичной окружности удовлетворяют уравнению:  (это следует из прямоугольного треугольника, катеты которого
(это следует из прямоугольного треугольника, катеты которого  , а гипотенуза равна 1; см. рис. 98). Отсюда
, а гипотенуза равна 1; см. рис. 98). Отсюда  где
где 
Из этой формулы следует, что: а) 
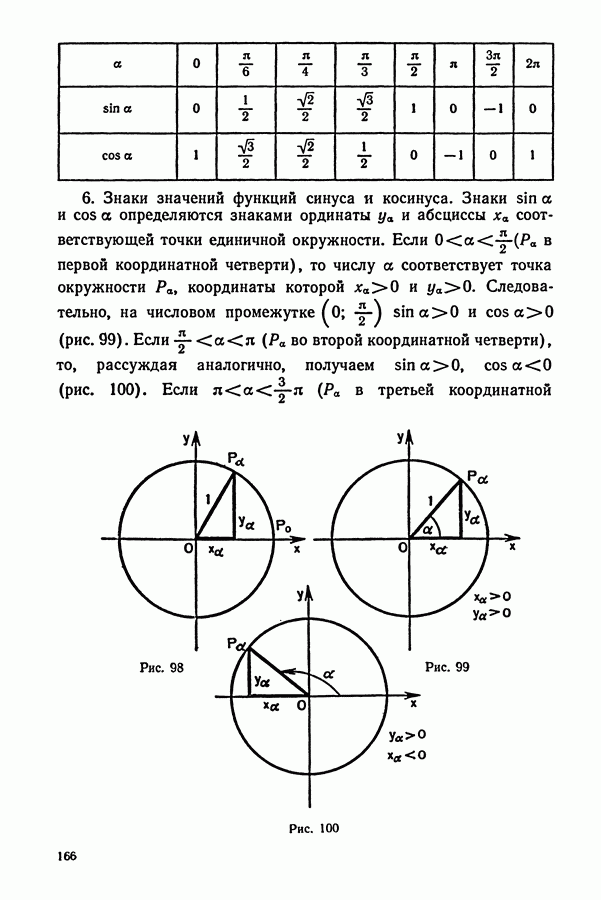
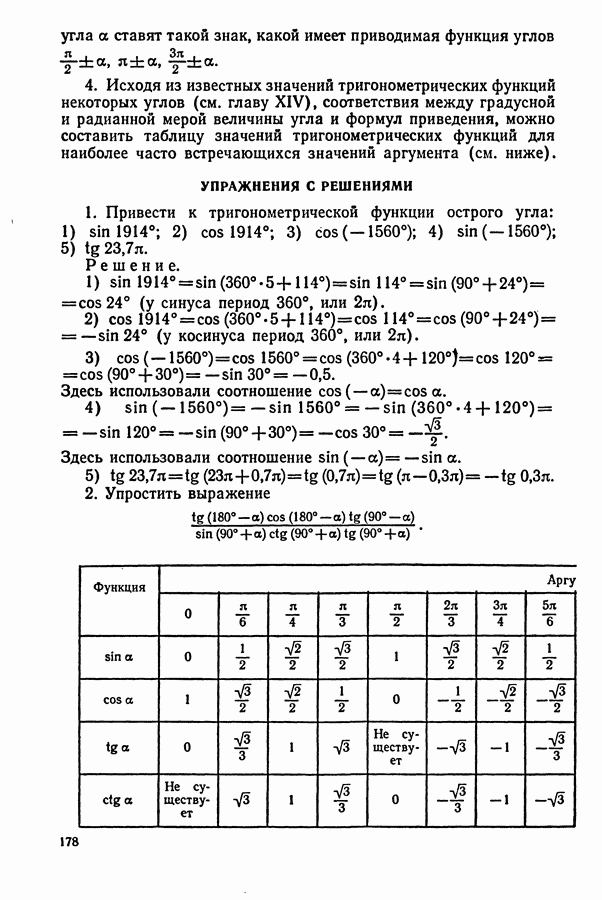
5. Значения синуса и косинуса некоторых чисел. В практических вычислениях часто используются значения синуса и косинуса, приведенные в таблице:

6. Знаки значений функций синуса и косинуса. Знаки  а определяются знаками ординаты
а определяются знаками ординаты  и абсциссы
и абсциссы  соответствующей точки единичной окружности. Если
соответствующей точки единичной окружности. Если  в первой координатной четверти), то числу а соответствует точка окружности
в первой координатной четверти), то числу а соответствует точка окружности  координаты которой
координаты которой  Следовательно, на числовом промежутке
Следовательно, на числовом промежутке  Если
Если  во второй координатной четверти), то, рассуждая аналогично, получаем
во второй координатной четверти), то, рассуждая аналогично, получаем  (рис. 100), Если
(рис. 100), Если  в третьей координатной
в третьей координатной


Рис. 101

Рис. 102

Рис. 103
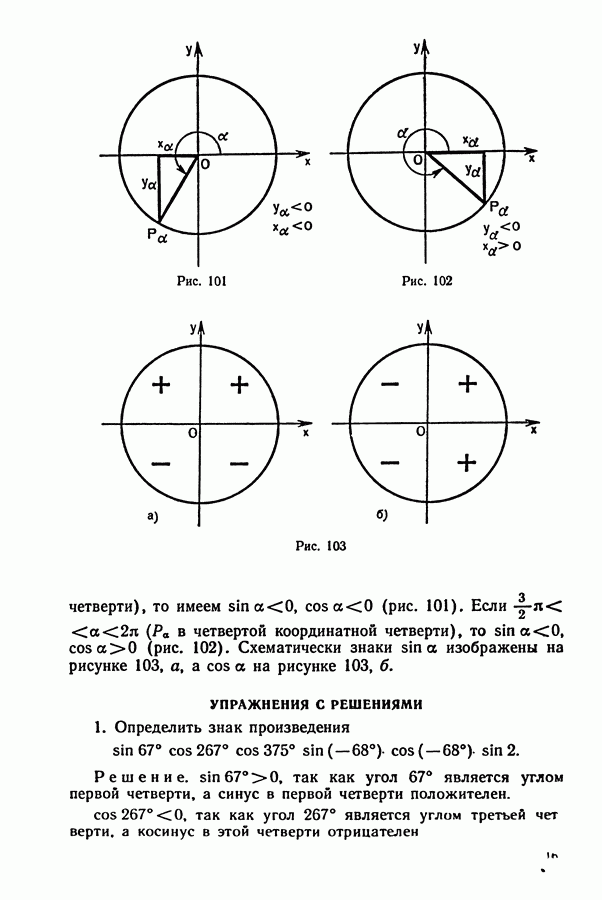
четверти), то имеем  (рис. 101). Если
(рис. 101). Если  в четвертой координатной четверти), то
в четвертой координатной четверти), то  (рис. 102). Схематически знаки
(рис. 102). Схематически знаки  изображены на рисунке 103, а, а
изображены на рисунке 103, а, а  на рисунке 103, б.
на рисунке 103, б.
УПРАЖНЕНИЯ С РЕШЕНИЯМИ
1. Определить знак произведения

Решение,  так как угол 67° является углом первой четверти, а синус в первой четверти положителен.
так как угол 67° является углом первой четверти, а синус в первой четверти положителен.
 так как угол 267° является углом третьей чет верти, а косинус в этой четверти отрицателен
так как угол 267° является углом третьей чет верти, а косинус в этой четверти отрицателен
 так как угол 375° является углом первой четверти, а косинус в этой четверти положителен.
так как угол 375° является углом первой четверти, а косинус в этой четверти положителен.
 так как угол —68° является углом четвертой четверти, а синус в этой четверти отрицателен.
так как угол —68° является углом четвертой четверти, а синус в этой четверти отрицателен.
 так как угол —68° является углом четвертой четверти, а косинус в этой четверти положителен.
так как угол —68° является углом четвертой четверти, а косинус в этой четверти положителен.
 так как угол, величина которого 2 радиана, является углом второй четверти, а синус во второй четверти положителен. Следовательно, произведение положительно.
так как угол, величина которого 2 радиана, является углом второй четверти, а синус во второй четверти положителен. Следовательно, произведение положительно.
2. Сравнить значения выражений:

Решение, 
Ответ. 
3. Доказать тождество

Доказательство. В левой части тождества произведем указанные действия и приведем подобные члены, получим:

Левую часть равенства преобразуем так:

Следовательно,  Тождество доказано.
Тождество доказано.
4. Вычислить значение  , если
, если  где
где 
Решение. Найдем значение косинуса, используя формулу  Имеем
Имеем

Выясним, какой знак надо оставить перед корнем. По условию  принадлежит III четверти, а косинус в этой четверти отрицателен. Следовательно, перед корнем надо оставить знак «минус». Итак,
принадлежит III четверти, а косинус в этой четверти отрицателен. Следовательно, перед корнем надо оставить знак «минус». Итак, 
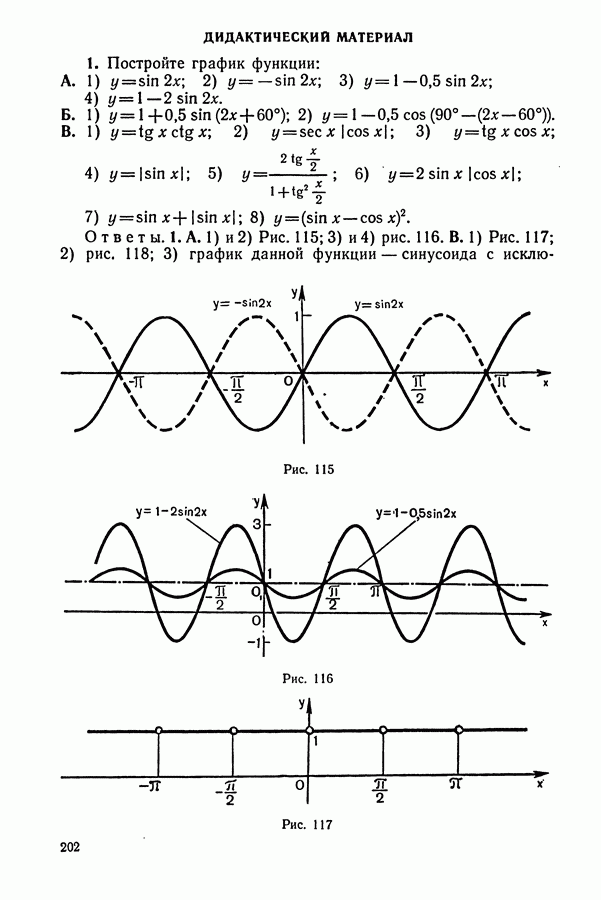
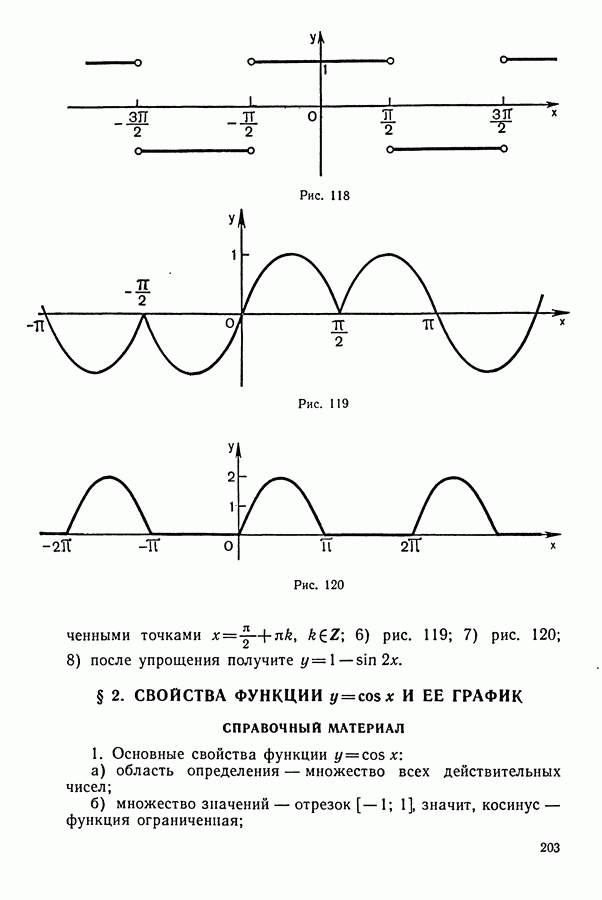
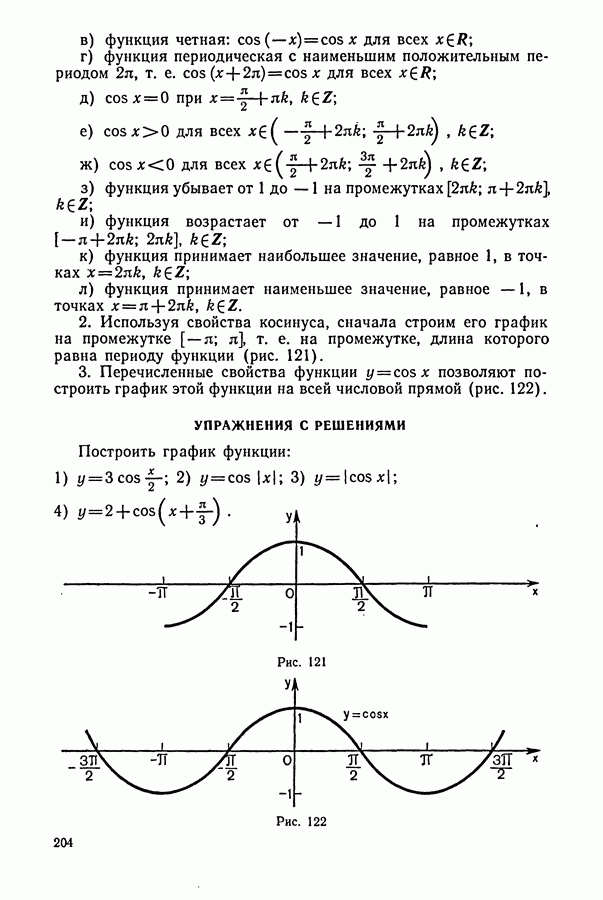
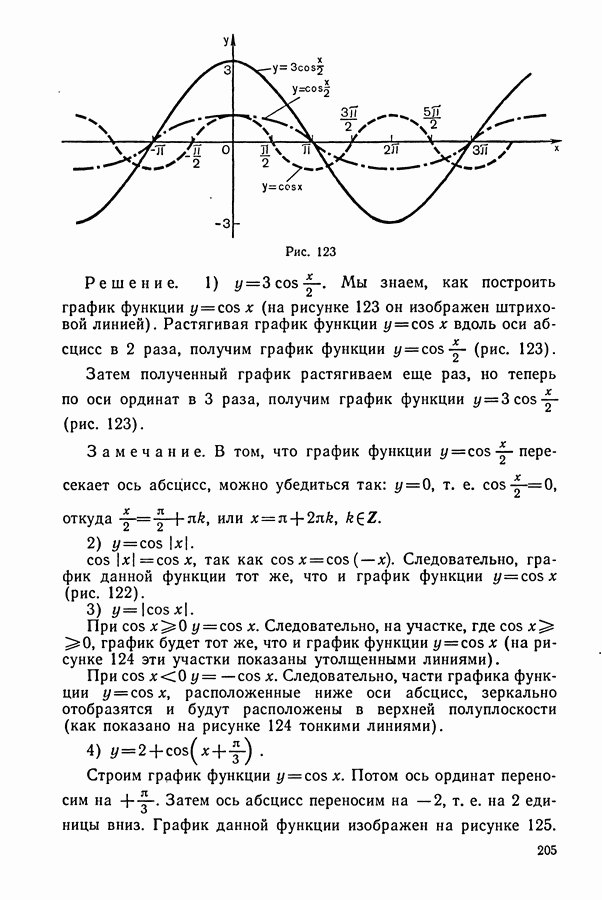
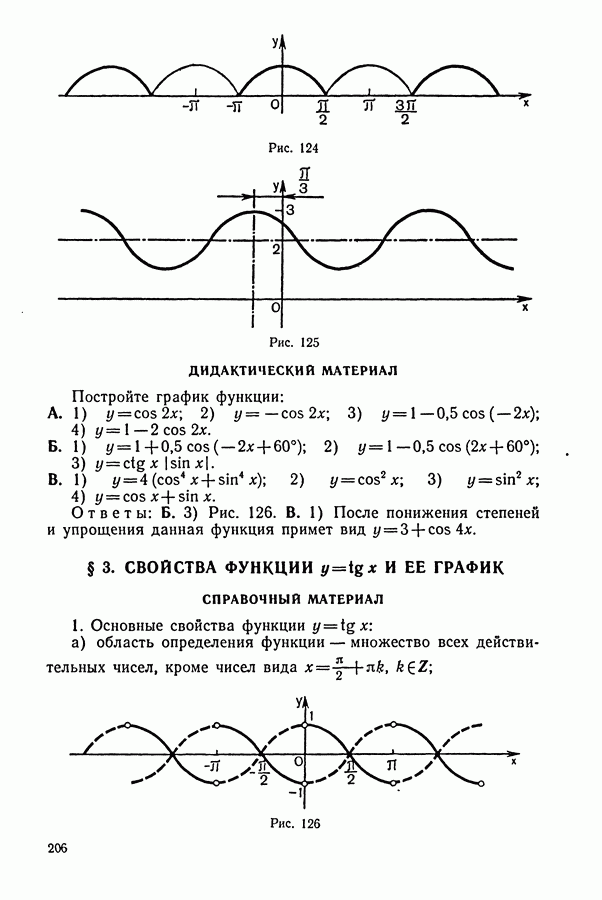
ДИДАКТИЧЕСКИЙ МАТЕРИАЛ
(см. скан)
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ГЛАВА I.
- § 1. НАТУРАЛЬНЫЕ ЧИСЛА И ДЕЙСТВИЯ НАД НИМИ
- § 2. СЛОЖЕНИЕ И ЗАКОНЫ СЛОЖЕНИЯ
- § 3. ВЫЧИТАНИЕ
- § 4. УМНОЖЕНИЕ И ЗАКОНЫ УМНОЖЕНИЯ
- § 5. ДЕЛЕНИЕ
- § 6. ПРИЗНАКИ ДЕЛИМОСТИ ЧИСЕЛ
- § 7. ПОНЯТИЕ МНОЖЕСТВА
- § 8. ОПЕРАЦИИ НАД МНОЖЕСТВАМИ
- § 9. ВЗАИМНО ОДНОЗНАЧНОЕ СООТВЕТСТВИЕ
- § 10. ПРОСТЫЕ И СОСТАВНЫЕ ЧИСЛА
- § 11. НАИБОЛЬШИЙ ОБЩИЙ ДЕЛИТЕЛЬ
- § 12. НАИМЕНЬШЕЕ ОБЩЕЕ КРАТНОЕ
- Контрольные вопросы
- ГЛАВА II
- § 1. ОБЫКНОВЕННЫЕ ДРОБИ
- § 2. ПРАВИЛЬНЫЕ И НЕПРАВИЛЬНЫЕ ДРОБИ
- § 3. ОСНОВНОЕ СВОЙСТВО ДРОБИ
- § 4. СЛОЖЕНИЕ И ВЫЧИТАНИЕ ДРОБЕЙ
- § 5. УМНОЖЕНИЕ ДРОБЕЙ
- § 6. ДЕЛЕНИЕ ДРОБЕЙ
- § 7. ДЕСЯТИЧНЫЕ ДРОБИ
- § 8. ОБРАЩЕНИЕ ДЕСЯТИЧНОЙ ДРОБИ В ОБЫКНОВЕННУЮ И ОБЫКНОВЕННОЙ В ДЕСЯТИЧНУЮ. ПЕРИОДИЧЕСКИЕ ДРОБИ
- § 9. ОТНОШЕНИЕ. ПРОПОРЦИЯ
- § 10. СВОЙСТВА ПРОПОРЦИИ
- § 11. ПРОЦЕНТ. ОСНОВНЫЕ ЗАДАЧИ НА ПРОЦЕНТЫ
- § 12. ДЕЛЕНИЕ ЧИСЛА НА ЧАСТИ, ПРЯМО И ОБРАТНО ПРОПОРЦИОНАЛЬНЫЕ ДАННЫМ ЧИСЛАМ
- Контрольные вопросы
- ГЛАВА III
- § 1. КООРДИНАТНАЯ ПРЯМАЯ
- § 2. МНОЖЕСТВО ЦЕЛЫХ ЧИСЕЛ
- § 3. МНОЖЕСТВО РАЦИОНАЛЬНЫХ ЧИСЕЛ
- § 4. МОДУЛЬ ЧИСЛА
- § 5. СРАВНЕНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ
- § 6. СЛОЖЕНИЕ И ВЫЧИТАНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ
- § 7. УМНОЖЕНИЕ И ДЕЛЕНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ
- § 8. ВОЗВЕДЕНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ В СТЕПЕНЬ С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ
- Контрольные вопросы
- ГЛАВА IV
- § 1. СВОЙСТВА СТЕПЕНИ С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ
- § 2. ЧИСЛОВЫЕ ВЫРАЖЕНИЯ
- § 3. ВЫРАЖЕНИЯ С ПЕРЕМЕННЫМИ
- § 4. ТОЖДЕСТВЕННО РАВНЫЕ ВЫРАЖЕНИЯ
- § 5. ОДНОЧЛЕНЫ
- § 6. МНОГОЧЛЕНЫ
- § 7. ПРЕОБРАЗОВАНИЕ СУММЫ И РАЗНОСТИ МНОГОЧЛЕНОВ
- § 8. УМНОЖЕНИЕ МНОГОЧЛЕНА НА ОДНОЧЛЕН И МНОГОЧЛЕНА НА МНОГОЧЛЕН
- § 9. РАЗЛОЖЕНИЕ МНОГОЧЛЕНА НА МНОЖИТЕЛИ СПОСОБОМ ВЫНЕСЕНИЯ ОБЩЕГО МНОЖИТЕЛЯ ЗА СКОБКИ
- § 10. РАЗЛОЖЕНИЕ МНОГОЧЛЕНА НА МНОЖИТЕЛИ СПОСОБОМ ГРУППИРОВКИ
- § 11. ФОРМУЛЫ СОКРАЩЕННОГО УМНОЖЕНИЯ
- Контрольные вопросы
- ГЛАВА V
- § 1. ДРОБЬ
- § 2. ЦЕЛЫЕ И ДРОБНЫЕ ВЫРАЖЕНИЯ
- § 3. ТОЖДЕСТВЕННОЕ ПРЕОБРАЗОВАНИЕ СУММЫ И РАЗНОСТИ ДВУХ ДРОБЕЙ
- § 4. ТОЖДЕСТВЕННОЕ ПРЕОБРАЗОВАНИЕ ПРОИЗВЕДЕНИЯ И ЧАСТНОГО ДВУХ ДРОБЕЙ
- § 5. СТЕПЕНЬ ДРОБИ
- Контрольные вопросы
- ГЛАВА VI
- § 1. ПОНЯТИЕ ОБ ИРРАЦИОНАЛЬНОМ ЧИСЛЕ
- § 2. РАЗВИТИЕ ПОНЯТИЯ О ЧИСЛЕ. МНОЖЕСТВО ДЕЙСТВИТЕЛЬНЫХ ЧИСЕЛ
- § 3. КОРЕНЬ СТЕПЕНИ ИЗ ДЕЙСТВИТЕЛЬНОГО ЧИСЛА
- § 4. АЛГОРИТМ ИЗВЛЕЧЕНИЯ КВАДРАТНОГО КОРНЯ ИЗ ЧИСЛА
- § 5. АРИФМЕТИЧЕСКИЕ ДЕЙСТВИЯ С ДЕЙСТВИТЕЛЬНЫМИ ЧИСЛАМИ
- § 6. ПРЕОБРАЗОВАНИЯ АРИФМЕТИЧЕСКИХ КОРНЕЙ
- § 7. СТЕПЕНЬ С ЦЕЛЫМ И ДРОБНЫМ ПОКАЗАТЕЛЕМ
- Контрольные вопросы
- ГЛАВА VII
- § 1. УРАВНЕНИЯ С ОДНОЙ ПЕРЕМЕННОЙ
- § 2. ПОНЯТИЕ О РАВНОСИЛЬНОСТИ УРАВНЕНИЙ
- § 3. СВОЙСТВА ЧИСЛОВЫХ РАВЕНСТВ И ТЕОРЕМЫ О РАВНОСИЛЬНОСТИ УРАВНЕНИЙ
- § 4. ЛИНЕЙНОЕ УРАВНЕНИЕ С ОДНОЙ ПЕРЕМЕННОЙ, СОДЕРЖАЩЕЕ ПАРАМЕТР
- Контрольные вопросы
- ГЛАВА VIII
- § 1. ПОНЯТИЕ ФУНКЦИИ
- § 2. СПОСОБЫ ЗАДАНИЯ ФУНКЦИИ
- § 3. МОНОТОННОСТЬ ФУНКЦИИ
- § 4. ЧЕТНЫЕ И НЕЧЕТНЫЕ ФУНКЦИИ СПРАВОЧНЫЙ МАТЕРИАЛ
- § 5. ПЕРИОДИЧЕСКИЕ ФУНКЦИИ
- § 6. ПРОМЕЖУТКИ ЗНАКОПОСТОЯНСТВА И КОРНИ ФУНКЦИИ
- Контрольные вопросы
- ГЛАВА IX
- § 1. ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ ГРАФИКОВ ФУНКЦИЙ
- § 2. ЛИНЕЙНАЯ ФУНКЦИЯ И ЕЕ ГРАФИК
- § 3. КВАДРАТИЧНАЯ ФУНКЦИЯ И ЕЕ ГРАФИК
- § 4. ФУНКЦИЯ y=k/x И ЕЕ ГРАФИК
- § 5. ДРОБНО-ЛИНЕЙНАЯ ФУНКЦИЯ И ЕЕ ГРАФИК
- Контрольные вопросы
- ГЛАВА X
- § 1. КВАДРАТНЫЕ УРАВНЕНИЯ
- § 2. ТЕОРЕМА ВИЕТА
- § 3. ГРАФИЧЕСКИЙ СПОСОБ РЕШЕНИЯ КВАДРАТНЫХ УРАВНЕНИЙ
- § 4. УРАВНЕНИЕ СО МНОГИМИ ПЕРЕМЕННЫМИ
- § 5. СИСТЕМЫ УРАВНЕНИЙ
- Контрольные вопросы
- ГЛАВА XI
- § 1. НЕРАВЕНСТВА
- § 2. ОСНОВНЫЕ СВОЙСТВА НЕРАВЕНСТВ
- § 3. ДЕЙСТВИЯ С НЕРАВЕНСТВАМИ
- § 4. ДОКАЗАТЕЛЬСТВА НЕРАВЕНСТВ
- § 5. НЕРАВЕНСТВА, СОДЕРЖАЩИЕ ПЕРЕМЕННУЮ
- § 6. РЕШЕНИЕ ЛИНЕЙНЫХ И КВАДРАТНЫХ НЕРАВЕНСТВ
- Контрольные вопросы
- ГЛАВА XII
- § 1. СИСТЕМЫ И СОВОКУПНОСТИ НЕРАВЕНСТВ
- § 2. НЕРАВЕНСТВА И СИСТЕМЫ НЕРАВЕНСТВ С ДВУМЯ ПЕРЕМЕННЫМИ
- § 3. РЕШЕНИЕ НЕРАВЕНСТВ, СОДЕРЖАЩИХ ПЕРЕМЕННУЮ ПОД ЗНАКОМ МОДУЛЯ
- § 4. РЕШЕНИЕ РАЦИОНАЛЬНЫХ НЕРАВЕНСТВ МЕТОДОМ ПРОМЕЖУТКОВ
- Контрольные вопросы
- ГЛАВА XIII
- § 1. ЧИСЛОВАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ
- § 2. АРИФМЕТИЧЕСКАЯ ПРОГРЕССИЯ
- § 3. ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИЯ
- § 4. СУММА БЕСКОНЕЧНОЙ ГЕОМЕТРИЧЕСКОЙ ПРОГРЕССИИ ПРИ |q|<1
- Контрольные вопросы
- ГЛАВА XIV
- § 1. ГРАДУСНОЕ ИЗМЕРЕНИЕ УГЛОВЫХ ВЕЛИЧИН
- § 2. РАДИАННОЕ ИЗМЕРЕНИЕ УГЛОВЫХ ВЕЛИЧИН
- § 3. СИНУС И КОСИНУС ЧИСЛОВОГО АРГУМЕНТА
- § 4. ТАНГЕНС И КОТАНГЕНС ЧИСЛОВОГО АРГУМЕНТА. СЕКАНС И КОСЕКАНС ЧИСЛА а
- § 5. ОСНОВНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ТОЖДЕСТВА
- § 6. ДОПОЛНИТЕЛЬНЫЕ СВОЙСТВА ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ
- Контрольные вопросы
- ГЛАВА XV
- § 1. ФОРМУЛЫ ПРИВЕДЕНИЯ
- § 2. ФОРМУЛЫ СЛОЖЕНИЯ
- § 3. ФОРМУЛЫ ДВОЙНОГО УГЛА СПРАВОЧНЫЙ МАТЕРИАЛ
- § 4. ПРЕОБРАЗОВАНИЕ ПРОИЗВЕДЕНИЯ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ В СУММУ
- § 5. ФОРМУЛЫ СУММЫ И РАЗНОСТИ ОДНОИМЕННЫХ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ
- § 6. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ ПОЛОВИННОГО АРГУМЕНТА
- § 7. ВЫРАЖЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ ЧЕРЕЗ ТАНГЕНС ПОЛОВИННОГО АРГУМЕНТА
- Контрольные вопросы
- ГЛАВА XVI
- § 1. СВОЙСТВА ФУНКЦИИ y = sin(x) И ЕЕ ГРАФИК
- § 2. СВОЙСТВА ФУНКЦИ И у = cos(x) И ЕЕ ГРАФИК
- § 3. СВОЙСТВА ФУНКЦИ И у=tg(x) И ЕЕ ГРАФИК
- § 4. СВОЙСТВА ФУНКЦИ И y=ctg(x) И ЕЕ ГРАФИК
- § 5. НАХОЖДЕНИЕ ПЕРИОДОВ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ
- Контрольные вопросы
- ГЛАВА XVII
- § 1. АРКСИНУС И АРККОСИНУС
- § 2. АРКТАНГЕНС И АРККОТАНГЕНС
- Контрольные вопросы
- ГЛАВА XVIII
- § 1. РЕШЕНИЕ УРАВНЕНИЙ ВИДА cos(x)=а
- § 2. РЕШЕНИЕ УРАВНЕНИЙ ВИДА sin(x)=a
- § 3. РЕШЕНИЕ УРАВНЕНИЙ ВИДА tg(х)=а
- § 4. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ, ПРИВОДИМЫХ К КВАДРАТНОМУ
- § 5. РЕШЕНИЕ ОДНОРОДНЫХ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ
- § 6. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ, РЕШАЕМЫЕ С ПОМОЩЬЮ ФОРМУЛ СЛОЖЕНИЯ, ПОНИЖЕНИЯ СТЕПЕНИ
- § 7. РЕШЕНИЕ СИСТЕМ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ
- Контрольные вопросы
- ГЛАВА XIX
- § 1. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ ВИДА sin(х) > а, sin(х) < а
- § 2. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ ВИДА cos(x) > a, cos(x) < a
- § 3. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ ВИДА tg(х) > a, tg(х) < a
- § 4. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ
- ГЛАВА XX
- § 1. ПРИРАЩЕНИЕ АРГУМЕНТА И ПРИРАЩЕНИЕ ФУНКЦИИ
- § 2. ПРЕДЕЛ ФУНКЦИИ
- § 3. НЕПРЕРЫВНОСТЬ ФУНКЦИИ
- § 4. ОПРЕДЕЛЕНИЕ ПРОИЗВОДНОЙ
- § 5. ПРОИЗВОДНАЯ СУММЫ, ПРОИЗВЕДЕНИЯ, ЧАСТНОГО
- § 6. ПРОИЗВОДНАЯ СТЕПЕННОЙ И СЛОЖНОЙ ФУНКЦИИ
- § 7. ПРОИЗВОДНЫЕ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ
- Контрольные вопросы
- ГЛАВА XXI
- § 1. ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ К НАХОЖДЕНИЮ ПРОМЕЖУТКОВ МОНОТОННОСТИ ФУНКЦИИ
- § 2. КРИТИЧЕСКИЕ ТОЧКИ ФУНКЦИИ, ЕЕ МАКСИМУМЫ И МИНИМУМЫ
- § 3. ОБЩАЯ СХЕМА ИССЛЕДОВАНИЯ ФУНКЦИИ
- § 4. ЗАДАЧИ НА НАХОЖДЕНИЕ НАИМЕНЬШЕГО И НАИБОЛЬШЕГО ЗНАЧЕНИЯ ФУНКЦИИ
- Контрольные вопросы
- ГЛАВА XXII
- § 1. ФОРМУЛЫ ПРИБЛИЖЕННЫХ ВЫЧИСЛЕНИЙ СПРАВОЧНЫЙ МАТЕРИАЛ
- § 2. КАСАТЕЛЬНАЯ К ГРАФИКУ ФУНКЦИИ
- § 3. СКОРОСТЬ И УСКОРЕНИЕ В ДАННЫЙ МОМЕНТ ВРЕМЕНИ
- § 4. ГРАФИКИ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ
- Контрольные вопросы
- ГЛАВА XXIII
- § 1. ПОТЕРЯННЫЕ И ПОСТОРОННИЕ КОРНИ ПРИ РЕШЕНИИ УРАВНЕНИЙ (НА ПРИМЕРАХ)
- § 2. ПОСТОРОННИЕ КОРНИ ИРРАЦИОНАЛЬНОГО УРАВНЕНИЯ (НА ПРИМЕРАХ)
- § 3. РЕШЕНИЕ ИРРАЦИОНАЛЬНЫХ УРАВНЕНИЙ
- § 4. РЕШЕНИЕ ИРРАЦИОНАЛЬНЫХ НЕРАВЕНСТВ СПРАВОЧНЫЙ МАТЕРИАЛ
- Контрольные вопросы
- ГЛАВА XXIV
- § 1. ПОКАЗАТЕЛЬНАЯ ФУНКЦИЯ, ЕЕ СВОЙСТВА И ГРАФИК
- § 2. ПОКАЗАТЕЛЬНЫЕ УРАВНЕНИЯ
- § 3. ПОКАЗАТЕЛЬНЫЕ НЕРАВЕНСТВА
- § 4. СИСТЕМЫ ПОКАЗАТЕЛЬНЫХ УРАВНЕНИЙ И НЕРАВЕНСТВ
- Контрольные вопросы
- ГЛАВА XXV
- § 1. ОБРАТНАЯ ФУНКЦИЯ
- § 2. ПОНЯТИЕ ЛОГАРИФМА
- § 3. СВОЙСТВА ЛОГАРИФМОВ
- § 4. ЛОГАРИФМИЧЕСКАЯ ФУНКЦИЯ, ЕЕ СВОЙСТВА И ГРАФИК
- § 5. ТЕОРЕМЫ О ЛОГАРИФМЕ ПРОИЗВЕДЕНИЯ, ЧАСТНОГО И СТЕПЕНИ. ФОРМУЛА ПЕРЕХОДА К НОВОМУ ОСНОВАНИЮ
- § 6. ДЕСЯТИЧНЫЕ ЛОГАРИФМЫ И ИХ СВОЙСТВА
- § 7. ЛОГАРИФМИРОВАНИЕ И ПОТЕНЦИРОВАНИЕ
- Контрольные вопросы
- ГЛАВА XXVI
- § 1. ЛОГАРИФМИЧЕСКИЕ УРАВНЕНИЯ
- § 2. ЛОГАРИФМИЧЕСКИЕ НЕРАВЕНСТВА
- § 3. СИСТЕМЫ ЛОГАРИФМИЧЕСКИХ УРАВНЕНИЙ И НЕРАВЕНСТВ
- § 4. ПРОИЗВОДНЫЕ ЛОГАРИФМИЧЕСКОЙ И ПОКАЗАТЕЛЬНОЙ ФУНКЦИЙ. ЧИСЛО e
- Контрольные вопросы
- ГЛАВА XXVII
- § 1. ПОНЯТИЕ ПЕРВООБРАЗНОЙ ФУНКЦИИ
- § 2. ОСНОВНОЕ СВОЙСТВО ПЕРВООБРАЗНОЙ ФУНКЦИИ
- § 3. ТРИ ПРАВИЛА НАХОЖДЕНИЯ ПЕРВООБРАЗНЫХ
- § 4. КРИВОЛИНЕЙНАЯ ТРАПЕЦИЯ И ЕЕ ПЛОЩАДЬ
- Контрольные вопросы
- ГЛАВА XXVIII
- § 1. ФОРМУЛА НЬЮТОНА—ЛЕЙБНИЦА
- § 2. ОСНОВНЫЕ ПРАВИЛА ИНТЕГРИРОВАНИЯ
- § 3. ВЫЧИСЛЕНИЕ ПЛОЩАДЕЙ С ПОМОЩЬЮ ИНТЕГРАЛА
- § 4. МЕХАНИЧЕСКИЕ И ФИЗИЧЕСКИЕ ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
- ПРИЛОЖЕНИЕ
- Введение
- 1. Задачи на движение
- 2. Задачи на совместную работу
- 3. Задачи на планирование
- 4. Задачи на зависимость между компонентами арифметических действий
- 5. Задачи на проценты
- 6. Задачи на смеси (сплавы)
- 7. Задачи на разбавление