§ 3. ОСНОВНЫЕ ТЕОРЕМЫ ДИНАМИКИ СИСТЕМЫ

1. Теорема об изменении количества движения системы и о движении центра масс системы.

Предположим, что среди всех возможных перемещений системы имеется поступательное перемещение всей системы, как одного твердого тела, параллельное какому-нибудь направлению. Не нарушая общности, всегда можно предполагать, что это перемещение направлено вдоль неподвижной оси х. Для такого возможного перемещения будем иметь

а потому общее уравнение динамики запишется следующим образом:

Оно будет представлять собой дифференциальное уравнение движения и легко преобразуется к виду

Представляя левую часть этого уравнения в виде

вектор Q с компонентами

назовем вектором количества движения системы. Тогда полученное уравнение движения можно будет записать так:

Из уравнения видно, что скорость изменения проекции количества движения системы на ось х равна сумме проекций на ту же ось всех активных сил, действующих на систему.

Преобразуем выражение для количества движения системы

где

Величину М будем называть массой системы, а произведение массы системы на скорость ее центра масс-количеством движения центра масс системы. Очевидно,

но, что количество движения системы равно количеству движения центра масс системы и мы можем сформулировать следующую теорему об изменении количества движения системы, или теорему о движении центра масс системы.

Теорема. Если связи допускают поступательное перемещение всей системы как одного целого вдоль неподвижной оси х, то центр масс системы будет двигаться в направлении оси х как материальная точка, масса которой равна массе всей системы М, на которую действуют все активные силы, действующие на систему.

Математически это запишется в виде уравнения

Если, кроме того, сумма проекций всех активных сил на ось х равна нулю, т. е.

то теорема дает первый интеграл уравнений движения. Вводя обозначение будем иметь

откуда

Интегрируя последнее уравнение, получаем

где — произвольные постоянные, зависящие от начальных условий.

Следствие. Если сумма проекций всех активных сил на ось х равна нулю, то центр масс системы движется вдоль оси х по линейному закону, как материальная точка, на которую не действуют никакие силы.

В этом заключается закон сохранения количества движения системы материальных точек, который можно представить в виде

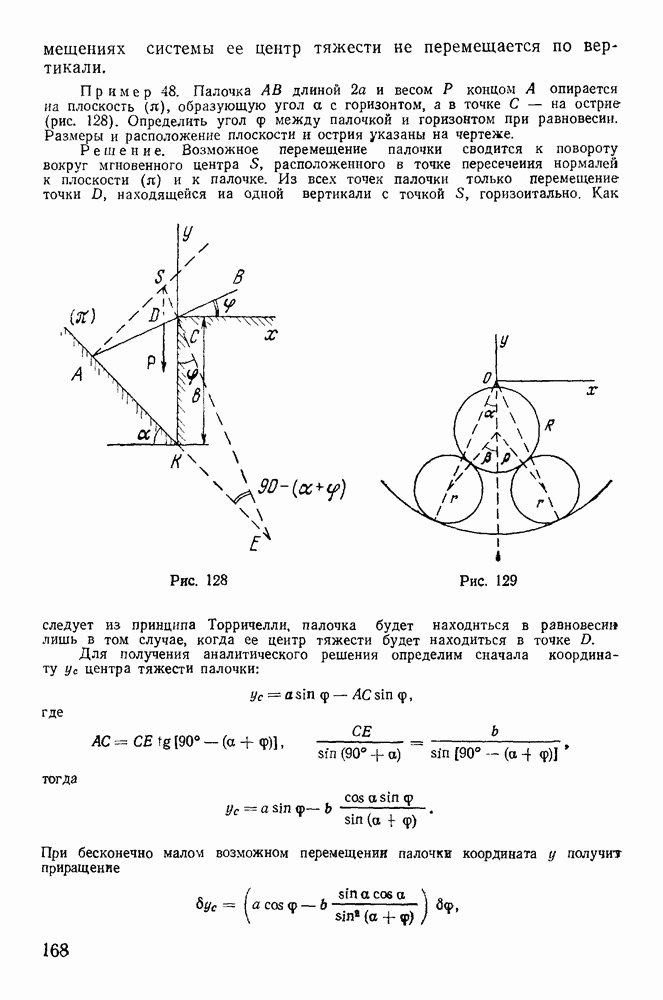
Пример 83. Тяжелая палочка АВ длины 2а опирается одним концом о гладкую горизонталную плоскость и находится в покое, поддерживаемая за

другой конец В. Когда конец В палочки отпускают, она начинает падать. Определить траекторию точки В палочки (рис. 184).

Среди возможных перемещений имеется поступательное перемещение палочки вдоль горизонтальной оси, которую примем за ось х.

Рис. 184

Проекция активных сил (веса) на эту ось равна нулю, поэтому центр тяжести движется вдоль оси х по закону

В начальный момент палочка находилась в покое, так что

откуда

т. е. центр тяжести палочки не перемещается по горизонтали. Выбирая новую систему координат так, чтобы вертикальная ось у, проходила через центр тяжести палочки, и обозначая через координаты точки В, будем иметь

т. е. траектория точки В — эллипс.

Замечания. 1. Установленная теорема имеет место лишь при условии, что связи допускают поступательное перемещение всей системы как одного твердого тела вдоль неподвижной оси х. Уравнение движения центра масс в этом случае получается из принципа Даламбера — Лагранжа, который не содержит реакций связей. Следовательно, реакции связей не войдут и в уравнение движения центра масс вдоль оси х.

2. Если связи, наложенные на систему материальных точек, допускают поступательное перемещение всей системы как вдоль оси х, так и вдоль осей у и то теорема о движении центра масс будет справедливой для всех трех направлений, и центр масс системы будет двигаться в пространстве как материальная точка, масса которой равна массе всей системы и на которую действуют все активные силы, приложенные к точкам системы, что можно представить в виде равнения

3. Разделим все силы, действующие на точки системы, на силы «внутренние» и силы «внешние». Под внутренними силами будем понимать силы взаимодействия между точками системы, а под внешними — силы, вызванные действием на точки системы других тел, не входящих в рассматриваемую систему. Тогда будем иметь

Если предположить, что все внутренние силы подчиняются третьему закону Ньютона, то для суммы проекций внутренних активных сил на оси х, у, z получим

а теорема о движении центра масс может быть сформулирована следующим образом.

Теорема. Если связи, наложенные на систему материальных точек, таковы, что среди возможных перемещений имеется поступательное перемещение всей системы как одного целого вдоль неподвижной оси х, то центр масс системы будет двигаться вдоль этой оси как материальная точка, масса которой равна сумме масс всех точек системы и на которую действуют все внешние активные силы, приложенные к точкам системы, т. е.

4. Внешние силы могут оказаться внутренними при рассмотрении более широкой системы. Так, папример, при рассмотрении движения падающих на Землю тел сила тяжести является силой внешней. Если же рассматривать систему «Земля — Луна», то сила, действующая со стороны Земли на Луну, и сила, действующая со стороны Луны на Землю, будут силами внутренними; внешними в этом случае будут силы действия Солнца на Луну и Землю.

Силы реакции также можно разделить на силы внутренние и внешние. Так, связи, наложенные на частицы абсолютно твердого тела, являются внутренними, и силы реакции, вызванные этими связями, суть внутренние силы реакции. Внешними называют такие связи, которые связывают рассматриваемую систему материальных точек с другими телами. Силы реакции,

вызываемые такими связями, называются внешними силами реакции.

5. Теорема о движении центра масс раскрывает реальный смысл теории движения одной материальной точки, которая рассматривалась выше. Такой точкой является центр масс системы.

Пример 84. Рассмотрим внутренние и внешние силы в задаче о движении системы, состоящей из маленького колесика, принимаемого за материальную точку с массой т., которое может свободно скользить по прямолинейному горизонтальному рельсу. С колесиком при помощи невесомого стержня длины соединена вторая материальная точка с массой так что стержень может вращаться вокруг точки в вертикальной плоскости (рис. 185).

Активными силами, действующими на систему, здесь будут силы тяжести и являющиеся внешними силами. Силы реакции можио разделить на внутренние силы взаимодействия и внешнюю силу действующую со стороны рельса на систему.

Рис. 185

Рис. 186

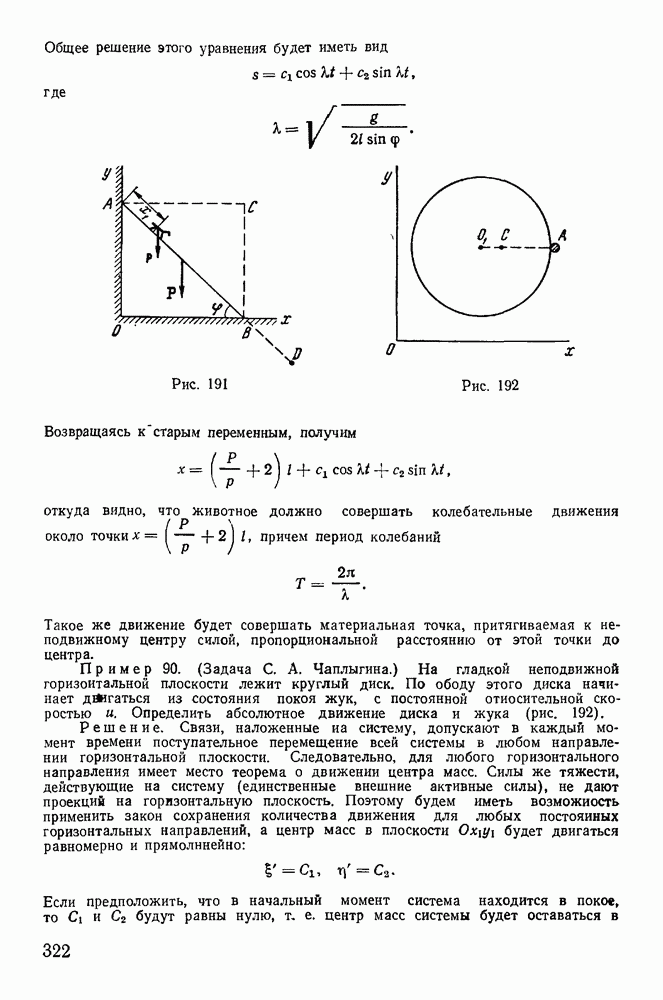
Пример 85. Задача двух тел. Рассмотрим в качестве примера движение системы Солнце — планета, считая их материальными точками, взаимно притягивающимися по закону Ньютона

где — масса планеты; М — масса Солнца (рис. 186). На систему не наложено никаких связей. Среди всех возможных перемещений системы имеются поступательные перемещения всей системы в любом направлении. Пренебрегая действием других небесных тел на рассматриваемую систему, из теоремы о движении центра масс получим, что центр масс системы движется равномерно и прямолинейно относительно любой инерциальной системы (не нарушая общности, можно предположить, что центр масс системы находится в покое). Обозначая через расстояние от центра масс О до планеты Р, а через — расстояние от центра масс до центра Солнца, будем иметь

или

где R — расстояние от планеты до Солнца. Выражая силу, действующую на планету, через расстояние от центра масс системы до планеты, получим

где

Теперь движение планеты можно рассматривать как движение материальной точки под действием силы притяжения к центру масс системы Солнце — планета. Такие движения подробно рассматривались в динамике материальной точки. Заметим, что для планеты Земля км. Так как радиус Солнца составляет около 696 тыс. км, то центр масс системы Солнце — Земля находится внутри Солнца. Движение планеты происходит по коническому сечению

где О — полярный угол; — постоянная живых сил; С — постоянная площадей, в одном из фокусов которого находится общий центр масс системы. Представляя это уравнение в виде

где

а и b — соответственно большая и малая полуоси эллиптической орбиты» найдем выражение секторной скорости через эти параметры

Площадь, заметаемая фокальным радиус-вектором планеты за время полного оборота, равна

откуда, подставив значение С, получим

или

т. е. отношение куба большой полуоси орбиты к квадрату периода обращения зависит от массы планеты и не является постоянной величиной, как это утверждалось в третьем законе Кеплера.

Иногда удобнее изучать движение планеты в подвижной системе с началом в центре Солнца и ориентированной по звездам (гелиоцентрическая система). В такой системе на планету кроме силы притяжения к Солнцу

будет действовать сила Кориолиса от переносного ускорения направленная тоже к Солнцу. Результирующая сила, действующая на планету;

также центральная и может быть представлена в виде

где

В этой системе движение происходит по эллиптической орбите, причем

Величины различны для различных планет. Например, для Земли

Для Юпитера

Вычислив соответственно для Земли и Юпитера, найдем

Задача о движении тела переменной массы.

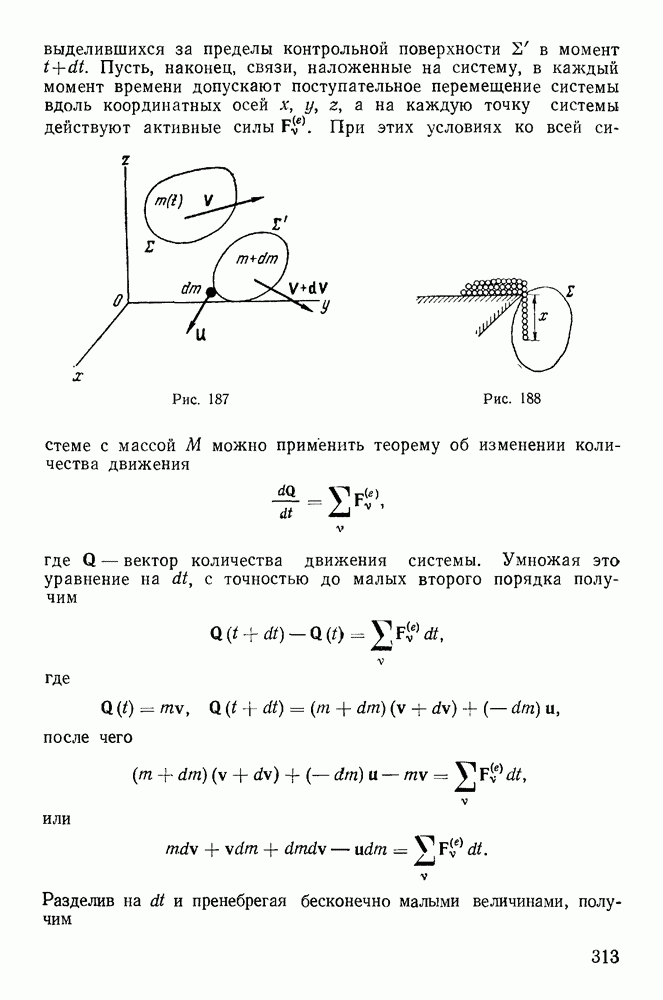
В качестве примера на применение теоремы об изменении количества движения рассмотрим задачу о движении системы материальных точек с переменной массой относительно неподвижной системы осей Пусть общая масса системы и вся система ограничена некоторой контрольной поверхностью . При движении системы некоторые из ее точек выходят за пределы этой контрольной поверхности (рис. 187). Обозначим через массу частиц, находящихся внутри контрольной поверхности в момент а через — приращение массы внутри контрольной поверхности за промежуток времени Массу частиц, выделившихся за пределы контрольной поверхности за интервал времени обозначим через Контрольная поверхность может перемещаться по отношению к системе координат и изменять свою форму. Через обозначим контрольную поверхность Б в момент

Пусть — скорость центра масс частиц, находящихся внутри контрольной поверхности в момент — скорость центра масс частиц, находящихся внутри контрольной поверхности в момент ; и -— абсолютная скорость центра масс частиц,

выделившихся за пределы контрольной поверхности в момент Пусть, наконец, связи, наложенные на систему, в каждый момент времени допускают поступательное перемещение системы вдоль координатных осей х, у, z, а на каждую точку системы действуют активные силы

Рис. 187

Рис. 188

При этих условиях ко всей системе с массой М можно применить теорему об изменении количества движения

где Q — вектор количества движения системы. Умножая это уравнение на с точностью до малых второго порядка получим

где

после чего

или

Разделив на и пренебрегая бесконечно малыми величинами, получим

Это уравнение определяет движение центра масс частиц, находящихся внутри контрольной поверхности. Впервые оно было полечено в 1897 г. И. В. Мещерским (1859—1935) в его магистерской диссертации, а поэтому и называется уравнением Мещерского.

Если с центром масс системы частиц, находящихся внутри контрольной поверхности, связать подвижную систему координат движущуюся поступательно, то разность будет представлять относительную скорость отбрасываемых частиц по отношению к системе При этом предполагается, что отделение частиц происходит за счет внутренних сил или в результате наложения (или снятия) новых связей, допускающих поступательное перемещение системы. Последний член в уравнении Мещерского имеет размерность силы. Этот член называется реактивной силой, действующей на систему частиц, остающихся внутри контрольной поверхности. Если для реактивной силы ввести обозначение Ф

то уравнение Мещерского перепишется в виде

Если обозначить через О вектор количества движения системы частиц, находящихся внутри контрольной поверхности 2, то будем иметь

откуда

после чего уравнение Мещерского получает вид

Последнее уравнение выражает теорему об изменении количества движения системы частиц, масса которой изменяется (система ограничена контрольной поверхностью).

Если абсолютная скорость отбрасываемых частиц равна нулю то уравнение Мещерского дает

В таком виде уравнение применяется в задачах небесной механики. Оно было получено в итальянским механиком Т. Леви-Чивита (1873—1941).

Теорема об изменении количества движения системы с переменной массой в последнем случае запишется также, как и для системы с постоянной массой

Если относительная скорость отбрасываемых частиц равна нулю, то уравнение Мещерского перепишется в виде

а теорема об изменении количества движения — в виде

Исторически первая задача динамики тел с переменной массой, решение которой приводится ниже, была рассмотрена в английским математиком Кэйли (1821—1895).

Пример 86 (Задача Кэйли) Определить движение тяжелой цепочки, свободный конец которой свешивается с горизонтального стола, тогда как не вступившая еще в движение часть цепочки свернута в клубок у самого края стола (рис 188).

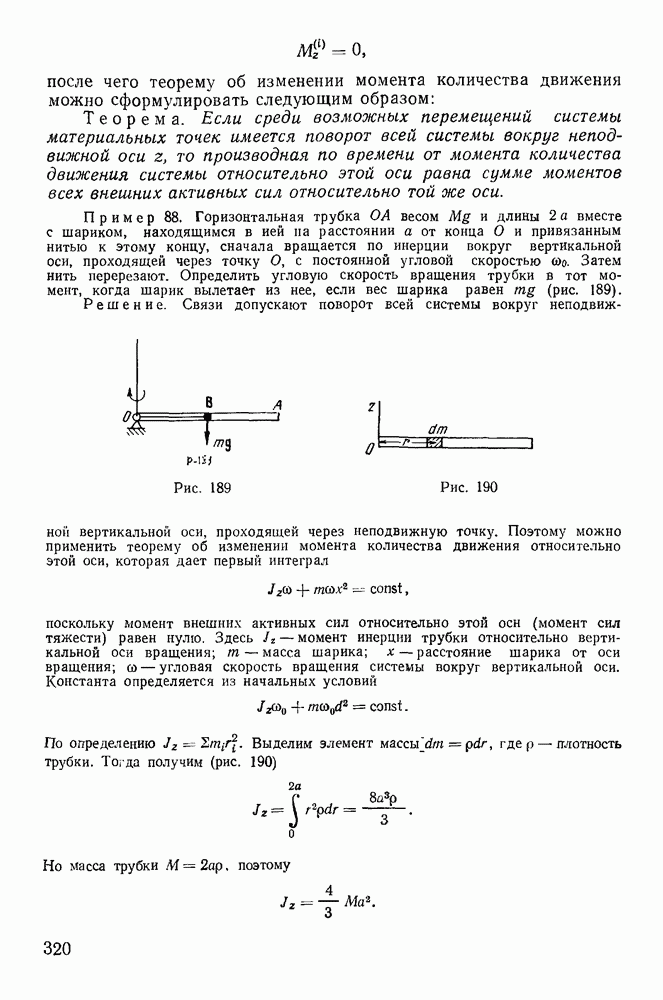
Пусть х — длина свешивающейся части цепочки Для присоединяющейся при движении массы имеем

где у — удельный вес цепочки Абсолютная скорость присоединяющейся массы равна До присоединения скорость равна нулю Уравнение Мещерского принимает вид

или

Принимая обозначения и учитывая, что будем иметь.

откуда, интегрируя, найдем

Постоянная определяется из начальных условий. Подставляя значение и, перепишем последнее уравнение в виде

В общем случае это уравнение с разделяющимися переменными не интегрируется в элементарных функциях. В частном случае, при имеем

откуда

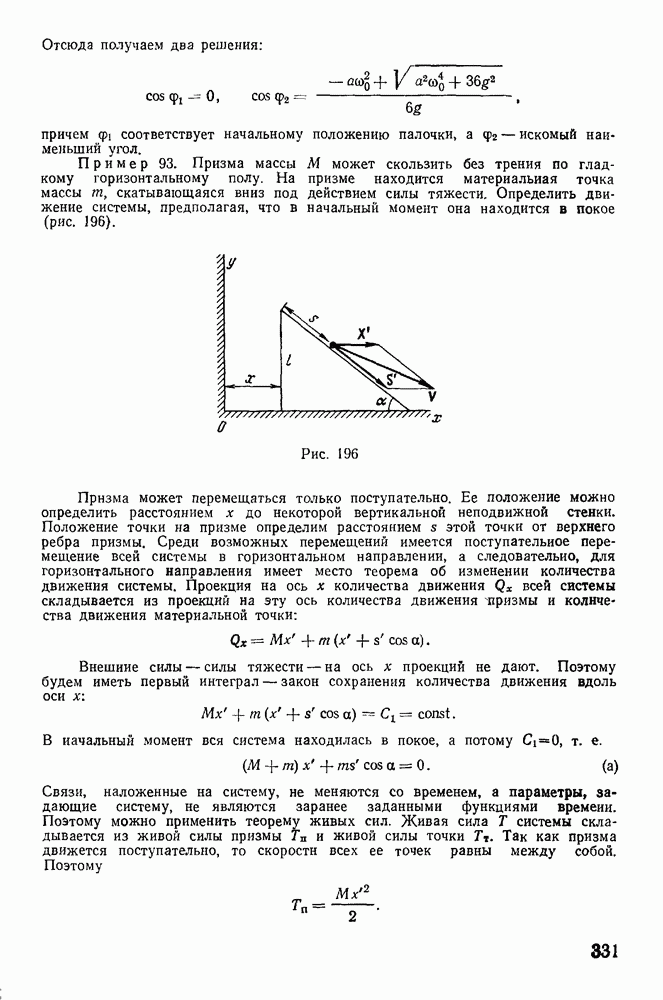
Пример 87. (Задача Циолковского.) Исследовать движение тела переменной массы в безвоздушном пространстве без воздействия внешних сил. Относительная скорость выбрасывания частиц за контрольную поверхность (скорость истечения) постоянна по величине и направлена коллинеарно вектору в сторону, противоположную направлению движения центра масс основной системы.

Уравнение Мещерского для этого случая получает вид

где — относительная скорость истечения частиц. Разделяя переменные, получим

откуда

Пусть при . Тогда приходим к формуле Циолковского

которая была впервые получена в 1903 г. К. Э. Циолковским (1857—1935). Из этой формулы видно, что скорость системы не зависит от режима изменения массы, а зависит лишь от ее расхода.