| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
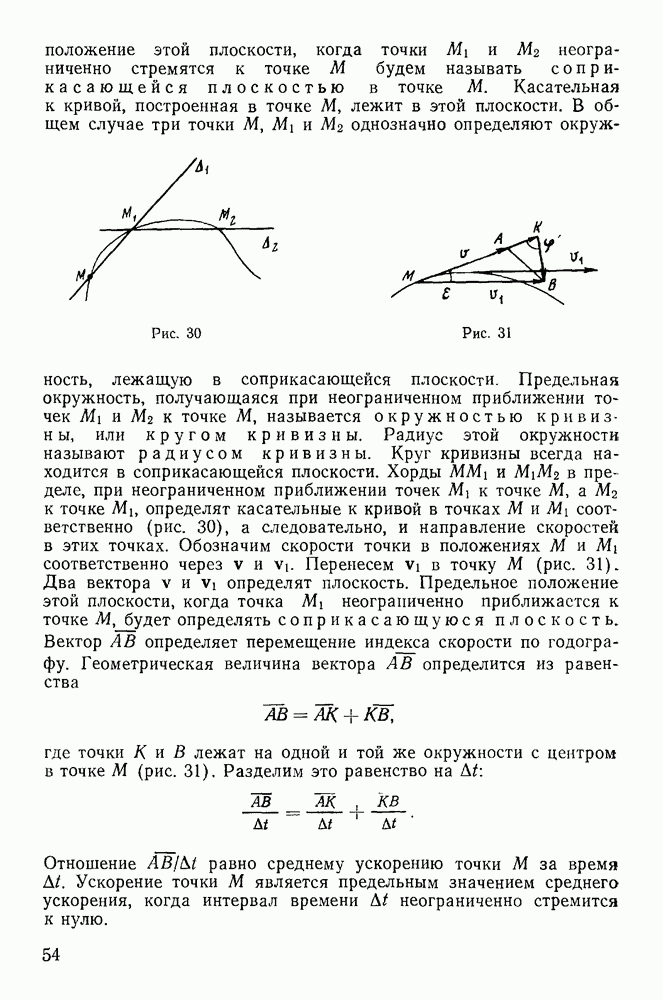
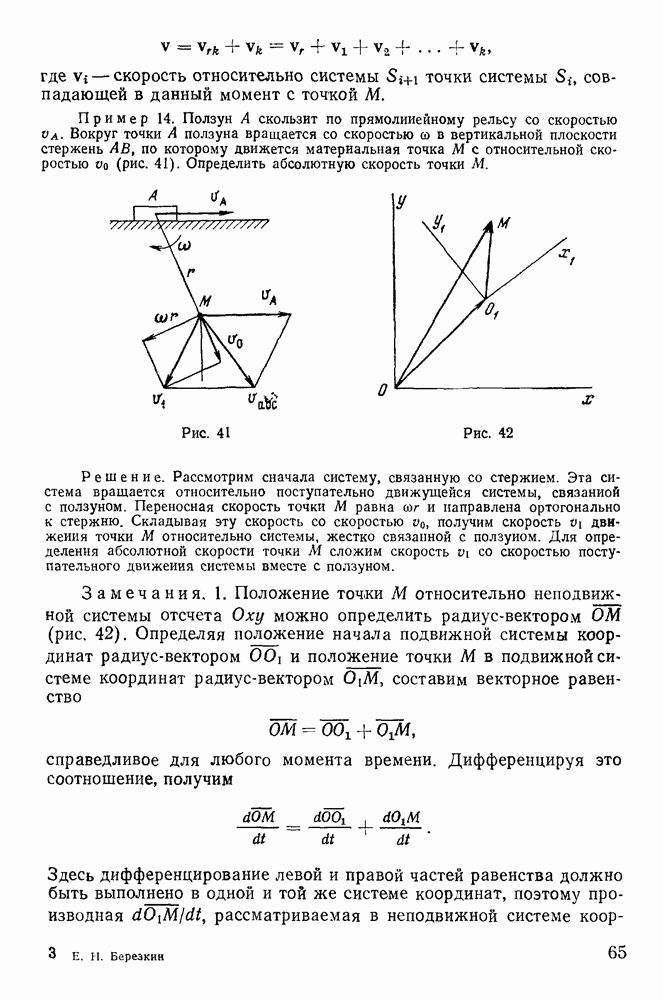
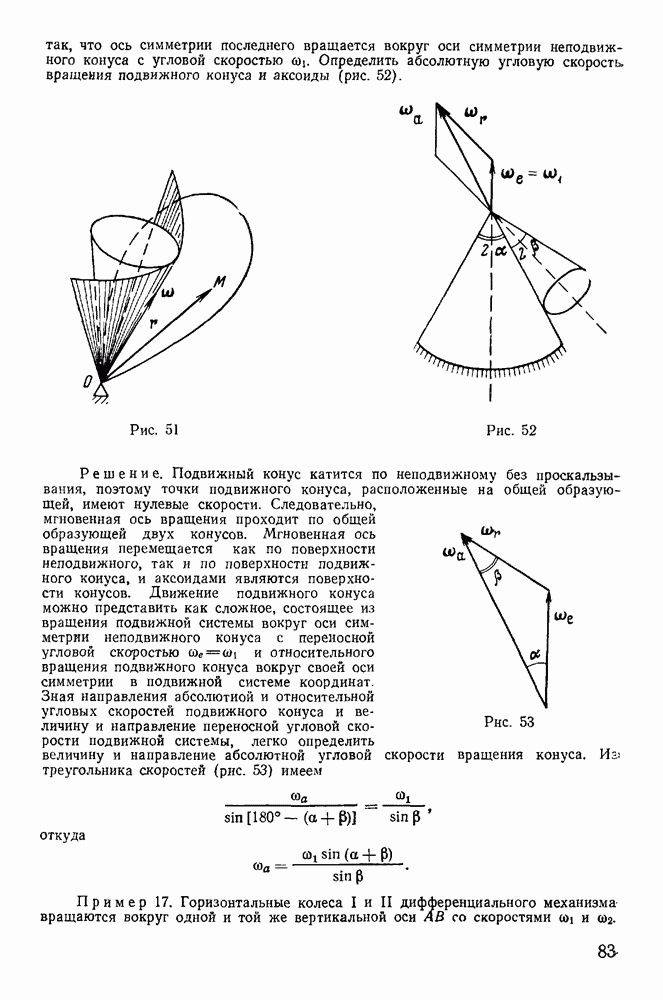
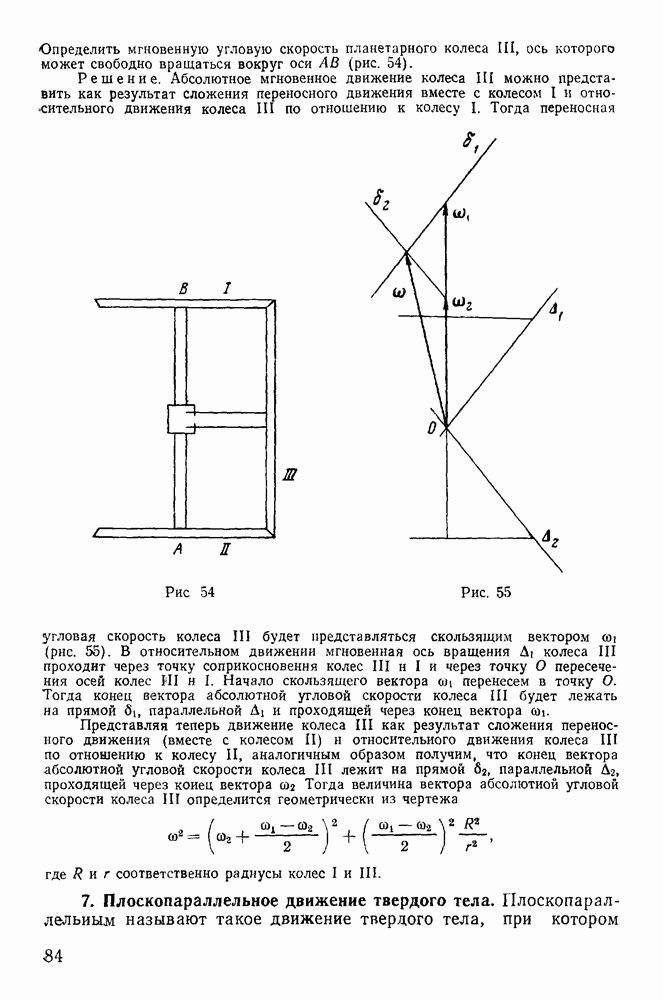
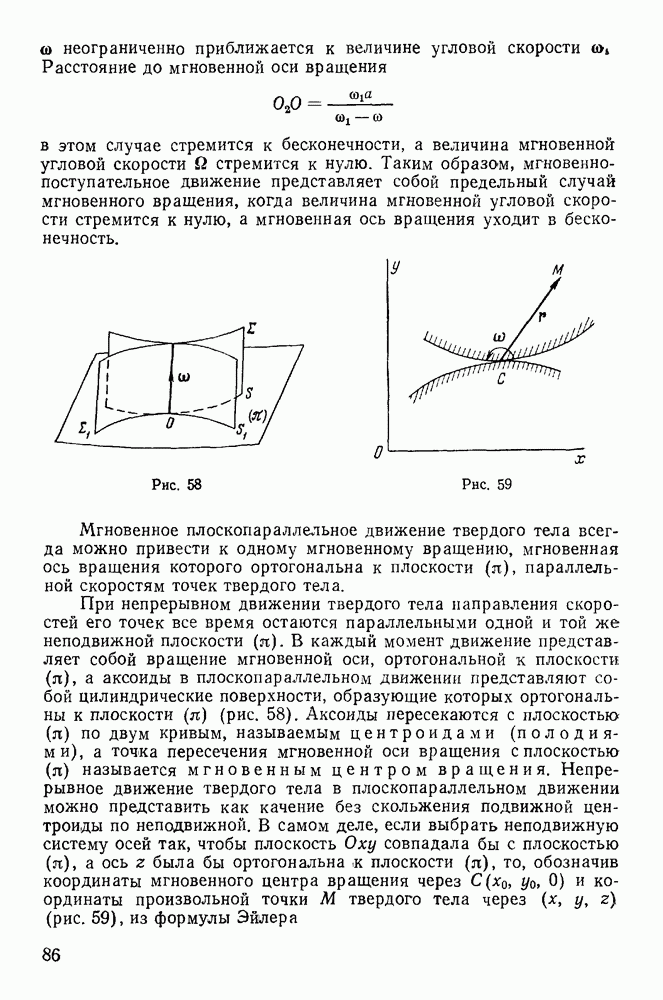
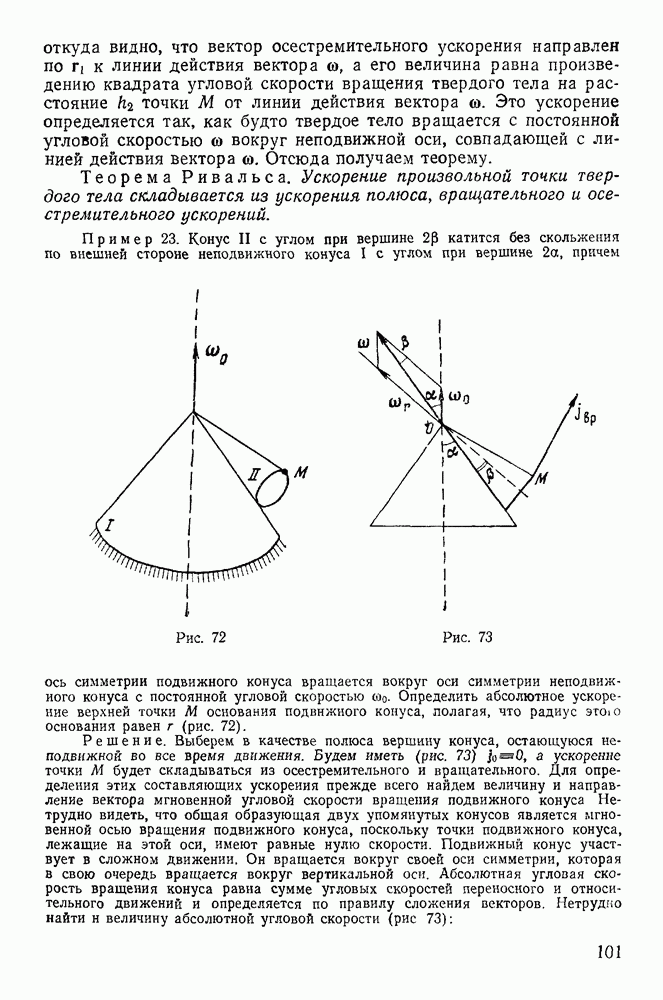
2. Мгновенный центр ускорений.
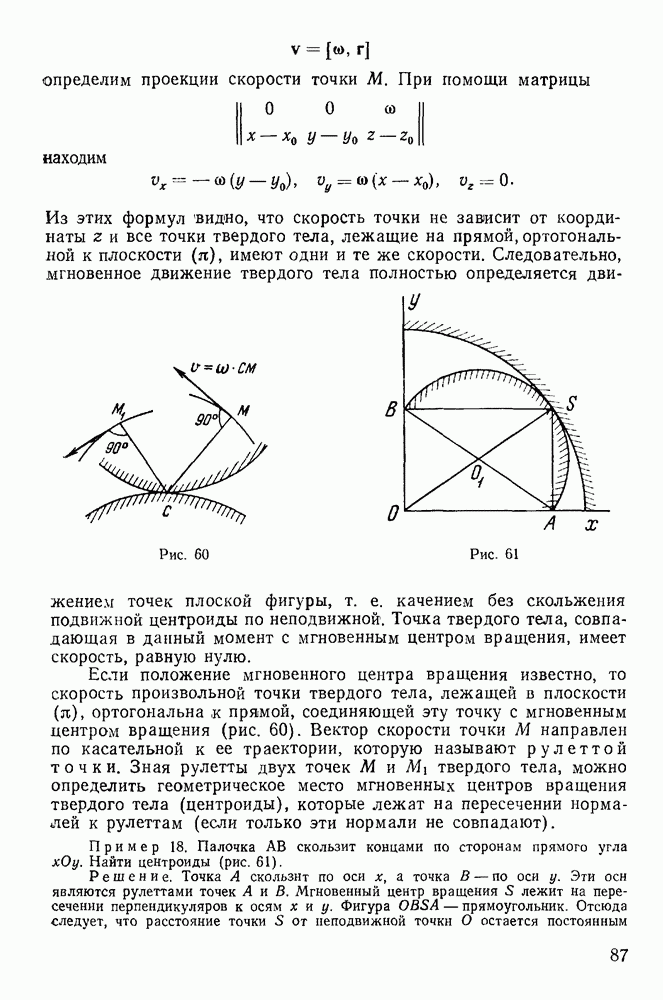
Мгновенным центром ускорений называется точка твердого тела, ускорение которой в данный момент времени равно нулю. Для определения такой точки рассмотрим ускорения точек твердого тела в плоскопараллельном движении. Обозначая через  проекции ускорения произвольной точки твердого тела на касательную и нормаль к траектории этой точки, будем иметь
проекции ускорения произвольной точки твердого тела на касательную и нормаль к траектории этой точки, будем иметь

Подставляя в эти соотношения значения  получим
получим

где  — угол между радиус-вектором точки М, построенным из мгновенного центра вращения, и направлением ускорения точки С (рис. 78). Введя обозначение
— угол между радиус-вектором точки М, построенным из мгновенного центра вращения, и направлением ускорения точки С (рис. 78). Введя обозначение  представим предыдущие формулы в виде
представим предыдущие формулы в виде

Если  — радиус кривизны рулетты точки М, то нормальное ускорение можно будет представить в виде
— радиус кривизны рулетты точки М, то нормальное ускорение можно будет представить в виде

Это выражение обращается в нуль при  или при
или при  . В последнем случае точка М является точкой перегибов. Если
. В последнем случае точка М является точкой перегибов. Если  то из уравнений (а) получим при
то из уравнений (а) получим при 

или

Величина  является одной и той же для всех точек твердого тела. Геометрическое место точек, удовлетворяющих уравнению
является одной и той же для всех точек твердого тела. Геометрическое место точек, удовлетворяющих уравнению  есть окружность радиуса
есть окружность радиуса  Рулетты на этой окружности имеют точки перегибов, поэтому полученную окружность
Рулетты на этой окружности имеют точки перегибов, поэтому полученную окружность
называют кругом перегибов, или кругом Лагира. Нормальные ускорения точек твердого тела, совпадающих с кругом Латра, равны нулю, а касательные ускорения проходят через точку К окружности, которую назовем полюсом перегибов.
Замечание. В случае поступательного движения твердого тела  и радиус круга Лагира стремится к бесконечности.
и радиус круга Лагира стремится к бесконечности.

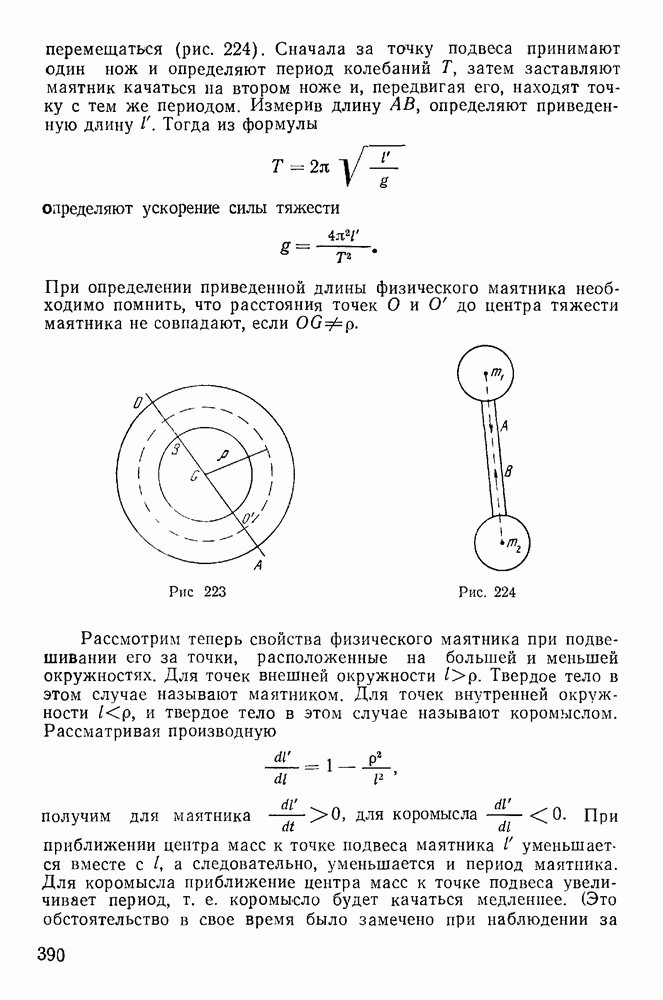
Рис. 78

Рис. 79
Рассмотрим теперь геометрическое место точек твердого тела, для которых обращается в нуль тангенциальное ускорение  . Пусть
. Пусть  тогда из формул (а) получим
тогда из формул (а) получим

Геометрическое место точек, удовлетворяющее этому уравнению, является окружностью радиуса  Если
Если  то радиус этой окружности неограниченно возрастает. Не будем рассматривать случай, когда
то радиус этой окружности неограниченно возрастает. Не будем рассматривать случай, когда  и
и  одновременно обращаются в нуль (случай поступательного движения), и будем предполагать, что эти величины отличны от нуля и конечны. На окружности обращаются в нуль касательные ускорения, и, следовательно, имеет место условие
одновременно обращаются в нуль (случай поступательного движения), и будем предполагать, что эти величины отличны от нуля и конечны. На окружности обращаются в нуль касательные ускорения, и, следовательно, имеет место условие

т. е. скорость принимает стационарное значение. Поэтому полученную окружность называют кругом стационарности (или кругом Бресса). Ускорения всех точек твердого тела, совпадающих с кругом Бресса, направлены к мгновенному центру вращения твердого тела. В точке  пересечения кругов Бресса и Лагира, обращаются в нуль и касательное и нормальное ускорения. Поэтому ускорение точки
пересечения кругов Бресса и Лагира, обращаются в нуль и касательное и нормальное ускорения. Поэтому ускорение точки  твердого телз равно нулю. Точка 5 является мгновенным центром ускорений твердого тела.
твердого телз равно нулю. Точка 5 является мгновенным центром ускорений твердого тела.
Круг стационарности и круг перегибов пересекаются в двух точках  и С. Но точка С является мгновенным центром вращения, а потому в ней будет равно нулю нормальное ускорение. Ускорение же
и С. Но точка С является мгновенным центром вращения, а потому в ней будет равно нулю нормальное ускорение. Ускорение же  точки С параллельно скорости точки С в момент
точки С параллельно скорости точки С в момент  т. е. направлено по касательной к траектории точки С и отлично от нуля. Определяя предельное значение ускорения при
т. е. направлено по касательной к траектории точки С и отлично от нуля. Определяя предельное значение ускорения при  заметим, что поскольку
заметим, что поскольку  то
то  и тогда
и тогда  .
.
Если связать подвижную систему координат с твердым телом, то из теоремы Кориолиса будем иметь  и ускорения точек твердого тела будут определяться формулой Ривальса
и ускорения точек твердого тела будут определяться формулой Ривальса

где  — радиус-вектор начала подвижной системы координат. Если за начало подвижной системы координат выбрать точку твердого тела, совпадающую с мгновенным центром ускорении,
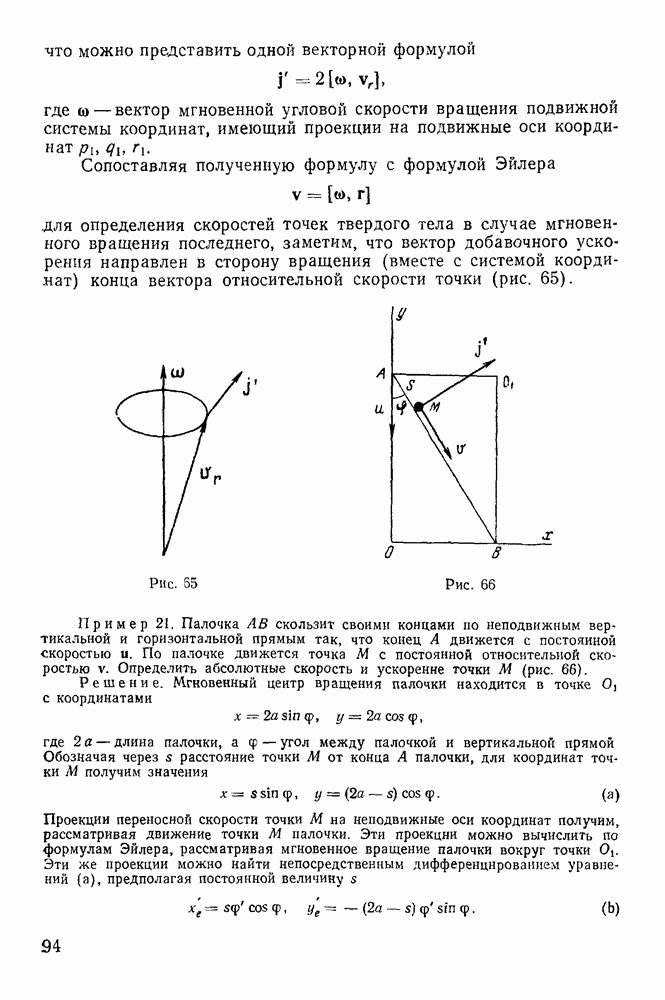
— радиус-вектор начала подвижной системы координат. Если за начало подвижной системы координат выбрать точку твердого тела, совпадающую с мгновенным центром ускорении,  и ускорения точек твердого тела будут распределяться так, как будто твердое тело вращается вокруг неподвижной оси, ортогональной к плоскости движения твердого тела и проходящей через мгновенный центр ускорений (рис. 79).
и ускорения точек твердого тела будут распределяться так, как будто твердое тело вращается вокруг неподвижной оси, ортогональной к плоскости движения твердого тела и проходящей через мгновенный центр ускорений (рис. 79).
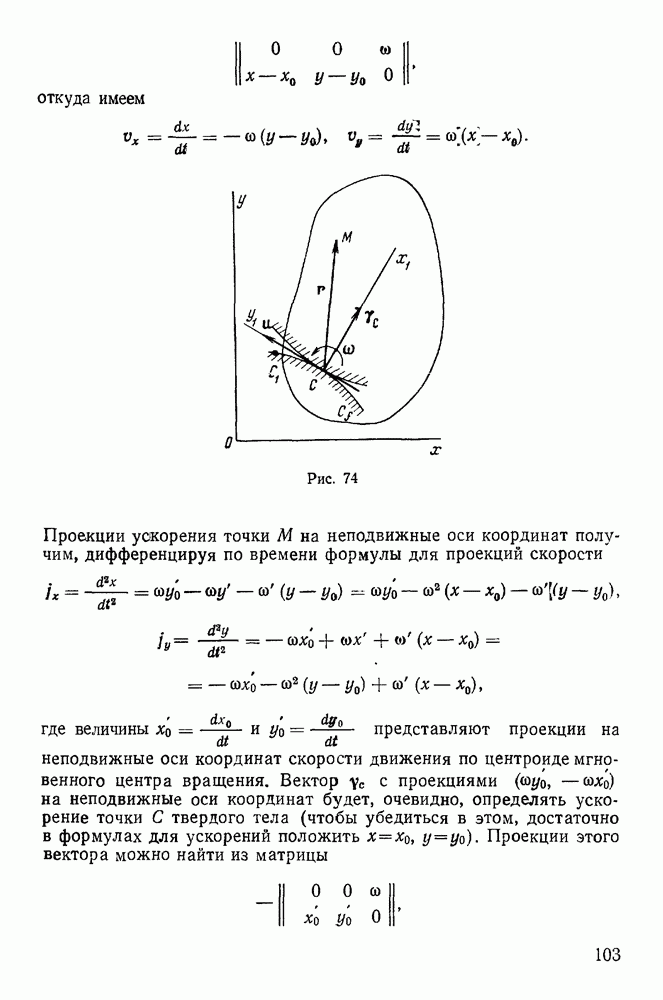
Формулы, определяющие мгновенный центр ускорений и ускорения произвольной точки твердого тела в плоскопараллельном движении, можно получить и непосредственно из формул Эйлера. Обозначая через  координаты мгновенного центра вращения твердого тела в неподвижной системе координат, а через х, у — координаты произвольной точки твердого тела, для проекций скоростей точек твердого тела получим равенства
координаты мгновенного центра вращения твердого тела в неподвижной системе координат, а через х, у — координаты произвольной точки твердого тела, для проекций скоростей точек твердого тела получим равенства

Отсюда для проекций ускорений точек твердого тела на неподвижные оси координат будем иметь следующие соотношения:

Обозначая через  координаты той точки твердого тела, ускорение которой равно нулю, для определения этих координат получим равенства
координаты той точки твердого тела, ускорение которой равно нулю, для определения этих координат получим равенства

Система линейных неоднородных алгебраических относительно разностей  уравнений имеет решение, если определитель системы отличен от нуля
уравнений имеет решение, если определитель системы отличен от нуля

Это условие выполняется, когда хотя бы одна из величин  или
или  отлична от нуля, что всегда имеет место, если движение твердого тела не является поступательным. В этом случае координаты точки твердого тела, ускорение которой равно нулю (мгновенного центра ускорений) определяются из равенств
отлична от нуля, что всегда имеет место, если движение твердого тела не является поступательным. В этом случае координаты точки твердого тела, ускорение которой равно нулю (мгновенного центра ускорений) определяются из равенств

Вычитая уравнения  из соответствующих уравнений
из соответствующих уравнений  получим уравнения для определения ускорений точек твердого тела
получим уравнения для определения ускорений точек твердого тела

Эти формулы допускают простое геометрическое истолкование: ускорения точек твердого тела распределяются так, как будто твердое тело вращается вокруг мгновенного центра ускорений, и могут быть представлены касательной и нормальной составляющими

где  - угловое ускорение твердого тела.
- угловое ускорение твердого тела.
Если обозначить через  угол между направлением ускорения и прямой, соединяющей точку М с мгновенным центром ускорений, то
угол между направлением ускорения и прямой, соединяющей точку М с мгновенным центром ускорений, то

т. е. этот угол является общим для всех точек твердого тела. Величина же ускорения

пропорциональна расстоянию точки до мгновенного центра ускорений.
Пример 27. Стержень АВ вращается с постоянной угловой скоростью  вокруг своего неподвижного конца в неподвижной плоскости
вокруг своего неподвижного конца в неподвижной плоскости  . В этой же
. В этой же
плоскости  вокруг точки С может вращаться стержень
вокруг точки С может вращаться стержень  Концы
Концы  стержней соединены шарнирно с третьим стержнем
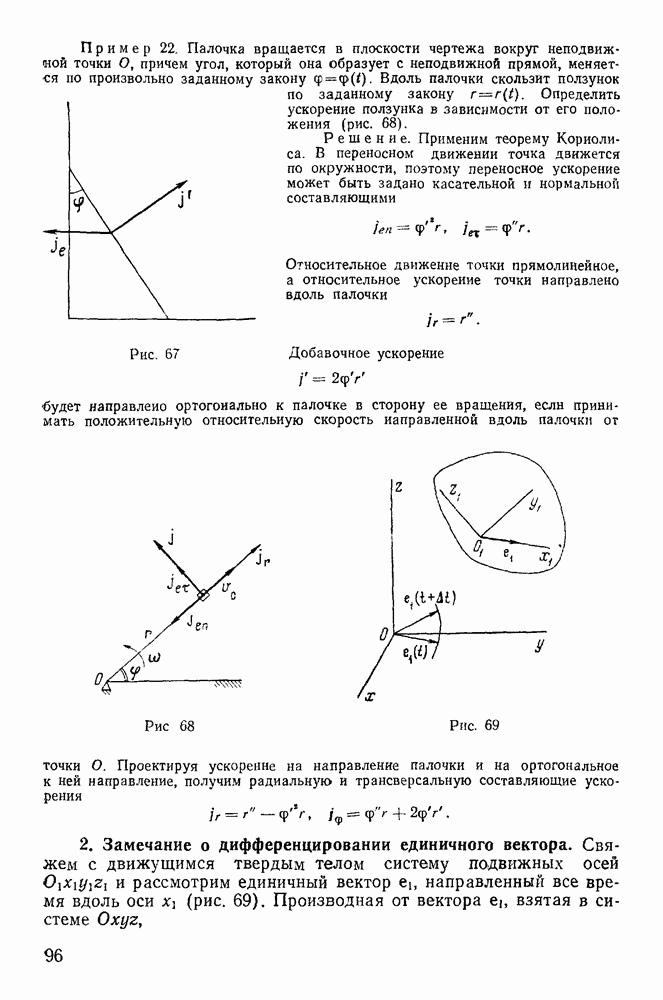
стержней соединены шарнирно с третьим стержнем  Определить ускорение точки D в тот момент, когда стержни АВ и DC параллельны между собой и ортогональны к отрезку
Определить ускорение точки D в тот момент, когда стержни АВ и DC параллельны между собой и ортогональны к отрезку  Длина стержня
Длина стержня  равна
равна  длина отрезка
длина отрезка  равна а (рис. 80)
равна а (рис. 80)
Решение. В рассматриваемом положении мгновенный центр вращения стержня  уходит в бесконечность, а его угловая скорость вращения равна нулю, т. е. стержень
уходит в бесконечность, а его угловая скорость вращения равна нулю, т. е. стержень  совершает мгновенно-поступательное движение. Скорости точек В и D равны по величине и по направлению
совершает мгновенно-поступательное движение. Скорости точек В и D равны по величине и по направлению


Рис. 80

Рис. 81
Точка D совершает движение по окружности радиуса  и ее центростремительное ускорение
и ее центростремительное ускорение

Вычислим ускорение точки D по формуле Рнвальса, принимая за полюс точку В стержня 

Здесь ускорение точки В будет только центростремительным при вращении вокруг точки А

Осестремительное ускорение точки D равно нулю, поскольку равна нулю мгновенная угловая скорость вращения стержня  Вращательное же ускорение точки
Вращательное же ускорение точки

содержит неизвестную величину в. Определяя центростремительную составляющую ускорения точки D из формулы  получим
получим

где

откуда

Тогда вращательная составляющая ускорения точки D

и полное ускорение точки  получит вид
получит вид

где

Пример 28. Квадрат  со стороной
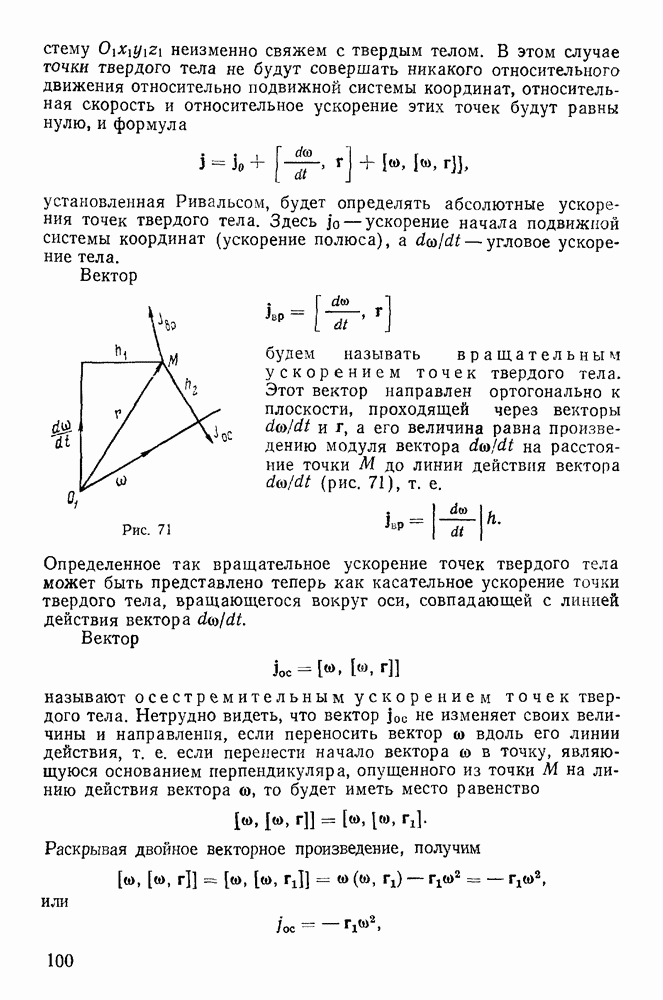
со стороной  совершает движение в плоскости чертежа. Найтн положение мгновенного центра ускорений и ускорение вершин его С и D, если известны в данный момент ускорения точек А и В (рис. 81).
совершает движение в плоскости чертежа. Найтн положение мгновенного центра ускорений и ускорение вершин его С и D, если известны в данный момент ускорения точек А и В (рис. 81).
Решение. Определим сначала мгновенную угловую скорость и угловое ускорение квадрата, воспользовавшись формулой Ривальса:

Проектируя это равенство на оси х и у, получим

откуда

Если величины  равны, то мгновенный центр ускорений находится в центре квадрата, а ускорения точек D и С направлены по сторонам квадрата и по величине равны ускорениям точек А и В.
равны, то мгновенный центр ускорений находится в центре квадрата, а ускорения точек D и С направлены по сторонам квадрата и по величине равны ускорениям точек А и В.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие
- Введение
- Глава I. ОСНОВЫ ТЕОРИИ ВЕКТОРОВ
- § 1. СВОБОДНЫЕ ВЕКТОРЫ
- 2. Сложение свободных векторов.
- 3. Проекция вектора на ось.
- 4. Инварианты системы свободных векторов.
- § 2. СКОЛЬЗЯЩИЕ ВЕКТОРЫ
- 2. Координаты скользящего вектора.
- 3. Момент скользящего вектора. Плюккеровы координаты.
- 4. Аналитическое определение момента скользящего вектора.
- 5. Проекция момента на ось.
- 6. Момент скользящего вектора относительно оси
- § 3. СИСТЕМА СКОЛЬЗЯЩИХ ВЕКТОРОВ
- 2. Произвольная система скользящих векторов. Элементарные операции.
- 3. Приведение системы скользящих векторов к простейшей эквивалентной форме.
- 4. Плоская система скользящих векторов.
- 5. Свойства системы параллельных скользящих векторов.
- § 4. ЗАКРЕПЛЕННЫЕ ВЕКТОРЫ
- § 5. ДИФФЕРЕНЦИРОВАНИЕ СВОБОДНОГО ВЕКТОРА ПО СКАЛЯРНОМУ АРГУМЕНТУ
- Глава II. КИНЕМАТИКА
- § 1. КИНЕМАТИКА ТОЧКИ
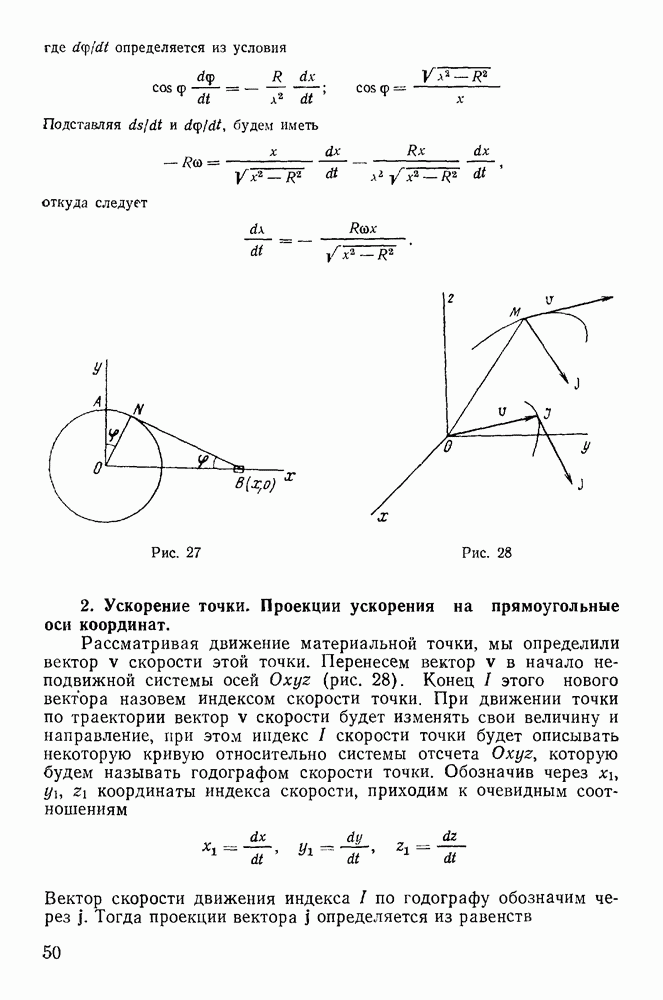
- 2. Ускорение точки. Проекции ускорения на прямоугольные оси координат.
- 3. Скорость и ускорение точки в полярных координатах.
- 4. Движение точки по окружности.
- 5. Проекции ускорения на оси естественного трехгранника.
- 6. Теорема о сложении скоростей в сложном движении точки.
- 7. Метод Роберваля построения касательных к плоским кривым.
- 8. Аналитическое доказательство теоремы о сложении скоростей.
- 9. Сложение скоростей в общем случае сложного движения точки.
- § 2. КИНЕМАТИКА АБСОЛЮТНО ТВЕРДОГО ТЕЛА
- 2. Элементарные движения твердого тела.
- 3. Мгновенные движения твердого тела.
- 4. Сложение мгновенно-поступательных и мгновенно-вращательных движений твердого тела.
- 5. Общий случай сложения мгновенно-поступательных и мгновенно-вращательных движений твердого тела. Непрерывное движение твердого тела.
- 6. Мгновенное движение твердого тела с одной неподвижной точкой.
- 7. Плоскопараллельное движение твердого тела.
- § 3. УСКОРЕНИЕ ТОЧКИ В СЛОЖНОМ ДВИЖЕНИИ
- 2. Замечание о дифференцировании единичного вектора.
- 3. Векторный вывод теоремы Кориолиса.
- 4. Теорема Ривальса.
- § 4. РАСПРЕДЕЛЕНИЕ УСКОРЕНИЙ В ПЛОСКОПАРАЛЛЕЛЬНОМ ДВИЖЕНИИ ТВЕРДОГО ТЕЛА
- 2. Мгновенный центр ускорений.
- § 5. КИНЕМАТИЧЕСКИЕ УРАВНЕНИЯ ЭЙЛЕРА
- Глава III. СТАТИКА
- I. ГЕОМЕТРИЧЕСКАЯ СТАТИКА
- § 1. АКСИОМЫ СТАТИКИ
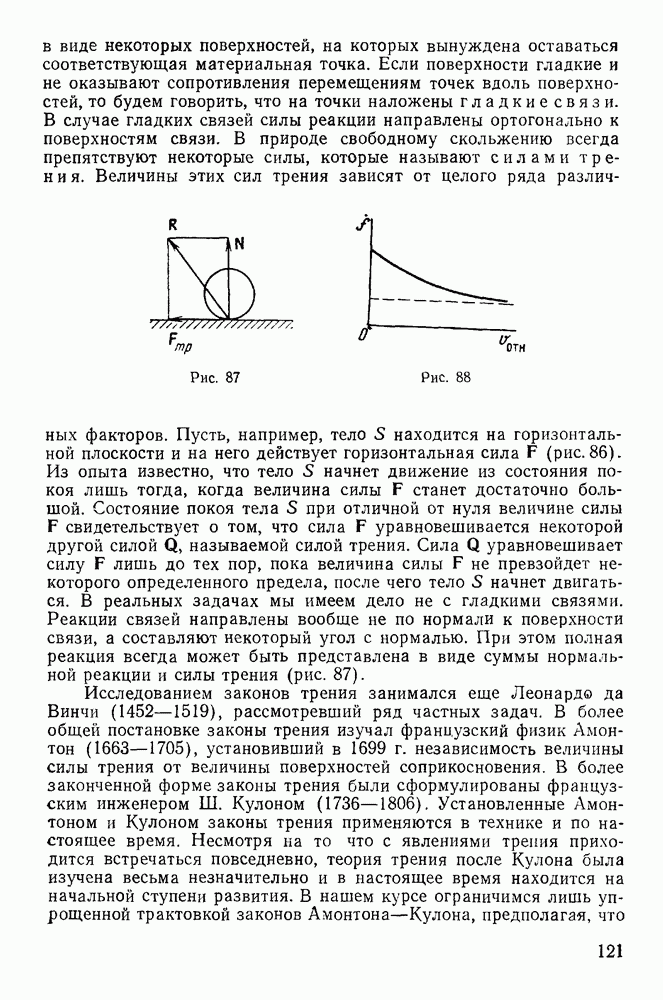
- § 2. ПОНЯТИЕ О СИЛЕ ТРЕНИЯ
- § 3. РАЗЛИЧНЫЕ ЗАДАЧИ СТАТИКИ
- 2. Равновесие трех сил.
- § 4. МОМЕНТ СИЛЫ
- 2. Момент силы относительно оси.
- 3. Теорема Вариньона для системы сходящихся сил.
- § 5. ПРОИЗВОЛЬНАЯ СИСТЕМА СИЛ, ДЕЙСТВУЮЩИХ НА ТВЕРДОЕ ТЕЛО
- § 6. УСЛОВИЯ РАВНОВЕСИЯ СИСТЕМЫ СИЛ, ДЕЙСТВУЮЩИХ НА ТВЕРДОЕ ТЕЛО
- § 7. ПРИВЕДЕНИЕ СИСТЕМЫ СИЛ, ДЕЙСТВУЮЩИХ НА ТВЕРДОЕ ТЕЛО, К ДИНАМЕ. УРАВНЕНИЯ РАВНОВЕСИЯ ТВЕРДОГО ТЕЛА
- § 8. УСЛОВИЯ РАВНОВЕСИЯ СИСТЕМЫ ТВЕРДЫХ ТЕЛ
- § 9. ПЛОСКАЯ СИСТЕМА СИЛ
- § 10. ЗАДАЧА О РАВНОВЕСИИ НЕСВОБОДНОГО ТВЕРДОГО ТЕЛА
- 2. Частные случаи равновесия твердого тела.
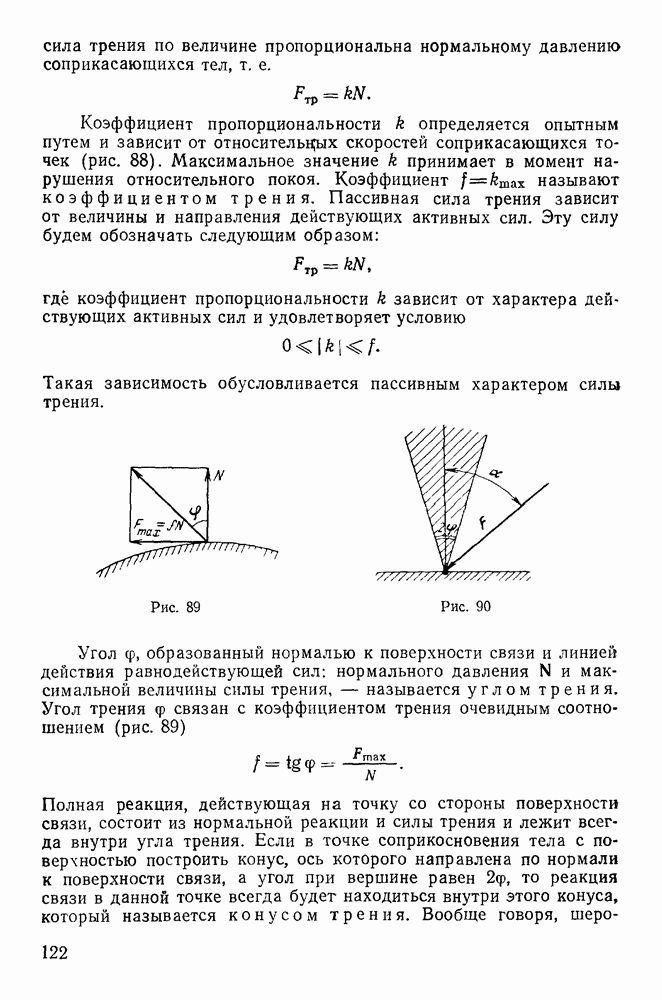
- § 11. ЗАДАЧА О РАВНОВЕСИИ ПРИ НАЛИЧИИ ТРЕНИЯ
- § 12. СИЛА ТЯЖЕСТИ И ЦЕНТР ТЯЖЕСТИ
- II. АНАЛИТИЧЕСКАЯ СТАТИКА
- § 1. РАБОТА СИЛЫ НА ПЕРЕМЕЩЕНИИ. СИЛОВАЯ ФУНКЦИЯ
- § 2. ПРИНЦИП ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ
- 2. Теорема Лагранжа о равновесии системы.
- 3. Принцип Торричелли.
- § 3. ОБЩИЕ ВОПРОСЫ АНАЛИТИЧЕСКОЙ СТАТИКИ
- 3. Общие теоремы о равновесии системы материальных точек.
- 4. Метод неопределенных множителей Лагранжа.
- 5. Определение реакций.
- § 4. ОПРЕДЕЛЕНИЕ РЕАКЦИЙ В ОБЩЕМ СЛУЧАЕ
- § 5. РАВНОВЕСИЕ НИТИ
- 2. Естественные уравнения равновесия нити.
- Глава IV. ДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ
- § 1. ОСНОВНЫЕ ЗАКОНЫ ДИНАМИКИ
- § 2. ДВЕ ОСНОВНЫЕ ЗАДАЧИ ДИНАМИКИ. УРАВНЕНИЯ ДВИЖЕНИЯ ТОЧКИ В ДЕКАРТОВЫХ ОСЯХ
- § 3. ЕСТЕСТВЕННЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ
- § 4. ОСНОВНЫЕ ТЕОРЕМЫ ДИНАМИКИ ДЛЯ СВОБОДНОЙ МАТЕРИАЛЬНОЙ ТОЧКИ
- 2. Теорема об изменении момента количества движения.
- 3. Следствия из теорем об изменении количества движения и момента количества движения материальной точки.
- 4. Теорема живых сил.
- 5. Интеграл живых сил.
- 6. Устойчивость равновесия. Теорема Лагранжа.
- § 5. ДВИЖЕНИЕ ТЯЖЕЛОЙ МАТЕРИАЛЬНОЙ ТОЧКИ В ПУСТОТЕ
- § 6. ДВИЖЕНИЕ МАТЕРИАЛЬНОЙ ТОЧКИ ПОД ДЕЙСТВИЕМ ЦЕНТРАЛЬНЫХ СИЛ
- 2. Формулы Бине
- 3. Задача о движении планет
- § 7. ДВИЖЕНИЕ ТОЧКИ В СОПРОТИВЛЯЮЩЕЙСЯ СРЕДЕ
- § 8. ДВИЖЕНИЕ НЕСВОБОДНОЙ МАТЕРИАЛЬНОЙ ТОЧКИ
- 2. Движение материальной точки по поверхности.
- § 9. ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЕ МАТЕРИАЛЬНОЙ ТОЧКИ
- 1. Теорема живых сил в относительном движении точки.
- 2. Уравнения относительного равновесия точки.
- 3. Равновесие материальной точки на поверхности Земли. Вес.
- 4. Задача о падении тяжелой точки в пустоте.
- 5. Маятник Фуко.
- § 10. ПРИНЦИП ДАЛАМБЕРА
- Глава V. ДИНАМИКА СИСТЕМЫ МАТЕРИАЛЬНЫХ ТОЧЕК
- § 1. УЧЕНИЕ О СВЯЗЯХ
- § 2. ПРИНЦИП ДАЛАМБЕРА — ЛАГРАНЖА
- § 3. ОСНОВНЫЕ ТЕОРЕМЫ ДИНАМИКИ СИСТЕМЫ
- 2. Теорема об изменении момента количества движения.
- 3. Теорема живых сил.
- § 4. ТЕОРЕМЫ О ДВИЖЕНИИ СИСТЕМЫ ОТНОСИТЕЛЬНО ОСЕЙ НЕИЗМЕННОГО НАПРАВЛЕНИЯ, ПРОХОДЯЩИХ ЧЕРЕЗ ЦЕНТР МАСС СИСТЕМЫ (ОСЕЙ КЕНИГА)
- 2. Теорема об изменении момента количества движения системы относительно осей Кёнига.
- 3. Теорема живых сил в движении системы относительно осей Кёнига.
- § 5. УРАВНЕНИЯ ЛАГРАНЖА ВТОРОГО РОДА
- 2. Случай существования силовой функции.
- 3. Замечание о лагранжевых координатах.
- § 6. ЭЛЕМЕНТАРНЫЕ СЛУЧАИ ИНТЕГРИРУЕМОСТИ УРАВНЕНИЙ ЛАГРАНЖА
- 2. Метод Рауса игнорирования циклических координат.
- 3. Обобщение теоремы и интеграла живых сил.
- § 7. ОПРЕДЕЛЕНИЕ РЕАКЦИЙ
- Глава VI. ДИНАМИКА ТВЕРДОГО ТЕЛА
- § 1. ТЕОРИЯ МОМЕНТОВ ИНЕРЦИИ
- 2. Момент инерции системы относительно произвольной оси, проходящей через заданную точку.
- 3. Эллипсоид инерции.
- 4. Определение главных осей инерции для произвольной точки.
- § 2. ВРАЩЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ОСИ
- § 3. ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА, ИМЕЮЩЕГО ОДНУ НЕПОДВИЖНУЮ ТОЧКУ
- 2. Уравнения движения твердого тела с одной неподвижной точкой.
- § 4. ДВИЖЕНИЕ ТЯЖЕЛОГО ТВЕРДОГО ТЕЛА ОКОЛО НЕПОДВИЖНОЙ ТОЧКИ
- 2. Интегрирование уравнений движения тяжелого твердого тела.
- 3. Случай Эйлера — Пуансо.
- Регулярная прецессия твердого тела в случае Эйлера.
- Геометрическая интерпретация Пуансо движения твердого тела в случае Эйлера.
- Устойчивость постоянных вращений твердого тела.
- 4. Случай Лагранжа.
- Особенные случаи движения твердого тела. Спящий волчок.
- Гироскоп. Приближенная теория.
- Некоторые применения гироскопов.
- Регулярная прецессия в случае Лагранжа.
- Вынужденная регулярная прецессия.
- 5. Случай Ковалевской.
- § 5. ОПРЕДЕЛЕНИЕ РЕАКЦИИ В СЛУЧАЕ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА С ОДНОЙ НЕПОДВИЖНОЙ ТОЧКОЙ
- § 6. УРАВНЕНИЯ ДВИЖЕНИЯ СВОБОДНОГО ТВЕРДОГО ТЕЛА
- § 7. ГИРОСТАТЫ
- Глава VII. АНАЛИТИЧЕСКАЯ ДИНАМИКА
- § 1. КАНОНИЧЕСКИЕ УРАВНЕНИЯ ГАМИЛЬТОНА
- 1. Преобразования Лежандра.
- 2. Канонические уравнения Гамильтона.
- 3. Функция Гамильтона и ее свойства.
- § 2. ПРИНЦИП ГАМИЛЬТОНА — ОСТРОГРАДСКОГО
- 2. Вывод канонических уравнений Гамильтона из принципа Гамильтона — Остроградского.
- 3. Принцип Гамильтона в форме Пуанкаре.
- § 3. ИНТЕГРИРОВАНИЕ КАНОНИЧЕСКИХ УРАВНЕНИЙ ГАМИЛЬТОНА
- 2. Канонические преобразования.
- 3. Бесконечно малые канонические преобразования.
- 4. Теорема Лиувилля.
- 5. Теорема Якоби.
- 6. Интегрирование уравнения Гамильтона—Якоби.
- Метод Имшенецкого разделения переменных.
- 7. Скобки Пуассона.
- § 4. ВАРИАЦИОННЫЕ ПРИНЦИПЫ МЕХАНИКИ
- 2. Принцип Лагранжа.
- 3. Принцип наименьшего действия в форме Якоби.
- Вывод уравнений Лагранжа второго рода из принципа Якоби.
- Сравнение принципа Якоби с принципом Гамильтона.
- 4. Оптико-механическая аналогия.
- 5. Интегральные инварианты.
- Линейные интегральные инварианты.
- Интегральный инвариант Пуанкаре — Картана.
- 6. Принцип наименьшего принуждения Гаусса. Уравнения Аппеля.
- 7. Уравнения Рауса.
- § 5. МАЛЫЕ КОЛЕБАНИЯ
- Затухающие колебания.
- Вынужденные колебания. Резонанс.
- Параметрический резонанс.
- Нелинейные колебания.
- Диссипативные системы.
- 2. Общий случай малых колебаний системы около положения устойчивого равновесия.
- Устойчивость равновесия. Теорема Лагранжа об устойчивости равновесия.
- Замечание об устойчивости стационарных движений.
- Малые колебания системы около положения устойчивого равновесия.
- Влияние диссипативных сил на малые колебания системы около устойчивого положения равновесия.
- § 6. УСТОЙЧИВОСТЬ ДВИЖЕНИЯ
- Прямой метод Ляпунова
- Теорема об асимптотической устойчивости.
- Теорема Четаева о неустойчивости движения.
- 2. Влияние новых связей на малые колебания системы около положения равновесия.
- 3. Влияние диссипативных сил на устойчивость равновесия.
- 4. Влияние гироскопических сил на устойчивость равновесия.
- § 7. ЭЛЕМЕНТЫ ТЕОРИИ ВОЗМУЩЕНИЙ
- Устойчивость консервативных систем.
- 2. Метод изменения произвольных постоянных.
- Глава VIII. ТЕОРИЯ УДАРА
- § 2. ТЕОРЕМЫ КАРНО
- § 3. ЗАДАЧА О ЦЕНТРЕ УДАРА
- § 4. ЗАДАЧА О БАЛЛИСТИЧЕСКОМ МАЯТНИКЕ
- § 5. УРАВНЕНИЯ ЛАГРАНЖА ДЛЯ УДАРА
- § 6. ЗАДАЧА ОБ УДАРЕ ПО ТВЕРДОМУ ТЕЛУ С ОДНОЙ НЕПОДВИЖНОЙ ТОЧКОЙ
- Глава IX. ЭЛЕМЕНТЫ СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- § 2. СПЕЦИАЛЬНЫЙ ПРИНЦИП ОТНОСИТЕЛЬНОСТИ ЭЙНШТЕЙНА
- § 3. ГРУППА ПРЕОБРАЗОВАНИЙ ЛОРЕНЦА
- § 4. ИНВАРИАНТНЫЕ ВЕЛИЧИНЫ В ТЕОРИИ ОТНОСИТЕЛЬНОСТИ. ЧЕТЫРЕХМЕРНЫЙ ВЕКТОР. МИР МИНКОВСКОГО
- § 5. РЕЛЯТИВИСТСКАЯ ДИНАМИКА
- Литература