| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 7. ОПРЕДЕЛЕНИЕ РЕАКЦИЙ
В ряде задач механики часто требуется определять не только движение системы, но и силы реакций, возникающие при таком движении. В некоторых случаях достаточно знать лишь часть сил реакций. Для определения сил реакций можно воспользоваться уже известными нам общими теоремами динамики системы. Заменяя наложенные на систему связи силами, эквивалентными по своему действию связям, можно рассматривать эту систему как освобожденную от связей. Действительное движение освобожденной системы происходит в соответствии с наложенными ранее связями, но при этом появляются новые возможные перемещения, которым раньше препятствовали наложенные связи. Эти новые возможные перемещения дают возможность так применять общие теоремы динамики системы, чтобы в соответствующие уравнения движения уже входили реакции связей (для этого достаточно применять теоремы на тех возможных перемещениях, на которых работа сил освобожденных реакций отлична от нуля).
В общем случае при освобождении системы от связей, появляется новое возможное перемещение, которому соответствует изменение некоторой новой лагранжевой координаты  сохраняющей постоянное значение в действительном движении системы.
сохраняющей постоянное значение в действительном движении системы.
Пусть положение неосвобожденной системы определяется  независимыми лагранжевыми координатами
независимыми лагранжевыми координатами  . Освобожденная система будет определяться
. Освобожденная система будет определяться  координатами
координатами  Для такой системы можно вычислить живую силу
Для такой системы можно вычислить живую силу

и, определив работу всех сил на новом возможном перемещении, соответствующем изменению координаты  найти соответствующую обобщенную силу
найти соответствующую обобщенную силу  . В эту обобщенную силу войдет и искомая реакция связи. Записывая теперь уравнения Лагранжа для координаты
. В эту обобщенную силу войдет и искомая реакция связи. Записывая теперь уравнения Лагранжа для координаты 

и принимая во внимание, что в действительном движении

получим уравнение для определения интересующей нас реакции.
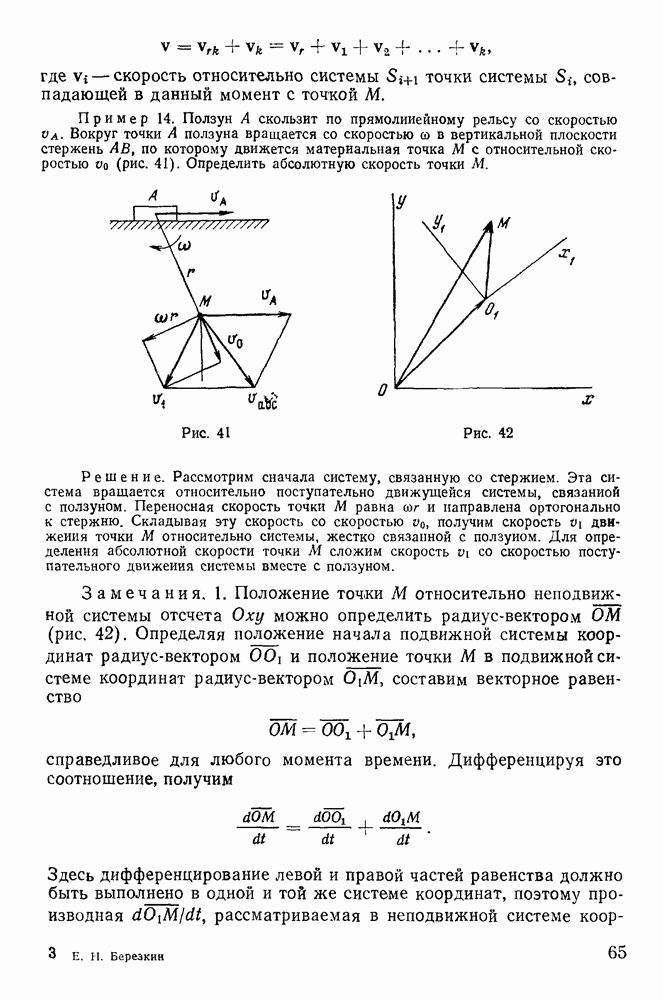
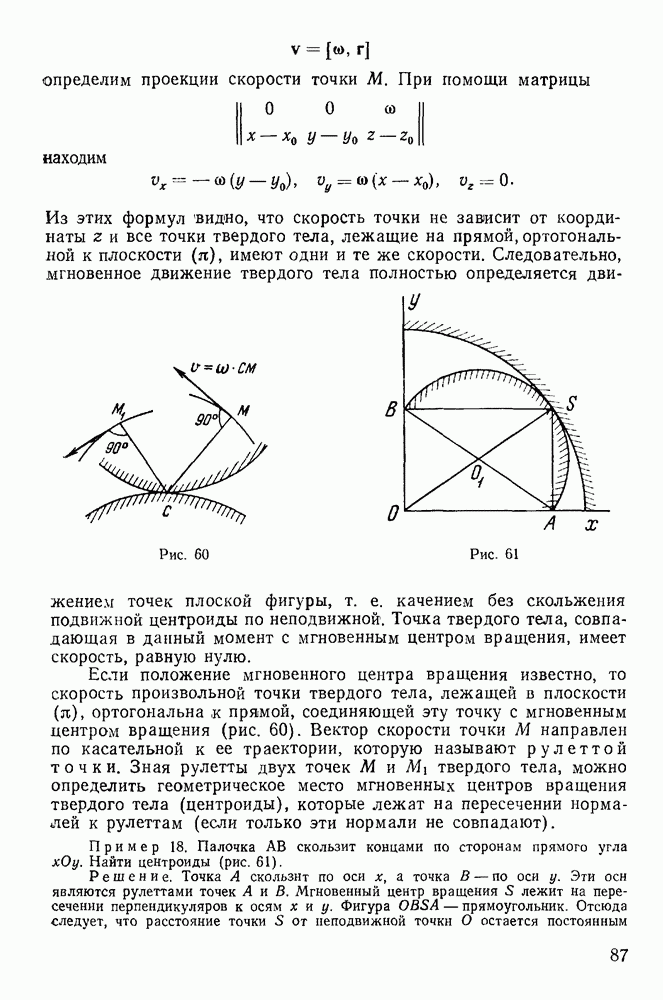
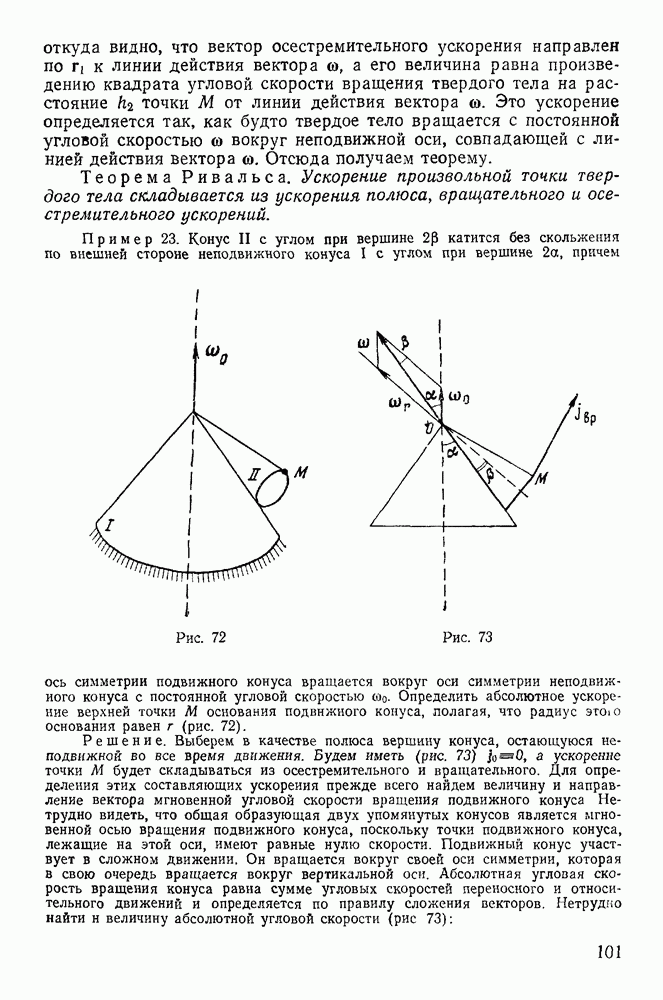
Пример 104. Тяжелая однородная палочка длины 21, опирающаяся одним концом на гладкую горизонтальную плоскость (рис. 208), начинает движение из состояния покоя, когда угол  Найти силу давления палочки на плоскость.
Найти силу давления палочки на плоскость.

Рис. 208
Определим сначала движение палочки. Связи, наложенные на систему, допускают поступательное перемещение палочкн вдоль неподвижной горизонтальной оси х. Применяя теорему о движении центра тяжести вдоль этой оси, получим

(где через  обозначена координата центра тяжести по оси х).
обозначена координата центра тяжести по оси х).
В начальный момент палочка находилась в покое, поэтому имеем

т. е. центр масс находится все время на одной и той же вертикальной прямой. Выберем неподвижную систему осей так, чтобы ось у совпадала с этой вертикальной прямой. Тогда центр масс все время будет оставаться на оси у.
Для определения движения остается найти зависимость угла  от времени. Но связи, наложенные на систему, не зависят явным образом от времени, и действительные перемещения находятся среди возможных. Следовательно, можно применить теорему живых сил, которая сразу дает интеграл живых сил
от времени. Но связи, наложенные на систему, не зависят явным образом от времени, и действительные перемещения находятся среди возможных. Следовательно, можно применить теорему живых сил, которая сразу дает интеграл живых сил

или

 — ордината центра масс;
— ордината центра масс;  — момент инерции палочки относительно оси, перпендикулярной к плоскости
— момент инерции палочки относительно оси, перпендикулярной к плоскости  и проходящей через центр масс. Определяя величины
и проходящей через центр масс. Определяя величины

и подставляя их значения в интеграл живых сил, получим

В начальный момент  тогда для
тогда для  имеем
имеем

Для определения реакции освободим систему от связи и введем силу реакции  Среди возможных перемещений теперь появляется поступательное перемещение палочкн вдоль оси у. Это дает возможность применить теорему о движении центра масс вдоль оси у
Среди возможных перемещений теперь появляется поступательное перемещение палочкн вдоль оси у. Это дает возможность применить теорему о движении центра масс вдоль оси у

откуда получаем

Подставляя сюда значение  имеем
имеем

где  определяются для действительного движения, стесненного связями. Эти значения можно выразить через
определяются для действительного движения, стесненного связями. Эти значения можно выразить через  при помощи интеграла живых сил. Дифференцируя последний по времени, для определения
при помощи интеграла живых сил. Дифференцируя последний по времени, для определения  получим уравнение
получим уравнение

После сокращения на  в начальный момент, когда
в начальный момент, когда  будем иметь
будем иметь 

откуда

Реакция  в начальный момент равна
в начальный момент равна

При  значение
значение  меньше веса палочки
меньше веса палочки  Например, при
Например, при  в начальный момент будем иметь
в начальный момент будем иметь

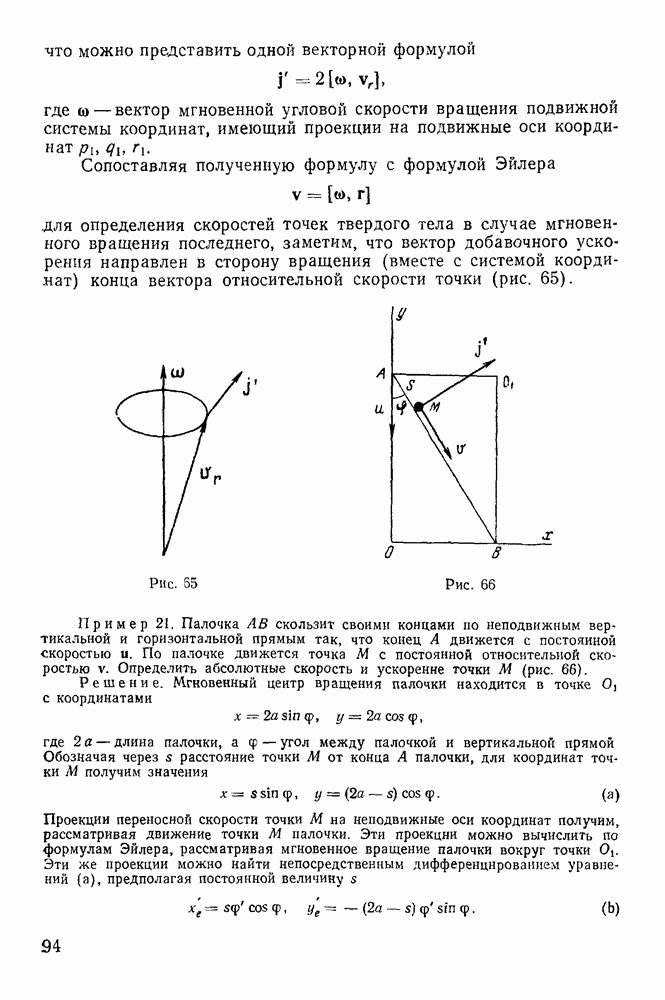
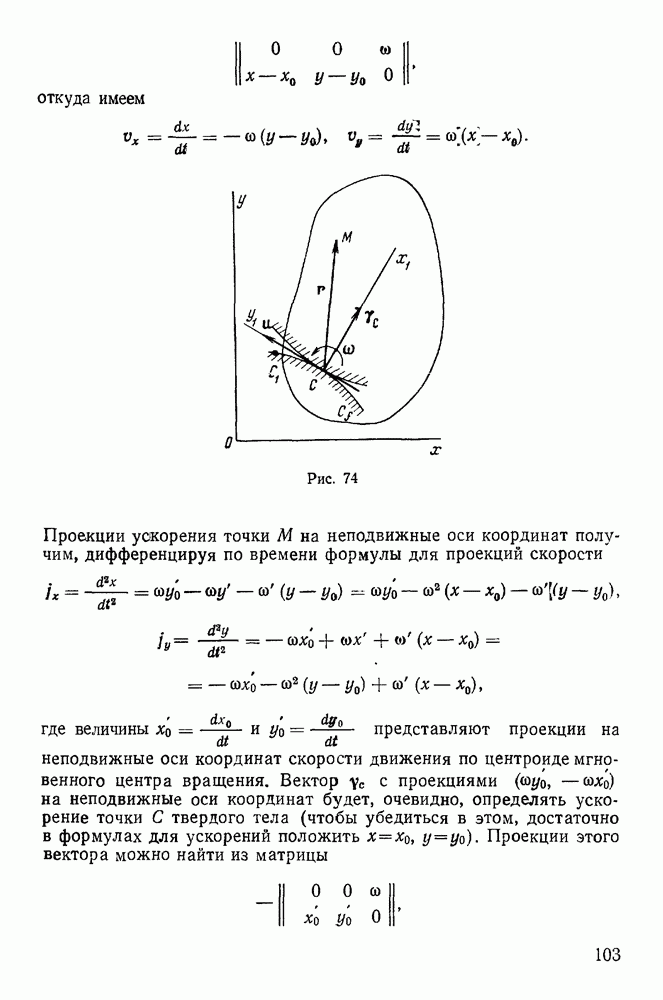
Пример 105, Однородная палочка АВ длины  и веса
и веса  положена в гладкий неподвижный полуцилиндр с горизонтальной осью, проходящей через точку О, причем
положена в гладкий неподвижный полуцилиндр с горизонтальной осью, проходящей через точку О, причем  Палочка движется под действием своего веса. Определить реакцию в точке А в зависимости от угла
Палочка движется под действием своего веса. Определить реакцию в точке А в зависимости от угла  где С — центр тяжести палочки. В начальный момент
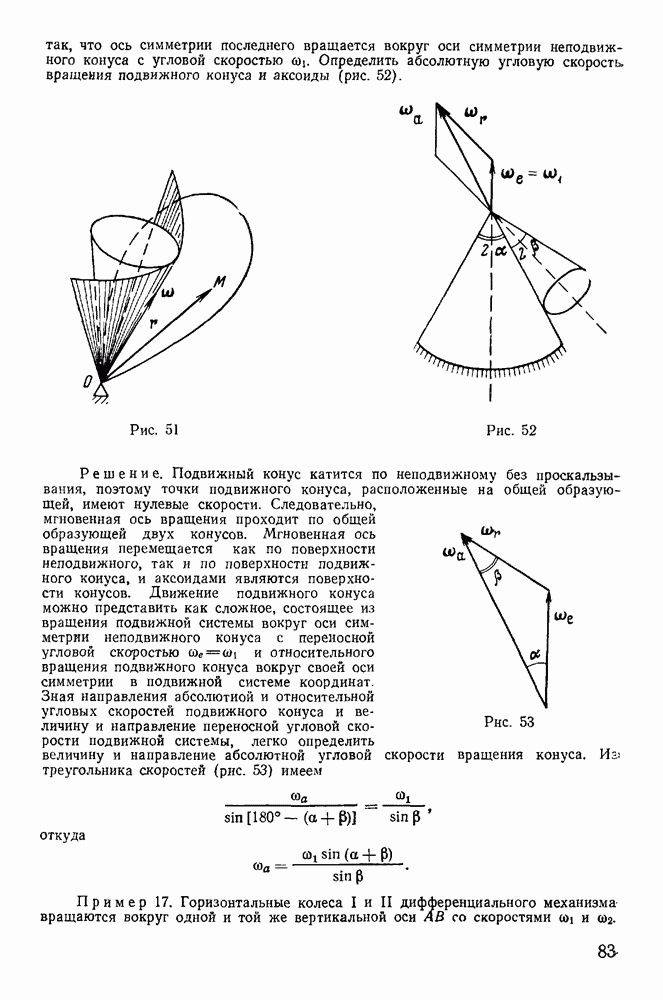
где С — центр тяжести палочки. В начальный момент  причем палочка находится в покое (рис. 209).
причем палочка находится в покое (рис. 209).
Связи, наложенные на систему (т. е. на палочку), идеальны и не зависят явно от времени, а активные силы (силы тяжести) обладают силовой функцией. При этих условиях существует интеграл живых сил

или

который полностью определяет движение палочки. Постоянная  находится из начальных условий:
находится из начальных условий:

Для определения реакции освободим палочку от связи в точке А, заменив ее действие силой  Будем рассматривать только движение палочки в плоскости чертежа. Возможное перемещение точки В палочки по направлению совпадает с касательной к окружности в точке В. Направим неподвижную ось
Будем рассматривать только движение палочки в плоскости чертежа. Возможное перемещение точки В палочки по направлению совпадает с касательной к окружности в точке В. Направим неподвижную ось  вдоль касательной в окружности в точке В в рассматриваемый момент времени. Освобожденная в точке А палочка может перемещаться поступательно вдоль оси
вдоль касательной в окружности в точке В в рассматриваемый момент времени. Освобожденная в точке А палочка может перемещаться поступательно вдоль оси  так что найдется возможное перемещение палочки, при котором перемещения всех точек палочки будут совпадать по величине и по направлению с перемещением точки В.
так что найдется возможное перемещение палочки, при котором перемещения всех точек палочки будут совпадать по величине и по направлению с перемещением точки В.

Рис. 209

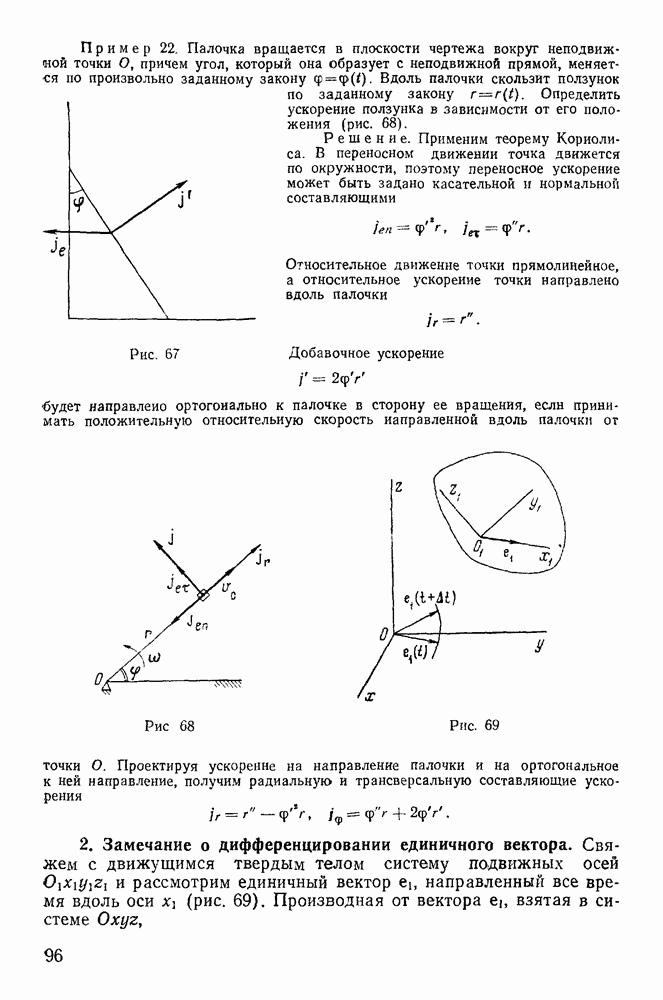
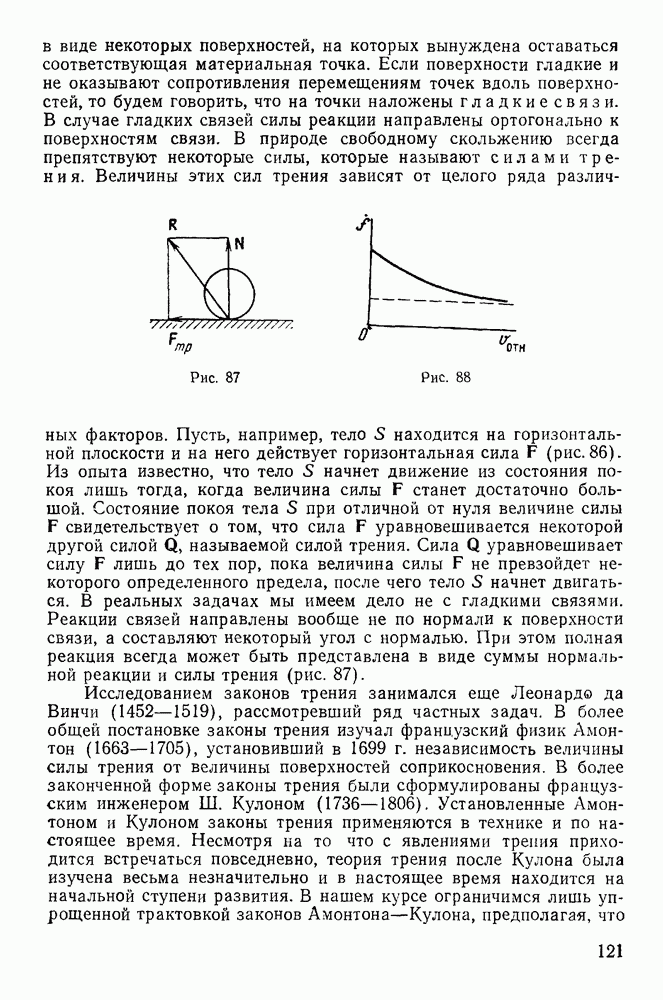
Рис. 210
Тогда можно применить теорему о движении центра масс для оси 

где  — проекция на ось х скорости о с центра тяжести палочки в ее действительном движении. Но
— проекция на ось х скорости о с центра тяжести палочки в ее действительном движении. Но

поэтому

где а — угол наклона палочки к оси х меняется во время движения. Отсюда

Но  рассматриваемый момент
рассматриваемый момент  тогда
тогда

Подставляя это значение в формулу для определения реакции, будем иметь

Определяя  с помощью интеграла живых сил и подставляя в предыдущую формулу, получим
с помощью интеграла живых сил и подставляя в предыдущую формулу, получим

Отсюда, при  , найдем
, найдем

Эту же задачу можно решить и при помощи уравнений Лагранжа второго рода. Для этого нужно вычислить живую силу и силовую функцию палочки:

после чего можно записать уравнение движения в форме Лагранжа, либо первый интеграл этого уравнения, каким будет интеграл живых сил.
Для определения реакции  заменим связь в точке
заменим связь в точке  силой. Среди возможных перемещений освобожденной системы будет такое, при котором изменяется угол
силой. Среди возможных перемещений освобожденной системы будет такое, при котором изменяется угол  Параметры
Параметры  можно рассматривать как лагранжевы координаты освобожденной системы. В новых параметрах живая сила имеет вид
можно рассматривать как лагранжевы координаты освобожденной системы. В новых параметрах живая сила имеет вид

Вычисляя работу всех сил, действующих на систему, на перемещении, соответствующем изменению угла  имеем
имеем

откуда

Дифференцируя живую силу  по
по 

и принимая во внимание, что в действительном движении  получим соответствующее координате О уравнение Лаграижа для действительного движения
получим соответствующее координате О уравнение Лаграижа для действительного движения

откуда определим N

После подстановки из уравнений движения значений  и соответствующих преобразований получим
и соответствующих преобразований получим

Пример 106. Концы однородного прямого стержня А В и длины  и массы
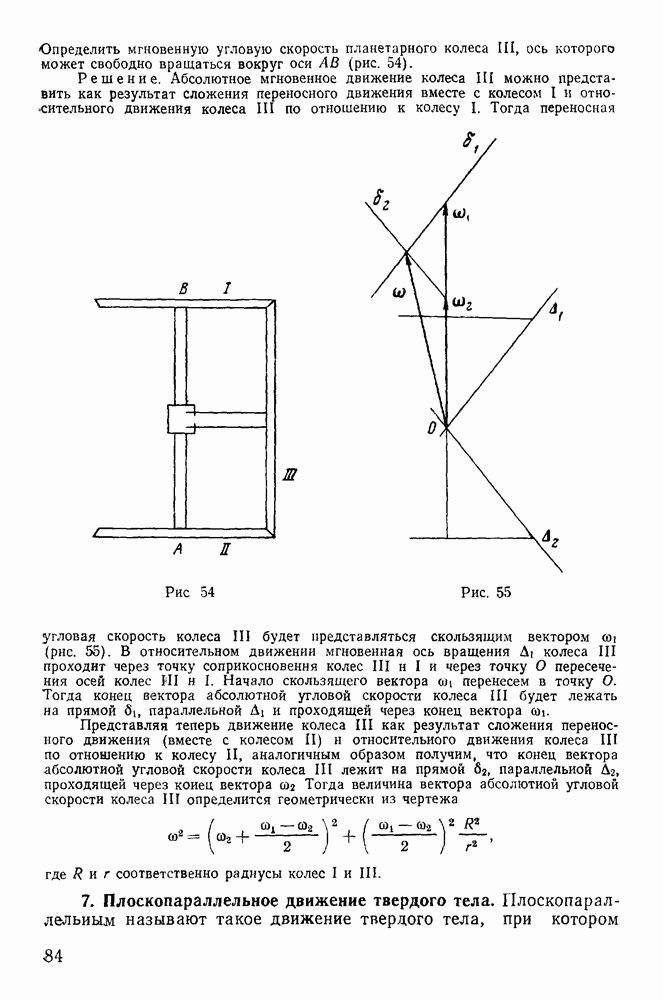
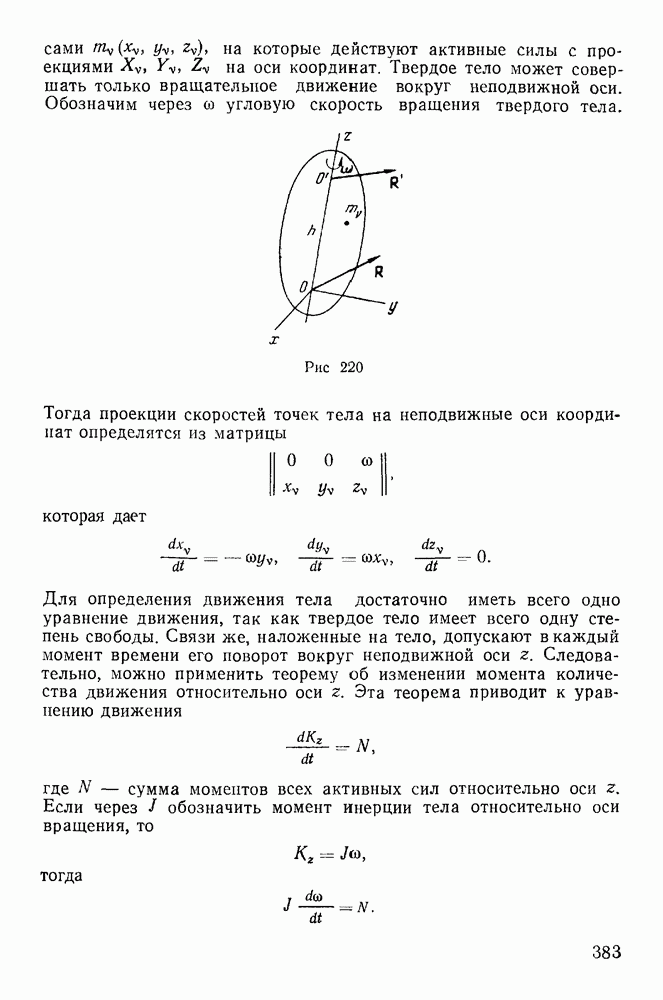
и массы  скользят без треиия по горизонтальному и вертикальному стержням рамки, вращающейся с постоянной угловой скоростью со вокруг вертикальной стороны (рис. 210). Определить вертикальное давление стержня на рамку в точке А.
скользят без треиия по горизонтальному и вертикальному стержням рамки, вращающейся с постоянной угловой скоростью со вокруг вертикальной стороны (рис. 210). Определить вертикальное давление стержня на рамку в точке А.
Принимая за лагранжеву координату угол наклона Ф стержня к горизонтальной стороне рамки, будем иметь

Движение стержня определяется из уравнения Лагранжа

которому отвечает первый интеграл (интеграл Якоби)

Для определения вертикального давления стержня на рамку освободим стержень в точке А от связи и введем силу  дав возможность точке А стержня перемещаться в вертикальном направлении. Обозначим вертикальную координату точки А через х. В действительном движении
дав возможность точке А стержня перемещаться в вертикальном направлении. Обозначим вертикальную координату точки А через х. В действительном движении  . Примем за лагранжевы координаты (при определении реакций) координаты
. Примем за лагранжевы координаты (при определении реакций) координаты  Тогда живая сила системы получит вид
Тогда живая сила системы получит вид

Обобщенная сила, соответствующая координате х

соответствующее уравнение Лагранжа (при  )
)

Определяя  из уравнений движения, будем иметь
из уравнений движения, будем иметь

Замечание. До сих пор при составлении дифференциальных уравнений движения системы материальных точек, мы предполагали, что на систему наложены идеальные связи. Такое предположение сильно сужает круг тех задач, которые могут быть разрешены методами динамики. В частности, связи с трением в ряде случаев являются неидеальными связями, а исключить все такие связи из рассмотрения практически невозможно.
Можно, однако, заметить, что все рассмотренные методы составления дифференциальных уравнений движения без особого труда распространяются и на системы с неидеальными связями. Для этого достаточно доопределить силы, действующие на систему, введя в рассмотрение неизвестные силы реакции связей, совершающие отличную от нуля работу на возможных перемещениях системы. После введения таких сил наложенные на систему связи могут уже рассматриваться как идеальные, и все рассмотренные методы составления дифференциальных уравнений движения будут применимы к такой системе.
Получающиеся таким путем дифференциальные уравнения движения в общем случае будут содержать лишние неизвестные, исключить которые не всегда просто. На помощь приходится привлекать экспериментальные факты, вносящие некоторую определенность в постановку задачи. Одним из таких экспериментальных фактов является, в частности, известный закон Кулона, устанавливающий зависимость касательных составляющих сил реакции связей от нормального давления. Составленные таким образом уравнения движения будут представлять собой сложную систему и дальнейшее исследование этой системы обычно проводится путем постепенного освобождения от лишних неизвестных. Исследование часто осложняется тем обстоятельством, что коэффициент трения не является постоянной величиной, а изменяется в зависимости от нагрузки.
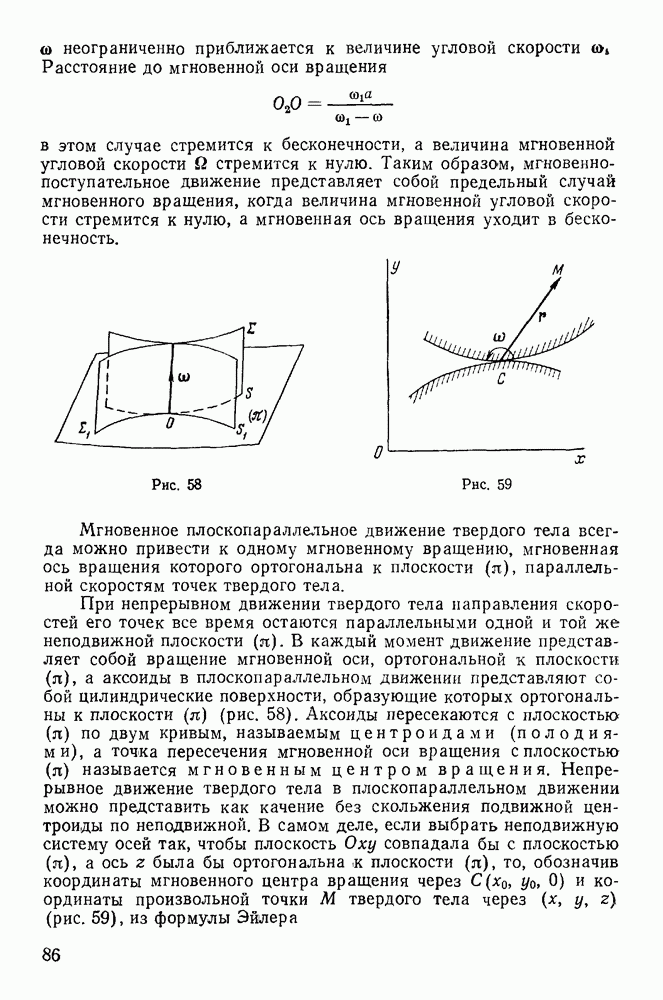
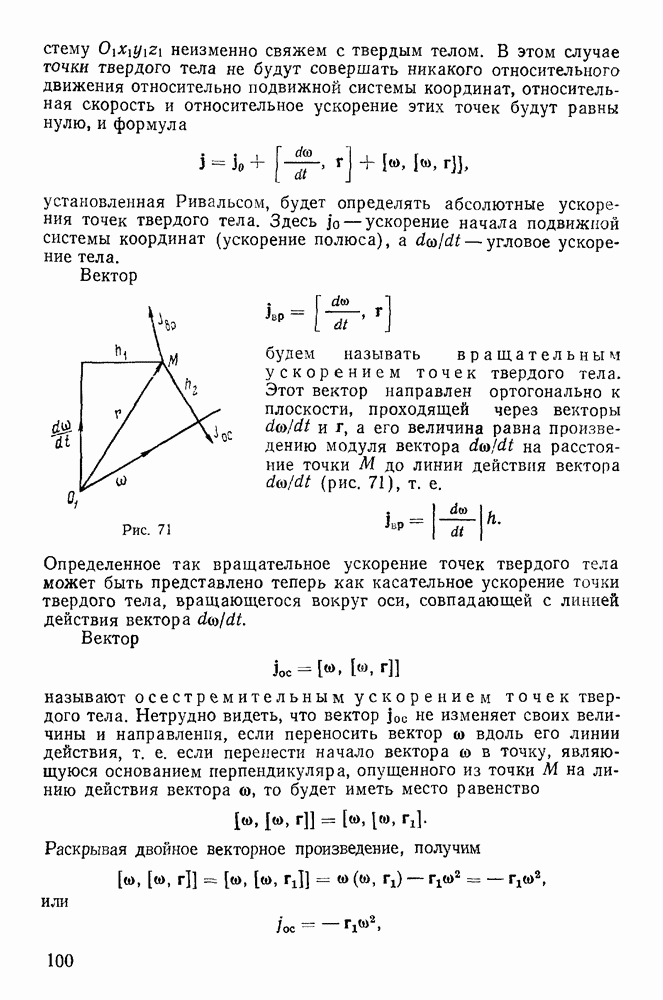
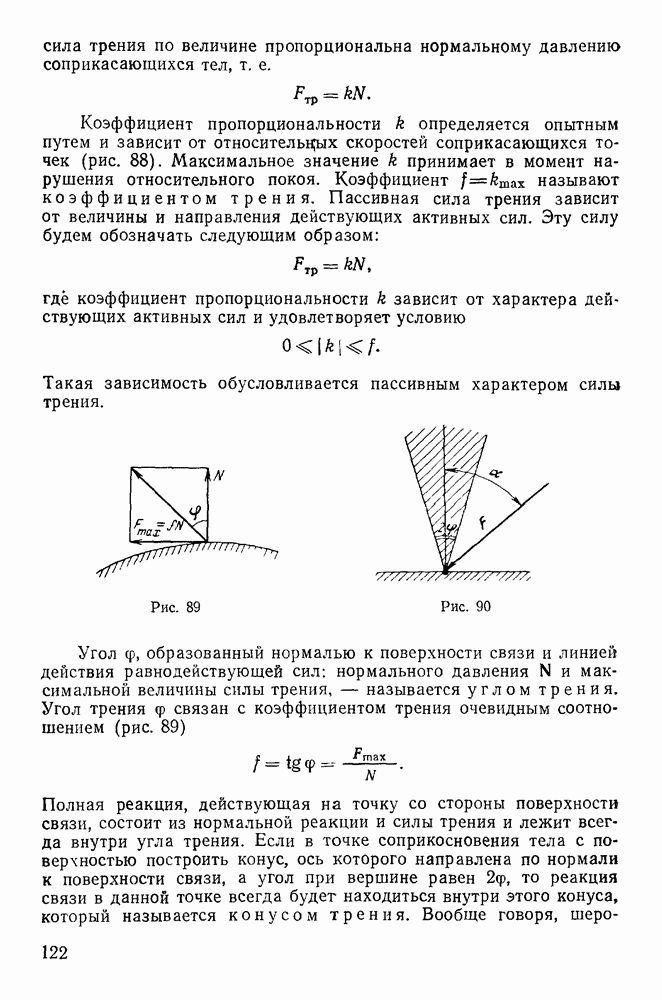
Пример 107. Определить движение однородного круглого диска, находящегося под действием силы тяжести и пущенного в вертикальной плоскости по горизонтальному рельсу  предполагая, что между диском и рельсом существует трение, определяемое законом Кулоиа (рис. 211).
предполагая, что между диском и рельсом существует трение, определяемое законом Кулоиа (рис. 211).
Наложенные на систему связи не являются идеальными и для того, чтобы применить общие теоремы, необходимо ввести в рассмотрение силы, препятствующие поступательному перемещению диска. Введя в рассмотрение неизвестную силу реакции F, направленную вдоль оси х, можно рассматривать рельс как совершенно гладкий. При этом среди возможных перемещений появляется поступательное перемещение диска вдоль оси х, что дает возможность применить теорему о движении центра масс, откуда

Полученное уравнение содержит две неизвестных величины: х и F. Из определения силы F по закону Кулона будем иметь

где  — вертикальная составляющая силы реакции;
— вертикальная составляющая силы реакции;  — коэффициент трения. Из теоремы о движении центра масс вдоль оси у получим, что
— коэффициент трения. Из теоремы о движении центра масс вдоль оси у получим, что 

Рис. 211
Таким образом, движение центра масс вдоль оси х будет определяться уравнением

Если теперь обозначить через  скорость точки обруча, находящейся в соприкосновении с рельсом, то будем иметь
скорость точки обруча, находящейся в соприкосновении с рельсом, то будем иметь

где  — угол поворота диска. Сила трения, определяемая по закону Кулона, направлена в сторону, противоположную направлению скорости и. Поэтому в уравнении движения будем считать, что
— угол поворота диска. Сила трения, определяемая по закону Кулона, направлена в сторону, противоположную направлению скорости и. Поэтому в уравнении движения будем считать, что  если
если  если
если  . Закон изменения угла
. Закон изменения угла  определим из теоремы об изменении момента количества движения
определим из теоремы об изменении момента количества движения

где  — радиус инерции диска относительно его центра масс,
— радиус инерции диска относительно его центра масс,  раднус диска. Подставляя F, будем иметь
раднус диска. Подставляя F, будем иметь

откуда без труда получим

Если в начальный момент выполняется условие

то скорость  убывает пропорционально времени и за конечное время обращается в нуль.
убывает пропорционально времени и за конечное время обращается в нуль.
Если в начальный момент выполняется условие

то  и уменьшается со временем разность
и уменьшается со временем разность  обращаясь в нуль за конечное время.
обращаясь в нуль за конечное время.
По достижении нулевого значения скорости  точки контакта, сила сопротивления F становится равной нулю (благодаря отсутствию проскальзывания) и дальнейшее движение происходит так, что разность
точки контакта, сила сопротивления F становится равной нулю (благодаря отсутствию проскальзывания) и дальнейшее движение происходит так, что разность  остается равной нулю.
остается равной нулю.
В частном случае, когда в начальный момент отрицательна и очень велика, при положительном  абсцисса х сначала возрастает со временем, пока скорость
абсцисса х сначала возрастает со временем, пока скорость  не обратится в нуль, после чего центр тяжести начинает неограниченно удаляться в сторону отрицательных значений х.
не обратится в нуль, после чего центр тяжести начинает неограниченно удаляться в сторону отрицательных значений х.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Введение
- Глава I. ОСНОВЫ ТЕОРИИ ВЕКТОРОВ
- § 1. СВОБОДНЫЕ ВЕКТОРЫ
- 2. Сложение свободных векторов.
- 3. Проекция вектора на ось.
- 4. Инварианты системы свободных векторов.
- § 2. СКОЛЬЗЯЩИЕ ВЕКТОРЫ
- 2. Координаты скользящего вектора.
- 3. Момент скользящего вектора. Плюккеровы координаты.
- 4. Аналитическое определение момента скользящего вектора.
- 5. Проекция момента на ось.
- 6. Момент скользящего вектора относительно оси
- § 3. СИСТЕМА СКОЛЬЗЯЩИХ ВЕКТОРОВ
- 2. Произвольная система скользящих векторов. Элементарные операции.
- 3. Приведение системы скользящих векторов к простейшей эквивалентной форме.
- 4. Плоская система скользящих векторов.
- 5. Свойства системы параллельных скользящих векторов.
- § 4. ЗАКРЕПЛЕННЫЕ ВЕКТОРЫ
- § 5. ДИФФЕРЕНЦИРОВАНИЕ СВОБОДНОГО ВЕКТОРА ПО СКАЛЯРНОМУ АРГУМЕНТУ
- Глава II. КИНЕМАТИКА
- § 1. КИНЕМАТИКА ТОЧКИ
- 2. Ускорение точки. Проекции ускорения на прямоугольные оси координат.
- 3. Скорость и ускорение точки в полярных координатах.
- 4. Движение точки по окружности.
- 5. Проекции ускорения на оси естественного трехгранника.
- 6. Теорема о сложении скоростей в сложном движении точки.
- 7. Метод Роберваля построения касательных к плоским кривым.
- 8. Аналитическое доказательство теоремы о сложении скоростей.
- 9. Сложение скоростей в общем случае сложного движения точки.
- § 2. КИНЕМАТИКА АБСОЛЮТНО ТВЕРДОГО ТЕЛА
- 2. Элементарные движения твердого тела.
- 3. Мгновенные движения твердого тела.
- 4. Сложение мгновенно-поступательных и мгновенно-вращательных движений твердого тела.
- 5. Общий случай сложения мгновенно-поступательных и мгновенно-вращательных движений твердого тела. Непрерывное движение твердого тела.
- 6. Мгновенное движение твердого тела с одной неподвижной точкой.
- 7. Плоскопараллельное движение твердого тела.
- § 3. УСКОРЕНИЕ ТОЧКИ В СЛОЖНОМ ДВИЖЕНИИ
- 2. Замечание о дифференцировании единичного вектора.
- 3. Векторный вывод теоремы Кориолиса.
- 4. Теорема Ривальса.
- § 4. РАСПРЕДЕЛЕНИЕ УСКОРЕНИЙ В ПЛОСКОПАРАЛЛЕЛЬНОМ ДВИЖЕНИИ ТВЕРДОГО ТЕЛА
- 2. Мгновенный центр ускорений.
- § 5. КИНЕМАТИЧЕСКИЕ УРАВНЕНИЯ ЭЙЛЕРА
- Глава III. СТАТИКА
- I. ГЕОМЕТРИЧЕСКАЯ СТАТИКА
- § 1. АКСИОМЫ СТАТИКИ
- § 2. ПОНЯТИЕ О СИЛЕ ТРЕНИЯ
- § 3. РАЗЛИЧНЫЕ ЗАДАЧИ СТАТИКИ
- 2. Равновесие трех сил.
- § 4. МОМЕНТ СИЛЫ
- 2. Момент силы относительно оси.
- 3. Теорема Вариньона для системы сходящихся сил.
- § 5. ПРОИЗВОЛЬНАЯ СИСТЕМА СИЛ, ДЕЙСТВУЮЩИХ НА ТВЕРДОЕ ТЕЛО
- § 6. УСЛОВИЯ РАВНОВЕСИЯ СИСТЕМЫ СИЛ, ДЕЙСТВУЮЩИХ НА ТВЕРДОЕ ТЕЛО
- § 7. ПРИВЕДЕНИЕ СИСТЕМЫ СИЛ, ДЕЙСТВУЮЩИХ НА ТВЕРДОЕ ТЕЛО, К ДИНАМЕ. УРАВНЕНИЯ РАВНОВЕСИЯ ТВЕРДОГО ТЕЛА
- § 8. УСЛОВИЯ РАВНОВЕСИЯ СИСТЕМЫ ТВЕРДЫХ ТЕЛ
- § 9. ПЛОСКАЯ СИСТЕМА СИЛ
- § 10. ЗАДАЧА О РАВНОВЕСИИ НЕСВОБОДНОГО ТВЕРДОГО ТЕЛА
- 2. Частные случаи равновесия твердого тела.
- § 11. ЗАДАЧА О РАВНОВЕСИИ ПРИ НАЛИЧИИ ТРЕНИЯ
- § 12. СИЛА ТЯЖЕСТИ И ЦЕНТР ТЯЖЕСТИ
- II. АНАЛИТИЧЕСКАЯ СТАТИКА
- § 1. РАБОТА СИЛЫ НА ПЕРЕМЕЩЕНИИ. СИЛОВАЯ ФУНКЦИЯ
- § 2. ПРИНЦИП ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ
- 2. Теорема Лагранжа о равновесии системы.
- 3. Принцип Торричелли.
- § 3. ОБЩИЕ ВОПРОСЫ АНАЛИТИЧЕСКОЙ СТАТИКИ
- 3. Общие теоремы о равновесии системы материальных точек.
- 4. Метод неопределенных множителей Лагранжа.
- 5. Определение реакций.
- § 4. ОПРЕДЕЛЕНИЕ РЕАКЦИЙ В ОБЩЕМ СЛУЧАЕ
- § 5. РАВНОВЕСИЕ НИТИ
- 2. Естественные уравнения равновесия нити.
- Глава IV. ДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ
- § 1. ОСНОВНЫЕ ЗАКОНЫ ДИНАМИКИ
- § 2. ДВЕ ОСНОВНЫЕ ЗАДАЧИ ДИНАМИКИ. УРАВНЕНИЯ ДВИЖЕНИЯ ТОЧКИ В ДЕКАРТОВЫХ ОСЯХ
- § 3. ЕСТЕСТВЕННЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ
- § 4. ОСНОВНЫЕ ТЕОРЕМЫ ДИНАМИКИ ДЛЯ СВОБОДНОЙ МАТЕРИАЛЬНОЙ ТОЧКИ
- 2. Теорема об изменении момента количества движения.
- 3. Следствия из теорем об изменении количества движения и момента количества движения материальной точки.
- 4. Теорема живых сил.
- 5. Интеграл живых сил.
- 6. Устойчивость равновесия. Теорема Лагранжа.
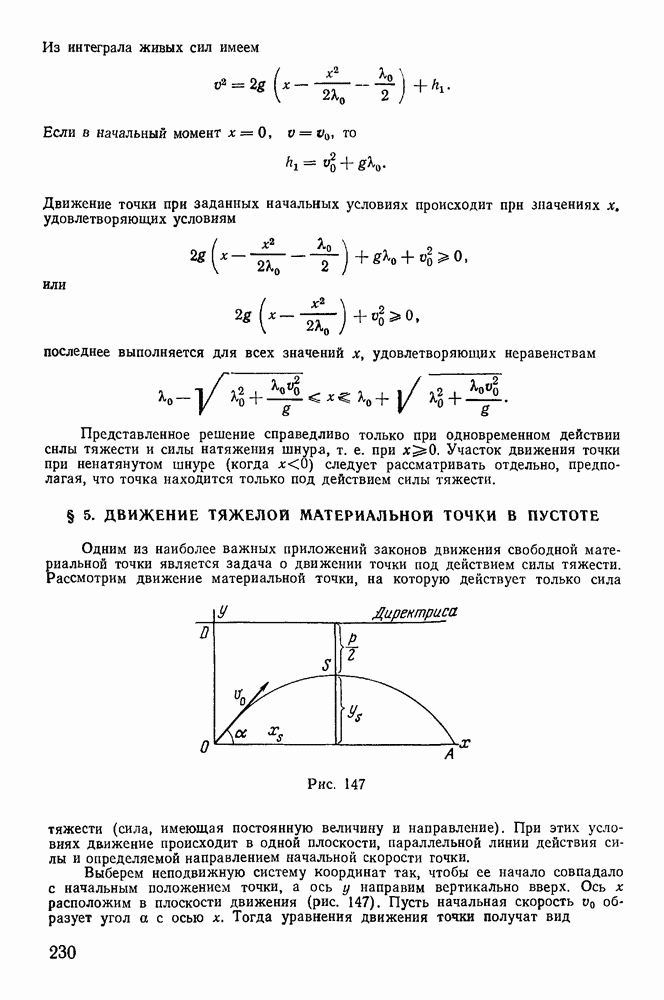
- § 5. ДВИЖЕНИЕ ТЯЖЕЛОЙ МАТЕРИАЛЬНОЙ ТОЧКИ В ПУСТОТЕ
- § 6. ДВИЖЕНИЕ МАТЕРИАЛЬНОЙ ТОЧКИ ПОД ДЕЙСТВИЕМ ЦЕНТРАЛЬНЫХ СИЛ
- 2. Формулы Бине
- 3. Задача о движении планет
- § 7. ДВИЖЕНИЕ ТОЧКИ В СОПРОТИВЛЯЮЩЕЙСЯ СРЕДЕ
- § 8. ДВИЖЕНИЕ НЕСВОБОДНОЙ МАТЕРИАЛЬНОЙ ТОЧКИ
- 2. Движение материальной точки по поверхности.
- § 9. ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЕ МАТЕРИАЛЬНОЙ ТОЧКИ
- 1. Теорема живых сил в относительном движении точки.
- 2. Уравнения относительного равновесия точки.
- 3. Равновесие материальной точки на поверхности Земли. Вес.
- 4. Задача о падении тяжелой точки в пустоте.
- 5. Маятник Фуко.
- § 10. ПРИНЦИП ДАЛАМБЕРА
- Глава V. ДИНАМИКА СИСТЕМЫ МАТЕРИАЛЬНЫХ ТОЧЕК
- § 1. УЧЕНИЕ О СВЯЗЯХ
- § 2. ПРИНЦИП ДАЛАМБЕРА — ЛАГРАНЖА
- § 3. ОСНОВНЫЕ ТЕОРЕМЫ ДИНАМИКИ СИСТЕМЫ
- 2. Теорема об изменении момента количества движения.
- 3. Теорема живых сил.
- § 4. ТЕОРЕМЫ О ДВИЖЕНИИ СИСТЕМЫ ОТНОСИТЕЛЬНО ОСЕЙ НЕИЗМЕННОГО НАПРАВЛЕНИЯ, ПРОХОДЯЩИХ ЧЕРЕЗ ЦЕНТР МАСС СИСТЕМЫ (ОСЕЙ КЕНИГА)
- 2. Теорема об изменении момента количества движения системы относительно осей Кёнига.
- 3. Теорема живых сил в движении системы относительно осей Кёнига.
- § 5. УРАВНЕНИЯ ЛАГРАНЖА ВТОРОГО РОДА
- 2. Случай существования силовой функции.
- 3. Замечание о лагранжевых координатах.
- § 6. ЭЛЕМЕНТАРНЫЕ СЛУЧАИ ИНТЕГРИРУЕМОСТИ УРАВНЕНИЙ ЛАГРАНЖА
- 2. Метод Рауса игнорирования циклических координат.
- 3. Обобщение теоремы и интеграла живых сил.
- § 7. ОПРЕДЕЛЕНИЕ РЕАКЦИЙ
- Глава VI. ДИНАМИКА ТВЕРДОГО ТЕЛА
- § 1. ТЕОРИЯ МОМЕНТОВ ИНЕРЦИИ
- 2. Момент инерции системы относительно произвольной оси, проходящей через заданную точку.
- 3. Эллипсоид инерции.
- 4. Определение главных осей инерции для произвольной точки.
- § 2. ВРАЩЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ОСИ
- § 3. ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА, ИМЕЮЩЕГО ОДНУ НЕПОДВИЖНУЮ ТОЧКУ
- 2. Уравнения движения твердого тела с одной неподвижной точкой.
- § 4. ДВИЖЕНИЕ ТЯЖЕЛОГО ТВЕРДОГО ТЕЛА ОКОЛО НЕПОДВИЖНОЙ ТОЧКИ
- 2. Интегрирование уравнений движения тяжелого твердого тела.
- 3. Случай Эйлера — Пуансо.
- Регулярная прецессия твердого тела в случае Эйлера.
- Геометрическая интерпретация Пуансо движения твердого тела в случае Эйлера.
- Устойчивость постоянных вращений твердого тела.
- 4. Случай Лагранжа.
- Особенные случаи движения твердого тела. Спящий волчок.
- Гироскоп. Приближенная теория.
- Некоторые применения гироскопов.
- Регулярная прецессия в случае Лагранжа.
- Вынужденная регулярная прецессия.
- 5. Случай Ковалевской.
- § 5. ОПРЕДЕЛЕНИЕ РЕАКЦИИ В СЛУЧАЕ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА С ОДНОЙ НЕПОДВИЖНОЙ ТОЧКОЙ
- § 6. УРАВНЕНИЯ ДВИЖЕНИЯ СВОБОДНОГО ТВЕРДОГО ТЕЛА
- § 7. ГИРОСТАТЫ
- Глава VII. АНАЛИТИЧЕСКАЯ ДИНАМИКА
- § 1. КАНОНИЧЕСКИЕ УРАВНЕНИЯ ГАМИЛЬТОНА
- 1. Преобразования Лежандра.
- 2. Канонические уравнения Гамильтона.
- 3. Функция Гамильтона и ее свойства.
- § 2. ПРИНЦИП ГАМИЛЬТОНА — ОСТРОГРАДСКОГО
- 2. Вывод канонических уравнений Гамильтона из принципа Гамильтона — Остроградского.
- 3. Принцип Гамильтона в форме Пуанкаре.
- § 3. ИНТЕГРИРОВАНИЕ КАНОНИЧЕСКИХ УРАВНЕНИЙ ГАМИЛЬТОНА
- 2. Канонические преобразования.
- 3. Бесконечно малые канонические преобразования.
- 4. Теорема Лиувилля.
- 5. Теорема Якоби.
- 6. Интегрирование уравнения Гамильтона—Якоби.
- Метод Имшенецкого разделения переменных.
- 7. Скобки Пуассона.
- § 4. ВАРИАЦИОННЫЕ ПРИНЦИПЫ МЕХАНИКИ
- 2. Принцип Лагранжа.
- 3. Принцип наименьшего действия в форме Якоби.
- Вывод уравнений Лагранжа второго рода из принципа Якоби.
- Сравнение принципа Якоби с принципом Гамильтона.
- 4. Оптико-механическая аналогия.
- 5. Интегральные инварианты.
- Линейные интегральные инварианты.
- Интегральный инвариант Пуанкаре — Картана.
- 6. Принцип наименьшего принуждения Гаусса. Уравнения Аппеля.
- 7. Уравнения Рауса.
- § 5. МАЛЫЕ КОЛЕБАНИЯ
- Затухающие колебания.
- Вынужденные колебания. Резонанс.
- Параметрический резонанс.
- Нелинейные колебания.
- Диссипативные системы.
- 2. Общий случай малых колебаний системы около положения устойчивого равновесия.
- Устойчивость равновесия. Теорема Лагранжа об устойчивости равновесия.
- Замечание об устойчивости стационарных движений.
- Малые колебания системы около положения устойчивого равновесия.
- Влияние диссипативных сил на малые колебания системы около устойчивого положения равновесия.
- § 6. УСТОЙЧИВОСТЬ ДВИЖЕНИЯ
- Прямой метод Ляпунова
- Теорема об асимптотической устойчивости.
- Теорема Четаева о неустойчивости движения.
- 2. Влияние новых связей на малые колебания системы около положения равновесия.
- 3. Влияние диссипативных сил на устойчивость равновесия.
- 4. Влияние гироскопических сил на устойчивость равновесия.
- § 7. ЭЛЕМЕНТЫ ТЕОРИИ ВОЗМУЩЕНИЙ
- Устойчивость консервативных систем.
- 2. Метод изменения произвольных постоянных.
- Глава VIII. ТЕОРИЯ УДАРА
- § 2. ТЕОРЕМЫ КАРНО
- § 3. ЗАДАЧА О ЦЕНТРЕ УДАРА
- § 4. ЗАДАЧА О БАЛЛИСТИЧЕСКОМ МАЯТНИКЕ
- § 5. УРАВНЕНИЯ ЛАГРАНЖА ДЛЯ УДАРА
- § 6. ЗАДАЧА ОБ УДАРЕ ПО ТВЕРДОМУ ТЕЛУ С ОДНОЙ НЕПОДВИЖНОЙ ТОЧКОЙ
- Глава IX. ЭЛЕМЕНТЫ СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- § 2. СПЕЦИАЛЬНЫЙ ПРИНЦИП ОТНОСИТЕЛЬНОСТИ ЭЙНШТЕЙНА
- § 3. ГРУППА ПРЕОБРАЗОВАНИЙ ЛОРЕНЦА
- § 4. ИНВАРИАНТНЫЕ ВЕЛИЧИНЫ В ТЕОРИИ ОТНОСИТЕЛЬНОСТИ. ЧЕТЫРЕХМЕРНЫЙ ВЕКТОР. МИР МИНКОВСКОГО
- § 5. РЕЛЯТИВИСТСКАЯ ДИНАМИКА
- Литература