Глава IX. ЭЛЕМЕНТЫ СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ

§ 1. ПОСТАНОВКА ЗАДАЧИ

В основе классической механики лежит уравнение Ньютона

где F — сила, действующая на частицу, являющаяся функцией времени, положения и скорости движения частицы, а длина и время измеряются в некоторой неподвижной системе отсчета.

Вопрос о выборе неподвижной системы отсчета возник в глубокой древности. Он обсуждался еще Аристотелем. Коперник (1473—1543) уже вводит понятие «преимущественной» системы отсчета, связанной с Солнцем и звездами. Наконец, Г. Галилей вводит понятие инерциальной системы координат и утверждает, что никакие механические опыты и наблюдения, производимые внутри этой инерциальной системы отсчета, не дают возможности решить вопрос о том, имеет ли система в целом прямолинейное равномерное движение или же она находится в покое. В этом утверждении заключается принцип относительности Галилея.

Принцип относительности Галилея связан с понятием закона инерции, согласно которому тела, не взаимодействующие с другими телами, продолжают оставаться в состоянии покоя или равномерного и прямолинейного движения До тех пор пока система координат не выбрана, закон инерции в том виде, в каком он здесь сформулирован, не имеет смысла. Для любого тела можно выбрать такую систему отсчета, относительно которой это тело, не испытывающее влияния других тел, движется неускоренно. Это инерциальная система отсчета. С физической точки зрения инерциальные системы отсчета существуют только приближенно. Так, для земных условий инерциальной может считаться система, образованная осями, проведенными из центра Земли и ориентированными по звездам.

Переход от одной системы к другой, движущейся относительно первой, определяется формулами преобразования. Если одна система движется относительно другой поступательно, прямолинейно и с постоянной скоростью, то, предполагая, что в начальный момент оси обеих систем параллельны и совпадают, будем иметь:

где — компоненты скорости системы относительно системы Это преобразование называют преобразованием Галилея. Предполагается, что время не зависит от выбора системы отсчета, так что (универсальное время), а а также, что расстояния между любыми двумя точками в данный момент времени не зависят от того, в какой системе они измеряются (что непосредственно следует из формул преобразования Галилея). Обозначая через координаты точки А, а через — координаты точки В, будем иметь

где x, у, z — координаты точек в подвижной системе.

По отношению к некоторой определенной инерциальной системе можно указать множество других инерциальных систем, получающихся одна из другой с помощью преобразования Галилея.

Уравнение Ньютона связано с предположением о существовании инерциальной системы отсчета, в которой на точку действуют только реальные силы. Неинерциальность системы можно объяснить наличием кориолисовых сил инерции, которые устраняются соответствующим выбором системы отсчета. Таким образом, если не выполняется закон инерции, то это может объясняться или выбором системы отсчета (неинерциальная система), или существованием некоторых реальных сил, природа которых пока не известна.

Записанное в некоторой инерциальной системе уравнение Ньютона остается инвариантным относительно любой другой инерциальной системы.

В XIX в начинает развиваться новая отрасль физики — электродинамика Максвелл (1831—1879) сформулировал законы электромагнетизма. Характер максвелловской теории электромагнетизма существенно отличается от механики Ньютона, и возникает вопрос о применимости принципа относительности Галилея к электродинамике.

Максвелл установил, что электромагнитные волны распространяются со скоростью, зависящей от свойств среды, заполняющей пространство, а в пустоте — с постоянной скоростью с.

Кроме того, было установлено, что свет является одним из видов электромагнитного излучения. Господствовавшая до

Максвелла теория Френеля (1788—1827) предполагала, что свет распространяется посредством колебаний упругого эфира. Теория Максвелла не требует наличия такой среды. Но уравнения Максвелла не удовлетворяют принципу относительности Галилея. Будучи справедливыми в одной какой-либо инерциальной системе, они перестают быть верными в другой инерциальной системе. Для разрешения этого противоречия нидерландским физиком Лоренцом (1853—1928) вновь вводится гипотеза эфира. Под эфиром понимается такая абстрактная среда, в которой всегда справедливы уравнения электродинамики Максвелла, и скорость света постоянна относительно неподвижного эфира. Для наблюдателя движущегося относительно неподвижного эфира, световые явления должны протекать иначе, чем для неподвижного наблюдателя.

Для экспериментальной проверки теории эфира делались попытки определить скорость движения Земли относительно эфира. Эксперимент такого рода был поставлен Майкельсоном и Морли в 1880 г. Идея эксперимента состояла в сравнении наблюдаемых скоростей света в двух различных направлениях. Предположения сводились к тому, что Земля не может служить привилегированной системой отсчета, так как она движется относительно Солнца со скоростью около Если даже в некоторый момент времени движение Земли совпадает с движением эфира (эфирным ветром), то через полгода скорость Земли относительно эфира будет равна около Движение это можно обнаружить, если измерить скорость света в двух перпендикулярных направлениях с относительной точностью, превышающей отношение (где v — скорость Земли, — скорость света), и если эксперимент осуществляется в течение периода, превышающего шесть месяцев.

Если обозначить через скорость Земли относительно эфира, то скорость света в направлении, противоположном направлению скорости Земли, будет равна а скорость света в противоположном направлении равна Если — путь света от источника до зеркала, то промежуток времени, за который свет пройдет до зеркала и обратно, будет

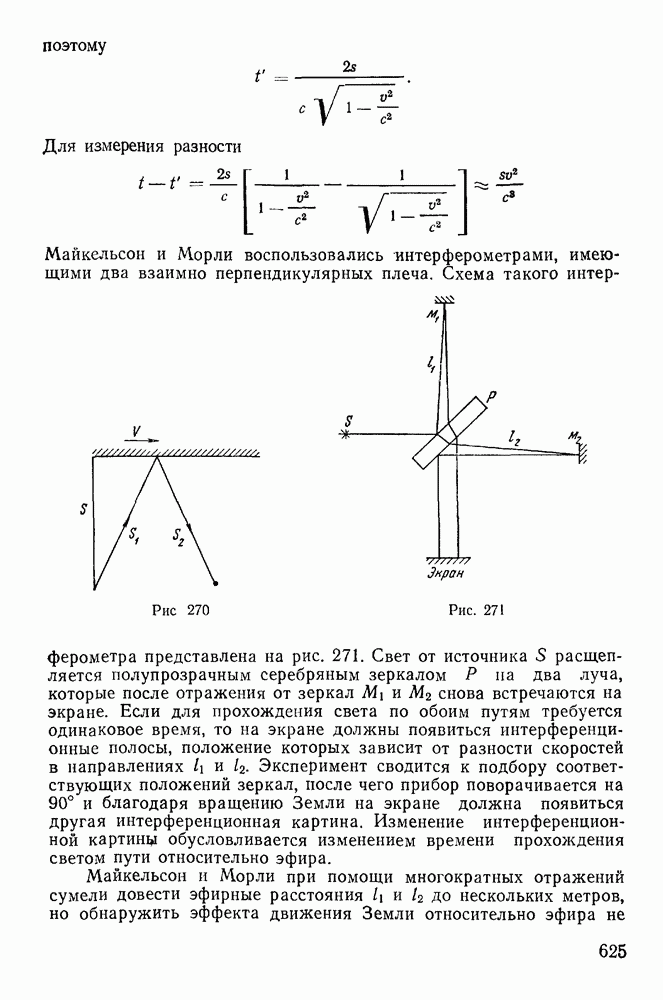
(луч света совпадает с линией вектора скорости Земли). Если скорость Земли ортогональна направлению луча (рис. 270), то за время движения света зеркало будет перемещаться, так что

где

поэтому

Для измерения разности

Майкельсон и Морли воспользовались интерферометрами, имеющими два взаимно перпендикулярных плеча. Схема такого интерферометра представлена на рис. 271.

Рис. 270

Рис. 271

Свет от источника расщепляется полупрозрачным серебряным зеркалом Р на два луча, которые после отражения от зеркал снова встречаются на экране. Если для прохождения света по обоим путям требуется одинаковое время, то на экране должны появиться интерференционные полосы, положение которых зависит от разности скоростей в направлениях Эксперимент сводится к подбору соответствующих положений зеркал, после чего прибор поворачивается на 90° и благодаря вращению Земли на экране должна появиться другая интерференционная картина. Изменение интерференционной картину обусловливается изменением времени прохождения светом пути относительно эфира.

Майкельсон и Морли при помощи многократных отражений сумели довести эфирные расстояния до нескольких метров, но обнаружить эффекта движения Земли относительно эфира не

удалось. Подобные опыты повторялись в течение десятилетий. Они показали, что обнаружить движение Земли относительно эфира невозможно. Предположение о том, что Земля увлекает прилегающий к ней эфир, не выдерживает критики, так как в этом случае видимые положения звезд смещались бы каждый год назад и вперед, но не так, как это наблюдается в действительности. Ирландский физик Фицджеральд (1851 —1901) и Лоренц сделали попытку объяснить полученный Майкельсоном и Морли результат, предположив, что длины всех физических тел, движущихся со скоростью относительно эфира, сокращаются в отношении Тогда при повороте интерферометра на 90° длина плеча его меняется так, что компенсируется ожидаемый эффект. Эта гипотеза, высказанная Лоренцом в 1892 г., сохраняет привилегированный характер определенной системы отсчета (эфира) и объясняет отрицательный результат опыта Майкельсона. При вычислении времени вместо необходимо взять величину после чего

так что разность обращается в нуль. Эта гипотеза не удовлетворяла и самого ее автора. Поэтому Лоренц поставил задачу найти такую группу преобразований, в которой основные уравнения Максвелла остаются неизменными. Эту задачу разрешил в 1905 г. французский математик и физик Анри Пуанкаре и в том же 1905 г. Альберт Эйнштейн (1879—1955).

Решение Пуанкаре.

Пуанкаре показал, что если первая система движется относительно второй прямолинейно и равномерно в направлении оси х, то для инвариантности уравнения Максвелла относительно выбора системы отсчета формулы преобразования должны иметь следующий вид:

Это преобразование называется преобразованием Лоренца. Для обратного преобразования получим

Уравнения Максвелла выражают закон распространения электромагнитных волн в свободном пространстве. Пусть X, Y, Z - проекции вектора напряженности электрического поля на

координатные оси, — соответствующие проекции вектора напряженности магнитного поля, тогда уравнения Максвелла запишутся в виде

Применяя преобразование Лоренца к первому уравнению первой группы, будем иметь

Подставляя сюда значения получим

откуда

Преобразуя первое уравнение второй группы, получим

или

Нетрудно видеть, что уравнения Максвелла сохраняют свою форму, если

Тогда преобразованные уравнения будут иметь такой же вид, как и первоначальные

Как видно из формул преобразования, векторы напряженности электрического и магнитного полей оказываются не инвариантными величинами. Это обстоятельство не является неожиданным, если вспомнить, что движущийся электрический заряд создает магнитное поле, которое отсутствует в системе отсчета, движущейся вместе с зарядом.

Уравнения Максвелла оказываются инвариантиыми относительно преобразования Лоренца Скорость же света принимается постоянной во всех системах координат.