3. Теорема живых сил.

Рассмотрим механическую систему, состоящую из материальных точек с массами координаты которых обозначим через Предположим, что к этим точкам приложены активные силы и что система стеснена идеальными связями.

В общем случае действительное перемещение системы может не находиться среди возможных перемещений. В самом деле, условия, накладываемые на действительные перемещения системы

не будут вообще совпадать с условиями, накладываемыми на возможные перемещения

если Могут встретиться такие случаи, когда действительное перемещение системы находится среди возможных. Это обстоятельство имеет место всякий раз, когда уравнения связей не зависят явным образом от времени. Если действительное перемещение системы находится среди возможных перемещений, то после подстановки в общее уравнение динамики

соответствующих возможных перемещений

будем иметь

откуда после соответствующих перестановок получим

Разделив и умножив левую часть на перепишем ее в виде

Выражение

называют живой силой или кинетической энергией системы. Предыдущее уравнение теперь приобретает вид

Этот результат можно сформулировать в виде теоремы.

Теорема. Если связи, наложенные на систему материальных точек, таковы, что действительное перемещение находится среди возможных, то дифференциал живой силы системы равен

сумме элементарных работ всех активных сил, действующих на точки системы, на действительном перемещении системы.

Необходимо отметить, что в правую часть полученного уравнения не входят силы реакции связей и рассматривается работа только одних активных сил на действительном перемещении точек системы. В правой части величины являются не произвольными дифференциалами координат, а действительными перемещениями точек системы.

Если активные силы таковы, что можно подобрать функцию

удовлетворяющим условиям

то говорят, что силы, действующие на точки системы, допускают силовую функцию или что силы консервативны. Тогда теорема живых сил получает вид

где — полный дифференциал силовой функции в действительном движении системы. Отсюда, интегрируя, получим

Последнее уравнение является первым интегралом уравнений движения, который называется интегралом живых сил. Величина представляет собой полную механическую энергию системы.

Интеграл живых сил существует, если действительные перемещения системы находятся среди возможных и если активные силы допускают не зависящую от времени силовую функцию.

Рассмотрим несколько примеров на определение живой силы системы и на применение теоремы живых сил.

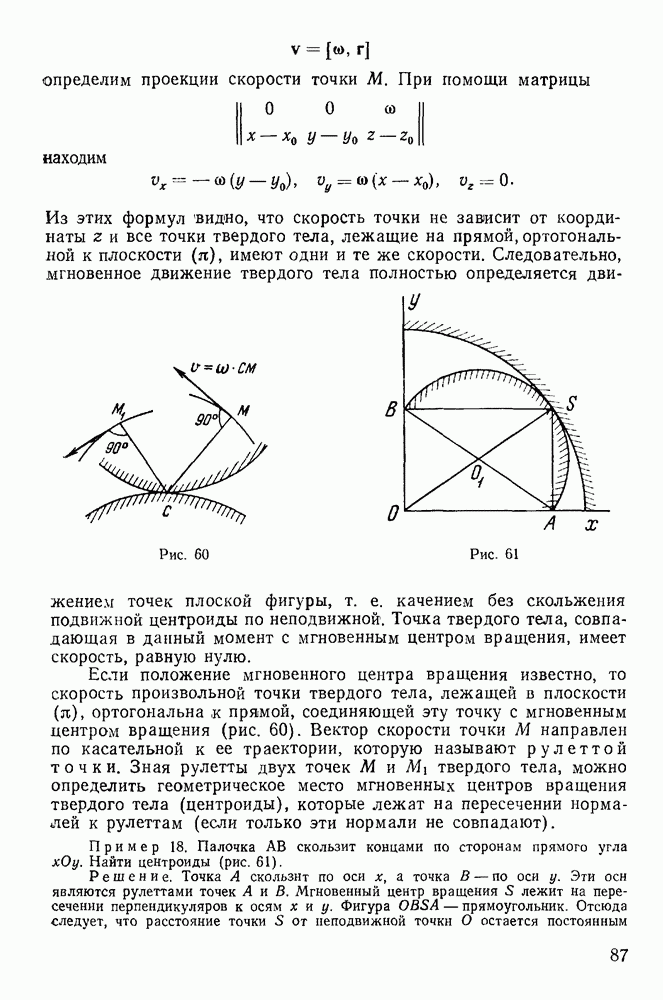
Пример 91. Вычислим живую силу твердого тела, вращающегося около неподвижной оси с угловой скоростью .

Обозначив через массу элементарной частицы твердого тела, а через — ее расстояние от оси вращения (рис. 193), будем иметь

после чего живая сила системы

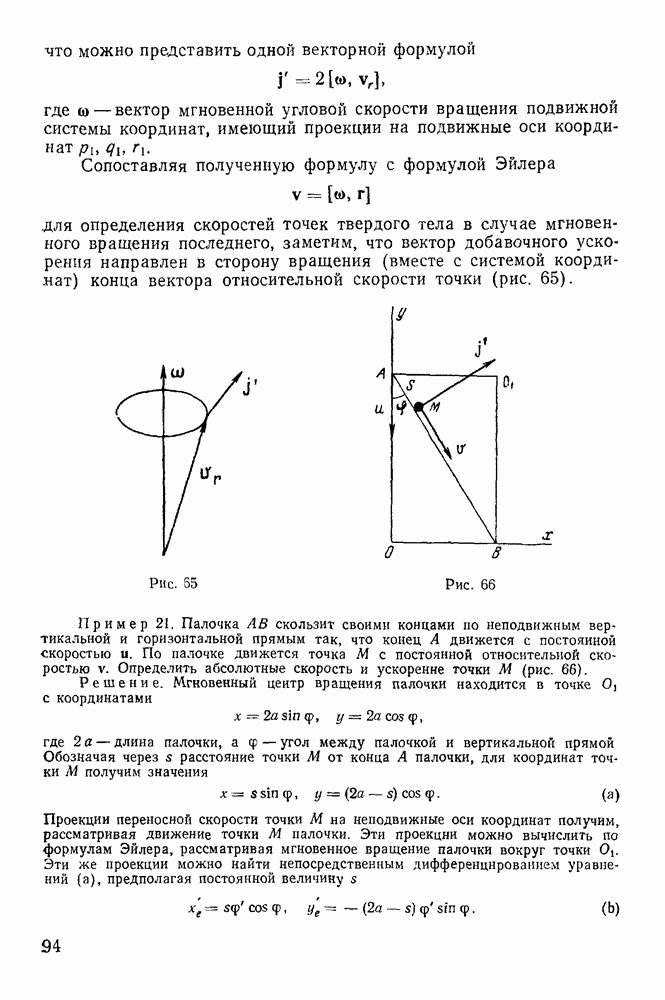
Пример 92. Однородная палочка массы и длины а может свободно вращаться в пространстве вокруг своего неподвижного конца. В начальный

момент ее приводят в горизонтальное положение и сообщают вращение в горизонтальной плоскости с угловой скоростью Найти, какой наименьший угол с вертикалью будет составлять палочка во время движения (рис. 194).

Связи, наложенные на систему, допускают поворот палочки вокруг вертикальной оси. Следовательно, применима теорема об изменении момента количества движения относительно этой оси. Внешними силами, действующими на палочку, являются силы тяжести. Момент этих сил относительно вертикальной оси равен нулю.

Рис. 193

Рис. 194

Рис. 195

Поэтому указанная теорема приводит к интегралу площадей

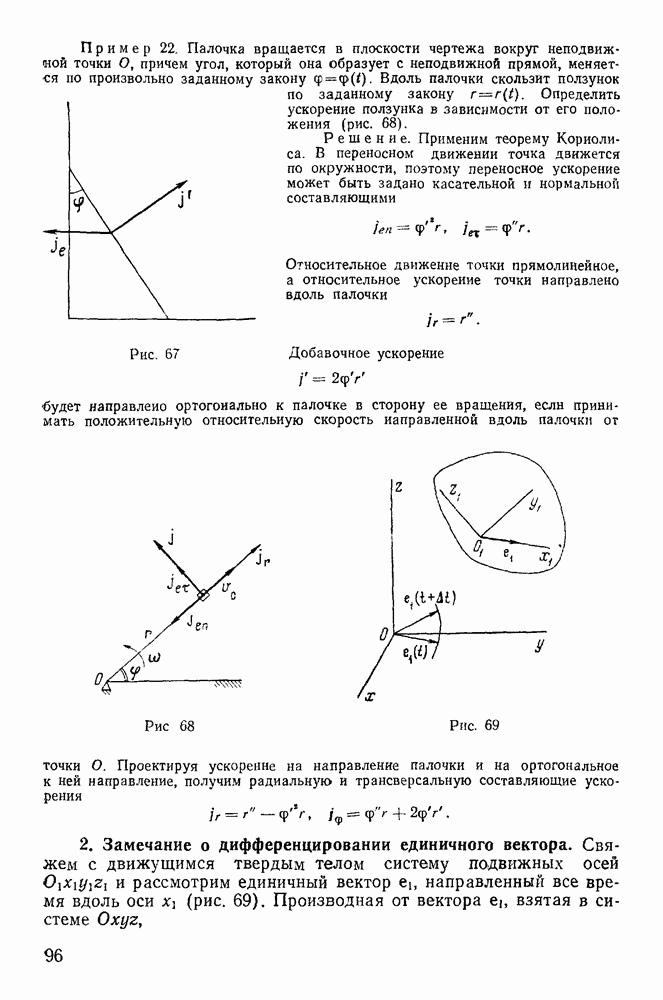
Положение палочки можно определить двумя независимыми параметрами: углом отклонения палочки от вертикальной оси и углом определяющим отклонение вертикальной плоскости в которой находится палочка, от неподвижной вертикальной плоскости, проходящей через ось вращения палочки (рис. 195). Количество движения элементарной частицы отстоящей от начала координат на расстоянии можно представить в виде двух составляющих: лежащей в вертикальной плоскости момент которой относительно вертикальной оси равен нулю, и составляющей которай лежит в горизонтальной плоскости и момент которой относительно вертикальной оси равен Момент количества движения всей палочки относительно вертикальной оси получим, суммируя элементарные моменты количества движения:

Запишем интеграл площадей в виде

или, принимая во внимание начальные условия

и сокращая на получим

Связи, наложенные на систему, не зависят явно от времени, а действующие активные силы консервативны, поэтому существует интеграл живых сил

По условиям задачи необходимо определить угол в тот момент, когда он примет наименьшее значение, т. е. при выполнении условия

В начальный момент палочка совершает мгновенное вращение вокруг вертикальной осн. Живая сила зависит лишь от распределения скоростей в данный момент времени. Поэтому для получим

где

т. е.

В тот момент, когда становится равным нулю, палочка снова совершает мгновенное вращение вокруг вертикальной оси так что

и из интеграла живых сил получаем

Исключая из уравнений (а) и (b) величину и сокращая уравнение на будем иметь

что можно переписать в виде

Отсюда получаем два решения:

причем соответствует начальному положению палочки, а — искомый наименьший угол.

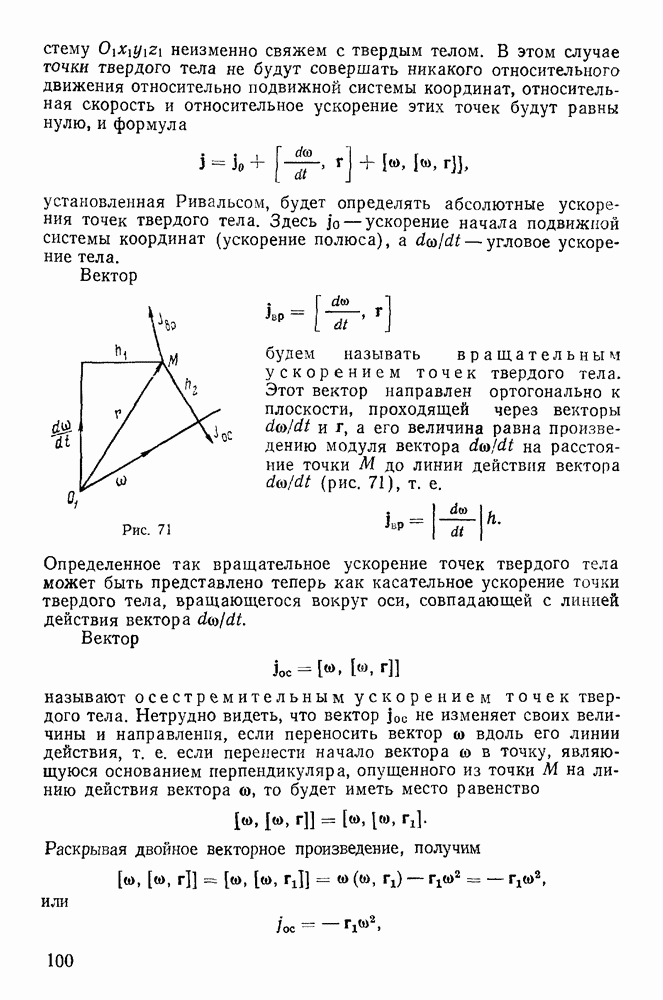
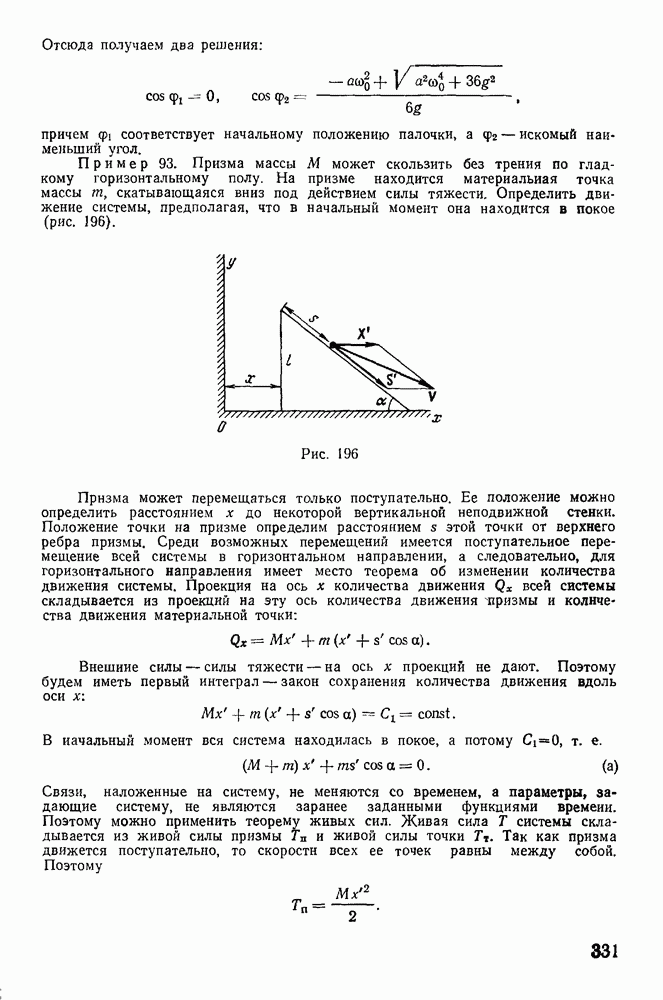
Пример 93. Призма массы М может скользить без трения по гладкому горизонтальному полу. На призме находится материальная точка массы скатывающаяся вниз под действием силы тяжести. Определить движение системы, предполагая, что в начальный момент она находится в покое (рис. 196).

Рис. 196

Призма может перемещаться только поступательно. Ее положение можно определить расстоянием х до некоторой вертикальной неподвижной стенки. Положение точки на призме определим расстоянием этой точки от верхнего ребра призмы. Среди возможных перемещений имеется поступательное перемещение всей системы в горизонтальном направлении, а следовательно, для горизонтального направления имеет место теорема об изменении количества движения системы. Проекция на ось х количества движения Q всей системы складывается из проекций на эту ось количества движения призмы и количества движения материальной точки:

Внешние силы — силы тяжести — на ось х проекций не дают. Поэтому будем иметь первый интеграл — закон сохранения количества движения вдоль оси

В начальный момент вся система находилась в покое, а потому т. е.

Связи, наложенные на систему, не меняются со временем, а параметры, задающие систему, не являются заранее заданными функциями времени. Поэтому можно применить теорему живых сил. Живая сила Т системы складывается из живой силы призмы и живой силы точки Тт. Так как призма движется поступательно, то скорости всех ее точек равны между собой. Поэтому

Живая сила точки равна где — абсолютная скорость точки, равная геометрической сумме ее переносной и относительной скоростей

Тогда

Активными силами, действующими на систему, являются только силы тяжести. Они допускают силовую функцию

где — постоянная ордината центра масс призмы; ордината материальной точки

и тогда

Произвольную постоянную подберем так, чтобы выполнялось условие

Тогда

Поекольку связи не зависят явно от времени, а силы допускают силовую функцию, будем иметь интеграл живых сил

или

В начальный момент система находилась в покое. Если этому состоянию соответствует значение то будем иметь и тогда

Уравнения (а) и полностью определяют движение системы, зависящее от изменения двух параметров х и . В самом деле, комбинируя уравнения (а) и (b), получим

исключая отсюда будем иметь

откуда, интегрируя найдем

Подставляя полученное значение в уравнение (а) и интегрируя, находим

где знак «минус» указывает на то, что координата х во время движения убивает.

Замечания. 1. Если к заданным силам добавить силы реакции связей, то систему можно будет рассматривать как свободную от связей. В этом случае для точек системы возможны любые перемещения и применима любая из рассмотренных выше теорем. Но в правые части формул, выражающих эти теоремы, будут теперь входить реакции связей, которые при составлении уравнений движения рассматриваются как некоторые заданные силы и которые являются неизвестными величинами в уравнениях движения.

2. При изучении динамики системы материальных точек очень большое значение имеет уменье пользоваться теоремами при решении конкретных задач, на основе анализа связей выбирать ту или иную теорему, решающую задачу о движении без введения в рассмотрение сил реакции связей, которые не определяют самого движения, а лишь накладывают ограничения на перемещения системы.