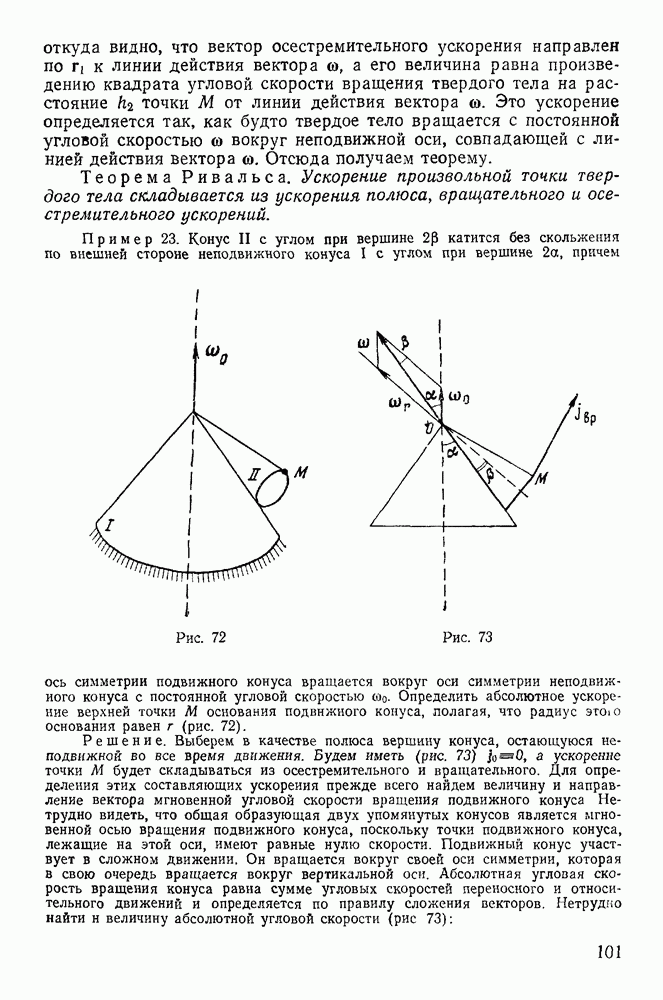
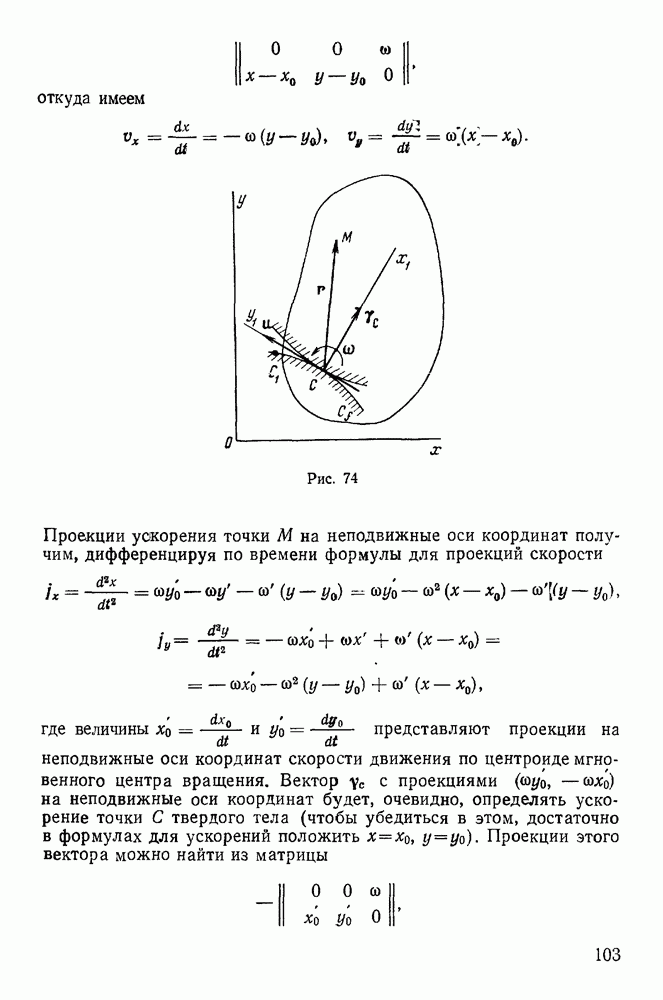
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 2. ВРАЩЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ОСИ
Задача о движении твердого тела вокруг неподвижной оси рассматривалась еще Гюйгенсом при разработке его замечательной теории движения физического маятника.
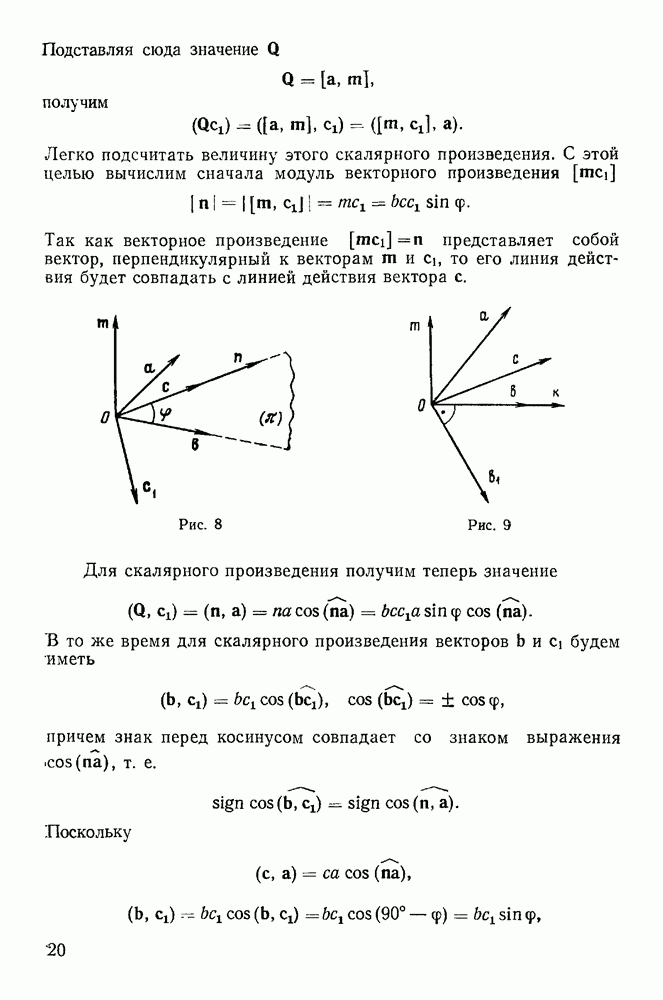
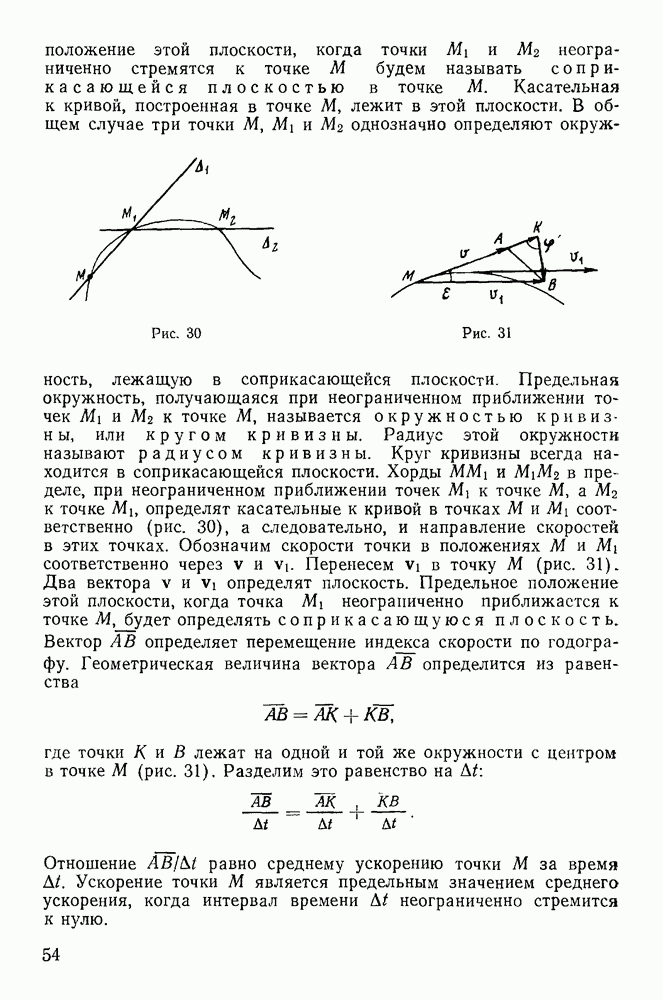
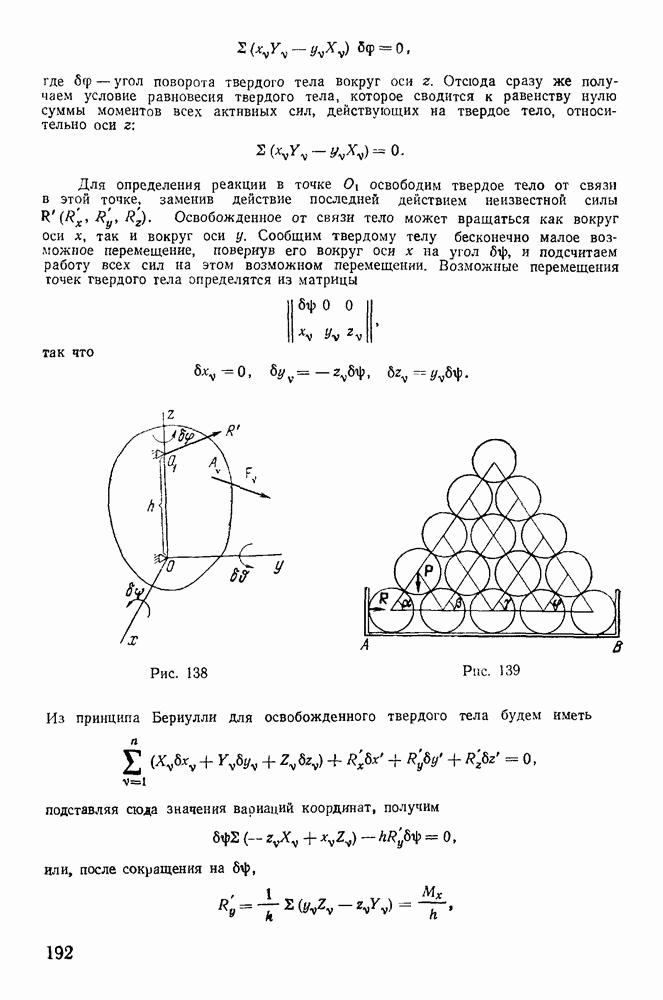
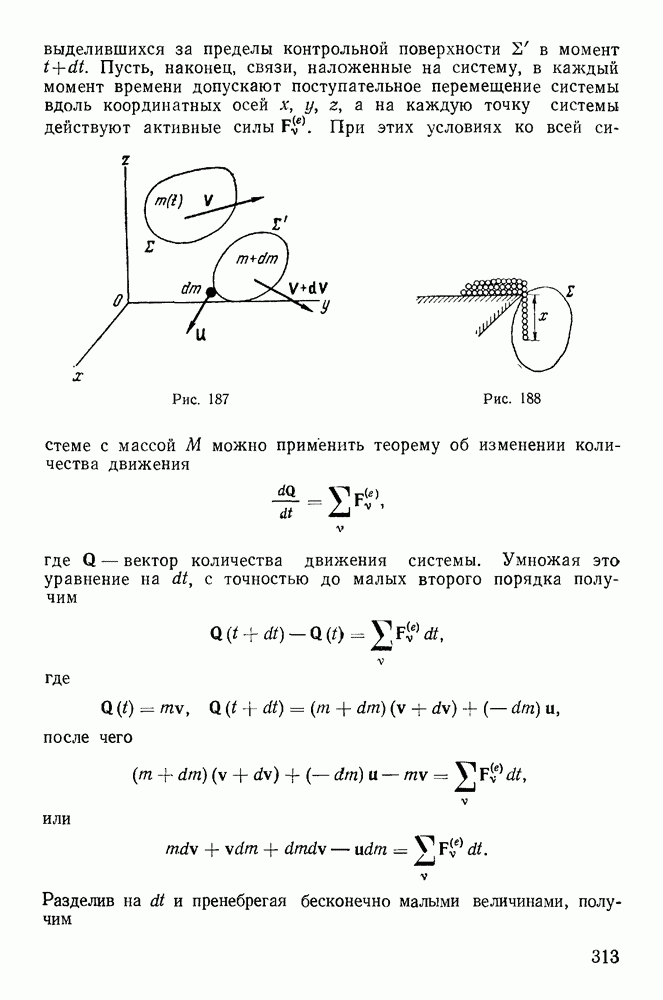
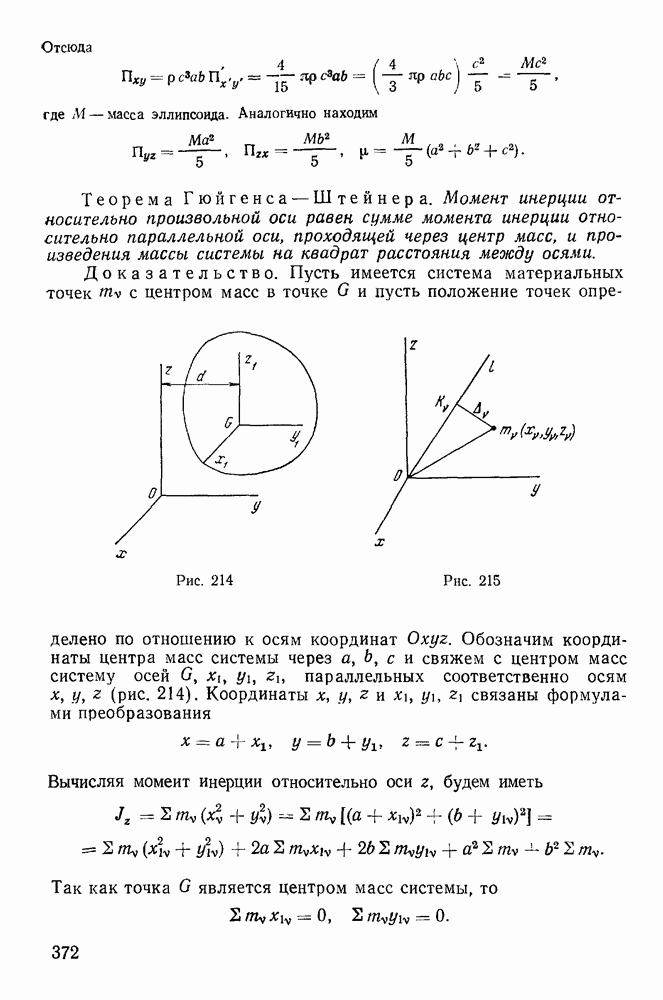
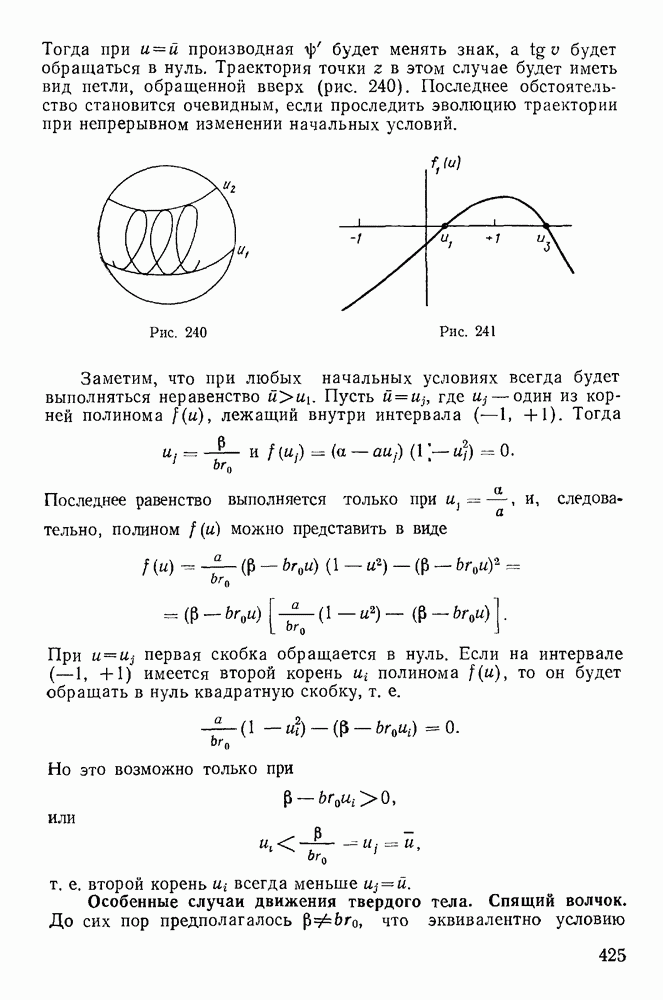
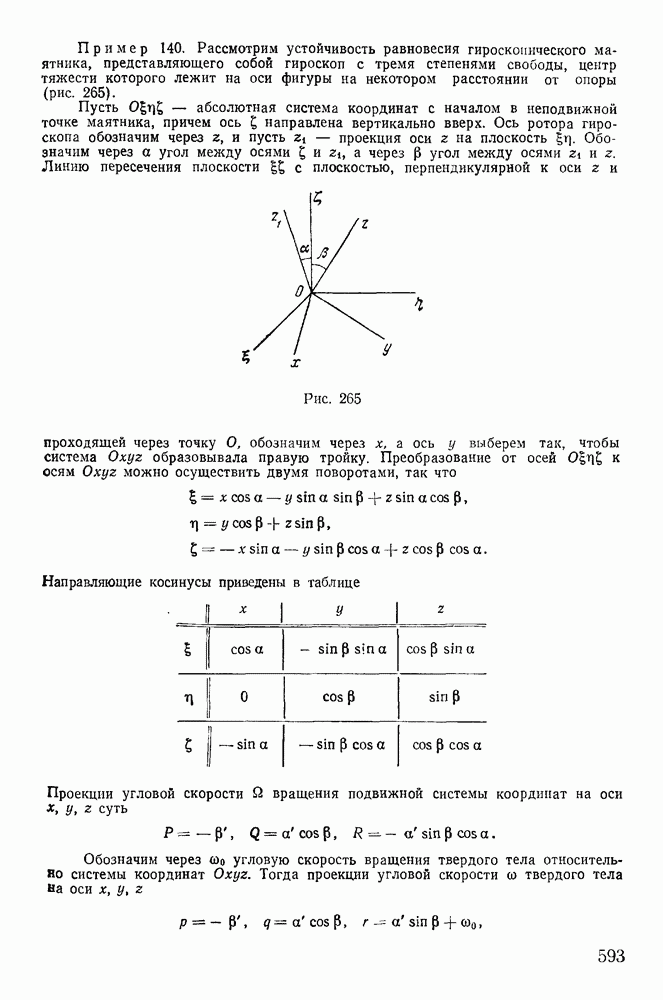
Представим себе абсолютно твердое тело, у которого закреплены две точки О и О (рис. 220). Прямая  являющаяся осью вращения тела, остается неизменной во все время движения тела как по отношению к самому телу, так и по отношению к некоторой неподвижной системе координат
являющаяся осью вращения тела, остается неизменной во все время движения тела как по отношению к самому телу, так и по отношению к некоторой неподвижной системе координат  . Для определенности выберем неподвижную систему координат с началом в точке О, направив ось
. Для определенности выберем неподвижную систему координат с началом в точке О, направив ось  вдоль оси вращения тела. Твердое тело будем рассматривать как совокупность материальных точек с
вдоль оси вращения тела. Твердое тело будем рассматривать как совокупность материальных точек с
массами  на которые действуют активные силы с проекциями
на которые действуют активные силы с проекциями  на оси координат. Твердое тело может совершать только вращательное движение вокруг неподвижной оси. Обозначим через со угловую скорость вращения твердого тела.
на оси координат. Твердое тело может совершать только вращательное движение вокруг неподвижной оси. Обозначим через со угловую скорость вращения твердого тела.

Рис. 220
Тогда проекции скоростей точек тела на неподвижные оси координат определятся из матрицы

которая дает

Для определения движения тела достаточно иметь всего одно уравнение движения, так как твердое тело имеет всего одну степень свободы. Связи же, наложенные на тело, допускают в каждый момент времени его поворот вокруг неподвижной оси  Следовательно, можно применить теорему об изменении момента количества движения относительно оси
Следовательно, можно применить теорему об изменении момента количества движения относительно оси  Эта теорема приводит к уравнению движения
Эта теорема приводит к уравнению движения

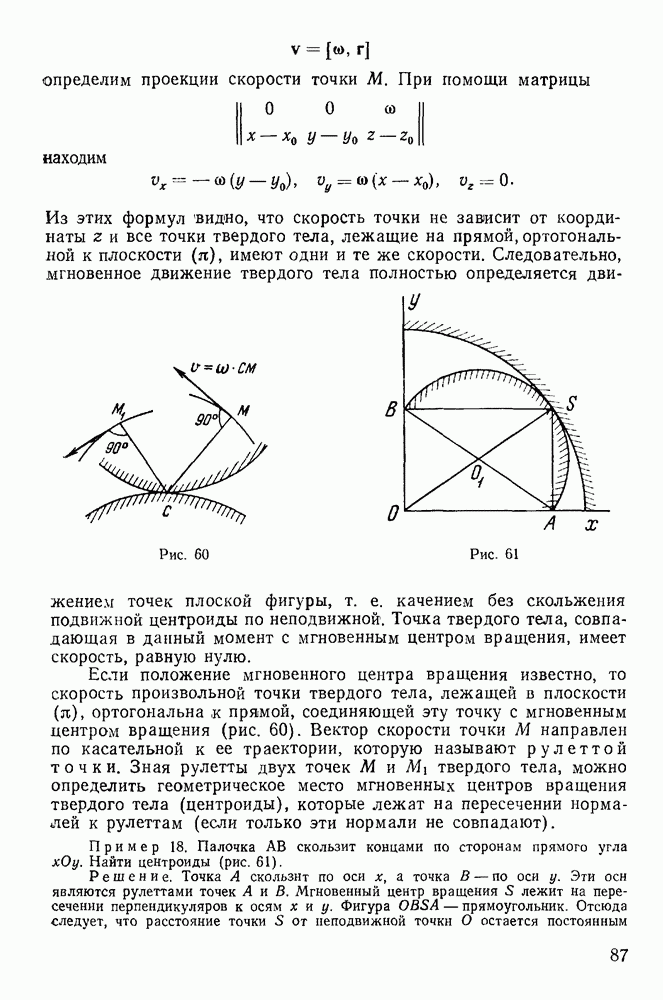
где  — сумма моментов всех активных сил относительно оси z. Если через
— сумма моментов всех активных сил относительно оси z. Если через  обозначить момент инерции тела относительно оси вращения, то
обозначить момент инерции тела относительно оси вращения, то

тогда

В технических задачах часто требуется определять величину опорных реакций. Обозначим через  и
и  силы реакций, приложенные в точках О и О; а через
силы реакций, приложенные в точках О и О; а через  — расстояние между точками О и О. Реакции
— расстояние между точками О и О. Реакции  и
и  будут иметь проекции на оси координат
будут иметь проекции на оси координат  Для определения сил реакций освободим систему (твердое тело) от связей, заменив связи неизвестными силами реакций
Для определения сил реакций освободим систему (твердое тело) от связей, заменив связи неизвестными силами реакций  и
и  действие которых эквивалентно действию связей. После освобождения от связей появятся новые возможные перемещения. В частности, будут возможны поступательные перемещения системы вдоль осей
действие которых эквивалентно действию связей. После освобождения от связей появятся новые возможные перемещения. В частности, будут возможны поступательные перемещения системы вдоль осей  и повороты системы вокруг осей х и у. Это дает возможность применить теорему об изменении количества движения и теорему об изменении момента количества движения, откуда получим следующие уравнения:
и повороты системы вокруг осей х и у. Это дает возможность применить теорему об изменении количества движения и теорему об изменении момента количества движения, откуда получим следующие уравнения:

где  — суммы моментов активных сил относительно осей
— суммы моментов активных сил относительно осей  Для определения шести неизвестных величин
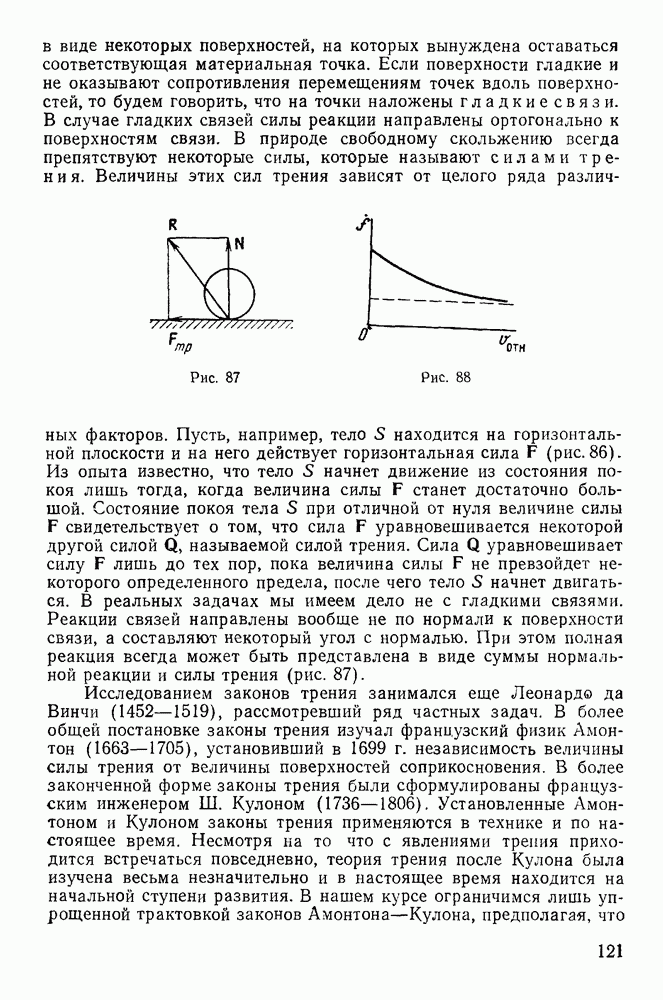
Для определения шести неизвестных величин  имеем пять уравнений. Задача определения реакций остается неразрешенной. В самом деле, реакции Z и Z одновременно препятствуют поступательному перемещению системы вдоль оси z. Именно эти реакции нельзя определить по отдельности, а можно определить только их сумму. В этом заключается неопределимость задачи. Из кинематических уравнений для проекций скорости получим реакции действительных ускорений точек тела:
имеем пять уравнений. Задача определения реакций остается неразрешенной. В самом деле, реакции Z и Z одновременно препятствуют поступательному перемещению системы вдоль оси z. Именно эти реакции нельзя определить по отдельности, а можно определить только их сумму. В этом заключается неопределимость задачи. Из кинематических уравнений для проекций скорости получим реакции действительных ускорений точек тела:

Подставляя эти значения в уравнения движения, будем иметь


Для определения четырех неизвестных X, Y, X, Y имеем четыре уравнения. Левые части этих уравнений являются известными функциями времени, поскольку движение системы, а следовательно, и закон изменения параметров системы, определяется из уравнения движения

Если выполняются условия

т. е. центр масс лежит на оси  являющейся главной центральной осью инерции, то левые части уравнений тождественно равны нулю и тогда реакции определяются, как в статике.
являющейся главной центральной осью инерции, то левые части уравнений тождественно равны нулю и тогда реакции определяются, как в статике.
Если ось  не является главной центральной осью инерции, то при движении твердого тела в левой части первых двух уравнений будут существовать отличные от нуля коэффициенты при
не является главной центральной осью инерции, то при движении твердого тела в левой части первых двух уравнений будут существовать отличные от нуля коэффициенты при  При больших значениях со эти коэффициенты представляют большие величины, следовательно и реакции тоже велики. Чтобы избежать больших реакций, ось вращения направляют по главной оси центрального эллипсоида инерции.
При больших значениях со эти коэффициенты представляют большие величины, следовательно и реакции тоже велики. Чтобы избежать больших реакций, ось вращения направляют по главной оси центрального эллипсоида инерции.
В частном случае, когда на твердое тело действуют активные силы, приводящиеся к равнодействующей, проходящей через точку О, уравнения движения дают

и твердое тело будет вращаться вокруг оси z с постоянной угловой скоростью. Рассмотрим в этом случае условия, при которых реакция в точке О обращается в нуль. Как видно из последних двух уравнений, это имеет место, если

т. е. ось  должна быть главной осью инерции для точки О. При выполнении указанных условий твердое тело будет вращаться вокруг оси
должна быть главной осью инерции для точки О. При выполнении указанных условий твердое тело будет вращаться вокруг оси  с постоянной угловой скоростью, не оказывая давления на вторую закрепленную точку. Такие оси называют постоянными, или перманентными, осями вращения твердого тела.
с постоянной угловой скоростью, не оказывая давления на вторую закрепленную точку. Такие оси называют постоянными, или перманентными, осями вращения твердого тела.
Предположим, что на твердое тело не действуют активные силы. Определим условия, при которых обе опорные реакции равны нулю. Условия эти следуют из уравнений движения и имеют вид

откуда следует, что ось  должна быть главной осью инерции и на ней должен находиться центр тяжести твердого тела. Такая ось является главной осью центрального эллипсоида инерции. Оси, при вращении вокруг которых твердое тело, на которое не действуют внешние силы, не оказывает давления на закрепленные точки этой оси, называются свободными, или естественными, осями. Нетрудно заметить, что три перманентные оси можно всегда найти для каждой точки твердого тела. Такими осями являются главные оси инерции для соответствующих точек твердого тела. Свободных осей у твердого тела только три — главные центральные оси инерции.
должна быть главной осью инерции и на ней должен находиться центр тяжести твердого тела. Такая ось является главной осью центрального эллипсоида инерции. Оси, при вращении вокруг которых твердое тело, на которое не действуют внешние силы, не оказывает давления на закрепленные точки этой оси, называются свободными, или естественными, осями. Нетрудно заметить, что три перманентные оси можно всегда найти для каждой точки твердого тела. Такими осями являются главные оси инерции для соответствующих точек твердого тела. Свободных осей у твердого тела только три — главные центральные оси инерции.
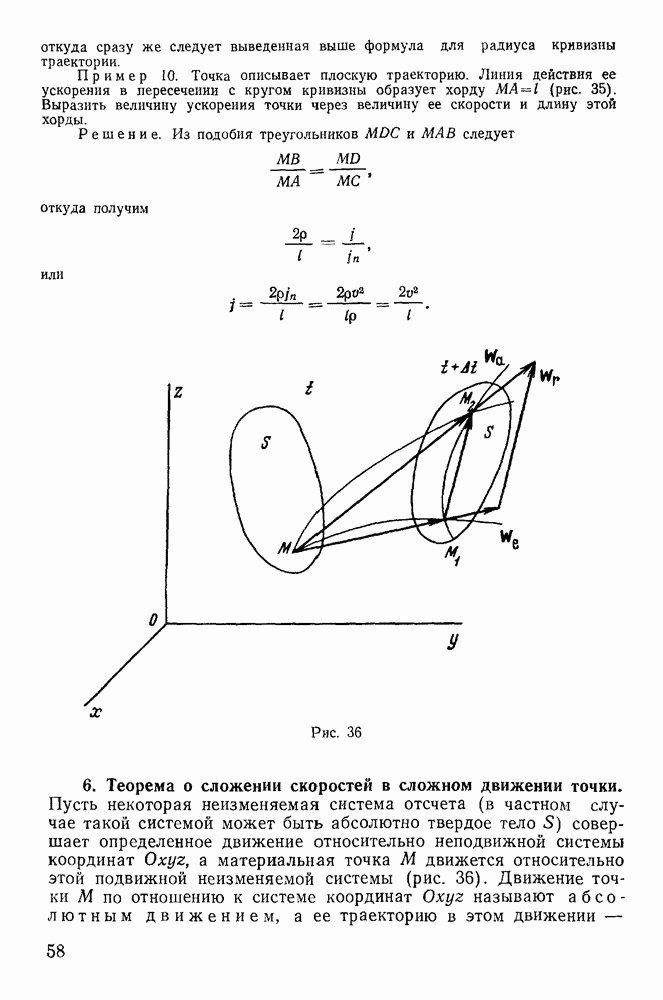
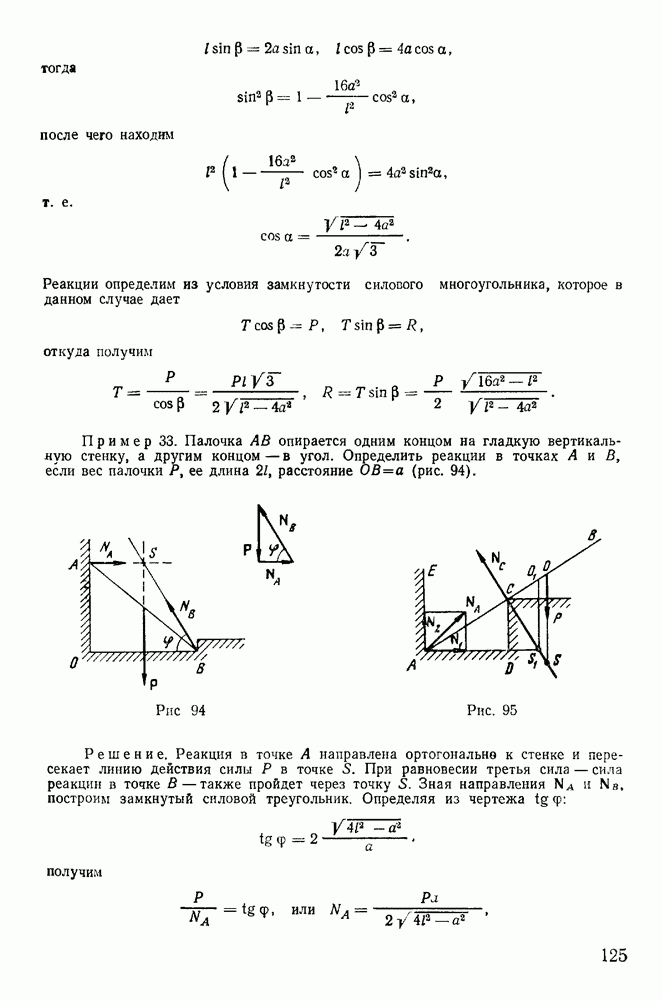
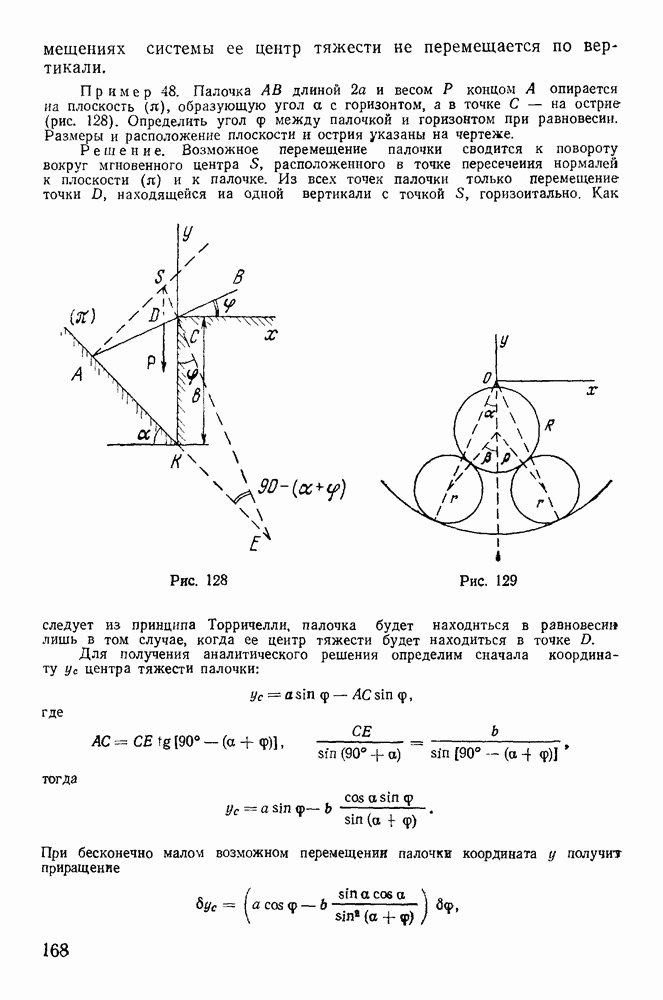
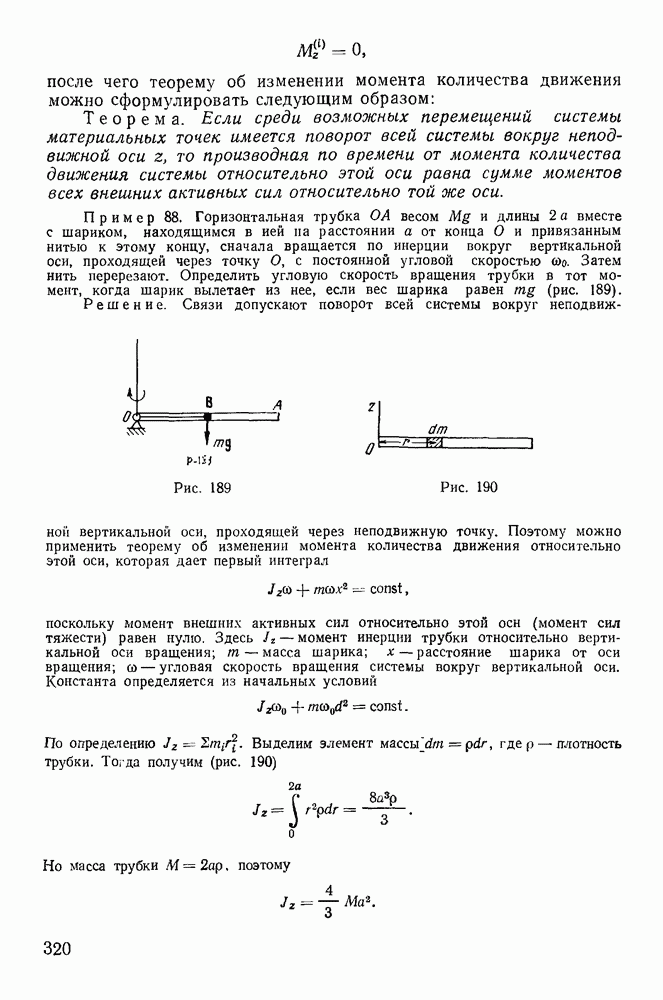
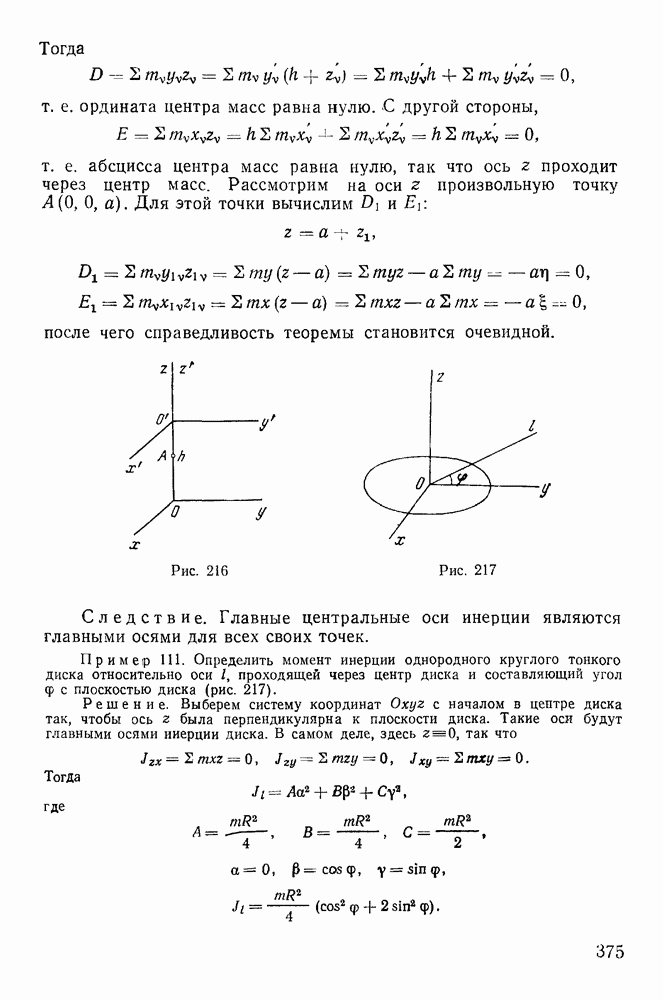
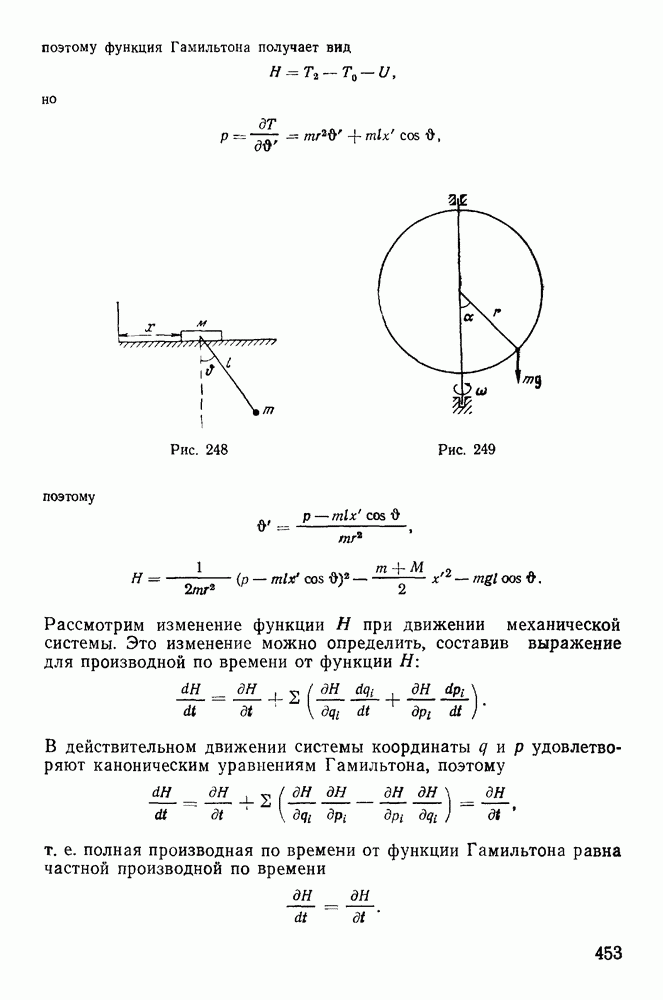
Пример 113. Однородный тонкий диск радиуса  и веса Р вращаетея вокруг вертикальной оси
и веса Р вращаетея вокруг вертикальной оси  с постоянной угловой скоростью
с постоянной угловой скоростью  Расстояние центра тяжести диска от оси вращения равно а. Ось симметрии диска образует с осью z угол а. Найдем реакции опор, предполагая, что расстояние между опорами равно
Расстояние центра тяжести диска от оси вращения равно а. Ось симметрии диска образует с осью z угол а. Найдем реакции опор, предполагая, что расстояние между опорами равно  (рис. 221)
(рис. 221)
Пусть в некоторый момент времени вертикальная плоскость симметрии диска совпадает с плоскостью  . Освободим точки
. Освободим точки  от связей и введем реакции
от связей и введем реакции  . К освобожденному твердому телу применим теорему о движении центра масс. Заметим, что центр масс диска совершает вращательное движение по горизонтальной окружности вокруг оси
. К освобожденному твердому телу применим теорему о движении центра масс. Заметим, что центр масс диска совершает вращательное движение по горизонтальной окружности вокруг оси  с постоянной угловой скоростью
с постоянной угловой скоростью  . Тогда вектор ускорения центра масс будет расположен в плоскости
. Тогда вектор ускорения центра масс будет расположен в плоскости  и направлен к оси вращения Величина его равна
и направлен к оси вращения Величина его равна

Из теоремы о движении центра масс имеем

Для получения недостающих уравнений применим теорему об изменении момента количества движения относительно осей х и у. Проекции момента количества движения на соответствующие оси имеют вид

Дифференцируя их, получим

Для полного решения задачи необходимо вычислить соответствующие произведения инерции. Выберем в качестве новых координатных осей  — центральные оси инерции диска, направив ось
— центральные оси инерции диска, направив ось  по оси симметрии диска, а ось
по оси симметрии диска, а ось  в вертикальной плоскости симметрии диска перпендикулярно к оси
в вертикальной плоскости симметрии диска перпендикулярно к оси  Координаты
Координаты  связаны простыми формулами преобразования (в рассматриваемый момент времени):
связаны простыми формулами преобразования (в рассматриваемый момент времени):

Для тонкого диска  так что
так что

Тогда произведения инерции примут вид

где


Рис. 221

Рис. 222
Подставляя эти значения в формулы для определения реакций, будем иметь

При

При

После того как определены реакции X и Y, реакции Х и У определяются сразу из теоремы о движении центра масс:

Физический маятник.
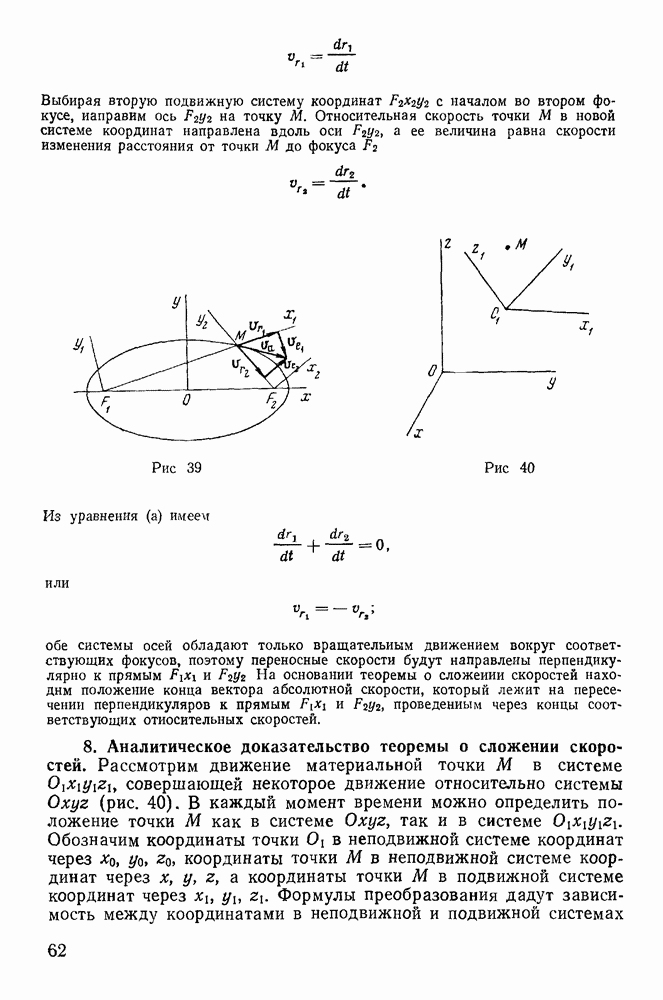
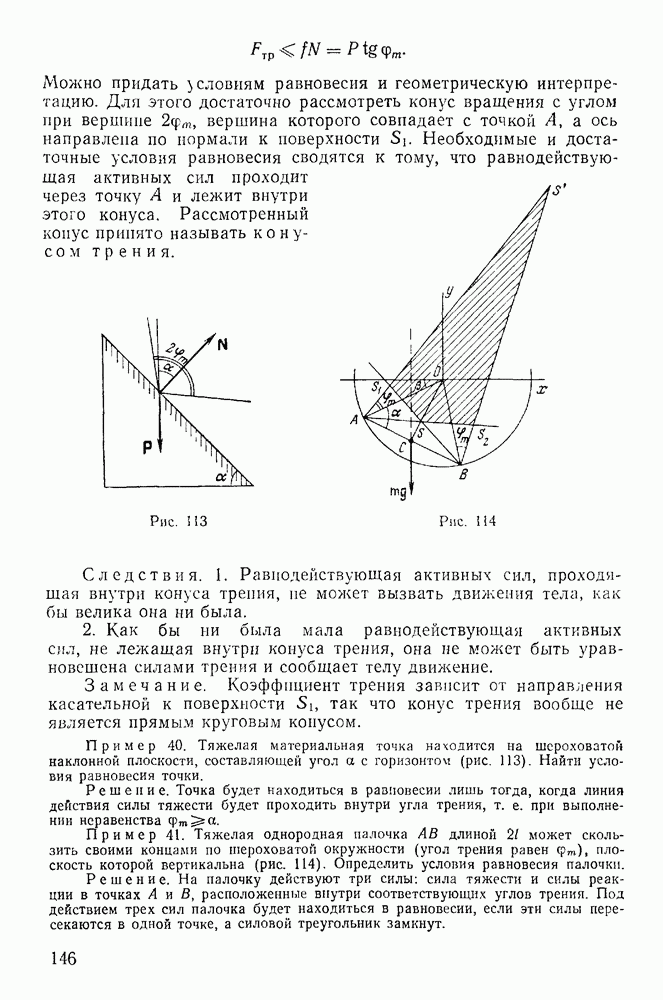
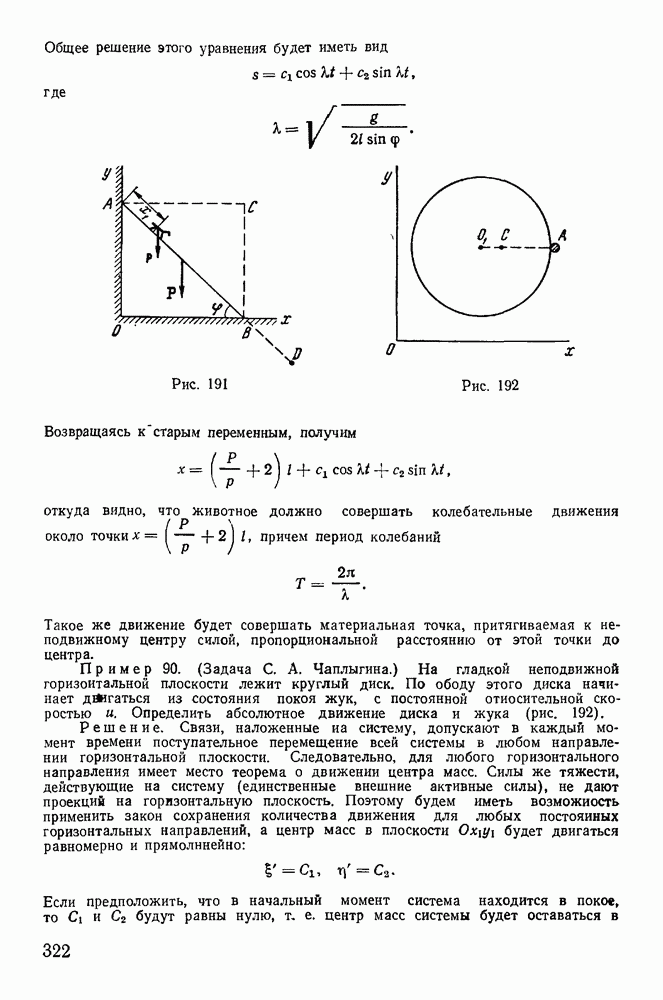
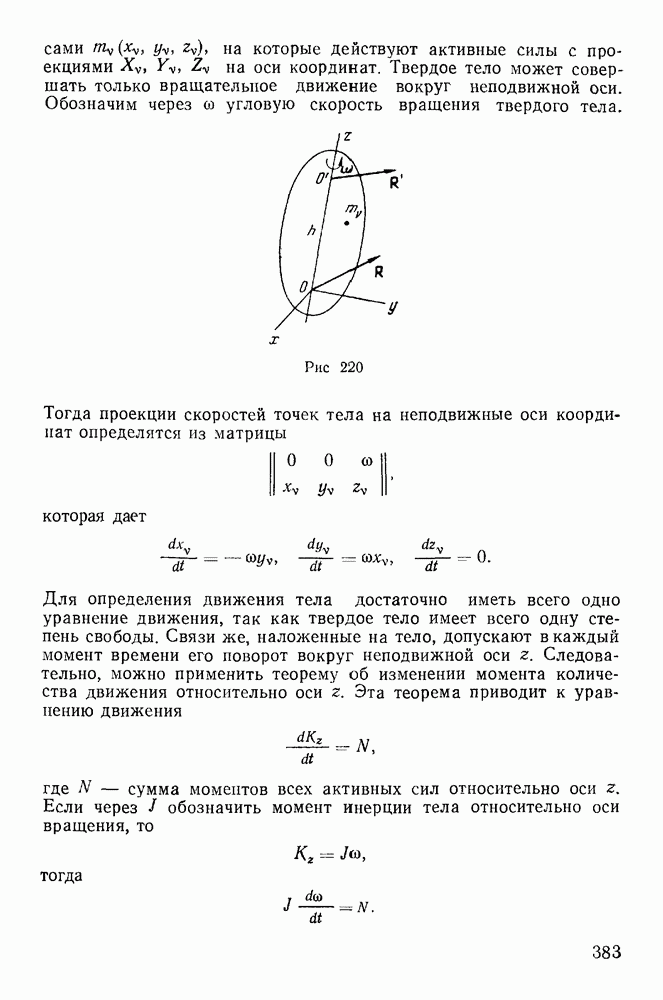
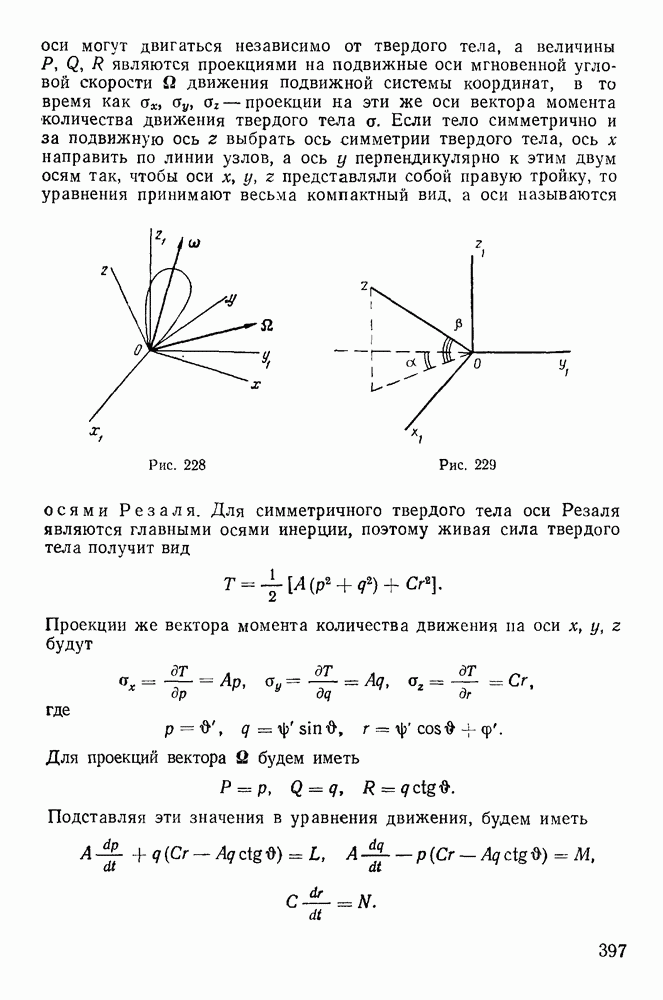
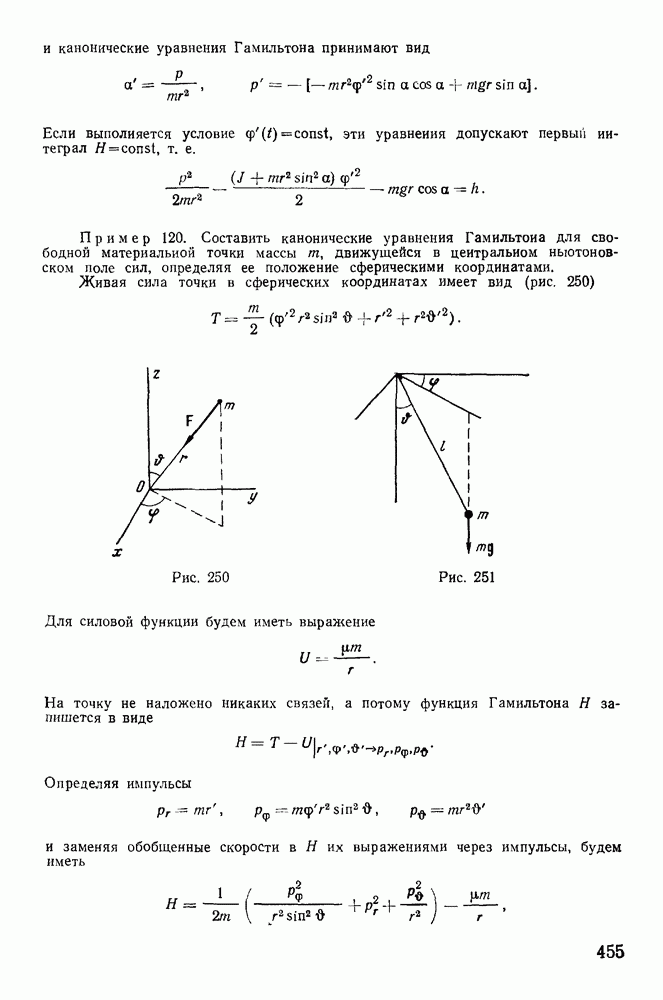
Физическим маятником называют тяжелое твердое тело, которое может свободно вращаться вокруг горизонтальной оси. Положение такого твердого тела определяется
углом  который образует плоскость, проходящая через ось вращения и центр тяжести, с вертикалью (рис. 222). Обозначим момент инерции твердого тела относительно оси вращения через
который образует плоскость, проходящая через ось вращения и центр тяжести, с вертикалью (рис. 222). Обозначим момент инерции твердого тела относительно оси вращения через  массу тела через М и пусть
массу тела через М и пусть

где  — радиус инерции маятника относительно оси вращения. Связи допускают поворот твердого тела вокруг горизонтальной оси, поэтому можно применить теорему об изменении момента количества движения относительно оси z
— радиус инерции маятника относительно оси вращения. Связи допускают поворот твердого тела вокруг горизонтальной оси, поэтому можно применить теорему об изменении момента количества движения относительно оси z

или

Полученное уравнение подобно по своей структуре уравнению движения математического маятника

Физический и математический маятники будут совершать колебания с одним и тем же периодом, если выполняется условие

Величина  называется приведенной длиной физического маятника. Построим на линии
называется приведенной длиной физического маятника. Построим на линии  точку О таким образом, чтобы имело место условие
точку О таким образом, чтобы имело место условие

Эту точку будем называть точкой качания (центром качания) физического маятника. Обозначим момент инерции твердого тела относительно оси, проходящей через центр масс и параллельной оси z, через  число
число  назовем центральным радиусом инерции. По теореме Гюйгенса — Штейнера будем иметь
назовем центральным радиусом инерции. По теореме Гюйгенса — Штейнера будем иметь

откуда

Подставляя это значение в формулу для приведенной длины физического маятника, получим

Отсюда видно, что I всегда больше, чем I, т. е. точка подвеса и центр качания расположены по разные стороны от центра тяжести твердого тела. Последнее условие можно переписать в виде

или

Полученная формула симметрична относительно точек О и О, а это значит, что последние можно поменять местами, т. е. при подвешивании маятника за точку О период останется прежним. При этом приведенная длина для точки О будет иметь вид

Отсюда непосредственно следует теорема Гюйгенса.
Теорема Гюйгенса. Точка подвеса физического маятника и центр качания суть точки взаимные. Если центр качания принять за точку подвеса, то прежняя точка подвеса будет центром качания. Период колебания маятника при этом не изменяется.
В формуле для приведенной длины физического маятника величина I меняется в зависимости от положения точки подвеса маятника:

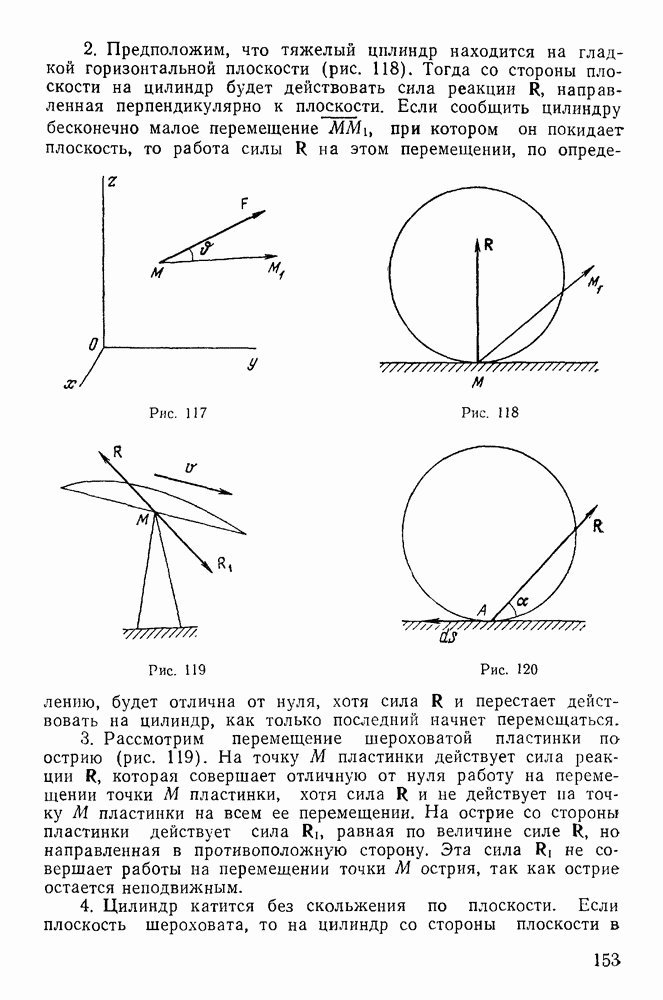
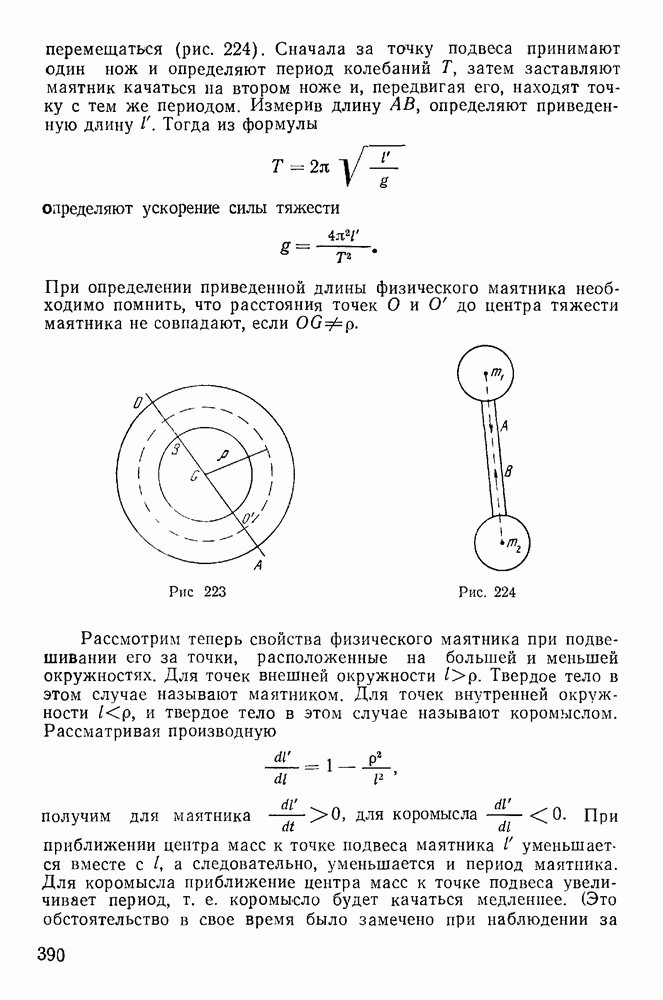
Следовательно, точки подвеса маятника, равноудаленные от центра тяжести, имеют одну и ту же приведенную длину, т. е. геометрическое место точек подвеса, обладающих одной и той же приведенной длиной (а следовательно, и одним периодом), суть две концентрических окружности с центром в центре тяжести (рис. 223). Между этими окружностями расположена окружность радиуса  (что следует из соотношения
(что следует из соотношения  На прямой 00 получим таким же образом четыре взаимные точки О, В, О, А, относительно которых маятник будет колебаться с одним периодом. Приведенной же длиной, очевидно, будет расстояние
На прямой 00 получим таким же образом четыре взаимные точки О, В, О, А, относительно которых маятник будет колебаться с одним периодом. Приведенной же длиной, очевидно, будет расстояние  или
или  т. е.
т. е.

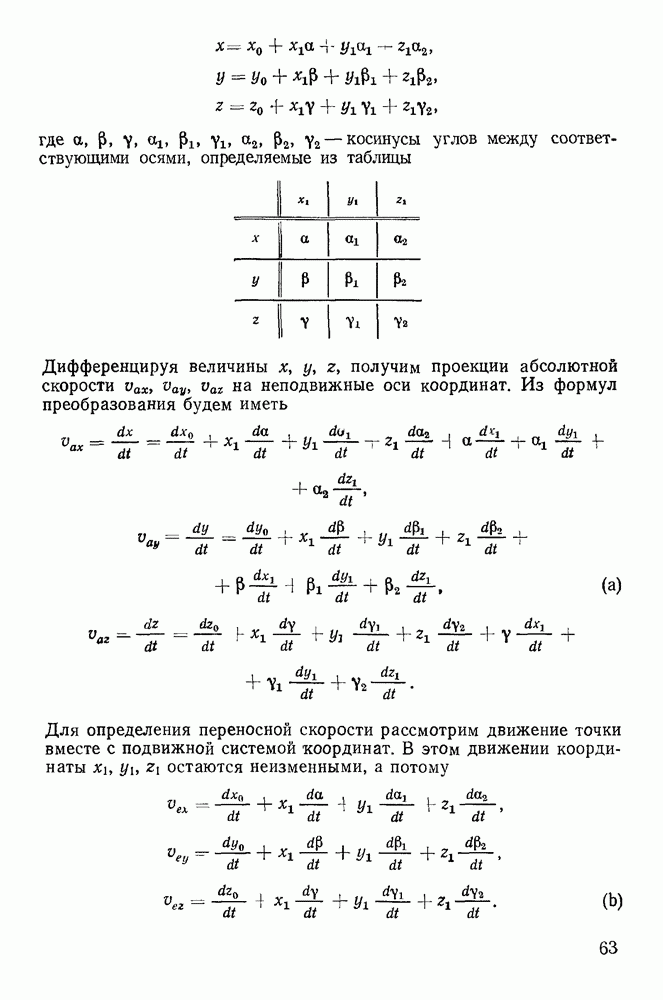
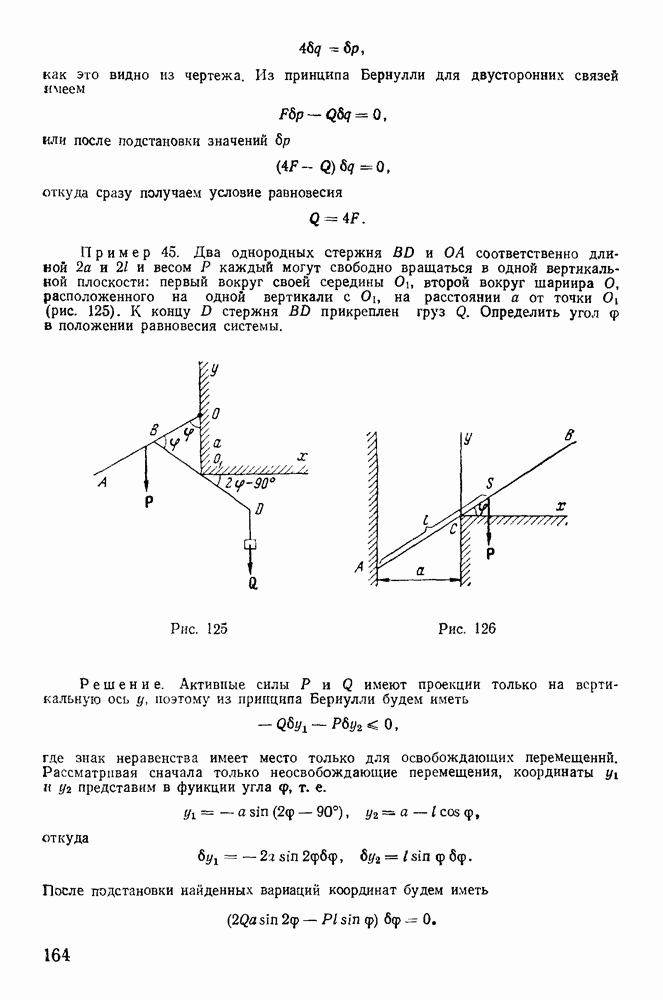
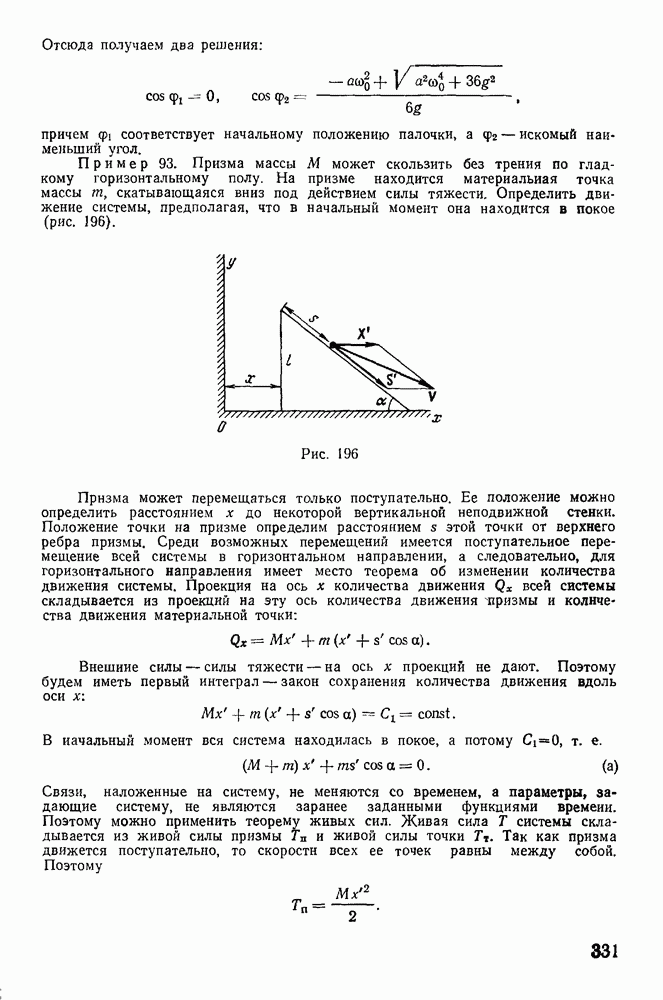
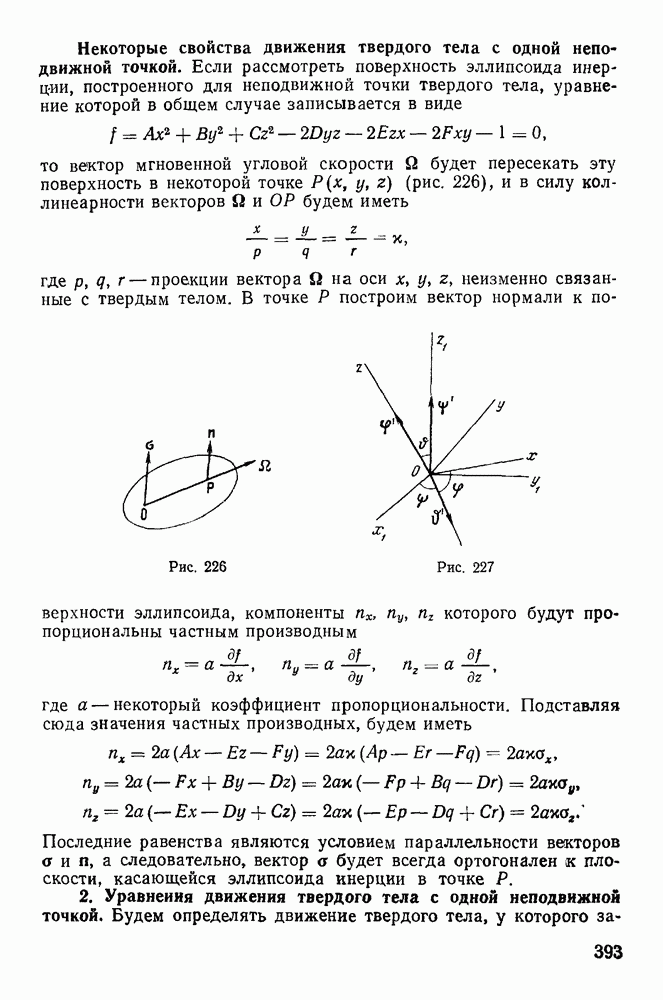
Обстоятельство это используется в оборотном маятнике Катера. Маятник состоит из двух шаров с разными массами. Между шарами на стержне укреплены два ножа, являющиеся точками подвеса маятника. Один из этих ножей неподвижен, другой может
перемещаться (рис. 224). Сначала за точку подвеса принимают один нож и определяют период колебаний Т, затем заставляют маятник качаться на втором ноже и, передвигая его, находят точку с тем же периодом. Измерив длину АВ, определяют приведенную длину Тогда из формулы

определяют ускорение силы тяжести

При определении приведенной длины физического маятника необходимо помнить, что расстояния точек О и О до центра тяжести маятника не совпадают, если 

Рис. 223

Рис. 224
Рассмотрим теперь свойства физического маятника при подвешивании его за точки, расположенные на большей и меньшей окружностях. Для точек внешней окружности  Твердое тело в этом случае называют маятником. Для точек внутренней окружности
Твердое тело в этом случае называют маятником. Для точек внутренней окружности  и твердое тело в этом случае называют коромыслом. Рассматривая производную
и твердое тело в этом случае называют коромыслом. Рассматривая производную

получим для маятника  для коромысла
для коромысла  При приближении центра масс к точке подвеса маятника
При приближении центра масс к точке подвеса маятника  уменьшается вместе с
уменьшается вместе с  а следовательно, уменьшается и период маятника. Для коромысла приближение центра масс к точке подвеса увеличивает период, т. е. коромысло будет качаться медленнее. (Это обстоятельство в свое время было замечено при наблюдении за
а следовательно, уменьшается и период маятника. Для коромысла приближение центра масс к точке подвеса увеличивает период, т. е. коромысло будет качаться медленнее. (Это обстоятельство в свое время было замечено при наблюдении за
часами Лондонского Вестминстерского аббатства, которые отставали. При уменьшении I часы сначала стали ходить быстрее. При дальнейшем уменьшении I часы стали замедлять свой ход.)
Задача о движении физического маятника является исторически первой разрешенной задачей динамики системы. Интерес к этой задаче возник в связи с вопросом об усовершенствовании часов и связан в первую очередь с именем Гюйгенса, хотя еще Галилей предлагал использовать маятник в качестве регулятора хода часов.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Введение
- Глава I. ОСНОВЫ ТЕОРИИ ВЕКТОРОВ
- § 1. СВОБОДНЫЕ ВЕКТОРЫ
- 2. Сложение свободных векторов.
- 3. Проекция вектора на ось.
- 4. Инварианты системы свободных векторов.
- § 2. СКОЛЬЗЯЩИЕ ВЕКТОРЫ
- 2. Координаты скользящего вектора.
- 3. Момент скользящего вектора. Плюккеровы координаты.
- 4. Аналитическое определение момента скользящего вектора.
- 5. Проекция момента на ось.
- 6. Момент скользящего вектора относительно оси
- § 3. СИСТЕМА СКОЛЬЗЯЩИХ ВЕКТОРОВ
- 2. Произвольная система скользящих векторов. Элементарные операции.
- 3. Приведение системы скользящих векторов к простейшей эквивалентной форме.
- 4. Плоская система скользящих векторов.
- 5. Свойства системы параллельных скользящих векторов.
- § 4. ЗАКРЕПЛЕННЫЕ ВЕКТОРЫ
- § 5. ДИФФЕРЕНЦИРОВАНИЕ СВОБОДНОГО ВЕКТОРА ПО СКАЛЯРНОМУ АРГУМЕНТУ
- Глава II. КИНЕМАТИКА
- § 1. КИНЕМАТИКА ТОЧКИ
- 2. Ускорение точки. Проекции ускорения на прямоугольные оси координат.
- 3. Скорость и ускорение точки в полярных координатах.
- 4. Движение точки по окружности.
- 5. Проекции ускорения на оси естественного трехгранника.
- 6. Теорема о сложении скоростей в сложном движении точки.
- 7. Метод Роберваля построения касательных к плоским кривым.
- 8. Аналитическое доказательство теоремы о сложении скоростей.
- 9. Сложение скоростей в общем случае сложного движения точки.
- § 2. КИНЕМАТИКА АБСОЛЮТНО ТВЕРДОГО ТЕЛА
- 2. Элементарные движения твердого тела.
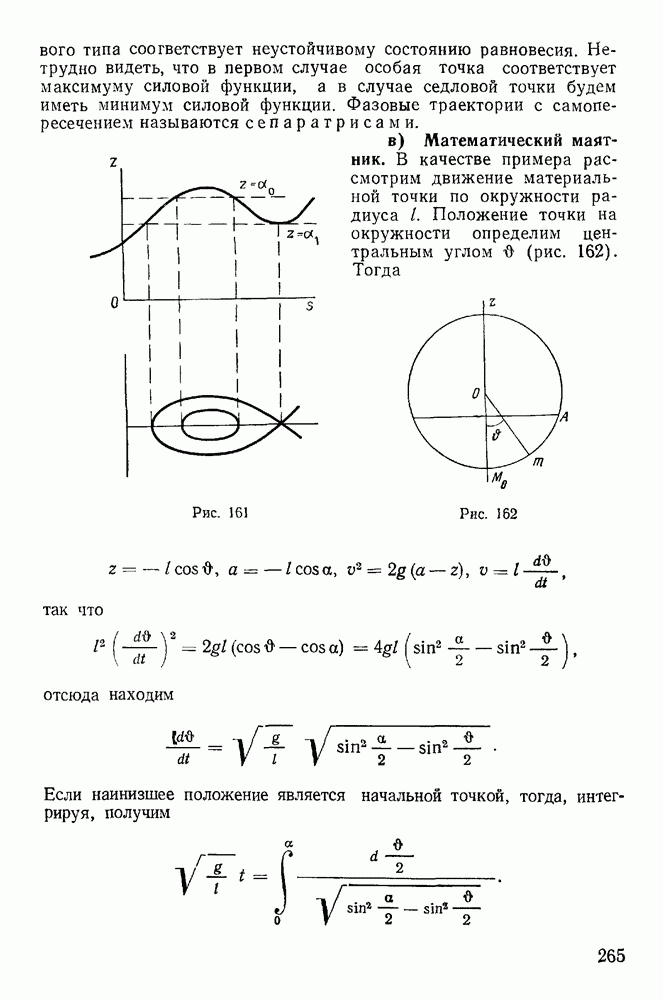
- 3. Мгновенные движения твердого тела.
- 4. Сложение мгновенно-поступательных и мгновенно-вращательных движений твердого тела.
- 5. Общий случай сложения мгновенно-поступательных и мгновенно-вращательных движений твердого тела. Непрерывное движение твердого тела.
- 6. Мгновенное движение твердого тела с одной неподвижной точкой.
- 7. Плоскопараллельное движение твердого тела.
- § 3. УСКОРЕНИЕ ТОЧКИ В СЛОЖНОМ ДВИЖЕНИИ
- 2. Замечание о дифференцировании единичного вектора.
- 3. Векторный вывод теоремы Кориолиса.
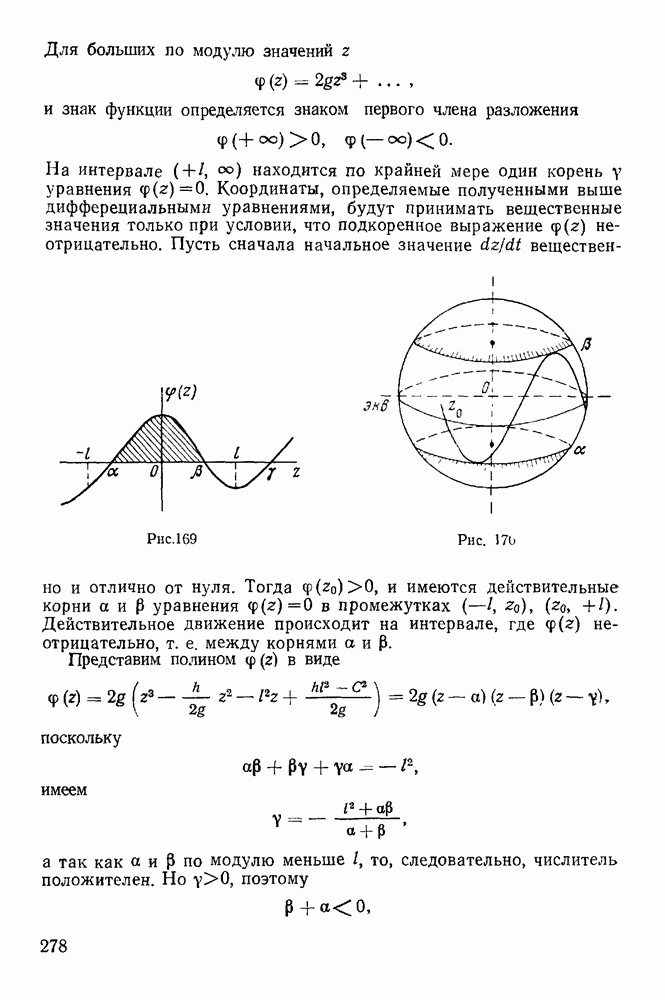
- 4. Теорема Ривальса.
- § 4. РАСПРЕДЕЛЕНИЕ УСКОРЕНИЙ В ПЛОСКОПАРАЛЛЕЛЬНОМ ДВИЖЕНИИ ТВЕРДОГО ТЕЛА
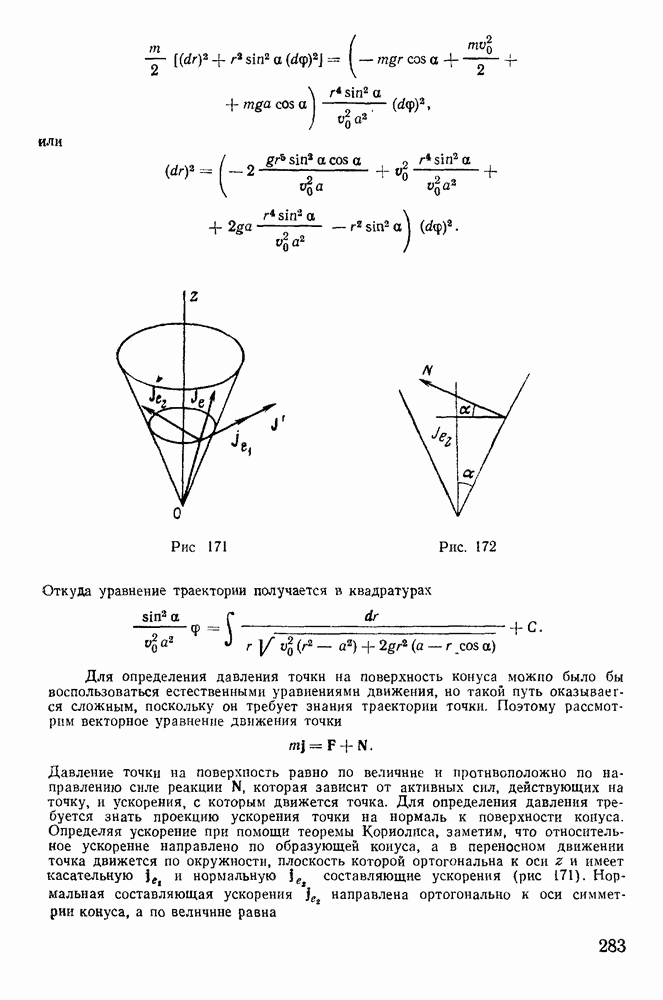
- 2. Мгновенный центр ускорений.
- § 5. КИНЕМАТИЧЕСКИЕ УРАВНЕНИЯ ЭЙЛЕРА
- Глава III. СТАТИКА
- I. ГЕОМЕТРИЧЕСКАЯ СТАТИКА
- § 1. АКСИОМЫ СТАТИКИ
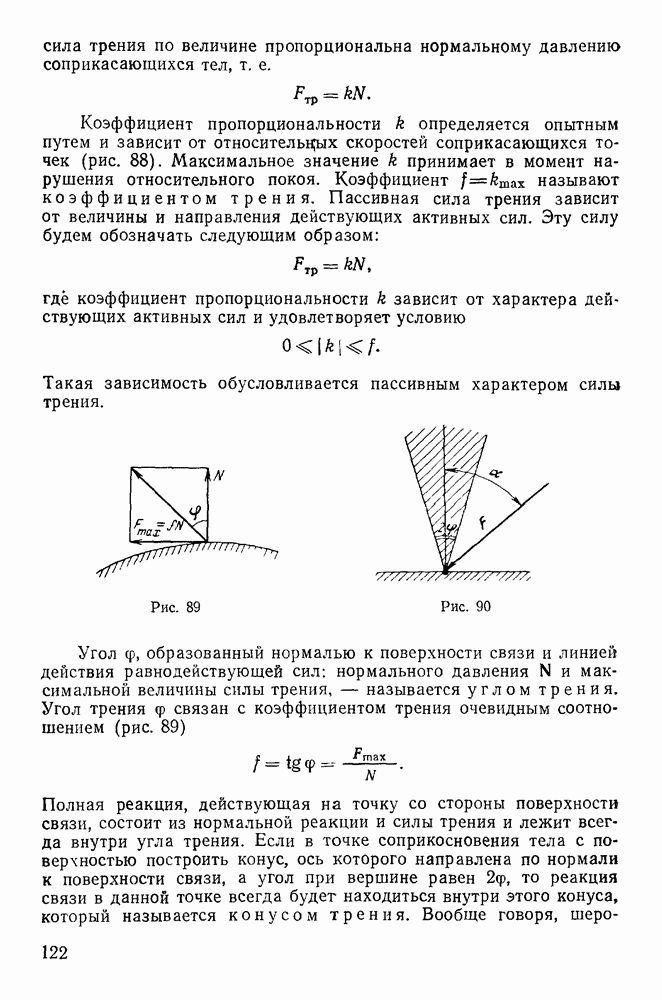
- § 2. ПОНЯТИЕ О СИЛЕ ТРЕНИЯ
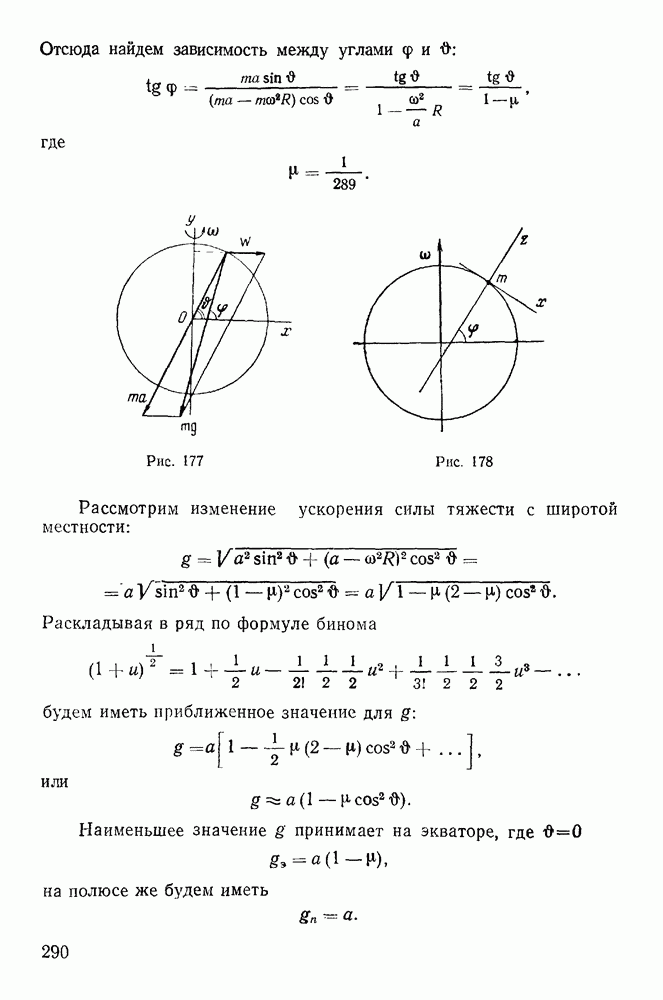
- § 3. РАЗЛИЧНЫЕ ЗАДАЧИ СТАТИКИ
- 2. Равновесие трех сил.
- § 4. МОМЕНТ СИЛЫ
- 2. Момент силы относительно оси.
- 3. Теорема Вариньона для системы сходящихся сил.
- § 5. ПРОИЗВОЛЬНАЯ СИСТЕМА СИЛ, ДЕЙСТВУЮЩИХ НА ТВЕРДОЕ ТЕЛО
- § 6. УСЛОВИЯ РАВНОВЕСИЯ СИСТЕМЫ СИЛ, ДЕЙСТВУЮЩИХ НА ТВЕРДОЕ ТЕЛО
- § 7. ПРИВЕДЕНИЕ СИСТЕМЫ СИЛ, ДЕЙСТВУЮЩИХ НА ТВЕРДОЕ ТЕЛО, К ДИНАМЕ. УРАВНЕНИЯ РАВНОВЕСИЯ ТВЕРДОГО ТЕЛА
- § 8. УСЛОВИЯ РАВНОВЕСИЯ СИСТЕМЫ ТВЕРДЫХ ТЕЛ
- § 9. ПЛОСКАЯ СИСТЕМА СИЛ
- § 10. ЗАДАЧА О РАВНОВЕСИИ НЕСВОБОДНОГО ТВЕРДОГО ТЕЛА
- 2. Частные случаи равновесия твердого тела.
- § 11. ЗАДАЧА О РАВНОВЕСИИ ПРИ НАЛИЧИИ ТРЕНИЯ
- § 12. СИЛА ТЯЖЕСТИ И ЦЕНТР ТЯЖЕСТИ
- II. АНАЛИТИЧЕСКАЯ СТАТИКА
- § 1. РАБОТА СИЛЫ НА ПЕРЕМЕЩЕНИИ. СИЛОВАЯ ФУНКЦИЯ
- § 2. ПРИНЦИП ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ
- 2. Теорема Лагранжа о равновесии системы.
- 3. Принцип Торричелли.
- § 3. ОБЩИЕ ВОПРОСЫ АНАЛИТИЧЕСКОЙ СТАТИКИ
- 3. Общие теоремы о равновесии системы материальных точек.
- 4. Метод неопределенных множителей Лагранжа.
- 5. Определение реакций.
- § 4. ОПРЕДЕЛЕНИЕ РЕАКЦИЙ В ОБЩЕМ СЛУЧАЕ
- § 5. РАВНОВЕСИЕ НИТИ
- 2. Естественные уравнения равновесия нити.
- Глава IV. ДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ
- § 1. ОСНОВНЫЕ ЗАКОНЫ ДИНАМИКИ
- § 2. ДВЕ ОСНОВНЫЕ ЗАДАЧИ ДИНАМИКИ. УРАВНЕНИЯ ДВИЖЕНИЯ ТОЧКИ В ДЕКАРТОВЫХ ОСЯХ
- § 3. ЕСТЕСТВЕННЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ
- § 4. ОСНОВНЫЕ ТЕОРЕМЫ ДИНАМИКИ ДЛЯ СВОБОДНОЙ МАТЕРИАЛЬНОЙ ТОЧКИ
- 2. Теорема об изменении момента количества движения.
- 3. Следствия из теорем об изменении количества движения и момента количества движения материальной точки.
- 4. Теорема живых сил.
- 5. Интеграл живых сил.
- 6. Устойчивость равновесия. Теорема Лагранжа.
- § 5. ДВИЖЕНИЕ ТЯЖЕЛОЙ МАТЕРИАЛЬНОЙ ТОЧКИ В ПУСТОТЕ
- § 6. ДВИЖЕНИЕ МАТЕРИАЛЬНОЙ ТОЧКИ ПОД ДЕЙСТВИЕМ ЦЕНТРАЛЬНЫХ СИЛ
- 2. Формулы Бине
- 3. Задача о движении планет
- § 7. ДВИЖЕНИЕ ТОЧКИ В СОПРОТИВЛЯЮЩЕЙСЯ СРЕДЕ
- § 8. ДВИЖЕНИЕ НЕСВОБОДНОЙ МАТЕРИАЛЬНОЙ ТОЧКИ
- 2. Движение материальной точки по поверхности.
- § 9. ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЕ МАТЕРИАЛЬНОЙ ТОЧКИ
- 1. Теорема живых сил в относительном движении точки.
- 2. Уравнения относительного равновесия точки.
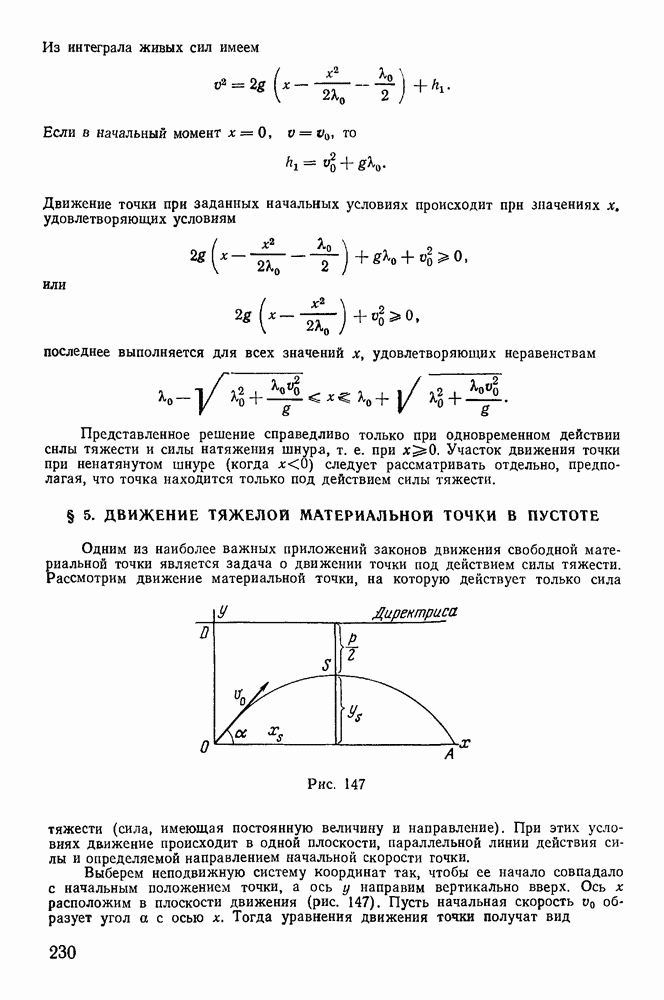
- 3. Равновесие материальной точки на поверхности Земли. Вес.
- 4. Задача о падении тяжелой точки в пустоте.
- 5. Маятник Фуко.
- § 10. ПРИНЦИП ДАЛАМБЕРА
- Глава V. ДИНАМИКА СИСТЕМЫ МАТЕРИАЛЬНЫХ ТОЧЕК
- § 1. УЧЕНИЕ О СВЯЗЯХ
- § 2. ПРИНЦИП ДАЛАМБЕРА — ЛАГРАНЖА
- § 3. ОСНОВНЫЕ ТЕОРЕМЫ ДИНАМИКИ СИСТЕМЫ
- 2. Теорема об изменении момента количества движения.
- 3. Теорема живых сил.
- § 4. ТЕОРЕМЫ О ДВИЖЕНИИ СИСТЕМЫ ОТНОСИТЕЛЬНО ОСЕЙ НЕИЗМЕННОГО НАПРАВЛЕНИЯ, ПРОХОДЯЩИХ ЧЕРЕЗ ЦЕНТР МАСС СИСТЕМЫ (ОСЕЙ КЕНИГА)
- 2. Теорема об изменении момента количества движения системы относительно осей Кёнига.
- 3. Теорема живых сил в движении системы относительно осей Кёнига.
- § 5. УРАВНЕНИЯ ЛАГРАНЖА ВТОРОГО РОДА
- 2. Случай существования силовой функции.
- 3. Замечание о лагранжевых координатах.
- § 6. ЭЛЕМЕНТАРНЫЕ СЛУЧАИ ИНТЕГРИРУЕМОСТИ УРАВНЕНИЙ ЛАГРАНЖА
- 2. Метод Рауса игнорирования циклических координат.
- 3. Обобщение теоремы и интеграла живых сил.
- § 7. ОПРЕДЕЛЕНИЕ РЕАКЦИЙ
- Глава VI. ДИНАМИКА ТВЕРДОГО ТЕЛА
- § 1. ТЕОРИЯ МОМЕНТОВ ИНЕРЦИИ
- 2. Момент инерции системы относительно произвольной оси, проходящей через заданную точку.
- 3. Эллипсоид инерции.
- 4. Определение главных осей инерции для произвольной точки.
- § 2. ВРАЩЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ОСИ
- § 3. ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА, ИМЕЮЩЕГО ОДНУ НЕПОДВИЖНУЮ ТОЧКУ
- 2. Уравнения движения твердого тела с одной неподвижной точкой.
- § 4. ДВИЖЕНИЕ ТЯЖЕЛОГО ТВЕРДОГО ТЕЛА ОКОЛО НЕПОДВИЖНОЙ ТОЧКИ
- 2. Интегрирование уравнений движения тяжелого твердого тела.
- 3. Случай Эйлера — Пуансо.
- Регулярная прецессия твердого тела в случае Эйлера.
- Геометрическая интерпретация Пуансо движения твердого тела в случае Эйлера.
- Устойчивость постоянных вращений твердого тела.
- 4. Случай Лагранжа.
- Особенные случаи движения твердого тела. Спящий волчок.
- Гироскоп. Приближенная теория.
- Некоторые применения гироскопов.
- Регулярная прецессия в случае Лагранжа.
- Вынужденная регулярная прецессия.
- 5. Случай Ковалевской.
- § 5. ОПРЕДЕЛЕНИЕ РЕАКЦИИ В СЛУЧАЕ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА С ОДНОЙ НЕПОДВИЖНОЙ ТОЧКОЙ
- § 6. УРАВНЕНИЯ ДВИЖЕНИЯ СВОБОДНОГО ТВЕРДОГО ТЕЛА
- § 7. ГИРОСТАТЫ
- Глава VII. АНАЛИТИЧЕСКАЯ ДИНАМИКА
- § 1. КАНОНИЧЕСКИЕ УРАВНЕНИЯ ГАМИЛЬТОНА
- 1. Преобразования Лежандра.
- 2. Канонические уравнения Гамильтона.
- 3. Функция Гамильтона и ее свойства.
- § 2. ПРИНЦИП ГАМИЛЬТОНА — ОСТРОГРАДСКОГО
- 2. Вывод канонических уравнений Гамильтона из принципа Гамильтона — Остроградского.
- 3. Принцип Гамильтона в форме Пуанкаре.
- § 3. ИНТЕГРИРОВАНИЕ КАНОНИЧЕСКИХ УРАВНЕНИЙ ГАМИЛЬТОНА
- 2. Канонические преобразования.
- 3. Бесконечно малые канонические преобразования.
- 4. Теорема Лиувилля.
- 5. Теорема Якоби.
- 6. Интегрирование уравнения Гамильтона—Якоби.
- Метод Имшенецкого разделения переменных.
- 7. Скобки Пуассона.
- § 4. ВАРИАЦИОННЫЕ ПРИНЦИПЫ МЕХАНИКИ
- 2. Принцип Лагранжа.
- 3. Принцип наименьшего действия в форме Якоби.
- Вывод уравнений Лагранжа второго рода из принципа Якоби.
- Сравнение принципа Якоби с принципом Гамильтона.
- 4. Оптико-механическая аналогия.
- 5. Интегральные инварианты.
- Линейные интегральные инварианты.
- Интегральный инвариант Пуанкаре — Картана.
- 6. Принцип наименьшего принуждения Гаусса. Уравнения Аппеля.
- 7. Уравнения Рауса.
- § 5. МАЛЫЕ КОЛЕБАНИЯ
- Затухающие колебания.
- Вынужденные колебания. Резонанс.
- Параметрический резонанс.
- Нелинейные колебания.
- Диссипативные системы.
- 2. Общий случай малых колебаний системы около положения устойчивого равновесия.
- Устойчивость равновесия. Теорема Лагранжа об устойчивости равновесия.
- Замечание об устойчивости стационарных движений.
- Малые колебания системы около положения устойчивого равновесия.
- Влияние диссипативных сил на малые колебания системы около устойчивого положения равновесия.
- § 6. УСТОЙЧИВОСТЬ ДВИЖЕНИЯ
- Прямой метод Ляпунова
- Теорема об асимптотической устойчивости.
- Теорема Четаева о неустойчивости движения.
- 2. Влияние новых связей на малые колебания системы около положения равновесия.
- 3. Влияние диссипативных сил на устойчивость равновесия.
- 4. Влияние гироскопических сил на устойчивость равновесия.
- § 7. ЭЛЕМЕНТЫ ТЕОРИИ ВОЗМУЩЕНИЙ
- Устойчивость консервативных систем.
- 2. Метод изменения произвольных постоянных.
- Глава VIII. ТЕОРИЯ УДАРА
- § 2. ТЕОРЕМЫ КАРНО
- § 3. ЗАДАЧА О ЦЕНТРЕ УДАРА
- § 4. ЗАДАЧА О БАЛЛИСТИЧЕСКОМ МАЯТНИКЕ
- § 5. УРАВНЕНИЯ ЛАГРАНЖА ДЛЯ УДАРА
- § 6. ЗАДАЧА ОБ УДАРЕ ПО ТВЕРДОМУ ТЕЛУ С ОДНОЙ НЕПОДВИЖНОЙ ТОЧКОЙ
- Глава IX. ЭЛЕМЕНТЫ СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- § 2. СПЕЦИАЛЬНЫЙ ПРИНЦИП ОТНОСИТЕЛЬНОСТИ ЭЙНШТЕЙНА
- § 3. ГРУППА ПРЕОБРАЗОВАНИЙ ЛОРЕНЦА
- § 4. ИНВАРИАНТНЫЕ ВЕЛИЧИНЫ В ТЕОРИИ ОТНОСИТЕЛЬНОСТИ. ЧЕТЫРЕХМЕРНЫЙ ВЕКТОР. МИР МИНКОВСКОГО
- § 5. РЕЛЯТИВИСТСКАЯ ДИНАМИКА
- Литература