2. Теорема об изменении момента количества движения.

В общем случае для системы, состоящей из материальных точек, на которую наложены идеальные связи, справедливо общее уравнение динамики

Пусть связи, наложенные на систему, допускают поворот всей системы, как одного тела, вокруг неподвижной оси (например, оси т. е. среди всех возможных перемещений системы будут находиться такие, проекции которых определяются матрицей

Отсюда для находим:

После подстановки этих возможных перемещений в общее уравнение динамики, получим

В силу произвольности отсюда следует

В левой части последнего уравнения стоит полная производная по времени от выражения

равного сумме моментов количества движения точек системы относительно оси . В дальнейшем это выражение будем называть моментом количества движения системы относительно оси Правая часть уравнения представляет сумму моментов всех активных сил, действующих на точки системы, относительно оси Обозначая эту сумму через перепишем полученное уравнение в виде

Оно представляет математическое выражение теоремы об изменении момента количества движения. Ее можно сформулировать так:

Теорема. Если среди всех возможных перемещений системы имеется поворот всей системы как твердого тела вокруг неподвижной оси z, то производная по времени от момента количества движения системы относительно этой оси будет равна сумме моментов всех активных сил, действующих на точки системы, относительно той же оси.

Следствия. 1. Пусть выполняется условие

т. е. сумма моментов всех активных сил, относительно оси равна нулю. Тогда теорема дает

откуда следует постоянство момента количества движения относительно оси т. е.

Полученное соотношение является первым интегралом уравнений движения системы и сохраняет постоянное значение во все время движения системы. Постоянная определяется из начальных условий. В этом и заключается закон площадей в динамике системы материальных точек, или закон сохранения момента количества движения.

Переходя от декартовых координат к полярным, интеграл площадей, как и в динамике точки, можно представить в виде

где — секторная скорость проекции v-той точки на основную координатную плоскость, или

В результате приходим к теореме.

Теорема. Если связи, наложенные на систему материальных точек, допускают поворот всей системы вокруг неподвижной оси, причем сумма моментов всех активных сил относительно этой оси равна нулю, то сумма произведений масс точек системы на секторные скорости их проекций на плоскость, перпендикулярную к оси возможного вращения, есть величина постоянная.

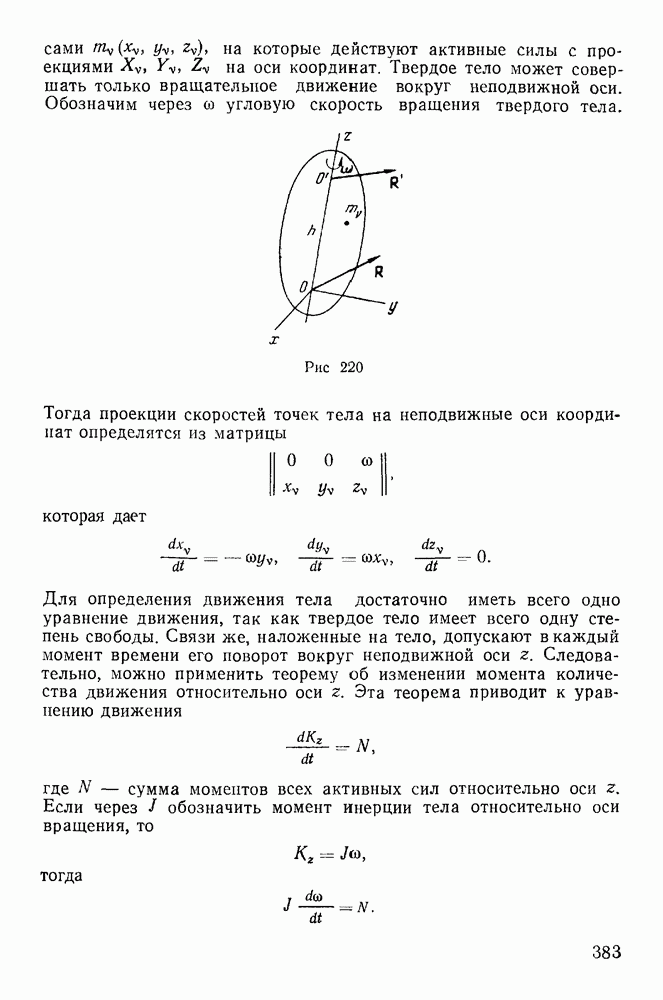
2. Предположим, что система материальных точек может только вращаться вокруг неподвижной оси (твердое тело на неподвижной оси). Обозначим через со угловую скорость вращения

системы. Тогда проекции скоростей точек системы определятся из формулы Эйлера

так что

Подставляя полученные значения составляющих скоростей в выражение для будем иметь

где

Выражение

назовем моментом инерции системы материальных точек относительно оси Из теоремы об изменении момента количества движения теперь будем иметь

Если, кроме того, сумма моментов всех активных сил относительно оси z равна нулю, т. е. то получаем первый интеграл уравнений движения

т. е. произведение момента инерции системы относительно оси z на угловую скорость вращения вокруг той же оси есть величина постоянная.

3. Если все активные силы, действующие на систему материальных точек, можно разделить на внутренние и внешние, причем внутренние силы — силы взаимодействия — определяются в соответствии с третьим законом Ньютона, то для моментов активных сил будем иметь

где — сумма моментов внутренних активных сил относительно оси — сумма моментов внешних активных сил относительно оси Так как моменты двух сил взаимодействия в соответствии с третьим законом Ньютона равны по величине и направлены в противоположные стороны, то для суммы моментов внутренних сил получим

после чего теорему об изменении момента количества движения можно сформулировать следующим образом:

Теорема. Если среди возможных перемещений системы материальных точек имеется поворот всей системы вокруг неподвижной оси z, то производная по времени от момента количества движения системы относительно этой оси равна сумме моментов всех внешних активных сил относительно той же оси.

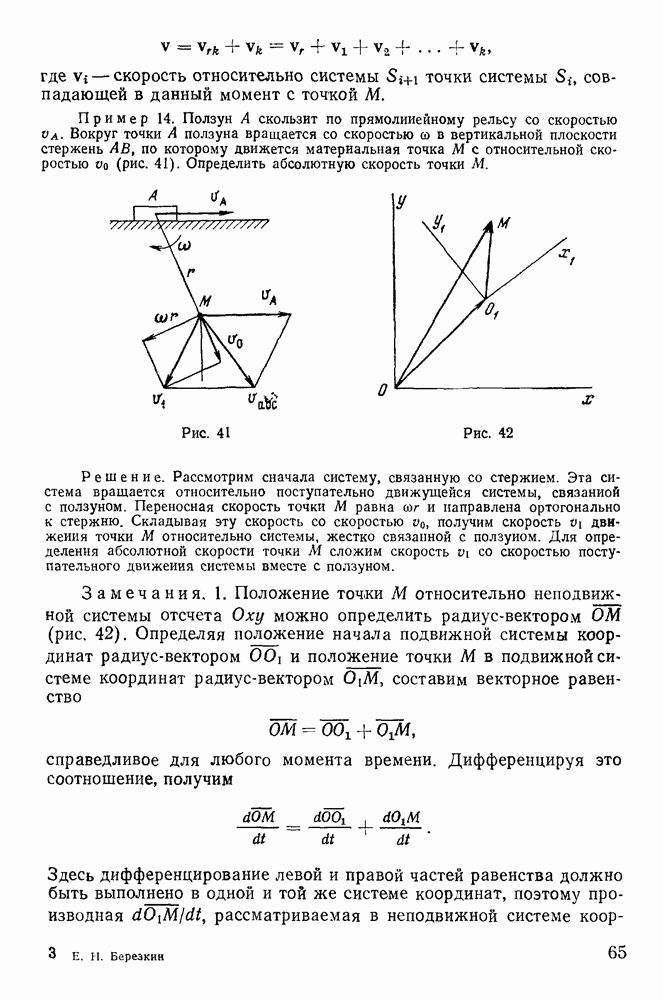
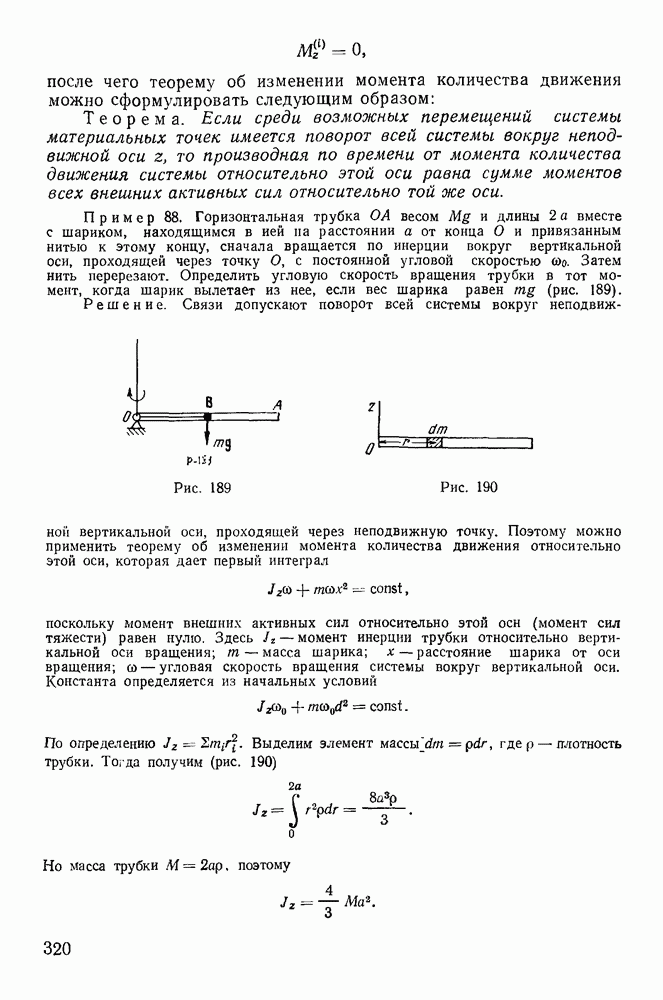
Пример 88. Горизонтальная трубка О А весом и длины 2 а вместе с шариком, находящимся в ней на расстоянии а от конца О и привязанным нитью к этому концу, сначала вращается по инерции вокруг вертикальной оси, проходящей через точку О, с постоянной угловой скоростью Затем нить перерезают. Определить угловую скорость вращения трубки в тот момент, когда шарик вылетает из нее, если вес шарика равен (рис. 189).

Решение.

Рис. 189

Рис. 190

Связи допускают поворот всей системы вокруг неподвижной вертикальной оси, проходящей через неподвижную точку. Поэтому можно применить теорему об изменении момента количества движения относительно этой оси, которая дает первый интеграл

поскольку момент внешних активных сил относительно этой осн (момент сил тяжести) равен нулю. Здесь 1г — момент инерции трубки относительно вертикальной оси вращения; — масса шарика; расстояние шарика от оси вращения; со — угловая скорость вращения системы вокруг вертикальной оси. Константа определяется из начальных условий

По определению Выделим элемент массы где — плотность трубки. Тогда получим (рис. 190)

Но Масса трубки поэтому

Подставляя это значение в полученный интеграл, будем иметь

откуда при получим

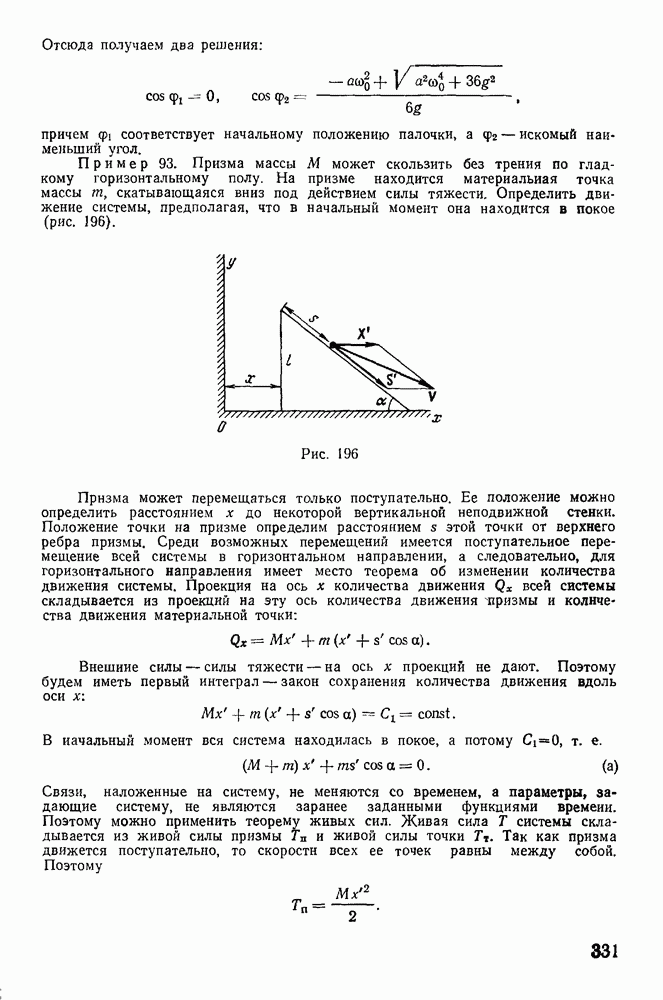
Пример 89. (Задача Н. Е. Жуковского.) По доске длины 21 и веса Р, опирающейся своими концами на гладкий горизонтальный пол и гладкую вертикальную стену, бежит животное весом Спрашивается, как оно должно бежать, чтобы доска не скользила (рис.

По условиям задачи животное должно бежать так, чтобы доска оставалась в покое. В рассматриваемом положении доски определим ее мгновенный центр вращения С. Так как доска во время движения системы остается в покое, точка С будет неподвижной по отношению к неподвижной системе координат Связи, наложенные на систему, допускают в каждый момент времени поворот всей системы вокруг горизонтальной оси, проходящей через точку С, и перпендикулярной к плоскости чертежа. Это дает возможность применить теорему об изменении момента количества движения системы относительно выбранной оси.

Вычислим сначала момент количества движения системы:

где — момент количества движения доски относительно точки С; — момент количества движения животного. Во все время движения имеем

Подсчитав сумму моментов всех сил относительно горизонтальной оси, проходящий через точку С,

запишем теорему об изменении момента количества движения

После подстановки найденного значения получаем

откуда

Замена

приводит к однородному линейному уравнению

Общее решение этого уравнения будет иметь вид

где

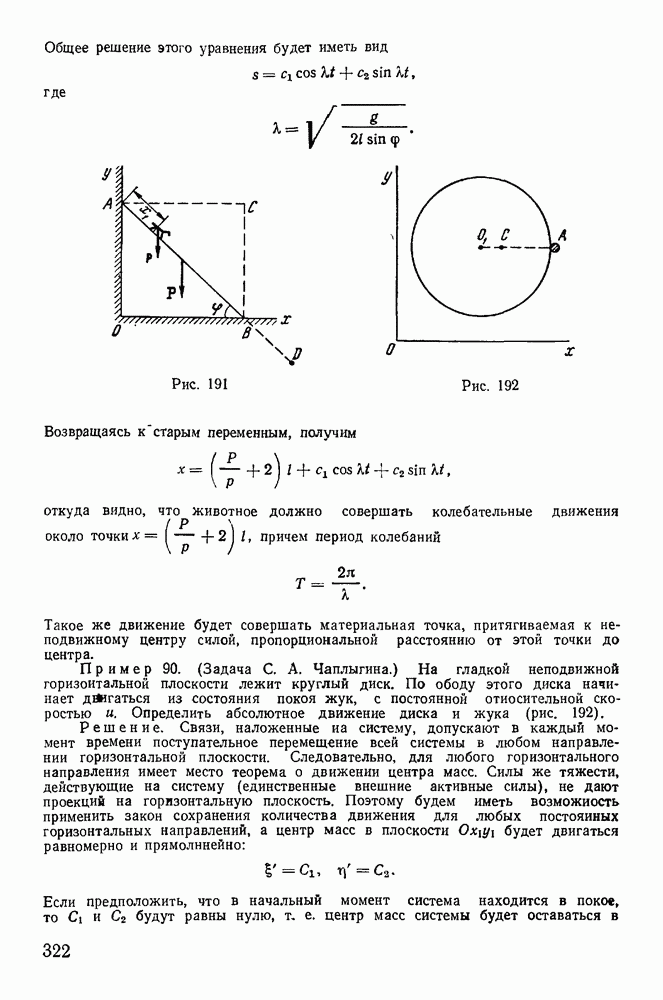
Рис. 191

Рис. 192

Возвращаясь к старым переменным, получим

откуда видно, что животное должно совершать колебательные движения около причем период колебаний

Такое же движение будет совершать материальная точка, притягиваемая к неподвижному центру силой, пропорциональной расстоянию от этой точки до центра.

Пример 90. (Задача С. А. Чаплыгина.) На гладкой неподвижной горизонтальной плоскости лежит круглый диск. По ободу этого диска начинает из состояния покоя жук, с постоянной относительной скоростью и. Определить абсолютное движение диска и жука (рис. 192).

Решение. Связи, наложенные на систему, допускают в каждый момент времени поступательное перемещение всей системы в любом направлении горизонтальной плоскости. Следовательно, для любого горизонтального направления имеет место теорема о движении центра масс. Силы же тяжести, действующие на систему (единственные внешние активные силы), не дают проекций на горизонтальную плоскость. Поэтому будем иметь возможность применить закон сохранения количества движения для любых постоянных горизонтальных направлений, а центр масс в плоскости будет двигаться равномерно и прямолинейно:

Если предположить, что в начальный момент система находится в покое, то будут равны нулю, т. е. центр масс системы будет оставаться в

покое во все время движения. Центр масс С лежит на прямой, соединяющей центр диска и жука. При этом имеет место соотношение

Обозначая через радиус диска, будем иметь

где

Поскольку величина х постоянна, центр масс диска должен находиться и» окружности радиуса х. Жук тоже должен находиться на окружности радиуса

Выберем неподвижную систему осей Схуг с началом в точке С. Выберем ось х так, чтобы в рассматриваемый момент времени жук находился на оси х, ось у направим перпендикулярно к оси х, а ось — по вертикали вверх. Пусть — скорость центра диска; и — относительная скорость жука; — абсолютная угловая скорость диска. Количество движения системы складывается из количества движения диска

и количества движения жука, равного произведению массы жука на его абсолютную скорость

Тогда проекции количества движения системы на оси координат (на основании закона сохранения количества движения) при заданных начальных условиях будут равны нулю:

Второе из полученных соотношений содержит две неизвестных величины . Для полного решения задачи необходимо иметь еще одно уравнение. Заметим, что связи, наложенные на систему, допускают вращение всей системы вокруг любой неподвижной вертикальной оси. Среди возможных вращений находится и вращение вокруг вертикальной неподвижной оси, проходящей через центр масс системы. Поэтому можно применить теорему об изменении момента количества движения системы относительно вертикальной оси Внешние силы — силы тяжести — не дают момента относительно этой оси. Следовательно,

Принимая во внимание, что в начальный момент система находится в покое, будем иметь

Вычислим сначала момент количества движения диска относительно оси

Определяя скорости по формуле Эйлера

где

для векторного произведения запишем матрицу

откуда получим

Подстановка этих значений в выражение для момента количества движения дает

Зная количество движения жука, легко найти его момент количества движения:

после чего интеграл площадей запишем в виде

Уравнения (а) и полностью определяют закон движения системы. Учитывая, что

и определяя из найденных первых интегралов уравнений движения неизпестные , будем иметь

Из этих формул видно, что первоначально выбранное направление угловой скорости не совпадает с действительным, так же как и направление скорости центра масс диска.

Полученные значения скоростей постоянны и зависят лишь от расположения масс системы. Следовательно, после начала движения жука центр масс диска движется с постоянной по величине скоростью, а его угловая скорость также постоянна.

Замечание. Если связи, наложенные на систему материальных точек, допускают поворот всей системы как твердого тела вокруг трех взаимно перпендикулярных осей, то будем иметь три уравнения, каждое из которых отвечает возможному вращению системы около одной из осей. Выбирая за указанные оси координатные оси будем иметь

Введем вектор К момента количества движения системы относительно начала координат, с проекциями

Тогда три скалярных уравнения можно будет заменить одним векторным

Результат можно сформулировать в виде следующей теоремы: Теорема. Производная от вектора момента количества движения равна сумме моментов внешних активных сил относительно начала координат.

Полученному результату можно дать и другую формулировку, принадлежащую А. Резалю (1828—1896).

Теорема. Скорость изменения вектора момента количества движения системы относительно начала координат равна сумме моментов внешних активных сил относительно того же начала

Теорема об изменении момента количества движения для системы частиц с переменной массой.

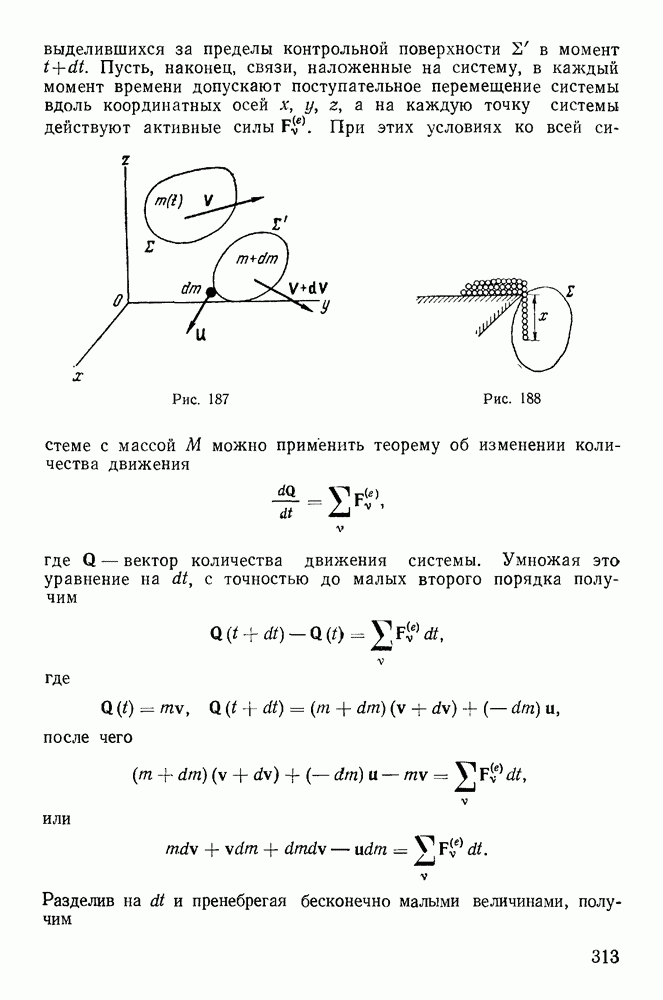
Рассмотрим движение системы материальных точек, ограниченных контрольной поверхностью 2, и предположим, что отдельные частицы системы могут выходить за пределы контрольной поверхности, а сама поверхность перемещается некоторым образом относительно инерциальной системы координат Обозначим через К вектор момента количества движения всей системы материальных точек относительно начала координат. Пусть — момент количества движения системы материальных точек, расположенных внутри контрольной поверхности момент количества движения системы частиц, находящихся вне контрольной поверхности. Кроме того, будем предполагать, что в момент

а в момент

Применяя теорему об изменении момента количества движения ко всей системе материальных точек, получим

где

Обозначая

и принимая во внимание, что

перепишем теорему об изменении момента количества движения в виде

где определяет «расход» момента количества движения через контрольную поверхность - в единицу времени. Полученная формула определяет изменение момента количества движения системы, ограниченной контрольной поверхностью, относительно инерциальной системы координат.