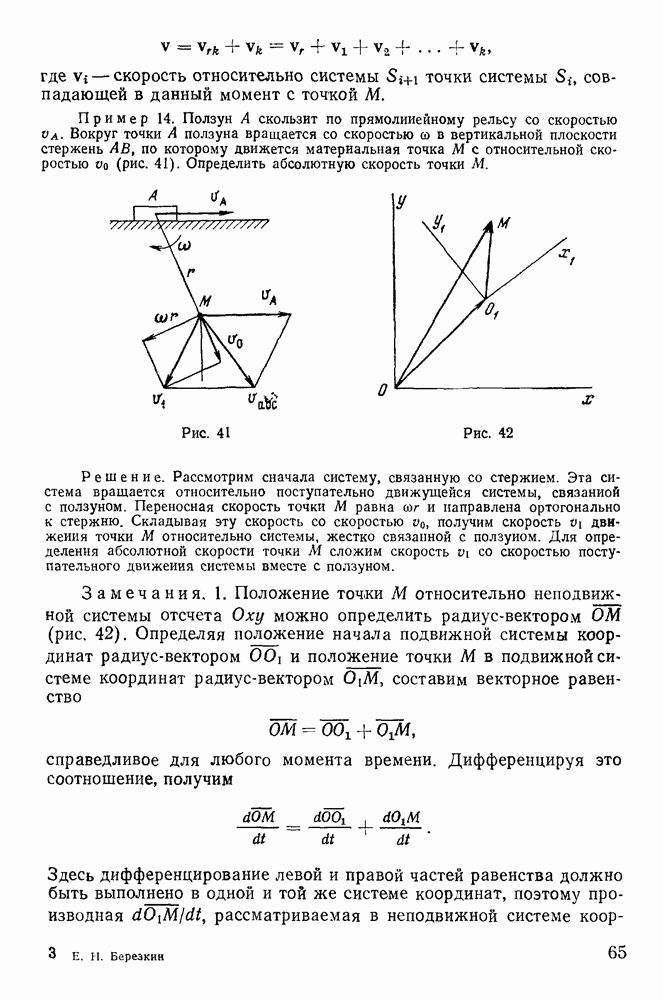
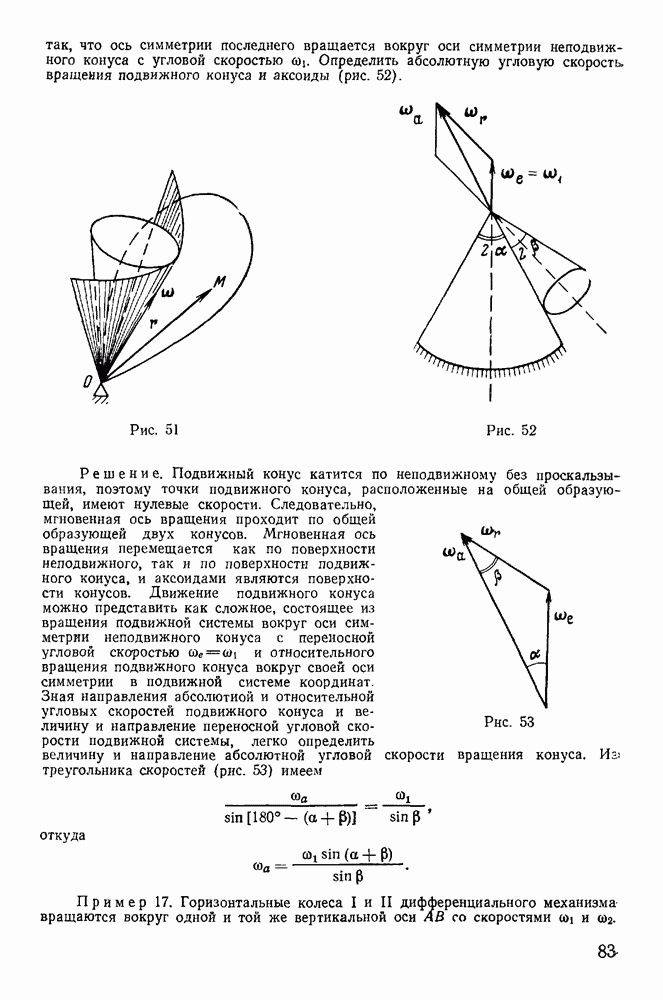
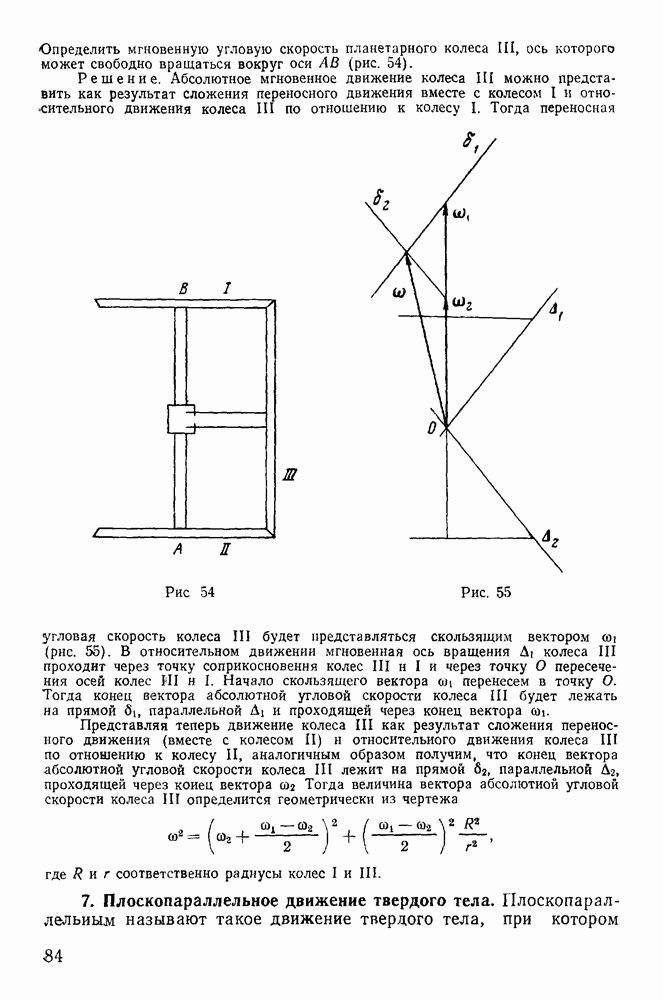
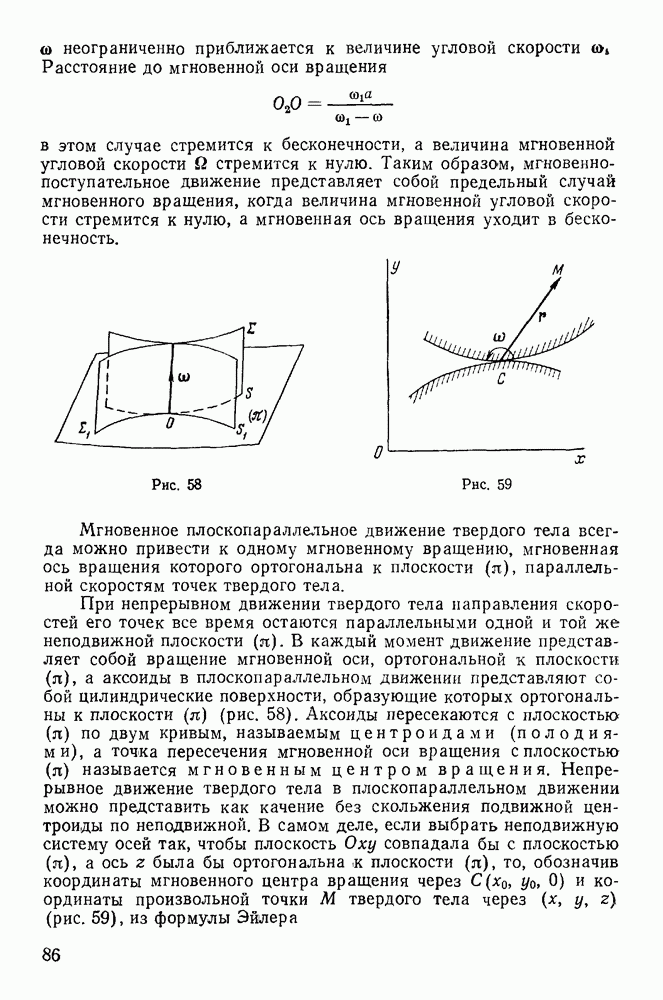
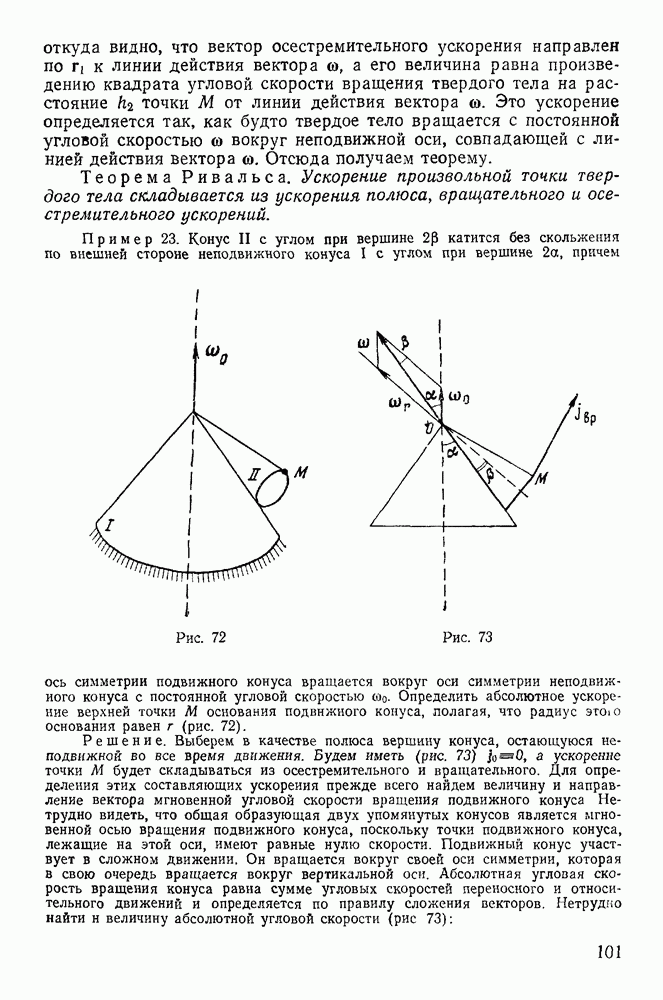
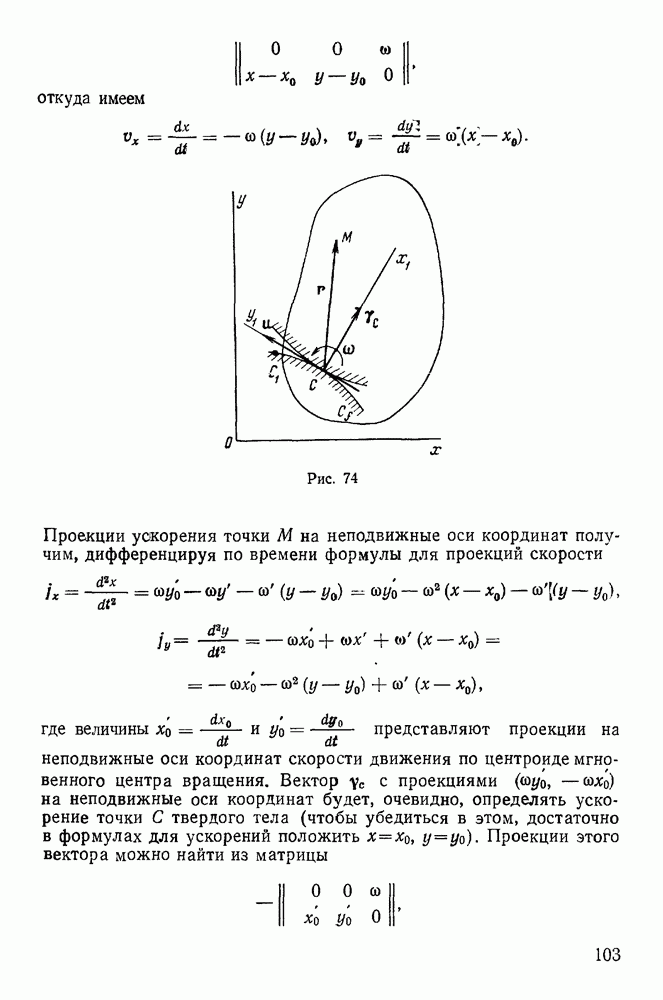
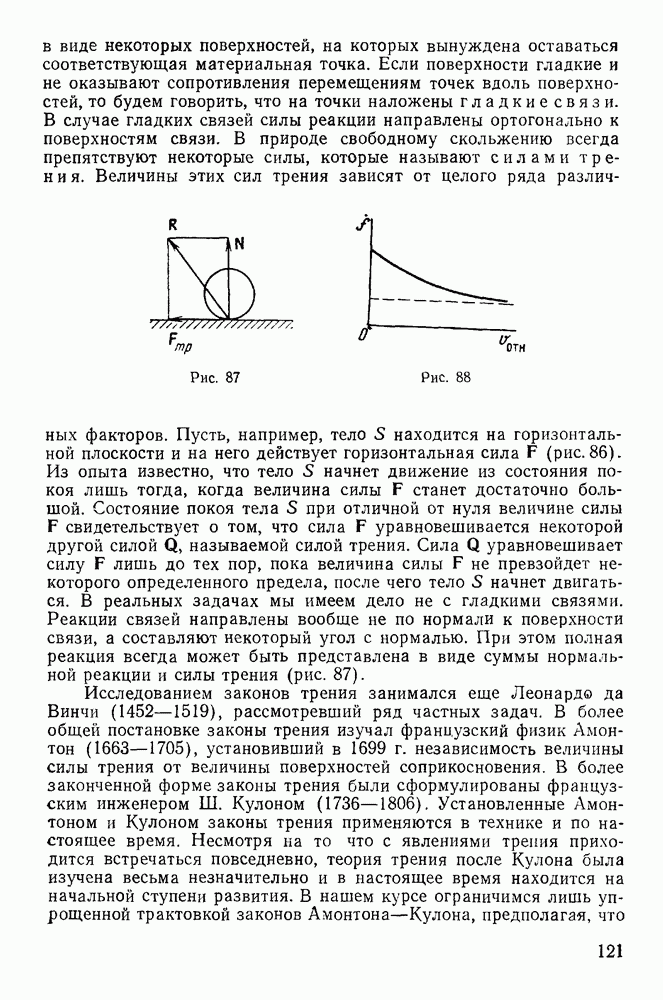
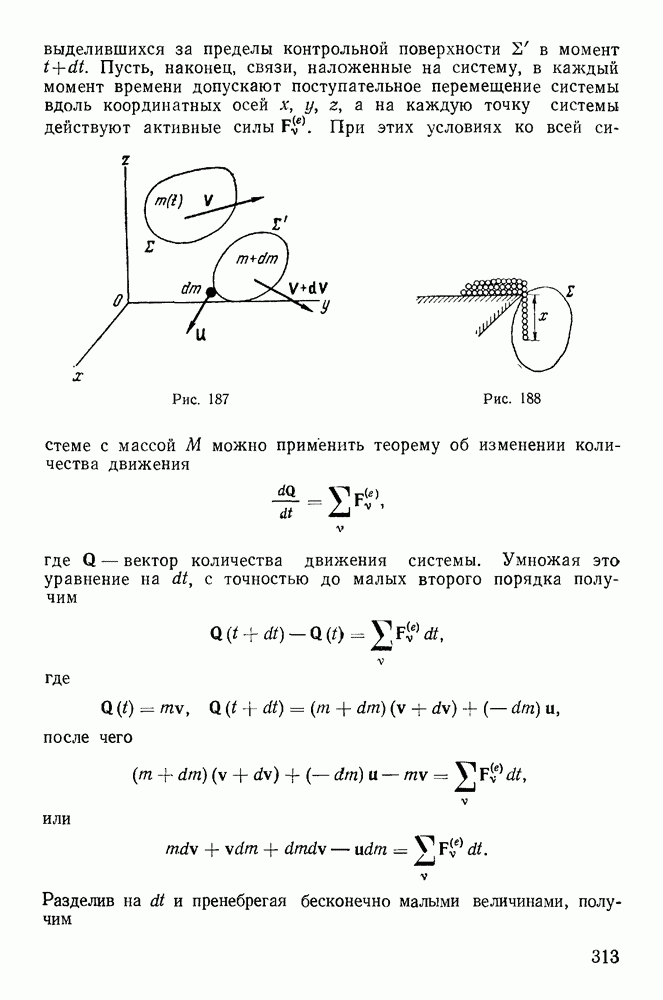
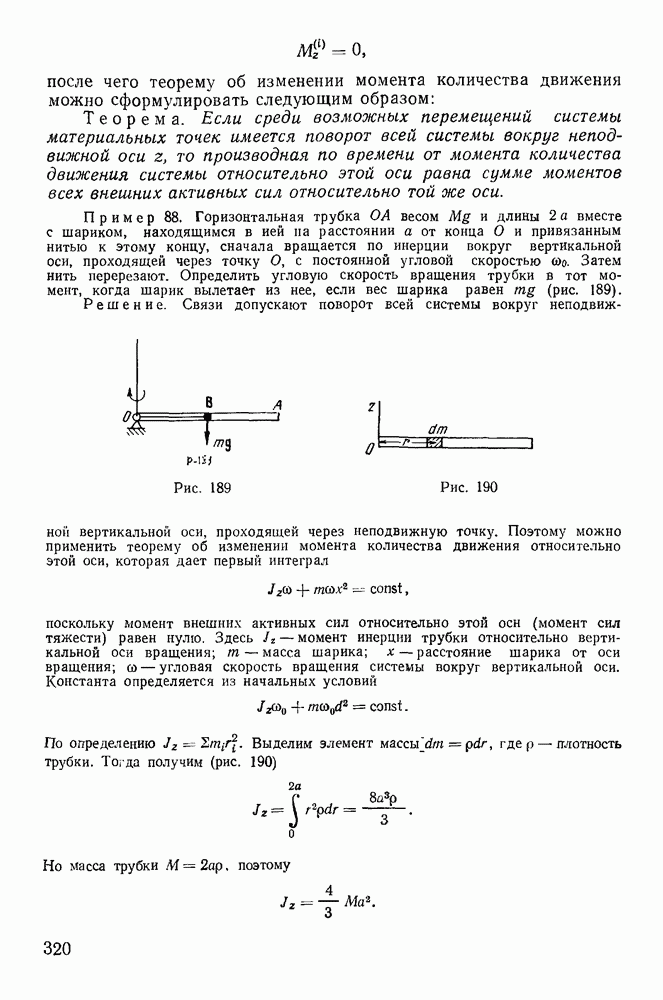
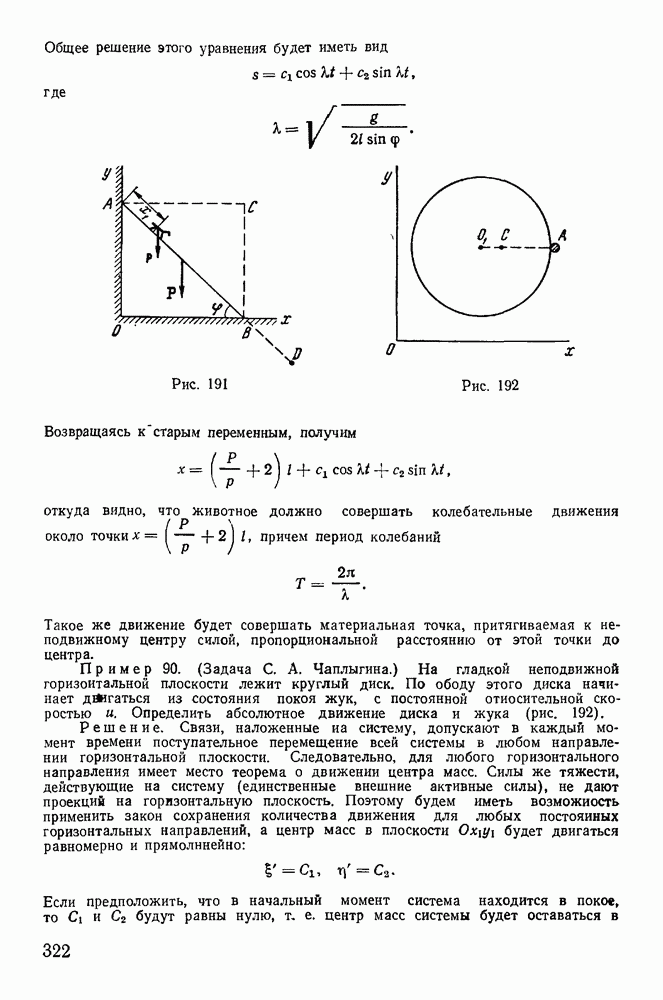
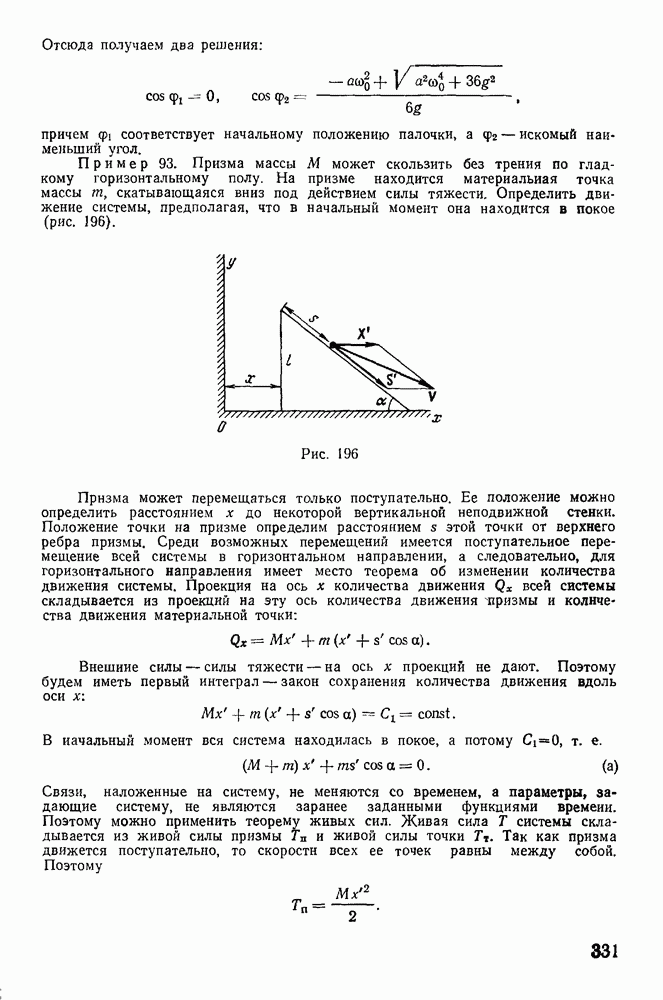
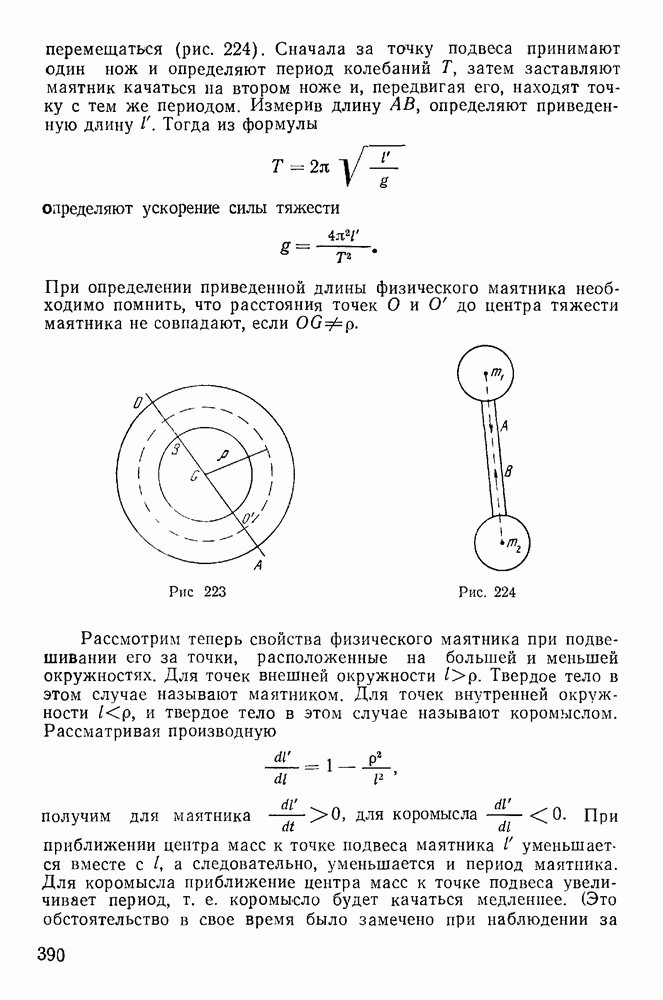
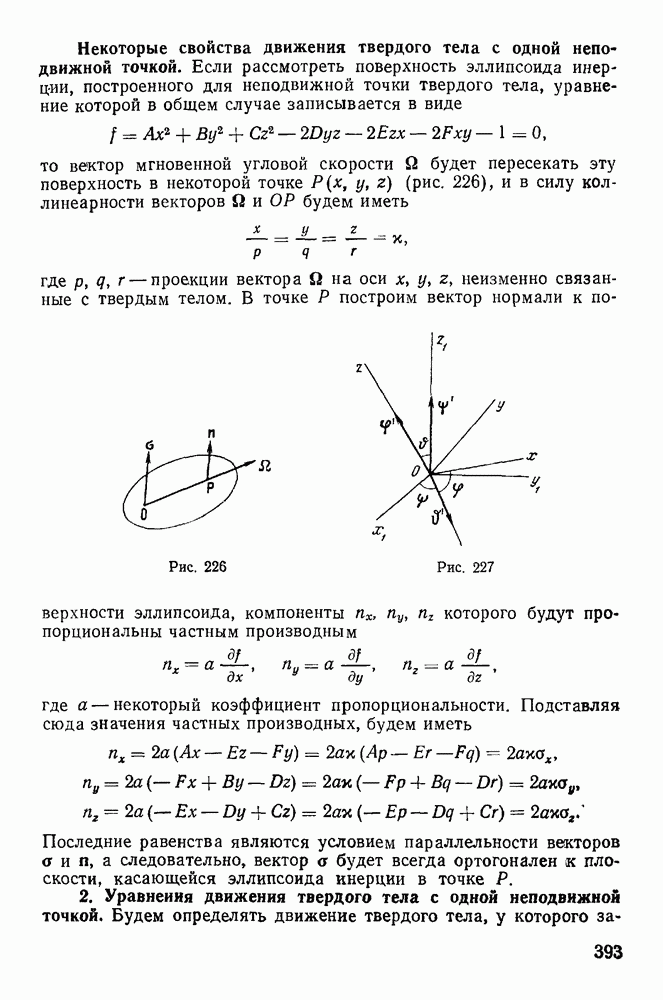
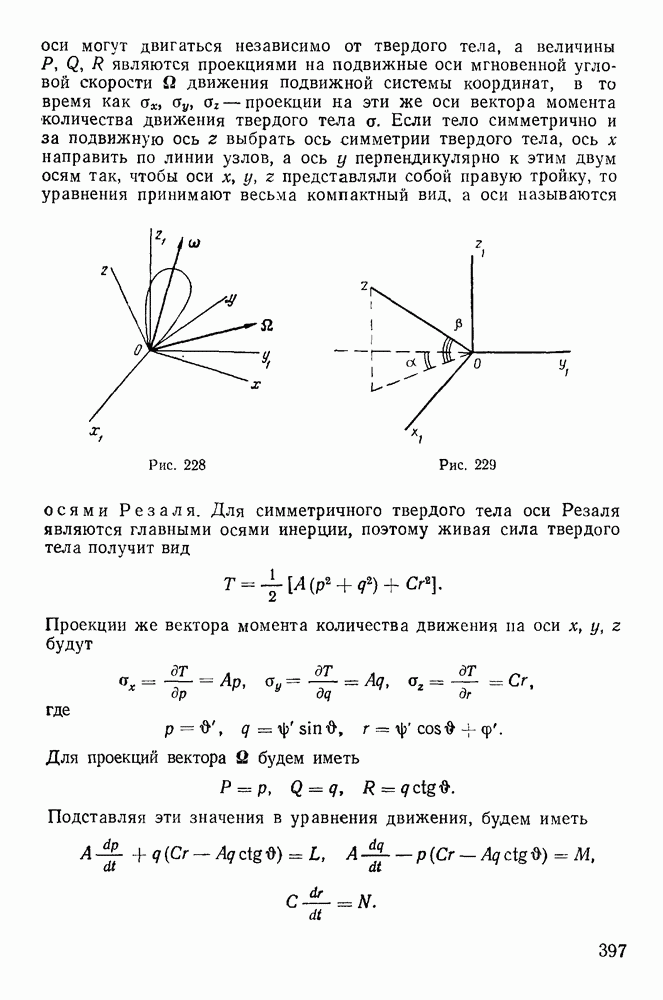
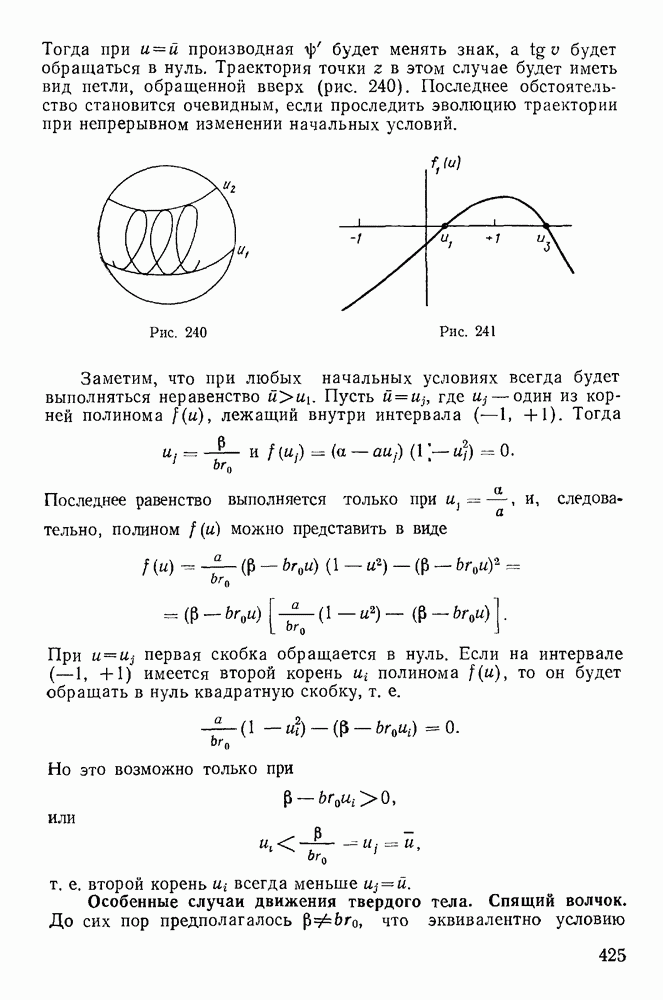
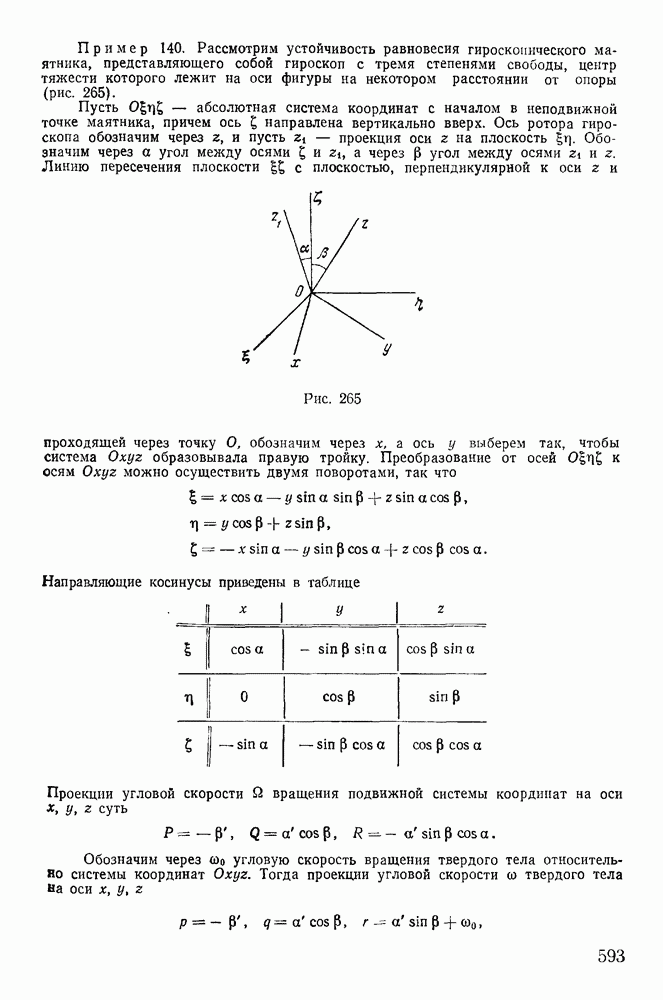
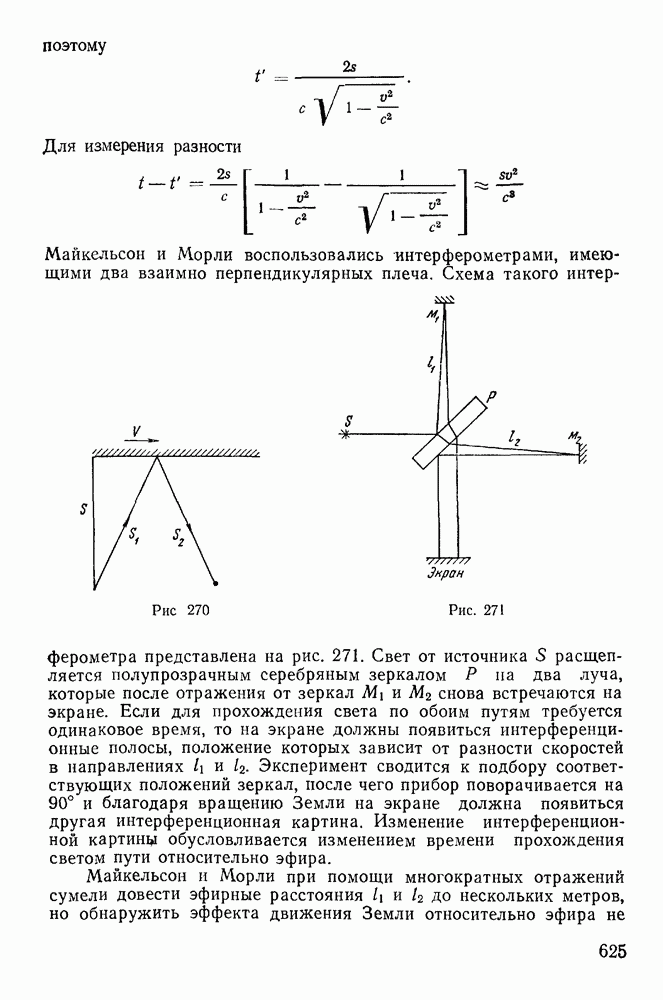
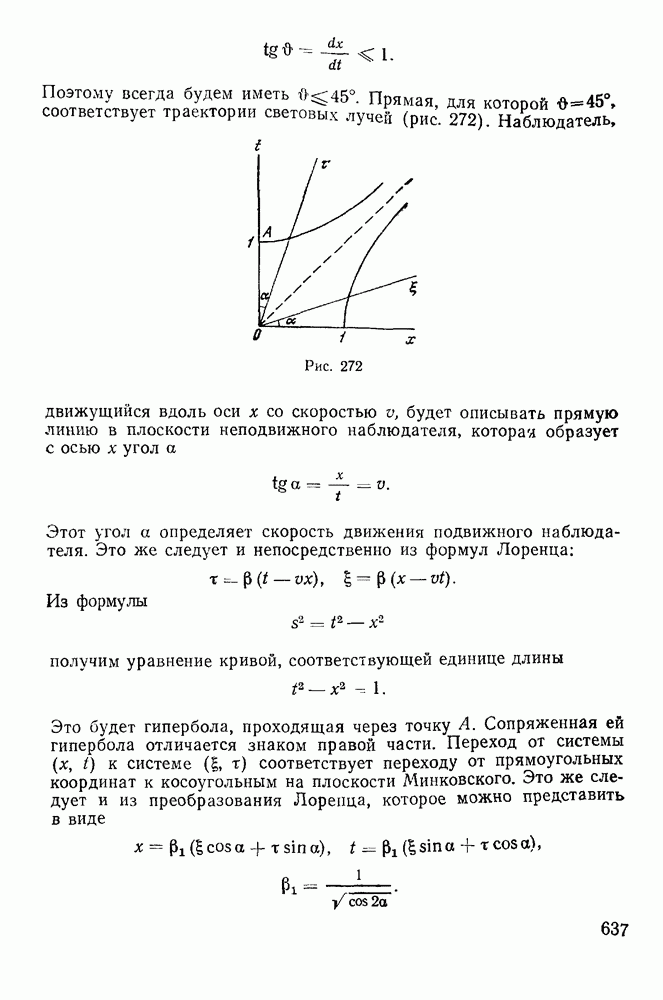
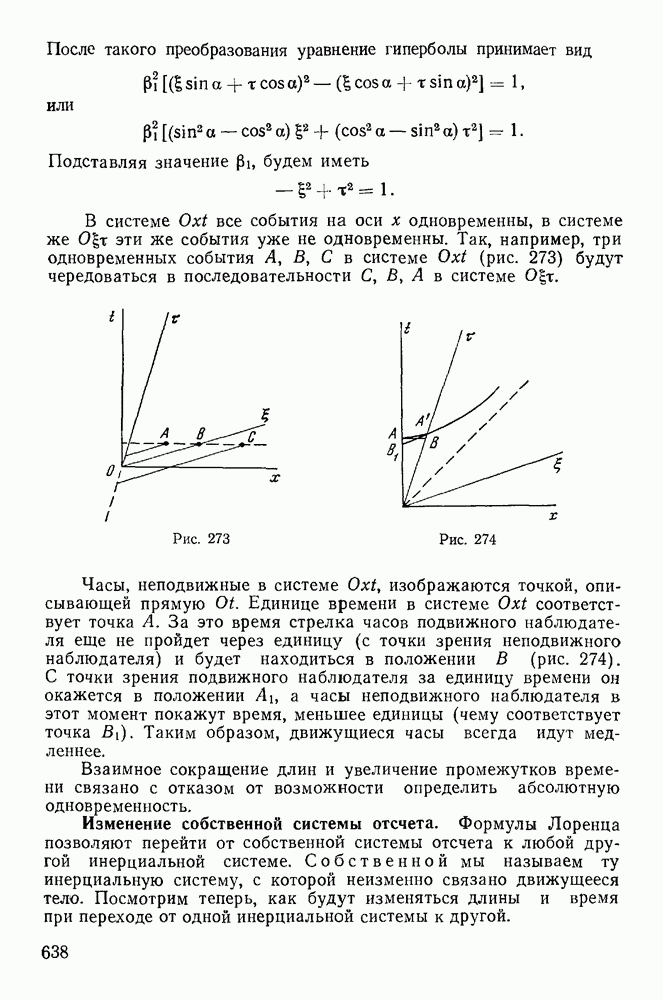
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
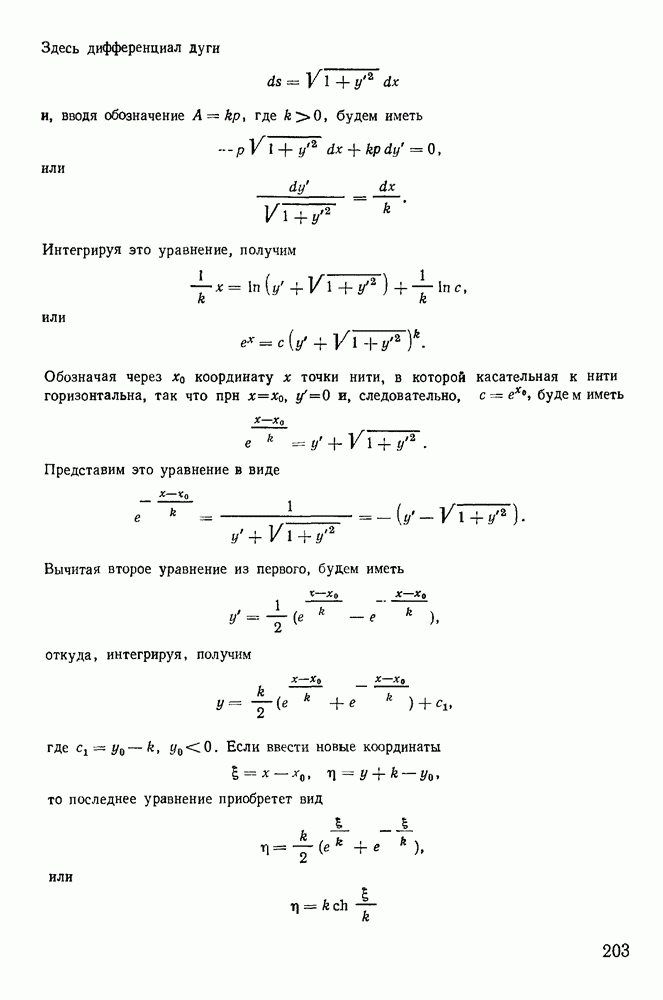
2. Движение материальной точки по поверхности.
Вторым важным для приложений случаем движения несвободной материальной точки является случай движения точки по поверхности.
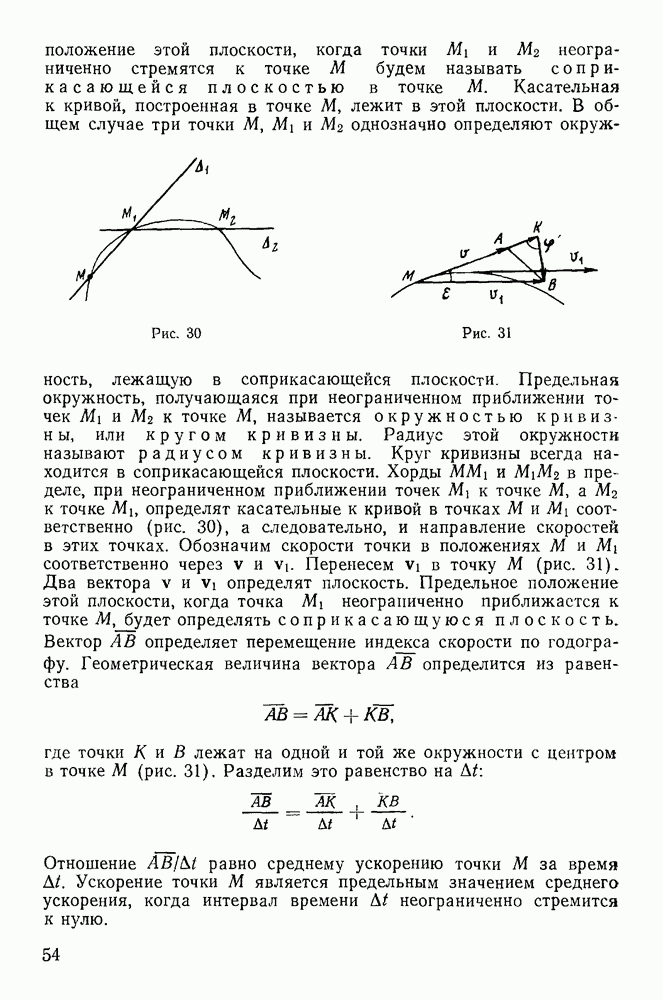
Предположим, что в своем движении материальная точка все время остается на некоторой гладкой поверхности

которая стесняет ее перемещения.

Рис. 164
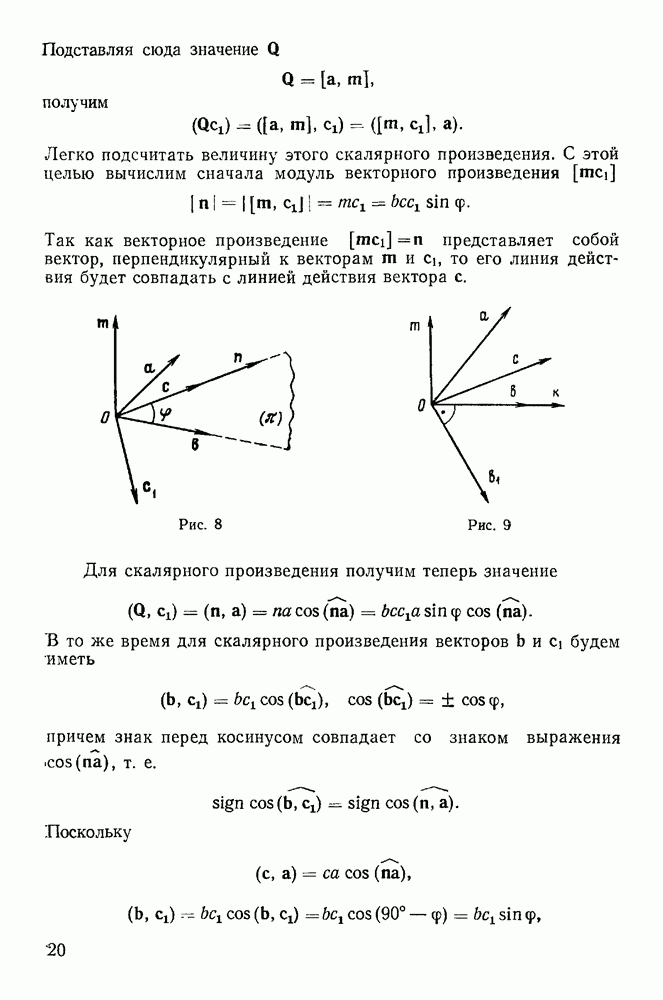
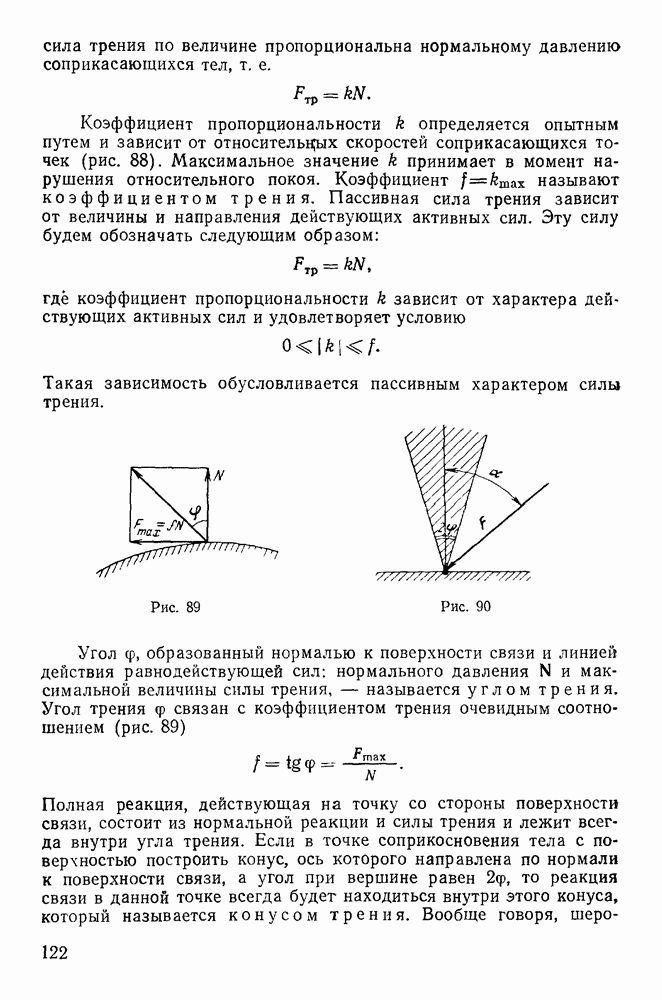
Форма и положение поверхности могут изменяться со временем, а сама поверхность оказывает воздействие на точку. Это воздействие можно определить некоторой силой, которую называют силой реакции. Она не препятствует перемещению точки по поверхности и направлена по нормали к поверхности (рис. 164), так как по предположению поверхность является гладкой. Аналитически это условие можно представить в виде

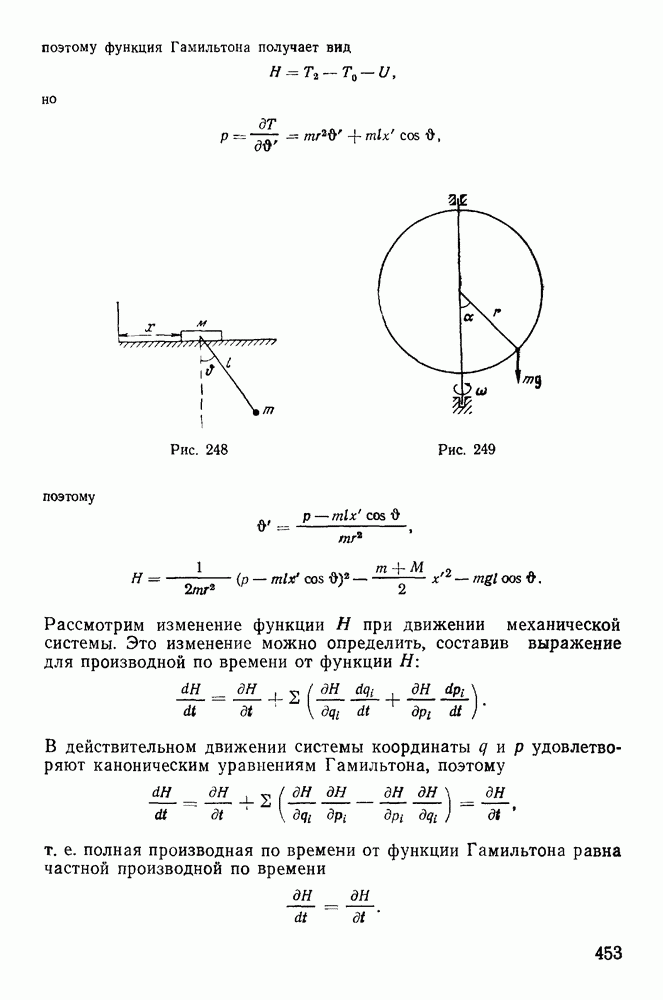
Движение точки полностью определяется двумя силами: активной силой F и силой реакции  а уравнения движения имеют вид
а уравнения движения имеют вид

Неизвестные величины  можно заменить одной неизвестной величиной К, после чего уравнения перепишутся следующим образом:
можно заменить одной неизвестной величиной К, после чего уравнения перепишутся следующим образом:

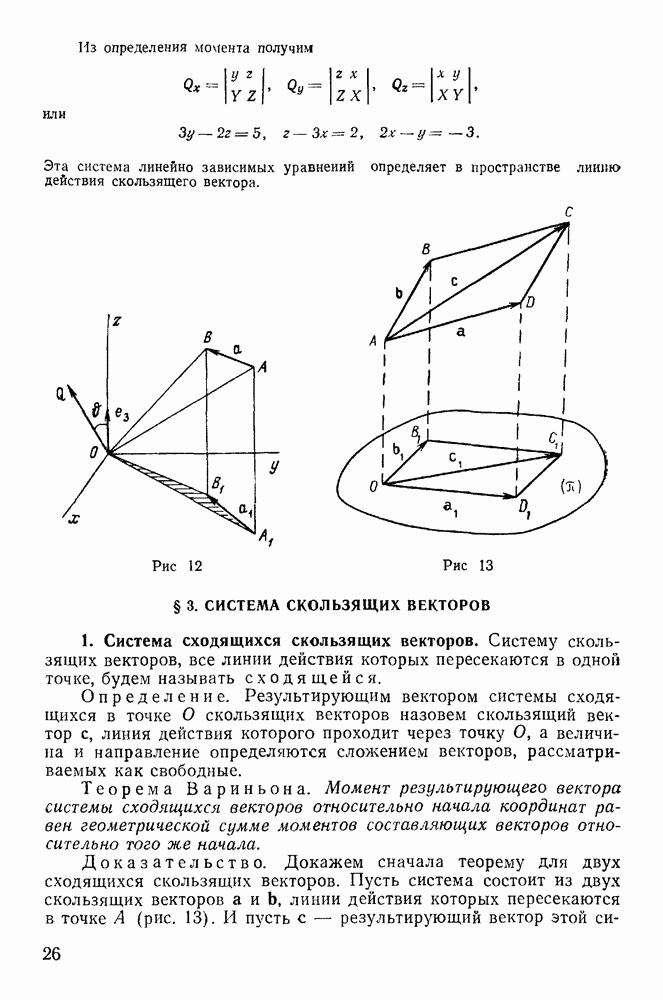
Уравнение  связывает координаты точки и является уравнением связи. Три уравнения движения вместе с уравнением связи полностью определяют движение материальной точки. Сами уравнения называются уравнениями Лагранжа с множителями.
связывает координаты точки и является уравнением связи. Три уравнения движения вместе с уравнением связи полностью определяют движение материальной точки. Сами уравнения называются уравнениями Лагранжа с множителями.
а) Теорема живых сил.
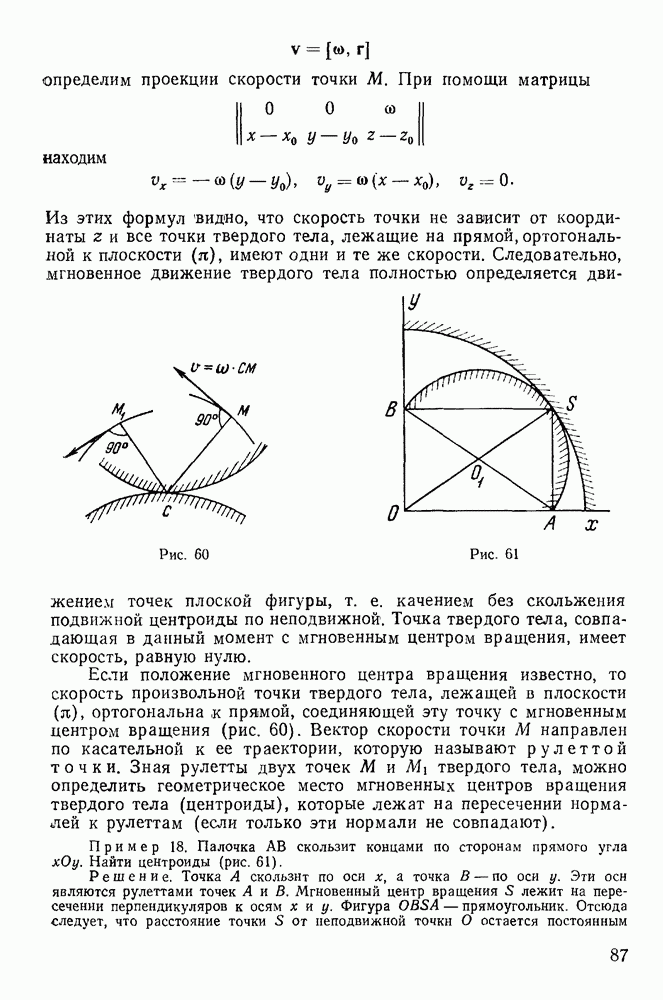
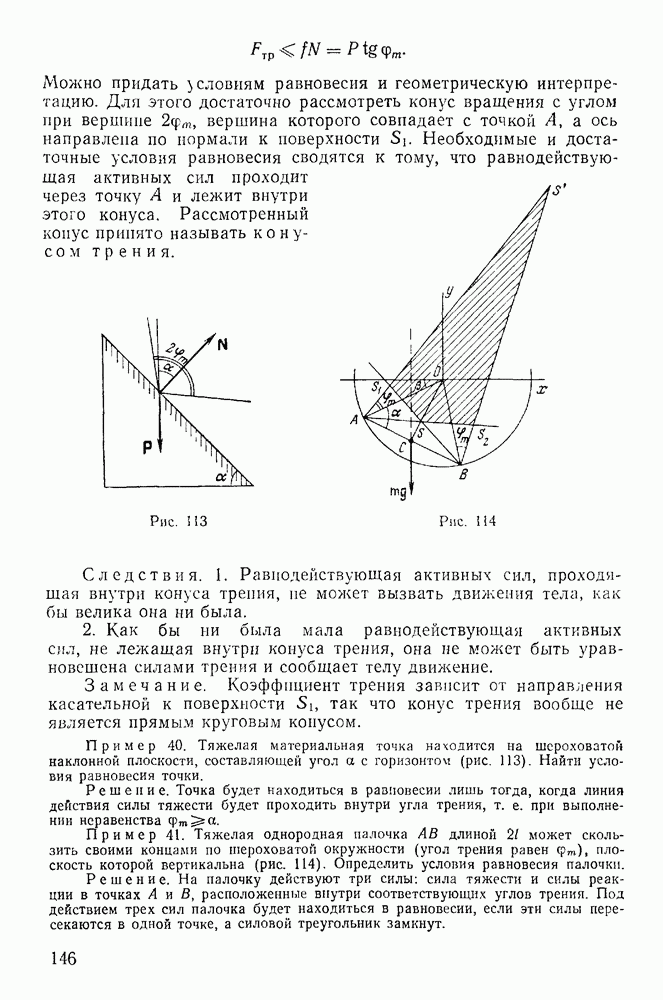
При изучении движения несвободной материальной точки большое значение имеют общие теоремы динамики материальной точки, и в первую очередь теорема живых сил.
Если точка вынуждена оставаться на поверхности

и определен закон движения точки, то ее координаты являются некоторыми функциями времени, после подстановки которых в уравнение связи, последнее становится тождеством. Дифференцируя это тождество по времени, будем иметь

Здесь  — проекции скорости точки на декартовы оси координат в действительном движении точки.
— проекции скорости точки на декартовы оси координат в действительном движении точки.
Чтобы получить теорему живых сил, умножим каждое из уравнений движения соответственно на  и сложим результат
и сложим результат

все это преобразуется к виду

и в результате получаем теорему живых сил для материальной точки, движущейся по поверхности.
Теорема. Изменение живой силы материальной точки равно работе заданных сил на действительном перемещении точки и некоторому дополнительному члену

представляющему работу сил реакций связи на действительном перемещении точки.
Если поверхность неподвижна и не изменяет своей формы, то

и теорема живых сил приобретает такой же вид, как и для свободной материальной точки, т. е.

Если, кроме того, активные силы обладают силовой функцией, то будет существовать интеграл живых сил

Для существования интеграла живых сил достаточно, чтобы связи не зависели явно от времени и активные силы обладали силовой функцией.
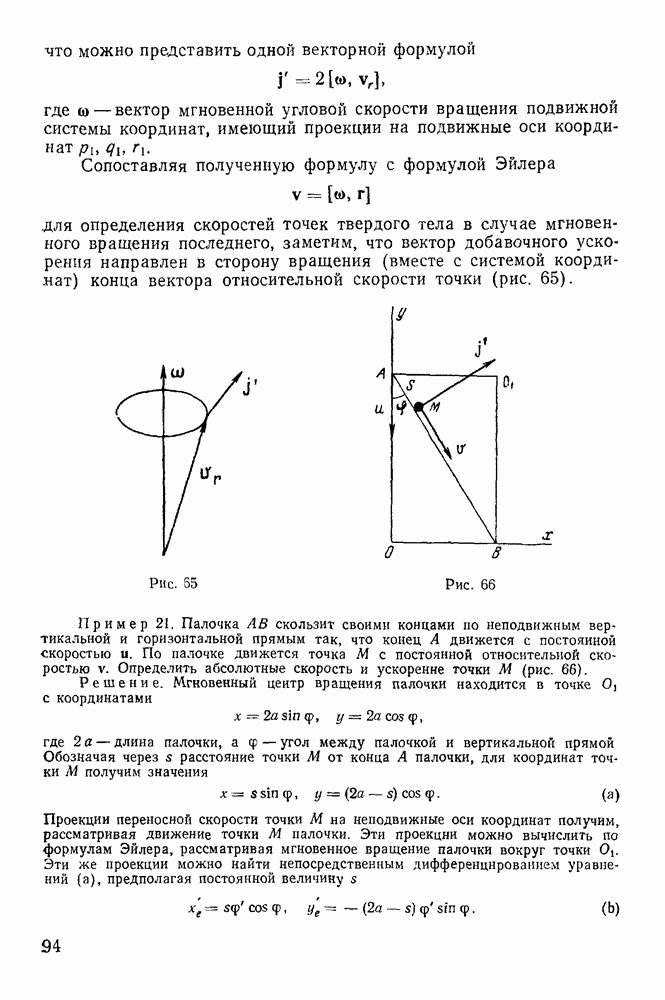
б) Естественные уравнения движения точки по поверхности.
Положение материальной точки на поверхности определяется двумя параметрами. Для нахождения зависимости этих параметров от времени необходимо иметь по крайней мере два дифференциальных уравнения движения. Одной теоремы живых сил теперь уже оказывается недостаточно. Уравнения движения в декартовых координатах часто оказываются очень сложными, поэтому приходится искать другие пути решения задачи о движении.
Предположим, что уравнение поверхности, на которой вынуждена оставаться материальная точка, не содержит явно времени. Точка  в своем движении по поверхности опишет некоторую траекторию, полностью расположенную на этой поверхности. Рассматривая уравнения движения в проекциях на естественные оси координат (рис. 165), замечаем, что касательная к траектории будет расположена в касательной плоскости к поверхности, а нормальная реакция будет давать проекции только на нормаль и (бинормаль
в своем движении по поверхности опишет некоторую траекторию, полностью расположенную на этой поверхности. Рассматривая уравнения движения в проекциях на естественные оси координат (рис. 165), замечаем, что касательная к траектории будет расположена в касательной плоскости к поверхности, а нормальная реакция будет давать проекции только на нормаль и (бинормаль

Если активная сила на точку не действует, т. е.  , то из первого уравнения находим
, то из первого уравнения находим

следовательно, точка будет двигаться по поверхности с постоянной скоростью. Из последнего уравнения движения следует, что  а потому реакция будет расположена в соприкасающейся плоскости, т. е. нормаль к траектории будет совпадать с нормалью к поверхности.
а потому реакция будет расположена в соприкасающейся плоскости, т. е. нормаль к траектории будет совпадать с нормалью к поверхности.

Рис. 165

Рис. 166
Кривые, обладающие этим свойством, называются геодезическими. Таким образом, если на точку, движущуюся по поверхности, активные силы не действуют, то точка движется по геодезической кривой с постоянной по величине скоростью.
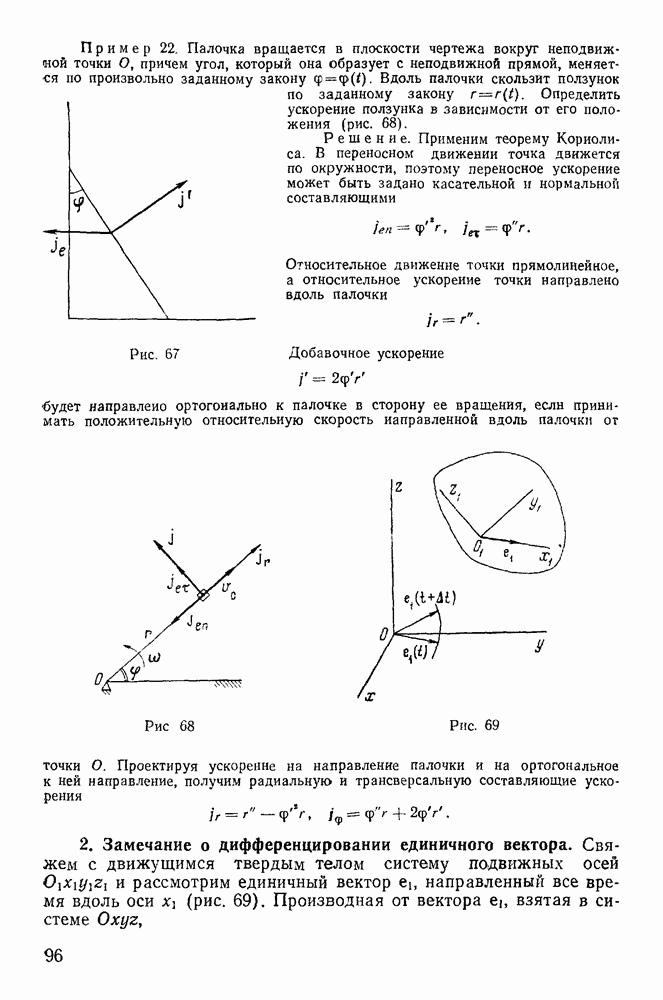
в) Движение точки по поверхности вращения.
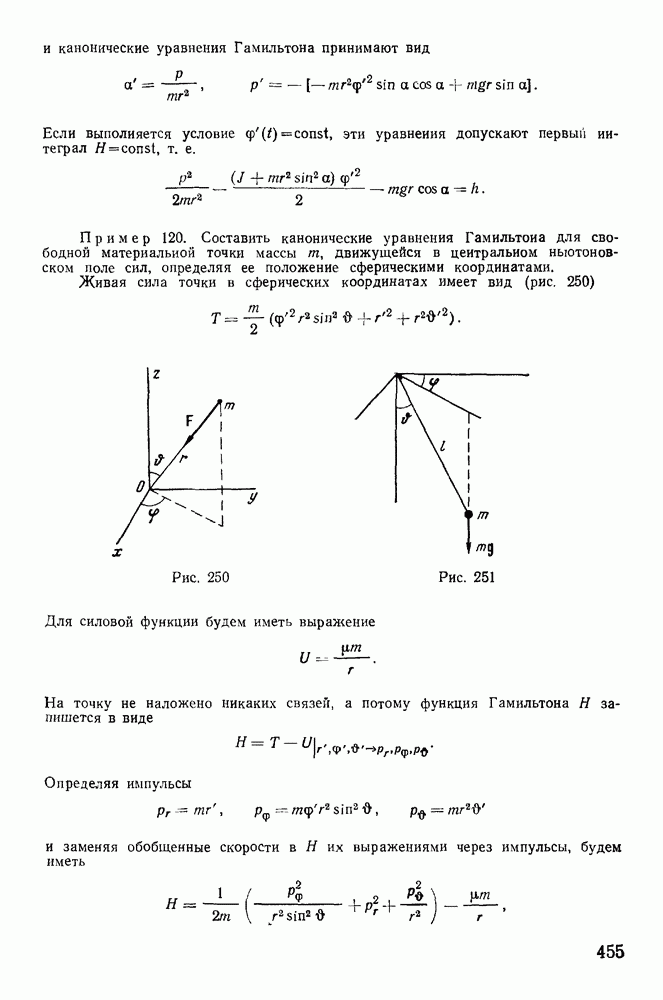
Теорема Клеро. В качестве примера рассмотрим движение материальной точки по поверхности вращения. Пусть ось z — ось симметрии поверхности. Если на точку не действуют активные силы, то точка будет двигаться по геодезической кривой  образующей с меридианом угол
образующей с меридианом угол  (рис. 166), причем движение происходит с постоянной по величине скоростью. Единственной силой, действующей на точку, будет сила нормальной реакции поверхности
(рис. 166), причем движение происходит с постоянной по величине скоростью. Единственной силой, действующей на точку, будет сила нормальной реакции поверхности  направленная ортогонально к поверхности. Линия действия этой силы пересекает ось
направленная ортогонально к поверхности. Линия действия этой силы пересекает ось  Из теоремы об изменении момента количества движения точки относительно оси z будем иметь
Из теоремы об изменении момента количества движения точки относительно оси z будем иметь

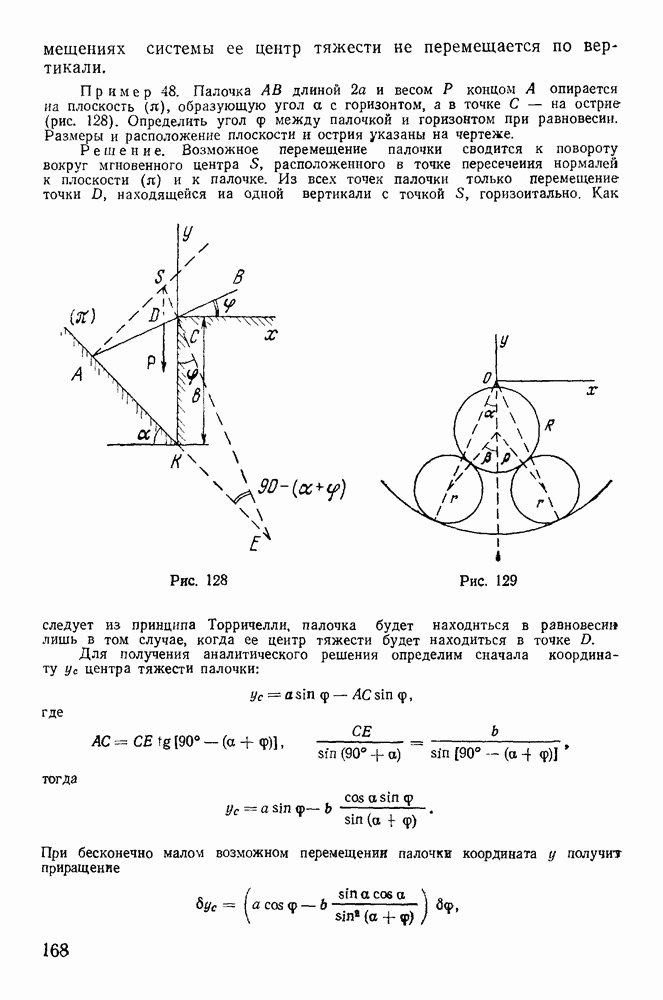
так что

Подставляя сюда явное выражение для момента количества движения, получим

Из постоянства массы и скорости отсюда сразу следует

т. е. вдоль геодезической линии поверхности вращения произведение радиуса параллели на синус азимута есть величина постоянная. В этом соотношении заключается теорема Клеро (1713—1765).
Геодезические линии поверхности вращения легко определить, если взять за систему отсчета цилиндрическую систему координат. В этой системе дифференциал дуги

Пусть поверхность задана уравнением

Из интеграла живых сил при отсутствии активных сил получаем

или

Подставляя сюда  из уравнения поверхности
из уравнения поверхности

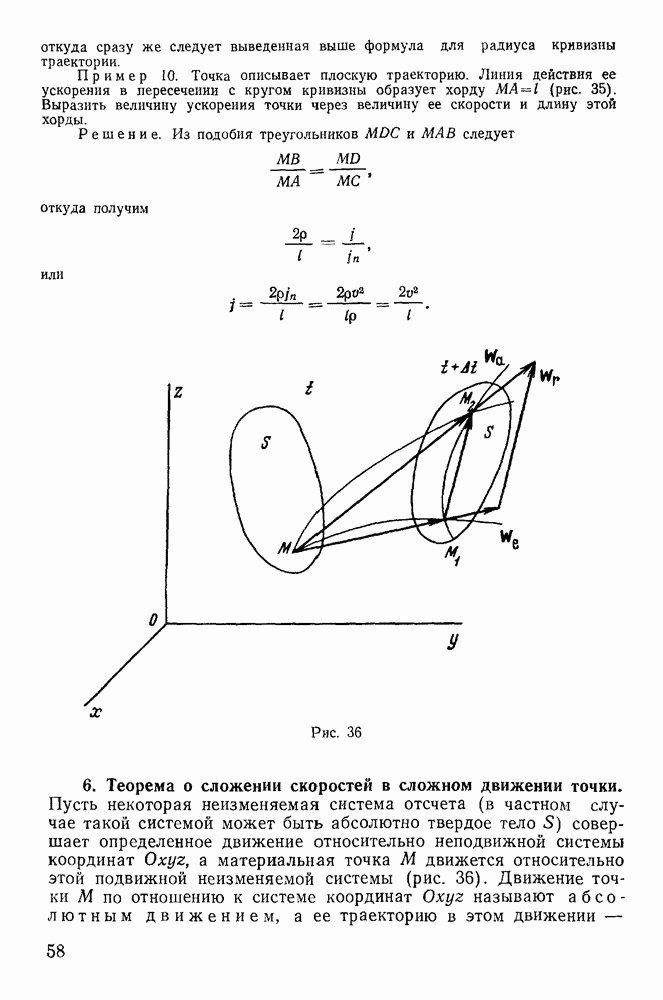
будем иметь

Из интеграла площадей имеем

Определяя отсюда  и подставляя в интеграл живых сил, получим
и подставляя в интеграл живых сил, получим

и после разделения переменных приходим к уравнению

интегрирование которого дает

Эти формулы определяют геодезическую кривую на поверхности вращения.
Замечания. 1. Уравнение  исключает из рассмотрения цилиндрические поверхности вращения
исключает из рассмотрения цилиндрические поверхности вращения  . В последнем случае
. В последнем случае  откуда
откуда

Исключая при помощи интеграла площадей время, найдем

и, интегрируя найденное уравнение, получим

Это и есть уравнение винтовой линии.
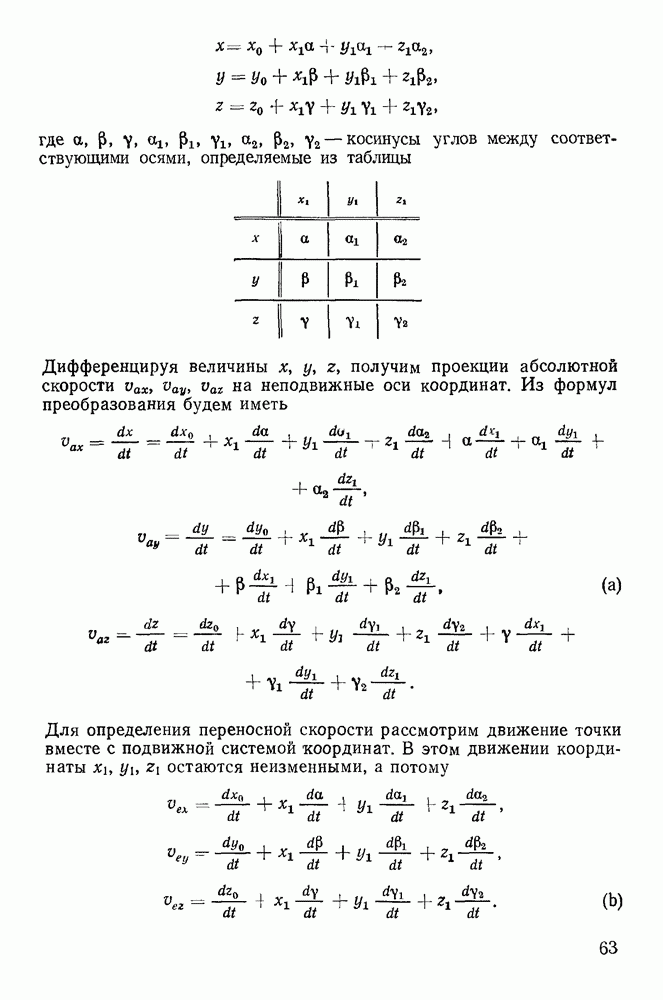
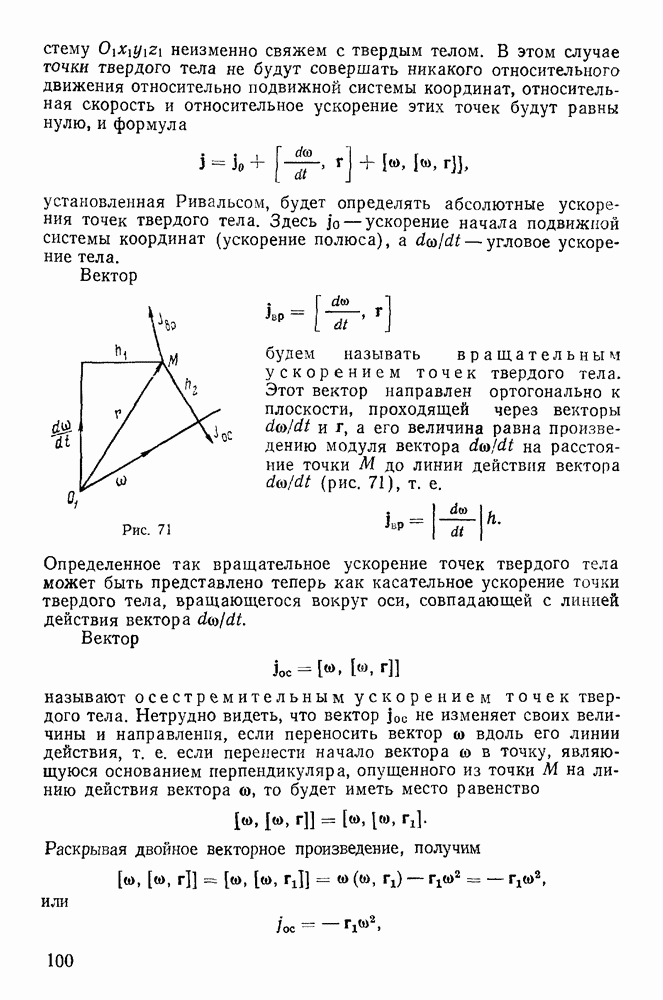
2. Можно уравнения движения точки отнести к специальным осям  имеющим начало в движущейся точке. Здесь
имеющим начало в движущейся точке. Здесь  - единичный вектор касательной к траектории точки, направленный в сторону движения;
- единичный вектор касательной к траектории точки, направленный в сторону движения;  — единичный вектор внутренней нормали к поверхности, а единичный вектор
— единичный вектор внутренней нормали к поверхности, а единичный вектор  расположен в касательной ллоскости перпендикулярно к
расположен в касательной ллоскости перпендикулярно к  так, чтобы векторы
так, чтобы векторы  образовывали правую систему (рис. 167). Обозначим через
образовывали правую систему (рис. 167). Обозначим через  угол между направлением главной нормали траектории
угол между направлением главной нормали траектории  и вектором
и вектором  Проектируя уравнения движения на оси
Проектируя уравнения движения на оси  получим
получим

Первое и второе уравнения определяют движение точки по поверхности, последнее же служит для определения реакции поверхности.
В целях дальнейшего преобразования уравнений рассмотрим произведение

Скалярное произведение  в силу ортогональности векторов равно нулю, так что
в силу ортогональности векторов равно нулю, так что

Для всех траекторий, имеющих одну и ту же касательную в точке, будем иметь

поэтому


Рис. 167

Рис. 168
Для траектории, расположенной в плоскости нормального сечения, имеем  Если обозначить через
Если обозначить через  радиус кривизны нормального сечения, то получим
радиус кривизны нормального сечения, то получим

т. е. радиус кривизны произвольной кривой на поверхности вращения по своей абсолютной величине равен проекции на ее соприкасающуюся плоскость радиуса кривизны нормального сечения, имеющего с траекторией общую касательную (теорема Менье). Теперь уравнения движения можно представить в виде

где  — радиус кривизны нормального сечения, а величина
— радиус кривизны нормального сечения, а величина  называется радиусом геодезической кривизны (рис. 168).
называется радиусом геодезической кривизны (рис. 168).
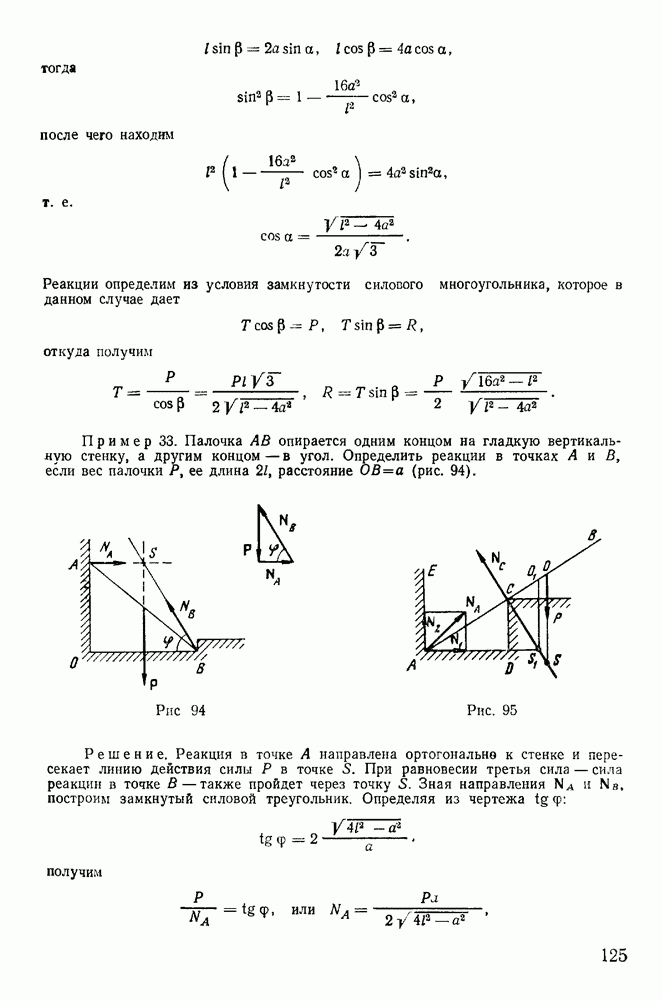
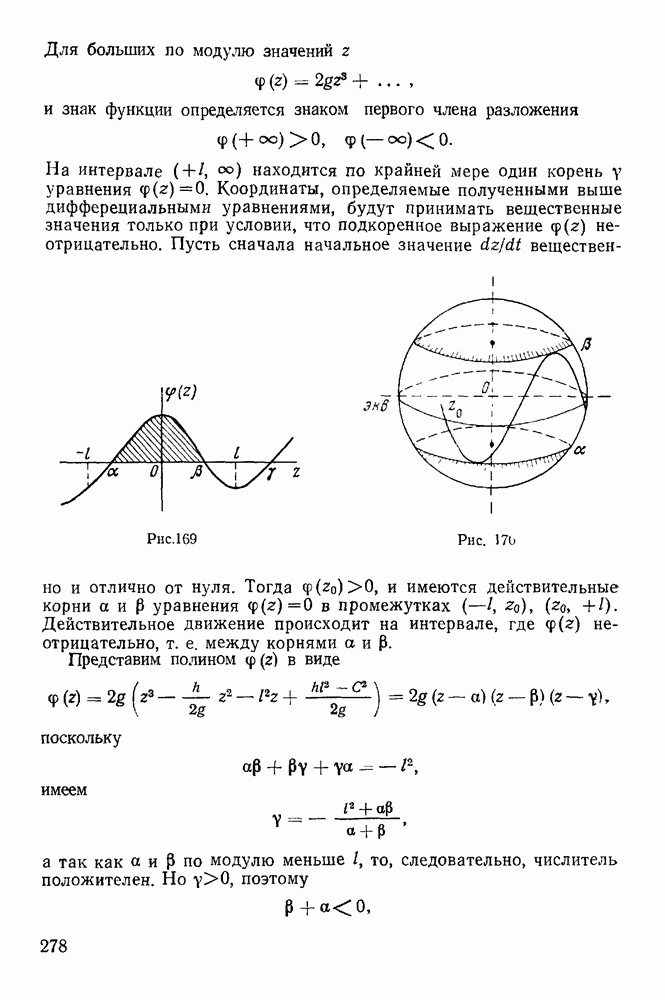
г) Сферический маятник.
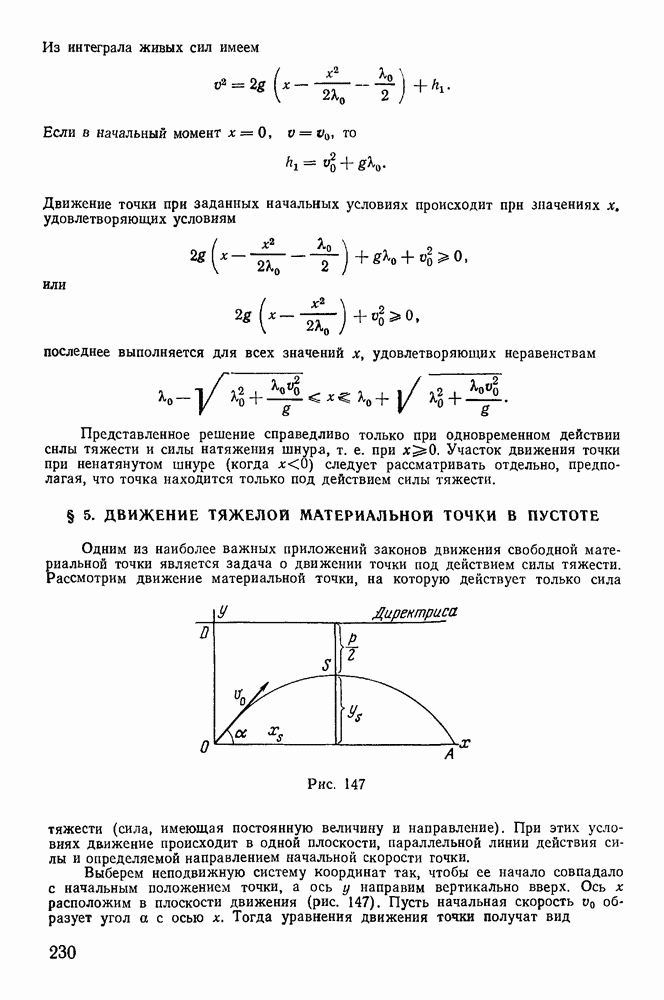
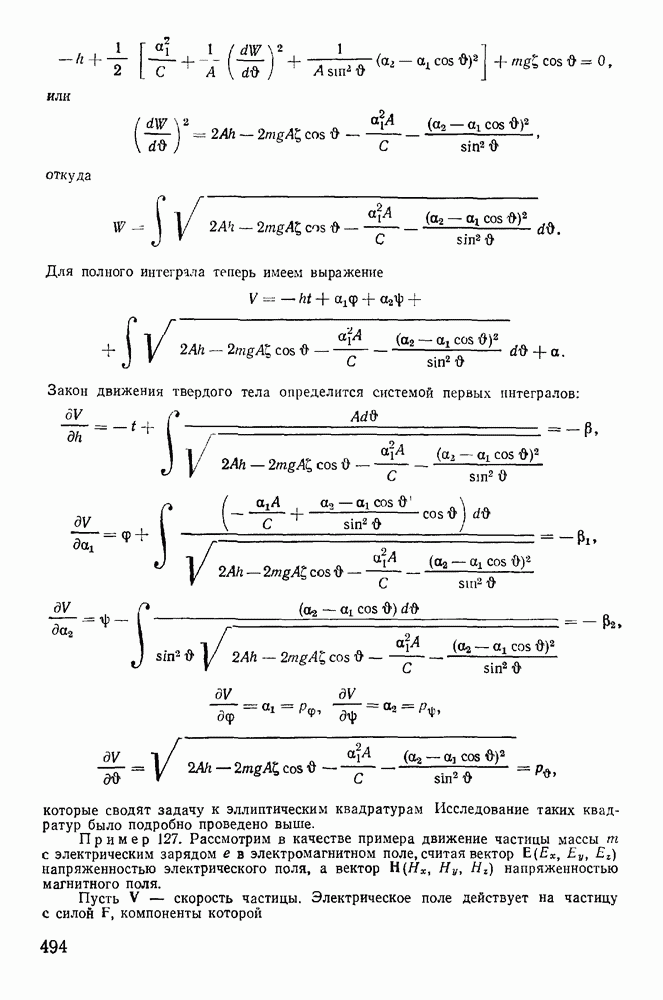
Рассмотрим задачу о движении тяжелой материальной точки по поверхности сферы. Связь эта может быть реализована в виде нерастяжимого и несжимаемого стержня, не имеющего массы, соединяющего точку с началом координат. На точку действует сила тяжести  и сила реакции
и сила реакции  направленная вдоль стержня. Если реакция всегда направлена
направленная вдоль стержня. Если реакция всегда направлена
к центру, то связь можно осуществить при помощи нерастяжимой идеальной нити. Уравнение связи имеет вид

и не содержит явно времени. Ось z направим вертикально вверх. Активная сила — сила тяжести — допускает существование силовой функции

а значит, существует интеграл живых сил

который можно представить в виде

Момент активных сил и сил реакции связи относительно оси z равен нулю, поэтому из теоремы об изменении момента количества движения относительно оси z имеем

откуда

или

где  секторная скорость точки.
секторная скорость точки.
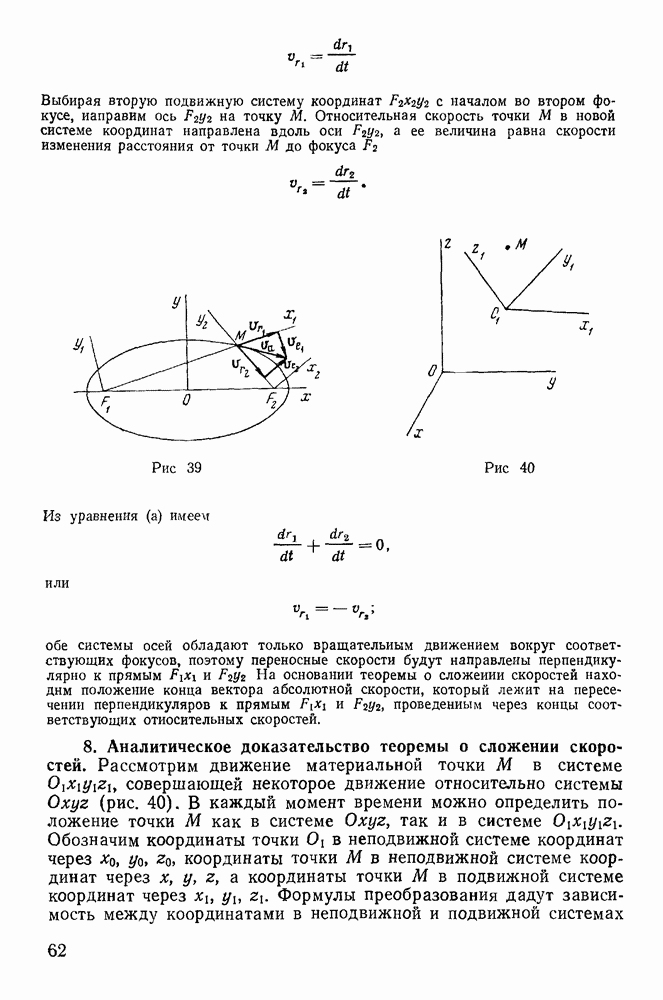
Задачу удобнее решать в цилиндрических координатах  . В этих координатах интеграл живых сил и интеграл площадей получают вид
. В этих координатах интеграл живых сил и интеграл площадей получают вид

Уравнение связи в цилиндрических координатах получает вид

откуда дифференцированием находим

Переписывая теперь интеграл живых сил

преобразуем его к виду

окончательно получим

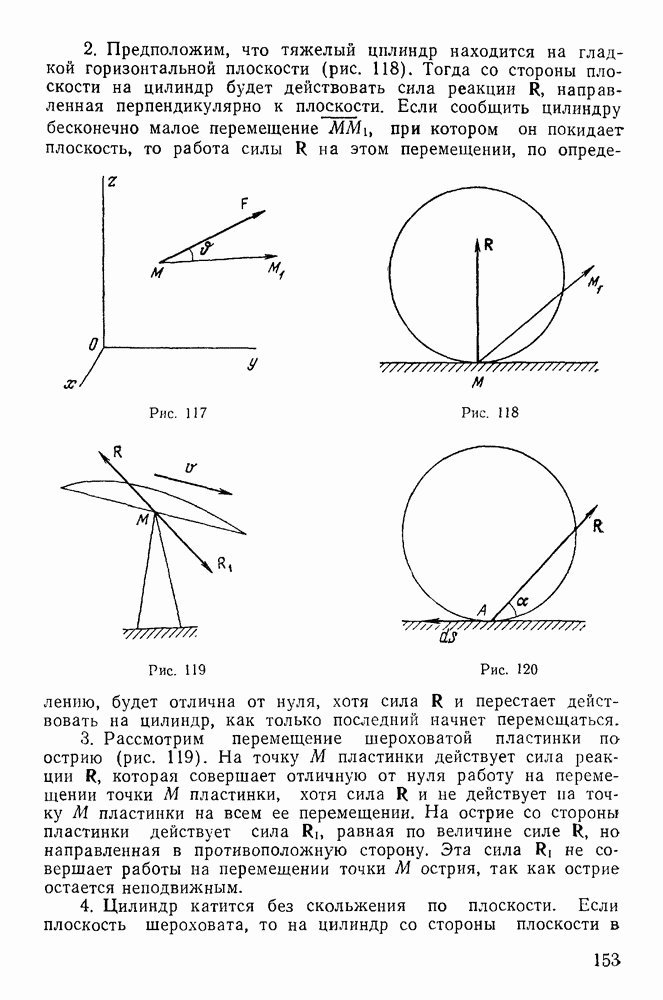
Полученное уравнение позволяет найти закон изменения координаты  Перепишем его в виде
Перепишем его в виде

где

Разделяя Переменные и интегрируя, получим

Так как  представляет собой многочлен третьей степени относительно z, то стоящий слева интеграл является эллиптическим. После того, как будет найдено
представляет собой многочлен третьей степени относительно z, то стоящий слева интеграл является эллиптическим. После того, как будет найдено  из последнего соотношения можно определить и уравнение траектории: с этой целью с помощью интеграла площадей исключим из дифференциального уравнения движения время и получим дифференциальное уравнение траектории
из последнего соотношения можно определить и уравнение траектории: с этой целью с помощью интеграла площадей исключим из дифференциального уравнения движения время и получим дифференциальное уравнение траектории

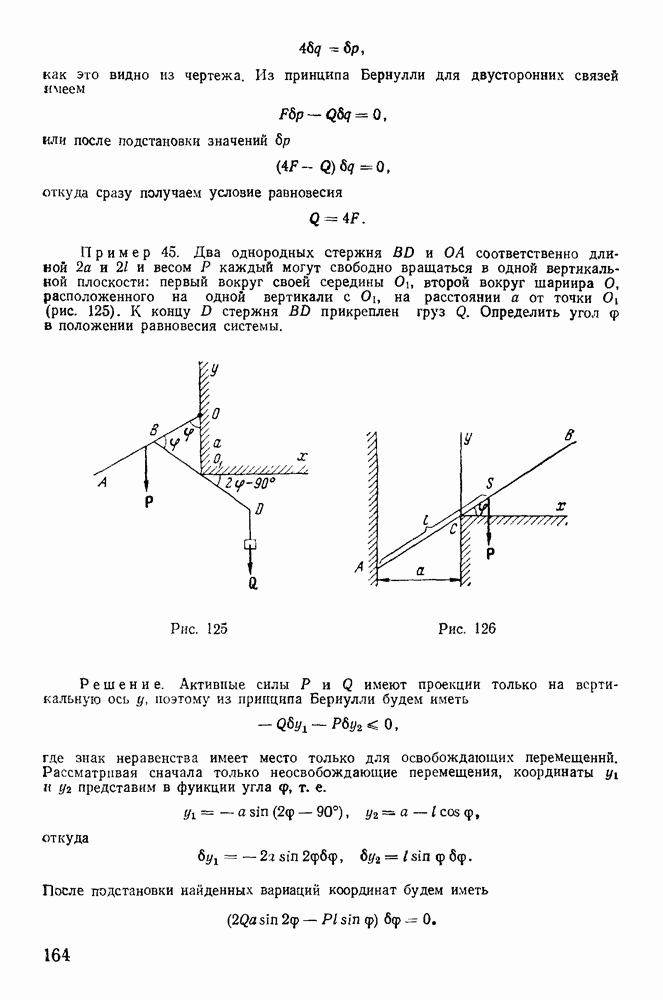
Как видно, задача об определении траектории также сводится к эллиптическим квадратурам.
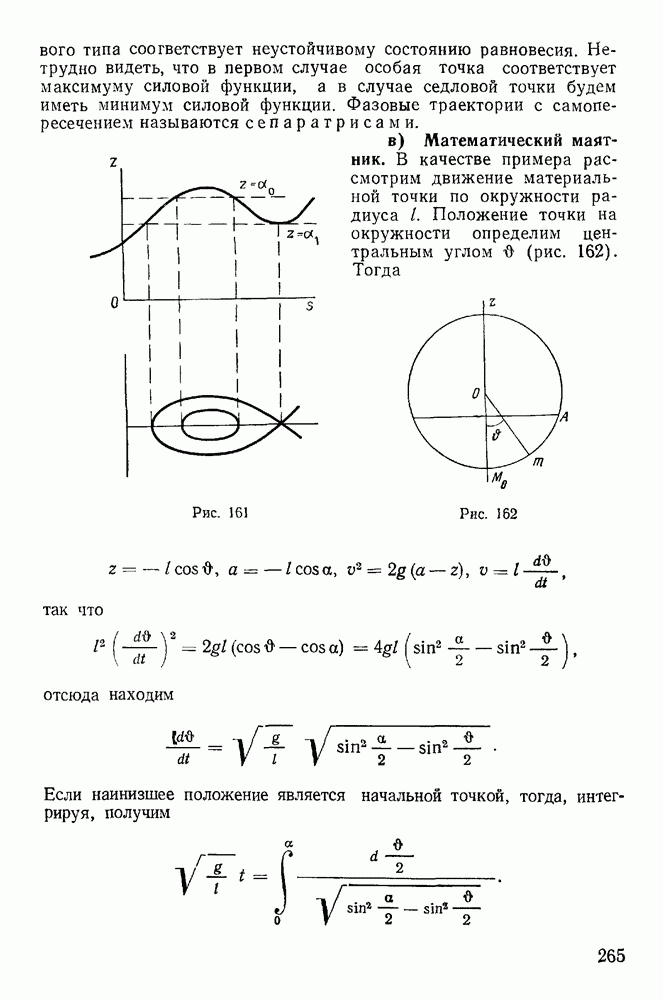
д) Качественное исследование движения сферического маятника.
Если вектор начальной скорости точки лежит в вертикальной плоскости, то движение будет происходить в той же плоскости. Для этого случая  т. е.
т. е.  Следовательно, задача сводится к обыкновенному математическому маятнику, который изучался выше.
Следовательно, задача сводится к обыкновенному математическому маятнику, который изучался выше.
Если  то, как видно из квадратур,
то, как видно из квадратур,  будет монотонной функцией относительно z. Для изучения закона изменения функции
будет монотонной функцией относительно z. Для изучения закона изменения функции  рассмотрим график (рис. 169) функции
рассмотрим график (рис. 169) функции

Нетрудно заметить, что

Для больших по модулю значений z

и знак функции определяется знаком первого члена разложения

На интервале  находится по крайней мере один корень у уравнения
находится по крайней мере один корень у уравнения  Координаты, определяемые полученными выше дифферециальными уравнениями, будут принимать вещественные значения только при условии, что подкоренное выражение
Координаты, определяемые полученными выше дифферециальными уравнениями, будут принимать вещественные значения только при условии, что подкоренное выражение  неотрицательно. Пусть сначала начальное значение
неотрицательно. Пусть сначала начальное значение  вещественно и отлично от нуля.
вещественно и отлично от нуля.

Рис. 169

Рис. 170
Тогда  и имеются действительные корни а и Р уравнения
и имеются действительные корни а и Р уравнения  в промежутках
в промежутках  Действительное движение происходит на интервале, где
Действительное движение происходит на интервале, где  неотрицательно, т. е. между корнями
неотрицательно, т. е. между корнями 
Представим полином  в виде
в виде

поскольку

имеем

а так как  и
и  по модулю меньше I, то, следовательно, числитель положителен. Но
по модулю меньше I, то, следовательно, числитель положителен. Но  поэтому
поэтому

отсюда следует, что по меньшей мере один из корни  отрицателен, т. е. во всяком случае
отрицателен, т. е. во всяком случае

Корень  может быть как положительным, так и отрицательным (рис. 170). Пусть для определенности при
может быть как положительным, так и отрицательным (рис. 170). Пусть для определенности при  координата z убывает. Тогда перед корнем надлежит взять знак минус, и z будет уменьшаться до тех пор, пока не достигнет значения а. Из интеграла площадей следует, что угол О изменяется лишь в одну сторону,
координата z убывает. Тогда перед корнем надлежит взять знак минус, и z будет уменьшаться до тех пор, пока не достигнет значения а. Из интеграла площадей следует, что угол О изменяется лишь в одну сторону,  может изменить знак лишь когда
может изменить знак лишь когда  обращается в нуль, т. е. при
обращается в нуль, т. е. при  или
или  Если в начальный момент
Если в начальный момент  то
то  является корнем уравнения
является корнем уравнения  и мы имеем критический случай. Дифференциальное уравнение для
и мы имеем критический случай. Дифференциальное уравнение для 

можно преобразовать к виду

или

Если  простые корни, то всюду
простые корни, то всюду  и тогда будет происходить изменение координаты z. Если а и Р — кратные корни, то
и тогда будет происходить изменение координаты z. Если а и Р — кратные корни, то  . В этом случае точка описывает окружность в плоскости, перпендикулярной к оси z.
. В этом случае точка описывает окружность в плоскости, перпендикулярной к оси z.
е) Определение реакции.
Реакция не входит в выражение для первых интегралов, и для ее определения следует исходить не из первых интегралов, а из самих уравнений движения материальной точки. Пусть  тогда, когда реакция направлена к центру. Тогда уравнения движения в проекциях на декартовы оси координат запишутся в виде
тогда, когда реакция направлена к центру. Тогда уравнения движения в проекциях на декартовы оси координат запишутся в виде

а интеграл живых сил

Умножая уравнения движения соответственно на х, у, z и складывая, получим

или

Дифференцируя по времени уравнение связи

будем иметь

Повторное дифференцирование дает

или

В результате приходим к следующему уравнению для определения реакции:

или

Отсюда видно, что в задаче о движении сферического маятника реакция кроме постоянной  зависит только от координаты
зависит только от координаты  Следовательно, на одинаковых параллелях реакции будут численно равны. Если при определении реакции получим во все время движения
Следовательно, на одинаковых параллелях реакции будут численно равны. Если при определении реакции получим во все время движения  (что всегда выполняется при
(что всегда выполняется при  то маятник можно осуществить при помощи гибкой нерастяжимой нити. Если же во время движения
то маятник можно осуществить при помощи гибкой нерастяжимой нити. Если же во время движения  обращается в нуль, то связь перестает быть натянутой, и после освобождения точки от связи приходим к новой механической задаче — задаче о движении свободной материальной точки.
обращается в нуль, то связь перестает быть натянутой, и после освобождения точки от связи приходим к новой механической задаче — задаче о движении свободной материальной точки.
ж) Малые колебания сферического маятника.
Запишем уравнения связи для сферического маятника в виде

откуда для отношения  получим значение
получим значение

и будем рассматривать малые отклонения маятника от вертикали, проходящей через начало координат. Тогда величина  будет оставаться малой по сравнению с единицей, и приближенно можно считать, что
будет оставаться малой по сравнению с единицей, и приближенно можно считать, что 
Верхнее положение точки является положением равновесия, но это положение неустойчиво, поскольку нижняя параллель всегда ниже экватора. Третье уравнение движения дает

или

При этом в положении равновесия  откуда
откуда  Если это условие не выполняется, то в силу того, что
Если это условие не выполняется, то в силу того, что

а  будем иметь
будем иметь  Тогда из уравнения движения имеем
Тогда из уравнения движения имеем

откуда

Но производная здесь не может неограниченно возрастать со временем, если  остается ограниченной величиной. Координаты х и у точки
остается ограниченной величиной. Координаты х и у точки  определяются приближенными уравнениями
определяются приближенными уравнениями

Принимая во внимание, что  представим эти уравнения в виде
представим эти уравнения в виде

Положив  получим общее решение системы уравнения движения
получим общее решение системы уравнения движения

Не нарушая общности, положим, что при  точка находится на оси х, а начальная скорость направлена перпендикулярно к этой оси. Тогда будем иметь
точка находится на оси х, а начальная скорость направлена перпендикулярно к этой оси. Тогда будем иметь

и соответствующее частное решение запишется в виде

Исключая время, получим уравнение,

которое представляет собой уравнение траектории проекции точки на плоскость  т. е. движение проекции точки происходит по эллиптической траектории.
т. е. движение проекции точки происходит по эллиптической траектории.
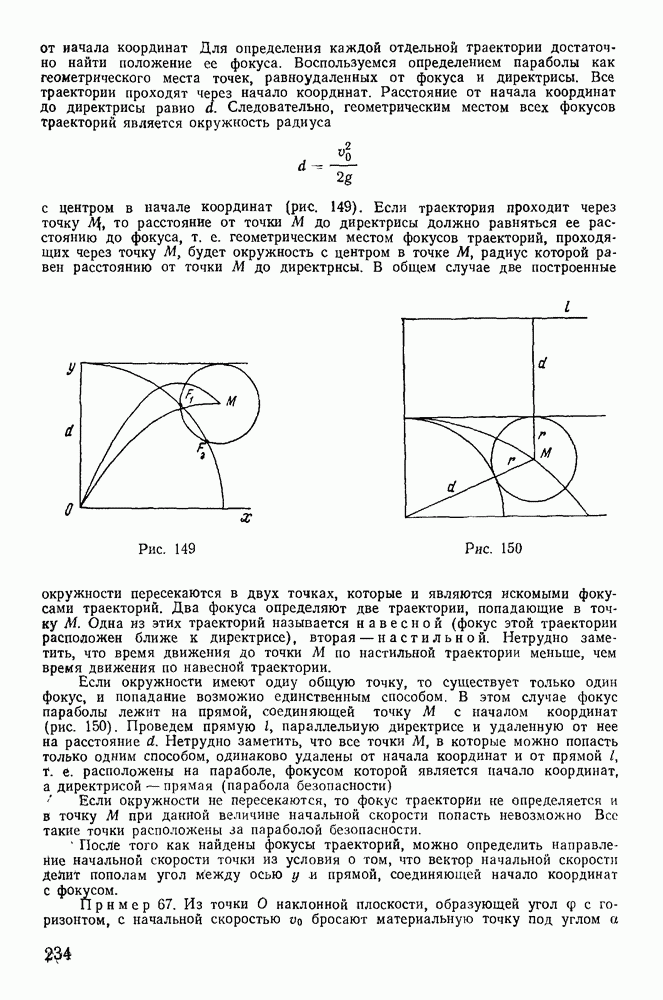
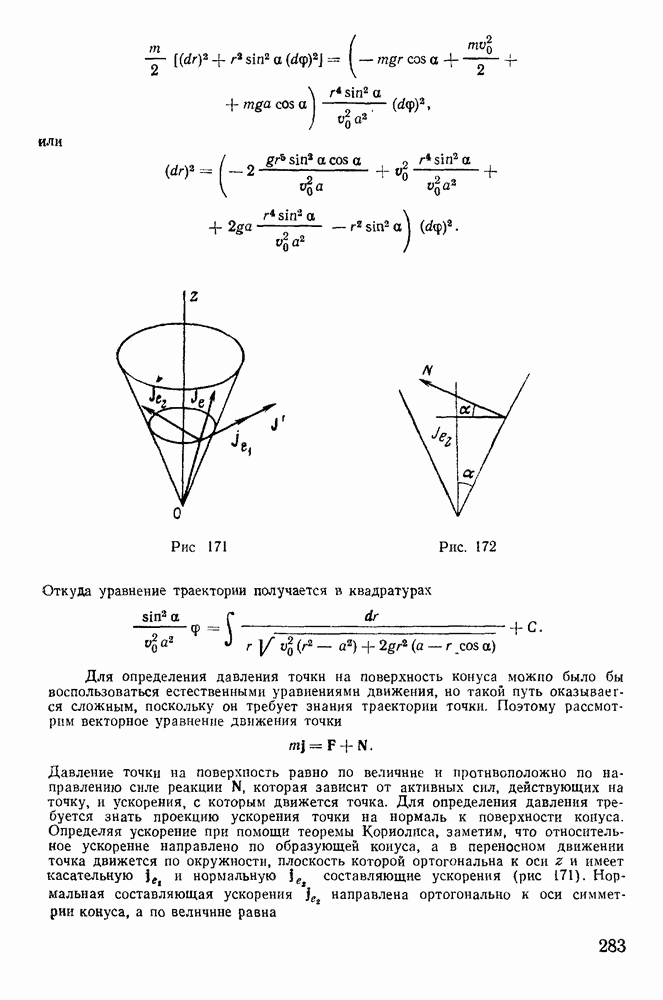
Пример 74. Тяжелая материальная точка движется по внутренней поверхности прямого кругового конуса, вершина которого обращена вниз, ось симметрии вертикальна, угол при вершине равен  . В начальный момент расстояние точки от вершины конуса равно а, начальная скорость равна
. В начальный момент расстояние точки от вершины конуса равно а, начальная скорость равна  и направлена перпендикулярно к образующей конуса. Определить траекторию точки и давление, оказываемое ею на поверхность конуса.
и направлена перпендикулярно к образующей конуса. Определить траекторию точки и давление, оказываемое ею на поверхность конуса.
Решение. Положение точки на поверхности конуса можно задать двумя координатами. В качестве таких координат выберем расстояние точки от вершины конуса  и угол
и угол  который образует вертикальная плоскость
который образует вертикальная плоскость  проходящая через ось симметрии конуса и точку М, с неподвижной плоскостью
проходящая через ось симметрии конуса и точку М, с неподвижной плоскостью  Рассматривая движение точки как сложное, состоящее из прямолинейного относительного движения в плоскости
Рассматривая движение точки как сложное, состоящее из прямолинейного относительного движения в плоскости  и переносного вращения вместе с плоскостью
и переносного вращения вместе с плоскостью  вокруг оси
вокруг оси  будем иметь
будем иметь

На точку действуют только сила тяжести и нормальная реакция гладкой поверхности, поэтому существует интеграл живых сил

Кроме того, действующие силы не создают момента относительно оси  поэтому существует интеграл площадей
поэтому существует интеграл площадей

Постоянные  и С выражаются через начальные данные
и С выражаются через начальные данные

Два первых интеграла позволяют определить траекторию точки на поверхности конуса. В самом деле, исключая время, получим

или


Рис. 171

Рис. 172
Откуда уравнение траектории получается в квадратурах

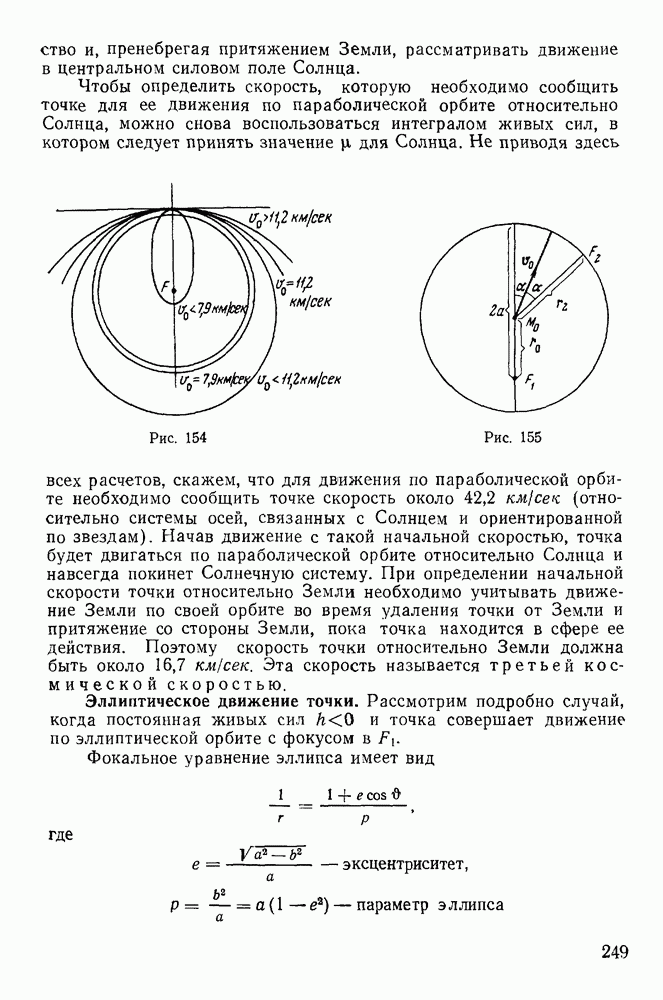
Для определения давления точки на поверхность конуса можно было бы воспользоваться естественными уравнениями движения, но такой путь оказывается сложным, поскольку он требует знания траектории точки. Поэтому рассмотрим векторное уравнение движения точки

Давление точки на поверхность равно по величине и противоположно по направлению силе реакции  которая зависит от активных сил, действующих на точку, и ускорения, с которым движется точка. Для определения давления требуется знать проекцию ускорения точки на нормаль к поверхности конуса. Определяя ускорение при помощи теоремы Кориолиса, заметим, что относительное ускорение направлено по образующей коиуса, а в переносном движении точка движется по окружности, плоскость которой ортогональна к оси z и имеет касательную
которая зависит от активных сил, действующих на точку, и ускорения, с которым движется точка. Для определения давления требуется знать проекцию ускорения точки на нормаль к поверхности конуса. Определяя ускорение при помощи теоремы Кориолиса, заметим, что относительное ускорение направлено по образующей коиуса, а в переносном движении точка движется по окружности, плоскость которой ортогональна к оси z и имеет касательную  и нормальную составляющие ускорения (рис 171). Нормальная составляющая ускорения
и нормальную составляющие ускорения (рис 171). Нормальная составляющая ускорения  направлена ортогонально к оси симметрии конуса, а по величине равна
направлена ортогонально к оси симметрии конуса, а по величине равна

Добавочное ускорение У коллинеарно с направлением ускорения  и численно равно
и численно равно

На нормаль к поверхности даег проекцию только составляющая ускорения  (рис. 172). Проектируя уравнение движения на нормаль к поверхности конуса, получим
(рис. 172). Проектируя уравнение движения на нормаль к поверхности конуса, получим

откуда

Определив  из интеграла площадей
из интеграла площадей

будем иметь

| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Введение
- Глава I. ОСНОВЫ ТЕОРИИ ВЕКТОРОВ
- § 1. СВОБОДНЫЕ ВЕКТОРЫ
- 2. Сложение свободных векторов.
- 3. Проекция вектора на ось.
- 4. Инварианты системы свободных векторов.
- § 2. СКОЛЬЗЯЩИЕ ВЕКТОРЫ
- 2. Координаты скользящего вектора.
- 3. Момент скользящего вектора. Плюккеровы координаты.
- 4. Аналитическое определение момента скользящего вектора.
- 5. Проекция момента на ось.
- 6. Момент скользящего вектора относительно оси
- § 3. СИСТЕМА СКОЛЬЗЯЩИХ ВЕКТОРОВ
- 2. Произвольная система скользящих векторов. Элементарные операции.
- 3. Приведение системы скользящих векторов к простейшей эквивалентной форме.
- 4. Плоская система скользящих векторов.
- 5. Свойства системы параллельных скользящих векторов.
- § 4. ЗАКРЕПЛЕННЫЕ ВЕКТОРЫ
- § 5. ДИФФЕРЕНЦИРОВАНИЕ СВОБОДНОГО ВЕКТОРА ПО СКАЛЯРНОМУ АРГУМЕНТУ
- Глава II. КИНЕМАТИКА
- § 1. КИНЕМАТИКА ТОЧКИ
- 2. Ускорение точки. Проекции ускорения на прямоугольные оси координат.
- 3. Скорость и ускорение точки в полярных координатах.
- 4. Движение точки по окружности.
- 5. Проекции ускорения на оси естественного трехгранника.
- 6. Теорема о сложении скоростей в сложном движении точки.
- 7. Метод Роберваля построения касательных к плоским кривым.
- 8. Аналитическое доказательство теоремы о сложении скоростей.
- 9. Сложение скоростей в общем случае сложного движения точки.
- § 2. КИНЕМАТИКА АБСОЛЮТНО ТВЕРДОГО ТЕЛА
- 2. Элементарные движения твердого тела.
- 3. Мгновенные движения твердого тела.
- 4. Сложение мгновенно-поступательных и мгновенно-вращательных движений твердого тела.
- 5. Общий случай сложения мгновенно-поступательных и мгновенно-вращательных движений твердого тела. Непрерывное движение твердого тела.
- 6. Мгновенное движение твердого тела с одной неподвижной точкой.
- 7. Плоскопараллельное движение твердого тела.
- § 3. УСКОРЕНИЕ ТОЧКИ В СЛОЖНОМ ДВИЖЕНИИ
- 2. Замечание о дифференцировании единичного вектора.
- 3. Векторный вывод теоремы Кориолиса.
- 4. Теорема Ривальса.
- § 4. РАСПРЕДЕЛЕНИЕ УСКОРЕНИЙ В ПЛОСКОПАРАЛЛЕЛЬНОМ ДВИЖЕНИИ ТВЕРДОГО ТЕЛА
- 2. Мгновенный центр ускорений.
- § 5. КИНЕМАТИЧЕСКИЕ УРАВНЕНИЯ ЭЙЛЕРА
- Глава III. СТАТИКА
- I. ГЕОМЕТРИЧЕСКАЯ СТАТИКА
- § 1. АКСИОМЫ СТАТИКИ
- § 2. ПОНЯТИЕ О СИЛЕ ТРЕНИЯ
- § 3. РАЗЛИЧНЫЕ ЗАДАЧИ СТАТИКИ
- 2. Равновесие трех сил.
- § 4. МОМЕНТ СИЛЫ
- 2. Момент силы относительно оси.
- 3. Теорема Вариньона для системы сходящихся сил.
- § 5. ПРОИЗВОЛЬНАЯ СИСТЕМА СИЛ, ДЕЙСТВУЮЩИХ НА ТВЕРДОЕ ТЕЛО
- § 6. УСЛОВИЯ РАВНОВЕСИЯ СИСТЕМЫ СИЛ, ДЕЙСТВУЮЩИХ НА ТВЕРДОЕ ТЕЛО
- § 7. ПРИВЕДЕНИЕ СИСТЕМЫ СИЛ, ДЕЙСТВУЮЩИХ НА ТВЕРДОЕ ТЕЛО, К ДИНАМЕ. УРАВНЕНИЯ РАВНОВЕСИЯ ТВЕРДОГО ТЕЛА
- § 8. УСЛОВИЯ РАВНОВЕСИЯ СИСТЕМЫ ТВЕРДЫХ ТЕЛ
- § 9. ПЛОСКАЯ СИСТЕМА СИЛ
- § 10. ЗАДАЧА О РАВНОВЕСИИ НЕСВОБОДНОГО ТВЕРДОГО ТЕЛА
- 2. Частные случаи равновесия твердого тела.
- § 11. ЗАДАЧА О РАВНОВЕСИИ ПРИ НАЛИЧИИ ТРЕНИЯ
- § 12. СИЛА ТЯЖЕСТИ И ЦЕНТР ТЯЖЕСТИ
- II. АНАЛИТИЧЕСКАЯ СТАТИКА
- § 1. РАБОТА СИЛЫ НА ПЕРЕМЕЩЕНИИ. СИЛОВАЯ ФУНКЦИЯ
- § 2. ПРИНЦИП ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ
- 2. Теорема Лагранжа о равновесии системы.
- 3. Принцип Торричелли.
- § 3. ОБЩИЕ ВОПРОСЫ АНАЛИТИЧЕСКОЙ СТАТИКИ
- 3. Общие теоремы о равновесии системы материальных точек.
- 4. Метод неопределенных множителей Лагранжа.
- 5. Определение реакций.
- § 4. ОПРЕДЕЛЕНИЕ РЕАКЦИЙ В ОБЩЕМ СЛУЧАЕ
- § 5. РАВНОВЕСИЕ НИТИ
- 2. Естественные уравнения равновесия нити.
- Глава IV. ДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ
- § 1. ОСНОВНЫЕ ЗАКОНЫ ДИНАМИКИ
- § 2. ДВЕ ОСНОВНЫЕ ЗАДАЧИ ДИНАМИКИ. УРАВНЕНИЯ ДВИЖЕНИЯ ТОЧКИ В ДЕКАРТОВЫХ ОСЯХ
- § 3. ЕСТЕСТВЕННЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ
- § 4. ОСНОВНЫЕ ТЕОРЕМЫ ДИНАМИКИ ДЛЯ СВОБОДНОЙ МАТЕРИАЛЬНОЙ ТОЧКИ
- 2. Теорема об изменении момента количества движения.
- 3. Следствия из теорем об изменении количества движения и момента количества движения материальной точки.
- 4. Теорема живых сил.
- 5. Интеграл живых сил.
- 6. Устойчивость равновесия. Теорема Лагранжа.
- § 5. ДВИЖЕНИЕ ТЯЖЕЛОЙ МАТЕРИАЛЬНОЙ ТОЧКИ В ПУСТОТЕ
- § 6. ДВИЖЕНИЕ МАТЕРИАЛЬНОЙ ТОЧКИ ПОД ДЕЙСТВИЕМ ЦЕНТРАЛЬНЫХ СИЛ
- 2. Формулы Бине
- 3. Задача о движении планет
- § 7. ДВИЖЕНИЕ ТОЧКИ В СОПРОТИВЛЯЮЩЕЙСЯ СРЕДЕ
- § 8. ДВИЖЕНИЕ НЕСВОБОДНОЙ МАТЕРИАЛЬНОЙ ТОЧКИ
- 2. Движение материальной точки по поверхности.
- § 9. ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЕ МАТЕРИАЛЬНОЙ ТОЧКИ
- 1. Теорема живых сил в относительном движении точки.
- 2. Уравнения относительного равновесия точки.
- 3. Равновесие материальной точки на поверхности Земли. Вес.
- 4. Задача о падении тяжелой точки в пустоте.
- 5. Маятник Фуко.
- § 10. ПРИНЦИП ДАЛАМБЕРА
- Глава V. ДИНАМИКА СИСТЕМЫ МАТЕРИАЛЬНЫХ ТОЧЕК
- § 1. УЧЕНИЕ О СВЯЗЯХ
- § 2. ПРИНЦИП ДАЛАМБЕРА — ЛАГРАНЖА
- § 3. ОСНОВНЫЕ ТЕОРЕМЫ ДИНАМИКИ СИСТЕМЫ
- 2. Теорема об изменении момента количества движения.
- 3. Теорема живых сил.
- § 4. ТЕОРЕМЫ О ДВИЖЕНИИ СИСТЕМЫ ОТНОСИТЕЛЬНО ОСЕЙ НЕИЗМЕННОГО НАПРАВЛЕНИЯ, ПРОХОДЯЩИХ ЧЕРЕЗ ЦЕНТР МАСС СИСТЕМЫ (ОСЕЙ КЕНИГА)
- 2. Теорема об изменении момента количества движения системы относительно осей Кёнига.
- 3. Теорема живых сил в движении системы относительно осей Кёнига.
- § 5. УРАВНЕНИЯ ЛАГРАНЖА ВТОРОГО РОДА
- 2. Случай существования силовой функции.
- 3. Замечание о лагранжевых координатах.
- § 6. ЭЛЕМЕНТАРНЫЕ СЛУЧАИ ИНТЕГРИРУЕМОСТИ УРАВНЕНИЙ ЛАГРАНЖА
- 2. Метод Рауса игнорирования циклических координат.
- 3. Обобщение теоремы и интеграла живых сил.
- § 7. ОПРЕДЕЛЕНИЕ РЕАКЦИЙ
- Глава VI. ДИНАМИКА ТВЕРДОГО ТЕЛА
- § 1. ТЕОРИЯ МОМЕНТОВ ИНЕРЦИИ
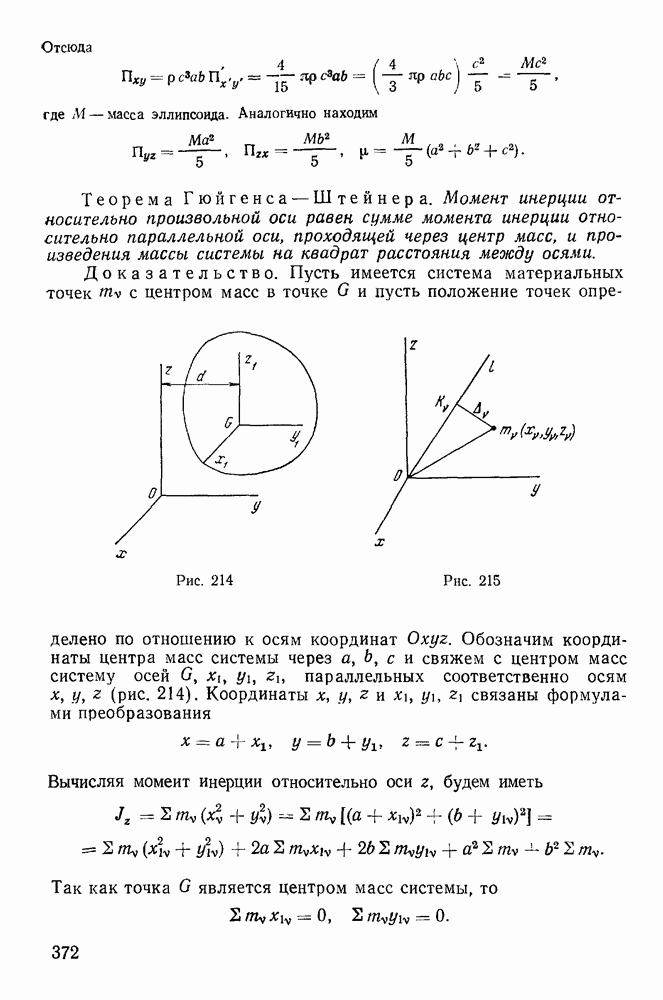
- 2. Момент инерции системы относительно произвольной оси, проходящей через заданную точку.
- 3. Эллипсоид инерции.
- 4. Определение главных осей инерции для произвольной точки.
- § 2. ВРАЩЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ОСИ
- § 3. ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА, ИМЕЮЩЕГО ОДНУ НЕПОДВИЖНУЮ ТОЧКУ
- 2. Уравнения движения твердого тела с одной неподвижной точкой.
- § 4. ДВИЖЕНИЕ ТЯЖЕЛОГО ТВЕРДОГО ТЕЛА ОКОЛО НЕПОДВИЖНОЙ ТОЧКИ
- 2. Интегрирование уравнений движения тяжелого твердого тела.
- 3. Случай Эйлера — Пуансо.
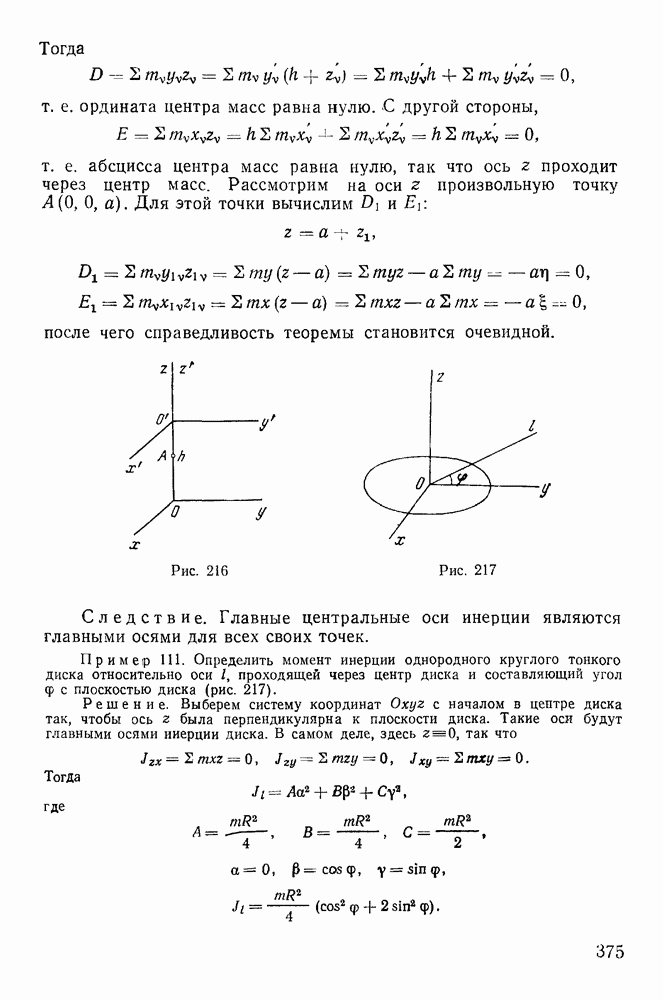
- Регулярная прецессия твердого тела в случае Эйлера.
- Геометрическая интерпретация Пуансо движения твердого тела в случае Эйлера.
- Устойчивость постоянных вращений твердого тела.
- 4. Случай Лагранжа.
- Особенные случаи движения твердого тела. Спящий волчок.
- Гироскоп. Приближенная теория.
- Некоторые применения гироскопов.
- Регулярная прецессия в случае Лагранжа.
- Вынужденная регулярная прецессия.
- 5. Случай Ковалевской.
- § 5. ОПРЕДЕЛЕНИЕ РЕАКЦИИ В СЛУЧАЕ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА С ОДНОЙ НЕПОДВИЖНОЙ ТОЧКОЙ
- § 6. УРАВНЕНИЯ ДВИЖЕНИЯ СВОБОДНОГО ТВЕРДОГО ТЕЛА
- § 7. ГИРОСТАТЫ
- Глава VII. АНАЛИТИЧЕСКАЯ ДИНАМИКА
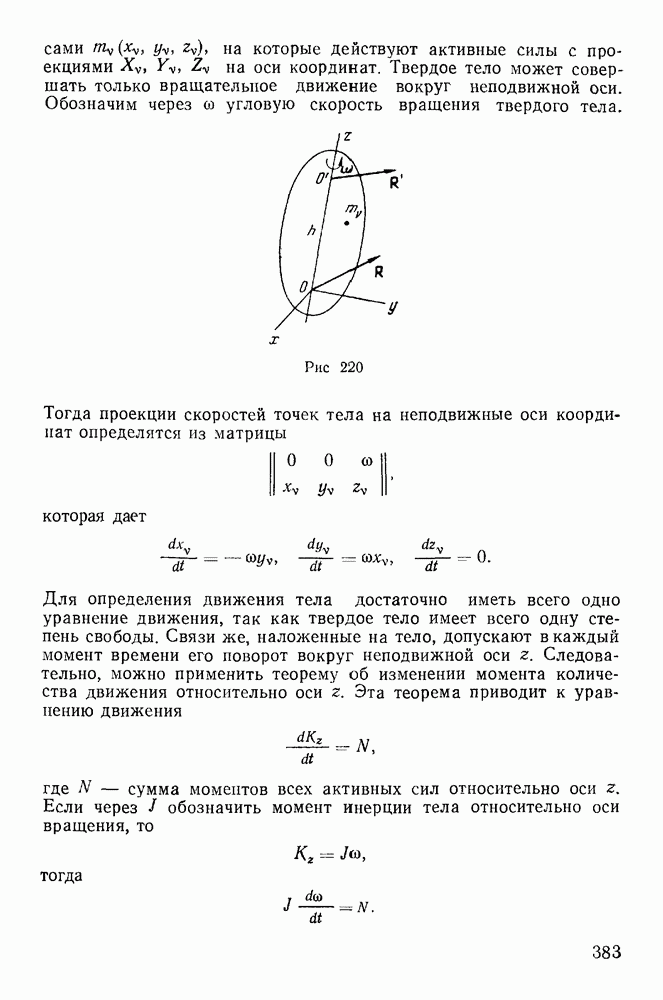
- § 1. КАНОНИЧЕСКИЕ УРАВНЕНИЯ ГАМИЛЬТОНА
- 1. Преобразования Лежандра.
- 2. Канонические уравнения Гамильтона.
- 3. Функция Гамильтона и ее свойства.
- § 2. ПРИНЦИП ГАМИЛЬТОНА — ОСТРОГРАДСКОГО
- 2. Вывод канонических уравнений Гамильтона из принципа Гамильтона — Остроградского.
- 3. Принцип Гамильтона в форме Пуанкаре.
- § 3. ИНТЕГРИРОВАНИЕ КАНОНИЧЕСКИХ УРАВНЕНИЙ ГАМИЛЬТОНА
- 2. Канонические преобразования.
- 3. Бесконечно малые канонические преобразования.
- 4. Теорема Лиувилля.
- 5. Теорема Якоби.
- 6. Интегрирование уравнения Гамильтона—Якоби.
- Метод Имшенецкого разделения переменных.
- 7. Скобки Пуассона.
- § 4. ВАРИАЦИОННЫЕ ПРИНЦИПЫ МЕХАНИКИ
- 2. Принцип Лагранжа.
- 3. Принцип наименьшего действия в форме Якоби.
- Вывод уравнений Лагранжа второго рода из принципа Якоби.
- Сравнение принципа Якоби с принципом Гамильтона.
- 4. Оптико-механическая аналогия.
- 5. Интегральные инварианты.
- Линейные интегральные инварианты.
- Интегральный инвариант Пуанкаре — Картана.
- 6. Принцип наименьшего принуждения Гаусса. Уравнения Аппеля.
- 7. Уравнения Рауса.
- § 5. МАЛЫЕ КОЛЕБАНИЯ
- Затухающие колебания.
- Вынужденные колебания. Резонанс.
- Параметрический резонанс.
- Нелинейные колебания.
- Диссипативные системы.
- 2. Общий случай малых колебаний системы около положения устойчивого равновесия.
- Устойчивость равновесия. Теорема Лагранжа об устойчивости равновесия.
- Замечание об устойчивости стационарных движений.
- Малые колебания системы около положения устойчивого равновесия.
- Влияние диссипативных сил на малые колебания системы около устойчивого положения равновесия.
- § 6. УСТОЙЧИВОСТЬ ДВИЖЕНИЯ
- Прямой метод Ляпунова
- Теорема об асимптотической устойчивости.
- Теорема Четаева о неустойчивости движения.
- 2. Влияние новых связей на малые колебания системы около положения равновесия.
- 3. Влияние диссипативных сил на устойчивость равновесия.
- 4. Влияние гироскопических сил на устойчивость равновесия.
- § 7. ЭЛЕМЕНТЫ ТЕОРИИ ВОЗМУЩЕНИЙ
- Устойчивость консервативных систем.
- 2. Метод изменения произвольных постоянных.
- Глава VIII. ТЕОРИЯ УДАРА
- § 2. ТЕОРЕМЫ КАРНО
- § 3. ЗАДАЧА О ЦЕНТРЕ УДАРА
- § 4. ЗАДАЧА О БАЛЛИСТИЧЕСКОМ МАЯТНИКЕ
- § 5. УРАВНЕНИЯ ЛАГРАНЖА ДЛЯ УДАРА
- § 6. ЗАДАЧА ОБ УДАРЕ ПО ТВЕРДОМУ ТЕЛУ С ОДНОЙ НЕПОДВИЖНОЙ ТОЧКОЙ
- Глава IX. ЭЛЕМЕНТЫ СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- § 2. СПЕЦИАЛЬНЫЙ ПРИНЦИП ОТНОСИТЕЛЬНОСТИ ЭЙНШТЕЙНА
- § 3. ГРУППА ПРЕОБРАЗОВАНИЙ ЛОРЕНЦА
- § 4. ИНВАРИАНТНЫЕ ВЕЛИЧИНЫ В ТЕОРИИ ОТНОСИТЕЛЬНОСТИ. ЧЕТЫРЕХМЕРНЫЙ ВЕКТОР. МИР МИНКОВСКОГО
- § 5. РЕЛЯТИВИСТСКАЯ ДИНАМИКА
- Литература