Малые колебания системы около положения устойчивого равновесия.

Рассмотрим малые колебания системы около положения ее устойчивого равновесия. Ограничиваясь лишь малыми движениями системы, будем предполагать, что величины остаются во все время движения настолько малыми, что при разложении в степенные ряды живой силы и силовой функции можно ограничиться лишь первыми членами разложения. Разложим в ряд коэффициенты в выражении живой силы:

где индекс 0 означает, что взяты значения величин, соответствующие При малых значениях можно использовать их приближенные значения

Тогда для живой силы получим приближенное значение

которое является однородной квадратичной формой относительно с постоянными коэффициентами.

Определяя силовую функцию так, чтобы в положении равновесия она обращалась в нуль, разложим ее в степенной ряд в окрестности положения равновесия

Пренебрегая в разложении членами выше второго порядка малости относительно и принимая во внимание, что в положении равновесия

получим приближенное значение силовой функции

где постоянные коэффициенты определяются из равенств

Воспользовавшись приближенными значениями силовой функции и живой силы, запишем уравнения Лагранжа второго рода

Задача определения движения в окрестности положения равновесия свелась к исследованию решений системы линейных однородных дифференциальных уравнений второго порядка с постоянными коэффициентами. Общее решение такой системы известно из курсов дифференциальных уравнений, и мы не будем останавливать на нем внимания.

Будем искать частное решение системы в виде

Тогда для определения коэффициентов А получим систему алгебраических уравнений

Отличное от нулевого решение такой системы существует только тогда, когда равен нулю определитель системы

Полученное уравнение называют характеристическим, или уравнением частот.

Можно найти такое преобразование координат, после которого живая сила и силовая функция будут представлены в виде

Для новых переменных будем иметь следующие уравнения Лагранжа:

Переменные в которых уравнения Лагранжа имеют указанный вид, называются главными, или нормальными, координатами.

Уравнения движения в нормальных координатах можно получить посредством линейной комбинации уравнений Лагранжа. Умножим каждое из уравнений движения

на неопределенный пока множитель и сложим полученные уравнения

Множители подберем так, чтобы имело место соотношение

Тогда уравнение примет вид

Преобразование должно выполняться для всех значений координат, а это возможно, если совпадают все коэффициенты преобразования, т. е.

или

Нетривиальные значения коэффициентов могут быть определены отсюда, если обращается в нуль определитель системы

Но этот определитель совпадает с уравнением частот. Определив корни этого уравнения, для каждого значения корня будем иметь систему коэффициентов зависящих по крайней мере от одного параметра. Относительно корней докажем следующую теорему, принадлежащую Сильвестру.

Теорема Сильвестра (1814—1897). Все корни уравнения частот вещественны.

Доказательство. Пусть — комплексный корень уравнения частот. Тогда для коэффициентов получим некоторые комплексные значения Для сопряженного корня будем иметь систему сопряженных значений которые определяются из уравнений

Умножая эти уравнения на и складывая результат умножения, получим

откуда

Этим и доказывается теорема.

Для каждого вещественного корня можно определить систему коэффициентов и тем самым координату х, удовлетворяющую уравнению

Теорема Вейерштрасса. Матрица определителя имеет простые элементарные делители.

Доказательство этого предложения можно провести при помощи известного метода Жордана. Предположим, что уравнения линейного преобразования имеют вид

Уравнение Лагранжа для координаты х запишем в виде

Так как

будем иметь

и при получим, как это было показано выше, уравнение

Последнее может быть только тогда, когда живая сила и силовая функция имеют вид

По определению, живая сила является знакоопределенной функцией. Поэтому выражение также является знакоопределенной положительной функцией от 1 переменных Переменные независимы, поэтому можно представить движение в пространстве переменных, где живая сила

и силовая функция

Уравнения Лагранжа для оставшихся переменных будут допускать по меньшей мере одно преобразование, подобное рассмотренному. Продолжая этот процесс, в итоге придем к следующему выражению для живой силы и силовой функции:

Причем среди величин могут оказаться равные между собой. После выполненных преобразований уравнения Лагранжа примут вид

а сами переменные оказываются главными координатами системы. Полученные уравнения системы интегрируются независимо одно от другого. Если в положении равновесия силовая функция имеет изолированный максимум, т. е. все то общее решение системы имеет следующую форму:

Если среди окажется хотя бы одно отрицательное, то будет существовать неограниченное частное решение, и предположение о том, что можно пренебрегать членами высшего порядка в разложениях живой силы и силовой функции системы, не будет оправдано. Существенным при выводе было предположение о том, что живая сила системы представляет собой знакоопределенную положительную функцию от обобщенных скоростей. Если это предположение не выполняется, то может оказаться, что нормальные координаты и не существуют.

Пример 135. Материальная точка массы привязана иягыо длины к неподвижной точке О и соединена со второй точкой той же массы при помощи нити длины а. Система находится в однородном поле силы тяжести. Определить частоты малых колебаний системы и нормальные колебания (рис. 264).

Рис. 264

Решение. Вводя в качестве обобщенных координат углы как указано На рис. 264, для живой силы получим следующее выражение:

Или приближенно

Силовую функцию задачи

Подбирая соответствующим образом константу, заменим выражение для силовой функции ее приближенным значением:

Уравнения Лагранжа для малых колебаний запишутся в виде

Здесь уравнение частот

можно переписать в виде

откуда

При — для определения величин имеем уравнение

или

откуда

так что можно положить

Для новой переменной

уравнение примет вид

где

При для определения величин приходим к уравнению

или

откуда

Для новой переменной

уравнение движения примет вид

где

В главных координатах решение имеет вид

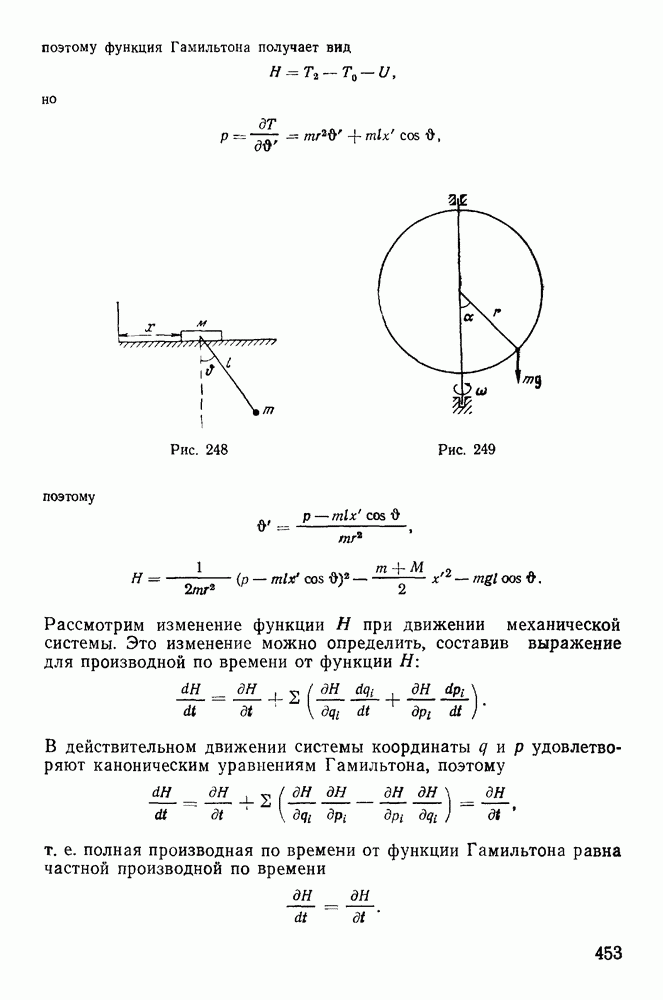
Пример 136. Трубка, согнутая в виде окружности, плоскость которой вертикальна, может свободно вращаться вокруг неподвижного вертикального диаметра. Внутри трубки находится шарик массы . Трубке сообщают начальную угловую скорость (Во вращения вокруг вертикального диаметра. При этом шарик находится в положении относительного равновесия, так что -Исследовать устойчивость относительного положения равновесия (см. рис. 249).

Решение. Принимая за обобщенные координаты угол поворота системы вокруг вертикальной оси и угол а между вертикалью и радиус-вектором шарика, для живой силы и силовой функции соответственно будем иметь

Угол представляет собой циклическую координату, которой соответствует первый интеграл

где для Р из начальных условий получим следующее значение:

Составим функцию Рауса

Полагая

где

приходим к задаче об относительном движении точки по окружности в поле сил с силовой функцией Положение «относительного» равновесия определяется уравнением

которое равносильно двум следующим уравнениям:

Из последнего уравнения находим после подстановки значения

откуда следует, что положение равновесия существует при

Если шарик поместить в положение, определяемое углом то при движения системы будет изменяться только циклическая координата а координата а будет сохранять постоянное значение. Такие движения, в которых все нециклические координаты сохраняют постоянное значение, Раус назвал стационарными. Для исследования устойчивости положений относительного равновесия рассмотрим вторую производную от функции

При получаем

Здесь

поэтому

т. e. силовая функция при имеет максимум, и положение равновесия устойчиво.

При имеем

если и положение равновесия неустойчиво.

Малые движения в окрестности устойчивого положения равновесия будут определяться уравнением

Общее решение этого уравнения имеет вид

где

Такие движения будут существовать, если в начальный момент при