| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2. Частные случаи равновесия твердого тела.
Рассматривая общие свойства равновесия твердого тела, отметим следующую теорему.
Теорема. Три силы уравновешивают твердое тело только в том случае, когда все они расположены в одной плоскости.
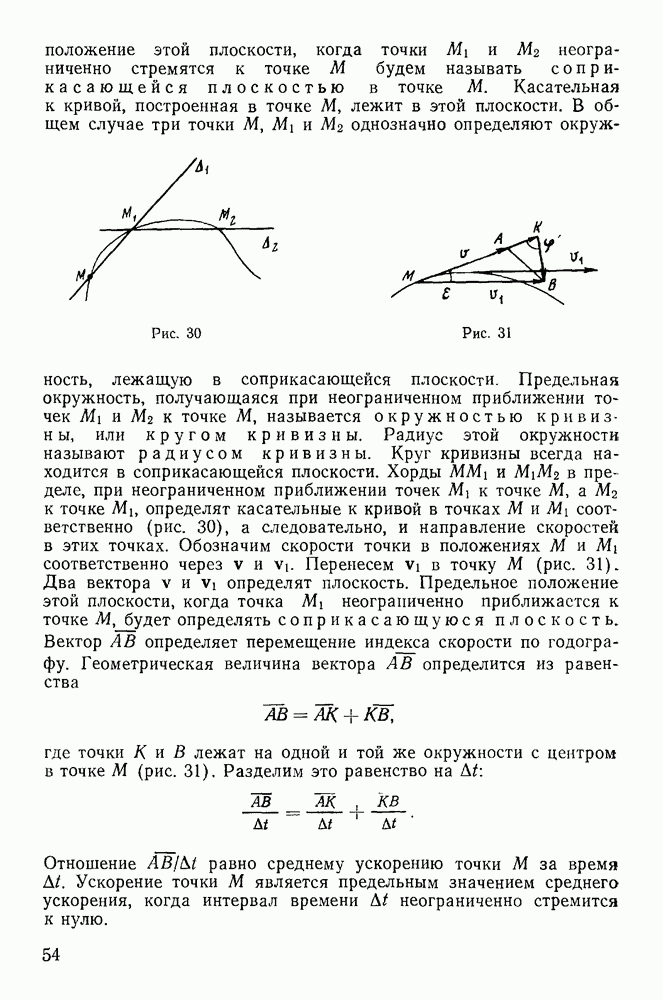
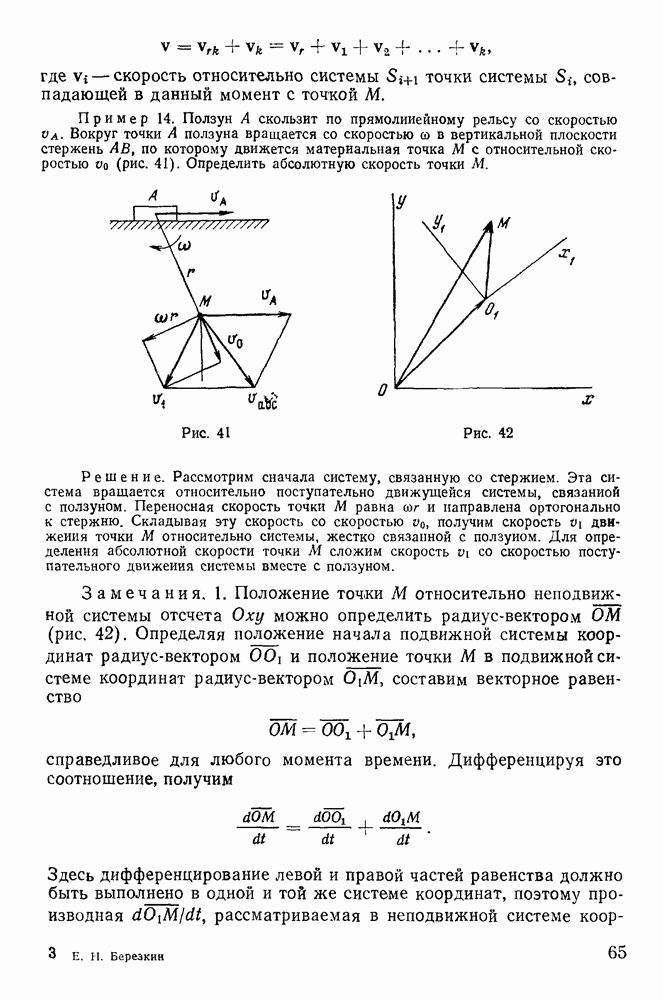
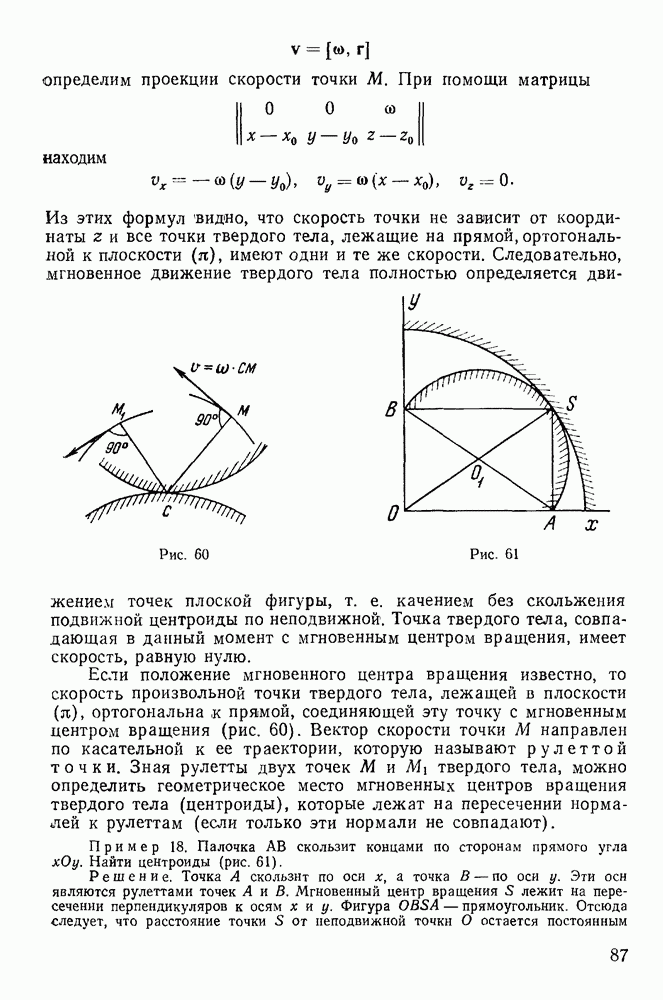
Доказательство. При приведении системы сил, действующих на твердое тело, к произвольной точке О результирующая сила и момент результирующей пары равны нулю, если твердое тело находится в равновесии. Выберем точку О на линии действия третьей силы (рис. 102). Тогда момент результирующей пары будет


Рис. 102
Но в положении равновесия  откуда
откуда

Направление вектора момента пары определяется плоскостью треугольника, а потому при равновесии плоскости треугольников  должны совпадать. Плоскости эти будут совпадать при приведении к любой точке на линии действия третьей силы. Это и доказывает теорему.
должны совпадать. Плоскости эти будут совпадать при приведении к любой точке на линии действия третьей силы. Это и доказывает теорему.
а) Условия равновесия твердого тела с одной неподвижной точкой.
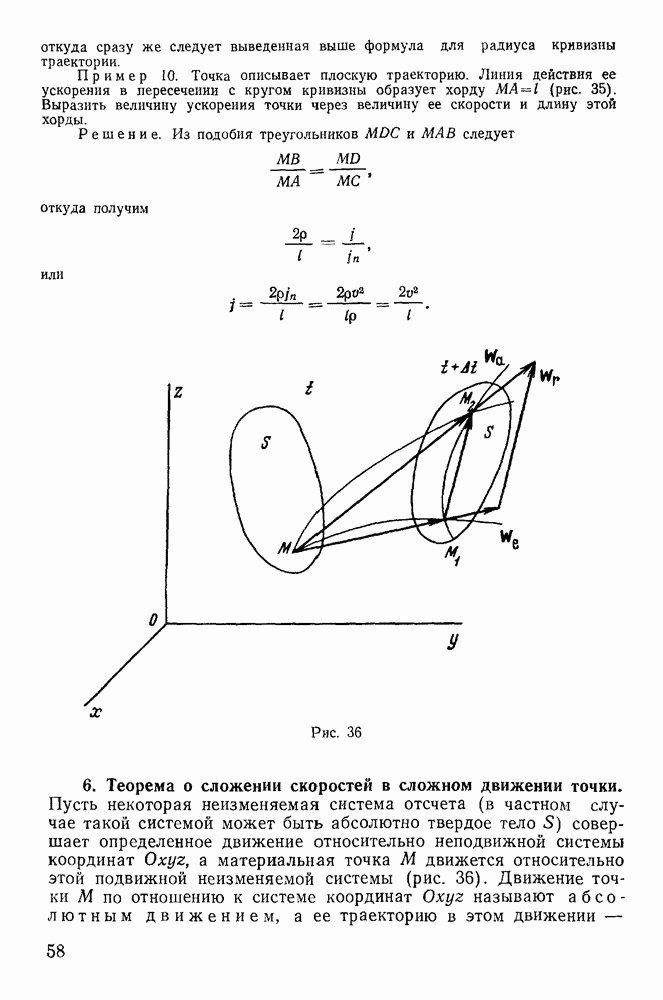
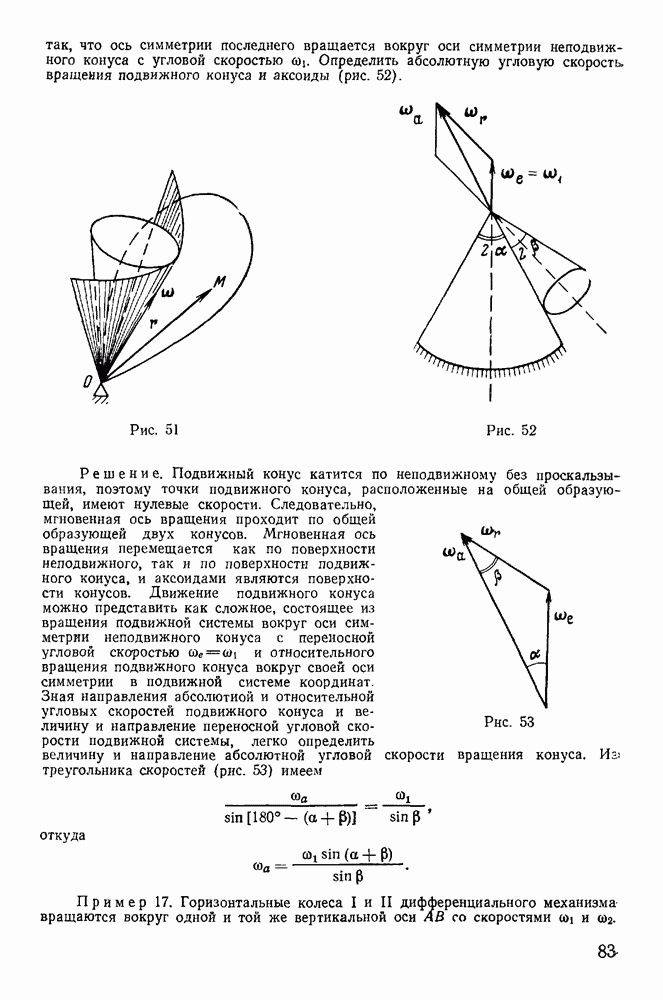
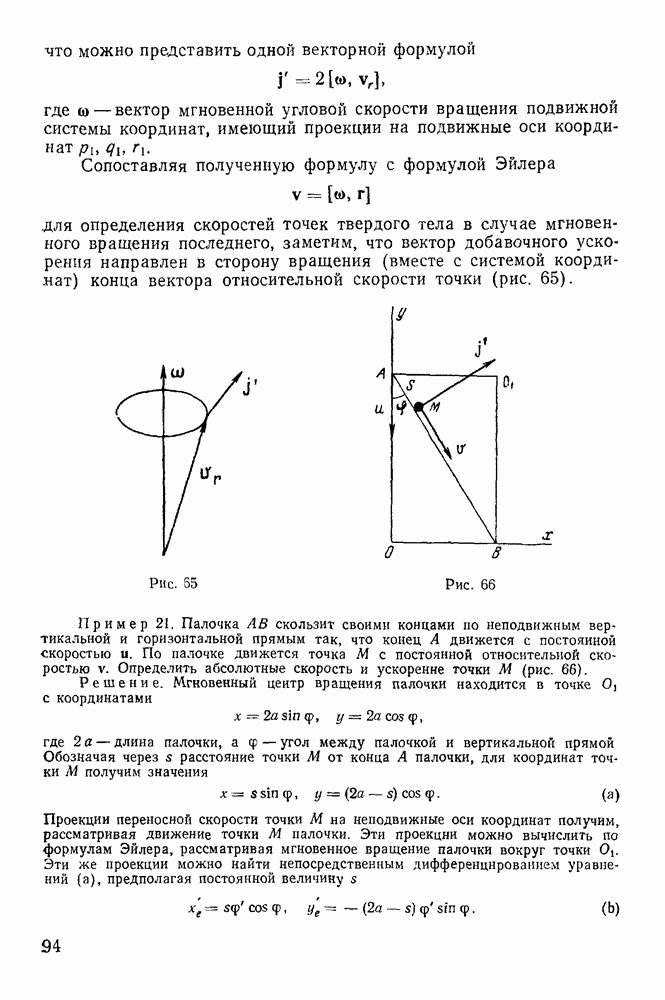
Предположим, что у твердого тела, равновесие которого изучается, закреплена одна точка. Выберем неподвижную прямоугольную систему координат  с началом в этой закрепленной точке (рис. 103). Предположим, что на каждый элемент твердого тела с массой
с началом в этой закрепленной точке (рис. 103). Предположим, что на каждый элемент твердого тела с массой  координаты которого обозначим через
координаты которого обозначим через  действует сила
действует сила  Через
Через  обозначим силу реакции в точке О. Выбирая за центр приведения неподвижную точку О, получим условия равновесия твердого тела, не включающие реакции связи
обозначим силу реакции в точке О. Выбирая за центр приведения неподвижную точку О, получим условия равновесия твердого тела, не включающие реакции связи

Приравнивая нулю результирующую силу, приходим к уравнениям для определения реакций связи

б) Условия равновесия твердого тела, способного вращаться вокруг неподвижной оси.
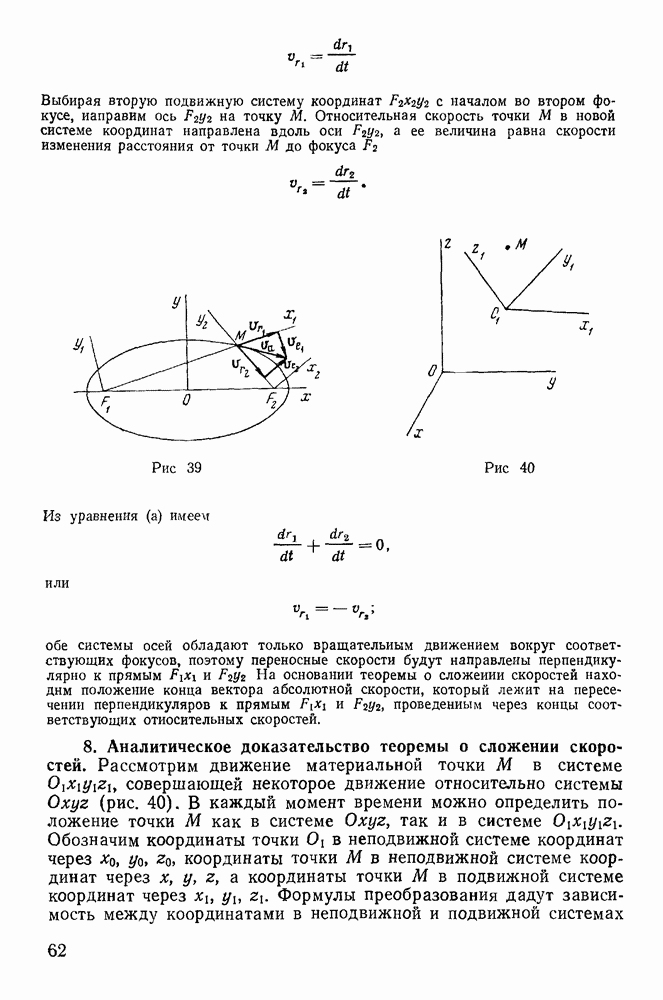
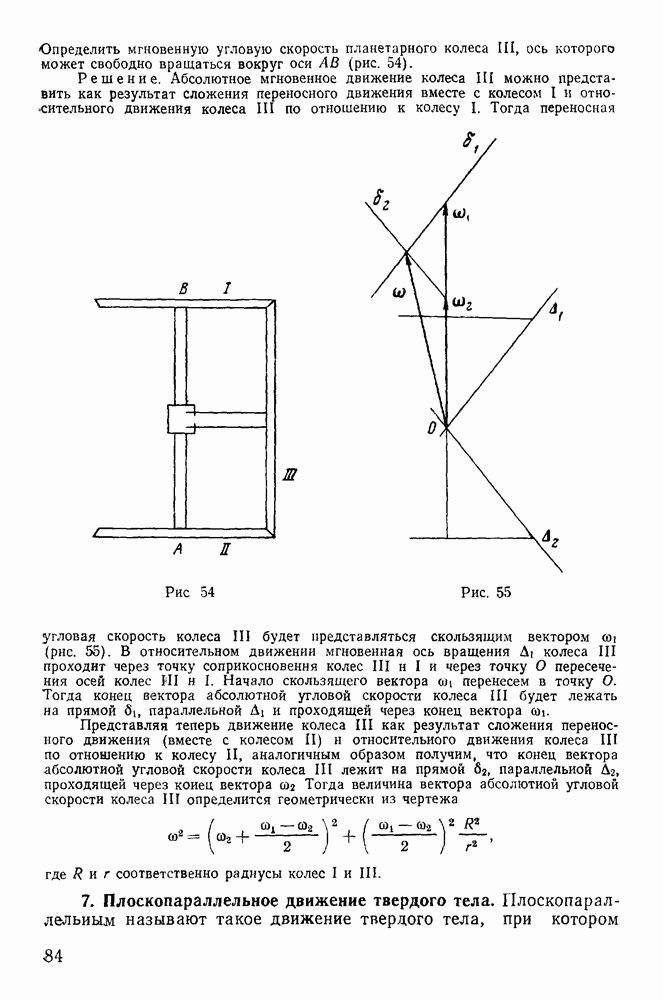
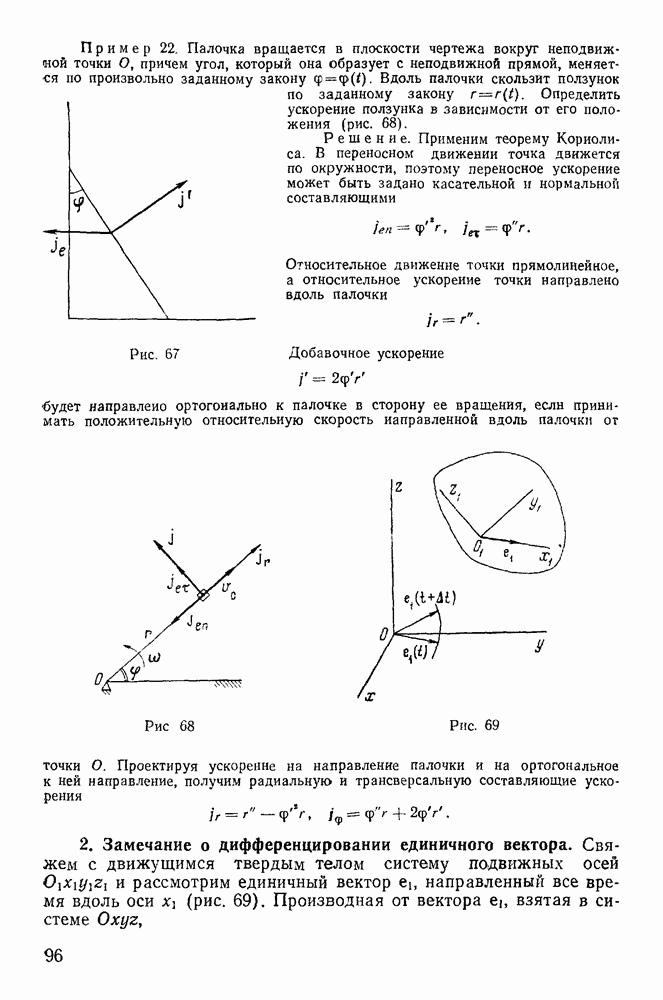
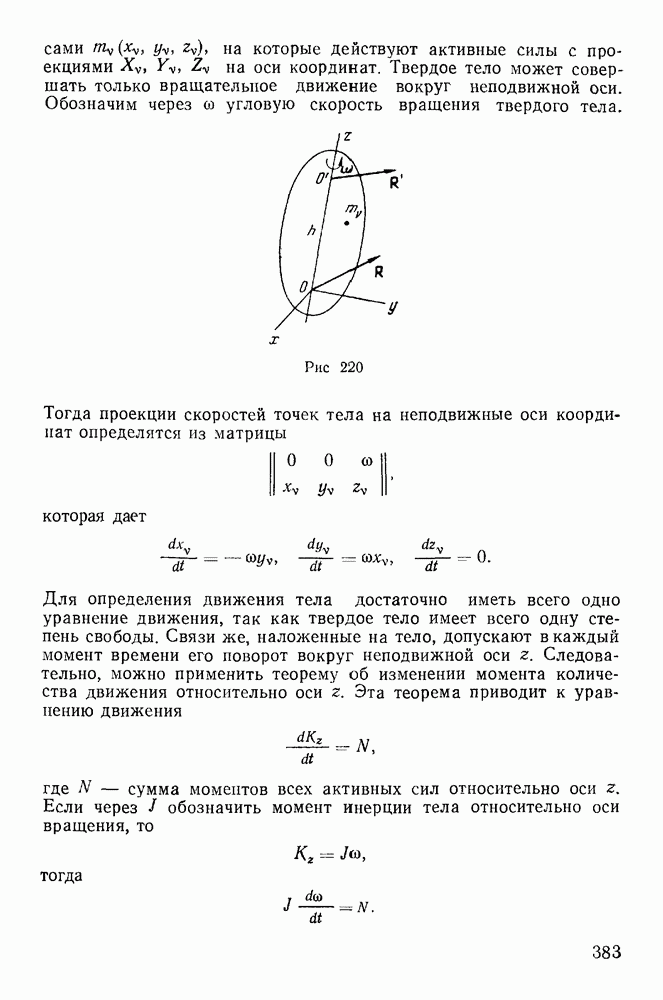
Неподвижность оси может быть достигнута закреплением двух точек тела О и  (рис. 104), хотя можно было бы закрепить и большее число точек, расположенных на одной прямой. Пусть на частицу
(рис. 104), хотя можно было бы закрепить и большее число точек, расположенных на одной прямой. Пусть на частицу  тела действует активная сила
тела действует активная сила
 Уравнения равновесия твердого тела можно получить, выбирая за центр приведения одну из неподвижных точек, например точку О. В качестве системы неподвижных осей выберем прямоугольные оси
Уравнения равновесия твердого тела можно получить, выбирая за центр приведения одну из неподвижных точек, например точку О. В качестве системы неподвижных осей выберем прямоугольные оси  с началом в точке О, причем ось z направим по прямой
с началом в точке О, причем ось z направим по прямой  Тогда уравнения равновесия получат вид
Тогда уравнения равновесия получат вид

где  — проекции силы
— проекции силы  на оси
на оси  — проекции силы реакции в точке О на эти же оси;
— проекции силы реакции в точке О на эти же оси;  проекции силы реакции в точке
проекции силы реакции в точке  на оси
на оси  — расстояние между точками О и
— расстояние между точками О и 

Рис. 103

Рис. 104
Рассматриваемое твердое тело может свободно вращаться вокруг оси  проходящей через две неподвижные точки, а его положение в пространстве определяется одним параметром, в качестве которого можно взять угол поворота твердого тела вокруг этой оси. Условием равновесия, определяющим этот параметр, является последнее уравнение системы
проходящей через две неподвижные точки, а его положение в пространстве определяется одним параметром, в качестве которого можно взять угол поворота твердого тела вокруг этой оси. Условием равновесия, определяющим этот параметр, является последнее уравнение системы

Пять остальных уравнений служат для определения шести неизвестных проекций сил реакции связи. Эта задача не может быть полностью разрешена из-за того, что уравнений оказывается меньше, чем неизвестных, подлежащих определению. Такого рода задачи называются статически неопределимыми. Равновесие твердого тела не изменится, если в точках О и  добавить две равные по величине и направленные в противоположные стороны по прямой
добавить две равные по величине и направленные в противоположные стороны по прямой  силы. Такие силы могут быть обусловлены начальными напряжениями. Если в точке
силы. Такие силы могут быть обусловлены начальными напряжениями. Если в точке  поставить цилиндрический подшипник так, чтобы реакция в точке
поставить цилиндрический подшипник так, чтобы реакция в точке  была направлена перпендикулярно к оси z, то задача станет статически определимой. Разрешить статически неопределимую задачу можно также, отказавшись от гипотезы абсолютно твердого тела, как это и делается в курсах сопротивления материалов.
была направлена перпендикулярно к оси z, то задача станет статически определимой. Разрешить статически неопределимую задачу можно также, отказавшись от гипотезы абсолютно твердого тела, как это и делается в курсах сопротивления материалов.
в) Условия равновесия твердого тела, способного перемещаться параллельно неподвижной плоскости.
Рассмотрим задачу о равновесии твердого тела, опирающегося несколькими своими точками на неподвижную гладкую плоскость  Силы реакции со стороны плоскости здесь будут действовать только на точки контакта и ортогональны к плоскости
Силы реакции со стороны плоскости здесь будут действовать только на точки контакта и ортогональны к плоскости  Обозначим точки контакта через а их координаты через
Обозначим точки контакта через а их координаты через  . Тогда уравнения равновесия получат вид
. Тогда уравнения равновесия получат вид

где  проекции активных сил на оси
проекции активных сил на оси  — координаты точек приложения активных сил,
— координаты точек приложения активных сил,  — сила реакции, действующая на точку
— сила реакции, действующая на точку  твердого тела.
твердого тела.
Два первых и последнее уравнения дают необходимые условия равновесия твердого тела. Три остальных уравнения определяют силы реакции, действующие на твердое тело. Очевидно, что из трех уравнений можно определить только три неизвестные силы реакции. Задача определения сил реакции в том случае, когда твердое тело касается плоскости более чем тремя точками, не может быть разрешена методами статики абсолютно твердого тела и является статически неопределимой задачей. Для разрешения такого рода задач необходимо вводить дополнительные гипотезы.
Рассмотрим частный случай, когда твердое тело опирается о плоскость только тремя своими точками. Для определения сил реакции имеем три уравнения, которые запишем в виде

Здесь

Система уравнений (а) обладает решением только в том случае, когда определитель системы отличен от нуля, т. е.

Отсюда видно, что задача определения реакций разрешима только тогда, когда все три точки не лежат на одной прямой. Если это условие не выполняется, задача определения реакций становится неразрешимой, и мы снова приходим к статически неопределимой задаче.
Из необходимых условий равновесия

следует, что в рассматриваемом случае система активных сил, действующих на твердое тело, приводится к одной результирующей силе, линия действия которой параллельна оси  Обозначая результирующую силу через F, а координаты точки пересечения ее линии действия с плоскостью
Обозначая результирующую силу через F, а координаты точки пересечения ее линии действия с плоскостью  через а и
через а и  уравнения для определения сил реакции запишем в виде
уравнения для определения сил реакции запишем в виде

где F проекции вектора F на ось  Из первого уравнения следует, что
Из первого уравнения следует, что  Два других уравнения после подстановки значения F можно переписать в виде
Два других уравнения после подстановки значения F можно переписать в виде

Эти уравнения определяют центр системы параллельных векторов  который, как известно, находится внутри треугольника, образованного точками приложения этих векторов, т. е. точками соприкосновения тела и плоскости. Полученные условия равновесия сводятся к тому, что линия действия результирующей силы F проходит внутри треугольника, образованного точками касания.
который, как известно, находится внутри треугольника, образованного точками приложения этих векторов, т. е. точками соприкосновения тела и плоскости. Полученные условия равновесия сводятся к тому, что линия действия результирующей силы F проходит внутри треугольника, образованного точками касания.
г) Замечание о статически неопределимых задачах.
Рассмотрим тот случай, когда определитель А обращается в нуль

т. е. когда выполняется условие

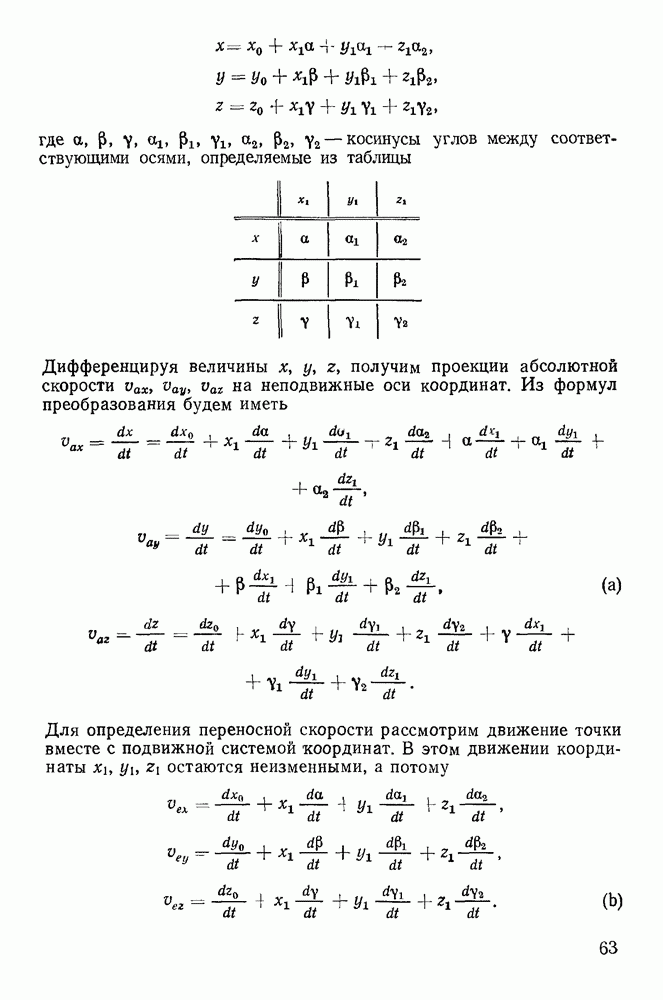
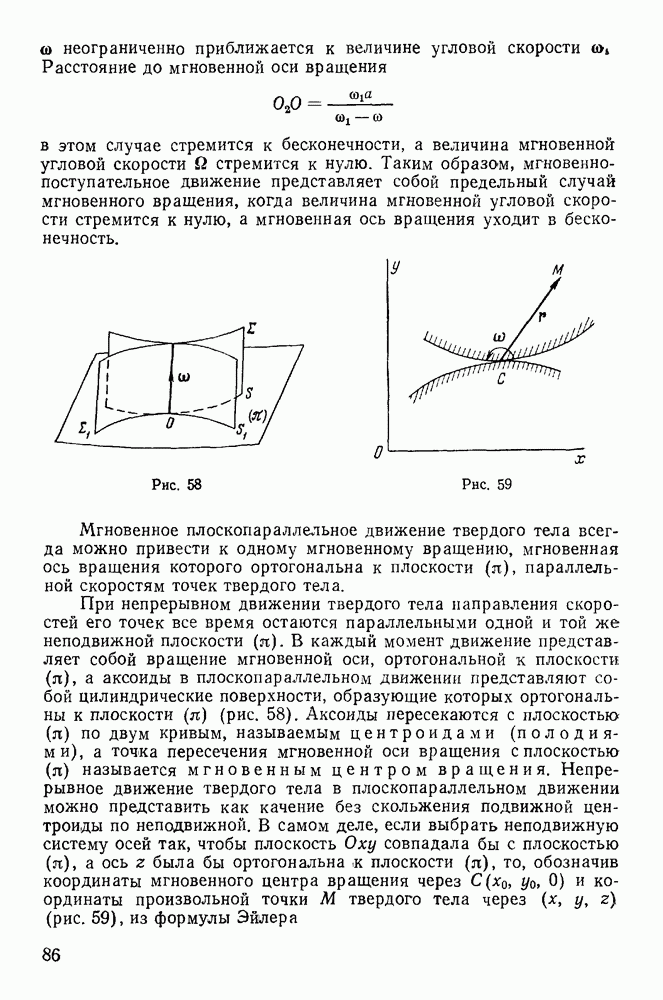
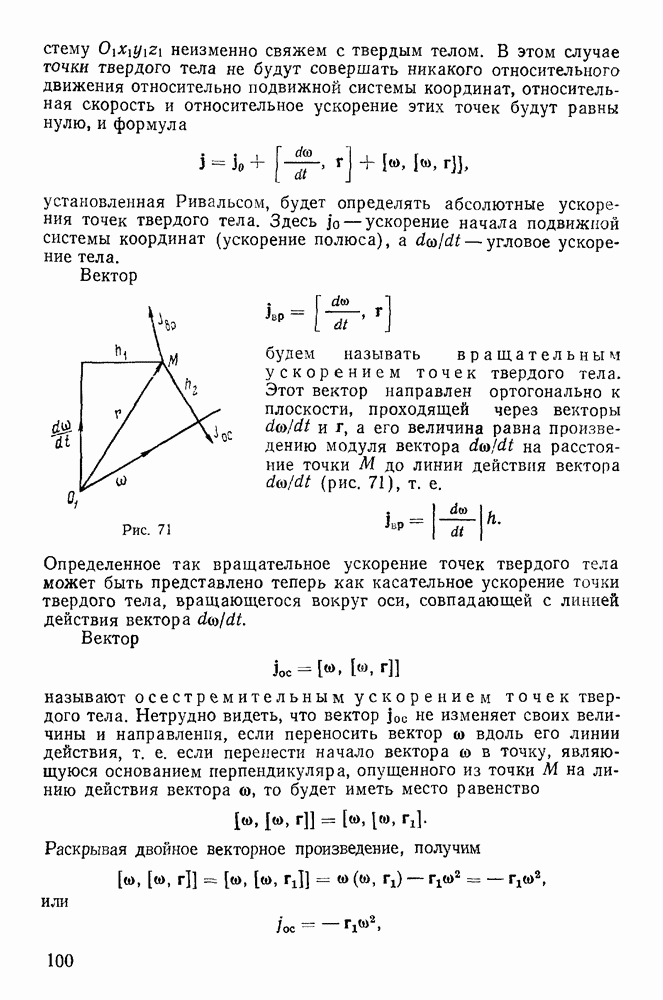
Последнее имеет место в случае, когда все три точки расположены на одной прямой (если точки не совпадают). Не нарушая общности, можно предположить, что все точки  расположены на оси х (рис. 105) и, следовательно,
расположены на оси х (рис. 105) и, следовательно,

Тогда уравнения для определения реакций примут вид

Последнее из этих уравнений дает условие равновесия активных сил, два первых уравнения служат для определения трех неизвестных реакций. Как уже отмечалось, задачи статики, в которых неизвестных больше, чем независимых уравнений равновесия, называются статически неопределимыми задачами.

Рис. 105

Рис. 106
Статическая неопределенность обусловливается излишними связями, накладываемыми на систему материальных точек, и может быть устранена освобождением системы от лишних связей. Такое освобождение системы от лишних связей осуществляется заменой связей силами, величины которых определяются из дополнительных условий, являющихся следствием вводимых физических гипотез. Так, например, рассматривая задачу о равновесии стержня, покоящегося на трех опорах, можно предположить, что одна из опор выполнена из упругого, легко деформируемого материала. Предположим, что возникающая при деформации сила сопротивления стержня подчинена закону Гука, а ее величина прямо пропорциональна величине сжатия опоры. Предположим, кроме того, что две другие опоры абсолютно жесткие, т. е. их деформации пренебрежимо малы. Обозначив через  длину несжатой опоры, а через
длину несжатой опоры, а через  длину опоры, когда на нее положен груз, силу, действующую со стороны опоры на балку, найдем из условия
длину опоры, когда на нее положен груз, силу, действующую со стороны опоры на балку, найдем из условия

Тогда уравнения для определения реакций получат вид

Отсюда сразу определяются неизвестные силы реакции 
Замечание. Статически неопределимые задачи могут стать статически определимыми, если систему частично освободить от некоторых связей.
Пример 38. Исследовать равновесие тяжелой абсолютно твердой палочки весом Р, закрепленной шарнирно в двух точках А и В (рис. 106).
Решение. Задача определения горизонтальных составляющих реакций в точках  оказывается неразрешимой (статически неопределимая задача). Если частично освободить палочку от связей, оставив в точке А шарнирное закрепление, а в точке В вместо шарнира ввести точечную опору, препятствующую перемещению палочки вниз, то задача станет статически определимой (предполагается, что палочка гладкая). Полученная статически определимая задача не эквивалентна первоначальной.
оказывается неразрешимой (статически неопределимая задача). Если частично освободить палочку от связей, оставив в точке А шарнирное закрепление, а в точке В вместо шарнира ввести точечную опору, препятствующую перемещению палочки вниз, то задача станет статически определимой (предполагается, что палочка гладкая). Полученная статически определимая задача не эквивалентна первоначальной.
В общем случае статически неопределимые задачи могут быть сделаны определимыми, если вместо гипотезы абсолютно твердого тела ввести гипотезу упругого тела, подчиняющегося закону Гука. Такого рода задачи решаются в курсах теории упругости и сопротивления материалов.
При исследовании равновесия системы абсолютно твердых тел статическая неопределимость может возникнуть как некоторое предельное положение системы.

Рис. 107

Рис. 108
Пример 39. Исследовать равновесие системы, состоящей из двух тяжелых однородных стержней, соединенных между собой шарнирно и закрепленных шарнирно в точках А и В (рис. 107), предполагая, что расстояние между точками А и В равно сумме длин стержней, так что оба стержня вытянуты в одну прямую линию.
Решение. Рассматриваемая задача является статически неопределимой, и реакции не могут быть найдены методами геометрической статики. Выбрав систему осей  как это показано на чертеже, и, обозначив через
как это показано на чертеже, и, обозначив через  соответствующие проекции реакций в точках А и В на эти оси, приведем систему сил, действующих на оба стержия, к точке А. Необходимые условия равновесия системы
соответствующие проекции реакций в точках А и В на эти оси, приведем систему сил, действующих на оба стержия, к точке А. Необходимые условия равновесия системы

Отсюда сразу получим  Для определения двух величин
Для определения двух величин  имеем только одно уравнение. Если же рассмотреть условия равновесия стержня
имеем только одно уравнение. Если же рассмотреть условия равновесия стержня  то, приводя систему сил, действующих на этот стержень, к точке С, будем иметь
то, приводя систему сил, действующих на этот стержень, к точке С, будем иметь

Отсюда находим  что при
что при  противоречит полученным ранее результатам. Новых условий для определения реакции
противоречит полученным ранее результатам. Новых условий для определения реакции  и в этом случае не получаем.
и в этом случае не получаем.
Противоречие устраняется, если отказаться от гипотезы абсолютно твердого тела или исключить условие о том, что расстояние между точками А и В равно сумме длин стержней. Рассмотрим это последнее предположение. Пусть расстояние АВ меньше суммы длин стержней (рис. 108). Тогда стержни образуют угол а с прямой, соединяющей точки А и В. Для определения реакций приведем сначала систему сил, действующих на оба стержня, к точке А. Тогда

Из этой системы уравнений следует, что

Приводя затем систему сил, действующих на стержень  к точке С, получим следующую систему уравнений:
к точке С, получим следующую систему уравнений:

которая дает

Реакции теперь полностью определяются (реакция в точке А находится из первой группы уравнений). Заметим, что при  величина реакции т. е. на стержень будут действовать очень большие растягивающие силы. В реальной задаче стержни не являются абсолютно твердыми, и эти усилия растягивают стержень так, что угол а при равновесии имеет конечное значение, отличное от нуля. Дальнейшее развитие изложенных положений можно найти в оригинальной монографии Пэнлеве «Лекции о трении».
величина реакции т. е. на стержень будут действовать очень большие растягивающие силы. В реальной задаче стержни не являются абсолютно твердыми, и эти усилия растягивают стержень так, что угол а при равновесии имеет конечное значение, отличное от нуля. Дальнейшее развитие изложенных положений можно найти в оригинальной монографии Пэнлеве «Лекции о трении».
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Введение
- Глава I. ОСНОВЫ ТЕОРИИ ВЕКТОРОВ
- § 1. СВОБОДНЫЕ ВЕКТОРЫ
- 2. Сложение свободных векторов.
- 3. Проекция вектора на ось.
- 4. Инварианты системы свободных векторов.
- § 2. СКОЛЬЗЯЩИЕ ВЕКТОРЫ
- 2. Координаты скользящего вектора.
- 3. Момент скользящего вектора. Плюккеровы координаты.
- 4. Аналитическое определение момента скользящего вектора.
- 5. Проекция момента на ось.
- 6. Момент скользящего вектора относительно оси
- § 3. СИСТЕМА СКОЛЬЗЯЩИХ ВЕКТОРОВ
- 2. Произвольная система скользящих векторов. Элементарные операции.
- 3. Приведение системы скользящих векторов к простейшей эквивалентной форме.
- 4. Плоская система скользящих векторов.
- 5. Свойства системы параллельных скользящих векторов.
- § 4. ЗАКРЕПЛЕННЫЕ ВЕКТОРЫ
- § 5. ДИФФЕРЕНЦИРОВАНИЕ СВОБОДНОГО ВЕКТОРА ПО СКАЛЯРНОМУ АРГУМЕНТУ
- Глава II. КИНЕМАТИКА
- § 1. КИНЕМАТИКА ТОЧКИ
- 2. Ускорение точки. Проекции ускорения на прямоугольные оси координат.
- 3. Скорость и ускорение точки в полярных координатах.
- 4. Движение точки по окружности.
- 5. Проекции ускорения на оси естественного трехгранника.
- 6. Теорема о сложении скоростей в сложном движении точки.
- 7. Метод Роберваля построения касательных к плоским кривым.
- 8. Аналитическое доказательство теоремы о сложении скоростей.
- 9. Сложение скоростей в общем случае сложного движения точки.
- § 2. КИНЕМАТИКА АБСОЛЮТНО ТВЕРДОГО ТЕЛА
- 2. Элементарные движения твердого тела.
- 3. Мгновенные движения твердого тела.
- 4. Сложение мгновенно-поступательных и мгновенно-вращательных движений твердого тела.
- 5. Общий случай сложения мгновенно-поступательных и мгновенно-вращательных движений твердого тела. Непрерывное движение твердого тела.
- 6. Мгновенное движение твердого тела с одной неподвижной точкой.
- 7. Плоскопараллельное движение твердого тела.
- § 3. УСКОРЕНИЕ ТОЧКИ В СЛОЖНОМ ДВИЖЕНИИ
- 2. Замечание о дифференцировании единичного вектора.
- 3. Векторный вывод теоремы Кориолиса.
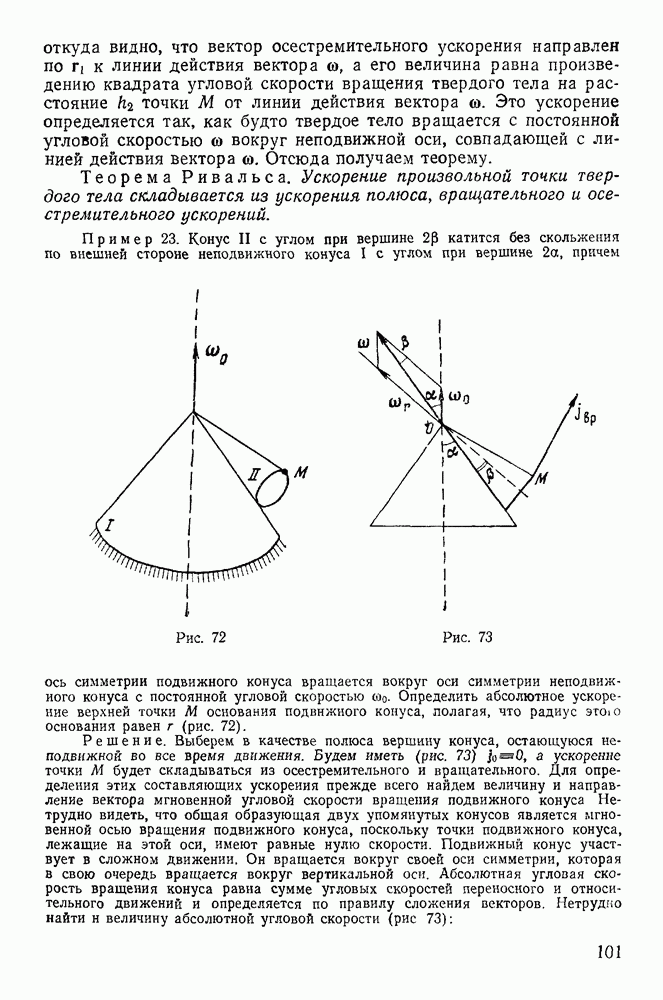
- 4. Теорема Ривальса.
- § 4. РАСПРЕДЕЛЕНИЕ УСКОРЕНИЙ В ПЛОСКОПАРАЛЛЕЛЬНОМ ДВИЖЕНИИ ТВЕРДОГО ТЕЛА
- 2. Мгновенный центр ускорений.
- § 5. КИНЕМАТИЧЕСКИЕ УРАВНЕНИЯ ЭЙЛЕРА
- Глава III. СТАТИКА
- I. ГЕОМЕТРИЧЕСКАЯ СТАТИКА
- § 1. АКСИОМЫ СТАТИКИ
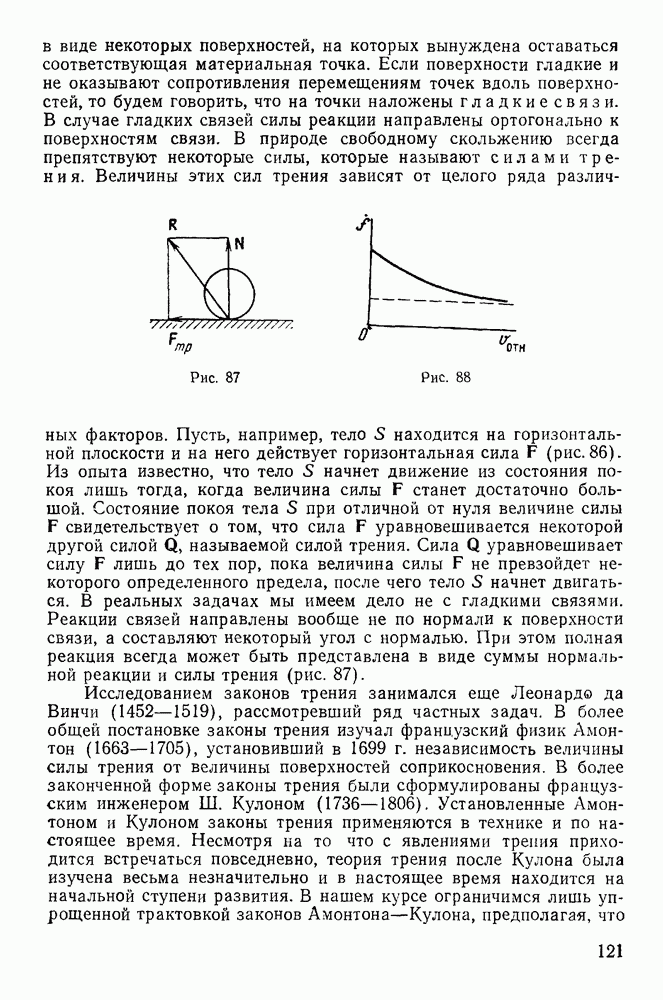
- § 2. ПОНЯТИЕ О СИЛЕ ТРЕНИЯ
- § 3. РАЗЛИЧНЫЕ ЗАДАЧИ СТАТИКИ
- 2. Равновесие трех сил.
- § 4. МОМЕНТ СИЛЫ
- 2. Момент силы относительно оси.
- 3. Теорема Вариньона для системы сходящихся сил.
- § 5. ПРОИЗВОЛЬНАЯ СИСТЕМА СИЛ, ДЕЙСТВУЮЩИХ НА ТВЕРДОЕ ТЕЛО
- § 6. УСЛОВИЯ РАВНОВЕСИЯ СИСТЕМЫ СИЛ, ДЕЙСТВУЮЩИХ НА ТВЕРДОЕ ТЕЛО
- § 7. ПРИВЕДЕНИЕ СИСТЕМЫ СИЛ, ДЕЙСТВУЮЩИХ НА ТВЕРДОЕ ТЕЛО, К ДИНАМЕ. УРАВНЕНИЯ РАВНОВЕСИЯ ТВЕРДОГО ТЕЛА
- § 8. УСЛОВИЯ РАВНОВЕСИЯ СИСТЕМЫ ТВЕРДЫХ ТЕЛ
- § 9. ПЛОСКАЯ СИСТЕМА СИЛ
- § 10. ЗАДАЧА О РАВНОВЕСИИ НЕСВОБОДНОГО ТВЕРДОГО ТЕЛА
- 2. Частные случаи равновесия твердого тела.
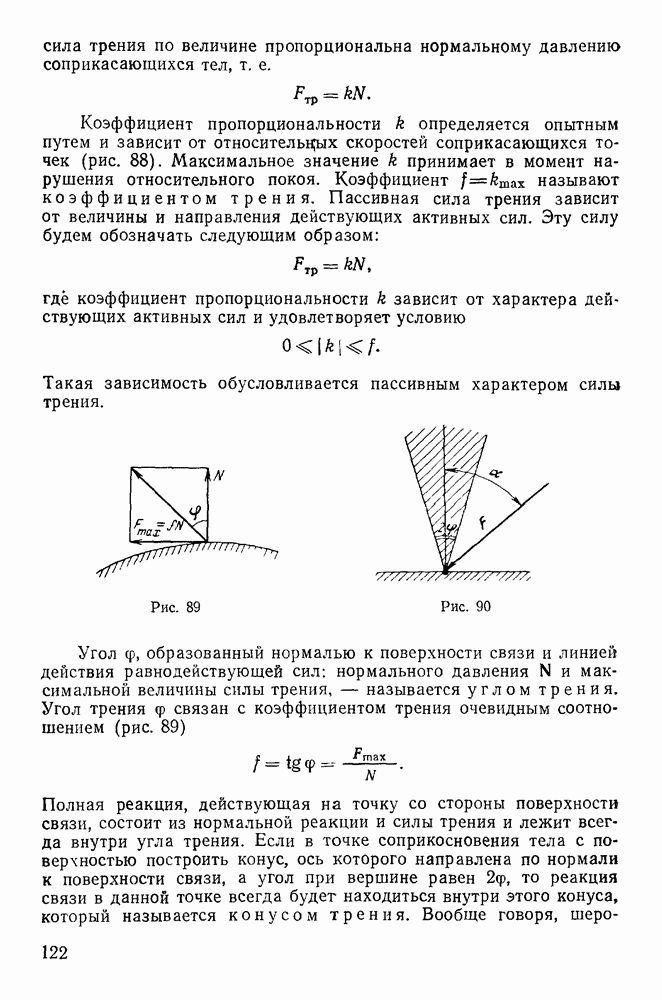
- § 11. ЗАДАЧА О РАВНОВЕСИИ ПРИ НАЛИЧИИ ТРЕНИЯ
- § 12. СИЛА ТЯЖЕСТИ И ЦЕНТР ТЯЖЕСТИ
- II. АНАЛИТИЧЕСКАЯ СТАТИКА
- § 1. РАБОТА СИЛЫ НА ПЕРЕМЕЩЕНИИ. СИЛОВАЯ ФУНКЦИЯ
- § 2. ПРИНЦИП ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ
- 2. Теорема Лагранжа о равновесии системы.
- 3. Принцип Торричелли.
- § 3. ОБЩИЕ ВОПРОСЫ АНАЛИТИЧЕСКОЙ СТАТИКИ
- 3. Общие теоремы о равновесии системы материальных точек.
- 4. Метод неопределенных множителей Лагранжа.
- 5. Определение реакций.
- § 4. ОПРЕДЕЛЕНИЕ РЕАКЦИЙ В ОБЩЕМ СЛУЧАЕ
- § 5. РАВНОВЕСИЕ НИТИ
- 2. Естественные уравнения равновесия нити.
- Глава IV. ДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ
- § 1. ОСНОВНЫЕ ЗАКОНЫ ДИНАМИКИ
- § 2. ДВЕ ОСНОВНЫЕ ЗАДАЧИ ДИНАМИКИ. УРАВНЕНИЯ ДВИЖЕНИЯ ТОЧКИ В ДЕКАРТОВЫХ ОСЯХ
- § 3. ЕСТЕСТВЕННЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ
- § 4. ОСНОВНЫЕ ТЕОРЕМЫ ДИНАМИКИ ДЛЯ СВОБОДНОЙ МАТЕРИАЛЬНОЙ ТОЧКИ
- 2. Теорема об изменении момента количества движения.
- 3. Следствия из теорем об изменении количества движения и момента количества движения материальной точки.
- 4. Теорема живых сил.
- 5. Интеграл живых сил.
- 6. Устойчивость равновесия. Теорема Лагранжа.
- § 5. ДВИЖЕНИЕ ТЯЖЕЛОЙ МАТЕРИАЛЬНОЙ ТОЧКИ В ПУСТОТЕ
- § 6. ДВИЖЕНИЕ МАТЕРИАЛЬНОЙ ТОЧКИ ПОД ДЕЙСТВИЕМ ЦЕНТРАЛЬНЫХ СИЛ
- 2. Формулы Бине
- 3. Задача о движении планет
- § 7. ДВИЖЕНИЕ ТОЧКИ В СОПРОТИВЛЯЮЩЕЙСЯ СРЕДЕ
- § 8. ДВИЖЕНИЕ НЕСВОБОДНОЙ МАТЕРИАЛЬНОЙ ТОЧКИ
- 2. Движение материальной точки по поверхности.
- § 9. ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЕ МАТЕРИАЛЬНОЙ ТОЧКИ
- 1. Теорема живых сил в относительном движении точки.
- 2. Уравнения относительного равновесия точки.
- 3. Равновесие материальной точки на поверхности Земли. Вес.
- 4. Задача о падении тяжелой точки в пустоте.
- 5. Маятник Фуко.
- § 10. ПРИНЦИП ДАЛАМБЕРА
- Глава V. ДИНАМИКА СИСТЕМЫ МАТЕРИАЛЬНЫХ ТОЧЕК
- § 1. УЧЕНИЕ О СВЯЗЯХ
- § 2. ПРИНЦИП ДАЛАМБЕРА — ЛАГРАНЖА
- § 3. ОСНОВНЫЕ ТЕОРЕМЫ ДИНАМИКИ СИСТЕМЫ
- 2. Теорема об изменении момента количества движения.
- 3. Теорема живых сил.
- § 4. ТЕОРЕМЫ О ДВИЖЕНИИ СИСТЕМЫ ОТНОСИТЕЛЬНО ОСЕЙ НЕИЗМЕННОГО НАПРАВЛЕНИЯ, ПРОХОДЯЩИХ ЧЕРЕЗ ЦЕНТР МАСС СИСТЕМЫ (ОСЕЙ КЕНИГА)
- 2. Теорема об изменении момента количества движения системы относительно осей Кёнига.
- 3. Теорема живых сил в движении системы относительно осей Кёнига.
- § 5. УРАВНЕНИЯ ЛАГРАНЖА ВТОРОГО РОДА
- 2. Случай существования силовой функции.
- 3. Замечание о лагранжевых координатах.
- § 6. ЭЛЕМЕНТАРНЫЕ СЛУЧАИ ИНТЕГРИРУЕМОСТИ УРАВНЕНИЙ ЛАГРАНЖА
- 2. Метод Рауса игнорирования циклических координат.
- 3. Обобщение теоремы и интеграла живых сил.
- § 7. ОПРЕДЕЛЕНИЕ РЕАКЦИЙ
- Глава VI. ДИНАМИКА ТВЕРДОГО ТЕЛА
- § 1. ТЕОРИЯ МОМЕНТОВ ИНЕРЦИИ
- 2. Момент инерции системы относительно произвольной оси, проходящей через заданную точку.
- 3. Эллипсоид инерции.
- 4. Определение главных осей инерции для произвольной точки.
- § 2. ВРАЩЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ОСИ
- § 3. ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА, ИМЕЮЩЕГО ОДНУ НЕПОДВИЖНУЮ ТОЧКУ
- 2. Уравнения движения твердого тела с одной неподвижной точкой.
- § 4. ДВИЖЕНИЕ ТЯЖЕЛОГО ТВЕРДОГО ТЕЛА ОКОЛО НЕПОДВИЖНОЙ ТОЧКИ
- 2. Интегрирование уравнений движения тяжелого твердого тела.
- 3. Случай Эйлера — Пуансо.
- Регулярная прецессия твердого тела в случае Эйлера.
- Геометрическая интерпретация Пуансо движения твердого тела в случае Эйлера.
- Устойчивость постоянных вращений твердого тела.
- 4. Случай Лагранжа.
- Особенные случаи движения твердого тела. Спящий волчок.
- Гироскоп. Приближенная теория.
- Некоторые применения гироскопов.
- Регулярная прецессия в случае Лагранжа.
- Вынужденная регулярная прецессия.
- 5. Случай Ковалевской.
- § 5. ОПРЕДЕЛЕНИЕ РЕАКЦИИ В СЛУЧАЕ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА С ОДНОЙ НЕПОДВИЖНОЙ ТОЧКОЙ
- § 6. УРАВНЕНИЯ ДВИЖЕНИЯ СВОБОДНОГО ТВЕРДОГО ТЕЛА
- § 7. ГИРОСТАТЫ
- Глава VII. АНАЛИТИЧЕСКАЯ ДИНАМИКА
- § 1. КАНОНИЧЕСКИЕ УРАВНЕНИЯ ГАМИЛЬТОНА
- 1. Преобразования Лежандра.
- 2. Канонические уравнения Гамильтона.
- 3. Функция Гамильтона и ее свойства.
- § 2. ПРИНЦИП ГАМИЛЬТОНА — ОСТРОГРАДСКОГО
- 2. Вывод канонических уравнений Гамильтона из принципа Гамильтона — Остроградского.
- 3. Принцип Гамильтона в форме Пуанкаре.
- § 3. ИНТЕГРИРОВАНИЕ КАНОНИЧЕСКИХ УРАВНЕНИЙ ГАМИЛЬТОНА
- 2. Канонические преобразования.
- 3. Бесконечно малые канонические преобразования.
- 4. Теорема Лиувилля.
- 5. Теорема Якоби.
- 6. Интегрирование уравнения Гамильтона—Якоби.
- Метод Имшенецкого разделения переменных.
- 7. Скобки Пуассона.
- § 4. ВАРИАЦИОННЫЕ ПРИНЦИПЫ МЕХАНИКИ
- 2. Принцип Лагранжа.
- 3. Принцип наименьшего действия в форме Якоби.
- Вывод уравнений Лагранжа второго рода из принципа Якоби.
- Сравнение принципа Якоби с принципом Гамильтона.
- 4. Оптико-механическая аналогия.
- 5. Интегральные инварианты.
- Линейные интегральные инварианты.
- Интегральный инвариант Пуанкаре — Картана.
- 6. Принцип наименьшего принуждения Гаусса. Уравнения Аппеля.
- 7. Уравнения Рауса.
- § 5. МАЛЫЕ КОЛЕБАНИЯ
- Затухающие колебания.
- Вынужденные колебания. Резонанс.
- Параметрический резонанс.
- Нелинейные колебания.
- Диссипативные системы.
- 2. Общий случай малых колебаний системы около положения устойчивого равновесия.
- Устойчивость равновесия. Теорема Лагранжа об устойчивости равновесия.
- Замечание об устойчивости стационарных движений.
- Малые колебания системы около положения устойчивого равновесия.
- Влияние диссипативных сил на малые колебания системы около устойчивого положения равновесия.
- § 6. УСТОЙЧИВОСТЬ ДВИЖЕНИЯ
- Прямой метод Ляпунова
- Теорема об асимптотической устойчивости.
- Теорема Четаева о неустойчивости движения.
- 2. Влияние новых связей на малые колебания системы около положения равновесия.
- 3. Влияние диссипативных сил на устойчивость равновесия.
- 4. Влияние гироскопических сил на устойчивость равновесия.
- § 7. ЭЛЕМЕНТЫ ТЕОРИИ ВОЗМУЩЕНИЙ
- Устойчивость консервативных систем.
- 2. Метод изменения произвольных постоянных.
- Глава VIII. ТЕОРИЯ УДАРА
- § 2. ТЕОРЕМЫ КАРНО
- § 3. ЗАДАЧА О ЦЕНТРЕ УДАРА
- § 4. ЗАДАЧА О БАЛЛИСТИЧЕСКОМ МАЯТНИКЕ
- § 5. УРАВНЕНИЯ ЛАГРАНЖА ДЛЯ УДАРА
- § 6. ЗАДАЧА ОБ УДАРЕ ПО ТВЕРДОМУ ТЕЛУ С ОДНОЙ НЕПОДВИЖНОЙ ТОЧКОЙ
- Глава IX. ЭЛЕМЕНТЫ СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- § 2. СПЕЦИАЛЬНЫЙ ПРИНЦИП ОТНОСИТЕЛЬНОСТИ ЭЙНШТЕЙНА
- § 3. ГРУППА ПРЕОБРАЗОВАНИЙ ЛОРЕНЦА
- § 4. ИНВАРИАНТНЫЕ ВЕЛИЧИНЫ В ТЕОРИИ ОТНОСИТЕЛЬНОСТИ. ЧЕТЫРЕХМЕРНЫЙ ВЕКТОР. МИР МИНКОВСКОГО
- § 5. РЕЛЯТИВИСТСКАЯ ДИНАМИКА
- Литература