| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 8. ДВИЖЕНИЕ НЕСВОБОДНОЙ МАТЕРИАЛЬНОЙ ТОЧКИ
В технических задачах большое значение имеют вопросы движения материальной точки, перемещения которой стесняются связями. Сюда относятся задачи о движении материальной точки по кривой и по поверхности.
1. Движение материальной точки по кривой.
Наиболее просто представляется движение материальной точки по кривой. Ее положение на кривой определяется всего одним параметром и для полного определения движения точки достаточно определить закон изменения этого параметра со временем.
Рассмотрим движение материальной точки по гладкой материальной кривой  , предполагая, что кривая может со временем менять свою форму и положение относительно системы отсчета
, предполагая, что кривая может со временем менять свою форму и положение относительно системы отсчета  в которой определены силы, действующие на материальную точку. Кроме активных сил на точку будут действовать еще и силы реакции связи. Так как кривая гладкая, то силы реакции не
в которой определены силы, действующие на материальную точку. Кроме активных сил на точку будут действовать еще и силы реакции связи. Так как кривая гладкая, то силы реакции не  препятствовать перемещению точки по кривой, и полная реакция кривой будет ортогональна к кривой.
препятствовать перемещению точки по кривой, и полная реакция кривой будет ортогональна к кривой.
Будем сначала предполагать, что кривая задана в пространстве, определяемом системой отсчета  уравнениями
уравнениями

т. е. представляется как геометрическое место точек пересечения двух поверхностей. Пусть  и
и  -нормали, проведенные в точке
-нормали, проведенные в точке  соответственно к поверхностям
соответственно к поверхностям  Вектор
Вектор  будет коллинеарен с вектором градиента к поверхности
будет коллинеарен с вектором градиента к поверхности  и его проекции будут пропорциональны частным производным
и его проекции будут пропорциональны частным производным

Вектор  имеет соответственно проекции, пропорциональные частным производным
имеет соответственно проекции, пропорциональные частным производным

Любая нормаль к кривой  будет лежать в плоскости нормалей
будет лежать в плоскости нормалей  Обозначая через
Обозначая через  силу реакции кривой
силу реакции кривой  на материальную точку, будем иметь
на материальную точку, будем иметь

Полагая, что на точку действует еще активная сила  получим уравнения движения точки
получим уравнения движения точки

Эти уравнения называются уравнениями Лагранжа первого рода.
а) Теорема живых сил.
Умножая уравнения движения соответственно на  и складывая их, получим в левой части
и складывая их, получим в левой части

В правой же части будем иметь 

Точка движется в соответствии с наложенными на нее связями, а координаты точки в каждый момент времени удовлетворяют уравнениям поверхностей

представляющих собой тождества по времени. Дифференцируя эти тождества, будем иметь

и окончательно получим

или после умножения на  теорему живых сил представим в виде
теорему живых сил представим в виде

Уравнение получает простой вид, когда связи, наложенные на точку, не зависят явно от времени. Тогда  , и уравнение запишется следующим образом:
, и уравнение запишется следующим образом:

В результате получаем, что если связи, наложенные на материальную точку, не зависят явно от времени, то теорема живых сил получает такой же вид, как и для свободной материальной точки. Если, кроме того, активные силы обладают силовой функцией, зависящей только от координат, т. е. существует функция  удовлетворяющая условиям
удовлетворяющая условиям

то правая часть уравнения живых сил будет представлять собой полный дифференциал от функции  и уравнение получит вид
и уравнение получит вид

отсюда сразу же получаем первый интеграл уравнений движения — интеграл живых сил

Постоянная живых сил  определяется из начальных условий. Мы получаем следующую теорему.
определяется из начальных условий. Мы получаем следующую теорему.
Теорема. Если связи, наложенные на материальную точку, вынужденную оставаться на материальной кривой, не зависят явно от времени, а действующие на точку активные силы обладают силовой функцией, то уравнения движения материальной точки допускают существование первого интеграла — интеграла живых сил.
б) Качественное исследование движения.
Положение материальной точки на кривой может быть определено одним параметром — длиной дуги кривой. Поэтому для решения задачи о движении материальной точки по кривой достаточно всего одного уравнения движения, вместо которого можно принять интеграл живых сил, если только он существует.
Рассмотрим задачу о движении тяжелой материальной точки М с массой  по неподвижной замкнутой кривой с непрерывно меняющейся касательной (рис. 160). В рассматриваемом случае связи, наложенные на материальную точку, не зависят явно от времени, а действующие силы обладают силовой функцией. Поэтому будет существовать интеграл живых сил
по неподвижной замкнутой кривой с непрерывно меняющейся касательной (рис. 160). В рассматриваемом случае связи, наложенные на материальную точку, не зависят явно от времени, а действующие силы обладают силовой функцией. Поэтому будет существовать интеграл живых сил


Рис. 160
Поскольку ось  направлена вертикально вверх, получим
направлена вертикально вверх, получим

или

Положив  перепишем интеграл в виде
перепишем интеграл в виде

Из этого соотношения видим, что скорость обращается в нуль только на горизонтальной плоскости

Обозначим эту плоскость через  Если через Р обозначить проекцию точки М на плоскость
Если через Р обозначить проекцию точки М на плоскость  то для скорости получим значение
то для скорости получим значение

откуда видно, что скорость определяется расстоянием точки М от плоскости 
Может оказаться, что плоскость  не имеет общих точек с кривой
не имеет общих точек с кривой  Если плоскость
Если плоскость  «выше» кривой, то скорость нигде не обращается в нуль, и точка будет двигаться сколь угодно долго по кривой. Ниже кривой плоскость
«выше» кривой, то скорость нигде не обращается в нуль, и точка будет двигаться сколь угодно долго по кривой. Ниже кривой плоскость  не может быть расположена, так как правая часть равенства
не может быть расположена, так как правая часть равенства  должна быть неотрицательна.
должна быть неотрицательна.
Предположим, что кривая  пересекает плоскость
пересекает плоскость  в точках А и А. Обозначая через
в точках А и А. Обозначая через  длину дуги, отсчитываемую от точки
длину дуги, отсчитываемую от точки  будем иметь
будем иметь

откуда

Уравнение кривой позволяет определить

а тогда в предыдущем уравнении можно разделить переменные

Пусть точка начинает свое движение из положения  Обозначим длину дуги
Обозначим длину дуги  через I. Обозначая через
через I. Обозначая через  дугу, определяющую положение точки в некоторый момент времени, и рассматривая
дугу, определяющую положение точки в некоторый момент времени, и рассматривая  как функцию
как функцию  разложим
разложим  в ряд Тэйлора в окрестности точки А
в ряд Тэйлора в окрестности точки А

Если производная от z по  в точке А отлична от нуля, то разложение
в точке А отлична от нуля, то разложение  будет начинаться с членов первого порядка малости относительно
будет начинаться с членов первого порядка малости относительно  а для величины
а для величины  получим выражение
получим выражение

Для точек, лежащих ниже плоскости  всегда будем иметь при этом
всегда будем иметь при этом

Рассмотрим интеграл

который определяет время движения точки из положения  в положение А Этот интеграл является несобственным, так как подынтегральная функция
в положение А Этот интеграл является несобственным, так как подынтегральная функция

где

при  неограниченно возрастает. На основании признака Коши при
неограниченно возрастает. На основании признака Коши при  интеграл будет сходиться, если функция
интеграл будет сходиться, если функция  является бесконечно большой порядка
является бесконечно большой порядка  по сравнению с
по сравнению с  и будет расходиться, если
и будет расходиться, если  будет порядка по сравнению с
будет порядка по сравнению с  .
.
Если в точке А первые  производных от функции
производных от функции  обращаются в нуль, то
обращаются в нуль, то

т. е. функция  будет иметь порядок
будет иметь порядок  При
При  интеграл
интеграл  сходится, а при
сходится, а при  интеграл расходится В первом случае время, необходимое для достижения точки А, определяется сходящимся интегралом. После достижения точки А движущаяся материальная точка возвращается к положению
интеграл расходится В первом случае время, необходимое для достижения точки А, определяется сходящимся интегралом. После достижения точки А движущаяся материальная точка возвращается к положению  которое она достигает со скоростью
которое она достигает со скоростью  и далее движется к точке А. Движение в этом случае будет иметь колебательный характер.
и далее движется к точке А. Движение в этом случае будет иметь колебательный характер.
Во втором случае, когда 12

движущаяся точка будет неограниченно приближаться к точке А, никогда ее не достигая.
Положение материальной точки на кривой определяется всего одним параметром. Такое движение называют однопараметрическим. Если действующие на точку силы обладают силовой функцией, то движение будет происходить в соответствии с интегралом живых сил. Для изображения состояния движения материальной точки удобно воспользоваться понятием фазовой плоскости, т. е. плоскости, на которой переменные  рассматриваются как декартовы координаты точки. Каждая точка фазовой плоскости изображает определенное состояние материальной точки, поэтому такую точку называют изображающей. При движении материальной точки изображающая точка будет описывать некоторую кривую, которая называется фазовой траекторией и не является действительной траекторией движения. Скорость движения изображающей точки называется фазовой скоростью, которая не является скоростью настоящей материальной точки.
рассматриваются как декартовы координаты точки. Каждая точка фазовой плоскости изображает определенное состояние материальной точки, поэтому такую точку называют изображающей. При движении материальной точки изображающая точка будет описывать некоторую кривую, которая называется фазовой траекторией и не является действительной траекторией движения. Скорость движения изображающей точки называется фазовой скоростью, которая не является скоростью настоящей материальной точки.
Если определить силовую функцию как  то интеграл живых сил
то интеграл живых сил

будет определять семейство фазовых траекторий на фазовой плоскости. Задание начального состояния движения материальной точки определяет  и однозначно определяет фазовую траекторию точки. Семейство фазовых траекторий является однопараметрическим семейством. Фазовые траектории, соответствующие различным начальным условиям (различным
и однозначно определяет фазовую траекторию точки. Семейство фазовых траекторий является однопараметрическим семейством. Фазовые траектории, соответствующие различным начальным условиям (различным  между собой не пересекаются, что следует из условия единственности решения уравнений движения. Движение изображающей точки по траектории происходит по часовой стрелке, так как в точках, где
между собой не пересекаются, что следует из условия единственности решения уравнений движения. Движение изображающей точки по траектории происходит по часовой стрелке, так как в точках, где  координата
координата  должна возрастать при движении изображающей точки. Состоянию покоя могут соответствовать только точки, находящиеся на оси
должна возрастать при движении изображающей точки. Состоянию покоя могут соответствовать только точки, находящиеся на оси  причем фазовые траектории пересекаются с осью
причем фазовые траектории пересекаются с осью  под прямым углом. Точки, в которых обращаются в нуль
под прямым углом. Точки, в которых обращаются в нуль  и производная
и производная  называются особыми точками фазовой плоскости. В особых точках скорость изображающей точки равна нулю. Все эти точки находятся на оси
называются особыми точками фазовой плоскости. В особых точках скорость изображающей точки равна нулю. Все эти точки находятся на оси  Зная совокупность фазовых траекторий, можно видеть всю картину возможных движений при различных начальных условиях.
Зная совокупность фазовых траекторий, можно видеть всю картину возможных движений при различных начальных условиях.
Перепишем интеграл живых сил в виде

где  При помощи этого интеграла легко можно построить фазовые траектории. В самом деле, нетрудно видеть, что все фазовые траектории симметричны относительно оси
При помощи этого интеграла легко можно построить фазовые траектории. В самом деле, нетрудно видеть, что все фазовые траектории симметричны относительно оси  Геометрическим местом точек, где касательные к фазовым кривым горизонтальны, будут точки, определяемые из уравнения
Геометрическим местом точек, где касательные к фазовым кривым горизонтальны, будут точки, определяемые из уравнения

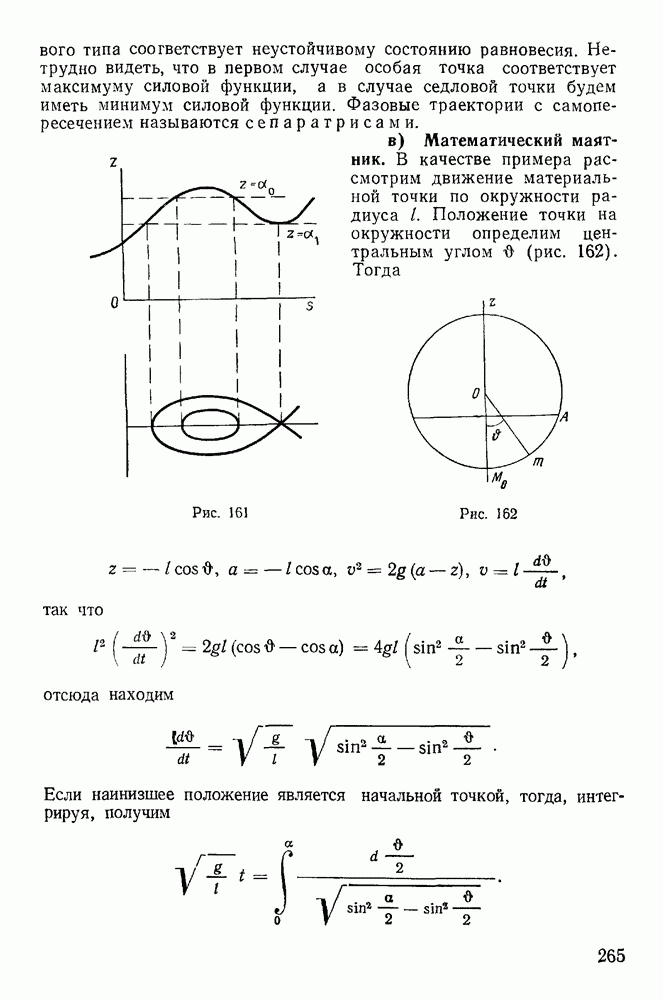
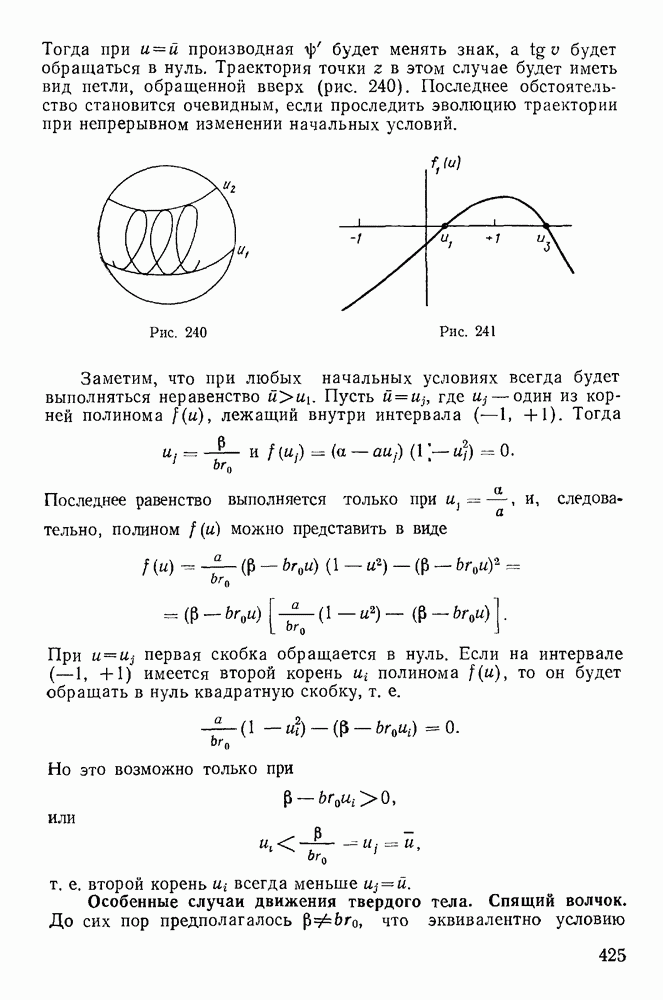
за исключением, быть может, особых точек. Можно предложить следующий способ построения фазовых траекторий. Построим сначала график функции  (рис. 161). Пусть некоторые начальные значения определяют постоянную
(рис. 161). Пусть некоторые начальные значения определяют постоянную  Построим горизонтальную прямую
Построим горизонтальную прямую  Разность
Разность  определяет
определяет  . Если провести другую прямую
. Если провести другую прямую  то получим другую фазовую траекторию. В результате такого построения на фазовой плоскости получим континуум замкнутых кривых, вложенных одна в другую и охватывающих выродившуюся в точку фазовую траекторию. Особая точка здесь соответствует положению равновесия материальной точки.
то получим другую фазовую траекторию. В результате такого построения на фазовой плоскости получим континуум замкнутых кривых, вложенных одна в другую и охватывающих выродившуюся в точку фазовую траекторию. Особая точка здесь соответствует положению равновесия материальной точки.
Особая точка типа «центр» будет соответствовать устойчивому положению равновесия материальной точки. Особая точка
седлового типа соответствует неустойчивому состоянию равновесия. Нетрудно видеть, что в первом случае особая точка соответствует максимуму силовой функции, а в случае седловой точки будем иметь минимум силовой функции. Фазовые траектории с самопересечением называются сепаратрисами.
в) Математический маятник.
В качестве примера рассмотрим движение материальной точки по окружности радиуса  Положение точки на окружности определим центральным углом
Положение точки на окружности определим центральным углом  (рис. 162). Тогда
(рис. 162). Тогда

Рис. 161

Рис. 162

так что

отсюда находим

Если наинизшее положение является начальной точкой, тогда, интегрируя, получим

Выполним замену переменной  и положим
и положим

Так как при  , кроме того,
, кроме того,

то

Таким образом, время движения материальной точки (четверть периода) выражается через эллиптический интеграл первого рода. Но выражение

можно разложить в ряд

и тогда задача сведется к вычислению интегралов типа

Отсюда для периода получим

Если амплитуда колебаний а достаточно мала, то в разложении для периода колебаний можно пренебрегать членами, содержащими  Приближенное значение периода в этом случае будет
Приближенное значение периода в этом случае будет

Если период вычисляется по этой формуле, то уже при амплитуде в 20° ошибка периода достигает 0,8%, при  при
при  Для математического маятника, длина которого
Для математического маятника, длина которого  при амплитуде 90° ошибка периода достигает 1 сек.
при амплитуде 90° ошибка периода достигает 1 сек.
г) Циклоидальный маятник.
Нидерландский математик и механик Христиан Гюйгенс (1629—1695) изобрел маятник, период колебаний которого не зависит от амплитуды колебаний (изохронный маятник). Оказалось, что период не зависит от амплитуды, если точка движется по циклоиде.
Циклоида представляет собой кривую, которую описывает точка обода круга, катящегося по неподвижной прямой (рис. 163).

Рис. 163
Пусть циклоида имеет горизонтальное основание, расположена в вертикальной плоскости и обращена своей вогнутостью вверх. За ось х примем неподвижную горизонтальную прямую, касающуюся циклоиды в нижней точке, ось у направим вертикально вверх. Уравнение циклоиды можно параметрически представить в виде

откуда

скорость точки

Применяя интеграл живых сил

получим

Пусть при  тогда
тогда  и интеграл живых сил приобретает вид
и интеграл живых сил приобретает вид

или

Полагая  получим
получим

откуда будем иметь

т. e. время движения точки до самого низшего положения не зависит от начального положения точки (от амплитуды).
д) Определение реакции.
Если для изучения движения точки по кривой применить естественные уравнения движения, то будем иметь одно уравнение, определяющее само движение точки, и два уравнения для определения реакции

Первое из этих уравнений эквивалентно теореме живых сил и приводит к интегралу живых сил, если выполнены условия существования последнего.
Пример 73. Шарик, масса которого равна  нанизан на горизонтальную проволочную окружность радиуса
нанизан на горизонтальную проволочную окружность радиуса  Зная коэффициент трения
Зная коэффициент трения  определить, какую начальную скорость нужно сообщить шарику, чтобы он сделал по окружности один полный оборот.
определить, какую начальную скорость нужно сообщить шарику, чтобы он сделал по окружности один полный оборот.
Решение. На точку действуют три силы: снла тяжести, нормальная реакция и сила трения. Составим уравнения движения точки

Последние два уравнения дают модуль полной реакции

При помощи этого соотношения приведем первое уравнение движения к виду

или

Разделяя переменные, будем иметь

Но

откуда

При 

или

откуда

Окончательно имеем

| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Введение
- Глава I. ОСНОВЫ ТЕОРИИ ВЕКТОРОВ
- § 1. СВОБОДНЫЕ ВЕКТОРЫ
- 2. Сложение свободных векторов.
- 3. Проекция вектора на ось.
- 4. Инварианты системы свободных векторов.
- § 2. СКОЛЬЗЯЩИЕ ВЕКТОРЫ
- 2. Координаты скользящего вектора.
- 3. Момент скользящего вектора. Плюккеровы координаты.
- 4. Аналитическое определение момента скользящего вектора.
- 5. Проекция момента на ось.
- 6. Момент скользящего вектора относительно оси
- § 3. СИСТЕМА СКОЛЬЗЯЩИХ ВЕКТОРОВ
- 2. Произвольная система скользящих векторов. Элементарные операции.
- 3. Приведение системы скользящих векторов к простейшей эквивалентной форме.
- 4. Плоская система скользящих векторов.
- 5. Свойства системы параллельных скользящих векторов.
- § 4. ЗАКРЕПЛЕННЫЕ ВЕКТОРЫ
- § 5. ДИФФЕРЕНЦИРОВАНИЕ СВОБОДНОГО ВЕКТОРА ПО СКАЛЯРНОМУ АРГУМЕНТУ
- Глава II. КИНЕМАТИКА
- § 1. КИНЕМАТИКА ТОЧКИ
- 2. Ускорение точки. Проекции ускорения на прямоугольные оси координат.
- 3. Скорость и ускорение точки в полярных координатах.
- 4. Движение точки по окружности.
- 5. Проекции ускорения на оси естественного трехгранника.
- 6. Теорема о сложении скоростей в сложном движении точки.
- 7. Метод Роберваля построения касательных к плоским кривым.
- 8. Аналитическое доказательство теоремы о сложении скоростей.
- 9. Сложение скоростей в общем случае сложного движения точки.
- § 2. КИНЕМАТИКА АБСОЛЮТНО ТВЕРДОГО ТЕЛА
- 2. Элементарные движения твердого тела.
- 3. Мгновенные движения твердого тела.
- 4. Сложение мгновенно-поступательных и мгновенно-вращательных движений твердого тела.
- 5. Общий случай сложения мгновенно-поступательных и мгновенно-вращательных движений твердого тела. Непрерывное движение твердого тела.
- 6. Мгновенное движение твердого тела с одной неподвижной точкой.
- 7. Плоскопараллельное движение твердого тела.
- § 3. УСКОРЕНИЕ ТОЧКИ В СЛОЖНОМ ДВИЖЕНИИ
- 2. Замечание о дифференцировании единичного вектора.
- 3. Векторный вывод теоремы Кориолиса.
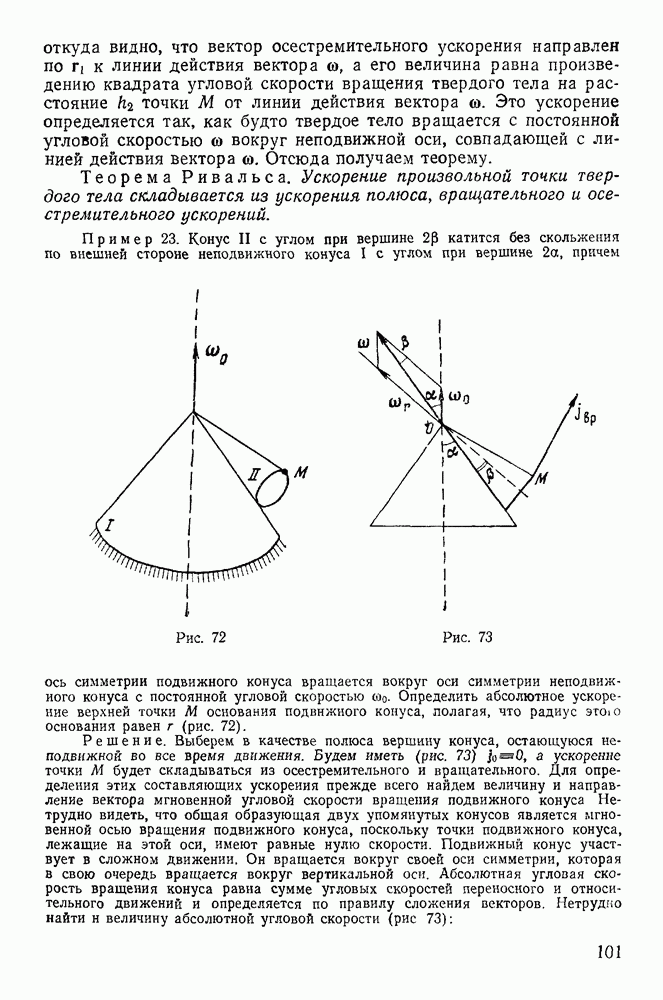
- 4. Теорема Ривальса.
- § 4. РАСПРЕДЕЛЕНИЕ УСКОРЕНИЙ В ПЛОСКОПАРАЛЛЕЛЬНОМ ДВИЖЕНИИ ТВЕРДОГО ТЕЛА
- 2. Мгновенный центр ускорений.
- § 5. КИНЕМАТИЧЕСКИЕ УРАВНЕНИЯ ЭЙЛЕРА
- Глава III. СТАТИКА
- I. ГЕОМЕТРИЧЕСКАЯ СТАТИКА
- § 1. АКСИОМЫ СТАТИКИ
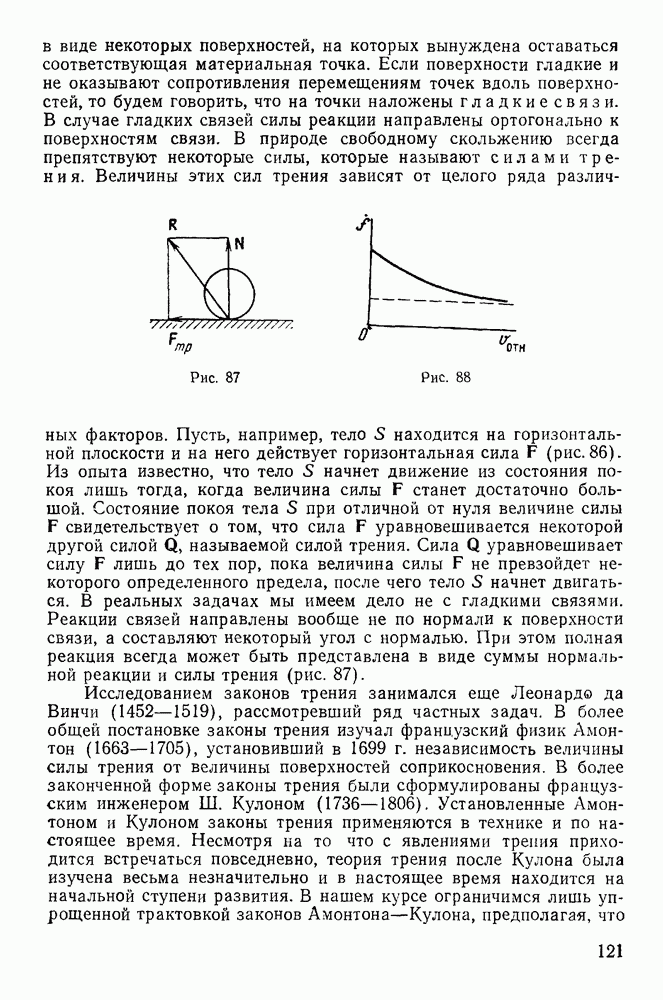
- § 2. ПОНЯТИЕ О СИЛЕ ТРЕНИЯ
- § 3. РАЗЛИЧНЫЕ ЗАДАЧИ СТАТИКИ
- 2. Равновесие трех сил.
- § 4. МОМЕНТ СИЛЫ
- 2. Момент силы относительно оси.
- 3. Теорема Вариньона для системы сходящихся сил.
- § 5. ПРОИЗВОЛЬНАЯ СИСТЕМА СИЛ, ДЕЙСТВУЮЩИХ НА ТВЕРДОЕ ТЕЛО
- § 6. УСЛОВИЯ РАВНОВЕСИЯ СИСТЕМЫ СИЛ, ДЕЙСТВУЮЩИХ НА ТВЕРДОЕ ТЕЛО
- § 7. ПРИВЕДЕНИЕ СИСТЕМЫ СИЛ, ДЕЙСТВУЮЩИХ НА ТВЕРДОЕ ТЕЛО, К ДИНАМЕ. УРАВНЕНИЯ РАВНОВЕСИЯ ТВЕРДОГО ТЕЛА
- § 8. УСЛОВИЯ РАВНОВЕСИЯ СИСТЕМЫ ТВЕРДЫХ ТЕЛ
- § 9. ПЛОСКАЯ СИСТЕМА СИЛ
- § 10. ЗАДАЧА О РАВНОВЕСИИ НЕСВОБОДНОГО ТВЕРДОГО ТЕЛА
- 2. Частные случаи равновесия твердого тела.
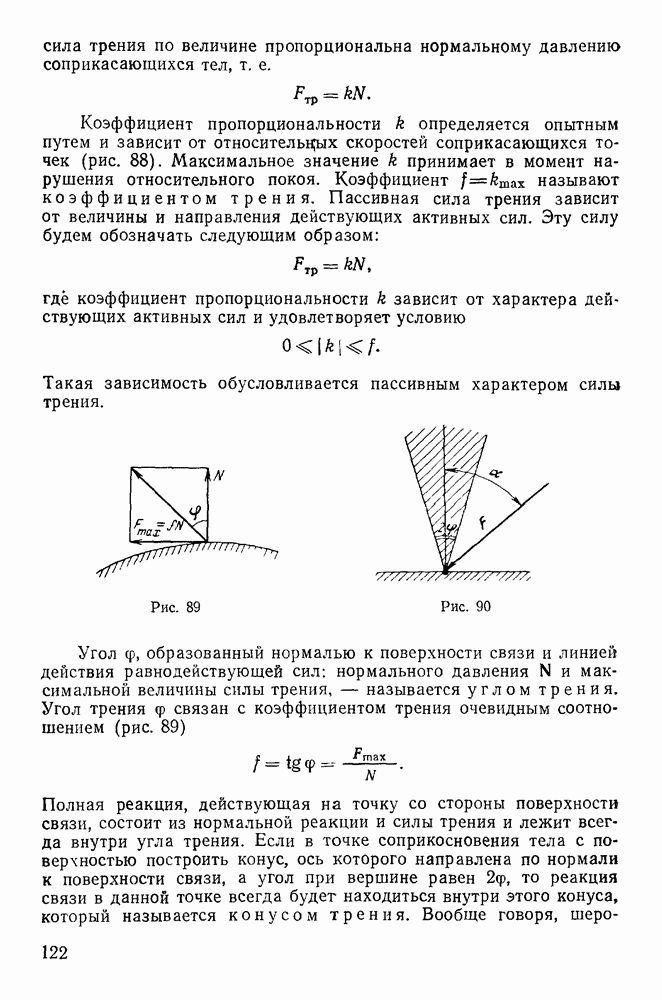
- § 11. ЗАДАЧА О РАВНОВЕСИИ ПРИ НАЛИЧИИ ТРЕНИЯ
- § 12. СИЛА ТЯЖЕСТИ И ЦЕНТР ТЯЖЕСТИ
- II. АНАЛИТИЧЕСКАЯ СТАТИКА
- § 1. РАБОТА СИЛЫ НА ПЕРЕМЕЩЕНИИ. СИЛОВАЯ ФУНКЦИЯ
- § 2. ПРИНЦИП ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ
- 2. Теорема Лагранжа о равновесии системы.
- 3. Принцип Торричелли.
- § 3. ОБЩИЕ ВОПРОСЫ АНАЛИТИЧЕСКОЙ СТАТИКИ
- 3. Общие теоремы о равновесии системы материальных точек.
- 4. Метод неопределенных множителей Лагранжа.
- 5. Определение реакций.
- § 4. ОПРЕДЕЛЕНИЕ РЕАКЦИЙ В ОБЩЕМ СЛУЧАЕ
- § 5. РАВНОВЕСИЕ НИТИ
- 2. Естественные уравнения равновесия нити.
- Глава IV. ДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ
- § 1. ОСНОВНЫЕ ЗАКОНЫ ДИНАМИКИ
- § 2. ДВЕ ОСНОВНЫЕ ЗАДАЧИ ДИНАМИКИ. УРАВНЕНИЯ ДВИЖЕНИЯ ТОЧКИ В ДЕКАРТОВЫХ ОСЯХ
- § 3. ЕСТЕСТВЕННЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ
- § 4. ОСНОВНЫЕ ТЕОРЕМЫ ДИНАМИКИ ДЛЯ СВОБОДНОЙ МАТЕРИАЛЬНОЙ ТОЧКИ
- 2. Теорема об изменении момента количества движения.
- 3. Следствия из теорем об изменении количества движения и момента количества движения материальной точки.
- 4. Теорема живых сил.
- 5. Интеграл живых сил.
- 6. Устойчивость равновесия. Теорема Лагранжа.
- § 5. ДВИЖЕНИЕ ТЯЖЕЛОЙ МАТЕРИАЛЬНОЙ ТОЧКИ В ПУСТОТЕ
- § 6. ДВИЖЕНИЕ МАТЕРИАЛЬНОЙ ТОЧКИ ПОД ДЕЙСТВИЕМ ЦЕНТРАЛЬНЫХ СИЛ
- 2. Формулы Бине
- 3. Задача о движении планет
- § 7. ДВИЖЕНИЕ ТОЧКИ В СОПРОТИВЛЯЮЩЕЙСЯ СРЕДЕ
- § 8. ДВИЖЕНИЕ НЕСВОБОДНОЙ МАТЕРИАЛЬНОЙ ТОЧКИ
- 2. Движение материальной точки по поверхности.
- § 9. ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЕ МАТЕРИАЛЬНОЙ ТОЧКИ
- 1. Теорема живых сил в относительном движении точки.
- 2. Уравнения относительного равновесия точки.
- 3. Равновесие материальной точки на поверхности Земли. Вес.
- 4. Задача о падении тяжелой точки в пустоте.
- 5. Маятник Фуко.
- § 10. ПРИНЦИП ДАЛАМБЕРА
- Глава V. ДИНАМИКА СИСТЕМЫ МАТЕРИАЛЬНЫХ ТОЧЕК
- § 1. УЧЕНИЕ О СВЯЗЯХ
- § 2. ПРИНЦИП ДАЛАМБЕРА — ЛАГРАНЖА
- § 3. ОСНОВНЫЕ ТЕОРЕМЫ ДИНАМИКИ СИСТЕМЫ
- 2. Теорема об изменении момента количества движения.
- 3. Теорема живых сил.
- § 4. ТЕОРЕМЫ О ДВИЖЕНИИ СИСТЕМЫ ОТНОСИТЕЛЬНО ОСЕЙ НЕИЗМЕННОГО НАПРАВЛЕНИЯ, ПРОХОДЯЩИХ ЧЕРЕЗ ЦЕНТР МАСС СИСТЕМЫ (ОСЕЙ КЕНИГА)
- 2. Теорема об изменении момента количества движения системы относительно осей Кёнига.
- 3. Теорема живых сил в движении системы относительно осей Кёнига.
- § 5. УРАВНЕНИЯ ЛАГРАНЖА ВТОРОГО РОДА
- 2. Случай существования силовой функции.
- 3. Замечание о лагранжевых координатах.
- § 6. ЭЛЕМЕНТАРНЫЕ СЛУЧАИ ИНТЕГРИРУЕМОСТИ УРАВНЕНИЙ ЛАГРАНЖА
- 2. Метод Рауса игнорирования циклических координат.
- 3. Обобщение теоремы и интеграла живых сил.
- § 7. ОПРЕДЕЛЕНИЕ РЕАКЦИЙ
- Глава VI. ДИНАМИКА ТВЕРДОГО ТЕЛА
- § 1. ТЕОРИЯ МОМЕНТОВ ИНЕРЦИИ
- 2. Момент инерции системы относительно произвольной оси, проходящей через заданную точку.
- 3. Эллипсоид инерции.
- 4. Определение главных осей инерции для произвольной точки.
- § 2. ВРАЩЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ОСИ
- § 3. ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА, ИМЕЮЩЕГО ОДНУ НЕПОДВИЖНУЮ ТОЧКУ
- 2. Уравнения движения твердого тела с одной неподвижной точкой.
- § 4. ДВИЖЕНИЕ ТЯЖЕЛОГО ТВЕРДОГО ТЕЛА ОКОЛО НЕПОДВИЖНОЙ ТОЧКИ
- 2. Интегрирование уравнений движения тяжелого твердого тела.
- 3. Случай Эйлера — Пуансо.
- Регулярная прецессия твердого тела в случае Эйлера.
- Геометрическая интерпретация Пуансо движения твердого тела в случае Эйлера.
- Устойчивость постоянных вращений твердого тела.
- 4. Случай Лагранжа.
- Особенные случаи движения твердого тела. Спящий волчок.
- Гироскоп. Приближенная теория.
- Некоторые применения гироскопов.
- Регулярная прецессия в случае Лагранжа.
- Вынужденная регулярная прецессия.
- 5. Случай Ковалевской.
- § 5. ОПРЕДЕЛЕНИЕ РЕАКЦИИ В СЛУЧАЕ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА С ОДНОЙ НЕПОДВИЖНОЙ ТОЧКОЙ
- § 6. УРАВНЕНИЯ ДВИЖЕНИЯ СВОБОДНОГО ТВЕРДОГО ТЕЛА
- § 7. ГИРОСТАТЫ
- Глава VII. АНАЛИТИЧЕСКАЯ ДИНАМИКА
- § 1. КАНОНИЧЕСКИЕ УРАВНЕНИЯ ГАМИЛЬТОНА
- 1. Преобразования Лежандра.
- 2. Канонические уравнения Гамильтона.
- 3. Функция Гамильтона и ее свойства.
- § 2. ПРИНЦИП ГАМИЛЬТОНА — ОСТРОГРАДСКОГО
- 2. Вывод канонических уравнений Гамильтона из принципа Гамильтона — Остроградского.
- 3. Принцип Гамильтона в форме Пуанкаре.
- § 3. ИНТЕГРИРОВАНИЕ КАНОНИЧЕСКИХ УРАВНЕНИЙ ГАМИЛЬТОНА
- 2. Канонические преобразования.
- 3. Бесконечно малые канонические преобразования.
- 4. Теорема Лиувилля.
- 5. Теорема Якоби.
- 6. Интегрирование уравнения Гамильтона—Якоби.
- Метод Имшенецкого разделения переменных.
- 7. Скобки Пуассона.
- § 4. ВАРИАЦИОННЫЕ ПРИНЦИПЫ МЕХАНИКИ
- 2. Принцип Лагранжа.
- 3. Принцип наименьшего действия в форме Якоби.
- Вывод уравнений Лагранжа второго рода из принципа Якоби.
- Сравнение принципа Якоби с принципом Гамильтона.
- 4. Оптико-механическая аналогия.
- 5. Интегральные инварианты.
- Линейные интегральные инварианты.
- Интегральный инвариант Пуанкаре — Картана.
- 6. Принцип наименьшего принуждения Гаусса. Уравнения Аппеля.
- 7. Уравнения Рауса.
- § 5. МАЛЫЕ КОЛЕБАНИЯ
- Затухающие колебания.
- Вынужденные колебания. Резонанс.
- Параметрический резонанс.
- Нелинейные колебания.
- Диссипативные системы.
- 2. Общий случай малых колебаний системы около положения устойчивого равновесия.
- Устойчивость равновесия. Теорема Лагранжа об устойчивости равновесия.
- Замечание об устойчивости стационарных движений.
- Малые колебания системы около положения устойчивого равновесия.
- Влияние диссипативных сил на малые колебания системы около устойчивого положения равновесия.
- § 6. УСТОЙЧИВОСТЬ ДВИЖЕНИЯ
- Прямой метод Ляпунова
- Теорема об асимптотической устойчивости.
- Теорема Четаева о неустойчивости движения.
- 2. Влияние новых связей на малые колебания системы около положения равновесия.
- 3. Влияние диссипативных сил на устойчивость равновесия.
- 4. Влияние гироскопических сил на устойчивость равновесия.
- § 7. ЭЛЕМЕНТЫ ТЕОРИИ ВОЗМУЩЕНИЙ
- Устойчивость консервативных систем.
- 2. Метод изменения произвольных постоянных.
- Глава VIII. ТЕОРИЯ УДАРА
- § 2. ТЕОРЕМЫ КАРНО
- § 3. ЗАДАЧА О ЦЕНТРЕ УДАРА
- § 4. ЗАДАЧА О БАЛЛИСТИЧЕСКОМ МАЯТНИКЕ
- § 5. УРАВНЕНИЯ ЛАГРАНЖА ДЛЯ УДАРА
- § 6. ЗАДАЧА ОБ УДАРЕ ПО ТВЕРДОМУ ТЕЛУ С ОДНОЙ НЕПОДВИЖНОЙ ТОЧКОЙ
- Глава IX. ЭЛЕМЕНТЫ СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- § 2. СПЕЦИАЛЬНЫЙ ПРИНЦИП ОТНОСИТЕЛЬНОСТИ ЭЙНШТЕЙНА
- § 3. ГРУППА ПРЕОБРАЗОВАНИЙ ЛОРЕНЦА
- § 4. ИНВАРИАНТНЫЕ ВЕЛИЧИНЫ В ТЕОРИИ ОТНОСИТЕЛЬНОСТИ. ЧЕТЫРЕХМЕРНЫЙ ВЕКТОР. МИР МИНКОВСКОГО
- § 5. РЕЛЯТИВИСТСКАЯ ДИНАМИКА
- Литература