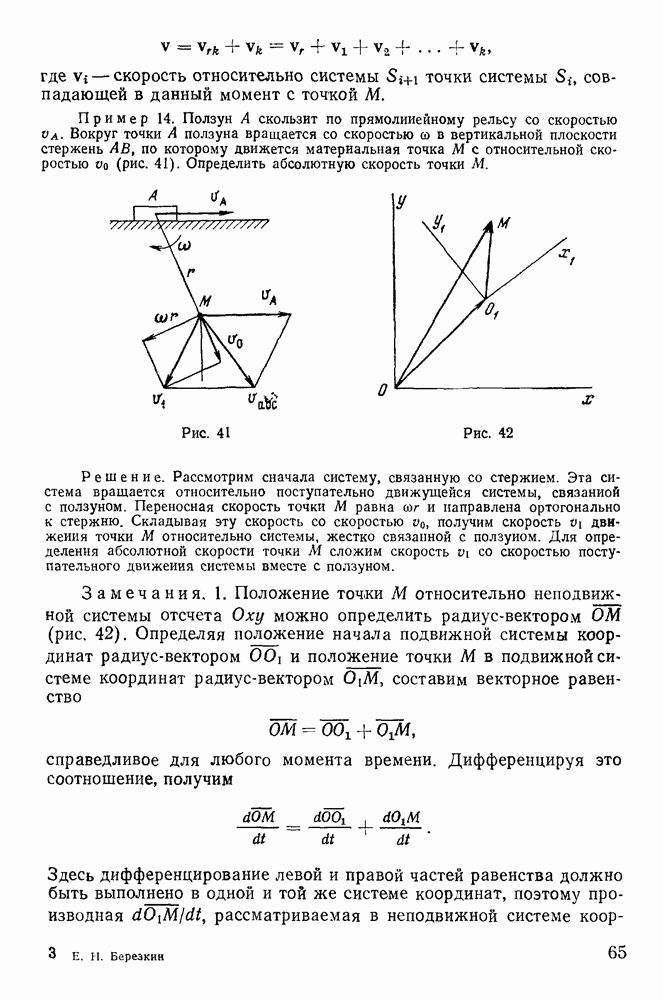
5. Общий случай сложения мгновенно-поступательных и мгновенно-вращательных движений твердого тела. Непрерывное движение твердого тела.

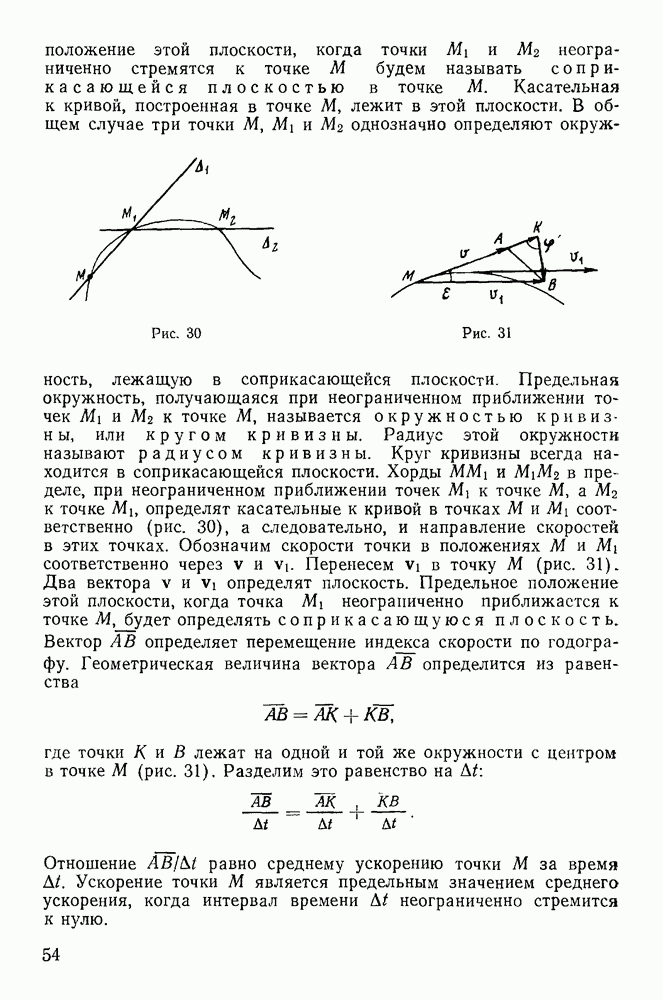
Рассмотрим сложное мгновенное движение твердого тела, состоящее из мгновенно-поступательных движений со скоростями и мгновенно-вращательных движений с угловыми скоростями (рис. 46), Пусть линии действия векторов проходят соответственно через точки

Теорема. Результирующее мгновенное движение твердого тела, участвующего одновременно в нескольких мгновенно-поступательных

и мгновенно-вращательных движениях, сводится к двум простейшим мгновенным движениям: одному мгновенно-поступательному и одному мгновенно-вращательному движению.

Доказательство. Твердое тело участвует в системе мгновенных движений. Добавим к этой системе движений еще два мгновенных движения, не изменяющих распределения скоростей в твердом теле. Такими движениями являются мгновенные вращения с угловыми скоростями линии действия которых совпадают и проходят через точку О. Тогда вектор с началом в точке и вектор проходящий через точку О, образуют пару вращений, эквивалентную одному мгновенно-поступательному движению со скоростью

Аналогичные построения проведем с каждым из векторов

Рис. 46

Рис. 47

Полученная новая система мгновенных движений твердого тела эквивалентна первоначальной системе и состоит из системы мгновенных вращений с угловыми скоростями линии действия которых проходят через начало координат, и системы мгновенно-поступательных движений со скоростями причем

Как было показано выше, система мгновенно-поступательных движений эквивалентна одному мгновенно-поступательному движению, скорость которого равна геометрической сумме составляющих скоростей мгновенно-поступательных движений

Система мгновенных вращений вокруг пересекающихся осей эквивалентна одному мгновенно-вращательному движению, угловая скорость которого равна геометрической сумме угловых скоростей составляющих мгновенных вращений, причем линия действия вектора проходит через точку пересечения линий действия составляющих векторов и т. е.

Этим доказана теорема о том, что результирующее движение твердого тела сводится к одному мгновенно-поступательному движению со скоростью и одному мгновенно-вращательному движению с угловой скоростью

а) Мгновенно-винтовое движение твердого тела.

Теорема. Сложное мгновенное движение твердого тела, состоящее из одного мгновенно-поступательного движения со скоростью и одного мгновенно-вращательного движения с угловой скоростью Q эквивалентно одному мгновенно-винтовому движению.

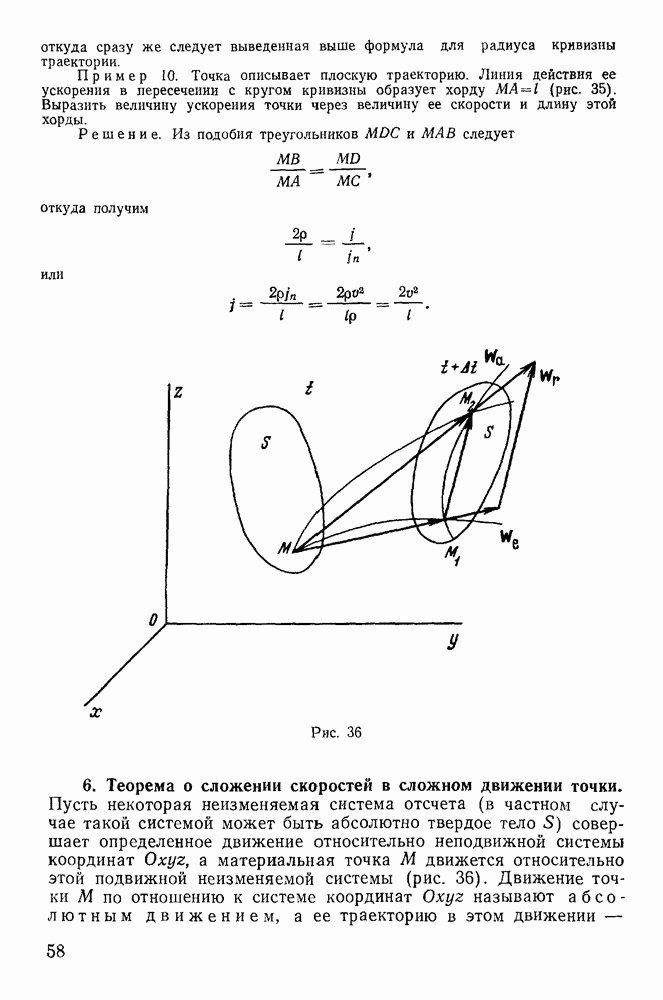
Доказательство. Рассмотрим мгновенное движение твердого тела, состоящее из мгновенного вращения с угловой скоростью линия действия которого проходит через точку О, и мгновеннопоступательного движения со скоростью (рис. 47). Представим вектор в виде суммы двух свободных векторов и , один из которых параллелен вектору а второй ортогонален вектору . В плоскости проходящей через линию действия вектора Q и ортогональной к вектору , выберем такую точку относительно которой момент вектора по величине совпадает с величиной вектора а по направлению противоположен направлению вектора . Положение точки определяется из условия

или

Умножив векторно это равенство на получим

или

Если, «роме того, потребовать, чтобы отрезок 001 был ортогонален к линии действия вектора то равенство можно будет переписать в виде

К рассматриваемой системе мгновенных движений твердого тела добавим два мгновенных вращения с угловыми скоростями и

, линии действия которых проходят через точку Полученная новая система мгновенных движений твердого тела эквивалентна первоначальной системе мгновенных движений. Но вектор проходящий через точку О, и вектор проходящий через точку образуют пару вращений, эквивалентную мгновенно-поступательному движению со скоростью

Результирующее движение состоит из одного мгновенного вращения с угловой скоростью , линия действия которой проходит через точку и системы мгновенно-поступательных движений со скоростями и Два последних мгновенно-поступательных движения эквивалентны одному мгновенно-поступательному движению со скоростью

коллинеарной с линией действия вектора

Мгновенное движение твердого тела, состоящее из таких мгновенно-вращательного и мгновенно-поступательного движений, у которых линии действия векторов мгновенно-угловой скорости и мгновенно-поступательной скорости коллинеарны, будем называть мгновенно-винтовым движением. Рассмотренное выше движение является мгновенно-винтовым движением твердого тела. Прямую линию твердого тела, для всех точек которой направление скорости совпадает с направлением мгновенно-угловой скорости твердого тела, будем называть винтовой осью. Отношение скорости поступательного движения тела вдоль винтовой оси к его угловой скорости

называют параметром винта. При будем иметь только одно мгновенное вращение, при мгновенно-поступательное движение. Мгновенно-винтовое движение определяет лишь состояние скоростей в данный момент времени, но не определяет полностью всего непрерывного движения твердого тела. Чтобы полностью определить движение, надо знать характер изменения скорости. Если же твердое тело действительно совершает винтовое движение, так что положение винтовой оси и параметры, определяющие состояние скоростей, не меняются, тогда за время т. е. за время одного полного оборота, тело продвинется вдоль винтовой оси на расстояние

число называют шагом винта

б) Теорема Эйлера.

Рассмотрим самый общий случай движения твердого тела и докажем теорему, принадлежащую Эйлеру, о распределении скоростей в твердом теле при произвольном движении.

Теорема. Произвольное мгновенное движение твердого тела в любой момент времени может быть представлено как сумма двух мгновенных движений: одного мгновенно-поступательного и одного мгновенно-вращательного.

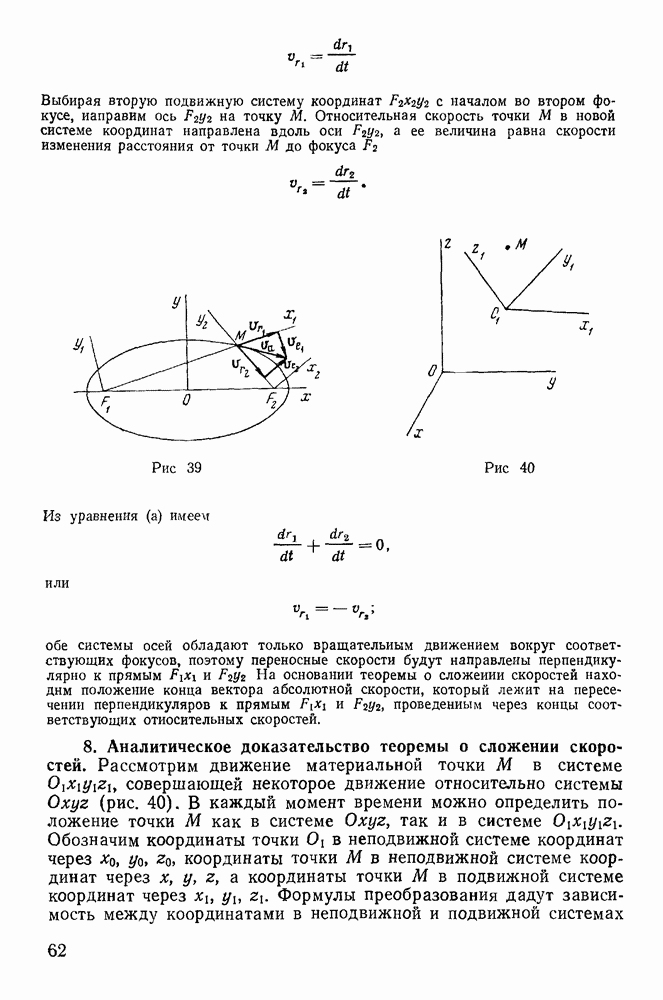
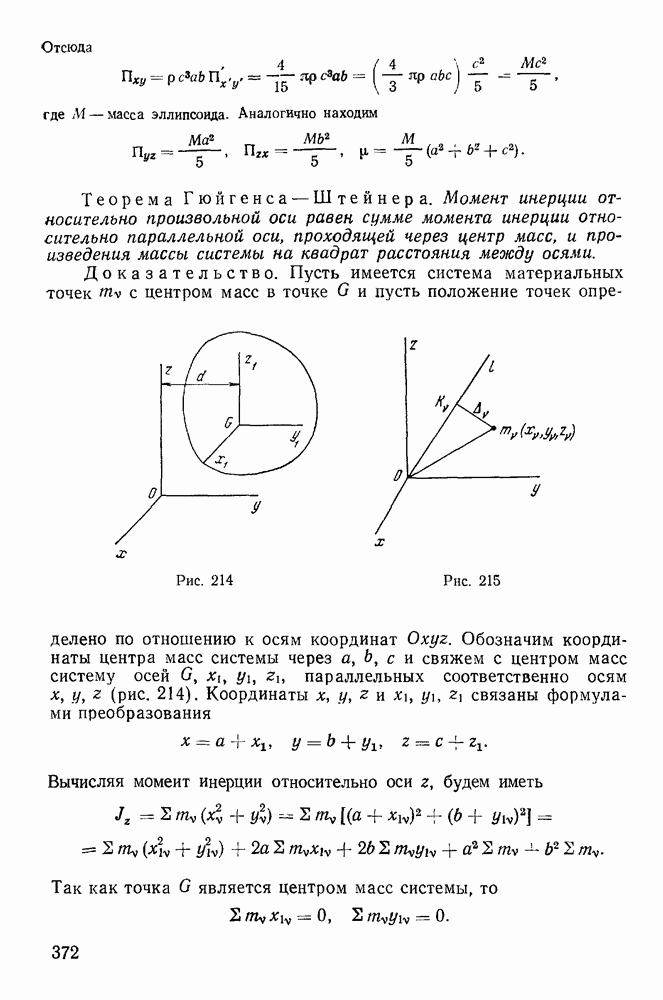
Доказательство. Будем рассматривать движение твердого тела относительно системы осей (рис. 48). С твердым телом свяжем жестко другую систему осей относительно которой оно не совершает движения. 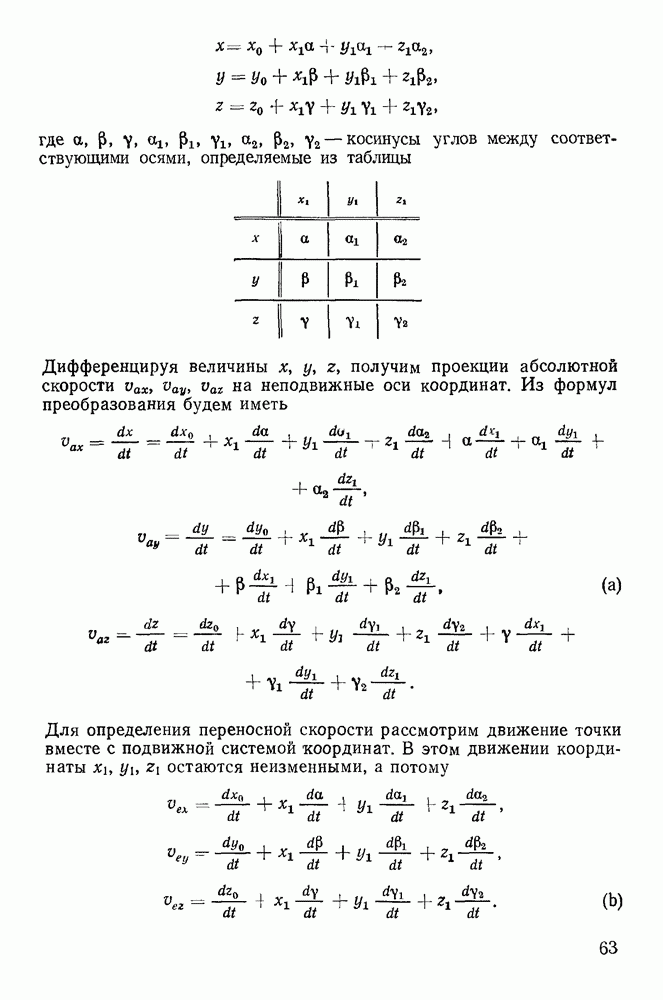Тогда движение твердого тела будет полностью определяться движением подвижной системы координат Выберем произвольную точку М твердого тела и рассмотрим ее движение относительно системы осей Координаты точки М в неподвижной системе отсчета обозначим через а ее координаты в системе, связанной с твердым телом, — через Через обозначим координаты точки Положение подвижной системы координат определяется положением точки и направляющими косинусами углов между осями подвижной и неподвижной систем координат. Эти направляющие косинусы можно задать таблицей:

Рис. 48

Координаты х, у, z точки М связаны с ее координатами известными формулами преобразования координат

Проекции скорости точки на неподвижные оси координат получим, дифференцируя координаты х, у, z по времени,

Чтобы придать формулам более симметричный вид, рассмотрим сначала проекции вектора абсолютной скорости точки М на подвижные оси Эти проекции найдем из уравнений

которые приводят к следующей формуле:

Аналогичным образом можно вывести формулы для Дифференцируя тождественное соотношение, связывающее направляющие косинусы

получим

Рассмотрим далее косинусы углов между подвижными осями координат

Дифференцируя эти соотношения по времени, приходим к следующему результату:

Проекции скорости точки М на оси запишутся в виде

(Последние два равенства легко получаются из первого циклической перестановкой индексов.) Введем единичные векторы направленные соответственно по осям Тогда вектор скорости точки М можно представить как сумму трех векторов

Пусть вектор представляет скорость точки относительно системы Если, кроме того, ввести вектор с проекциями на подвижные оси и вектор с проекциями то сумму векторов

можно будет представить в виде определителя

и окончательно скорость точки М определится формулой

которая называется формулой Эйлера. Формула показывает, что скорость произвольной точки твердого тела складывается из скоростей начала подвижной системы координат (общей для всех точек твердого тела) и скорости, определяемой векторным произведением Последняя формула соответствует случаю мгновенновращательного движения твердого тела, причем вектор представляет мгновенную угловую скорость вращения твердого тела относительно системы осей, совершающей поступательное движение вместе с точкой . В результате в самом общем случае мгновенное движение твердого тела сводится к одному мгновенно-поступательному движению со скоростью произвольной точки неизменно связанной с твердым телом (ее иногда называют полюсом), и одному мгновенному вращательному движению с угловой скоростью и, вектор которой проходит через точку Этим и доказана теорема Эйлера.

Замечание. Скорость произвольной точки твердого тела, определяемую формулой Эйлера, можно рассматривать как скорость движения материальной точки в сложном движении в соответствии с теоремой о сложении скоростей. При этом одно из

рассмотренных мгновенных движений твердого тела будет являться переносным, а другое — относительным, и в каждый момент мгновенное движение твердого тела можно представить как мгновенно-вращательное движение с угловой скоростью относительно системы осей движущейся поступательно со скоростью точки О]. В некоторых случаях удобнее представлять мгновенное движение как мгновенное вращение подвижной системы осей, относительно которой твердое тело совершает мгновенно-поступательное движение.

в) Уравнение винтовой оси. Аксоиды. Непрерывное движение твердого тела.

Из теоремы Эйлера следует, что произвольное мгновенное движение твердого тела всегда может быть сведено к одному мгновенно-винтовому движению.

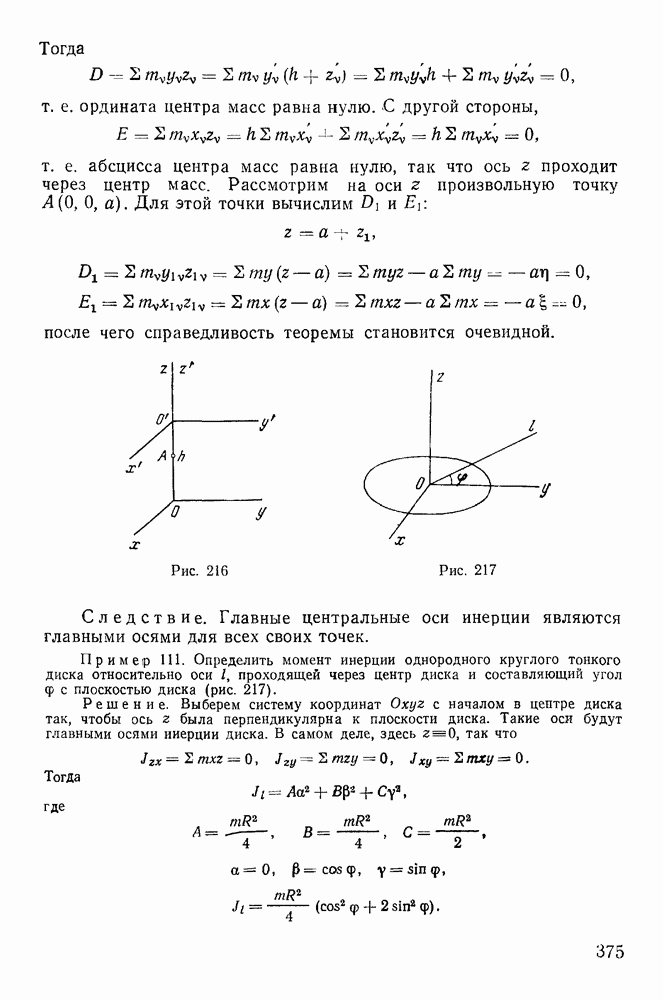
Рассмотрим самый общий случай мгновенного движения твердого тела, эквивалентного мгновенно-поступательному движению со скоростью и мгновенно-вращательному движению с угловой скоростью . Такое мгновенное движение сводится к мгновенновинтовому движению, в котором скорости точек твердого тела, лежащих на винтовой оси, параллельны вектору мгновенной угловой скорости (рис. 49). Условие параллельности векторов записанное через проекции на оси неизменно связанные с твердым телом, получает вид

Если обозначить координаты точек винтовой оси в подвижной системе через то по формуле Эйлера найдем

Подставляя эти значения в условие параллельности векторов, имеем

Полученное уравнение определяет координаты точек твердого тела, расположенных на винтовой оси, относительно системы связанной с твердым телом.

Можно найти уравнение винтовой оси и в системе неподвижных осей Обозначим через проекции вектора и на неподвижные оси х, у, z. Проекции скорости точки находящейся на винтовой оси, на оси х, у, z определим из формулы Эйлера

где вектор имеет проекции на неподвижные оси Тогда для проекций скорости получим

а уравнение винтовой оси в неподвижной системе координат приобретает вид

Рис. 49

Рис. 50

Уравнения (а) и (b) определяют одну и ту же прямую линию— винтовую ось. Но при движении твердого тела мгновенное распределение скоростей непрерывно меняется со временем. При этом изменяются величины При непрерывном изменении коэффициентов уравнения (а) и (Ь) в каждый следующий момент будут вообще определять уже другую прямую. Геометрическое место мгновенных винтовых осей в неподвижном пространстве называют неподвижным аксоидом, а геометрическое место мгновенных винтовых осей, определенных относительно системы отсчета подвижным аксоидом. Эти геометрические места (аксоиды) представляют собой линейчатые поверхности, имеющие в каждый момент по меньшей мере одну общую прямую — мгновенную винтовую ось.

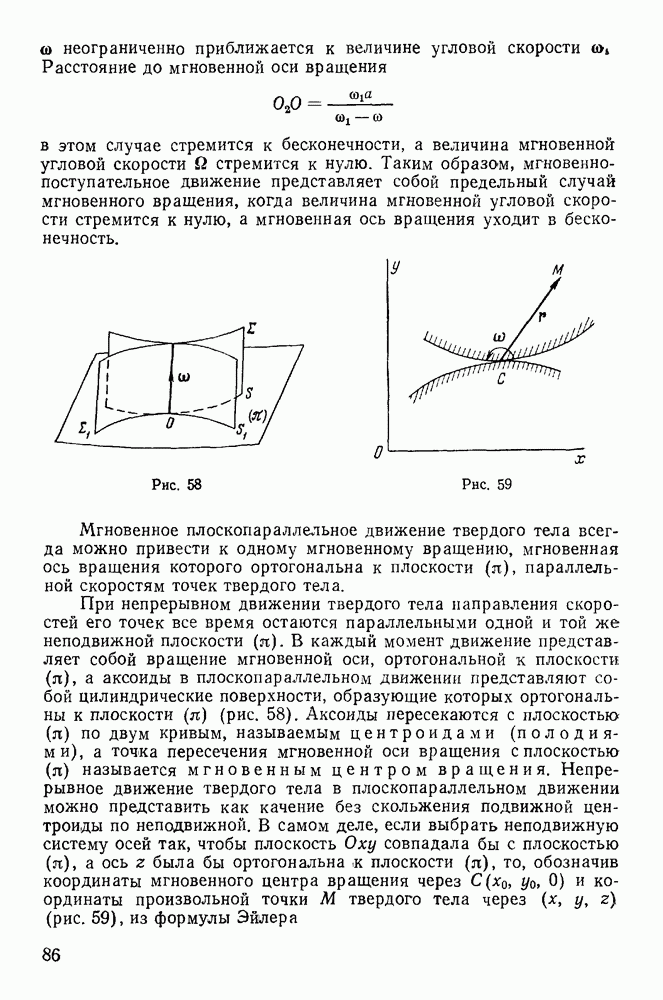
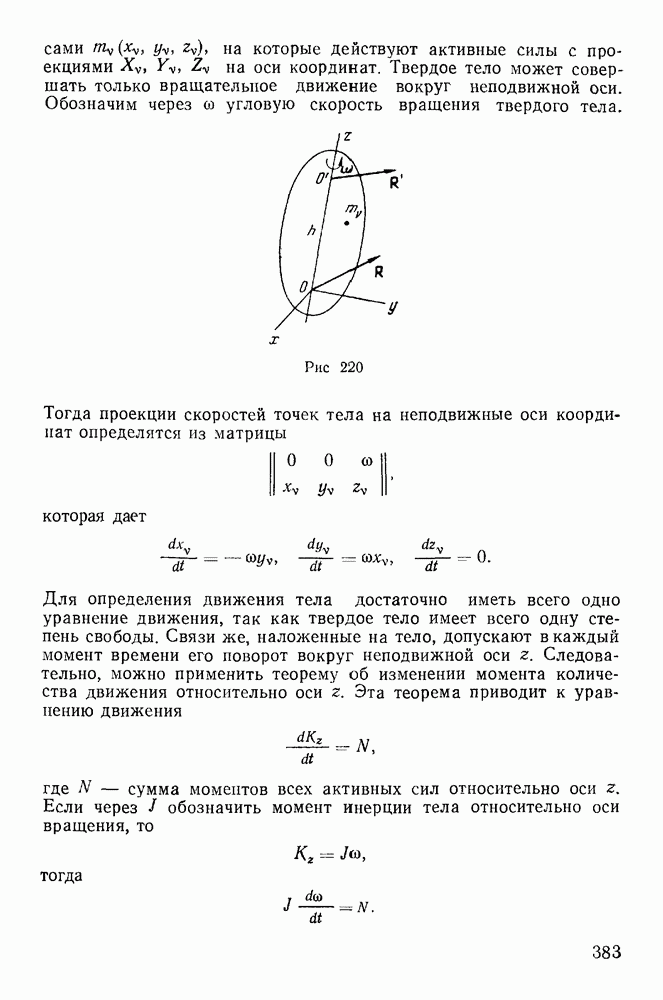
Покажем, что подвижный и неподвижный аксоиды имеют общую соприкасающуюся плоскость, проходящую через мгновенную

винтовую ось. В самом деле, пусть неподвижный аксоид X и Подвижный аксоид имеют общую винтовую ось А (рис. 50). Рассмотрим движение некоторой точки М, остающейся все время на винтовой оси. Пусть — траектория этой точки на неподвижном аксоиде X и траектория точки М на подвижном аксоиде. Абсолютная скорость точки М направлена по касательной к абсолютной траектории точки М. Относительная скорость направлена по касательной к относительной траектории точки. Переносная скорость — это скорость точки подвижного аксоида, совпадающей в данный момент с точкой М. Но эта точка лежит на винтовой оси, а потому и переносная скорость направлена вдоль винтовой оси. Касательная плоскость к неподвижному аксоиду будет определяться векторами а касательная плоскость к подвижному аксоиду — векторами Но по теореме о сложении скоростей имеем

т. е. вектор лежит в касательной плоскости к подвижному аксоиду, а следовательно, касательные плоскости совпадают. Непрерывное движение твердого тела можно теперь представить как качение подвижного аксоида по неподвижному аксоиду Б с проскальзыванием вдоль мгновенной винтовой оси.