| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
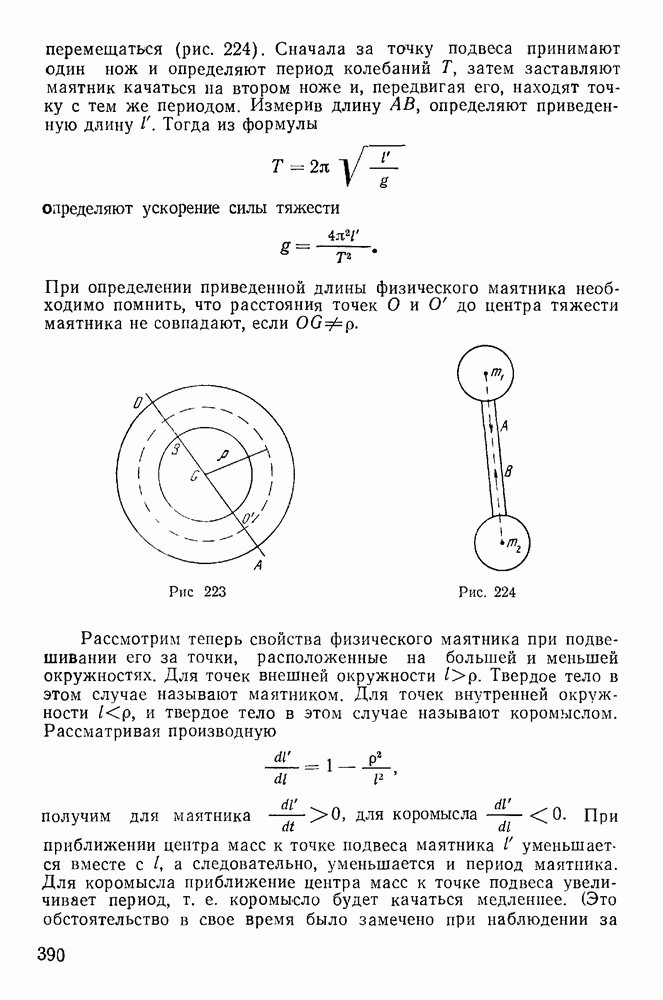
§ 11. ЗАДАЧА О РАВНОВЕСИИ ПРИ НАЛИЧИИ ТРЕНИЯ
До сих пор мы рассматривали равновесие преимущественно идеальных механических систем, предполагая, что поверхности соприкасающихся тел являются абсолютно гладкими и что всякое трение между соприкасающимися телами отсутствует, а сами тела — абсолютно твердые. Такие предположения лишь приближенно соответствуют действительности. В частности, в реальных задачах невозможно полностью исключить влияние сил трения. Применение же законов статики к решению практических задач о равновесии механических систем без учета сил трения может привести к результатам, мало соответствующим действительности.
Силы трения существенно отличаются от всех других сил. Они возникают в тех случаях, когда активные силы способны создать
относительное движение соприкасающихся тел. Не останавливаясь подробно на вопросах о происхождении и физической природе сил трения, ограничимся лишь изучением некоторых их свойств и той роли, которую они играют при исследовании равновесия и движения механических систем.
Силы трения в статике будем определять в соответствии с законами Амонтона—Кулона, сущность которых была изложена выше. Это грубое предположение достаточно хорошо согласуется с экспериментальными данными.

Рис. 109

Рис. 110
Аналитический метод решения задач статики при наличии сил трения сохраняется таким же, как и при отсутствии сил трения, но из-за того, что силы трения не определяются однозначно, условия равновесия при наличии сил трения выражаются неравенствами. Это говорит о том, что при наличии трения существует не одно, а целое множество смежных положений равновесия исследуемой системы. Задача о равновесии сводится теперь к отысканию границ области равновесия.
Рассматривая абсолютно твердые и идеально гладкие тела, мы предполагали, что два тела, находящиеся в равновесии, могут соприкасаться друг с другом в одной точке и свободно скользить одно относительно другого. Такое предположение противоречит опытным данным. Реальные тела не являются ни абсолютно твердыми, ни абсолютно гладкими. В действительности соприкосновение тел никогда не происходит в одной точке, ибо соприкасающиеся тела испытывают деформации и, как бы малы ни были последние, соприкасание тел происходит по некоторой площадке, размерами которой обычно пренебрегают.
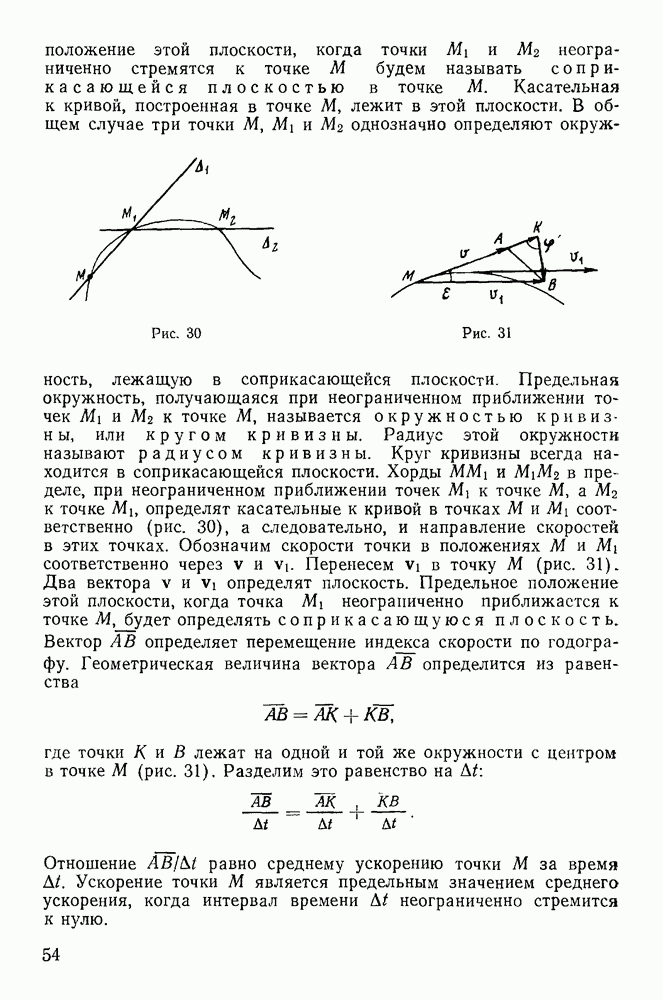
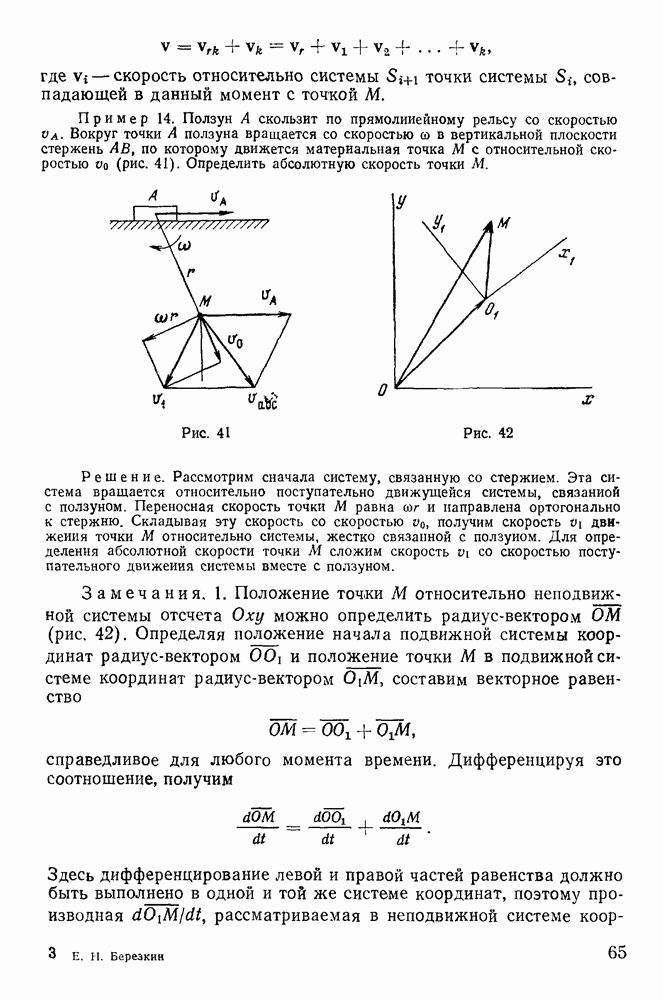
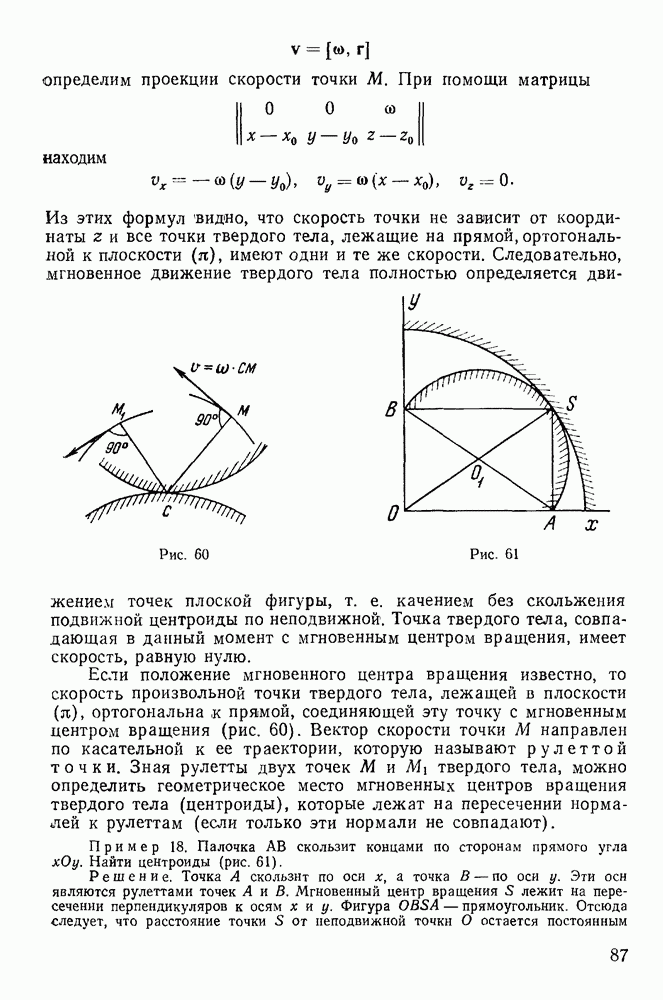
Рассмотрим два твердых тела А и В, находящиеся в соприкосновении, и пусть О — точка контакта (рис. 109). Мгновенное движение тела В относительно тела А всегда может быть сведено
к мгновенно-поступательному движению с относительной скоростью  точки О тела В и к мгновенно-вращательному движению тела В с относительной угловой скоростью
точки О тела В и к мгновенно-вращательному движению тела В с относительной угловой скоростью  линия действия которой проходит через точку О. Вектор
линия действия которой проходит через точку О. Вектор  можно представить в виде суммы двух векторов
можно представить в виде суммы двух векторов

причем  лежит в общей касательной плоскости
лежит в общей касательной плоскости  а
а  ортогонален к плоскости
ортогонален к плоскости  Вектор ом будем называть вектором скорости качения, а вектор
Вектор ом будем называть вектором скорости качения, а вектор  — вектором скорости верчения тела. Мгновенное движение тела В относительно тела А теперь можно представить как совокупность трех движений: скольжения, качения и верчения. Совокупность действующих на находящееся в равновесии тело В активных сил может быть приведена к одной результирующей силе F, линия действия которой проходит через точку О, и паре с моментом
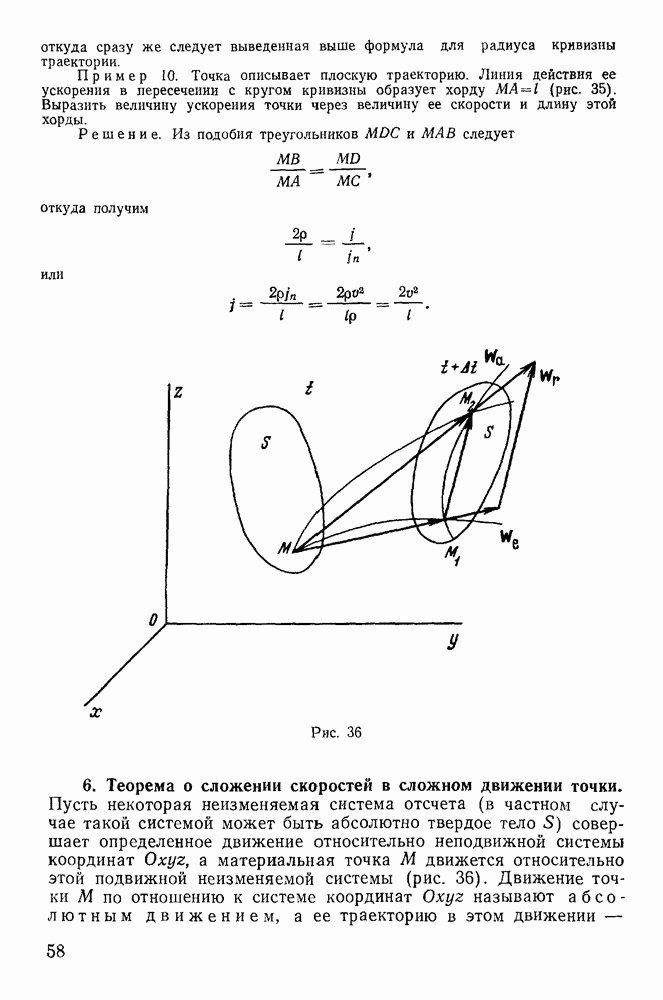
— вектором скорости верчения тела. Мгновенное движение тела В относительно тела А теперь можно представить как совокупность трех движений: скольжения, качения и верчения. Совокупность действующих на находящееся в равновесии тело В активных сил может быть приведена к одной результирующей силе F, линия действия которой проходит через точку О, и паре с моментом  Действие этой системы сил уравновешивается силами реакций со стороны тела А, которые таким образом сводятся к результирующей силе
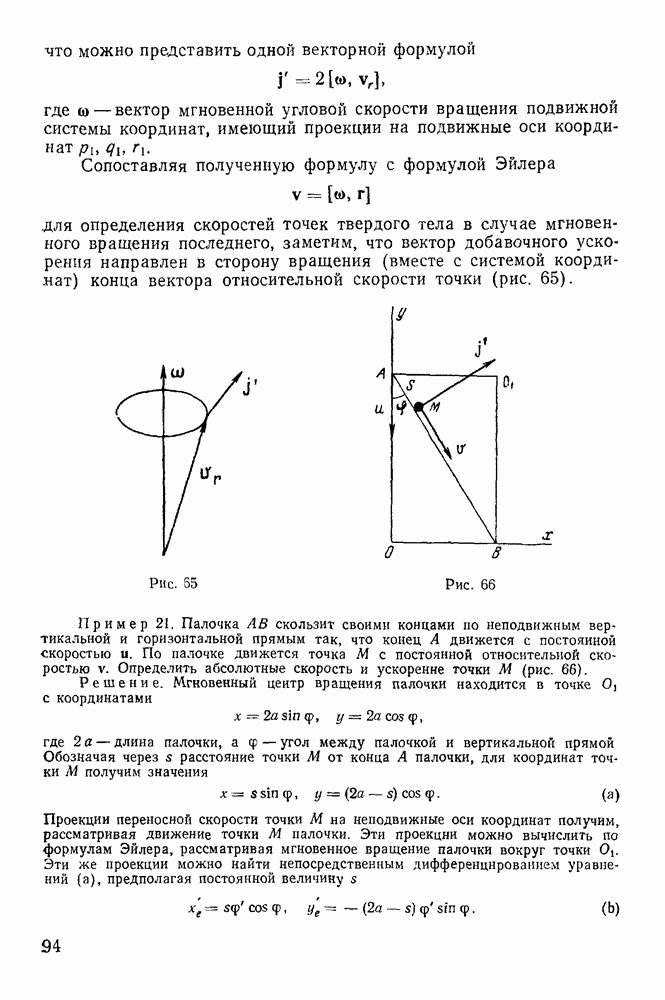
Действие этой системы сил уравновешивается силами реакций со стороны тела А, которые таким образом сводятся к результирующей силе  линия действия которой совпадает с линией действия силы F, и результирующей паре с моментом
линия действия которой совпадает с линией действия силы F, и результирующей паре с моментом  (рис. 110), удовлетворяющих условиям
(рис. 110), удовлетворяющих условиям

Разложим силу  и момент пары
и момент пары  на составляющие, расположенные в плоскости
на составляющие, расположенные в плоскости  и ортогональные к ней
и ортогональные к ней

Составляющую  направленную по нормали к соприкасающейся плоскости
направленную по нормали к соприкасающейся плоскости  назовем нормальной реакцией. Эта сила препятствует взаимному проникновению тел. Составляющую
назовем нормальной реакцией. Эта сила препятствует взаимному проникновению тел. Составляющую  лежащую в плоскости
лежащую в плоскости  будем называть силой трения скольжения, или просто трением скольжения. Эта сила препятствует проскальзыванию тела В по телу А. Составляющую
будем называть силой трения скольжения, или просто трением скольжения. Эта сила препятствует проскальзыванию тела В по телу А. Составляющую  ортогональную к плоскости
ортогональную к плоскости  и препятствующую верчению тела, назовем парой трения верчения. Наконец, составляющую
и препятствующую верчению тела, назовем парой трения верчения. Наконец, составляющую  параллельную плоскости
параллельную плоскости  и препятствующую качению тела, назовем парой трения качения. Заметим, что влияние пар
и препятствующую качению тела, назовем парой трения качения. Заметим, что влияние пар  вообще очень мало по сравнению с влиянием сил
вообще очень мало по сравнению с влиянием сил  поэтому рассмотрим сначала те задачи, в которых этими парами можно пренебрегать.
поэтому рассмотрим сначала те задачи, в которых этими парами можно пренебрегать.
Хотя реальные тела не являются абсолютно твердыми и в общем случае касание тел А и В происходит по некоторой площадке, тем не менее в ряде задач можно пренебречь размерами этой площадки и с достаточной степенью точности считать тела А и В абсолютно твердыми, а их касание происходящим в одной точке. Кроме того, будем предполагать, что со стороны тела В на тело А действует рассмотренная выше система сил.
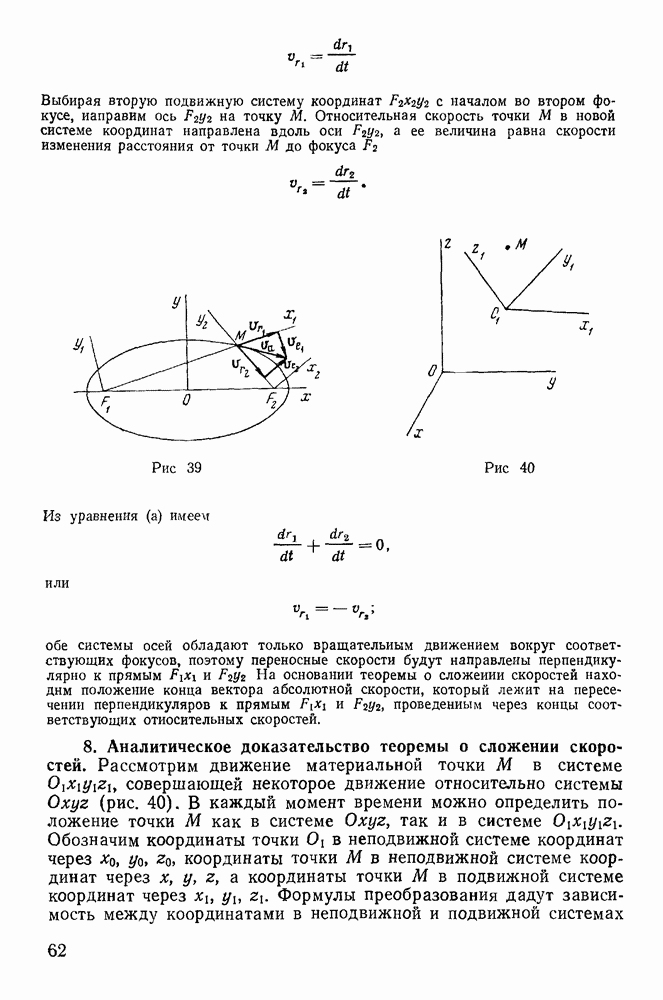
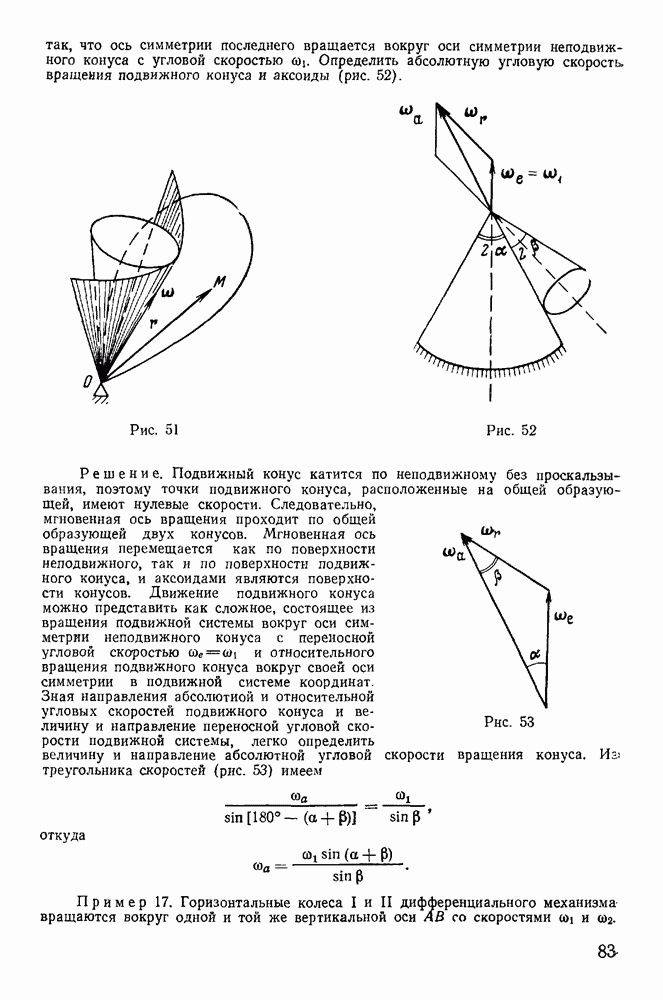
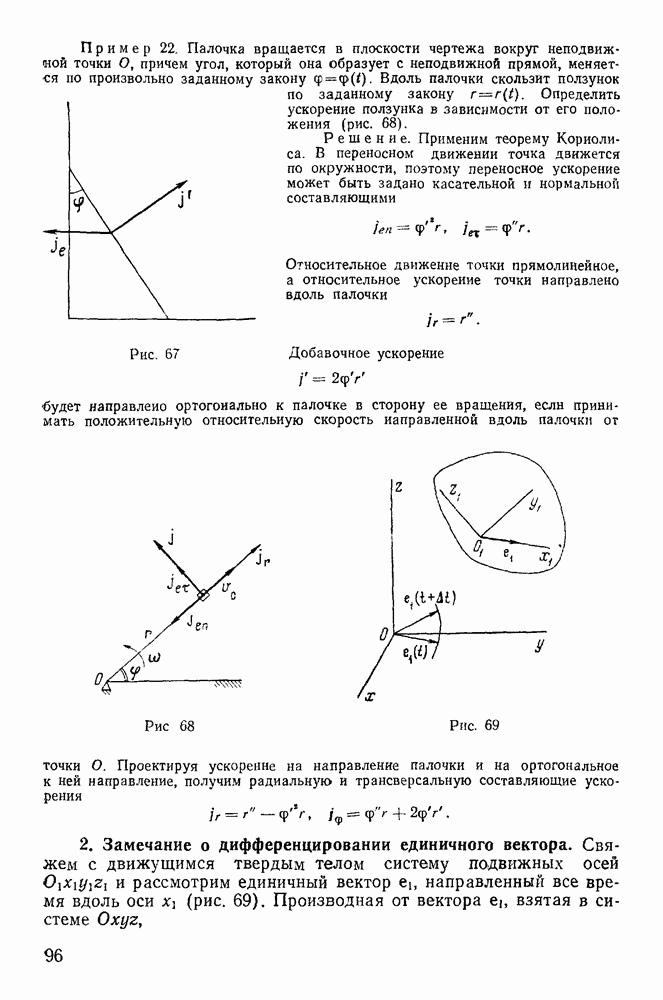
Пусть тело  под действием активных сил находится в равновесии на поверхности
под действием активных сил находится в равновесии на поверхности  касаясь последней в точке А (рис. 111). Действующая на тело
касаясь последней в точке А (рис. 111). Действующая на тело  со стороны поверхности
со стороны поверхности  полная реакция
полная реакция  складывается из нормальной реакции
складывается из нормальной реакции  и силы трения
и силы трения  Направление последней заранее неизвестно, а максимальное значение, определенное в соответствии с законом Амонтона—Кулона,
Направление последней заранее неизвестно, а максимальное значение, определенное в соответствии с законом Амонтона—Кулона,  где
где  — коэффициент трения скольжения.
— коэффициент трения скольжения.

Рис. 111

Рис. 112
Угол  между направлениями полной реакции
между направлениями полной реакции  и нормальной реакции
и нормальной реакции  никогда не превосходит угла трения
никогда не превосходит угла трения  который определяется из условия
который определяется из условия

Для равновесия тела  необходимо, чтобы уравновешивались все силы, действующие на тело
необходимо, чтобы уравновешивались все силы, действующие на тело  Последнее возможно лишь в случае, когда все действующие на тело силы приводятся к одной равнодействующей силе F, линия действия которой проходит через точку А, по величине, равной силе реакции
Последнее возможно лишь в случае, когда все действующие на тело силы приводятся к одной равнодействующей силе F, линия действия которой проходит через точку А, по величине, равной силе реакции  и противоположной по направлению. Сила F должна «прижимать» тело
и противоположной по направлению. Сила F должна «прижимать» тело  к поверхности
к поверхности  и образовывать с нормалью к поверхности
и образовывать с нормалью к поверхности  угол, меньший угла трения.
угол, меньший угла трения.
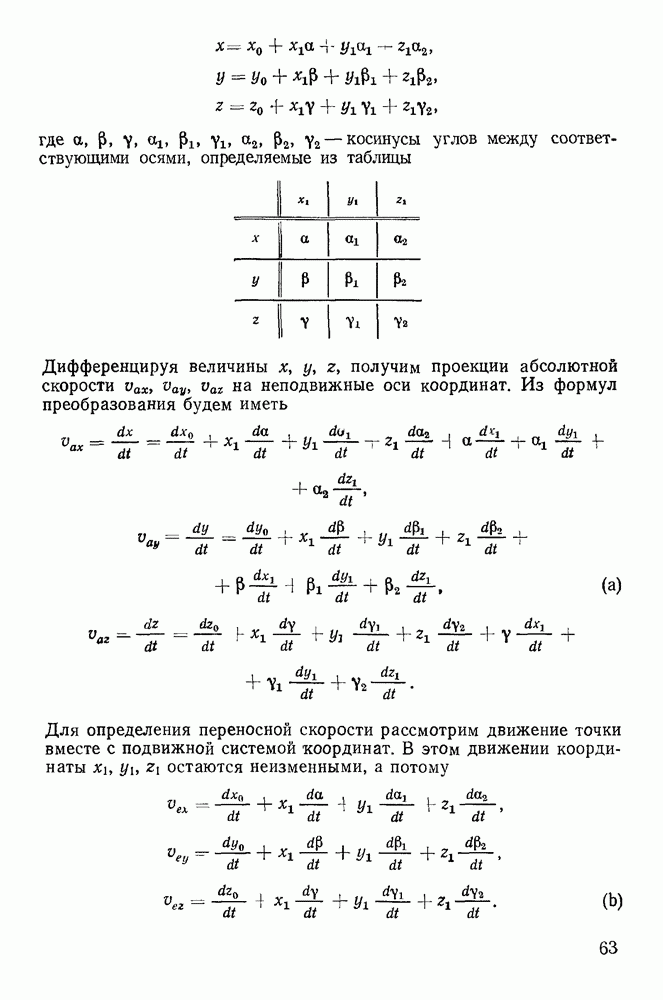
Эти необходимые условия оказываются и достаточными, так как если они выполнены, то равнодействующую силу F можно разложить на составляющие: нормальную Р и касательную Q (рис. 112). Сила Р уравновешивается силой нормальной реакции  так что
так что  Сила
Сила  где
где  не может вызывать скольжения тела
не может вызывать скольжения тела  по поверхности
по поверхности  поскольку она остается меньше максимальной силы трения
поскольку она остается меньше максимальной силы трения

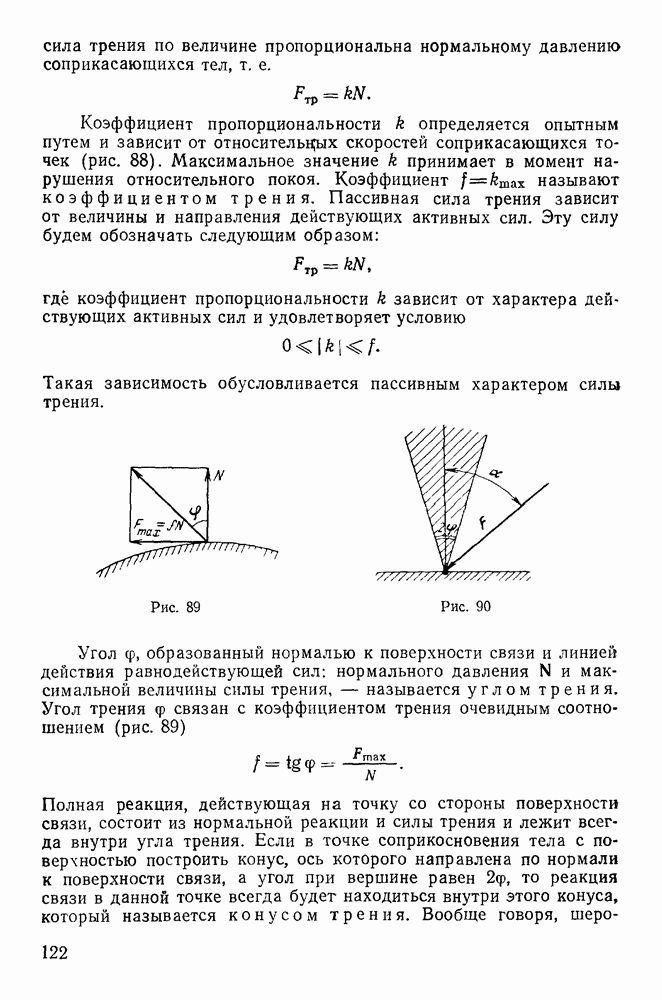
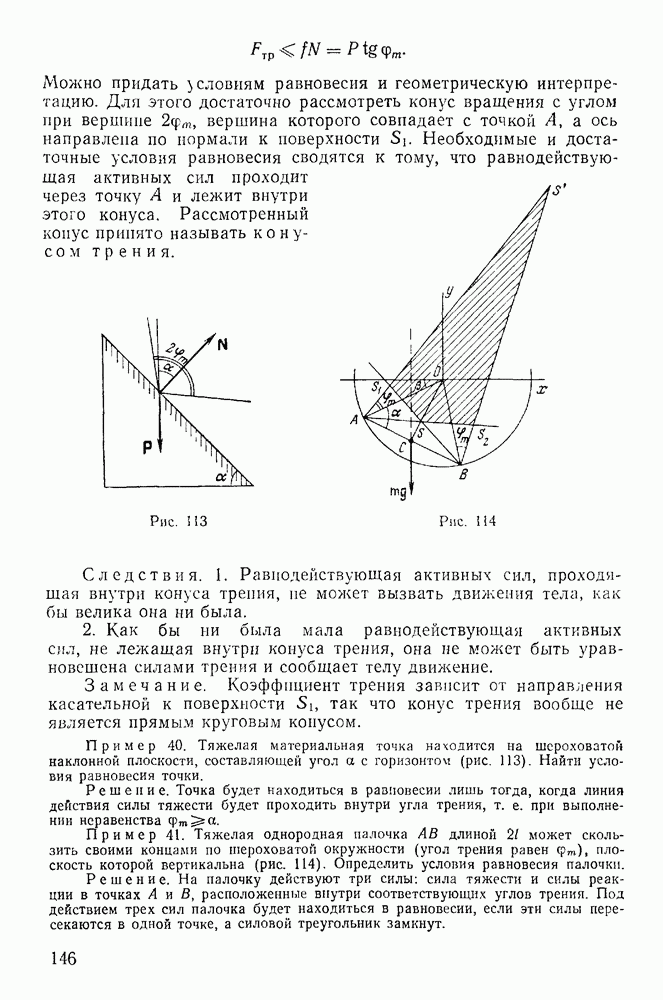
Можно придать условиям равновесия и геометрическую интерпретацию. Для этого достаточно рассмотреть конус вращения с углом при вершине  вершина которого совпадает с точкой А, а ось направлена по нормали к поверхности
вершина которого совпадает с точкой А, а ось направлена по нормали к поверхности  Необходимые и достаточные условия равновесия сводятся к тому, что равнодействующая активных сил проходит через точку А и лежит внутри этого конуса. Рассмотренный конус принято называть конусом трения.
Необходимые и достаточные условия равновесия сводятся к тому, что равнодействующая активных сил проходит через точку А и лежит внутри этого конуса. Рассмотренный конус принято называть конусом трения.

Рис. 113

Рис. 114
Следствия. 1. Равнодействующая активных сил, проходящая внутри конуса трения, не может вызвать движения тела, как бы велика она ни была.
2. Как бы ни была мала равнодействующая активных сил, не лежащая внутри конуса трения, она не может быть уравновешена силами трения и сообщает телу движение.
Замечание. Коэффициент трения зависит от направления касательной к поверхности  так что конус трения вообще не является прямым круговым конусом.
так что конус трения вообще не является прямым круговым конусом.
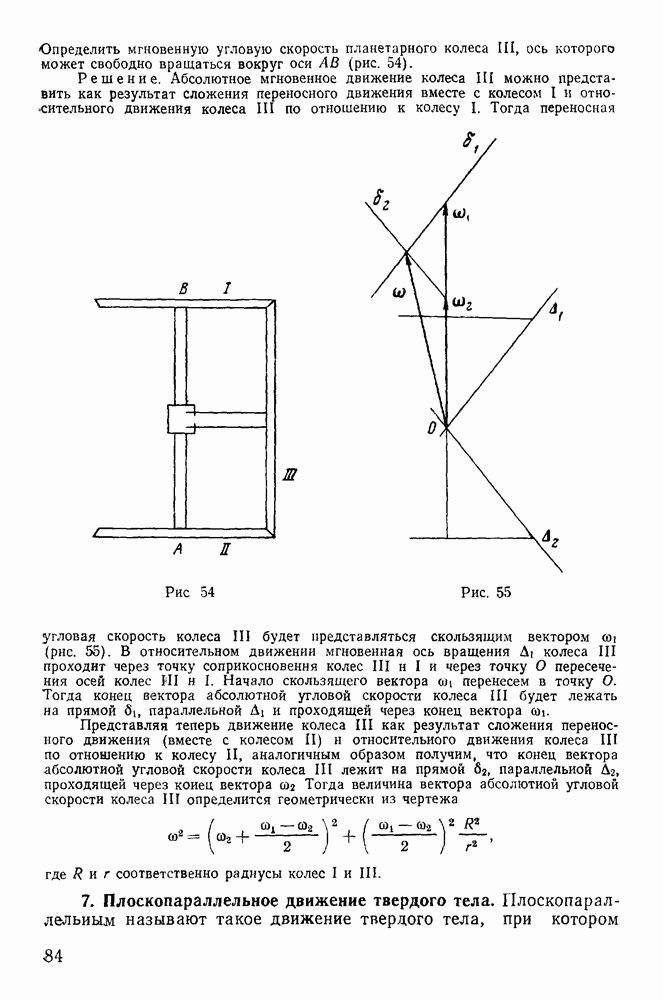
Пример 40. Тяжелая материальная точка находится на шероховатой наклонной плоскости, составляющей угол а с горизонтом (рис. 113). Найти условия равновесия точки.
Решение. Точка будет находиться в равновесии лишь тогда, когда линия действия силы тяжести будет проходить внутри угла трения, т. е. при выполнении неравенства 
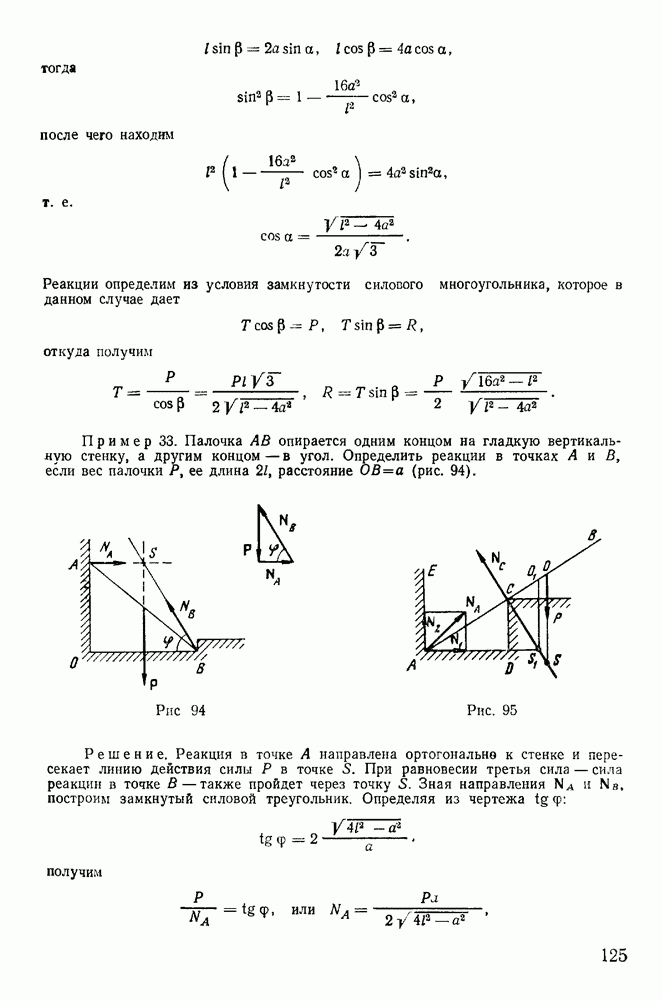
Пример 41. Тяжелая однородная палочка АВ длиной  может скользить своими концами по шероховатой окружности (угол трения равен
может скользить своими концами по шероховатой окружности (угол трения равен  плоскость которой вертикальна (рис. 114). Определить условия равновесия палочки.
плоскость которой вертикальна (рис. 114). Определить условия равновесия палочки.
Решение. На палочку действуют три силы: сила тяжести и силы реакции в точках А и В, расположенные внутри соответствующих углов трения. Под действием трех сил палочка будет находиться в равновесии, если эти силы пересекаются в одной точке, а силовой треугольник замкнут.
Построим в точках А и В углы трения  Получим часть плоскости
Получим часть плоскости  заключенную внутри того и другого угла. Первое из условий равновесия может быть выполнено лишь в случае, когда линия действия силы тяжести пересекает фигуру
заключенную внутри того и другого угла. Первое из условий равновесия может быть выполнено лишь в случае, когда линия действия силы тяжести пересекает фигуру  Аналитически это условие можно записать в виде
Аналитически это условие можно записать в виде

где  — абсцисса центра палочки. Обозначив через Р угол между горизонтальным радиусом окружности и прямой
— абсцисса центра палочки. Обозначив через Р угол между горизонтальным радиусом окружности и прямой  соединяющей центр окружности с центром палочки, а через а — угол между прямой
соединяющей центр окружности с центром палочки, а через а — угол между прямой  и палочкой, и опуская
и палочкой, и опуская  иидекс
иидекс  полученное условие представим в виде
полученное условие представим в виде

откуда окончательно получаем условия равновесия

Условия  определяют не одно положение равновесия, а целую область возможных положений равновесия. Условия эти являются и достаточными. В самом Деле, перенося силу
определяют не одно положение равновесия, а целую область возможных положений равновесия. Условия эти являются и достаточными. В самом Деле, перенося силу  в произвольную точку заштрихованной области, заметим, что эта сила всегда может быть уравновешена силами реакции.
в произвольную точку заштрихованной области, заметим, что эта сила всегда может быть уравновешена силами реакции.
В частном случае при  условие
условие  становится особенно наглядным
становится особенно наглядным

откуда следует

или

Если трение отсутствует, т. е.  условие
условие  сводится к уравнению
сводится к уравнению

которое преобразуется к виду

Последнее уравнение определяет единственное положение равновесия, соответствующее горизонтальному положению палочки.
При наличи сил трения задача определения положения равновесия и сил реакций однозначно не разрешается.
Замечание о трении качения.
Как уже отмечалось, трение качения возникает при качении одного тела по другому. Возникновение этого трения можно грубо объяснить тем, что поверхности соприкасающихся тел не являются абсолютно твердыми и несколько деформируются. Законы трения качения, основанные на этом предположении Кулоном и Мореном, представляют грубое приближение к действительности.
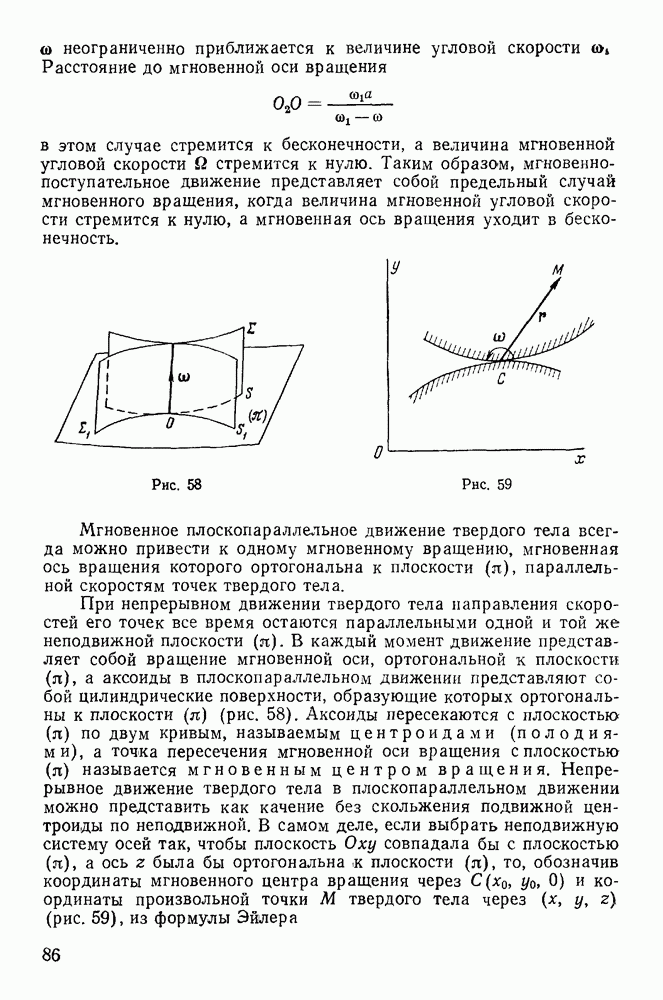
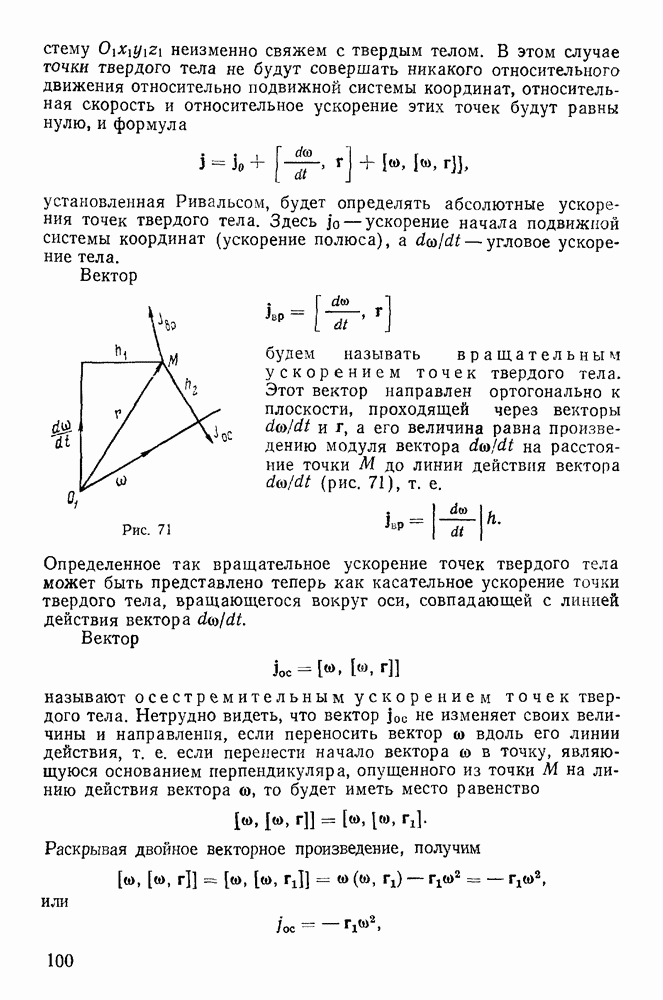
Рассмотрим в качестве примера задачу о качении колеса по прямолинейному горизонтальному рельсу, предполагая, что кроме силы тяжести на колесо действует еще некоторая система сил, расположенных в плоскости колеса. Действующие силы вообще несколько деформируют как само колесо, так и рельс, и для возможности качения по рельсу необходимо приложить некоторое усилие. Возникающее сопротивление свободному качению обычно и называют трением качения.

Рис. 115

Рис. 116
Такое объяснение явления трения связано с отказом от гипотезы абсолютно твердого тела, что вызывает необходимость пересмотра основных принципов статики твердого тела, в основе которых лежит эта гипотеза. Поэтому, сохраняя гипотезу абсолютно твердого тела, будем предполагать, что соприкасание тел происходит в одной точке и всякие деформации тел отсутствуют. Обозначим через А точку касания колеса и плоскости (рис. 115). Приводя систему сил, действующих на колесо, к точке А, в общем случае получим результирующую силу F и пару сил с моментом  перпендикулярным к плоскости колеса. Раскладывая силу F на
перпендикулярным к плоскости колеса. Раскладывая силу F на  нормальную к рельсу, и
нормальную к рельсу, и  параллельную рельсу, заметим, что сила
параллельную рельсу, заметим, что сила  будет вызывать скольжение колеса, а пара — его вращение. Для отсутствия скольжения достаточно выполнения неравенства.
будет вызывать скольжение колеса, а пара — его вращение. Для отсутствия скольжения достаточно выполнения неравенства.

где  — коэффициент трения скольжения. При выполнении этого условия колесо еще не будет находиться в равновесии, пока не уравновешена пара. Опыт показывает, что колесо не начнет катиться до тех пор, пока момент пары
— коэффициент трения скольжения. При выполнении этого условия колесо еще не будет находиться в равновесии, пока не уравновешена пара. Опыт показывает, что колесо не начнет катиться до тех пор, пока момент пары  не превзойдет некоторого предельного значения
не превзойдет некоторого предельного значения

Величина 6 называется коэффициентом трения качения. Этот коэффициент не зависит от величины силы F и радиуса
кривизны катящегося предмета, а зависит лишь от физических свойств соприкасающихся тел. Обычно вводится гипотеза, что кроме активных сил на твердое тело действуют нормальная сила реакции  уравновешивающая действие силы сила трения скольжения, уравновешивающая действие силы
уравновешивающая действие силы сила трения скольжения, уравновешивающая действие силы  и пара сил, называемая парой трения качения, которая уравновешивает пару с моментом т. Для равновесия достаточно выполнения двух неравенств
и пара сил, называемая парой трения качения, которая уравновешивает пару с моментом т. Для равновесия достаточно выполнения двух неравенств

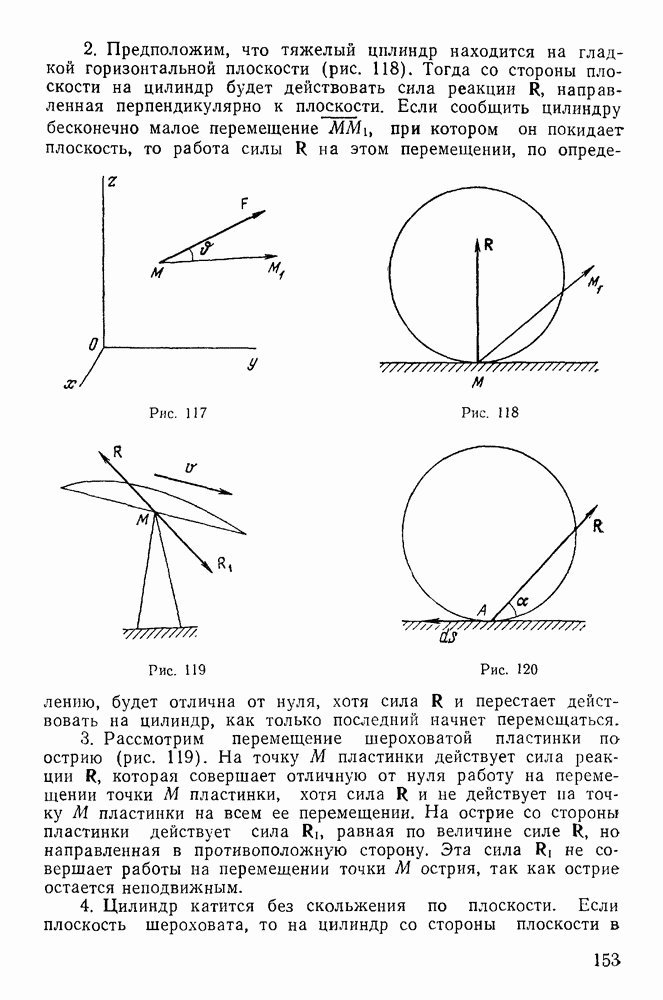
Заметим, что в большинстве случаев трение качения оказывается значительно меньшим, чем трение скольжения, и при решении практических задач им часто можно пренебрегать.
Замечание о трении верчения.
Рассмотрим тяжелый шар, лежащий на горизонтальной плоскости и касающийся ее в точке С (рис. 116), так что  — вертикальный радиус шара. Вращение шара вокруг вертикального радиуса называют верчением. Приводя систему активных сил, действующих на шар, к точке С, в общем случае получим результирующую силу, проходящую через точку С, и пару с моментом
— вертикальный радиус шара. Вращение шара вокруг вертикального радиуса называют верчением. Приводя систему активных сил, действующих на шар, к точке С, в общем случае получим результирующую силу, проходящую через точку С, и пару с моментом  Предположим, для простоты, что момент пары параллелен вертикальному радиусу шара. Раскладывая, как это уже делалось выше, результирующую силу на составляющие, одна из которых
Предположим, для простоты, что момент пары параллелен вертикальному радиусу шара. Раскладывая, как это уже делалось выше, результирующую силу на составляющие, одна из которых  параллельна горизонтальной плоскости, а вторая
параллельна горизонтальной плоскости, а вторая  ей ортогональна, заметим, что сила
ей ортогональна, заметим, что сила  уравновешивается нормальной реакцией плоскости, сила
уравновешивается нормальной реакцией плоскости, сила  — силой трения скольжения, и для полного равновесия шара необходимо
— силой трения скольжения, и для полного равновесия шара необходимо  уравновесить пару. Как известно из опыта, если момент пары, стремящийся привести шар в верчение, достаточно мал, то шар вертеться не начнет. Действию активной силы в этом случае препятствует некоторая пара сил реакций, называемая трением верчения. Предельный момент трения верчения можно представить в виде произведения некоторого коэффициента
уравновесить пару. Как известно из опыта, если момент пары, стремящийся привести шар в верчение, достаточно мал, то шар вертеться не начнет. Действию активной силы в этом случае препятствует некоторая пара сил реакций, называемая трением верчения. Предельный момент трения верчения можно представить в виде произведения некоторого коэффициента  называемого коэффициентом трения верчения и определяемого экспериментально, на нормальную составляющую результирующей активной силы, т. е.
называемого коэффициентом трения верчения и определяемого экспериментально, на нормальную составляющую результирующей активной силы, т. е.  Коэффициент трения верчения обычно величина малая, в 5—10 раз меньшая коэффициента трения качения. Условия равновесия сводятся к двум неравенствам:
Коэффициент трения верчения обычно величина малая, в 5—10 раз меньшая коэффициента трения качения. Условия равновесия сводятся к двум неравенствам:

| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Введение
- Глава I. ОСНОВЫ ТЕОРИИ ВЕКТОРОВ
- § 1. СВОБОДНЫЕ ВЕКТОРЫ
- 2. Сложение свободных векторов.
- 3. Проекция вектора на ось.
- 4. Инварианты системы свободных векторов.
- § 2. СКОЛЬЗЯЩИЕ ВЕКТОРЫ
- 2. Координаты скользящего вектора.
- 3. Момент скользящего вектора. Плюккеровы координаты.
- 4. Аналитическое определение момента скользящего вектора.
- 5. Проекция момента на ось.
- 6. Момент скользящего вектора относительно оси
- § 3. СИСТЕМА СКОЛЬЗЯЩИХ ВЕКТОРОВ
- 2. Произвольная система скользящих векторов. Элементарные операции.
- 3. Приведение системы скользящих векторов к простейшей эквивалентной форме.
- 4. Плоская система скользящих векторов.
- 5. Свойства системы параллельных скользящих векторов.
- § 4. ЗАКРЕПЛЕННЫЕ ВЕКТОРЫ
- § 5. ДИФФЕРЕНЦИРОВАНИЕ СВОБОДНОГО ВЕКТОРА ПО СКАЛЯРНОМУ АРГУМЕНТУ
- Глава II. КИНЕМАТИКА
- § 1. КИНЕМАТИКА ТОЧКИ
- 2. Ускорение точки. Проекции ускорения на прямоугольные оси координат.
- 3. Скорость и ускорение точки в полярных координатах.
- 4. Движение точки по окружности.
- 5. Проекции ускорения на оси естественного трехгранника.
- 6. Теорема о сложении скоростей в сложном движении точки.
- 7. Метод Роберваля построения касательных к плоским кривым.
- 8. Аналитическое доказательство теоремы о сложении скоростей.
- 9. Сложение скоростей в общем случае сложного движения точки.
- § 2. КИНЕМАТИКА АБСОЛЮТНО ТВЕРДОГО ТЕЛА
- 2. Элементарные движения твердого тела.
- 3. Мгновенные движения твердого тела.
- 4. Сложение мгновенно-поступательных и мгновенно-вращательных движений твердого тела.
- 5. Общий случай сложения мгновенно-поступательных и мгновенно-вращательных движений твердого тела. Непрерывное движение твердого тела.
- 6. Мгновенное движение твердого тела с одной неподвижной точкой.
- 7. Плоскопараллельное движение твердого тела.
- § 3. УСКОРЕНИЕ ТОЧКИ В СЛОЖНОМ ДВИЖЕНИИ
- 2. Замечание о дифференцировании единичного вектора.
- 3. Векторный вывод теоремы Кориолиса.
- 4. Теорема Ривальса.
- § 4. РАСПРЕДЕЛЕНИЕ УСКОРЕНИЙ В ПЛОСКОПАРАЛЛЕЛЬНОМ ДВИЖЕНИИ ТВЕРДОГО ТЕЛА
- 2. Мгновенный центр ускорений.
- § 5. КИНЕМАТИЧЕСКИЕ УРАВНЕНИЯ ЭЙЛЕРА
- Глава III. СТАТИКА
- I. ГЕОМЕТРИЧЕСКАЯ СТАТИКА
- § 1. АКСИОМЫ СТАТИКИ
- § 2. ПОНЯТИЕ О СИЛЕ ТРЕНИЯ
- § 3. РАЗЛИЧНЫЕ ЗАДАЧИ СТАТИКИ
- 2. Равновесие трех сил.
- § 4. МОМЕНТ СИЛЫ
- 2. Момент силы относительно оси.
- 3. Теорема Вариньона для системы сходящихся сил.
- § 5. ПРОИЗВОЛЬНАЯ СИСТЕМА СИЛ, ДЕЙСТВУЮЩИХ НА ТВЕРДОЕ ТЕЛО
- § 6. УСЛОВИЯ РАВНОВЕСИЯ СИСТЕМЫ СИЛ, ДЕЙСТВУЮЩИХ НА ТВЕРДОЕ ТЕЛО
- § 7. ПРИВЕДЕНИЕ СИСТЕМЫ СИЛ, ДЕЙСТВУЮЩИХ НА ТВЕРДОЕ ТЕЛО, К ДИНАМЕ. УРАВНЕНИЯ РАВНОВЕСИЯ ТВЕРДОГО ТЕЛА
- § 8. УСЛОВИЯ РАВНОВЕСИЯ СИСТЕМЫ ТВЕРДЫХ ТЕЛ
- § 9. ПЛОСКАЯ СИСТЕМА СИЛ
- § 10. ЗАДАЧА О РАВНОВЕСИИ НЕСВОБОДНОГО ТВЕРДОГО ТЕЛА
- 2. Частные случаи равновесия твердого тела.
- § 11. ЗАДАЧА О РАВНОВЕСИИ ПРИ НАЛИЧИИ ТРЕНИЯ
- § 12. СИЛА ТЯЖЕСТИ И ЦЕНТР ТЯЖЕСТИ
- II. АНАЛИТИЧЕСКАЯ СТАТИКА
- § 1. РАБОТА СИЛЫ НА ПЕРЕМЕЩЕНИИ. СИЛОВАЯ ФУНКЦИЯ
- § 2. ПРИНЦИП ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ
- 2. Теорема Лагранжа о равновесии системы.
- 3. Принцип Торричелли.
- § 3. ОБЩИЕ ВОПРОСЫ АНАЛИТИЧЕСКОЙ СТАТИКИ
- 3. Общие теоремы о равновесии системы материальных точек.
- 4. Метод неопределенных множителей Лагранжа.
- 5. Определение реакций.
- § 4. ОПРЕДЕЛЕНИЕ РЕАКЦИЙ В ОБЩЕМ СЛУЧАЕ
- § 5. РАВНОВЕСИЕ НИТИ
- 2. Естественные уравнения равновесия нити.
- Глава IV. ДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ
- § 1. ОСНОВНЫЕ ЗАКОНЫ ДИНАМИКИ
- § 2. ДВЕ ОСНОВНЫЕ ЗАДАЧИ ДИНАМИКИ. УРАВНЕНИЯ ДВИЖЕНИЯ ТОЧКИ В ДЕКАРТОВЫХ ОСЯХ
- § 3. ЕСТЕСТВЕННЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ
- § 4. ОСНОВНЫЕ ТЕОРЕМЫ ДИНАМИКИ ДЛЯ СВОБОДНОЙ МАТЕРИАЛЬНОЙ ТОЧКИ
- 2. Теорема об изменении момента количества движения.
- 3. Следствия из теорем об изменении количества движения и момента количества движения материальной точки.
- 4. Теорема живых сил.
- 5. Интеграл живых сил.
- 6. Устойчивость равновесия. Теорема Лагранжа.
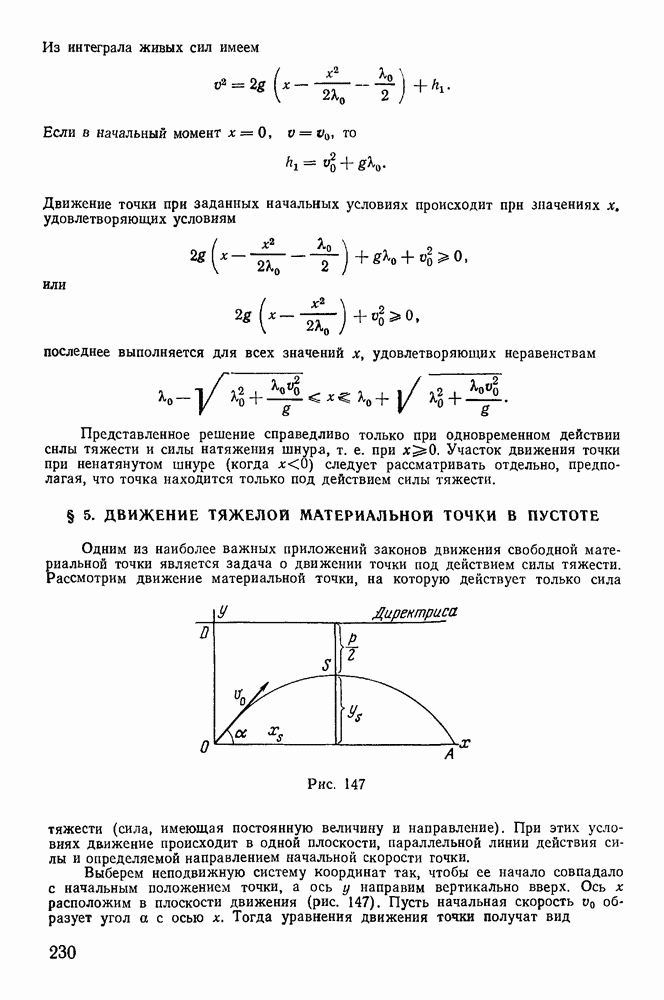
- § 5. ДВИЖЕНИЕ ТЯЖЕЛОЙ МАТЕРИАЛЬНОЙ ТОЧКИ В ПУСТОТЕ
- § 6. ДВИЖЕНИЕ МАТЕРИАЛЬНОЙ ТОЧКИ ПОД ДЕЙСТВИЕМ ЦЕНТРАЛЬНЫХ СИЛ
- 2. Формулы Бине
- 3. Задача о движении планет
- § 7. ДВИЖЕНИЕ ТОЧКИ В СОПРОТИВЛЯЮЩЕЙСЯ СРЕДЕ
- § 8. ДВИЖЕНИЕ НЕСВОБОДНОЙ МАТЕРИАЛЬНОЙ ТОЧКИ
- 2. Движение материальной точки по поверхности.
- § 9. ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЕ МАТЕРИАЛЬНОЙ ТОЧКИ
- 1. Теорема живых сил в относительном движении точки.
- 2. Уравнения относительного равновесия точки.
- 3. Равновесие материальной точки на поверхности Земли. Вес.
- 4. Задача о падении тяжелой точки в пустоте.
- 5. Маятник Фуко.
- § 10. ПРИНЦИП ДАЛАМБЕРА
- Глава V. ДИНАМИКА СИСТЕМЫ МАТЕРИАЛЬНЫХ ТОЧЕК
- § 1. УЧЕНИЕ О СВЯЗЯХ
- § 2. ПРИНЦИП ДАЛАМБЕРА — ЛАГРАНЖА
- § 3. ОСНОВНЫЕ ТЕОРЕМЫ ДИНАМИКИ СИСТЕМЫ
- 2. Теорема об изменении момента количества движения.
- 3. Теорема живых сил.
- § 4. ТЕОРЕМЫ О ДВИЖЕНИИ СИСТЕМЫ ОТНОСИТЕЛЬНО ОСЕЙ НЕИЗМЕННОГО НАПРАВЛЕНИЯ, ПРОХОДЯЩИХ ЧЕРЕЗ ЦЕНТР МАСС СИСТЕМЫ (ОСЕЙ КЕНИГА)
- 2. Теорема об изменении момента количества движения системы относительно осей Кёнига.
- 3. Теорема живых сил в движении системы относительно осей Кёнига.
- § 5. УРАВНЕНИЯ ЛАГРАНЖА ВТОРОГО РОДА
- 2. Случай существования силовой функции.
- 3. Замечание о лагранжевых координатах.
- § 6. ЭЛЕМЕНТАРНЫЕ СЛУЧАИ ИНТЕГРИРУЕМОСТИ УРАВНЕНИЙ ЛАГРАНЖА
- 2. Метод Рауса игнорирования циклических координат.
- 3. Обобщение теоремы и интеграла живых сил.
- § 7. ОПРЕДЕЛЕНИЕ РЕАКЦИЙ
- Глава VI. ДИНАМИКА ТВЕРДОГО ТЕЛА
- § 1. ТЕОРИЯ МОМЕНТОВ ИНЕРЦИИ
- 2. Момент инерции системы относительно произвольной оси, проходящей через заданную точку.
- 3. Эллипсоид инерции.
- 4. Определение главных осей инерции для произвольной точки.
- § 2. ВРАЩЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ОСИ
- § 3. ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА, ИМЕЮЩЕГО ОДНУ НЕПОДВИЖНУЮ ТОЧКУ
- 2. Уравнения движения твердого тела с одной неподвижной точкой.
- § 4. ДВИЖЕНИЕ ТЯЖЕЛОГО ТВЕРДОГО ТЕЛА ОКОЛО НЕПОДВИЖНОЙ ТОЧКИ
- 2. Интегрирование уравнений движения тяжелого твердого тела.
- 3. Случай Эйлера — Пуансо.
- Регулярная прецессия твердого тела в случае Эйлера.
- Геометрическая интерпретация Пуансо движения твердого тела в случае Эйлера.
- Устойчивость постоянных вращений твердого тела.
- 4. Случай Лагранжа.
- Особенные случаи движения твердого тела. Спящий волчок.
- Гироскоп. Приближенная теория.
- Некоторые применения гироскопов.
- Регулярная прецессия в случае Лагранжа.
- Вынужденная регулярная прецессия.
- 5. Случай Ковалевской.
- § 5. ОПРЕДЕЛЕНИЕ РЕАКЦИИ В СЛУЧАЕ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА С ОДНОЙ НЕПОДВИЖНОЙ ТОЧКОЙ
- § 6. УРАВНЕНИЯ ДВИЖЕНИЯ СВОБОДНОГО ТВЕРДОГО ТЕЛА
- § 7. ГИРОСТАТЫ
- Глава VII. АНАЛИТИЧЕСКАЯ ДИНАМИКА
- § 1. КАНОНИЧЕСКИЕ УРАВНЕНИЯ ГАМИЛЬТОНА
- 1. Преобразования Лежандра.
- 2. Канонические уравнения Гамильтона.
- 3. Функция Гамильтона и ее свойства.
- § 2. ПРИНЦИП ГАМИЛЬТОНА — ОСТРОГРАДСКОГО
- 2. Вывод канонических уравнений Гамильтона из принципа Гамильтона — Остроградского.
- 3. Принцип Гамильтона в форме Пуанкаре.
- § 3. ИНТЕГРИРОВАНИЕ КАНОНИЧЕСКИХ УРАВНЕНИЙ ГАМИЛЬТОНА
- 2. Канонические преобразования.
- 3. Бесконечно малые канонические преобразования.
- 4. Теорема Лиувилля.
- 5. Теорема Якоби.
- 6. Интегрирование уравнения Гамильтона—Якоби.
- Метод Имшенецкого разделения переменных.
- 7. Скобки Пуассона.
- § 4. ВАРИАЦИОННЫЕ ПРИНЦИПЫ МЕХАНИКИ
- 2. Принцип Лагранжа.
- 3. Принцип наименьшего действия в форме Якоби.
- Вывод уравнений Лагранжа второго рода из принципа Якоби.
- Сравнение принципа Якоби с принципом Гамильтона.
- 4. Оптико-механическая аналогия.
- 5. Интегральные инварианты.
- Линейные интегральные инварианты.
- Интегральный инвариант Пуанкаре — Картана.
- 6. Принцип наименьшего принуждения Гаусса. Уравнения Аппеля.
- 7. Уравнения Рауса.
- § 5. МАЛЫЕ КОЛЕБАНИЯ
- Затухающие колебания.
- Вынужденные колебания. Резонанс.
- Параметрический резонанс.
- Нелинейные колебания.
- Диссипативные системы.
- 2. Общий случай малых колебаний системы около положения устойчивого равновесия.
- Устойчивость равновесия. Теорема Лагранжа об устойчивости равновесия.
- Замечание об устойчивости стационарных движений.
- Малые колебания системы около положения устойчивого равновесия.
- Влияние диссипативных сил на малые колебания системы около устойчивого положения равновесия.
- § 6. УСТОЙЧИВОСТЬ ДВИЖЕНИЯ
- Прямой метод Ляпунова
- Теорема об асимптотической устойчивости.
- Теорема Четаева о неустойчивости движения.
- 2. Влияние новых связей на малые колебания системы около положения равновесия.
- 3. Влияние диссипативных сил на устойчивость равновесия.
- 4. Влияние гироскопических сил на устойчивость равновесия.
- § 7. ЭЛЕМЕНТЫ ТЕОРИИ ВОЗМУЩЕНИЙ
- Устойчивость консервативных систем.
- 2. Метод изменения произвольных постоянных.
- Глава VIII. ТЕОРИЯ УДАРА
- § 2. ТЕОРЕМЫ КАРНО
- § 3. ЗАДАЧА О ЦЕНТРЕ УДАРА
- § 4. ЗАДАЧА О БАЛЛИСТИЧЕСКОМ МАЯТНИКЕ
- § 5. УРАВНЕНИЯ ЛАГРАНЖА ДЛЯ УДАРА
- § 6. ЗАДАЧА ОБ УДАРЕ ПО ТВЕРДОМУ ТЕЛУ С ОДНОЙ НЕПОДВИЖНОЙ ТОЧКОЙ
- Глава IX. ЭЛЕМЕНТЫ СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- § 2. СПЕЦИАЛЬНЫЙ ПРИНЦИП ОТНОСИТЕЛЬНОСТИ ЭЙНШТЕЙНА
- § 3. ГРУППА ПРЕОБРАЗОВАНИЙ ЛОРЕНЦА
- § 4. ИНВАРИАНТНЫЕ ВЕЛИЧИНЫ В ТЕОРИИ ОТНОСИТЕЛЬНОСТИ. ЧЕТЫРЕХМЕРНЫЙ ВЕКТОР. МИР МИНКОВСКОГО
- § 5. РЕЛЯТИВИСТСКАЯ ДИНАМИКА
- Литература