| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
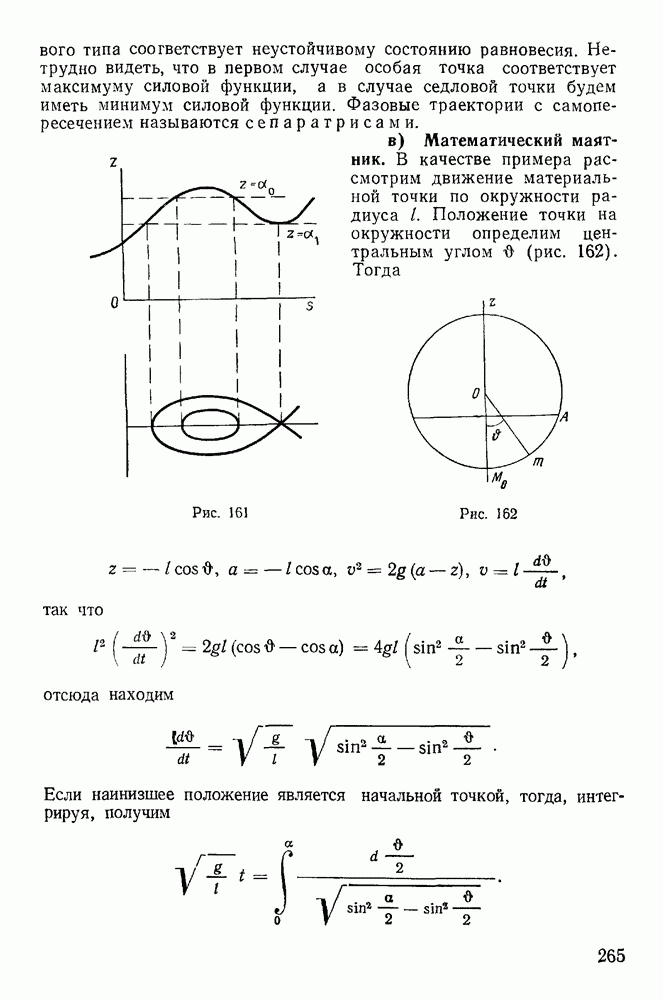
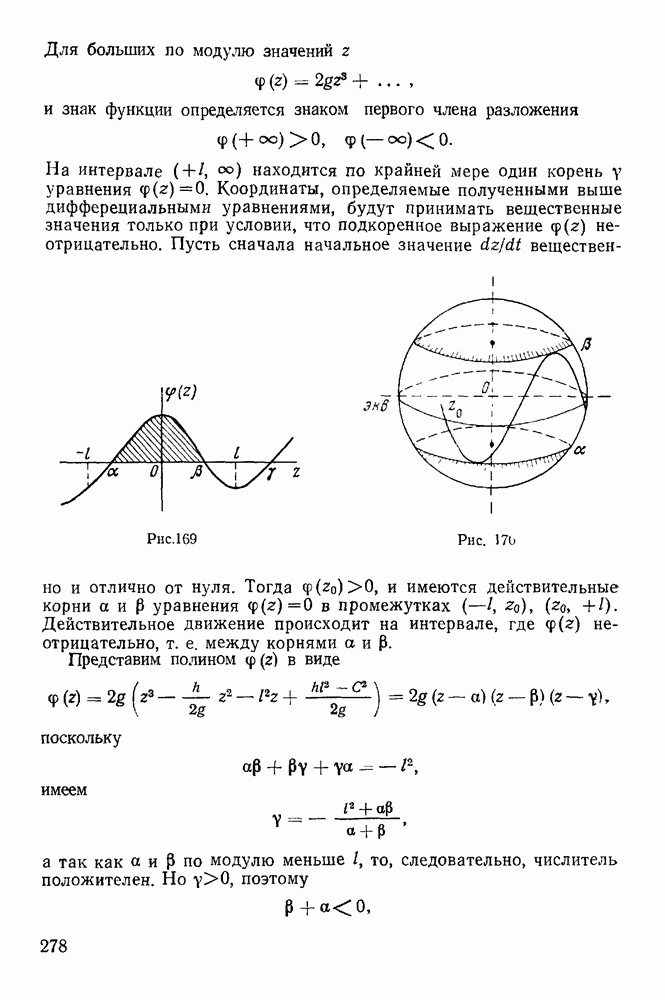
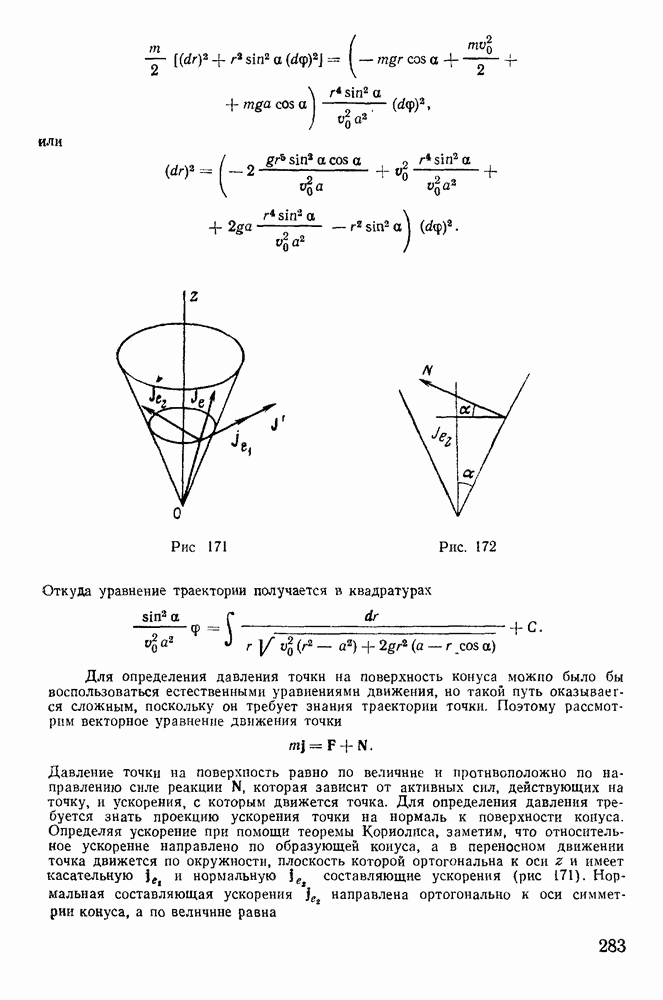
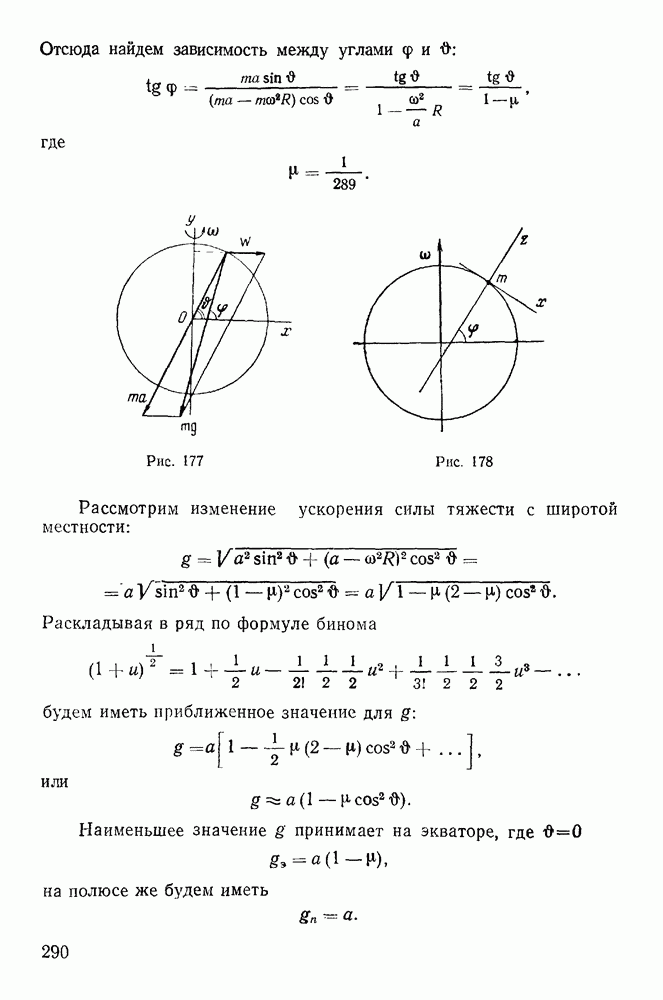
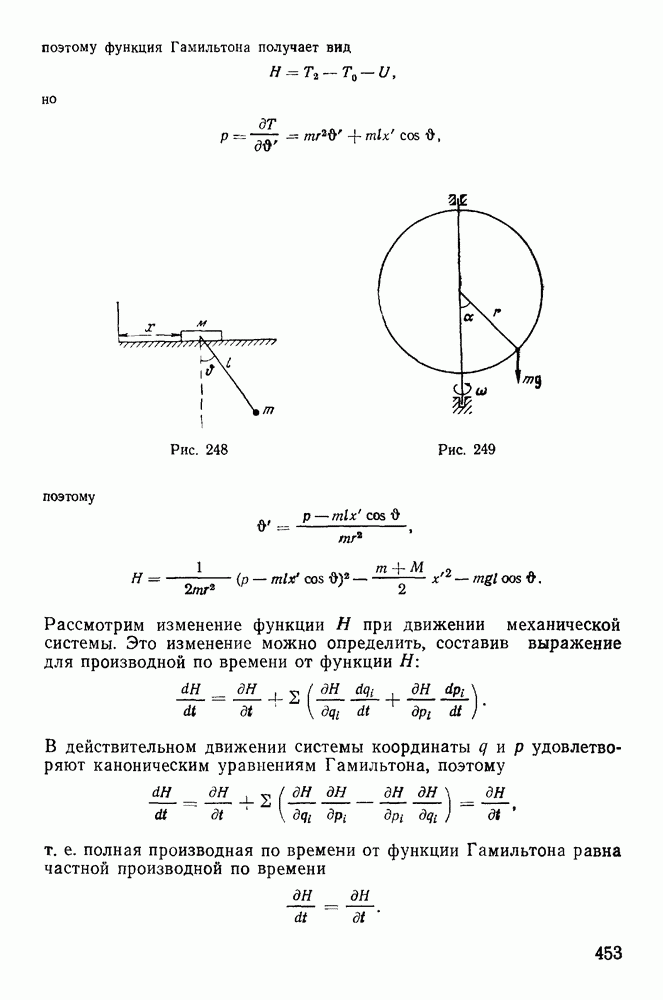
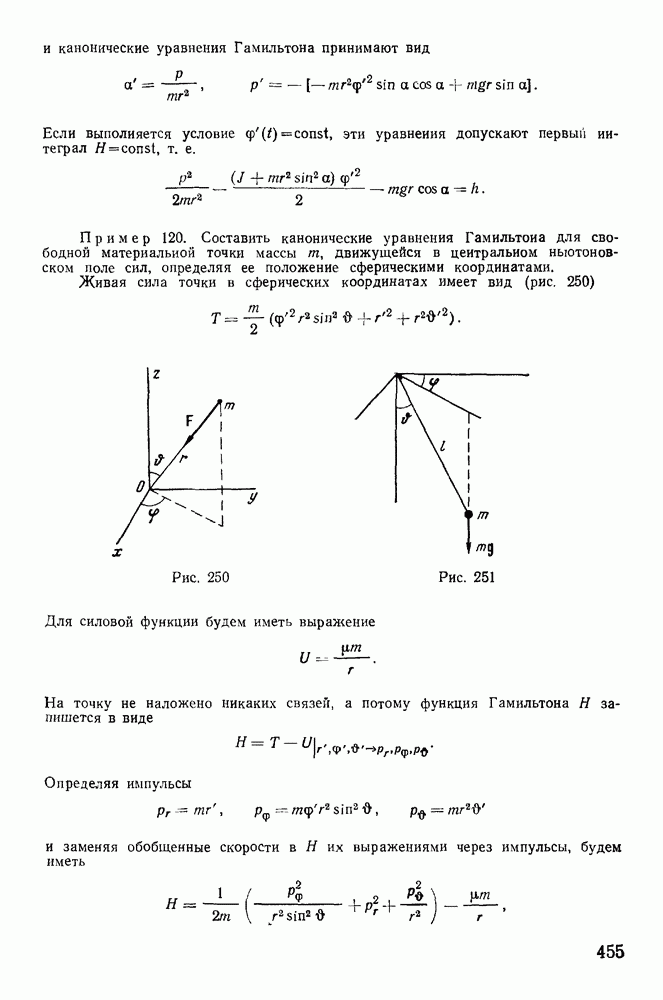
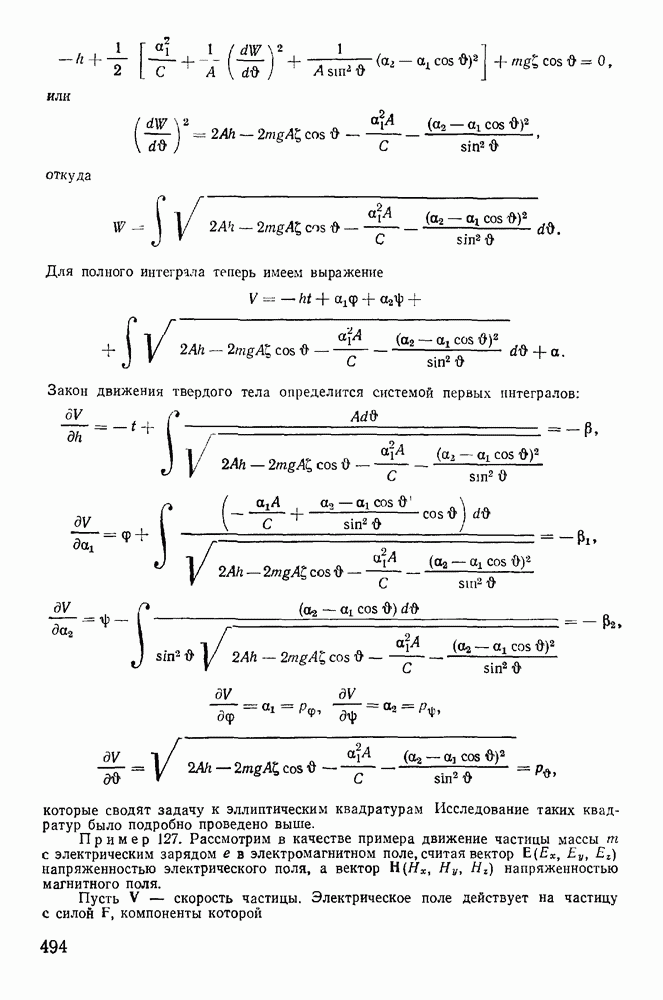
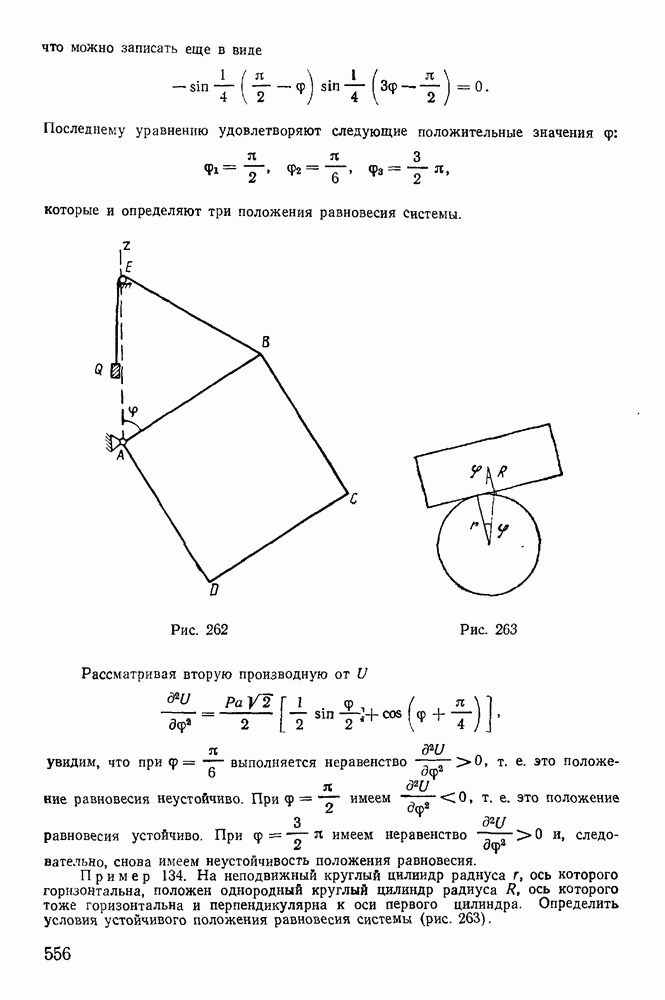
7. Скобки Пуассона.
Рассмотрим некоторые свойства первых интегралов канонических уравнений Гамильтона:

Функция  называется первым интегралом канонических уравнений Гамильтона, если она сохраняет постоянное значение на всяком конкретном движении системы (постоянная меняется при переходе от одного движения системы к другому). Производная от функции
называется первым интегралом канонических уравнений Гамильтона, если она сохраняет постоянное значение на всяком конкретном движении системы (постоянная меняется при переходе от одного движения системы к другому). Производная от функции  взятая в силу системы канонических уравнений Гамильтона, тождественно обращается в нуль, т. е.
взятая в силу системы канонических уравнений Гамильтона, тождественно обращается в нуль, т. е.

Очевидно, что если функции  являются первыми интегралами уравнений движения, то произвольная функция от этих интегралов
являются первыми интегралами уравнений движения, то произвольная функция от этих интегралов

также будет первым интегралом. (В дальнейшем нас будут интересовать только независимые интегралы.) Метод Пуассона дает возможность по двум первым интегралам канонических уравнений Гамильтона найти еще один первый интеграл, который может вообще оказаться некоторой функцией двух первых.
Чтобы пояснить метод, введем понятие скобок Пуассона. Пусть имеются две произвольные функции  Выражение
Выражение

называется скобками Пуассона.
Условие, что функция  является первым интегралом канонических уравнений Гамильтона, с помощью скобок Пуассона запишется следующим образом:
является первым интегралом канонических уравнений Гамильтона, с помощью скобок Пуассона запишется следующим образом:

Из определения скобок Пуассона вытекают следующие их свойства:


Все эти свойства очевидны, за исключением соотношения 4), называемого тождеством Пуассона. Доказать его можно непосредственным вычислением двойных скобок Пуассона. Можно также воспользоваться следующими соображениями. В скобке Пуассона  операция дифференцирования выполняется дважды над функциями
операция дифференцирования выполняется дважды над функциями  а вся скобка представляем собой линейную однородную функцию производных второго порядка от
а вся скобка представляем собой линейную однородную функцию производных второго порядка от  Таким образом, левая часть тождества Пуассона является линейной функцией вторых производных от всех трех функций
Таким образом, левая часть тождества Пуассона является линейной функцией вторых производных от всех трех функций  Соберем вместе члены, содержащие вторые производные от функции
Соберем вместе члены, содержащие вторые производные от функции  Они войдут в выражение
Они войдут в выражение

Введем линейные дифференциальные операторы

Тогда

Легко видеть, что такая комбинация линейных операторов не может содержать вторых производных от  Обозначая для упрощения вычислений координаты и импульсы через
Обозначая для упрощения вычислений координаты и импульсы через  и представляя
и представляя

будем иметь

Разность этих операторов

есть снова оператор, содержащий только первые производные. Поэтому в левой части тождества Пуассона сокращаются все члены со вторыми производными от х, то же самое относится, очевидно,
и функциям  Следовательно, левая часть тождественно равна нулю.
Следовательно, левая часть тождественно равна нулю.
Теорема Пуассона. Если  — первые интегралы канонических уравнений Гамильтона, то скобка Пуассона
— первые интегралы канонических уравнений Гамильтона, то скобка Пуассона  также является первым интегралом канонических уравнений Гамильтона.
также является первым интегралом канонических уравнений Гамильтона.
Доказательство. Если  — первые интегралы, то для них выполняются соотношения
— первые интегралы, то для них выполняются соотношения

Из пятого свойства скобок Пуассона теперь имеем

Подставляя в правую часть значения производных  и
и  получим
получим

или, на основании тождества Пуассона,

Последнее равенство означает, что скобка  является первым интегралом канонических уравнений.
является первым интегралом канонических уравнений.
Теорема Пуассона дает правило, позволяющее из двух первых интегралов получать третий При этом не всегда получается новый интеграл. Часто оказывается, что скобка Пуассона от двух первых интегралов или является линейной функцией уже найденных интегралов, или тождественно обращается в нуль.
Замечание. Если функция Н не зависит явно от времени, то имеет место интеграл Якоби

Если, кроме того, известен еще один первый интеграл канонических уравнений Гамильтона

то скобка Пуассона  тоже будет представлять первый интеграл канонических уравнений Гамильтона. Но так как Ф — первый интеграл, то
тоже будет представлять первый интеграл канонических уравнений Гамильтона. Но так как Ф — первый интеграл, то

и, следовательно, на интегральной кривой будет выполняться соотношение

откуда следует, что функция  будет представлять собой первый интеграл канонических уравнений Гамильтона.
будет представлять собой первый интеграл канонических уравнений Гамильтона.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие
- Введение
- Глава I. ОСНОВЫ ТЕОРИИ ВЕКТОРОВ
- § 1. СВОБОДНЫЕ ВЕКТОРЫ
- 2. Сложение свободных векторов.
- 3. Проекция вектора на ось.
- 4. Инварианты системы свободных векторов.
- § 2. СКОЛЬЗЯЩИЕ ВЕКТОРЫ
- 2. Координаты скользящего вектора.
- 3. Момент скользящего вектора. Плюккеровы координаты.
- 4. Аналитическое определение момента скользящего вектора.
- 5. Проекция момента на ось.
- 6. Момент скользящего вектора относительно оси
- § 3. СИСТЕМА СКОЛЬЗЯЩИХ ВЕКТОРОВ
- 2. Произвольная система скользящих векторов. Элементарные операции.
- 3. Приведение системы скользящих векторов к простейшей эквивалентной форме.
- 4. Плоская система скользящих векторов.
- 5. Свойства системы параллельных скользящих векторов.
- § 4. ЗАКРЕПЛЕННЫЕ ВЕКТОРЫ
- § 5. ДИФФЕРЕНЦИРОВАНИЕ СВОБОДНОГО ВЕКТОРА ПО СКАЛЯРНОМУ АРГУМЕНТУ
- Глава II. КИНЕМАТИКА
- § 1. КИНЕМАТИКА ТОЧКИ
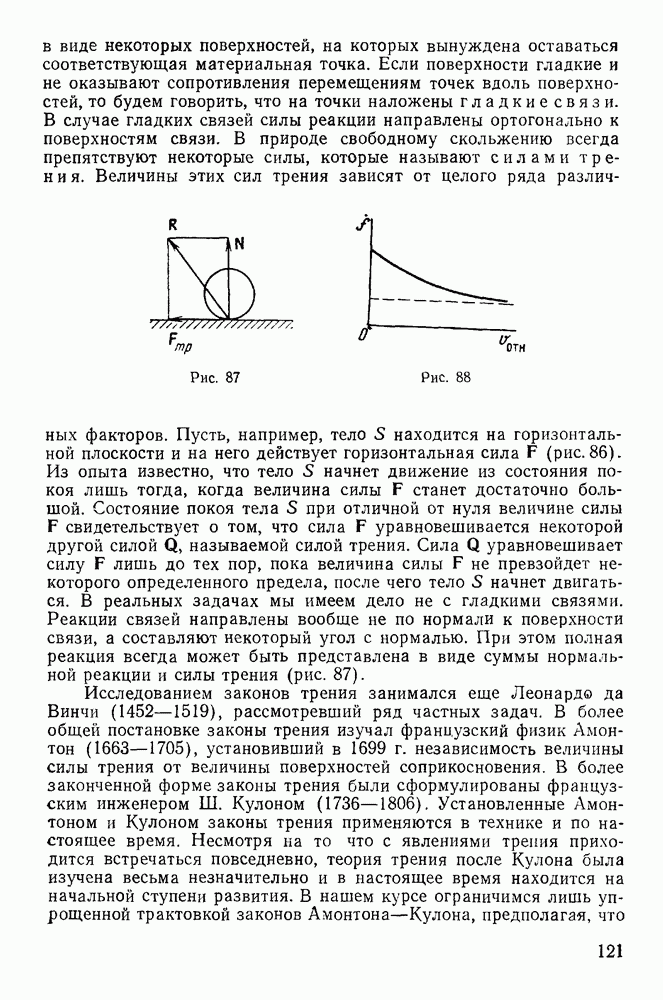
- 2. Ускорение точки. Проекции ускорения на прямоугольные оси координат.
- 3. Скорость и ускорение точки в полярных координатах.
- 4. Движение точки по окружности.
- 5. Проекции ускорения на оси естественного трехгранника.
- 6. Теорема о сложении скоростей в сложном движении точки.
- 7. Метод Роберваля построения касательных к плоским кривым.
- 8. Аналитическое доказательство теоремы о сложении скоростей.
- 9. Сложение скоростей в общем случае сложного движения точки.
- § 2. КИНЕМАТИКА АБСОЛЮТНО ТВЕРДОГО ТЕЛА
- 2. Элементарные движения твердого тела.
- 3. Мгновенные движения твердого тела.
- 4. Сложение мгновенно-поступательных и мгновенно-вращательных движений твердого тела.
- 5. Общий случай сложения мгновенно-поступательных и мгновенно-вращательных движений твердого тела. Непрерывное движение твердого тела.
- 6. Мгновенное движение твердого тела с одной неподвижной точкой.
- 7. Плоскопараллельное движение твердого тела.
- § 3. УСКОРЕНИЕ ТОЧКИ В СЛОЖНОМ ДВИЖЕНИИ
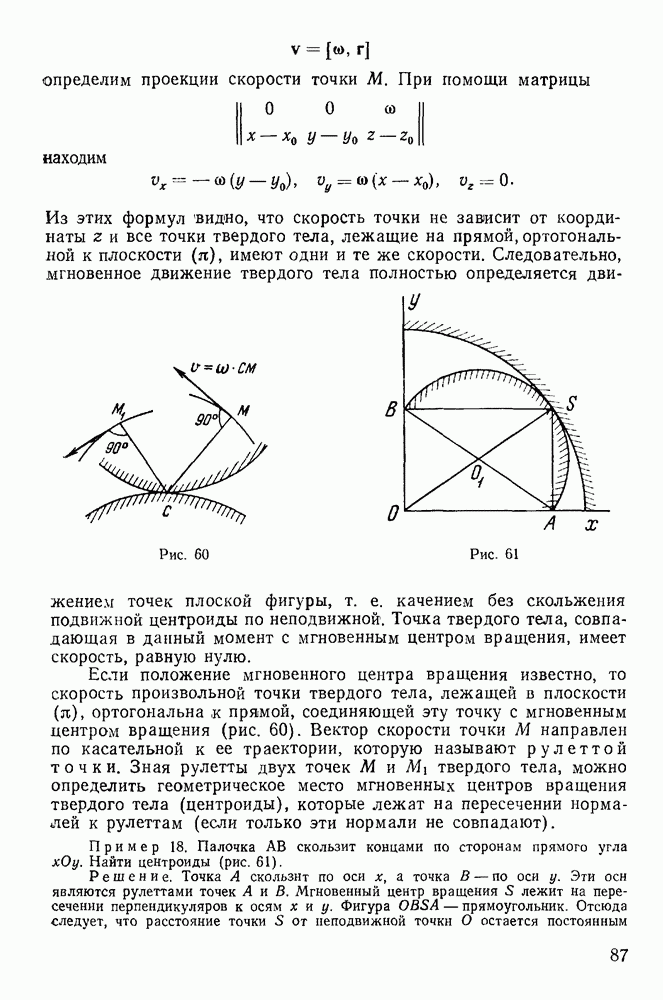
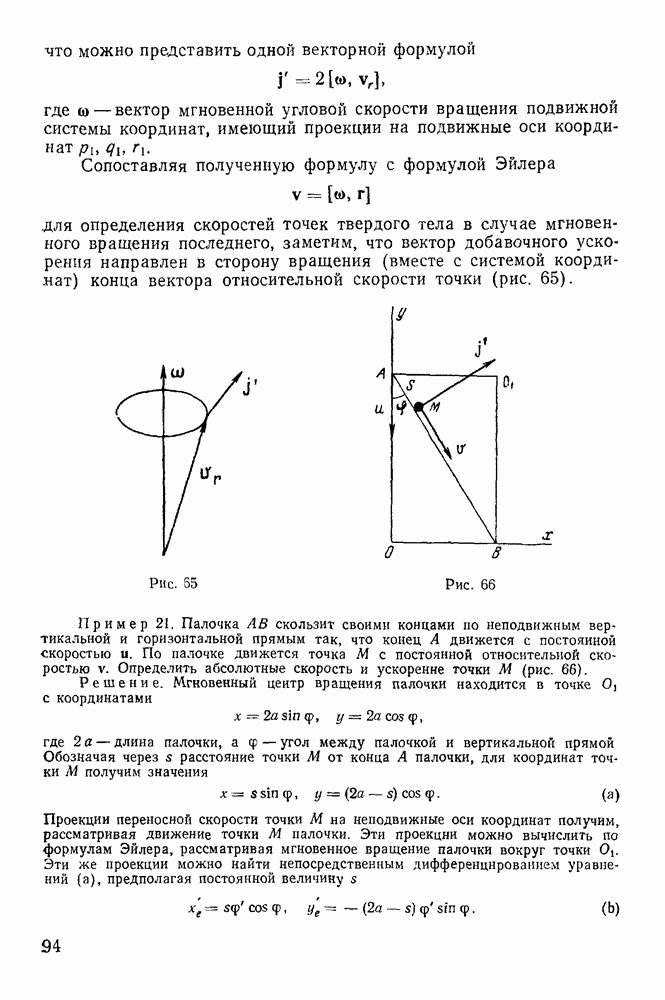
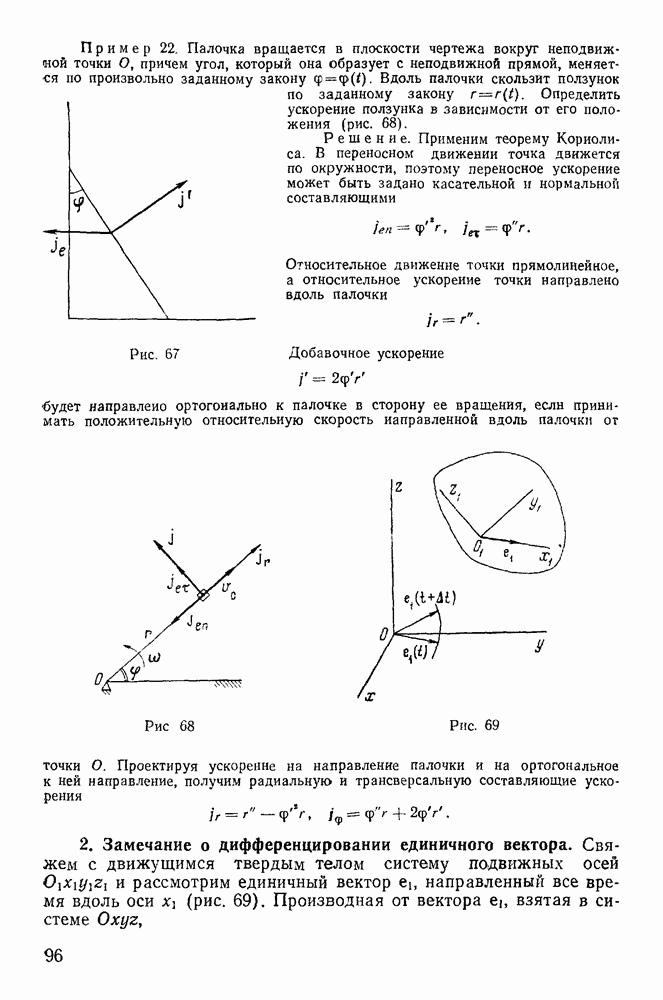
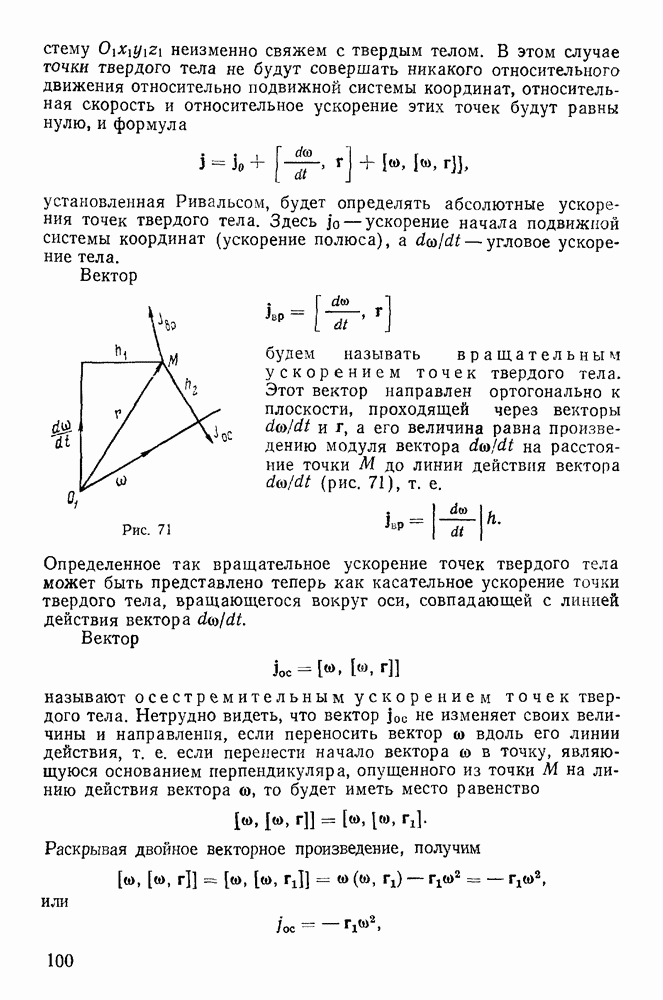
- 2. Замечание о дифференцировании единичного вектора.
- 3. Векторный вывод теоремы Кориолиса.
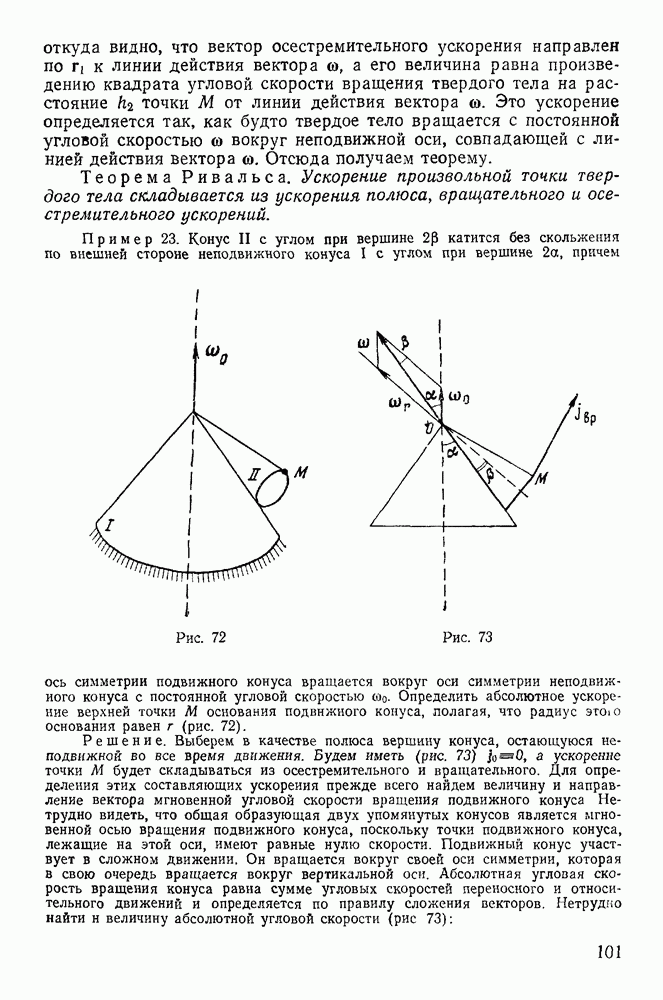
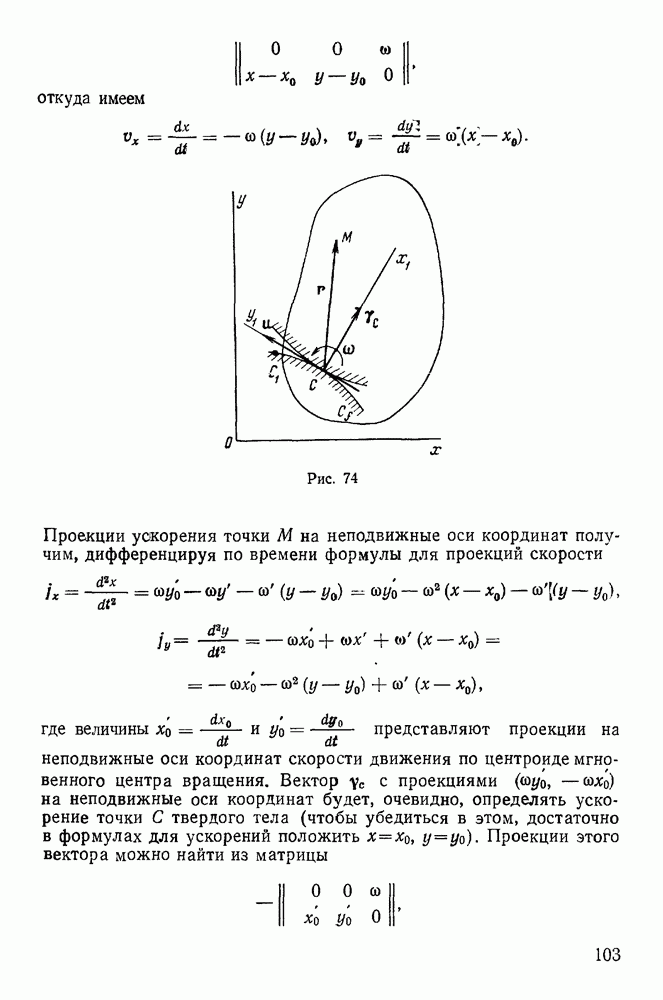
- 4. Теорема Ривальса.
- § 4. РАСПРЕДЕЛЕНИЕ УСКОРЕНИЙ В ПЛОСКОПАРАЛЛЕЛЬНОМ ДВИЖЕНИИ ТВЕРДОГО ТЕЛА
- 2. Мгновенный центр ускорений.
- § 5. КИНЕМАТИЧЕСКИЕ УРАВНЕНИЯ ЭЙЛЕРА
- Глава III. СТАТИКА
- I. ГЕОМЕТРИЧЕСКАЯ СТАТИКА
- § 1. АКСИОМЫ СТАТИКИ
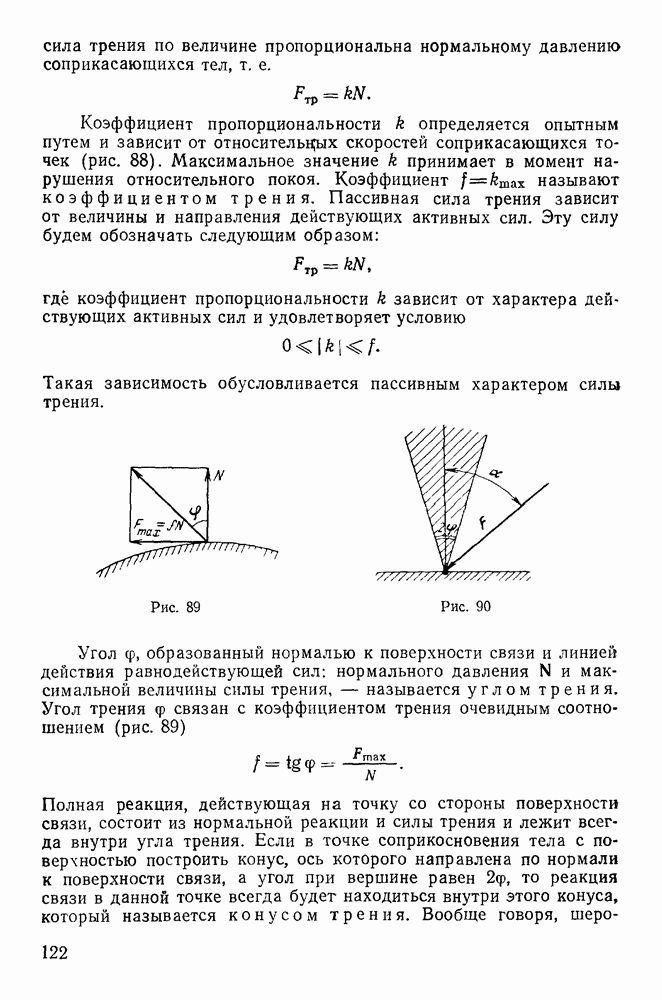
- § 2. ПОНЯТИЕ О СИЛЕ ТРЕНИЯ
- § 3. РАЗЛИЧНЫЕ ЗАДАЧИ СТАТИКИ
- 2. Равновесие трех сил.
- § 4. МОМЕНТ СИЛЫ
- 2. Момент силы относительно оси.
- 3. Теорема Вариньона для системы сходящихся сил.
- § 5. ПРОИЗВОЛЬНАЯ СИСТЕМА СИЛ, ДЕЙСТВУЮЩИХ НА ТВЕРДОЕ ТЕЛО
- § 6. УСЛОВИЯ РАВНОВЕСИЯ СИСТЕМЫ СИЛ, ДЕЙСТВУЮЩИХ НА ТВЕРДОЕ ТЕЛО
- § 7. ПРИВЕДЕНИЕ СИСТЕМЫ СИЛ, ДЕЙСТВУЮЩИХ НА ТВЕРДОЕ ТЕЛО, К ДИНАМЕ. УРАВНЕНИЯ РАВНОВЕСИЯ ТВЕРДОГО ТЕЛА
- § 8. УСЛОВИЯ РАВНОВЕСИЯ СИСТЕМЫ ТВЕРДЫХ ТЕЛ
- § 9. ПЛОСКАЯ СИСТЕМА СИЛ
- § 10. ЗАДАЧА О РАВНОВЕСИИ НЕСВОБОДНОГО ТВЕРДОГО ТЕЛА
- 2. Частные случаи равновесия твердого тела.
- § 11. ЗАДАЧА О РАВНОВЕСИИ ПРИ НАЛИЧИИ ТРЕНИЯ
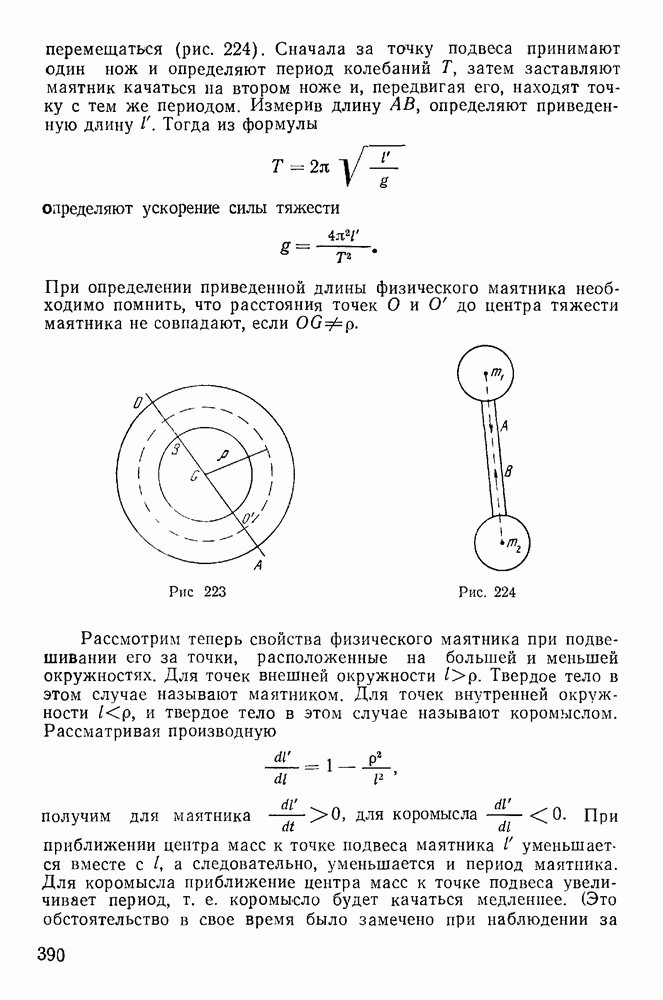
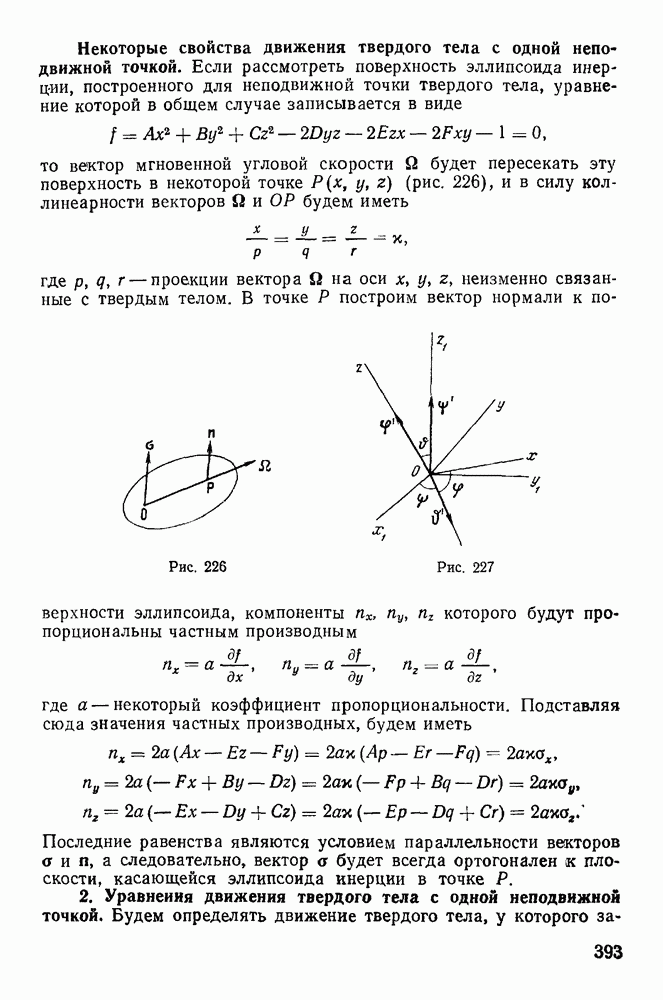
- § 12. СИЛА ТЯЖЕСТИ И ЦЕНТР ТЯЖЕСТИ
- II. АНАЛИТИЧЕСКАЯ СТАТИКА
- § 1. РАБОТА СИЛЫ НА ПЕРЕМЕЩЕНИИ. СИЛОВАЯ ФУНКЦИЯ
- § 2. ПРИНЦИП ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ
- 2. Теорема Лагранжа о равновесии системы.
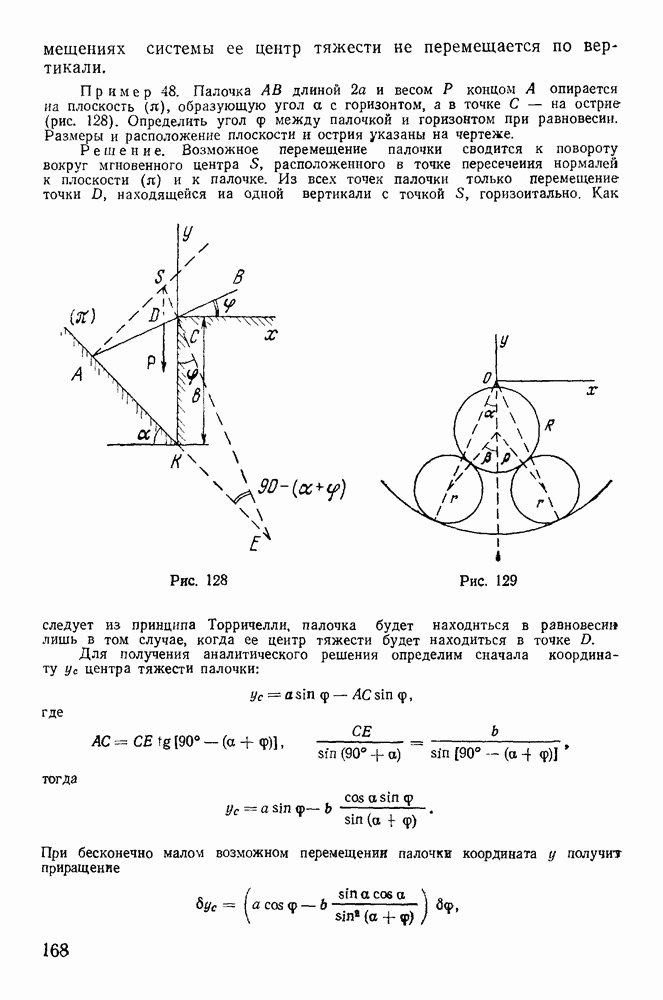
- 3. Принцип Торричелли.
- § 3. ОБЩИЕ ВОПРОСЫ АНАЛИТИЧЕСКОЙ СТАТИКИ
- 3. Общие теоремы о равновесии системы материальных точек.
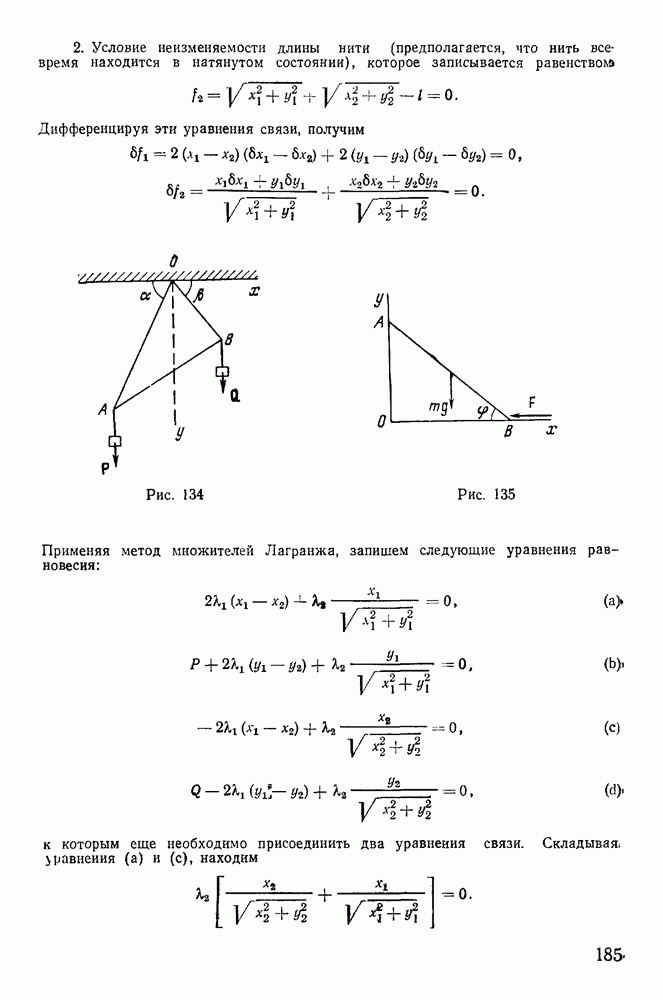
- 4. Метод неопределенных множителей Лагранжа.
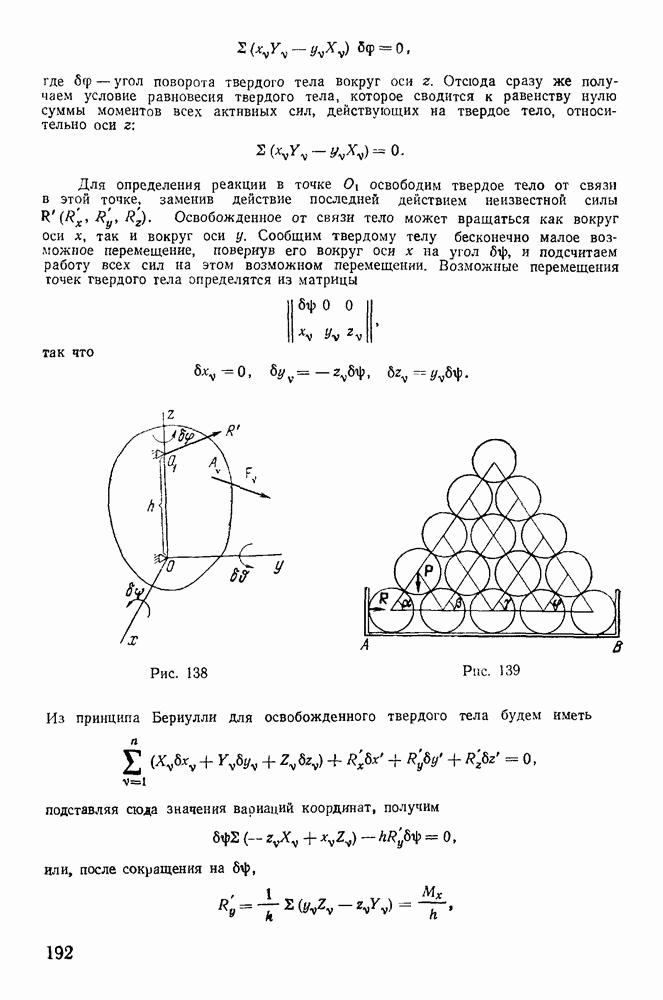
- 5. Определение реакций.
- § 4. ОПРЕДЕЛЕНИЕ РЕАКЦИЙ В ОБЩЕМ СЛУЧАЕ
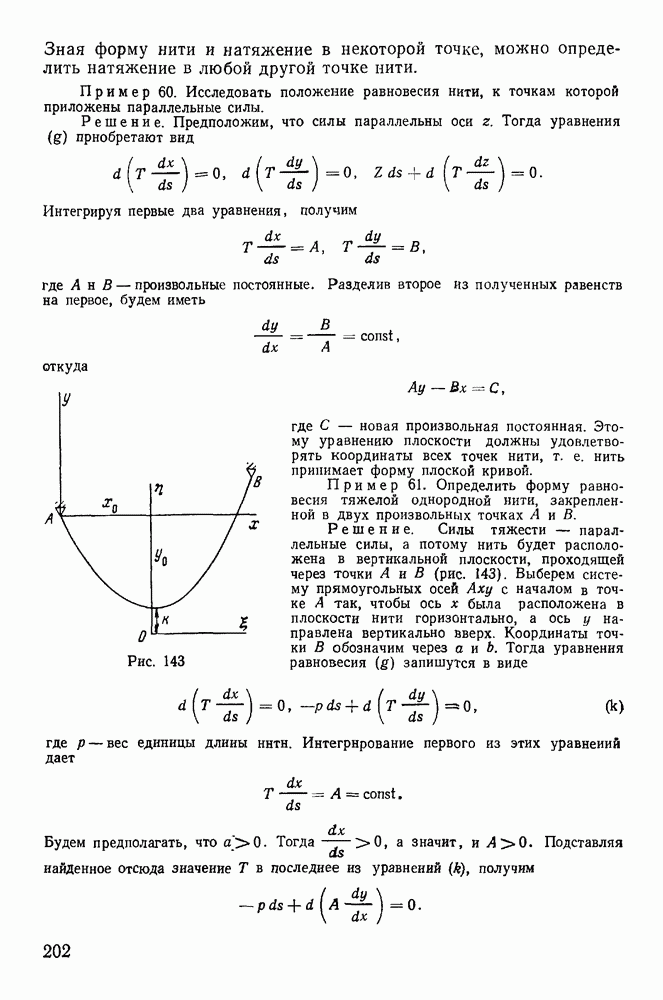
- § 5. РАВНОВЕСИЕ НИТИ
- 2. Естественные уравнения равновесия нити.
- Глава IV. ДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ
- § 1. ОСНОВНЫЕ ЗАКОНЫ ДИНАМИКИ
- § 2. ДВЕ ОСНОВНЫЕ ЗАДАЧИ ДИНАМИКИ. УРАВНЕНИЯ ДВИЖЕНИЯ ТОЧКИ В ДЕКАРТОВЫХ ОСЯХ
- § 3. ЕСТЕСТВЕННЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ
- § 4. ОСНОВНЫЕ ТЕОРЕМЫ ДИНАМИКИ ДЛЯ СВОБОДНОЙ МАТЕРИАЛЬНОЙ ТОЧКИ
- 2. Теорема об изменении момента количества движения.
- 3. Следствия из теорем об изменении количества движения и момента количества движения материальной точки.
- 4. Теорема живых сил.
- 5. Интеграл живых сил.
- 6. Устойчивость равновесия. Теорема Лагранжа.
- § 5. ДВИЖЕНИЕ ТЯЖЕЛОЙ МАТЕРИАЛЬНОЙ ТОЧКИ В ПУСТОТЕ
- § 6. ДВИЖЕНИЕ МАТЕРИАЛЬНОЙ ТОЧКИ ПОД ДЕЙСТВИЕМ ЦЕНТРАЛЬНЫХ СИЛ
- 2. Формулы Бине
- 3. Задача о движении планет
- § 7. ДВИЖЕНИЕ ТОЧКИ В СОПРОТИВЛЯЮЩЕЙСЯ СРЕДЕ
- § 8. ДВИЖЕНИЕ НЕСВОБОДНОЙ МАТЕРИАЛЬНОЙ ТОЧКИ
- 2. Движение материальной точки по поверхности.
- § 9. ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЕ МАТЕРИАЛЬНОЙ ТОЧКИ
- 1. Теорема живых сил в относительном движении точки.
- 2. Уравнения относительного равновесия точки.
- 3. Равновесие материальной точки на поверхности Земли. Вес.
- 4. Задача о падении тяжелой точки в пустоте.
- 5. Маятник Фуко.
- § 10. ПРИНЦИП ДАЛАМБЕРА
- Глава V. ДИНАМИКА СИСТЕМЫ МАТЕРИАЛЬНЫХ ТОЧЕК
- § 1. УЧЕНИЕ О СВЯЗЯХ
- § 2. ПРИНЦИП ДАЛАМБЕРА — ЛАГРАНЖА
- § 3. ОСНОВНЫЕ ТЕОРЕМЫ ДИНАМИКИ СИСТЕМЫ
- 2. Теорема об изменении момента количества движения.
- 3. Теорема живых сил.
- § 4. ТЕОРЕМЫ О ДВИЖЕНИИ СИСТЕМЫ ОТНОСИТЕЛЬНО ОСЕЙ НЕИЗМЕННОГО НАПРАВЛЕНИЯ, ПРОХОДЯЩИХ ЧЕРЕЗ ЦЕНТР МАСС СИСТЕМЫ (ОСЕЙ КЕНИГА)
- 2. Теорема об изменении момента количества движения системы относительно осей Кёнига.
- 3. Теорема живых сил в движении системы относительно осей Кёнига.
- § 5. УРАВНЕНИЯ ЛАГРАНЖА ВТОРОГО РОДА
- 2. Случай существования силовой функции.
- 3. Замечание о лагранжевых координатах.
- § 6. ЭЛЕМЕНТАРНЫЕ СЛУЧАИ ИНТЕГРИРУЕМОСТИ УРАВНЕНИЙ ЛАГРАНЖА
- 2. Метод Рауса игнорирования циклических координат.
- 3. Обобщение теоремы и интеграла живых сил.
- § 7. ОПРЕДЕЛЕНИЕ РЕАКЦИЙ
- Глава VI. ДИНАМИКА ТВЕРДОГО ТЕЛА
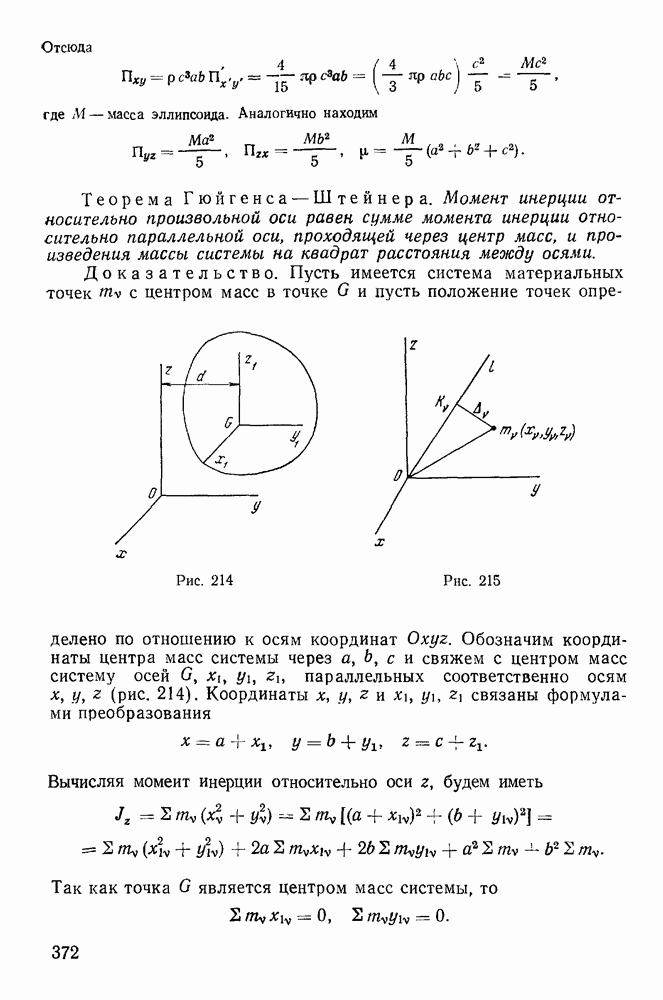
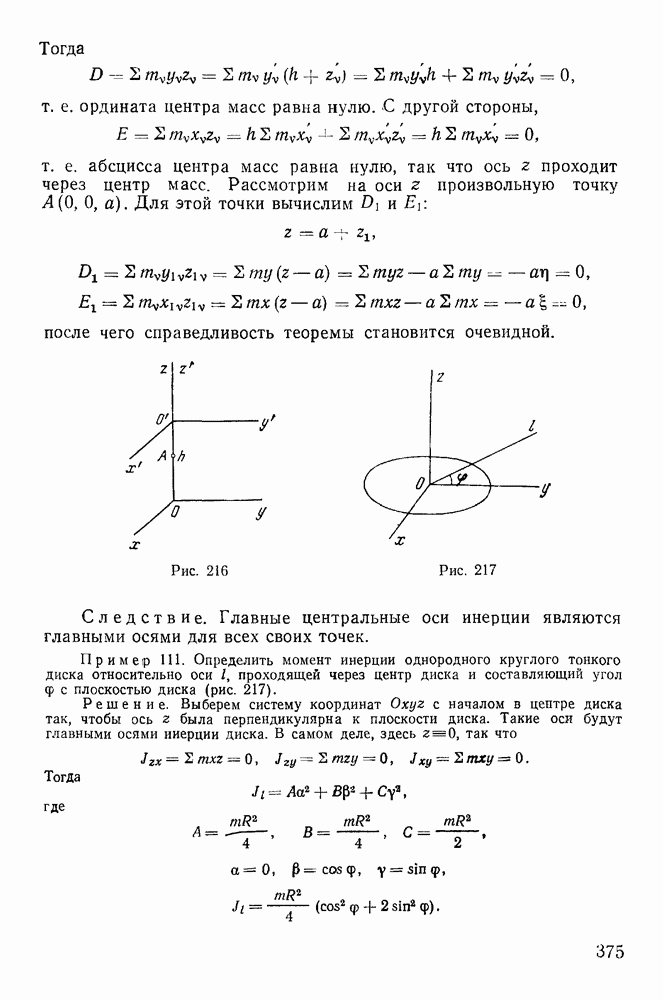
- § 1. ТЕОРИЯ МОМЕНТОВ ИНЕРЦИИ
- 2. Момент инерции системы относительно произвольной оси, проходящей через заданную точку.
- 3. Эллипсоид инерции.
- 4. Определение главных осей инерции для произвольной точки.
- § 2. ВРАЩЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ОСИ
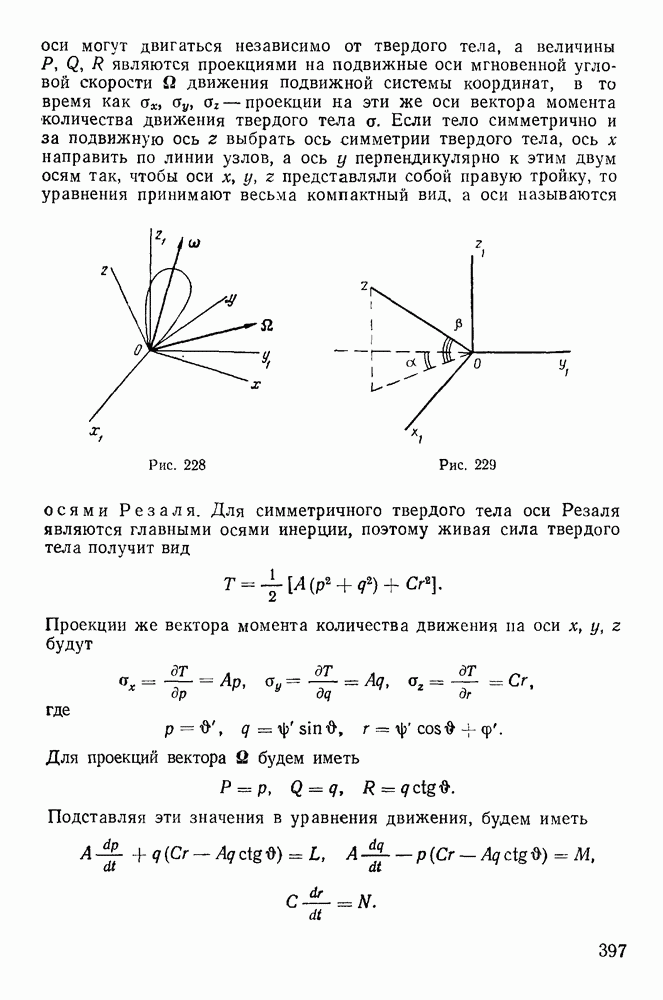
- § 3. ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА, ИМЕЮЩЕГО ОДНУ НЕПОДВИЖНУЮ ТОЧКУ
- 2. Уравнения движения твердого тела с одной неподвижной точкой.
- § 4. ДВИЖЕНИЕ ТЯЖЕЛОГО ТВЕРДОГО ТЕЛА ОКОЛО НЕПОДВИЖНОЙ ТОЧКИ
- 2. Интегрирование уравнений движения тяжелого твердого тела.
- 3. Случай Эйлера — Пуансо.
- Регулярная прецессия твердого тела в случае Эйлера.
- Геометрическая интерпретация Пуансо движения твердого тела в случае Эйлера.
- Устойчивость постоянных вращений твердого тела.
- 4. Случай Лагранжа.
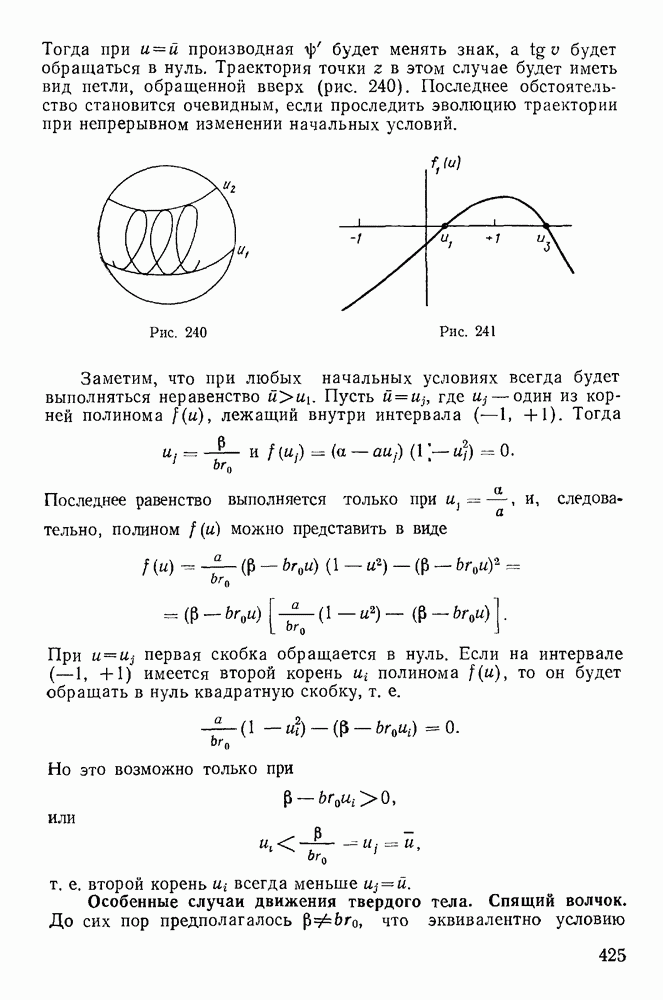
- Особенные случаи движения твердого тела. Спящий волчок.
- Гироскоп. Приближенная теория.
- Некоторые применения гироскопов.
- Регулярная прецессия в случае Лагранжа.
- Вынужденная регулярная прецессия.
- 5. Случай Ковалевской.
- § 5. ОПРЕДЕЛЕНИЕ РЕАКЦИИ В СЛУЧАЕ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА С ОДНОЙ НЕПОДВИЖНОЙ ТОЧКОЙ
- § 6. УРАВНЕНИЯ ДВИЖЕНИЯ СВОБОДНОГО ТВЕРДОГО ТЕЛА
- § 7. ГИРОСТАТЫ
- Глава VII. АНАЛИТИЧЕСКАЯ ДИНАМИКА
- § 1. КАНОНИЧЕСКИЕ УРАВНЕНИЯ ГАМИЛЬТОНА
- 1. Преобразования Лежандра.
- 2. Канонические уравнения Гамильтона.
- 3. Функция Гамильтона и ее свойства.
- § 2. ПРИНЦИП ГАМИЛЬТОНА — ОСТРОГРАДСКОГО
- 2. Вывод канонических уравнений Гамильтона из принципа Гамильтона — Остроградского.
- 3. Принцип Гамильтона в форме Пуанкаре.
- § 3. ИНТЕГРИРОВАНИЕ КАНОНИЧЕСКИХ УРАВНЕНИЙ ГАМИЛЬТОНА
- 2. Канонические преобразования.
- 3. Бесконечно малые канонические преобразования.
- 4. Теорема Лиувилля.
- 5. Теорема Якоби.
- 6. Интегрирование уравнения Гамильтона—Якоби.
- Метод Имшенецкого разделения переменных.
- 7. Скобки Пуассона.
- § 4. ВАРИАЦИОННЫЕ ПРИНЦИПЫ МЕХАНИКИ
- 2. Принцип Лагранжа.
- 3. Принцип наименьшего действия в форме Якоби.
- Вывод уравнений Лагранжа второго рода из принципа Якоби.
- Сравнение принципа Якоби с принципом Гамильтона.
- 4. Оптико-механическая аналогия.
- 5. Интегральные инварианты.
- Линейные интегральные инварианты.
- Интегральный инвариант Пуанкаре — Картана.
- 6. Принцип наименьшего принуждения Гаусса. Уравнения Аппеля.
- 7. Уравнения Рауса.
- § 5. МАЛЫЕ КОЛЕБАНИЯ
- Затухающие колебания.
- Вынужденные колебания. Резонанс.
- Параметрический резонанс.
- Нелинейные колебания.
- Диссипативные системы.
- 2. Общий случай малых колебаний системы около положения устойчивого равновесия.
- Устойчивость равновесия. Теорема Лагранжа об устойчивости равновесия.
- Замечание об устойчивости стационарных движений.
- Малые колебания системы около положения устойчивого равновесия.
- Влияние диссипативных сил на малые колебания системы около устойчивого положения равновесия.
- § 6. УСТОЙЧИВОСТЬ ДВИЖЕНИЯ
- Прямой метод Ляпунова
- Теорема об асимптотической устойчивости.
- Теорема Четаева о неустойчивости движения.
- 2. Влияние новых связей на малые колебания системы около положения равновесия.
- 3. Влияние диссипативных сил на устойчивость равновесия.
- 4. Влияние гироскопических сил на устойчивость равновесия.
- § 7. ЭЛЕМЕНТЫ ТЕОРИИ ВОЗМУЩЕНИЙ
- Устойчивость консервативных систем.
- 2. Метод изменения произвольных постоянных.
- Глава VIII. ТЕОРИЯ УДАРА
- § 2. ТЕОРЕМЫ КАРНО
- § 3. ЗАДАЧА О ЦЕНТРЕ УДАРА
- § 4. ЗАДАЧА О БАЛЛИСТИЧЕСКОМ МАЯТНИКЕ
- § 5. УРАВНЕНИЯ ЛАГРАНЖА ДЛЯ УДАРА
- § 6. ЗАДАЧА ОБ УДАРЕ ПО ТВЕРДОМУ ТЕЛУ С ОДНОЙ НЕПОДВИЖНОЙ ТОЧКОЙ
- Глава IX. ЭЛЕМЕНТЫ СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- § 2. СПЕЦИАЛЬНЫЙ ПРИНЦИП ОТНОСИТЕЛЬНОСТИ ЭЙНШТЕЙНА
- § 3. ГРУППА ПРЕОБРАЗОВАНИЙ ЛОРЕНЦА
- § 4. ИНВАРИАНТНЫЕ ВЕЛИЧИНЫ В ТЕОРИИ ОТНОСИТЕЛЬНОСТИ. ЧЕТЫРЕХМЕРНЫЙ ВЕКТОР. МИР МИНКОВСКОГО
- § 5. РЕЛЯТИВИСТСКАЯ ДИНАМИКА
- Литература