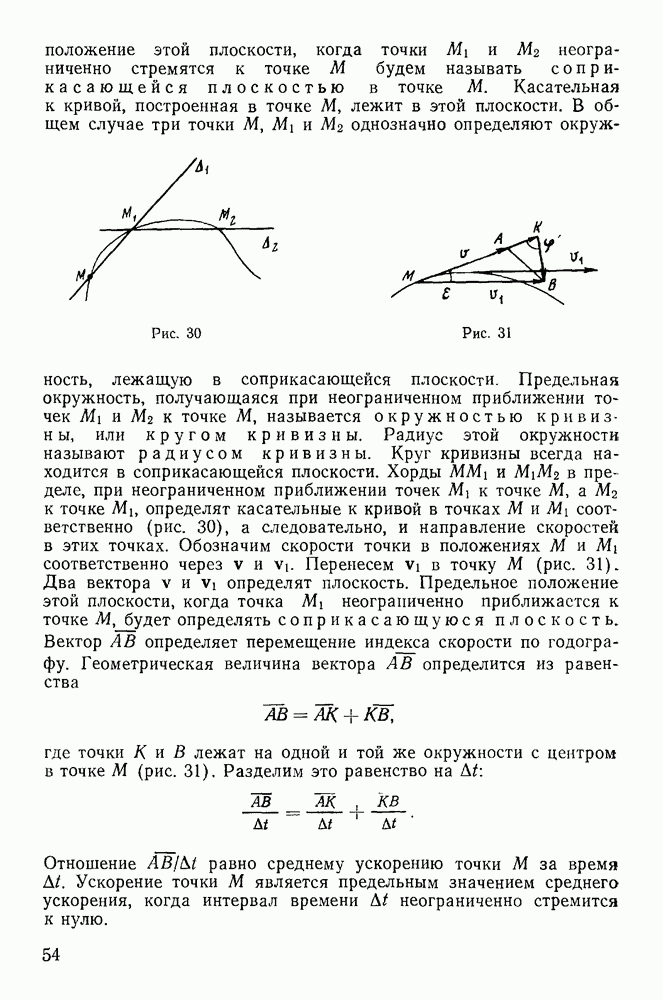
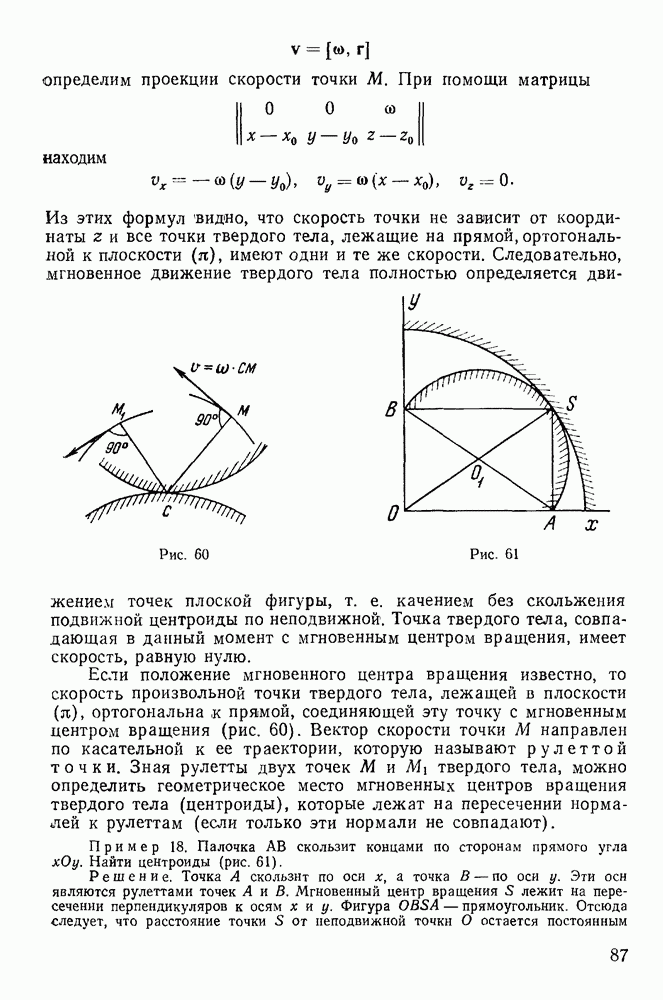
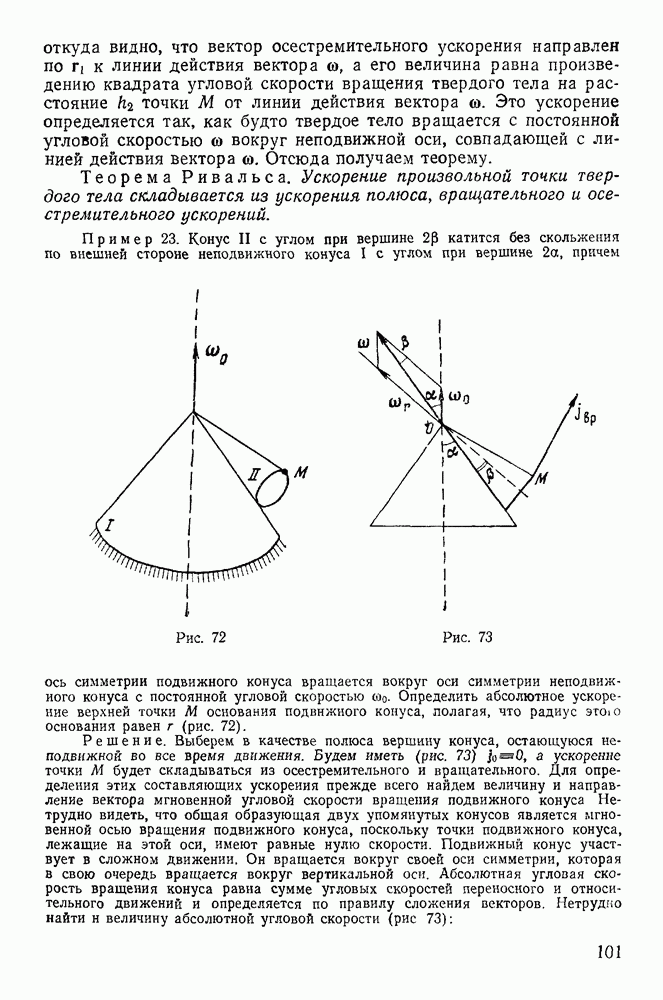
§ 5. ДВИЖЕНИЕ ТЯЖЕЛОЙ МАТЕРИАЛЬНОЙ ТОЧКИ В ПУСТОТЕ

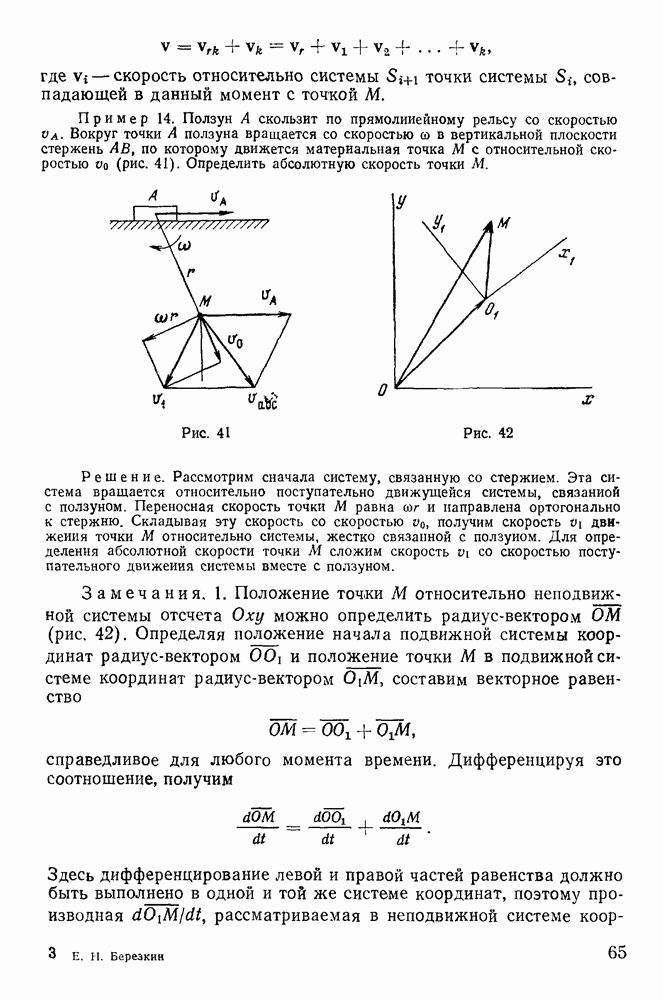
Одним из наиболее важных приложений законов движения свободной материальной точки является задача о движении точки под действием силы тяжести. Рассмотрим движение материальной точки, на которую действует только сила тяжести (сила, имеющая постоянную величину и направление).

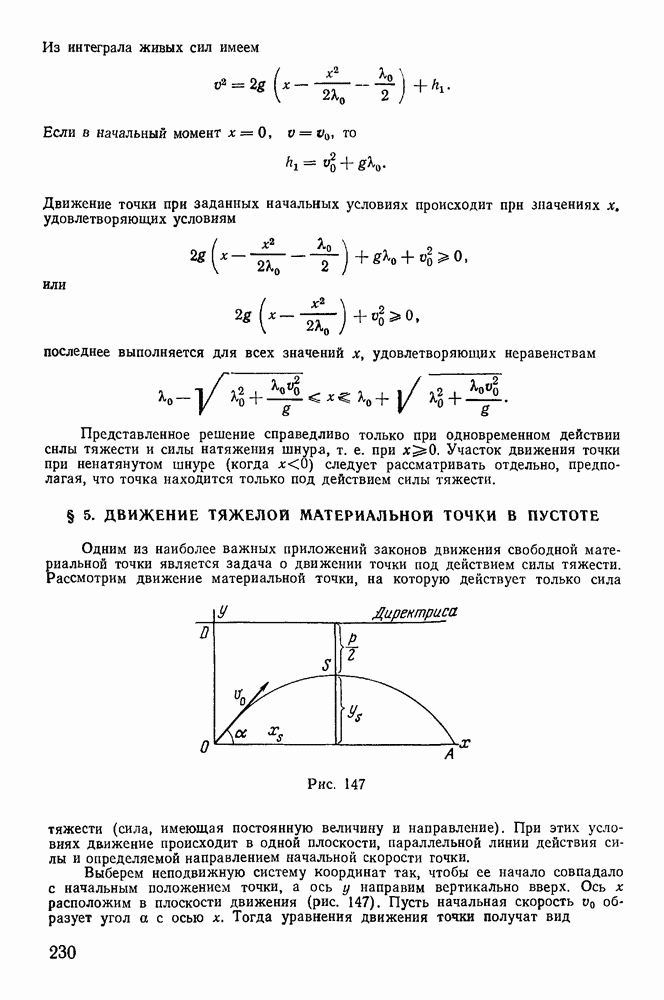
Рис. 147

При этих условиях движение происходит в одной плоскости, параллельной линии действия силы и определяемой направлением начальной скорости гочки.

Выберем неподвижную систему координат так, чтобы ее начало совпадало с начальным положением точки, а ось у направим вертикально вверх. Ось х расположим в плоскости движения (рис. 147). Пусть начальная скорость образует угол а с осью х. Тогда уравнения движения точки получат вид

Из первого уравнения получим

Интегрируя второе уравнение, будем иметь

Исключая отсюда время, получим уравнение траектории

которое представляет собой уравнение параболы с параметром

Точка вершины параболы может быть определена из условия

т. е.

откуда

Подставляя это значение в уравнение параболы, определим ординату вершины

Отсюда видно, что траектория точки является параболой, ось которой проходит через точку 5 и параллельна оси у. Дальность полета по горизонтали

Очевидно, что максимальная дальность полета обеспечивается при т. е. при . В этом случае

Заметим, что расстояние от начала координат до директрисы параболы зависит только от величины начальной скорости точки. В самом деле,

Свойства траектории. Перепишем уравнение параболы в виде

или, принимая во внимание, что

Вид траектории зависит от . При различных значениях получим семейство траекторий, имеющих одну и ту же директрису. Исключая параметр из уравнений

найдем уравнение огибающей семейства траекторий. Здесь

откуда

Подставляя это значение в уравнение получим уравнение огибающей

или

Заметим, что огибающая семейства траекторий является параболой, параметр которой

а ось вертикальна и совпадает с осью у. Расстояние от начала координат до вершины огибающей

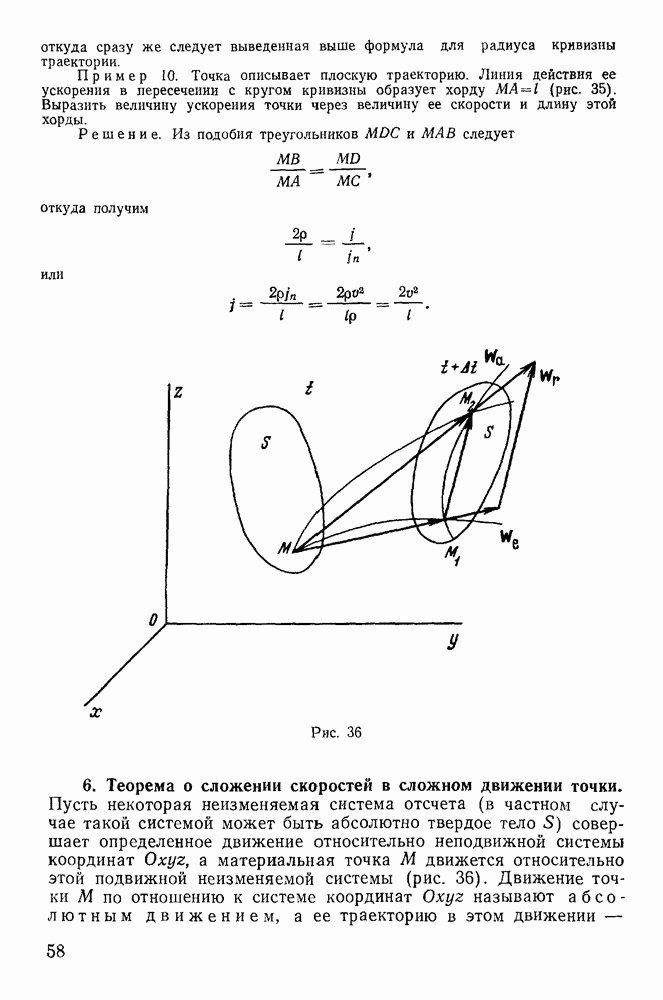
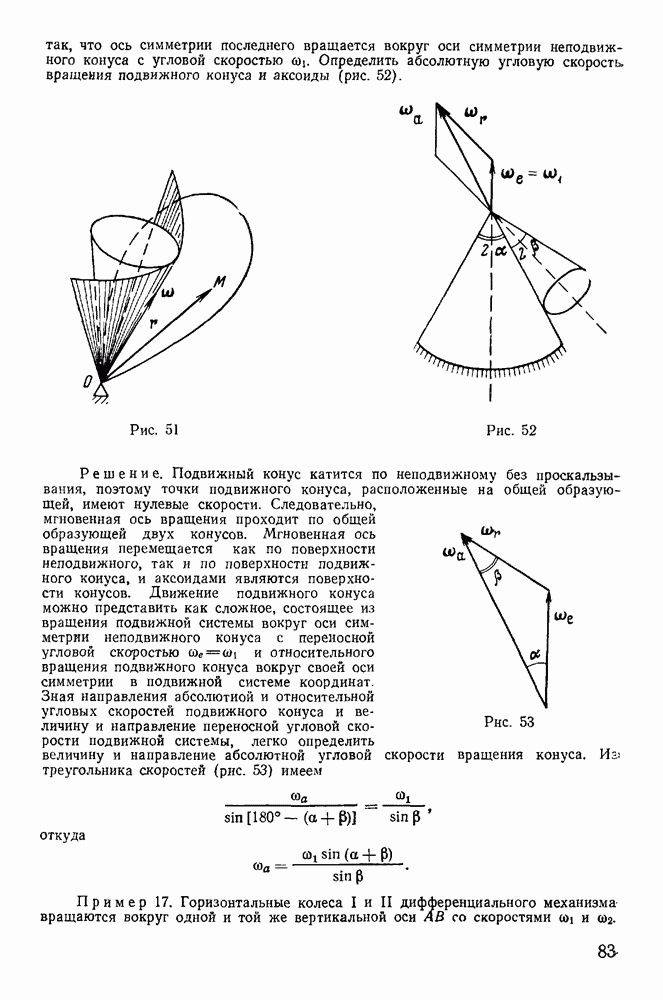
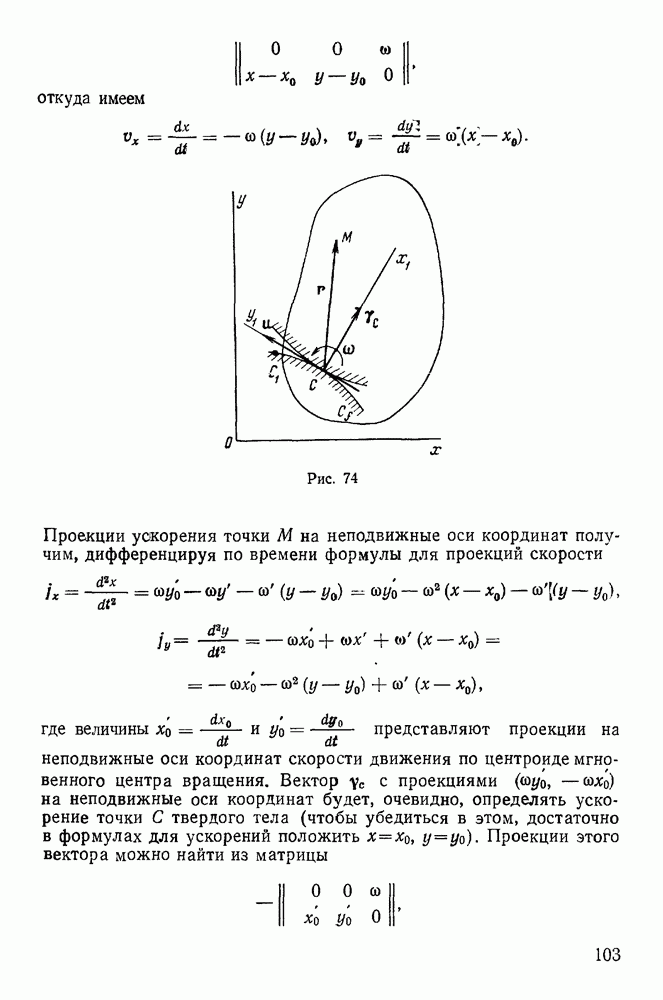
равно расстоянию до директрисы семейства траекторий, а начало координат является фокусом огибающей параболы. Все траектории семейства расположены внутри огибающей параболы (рис. 148), так что, изменяя угол бросания, при заданной начальной скорости никогда нельзя попасть в точки, расположенные за огибающей. В связи с этим огибающая парабола называется параболой безопасности.

Рис. 148

Задача попадания. Рассмотрим задачу попадания с заданной начальной скоростью в некоторую точку пространства Для того чтобы можно было попасть в точку М, координаты этой точки должны удовлетворять уравнению траектории

Разрешая это уравнение относительно , найдем угол бросания, необходимый для того, чтобы траектория прошла через точку М:

Решение зависит от знака дискриминанта

Если то для а получаем два действительных различных значения, и в точку М можно будет попасть двумя различными способами, бросая ее под углами к горизонту.

Если то корнн кратные, т. е. имеется только одна траектория, проходящая через точку М. Раскрывая равенство получим

что совпадает с уравнением огибающей. Это значит, что точка М расположена на параболе безопасности.

Для точек, расположенных за параболой безопасности, дискриминант отрицателен. В этом случае для а не существует действительных значений, и никакая действительная траектория не может проходить через точку .

Рассмотренному решению можно дать простое геометрическое истолкование. Как уже отмечалось, все траектории точек, имеющих одну и ту же величину начальной скорости, имеют общую директрису, расположенную на расстоянии

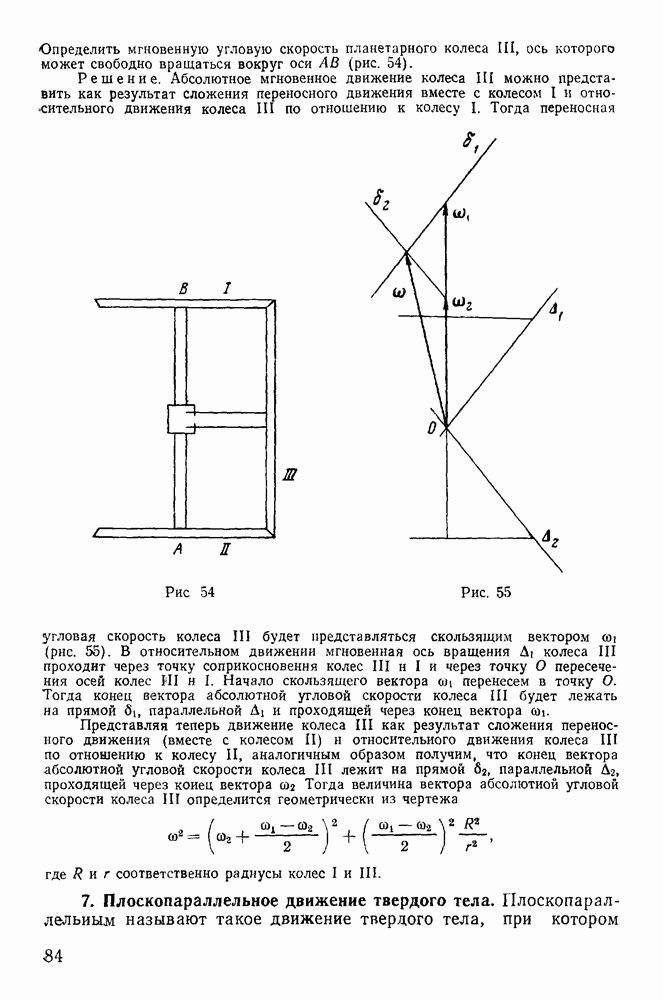
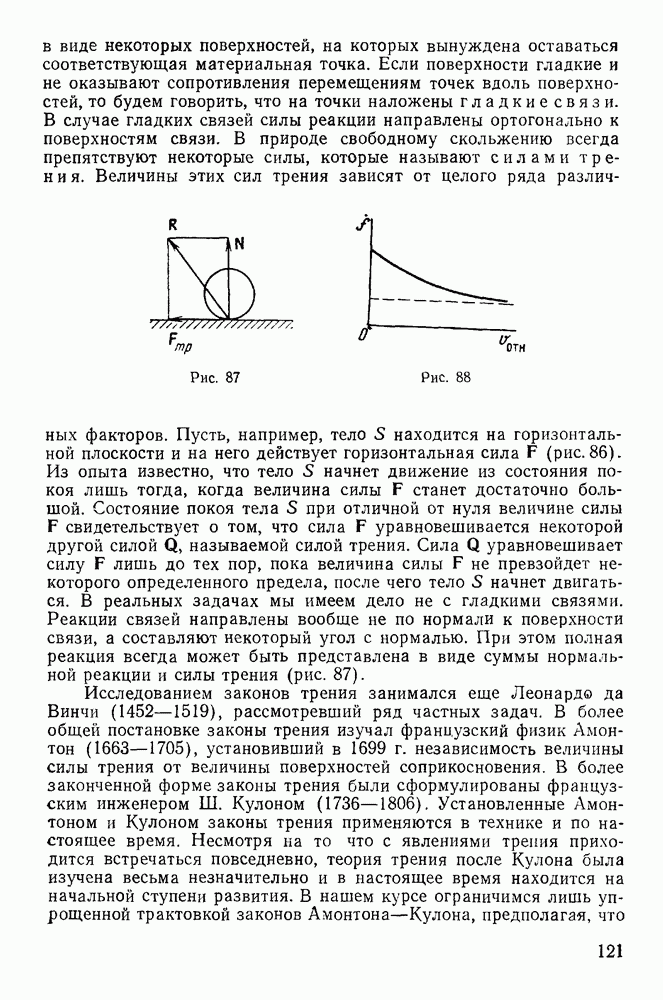
от начала координат Для определения каждой отдельной траектории достаточно найти положение ее фокуса. Воспользуемся определением параболы как геометрического места точек, равноудаленных от фокуса и директрисы. Все траектории проходят через начало координат. Расстояние от начала координат до директрисы равно Следовательно, геометрическим местом всех фокусов траекторий является окружность радиуса

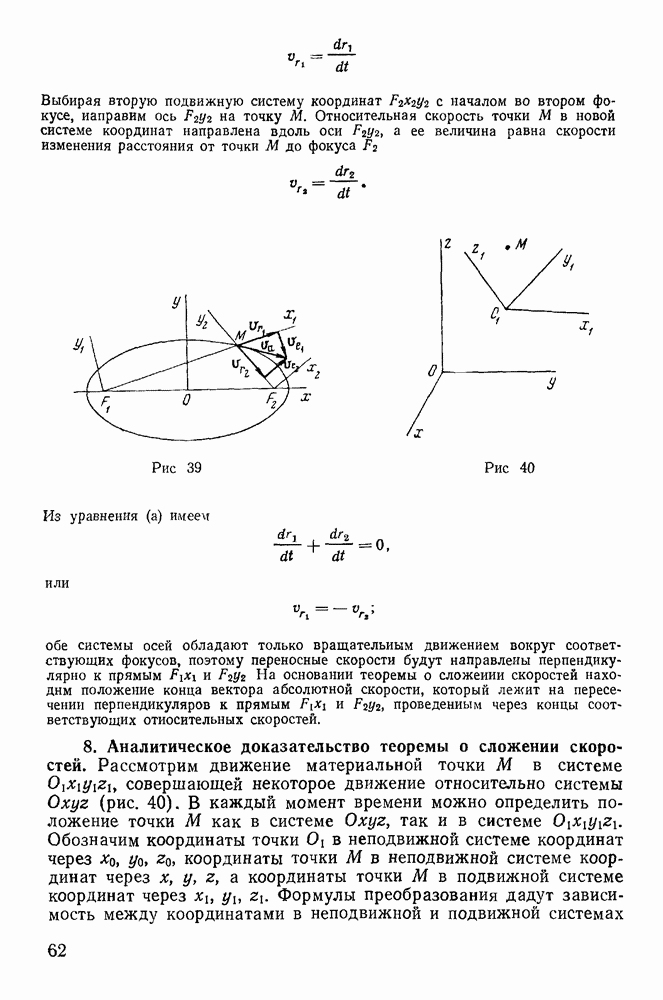
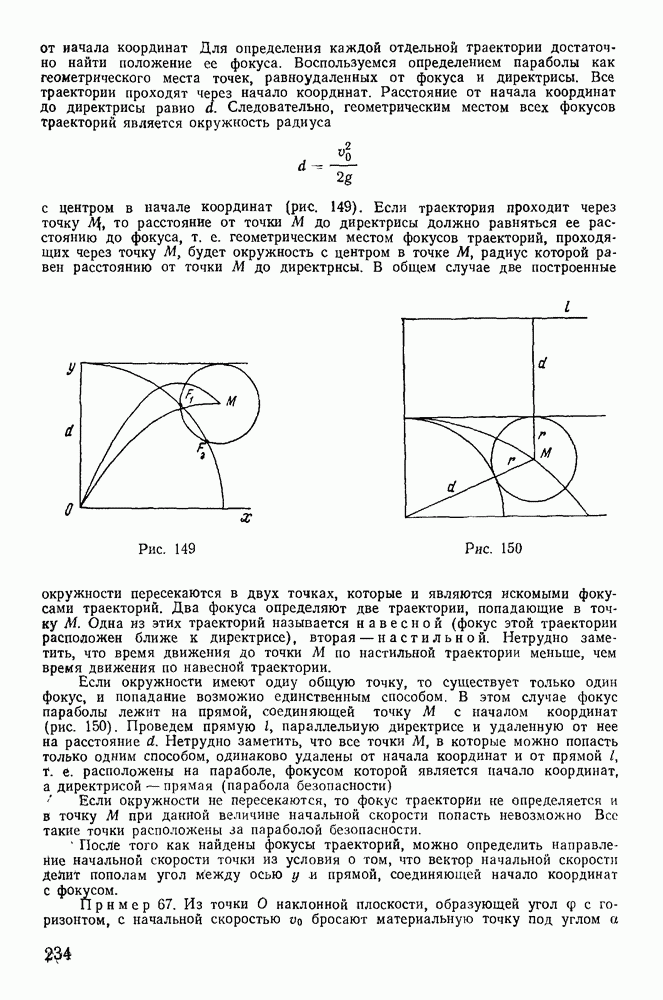
с центром в начале координат (рис. 149). Если траектория проходит через точку то расстояние от точки М до директрисы должно равняться ее расстоянию до фокуса, т. е. геометрическим местом фокусов траекторий, проходящих через точку М, будет окружность с центром в точке М, радиус которой равен расстоянию от точки М до директрисы.

Рис. 149

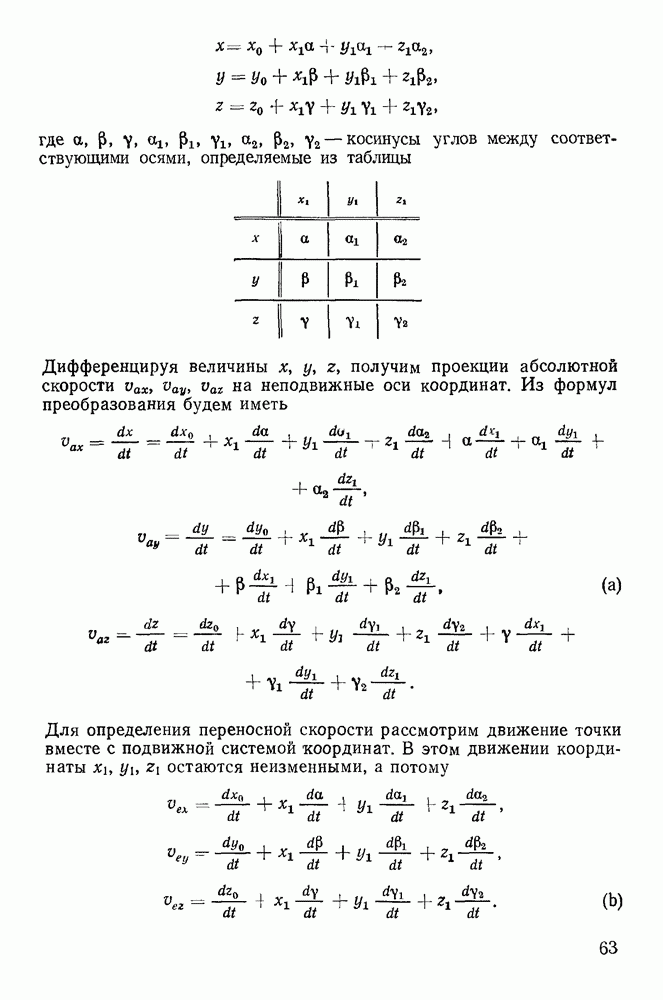
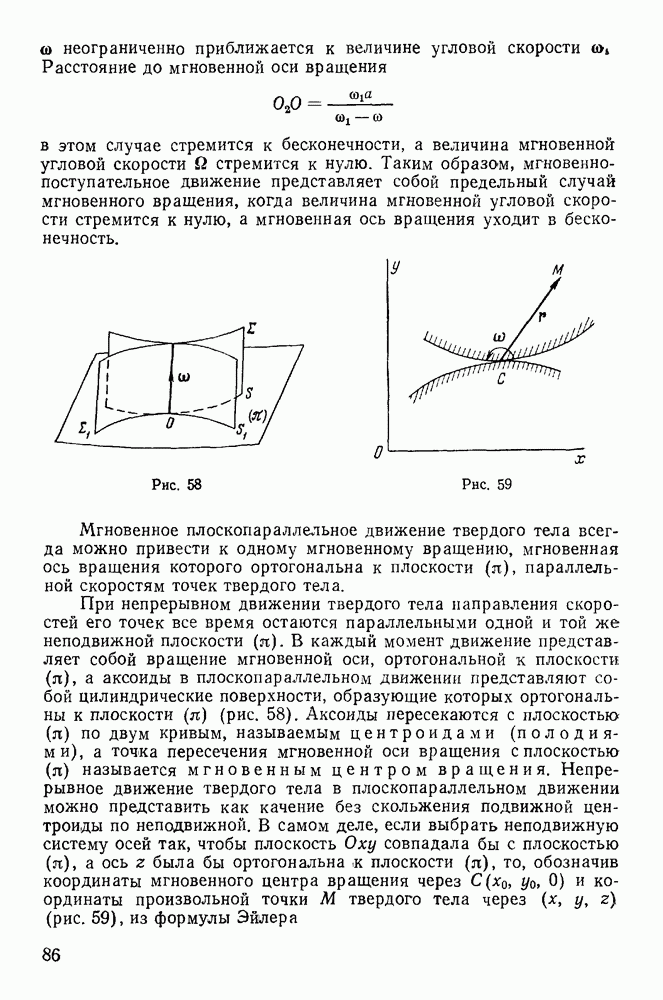
Рис. 150

В общем случае две построенные окружности пересекаются в двух точках, которые и являются искомыми фокусами траекторий. Два фокуса определяют две траектории, попадающие в точку М. Одна из этих траекторий называется навесной (фокус этой траектории расположен ближе к директрисе), вторая — настильной. Нетрудно заметить, что время движения до точки М по настильной траектории меньше, чем время движения по навесной траектории.

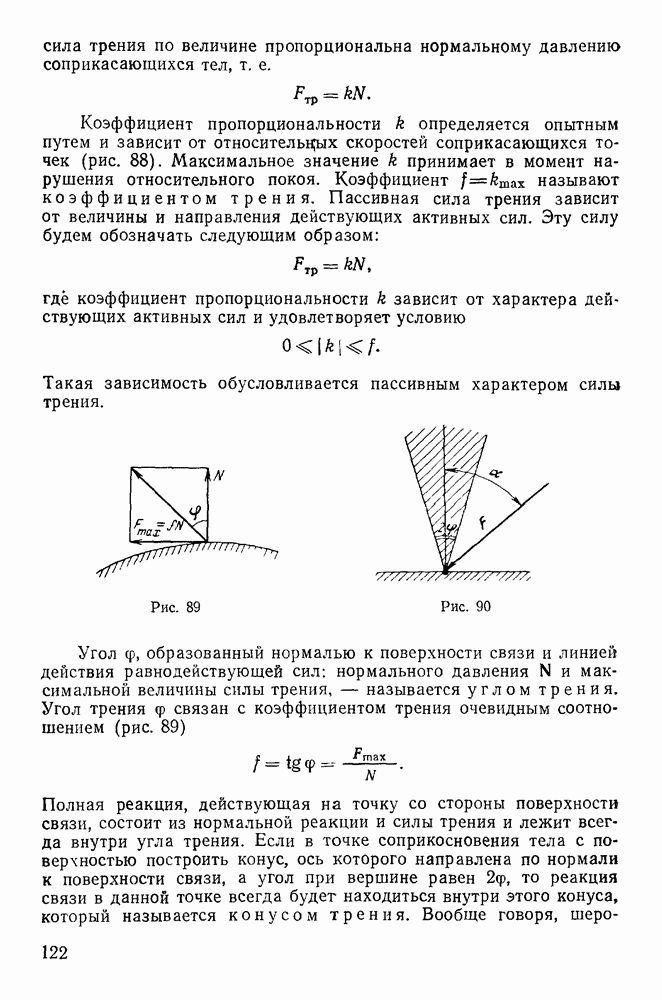
Если окружности имеют одну общую точку, то существует только один фокус, и попадание возможно единственным способом. В этом случае фокус параболы лежит на прямой, соединяющей точку М с началом координат (рис. 150). Проведем прямую I, параллельную директрисе и удаленную от нее на расстояние Нетрудно заметить, что все точки М, в которые можно попасть только одним способом, одинаково удалены от начала координат и от прямой I, т. е. расположены на параболе, фокусом которой является начало координат, а директрисой — прямая (парабола безопасности)

Если окружности не пересекаются, то фокус траектории не определяется и в точку М при данной величине начальной скорости попасть невозможно Все такие точки расположены за параболой безопасности.

После того как найдены фокусы траекторий, можно определить направление начальной скорости точки из условия о том, что вектор начальной скорости пополам угол лгёжду осью прямой, соединяющей начало координат с фокусом.

Пример 67. Из точки О наклонной плоскости, образующей угол с горизонтом, с начальной скоростью бросают материальную точку под углом а

к горизонту таким образом, что точка падает на наклонную плоскость под прямым углом (рис. 151). Определить угол а.

Решение. Систему осей выберем так, чтобы ось х была направлена вдоль наклонной плоскости. Тогда уравнения движения примут вид

Рис. 151

Сокращая на и интегрируя, получим

В начальный момент поэтому Дифференцируя найденные зависимости, имеем

откуда

Точка падает на наклонную плоскость под прямым углом, т. е. в момент падения или

откуда

В момент падения т. е.

что можно представить в виде

Решение — соответствует моменту времени Приравнивая нулю квадратную скобку, получаем

Разделив на , будем иметь

или

Пример 68. Материальная точка брошена вертикально вверх в среде, сопротивление которой пропорционально квадрату скорости точки, с начальной скоростью . С какой скоростью точка вернется на Землю?

Решение. Ось х направим вертикально вверх. Тогда для точки, движущейся вверх, будем иметь дифференциальное уравнение

которое можно преобразовать к виду

Интегрируя, найдем

или

Точка будет двигаться вверх до тех пор, пока ее скорость не станет равной нулю. Обозначив максимальную высоту подъема через будем иметь

Для падающей точки уравнение движения запишется уже иначе:

его можно преобразовать к виду

причем все время движения будет выполняться неравенство

Разделяя переменные, получим

откуда

или

Если

то

При из соотношения

получим значение скорости