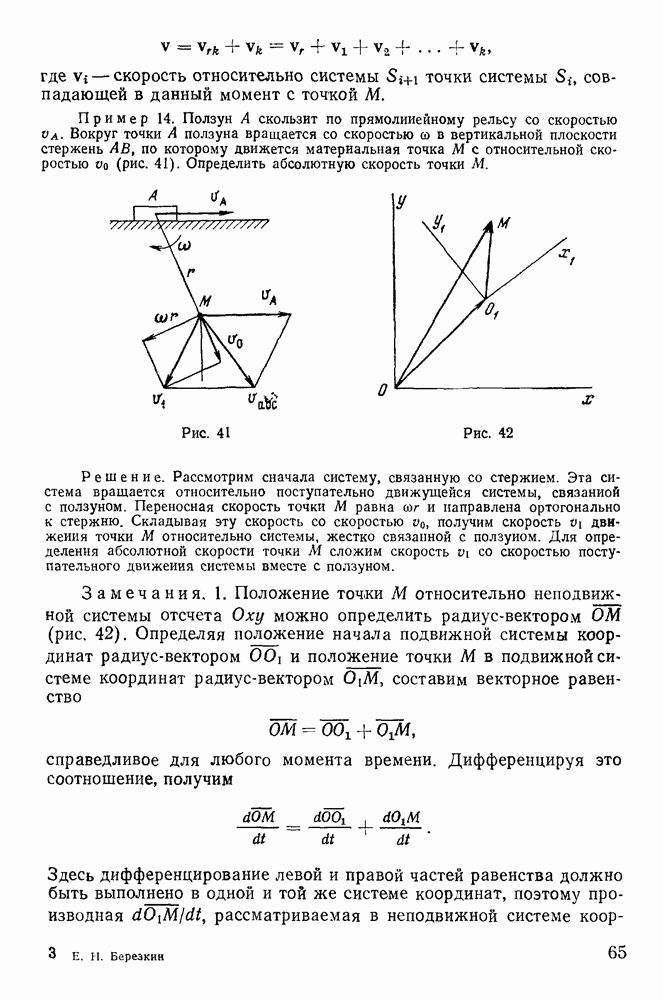
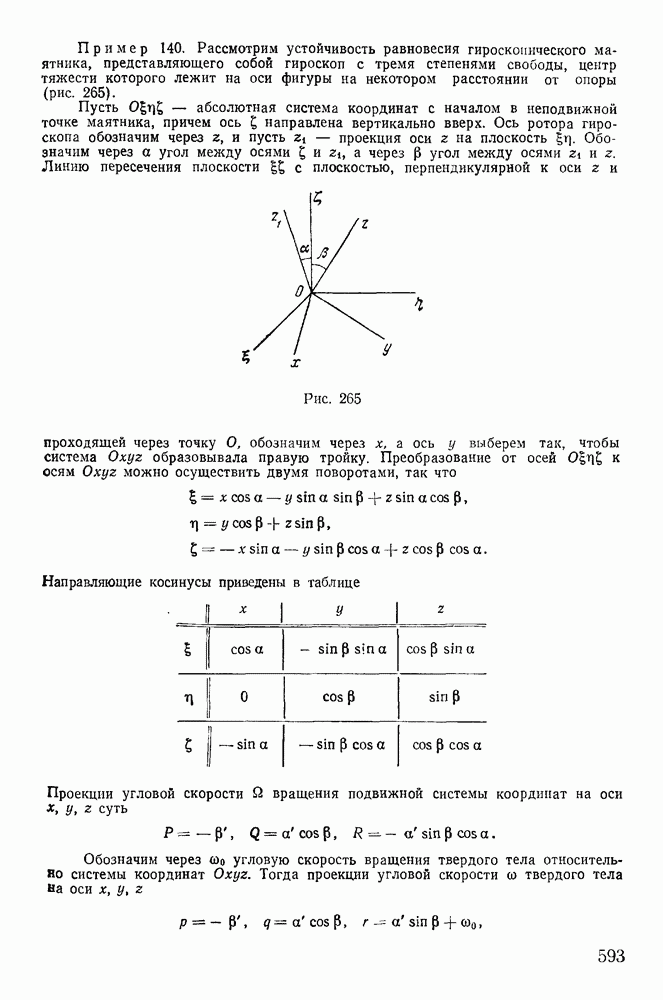
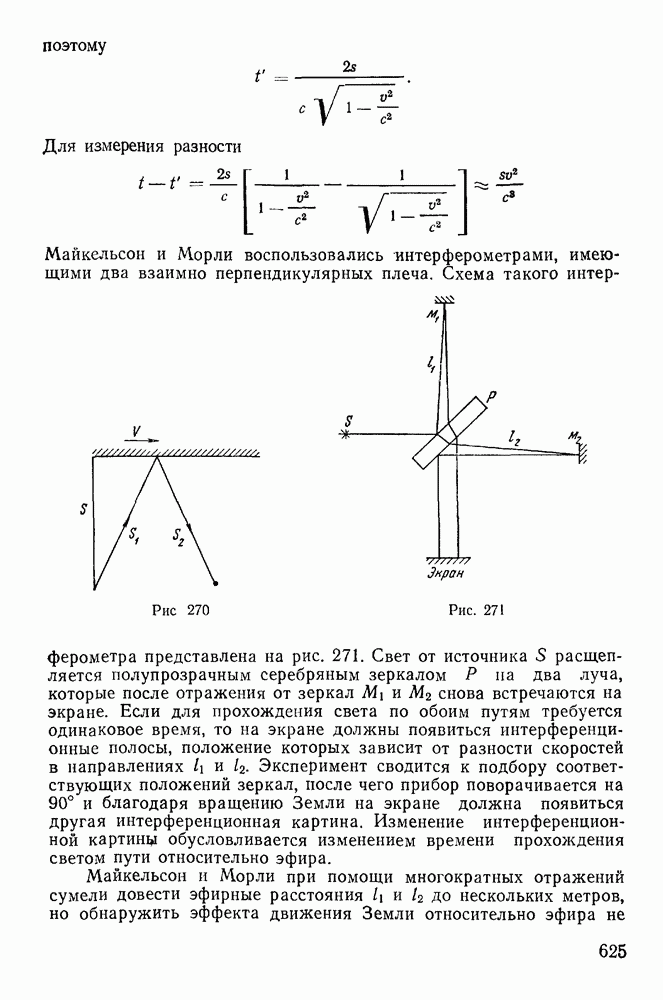
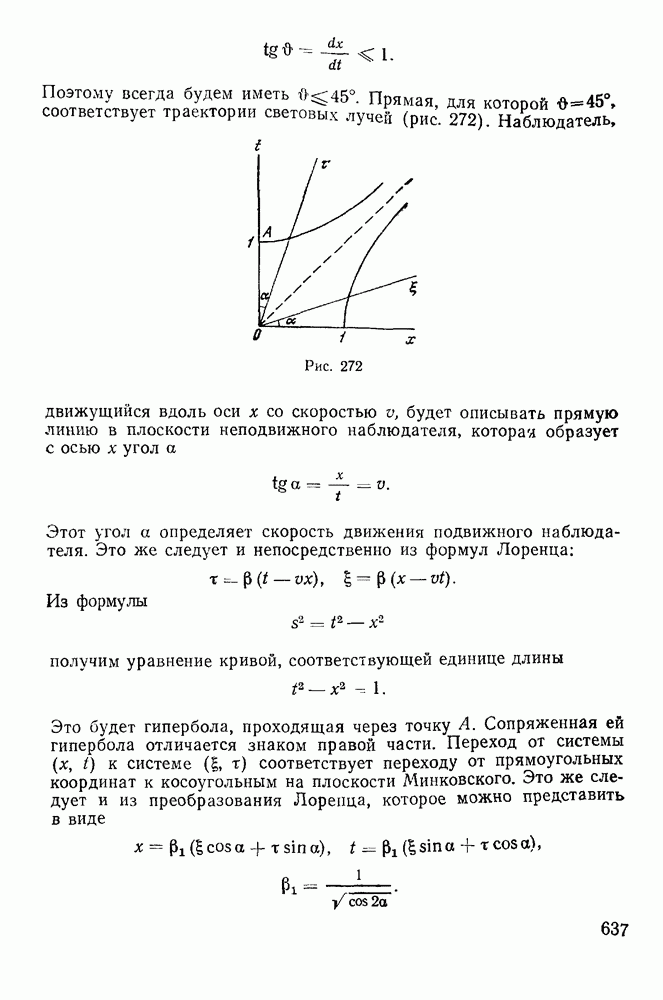
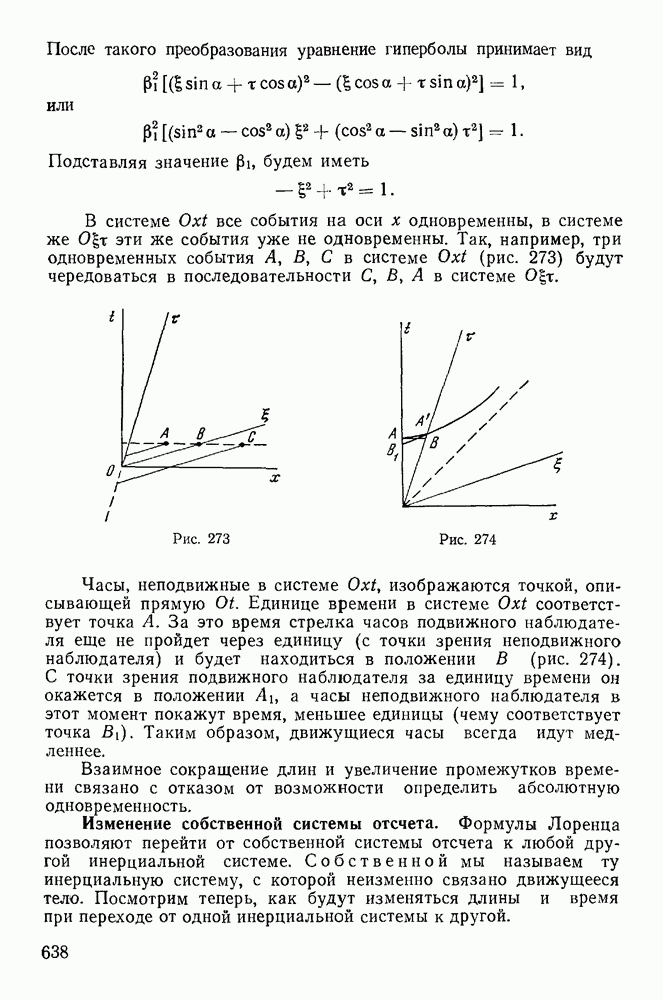
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 2. ПРИНЦИП ГАМИЛЬТОНА - ОСТРОГРАДСКОГО
1. Принцип Гамильтона—Остроградского
В настоящее время стал одним из основополагающих принципов механики. Для голономных механических систем он может быть непосредственно получен как следствие принципа Даламбера — Лагранжа. В свою очередь, все свойства движения голономных механических систем могут быть получены из принципа Гамильтона — Остроградского.
Рассмотрим движение системы материальных точек  относительно некоторой инерциальной системы отсчета
относительно некоторой инерциальной системы отсчета  под действием активных сил
под действием активных сил  Пусть возможные перемещения точек системы стеснены идеальными голономными связями. Обозначим декартовы координаты точки
Пусть возможные перемещения точек системы стеснены идеальными голономными связями. Обозначим декартовы координаты точки  через
через  а независимые лагранжевы координаты через
а независимые лагранжевы координаты через  Зависимость между декартовыми и лагранжевыми координатами задается соотношениями
Зависимость между декартовыми и лагранжевыми координатами задается соотношениями

В дальнейшем будем предполагать, что координаты  представляются однозначными, непрерывными и сколь угодно раз дифференцируемыми функциями переменных
представляются однозначными, непрерывными и сколь угодно раз дифференцируемыми функциями переменных  Кроме того, будем предполагать, что из каждого положения системы параметры
Кроме того, будем предполагать, что из каждого положения системы параметры  могут изменяться как в положительном, так и в отрицательном направлении. Движение системы будем рассматривать начиная с некоторого момента времени
могут изменяться как в положительном, так и в отрицательном направлении. Движение системы будем рассматривать начиная с некоторого момента времени  до момента
до момента  Пусть начальному положению системы отвечают значения
Пусть начальному положению системы отвечают значения
лагранжевых координат  а положению системы в момент
а положению системы в момент  — значения
— значения  Введем в рассмотрение
Введем в рассмотрение  -мерное расширенное пространство координат
-мерное расширенное пространство координат  и времени
и времени  в котором каждому конкретному положению системы отвечает одна точка. В таком расширенном
в котором каждому конкретному положению системы отвечает одна точка. В таком расширенном  -мерном пространстве движение системы представляется некоторой кривой, которую в дальнейшем будем называть траекторией системы. Начальному и конечному положениям системы здесь будут соответствовать две точки
-мерном пространстве движение системы представляется некоторой кривой, которую в дальнейшем будем называть траекторией системы. Начальному и конечному положениям системы здесь будут соответствовать две точки  . В действительном движении системы из положения
. В действительном движении системы из положения  в положение
в положение  лагранжевы координаты непрерывно изменяются, определяя в
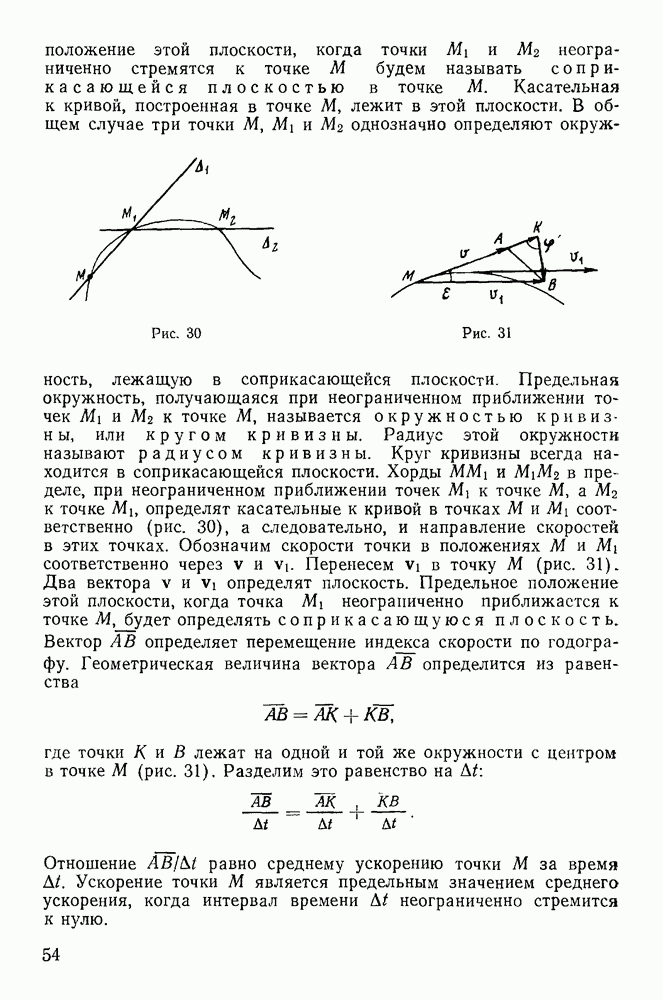
лагранжевы координаты непрерывно изменяются, определяя в  -мерном пространстве кривую, которую будем называть действительнойтраекторией системы. Можно заставить перемещаться систему в соответствии с наложенными на систему связями из положения
-мерном пространстве кривую, которую будем называть действительнойтраекторией системы. Можно заставить перемещаться систему в соответствии с наложенными на систему связями из положения  в положение
в положение  за тот же интервал времени, но по другой траектории, близкой к действительной, не заботясь о том, чтобы удовлетворялись уравнения движения. Такую траекторию в
за тот же интервал времени, но по другой траектории, близкой к действительной, не заботясь о том, чтобы удовлетворялись уравнения движения. Такую траекторию в  -мерном пространстве назовем окольной траекторией. Сравнивая движения по действительной и окольным траекториям, зададимся целью определить действительную траекторию среди окольных. Пусть положение системы в момент
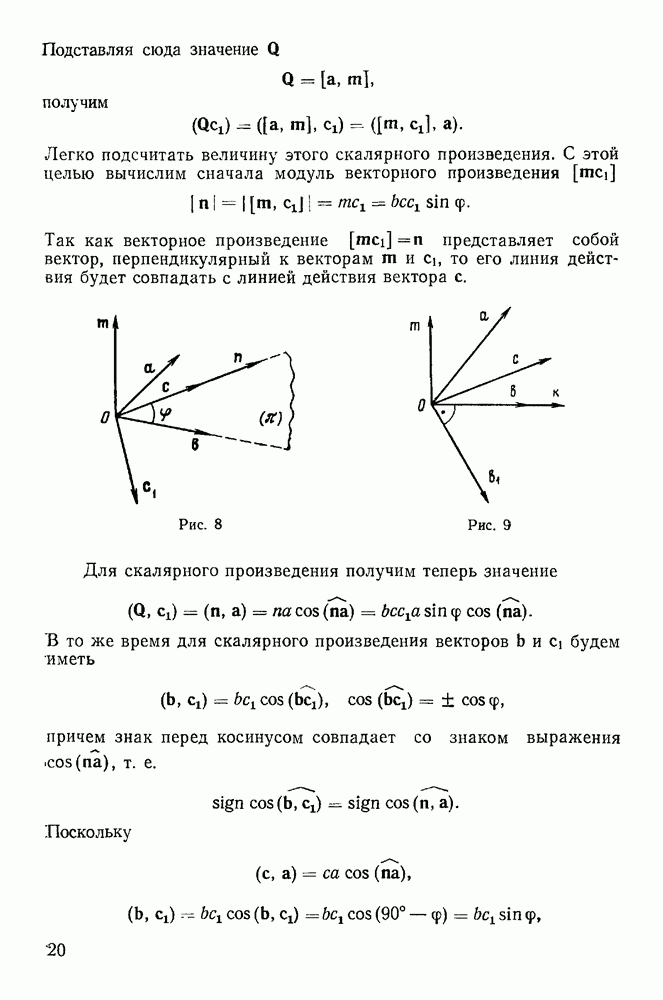
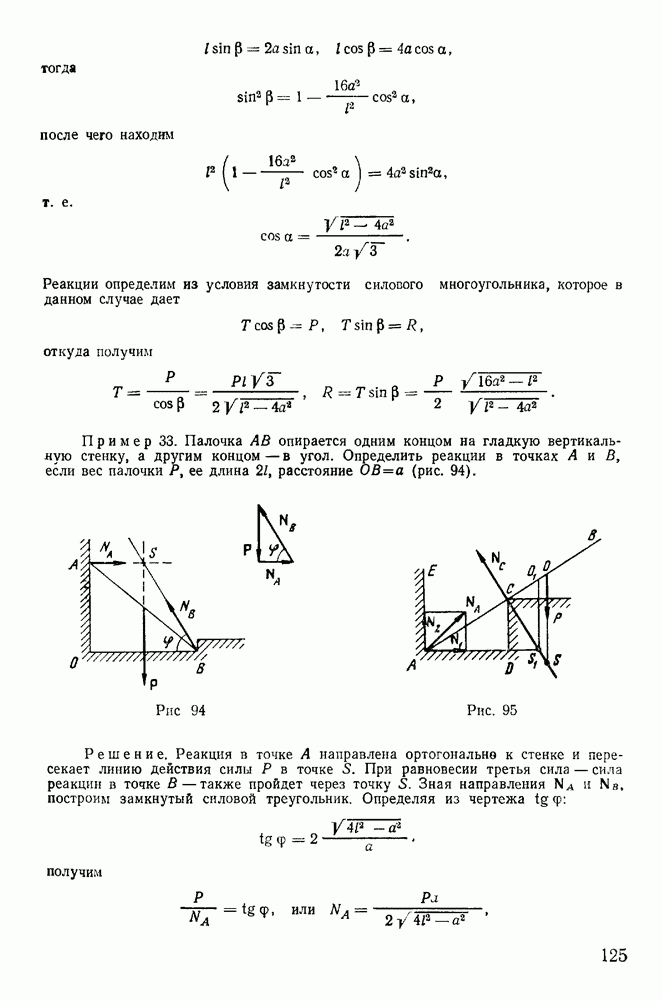
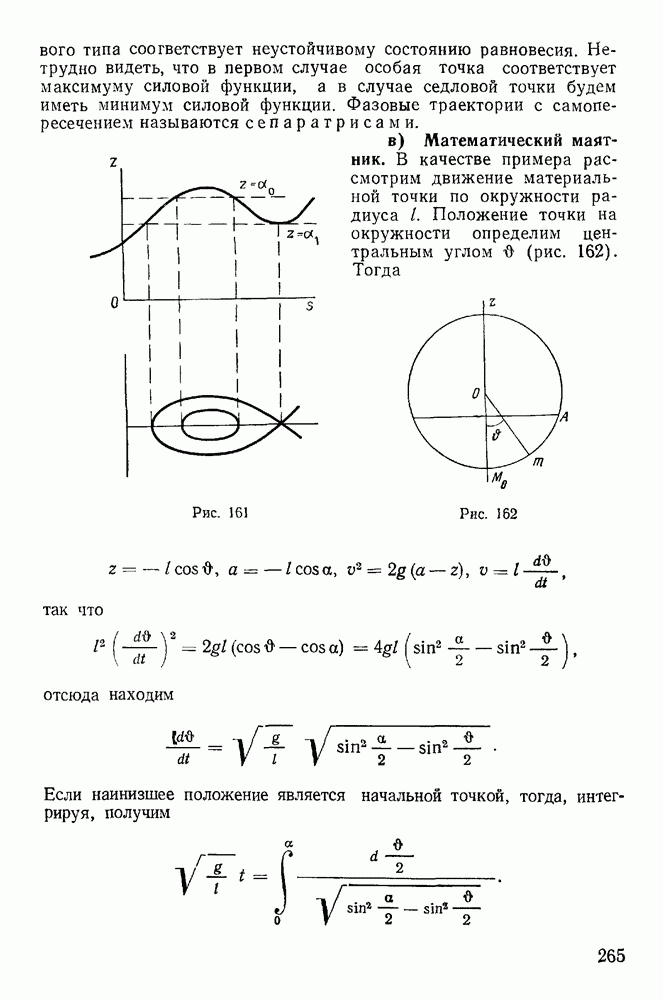
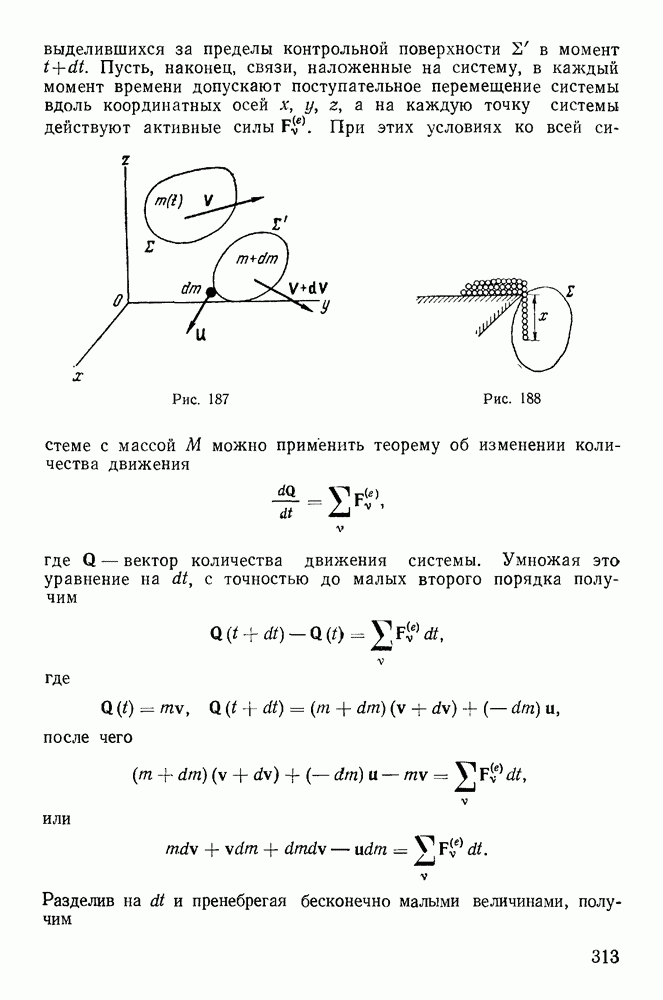
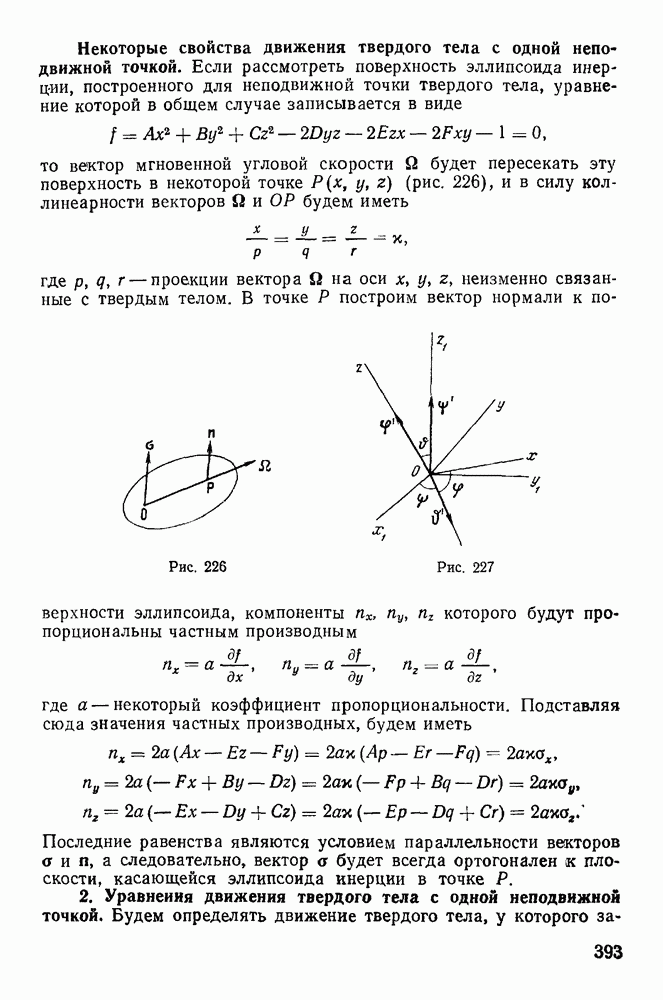
-мерном пространстве назовем окольной траекторией. Сравнивая движения по действительной и окольным траекториям, зададимся целью определить действительную траекторию среди окольных. Пусть положение системы в момент  на действительной траектории отмечается точкой Р, а положение системы в тот же момент времени на окольной траектории — точкой Р (рис. 252).
на действительной траектории отмечается точкой Р, а положение системы в тот же момент времени на окольной траектории — точкой Р (рис. 252).

Рис. 252
Отрезок  соединяющий две точки на различных траекториях в один и тот же момент времени, будет представлять возможное перемещение системы в момент
соединяющий две точки на различных траекториях в один и тот же момент времени, будет представлять возможное перемещение системы в момент  Он соответствует изменению лагранжевых координат в момент
Он соответствует изменению лагранжевых координат в момент  при переходе из положения Р в положение Р на величину
при переходе из положения Р в положение Р на величину  Возможному перемещению системы будут отвечать вариации декартовых координат
Возможному перемещению системы будут отвечать вариации декартовых координат  которые могут быть выражены через вариации координат Лагранжа в виде равенств
которые могут быть выражены через вариации координат Лагранжа в виде равенств

Рассмотрим произвольное однопараметрическое семейство «траекторий»

каждая из которых соединяет точки  проходя через них в моменты времени
проходя через них в моменты времени  соответственно, и пусть значению параметра
соответственно, и пусть значению параметра  отвечает действительная траектория (прямой путь), которую проходит система за время
отвечает действительная траектория (прямой путь), которую проходит система за время  из положения
из положения  в положение
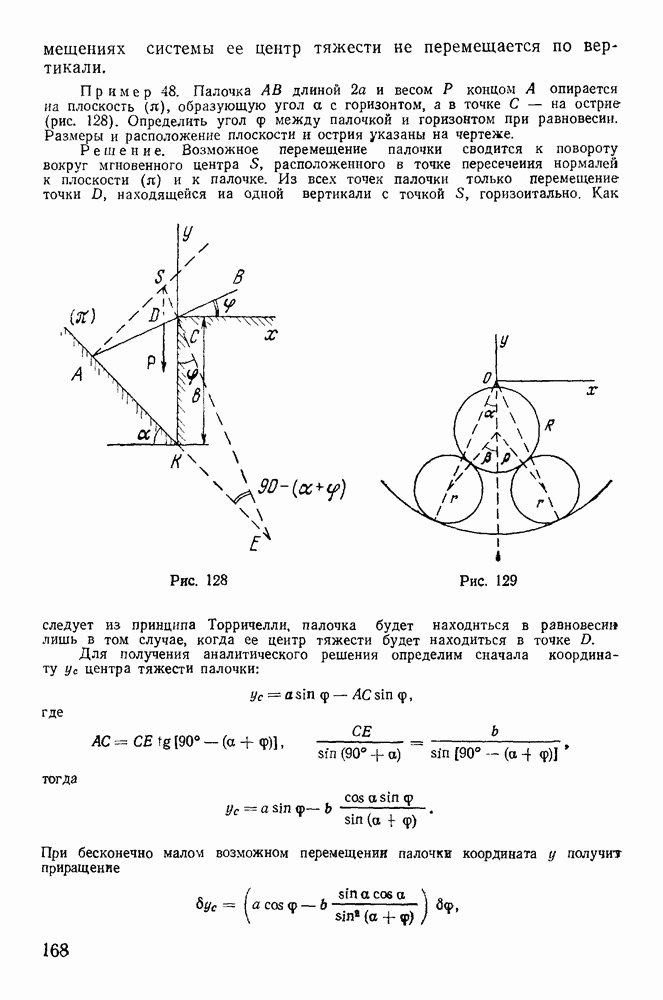
в положение  Значениям а, отличным от нуля, отвечают «окольные» траектории (окольные пути), т. е. все остальные траектории, соединяющие точки
Значениям а, отличным от нуля, отвечают «окольные» траектории (окольные пути), т. е. все остальные траектории, соединяющие точки  за время
за время  Перемещению системы вдоль какой-либо траектории будет соответствовать изменение лагранжевых координат за счет изменения времени
Перемещению системы вдоль какой-либо траектории будет соответствовать изменение лагранжевых координат за счет изменения времени  когда параметр а остается неизменным. Параметр а будет меняться лишь при переходе с одной траектории на другую. Вариация координаты
когда параметр а остается неизменным. Параметр а будет меняться лишь при переходе с одной траектории на другую. Вариация координаты  будет теперь определяться следующим образом:
будет теперь определяться следующим образом:

а производная по времени от координаты  будет иметь вид
будет иметь вид

Пусть лагранжевы координаты  являются однозначными непрерывными дифференцируемыми функциями от
являются однозначными непрерывными дифференцируемыми функциями от  . Тогда
. Тогда

или

Полученные соотношения в механике называются «перестановочными». Операции дифференцирования перестановочны только тогда, когда все координаты  независимы и не связаны неинтегрируемыми соотношениями.
независимы и не связаны неинтегрируемыми соотношениями.
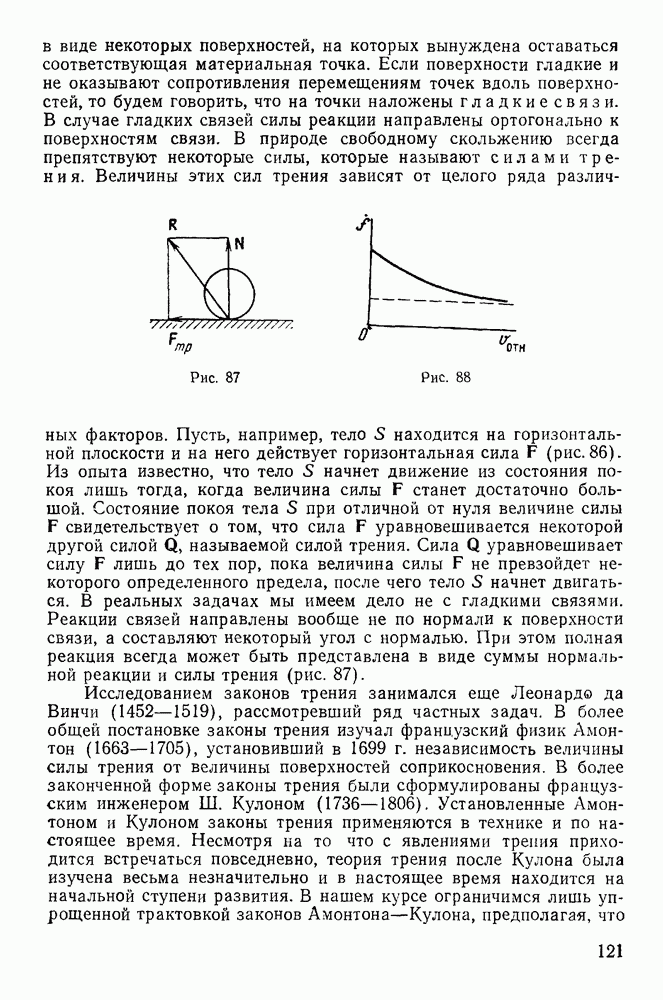
Покажем, что перестановочность операций варьирования и дифференцирования выполняется и для декартовых координат. Пусть

Тогда

Рассмотрим производную по времени от 

С другой стороны,

Вычитая второе равенство из первого, получим

откуда следует

т. e. операции дифференцирования и варьирования перестановочны и для декартовых координат, если на систему материальных точек наложены только голономные идеальные связи.
Перейдем к определению действительной траектории среди всех окольных. Действительное движение системы происходит в соответствии с принципом Даламбера — Лагранжа

который определяет «тенденцию» истинного движения (действительного движения) в каждый момент времени. Рассмотрим интеграл

взятый вдоль действительной траектории системы. Все сравниваемые траектории системы начинаются в один и тот же момент времени и из одной и той же точки  -мерного пространства. Все они оканчиваются в одной и той же точке в один и тот же момент времени. Поэтому на концах траекторий при
-мерного пространства. Все они оканчиваются в одной и той же точке в один и тот же момент времени. Поэтому на концах траекторий при  будут выполняться условия
будут выполняться условия

Преобразуем полученное уравнение, проинтегрировав по частям выражение

а так как на концах траектории вариации  обращаются в нуль, будем иметь
обращаются в нуль, будем иметь

В силу перестановочности операций дифференцирования и варьирования, имеем

после чего уравнение принимает вид

или

В таком виде полученное уравнение выражает «принцип наименьшего действия» Гамильтона для общих механических систем. На действительной траектории системы обращается в нуль интеграл от функции

Если силы, действующие на систему, обладают силовой функцией  , то имеет место соотношение
, то имеет место соотношение

а выведенное выше уравнение принимает вид

Так как варьирование не связано с изменением времени, то операции варьирования и интегрирования можно поменять местами:

т. e. интеграл  на действительной траектории имеет стационарное значение.
на действительной траектории имеет стационарное значение.
Мы показали необходимость стационарного значения интеграла на действительной траектории. Покажем, что обращение вариации интеграла в нуль является достаточным условием действительного движения системы. Для этого достаточно из принципа Гамильтона получить уравнения движения системы.
Рассмотрим механическую систему с голономными идеальными связями, положение которой определяется лагранжевыми координатами  а живая сила
а живая сила

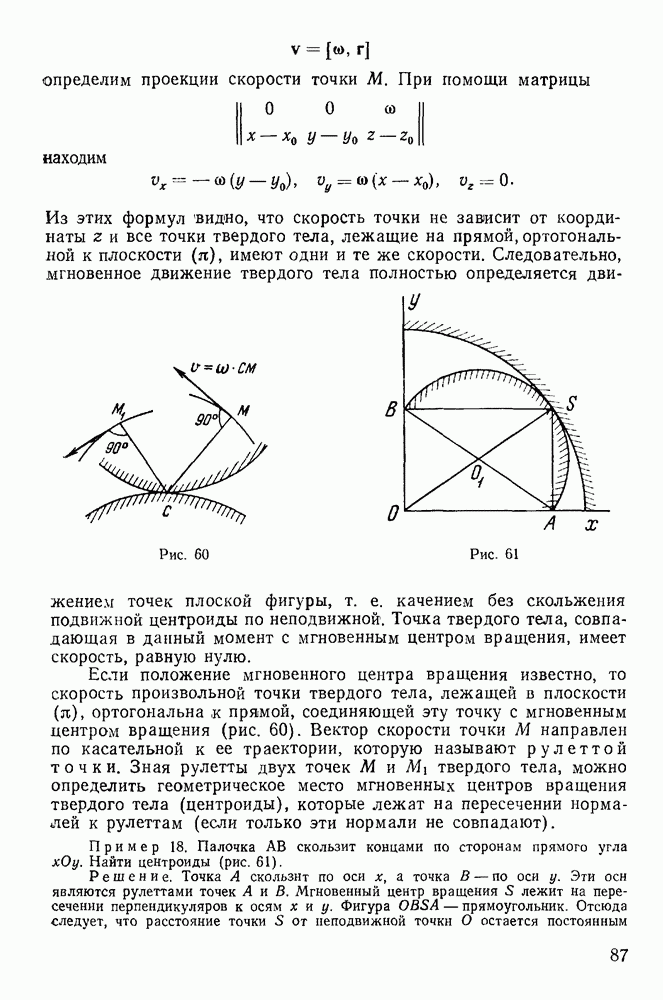
зависит от обобщенных скоростей, координат и времени. Принимая во внимание известное соотношение

перепишем принцип Гамильтона в виде

Выполняя варьирование живой силы

и интегрируя затем по частям

так как на концах интервала вариации координат равны нулю, из принципа Гамильтона получим

или

Вариации  произвольны и независимы внутри интервала
произвольны и независимы внутри интервала  а тогда в силу основной леммы вариационного исчисления равенство будет возможно только тогда, когда все коэффициенты при
а тогда в силу основной леммы вариационного исчисления равенство будет возможно только тогда, когда все коэффициенты при  обращаются в нуль, т. е. когда выполняются условия
обращаются в нуль, т. е. когда выполняются условия

Полученные уравнения должны выполняться в действительном движении механической системы. Достаточность принципа Гамильтона доказывается тем, что эти уравнения являются уравнениями Лагранжа второго рода, описывающими движение механической системы, на которую наложены голономные идеальные связи.
Принцип Гамильтона для механических систем с голономными идеальными связями можно теперь сформулировать следующим образом:
Действительное движение системы с голономными идеальными связями между двумя заданными положениями отличается от кинематически возможных между этими положениями движений, совершаемых за тот же промежуток времени, тем, что на действительном движении обращается в нуль интеграл

для всех значений  удовлетворяющих указанным условиям.
удовлетворяющих указанным условиям.
Принцип Гамильтона может быть принят в качестве основного принципа механики систем с идеальными голономными связями. Мы доказали, что интеграл принимает стационарное значение на действительной траектории системы, но при некоторых ограничениях можно показать, что действительная траектория не только является экстремалью, но и доставляет наименьшее значение интегралу

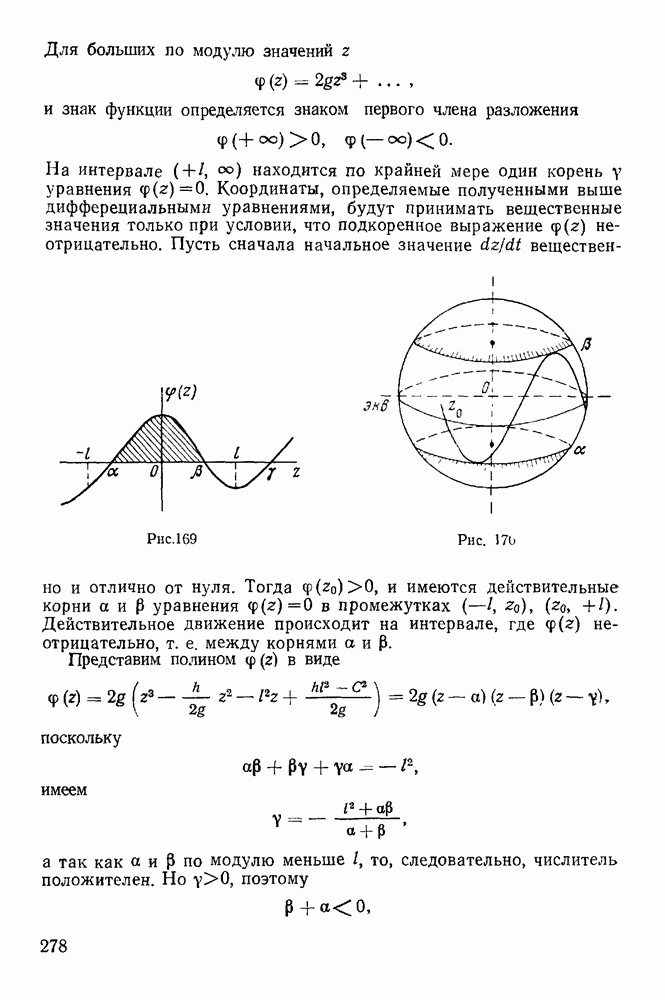
Вопрос о характере экстремума не имеет существенного значения при выводе уравнений движения. Но существуют задачи, в которых использование свойств минимальности играет большое, значение. Если произвольно выбирать начальное и конечное положения системы, то может оказаться, что эти два положения невозможно соединить действительной траекторией или, как говорят, «прямым путем». Так, например, при прямолинейном движении точки в поле тяготения будем иметь

Положения точки  не могут быть соединены прямым путем за время
не могут быть соединены прямым путем за время 
В общем случае между двумя данными положениями можно провести несколько отличных друг от друга прямых путей, по которым движение происходит за одно и то же время. Если два положения  таковы, что могут быть соединены между собой несколькими различными прямыми путями, то такие положения называются сопряженными кинетическими фокусами.
таковы, что могут быть соединены между собой несколькими различными прямыми путями, то такие положения называются сопряженными кинетическими фокусами.
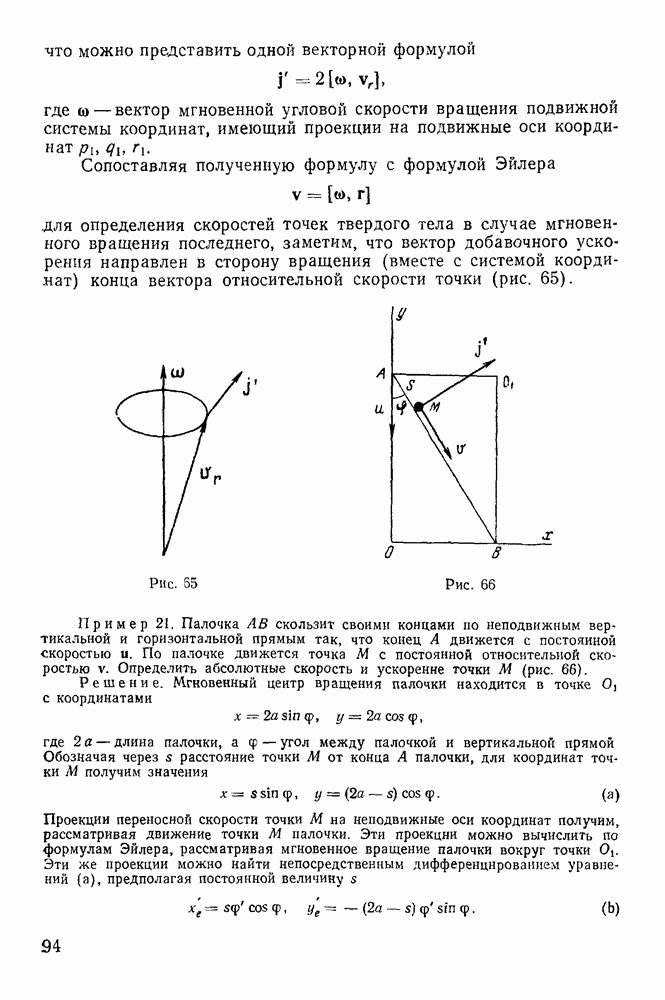
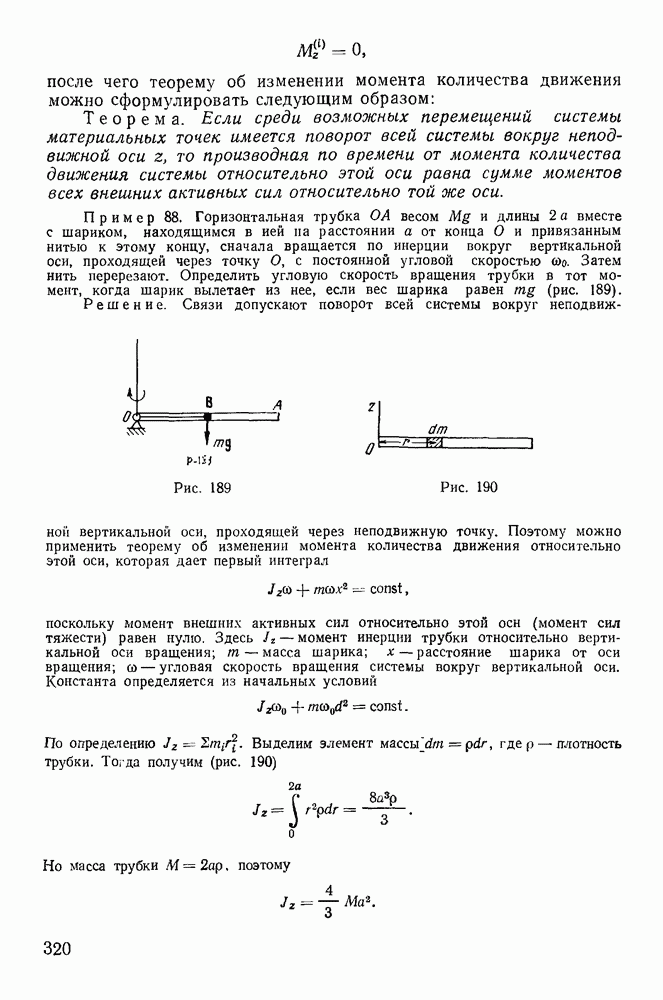
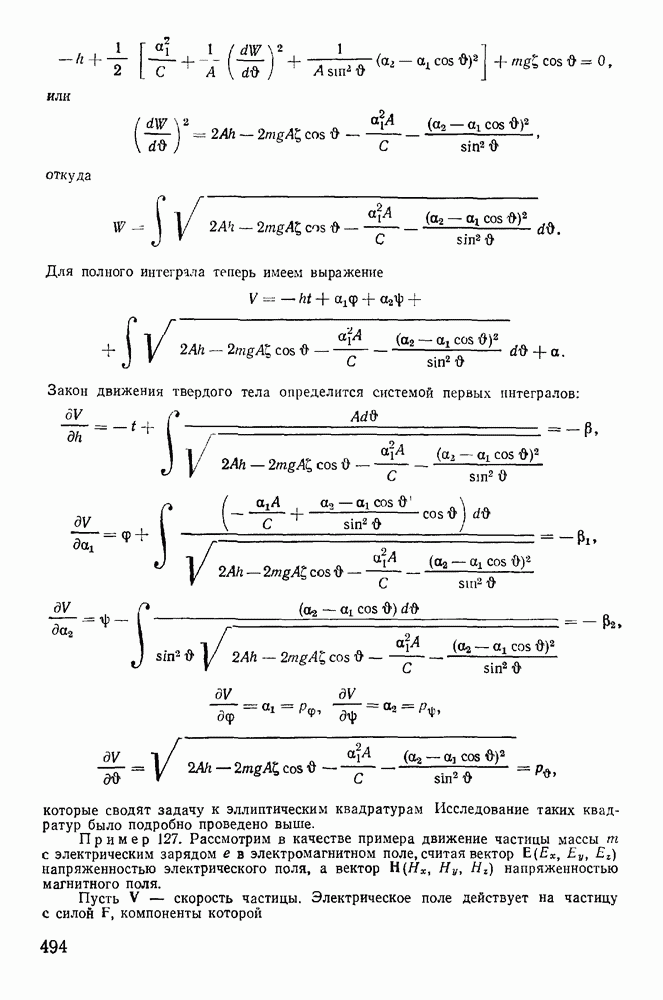
Рассмотрим в качестве примера движение несвободной материальной точки массы  вынужденной оставаться на поверхности сферы радиуса
вынужденной оставаться на поверхности сферы радиуса  при отсутствии силового поля. В сферических координатах кинетическая энергия точки
при отсутствии силового поля. В сферических координатах кинетическая энергия точки

Так как координата  является циклической, ей соответствует циклический интеграл
является циклической, ей соответствует циклический интеграл

Известно, что при отсутствии силового поля точка движется по геодезической кривой. Такими геодезическими кривыми в данном случае являются дуги больших кругов. Таким образом, прямое движение — это движение точки по дуге большого круга. Не нарушая общности, можно всегда предположить, что во все время, движения выполняется условие  откуда следует
откуда следует  Тогда в действительном движении будет выполняться условие
Тогда в действительном движении будет выполняться условие  т. е. прямой путь будет представлять равномерное движение точки по дуге большого круга. Обозначая через W интеграл
т. е. прямой путь будет представлять равномерное движение точки по дуге большого круга. Обозначая через W интеграл

будем иметь

В окольном движении

поэтому

где  — окольный путь;
— окольный путь;  — прямой путь. Если точки
— прямой путь. Если точки  являются диаметрально противоположными точками, то они будут сопряженными кинетическими фокусами. Во всех остальных случаях окольная дуга всегда будет больше дуги большого круга. Если расстояние между
являются диаметрально противоположными точками, то они будут сопряженными кинетическими фокусами. Во всех остальных случаях окольная дуга всегда будет больше дуги большого круга. Если расстояние между  больше, чем
больше, чем  , то окольный путь может стать короче прямого и действие не будет иметь минимума.
, то окольный путь может стать короче прямого и действие не будет иметь минимума.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Введение
- Глава I. ОСНОВЫ ТЕОРИИ ВЕКТОРОВ
- § 1. СВОБОДНЫЕ ВЕКТОРЫ
- 2. Сложение свободных векторов.
- 3. Проекция вектора на ось.
- 4. Инварианты системы свободных векторов.
- § 2. СКОЛЬЗЯЩИЕ ВЕКТОРЫ
- 2. Координаты скользящего вектора.
- 3. Момент скользящего вектора. Плюккеровы координаты.
- 4. Аналитическое определение момента скользящего вектора.
- 5. Проекция момента на ось.
- 6. Момент скользящего вектора относительно оси
- § 3. СИСТЕМА СКОЛЬЗЯЩИХ ВЕКТОРОВ
- 2. Произвольная система скользящих векторов. Элементарные операции.
- 3. Приведение системы скользящих векторов к простейшей эквивалентной форме.
- 4. Плоская система скользящих векторов.
- 5. Свойства системы параллельных скользящих векторов.
- § 4. ЗАКРЕПЛЕННЫЕ ВЕКТОРЫ
- § 5. ДИФФЕРЕНЦИРОВАНИЕ СВОБОДНОГО ВЕКТОРА ПО СКАЛЯРНОМУ АРГУМЕНТУ
- Глава II. КИНЕМАТИКА
- § 1. КИНЕМАТИКА ТОЧКИ
- 2. Ускорение точки. Проекции ускорения на прямоугольные оси координат.
- 3. Скорость и ускорение точки в полярных координатах.
- 4. Движение точки по окружности.
- 5. Проекции ускорения на оси естественного трехгранника.
- 6. Теорема о сложении скоростей в сложном движении точки.
- 7. Метод Роберваля построения касательных к плоским кривым.
- 8. Аналитическое доказательство теоремы о сложении скоростей.
- 9. Сложение скоростей в общем случае сложного движения точки.
- § 2. КИНЕМАТИКА АБСОЛЮТНО ТВЕРДОГО ТЕЛА
- 2. Элементарные движения твердого тела.
- 3. Мгновенные движения твердого тела.
- 4. Сложение мгновенно-поступательных и мгновенно-вращательных движений твердого тела.
- 5. Общий случай сложения мгновенно-поступательных и мгновенно-вращательных движений твердого тела. Непрерывное движение твердого тела.
- 6. Мгновенное движение твердого тела с одной неподвижной точкой.
- 7. Плоскопараллельное движение твердого тела.
- § 3. УСКОРЕНИЕ ТОЧКИ В СЛОЖНОМ ДВИЖЕНИИ
- 2. Замечание о дифференцировании единичного вектора.
- 3. Векторный вывод теоремы Кориолиса.
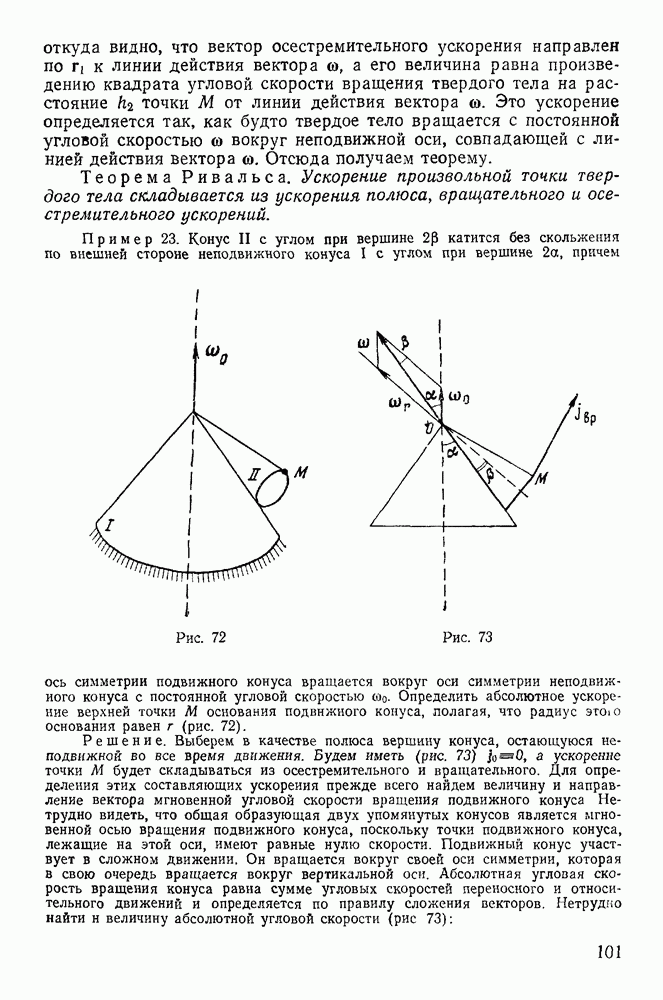
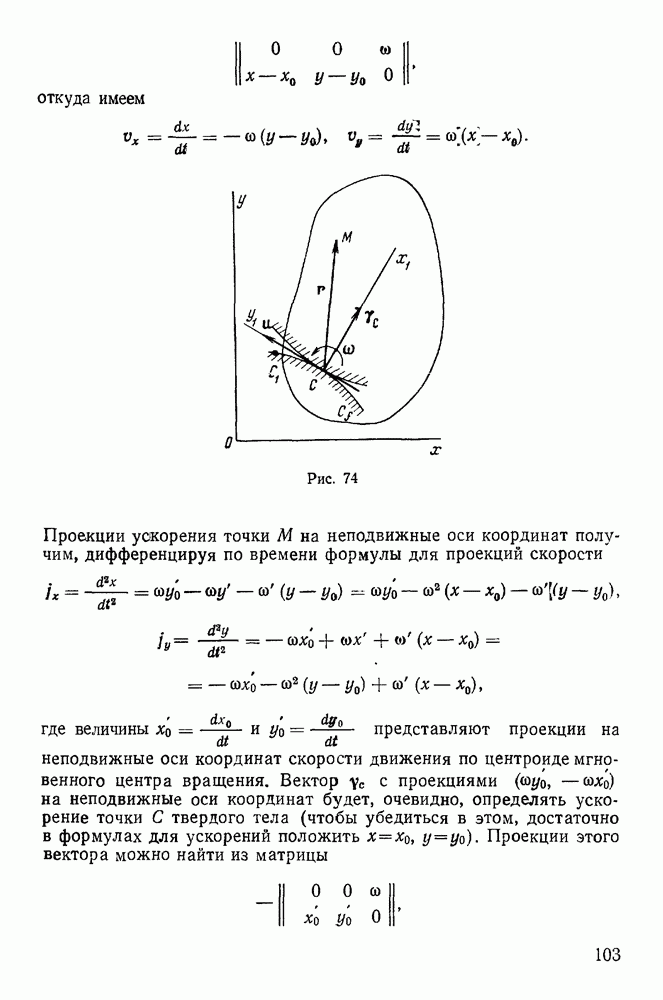
- 4. Теорема Ривальса.
- § 4. РАСПРЕДЕЛЕНИЕ УСКОРЕНИЙ В ПЛОСКОПАРАЛЛЕЛЬНОМ ДВИЖЕНИИ ТВЕРДОГО ТЕЛА
- 2. Мгновенный центр ускорений.
- § 5. КИНЕМАТИЧЕСКИЕ УРАВНЕНИЯ ЭЙЛЕРА
- Глава III. СТАТИКА
- I. ГЕОМЕТРИЧЕСКАЯ СТАТИКА
- § 1. АКСИОМЫ СТАТИКИ
- § 2. ПОНЯТИЕ О СИЛЕ ТРЕНИЯ
- § 3. РАЗЛИЧНЫЕ ЗАДАЧИ СТАТИКИ
- 2. Равновесие трех сил.
- § 4. МОМЕНТ СИЛЫ
- 2. Момент силы относительно оси.
- 3. Теорема Вариньона для системы сходящихся сил.
- § 5. ПРОИЗВОЛЬНАЯ СИСТЕМА СИЛ, ДЕЙСТВУЮЩИХ НА ТВЕРДОЕ ТЕЛО
- § 6. УСЛОВИЯ РАВНОВЕСИЯ СИСТЕМЫ СИЛ, ДЕЙСТВУЮЩИХ НА ТВЕРДОЕ ТЕЛО
- § 7. ПРИВЕДЕНИЕ СИСТЕМЫ СИЛ, ДЕЙСТВУЮЩИХ НА ТВЕРДОЕ ТЕЛО, К ДИНАМЕ. УРАВНЕНИЯ РАВНОВЕСИЯ ТВЕРДОГО ТЕЛА
- § 8. УСЛОВИЯ РАВНОВЕСИЯ СИСТЕМЫ ТВЕРДЫХ ТЕЛ
- § 9. ПЛОСКАЯ СИСТЕМА СИЛ
- § 10. ЗАДАЧА О РАВНОВЕСИИ НЕСВОБОДНОГО ТВЕРДОГО ТЕЛА
- 2. Частные случаи равновесия твердого тела.
- § 11. ЗАДАЧА О РАВНОВЕСИИ ПРИ НАЛИЧИИ ТРЕНИЯ
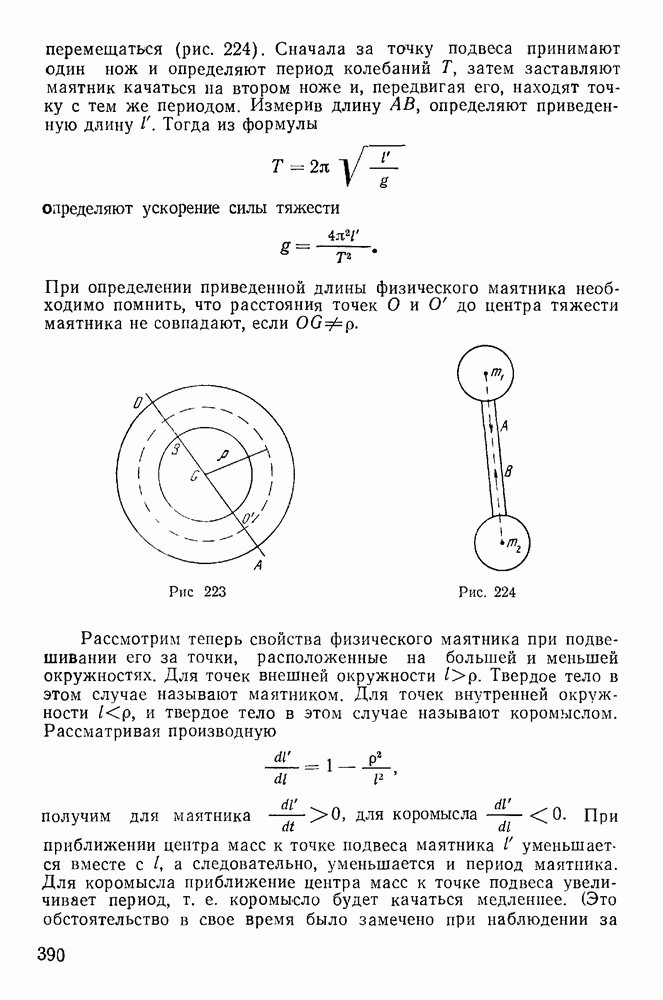
- § 12. СИЛА ТЯЖЕСТИ И ЦЕНТР ТЯЖЕСТИ
- II. АНАЛИТИЧЕСКАЯ СТАТИКА
- § 1. РАБОТА СИЛЫ НА ПЕРЕМЕЩЕНИИ. СИЛОВАЯ ФУНКЦИЯ
- § 2. ПРИНЦИП ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ
- 2. Теорема Лагранжа о равновесии системы.
- 3. Принцип Торричелли.
- § 3. ОБЩИЕ ВОПРОСЫ АНАЛИТИЧЕСКОЙ СТАТИКИ
- 3. Общие теоремы о равновесии системы материальных точек.
- 4. Метод неопределенных множителей Лагранжа.
- 5. Определение реакций.
- § 4. ОПРЕДЕЛЕНИЕ РЕАКЦИЙ В ОБЩЕМ СЛУЧАЕ
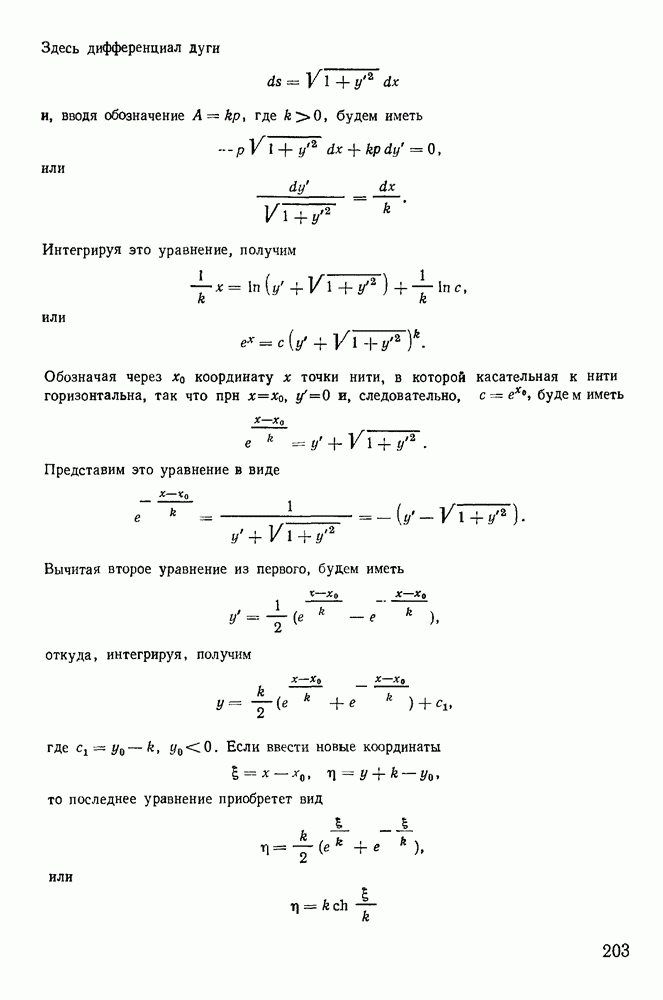
- § 5. РАВНОВЕСИЕ НИТИ
- 2. Естественные уравнения равновесия нити.
- Глава IV. ДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ
- § 1. ОСНОВНЫЕ ЗАКОНЫ ДИНАМИКИ
- § 2. ДВЕ ОСНОВНЫЕ ЗАДАЧИ ДИНАМИКИ. УРАВНЕНИЯ ДВИЖЕНИЯ ТОЧКИ В ДЕКАРТОВЫХ ОСЯХ
- § 3. ЕСТЕСТВЕННЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ
- § 4. ОСНОВНЫЕ ТЕОРЕМЫ ДИНАМИКИ ДЛЯ СВОБОДНОЙ МАТЕРИАЛЬНОЙ ТОЧКИ
- 2. Теорема об изменении момента количества движения.
- 3. Следствия из теорем об изменении количества движения и момента количества движения материальной точки.
- 4. Теорема живых сил.
- 5. Интеграл живых сил.
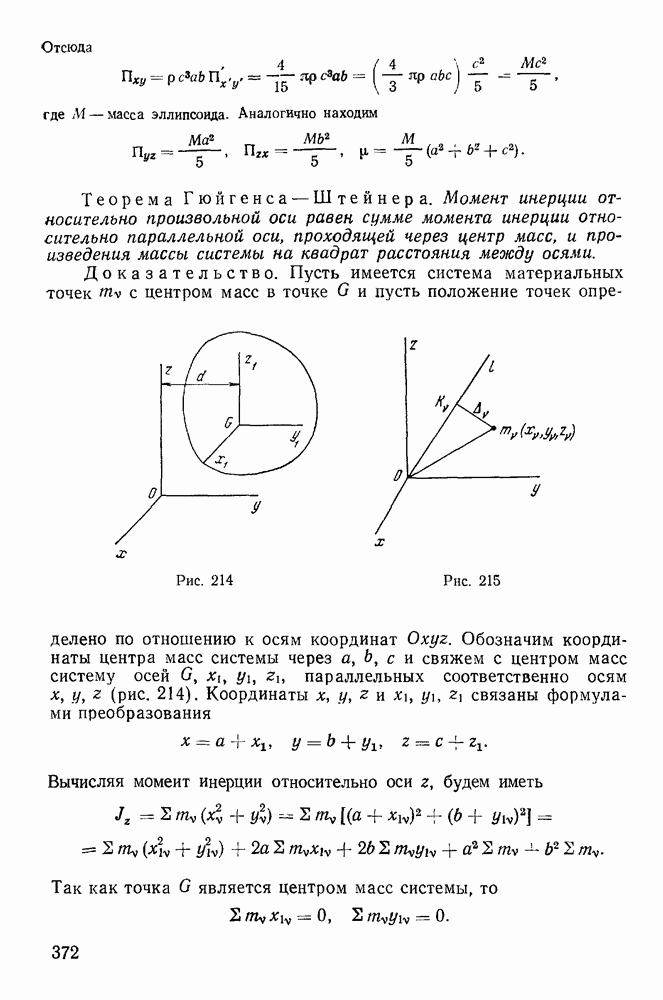
- 6. Устойчивость равновесия. Теорема Лагранжа.
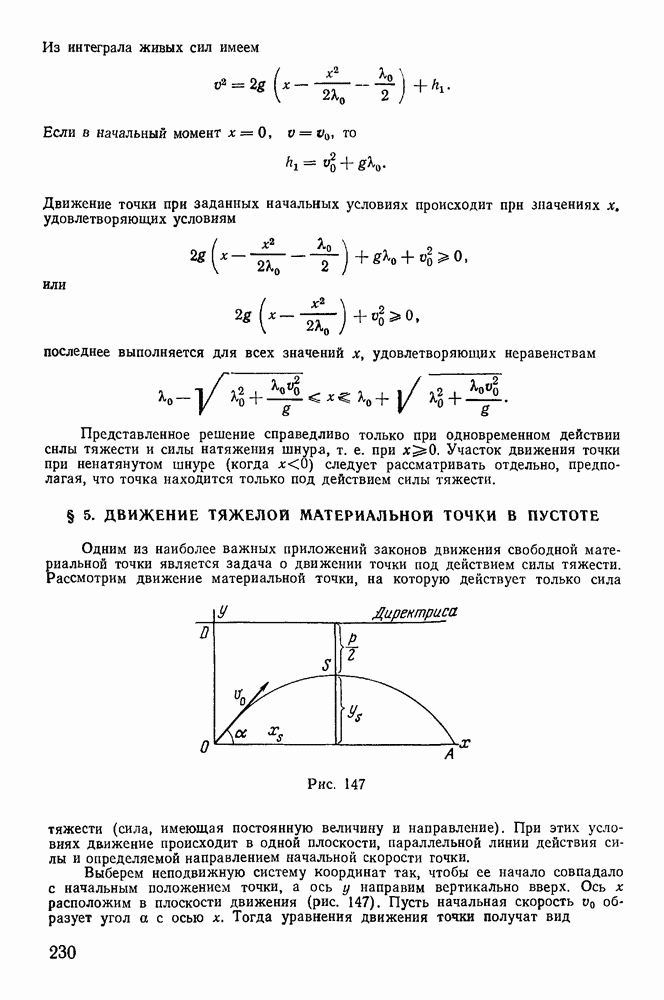
- § 5. ДВИЖЕНИЕ ТЯЖЕЛОЙ МАТЕРИАЛЬНОЙ ТОЧКИ В ПУСТОТЕ
- § 6. ДВИЖЕНИЕ МАТЕРИАЛЬНОЙ ТОЧКИ ПОД ДЕЙСТВИЕМ ЦЕНТРАЛЬНЫХ СИЛ
- 2. Формулы Бине
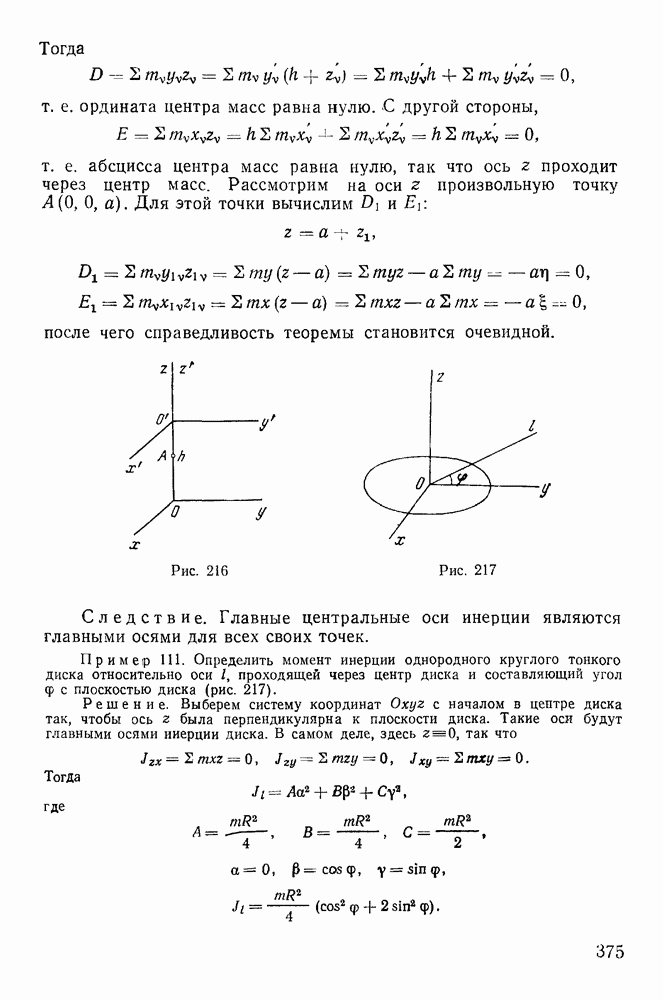
- 3. Задача о движении планет
- § 7. ДВИЖЕНИЕ ТОЧКИ В СОПРОТИВЛЯЮЩЕЙСЯ СРЕДЕ
- § 8. ДВИЖЕНИЕ НЕСВОБОДНОЙ МАТЕРИАЛЬНОЙ ТОЧКИ
- 2. Движение материальной точки по поверхности.
- § 9. ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЕ МАТЕРИАЛЬНОЙ ТОЧКИ
- 1. Теорема живых сил в относительном движении точки.
- 2. Уравнения относительного равновесия точки.
- 3. Равновесие материальной точки на поверхности Земли. Вес.
- 4. Задача о падении тяжелой точки в пустоте.
- 5. Маятник Фуко.
- § 10. ПРИНЦИП ДАЛАМБЕРА
- Глава V. ДИНАМИКА СИСТЕМЫ МАТЕРИАЛЬНЫХ ТОЧЕК
- § 1. УЧЕНИЕ О СВЯЗЯХ
- § 2. ПРИНЦИП ДАЛАМБЕРА — ЛАГРАНЖА
- § 3. ОСНОВНЫЕ ТЕОРЕМЫ ДИНАМИКИ СИСТЕМЫ
- 2. Теорема об изменении момента количества движения.
- 3. Теорема живых сил.
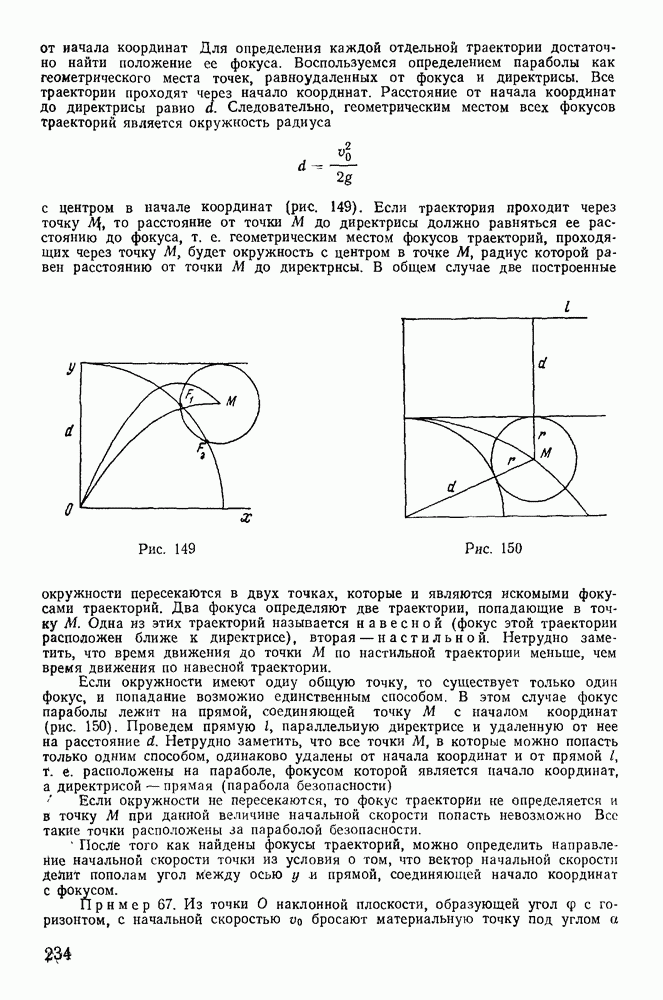
- § 4. ТЕОРЕМЫ О ДВИЖЕНИИ СИСТЕМЫ ОТНОСИТЕЛЬНО ОСЕЙ НЕИЗМЕННОГО НАПРАВЛЕНИЯ, ПРОХОДЯЩИХ ЧЕРЕЗ ЦЕНТР МАСС СИСТЕМЫ (ОСЕЙ КЕНИГА)
- 2. Теорема об изменении момента количества движения системы относительно осей Кёнига.
- 3. Теорема живых сил в движении системы относительно осей Кёнига.
- § 5. УРАВНЕНИЯ ЛАГРАНЖА ВТОРОГО РОДА
- 2. Случай существования силовой функции.
- 3. Замечание о лагранжевых координатах.
- § 6. ЭЛЕМЕНТАРНЫЕ СЛУЧАИ ИНТЕГРИРУЕМОСТИ УРАВНЕНИЙ ЛАГРАНЖА
- 2. Метод Рауса игнорирования циклических координат.
- 3. Обобщение теоремы и интеграла живых сил.
- § 7. ОПРЕДЕЛЕНИЕ РЕАКЦИЙ
- Глава VI. ДИНАМИКА ТВЕРДОГО ТЕЛА
- § 1. ТЕОРИЯ МОМЕНТОВ ИНЕРЦИИ
- 2. Момент инерции системы относительно произвольной оси, проходящей через заданную точку.
- 3. Эллипсоид инерции.
- 4. Определение главных осей инерции для произвольной точки.
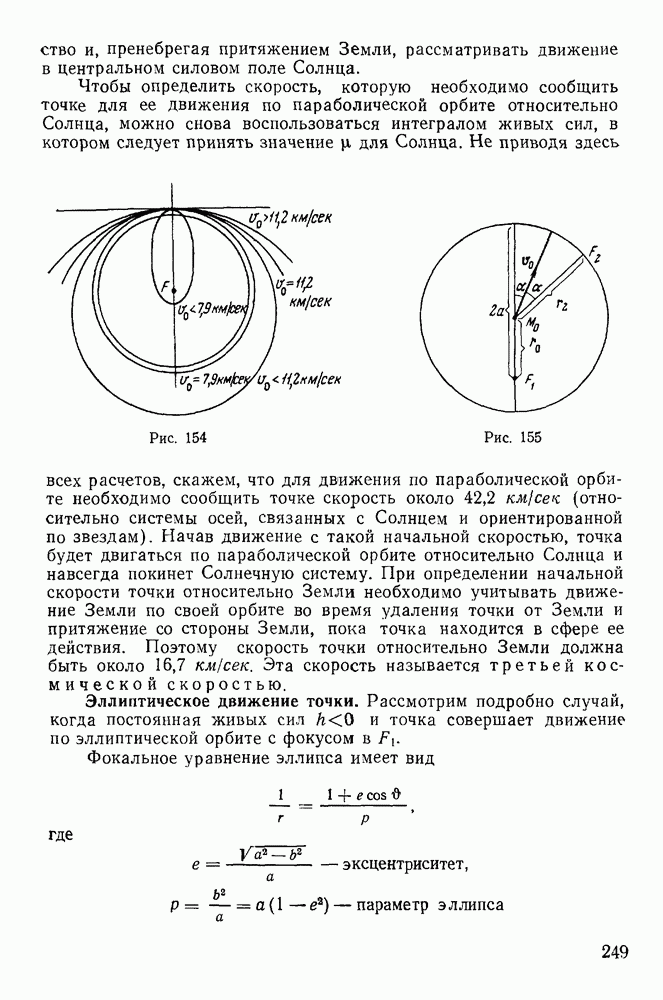
- § 2. ВРАЩЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ОСИ
- § 3. ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА, ИМЕЮЩЕГО ОДНУ НЕПОДВИЖНУЮ ТОЧКУ
- 2. Уравнения движения твердого тела с одной неподвижной точкой.
- § 4. ДВИЖЕНИЕ ТЯЖЕЛОГО ТВЕРДОГО ТЕЛА ОКОЛО НЕПОДВИЖНОЙ ТОЧКИ
- 2. Интегрирование уравнений движения тяжелого твердого тела.
- 3. Случай Эйлера — Пуансо.
- Регулярная прецессия твердого тела в случае Эйлера.
- Геометрическая интерпретация Пуансо движения твердого тела в случае Эйлера.
- Устойчивость постоянных вращений твердого тела.
- 4. Случай Лагранжа.
- Особенные случаи движения твердого тела. Спящий волчок.
- Гироскоп. Приближенная теория.
- Некоторые применения гироскопов.
- Регулярная прецессия в случае Лагранжа.
- Вынужденная регулярная прецессия.
- 5. Случай Ковалевской.
- § 5. ОПРЕДЕЛЕНИЕ РЕАКЦИИ В СЛУЧАЕ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА С ОДНОЙ НЕПОДВИЖНОЙ ТОЧКОЙ
- § 6. УРАВНЕНИЯ ДВИЖЕНИЯ СВОБОДНОГО ТВЕРДОГО ТЕЛА
- § 7. ГИРОСТАТЫ
- Глава VII. АНАЛИТИЧЕСКАЯ ДИНАМИКА
- § 1. КАНОНИЧЕСКИЕ УРАВНЕНИЯ ГАМИЛЬТОНА
- 1. Преобразования Лежандра.
- 2. Канонические уравнения Гамильтона.
- 3. Функция Гамильтона и ее свойства.
- § 2. ПРИНЦИП ГАМИЛЬТОНА — ОСТРОГРАДСКОГО
- 2. Вывод канонических уравнений Гамильтона из принципа Гамильтона — Остроградского.
- 3. Принцип Гамильтона в форме Пуанкаре.
- § 3. ИНТЕГРИРОВАНИЕ КАНОНИЧЕСКИХ УРАВНЕНИЙ ГАМИЛЬТОНА
- 2. Канонические преобразования.
- 3. Бесконечно малые канонические преобразования.
- 4. Теорема Лиувилля.
- 5. Теорема Якоби.
- 6. Интегрирование уравнения Гамильтона—Якоби.
- Метод Имшенецкого разделения переменных.
- 7. Скобки Пуассона.
- § 4. ВАРИАЦИОННЫЕ ПРИНЦИПЫ МЕХАНИКИ
- 2. Принцип Лагранжа.
- 3. Принцип наименьшего действия в форме Якоби.
- Вывод уравнений Лагранжа второго рода из принципа Якоби.
- Сравнение принципа Якоби с принципом Гамильтона.
- 4. Оптико-механическая аналогия.
- 5. Интегральные инварианты.
- Линейные интегральные инварианты.
- Интегральный инвариант Пуанкаре — Картана.
- 6. Принцип наименьшего принуждения Гаусса. Уравнения Аппеля.
- 7. Уравнения Рауса.
- § 5. МАЛЫЕ КОЛЕБАНИЯ
- Затухающие колебания.
- Вынужденные колебания. Резонанс.
- Параметрический резонанс.
- Нелинейные колебания.
- Диссипативные системы.
- 2. Общий случай малых колебаний системы около положения устойчивого равновесия.
- Устойчивость равновесия. Теорема Лагранжа об устойчивости равновесия.
- Замечание об устойчивости стационарных движений.
- Малые колебания системы около положения устойчивого равновесия.
- Влияние диссипативных сил на малые колебания системы около устойчивого положения равновесия.
- § 6. УСТОЙЧИВОСТЬ ДВИЖЕНИЯ
- Прямой метод Ляпунова
- Теорема об асимптотической устойчивости.
- Теорема Четаева о неустойчивости движения.
- 2. Влияние новых связей на малые колебания системы около положения равновесия.
- 3. Влияние диссипативных сил на устойчивость равновесия.
- 4. Влияние гироскопических сил на устойчивость равновесия.
- § 7. ЭЛЕМЕНТЫ ТЕОРИИ ВОЗМУЩЕНИЙ
- Устойчивость консервативных систем.
- 2. Метод изменения произвольных постоянных.
- Глава VIII. ТЕОРИЯ УДАРА
- § 2. ТЕОРЕМЫ КАРНО
- § 3. ЗАДАЧА О ЦЕНТРЕ УДАРА
- § 4. ЗАДАЧА О БАЛЛИСТИЧЕСКОМ МАЯТНИКЕ
- § 5. УРАВНЕНИЯ ЛАГРАНЖА ДЛЯ УДАРА
- § 6. ЗАДАЧА ОБ УДАРЕ ПО ТВЕРДОМУ ТЕЛУ С ОДНОЙ НЕПОДВИЖНОЙ ТОЧКОЙ
- Глава IX. ЭЛЕМЕНТЫ СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- § 2. СПЕЦИАЛЬНЫЙ ПРИНЦИП ОТНОСИТЕЛЬНОСТИ ЭЙНШТЕЙНА
- § 3. ГРУППА ПРЕОБРАЗОВАНИЙ ЛОРЕНЦА
- § 4. ИНВАРИАНТНЫЕ ВЕЛИЧИНЫ В ТЕОРИИ ОТНОСИТЕЛЬНОСТИ. ЧЕТЫРЕХМЕРНЫЙ ВЕКТОР. МИР МИНКОВСКОГО
- § 5. РЕЛЯТИВИСТСКАЯ ДИНАМИКА
- Литература