| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
4. О ПРИМЕНЕНИИ ПРЯМОГО МЕТОДА ЛЯПУНОВА К АНАЛИЗУ УСТОЙЧИВОСТИ ОДНОГО КЛАССА СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
Постановка задачи. Прямой метод в теории регулирования стали применять после опубликования работы А. И. Лурье и В. Н. Постникова о решении одной частной задачи. Позднее А. И. Лурье развил излагаемый ниже алгоритм построения функции Ляпунова, разрешающей задачу устойчивости для одного класса регулируемых систем. Эти исследования были затем продолжены и развиты рядом советских ученых.
Итак, рассмотрим систему регулирования, возмущенное движение которой описывается уравнениями

где  — постоянные;
— постоянные;
 — координаты объекта регулирования;
— координаты объекта регулирования;
 — координата регулирующего органа; тк — постоянные регулирующего органа;
— координата регулирующего органа; тк — постоянные регулирующего органа;
 — постоянные регулятора;
— постоянные регулятора;
 — управляющий сигнал, формируемый измерительными органами регулятора, которые предполагаются идеальными.
— управляющий сигнал, формируемый измерительными органами регулятора, которые предполагаются идеальными.
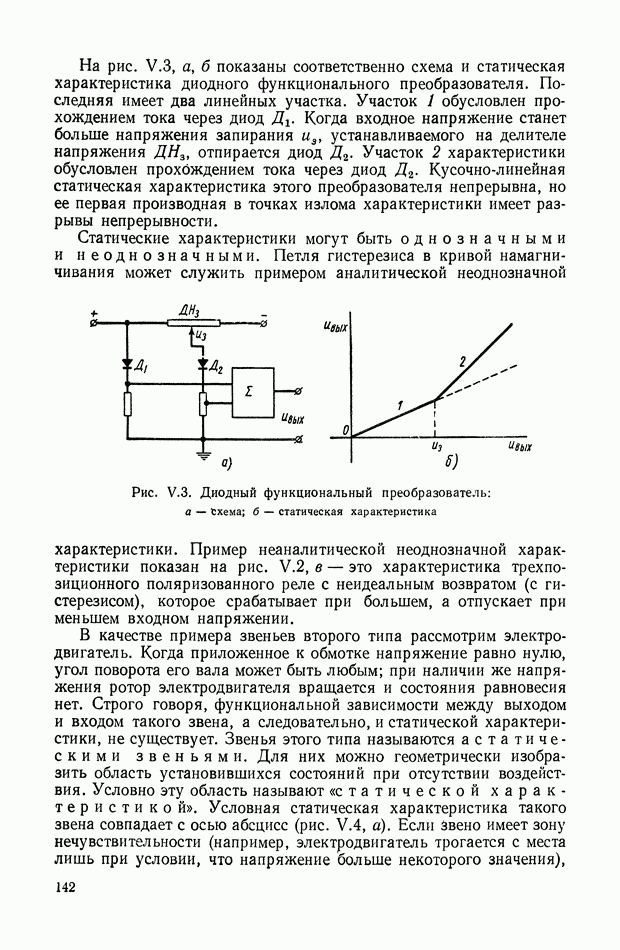
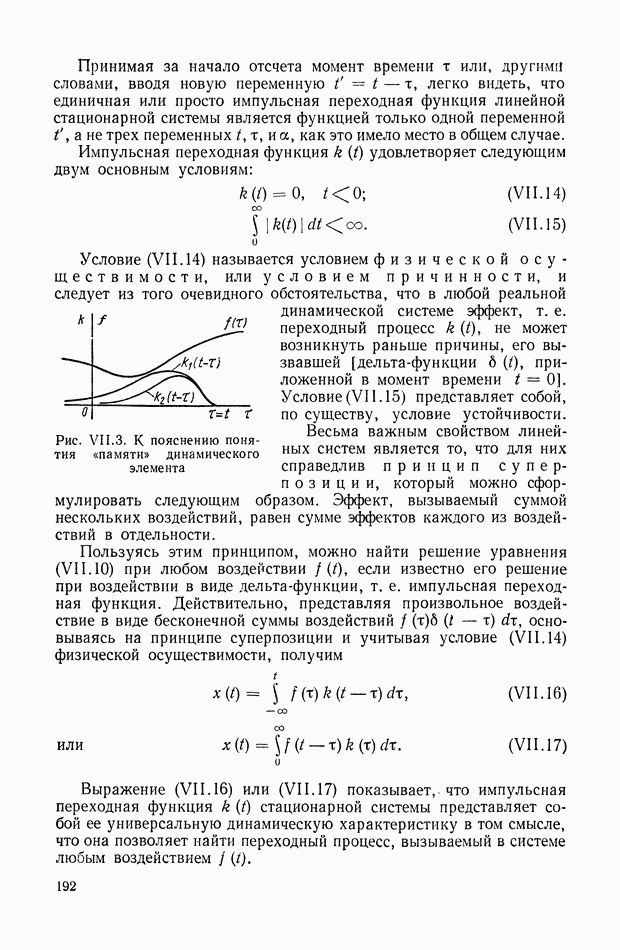
Функция  описывает скорость перестановки регулирующего органа из одного положения в другое в соответствии со значением управляющего сигнала о (см. рис. XI.2). Рассматриваемая
описывает скорость перестановки регулирующего органа из одного положения в другое в соответствии со значением управляющего сигнала о (см. рис. XI.2). Рассматриваемая
функция однозначная, ограниченная, обладающая следующими свойствами:  при
при  при
при 
Условимся, что такие функции образуют класс А функций.
В некоторых случаях, оговоренных особо, будет идти речь о таких функциях  , которые в дополнение к сказанному обладают следующими свойствами:
, которые в дополнение к сказанному обладают следующими свойствами:

Условимся, что эти функции образуют подкласс А функций  в классе А.
в классе А.
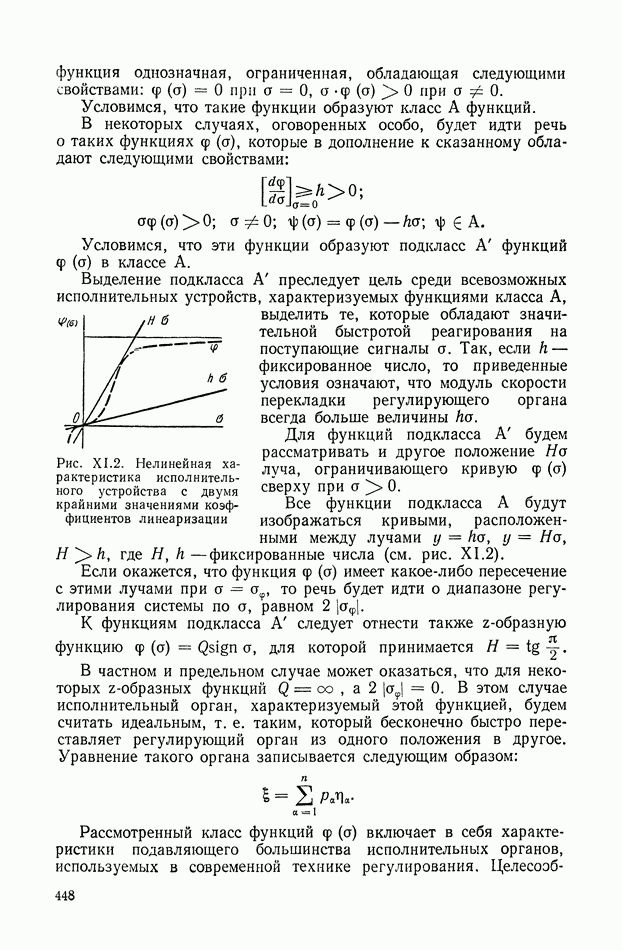
Выделение подкласса А преследует цель среди всевозможных исполнительных устройств, характеризуемых функциями класса А, выделить те, которые обладают значительной быстротой реагирования на поступающие сигналы  . Так, если
. Так, если  — фиксированное число, то приведенные условия означают, что модуль скорости перекладки регулирующего органа всегда больше величины
— фиксированное число, то приведенные условия означают, что модуль скорости перекладки регулирующего органа всегда больше величины 

Рис. XI.2. Нелинейная характеристика исполнительного устройства с двумя крайними значениями коэффициентов линеаризации
Для функций подкласса А будем рассматривать и другое положение Но луча, ограничивающего кривую  сверху при
сверху при  .
.
Все функции подкласса А будут изображаться кривыми, расположенными между лучами  где
где  — фиксированные числа (см. рис. XI.2).
— фиксированные числа (см. рис. XI.2).
Если окажется, что функция  имеет какое-либо пересечение с этими лучами при
имеет какое-либо пересечение с этими лучами при  то речь будет идти о диапазоне регулирования системы по а, равном
то речь будет идти о диапазоне регулирования системы по а, равном 
К функциям подкласса А следует отнести также  -образную функцию
-образную функцию  , для которой принимается
, для которой принимается  .
.
В частном и предельном случае может оказаться, что для некоторых  -образных функций
-образных функций  . В этом случае исполнительный орган, характеризуемый этой функцией, будем считать идеальным, т. е. таким, который бесконечно быстро переставляет регулирующий орган из одного положения в другое. Уравнение такого органа записывается следующим образом:
. В этом случае исполнительный орган, характеризуемый этой функцией, будем считать идеальным, т. е. таким, который бесконечно быстро переставляет регулирующий орган из одного положения в другое. Уравнение такого органа записывается следующим образом:

Рассмотренный класс функций  включает в себя характеристики подавляющего большинства исполнительных органов, используемых в современной технике регулирования,
включает в себя характеристики подавляющего большинства исполнительных органов, используемых в современной технике регулирования,
Целесообразность объединения этих характеристик одним классом функций подтверждается следующим весьма важным соображением.
Обычно определение функций  производится экспериментально, путем графической записи скорости хода исполнительного органа в так называемом статическом режиме, когда величина о принимает известные фиксированные, дискретные значения. При такой записи получается как бы семейство функций
производится экспериментально, путем графической записи скорости хода исполнительного органа в так называемом статическом режиме, когда величина о принимает известные фиксированные, дискретные значения. При такой записи получается как бы семейство функций  , зависящее от приложенной фиксированной нагрузки.
, зависящее от приложенной фиксированной нагрузки.
Однако фактические условия работы исполнительных органов включают в себя непрерывное изменение действующей нагрузки. Ее действие на исполнительный орган сводится к заметному искажению вида функции  записанной в статическом режиме. Это искажение не может быть полностью учтено, несмотря на то, что оно не меняет определенного выше класса функций
записанной в статическом режиме. Это искажение не может быть полностью учтено, несмотря на то, что оно не меняет определенного выше класса функций  .
.
В то же время особенно сильные искажения функции  в процессе регулирования могут происходить в результате колебания уровня энергии внешнего источника питания регулятора. Следовательно, в каждой частной задаче невозможно строго фиксировать функцию
в процессе регулирования могут происходить в результате колебания уровня энергии внешнего источника питания регулятора. Следовательно, в каждой частной задаче невозможно строго фиксировать функцию  и тем более корректно проводить и линеаризацию ее коррекции, строго фиксируя коэффициент линейного приближения. Приведенные рассуждения показывают, что в подобных задачах всегда можно определить функцию
и тем более корректно проводить и линеаризацию ее коррекции, строго фиксируя коэффициент линейного приближения. Приведенные рассуждения показывают, что в подобных задачах всегда можно определить функцию  лишь с точностью ее принадлежности к классу А или подклассу А функций. Этого определения будет вполне достаточно, если основные задачи теории автоматического регулирования решать на основе прямого метода Ляпунова.
лишь с точностью ее принадлежности к классу А или подклассу А функций. Этого определения будет вполне достаточно, если основные задачи теории автоматического регулирования решать на основе прямого метода Ляпунова.
Для окончательной формулировки задачи допустим, что возмущенное движение системы регулирования описывается уравнениями (XI. 17). Требуется найти условия, которые следует наложить на параметры регулятора, выполнение которых гарантирует устойчивость установившегося состояния системы автоматического регулирования, описываемого очевидным решением уравнений (XI. 17), каковы бы ни были возмущения и функции класса А или подкласса А.
Построение функции Ляпунова. Изложим метод построения функции Ляпунова для регулируемых систем, обладающих устойчивостью при выключенном регуляторе.
Функции Ляпунова удобнее строить, если уравнения задачи приведены к так называемой канонической форме.
С этой целью рассмотрим линейную подстановку

Дифференцируя  после исключения с помощью уравнений (XI. 17) величин
после исключения с помощью уравнений (XI. 17) величин  находим
находим

Придавая уравнениям в новых переменных каноническую форму

подберем постоянные  так, чтобы удовлетворялись соотношения
так, чтобы удовлетворялись соотношения

где  — параметры преобразования, определение которых сводится к следующему.
— параметры преобразования, определение которых сводится к следующему.
Первые  соотношений (XI. 196) следует рассматривать как линейные однородные уравнения относительно неизвестных Как известно, они тогда лишь имеют ненулевые решения, когда их определитель равен нулю.
соотношений (XI. 196) следует рассматривать как линейные однородные уравнения относительно неизвестных Как известно, они тогда лишь имеют ненулевые решения, когда их определитель равен нулю.
Таким образом, для того чтобы привести уравнения (XI. 17) к каноническому виду, мы должны выбрать числа как корни уравнения

Для завершения преобразования уравнений (XI. 17) остается выразить о через новые переменные. С этой целью из соотношений (XI. 196) необходимо определить все значения и разрешить соотношения (XI. 18) относительно старых переменных. При этом могут встретиться различные случаи в зависимости от корней уравнения  Ниже будут рассмотрены лишь регулируемые системы, для которых корни
Ниже будут рассмотрены лишь регулируемые системы, для которых корни  — вещественные,
— вещественные,  — попарно сопряженные комплексные, и все простые обладают свойством
— попарно сопряженные комплексные, и все простые обладают свойством

Для краткости такие системы назовем собственно устойчивыми.
В этом случае преобразование (XI. 18) является неособым, вследствие чего можем найти

С помощью этих соотношений, дифференцируя величину а, получим

где постоянные можно выбирать.
Следовательно, преобразование позволяет поставить вопрос об устойчивости невозмущенного движения системы регулирования (XI. 17), описываемого очевидным решением  уравнений (XI. 196). Для разрешения вопроса по прямому методу Ляпунова рассмотрим функцию
уравнений (XI. 196). Для разрешения вопроса по прямому методу Ляпунова рассмотрим функцию

где  — вещественные,
— вещественные,  — попарно сопряженные комплексные и в остальном произвольные постоянные.
— попарно сопряженные комплексные и в остальном произвольные постоянные.
Поскольку очевидно, что

то при любых значениях К на основании тождества

заключаем, что функция V принимает только вещественные и всюду положительные значения, обращаясь в нуль лишь в точке  Ее полная производная имеет вид
Ее полная производная имеет вид

Учитывая, что

и, добавляя в правую часть выражения величину  эквивалентную нулю, получим
эквивалентную нулю, получим

Если постоянные  определить при помощи следующего уравнения:
определить при помощи следующего уравнения:

то полная производная примет вид

и, очевидно, будет являться знакопостоянной функцией, принимая всюду отрицательные или нулевые значения.
Итак, можно сформулировать следующую теорему [6]: если постоянные регулятора таковы, что система квадратных уравнений (XI. 21), в которой  — вещественные, а
— вещественные, а  — соответственно попарно сопряженные комплексные числа, имеет хотя бы одну систему решений, содержащую
— соответственно попарно сопряженные комплексные числа, имеет хотя бы одну систему решений, содержащую  вещественных и
вещественных и  попарно сопряженных комплексных чисел, то установившееся состояние системы автоматического регулирования обладает устойчивостью в большом, какова бы ни была функция
попарно сопряженных комплексных чисел, то установившееся состояние системы автоматического регулирования обладает устойчивостью в большом, какова бы ни была функция  класса А.
класса А.
Можно доказать, что эта устойчивость асимптотическая. Если среди вещественных корней окажется один, например  равный нулю, то в функции V следует опустить член
равный нулю, то в функции V следует опустить член  и вместо него написать
и вместо него написать  где
где  этом случае в уравнениях (XI. 21) первое из них заменится уравнением
этом случае в уравнениях (XI. 21) первое из них заменится уравнением  которое наложит на
которое наложит на  условие
условие 
Для построения критерия устойчивости фактически нет необходимости решать уравнения (XI. 21), достаточно лишь найти условие их разрешимости. Как показывают примеры, эти условия сводятся к выполнению М совокупных неравенств, содержащих параметры объекта регулирования и регулятора, входящие в постоянные 
В работе [6] предлагается следующая формула для определения этих постоянных:

где  — производная по X определителя
— производная по X определителя  — значение определителя
— значение определителя  при
при  в котором строка элементов с номером
в котором строка элементов с номером  замещена числами
замещена числами 
Для краткости мы не останавливаемся на выводе этих важных формул, позволяющих в каждой частной задаче миновать все промежуточные выкладки и сразу же приступить к формированию искомого критерия устойчивости, как только будут написаны исходные уравнения.
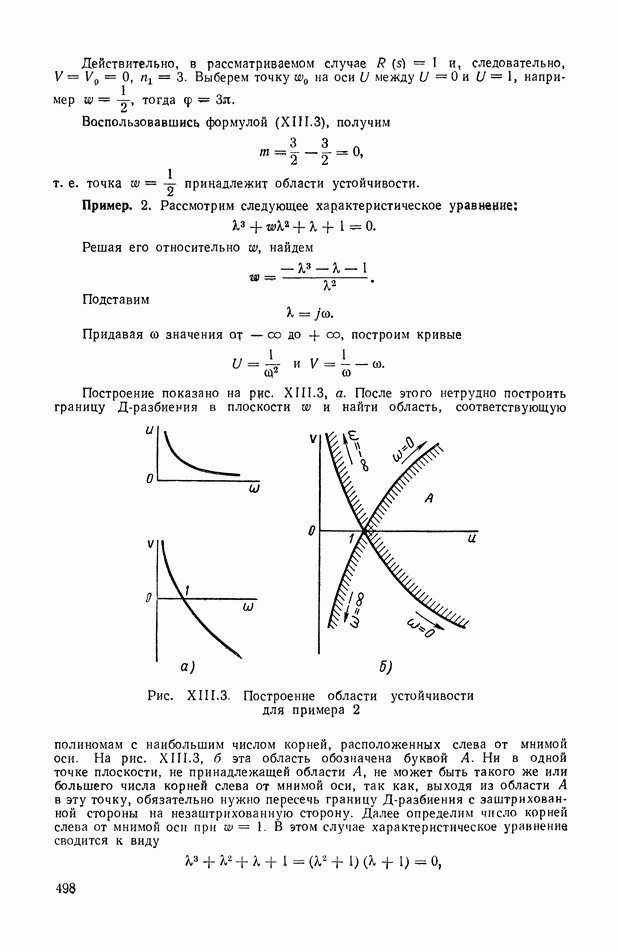
В качестве примера приложения метода рассмотрим задачу о возмущенных движениях системы автоматического регулирования, описываемую уравнениями

где  — координата;
— координата;
 — постоянные объекта регулирования;
— постоянные объекта регулирования;
 — координата регулирующего органа;
— координата регулирующего органа;
 — постоянные регулятора, физический смысл которых ясен из написания а;
— постоянные регулятора, физический смысл которых ясен из написания а;
 — функция класса А.
— функция класса А.
Установившееся состояние системы определяется следующими величинами:

Для того чтобы привести уравнения (XI. 22) к форме уравнений (XI. 17), примем, что

После исключения в выражении для а величины получим

где

Составим уравнение  тогда получим
тогда получим

откуда найдем

и

Очевидно, все корни  будут иметь отрицательные вещественные части, если
будут иметь отрицательные вещественные части, если 
Далее образуем определители 

Применяя формулы (XI. 22), получим

В соответствии с уравнениями имеем

Нетрудно показать, что эти уравнения непременно удовлетворяют условиям теоремы, если выполняются следующие неравенства:

Если воспользоваться обозначениями формул (XI. 23) и (XI. 23а), то последние неравенства легко привести к следующему окончательному виду:

Не имея здесь возможности останавливаться более подробно на применении прямого метода Ляпунова к исследованию устойчивости систем автоматического регулирования, мы отсылаем читателя, интересующегося этим вопросом, к специальной литературе [1,4,5].
В настоящее время учение Ляпунова об устойчивости движения развилось в самостоятельную обширную дисциплину большого прикладного значения.
Идеи Ляпунова получили свое дальнейшее развитие главным образом в трудах советских ученых и изложены в монографиях [2, 3, 7, 8].
ЛИТЕРАТУРА
(см. скан)
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- РАЗДЕЛ I. ОБЩИЕ СВЕДЕНИЯ. МЕТОДЫ МАТЕМАТИЧЕСКОГО ОПИСАНИЯ И СТРУКТУРНОГО ПРЕОБРАЗОВАНИЯ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- ГЛАВА I. ОЧЕРК О РАЗВИТИИ ТЕОРИИ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ В СССР
- 1. ТЕОРИЯ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ В ДОРЕВОЛЮЦИОННЫЙ ПЕРИОД
- 2. РАЗВИТИЕ ТЕОРИИ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ПОСЛЕ ОКТЯБРЬСКОЙ СОЦИАЛИСТИЧЕСКОЙ РЕВОЛЮЦИИ
- ГЛАВА II. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ ТЕОРИИ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. СУЩНОСТЬ ПРОБЛЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- 2. ПРОБЛЕМА РЕГУЛИРОВАНИЯ КАК ЧАСТНЫЙ СЛУЧАЙ ПРОБЛЕМЫ УПРАВЛЕНИЯ
- 3. ОСНОВНОЙ ПРИНЦИП ДЕЙСТВИЯ И ОПРЕДЕЛЕНИЕ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 4. КЛАССИФИКАЦИЯ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ В ЗАВИСИМОСТИ ОТ УПРАВЛЯЮЩЕГО ВОЗДЕЙСТВИЯ
- 5. ОСНОВНЫЕ УСТРОЙСТВА СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ И ИХ КЛАССИФИКАЦИЯ ПО НАЗНАЧЕНИЮ
- 6. КЛАССИФИКАЦИЯ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ В ЗАВИСИМОСТИ ОТ ХАРАКТЕРА СИГНАЛОВ
- 7. КЛАССИФИКАЦИЯ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ В ЗАВИСИМОСТИ ОТ ИДЕАЛИЗАЦИИ, ПРИНЯТОЙ ПРИ ИХ МАТЕМАТИЧЕСКОМ ОПИСАНИИ
- 8. СТРУКТУРНЫЕ СХЕМЫ, ОДНОКОНТУРНЫЕ И МНОГОКОНТУРНЫЕ, НЕСВЯЗАННЫЕ И СВЯЗАННЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 9. КЛАССИФИКАЦИЯ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ В ЗАВИСИМОСТИ ОТ ХАРАКТЕРА КОНТРОЛИРУЕМЫХ ИЗМЕНЕНИЙ
- 10. ТРЕБОВАНИЯ, ПРЕДЪЯВЛЯЕМЫЕ К ДИНАМИЧЕСКИМ СВОЙСТВАМ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- ГЛАВА III. ОСНОВНЫЕ УСТРОЙСТВА И ТИПОВЫЕ СХЕМЫ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. КРАТКАЯ ХАРАКТЕРИСТИКА УСТРОЙСТВ, ИЗ КОТОРЫХ СОСТОЯТ СИСТЕМЫ РЕГУЛИРОВАНИЯ
- 2. СИСТЕМА АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ СКОРОСТИ ГИДРОТУРБИНЫ
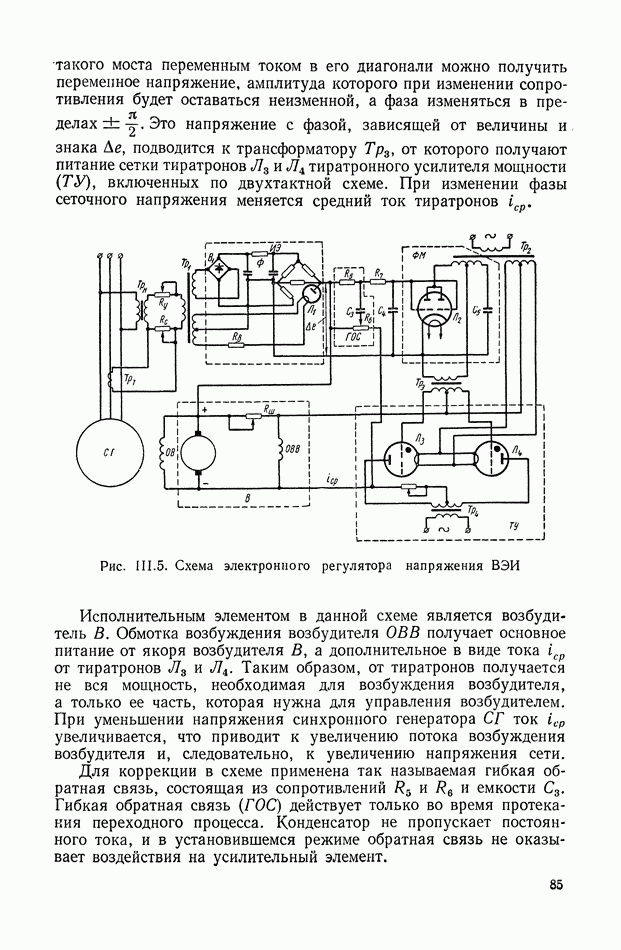
- 3. ЭЛЕКТРОННЫЙ РЕГУЛЯТОР НАПРЯЖЕНИЯ ВЭИ
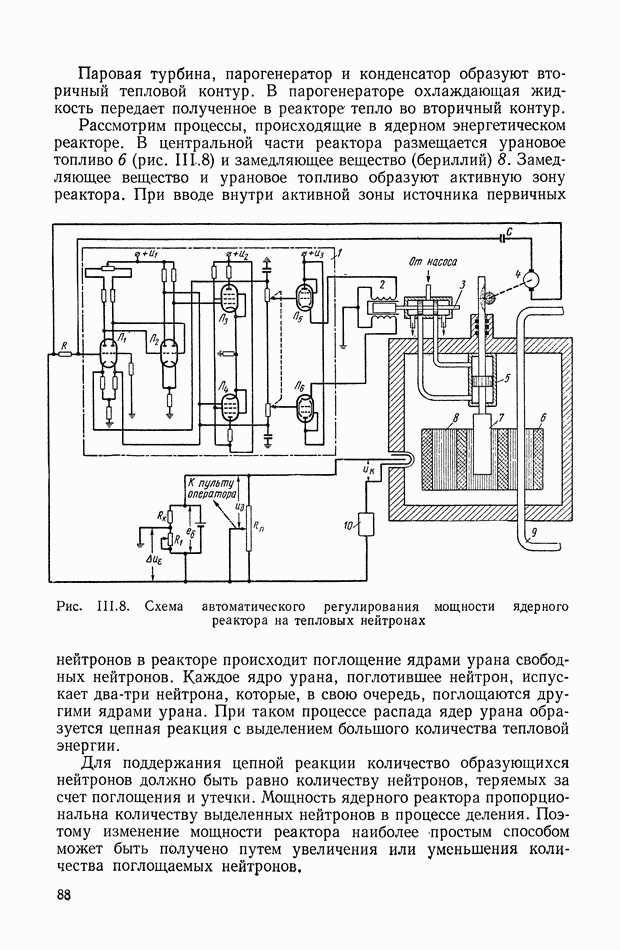
- 4. СИСТЕМА АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ЯДЕРНОГО РЕАКТОРА ПО МОЩНОСТИ
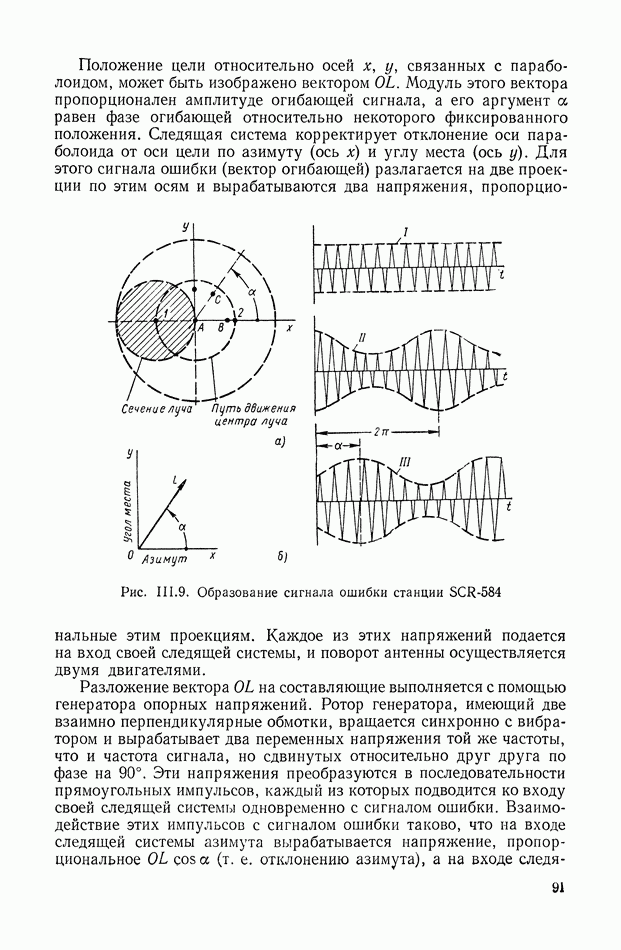
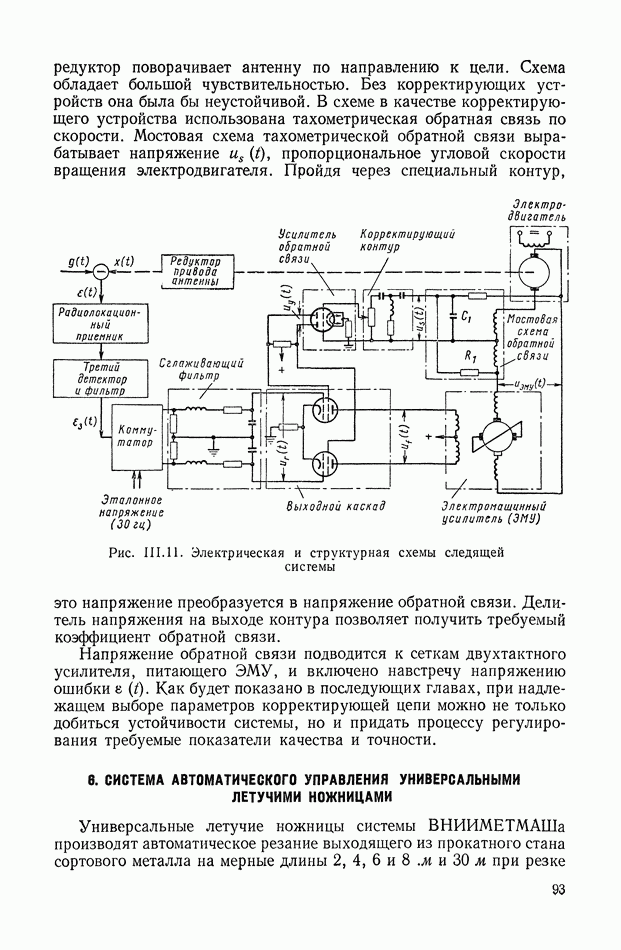
- 5. СЛЕДЯЩАЯ СИСТЕМА РАДИОЛОКАЦИОННОЙ СТАНЦИИ
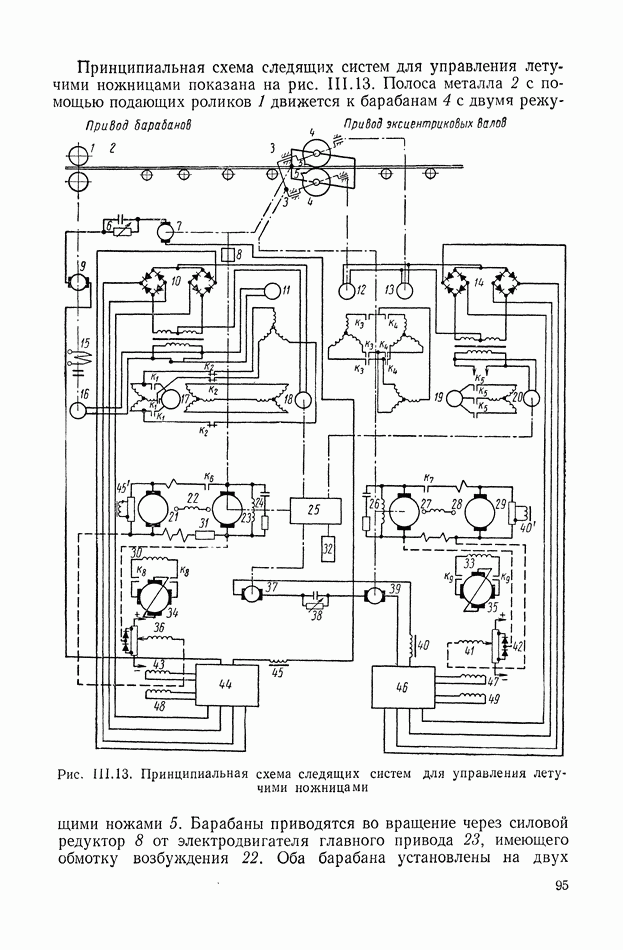
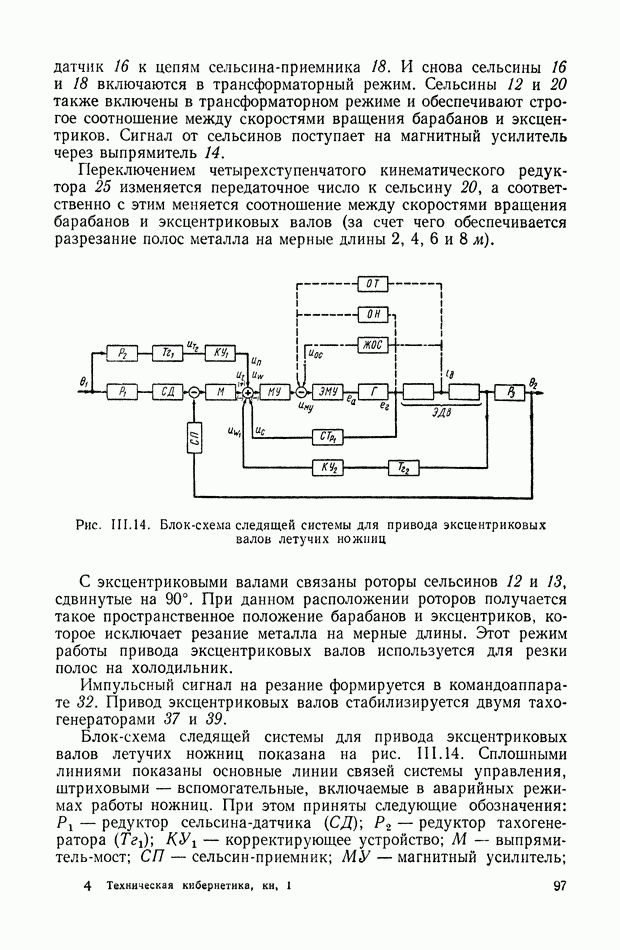
- 6. СИСТЕМА АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ УНИВЕРСАЛЬНЫМИ ЛЕТУЧИМИ НОЖНИЦАМИ
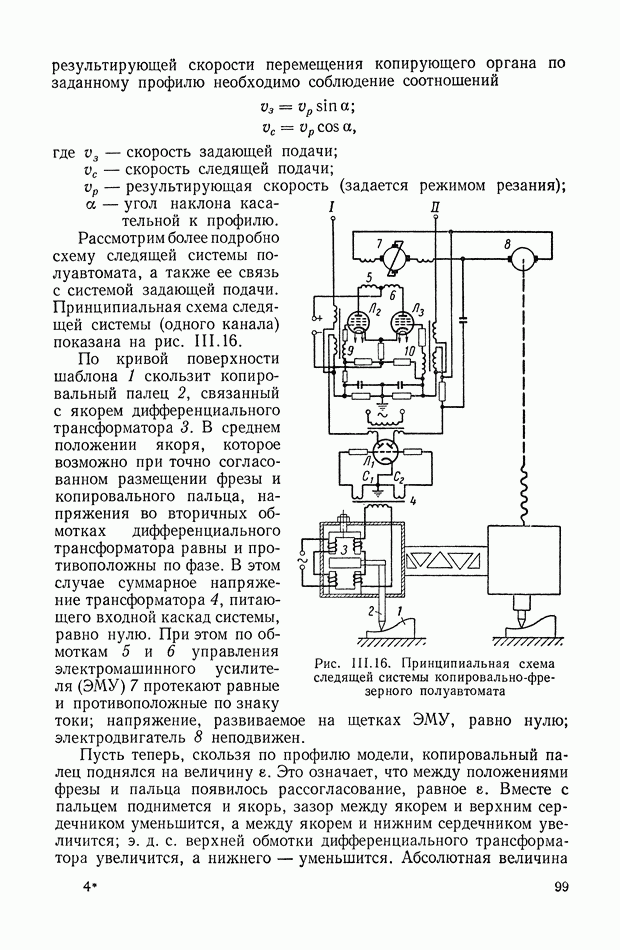
- 7. СЛЕДЯЩАЯ СИСТЕМА КОПИРОВАЛЬНО-ФРЕЗЕРНОГО ПОЛУАВТОМАТА
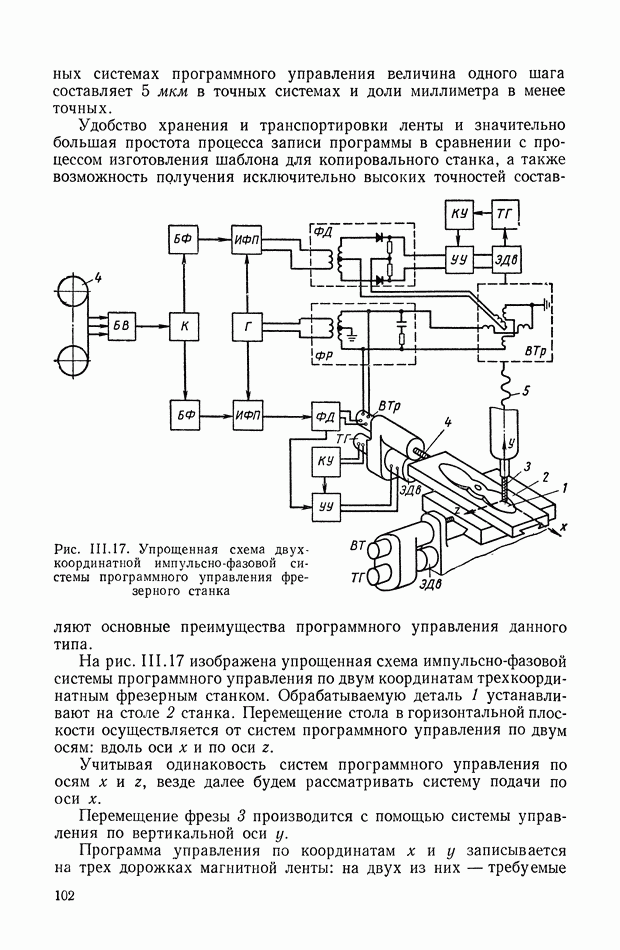
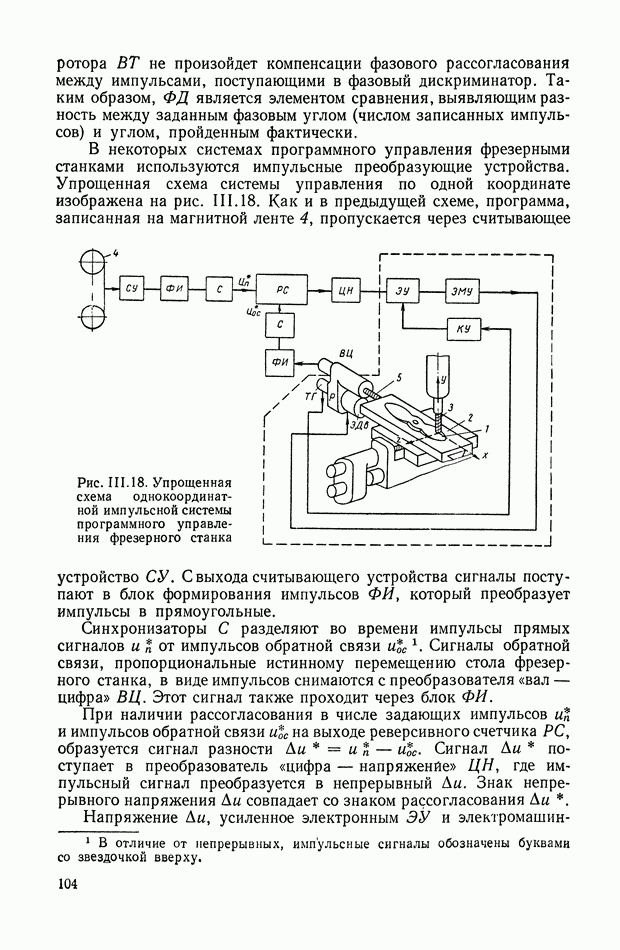
- 8. ПРОГРАММНОЕ УПРАВЛЕНИЕ МЕТАЛЛОРЕЖУЩИМИ СТАНКАМИ
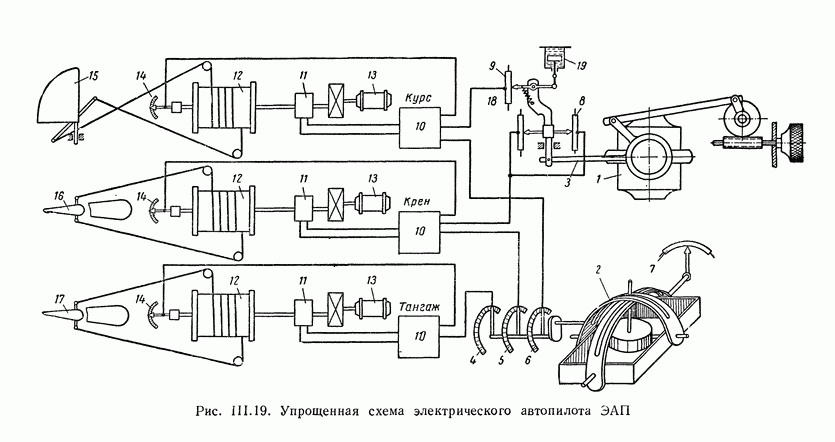
- 9. ПРИНЦИП ДЕЙСТВИЯ ЭЛЕКТРИЧЕСКОГО АВТОПИЛОТА
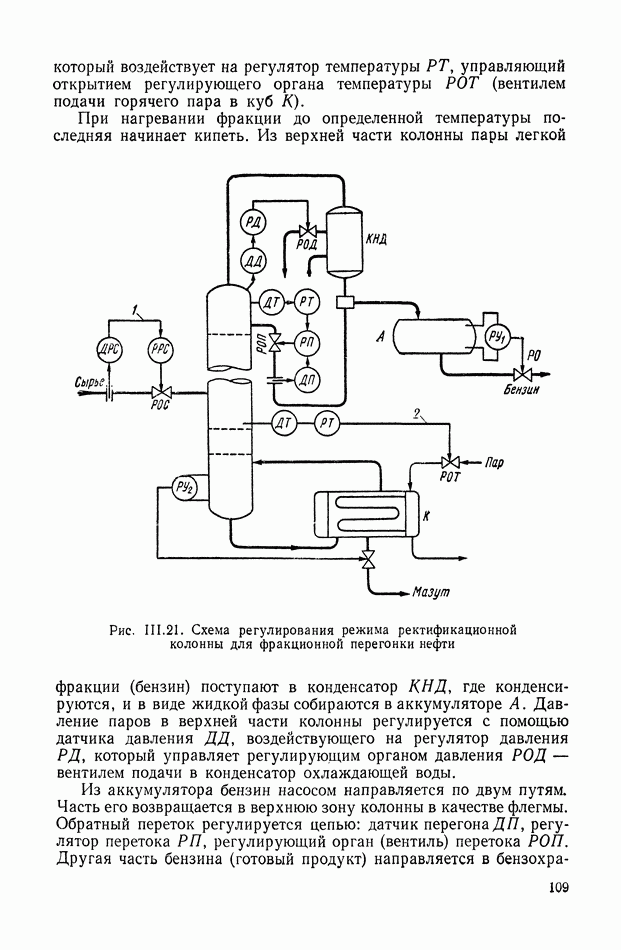
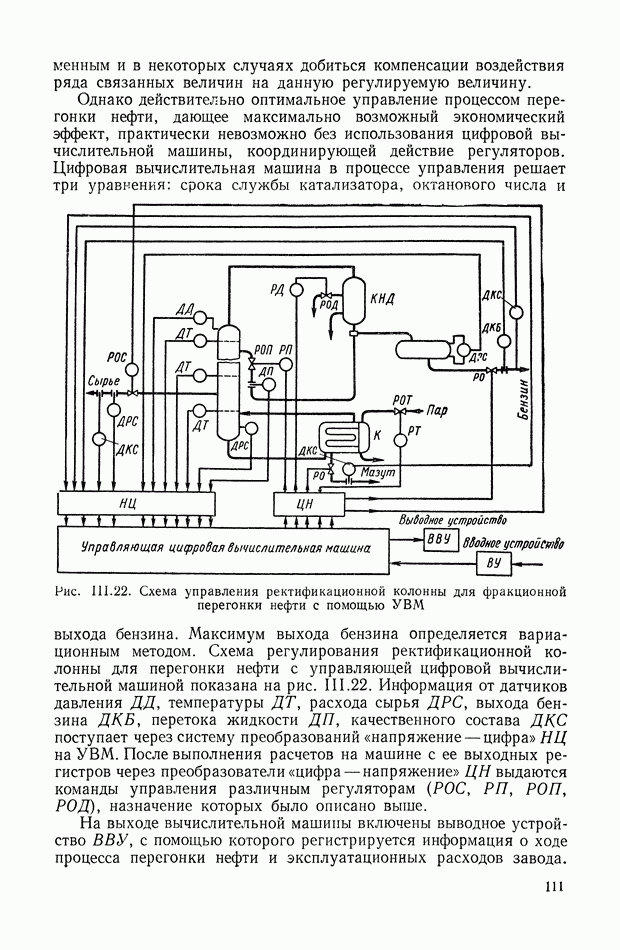
- 10. РЕГУЛИРОВАНИЕ МНОГИХ ВЕЛИЧИН ПРИ АВТОМАТИЧЕСКОМ УПРАВЛЕНИИ ПЕРЕГОНКОЙ НЕФТИ
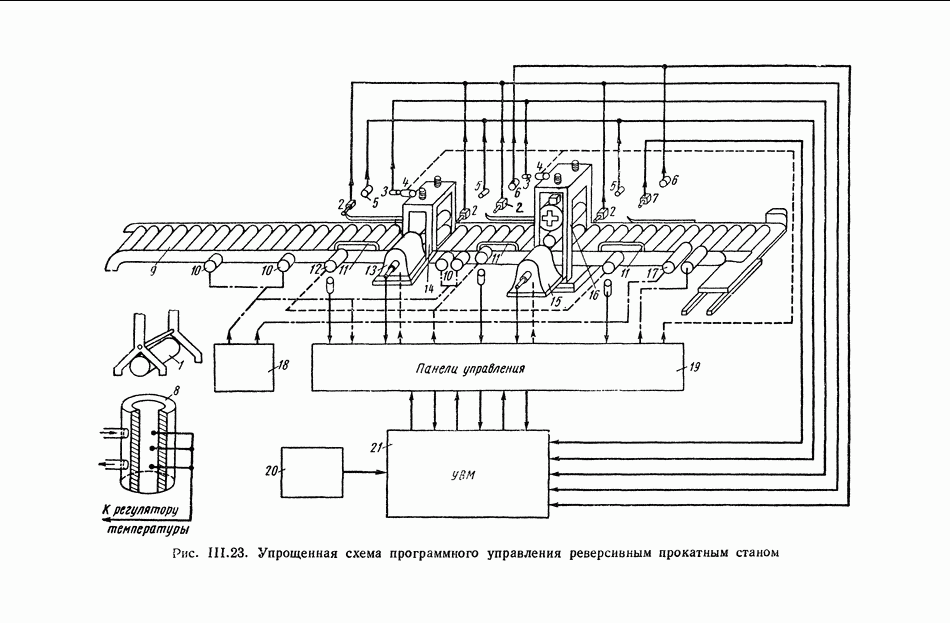
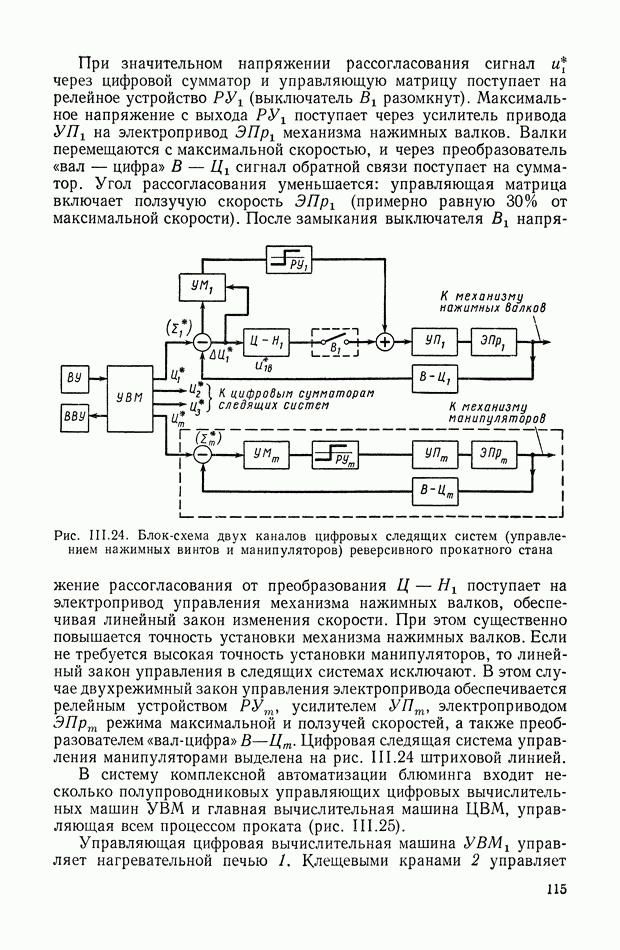
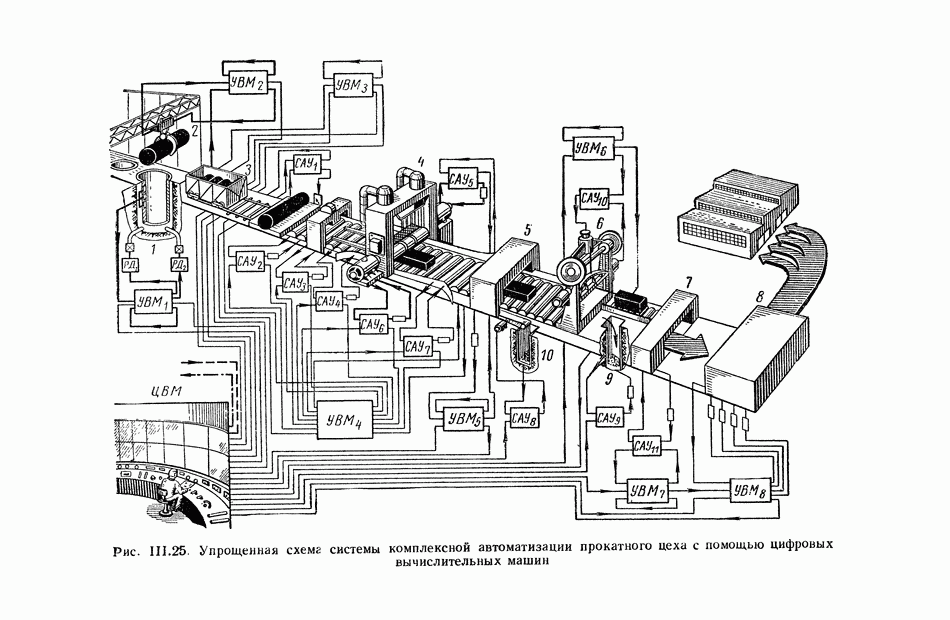
- 11. СИСТЕМА АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ РЕВЕРСИВНЫМ ПРОКАТНЫМ СТАНОМ С ИСПОЛЬЗОВАНИЕМ ЦИФРОВОЙ ВЫЧИСЛИТЕЛЬНОЙ МАШИНЫ
- ГЛАВА IV. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ЛАГРАНЖА ВТОРОГО РОДА
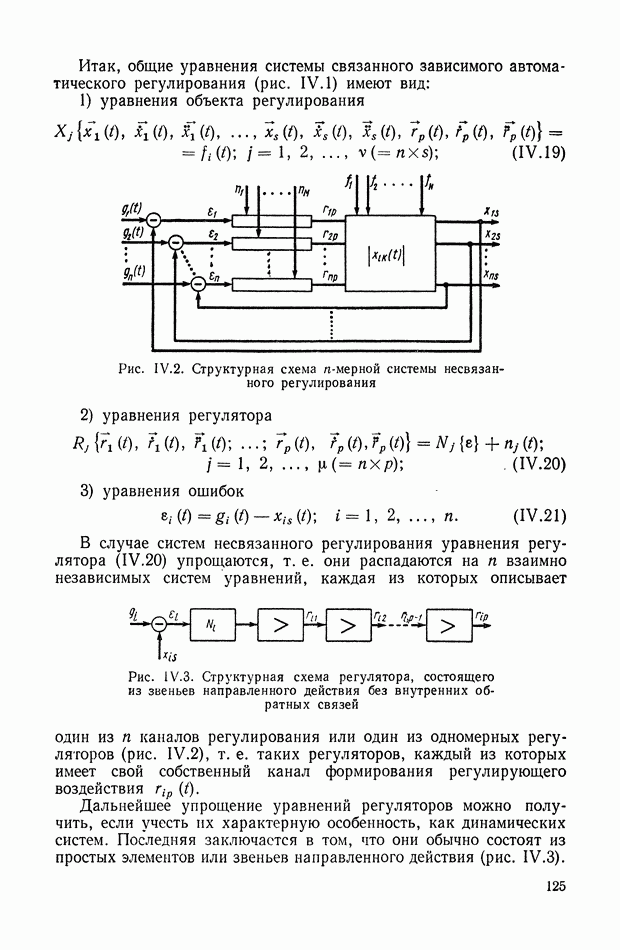
- 2. ОБЩИЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 3. ОБЩИЕ ЛИНЕАРИЗОВАННЫЕ УРАВНЕНИЯ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 4. ПРИМЕР СОСТАВЛЕНИЯ УРАВНЕНИЯ ОБЪЕКТА РЕГУЛИРОВАНИЯ
- ГЛАВА V. СТАТИКА СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. СТАТИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПРОСТЕЙШИХ ЗВЕНЬЕВ
- 2. СТАТИЧЕСКИЕ ХАРАКТЕРИСТИКИ ОСНОВНЫХ ТИПОВ СОЕДИНЕНИЙ ЗВЕНЬЕВ
- 3. КОРРЕКЦИЯ СТАТИЧЕСКИХ ХАРАКТЕРИСТИК
- Статическая характеристика замкнутой одномерной системы регулирования.
- Статическая характеристика линейной замкнутой системы.
- 4. СТАТИЗМ РЕГУЛИРОВАНИЯ
- 5. СТАТИКА ЛИНЕЙНЫХ СИСТЕМ С НЕСКОЛЬКИМИ РЕГУЛИРУЕМЫМИ ВЕЛИЧИНАМИ
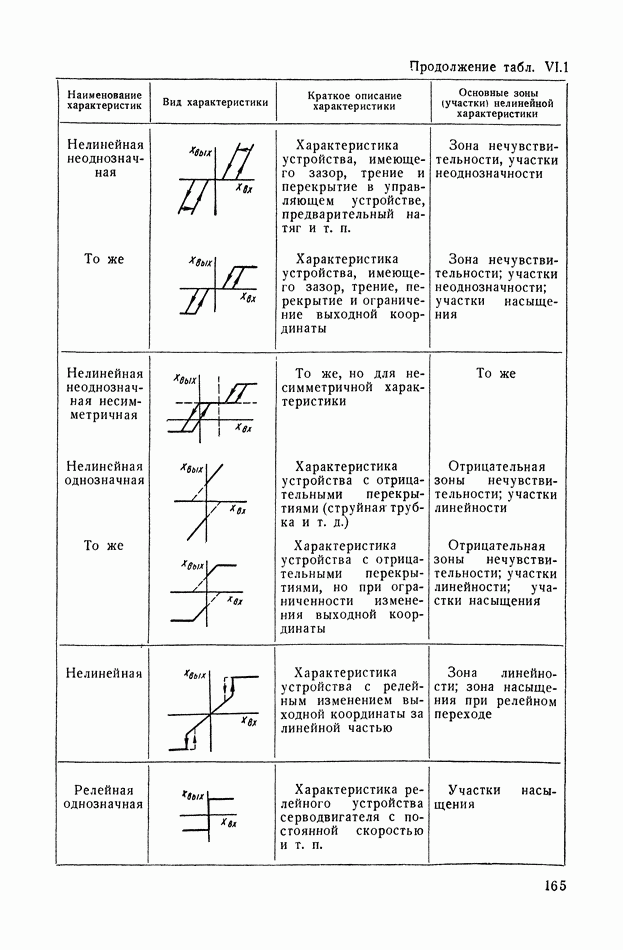
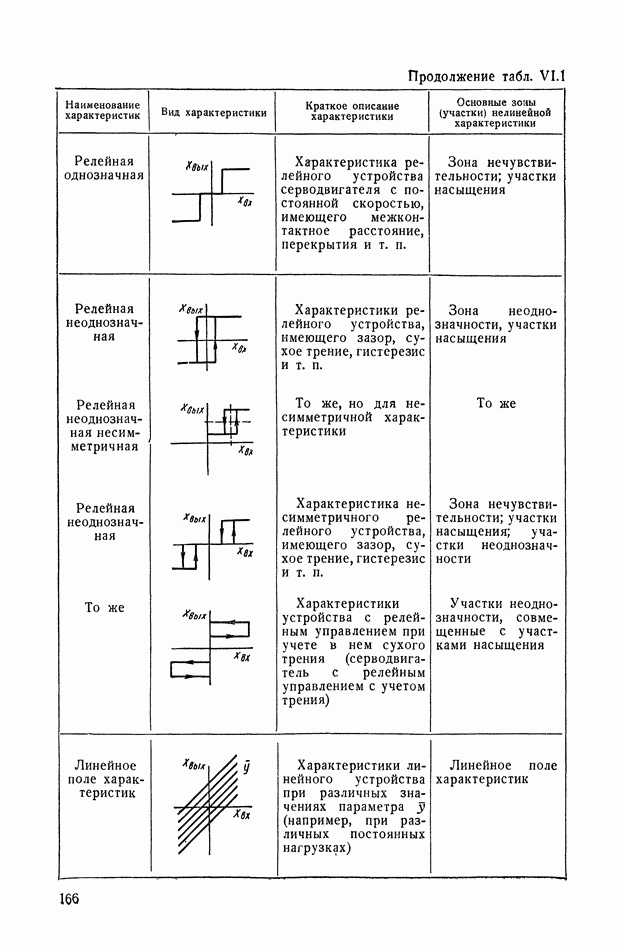
- ГЛАВА VI. ТИПИЧНЫЕ НЕЛИНЕЙНЫЕ СТАТИЧЕСКИЕ ХАРАКТЕРИСТИКИ ТИПОВЫХ ЗВЕНЬЕВ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. НЕЛИНЕЙНЫЕ ХАРАКТЕРИСТИКИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 2. ВИДЫ ТИПИЧНЫХ НЕЛИНЕЙНЫХ СТАТИЧЕСКИХ ХАРАКТЕРИСТИК СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 3. ТИПИЧНЫЕ НЕЛИНЕЙНЫЕ ХАРАКТЕРИСТИКИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 4. ЗОНЫ НЕЧУВСТВИТЕЛЬНОСТИ
- 5. ЗОНЫ ЛИНЕЙНОСТИ И НЕОДНОЗНАЧНОСТИ
- 6. ЗОНЫ НАСЫЩЕНИЯ
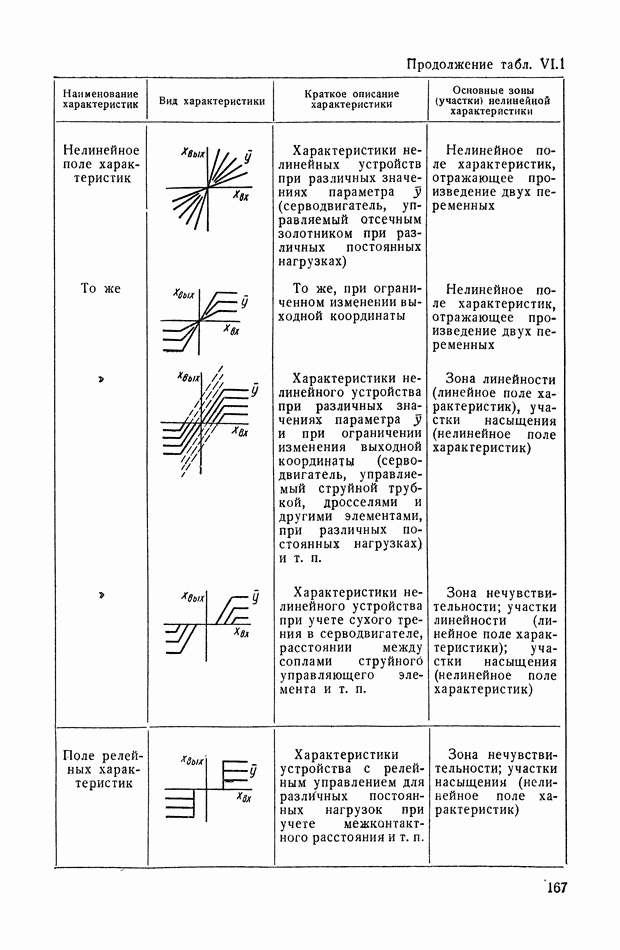
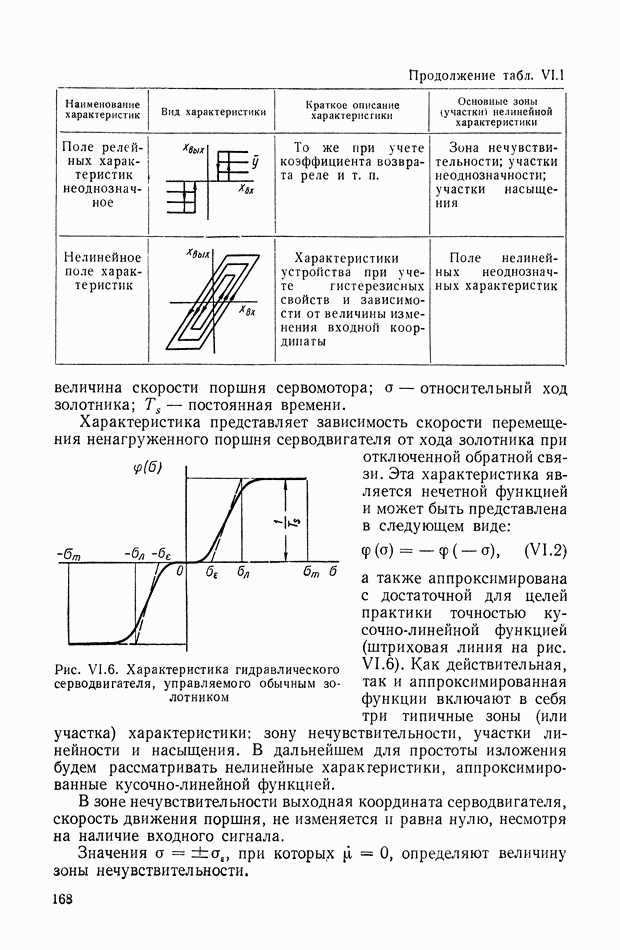
- 7. ПОЛЕ КРИВЫХ, ПРЕДСТАВЛЯЮЩИХ ХАРАКТЕРИСТИКУ СЕРВОДВИГАТЕЛЯ
- 8. ЭКСПЕРИМЕНТАЛЬНОЕ ВЫЯВЛЕНИЕ НЕЛИНЕЙНОСТИ ХАРАКТЕРИСТИК СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- ГЛАВА VII. ПЕРЕХОДНЫЕ ФУНКЦИИ, ПЕРЕДАТОЧНЫЕ ФУНКЦИИ И ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ДИНАМИЧЕСКИХ ЭЛЕМЕНТОВ
- 1. КЛАССИФИКАЦИЯ ДИНАМИЧЕСКИХ ЭЛЕМЕНТОВ
- 2. ОБЩЕЕ ОПРЕДЕЛЕНИЕ ИМПУЛЬСНОЙ ПЕРЕХОДНОЙ И ПЕРЕДАТОЧНОЙ ФУНКЦИЙ ДИНАМИЧЕСКОЙ СИСТЕМЫ ИЛИ ДИНАМИЧЕСКОГО ЭЛЕМЕНТА
- 3. ИМПУЛЬСНАЯ ПЕРЕХОДНАЯ ФУНКЦИЯ НЕПРЕРЫВНОЙ СТАЦИОНАРНОЙ ЛИНЕЙНОЙ СИСТЕМЫ
- 4. ПЕРЕДАТОЧНАЯ ФУНКЦИЯ НЕПРЕРЫВНОЙ ЛИНЕЙНОЙ СТАЦИОНАРНОЙ СИСТЕМЫ
- 5. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЛИНЕЙНОЙ СТАЦИОНАРНОЙ НЕПРЕРЫВНОЙ ДИНАМИЧЕСКОЙ СИСТЕМЫ
- 6. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДИНАМИЧЕСКОГО ЭЛЕМЕНТА С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
- 7. ПРИМЕНЕНИЕ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА К РЕШЕНИЮ УРАВНЕНИЙ ЭЛЕМЕНТА С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
- 8. ПЕРЕДАТОЧНАЯ ФУНКЦИЯ ДИНАМИЧЕСКОГО ЭЛЕМЕНТА С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
- 9. ПЕРЕДАТОЧНАЯ ФУНКЦИЯ ПОСЛЕДОВАТЕЛЬНОГО СОЕДИНЕНИЯ ДИНАМИЧЕСКИХ ЭЛЕМЕНТОВ С СОСРЕДОТОЧЕННЫМИ И С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
- 10. ПЕРЕДАТОЧНАЯ ФУНКЦИЯ ЗАПАЗДЫВАЮЩЕГО ЭЛЕМЕНТА
- 11. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЭЛЕМЕНТА С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
- 12. ИМПУЛЬСНАЯ ПЕРЕХОДНАЯ ФУНКЦИЯ ДИНАМИЧЕСКОГО ЭЛЕМЕНТА С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
- 13. ПЕРЕДАТОЧНАЯ ФУНКЦИЯ СИСТЕМЫ С ГАРМОНИЧЕСКОЙ МОДУЛЯЦИЕЙ
- 14 ИМПУЛЬСНАЯ ПЕРЕХОДНАЯ И ПЕРЕДАТОЧНАЯ ФУНКЦИИ ДИСКРЕТНОЙ ЛИНЕЙНОЙ СТАЦИОНАРНОЙ СИСТЕМЫ
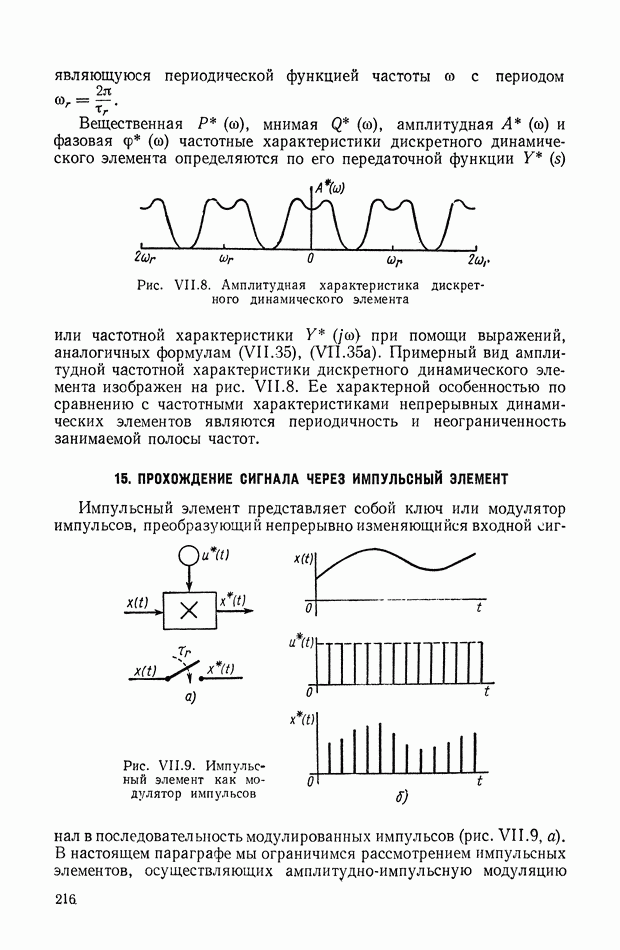
- 15. ПРОХОЖДЕНИЕ СИГНАЛА ЧЕРЕЗ ИМПУЛЬСНЫЙ ЭЛЕМЕНТ
- 16. ПОСЛЕДОВАТЕЛЬНОЕ СОЕДИНЕНИЕ ИМПУЛЬСНОГО ЭЛЕМЕНТА И НЕПРЕРЫВНОГО ДИНАМИЧЕСКОГО ЭЛЕМЕНТА
- 17. ИМПУЛЬСНАЯ ПЕРЕХОДНАЯ ФУНКЦИЯ ЛИНЕЙНОЙ НЕСТАЦИОНАРНОЙ СИСТЕМЫ (СИСТЕМЫ С ПЕРЕМЕННЫМИ ПАРАМЕТРАМИ)
- 18. ПЕРЕДАТОЧНАЯ ФУНКЦИЯ НЕПРЕРЫВНОЙ ЛИНЕЙНОЙ НЕСТАЦИОНАРНОЙ СИСТЕМЫ
- 19. МНОГОМЕРНЫЕ ИМПУЛЬСНЫЕ ПЕРЕХОДНЫЕ И ПЕРЕДАТОЧНЫЕ ФУНКЦИИ НЕЛИНЕЙНЫХ СИСТЕМ
- 20. МНОГОМЕРНЫЕ ПЕРЕДАТОЧНЫЕ ФУНКЦИИ НЕЛИНЕЙНЫХ СИСТЕМ
- ГЛАВА VIII. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ, ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ И ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ НЕПРЕРЫВНЫХ ЛИНЕЙНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
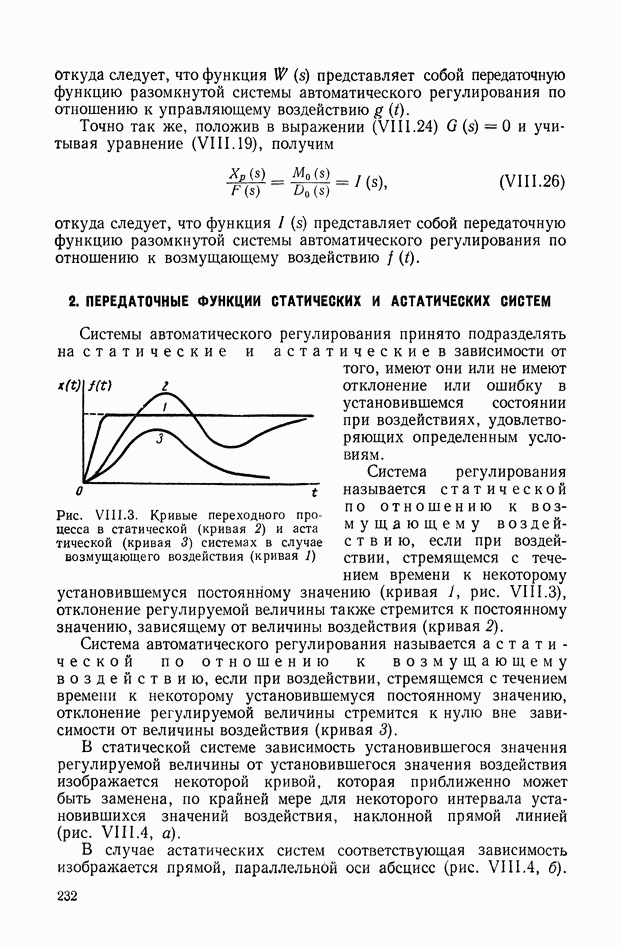
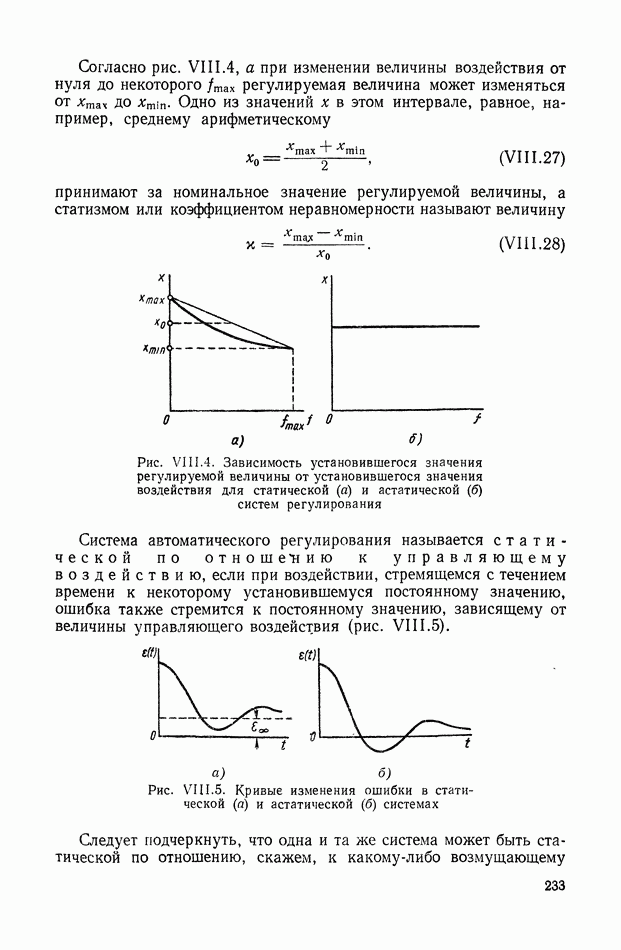
- 2. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ СТАТИЧЕСКИХ И АСТАТИЧЕСКИХ СИСТЕМ
- 3. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ
- 4. ВЗАИМНАЯ СВЯЗЬ МЕЖДУ ЧАСТОТНЫМИ ХАРАКТЕРИСТИКАМИ ЗАМКНУТОЙ И РАЗОМКНУТОЙ СИСТЕМЫ
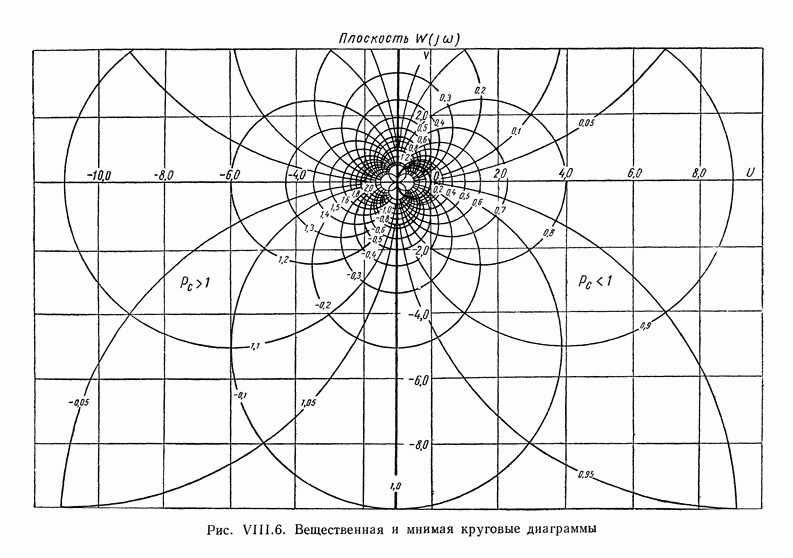
- 5. КРУГОВЫЕ ДИАГРАММЫ
- 6. НОМОГРАММЫ ЗАМЫКАНИЯ
- 7. УСЛОВИЯ ОДНОЗНАЧНОЙ связи МЕЖДУ ЧАСТОТНЫМИ ХАРАКТЕРИСТИКАМИ
- 8. ОПРЕДЕЛЕНИЕ ПЕРЕДАТОЧНОЙ ФУНКЦИИ ПО ОДНОЙ ИЗ ЧАСТОТНЫХ ХАРАКТЕРИСТИК, ЗАДАННОЙ АНАЛИТИЧЕСКИ
- 9. ФОРМУЛА ДЛЯ ВЫЧИСЛЕНИЯ ФАЗОВОЙ ЧАСТОТНОЙ ХАРАКТЕРИСТИКИ ПО ЗАДАННОЙ АМПЛИТУДНОЙ ЧАСТОТНОЙ ХАРАКТЕРИСТИКЕ
- 10. ЗАВИСИМОСТЬ МЕЖДУ ЛОГАРИФМИЧЕСКОЙ АМПЛИТУДНОЙ И ФАЗОВОЙ ЧАСТОТНЫМИ ХАРАКТЕРИСТИКАМИ
- 11. ГРАФИЧЕСКИЙ МЕТОД ОПРЕДЕЛЕНИЯ ФАЗОВОЙ ХАРАКТЕРИСТИКИ ПО ЗАДАННОЙ АМПЛИТУДНОЙ ХАРАКТЕРИСТИКЕ
- 12. ИНТЕГРАЛЬНЫЕ ВЫРАЖЕНИЯ ДЛЯ ОШИБКИ И ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 13. ТИПОВЫЕ ЗВЕНЬЯ
- 14. АПЕРИОДИЧЕСКОЕ ЗВЕНО
- 15. КОЛЕБАТЕЛЬНОЕ ЗВЕНО
- 16. ИНТЕГРИРУЮЩЕЕ ЗВЕНО
- 17. ДИФФЕРЕНЦИРУЮЩЕЕ ЗВЕНО ПЕРВОГО ПОРЯДКА
- 18. ДИФФЕРЕНЦИРУЮЩЕЕ ЗВЕНО ВТОРОГО ПОРЯДКА
- 19. КОЭФФИЦИЕНТЫ ОШИБКИ
- ГЛАВА IX. МЕТОДЫ СТРУКТУРНЫХ ПРЕОБРАЗОВАНИЙ В СИСТЕМАХ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. ГРАФИЧЕСКИЕ ИЗОБРАЖЕНИЯ УСЛОВИЙ ПРЕОБРАЗОВАНИЯ СИГНАЛОВ
- 2. СХЕМЫ С ЭЛЕМЕНТАМИ, ОБЛАДАЮЩИМИ И НЕ ОБЛАДАЮЩИМИ СВОЙСТВОМ НАПРАВЛЕННОСТИ ДЕЙСТВИЯ
- 3. ДЕТАЛИЗИРОВАННЫЕ СТРУКТУРЫ
- 4. ПРЕОБРАЗОВАНИЯ МНОГОКОНТУРНЫХ СТРУКТУРНЫХ СХЕМ, ДОПУСКАЮЩИХ ПОСЛЕДОВАТЕЛЬНОЕ ПРИМЕНЕНИЕ ПРАВИЛ СВЕРТЫВАНИЯ КОНТУРОВ, И НЕКОТОРЫЕ ЭКВИВАЛЕНТНЫЕ ПРЕОБРАЗОВАНИЯ
- 5. ПРЕОБРАЗОВАНИЯ ПЕРЕКРЕСТНЫХ СТРУКТУРНЫХ СХЕМ МЕТОДОМ РАЗВЯЗКИ КОНТУРОВ И НЕКОТОРЫЕ ЭКВИВАЛЕНТНЫЕ ПРЕОБРАЗОВАНИЯ
- 6. ПРИМЕНЕНИЕ СТРУКТУРНЫХ МЕТОДОВ ДЛЯ ОПРЕДЕЛЕНИЯ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ МНОГОКОНТУРНЫХ СИСТЕМ
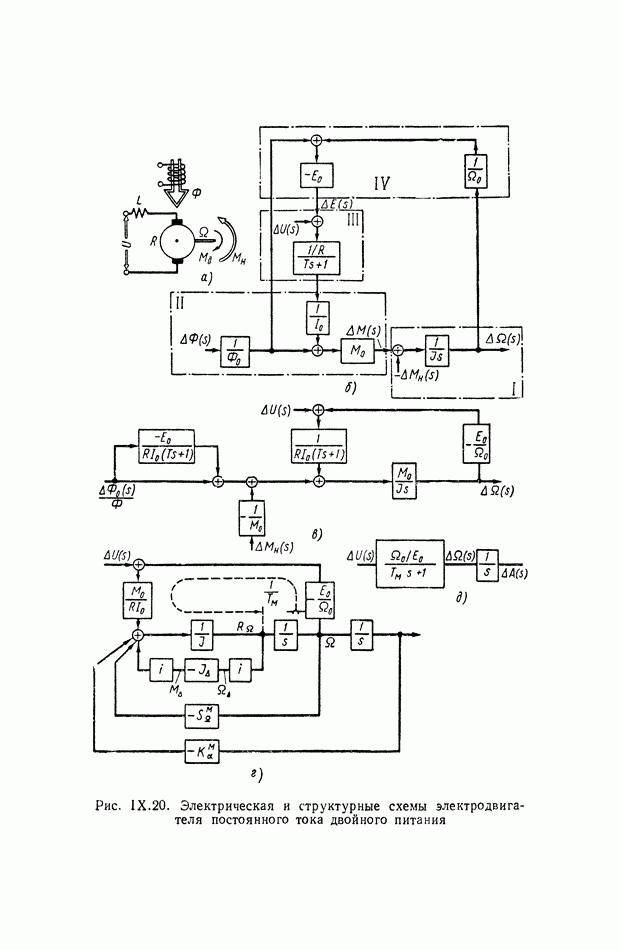
- 7. СОСТАВЛЕНИЕ И ПРЕОБРАЗОВАНИЕ СТРУКТУРНОЙ СХЕМЫ НА ПРИМЕРЕ ЭЛЕКТРОДВИГАТЕЛЯ ПОСТОЯННОГО ТОКА ДВОЙНОГО ПИТАНИЯ
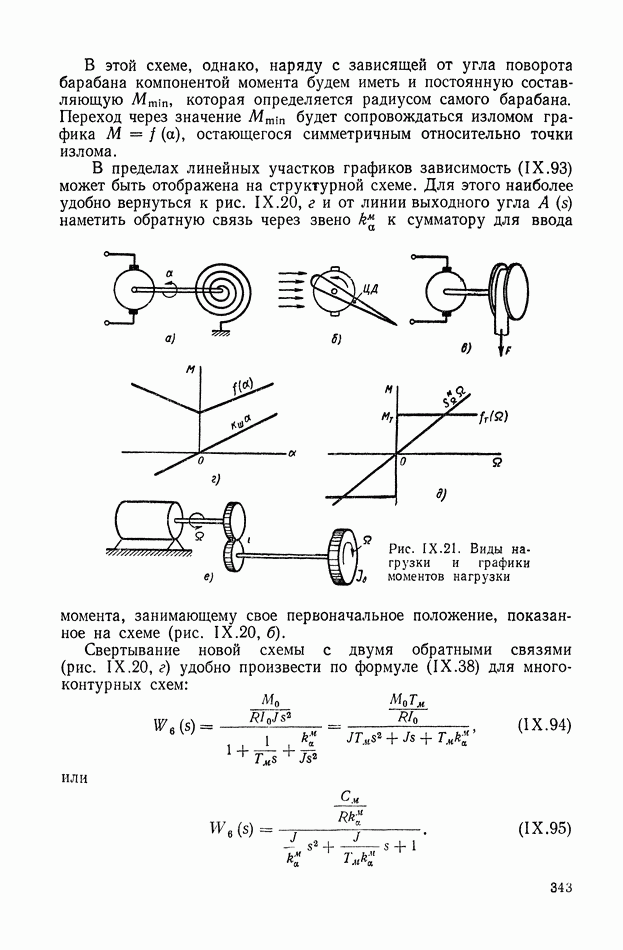
- Учет зависимости момента нагрузки от угла поворота вала и его производных по времени.
- 8. СТРУКТУРНЫЕ СХЕМЫ МЕХАНИЧЕСКИХ ОБЪЕКТОВ РЕГУЛИРОВАНИЯ С РЕДУКТОРАМИ, ДИФФЕРЕНЦИАЛАМИ И УПРУГИМИ ЭЛЕМЕНТАМИ В СИЛОВЫХ ПЕРЕДАЧАХ
- 9. ПРАВИЛА СТРУКТУРНЫХ ПРЕОБРАЗОВАНИЙ ДЛЯ СИСТЕМ С ПЕРЕМЕННЫМИ ПАРАМЕТРАМИ
- 10. ФУНКЦИОНАЛЬНЫЕ СТРУКТУРНЫЕ СХЕМЫ ДЛЯ АНАЛИЗА СОВМЕСТНЫХ СТАТИЧЕСКИХ ХАРАКТЕРИСТИК НЕЛИНЕЙНЫХ ЗВЕНЬЕВ
- ГЛАВА X. ПРИМЕРЫ СОСТАВЛЕНИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ, СТРУКТУРНЫХ СХЕМ И ПЕРЕДАТОЧНЫХ ФУНКЦИЙ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. СИСТЕМА АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ СКОРОСТИ ВРАЩЕНИЯ ГИДРОТУРБИНЫ
- 2. ЭЛЕКТРОННЫЙ РЕГУЛЯТОР НАПРЯЖЕНИЯ ВЭИ
- 3. СИСТЕМА АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ МОЩНОСТИ ЯДЕРНОГО ЭНЕРГЕТИЧЕСКОГО РЕАКТОРА НА ТЕПЛОВЫХ НЕЙТРОНАХ
- 4. СЛЕДЯЩАЯ СИСТЕМА РАДИОЛОКАЦИОННОЙ СТАНЦИИ
- 5. СИСТЕМА АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ УНИВЕРСАЛЬНЫХ ЛЕТУЧИХ НОЖНИЦ
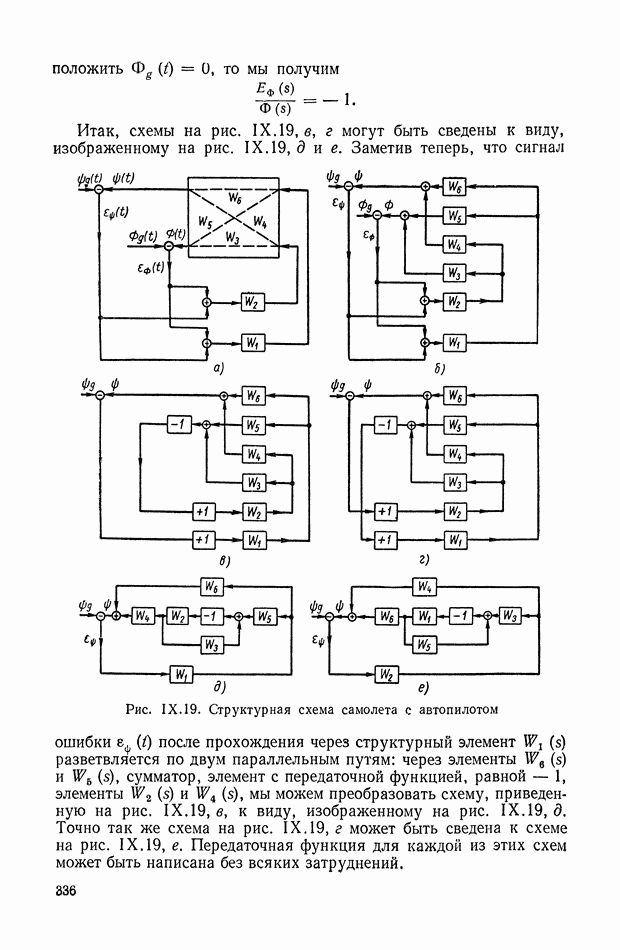
- 6. САМОЛЕТ С АВТОПИЛОТОМ
- 7. СЛЕДЯЩАЯ СИСТЕМА КОПИРОВАЛЬНО-ФРЕЗЕРНОГО СТАНКА
- РАЗДЕЛ II. АНАЛИЗ УСТОЙЧИВОСТИ НЕПРЕРЫВНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- ГЛАВА XI. ОБЩАЯ ПОСТАНОВКА ЗАДАЧИ УСТОЙЧИВОСТИ ПО ЛЯПУНОВУ И АНАЛИЗ УСТОЙЧИВОСТИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. ПОСТАНОВКА ЗАДАЧИ ОБ УСТОЙЧИВОСТИ В ТЕОРИИ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 2. ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ УСТАНОВИВШИХСЯ ДВИЖЕНИЙ ПО УРАВНЕНИЮ ПЕРВОГО ПРИБЛИЖЕНИЯ
- 3. О ПРЯМОМ МЕТОДЕ ЛЯПУНОВА
- 4. О ПРИМЕНЕНИИ ПРЯМОГО МЕТОДА ЛЯПУНОВА К АНАЛИЗУ УСТОЙЧИВОСТИ ОДНОГО КЛАССА СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- ГЛАВА XII. КРИТЕРИИ И МЕТОДЫ АНАЛИЗА УСТОЙЧИВОСТИ ЛИНЕАРИЗОВАННЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЙ
- 1. УСТОЙЧИВОСТЬ И ПРИНЦИП АРГУМЕНТА
- 2. КРИТЕРИЙ УСТОЙЧИВОСТИ МИХАЙЛОВА
- 3. КРИТЕРИЙ УСТОЙЧИВОСТИ РАУСА И ГУРВИЦА
- 4. ЧАСТОТНЫЙ КРИТЕРИЙ УСТОЙЧИВОСТИ
- 5. ОБОБЩЕНИЕ ЧАСТОТНОГО КРИТЕРИЯ НА АСТАТИЧЕСКИЕ СИСТЕМЫ
- 6. ОБОБЩЕНИЕ ЧАСТОТНОГО КРИТЕРИЯ НА СЛУЧАЙ, КОГДА РАЗОМКНУТАЯ СИСТЕМА НЕУСТОЙЧИВА
- 7. ЧАСТОТНЫЙ КРИТЕРИЙ УСТОЙЧИВОСТИ ДЛЯ ОБРАТНОЙ АМПЛИТУДНО-ФАЗОВОЙ ХАРАКТЕРИСТИКИ
- 8. АНАЛИЗ УСТОЙЧИВОСТИ ОДНОКОНТУРНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ПО ИХ ЛОГАРИФМИЧЕСКИМ ЧАСТОТНЫМ ХАРАКТЕРИСТИКАМ
- 9. ПРИБЛИЖЕННЫЙ СПОСОБ ПОСТРОЕНИЯ ЛОГАРИФМИЧЕСКИХ ЧАСТОТНЫХ ХАРАКТЕРИСТИК ОДНОКОНТУРНЫХ СИСТЕМ
- 10. ОБОБЩЕНИЕ ЧАСТОТНОГО КРИТЕРИЯ УСТОЙЧИВОСТИ НА МНОГОКОНТУРНЫЕ СИСТЕМЫ
- 11. АНАЛИЗ УСТОЙЧИВОСТИ МНОГОКОНТУРНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ПРИ ПОМОЩИ ЛОГАРИФМИЧЕСКИХ ЧАСТОТНЫХ ХАРАКТЕРИСТИК
- ГЛАВА XIII. ВЫДЕЛЕНИЕ ОБЛАСТЕЙ УСТОЙЧИВОСТИ
- 1. ПОНЯТИЕ О Д-РАЗБИЕНИИ ПРОСТРАНСТВА КОЭФФИЦИЕНТОВ ХАРАКТЕРИСТИЧЕСКОГО УРАВНЕНИЯ И ПРОСТРАНСТВА ПАРАМЕТРОВ
- 2. Д-РАЗБИЕНИЕ ПЛОСКОСТИ ОДНОГО КОМПЛЕКСНОГО ПАРАМЕТРА
- 3. СВЯЗЬ Д-РАЗБИЕНИЯ С КРИТЕРИЯМИ УСТОЙЧИВОСТИ
- 4. Д-РАЗБИЕНИЕ ПЛОСКОСТИ ДВУХ ДЕЙСТВИТЕЛЬНЫХ ПАРАМЕТРОВ (ДИАГРАММА ВЫШНЕГРАДСКОГО)
- 5. УСЛОВИЯ СУЩЕСТВОВАНИЯ ОБЛАСТИ УСТОЙЧИВОСТИ
- ГЛАВА XIV. ПРИМЕРЫ АНАЛИЗА УСТОЙЧИВОСТИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. СИСТЕМА АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ СКОРОСТИ ВРАЩЕНИЯ ГИДРОТУРБИНЫ
- 2. СЛЕДЯЩАЯ СИСТЕМА КОПИРОВАЛЬНО-ФРЕЗЕРНОГО СТАНКА
- 3. СИСТЕМА АВТОМАТИЧЕСКОЙ СТАБИЛИЗАЦИИ САМОЛЕТА (АВТОПИЛОТ)
- 4. СИСТЕМА АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ МОЩНОСТИ ЯДЕРНОГО ЭНЕРГЕТИЧЕСКОГО РЕАКТОРА
- РАЗДЕЛ III. АНАЛИЗ ПЕРЕХОДНЫХ ПРОЦЕССОВ И КАЧЕСТВА ЛИНЕЙНЫХ НЕПРЕРЫВНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- ГЛАВА XV. ЧАСТОТНЫЙ МЕТОД АНАЛИЗА ПЕРЕХОДНЫХ ПРОЦЕССОВ
- 1. ОБОБЩЕННЫЕ ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ И ИХ СВЯЗЬ С ПЕРЕХОДНЫМИ ПРОЦЕССАМИ
- 2. ОПРЕДЕЛЕНИЕ ОБОБЩЕННЫХ ЧАСТОТНЫХ ХАРАКТЕРИСТИК В ОБЩЕМ СЛУЧАЕ
- 3. СЛУЧАЙ, КОГДА ФУНКЦИЯ X(s) НЕ СОДЕРЖИТ ОСОБЕННОСТЕЙ ВО ВСЕЙ ПРАВОЙ ПОЛУПЛОСКОСТИ И НА МНИМОЙ ОСИ
- 4. СВЯЗЬ МЕЖДУ ЧАСТОТНЫМИ ХАРАКТЕРИСТИКАМИ P(w), Q(w) И ИМПУЛЬСНОЙ ПЕРЕХОДНОЙ ФУНКЦИЕЙ k(t)
- 5. СЛУЧАЙ, КОГДА ВСЕ ПОЛЮСА ФУНКЦИИ X(s) РАСПОЛОЖЕНЫ В ЛЕВОЙ ПОЛУПЛОСКОСТИ, ЗА ИСКЛЮЧЕНИЕМ ПОЛЮСА В НАЧАЛЕ КООРДИНАТ
- 6. СВЯЗЬ МЕЖДУ ЧАСТОТНЫМИ ХАРАКТЕРИСТИКАМИ И ПЕРЕХОДНОЙ ФУНКЦИЕЙ h(t)
- 7. СЛУЧАЙ, КОГДА ФУНКЦИЯ X(s) ИМЕЕТ ДВА СОПРЯЖЕННЫХ ПОЛЮСА НА МНИМОЙ ОСИ
- 8. АНАЛИЗ ПЕРЕХОДНЫХ ПРОЦЕССОВ МЕТОДОМ ТРАПЕЦЕИДАЛЬНЫХ ЧАСТОТНЫХ ХАРАКТЕРИСТИК
- 9. О НЕКОТОРЫХ ЧАСТНЫХ СЛУЧАЯХ МЕТОДА ТРАПЕЦЕИДАЛЬНЫХ ЧАСТОТНЫХ ХАРАКТЕРИСТИК
- 10. ОБ УСЛОВИЯХ ПРИМЕНИМОСТИ ЧАСТОТНОГО МЕТОДА АНАЛИЗА ПЕРЕХОДНЫХ ПРОЦЕССОВ
- 11. ОПРЕДЕЛЕНИЕ ДИСКРЕТНЫХ ЗНАЧЕНИЙ ПЕРЕХОДНОЙ ФУНКЦИИ
- ГЛАВА XVI. ЧАСТОТНЫЙ МЕТОД АНАЛИЗА КАЧЕСТВА
- 1. ЧАСТОТНЫЙ КРИТЕРИЙ КАЧЕСТВА РЕГУЛИРОВАНИЯ
- 2. ЧАСТОТНЫЙ КРИТЕРИЙ ОТСУТСТВИЯ ПЕРЕРЕГУЛИРОВАНИЙ И ЧАСТОТНЫЙ КРИТЕРИЙ МОНОТОННОСТИ
- 3. О ПРОВЕРКЕ ВЫПОЛНЕНИЯ СФОРМУЛИРОВАННЫХ КРИТЕРИЕВ
- 4. НЕКОТОРЫЕ ПРИЗНАКИ НЕУДОВЛЕТВОРЕНИЯ КРИТЕРИЕВ КАЧЕСТВА И КРИТЕРИЕВ ОТСУТСТВИЯ ПЕРЕРЕГУЛИРОВАНИЙ И МОНОТОННОСТИ
- 5. НЕКОТОРЫЕ ЭЛЕМЕНТАРНЫЕ СВОЙСТВА ЧАСТОТНЫХ ХАРАКТЕРИСТИК
- 6. ДОСТАТОЧНЫЕ УСЛОВИЯ ДЛЯ МАЛЫХ ПЕРЕРЕГУЛИРОВАНИЙ И НЕОБХОДИМЫЕ УСЛОВИЯ ДЛЯ ОТСУТСТВИЯ ПЕРЕРЕГУЛИРОВАНИЙ
- 7. КРИТЕРИЙ, ОПРЕДЕЛЯЮЩИЙ ДОСТАТОЧНЫЕ УСЛОВИЯ ДЛЯ МОНОТОННОСТИ
- 8. ОЦЕНКИ ВЕЛИЧИНЫ ПЕРЕРЕГУЛИРОВАНИЯ И ВРЕМЕНИ ПЕРЕХОДНОГО ПРОЦЕССА
- 9. ОЦЕНКА АБСОЛЮТНОГО ЗНАЧЕНИЯ РАЗНОСТИ МЕЖДУ ПЕРЕХОДНЫМИ ФУНКЦИЯМИ ПО СООТВЕТСТВУЮЩИМ ИМ ЧАСТОТНЫМ ХАРАКТЕРИСТИКАМ
- 10. СВЯЗЬ МЕЖДУ СВОЙСТВАМИ АМПЛИТУДНО-ФАЗОВОЙ ХАРАКТЕРИСТИКИ РАЗОМКНУТОЙ СИСТЕМЫ И КАЧЕСТВОМ
- 11. ТРЕБОВАНИЯ К ЧАСТОТНЫМ ХАРАКТЕРИСТИКАМ, ОБЕСПЕЧИВАЮЩИЕ ВЫСОКУЮ ТОЧНОСТЬ В СЛЕДЯЩИХ СИСТЕМАХ
- 12. СВЯЗЬ МЕЖДУ СВОЙСТВАМИ ЛОГАРИФМИЧЕСКОЙ АМПЛИТУДНОЙ ХАРАКТЕРИСТИКИ И КАЧЕСТВОМ
- 13. ОПРЕДЕЛЕНИЕ ВЕЛИЧИНЫ ПЕРЕДАТОЧНОГО КОЭФФИЦИЕНТА ИЛИ ДОБРОТНОСТИ ПО ЛОГАРИФМИЧЕСКОЙ АМПЛИТУДНОЙ ХАРАКТЕРИСТИКЕ
- 14. ОПРЕДЕЛЕНИЕ УСТАНОВИВШЕЙСЯ ОШИБКИ ПРИ ГАРМОНИЧЕСКОМ УПРАВЛЯЮЩЕМ ВОЗДЕЙСТВИИ ПО ЛОГАРИФМИЧЕСКОЙ АМПЛИТУДНОЙ ХАРАКТЕРИСТИКЕ
- 15. ПРИБЛИЖЕННЫЙ СПОСОБ ВЫЧИСЛЕНИЯ ПЕРЕХОДНОГО ПРОЦЕССА ПО СОПРЯГАЮЩИМ ЧАСТОТАМ ЛОГАРИФМИЧЕСКОЙ АМПЛИТУДНОЙ ЧАСТОТНОЙ ХАРАКТЕРИСТИКИ
- 16. НОМОГРАММА ДЛЯ ОПРЕДЕЛЕНИЯ ЗАПАСА УСТОЙЧИВОСТИ, ПОКАЗАТЕЛЕЙ КАЧЕСТВА И КОЭФФИЦИЕНТОВ ОШИБОК ПО ВИДУ ЛОГАРИФМИЧЕСКОЙ АМПЛИТУДНОЙ ХАРАКТЕРИСТИКИ
- ГЛАВА XVII. СВЯЗЬ МЕЖДУ КАЧЕСТВОМ ПЕРЕХОДНОГО ПРОЦЕССА И РАСПРЕДЕЛЕНИЕМ НУЛЕЙ И ПОЛЮСОВ ПЕРЕДАТОЧНОЙ ФУНКЦИИ. МЕТОД КОРНЕВЫХ ГОДОГРАФОВ
- 2. АНАЛИЗ РАСПРЕДЕЛЕНИЯ КОРНЕЙ ХАРАКТЕРИСТИЧЕСКОГО УРАВНЕНИЯ СИСТЕМЫ И ОЦЕНКА КАЧЕСТВА ПЕРЕХОДНОГО ПРОЦЕССА
- 3. ГЕОМЕТРИЧЕСКИЙ МЕТОД ПОСТРОЕНИЯ КОРНЕВОГО ГОДОГРАФА
- 4. АНАЛИТИЧЕСКОЕ ПОСТРОЕНИЕ ГЕОМЕТРИЧЕСКОГО МЕСТА КОРНЕЙ
- 5. ОПРЕДЕЛЕНИЕ ОБЛАСТЕЙ УСТОЙЧИВОСТИ ЛИНЕЙНЫХ СИСТЕМ МЕТОДОМ КОРНЕВОГО ГОДОГРАФА
- 6. ОЦЕНКИ ПАРАМЕТРОВ ПЕРЕХОДНОЙ И ЧАСТОТНОЙ ХАРАКТЕРИСТИК ПО КОРНЕВОМУ ГОДОГРАФУ
- 7. ВЛИЯНИЕ РАСПОЛОЖЕНИЯ НУЛЕЙ И ПОЛЮСОВ ЗАМКНУТОЙ СИСТЕМЫ НА ПЕРЕХОДНУЮ ХАРАКТЕРИСТИКУ h(t)
- 8. ВЛИЯНИЕ РАСПОЛОЖЕНИЯ НУЛЕЙ И ПОЛЮСОВ ЗАМКНУТОЙ СИСТЕМЫ НА ЕЕ ПОЛОСУ ЧАСТОТ
- 9. КОРНЕВОЙ ГОДОГРАФ И ПЕРЕХОДНАЯ ХАРАКТЕРИСТИКА СИСТЕМЫ ПРИ ВОЗМУЩЕНИЯХ, ПРИЛОЖЕННЫХ НЕ К ОСНОВНОМУ ВХОДУ СИСТЕМЫ
- 10. ВЛИЯНИЕ РАСПРЕДЕЛЕНИЯ НУЛЕЙ И ПОЛЮСОВ ПЕРЕДАТОЧНОЙ ФУНКЦИИ НА КАЧЕСТВО ПЕРЕХОДНОГО ПРОЦЕССА ПРИ НАЛИЧИИ ВНЕШНЕГО ВОЗДЕЙСТВИЯ
- ГЛАВА XVIII. МЕТОД ЛОГАРИФМИЧЕСКИХ КОРНЕВЫХ ГОДОГРАФОВ
- 2. ОПРЕДЕЛЕНИЕ КОРНЕЙ ЗАМКНУТОЙ СИСТЕМЫ ПО ЛОГАРИФМИЧЕСКОЙ АМПЛИТУДНОЙ КОМПЛЕКСНО-ЧАСТОТНОЙ ХАРАКТЕРИСТИКЕ РАЗОМКНУТОЙ СИСТЕМЫ
- 3. ЛОГАРИФМИЧЕСКИЕ КОРНЕВЫЕ ГОДОГРАФЫ
- 4. ЛОГАРИФМИЧЕСКИЕ КОМПЛЕКСНО-ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЗВЕНЬЕВ ВТОРОГО ПОРЯДКА
- 5. ПРИМЕР ПОСТРОЕНИЯ ЛОГАРИФМИЧЕСКОГО КОРНЕВОГО ГОДОГРАФА
- ГЛАВА XIX. ИНТЕГРАЛЬНЫЕ ОЦЕНКИ И КРИТЕРИИ КАЧЕСТВА РЕГУЛИРОВАНИЯ
- 2. МЕТОДИКА ПРИМЕНЕНИЯ ИНТЕГРАЛЬНЫХ КВАДРАТИЧНЫХ ОЦЕНОК
- 3. ЛИНЕЙНЫЕ ИНТЕГРАЛЬНЫЕ ОЦЕНКИ
- ПРИЛОЖЕНИЕ
- БИБЛИОГРАФИЯ ПО РАЗДЕЛАМ КНИГИ