| << Предыдущий параграф | Следующий параграф >> |
Пред.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
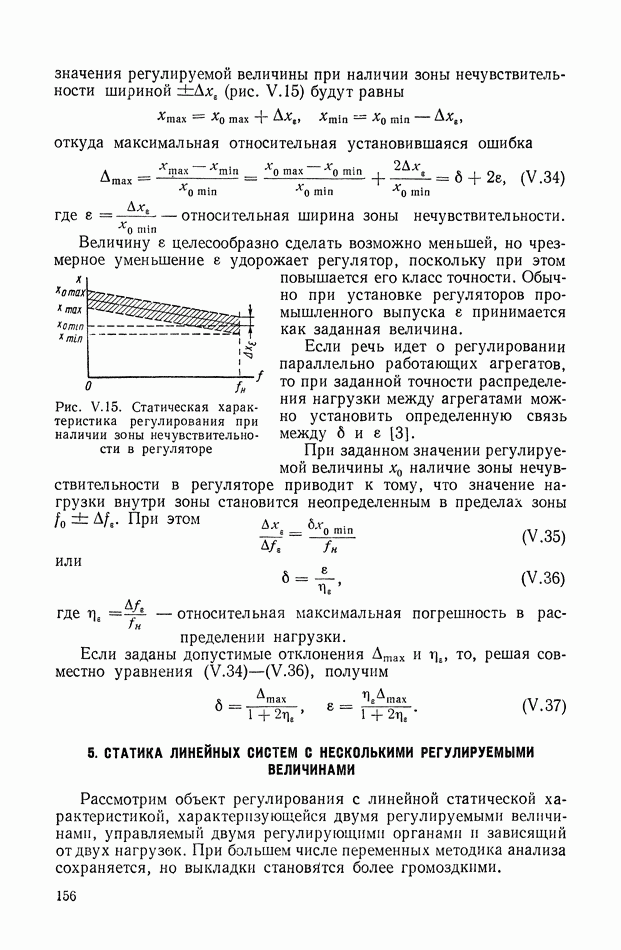
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
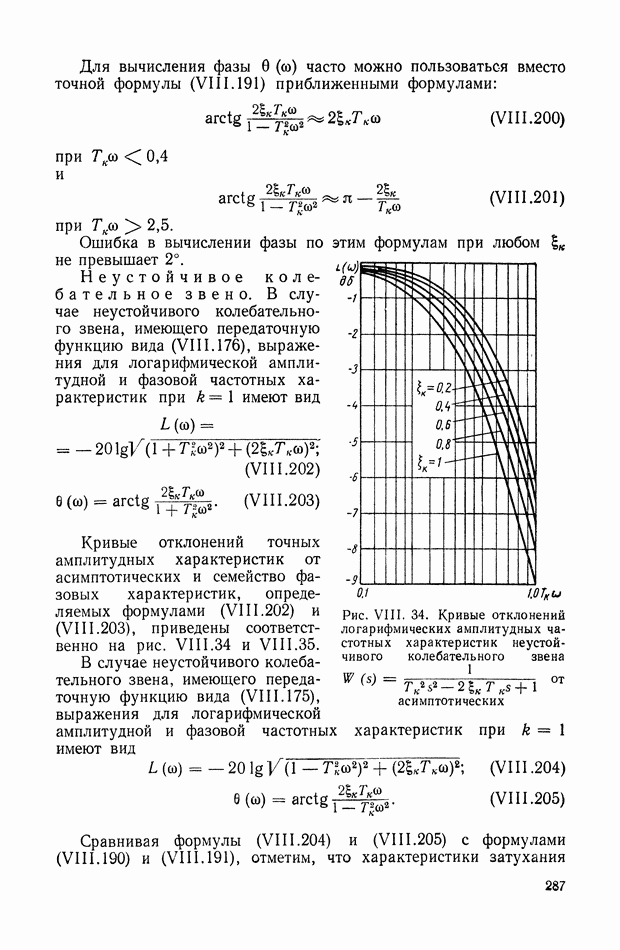
287
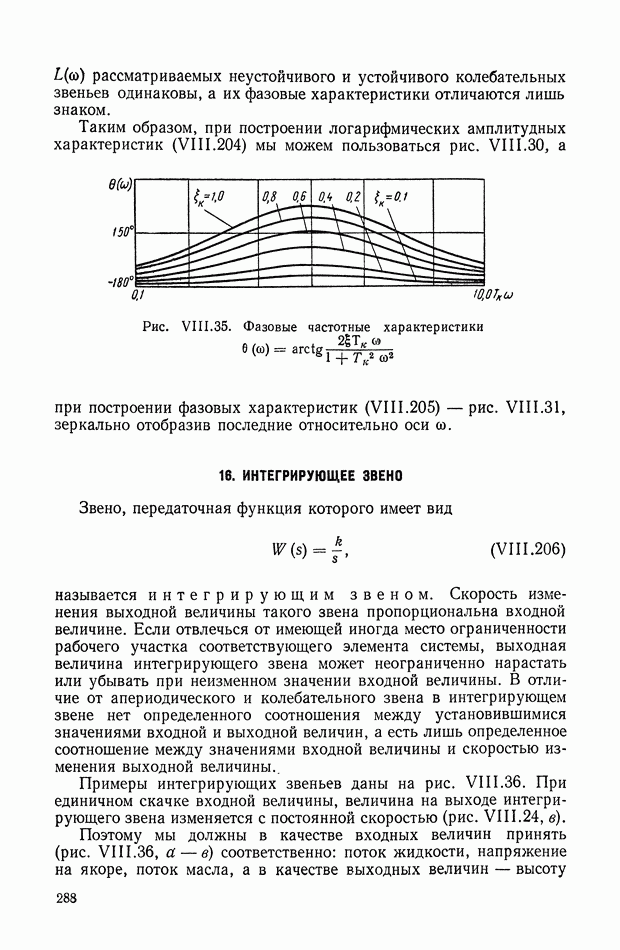
288
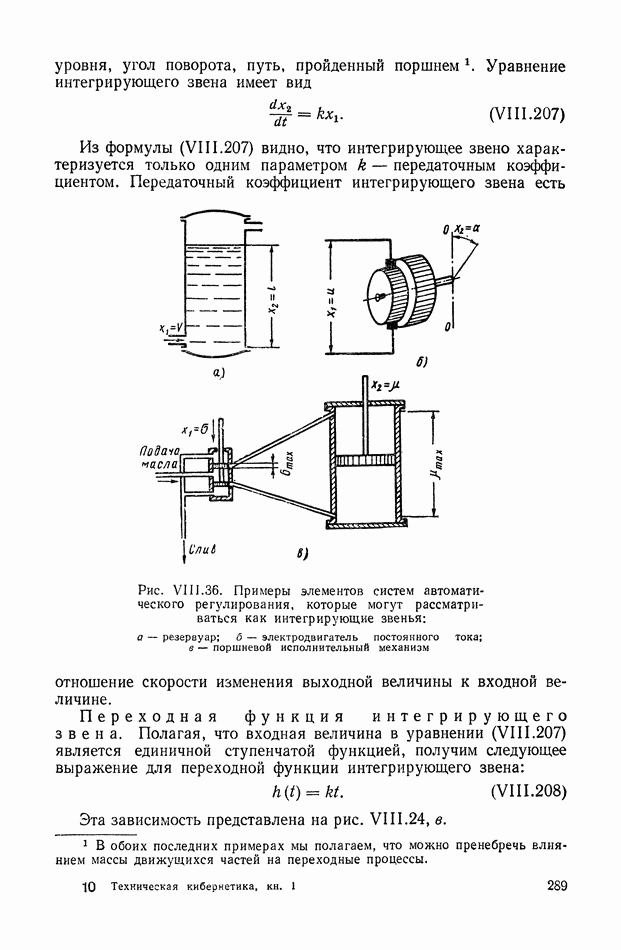
289
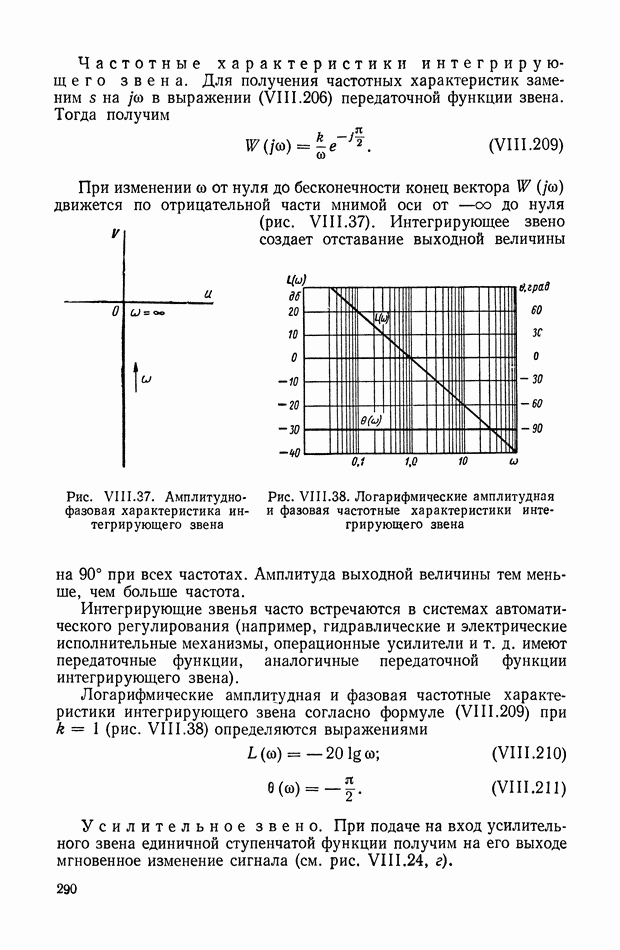
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
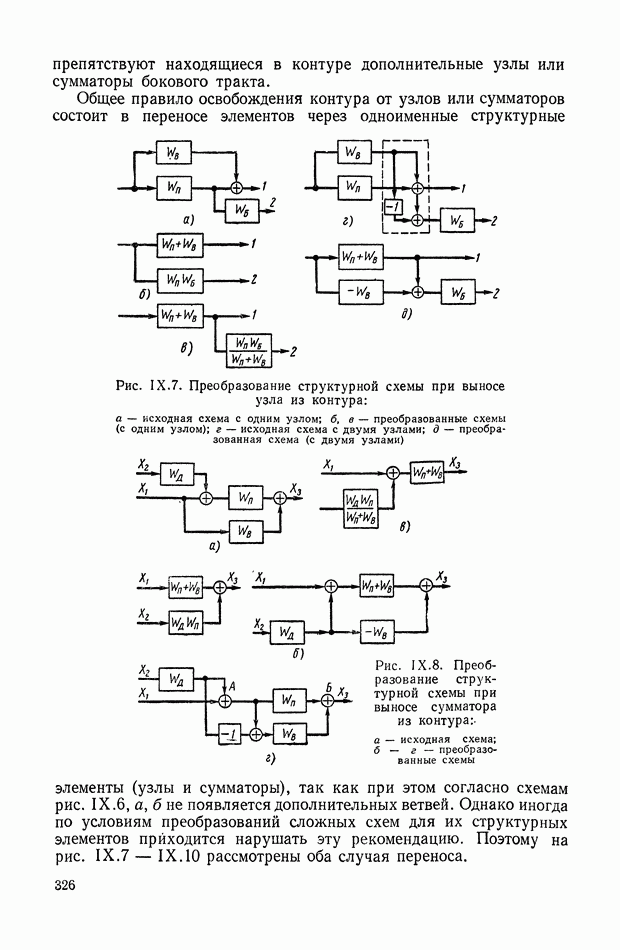
326
327
328
329
330
331
332
333
334
335
336
337
338
339
340
341
342
343
344
345
346
347
348
349
350
351
352
353
354
355
356
357
358
359
360
361
362
363
364
365
366
367
368
369
370
371
372
373
374
375
376
377
378
379
380
381
382
383
384
385
386
387
388
389
390
391
392
393
394
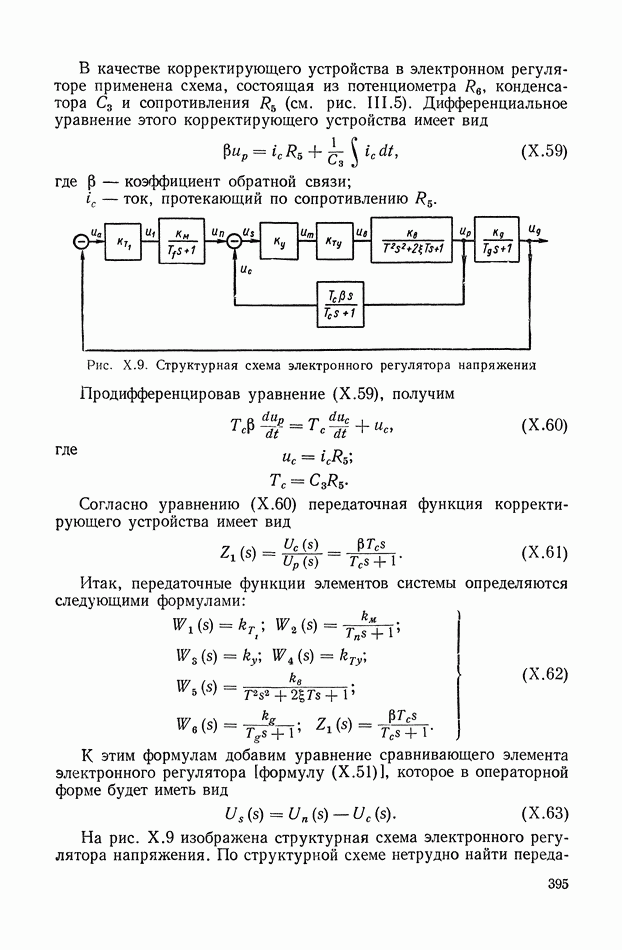
395
396
397
398
399
400
401
402
403
404
405
406
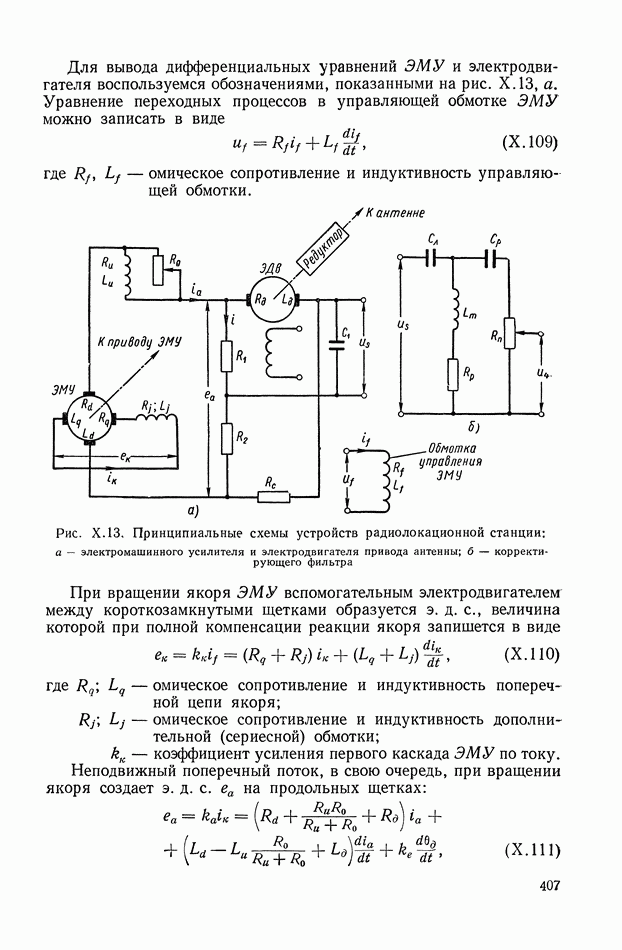
407
408
409
410
411
412
413
414
415
416
417
418
419
420
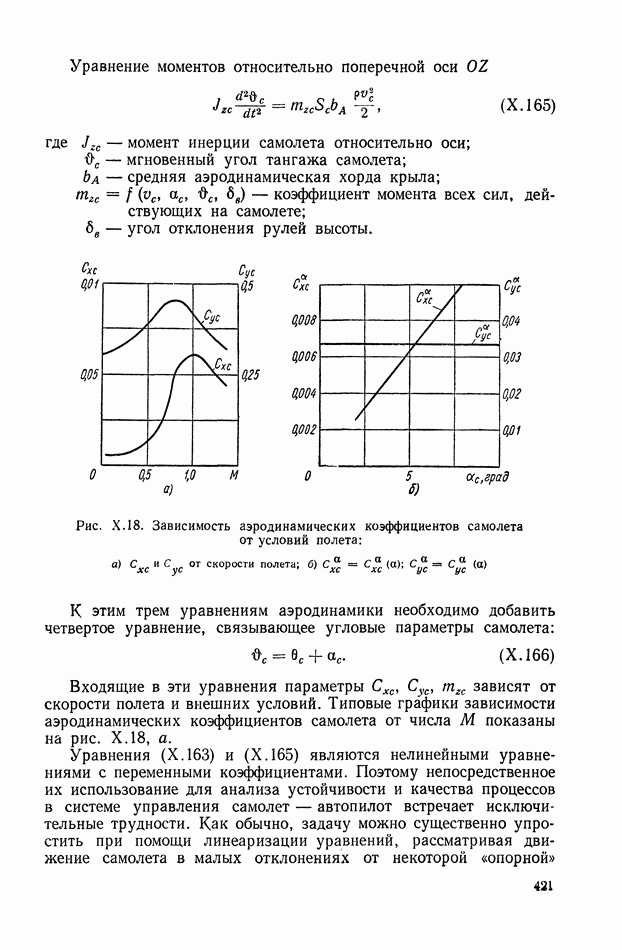
421
422
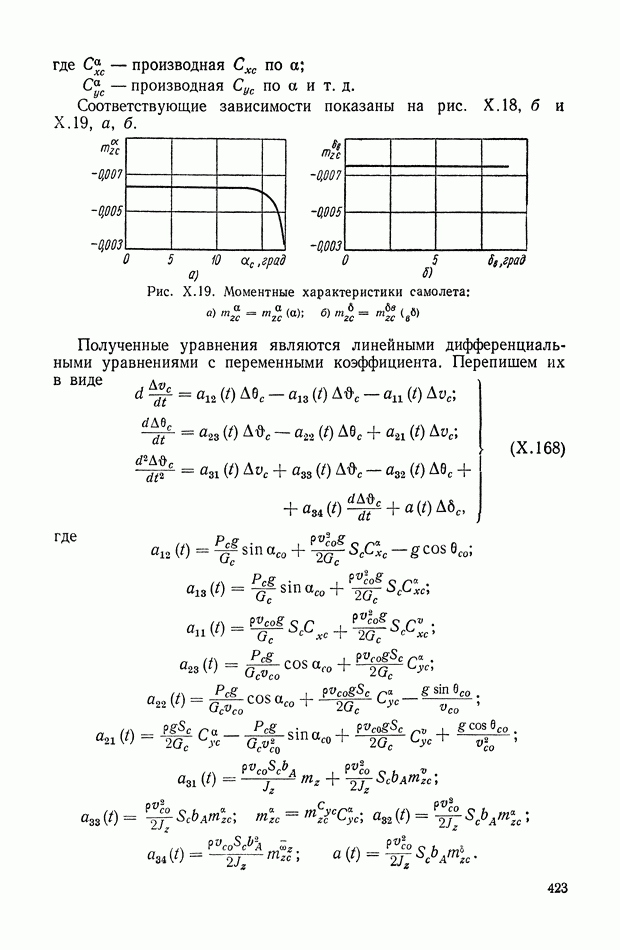
423
424
425
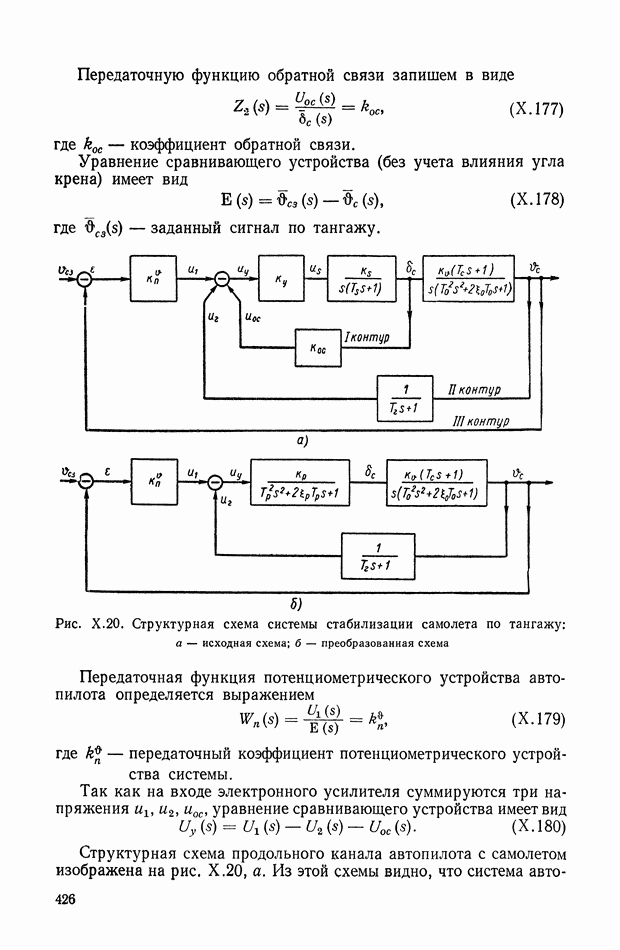
426
427
428
429
430
431
432
433
434
435
436
437
438
439
440
441
442
443
444
445
446
447
448
449
450
451
452
453
454
455
456
457
458
459
460
461
462
463
464
465
466
467
468
469
470
471
472
473
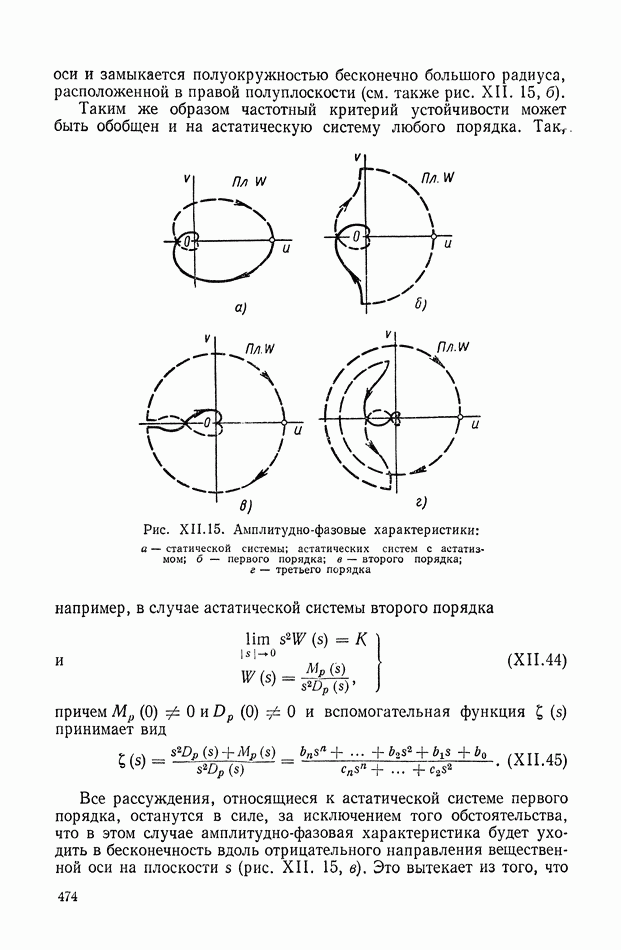
474
475
476
477
478
479
480
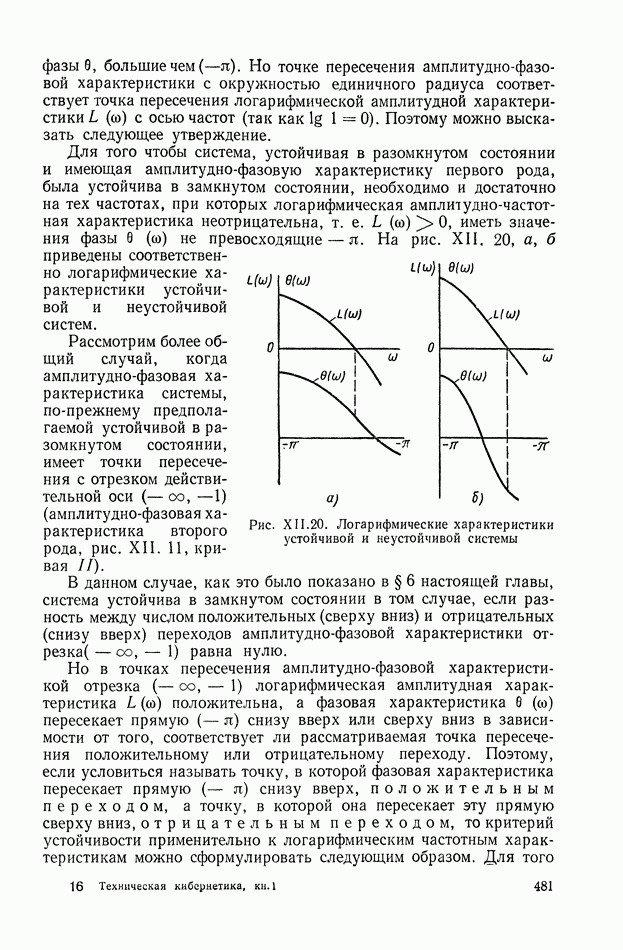
481
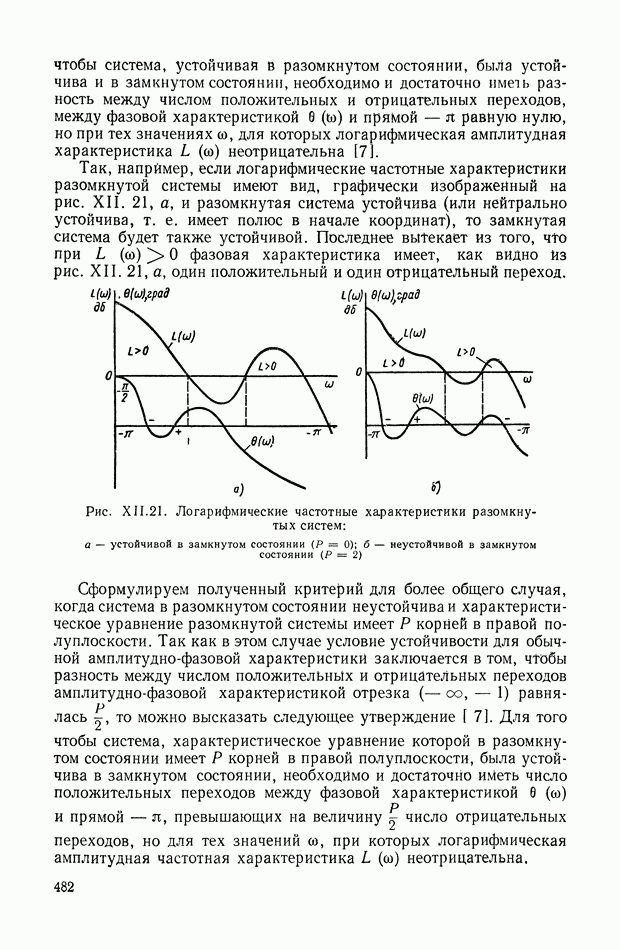
482
483
484
485
486
487
488
489
490
491
492
493
494
495
496
497
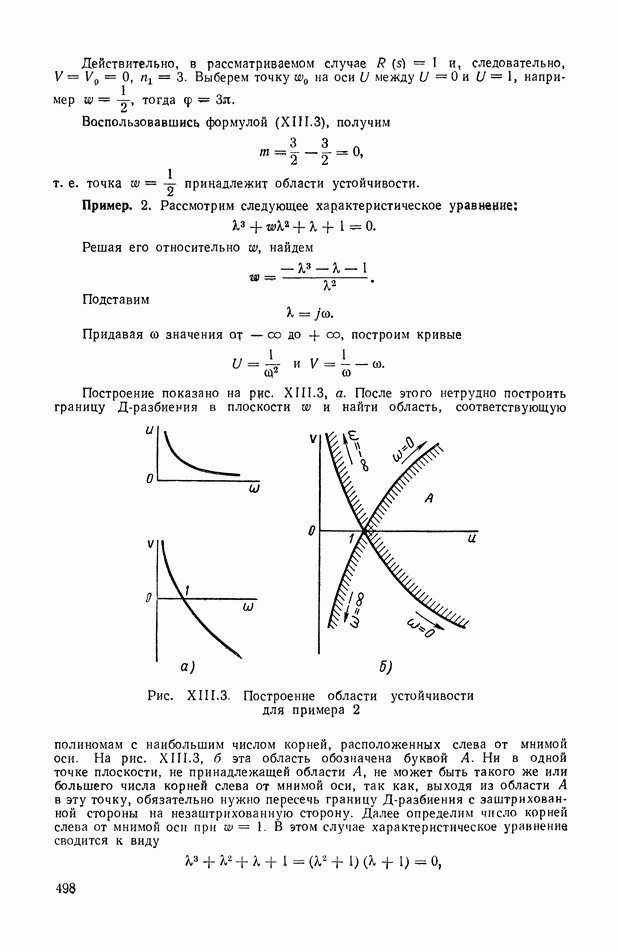
498
499
500
501
502
503
504
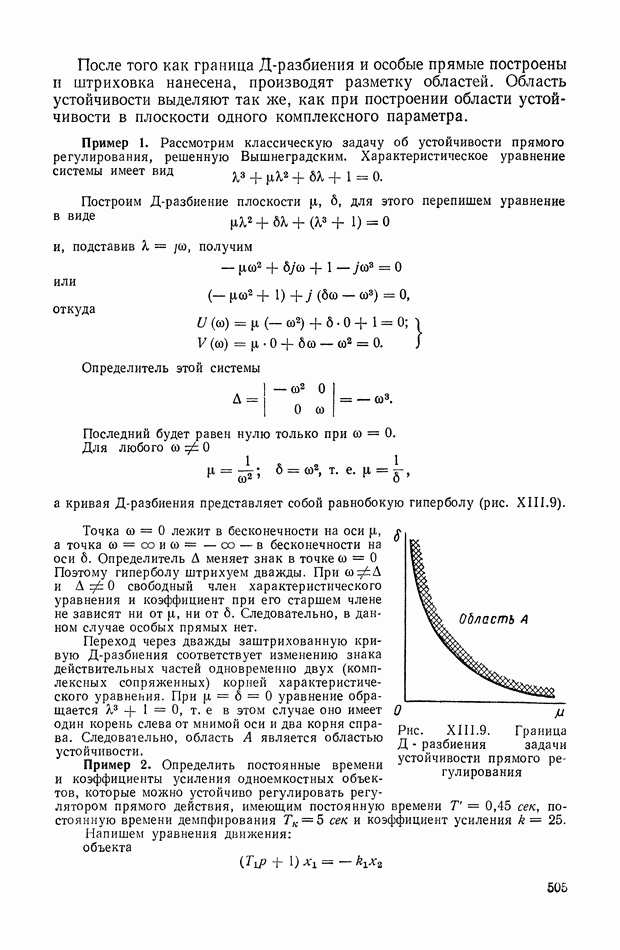
505
506
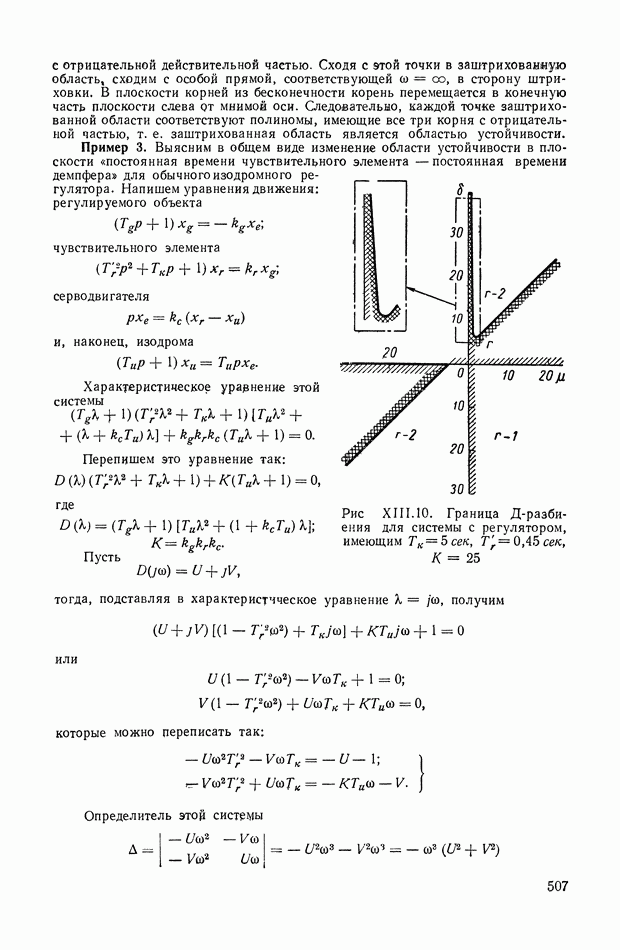
507
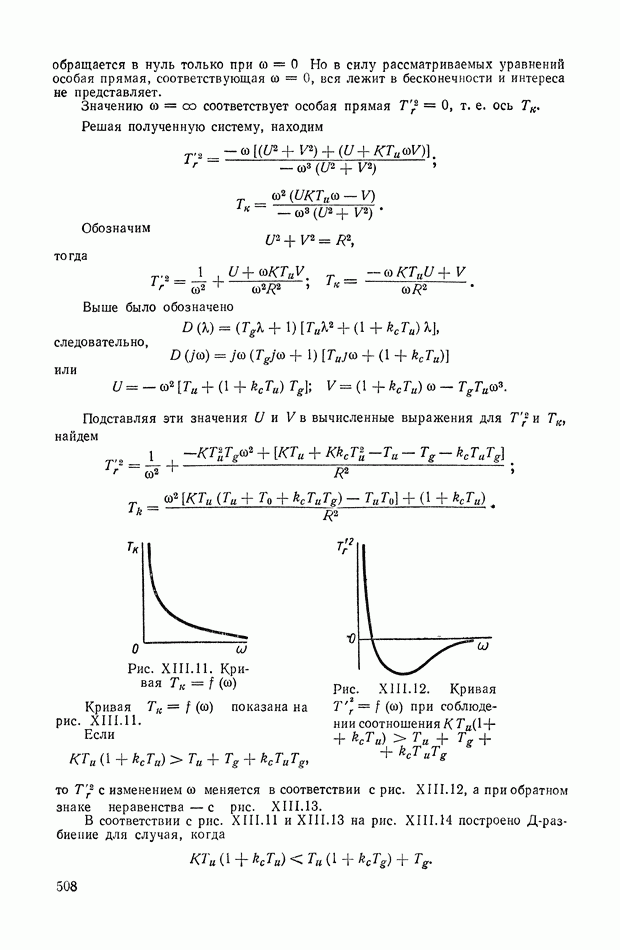
508
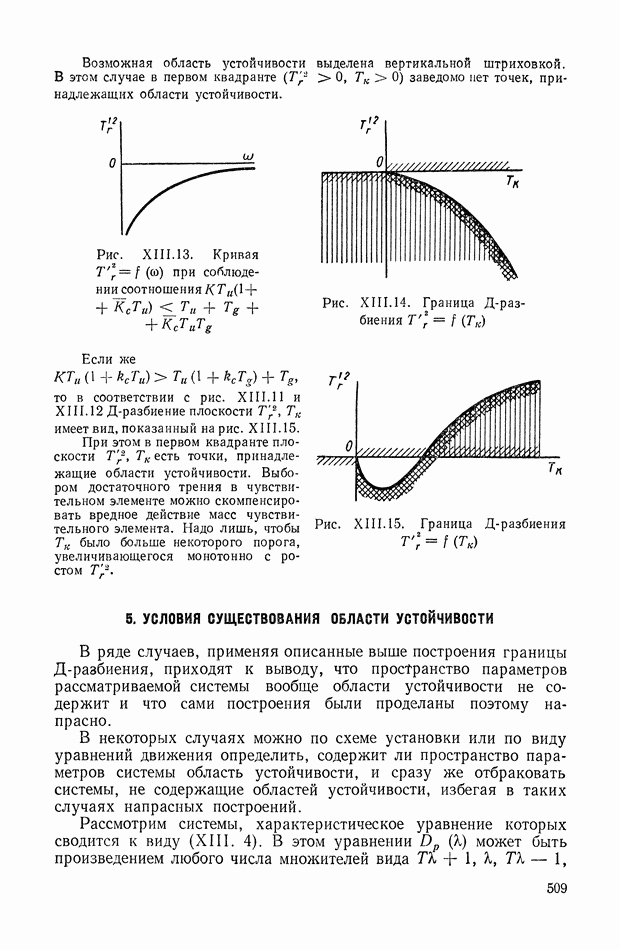
509
510
511
512
513
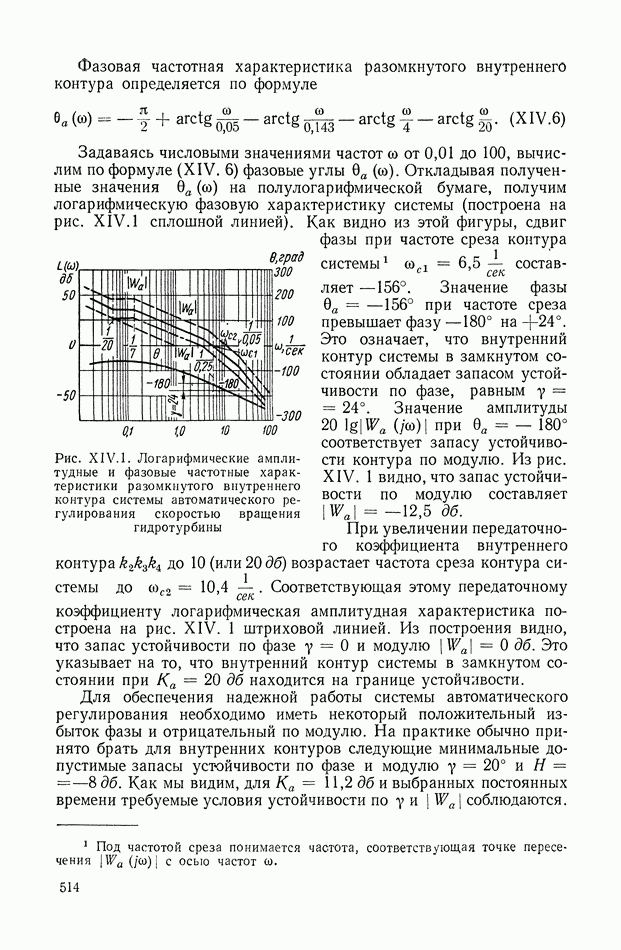
514
515
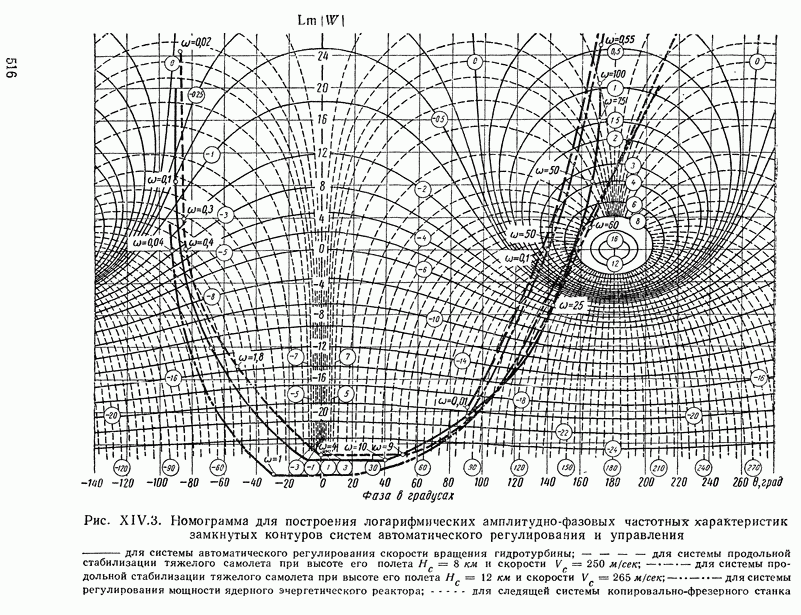
516
517
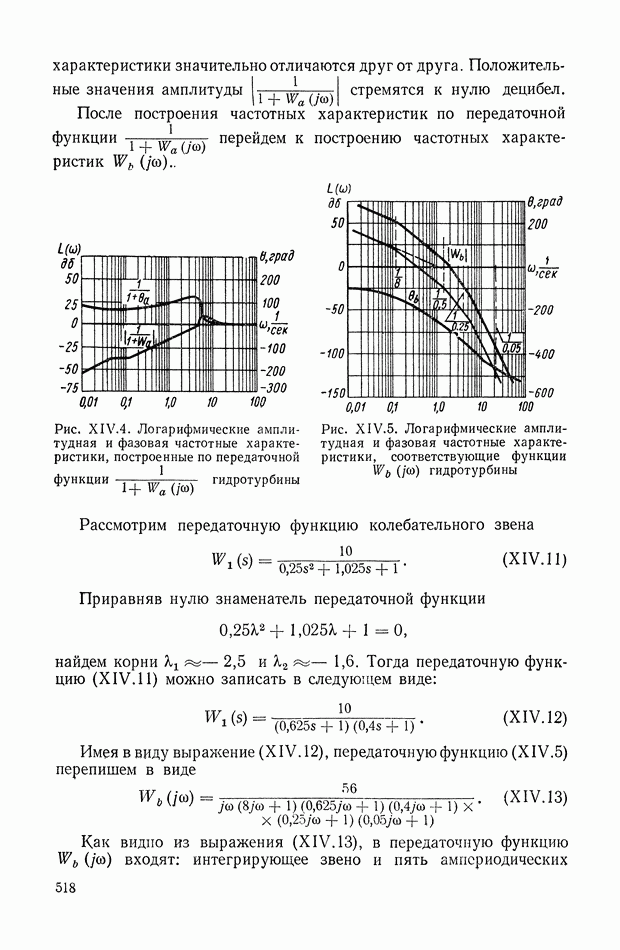
518
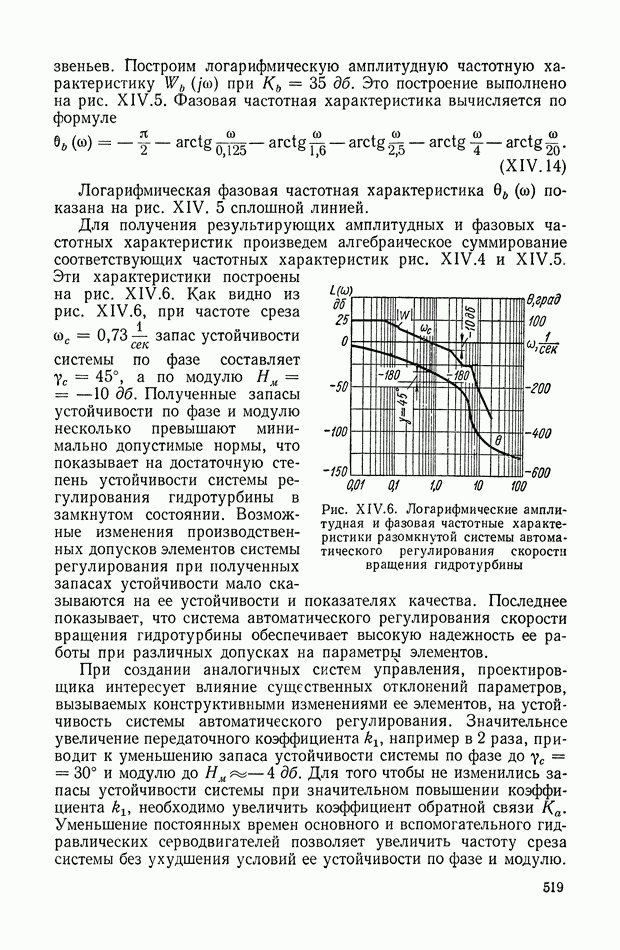
519
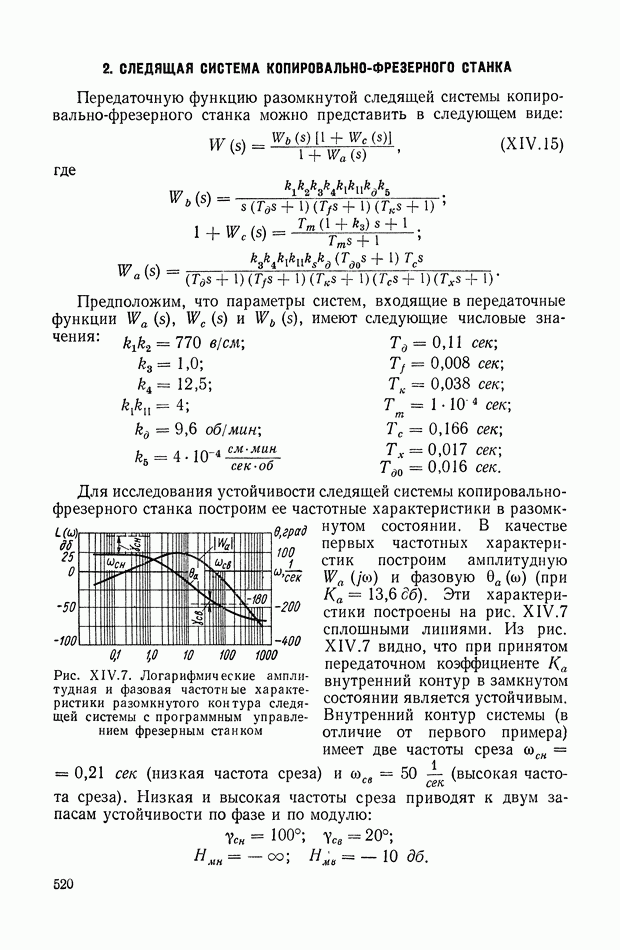
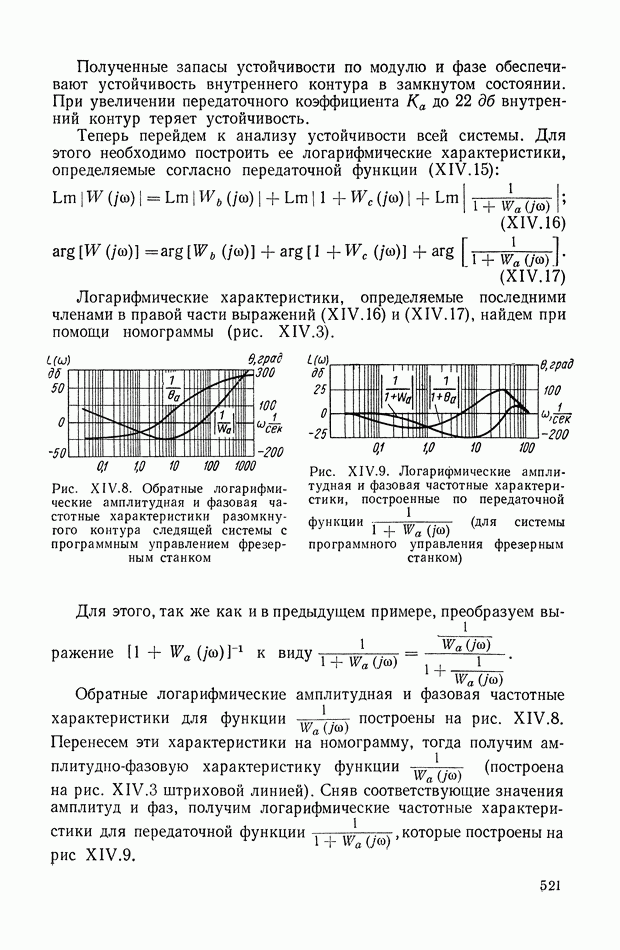
520
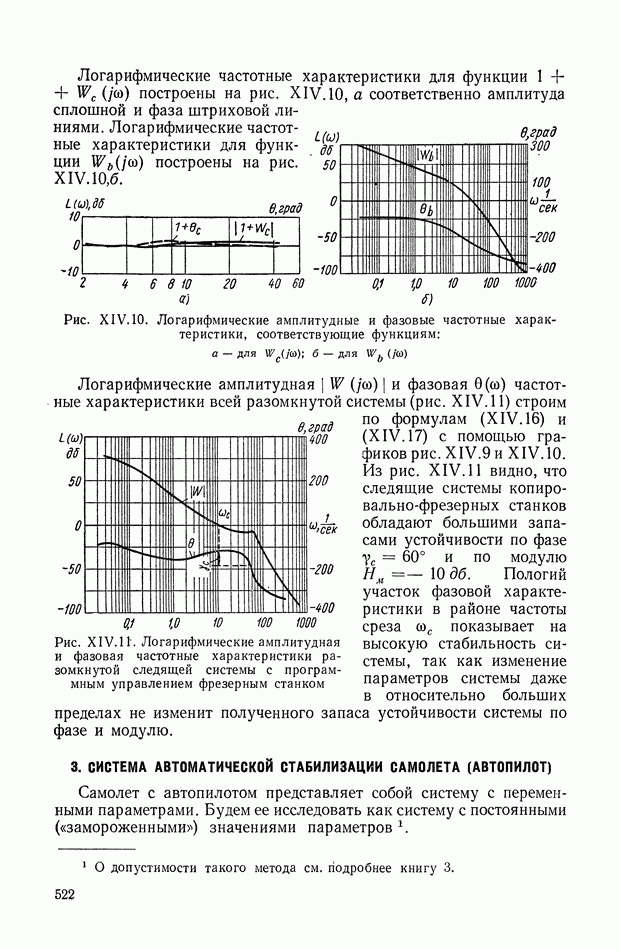
521
522
523
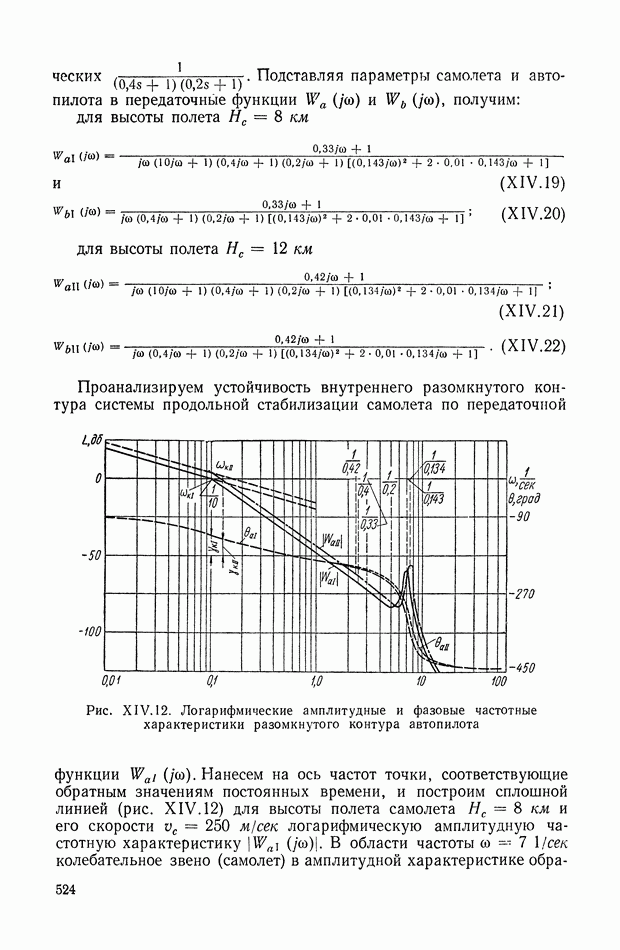
524
525
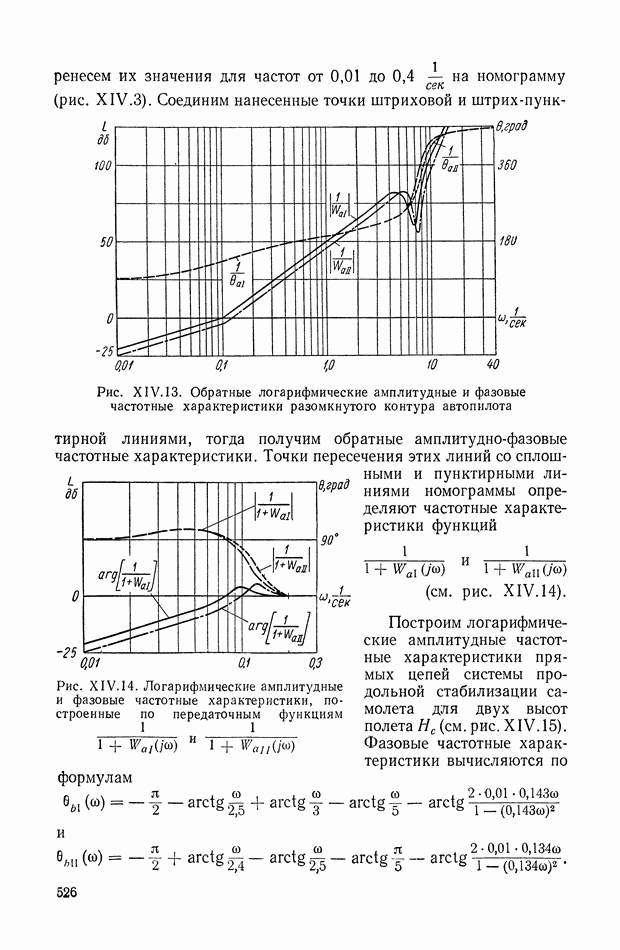
526
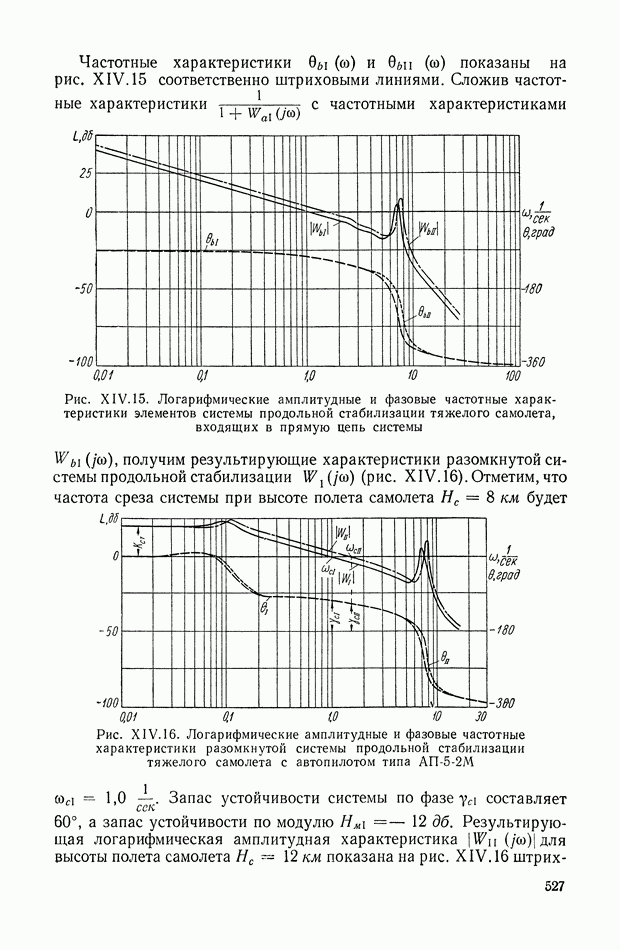
527
528
529
530
531
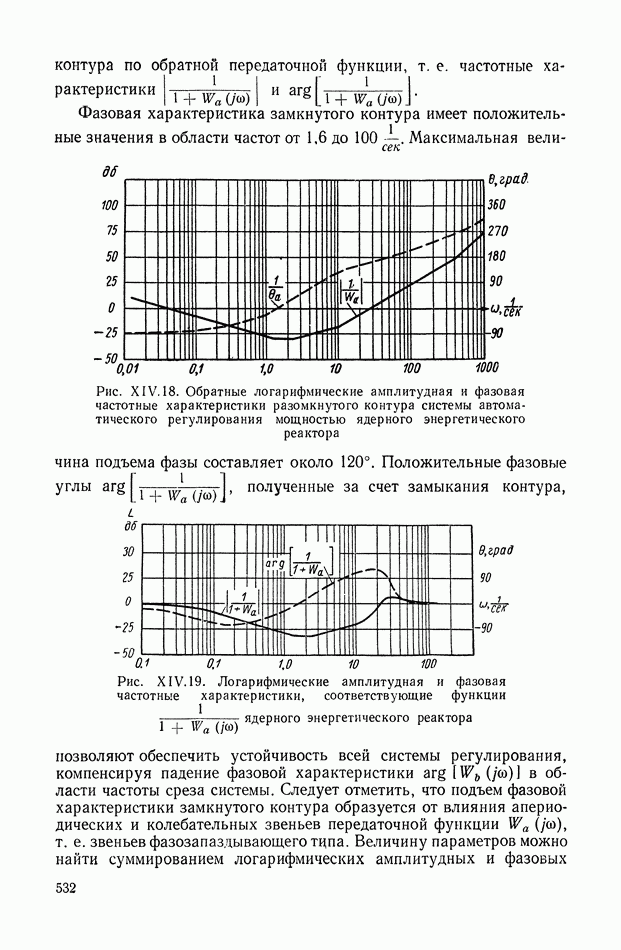
532
533
534
535
536
537
538
539
540
541
542
543
544
545
546
547
548
549
550
551
552
553
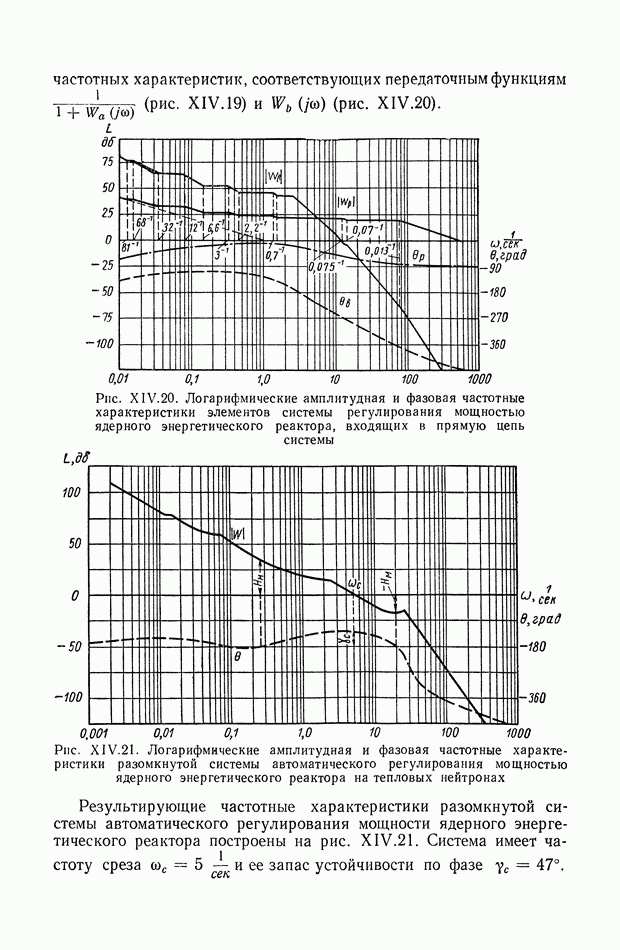
554
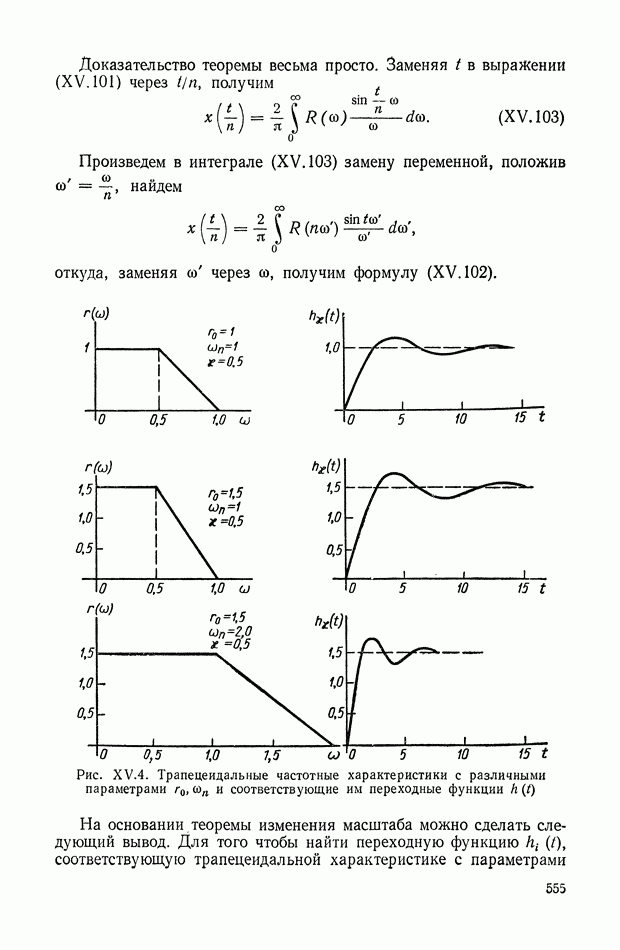
555
556
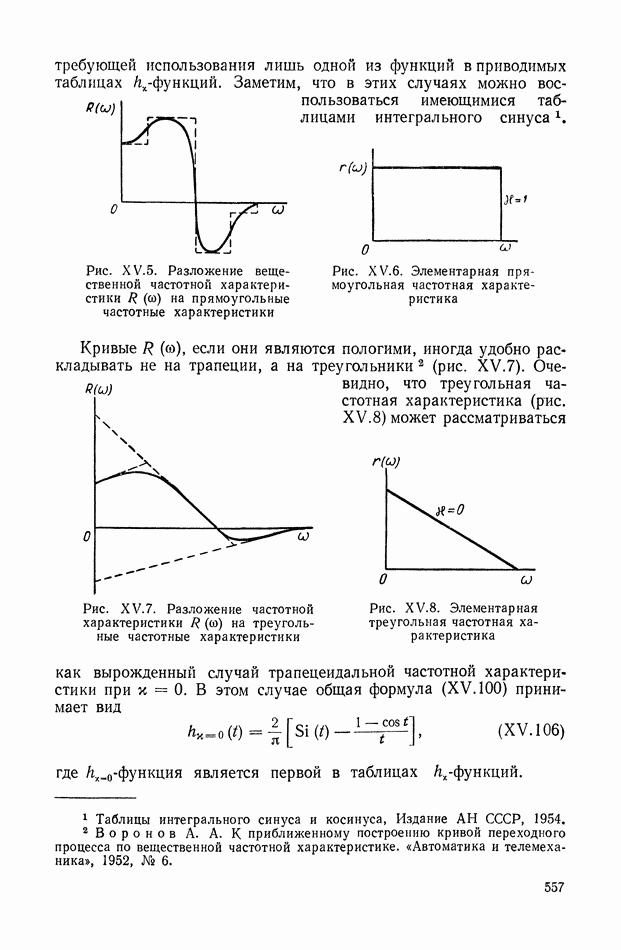
557
558
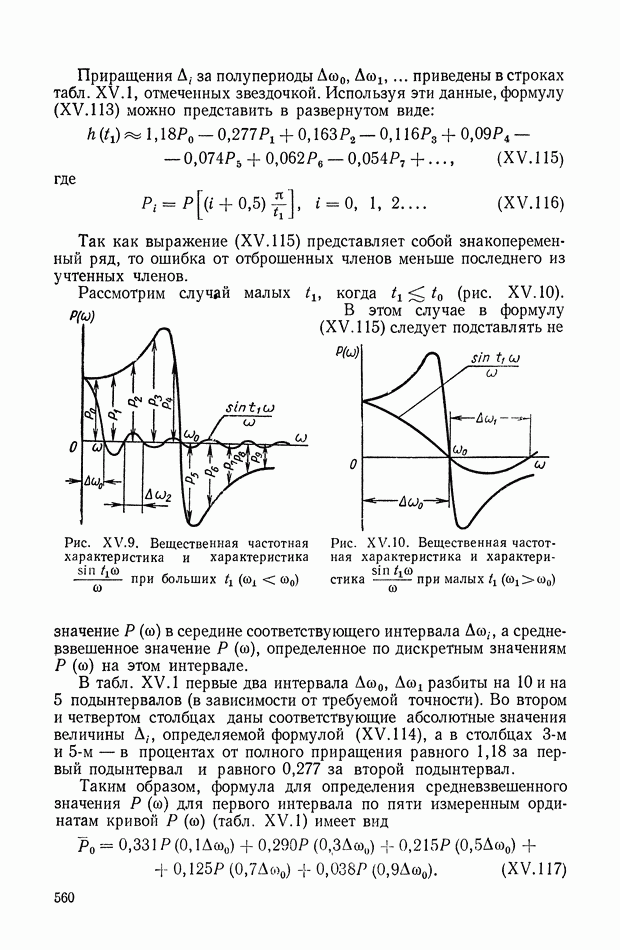
559
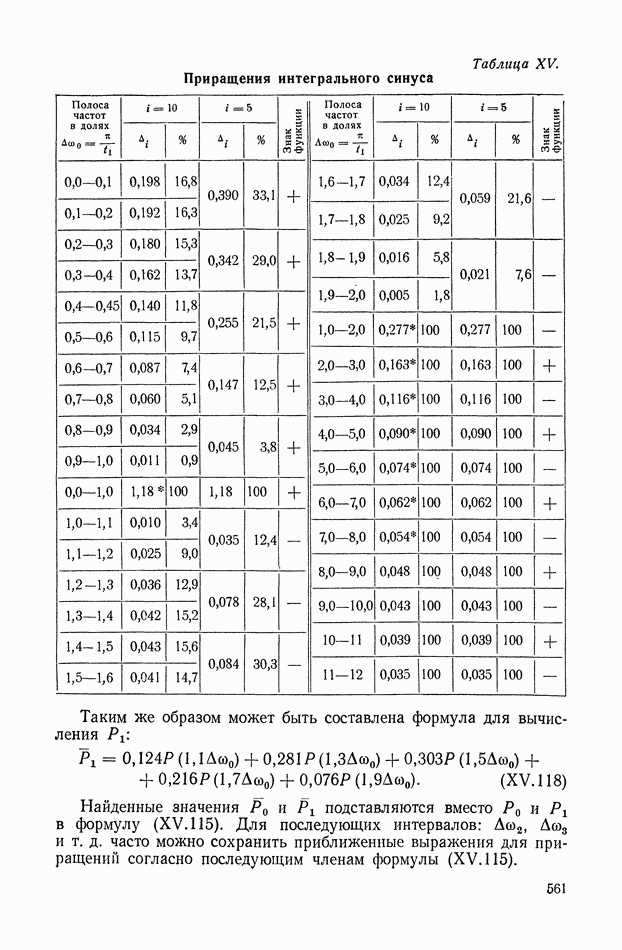
560
561
562
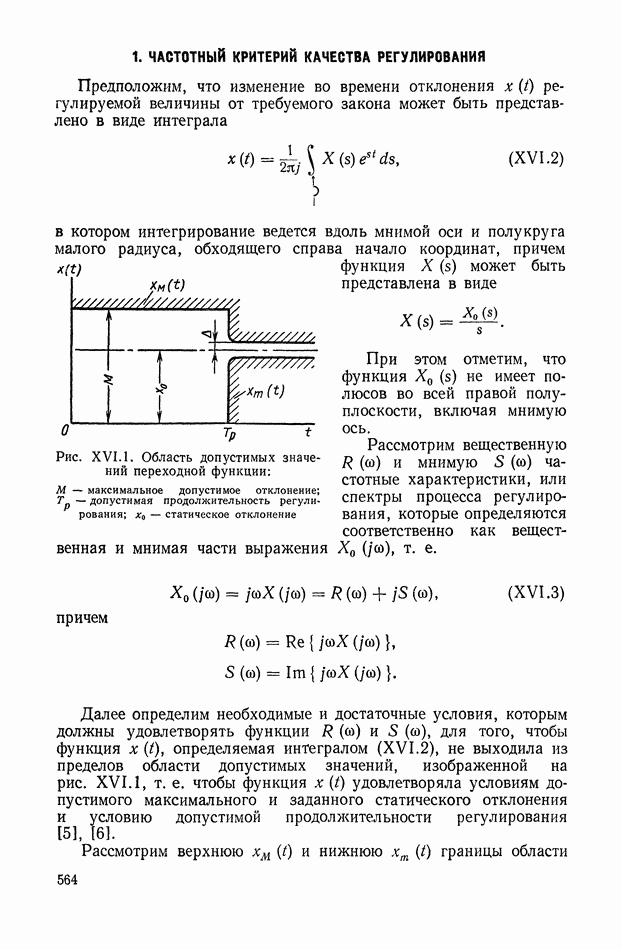
563
564
565
566
567
568
569
570
571
572
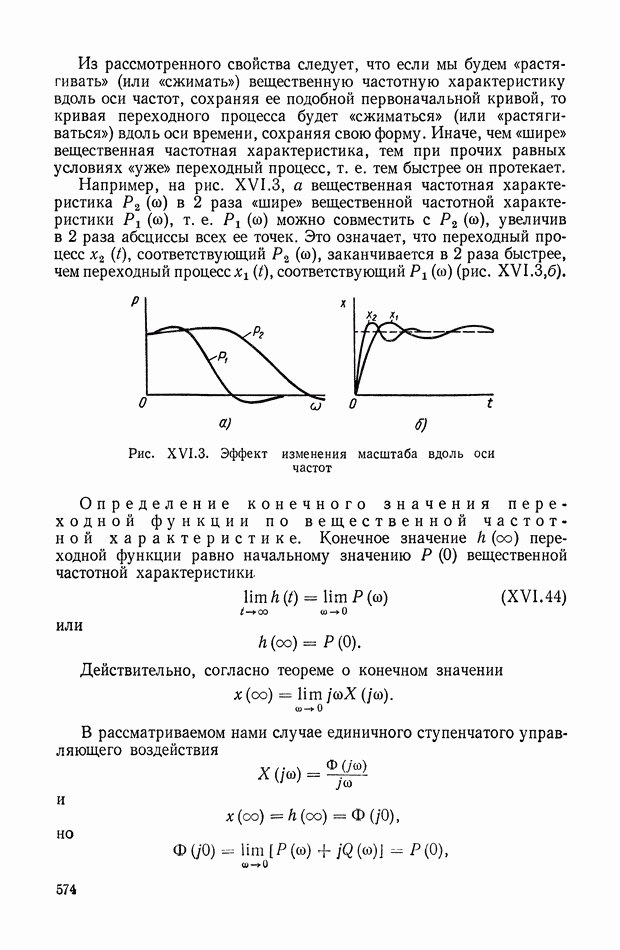
573
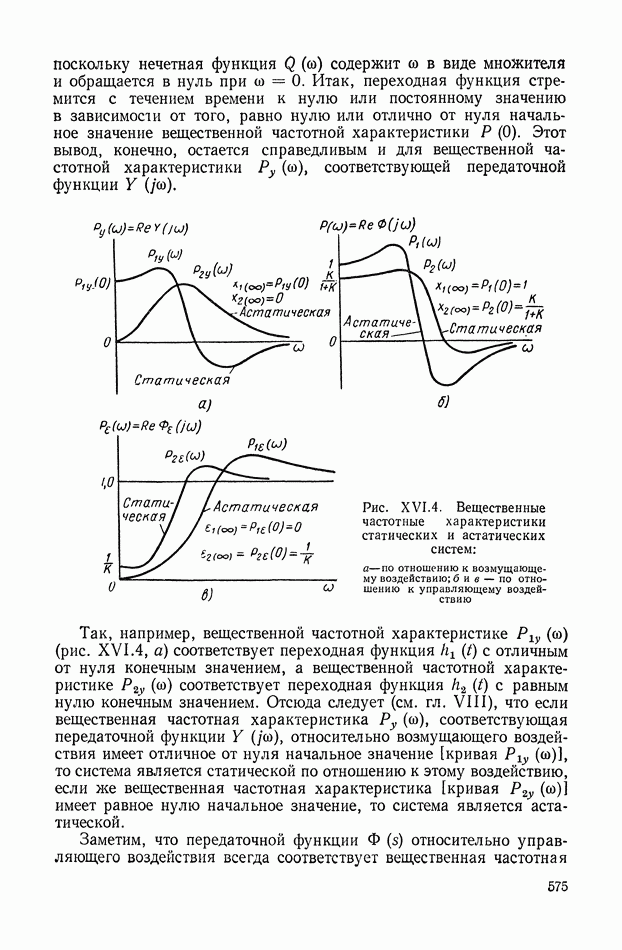
574
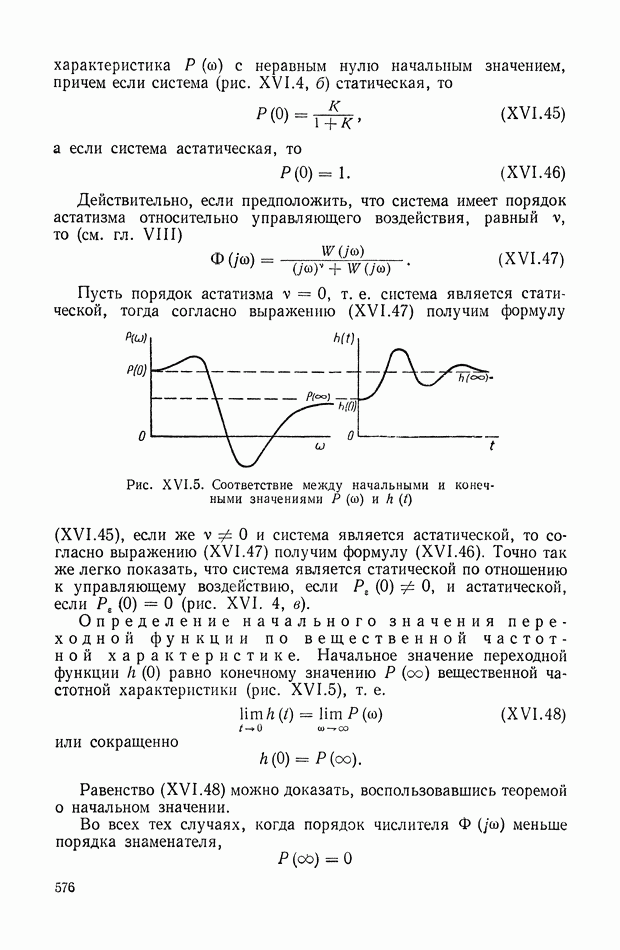
575
576
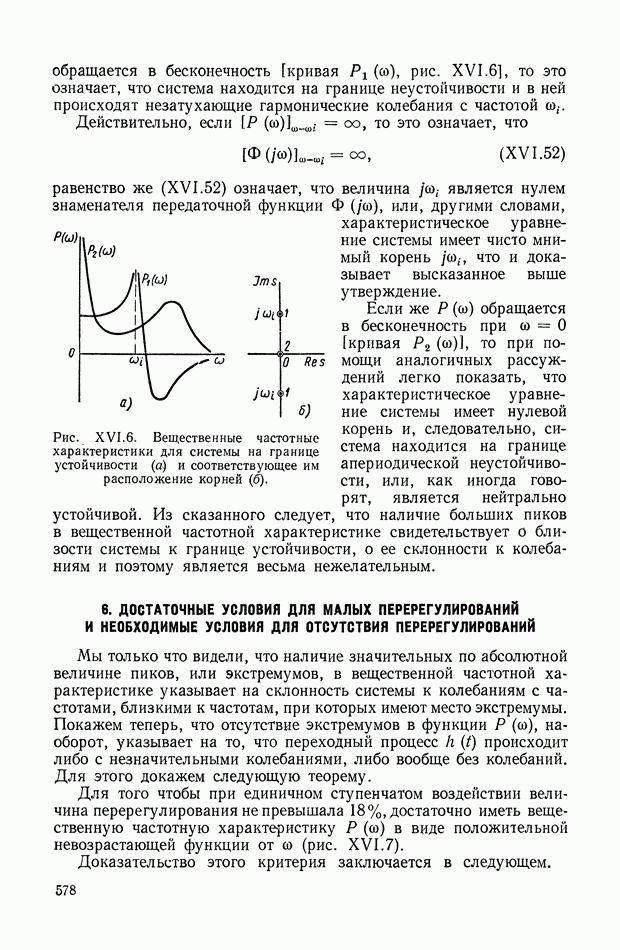
577
578
579
580
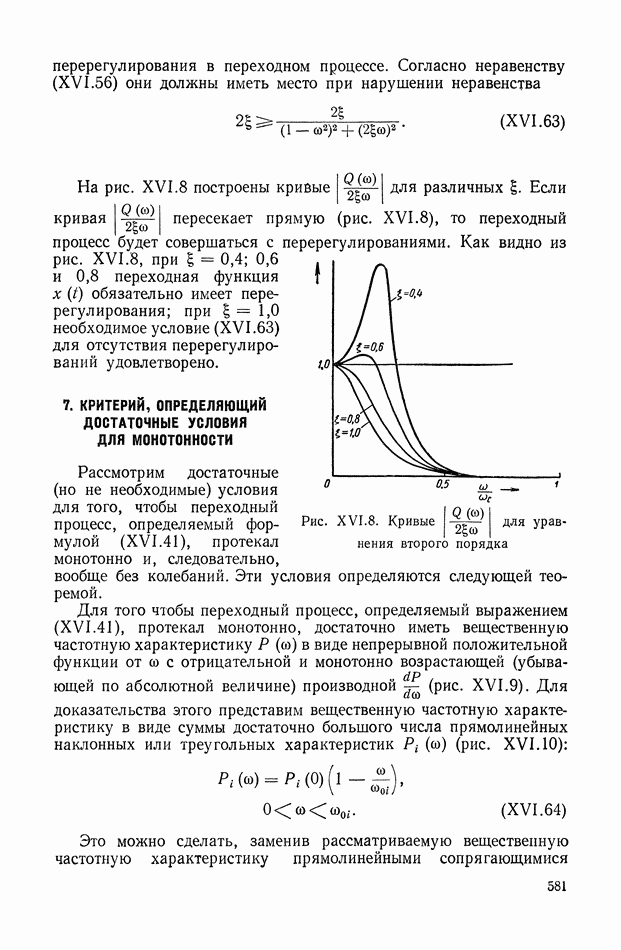
581
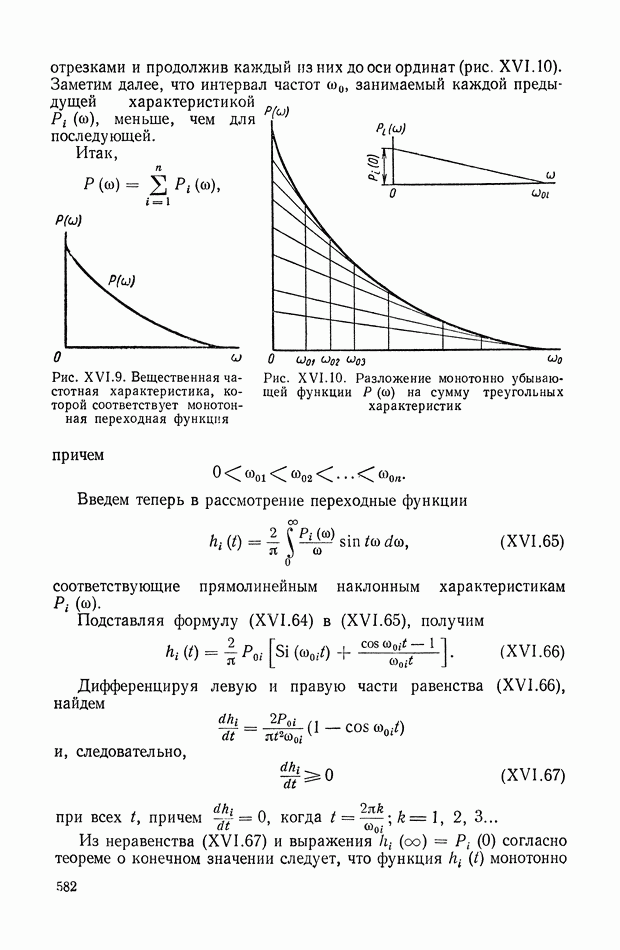
582
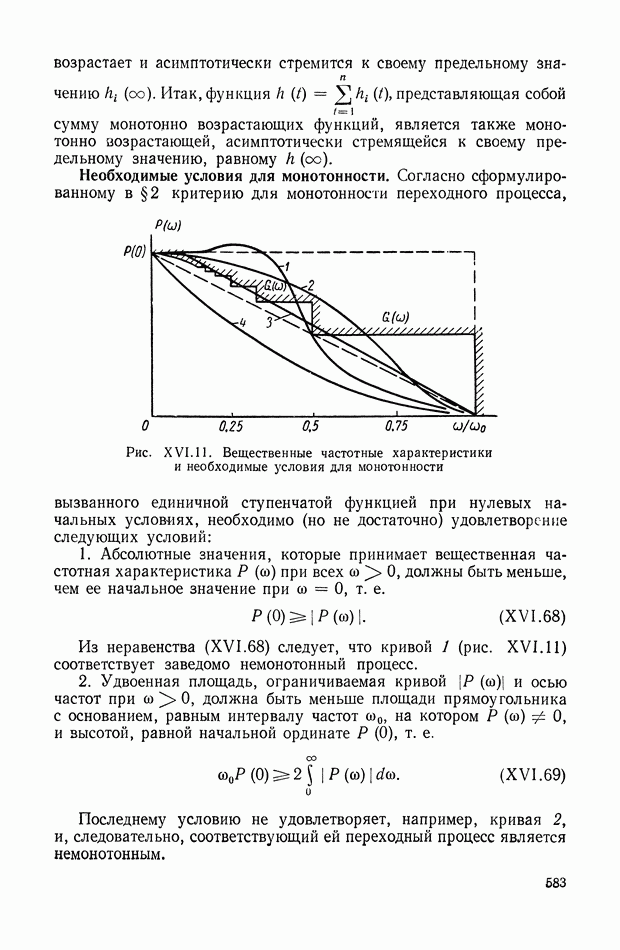
583
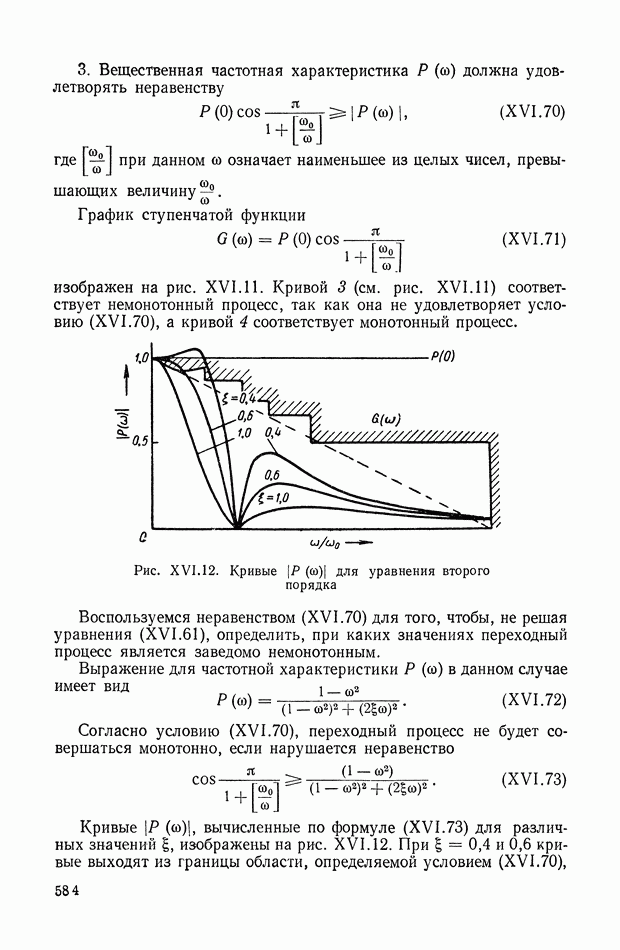
584
585
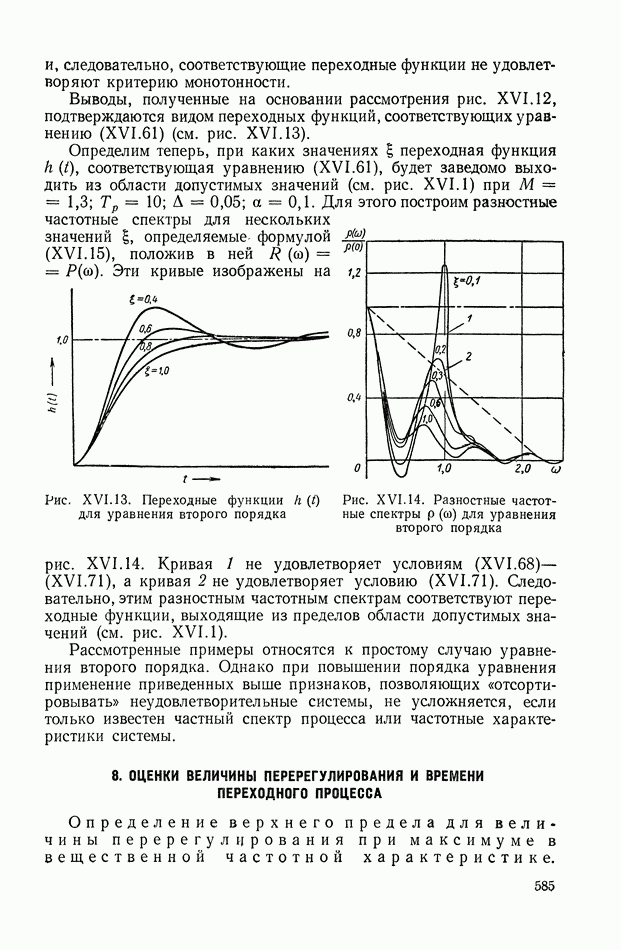
586
587
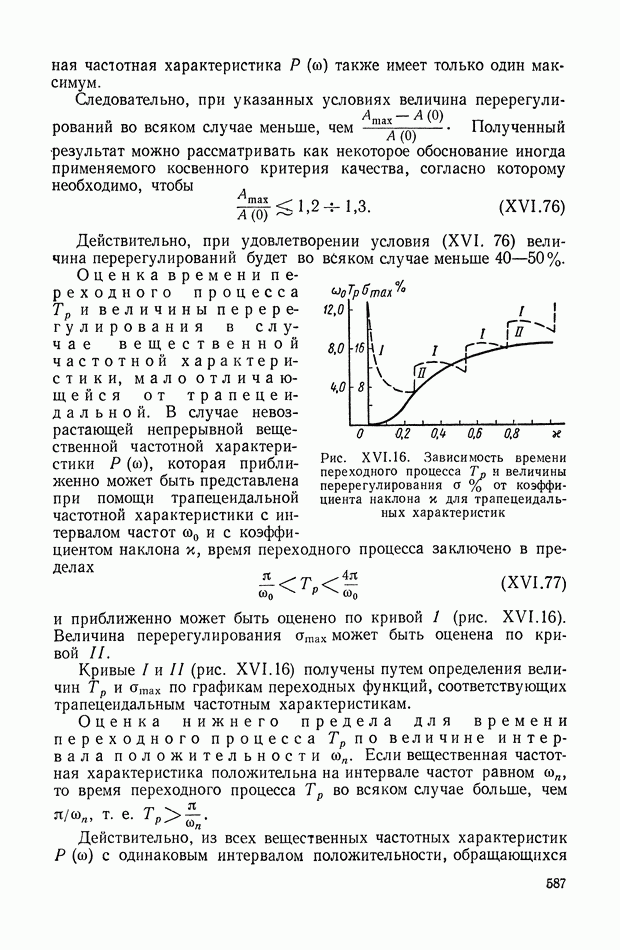
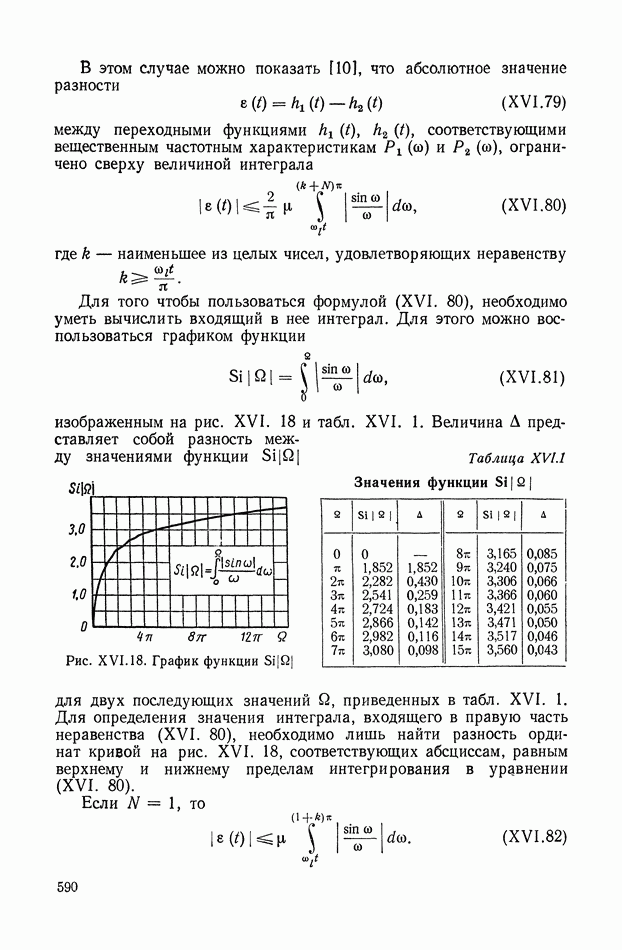
588
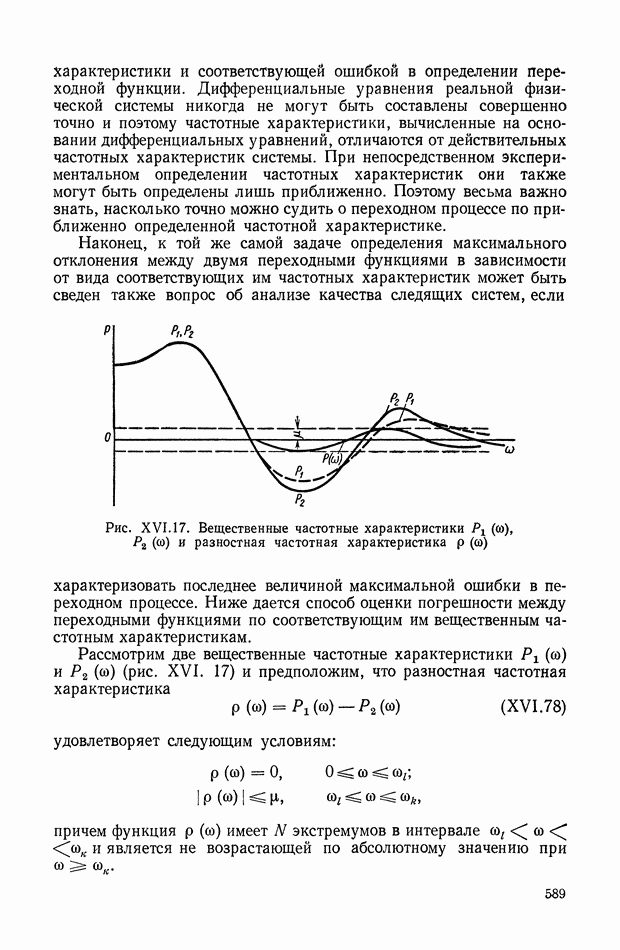
589
590
591
592
593
594
595
596
597
598
599
600
601
602
603
604
605
606
607
608
609
610
611
612
613
614
615
616
617
618
619
620
621
622
623
624
625
626
627
628
629
630
631
632
633
634
635
636
637
638
639
640
641
642
643
644
645
646
647
648
649
650
651
652
653
654
655
656
657
658
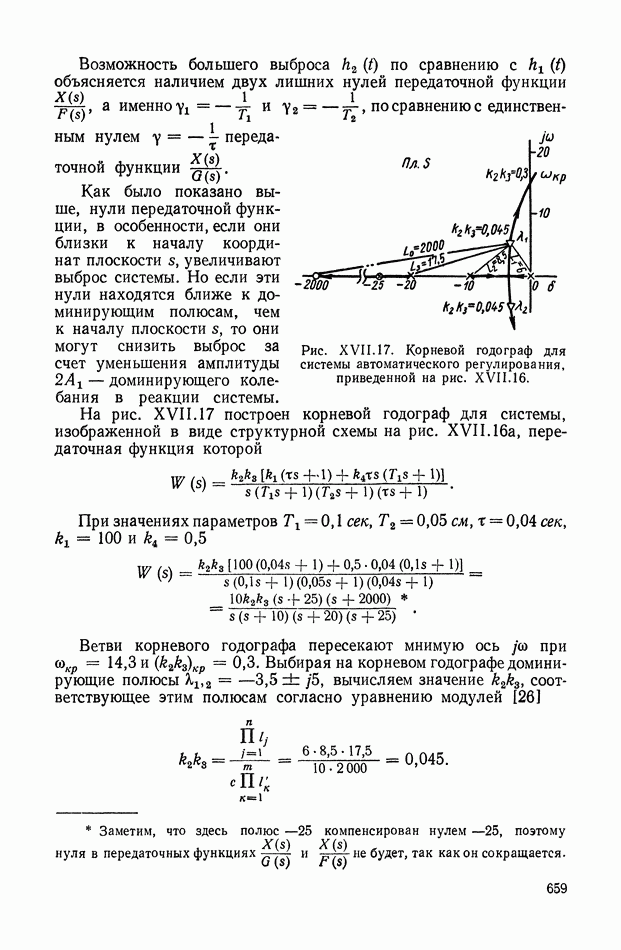
659
660
661
662
663
664
665
666
667
668
669
670
671
672
673
674
675
676
677
678
679
680
681
682
683
684
685
686
687
688
689
690
691
692
693
694
695
696
697
698
699
700
701
702
703
704
705
706
707
708
709
710
711
712
713
714
715
716
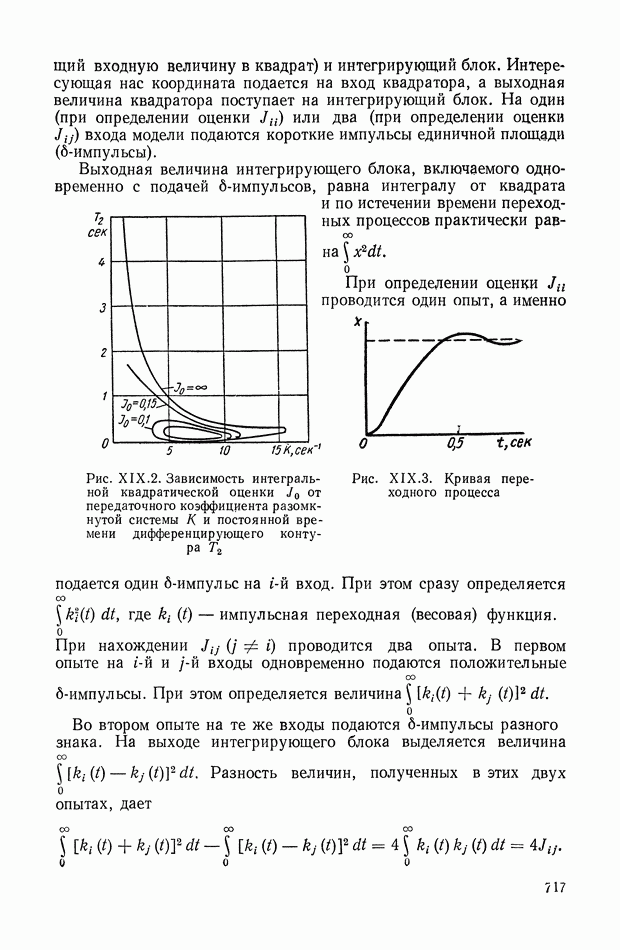
717
718
719
720
721
722
723
724
725
726
727
728
729
730
731
732
733
734
735
736
737
738
739
740
741
742
743
744
745
746
747
748
749
750
751
752
753
754
755
756
757
758
759
760
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
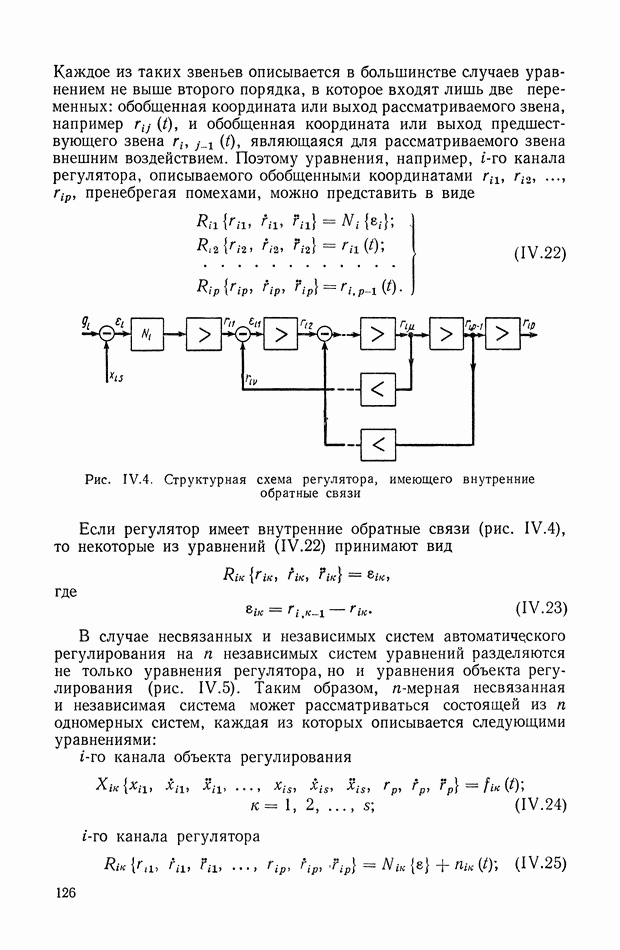
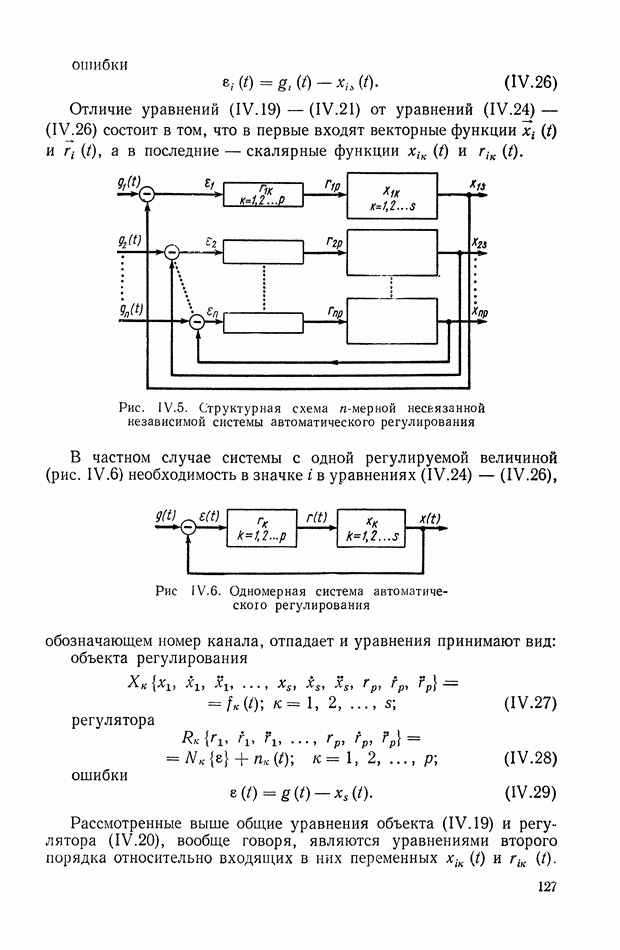
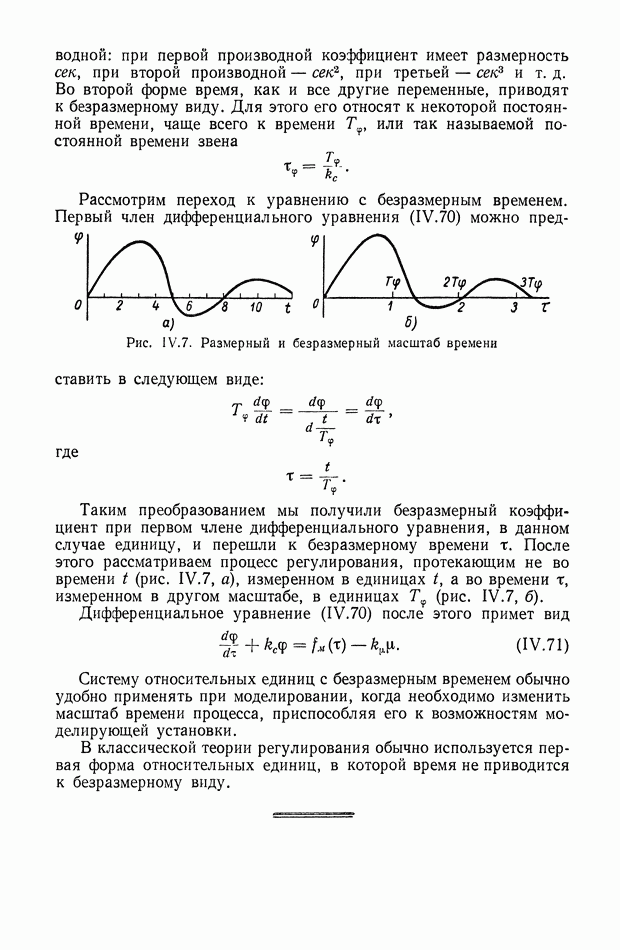
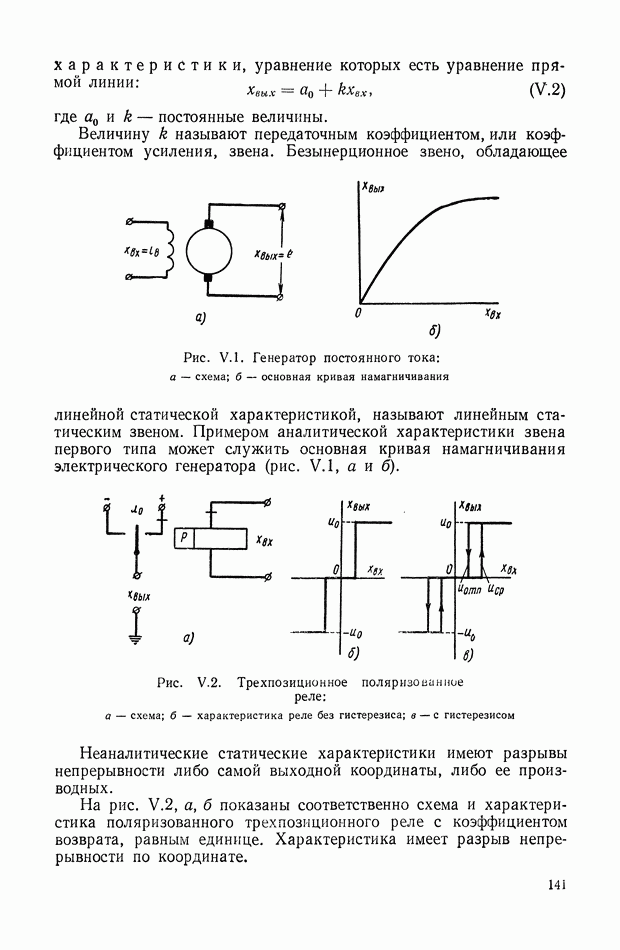
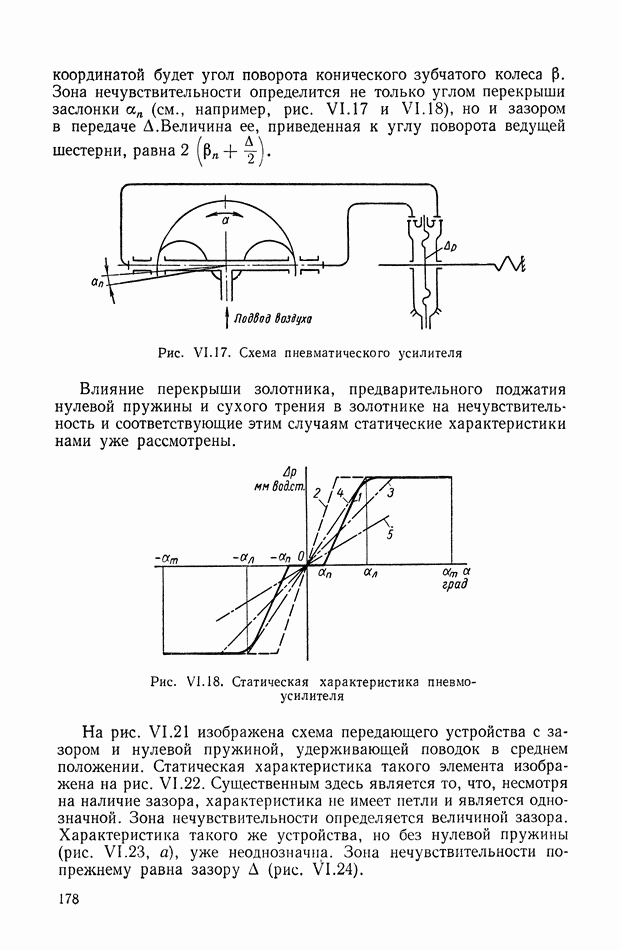
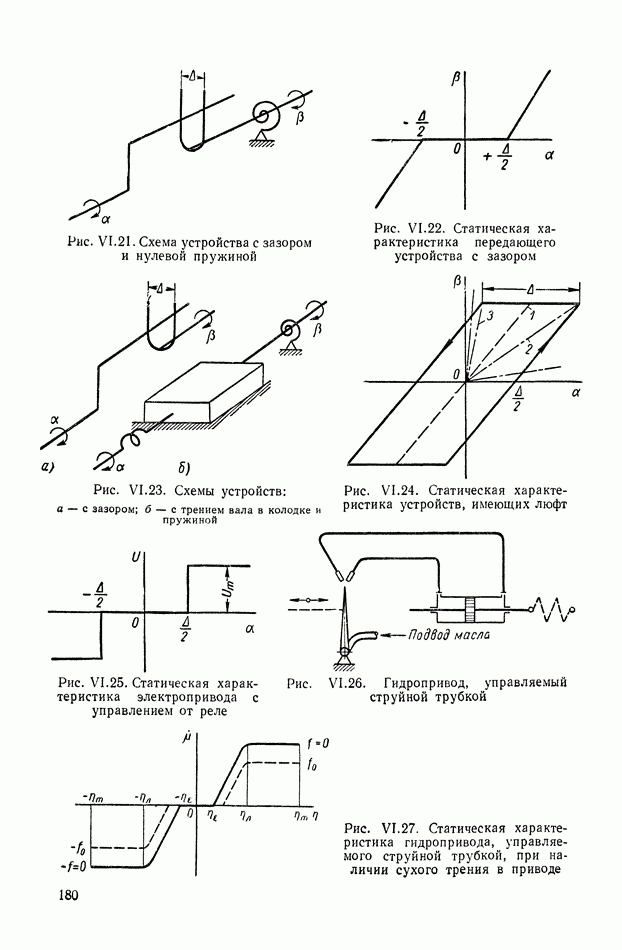
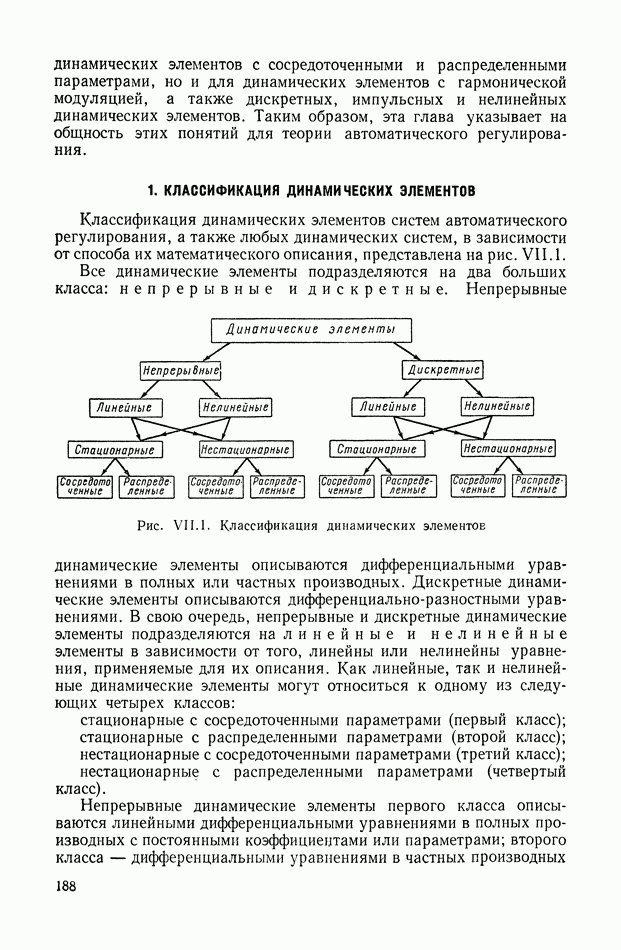
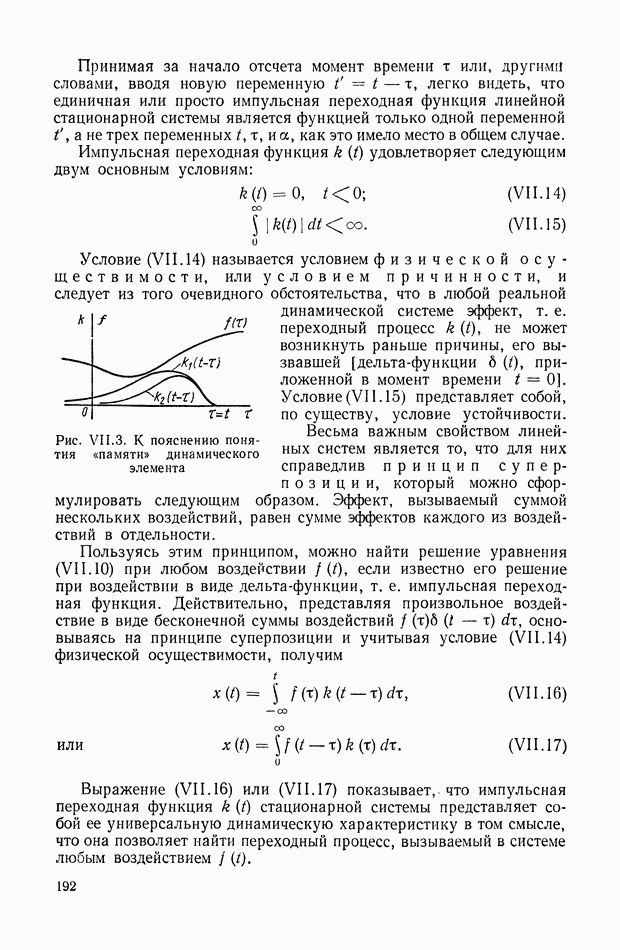
13. ТИПОВЫЕ ЗВЕНЬЯ
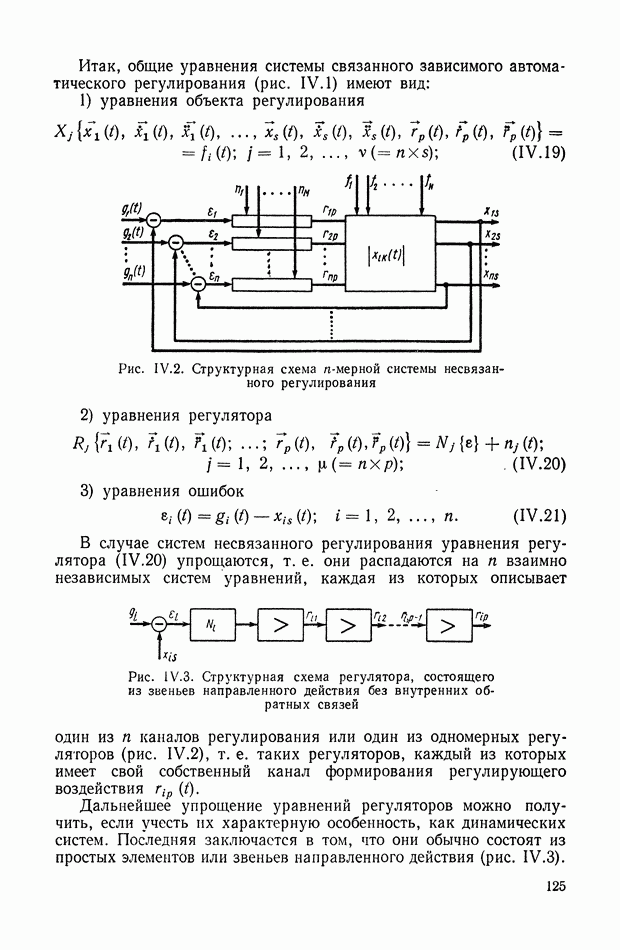
При анализе динамических свойств систем автоматического регулирования часто оказывается удобным вводить в рассмотрение понятие типовых звеньев как некоторых простейших составных частей динамического элемента. [2], [7]. В случае стационарных линейных динамических элементов с сосредоточенными параметрами понятие типовых звеньев может быть введено следующим образом.
Как это было показано выше, передаточная функция такого динамического элемента представляет собой дробно-рациональную функцию от  вида
вида

Если теперь предположить, что нам известны все корни как числителя, так и знаменателя в выражении (VIII.151), то, разлагая его на множители, получим

Предполагая теперь, что числитель имеет  нулевых корней, преобразуя сомножители числителя и знаменателя, соответствующие вещественным корням
нулевых корней, преобразуя сомножители числителя и знаменателя, соответствующие вещественным корням  к виду
к виду

где

и преобразуя сомножители числителя и знаменателя, соответствующие комплексным сопряженным корням, к виду

где

а также

где

вместо выражения (VIII. 151) можем написать

В соответствии с этой формой выражения для передаточной функции, содержащей шесть видов сомножителей, любой структурный элемент можно рассматривать как последовательное соединение в общем случае шести типов элементарных структурных звеньев.
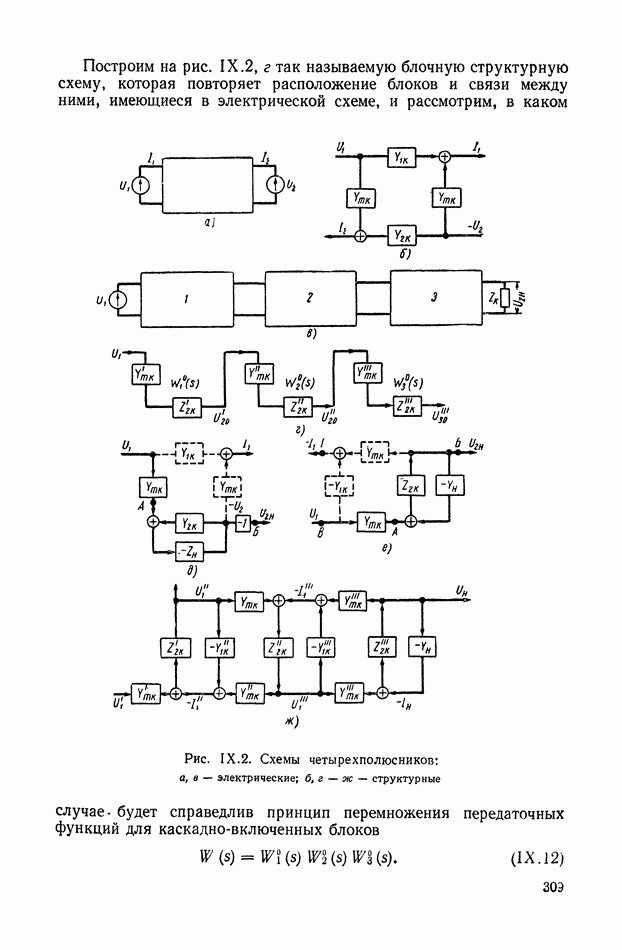
Следует подчеркнуть, что расчленение систем регулирования на типовые звенья имеет под собой не только формальную математическую, но и техническую основу, заключающуюся в следующем. Несмотря на то, что функциональные устройства, входящие в состав системы регулирования, могут иметь самое различное конструктивное оформление и принцип действия, их математическое описание часто сводится к дифференциальным уравнениям первого или второго порядка. Поэтому передаточные функции этих устройств также имеют первый или второй порядок, причем коэффициенты, входящие в выражения для передаточных функций, непосредственно связаны с конструктивными параметрами устройства. Функциональные устройства, входящие в состав системы регулирования, часто обладают свойством направленности действия, благодаря которому (о чем подробнее говорится ниже) передаточные функции последовательного соединения таких устройств могут быть получены как результат перемножения передаточных функций каждого из устройств, без изменения их вида. Именно, вследствие этого обстоятельства передаточные функции сложных динамических элементов систем регулирования часто имеют вид выражения (VIII. 152), состоящего
из произведения простых сомножителей первого или второго порядка. Другими словами, целесообразность расчленения динамического элемента на типовые звенья объясняется особенностью технической реализации систем регулирования, состоящих обычно из совокупности сравнительно не сложных устройств направленного действия.
Звенья, имеющие передаточные функции, соответствующие трем типам сомножителей, входящих в знаменатель, будем называть соответственно интегрирующими, апериодическими и колебательными. 1
Если все члены какого-либо сомножителя в знаменателе выражения (VIII .152) положительны, то оно соответствует устойчивому звену, а если хотя бы один из них отрицателен, то неустойчивому.
При дальнейшем изложении там, где это не может вызвать недоразумений, мы будем для краткости опускать слово «устойчивые», говоря об устойчивых звеньях. Звенья, имеющие передаточные функции, соответствующие трем типам сомножителей, входящих в числитель, будем называть соответственно усилительными, дифференцирующими первого порядка идифференцирующими второго порядка.
Так как звенья имеют различные передаточные функции, то они различаются и по виду переходного процесса, возникающего при изменении входной величины. Для исследования и сравнения звеньев принято, помимо их передаточных функций, рассматривать переходный процесс при определенном стандартном типе возмущения, а именно — при скачкообразном изменении входной величины на единицу и при нулевых начальных условиях (звено в покое), т. е. при единичном ступенчатом воздействии. Функция, определяющая изменение величины на выходе звена при этих условиях, называется переходной функцией звена. Очевидно, что импульсная переходная функция является производной от переходной функции.
Перейдем к рассмотрению передаточных функций, частотных характеристик и переходных функций типовых звеньев.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- РАЗДЕЛ I. ОБЩИЕ СВЕДЕНИЯ. МЕТОДЫ МАТЕМАТИЧЕСКОГО ОПИСАНИЯ И СТРУКТУРНОГО ПРЕОБРАЗОВАНИЯ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- ГЛАВА I. ОЧЕРК О РАЗВИТИИ ТЕОРИИ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ В СССР
- 1. ТЕОРИЯ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ В ДОРЕВОЛЮЦИОННЫЙ ПЕРИОД
- 2. РАЗВИТИЕ ТЕОРИИ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ПОСЛЕ ОКТЯБРЬСКОЙ СОЦИАЛИСТИЧЕСКОЙ РЕВОЛЮЦИИ
- ГЛАВА II. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ ТЕОРИИ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. СУЩНОСТЬ ПРОБЛЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- 2. ПРОБЛЕМА РЕГУЛИРОВАНИЯ КАК ЧАСТНЫЙ СЛУЧАЙ ПРОБЛЕМЫ УПРАВЛЕНИЯ
- 3. ОСНОВНОЙ ПРИНЦИП ДЕЙСТВИЯ И ОПРЕДЕЛЕНИЕ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 4. КЛАССИФИКАЦИЯ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ В ЗАВИСИМОСТИ ОТ УПРАВЛЯЮЩЕГО ВОЗДЕЙСТВИЯ
- 5. ОСНОВНЫЕ УСТРОЙСТВА СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ И ИХ КЛАССИФИКАЦИЯ ПО НАЗНАЧЕНИЮ
- 6. КЛАССИФИКАЦИЯ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ В ЗАВИСИМОСТИ ОТ ХАРАКТЕРА СИГНАЛОВ
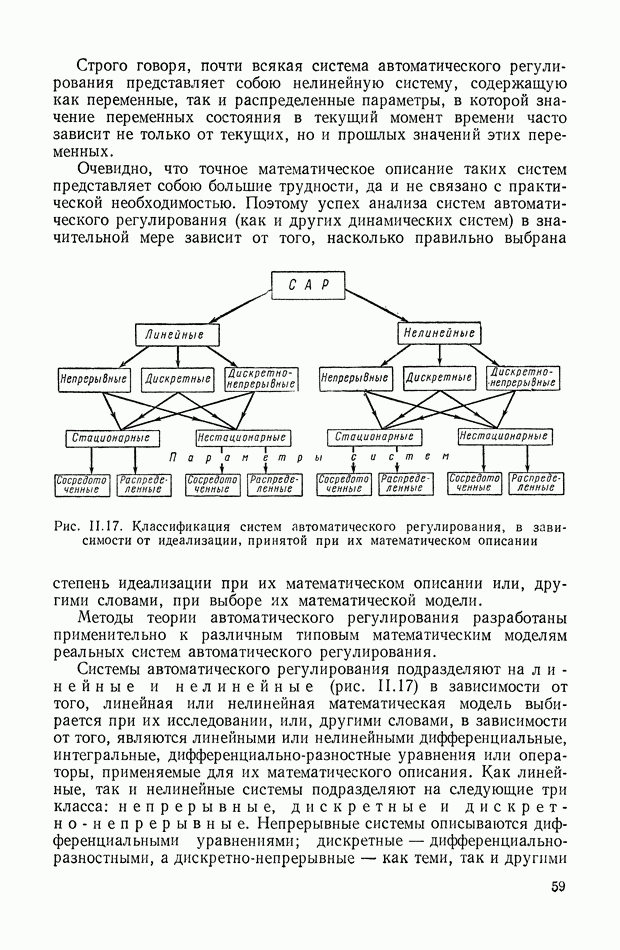
- 7. КЛАССИФИКАЦИЯ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ В ЗАВИСИМОСТИ ОТ ИДЕАЛИЗАЦИИ, ПРИНЯТОЙ ПРИ ИХ МАТЕМАТИЧЕСКОМ ОПИСАНИИ
- 8. СТРУКТУРНЫЕ СХЕМЫ, ОДНОКОНТУРНЫЕ И МНОГОКОНТУРНЫЕ, НЕСВЯЗАННЫЕ И СВЯЗАННЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
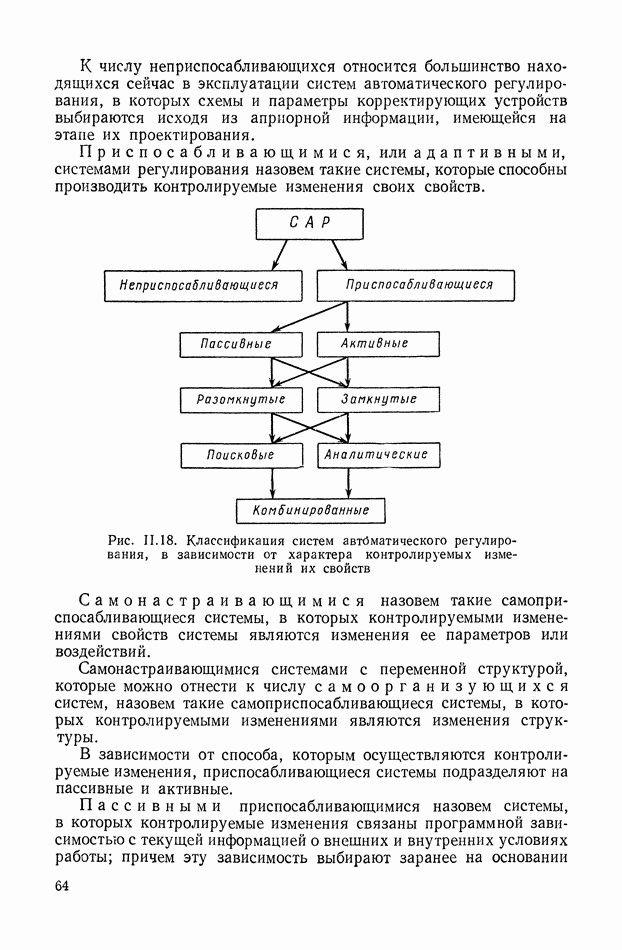
- 9. КЛАССИФИКАЦИЯ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ В ЗАВИСИМОСТИ ОТ ХАРАКТЕРА КОНТРОЛИРУЕМЫХ ИЗМЕНЕНИЙ
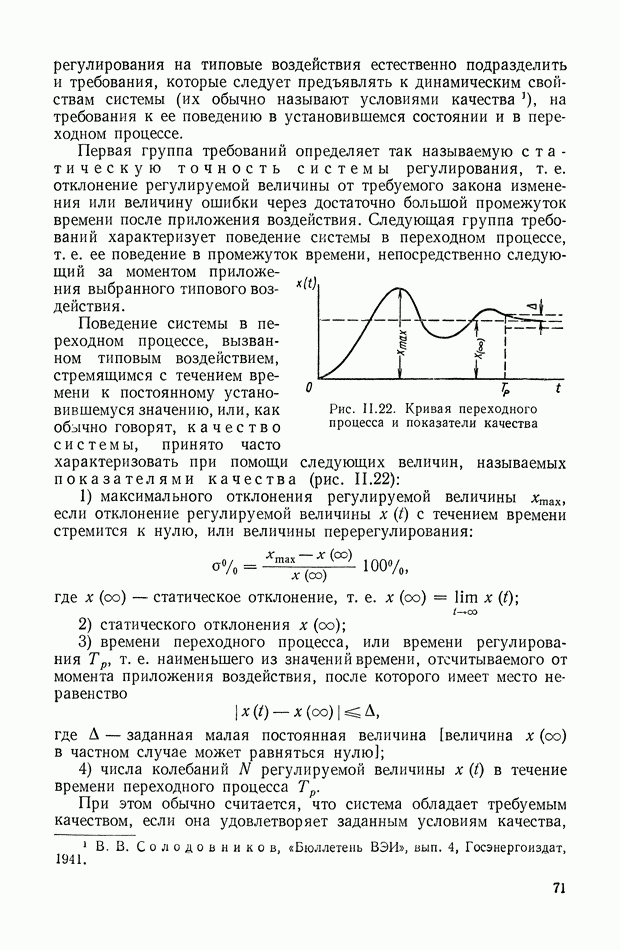
- 10. ТРЕБОВАНИЯ, ПРЕДЪЯВЛЯЕМЫЕ К ДИНАМИЧЕСКИМ СВОЙСТВАМ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- ГЛАВА III. ОСНОВНЫЕ УСТРОЙСТВА И ТИПОВЫЕ СХЕМЫ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. КРАТКАЯ ХАРАКТЕРИСТИКА УСТРОЙСТВ, ИЗ КОТОРЫХ СОСТОЯТ СИСТЕМЫ РЕГУЛИРОВАНИЯ
- 2. СИСТЕМА АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ СКОРОСТИ ГИДРОТУРБИНЫ
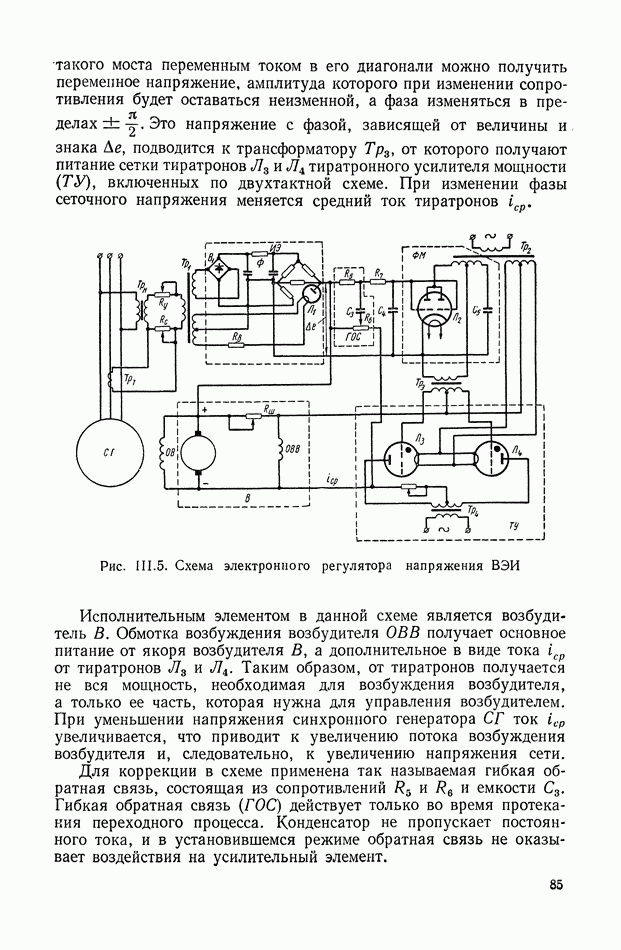
- 3. ЭЛЕКТРОННЫЙ РЕГУЛЯТОР НАПРЯЖЕНИЯ ВЭИ
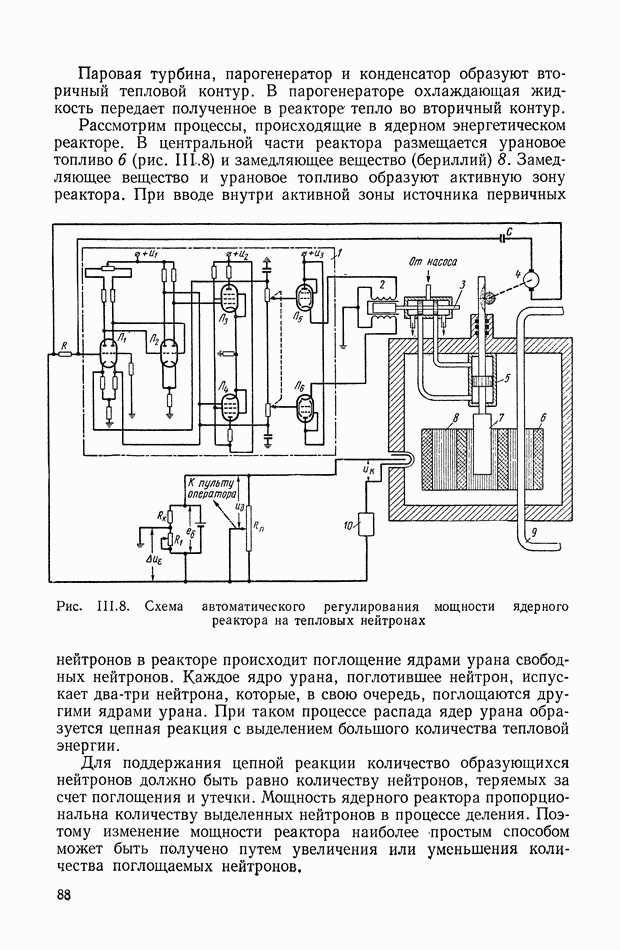
- 4. СИСТЕМА АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ЯДЕРНОГО РЕАКТОРА ПО МОЩНОСТИ
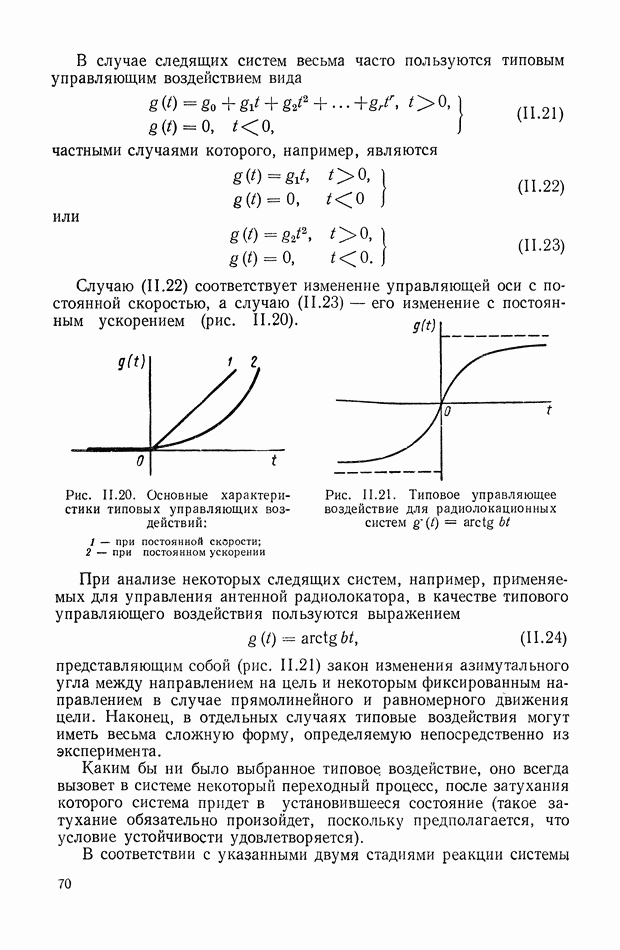
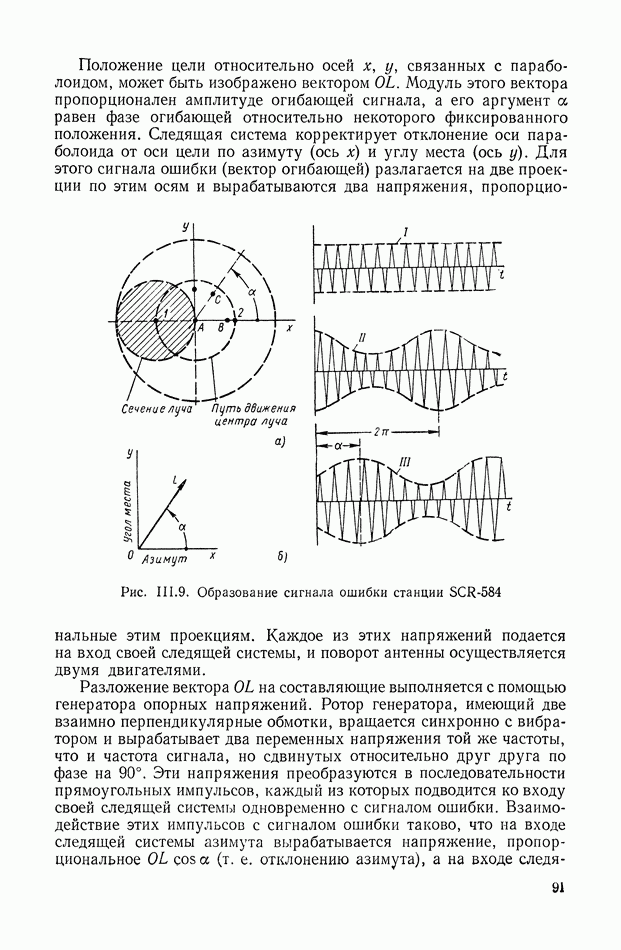
- 5. СЛЕДЯЩАЯ СИСТЕМА РАДИОЛОКАЦИОННОЙ СТАНЦИИ
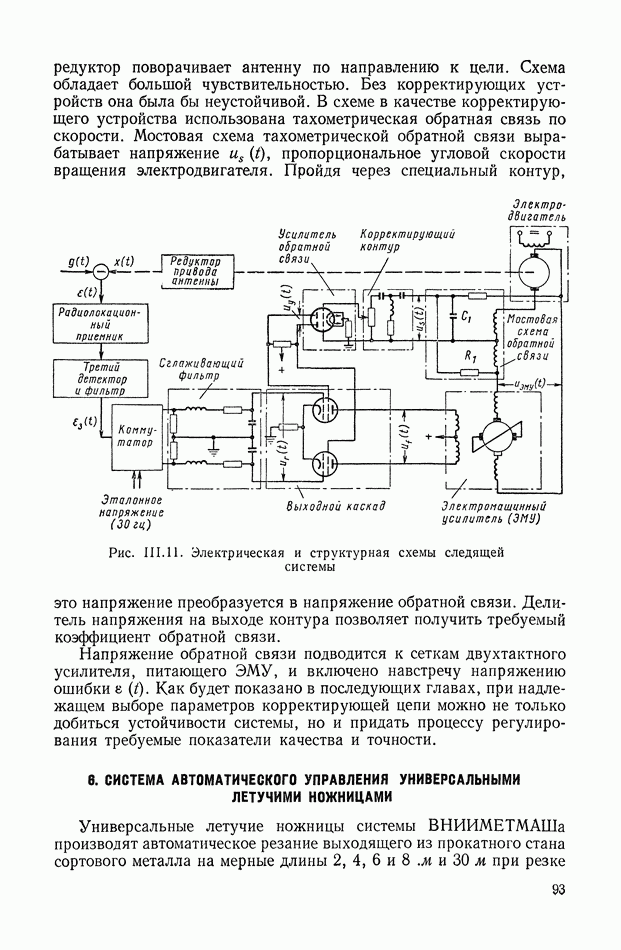
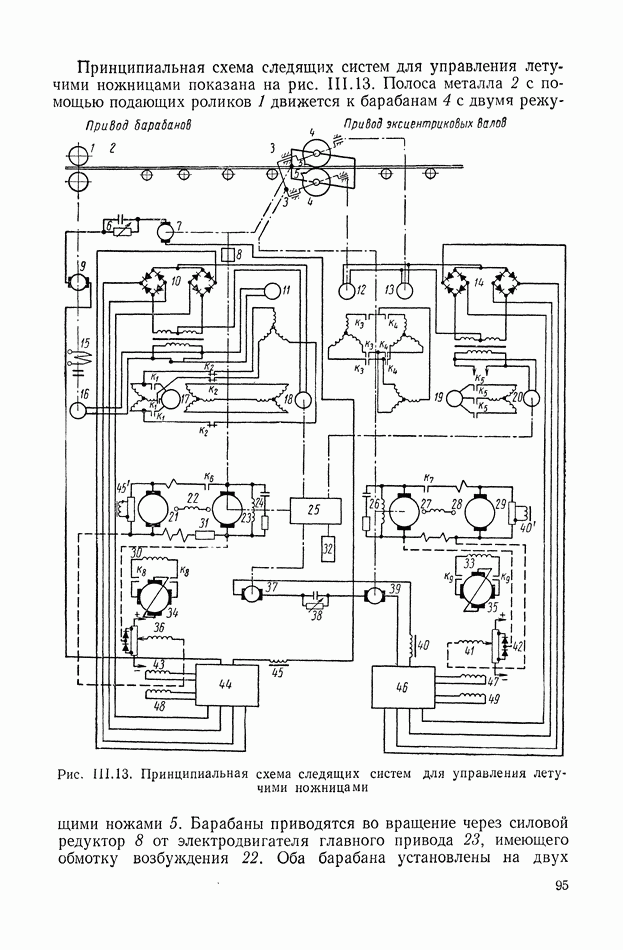
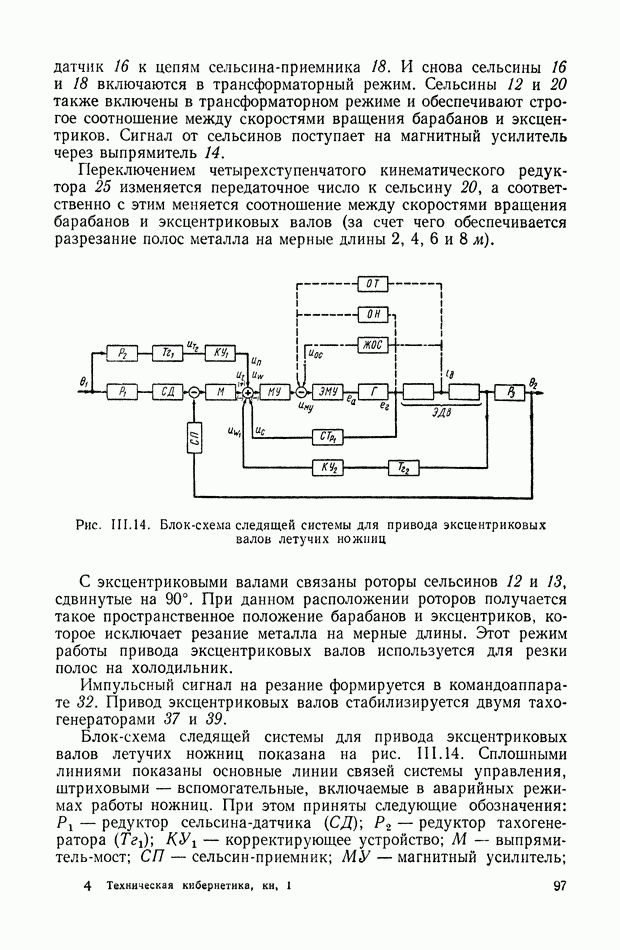
- 6. СИСТЕМА АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ УНИВЕРСАЛЬНЫМИ ЛЕТУЧИМИ НОЖНИЦАМИ
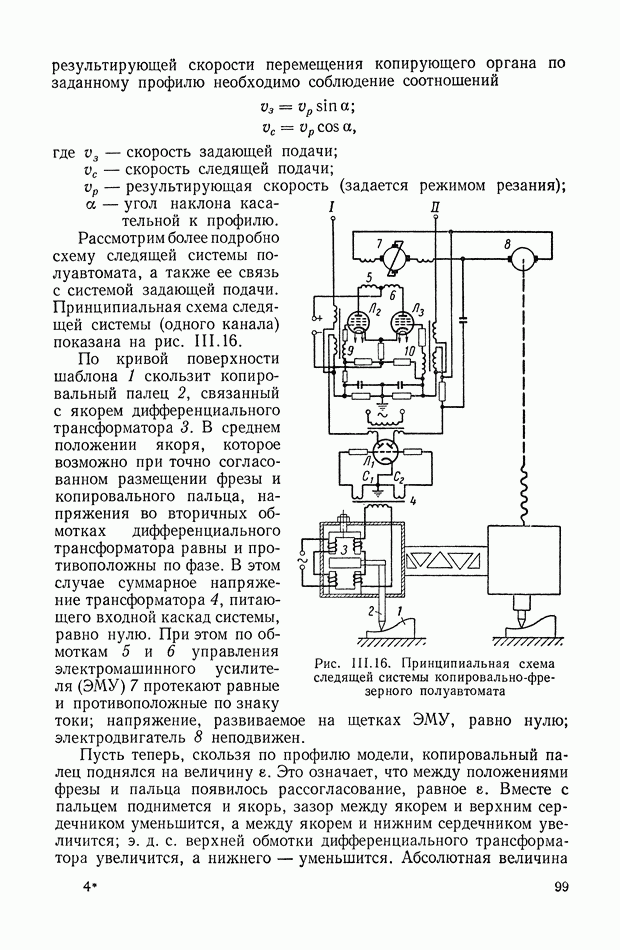
- 7. СЛЕДЯЩАЯ СИСТЕМА КОПИРОВАЛЬНО-ФРЕЗЕРНОГО ПОЛУАВТОМАТА
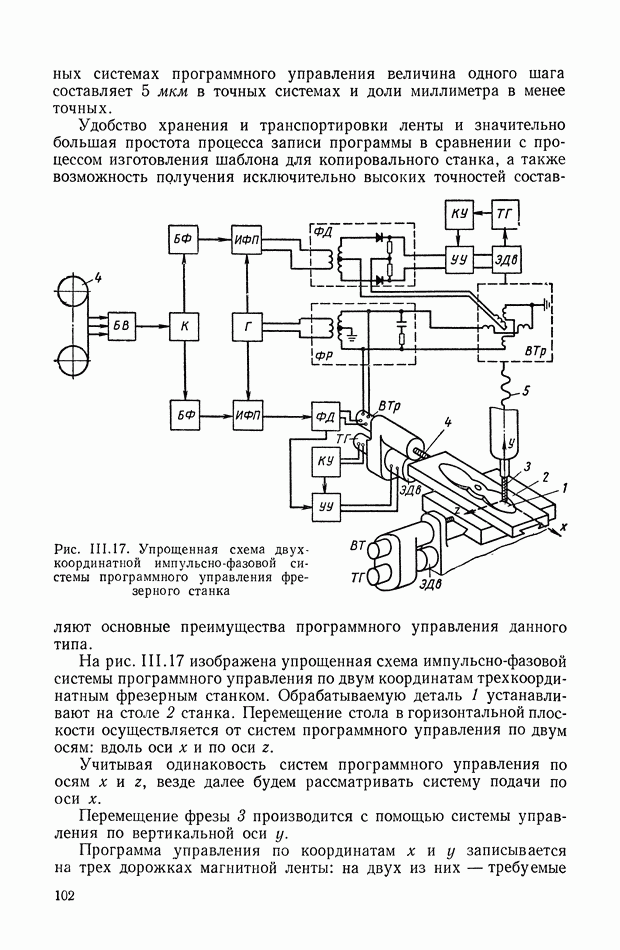
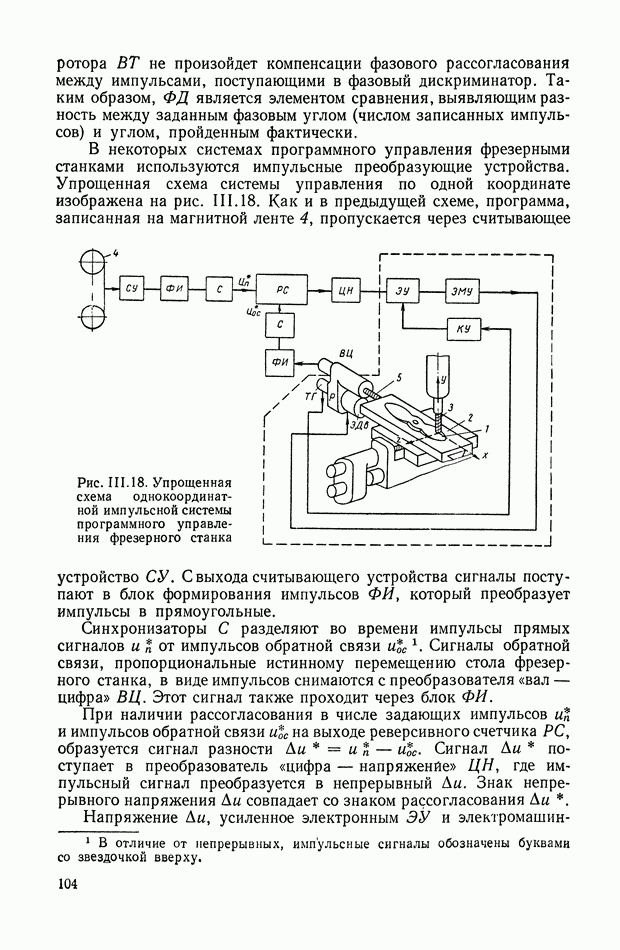
- 8. ПРОГРАММНОЕ УПРАВЛЕНИЕ МЕТАЛЛОРЕЖУЩИМИ СТАНКАМИ
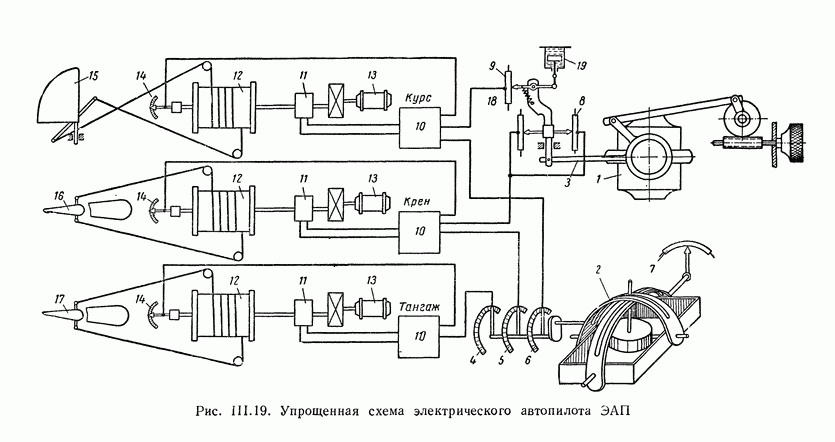
- 9. ПРИНЦИП ДЕЙСТВИЯ ЭЛЕКТРИЧЕСКОГО АВТОПИЛОТА
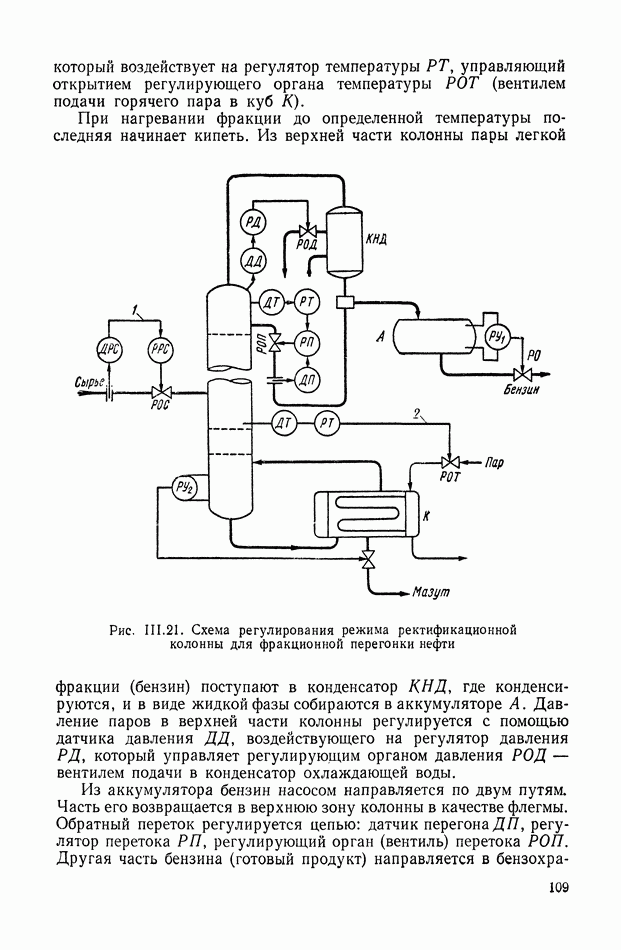
- 10. РЕГУЛИРОВАНИЕ МНОГИХ ВЕЛИЧИН ПРИ АВТОМАТИЧЕСКОМ УПРАВЛЕНИИ ПЕРЕГОНКОЙ НЕФТИ
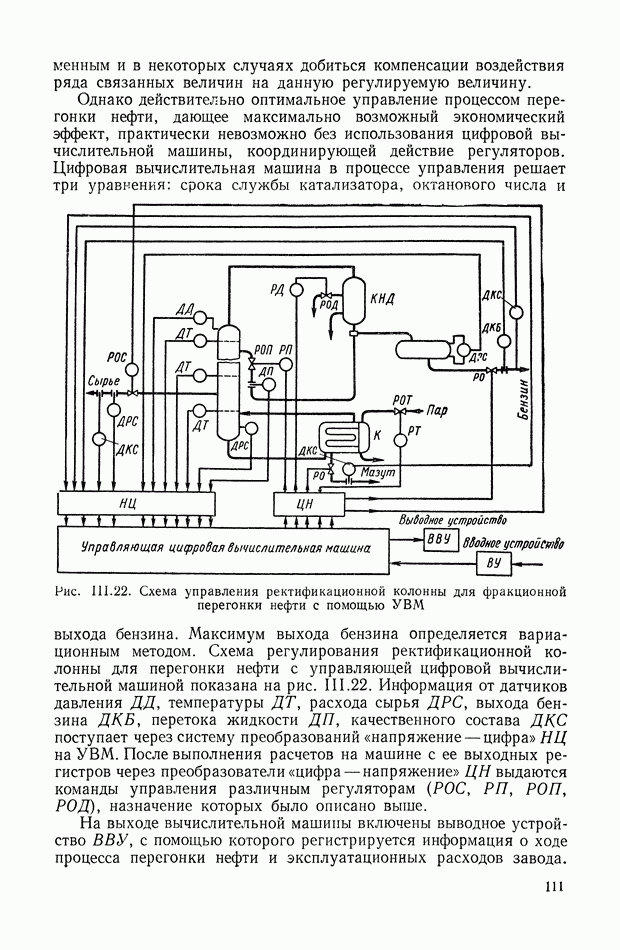
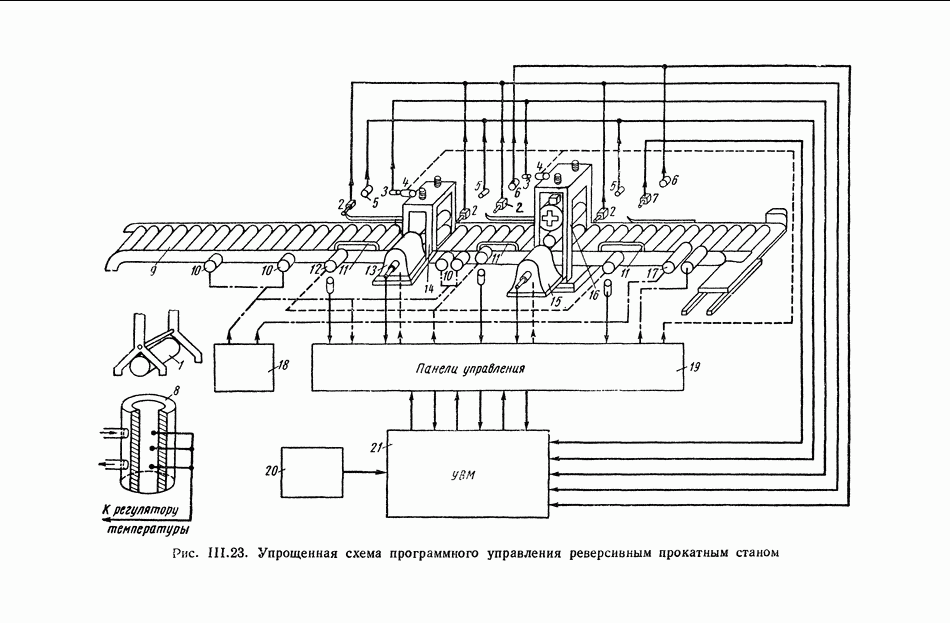
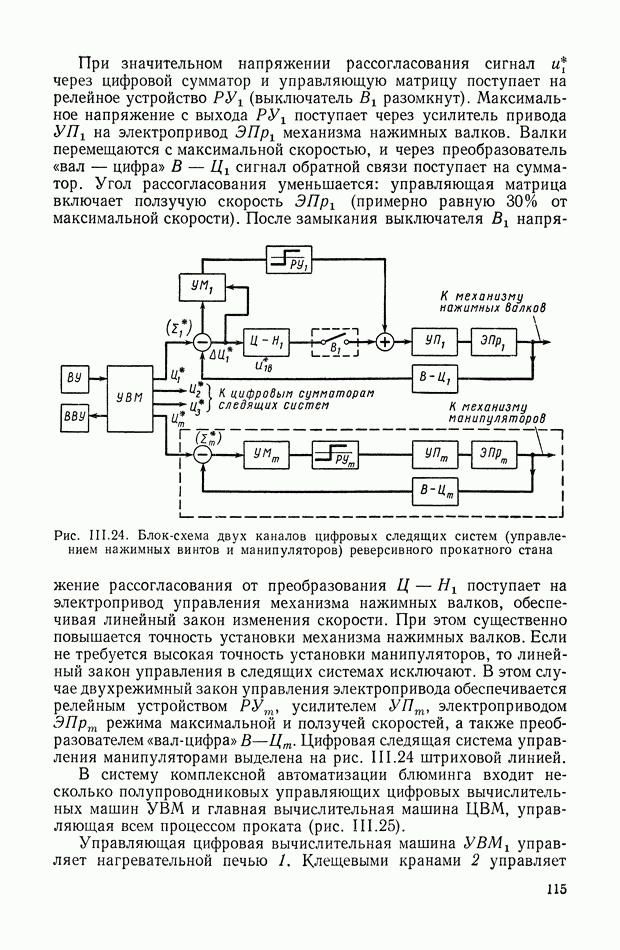
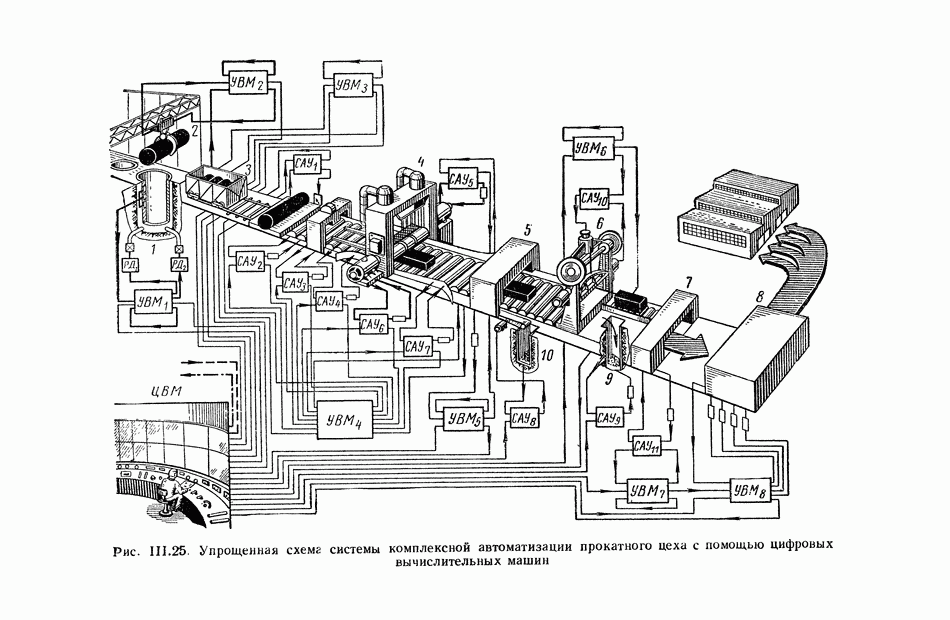
- 11. СИСТЕМА АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ РЕВЕРСИВНЫМ ПРОКАТНЫМ СТАНОМ С ИСПОЛЬЗОВАНИЕМ ЦИФРОВОЙ ВЫЧИСЛИТЕЛЬНОЙ МАШИНЫ
- ГЛАВА IV. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ЛАГРАНЖА ВТОРОГО РОДА
- 2. ОБЩИЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 3. ОБЩИЕ ЛИНЕАРИЗОВАННЫЕ УРАВНЕНИЯ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 4. ПРИМЕР СОСТАВЛЕНИЯ УРАВНЕНИЯ ОБЪЕКТА РЕГУЛИРОВАНИЯ
- ГЛАВА V. СТАТИКА СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. СТАТИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПРОСТЕЙШИХ ЗВЕНЬЕВ
- 2. СТАТИЧЕСКИЕ ХАРАКТЕРИСТИКИ ОСНОВНЫХ ТИПОВ СОЕДИНЕНИЙ ЗВЕНЬЕВ
- 3. КОРРЕКЦИЯ СТАТИЧЕСКИХ ХАРАКТЕРИСТИК
- Статическая характеристика замкнутой одномерной системы регулирования.
- Статическая характеристика линейной замкнутой системы.
- 4. СТАТИЗМ РЕГУЛИРОВАНИЯ
- 5. СТАТИКА ЛИНЕЙНЫХ СИСТЕМ С НЕСКОЛЬКИМИ РЕГУЛИРУЕМЫМИ ВЕЛИЧИНАМИ
- ГЛАВА VI. ТИПИЧНЫЕ НЕЛИНЕЙНЫЕ СТАТИЧЕСКИЕ ХАРАКТЕРИСТИКИ ТИПОВЫХ ЗВЕНЬЕВ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. НЕЛИНЕЙНЫЕ ХАРАКТЕРИСТИКИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
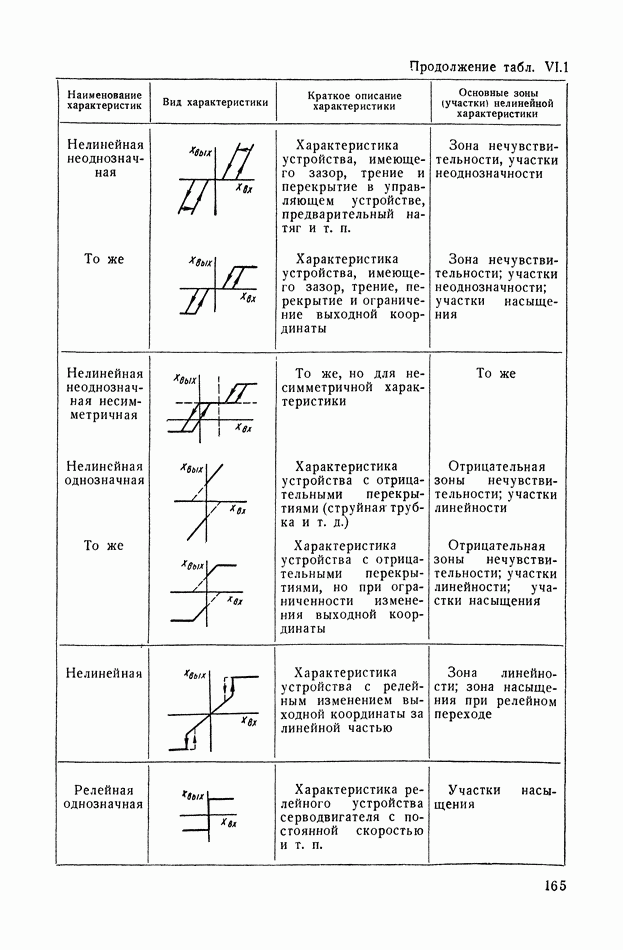
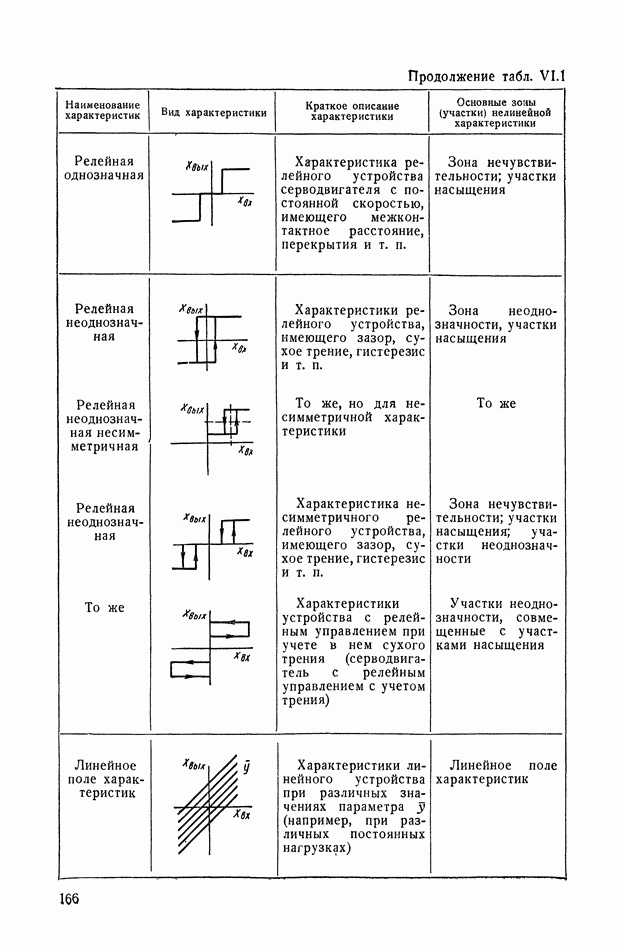
- 2. ВИДЫ ТИПИЧНЫХ НЕЛИНЕЙНЫХ СТАТИЧЕСКИХ ХАРАКТЕРИСТИК СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
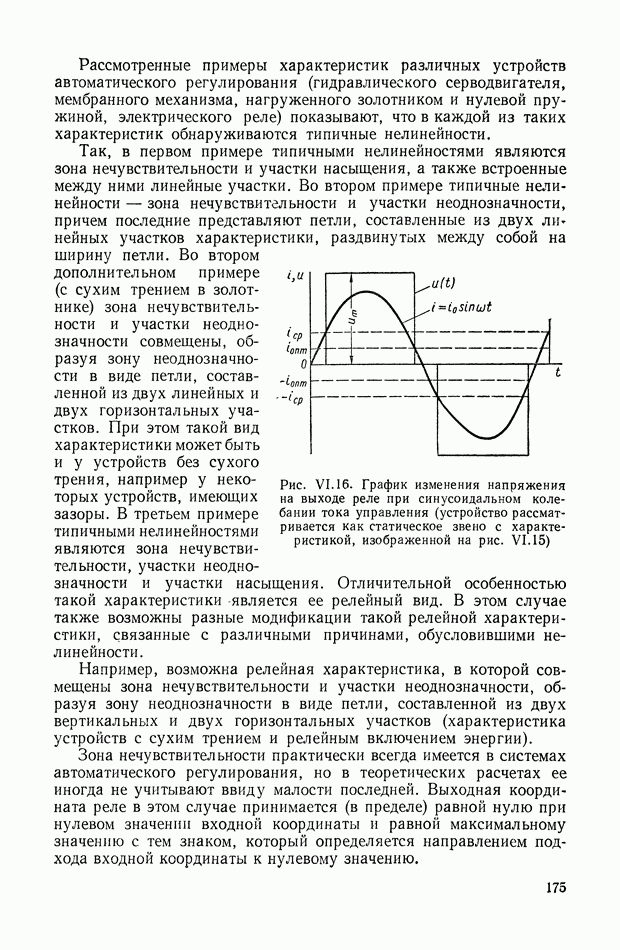
- 3. ТИПИЧНЫЕ НЕЛИНЕЙНЫЕ ХАРАКТЕРИСТИКИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 4. ЗОНЫ НЕЧУВСТВИТЕЛЬНОСТИ
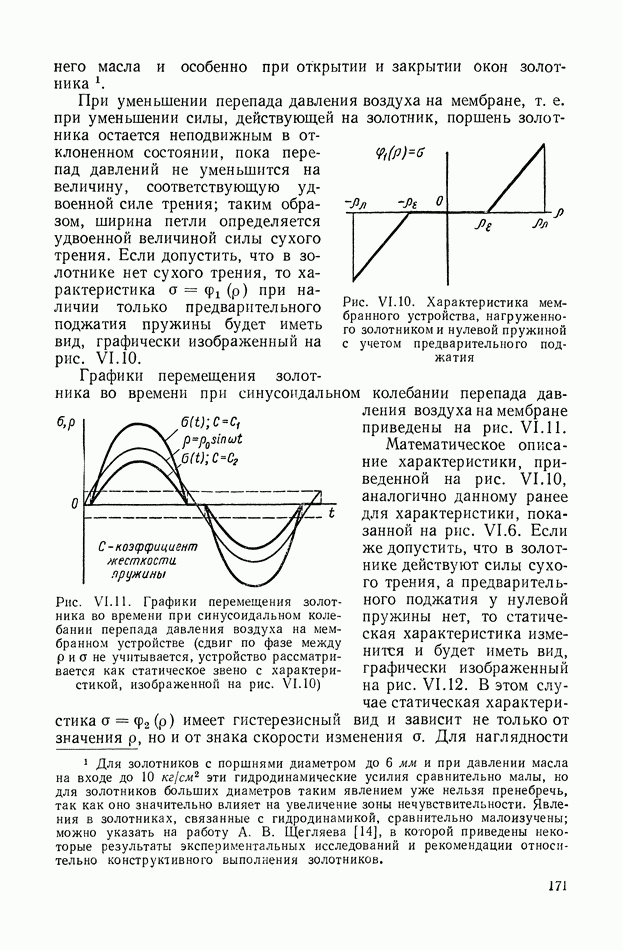
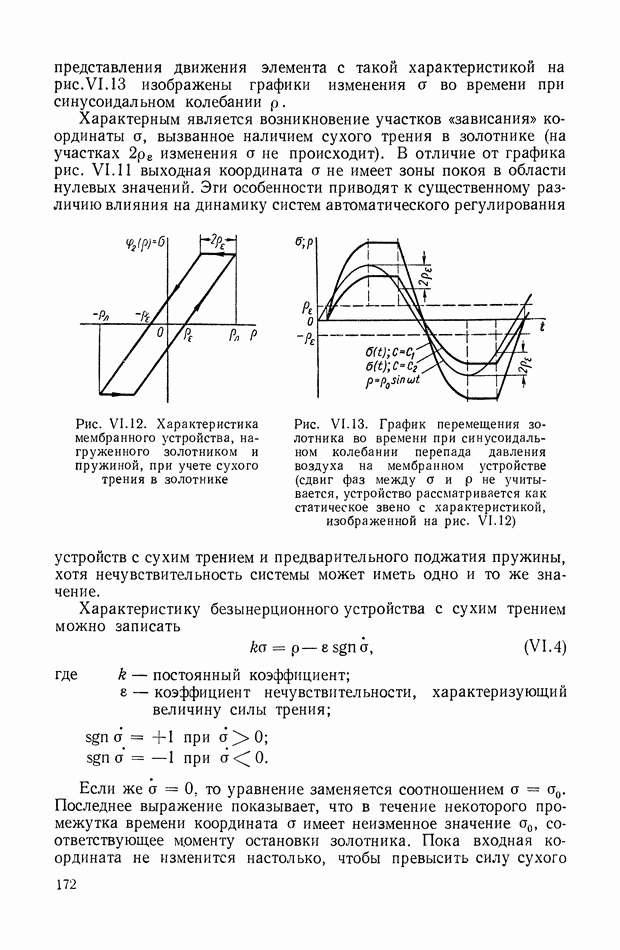
- 5. ЗОНЫ ЛИНЕЙНОСТИ И НЕОДНОЗНАЧНОСТИ
- 6. ЗОНЫ НАСЫЩЕНИЯ
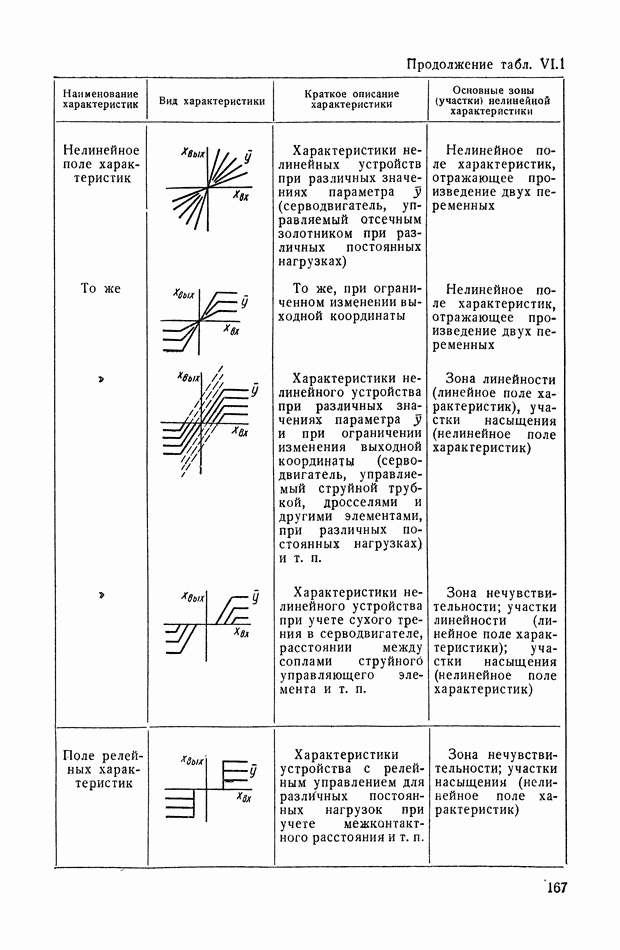
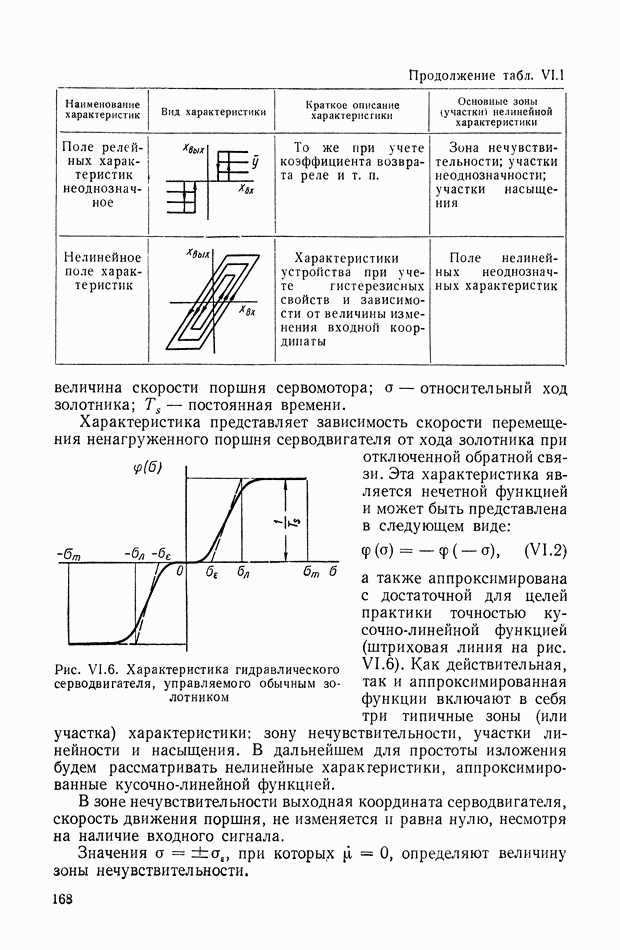
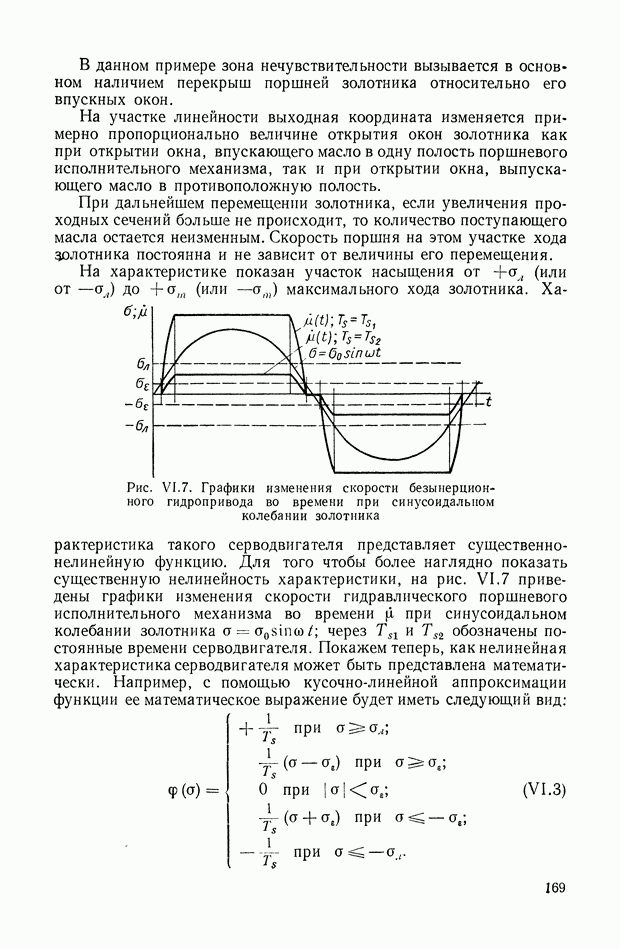
- 7. ПОЛЕ КРИВЫХ, ПРЕДСТАВЛЯЮЩИХ ХАРАКТЕРИСТИКУ СЕРВОДВИГАТЕЛЯ
- 8. ЭКСПЕРИМЕНТАЛЬНОЕ ВЫЯВЛЕНИЕ НЕЛИНЕЙНОСТИ ХАРАКТЕРИСТИК СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- ГЛАВА VII. ПЕРЕХОДНЫЕ ФУНКЦИИ, ПЕРЕДАТОЧНЫЕ ФУНКЦИИ И ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ДИНАМИЧЕСКИХ ЭЛЕМЕНТОВ
- 1. КЛАССИФИКАЦИЯ ДИНАМИЧЕСКИХ ЭЛЕМЕНТОВ
- 2. ОБЩЕЕ ОПРЕДЕЛЕНИЕ ИМПУЛЬСНОЙ ПЕРЕХОДНОЙ И ПЕРЕДАТОЧНОЙ ФУНКЦИЙ ДИНАМИЧЕСКОЙ СИСТЕМЫ ИЛИ ДИНАМИЧЕСКОГО ЭЛЕМЕНТА
- 3. ИМПУЛЬСНАЯ ПЕРЕХОДНАЯ ФУНКЦИЯ НЕПРЕРЫВНОЙ СТАЦИОНАРНОЙ ЛИНЕЙНОЙ СИСТЕМЫ
- 4. ПЕРЕДАТОЧНАЯ ФУНКЦИЯ НЕПРЕРЫВНОЙ ЛИНЕЙНОЙ СТАЦИОНАРНОЙ СИСТЕМЫ
- 5. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЛИНЕЙНОЙ СТАЦИОНАРНОЙ НЕПРЕРЫВНОЙ ДИНАМИЧЕСКОЙ СИСТЕМЫ
- 6. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДИНАМИЧЕСКОГО ЭЛЕМЕНТА С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
- 7. ПРИМЕНЕНИЕ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА К РЕШЕНИЮ УРАВНЕНИЙ ЭЛЕМЕНТА С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
- 8. ПЕРЕДАТОЧНАЯ ФУНКЦИЯ ДИНАМИЧЕСКОГО ЭЛЕМЕНТА С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
- 9. ПЕРЕДАТОЧНАЯ ФУНКЦИЯ ПОСЛЕДОВАТЕЛЬНОГО СОЕДИНЕНИЯ ДИНАМИЧЕСКИХ ЭЛЕМЕНТОВ С СОСРЕДОТОЧЕННЫМИ И С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
- 10. ПЕРЕДАТОЧНАЯ ФУНКЦИЯ ЗАПАЗДЫВАЮЩЕГО ЭЛЕМЕНТА
- 11. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЭЛЕМЕНТА С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
- 12. ИМПУЛЬСНАЯ ПЕРЕХОДНАЯ ФУНКЦИЯ ДИНАМИЧЕСКОГО ЭЛЕМЕНТА С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
- 13. ПЕРЕДАТОЧНАЯ ФУНКЦИЯ СИСТЕМЫ С ГАРМОНИЧЕСКОЙ МОДУЛЯЦИЕЙ
- 14 ИМПУЛЬСНАЯ ПЕРЕХОДНАЯ И ПЕРЕДАТОЧНАЯ ФУНКЦИИ ДИСКРЕТНОЙ ЛИНЕЙНОЙ СТАЦИОНАРНОЙ СИСТЕМЫ
- 15. ПРОХОЖДЕНИЕ СИГНАЛА ЧЕРЕЗ ИМПУЛЬСНЫЙ ЭЛЕМЕНТ
- 16. ПОСЛЕДОВАТЕЛЬНОЕ СОЕДИНЕНИЕ ИМПУЛЬСНОГО ЭЛЕМЕНТА И НЕПРЕРЫВНОГО ДИНАМИЧЕСКОГО ЭЛЕМЕНТА
- 17. ИМПУЛЬСНАЯ ПЕРЕХОДНАЯ ФУНКЦИЯ ЛИНЕЙНОЙ НЕСТАЦИОНАРНОЙ СИСТЕМЫ (СИСТЕМЫ С ПЕРЕМЕННЫМИ ПАРАМЕТРАМИ)
- 18. ПЕРЕДАТОЧНАЯ ФУНКЦИЯ НЕПРЕРЫВНОЙ ЛИНЕЙНОЙ НЕСТАЦИОНАРНОЙ СИСТЕМЫ
- 19. МНОГОМЕРНЫЕ ИМПУЛЬСНЫЕ ПЕРЕХОДНЫЕ И ПЕРЕДАТОЧНЫЕ ФУНКЦИИ НЕЛИНЕЙНЫХ СИСТЕМ
- 20. МНОГОМЕРНЫЕ ПЕРЕДАТОЧНЫЕ ФУНКЦИИ НЕЛИНЕЙНЫХ СИСТЕМ
- ГЛАВА VIII. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ, ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ И ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ НЕПРЕРЫВНЫХ ЛИНЕЙНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 2. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ СТАТИЧЕСКИХ И АСТАТИЧЕСКИХ СИСТЕМ
- 3. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ
- 4. ВЗАИМНАЯ СВЯЗЬ МЕЖДУ ЧАСТОТНЫМИ ХАРАКТЕРИСТИКАМИ ЗАМКНУТОЙ И РАЗОМКНУТОЙ СИСТЕМЫ
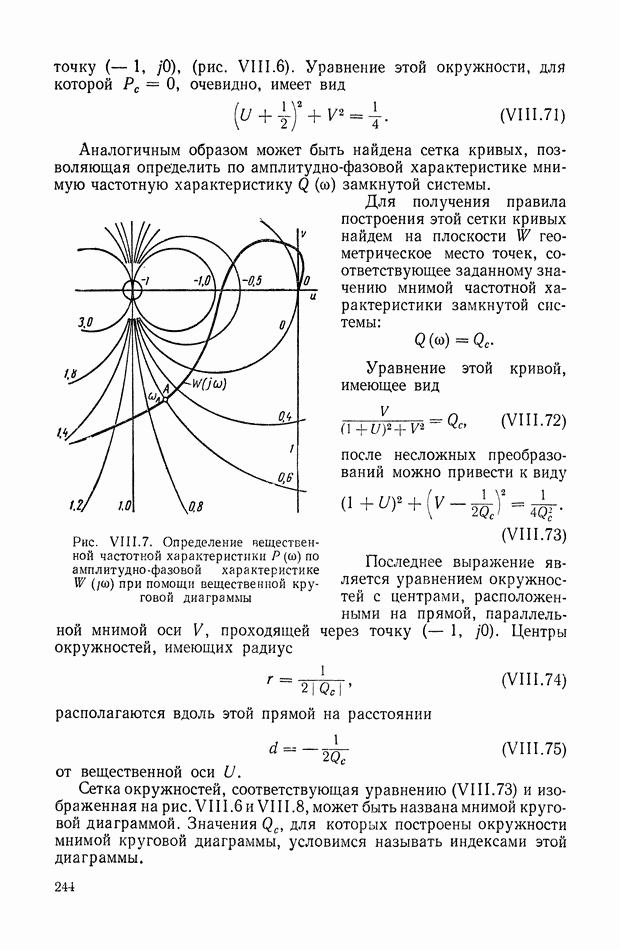
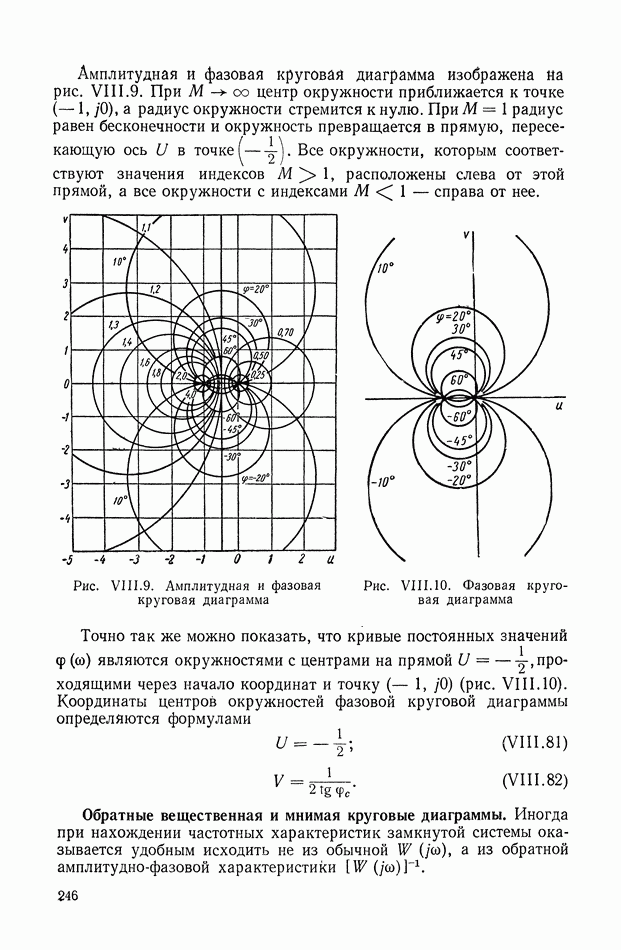
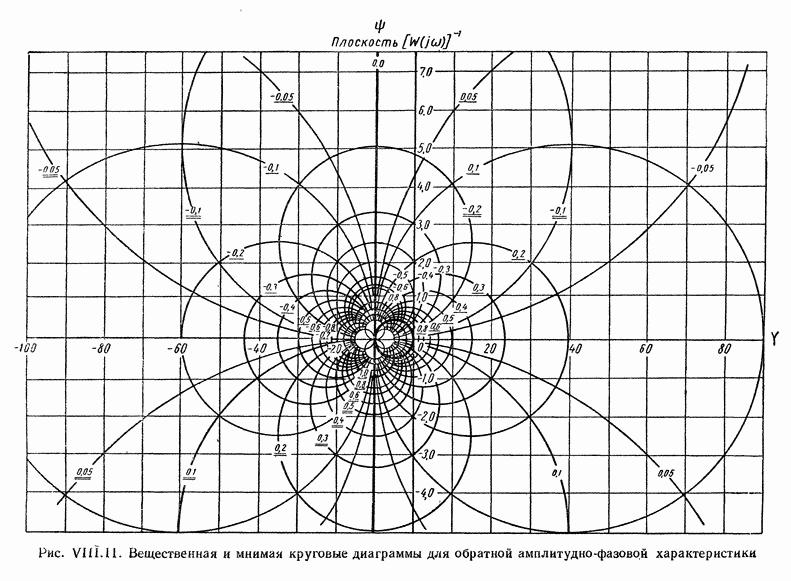
- 5. КРУГОВЫЕ ДИАГРАММЫ
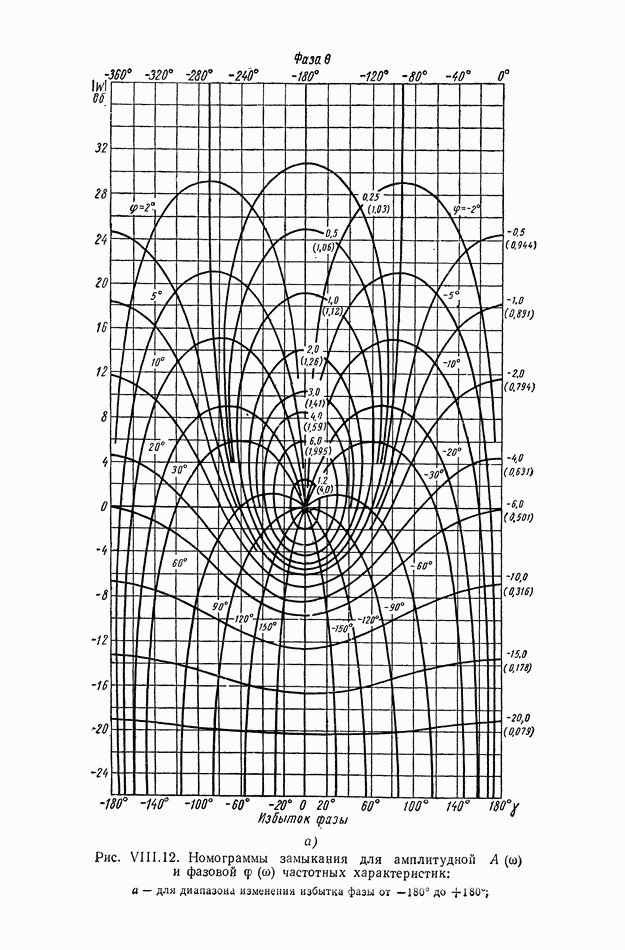
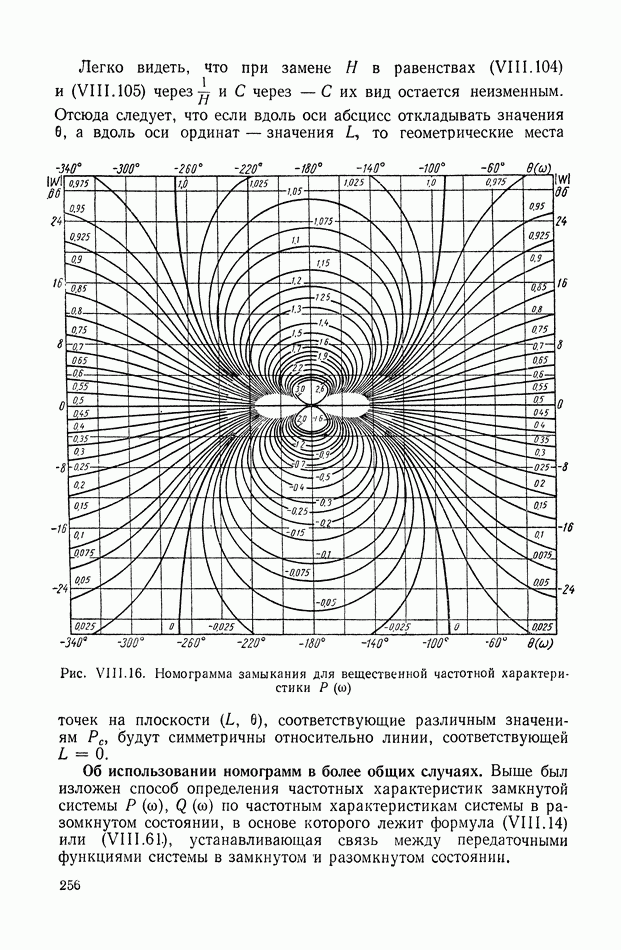
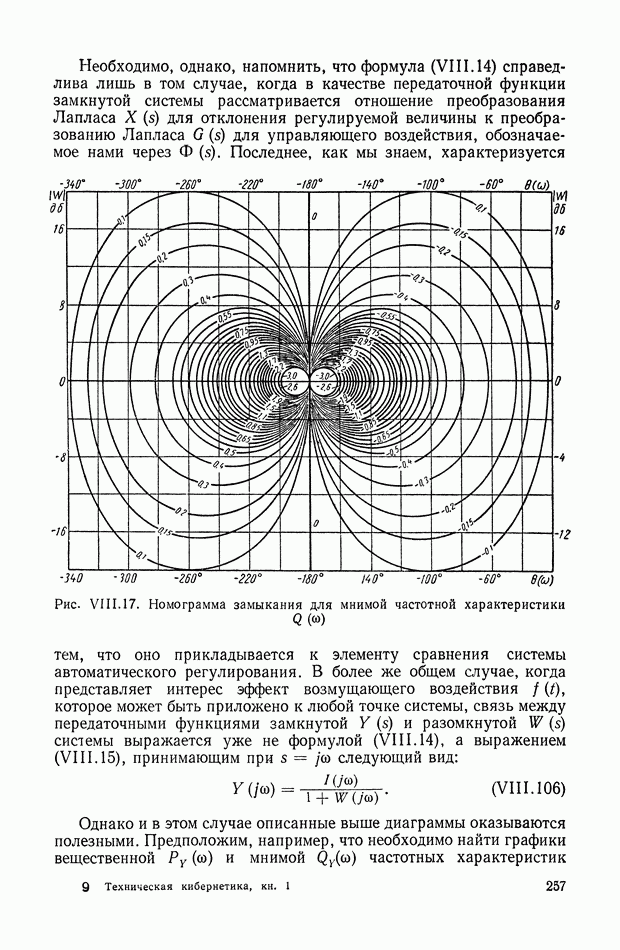
- 6. НОМОГРАММЫ ЗАМЫКАНИЯ
- 7. УСЛОВИЯ ОДНОЗНАЧНОЙ связи МЕЖДУ ЧАСТОТНЫМИ ХАРАКТЕРИСТИКАМИ
- 8. ОПРЕДЕЛЕНИЕ ПЕРЕДАТОЧНОЙ ФУНКЦИИ ПО ОДНОЙ ИЗ ЧАСТОТНЫХ ХАРАКТЕРИСТИК, ЗАДАННОЙ АНАЛИТИЧЕСКИ
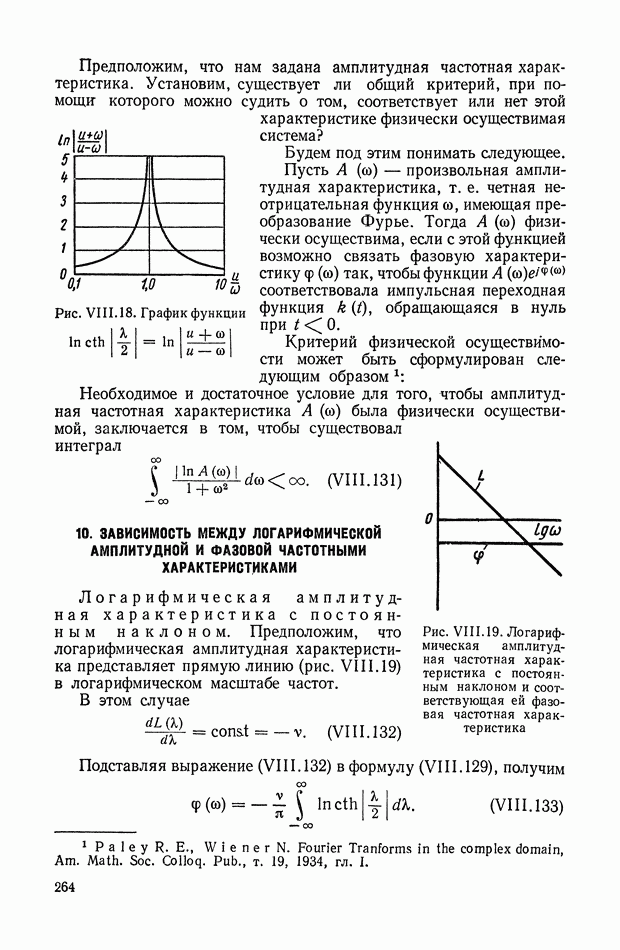
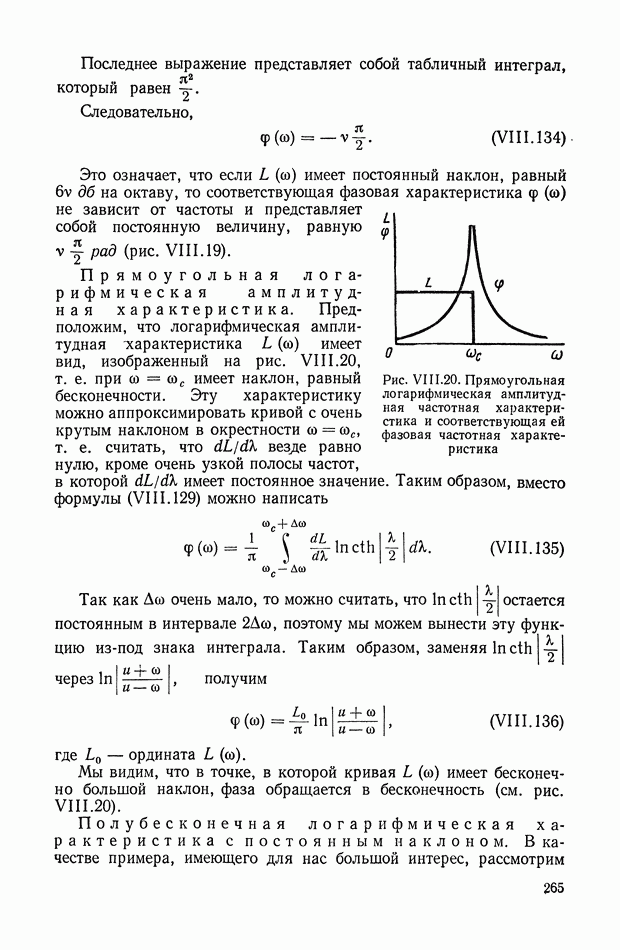
- 9. ФОРМУЛА ДЛЯ ВЫЧИСЛЕНИЯ ФАЗОВОЙ ЧАСТОТНОЙ ХАРАКТЕРИСТИКИ ПО ЗАДАННОЙ АМПЛИТУДНОЙ ЧАСТОТНОЙ ХАРАКТЕРИСТИКЕ
- 10. ЗАВИСИМОСТЬ МЕЖДУ ЛОГАРИФМИЧЕСКОЙ АМПЛИТУДНОЙ И ФАЗОВОЙ ЧАСТОТНЫМИ ХАРАКТЕРИСТИКАМИ
- 11. ГРАФИЧЕСКИЙ МЕТОД ОПРЕДЕЛЕНИЯ ФАЗОВОЙ ХАРАКТЕРИСТИКИ ПО ЗАДАННОЙ АМПЛИТУДНОЙ ХАРАКТЕРИСТИКЕ
- 12. ИНТЕГРАЛЬНЫЕ ВЫРАЖЕНИЯ ДЛЯ ОШИБКИ И ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 13. ТИПОВЫЕ ЗВЕНЬЯ
- 14. АПЕРИОДИЧЕСКОЕ ЗВЕНО
- 15. КОЛЕБАТЕЛЬНОЕ ЗВЕНО
- 16. ИНТЕГРИРУЮЩЕЕ ЗВЕНО
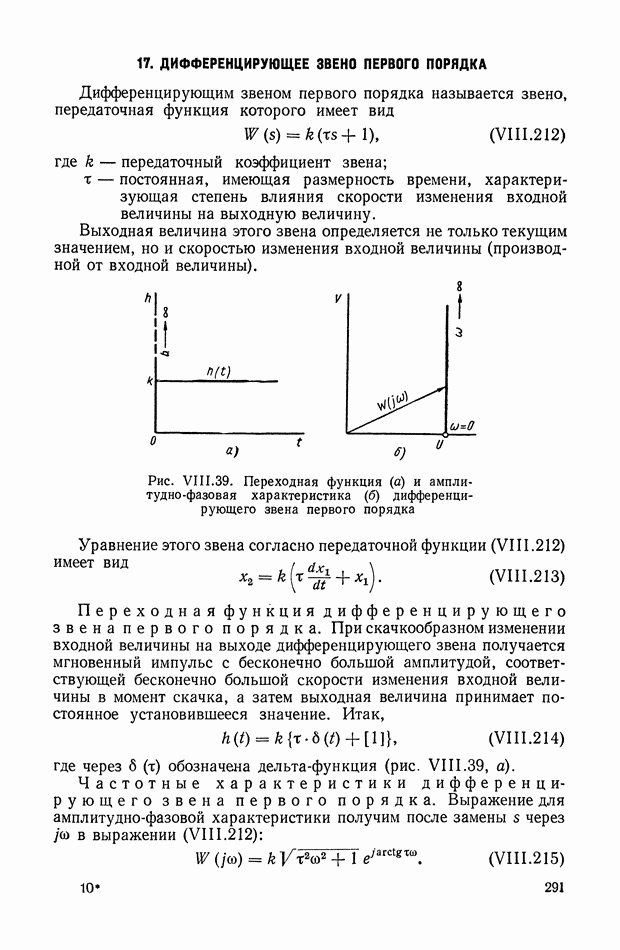
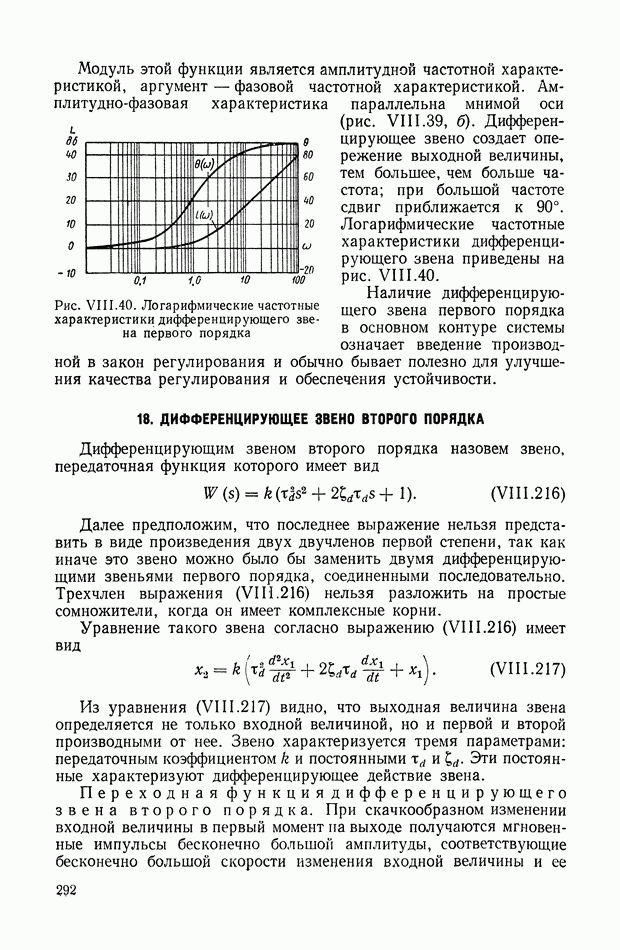
- 17. ДИФФЕРЕНЦИРУЮЩЕЕ ЗВЕНО ПЕРВОГО ПОРЯДКА
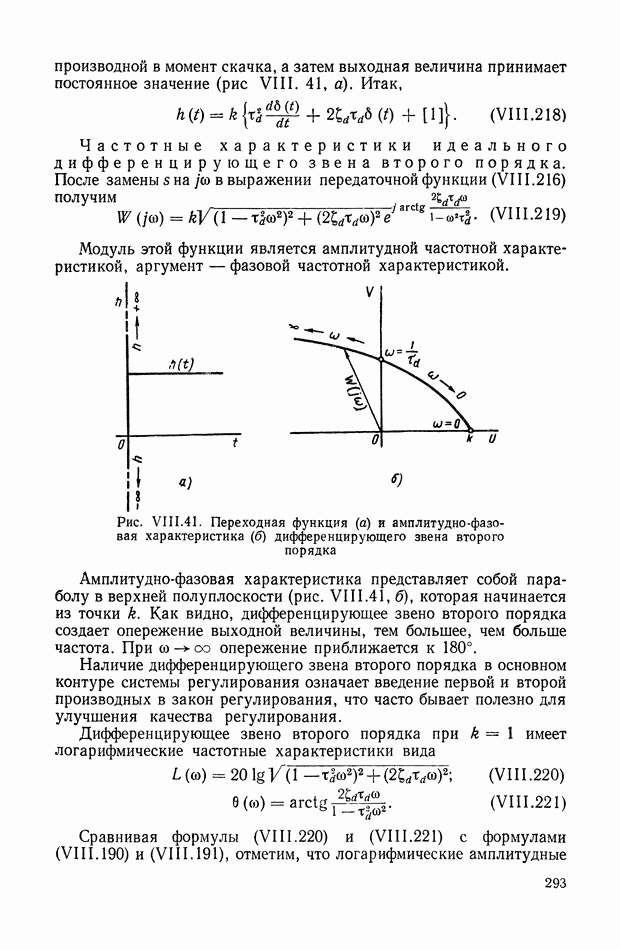
- 18. ДИФФЕРЕНЦИРУЮЩЕЕ ЗВЕНО ВТОРОГО ПОРЯДКА
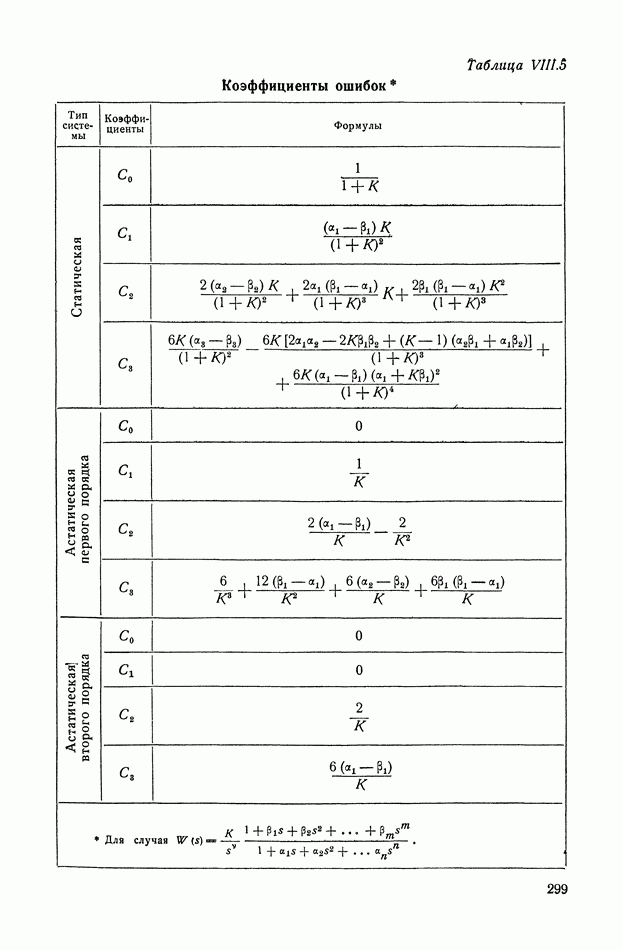
- 19. КОЭФФИЦИЕНТЫ ОШИБКИ
- ГЛАВА IX. МЕТОДЫ СТРУКТУРНЫХ ПРЕОБРАЗОВАНИЙ В СИСТЕМАХ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. ГРАФИЧЕСКИЕ ИЗОБРАЖЕНИЯ УСЛОВИЙ ПРЕОБРАЗОВАНИЯ СИГНАЛОВ
- 2. СХЕМЫ С ЭЛЕМЕНТАМИ, ОБЛАДАЮЩИМИ И НЕ ОБЛАДАЮЩИМИ СВОЙСТВОМ НАПРАВЛЕННОСТИ ДЕЙСТВИЯ
- 3. ДЕТАЛИЗИРОВАННЫЕ СТРУКТУРЫ
- 4. ПРЕОБРАЗОВАНИЯ МНОГОКОНТУРНЫХ СТРУКТУРНЫХ СХЕМ, ДОПУСКАЮЩИХ ПОСЛЕДОВАТЕЛЬНОЕ ПРИМЕНЕНИЕ ПРАВИЛ СВЕРТЫВАНИЯ КОНТУРОВ, И НЕКОТОРЫЕ ЭКВИВАЛЕНТНЫЕ ПРЕОБРАЗОВАНИЯ
- 5. ПРЕОБРАЗОВАНИЯ ПЕРЕКРЕСТНЫХ СТРУКТУРНЫХ СХЕМ МЕТОДОМ РАЗВЯЗКИ КОНТУРОВ И НЕКОТОРЫЕ ЭКВИВАЛЕНТНЫЕ ПРЕОБРАЗОВАНИЯ
- 6. ПРИМЕНЕНИЕ СТРУКТУРНЫХ МЕТОДОВ ДЛЯ ОПРЕДЕЛЕНИЯ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ МНОГОКОНТУРНЫХ СИСТЕМ
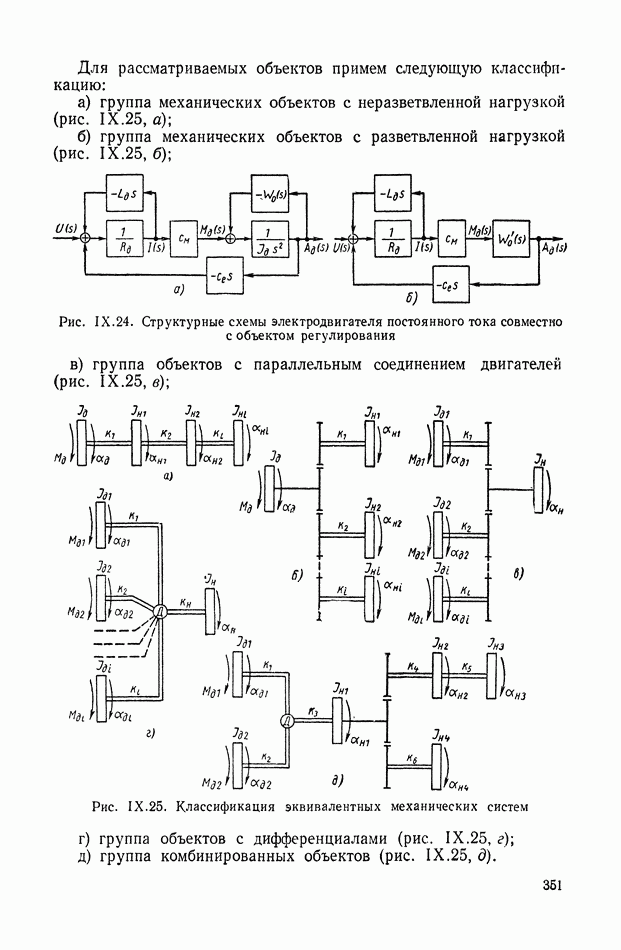
- 7. СОСТАВЛЕНИЕ И ПРЕОБРАЗОВАНИЕ СТРУКТУРНОЙ СХЕМЫ НА ПРИМЕРЕ ЭЛЕКТРОДВИГАТЕЛЯ ПОСТОЯННОГО ТОКА ДВОЙНОГО ПИТАНИЯ
- Учет зависимости момента нагрузки от угла поворота вала и его производных по времени.
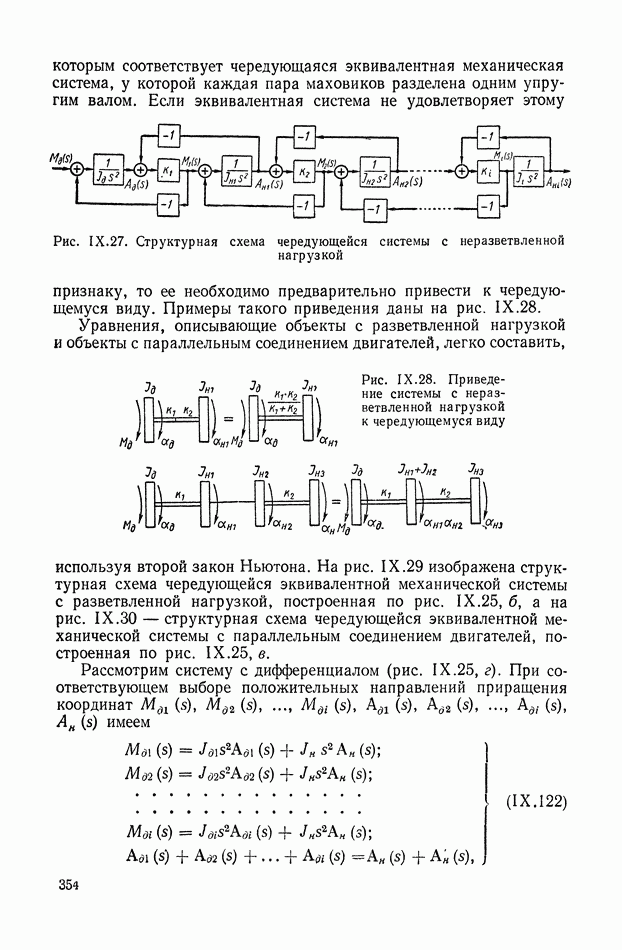
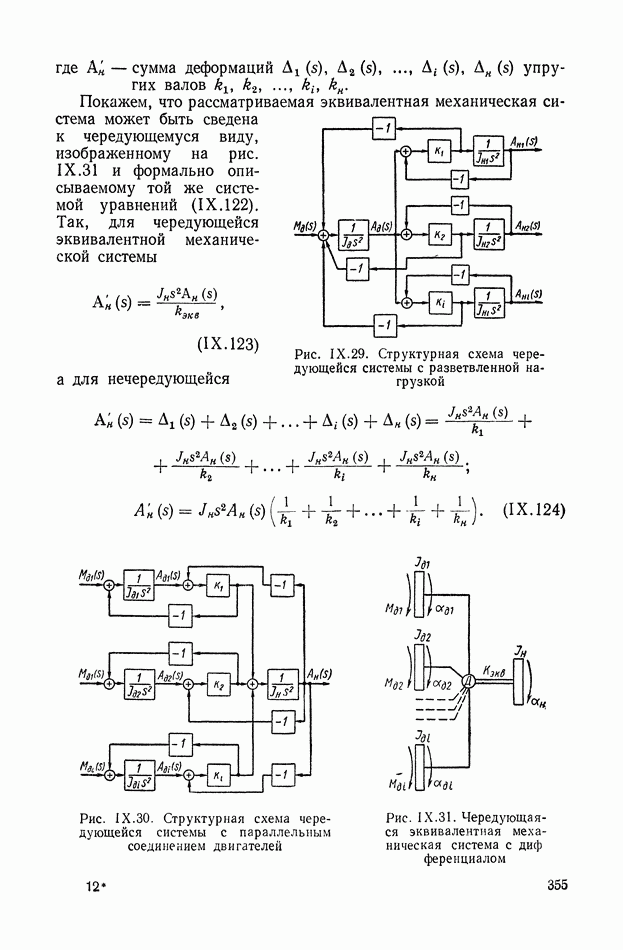
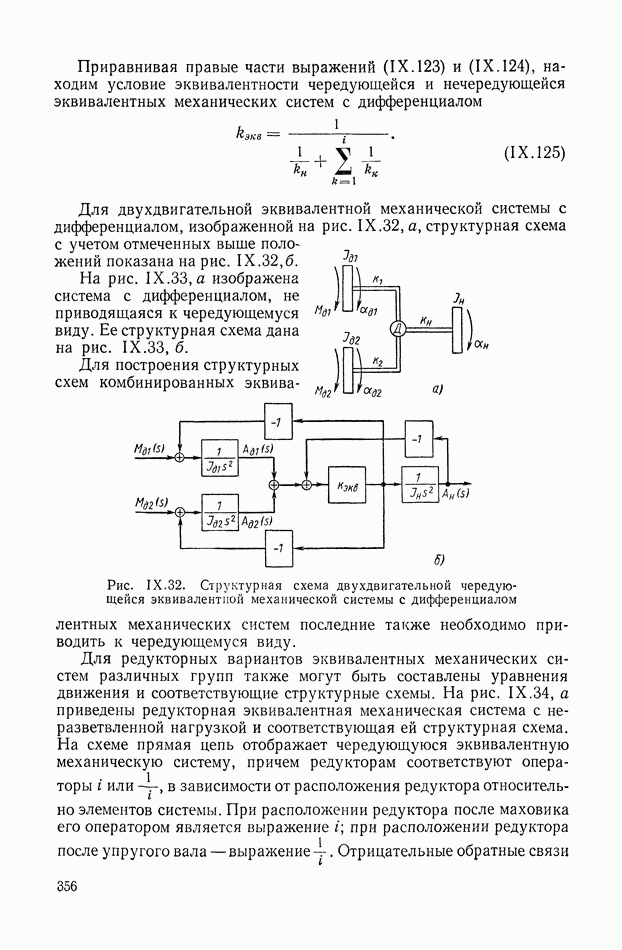
- 8. СТРУКТУРНЫЕ СХЕМЫ МЕХАНИЧЕСКИХ ОБЪЕКТОВ РЕГУЛИРОВАНИЯ С РЕДУКТОРАМИ, ДИФФЕРЕНЦИАЛАМИ И УПРУГИМИ ЭЛЕМЕНТАМИ В СИЛОВЫХ ПЕРЕДАЧАХ
- 9. ПРАВИЛА СТРУКТУРНЫХ ПРЕОБРАЗОВАНИЙ ДЛЯ СИСТЕМ С ПЕРЕМЕННЫМИ ПАРАМЕТРАМИ
- 10. ФУНКЦИОНАЛЬНЫЕ СТРУКТУРНЫЕ СХЕМЫ ДЛЯ АНАЛИЗА СОВМЕСТНЫХ СТАТИЧЕСКИХ ХАРАКТЕРИСТИК НЕЛИНЕЙНЫХ ЗВЕНЬЕВ
- ГЛАВА X. ПРИМЕРЫ СОСТАВЛЕНИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ, СТРУКТУРНЫХ СХЕМ И ПЕРЕДАТОЧНЫХ ФУНКЦИЙ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. СИСТЕМА АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ СКОРОСТИ ВРАЩЕНИЯ ГИДРОТУРБИНЫ
- 2. ЭЛЕКТРОННЫЙ РЕГУЛЯТОР НАПРЯЖЕНИЯ ВЭИ
- 3. СИСТЕМА АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ МОЩНОСТИ ЯДЕРНОГО ЭНЕРГЕТИЧЕСКОГО РЕАКТОРА НА ТЕПЛОВЫХ НЕЙТРОНАХ
- 4. СЛЕДЯЩАЯ СИСТЕМА РАДИОЛОКАЦИОННОЙ СТАНЦИИ
- 5. СИСТЕМА АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ УНИВЕРСАЛЬНЫХ ЛЕТУЧИХ НОЖНИЦ
- 6. САМОЛЕТ С АВТОПИЛОТОМ
- 7. СЛЕДЯЩАЯ СИСТЕМА КОПИРОВАЛЬНО-ФРЕЗЕРНОГО СТАНКА
- РАЗДЕЛ II. АНАЛИЗ УСТОЙЧИВОСТИ НЕПРЕРЫВНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- ГЛАВА XI. ОБЩАЯ ПОСТАНОВКА ЗАДАЧИ УСТОЙЧИВОСТИ ПО ЛЯПУНОВУ И АНАЛИЗ УСТОЙЧИВОСТИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. ПОСТАНОВКА ЗАДАЧИ ОБ УСТОЙЧИВОСТИ В ТЕОРИИ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 2. ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ УСТАНОВИВШИХСЯ ДВИЖЕНИЙ ПО УРАВНЕНИЮ ПЕРВОГО ПРИБЛИЖЕНИЯ
- 3. О ПРЯМОМ МЕТОДЕ ЛЯПУНОВА
- 4. О ПРИМЕНЕНИИ ПРЯМОГО МЕТОДА ЛЯПУНОВА К АНАЛИЗУ УСТОЙЧИВОСТИ ОДНОГО КЛАССА СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- ГЛАВА XII. КРИТЕРИИ И МЕТОДЫ АНАЛИЗА УСТОЙЧИВОСТИ ЛИНЕАРИЗОВАННЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЙ
- 1. УСТОЙЧИВОСТЬ И ПРИНЦИП АРГУМЕНТА
- 2. КРИТЕРИЙ УСТОЙЧИВОСТИ МИХАЙЛОВА
- 3. КРИТЕРИЙ УСТОЙЧИВОСТИ РАУСА И ГУРВИЦА
- 4. ЧАСТОТНЫЙ КРИТЕРИЙ УСТОЙЧИВОСТИ
- 5. ОБОБЩЕНИЕ ЧАСТОТНОГО КРИТЕРИЯ НА АСТАТИЧЕСКИЕ СИСТЕМЫ
- 6. ОБОБЩЕНИЕ ЧАСТОТНОГО КРИТЕРИЯ НА СЛУЧАЙ, КОГДА РАЗОМКНУТАЯ СИСТЕМА НЕУСТОЙЧИВА
- 7. ЧАСТОТНЫЙ КРИТЕРИЙ УСТОЙЧИВОСТИ ДЛЯ ОБРАТНОЙ АМПЛИТУДНО-ФАЗОВОЙ ХАРАКТЕРИСТИКИ
- 8. АНАЛИЗ УСТОЙЧИВОСТИ ОДНОКОНТУРНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ПО ИХ ЛОГАРИФМИЧЕСКИМ ЧАСТОТНЫМ ХАРАКТЕРИСТИКАМ
- 9. ПРИБЛИЖЕННЫЙ СПОСОБ ПОСТРОЕНИЯ ЛОГАРИФМИЧЕСКИХ ЧАСТОТНЫХ ХАРАКТЕРИСТИК ОДНОКОНТУРНЫХ СИСТЕМ
- 10. ОБОБЩЕНИЕ ЧАСТОТНОГО КРИТЕРИЯ УСТОЙЧИВОСТИ НА МНОГОКОНТУРНЫЕ СИСТЕМЫ
- 11. АНАЛИЗ УСТОЙЧИВОСТИ МНОГОКОНТУРНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ПРИ ПОМОЩИ ЛОГАРИФМИЧЕСКИХ ЧАСТОТНЫХ ХАРАКТЕРИСТИК
- ГЛАВА XIII. ВЫДЕЛЕНИЕ ОБЛАСТЕЙ УСТОЙЧИВОСТИ
- 1. ПОНЯТИЕ О Д-РАЗБИЕНИИ ПРОСТРАНСТВА КОЭФФИЦИЕНТОВ ХАРАКТЕРИСТИЧЕСКОГО УРАВНЕНИЯ И ПРОСТРАНСТВА ПАРАМЕТРОВ
- 2. Д-РАЗБИЕНИЕ ПЛОСКОСТИ ОДНОГО КОМПЛЕКСНОГО ПАРАМЕТРА
- 3. СВЯЗЬ Д-РАЗБИЕНИЯ С КРИТЕРИЯМИ УСТОЙЧИВОСТИ
- 4. Д-РАЗБИЕНИЕ ПЛОСКОСТИ ДВУХ ДЕЙСТВИТЕЛЬНЫХ ПАРАМЕТРОВ (ДИАГРАММА ВЫШНЕГРАДСКОГО)
- 5. УСЛОВИЯ СУЩЕСТВОВАНИЯ ОБЛАСТИ УСТОЙЧИВОСТИ
- ГЛАВА XIV. ПРИМЕРЫ АНАЛИЗА УСТОЙЧИВОСТИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. СИСТЕМА АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ СКОРОСТИ ВРАЩЕНИЯ ГИДРОТУРБИНЫ
- 2. СЛЕДЯЩАЯ СИСТЕМА КОПИРОВАЛЬНО-ФРЕЗЕРНОГО СТАНКА
- 3. СИСТЕМА АВТОМАТИЧЕСКОЙ СТАБИЛИЗАЦИИ САМОЛЕТА (АВТОПИЛОТ)
- 4. СИСТЕМА АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ МОЩНОСТИ ЯДЕРНОГО ЭНЕРГЕТИЧЕСКОГО РЕАКТОРА
- РАЗДЕЛ III. АНАЛИЗ ПЕРЕХОДНЫХ ПРОЦЕССОВ И КАЧЕСТВА ЛИНЕЙНЫХ НЕПРЕРЫВНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- ГЛАВА XV. ЧАСТОТНЫЙ МЕТОД АНАЛИЗА ПЕРЕХОДНЫХ ПРОЦЕССОВ
- 1. ОБОБЩЕННЫЕ ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ И ИХ СВЯЗЬ С ПЕРЕХОДНЫМИ ПРОЦЕССАМИ
- 2. ОПРЕДЕЛЕНИЕ ОБОБЩЕННЫХ ЧАСТОТНЫХ ХАРАКТЕРИСТИК В ОБЩЕМ СЛУЧАЕ
- 3. СЛУЧАЙ, КОГДА ФУНКЦИЯ X(s) НЕ СОДЕРЖИТ ОСОБЕННОСТЕЙ ВО ВСЕЙ ПРАВОЙ ПОЛУПЛОСКОСТИ И НА МНИМОЙ ОСИ
- 4. СВЯЗЬ МЕЖДУ ЧАСТОТНЫМИ ХАРАКТЕРИСТИКАМИ P(w), Q(w) И ИМПУЛЬСНОЙ ПЕРЕХОДНОЙ ФУНКЦИЕЙ k(t)
- 5. СЛУЧАЙ, КОГДА ВСЕ ПОЛЮСА ФУНКЦИИ X(s) РАСПОЛОЖЕНЫ В ЛЕВОЙ ПОЛУПЛОСКОСТИ, ЗА ИСКЛЮЧЕНИЕМ ПОЛЮСА В НАЧАЛЕ КООРДИНАТ
- 6. СВЯЗЬ МЕЖДУ ЧАСТОТНЫМИ ХАРАКТЕРИСТИКАМИ И ПЕРЕХОДНОЙ ФУНКЦИЕЙ h(t)
- 7. СЛУЧАЙ, КОГДА ФУНКЦИЯ X(s) ИМЕЕТ ДВА СОПРЯЖЕННЫХ ПОЛЮСА НА МНИМОЙ ОСИ
- 8. АНАЛИЗ ПЕРЕХОДНЫХ ПРОЦЕССОВ МЕТОДОМ ТРАПЕЦЕИДАЛЬНЫХ ЧАСТОТНЫХ ХАРАКТЕРИСТИК
- 9. О НЕКОТОРЫХ ЧАСТНЫХ СЛУЧАЯХ МЕТОДА ТРАПЕЦЕИДАЛЬНЫХ ЧАСТОТНЫХ ХАРАКТЕРИСТИК
- 10. ОБ УСЛОВИЯХ ПРИМЕНИМОСТИ ЧАСТОТНОГО МЕТОДА АНАЛИЗА ПЕРЕХОДНЫХ ПРОЦЕССОВ
- 11. ОПРЕДЕЛЕНИЕ ДИСКРЕТНЫХ ЗНАЧЕНИЙ ПЕРЕХОДНОЙ ФУНКЦИИ
- ГЛАВА XVI. ЧАСТОТНЫЙ МЕТОД АНАЛИЗА КАЧЕСТВА
- 1. ЧАСТОТНЫЙ КРИТЕРИЙ КАЧЕСТВА РЕГУЛИРОВАНИЯ
- 2. ЧАСТОТНЫЙ КРИТЕРИЙ ОТСУТСТВИЯ ПЕРЕРЕГУЛИРОВАНИЙ И ЧАСТОТНЫЙ КРИТЕРИЙ МОНОТОННОСТИ
- 3. О ПРОВЕРКЕ ВЫПОЛНЕНИЯ СФОРМУЛИРОВАННЫХ КРИТЕРИЕВ
- 4. НЕКОТОРЫЕ ПРИЗНАКИ НЕУДОВЛЕТВОРЕНИЯ КРИТЕРИЕВ КАЧЕСТВА И КРИТЕРИЕВ ОТСУТСТВИЯ ПЕРЕРЕГУЛИРОВАНИЙ И МОНОТОННОСТИ
- 5. НЕКОТОРЫЕ ЭЛЕМЕНТАРНЫЕ СВОЙСТВА ЧАСТОТНЫХ ХАРАКТЕРИСТИК
- 6. ДОСТАТОЧНЫЕ УСЛОВИЯ ДЛЯ МАЛЫХ ПЕРЕРЕГУЛИРОВАНИЙ И НЕОБХОДИМЫЕ УСЛОВИЯ ДЛЯ ОТСУТСТВИЯ ПЕРЕРЕГУЛИРОВАНИЙ
- 7. КРИТЕРИЙ, ОПРЕДЕЛЯЮЩИЙ ДОСТАТОЧНЫЕ УСЛОВИЯ ДЛЯ МОНОТОННОСТИ
- 8. ОЦЕНКИ ВЕЛИЧИНЫ ПЕРЕРЕГУЛИРОВАНИЯ И ВРЕМЕНИ ПЕРЕХОДНОГО ПРОЦЕССА
- 9. ОЦЕНКА АБСОЛЮТНОГО ЗНАЧЕНИЯ РАЗНОСТИ МЕЖДУ ПЕРЕХОДНЫМИ ФУНКЦИЯМИ ПО СООТВЕТСТВУЮЩИМ ИМ ЧАСТОТНЫМ ХАРАКТЕРИСТИКАМ
- 10. СВЯЗЬ МЕЖДУ СВОЙСТВАМИ АМПЛИТУДНО-ФАЗОВОЙ ХАРАКТЕРИСТИКИ РАЗОМКНУТОЙ СИСТЕМЫ И КАЧЕСТВОМ
- 11. ТРЕБОВАНИЯ К ЧАСТОТНЫМ ХАРАКТЕРИСТИКАМ, ОБЕСПЕЧИВАЮЩИЕ ВЫСОКУЮ ТОЧНОСТЬ В СЛЕДЯЩИХ СИСТЕМАХ
- 12. СВЯЗЬ МЕЖДУ СВОЙСТВАМИ ЛОГАРИФМИЧЕСКОЙ АМПЛИТУДНОЙ ХАРАКТЕРИСТИКИ И КАЧЕСТВОМ
- 13. ОПРЕДЕЛЕНИЕ ВЕЛИЧИНЫ ПЕРЕДАТОЧНОГО КОЭФФИЦИЕНТА ИЛИ ДОБРОТНОСТИ ПО ЛОГАРИФМИЧЕСКОЙ АМПЛИТУДНОЙ ХАРАКТЕРИСТИКЕ
- 14. ОПРЕДЕЛЕНИЕ УСТАНОВИВШЕЙСЯ ОШИБКИ ПРИ ГАРМОНИЧЕСКОМ УПРАВЛЯЮЩЕМ ВОЗДЕЙСТВИИ ПО ЛОГАРИФМИЧЕСКОЙ АМПЛИТУДНОЙ ХАРАКТЕРИСТИКЕ
- 15. ПРИБЛИЖЕННЫЙ СПОСОБ ВЫЧИСЛЕНИЯ ПЕРЕХОДНОГО ПРОЦЕССА ПО СОПРЯГАЮЩИМ ЧАСТОТАМ ЛОГАРИФМИЧЕСКОЙ АМПЛИТУДНОЙ ЧАСТОТНОЙ ХАРАКТЕРИСТИКИ
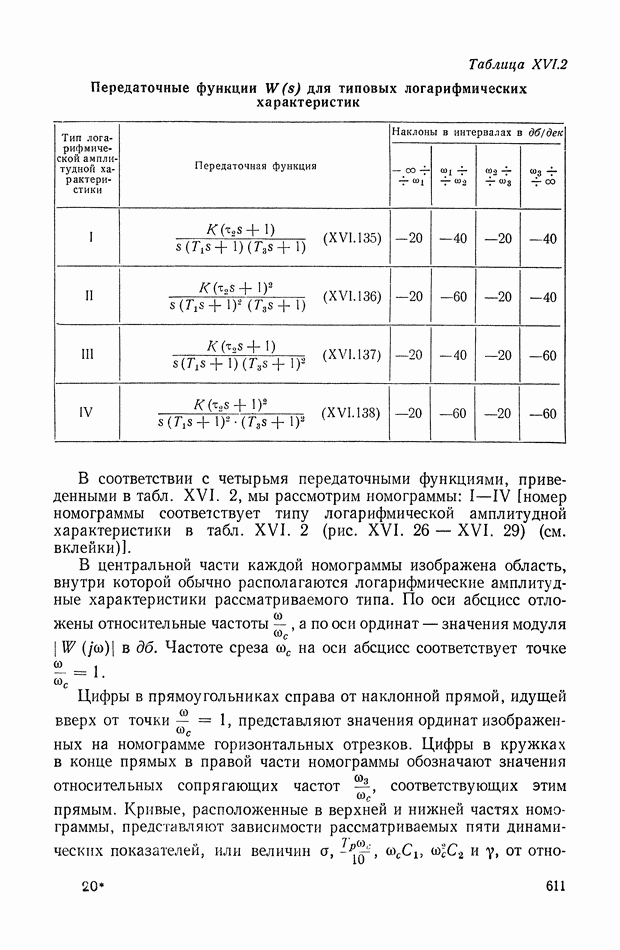
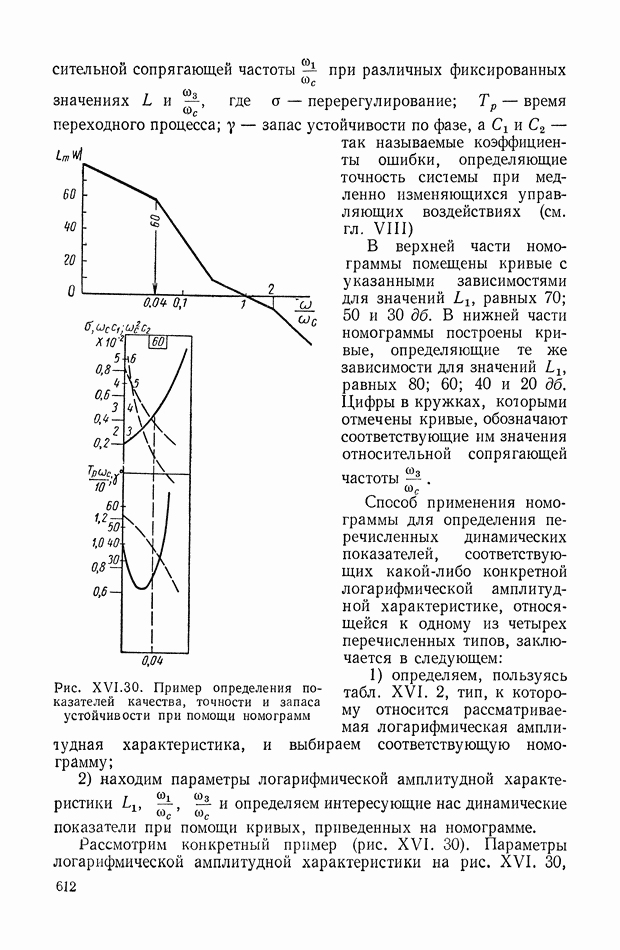
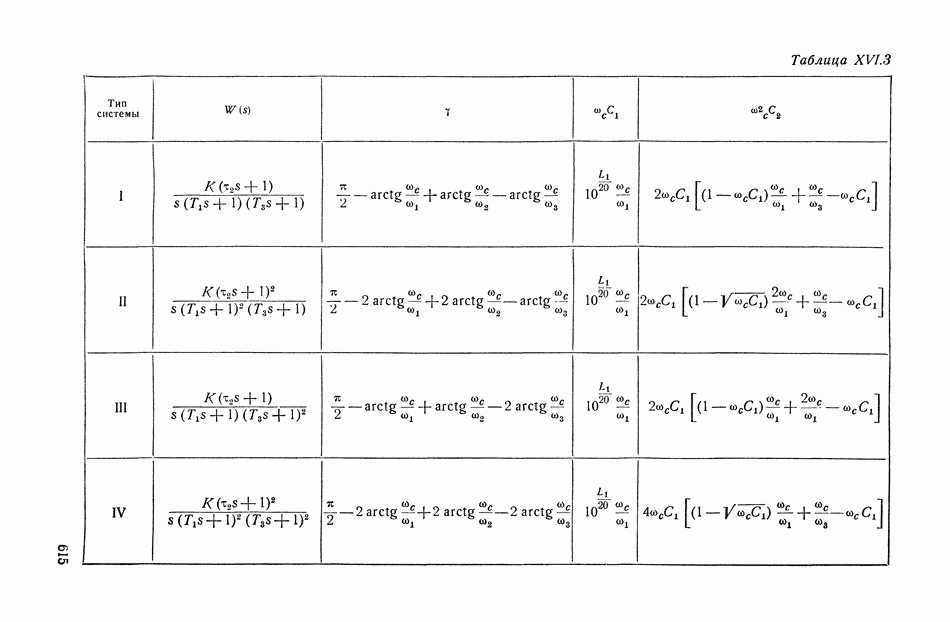
- 16. НОМОГРАММА ДЛЯ ОПРЕДЕЛЕНИЯ ЗАПАСА УСТОЙЧИВОСТИ, ПОКАЗАТЕЛЕЙ КАЧЕСТВА И КОЭФФИЦИЕНТОВ ОШИБОК ПО ВИДУ ЛОГАРИФМИЧЕСКОЙ АМПЛИТУДНОЙ ХАРАКТЕРИСТИКИ
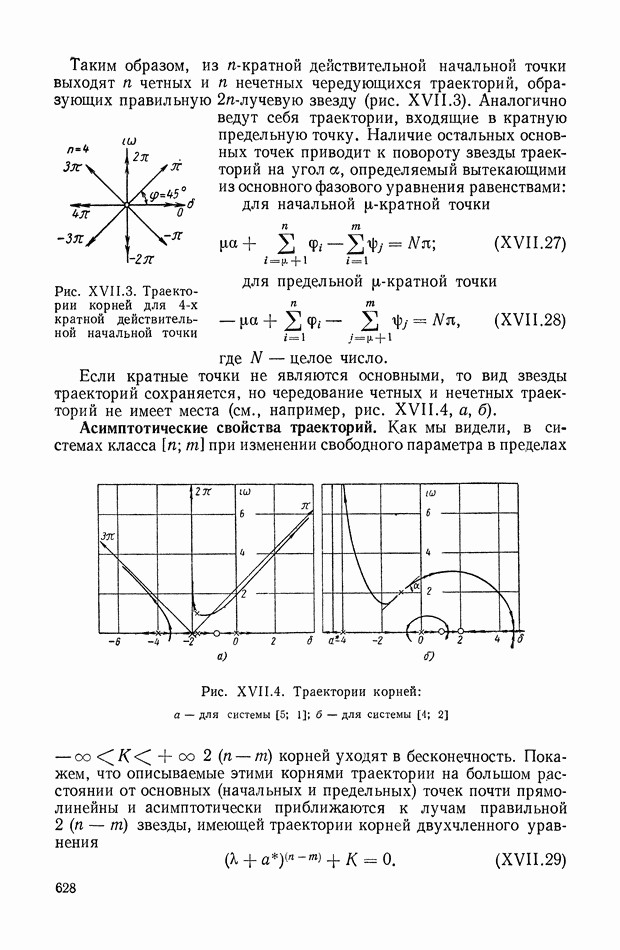
- ГЛАВА XVII. СВЯЗЬ МЕЖДУ КАЧЕСТВОМ ПЕРЕХОДНОГО ПРОЦЕССА И РАСПРЕДЕЛЕНИЕМ НУЛЕЙ И ПОЛЮСОВ ПЕРЕДАТОЧНОЙ ФУНКЦИИ. МЕТОД КОРНЕВЫХ ГОДОГРАФОВ
- 2. АНАЛИЗ РАСПРЕДЕЛЕНИЯ КОРНЕЙ ХАРАКТЕРИСТИЧЕСКОГО УРАВНЕНИЯ СИСТЕМЫ И ОЦЕНКА КАЧЕСТВА ПЕРЕХОДНОГО ПРОЦЕССА
- 3. ГЕОМЕТРИЧЕСКИЙ МЕТОД ПОСТРОЕНИЯ КОРНЕВОГО ГОДОГРАФА
- 4. АНАЛИТИЧЕСКОЕ ПОСТРОЕНИЕ ГЕОМЕТРИЧЕСКОГО МЕСТА КОРНЕЙ
- 5. ОПРЕДЕЛЕНИЕ ОБЛАСТЕЙ УСТОЙЧИВОСТИ ЛИНЕЙНЫХ СИСТЕМ МЕТОДОМ КОРНЕВОГО ГОДОГРАФА
- 6. ОЦЕНКИ ПАРАМЕТРОВ ПЕРЕХОДНОЙ И ЧАСТОТНОЙ ХАРАКТЕРИСТИК ПО КОРНЕВОМУ ГОДОГРАФУ
- 7. ВЛИЯНИЕ РАСПОЛОЖЕНИЯ НУЛЕЙ И ПОЛЮСОВ ЗАМКНУТОЙ СИСТЕМЫ НА ПЕРЕХОДНУЮ ХАРАКТЕРИСТИКУ h(t)
- 8. ВЛИЯНИЕ РАСПОЛОЖЕНИЯ НУЛЕЙ И ПОЛЮСОВ ЗАМКНУТОЙ СИСТЕМЫ НА ЕЕ ПОЛОСУ ЧАСТОТ
- 9. КОРНЕВОЙ ГОДОГРАФ И ПЕРЕХОДНАЯ ХАРАКТЕРИСТИКА СИСТЕМЫ ПРИ ВОЗМУЩЕНИЯХ, ПРИЛОЖЕННЫХ НЕ К ОСНОВНОМУ ВХОДУ СИСТЕМЫ
- 10. ВЛИЯНИЕ РАСПРЕДЕЛЕНИЯ НУЛЕЙ И ПОЛЮСОВ ПЕРЕДАТОЧНОЙ ФУНКЦИИ НА КАЧЕСТВО ПЕРЕХОДНОГО ПРОЦЕССА ПРИ НАЛИЧИИ ВНЕШНЕГО ВОЗДЕЙСТВИЯ
- ГЛАВА XVIII. МЕТОД ЛОГАРИФМИЧЕСКИХ КОРНЕВЫХ ГОДОГРАФОВ
- 2. ОПРЕДЕЛЕНИЕ КОРНЕЙ ЗАМКНУТОЙ СИСТЕМЫ ПО ЛОГАРИФМИЧЕСКОЙ АМПЛИТУДНОЙ КОМПЛЕКСНО-ЧАСТОТНОЙ ХАРАКТЕРИСТИКЕ РАЗОМКНУТОЙ СИСТЕМЫ
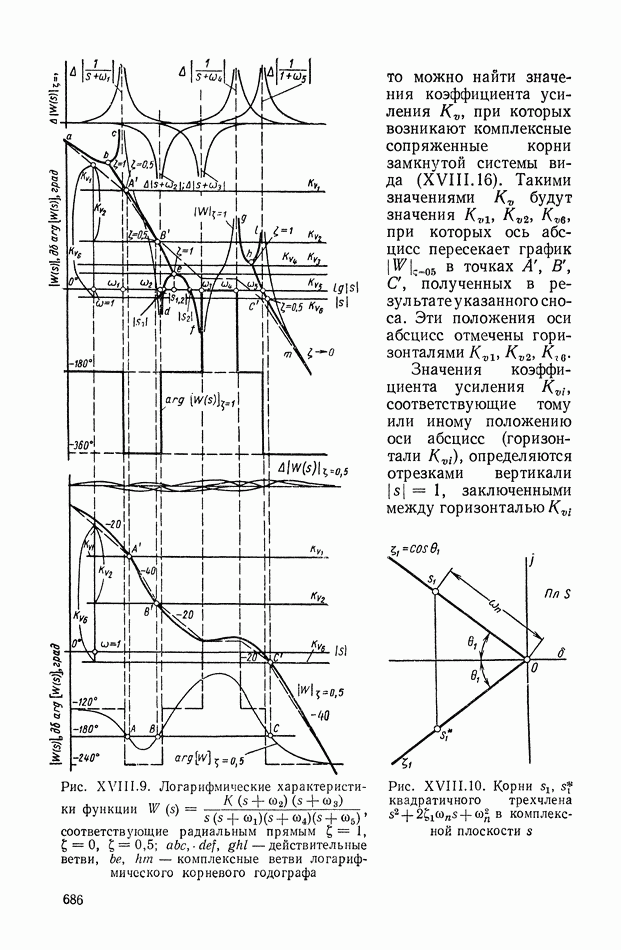
- 3. ЛОГАРИФМИЧЕСКИЕ КОРНЕВЫЕ ГОДОГРАФЫ
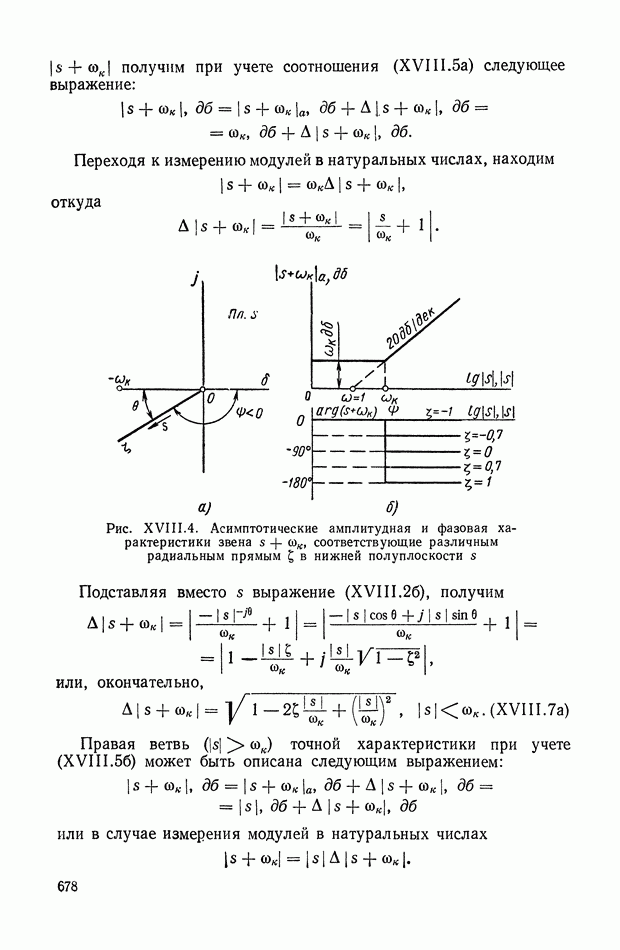
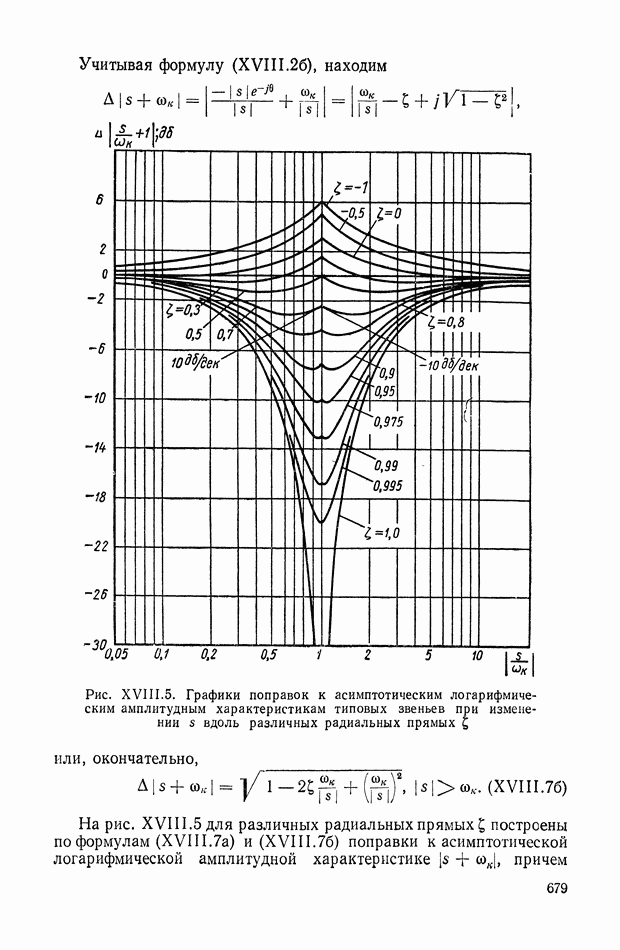
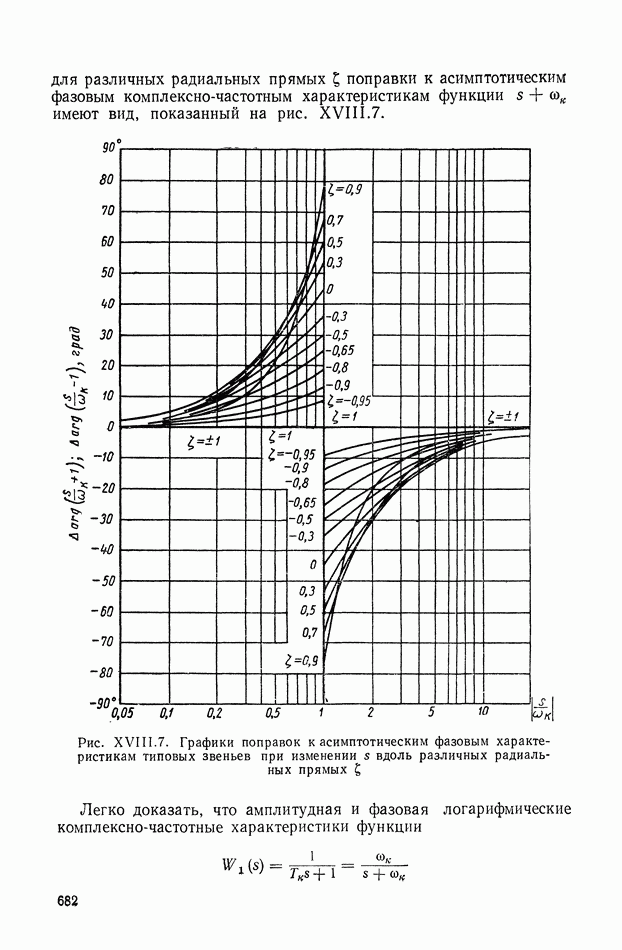
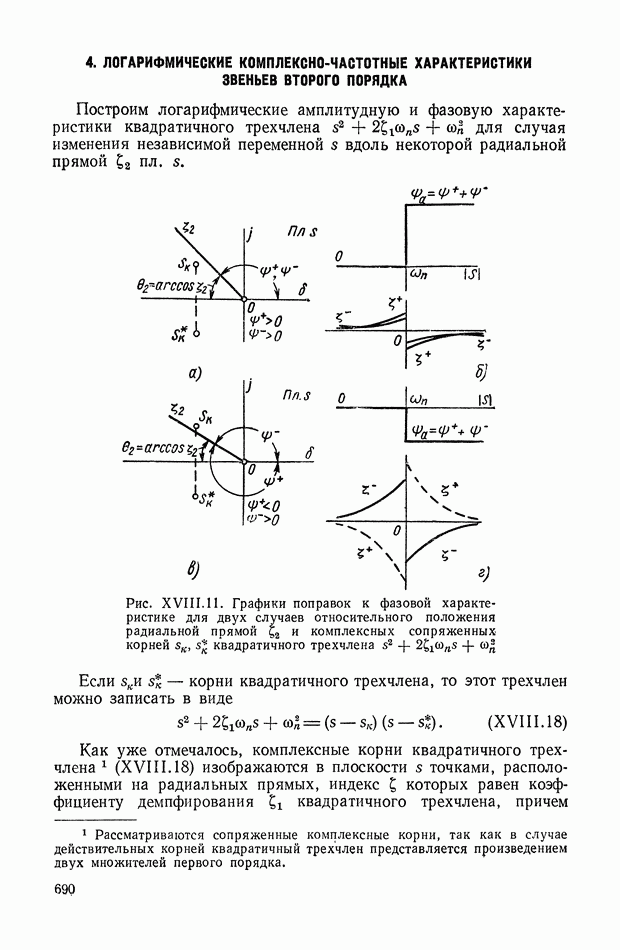
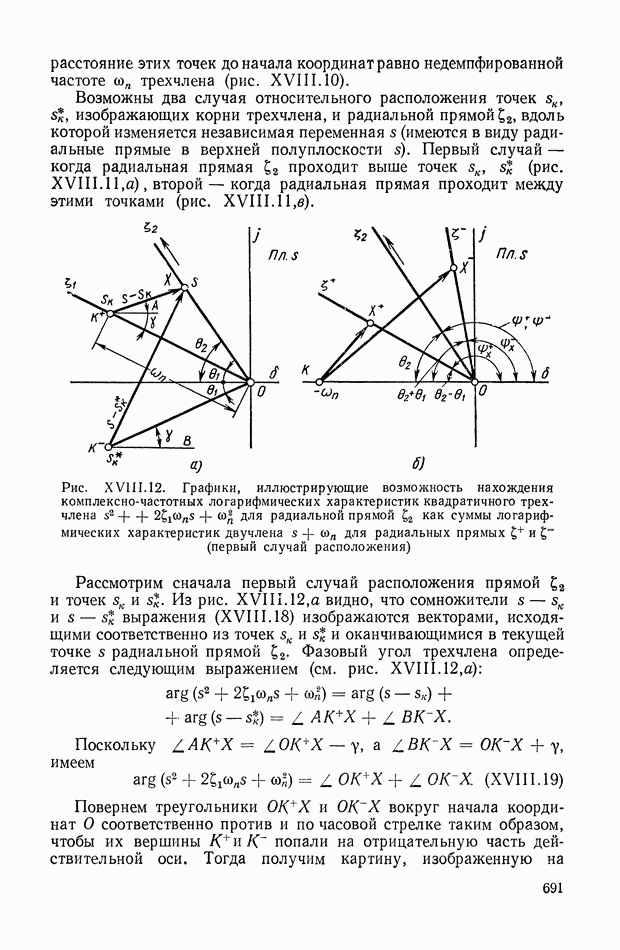
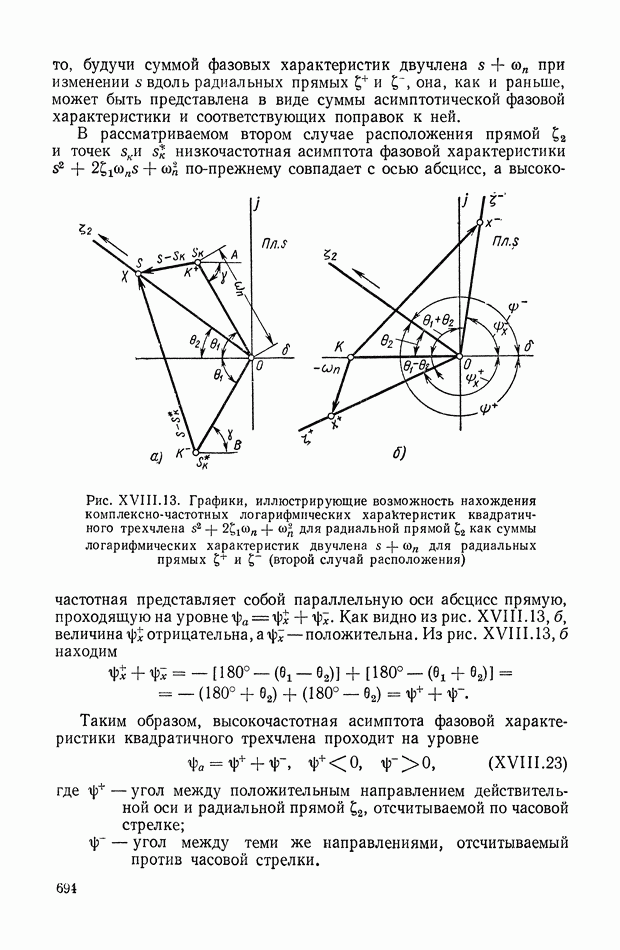
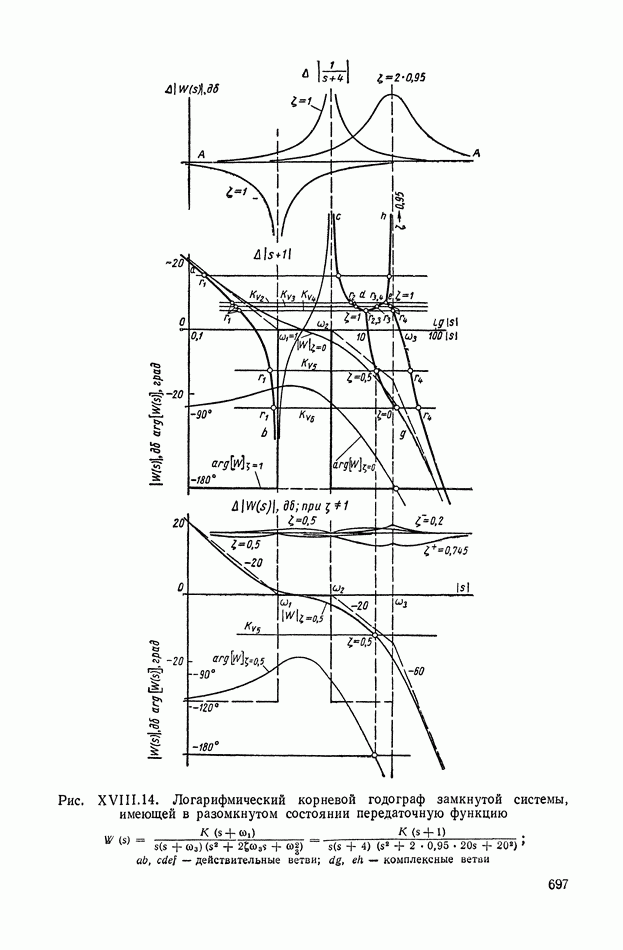
- 4. ЛОГАРИФМИЧЕСКИЕ КОМПЛЕКСНО-ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЗВЕНЬЕВ ВТОРОГО ПОРЯДКА
- 5. ПРИМЕР ПОСТРОЕНИЯ ЛОГАРИФМИЧЕСКОГО КОРНЕВОГО ГОДОГРАФА
- ГЛАВА XIX. ИНТЕГРАЛЬНЫЕ ОЦЕНКИ И КРИТЕРИИ КАЧЕСТВА РЕГУЛИРОВАНИЯ
- 2. МЕТОДИКА ПРИМЕНЕНИЯ ИНТЕГРАЛЬНЫХ КВАДРАТИЧНЫХ ОЦЕНОК
- 3. ЛИНЕЙНЫЕ ИНТЕГРАЛЬНЫЕ ОЦЕНКИ
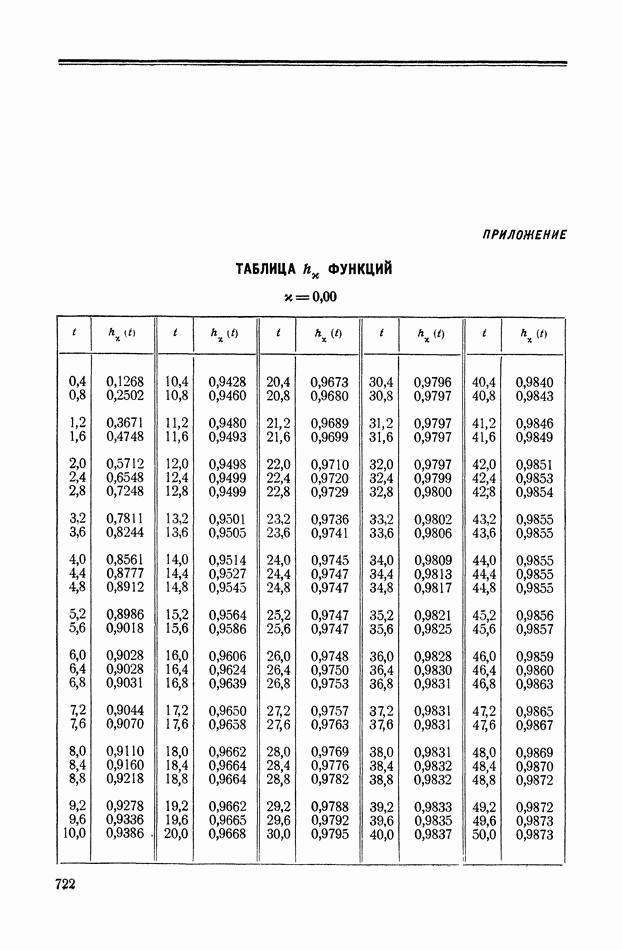
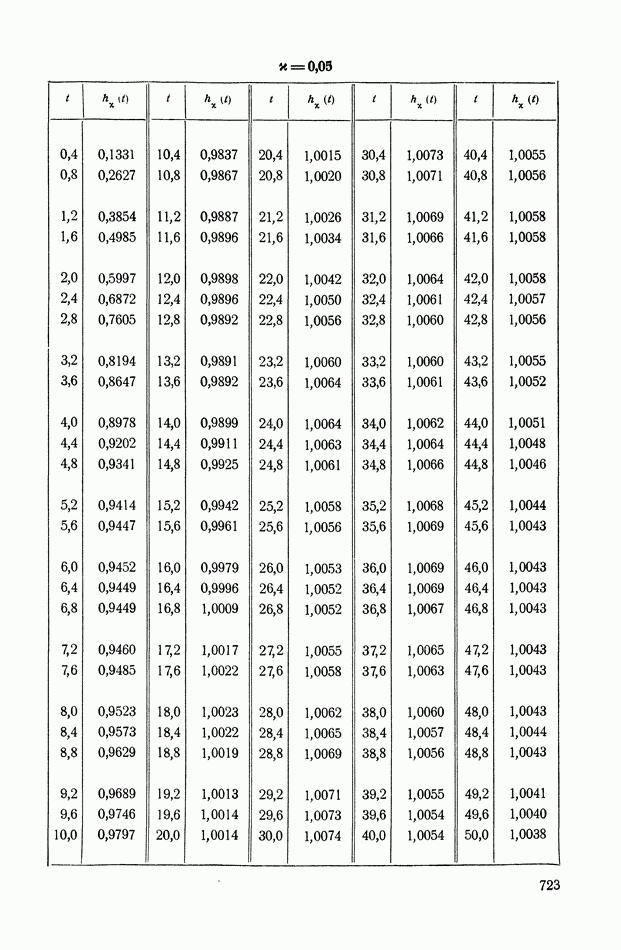
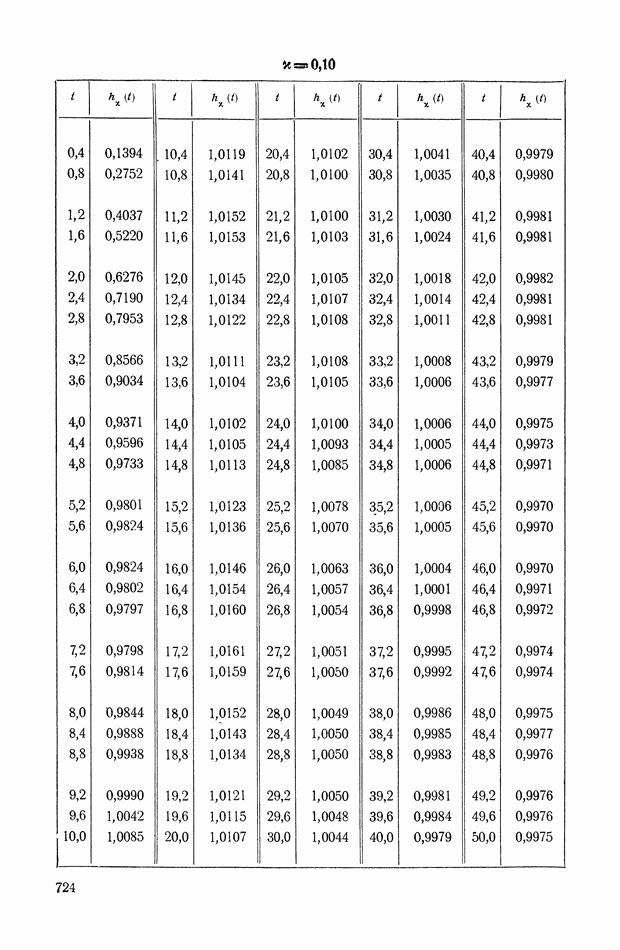
- ПРИЛОЖЕНИЕ
- БИБЛИОГРАФИЯ ПО РАЗДЕЛАМ КНИГИ