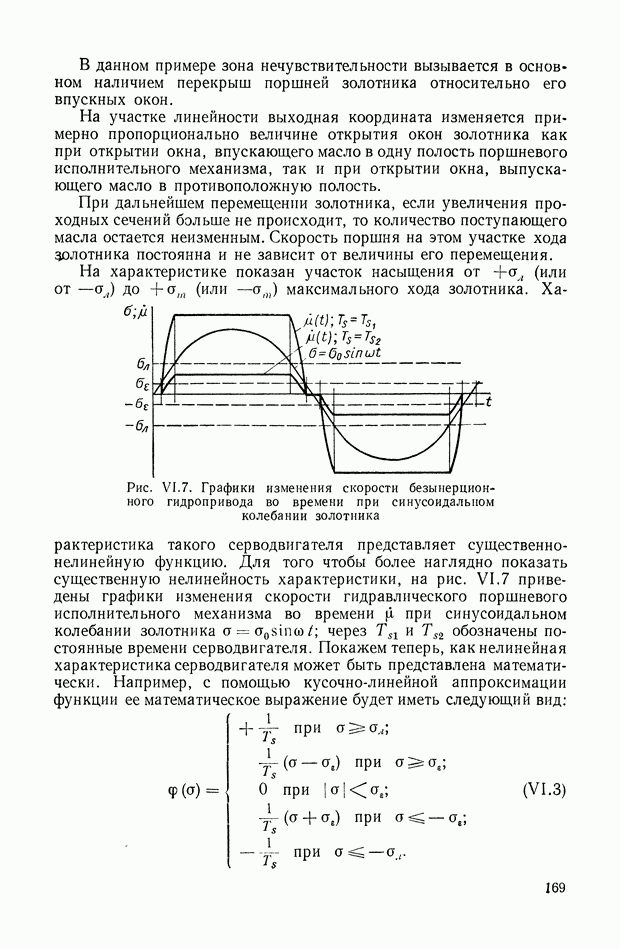
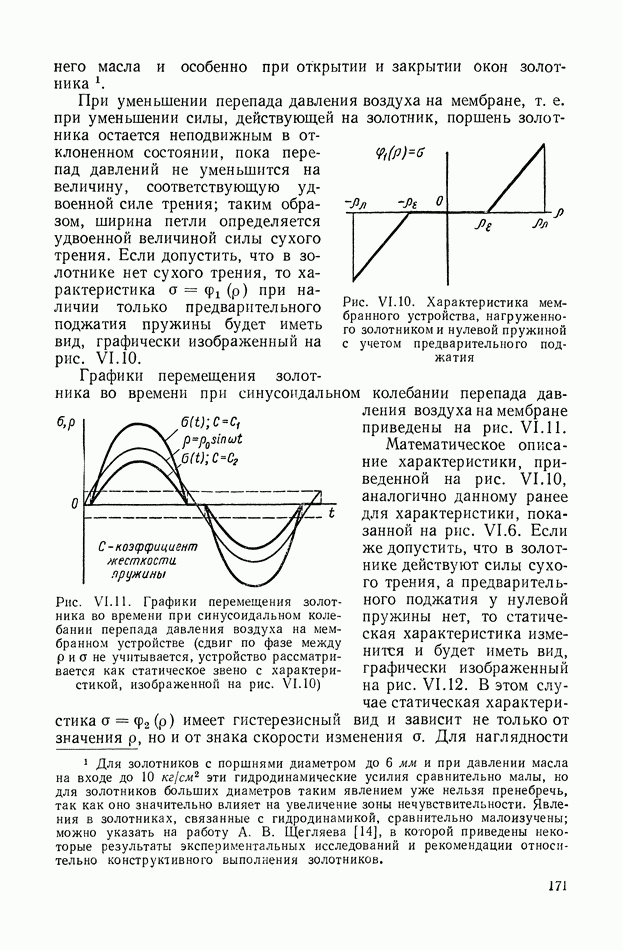
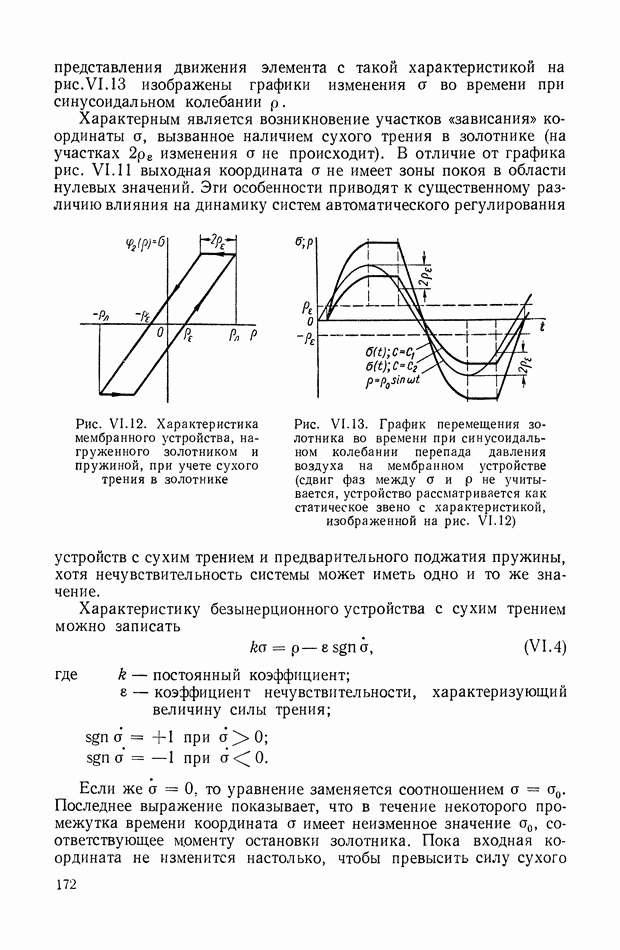
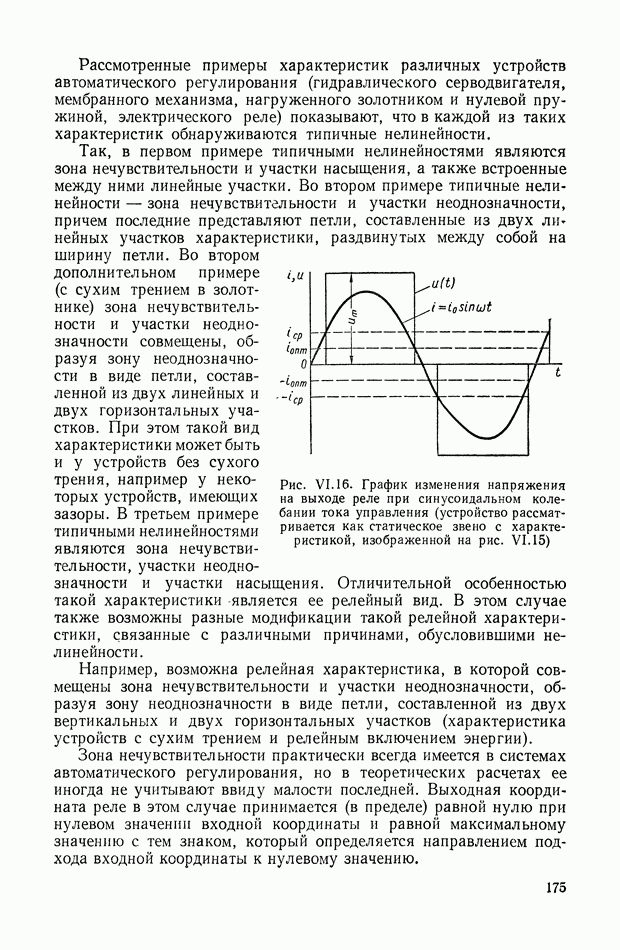
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
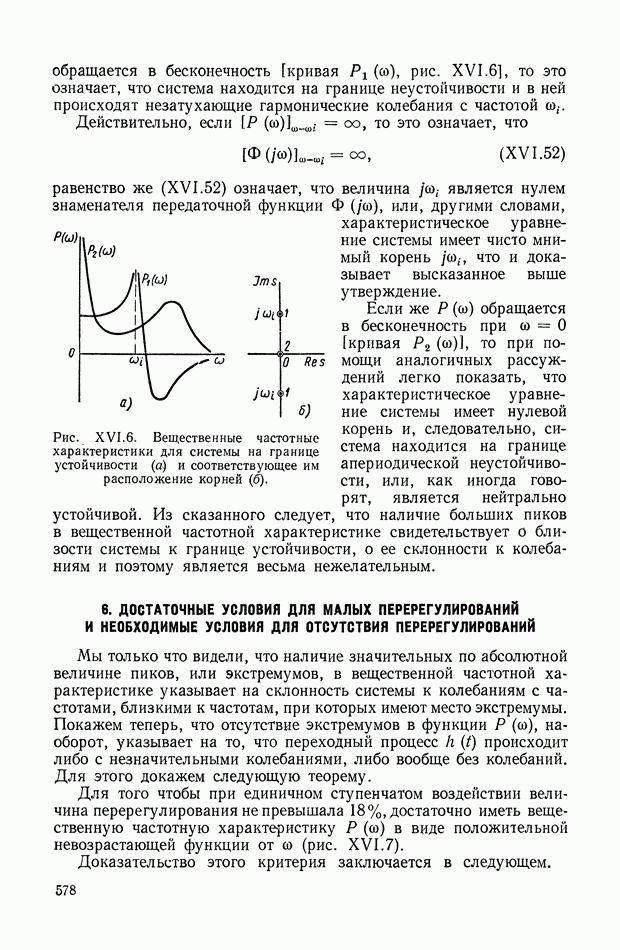
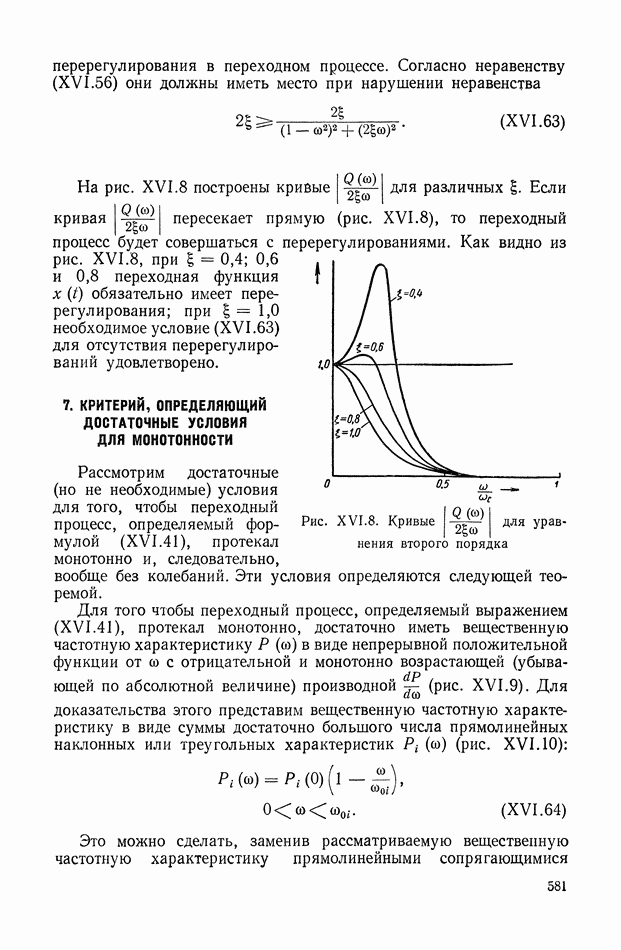
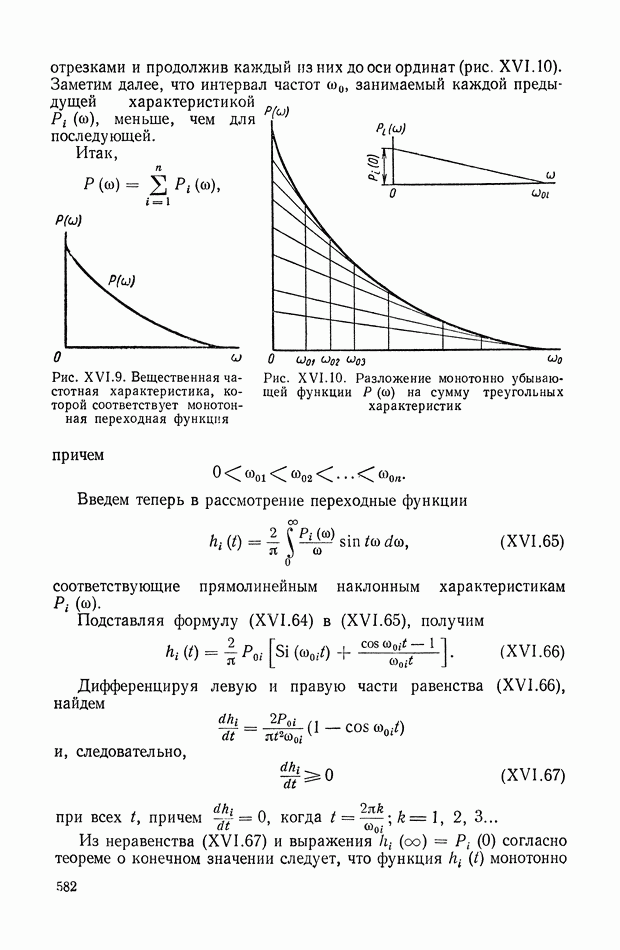
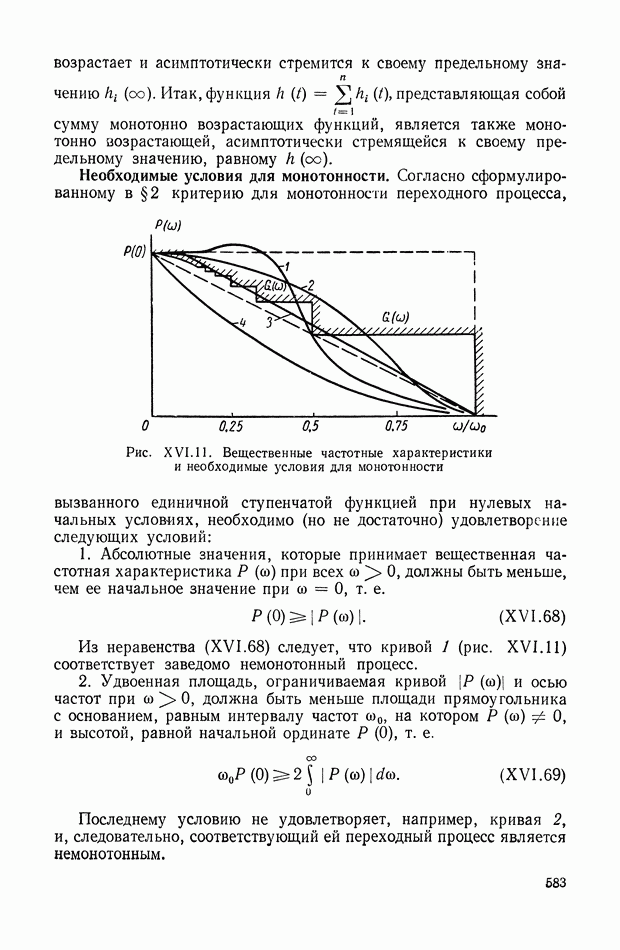
10. ТРЕБОВАНИЯ, ПРЕДЪЯВЛЯЕМЫЕ К ДИНАМИЧЕСКИМ СВОЙСТВАМ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
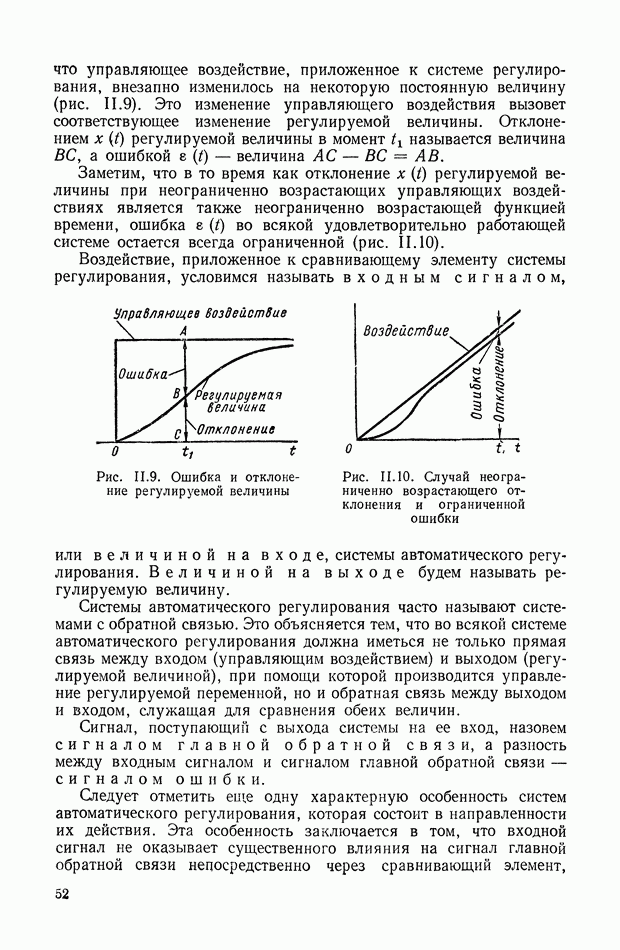
Согласно данному выше определению, основным требованием, предъявляемым к системам автоматического регулирования, является сохранение в допустимых пределах ошибки между требуемыми и действительными изменениями регулируемых переменных.
Системы, для которых эти ошибки равны нулю во все моменты времени, называются идеальными. На практике осуществление идеальных систем регулирования, согласно самому принципу их действия, основанному на измерении этих ошибок, невозможно.
Поэтому, так же как и в рассмотренном выше общем случае многомерных систем автоматического управления, при проектировании систем автоматического регулирования весьма полезным оказывается введение того или иного критерия эффективности или качества регулирования, определяющего оптимальные условия работы системы.
Критерии качества регулирования весьма разнообразны, причем их выбор зависит от конкретных условий работы системы. Эти критерии рассматриваются в последующих главах книги. Здесь целесообразно ограничиться лишь некоторыми общими замечаниями.
Не только идеальная, но и оптимальная система автоматического регулирования, удовлетворяющая принятому критерию качества, т. е. обеспечивающая экстремум принятого показателя качества, может быть реализована лишь с большей или меньшей степенью приближения. Поэтому оптимальная система может рассматриваться как своего рода предел, «начало отсчета», к которому нужно стремиться, но который нельзя реализовать совершенно точно. При этом чем выше эта степень приближения, т. е. чем меньше отклонения регулируемых переменных и чем, следовательно, выше качество, тем сложнее оказывается система регулирования. В связи с этим задача проектирования систем автоматического регулирования, так же как и решение почти любой инженерной задачи, сводится к нахождению разумного компромисса между стремлением получить возможно более высокое качество работы и стремлением достигнуть решения этой задачи возможно более простыми техническими средствами. Кроме того, нужно иметь в виду, что решение задачи оптимизации иногда представляет собою большие трудности и не всегда необходимо на практике.
Вследствие этого при расчете и проектировании системы автоматического регулирования, наряду с критерием качества регулирования, определяющим оптимальные условия работы, необходимо располагать требованиями, определяющими допустимые условия работы системы.
Так как требования, предъявляемые к поведению систем регулирования в динамике, зависят от их назначения, характера воздействия, конкретных условий и т. д., то они могут быть самыми различными. Их можно подразделить на следующие четыре категории:
требования к запасу устойчивости системы;
требования к величине ошибок в установившемся состоянии или к статической точности;
требования к поведению системы в переходном процессе (эти требования обычно называются условиями качества);
требования к динамической точности системы, т. е. к величине ошибок при наличии непрерывно изменяющихся воздействий.
Поясним вкратце смысл каждой из указанных выше категорий требований.
Системы регулирования вследствие самого принципа их действия, благодаря которому часть энергии с их выхода может возвращаться обратно на вход, являются системами, склонными к колебаниям.
Рассмотрим, например, самолет, снабженный автоматом курса, реагирующим на отклонения самолета от требуемого направления. Предположим, что в начальный момент времени благодаря действию тех или иных возмущающих причин продольная ось самолета не совпадает с требуемым направлением движения. Тогда чувствительный элемент автомата курса выработает сигнал, который заставит отклониться руль направления.
В результате отклонения руля от нейтрали возникает вращающий момент, который будет стремиться возвратить самолет на заданный курс. Однако в момент, когда продольная ось самолета совпадет с требуемым направлением движения, его вращательное движение не прекратится. Это произойдет, во-первых, потому, что самолет, имеющий значительный момент инерции, будет обладать при подходе к заданному курсу определенным запасом кинетической энергии, и, во-вторых, потому, что автомат курса, обладающий некоторым запаздыванием, возвратит руль в нейтральное положение лишь через некоторый промежуток времени после того, как продольная ось самолета совпадет с заданным курсом.
Вследствие указанных причин самолет будет отклоняться от заданного курса в направлении, противоположном первоначальному отклонению, до тех пор, пока автомат курса не произведет перекладку руля и пока в результате этого не разовьется вращающий момент, достаточный для того, чтобы заставить самолет опять стремиться к заданному курсу. Теперь самолет подойдет к нему уже с другой стороны, и по тем же причинам, которые были приведены выше, опять возникнет отклонение от заданного курса, имеющее тот же знак, что и первоначальное отклонение. Затем весь процесс повторится снова и т. д. При этом если демпфирование самолета невелико, а его инерция и запаздывание автомата курса значительны, то амплитуда колебаний самолета относительно заданного курса будет постепенно возрастать и, таким образом, сохранение требуемого курса не сможет быть достигнуто.
Приведенный пример показывает, что принцип обратной связи, лежащей в основе действия систем регулирования, может превратиться из средства подавления колебаний и уменьшения ошибки в средство генерации колебаний и увеличения ошибки. Из этого примера также видно, что для удовлетворительной работы системы регулирования прежде всего необходимо, чтобы она была устойчива, т. е. система должна обладать свойством, при котором начальные отклонения регулируемой величины от требуемого закона изменения должны стремиться к нулю с течением времени. Поэтому требование устойчивости является первым и важнейшим условием нормальной работы систем регулирования. При этом необходимо
подчеркнуть, что требование устойчивости должно удовлетворяться с некоторым запасом, предусматривающим возможные изменения параметров системы во время ее работы.
Однако понятие устойчивости, связанное, как мы видели, с рассмотрением поведения систем в отсутствии воздействий, является лишь необходимым, но далеко не достаточным для характеристики динамических свойств систем регулирования в реальных условиях их работы, при наличии воздействий. Для того чтобы охарактеризовать эти динамические свойства, необходимо прежде всего уточнить вопрос о том, какие воздействия следует иметь в виду, так как поведение системы регулирования, конечно, существенно зависит от величины и характера изменения воздействий. Решение этого вопроса вызывает определенные трудности, так как обычно воздействия, приложенные к системам регулирования, представляют собой непрерывно изменяющиеся функции времени, точный закон изменения которых невозможно предугадать. Однако при внимательном рассмотрении конкретных условий работы системы часто все же оказывается возможным выбрать среди всего многообразия возможных воздействий та кое, которое являлось бы наиболее типичным или наиболее неблагоприятным. Выбрав такое типичное воздействие и изучив вызываемый им переходный процесс, можно составить себе довольно полное представление о динамических свойствах системы.

Рис. II.19. Единичное ступенчатое воздействие
В виде типового воздействия при анализе динамики систем автоматического регулирования весьма часто выбирают так называемое ступенчатое воздействие, или единичный скачок (рис. 11.19). Такого рода воздействию соответствуют, например, сбросы или набросы нагрузки в системах регулирования скорости двигателей, отказ мотора в системе двухмоторный самолет — автомат курса, внезапное изменение положения задающей оси в следящих системах и т. д.
Иногда типовым воздействием служит воздействие в форме дельтафункции, т. е. импульса произвольной формы, имеющего определенную площадь и весьма малую продолжительность по сравнению с ожидаемой продолжительностью переходного процесса. В реальных условиях такого рода воздействие может иметь место, например, в случае внезапного вхождения самолета в струю воздуха, движущегося перпендикулярно траектории движения самолета. Другим примером может служить импульсная нагрузка, которая возникает на валу двигателя в следящем приводе, служащем для управления летучими ножницами в стане горячей прокатки при разрезании полосы на листы и т. д.
В случае следящих систем весьма часто пользуются типовым управляющим воздействием вида

частными случаями которого, например, являются

или

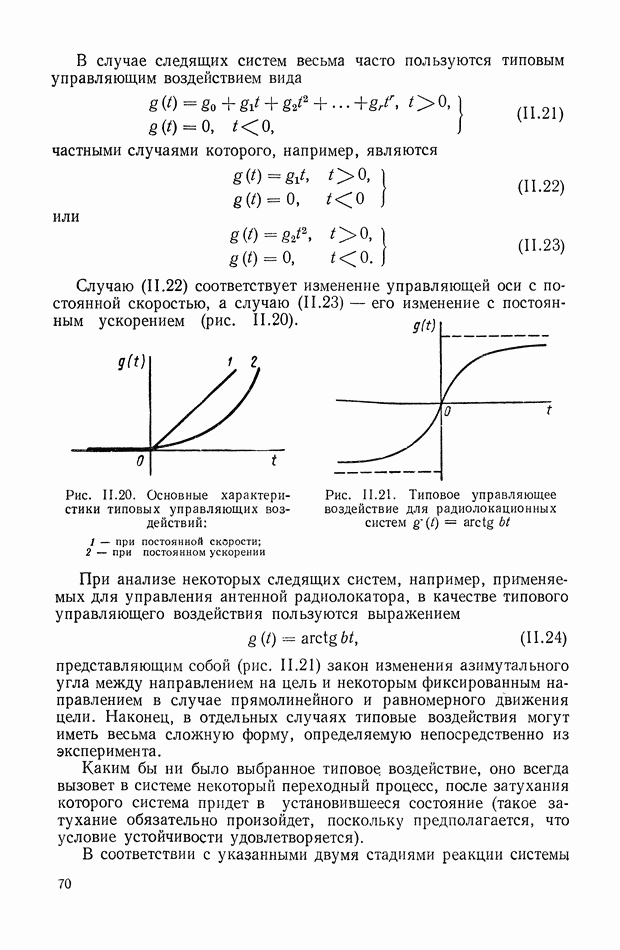
Случаю (11.22) соответствует изменение управляющей оси с постоянной скоростью, а случаю (11.23) — его изменение с постоянным ускорением (рис. II ,20).

Рис. 11.20. Основные характеристики типовых управляющих воздействий: 1 — при постоянной скорости; 2 — при постоянном ускорении

Рис. 11.21. Типовое управляющее воздействие для радиолокационных систем 
При анализе некоторых следящих систем, например, применяемых для управления антенной радиолокатора, в качестве типового управляющего воздействия пользуются выражением

представляющим собой (рис. 11.21) закон изменения азимутального угла между направлением на цель и некоторым фиксированным направлением в случае прямолинейного и равномерного движения цели. Наконец, в отдельных случаях типовые воздействия могут иметь весьма сложную форму, определяемую непосредственно из эксперимента.
Каким бы ни было выбранное типовое воздействие, оно всегда вызовет в системе некоторый переходный процесс, после затухания которого система придет в установившееся состояние (такое затухание обязательно произойдет, поскольку предполагается, что условие устойчивости удовлетворяется).
В соответствии с указанными двумя стадиями реакции системы
регулирования на типовые воздействия естественно подразделить и требования, которые следует предъявлять к динамическим свойствам системы (их обычно называют условиями качества 3), на требования к ее поведению в установившемся состоянии и в переходном процессе.
Первая группа требований определяет так называемую статическую точность системы регулирования, т. е. отклонение регулируемой величины от требуемого закона изменения или величину ошибки через достаточно большой промежуток времени после приложения воздействия. Следующая группа требований характеризует поведение системы в переходном процессе, т. е. ее поведение в промежуток времени, непосредственно следующий за моментом приложения выбранного типового воздействия.
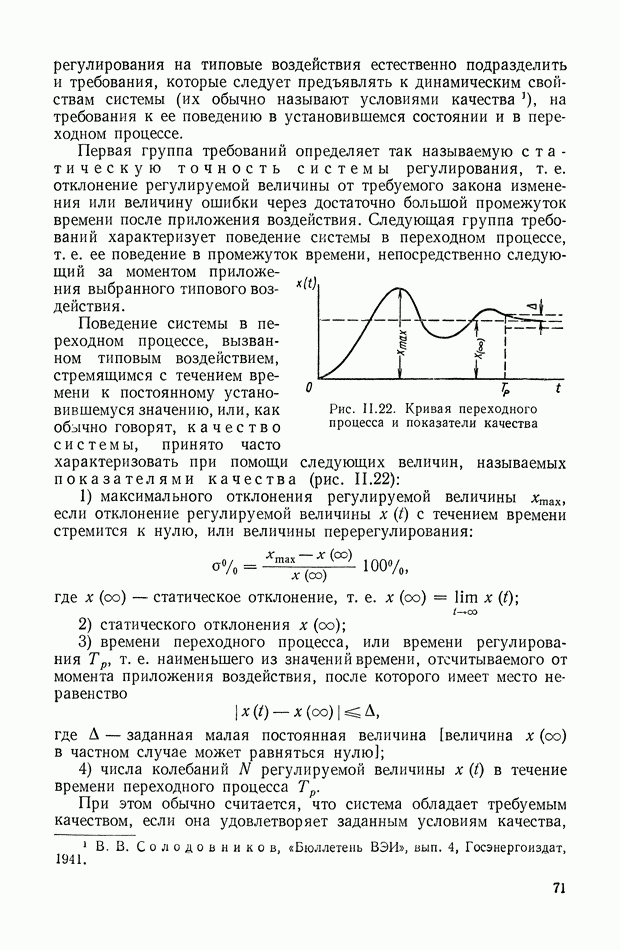
Поведение системы в переходном процессе, вызванном типовым воздействием, стремящимся с течением времени к постоянному установившемуся значению, или, как обычно говорят, качество системы, принято часто характеризовать при помощи следующих величин, называемых показателями качества (рис. 11.22):

Рис. 11.22. Кривая переходного процесса и показатели качества
1) максимального отклонения регулируемой величины  если отклонение регулируемой величины
если отклонение регулируемой величины  с течением времени стремится к нулю, или величины перерегулирования:
с течением времени стремится к нулю, или величины перерегулирования:

где  — статическое отклонение, т. е.
— статическое отклонение, т. е. 
2) статического отклонения 
3) времени переходного процесса, или времени регулирования  т. е. наименьшего из значений времени, отсчитываемого от момента приложения воздействия, после которого имеет место неравенство
т. е. наименьшего из значений времени, отсчитываемого от момента приложения воздействия, после которого имеет место неравенство

где  — заданная малая постоянная величина [величина
— заданная малая постоянная величина [величина  в частном случае может равняться нулю];
в частном случае может равняться нулю];
4) числа колебаний  регулируемой величины
регулируемой величины  в течение времени переходного процесса
в течение времени переходного процесса 
При этом обычно считается, что система обладает требуемым качеством, если она удовлетворяет заданным условиям качества,
т. е. если показатели качества не превышают некоторых заранее заданных значений.
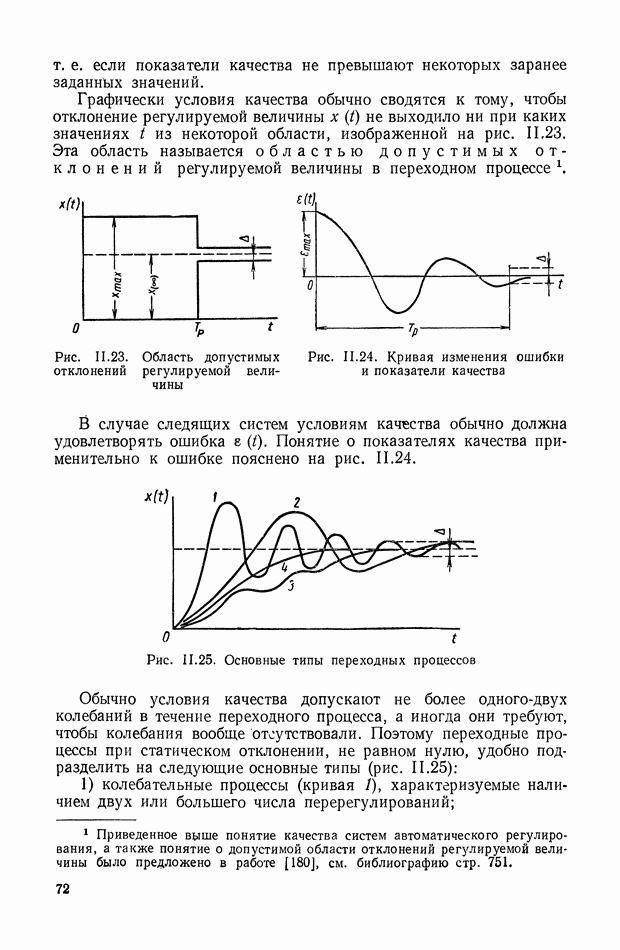
Графически условия качества обычно сводятся к тому, чтобы отклонение регулируемой величины  не выходило ни при каких значениях
не выходило ни при каких значениях  из некоторой области, изображенной на рис. 11,23. Эта область называется областью допустимых отклонений регулируемой величины в переходном процессе.
из некоторой области, изображенной на рис. 11,23. Эта область называется областью допустимых отклонений регулируемой величины в переходном процессе.

Рис. 11.23. Область допустимых отклонений регулируемой величины

Рис. 11.24. Кривая изменения ошибки и показатели качества
В случае следящих систем условиям качества обычно должна удовлетворять ошибка  Понятие о показателях качества применительно к ошибке пояснено на рис. II.24.
Понятие о показателях качества применительно к ошибке пояснено на рис. II.24.

Рис. 11.25. Основные типы переходных процессов
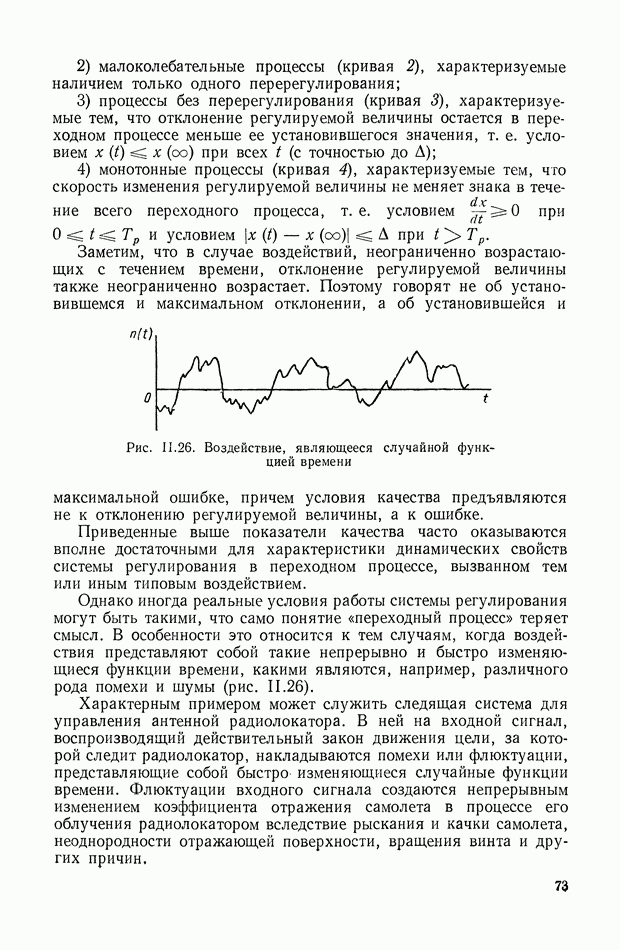
Обычно условия качества допускают не более одного-двух колебаний в течение переходного процесса, а иногда они требуют, чтобы колебания вообще отсутствовали. Поэтому переходные процессы при статическом отклонении, не равном нулю, удобно подразделить на следующие основные типы (рис. II.25):
1) колебательные процессы (кривая  ), характеризуемые наличием двух или большего числа перерегулирований;
), характеризуемые наличием двух или большего числа перерегулирований;
2) малоколебательные процессы (кривая 2), характеризуемые наличием только одного перерегулирования;
3) процессы без перерегулирования (кривая 3), характеризуемые тем, что отклонение регулируемой величины остается в переходном процессе меньше ее установившегося значения, т. е. условием  при всех
при всех  (с точностью до А);
(с точностью до А);
4) монотонные процессы (кривая 4), характеризуемые тем, что скорость изменения регулируемой величины не меняет знака в течение всего переходного процесса, т. е. условием при  и условием
и условием  при
при 
Заметим, что в случае воздействий, неограниченно возрастающих с течением времени, отклонение регулируемой величины также неограниченно возрастает.

Рис. 11.26. Воздействие, являющееся случайной функцией времени
Поэтому говорят не об установившемся и максимальном отклонении, а об установившейся и максимальной ошибке, причем условия качества предъявляются не к отклонению регулируемой величины, а к ошибке.
Приведенные выше показатели качества часто оказываются вполне достаточными для характеристики динамических свойств системы регулирования в переходном процессе, вызванном тем или иным типовым воздействием.
Однако иногда реальные условия работы системы регулирования могут быть такими, что само понятие «переходный процесс» теряет смысл. В особенности это относится к тем случаям, когда воздействия представляют собой такие непрерывно и быстро изменяющиеся функции времени, какими являются, например, различного рода помехи и шумы (рис. II.26).
Характерным примером может служить следящая система для управления антенной радиолокатора. В ней на входной сигнал, воспроизводящий действительный закон движения цели, за которой следит радиолокатор, накладываются помехи или флюктуации, представляющие собой быстро изменяющиеся случайные функции времени. Флюктуации входного сигнала создаются непрерывным изменением коэффициента отражения самолета в процессе его облучения радиолокатором вследствие рыскания и качки самолета, неоднородности отражающей поверхности, вращения винта и других причин.
Такого рода воздействия при анализе не могут быть заменены типовым воздействием в виде заданной функции времени, и в то же время ими нельзя пренебречь, так как от них существенным образом зависит общая величина ошибки системы.
При этом такие показатели качества, как время переходного процесса, статическое отклонение, число колебаний, а также перерегулирование, теряют смысл, и сохраняет значение лишь максимальное отклонение хтах, характеризующее в отличие от  не статическую точность системы в установившемся состоянии, а ее динамическую точность в неустановившемся состоянии.
не статическую точность системы в установившемся состоянии, а ее динамическую точность в неустановившемся состоянии.
Следует, однако, заметить, что как вследствие трудности оценки максимальных значений хтах, так и вследствие того, что последние часто недостаточны для характеристики работы системы при непрерывно изменяющихся случайных воздействиях, в этих случаях обычно вводят в рассмотрение некоторые средние значения от  определяющие динамическую точность системы в статистическом смысле для некоторых промежутков времени (подробнее об этом см. в книге 2, гл. I).
определяющие динамическую точность системы в статистическом смысле для некоторых промежутков времени (подробнее об этом см. в книге 2, гл. I).
Примером такого рода показателей качества могут служить средние квадратические значения отклонений регулируемой величины или ошибки.
Обычно системы регулирования наряду с требованиями к динамическим свойствам должны удовлетворять ряду требований, связанных с условиями их эксплуатации.
Эти требования часто имеют решающее значение при выборе элементов систем регулирования. При этом, поскольку каждое конкретное устройство обладает своими динамическими характеристиками, ясно, что эксплуатационные требования имеют существенное влияние на динамические свойства системы и что, следовательно, к анализу динамики нужно переходить лишь тогда, когда имеется уверенность в том, что элементы системы регулирования выбраны с учетом этих требований.
Ввиду многообразия условий эксплуатации, в которых приходится работать различным системам регулирования, мы не имеем возможности останавливаться на этом вопросе сколько-нибудь подробно, но считаем необходимым подчеркнуть, что анализ условий эксплуатации и вытекающих из них требований должен предшествовать проектированию любой системы регулирования.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- РАЗДЕЛ I. ОБЩИЕ СВЕДЕНИЯ. МЕТОДЫ МАТЕМАТИЧЕСКОГО ОПИСАНИЯ И СТРУКТУРНОГО ПРЕОБРАЗОВАНИЯ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- ГЛАВА I. ОЧЕРК О РАЗВИТИИ ТЕОРИИ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ В СССР
- 1. ТЕОРИЯ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ В ДОРЕВОЛЮЦИОННЫЙ ПЕРИОД
- 2. РАЗВИТИЕ ТЕОРИИ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ПОСЛЕ ОКТЯБРЬСКОЙ СОЦИАЛИСТИЧЕСКОЙ РЕВОЛЮЦИИ
- ГЛАВА II. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ ТЕОРИИ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. СУЩНОСТЬ ПРОБЛЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- 2. ПРОБЛЕМА РЕГУЛИРОВАНИЯ КАК ЧАСТНЫЙ СЛУЧАЙ ПРОБЛЕМЫ УПРАВЛЕНИЯ
- 3. ОСНОВНОЙ ПРИНЦИП ДЕЙСТВИЯ И ОПРЕДЕЛЕНИЕ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 4. КЛАССИФИКАЦИЯ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ В ЗАВИСИМОСТИ ОТ УПРАВЛЯЮЩЕГО ВОЗДЕЙСТВИЯ
- 5. ОСНОВНЫЕ УСТРОЙСТВА СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ И ИХ КЛАССИФИКАЦИЯ ПО НАЗНАЧЕНИЮ
- 6. КЛАССИФИКАЦИЯ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ В ЗАВИСИМОСТИ ОТ ХАРАКТЕРА СИГНАЛОВ
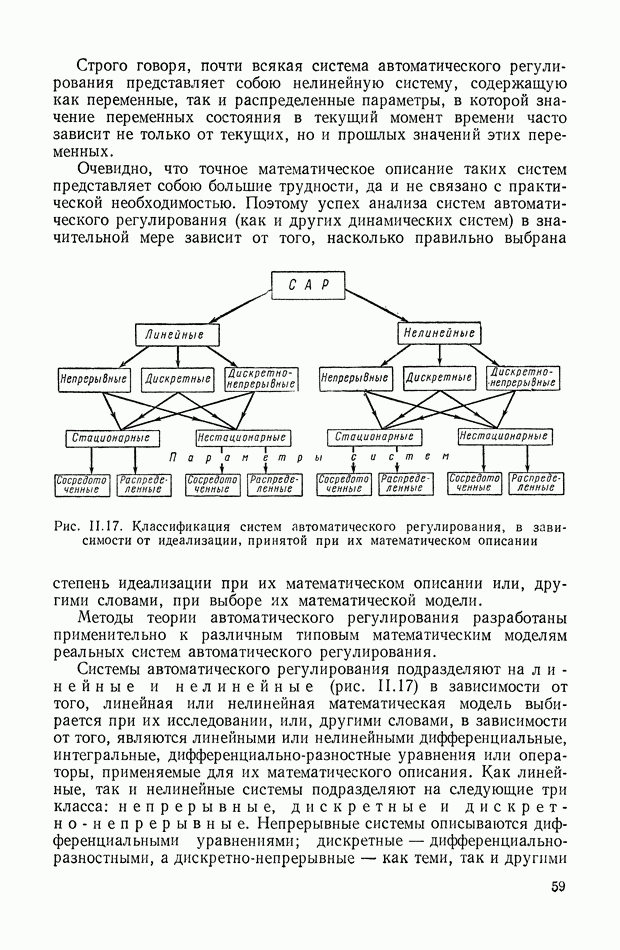
- 7. КЛАССИФИКАЦИЯ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ В ЗАВИСИМОСТИ ОТ ИДЕАЛИЗАЦИИ, ПРИНЯТОЙ ПРИ ИХ МАТЕМАТИЧЕСКОМ ОПИСАНИИ
- 8. СТРУКТУРНЫЕ СХЕМЫ, ОДНОКОНТУРНЫЕ И МНОГОКОНТУРНЫЕ, НЕСВЯЗАННЫЕ И СВЯЗАННЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
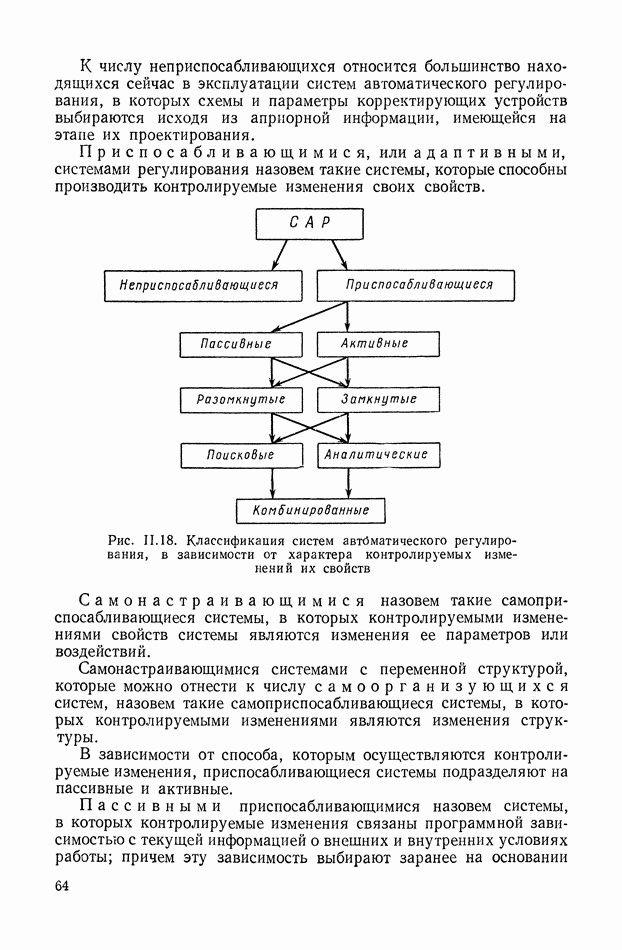
- 9. КЛАССИФИКАЦИЯ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ В ЗАВИСИМОСТИ ОТ ХАРАКТЕРА КОНТРОЛИРУЕМЫХ ИЗМЕНЕНИЙ
- 10. ТРЕБОВАНИЯ, ПРЕДЪЯВЛЯЕМЫЕ К ДИНАМИЧЕСКИМ СВОЙСТВАМ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- ГЛАВА III. ОСНОВНЫЕ УСТРОЙСТВА И ТИПОВЫЕ СХЕМЫ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. КРАТКАЯ ХАРАКТЕРИСТИКА УСТРОЙСТВ, ИЗ КОТОРЫХ СОСТОЯТ СИСТЕМЫ РЕГУЛИРОВАНИЯ
- 2. СИСТЕМА АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ СКОРОСТИ ГИДРОТУРБИНЫ
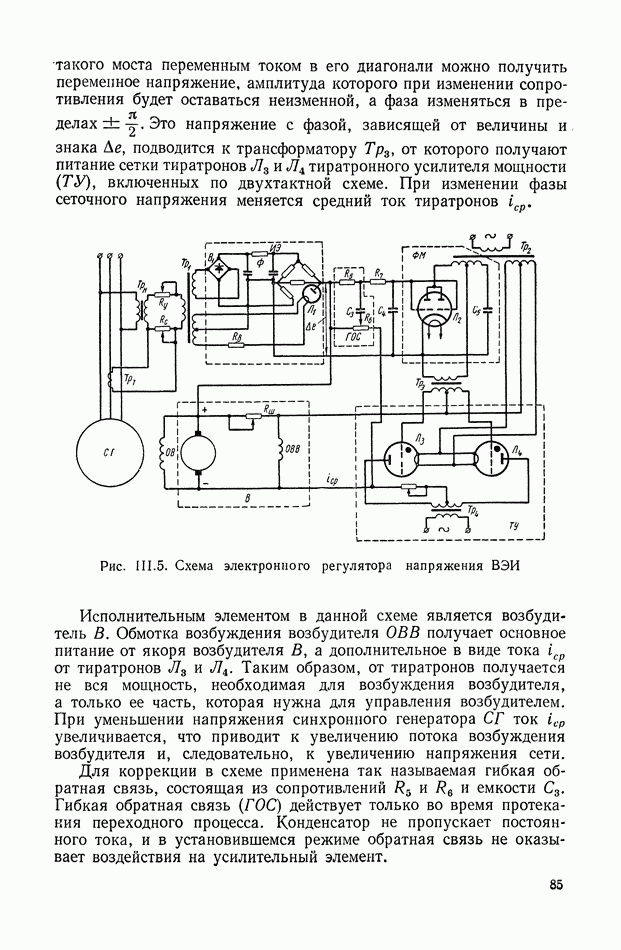
- 3. ЭЛЕКТРОННЫЙ РЕГУЛЯТОР НАПРЯЖЕНИЯ ВЭИ
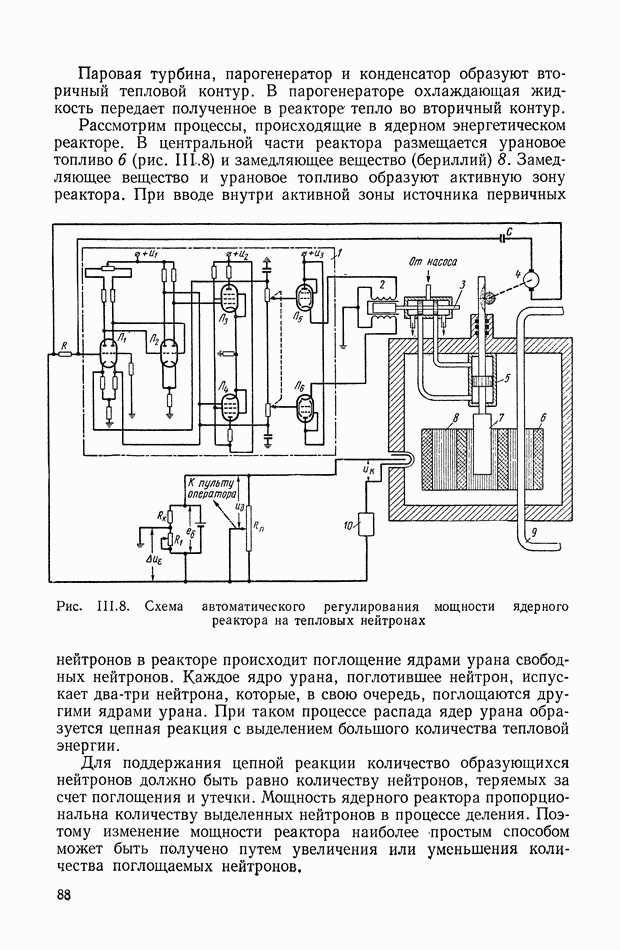
- 4. СИСТЕМА АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ЯДЕРНОГО РЕАКТОРА ПО МОЩНОСТИ
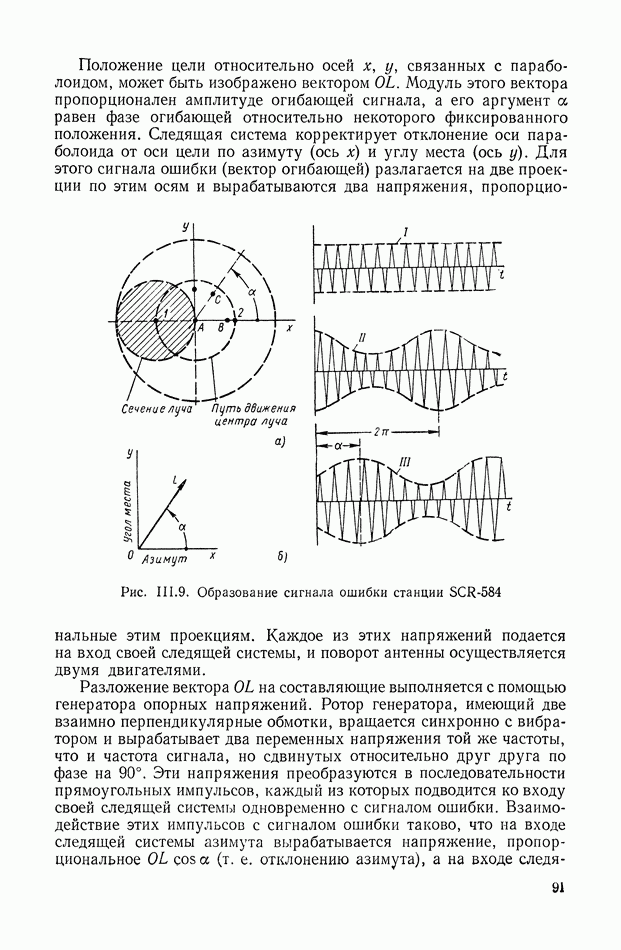
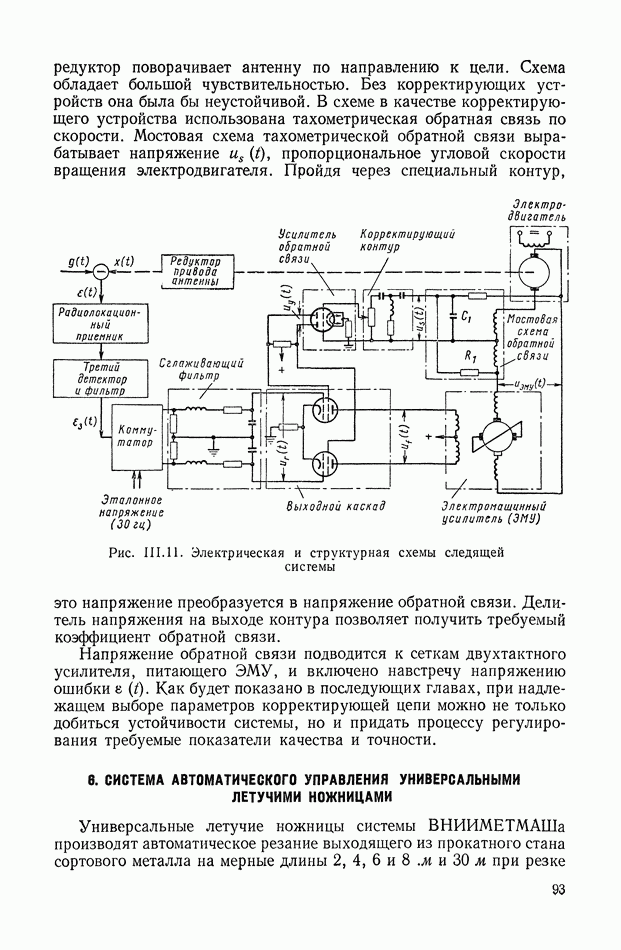
- 5. СЛЕДЯЩАЯ СИСТЕМА РАДИОЛОКАЦИОННОЙ СТАНЦИИ
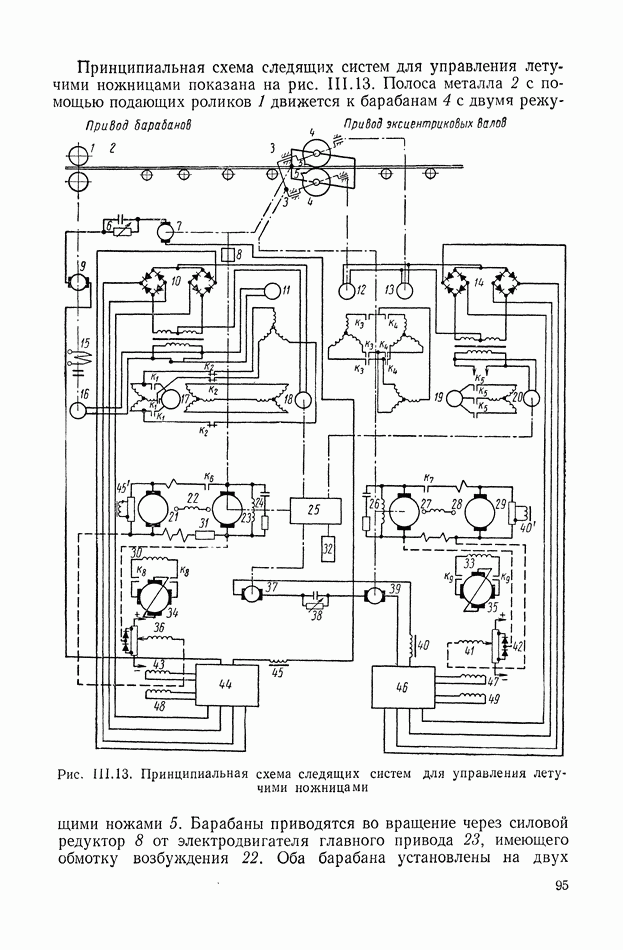
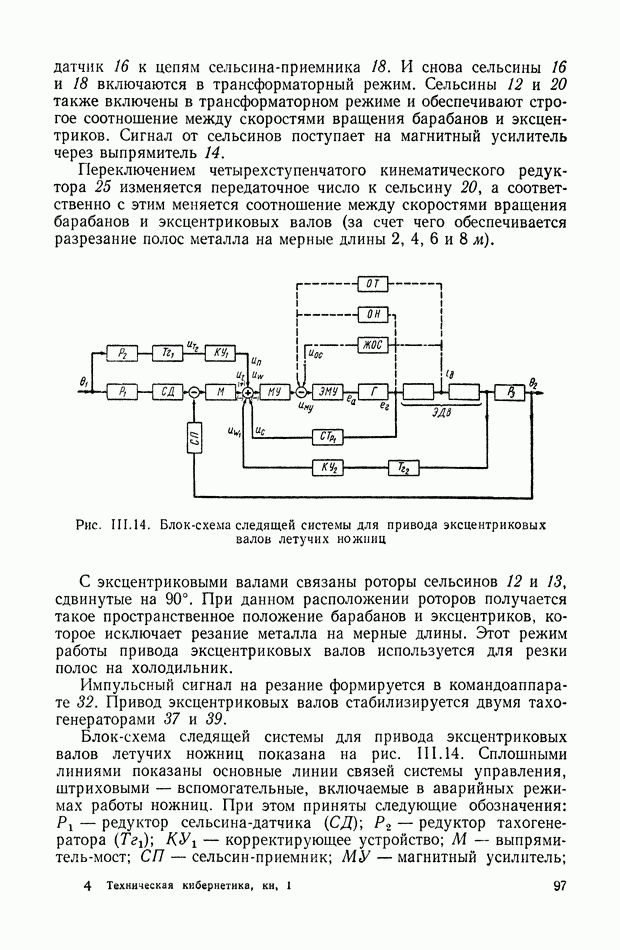
- 6. СИСТЕМА АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ УНИВЕРСАЛЬНЫМИ ЛЕТУЧИМИ НОЖНИЦАМИ
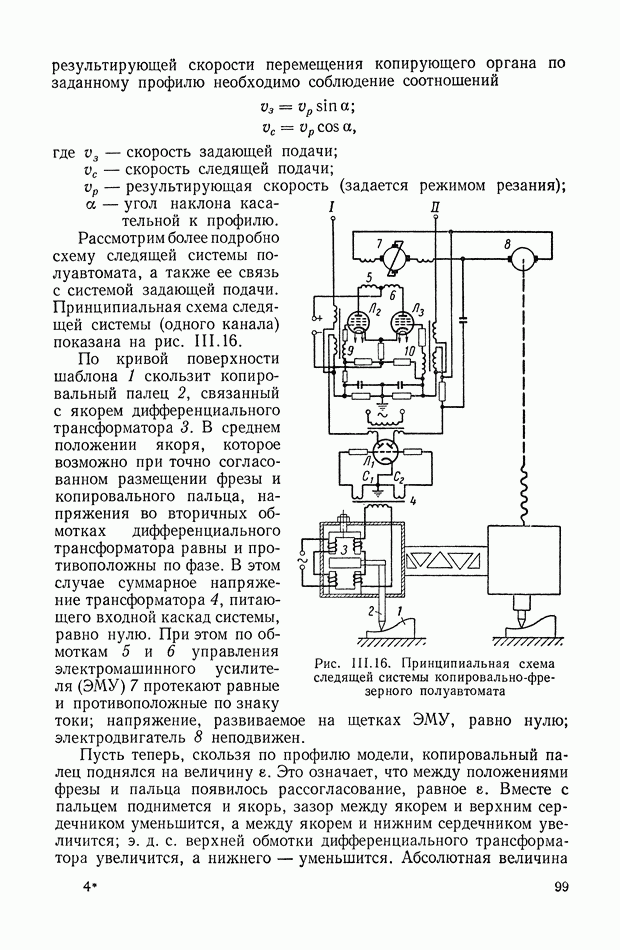
- 7. СЛЕДЯЩАЯ СИСТЕМА КОПИРОВАЛЬНО-ФРЕЗЕРНОГО ПОЛУАВТОМАТА
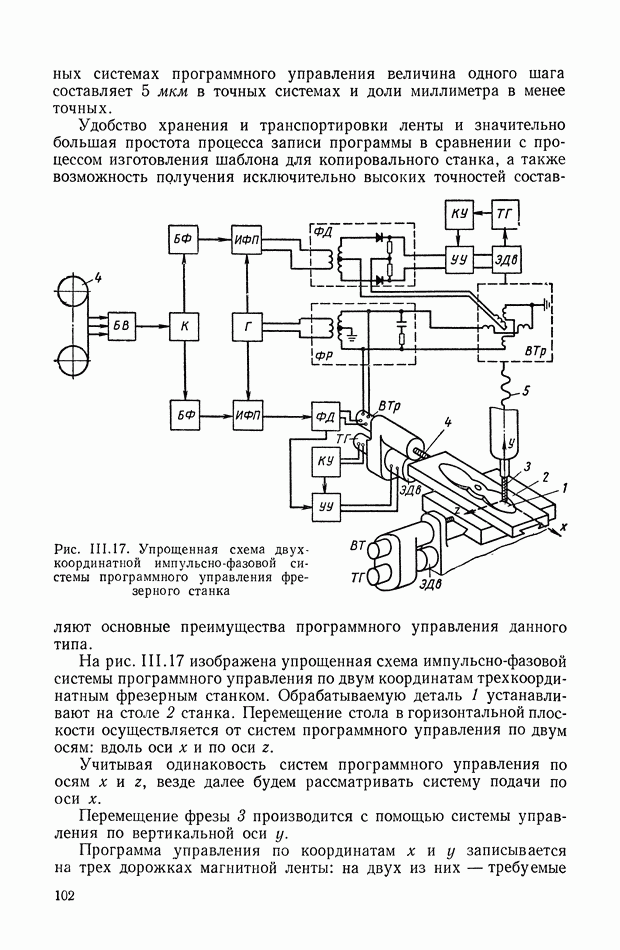
- 8. ПРОГРАММНОЕ УПРАВЛЕНИЕ МЕТАЛЛОРЕЖУЩИМИ СТАНКАМИ
- 9. ПРИНЦИП ДЕЙСТВИЯ ЭЛЕКТРИЧЕСКОГО АВТОПИЛОТА
- 10. РЕГУЛИРОВАНИЕ МНОГИХ ВЕЛИЧИН ПРИ АВТОМАТИЧЕСКОМ УПРАВЛЕНИИ ПЕРЕГОНКОЙ НЕФТИ
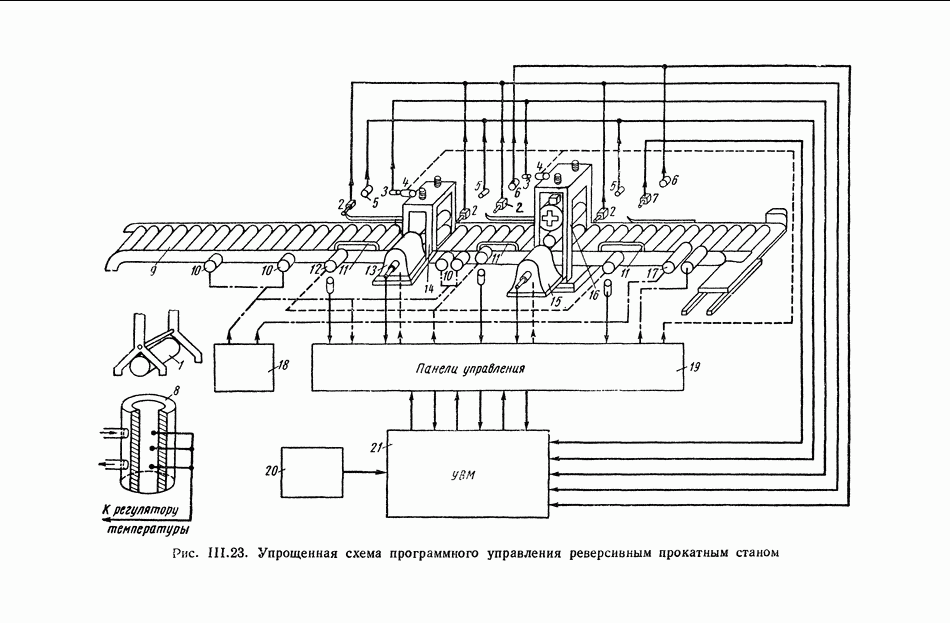
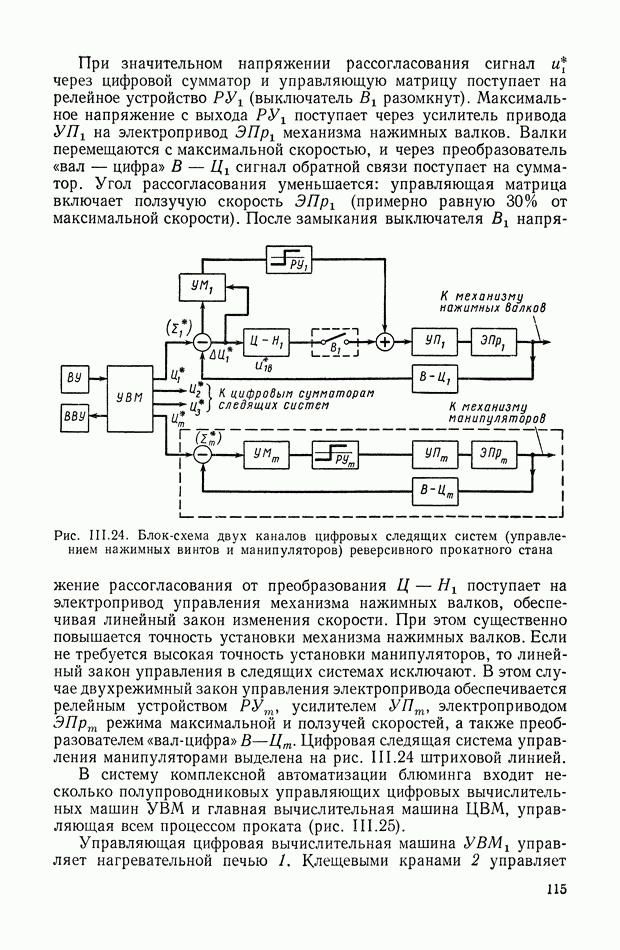
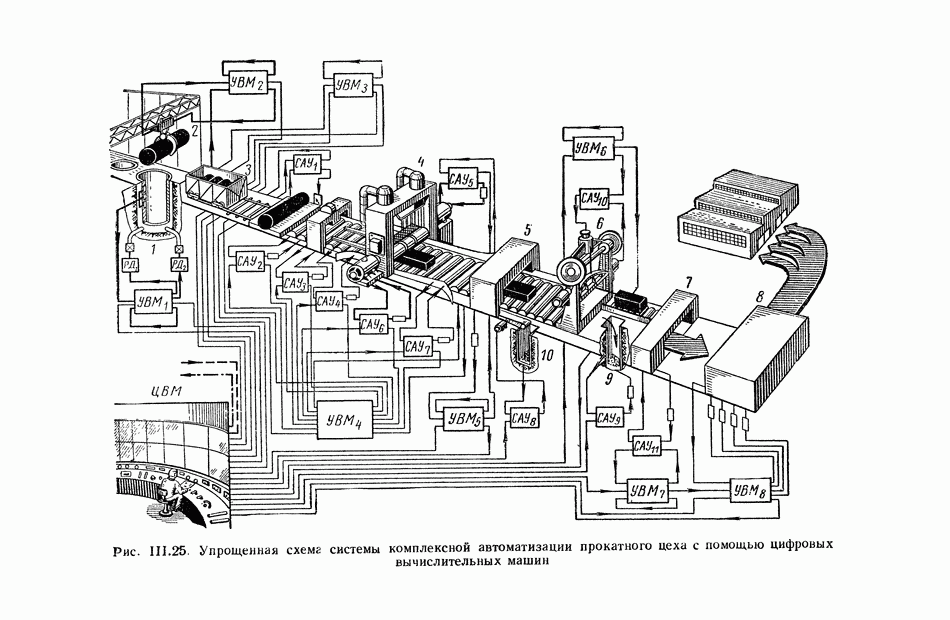
- 11. СИСТЕМА АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ РЕВЕРСИВНЫМ ПРОКАТНЫМ СТАНОМ С ИСПОЛЬЗОВАНИЕМ ЦИФРОВОЙ ВЫЧИСЛИТЕЛЬНОЙ МАШИНЫ
- ГЛАВА IV. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ЛАГРАНЖА ВТОРОГО РОДА
- 2. ОБЩИЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 3. ОБЩИЕ ЛИНЕАРИЗОВАННЫЕ УРАВНЕНИЯ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 4. ПРИМЕР СОСТАВЛЕНИЯ УРАВНЕНИЯ ОБЪЕКТА РЕГУЛИРОВАНИЯ
- ГЛАВА V. СТАТИКА СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. СТАТИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПРОСТЕЙШИХ ЗВЕНЬЕВ
- 2. СТАТИЧЕСКИЕ ХАРАКТЕРИСТИКИ ОСНОВНЫХ ТИПОВ СОЕДИНЕНИЙ ЗВЕНЬЕВ
- 3. КОРРЕКЦИЯ СТАТИЧЕСКИХ ХАРАКТЕРИСТИК
- Статическая характеристика замкнутой одномерной системы регулирования.
- Статическая характеристика линейной замкнутой системы.
- 4. СТАТИЗМ РЕГУЛИРОВАНИЯ
- 5. СТАТИКА ЛИНЕЙНЫХ СИСТЕМ С НЕСКОЛЬКИМИ РЕГУЛИРУЕМЫМИ ВЕЛИЧИНАМИ
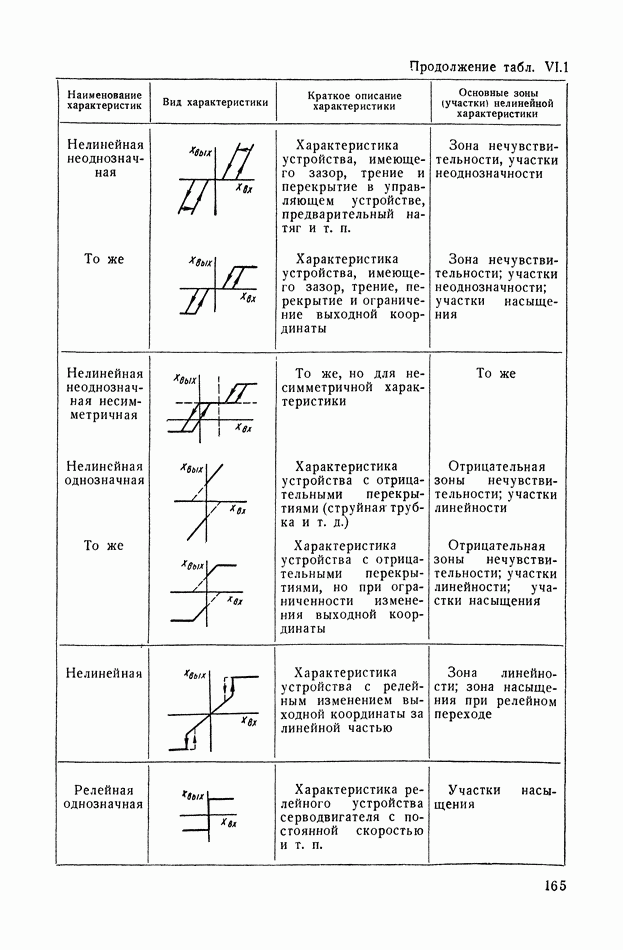
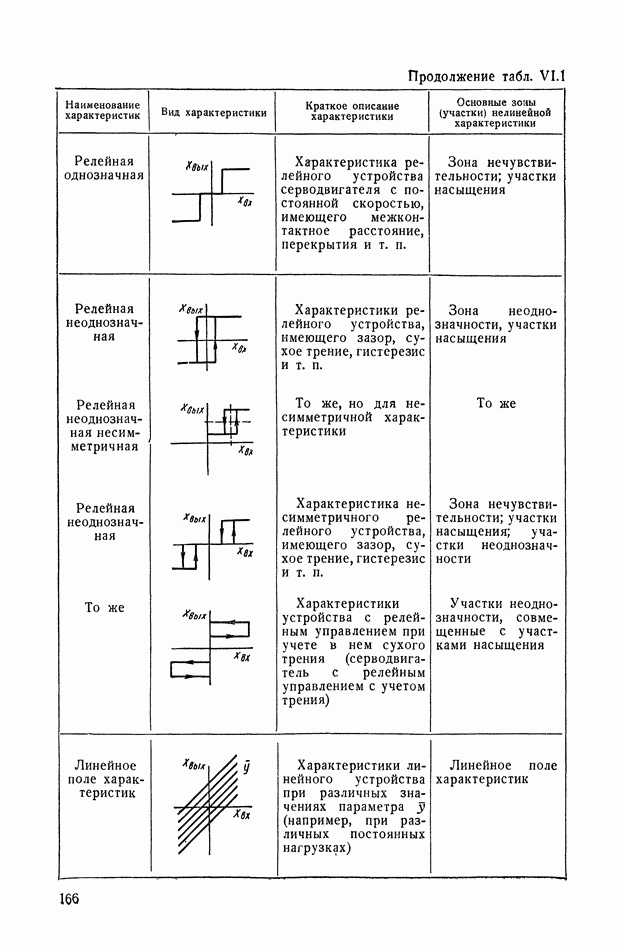
- ГЛАВА VI. ТИПИЧНЫЕ НЕЛИНЕЙНЫЕ СТАТИЧЕСКИЕ ХАРАКТЕРИСТИКИ ТИПОВЫХ ЗВЕНЬЕВ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. НЕЛИНЕЙНЫЕ ХАРАКТЕРИСТИКИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 2. ВИДЫ ТИПИЧНЫХ НЕЛИНЕЙНЫХ СТАТИЧЕСКИХ ХАРАКТЕРИСТИК СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 3. ТИПИЧНЫЕ НЕЛИНЕЙНЫЕ ХАРАКТЕРИСТИКИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 4. ЗОНЫ НЕЧУВСТВИТЕЛЬНОСТИ
- 5. ЗОНЫ ЛИНЕЙНОСТИ И НЕОДНОЗНАЧНОСТИ
- 6. ЗОНЫ НАСЫЩЕНИЯ
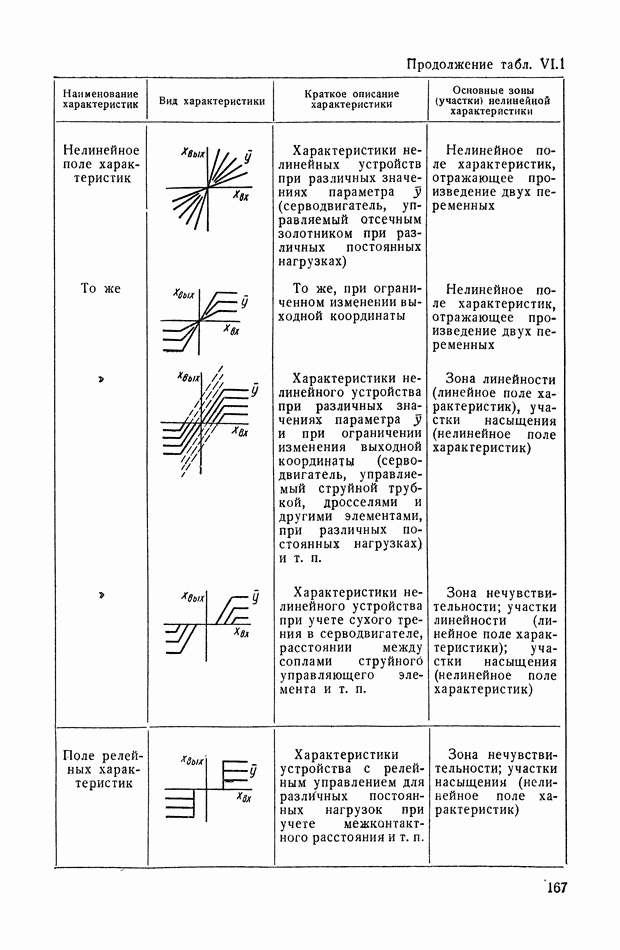
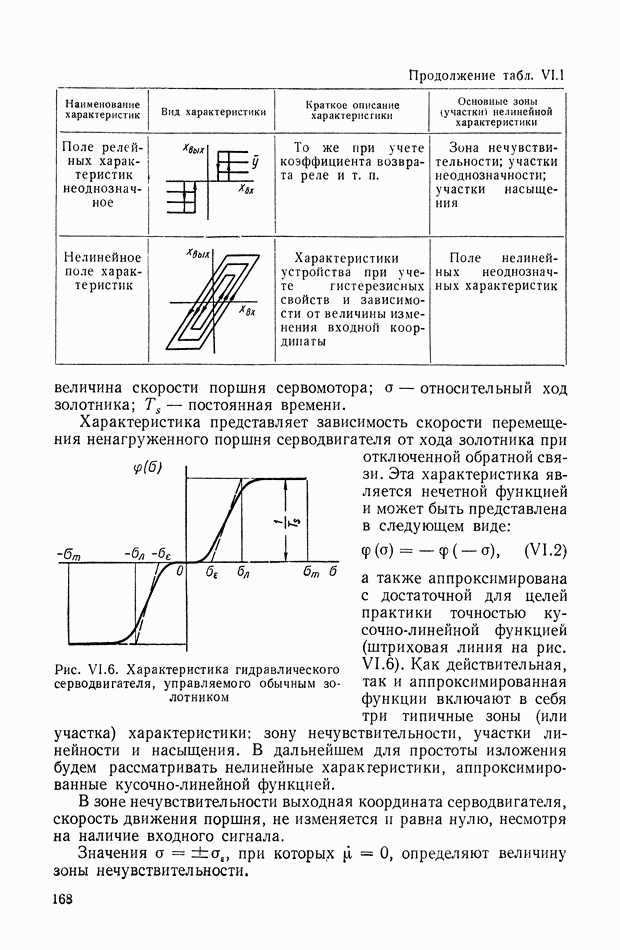
- 7. ПОЛЕ КРИВЫХ, ПРЕДСТАВЛЯЮЩИХ ХАРАКТЕРИСТИКУ СЕРВОДВИГАТЕЛЯ
- 8. ЭКСПЕРИМЕНТАЛЬНОЕ ВЫЯВЛЕНИЕ НЕЛИНЕЙНОСТИ ХАРАКТЕРИСТИК СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- ГЛАВА VII. ПЕРЕХОДНЫЕ ФУНКЦИИ, ПЕРЕДАТОЧНЫЕ ФУНКЦИИ И ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ДИНАМИЧЕСКИХ ЭЛЕМЕНТОВ
- 1. КЛАССИФИКАЦИЯ ДИНАМИЧЕСКИХ ЭЛЕМЕНТОВ
- 2. ОБЩЕЕ ОПРЕДЕЛЕНИЕ ИМПУЛЬСНОЙ ПЕРЕХОДНОЙ И ПЕРЕДАТОЧНОЙ ФУНКЦИЙ ДИНАМИЧЕСКОЙ СИСТЕМЫ ИЛИ ДИНАМИЧЕСКОГО ЭЛЕМЕНТА
- 3. ИМПУЛЬСНАЯ ПЕРЕХОДНАЯ ФУНКЦИЯ НЕПРЕРЫВНОЙ СТАЦИОНАРНОЙ ЛИНЕЙНОЙ СИСТЕМЫ
- 4. ПЕРЕДАТОЧНАЯ ФУНКЦИЯ НЕПРЕРЫВНОЙ ЛИНЕЙНОЙ СТАЦИОНАРНОЙ СИСТЕМЫ
- 5. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЛИНЕЙНОЙ СТАЦИОНАРНОЙ НЕПРЕРЫВНОЙ ДИНАМИЧЕСКОЙ СИСТЕМЫ
- 6. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДИНАМИЧЕСКОГО ЭЛЕМЕНТА С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
- 7. ПРИМЕНЕНИЕ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА К РЕШЕНИЮ УРАВНЕНИЙ ЭЛЕМЕНТА С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
- 8. ПЕРЕДАТОЧНАЯ ФУНКЦИЯ ДИНАМИЧЕСКОГО ЭЛЕМЕНТА С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
- 9. ПЕРЕДАТОЧНАЯ ФУНКЦИЯ ПОСЛЕДОВАТЕЛЬНОГО СОЕДИНЕНИЯ ДИНАМИЧЕСКИХ ЭЛЕМЕНТОВ С СОСРЕДОТОЧЕННЫМИ И С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
- 10. ПЕРЕДАТОЧНАЯ ФУНКЦИЯ ЗАПАЗДЫВАЮЩЕГО ЭЛЕМЕНТА
- 11. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЭЛЕМЕНТА С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
- 12. ИМПУЛЬСНАЯ ПЕРЕХОДНАЯ ФУНКЦИЯ ДИНАМИЧЕСКОГО ЭЛЕМЕНТА С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
- 13. ПЕРЕДАТОЧНАЯ ФУНКЦИЯ СИСТЕМЫ С ГАРМОНИЧЕСКОЙ МОДУЛЯЦИЕЙ
- 14 ИМПУЛЬСНАЯ ПЕРЕХОДНАЯ И ПЕРЕДАТОЧНАЯ ФУНКЦИИ ДИСКРЕТНОЙ ЛИНЕЙНОЙ СТАЦИОНАРНОЙ СИСТЕМЫ
- 15. ПРОХОЖДЕНИЕ СИГНАЛА ЧЕРЕЗ ИМПУЛЬСНЫЙ ЭЛЕМЕНТ
- 16. ПОСЛЕДОВАТЕЛЬНОЕ СОЕДИНЕНИЕ ИМПУЛЬСНОГО ЭЛЕМЕНТА И НЕПРЕРЫВНОГО ДИНАМИЧЕСКОГО ЭЛЕМЕНТА
- 17. ИМПУЛЬСНАЯ ПЕРЕХОДНАЯ ФУНКЦИЯ ЛИНЕЙНОЙ НЕСТАЦИОНАРНОЙ СИСТЕМЫ (СИСТЕМЫ С ПЕРЕМЕННЫМИ ПАРАМЕТРАМИ)
- 18. ПЕРЕДАТОЧНАЯ ФУНКЦИЯ НЕПРЕРЫВНОЙ ЛИНЕЙНОЙ НЕСТАЦИОНАРНОЙ СИСТЕМЫ
- 19. МНОГОМЕРНЫЕ ИМПУЛЬСНЫЕ ПЕРЕХОДНЫЕ И ПЕРЕДАТОЧНЫЕ ФУНКЦИИ НЕЛИНЕЙНЫХ СИСТЕМ
- 20. МНОГОМЕРНЫЕ ПЕРЕДАТОЧНЫЕ ФУНКЦИИ НЕЛИНЕЙНЫХ СИСТЕМ
- ГЛАВА VIII. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ, ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ И ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ НЕПРЕРЫВНЫХ ЛИНЕЙНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 2. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ СТАТИЧЕСКИХ И АСТАТИЧЕСКИХ СИСТЕМ
- 3. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ
- 4. ВЗАИМНАЯ СВЯЗЬ МЕЖДУ ЧАСТОТНЫМИ ХАРАКТЕРИСТИКАМИ ЗАМКНУТОЙ И РАЗОМКНУТОЙ СИСТЕМЫ
- 5. КРУГОВЫЕ ДИАГРАММЫ
- 6. НОМОГРАММЫ ЗАМЫКАНИЯ
- 7. УСЛОВИЯ ОДНОЗНАЧНОЙ связи МЕЖДУ ЧАСТОТНЫМИ ХАРАКТЕРИСТИКАМИ
- 8. ОПРЕДЕЛЕНИЕ ПЕРЕДАТОЧНОЙ ФУНКЦИИ ПО ОДНОЙ ИЗ ЧАСТОТНЫХ ХАРАКТЕРИСТИК, ЗАДАННОЙ АНАЛИТИЧЕСКИ
- 9. ФОРМУЛА ДЛЯ ВЫЧИСЛЕНИЯ ФАЗОВОЙ ЧАСТОТНОЙ ХАРАКТЕРИСТИКИ ПО ЗАДАННОЙ АМПЛИТУДНОЙ ЧАСТОТНОЙ ХАРАКТЕРИСТИКЕ
- 10. ЗАВИСИМОСТЬ МЕЖДУ ЛОГАРИФМИЧЕСКОЙ АМПЛИТУДНОЙ И ФАЗОВОЙ ЧАСТОТНЫМИ ХАРАКТЕРИСТИКАМИ
- 11. ГРАФИЧЕСКИЙ МЕТОД ОПРЕДЕЛЕНИЯ ФАЗОВОЙ ХАРАКТЕРИСТИКИ ПО ЗАДАННОЙ АМПЛИТУДНОЙ ХАРАКТЕРИСТИКЕ
- 12. ИНТЕГРАЛЬНЫЕ ВЫРАЖЕНИЯ ДЛЯ ОШИБКИ И ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 13. ТИПОВЫЕ ЗВЕНЬЯ
- 14. АПЕРИОДИЧЕСКОЕ ЗВЕНО
- 15. КОЛЕБАТЕЛЬНОЕ ЗВЕНО
- 16. ИНТЕГРИРУЮЩЕЕ ЗВЕНО
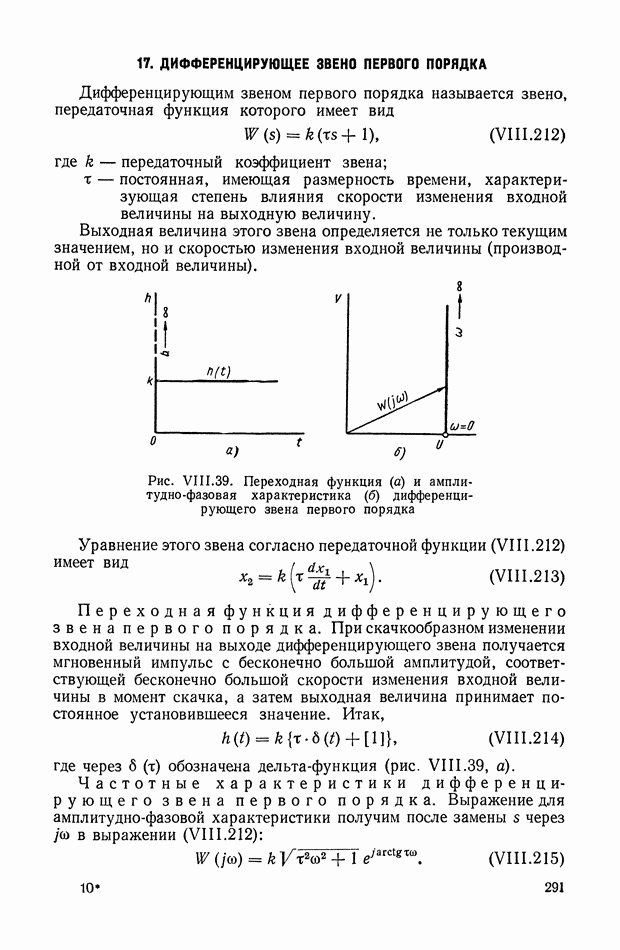
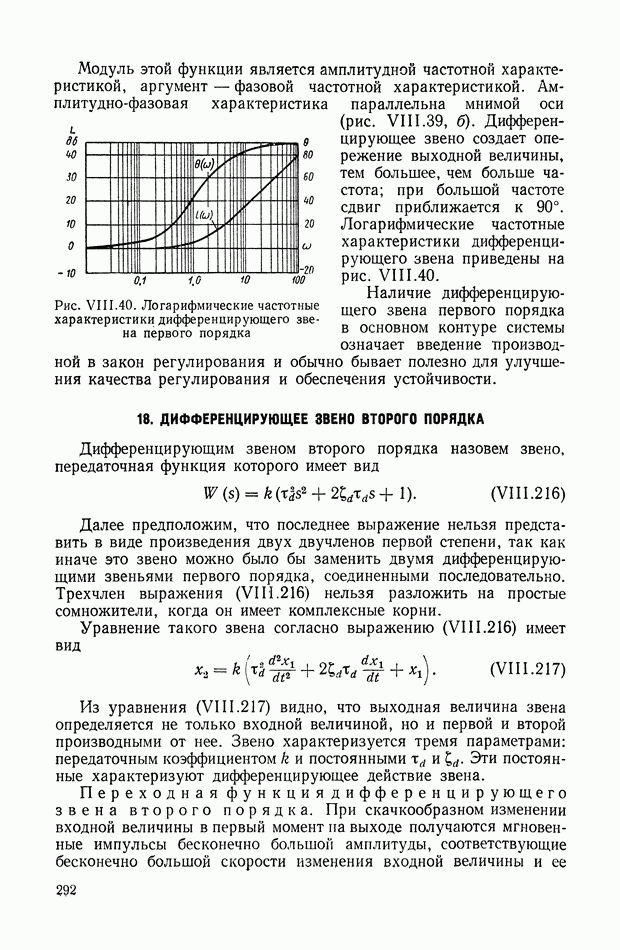
- 17. ДИФФЕРЕНЦИРУЮЩЕЕ ЗВЕНО ПЕРВОГО ПОРЯДКА
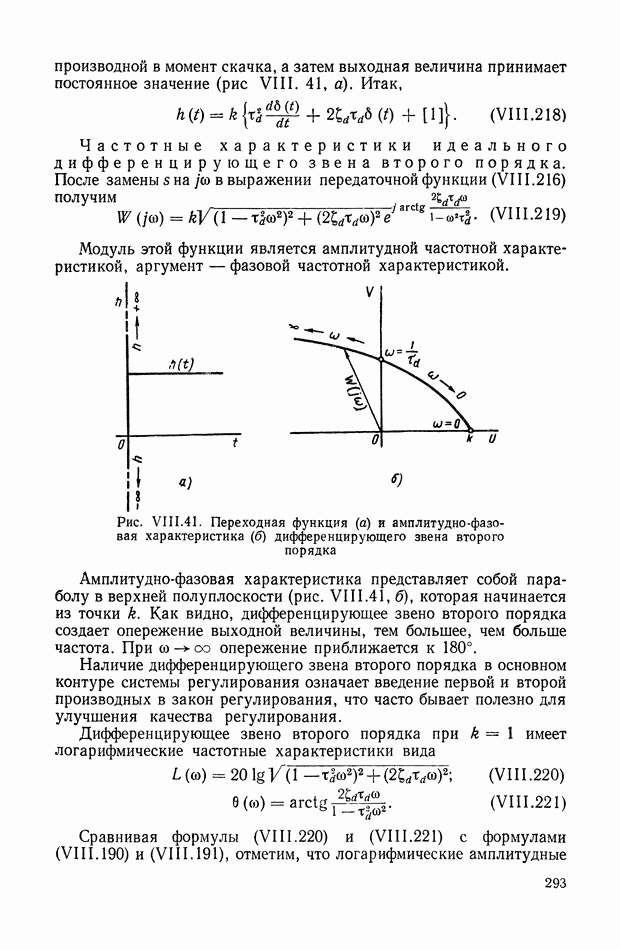
- 18. ДИФФЕРЕНЦИРУЮЩЕЕ ЗВЕНО ВТОРОГО ПОРЯДКА
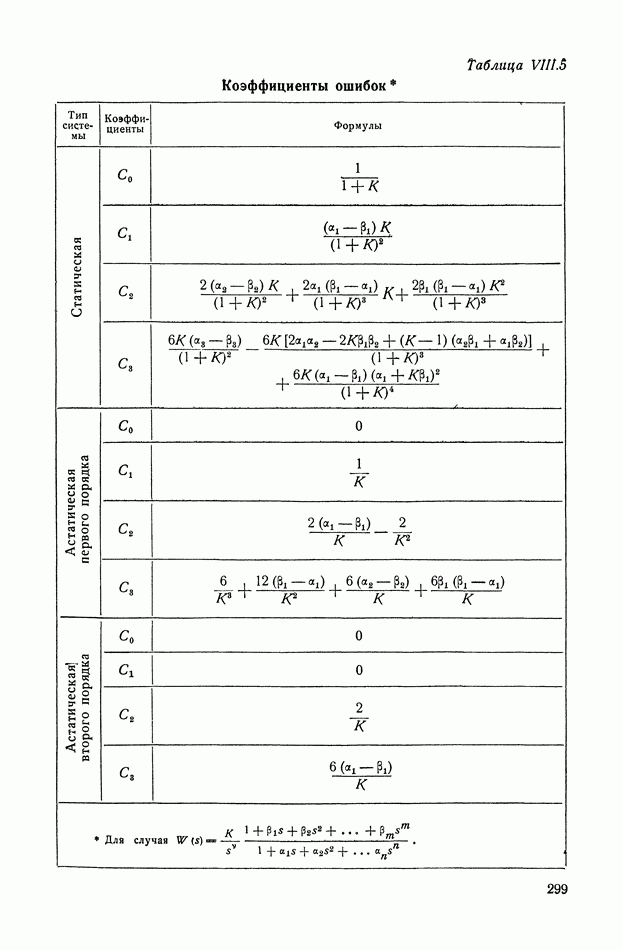
- 19. КОЭФФИЦИЕНТЫ ОШИБКИ
- ГЛАВА IX. МЕТОДЫ СТРУКТУРНЫХ ПРЕОБРАЗОВАНИЙ В СИСТЕМАХ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. ГРАФИЧЕСКИЕ ИЗОБРАЖЕНИЯ УСЛОВИЙ ПРЕОБРАЗОВАНИЯ СИГНАЛОВ
- 2. СХЕМЫ С ЭЛЕМЕНТАМИ, ОБЛАДАЮЩИМИ И НЕ ОБЛАДАЮЩИМИ СВОЙСТВОМ НАПРАВЛЕННОСТИ ДЕЙСТВИЯ
- 3. ДЕТАЛИЗИРОВАННЫЕ СТРУКТУРЫ
- 4. ПРЕОБРАЗОВАНИЯ МНОГОКОНТУРНЫХ СТРУКТУРНЫХ СХЕМ, ДОПУСКАЮЩИХ ПОСЛЕДОВАТЕЛЬНОЕ ПРИМЕНЕНИЕ ПРАВИЛ СВЕРТЫВАНИЯ КОНТУРОВ, И НЕКОТОРЫЕ ЭКВИВАЛЕНТНЫЕ ПРЕОБРАЗОВАНИЯ
- 5. ПРЕОБРАЗОВАНИЯ ПЕРЕКРЕСТНЫХ СТРУКТУРНЫХ СХЕМ МЕТОДОМ РАЗВЯЗКИ КОНТУРОВ И НЕКОТОРЫЕ ЭКВИВАЛЕНТНЫЕ ПРЕОБРАЗОВАНИЯ
- 6. ПРИМЕНЕНИЕ СТРУКТУРНЫХ МЕТОДОВ ДЛЯ ОПРЕДЕЛЕНИЯ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ МНОГОКОНТУРНЫХ СИСТЕМ
- 7. СОСТАВЛЕНИЕ И ПРЕОБРАЗОВАНИЕ СТРУКТУРНОЙ СХЕМЫ НА ПРИМЕРЕ ЭЛЕКТРОДВИГАТЕЛЯ ПОСТОЯННОГО ТОКА ДВОЙНОГО ПИТАНИЯ
- Учет зависимости момента нагрузки от угла поворота вала и его производных по времени.
- 8. СТРУКТУРНЫЕ СХЕМЫ МЕХАНИЧЕСКИХ ОБЪЕКТОВ РЕГУЛИРОВАНИЯ С РЕДУКТОРАМИ, ДИФФЕРЕНЦИАЛАМИ И УПРУГИМИ ЭЛЕМЕНТАМИ В СИЛОВЫХ ПЕРЕДАЧАХ
- 9. ПРАВИЛА СТРУКТУРНЫХ ПРЕОБРАЗОВАНИЙ ДЛЯ СИСТЕМ С ПЕРЕМЕННЫМИ ПАРАМЕТРАМИ
- 10. ФУНКЦИОНАЛЬНЫЕ СТРУКТУРНЫЕ СХЕМЫ ДЛЯ АНАЛИЗА СОВМЕСТНЫХ СТАТИЧЕСКИХ ХАРАКТЕРИСТИК НЕЛИНЕЙНЫХ ЗВЕНЬЕВ
- ГЛАВА X. ПРИМЕРЫ СОСТАВЛЕНИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ, СТРУКТУРНЫХ СХЕМ И ПЕРЕДАТОЧНЫХ ФУНКЦИЙ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. СИСТЕМА АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ СКОРОСТИ ВРАЩЕНИЯ ГИДРОТУРБИНЫ
- 2. ЭЛЕКТРОННЫЙ РЕГУЛЯТОР НАПРЯЖЕНИЯ ВЭИ
- 3. СИСТЕМА АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ МОЩНОСТИ ЯДЕРНОГО ЭНЕРГЕТИЧЕСКОГО РЕАКТОРА НА ТЕПЛОВЫХ НЕЙТРОНАХ
- 4. СЛЕДЯЩАЯ СИСТЕМА РАДИОЛОКАЦИОННОЙ СТАНЦИИ
- 5. СИСТЕМА АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ УНИВЕРСАЛЬНЫХ ЛЕТУЧИХ НОЖНИЦ
- 6. САМОЛЕТ С АВТОПИЛОТОМ
- 7. СЛЕДЯЩАЯ СИСТЕМА КОПИРОВАЛЬНО-ФРЕЗЕРНОГО СТАНКА
- РАЗДЕЛ II. АНАЛИЗ УСТОЙЧИВОСТИ НЕПРЕРЫВНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- ГЛАВА XI. ОБЩАЯ ПОСТАНОВКА ЗАДАЧИ УСТОЙЧИВОСТИ ПО ЛЯПУНОВУ И АНАЛИЗ УСТОЙЧИВОСТИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. ПОСТАНОВКА ЗАДАЧИ ОБ УСТОЙЧИВОСТИ В ТЕОРИИ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 2. ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ УСТАНОВИВШИХСЯ ДВИЖЕНИЙ ПО УРАВНЕНИЮ ПЕРВОГО ПРИБЛИЖЕНИЯ
- 3. О ПРЯМОМ МЕТОДЕ ЛЯПУНОВА
- 4. О ПРИМЕНЕНИИ ПРЯМОГО МЕТОДА ЛЯПУНОВА К АНАЛИЗУ УСТОЙЧИВОСТИ ОДНОГО КЛАССА СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- ГЛАВА XII. КРИТЕРИИ И МЕТОДЫ АНАЛИЗА УСТОЙЧИВОСТИ ЛИНЕАРИЗОВАННЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЙ
- 1. УСТОЙЧИВОСТЬ И ПРИНЦИП АРГУМЕНТА
- 2. КРИТЕРИЙ УСТОЙЧИВОСТИ МИХАЙЛОВА
- 3. КРИТЕРИЙ УСТОЙЧИВОСТИ РАУСА И ГУРВИЦА
- 4. ЧАСТОТНЫЙ КРИТЕРИЙ УСТОЙЧИВОСТИ
- 5. ОБОБЩЕНИЕ ЧАСТОТНОГО КРИТЕРИЯ НА АСТАТИЧЕСКИЕ СИСТЕМЫ
- 6. ОБОБЩЕНИЕ ЧАСТОТНОГО КРИТЕРИЯ НА СЛУЧАЙ, КОГДА РАЗОМКНУТАЯ СИСТЕМА НЕУСТОЙЧИВА
- 7. ЧАСТОТНЫЙ КРИТЕРИЙ УСТОЙЧИВОСТИ ДЛЯ ОБРАТНОЙ АМПЛИТУДНО-ФАЗОВОЙ ХАРАКТЕРИСТИКИ
- 8. АНАЛИЗ УСТОЙЧИВОСТИ ОДНОКОНТУРНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ПО ИХ ЛОГАРИФМИЧЕСКИМ ЧАСТОТНЫМ ХАРАКТЕРИСТИКАМ
- 9. ПРИБЛИЖЕННЫЙ СПОСОБ ПОСТРОЕНИЯ ЛОГАРИФМИЧЕСКИХ ЧАСТОТНЫХ ХАРАКТЕРИСТИК ОДНОКОНТУРНЫХ СИСТЕМ
- 10. ОБОБЩЕНИЕ ЧАСТОТНОГО КРИТЕРИЯ УСТОЙЧИВОСТИ НА МНОГОКОНТУРНЫЕ СИСТЕМЫ
- 11. АНАЛИЗ УСТОЙЧИВОСТИ МНОГОКОНТУРНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ПРИ ПОМОЩИ ЛОГАРИФМИЧЕСКИХ ЧАСТОТНЫХ ХАРАКТЕРИСТИК
- ГЛАВА XIII. ВЫДЕЛЕНИЕ ОБЛАСТЕЙ УСТОЙЧИВОСТИ
- 1. ПОНЯТИЕ О Д-РАЗБИЕНИИ ПРОСТРАНСТВА КОЭФФИЦИЕНТОВ ХАРАКТЕРИСТИЧЕСКОГО УРАВНЕНИЯ И ПРОСТРАНСТВА ПАРАМЕТРОВ
- 2. Д-РАЗБИЕНИЕ ПЛОСКОСТИ ОДНОГО КОМПЛЕКСНОГО ПАРАМЕТРА
- 3. СВЯЗЬ Д-РАЗБИЕНИЯ С КРИТЕРИЯМИ УСТОЙЧИВОСТИ
- 4. Д-РАЗБИЕНИЕ ПЛОСКОСТИ ДВУХ ДЕЙСТВИТЕЛЬНЫХ ПАРАМЕТРОВ (ДИАГРАММА ВЫШНЕГРАДСКОГО)
- 5. УСЛОВИЯ СУЩЕСТВОВАНИЯ ОБЛАСТИ УСТОЙЧИВОСТИ
- ГЛАВА XIV. ПРИМЕРЫ АНАЛИЗА УСТОЙЧИВОСТИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. СИСТЕМА АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ СКОРОСТИ ВРАЩЕНИЯ ГИДРОТУРБИНЫ
- 2. СЛЕДЯЩАЯ СИСТЕМА КОПИРОВАЛЬНО-ФРЕЗЕРНОГО СТАНКА
- 3. СИСТЕМА АВТОМАТИЧЕСКОЙ СТАБИЛИЗАЦИИ САМОЛЕТА (АВТОПИЛОТ)
- 4. СИСТЕМА АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ МОЩНОСТИ ЯДЕРНОГО ЭНЕРГЕТИЧЕСКОГО РЕАКТОРА
- РАЗДЕЛ III. АНАЛИЗ ПЕРЕХОДНЫХ ПРОЦЕССОВ И КАЧЕСТВА ЛИНЕЙНЫХ НЕПРЕРЫВНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- ГЛАВА XV. ЧАСТОТНЫЙ МЕТОД АНАЛИЗА ПЕРЕХОДНЫХ ПРОЦЕССОВ
- 1. ОБОБЩЕННЫЕ ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ И ИХ СВЯЗЬ С ПЕРЕХОДНЫМИ ПРОЦЕССАМИ
- 2. ОПРЕДЕЛЕНИЕ ОБОБЩЕННЫХ ЧАСТОТНЫХ ХАРАКТЕРИСТИК В ОБЩЕМ СЛУЧАЕ
- 3. СЛУЧАЙ, КОГДА ФУНКЦИЯ X(s) НЕ СОДЕРЖИТ ОСОБЕННОСТЕЙ ВО ВСЕЙ ПРАВОЙ ПОЛУПЛОСКОСТИ И НА МНИМОЙ ОСИ
- 4. СВЯЗЬ МЕЖДУ ЧАСТОТНЫМИ ХАРАКТЕРИСТИКАМИ P(w), Q(w) И ИМПУЛЬСНОЙ ПЕРЕХОДНОЙ ФУНКЦИЕЙ k(t)
- 5. СЛУЧАЙ, КОГДА ВСЕ ПОЛЮСА ФУНКЦИИ X(s) РАСПОЛОЖЕНЫ В ЛЕВОЙ ПОЛУПЛОСКОСТИ, ЗА ИСКЛЮЧЕНИЕМ ПОЛЮСА В НАЧАЛЕ КООРДИНАТ
- 6. СВЯЗЬ МЕЖДУ ЧАСТОТНЫМИ ХАРАКТЕРИСТИКАМИ И ПЕРЕХОДНОЙ ФУНКЦИЕЙ h(t)
- 7. СЛУЧАЙ, КОГДА ФУНКЦИЯ X(s) ИМЕЕТ ДВА СОПРЯЖЕННЫХ ПОЛЮСА НА МНИМОЙ ОСИ
- 8. АНАЛИЗ ПЕРЕХОДНЫХ ПРОЦЕССОВ МЕТОДОМ ТРАПЕЦЕИДАЛЬНЫХ ЧАСТОТНЫХ ХАРАКТЕРИСТИК
- 9. О НЕКОТОРЫХ ЧАСТНЫХ СЛУЧАЯХ МЕТОДА ТРАПЕЦЕИДАЛЬНЫХ ЧАСТОТНЫХ ХАРАКТЕРИСТИК
- 10. ОБ УСЛОВИЯХ ПРИМЕНИМОСТИ ЧАСТОТНОГО МЕТОДА АНАЛИЗА ПЕРЕХОДНЫХ ПРОЦЕССОВ
- 11. ОПРЕДЕЛЕНИЕ ДИСКРЕТНЫХ ЗНАЧЕНИЙ ПЕРЕХОДНОЙ ФУНКЦИИ
- ГЛАВА XVI. ЧАСТОТНЫЙ МЕТОД АНАЛИЗА КАЧЕСТВА
- 1. ЧАСТОТНЫЙ КРИТЕРИЙ КАЧЕСТВА РЕГУЛИРОВАНИЯ
- 2. ЧАСТОТНЫЙ КРИТЕРИЙ ОТСУТСТВИЯ ПЕРЕРЕГУЛИРОВАНИЙ И ЧАСТОТНЫЙ КРИТЕРИЙ МОНОТОННОСТИ
- 3. О ПРОВЕРКЕ ВЫПОЛНЕНИЯ СФОРМУЛИРОВАННЫХ КРИТЕРИЕВ
- 4. НЕКОТОРЫЕ ПРИЗНАКИ НЕУДОВЛЕТВОРЕНИЯ КРИТЕРИЕВ КАЧЕСТВА И КРИТЕРИЕВ ОТСУТСТВИЯ ПЕРЕРЕГУЛИРОВАНИЙ И МОНОТОННОСТИ
- 5. НЕКОТОРЫЕ ЭЛЕМЕНТАРНЫЕ СВОЙСТВА ЧАСТОТНЫХ ХАРАКТЕРИСТИК
- 6. ДОСТАТОЧНЫЕ УСЛОВИЯ ДЛЯ МАЛЫХ ПЕРЕРЕГУЛИРОВАНИЙ И НЕОБХОДИМЫЕ УСЛОВИЯ ДЛЯ ОТСУТСТВИЯ ПЕРЕРЕГУЛИРОВАНИЙ
- 7. КРИТЕРИЙ, ОПРЕДЕЛЯЮЩИЙ ДОСТАТОЧНЫЕ УСЛОВИЯ ДЛЯ МОНОТОННОСТИ
- 8. ОЦЕНКИ ВЕЛИЧИНЫ ПЕРЕРЕГУЛИРОВАНИЯ И ВРЕМЕНИ ПЕРЕХОДНОГО ПРОЦЕССА
- 9. ОЦЕНКА АБСОЛЮТНОГО ЗНАЧЕНИЯ РАЗНОСТИ МЕЖДУ ПЕРЕХОДНЫМИ ФУНКЦИЯМИ ПО СООТВЕТСТВУЮЩИМ ИМ ЧАСТОТНЫМ ХАРАКТЕРИСТИКАМ
- 10. СВЯЗЬ МЕЖДУ СВОЙСТВАМИ АМПЛИТУДНО-ФАЗОВОЙ ХАРАКТЕРИСТИКИ РАЗОМКНУТОЙ СИСТЕМЫ И КАЧЕСТВОМ
- 11. ТРЕБОВАНИЯ К ЧАСТОТНЫМ ХАРАКТЕРИСТИКАМ, ОБЕСПЕЧИВАЮЩИЕ ВЫСОКУЮ ТОЧНОСТЬ В СЛЕДЯЩИХ СИСТЕМАХ
- 12. СВЯЗЬ МЕЖДУ СВОЙСТВАМИ ЛОГАРИФМИЧЕСКОЙ АМПЛИТУДНОЙ ХАРАКТЕРИСТИКИ И КАЧЕСТВОМ
- 13. ОПРЕДЕЛЕНИЕ ВЕЛИЧИНЫ ПЕРЕДАТОЧНОГО КОЭФФИЦИЕНТА ИЛИ ДОБРОТНОСТИ ПО ЛОГАРИФМИЧЕСКОЙ АМПЛИТУДНОЙ ХАРАКТЕРИСТИКЕ
- 14. ОПРЕДЕЛЕНИЕ УСТАНОВИВШЕЙСЯ ОШИБКИ ПРИ ГАРМОНИЧЕСКОМ УПРАВЛЯЮЩЕМ ВОЗДЕЙСТВИИ ПО ЛОГАРИФМИЧЕСКОЙ АМПЛИТУДНОЙ ХАРАКТЕРИСТИКЕ
- 15. ПРИБЛИЖЕННЫЙ СПОСОБ ВЫЧИСЛЕНИЯ ПЕРЕХОДНОГО ПРОЦЕССА ПО СОПРЯГАЮЩИМ ЧАСТОТАМ ЛОГАРИФМИЧЕСКОЙ АМПЛИТУДНОЙ ЧАСТОТНОЙ ХАРАКТЕРИСТИКИ
- 16. НОМОГРАММА ДЛЯ ОПРЕДЕЛЕНИЯ ЗАПАСА УСТОЙЧИВОСТИ, ПОКАЗАТЕЛЕЙ КАЧЕСТВА И КОЭФФИЦИЕНТОВ ОШИБОК ПО ВИДУ ЛОГАРИФМИЧЕСКОЙ АМПЛИТУДНОЙ ХАРАКТЕРИСТИКИ
- ГЛАВА XVII. СВЯЗЬ МЕЖДУ КАЧЕСТВОМ ПЕРЕХОДНОГО ПРОЦЕССА И РАСПРЕДЕЛЕНИЕМ НУЛЕЙ И ПОЛЮСОВ ПЕРЕДАТОЧНОЙ ФУНКЦИИ. МЕТОД КОРНЕВЫХ ГОДОГРАФОВ
- 2. АНАЛИЗ РАСПРЕДЕЛЕНИЯ КОРНЕЙ ХАРАКТЕРИСТИЧЕСКОГО УРАВНЕНИЯ СИСТЕМЫ И ОЦЕНКА КАЧЕСТВА ПЕРЕХОДНОГО ПРОЦЕССА
- 3. ГЕОМЕТРИЧЕСКИЙ МЕТОД ПОСТРОЕНИЯ КОРНЕВОГО ГОДОГРАФА
- 4. АНАЛИТИЧЕСКОЕ ПОСТРОЕНИЕ ГЕОМЕТРИЧЕСКОГО МЕСТА КОРНЕЙ
- 5. ОПРЕДЕЛЕНИЕ ОБЛАСТЕЙ УСТОЙЧИВОСТИ ЛИНЕЙНЫХ СИСТЕМ МЕТОДОМ КОРНЕВОГО ГОДОГРАФА
- 6. ОЦЕНКИ ПАРАМЕТРОВ ПЕРЕХОДНОЙ И ЧАСТОТНОЙ ХАРАКТЕРИСТИК ПО КОРНЕВОМУ ГОДОГРАФУ
- 7. ВЛИЯНИЕ РАСПОЛОЖЕНИЯ НУЛЕЙ И ПОЛЮСОВ ЗАМКНУТОЙ СИСТЕМЫ НА ПЕРЕХОДНУЮ ХАРАКТЕРИСТИКУ h(t)
- 8. ВЛИЯНИЕ РАСПОЛОЖЕНИЯ НУЛЕЙ И ПОЛЮСОВ ЗАМКНУТОЙ СИСТЕМЫ НА ЕЕ ПОЛОСУ ЧАСТОТ
- 9. КОРНЕВОЙ ГОДОГРАФ И ПЕРЕХОДНАЯ ХАРАКТЕРИСТИКА СИСТЕМЫ ПРИ ВОЗМУЩЕНИЯХ, ПРИЛОЖЕННЫХ НЕ К ОСНОВНОМУ ВХОДУ СИСТЕМЫ
- 10. ВЛИЯНИЕ РАСПРЕДЕЛЕНИЯ НУЛЕЙ И ПОЛЮСОВ ПЕРЕДАТОЧНОЙ ФУНКЦИИ НА КАЧЕСТВО ПЕРЕХОДНОГО ПРОЦЕССА ПРИ НАЛИЧИИ ВНЕШНЕГО ВОЗДЕЙСТВИЯ
- ГЛАВА XVIII. МЕТОД ЛОГАРИФМИЧЕСКИХ КОРНЕВЫХ ГОДОГРАФОВ
- 2. ОПРЕДЕЛЕНИЕ КОРНЕЙ ЗАМКНУТОЙ СИСТЕМЫ ПО ЛОГАРИФМИЧЕСКОЙ АМПЛИТУДНОЙ КОМПЛЕКСНО-ЧАСТОТНОЙ ХАРАКТЕРИСТИКЕ РАЗОМКНУТОЙ СИСТЕМЫ
- 3. ЛОГАРИФМИЧЕСКИЕ КОРНЕВЫЕ ГОДОГРАФЫ
- 4. ЛОГАРИФМИЧЕСКИЕ КОМПЛЕКСНО-ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЗВЕНЬЕВ ВТОРОГО ПОРЯДКА
- 5. ПРИМЕР ПОСТРОЕНИЯ ЛОГАРИФМИЧЕСКОГО КОРНЕВОГО ГОДОГРАФА
- ГЛАВА XIX. ИНТЕГРАЛЬНЫЕ ОЦЕНКИ И КРИТЕРИИ КАЧЕСТВА РЕГУЛИРОВАНИЯ
- 2. МЕТОДИКА ПРИМЕНЕНИЯ ИНТЕГРАЛЬНЫХ КВАДРАТИЧНЫХ ОЦЕНОК
- 3. ЛИНЕЙНЫЕ ИНТЕГРАЛЬНЫЕ ОЦЕНКИ
- ПРИЛОЖЕНИЕ
- БИБЛИОГРАФИЯ ПО РАЗДЕЛАМ КНИГИ