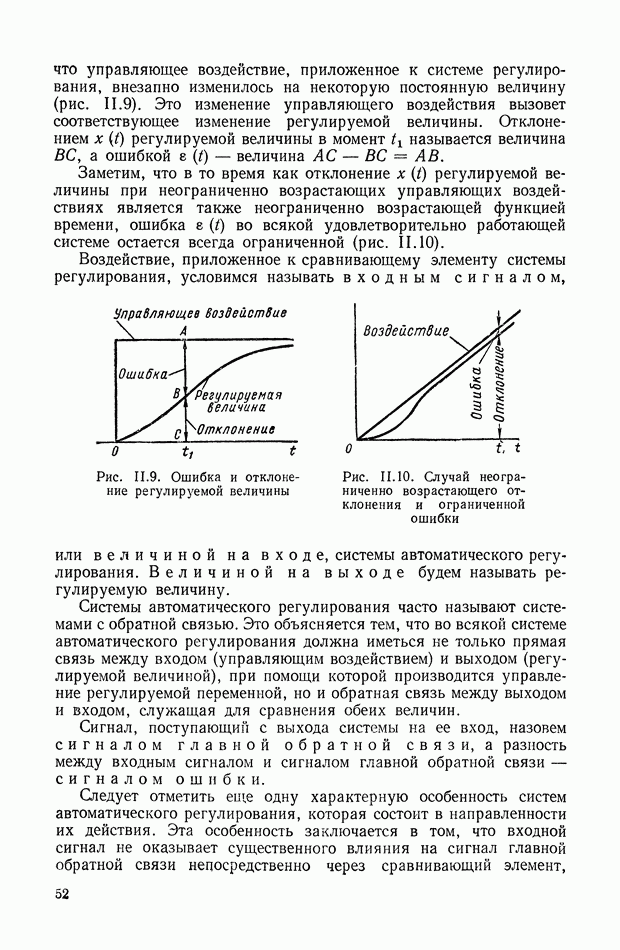
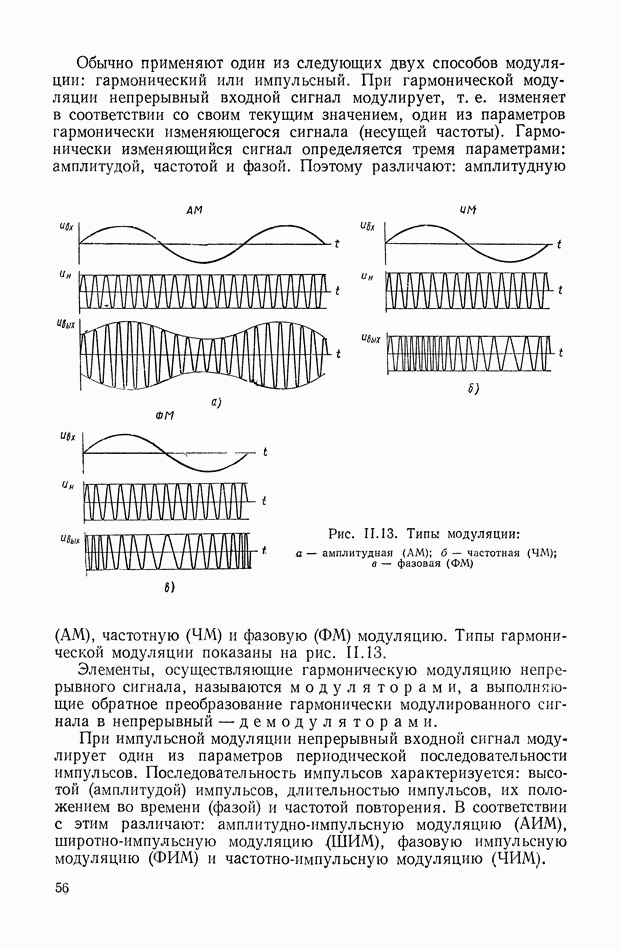
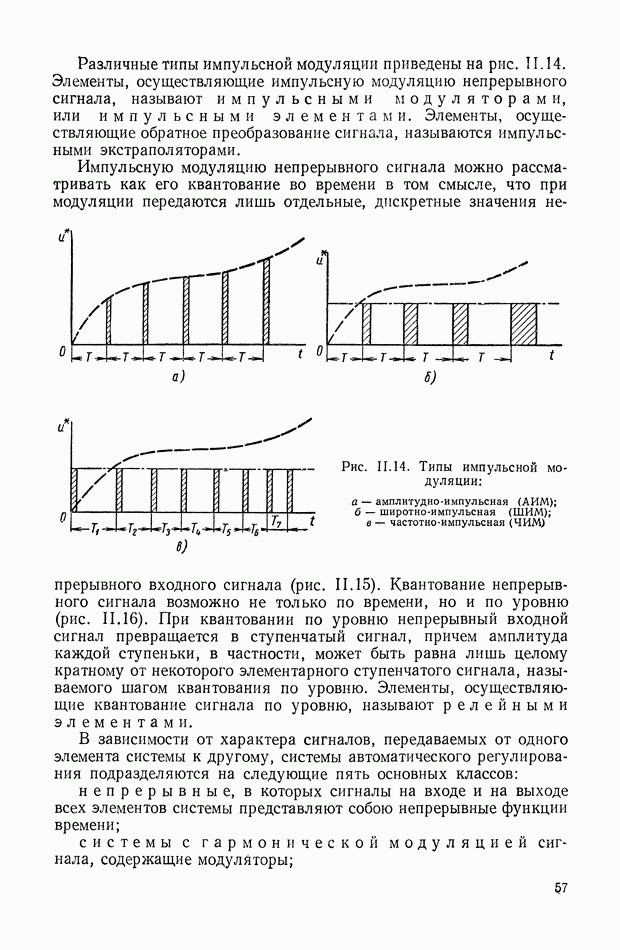
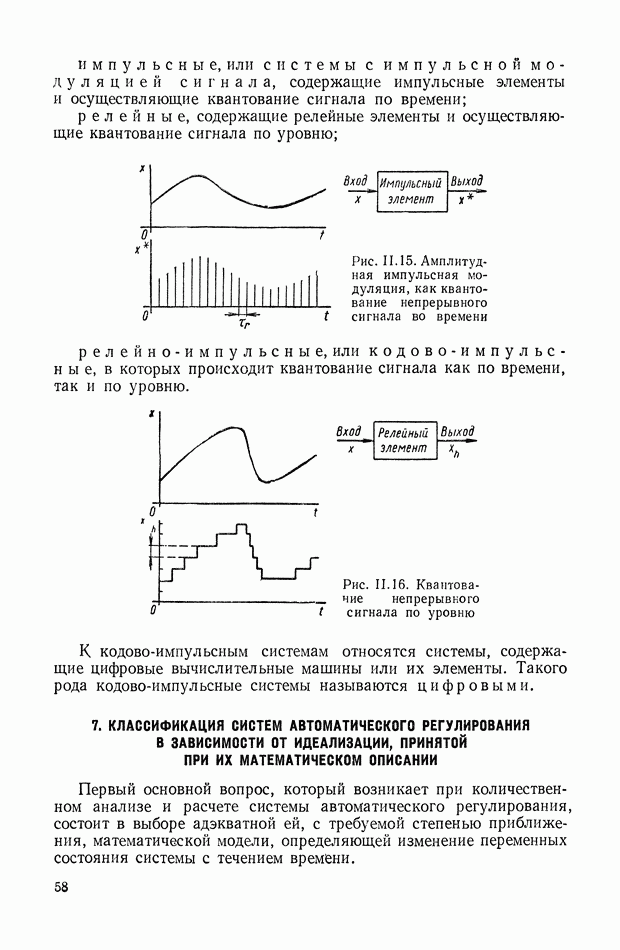
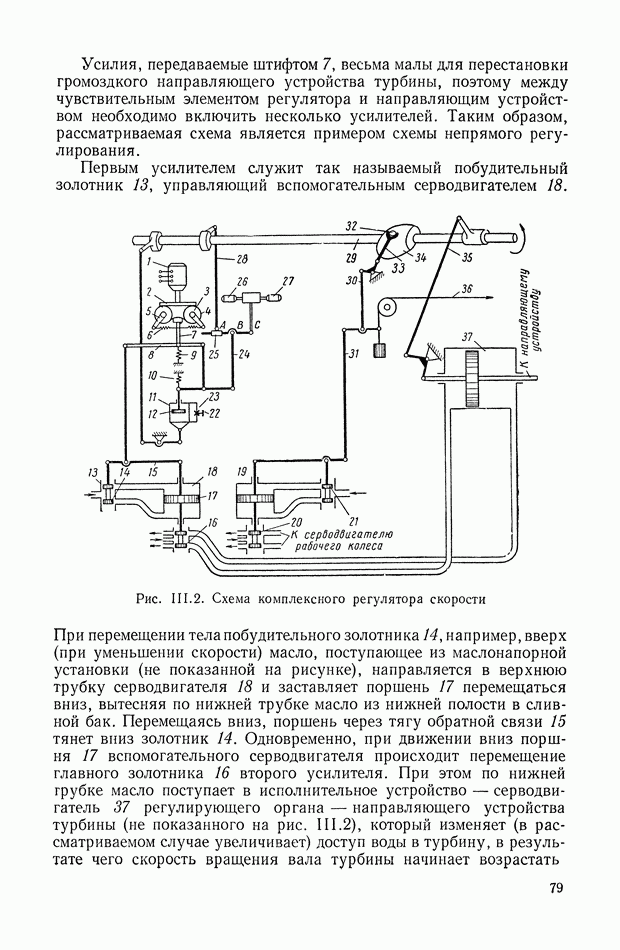
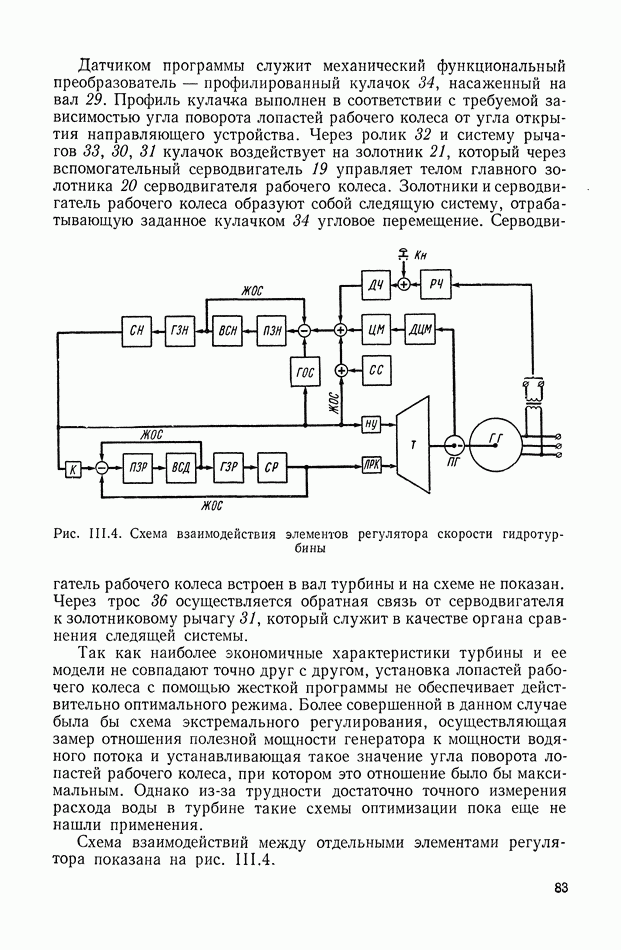
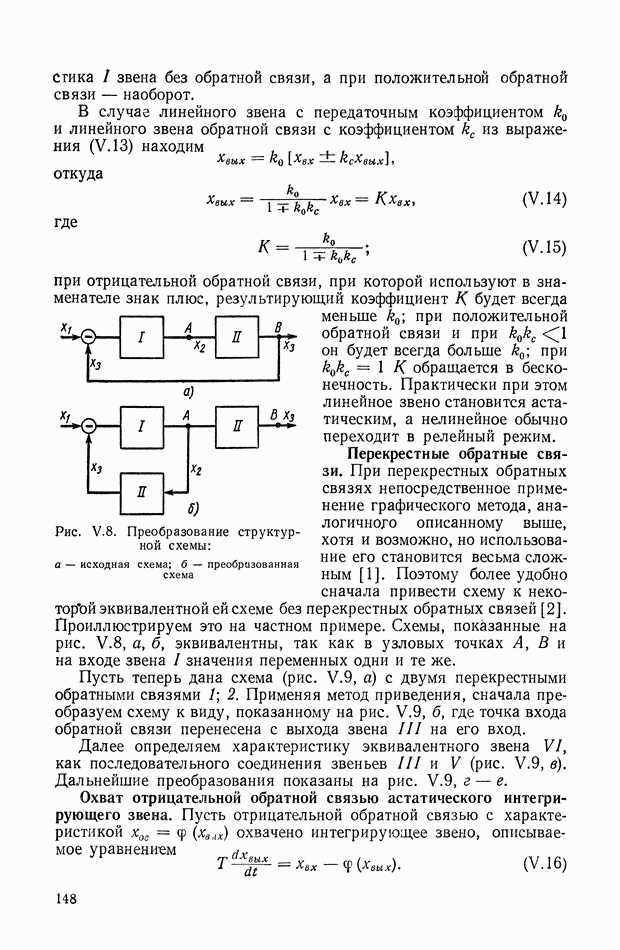
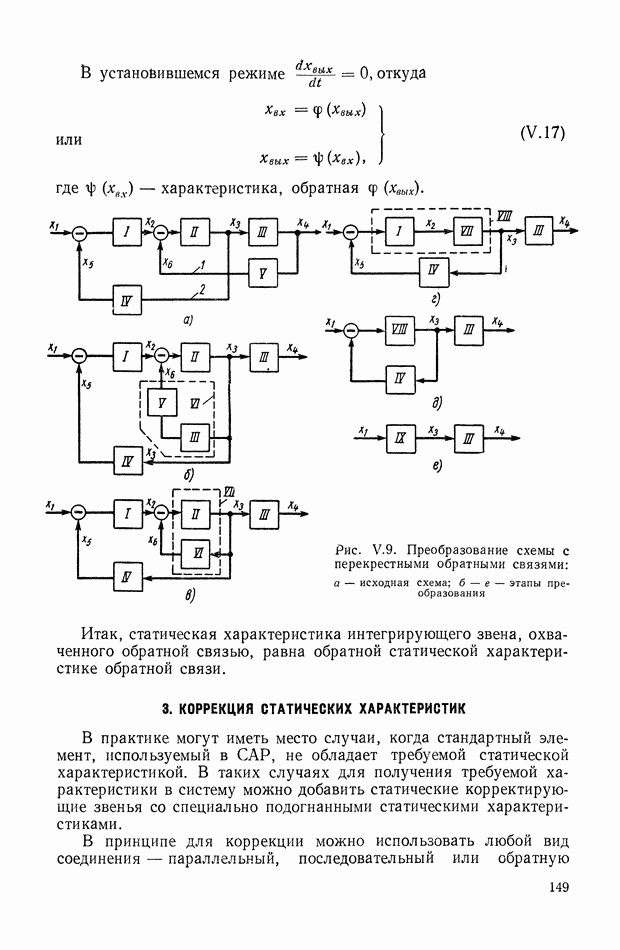
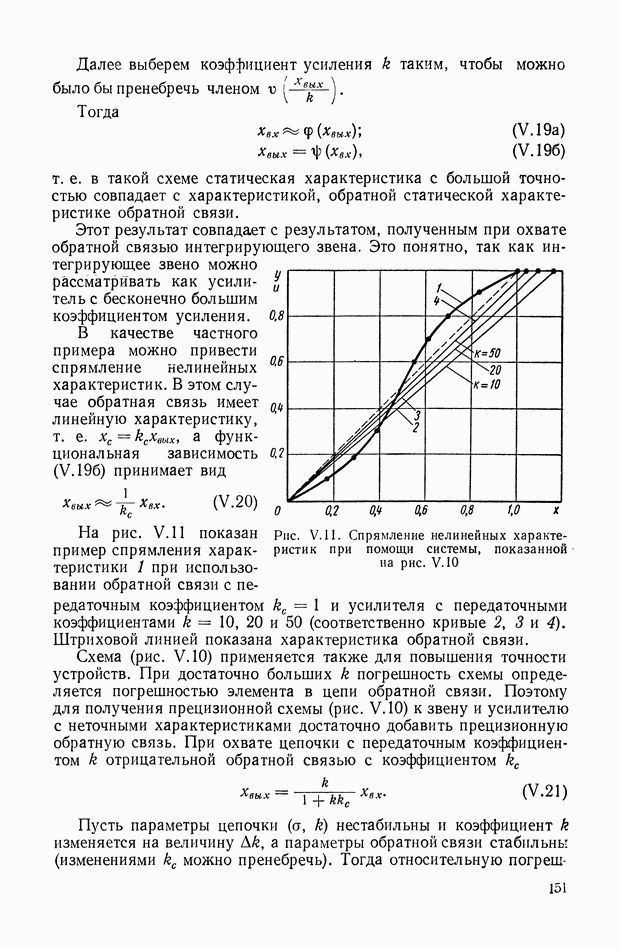
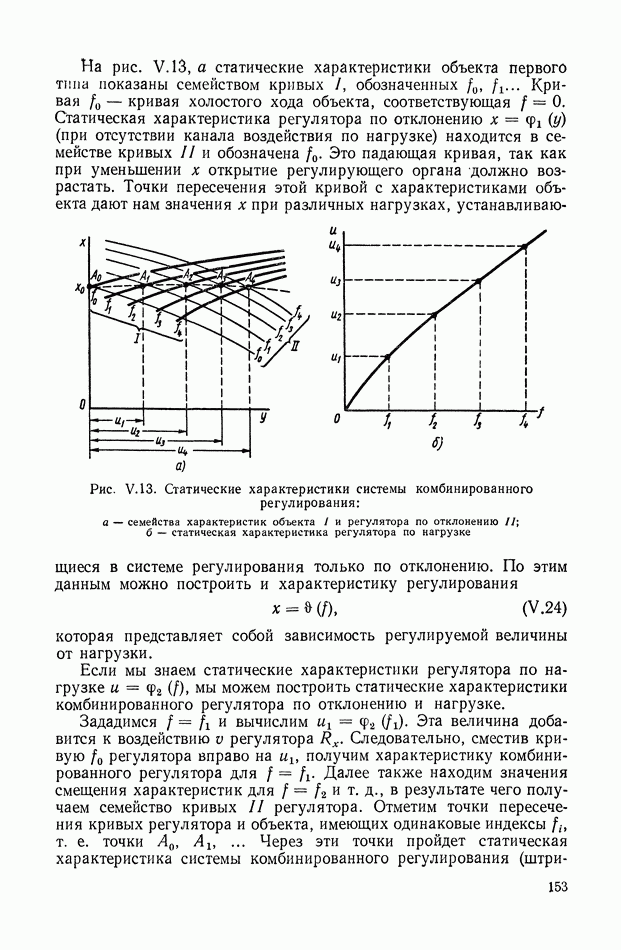
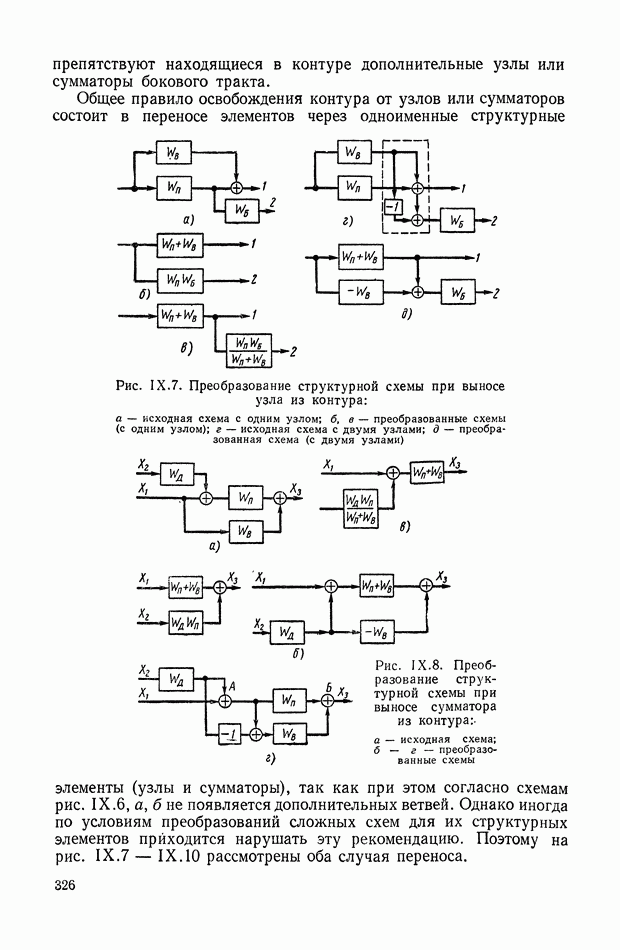
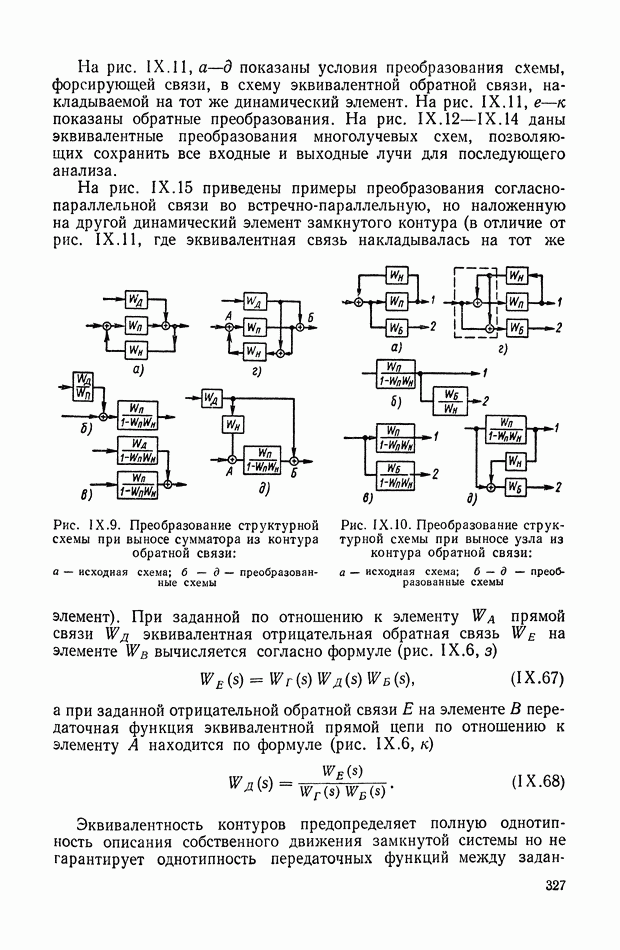
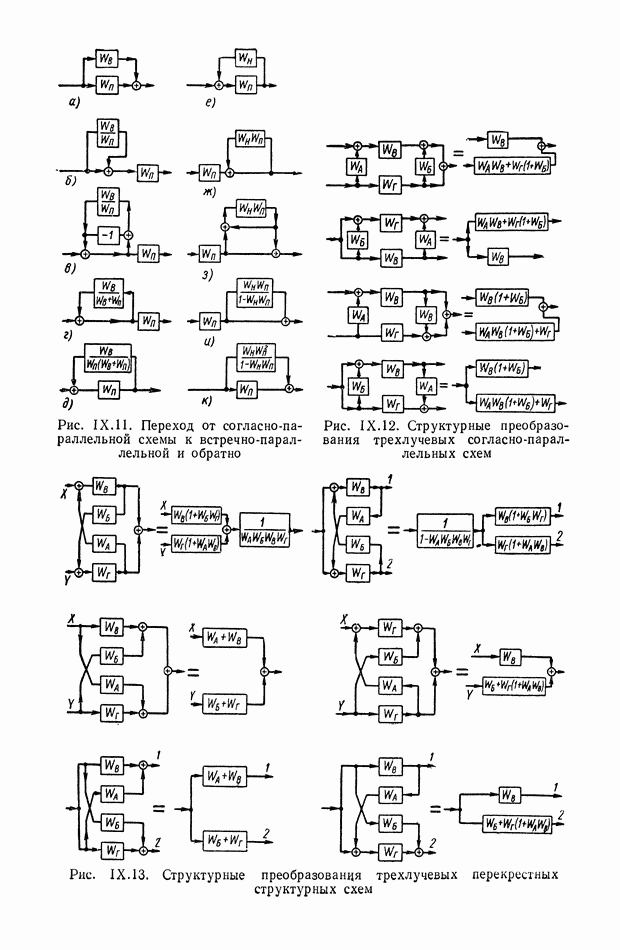
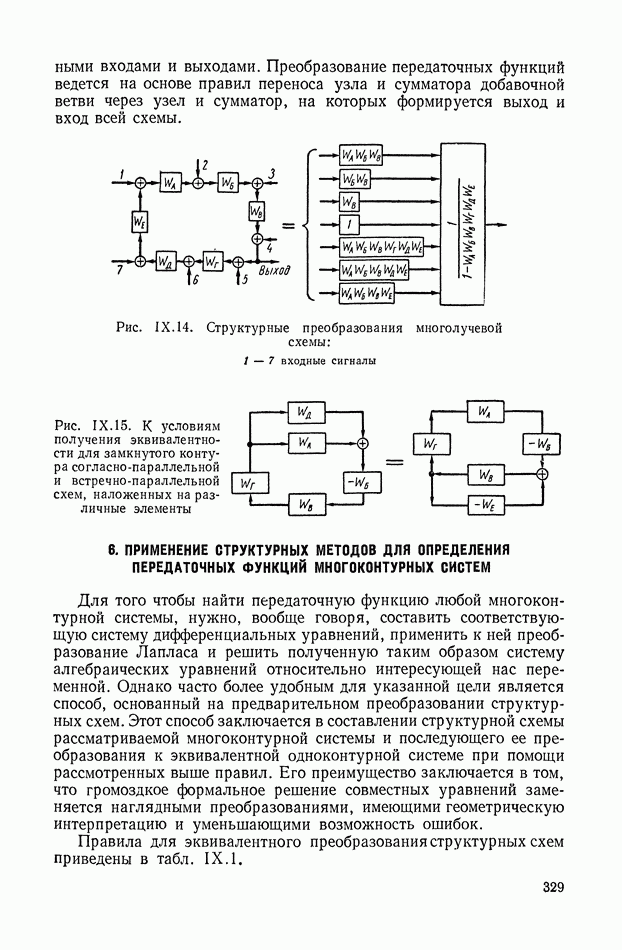
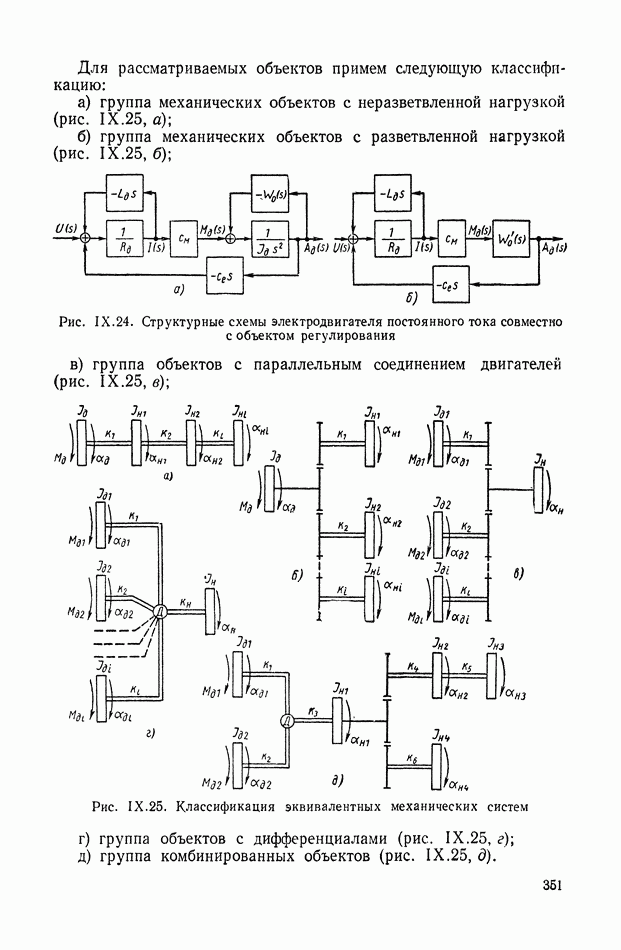
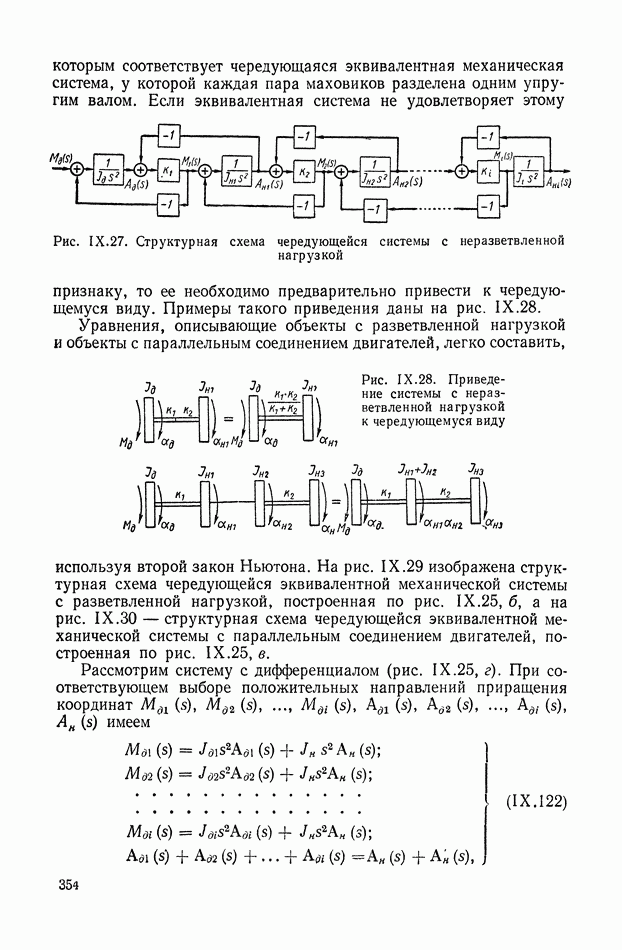
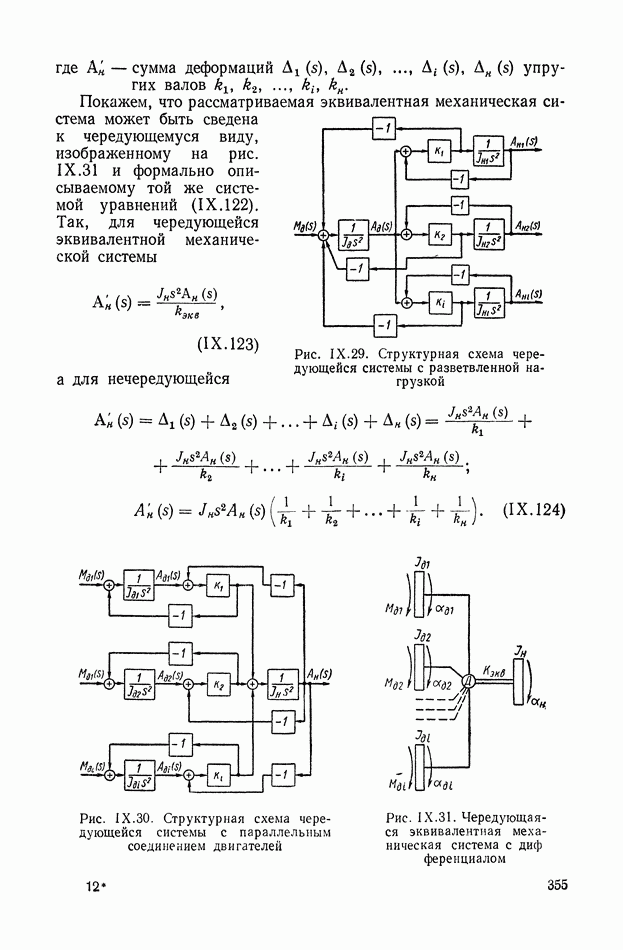
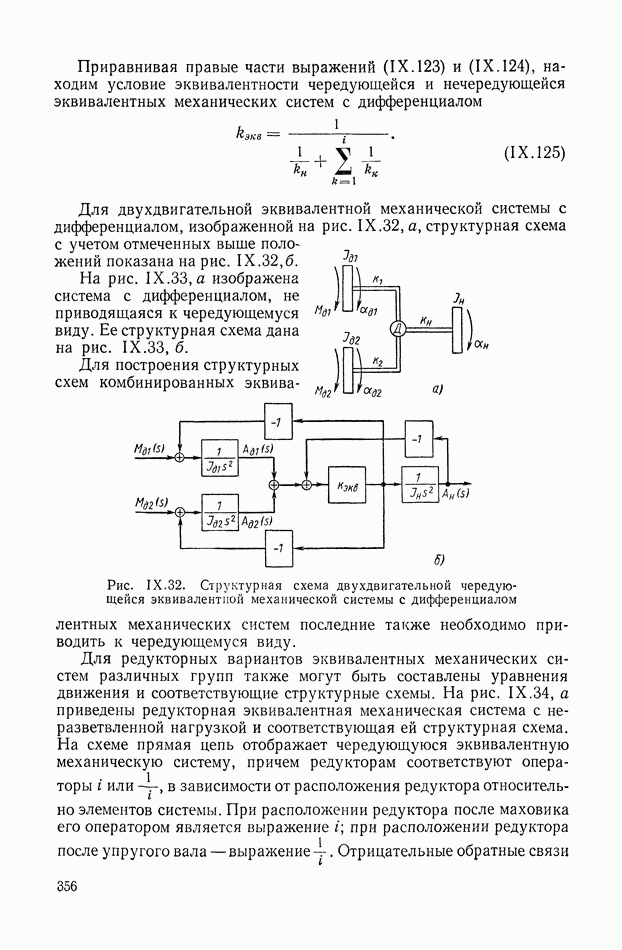
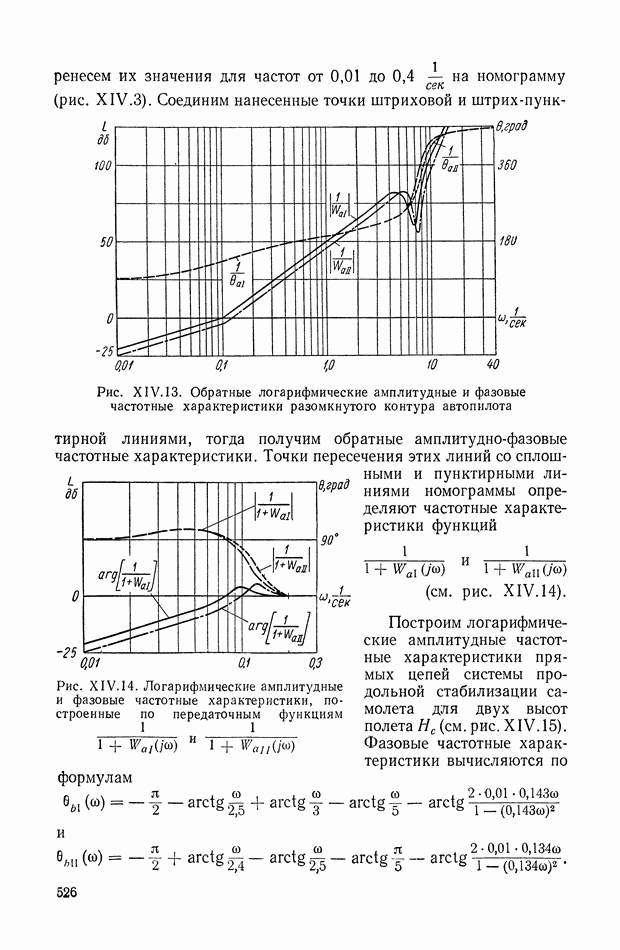
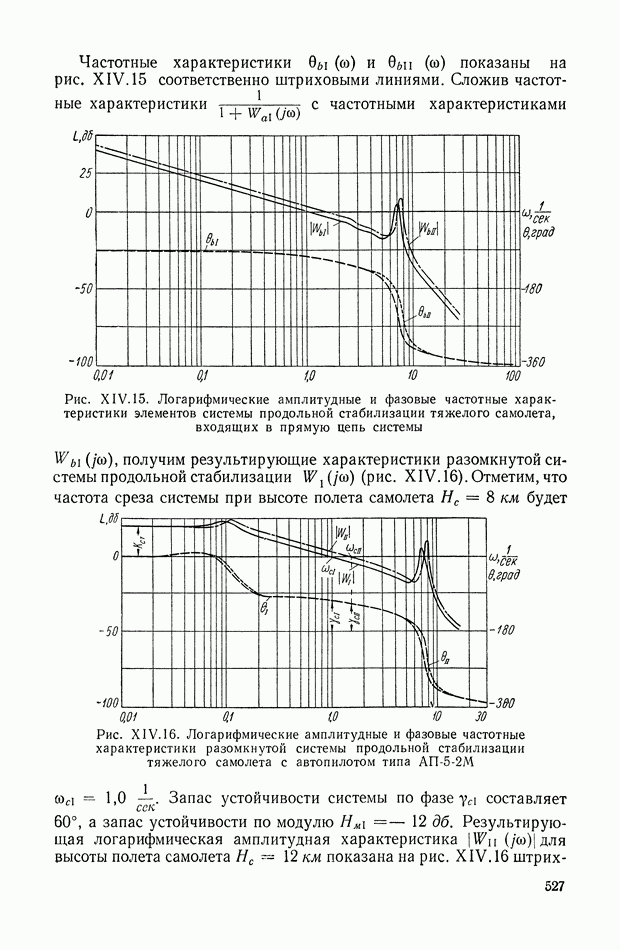
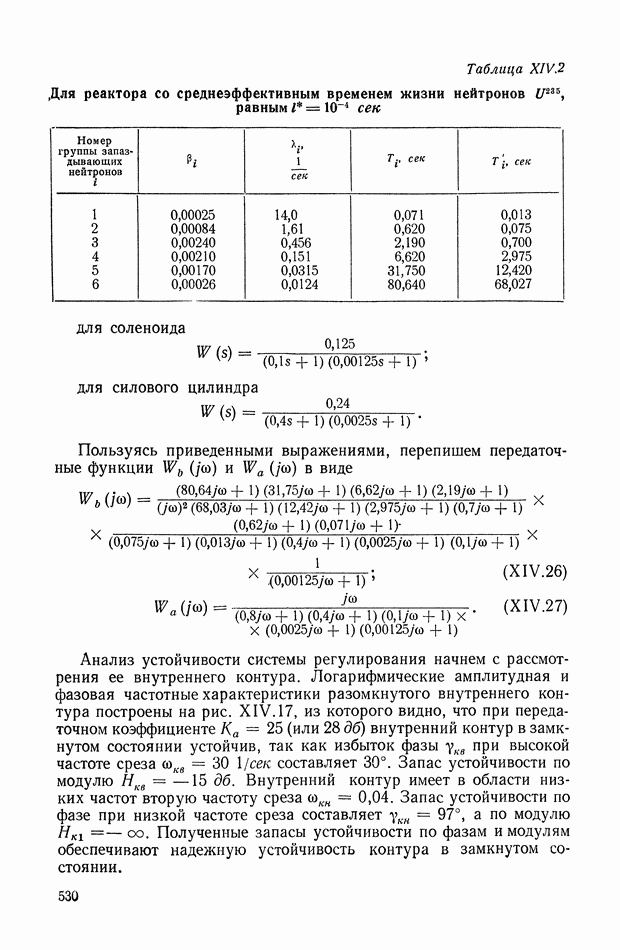
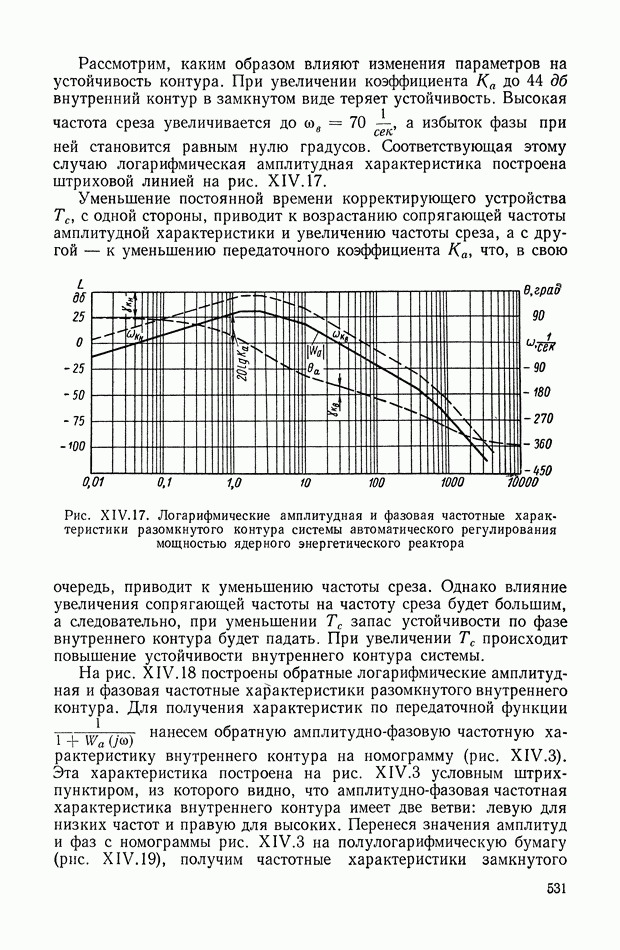
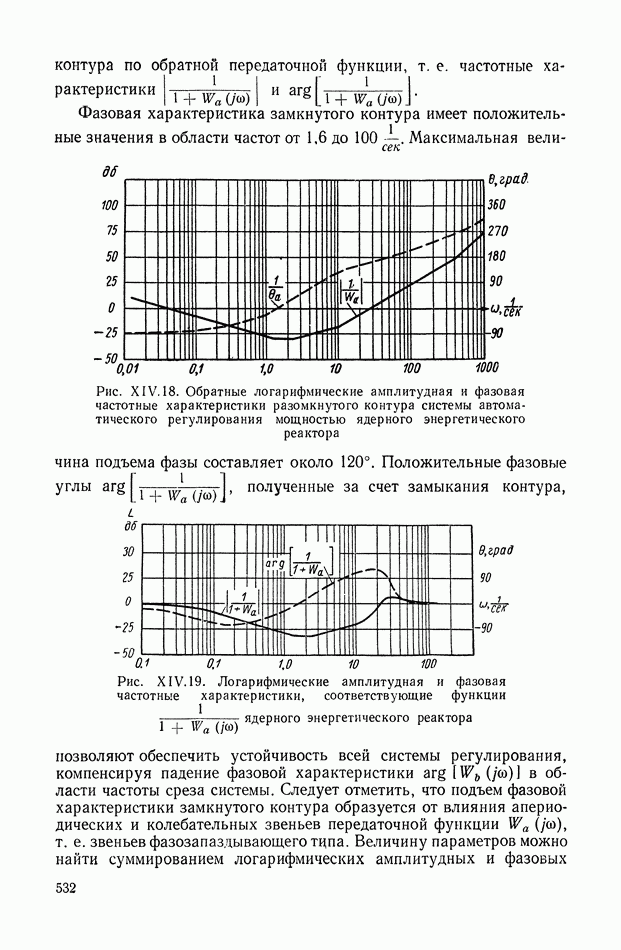
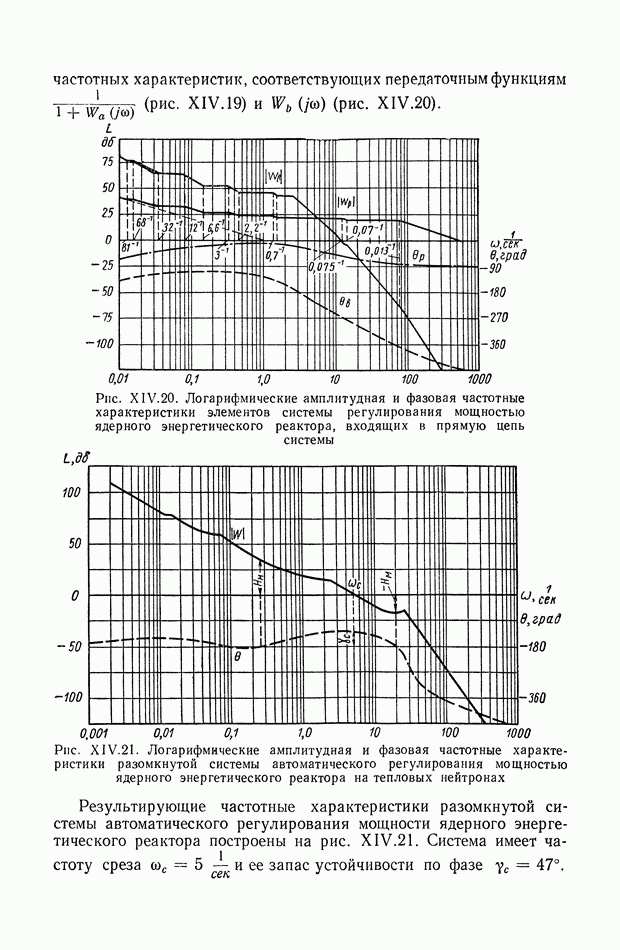
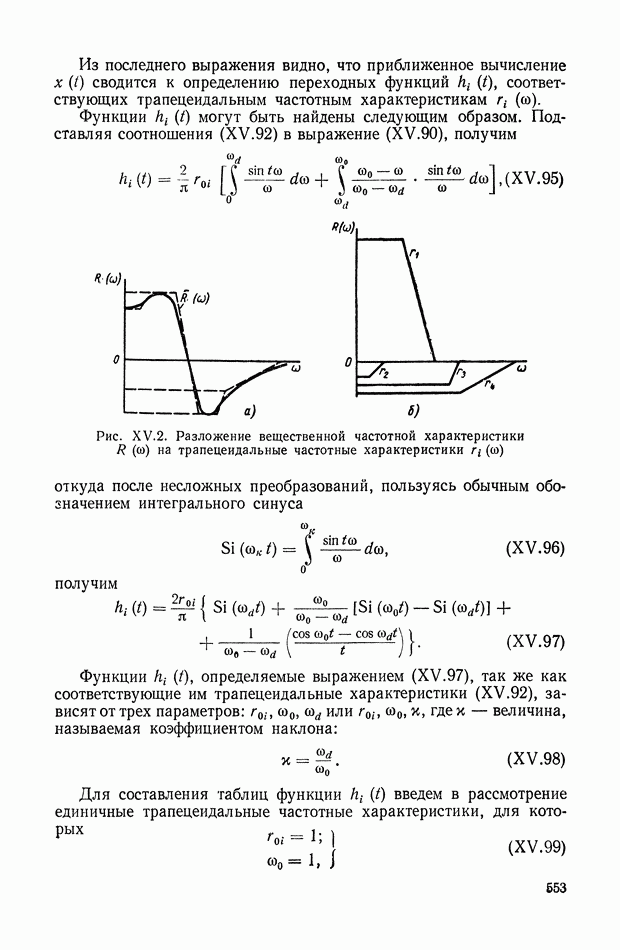
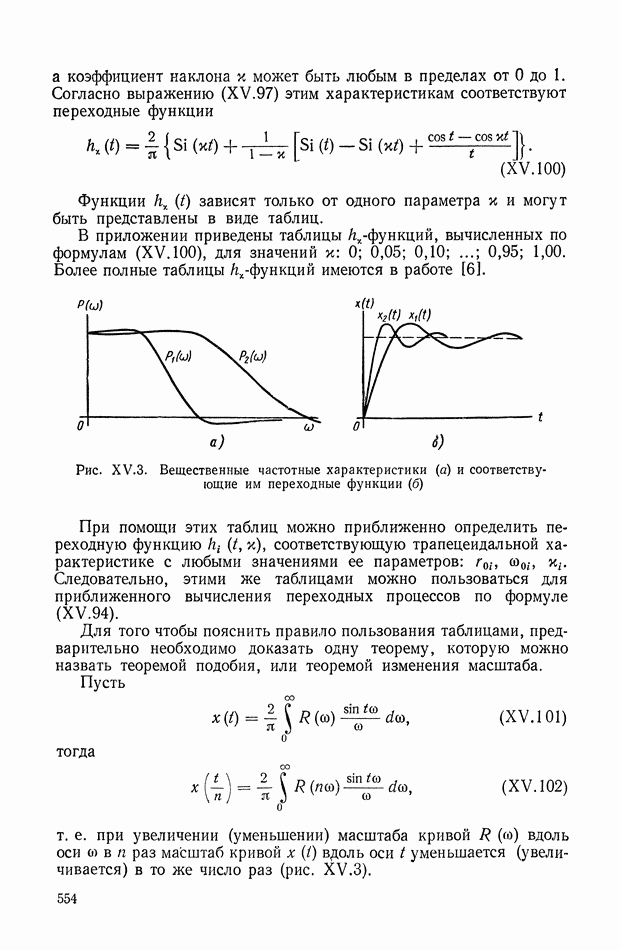
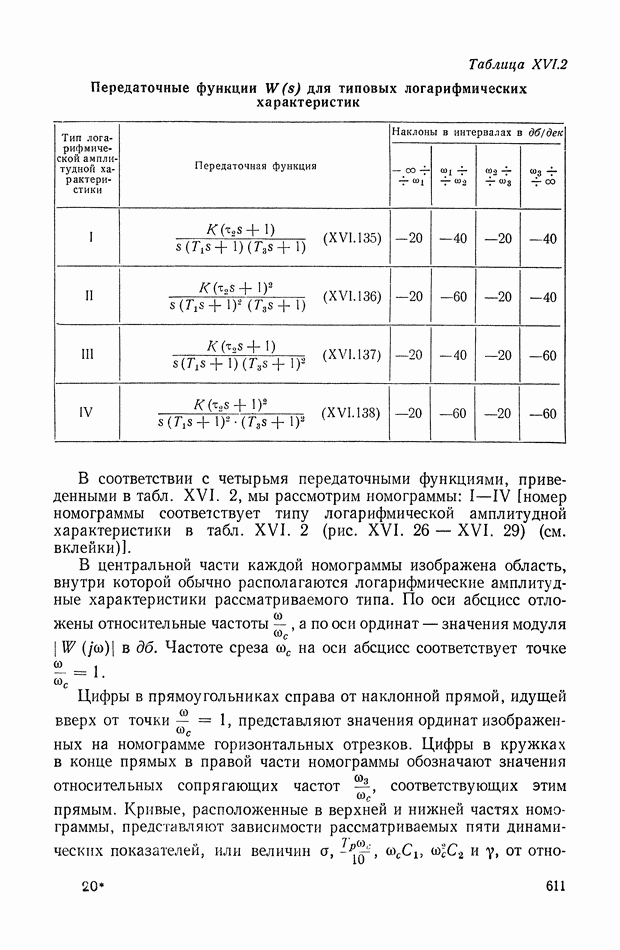
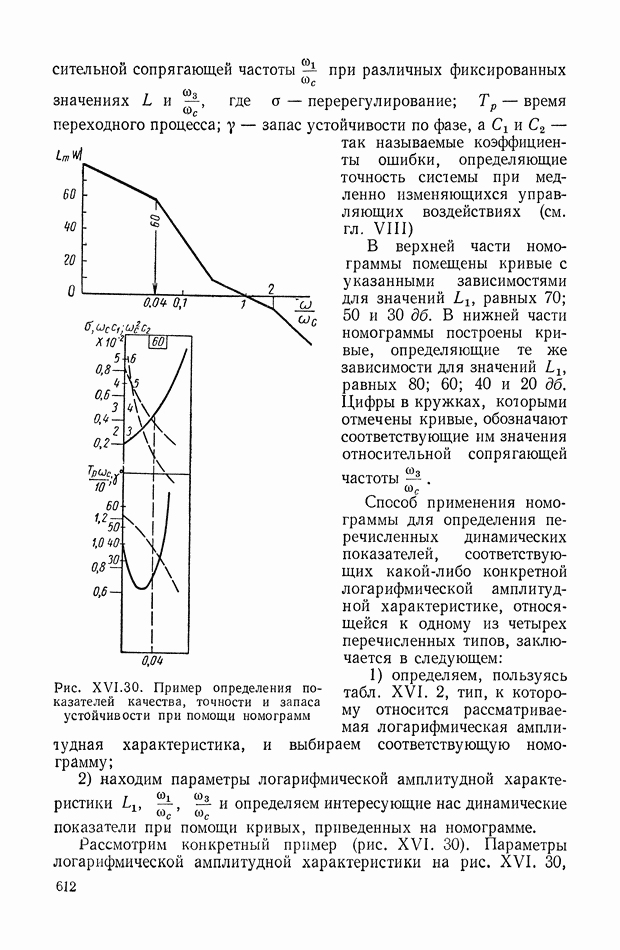
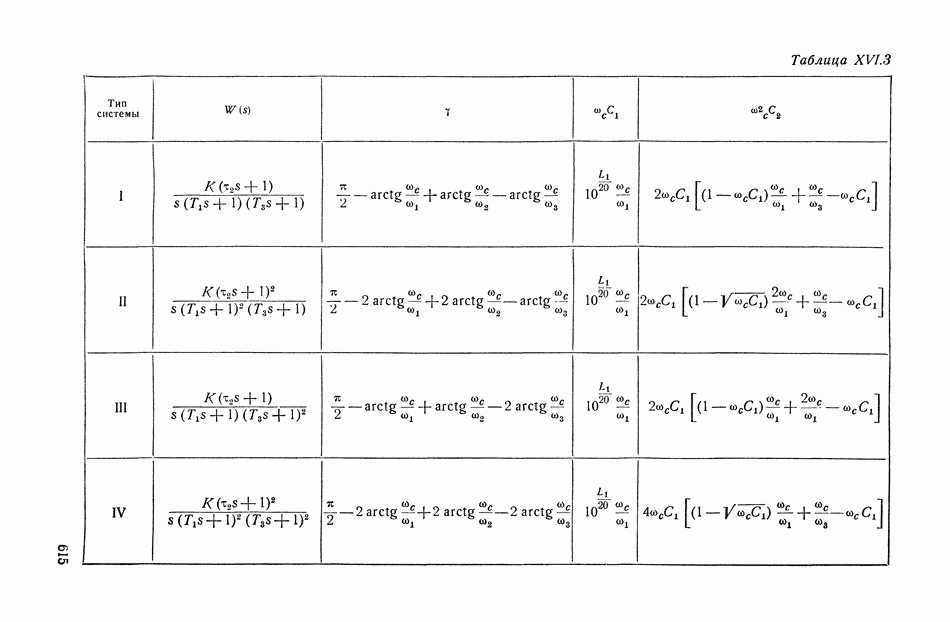
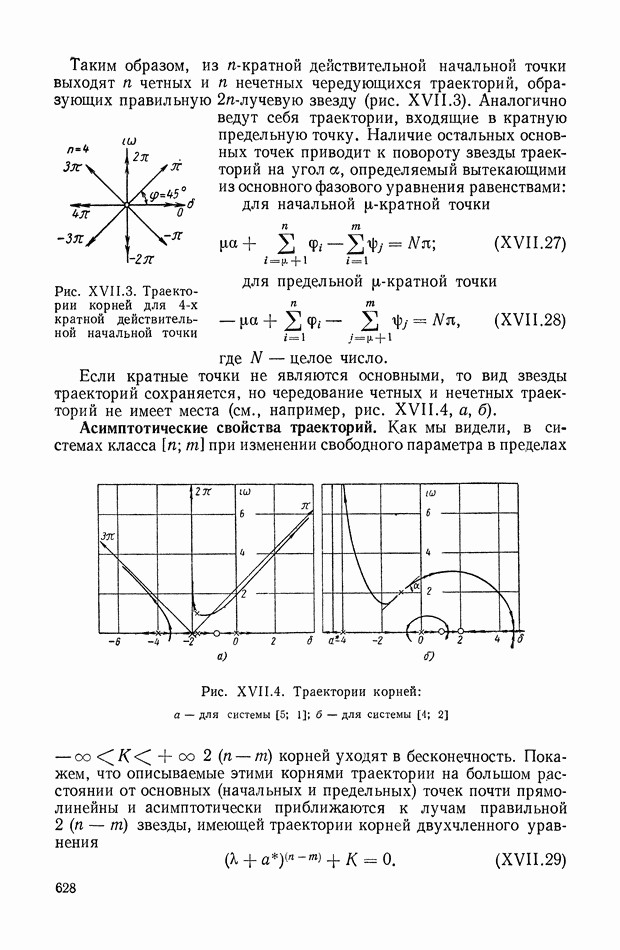
| << Предыдущий параграф | Следующий параграф >> |
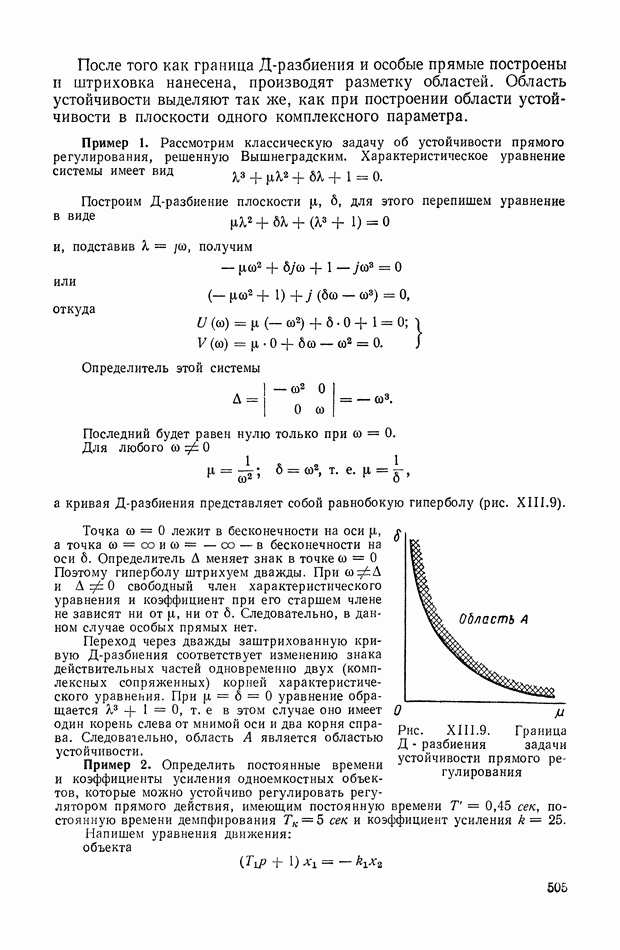
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
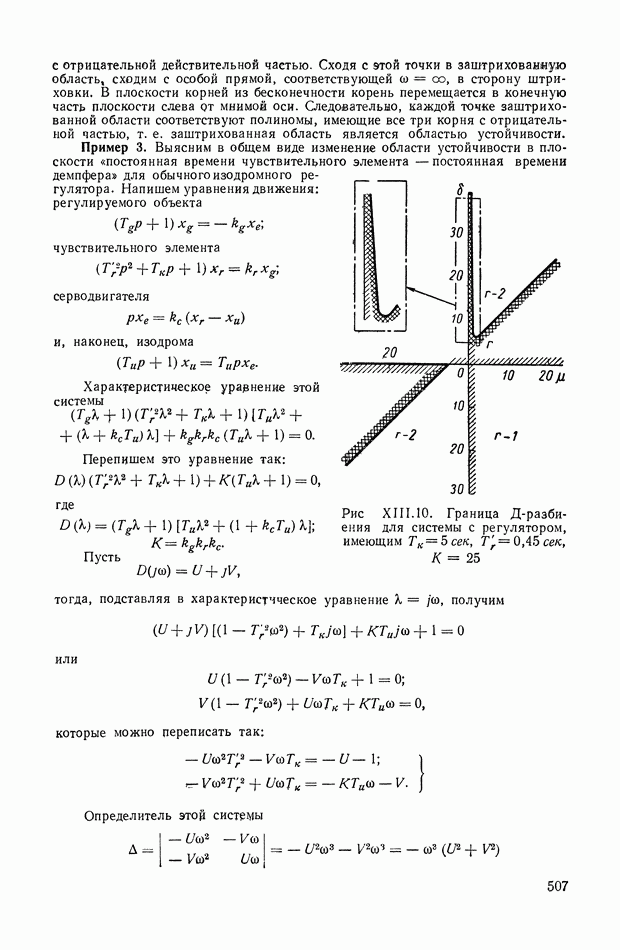
ГЛАВА II. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ ТЕОРИИ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
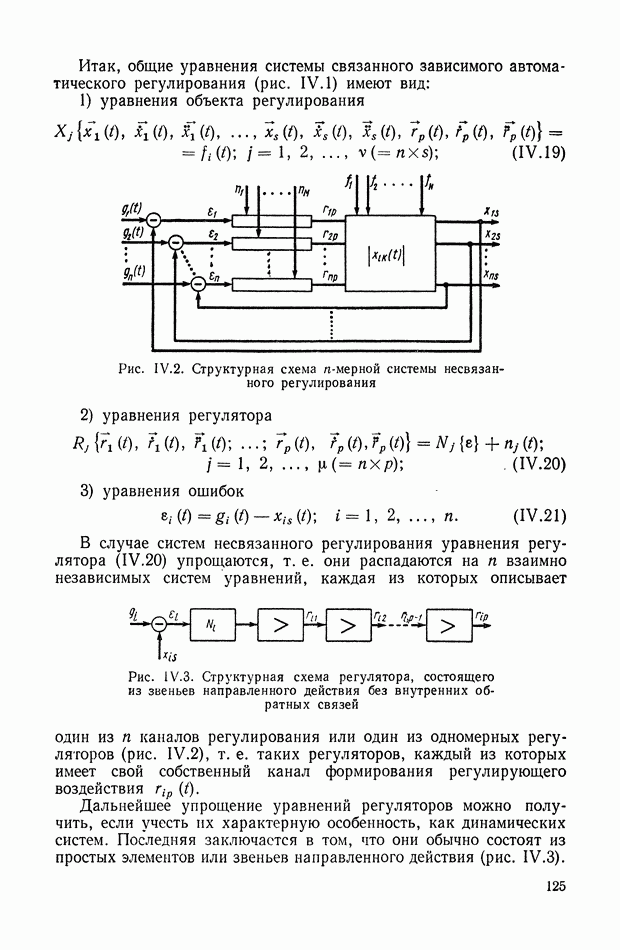
Настоящая глава посвящена изложению основных понятий и определений теории автоматического регулирования. Проблему автоматического регулирования можно рассматривать как частный случай проблемы автоматического управления. Системы автоматического регулирования представляют собою определенный класс динамических систем, а именно: класс замкнутых активных динамических систем направленного действия. Классификация систем автоматического регулирования может быть дана в зависимости: от характера управляющих воздействий, от содержащихся в них элементов для преобразования сигналов, от идеализации, принятой при математическом описании, от характера контролируемыхизменений их свойств. Классификация устройств, из которых состоят системы автоматического регулирования, обычно дается по функциональному признаку. Очень важным понятием теории регулирования является понятие структурной схемы и структурных элементов. Требования, предъявляемые к динамическим свойствам систем автоматического регулирования, разнообразны и зависят от конкретных условий их работы.
1. СУЩНОСТЬ ПРОБЛЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
Проблема регулирования может рассматриваться как частный случай проблемы управления. Поэтому остановимся прежде всего на формулировке последней.
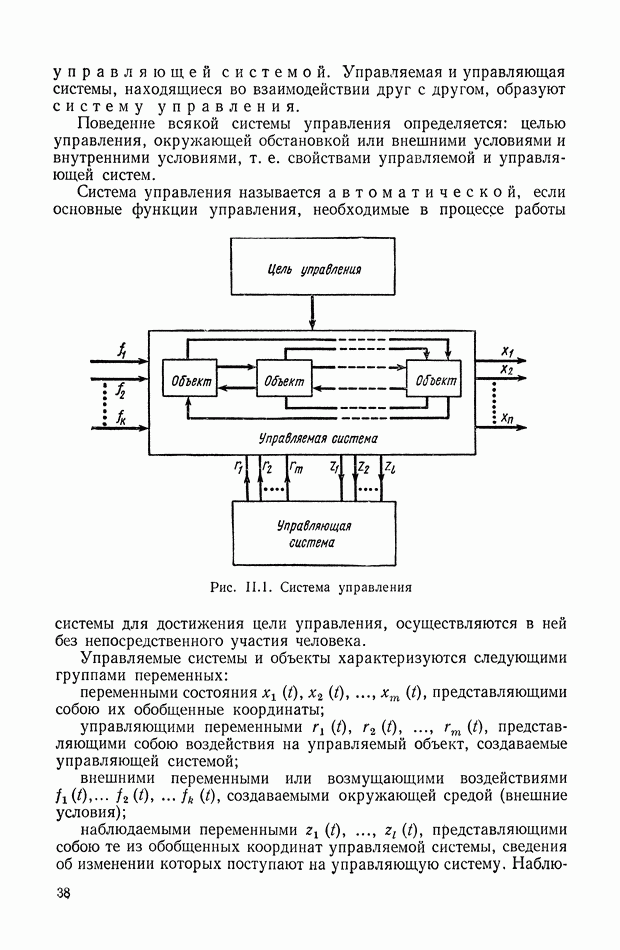
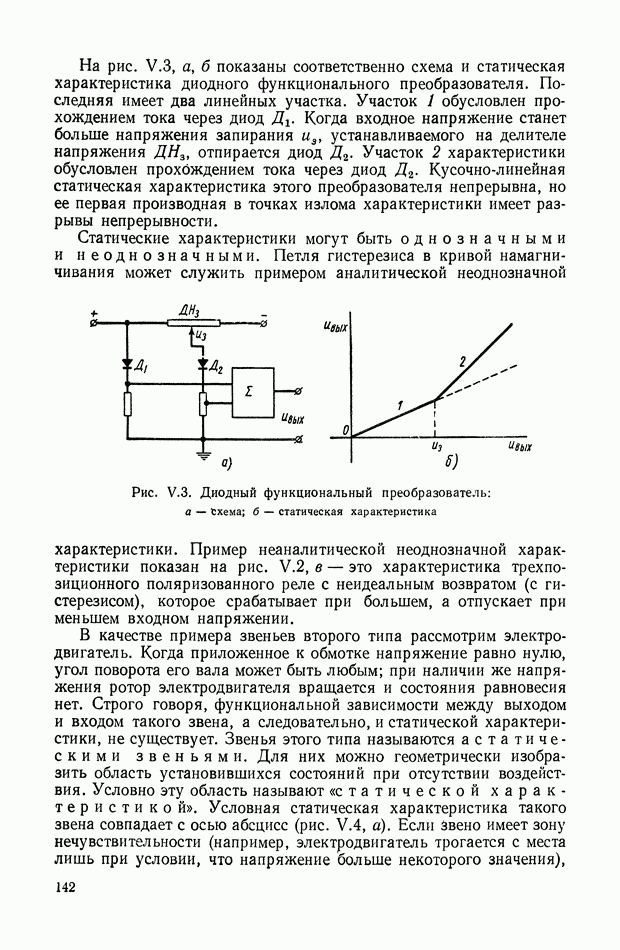
Всякий процесс управления подразумевает наличие одного или нескольких объектов управления и управляющей ими системы. Совокупность нескольких управляемых объектов, объединенных единством цели управления, назовем управляемой системой (рис. II. 1). В качестве управляемой системы можно рассматривать, например, цех завода, состоящий из ряда взаимодействующих друг с другом и управляемых в соответствии с единой целью агрегатов и машин. Совокупность средств, стремящихся обеспечить выполнение управляемой системой определенной цели, назовем
управляющей системой. Управляемая и управляющая системы, находящиеся во взаимодействии друг с другом, образуют систему управления.
Поведение всякой системы управления определяется: целью управления, окружающей обстановкой или внешними условиями и внутренними условиями, т. е. свойствами управляемой и управляющей систем.
Система управления называется автоматической, если основные функции управления, необходимые в процессе работы системы для достижения цели управления, осуществляются в ней без непосредственного участия человека.

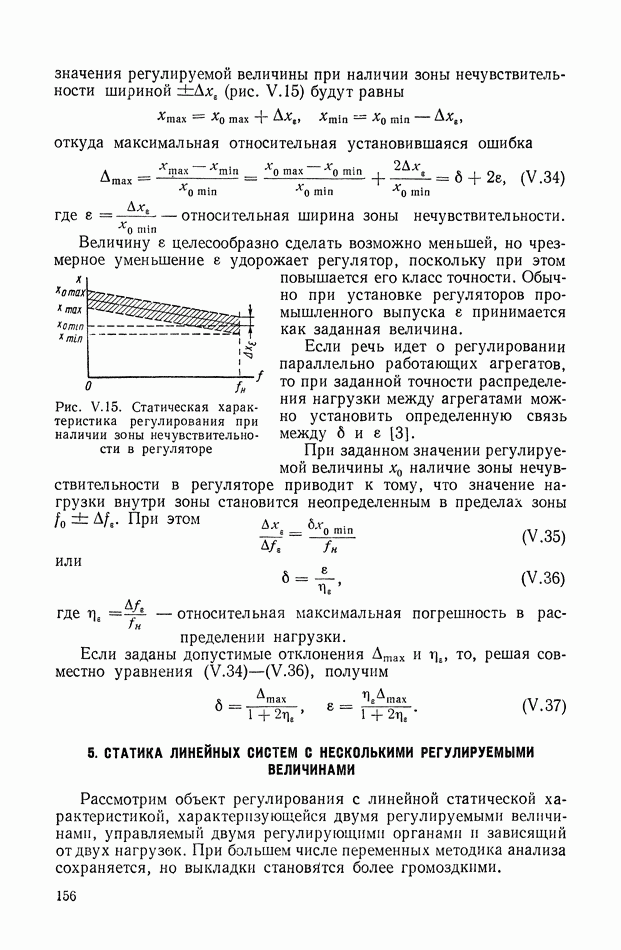
Рис. II. 1. Система управления
Управляемые системы и объекты характеризуются следующими группами переменных:
переменными состояния  представляющими собою их обобщенные координаты;
представляющими собою их обобщенные координаты;
управляющими переменными  представляющими собою воздействия на управляемый объект, создаваемые управляющей системой;
представляющими собою воздействия на управляемый объект, создаваемые управляющей системой;
внешними переменными или возмущающими воздействиями  создаваемыми окружающей средой (внешние условия);
создаваемыми окружающей средой (внешние условия);
наблюдаемыми переменными  представляющими собою те из обобщенных координат управляемой системы, сведения об изменении которых поступают на управляющую систему.
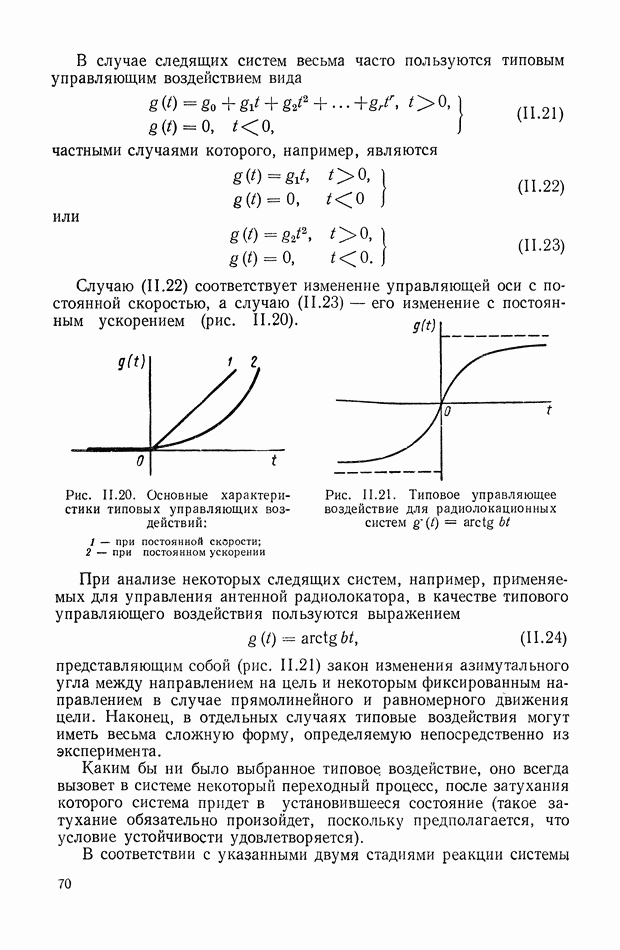
представляющими собою те из обобщенных координат управляемой системы, сведения об изменении которых поступают на управляющую систему.
Наблюдаемыми переменными, в частности, могут быть переменные состояния 
Условимся рассматривать эти переменные как компоненты многомерных векторных функций:

и называть вектора  соответственно, векторами состояния, управления, возмущения и наблюдения.
соответственно, векторами состояния, управления, возмущения и наблюдения.
В дальнейшем для упрощения предположим, что вектор состояния совпадает с вектором наблюдения.
В любой момент времени  состояние управляемой системы является функцией начального состояния
состояние управляемой системы является функцией начального состояния  и векторов
и векторов 

Уравнение (II. 1) эквивалентно системе из  зависимостей:
зависимостей:

где 
Уравнения (II. 1) и (11.1а) можно рассматривать как уравнения математической модели управляемой системы. Для систем, описываемых дифференциальными уравнениями, приведенные выше уравнения можно привести к следующему виду:

или

где влияние вектора возмущений  учтено явной зависимостью оператора X от времени
учтено явной зависимостью оператора X от времени 
Часто на изменения вектора состояния  (или на его производные) и вектора управления
(или на его производные) и вектора управления  накладываются ограничения
накладываются ограничения

которые означают, что изменения векторов  должны быть ограничены замкнутыми областями
должны быть ограничены замкнутыми областями  соответственно векторного пространства состояний и векторного пространства управлений.
соответственно векторного пространства состояний и векторного пространства управлений.
Предположим, что цель управления определяется экстремумом некоторого функционала  , называемого в дальнейшем показателем цели управления:
, называемого в дальнейшем показателем цели управления:

Решение проблемы управления состоит в том, чтобы найти вектор управления  обеспечивающий выполнение условия
обеспечивающий выполнение условия

и одновременно удовлетворяющий ограничениям и связям, налагаемым внутренними свойствами системы.
Решение этой экстремальной проблемы ввиду ее трудности можно представить себе основанным на методе последовательных приближений, причем первое и второе приближения определяются в результате:
а) этапа идеальной, или первичной оптимизации, состоящего в нахождении идеального, но обычно нереализуемого вектора управления 
б) этапа вторичной оптимизации, или оптимизации качества управления, состоящего в нахождений оптимального и в то же время реализуемого вектора управления 
Этап первичной оптимизации заключается в том, что экстремальная задача (II.5) решается в идеализированной постановке, учитывающей лишь важнейшие свойства системы управления.
Так, например, можно представить себе, что на этом этапе учитываются лишь ограничения вида (II.3) или, что помимо этих ограничений, решение экстремальной задачи должно удовлетворять еще определенным зависимостям, например, вида

называемым уравнениями идеальной модели системы управления.
Вектор управления  удовлетворяющий принятой идеализированной постановке проблемы, назовем идеальным вектором управления
удовлетворяющий принятой идеализированной постановке проблемы, назовем идеальным вектором управления  а его зависимость от вектора состояния и вектора возмущения
а его зависимость от вектора состояния и вектора возмущения

идеальным алгоритмов управления.
Подставляя выражение (II.7) в уравнение (II.6) и решая последнее относительно  можно найти идеальный вектор состояния
можно найти идеальный вектор состояния 
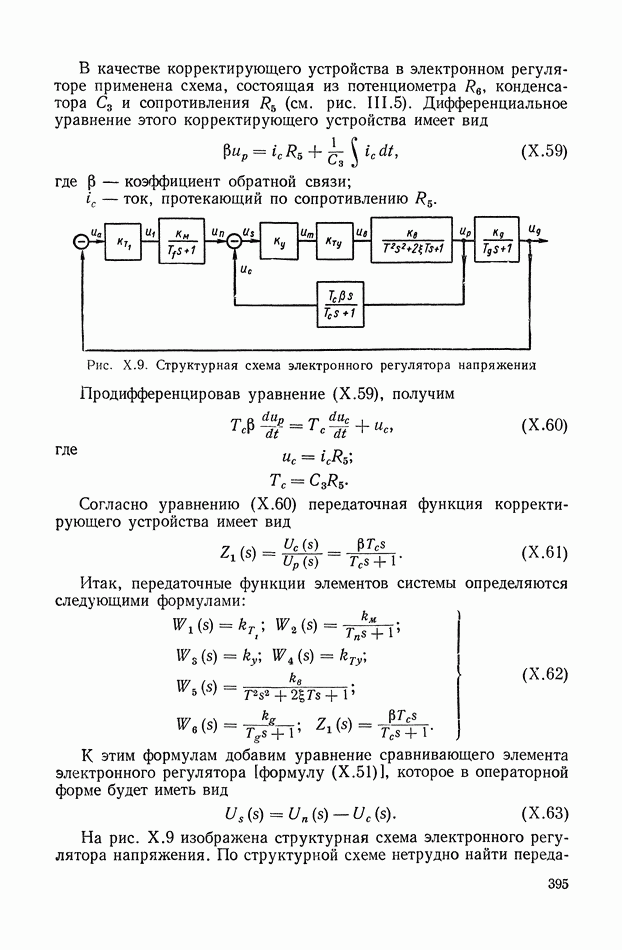
Идеальный алгоритм управления, как это было указано, можно рассматривать как первое приближение к решению проблемы управления, причем обычно он практически нереализуем.
Этап вторичной оптимизации заключается в том, чтобы получить решение, наименее отличающееся от идеального и в то же время учитывающее возможно более полно ограничения и связи, налагаемые свойствами системы управления, т. е. в том, чтобы получить не только оптимальное, но и реализуемое решение.
Для количественной характеристики отношения оптимального реализуемого решения от идеального введем величину, которая может быть названа показателем качества управления и представляет собою функционал вида

где  — экстремум показателя цели управления (II.4), соответствующий идеальной системе управления;
— экстремум показателя цели управления (II.4), соответствующий идеальной системе управления;
Е — значение показателя цели управления, обеспечиваемое реальной системой.
Стремление обеспечить минимум величины  обычно вступает в противоречие с имеющимися условиями реализуемости управляющей системы, которые могут характеризоваться ее сложностью, стоимостью, надежностью и т. д. Действительно, чем выше качество управления, т. е. чем выше точность аппроксимации идеального алгоритма управления, тем обычно сложнее, дороже и ненадежнее управляющая система, тем большего количества оборудования она требует для своей реализации. Поэтому основная задача синтеза управляющих систем состоит в том, чтобы достигнуть наивыгоднейших условий компромисса между противоречивыми требованиями качества и реализуемости управления.
обычно вступает в противоречие с имеющимися условиями реализуемости управляющей системы, которые могут характеризоваться ее сложностью, стоимостью, надежностью и т. д. Действительно, чем выше качество управления, т. е. чем выше точность аппроксимации идеального алгоритма управления, тем обычно сложнее, дороже и ненадежнее управляющая система, тем большего количества оборудования она требует для своей реализации. Поэтому основная задача синтеза управляющих систем состоит в том, чтобы достигнуть наивыгоднейших условий компромисса между противоречивыми требованиями качества и реализуемости управления.
Сказанное выше можно сформулировать также следующим образом.
Введем в рассмотрение величину Р, представляющую собою основную характеристику условий реализуемости управляющей системы (например, меру ее стоимости, сложности, ненадежности и т. д. или обобщенную меру совокупности всех этих качеств). Показателем, характеризующим эффективность управления, можно тогда назвать функционал

в частном случае имеющий вид

где  — некоторый весовой коэффициент»
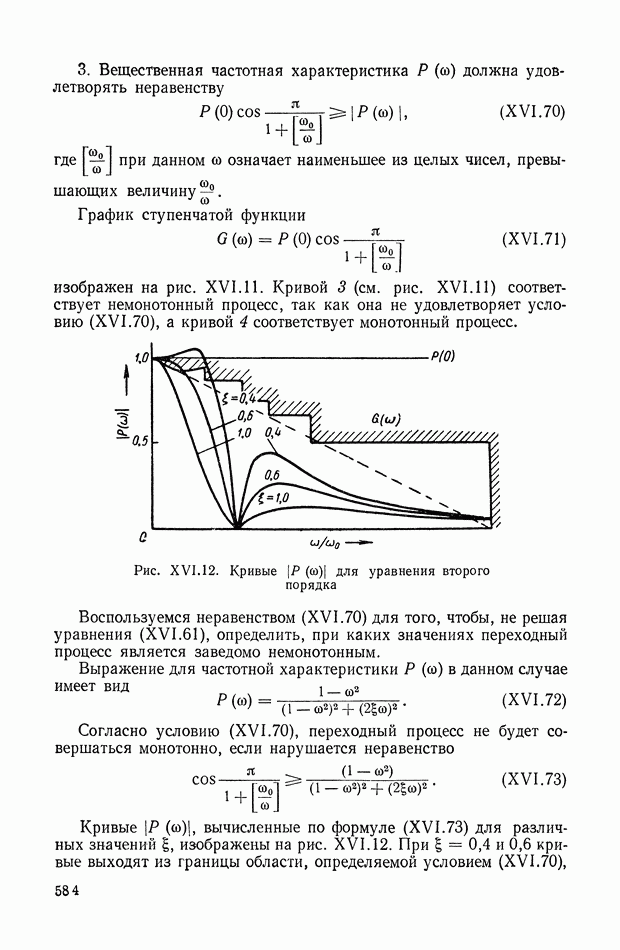
— некоторый весовой коэффициент»
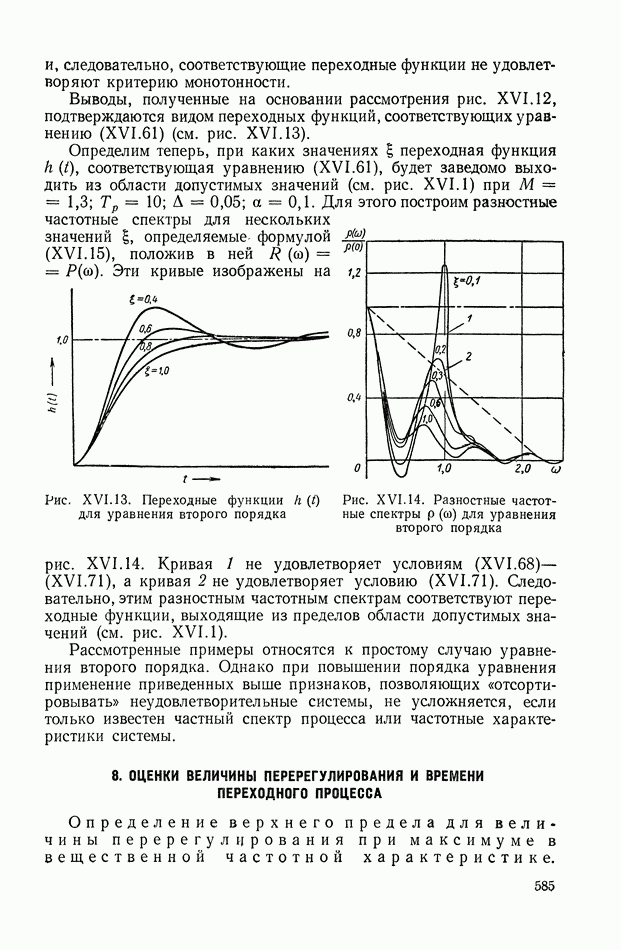
Итак, задачей вторичной оптимизации назовем задачу определения вектора управления  обеспечивающего минимум величины С:
обеспечивающего минимум величины С:

и одновременно удовлетворяющего уравнениям математической модели управляемой системы (II. 1) или (II.2), а также ограничениям (II.3). Оптимальный реализуемый алгоритм управления представим в виде

Частные случаи этой формулировки задачи вторичной оптимизации сводятся к тому, чтобы найти вектор управления  обеспечивающий минимум величины
обеспечивающий минимум величины  при заданной величине Р, т. е.
при заданной величине Р, т. е.

или, наоборот, минимум величины  при заданной величине
при заданной величине  т. е.
т. е.

Подводя итоги, можно дать следующую формулировку проблемы управления: проблема управления состоит в определении и реализации вектора управления  обеспечивающего экстремум показателя эффективности управления (II.9) при достижении цели управления (11.5) и удовлетворяющего имеющимся связям [например, вида (II.2)] и ограничениям [например, вида (II.3)].
обеспечивающего экстремум показателя эффективности управления (II.9) при достижении цели управления (11.5) и удовлетворяющего имеющимся связям [например, вида (II.2)] и ограничениям [например, вида (II.3)].
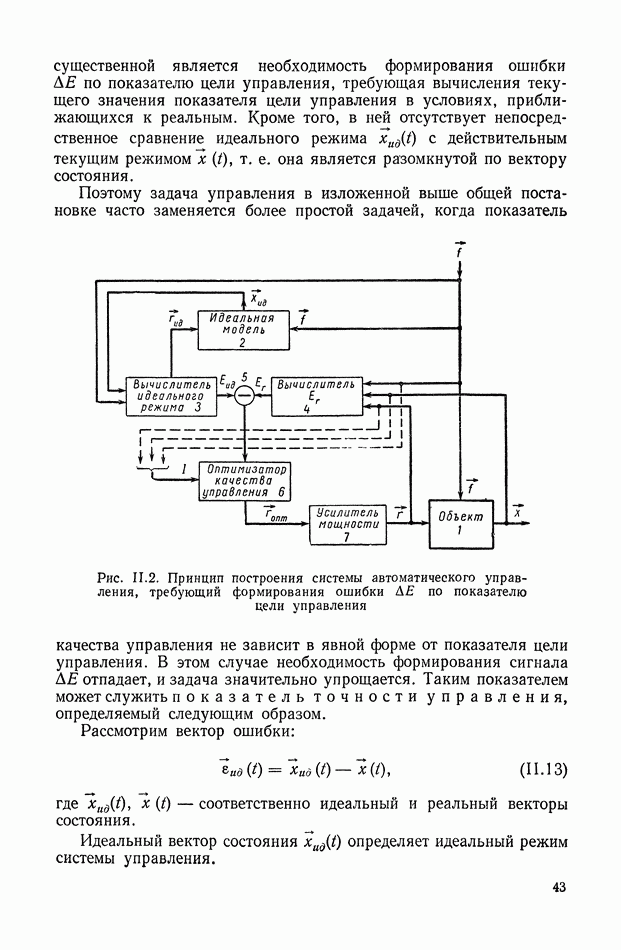
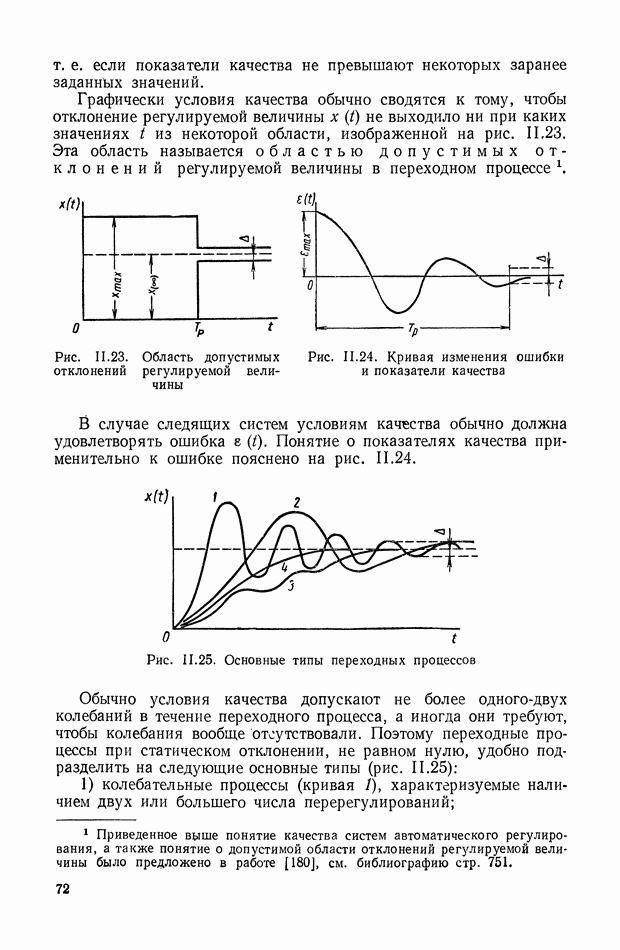
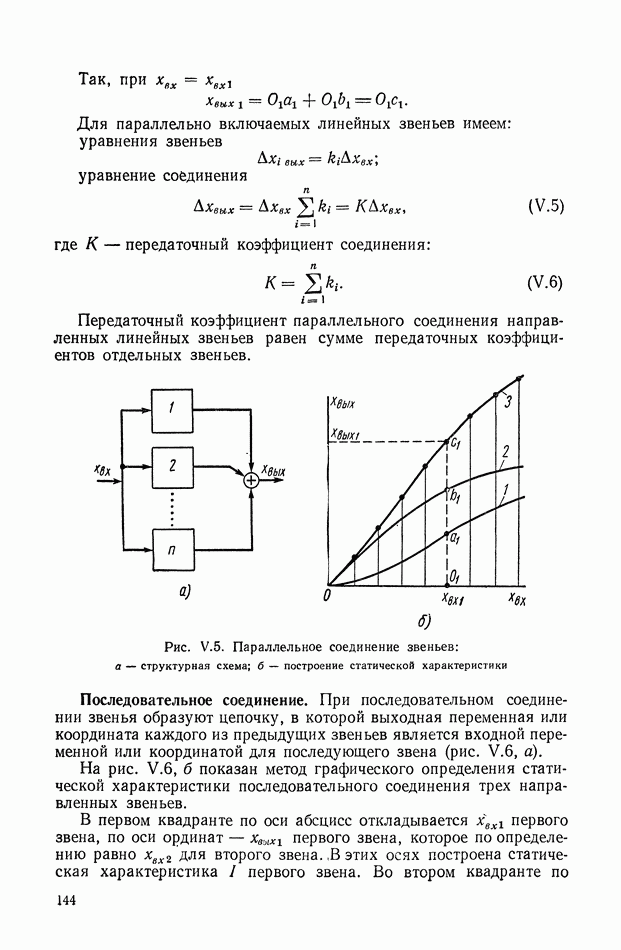
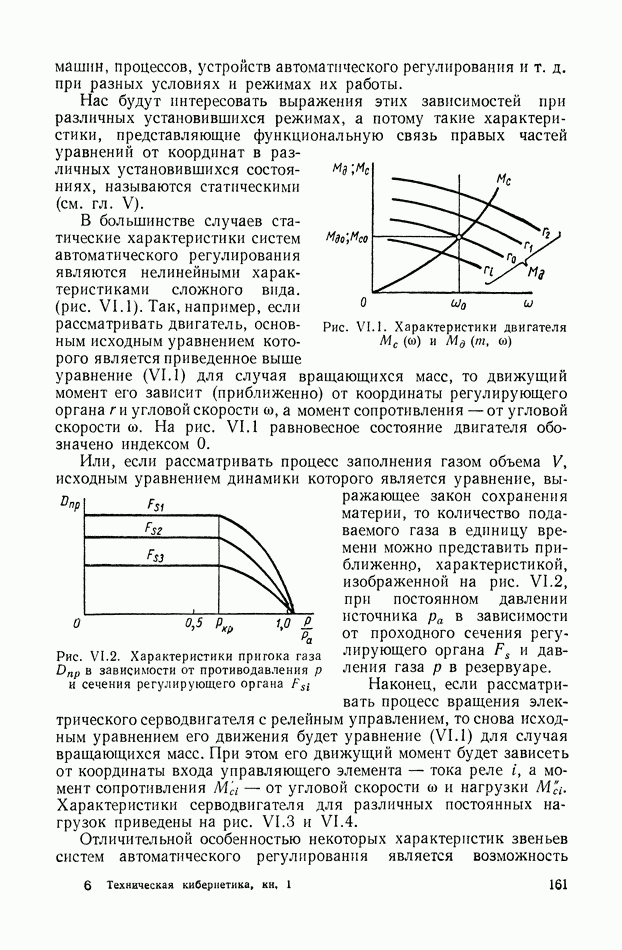
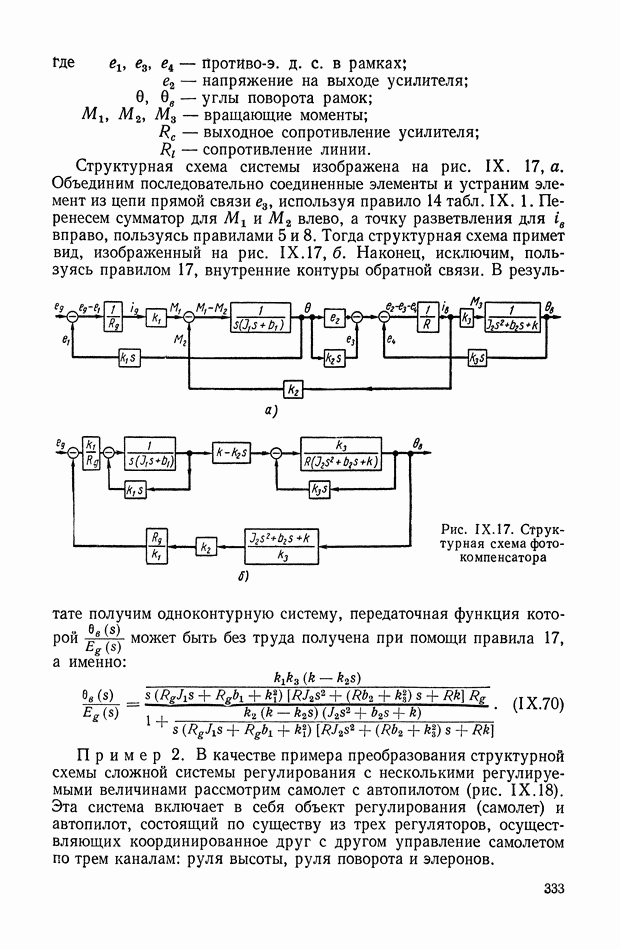
На рис. II.2 приведена схема, поясняющая приведенную выше формулировку проблемы управления и способ реализации вектора управления  Управляемый объект 1 находится под влиянием вектора возмущений
Управляемый объект 1 находится под влиянием вектора возмущений  и зектора управления
и зектора управления  Интересующее нас состояние объекта описывается вектором состояния
Интересующее нас состояние объекта описывается вектором состояния  Идеальная модель 2 реализует уравнения (II.6) с учетом ограничений (II.3). Вычислитель идеального режима 3 решает вариационную проблему (II.5) в принятой идеальной постановке, определяя
Идеальная модель 2 реализует уравнения (II.6) с учетом ограничений (II.3). Вычислитель идеального режима 3 решает вариационную проблему (II.5) в принятой идеальной постановке, определяя  и идеальный показатель цели управления
и идеальный показатель цели управления  Вычислитель 4 по известным
Вычислитель 4 по известным  определяет приближенное значение действительного показателя цели управления
определяет приближенное значение действительного показателя цели управления  Сигналы, пропорциональные
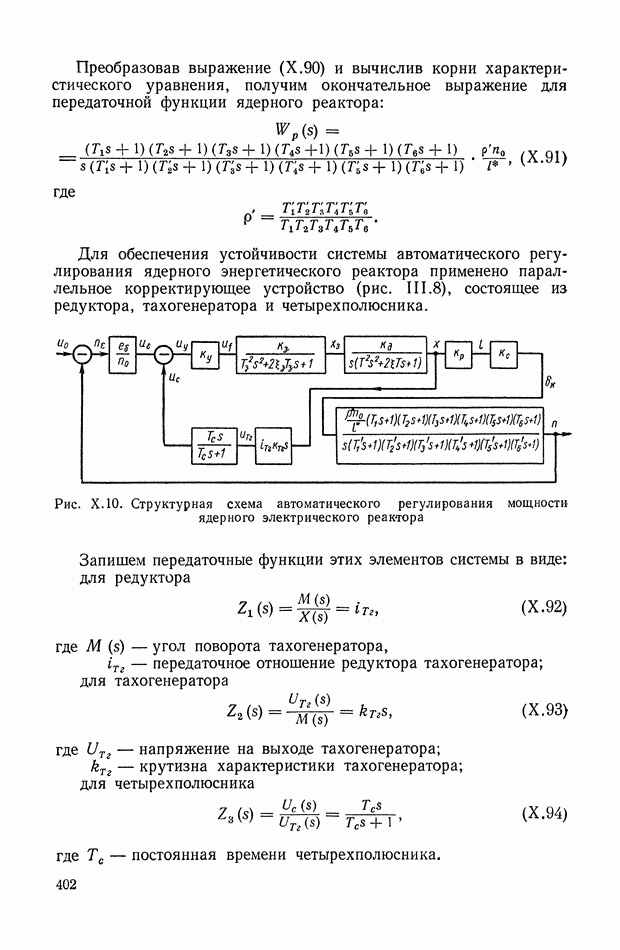
Сигналы, пропорциональные  сравниваются в устройстве 5, и сигнал ошибки
сравниваются в устройстве 5, и сигнал ошибки  по показателю цели управления, совместно с необходимой добавочной информацией
по показателю цели управления, совместно с необходимой добавочной информацией  поступает на оптимизатор качества, или эффективности управления
поступает на оптимизатор качества, или эффективности управления  который решает вариационную задачу (11.10), определяя оптимальный вектор управления
который решает вариационную задачу (11.10), определяя оптимальный вектор управления  Для реализации вектора
Для реализации вектора  обычно необходимы усилители мощности с обратной связью 7.
обычно необходимы усилители мощности с обратной связью 7.
Реализация системы управления, по этому принципу (рис. II.2), представляет собою большие трудности. Одной из наиболее
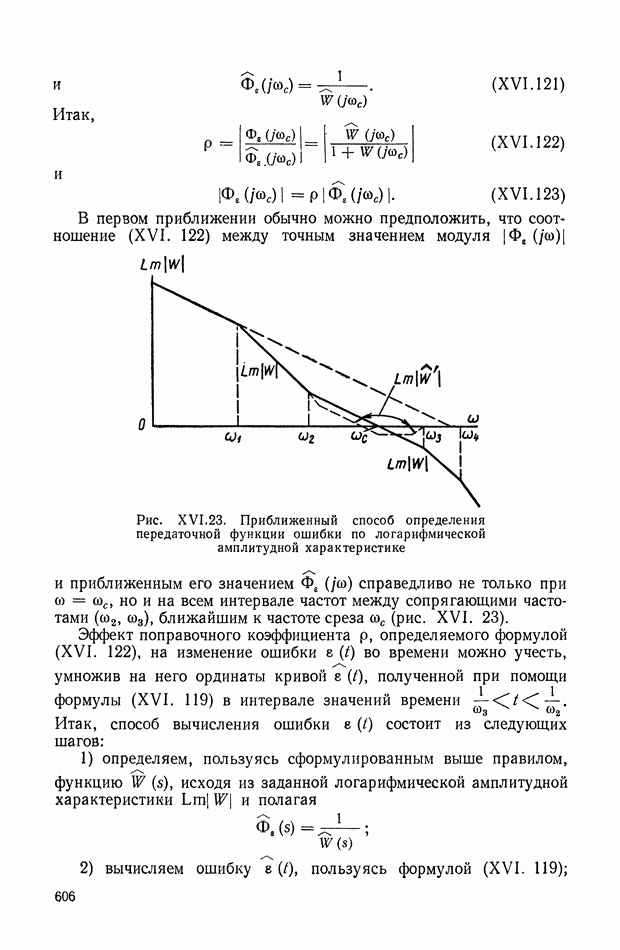
существенной является необходимость формирования ошибки  по показателю цели управления, требующая вычисления текущего значения показателя цели управления в условиях, приближающихся к реальным. Кроме того, в ней отсутствует непосредственное сравнение идеального режима
по показателю цели управления, требующая вычисления текущего значения показателя цели управления в условиях, приближающихся к реальным. Кроме того, в ней отсутствует непосредственное сравнение идеального режима  с действительным текущим режимом
с действительным текущим режимом  т. е. она является разомкнутой по вектору состояния.
т. е. она является разомкнутой по вектору состояния.
Поэтому задача управления в изложенной выше общей постановке часто заменяется более простой задачей, когда показатель качества управления не зависит в явной форме от показателя цели управления.

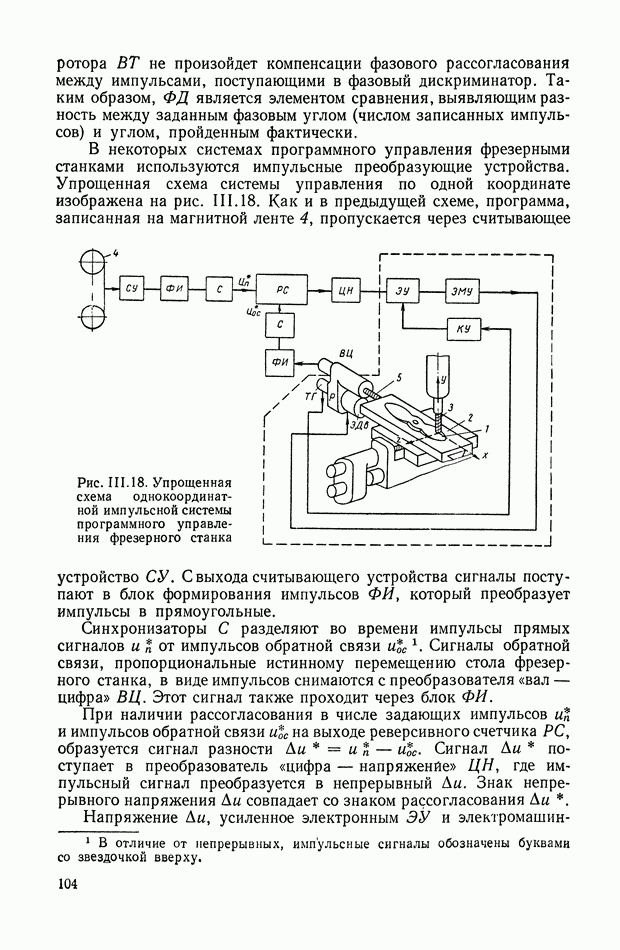
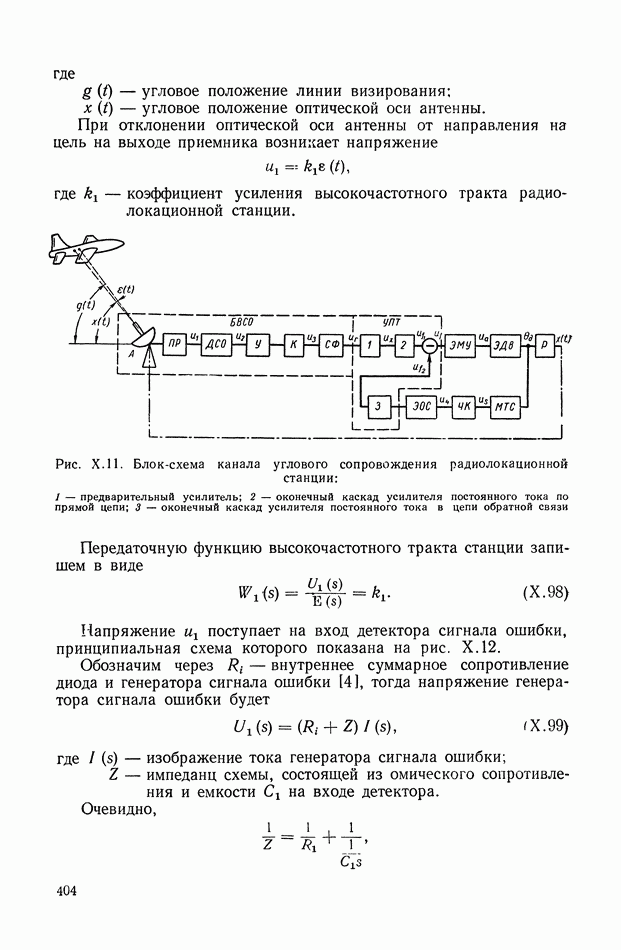
Рис. 11.2. Принцип построения системы автоматического управления, требующий формирования ошибки  по показателю цели управления
по показателю цели управления
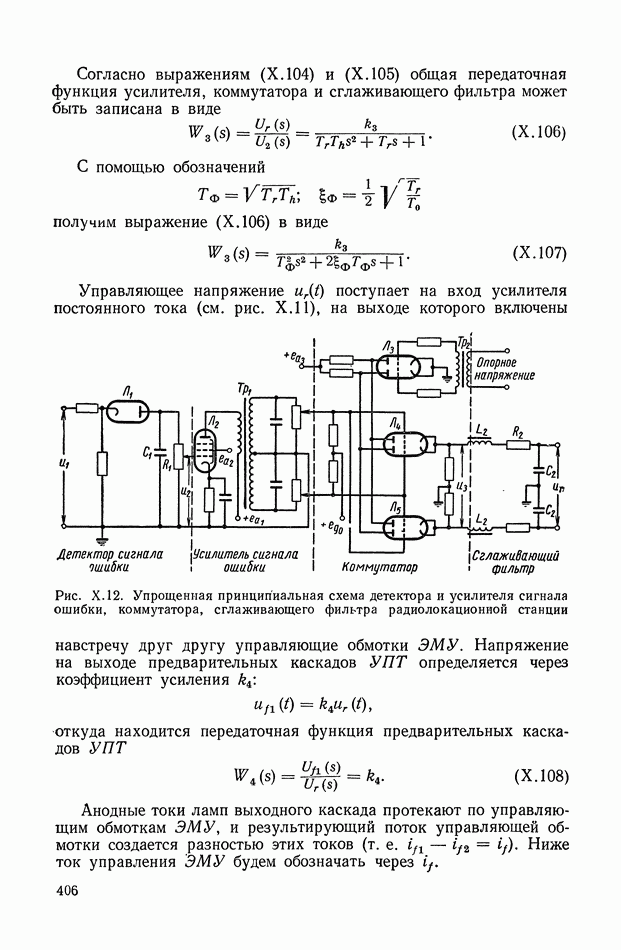
В этом случае необходимость формирования сигнала  отпадает, и задача значительно упрощается. Таким показателем может служить показатель точности управления, определяемый следующим образом.
отпадает, и задача значительно упрощается. Таким показателем может служить показатель точности управления, определяемый следующим образом.
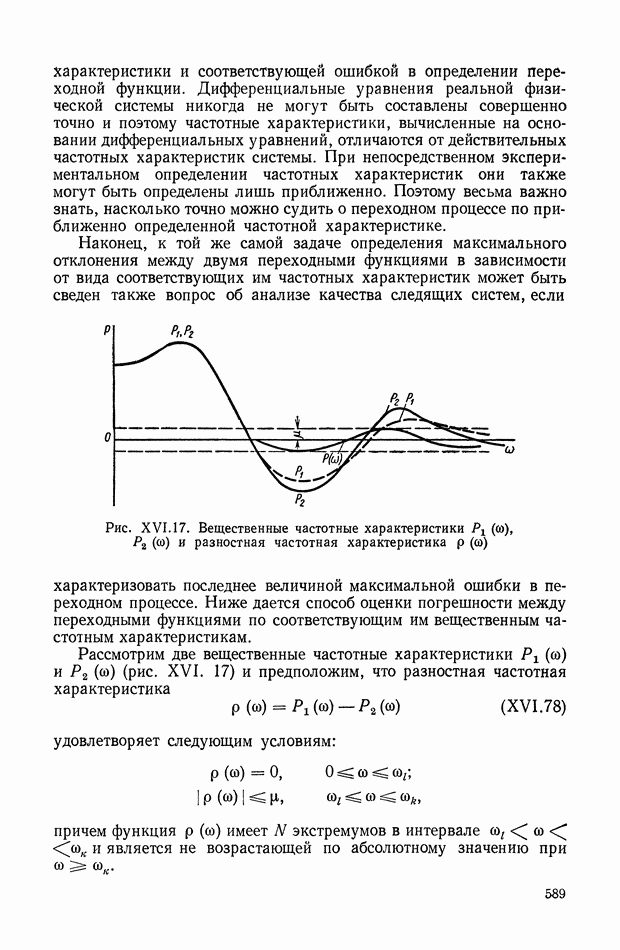
Рассмотрим вектор ошибки:

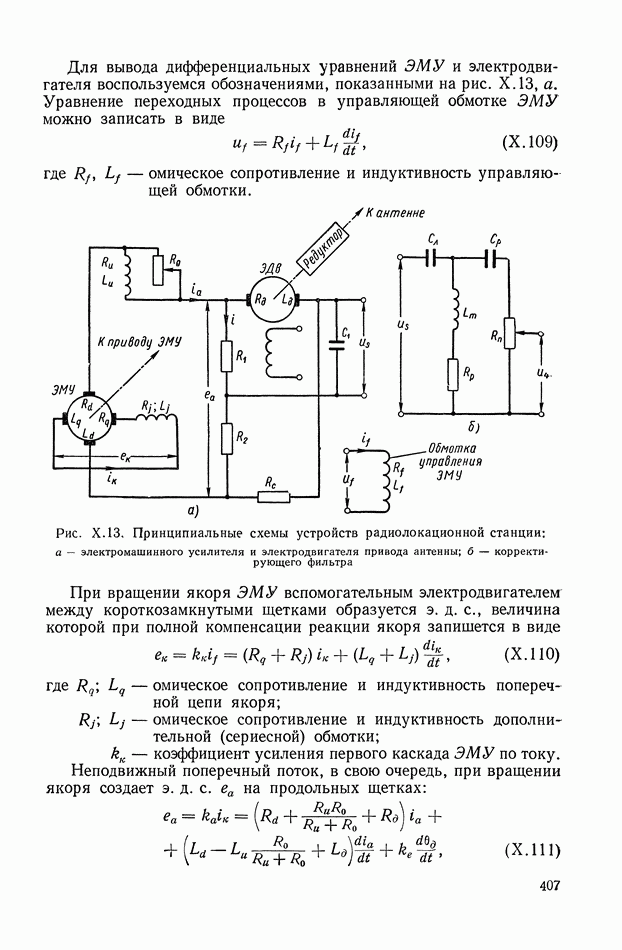
где  — соответственно идеальный и реальный векторы состояния.
— соответственно идеальный и реальный векторы состояния.
Идеальный вектор состояния  определяет идеальный режим системы управления.
определяет идеальный режим системы управления.
Показателем точности назовем функционал от ошибки

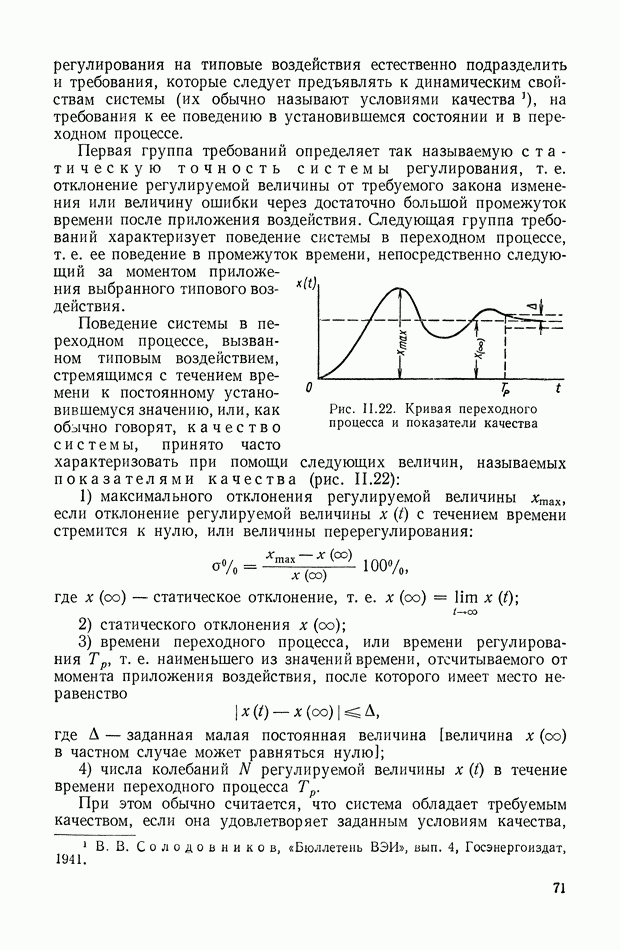
Очевидно, что решение задачи минимизации функционала (11.14) значительно проще минимизации функционала (II.8).
В качестве показателя точности обычно выбирается функционал вида

где  — некоторая непрерывная функция от гид.
— некоторая непрерывная функция от гид.
Функционал  является мерой отклонения на интервале
является мерой отклонения на интервале  действительного вектора состояния х от идеального вектора состояния
действительного вектора состояния х от идеального вектора состояния  совместимого с имеющимися ограничениями на изменения вектора
совместимого с имеющимися ограничениями на изменения вектора 
Заметим, что если представляет интерес мера полного отклонения на достаточно большом интервале времени, то вместо функционала (11.15) с конечными пределами рассматривается функционал вида

с бесконечными пределами.
Возможен также и другой предельный случай, когда интерес представляет мера ошибки  лишь в определенный момент времени
лишь в определенный момент времени  В этом случае
В этом случае

при 
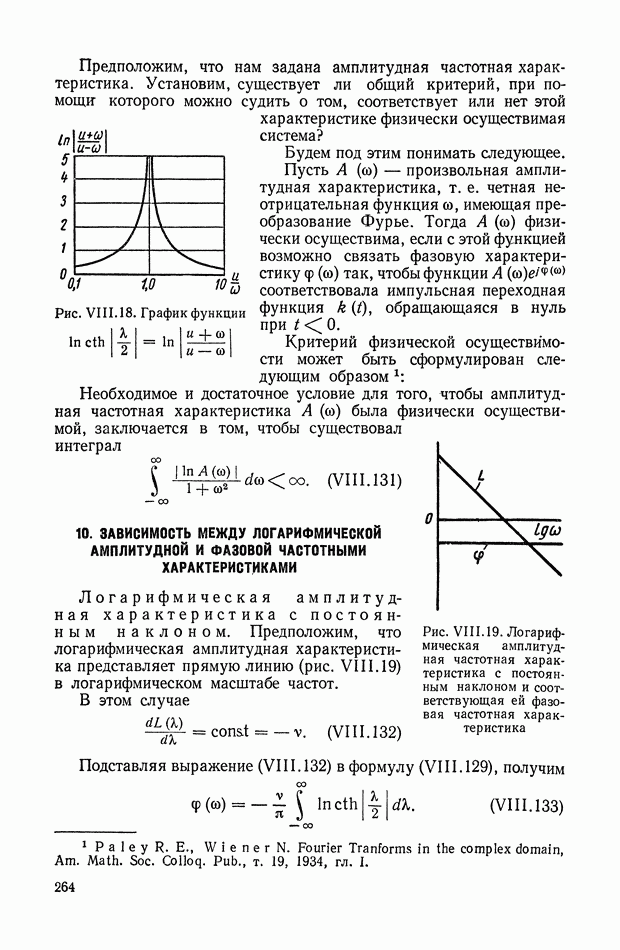
Решение задачи на минимум функционала (11.14) при имеющихся ограничениях и связях позволяет найти вектор состояния, который мы назовем оптимальным и обозначим через  Оптимальный вектор состояния
Оптимальный вектор состояния  называется также вектором задания и обозначается через
называется также вектором задания и обозначается через 
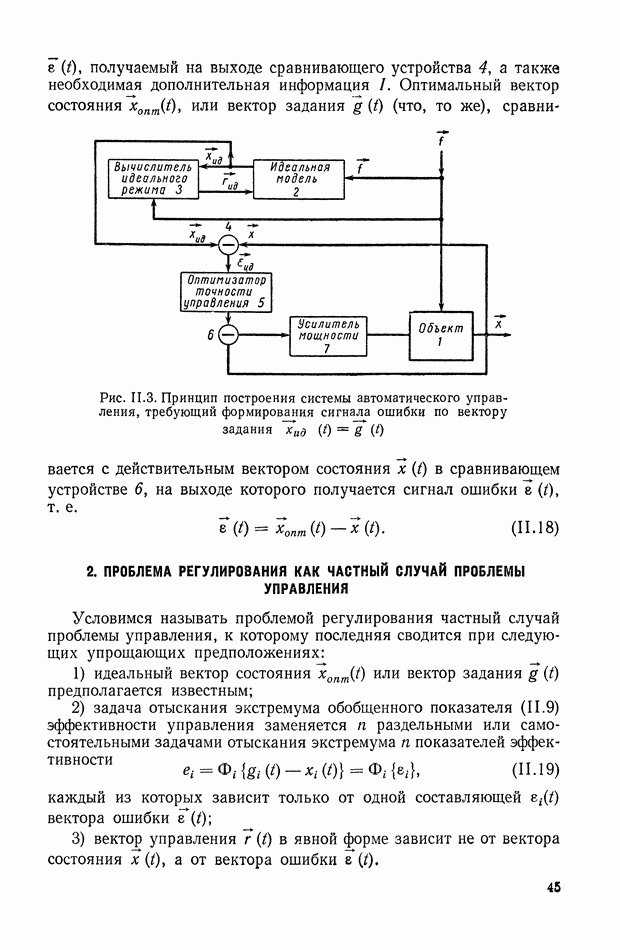
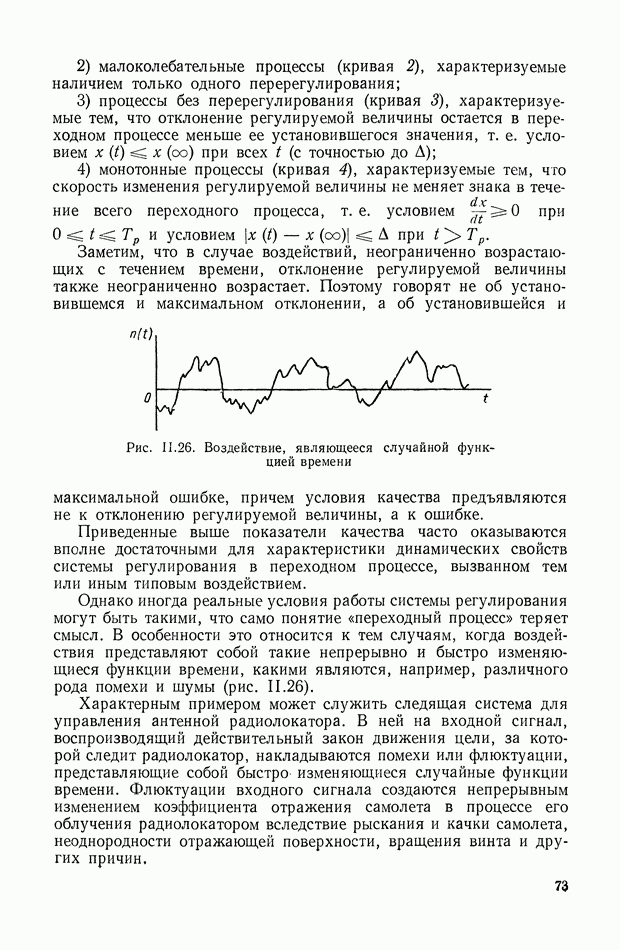
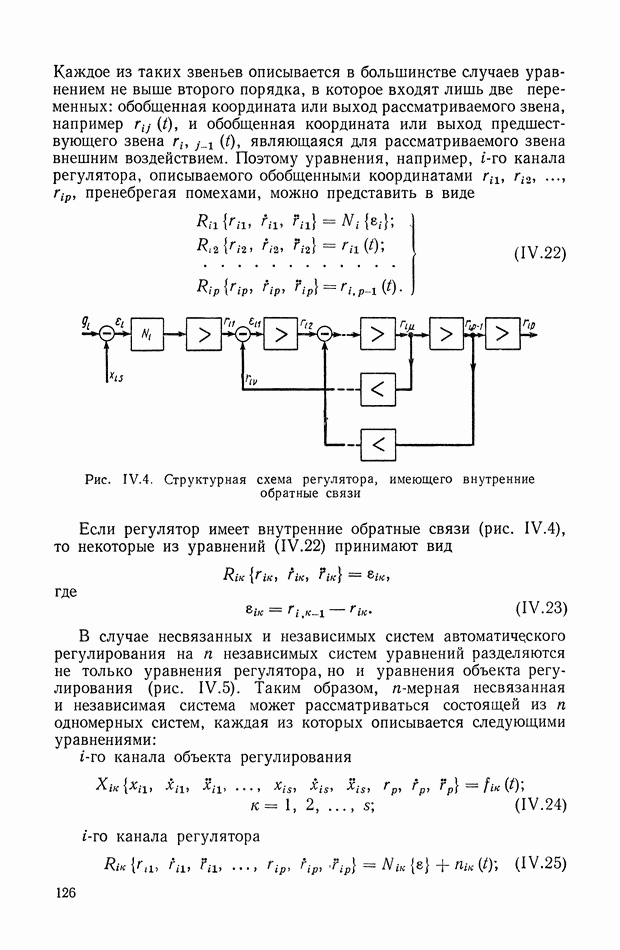
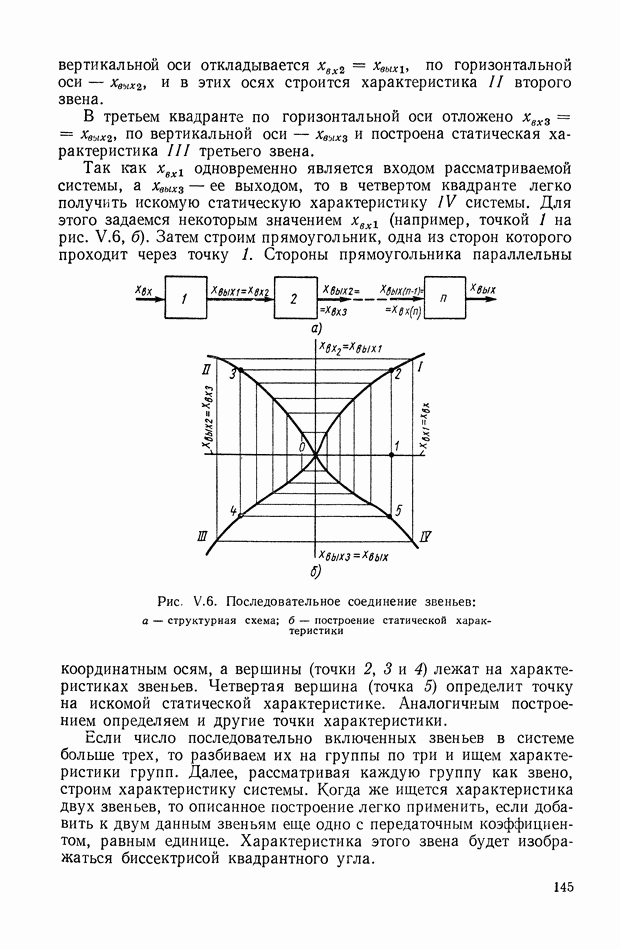
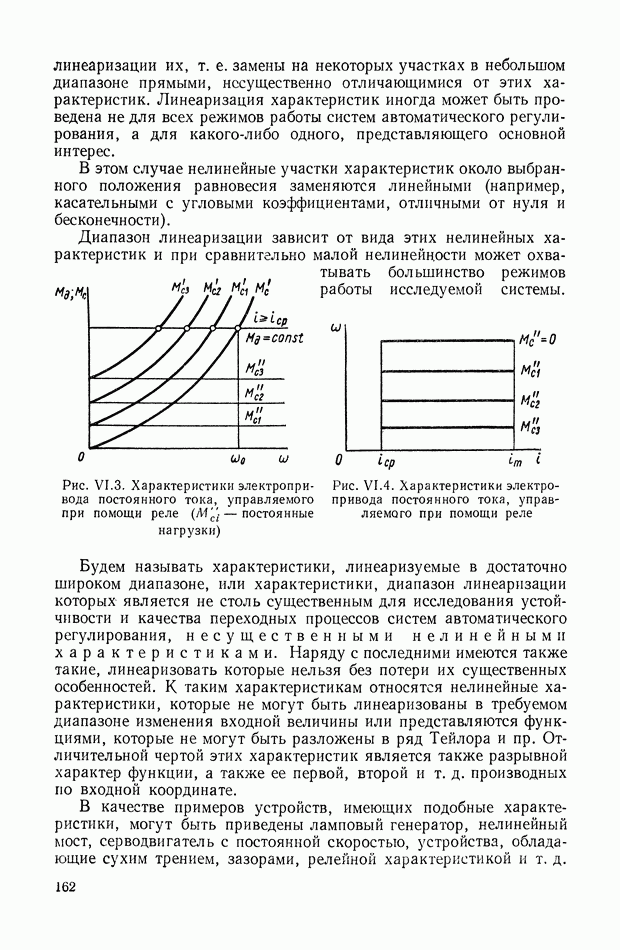
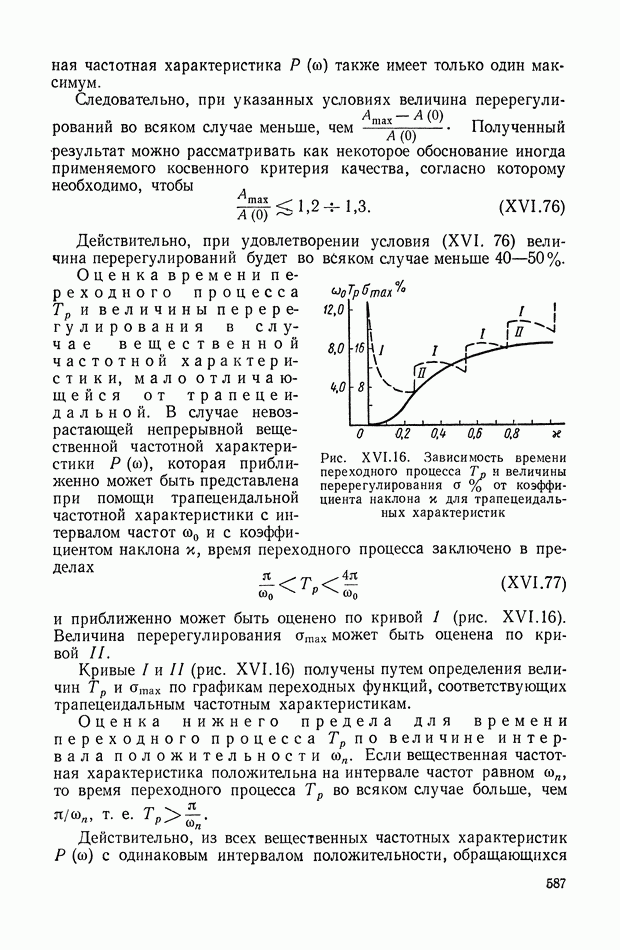
На рис. II.3 изображена схема, поясняющая рассмотренный выше принцип управления, когда показателем эффективности управления является показатель точности (11.14). Здесь, так же как и на рис. II.2, имеется объект регулирования 1, идеальная модель 2, вычислитель идеального режима 3, усилитель мощности 7, но цепь для формирования сигнала ошибки  по показателю цели управления уже оказывается не нужной, что существенно упрощает систему.
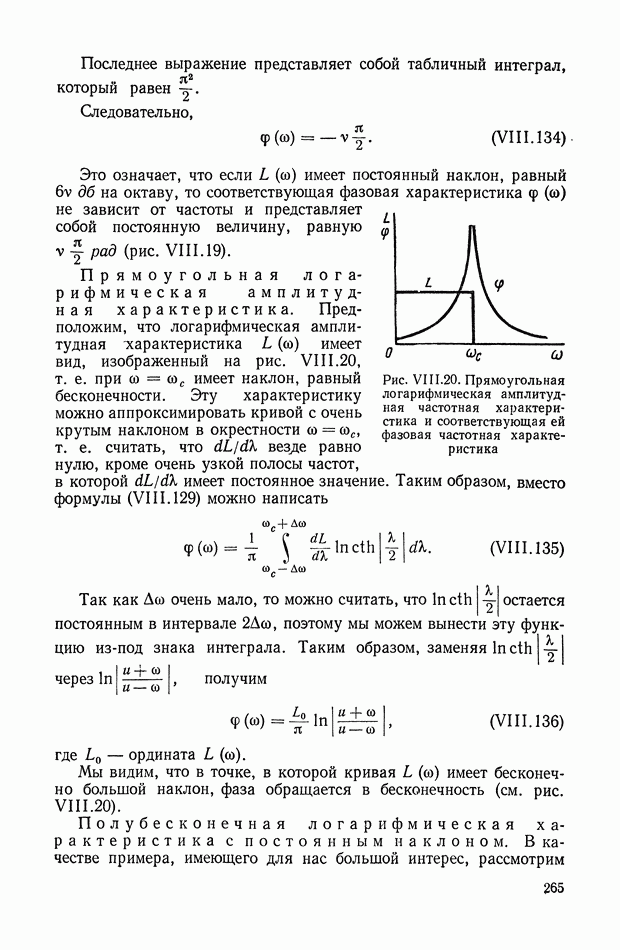
по показателю цели управления уже оказывается не нужной, что существенно упрощает систему.
Оптимизатор качества управления 6 (рис. II.2) в рассматриваемом случае (рис. II.3) сводится к оптимизатору точности управления 5, входными сигналами для которого является сигнал ошибки
 получаемый на выходе сравнивающего устройства 4, а также необходимая дополнительная информация
получаемый на выходе сравнивающего устройства 4, а также необходимая дополнительная информация 

Рис. II.3. Принцип построения системы автоматического управления, требующий формирования сигнала ошибки по вектору задания 
Оптимальный вектор состояния  или вектор задания
или вектор задания  то же), сравнивается с действительным вектором состояния
то же), сравнивается с действительным вектором состояния  в сравнивающем устройстве 6, на выходе которого получается сигнал ошибки
в сравнивающем устройстве 6, на выходе которого получается сигнал ошибки  т. е.
т. е.

| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- РАЗДЕЛ I. ОБЩИЕ СВЕДЕНИЯ. МЕТОДЫ МАТЕМАТИЧЕСКОГО ОПИСАНИЯ И СТРУКТУРНОГО ПРЕОБРАЗОВАНИЯ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- ГЛАВА I. ОЧЕРК О РАЗВИТИИ ТЕОРИИ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ В СССР
- 1. ТЕОРИЯ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ В ДОРЕВОЛЮЦИОННЫЙ ПЕРИОД
- 2. РАЗВИТИЕ ТЕОРИИ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ПОСЛЕ ОКТЯБРЬСКОЙ СОЦИАЛИСТИЧЕСКОЙ РЕВОЛЮЦИИ
- ГЛАВА II. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ ТЕОРИИ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. СУЩНОСТЬ ПРОБЛЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- 2. ПРОБЛЕМА РЕГУЛИРОВАНИЯ КАК ЧАСТНЫЙ СЛУЧАЙ ПРОБЛЕМЫ УПРАВЛЕНИЯ
- 3. ОСНОВНОЙ ПРИНЦИП ДЕЙСТВИЯ И ОПРЕДЕЛЕНИЕ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 4. КЛАССИФИКАЦИЯ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ В ЗАВИСИМОСТИ ОТ УПРАВЛЯЮЩЕГО ВОЗДЕЙСТВИЯ
- 5. ОСНОВНЫЕ УСТРОЙСТВА СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ И ИХ КЛАССИФИКАЦИЯ ПО НАЗНАЧЕНИЮ
- 6. КЛАССИФИКАЦИЯ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ В ЗАВИСИМОСТИ ОТ ХАРАКТЕРА СИГНАЛОВ
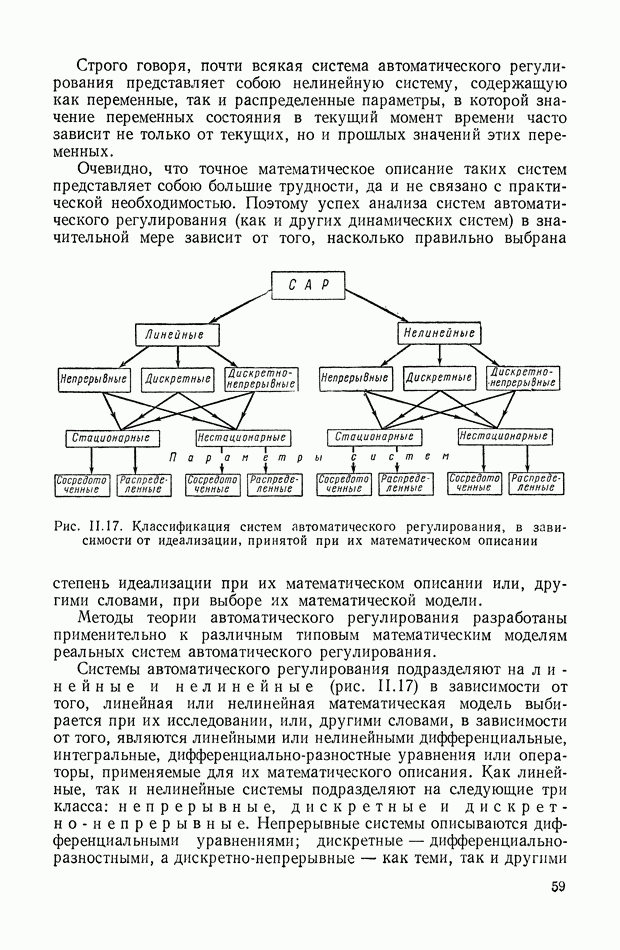
- 7. КЛАССИФИКАЦИЯ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ В ЗАВИСИМОСТИ ОТ ИДЕАЛИЗАЦИИ, ПРИНЯТОЙ ПРИ ИХ МАТЕМАТИЧЕСКОМ ОПИСАНИИ
- 8. СТРУКТУРНЫЕ СХЕМЫ, ОДНОКОНТУРНЫЕ И МНОГОКОНТУРНЫЕ, НЕСВЯЗАННЫЕ И СВЯЗАННЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
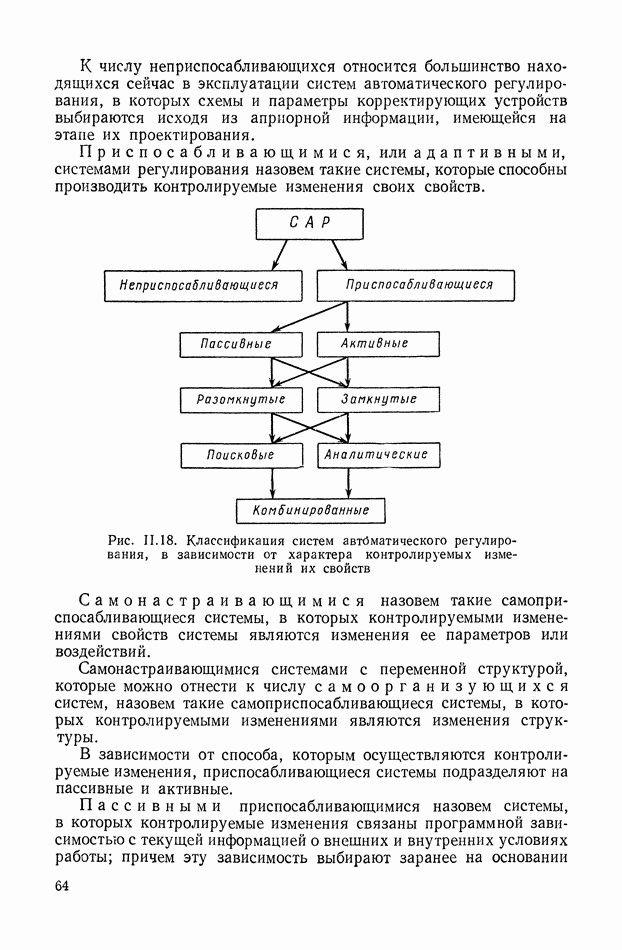
- 9. КЛАССИФИКАЦИЯ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ В ЗАВИСИМОСТИ ОТ ХАРАКТЕРА КОНТРОЛИРУЕМЫХ ИЗМЕНЕНИЙ
- 10. ТРЕБОВАНИЯ, ПРЕДЪЯВЛЯЕМЫЕ К ДИНАМИЧЕСКИМ СВОЙСТВАМ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- ГЛАВА III. ОСНОВНЫЕ УСТРОЙСТВА И ТИПОВЫЕ СХЕМЫ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. КРАТКАЯ ХАРАКТЕРИСТИКА УСТРОЙСТВ, ИЗ КОТОРЫХ СОСТОЯТ СИСТЕМЫ РЕГУЛИРОВАНИЯ
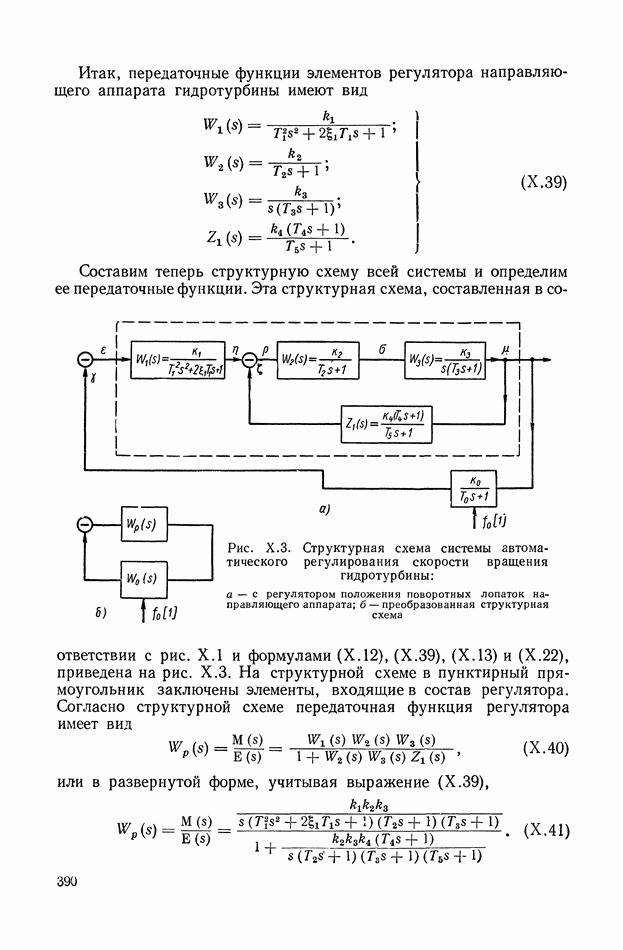
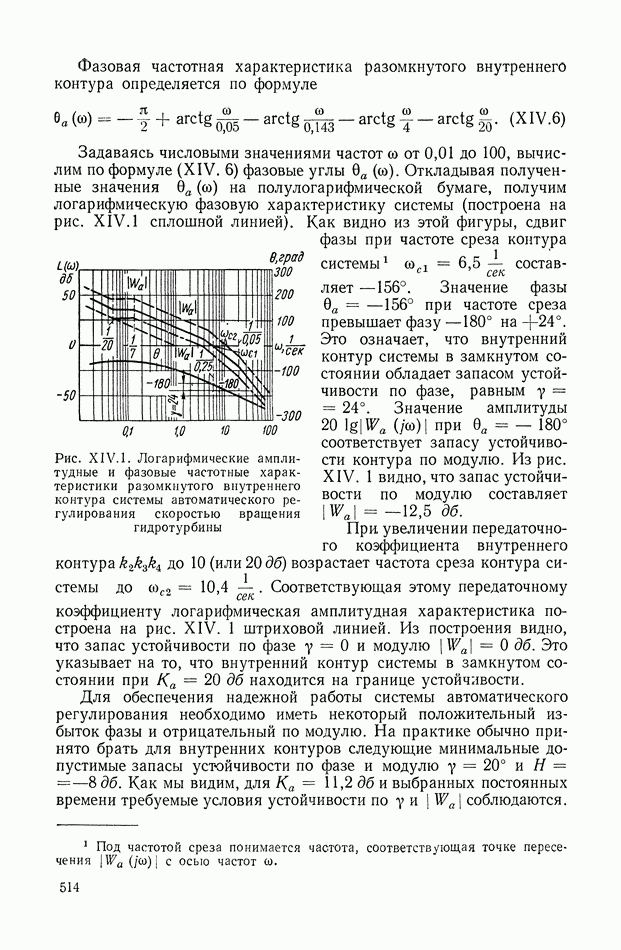
- 2. СИСТЕМА АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ СКОРОСТИ ГИДРОТУРБИНЫ
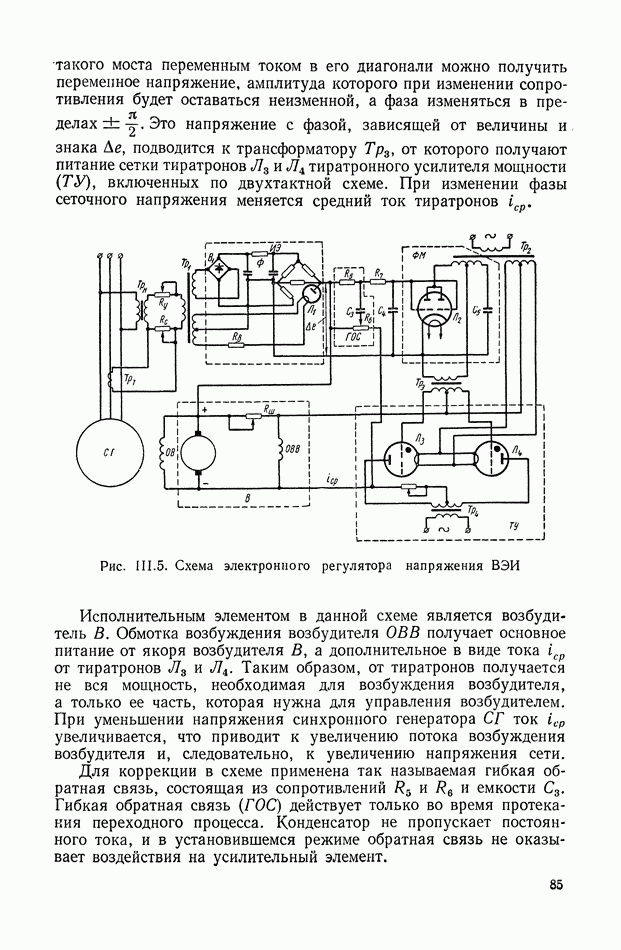
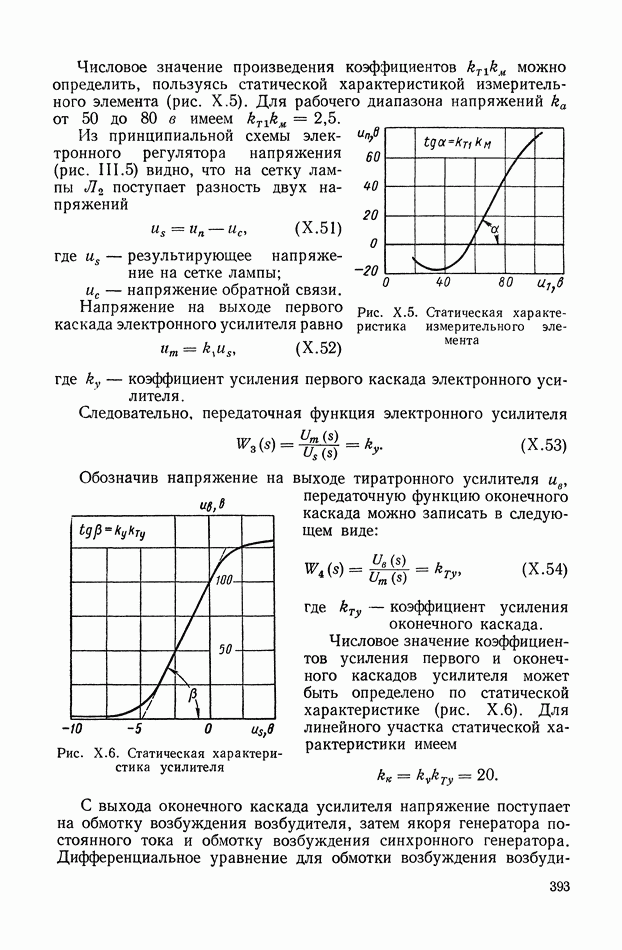
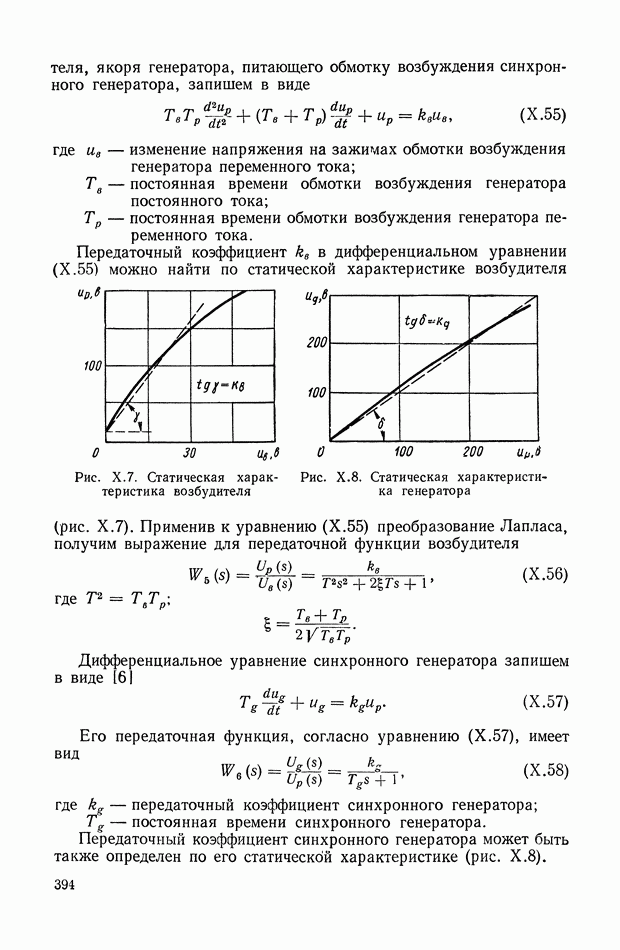
- 3. ЭЛЕКТРОННЫЙ РЕГУЛЯТОР НАПРЯЖЕНИЯ ВЭИ
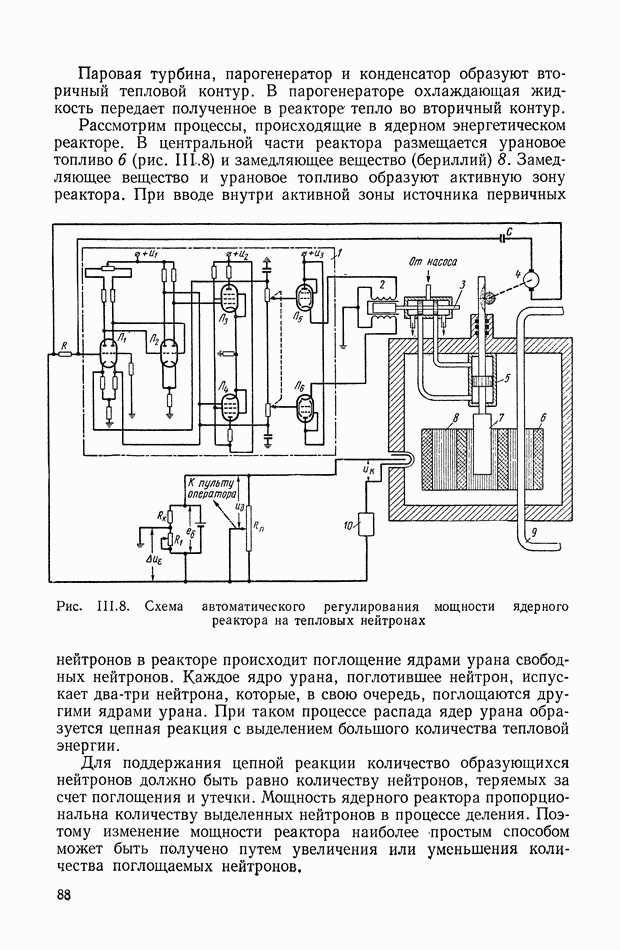
- 4. СИСТЕМА АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ЯДЕРНОГО РЕАКТОРА ПО МОЩНОСТИ
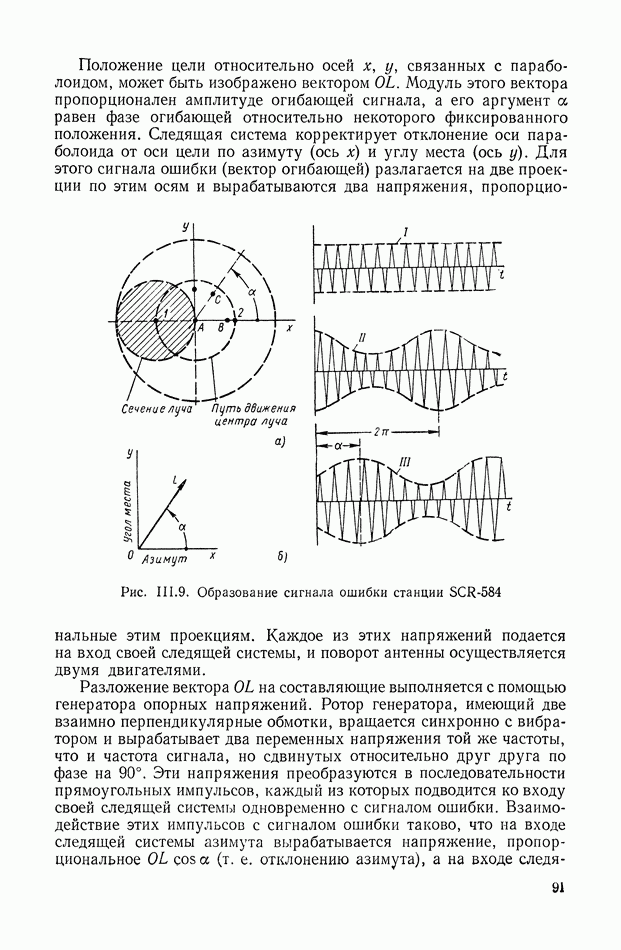
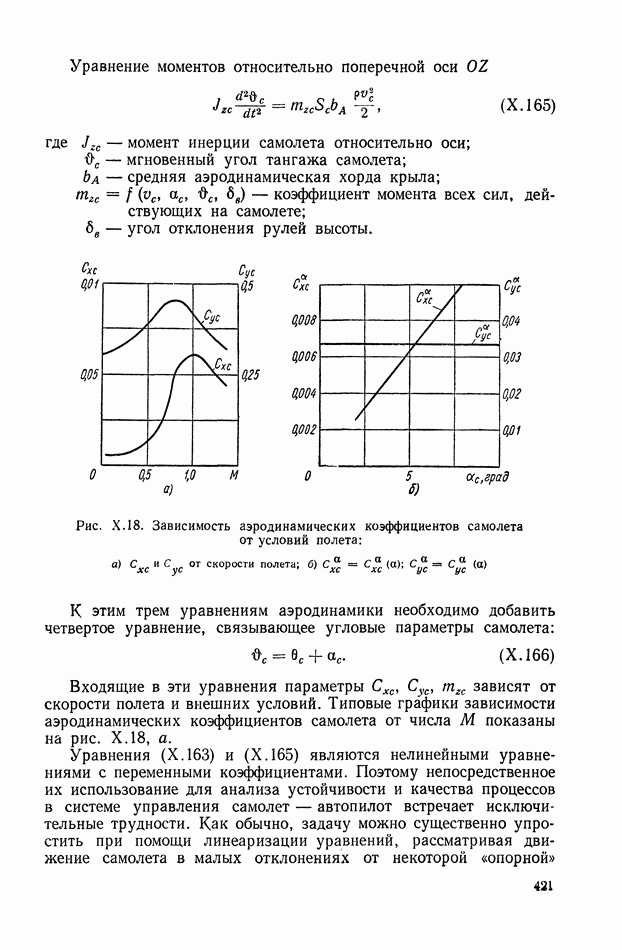
- 5. СЛЕДЯЩАЯ СИСТЕМА РАДИОЛОКАЦИОННОЙ СТАНЦИИ
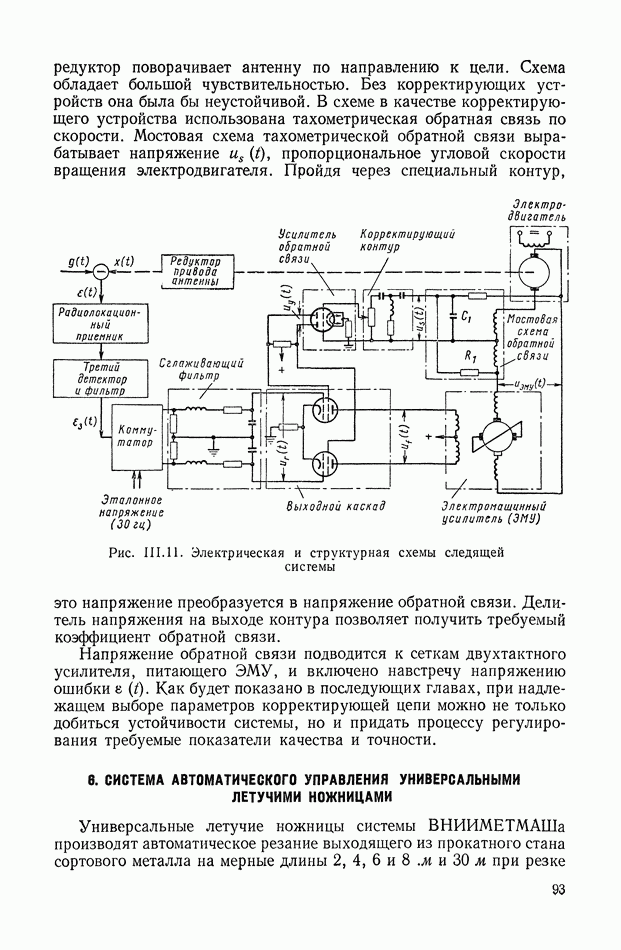
- 6. СИСТЕМА АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ УНИВЕРСАЛЬНЫМИ ЛЕТУЧИМИ НОЖНИЦАМИ
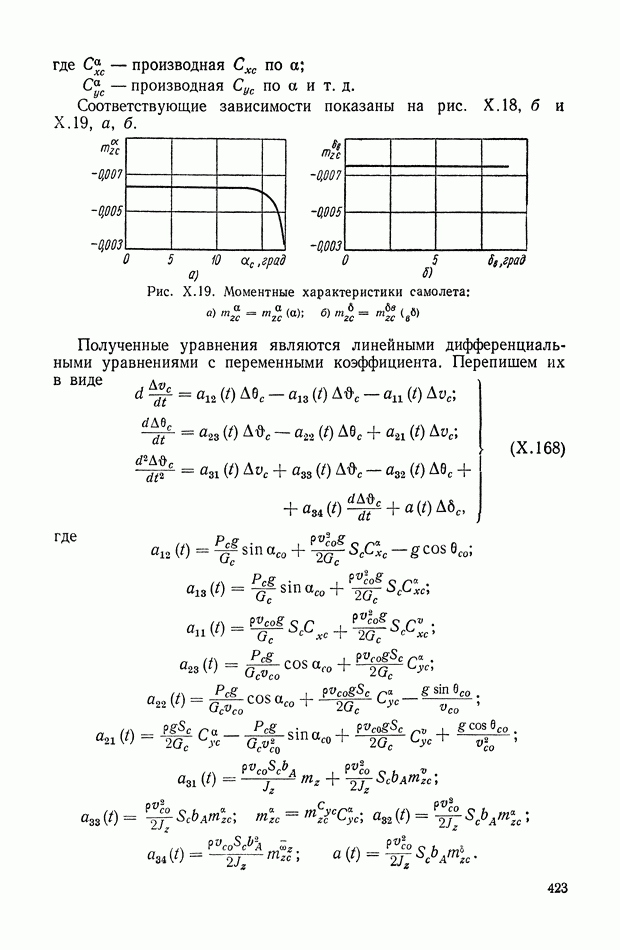
- 7. СЛЕДЯЩАЯ СИСТЕМА КОПИРОВАЛЬНО-ФРЕЗЕРНОГО ПОЛУАВТОМАТА
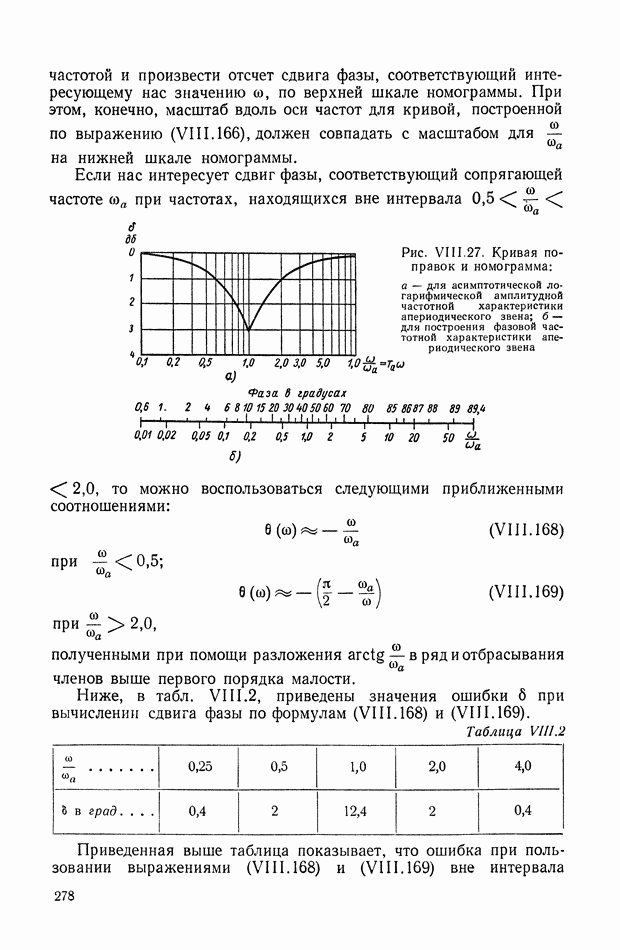
- 8. ПРОГРАММНОЕ УПРАВЛЕНИЕ МЕТАЛЛОРЕЖУЩИМИ СТАНКАМИ
- 9. ПРИНЦИП ДЕЙСТВИЯ ЭЛЕКТРИЧЕСКОГО АВТОПИЛОТА
- 10. РЕГУЛИРОВАНИЕ МНОГИХ ВЕЛИЧИН ПРИ АВТОМАТИЧЕСКОМ УПРАВЛЕНИИ ПЕРЕГОНКОЙ НЕФТИ
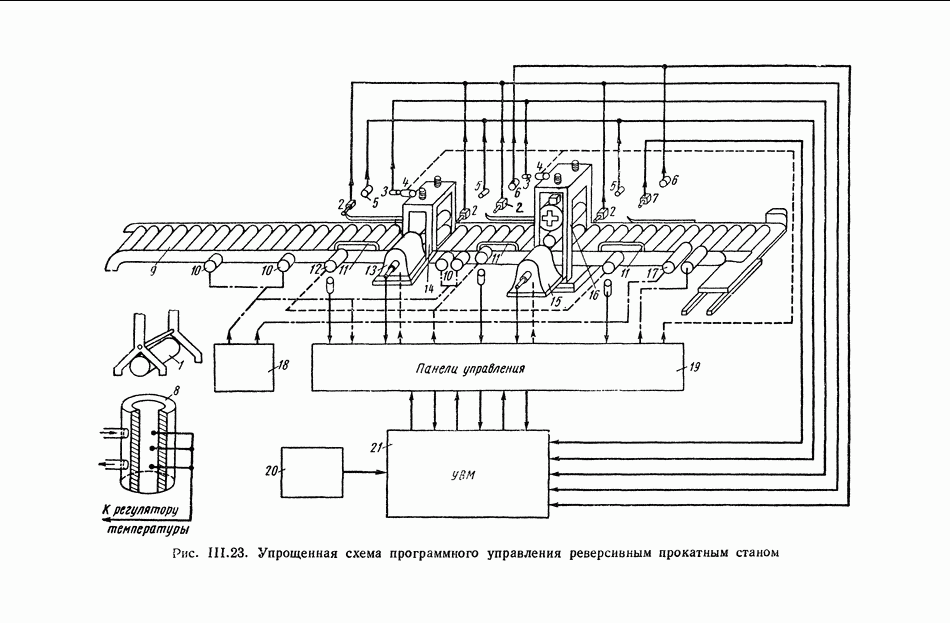
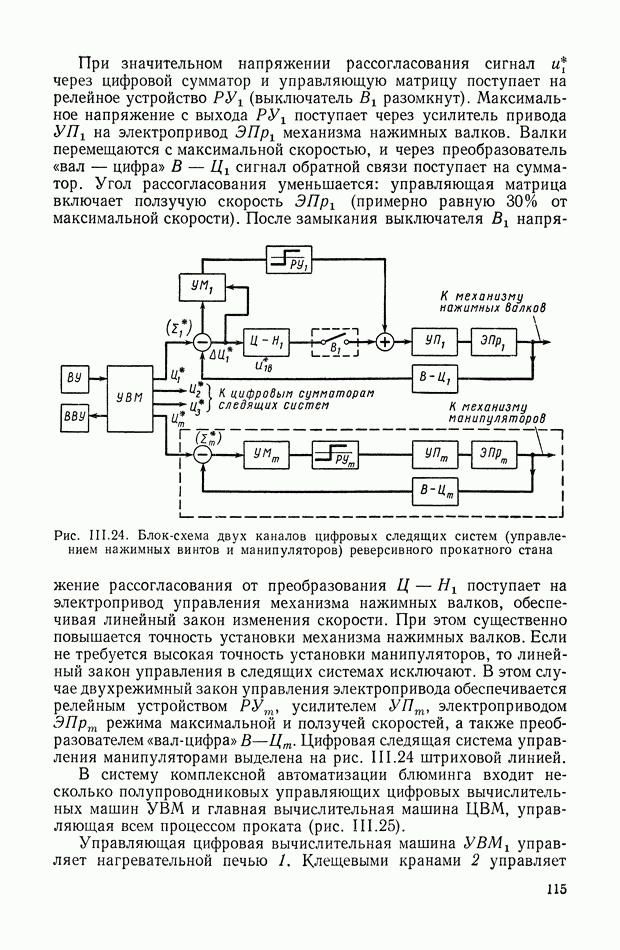
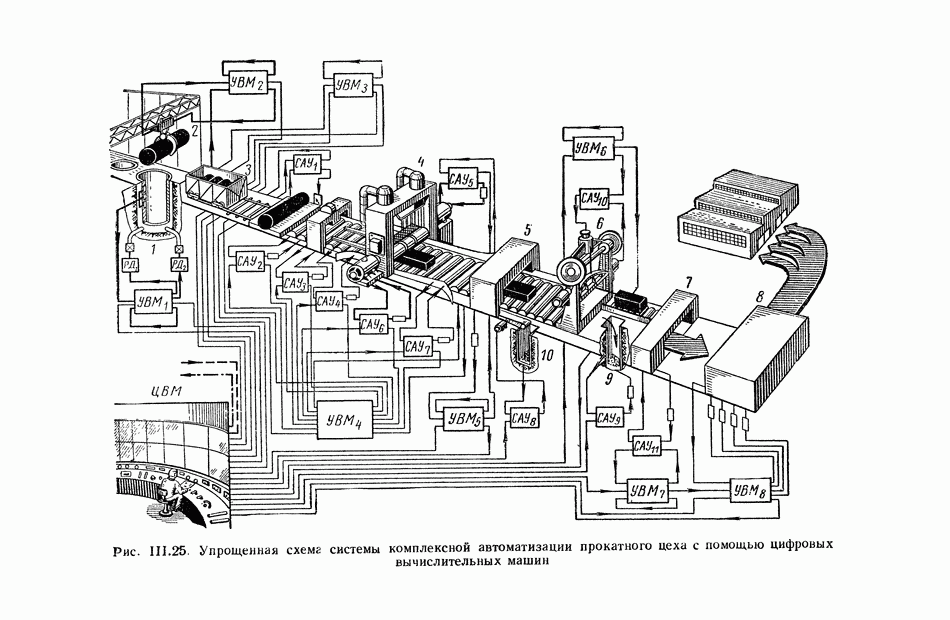
- 11. СИСТЕМА АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ РЕВЕРСИВНЫМ ПРОКАТНЫМ СТАНОМ С ИСПОЛЬЗОВАНИЕМ ЦИФРОВОЙ ВЫЧИСЛИТЕЛЬНОЙ МАШИНЫ
- ГЛАВА IV. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ЛАГРАНЖА ВТОРОГО РОДА
- 2. ОБЩИЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 3. ОБЩИЕ ЛИНЕАРИЗОВАННЫЕ УРАВНЕНИЯ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
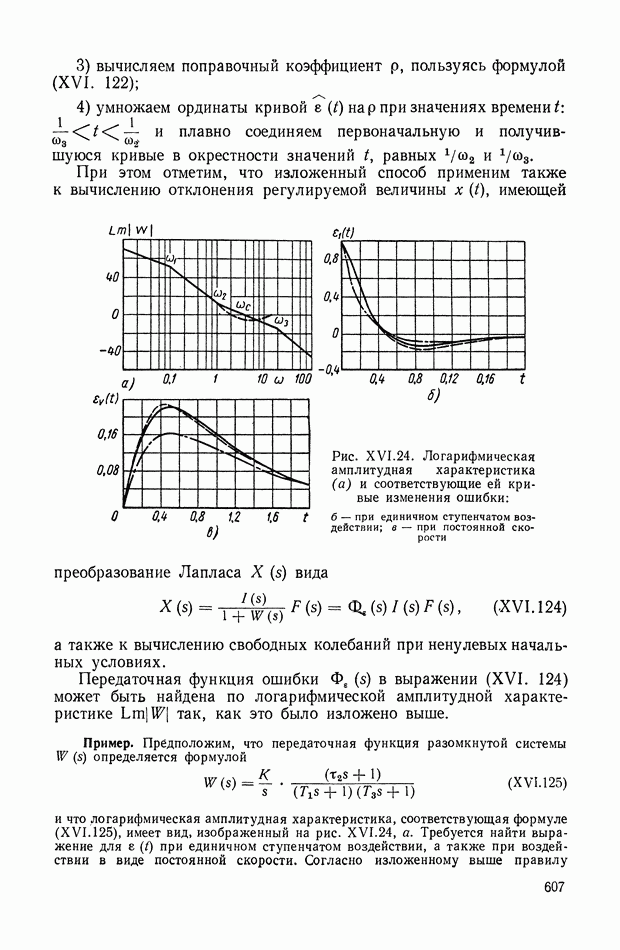
- 4. ПРИМЕР СОСТАВЛЕНИЯ УРАВНЕНИЯ ОБЪЕКТА РЕГУЛИРОВАНИЯ
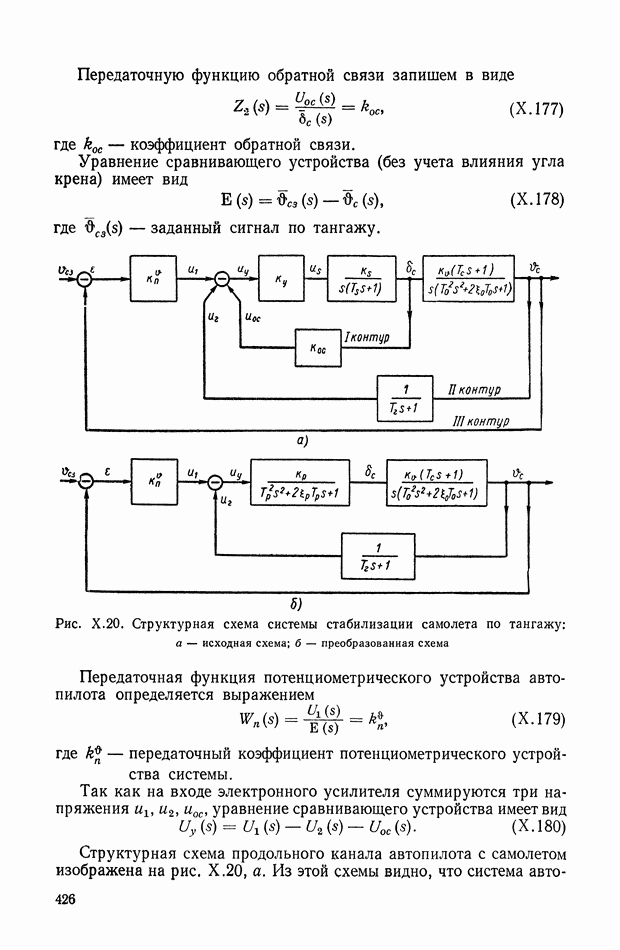
- ГЛАВА V. СТАТИКА СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. СТАТИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПРОСТЕЙШИХ ЗВЕНЬЕВ
- 2. СТАТИЧЕСКИЕ ХАРАКТЕРИСТИКИ ОСНОВНЫХ ТИПОВ СОЕДИНЕНИЙ ЗВЕНЬЕВ
- 3. КОРРЕКЦИЯ СТАТИЧЕСКИХ ХАРАКТЕРИСТИК
- Статическая характеристика замкнутой одномерной системы регулирования.
- Статическая характеристика линейной замкнутой системы.
- 4. СТАТИЗМ РЕГУЛИРОВАНИЯ
- 5. СТАТИКА ЛИНЕЙНЫХ СИСТЕМ С НЕСКОЛЬКИМИ РЕГУЛИРУЕМЫМИ ВЕЛИЧИНАМИ
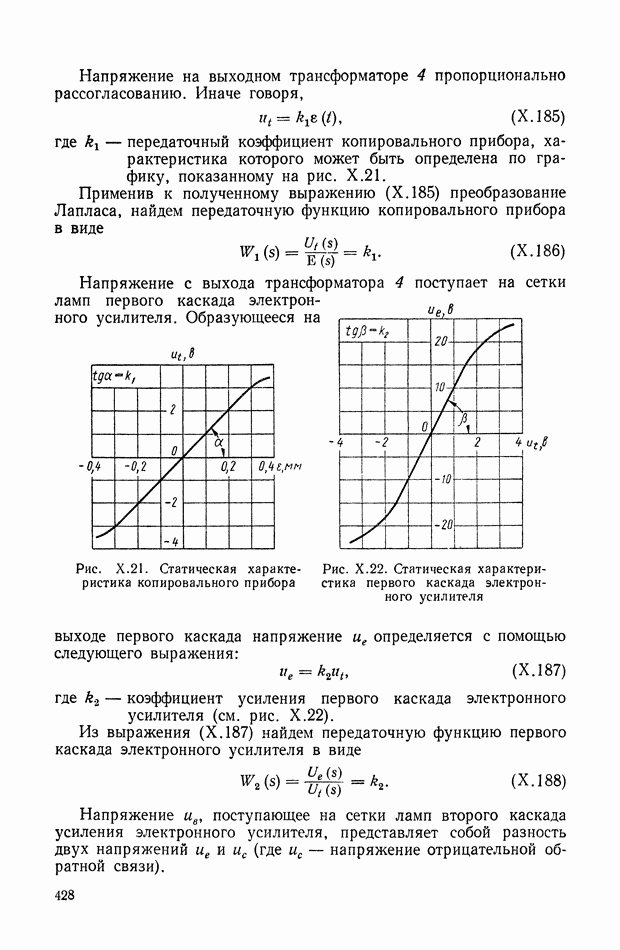
- ГЛАВА VI. ТИПИЧНЫЕ НЕЛИНЕЙНЫЕ СТАТИЧЕСКИЕ ХАРАКТЕРИСТИКИ ТИПОВЫХ ЗВЕНЬЕВ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
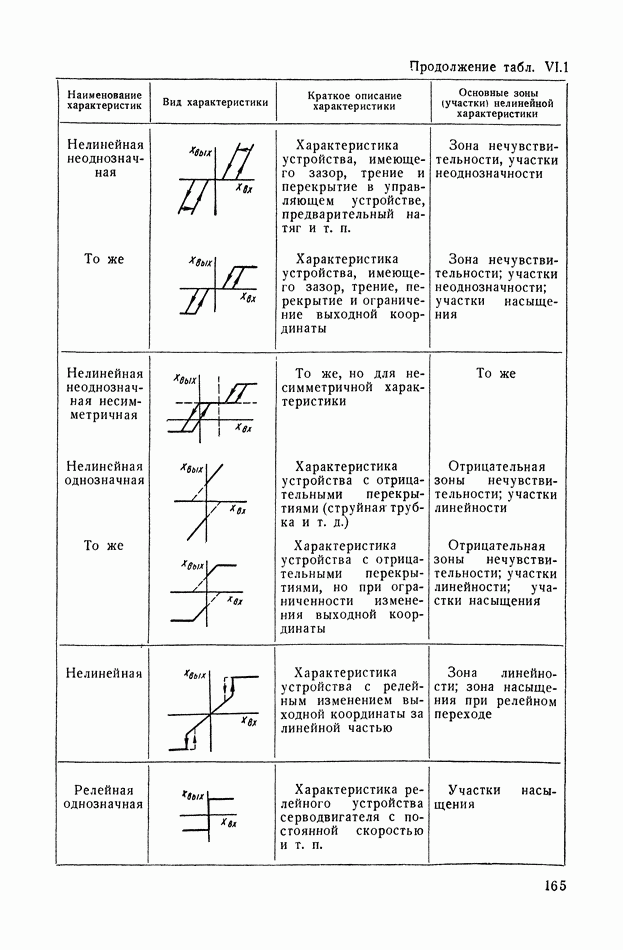
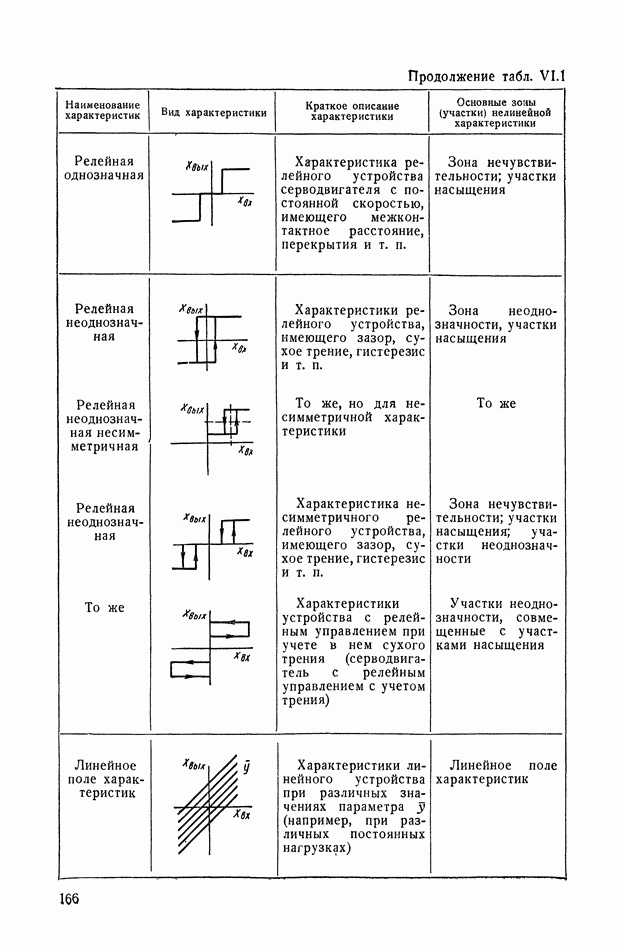
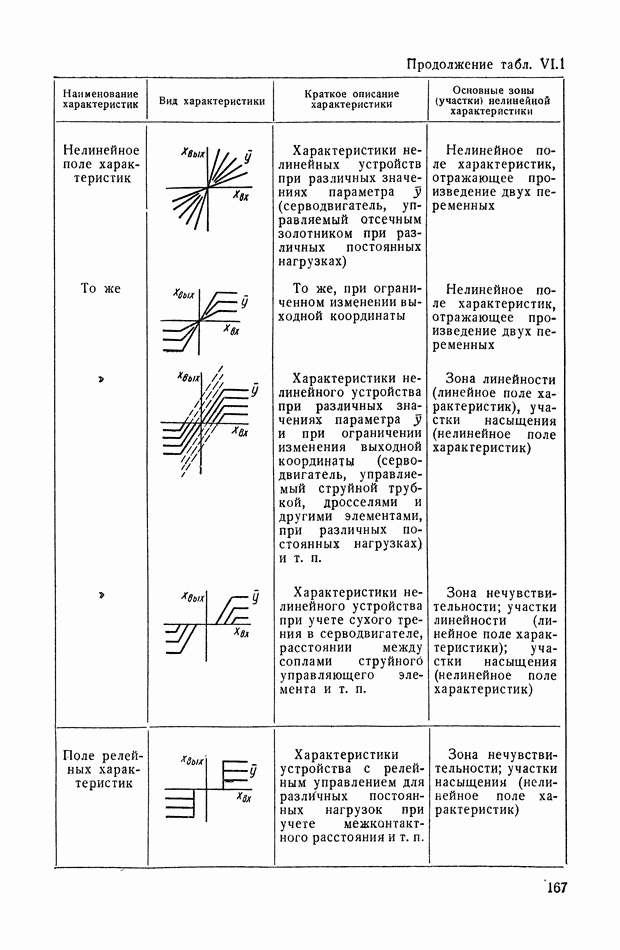
- 1. НЕЛИНЕЙНЫЕ ХАРАКТЕРИСТИКИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
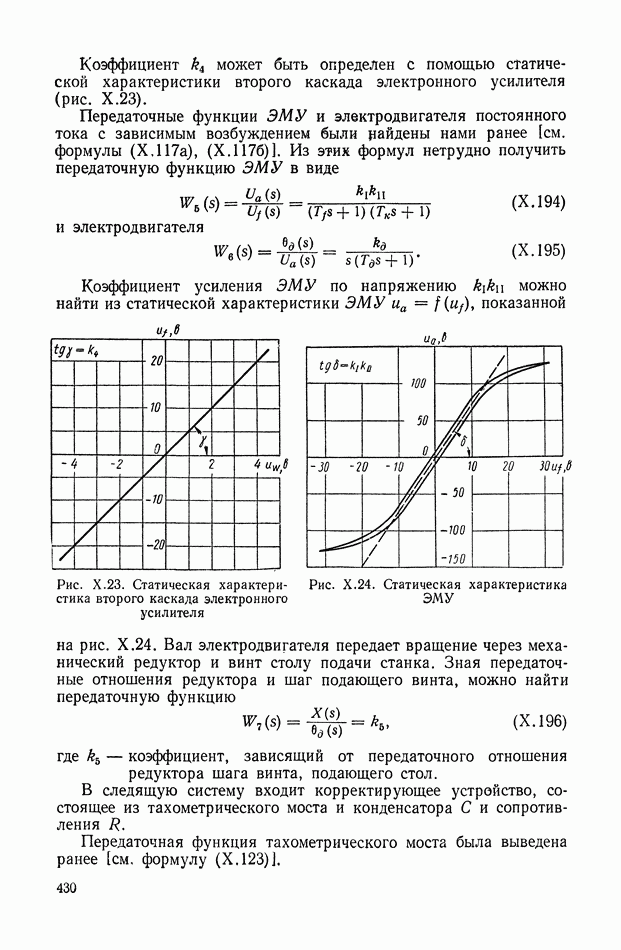
- 2. ВИДЫ ТИПИЧНЫХ НЕЛИНЕЙНЫХ СТАТИЧЕСКИХ ХАРАКТЕРИСТИК СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 3. ТИПИЧНЫЕ НЕЛИНЕЙНЫЕ ХАРАКТЕРИСТИКИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
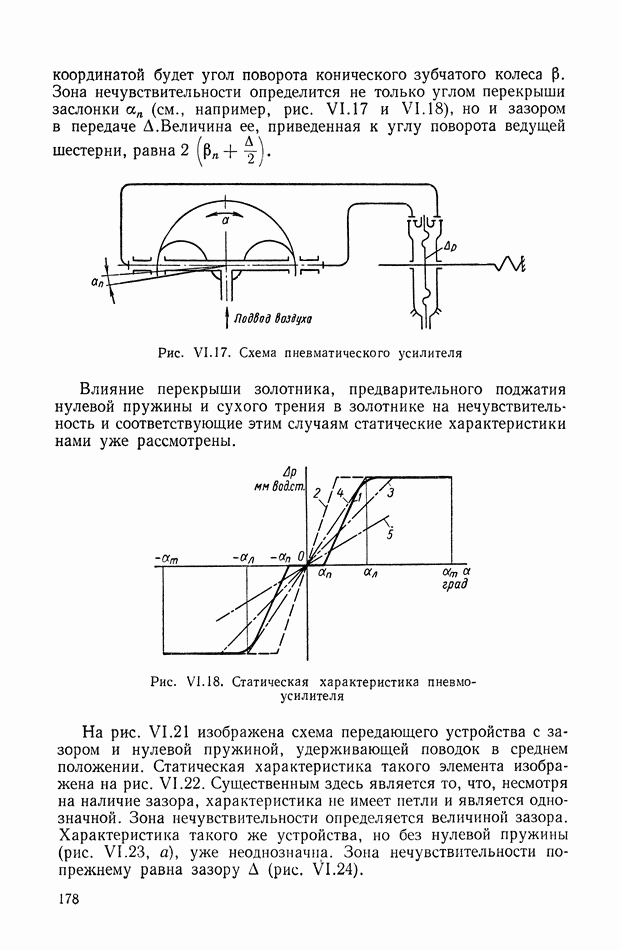
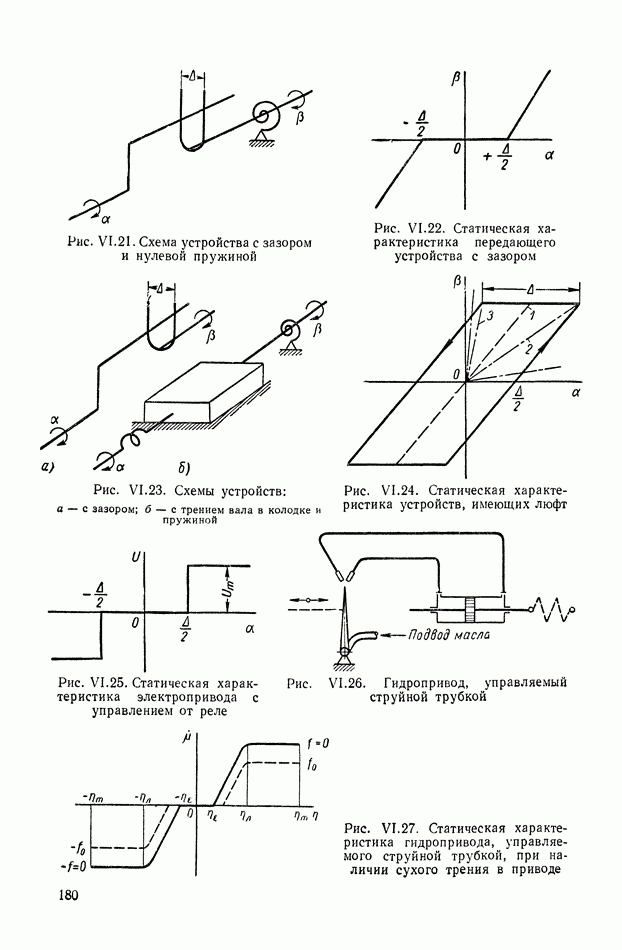
- 4. ЗОНЫ НЕЧУВСТВИТЕЛЬНОСТИ
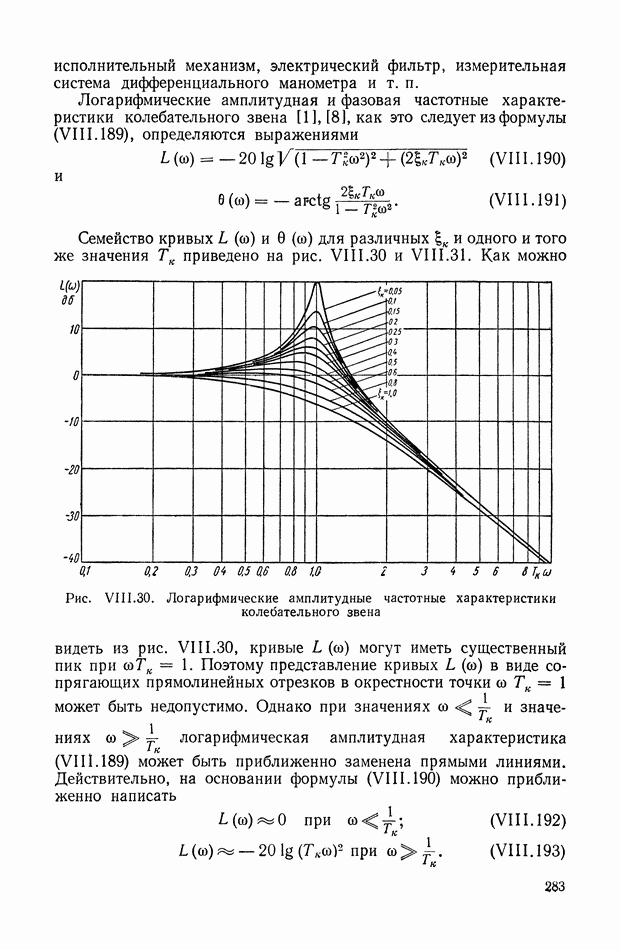
- 5. ЗОНЫ ЛИНЕЙНОСТИ И НЕОДНОЗНАЧНОСТИ
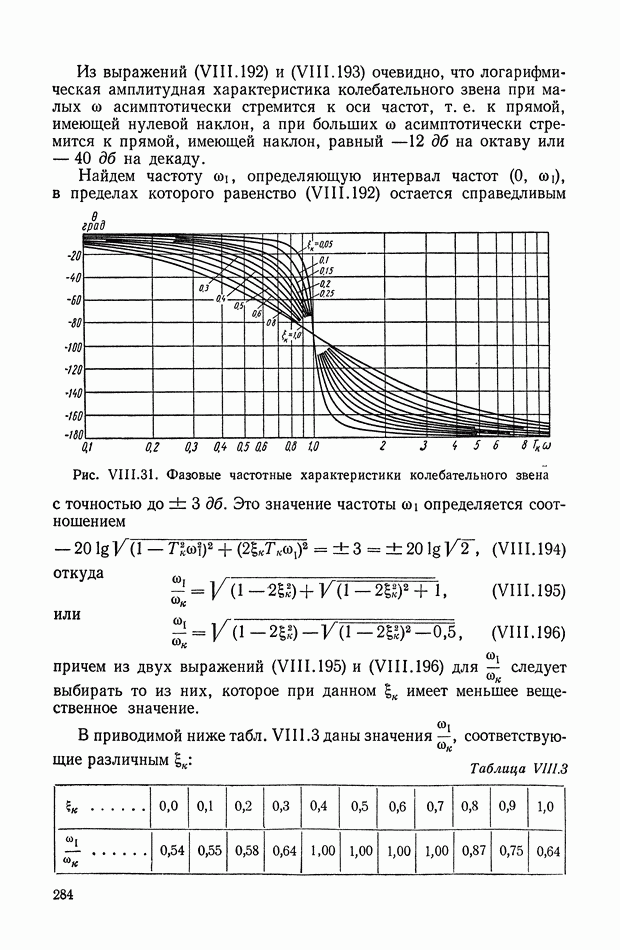
- 6. ЗОНЫ НАСЫЩЕНИЯ
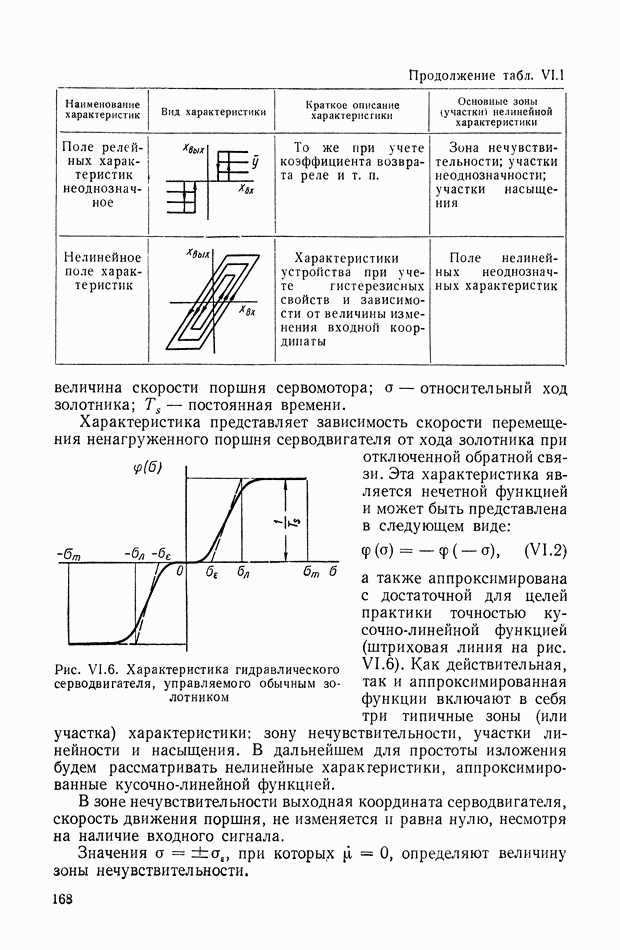
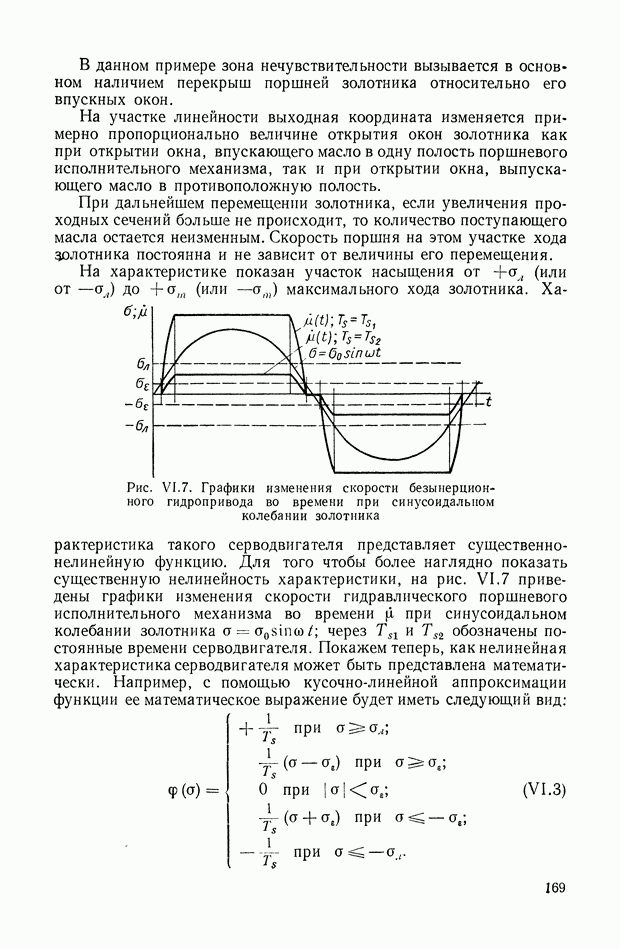
- 7. ПОЛЕ КРИВЫХ, ПРЕДСТАВЛЯЮЩИХ ХАРАКТЕРИСТИКУ СЕРВОДВИГАТЕЛЯ
- 8. ЭКСПЕРИМЕНТАЛЬНОЕ ВЫЯВЛЕНИЕ НЕЛИНЕЙНОСТИ ХАРАКТЕРИСТИК СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
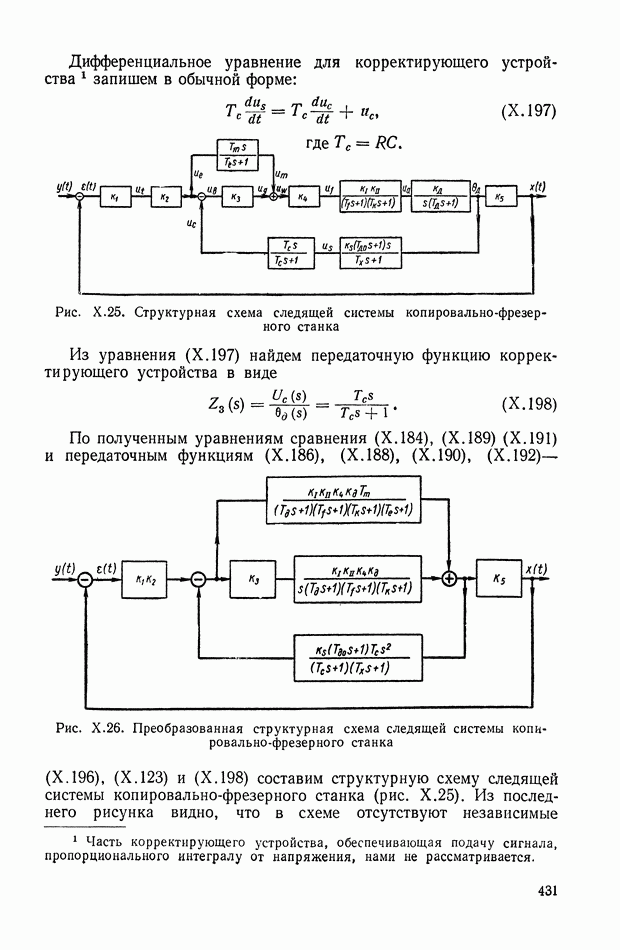
- ГЛАВА VII. ПЕРЕХОДНЫЕ ФУНКЦИИ, ПЕРЕДАТОЧНЫЕ ФУНКЦИИ И ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ДИНАМИЧЕСКИХ ЭЛЕМЕНТОВ
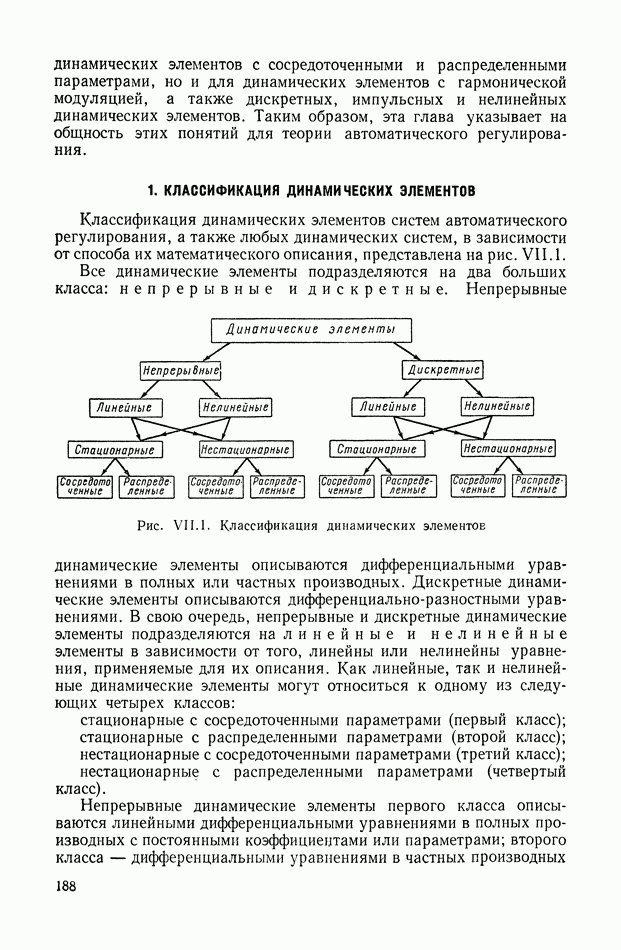
- 1. КЛАССИФИКАЦИЯ ДИНАМИЧЕСКИХ ЭЛЕМЕНТОВ
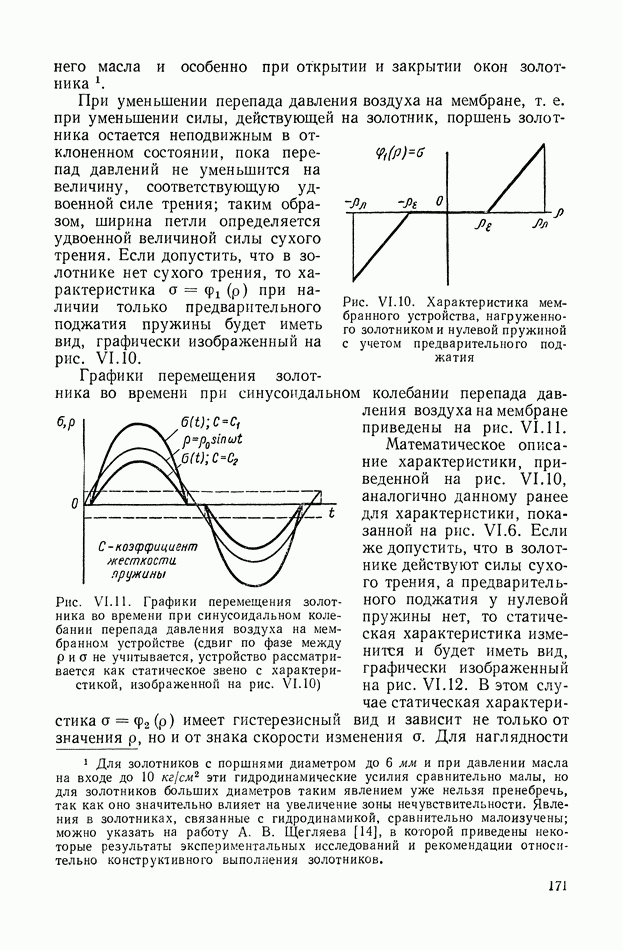
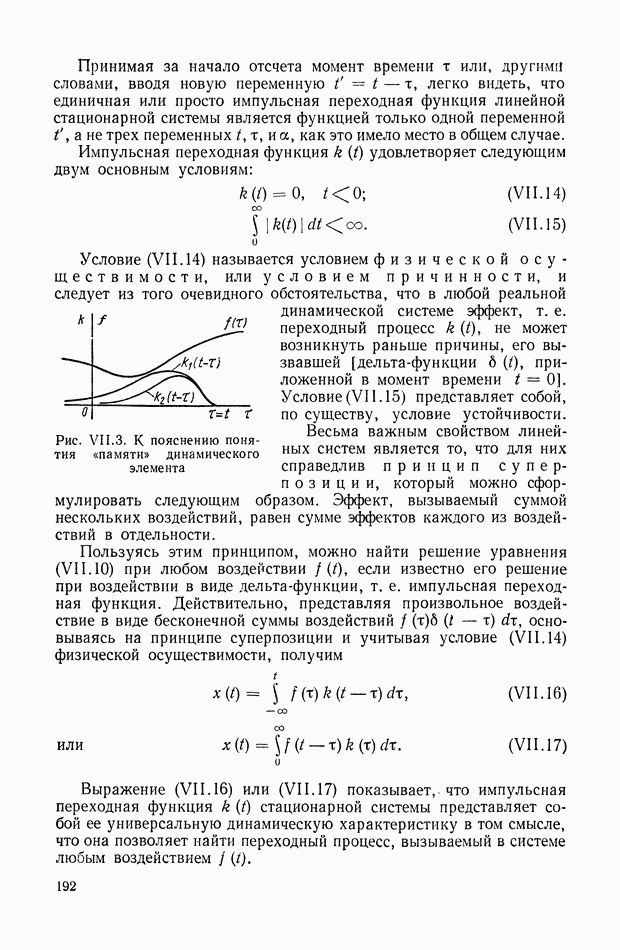
- 2. ОБЩЕЕ ОПРЕДЕЛЕНИЕ ИМПУЛЬСНОЙ ПЕРЕХОДНОЙ И ПЕРЕДАТОЧНОЙ ФУНКЦИЙ ДИНАМИЧЕСКОЙ СИСТЕМЫ ИЛИ ДИНАМИЧЕСКОГО ЭЛЕМЕНТА
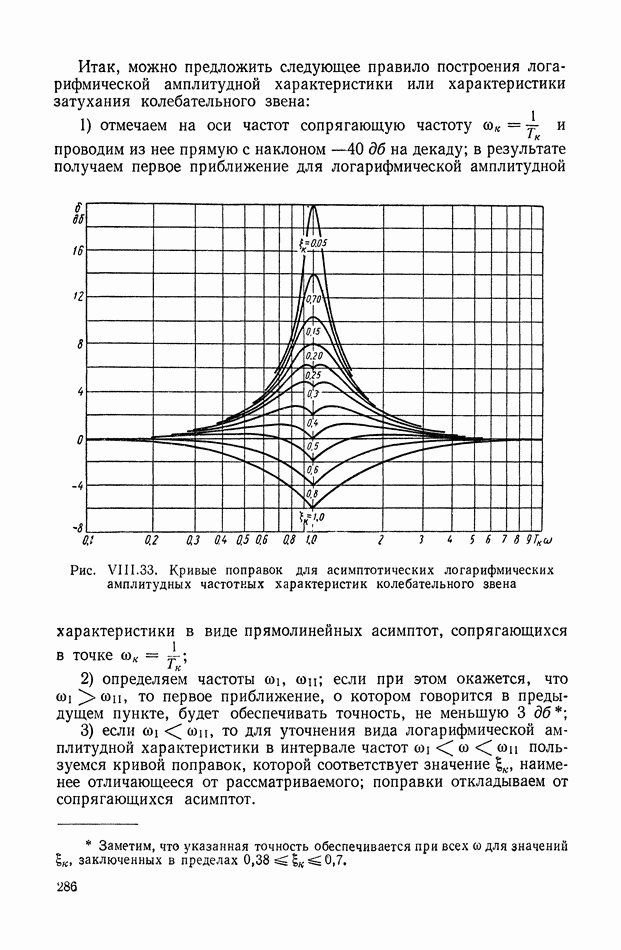
- 3. ИМПУЛЬСНАЯ ПЕРЕХОДНАЯ ФУНКЦИЯ НЕПРЕРЫВНОЙ СТАЦИОНАРНОЙ ЛИНЕЙНОЙ СИСТЕМЫ
- 4. ПЕРЕДАТОЧНАЯ ФУНКЦИЯ НЕПРЕРЫВНОЙ ЛИНЕЙНОЙ СТАЦИОНАРНОЙ СИСТЕМЫ
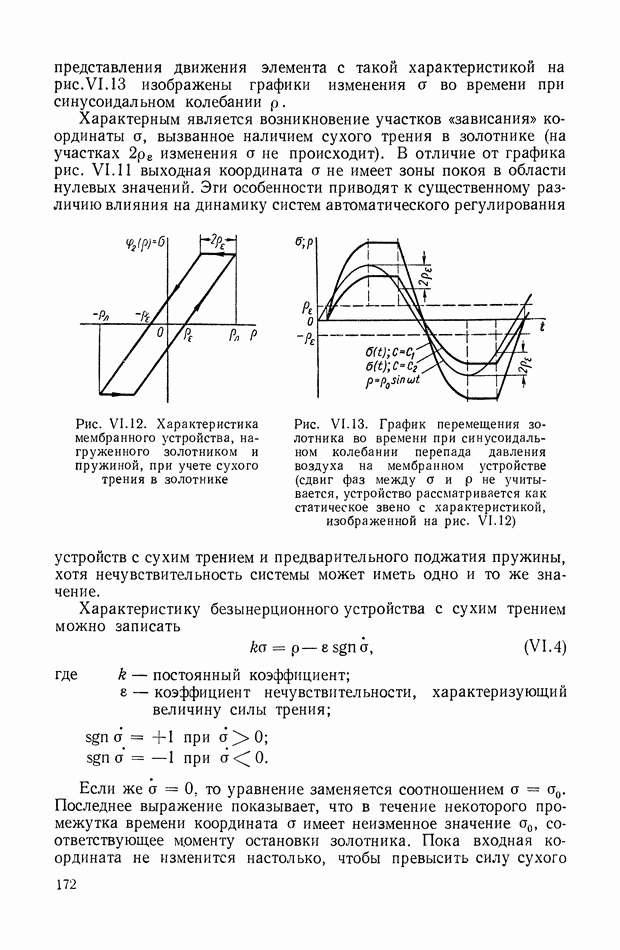
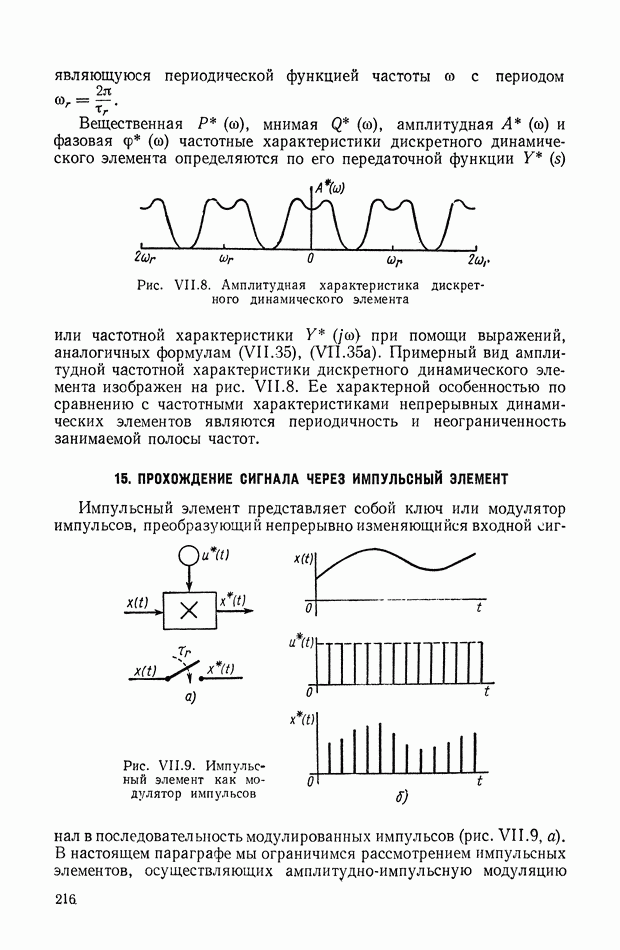
- 5. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЛИНЕЙНОЙ СТАЦИОНАРНОЙ НЕПРЕРЫВНОЙ ДИНАМИЧЕСКОЙ СИСТЕМЫ
- 6. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДИНАМИЧЕСКОГО ЭЛЕМЕНТА С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
- 7. ПРИМЕНЕНИЕ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА К РЕШЕНИЮ УРАВНЕНИЙ ЭЛЕМЕНТА С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
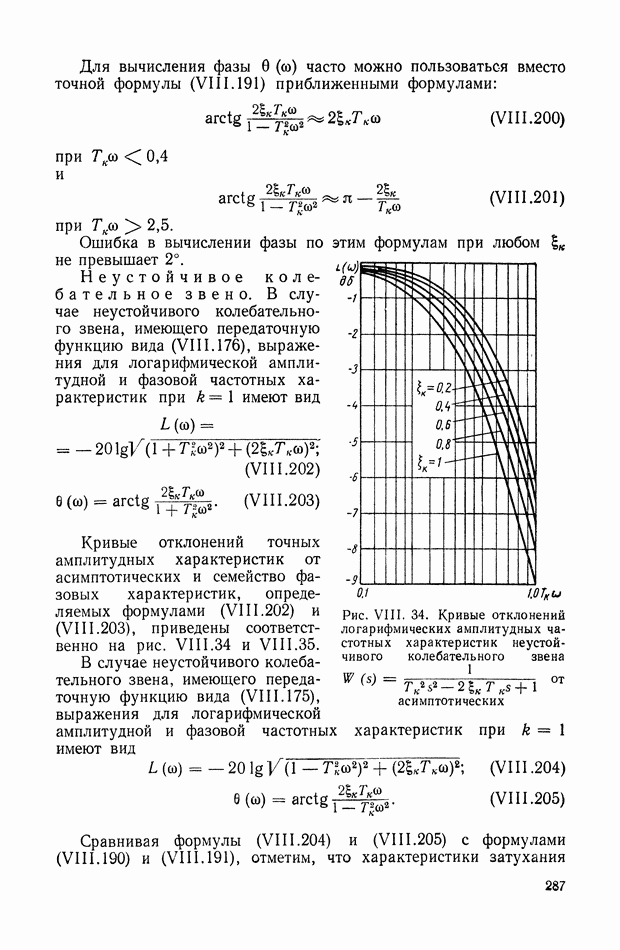
- 8. ПЕРЕДАТОЧНАЯ ФУНКЦИЯ ДИНАМИЧЕСКОГО ЭЛЕМЕНТА С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
- 9. ПЕРЕДАТОЧНАЯ ФУНКЦИЯ ПОСЛЕДОВАТЕЛЬНОГО СОЕДИНЕНИЯ ДИНАМИЧЕСКИХ ЭЛЕМЕНТОВ С СОСРЕДОТОЧЕННЫМИ И С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
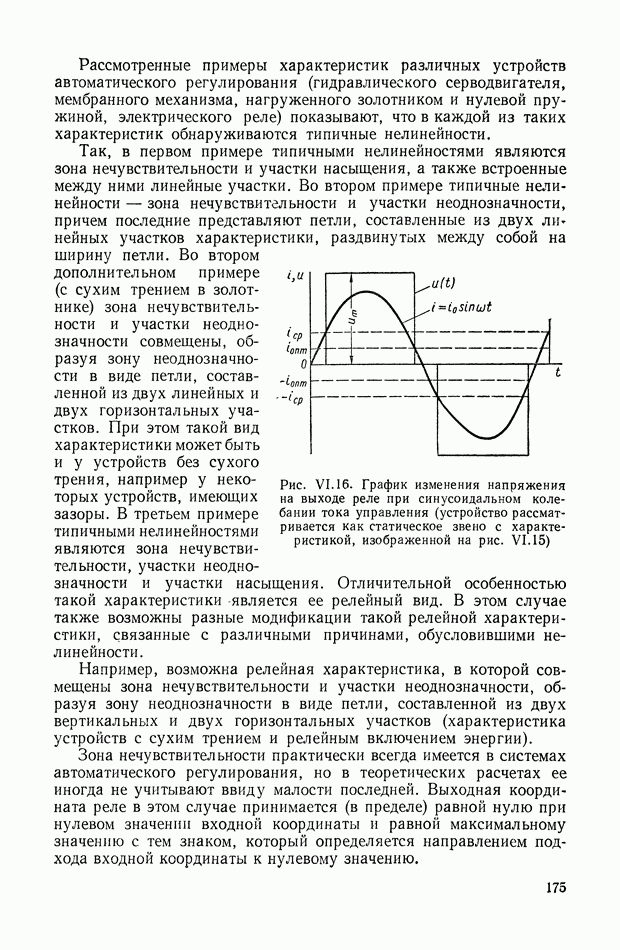
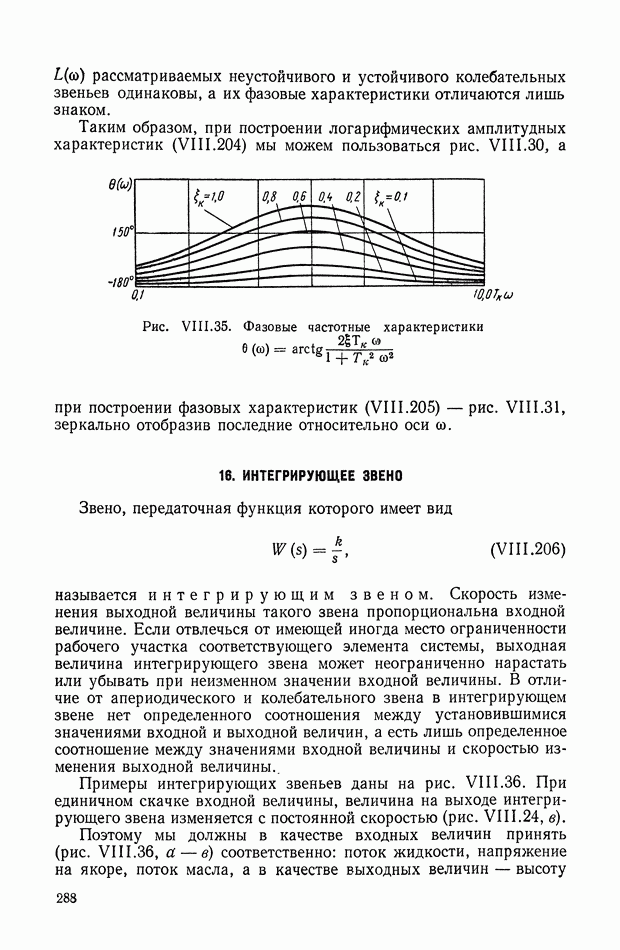
- 10. ПЕРЕДАТОЧНАЯ ФУНКЦИЯ ЗАПАЗДЫВАЮЩЕГО ЭЛЕМЕНТА
- 11. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЭЛЕМЕНТА С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
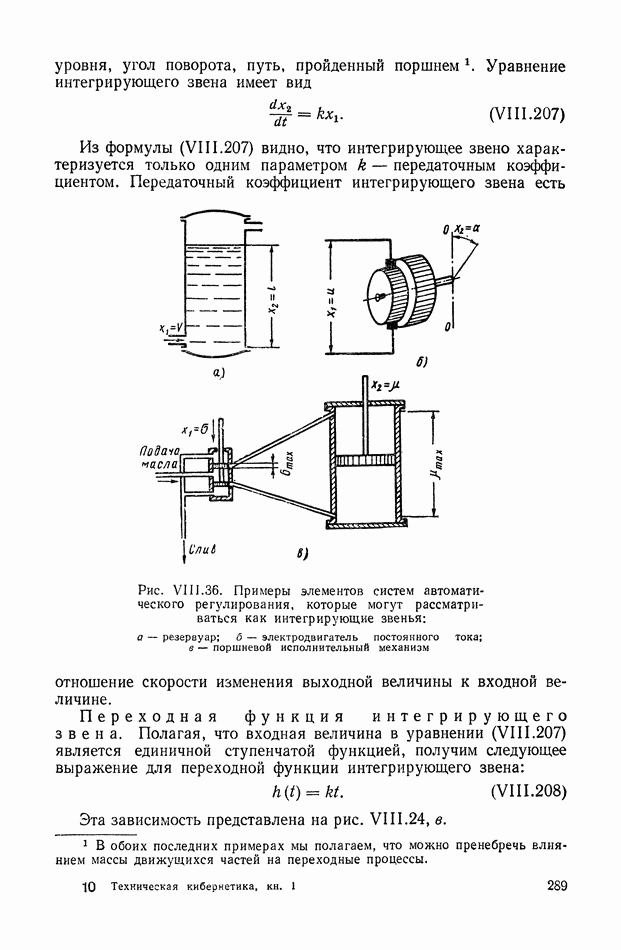
- 12. ИМПУЛЬСНАЯ ПЕРЕХОДНАЯ ФУНКЦИЯ ДИНАМИЧЕСКОГО ЭЛЕМЕНТА С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
- 13. ПЕРЕДАТОЧНАЯ ФУНКЦИЯ СИСТЕМЫ С ГАРМОНИЧЕСКОЙ МОДУЛЯЦИЕЙ
- 14 ИМПУЛЬСНАЯ ПЕРЕХОДНАЯ И ПЕРЕДАТОЧНАЯ ФУНКЦИИ ДИСКРЕТНОЙ ЛИНЕЙНОЙ СТАЦИОНАРНОЙ СИСТЕМЫ
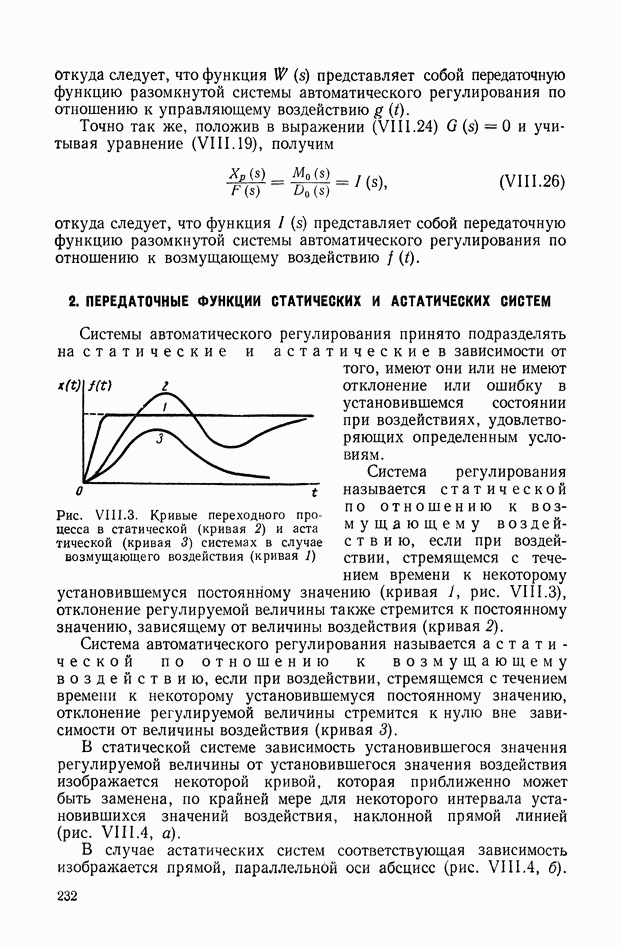
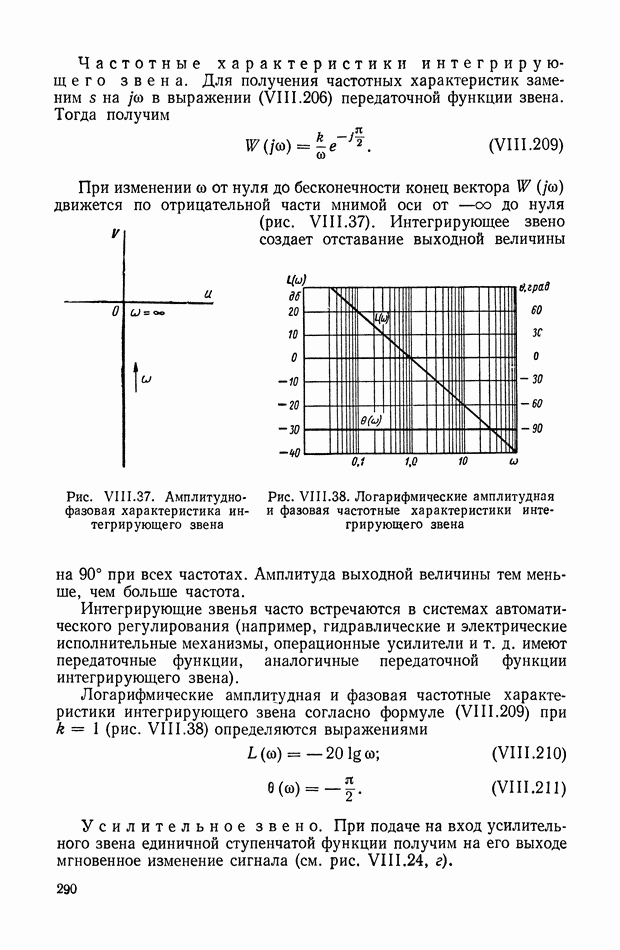
- 15. ПРОХОЖДЕНИЕ СИГНАЛА ЧЕРЕЗ ИМПУЛЬСНЫЙ ЭЛЕМЕНТ
- 16. ПОСЛЕДОВАТЕЛЬНОЕ СОЕДИНЕНИЕ ИМПУЛЬСНОГО ЭЛЕМЕНТА И НЕПРЕРЫВНОГО ДИНАМИЧЕСКОГО ЭЛЕМЕНТА
- 17. ИМПУЛЬСНАЯ ПЕРЕХОДНАЯ ФУНКЦИЯ ЛИНЕЙНОЙ НЕСТАЦИОНАРНОЙ СИСТЕМЫ (СИСТЕМЫ С ПЕРЕМЕННЫМИ ПАРАМЕТРАМИ)
- 18. ПЕРЕДАТОЧНАЯ ФУНКЦИЯ НЕПРЕРЫВНОЙ ЛИНЕЙНОЙ НЕСТАЦИОНАРНОЙ СИСТЕМЫ
- 19. МНОГОМЕРНЫЕ ИМПУЛЬСНЫЕ ПЕРЕХОДНЫЕ И ПЕРЕДАТОЧНЫЕ ФУНКЦИИ НЕЛИНЕЙНЫХ СИСТЕМ
- 20. МНОГОМЕРНЫЕ ПЕРЕДАТОЧНЫЕ ФУНКЦИИ НЕЛИНЕЙНЫХ СИСТЕМ
- ГЛАВА VIII. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ, ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ И ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ НЕПРЕРЫВНЫХ ЛИНЕЙНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
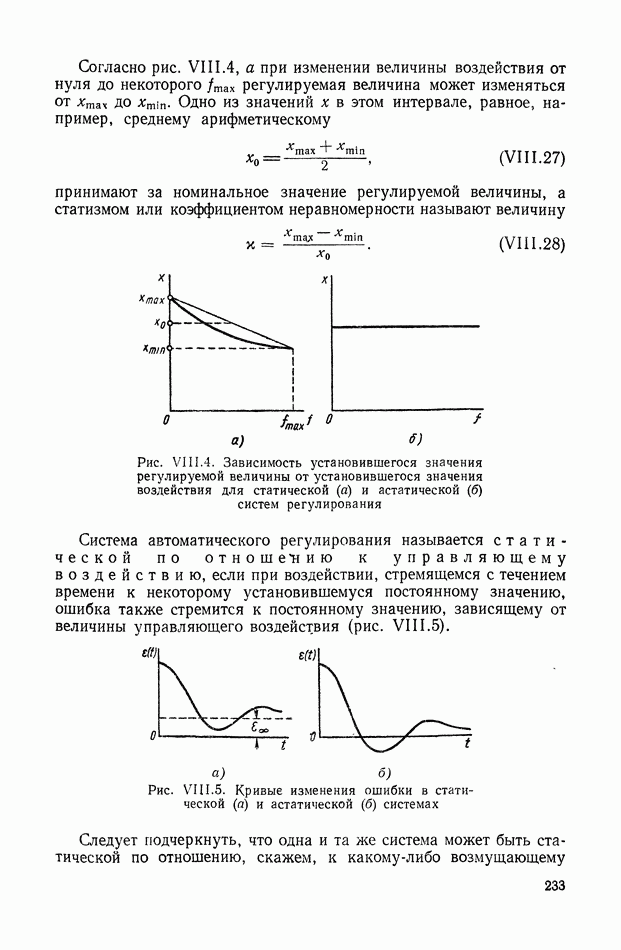
- 2. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ СТАТИЧЕСКИХ И АСТАТИЧЕСКИХ СИСТЕМ
- 3. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ
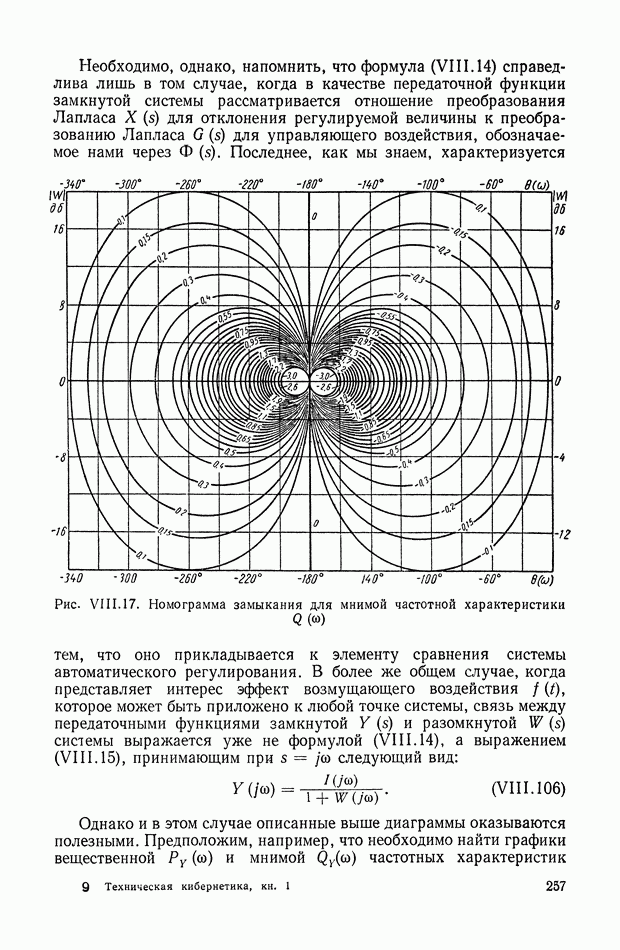
- 4. ВЗАИМНАЯ СВЯЗЬ МЕЖДУ ЧАСТОТНЫМИ ХАРАКТЕРИСТИКАМИ ЗАМКНУТОЙ И РАЗОМКНУТОЙ СИСТЕМЫ
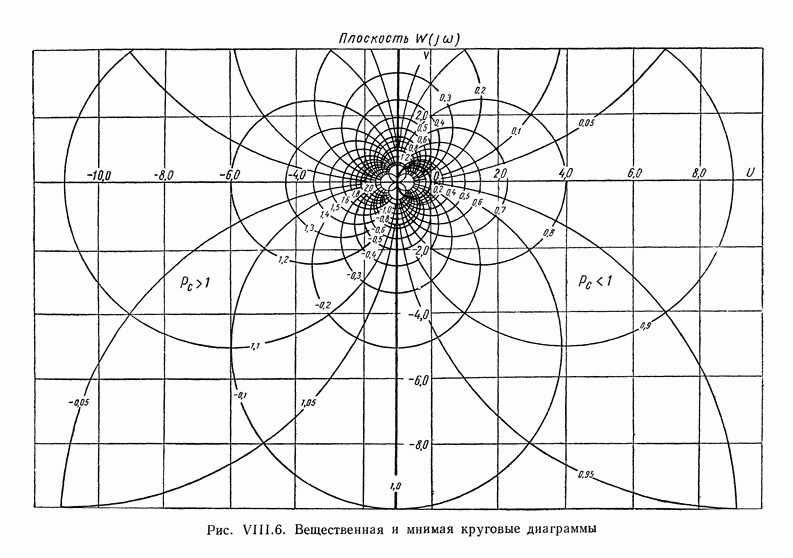
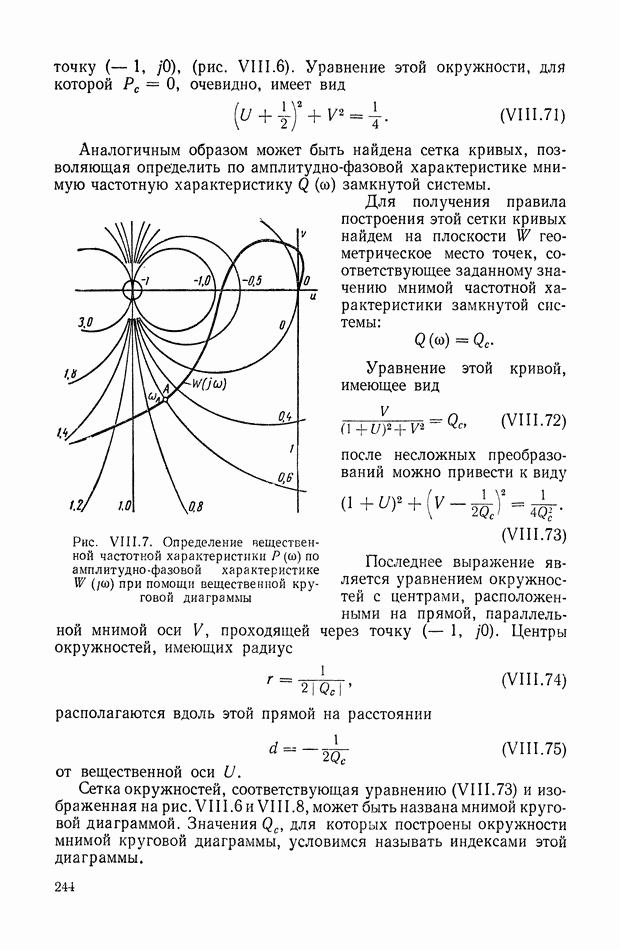
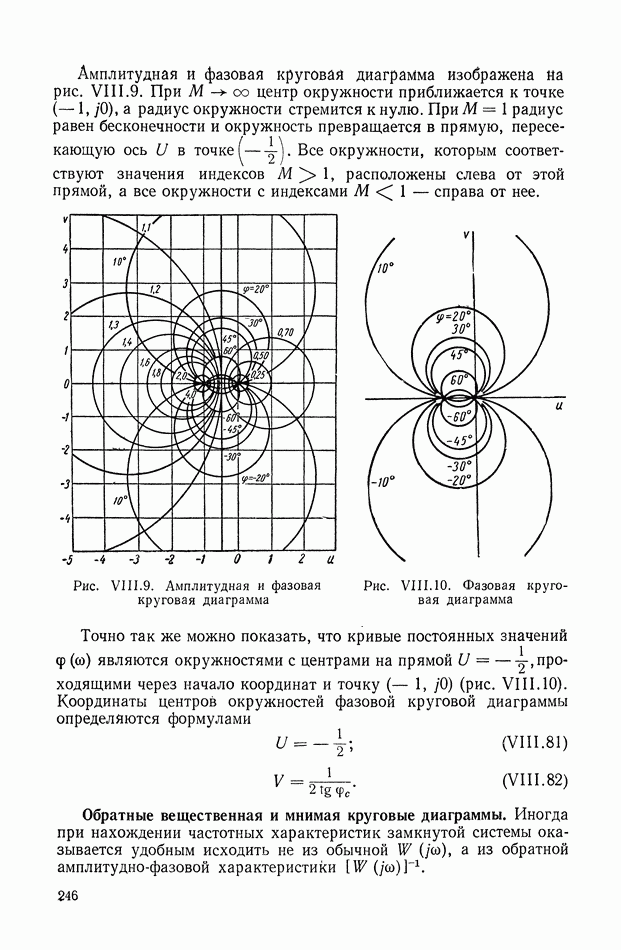
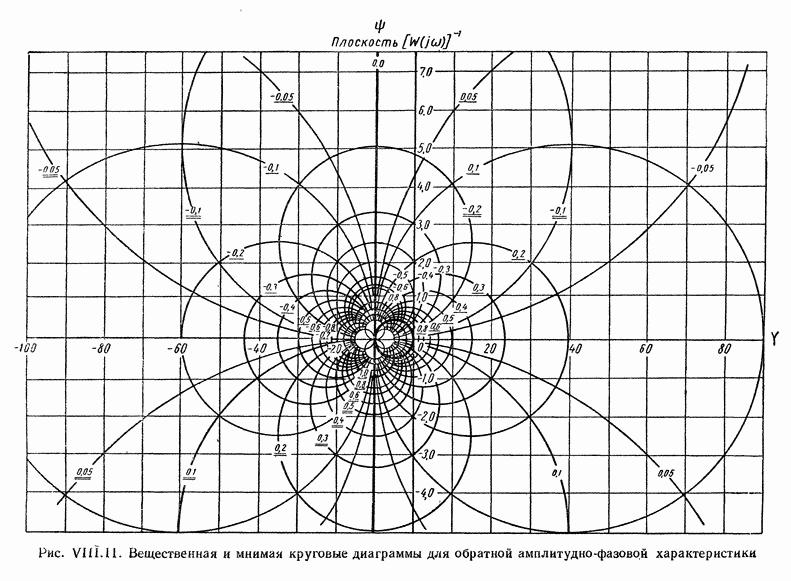
- 5. КРУГОВЫЕ ДИАГРАММЫ
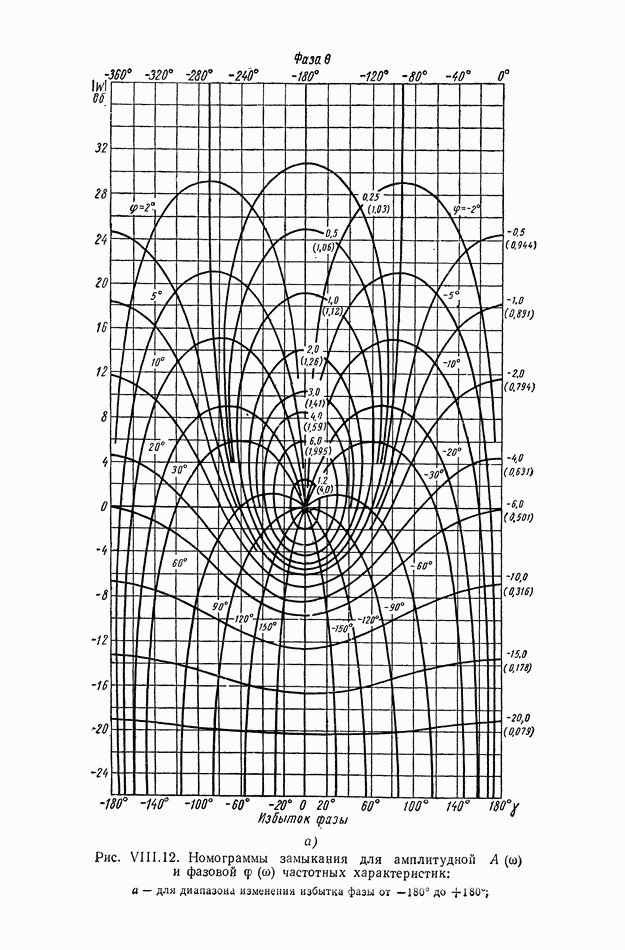
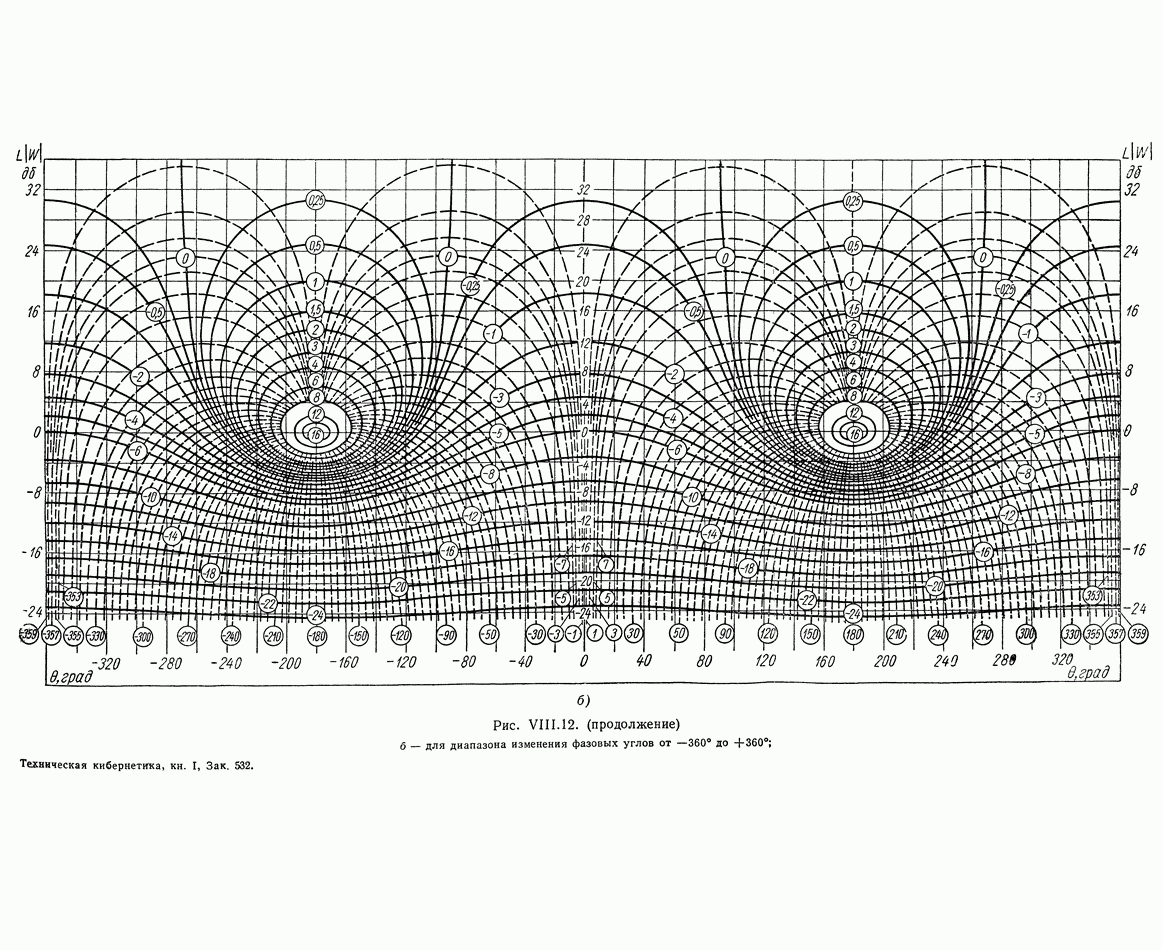
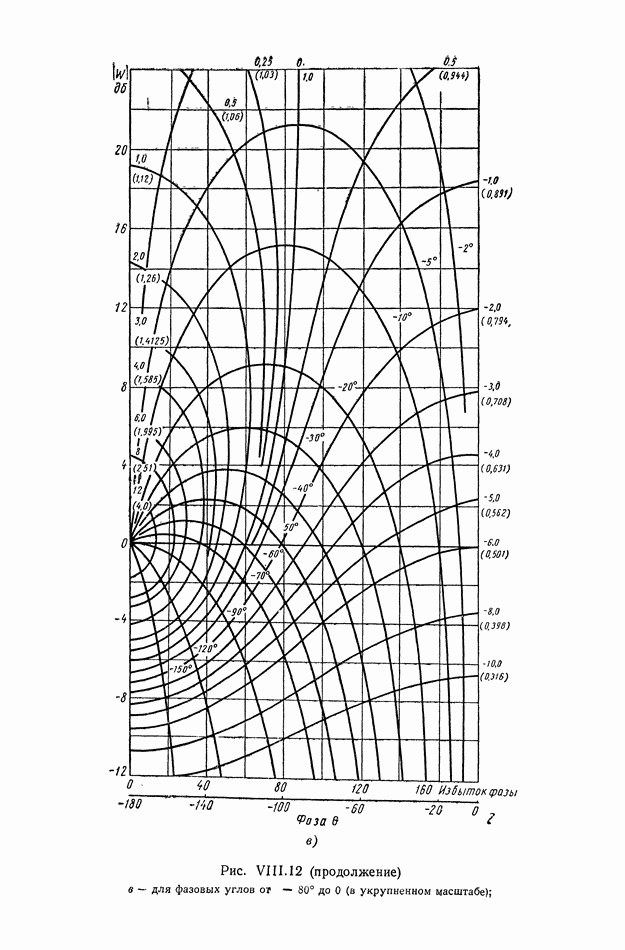
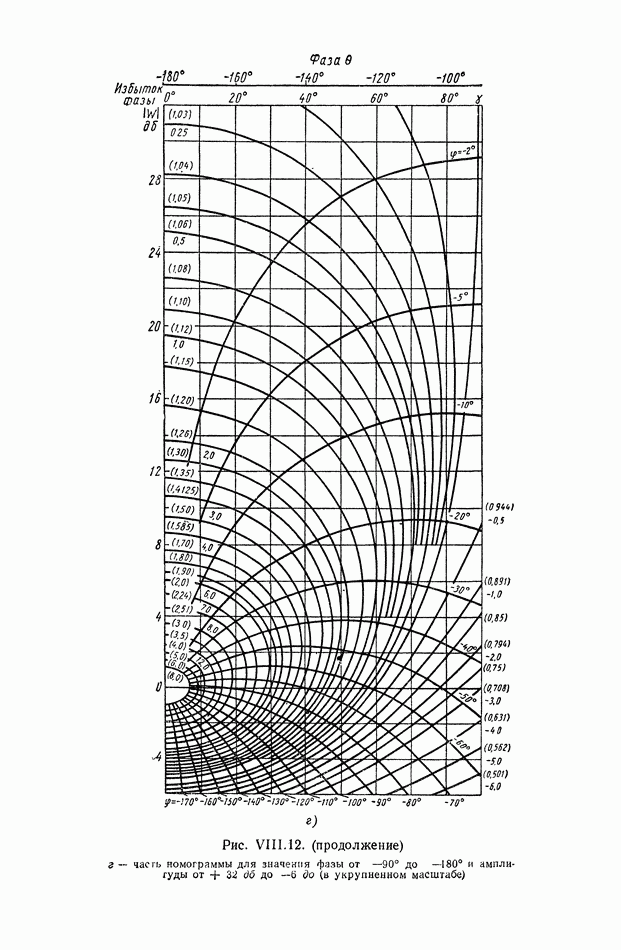
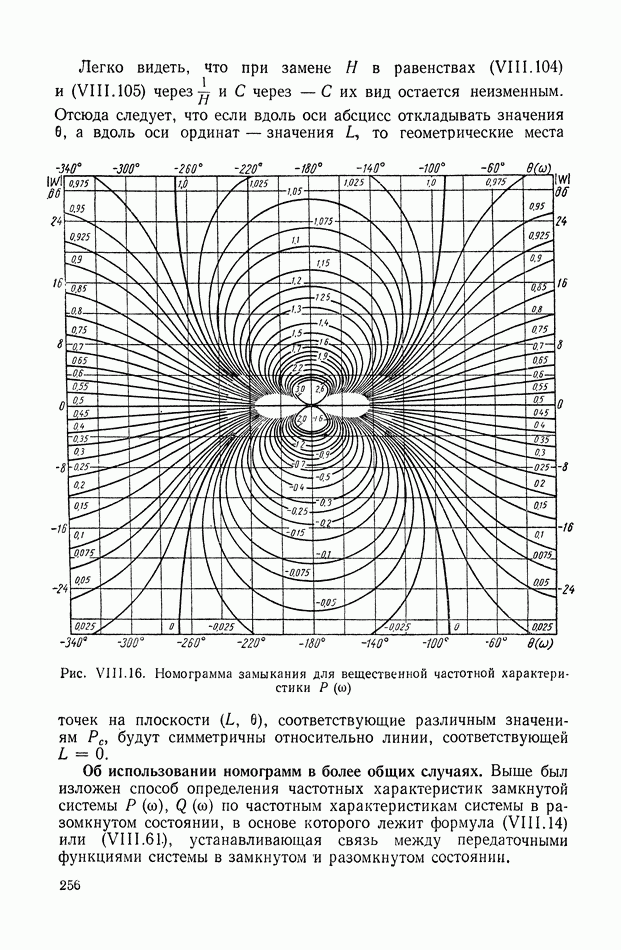
- 6. НОМОГРАММЫ ЗАМЫКАНИЯ
- 7. УСЛОВИЯ ОДНОЗНАЧНОЙ связи МЕЖДУ ЧАСТОТНЫМИ ХАРАКТЕРИСТИКАМИ
- 8. ОПРЕДЕЛЕНИЕ ПЕРЕДАТОЧНОЙ ФУНКЦИИ ПО ОДНОЙ ИЗ ЧАСТОТНЫХ ХАРАКТЕРИСТИК, ЗАДАННОЙ АНАЛИТИЧЕСКИ
- 9. ФОРМУЛА ДЛЯ ВЫЧИСЛЕНИЯ ФАЗОВОЙ ЧАСТОТНОЙ ХАРАКТЕРИСТИКИ ПО ЗАДАННОЙ АМПЛИТУДНОЙ ЧАСТОТНОЙ ХАРАКТЕРИСТИКЕ
- 10. ЗАВИСИМОСТЬ МЕЖДУ ЛОГАРИФМИЧЕСКОЙ АМПЛИТУДНОЙ И ФАЗОВОЙ ЧАСТОТНЫМИ ХАРАКТЕРИСТИКАМИ
- 11. ГРАФИЧЕСКИЙ МЕТОД ОПРЕДЕЛЕНИЯ ФАЗОВОЙ ХАРАКТЕРИСТИКИ ПО ЗАДАННОЙ АМПЛИТУДНОЙ ХАРАКТЕРИСТИКЕ
- 12. ИНТЕГРАЛЬНЫЕ ВЫРАЖЕНИЯ ДЛЯ ОШИБКИ И ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 13. ТИПОВЫЕ ЗВЕНЬЯ
- 14. АПЕРИОДИЧЕСКОЕ ЗВЕНО
- 15. КОЛЕБАТЕЛЬНОЕ ЗВЕНО
- 16. ИНТЕГРИРУЮЩЕЕ ЗВЕНО
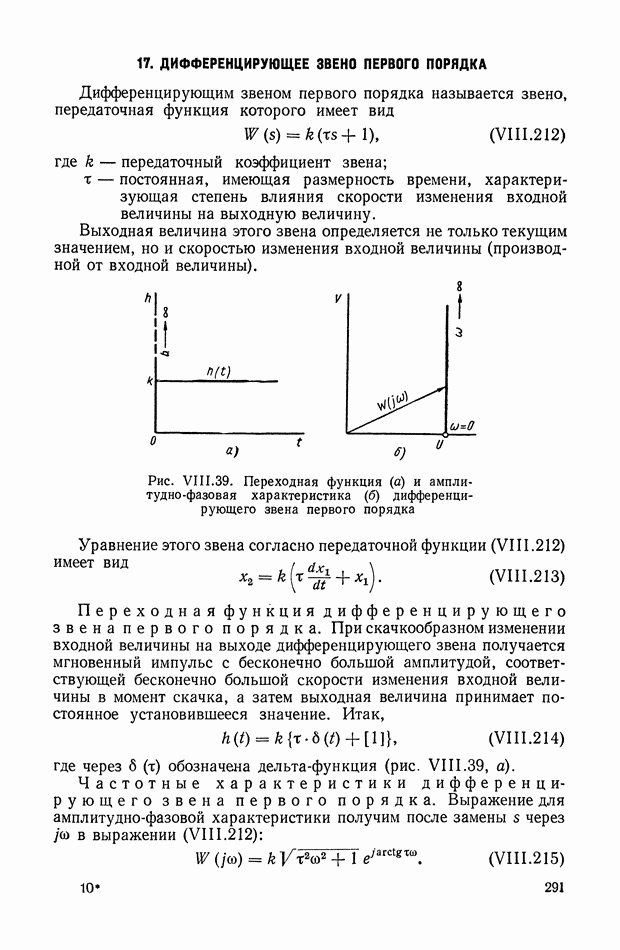
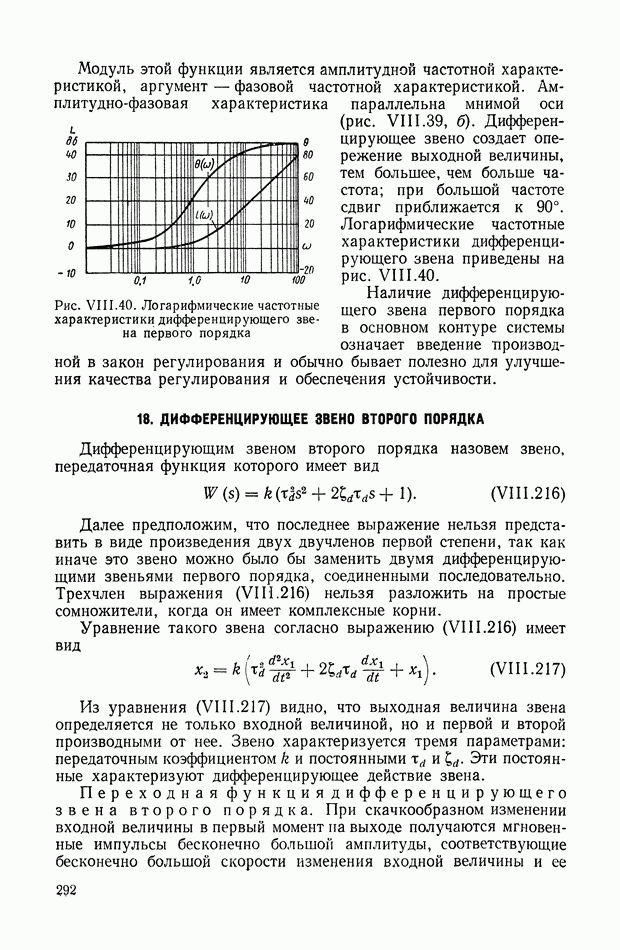
- 17. ДИФФЕРЕНЦИРУЮЩЕЕ ЗВЕНО ПЕРВОГО ПОРЯДКА
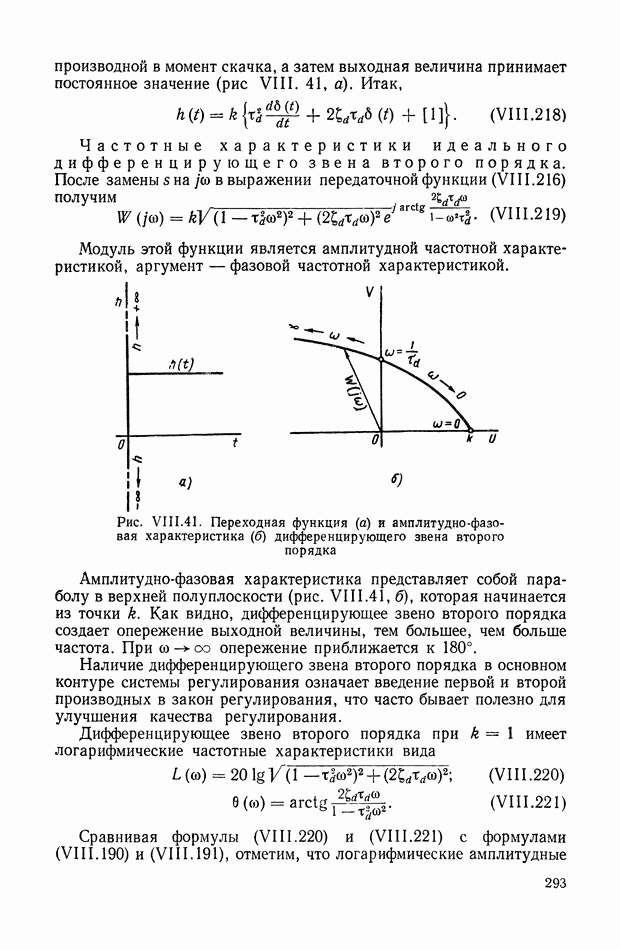
- 18. ДИФФЕРЕНЦИРУЮЩЕЕ ЗВЕНО ВТОРОГО ПОРЯДКА
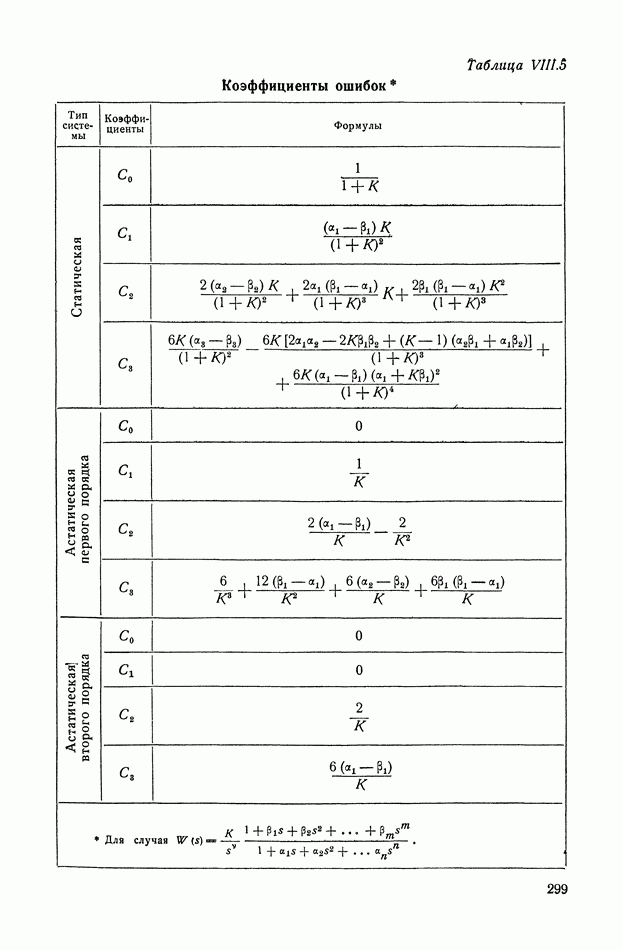
- 19. КОЭФФИЦИЕНТЫ ОШИБКИ
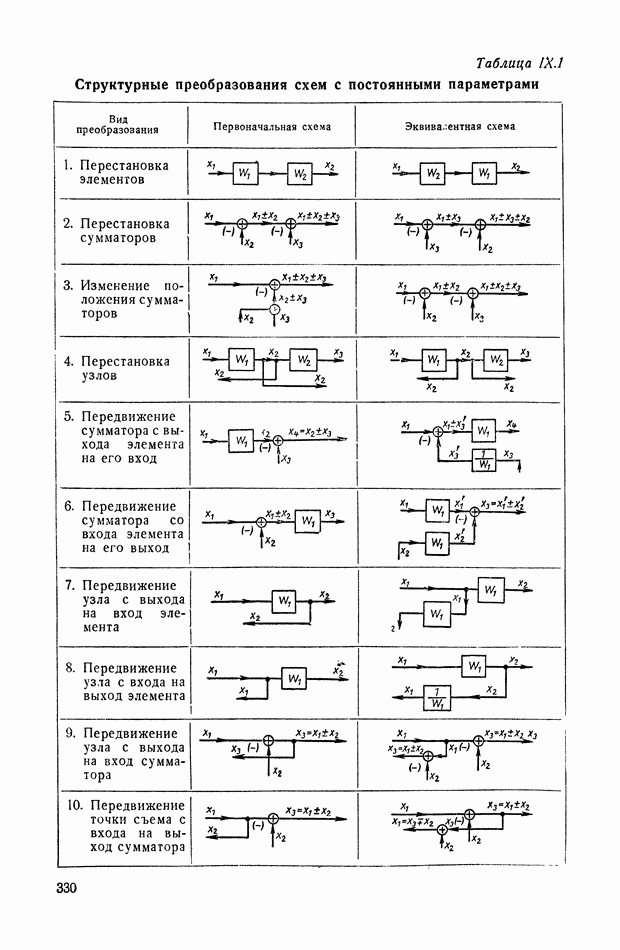
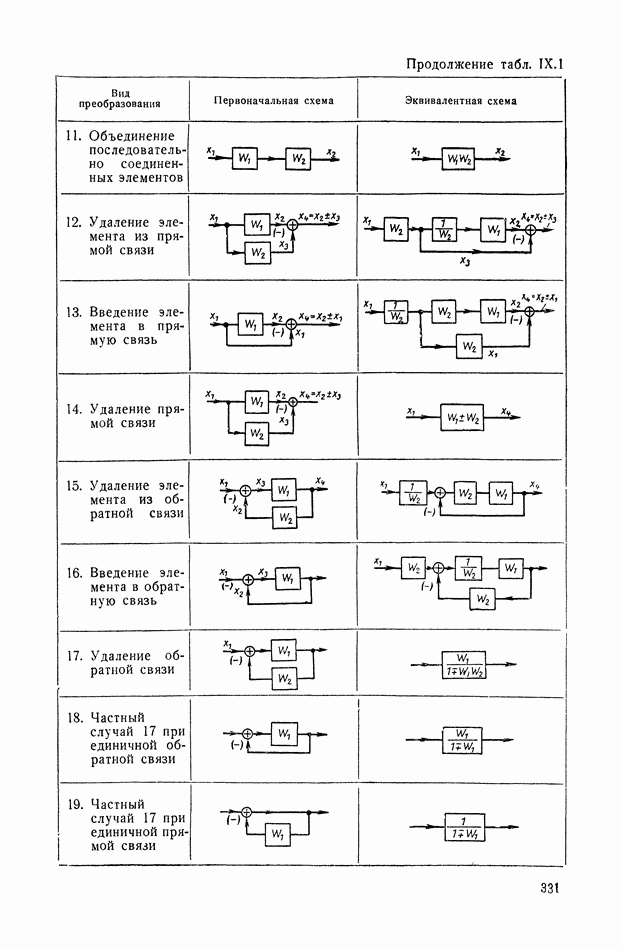
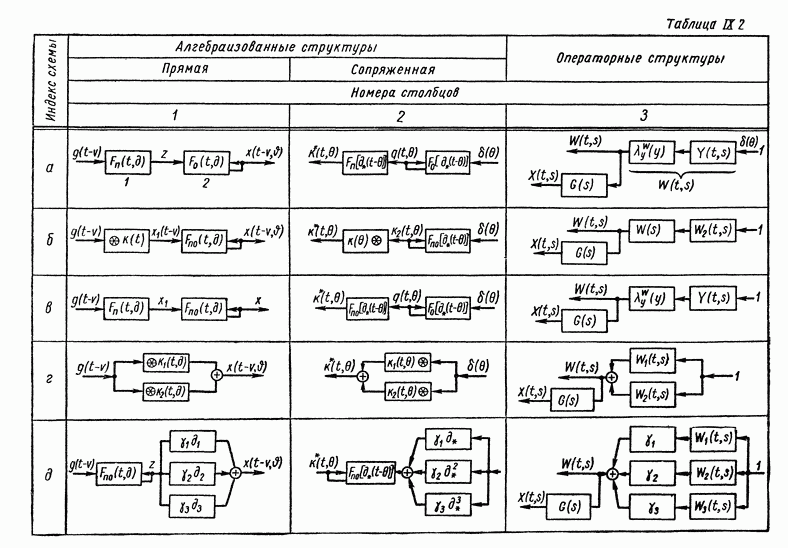
- ГЛАВА IX. МЕТОДЫ СТРУКТУРНЫХ ПРЕОБРАЗОВАНИЙ В СИСТЕМАХ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
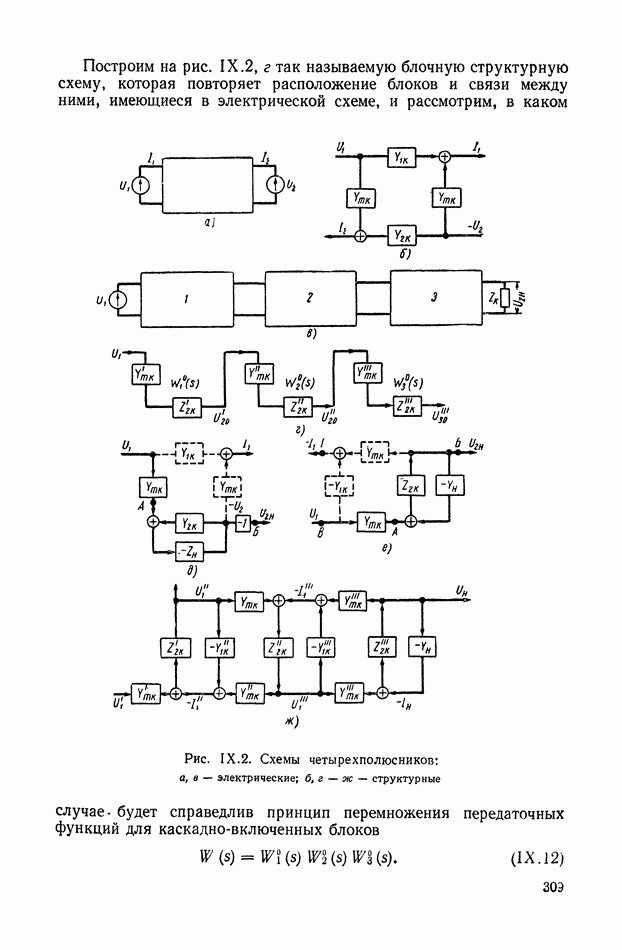
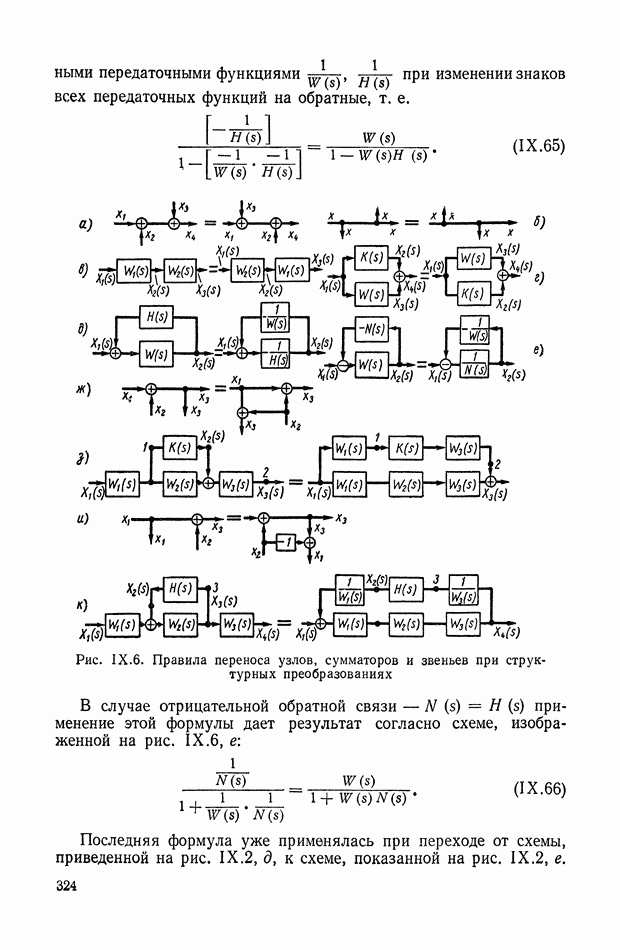
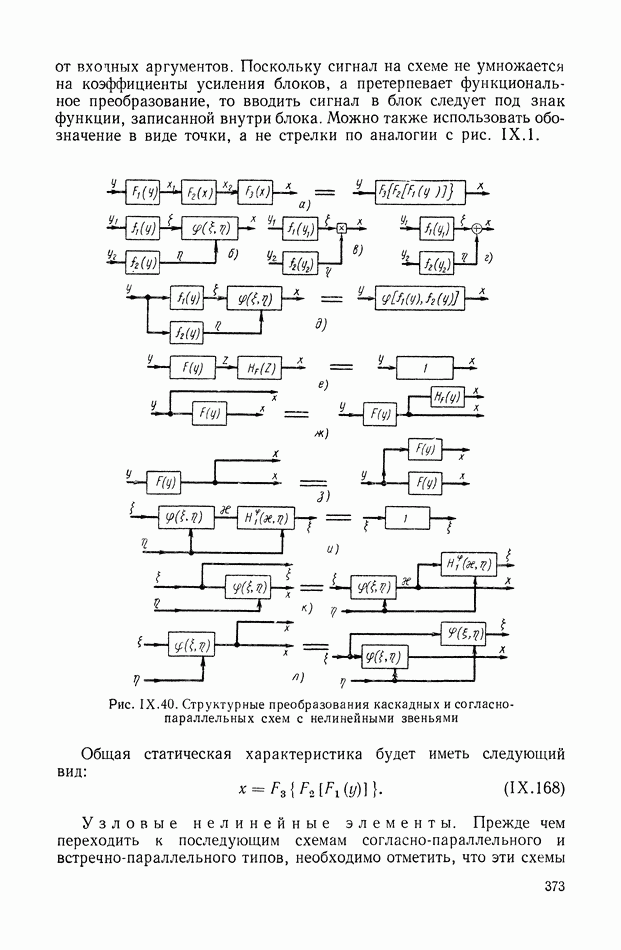
- 1. ГРАФИЧЕСКИЕ ИЗОБРАЖЕНИЯ УСЛОВИЙ ПРЕОБРАЗОВАНИЯ СИГНАЛОВ
- 2. СХЕМЫ С ЭЛЕМЕНТАМИ, ОБЛАДАЮЩИМИ И НЕ ОБЛАДАЮЩИМИ СВОЙСТВОМ НАПРАВЛЕННОСТИ ДЕЙСТВИЯ
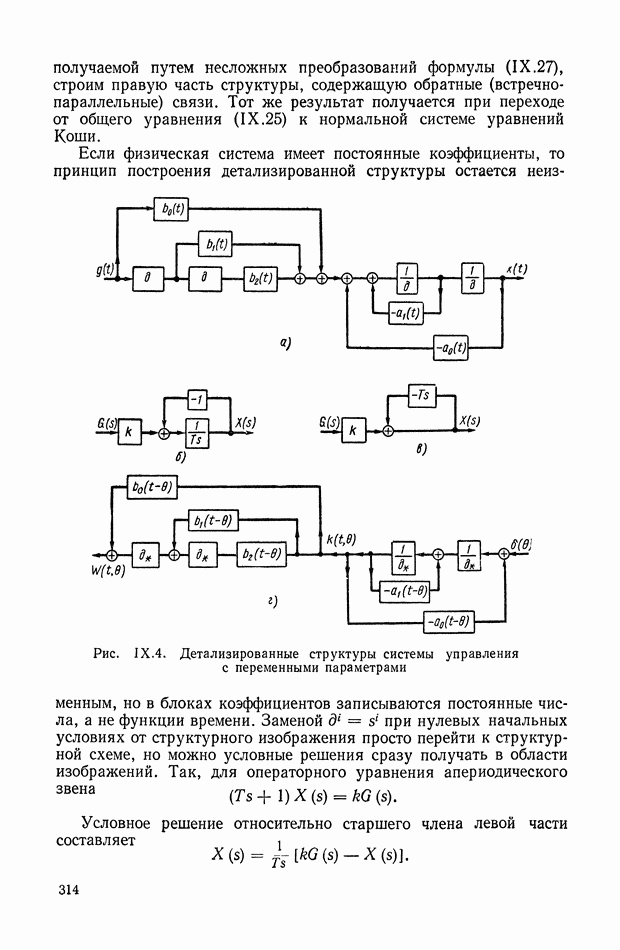
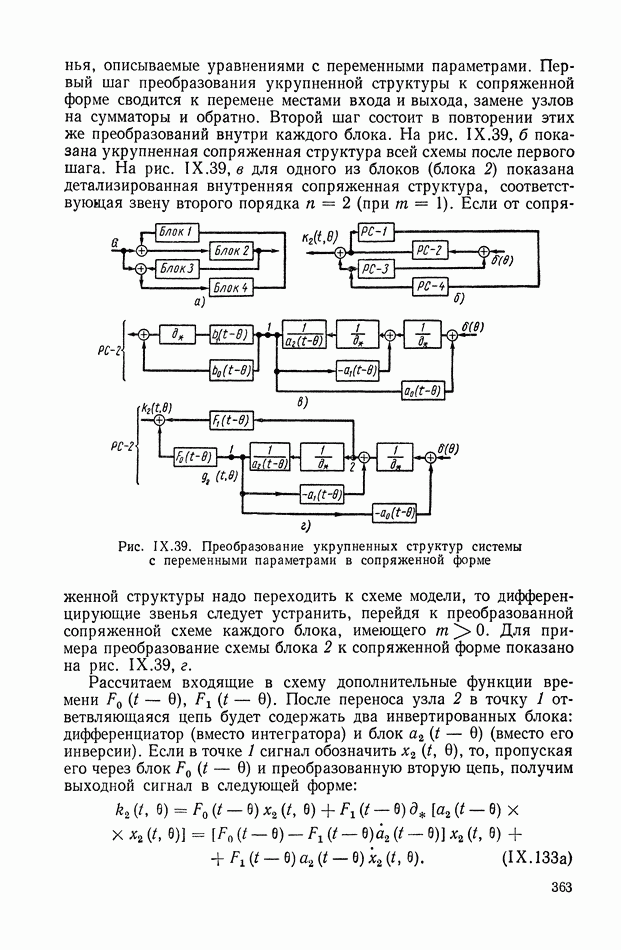
- 3. ДЕТАЛИЗИРОВАННЫЕ СТРУКТУРЫ
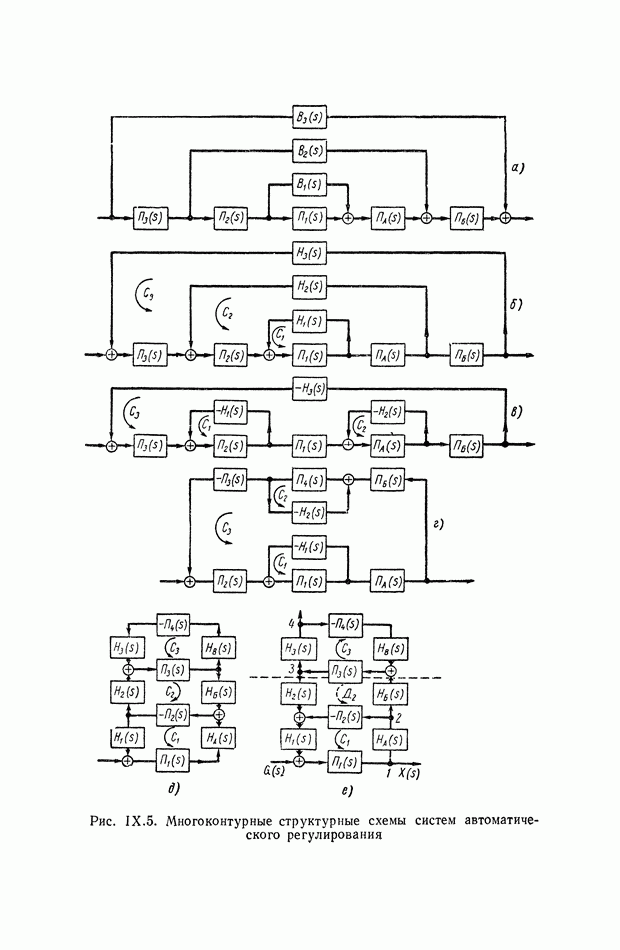
- 4. ПРЕОБРАЗОВАНИЯ МНОГОКОНТУРНЫХ СТРУКТУРНЫХ СХЕМ, ДОПУСКАЮЩИХ ПОСЛЕДОВАТЕЛЬНОЕ ПРИМЕНЕНИЕ ПРАВИЛ СВЕРТЫВАНИЯ КОНТУРОВ, И НЕКОТОРЫЕ ЭКВИВАЛЕНТНЫЕ ПРЕОБРАЗОВАНИЯ
- 5. ПРЕОБРАЗОВАНИЯ ПЕРЕКРЕСТНЫХ СТРУКТУРНЫХ СХЕМ МЕТОДОМ РАЗВЯЗКИ КОНТУРОВ И НЕКОТОРЫЕ ЭКВИВАЛЕНТНЫЕ ПРЕОБРАЗОВАНИЯ
- 6. ПРИМЕНЕНИЕ СТРУКТУРНЫХ МЕТОДОВ ДЛЯ ОПРЕДЕЛЕНИЯ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ МНОГОКОНТУРНЫХ СИСТЕМ
- 7. СОСТАВЛЕНИЕ И ПРЕОБРАЗОВАНИЕ СТРУКТУРНОЙ СХЕМЫ НА ПРИМЕРЕ ЭЛЕКТРОДВИГАТЕЛЯ ПОСТОЯННОГО ТОКА ДВОЙНОГО ПИТАНИЯ
- Учет зависимости момента нагрузки от угла поворота вала и его производных по времени.
- 8. СТРУКТУРНЫЕ СХЕМЫ МЕХАНИЧЕСКИХ ОБЪЕКТОВ РЕГУЛИРОВАНИЯ С РЕДУКТОРАМИ, ДИФФЕРЕНЦИАЛАМИ И УПРУГИМИ ЭЛЕМЕНТАМИ В СИЛОВЫХ ПЕРЕДАЧАХ
- 9. ПРАВИЛА СТРУКТУРНЫХ ПРЕОБРАЗОВАНИЙ ДЛЯ СИСТЕМ С ПЕРЕМЕННЫМИ ПАРАМЕТРАМИ
- 10. ФУНКЦИОНАЛЬНЫЕ СТРУКТУРНЫЕ СХЕМЫ ДЛЯ АНАЛИЗА СОВМЕСТНЫХ СТАТИЧЕСКИХ ХАРАКТЕРИСТИК НЕЛИНЕЙНЫХ ЗВЕНЬЕВ
- ГЛАВА X. ПРИМЕРЫ СОСТАВЛЕНИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ, СТРУКТУРНЫХ СХЕМ И ПЕРЕДАТОЧНЫХ ФУНКЦИЙ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. СИСТЕМА АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ СКОРОСТИ ВРАЩЕНИЯ ГИДРОТУРБИНЫ
- 2. ЭЛЕКТРОННЫЙ РЕГУЛЯТОР НАПРЯЖЕНИЯ ВЭИ
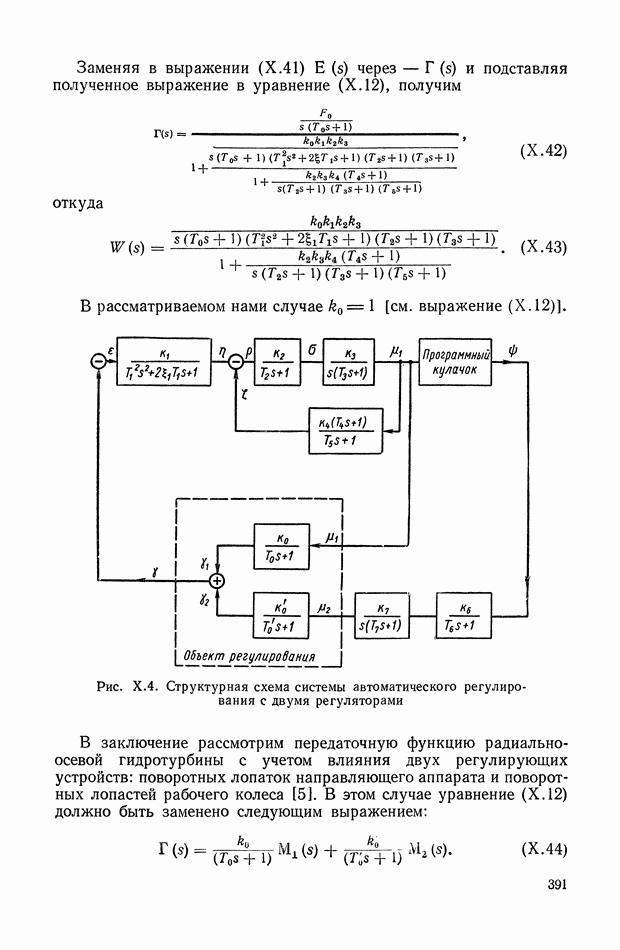
- 3. СИСТЕМА АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ МОЩНОСТИ ЯДЕРНОГО ЭНЕРГЕТИЧЕСКОГО РЕАКТОРА НА ТЕПЛОВЫХ НЕЙТРОНАХ
- 4. СЛЕДЯЩАЯ СИСТЕМА РАДИОЛОКАЦИОННОЙ СТАНЦИИ
- 5. СИСТЕМА АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ УНИВЕРСАЛЬНЫХ ЛЕТУЧИХ НОЖНИЦ
- 6. САМОЛЕТ С АВТОПИЛОТОМ
- 7. СЛЕДЯЩАЯ СИСТЕМА КОПИРОВАЛЬНО-ФРЕЗЕРНОГО СТАНКА
- РАЗДЕЛ II. АНАЛИЗ УСТОЙЧИВОСТИ НЕПРЕРЫВНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- ГЛАВА XI. ОБЩАЯ ПОСТАНОВКА ЗАДАЧИ УСТОЙЧИВОСТИ ПО ЛЯПУНОВУ И АНАЛИЗ УСТОЙЧИВОСТИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. ПОСТАНОВКА ЗАДАЧИ ОБ УСТОЙЧИВОСТИ В ТЕОРИИ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 2. ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ УСТАНОВИВШИХСЯ ДВИЖЕНИЙ ПО УРАВНЕНИЮ ПЕРВОГО ПРИБЛИЖЕНИЯ
- 3. О ПРЯМОМ МЕТОДЕ ЛЯПУНОВА
- 4. О ПРИМЕНЕНИИ ПРЯМОГО МЕТОДА ЛЯПУНОВА К АНАЛИЗУ УСТОЙЧИВОСТИ ОДНОГО КЛАССА СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- ГЛАВА XII. КРИТЕРИИ И МЕТОДЫ АНАЛИЗА УСТОЙЧИВОСТИ ЛИНЕАРИЗОВАННЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЙ
- 1. УСТОЙЧИВОСТЬ И ПРИНЦИП АРГУМЕНТА
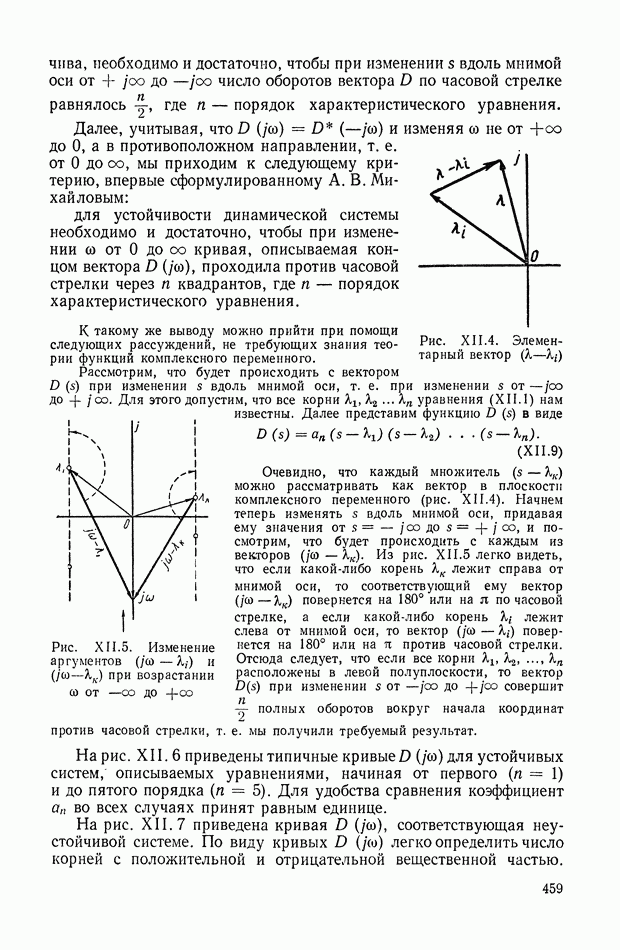
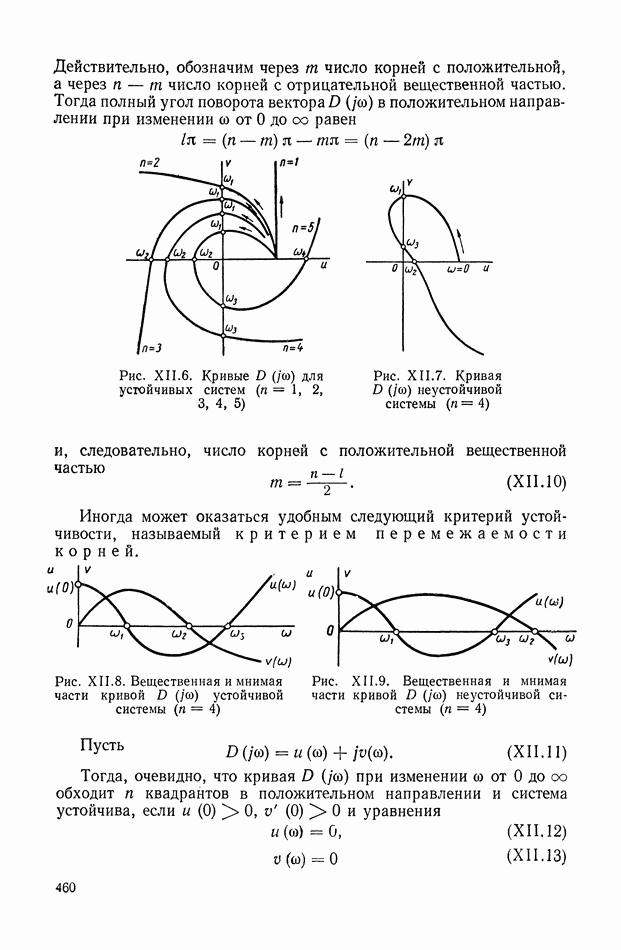
- 2. КРИТЕРИЙ УСТОЙЧИВОСТИ МИХАЙЛОВА
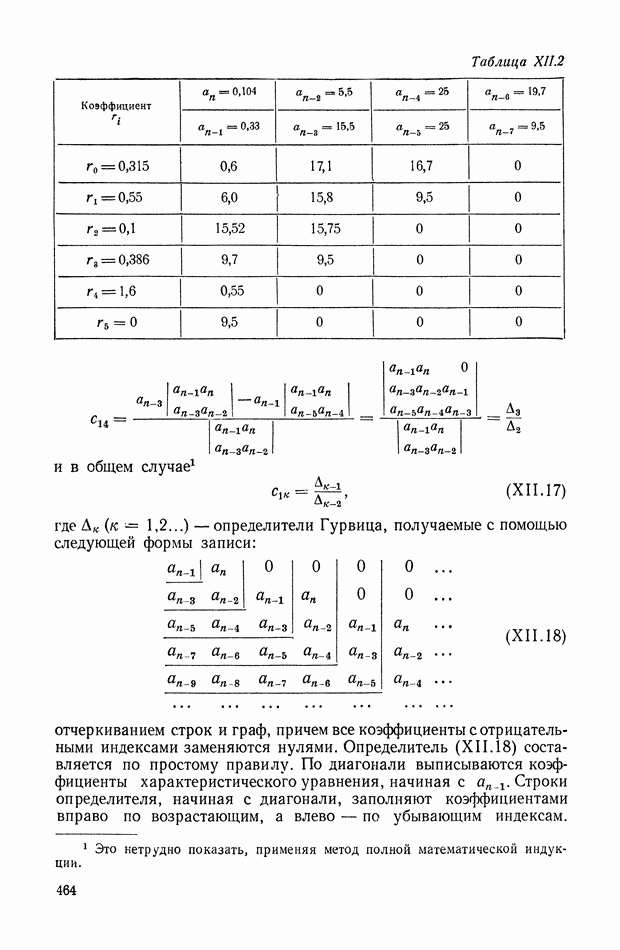
- 3. КРИТЕРИЙ УСТОЙЧИВОСТИ РАУСА И ГУРВИЦА
- 4. ЧАСТОТНЫЙ КРИТЕРИЙ УСТОЙЧИВОСТИ
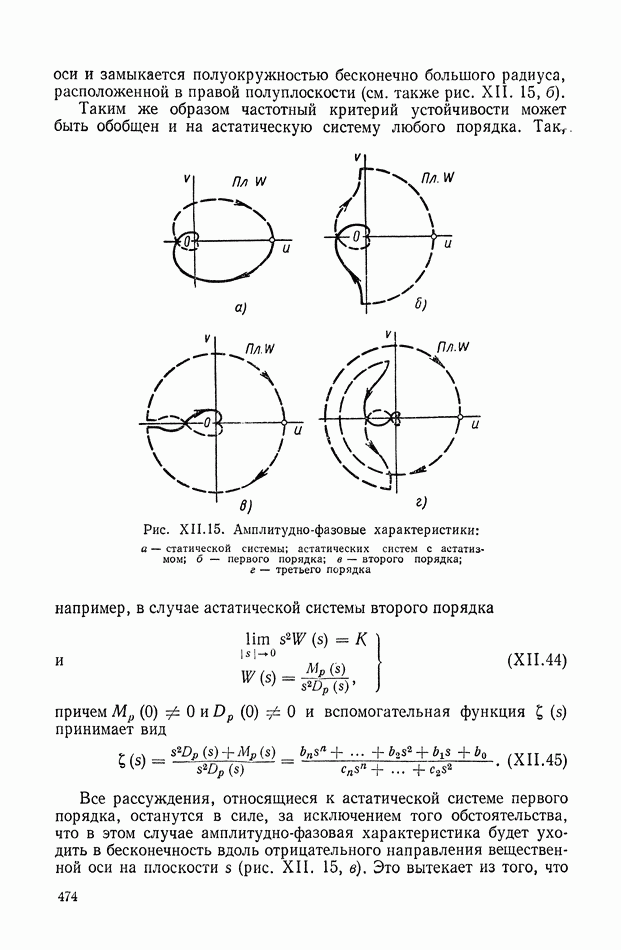
- 5. ОБОБЩЕНИЕ ЧАСТОТНОГО КРИТЕРИЯ НА АСТАТИЧЕСКИЕ СИСТЕМЫ
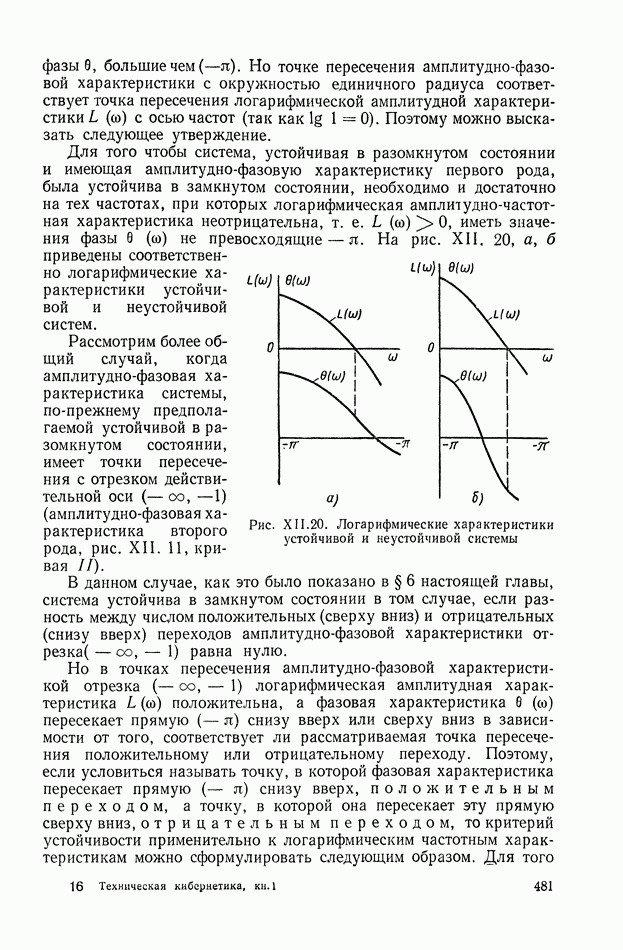
- 6. ОБОБЩЕНИЕ ЧАСТОТНОГО КРИТЕРИЯ НА СЛУЧАЙ, КОГДА РАЗОМКНУТАЯ СИСТЕМА НЕУСТОЙЧИВА
- 7. ЧАСТОТНЫЙ КРИТЕРИЙ УСТОЙЧИВОСТИ ДЛЯ ОБРАТНОЙ АМПЛИТУДНО-ФАЗОВОЙ ХАРАКТЕРИСТИКИ
- 8. АНАЛИЗ УСТОЙЧИВОСТИ ОДНОКОНТУРНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ПО ИХ ЛОГАРИФМИЧЕСКИМ ЧАСТОТНЫМ ХАРАКТЕРИСТИКАМ
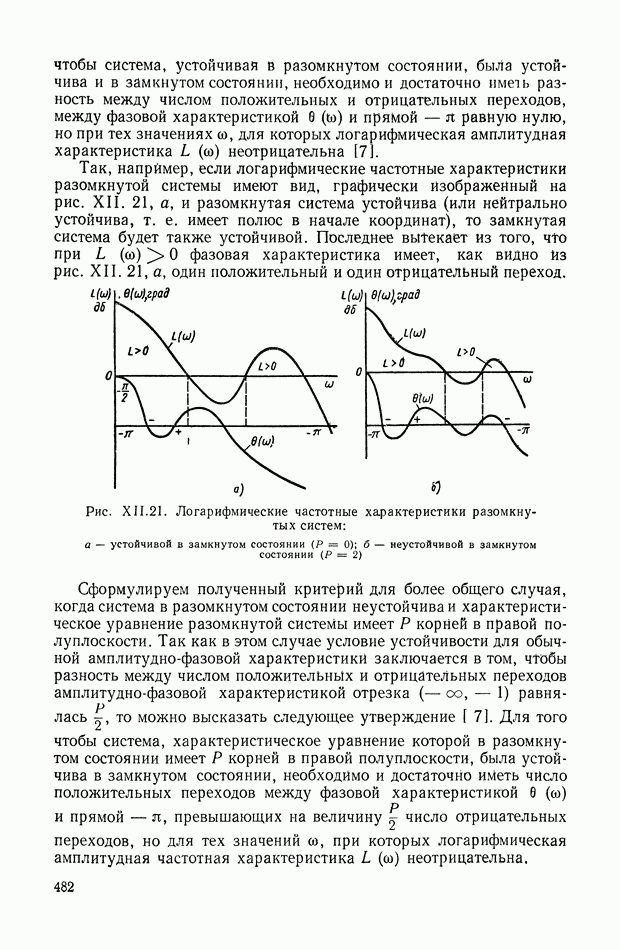
- 9. ПРИБЛИЖЕННЫЙ СПОСОБ ПОСТРОЕНИЯ ЛОГАРИФМИЧЕСКИХ ЧАСТОТНЫХ ХАРАКТЕРИСТИК ОДНОКОНТУРНЫХ СИСТЕМ
- 10. ОБОБЩЕНИЕ ЧАСТОТНОГО КРИТЕРИЯ УСТОЙЧИВОСТИ НА МНОГОКОНТУРНЫЕ СИСТЕМЫ
- 11. АНАЛИЗ УСТОЙЧИВОСТИ МНОГОКОНТУРНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ПРИ ПОМОЩИ ЛОГАРИФМИЧЕСКИХ ЧАСТОТНЫХ ХАРАКТЕРИСТИК
- ГЛАВА XIII. ВЫДЕЛЕНИЕ ОБЛАСТЕЙ УСТОЙЧИВОСТИ
- 1. ПОНЯТИЕ О Д-РАЗБИЕНИИ ПРОСТРАНСТВА КОЭФФИЦИЕНТОВ ХАРАКТЕРИСТИЧЕСКОГО УРАВНЕНИЯ И ПРОСТРАНСТВА ПАРАМЕТРОВ
- 2. Д-РАЗБИЕНИЕ ПЛОСКОСТИ ОДНОГО КОМПЛЕКСНОГО ПАРАМЕТРА
- 3. СВЯЗЬ Д-РАЗБИЕНИЯ С КРИТЕРИЯМИ УСТОЙЧИВОСТИ
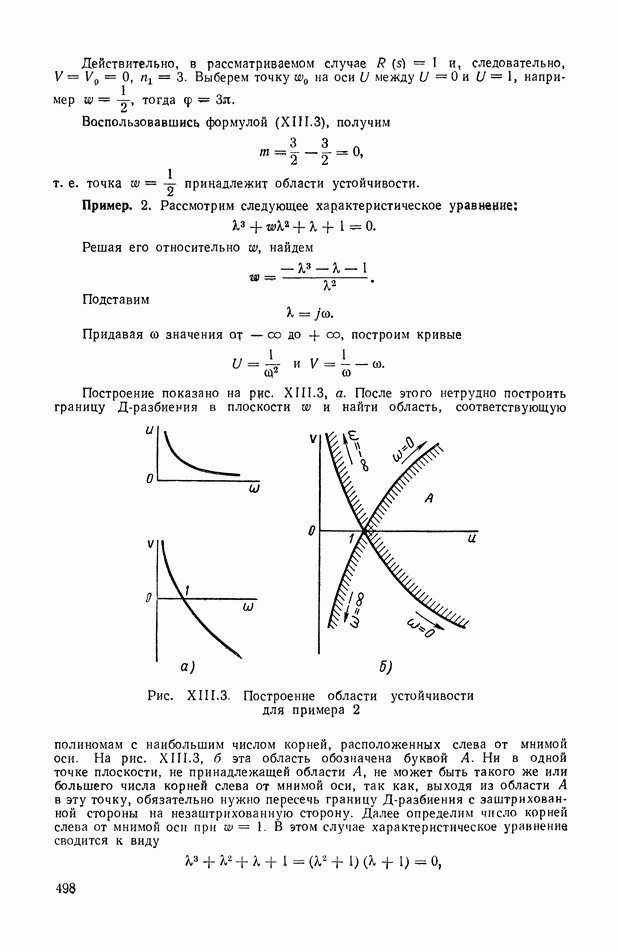
- 4. Д-РАЗБИЕНИЕ ПЛОСКОСТИ ДВУХ ДЕЙСТВИТЕЛЬНЫХ ПАРАМЕТРОВ (ДИАГРАММА ВЫШНЕГРАДСКОГО)
- 5. УСЛОВИЯ СУЩЕСТВОВАНИЯ ОБЛАСТИ УСТОЙЧИВОСТИ
- ГЛАВА XIV. ПРИМЕРЫ АНАЛИЗА УСТОЙЧИВОСТИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. СИСТЕМА АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ СКОРОСТИ ВРАЩЕНИЯ ГИДРОТУРБИНЫ
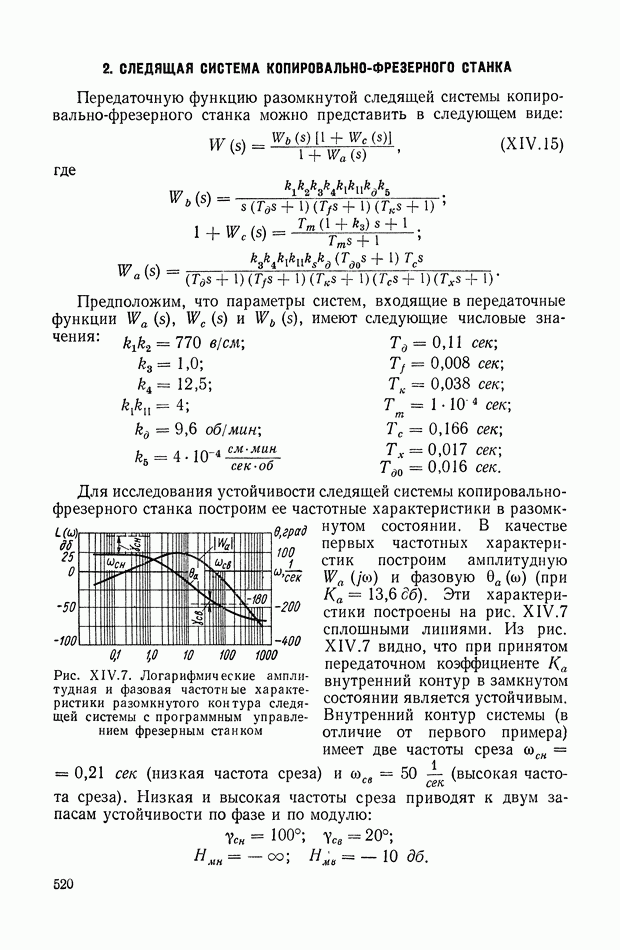
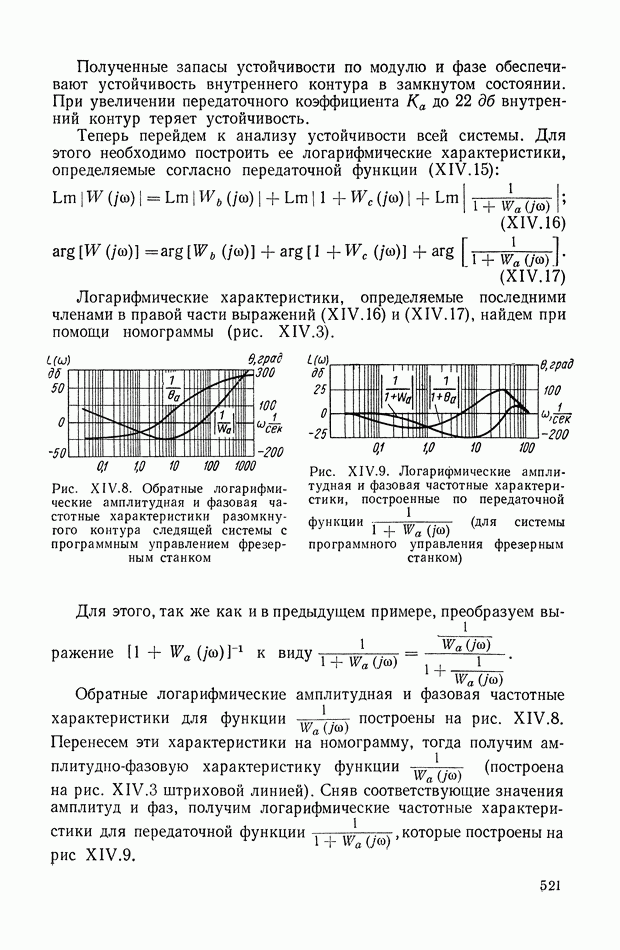
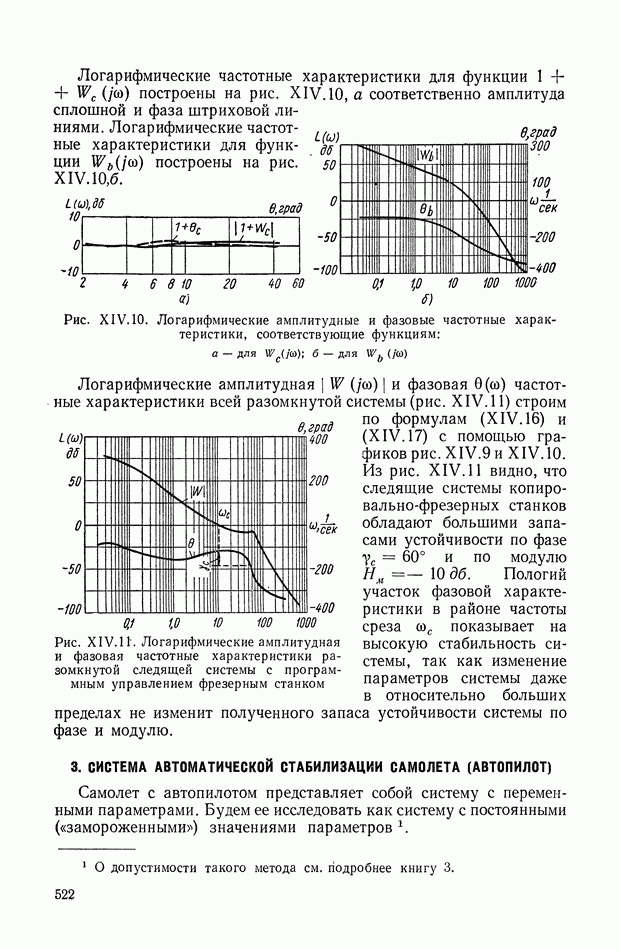
- 2. СЛЕДЯЩАЯ СИСТЕМА КОПИРОВАЛЬНО-ФРЕЗЕРНОГО СТАНКА
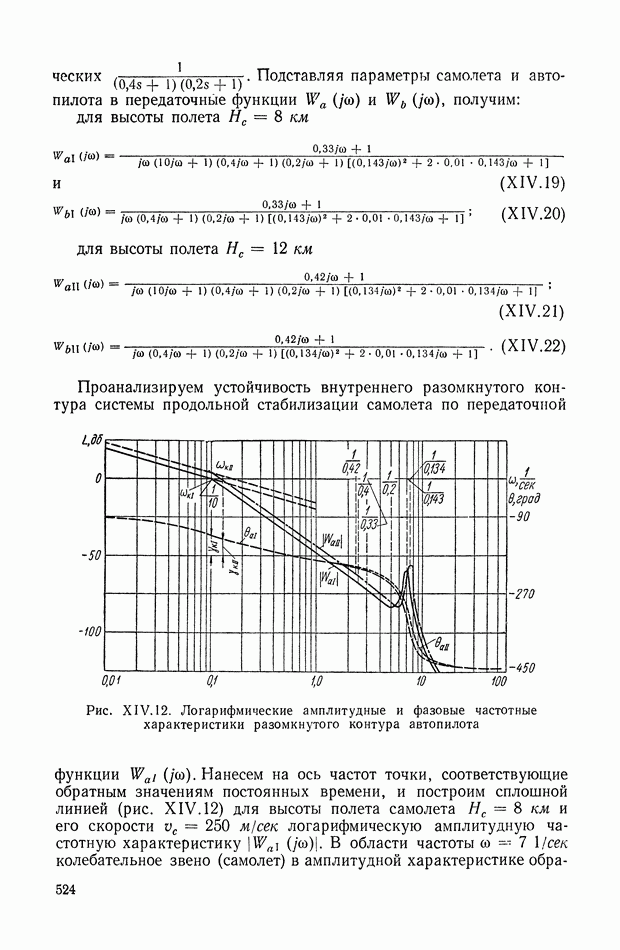
- 3. СИСТЕМА АВТОМАТИЧЕСКОЙ СТАБИЛИЗАЦИИ САМОЛЕТА (АВТОПИЛОТ)
- 4. СИСТЕМА АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ МОЩНОСТИ ЯДЕРНОГО ЭНЕРГЕТИЧЕСКОГО РЕАКТОРА
- РАЗДЕЛ III. АНАЛИЗ ПЕРЕХОДНЫХ ПРОЦЕССОВ И КАЧЕСТВА ЛИНЕЙНЫХ НЕПРЕРЫВНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- ГЛАВА XV. ЧАСТОТНЫЙ МЕТОД АНАЛИЗА ПЕРЕХОДНЫХ ПРОЦЕССОВ
- 1. ОБОБЩЕННЫЕ ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ И ИХ СВЯЗЬ С ПЕРЕХОДНЫМИ ПРОЦЕССАМИ
- 2. ОПРЕДЕЛЕНИЕ ОБОБЩЕННЫХ ЧАСТОТНЫХ ХАРАКТЕРИСТИК В ОБЩЕМ СЛУЧАЕ
- 3. СЛУЧАЙ, КОГДА ФУНКЦИЯ X(s) НЕ СОДЕРЖИТ ОСОБЕННОСТЕЙ ВО ВСЕЙ ПРАВОЙ ПОЛУПЛОСКОСТИ И НА МНИМОЙ ОСИ
- 4. СВЯЗЬ МЕЖДУ ЧАСТОТНЫМИ ХАРАКТЕРИСТИКАМИ P(w), Q(w) И ИМПУЛЬСНОЙ ПЕРЕХОДНОЙ ФУНКЦИЕЙ k(t)
- 5. СЛУЧАЙ, КОГДА ВСЕ ПОЛЮСА ФУНКЦИИ X(s) РАСПОЛОЖЕНЫ В ЛЕВОЙ ПОЛУПЛОСКОСТИ, ЗА ИСКЛЮЧЕНИЕМ ПОЛЮСА В НАЧАЛЕ КООРДИНАТ
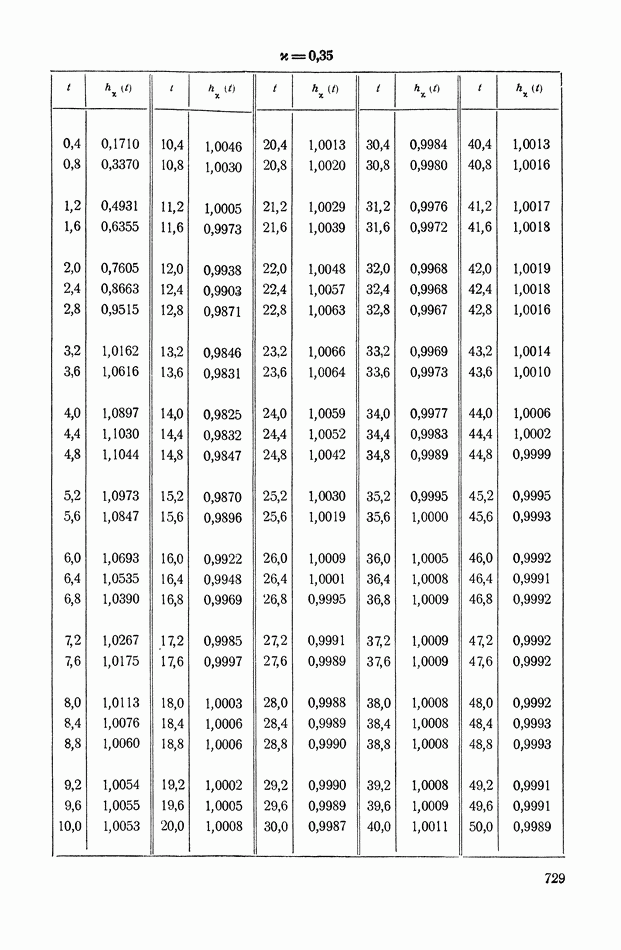
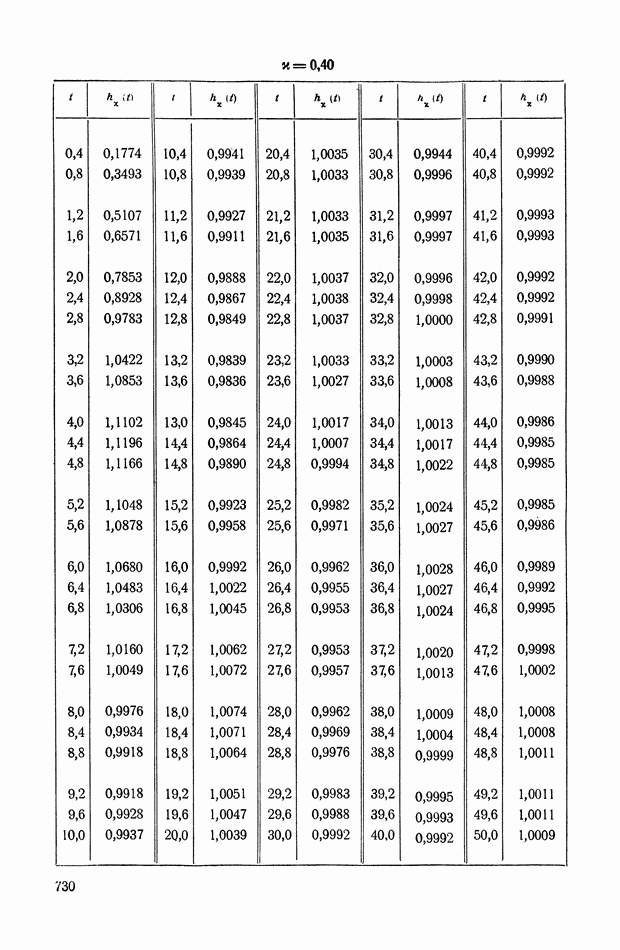
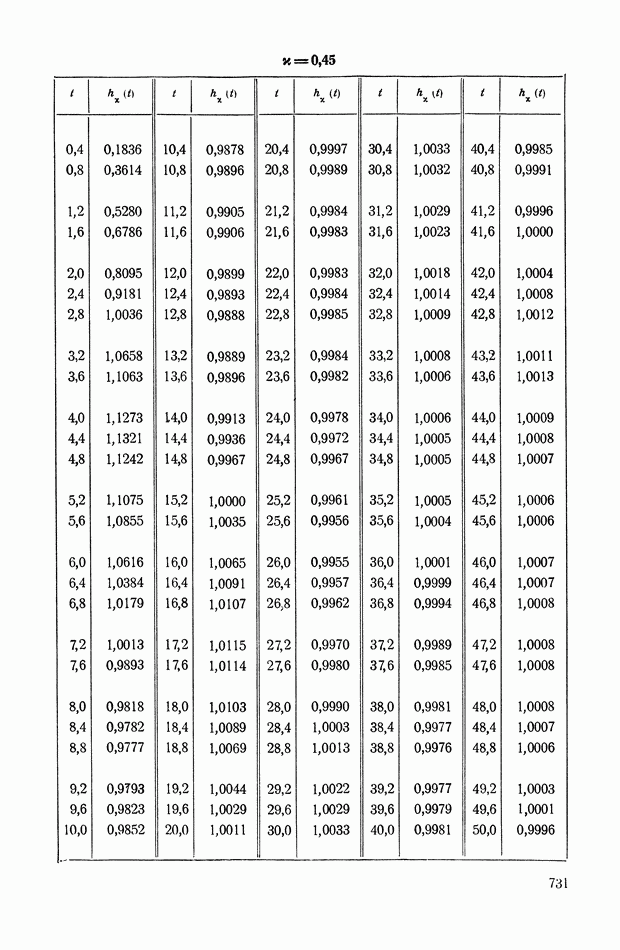
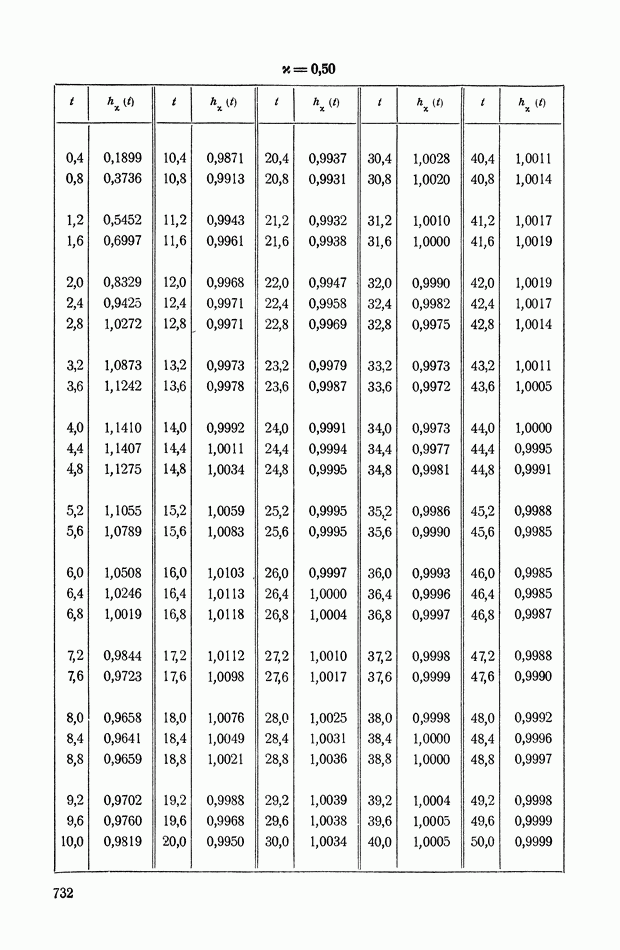
- 6. СВЯЗЬ МЕЖДУ ЧАСТОТНЫМИ ХАРАКТЕРИСТИКАМИ И ПЕРЕХОДНОЙ ФУНКЦИЕЙ h(t)
- 7. СЛУЧАЙ, КОГДА ФУНКЦИЯ X(s) ИМЕЕТ ДВА СОПРЯЖЕННЫХ ПОЛЮСА НА МНИМОЙ ОСИ
- 8. АНАЛИЗ ПЕРЕХОДНЫХ ПРОЦЕССОВ МЕТОДОМ ТРАПЕЦЕИДАЛЬНЫХ ЧАСТОТНЫХ ХАРАКТЕРИСТИК
- 9. О НЕКОТОРЫХ ЧАСТНЫХ СЛУЧАЯХ МЕТОДА ТРАПЕЦЕИДАЛЬНЫХ ЧАСТОТНЫХ ХАРАКТЕРИСТИК
- 10. ОБ УСЛОВИЯХ ПРИМЕНИМОСТИ ЧАСТОТНОГО МЕТОДА АНАЛИЗА ПЕРЕХОДНЫХ ПРОЦЕССОВ
- 11. ОПРЕДЕЛЕНИЕ ДИСКРЕТНЫХ ЗНАЧЕНИЙ ПЕРЕХОДНОЙ ФУНКЦИИ
- ГЛАВА XVI. ЧАСТОТНЫЙ МЕТОД АНАЛИЗА КАЧЕСТВА
- 1. ЧАСТОТНЫЙ КРИТЕРИЙ КАЧЕСТВА РЕГУЛИРОВАНИЯ
- 2. ЧАСТОТНЫЙ КРИТЕРИЙ ОТСУТСТВИЯ ПЕРЕРЕГУЛИРОВАНИЙ И ЧАСТОТНЫЙ КРИТЕРИЙ МОНОТОННОСТИ
- 3. О ПРОВЕРКЕ ВЫПОЛНЕНИЯ СФОРМУЛИРОВАННЫХ КРИТЕРИЕВ
- 4. НЕКОТОРЫЕ ПРИЗНАКИ НЕУДОВЛЕТВОРЕНИЯ КРИТЕРИЕВ КАЧЕСТВА И КРИТЕРИЕВ ОТСУТСТВИЯ ПЕРЕРЕГУЛИРОВАНИЙ И МОНОТОННОСТИ
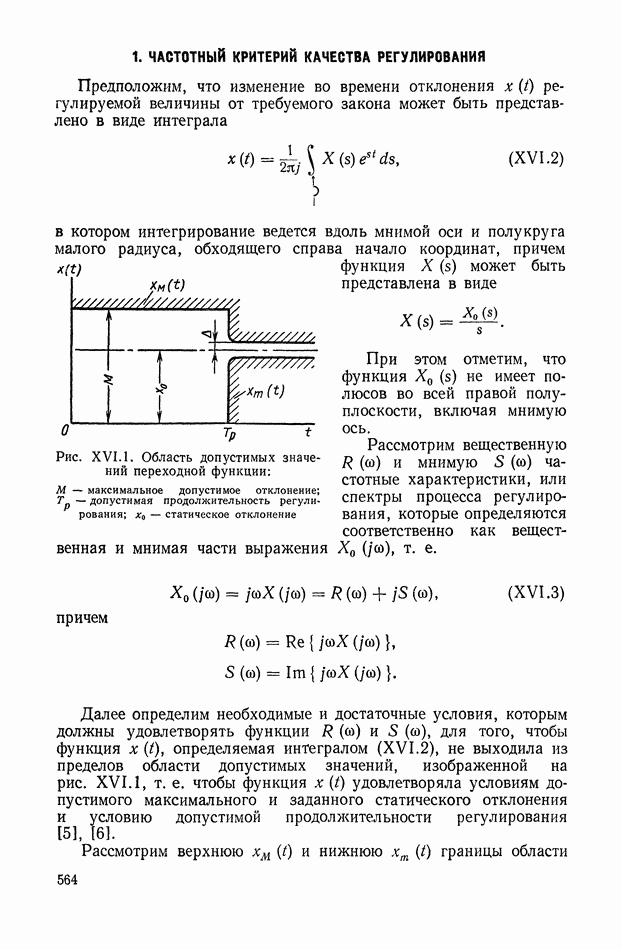
- 5. НЕКОТОРЫЕ ЭЛЕМЕНТАРНЫЕ СВОЙСТВА ЧАСТОТНЫХ ХАРАКТЕРИСТИК
- 6. ДОСТАТОЧНЫЕ УСЛОВИЯ ДЛЯ МАЛЫХ ПЕРЕРЕГУЛИРОВАНИЙ И НЕОБХОДИМЫЕ УСЛОВИЯ ДЛЯ ОТСУТСТВИЯ ПЕРЕРЕГУЛИРОВАНИЙ
- 7. КРИТЕРИЙ, ОПРЕДЕЛЯЮЩИЙ ДОСТАТОЧНЫЕ УСЛОВИЯ ДЛЯ МОНОТОННОСТИ
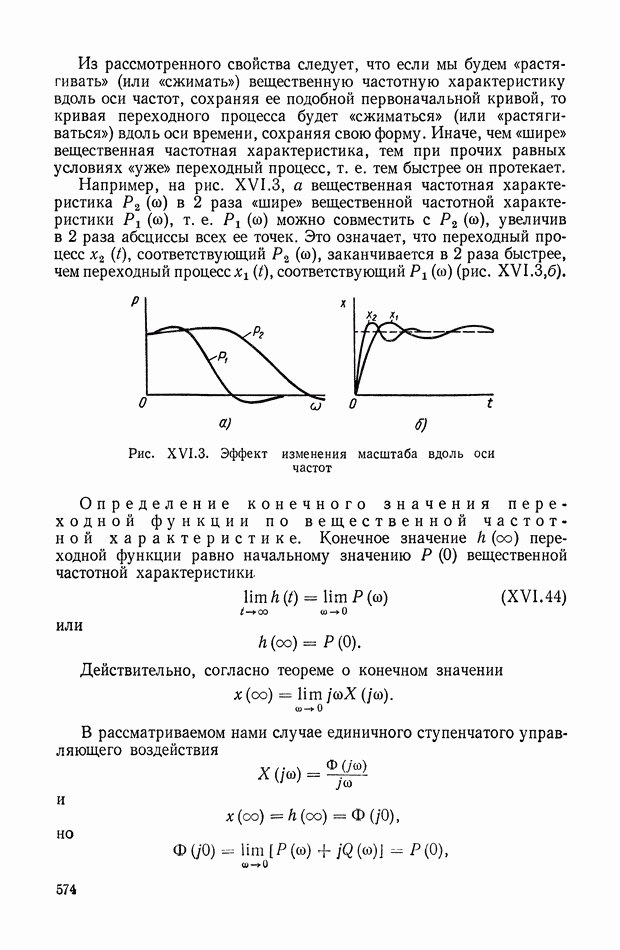
- 8. ОЦЕНКИ ВЕЛИЧИНЫ ПЕРЕРЕГУЛИРОВАНИЯ И ВРЕМЕНИ ПЕРЕХОДНОГО ПРОЦЕССА
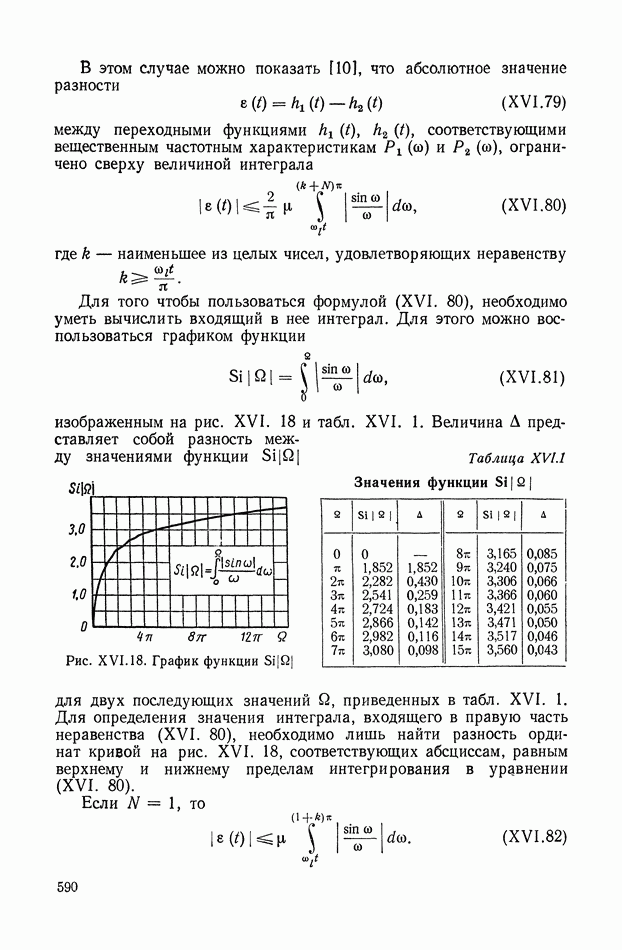
- 9. ОЦЕНКА АБСОЛЮТНОГО ЗНАЧЕНИЯ РАЗНОСТИ МЕЖДУ ПЕРЕХОДНЫМИ ФУНКЦИЯМИ ПО СООТВЕТСТВУЮЩИМ ИМ ЧАСТОТНЫМ ХАРАКТЕРИСТИКАМ
- 10. СВЯЗЬ МЕЖДУ СВОЙСТВАМИ АМПЛИТУДНО-ФАЗОВОЙ ХАРАКТЕРИСТИКИ РАЗОМКНУТОЙ СИСТЕМЫ И КАЧЕСТВОМ
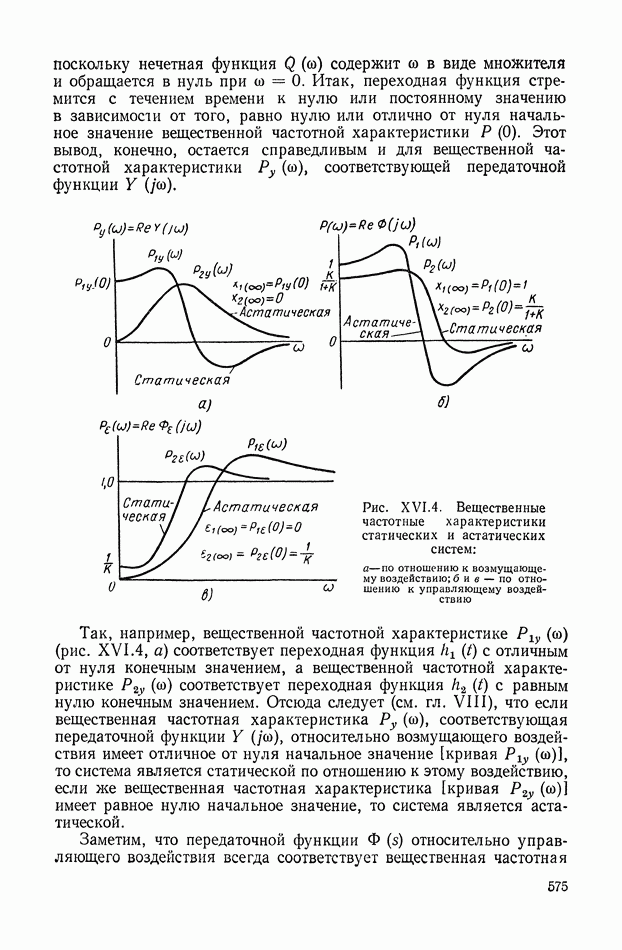
- 11. ТРЕБОВАНИЯ К ЧАСТОТНЫМ ХАРАКТЕРИСТИКАМ, ОБЕСПЕЧИВАЮЩИЕ ВЫСОКУЮ ТОЧНОСТЬ В СЛЕДЯЩИХ СИСТЕМАХ
- 12. СВЯЗЬ МЕЖДУ СВОЙСТВАМИ ЛОГАРИФМИЧЕСКОЙ АМПЛИТУДНОЙ ХАРАКТЕРИСТИКИ И КАЧЕСТВОМ
- 13. ОПРЕДЕЛЕНИЕ ВЕЛИЧИНЫ ПЕРЕДАТОЧНОГО КОЭФФИЦИЕНТА ИЛИ ДОБРОТНОСТИ ПО ЛОГАРИФМИЧЕСКОЙ АМПЛИТУДНОЙ ХАРАКТЕРИСТИКЕ
- 14. ОПРЕДЕЛЕНИЕ УСТАНОВИВШЕЙСЯ ОШИБКИ ПРИ ГАРМОНИЧЕСКОМ УПРАВЛЯЮЩЕМ ВОЗДЕЙСТВИИ ПО ЛОГАРИФМИЧЕСКОЙ АМПЛИТУДНОЙ ХАРАКТЕРИСТИКЕ
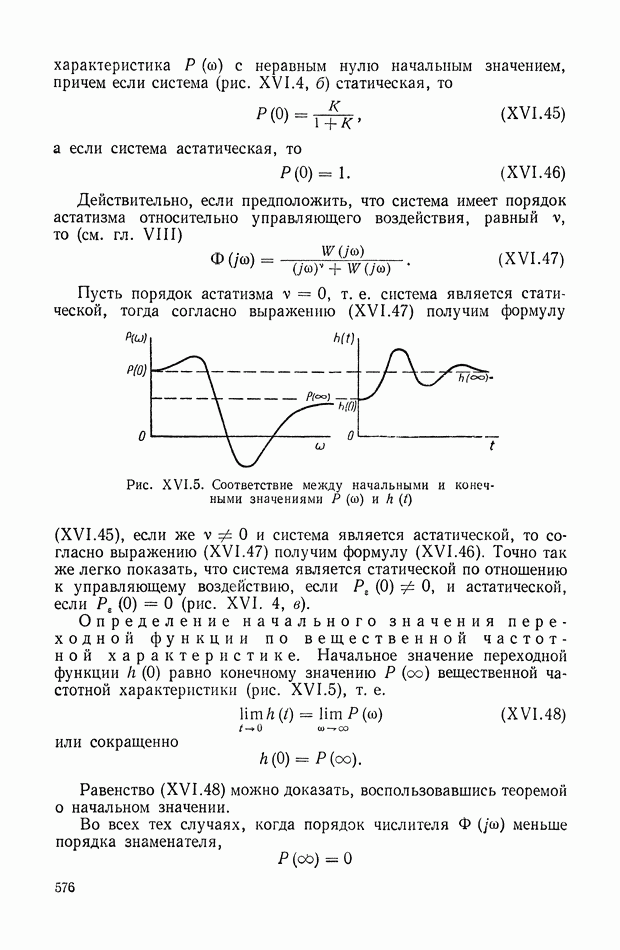
- 15. ПРИБЛИЖЕННЫЙ СПОСОБ ВЫЧИСЛЕНИЯ ПЕРЕХОДНОГО ПРОЦЕССА ПО СОПРЯГАЮЩИМ ЧАСТОТАМ ЛОГАРИФМИЧЕСКОЙ АМПЛИТУДНОЙ ЧАСТОТНОЙ ХАРАКТЕРИСТИКИ
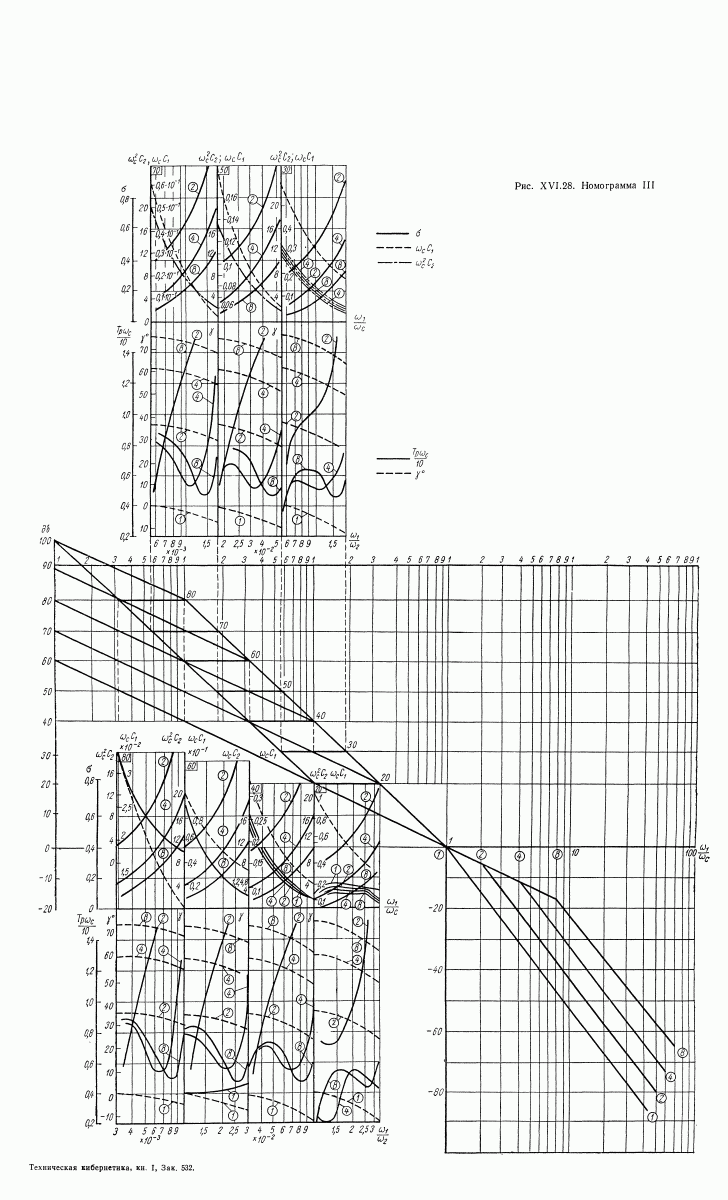
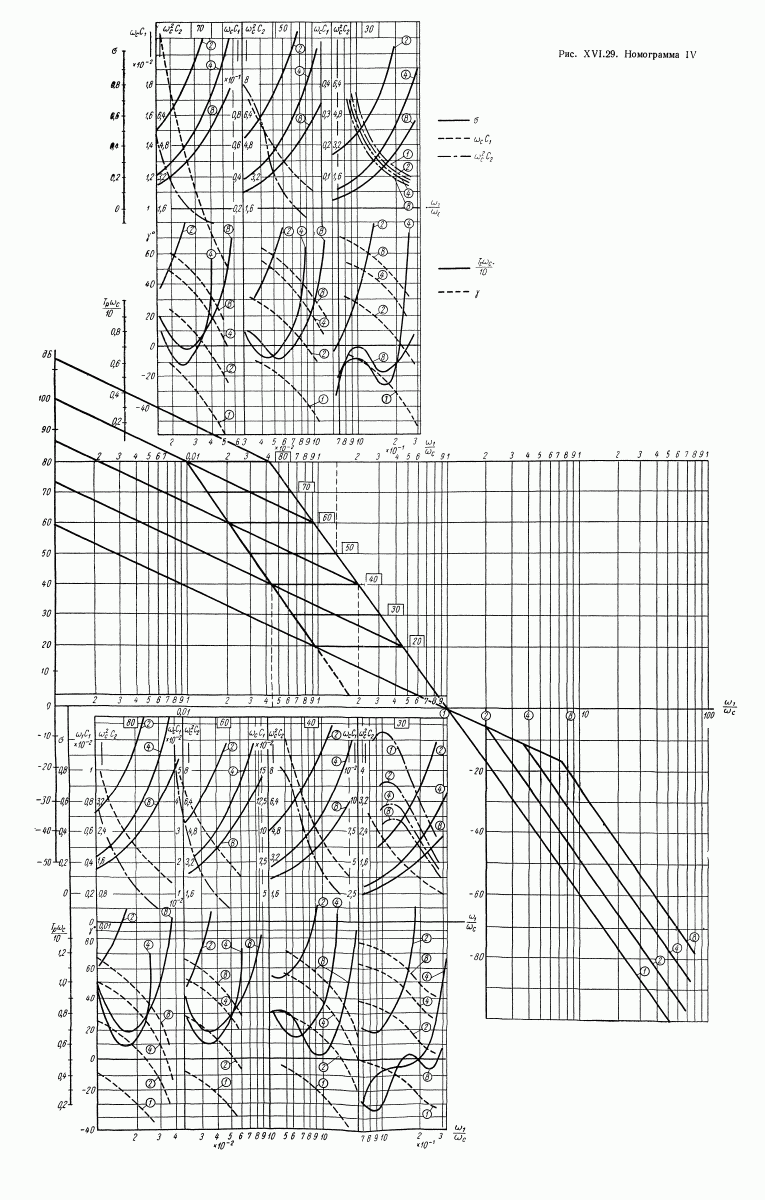
- 16. НОМОГРАММА ДЛЯ ОПРЕДЕЛЕНИЯ ЗАПАСА УСТОЙЧИВОСТИ, ПОКАЗАТЕЛЕЙ КАЧЕСТВА И КОЭФФИЦИЕНТОВ ОШИБОК ПО ВИДУ ЛОГАРИФМИЧЕСКОЙ АМПЛИТУДНОЙ ХАРАКТЕРИСТИКИ
- ГЛАВА XVII. СВЯЗЬ МЕЖДУ КАЧЕСТВОМ ПЕРЕХОДНОГО ПРОЦЕССА И РАСПРЕДЕЛЕНИЕМ НУЛЕЙ И ПОЛЮСОВ ПЕРЕДАТОЧНОЙ ФУНКЦИИ. МЕТОД КОРНЕВЫХ ГОДОГРАФОВ
- 2. АНАЛИЗ РАСПРЕДЕЛЕНИЯ КОРНЕЙ ХАРАКТЕРИСТИЧЕСКОГО УРАВНЕНИЯ СИСТЕМЫ И ОЦЕНКА КАЧЕСТВА ПЕРЕХОДНОГО ПРОЦЕССА
- 3. ГЕОМЕТРИЧЕСКИЙ МЕТОД ПОСТРОЕНИЯ КОРНЕВОГО ГОДОГРАФА
- 4. АНАЛИТИЧЕСКОЕ ПОСТРОЕНИЕ ГЕОМЕТРИЧЕСКОГО МЕСТА КОРНЕЙ
- 5. ОПРЕДЕЛЕНИЕ ОБЛАСТЕЙ УСТОЙЧИВОСТИ ЛИНЕЙНЫХ СИСТЕМ МЕТОДОМ КОРНЕВОГО ГОДОГРАФА
- 6. ОЦЕНКИ ПАРАМЕТРОВ ПЕРЕХОДНОЙ И ЧАСТОТНОЙ ХАРАКТЕРИСТИК ПО КОРНЕВОМУ ГОДОГРАФУ
- 7. ВЛИЯНИЕ РАСПОЛОЖЕНИЯ НУЛЕЙ И ПОЛЮСОВ ЗАМКНУТОЙ СИСТЕМЫ НА ПЕРЕХОДНУЮ ХАРАКТЕРИСТИКУ h(t)
- 8. ВЛИЯНИЕ РАСПОЛОЖЕНИЯ НУЛЕЙ И ПОЛЮСОВ ЗАМКНУТОЙ СИСТЕМЫ НА ЕЕ ПОЛОСУ ЧАСТОТ
- 9. КОРНЕВОЙ ГОДОГРАФ И ПЕРЕХОДНАЯ ХАРАКТЕРИСТИКА СИСТЕМЫ ПРИ ВОЗМУЩЕНИЯХ, ПРИЛОЖЕННЫХ НЕ К ОСНОВНОМУ ВХОДУ СИСТЕМЫ
- 10. ВЛИЯНИЕ РАСПРЕДЕЛЕНИЯ НУЛЕЙ И ПОЛЮСОВ ПЕРЕДАТОЧНОЙ ФУНКЦИИ НА КАЧЕСТВО ПЕРЕХОДНОГО ПРОЦЕССА ПРИ НАЛИЧИИ ВНЕШНЕГО ВОЗДЕЙСТВИЯ
- ГЛАВА XVIII. МЕТОД ЛОГАРИФМИЧЕСКИХ КОРНЕВЫХ ГОДОГРАФОВ
- 2. ОПРЕДЕЛЕНИЕ КОРНЕЙ ЗАМКНУТОЙ СИСТЕМЫ ПО ЛОГАРИФМИЧЕСКОЙ АМПЛИТУДНОЙ КОМПЛЕКСНО-ЧАСТОТНОЙ ХАРАКТЕРИСТИКЕ РАЗОМКНУТОЙ СИСТЕМЫ
- 3. ЛОГАРИФМИЧЕСКИЕ КОРНЕВЫЕ ГОДОГРАФЫ
- 4. ЛОГАРИФМИЧЕСКИЕ КОМПЛЕКСНО-ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЗВЕНЬЕВ ВТОРОГО ПОРЯДКА
- 5. ПРИМЕР ПОСТРОЕНИЯ ЛОГАРИФМИЧЕСКОГО КОРНЕВОГО ГОДОГРАФА
- ГЛАВА XIX. ИНТЕГРАЛЬНЫЕ ОЦЕНКИ И КРИТЕРИИ КАЧЕСТВА РЕГУЛИРОВАНИЯ
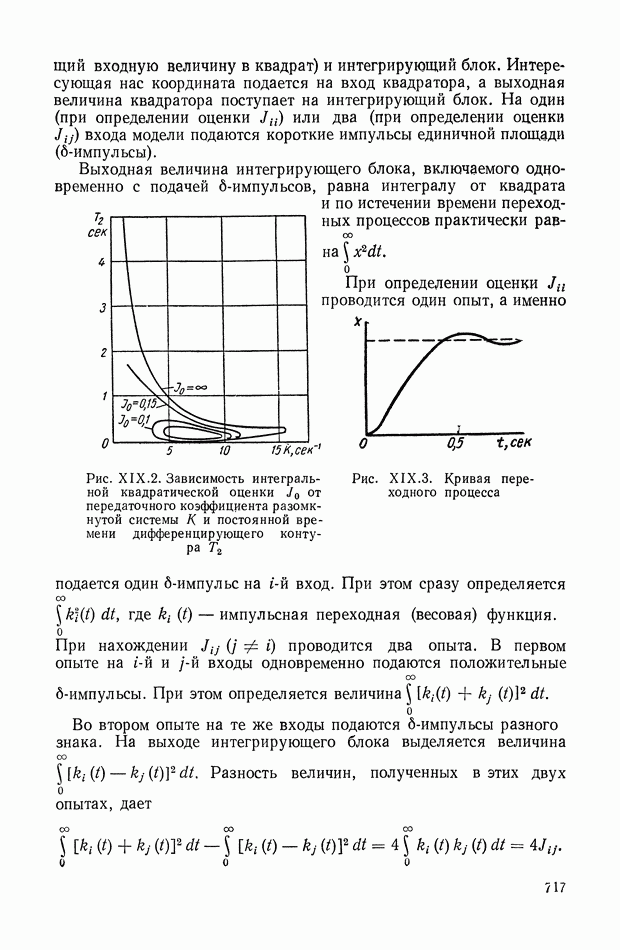
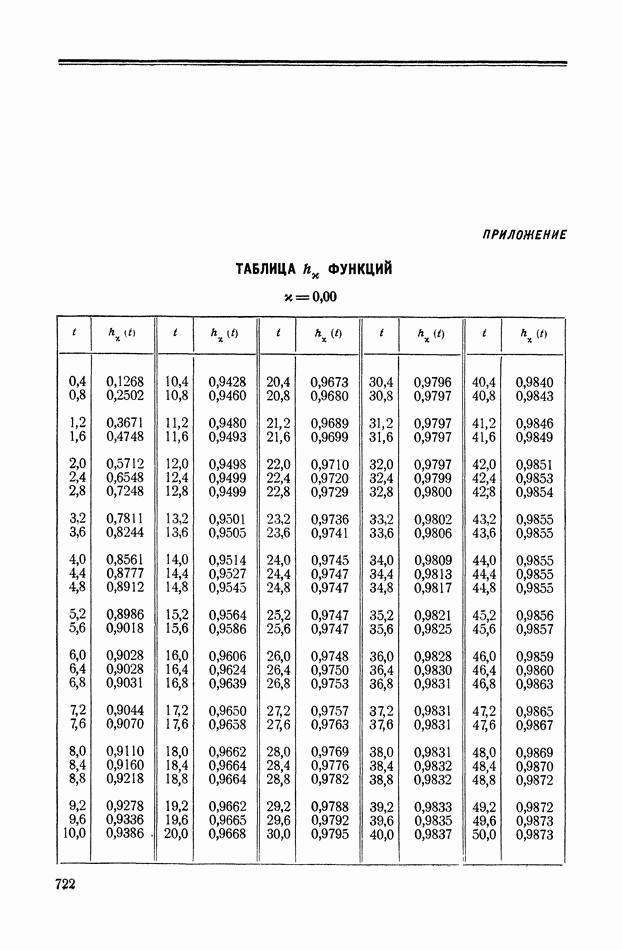
- 2. МЕТОДИКА ПРИМЕНЕНИЯ ИНТЕГРАЛЬНЫХ КВАДРАТИЧНЫХ ОЦЕНОК
- 3. ЛИНЕЙНЫЕ ИНТЕГРАЛЬНЫЕ ОЦЕНКИ
- ПРИЛОЖЕНИЕ
- БИБЛИОГРАФИЯ ПО РАЗДЕЛАМ КНИГИ