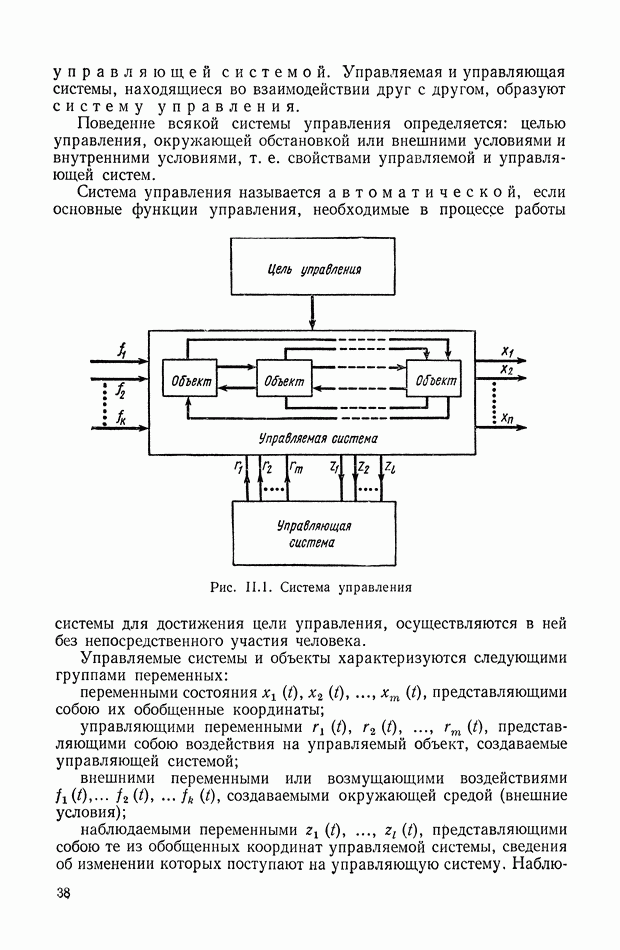
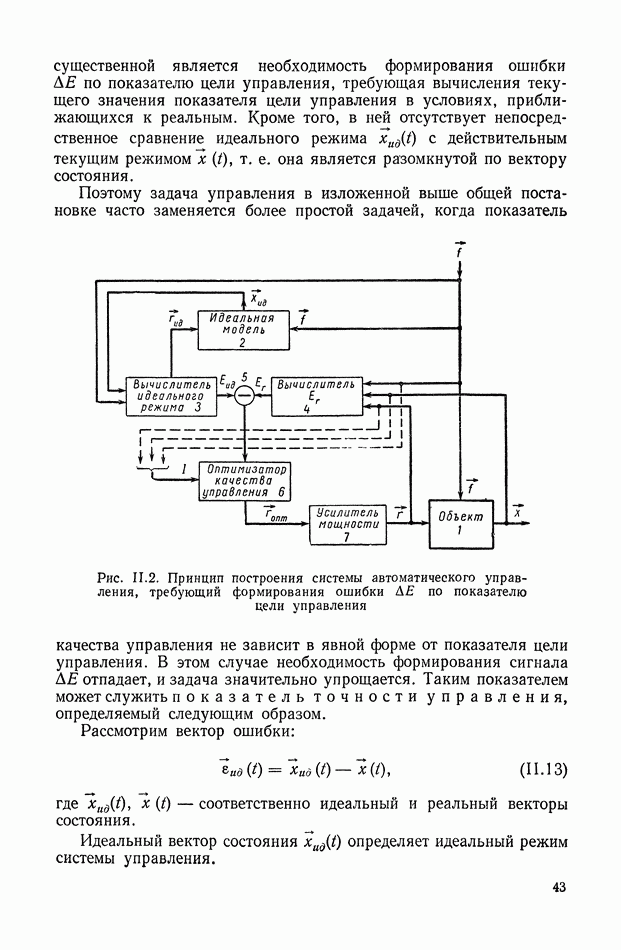
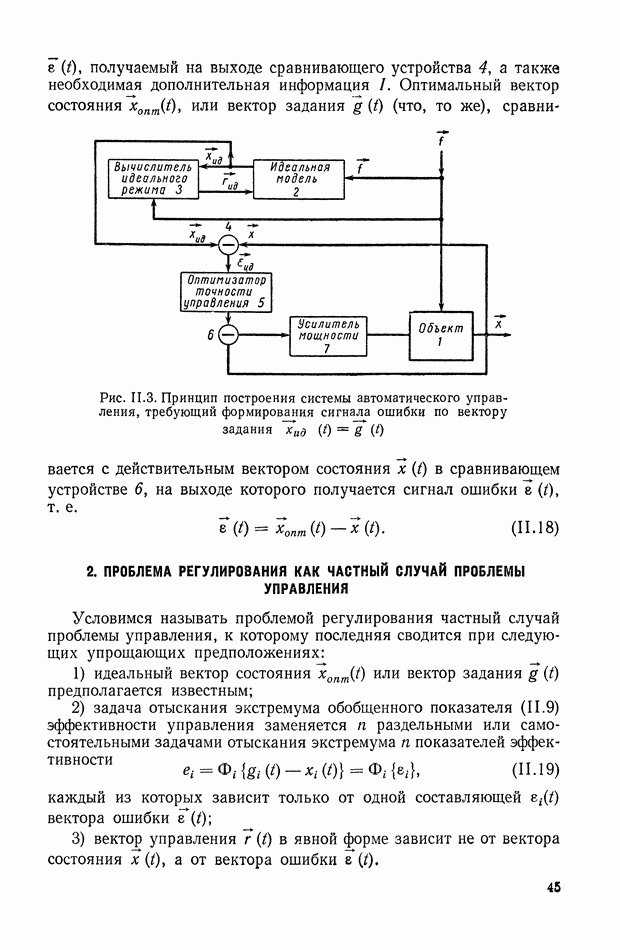
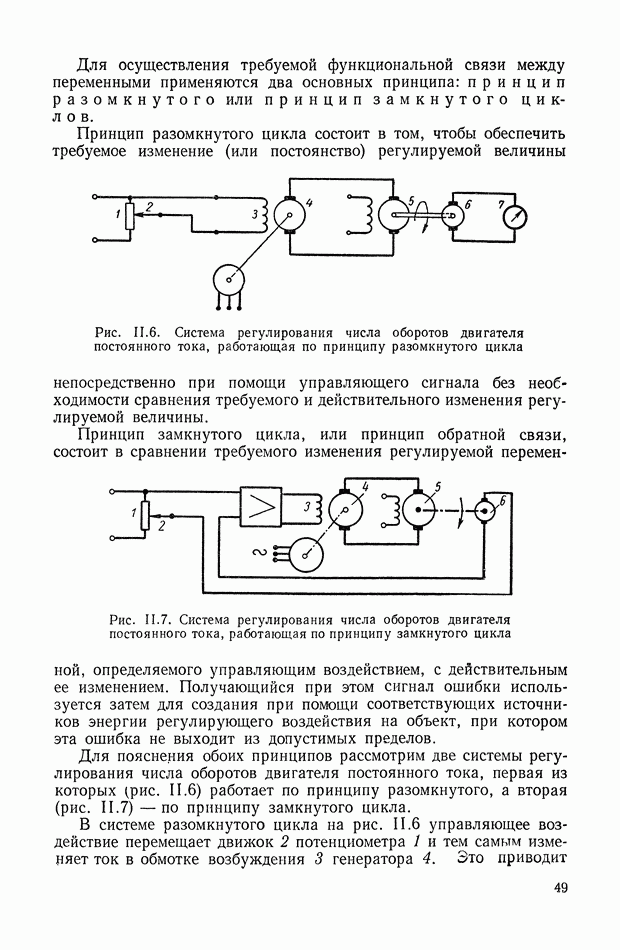
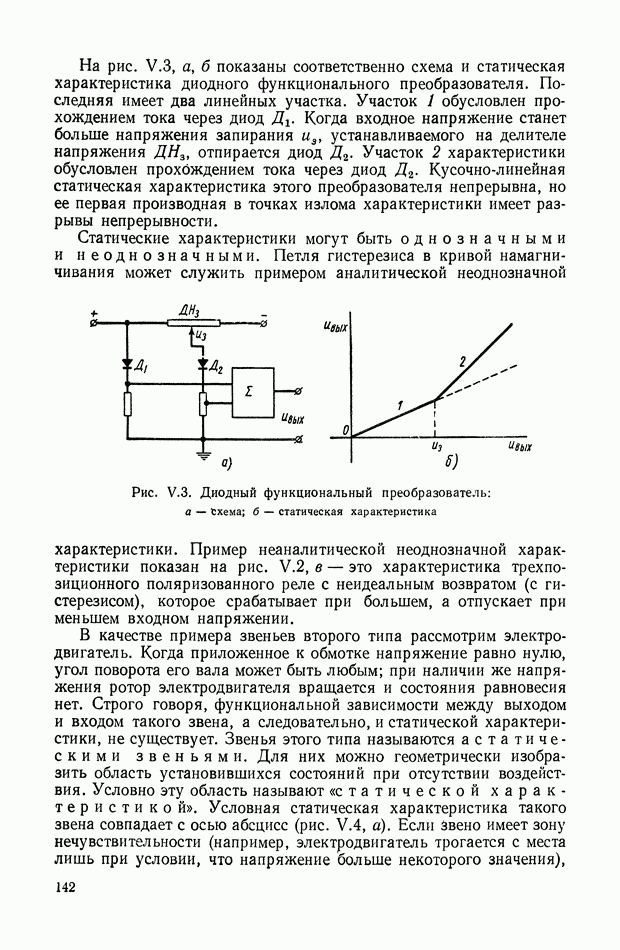
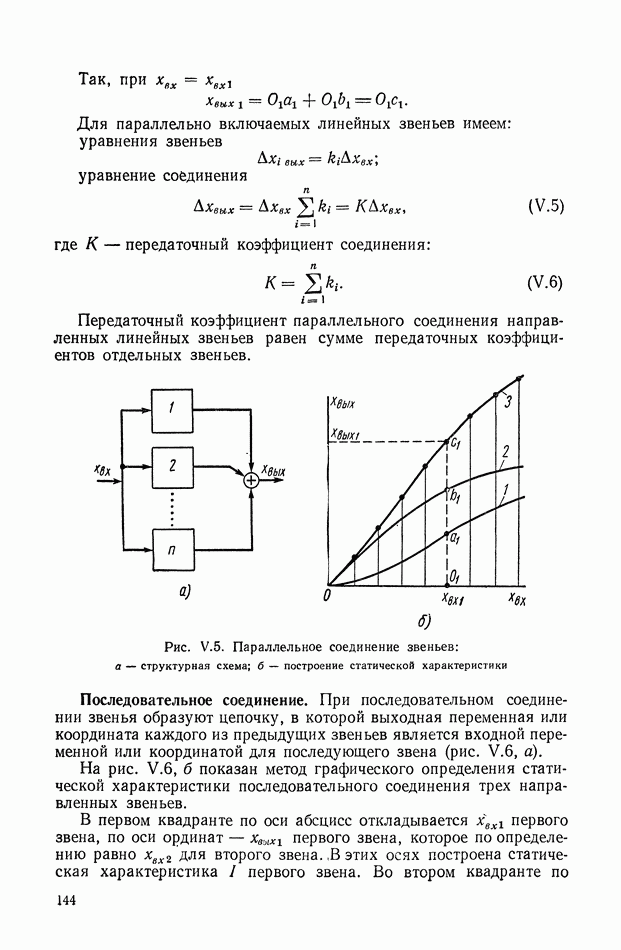
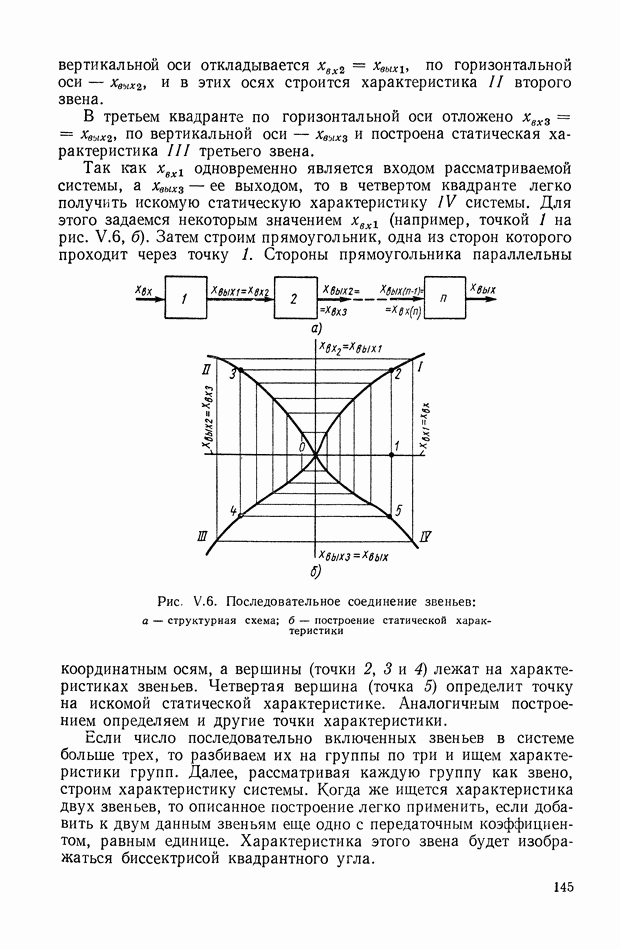
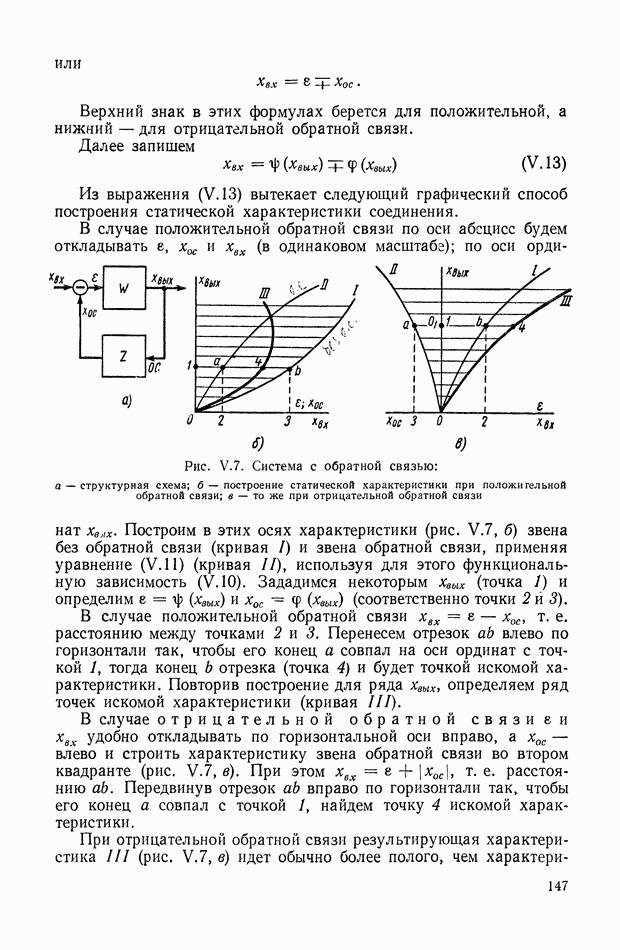
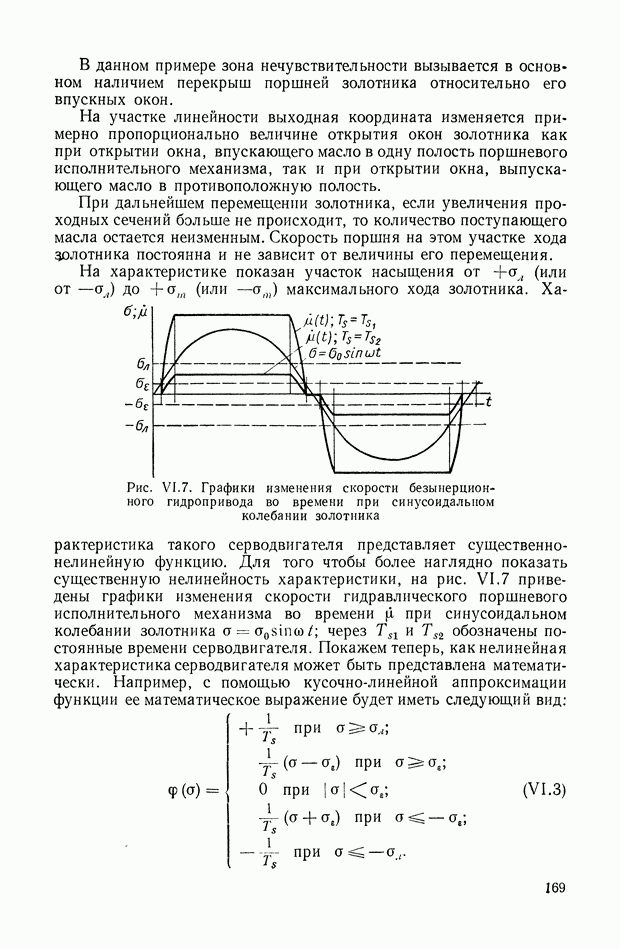
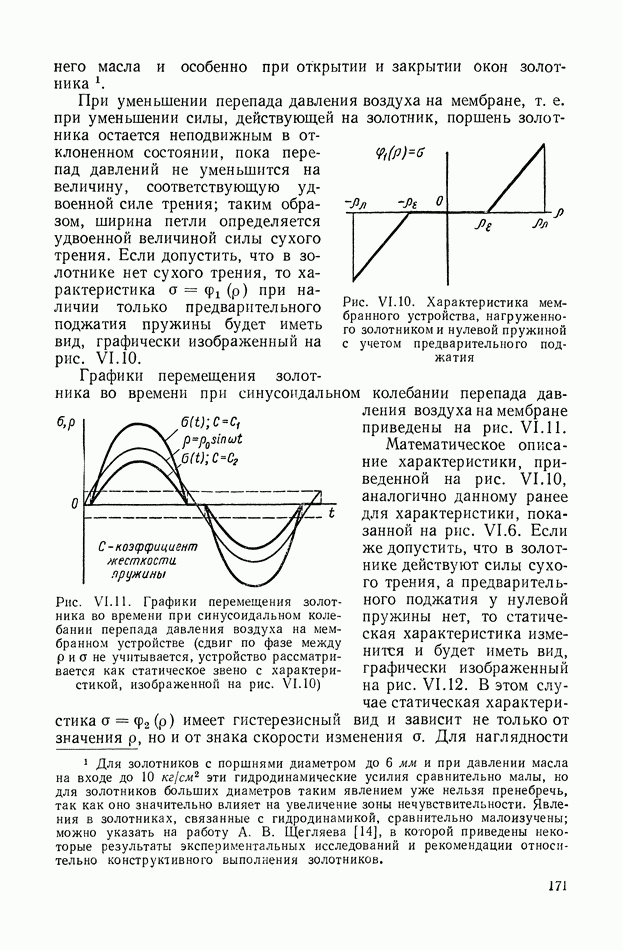
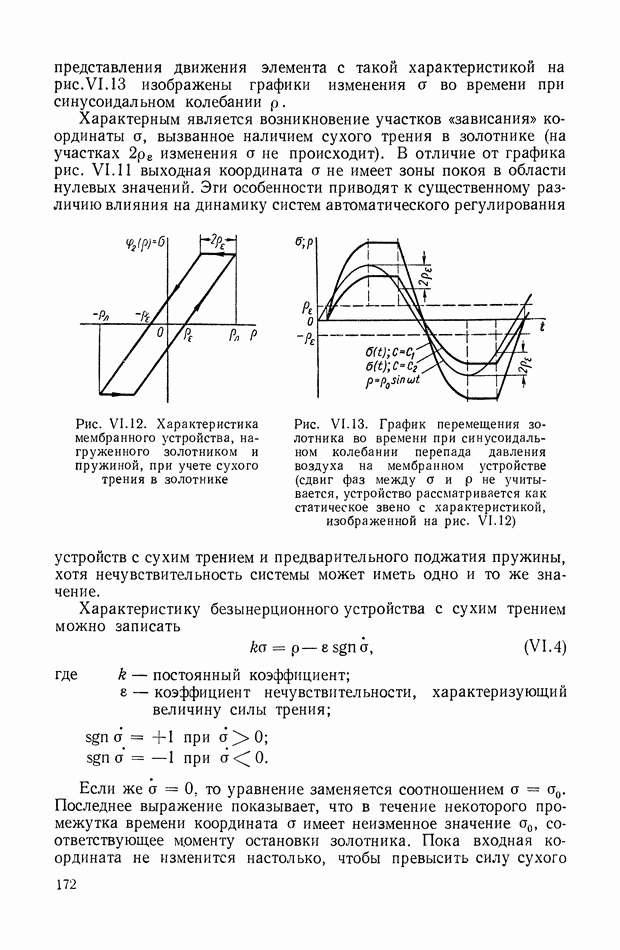
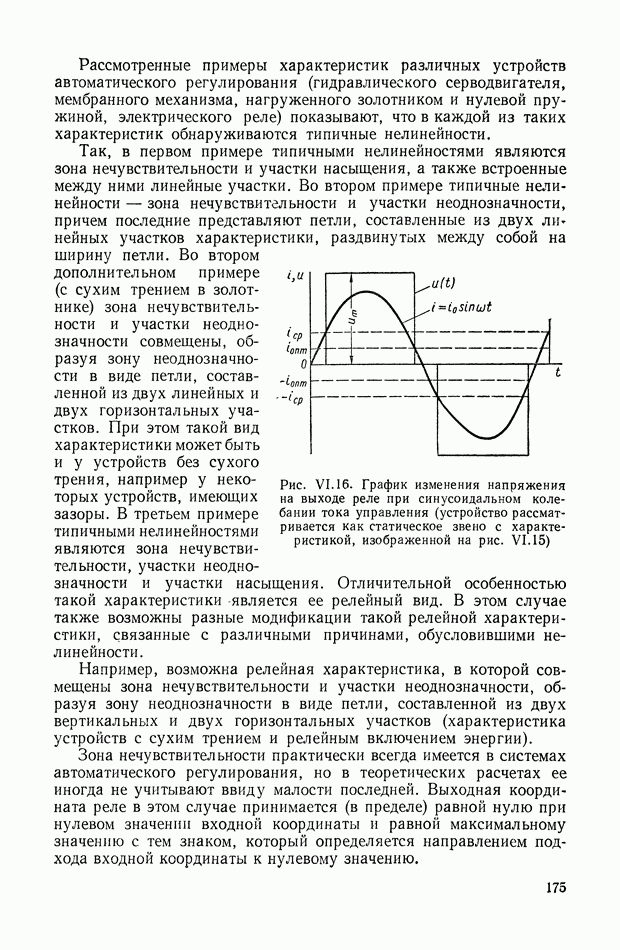
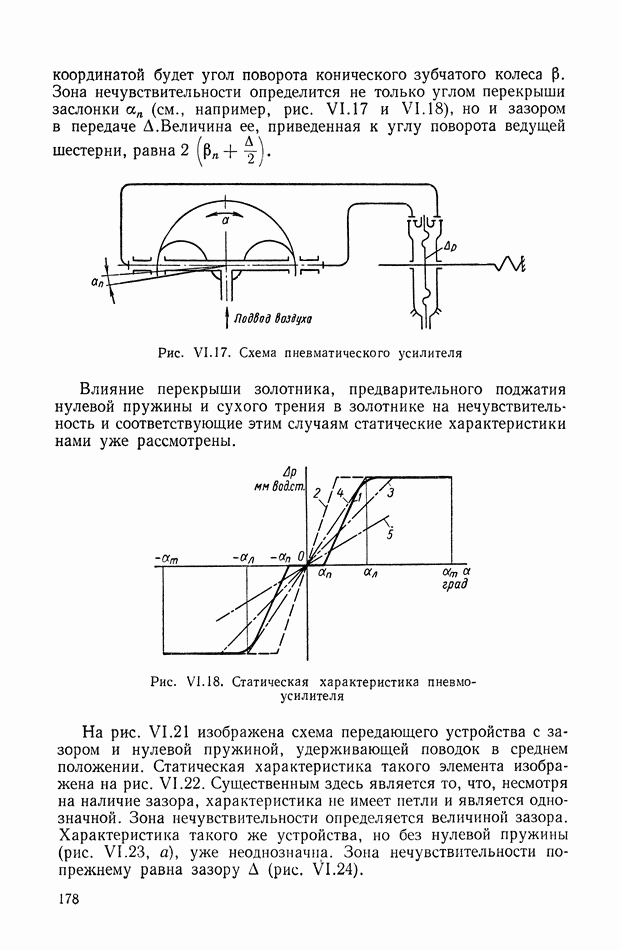
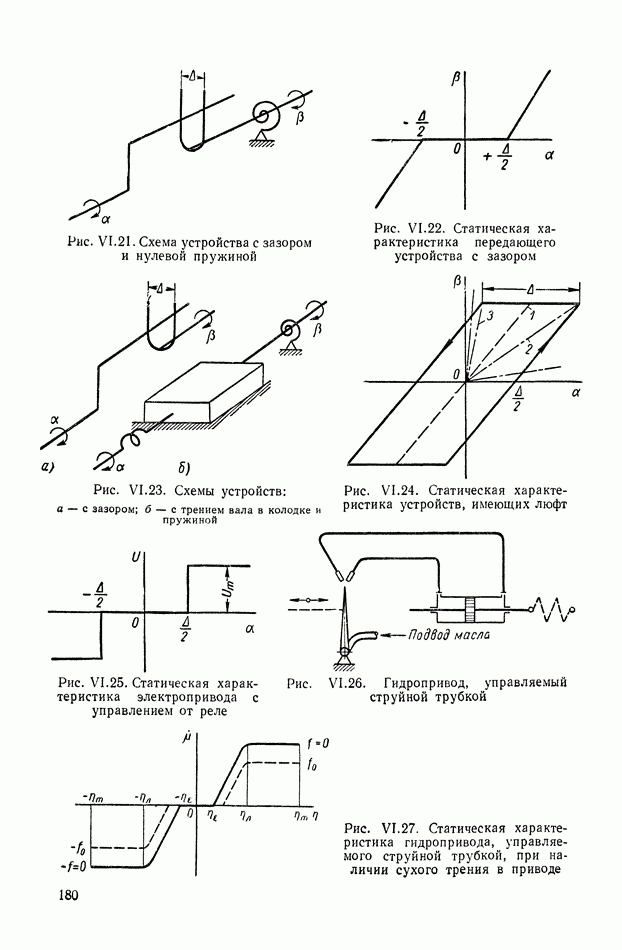
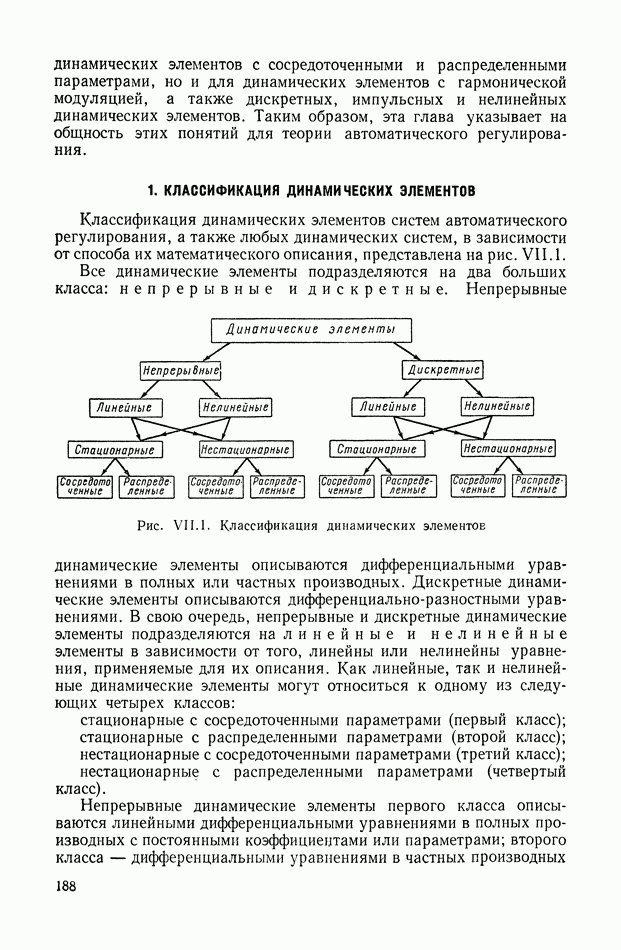
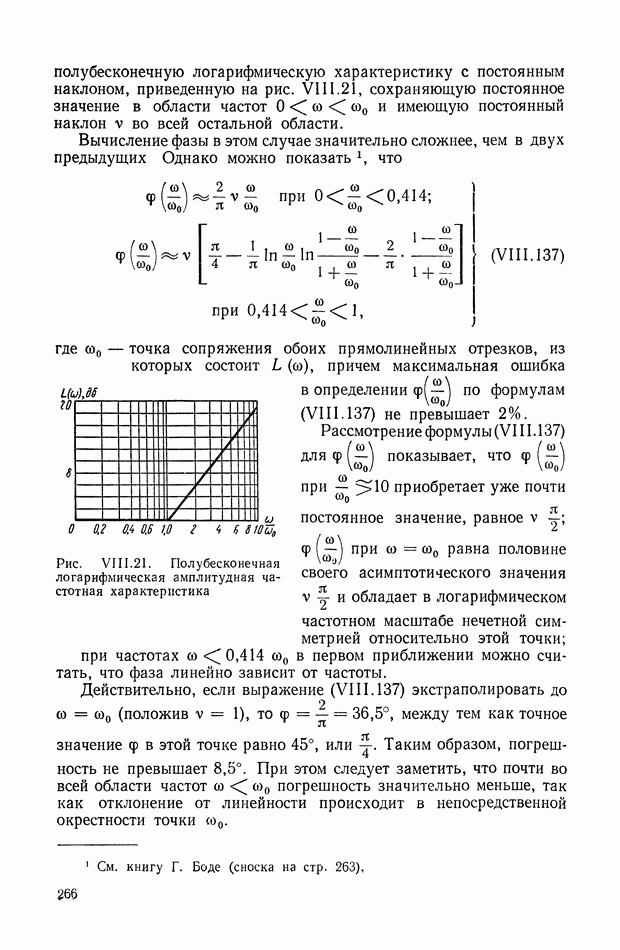
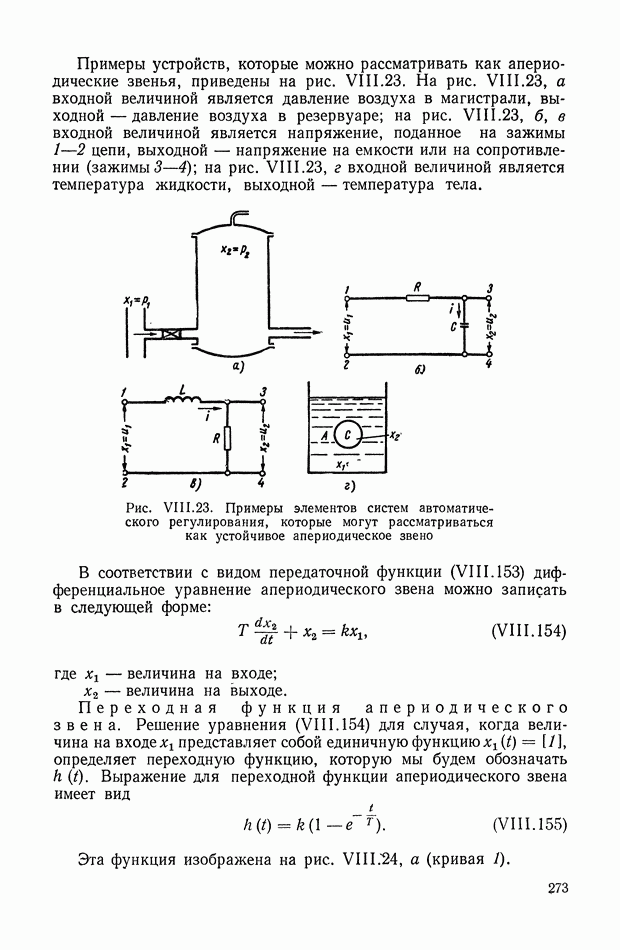
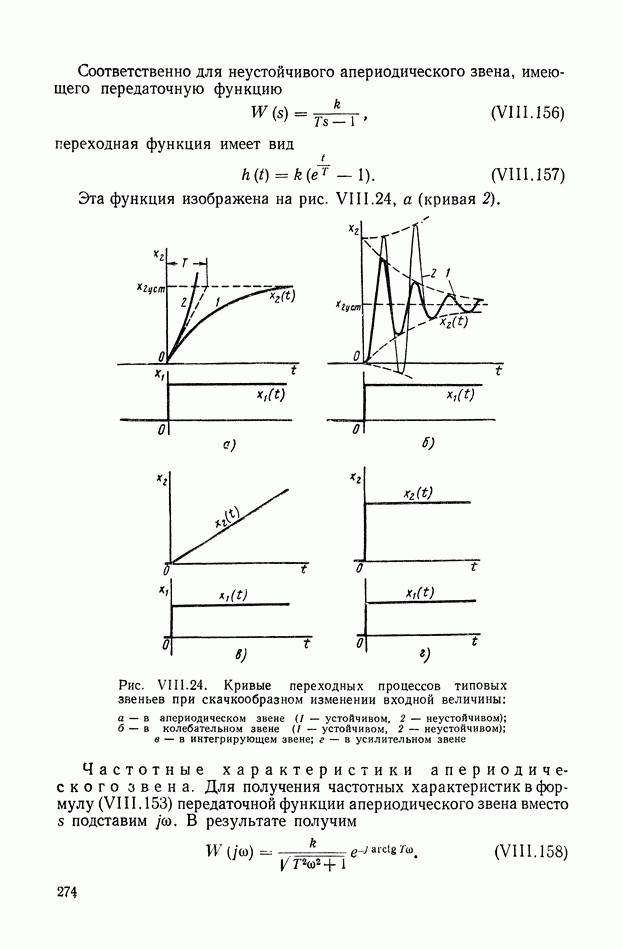
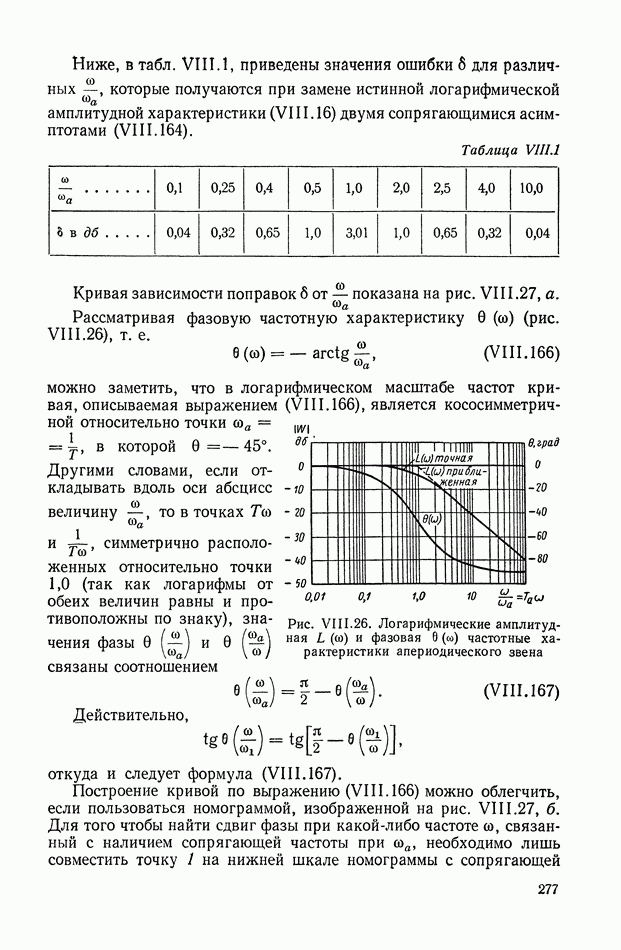
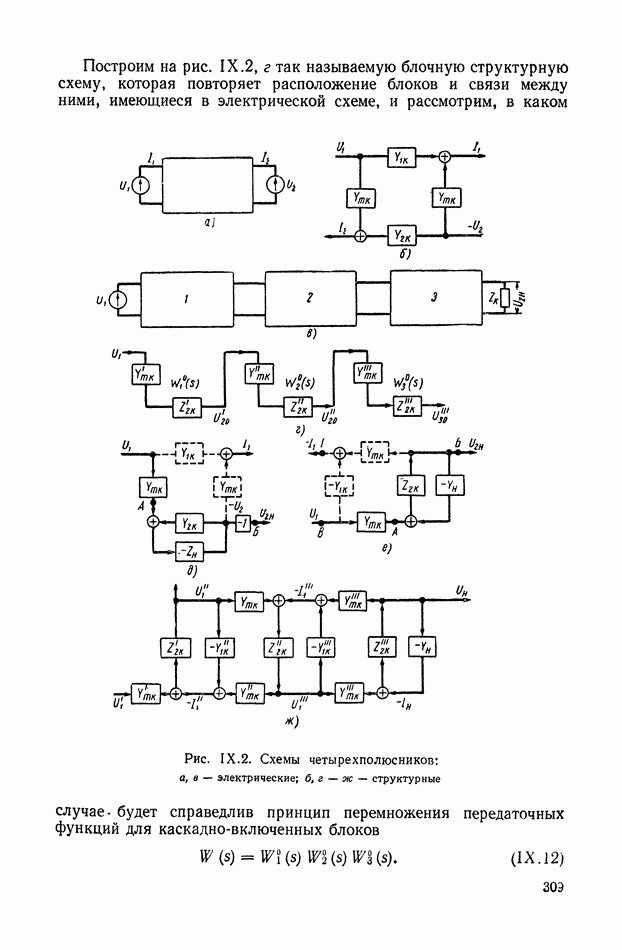
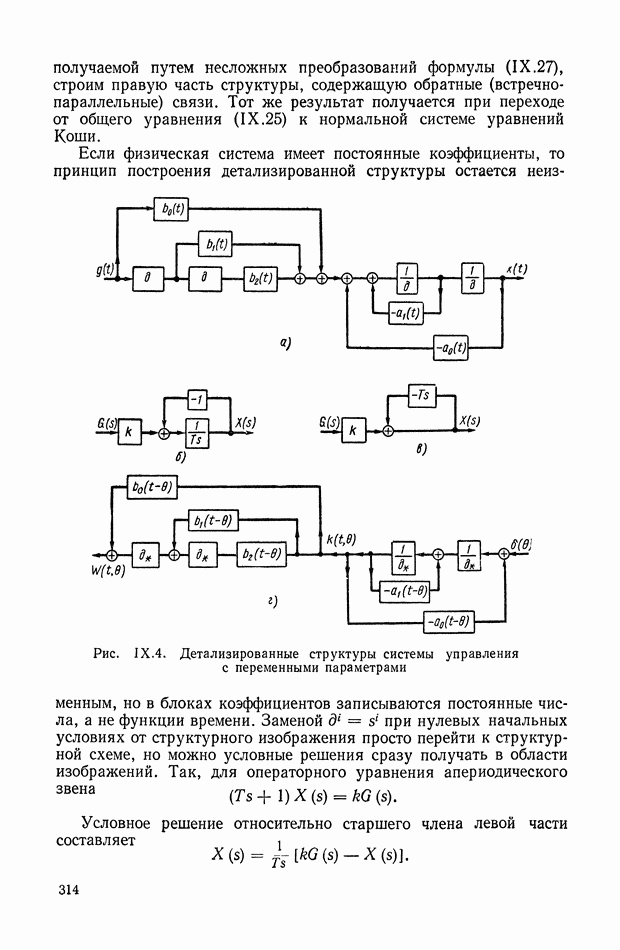
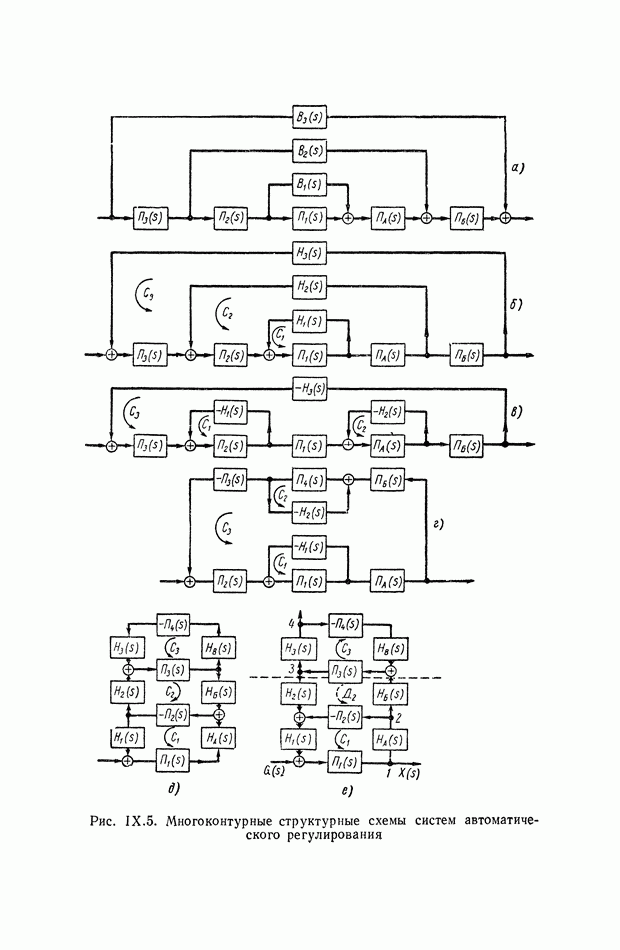
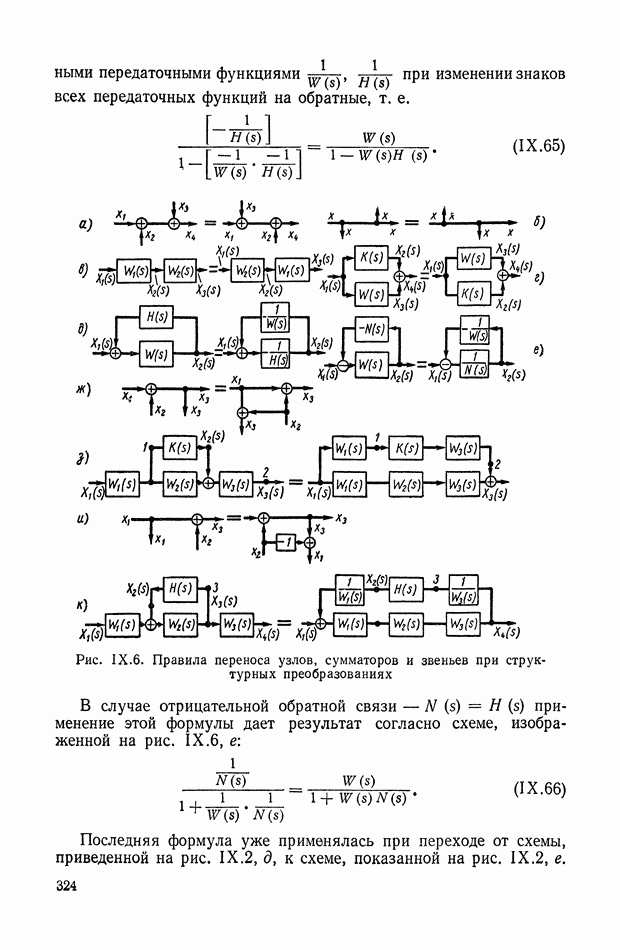
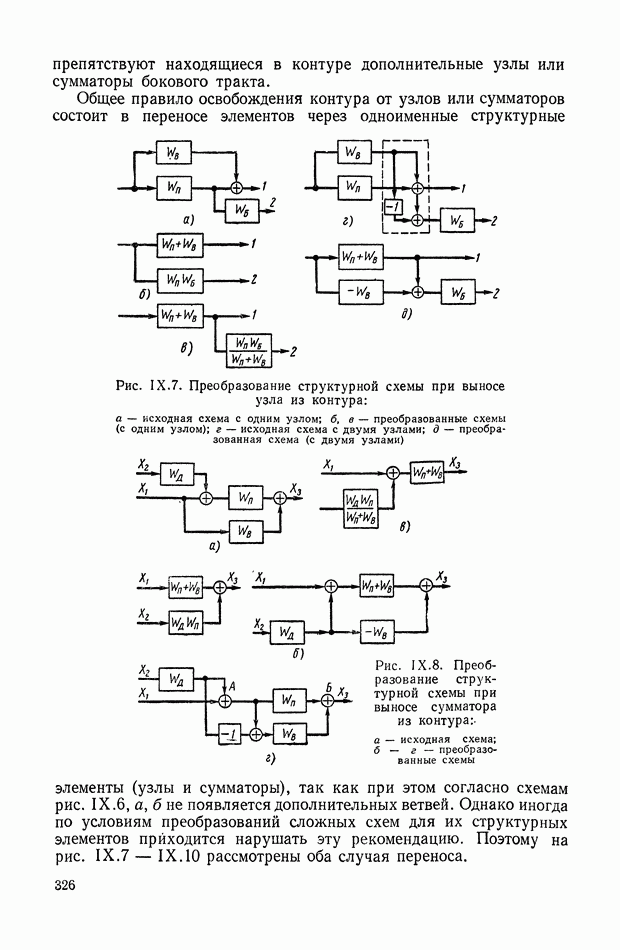
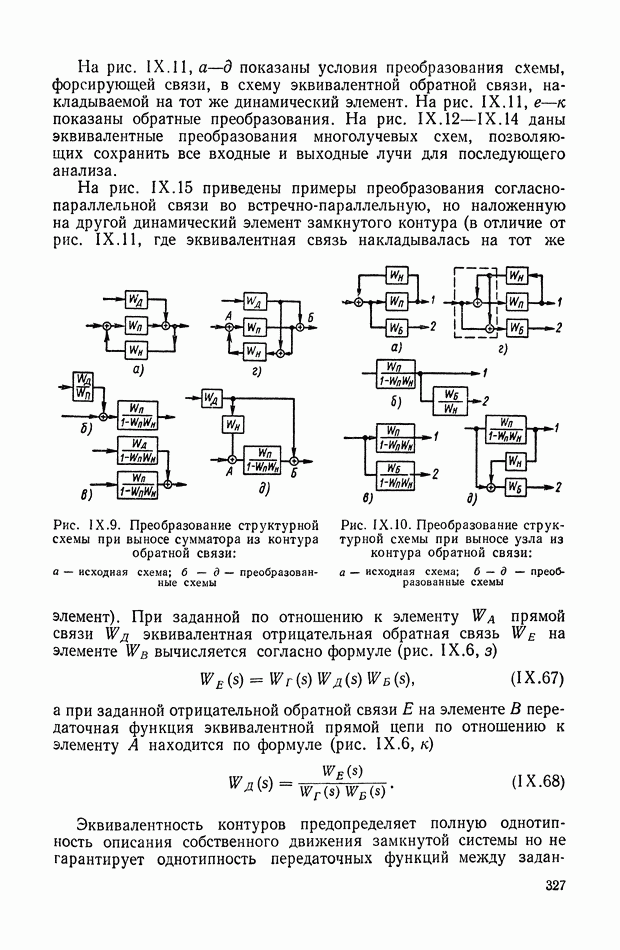
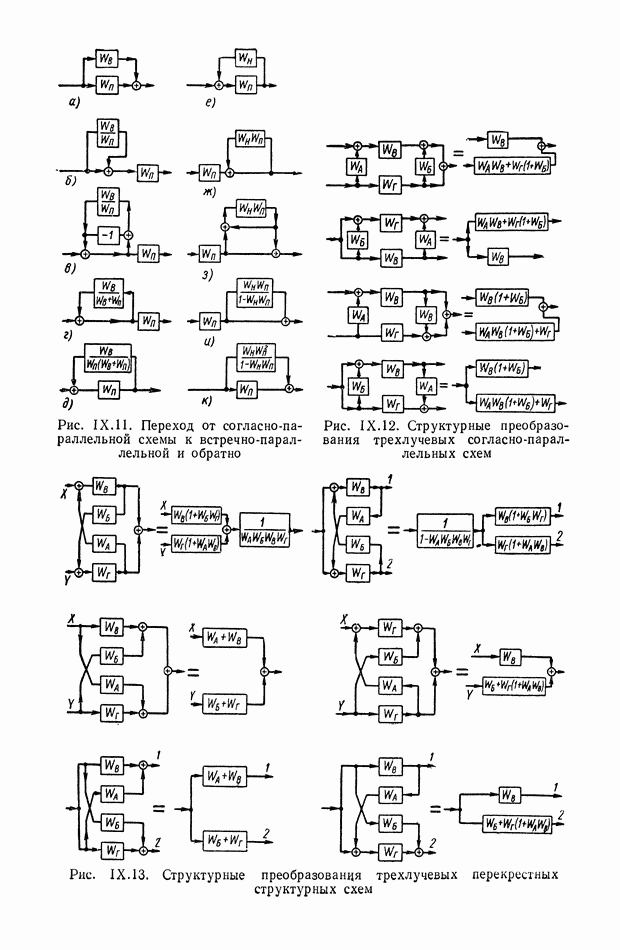
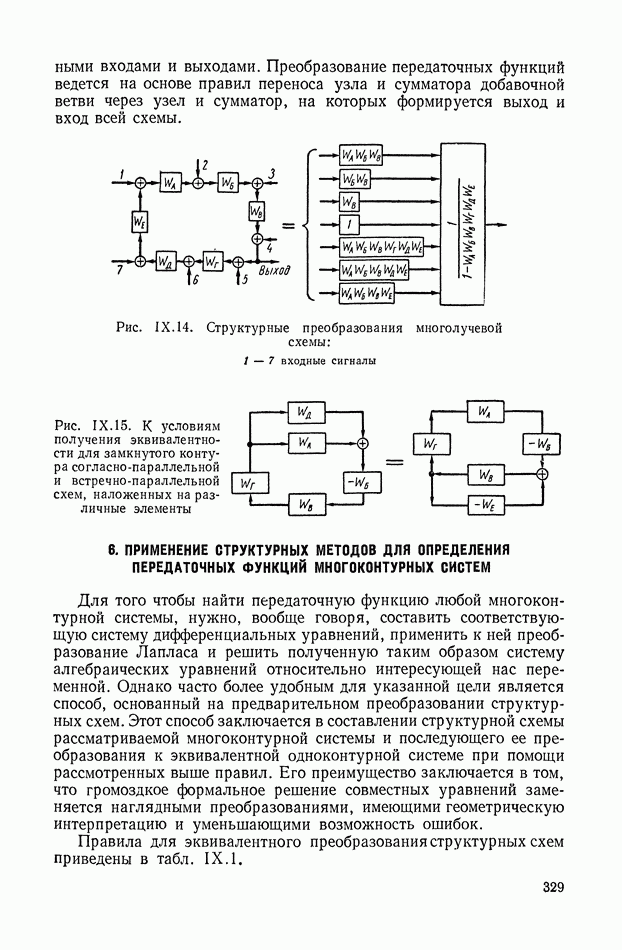
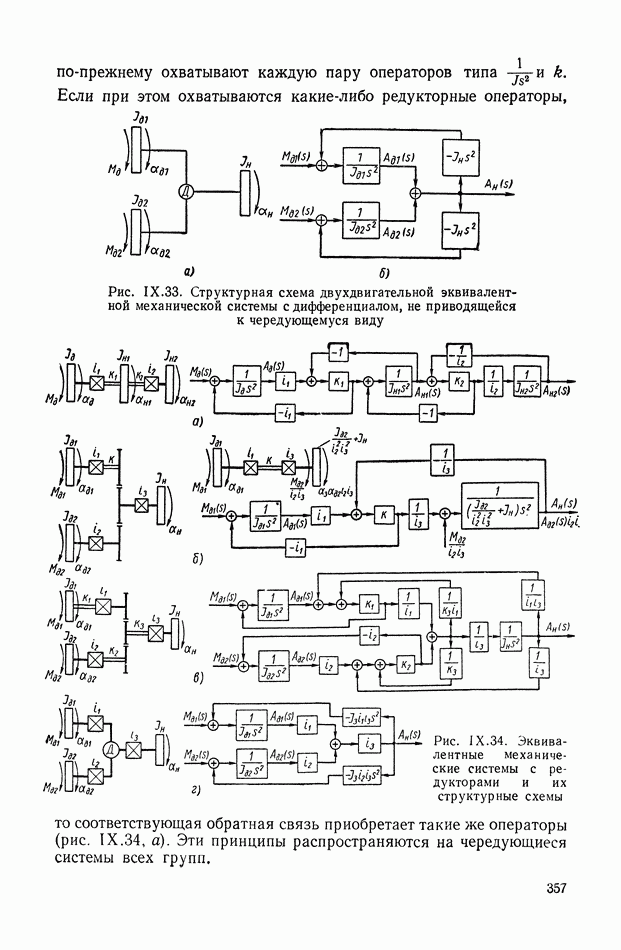
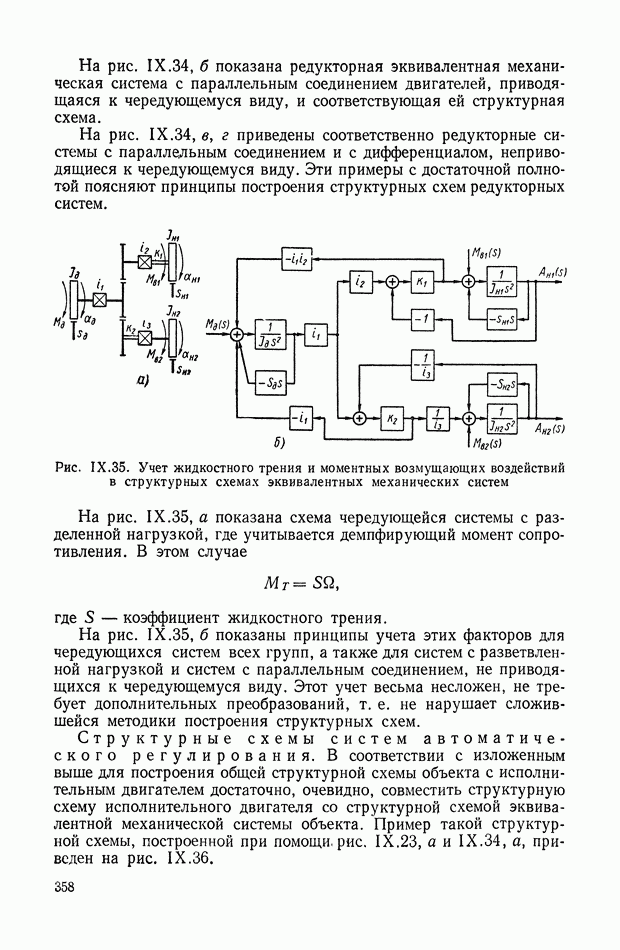
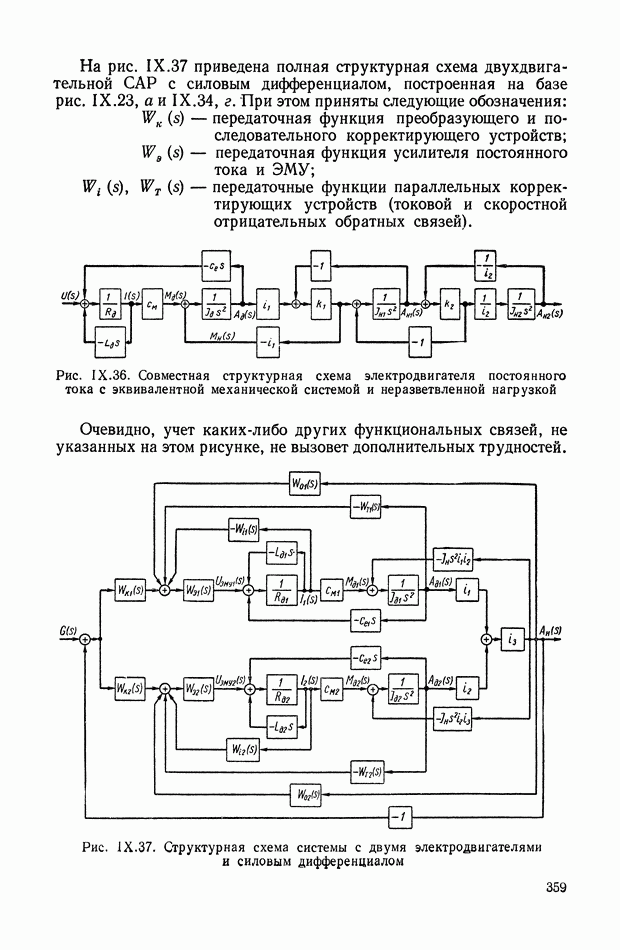
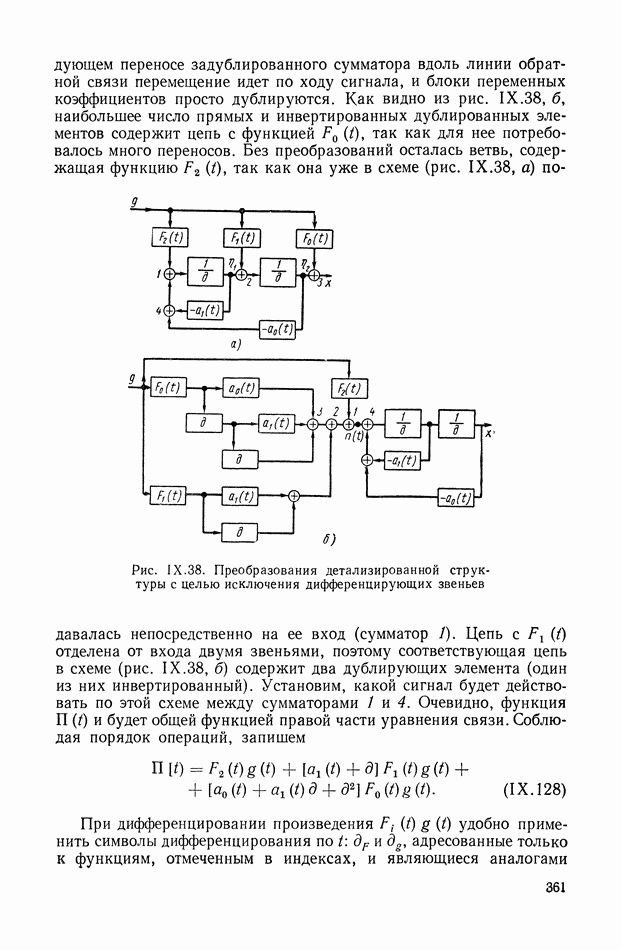
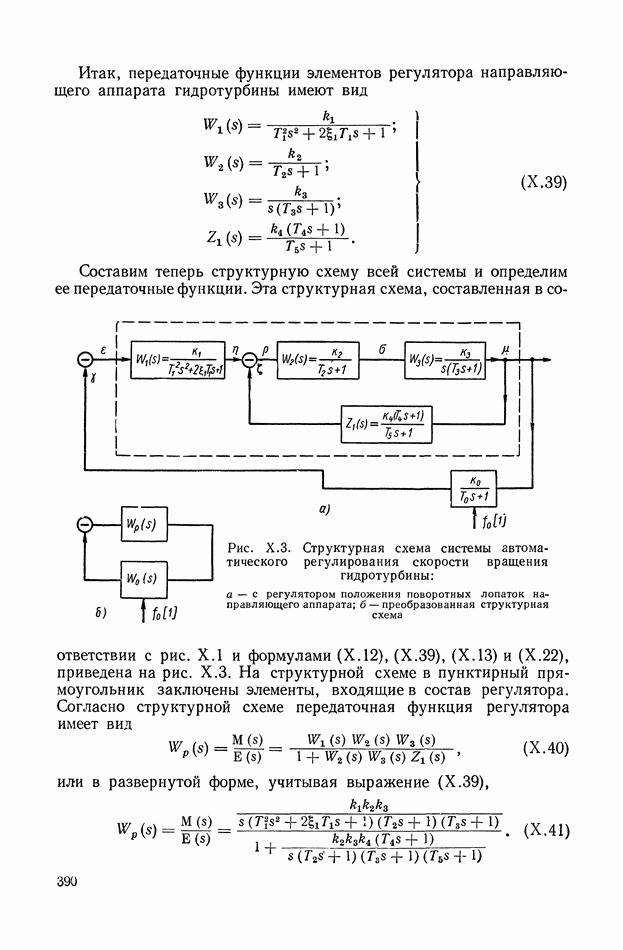
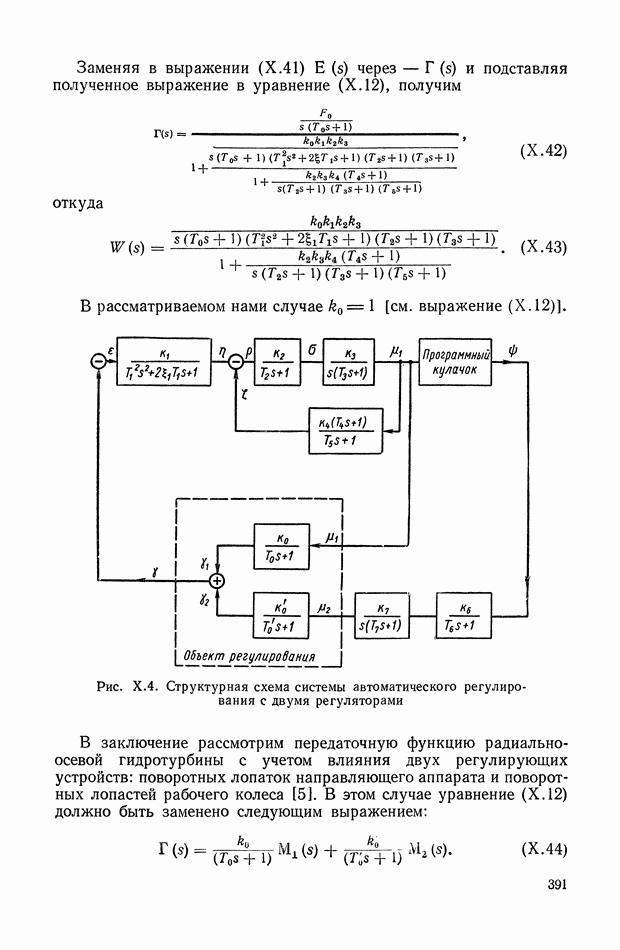
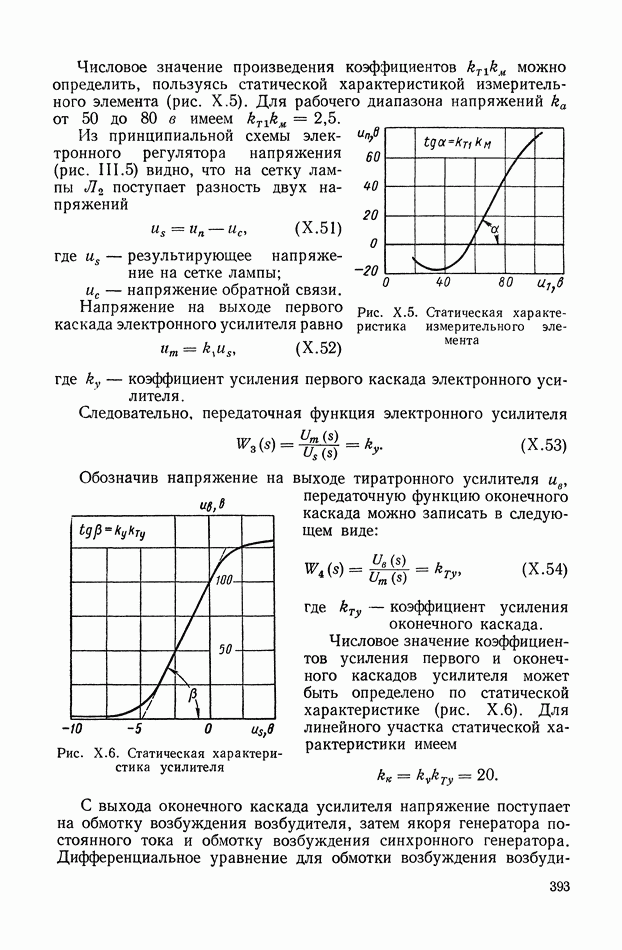
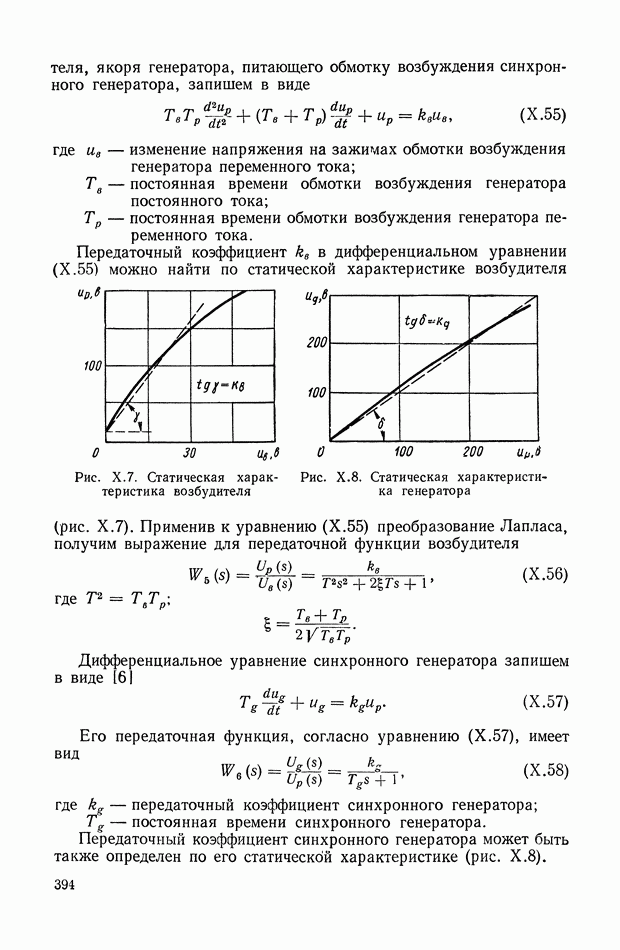
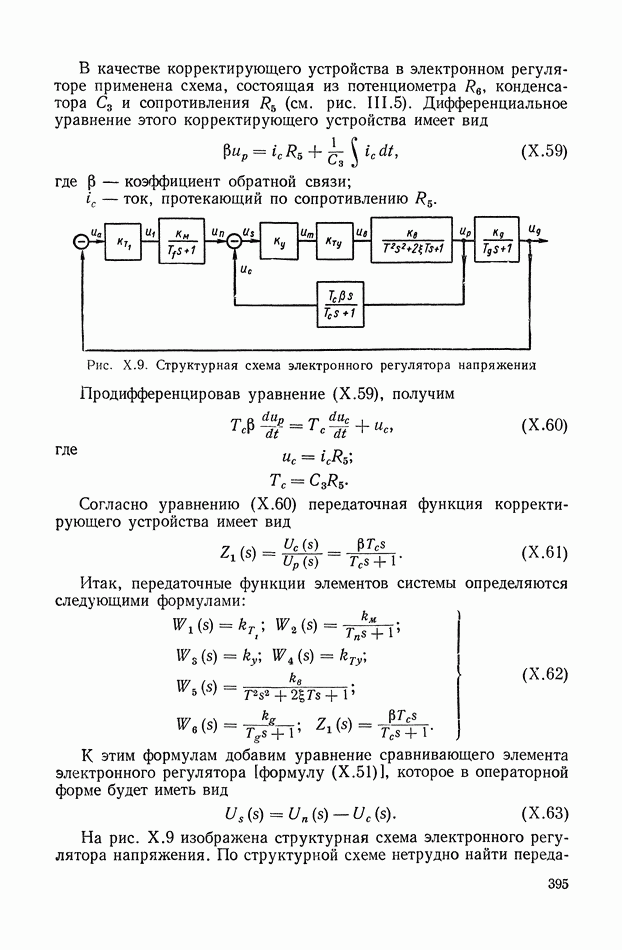
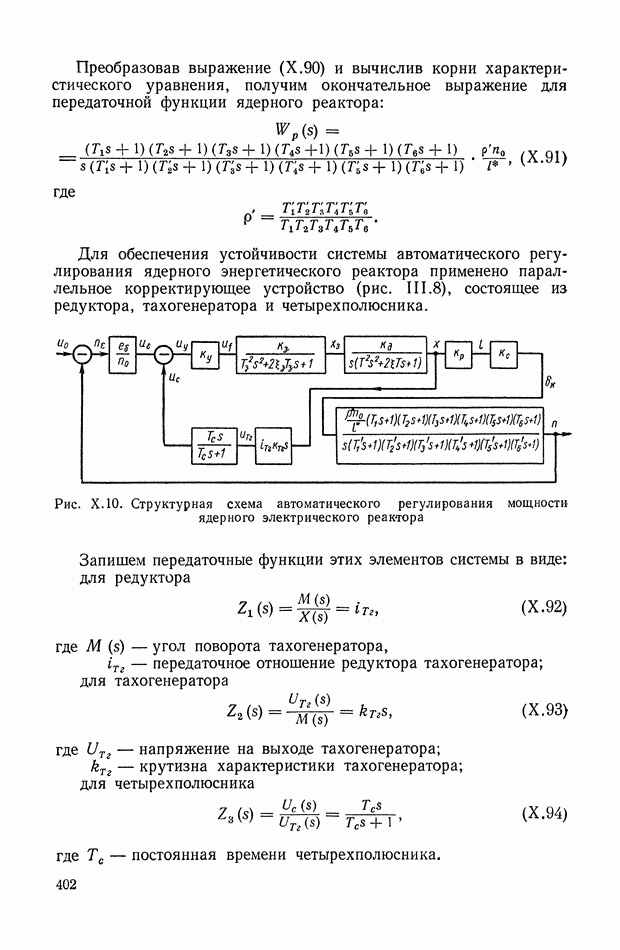
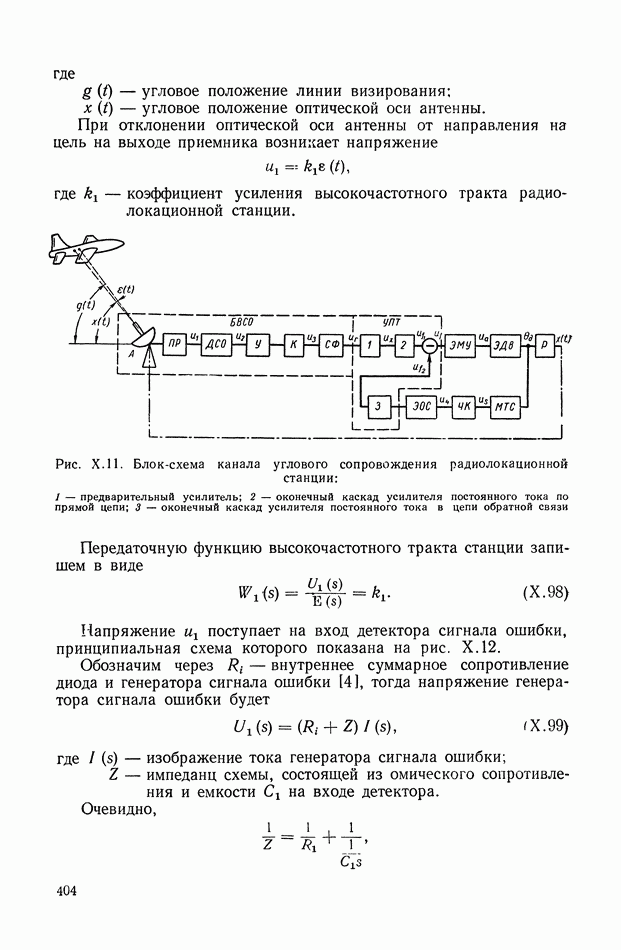
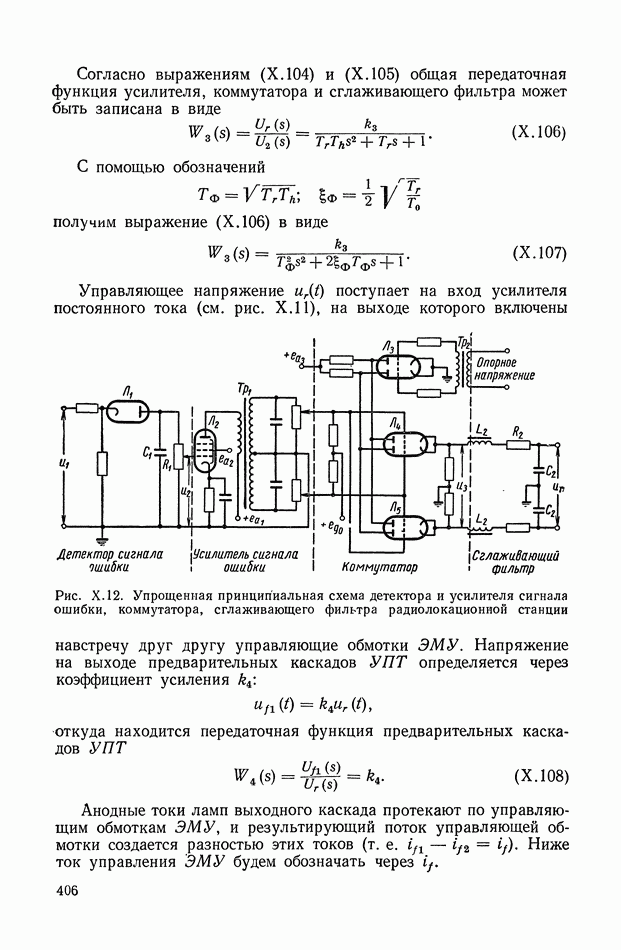
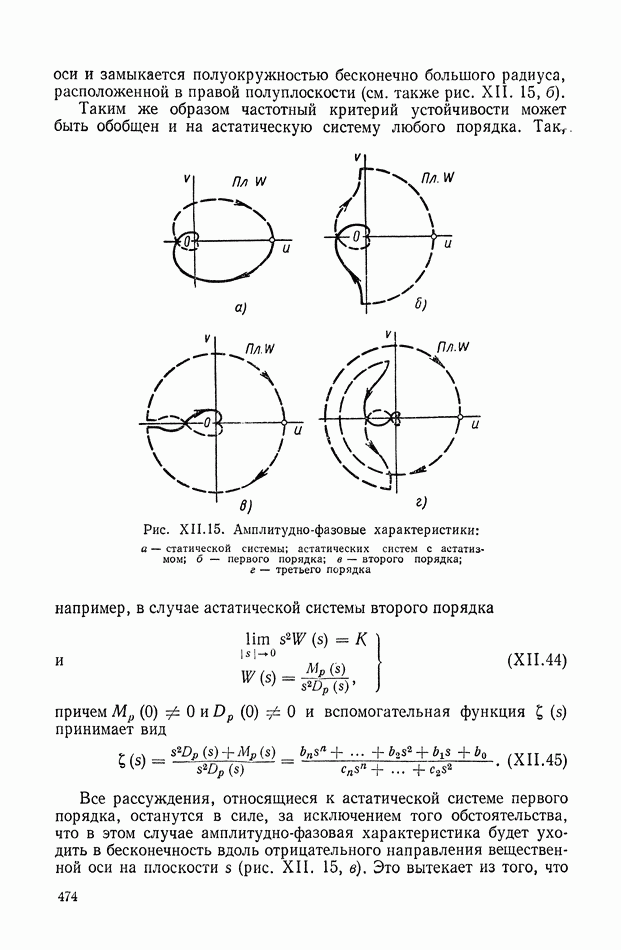
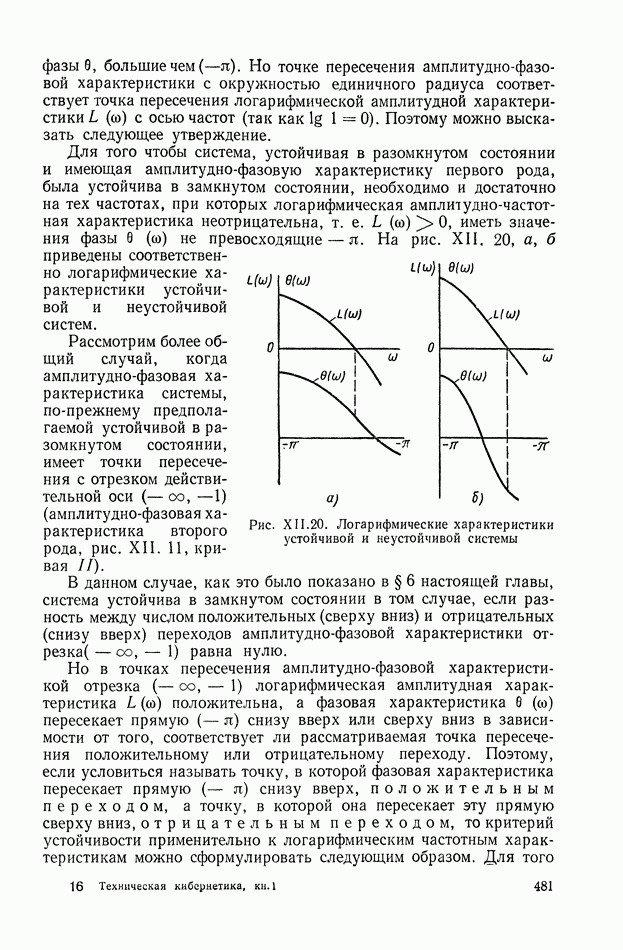
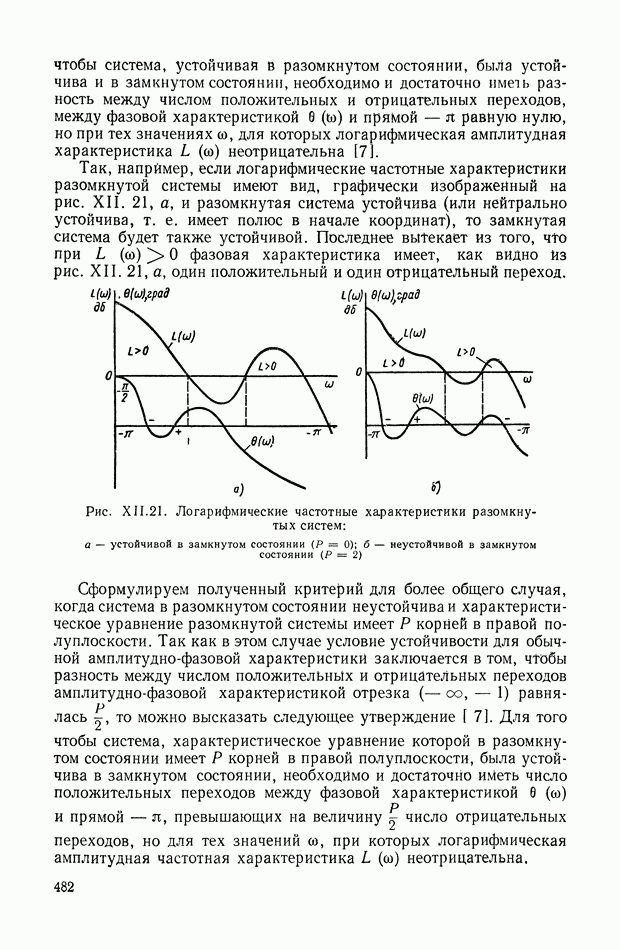
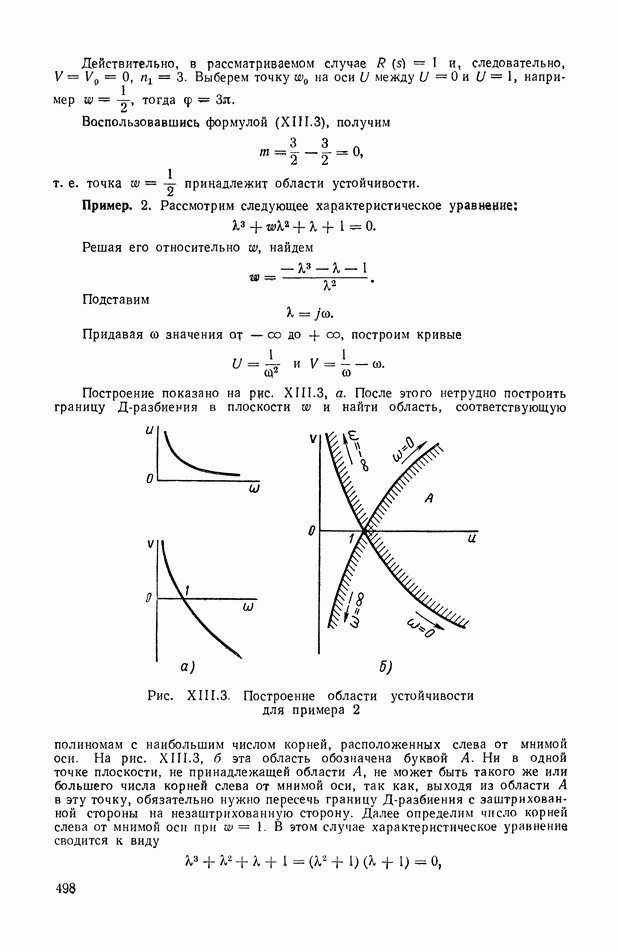
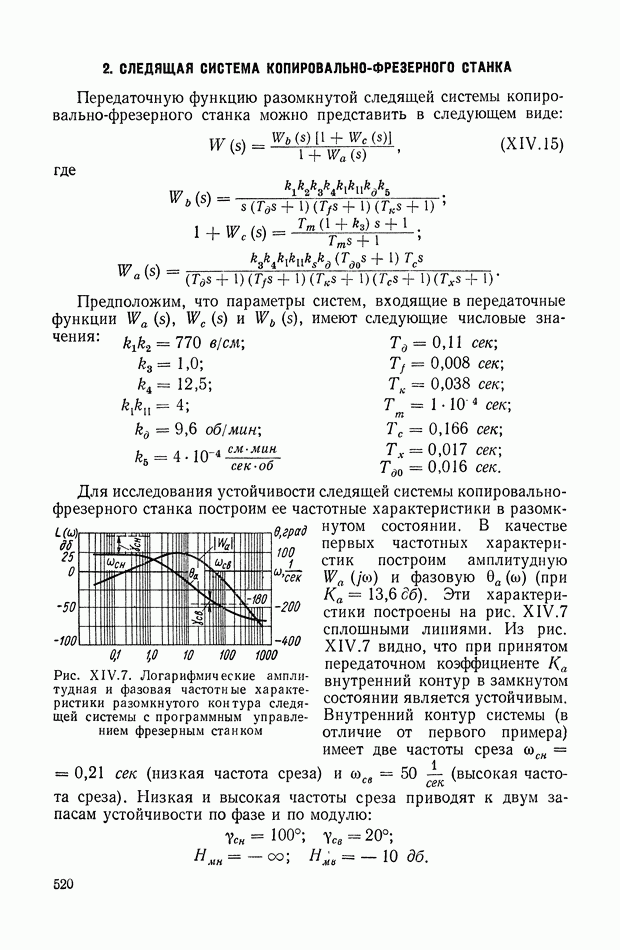
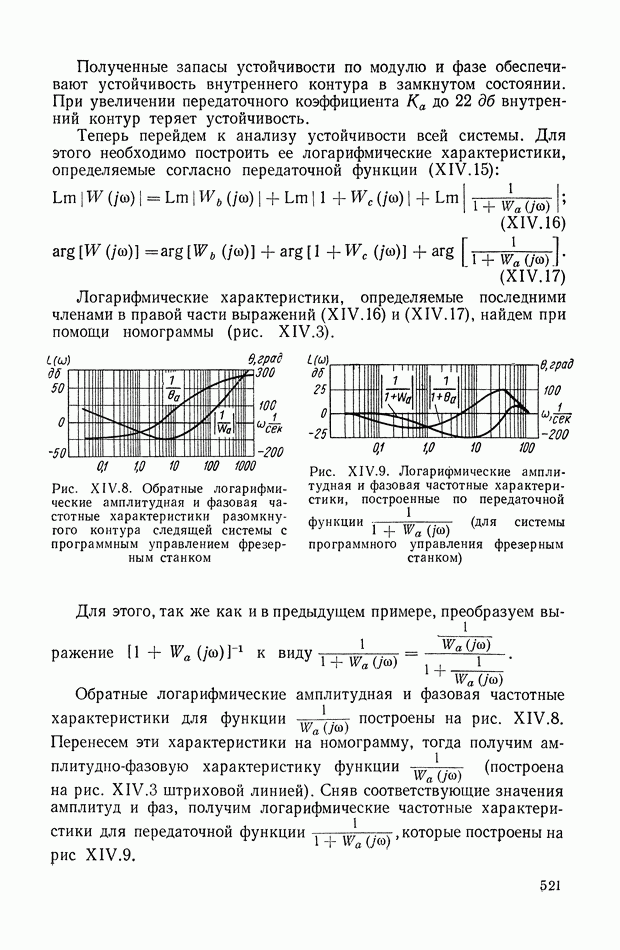
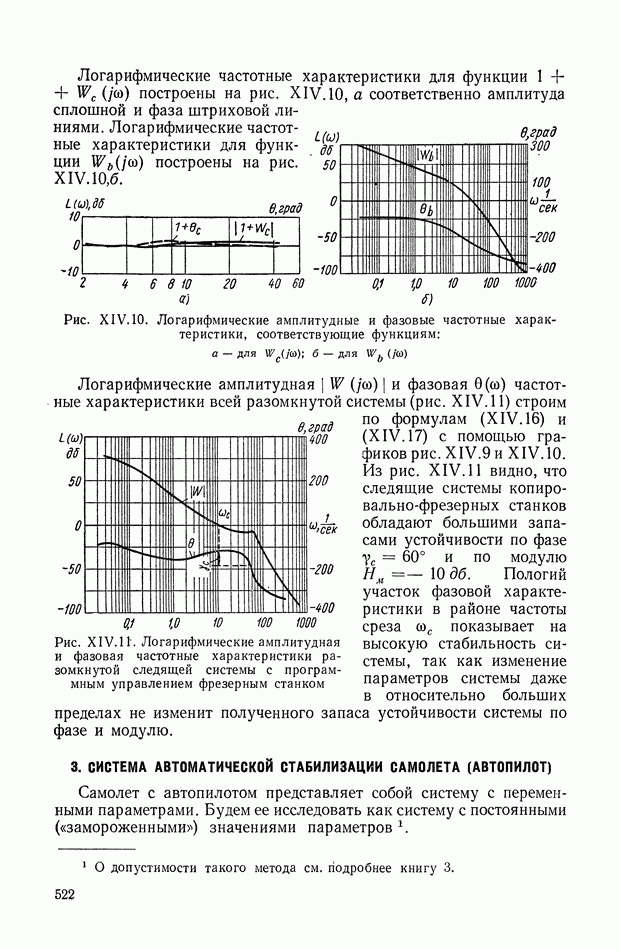
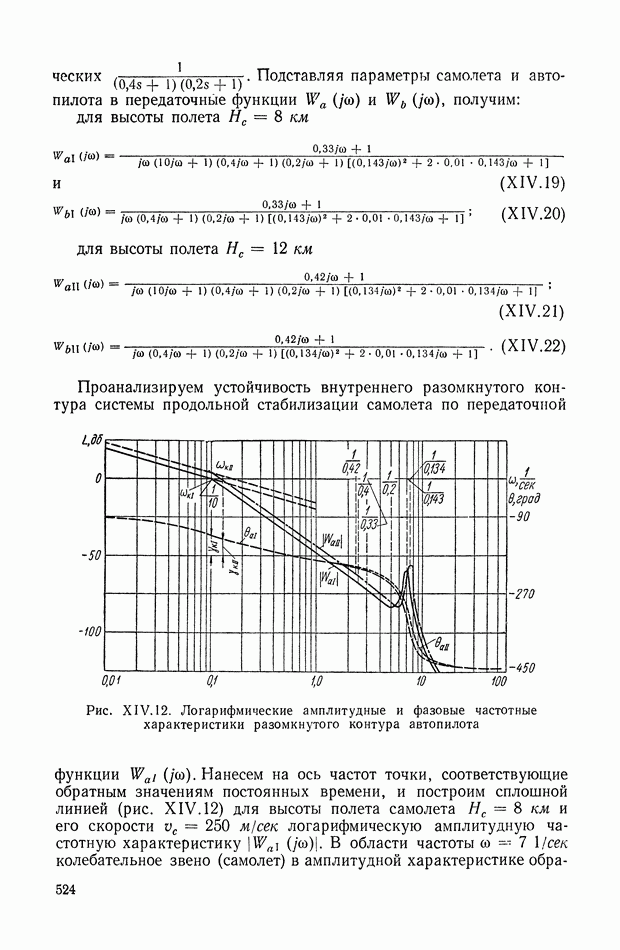
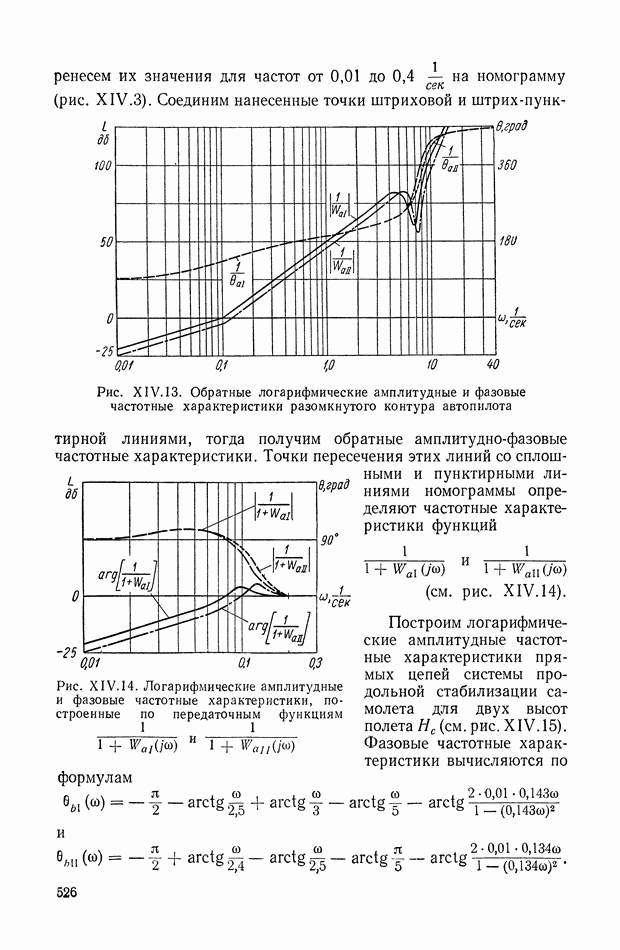
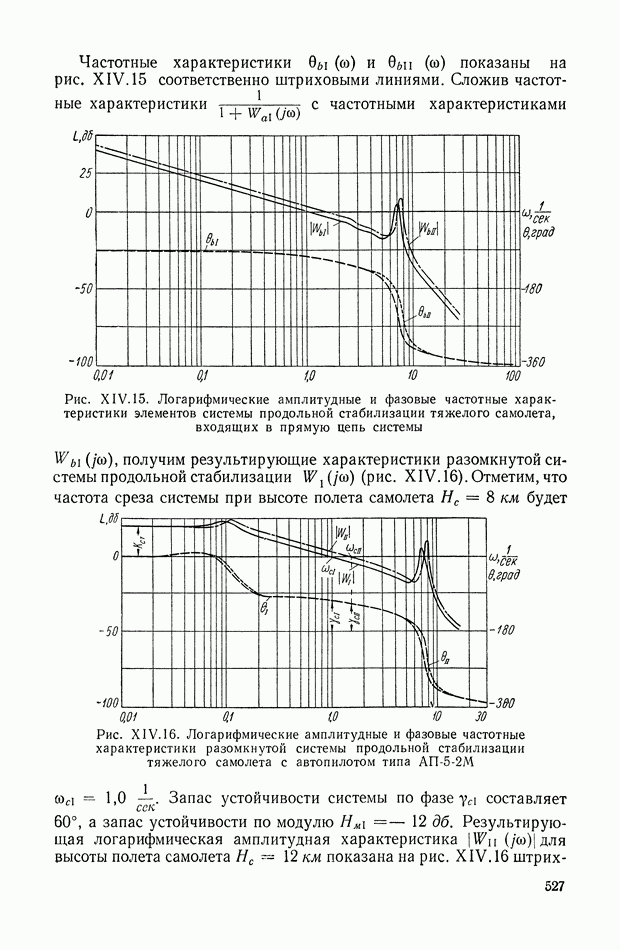
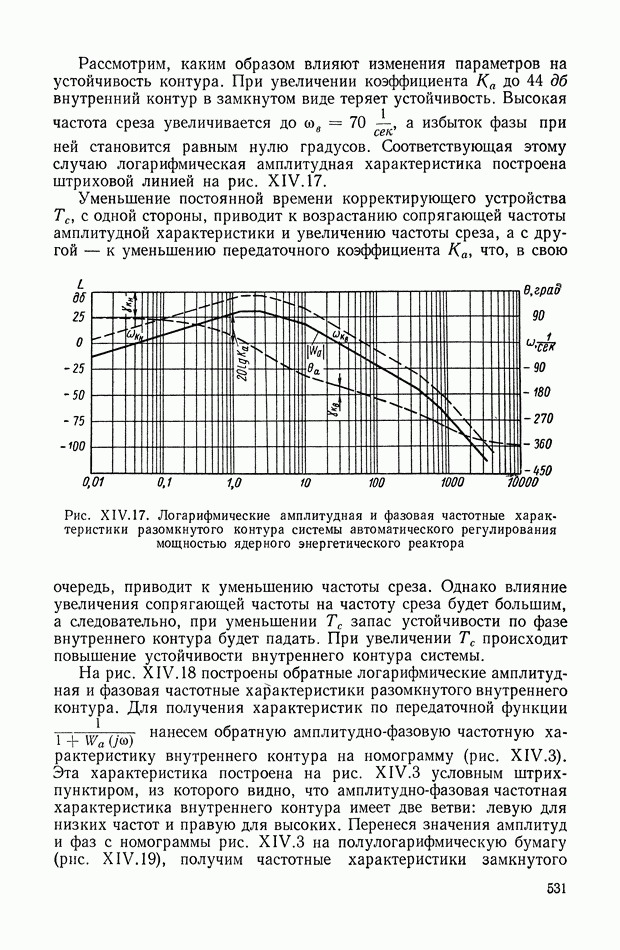
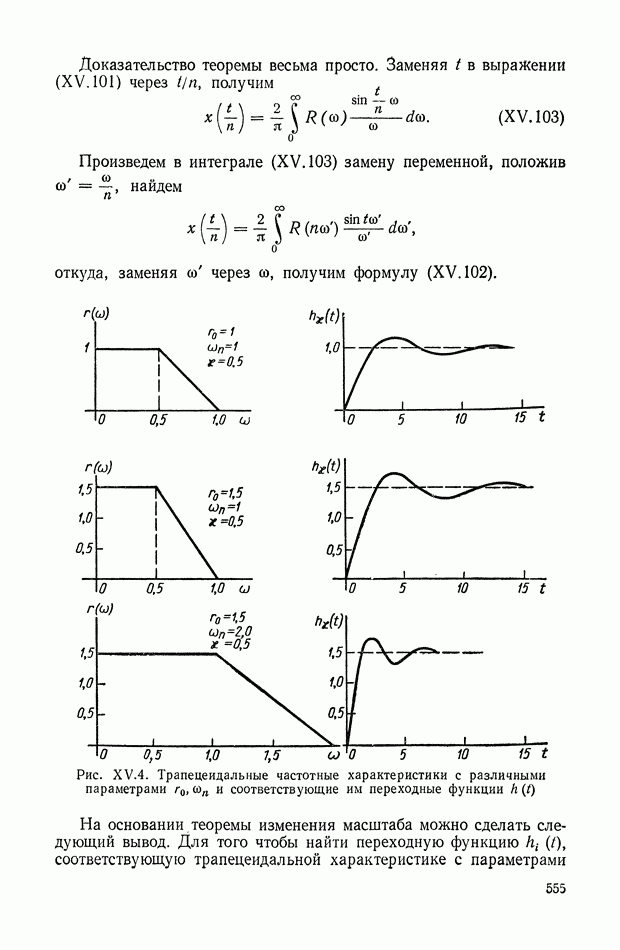
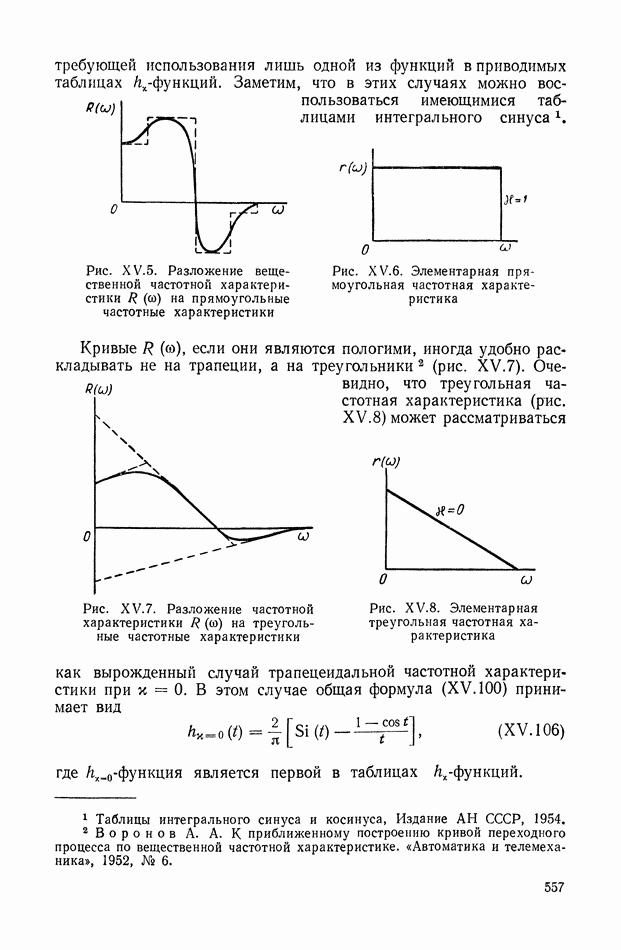
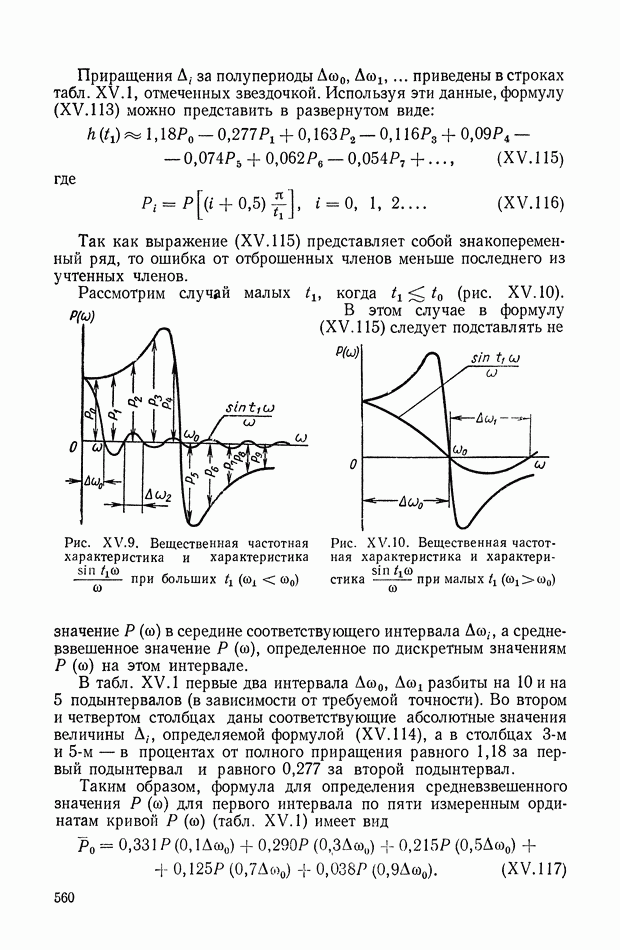
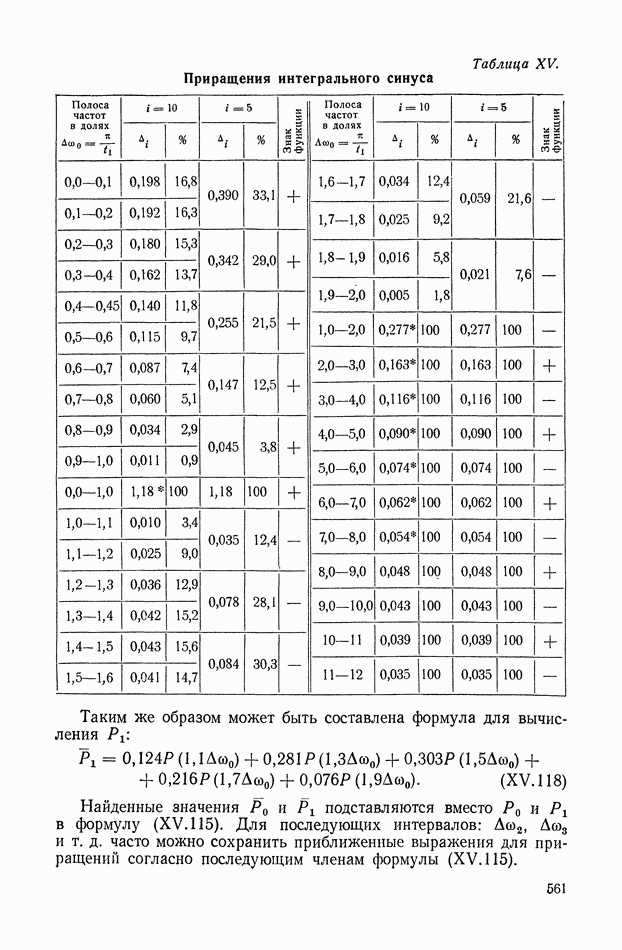
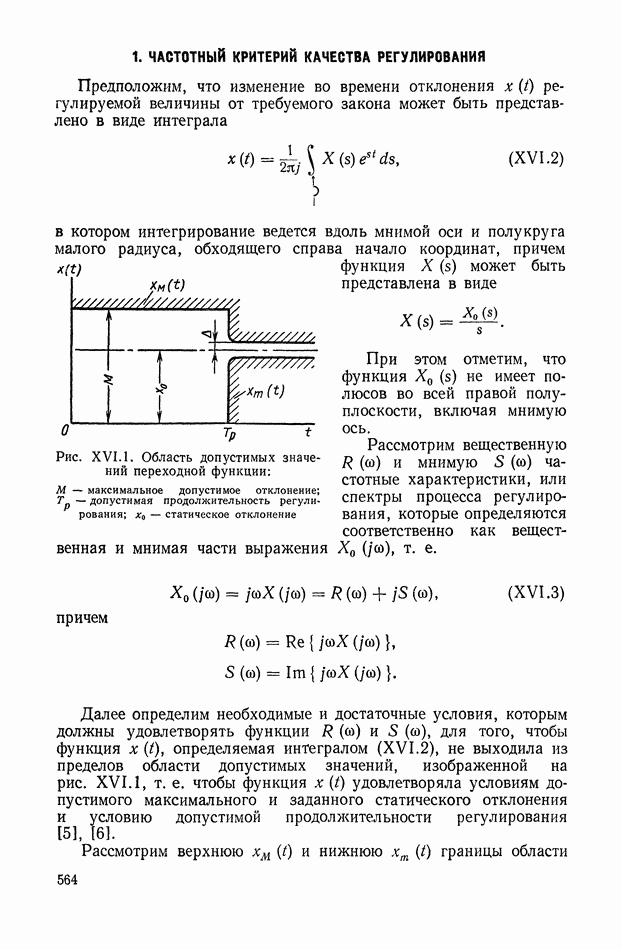
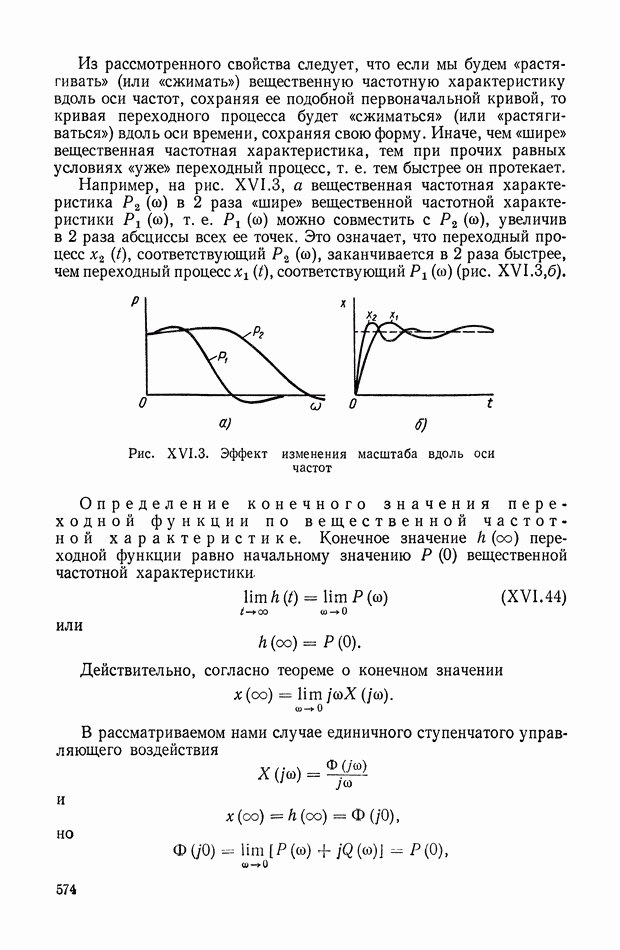
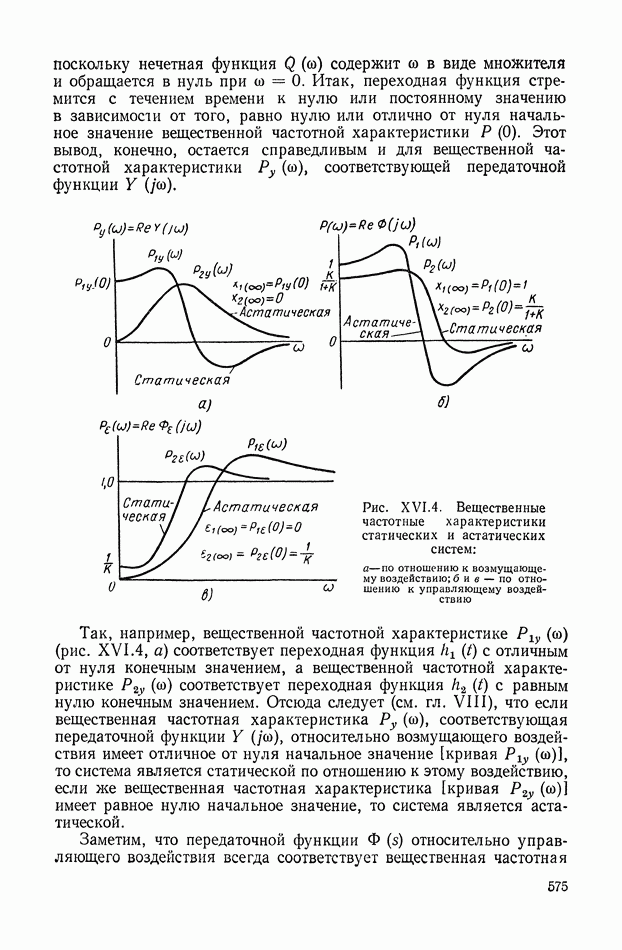
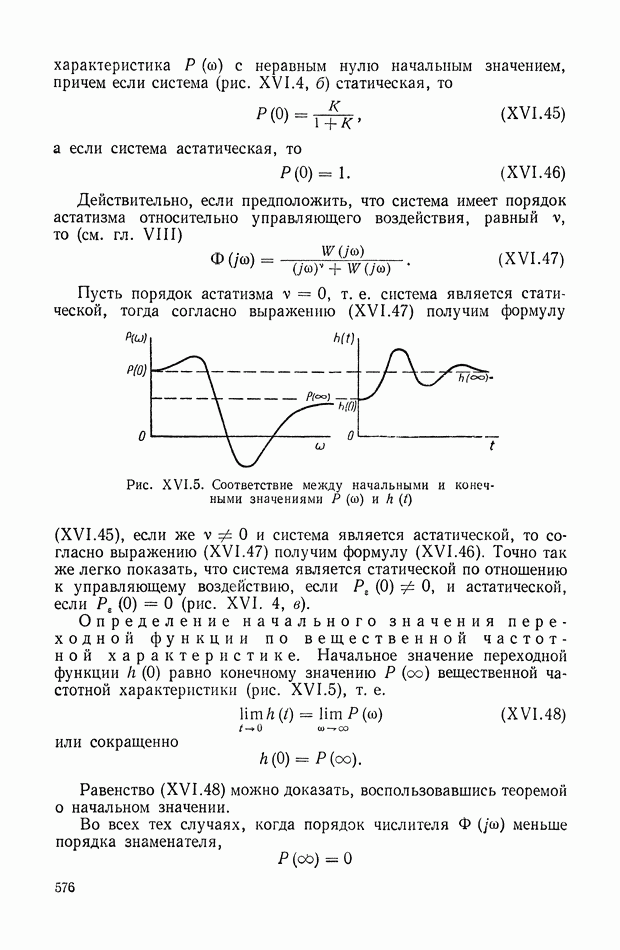
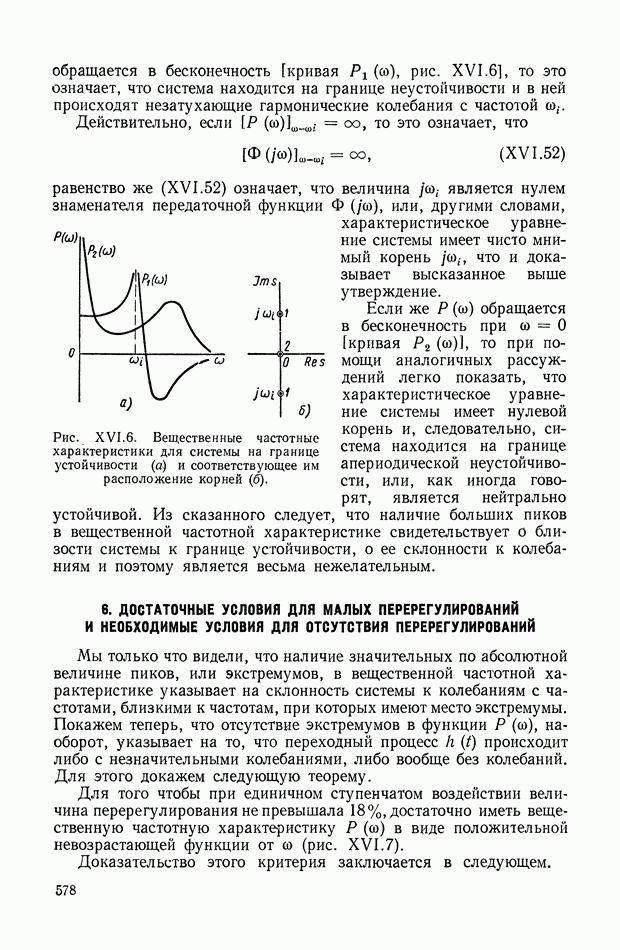
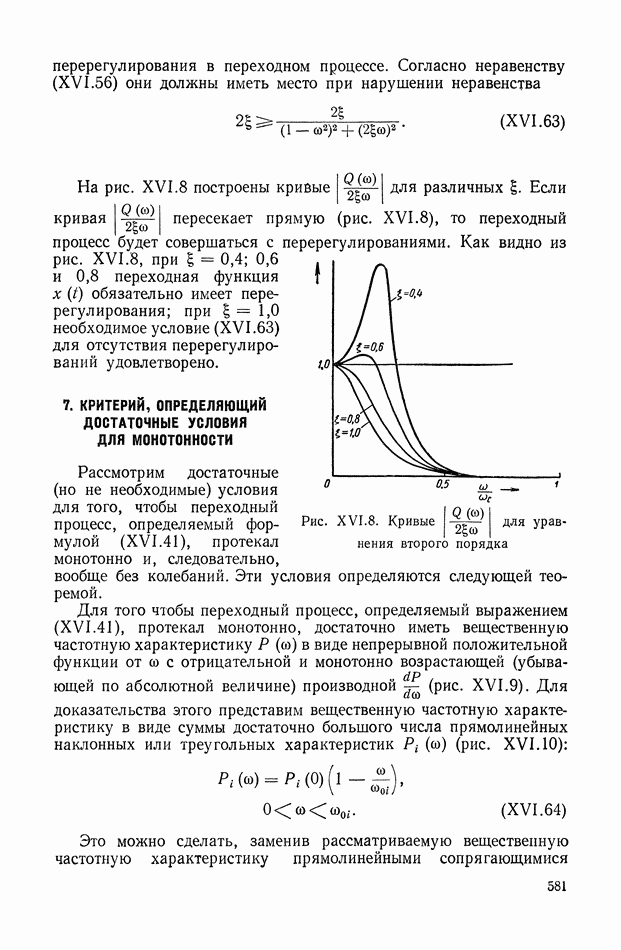
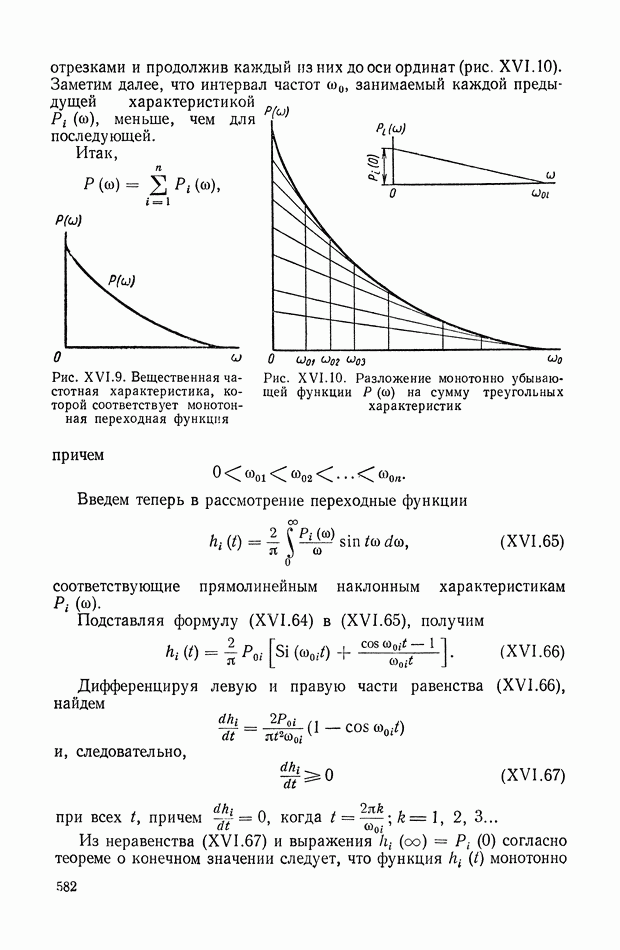
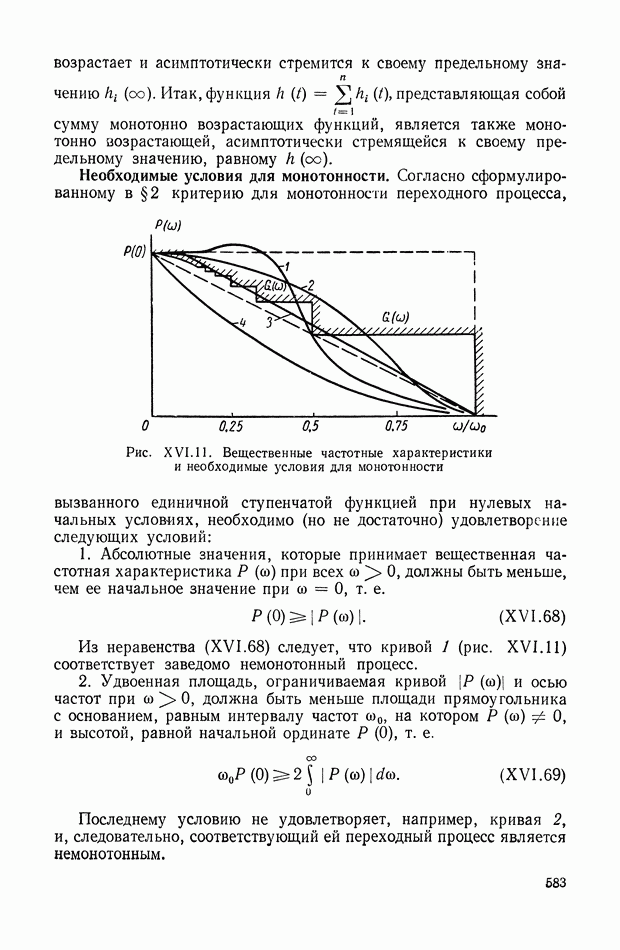
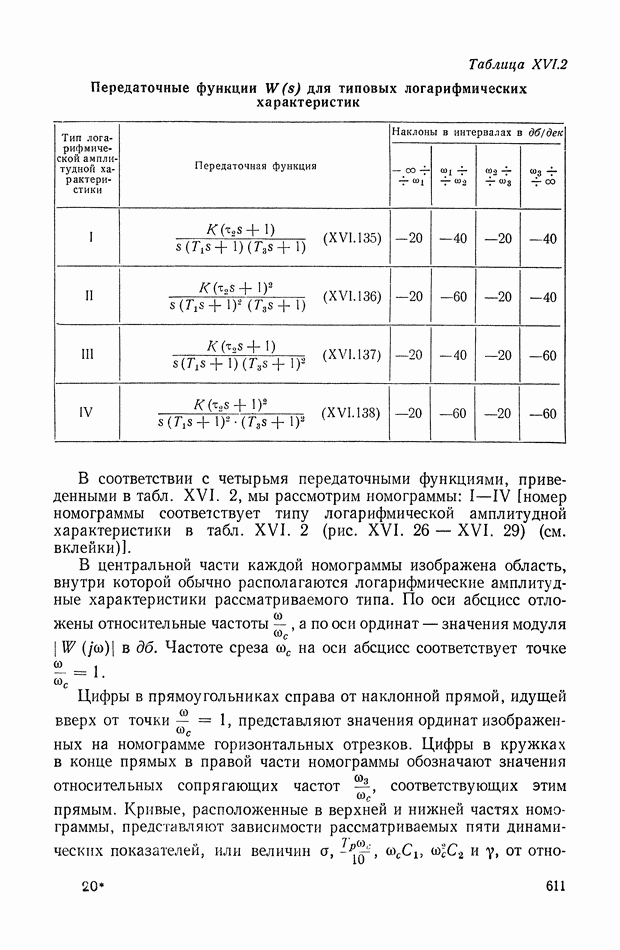
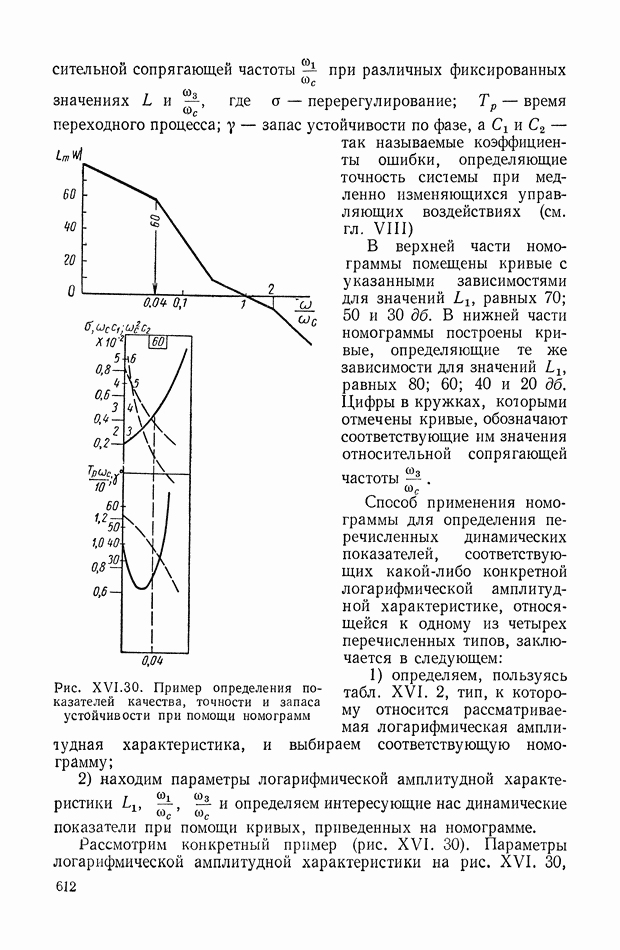
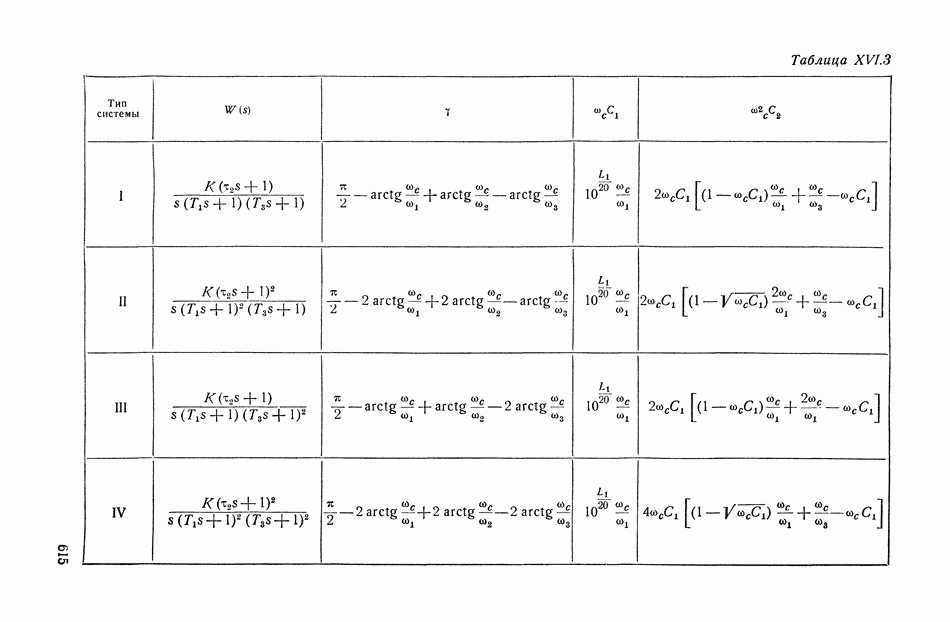
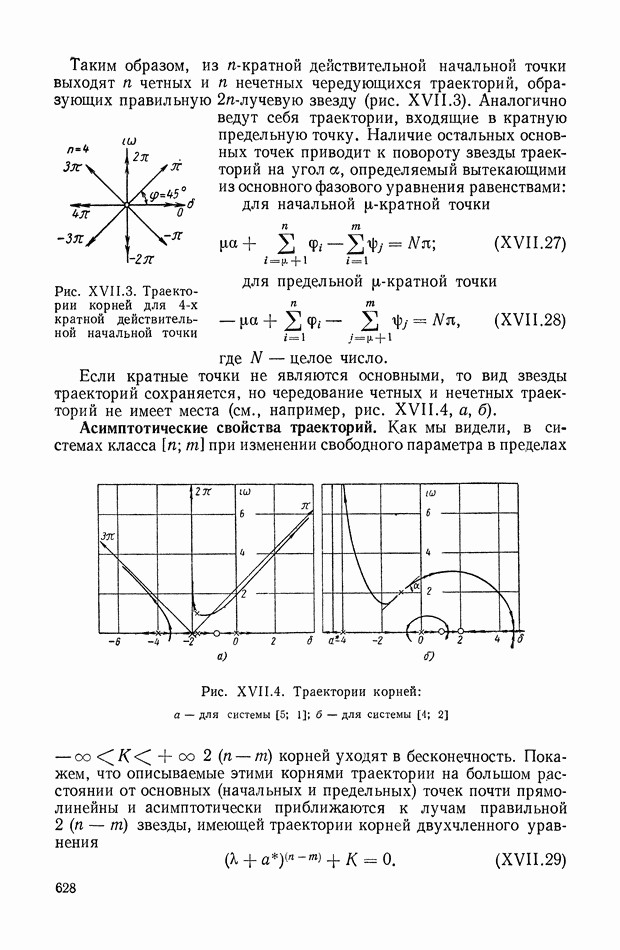
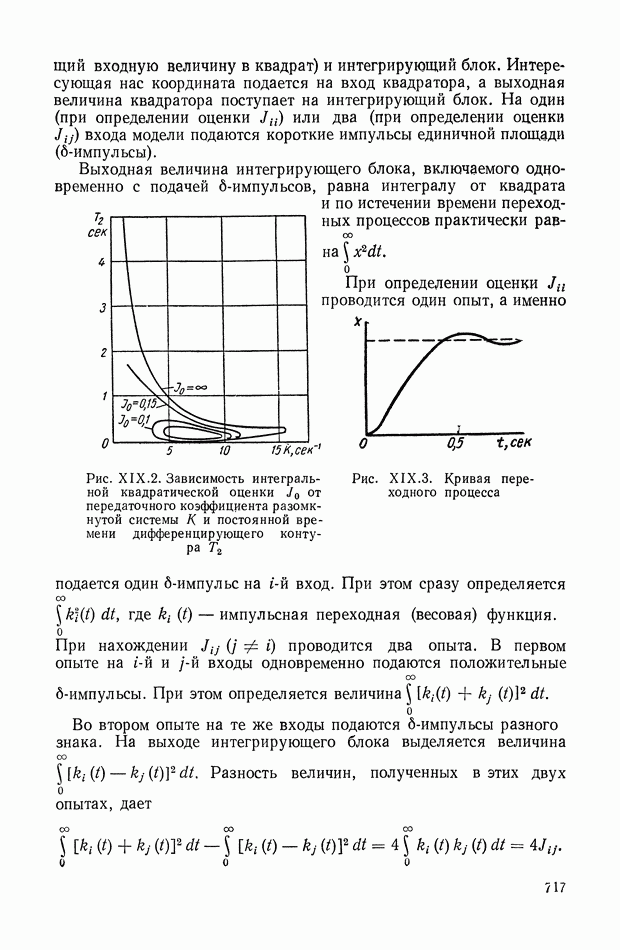
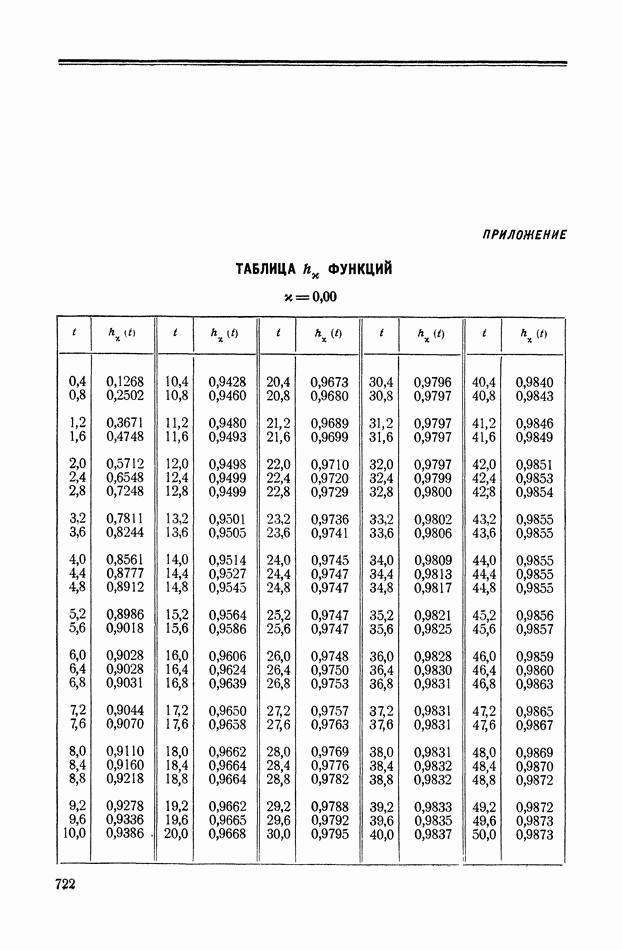
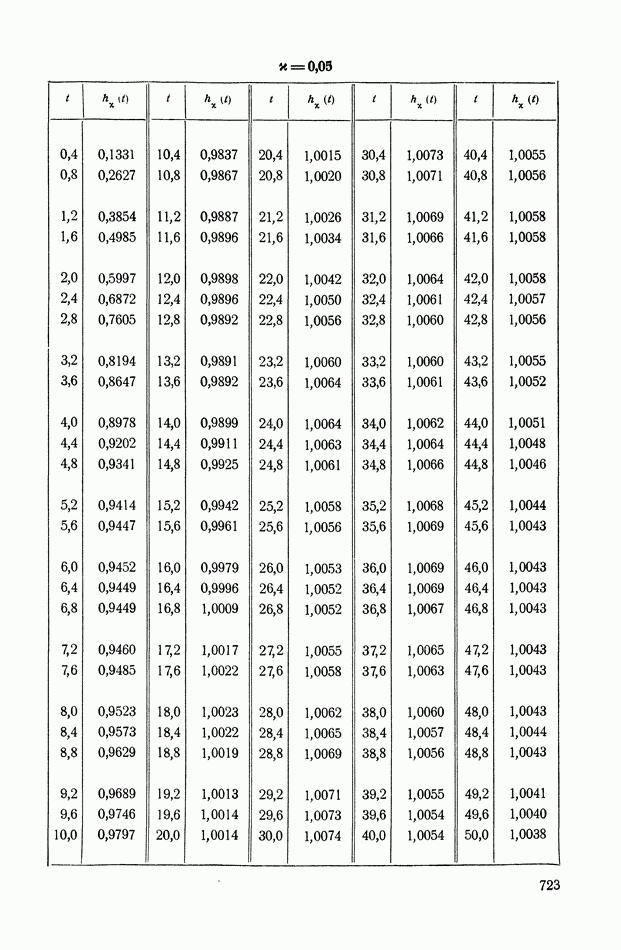
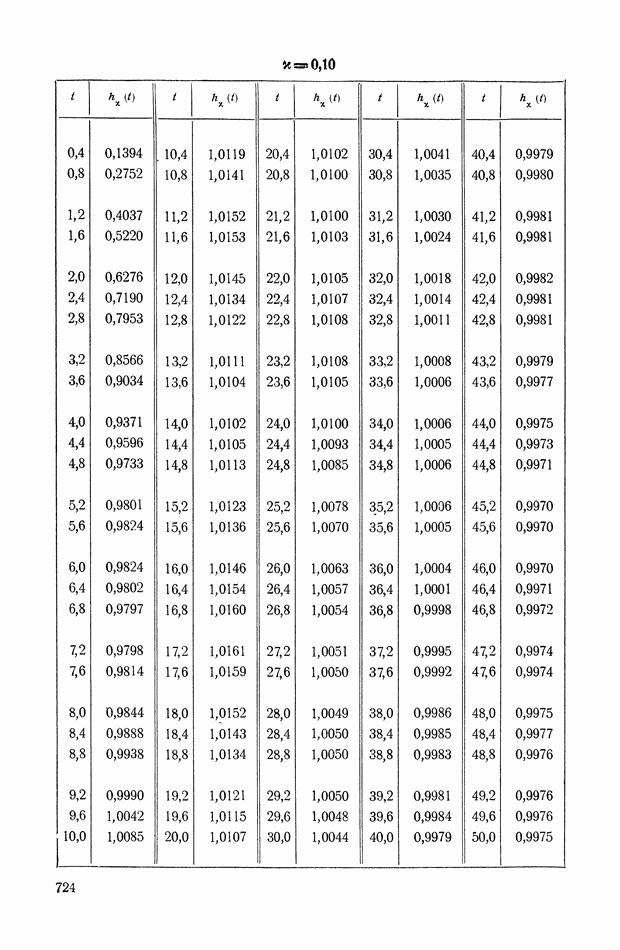
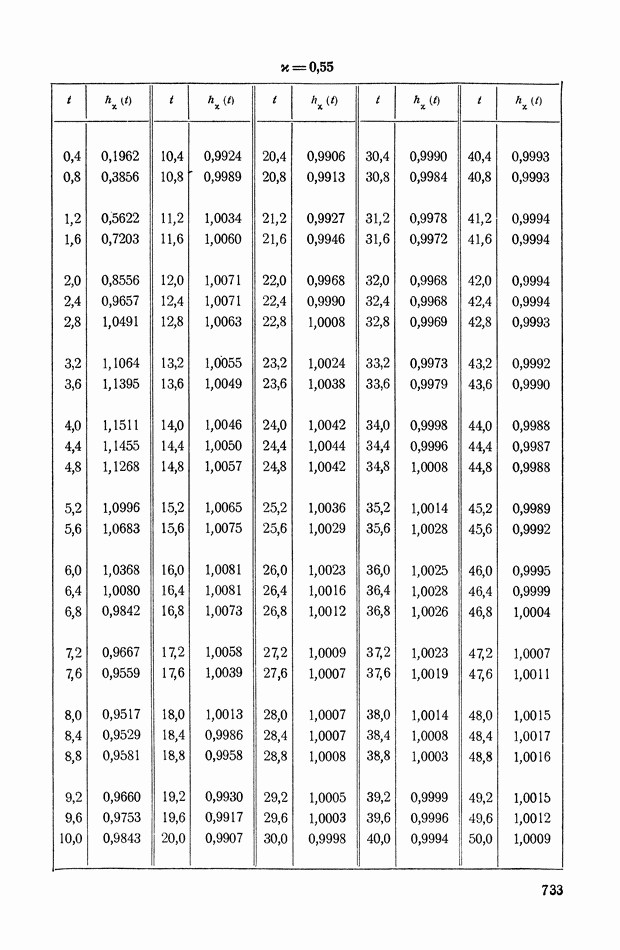
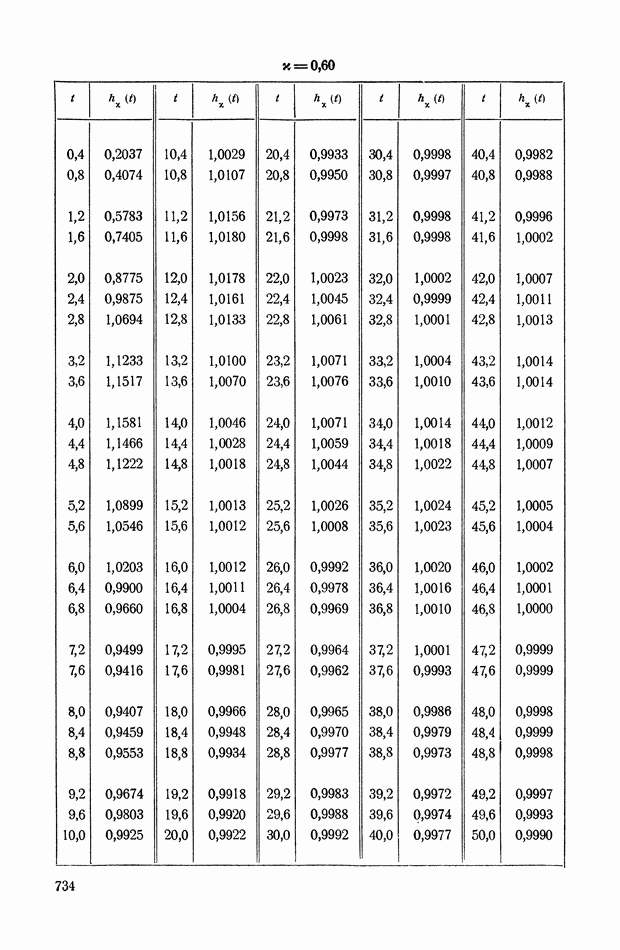
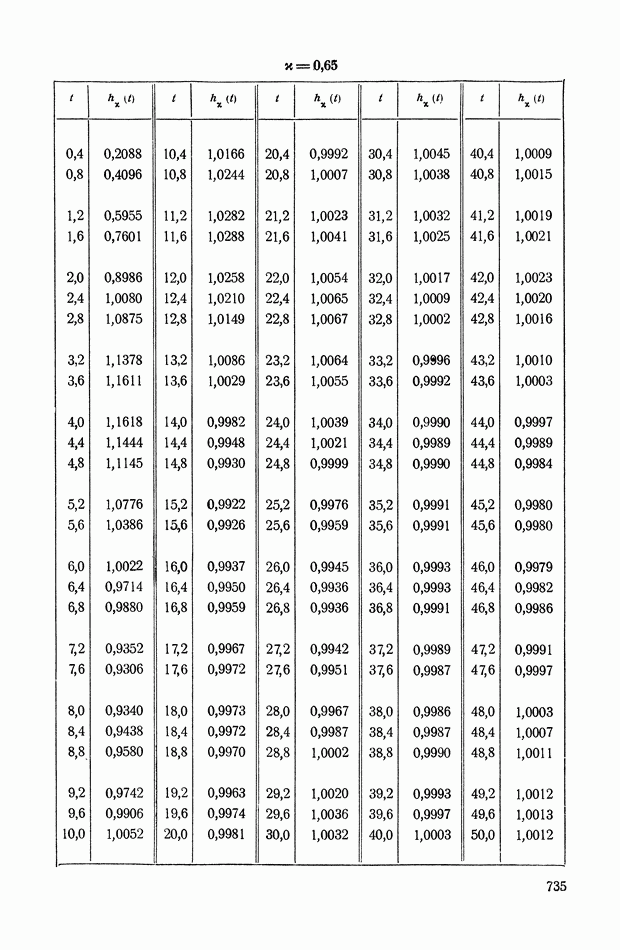
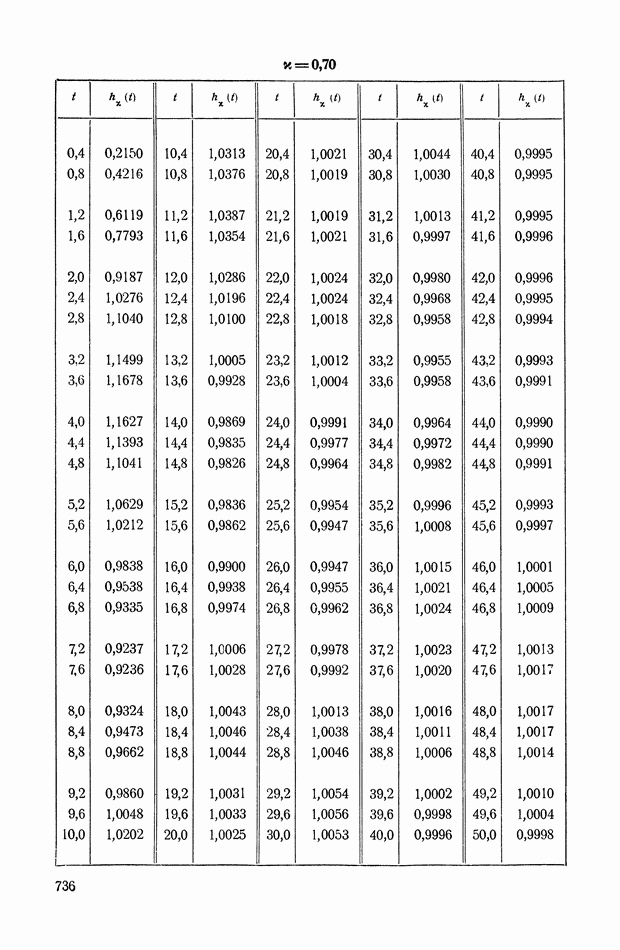
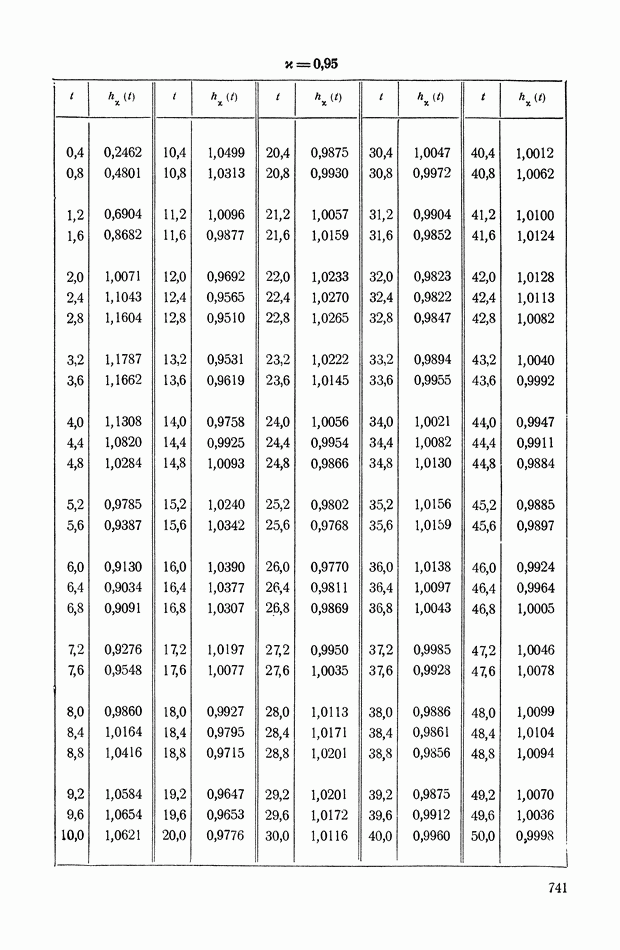
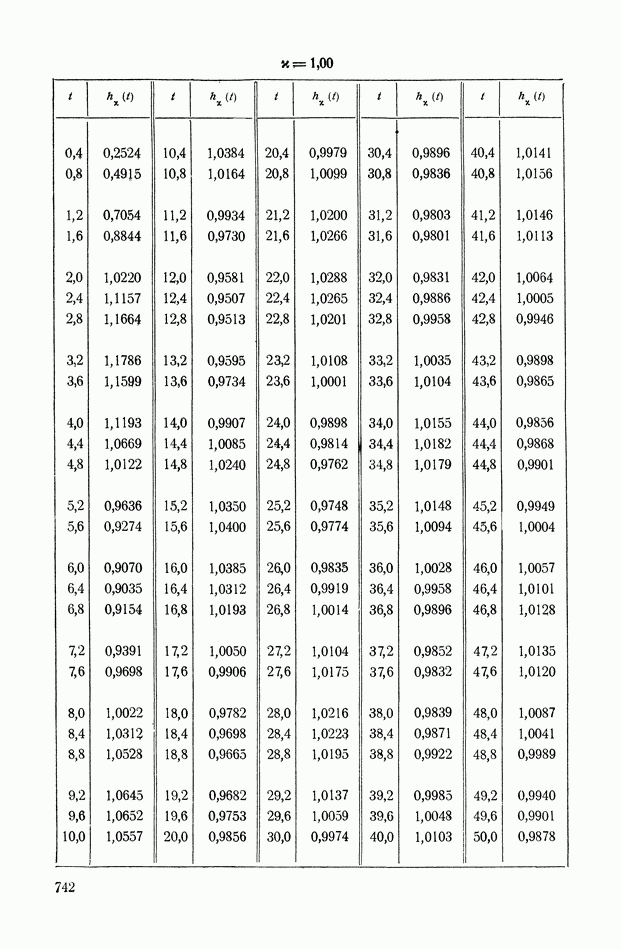
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
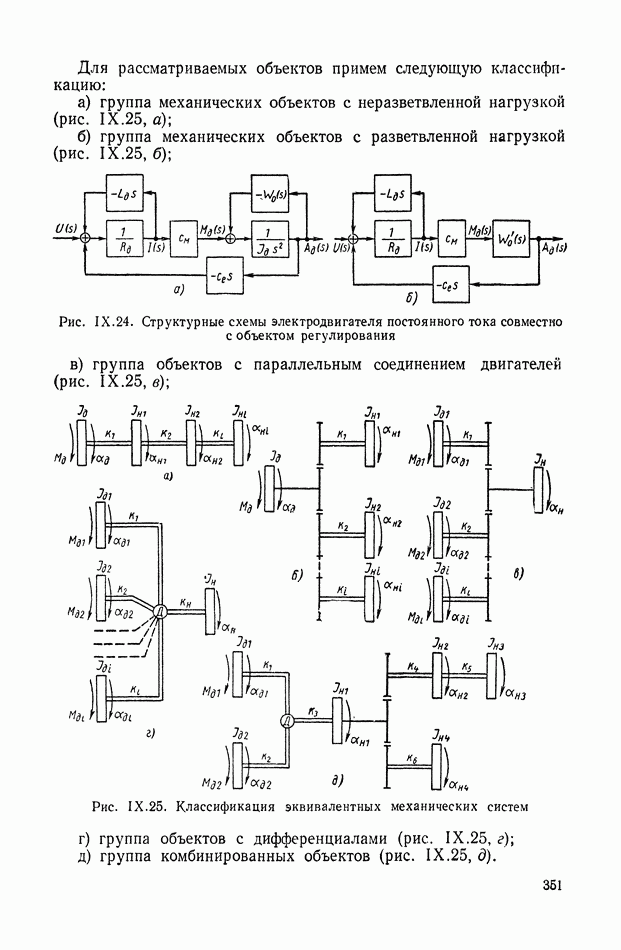
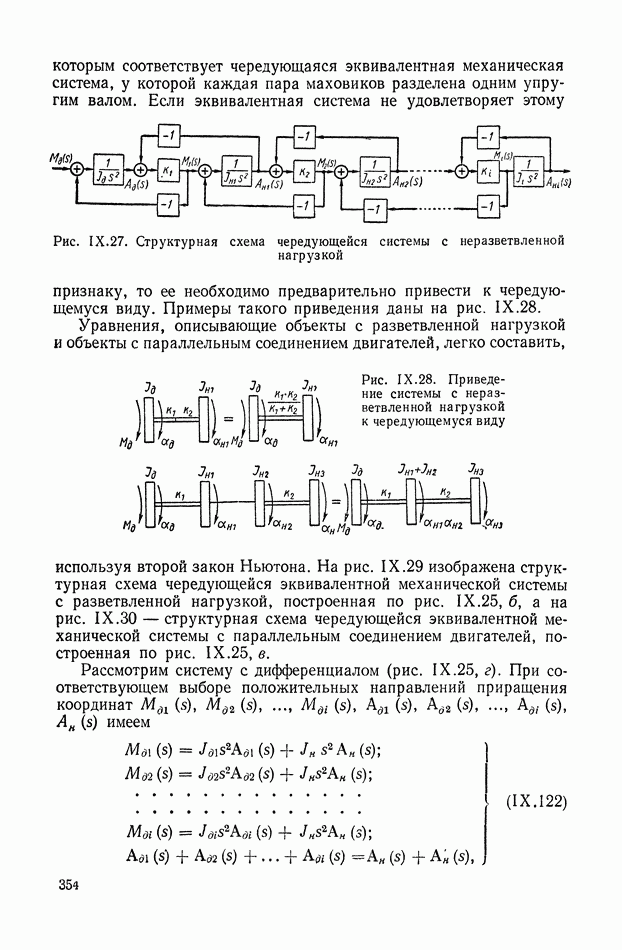
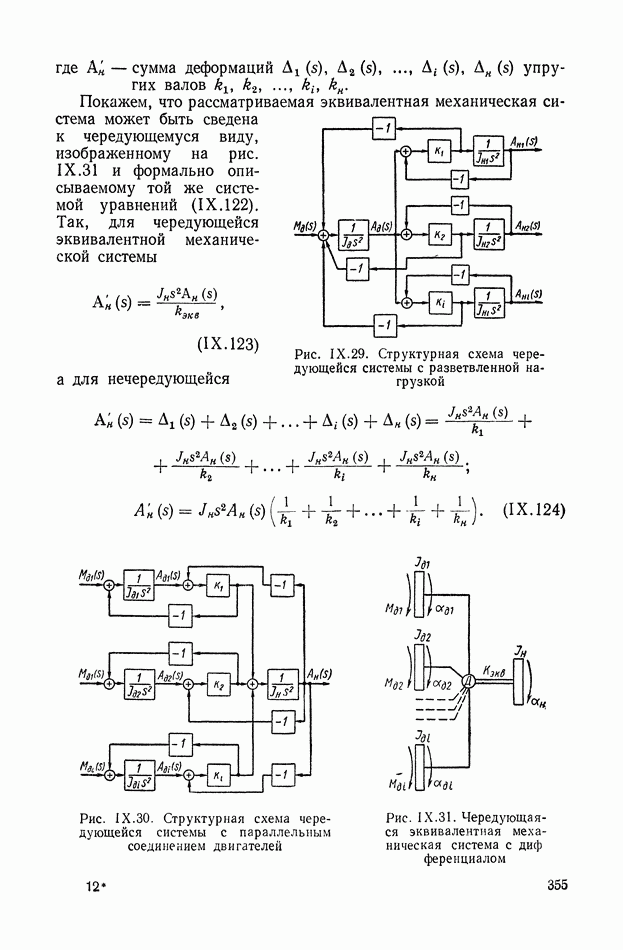
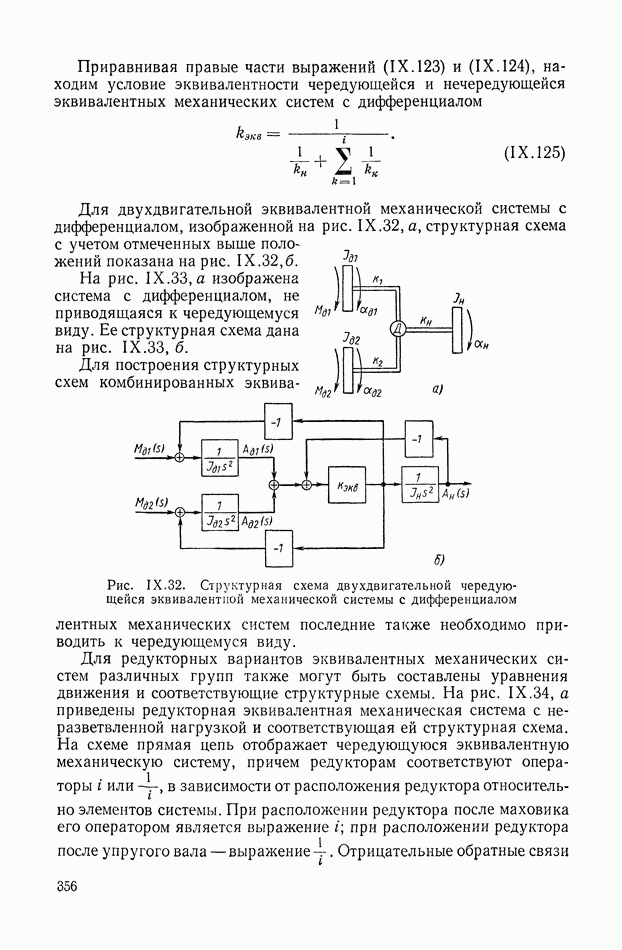
ГЛАВА XIX. ИНТЕГРАЛЬНЫЕ ОЦЕНКИ И КРИТЕРИИ КАЧЕСТВА РЕГУЛИРОВАНИЯ
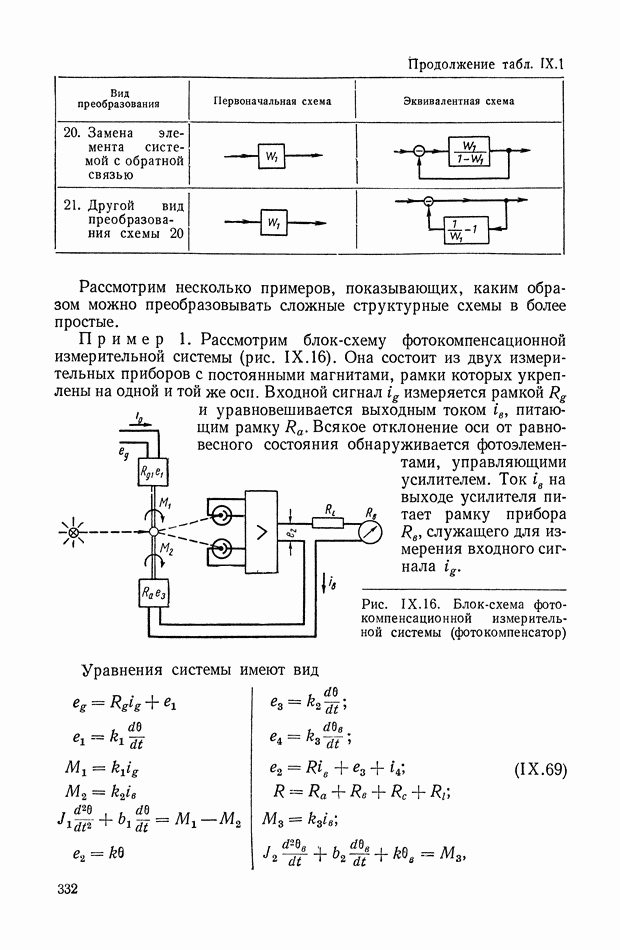
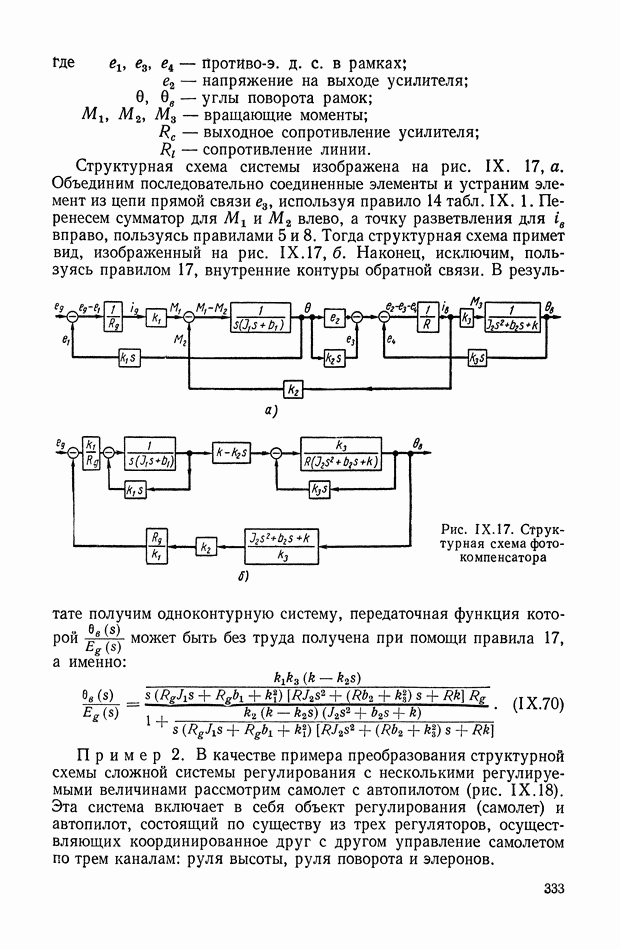
Метод интегральных критериев и оценок качества регулирования можно отнести к аналитическим методам, хотя в сложных случаях он требует значительных численных расчетов и эффективен при использовании аналоговых или цифровых вычислительных машин. Его с равным успехом можно применить как для линейных непрерывных, так и линейных импульсных систем. Интегральные критерии оптимальности используются и при решении общих задач синтеза нелинейных систем. Ниже данный метод рассматривается в основном применительно к линейным стационарным непрерывным системам.
Интегральной оценкой называется определенный интеграл по времени некоторой функции от координат системы. Если состояние системы характеризуется координатами  то интегральной квадратичной оценкой общего вида называется интеграл от квадратичной формы этих координат:
то интегральной квадратичной оценкой общего вида называется интеграл от квадратичной формы этих координат:

где  — заданные коэффициенты квадратичной формы;
— заданные коэффициенты квадратичной формы;  — также интегральные квадратичные оценки.
— также интегральные квадратичные оценки.
Для системы, состояние которой характеризуется одной величиной  и ее производными, интегральными квадратичными оценками служат
и ее производными, интегральными квадратичными оценками служат

или в более общем случае

где  - постоянные величины, имеющие размерность времени.
- постоянные величины, имеющие размерность времени.
Линейными интегральными оценками называются определенные интегралы по времени линейных функций координат или произведений этих функций на заданные функции времени. Так, линейными интегральными оценками являются

Помимо указанных квадратичных и линейных оценок, в теории оптимальных систем используются также функционалы более общего вида

где  — заданная функция.
— заданная функция.
Эти функционалы также являются интегральными критериями.
1. ВЫЧИСЛЕНИЕ ИНТЕГРАЛЬНЫХ КВАДРАТИЧНЫХ ОЦЕНОК
Способы, использующие систему дифференциальных уравнений. Пусть собственное движение линейной устойчивой стационарной системы описывается  уравнениями первого порядка:
уравнениями первого порядка:

Умножив каждое из этих уравнений на  и проинтегрировав в пределах от 0 до
и проинтегрировав в пределах от 0 до  получим
получим

где

Если не принимать во внимание соотношения  то
то  уравнений (XVIII.2) содержат
уравнений (XVIII.2) содержат  неизвестных
неизвестных  неизвестных вида
неизвестных вида 
Число уравнений становится равным числу неизвестных, если, интегрируя по частям, записать

Обозначая  и учитывая, что в силу условия устойчивости
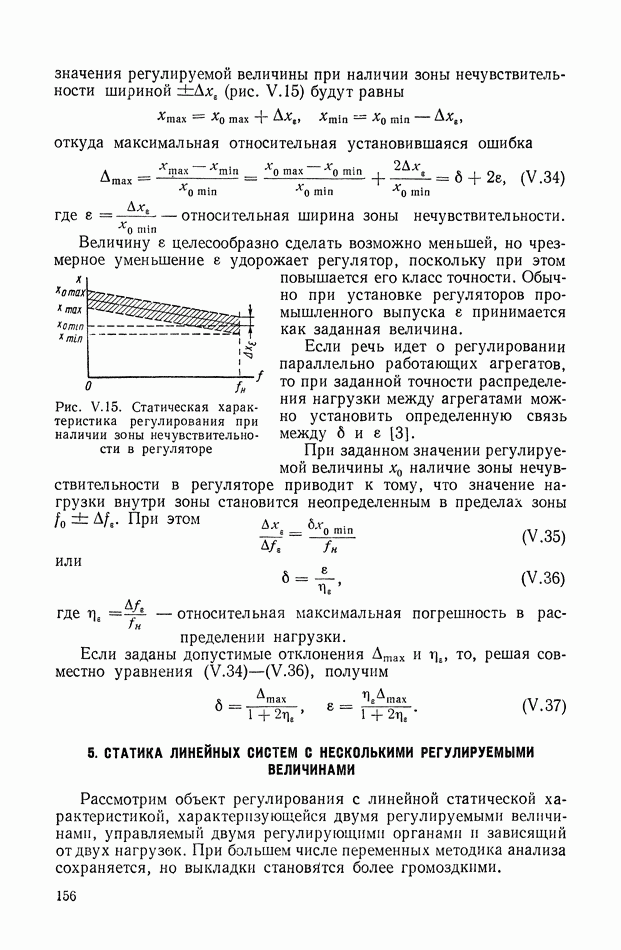
и учитывая, что в силу условия устойчивости  последние уравнения представим в виде
последние уравнения представим в виде

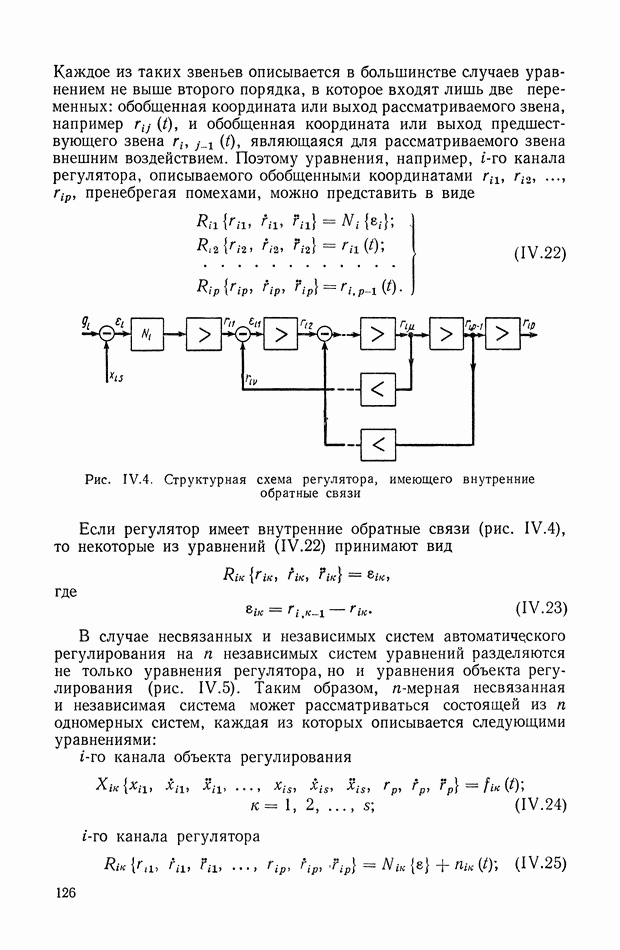
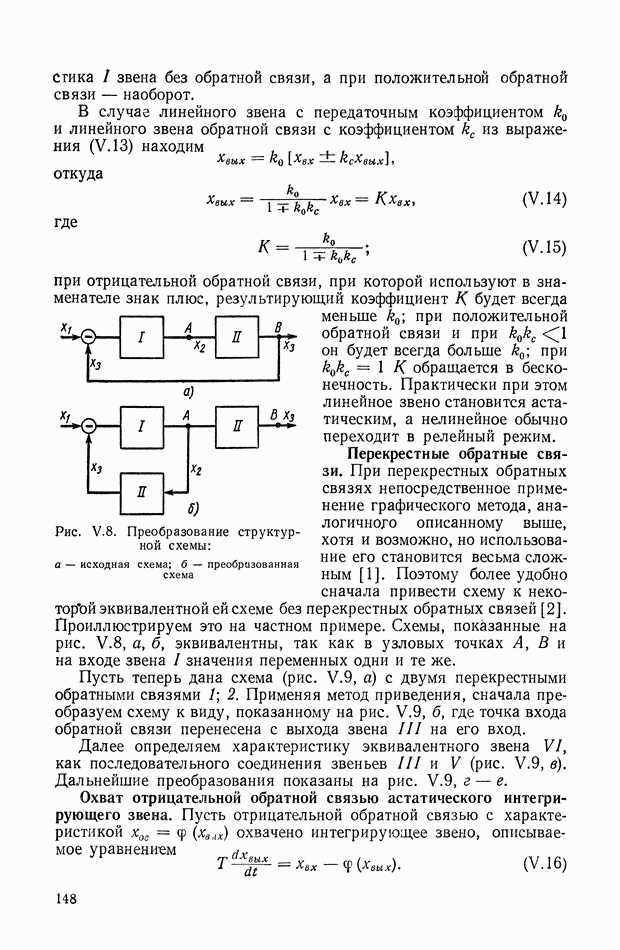
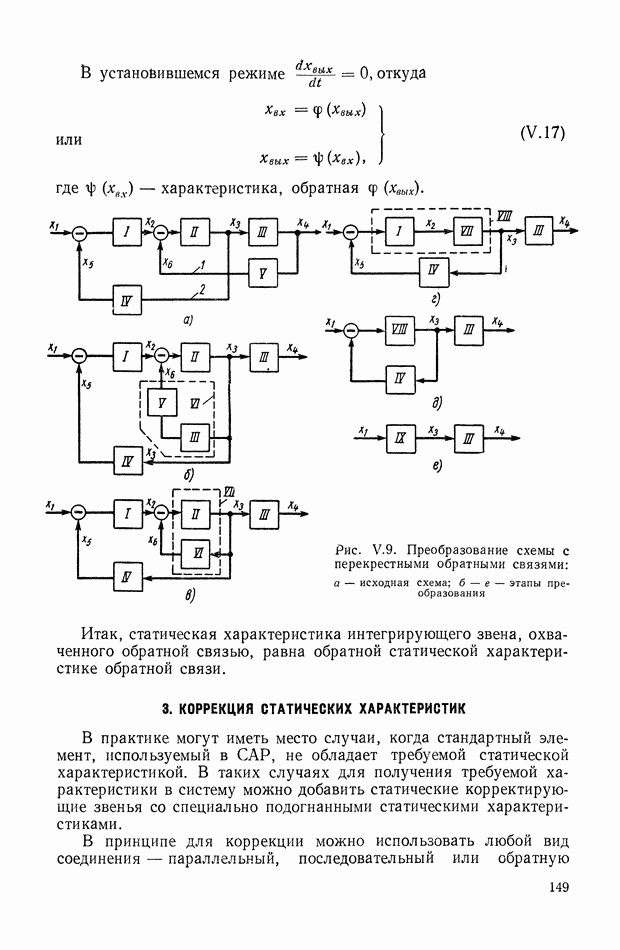
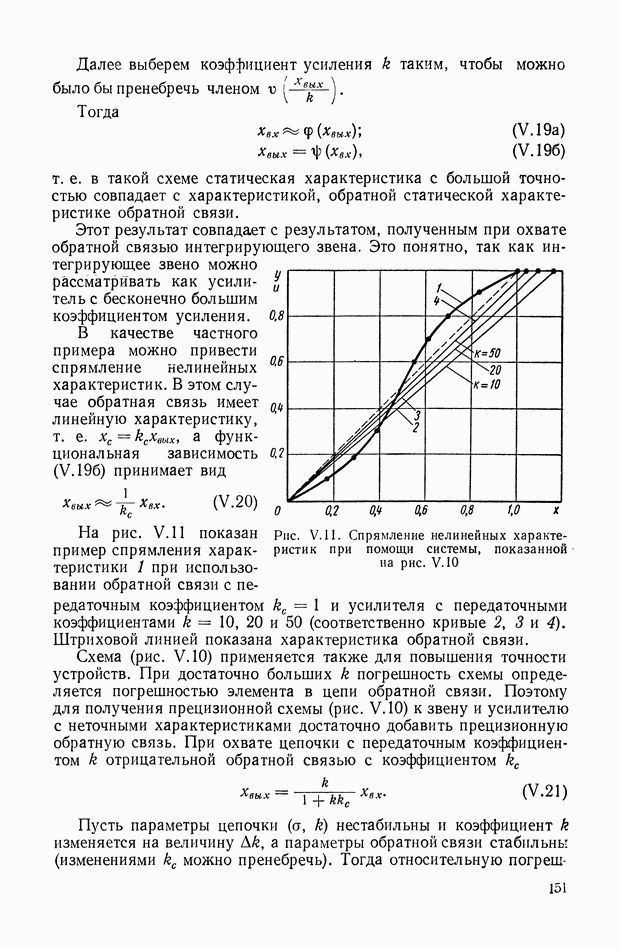
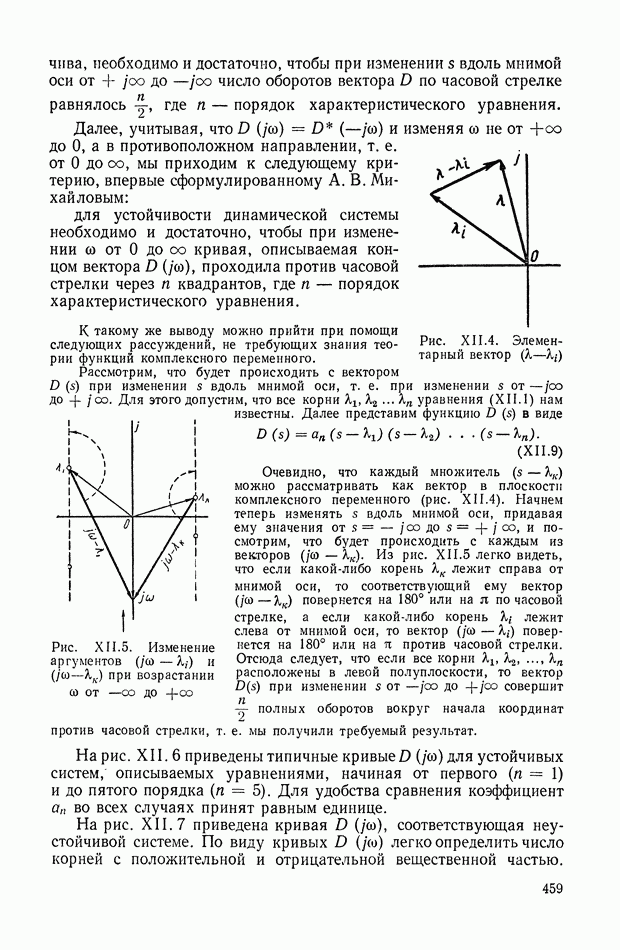
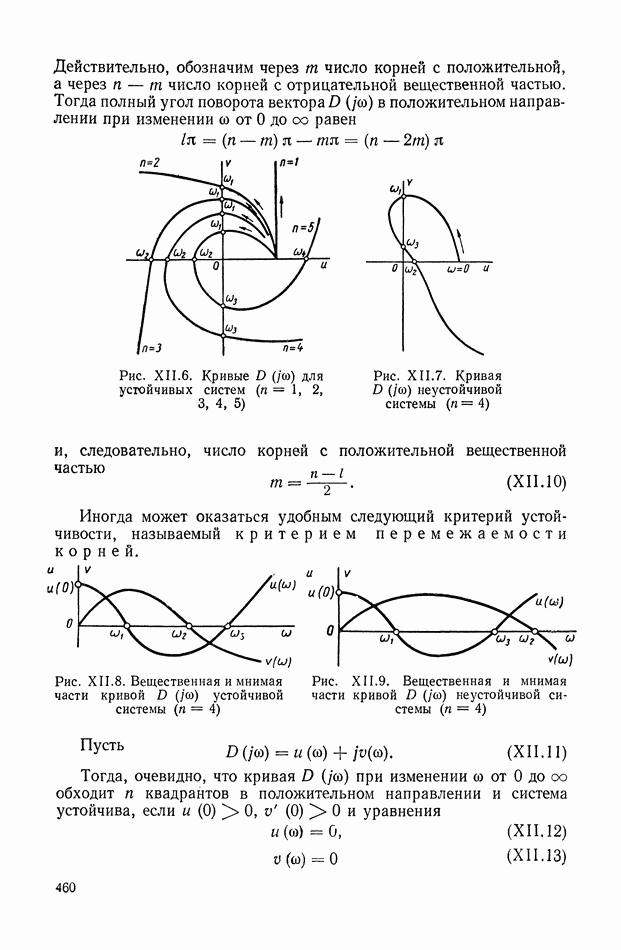
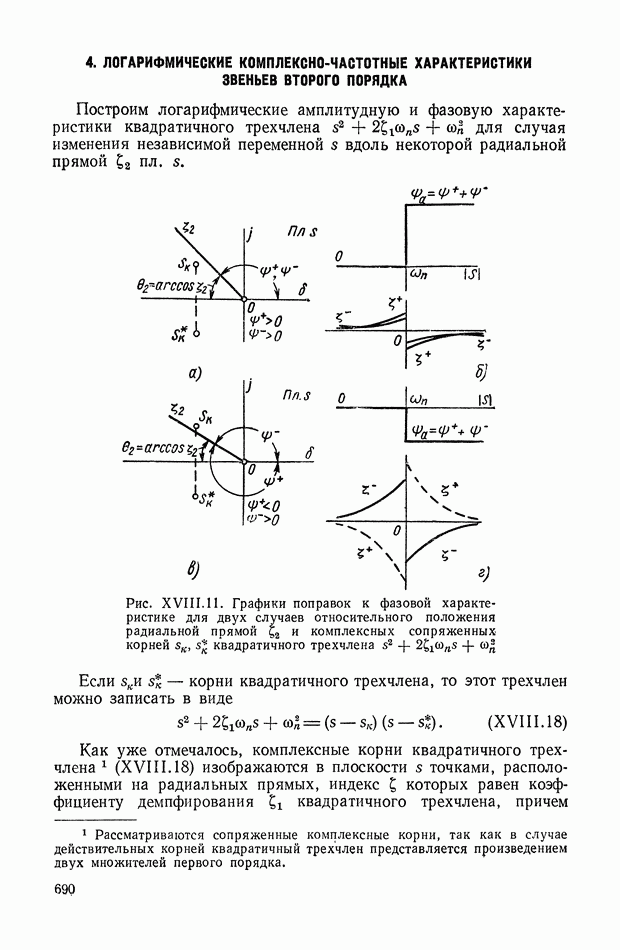
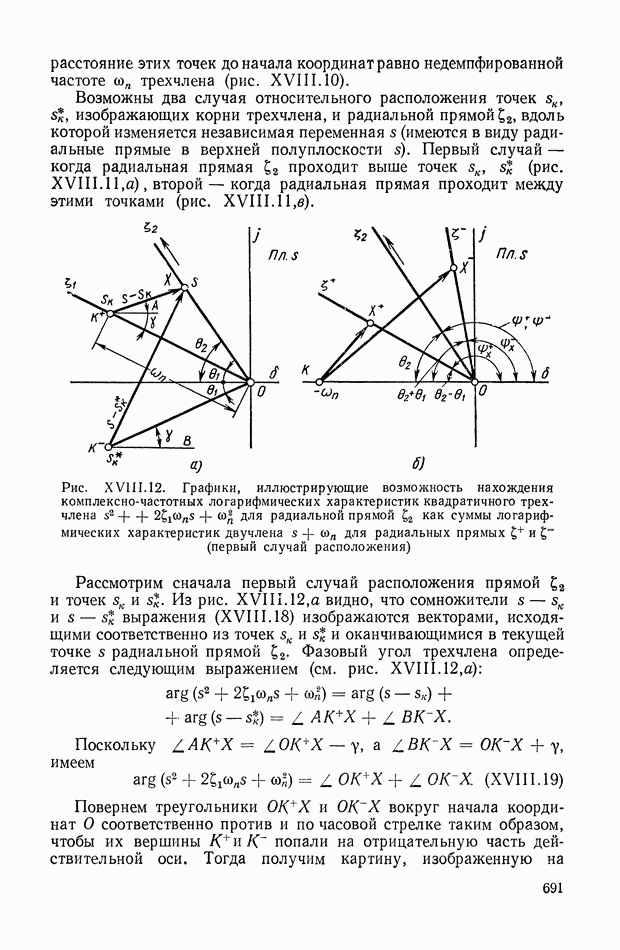
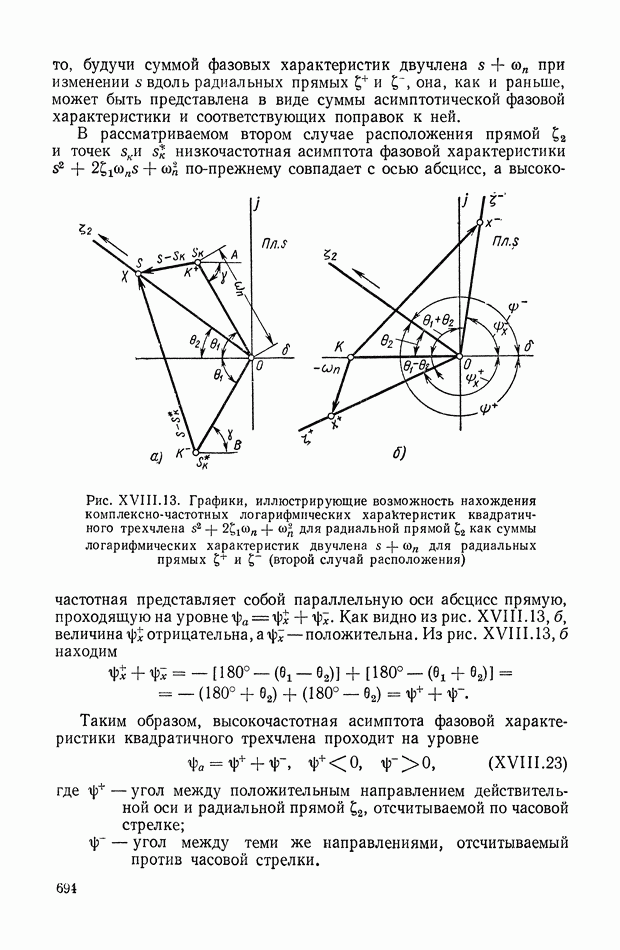
Уравнения (XIX.2), (XIX.3) представляют собой замкнутую систему уравнений. Можно показать, что из условия устойчивости вытекает неравенство нулю главного определителя этой системы уравнений. Таким образом, линейные уравнения (XIX.2), (XIX.3) для устойчивой системы всегда разрешимы и определяют все интегральные оценки  вместе с величинами
вместе с величинами  Этот способ впервые был предложен в работе, посвященной исследованию переходных процессов в электрических связанных контурах [13].
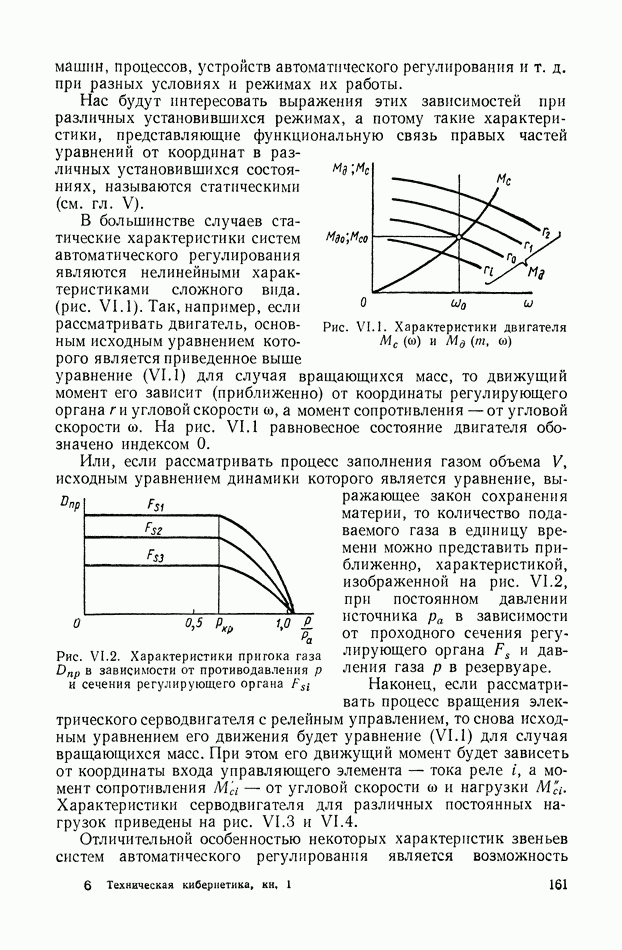
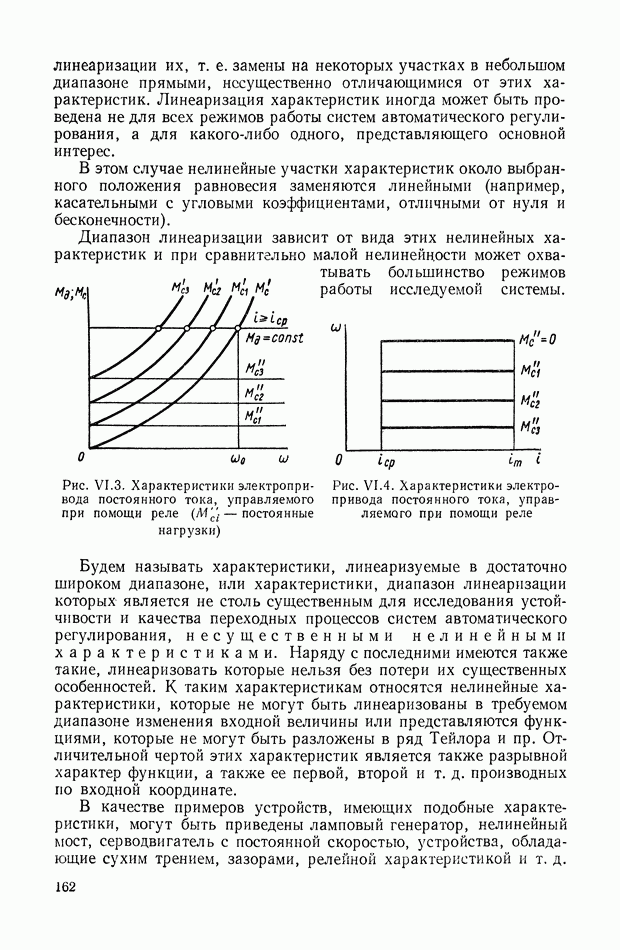
Этот способ впервые был предложен в работе, посвященной исследованию переходных процессов в электрических связанных контурах [13].
Переставив индексы в уравнении  а затем сложив полученное таким образом уравнение с первоначальным и использовав выражение (XVIII.3), исключаем неизвестные вида
а затем сложив полученное таким образом уравнение с первоначальным и использовав выражение (XVIII.3), исключаем неизвестные вида 

Особенно компактна матричная форма записи этой системы уравнений:

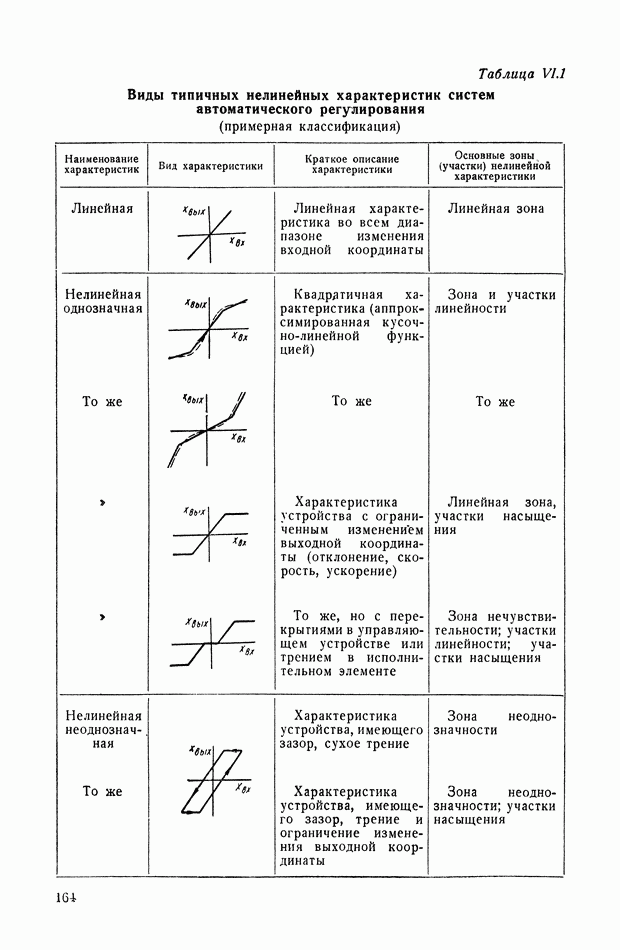
где  — квадратные матрицы; индекс Т обозначает транспонированную матрицу.
— квадратные матрицы; индекс Т обозначает транспонированную матрицу.
Известно, что  Но
Но  поэтому матричное уравнение можно представить также в виде
поэтому матричное уравнение можно представить также в виде

Несмотря на компактную форму выражения (XIX.5) или (XIX.6) для уравнений интегральных квадратичных оценок, развернутые выражения этих оценок через коэффициенты  и начальные условия громоздки. Это обусловливает то, что запись окончательных
и начальные условия громоздки. Это обусловливает то, что запись окончательных
формул для  в общем развернутом виде нецелесообразна. Таким образом, данное решение задачи определения интегральных квадратичных оценок носит характер скорее алгоритма, чем окончательных формул.
в общем развернутом виде нецелесообразна. Таким образом, данное решение задачи определения интегральных квадратичных оценок носит характер скорее алгоритма, чем окончательных формул.
Другим недостатком данного способа является то, что в нем рассматриваются только однородные дифференциальные уравнения или дифференциальные уравнения, приводимые к однородным. Для применения данного способа к переходным процессам, вызванным ступенчатыми или импульсными воздействиями, необходимо учитывать влияние этих воздействий путем преобразования в эквивалентные начальные условия.
В работе [17] был предложен способ вычисления интегральных квадратичных оценок, который по объему необходимых преобразований эквивалентен изложенному, но раскрывает некоторую связь этих оценок с функцией Ляпунова. Этот способ заключается в следующем. Допустим, что требуется определить оценку  для решения системы дифференциальных уравнений (XIX.1) при заданных начальных условиях.
для решения системы дифференциальных уравнений (XIX.1) при заданных начальных условиях.
Будем искать квадратичную форму

производная по времени которой может быть определена из системы дифференциальных уравнений (XIX.I) в виде х:

Тогда для устойчивой системы

Равенство (XIX.8) будет иметь место при любых х, только если

где  не равны
не равны 
В матричной форме эти уравнения имеют вид

где  — так называемая матричная единица, т. е. матрица, у которой единственным отличным от нуля элементом является единица, стоящая в
— так называемая матричная единица, т. е. матрица, у которой единственным отличным от нуля элементом является единица, стоящая в  строке
строке  столбце.
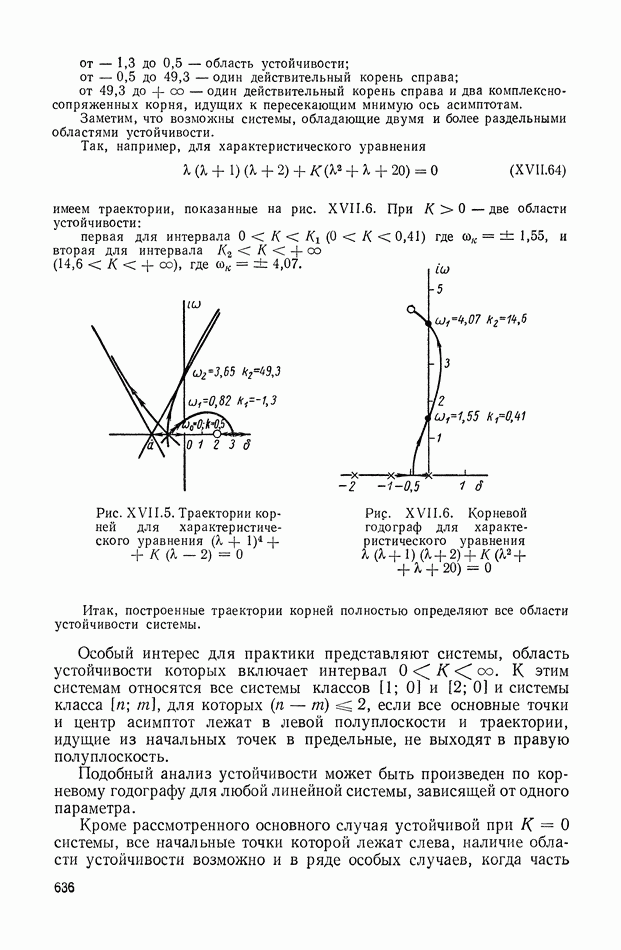
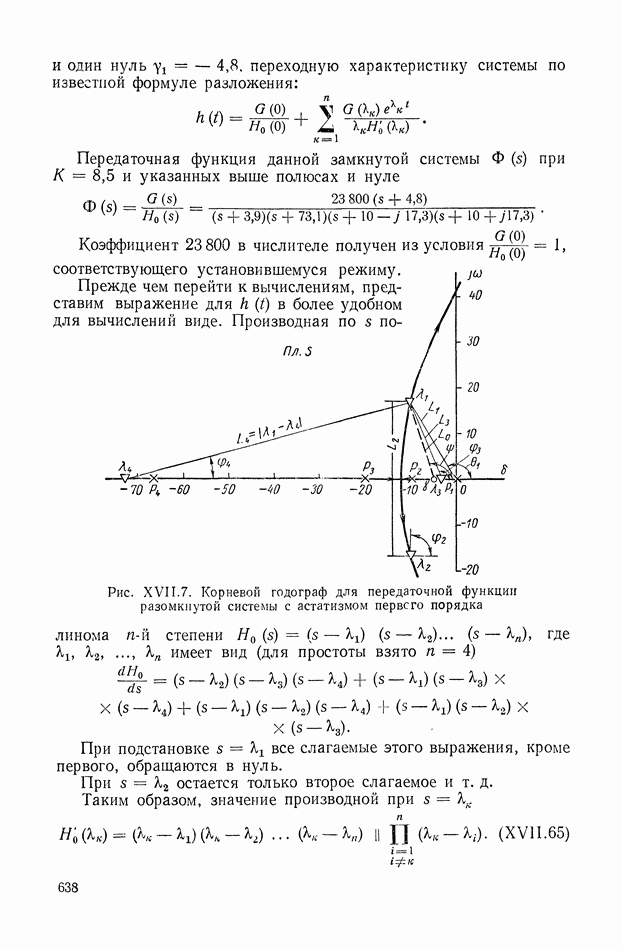
столбце.
Строго говоря, для матрицы В и ее элементов  следовало бы ввести дополнительные индексы
следовало бы ввести дополнительные индексы  Однако во избежание громоздких индексов мы не будем этого делать.
Однако во избежание громоздких индексов мы не будем этого делать.
Итак, интегральная квадратичная оценка равна квадратичной форме начальных значений координат:

матрица коэффициентов которой определяется уравнением вида

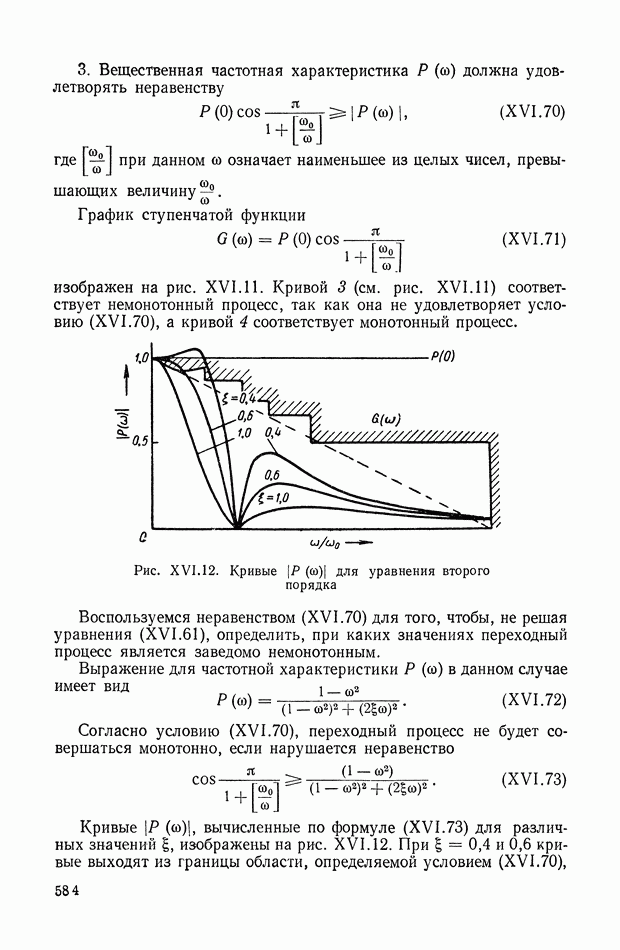
Уравнения (XIX.10), (XIX.11) эквивалентны уравнению (XIX.6) в том отношении, что из выражений (XIX.10), (XIX.11) можно получить уравнение (XIX.6) и наоборот. Что касается объема вычислений при решении уравнений (XIX.6) и (XIX.10), (XIX.11), то он примерно одинаков. В первом случае необходимо решить систему  линейных алгебраических уравнений (с учетом
линейных алгебраических уравнений (с учетом  систему
систему  уравнений) относительно интересующей нас оценки
уравнений) относительно интересующей нас оценки  Правые части всех уравнений, при
Правые части всех уравнений, при  здесь отличны от нуля.
здесь отличны от нуля.
Во втором случае необходимо решить аналогичную систему уравнений, в которой, однако, лишь одна правая часть отлична от нуля. В этом отношении решение уравнения (XIX. 11) проще, чем решение уравнения (XIX.6). Зато уравнение (XIX.11) необходимо решить относительно всех неизвестных, входящих в матрицу В, так как эти величины фигурируют в окончательном выражении (XIX.10).
Если требуется вычислить более общую интегральную квадратичную оценку, а именно, интегральную оценку §  квадратичной формы
квадратичной формы

где  — заданные величины, то при первом способе решают уравнение (XIХ.6) и используют соотношение
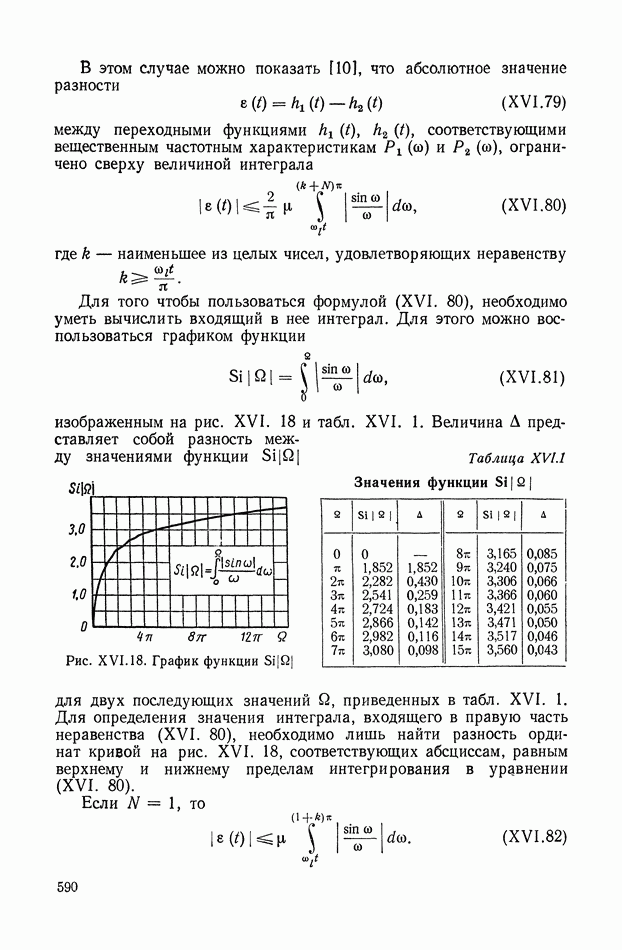
— заданные величины, то при первом способе решают уравнение (XIХ.6) и используют соотношение

При втором способе ищут квадратичную форму выражения (XIX.7), производная которой в силу исходных дифференциальных уравнений была бы равна —V. При этом вместо матричного уравнения (XIX. 11) получают матричное уравнение вида

Сама же интегральная оценка определяется по прежней формуле 

Если V — определенно положительная функция, а именно такой выбирается функция интегральной оценки, то, как видно из выражения (XIX. 13),  также определенно положительная функция. Производная по времени функции
также определенно положительная функция. Производная по времени функции  ввиду соотношения
ввиду соотношения  определенно отрицательна. Известно, что определенно положительная функция, производная по времени которой в силу данных дифференциальных уравнений определенно отрицательна, является функцией Ляпунова. Итак, интегральная оценка определенно положительной квадратичной формы координат устойчивой линейной системы равна функции Ляпунова от начальных значений координат системы. Коэффициенты квадратичной формы, выражающей указанную функцию Ляпунова, определяют по уравнению (XIX.12).
определенно отрицательна. Известно, что определенно положительная функция, производная по времени которой в силу данных дифференциальных уравнений определенно отрицательна, является функцией Ляпунова. Итак, интегральная оценка определенно положительной квадратичной формы координат устойчивой линейной системы равна функции Ляпунова от начальных значений координат системы. Коэффициенты квадратичной формы, выражающей указанную функцию Ляпунова, определяют по уравнению (XIX.12).
Как уже отмечалось, буквенное выражение решения уравнения (XIX. 12) в общем случае весьма громоздко и в развернутом виде никогда не используется.
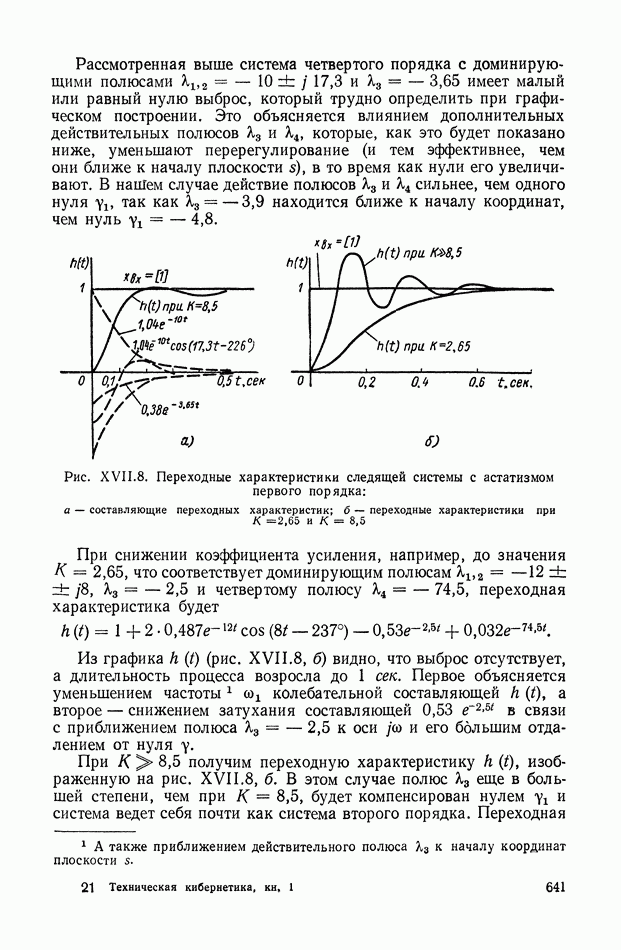
Способы, использующие преобразование Лапласа. В современной линейной теории регулирования чаще оперируют с передаточными функциями и преобразованиями Лапласа или Фурье, чем с дифференциальными уравнениями системы и начальными условиями. Поэтому наибольшее применение имеют те способы вычисления интегральных оценок, которые позволяют находить эти оценки непосредственно по изображениям оригиналов-координат.
Пусть преобразования Лапласа двух функций  есть дробно-рациональные функции:
есть дробно-рациональные функции:

имеющие общий знаменатель, полюса с отрицательными действительными частями и 
В частности, этим условиям удовлетворяют изображения любой пары координат однородной системы уравнений (XIX.1). Интегральная оценка

с помощью обратного преобразования Лапласа

может быть представлена в виде

Таким образом,

Согласно формуле (XIX. 14) подынтегральное выражение имеет вид

где

причем  содержит лишь четные степени
содержит лишь четные степени  , а
, а  — нечетные степени.
— нечетные степени.
Очевидно, что

поэтому

где

Интеграл (XIX. 16) сразу может быть представлен в виде суммы вычетов. Однако задача заключается в том, чтобы эту сумму выразить через коэффициенты исходных изображений.
В работах [1,2] приведен способ решения этой задачи и даны развернутые выражения интегральных квадратичных оценок через коэффициенты, аналогичные  (для
(для  от 1 до 7). В ряде случаев требуются общие выражения (для произвольного
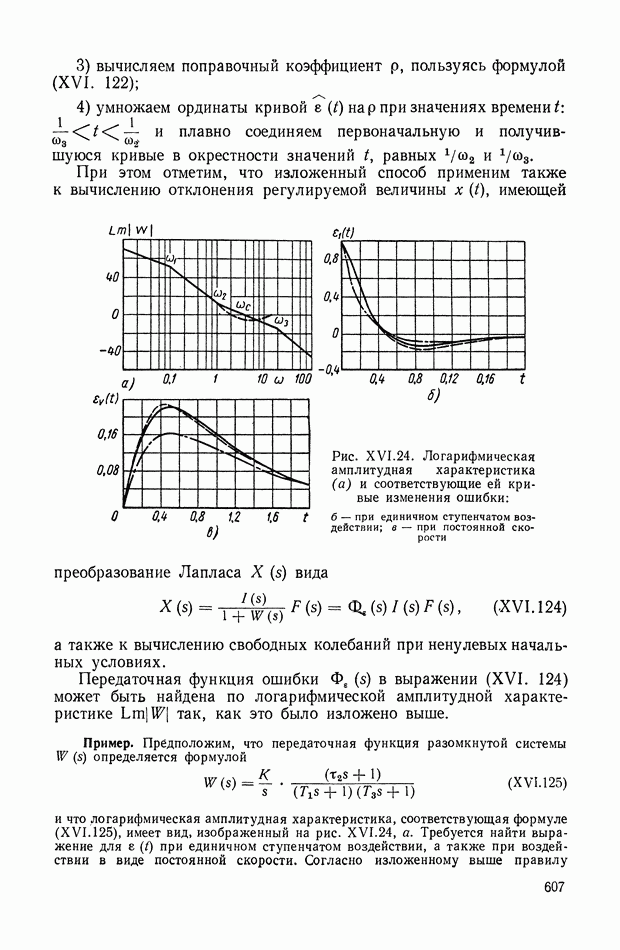
от 1 до 7). В ряде случаев требуются общие выражения (для произвольного  интегральных квадратичных оценок через коэффициенты преобразования Лапласа или коэффициенты передаточной функции. Такие выражения были получены также в работе [5]. Первоначально задача решалась применительно к интегральной квадратичной оценке переходной составляющей реакции системы на ступенчатое воздействие. Это наложило определенный отпечаток на вид нижеследующей формулы.
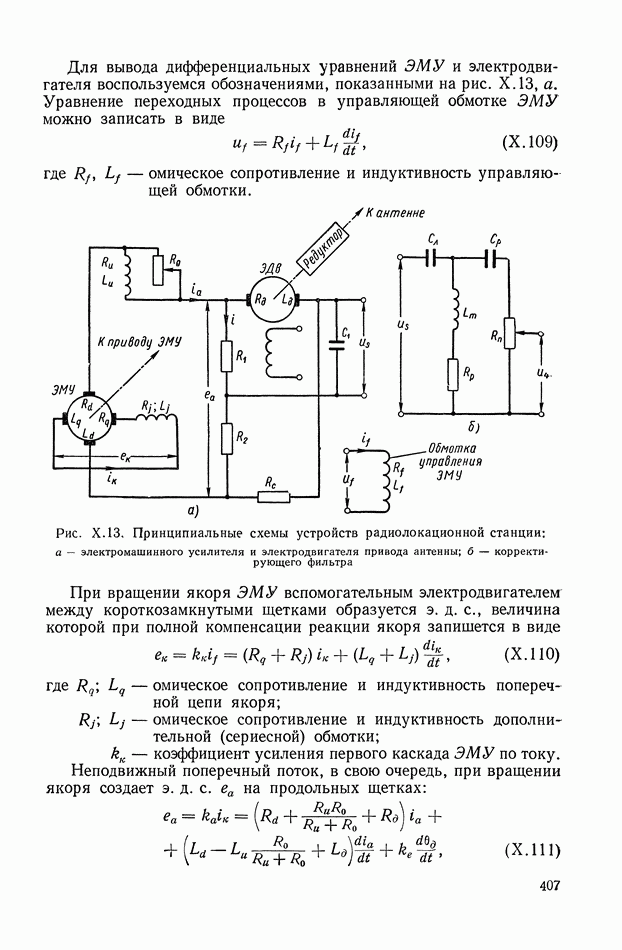
интегральных квадратичных оценок через коэффициенты преобразования Лапласа или коэффициенты передаточной функции. Такие выражения были получены также в работе [5]. Первоначально задача решалась применительно к интегральной квадратичной оценке переходной составляющей реакции системы на ступенчатое воздействие. Это наложило определенный отпечаток на вид нижеследующей формулы.
Если функция  имеет дробно-рациональное преобразование Лапласа
имеет дробно-рациональное преобразование Лапласа

и корни уравнения

обладают отрицательными действительными частями, то

где

 - определитель, получающийся из А заменой
- определитель, получающийся из А заменой  -гостолбца столбцом
-гостолбца столбцом  Определитель А равен старшему определителю Гурвица и обращается в нуль на соответствующем
Определитель А равен старшему определителю Гурвица и обращается в нуль на соответствующем
участке границы области устойчивости. Если  то преобразование Лапласа имеет вид
то преобразование Лапласа имеет вид

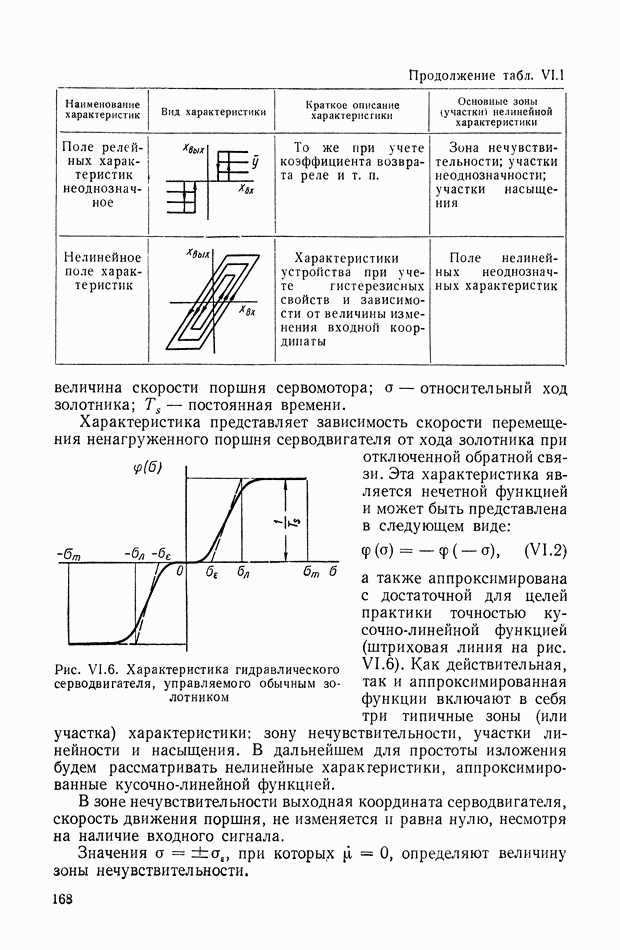
Предельное значение  в этом случае равно нулю, т. е.
в этом случае равно нулю, т. е.  Формула (XIX.19) принимает вид
Формула (XIX.19) принимает вид

Эту формулу можно еще упростить, если обратить внимание на то, что

где

 — минор
— минор  элемента верхней строки определителя
элемента верхней строки определителя  .
.
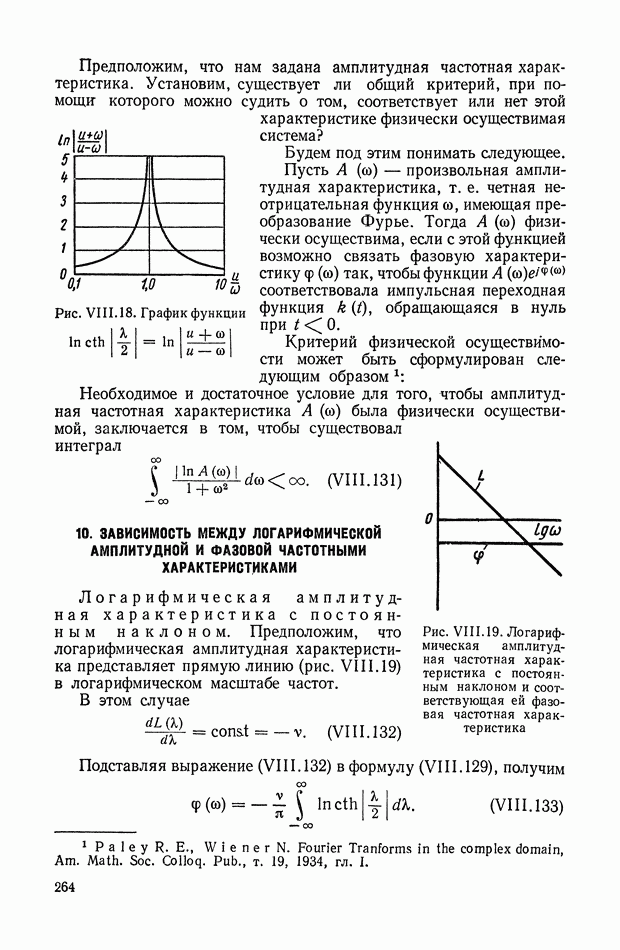
Таким образом,

или

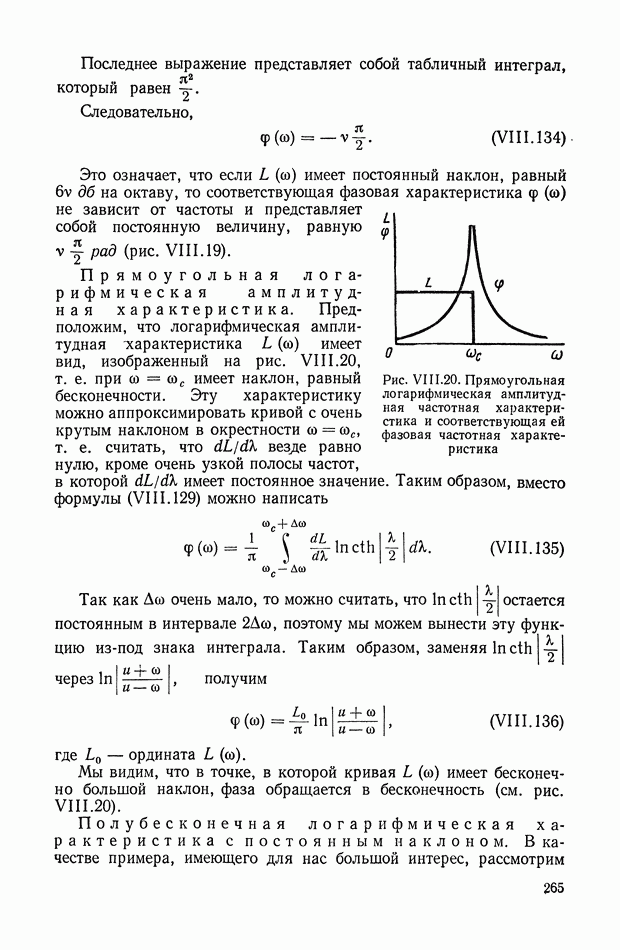
где  — определитель, получающийся из
— определитель, получающийся из  заменой верхней строки строкой
заменой верхней строки строкой  Формула (XIX.22) в работе [5] получена для случая
Формула (XIX.22) в работе [5] получена для случая  Для случая
Для случая  в работах [5 — 7 и 9] рекомендуется применять несколько более громоздкую формулу.
в работах [5 — 7 и 9] рекомендуется применять несколько более громоздкую формулу.
Покажем, что для случая  можно применять формулы, аналогичные (XIX.22), (XIX.23). Попутно поясним методику вывода формул на основе общих матричных уравнений (XIX.6). Первоначально рассмотрим функцию
можно применять формулы, аналогичные (XIX.22), (XIX.23). Попутно поясним методику вывода формул на основе общих матричных уравнений (XIX.6). Первоначально рассмотрим функцию  преобразование Лапласа которой имеет вид
преобразование Лапласа которой имеет вид

Очевидно, что  есть решение дифференциального уравнения
есть решение дифференциального уравнения

при начальных условиях

Заменой переменных  это уравнение преобразуем в систему дифференциальных уравнений вида
это уравнение преобразуем в систему дифференциальных уравнений вида

при начальных условиях

Таким образом, матрица А [см. уравнение (XIX.6)] в этом случае имеет вид

а матрица  пропорциональна матричной единице, где единственным отличным от нуля элементом является элемент последней строки и последнего столбца:
пропорциональна матричной единице, где единственным отличным от нуля элементом является элемент последней строки и последнего столбца:

Теперь можно записать для данного случая матричное уравнение (XIX.6). Однако предварительно целесообразно упростить искомую матрицы интегральных оценок  Действительно, при начальных условиях (XIX.25)
Действительно, при начальных условиях (XIX.25)

Эти формулы можно получить простым последовательным интегрированием по частям.
В соответствии с этим матрицу  можно записать в виде
можно записать в виде

Вычислив произведение матриц  а затем произведя транспонирование и сложение, можно убедиться, что все элементы матрицы
а затем произведя транспонирование и сложение, можно убедиться, что все элементы матрицы  кроме элементов нижней строки и последнего столбца, равны нулю. Приравнивание элементов последней строки (столбца) этой матрицы элементам последней строки (столбца) матрицы
кроме элементов нижней строки и последнего столбца, равны нулю. Приравнивание элементов последней строки (столбца) этой матрицы элементам последней строки (столбца) матрицы

дает следующую систему уравнения:

Решение этой системы уравнений есть

где А — главный определитель (XIX.20);
 — алгебраическое дополнение элемента
— алгебраическое дополнение элемента  строки
строки  столбца этого определителя.
столбца этого определителя.
Если  имеет преобразование Лапласа
имеет преобразование Лапласа

то очевидно

Поэтому с учетом выражений (XIX.25), (XIX.26)

Подставляя сюда выражение (XIX.27), получаем

где  получается из определителя
получается из определителя  заменой нижней строки строкой
заменой нижней строки строкой 
Эта формула справедлива и при  если в ней полагать
если в ней полагать  а стало быть
а стало быть 
При этом путем простых преобразований формула (XIX.29) превращается в формулу (XIX.22).
Для интегральной оценки произведения двух функций вида (XIX. 14) также справедлива формула

где  имеют выражения (XIX. 17).
имеют выражения (XIX. 17).
Если не принимать во внимание различия в обозначениях, то формула (XIX.29) с точностью до простейших алгебраических преобразований совпадает с формулой, приведенной в работах [4 и 12]. Итак, формула (XIX.29) является достаточно общей и в то же время компактной и легкой для запоминания. Что касается формулы для случая  приводимой в [5—7, 9], то она, разумеется, в конечном итоге дает тот же результат, что и формула (XIX.29), но имеет более громоздкий вид.
приводимой в [5—7, 9], то она, разумеется, в конечном итоге дает тот же результат, что и формула (XIX.29), но имеет более громоздкий вид.
Подводя итоги, можно дать следующие рекомендации. Если изображение интересующей нас координаты имеет вид выражения (XIX. 18), то для интегральной квадратичной оценки переходной погрешности целесообразно применять формулу (XIX.19). Если же изображение координаты х имеет вид

где произвольное число коэффициентов  может быть равно нулю, то целесообразно применять формулу (XIX.29).
может быть равно нулю, то целесообразно применять формулу (XIX.29).
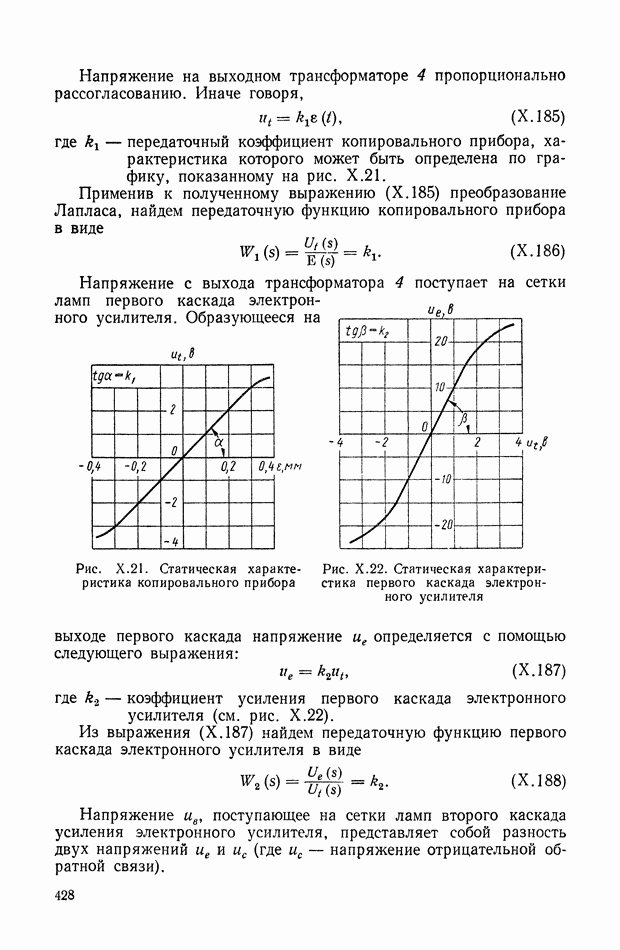
Следует отметить, что рассматриваемые в этом параграфе формулы позволяют вычислять интегралы более общего вида

где  имеет дробно-рациональное преобразование Лапласа типа (XVIII.30) с полюсами
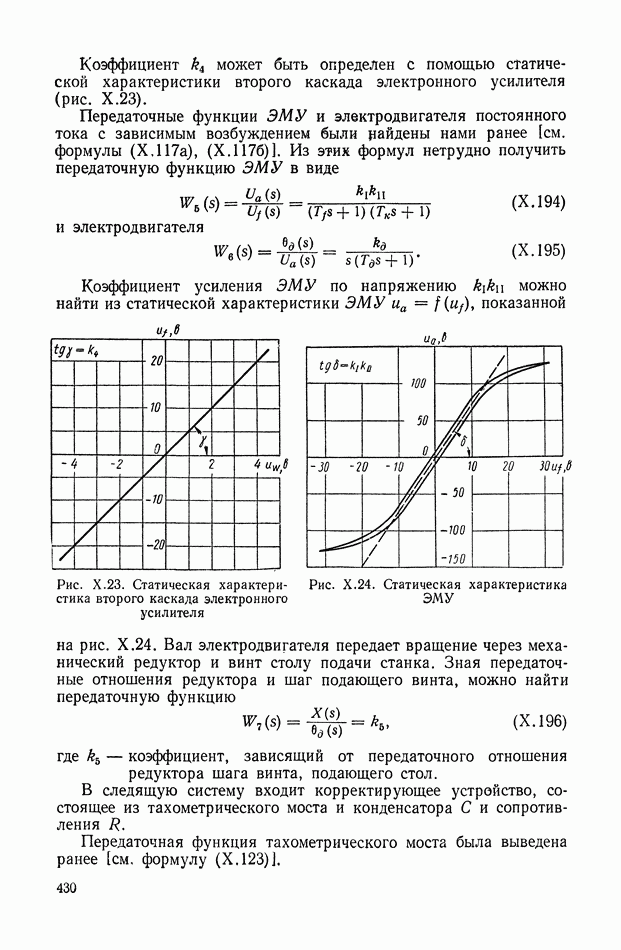
имеет дробно-рациональное преобразование Лапласа типа (XVIII.30) с полюсами  — действительные или комплексные попарно сопряженные числа, такие, что все суммы
— действительные или комплексные попарно сопряженные числа, такие, что все суммы  имеют отрицательные действительные части;
имеют отрицательные действительные части;  — полиномы любой степени по
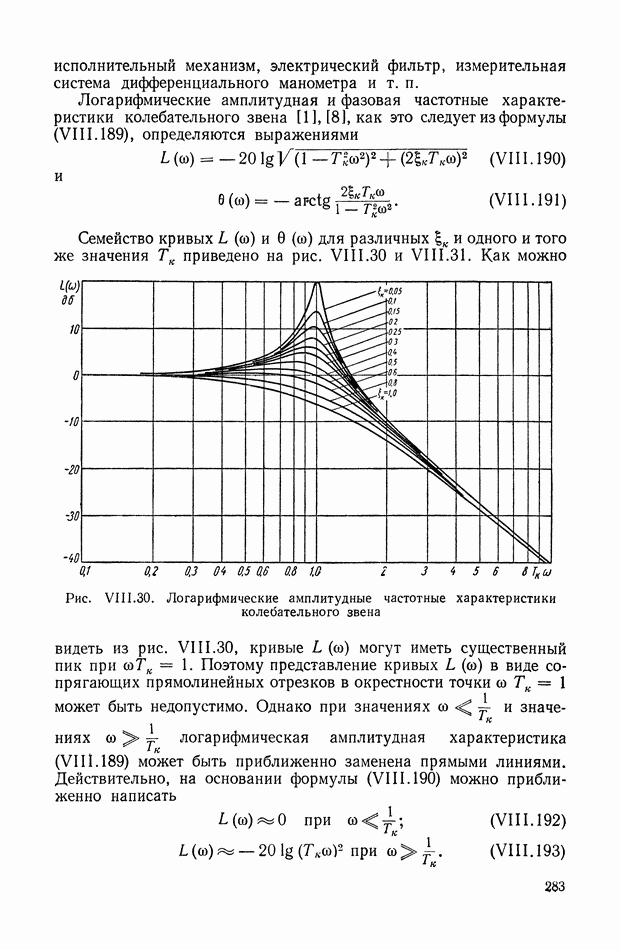
— полиномы любой степени по 
Действительно, если преобразование Лапласа функции  есть дробно-рациональная функция типа (XIX.30), то можно применять указанные формулы.
есть дробно-рациональная функция типа (XIX.30), то можно применять указанные формулы.
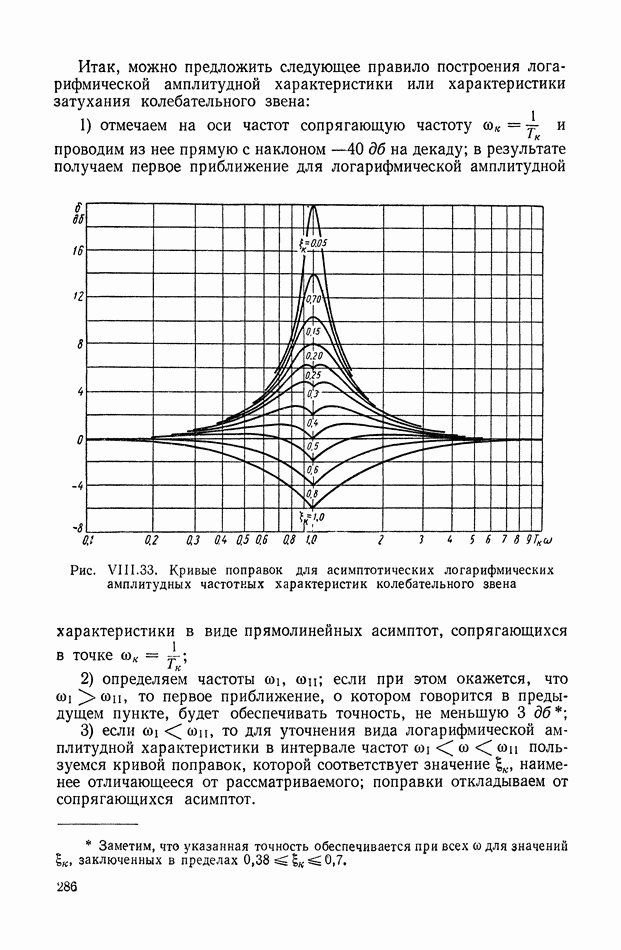
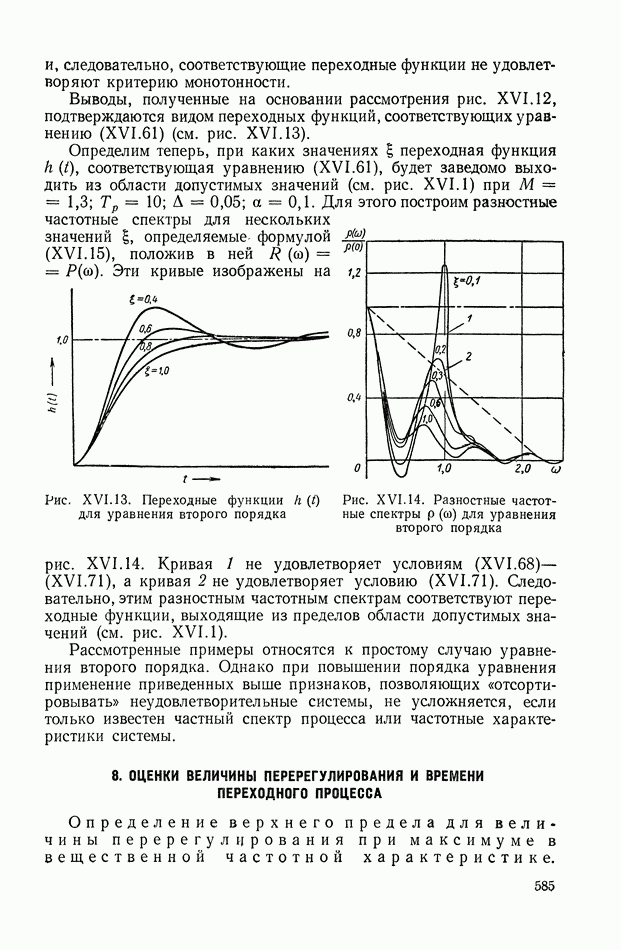
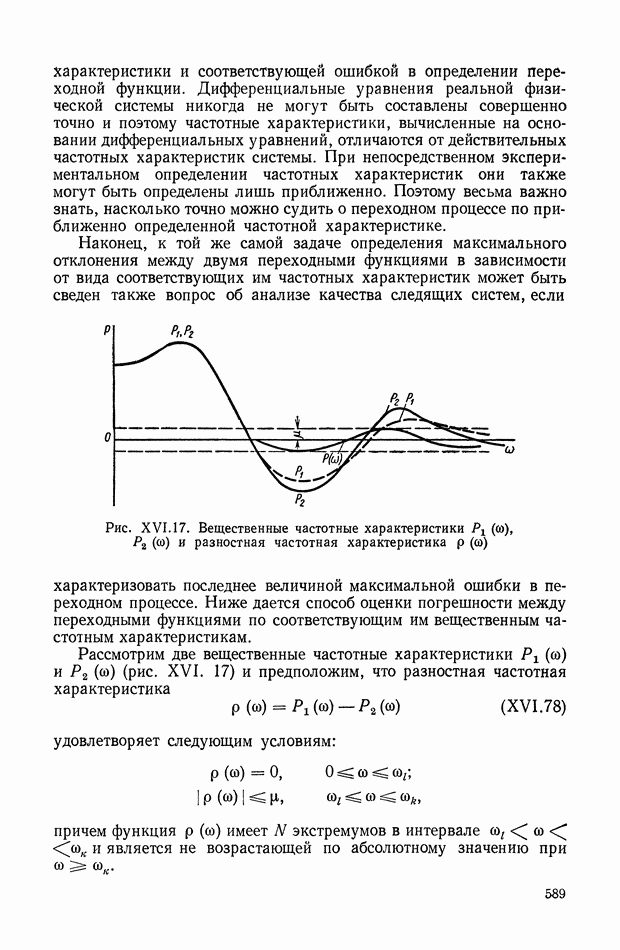
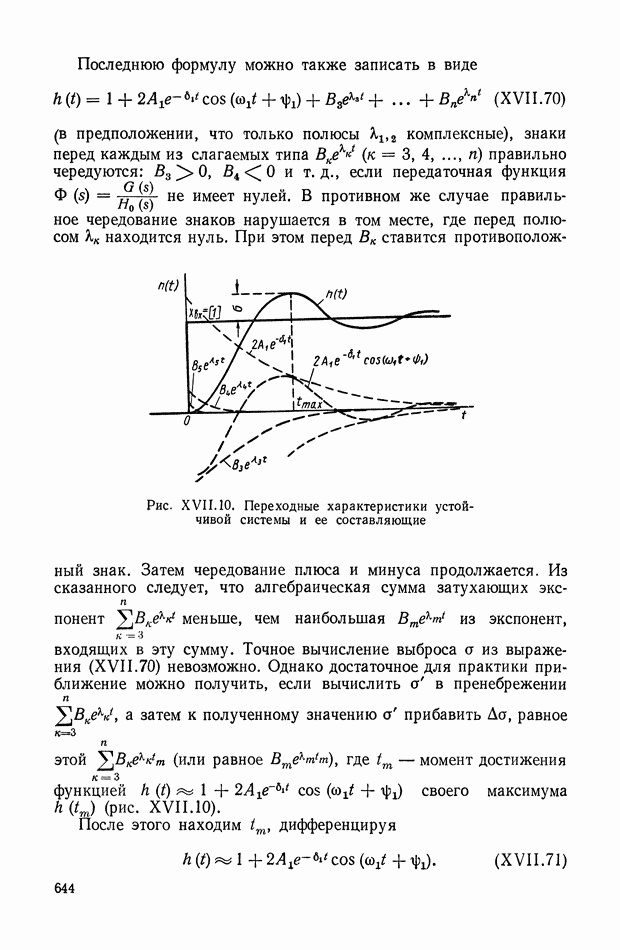
Формулы (XIX.19), (XIX.22), (XIX.29) и излагаемая ниже методика их применения прочно вошли в теорию автоматического регулирования и используются во многих исследованиях.
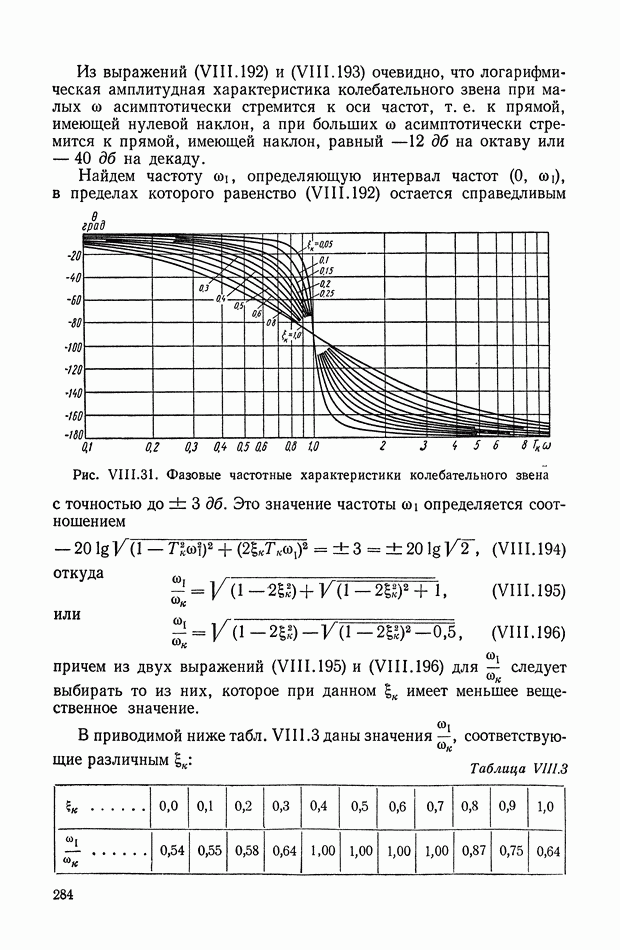
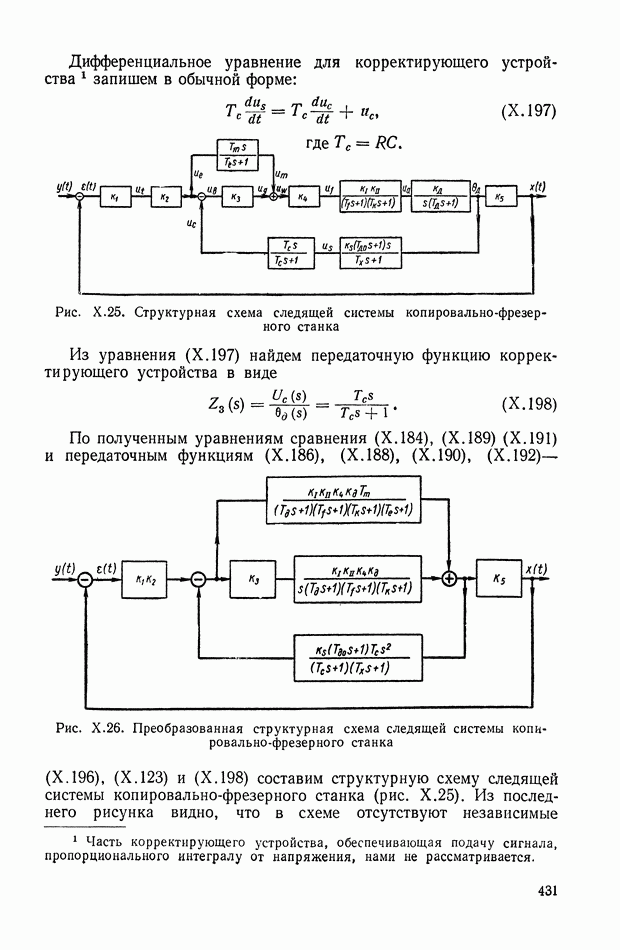
В последнее время значительные результаты в области алгебры интегральных квадратичных оценок получены в работах [21], [22], в которых исследована связь этих оценок с другими критериями качества, а также рассмотрены условия существования точки экстремума интегральной оценки в пространстве коэффициентов и др.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- РАЗДЕЛ I. ОБЩИЕ СВЕДЕНИЯ. МЕТОДЫ МАТЕМАТИЧЕСКОГО ОПИСАНИЯ И СТРУКТУРНОГО ПРЕОБРАЗОВАНИЯ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- ГЛАВА I. ОЧЕРК О РАЗВИТИИ ТЕОРИИ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ В СССР
- 1. ТЕОРИЯ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ В ДОРЕВОЛЮЦИОННЫЙ ПЕРИОД
- 2. РАЗВИТИЕ ТЕОРИИ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ПОСЛЕ ОКТЯБРЬСКОЙ СОЦИАЛИСТИЧЕСКОЙ РЕВОЛЮЦИИ
- ГЛАВА II. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ ТЕОРИИ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. СУЩНОСТЬ ПРОБЛЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- 2. ПРОБЛЕМА РЕГУЛИРОВАНИЯ КАК ЧАСТНЫЙ СЛУЧАЙ ПРОБЛЕМЫ УПРАВЛЕНИЯ
- 3. ОСНОВНОЙ ПРИНЦИП ДЕЙСТВИЯ И ОПРЕДЕЛЕНИЕ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 4. КЛАССИФИКАЦИЯ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ В ЗАВИСИМОСТИ ОТ УПРАВЛЯЮЩЕГО ВОЗДЕЙСТВИЯ
- 5. ОСНОВНЫЕ УСТРОЙСТВА СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ И ИХ КЛАССИФИКАЦИЯ ПО НАЗНАЧЕНИЮ
- 6. КЛАССИФИКАЦИЯ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ В ЗАВИСИМОСТИ ОТ ХАРАКТЕРА СИГНАЛОВ
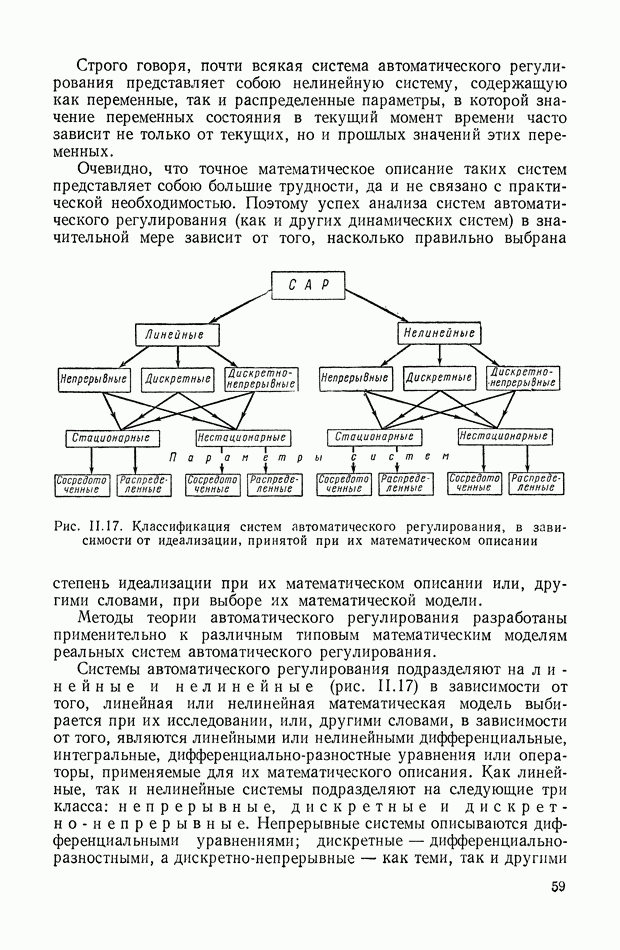
- 7. КЛАССИФИКАЦИЯ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ В ЗАВИСИМОСТИ ОТ ИДЕАЛИЗАЦИИ, ПРИНЯТОЙ ПРИ ИХ МАТЕМАТИЧЕСКОМ ОПИСАНИИ
- 8. СТРУКТУРНЫЕ СХЕМЫ, ОДНОКОНТУРНЫЕ И МНОГОКОНТУРНЫЕ, НЕСВЯЗАННЫЕ И СВЯЗАННЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
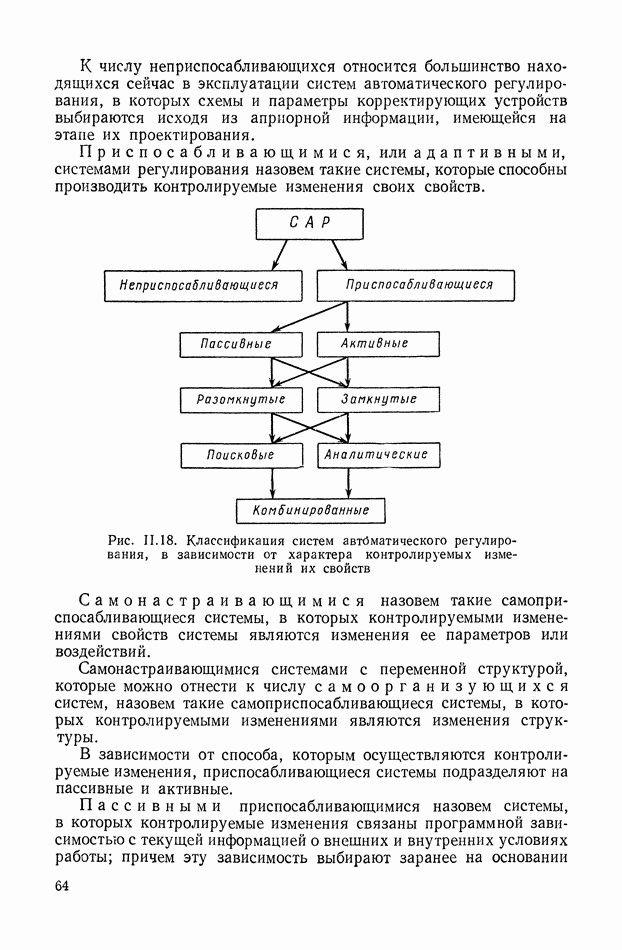
- 9. КЛАССИФИКАЦИЯ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ В ЗАВИСИМОСТИ ОТ ХАРАКТЕРА КОНТРОЛИРУЕМЫХ ИЗМЕНЕНИЙ
- 10. ТРЕБОВАНИЯ, ПРЕДЪЯВЛЯЕМЫЕ К ДИНАМИЧЕСКИМ СВОЙСТВАМ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- ГЛАВА III. ОСНОВНЫЕ УСТРОЙСТВА И ТИПОВЫЕ СХЕМЫ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
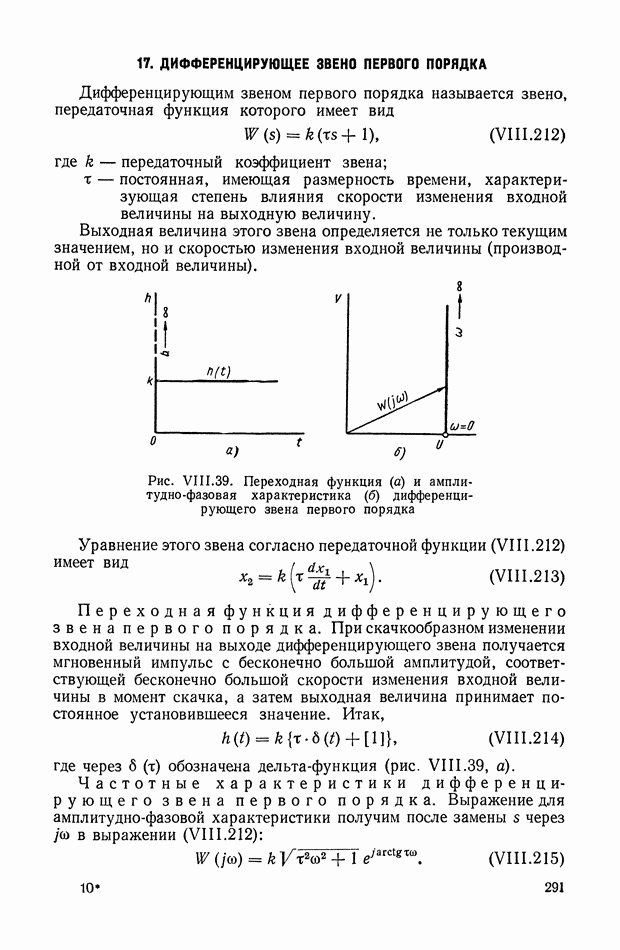
- 1. КРАТКАЯ ХАРАКТЕРИСТИКА УСТРОЙСТВ, ИЗ КОТОРЫХ СОСТОЯТ СИСТЕМЫ РЕГУЛИРОВАНИЯ
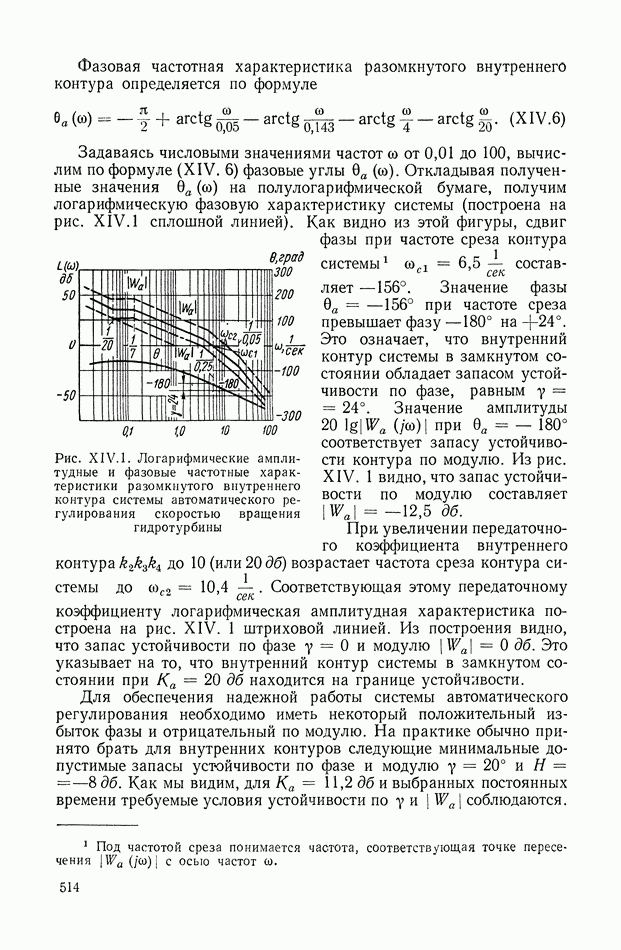
- 2. СИСТЕМА АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ СКОРОСТИ ГИДРОТУРБИНЫ
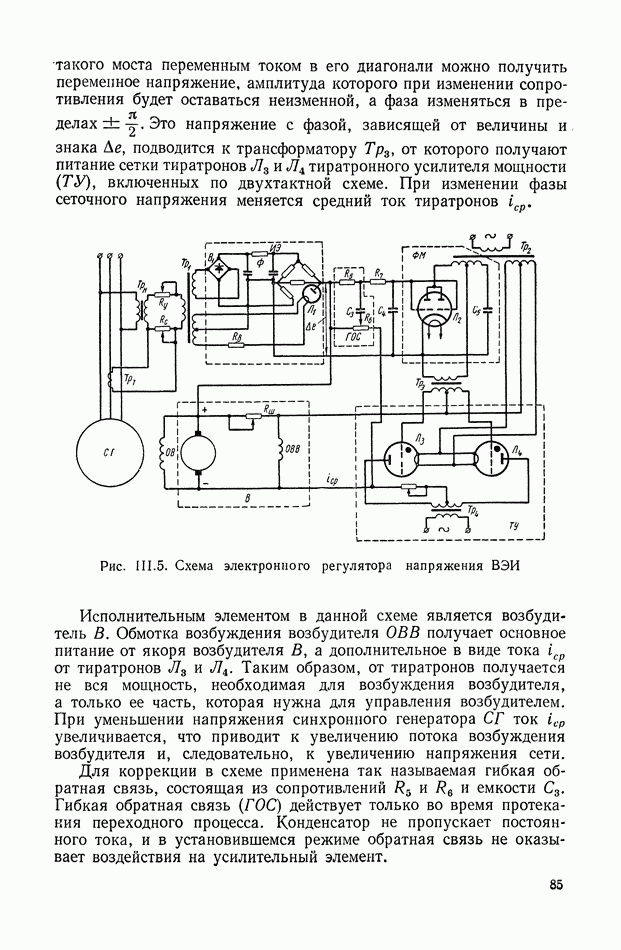
- 3. ЭЛЕКТРОННЫЙ РЕГУЛЯТОР НАПРЯЖЕНИЯ ВЭИ
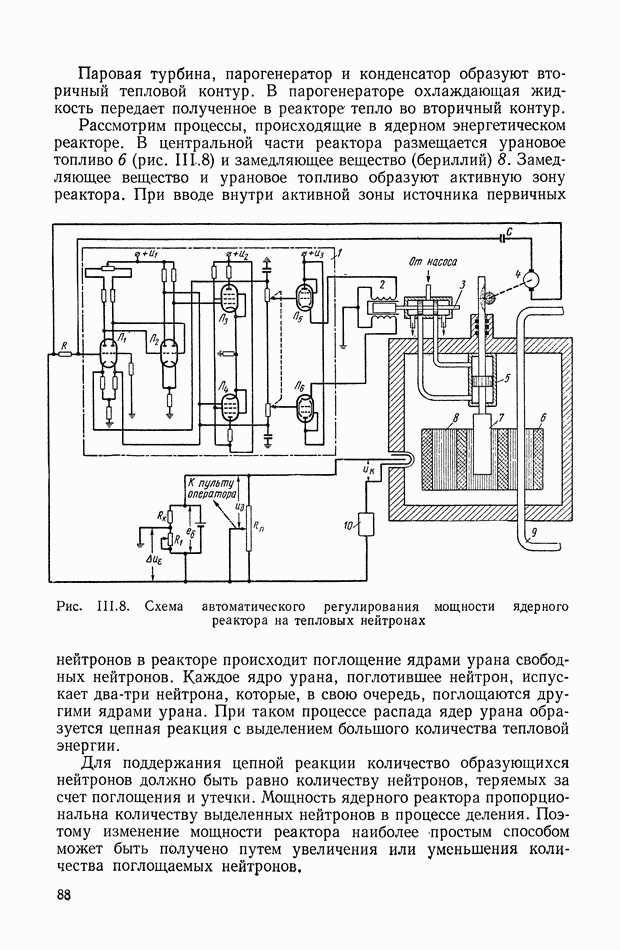
- 4. СИСТЕМА АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ЯДЕРНОГО РЕАКТОРА ПО МОЩНОСТИ
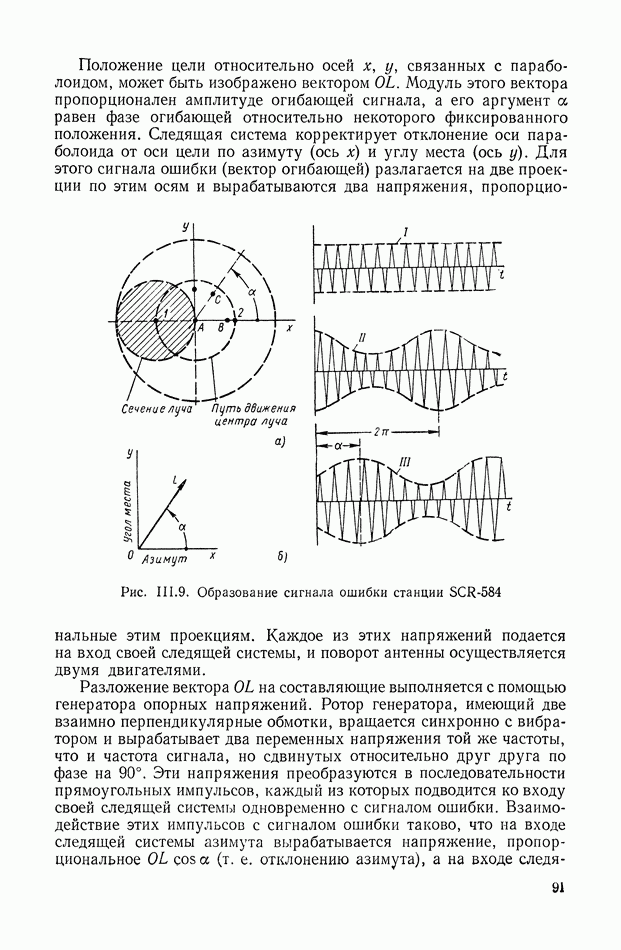
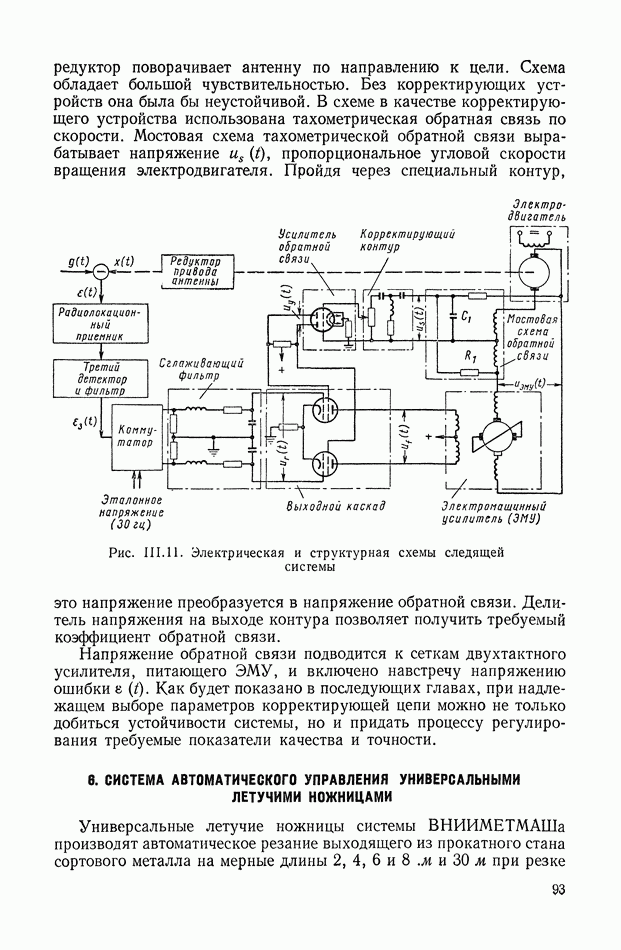
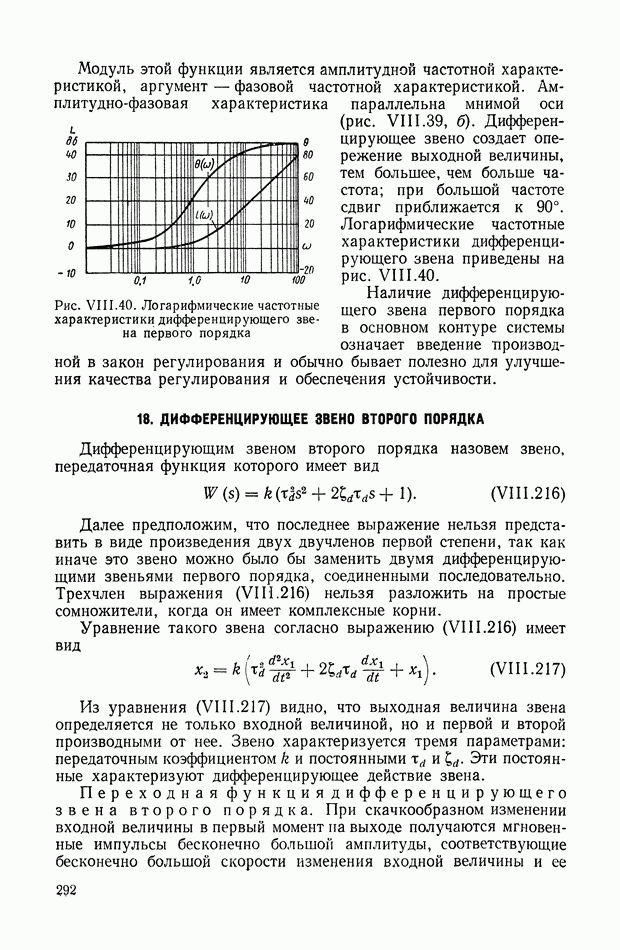
- 5. СЛЕДЯЩАЯ СИСТЕМА РАДИОЛОКАЦИОННОЙ СТАНЦИИ
- 6. СИСТЕМА АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ УНИВЕРСАЛЬНЫМИ ЛЕТУЧИМИ НОЖНИЦАМИ
- 7. СЛЕДЯЩАЯ СИСТЕМА КОПИРОВАЛЬНО-ФРЕЗЕРНОГО ПОЛУАВТОМАТА
- 8. ПРОГРАММНОЕ УПРАВЛЕНИЕ МЕТАЛЛОРЕЖУЩИМИ СТАНКАМИ
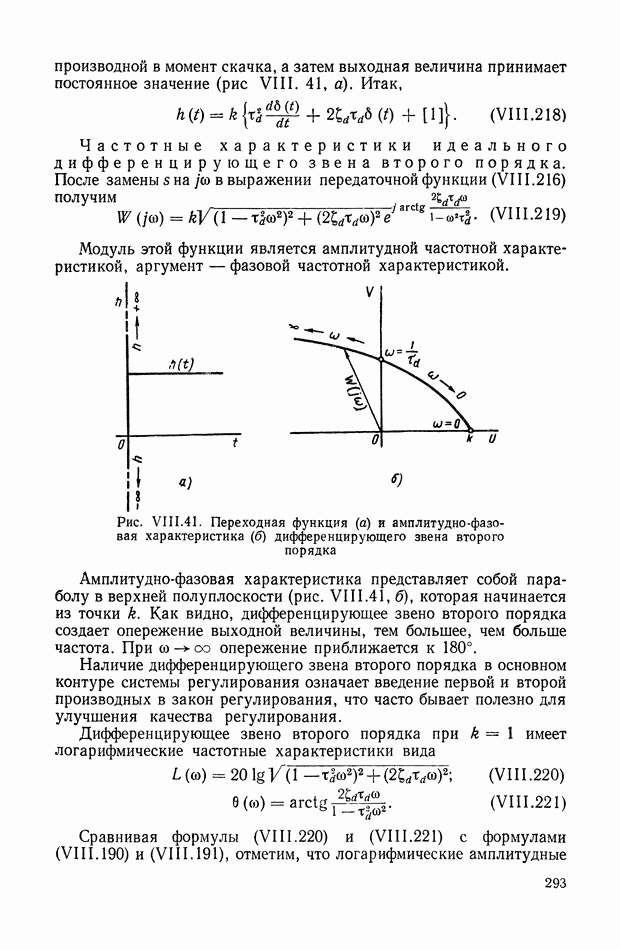
- 9. ПРИНЦИП ДЕЙСТВИЯ ЭЛЕКТРИЧЕСКОГО АВТОПИЛОТА
- 10. РЕГУЛИРОВАНИЕ МНОГИХ ВЕЛИЧИН ПРИ АВТОМАТИЧЕСКОМ УПРАВЛЕНИИ ПЕРЕГОНКОЙ НЕФТИ
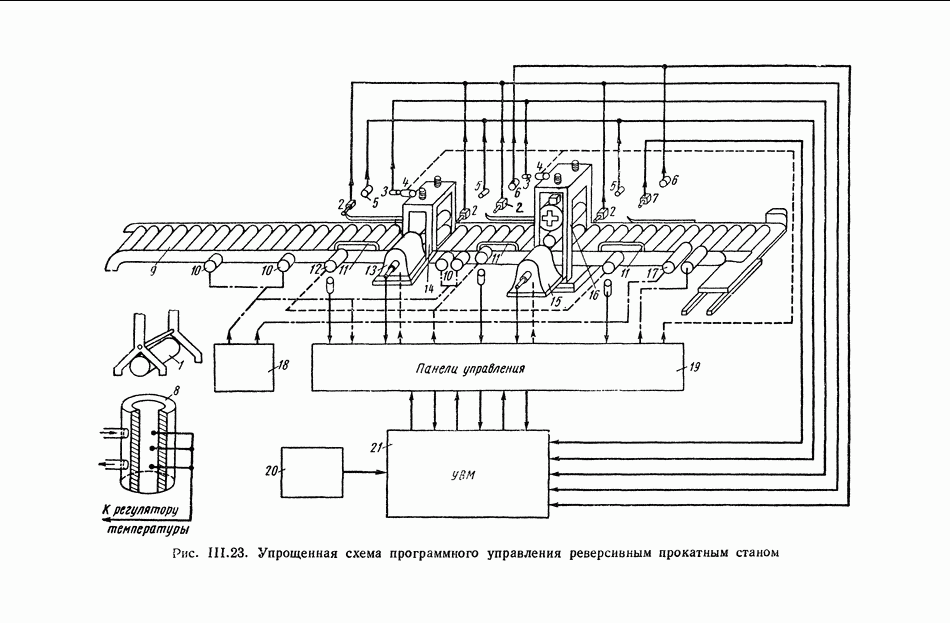
- 11. СИСТЕМА АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ РЕВЕРСИВНЫМ ПРОКАТНЫМ СТАНОМ С ИСПОЛЬЗОВАНИЕМ ЦИФРОВОЙ ВЫЧИСЛИТЕЛЬНОЙ МАШИНЫ
- ГЛАВА IV. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ЛАГРАНЖА ВТОРОГО РОДА
- 2. ОБЩИЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 3. ОБЩИЕ ЛИНЕАРИЗОВАННЫЕ УРАВНЕНИЯ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 4. ПРИМЕР СОСТАВЛЕНИЯ УРАВНЕНИЯ ОБЪЕКТА РЕГУЛИРОВАНИЯ
- ГЛАВА V. СТАТИКА СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. СТАТИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПРОСТЕЙШИХ ЗВЕНЬЕВ
- 2. СТАТИЧЕСКИЕ ХАРАКТЕРИСТИКИ ОСНОВНЫХ ТИПОВ СОЕДИНЕНИЙ ЗВЕНЬЕВ
- 3. КОРРЕКЦИЯ СТАТИЧЕСКИХ ХАРАКТЕРИСТИК
- Статическая характеристика замкнутой одномерной системы регулирования.
- Статическая характеристика линейной замкнутой системы.
- 4. СТАТИЗМ РЕГУЛИРОВАНИЯ
- 5. СТАТИКА ЛИНЕЙНЫХ СИСТЕМ С НЕСКОЛЬКИМИ РЕГУЛИРУЕМЫМИ ВЕЛИЧИНАМИ
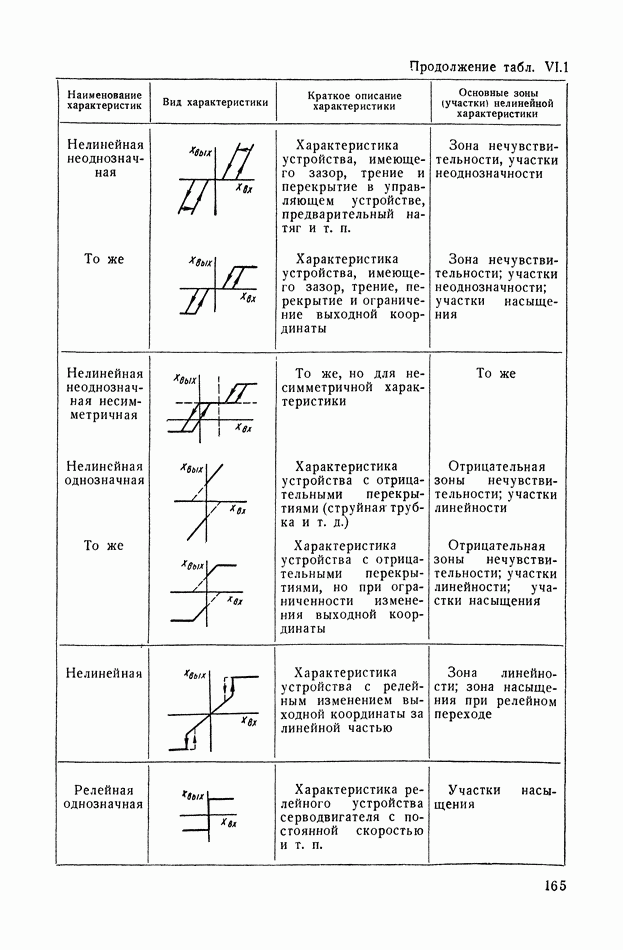
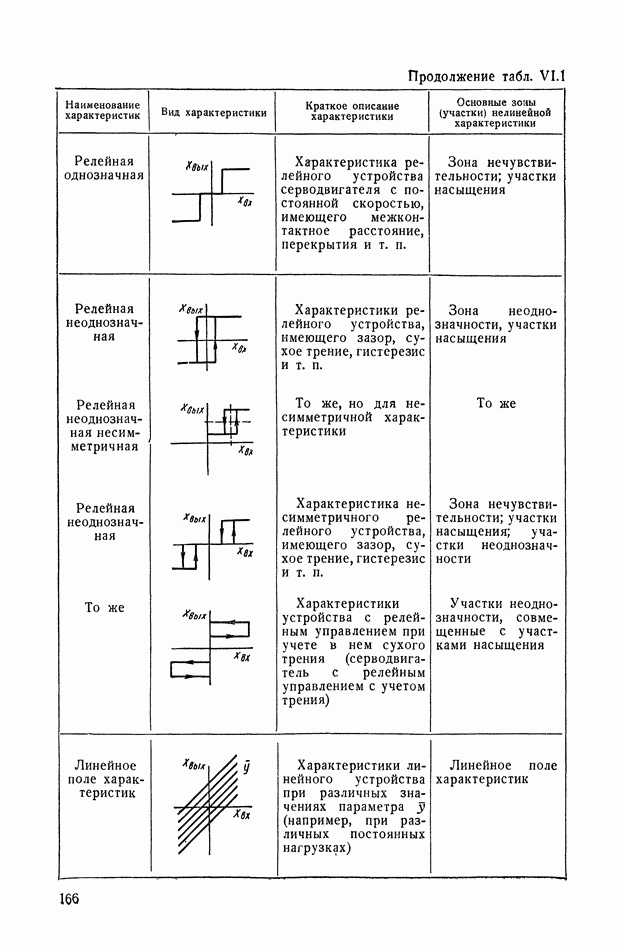
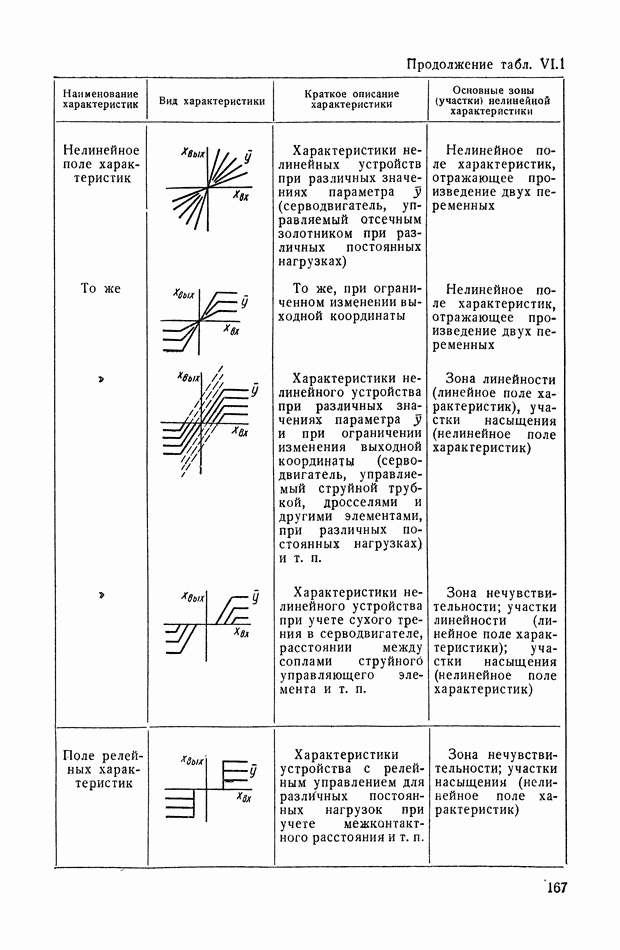
- ГЛАВА VI. ТИПИЧНЫЕ НЕЛИНЕЙНЫЕ СТАТИЧЕСКИЕ ХАРАКТЕРИСТИКИ ТИПОВЫХ ЗВЕНЬЕВ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. НЕЛИНЕЙНЫЕ ХАРАКТЕРИСТИКИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 2. ВИДЫ ТИПИЧНЫХ НЕЛИНЕЙНЫХ СТАТИЧЕСКИХ ХАРАКТЕРИСТИК СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 3. ТИПИЧНЫЕ НЕЛИНЕЙНЫЕ ХАРАКТЕРИСТИКИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 4. ЗОНЫ НЕЧУВСТВИТЕЛЬНОСТИ
- 5. ЗОНЫ ЛИНЕЙНОСТИ И НЕОДНОЗНАЧНОСТИ
- 6. ЗОНЫ НАСЫЩЕНИЯ
- 7. ПОЛЕ КРИВЫХ, ПРЕДСТАВЛЯЮЩИХ ХАРАКТЕРИСТИКУ СЕРВОДВИГАТЕЛЯ
- 8. ЭКСПЕРИМЕНТАЛЬНОЕ ВЫЯВЛЕНИЕ НЕЛИНЕЙНОСТИ ХАРАКТЕРИСТИК СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- ГЛАВА VII. ПЕРЕХОДНЫЕ ФУНКЦИИ, ПЕРЕДАТОЧНЫЕ ФУНКЦИИ И ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ДИНАМИЧЕСКИХ ЭЛЕМЕНТОВ
- 1. КЛАССИФИКАЦИЯ ДИНАМИЧЕСКИХ ЭЛЕМЕНТОВ
- 2. ОБЩЕЕ ОПРЕДЕЛЕНИЕ ИМПУЛЬСНОЙ ПЕРЕХОДНОЙ И ПЕРЕДАТОЧНОЙ ФУНКЦИЙ ДИНАМИЧЕСКОЙ СИСТЕМЫ ИЛИ ДИНАМИЧЕСКОГО ЭЛЕМЕНТА
- 3. ИМПУЛЬСНАЯ ПЕРЕХОДНАЯ ФУНКЦИЯ НЕПРЕРЫВНОЙ СТАЦИОНАРНОЙ ЛИНЕЙНОЙ СИСТЕМЫ
- 4. ПЕРЕДАТОЧНАЯ ФУНКЦИЯ НЕПРЕРЫВНОЙ ЛИНЕЙНОЙ СТАЦИОНАРНОЙ СИСТЕМЫ
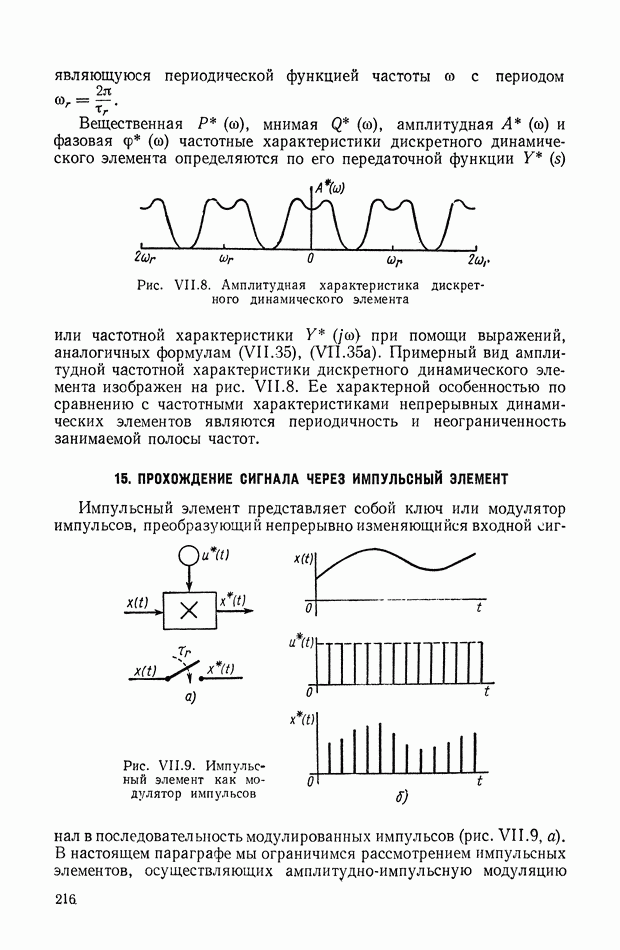
- 5. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЛИНЕЙНОЙ СТАЦИОНАРНОЙ НЕПРЕРЫВНОЙ ДИНАМИЧЕСКОЙ СИСТЕМЫ
- 6. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДИНАМИЧЕСКОГО ЭЛЕМЕНТА С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
- 7. ПРИМЕНЕНИЕ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА К РЕШЕНИЮ УРАВНЕНИЙ ЭЛЕМЕНТА С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
- 8. ПЕРЕДАТОЧНАЯ ФУНКЦИЯ ДИНАМИЧЕСКОГО ЭЛЕМЕНТА С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
- 9. ПЕРЕДАТОЧНАЯ ФУНКЦИЯ ПОСЛЕДОВАТЕЛЬНОГО СОЕДИНЕНИЯ ДИНАМИЧЕСКИХ ЭЛЕМЕНТОВ С СОСРЕДОТОЧЕННЫМИ И С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
- 10. ПЕРЕДАТОЧНАЯ ФУНКЦИЯ ЗАПАЗДЫВАЮЩЕГО ЭЛЕМЕНТА
- 11. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЭЛЕМЕНТА С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
- 12. ИМПУЛЬСНАЯ ПЕРЕХОДНАЯ ФУНКЦИЯ ДИНАМИЧЕСКОГО ЭЛЕМЕНТА С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
- 13. ПЕРЕДАТОЧНАЯ ФУНКЦИЯ СИСТЕМЫ С ГАРМОНИЧЕСКОЙ МОДУЛЯЦИЕЙ
- 14 ИМПУЛЬСНАЯ ПЕРЕХОДНАЯ И ПЕРЕДАТОЧНАЯ ФУНКЦИИ ДИСКРЕТНОЙ ЛИНЕЙНОЙ СТАЦИОНАРНОЙ СИСТЕМЫ
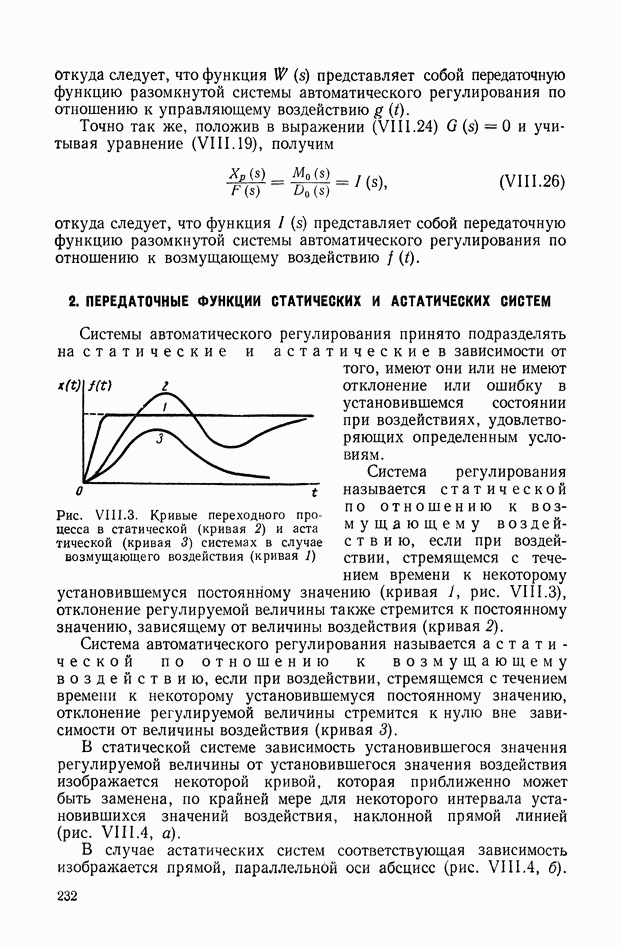
- 15. ПРОХОЖДЕНИЕ СИГНАЛА ЧЕРЕЗ ИМПУЛЬСНЫЙ ЭЛЕМЕНТ
- 16. ПОСЛЕДОВАТЕЛЬНОЕ СОЕДИНЕНИЕ ИМПУЛЬСНОГО ЭЛЕМЕНТА И НЕПРЕРЫВНОГО ДИНАМИЧЕСКОГО ЭЛЕМЕНТА
- 17. ИМПУЛЬСНАЯ ПЕРЕХОДНАЯ ФУНКЦИЯ ЛИНЕЙНОЙ НЕСТАЦИОНАРНОЙ СИСТЕМЫ (СИСТЕМЫ С ПЕРЕМЕННЫМИ ПАРАМЕТРАМИ)
- 18. ПЕРЕДАТОЧНАЯ ФУНКЦИЯ НЕПРЕРЫВНОЙ ЛИНЕЙНОЙ НЕСТАЦИОНАРНОЙ СИСТЕМЫ
- 19. МНОГОМЕРНЫЕ ИМПУЛЬСНЫЕ ПЕРЕХОДНЫЕ И ПЕРЕДАТОЧНЫЕ ФУНКЦИИ НЕЛИНЕЙНЫХ СИСТЕМ
- 20. МНОГОМЕРНЫЕ ПЕРЕДАТОЧНЫЕ ФУНКЦИИ НЕЛИНЕЙНЫХ СИСТЕМ
- ГЛАВА VIII. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ, ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ И ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ НЕПРЕРЫВНЫХ ЛИНЕЙНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
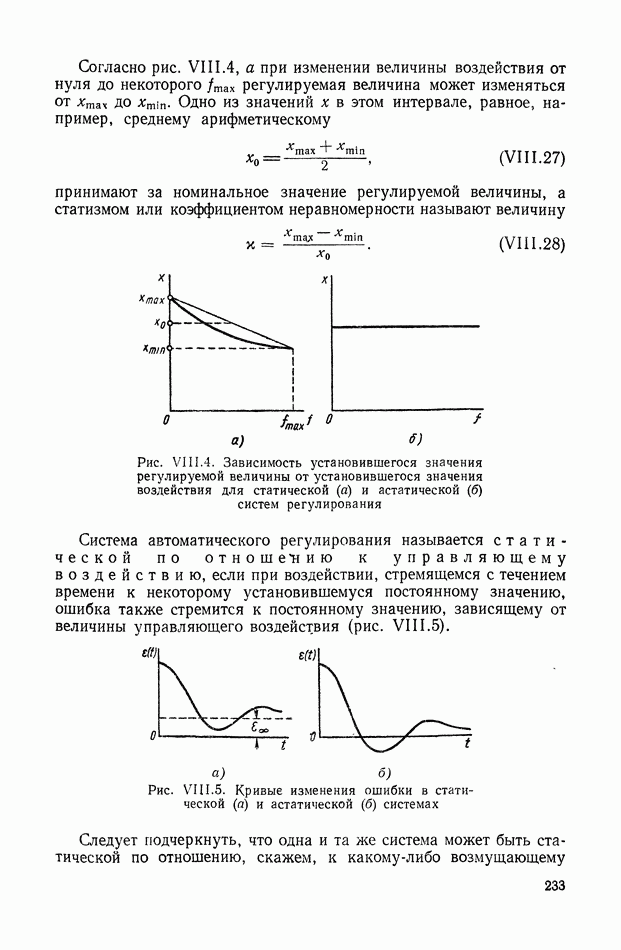
- 2. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ СТАТИЧЕСКИХ И АСТАТИЧЕСКИХ СИСТЕМ
- 3. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ
- 4. ВЗАИМНАЯ СВЯЗЬ МЕЖДУ ЧАСТОТНЫМИ ХАРАКТЕРИСТИКАМИ ЗАМКНУТОЙ И РАЗОМКНУТОЙ СИСТЕМЫ
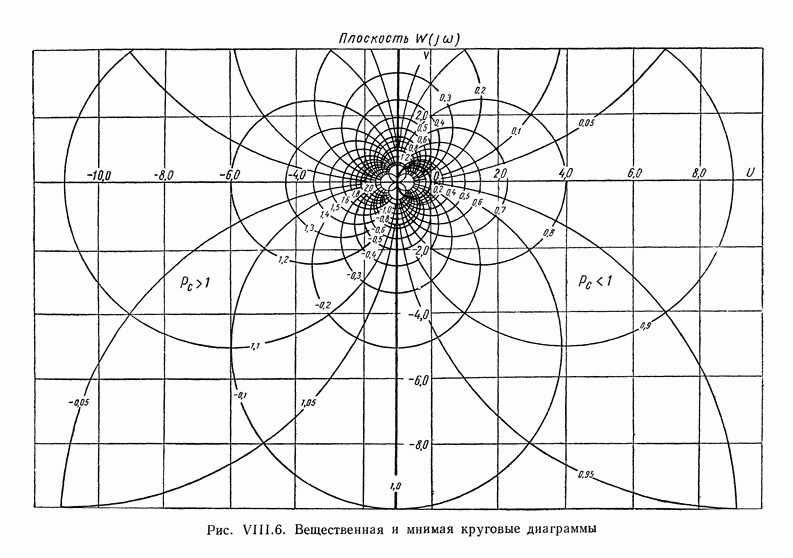
- 5. КРУГОВЫЕ ДИАГРАММЫ
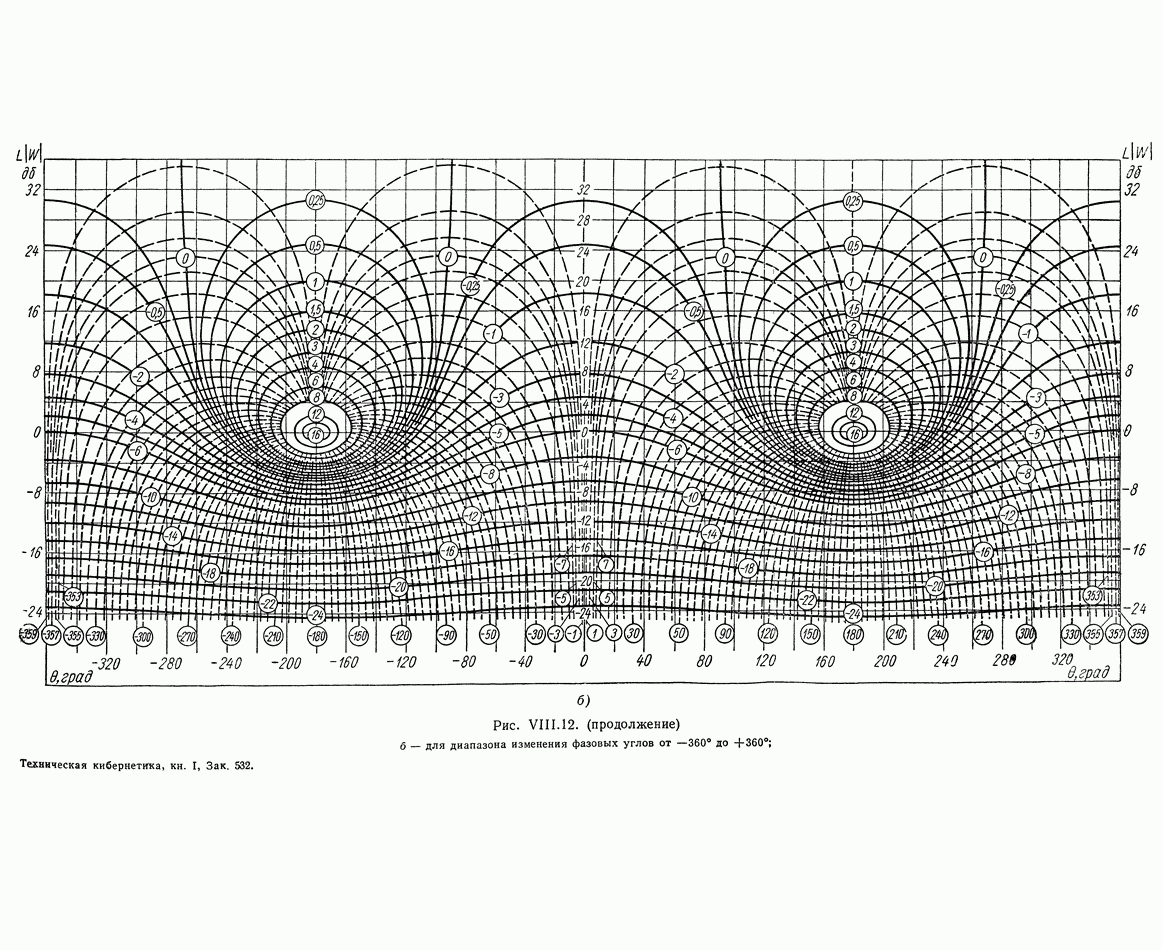
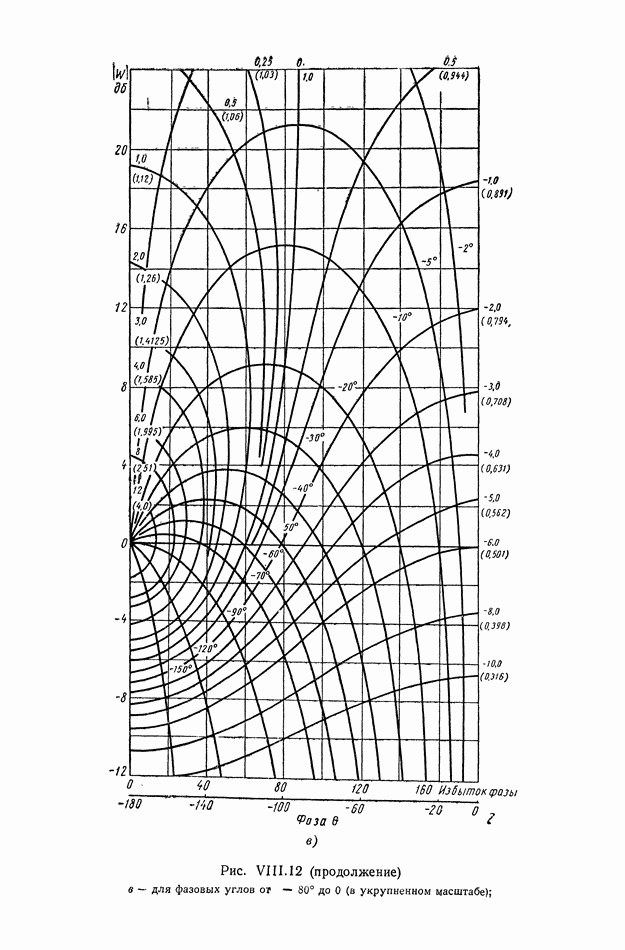
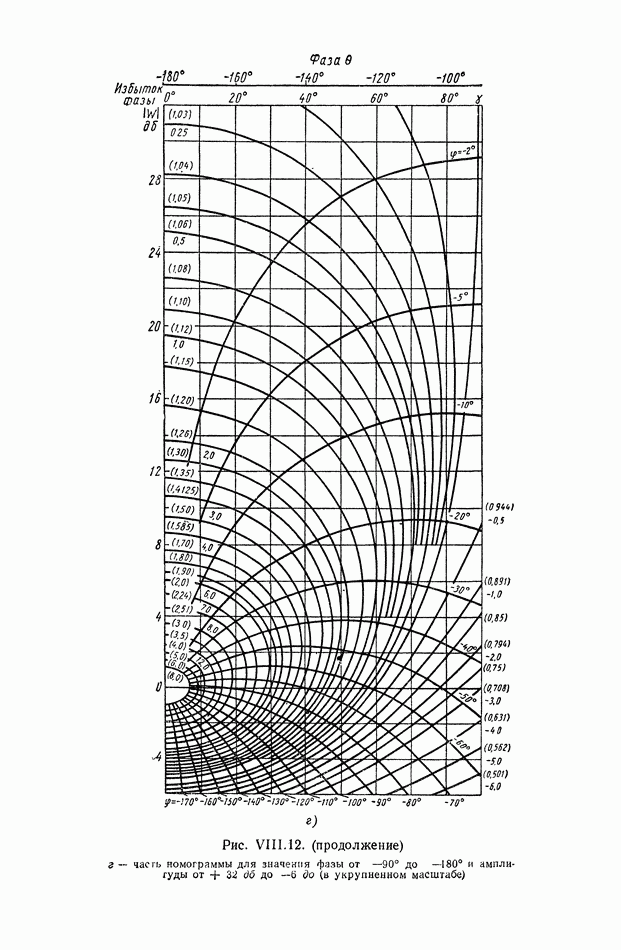
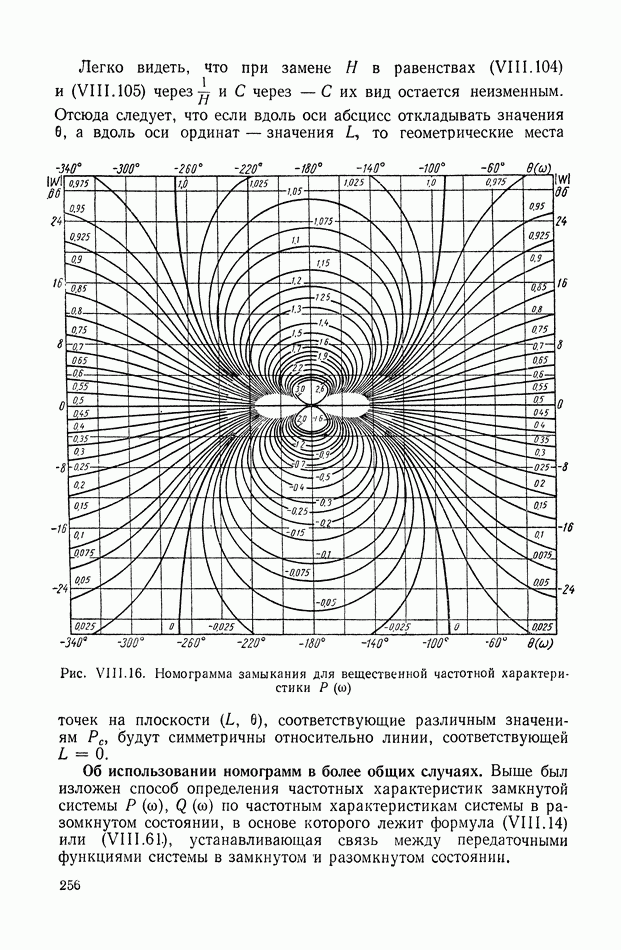
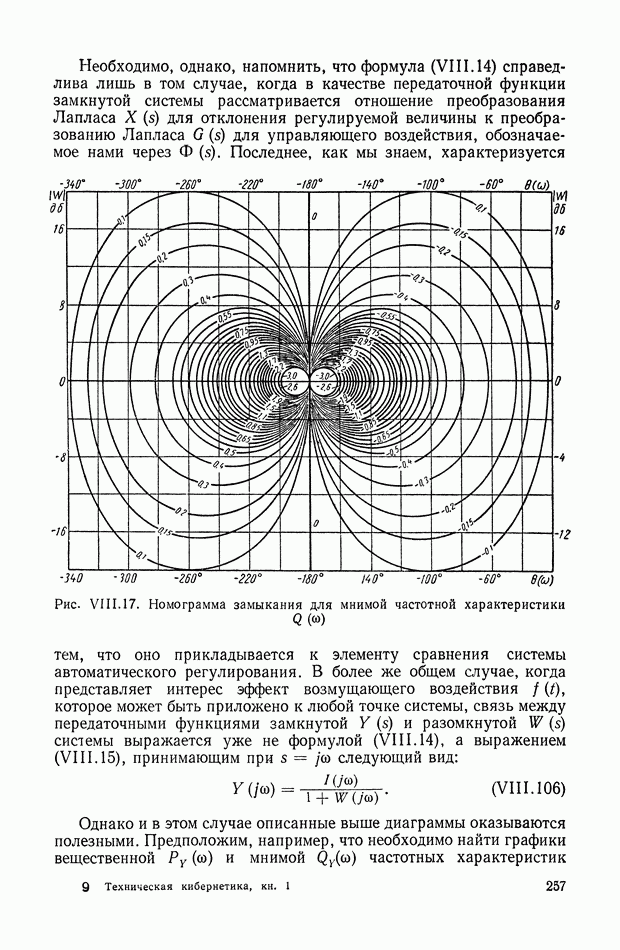
- 6. НОМОГРАММЫ ЗАМЫКАНИЯ
- 7. УСЛОВИЯ ОДНОЗНАЧНОЙ связи МЕЖДУ ЧАСТОТНЫМИ ХАРАКТЕРИСТИКАМИ
- 8. ОПРЕДЕЛЕНИЕ ПЕРЕДАТОЧНОЙ ФУНКЦИИ ПО ОДНОЙ ИЗ ЧАСТОТНЫХ ХАРАКТЕРИСТИК, ЗАДАННОЙ АНАЛИТИЧЕСКИ
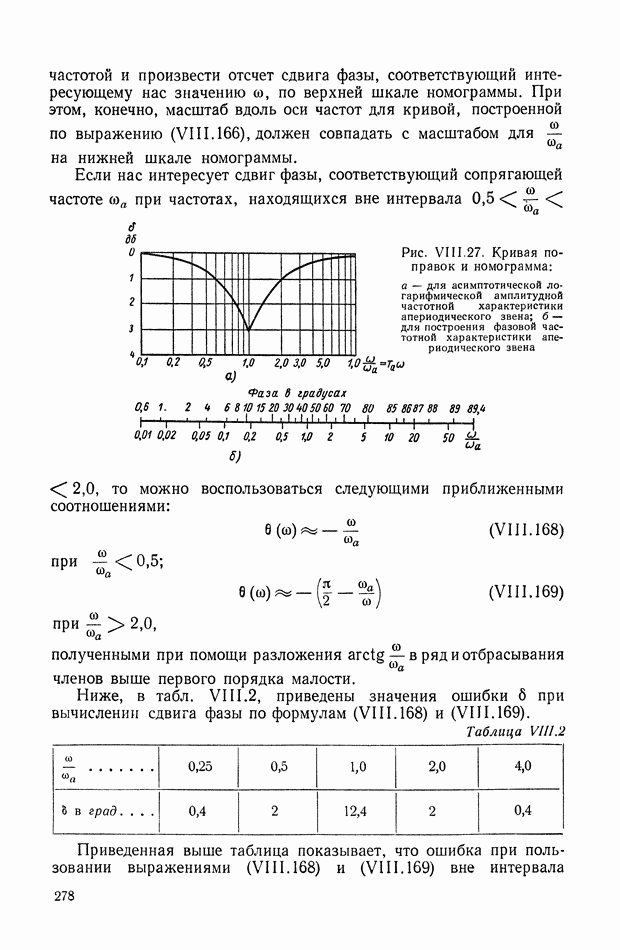
- 9. ФОРМУЛА ДЛЯ ВЫЧИСЛЕНИЯ ФАЗОВОЙ ЧАСТОТНОЙ ХАРАКТЕРИСТИКИ ПО ЗАДАННОЙ АМПЛИТУДНОЙ ЧАСТОТНОЙ ХАРАКТЕРИСТИКЕ
- 10. ЗАВИСИМОСТЬ МЕЖДУ ЛОГАРИФМИЧЕСКОЙ АМПЛИТУДНОЙ И ФАЗОВОЙ ЧАСТОТНЫМИ ХАРАКТЕРИСТИКАМИ
- 11. ГРАФИЧЕСКИЙ МЕТОД ОПРЕДЕЛЕНИЯ ФАЗОВОЙ ХАРАКТЕРИСТИКИ ПО ЗАДАННОЙ АМПЛИТУДНОЙ ХАРАКТЕРИСТИКЕ
- 12. ИНТЕГРАЛЬНЫЕ ВЫРАЖЕНИЯ ДЛЯ ОШИБКИ И ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 13. ТИПОВЫЕ ЗВЕНЬЯ
- 14. АПЕРИОДИЧЕСКОЕ ЗВЕНО
- 15. КОЛЕБАТЕЛЬНОЕ ЗВЕНО
- 16. ИНТЕГРИРУЮЩЕЕ ЗВЕНО
- 17. ДИФФЕРЕНЦИРУЮЩЕЕ ЗВЕНО ПЕРВОГО ПОРЯДКА
- 18. ДИФФЕРЕНЦИРУЮЩЕЕ ЗВЕНО ВТОРОГО ПОРЯДКА
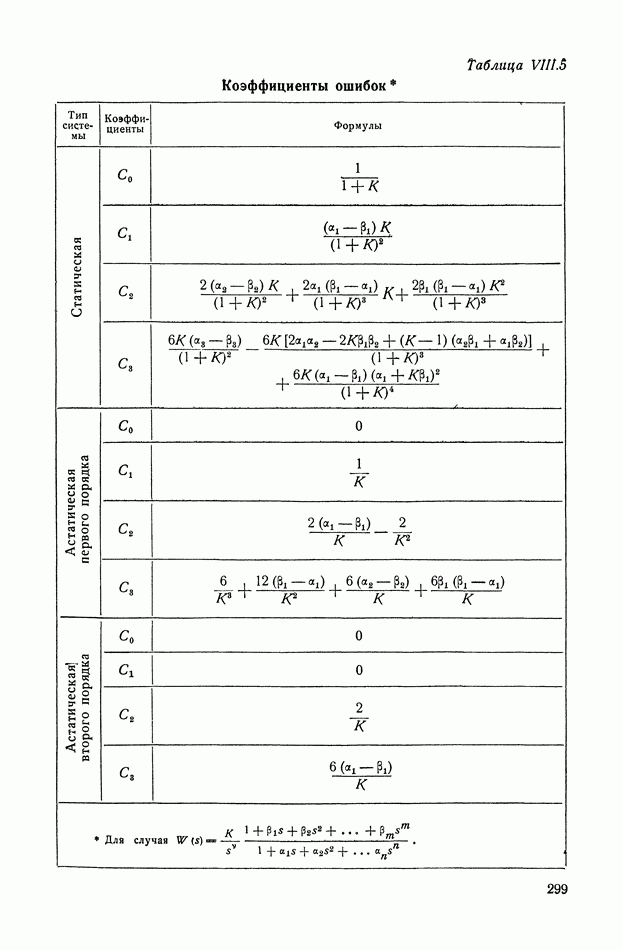
- 19. КОЭФФИЦИЕНТЫ ОШИБКИ
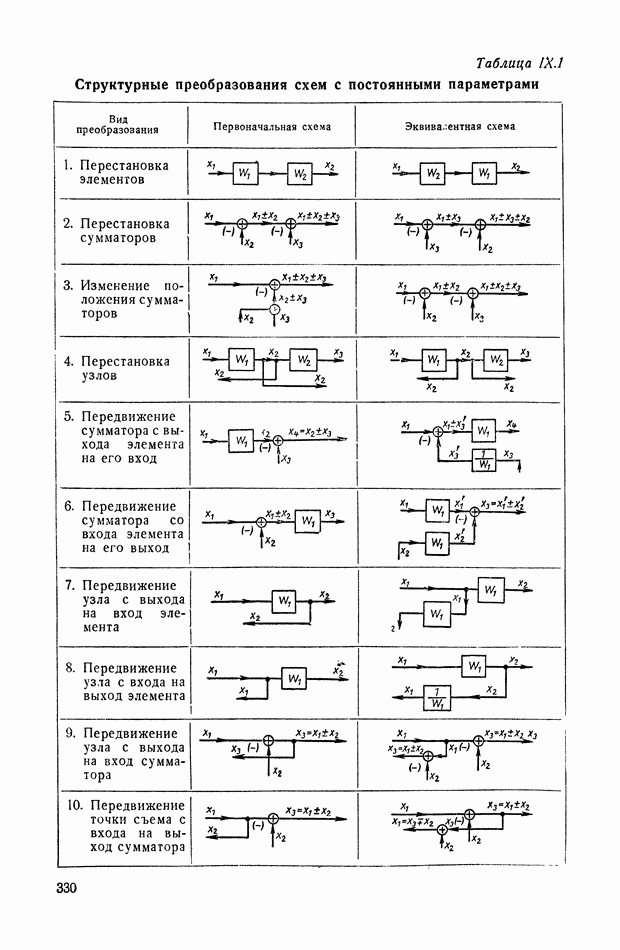
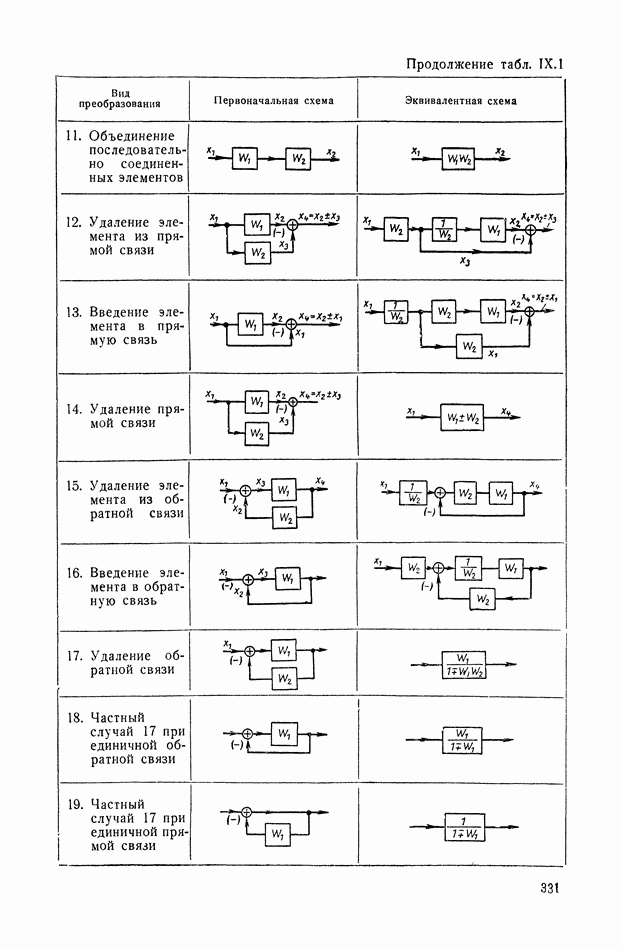
- ГЛАВА IX. МЕТОДЫ СТРУКТУРНЫХ ПРЕОБРАЗОВАНИЙ В СИСТЕМАХ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. ГРАФИЧЕСКИЕ ИЗОБРАЖЕНИЯ УСЛОВИЙ ПРЕОБРАЗОВАНИЯ СИГНАЛОВ
- 2. СХЕМЫ С ЭЛЕМЕНТАМИ, ОБЛАДАЮЩИМИ И НЕ ОБЛАДАЮЩИМИ СВОЙСТВОМ НАПРАВЛЕННОСТИ ДЕЙСТВИЯ
- 3. ДЕТАЛИЗИРОВАННЫЕ СТРУКТУРЫ
- 4. ПРЕОБРАЗОВАНИЯ МНОГОКОНТУРНЫХ СТРУКТУРНЫХ СХЕМ, ДОПУСКАЮЩИХ ПОСЛЕДОВАТЕЛЬНОЕ ПРИМЕНЕНИЕ ПРАВИЛ СВЕРТЫВАНИЯ КОНТУРОВ, И НЕКОТОРЫЕ ЭКВИВАЛЕНТНЫЕ ПРЕОБРАЗОВАНИЯ
- 5. ПРЕОБРАЗОВАНИЯ ПЕРЕКРЕСТНЫХ СТРУКТУРНЫХ СХЕМ МЕТОДОМ РАЗВЯЗКИ КОНТУРОВ И НЕКОТОРЫЕ ЭКВИВАЛЕНТНЫЕ ПРЕОБРАЗОВАНИЯ
- 6. ПРИМЕНЕНИЕ СТРУКТУРНЫХ МЕТОДОВ ДЛЯ ОПРЕДЕЛЕНИЯ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ МНОГОКОНТУРНЫХ СИСТЕМ
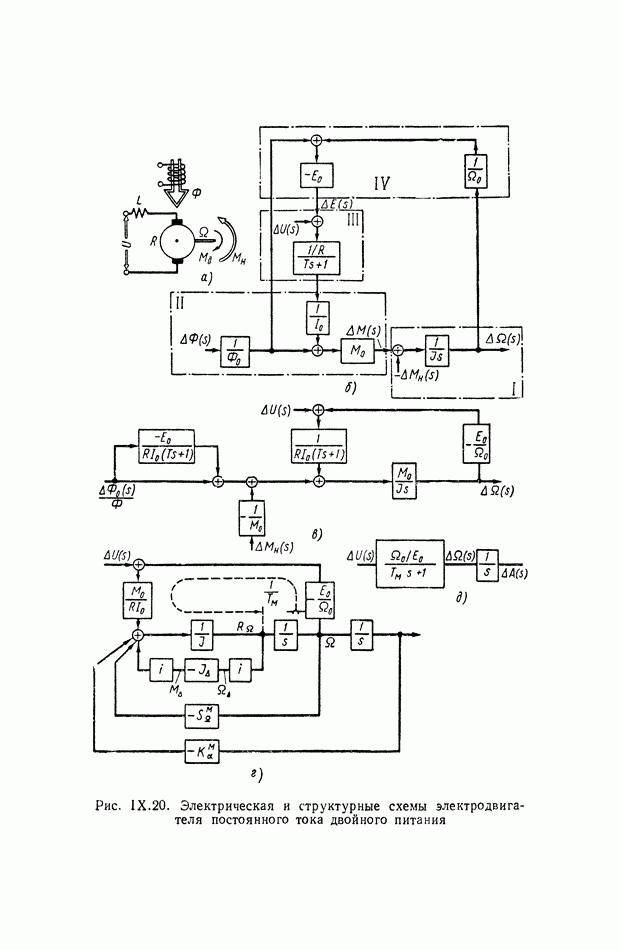
- 7. СОСТАВЛЕНИЕ И ПРЕОБРАЗОВАНИЕ СТРУКТУРНОЙ СХЕМЫ НА ПРИМЕРЕ ЭЛЕКТРОДВИГАТЕЛЯ ПОСТОЯННОГО ТОКА ДВОЙНОГО ПИТАНИЯ
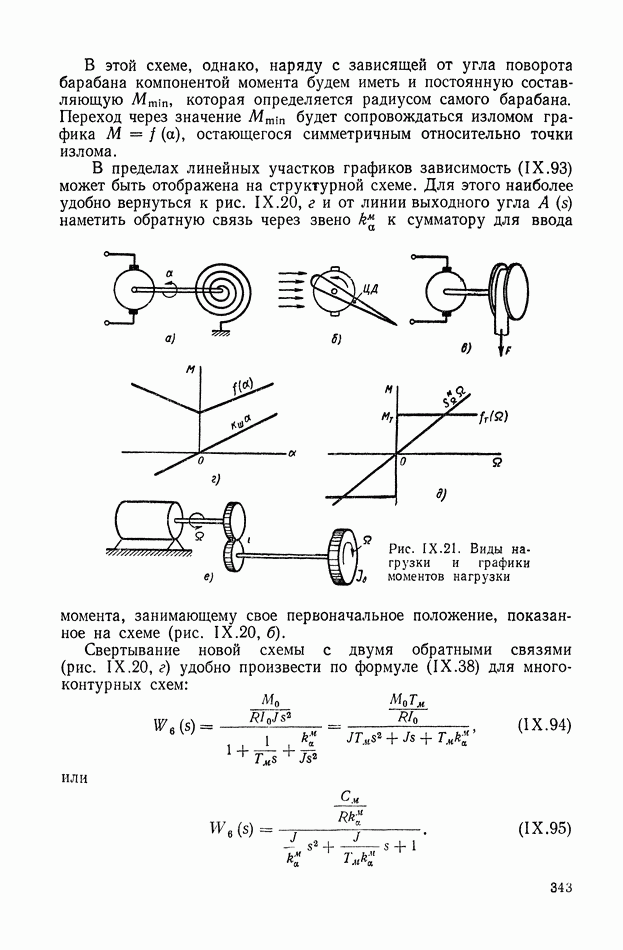
- Учет зависимости момента нагрузки от угла поворота вала и его производных по времени.
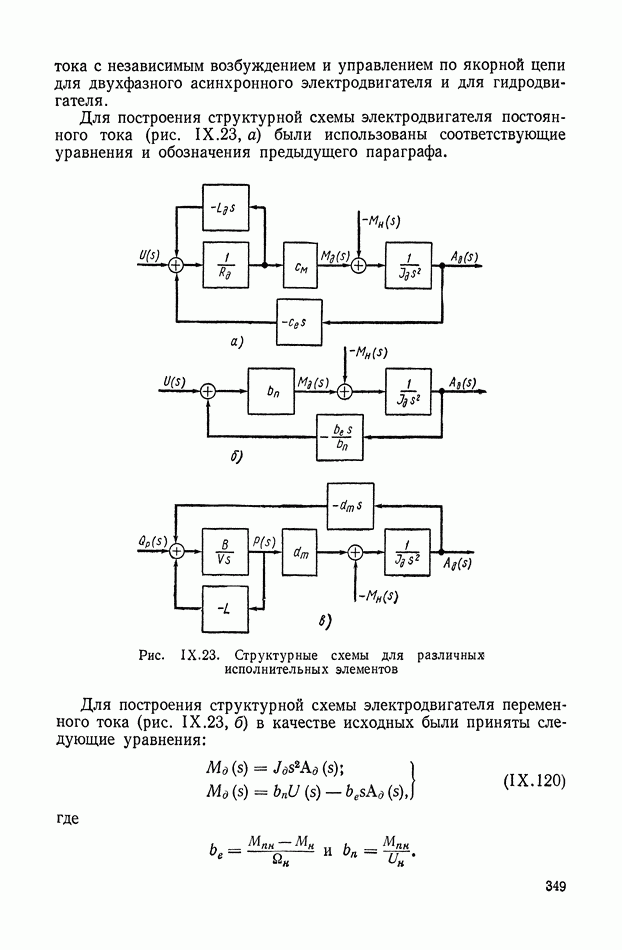
- 8. СТРУКТУРНЫЕ СХЕМЫ МЕХАНИЧЕСКИХ ОБЪЕКТОВ РЕГУЛИРОВАНИЯ С РЕДУКТОРАМИ, ДИФФЕРЕНЦИАЛАМИ И УПРУГИМИ ЭЛЕМЕНТАМИ В СИЛОВЫХ ПЕРЕДАЧАХ
- 9. ПРАВИЛА СТРУКТУРНЫХ ПРЕОБРАЗОВАНИЙ ДЛЯ СИСТЕМ С ПЕРЕМЕННЫМИ ПАРАМЕТРАМИ
- 10. ФУНКЦИОНАЛЬНЫЕ СТРУКТУРНЫЕ СХЕМЫ ДЛЯ АНАЛИЗА СОВМЕСТНЫХ СТАТИЧЕСКИХ ХАРАКТЕРИСТИК НЕЛИНЕЙНЫХ ЗВЕНЬЕВ
- ГЛАВА X. ПРИМЕРЫ СОСТАВЛЕНИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ, СТРУКТУРНЫХ СХЕМ И ПЕРЕДАТОЧНЫХ ФУНКЦИЙ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. СИСТЕМА АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ СКОРОСТИ ВРАЩЕНИЯ ГИДРОТУРБИНЫ
- 2. ЭЛЕКТРОННЫЙ РЕГУЛЯТОР НАПРЯЖЕНИЯ ВЭИ
- 3. СИСТЕМА АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ МОЩНОСТИ ЯДЕРНОГО ЭНЕРГЕТИЧЕСКОГО РЕАКТОРА НА ТЕПЛОВЫХ НЕЙТРОНАХ
- 4. СЛЕДЯЩАЯ СИСТЕМА РАДИОЛОКАЦИОННОЙ СТАНЦИИ
- 5. СИСТЕМА АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ УНИВЕРСАЛЬНЫХ ЛЕТУЧИХ НОЖНИЦ
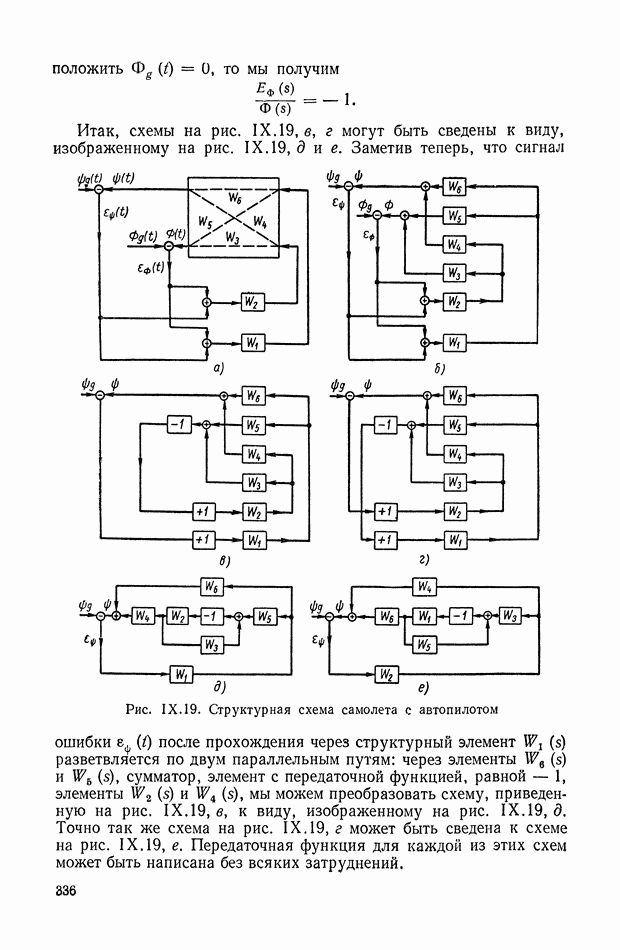
- 6. САМОЛЕТ С АВТОПИЛОТОМ
- 7. СЛЕДЯЩАЯ СИСТЕМА КОПИРОВАЛЬНО-ФРЕЗЕРНОГО СТАНКА
- РАЗДЕЛ II. АНАЛИЗ УСТОЙЧИВОСТИ НЕПРЕРЫВНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- ГЛАВА XI. ОБЩАЯ ПОСТАНОВКА ЗАДАЧИ УСТОЙЧИВОСТИ ПО ЛЯПУНОВУ И АНАЛИЗ УСТОЙЧИВОСТИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. ПОСТАНОВКА ЗАДАЧИ ОБ УСТОЙЧИВОСТИ В ТЕОРИИ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 2. ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ УСТАНОВИВШИХСЯ ДВИЖЕНИЙ ПО УРАВНЕНИЮ ПЕРВОГО ПРИБЛИЖЕНИЯ
- 3. О ПРЯМОМ МЕТОДЕ ЛЯПУНОВА
- 4. О ПРИМЕНЕНИИ ПРЯМОГО МЕТОДА ЛЯПУНОВА К АНАЛИЗУ УСТОЙЧИВОСТИ ОДНОГО КЛАССА СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- ГЛАВА XII. КРИТЕРИИ И МЕТОДЫ АНАЛИЗА УСТОЙЧИВОСТИ ЛИНЕАРИЗОВАННЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЙ
- 1. УСТОЙЧИВОСТЬ И ПРИНЦИП АРГУМЕНТА
- 2. КРИТЕРИЙ УСТОЙЧИВОСТИ МИХАЙЛОВА
- 3. КРИТЕРИЙ УСТОЙЧИВОСТИ РАУСА И ГУРВИЦА
- 4. ЧАСТОТНЫЙ КРИТЕРИЙ УСТОЙЧИВОСТИ
- 5. ОБОБЩЕНИЕ ЧАСТОТНОГО КРИТЕРИЯ НА АСТАТИЧЕСКИЕ СИСТЕМЫ
- 6. ОБОБЩЕНИЕ ЧАСТОТНОГО КРИТЕРИЯ НА СЛУЧАЙ, КОГДА РАЗОМКНУТАЯ СИСТЕМА НЕУСТОЙЧИВА
- 7. ЧАСТОТНЫЙ КРИТЕРИЙ УСТОЙЧИВОСТИ ДЛЯ ОБРАТНОЙ АМПЛИТУДНО-ФАЗОВОЙ ХАРАКТЕРИСТИКИ
- 8. АНАЛИЗ УСТОЙЧИВОСТИ ОДНОКОНТУРНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ПО ИХ ЛОГАРИФМИЧЕСКИМ ЧАСТОТНЫМ ХАРАКТЕРИСТИКАМ
- 9. ПРИБЛИЖЕННЫЙ СПОСОБ ПОСТРОЕНИЯ ЛОГАРИФМИЧЕСКИХ ЧАСТОТНЫХ ХАРАКТЕРИСТИК ОДНОКОНТУРНЫХ СИСТЕМ
- 10. ОБОБЩЕНИЕ ЧАСТОТНОГО КРИТЕРИЯ УСТОЙЧИВОСТИ НА МНОГОКОНТУРНЫЕ СИСТЕМЫ
- 11. АНАЛИЗ УСТОЙЧИВОСТИ МНОГОКОНТУРНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ПРИ ПОМОЩИ ЛОГАРИФМИЧЕСКИХ ЧАСТОТНЫХ ХАРАКТЕРИСТИК
- ГЛАВА XIII. ВЫДЕЛЕНИЕ ОБЛАСТЕЙ УСТОЙЧИВОСТИ
- 1. ПОНЯТИЕ О Д-РАЗБИЕНИИ ПРОСТРАНСТВА КОЭФФИЦИЕНТОВ ХАРАКТЕРИСТИЧЕСКОГО УРАВНЕНИЯ И ПРОСТРАНСТВА ПАРАМЕТРОВ
- 2. Д-РАЗБИЕНИЕ ПЛОСКОСТИ ОДНОГО КОМПЛЕКСНОГО ПАРАМЕТРА
- 3. СВЯЗЬ Д-РАЗБИЕНИЯ С КРИТЕРИЯМИ УСТОЙЧИВОСТИ
- 4. Д-РАЗБИЕНИЕ ПЛОСКОСТИ ДВУХ ДЕЙСТВИТЕЛЬНЫХ ПАРАМЕТРОВ (ДИАГРАММА ВЫШНЕГРАДСКОГО)
- 5. УСЛОВИЯ СУЩЕСТВОВАНИЯ ОБЛАСТИ УСТОЙЧИВОСТИ
- ГЛАВА XIV. ПРИМЕРЫ АНАЛИЗА УСТОЙЧИВОСТИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. СИСТЕМА АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ СКОРОСТИ ВРАЩЕНИЯ ГИДРОТУРБИНЫ
- 2. СЛЕДЯЩАЯ СИСТЕМА КОПИРОВАЛЬНО-ФРЕЗЕРНОГО СТАНКА
- 3. СИСТЕМА АВТОМАТИЧЕСКОЙ СТАБИЛИЗАЦИИ САМОЛЕТА (АВТОПИЛОТ)
- 4. СИСТЕМА АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ МОЩНОСТИ ЯДЕРНОГО ЭНЕРГЕТИЧЕСКОГО РЕАКТОРА
- РАЗДЕЛ III. АНАЛИЗ ПЕРЕХОДНЫХ ПРОЦЕССОВ И КАЧЕСТВА ЛИНЕЙНЫХ НЕПРЕРЫВНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- ГЛАВА XV. ЧАСТОТНЫЙ МЕТОД АНАЛИЗА ПЕРЕХОДНЫХ ПРОЦЕССОВ
- 1. ОБОБЩЕННЫЕ ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ И ИХ СВЯЗЬ С ПЕРЕХОДНЫМИ ПРОЦЕССАМИ
- 2. ОПРЕДЕЛЕНИЕ ОБОБЩЕННЫХ ЧАСТОТНЫХ ХАРАКТЕРИСТИК В ОБЩЕМ СЛУЧАЕ
- 3. СЛУЧАЙ, КОГДА ФУНКЦИЯ X(s) НЕ СОДЕРЖИТ ОСОБЕННОСТЕЙ ВО ВСЕЙ ПРАВОЙ ПОЛУПЛОСКОСТИ И НА МНИМОЙ ОСИ
- 4. СВЯЗЬ МЕЖДУ ЧАСТОТНЫМИ ХАРАКТЕРИСТИКАМИ P(w), Q(w) И ИМПУЛЬСНОЙ ПЕРЕХОДНОЙ ФУНКЦИЕЙ k(t)
- 5. СЛУЧАЙ, КОГДА ВСЕ ПОЛЮСА ФУНКЦИИ X(s) РАСПОЛОЖЕНЫ В ЛЕВОЙ ПОЛУПЛОСКОСТИ, ЗА ИСКЛЮЧЕНИЕМ ПОЛЮСА В НАЧАЛЕ КООРДИНАТ
- 6. СВЯЗЬ МЕЖДУ ЧАСТОТНЫМИ ХАРАКТЕРИСТИКАМИ И ПЕРЕХОДНОЙ ФУНКЦИЕЙ h(t)
- 7. СЛУЧАЙ, КОГДА ФУНКЦИЯ X(s) ИМЕЕТ ДВА СОПРЯЖЕННЫХ ПОЛЮСА НА МНИМОЙ ОСИ
- 8. АНАЛИЗ ПЕРЕХОДНЫХ ПРОЦЕССОВ МЕТОДОМ ТРАПЕЦЕИДАЛЬНЫХ ЧАСТОТНЫХ ХАРАКТЕРИСТИК
- 9. О НЕКОТОРЫХ ЧАСТНЫХ СЛУЧАЯХ МЕТОДА ТРАПЕЦЕИДАЛЬНЫХ ЧАСТОТНЫХ ХАРАКТЕРИСТИК
- 10. ОБ УСЛОВИЯХ ПРИМЕНИМОСТИ ЧАСТОТНОГО МЕТОДА АНАЛИЗА ПЕРЕХОДНЫХ ПРОЦЕССОВ
- 11. ОПРЕДЕЛЕНИЕ ДИСКРЕТНЫХ ЗНАЧЕНИЙ ПЕРЕХОДНОЙ ФУНКЦИИ
- ГЛАВА XVI. ЧАСТОТНЫЙ МЕТОД АНАЛИЗА КАЧЕСТВА
- 1. ЧАСТОТНЫЙ КРИТЕРИЙ КАЧЕСТВА РЕГУЛИРОВАНИЯ
- 2. ЧАСТОТНЫЙ КРИТЕРИЙ ОТСУТСТВИЯ ПЕРЕРЕГУЛИРОВАНИЙ И ЧАСТОТНЫЙ КРИТЕРИЙ МОНОТОННОСТИ
- 3. О ПРОВЕРКЕ ВЫПОЛНЕНИЯ СФОРМУЛИРОВАННЫХ КРИТЕРИЕВ
- 4. НЕКОТОРЫЕ ПРИЗНАКИ НЕУДОВЛЕТВОРЕНИЯ КРИТЕРИЕВ КАЧЕСТВА И КРИТЕРИЕВ ОТСУТСТВИЯ ПЕРЕРЕГУЛИРОВАНИЙ И МОНОТОННОСТИ
- 5. НЕКОТОРЫЕ ЭЛЕМЕНТАРНЫЕ СВОЙСТВА ЧАСТОТНЫХ ХАРАКТЕРИСТИК
- 6. ДОСТАТОЧНЫЕ УСЛОВИЯ ДЛЯ МАЛЫХ ПЕРЕРЕГУЛИРОВАНИЙ И НЕОБХОДИМЫЕ УСЛОВИЯ ДЛЯ ОТСУТСТВИЯ ПЕРЕРЕГУЛИРОВАНИЙ
- 7. КРИТЕРИЙ, ОПРЕДЕЛЯЮЩИЙ ДОСТАТОЧНЫЕ УСЛОВИЯ ДЛЯ МОНОТОННОСТИ
- 8. ОЦЕНКИ ВЕЛИЧИНЫ ПЕРЕРЕГУЛИРОВАНИЯ И ВРЕМЕНИ ПЕРЕХОДНОГО ПРОЦЕССА
- 9. ОЦЕНКА АБСОЛЮТНОГО ЗНАЧЕНИЯ РАЗНОСТИ МЕЖДУ ПЕРЕХОДНЫМИ ФУНКЦИЯМИ ПО СООТВЕТСТВУЮЩИМ ИМ ЧАСТОТНЫМ ХАРАКТЕРИСТИКАМ
- 10. СВЯЗЬ МЕЖДУ СВОЙСТВАМИ АМПЛИТУДНО-ФАЗОВОЙ ХАРАКТЕРИСТИКИ РАЗОМКНУТОЙ СИСТЕМЫ И КАЧЕСТВОМ
- 11. ТРЕБОВАНИЯ К ЧАСТОТНЫМ ХАРАКТЕРИСТИКАМ, ОБЕСПЕЧИВАЮЩИЕ ВЫСОКУЮ ТОЧНОСТЬ В СЛЕДЯЩИХ СИСТЕМАХ
- 12. СВЯЗЬ МЕЖДУ СВОЙСТВАМИ ЛОГАРИФМИЧЕСКОЙ АМПЛИТУДНОЙ ХАРАКТЕРИСТИКИ И КАЧЕСТВОМ
- 13. ОПРЕДЕЛЕНИЕ ВЕЛИЧИНЫ ПЕРЕДАТОЧНОГО КОЭФФИЦИЕНТА ИЛИ ДОБРОТНОСТИ ПО ЛОГАРИФМИЧЕСКОЙ АМПЛИТУДНОЙ ХАРАКТЕРИСТИКЕ
- 14. ОПРЕДЕЛЕНИЕ УСТАНОВИВШЕЙСЯ ОШИБКИ ПРИ ГАРМОНИЧЕСКОМ УПРАВЛЯЮЩЕМ ВОЗДЕЙСТВИИ ПО ЛОГАРИФМИЧЕСКОЙ АМПЛИТУДНОЙ ХАРАКТЕРИСТИКЕ
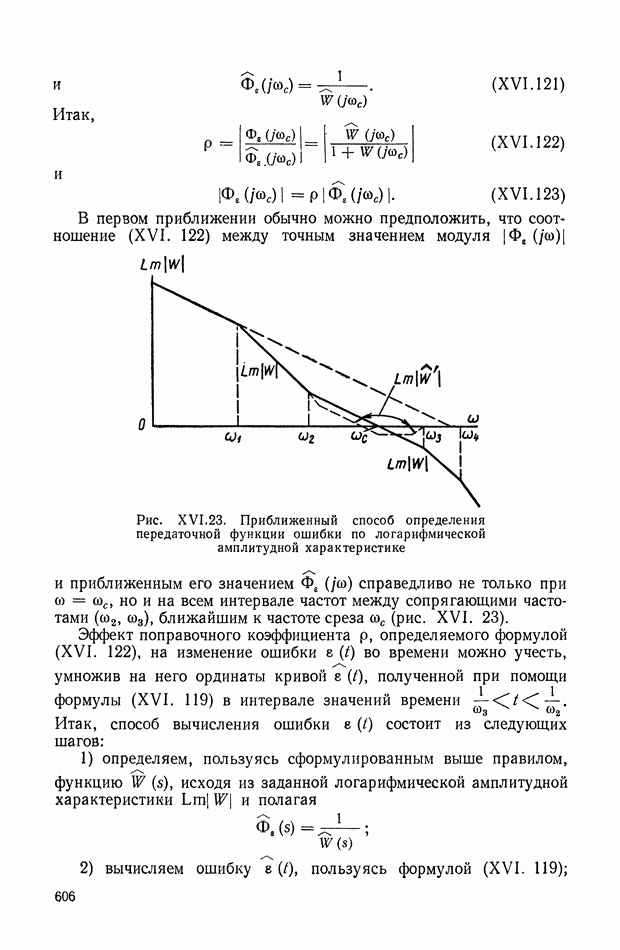
- 15. ПРИБЛИЖЕННЫЙ СПОСОБ ВЫЧИСЛЕНИЯ ПЕРЕХОДНОГО ПРОЦЕССА ПО СОПРЯГАЮЩИМ ЧАСТОТАМ ЛОГАРИФМИЧЕСКОЙ АМПЛИТУДНОЙ ЧАСТОТНОЙ ХАРАКТЕРИСТИКИ
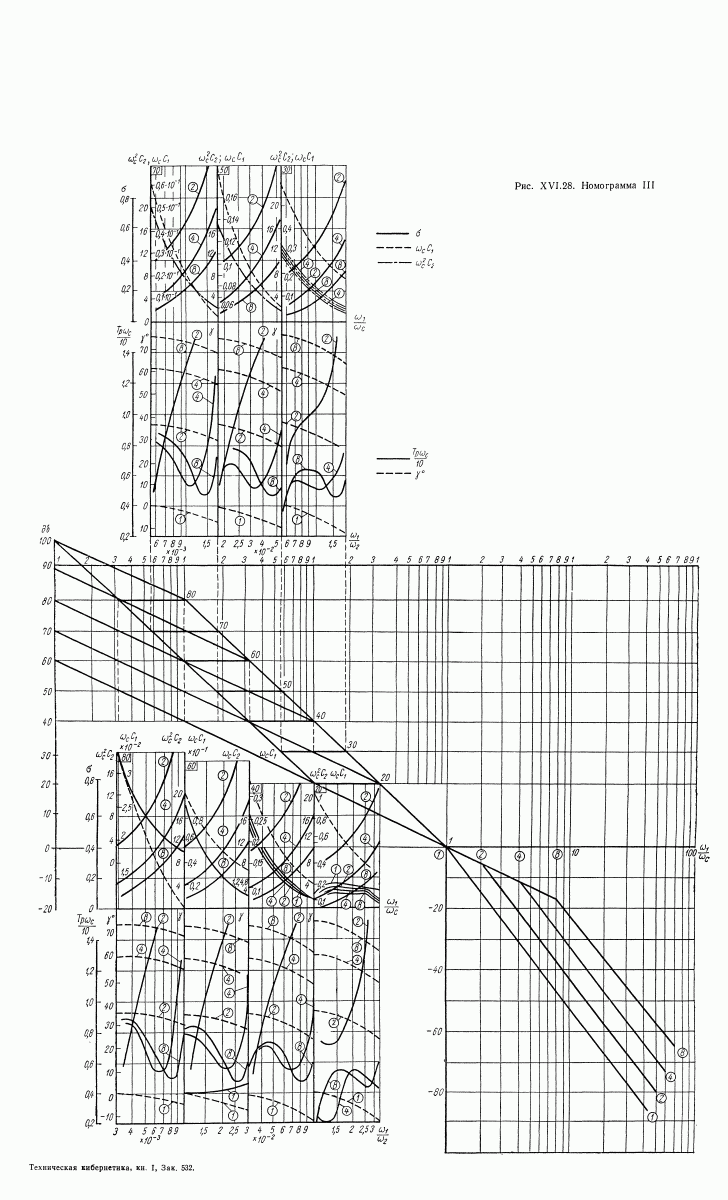
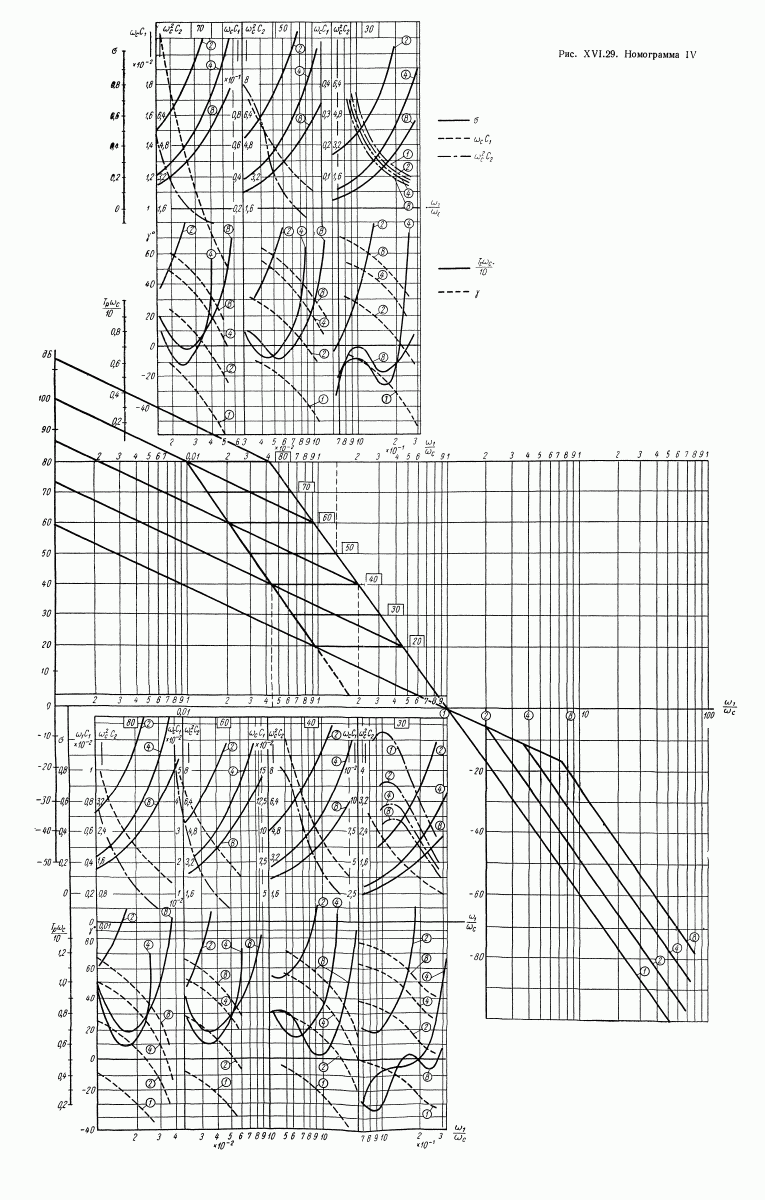
- 16. НОМОГРАММА ДЛЯ ОПРЕДЕЛЕНИЯ ЗАПАСА УСТОЙЧИВОСТИ, ПОКАЗАТЕЛЕЙ КАЧЕСТВА И КОЭФФИЦИЕНТОВ ОШИБОК ПО ВИДУ ЛОГАРИФМИЧЕСКОЙ АМПЛИТУДНОЙ ХАРАКТЕРИСТИКИ
- ГЛАВА XVII. СВЯЗЬ МЕЖДУ КАЧЕСТВОМ ПЕРЕХОДНОГО ПРОЦЕССА И РАСПРЕДЕЛЕНИЕМ НУЛЕЙ И ПОЛЮСОВ ПЕРЕДАТОЧНОЙ ФУНКЦИИ. МЕТОД КОРНЕВЫХ ГОДОГРАФОВ
- 2. АНАЛИЗ РАСПРЕДЕЛЕНИЯ КОРНЕЙ ХАРАКТЕРИСТИЧЕСКОГО УРАВНЕНИЯ СИСТЕМЫ И ОЦЕНКА КАЧЕСТВА ПЕРЕХОДНОГО ПРОЦЕССА
- 3. ГЕОМЕТРИЧЕСКИЙ МЕТОД ПОСТРОЕНИЯ КОРНЕВОГО ГОДОГРАФА
- 4. АНАЛИТИЧЕСКОЕ ПОСТРОЕНИЕ ГЕОМЕТРИЧЕСКОГО МЕСТА КОРНЕЙ
- 5. ОПРЕДЕЛЕНИЕ ОБЛАСТЕЙ УСТОЙЧИВОСТИ ЛИНЕЙНЫХ СИСТЕМ МЕТОДОМ КОРНЕВОГО ГОДОГРАФА
- 6. ОЦЕНКИ ПАРАМЕТРОВ ПЕРЕХОДНОЙ И ЧАСТОТНОЙ ХАРАКТЕРИСТИК ПО КОРНЕВОМУ ГОДОГРАФУ
- 7. ВЛИЯНИЕ РАСПОЛОЖЕНИЯ НУЛЕЙ И ПОЛЮСОВ ЗАМКНУТОЙ СИСТЕМЫ НА ПЕРЕХОДНУЮ ХАРАКТЕРИСТИКУ h(t)
- 8. ВЛИЯНИЕ РАСПОЛОЖЕНИЯ НУЛЕЙ И ПОЛЮСОВ ЗАМКНУТОЙ СИСТЕМЫ НА ЕЕ ПОЛОСУ ЧАСТОТ
- 9. КОРНЕВОЙ ГОДОГРАФ И ПЕРЕХОДНАЯ ХАРАКТЕРИСТИКА СИСТЕМЫ ПРИ ВОЗМУЩЕНИЯХ, ПРИЛОЖЕННЫХ НЕ К ОСНОВНОМУ ВХОДУ СИСТЕМЫ
- 10. ВЛИЯНИЕ РАСПРЕДЕЛЕНИЯ НУЛЕЙ И ПОЛЮСОВ ПЕРЕДАТОЧНОЙ ФУНКЦИИ НА КАЧЕСТВО ПЕРЕХОДНОГО ПРОЦЕССА ПРИ НАЛИЧИИ ВНЕШНЕГО ВОЗДЕЙСТВИЯ
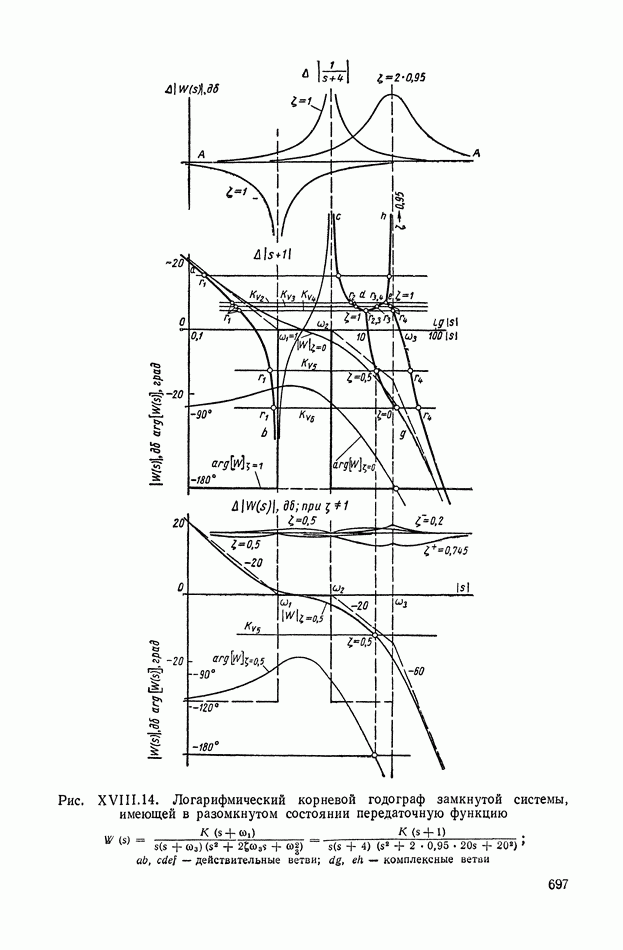
- ГЛАВА XVIII. МЕТОД ЛОГАРИФМИЧЕСКИХ КОРНЕВЫХ ГОДОГРАФОВ
- 2. ОПРЕДЕЛЕНИЕ КОРНЕЙ ЗАМКНУТОЙ СИСТЕМЫ ПО ЛОГАРИФМИЧЕСКОЙ АМПЛИТУДНОЙ КОМПЛЕКСНО-ЧАСТОТНОЙ ХАРАКТЕРИСТИКЕ РАЗОМКНУТОЙ СИСТЕМЫ
- 3. ЛОГАРИФМИЧЕСКИЕ КОРНЕВЫЕ ГОДОГРАФЫ
- 4. ЛОГАРИФМИЧЕСКИЕ КОМПЛЕКСНО-ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЗВЕНЬЕВ ВТОРОГО ПОРЯДКА
- 5. ПРИМЕР ПОСТРОЕНИЯ ЛОГАРИФМИЧЕСКОГО КОРНЕВОГО ГОДОГРАФА
- ГЛАВА XIX. ИНТЕГРАЛЬНЫЕ ОЦЕНКИ И КРИТЕРИИ КАЧЕСТВА РЕГУЛИРОВАНИЯ
- 2. МЕТОДИКА ПРИМЕНЕНИЯ ИНТЕГРАЛЬНЫХ КВАДРАТИЧНЫХ ОЦЕНОК
- 3. ЛИНЕЙНЫЕ ИНТЕГРАЛЬНЫЕ ОЦЕНКИ
- ПРИЛОЖЕНИЕ
- БИБЛИОГРАФИЯ ПО РАЗДЕЛАМ КНИГИ