| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
3. ГЕОМЕТРИЧЕСКИЙ МЕТОД ПОСТРОЕНИЯ КОРНЕВОГО ГОДОГРАФА
Рассмотрим передаточную функцию замкнутой системы [5]

где  — целые полиномы от
— целые полиномы от  соответственно со степенями порядков
соответственно со степенями порядков  с действительными коэффициентами.
с действительными коэффициентами.
Приравняв нулю числитель передаточной функции, получим уравнение, определяющее нули:

а приравняв нулю знаменатель, получим характеристическое уравнение

Условимся называть последнее уравнение уравнением системы класса 
В рассматриваемых системах характеристические уравнения (XVII. 10) зависят от одного действительного свободного параметра, линейно входящего в некоторые его коэффициенты. Поэтому выражение (XVI 1.10) определяет целое семейство уравнений, зависящее от одного свободного параметра К. При непрерывном изменении  непрерывно изменяются корни этого уравнения, а вместе с тем и устойчивость и передаточные свойства системы.
непрерывно изменяются корни этого уравнения, а вместе с тем и устойчивость и передаточные свойства системы.
При  корни характеристического уравнения совпадают с корнями уравнения
корни характеристического уравнения совпадают с корнями уравнения

Обозначим эти корни буквами

и назовем их начальными точками траекторий корней.
При  корни характеристического уравнения совпадают с корнями уравнения
корни характеристического уравнения совпадают с корнями уравнения

Обозначим эти корни буквами

и назовем их предельными точками траекторий корней.
Если обратная связь жесткая и свободным параметром является коэффициент усиления системы, то все начальные точки совпадают с полюсами, а предельные — с нулями передаточной функции разомкнутой системы. В более общем случае гибких обратных связей или многоконтурных систем эти условия нарушаются.
Совокупность  начальных и
начальных и  предельных точек системы класса
предельных точек системы класса  будем далее называть основными точками траекторий корней, так как они однозначно определяют все геометрическое место корней уравнения (XVII. 10) при изменении свободного параметра в пределах —
будем далее называть основными точками траекторий корней, так как они однозначно определяют все геометрическое место корней уравнения (XVII. 10) при изменении свободного параметра в пределах — 
Уравнения нулей, полюсов и основных точек всегда являются алгебраическими уравнениями с действительными коэффициентами, все корни которых могут быть только действительными или комплексно-сопряженными. Поэтому на плоскости комплексного переменного  все нули, полюса и основные точки расположены симметрично относительно действительной оси.
все нули, полюса и основные точки расположены симметрично относительно действительной оси.
Так как знак свободного параметра определяется структурой системы, то практически рационально рассматривать порознь геометрические места корней при положительных и отрицательных значениях параметра. Условимся первое геометрическое место корней называть положительным, а второе — отрицательным годографом семейства корней системы (XVII. 10). Так как при непрерывном изменении свободного параметра уравнения (XVII. 10) корни его изменяются также непрерывно, то как положительный, так и отрицательный годограф системы  порядка состоит из
порядка состоит из  непрерывных траекторий, каждая из которых описывается одним из корней уравнения (XVII. 10) при изменении параметра соответственно от нуля
непрерывных траекторий, каждая из которых описывается одним из корней уравнения (XVII. 10) при изменении параметра соответственно от нуля 
Общие свойства геометрического места корней семейства уравнений, линейно зависящего от одного параметра. Если исследуемая линейная система состоит из детерминированных типовых звеньев первого и второго порядков (апериодических и колебательных), то основные точки ее характеристического уравнения нам заданы. В противном случае они могут быть найдены из уравнений (XVI 1.11) и (XVII. 13). Зная основные точки, мы можем записать исходное уравнение (XVI 1.10) в следующем виде:

При значении свободного параметра, равном нулю  все корни этого уравнения совпадают с начальными точками
все корни этого уравнения совпадают с начальными точками  При
При  имеем, что
имеем, что  корней выражения (XVII. 15) совпадает с
корней выражения (XVII. 15) совпадает с  предельными точками, а остальные
предельными точками, а остальные  корней равны бесконечности.
корней равны бесконечности.
При непрерывном изменении свободного параметра исходного уравнения (XVII. 10) или (XVI 1.15) от  до
до  из
из
каждой из  начальных точек
начальных точек  выходит корень, описывающий на плоскости комплексного переменного
выходит корень, описывающий на плоскости комплексного переменного  ко непрерывную траекторию. Из
ко непрерывную траекторию. Из  этих траекторий
этих траекторий  заканчиваются в
заканчиваются в  предельных точках
предельных точках  а остальные уходят в бесконечность. Все
а остальные уходят в бесконечность. Все  этих траекторий образуют положительный годограф системы.
этих траекторий образуют положительный годограф системы.
Аналогично, при непрерывном уменьшении К от нуля до  из тех же начальных точек выходят
из тех же начальных точек выходят  новых корней, двигающихся по
новых корней, двигающихся по  новым траекториям, из которых
новым траекториям, из которых  оканчиваются в предельных точках,
оканчиваются в предельных точках,  в бесконечности. Эти траектории образуют отрицательный годограф системы.
в бесконечности. Эти траектории образуют отрицательный годограф системы.
Из уравнения (XVI 1.15) следует, что форма кривой геометрического места корней не зависит от выбора нулевого значения для отсчета параметра К и от положения мнимой оси относительно геометрического места корней. Основываясь на этом свойстве покажем следующее.
1. Любую группу корней характеристического уравнения (XVI 1.10) при фиксированном значении свободного параметра  можно принять за начальные точки траекторий корней. Предельные точки при этом не изменяются. Действительно, прибавим и вычтем из уравнения (XVII.10) два равных полинома
можно принять за начальные точки траекторий корней. Предельные точки при этом не изменяются. Действительно, прибавим и вычтем из уравнения (XVII.10) два равных полинома  В этом случае можем записать
В этом случае можем записать

или

По определению, начальными точками траекторий корней последнего уравнения являются корни уравнения (XVI 1.10) при  . Предельные же точки уравнений (XVII. 10) и (XVII. 16) совпадают. Это позволяет в случае, когда полиномы
. Предельные же точки уравнений (XVII. 10) и (XVII. 16) совпадают. Это позволяет в случае, когда полиномы  содержат свободные члены, упростить характеристическое уравнение (XVII.10), приведя его к виду
содержат свободные члены, упростить характеристическое уравнение (XVII.10), приведя его к виду

в котором одна из начальных точек равна нулю.
2. Конфигурация геометрического места корней семейства характеристических уравнений (XVII. 10) не зависит от положения мнимой оси.
Из уравнения (XVI 1.15) видно, что конфигурация траекторий на плоскости комплексного переменного определяется лишь расстояниями точек траекторий корней от основных точек. Разности, очевидно, не зависят от положения начала координат и мнимой оси. Так как перемещение мнимой оси на произвольную действительную величину а изменяет лишь абсциссы основных точек, то любое уравнение семейства

определяет то же геометрическое место корней, что и уравнение (XVII. 15). Это свойство независимости кривой геометрического места корней от смещения мнимой оси позволяет выбрать для построения траекторий наиболее удобное для исследования уравнение.
Вывод основного фазового уравнения геометрического места корней [21, 31]. Возьмем характеристическое уравнение в виде (XVII. 15), явно содержащем основные точки, и, подставив в него значение любой точки геометрического места корней  получим тождество
получим тождество

Представим входящие сюда разности через их модули и фазы в виде

и подставим их в выражение (XVI 1.19), тогда получим

Так как параметр К принимает лишь действительные значения, то и правая часть тождества (XVI 1.20) должна быть действительным числом. Это будет иметь место, если фазы  и удовлетворяют условию
и удовлетворяют условию

Таким образом, только те точки комплексной плоскости являются корнями уравнения (XVII. 15) и принадлежат геометрическому месту корней, для которых выполняется соотношение (XVII.21). Последнее и является искомым основным фазовым уравнением всего геометрического места корней семейства уравнений (XVII. 15).
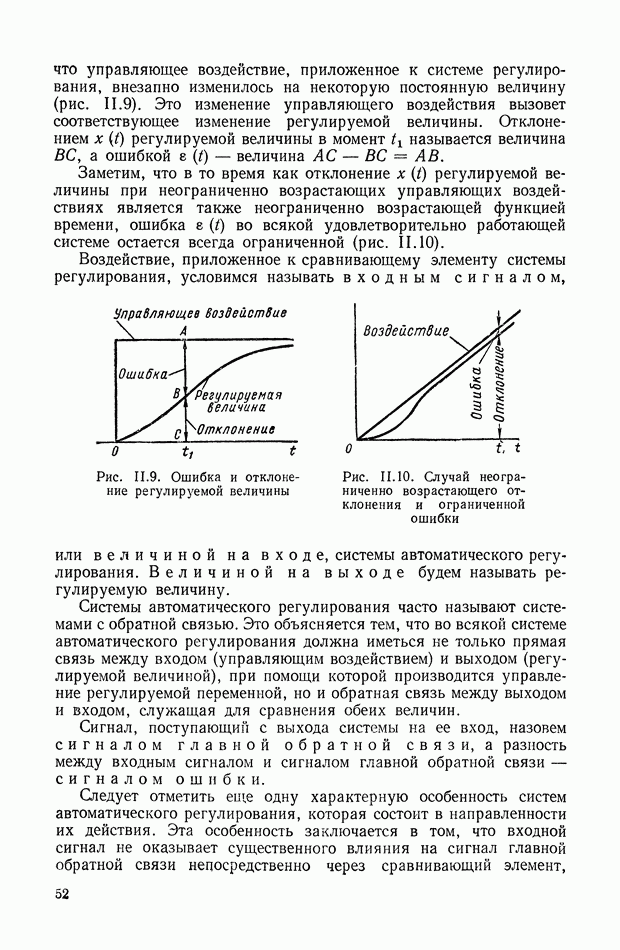
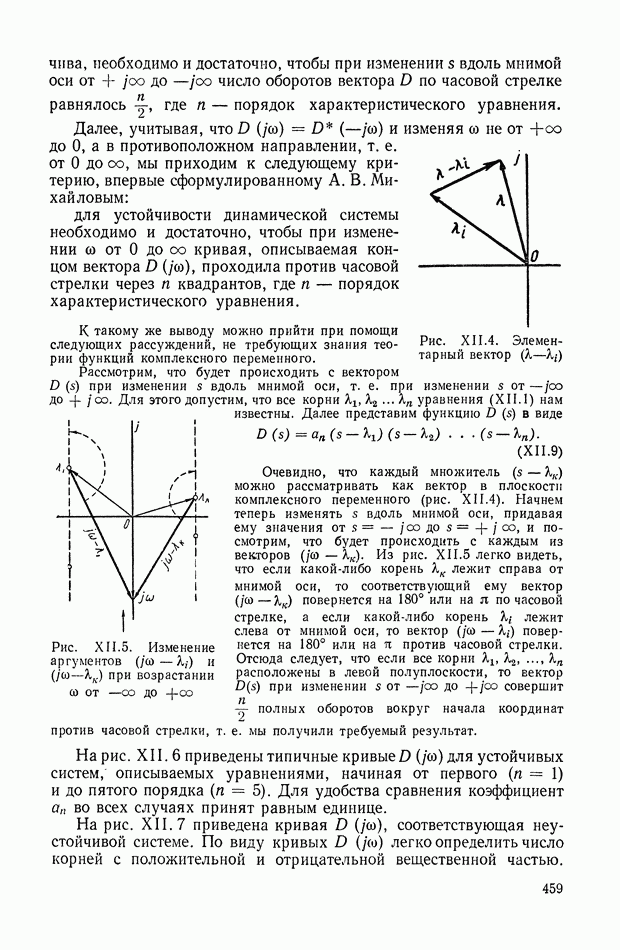
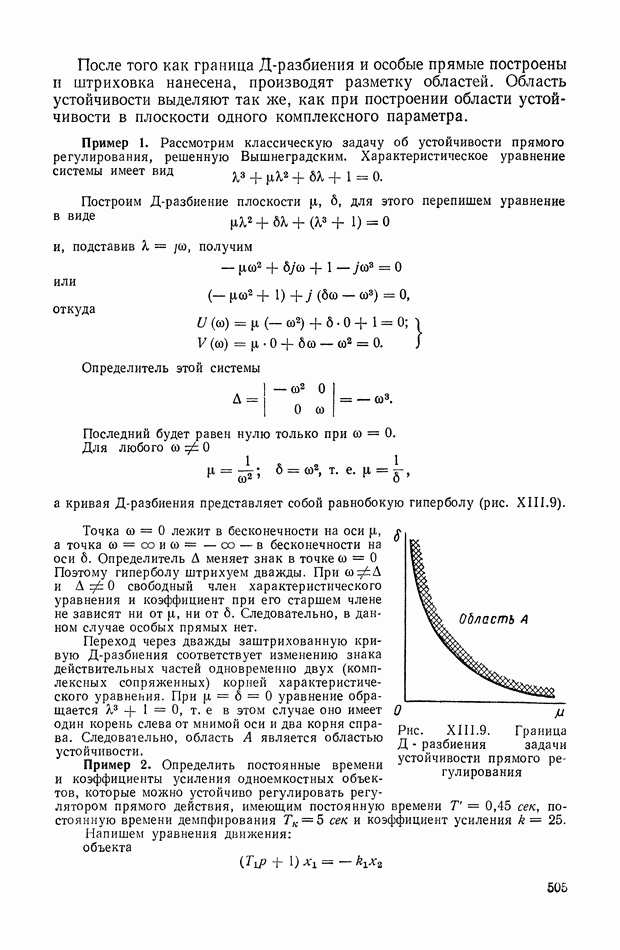
Уравнение (XVII.21) имеет простой геометрический смысл: только те точки комплексной плоскости  лежат на траекториях корней уравнения (XVII. 15), для которых сумма углов
лежат на траекториях корней уравнения (XVII. 15), для которых сумма углов  образованных комплексными векторами
образованных комплексными векторами  проведенными из начальных точек в исследуемую точку
проведенными из начальных точек в исследуемую точку  с положительным направлением действительной оси, минус сумма углов образованных аналогичными векторами
с положительным направлением действительной оси, минус сумма углов образованных аналогичными векторами  проведенными из предельных точек, равна нулю или целому кратному
проведенными из предельных точек, равна нулю или целому кратному  (рис. XVII. 1).
(рис. XVII. 1).
Подставив уравнение (XVII.21) в выражение (XVII.20), получим 

Эта формула определяет значение параметра, соответствующее корню  и показывает, что положительные значения свободного параметра соответствуют нечетным
и показывает, что положительные значения свободного параметра соответствуют нечетным  а отрицательные — четным.
а отрицательные — четным.
Таким образом, положительный годограф состоит из  нечетных траекторий, для которых в основном фазовом уравнении
нечетных траекторий, для которых в основном фазовом уравнении  принимает нечетные целые значения, а отрицательный — из
принимает нечетные целые значения, а отрицательный — из  четных траекторий, вдоль которых
четных траекторий, вдоль которых  четно. Ввиду этого будем далее называть годограф корней при
четно. Ввиду этого будем далее называть годограф корней при  четным (отрицательным), а годограф корней при
четным (отрицательным), а годограф корней при  — нечетным (положительным) годографом системы. На основании этого равенство (XVI 1.22) может быть записано в виде
— нечетным (положительным) годографом системы. На основании этого равенство (XVI 1.22) может быть записано в виде


Рис. XVII.1. Определение точки корневого годографа по основным точкам
Равенство (XVI  так же как формула (XVI 1.21), имеет простой геометрический смысл. Оно показывает, что значение свободного параметра К в любой точке траектории корней
так же как формула (XVI 1.21), имеет простой геометрический смысл. Оно показывает, что значение свободного параметра К в любой точке траектории корней  равно произведению длин
равно произведению длин  векторов, соединяющих все начальные точки с корнем
векторов, соединяющих все начальные точки с корнем  деленному на произведение длин векторов, соединяющих
деленному на произведение длин векторов, соединяющих  предельных точек с этим корнем. Знак К положителен, если
предельных точек с этим корнем. Знак К положителен, если  лежит на нечетной, и отрицателен, если 5 лежит на четной траектории корней. Это графическое пояснение равенства (XVI 1.23) весьма удобно для вычисления значения параметра, соответствующего данной точке траектории. Условимся ниже называть равенство (XVI 1.23) формулой параметра.
лежит на нечетной, и отрицателен, если 5 лежит на четной траектории корней. Это графическое пояснение равенства (XVI 1.23) весьма удобно для вычисления значения параметра, соответствующего данной точке траектории. Условимся ниже называть равенство (XVI 1.23) формулой параметра.
Применение основного фазового уравнения траекторий для разбиения действительной оси плоскости комплексного переменного на траектории корней. Из уравнения (XVII.21) вытекает ряд следствий, имеющих большое значение для построения траекторий корней.
1. Любая точка действительной оси принадлежит геометрическому месту корней. Действительно, любая основная точка дает в точке  лежащей на действительной оси справа от нее, угол равный нулю, а слева — угол
лежащей на действительной оси справа от нее, угол равный нулю, а слева — угол  . Любая же пара комплексно-сопряженных основных точек дает
. Любая же пара комплексно-сопряженных основных точек дает
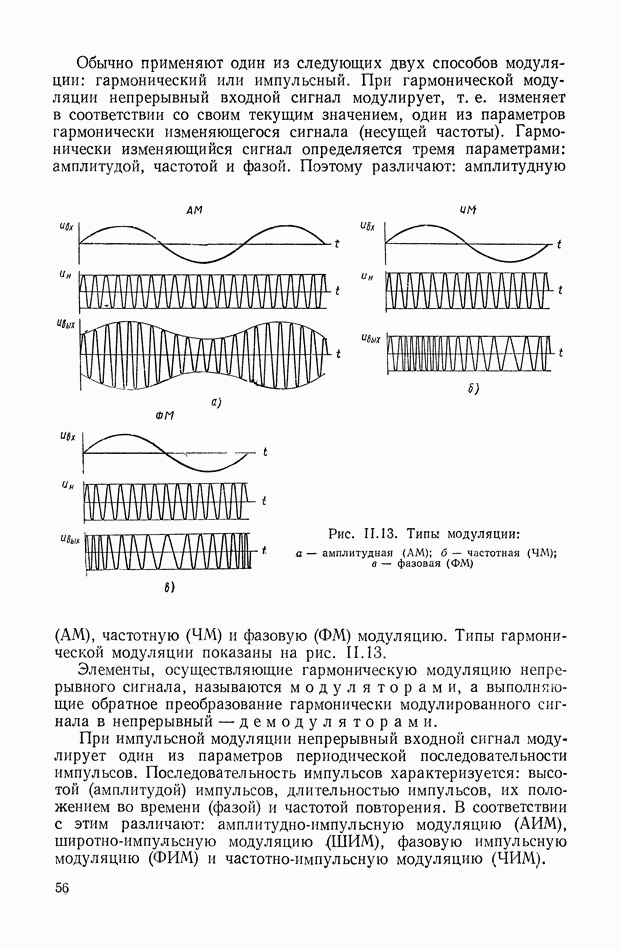
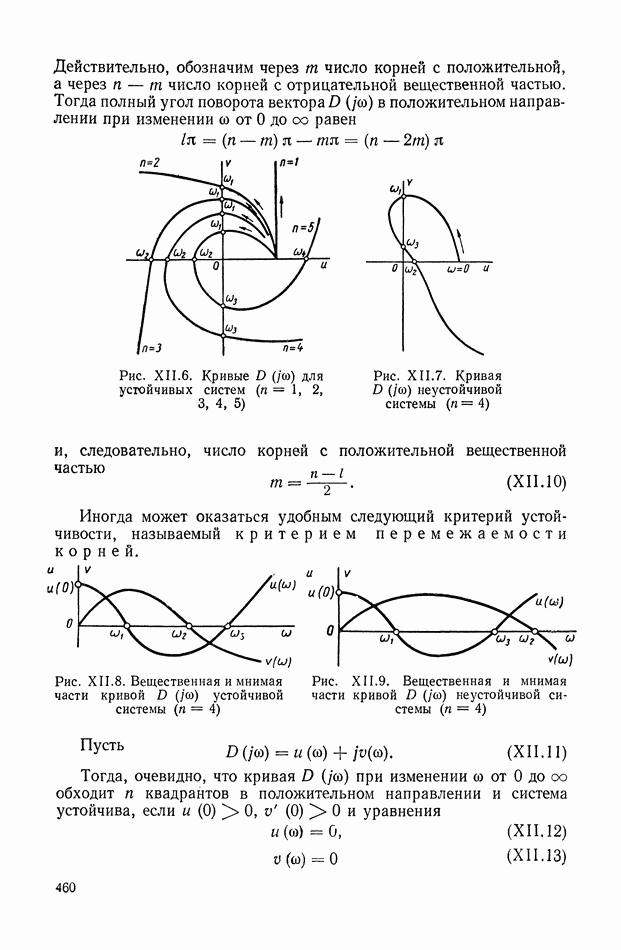
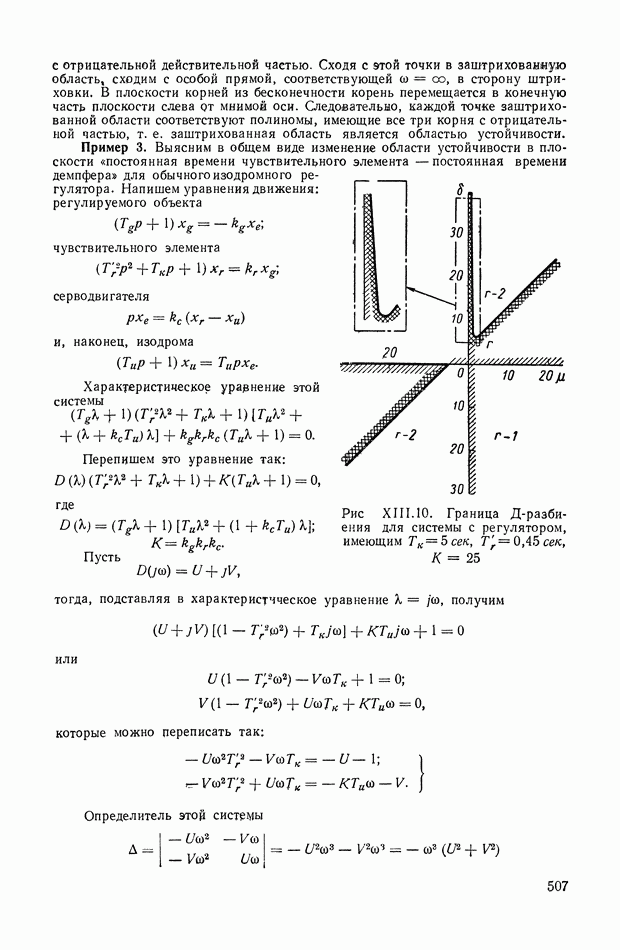
в любой точке  лежащей на действительной оси, сумму углов, равную нулю. Благодаря этому при применении основного фазового уравнения (XVI 1.21) к точкам действительной оси достаточно учитывать только влияние действительных начальных и предельных точек (рис. XVI 1.2). Вправо от первой основной точки кг лежит нулевая траектория; между
лежащей на действительной оси, сумму углов, равную нулю. Благодаря этому при применении основного фазового уравнения (XVI 1.21) к точкам действительной оси достаточно учитывать только влияние действительных начальных и предельных точек (рис. XVI 1.2). Вправо от первой основной точки кг лежит нулевая траектория; между  траектория
траектория  Таким образом, вся действительная ось разбита основными точками на пять траекторий: две четные и три нечетные.
Таким образом, вся действительная ось разбита основными точками на пять траекторий: две четные и три нечетные.
Одинарными стрелками из рис. XVI 1.2 обозначено направление движения корней при К увеличивающемся, а двойными — при К уменьшающемся от нуля. Из рис. XVI 1.2 видно, что при К 0 два корня, двигающихся навстречу друг другу, встречаются в некоторой точке  образуя двукратный корень, из которого при дальнейшем увеличении К возникает пара комплексно-сопряженных корней.
образуя двукратный корень, из которого при дальнейшем увеличении К возникает пара комплексно-сопряженных корней.

Рис. XVII.2. Разбиение действительной оси основными точками на траектории (две четных и три нечетных)
2. Кратными могут быть лишь точки, удовлетворяющие как исходному уравнению (XVII. 10), так и его производной. Исключив из этой системы свободный параметр, мы получим уравнение возможных кратных точек траекторий корней:

Конечно, только те корни уравнения (XVI 1.24) будут кратными точками геометрического места корней, которые лежат на образующих его траекториях. Поэтому кратными будут лишь точки комплексной плоскости, удовлетворяющие одновременно как уравнению (XVI 1.24), так и основному фазовому уравнению траекторий (XVII.21).
Все точки действительной оси лежат на траекториях корней, поэтому все действительные корни уравнения (XVI 1.24) всегда являются кратными точками геометрического места корней.
Поведение траекторий корней вблизи кратных точек. Для выяснения поведения траекторий вблизи кратных основных точек рассмотрим характеристическое уравнение вида

При  это уравнение имеет
это уравнение имеет  -кратную начальную точку в начале координат и не имеет предельных точек. Согласно основному фазовому уравнению (XVI 1.21) траекториями будут прямые, выходящие из этой начальной точки под углами к действительной оси:
-кратную начальную точку в начале координат и не имеет предельных точек. Согласно основному фазовому уравнению (XVI 1.21) траекториями будут прямые, выходящие из этой начальной точки под углами к действительной оси:

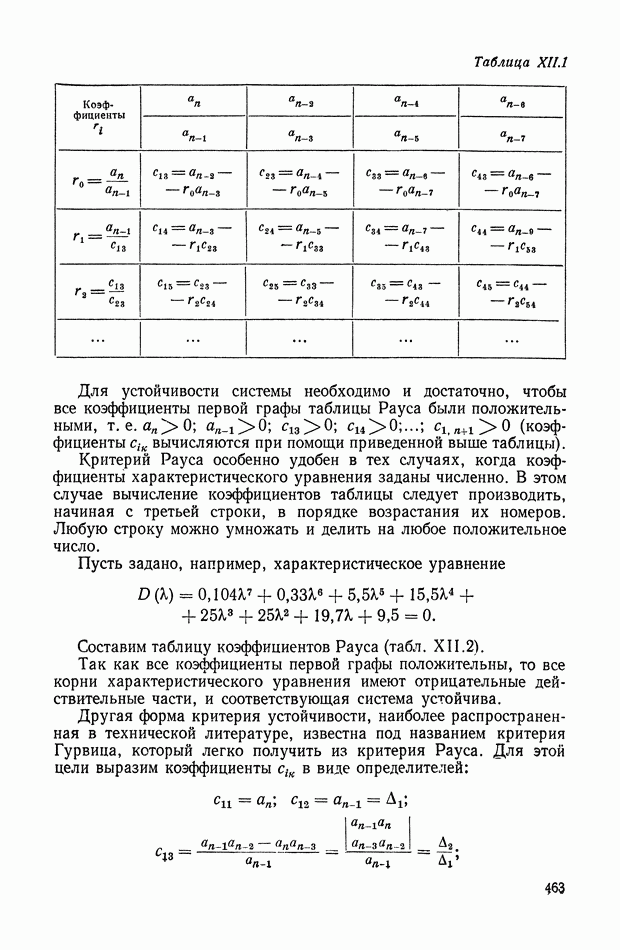
Таким образом, из  -кратиой действительной начальной точки выходят
-кратиой действительной начальной точки выходят  четных и
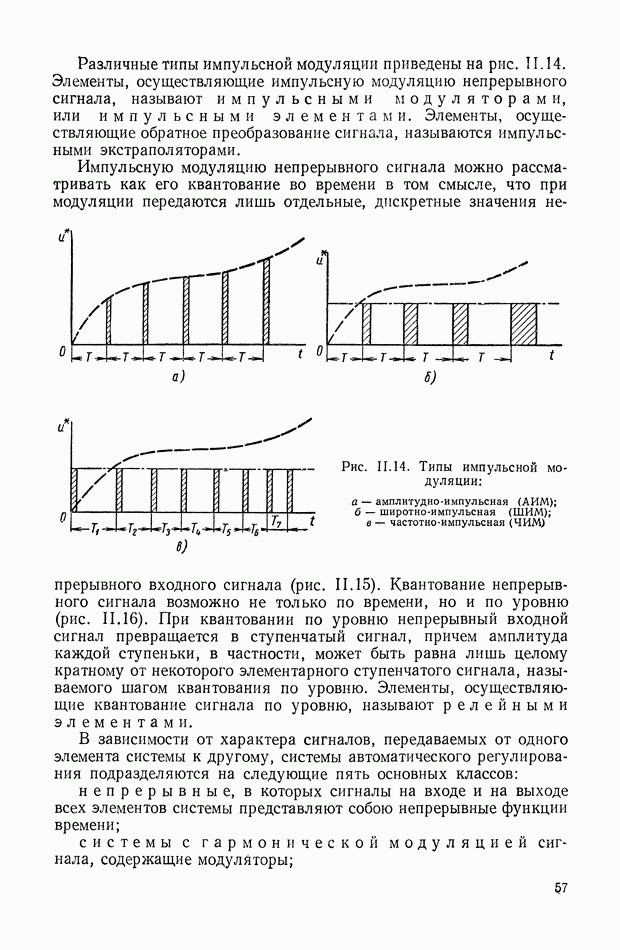
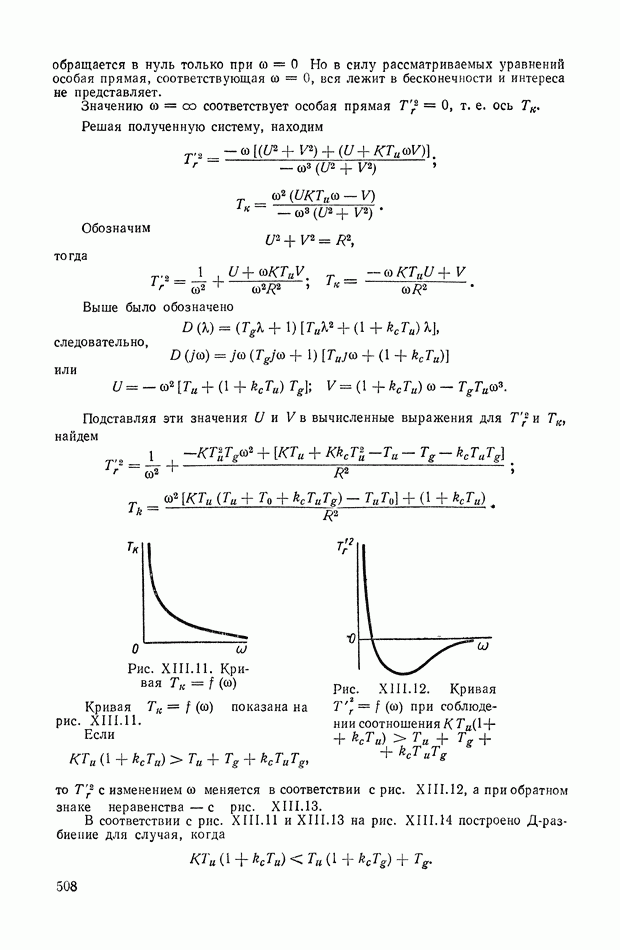
четных и  нечетных чередующихся траекторий, образующих правильную
нечетных чередующихся траекторий, образующих правильную  -лучевую звезду (рис. XVI 1.3). Аналогично ведут себя траектории, входящие в кратную предельную точку. Наличие остальных основных точек приводит к повороту звезды траекторий на угол а, определяемый вытекающими из основного фазового уравнения равенствами: для начальной (х-кратной точки
-лучевую звезду (рис. XVI 1.3). Аналогично ведут себя траектории, входящие в кратную предельную точку. Наличие остальных основных точек приводит к повороту звезды траекторий на угол а, определяемый вытекающими из основного фазового уравнения равенствами: для начальной (х-кратной точки

для предельной  -кратной точки
-кратной точки

где  — целое число.
— целое число.
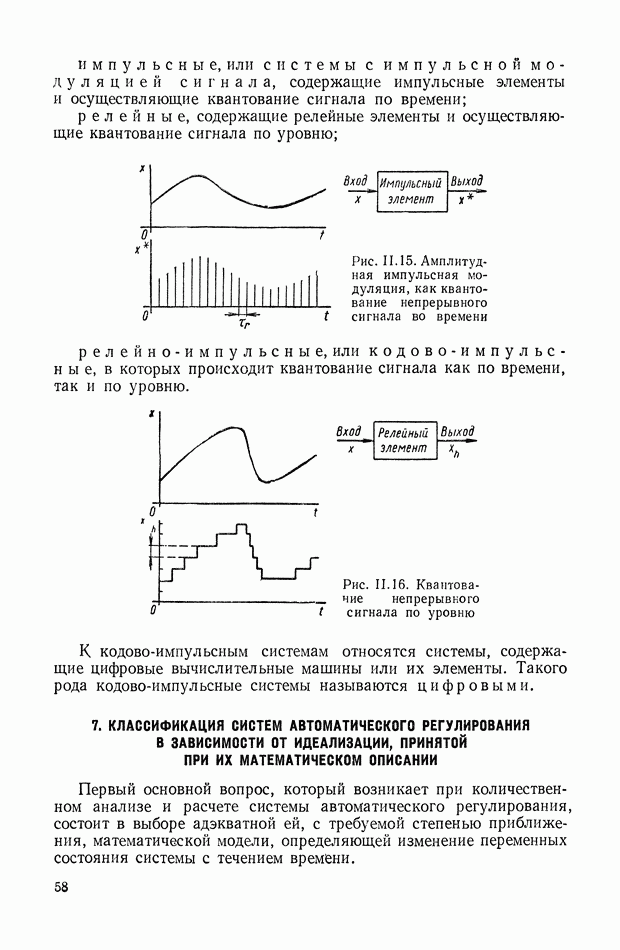
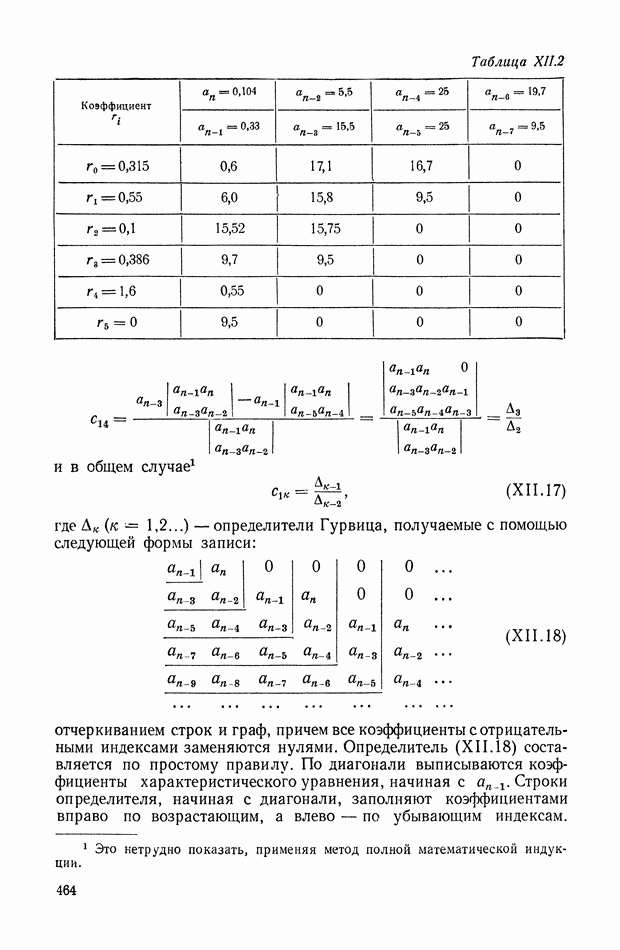
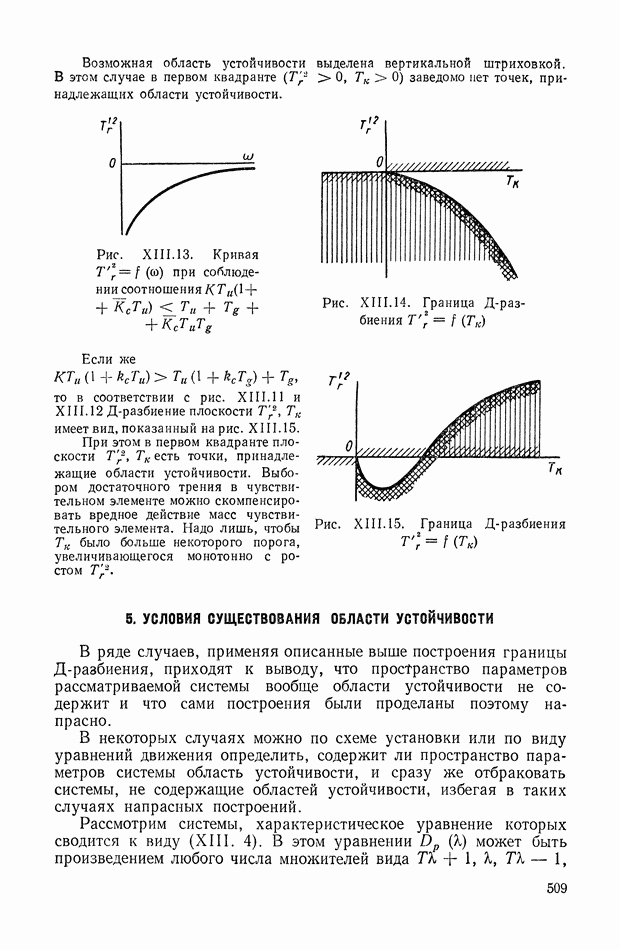
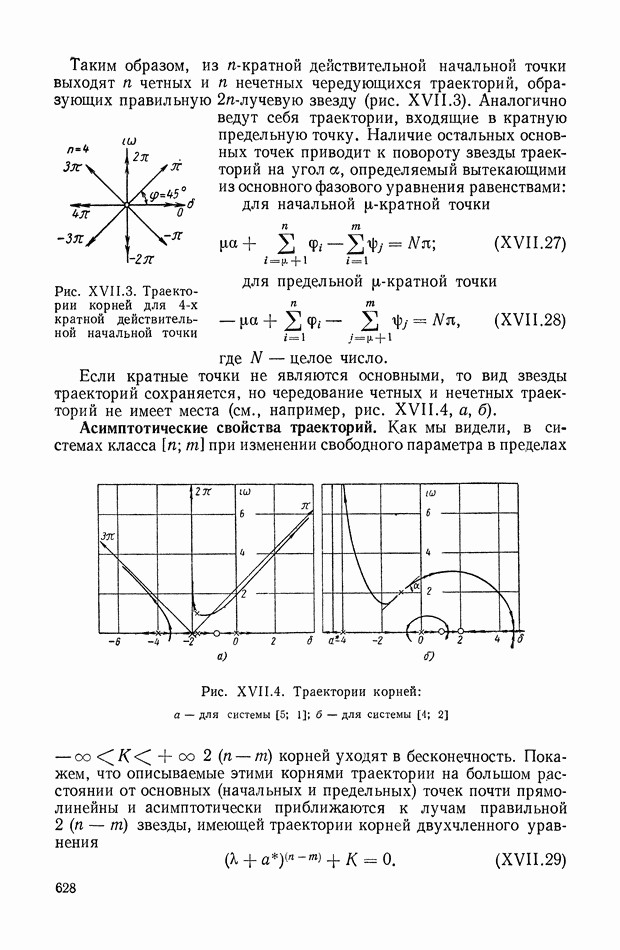
Если кратные точки не являются основными, то вид звезды траекторий сохраняется, но чередование четных и нечетных траекторий не имеет места (см., например, рис. XVI 1.4, а, б).
Асимптотические свойства траекторий. Как мы видели, в системах класса  при изменении свободного параметра в пределах
при изменении свободного параметра в пределах  корней уходят в бесконечность.
корней уходят в бесконечность.

Рис. XVI 1.3. Траектории корней для 4-х кратной действительной начальной точки

Рис. XVII.4. Траектории корней: а — для системы [5; 1]; б — для системы [4; 2]
Покажем, что описываемые этими корнями траектории на большом расстоянии от основных (начальных и предельных) точек почти прямолинейны и асимптотически приближаются к лучам правильной  звезды, имеющей траектории корней двухчленного уравнения
звезды, имеющей траектории корней двухчленного уравнения

Параметр а этого уравнения связан с основными точками системы (XVI 1.10) соотношением

Приведем доказательство этого положения, пользуясь гидродинамической аналогией. При этом любая пара, образованная совпадающими полюсом и нулем, компенсирует друг друга (анигилирует) подобно единичному источнику и стоку. При рассмотрении движения из бесконечности все конечные основные точки представляются совпадающими и эквивалентными  -кратному источнику, расположенному в «центре тяжести» единичных источников и стоков. Такое рассмотрение непосредственно приводит к формуле (XVII.30) и уравнению (XVII.29), имеющему
-кратному источнику, расположенному в «центре тяжести» единичных источников и стоков. Такое рассмотрение непосредственно приводит к формуле (XVII.30) и уравнению (XVII.29), имеющему  прямолинейных траекторий, уходящих в бесконечность.
прямолинейных траекторий, уходящих в бесконечность.
Из сказанного выше имеем следующие асимптотические свойства траекторий корней. При неограниченном увеличении по абсолютной величине свободного параметра уравнения (XVII. 15)  его корней уходят в бесконечность по
его корней уходят в бесконечность по  траекториям, асимптотически приближающимся к лучам звезды, состоящей из
траекториям, асимптотически приближающимся к лучам звезды, состоящей из  чередующихся четных и нечетных прямолинейных асимптот, расходящихся из центра асимптот а, определяемого соотношением (XVI 1.30), под углами
чередующихся четных и нечетных прямолинейных асимптот, расходящихся из центра асимптот а, определяемого соотношением (XVI 1.30), под углами

Если исходное характеристическое уравнение (XVII. 10) задано в развернутом виде

то центр асимптот определяется формулой

Геометрический метод построения траектории корней. Рассмотренные выше свойства траекторий корней позволяют сравнительно просто строить качественную картину геометрического места корней. Пусть нам задано семейство характеристических уравнений, явно содержащих основные точки [уравнение (XVII. 15)].
Последнее условие не налагает существенных ограничений, так как в большинстве случаев исследуемая система состоит из детерминированных типовых звеньев, полюсы и нули которых известны.
Построение геометрического места корней проводим в следующем порядке:
1) начальные  и предельные
и предельные  точки нанесем на плоскости комплексного переменного
точки нанесем на плоскости комплексного переменного  и разобьем действительную ось на четные и нечетные траектории. При этом качественно определяется часть действительных двойных точек и направление выхода и входа в них комплексно-сопряженных траекторий;
и разобьем действительную ось на четные и нечетные траектории. При этом качественно определяется часть действительных двойных точек и направление выхода и входа в них комплексно-сопряженных траекторий;
2) там же нанесем центр асимптот а в соответствии с соотношением (XVI 1.30), через который проведем  асимптот под углами к действительной оси, определяемыми по формуле (XVII.31);
асимптот под углами к действительной оси, определяемыми по формуле (XVII.31);
3) воспользовавшись основным фазовым уравнением (XVI 1.21), определим направления выхода и входа траекторий в простые и кратные основные точки и нанесем эти направления на график геометрического места корней.
Эти данные достаточны для качественного построения геометрического места корней, определяемых характеристическим уравнением невысокого порядка. Уточнить построенные траектории для ряда точек можно с помощью транспортира и линейки.
Для графического построения точек траекторий по основному фазовому уравнению Эвансом [7], [32] разработана специальная линейка. Она позволяет быстро подсчитывать сумму углов  и значение параметра К для произвольной точки комплексной плоскости. Применив ее к точкам пересечения траекторий корней с мнимой осью или для ряда выбранных прямых, параллельных мнимой оси, можно быстро уточнить форму траектории. Эти траектории могут быть также построены аналитическим методом, описанным ниже. После уточнения вида траекторий корней, на основании формулы (XVI 1.23), вычисляем значения свободного параметра К для интересующих нас точек траектории
и значение параметра К для произвольной точки комплексной плоскости. Применив ее к точкам пересечения траекторий корней с мнимой осью или для ряда выбранных прямых, параллельных мнимой оси, можно быстро уточнить форму траектории. Эти траектории могут быть также построены аналитическим методом, описанным ниже. После уточнения вида траекторий корней, на основании формулы (XVI 1.23), вычисляем значения свободного параметра К для интересующих нас точек траектории 
В качестве примера рассмотрим систему класса [5; 1], характеристическое уравнение которой имеет вид

На плоскости  нанесены основные начальные и предельные точки системы (рис. XVI 1.4а). Действительная ось разбивается на три четные (двойные стрелки) и две нечетные (одинарные стрелки) траектории. При этом, примерно, положение двойного корня соответствует
нанесены основные начальные и предельные точки системы (рис. XVI 1.4а). Действительная ось разбивается на три четные (двойные стрелки) и две нечетные (одинарные стрелки) траектории. При этом, примерно, положение двойного корня соответствует  Центр асимптот в соответствии с формулой (XVII.30) помещается на действительной оси в точке
Центр асимптот в соответствии с формулой (XVII.30) помещается на действительной оси в точке  Так как
Так как  то асимптоты соответствуют системе четвертого порядка. Проводим их под углом 45° друг к другу, после чего произведем разметку стрелками четных и нечетных асимптот (рис. XVII.4a).
то асимптоты соответствуют системе четвертого порядка. Проводим их под углом 45° друг к другу, после чего произведем разметку стрелками четных и нечетных асимптот (рис. XVII.4a).
Далее с помощью основного фазового уравнения определяем направление выхода траекторий из пары комплексно-сопряженных точек. Воспользовавшись построенным таким образом скелетом траекторий, качественно проводим комплексно-сопряженные четные и нечетные траектории системы. При этом качественно намечается положение пары комплексно-сопряженных критических частот.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- РАЗДЕЛ I. ОБЩИЕ СВЕДЕНИЯ. МЕТОДЫ МАТЕМАТИЧЕСКОГО ОПИСАНИЯ И СТРУКТУРНОГО ПРЕОБРАЗОВАНИЯ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- ГЛАВА I. ОЧЕРК О РАЗВИТИИ ТЕОРИИ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ В СССР
- 1. ТЕОРИЯ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ В ДОРЕВОЛЮЦИОННЫЙ ПЕРИОД
- 2. РАЗВИТИЕ ТЕОРИИ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ПОСЛЕ ОКТЯБРЬСКОЙ СОЦИАЛИСТИЧЕСКОЙ РЕВОЛЮЦИИ
- ГЛАВА II. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ ТЕОРИИ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. СУЩНОСТЬ ПРОБЛЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- 2. ПРОБЛЕМА РЕГУЛИРОВАНИЯ КАК ЧАСТНЫЙ СЛУЧАЙ ПРОБЛЕМЫ УПРАВЛЕНИЯ
- 3. ОСНОВНОЙ ПРИНЦИП ДЕЙСТВИЯ И ОПРЕДЕЛЕНИЕ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 4. КЛАССИФИКАЦИЯ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ В ЗАВИСИМОСТИ ОТ УПРАВЛЯЮЩЕГО ВОЗДЕЙСТВИЯ
- 5. ОСНОВНЫЕ УСТРОЙСТВА СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ И ИХ КЛАССИФИКАЦИЯ ПО НАЗНАЧЕНИЮ
- 6. КЛАССИФИКАЦИЯ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ В ЗАВИСИМОСТИ ОТ ХАРАКТЕРА СИГНАЛОВ
- 7. КЛАССИФИКАЦИЯ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ В ЗАВИСИМОСТИ ОТ ИДЕАЛИЗАЦИИ, ПРИНЯТОЙ ПРИ ИХ МАТЕМАТИЧЕСКОМ ОПИСАНИИ
- 8. СТРУКТУРНЫЕ СХЕМЫ, ОДНОКОНТУРНЫЕ И МНОГОКОНТУРНЫЕ, НЕСВЯЗАННЫЕ И СВЯЗАННЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 9. КЛАССИФИКАЦИЯ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ В ЗАВИСИМОСТИ ОТ ХАРАКТЕРА КОНТРОЛИРУЕМЫХ ИЗМЕНЕНИЙ
- 10. ТРЕБОВАНИЯ, ПРЕДЪЯВЛЯЕМЫЕ К ДИНАМИЧЕСКИМ СВОЙСТВАМ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- ГЛАВА III. ОСНОВНЫЕ УСТРОЙСТВА И ТИПОВЫЕ СХЕМЫ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. КРАТКАЯ ХАРАКТЕРИСТИКА УСТРОЙСТВ, ИЗ КОТОРЫХ СОСТОЯТ СИСТЕМЫ РЕГУЛИРОВАНИЯ
- 2. СИСТЕМА АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ СКОРОСТИ ГИДРОТУРБИНЫ
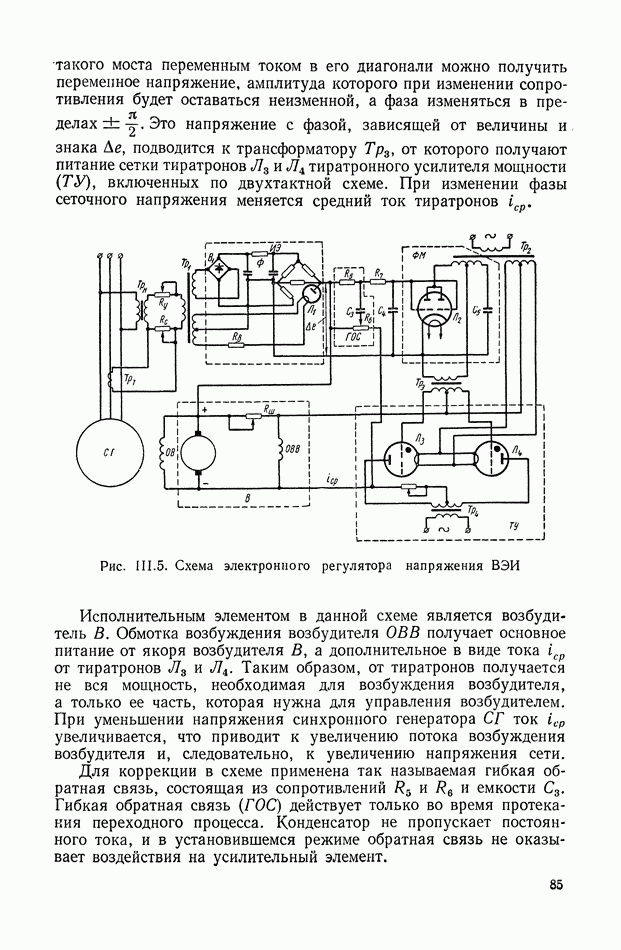
- 3. ЭЛЕКТРОННЫЙ РЕГУЛЯТОР НАПРЯЖЕНИЯ ВЭИ
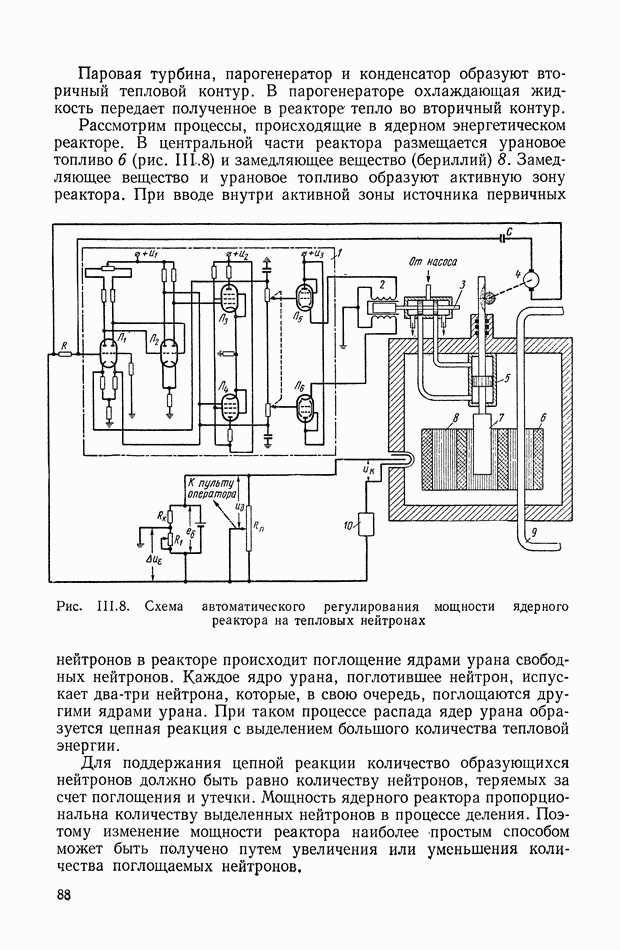
- 4. СИСТЕМА АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ЯДЕРНОГО РЕАКТОРА ПО МОЩНОСТИ
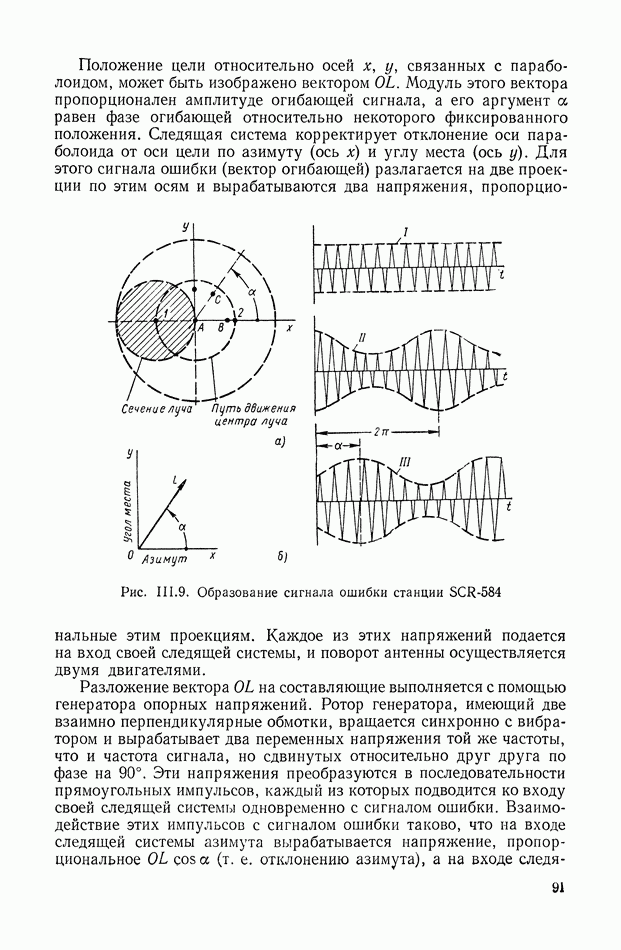
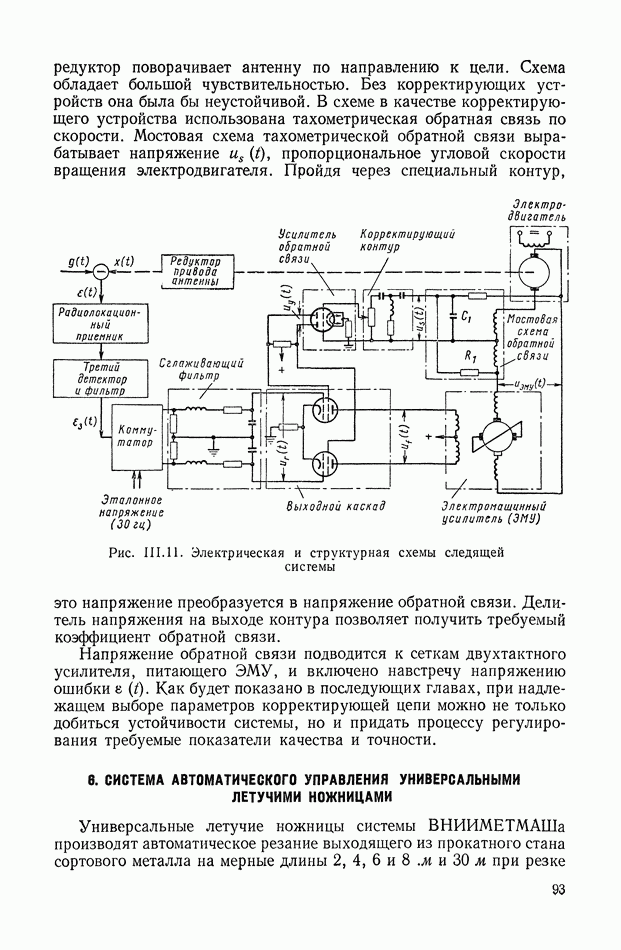
- 5. СЛЕДЯЩАЯ СИСТЕМА РАДИОЛОКАЦИОННОЙ СТАНЦИИ
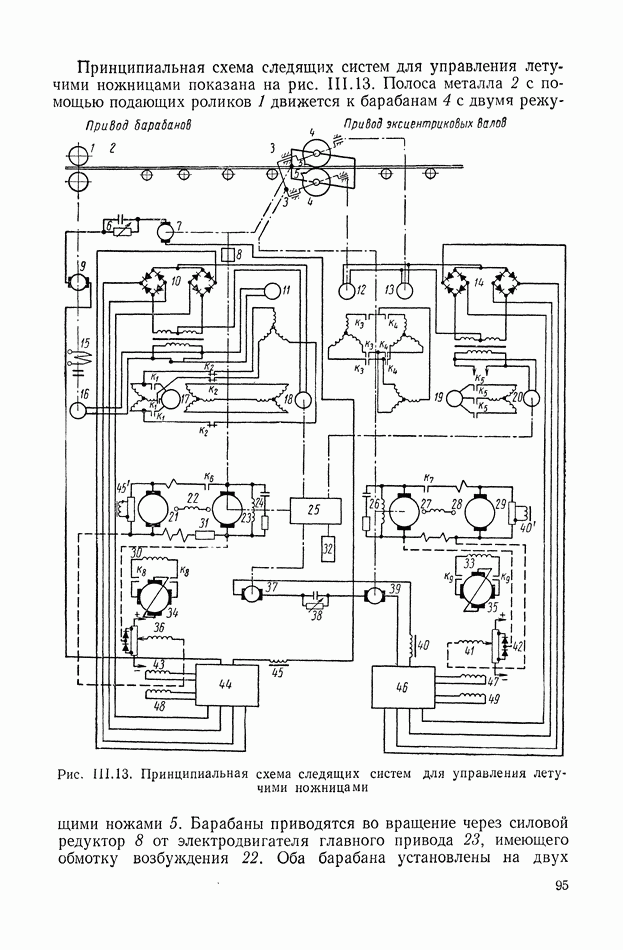
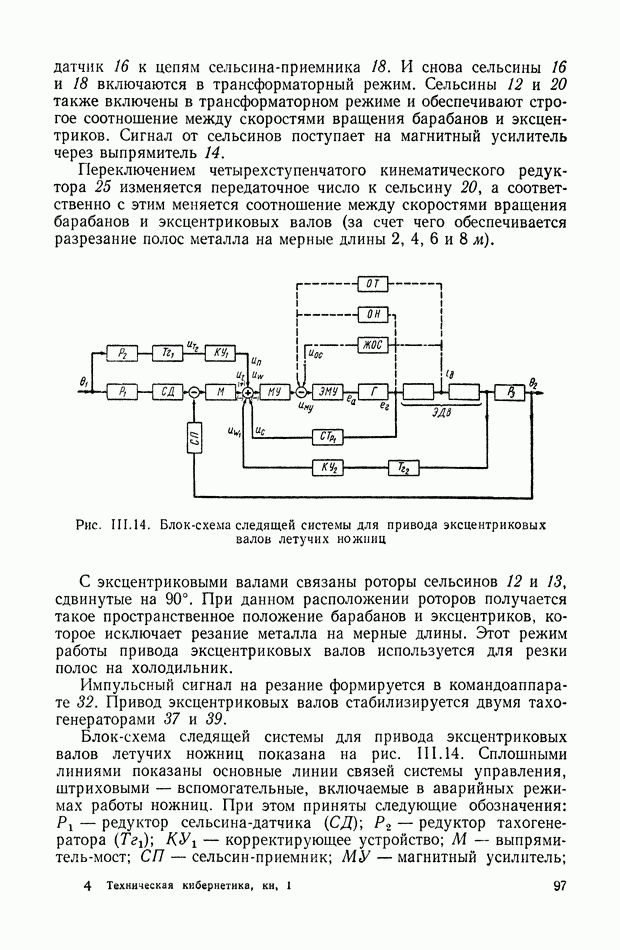
- 6. СИСТЕМА АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ УНИВЕРСАЛЬНЫМИ ЛЕТУЧИМИ НОЖНИЦАМИ
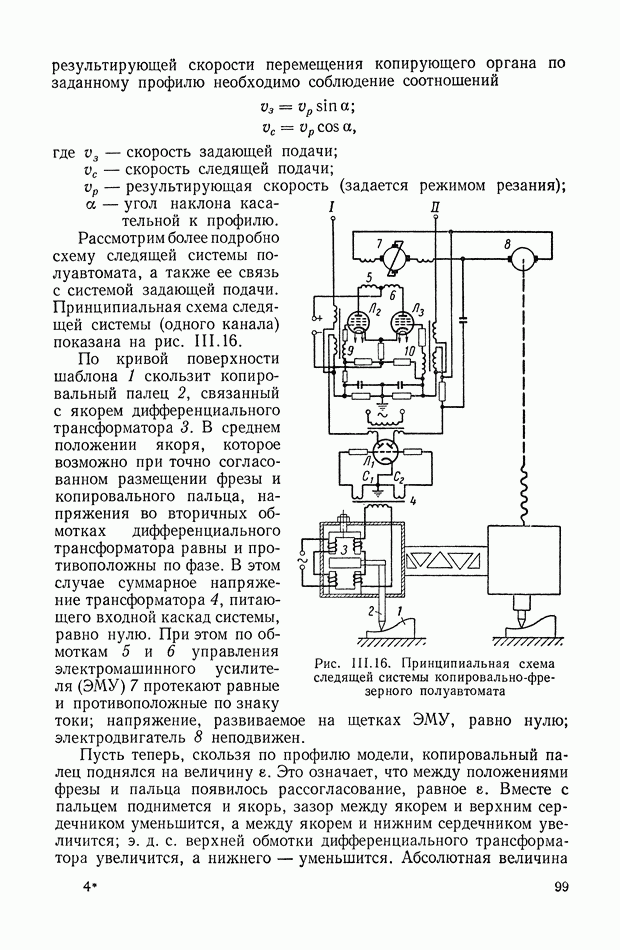
- 7. СЛЕДЯЩАЯ СИСТЕМА КОПИРОВАЛЬНО-ФРЕЗЕРНОГО ПОЛУАВТОМАТА
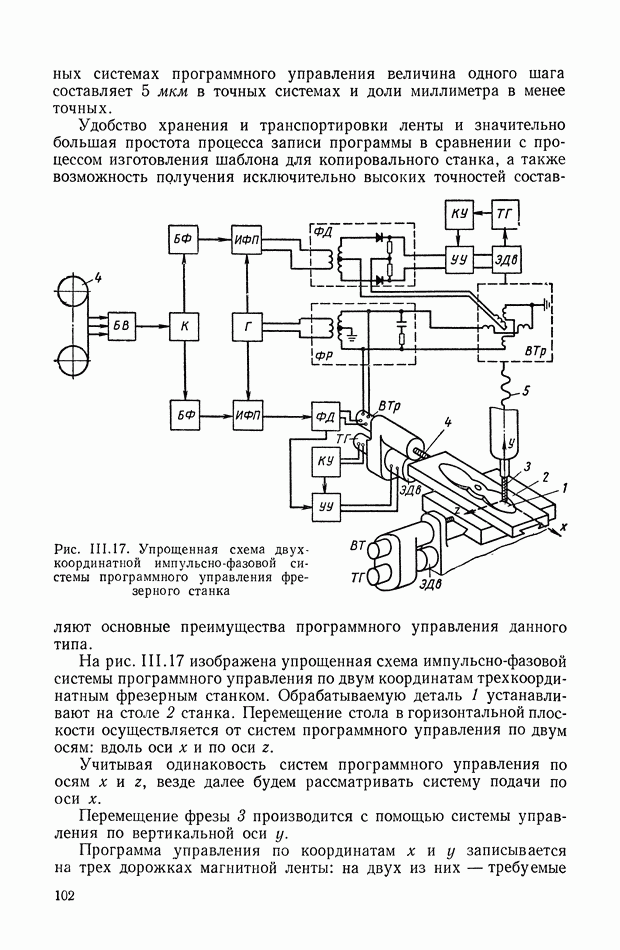
- 8. ПРОГРАММНОЕ УПРАВЛЕНИЕ МЕТАЛЛОРЕЖУЩИМИ СТАНКАМИ
- 9. ПРИНЦИП ДЕЙСТВИЯ ЭЛЕКТРИЧЕСКОГО АВТОПИЛОТА
- 10. РЕГУЛИРОВАНИЕ МНОГИХ ВЕЛИЧИН ПРИ АВТОМАТИЧЕСКОМ УПРАВЛЕНИИ ПЕРЕГОНКОЙ НЕФТИ
- 11. СИСТЕМА АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ РЕВЕРСИВНЫМ ПРОКАТНЫМ СТАНОМ С ИСПОЛЬЗОВАНИЕМ ЦИФРОВОЙ ВЫЧИСЛИТЕЛЬНОЙ МАШИНЫ
- ГЛАВА IV. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ЛАГРАНЖА ВТОРОГО РОДА
- 2. ОБЩИЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 3. ОБЩИЕ ЛИНЕАРИЗОВАННЫЕ УРАВНЕНИЯ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 4. ПРИМЕР СОСТАВЛЕНИЯ УРАВНЕНИЯ ОБЪЕКТА РЕГУЛИРОВАНИЯ
- ГЛАВА V. СТАТИКА СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. СТАТИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПРОСТЕЙШИХ ЗВЕНЬЕВ
- 2. СТАТИЧЕСКИЕ ХАРАКТЕРИСТИКИ ОСНОВНЫХ ТИПОВ СОЕДИНЕНИЙ ЗВЕНЬЕВ
- 3. КОРРЕКЦИЯ СТАТИЧЕСКИХ ХАРАКТЕРИСТИК
- Статическая характеристика замкнутой одномерной системы регулирования.
- Статическая характеристика линейной замкнутой системы.
- 4. СТАТИЗМ РЕГУЛИРОВАНИЯ
- 5. СТАТИКА ЛИНЕЙНЫХ СИСТЕМ С НЕСКОЛЬКИМИ РЕГУЛИРУЕМЫМИ ВЕЛИЧИНАМИ
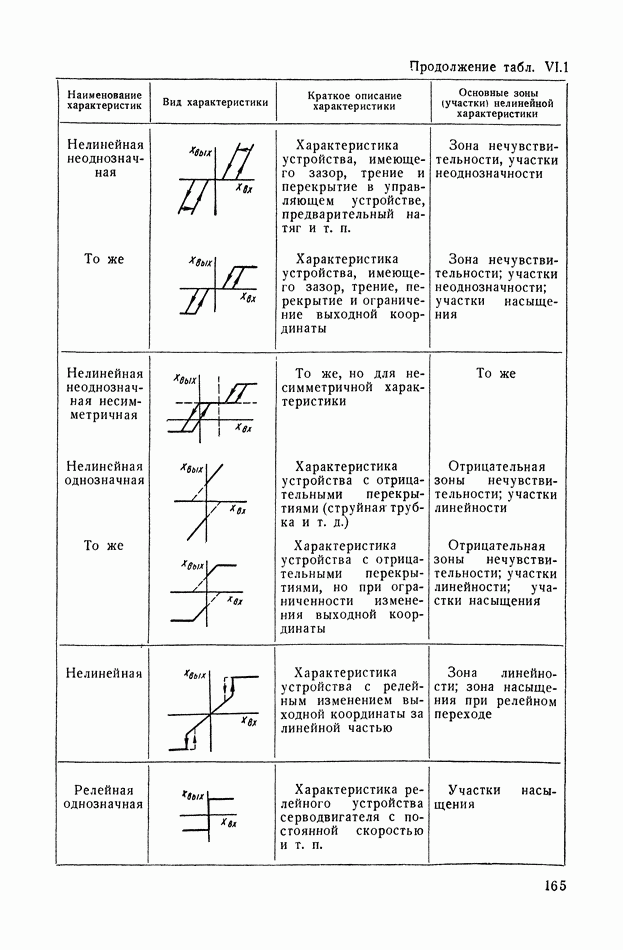
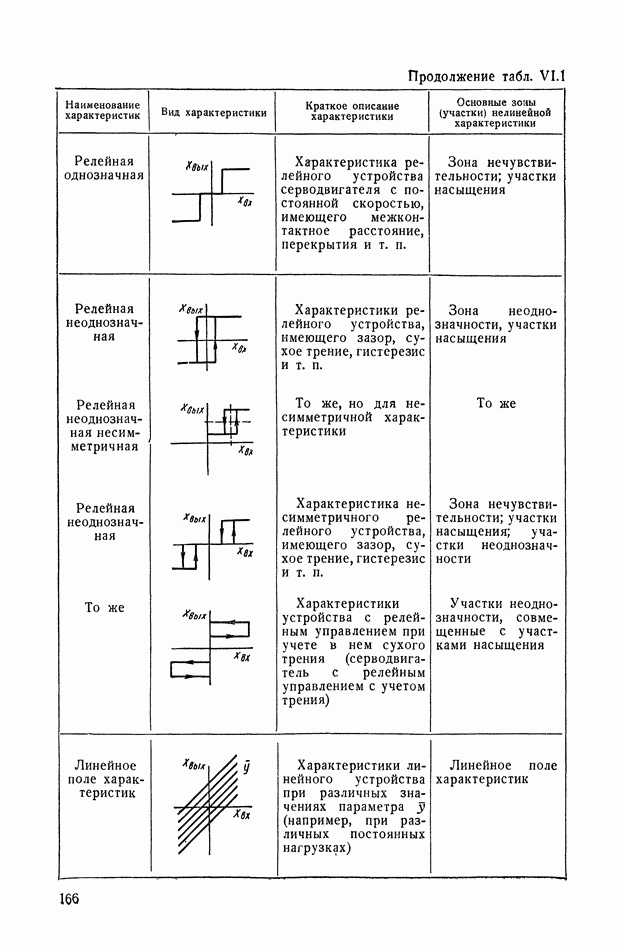
- ГЛАВА VI. ТИПИЧНЫЕ НЕЛИНЕЙНЫЕ СТАТИЧЕСКИЕ ХАРАКТЕРИСТИКИ ТИПОВЫХ ЗВЕНЬЕВ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. НЕЛИНЕЙНЫЕ ХАРАКТЕРИСТИКИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 2. ВИДЫ ТИПИЧНЫХ НЕЛИНЕЙНЫХ СТАТИЧЕСКИХ ХАРАКТЕРИСТИК СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 3. ТИПИЧНЫЕ НЕЛИНЕЙНЫЕ ХАРАКТЕРИСТИКИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 4. ЗОНЫ НЕЧУВСТВИТЕЛЬНОСТИ
- 5. ЗОНЫ ЛИНЕЙНОСТИ И НЕОДНОЗНАЧНОСТИ
- 6. ЗОНЫ НАСЫЩЕНИЯ
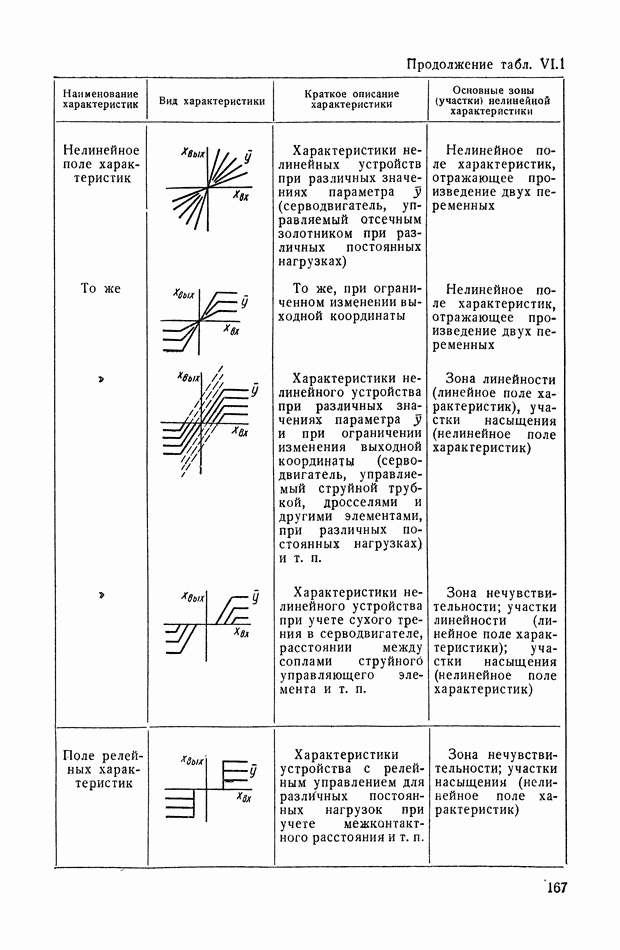
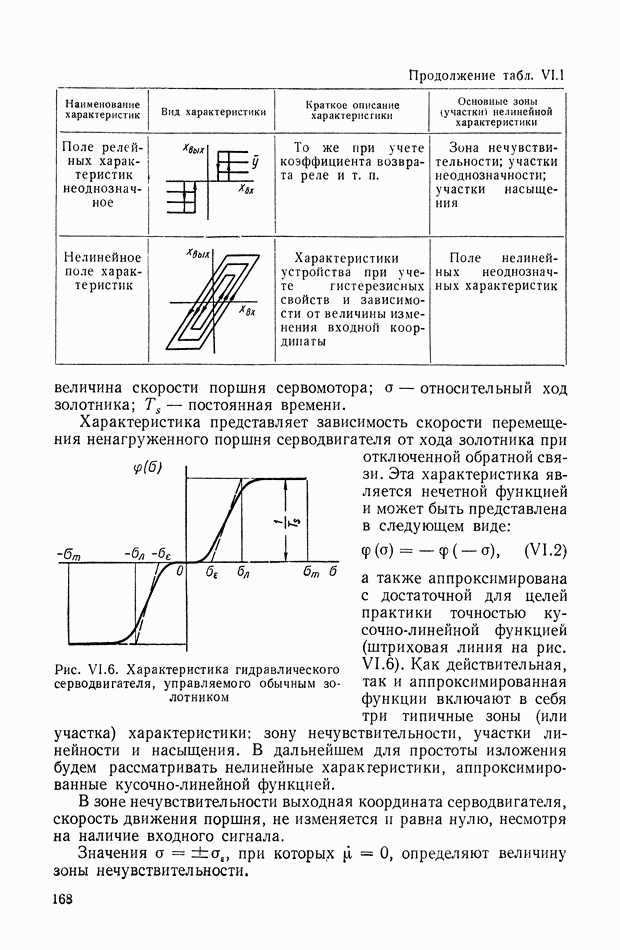
- 7. ПОЛЕ КРИВЫХ, ПРЕДСТАВЛЯЮЩИХ ХАРАКТЕРИСТИКУ СЕРВОДВИГАТЕЛЯ
- 8. ЭКСПЕРИМЕНТАЛЬНОЕ ВЫЯВЛЕНИЕ НЕЛИНЕЙНОСТИ ХАРАКТЕРИСТИК СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- ГЛАВА VII. ПЕРЕХОДНЫЕ ФУНКЦИИ, ПЕРЕДАТОЧНЫЕ ФУНКЦИИ И ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ДИНАМИЧЕСКИХ ЭЛЕМЕНТОВ
- 1. КЛАССИФИКАЦИЯ ДИНАМИЧЕСКИХ ЭЛЕМЕНТОВ
- 2. ОБЩЕЕ ОПРЕДЕЛЕНИЕ ИМПУЛЬСНОЙ ПЕРЕХОДНОЙ И ПЕРЕДАТОЧНОЙ ФУНКЦИЙ ДИНАМИЧЕСКОЙ СИСТЕМЫ ИЛИ ДИНАМИЧЕСКОГО ЭЛЕМЕНТА
- 3. ИМПУЛЬСНАЯ ПЕРЕХОДНАЯ ФУНКЦИЯ НЕПРЕРЫВНОЙ СТАЦИОНАРНОЙ ЛИНЕЙНОЙ СИСТЕМЫ
- 4. ПЕРЕДАТОЧНАЯ ФУНКЦИЯ НЕПРЕРЫВНОЙ ЛИНЕЙНОЙ СТАЦИОНАРНОЙ СИСТЕМЫ
- 5. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЛИНЕЙНОЙ СТАЦИОНАРНОЙ НЕПРЕРЫВНОЙ ДИНАМИЧЕСКОЙ СИСТЕМЫ
- 6. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДИНАМИЧЕСКОГО ЭЛЕМЕНТА С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
- 7. ПРИМЕНЕНИЕ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА К РЕШЕНИЮ УРАВНЕНИЙ ЭЛЕМЕНТА С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
- 8. ПЕРЕДАТОЧНАЯ ФУНКЦИЯ ДИНАМИЧЕСКОГО ЭЛЕМЕНТА С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
- 9. ПЕРЕДАТОЧНАЯ ФУНКЦИЯ ПОСЛЕДОВАТЕЛЬНОГО СОЕДИНЕНИЯ ДИНАМИЧЕСКИХ ЭЛЕМЕНТОВ С СОСРЕДОТОЧЕННЫМИ И С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
- 10. ПЕРЕДАТОЧНАЯ ФУНКЦИЯ ЗАПАЗДЫВАЮЩЕГО ЭЛЕМЕНТА
- 11. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЭЛЕМЕНТА С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
- 12. ИМПУЛЬСНАЯ ПЕРЕХОДНАЯ ФУНКЦИЯ ДИНАМИЧЕСКОГО ЭЛЕМЕНТА С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
- 13. ПЕРЕДАТОЧНАЯ ФУНКЦИЯ СИСТЕМЫ С ГАРМОНИЧЕСКОЙ МОДУЛЯЦИЕЙ
- 14 ИМПУЛЬСНАЯ ПЕРЕХОДНАЯ И ПЕРЕДАТОЧНАЯ ФУНКЦИИ ДИСКРЕТНОЙ ЛИНЕЙНОЙ СТАЦИОНАРНОЙ СИСТЕМЫ
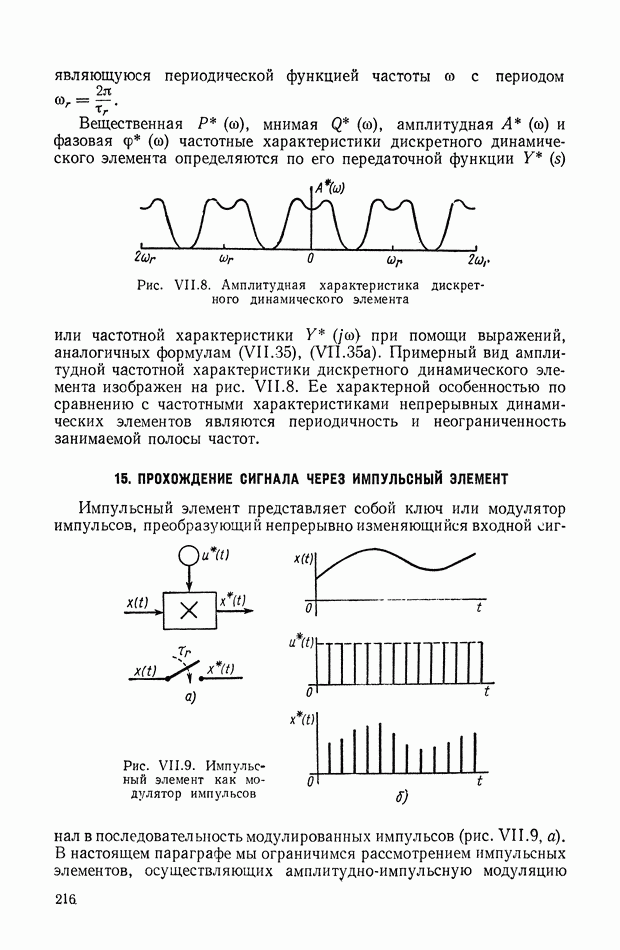
- 15. ПРОХОЖДЕНИЕ СИГНАЛА ЧЕРЕЗ ИМПУЛЬСНЫЙ ЭЛЕМЕНТ
- 16. ПОСЛЕДОВАТЕЛЬНОЕ СОЕДИНЕНИЕ ИМПУЛЬСНОГО ЭЛЕМЕНТА И НЕПРЕРЫВНОГО ДИНАМИЧЕСКОГО ЭЛЕМЕНТА
- 17. ИМПУЛЬСНАЯ ПЕРЕХОДНАЯ ФУНКЦИЯ ЛИНЕЙНОЙ НЕСТАЦИОНАРНОЙ СИСТЕМЫ (СИСТЕМЫ С ПЕРЕМЕННЫМИ ПАРАМЕТРАМИ)
- 18. ПЕРЕДАТОЧНАЯ ФУНКЦИЯ НЕПРЕРЫВНОЙ ЛИНЕЙНОЙ НЕСТАЦИОНАРНОЙ СИСТЕМЫ
- 19. МНОГОМЕРНЫЕ ИМПУЛЬСНЫЕ ПЕРЕХОДНЫЕ И ПЕРЕДАТОЧНЫЕ ФУНКЦИИ НЕЛИНЕЙНЫХ СИСТЕМ
- 20. МНОГОМЕРНЫЕ ПЕРЕДАТОЧНЫЕ ФУНКЦИИ НЕЛИНЕЙНЫХ СИСТЕМ
- ГЛАВА VIII. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ, ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ И ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ НЕПРЕРЫВНЫХ ЛИНЕЙНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
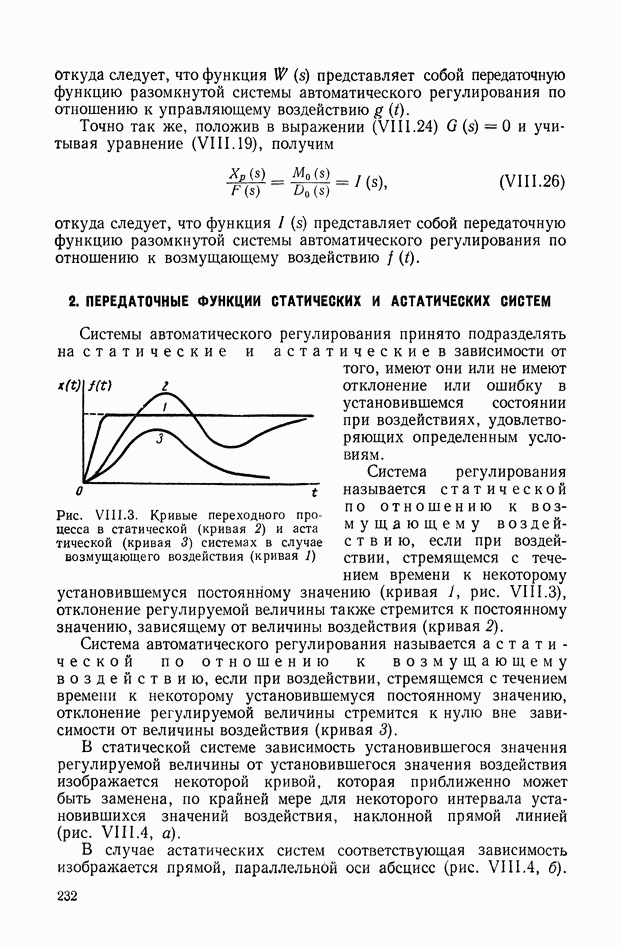
- 2. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ СТАТИЧЕСКИХ И АСТАТИЧЕСКИХ СИСТЕМ
- 3. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ
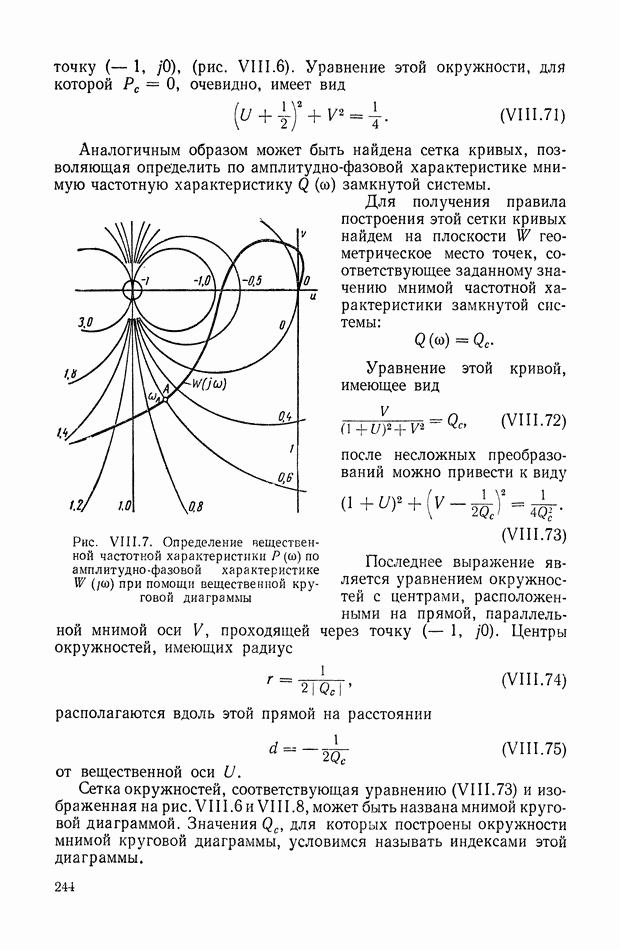
- 4. ВЗАИМНАЯ СВЯЗЬ МЕЖДУ ЧАСТОТНЫМИ ХАРАКТЕРИСТИКАМИ ЗАМКНУТОЙ И РАЗОМКНУТОЙ СИСТЕМЫ
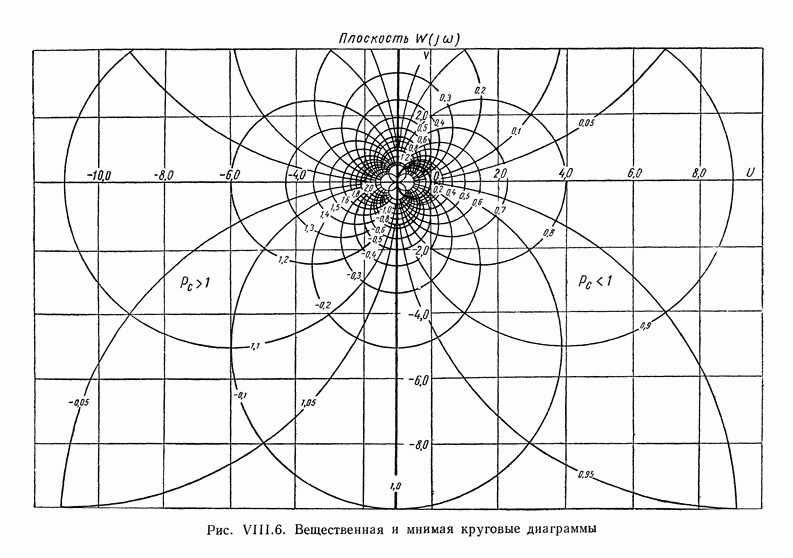
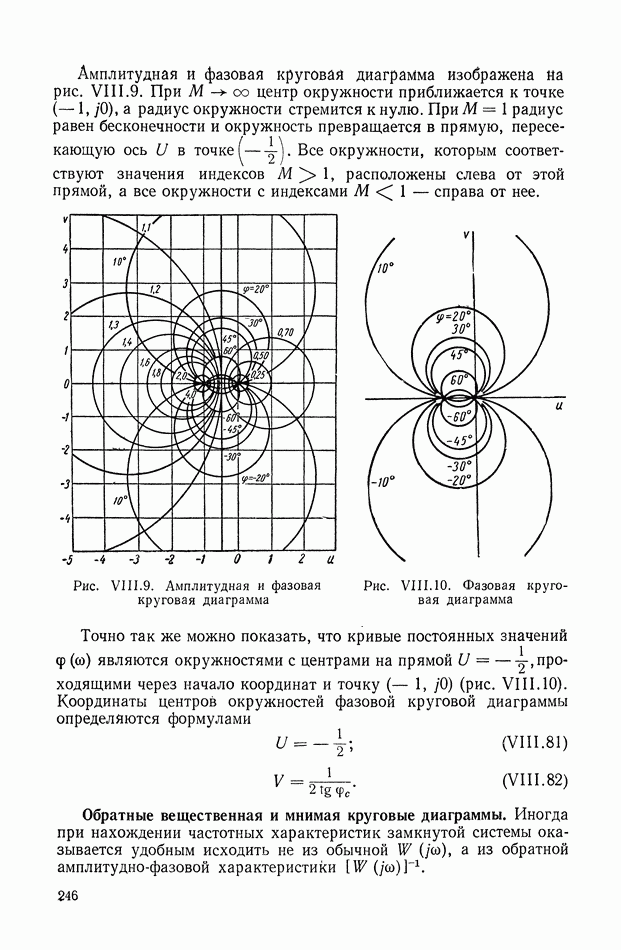
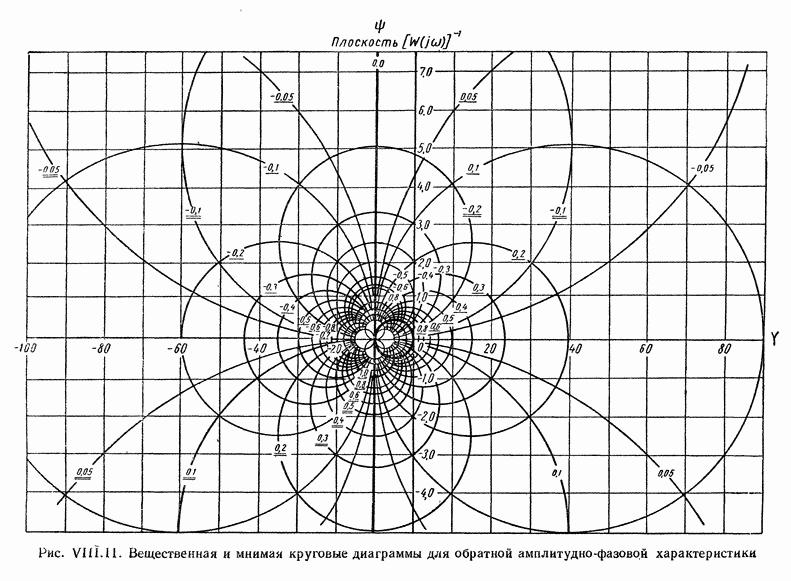
- 5. КРУГОВЫЕ ДИАГРАММЫ
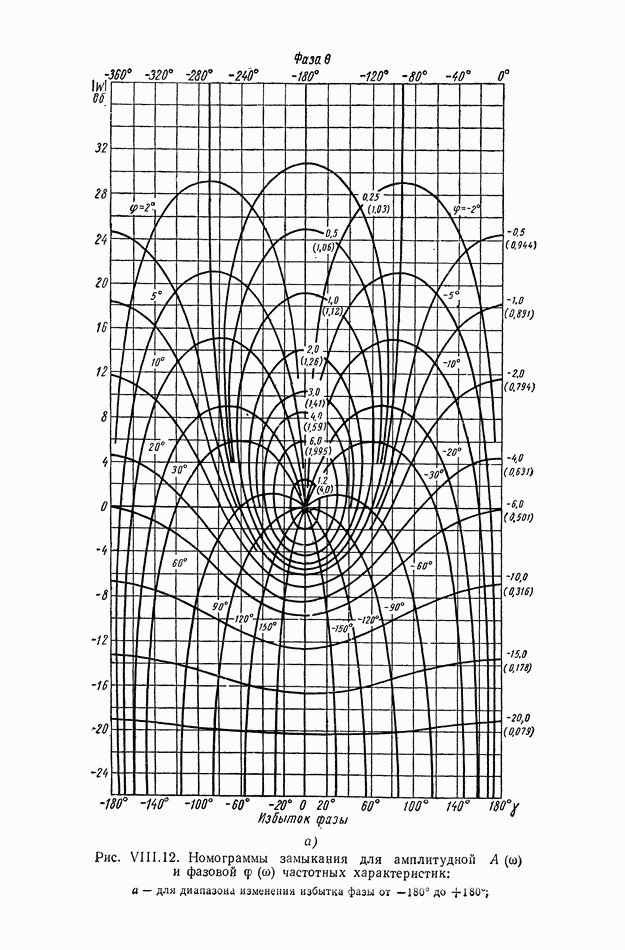
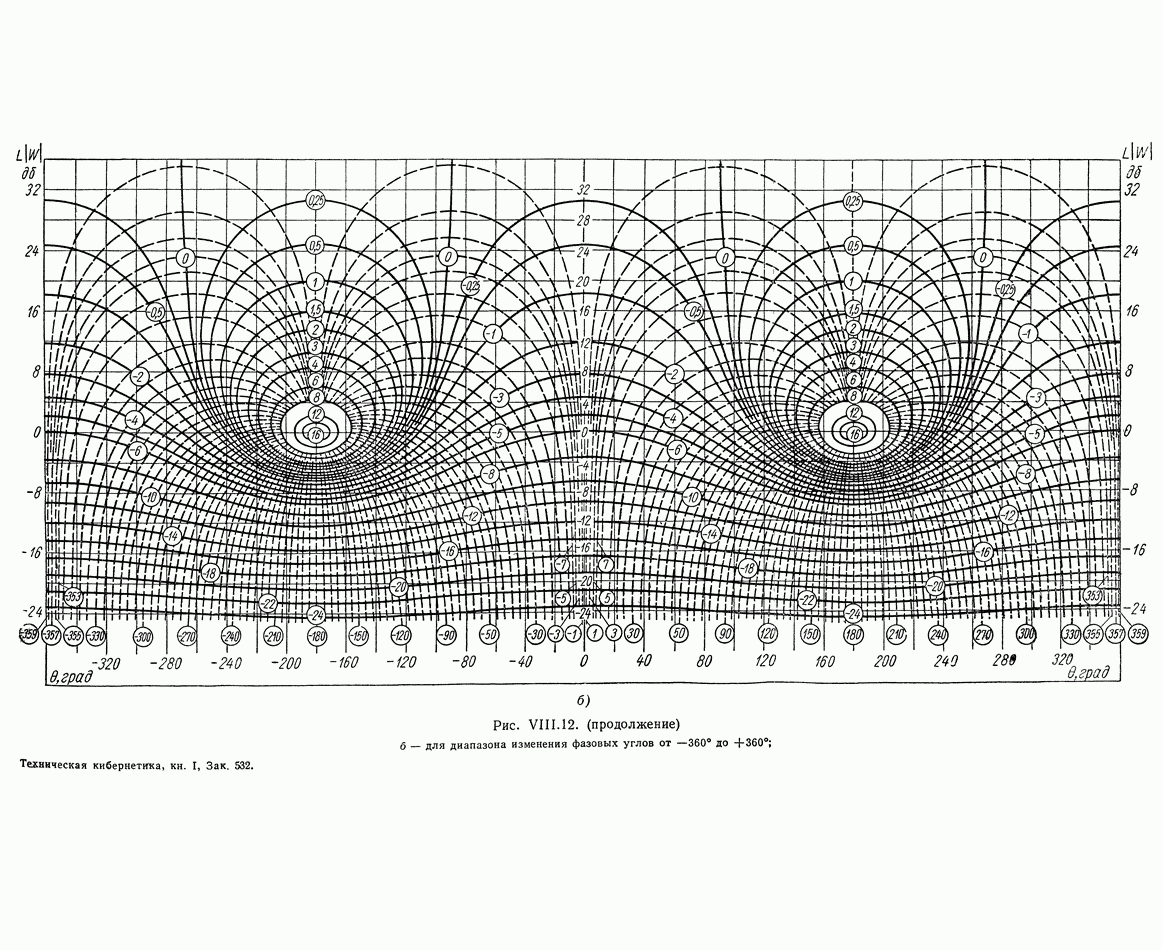
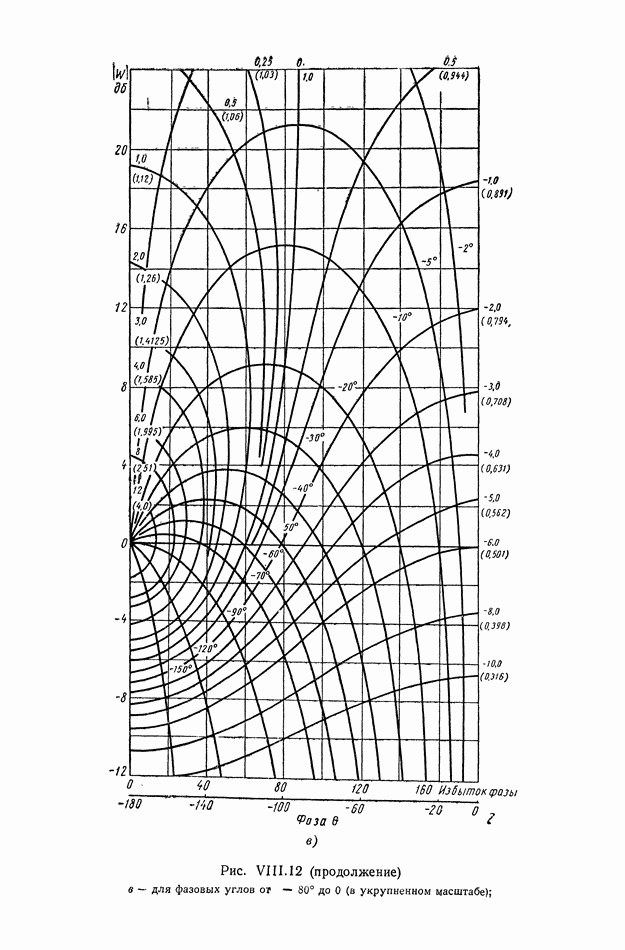
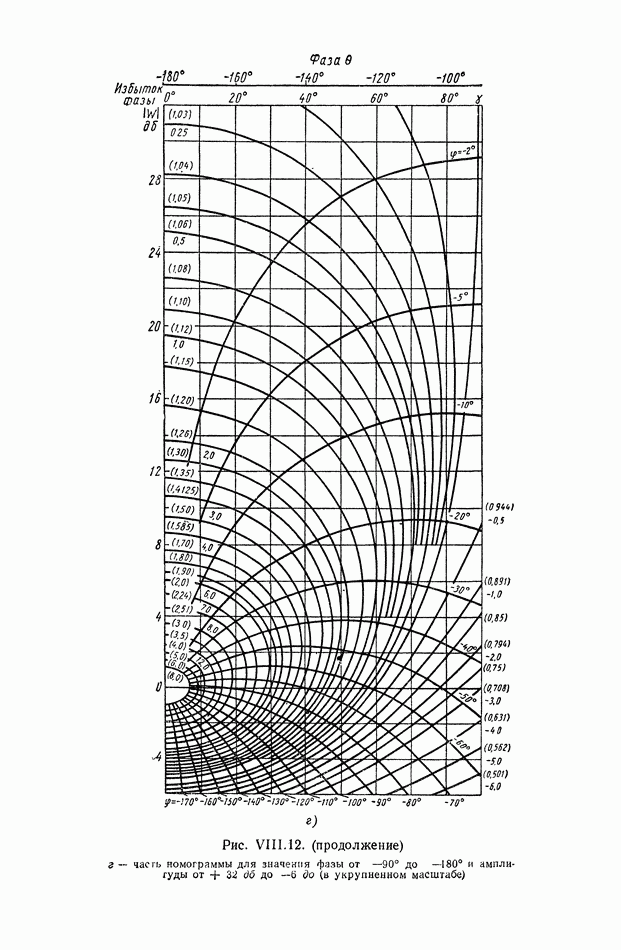
- 6. НОМОГРАММЫ ЗАМЫКАНИЯ
- 7. УСЛОВИЯ ОДНОЗНАЧНОЙ связи МЕЖДУ ЧАСТОТНЫМИ ХАРАКТЕРИСТИКАМИ
- 8. ОПРЕДЕЛЕНИЕ ПЕРЕДАТОЧНОЙ ФУНКЦИИ ПО ОДНОЙ ИЗ ЧАСТОТНЫХ ХАРАКТЕРИСТИК, ЗАДАННОЙ АНАЛИТИЧЕСКИ
- 9. ФОРМУЛА ДЛЯ ВЫЧИСЛЕНИЯ ФАЗОВОЙ ЧАСТОТНОЙ ХАРАКТЕРИСТИКИ ПО ЗАДАННОЙ АМПЛИТУДНОЙ ЧАСТОТНОЙ ХАРАКТЕРИСТИКЕ
- 10. ЗАВИСИМОСТЬ МЕЖДУ ЛОГАРИФМИЧЕСКОЙ АМПЛИТУДНОЙ И ФАЗОВОЙ ЧАСТОТНЫМИ ХАРАКТЕРИСТИКАМИ
- 11. ГРАФИЧЕСКИЙ МЕТОД ОПРЕДЕЛЕНИЯ ФАЗОВОЙ ХАРАКТЕРИСТИКИ ПО ЗАДАННОЙ АМПЛИТУДНОЙ ХАРАКТЕРИСТИКЕ
- 12. ИНТЕГРАЛЬНЫЕ ВЫРАЖЕНИЯ ДЛЯ ОШИБКИ И ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 13. ТИПОВЫЕ ЗВЕНЬЯ
- 14. АПЕРИОДИЧЕСКОЕ ЗВЕНО
- 15. КОЛЕБАТЕЛЬНОЕ ЗВЕНО
- 16. ИНТЕГРИРУЮЩЕЕ ЗВЕНО
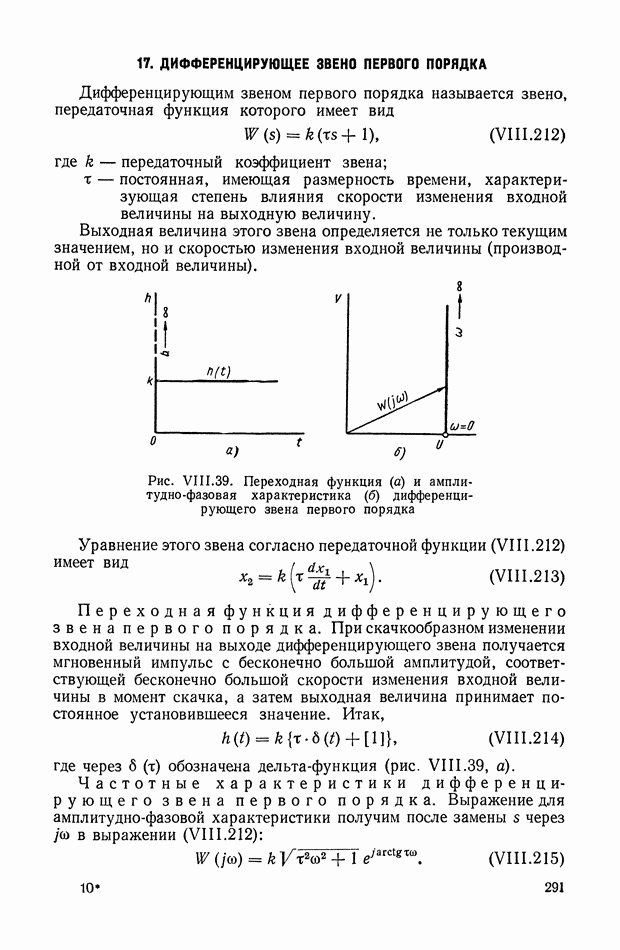
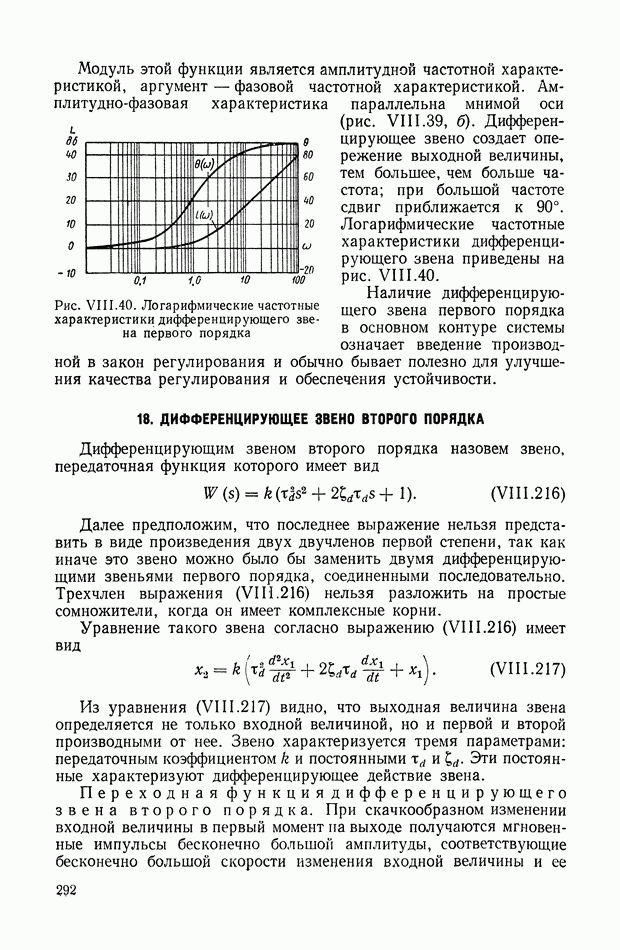
- 17. ДИФФЕРЕНЦИРУЮЩЕЕ ЗВЕНО ПЕРВОГО ПОРЯДКА
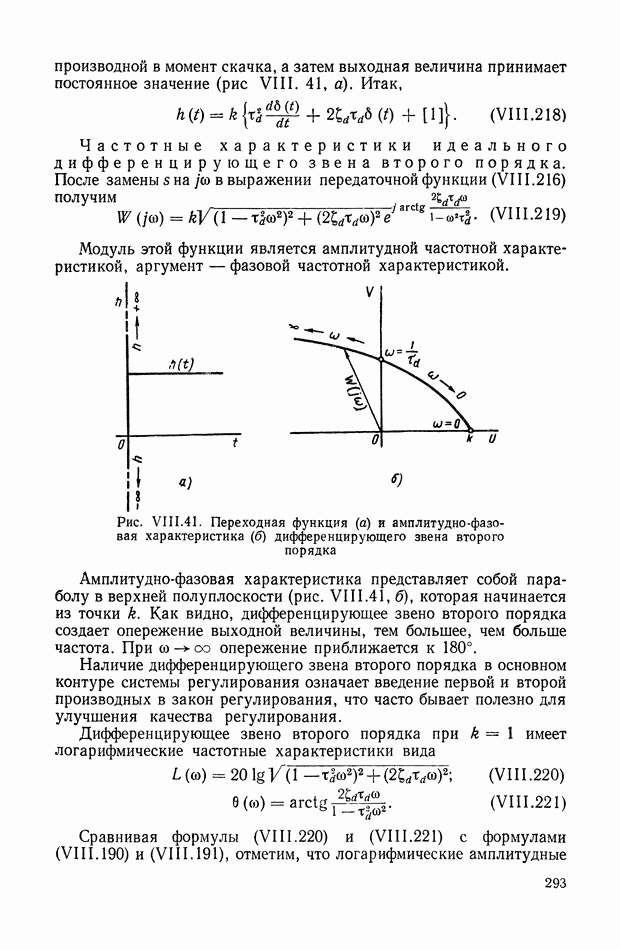
- 18. ДИФФЕРЕНЦИРУЮЩЕЕ ЗВЕНО ВТОРОГО ПОРЯДКА
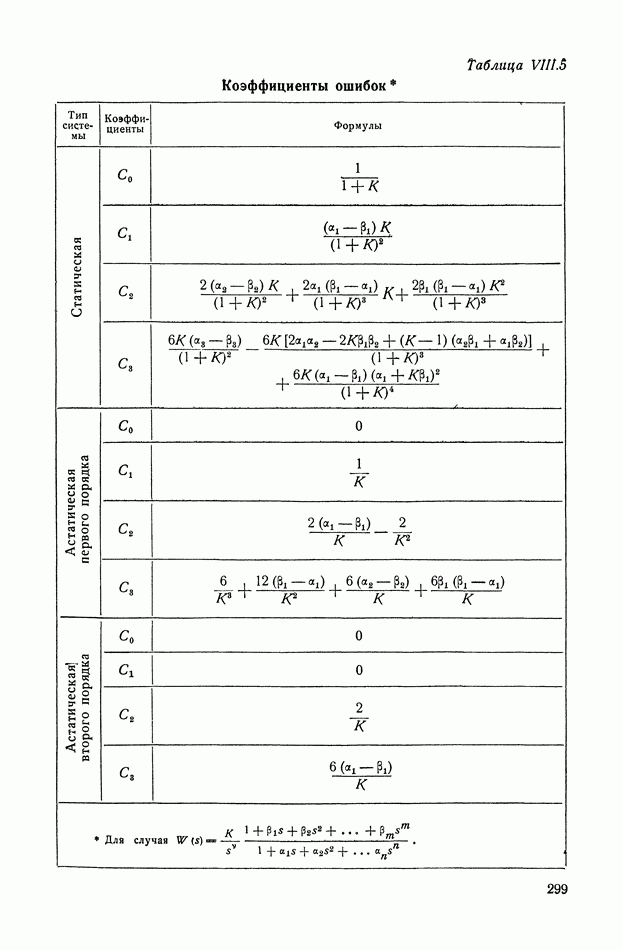
- 19. КОЭФФИЦИЕНТЫ ОШИБКИ
- ГЛАВА IX. МЕТОДЫ СТРУКТУРНЫХ ПРЕОБРАЗОВАНИЙ В СИСТЕМАХ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. ГРАФИЧЕСКИЕ ИЗОБРАЖЕНИЯ УСЛОВИЙ ПРЕОБРАЗОВАНИЯ СИГНАЛОВ
- 2. СХЕМЫ С ЭЛЕМЕНТАМИ, ОБЛАДАЮЩИМИ И НЕ ОБЛАДАЮЩИМИ СВОЙСТВОМ НАПРАВЛЕННОСТИ ДЕЙСТВИЯ
- 3. ДЕТАЛИЗИРОВАННЫЕ СТРУКТУРЫ
- 4. ПРЕОБРАЗОВАНИЯ МНОГОКОНТУРНЫХ СТРУКТУРНЫХ СХЕМ, ДОПУСКАЮЩИХ ПОСЛЕДОВАТЕЛЬНОЕ ПРИМЕНЕНИЕ ПРАВИЛ СВЕРТЫВАНИЯ КОНТУРОВ, И НЕКОТОРЫЕ ЭКВИВАЛЕНТНЫЕ ПРЕОБРАЗОВАНИЯ
- 5. ПРЕОБРАЗОВАНИЯ ПЕРЕКРЕСТНЫХ СТРУКТУРНЫХ СХЕМ МЕТОДОМ РАЗВЯЗКИ КОНТУРОВ И НЕКОТОРЫЕ ЭКВИВАЛЕНТНЫЕ ПРЕОБРАЗОВАНИЯ
- 6. ПРИМЕНЕНИЕ СТРУКТУРНЫХ МЕТОДОВ ДЛЯ ОПРЕДЕЛЕНИЯ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ МНОГОКОНТУРНЫХ СИСТЕМ
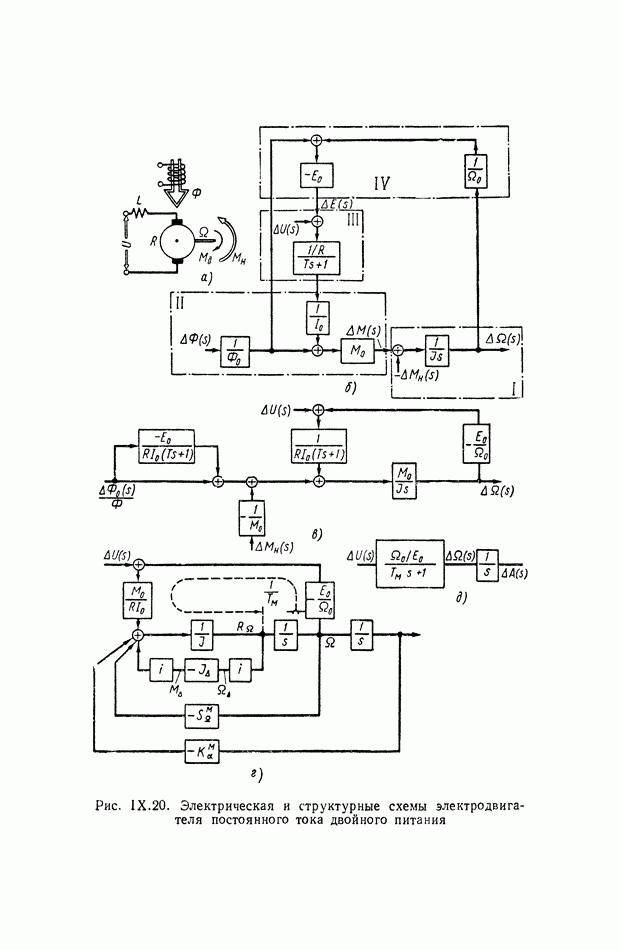
- 7. СОСТАВЛЕНИЕ И ПРЕОБРАЗОВАНИЕ СТРУКТУРНОЙ СХЕМЫ НА ПРИМЕРЕ ЭЛЕКТРОДВИГАТЕЛЯ ПОСТОЯННОГО ТОКА ДВОЙНОГО ПИТАНИЯ
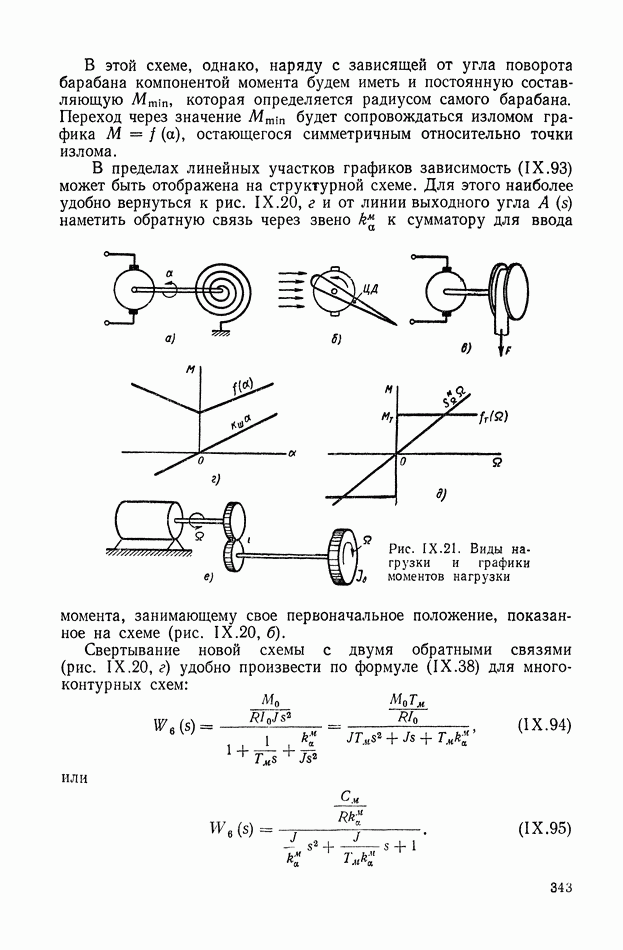
- Учет зависимости момента нагрузки от угла поворота вала и его производных по времени.
- 8. СТРУКТУРНЫЕ СХЕМЫ МЕХАНИЧЕСКИХ ОБЪЕКТОВ РЕГУЛИРОВАНИЯ С РЕДУКТОРАМИ, ДИФФЕРЕНЦИАЛАМИ И УПРУГИМИ ЭЛЕМЕНТАМИ В СИЛОВЫХ ПЕРЕДАЧАХ
- 9. ПРАВИЛА СТРУКТУРНЫХ ПРЕОБРАЗОВАНИЙ ДЛЯ СИСТЕМ С ПЕРЕМЕННЫМИ ПАРАМЕТРАМИ
- 10. ФУНКЦИОНАЛЬНЫЕ СТРУКТУРНЫЕ СХЕМЫ ДЛЯ АНАЛИЗА СОВМЕСТНЫХ СТАТИЧЕСКИХ ХАРАКТЕРИСТИК НЕЛИНЕЙНЫХ ЗВЕНЬЕВ
- ГЛАВА X. ПРИМЕРЫ СОСТАВЛЕНИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ, СТРУКТУРНЫХ СХЕМ И ПЕРЕДАТОЧНЫХ ФУНКЦИЙ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. СИСТЕМА АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ СКОРОСТИ ВРАЩЕНИЯ ГИДРОТУРБИНЫ
- 2. ЭЛЕКТРОННЫЙ РЕГУЛЯТОР НАПРЯЖЕНИЯ ВЭИ
- 3. СИСТЕМА АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ МОЩНОСТИ ЯДЕРНОГО ЭНЕРГЕТИЧЕСКОГО РЕАКТОРА НА ТЕПЛОВЫХ НЕЙТРОНАХ
- 4. СЛЕДЯЩАЯ СИСТЕМА РАДИОЛОКАЦИОННОЙ СТАНЦИИ
- 5. СИСТЕМА АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ УНИВЕРСАЛЬНЫХ ЛЕТУЧИХ НОЖНИЦ
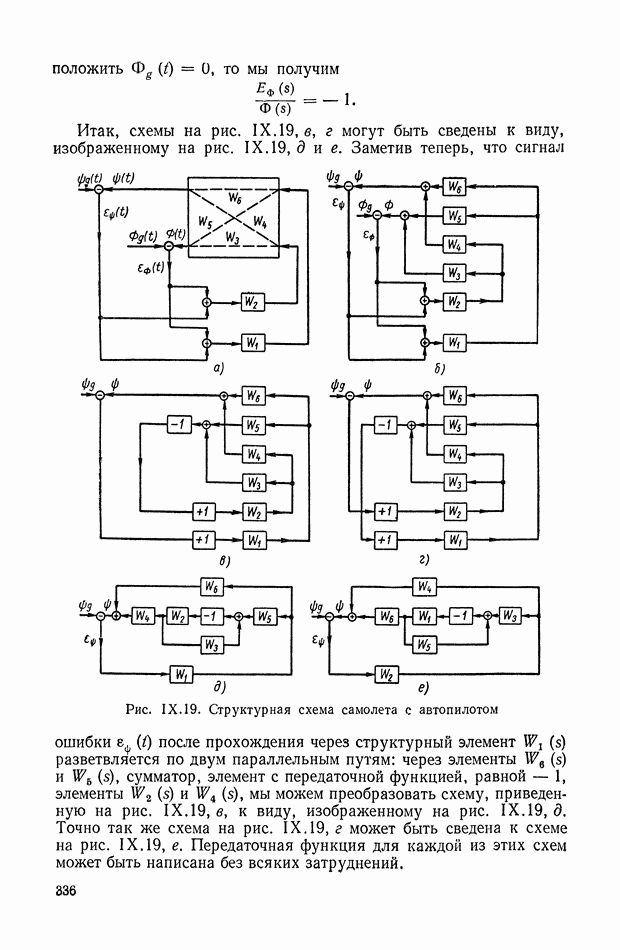
- 6. САМОЛЕТ С АВТОПИЛОТОМ
- 7. СЛЕДЯЩАЯ СИСТЕМА КОПИРОВАЛЬНО-ФРЕЗЕРНОГО СТАНКА
- РАЗДЕЛ II. АНАЛИЗ УСТОЙЧИВОСТИ НЕПРЕРЫВНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- ГЛАВА XI. ОБЩАЯ ПОСТАНОВКА ЗАДАЧИ УСТОЙЧИВОСТИ ПО ЛЯПУНОВУ И АНАЛИЗ УСТОЙЧИВОСТИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. ПОСТАНОВКА ЗАДАЧИ ОБ УСТОЙЧИВОСТИ В ТЕОРИИ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 2. ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ УСТАНОВИВШИХСЯ ДВИЖЕНИЙ ПО УРАВНЕНИЮ ПЕРВОГО ПРИБЛИЖЕНИЯ
- 3. О ПРЯМОМ МЕТОДЕ ЛЯПУНОВА
- 4. О ПРИМЕНЕНИИ ПРЯМОГО МЕТОДА ЛЯПУНОВА К АНАЛИЗУ УСТОЙЧИВОСТИ ОДНОГО КЛАССА СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- ГЛАВА XII. КРИТЕРИИ И МЕТОДЫ АНАЛИЗА УСТОЙЧИВОСТИ ЛИНЕАРИЗОВАННЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЙ
- 1. УСТОЙЧИВОСТЬ И ПРИНЦИП АРГУМЕНТА
- 2. КРИТЕРИЙ УСТОЙЧИВОСТИ МИХАЙЛОВА
- 3. КРИТЕРИЙ УСТОЙЧИВОСТИ РАУСА И ГУРВИЦА
- 4. ЧАСТОТНЫЙ КРИТЕРИЙ УСТОЙЧИВОСТИ
- 5. ОБОБЩЕНИЕ ЧАСТОТНОГО КРИТЕРИЯ НА АСТАТИЧЕСКИЕ СИСТЕМЫ
- 6. ОБОБЩЕНИЕ ЧАСТОТНОГО КРИТЕРИЯ НА СЛУЧАЙ, КОГДА РАЗОМКНУТАЯ СИСТЕМА НЕУСТОЙЧИВА
- 7. ЧАСТОТНЫЙ КРИТЕРИЙ УСТОЙЧИВОСТИ ДЛЯ ОБРАТНОЙ АМПЛИТУДНО-ФАЗОВОЙ ХАРАКТЕРИСТИКИ
- 8. АНАЛИЗ УСТОЙЧИВОСТИ ОДНОКОНТУРНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ПО ИХ ЛОГАРИФМИЧЕСКИМ ЧАСТОТНЫМ ХАРАКТЕРИСТИКАМ
- 9. ПРИБЛИЖЕННЫЙ СПОСОБ ПОСТРОЕНИЯ ЛОГАРИФМИЧЕСКИХ ЧАСТОТНЫХ ХАРАКТЕРИСТИК ОДНОКОНТУРНЫХ СИСТЕМ
- 10. ОБОБЩЕНИЕ ЧАСТОТНОГО КРИТЕРИЯ УСТОЙЧИВОСТИ НА МНОГОКОНТУРНЫЕ СИСТЕМЫ
- 11. АНАЛИЗ УСТОЙЧИВОСТИ МНОГОКОНТУРНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ПРИ ПОМОЩИ ЛОГАРИФМИЧЕСКИХ ЧАСТОТНЫХ ХАРАКТЕРИСТИК
- ГЛАВА XIII. ВЫДЕЛЕНИЕ ОБЛАСТЕЙ УСТОЙЧИВОСТИ
- 1. ПОНЯТИЕ О Д-РАЗБИЕНИИ ПРОСТРАНСТВА КОЭФФИЦИЕНТОВ ХАРАКТЕРИСТИЧЕСКОГО УРАВНЕНИЯ И ПРОСТРАНСТВА ПАРАМЕТРОВ
- 2. Д-РАЗБИЕНИЕ ПЛОСКОСТИ ОДНОГО КОМПЛЕКСНОГО ПАРАМЕТРА
- 3. СВЯЗЬ Д-РАЗБИЕНИЯ С КРИТЕРИЯМИ УСТОЙЧИВОСТИ
- 4. Д-РАЗБИЕНИЕ ПЛОСКОСТИ ДВУХ ДЕЙСТВИТЕЛЬНЫХ ПАРАМЕТРОВ (ДИАГРАММА ВЫШНЕГРАДСКОГО)
- 5. УСЛОВИЯ СУЩЕСТВОВАНИЯ ОБЛАСТИ УСТОЙЧИВОСТИ
- ГЛАВА XIV. ПРИМЕРЫ АНАЛИЗА УСТОЙЧИВОСТИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. СИСТЕМА АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ СКОРОСТИ ВРАЩЕНИЯ ГИДРОТУРБИНЫ
- 2. СЛЕДЯЩАЯ СИСТЕМА КОПИРОВАЛЬНО-ФРЕЗЕРНОГО СТАНКА
- 3. СИСТЕМА АВТОМАТИЧЕСКОЙ СТАБИЛИЗАЦИИ САМОЛЕТА (АВТОПИЛОТ)
- 4. СИСТЕМА АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ МОЩНОСТИ ЯДЕРНОГО ЭНЕРГЕТИЧЕСКОГО РЕАКТОРА
- РАЗДЕЛ III. АНАЛИЗ ПЕРЕХОДНЫХ ПРОЦЕССОВ И КАЧЕСТВА ЛИНЕЙНЫХ НЕПРЕРЫВНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- ГЛАВА XV. ЧАСТОТНЫЙ МЕТОД АНАЛИЗА ПЕРЕХОДНЫХ ПРОЦЕССОВ
- 1. ОБОБЩЕННЫЕ ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ И ИХ СВЯЗЬ С ПЕРЕХОДНЫМИ ПРОЦЕССАМИ
- 2. ОПРЕДЕЛЕНИЕ ОБОБЩЕННЫХ ЧАСТОТНЫХ ХАРАКТЕРИСТИК В ОБЩЕМ СЛУЧАЕ
- 3. СЛУЧАЙ, КОГДА ФУНКЦИЯ X(s) НЕ СОДЕРЖИТ ОСОБЕННОСТЕЙ ВО ВСЕЙ ПРАВОЙ ПОЛУПЛОСКОСТИ И НА МНИМОЙ ОСИ
- 4. СВЯЗЬ МЕЖДУ ЧАСТОТНЫМИ ХАРАКТЕРИСТИКАМИ P(w), Q(w) И ИМПУЛЬСНОЙ ПЕРЕХОДНОЙ ФУНКЦИЕЙ k(t)
- 5. СЛУЧАЙ, КОГДА ВСЕ ПОЛЮСА ФУНКЦИИ X(s) РАСПОЛОЖЕНЫ В ЛЕВОЙ ПОЛУПЛОСКОСТИ, ЗА ИСКЛЮЧЕНИЕМ ПОЛЮСА В НАЧАЛЕ КООРДИНАТ
- 6. СВЯЗЬ МЕЖДУ ЧАСТОТНЫМИ ХАРАКТЕРИСТИКАМИ И ПЕРЕХОДНОЙ ФУНКЦИЕЙ h(t)
- 7. СЛУЧАЙ, КОГДА ФУНКЦИЯ X(s) ИМЕЕТ ДВА СОПРЯЖЕННЫХ ПОЛЮСА НА МНИМОЙ ОСИ
- 8. АНАЛИЗ ПЕРЕХОДНЫХ ПРОЦЕССОВ МЕТОДОМ ТРАПЕЦЕИДАЛЬНЫХ ЧАСТОТНЫХ ХАРАКТЕРИСТИК
- 9. О НЕКОТОРЫХ ЧАСТНЫХ СЛУЧАЯХ МЕТОДА ТРАПЕЦЕИДАЛЬНЫХ ЧАСТОТНЫХ ХАРАКТЕРИСТИК
- 10. ОБ УСЛОВИЯХ ПРИМЕНИМОСТИ ЧАСТОТНОГО МЕТОДА АНАЛИЗА ПЕРЕХОДНЫХ ПРОЦЕССОВ
- 11. ОПРЕДЕЛЕНИЕ ДИСКРЕТНЫХ ЗНАЧЕНИЙ ПЕРЕХОДНОЙ ФУНКЦИИ
- ГЛАВА XVI. ЧАСТОТНЫЙ МЕТОД АНАЛИЗА КАЧЕСТВА
- 1. ЧАСТОТНЫЙ КРИТЕРИЙ КАЧЕСТВА РЕГУЛИРОВАНИЯ
- 2. ЧАСТОТНЫЙ КРИТЕРИЙ ОТСУТСТВИЯ ПЕРЕРЕГУЛИРОВАНИЙ И ЧАСТОТНЫЙ КРИТЕРИЙ МОНОТОННОСТИ
- 3. О ПРОВЕРКЕ ВЫПОЛНЕНИЯ СФОРМУЛИРОВАННЫХ КРИТЕРИЕВ
- 4. НЕКОТОРЫЕ ПРИЗНАКИ НЕУДОВЛЕТВОРЕНИЯ КРИТЕРИЕВ КАЧЕСТВА И КРИТЕРИЕВ ОТСУТСТВИЯ ПЕРЕРЕГУЛИРОВАНИЙ И МОНОТОННОСТИ
- 5. НЕКОТОРЫЕ ЭЛЕМЕНТАРНЫЕ СВОЙСТВА ЧАСТОТНЫХ ХАРАКТЕРИСТИК
- 6. ДОСТАТОЧНЫЕ УСЛОВИЯ ДЛЯ МАЛЫХ ПЕРЕРЕГУЛИРОВАНИЙ И НЕОБХОДИМЫЕ УСЛОВИЯ ДЛЯ ОТСУТСТВИЯ ПЕРЕРЕГУЛИРОВАНИЙ
- 7. КРИТЕРИЙ, ОПРЕДЕЛЯЮЩИЙ ДОСТАТОЧНЫЕ УСЛОВИЯ ДЛЯ МОНОТОННОСТИ
- 8. ОЦЕНКИ ВЕЛИЧИНЫ ПЕРЕРЕГУЛИРОВАНИЯ И ВРЕМЕНИ ПЕРЕХОДНОГО ПРОЦЕССА
- 9. ОЦЕНКА АБСОЛЮТНОГО ЗНАЧЕНИЯ РАЗНОСТИ МЕЖДУ ПЕРЕХОДНЫМИ ФУНКЦИЯМИ ПО СООТВЕТСТВУЮЩИМ ИМ ЧАСТОТНЫМ ХАРАКТЕРИСТИКАМ
- 10. СВЯЗЬ МЕЖДУ СВОЙСТВАМИ АМПЛИТУДНО-ФАЗОВОЙ ХАРАКТЕРИСТИКИ РАЗОМКНУТОЙ СИСТЕМЫ И КАЧЕСТВОМ
- 11. ТРЕБОВАНИЯ К ЧАСТОТНЫМ ХАРАКТЕРИСТИКАМ, ОБЕСПЕЧИВАЮЩИЕ ВЫСОКУЮ ТОЧНОСТЬ В СЛЕДЯЩИХ СИСТЕМАХ
- 12. СВЯЗЬ МЕЖДУ СВОЙСТВАМИ ЛОГАРИФМИЧЕСКОЙ АМПЛИТУДНОЙ ХАРАКТЕРИСТИКИ И КАЧЕСТВОМ
- 13. ОПРЕДЕЛЕНИЕ ВЕЛИЧИНЫ ПЕРЕДАТОЧНОГО КОЭФФИЦИЕНТА ИЛИ ДОБРОТНОСТИ ПО ЛОГАРИФМИЧЕСКОЙ АМПЛИТУДНОЙ ХАРАКТЕРИСТИКЕ
- 14. ОПРЕДЕЛЕНИЕ УСТАНОВИВШЕЙСЯ ОШИБКИ ПРИ ГАРМОНИЧЕСКОМ УПРАВЛЯЮЩЕМ ВОЗДЕЙСТВИИ ПО ЛОГАРИФМИЧЕСКОЙ АМПЛИТУДНОЙ ХАРАКТЕРИСТИКЕ
- 15. ПРИБЛИЖЕННЫЙ СПОСОБ ВЫЧИСЛЕНИЯ ПЕРЕХОДНОГО ПРОЦЕССА ПО СОПРЯГАЮЩИМ ЧАСТОТАМ ЛОГАРИФМИЧЕСКОЙ АМПЛИТУДНОЙ ЧАСТОТНОЙ ХАРАКТЕРИСТИКИ
- 16. НОМОГРАММА ДЛЯ ОПРЕДЕЛЕНИЯ ЗАПАСА УСТОЙЧИВОСТИ, ПОКАЗАТЕЛЕЙ КАЧЕСТВА И КОЭФФИЦИЕНТОВ ОШИБОК ПО ВИДУ ЛОГАРИФМИЧЕСКОЙ АМПЛИТУДНОЙ ХАРАКТЕРИСТИКИ
- ГЛАВА XVII. СВЯЗЬ МЕЖДУ КАЧЕСТВОМ ПЕРЕХОДНОГО ПРОЦЕССА И РАСПРЕДЕЛЕНИЕМ НУЛЕЙ И ПОЛЮСОВ ПЕРЕДАТОЧНОЙ ФУНКЦИИ. МЕТОД КОРНЕВЫХ ГОДОГРАФОВ
- 2. АНАЛИЗ РАСПРЕДЕЛЕНИЯ КОРНЕЙ ХАРАКТЕРИСТИЧЕСКОГО УРАВНЕНИЯ СИСТЕМЫ И ОЦЕНКА КАЧЕСТВА ПЕРЕХОДНОГО ПРОЦЕССА
- 3. ГЕОМЕТРИЧЕСКИЙ МЕТОД ПОСТРОЕНИЯ КОРНЕВОГО ГОДОГРАФА
- 4. АНАЛИТИЧЕСКОЕ ПОСТРОЕНИЕ ГЕОМЕТРИЧЕСКОГО МЕСТА КОРНЕЙ
- 5. ОПРЕДЕЛЕНИЕ ОБЛАСТЕЙ УСТОЙЧИВОСТИ ЛИНЕЙНЫХ СИСТЕМ МЕТОДОМ КОРНЕВОГО ГОДОГРАФА
- 6. ОЦЕНКИ ПАРАМЕТРОВ ПЕРЕХОДНОЙ И ЧАСТОТНОЙ ХАРАКТЕРИСТИК ПО КОРНЕВОМУ ГОДОГРАФУ
- 7. ВЛИЯНИЕ РАСПОЛОЖЕНИЯ НУЛЕЙ И ПОЛЮСОВ ЗАМКНУТОЙ СИСТЕМЫ НА ПЕРЕХОДНУЮ ХАРАКТЕРИСТИКУ h(t)
- 8. ВЛИЯНИЕ РАСПОЛОЖЕНИЯ НУЛЕЙ И ПОЛЮСОВ ЗАМКНУТОЙ СИСТЕМЫ НА ЕЕ ПОЛОСУ ЧАСТОТ
- 9. КОРНЕВОЙ ГОДОГРАФ И ПЕРЕХОДНАЯ ХАРАКТЕРИСТИКА СИСТЕМЫ ПРИ ВОЗМУЩЕНИЯХ, ПРИЛОЖЕННЫХ НЕ К ОСНОВНОМУ ВХОДУ СИСТЕМЫ
- 10. ВЛИЯНИЕ РАСПРЕДЕЛЕНИЯ НУЛЕЙ И ПОЛЮСОВ ПЕРЕДАТОЧНОЙ ФУНКЦИИ НА КАЧЕСТВО ПЕРЕХОДНОГО ПРОЦЕССА ПРИ НАЛИЧИИ ВНЕШНЕГО ВОЗДЕЙСТВИЯ
- ГЛАВА XVIII. МЕТОД ЛОГАРИФМИЧЕСКИХ КОРНЕВЫХ ГОДОГРАФОВ
- 2. ОПРЕДЕЛЕНИЕ КОРНЕЙ ЗАМКНУТОЙ СИСТЕМЫ ПО ЛОГАРИФМИЧЕСКОЙ АМПЛИТУДНОЙ КОМПЛЕКСНО-ЧАСТОТНОЙ ХАРАКТЕРИСТИКЕ РАЗОМКНУТОЙ СИСТЕМЫ
- 3. ЛОГАРИФМИЧЕСКИЕ КОРНЕВЫЕ ГОДОГРАФЫ
- 4. ЛОГАРИФМИЧЕСКИЕ КОМПЛЕКСНО-ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЗВЕНЬЕВ ВТОРОГО ПОРЯДКА
- 5. ПРИМЕР ПОСТРОЕНИЯ ЛОГАРИФМИЧЕСКОГО КОРНЕВОГО ГОДОГРАФА
- ГЛАВА XIX. ИНТЕГРАЛЬНЫЕ ОЦЕНКИ И КРИТЕРИИ КАЧЕСТВА РЕГУЛИРОВАНИЯ
- 2. МЕТОДИКА ПРИМЕНЕНИЯ ИНТЕГРАЛЬНЫХ КВАДРАТИЧНЫХ ОЦЕНОК
- 3. ЛИНЕЙНЫЕ ИНТЕГРАЛЬНЫЕ ОЦЕНКИ
- ПРИЛОЖЕНИЕ
- БИБЛИОГРАФИЯ ПО РАЗДЕЛАМ КНИГИ