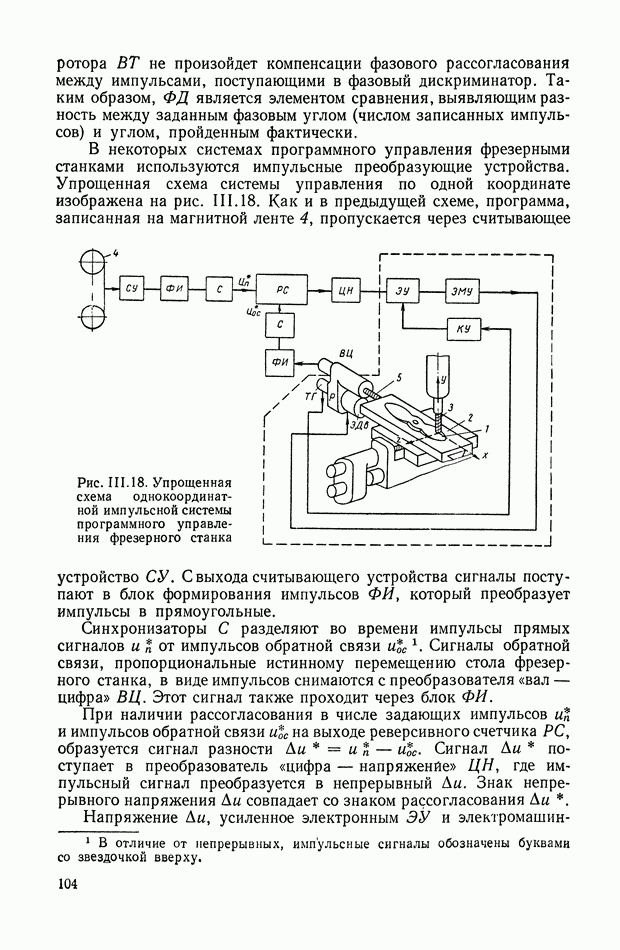
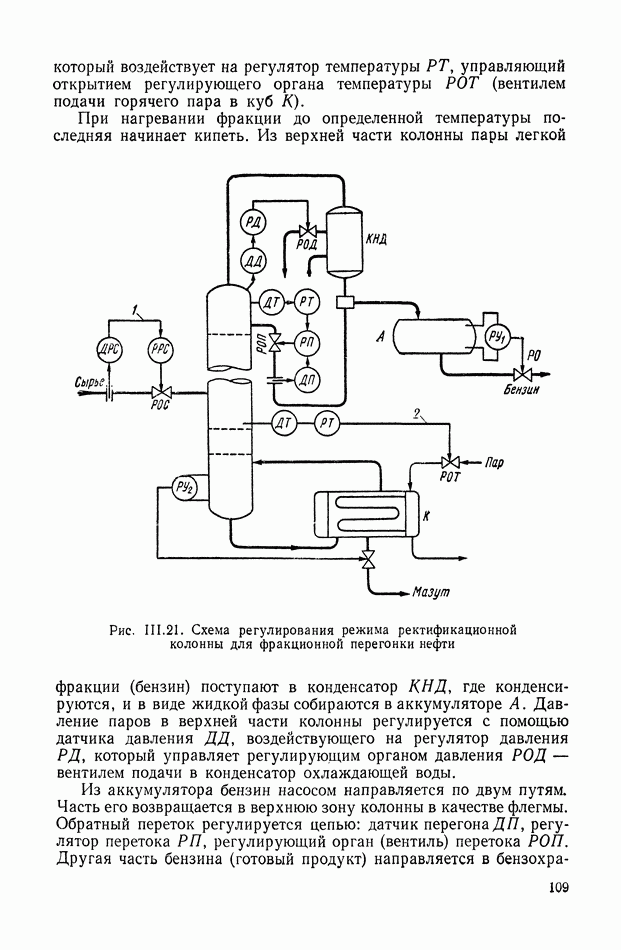
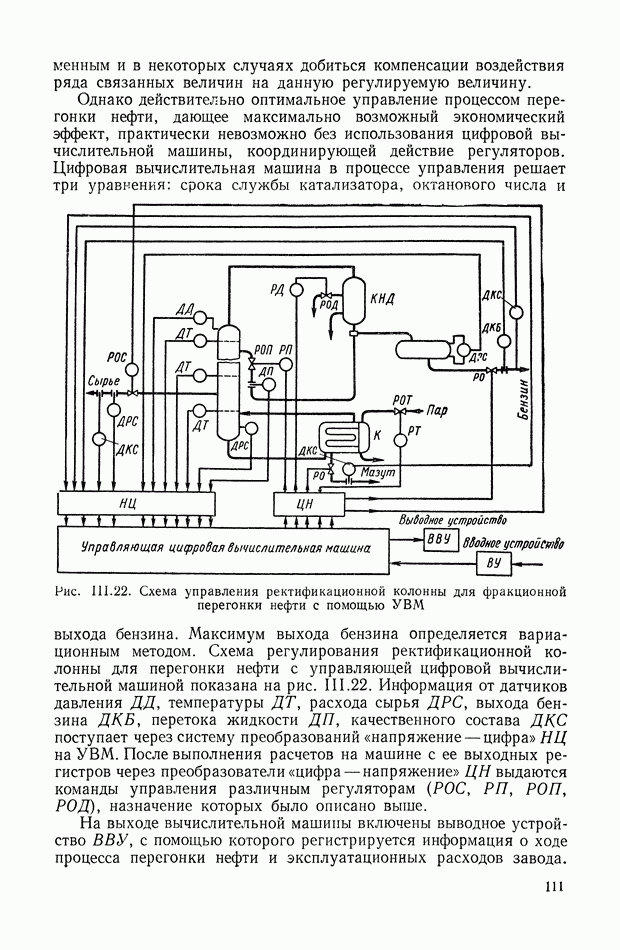
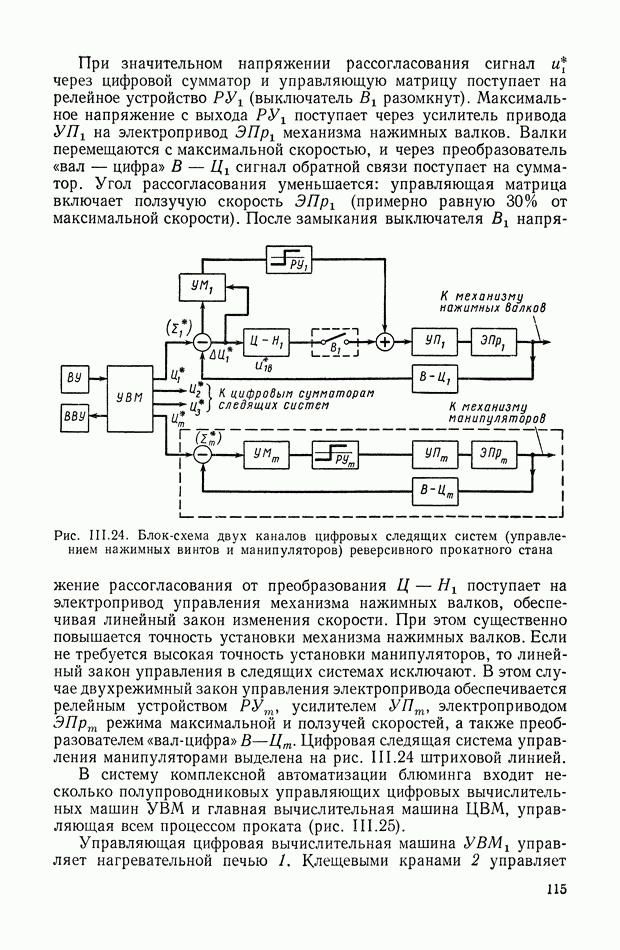
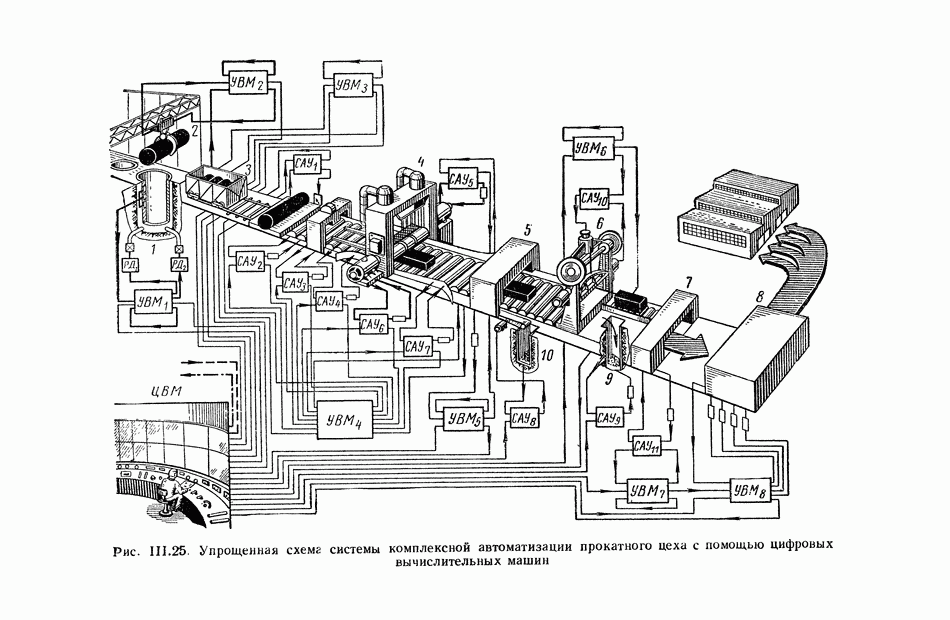
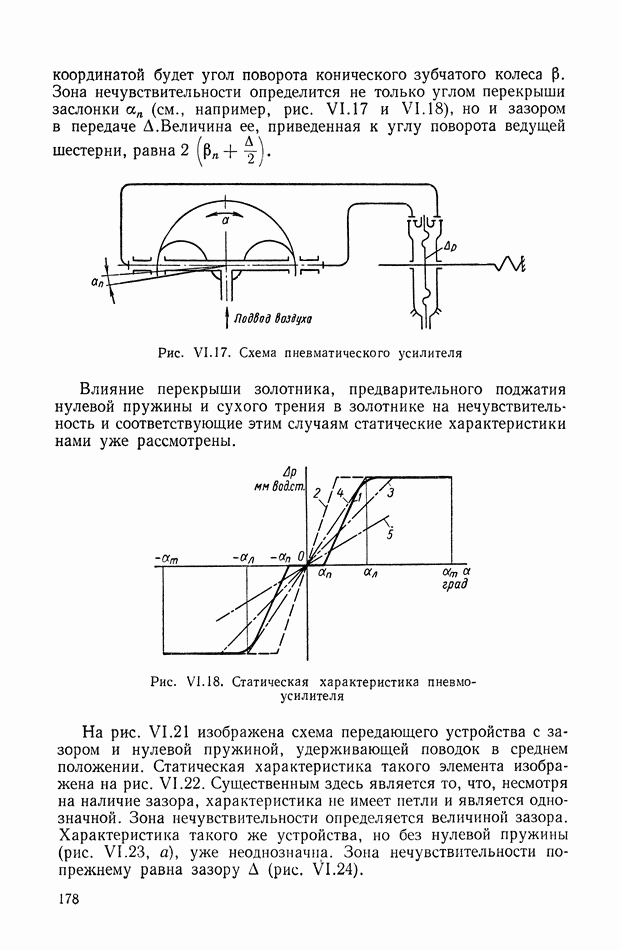
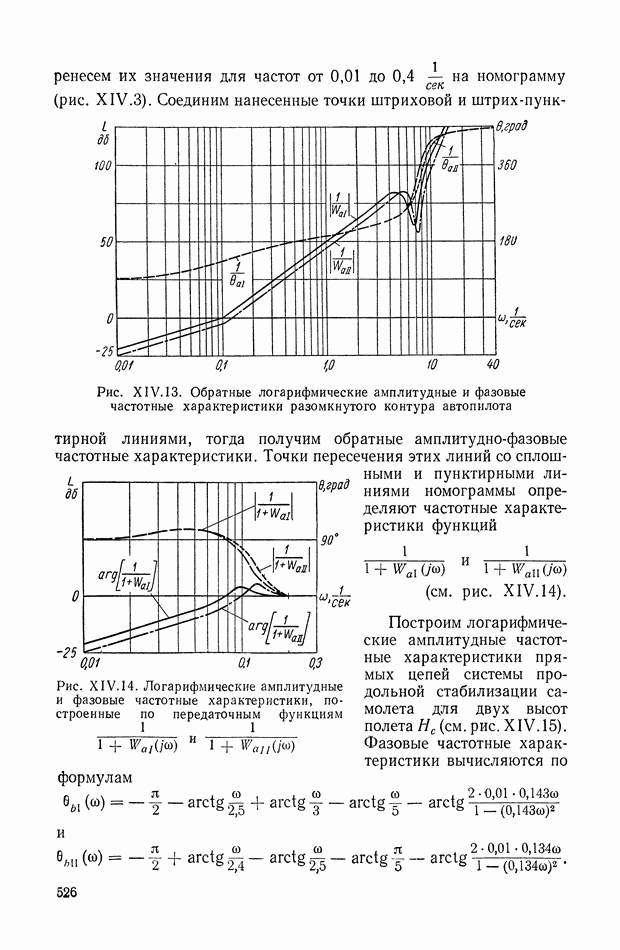
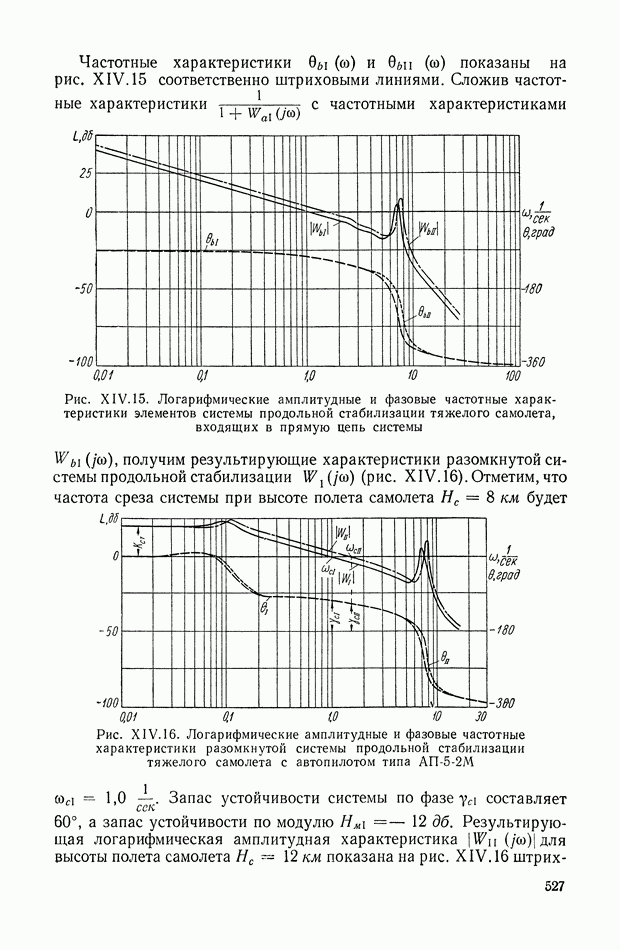
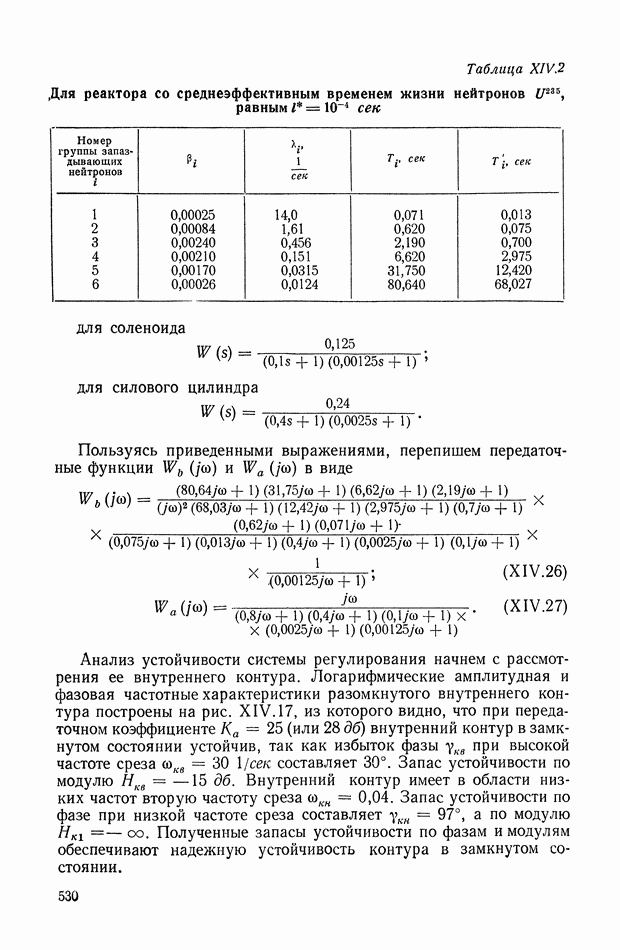
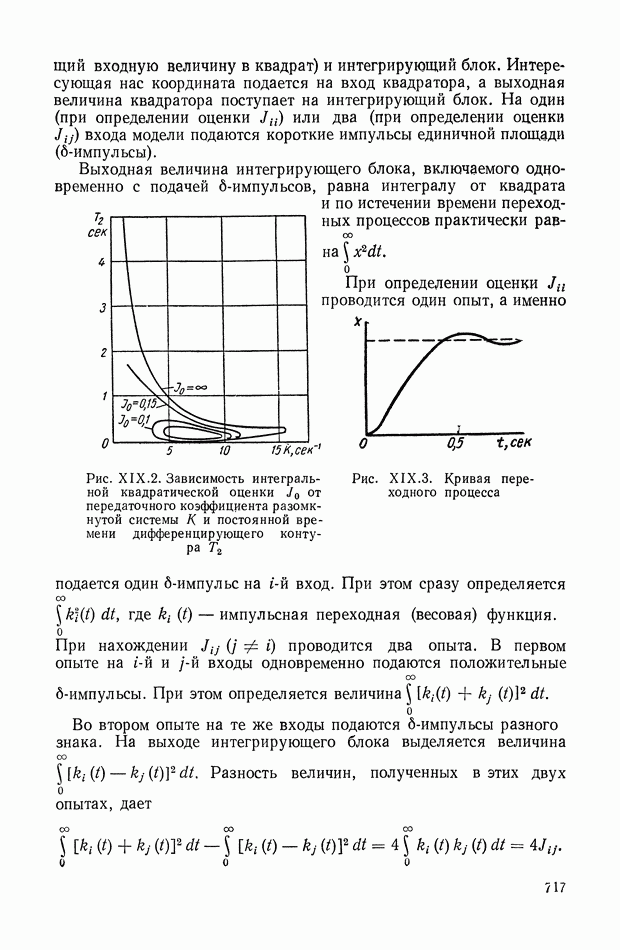
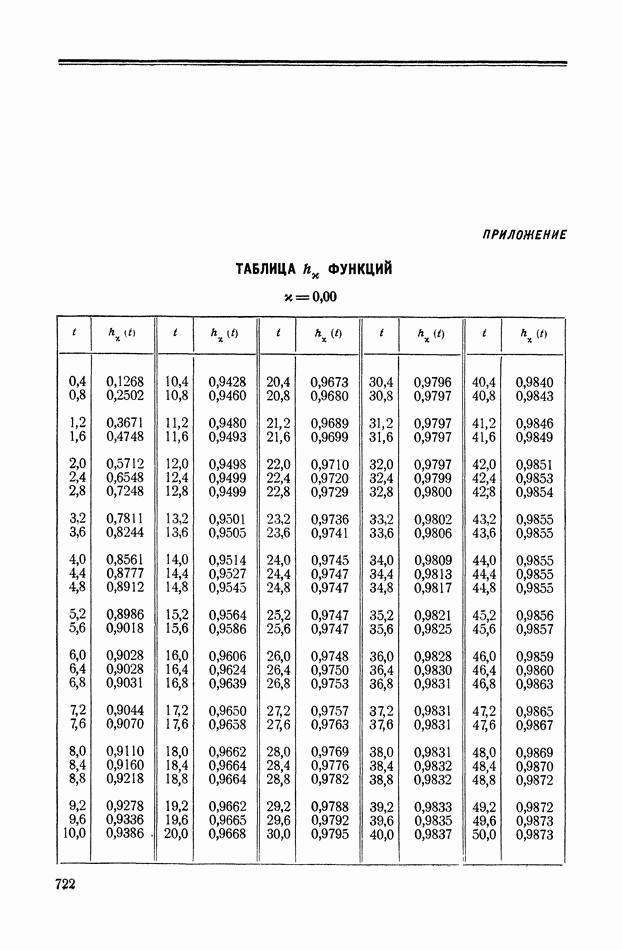
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
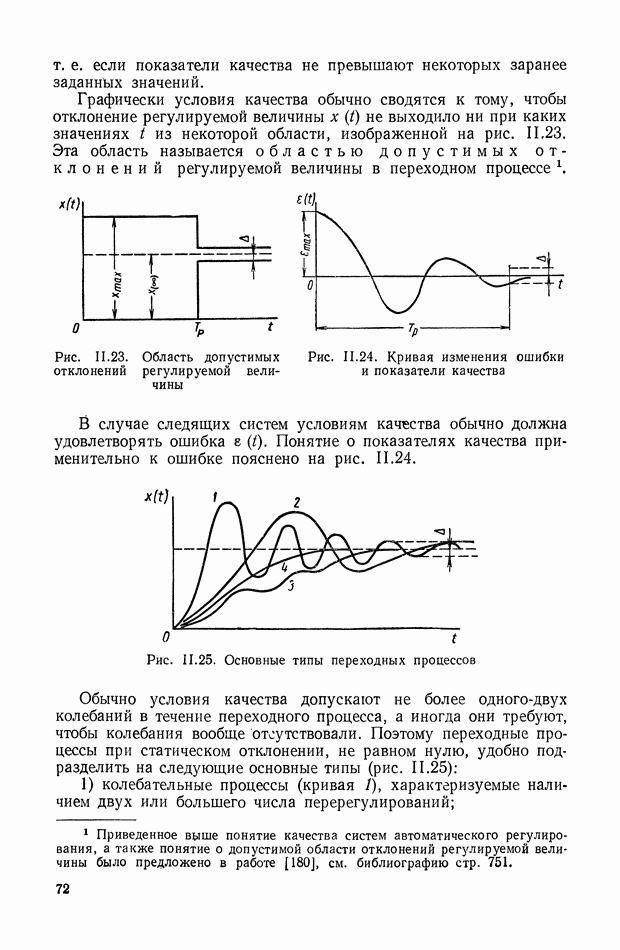
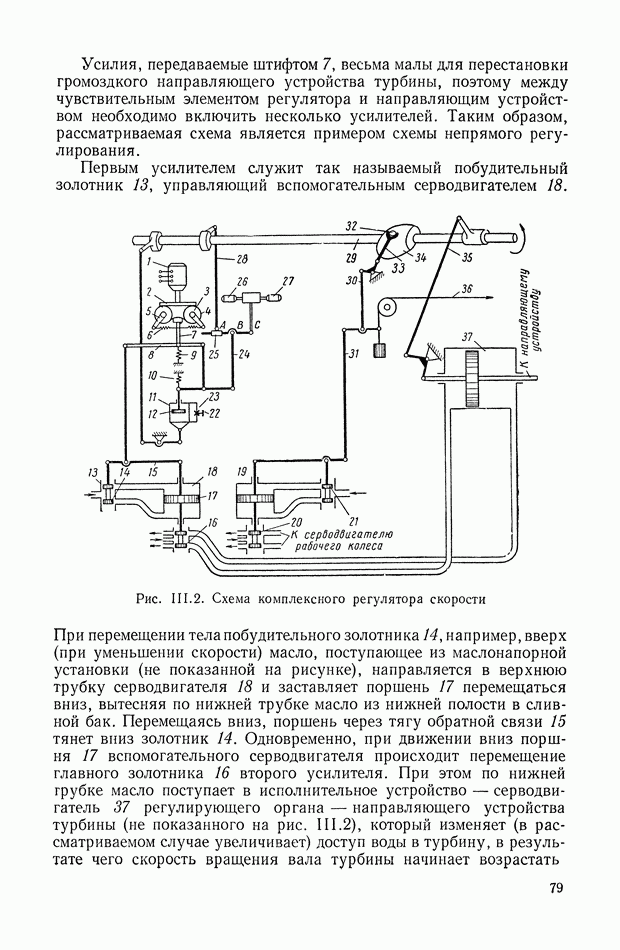
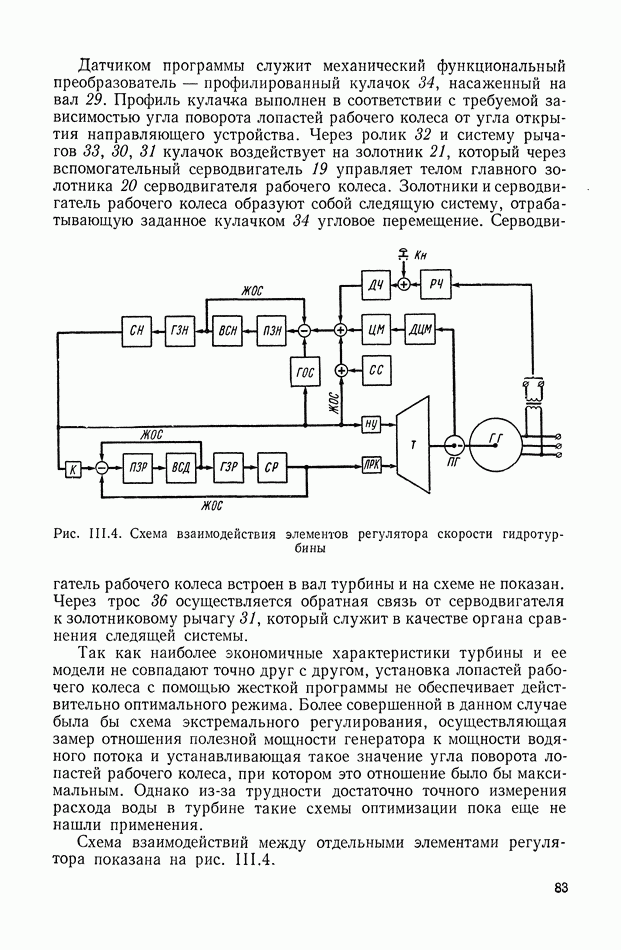
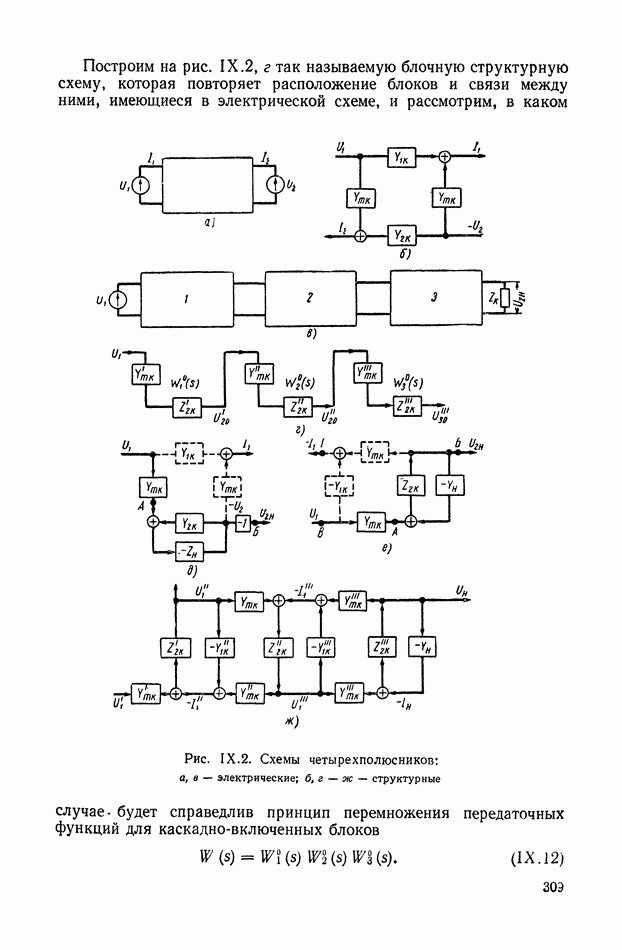
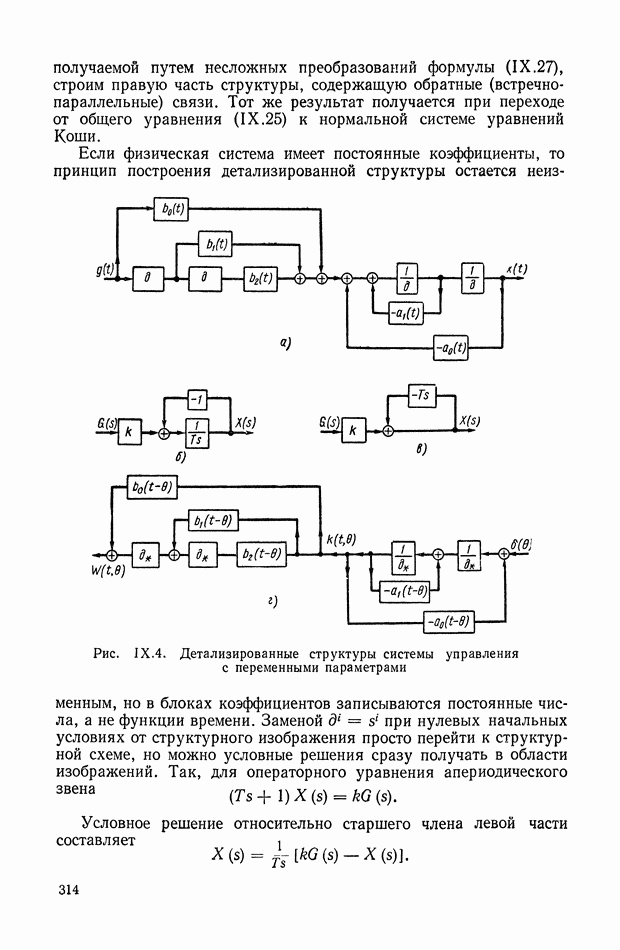
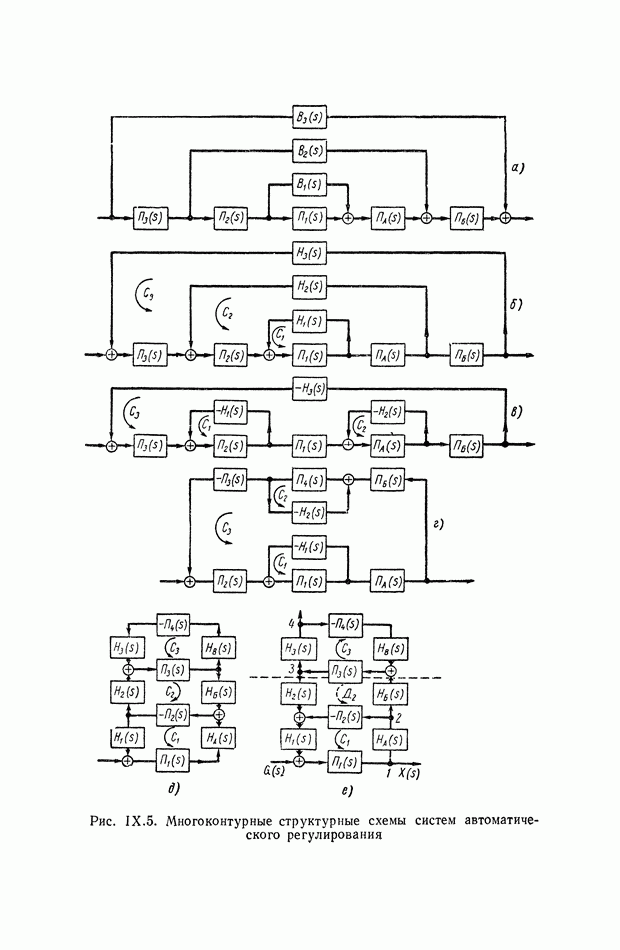
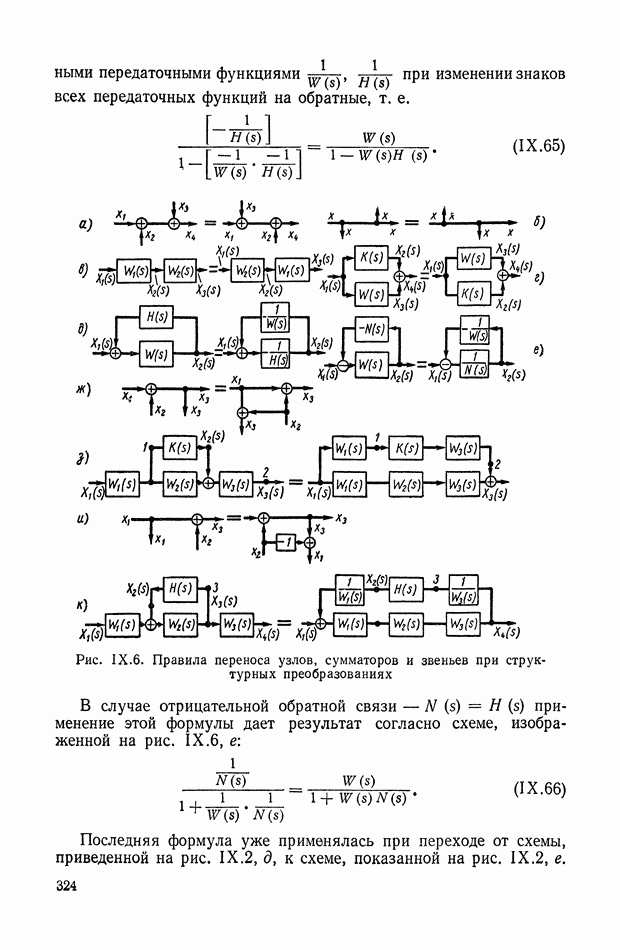
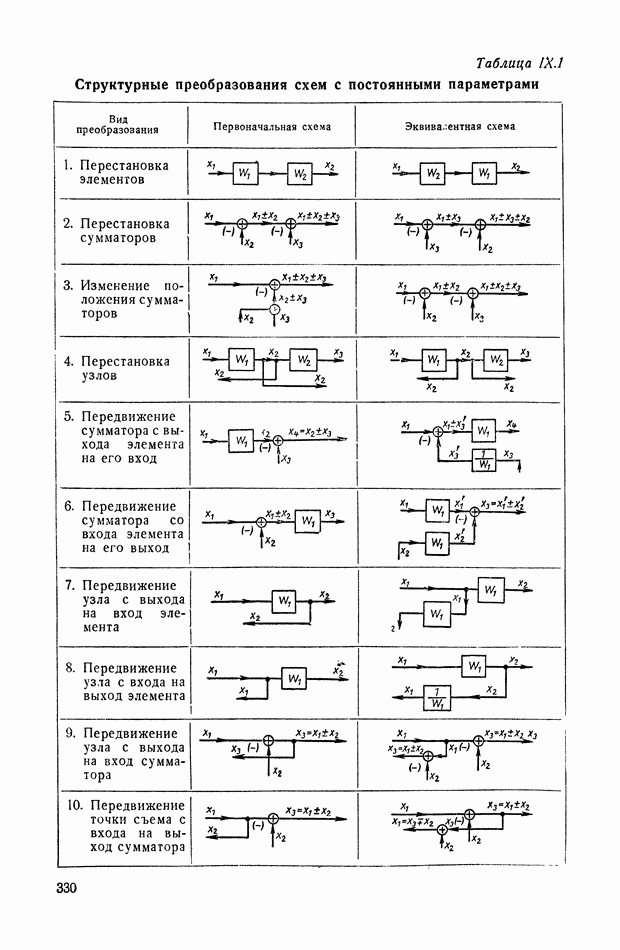
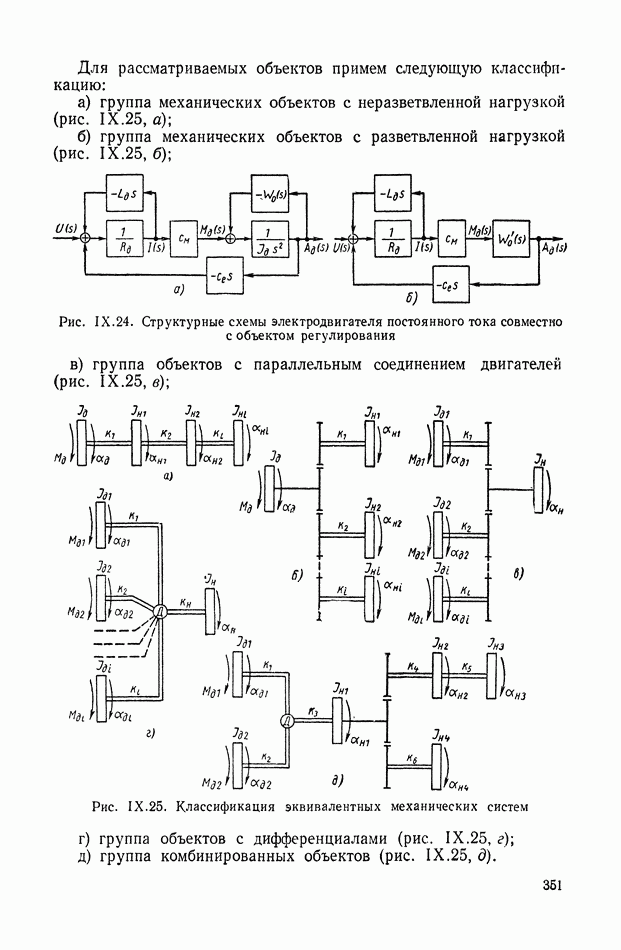
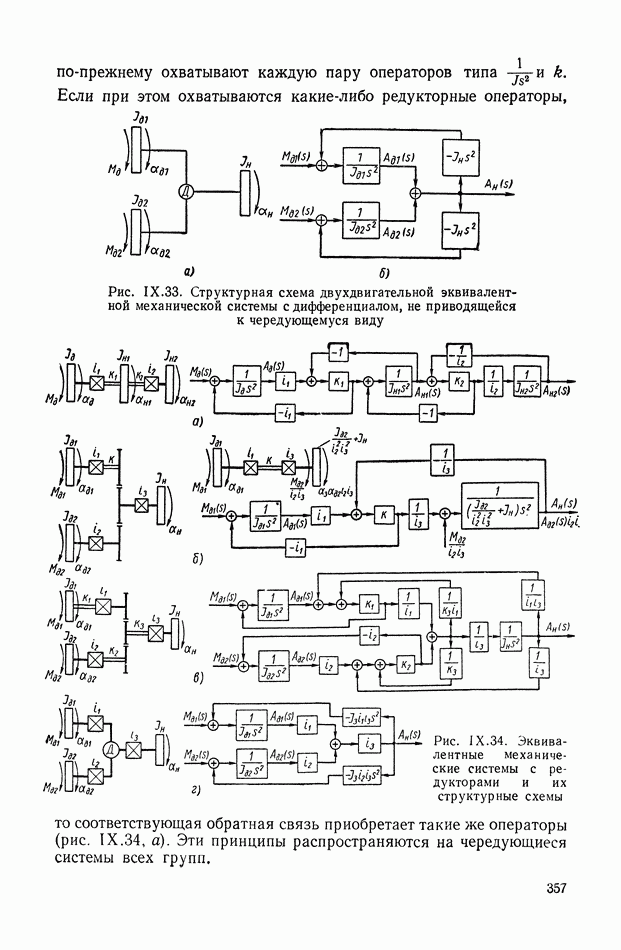
9. ПРАВИЛА СТРУКТУРНЫХ ПРЕОБРАЗОВАНИЙ ДЛЯ СИСТЕМ С ПЕРЕМЕННЫМИ ПАРАМЕТРАМИ
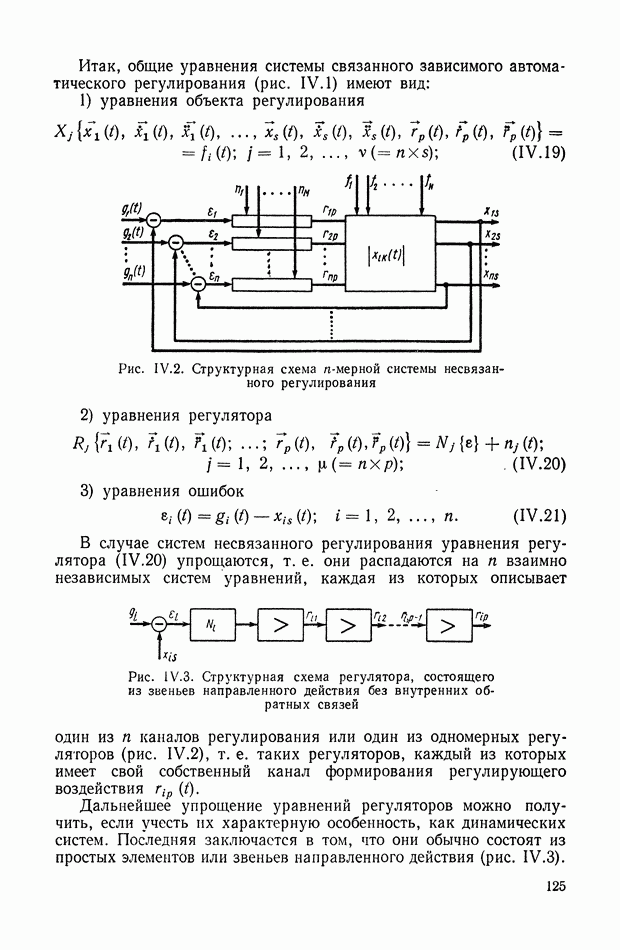
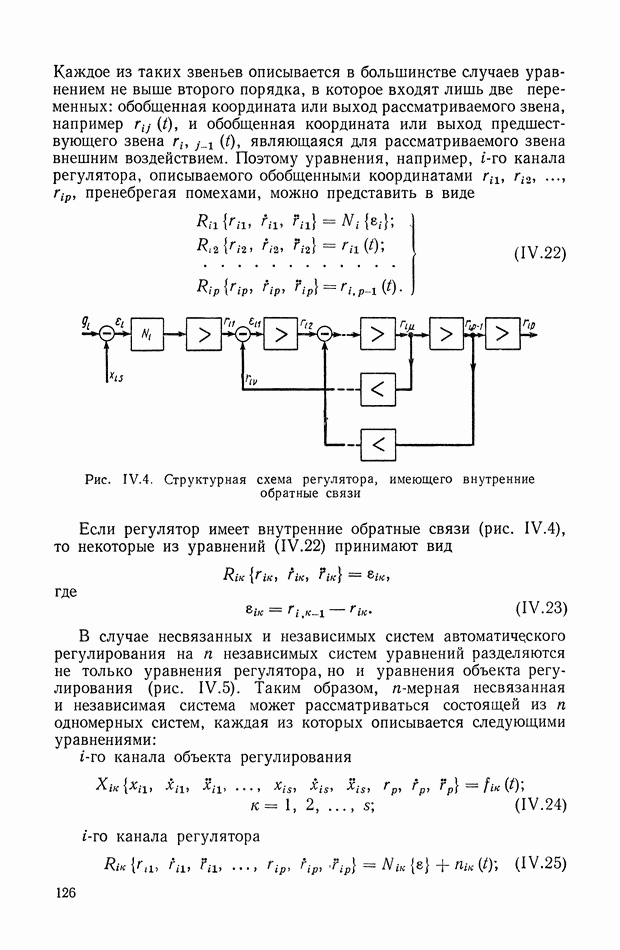
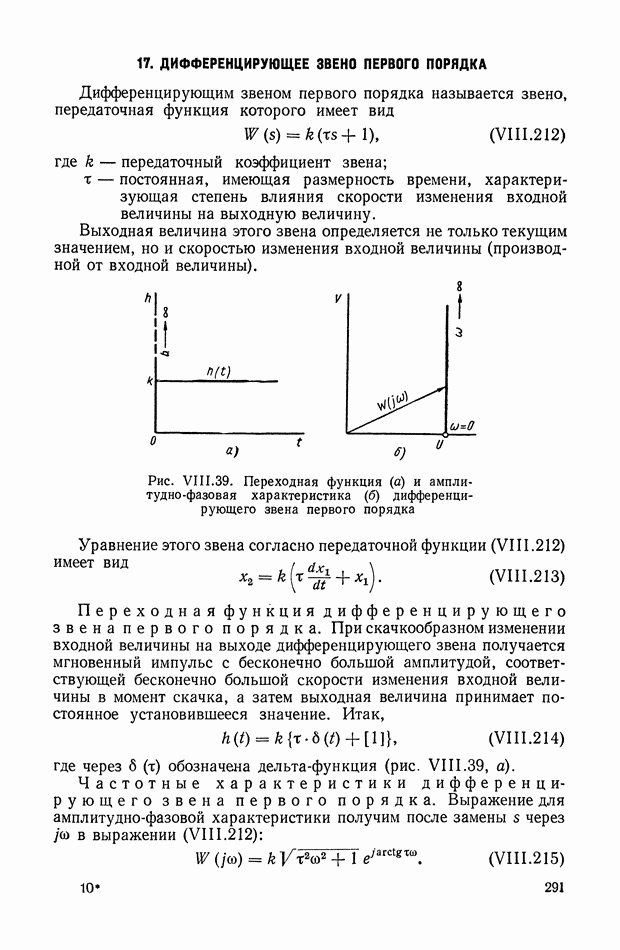
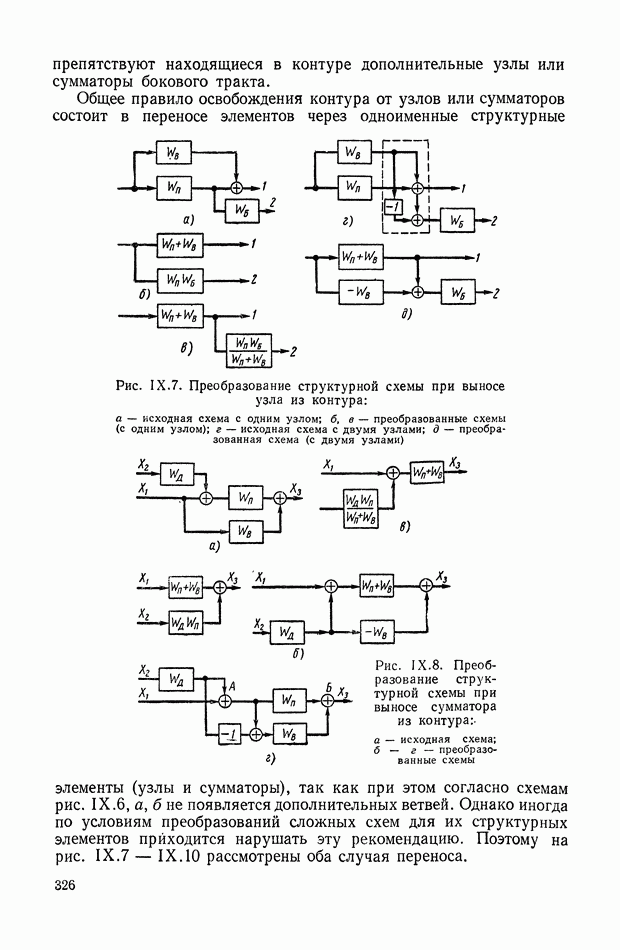
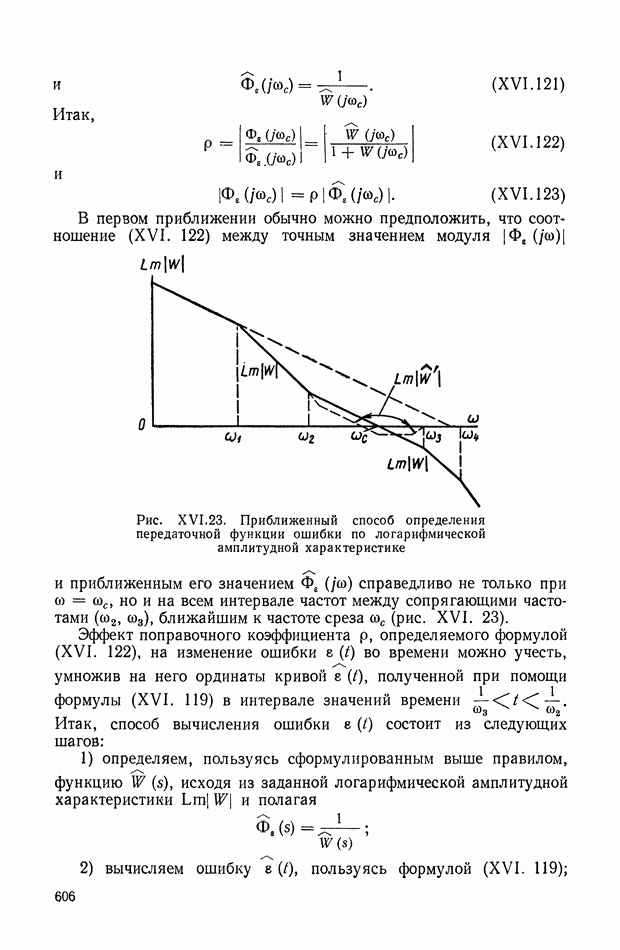
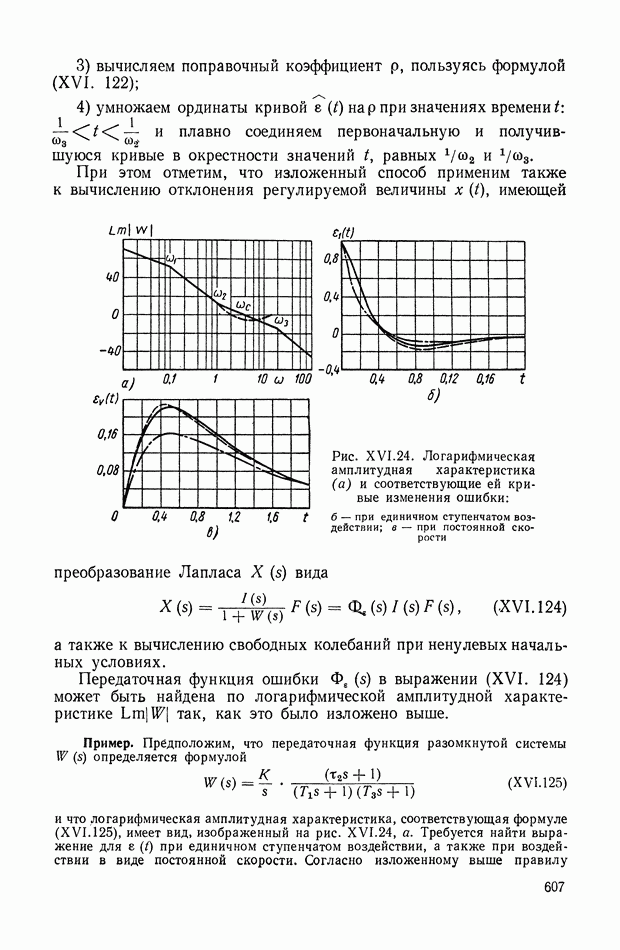
Устранение дифференцирующих звеньев в детализированных структурных изображениях. При получении детализированной структуры уравнения с развитой правой частью на основе условно-разрешенной формы (см. § 4) не удается избежать в структуре дифференцирующих звеньев, которые неудобны при моделировании. Рассмотрим преобразованную детализированную структуру, приведенную на рис. IX.38, а. Интегрирующие элементы схемы  и обратные связи
и обратные связи  соответствуют структуре приведенного уравнения связи
соответствуют структуре приведенного уравнения связи  порядка.
порядка.
Элементы схемы  отражают преобразованные условия подачи входного сигнала в новые точки схемы через блоки переменных коэффициентов. Определим, какому виду правой части уравнения связи отвечает такая преобразованная детализированная структура. Для этого перенесем сумматоры 2, 3 на вход схемы, как показано на рис. IX.38, б. Поскольку перенос сумматора производится против хода сигнала в основном тракте, то при переходе через каждый узел и звено осуществляется принцип нейтрализации или инверсного дублирования, рассмотренный в § 6. Так, инверсия интегратора ддет дифференциатор
отражают преобразованные условия подачи входного сигнала в новые точки схемы через блоки переменных коэффициентов. Определим, какому виду правой части уравнения связи отвечает такая преобразованная детализированная структура. Для этого перенесем сумматоры 2, 3 на вход схемы, как показано на рис. IX.38, б. Поскольку перенос сумматора производится против хода сигнала в основном тракте, то при переходе через каждый узел и звено осуществляется принцип нейтрализации или инверсного дублирования, рассмотренный в § 6. Так, инверсия интегратора ддет дифференциатор  а инверсия сумматора меняет знак в ответвляющихся линиях обратных связей. При последующем
а инверсия сумматора меняет знак в ответвляющихся линиях обратных связей. При последующем
переносе задублированного сумматора вдоль линии обратной связи перемещение идет по ходу сигнала, и блоки переменных коэффициентов просто дублируются. Как видно из рис. IX.38, б, наибольшее число прямых и инвертированных дублированных элементов содержит цепь с функцией  так как для нее потребовалось много переносов. Без преобразований осталась ветвь, содержащая функцию
так как для нее потребовалось много переносов. Без преобразований осталась ветвь, содержащая функцию  так как она Уже в схеме (рис. IX.38, а) подавалась непосредственно на ее вход (сумматор 1).
так как она Уже в схеме (рис. IX.38, а) подавалась непосредственно на ее вход (сумматор 1).

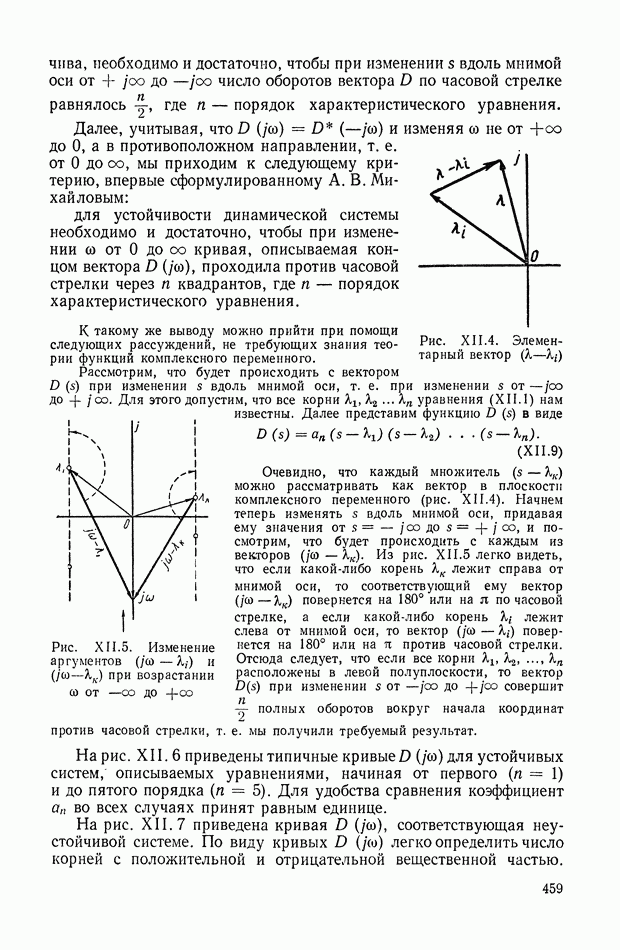
Рис. IX.38. Преобразования детализированной структуры с целью исключения дифференцирующих звеньев
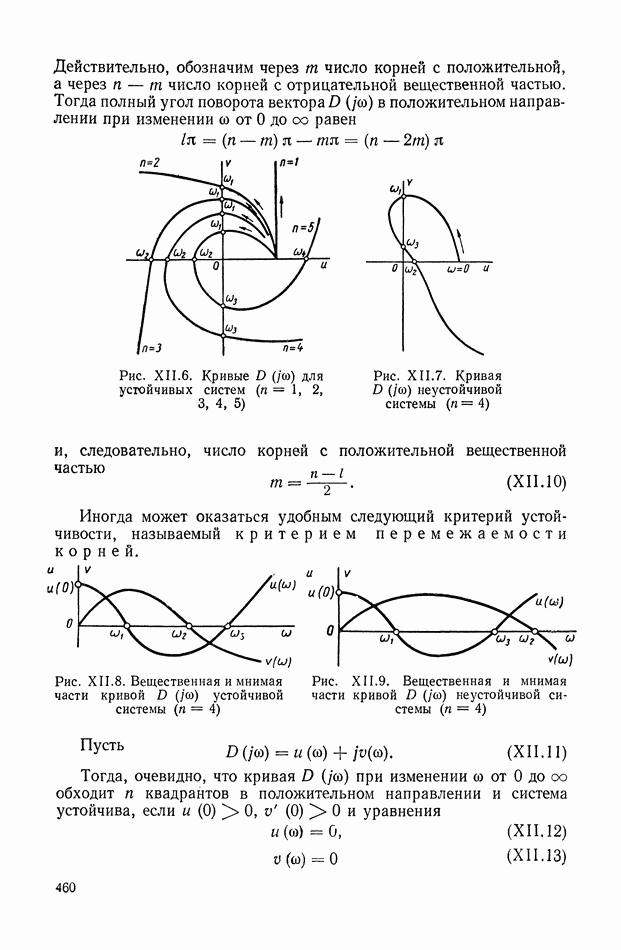
Цепь с  отделена от входа двумя звеньями, поэтому соответствующая цепь в схеме (рис. IX.38, б) содержит два дублирующих элемента (один из них инвертированный). Установим, какой сигнал будет действовать по этой схеме между сумматорами 1 и 4. Очевидно, функция
отделена от входа двумя звеньями, поэтому соответствующая цепь в схеме (рис. IX.38, б) содержит два дублирующих элемента (один из них инвертированный). Установим, какой сигнал будет действовать по этой схеме между сумматорами 1 и 4. Очевидно, функция  и будет общей функцией правой части уравнения связи. Соблюдая порядок операций, запишем
и будет общей функцией правой части уравнения связи. Соблюдая порядок операций, запишем

При дифференцировании произведения  удобно применить символы дифференцирования по
удобно применить символы дифференцирования по  адресованные только к функциям, отмеченным в индексах, и являющиеся аналогами
адресованные только к функциям, отмеченным в индексах, и являющиеся аналогами
частных производных. На основе этих обозначений перепишем формулу Лейбница для производной от двух сомножителей:

Применяя обозначения (IX.129а) и (IX.1296) вформуле (IX.128), получим

Далее реализуем операцию дифференцирования, адресованную к  в форме
в форме

а символ  оставим непреобразованным, сгруппировав члены с одинаковыми показателями степени
оставим непреобразованным, сгруппировав члены с одинаковыми показателями степени 

Поскольку правая часть уравнения связи для  обычно записывается так:
обычно записывается так:

где индекс  символа дифференцирования опущен, то, решая уравнения балансов коэффициентов при одинаковых степенях
символа дифференцирования опущен, то, решая уравнения балансов коэффициентов при одинаковых степенях  в уравнениях
в уравнениях  получим
получим

Эти уравнения последовательно решаются для функций  и позволяют по правой части уравнения (IX. 131) строить преобразованную детализированную структуру (рис. IX.38, а) без дифференциаторов, но с дополнительными связями, содержащими найденные функции
и позволяют по правой части уравнения (IX. 131) строить преобразованную детализированную структуру (рис. IX.38, а) без дифференциаторов, но с дополнительными связями, содержащими найденные функции 
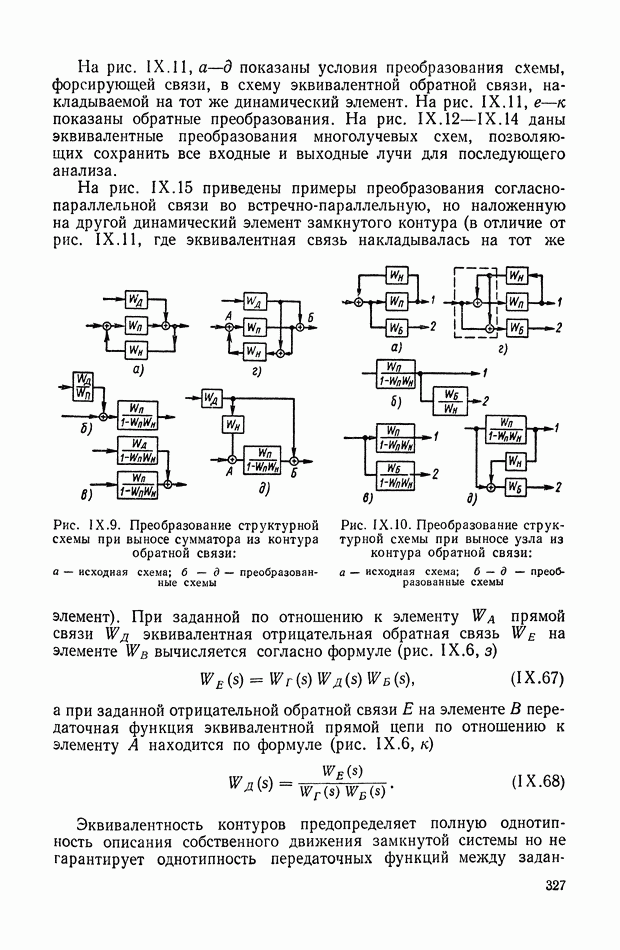
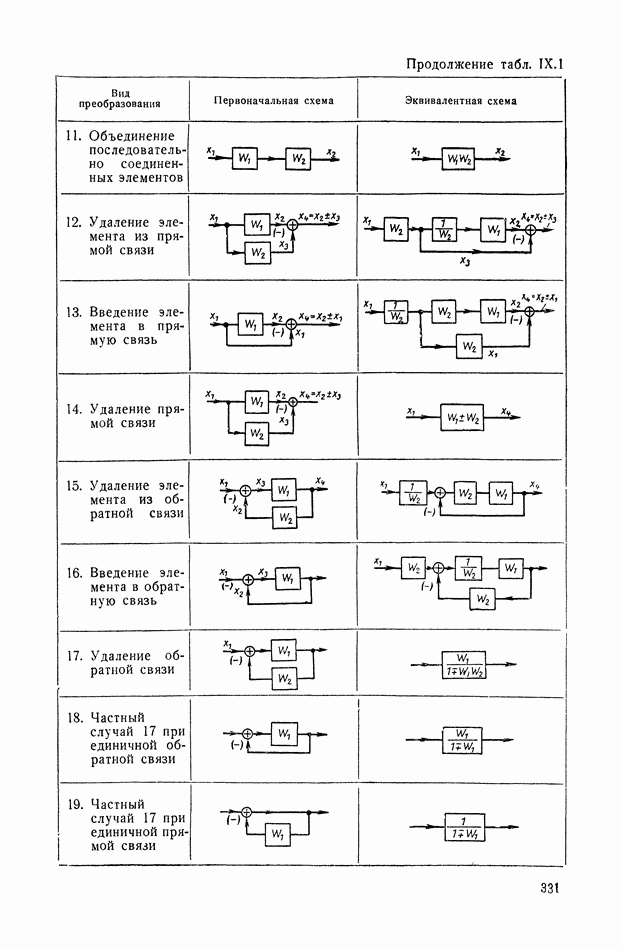
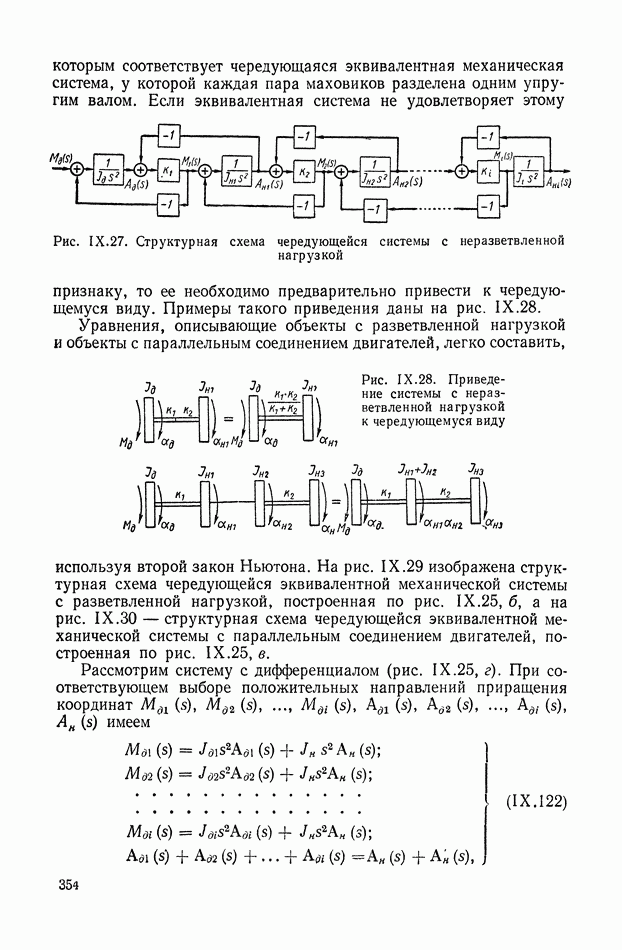
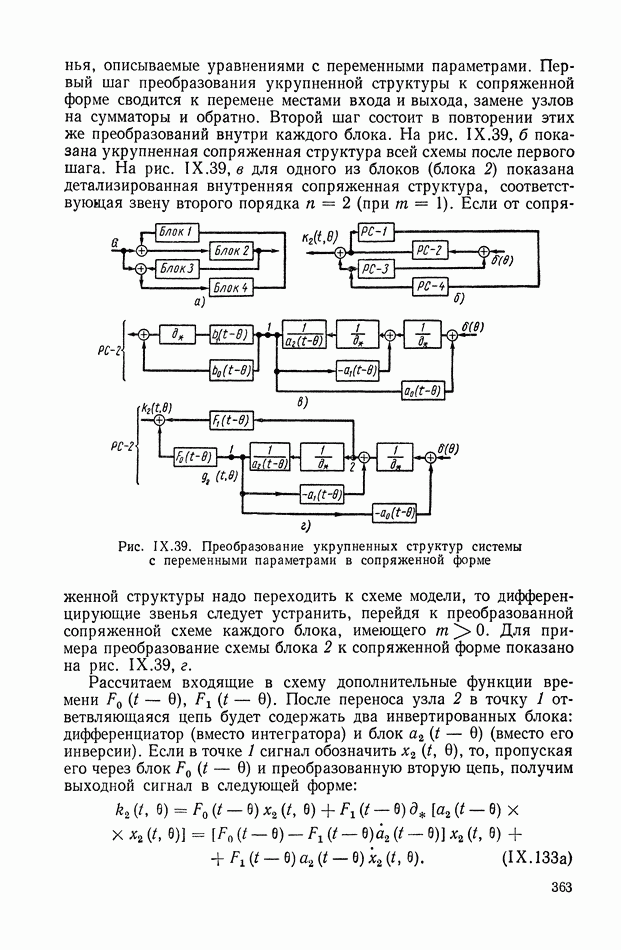
Преобразование сложных переменных структур к сопряженной форме. Приведенные в § 4 правила перехода от детализированной структуры переменной системы к сопряженной ей структуре могут быть развиты и многократно применены для укрупненных структур, например, типа, показанного на рис. IX.39, а, где блоками 1—4 схемы служат
звенья, описываемые уравнениями с переменными параметрами. Первый шаг преобразования укрупненной структуры к сопряженной форме сводится к перемене местами входа и выхода, замене узлов на сумматоры и обратно. Второй шаг состоит в повторении этих же преобразований внутри каждого блока. На рис. IX.39, б показана укрупненная сопряженная структура всей схемы после первого шага. На рис. IX.39, в для одного из блоков (блока 2) показана детализированная внутренняя сопряженная структура, соответствующая звену второго порядка 

Рис. IX.39. Преобразование укрупненных структур системы с переменными параметрами в сопряженной форме
Если от сопряженной структуры надо переходить к схеме модели, то дифференцирующие звенья следует устранить, перейдя к преобразованной сопряженной схеме каждого блока, имеющего  Для примера преобразование схемы блока 2 к сопряженной форме показано на рис. IX.39, г.
Для примера преобразование схемы блока 2 к сопряженной форме показано на рис. IX.39, г.
Рассчитаем входящие в схему дополнительные функции времени  После переноса узла 2 в точку 1 ответвляющаяся цепь будет содержать два инвертированных блока: дифференциатор (вместо интегратора) и блок
После переноса узла 2 в точку 1 ответвляющаяся цепь будет содержать два инвертированных блока: дифференциатор (вместо интегратора) и блок  (вместо его инверсии). Если в точке 1 сигнал обозначить
(вместо его инверсии). Если в точке 1 сигнал обозначить  то, пропуская его через блок
то, пропуская его через блок  и преобразованную вторую цепь, получим выходной сигнал в следующей форме:
и преобразованную вторую цепь, получим выходной сигнал в следующей форме:

Так как в схеме (рис. IX.39) имеется следующее соотношение:

решая уравнения балансов для двух последних уравнений (IX. 133а) и (IX. 1336), получим сначала одну неизвестную функцию

а затем вторую

Таким путем определяются все коэффициенты в дополнительных цепях преобразованных структур типа рис. IX.39, г. Если в исходной схеме встречаются звенья с постоянными параметрами, то они могут быть подключены в сопряженную модель в виде реальной аппаратуры, так как для случая постоянства параметров преобразование к сопряженной форме схему звена не изменяет.
Преобразования параметрическихструк-турных схем. Этот раздел связан прежде всего с понятием параметрической передаточной функции  (см. рис. IX.1, и). При этом отметим, что введение в состав постоянной системы хотя бы одного переменного безынерционного коэффициента
(см. рис. IX.1, и). При этом отметим, что введение в состав постоянной системы хотя бы одного переменного безынерционного коэффициента  лишает преобразование Лапласа
лишает преобразование Лапласа  переводящего описание реакции системы из временной области
переводящего описание реакции системы из временной области  в область комплексного переменного
в область комплексного переменного  его основных преимуществ. В переменных системах нельзя получить алгебраическую связь между изображением реакции и воздействия и характеризовать передаточные свойства системы передаточной функцией, независящей от вида сигналов.
его основных преимуществ. В переменных системах нельзя получить алгебраическую связь между изображением реакции и воздействия и характеризовать передаточные свойства системы передаточной функцией, независящей от вида сигналов.
Приведенные на рис. IX.1, и, к структуры несколько расширяют возможности структурного анализа переменных систем на основе применения метода  -преобразования в области комплексного переменного
-преобразования в области комплексного переменного  но не приближают исследователя к получению передаточной функции. Действительно, рассмотрим для упрощения анализа схему из двух элементов, содержащую входной стационарный элемент с передаточной функцией
но не приближают исследователя к получению передаточной функции. Действительно, рассмотрим для упрощения анализа схему из двух элементов, содержащую входной стационарный элемент с передаточной функцией  и переменный коэффициент
и переменный коэффициент  на выходе системы. Подавая на вход такой системы воздействие
на выходе системы. Подавая на вход такой системы воздействие  получим реакцию
получим реакцию

в форме изображения по Лапласу ( -изображения). Однако полученное решение не позволяет из отношения изображений
-изображения). Однако полученное решение не позволяет из отношения изображений

выделить сомножитель, независящий от входного сигнала и играющий роль передаточной функции. Эта задача решается при переходе ко второму временному аргументу 0 — рабочему интервалу. Функции этого аргумента обозначают звездочкой  также как и изображения по Лапласу
также как и изображения по Лапласу  переводящие функции, являющиеся решением сопряженных уравнений, из области временного аргумента 0 в область комплексного аргумента
переводящие функции, являющиеся решением сопряженных уравнений, из области временного аргумента 0 в область комплексного аргумента  Структурные схемы в ряде случаев облегчают получение параметрической передаточной функции системы при известных параметрических передаточных функциях элементов и повышают наглядность этой операции. Перейдем к рассмотрению некоторых типовых схем.
Структурные схемы в ряде случаев облегчают получение параметрической передаточной функции системы при известных параметрических передаточных функциях элементов и повышают наглядность этой операции. Перейдем к рассмотрению некоторых типовых схем.
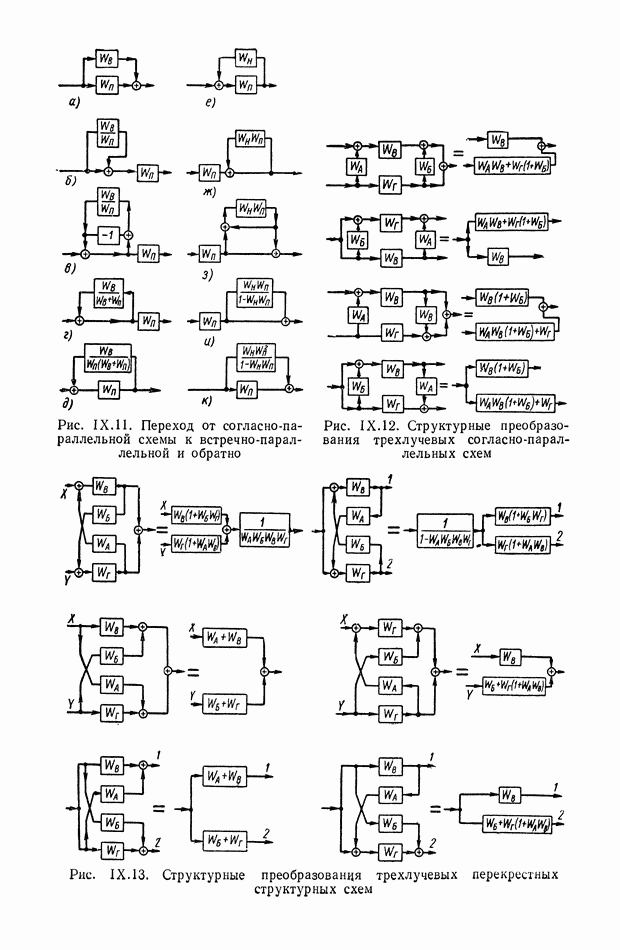
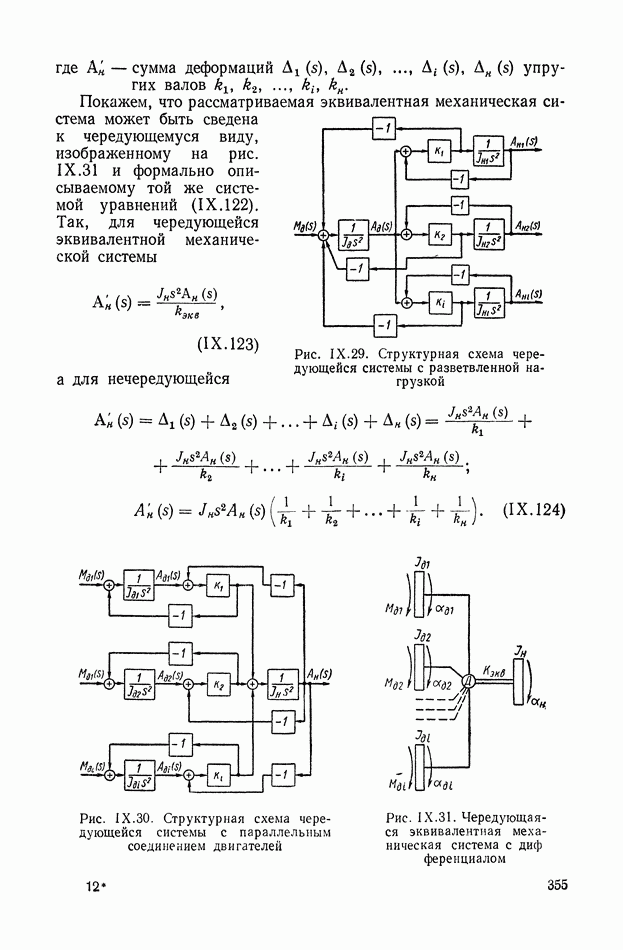
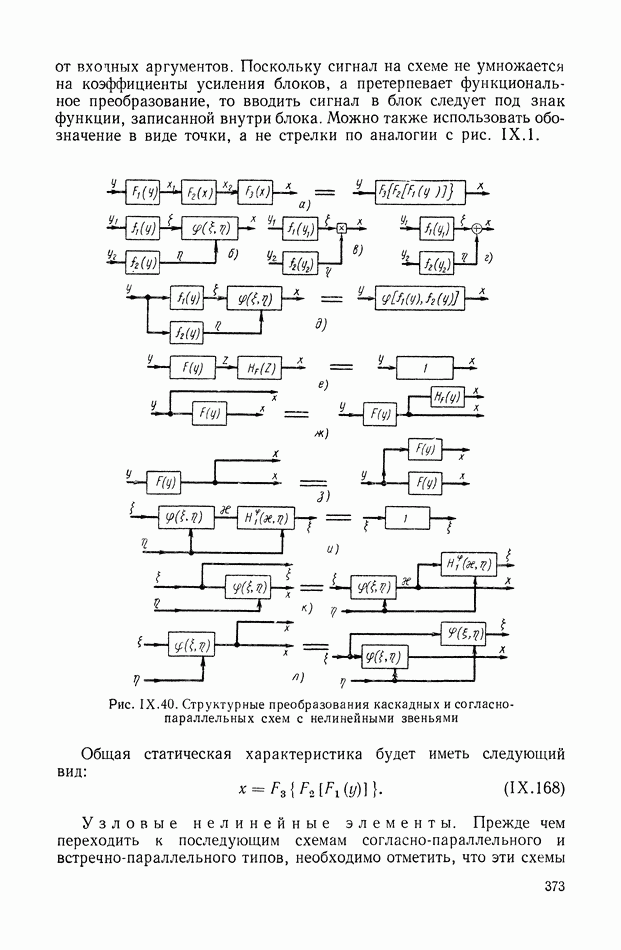
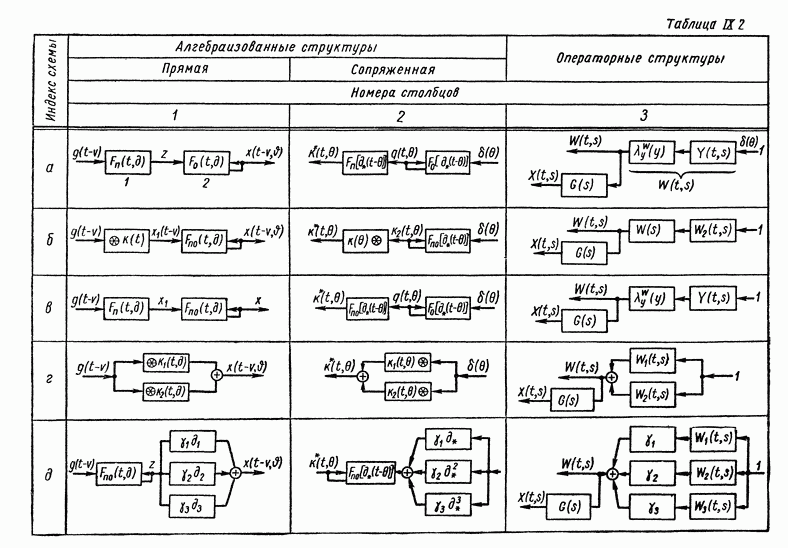
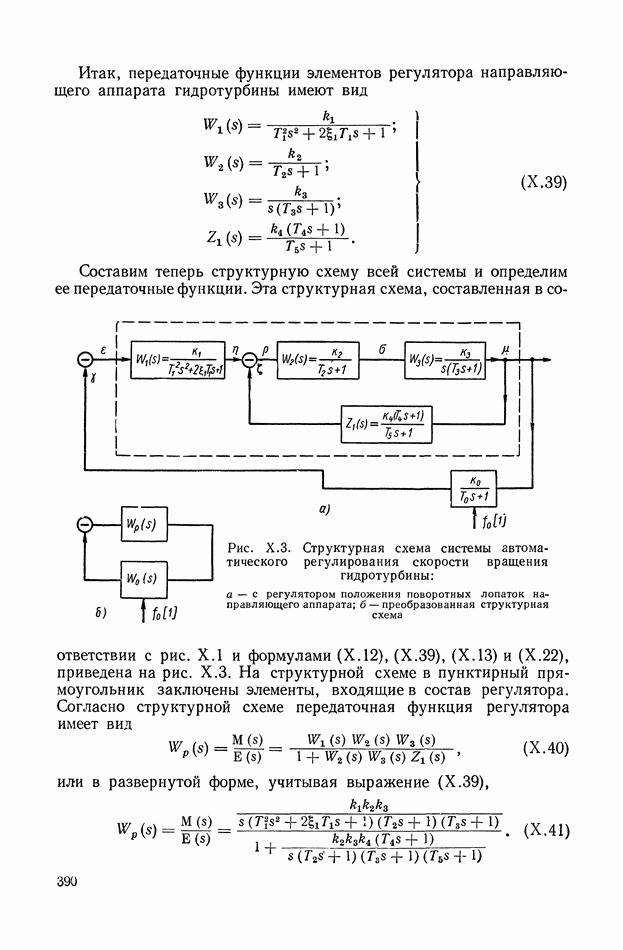
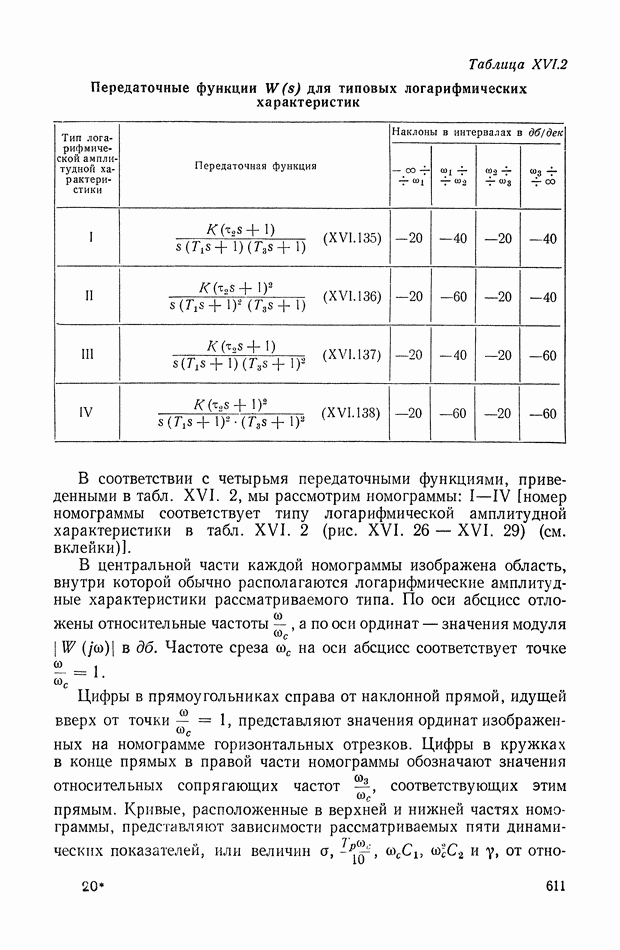
В табл. IX.2 приведены примеры структурных преобразований каскадных и согласно-параллельных схем соединений динамических элементов (см. стр. 379).
В 1-м столбце приведены физические или прямые схемы соединения элементов и заданы их уравнения в алгебраизованной форме. Во  столбце иллюстрируется структура весовой функции той же схемы, но в сопряженной форме, причем уравнения динамических элементов заданы для области второго — временного аргумента. В 3-м столбце показаны условия перехода к операторной структурной схеме, возбуждаемой импульсом, который имеет единичное изображение
столбце иллюстрируется структура весовой функции той же схемы, но в сопряженной форме, причем уравнения динамических элементов заданы для области второго — временного аргумента. В 3-м столбце показаны условия перехода к операторной структурной схеме, возбуждаемой импульсом, который имеет единичное изображение 
В табл. IX.2 включены в основном случаи, когда в уравнениях динамических элементов имеются некоторые упрощения, позволяющие наглядно иллюстрировать структурные преобразования.
Рассмотрим каждый из этих случаев. Схемы будем различать по индексу  и номеру столбца (1—3).
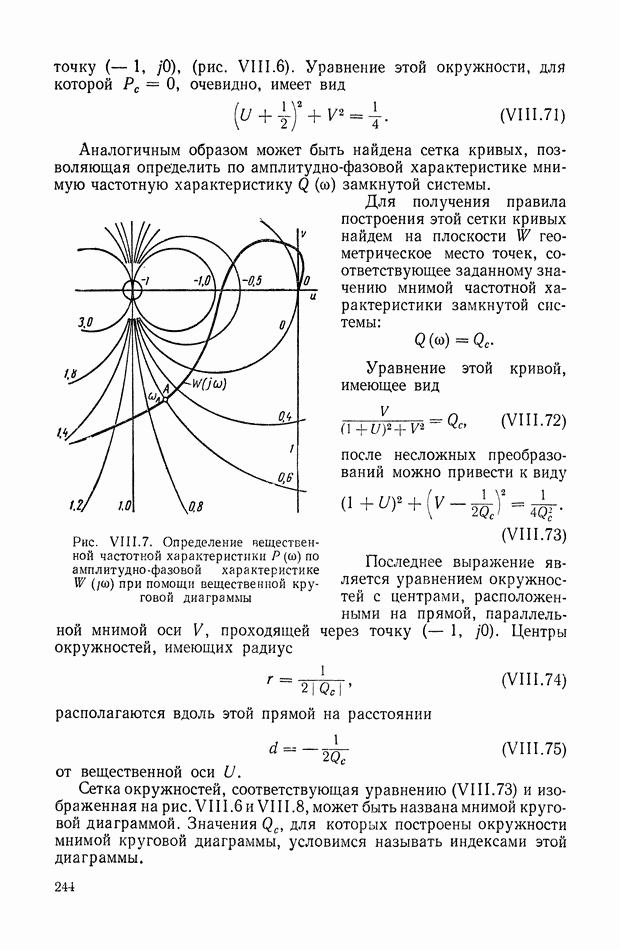
и номеру столбца (1—3).
Каскадные схемы (а — в). Входной элемент задан уравнением с приведенной левой частью, и выходной элемент описывается уравнением с приведенной правой частью. Уравнения динамических элементов запишем сначала во временной области в общей форме:

где входное воздействие  задано процессом установленной формы, но с произвольным смещением Ф относительно момента
задано процессом установленной формы, но с произвольным смещением Ф относительно момента  являющегося началом изменения переменных коэффициентов системы. Решение уравнения (IX. 136) обозначено
являющегося началом изменения переменных коэффициентов системы. Решение уравнения (IX. 136) обозначено  . Решение уравнения (IX.137) на входной единичный импульс
. Решение уравнения (IX.137) на входной единичный импульс  называется приведенной весовой функцией
называется приведенной весовой функцией  , так как вся правая часть уравнения (IX. 137) сведена в одну функцию
, так как вся правая часть уравнения (IX. 137) сведена в одну функцию  На схеме
На схеме  структурные свойства элементов записаны по аналогии с рис. IX. 1, ж
структурные свойства элементов записаны по аналогии с рис. IX. 1, ж
в виде функций  , характеризующих прямые и обратные связи в исходных детализированных структурах, соответствующих этим звеньям.
, характеризующих прямые и обратные связи в исходных детализированных структурах, соответствующих этим звеньям.
Перейдем теперь от прямой структуры  (табл. IX.2) к сопряженной структуре
(табл. IX.2) к сопряженной структуре  Согласно правилам преобразования к сопряженной форме начинать надо со второго элемента и его уравнения в сопряженной форме:
Согласно правилам преобразования к сопряженной форме начинать надо со второго элемента и его уравнения в сопряженной форме:

где

его решением служит параметрическая приведенная весовая функция 
На структурной схеме  получение функции
получение функции  связано с преобразованием
связано с преобразованием  отображающим детализированную сопряженную структуру с обратными связями.
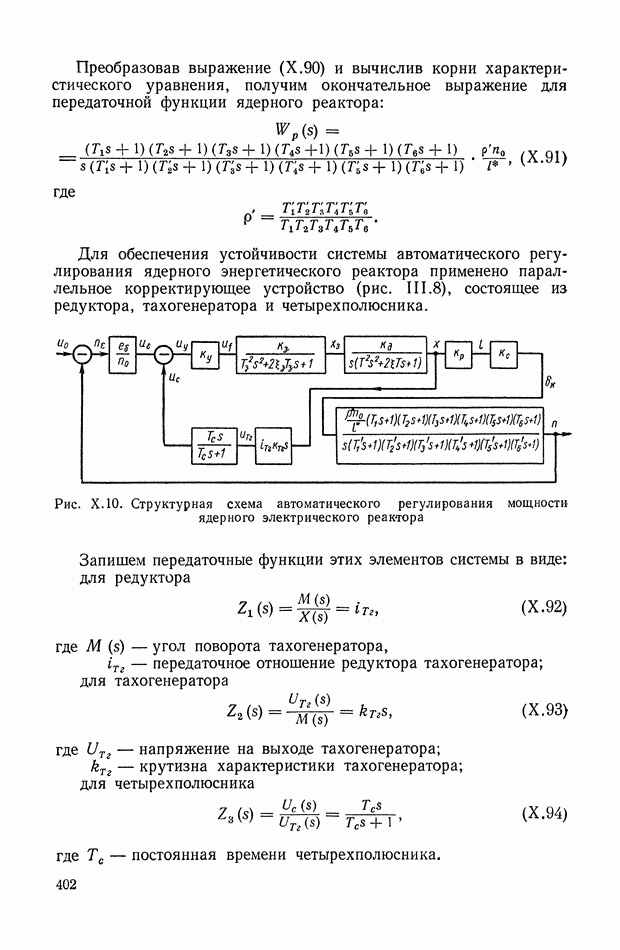
отображающим детализированную сопряженную структуру с обратными связями.
Далее следует обратиться к элементу (IX. 136); его реакция на смещенный импульс  определится из формулы
определится из формулы

Правая часть этой формулы получена на основе дифференцирующих свойств импульсов высокого порядка.
Переход к рабочему интервалу  дает сопряженное уравнение
дает сопряженное уравнение

Детализированная структура, соответствующая этой формуле, не имеет обратных связей, что отмечено индексом  в символе преобразования
в символе преобразования  Последовательность преобразований сигнала в сопряженной схеме
Последовательность преобразований сигнала в сопряженной схеме  обратна последовательности преобразований в прямой схеме
обратна последовательности преобразований в прямой схеме 
Для получения полной параметрической весовой функции на выходе сопряженной схемы  в уравнении (IX. 140) вместо одного импульса надо подставить реакцию на него второго элемента, т. е.
в уравнении (IX. 140) вместо одного импульса надо подставить реакцию на него второго элемента, т. е.  , что дает
, что дает

Итак, два уравнения (IX.138) и (IX. 141) отображают преобразования импульса сопряженной схемой в области второго временного аргумента  .
.
Допустим далее, что из уравнения (IX. 138) после  -преобразования в явной форме найдена приведенная параметрическая передаточная функция
-преобразования в явной форме найдена приведенная параметрическая передаточная функция  тогда преобразования импульса в области изображения можно отобразить на параметрической структуре
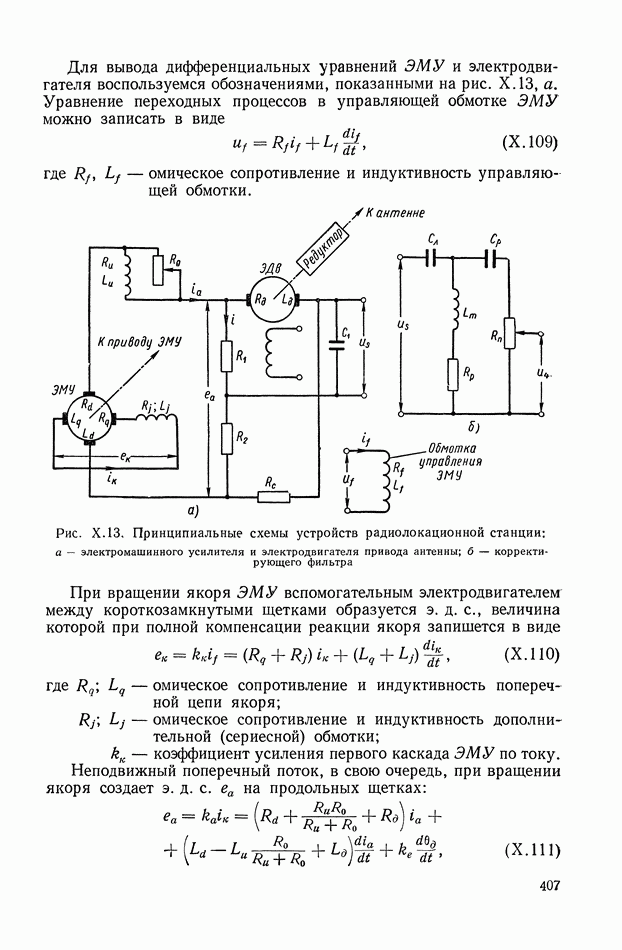
тогда преобразования импульса в области изображения можно отобразить на параметрической структуре  Теперь остается перейти к
Теперь остается перейти к  -изображениям в формуле (IX. 141). Для этого надо задать коэффициенты
-изображениям в формуле (IX. 141). Для этого надо задать коэффициенты  в форме конкретных функций. Так, при задании коэффициентов степенными рядами
в форме конкретных функций. Так, при задании коэффициентов степенными рядами

можно в формуле (IX. 141) сначала преобразовать по Лапласу приведенную весовую функцию, получив  а затем учесть добавочные операции:
а затем учесть добавочные операции:
дифференцирование этой параметрической передаточной функции по аргументу  в связи с умножением оригиналов на степень аргумента
в связи с умножением оригиналов на степень аргумента  ;
;
умножение на постоянные для второго временного аргумента функции 
умножение на  соответственно кратности дифференцирования
соответственно кратности дифференцирования  в области оригинала;
в области оригинала;
двукратное суммирование согласно формулам (IX. 139) и (IX. 140).
Итак, 

Все эти преобразования в области комплексного аргумента  могут быть обозначены общим символом переводящим приведенную параметрическую передаточную функцию в полную
могут быть обозначены общим символом переводящим приведенную параметрическую передаточную функцию в полную

Это преобразование записано на схеме  в верхней цепочке. Весовая функция такой системы получается на выходе цепочки при задании на входе схемы импульса
в верхней цепочке. Весовая функция такой системы получается на выходе цепочки при задании на входе схемы импульса  Изображение реакции в заданной точке наблюдения на любой входной процесс установленной формы с произвольным рабочим интервалом составит
Изображение реакции в заданной точке наблюдения на любой входной процесс установленной формы с произвольным рабочим интервалом составит

Это домножение на изображение входного процесса показано на структурной схеме  слева внизу, т. е. в конце цикла
слева внизу, т. е. в конце цикла
преобразования  -изображений. Таким образом, в параметрической структурной схеме последовательность участия элементов в преобразованиях изображений обратна последовательности, имеющейся в блочной схеме в области временного аргумента
-изображений. Таким образом, в параметрической структурной схеме последовательность участия элементов в преобразованиях изображений обратна последовательности, имеющейся в блочной схеме в области временного аргумента  и соответствует последовательности, имеющейся в сопряженной структуре
и соответствует последовательности, имеющейся в сопряженной структуре  Если речь идет только об общей параметрической передаточной функций схемы, то расположение входа и выхода не принципиально, что видно из сравнения рис.
Если речь идет только об общей параметрической передаточной функций схемы, то расположение входа и выхода не принципиально, что видно из сравнения рис.  и
и  Если входной элемент в схеме а содержит только один безынерционный коэффициент
Если входной элемент в схеме а содержит только один безынерционный коэффициент  при
при  то из суммы выражения (IX. 143) следует использовать только одно слагаемое при
то из суммы выражения (IX. 143) следует использовать только одно слагаемое при 

При задании коэффициента  трансцендентной функцией, например
трансцендентной функцией, например  после реверса аргумента
после реверса аргумента

коэффициент распадается на произведение двух функций с независимыми аргументами. В этом случае  -преобразование следует определить по сомножителю
-преобразование следует определить по сомножителю  в области оригинала, что дает в области изображений
в области оригинала, что дает в области изображений  Для экспоненциального масштаба получаем
Для экспоненциального масштаба получаем

Двухкаскадная схема со стационарным входным элементом. Во временной области сигнал  согласно схеме
согласно схеме  преобразуется постоянным звеном в сигнал
преобразуется постоянным звеном в сигнал  по формуле свертки
по формуле свертки

и имеет  -изображение
-изображение

поскольку его величина в момент наблюдения зависит только от рабочего интервала. Поэтому первый этап преобразования достаточно просто изображается на входе прямой структуры  , на выходах сопряженной структуры
, на выходах сопряженной структуры  и параметрической структурной схемы
и параметрической структурной схемы  Далее, в области первого и второго временных аргументов снова свойства переменных звеньев отображены через сокращенные символы детализированных структур одновременно с прямыми
Далее, в области первого и второго временных аргументов снова свойства переменных звеньев отображены через сокращенные символы детализированных структур одновременно с прямыми  и обратными
и обратными  связями
связями  для схемы
для схемы  для сопряженной схемы
для сопряженной схемы 
Операция  объединяет две отдельные операции
объединяет две отдельные операции  имеющиеся на схемах
имеющиеся на схемах  и
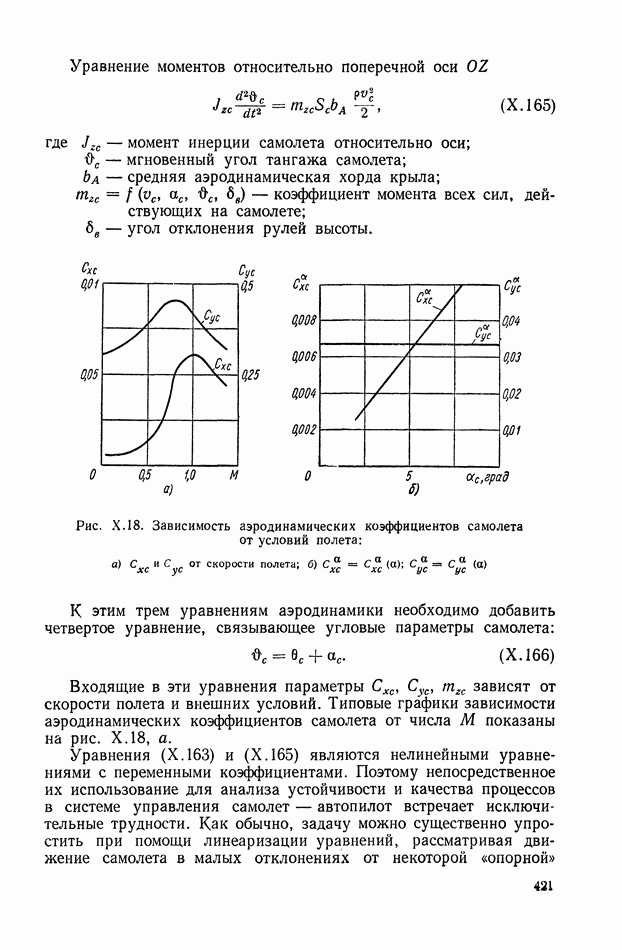
и 
Для области изображений (рис. IX. 1, з) имеем параметрическое изображение реакции

или с учетом выражения (IX. 148)

На структурной схеме  показана последовательность преобразования изображений звеньями также в обратном по сравнению со схемой
показана последовательность преобразования изображений звеньями также в обратном по сравнению со схемой  порядке соответственно правилам преобразований к сопряженной форме.
порядке соответственно правилам преобразований к сопряженной форме.
Входной переменный элемент с приведенной левой частью. Условия задания аналогичны схеме  но с другими исходными уравнениями:
но с другими исходными уравнениями:

Второй элемент можно представить в виде двух элементов с приведенными уравнениями, включенными согласно схеме 

Уравнения (IX. 150) и (IX. 153) могут быть объединены в одно прямой подстановкой, которая для импульсного входа будет иметь

Проводя дифференцирование произведений под знаком внутренней суммы по формуле Лейбница, получим

Внесем теперь коэффициенты  под общий символ трех сумм и используем правила умножения производной от импульса на непрерывную функцию
под общий символ трех сумм и используем правила умножения производной от импульса на непрерывную функцию  при одновременном реверсе аргумента
при одновременном реверсе аргумента  что изменяет и вид функции
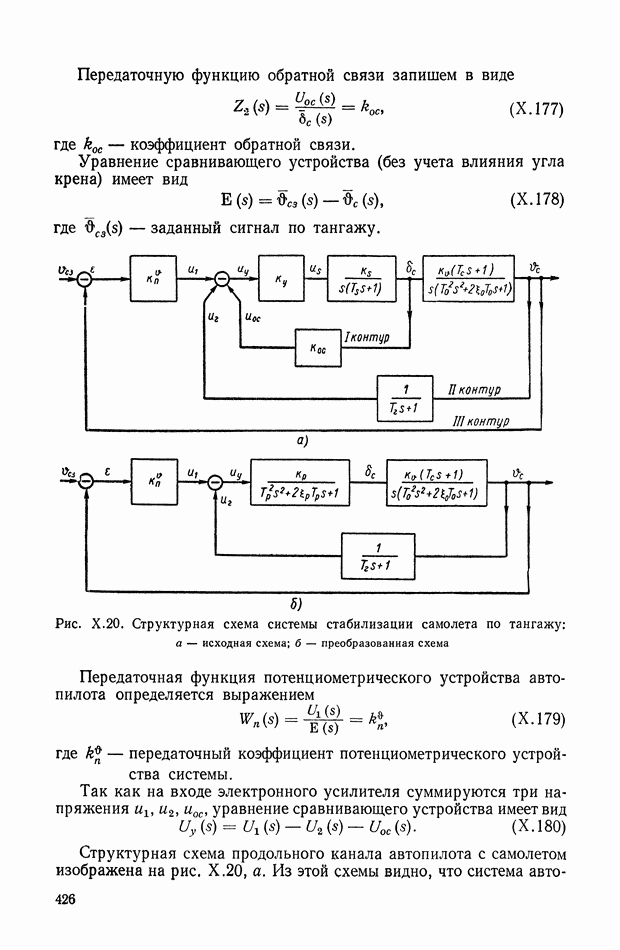
что изменяет и вид функции

Если снова переход от одного импульса к сложной функции  понимать как
понимать как  -преобразование, то это же преобразование остается для перехода от функции
-преобразование, то это же преобразование остается для перехода от функции  к функции к
к функции к  т. е.
т. е.

При переходе к  -изображениям в произведении функций
-изображениям в произведении функций  должны быть выделены сомножители, являющиеся известными функциями от
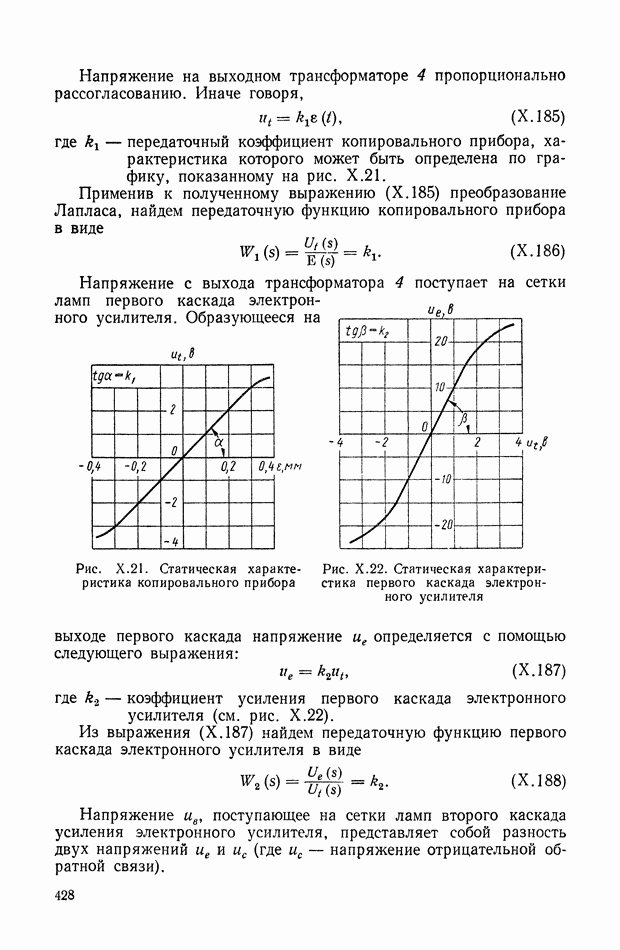
должны быть выделены сомножители, являющиеся известными функциями от  . Это можно осуществить, например, при разложении указанных произведений в ряды по степеням 0 аналогично выражению (IX. 142), тогда получим связь между изображениями:
. Это можно осуществить, например, при разложении указанных произведений в ряды по степеням 0 аналогично выражению (IX. 142), тогда получим связь между изображениями:

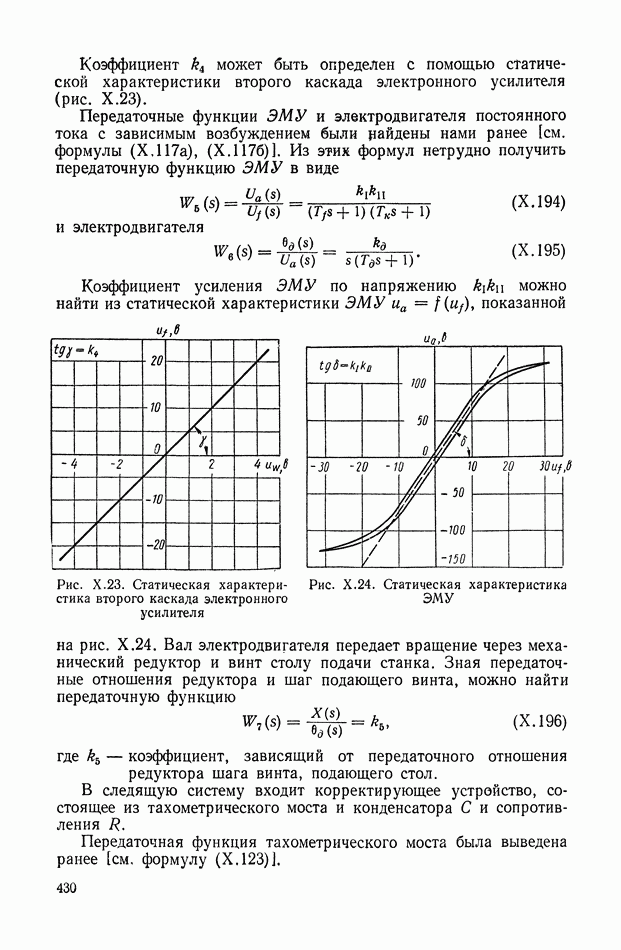
показанную на схеме  для импульсного и для произвольного входов.
для импульсного и для произвольного входов.
В простейшем случае, если звено 1 характеризуется только переменным коэффициентом усиления

предыдущая формула несколько упрощается, т. е.

Если произведение коэффициентов  содержит не только степени
содержит не только степени  , но и другие функции второго аргумента, то для перехода от
, но и другие функции второго аргумента, то для перехода от  используются дополнительные формы
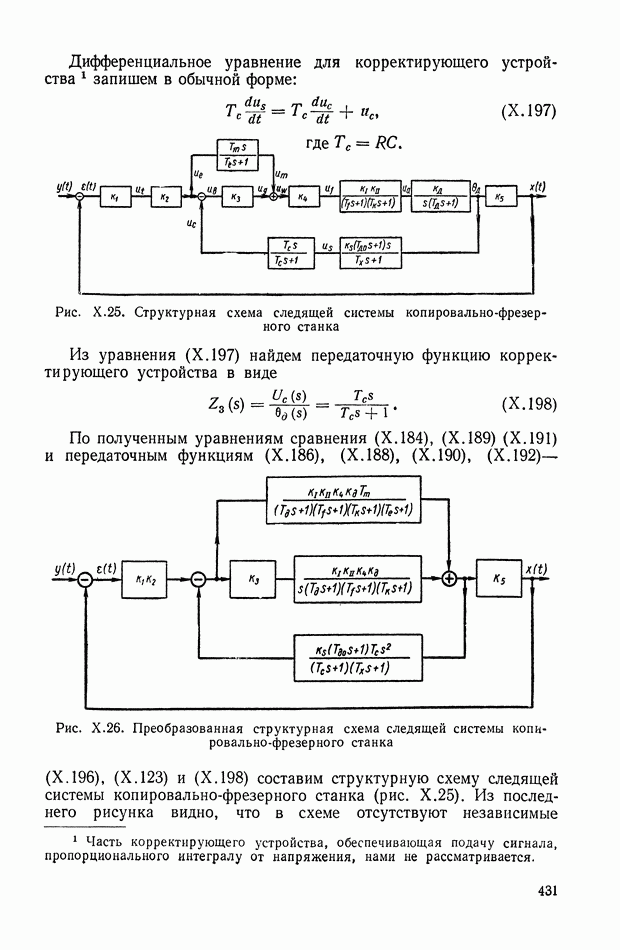
используются дополнительные формы  -преобразования.
-преобразования.
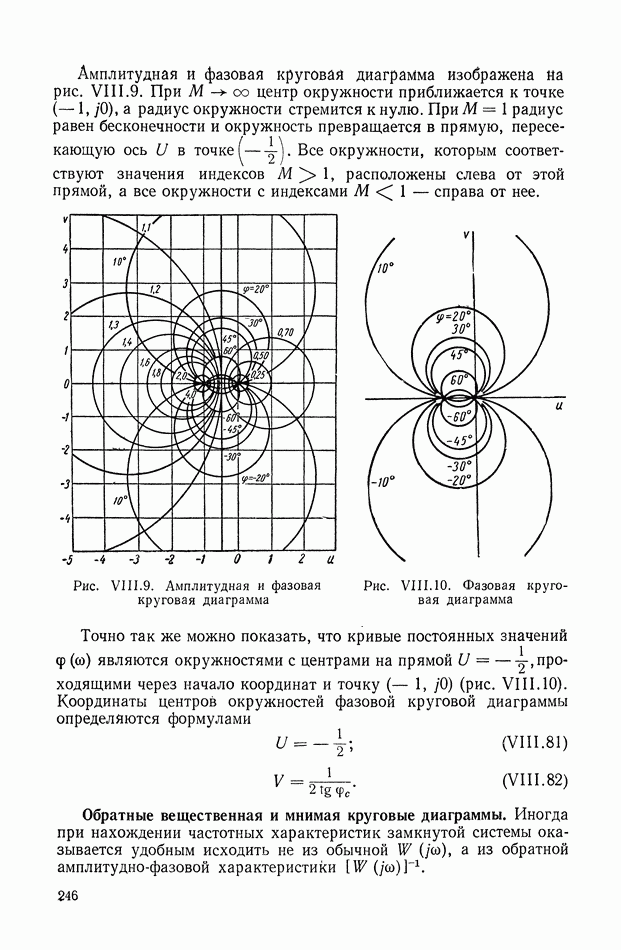
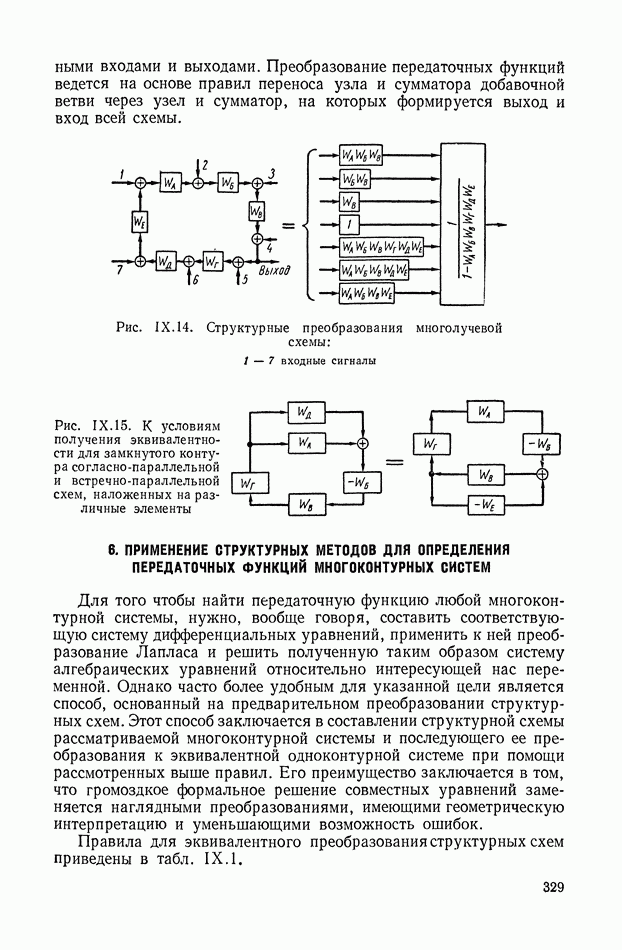
Согласно-параллельная схема (г). Согласно-параллельная схема  преобразуется в сопряженную схему
преобразуется в сопряженную схему  и затем в структурную схему
и затем в структурную схему  путем перехода от весовых функций звеньев к их параметрическим передаточным функциям и изменениям связей согласно правилам преобразований к сопряженной форме. При подаче на вход схемы
путем перехода от весовых функций звеньев к их параметрическим передаточным функциям и изменениям связей согласно правилам преобразований к сопряженной форме. При подаче на вход схемы  единичного импульса, имеющего единичное изображение, изображение реакции на выходе будет параметрической передаточной функцией согласно-параллельной схемы, которая легко свертывается к виду
единичного импульса, имеющего единичное изображение, изображение реакции на выходе будет параметрической передаточной функцией согласно-параллельной схемы, которая легко свертывается к виду

Двухкаскадная схема из входного переменного элемента и группы выходных дифференцирующих параллельно включенных элементов (д). Зададимся уравнениями элементов

В уравнении (IX. 158) поделим все коэффициенты на младший коэффициент левой части 

где нормированные коэффициенты обозначены

Далее произведем однократное дифференцирование

тогда, рассматривая  как самостоятельную функцию, из выражения (IX. 161) можно найти параметрическую передаточную функцию
как самостоятельную функцию, из выражения (IX. 161) можно найти параметрическую передаточную функцию

Заметим теперь, что в уравнении (IX. 161) при  имеется коэффициент
имеется коэффициент  , снова освобождаемся от этого коэффициента путем нормирования уравнения (IX.161), что дает
, снова освобождаемся от этого коэффициента путем нормирования уравнения (IX.161), что дает

где

Следующее дифференцирование выражения (IX. 163) приводит к результату 

Обозначая  из последнего выражения можно найти новую параметрическую передаточную функцию в виде
из последнего выражения можно найти новую параметрическую передаточную функцию в виде

Далее, нормируя выражение (IX. 165) и проводя дифференцирование, можно аналогичным путем найти следующую параметрическую передаточную функцию:

где 
Общая параметрическая передаточная функция схемы на основании выражения (IX. 159) будет иметь вид

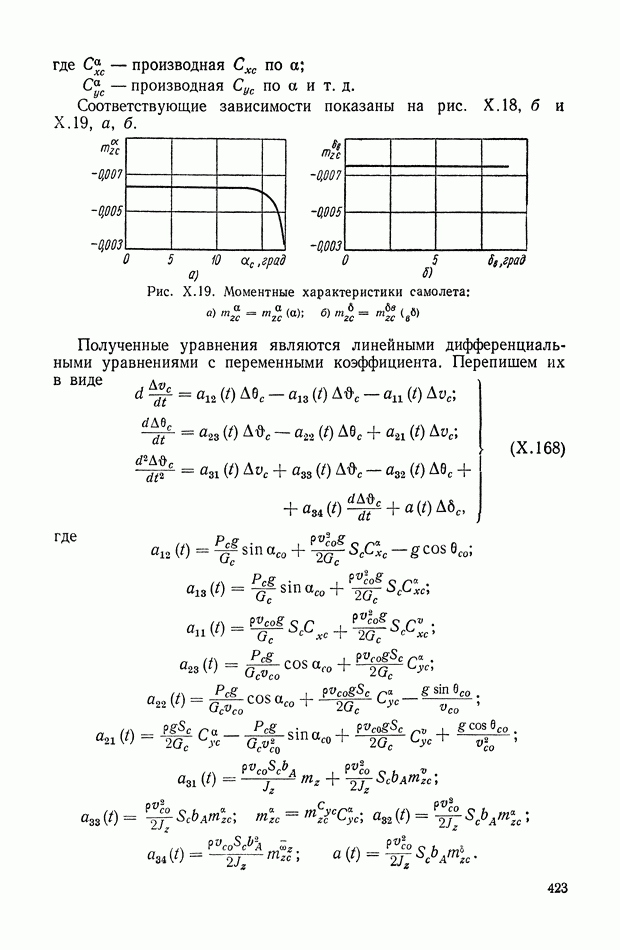
По выведенным формулам построены временная структура  сопряженная
сопряженная  и параметрическая структурная схема
и параметрическая структурная схема  Нетрудно заметить, что присоединение даже одного дифференцирующего звена к переменной системе требует сложных аналитических преобразований уравнений системы для получения общей структуры. При более сложных схемах, чем
Нетрудно заметить, что присоединение даже одного дифференцирующего звена к переменной системе требует сложных аналитических преобразований уравнений системы для получения общей структуры. При более сложных схемах, чем  общее представление о системе возможно получить только на основе аналитических преобразований, которые могут сочетаться со структурными представлениями.
общее представление о системе возможно получить только на основе аналитических преобразований, которые могут сочетаться со структурными представлениями.
Следует отметить, что все структурные преобразования схем систем с постоянными коэффициентами, основанные на принципе прямого дублирования, сохраняются и для переменных систем.
Структурные преобразования, требовавшие в случае постоянных систем инверсного дублирования, проводятся и для переменных систем. В этом случае также появляются инверсные операции.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- РАЗДЕЛ I. ОБЩИЕ СВЕДЕНИЯ. МЕТОДЫ МАТЕМАТИЧЕСКОГО ОПИСАНИЯ И СТРУКТУРНОГО ПРЕОБРАЗОВАНИЯ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- ГЛАВА I. ОЧЕРК О РАЗВИТИИ ТЕОРИИ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ В СССР
- 1. ТЕОРИЯ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ В ДОРЕВОЛЮЦИОННЫЙ ПЕРИОД
- 2. РАЗВИТИЕ ТЕОРИИ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ПОСЛЕ ОКТЯБРЬСКОЙ СОЦИАЛИСТИЧЕСКОЙ РЕВОЛЮЦИИ
- ГЛАВА II. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ ТЕОРИИ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
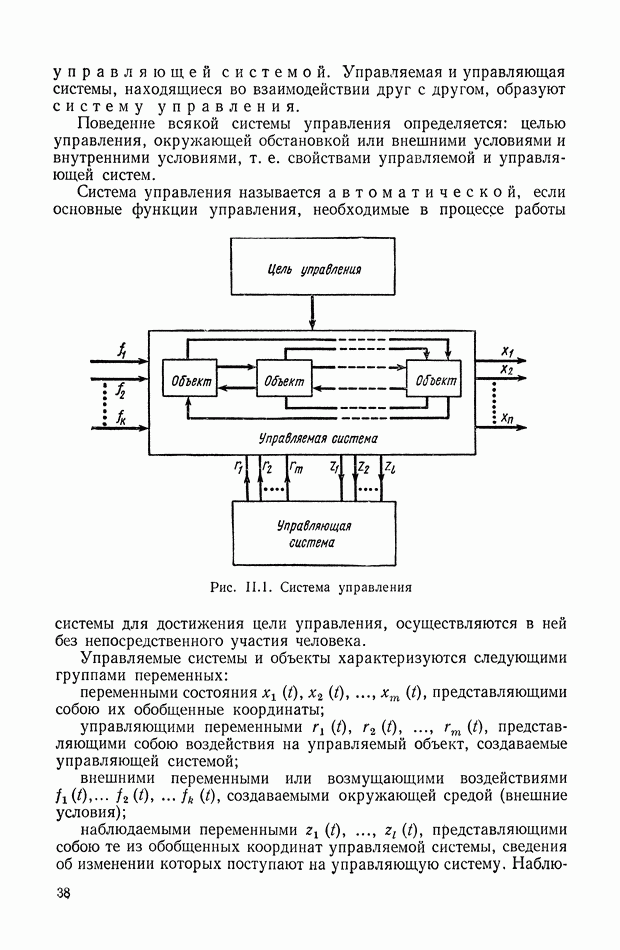
- 1. СУЩНОСТЬ ПРОБЛЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
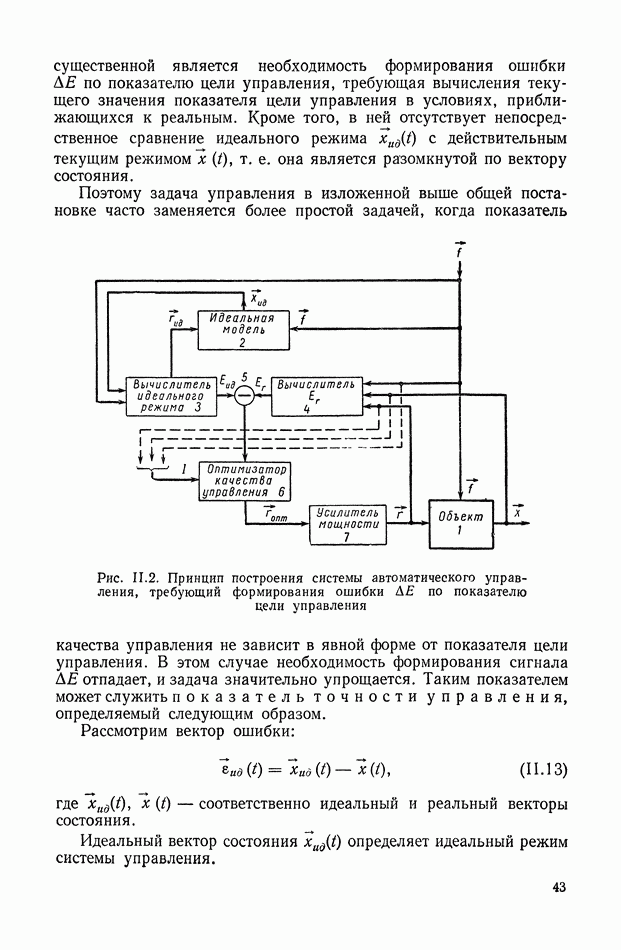
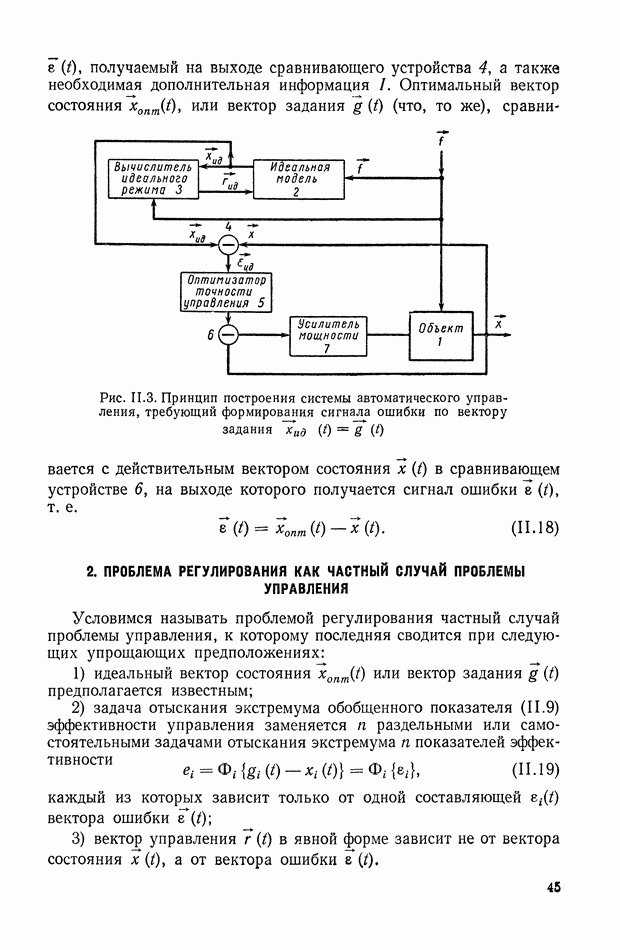
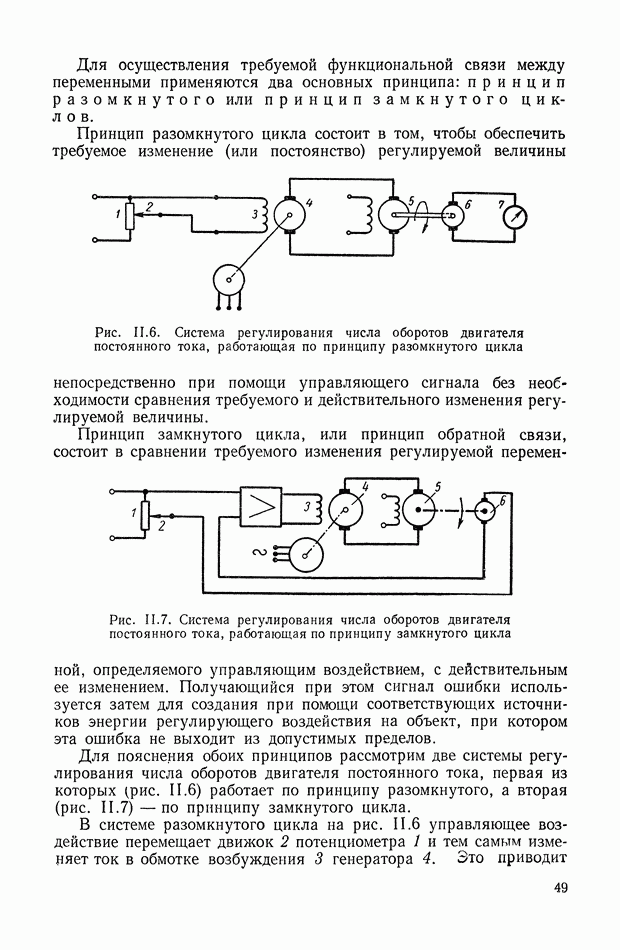
- 2. ПРОБЛЕМА РЕГУЛИРОВАНИЯ КАК ЧАСТНЫЙ СЛУЧАЙ ПРОБЛЕМЫ УПРАВЛЕНИЯ
- 3. ОСНОВНОЙ ПРИНЦИП ДЕЙСТВИЯ И ОПРЕДЕЛЕНИЕ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 4. КЛАССИФИКАЦИЯ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ В ЗАВИСИМОСТИ ОТ УПРАВЛЯЮЩЕГО ВОЗДЕЙСТВИЯ
- 5. ОСНОВНЫЕ УСТРОЙСТВА СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ И ИХ КЛАССИФИКАЦИЯ ПО НАЗНАЧЕНИЮ
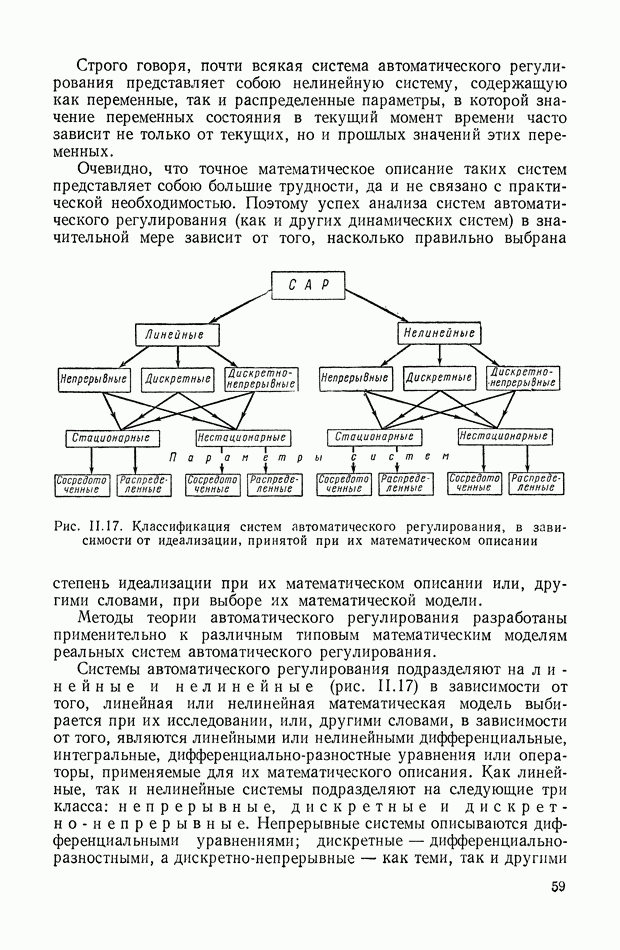
- 6. КЛАССИФИКАЦИЯ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ В ЗАВИСИМОСТИ ОТ ХАРАКТЕРА СИГНАЛОВ
- 7. КЛАССИФИКАЦИЯ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ В ЗАВИСИМОСТИ ОТ ИДЕАЛИЗАЦИИ, ПРИНЯТОЙ ПРИ ИХ МАТЕМАТИЧЕСКОМ ОПИСАНИИ
- 8. СТРУКТУРНЫЕ СХЕМЫ, ОДНОКОНТУРНЫЕ И МНОГОКОНТУРНЫЕ, НЕСВЯЗАННЫЕ И СВЯЗАННЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
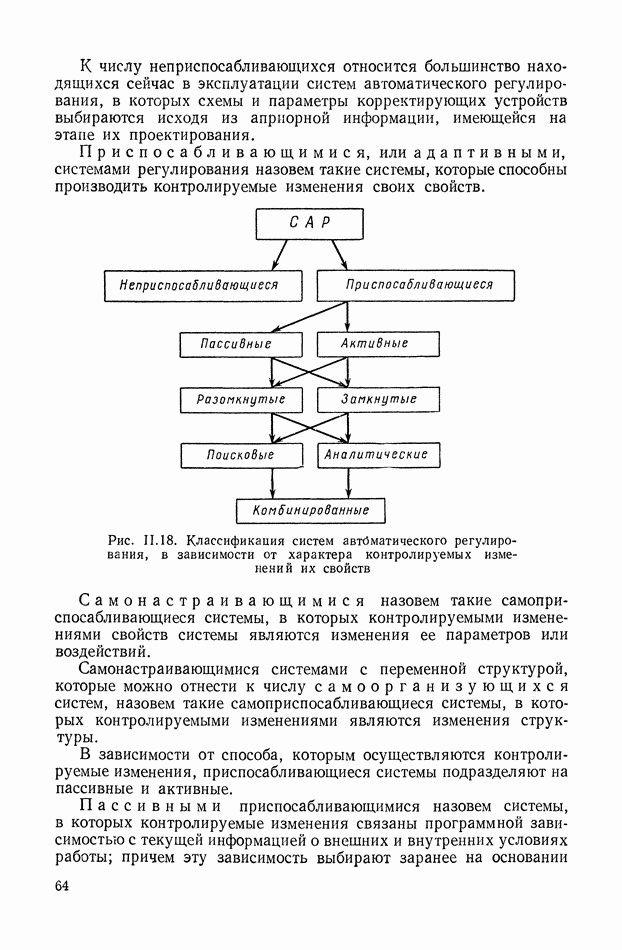
- 9. КЛАССИФИКАЦИЯ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ В ЗАВИСИМОСТИ ОТ ХАРАКТЕРА КОНТРОЛИРУЕМЫХ ИЗМЕНЕНИЙ
- 10. ТРЕБОВАНИЯ, ПРЕДЪЯВЛЯЕМЫЕ К ДИНАМИЧЕСКИМ СВОЙСТВАМ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- ГЛАВА III. ОСНОВНЫЕ УСТРОЙСТВА И ТИПОВЫЕ СХЕМЫ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. КРАТКАЯ ХАРАКТЕРИСТИКА УСТРОЙСТВ, ИЗ КОТОРЫХ СОСТОЯТ СИСТЕМЫ РЕГУЛИРОВАНИЯ
- 2. СИСТЕМА АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ СКОРОСТИ ГИДРОТУРБИНЫ
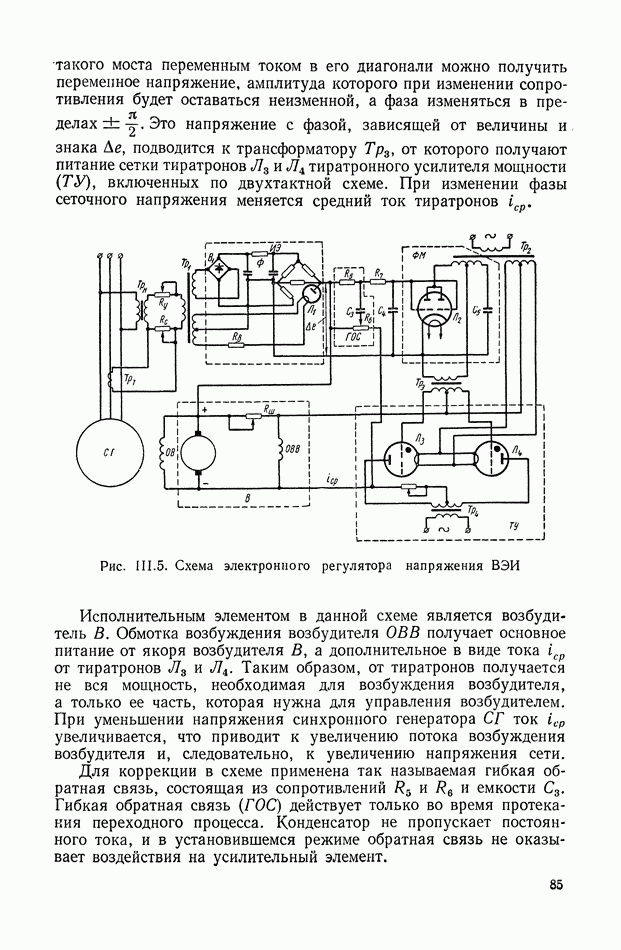
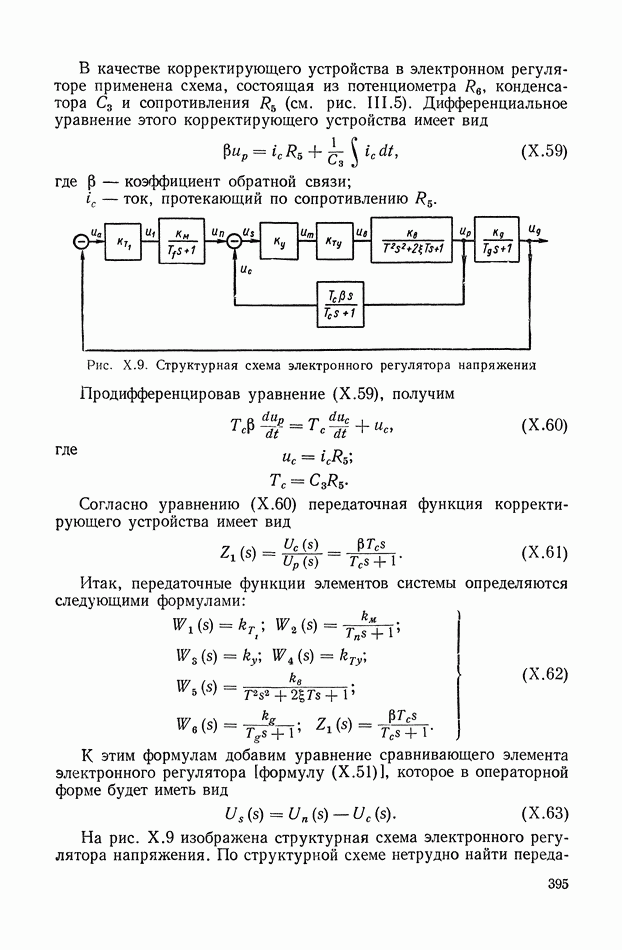
- 3. ЭЛЕКТРОННЫЙ РЕГУЛЯТОР НАПРЯЖЕНИЯ ВЭИ
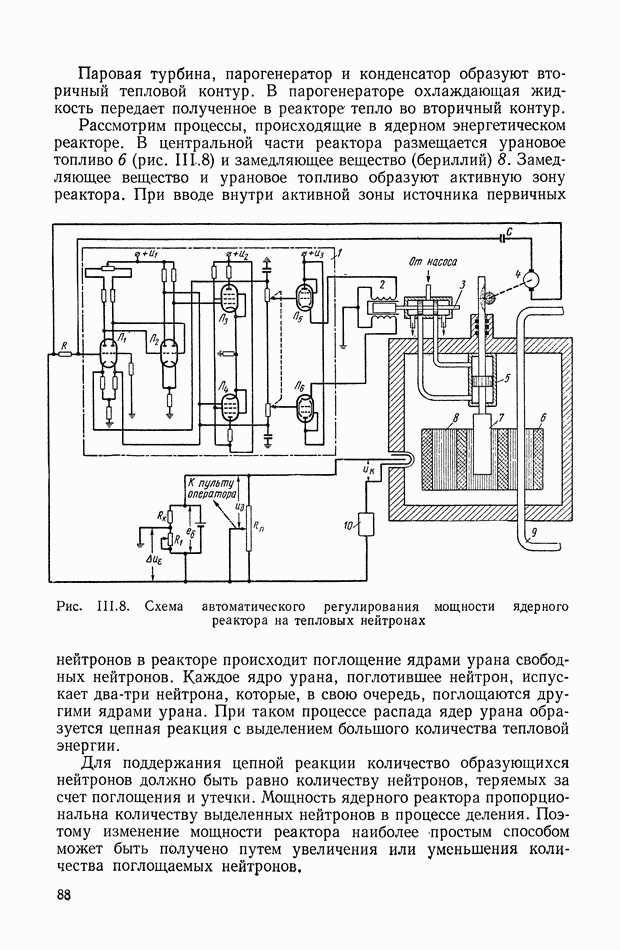
- 4. СИСТЕМА АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ЯДЕРНОГО РЕАКТОРА ПО МОЩНОСТИ
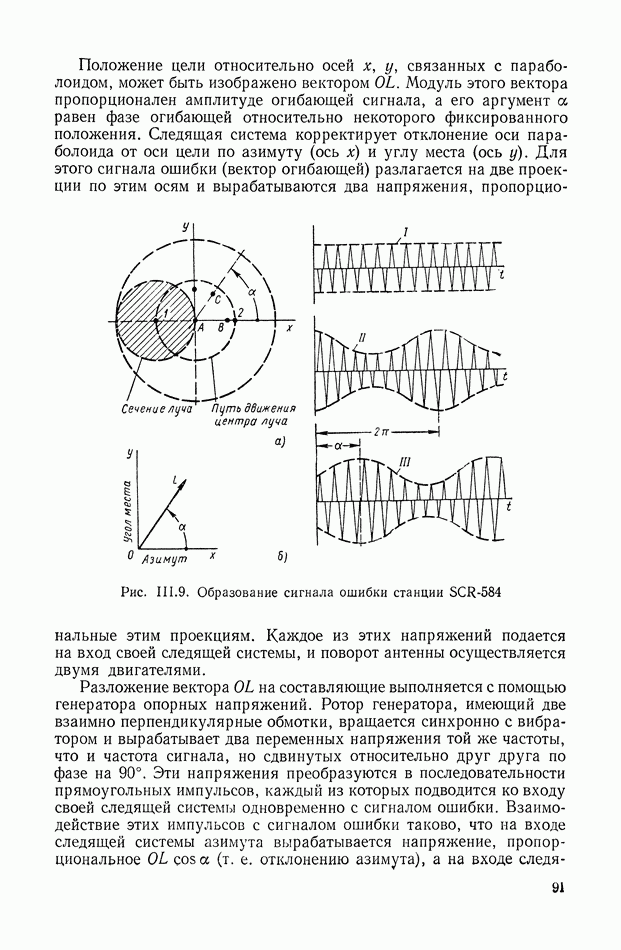
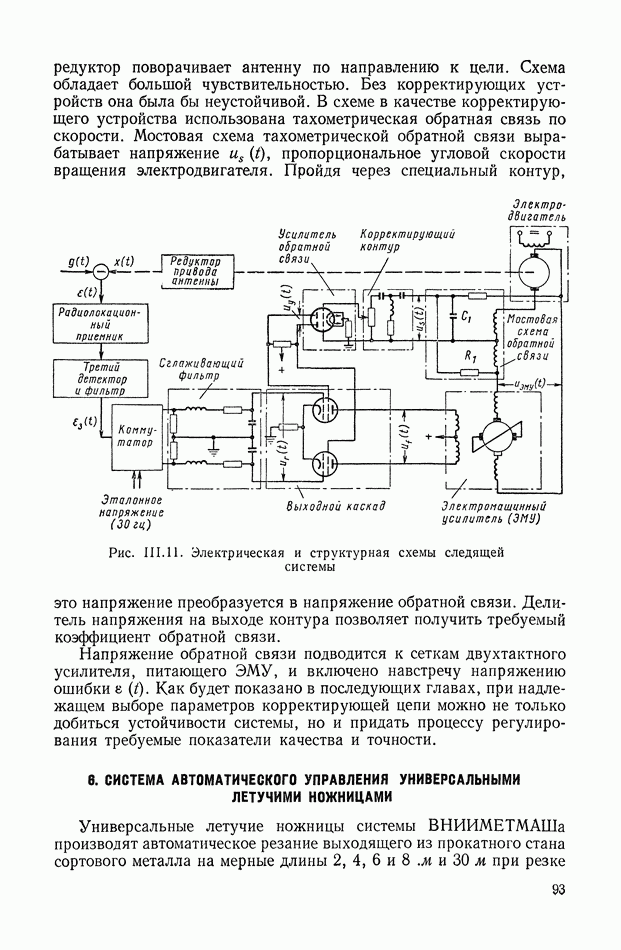
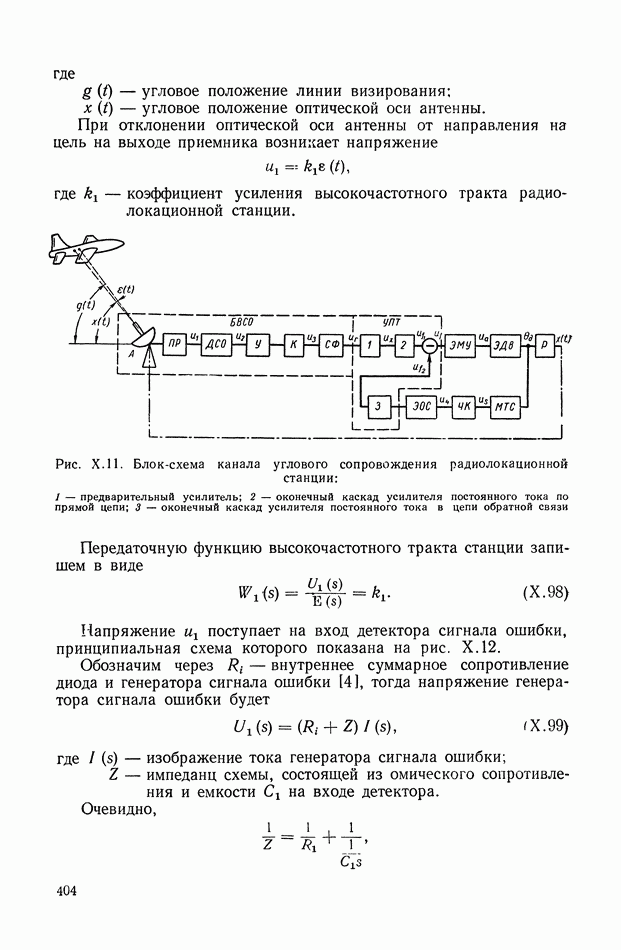
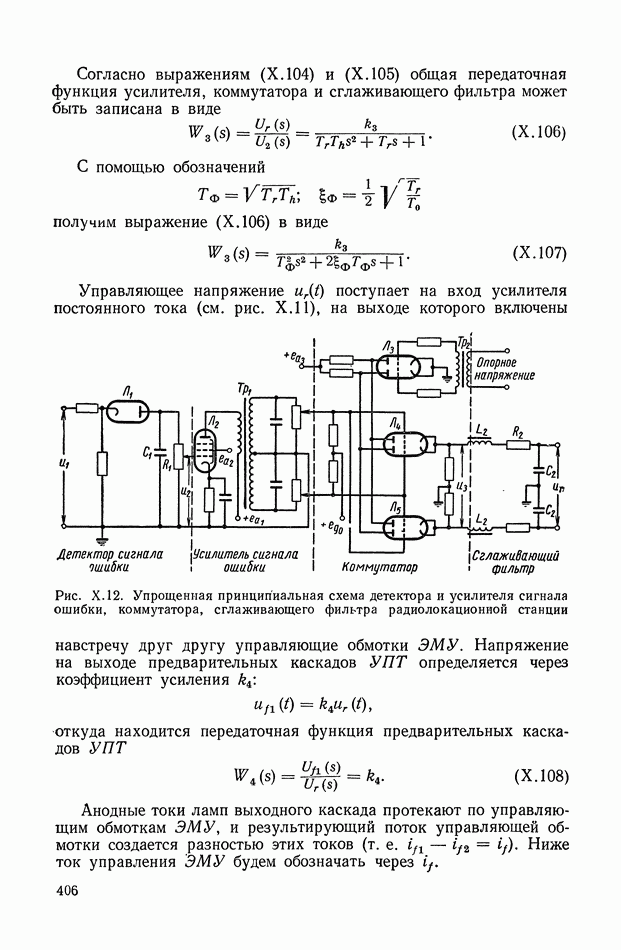
- 5. СЛЕДЯЩАЯ СИСТЕМА РАДИОЛОКАЦИОННОЙ СТАНЦИИ
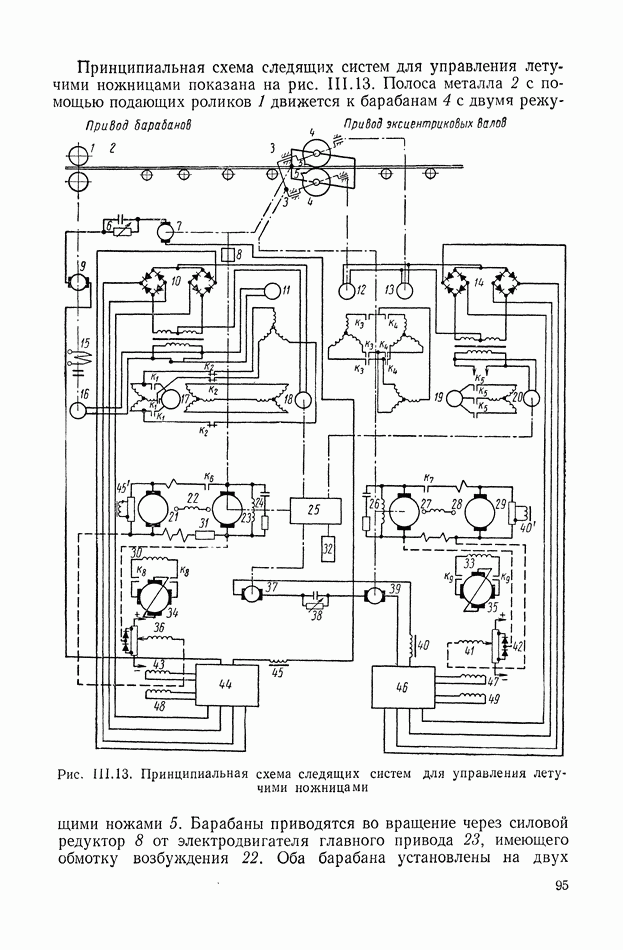
- 6. СИСТЕМА АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ УНИВЕРСАЛЬНЫМИ ЛЕТУЧИМИ НОЖНИЦАМИ
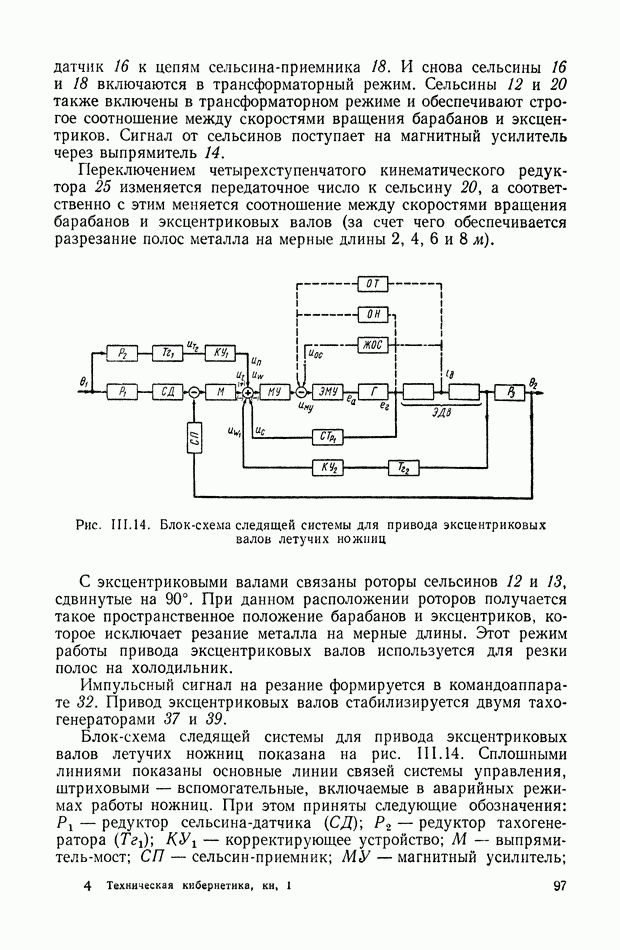
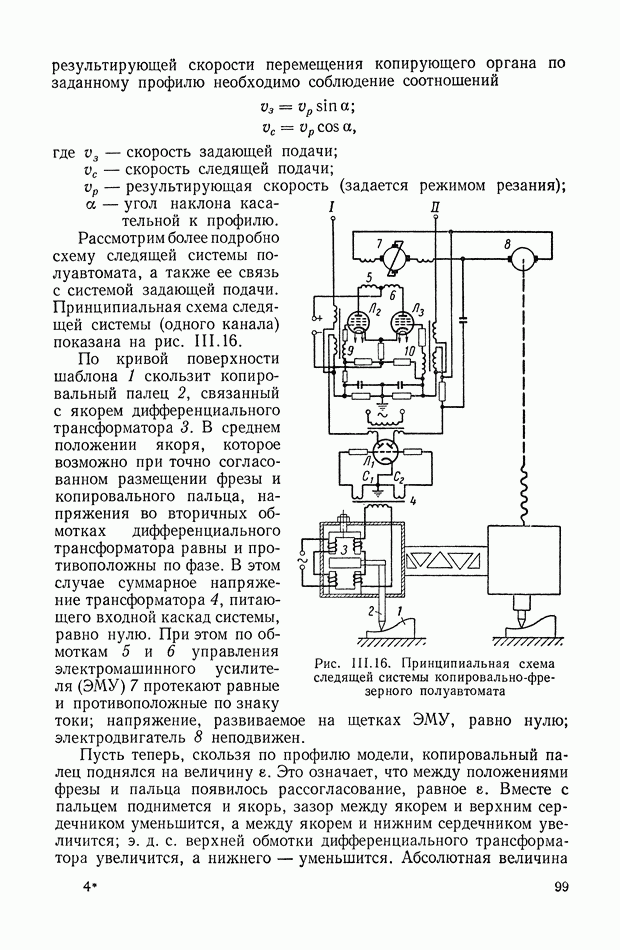
- 7. СЛЕДЯЩАЯ СИСТЕМА КОПИРОВАЛЬНО-ФРЕЗЕРНОГО ПОЛУАВТОМАТА
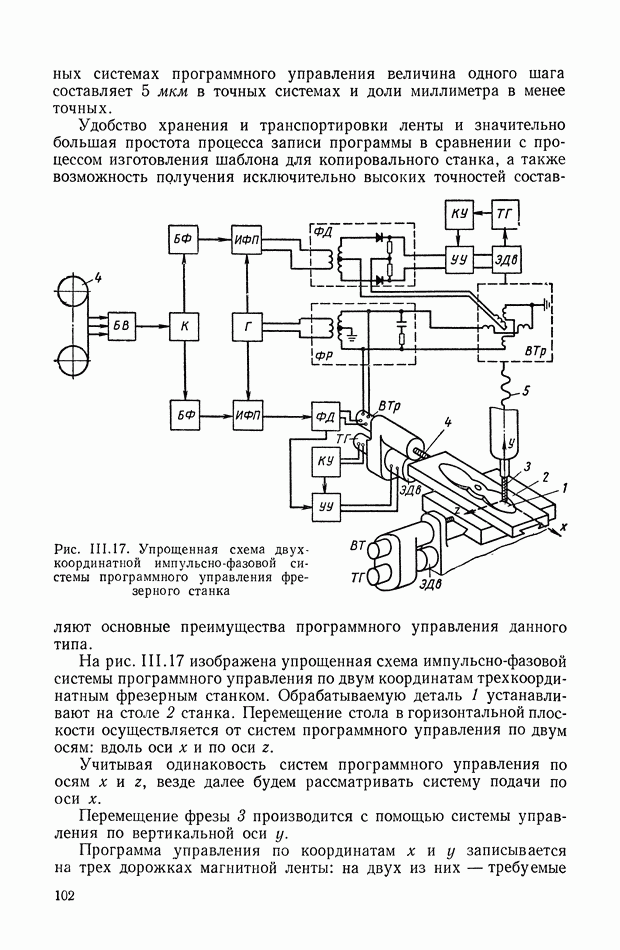
- 8. ПРОГРАММНОЕ УПРАВЛЕНИЕ МЕТАЛЛОРЕЖУЩИМИ СТАНКАМИ
- 9. ПРИНЦИП ДЕЙСТВИЯ ЭЛЕКТРИЧЕСКОГО АВТОПИЛОТА
- 10. РЕГУЛИРОВАНИЕ МНОГИХ ВЕЛИЧИН ПРИ АВТОМАТИЧЕСКОМ УПРАВЛЕНИИ ПЕРЕГОНКОЙ НЕФТИ
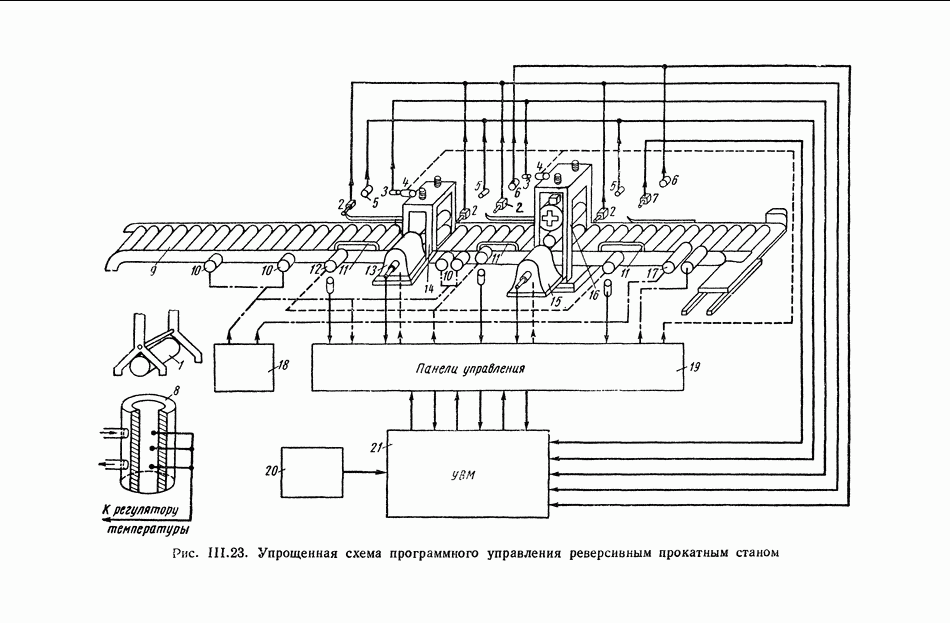
- 11. СИСТЕМА АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ РЕВЕРСИВНЫМ ПРОКАТНЫМ СТАНОМ С ИСПОЛЬЗОВАНИЕМ ЦИФРОВОЙ ВЫЧИСЛИТЕЛЬНОЙ МАШИНЫ
- ГЛАВА IV. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ЛАГРАНЖА ВТОРОГО РОДА
- 2. ОБЩИЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 3. ОБЩИЕ ЛИНЕАРИЗОВАННЫЕ УРАВНЕНИЯ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 4. ПРИМЕР СОСТАВЛЕНИЯ УРАВНЕНИЯ ОБЪЕКТА РЕГУЛИРОВАНИЯ
- ГЛАВА V. СТАТИКА СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. СТАТИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПРОСТЕЙШИХ ЗВЕНЬЕВ
- 2. СТАТИЧЕСКИЕ ХАРАКТЕРИСТИКИ ОСНОВНЫХ ТИПОВ СОЕДИНЕНИЙ ЗВЕНЬЕВ
- 3. КОРРЕКЦИЯ СТАТИЧЕСКИХ ХАРАКТЕРИСТИК
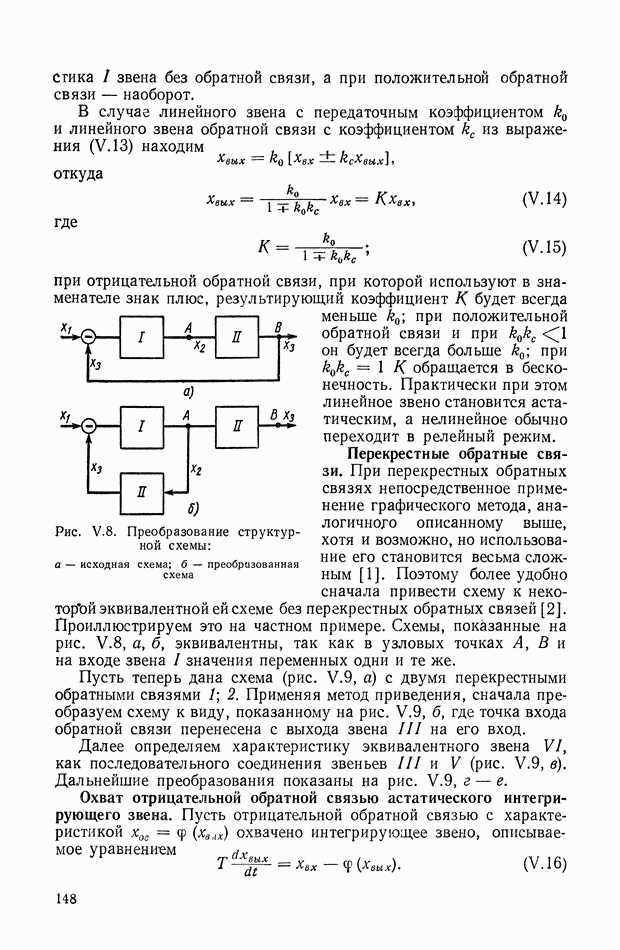
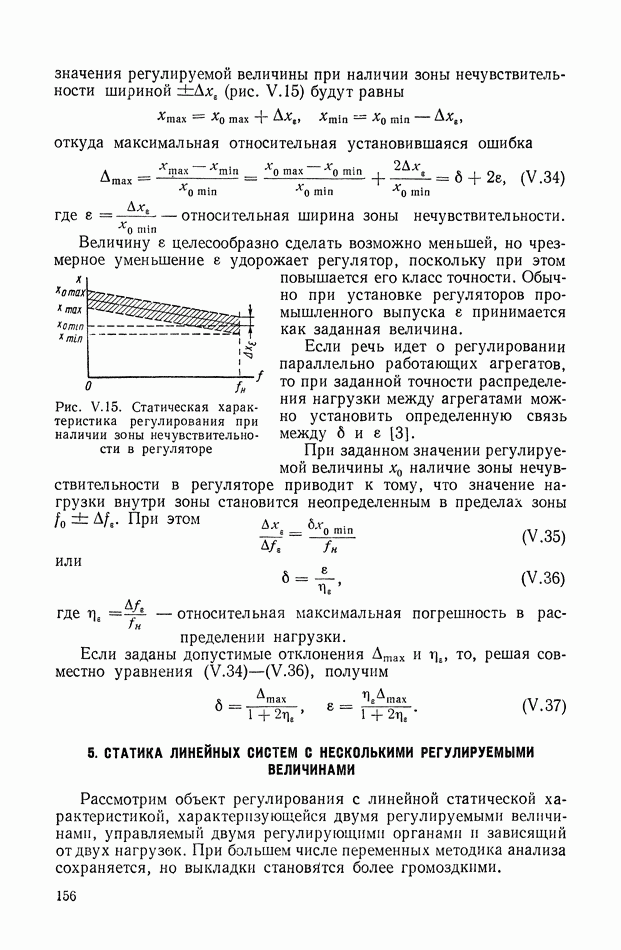
- Статическая характеристика замкнутой одномерной системы регулирования.
- Статическая характеристика линейной замкнутой системы.
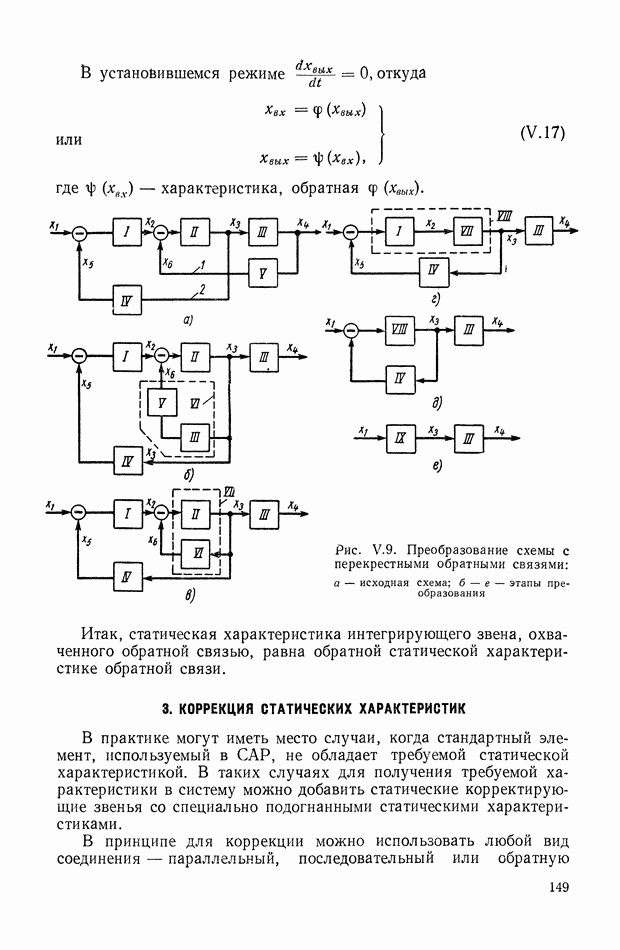
- 4. СТАТИЗМ РЕГУЛИРОВАНИЯ
- 5. СТАТИКА ЛИНЕЙНЫХ СИСТЕМ С НЕСКОЛЬКИМИ РЕГУЛИРУЕМЫМИ ВЕЛИЧИНАМИ
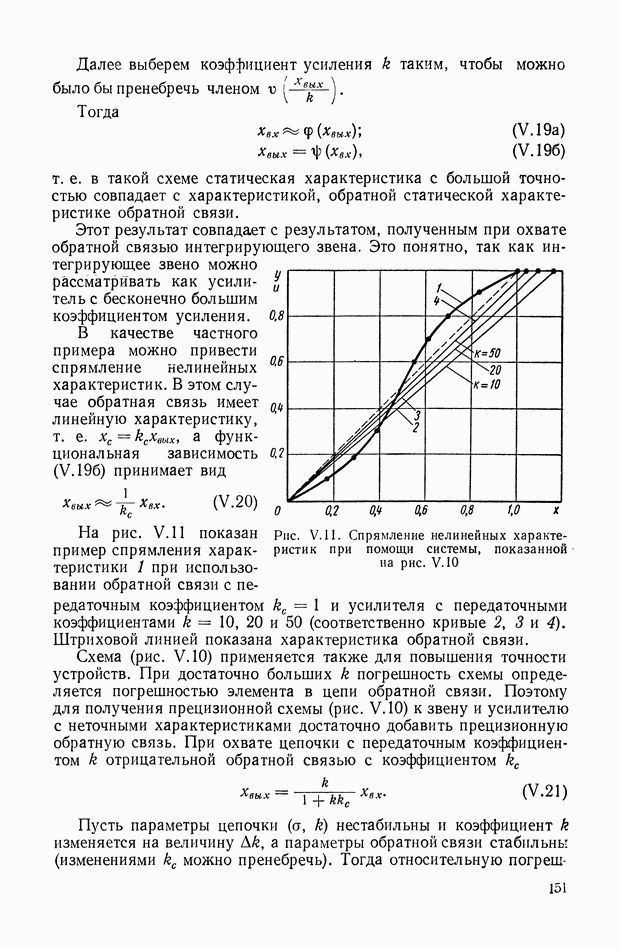
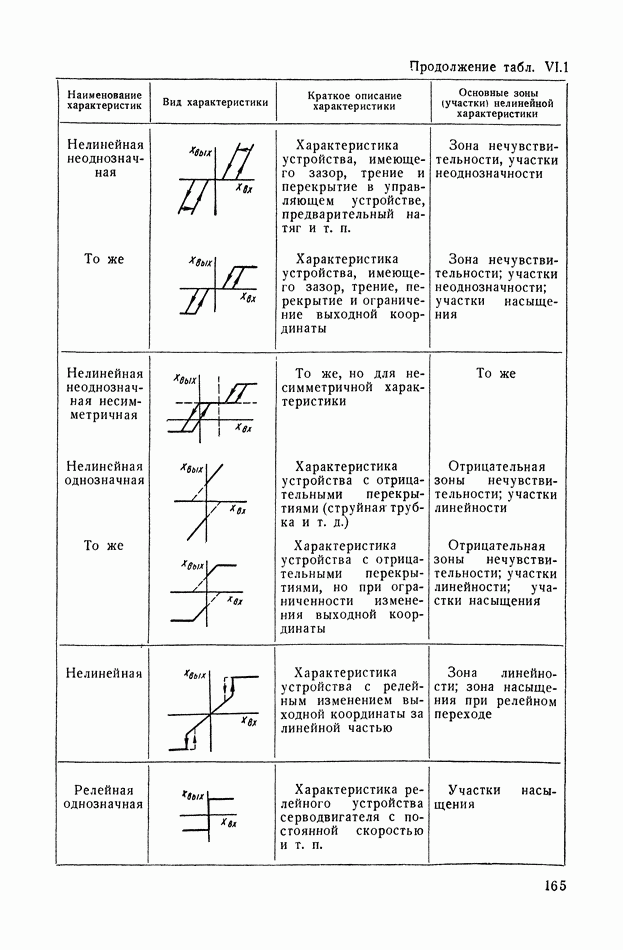
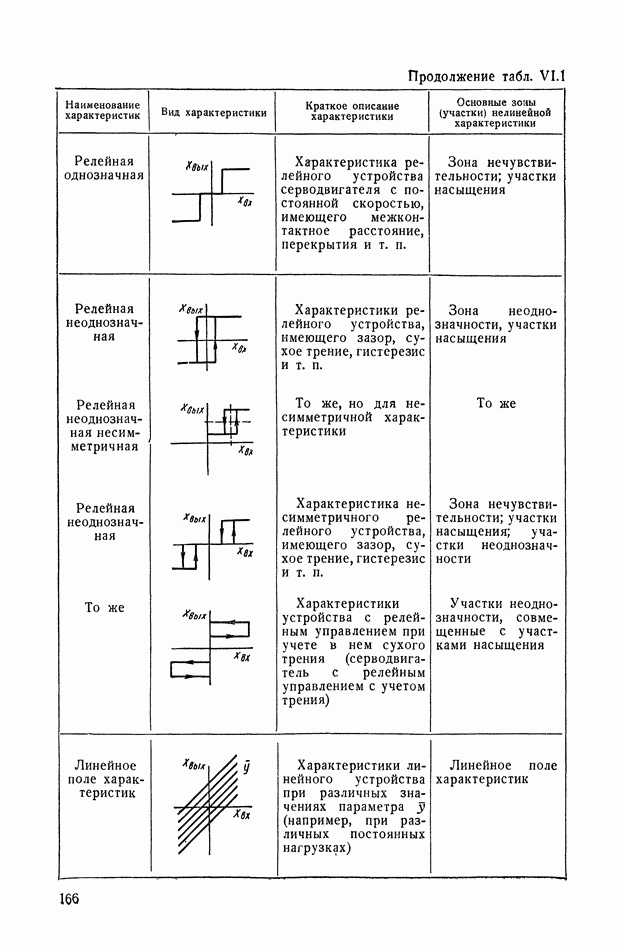
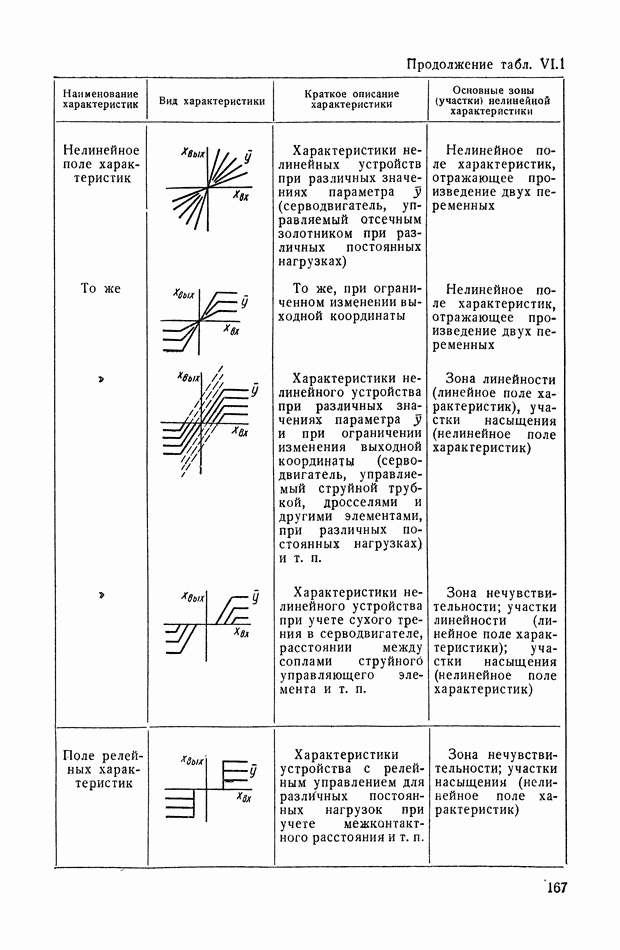
- ГЛАВА VI. ТИПИЧНЫЕ НЕЛИНЕЙНЫЕ СТАТИЧЕСКИЕ ХАРАКТЕРИСТИКИ ТИПОВЫХ ЗВЕНЬЕВ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
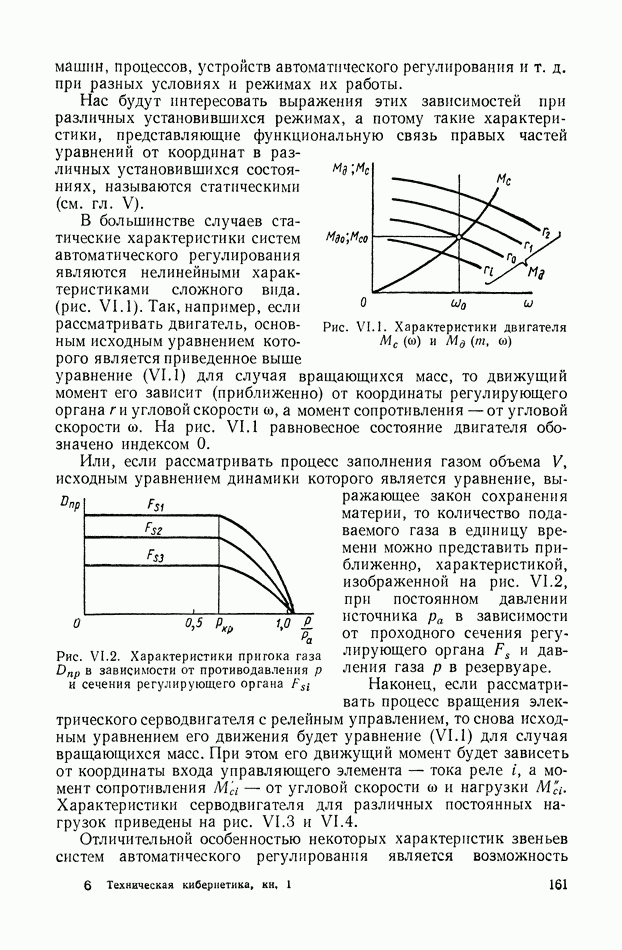
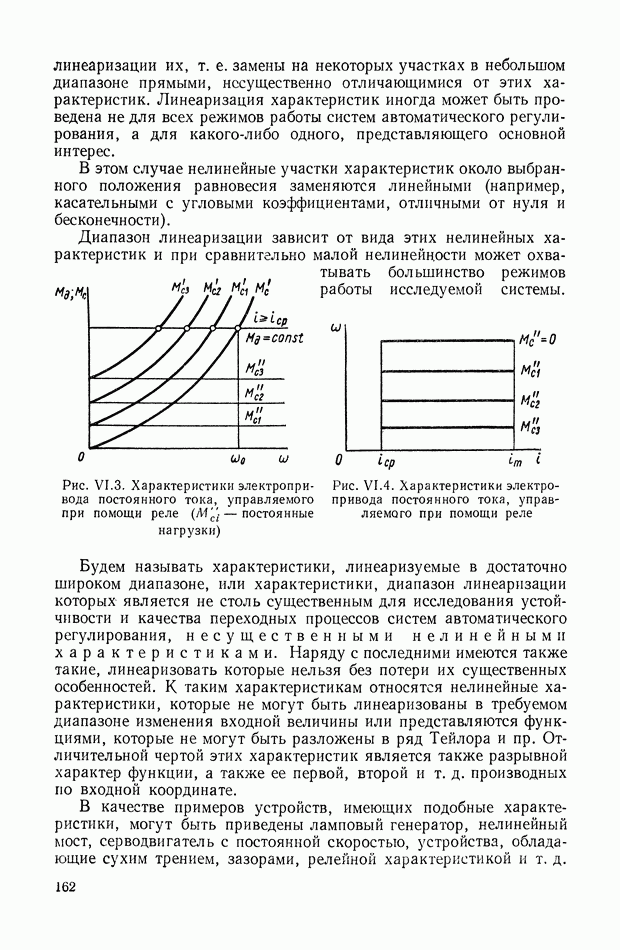
- 1. НЕЛИНЕЙНЫЕ ХАРАКТЕРИСТИКИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
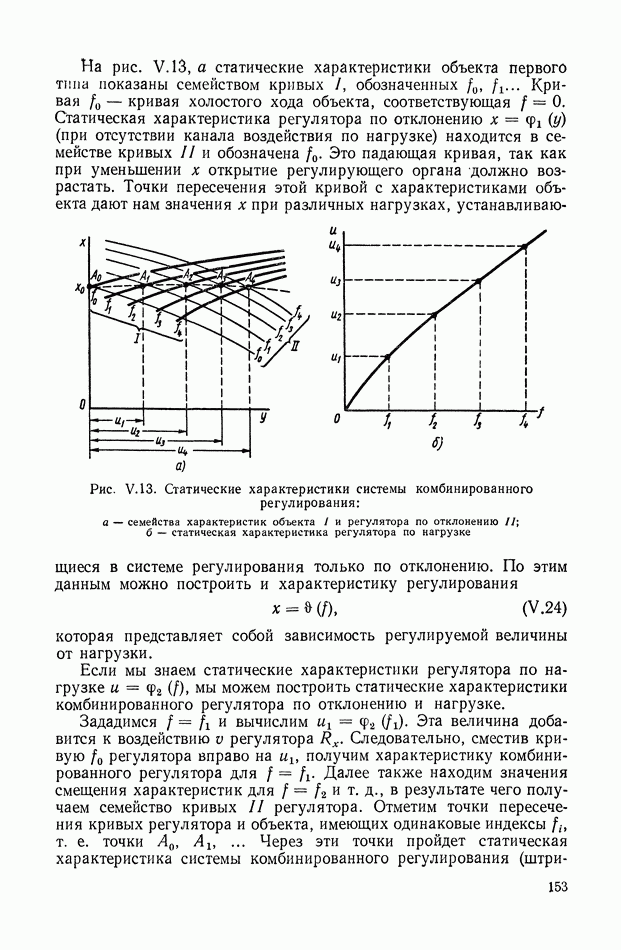
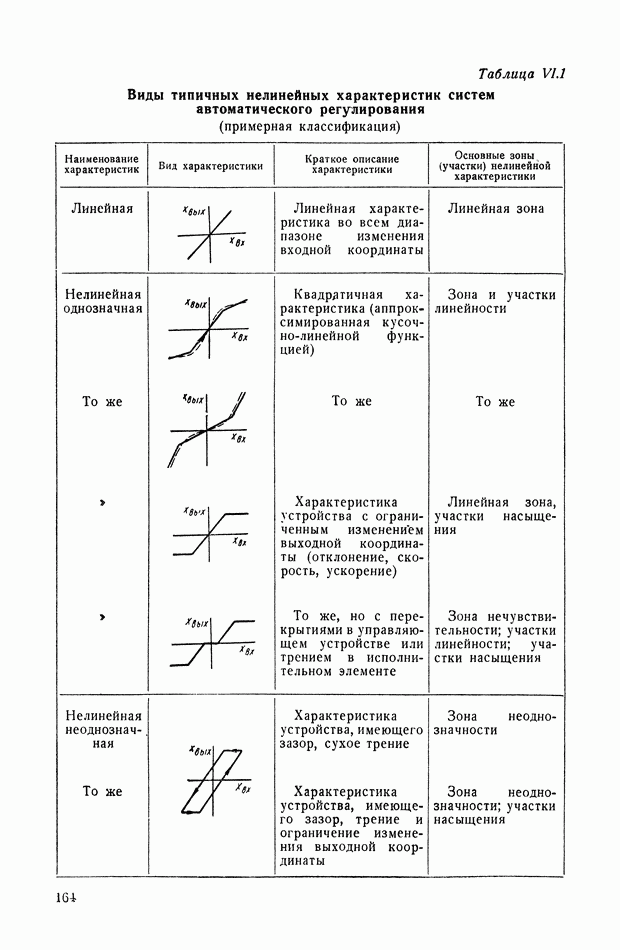
- 2. ВИДЫ ТИПИЧНЫХ НЕЛИНЕЙНЫХ СТАТИЧЕСКИХ ХАРАКТЕРИСТИК СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
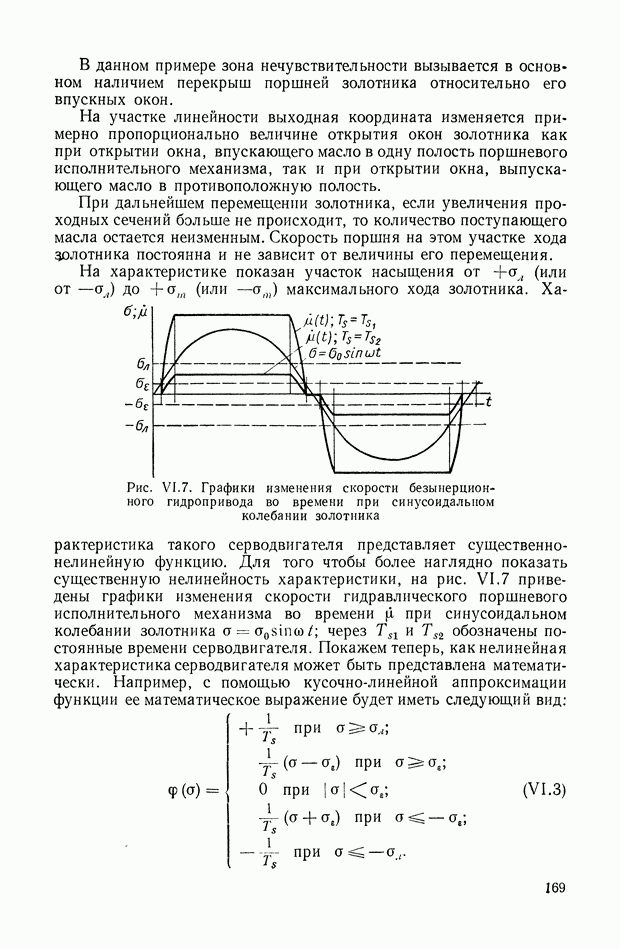
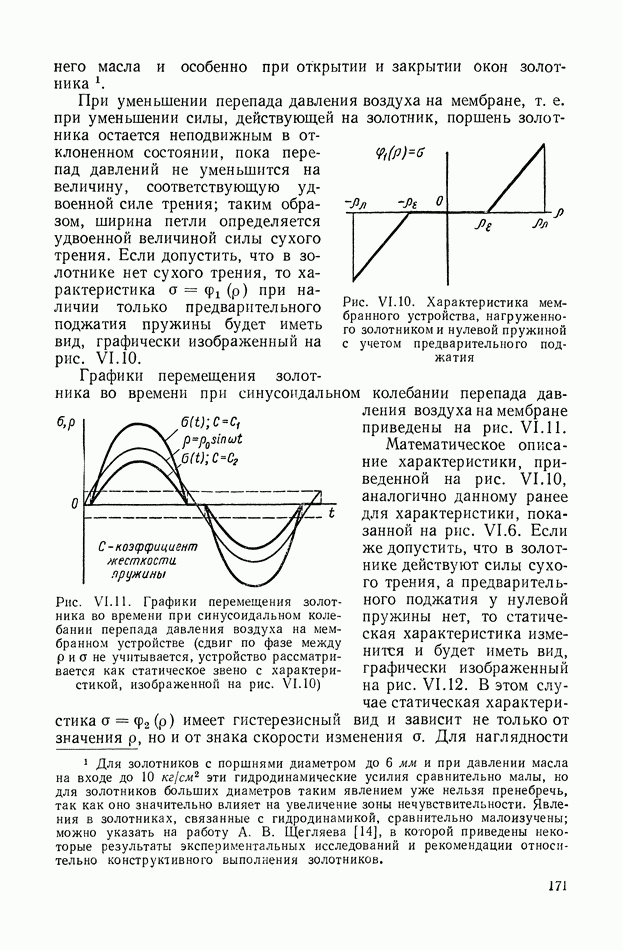
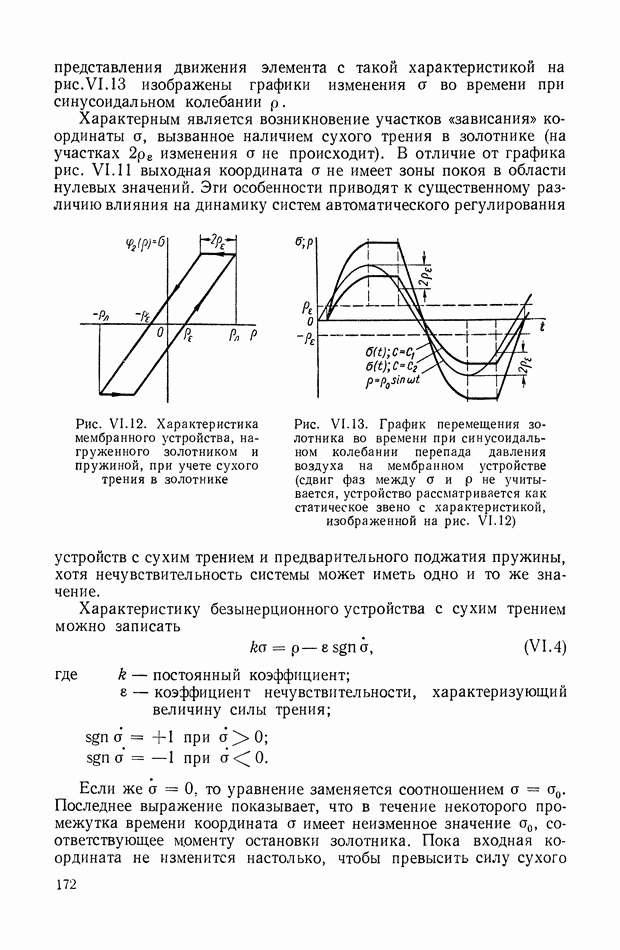
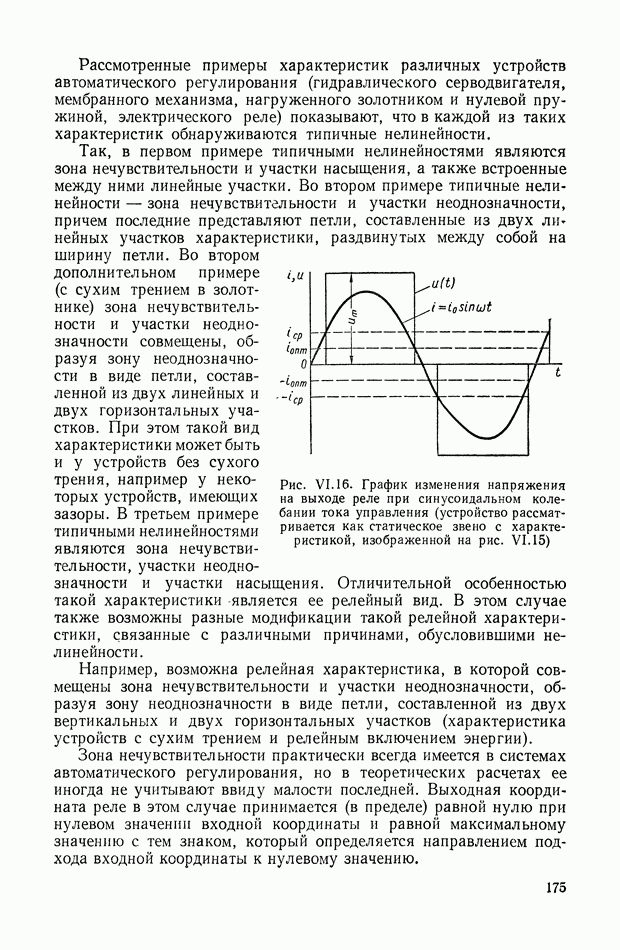
- 3. ТИПИЧНЫЕ НЕЛИНЕЙНЫЕ ХАРАКТЕРИСТИКИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
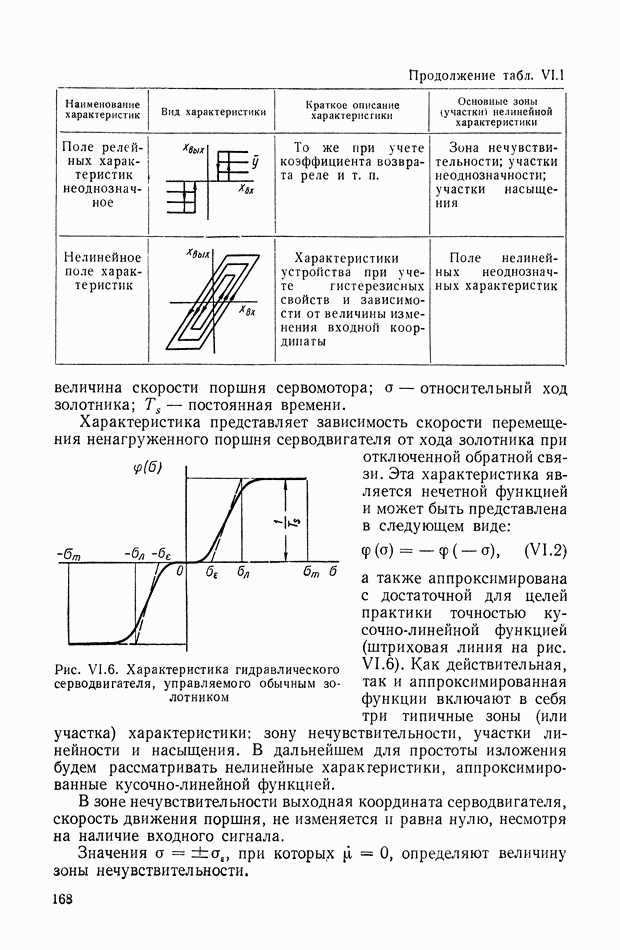
- 4. ЗОНЫ НЕЧУВСТВИТЕЛЬНОСТИ
- 5. ЗОНЫ ЛИНЕЙНОСТИ И НЕОДНОЗНАЧНОСТИ
- 6. ЗОНЫ НАСЫЩЕНИЯ
- 7. ПОЛЕ КРИВЫХ, ПРЕДСТАВЛЯЮЩИХ ХАРАКТЕРИСТИКУ СЕРВОДВИГАТЕЛЯ
- 8. ЭКСПЕРИМЕНТАЛЬНОЕ ВЫЯВЛЕНИЕ НЕЛИНЕЙНОСТИ ХАРАКТЕРИСТИК СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- ГЛАВА VII. ПЕРЕХОДНЫЕ ФУНКЦИИ, ПЕРЕДАТОЧНЫЕ ФУНКЦИИ И ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ДИНАМИЧЕСКИХ ЭЛЕМЕНТОВ
- 1. КЛАССИФИКАЦИЯ ДИНАМИЧЕСКИХ ЭЛЕМЕНТОВ
- 2. ОБЩЕЕ ОПРЕДЕЛЕНИЕ ИМПУЛЬСНОЙ ПЕРЕХОДНОЙ И ПЕРЕДАТОЧНОЙ ФУНКЦИЙ ДИНАМИЧЕСКОЙ СИСТЕМЫ ИЛИ ДИНАМИЧЕСКОГО ЭЛЕМЕНТА
- 3. ИМПУЛЬСНАЯ ПЕРЕХОДНАЯ ФУНКЦИЯ НЕПРЕРЫВНОЙ СТАЦИОНАРНОЙ ЛИНЕЙНОЙ СИСТЕМЫ
- 4. ПЕРЕДАТОЧНАЯ ФУНКЦИЯ НЕПРЕРЫВНОЙ ЛИНЕЙНОЙ СТАЦИОНАРНОЙ СИСТЕМЫ
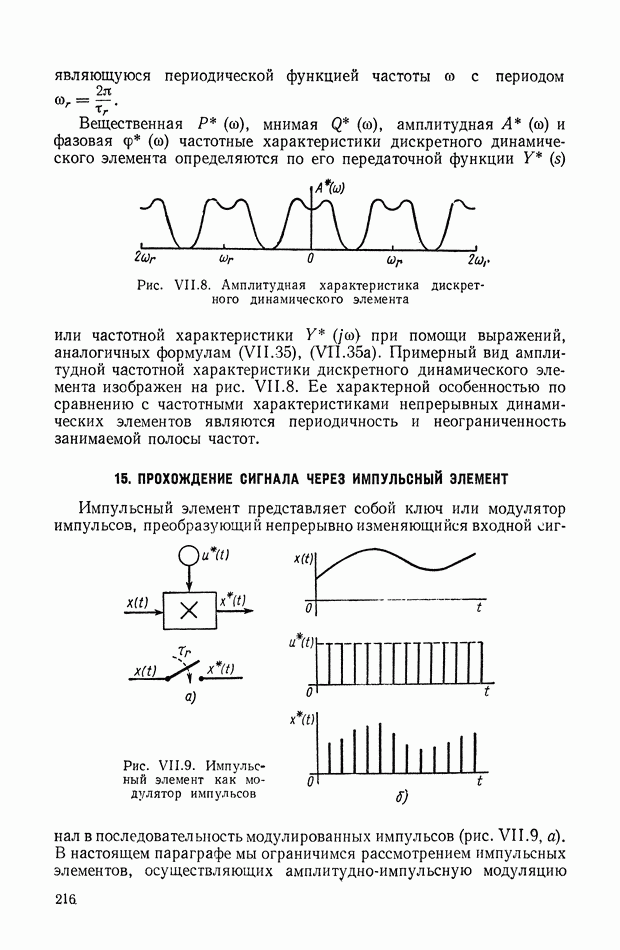
- 5. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЛИНЕЙНОЙ СТАЦИОНАРНОЙ НЕПРЕРЫВНОЙ ДИНАМИЧЕСКОЙ СИСТЕМЫ
- 6. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДИНАМИЧЕСКОГО ЭЛЕМЕНТА С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
- 7. ПРИМЕНЕНИЕ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА К РЕШЕНИЮ УРАВНЕНИЙ ЭЛЕМЕНТА С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
- 8. ПЕРЕДАТОЧНАЯ ФУНКЦИЯ ДИНАМИЧЕСКОГО ЭЛЕМЕНТА С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
- 9. ПЕРЕДАТОЧНАЯ ФУНКЦИЯ ПОСЛЕДОВАТЕЛЬНОГО СОЕДИНЕНИЯ ДИНАМИЧЕСКИХ ЭЛЕМЕНТОВ С СОСРЕДОТОЧЕННЫМИ И С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
- 10. ПЕРЕДАТОЧНАЯ ФУНКЦИЯ ЗАПАЗДЫВАЮЩЕГО ЭЛЕМЕНТА
- 11. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЭЛЕМЕНТА С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
- 12. ИМПУЛЬСНАЯ ПЕРЕХОДНАЯ ФУНКЦИЯ ДИНАМИЧЕСКОГО ЭЛЕМЕНТА С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
- 13. ПЕРЕДАТОЧНАЯ ФУНКЦИЯ СИСТЕМЫ С ГАРМОНИЧЕСКОЙ МОДУЛЯЦИЕЙ
- 14 ИМПУЛЬСНАЯ ПЕРЕХОДНАЯ И ПЕРЕДАТОЧНАЯ ФУНКЦИИ ДИСКРЕТНОЙ ЛИНЕЙНОЙ СТАЦИОНАРНОЙ СИСТЕМЫ
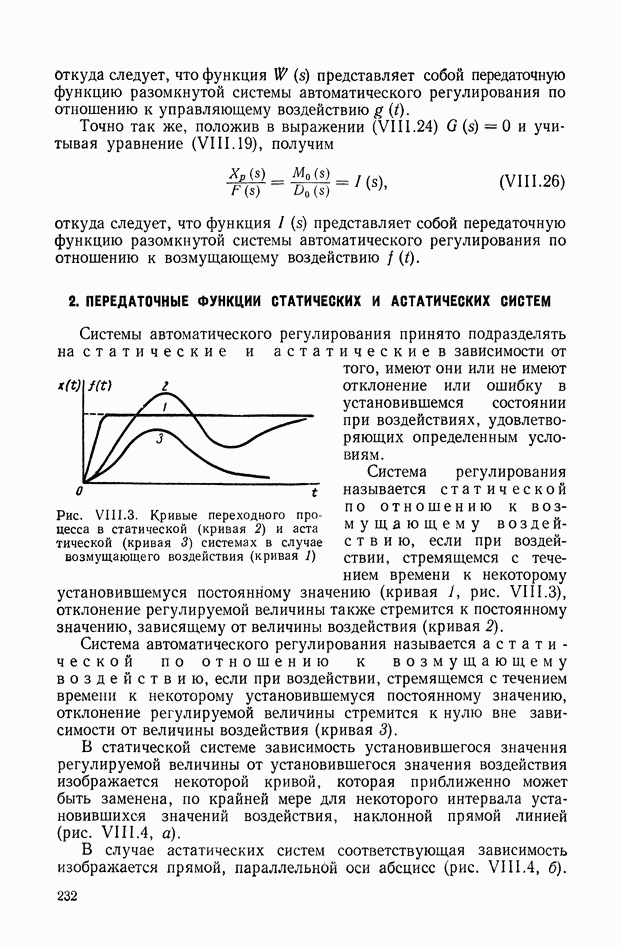
- 15. ПРОХОЖДЕНИЕ СИГНАЛА ЧЕРЕЗ ИМПУЛЬСНЫЙ ЭЛЕМЕНТ
- 16. ПОСЛЕДОВАТЕЛЬНОЕ СОЕДИНЕНИЕ ИМПУЛЬСНОГО ЭЛЕМЕНТА И НЕПРЕРЫВНОГО ДИНАМИЧЕСКОГО ЭЛЕМЕНТА
- 17. ИМПУЛЬСНАЯ ПЕРЕХОДНАЯ ФУНКЦИЯ ЛИНЕЙНОЙ НЕСТАЦИОНАРНОЙ СИСТЕМЫ (СИСТЕМЫ С ПЕРЕМЕННЫМИ ПАРАМЕТРАМИ)
- 18. ПЕРЕДАТОЧНАЯ ФУНКЦИЯ НЕПРЕРЫВНОЙ ЛИНЕЙНОЙ НЕСТАЦИОНАРНОЙ СИСТЕМЫ
- 19. МНОГОМЕРНЫЕ ИМПУЛЬСНЫЕ ПЕРЕХОДНЫЕ И ПЕРЕДАТОЧНЫЕ ФУНКЦИИ НЕЛИНЕЙНЫХ СИСТЕМ
- 20. МНОГОМЕРНЫЕ ПЕРЕДАТОЧНЫЕ ФУНКЦИИ НЕЛИНЕЙНЫХ СИСТЕМ
- ГЛАВА VIII. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ, ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ И ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ НЕПРЕРЫВНЫХ ЛИНЕЙНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
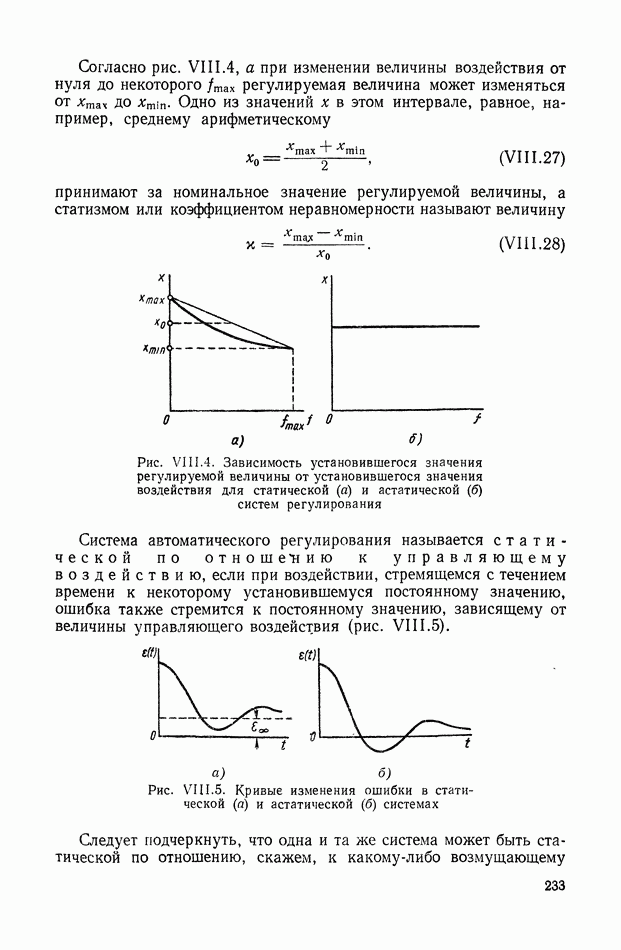
- 2. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ СТАТИЧЕСКИХ И АСТАТИЧЕСКИХ СИСТЕМ
- 3. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ
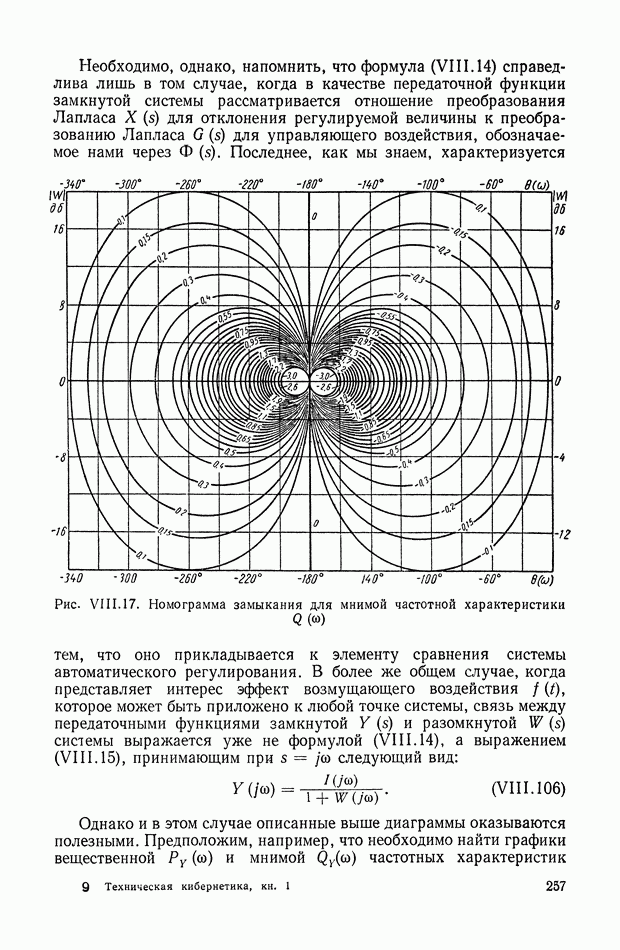
- 4. ВЗАИМНАЯ СВЯЗЬ МЕЖДУ ЧАСТОТНЫМИ ХАРАКТЕРИСТИКАМИ ЗАМКНУТОЙ И РАЗОМКНУТОЙ СИСТЕМЫ
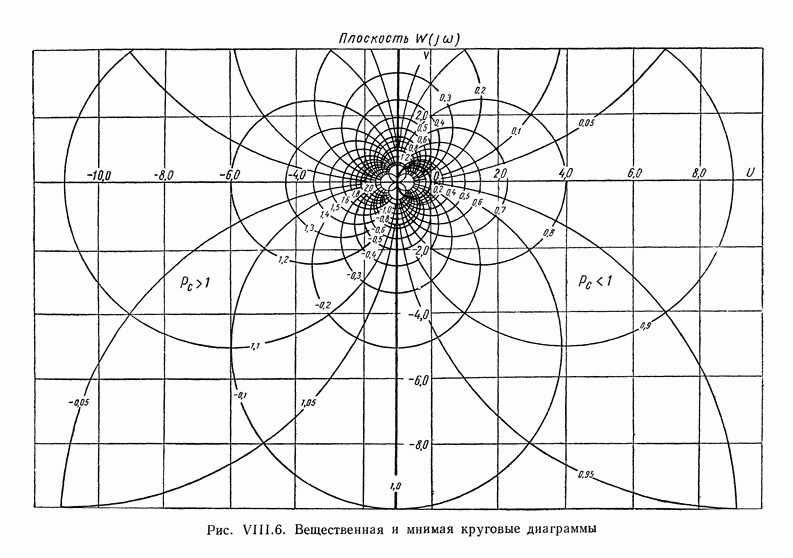
- 5. КРУГОВЫЕ ДИАГРАММЫ
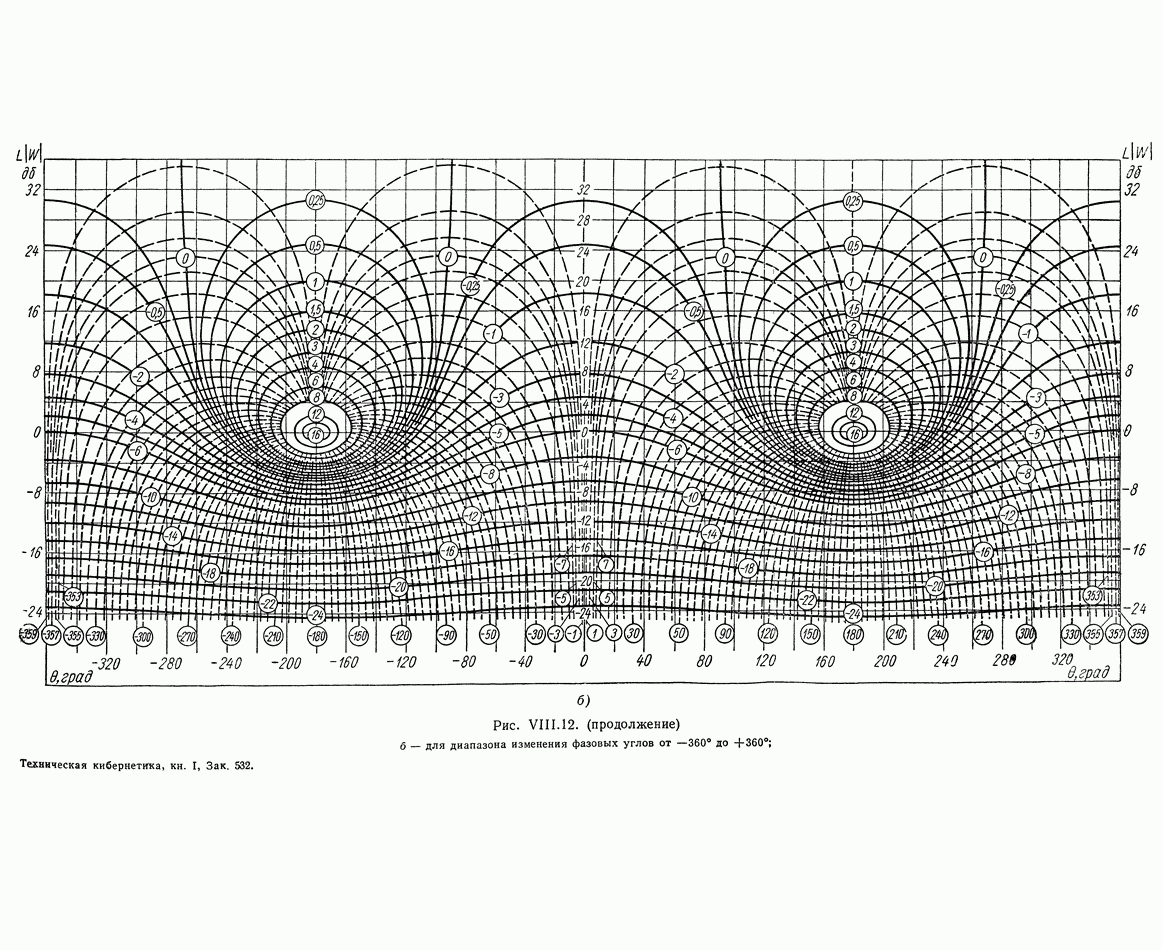
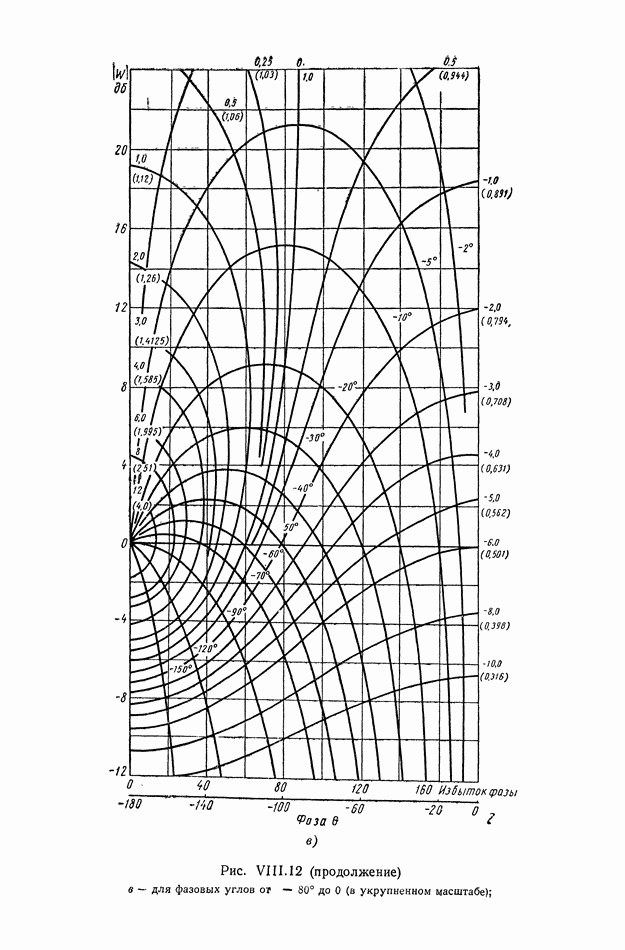
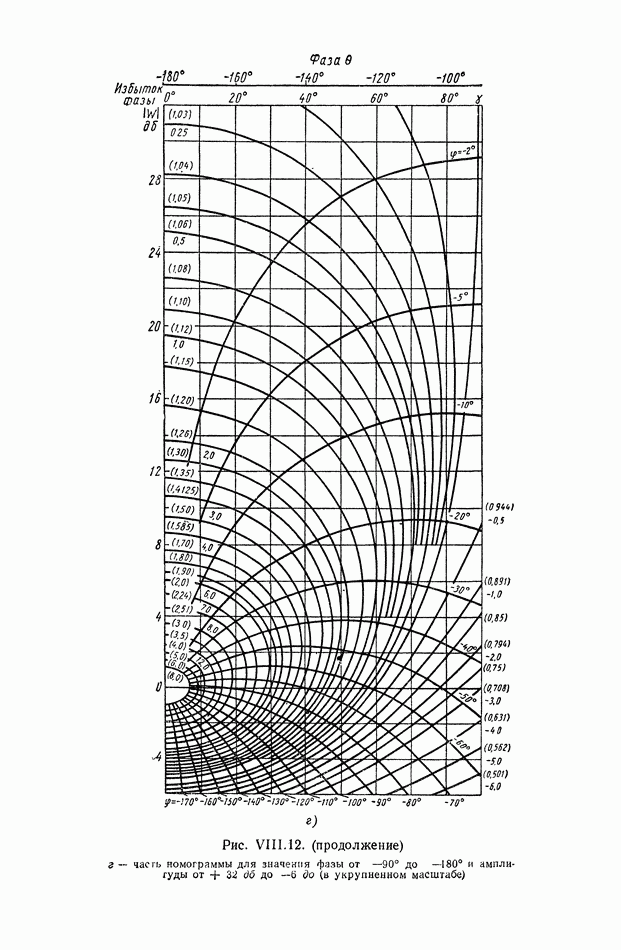
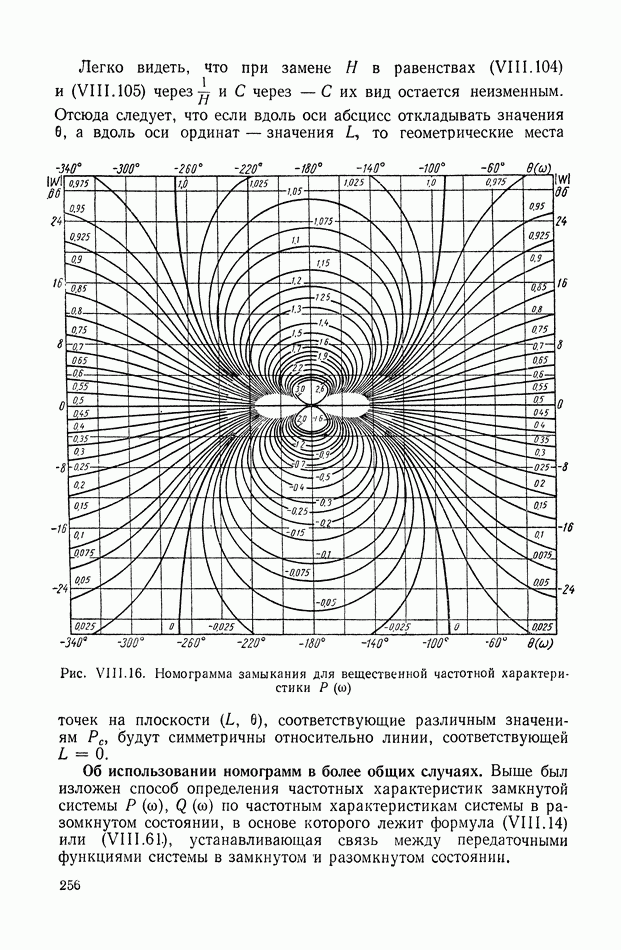
- 6. НОМОГРАММЫ ЗАМЫКАНИЯ
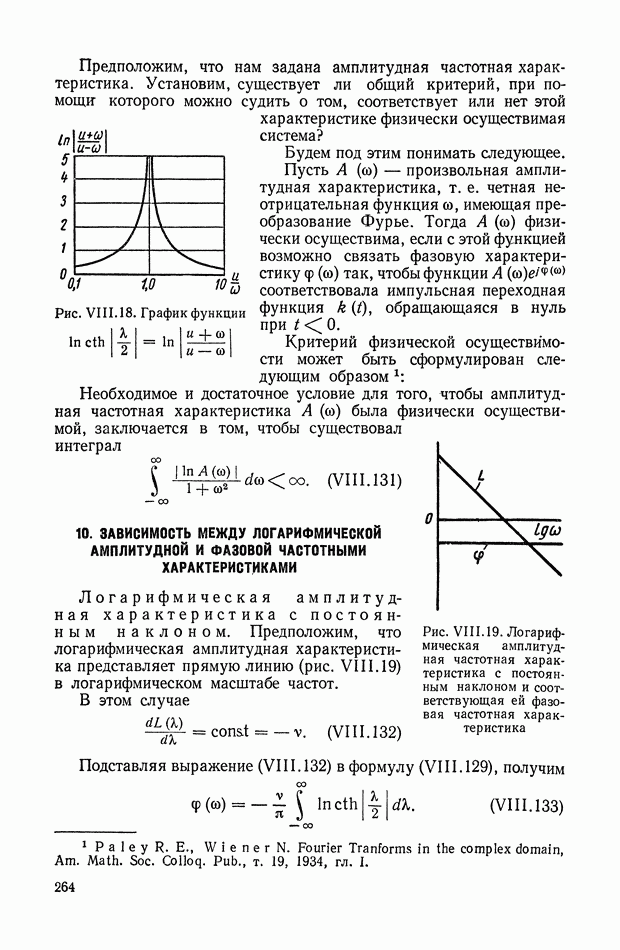
- 7. УСЛОВИЯ ОДНОЗНАЧНОЙ связи МЕЖДУ ЧАСТОТНЫМИ ХАРАКТЕРИСТИКАМИ
- 8. ОПРЕДЕЛЕНИЕ ПЕРЕДАТОЧНОЙ ФУНКЦИИ ПО ОДНОЙ ИЗ ЧАСТОТНЫХ ХАРАКТЕРИСТИК, ЗАДАННОЙ АНАЛИТИЧЕСКИ
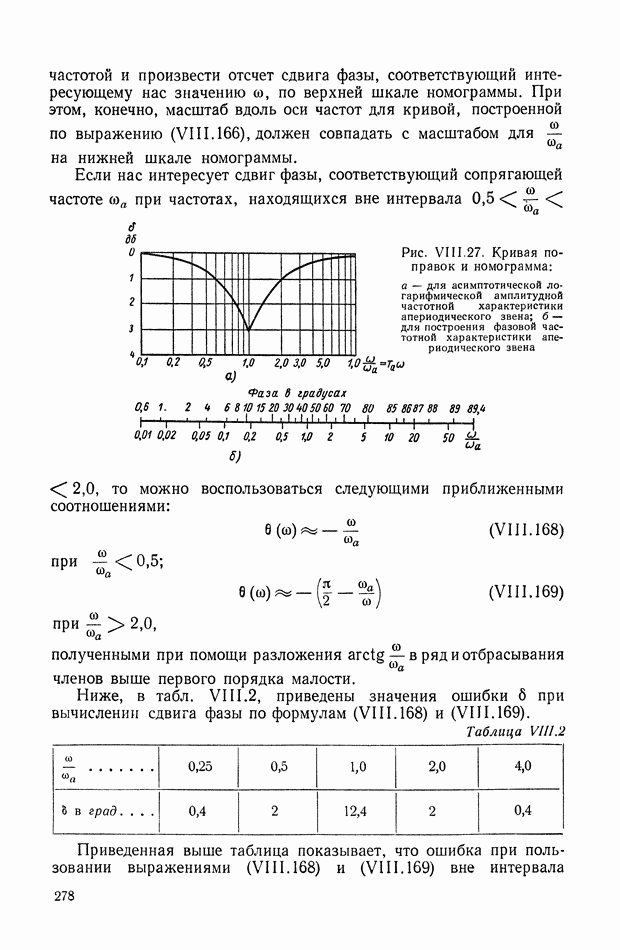
- 9. ФОРМУЛА ДЛЯ ВЫЧИСЛЕНИЯ ФАЗОВОЙ ЧАСТОТНОЙ ХАРАКТЕРИСТИКИ ПО ЗАДАННОЙ АМПЛИТУДНОЙ ЧАСТОТНОЙ ХАРАКТЕРИСТИКЕ
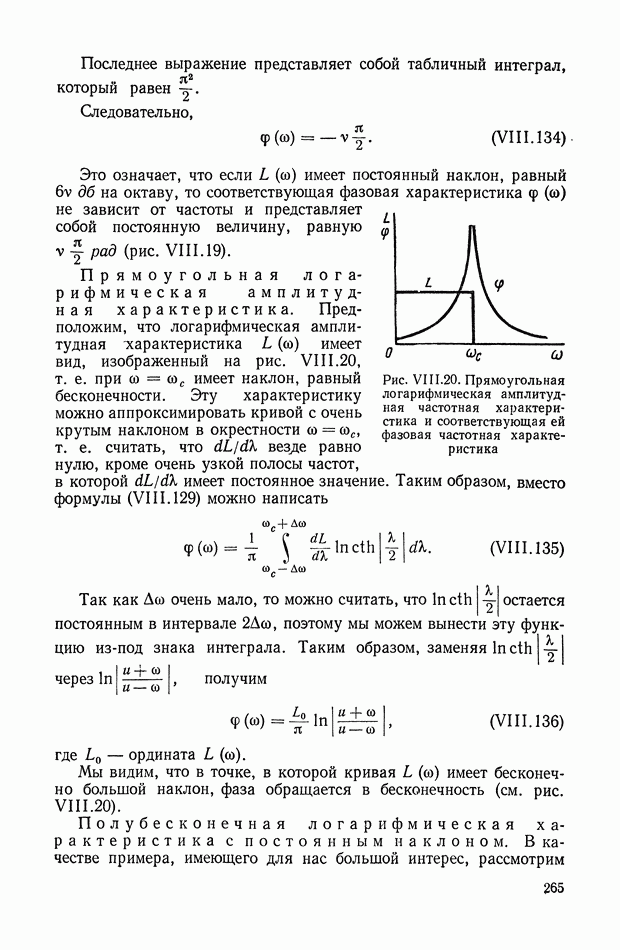
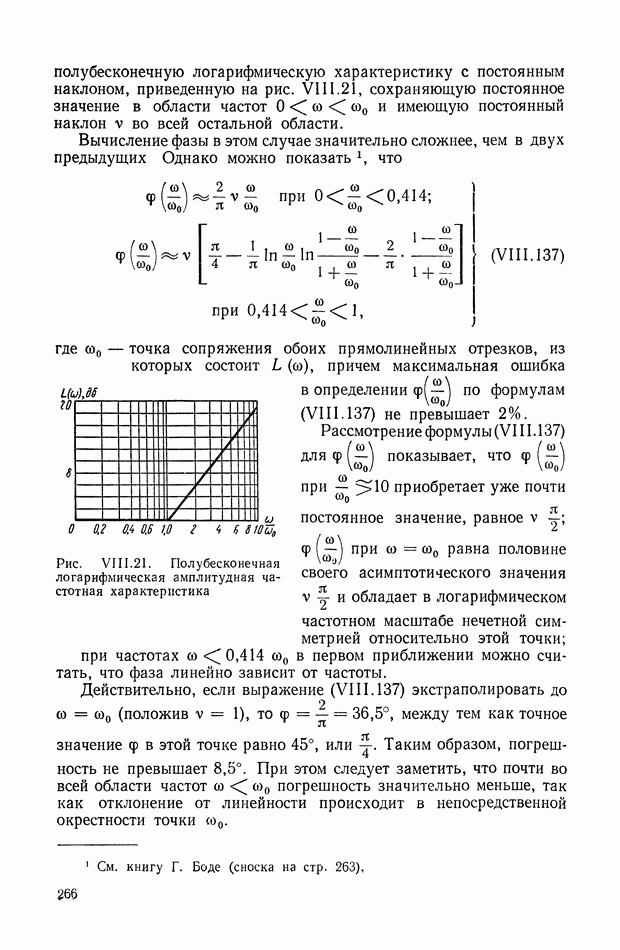
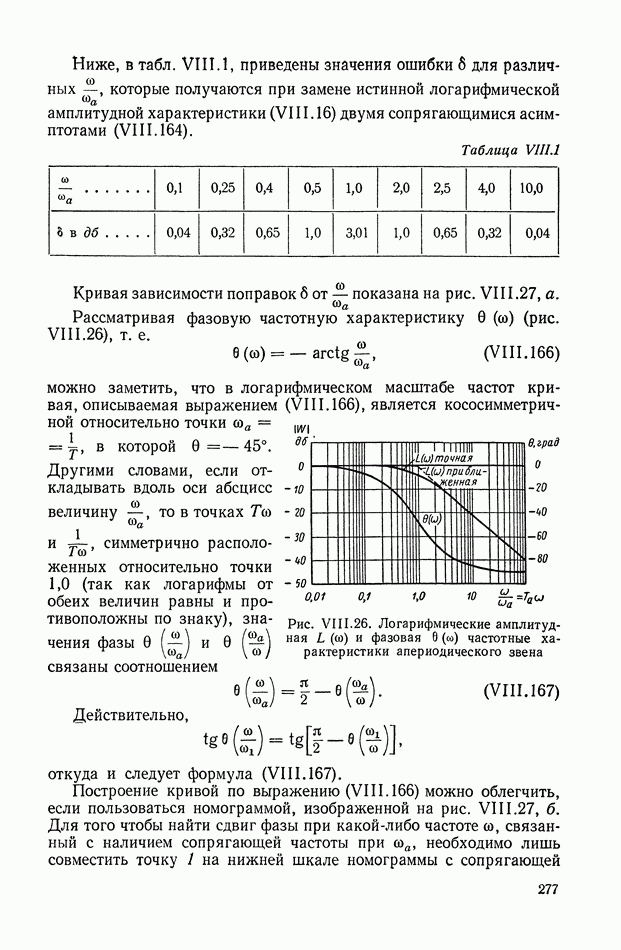
- 10. ЗАВИСИМОСТЬ МЕЖДУ ЛОГАРИФМИЧЕСКОЙ АМПЛИТУДНОЙ И ФАЗОВОЙ ЧАСТОТНЫМИ ХАРАКТЕРИСТИКАМИ
- 11. ГРАФИЧЕСКИЙ МЕТОД ОПРЕДЕЛЕНИЯ ФАЗОВОЙ ХАРАКТЕРИСТИКИ ПО ЗАДАННОЙ АМПЛИТУДНОЙ ХАРАКТЕРИСТИКЕ
- 12. ИНТЕГРАЛЬНЫЕ ВЫРАЖЕНИЯ ДЛЯ ОШИБКИ И ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 13. ТИПОВЫЕ ЗВЕНЬЯ
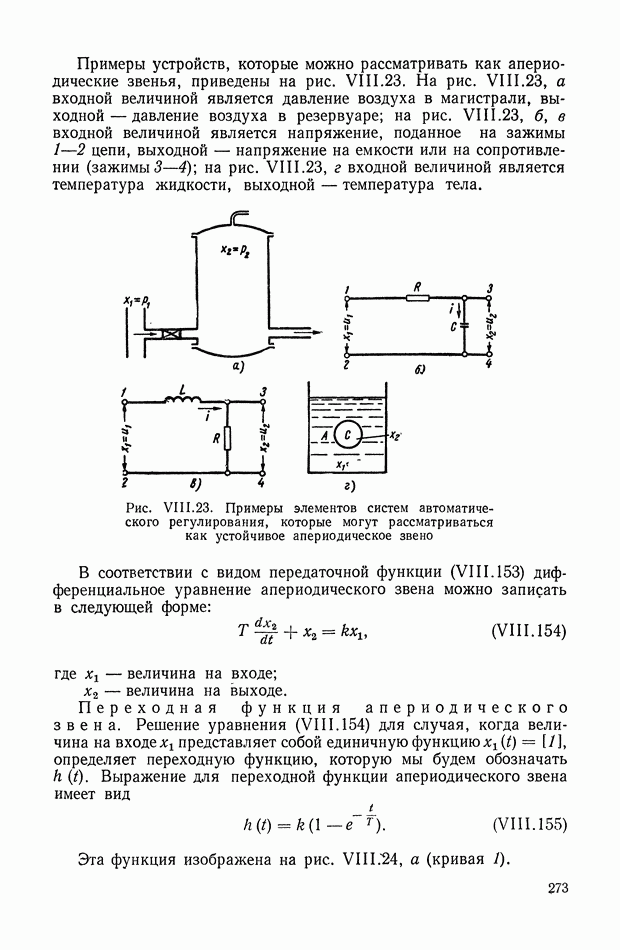
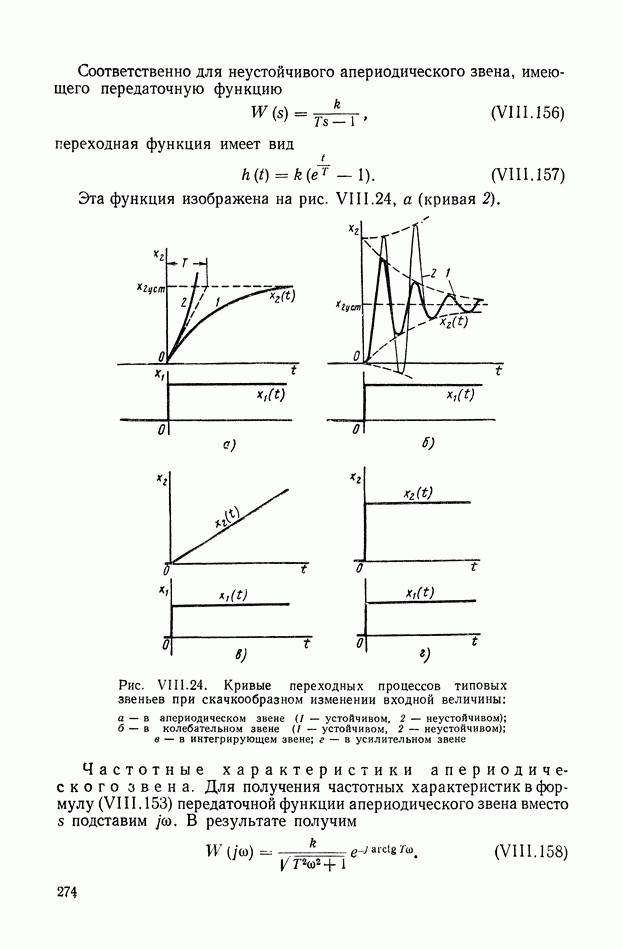
- 14. АПЕРИОДИЧЕСКОЕ ЗВЕНО
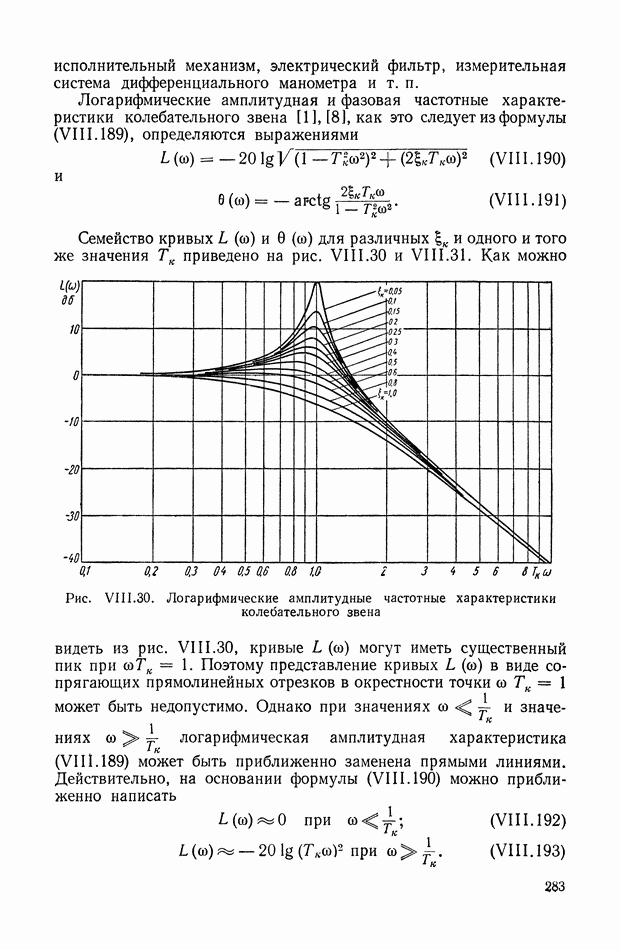
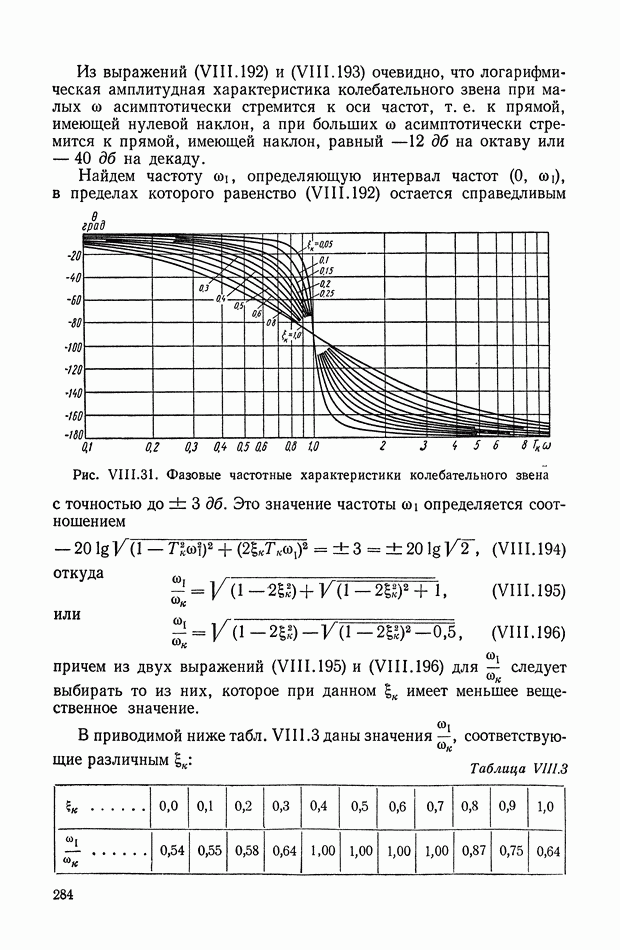
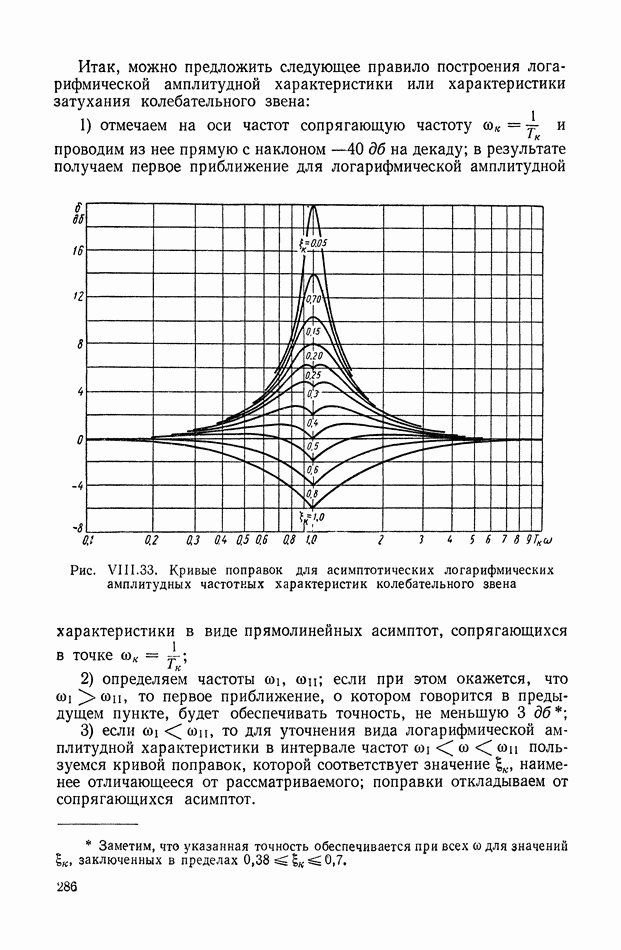
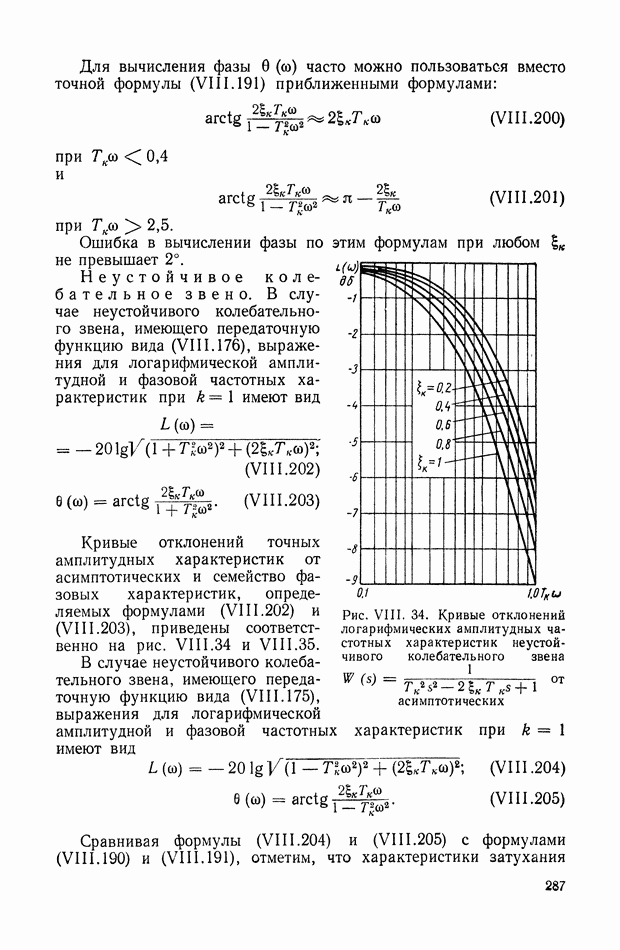
- 15. КОЛЕБАТЕЛЬНОЕ ЗВЕНО
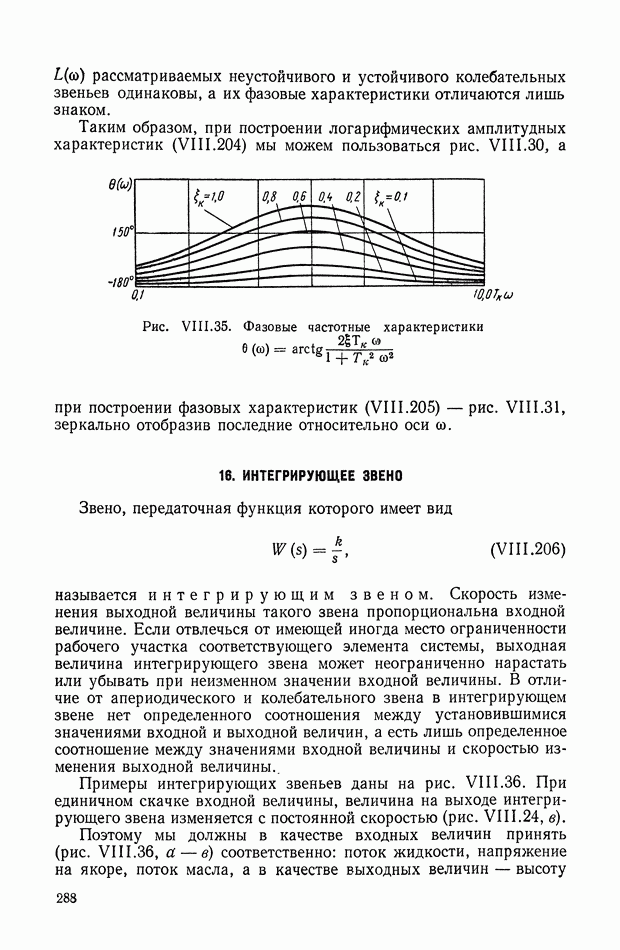
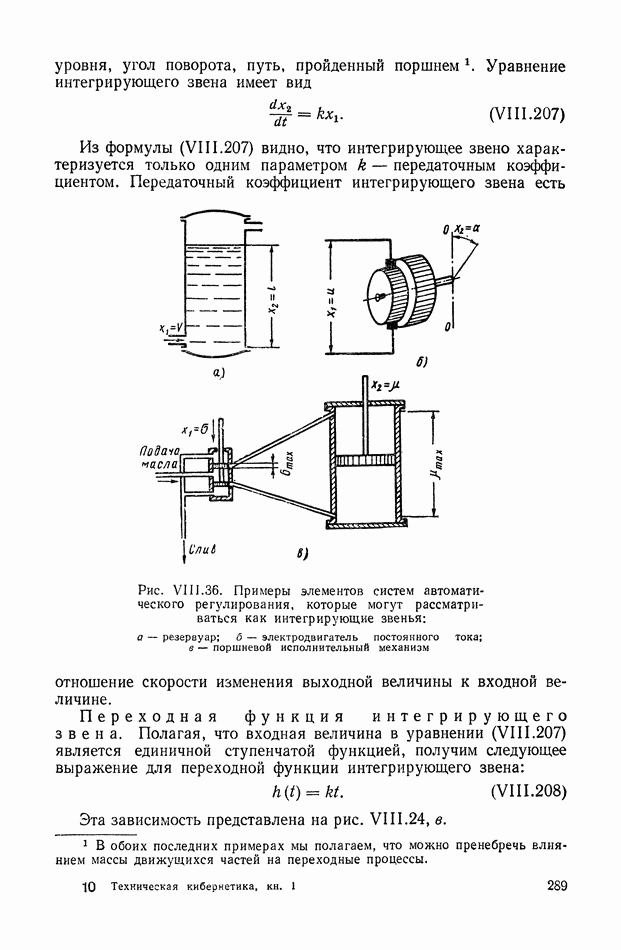
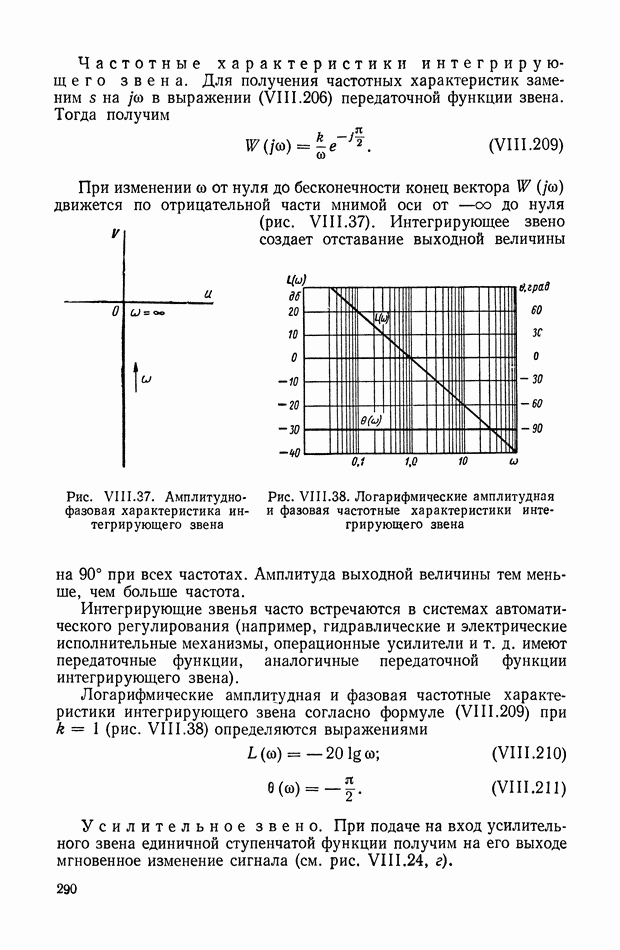
- 16. ИНТЕГРИРУЮЩЕЕ ЗВЕНО
- 17. ДИФФЕРЕНЦИРУЮЩЕЕ ЗВЕНО ПЕРВОГО ПОРЯДКА
- 18. ДИФФЕРЕНЦИРУЮЩЕЕ ЗВЕНО ВТОРОГО ПОРЯДКА
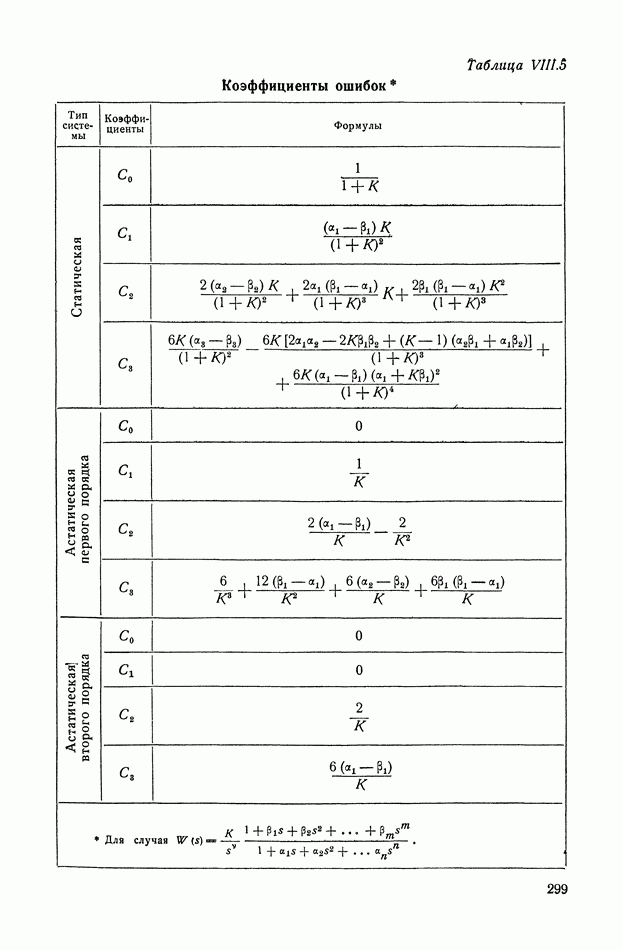
- 19. КОЭФФИЦИЕНТЫ ОШИБКИ
- ГЛАВА IX. МЕТОДЫ СТРУКТУРНЫХ ПРЕОБРАЗОВАНИЙ В СИСТЕМАХ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. ГРАФИЧЕСКИЕ ИЗОБРАЖЕНИЯ УСЛОВИЙ ПРЕОБРАЗОВАНИЯ СИГНАЛОВ
- 2. СХЕМЫ С ЭЛЕМЕНТАМИ, ОБЛАДАЮЩИМИ И НЕ ОБЛАДАЮЩИМИ СВОЙСТВОМ НАПРАВЛЕННОСТИ ДЕЙСТВИЯ
- 3. ДЕТАЛИЗИРОВАННЫЕ СТРУКТУРЫ
- 4. ПРЕОБРАЗОВАНИЯ МНОГОКОНТУРНЫХ СТРУКТУРНЫХ СХЕМ, ДОПУСКАЮЩИХ ПОСЛЕДОВАТЕЛЬНОЕ ПРИМЕНЕНИЕ ПРАВИЛ СВЕРТЫВАНИЯ КОНТУРОВ, И НЕКОТОРЫЕ ЭКВИВАЛЕНТНЫЕ ПРЕОБРАЗОВАНИЯ
- 5. ПРЕОБРАЗОВАНИЯ ПЕРЕКРЕСТНЫХ СТРУКТУРНЫХ СХЕМ МЕТОДОМ РАЗВЯЗКИ КОНТУРОВ И НЕКОТОРЫЕ ЭКВИВАЛЕНТНЫЕ ПРЕОБРАЗОВАНИЯ
- 6. ПРИМЕНЕНИЕ СТРУКТУРНЫХ МЕТОДОВ ДЛЯ ОПРЕДЕЛЕНИЯ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ МНОГОКОНТУРНЫХ СИСТЕМ
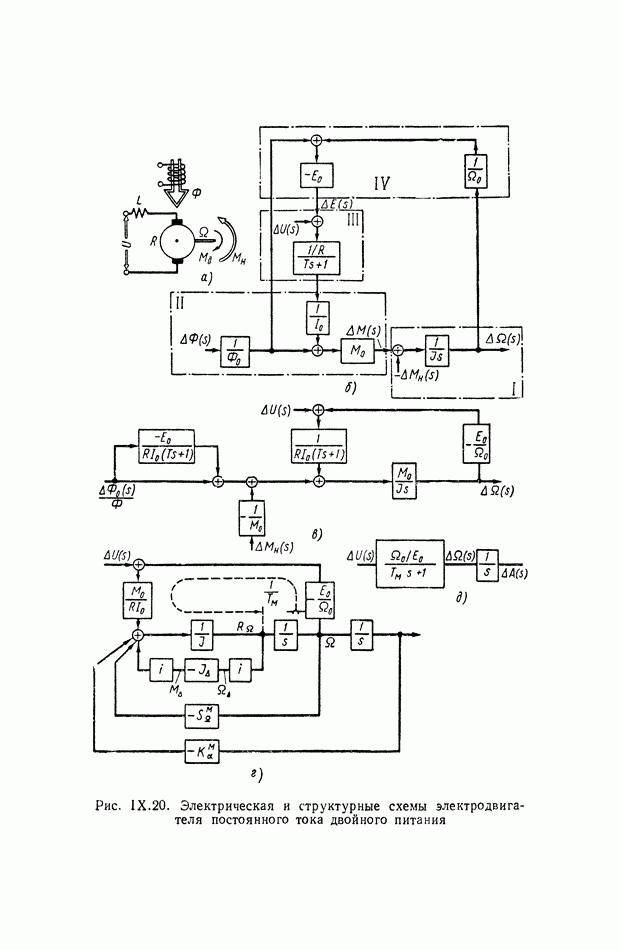
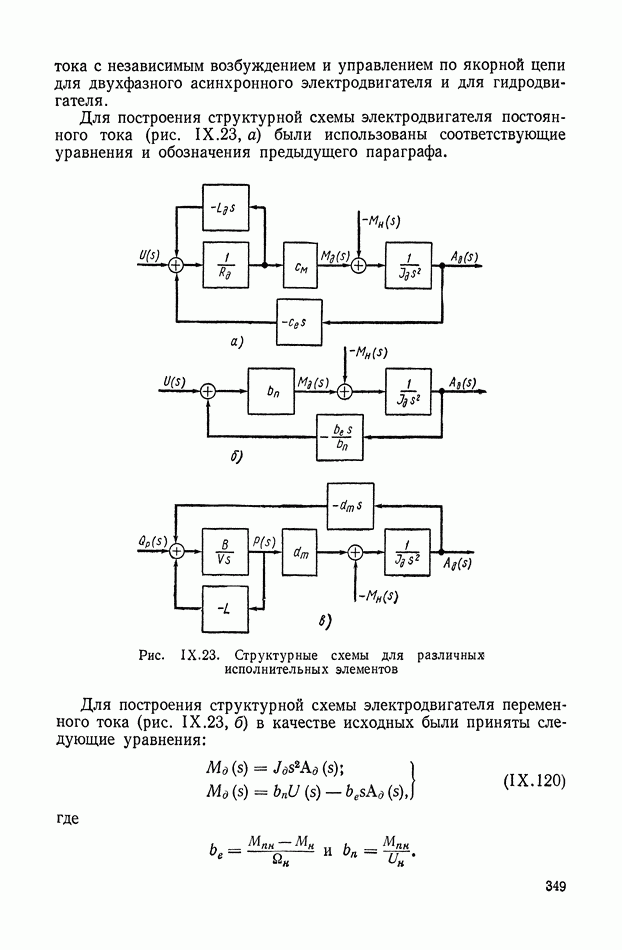
- 7. СОСТАВЛЕНИЕ И ПРЕОБРАЗОВАНИЕ СТРУКТУРНОЙ СХЕМЫ НА ПРИМЕРЕ ЭЛЕКТРОДВИГАТЕЛЯ ПОСТОЯННОГО ТОКА ДВОЙНОГО ПИТАНИЯ
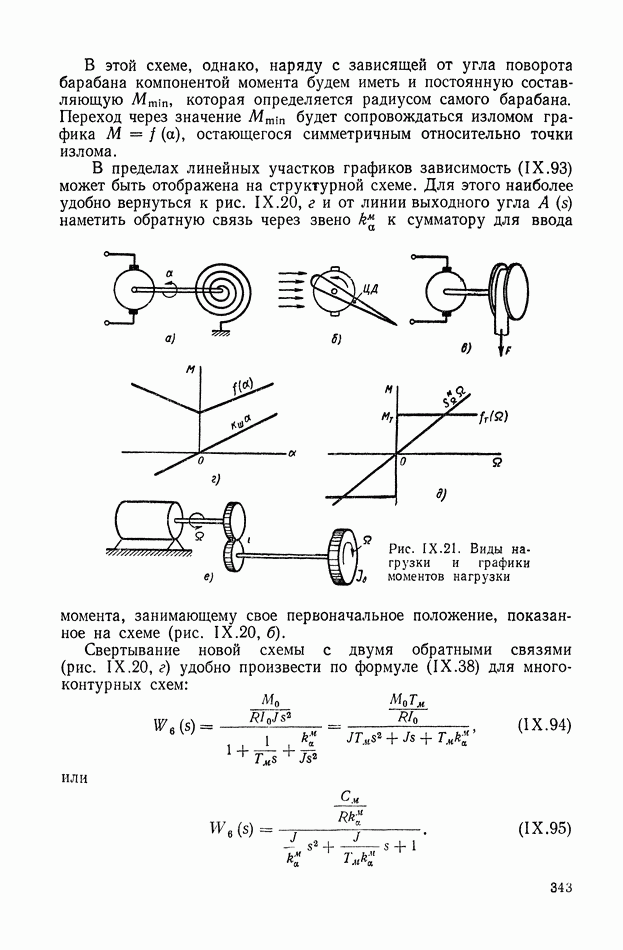
- Учет зависимости момента нагрузки от угла поворота вала и его производных по времени.
- 8. СТРУКТУРНЫЕ СХЕМЫ МЕХАНИЧЕСКИХ ОБЪЕКТОВ РЕГУЛИРОВАНИЯ С РЕДУКТОРАМИ, ДИФФЕРЕНЦИАЛАМИ И УПРУГИМИ ЭЛЕМЕНТАМИ В СИЛОВЫХ ПЕРЕДАЧАХ
- 9. ПРАВИЛА СТРУКТУРНЫХ ПРЕОБРАЗОВАНИЙ ДЛЯ СИСТЕМ С ПЕРЕМЕННЫМИ ПАРАМЕТРАМИ
- 10. ФУНКЦИОНАЛЬНЫЕ СТРУКТУРНЫЕ СХЕМЫ ДЛЯ АНАЛИЗА СОВМЕСТНЫХ СТАТИЧЕСКИХ ХАРАКТЕРИСТИК НЕЛИНЕЙНЫХ ЗВЕНЬЕВ
- ГЛАВА X. ПРИМЕРЫ СОСТАВЛЕНИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ, СТРУКТУРНЫХ СХЕМ И ПЕРЕДАТОЧНЫХ ФУНКЦИЙ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. СИСТЕМА АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ СКОРОСТИ ВРАЩЕНИЯ ГИДРОТУРБИНЫ
- 2. ЭЛЕКТРОННЫЙ РЕГУЛЯТОР НАПРЯЖЕНИЯ ВЭИ
- 3. СИСТЕМА АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ МОЩНОСТИ ЯДЕРНОГО ЭНЕРГЕТИЧЕСКОГО РЕАКТОРА НА ТЕПЛОВЫХ НЕЙТРОНАХ
- 4. СЛЕДЯЩАЯ СИСТЕМА РАДИОЛОКАЦИОННОЙ СТАНЦИИ
- 5. СИСТЕМА АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ УНИВЕРСАЛЬНЫХ ЛЕТУЧИХ НОЖНИЦ
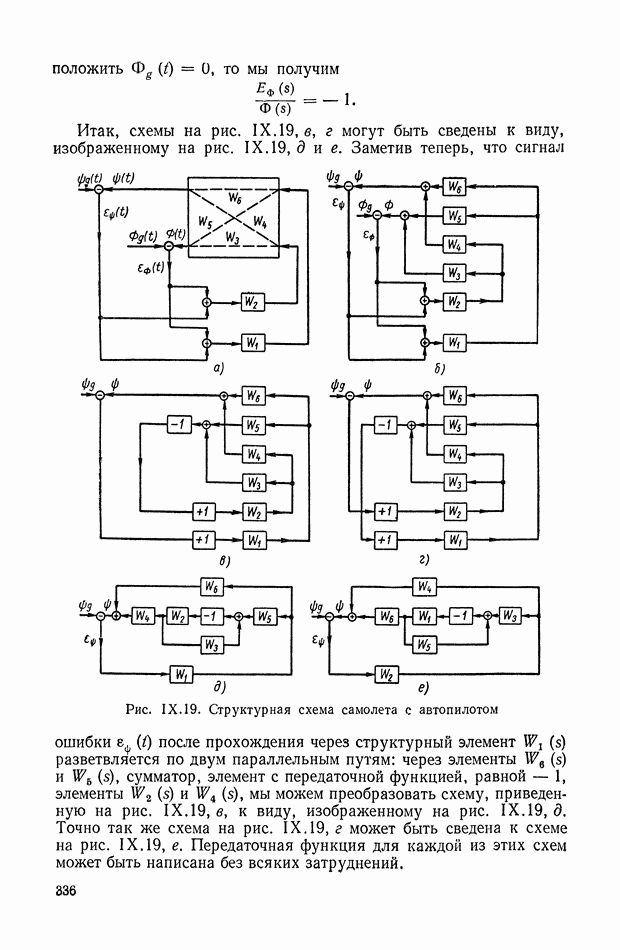
- 6. САМОЛЕТ С АВТОПИЛОТОМ
- 7. СЛЕДЯЩАЯ СИСТЕМА КОПИРОВАЛЬНО-ФРЕЗЕРНОГО СТАНКА
- РАЗДЕЛ II. АНАЛИЗ УСТОЙЧИВОСТИ НЕПРЕРЫВНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- ГЛАВА XI. ОБЩАЯ ПОСТАНОВКА ЗАДАЧИ УСТОЙЧИВОСТИ ПО ЛЯПУНОВУ И АНАЛИЗ УСТОЙЧИВОСТИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. ПОСТАНОВКА ЗАДАЧИ ОБ УСТОЙЧИВОСТИ В ТЕОРИИ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 2. ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ УСТАНОВИВШИХСЯ ДВИЖЕНИЙ ПО УРАВНЕНИЮ ПЕРВОГО ПРИБЛИЖЕНИЯ
- 3. О ПРЯМОМ МЕТОДЕ ЛЯПУНОВА
- 4. О ПРИМЕНЕНИИ ПРЯМОГО МЕТОДА ЛЯПУНОВА К АНАЛИЗУ УСТОЙЧИВОСТИ ОДНОГО КЛАССА СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- ГЛАВА XII. КРИТЕРИИ И МЕТОДЫ АНАЛИЗА УСТОЙЧИВОСТИ ЛИНЕАРИЗОВАННЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЙ
- 1. УСТОЙЧИВОСТЬ И ПРИНЦИП АРГУМЕНТА
- 2. КРИТЕРИЙ УСТОЙЧИВОСТИ МИХАЙЛОВА
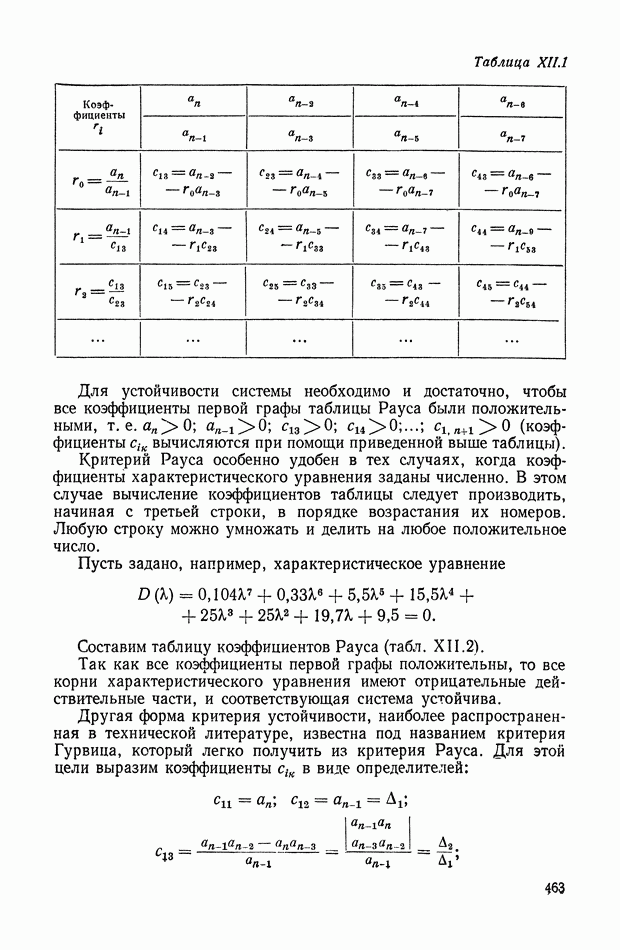
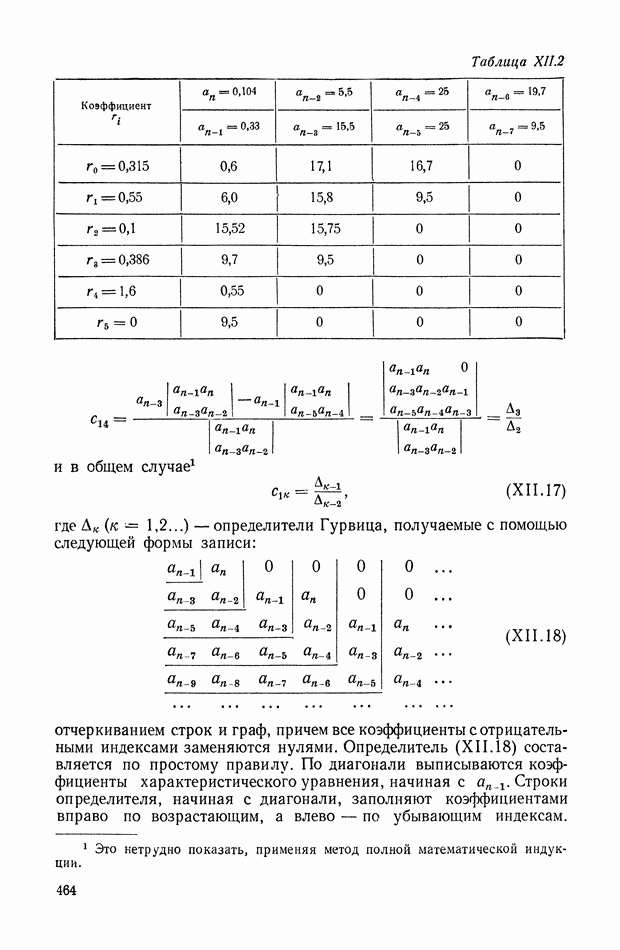
- 3. КРИТЕРИЙ УСТОЙЧИВОСТИ РАУСА И ГУРВИЦА
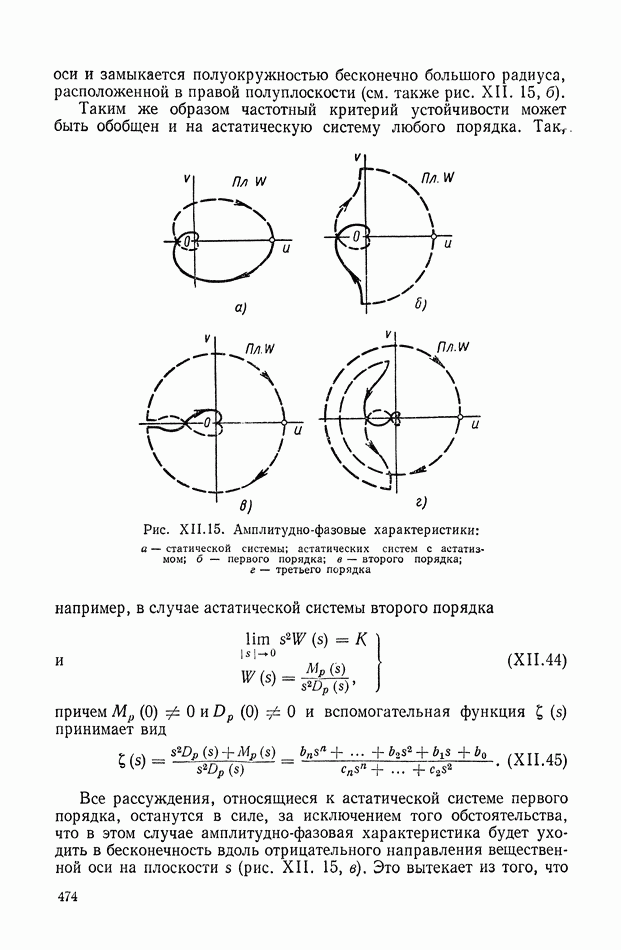
- 4. ЧАСТОТНЫЙ КРИТЕРИЙ УСТОЙЧИВОСТИ
- 5. ОБОБЩЕНИЕ ЧАСТОТНОГО КРИТЕРИЯ НА АСТАТИЧЕСКИЕ СИСТЕМЫ
- 6. ОБОБЩЕНИЕ ЧАСТОТНОГО КРИТЕРИЯ НА СЛУЧАЙ, КОГДА РАЗОМКНУТАЯ СИСТЕМА НЕУСТОЙЧИВА
- 7. ЧАСТОТНЫЙ КРИТЕРИЙ УСТОЙЧИВОСТИ ДЛЯ ОБРАТНОЙ АМПЛИТУДНО-ФАЗОВОЙ ХАРАКТЕРИСТИКИ
- 8. АНАЛИЗ УСТОЙЧИВОСТИ ОДНОКОНТУРНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ПО ИХ ЛОГАРИФМИЧЕСКИМ ЧАСТОТНЫМ ХАРАКТЕРИСТИКАМ
- 9. ПРИБЛИЖЕННЫЙ СПОСОБ ПОСТРОЕНИЯ ЛОГАРИФМИЧЕСКИХ ЧАСТОТНЫХ ХАРАКТЕРИСТИК ОДНОКОНТУРНЫХ СИСТЕМ
- 10. ОБОБЩЕНИЕ ЧАСТОТНОГО КРИТЕРИЯ УСТОЙЧИВОСТИ НА МНОГОКОНТУРНЫЕ СИСТЕМЫ
- 11. АНАЛИЗ УСТОЙЧИВОСТИ МНОГОКОНТУРНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ПРИ ПОМОЩИ ЛОГАРИФМИЧЕСКИХ ЧАСТОТНЫХ ХАРАКТЕРИСТИК
- ГЛАВА XIII. ВЫДЕЛЕНИЕ ОБЛАСТЕЙ УСТОЙЧИВОСТИ
- 1. ПОНЯТИЕ О Д-РАЗБИЕНИИ ПРОСТРАНСТВА КОЭФФИЦИЕНТОВ ХАРАКТЕРИСТИЧЕСКОГО УРАВНЕНИЯ И ПРОСТРАНСТВА ПАРАМЕТРОВ
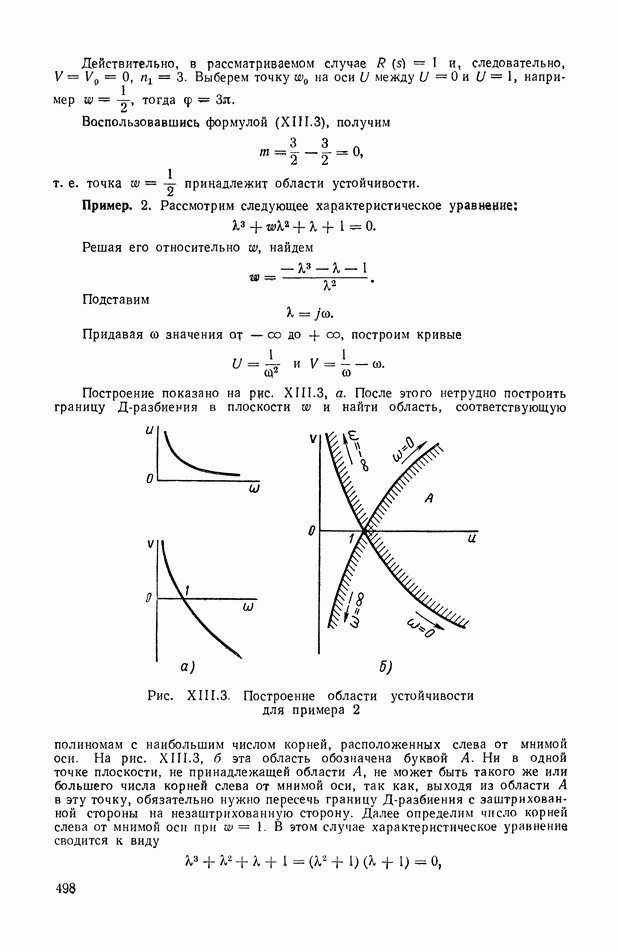
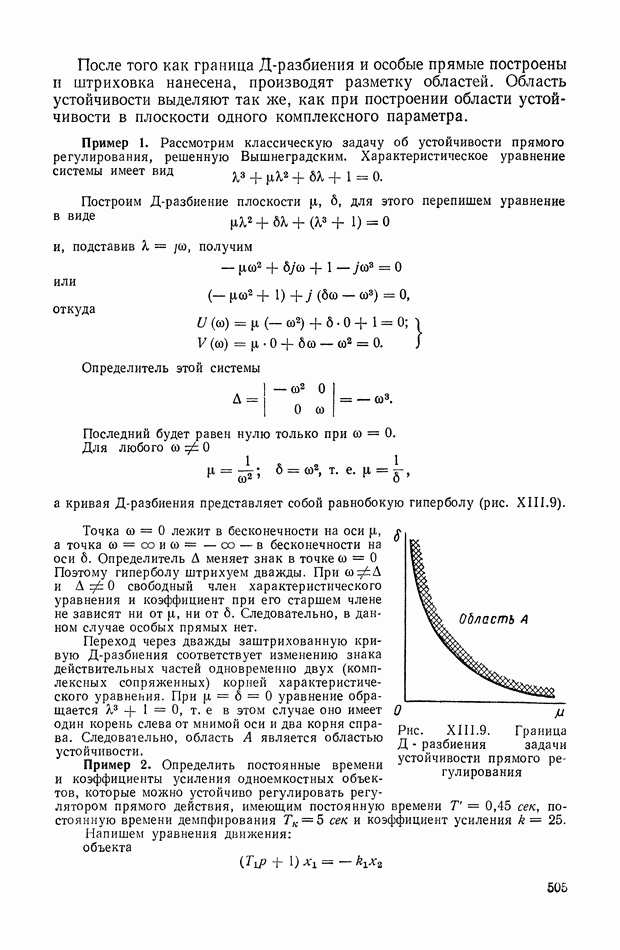
- 2. Д-РАЗБИЕНИЕ ПЛОСКОСТИ ОДНОГО КОМПЛЕКСНОГО ПАРАМЕТРА
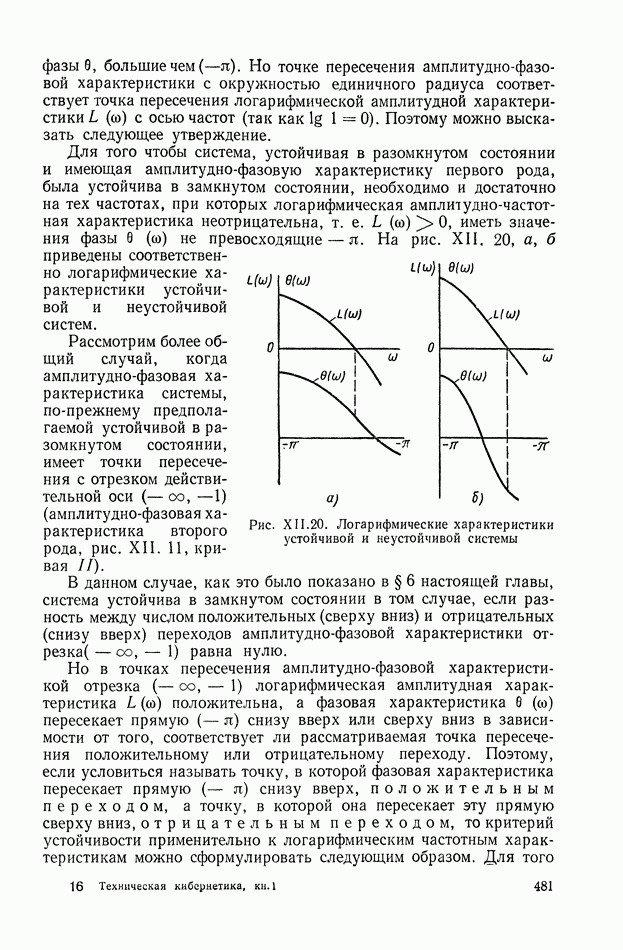
- 3. СВЯЗЬ Д-РАЗБИЕНИЯ С КРИТЕРИЯМИ УСТОЙЧИВОСТИ
- 4. Д-РАЗБИЕНИЕ ПЛОСКОСТИ ДВУХ ДЕЙСТВИТЕЛЬНЫХ ПАРАМЕТРОВ (ДИАГРАММА ВЫШНЕГРАДСКОГО)
- 5. УСЛОВИЯ СУЩЕСТВОВАНИЯ ОБЛАСТИ УСТОЙЧИВОСТИ
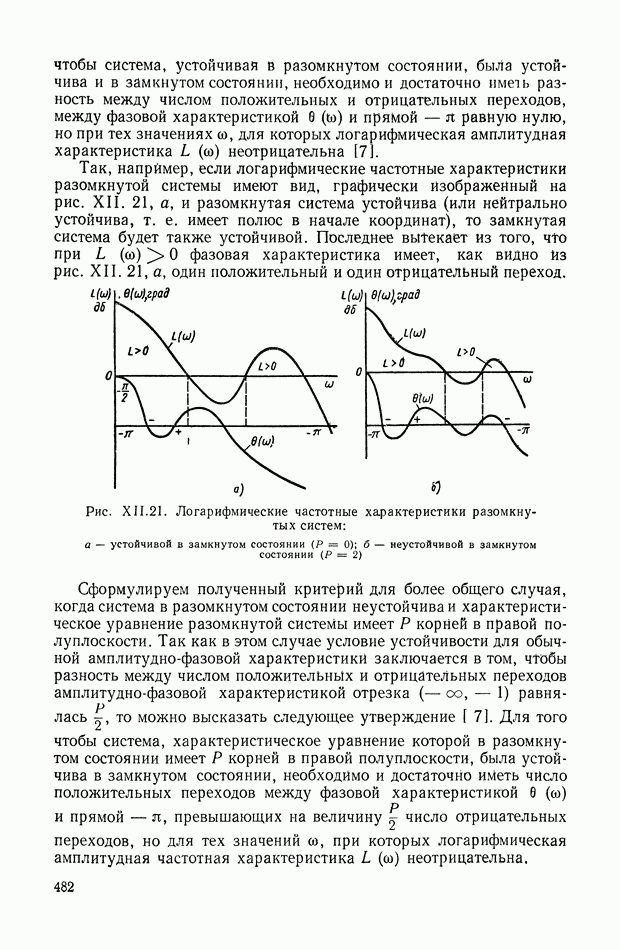
- ГЛАВА XIV. ПРИМЕРЫ АНАЛИЗА УСТОЙЧИВОСТИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
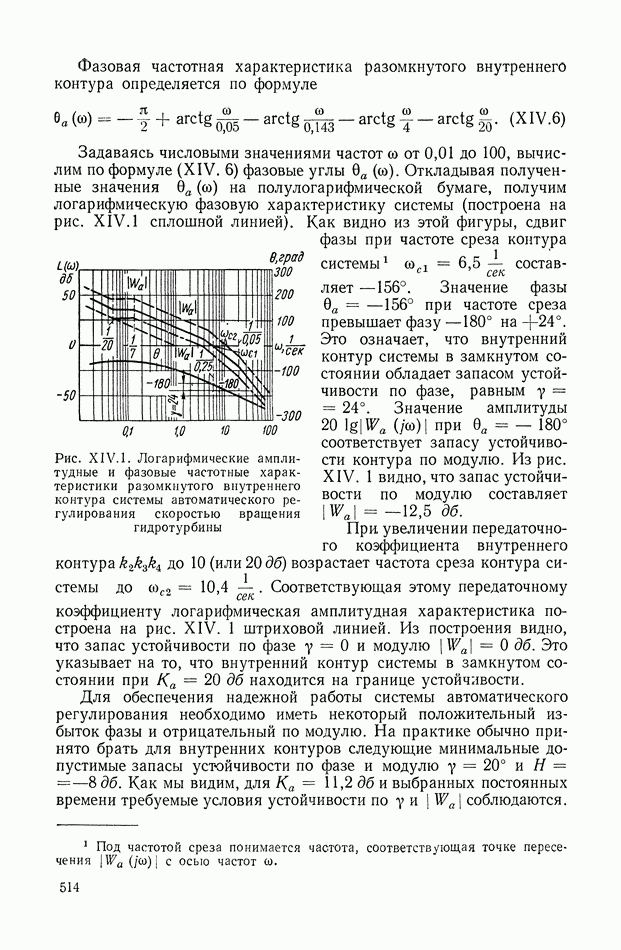
- 1. СИСТЕМА АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ СКОРОСТИ ВРАЩЕНИЯ ГИДРОТУРБИНЫ
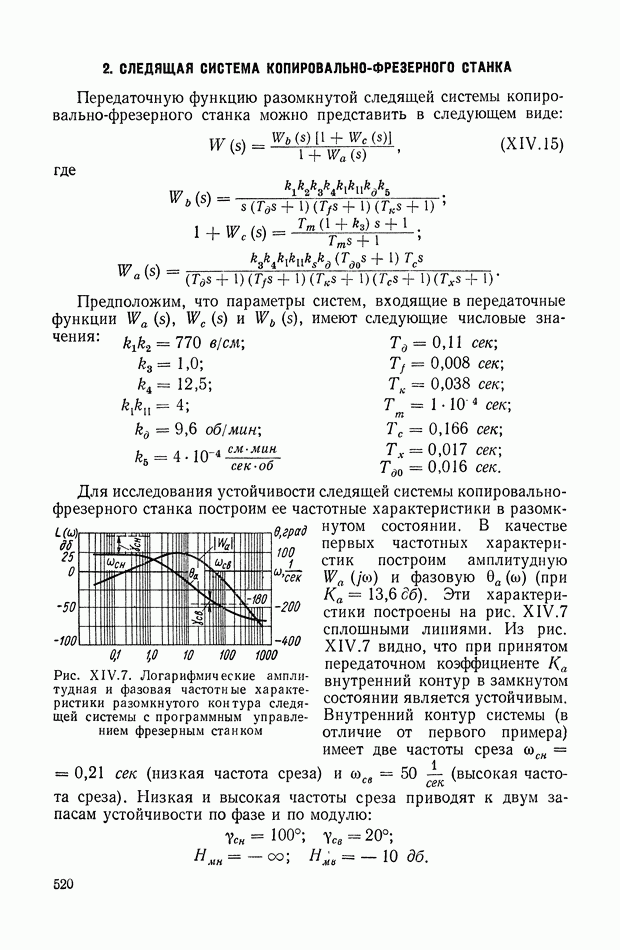
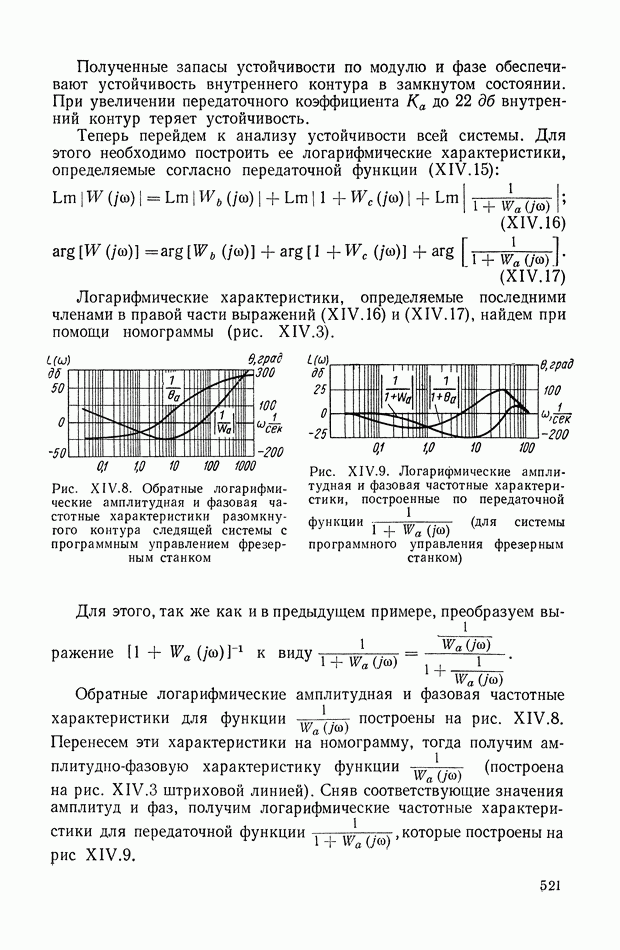
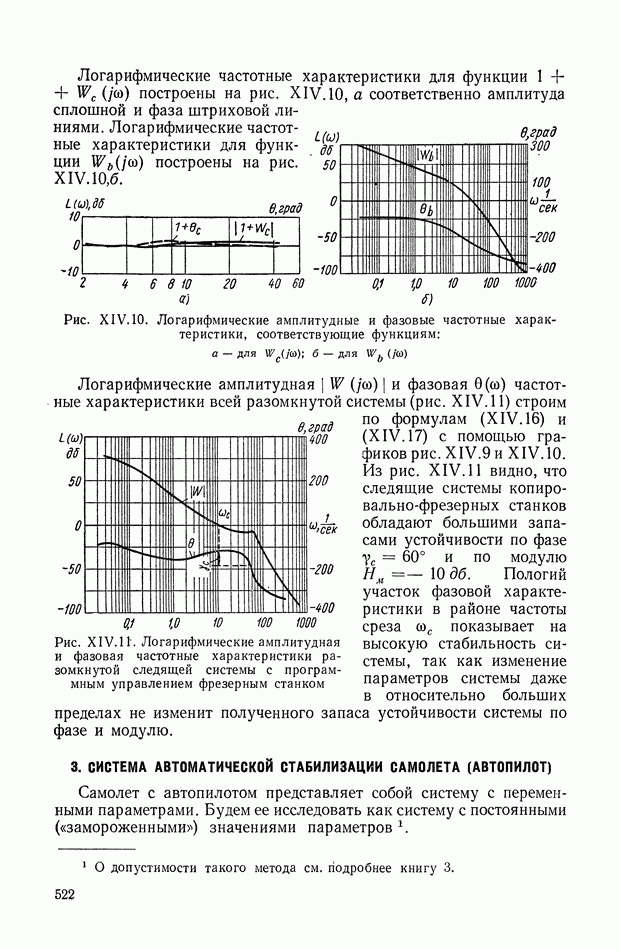
- 2. СЛЕДЯЩАЯ СИСТЕМА КОПИРОВАЛЬНО-ФРЕЗЕРНОГО СТАНКА
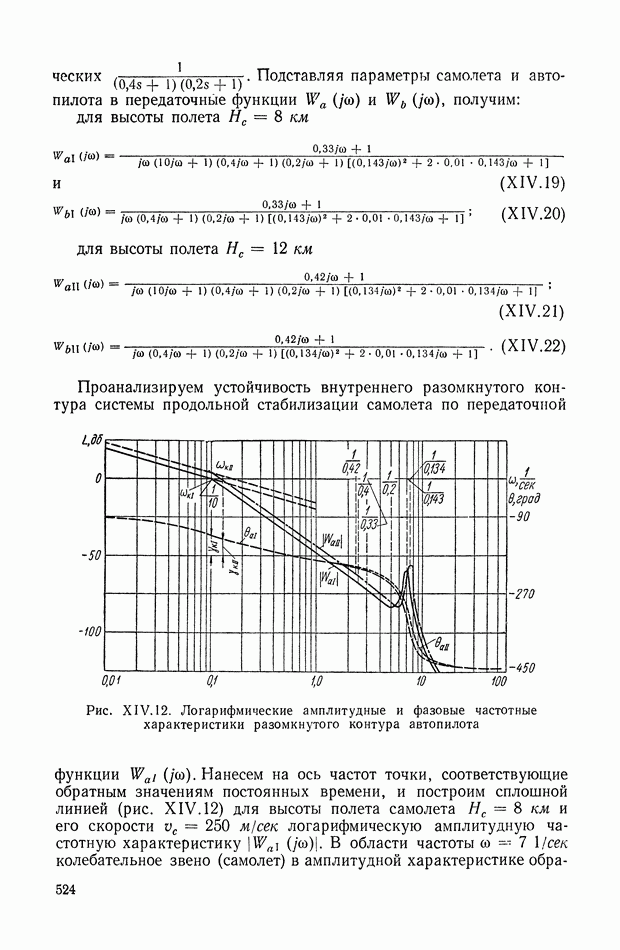
- 3. СИСТЕМА АВТОМАТИЧЕСКОЙ СТАБИЛИЗАЦИИ САМОЛЕТА (АВТОПИЛОТ)
- 4. СИСТЕМА АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ МОЩНОСТИ ЯДЕРНОГО ЭНЕРГЕТИЧЕСКОГО РЕАКТОРА
- РАЗДЕЛ III. АНАЛИЗ ПЕРЕХОДНЫХ ПРОЦЕССОВ И КАЧЕСТВА ЛИНЕЙНЫХ НЕПРЕРЫВНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- ГЛАВА XV. ЧАСТОТНЫЙ МЕТОД АНАЛИЗА ПЕРЕХОДНЫХ ПРОЦЕССОВ
- 1. ОБОБЩЕННЫЕ ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ И ИХ СВЯЗЬ С ПЕРЕХОДНЫМИ ПРОЦЕССАМИ
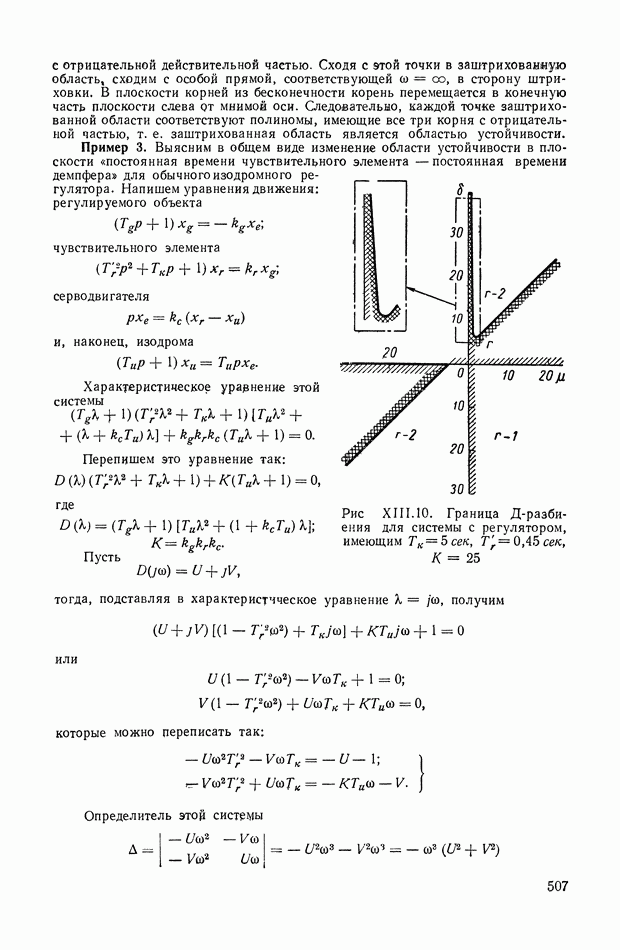
- 2. ОПРЕДЕЛЕНИЕ ОБОБЩЕННЫХ ЧАСТОТНЫХ ХАРАКТЕРИСТИК В ОБЩЕМ СЛУЧАЕ
- 3. СЛУЧАЙ, КОГДА ФУНКЦИЯ X(s) НЕ СОДЕРЖИТ ОСОБЕННОСТЕЙ ВО ВСЕЙ ПРАВОЙ ПОЛУПЛОСКОСТИ И НА МНИМОЙ ОСИ
- 4. СВЯЗЬ МЕЖДУ ЧАСТОТНЫМИ ХАРАКТЕРИСТИКАМИ P(w), Q(w) И ИМПУЛЬСНОЙ ПЕРЕХОДНОЙ ФУНКЦИЕЙ k(t)
- 5. СЛУЧАЙ, КОГДА ВСЕ ПОЛЮСА ФУНКЦИИ X(s) РАСПОЛОЖЕНЫ В ЛЕВОЙ ПОЛУПЛОСКОСТИ, ЗА ИСКЛЮЧЕНИЕМ ПОЛЮСА В НАЧАЛЕ КООРДИНАТ
- 6. СВЯЗЬ МЕЖДУ ЧАСТОТНЫМИ ХАРАКТЕРИСТИКАМИ И ПЕРЕХОДНОЙ ФУНКЦИЕЙ h(t)
- 7. СЛУЧАЙ, КОГДА ФУНКЦИЯ X(s) ИМЕЕТ ДВА СОПРЯЖЕННЫХ ПОЛЮСА НА МНИМОЙ ОСИ
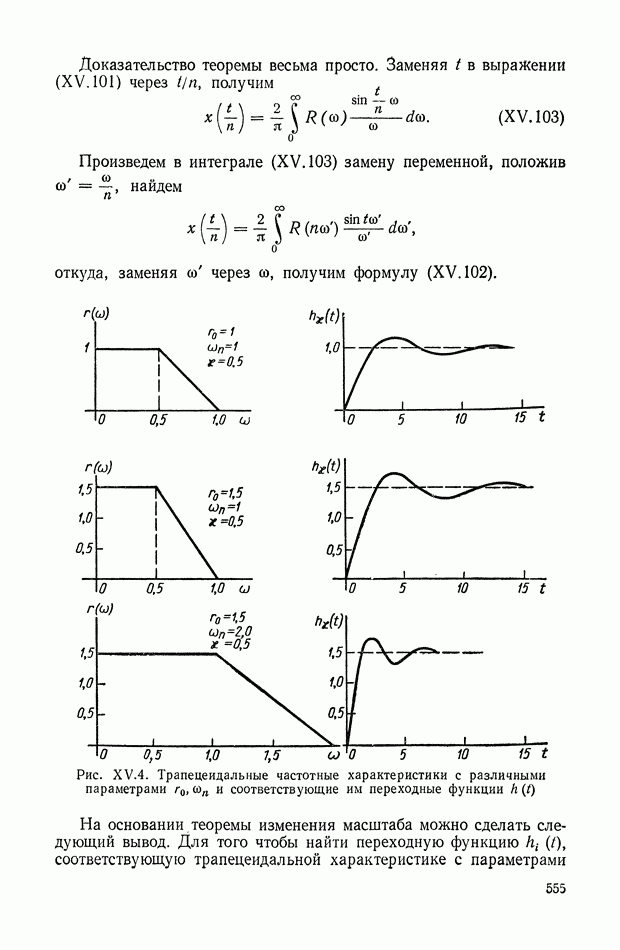
- 8. АНАЛИЗ ПЕРЕХОДНЫХ ПРОЦЕССОВ МЕТОДОМ ТРАПЕЦЕИДАЛЬНЫХ ЧАСТОТНЫХ ХАРАКТЕРИСТИК
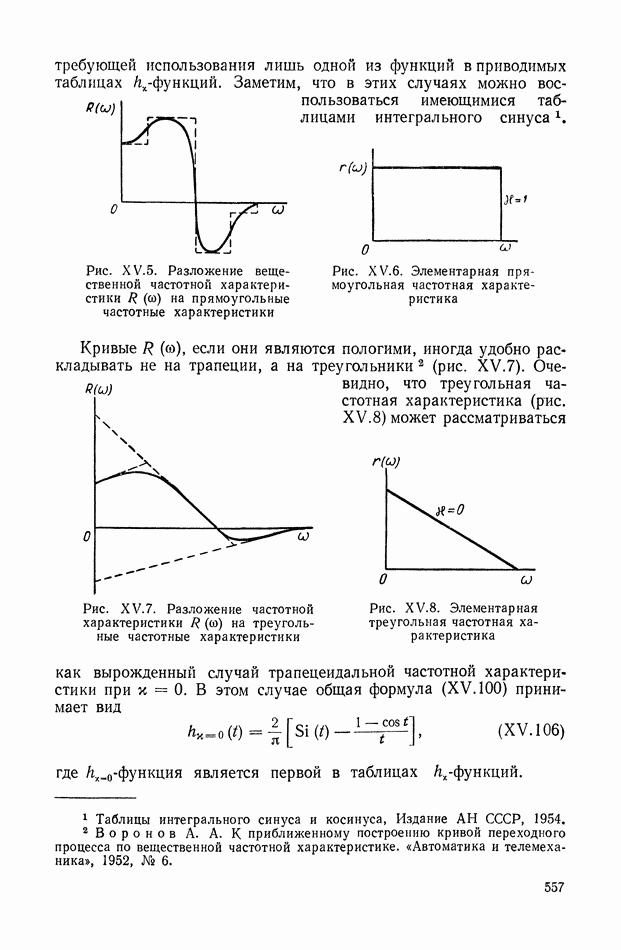
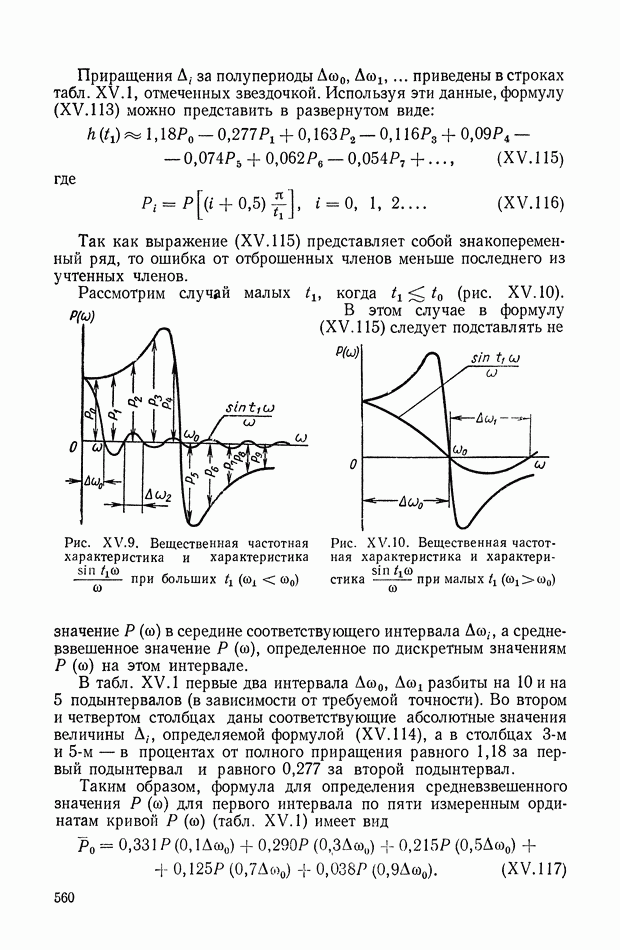
- 9. О НЕКОТОРЫХ ЧАСТНЫХ СЛУЧАЯХ МЕТОДА ТРАПЕЦЕИДАЛЬНЫХ ЧАСТОТНЫХ ХАРАКТЕРИСТИК
- 10. ОБ УСЛОВИЯХ ПРИМЕНИМОСТИ ЧАСТОТНОГО МЕТОДА АНАЛИЗА ПЕРЕХОДНЫХ ПРОЦЕССОВ
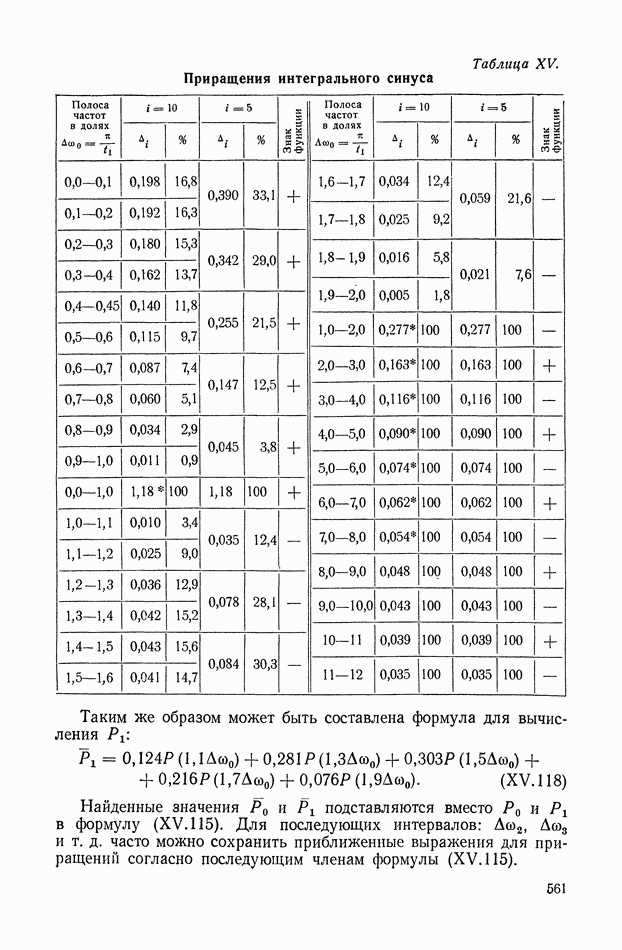
- 11. ОПРЕДЕЛЕНИЕ ДИСКРЕТНЫХ ЗНАЧЕНИЙ ПЕРЕХОДНОЙ ФУНКЦИИ
- ГЛАВА XVI. ЧАСТОТНЫЙ МЕТОД АНАЛИЗА КАЧЕСТВА
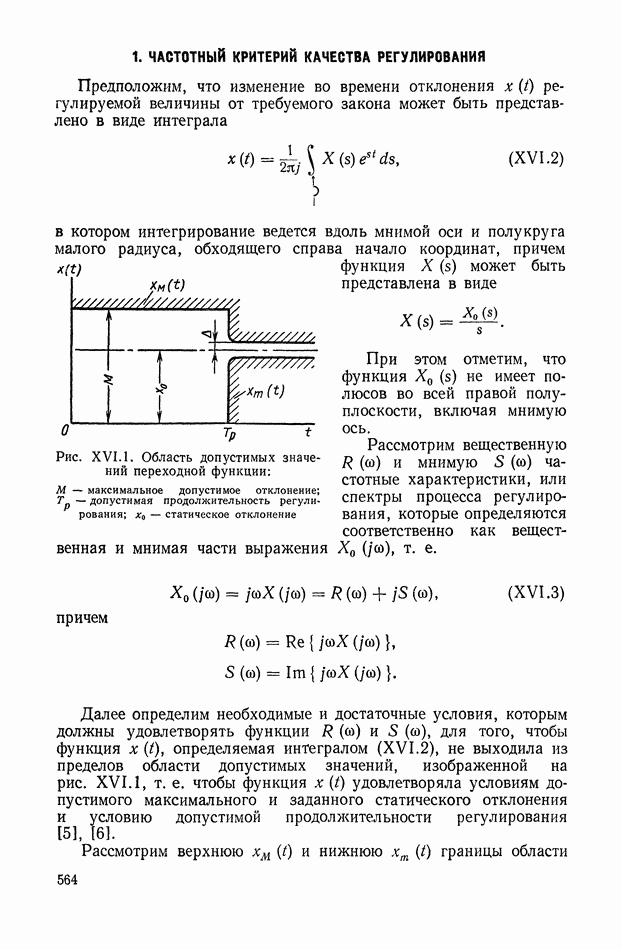
- 1. ЧАСТОТНЫЙ КРИТЕРИЙ КАЧЕСТВА РЕГУЛИРОВАНИЯ
- 2. ЧАСТОТНЫЙ КРИТЕРИЙ ОТСУТСТВИЯ ПЕРЕРЕГУЛИРОВАНИЙ И ЧАСТОТНЫЙ КРИТЕРИЙ МОНОТОННОСТИ
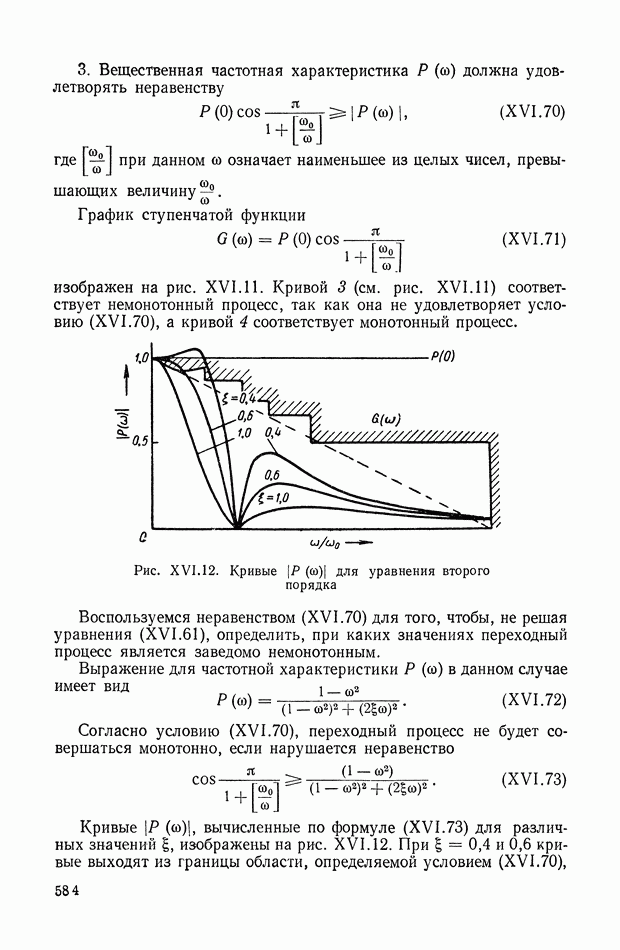
- 3. О ПРОВЕРКЕ ВЫПОЛНЕНИЯ СФОРМУЛИРОВАННЫХ КРИТЕРИЕВ
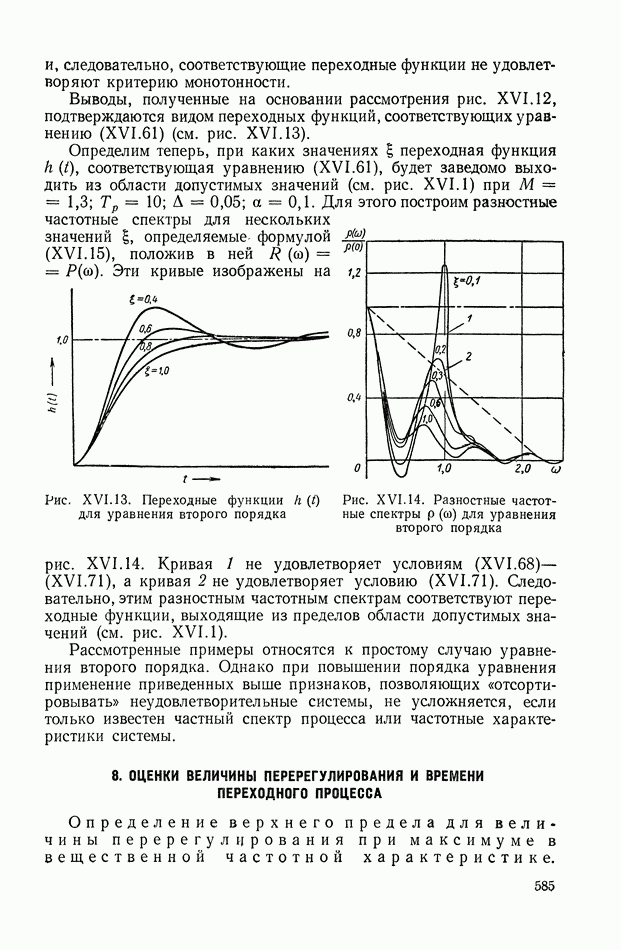
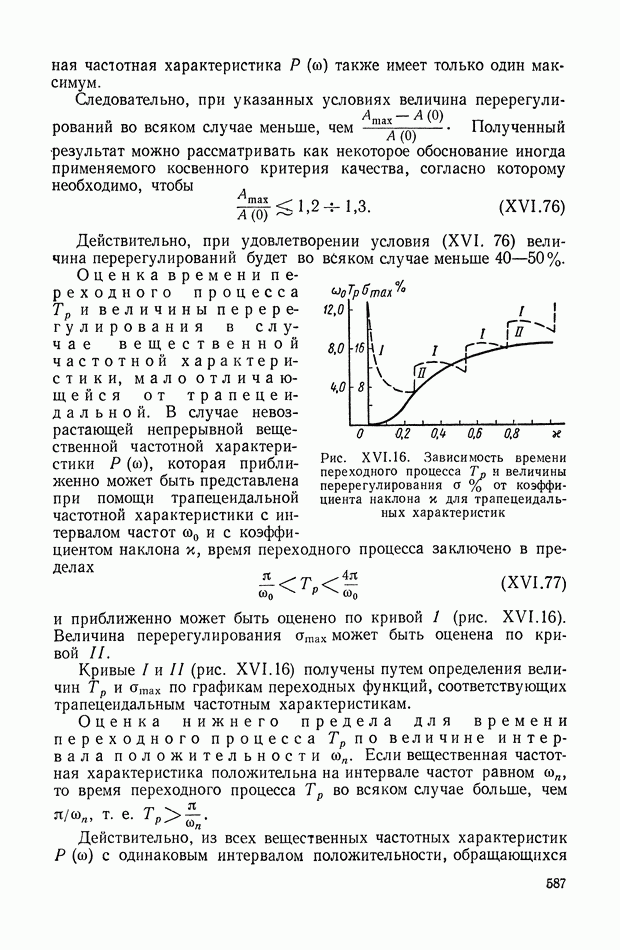
- 4. НЕКОТОРЫЕ ПРИЗНАКИ НЕУДОВЛЕТВОРЕНИЯ КРИТЕРИЕВ КАЧЕСТВА И КРИТЕРИЕВ ОТСУТСТВИЯ ПЕРЕРЕГУЛИРОВАНИЙ И МОНОТОННОСТИ
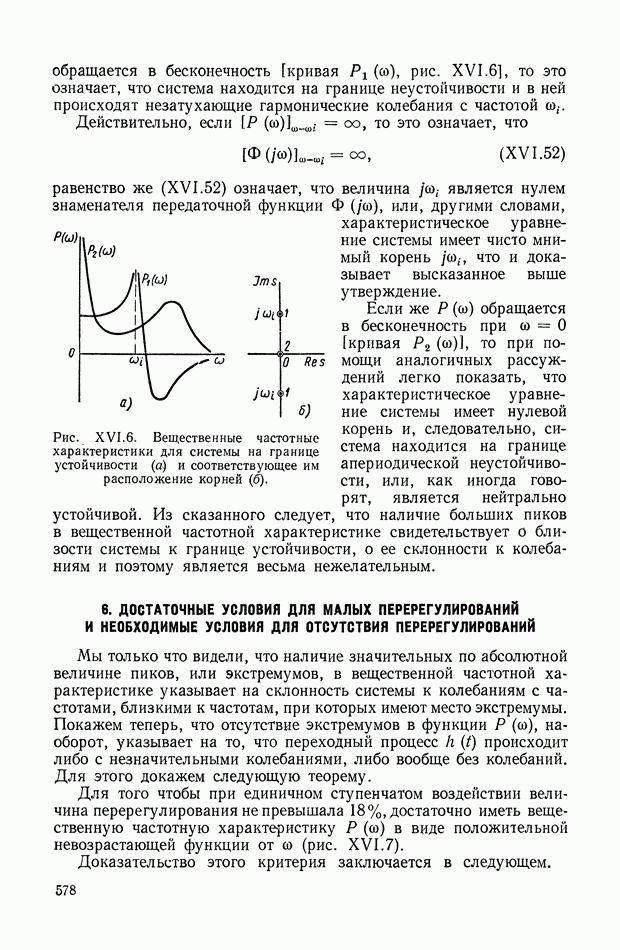
- 5. НЕКОТОРЫЕ ЭЛЕМЕНТАРНЫЕ СВОЙСТВА ЧАСТОТНЫХ ХАРАКТЕРИСТИК
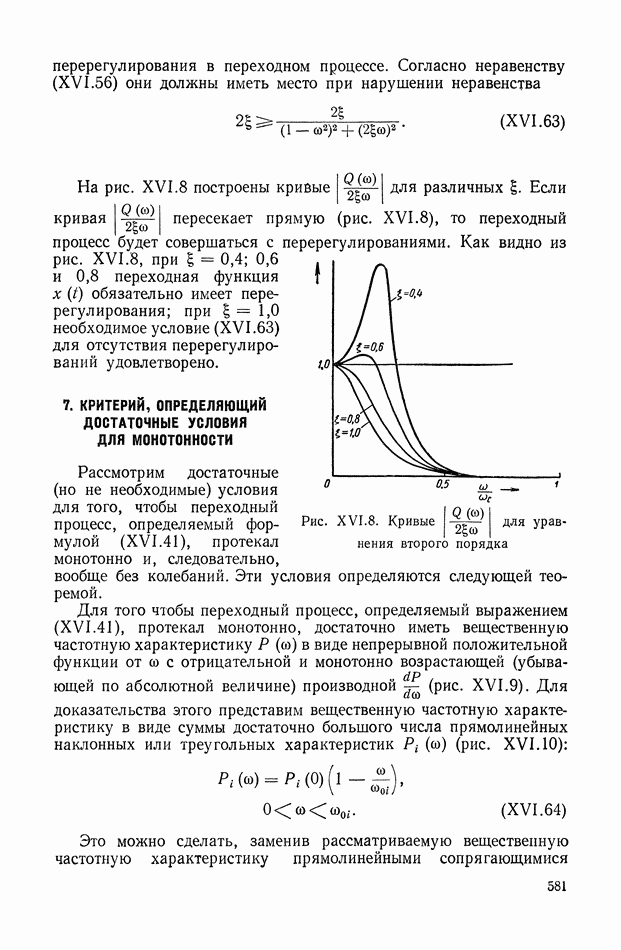
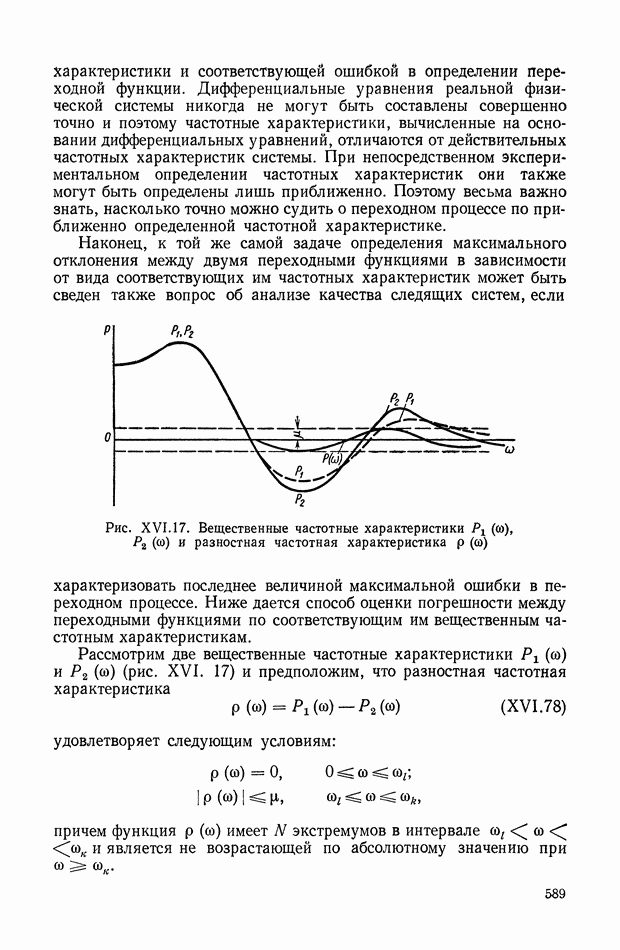
- 6. ДОСТАТОЧНЫЕ УСЛОВИЯ ДЛЯ МАЛЫХ ПЕРЕРЕГУЛИРОВАНИЙ И НЕОБХОДИМЫЕ УСЛОВИЯ ДЛЯ ОТСУТСТВИЯ ПЕРЕРЕГУЛИРОВАНИЙ
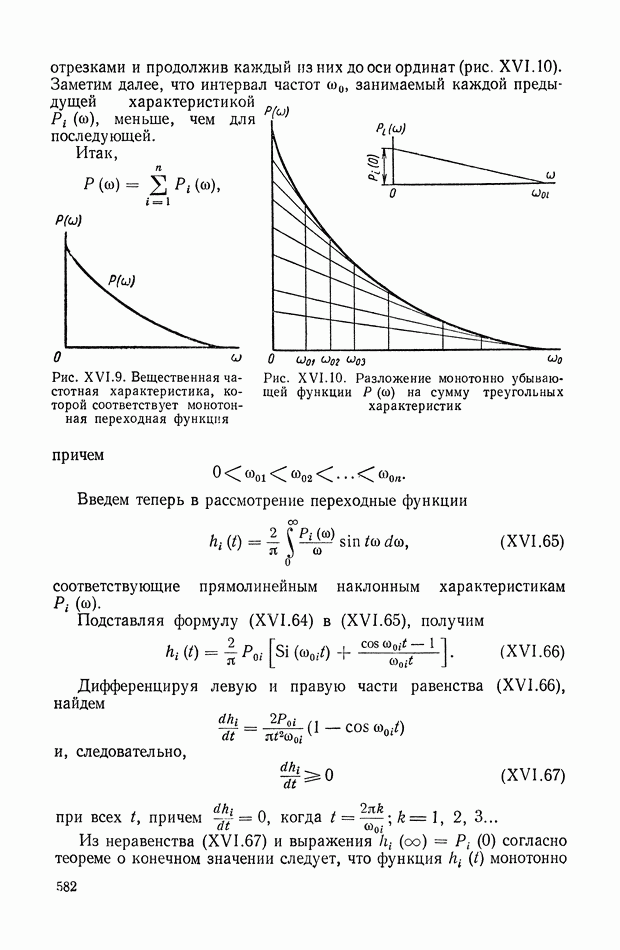
- 7. КРИТЕРИЙ, ОПРЕДЕЛЯЮЩИЙ ДОСТАТОЧНЫЕ УСЛОВИЯ ДЛЯ МОНОТОННОСТИ
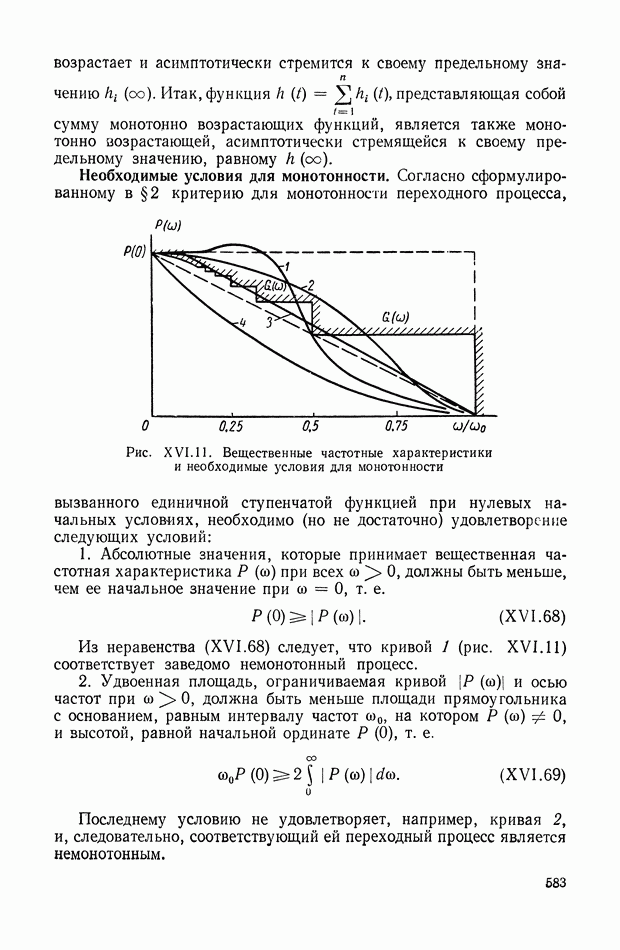
- 8. ОЦЕНКИ ВЕЛИЧИНЫ ПЕРЕРЕГУЛИРОВАНИЯ И ВРЕМЕНИ ПЕРЕХОДНОГО ПРОЦЕССА
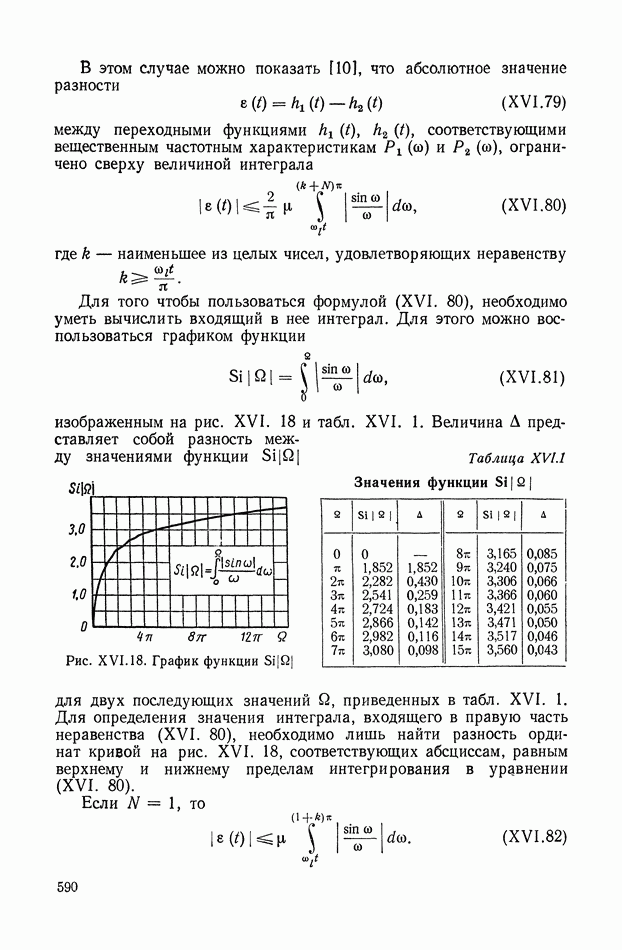
- 9. ОЦЕНКА АБСОЛЮТНОГО ЗНАЧЕНИЯ РАЗНОСТИ МЕЖДУ ПЕРЕХОДНЫМИ ФУНКЦИЯМИ ПО СООТВЕТСТВУЮЩИМ ИМ ЧАСТОТНЫМ ХАРАКТЕРИСТИКАМ
- 10. СВЯЗЬ МЕЖДУ СВОЙСТВАМИ АМПЛИТУДНО-ФАЗОВОЙ ХАРАКТЕРИСТИКИ РАЗОМКНУТОЙ СИСТЕМЫ И КАЧЕСТВОМ
- 11. ТРЕБОВАНИЯ К ЧАСТОТНЫМ ХАРАКТЕРИСТИКАМ, ОБЕСПЕЧИВАЮЩИЕ ВЫСОКУЮ ТОЧНОСТЬ В СЛЕДЯЩИХ СИСТЕМАХ
- 12. СВЯЗЬ МЕЖДУ СВОЙСТВАМИ ЛОГАРИФМИЧЕСКОЙ АМПЛИТУДНОЙ ХАРАКТЕРИСТИКИ И КАЧЕСТВОМ
- 13. ОПРЕДЕЛЕНИЕ ВЕЛИЧИНЫ ПЕРЕДАТОЧНОГО КОЭФФИЦИЕНТА ИЛИ ДОБРОТНОСТИ ПО ЛОГАРИФМИЧЕСКОЙ АМПЛИТУДНОЙ ХАРАКТЕРИСТИКЕ
- 14. ОПРЕДЕЛЕНИЕ УСТАНОВИВШЕЙСЯ ОШИБКИ ПРИ ГАРМОНИЧЕСКОМ УПРАВЛЯЮЩЕМ ВОЗДЕЙСТВИИ ПО ЛОГАРИФМИЧЕСКОЙ АМПЛИТУДНОЙ ХАРАКТЕРИСТИКЕ
- 15. ПРИБЛИЖЕННЫЙ СПОСОБ ВЫЧИСЛЕНИЯ ПЕРЕХОДНОГО ПРОЦЕССА ПО СОПРЯГАЮЩИМ ЧАСТОТАМ ЛОГАРИФМИЧЕСКОЙ АМПЛИТУДНОЙ ЧАСТОТНОЙ ХАРАКТЕРИСТИКИ
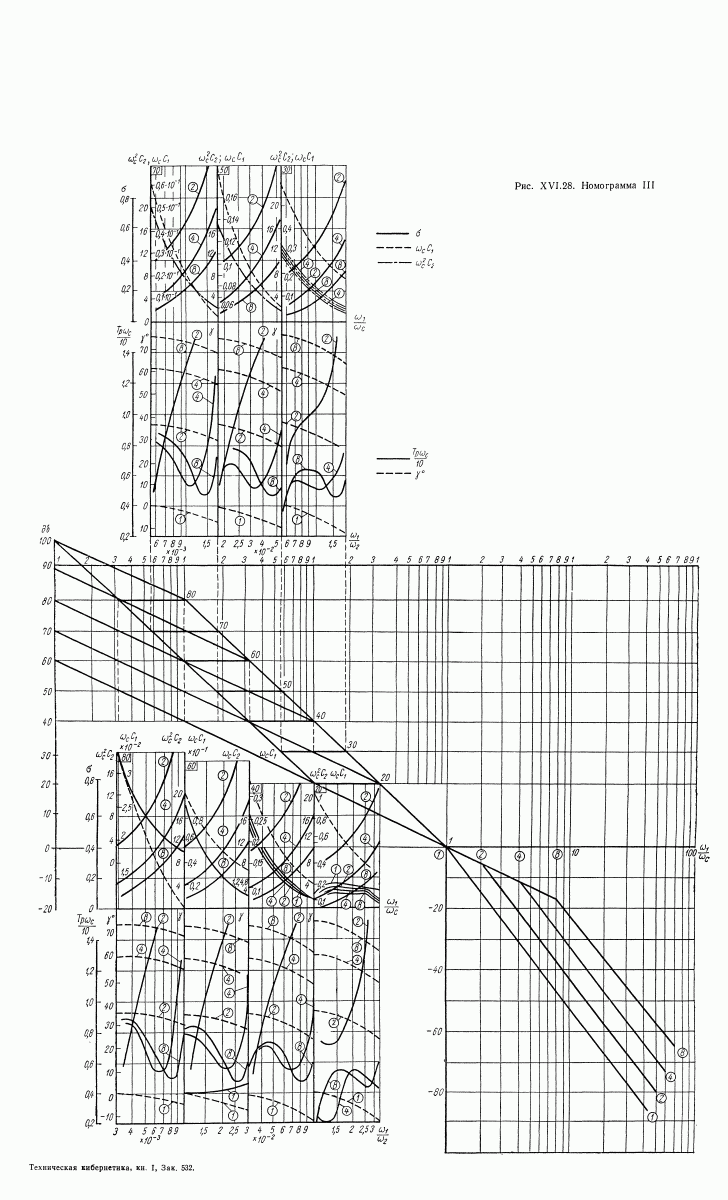
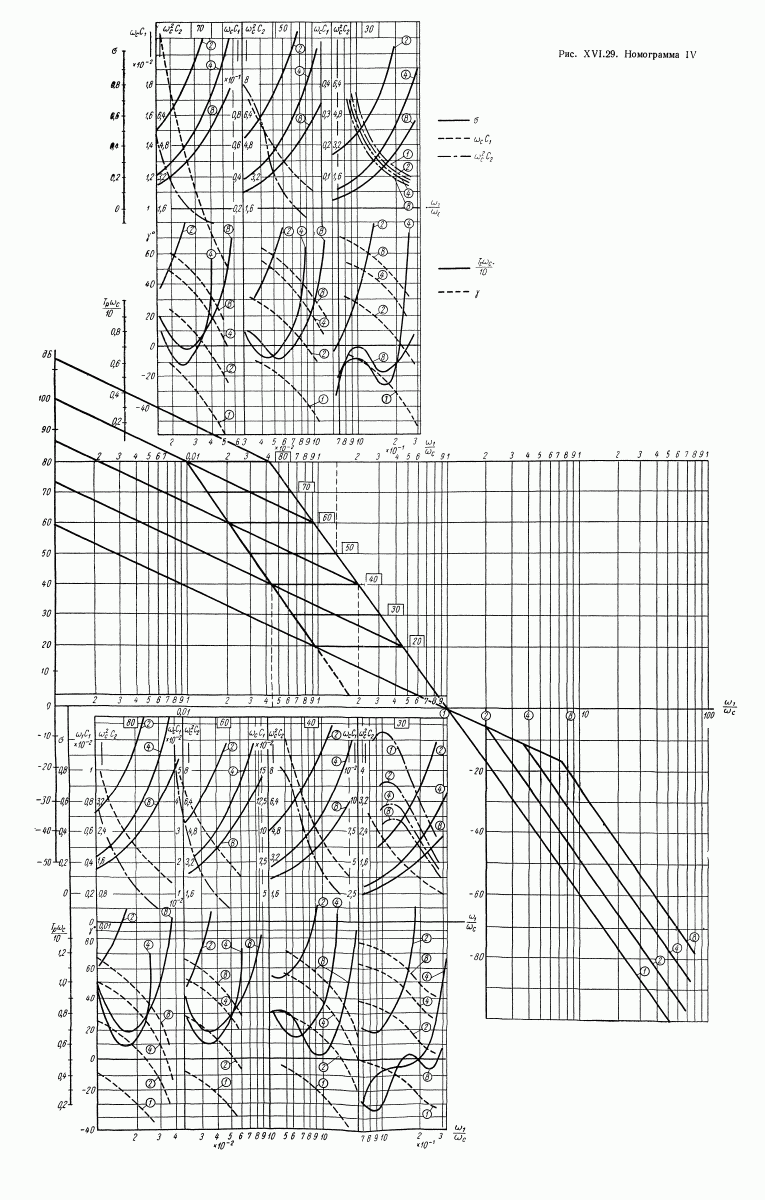
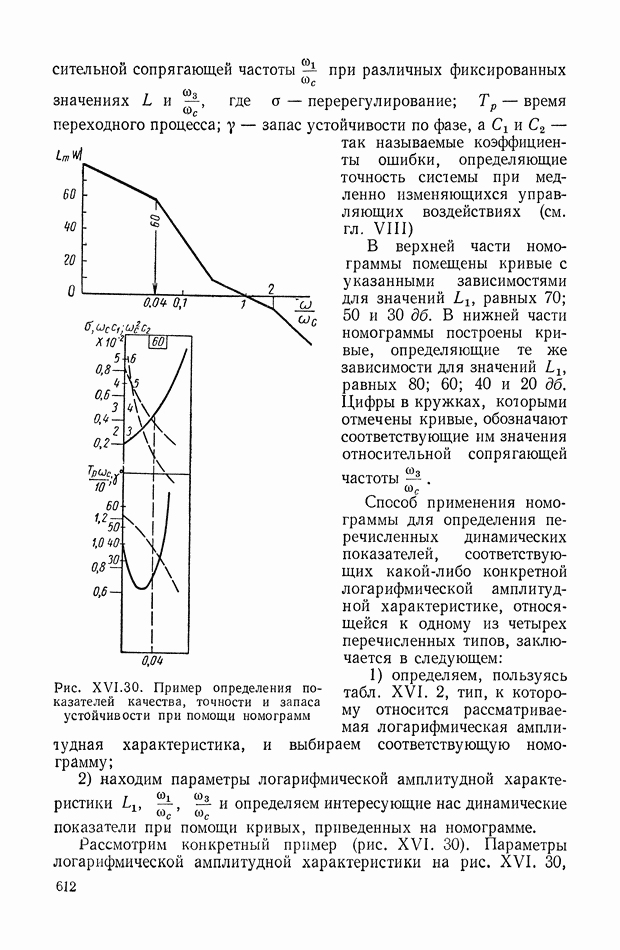
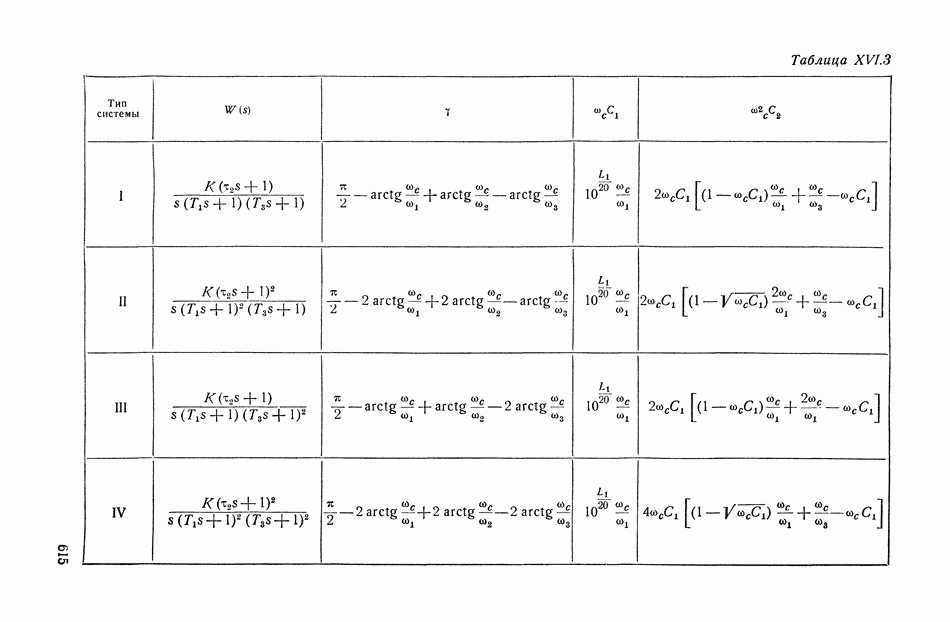
- 16. НОМОГРАММА ДЛЯ ОПРЕДЕЛЕНИЯ ЗАПАСА УСТОЙЧИВОСТИ, ПОКАЗАТЕЛЕЙ КАЧЕСТВА И КОЭФФИЦИЕНТОВ ОШИБОК ПО ВИДУ ЛОГАРИФМИЧЕСКОЙ АМПЛИТУДНОЙ ХАРАКТЕРИСТИКИ
- ГЛАВА XVII. СВЯЗЬ МЕЖДУ КАЧЕСТВОМ ПЕРЕХОДНОГО ПРОЦЕССА И РАСПРЕДЕЛЕНИЕМ НУЛЕЙ И ПОЛЮСОВ ПЕРЕДАТОЧНОЙ ФУНКЦИИ. МЕТОД КОРНЕВЫХ ГОДОГРАФОВ
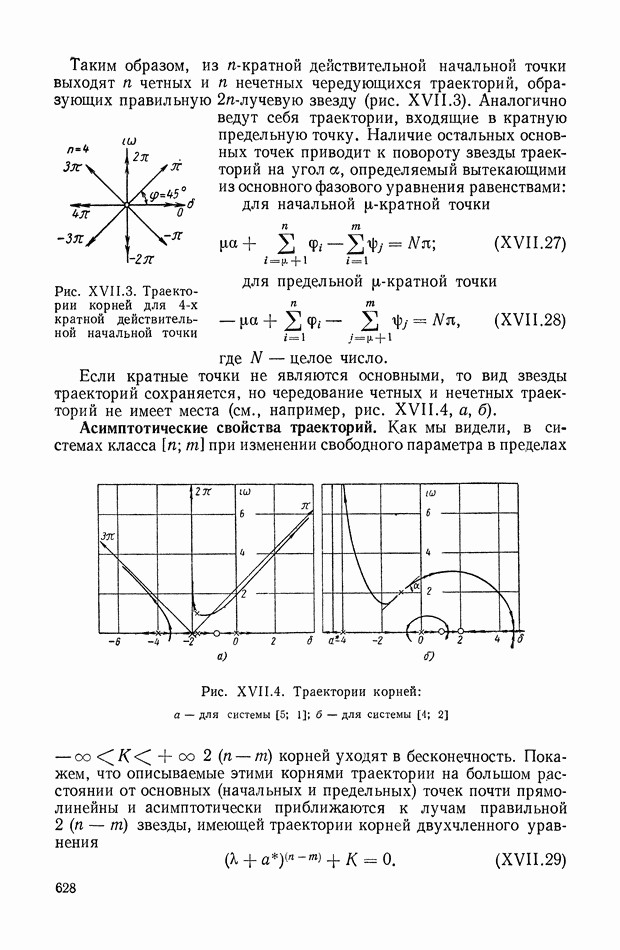
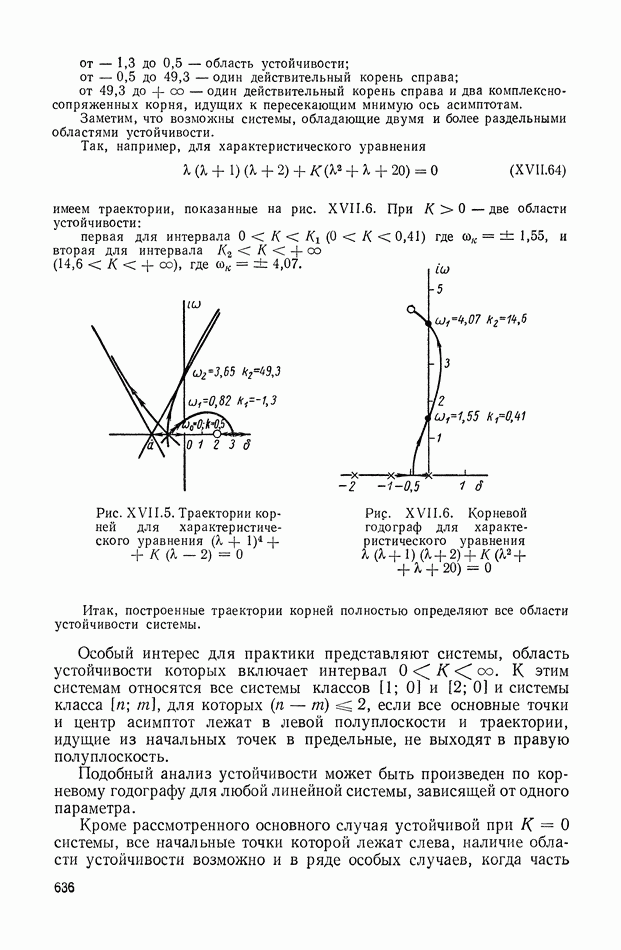
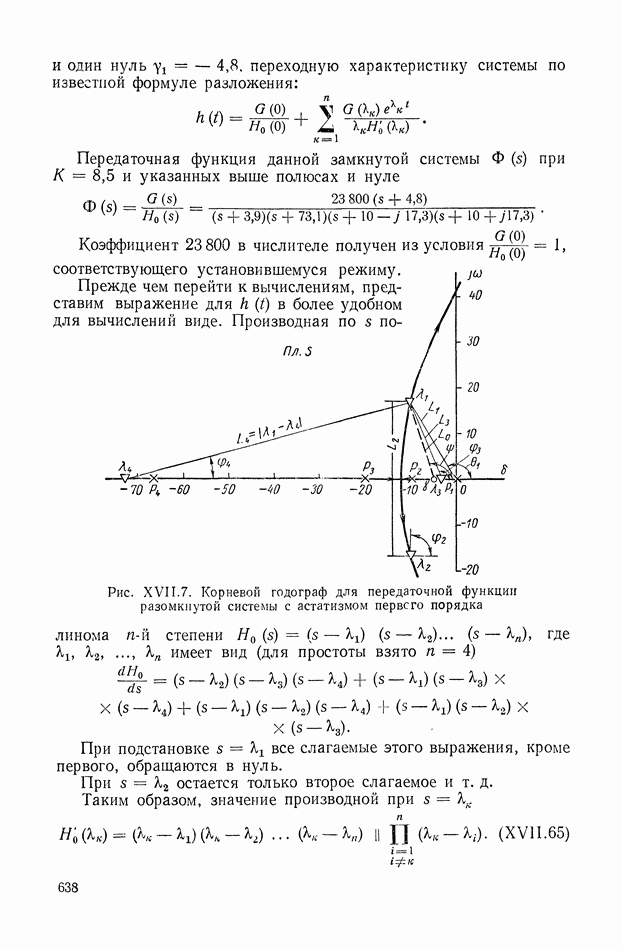
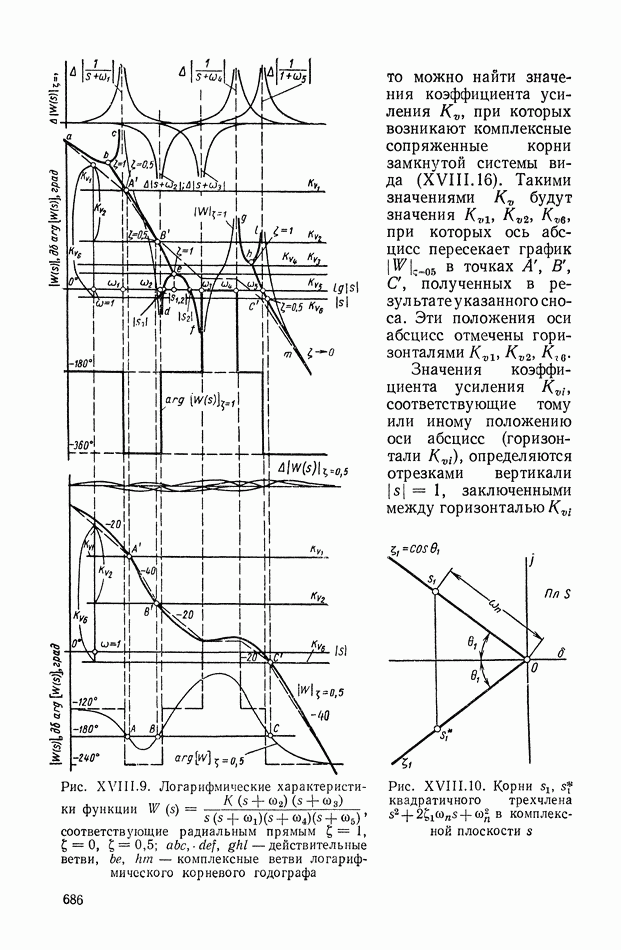
- 2. АНАЛИЗ РАСПРЕДЕЛЕНИЯ КОРНЕЙ ХАРАКТЕРИСТИЧЕСКОГО УРАВНЕНИЯ СИСТЕМЫ И ОЦЕНКА КАЧЕСТВА ПЕРЕХОДНОГО ПРОЦЕССА
- 3. ГЕОМЕТРИЧЕСКИЙ МЕТОД ПОСТРОЕНИЯ КОРНЕВОГО ГОДОГРАФА
- 4. АНАЛИТИЧЕСКОЕ ПОСТРОЕНИЕ ГЕОМЕТРИЧЕСКОГО МЕСТА КОРНЕЙ
- 5. ОПРЕДЕЛЕНИЕ ОБЛАСТЕЙ УСТОЙЧИВОСТИ ЛИНЕЙНЫХ СИСТЕМ МЕТОДОМ КОРНЕВОГО ГОДОГРАФА
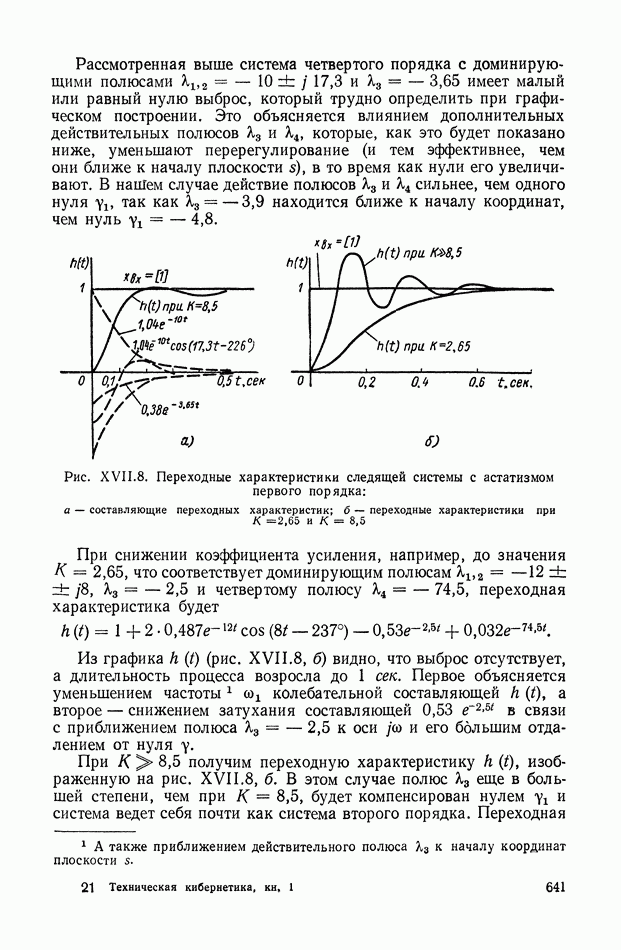
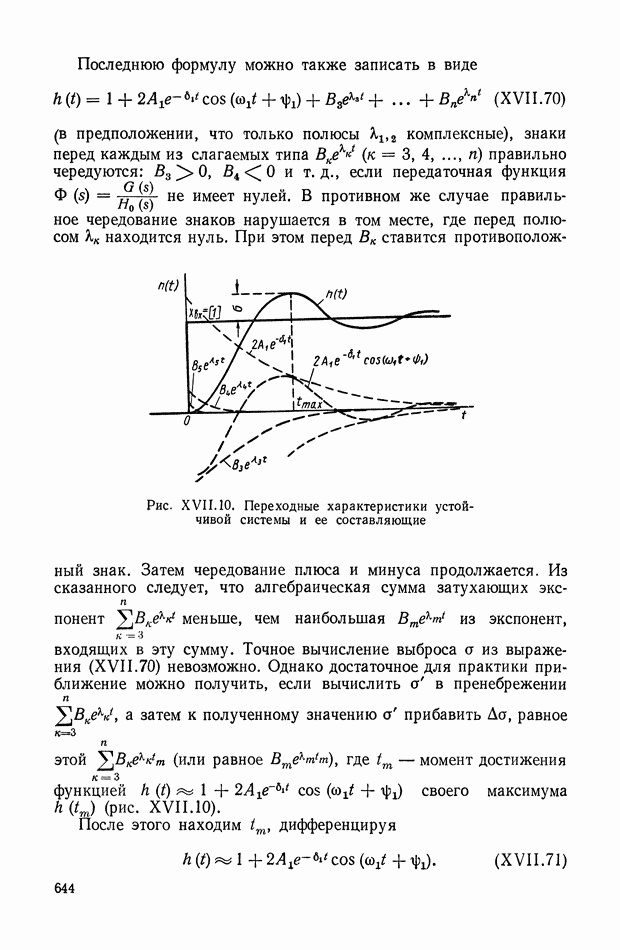
- 6. ОЦЕНКИ ПАРАМЕТРОВ ПЕРЕХОДНОЙ И ЧАСТОТНОЙ ХАРАКТЕРИСТИК ПО КОРНЕВОМУ ГОДОГРАФУ
- 7. ВЛИЯНИЕ РАСПОЛОЖЕНИЯ НУЛЕЙ И ПОЛЮСОВ ЗАМКНУТОЙ СИСТЕМЫ НА ПЕРЕХОДНУЮ ХАРАКТЕРИСТИКУ h(t)
- 8. ВЛИЯНИЕ РАСПОЛОЖЕНИЯ НУЛЕЙ И ПОЛЮСОВ ЗАМКНУТОЙ СИСТЕМЫ НА ЕЕ ПОЛОСУ ЧАСТОТ
- 9. КОРНЕВОЙ ГОДОГРАФ И ПЕРЕХОДНАЯ ХАРАКТЕРИСТИКА СИСТЕМЫ ПРИ ВОЗМУЩЕНИЯХ, ПРИЛОЖЕННЫХ НЕ К ОСНОВНОМУ ВХОДУ СИСТЕМЫ
- 10. ВЛИЯНИЕ РАСПРЕДЕЛЕНИЯ НУЛЕЙ И ПОЛЮСОВ ПЕРЕДАТОЧНОЙ ФУНКЦИИ НА КАЧЕСТВО ПЕРЕХОДНОГО ПРОЦЕССА ПРИ НАЛИЧИИ ВНЕШНЕГО ВОЗДЕЙСТВИЯ
- ГЛАВА XVIII. МЕТОД ЛОГАРИФМИЧЕСКИХ КОРНЕВЫХ ГОДОГРАФОВ
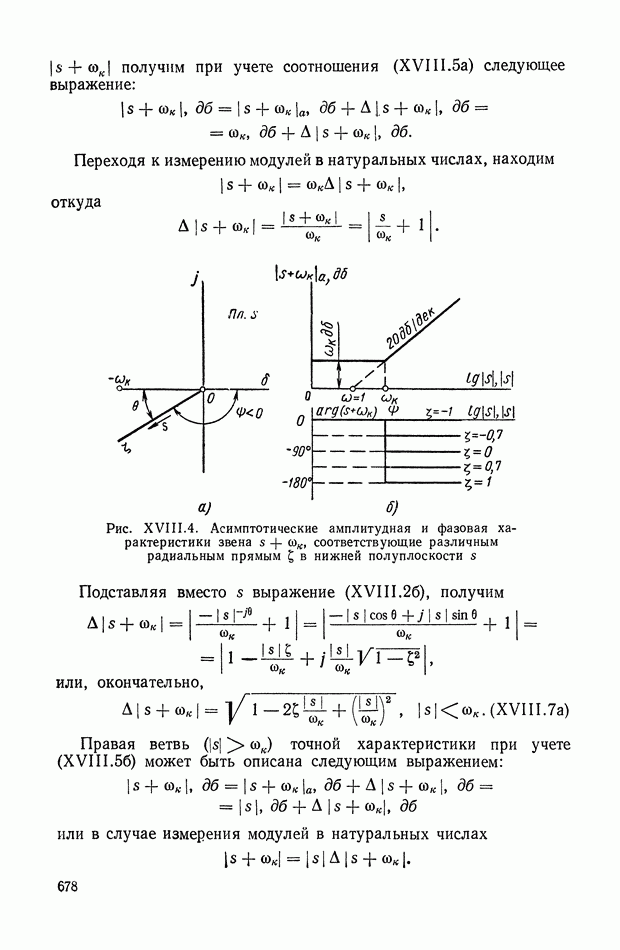
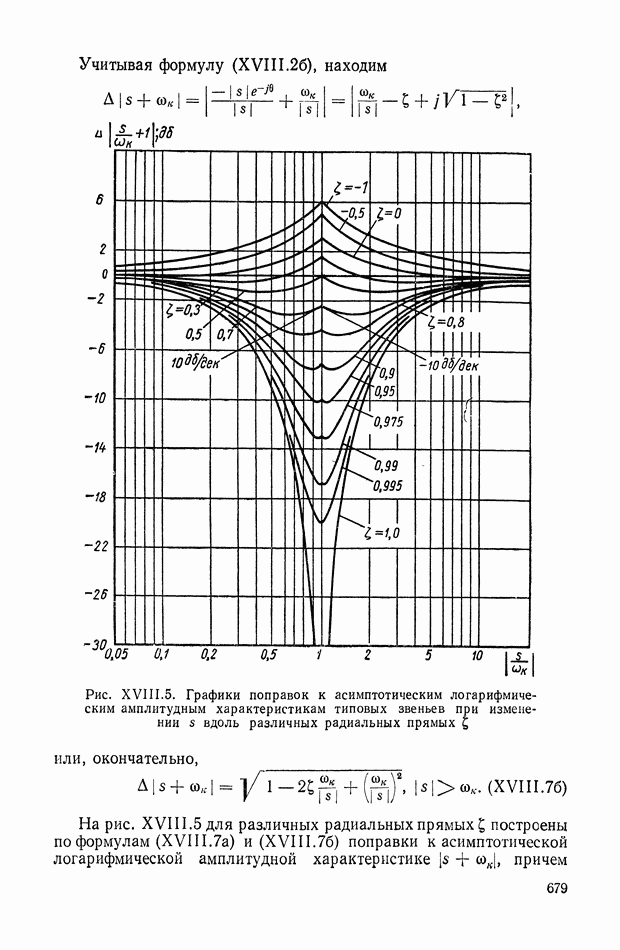
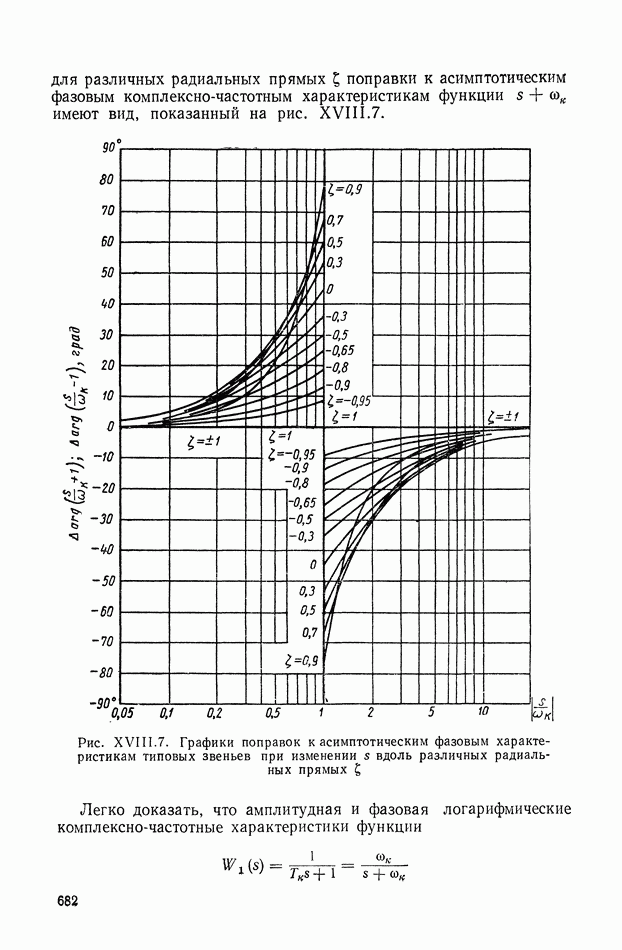
- 2. ОПРЕДЕЛЕНИЕ КОРНЕЙ ЗАМКНУТОЙ СИСТЕМЫ ПО ЛОГАРИФМИЧЕСКОЙ АМПЛИТУДНОЙ КОМПЛЕКСНО-ЧАСТОТНОЙ ХАРАКТЕРИСТИКЕ РАЗОМКНУТОЙ СИСТЕМЫ
- 3. ЛОГАРИФМИЧЕСКИЕ КОРНЕВЫЕ ГОДОГРАФЫ
- 4. ЛОГАРИФМИЧЕСКИЕ КОМПЛЕКСНО-ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЗВЕНЬЕВ ВТОРОГО ПОРЯДКА
- 5. ПРИМЕР ПОСТРОЕНИЯ ЛОГАРИФМИЧЕСКОГО КОРНЕВОГО ГОДОГРАФА
- ГЛАВА XIX. ИНТЕГРАЛЬНЫЕ ОЦЕНКИ И КРИТЕРИИ КАЧЕСТВА РЕГУЛИРОВАНИЯ
- 2. МЕТОДИКА ПРИМЕНЕНИЯ ИНТЕГРАЛЬНЫХ КВАДРАТИЧНЫХ ОЦЕНОК
- 3. ЛИНЕЙНЫЕ ИНТЕГРАЛЬНЫЕ ОЦЕНКИ
- ПРИЛОЖЕНИЕ
- БИБЛИОГРАФИЯ ПО РАЗДЕЛАМ КНИГИ