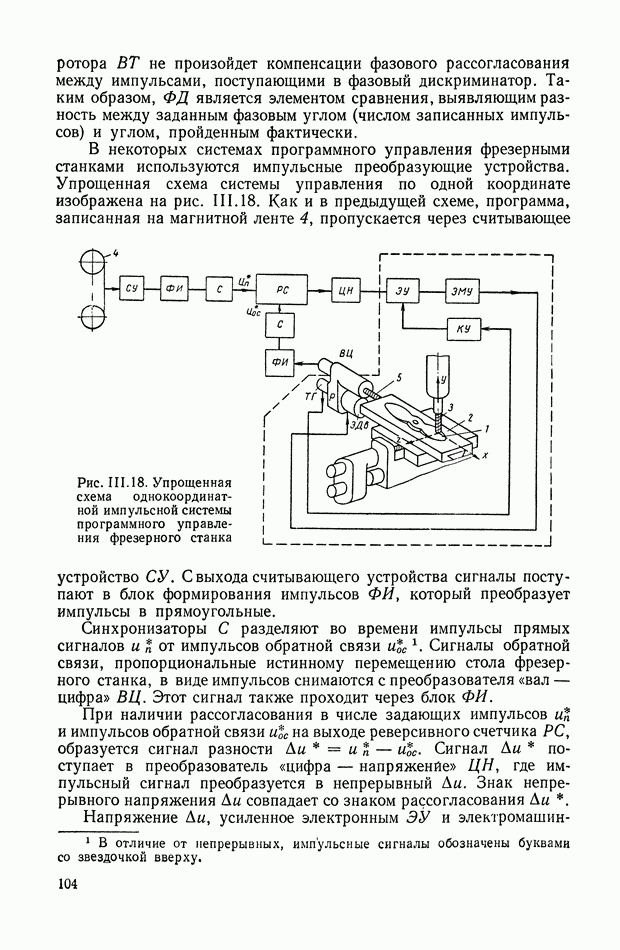
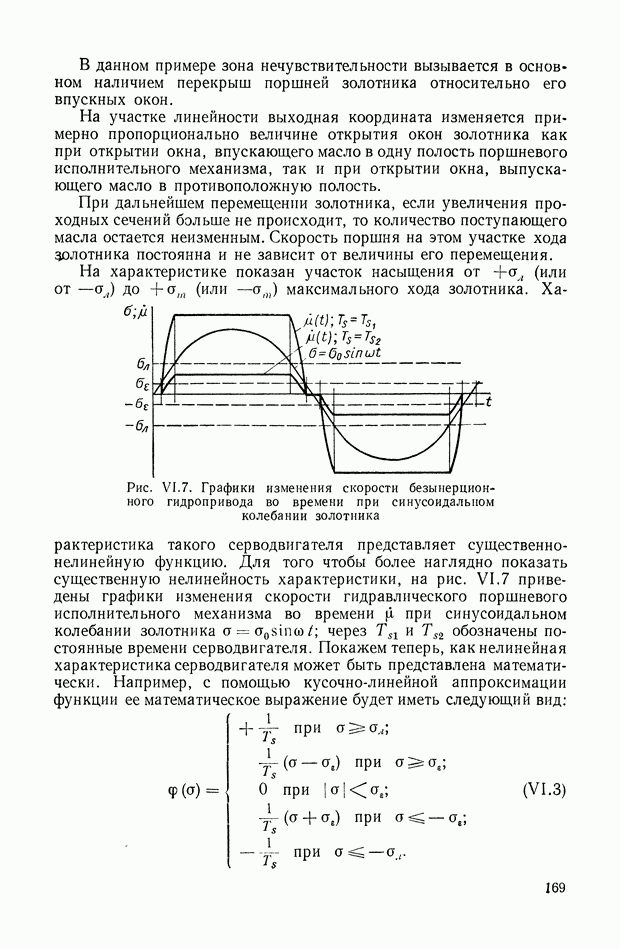
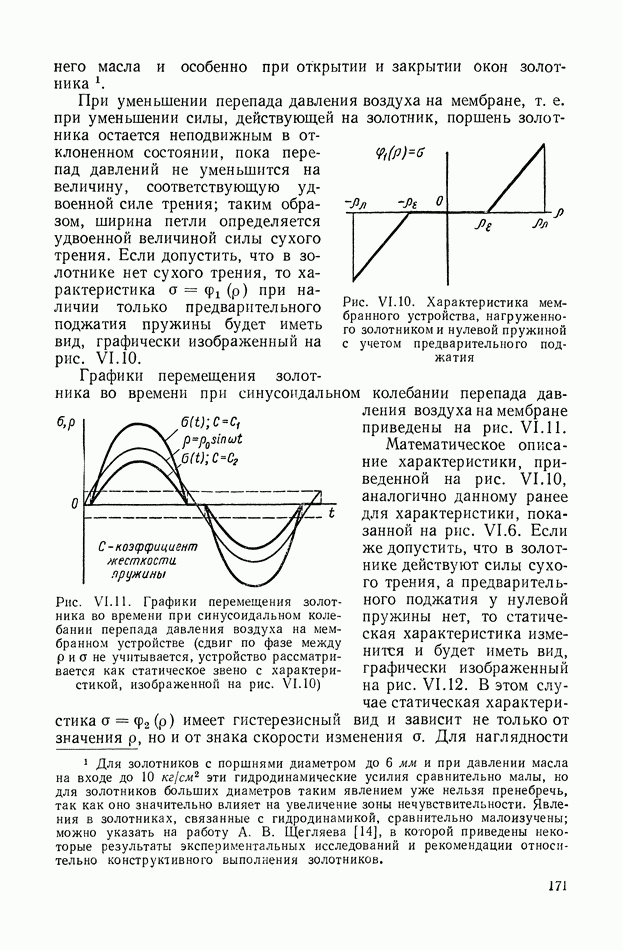
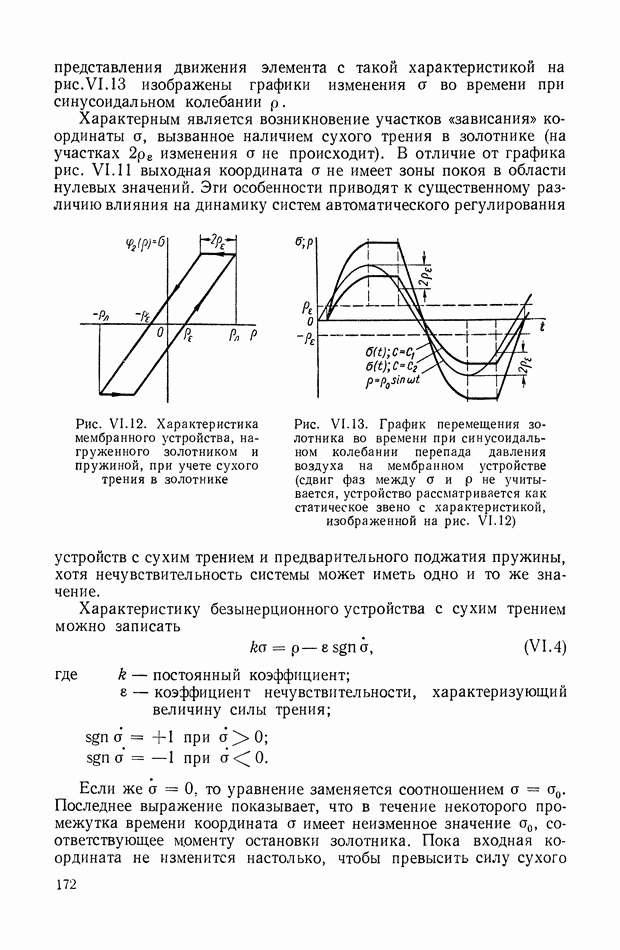
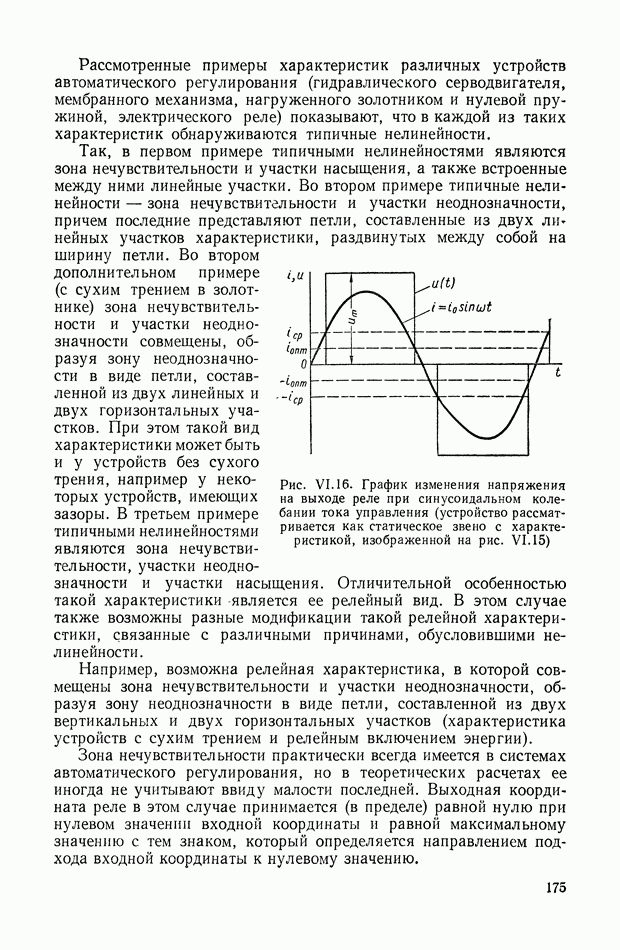
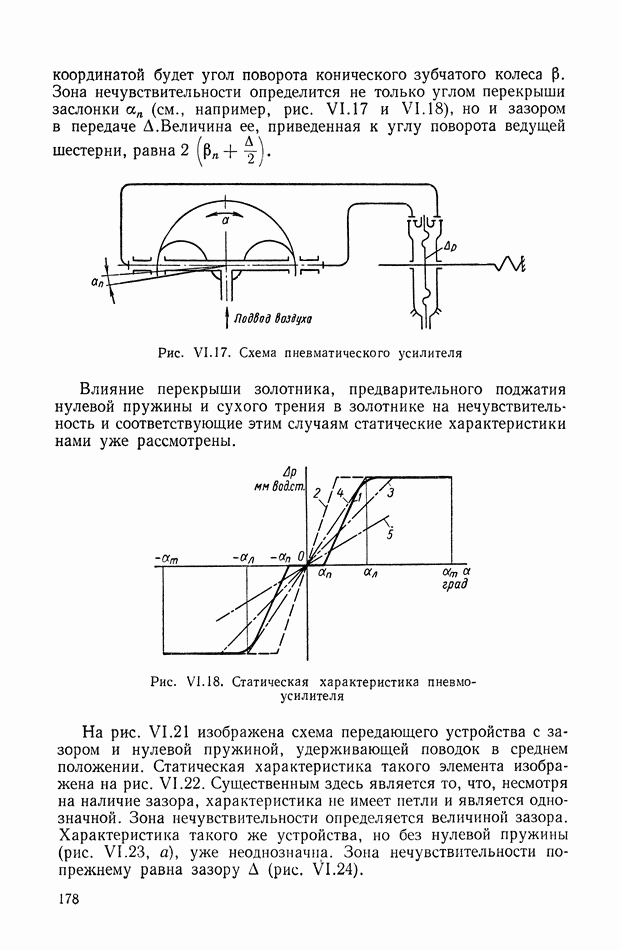
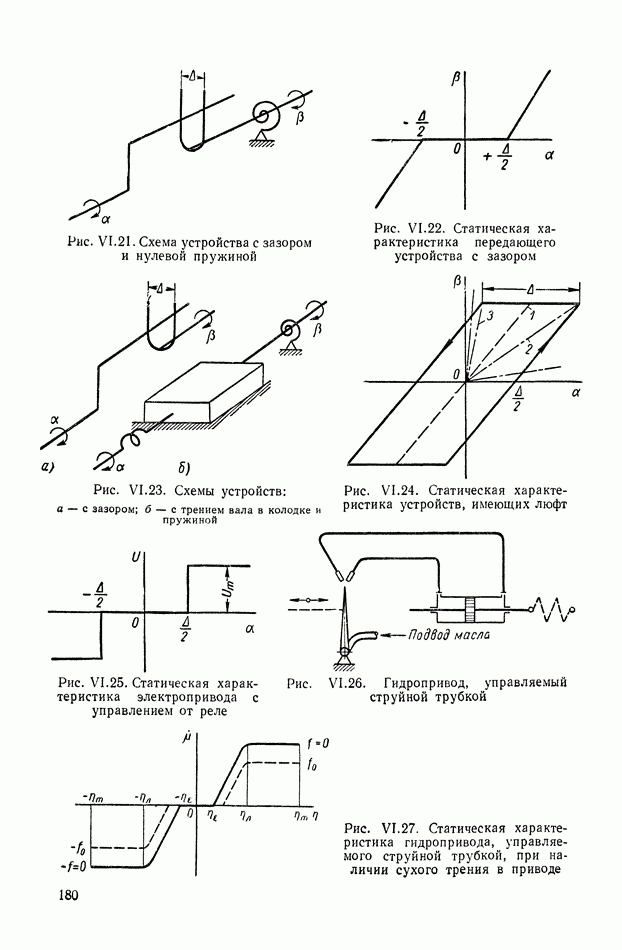
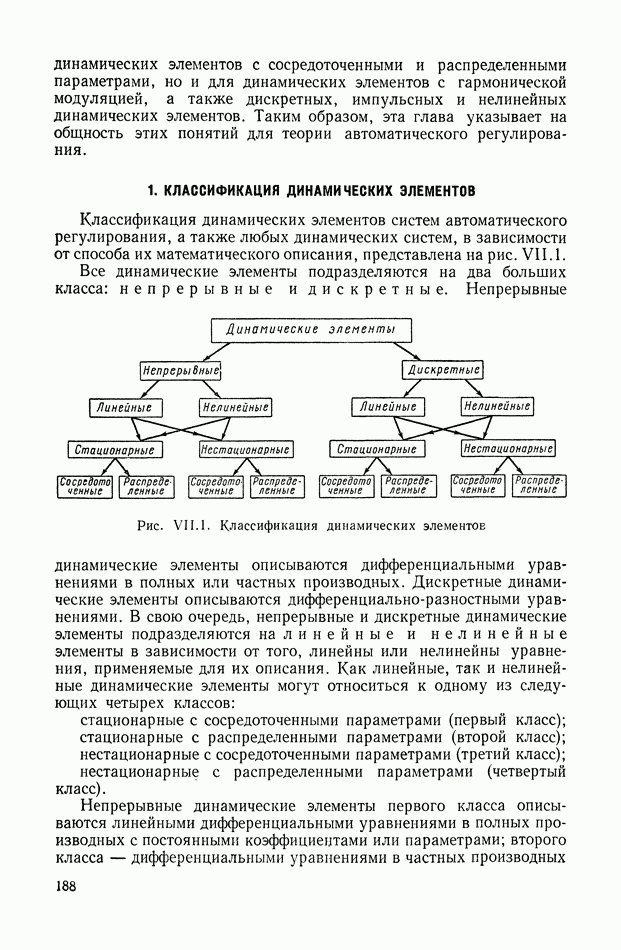
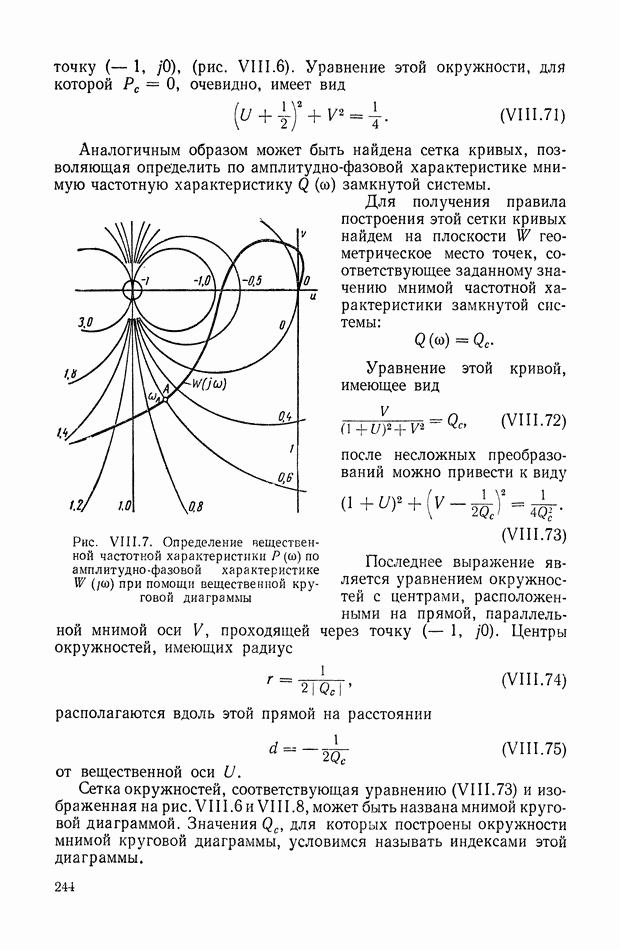
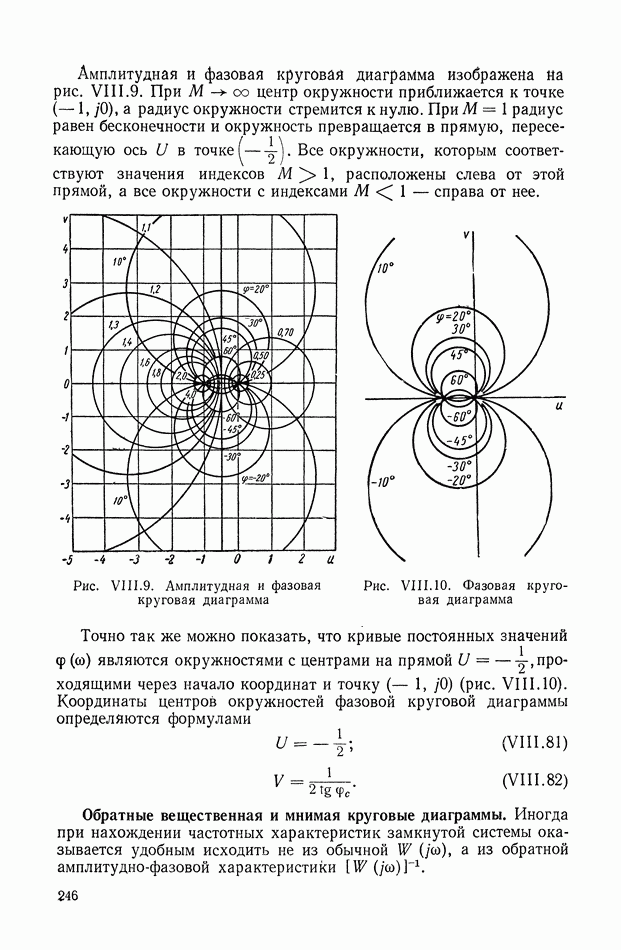
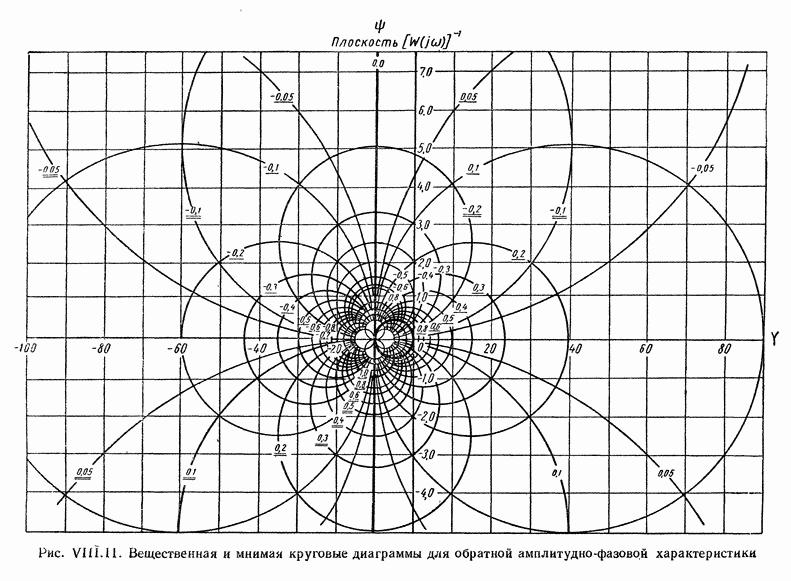
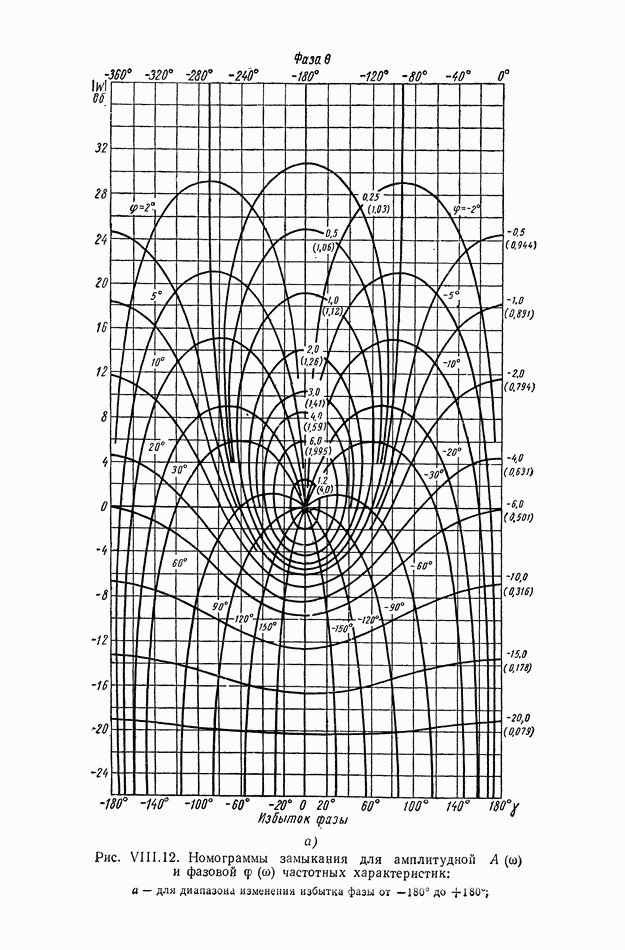
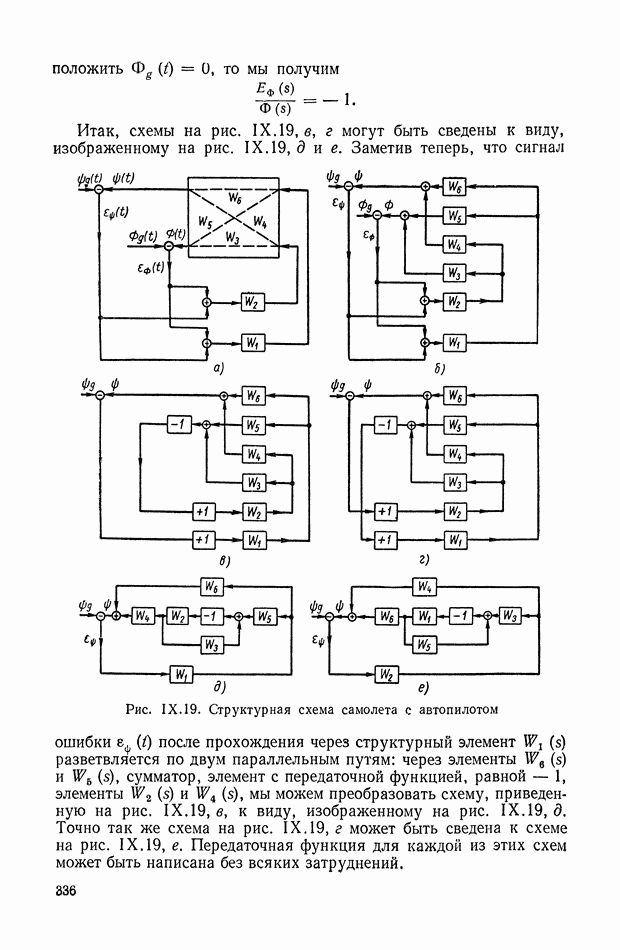
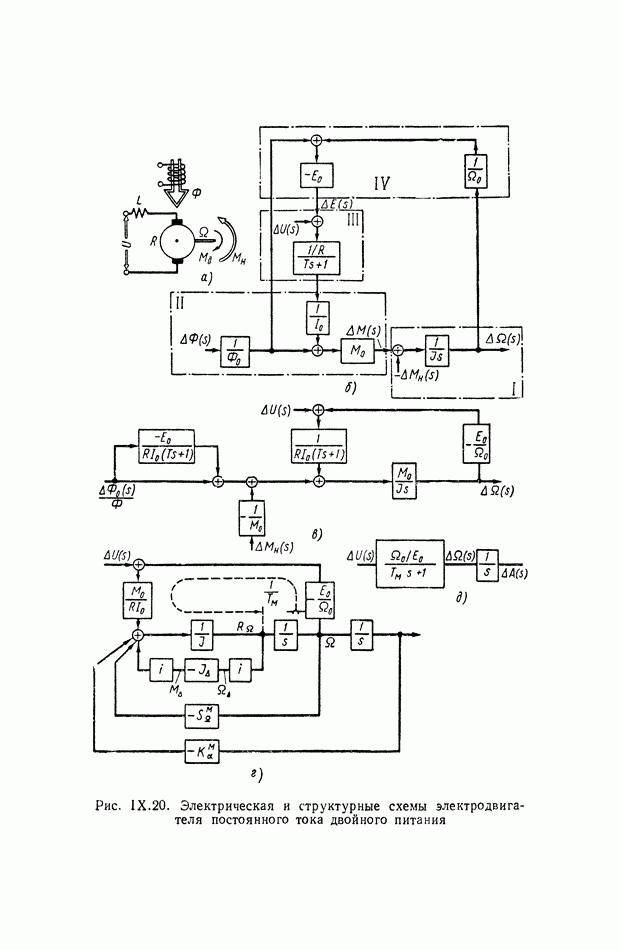
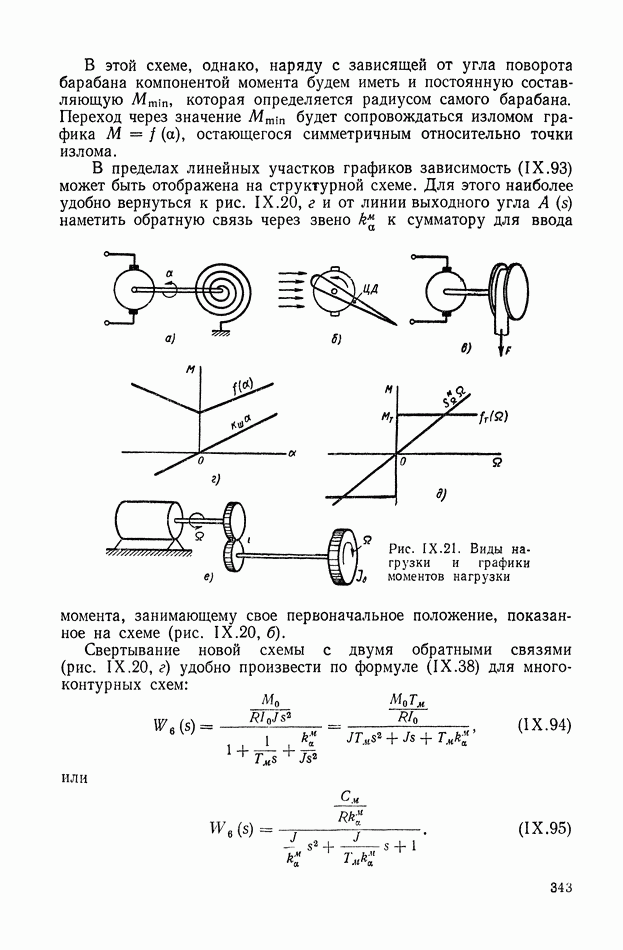
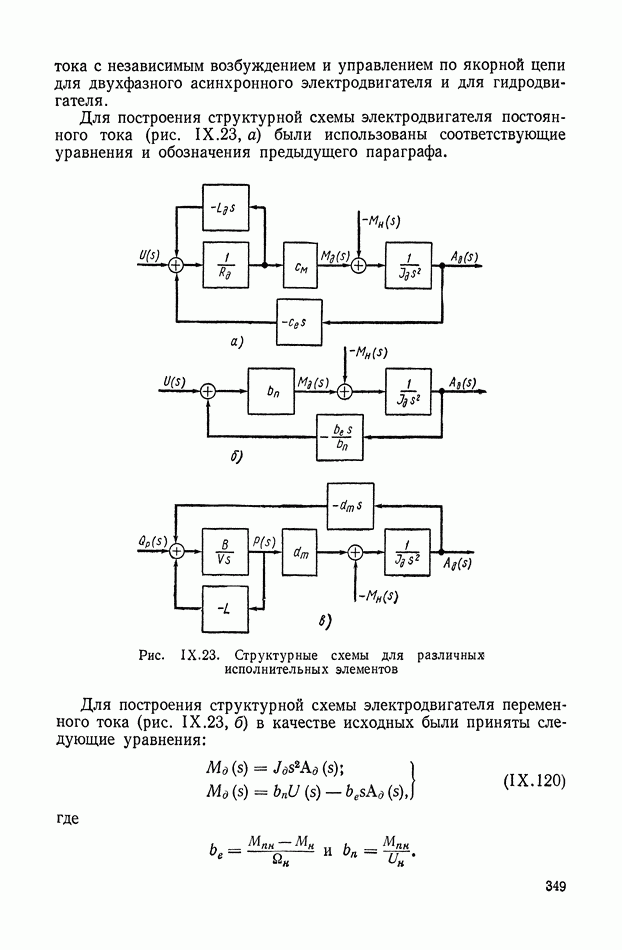
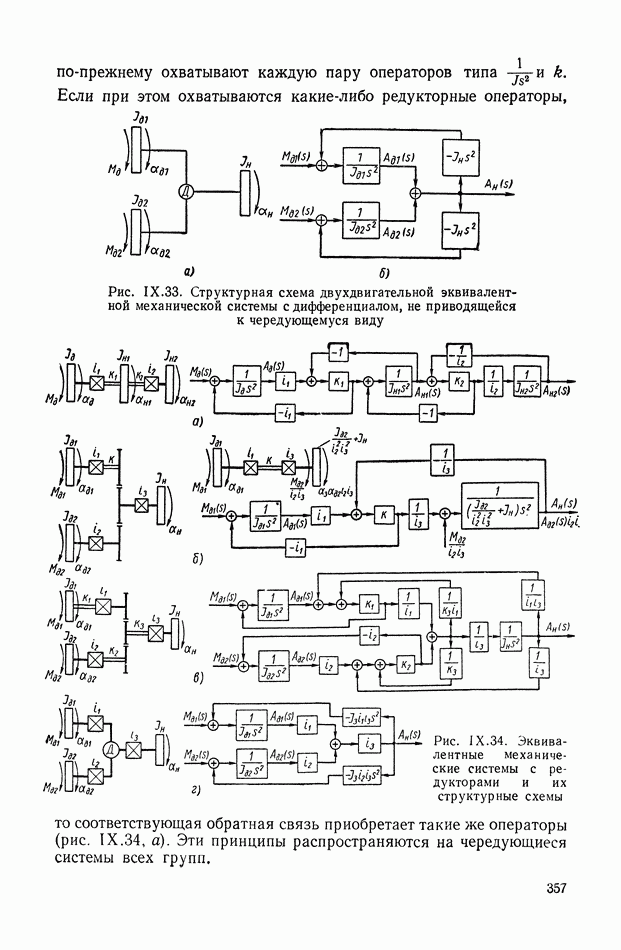
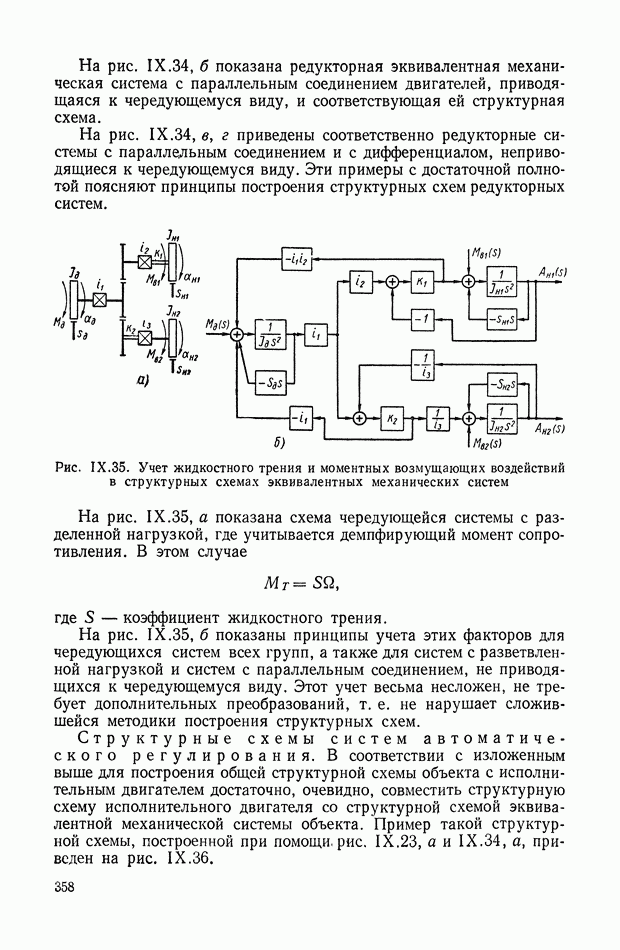
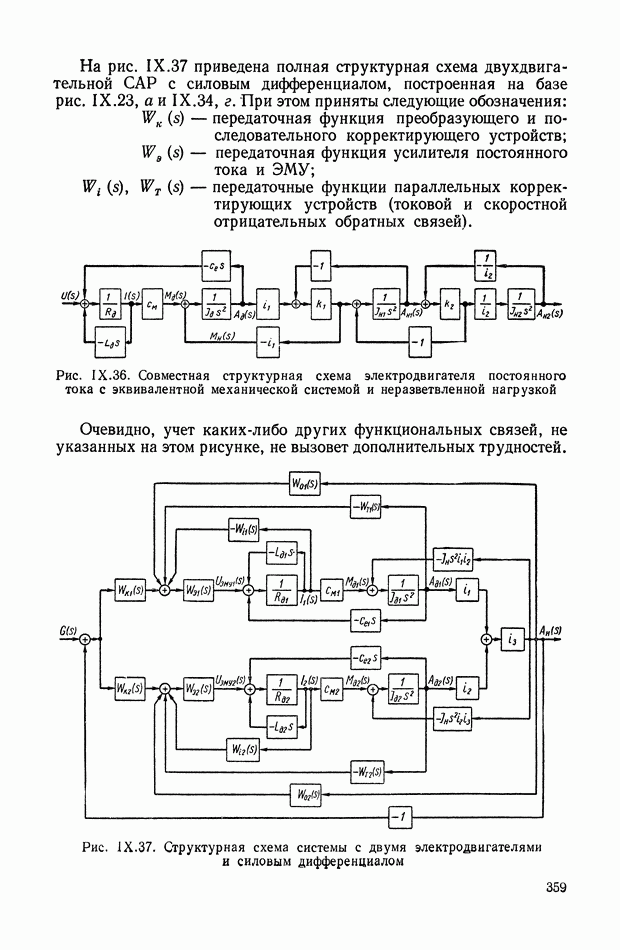
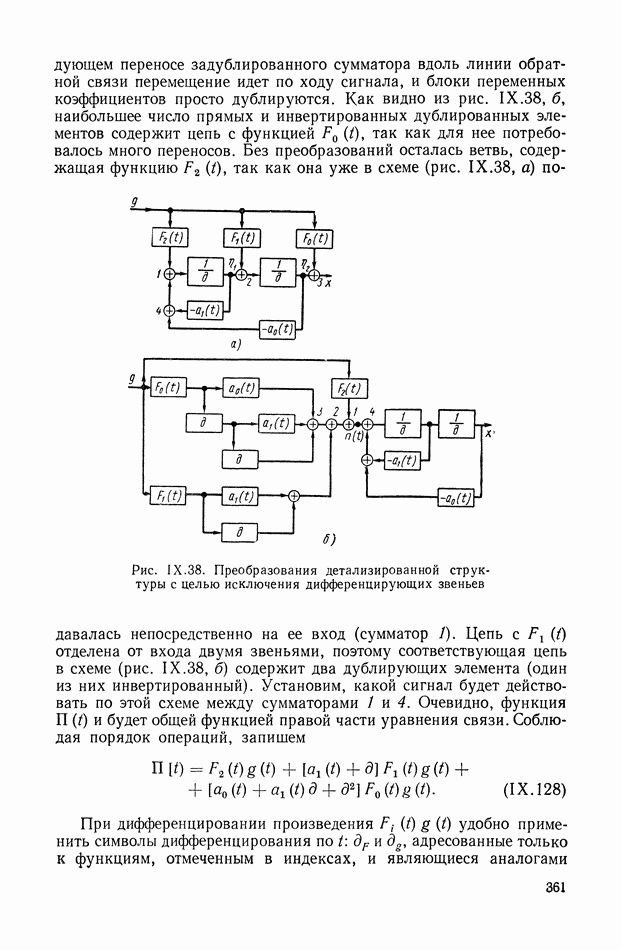
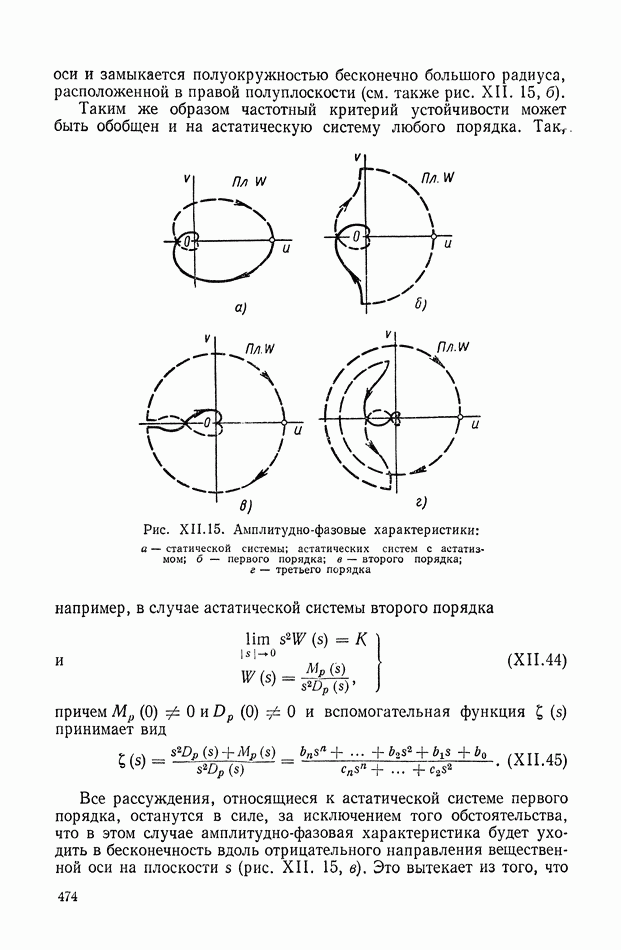
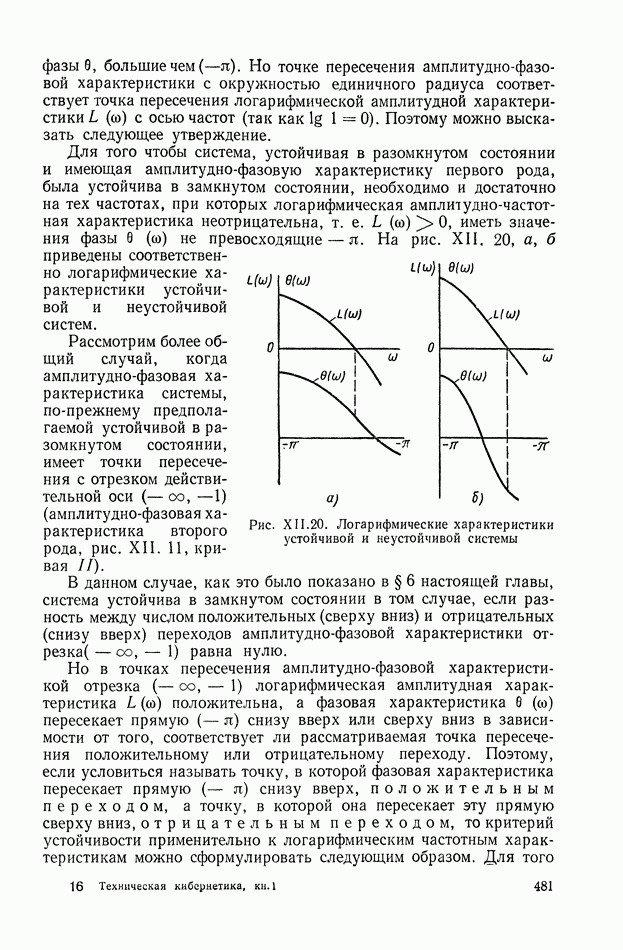
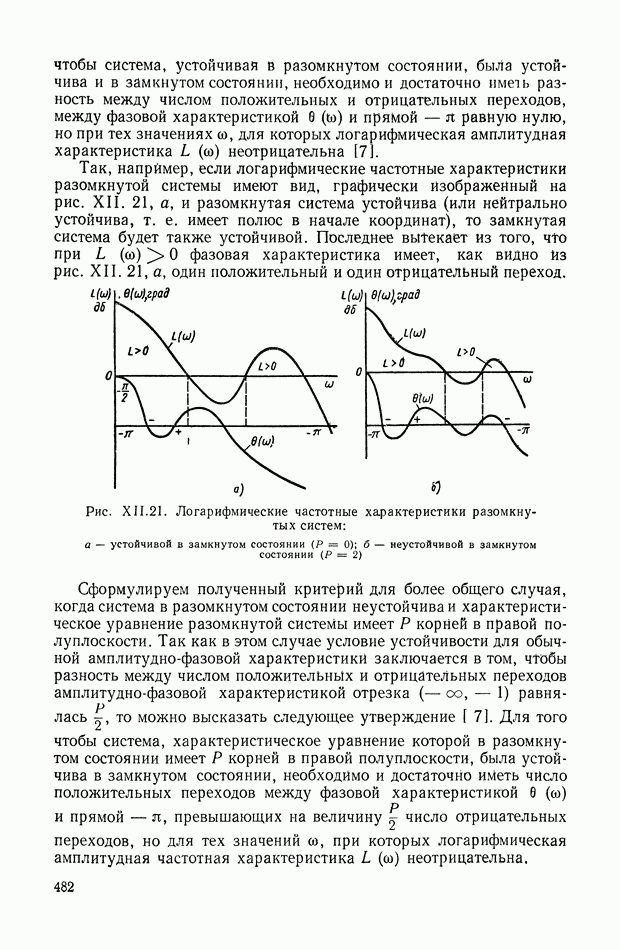
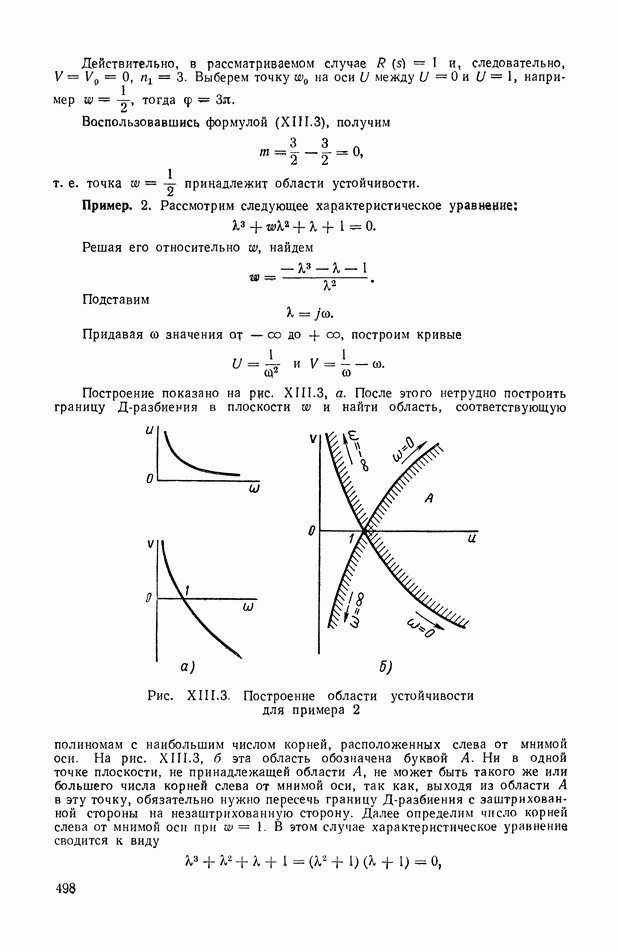
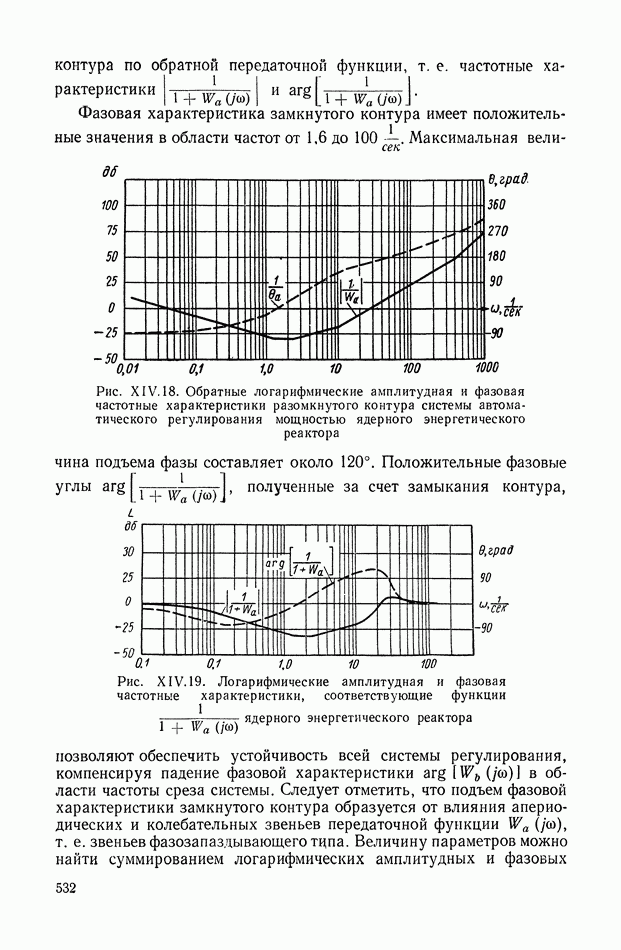
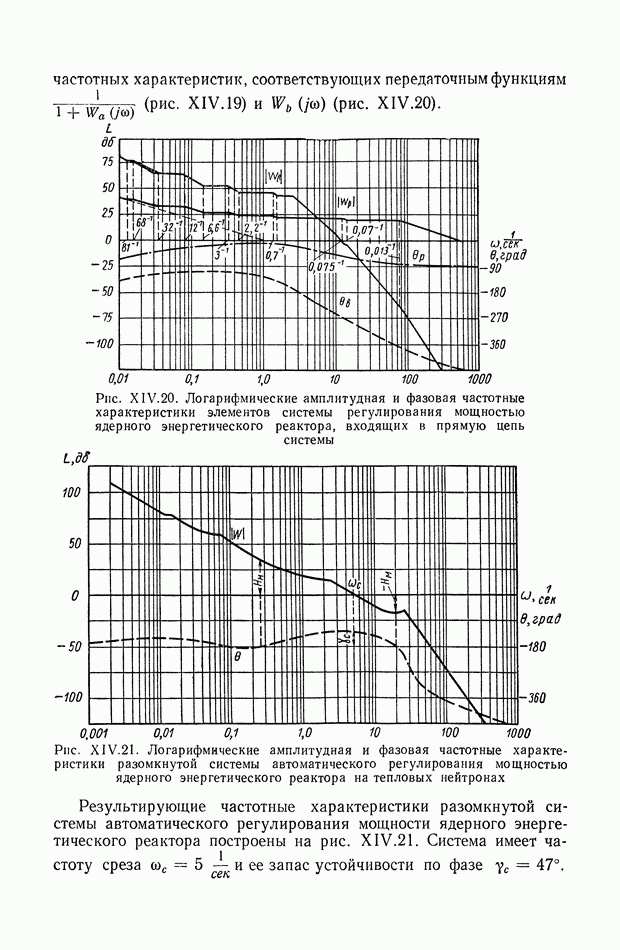
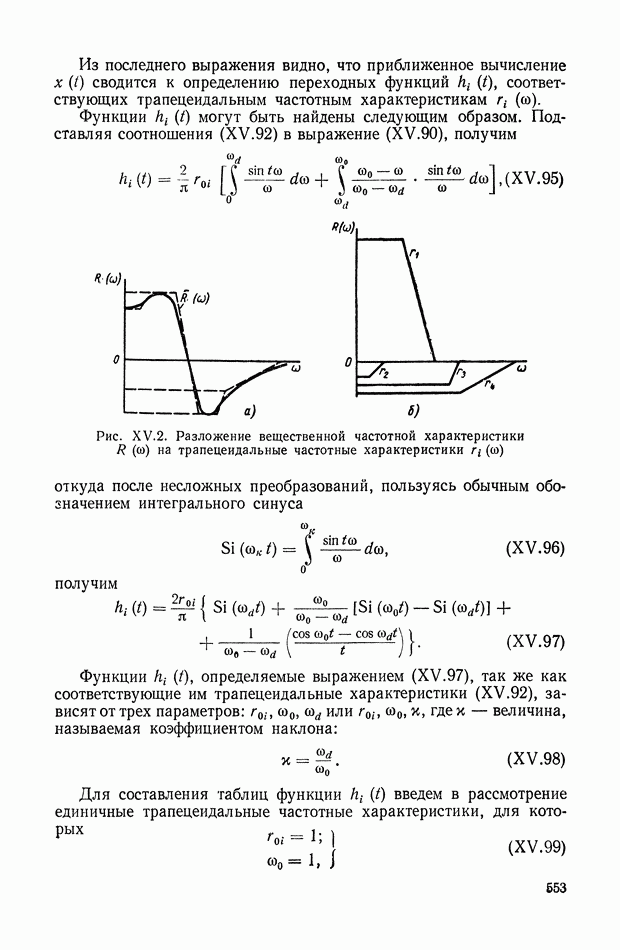
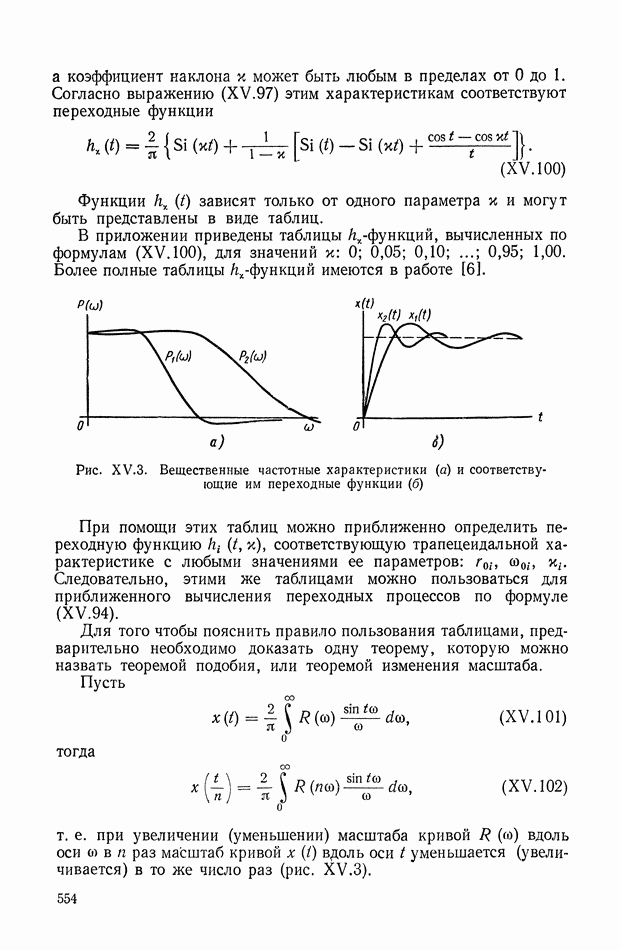
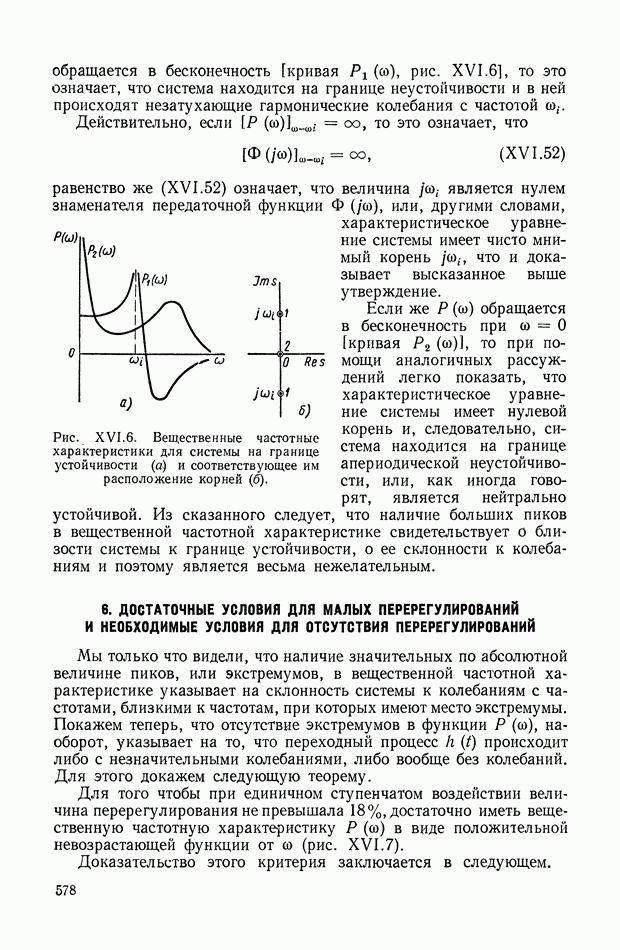
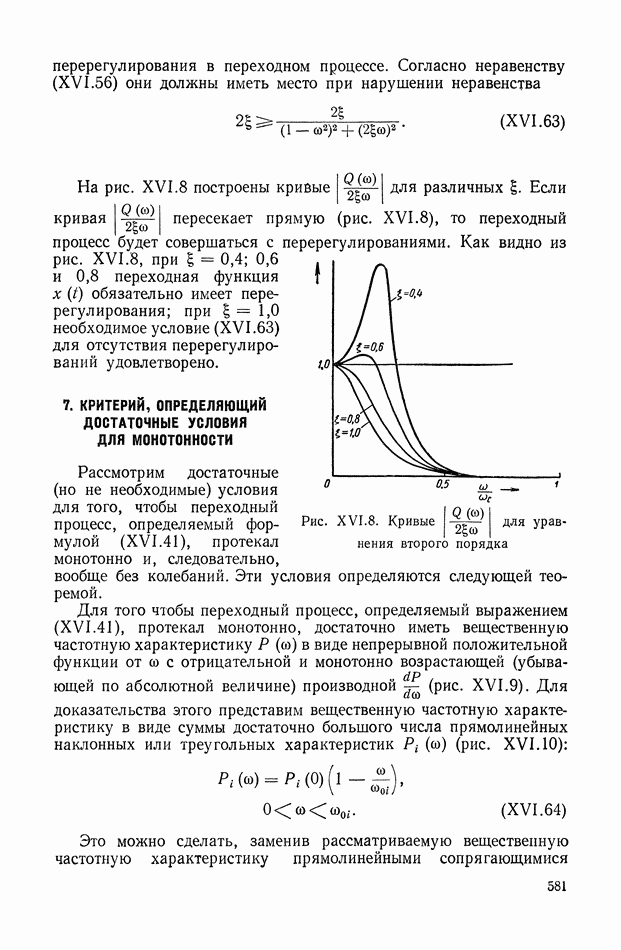
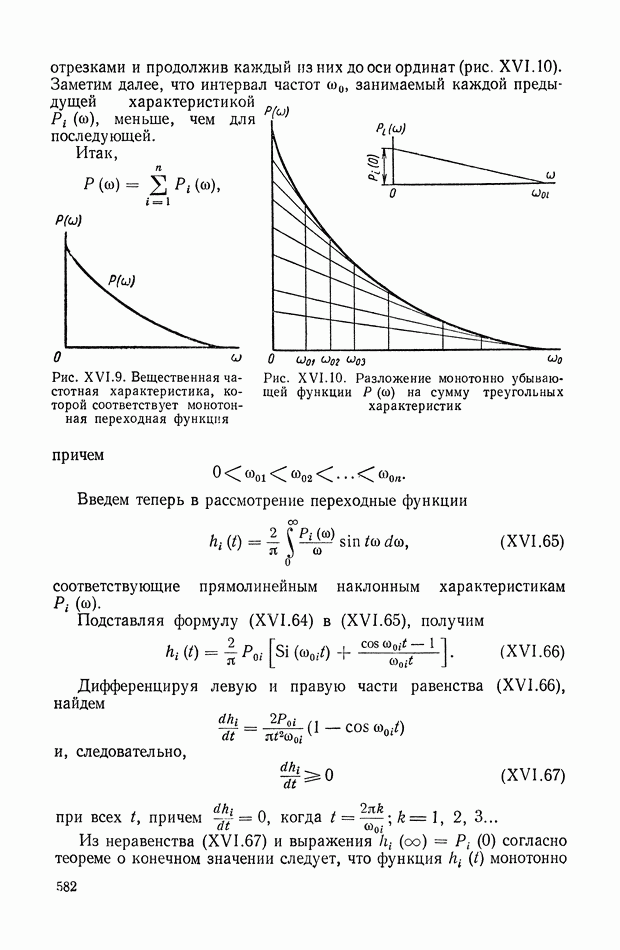
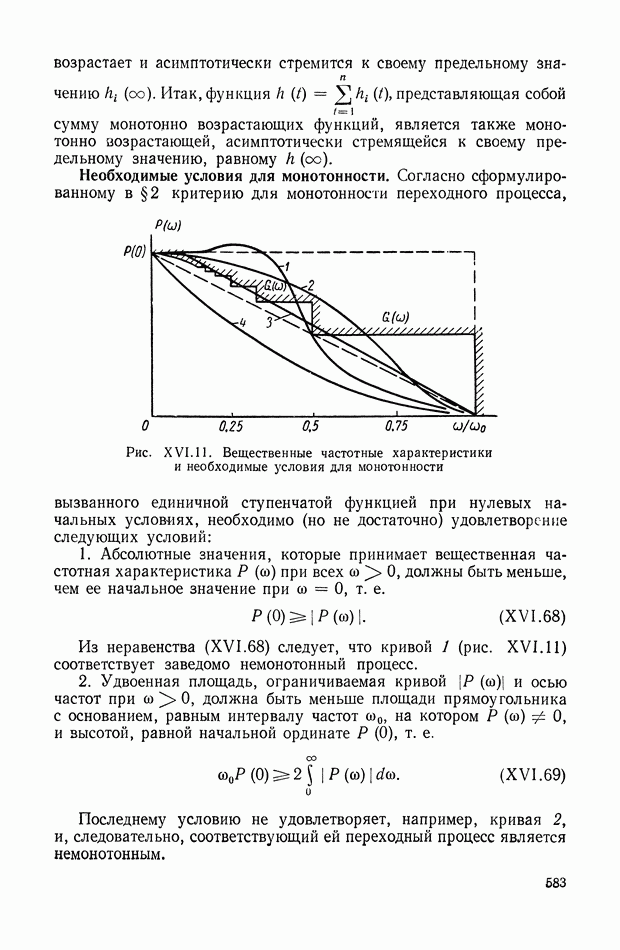
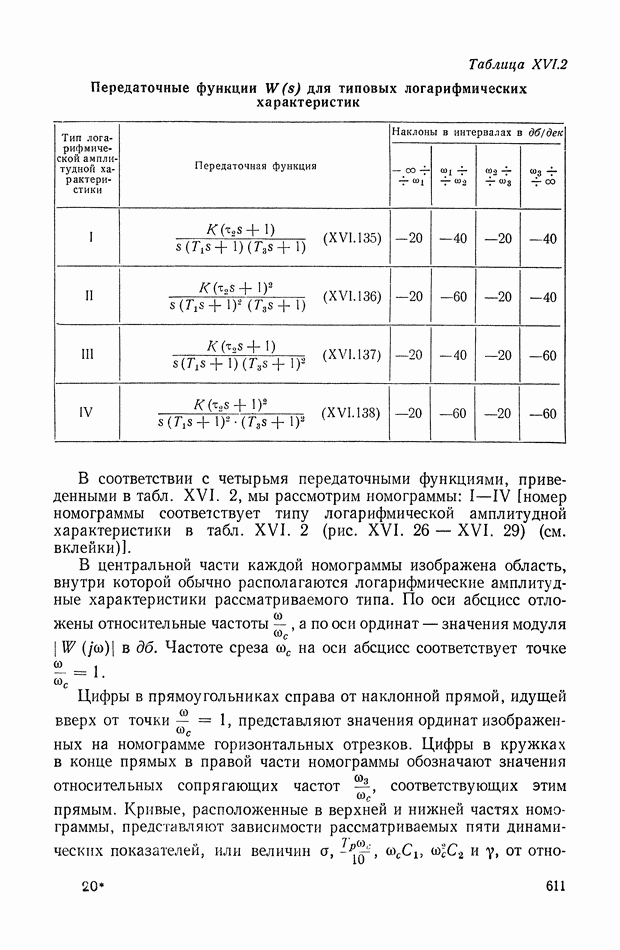
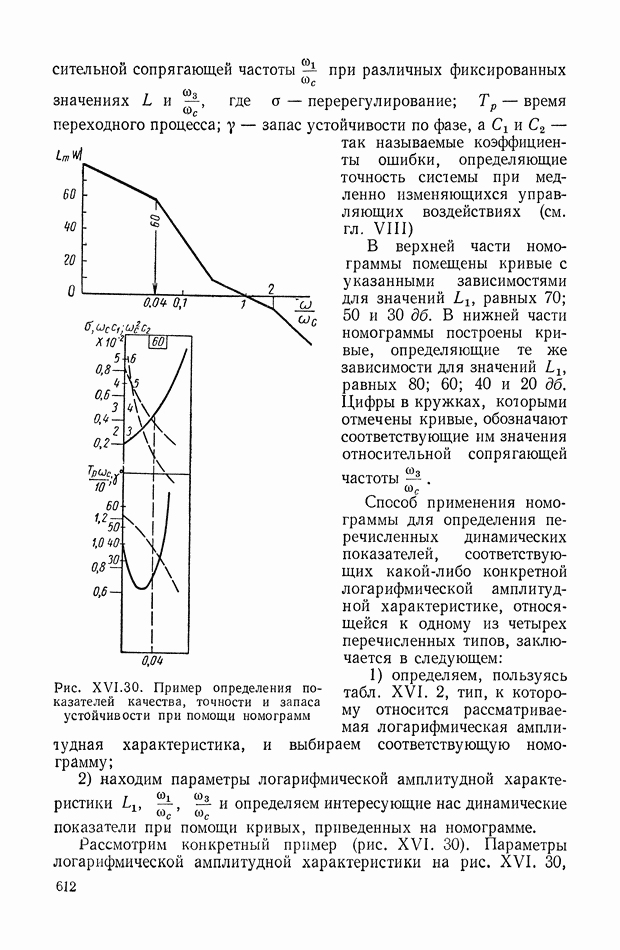
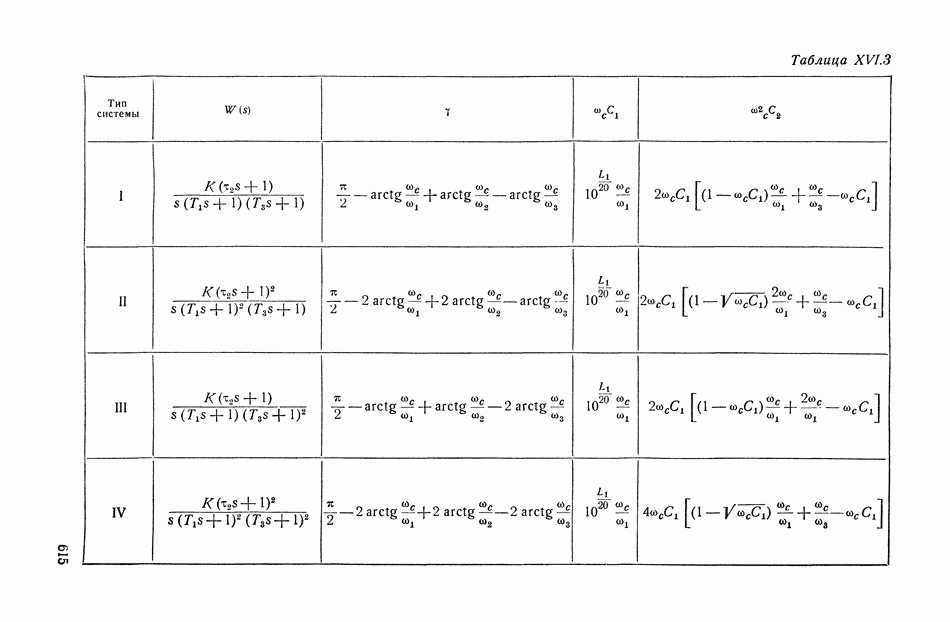
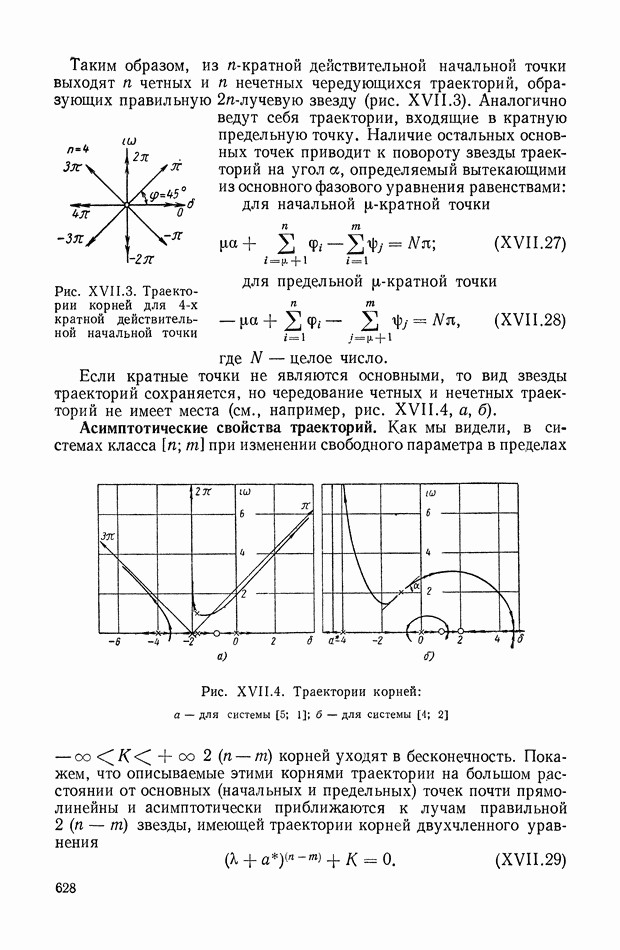
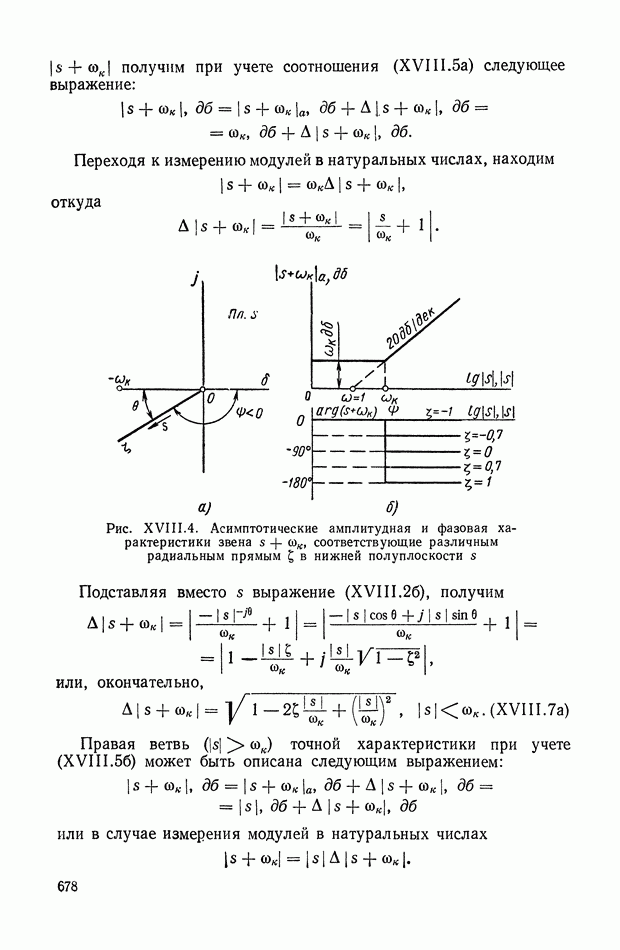
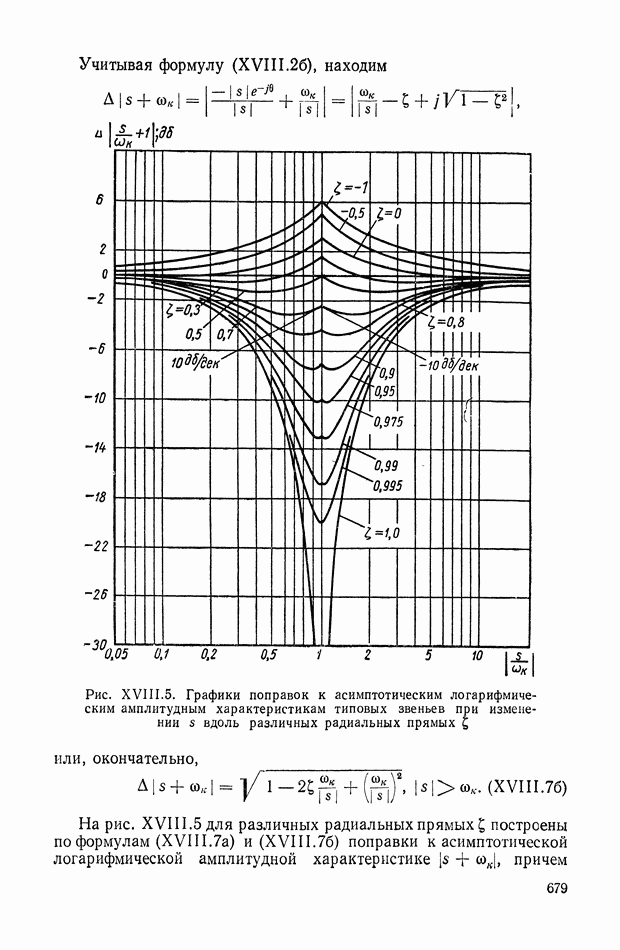
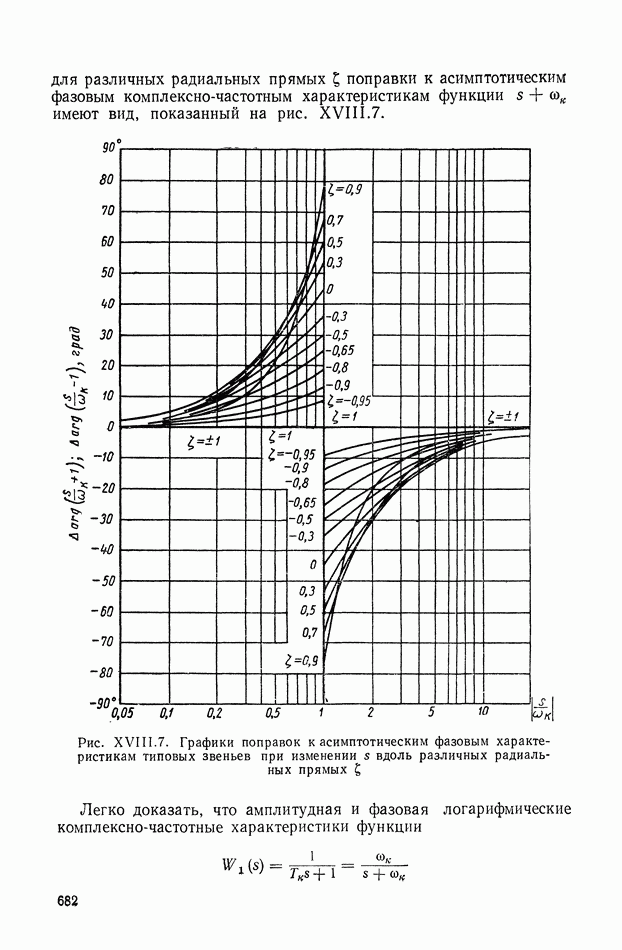
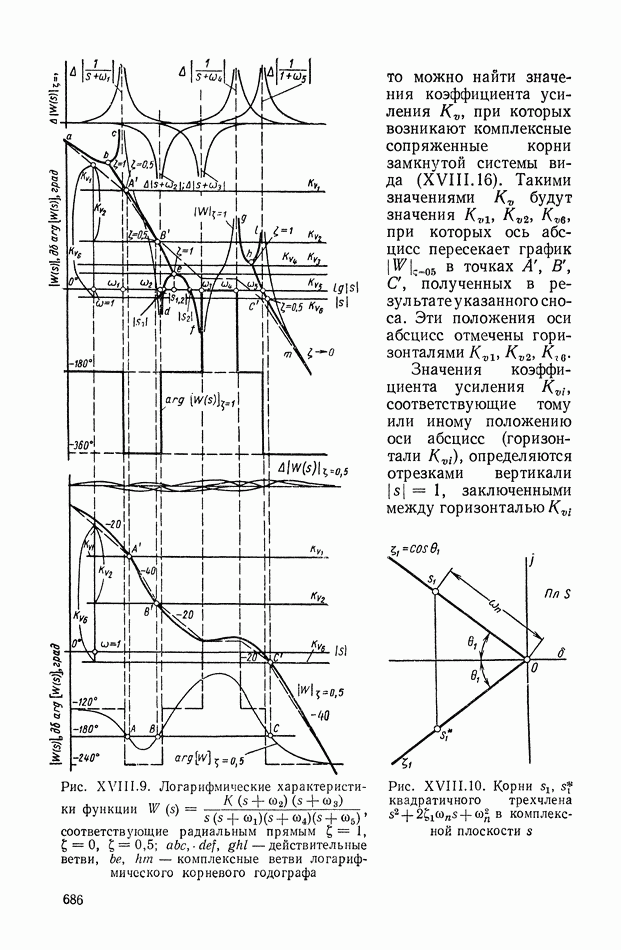
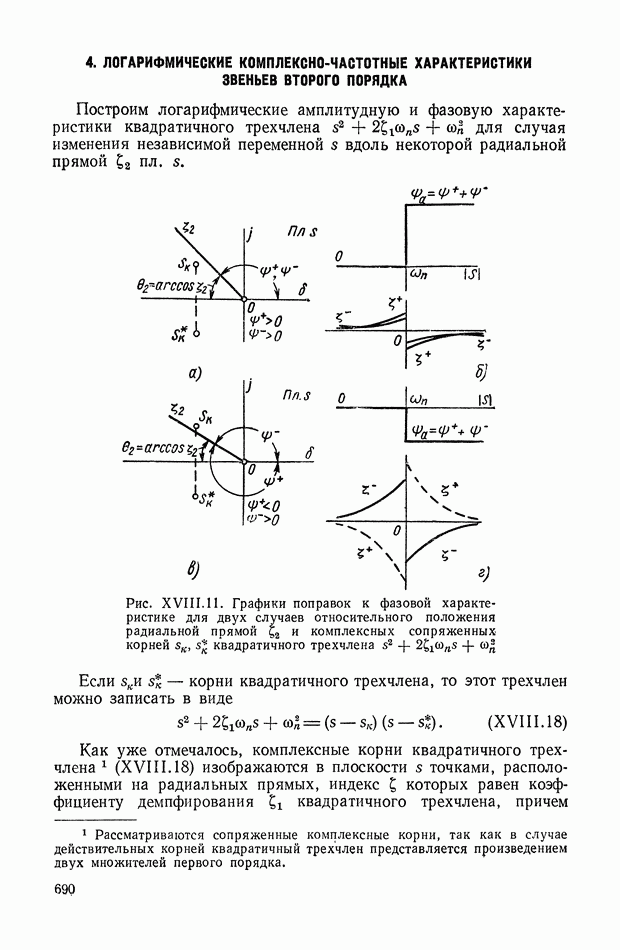
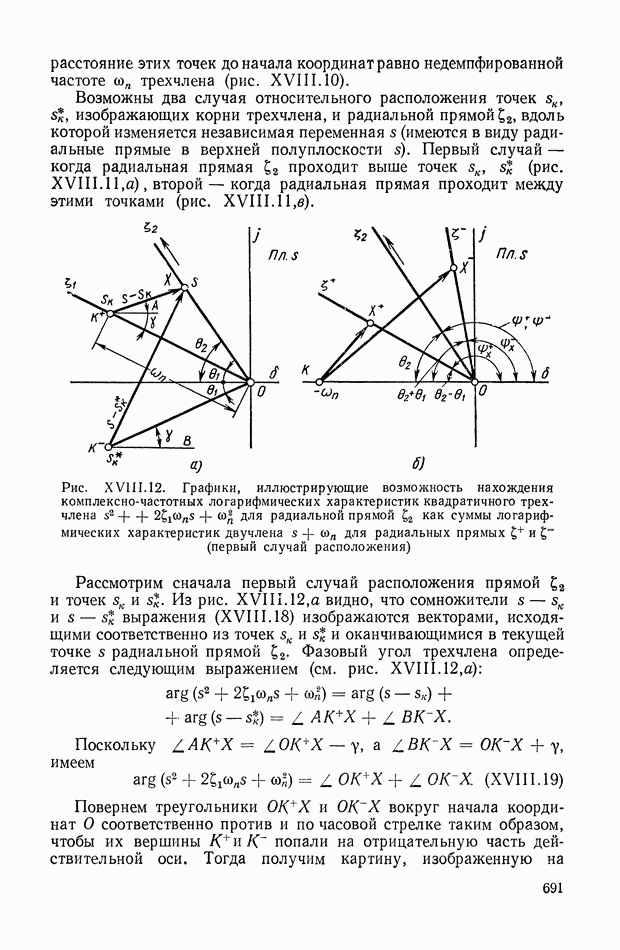
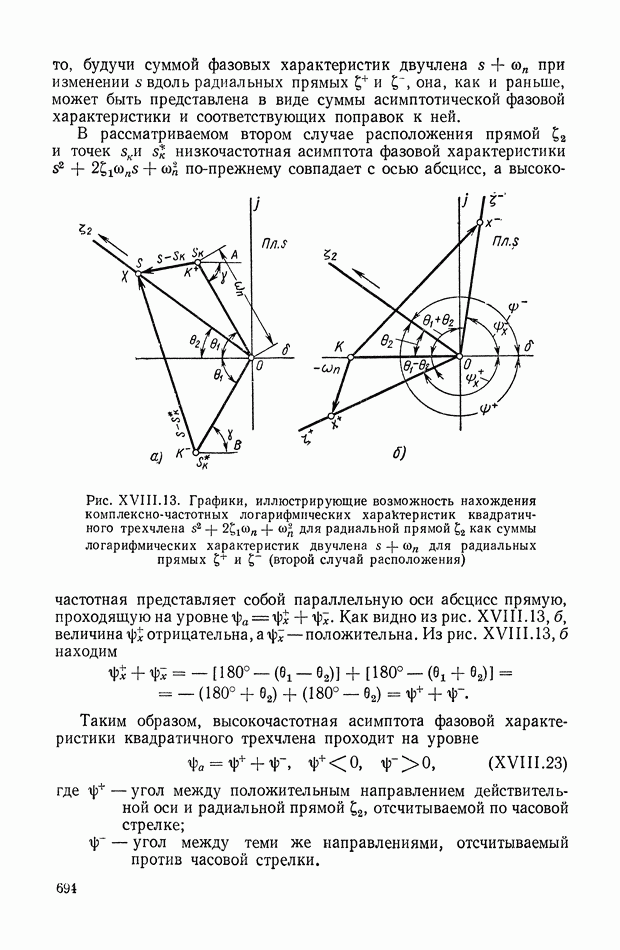
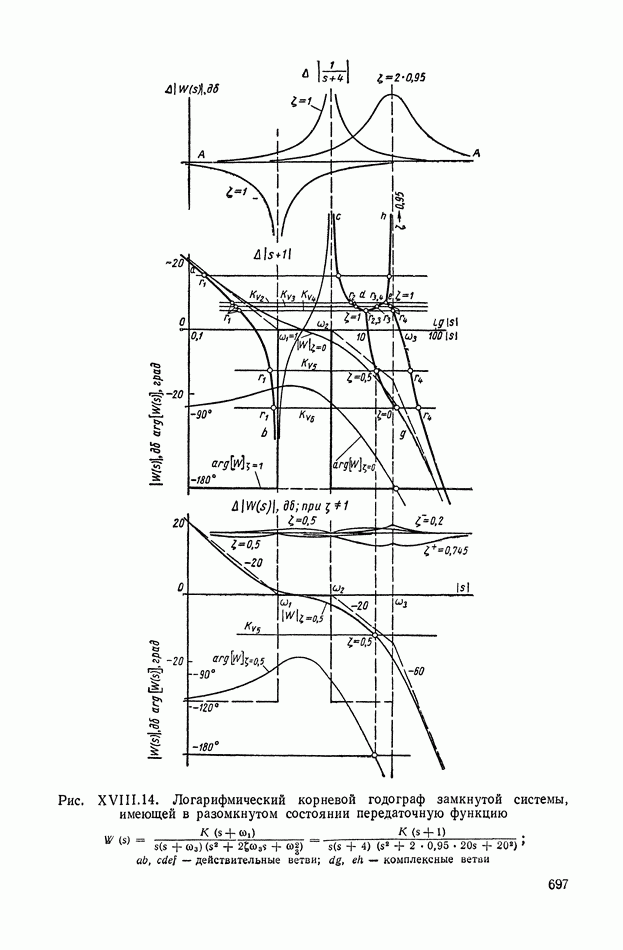
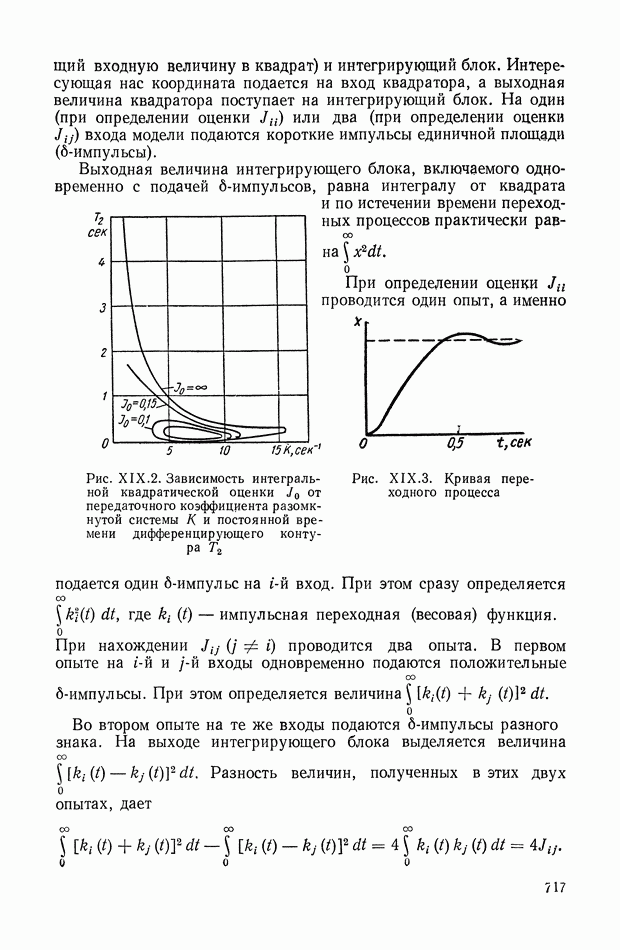
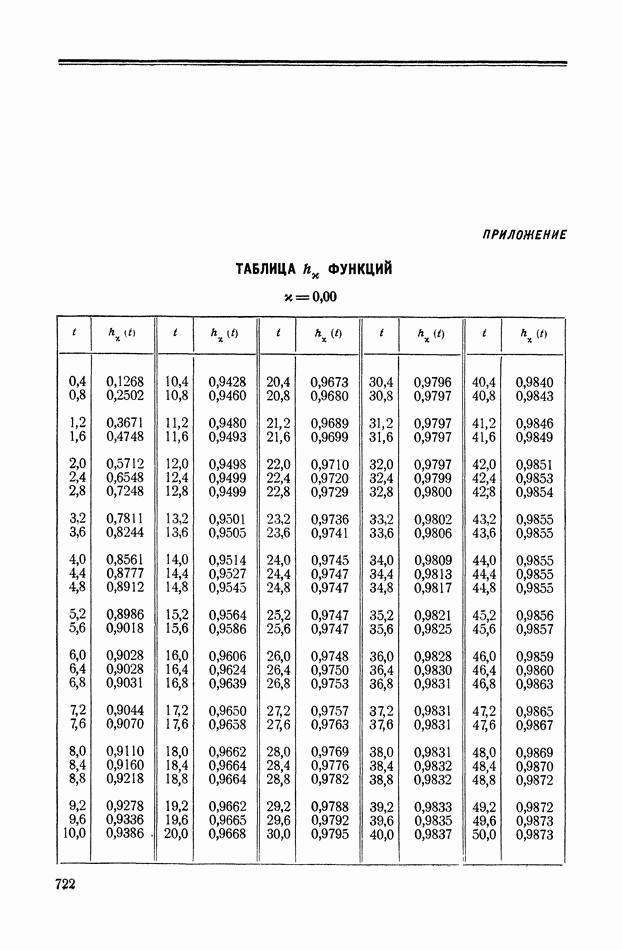
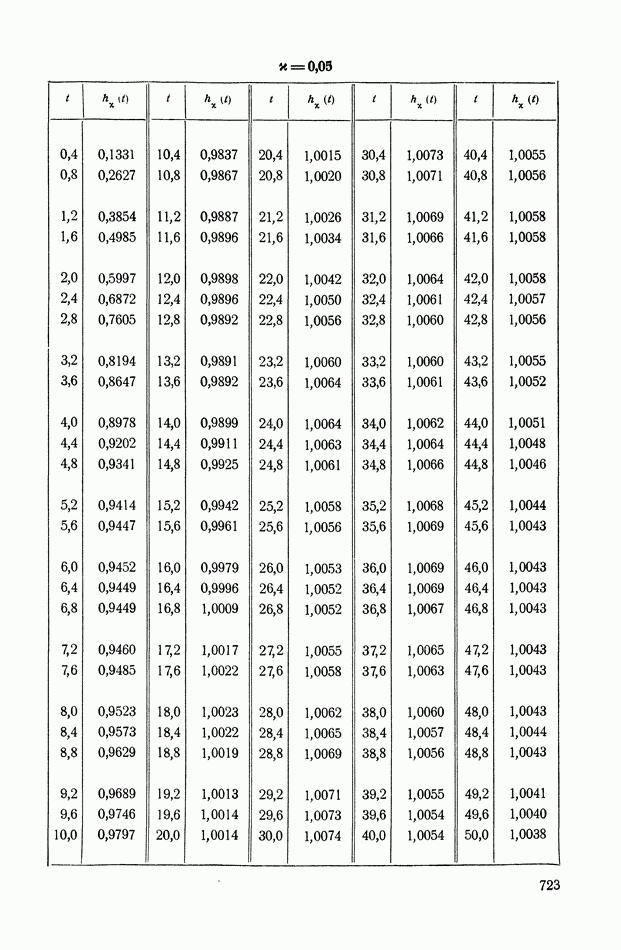
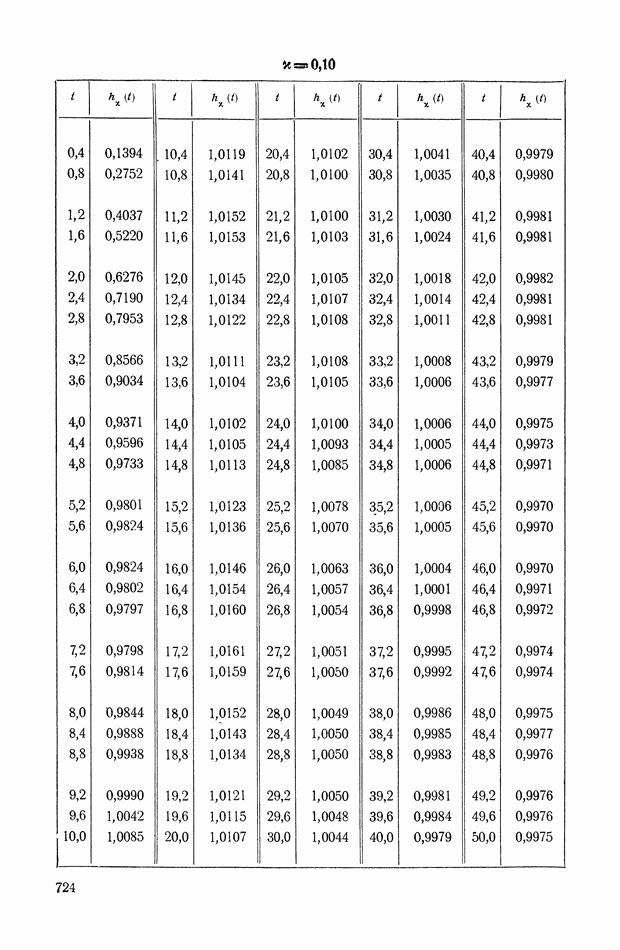
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
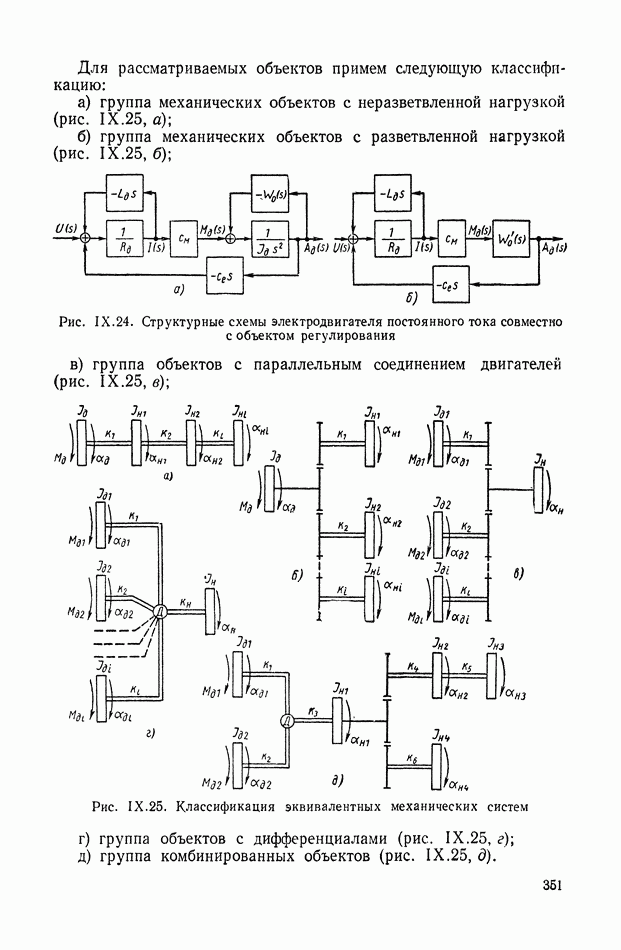
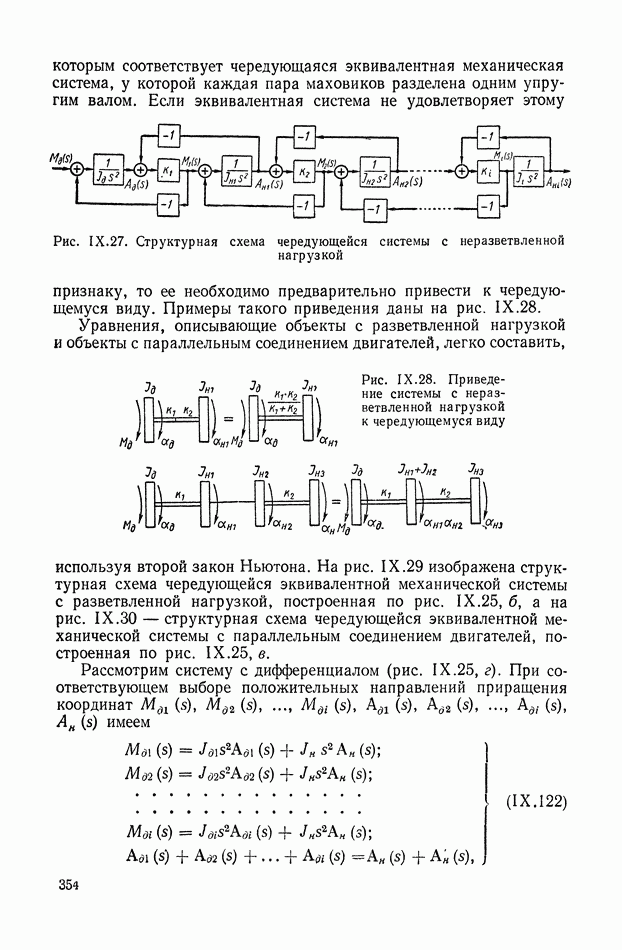
2. РАЗВИТИЕ ТЕОРИИ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ПОСЛЕ ОКТЯБРЬСКОЙ СОЦИАЛИСТИЧЕСКОЙ РЕВОЛЮЦИИ
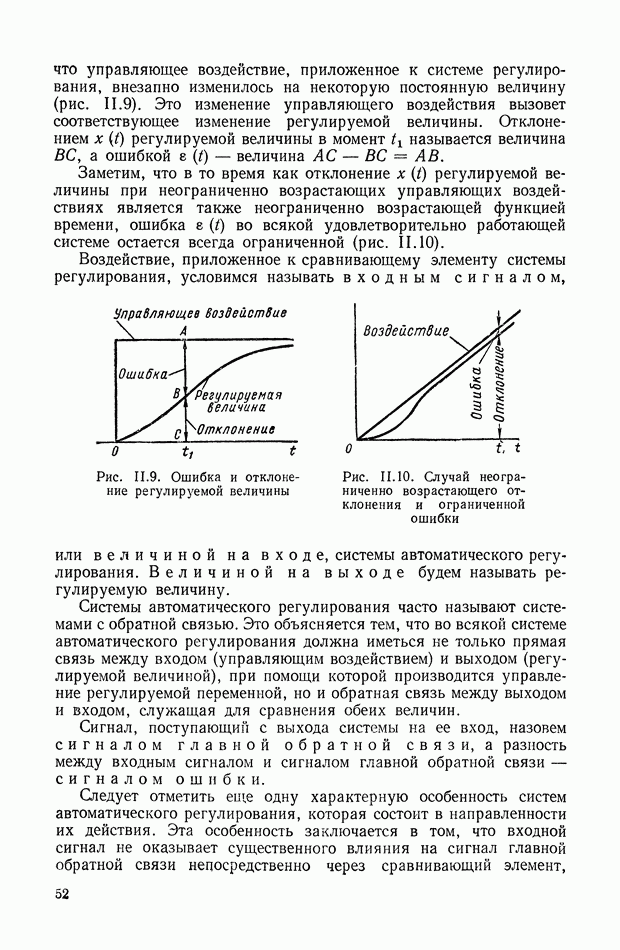
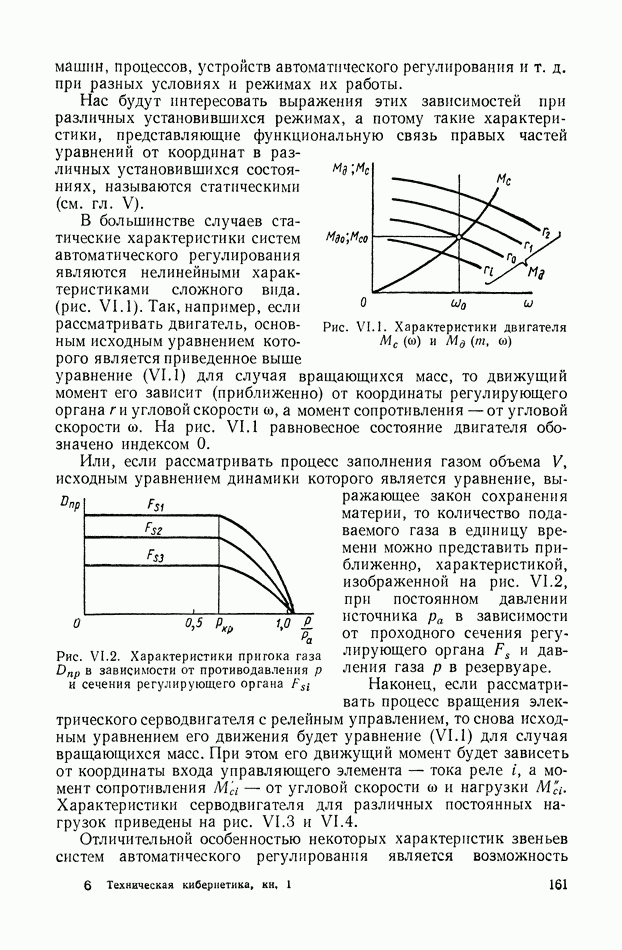
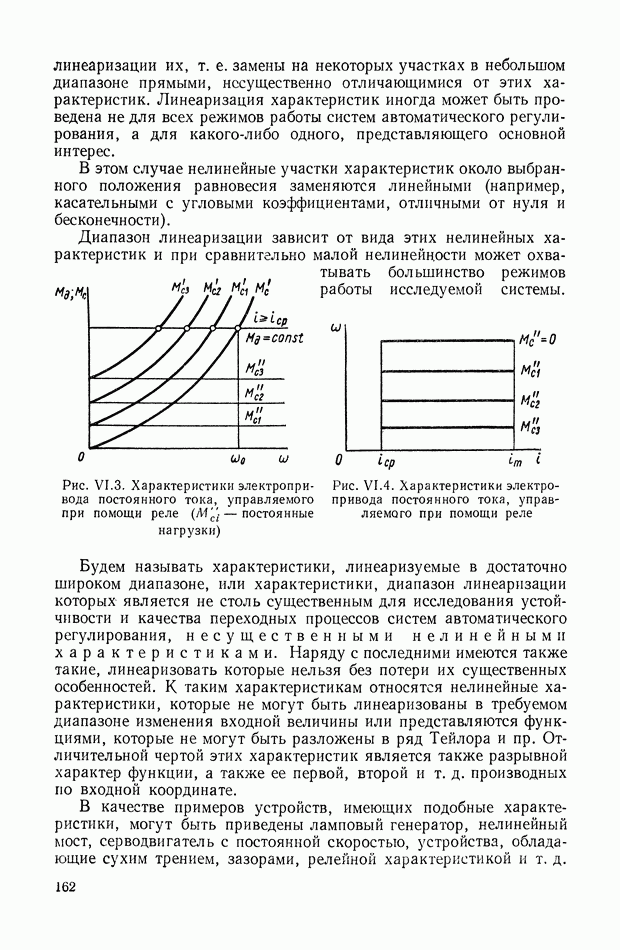
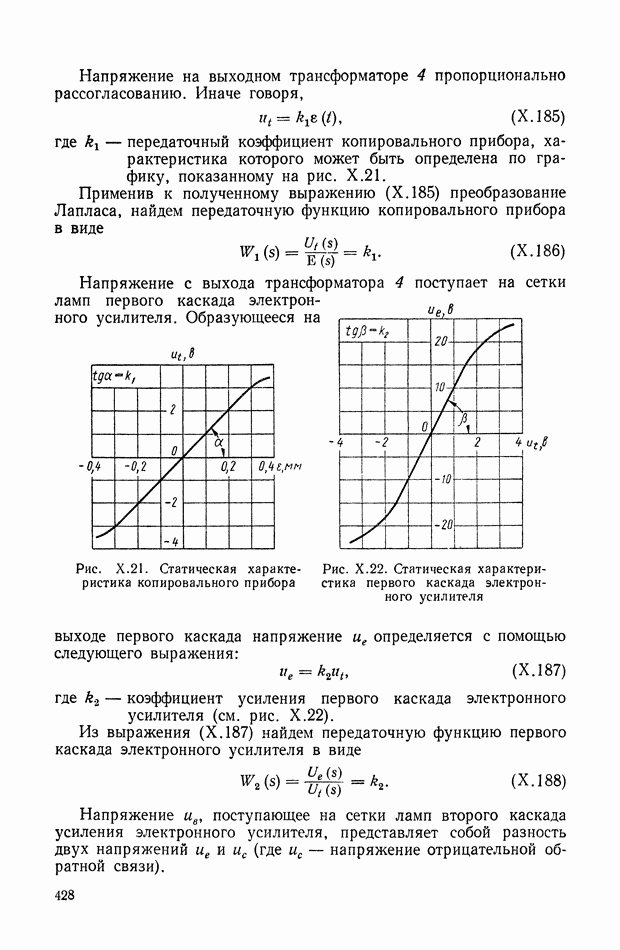
В первые годы после Октябрьской Социалистической революции работы по автоматическому регулированию проводились в основном в высших учебных заведениях страны. Так, в Ленинградском технологическом институте крупный инженер и ученый И. Н. Вознесенский проводит многочисленные исследования в области систем автоматического регулирования паровых и гидравлических турбин. В 1922 г. им были опубликованы две статьи: «О регуляторах непрямого действия» [23] и «Быстродействующие сервомоторы» [22], где излагаются основы линейной теории регуляторов и сервомоторов; даются конкретные инженерные рекомендации по выбору схем и параметров турбин и регуляторов.
В 1924 г. в трудах Днепропетровского горного института К. Э. Рерих [173], а затем Я. И. Грдина [40] публикуют статьи, посвященные исследованиям прерывистых регуляторов быстроходных машин [41]. К. Э. Рерих рассматривает динамику процессов регулирования паровых машин с переменной отсечкой пара, пользуясь для этого разностными уравнениями. Из анализа этих уравнений он приходит к формуле, связывающей постоянную времени регулятора, постоянную времени паровой машины с коэффициентом неравномерности регулятора. Я. И. Грдина показывает,
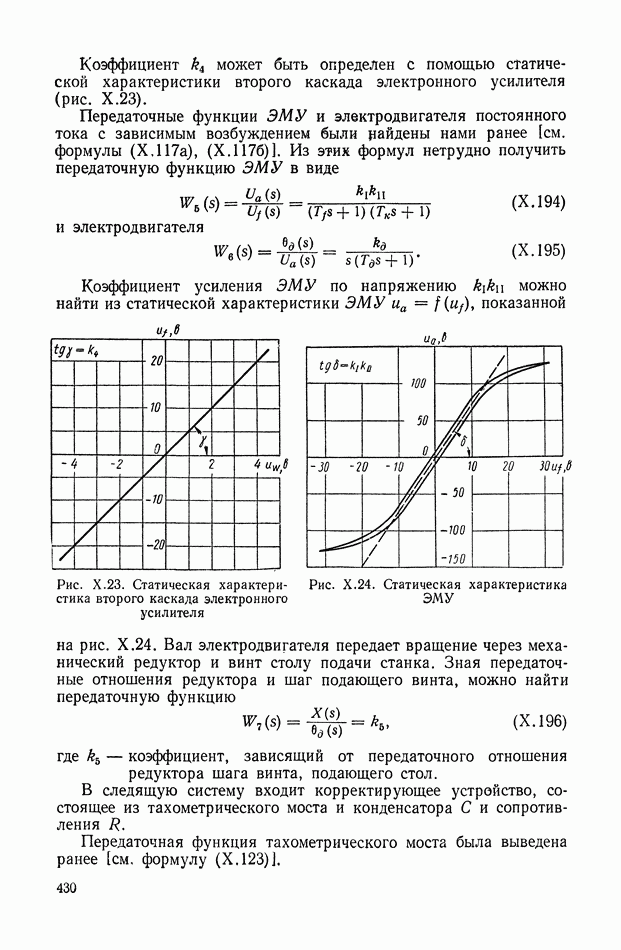
что с помощью этой формулы могут выбираться параметры регулятора и паровой машины для достаточно широкого диапазона ее работы. Ему удается выяснить, насколько расширяется область устойчивой работы системы от действия сухого трения регулятора и дополнительного трения катаракта. Он также рассмотрел устойчивость прерывистых систем регулирования паровых машин [41]. В эти годы отечественная промышленность сделала важный шаг в развитии регуляторостроения. На ряде предприятий осваивается выпуск серийных регуляторов. Так, например, первый регулятор для водяной турбины был изготовлен в 1925 г., а в 1927 г. построена партия термоэлектрических регуляторов.
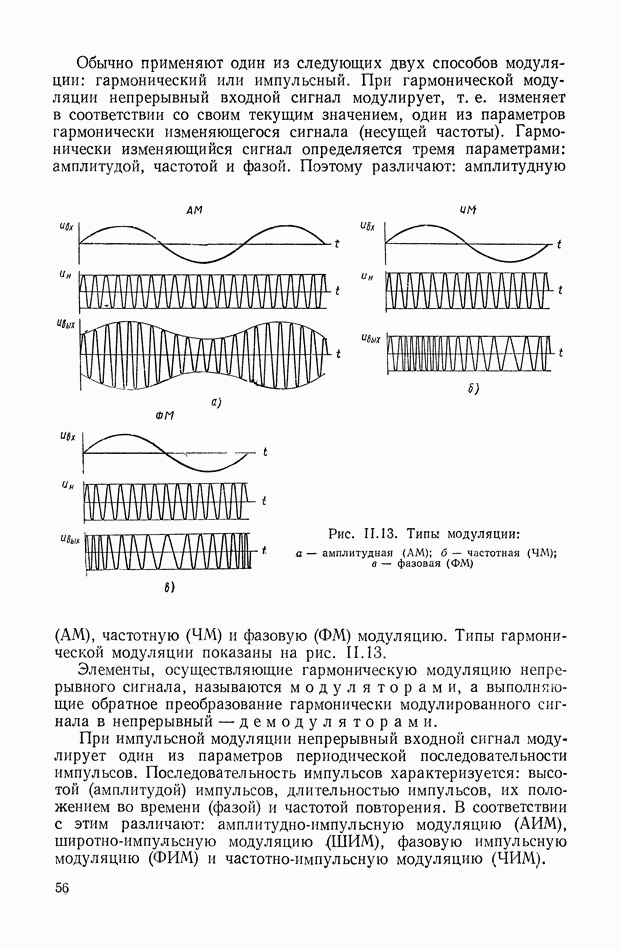
В 1930 г. Е. Л. Николаи издает учебник по теории автоматического регулирования [126], в котором рассматривает динамику процессов для регуляторов прямого и непрямого действия с помощью дифференциальных уравнений в вариациях. Там же были даны рекомендации по наивыгоднейшим с точки зрения устойчивости параметрам паровой машины, регулятора и гидравлического серводвигателя. Рассматривая схемы непрерывных систем прямого регулирования, Е. Л. Николаи оценивает влияние сухого трения на сходимость процессов и определяет минимальную величину коэффициента нечувствительности, при котором колебания регулятора затухают [125]. Для практического использования этих результатов им был дан график, разбивающий плоскость на области устойчивых и неустойчивых состояний, в зависимости от обобщенных коэффициентов неравномерности и нечувствительности.
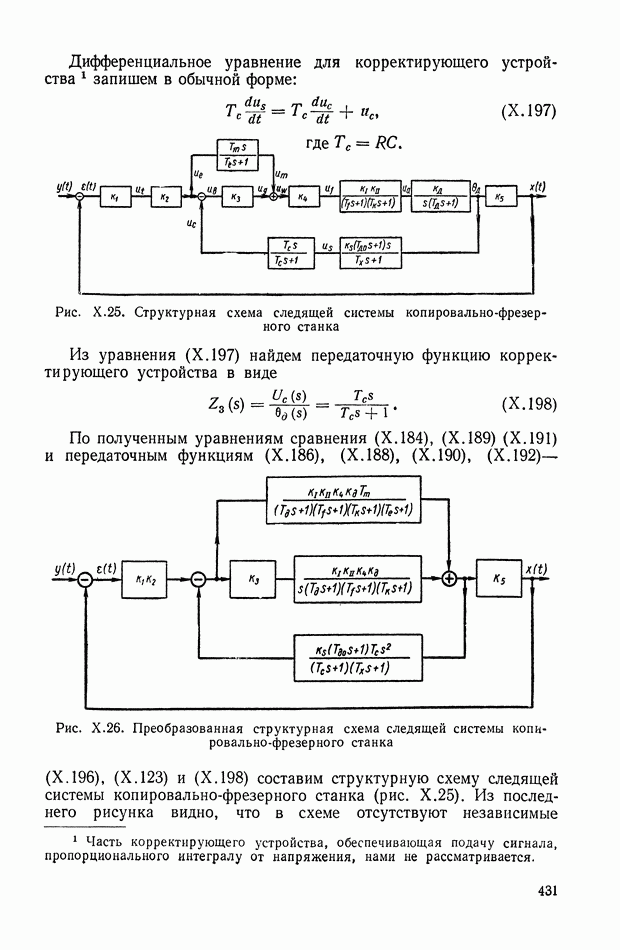
Большое значение для развития отечественного регуляторостроения имело создание в начале 30-х годов научно-исследовательских институтов: Центрального котлотурбиккого, Всесоюзного электротехнического и Всесоюзного теплотехнического.
В 1934 г. И. Н. Вознесенский впервые предложил принцип автономности для систем автоматического регулирования с несколькими регулируемыми параметрами [24]. Ему удается найти математические зависимости, определяющие условия автономности систем непрямого регулирования. В эти же годы он создает методику выбора рациональных кинематических связей в системах прямого регулирования [25]. Развивая теоретические положения этих двух работ, И. Н. Вознесенский в 1938 г. обобщил полученные им результаты на объекты с  параметрами [26], где показал, что путем выбора надлежащих кинематических связей обеспечивается автономность в сложкых системах автоматического регулирования [27].
параметрами [26], где показал, что путем выбора надлежащих кинематических связей обеспечивается автономность в сложкых системах автоматического регулирования [27].
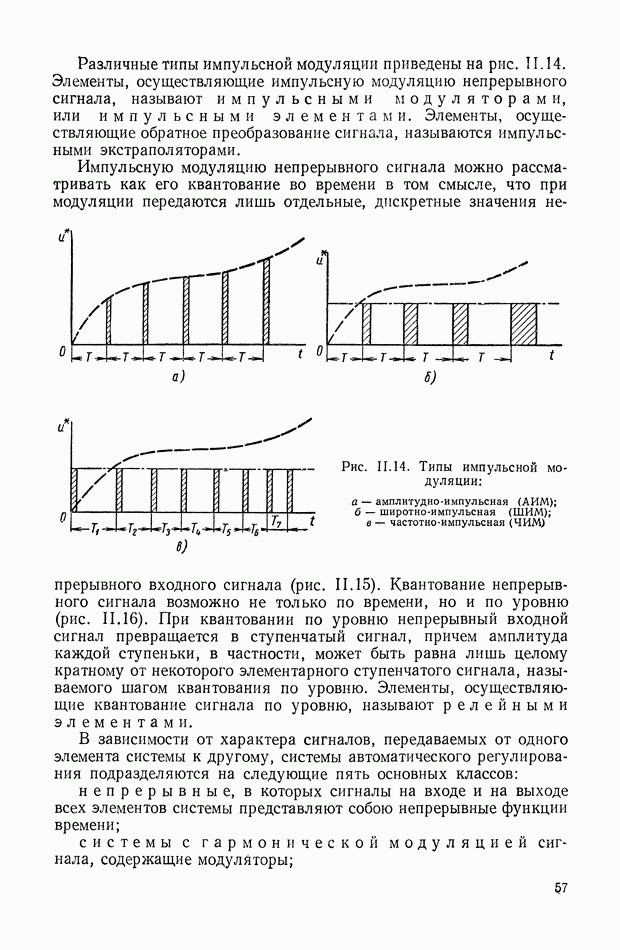
Оценивая деятельность такого крупного ученого, каким был И. Н. Вознесенский, нельзя не сказать о его инженерной деятельности в области регуляторостроения [54], [146]. Первые отечественные высококачественные регуляторы мощных турбин были созданы еще в 1923 г. по чертежам, разработанным И. Н. Вознесенским. Это позволило в последующие годы отечественному турбостроению занять ведущее место в мире.
С 1932 г. в периодической печати появляются многочисленные работы другого крупного ученого В. С. Кулебакина, развивающего теорию автоматического регулирования применительно к электрическим машинам и регуляторам [21], [150]. Первые работы В. С. Кулебакина откосились к теории вибрационных регуляторов электрических машин [82], где по соотношениям периодов замыканий и размыканий, учету времени запаздывания вспомогательного реле выбираются допустимые частоты вибраций контактов и амплитуды пульсаций напряжения возбудителя для различных режимов работы электрических машин. В последующих работах он рассматривает установившиеся и переходные режимы возбуждения синхронных машин, устанавливает определенные соотношения по скорости возбуждения в зависимости от применяемых схем включения возбудителей, а также определяет условия устойчивости параллельно работающих синхронных машин [83]. В 1940 г. В. С. Кулебакин в ряде своих статей [84], [85] высказывает некоторые соображения по выбору типов регуляторов под заданные характеристики объектов регулирования, что явилось дальнейшим шагом в проблеме синтеза автоматических систем. Большую известность получили его работы в области самолетных вибрационных регуляторов [86] и специальных электрических машин [87], [232].
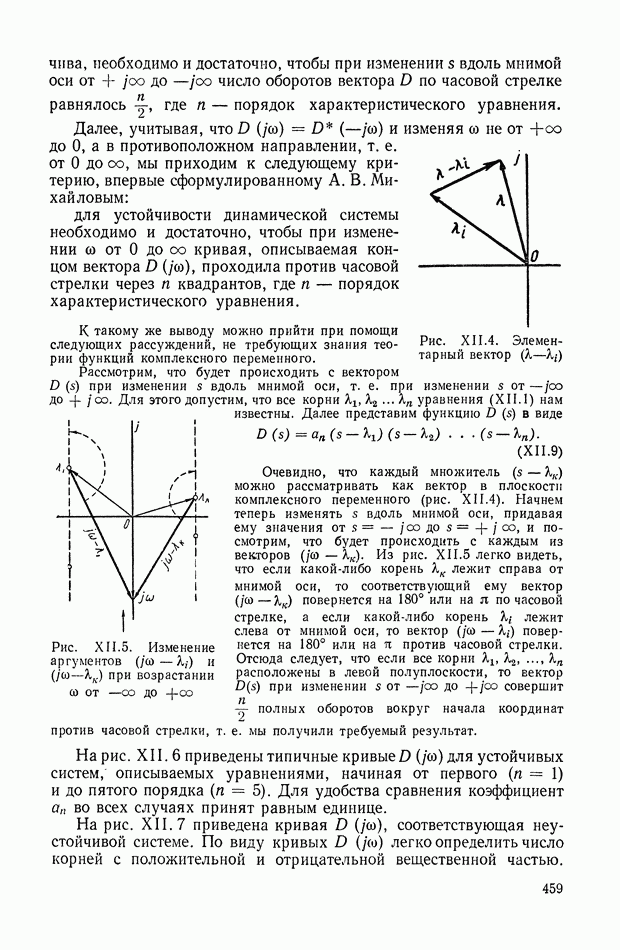
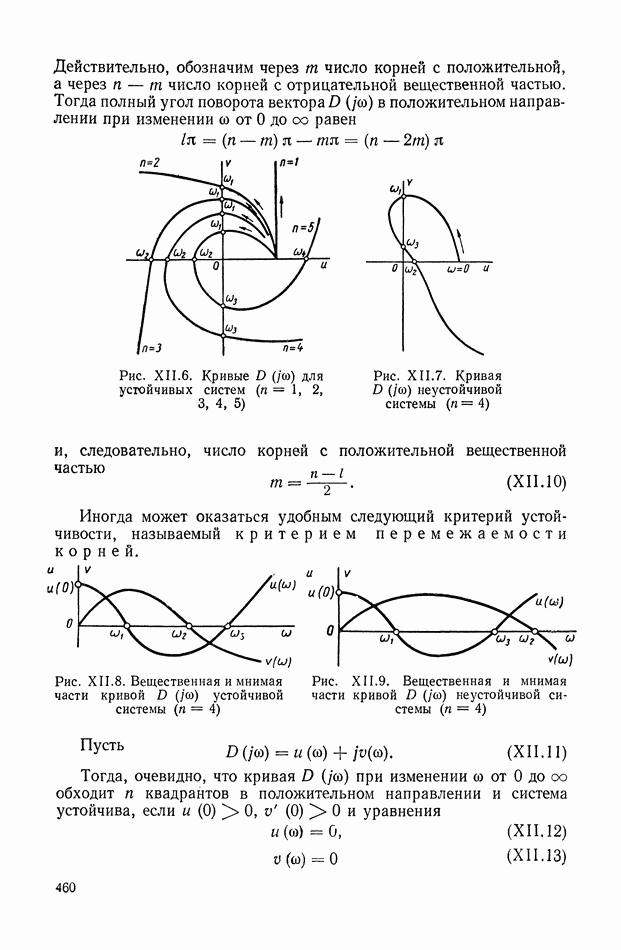
Исключительно важную роль в развитии теории автоматического регулирования сыграли работы А. В. Михайлова, которые были выполнены во Всесоюзном электротехническом институте в 1936 г. Они послужили основой для создания и развития частотных методов в теории регулирования [134] и были опубликованы в 1938 г. [118], [119]. Он впервые обратил внимание на общность теории ламповых усилителей с обратной связью, разработанную Г. Найквистом [249], с теорией линейных систем автоматического регулирования и предложил использовать частотный критерий устойчивости для анализа устойчивости автоматических систем. В своих работах [120], [121] А. В. Михайлов предложил новый критерий устойчивости линейных систем, основанный на графическом представлении функции комплексного переменного, представляющей собой левую часть характеристического уравнения, и показал его связь с критерием А. Гурвица. Ему также принадлежат идеи типизации динамических звеньев систем автоматического регулирования и структурных методов анализа.
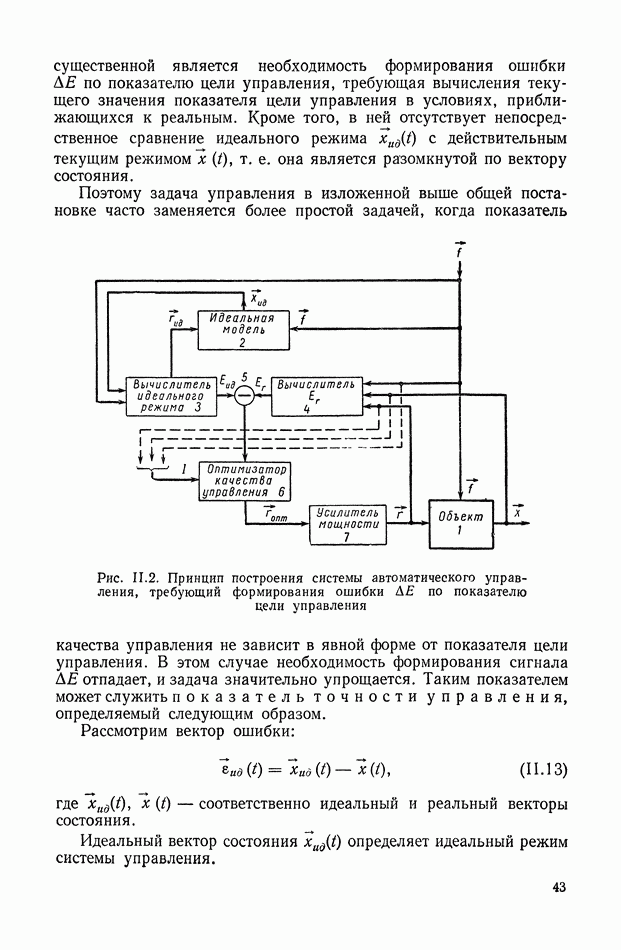
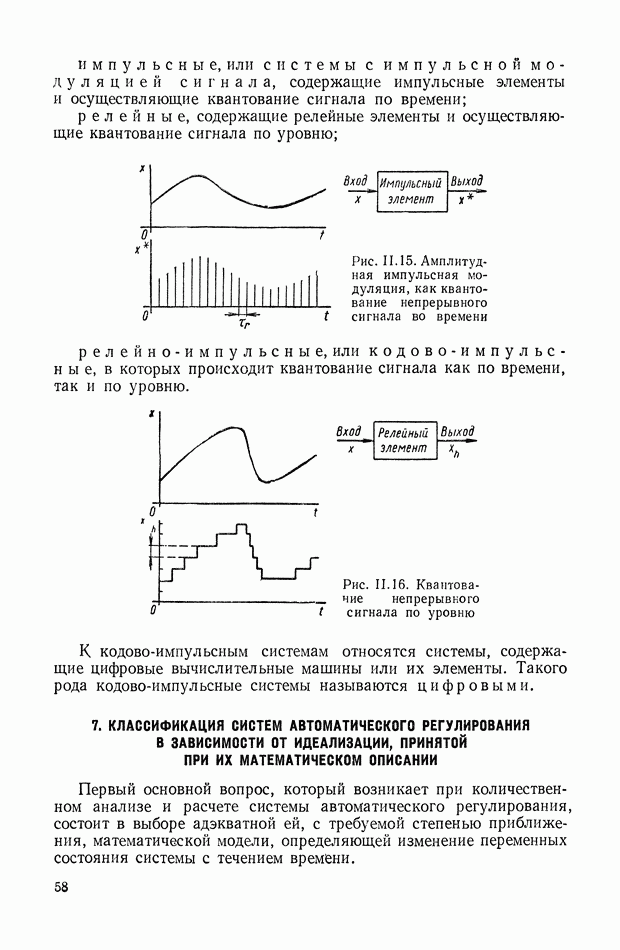
В результате дальнейшего развития техники в этот период назрела острая необходимость в методах исследования качества и точности регулирования при возмущающих воздействиях.
В 1939 г. В. В. Солодовников сформулировал условия качества регулирования и применил преобразование Лапласа для получения общих уравнений системы регулирования в операторной форме
и разработал основы частотного метода анализа качества [180]. Им же частотный метод анализа устойчивости и качества был обобщен на системы с распределенными параметрами [182].
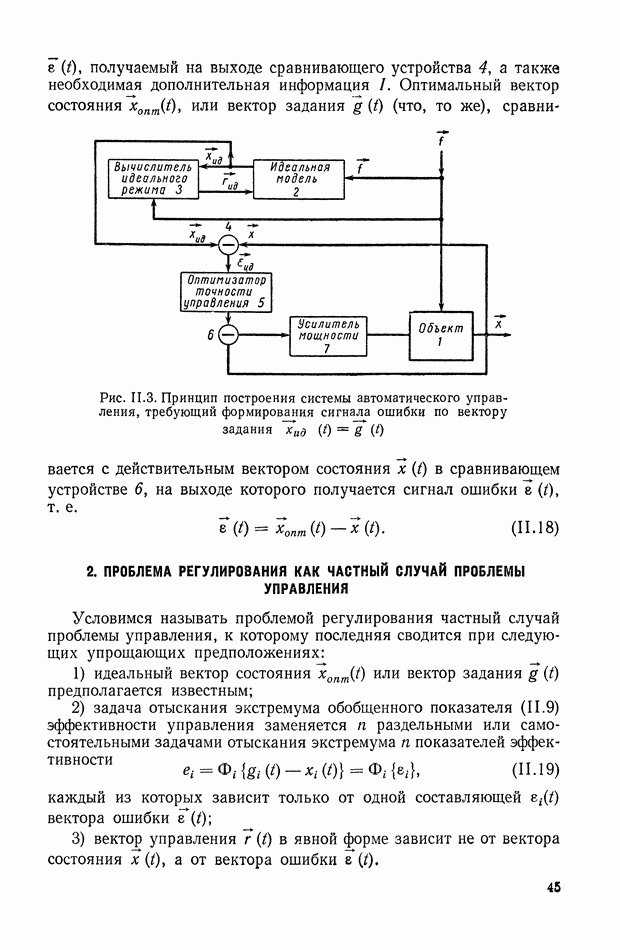
В 1938 г. известным ученым Г. В. Щипановым были сформулированы условия полной компенсации вынужденной составляющей отклонений регулируемого параметра, вызываемых внешним возмущением, изменяющимся произвольно [208], [233], [234]. Эти работы привлекли внимание такого крупного математика, как Н. Н. Лузина [101 ] и его ученика П. И. Кузнецова. С помощью теории матриц они доказали теоремы о полной и частичной компенсации возмущений и ввели новое название принципа компенсации Щипанова — принцип инвариантности.
Нелинейная теория регулирования получила значительное развитие в послевоенные годы. Но это было достигнуто при помощи методов, разработанных гораздо раньше применительно к задачам механики и теории колебаний. Этими методами явились: уже упоминавшийся выше второй метод Ляпунова [111]-[116], метод фазового пространства [7] и методы малого параметра [И], [16], [20].
В 1932 г. выдающиеся ученые Н. М. Крылов и Н. Н. Боголюбов создали метод гармонического баланса. В основу этого метода были положены асимптотические разложения, представляющие собой дальнейшее развитие методов теории возмущений [76], [77], [78]. Впервые этот метод был применен для решения нелинейных задач теории регулирования Л. С. Гольдфарбом в 1940 г.
Рассматривая процессы в ламповом генераторе, как в нелинейной динамической системе, известный физик А. А. Андронов и ряд других советских ученых разработали методы исследований нелинейных колебаний на основе понятия фазового пространства [1], [37], [128].
В этот период были опубликованы «Введение в нелинейную механику» Н. М. Крылова и Н. Н. Боголюбова [79] и «Теория колебаний» А. А. Андронова, А. А. Витте и С. Э. Хайкина [8], которые получили мировую известность. Основные теоретические положения, высказанные в этих работах, позволили отечественным ученым в последующие годы создать основы теории нелинейных систем автоматического регулирования.
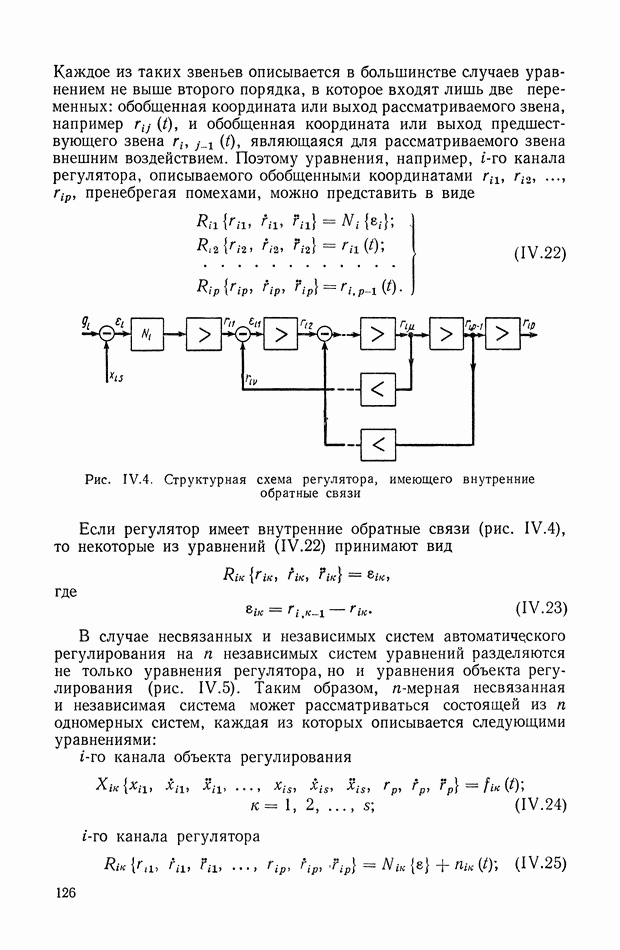
Развитие военной техники и промышленности в период Великой Отечественной войны сыграло большую роль в формировании теории автоматического регулирования. Созданные в эти годы многочисленные системы автоматического регулирования успешно работали в машиностроении, металлургии, энергетике и других отраслях народного хозяйства. С этого времени начинается период массового применения регуляторов и следящих систем в промышленности, что естественно накладывает определенное влияние на развитие теории регулирования. Теория автоматического
регулирования становится дисциплиной, необходимой для широкого круга инженеров и конструкторов. В это время (1945-1953 гг.) частотный метод анализа и синтеза, дающий единую и взаимосвязанную методику решения основных задач линейной теории регулирования, приобретает в значительной мере законченную форму, благодаря работам В. В. Солодовникова [183]-[192]. Этот метод становится основным методом расчета и проектирования систем автоматического регулирования, допускающих линеаризацию.
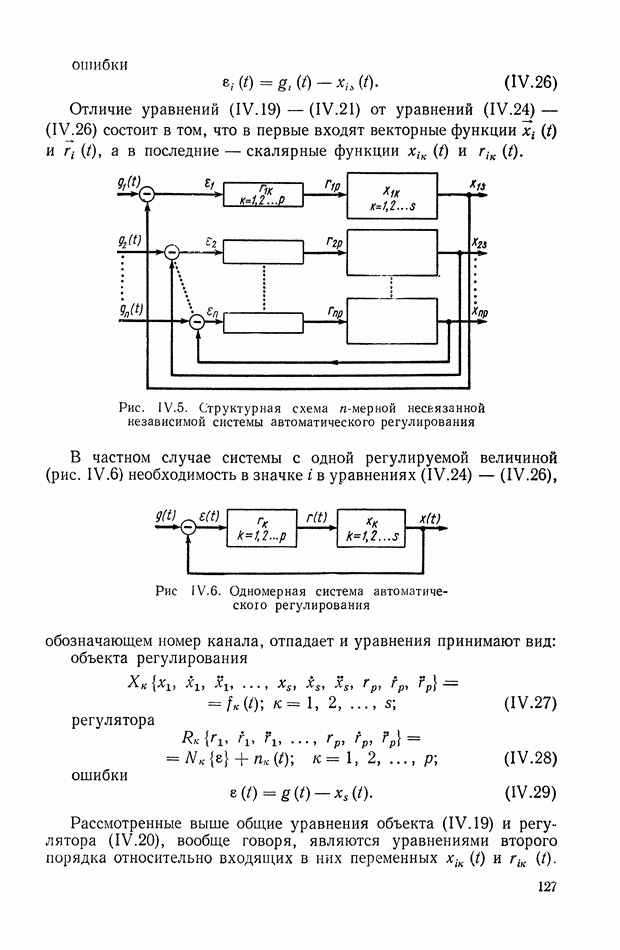
Важнейшими результатами, полученными в данном направлении, являются: обобщение частотного метода на ненулевые начальные условия и широкий класс типовых воздействий [185], установление свойств критериев и теорем, позволяющих судить о качестве и характере переходного процесса непосредственно по виду частотных характеристик [187], разработка метода трапецеидальных частотных характеристик для построения переходных процессов [188], [195], и создание метода синтеза корректирующих устройств [190], [192] при помощи логарифмических частотных характеристик [184]. В это же время (1947-1948 гг.) Ю. И. Неймарк развил метод Д-разбиения плоскости двух параметров для линеаризованной системы, позволяющей выделять области устойчивости [123], [124]. Он же показал, что все известные критерии устойчивости линейных систем можно рассматривать как различные формы  -разбиения.
-разбиения.
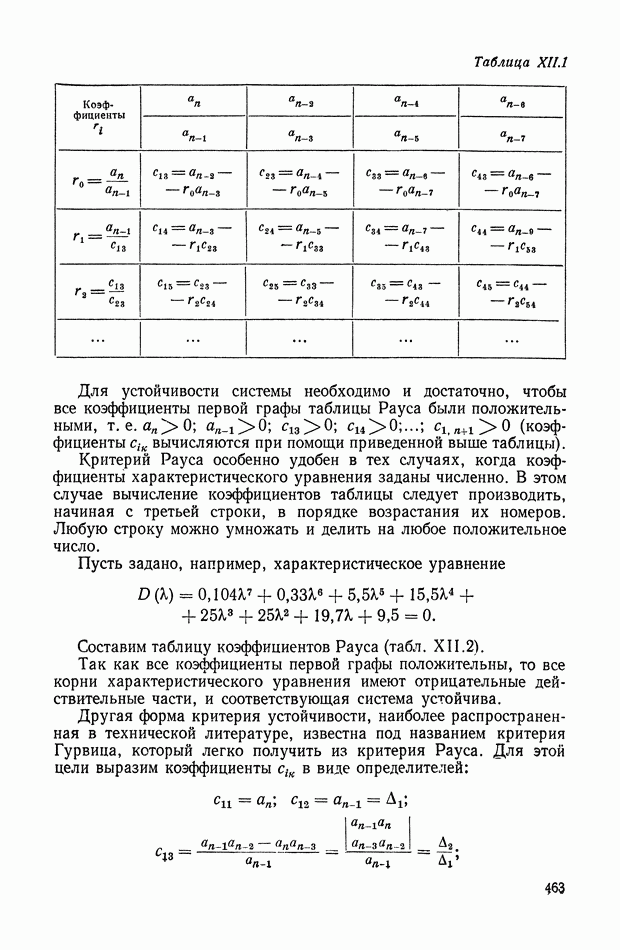
Наряду с частотными методами развивались методы анализа качества процессов регулирования, основанные на исследовании расположения полюсов и нулей передаточной функции и методы интегральных оценок. В частности, Я. 3. Цыпкиным и П. В. Бромбергом было введено понятие степени устойчивости, а С. П. Стрелковым исследовано влияние расположения полюсов и нулей на качество воспроизведения внешних воздействий.
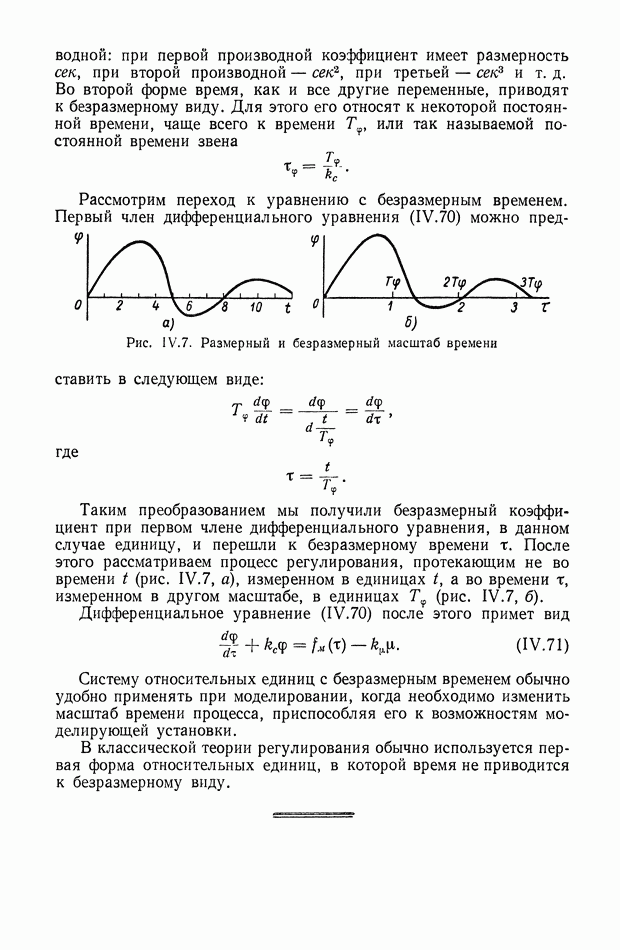
Первое применение метода интегральных оценок в теории регулирования было сделано В. С. Кулебакиным, предложившим в 1940 г. оцекивать качество переходного процесса по ограничиваемой им площади [84], [85]. Позже этот метод получил существенное развитие в работах А. А. Красовского и А. А. Фельдбаума.
Широкое применение следящих систем, работающих в условиях помех, выдвигает, как одну из главных задач теории регулирования, решение проблем динамической точкости следящих систем, находящихся под влиянием случайных воздействий. В 1950 г. В. В. Солодовников, основываясь на классических работах А. Н. Колмогорова, А. Я. Хинчина и Н. Винера, в которых были
заложены математические основы теории стационарных случайных процессов и решения проблем интерполяции и экстраполяции, опубликовал монографию «Введение в статистическую динамику систем автоматического управления» [191]. Эта книга послужила основой для формирования нового раздела теории автоматического регулирования.
В последующие годы им разрабатывается методика синтеза систем автоматического регулирования с постоянными [190], [193], [194] и переменными [200] параметрами при наличии помех по заданным требованиям к качеству и динамической точности [192], а также принцип построения и теория аналитических самонастраивающихся систем [196], [201].
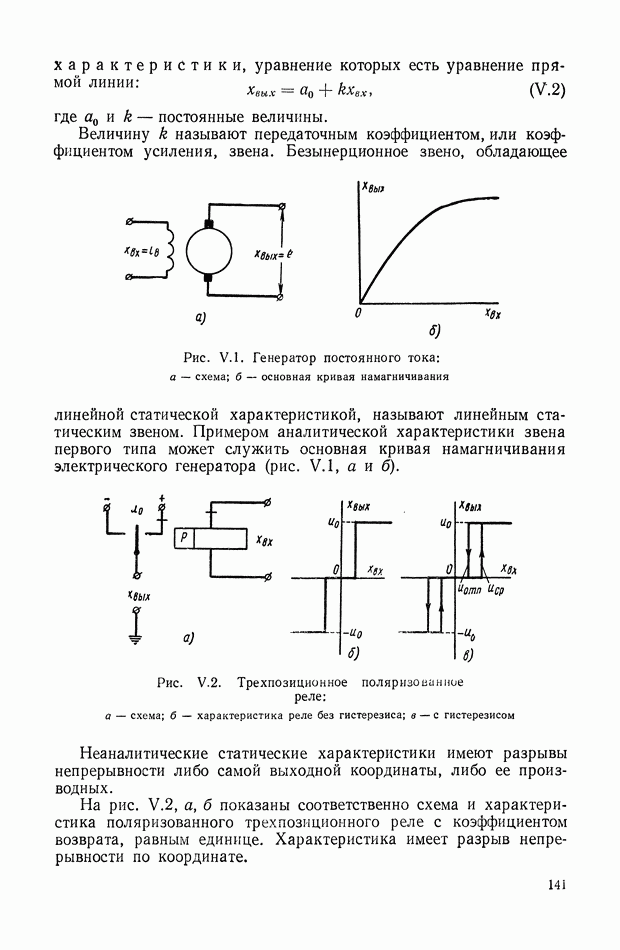
В 1950 г. В. С. Пугачевым был разработан математический аппарат для анализа динамических систем, находящихся под влиянием случайных воздействий, не связанный с предположением об их стационарности. Он также предложил способ представления случайных функций в виде канонических разложений [165], [166], которые он применил для определения оптимальных линейных [167] и нелинейных систем автоматического регулирования. В своих последующих работах он разрабатывает методы определения оптимальных систем по произвольному [168] и по общему Байессву [169] критериям, уменьшающим число ограничений, накладываемых на системы. Значительный интерес представляют работы В. С. Пугачева, посвященные созданию метода анализа одномерных и многомерных систем регулирования, находящихся под влиянием нестационарных случайных воздействий [170].
Теоретические основы дискретных систем автоматического регулирования развиваются Я. 3. Цыпкиным [215], который еще в 1948 г. предлагает частотный критерий устойчивости дискретных систем, а затем на основе дискретного преобразования Лапласа создает основы общей теории таких систем, формально подобную теории линейных непрерывных систем. Начиная с 1952 г., им успешно были решены проблемы качества [216]-[218], [225] и динамической точности [219] дискретных систем. Большой интерес представляют его работы, посвященные методам синтеза дискретных корректирующих устройств [222], дискретным системам с экстраполирующими устройствами [223]. В 1958 г. выходит книга «Теория импульсных систем», в которой Я. 3. Цыпкин с единых позиций излагает общую теорию анализа и синтеза дискретных систем управления. Эта книга представляла собой наиболее полную монографию, посвященную теории линейных импульсных систем. В теории релейных систем автоматического регулирования
Я. 3. Цыпкин разработал точный метод решения задачи о вынужденных колебаниях [217]. В своих работах, посвященных исследованию устойчивости периодических режимов, он распространяет частотные методы анализа и синтеза на релейные системы регулирования [218], [220], [221].
Значительные научные результаты в теории релейных систем регулирования были получены А. А. Фельдбаумом. Он использовал фазовую плоскость для исследования влияния неоднозначной релейной характеристики и различных видов обратных связей на поведение релейных автоматических систем [204], [205]. Развивая эти направления, он поставил и в 1955 г. решил задачу синтеза оптимальных релейных систем регулирования [206].
Общее решение проблемы оптимальных по быстродействию систем автоматического регулирования было дано в работах Л. С. Понтрягина и его учеников (1956-1960 гг.), сформулировавших принцип максимума [148], [149].
Методом медленно меняющихся функций Г. С. Поспелов исследовал релейные системы автоматического регулирования и показал на возможность получения в них режимов вибрационной линеаризации [161], [162]. Он также разработал некоторые способы подавления автоколебаний в релейных системах [163].
Теория нелинейных систем автоматического регулирования развивается по трем направлениям: дальнейшее совершенствование второго метода Ляпунова, методов фазового пространства и малого параметра.
Н. Г. Четаев, используя метод Ляпунова, формулирует задачу устойчивости на конечном интервале [229]; развивает теорию характеристических чисел; показывает на аналитические и геометрические возможности прямого метода [230]. А. И. Лурье предложил метод построения функций Ляпунова, основываясь на приведении уравнений систем автоматического регулирования к канонической форме [107]. Этот метод, доведенный А. И. Лурье до рабочего алгоритма, существенным образом упрощает задачу анализа устойчивости одного из классов нелинейных систем [105]-[108].
А. М. Летов, используя идеи Ляпунова по оценке времени затухания переходного процесса, предложил способ отыскания экстремальных значений квадратичной формы замкнутой поверхности для оценки качества нелинейных систем регулирования [97], [98], [100]. Вслед за этими работами появляются статьи и книги
Н. П. Еругина и В. И. Зубова, в которых они дали наиболее полное решение проблемы обращения в теории устойчивости Ляпунова [45], [53].
В 1953 г. В. И. Зубов [50] предлагает применять в нелинейных системах метод кажущейся линеаризации, позволяющий иногда
достаточно просто анализировать устойчивость нелинейных систем [52].
Методы определения режимов автоколебаний в нелинейных системах были разработаны А. А. Андроновым [1], [3], [244]. С помощью метода точечных преобразований он исследовал фазовое пространство ряда нелинейных систем автоматического регулирования, имеющих большое практическое значение. В наиболее полном виде им были исследованы: системы непрямого регулирования с учетом сухого трения в чувствительном элементе [7], системы стабилизации самолета с рулевыми приводами, имеющими постоянную скорость и зону нечувствительности, а также некоторые другие системы [8]. В последующие годы это направление, связанное с построением фазового пространства, успешно развивается
В. В. Петровым. Совместно с Г. М. Улановым им были исследованы системы регулирования с одной и несколькими нелинейностями, для которых впервые использовались многолистные фазовые поверхности [141]-[143]. С помощью многолистной поверхности он исследует скользящие, или пульсирующие, режимы, устанавливая общность скользящих и оптимальных режимов [144].
В. В. Петров предложил применять метод вырожденных циклов для определения границы устойчивости двухкаскадных нелинейных сервомеханизмов [145].
Известный ученый Б. В. Булгаков еще в 1942 г. рассмотрел возможность применения метода А. Пуанкаре [250] к определению периодических режимов в нелинейных системах [15]. Периодические решения по этому методу находятся в виде рядов по степеням малого параметра [16]. Им был разработан метод получения приближенных («укороченных») уравнений для нелинейных систем, позволяющий исследовать не только периодические процессы, но и процессы установления [20]. Важное значение для синтеза нелинейных систем имеет работа Б. В. Булгакова «Автоколебания регулируемых систем», где ставится и решается задача выбора нелинейной функции, предотвращающей возникновение автоколебаний в системе автоматического регулирования [15].
В области линейной теории Б. В. Булгаков разрабатывает методы оценки возмущений в системах (метод накопления) [17], [18] и некоторые вопросы синтеза корректирующих устройств [19]. Изданная в 1949 г. монография Б. В. Булгакова «Колебания» посвящена рассмотрению методов расчета систем автоматического регулирования.
Значительное развитие получают приближенные способы анализа нелинейных систем регулирования, основанные на методе гармонического баланса Н. М. Крылова и Н. Н. Боголюбова. Используя амплитудно-фазовую частотную характеристику
линейной части системы и эквивалентные характеристики нелинейной части, Л. С. Гольдфарб предлагает метод определения автоколебаний в системах автоматического регулирования [33], [35]. С помощью этого метода он исследует вибрационные регуляторы [34], системы регулирования с исполнительными двигателями, имеющими ограничение скорости [36].
Существенные результаты, полученные советской школой в области автоматического регулирования к началу 60-х годов, были обобщены и систематизированы в получившем широкую известность коллективном труде «Основы автоматического регулирования. Теория», вышедшем в 1954 г.
Развивая идеи Н. М. Крылова и Н. Н. Боголюбова, Е. П. Попов создает теорию гармонической линеаризации [151], [158], получившую в последующие годы широкое практическое применение. Ему также принадлежит способ определения автоколебаний, основанный на применении годографа Михайлова линейной части и эквивалентной передаточной функции нелинейной части системы [153], [155]. В 1953 г. он распространяет методы гармонической линеаризации на системы с несколькими нелинейностями. В своих последующих работах ему удается разработать метод, позволяющий уточнять результаты первого приближения, при определении амплитуд и частот автоколебаний, за счет учета высших гармоник [152], [154]. Весьма важны результаты, полученные Е. П. Поповым при исследовании режимов автоколебаний нелинейных систем, на вход которых действуют различного рода внешние воздействия [156]. В качестве внешних воздействий он рассматривает сначала вибрации, а затем и медленно меняющиеся случайные воздействия, создав тем самым единый аппарат линеаризации (гармонический и статистический). Е. П. Попов обобщает асимптотический метод Крылова — Боголюбова на исследование переходных процессов в нелинейных системах [157], [159]. В 1960 г. Е. П. Попов совместно с И. П. Пальтовым публикует книгу «Приближенные методы исследования нелинейных автоматических систем».
Значительный вклад в статистическую теорию нелинейных систем регулирования был сделан П. И. Кузнецовым [81], который применил статистические методы к исследованию нелинейных систем, учитывая распределение характеристических функций и моментов при наличии многократных корреляций между ними.
Анализируя встречающиеся на практике плотности вероятности, незначительно отличающиеся от нормальной, ему удалось представить их в виде ряда по многомерным ортогональным полиномам Эрмита. Развивая эти теоретические положения, П. И. Кузнецову удается показать, что при линейных и нелинейных преобразованиях случайных процессов коэффициенты разложения, т. е. квазимоменты, преобразуются в линейные. С целью упрощения методики синтеза нелинейных систем в его работах даны формулы для определения плотности вероятности, корреляционных и моментных
функций при линейных и нелинейных (полиноминальных) преобразованиях случайных процессов. Ему также удалось решить задачу выбора параметров системы, обеспечивающих воспроизведение полезных сигналов при наличии шумов с минимальной среднеквадратичной погрешностью [80].
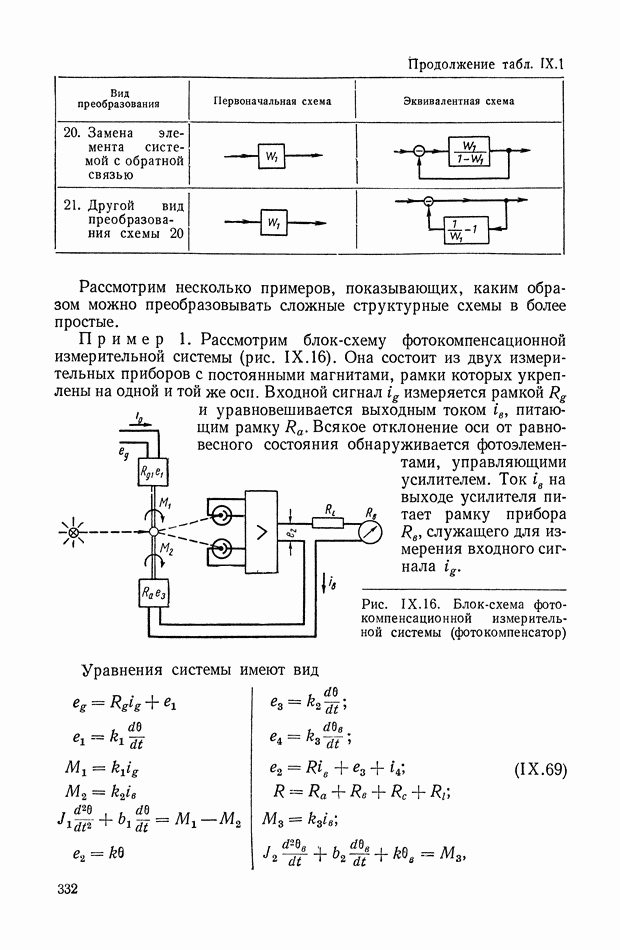
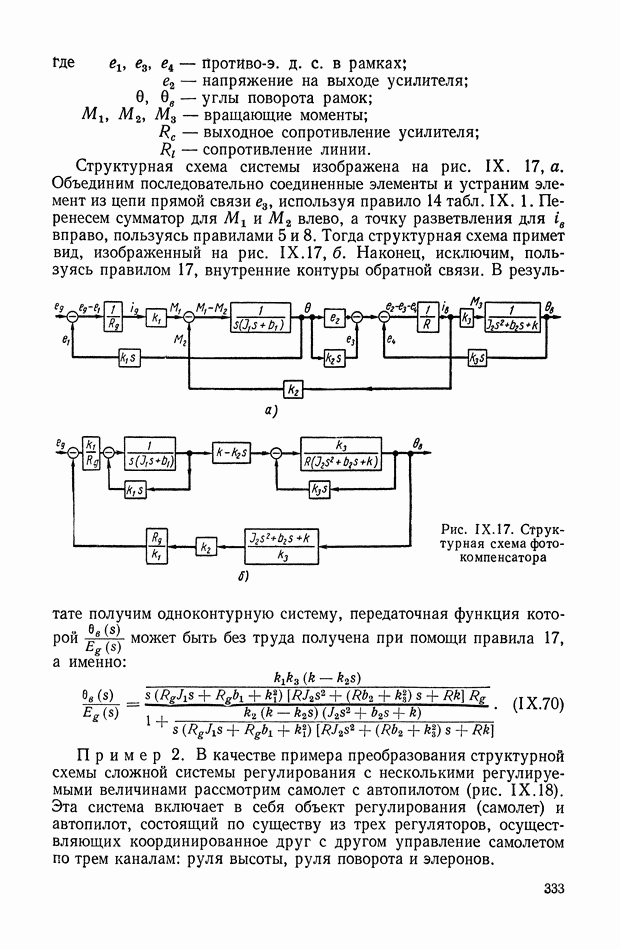
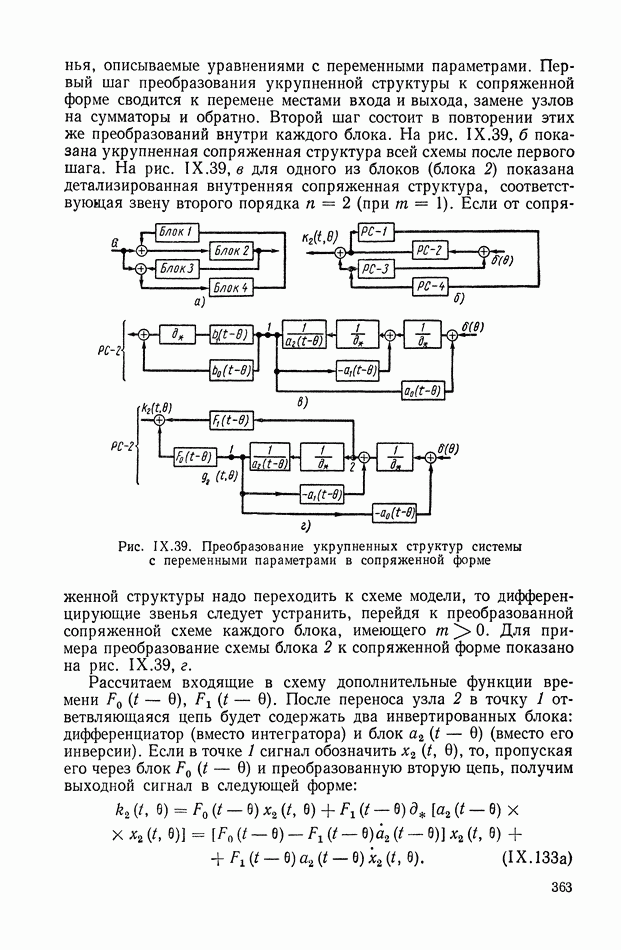
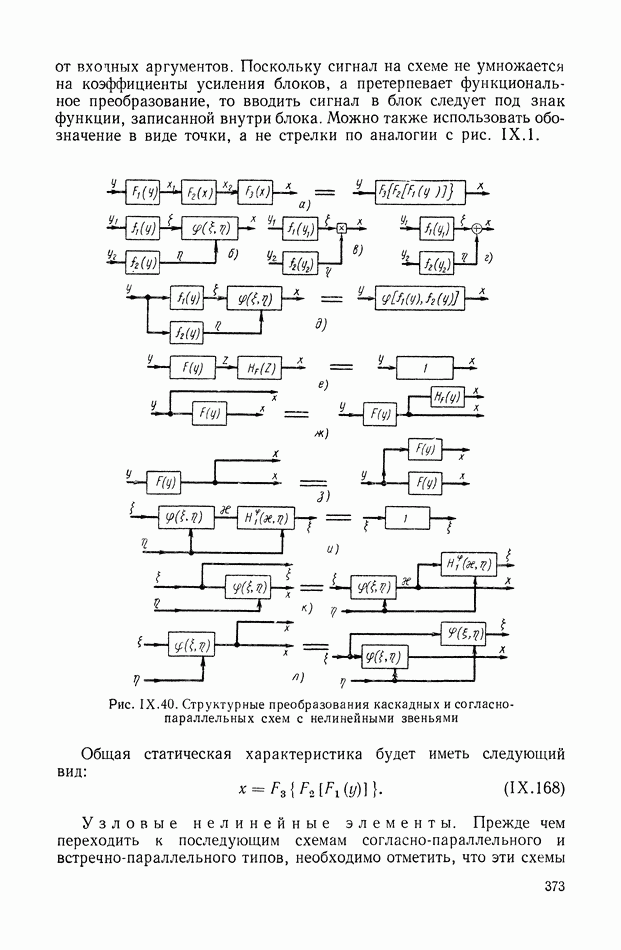
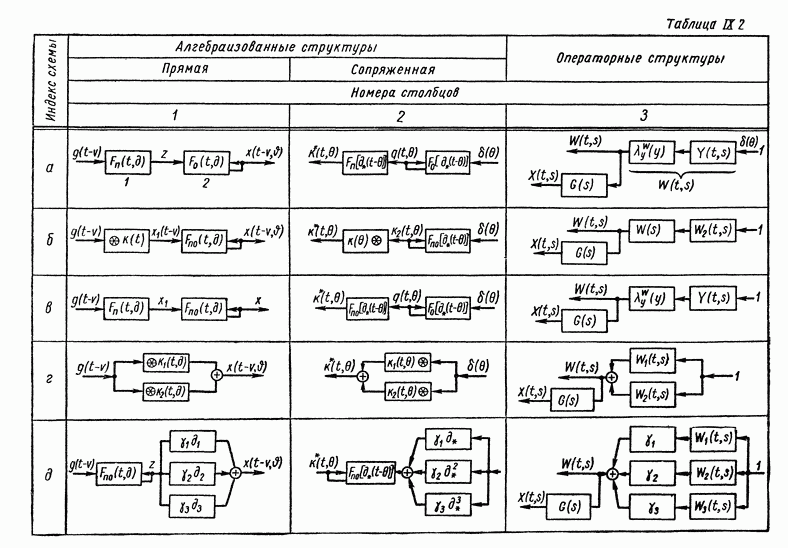
Развивая матричные методы в теории автоматического регулирования, Б. Н. Петров в 1945 г. предложил способы преобразования структурных схем, без применения которых в настоящее время невозможен расчет и проектирование реальных систем регулирования [129], [130], [133]. Кроме того, он разработал на основе метода С. А. Чаплыгина аналитические способы анализа систем автоматического регулирования, описываемых дифференциальными уравнениями второго порядка с переменными параметрами [132], [133].
На основе обобщенных представлений линейных систем А. С. Шаталов разработал способы структурных преобразований систем автоматического регулирования.
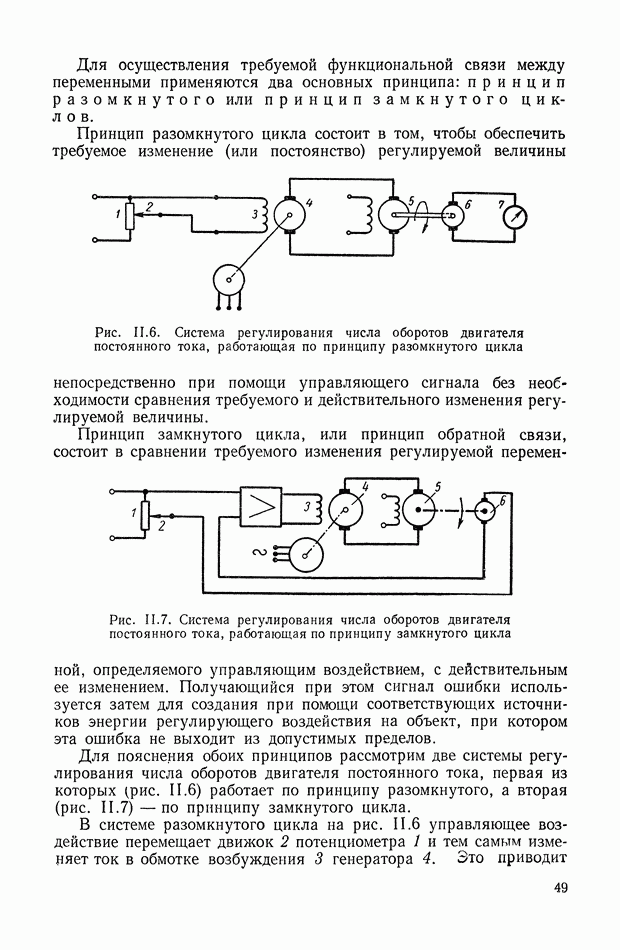
Важным направлением теории автоматического регулирования, по-прежнему, является теория инвариантности. В классе систем регулирования, работающих по отклонению с одним регулируемым параметром, задача абсолютной инвариантности может быть решена только при бесконечно большом коэффициенте усиления. Невозможность получения этого на практике выдвигает задачу о частичной инвариантности. Решению этой задачи с точностью до в посвящены работы Н. Н. Лузина и П. И. Кузнецова [102], опубликованные в 1946-1951гг.
Создание систем, инвариантных до  следует рассматривать как одно из основных направлений достижения независимости динамических свойств системы от внешних воздействий. Постановка задачи о компенсации внешних возмущений с точностью до значений, обусловленных старшими производными от внешних возмущений, была высказана Б. А. Рябовым еще в 1939 г. [175], [176].
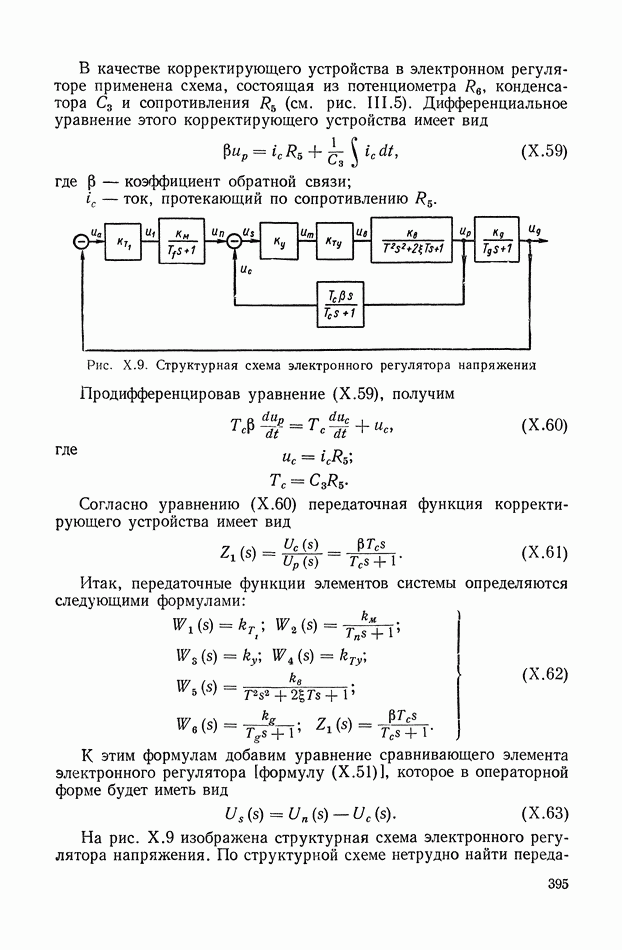
следует рассматривать как одно из основных направлений достижения независимости динамических свойств системы от внешних воздействий. Постановка задачи о компенсации внешних возмущений с точностью до значений, обусловленных старшими производными от внешних возмущений, была высказана Б. А. Рябовым еще в 1939 г. [175], [176].
В эти же годы В. С. Кулебакин разрабатывает общие принципы физической реализуемости инвариантных систем [88]-[90]. Одно из центральных мест в его теории занимает К ( -изображение. С помощью физической реализации идей К (
-изображение. С помощью физической реализации идей К ( -изображения можно обеспечить полную инвариантность систем регулирования по отношению к возмущающему воздействию [91], [92]. При дальнейшем развитии этого направления В. С. Кулебакин приходит к методам синтеза инвариантных систем регулирования [93]. Многочисленные работы В. С. Кулебакина [94]-[96] и А. Г. Ивахненко [55]-[59] посвящены теоретическим методам выбора структур и параметров комбинированных систем управления.
-изображения можно обеспечить полную инвариантность систем регулирования по отношению к возмущающему воздействию [91], [92]. При дальнейшем развитии этого направления В. С. Кулебакин приходит к методам синтеза инвариантных систем регулирования [93]. Многочисленные работы В. С. Кулебакина [94]-[96] и А. Г. Ивахненко [55]-[59] посвящены теоретическим методам выбора структур и параметров комбинированных систем управления.
В 1956 г. Б. Н. Петров предлагает критерий физической осуществимости абсолютно инвариантных систем, на основе которого в настоящее время проектируются высококачественные системы автоматического регулирования. В последующих работах, выполненных в 1960-1965 гг., он разрабатывает принципы создания двухканальных систем регулирования, инвариантных к возмущающему воздействию [136]-[139].
Первые работы в области экстремальных систем регулирования были выполнены В. В. Казакевичем [67]. В них он рассмотрел различные схемы релейных экстремальных регуляторов, исследовал влияние коммутатора, зазора в механической передаче, запаздывания и времени выбега в серводвигателе на периодическом участке движения. Ему также принадлежат способы улучшения устойчивости и качества систем экстремального регулирования [64]-[66].
Существенные результаты в теории экстремальных регуляторов были получены А. А. Красовским, который рассмотрел динамические режимы квазистационарных экстремальных регуляторов в нормальных и форсированных режимах [72], [74]. Он решил общую задачу синтеза линейной непрерывной системы экстремального регулирования [73], [75].
В связи с усложнением объектов регулирования и необходимостью автоматизации процессов, не имеющих математического описания, большое развитие получают экспериментальные статистические методы определения динамических характеристик в процессе нормальной эксплуатации, основанные на применении средств вычислительной техники [198].
Наряду с теорией поисковых самонастраивающихся систем начинает формироваться теория аналитических самонастраивающихся систем [196], [197], [201].
Говоря об истории теории автоматического регулирования, нельзя не отметить роль Института автоматики и телемеханики [209], где в течение многих лет работали и работают наиболее крупные советские ученые по автоматическому регулированию: В. С. Кулебакин, В. А. Трапезников, Б. Н. Петров, Б. С. Сотсков, В. В. Солодовников, Я. 3. Цыпкин, А. М. Летов, В. В. Петров и многие другие.
Заканчивая на этом краткий исторический очерк развития теории автоматического регулирования в СССР, необходимо, прежде всего, отметить, что последний не претендует на полноту, и многие интересные результаты не нашли в нем освещения.
Это объясняется следующими причинами. Во-первых, полное исследование истории развития теории регулирования в СССР — достаточно обширная тема, чтобы ее можно было бы осветить в пределах одной главы. Во-вторых, в этот очерк намеренно не включены многие из результатов, полученных за последние годы, поскольку они, согласно принятой нами терминологии, относятся уже скорее к теории
управления, чем к теории регулирования и, следовательно, выходят за рамки настоящей книги.
Большую роль в формировании теории автоматического регулирования сыграли Всесоюзные совещания (первое — 1940 г., второе — 1953 г. [134]; третье — 1965 г.).
Современная теория автоматического регулирования располагает мощными методами анализа и синтеза, позволяющими создавать высококачественные и высоконадежные автоматические системы и регуляторы.
Теория автоматического регулирования является одной из основных наук, имеющих исключительно важное значение для формирования инженерных знаний, поэтому в настоящее время в нашей стране нет ни одного высшего технического учебного заведения, где не преподавалась бы теория автоматического регулирования.
Дальнейшее развитие теории автоматического регулирования с помощью современных методов и цифровых вычислительных машин позволит создавать более совершенные автоматические системы, значительно повышающие уровень промышленного производства.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- РАЗДЕЛ I. ОБЩИЕ СВЕДЕНИЯ. МЕТОДЫ МАТЕМАТИЧЕСКОГО ОПИСАНИЯ И СТРУКТУРНОГО ПРЕОБРАЗОВАНИЯ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- ГЛАВА I. ОЧЕРК О РАЗВИТИИ ТЕОРИИ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ В СССР
- 1. ТЕОРИЯ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ В ДОРЕВОЛЮЦИОННЫЙ ПЕРИОД
- 2. РАЗВИТИЕ ТЕОРИИ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ПОСЛЕ ОКТЯБРЬСКОЙ СОЦИАЛИСТИЧЕСКОЙ РЕВОЛЮЦИИ
- ГЛАВА II. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ ТЕОРИИ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
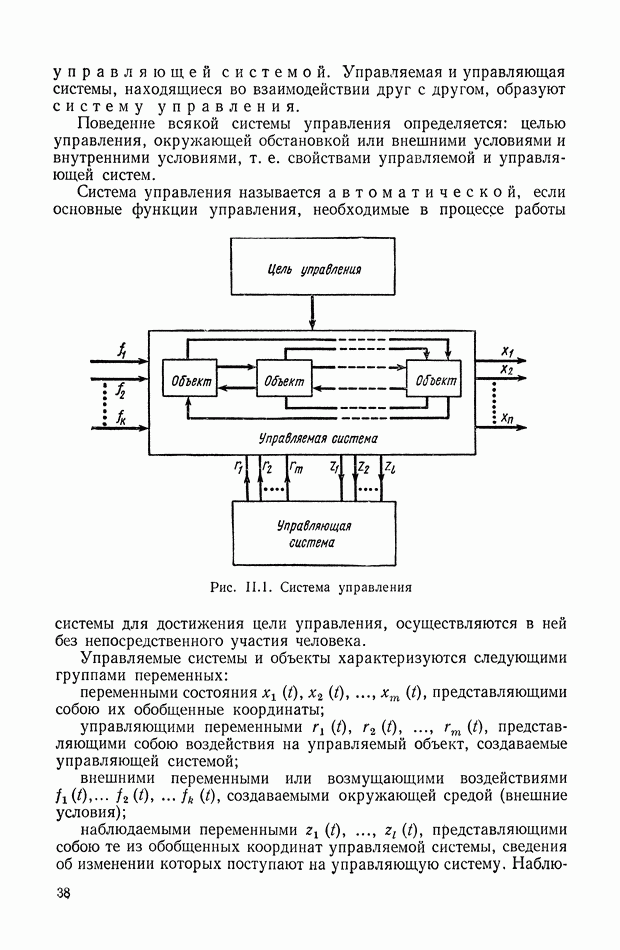
- 1. СУЩНОСТЬ ПРОБЛЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- 2. ПРОБЛЕМА РЕГУЛИРОВАНИЯ КАК ЧАСТНЫЙ СЛУЧАЙ ПРОБЛЕМЫ УПРАВЛЕНИЯ
- 3. ОСНОВНОЙ ПРИНЦИП ДЕЙСТВИЯ И ОПРЕДЕЛЕНИЕ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 4. КЛАССИФИКАЦИЯ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ В ЗАВИСИМОСТИ ОТ УПРАВЛЯЮЩЕГО ВОЗДЕЙСТВИЯ
- 5. ОСНОВНЫЕ УСТРОЙСТВА СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ И ИХ КЛАССИФИКАЦИЯ ПО НАЗНАЧЕНИЮ
- 6. КЛАССИФИКАЦИЯ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ В ЗАВИСИМОСТИ ОТ ХАРАКТЕРА СИГНАЛОВ
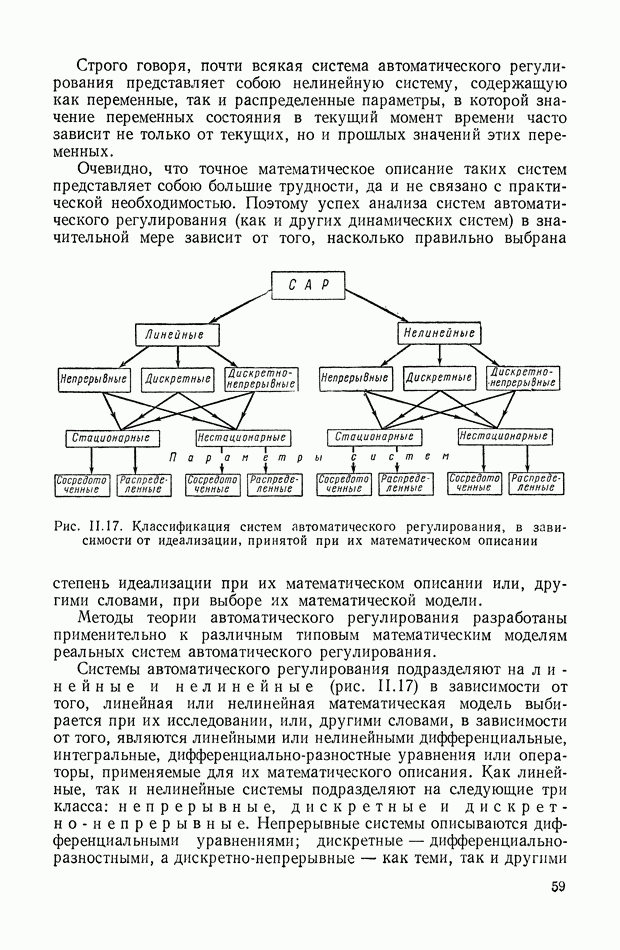
- 7. КЛАССИФИКАЦИЯ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ В ЗАВИСИМОСТИ ОТ ИДЕАЛИЗАЦИИ, ПРИНЯТОЙ ПРИ ИХ МАТЕМАТИЧЕСКОМ ОПИСАНИИ
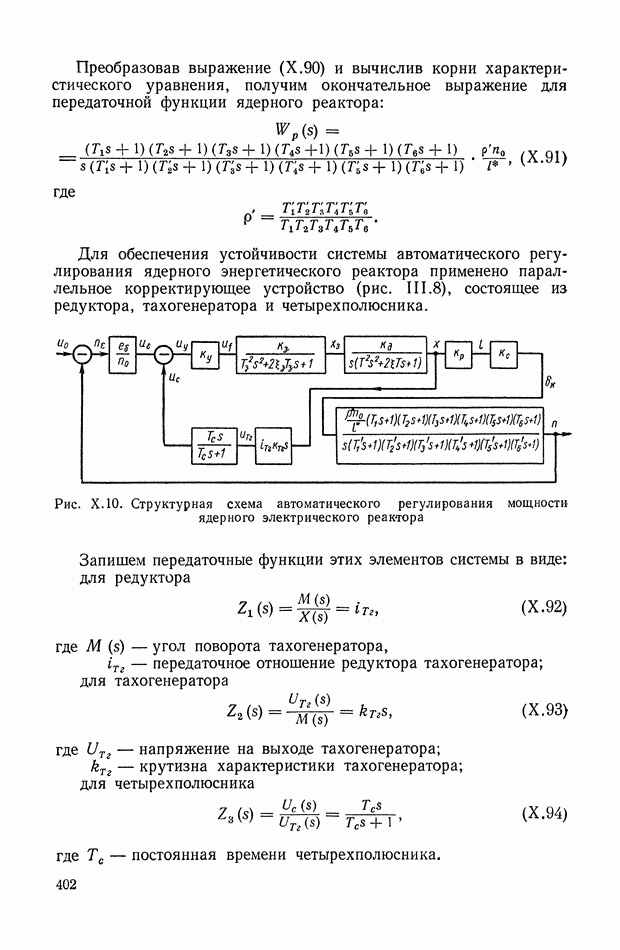
- 8. СТРУКТУРНЫЕ СХЕМЫ, ОДНОКОНТУРНЫЕ И МНОГОКОНТУРНЫЕ, НЕСВЯЗАННЫЕ И СВЯЗАННЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
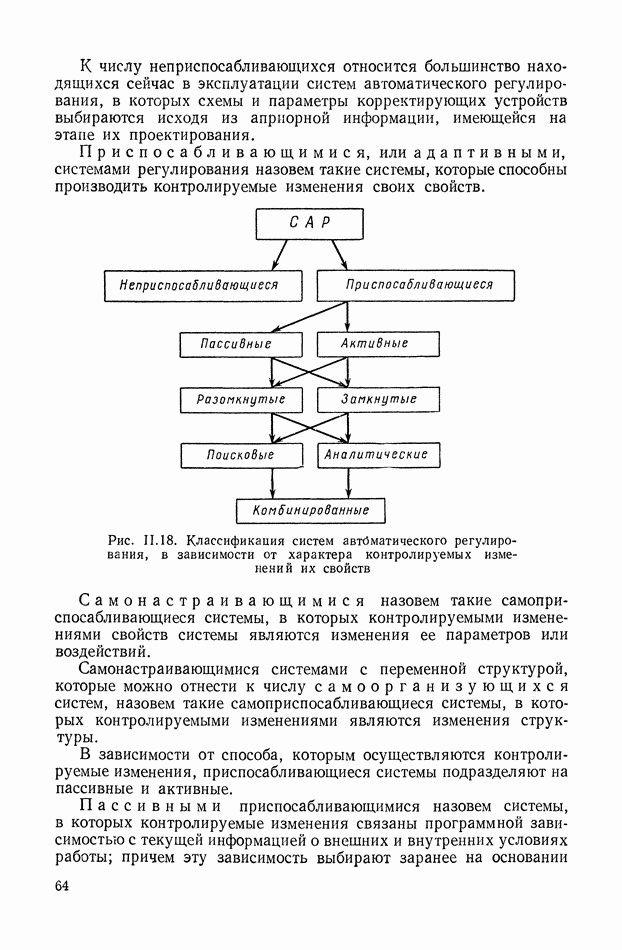
- 9. КЛАССИФИКАЦИЯ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ В ЗАВИСИМОСТИ ОТ ХАРАКТЕРА КОНТРОЛИРУЕМЫХ ИЗМЕНЕНИЙ
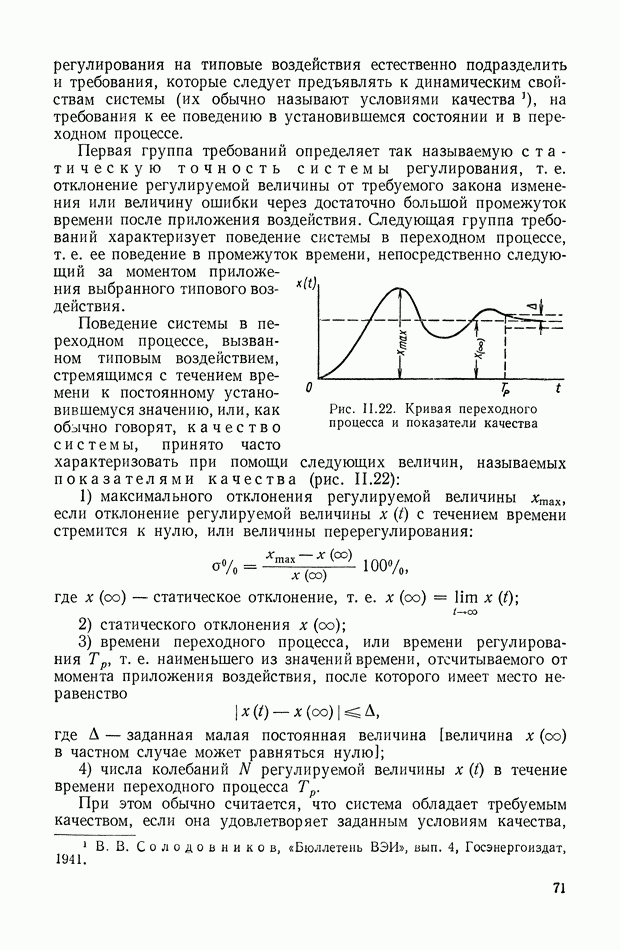
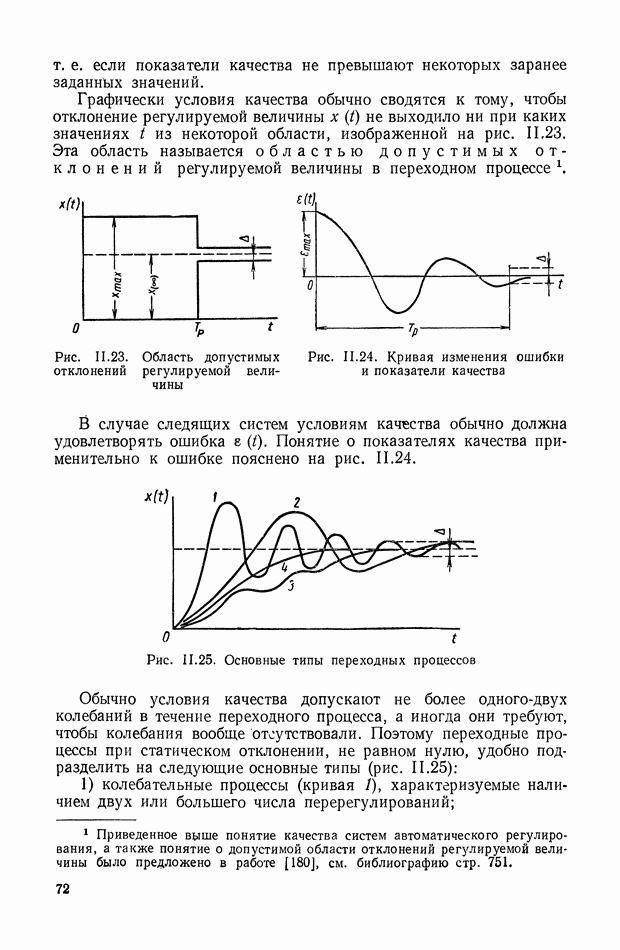
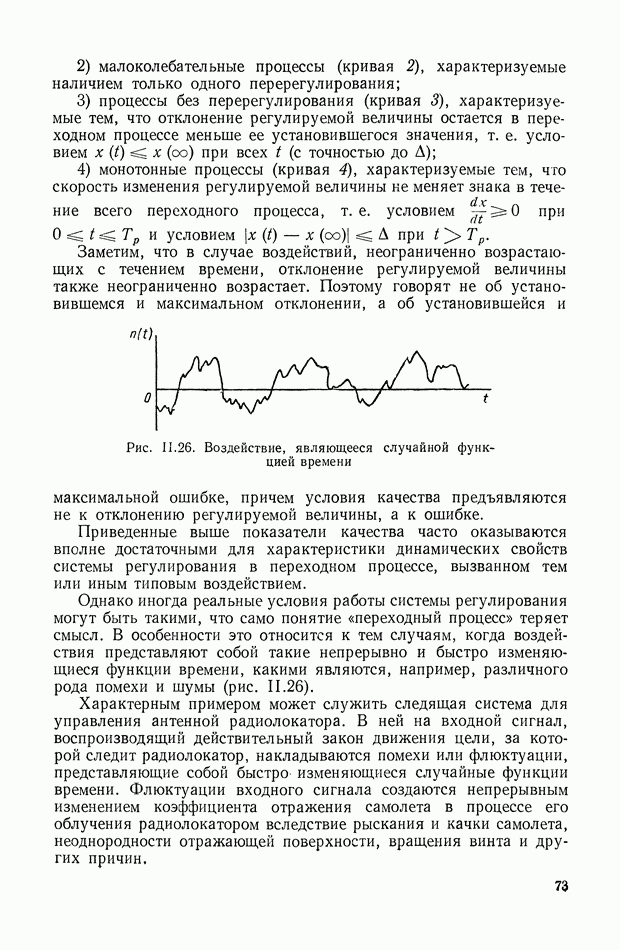
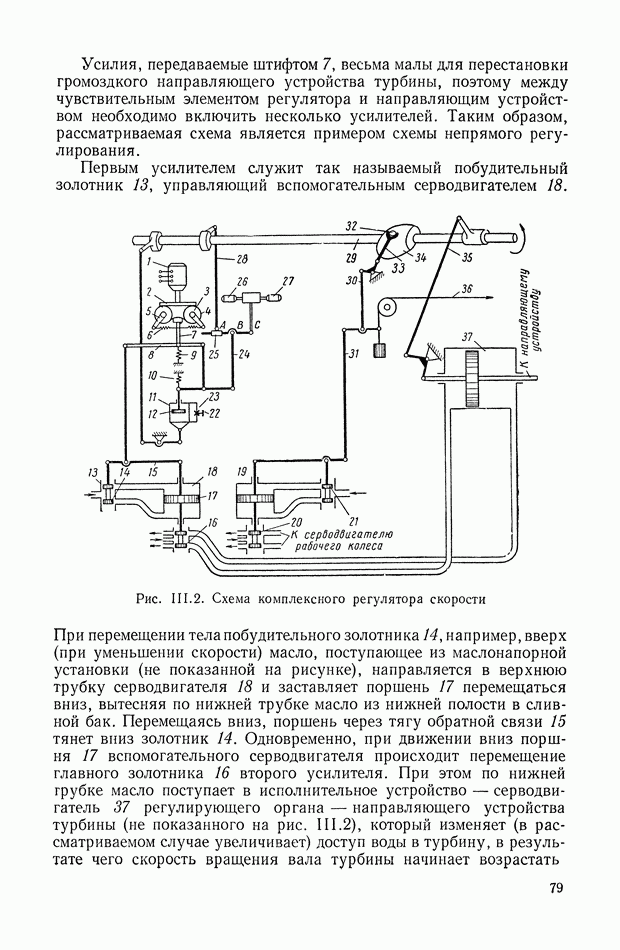
- 10. ТРЕБОВАНИЯ, ПРЕДЪЯВЛЯЕМЫЕ К ДИНАМИЧЕСКИМ СВОЙСТВАМ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- ГЛАВА III. ОСНОВНЫЕ УСТРОЙСТВА И ТИПОВЫЕ СХЕМЫ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. КРАТКАЯ ХАРАКТЕРИСТИКА УСТРОЙСТВ, ИЗ КОТОРЫХ СОСТОЯТ СИСТЕМЫ РЕГУЛИРОВАНИЯ
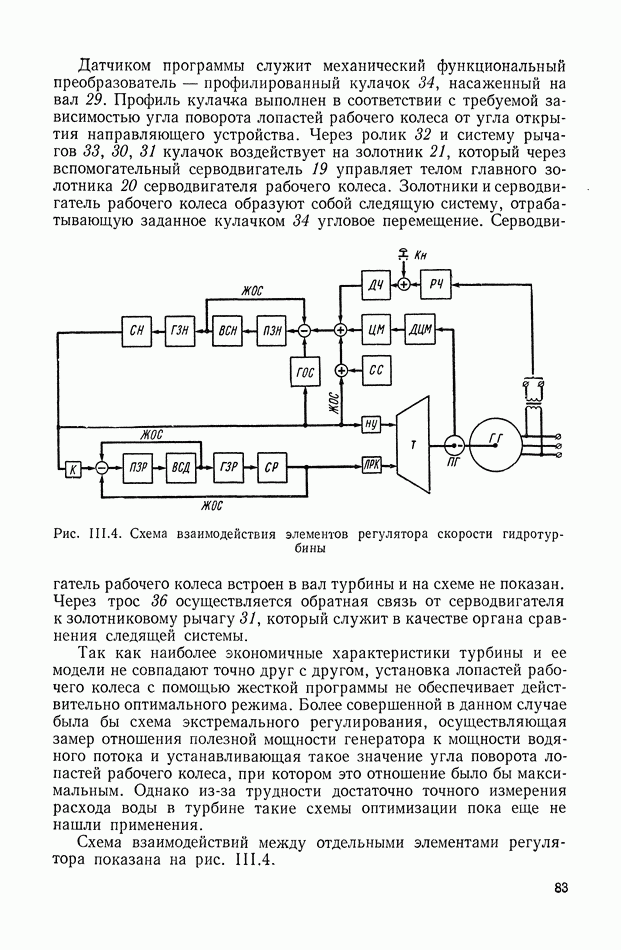
- 2. СИСТЕМА АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ СКОРОСТИ ГИДРОТУРБИНЫ
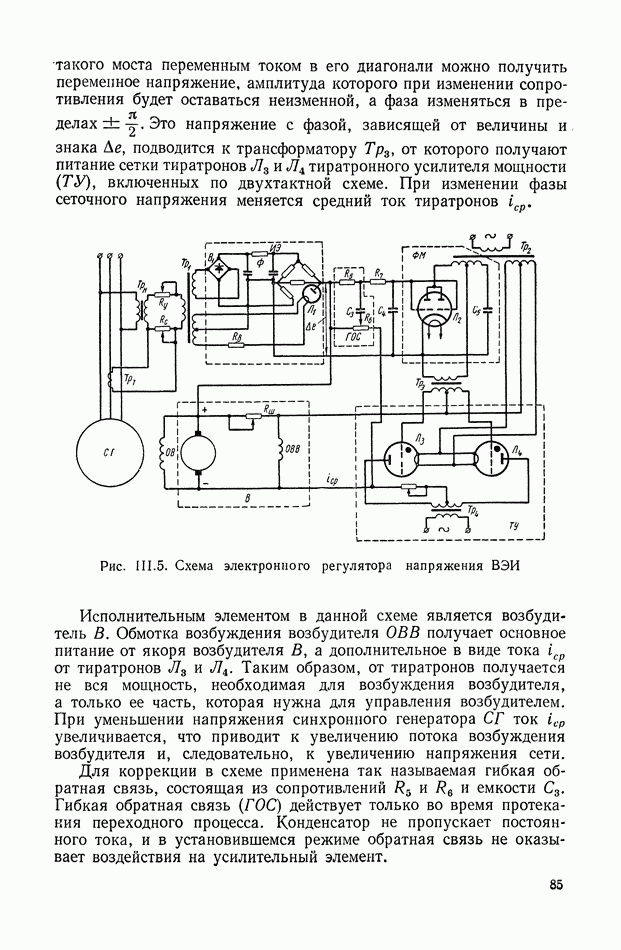
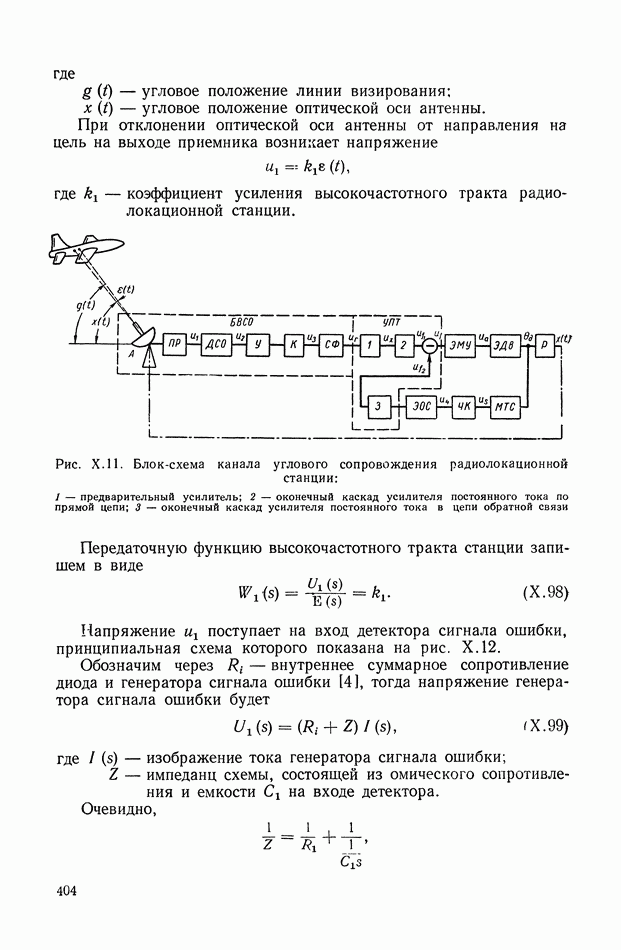
- 3. ЭЛЕКТРОННЫЙ РЕГУЛЯТОР НАПРЯЖЕНИЯ ВЭИ
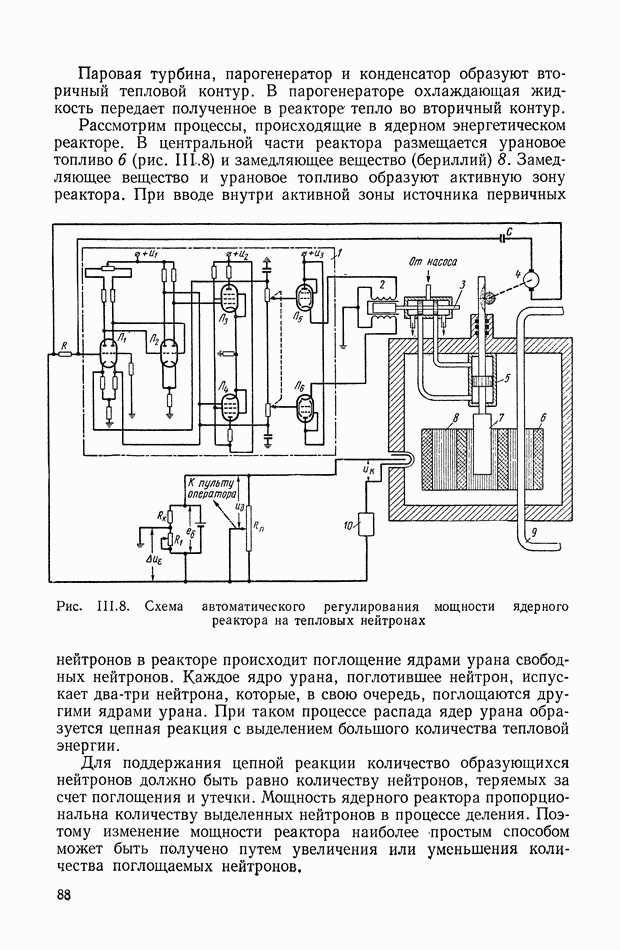
- 4. СИСТЕМА АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ЯДЕРНОГО РЕАКТОРА ПО МОЩНОСТИ
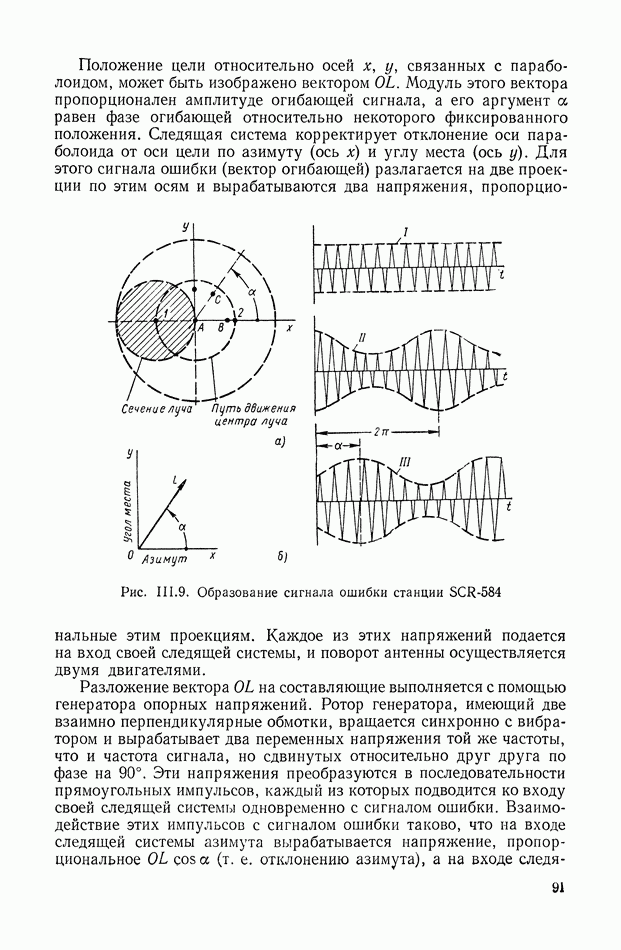
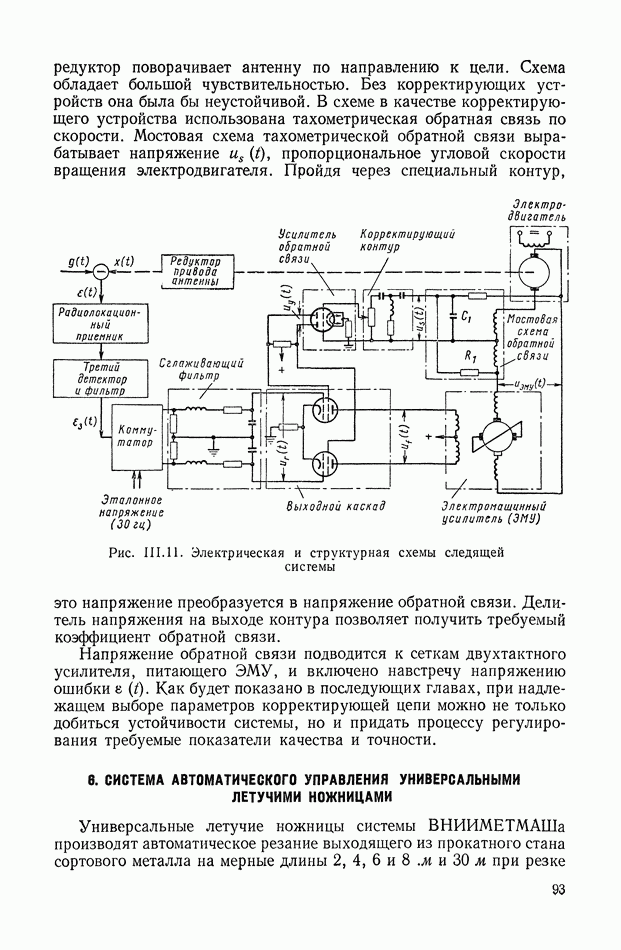
- 5. СЛЕДЯЩАЯ СИСТЕМА РАДИОЛОКАЦИОННОЙ СТАНЦИИ
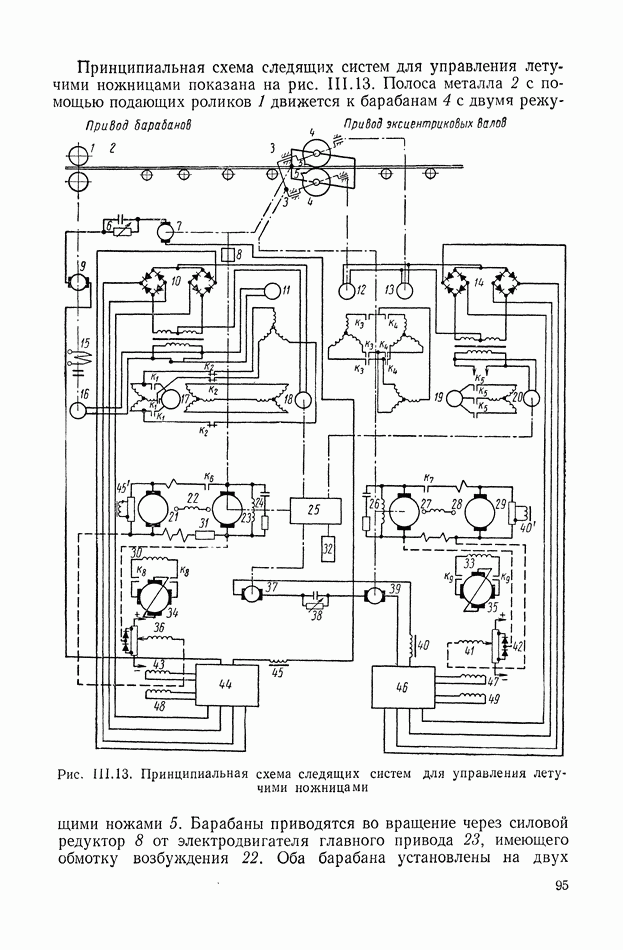
- 6. СИСТЕМА АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ УНИВЕРСАЛЬНЫМИ ЛЕТУЧИМИ НОЖНИЦАМИ
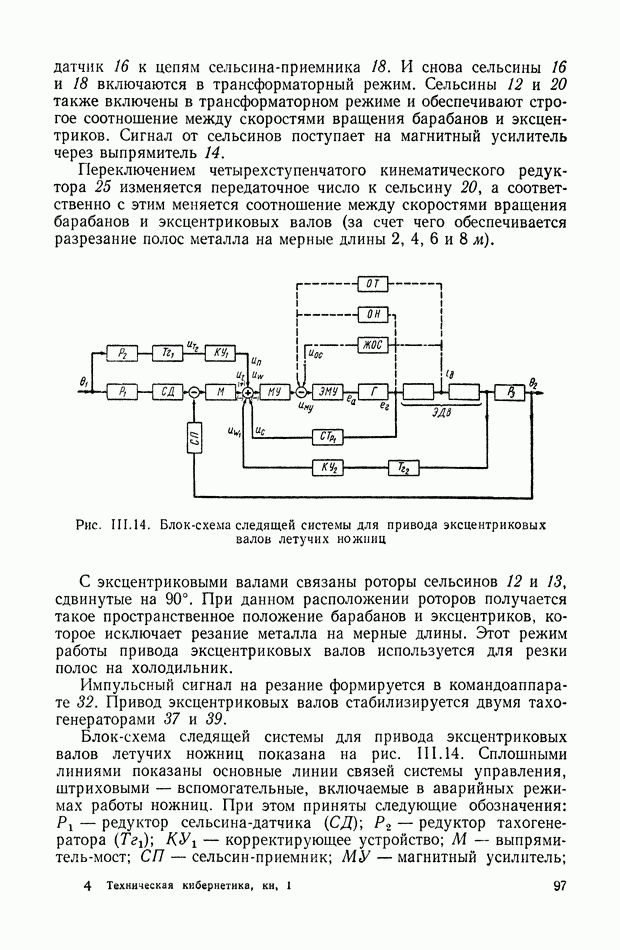
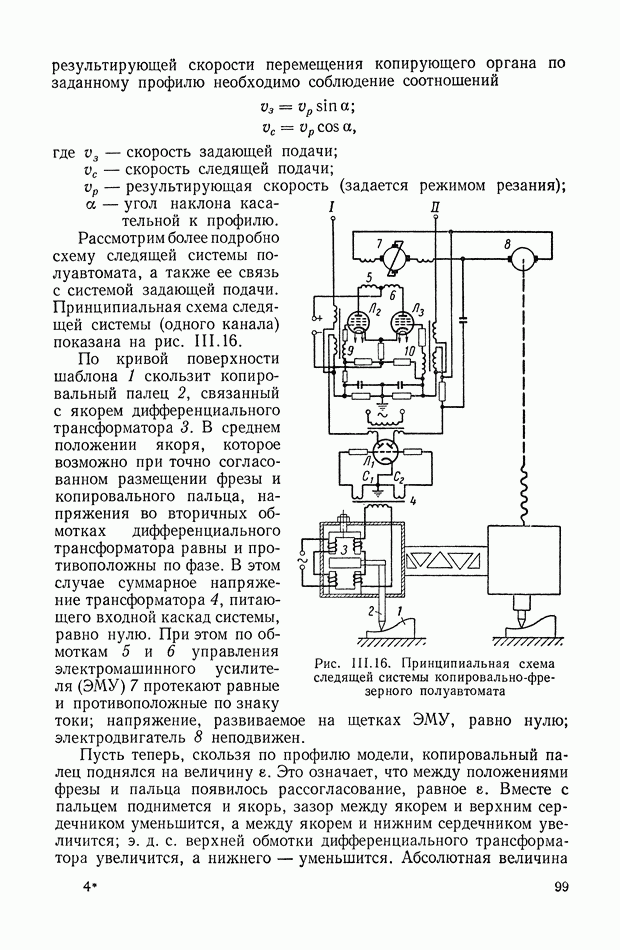
- 7. СЛЕДЯЩАЯ СИСТЕМА КОПИРОВАЛЬНО-ФРЕЗЕРНОГО ПОЛУАВТОМАТА
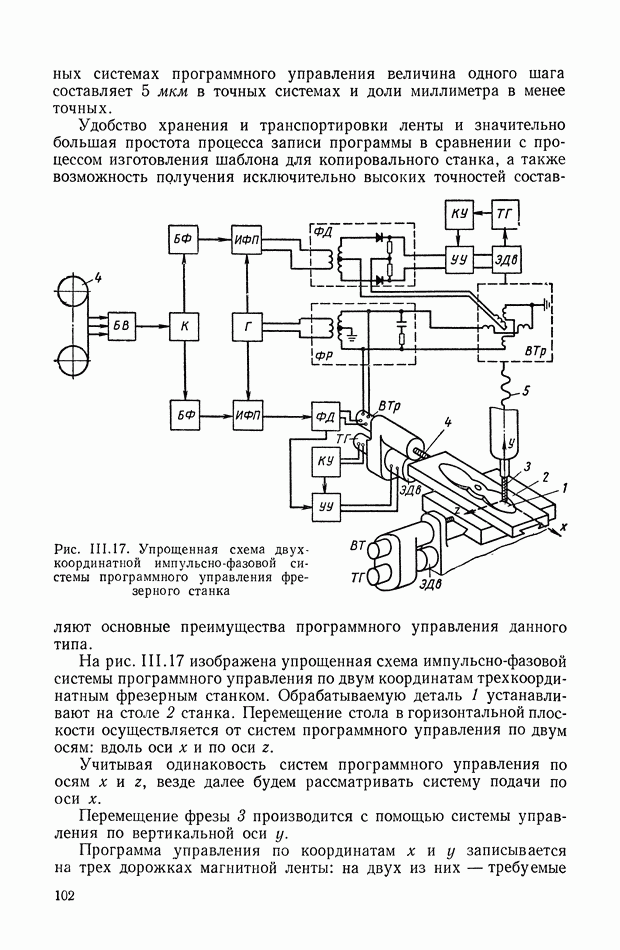
- 8. ПРОГРАММНОЕ УПРАВЛЕНИЕ МЕТАЛЛОРЕЖУЩИМИ СТАНКАМИ
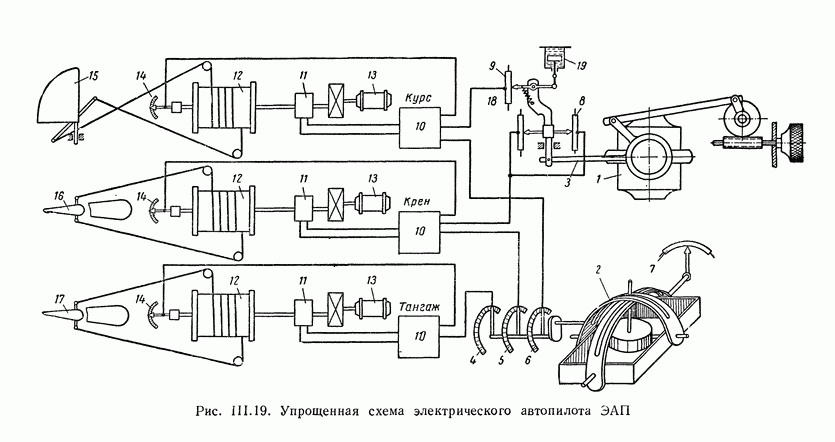
- 9. ПРИНЦИП ДЕЙСТВИЯ ЭЛЕКТРИЧЕСКОГО АВТОПИЛОТА
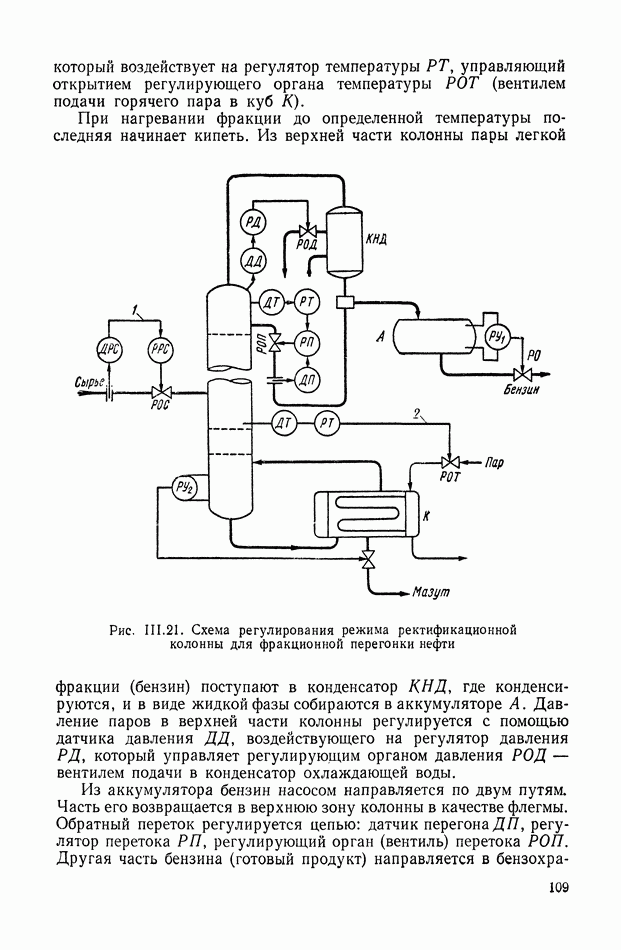
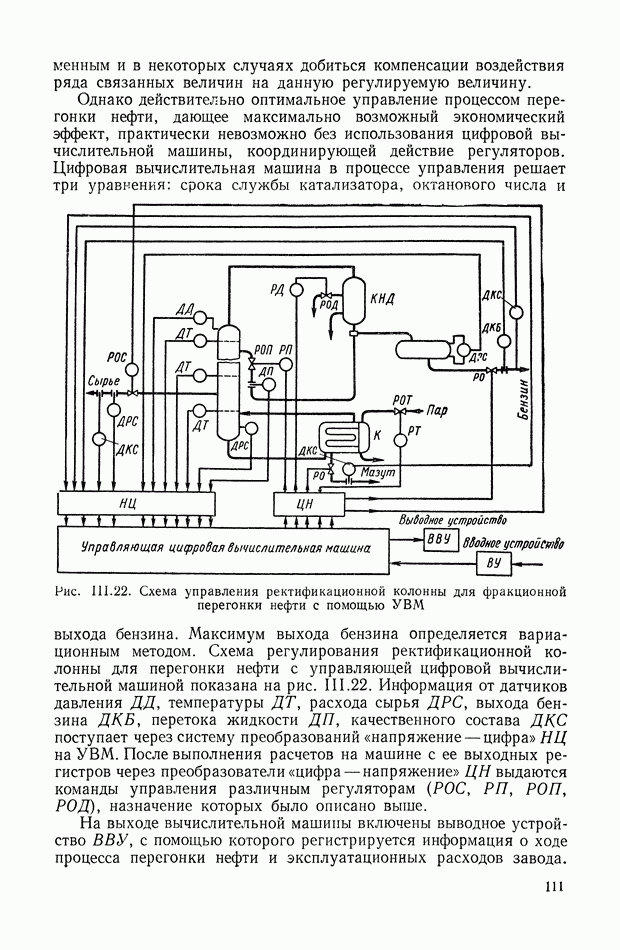
- 10. РЕГУЛИРОВАНИЕ МНОГИХ ВЕЛИЧИН ПРИ АВТОМАТИЧЕСКОМ УПРАВЛЕНИИ ПЕРЕГОНКОЙ НЕФТИ
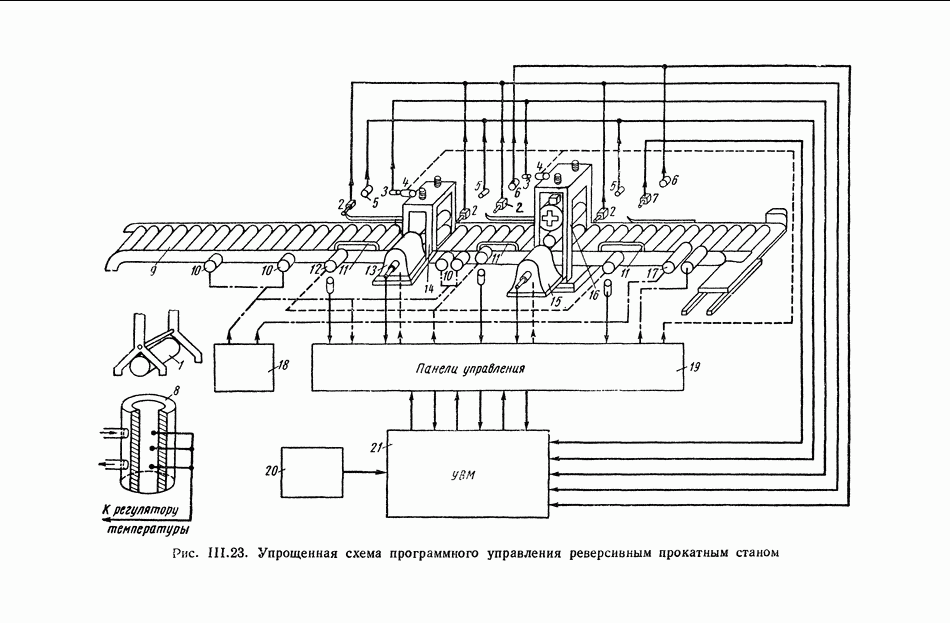
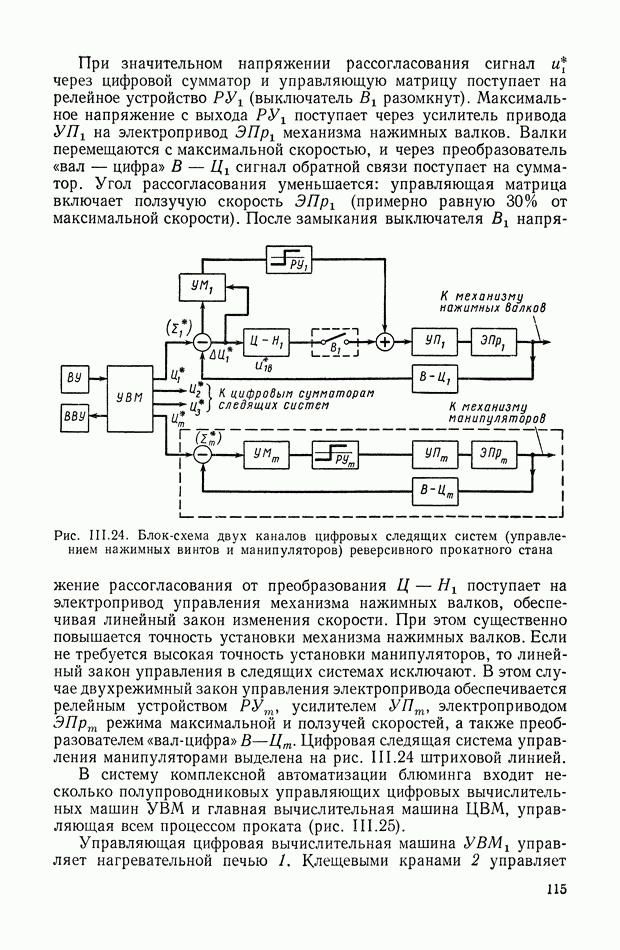
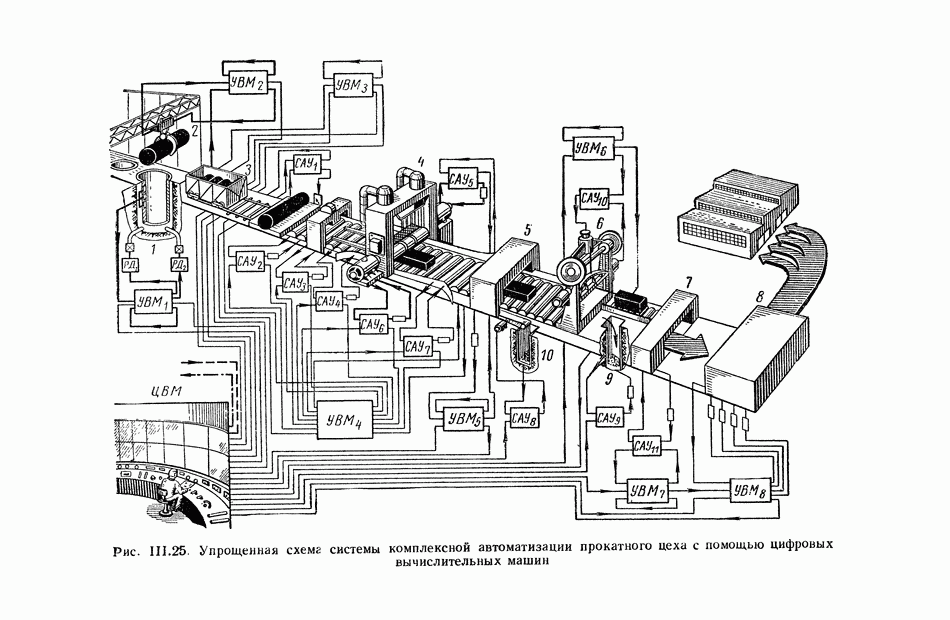
- 11. СИСТЕМА АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ РЕВЕРСИВНЫМ ПРОКАТНЫМ СТАНОМ С ИСПОЛЬЗОВАНИЕМ ЦИФРОВОЙ ВЫЧИСЛИТЕЛЬНОЙ МАШИНЫ
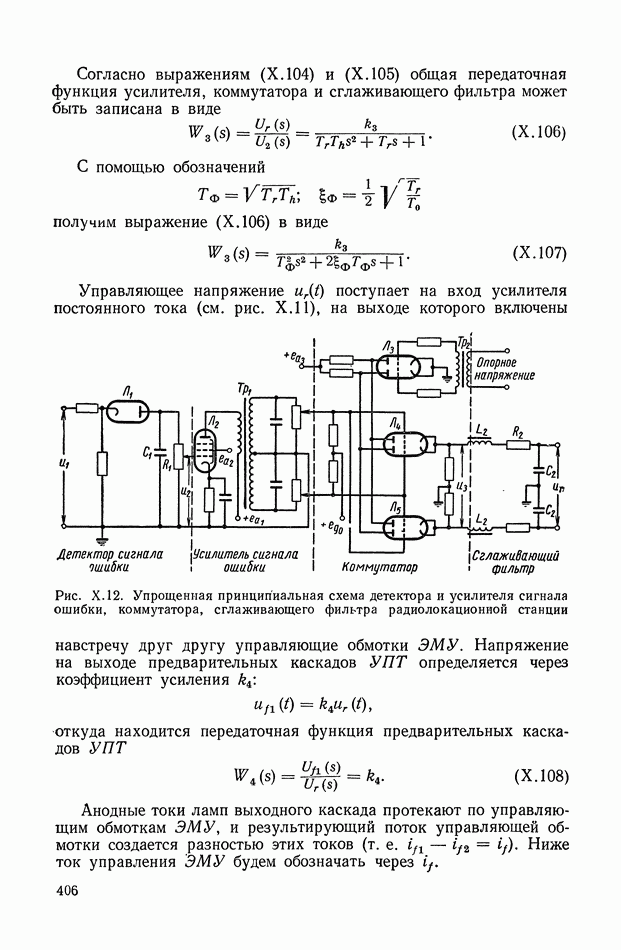
- ГЛАВА IV. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ЛАГРАНЖА ВТОРОГО РОДА
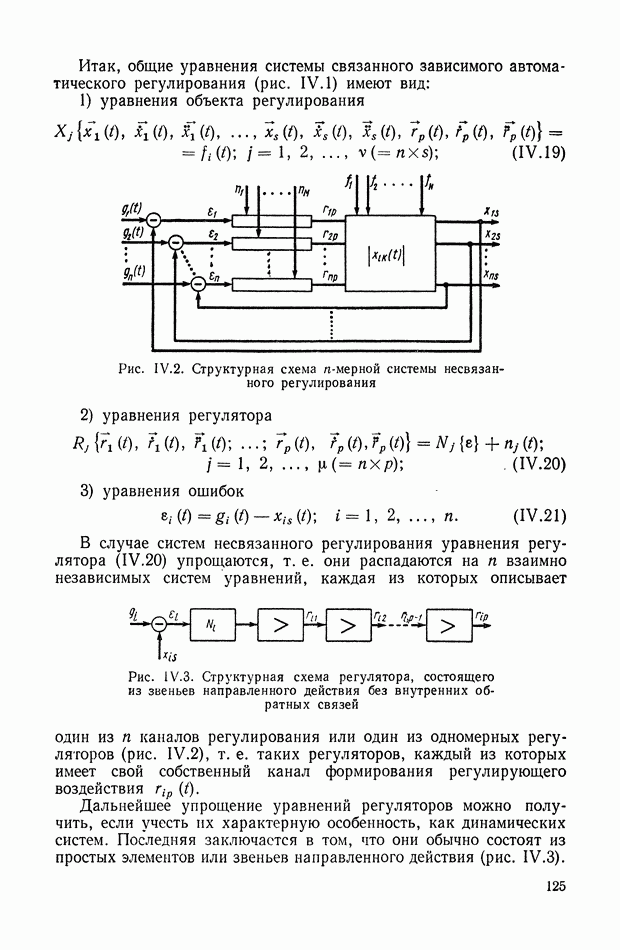
- 2. ОБЩИЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
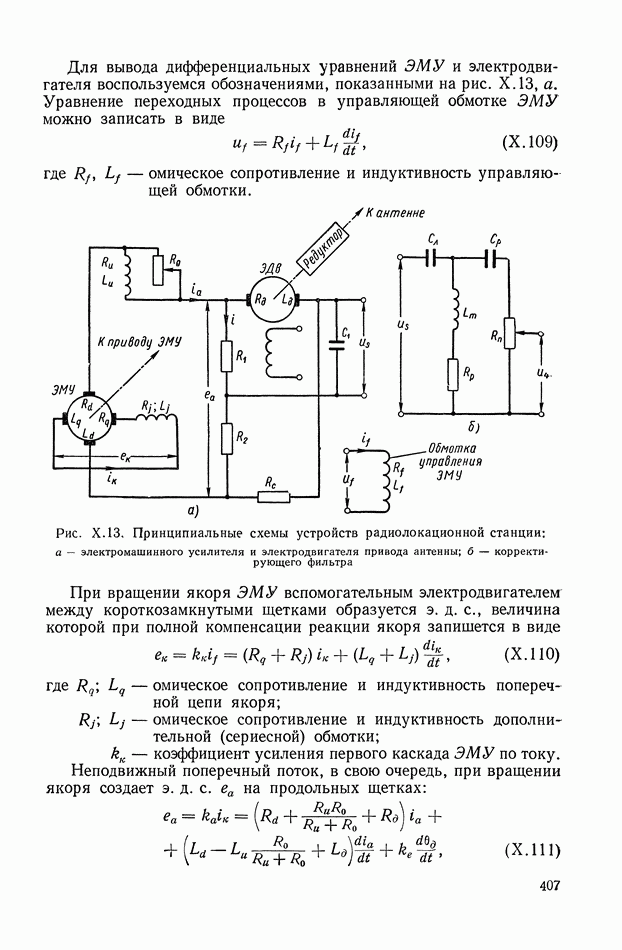
- 3. ОБЩИЕ ЛИНЕАРИЗОВАННЫЕ УРАВНЕНИЯ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 4. ПРИМЕР СОСТАВЛЕНИЯ УРАВНЕНИЯ ОБЪЕКТА РЕГУЛИРОВАНИЯ
- ГЛАВА V. СТАТИКА СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. СТАТИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПРОСТЕЙШИХ ЗВЕНЬЕВ
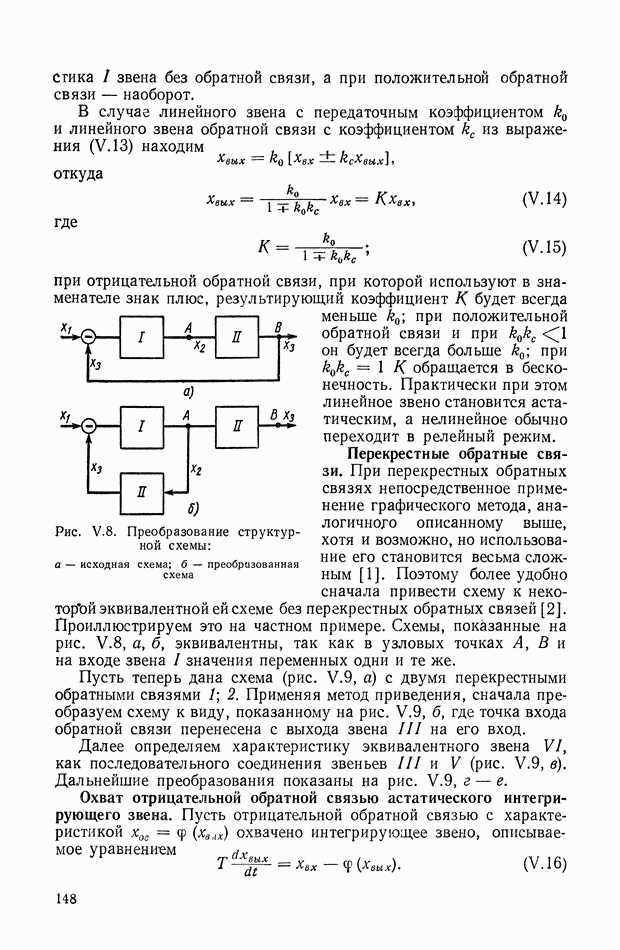
- 2. СТАТИЧЕСКИЕ ХАРАКТЕРИСТИКИ ОСНОВНЫХ ТИПОВ СОЕДИНЕНИЙ ЗВЕНЬЕВ
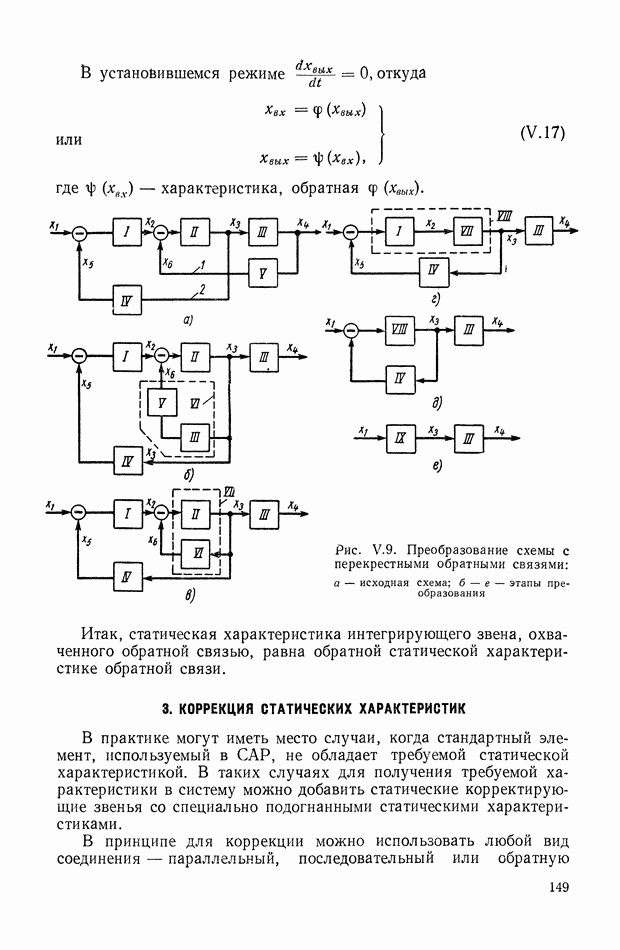
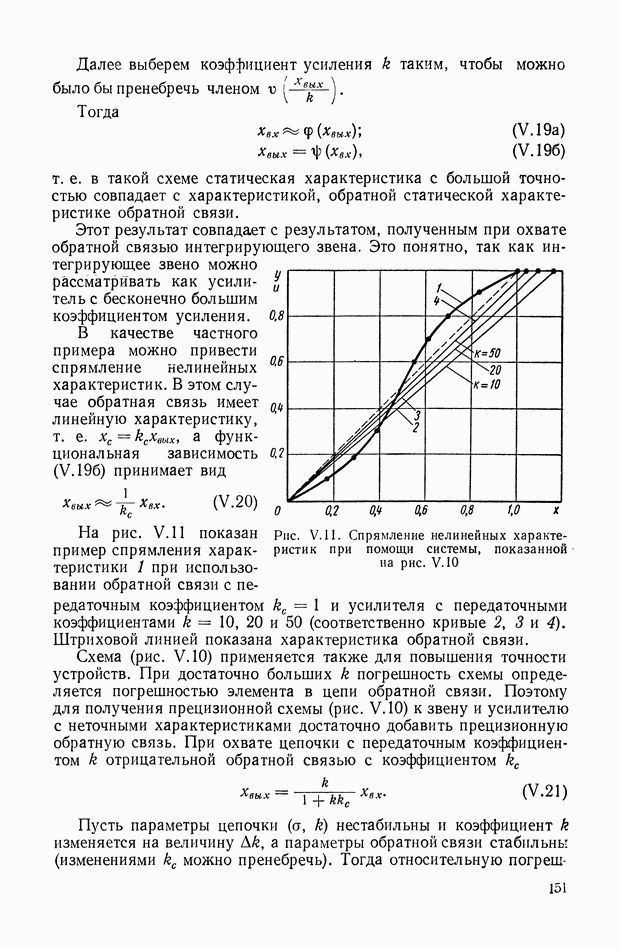
- 3. КОРРЕКЦИЯ СТАТИЧЕСКИХ ХАРАКТЕРИСТИК
- Статическая характеристика замкнутой одномерной системы регулирования.
- Статическая характеристика линейной замкнутой системы.
- 4. СТАТИЗМ РЕГУЛИРОВАНИЯ
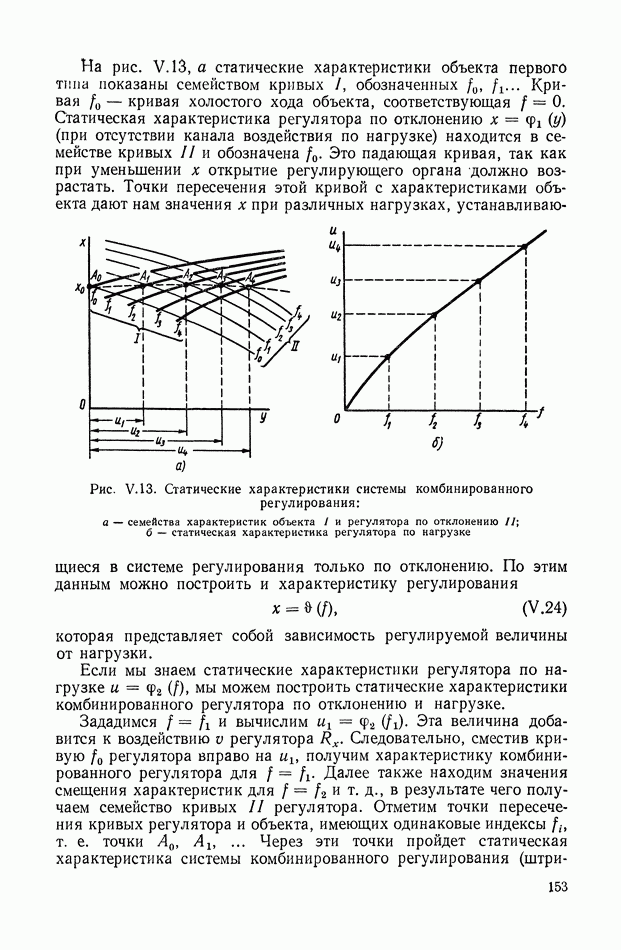
- 5. СТАТИКА ЛИНЕЙНЫХ СИСТЕМ С НЕСКОЛЬКИМИ РЕГУЛИРУЕМЫМИ ВЕЛИЧИНАМИ
- ГЛАВА VI. ТИПИЧНЫЕ НЕЛИНЕЙНЫЕ СТАТИЧЕСКИЕ ХАРАКТЕРИСТИКИ ТИПОВЫХ ЗВЕНЬЕВ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
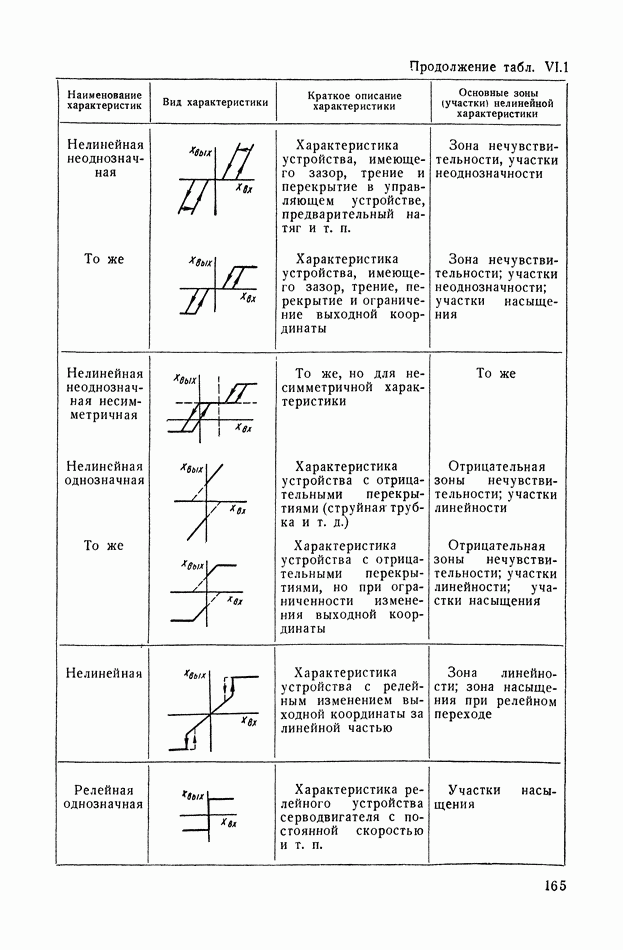
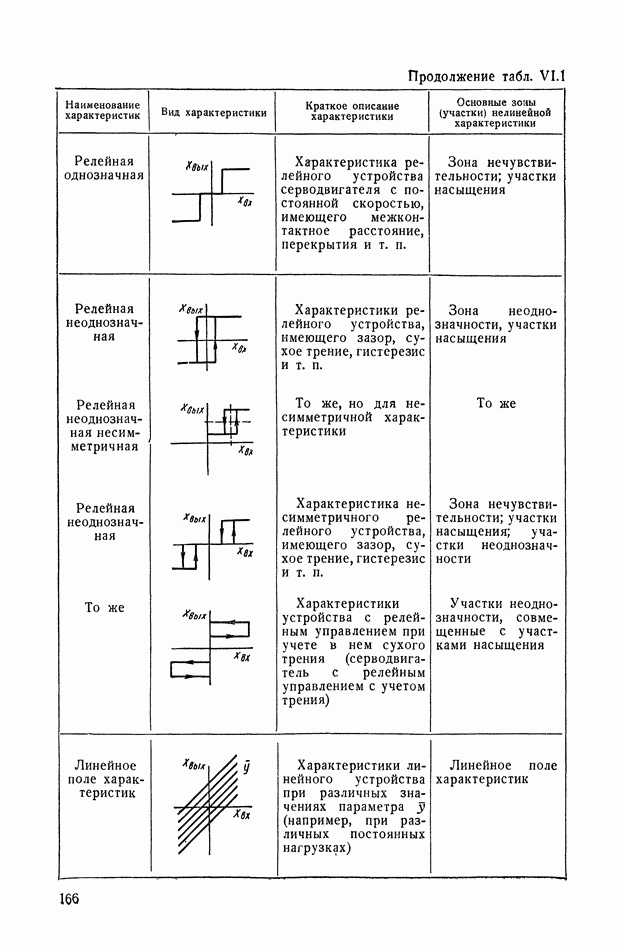
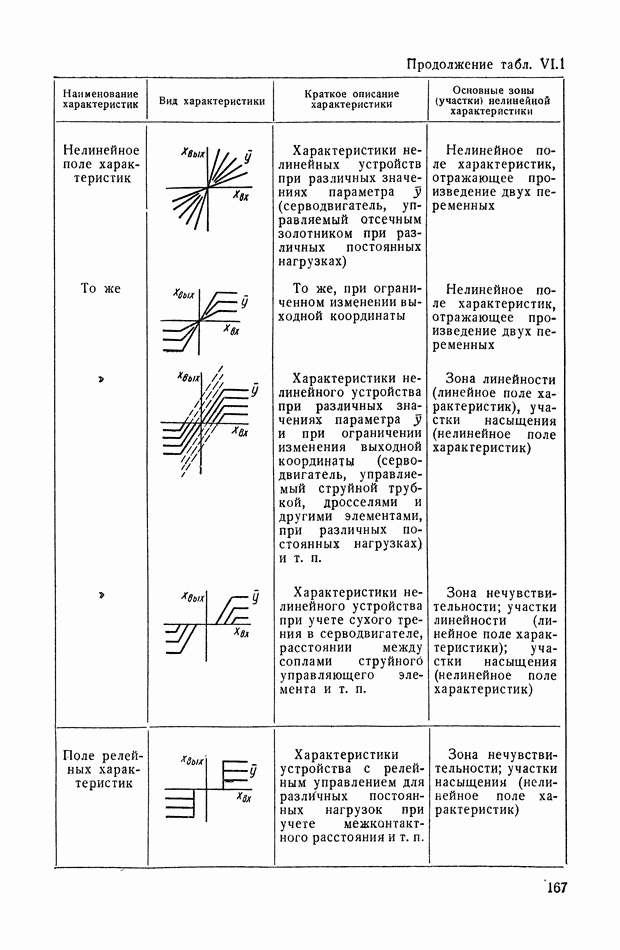
- 1. НЕЛИНЕЙНЫЕ ХАРАКТЕРИСТИКИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
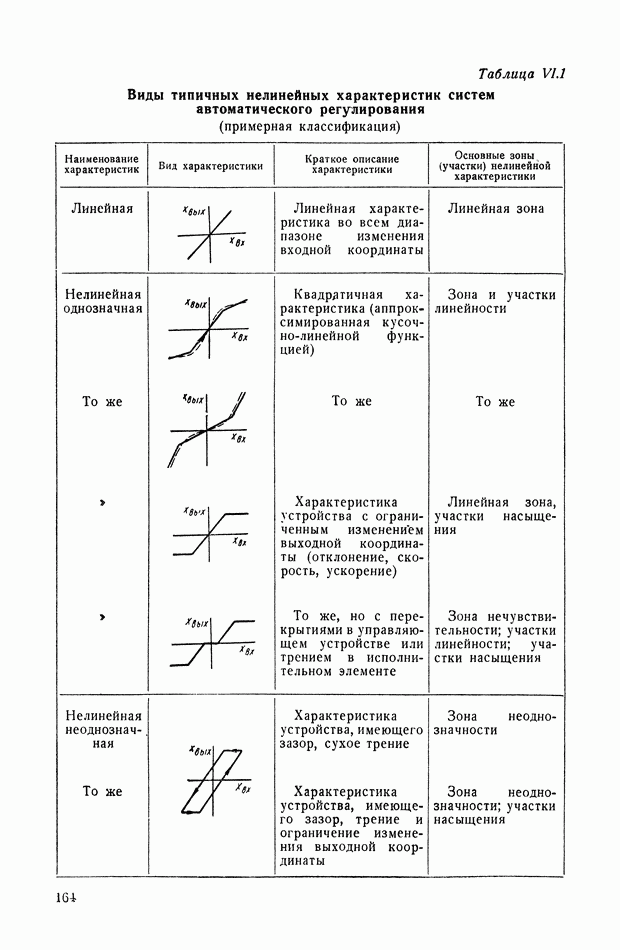
- 2. ВИДЫ ТИПИЧНЫХ НЕЛИНЕЙНЫХ СТАТИЧЕСКИХ ХАРАКТЕРИСТИК СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 3. ТИПИЧНЫЕ НЕЛИНЕЙНЫЕ ХАРАКТЕРИСТИКИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
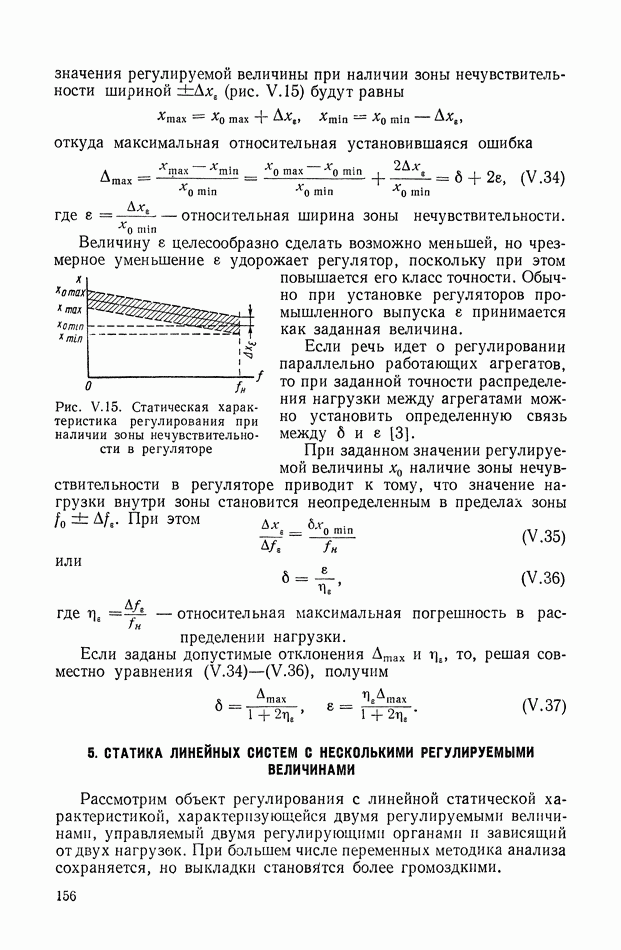
- 4. ЗОНЫ НЕЧУВСТВИТЕЛЬНОСТИ
- 5. ЗОНЫ ЛИНЕЙНОСТИ И НЕОДНОЗНАЧНОСТИ
- 6. ЗОНЫ НАСЫЩЕНИЯ
- 7. ПОЛЕ КРИВЫХ, ПРЕДСТАВЛЯЮЩИХ ХАРАКТЕРИСТИКУ СЕРВОДВИГАТЕЛЯ
- 8. ЭКСПЕРИМЕНТАЛЬНОЕ ВЫЯВЛЕНИЕ НЕЛИНЕЙНОСТИ ХАРАКТЕРИСТИК СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
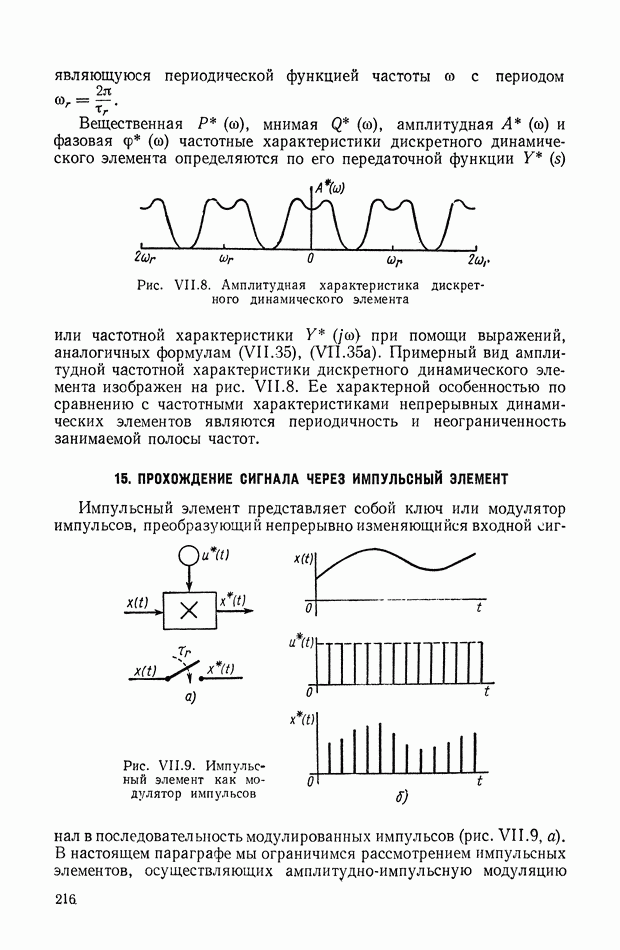
- ГЛАВА VII. ПЕРЕХОДНЫЕ ФУНКЦИИ, ПЕРЕДАТОЧНЫЕ ФУНКЦИИ И ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ДИНАМИЧЕСКИХ ЭЛЕМЕНТОВ
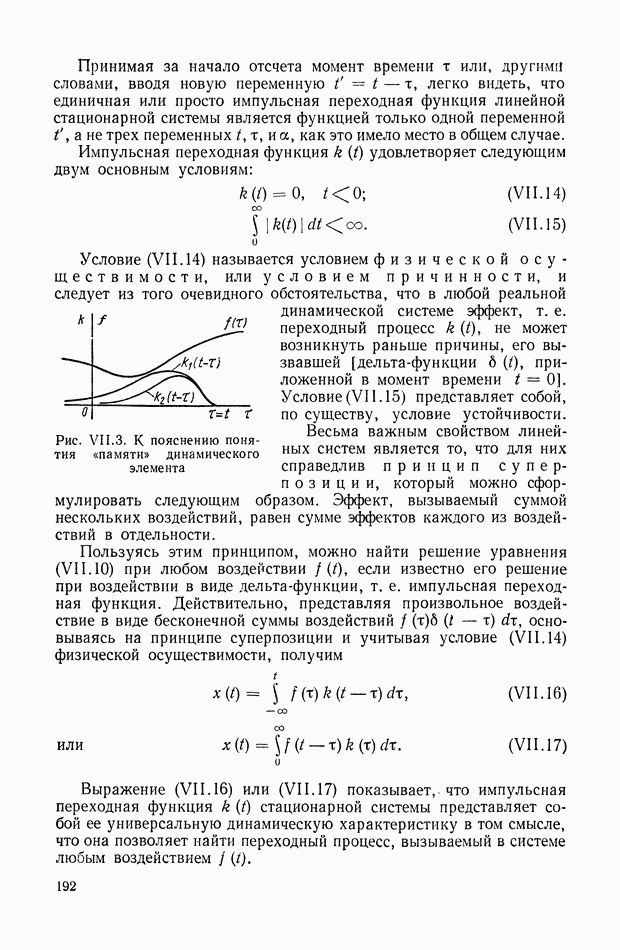
- 1. КЛАССИФИКАЦИЯ ДИНАМИЧЕСКИХ ЭЛЕМЕНТОВ
- 2. ОБЩЕЕ ОПРЕДЕЛЕНИЕ ИМПУЛЬСНОЙ ПЕРЕХОДНОЙ И ПЕРЕДАТОЧНОЙ ФУНКЦИЙ ДИНАМИЧЕСКОЙ СИСТЕМЫ ИЛИ ДИНАМИЧЕСКОГО ЭЛЕМЕНТА
- 3. ИМПУЛЬСНАЯ ПЕРЕХОДНАЯ ФУНКЦИЯ НЕПРЕРЫВНОЙ СТАЦИОНАРНОЙ ЛИНЕЙНОЙ СИСТЕМЫ
- 4. ПЕРЕДАТОЧНАЯ ФУНКЦИЯ НЕПРЕРЫВНОЙ ЛИНЕЙНОЙ СТАЦИОНАРНОЙ СИСТЕМЫ
- 5. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЛИНЕЙНОЙ СТАЦИОНАРНОЙ НЕПРЕРЫВНОЙ ДИНАМИЧЕСКОЙ СИСТЕМЫ
- 6. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДИНАМИЧЕСКОГО ЭЛЕМЕНТА С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
- 7. ПРИМЕНЕНИЕ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА К РЕШЕНИЮ УРАВНЕНИЙ ЭЛЕМЕНТА С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
- 8. ПЕРЕДАТОЧНАЯ ФУНКЦИЯ ДИНАМИЧЕСКОГО ЭЛЕМЕНТА С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
- 9. ПЕРЕДАТОЧНАЯ ФУНКЦИЯ ПОСЛЕДОВАТЕЛЬНОГО СОЕДИНЕНИЯ ДИНАМИЧЕСКИХ ЭЛЕМЕНТОВ С СОСРЕДОТОЧЕННЫМИ И С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
- 10. ПЕРЕДАТОЧНАЯ ФУНКЦИЯ ЗАПАЗДЫВАЮЩЕГО ЭЛЕМЕНТА
- 11. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЭЛЕМЕНТА С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
- 12. ИМПУЛЬСНАЯ ПЕРЕХОДНАЯ ФУНКЦИЯ ДИНАМИЧЕСКОГО ЭЛЕМЕНТА С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
- 13. ПЕРЕДАТОЧНАЯ ФУНКЦИЯ СИСТЕМЫ С ГАРМОНИЧЕСКОЙ МОДУЛЯЦИЕЙ
- 14 ИМПУЛЬСНАЯ ПЕРЕХОДНАЯ И ПЕРЕДАТОЧНАЯ ФУНКЦИИ ДИСКРЕТНОЙ ЛИНЕЙНОЙ СТАЦИОНАРНОЙ СИСТЕМЫ
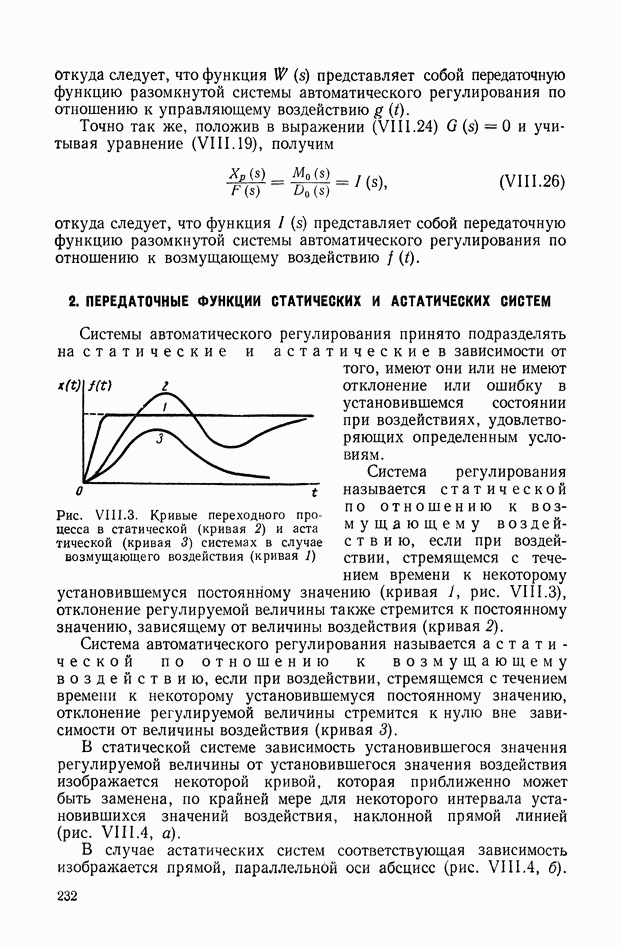
- 15. ПРОХОЖДЕНИЕ СИГНАЛА ЧЕРЕЗ ИМПУЛЬСНЫЙ ЭЛЕМЕНТ
- 16. ПОСЛЕДОВАТЕЛЬНОЕ СОЕДИНЕНИЕ ИМПУЛЬСНОГО ЭЛЕМЕНТА И НЕПРЕРЫВНОГО ДИНАМИЧЕСКОГО ЭЛЕМЕНТА
- 17. ИМПУЛЬСНАЯ ПЕРЕХОДНАЯ ФУНКЦИЯ ЛИНЕЙНОЙ НЕСТАЦИОНАРНОЙ СИСТЕМЫ (СИСТЕМЫ С ПЕРЕМЕННЫМИ ПАРАМЕТРАМИ)
- 18. ПЕРЕДАТОЧНАЯ ФУНКЦИЯ НЕПРЕРЫВНОЙ ЛИНЕЙНОЙ НЕСТАЦИОНАРНОЙ СИСТЕМЫ
- 19. МНОГОМЕРНЫЕ ИМПУЛЬСНЫЕ ПЕРЕХОДНЫЕ И ПЕРЕДАТОЧНЫЕ ФУНКЦИИ НЕЛИНЕЙНЫХ СИСТЕМ
- 20. МНОГОМЕРНЫЕ ПЕРЕДАТОЧНЫЕ ФУНКЦИИ НЕЛИНЕЙНЫХ СИСТЕМ
- ГЛАВА VIII. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ, ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ И ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ НЕПРЕРЫВНЫХ ЛИНЕЙНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
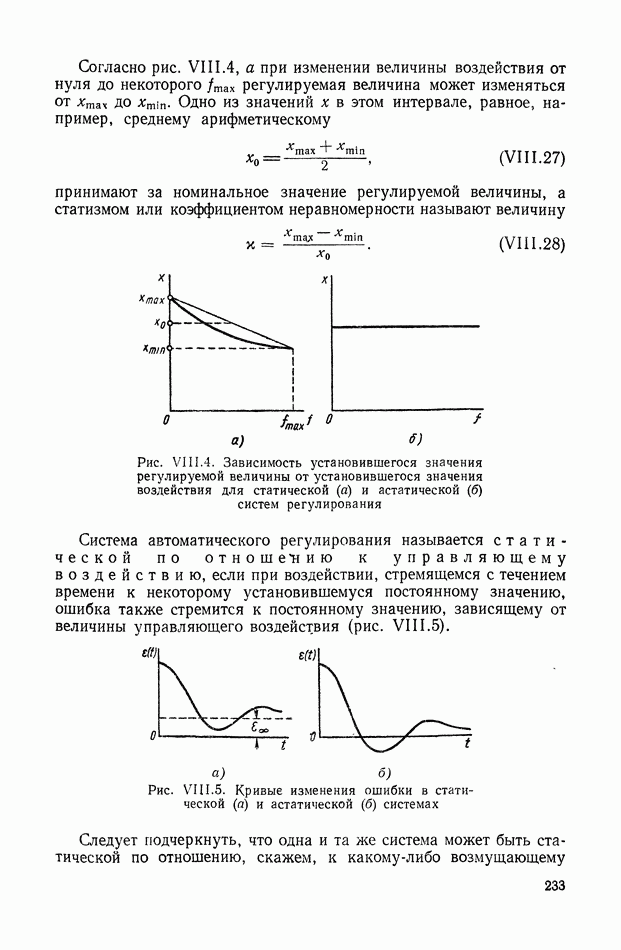
- 2. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ СТАТИЧЕСКИХ И АСТАТИЧЕСКИХ СИСТЕМ
- 3. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ
- 4. ВЗАИМНАЯ СВЯЗЬ МЕЖДУ ЧАСТОТНЫМИ ХАРАКТЕРИСТИКАМИ ЗАМКНУТОЙ И РАЗОМКНУТОЙ СИСТЕМЫ
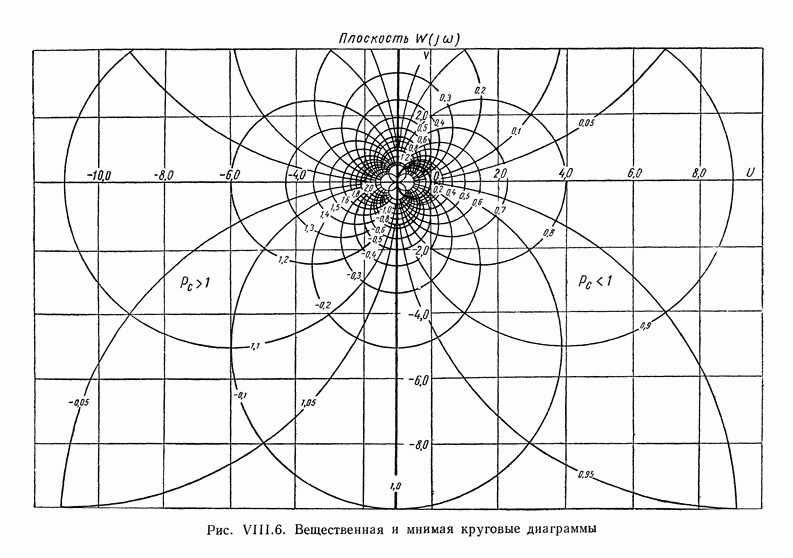
- 5. КРУГОВЫЕ ДИАГРАММЫ
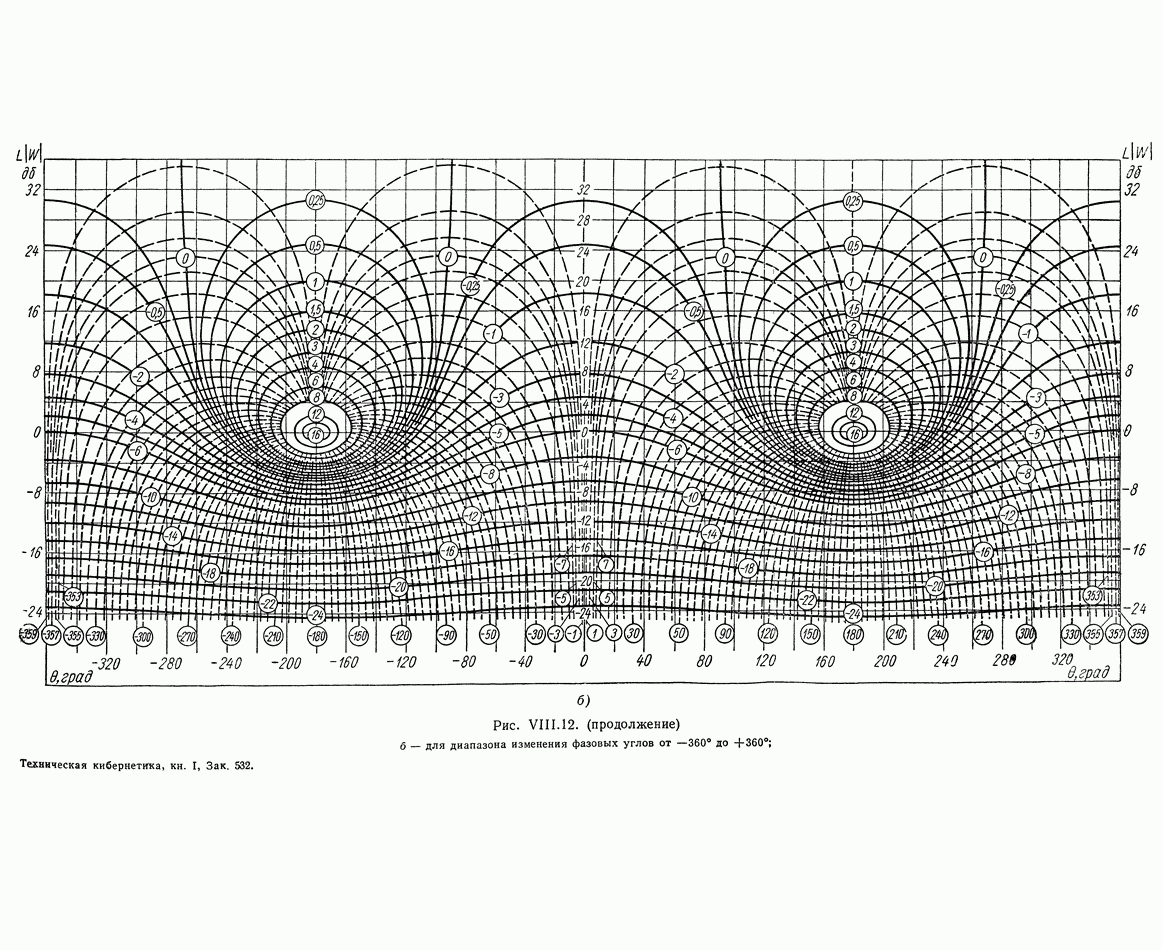
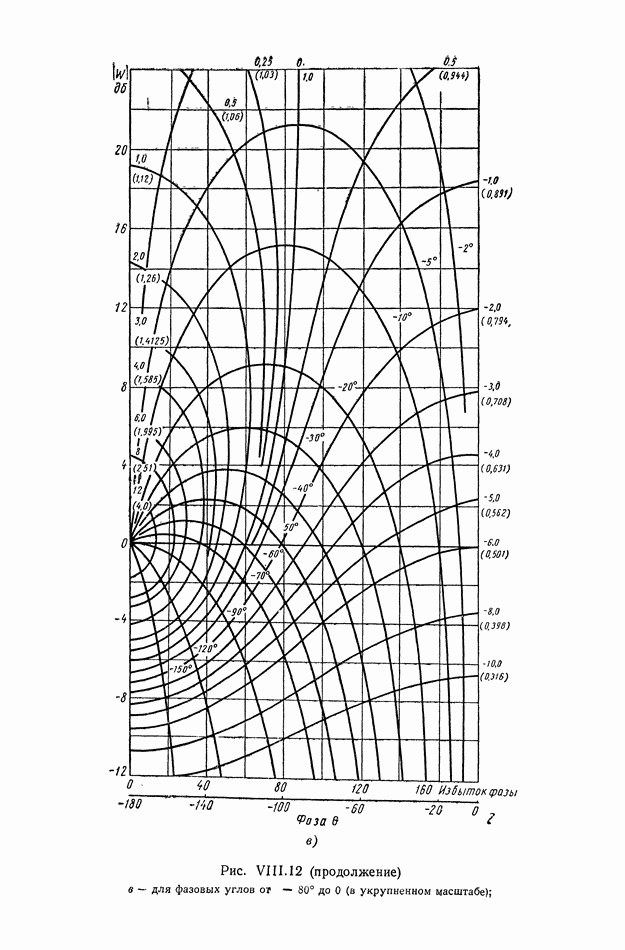
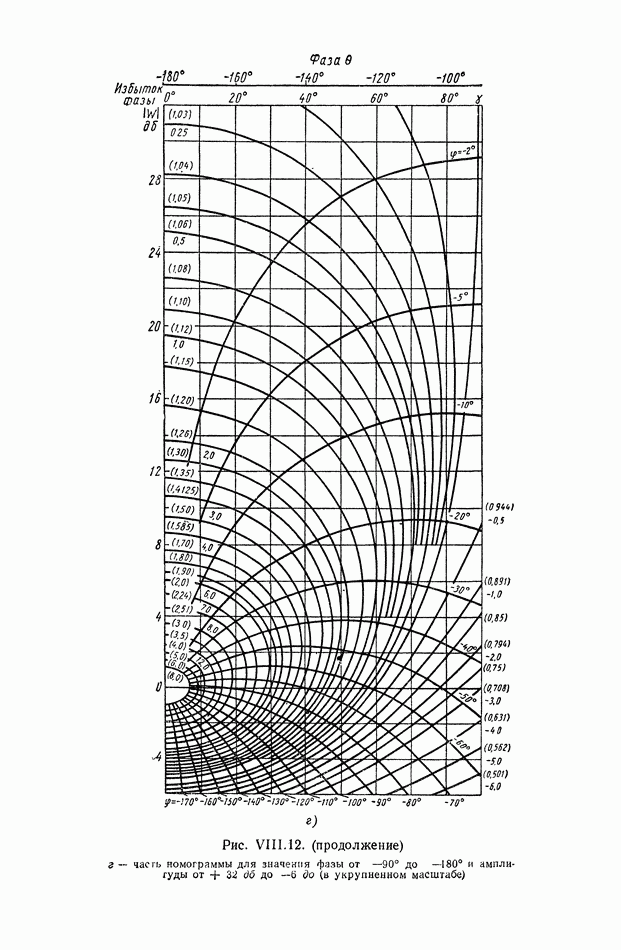
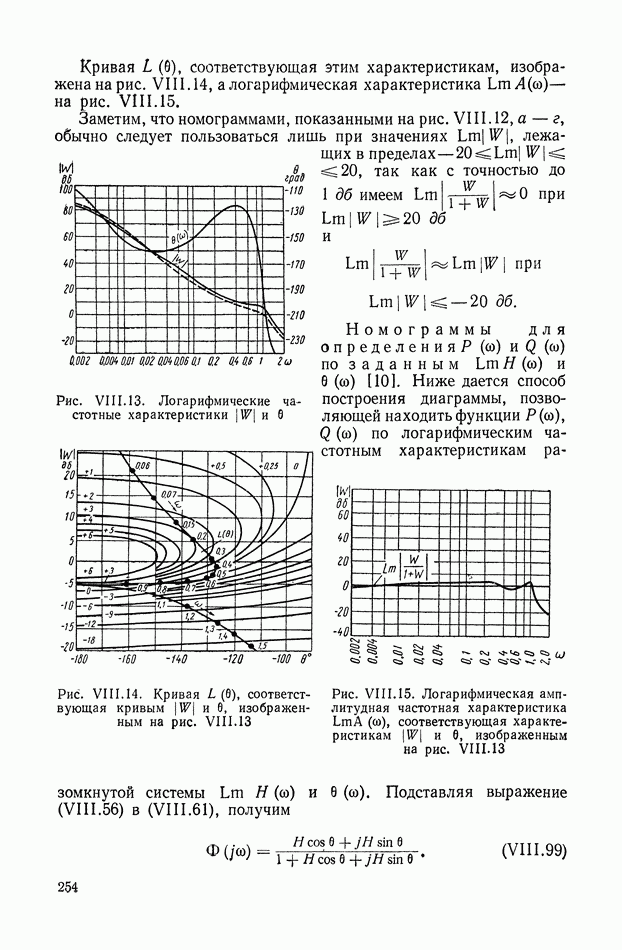
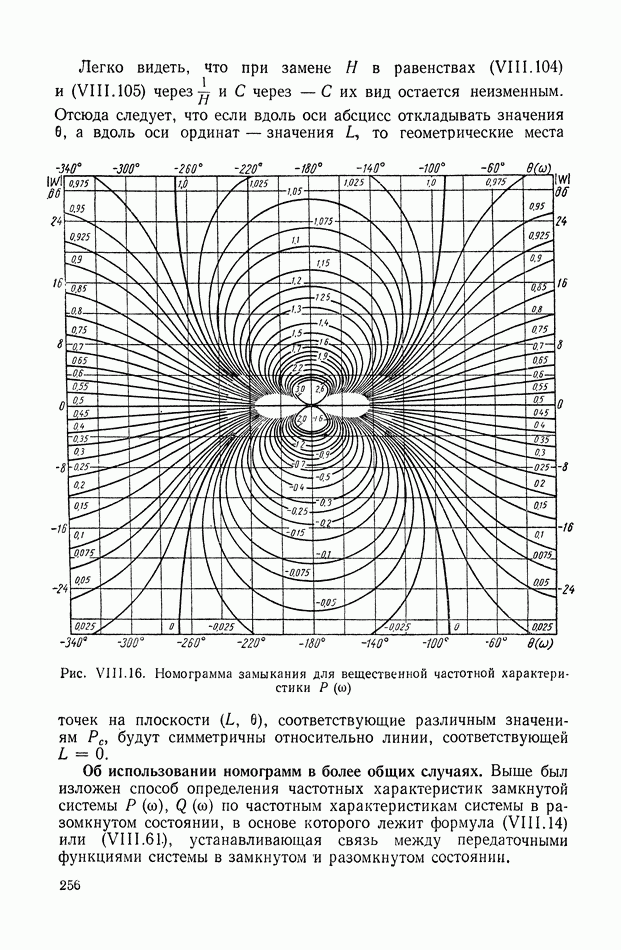
- 6. НОМОГРАММЫ ЗАМЫКАНИЯ
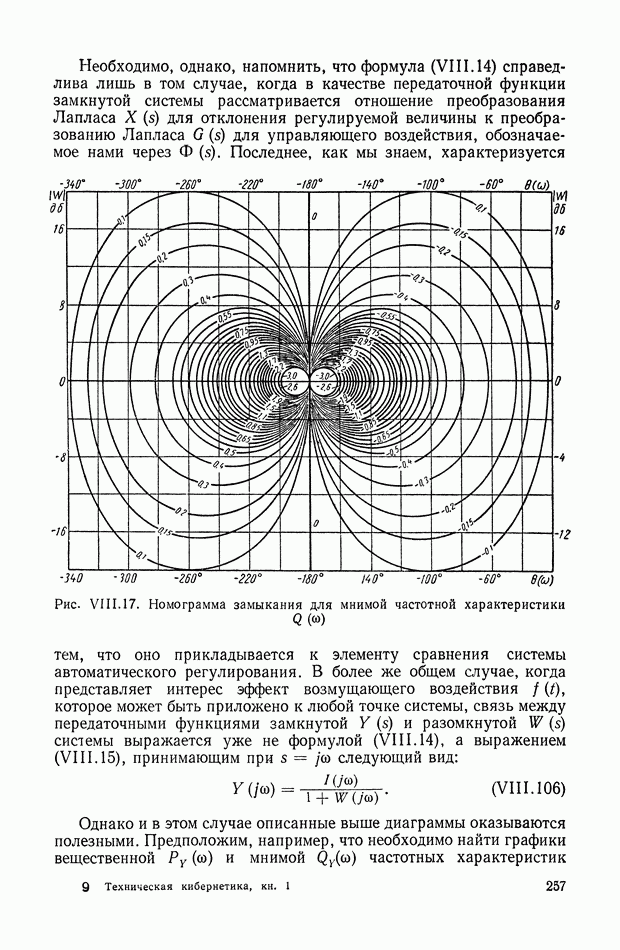
- 7. УСЛОВИЯ ОДНОЗНАЧНОЙ связи МЕЖДУ ЧАСТОТНЫМИ ХАРАКТЕРИСТИКАМИ
- 8. ОПРЕДЕЛЕНИЕ ПЕРЕДАТОЧНОЙ ФУНКЦИИ ПО ОДНОЙ ИЗ ЧАСТОТНЫХ ХАРАКТЕРИСТИК, ЗАДАННОЙ АНАЛИТИЧЕСКИ
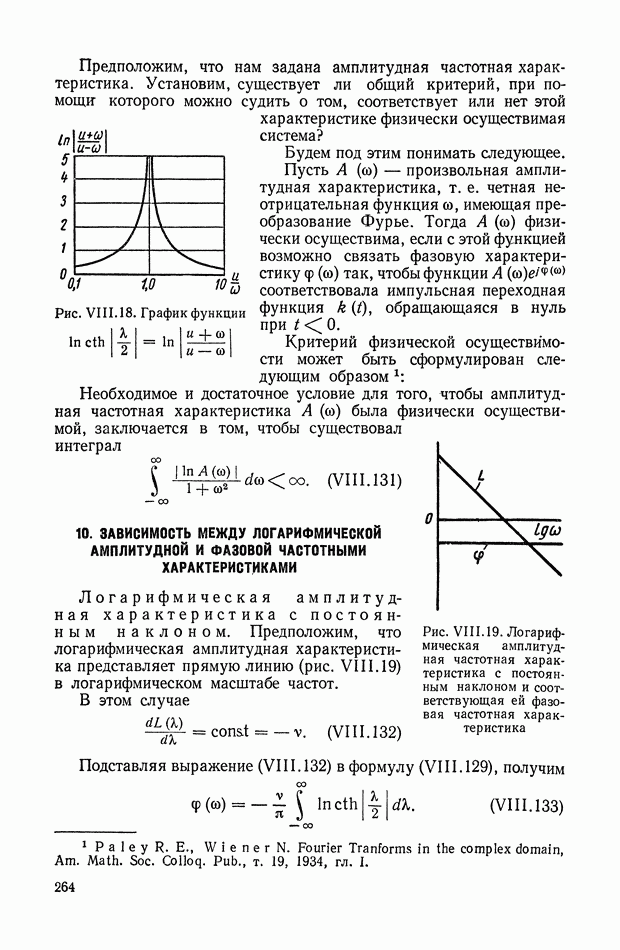
- 9. ФОРМУЛА ДЛЯ ВЫЧИСЛЕНИЯ ФАЗОВОЙ ЧАСТОТНОЙ ХАРАКТЕРИСТИКИ ПО ЗАДАННОЙ АМПЛИТУДНОЙ ЧАСТОТНОЙ ХАРАКТЕРИСТИКЕ
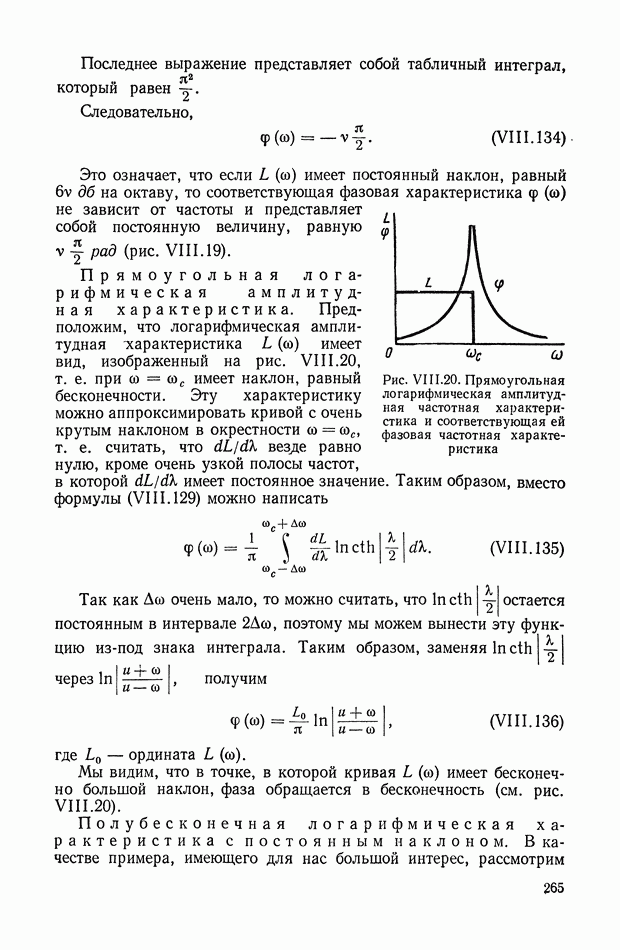
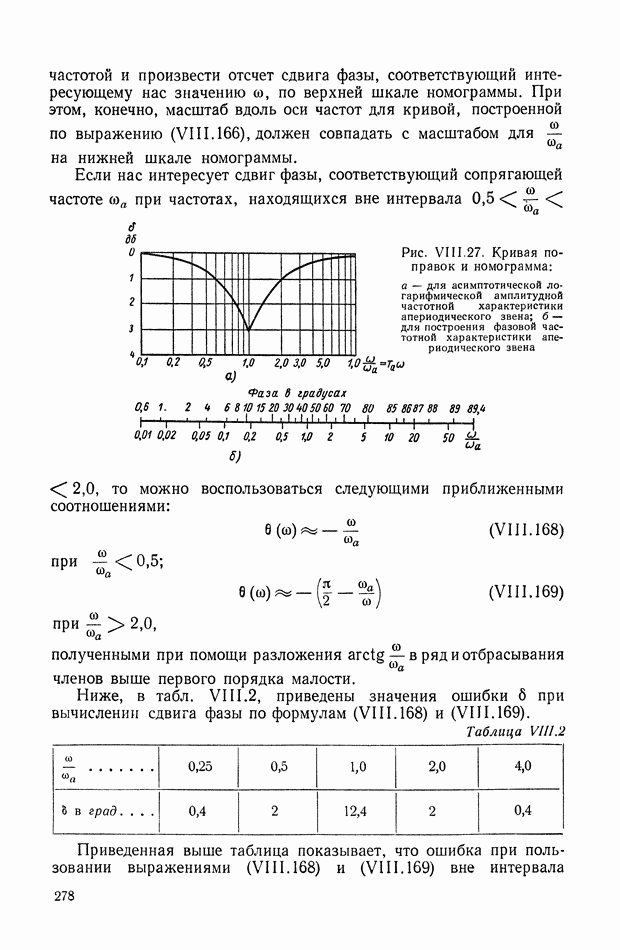
- 10. ЗАВИСИМОСТЬ МЕЖДУ ЛОГАРИФМИЧЕСКОЙ АМПЛИТУДНОЙ И ФАЗОВОЙ ЧАСТОТНЫМИ ХАРАКТЕРИСТИКАМИ
- 11. ГРАФИЧЕСКИЙ МЕТОД ОПРЕДЕЛЕНИЯ ФАЗОВОЙ ХАРАКТЕРИСТИКИ ПО ЗАДАННОЙ АМПЛИТУДНОЙ ХАРАКТЕРИСТИКЕ
- 12. ИНТЕГРАЛЬНЫЕ ВЫРАЖЕНИЯ ДЛЯ ОШИБКИ И ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 13. ТИПОВЫЕ ЗВЕНЬЯ
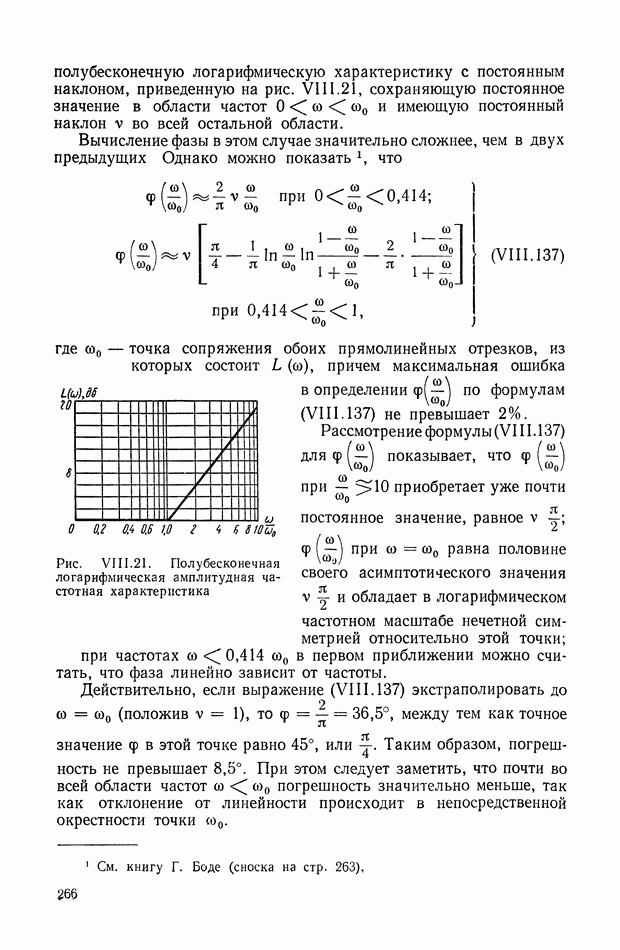
- 14. АПЕРИОДИЧЕСКОЕ ЗВЕНО
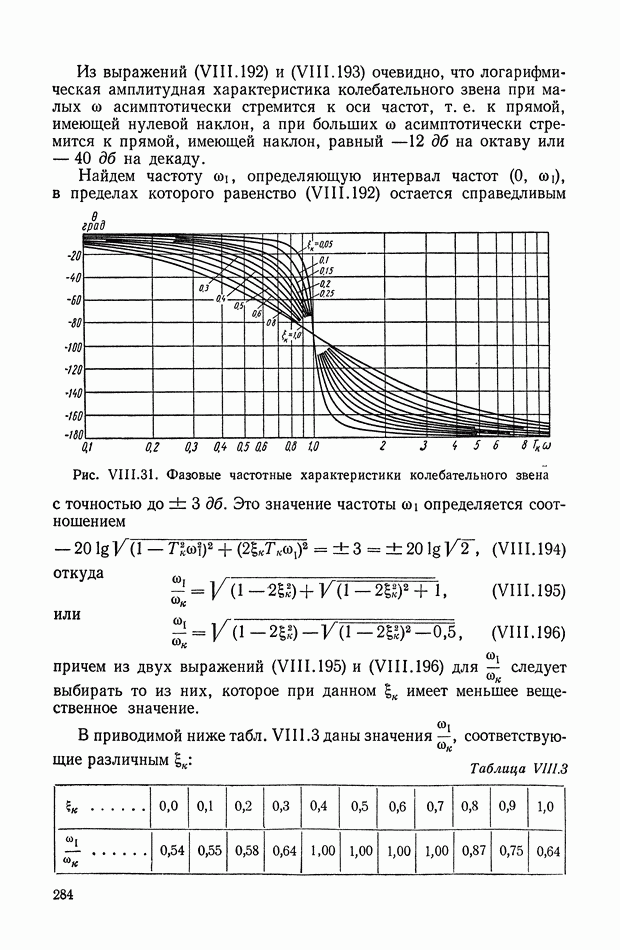
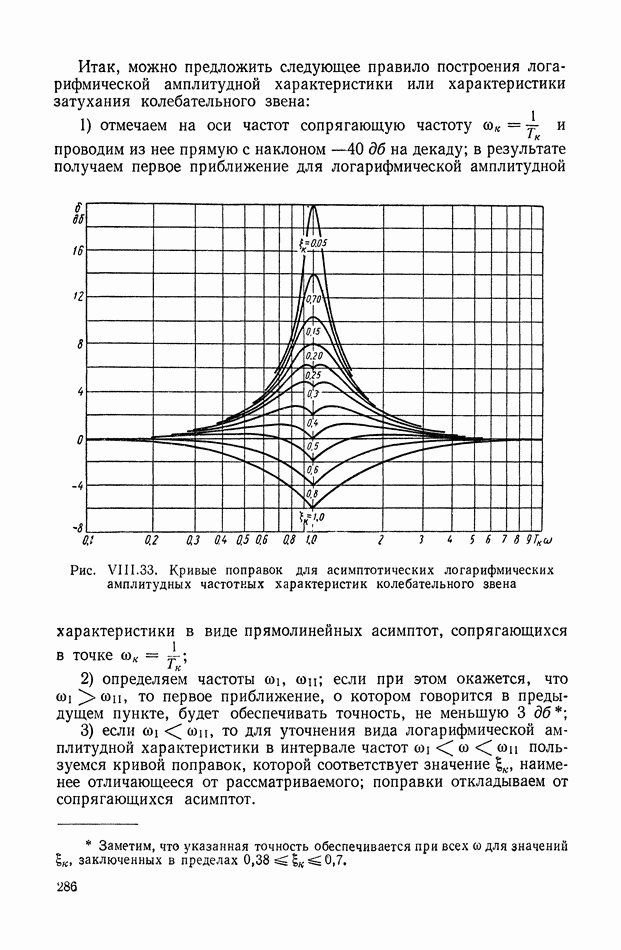
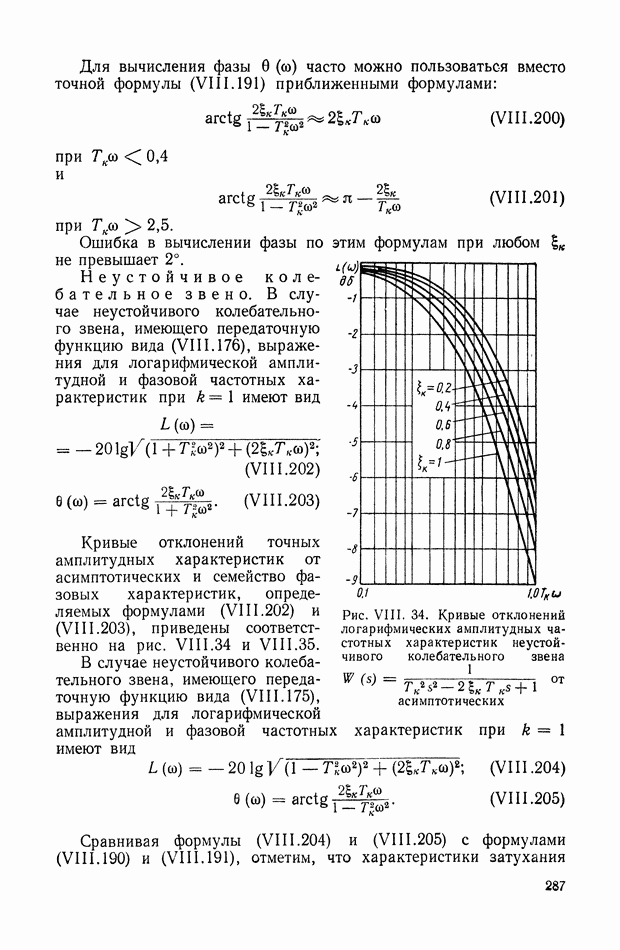
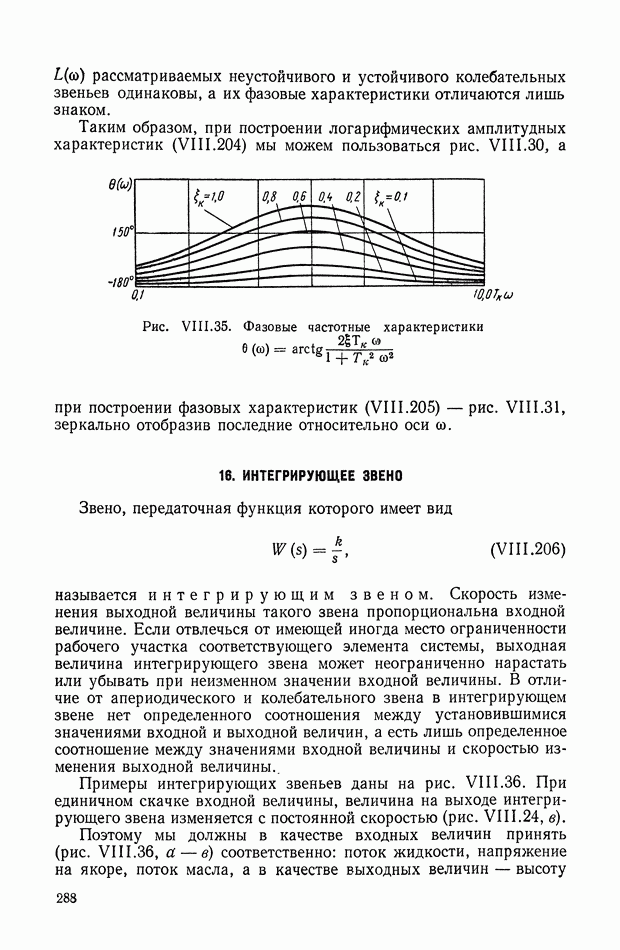
- 15. КОЛЕБАТЕЛЬНОЕ ЗВЕНО
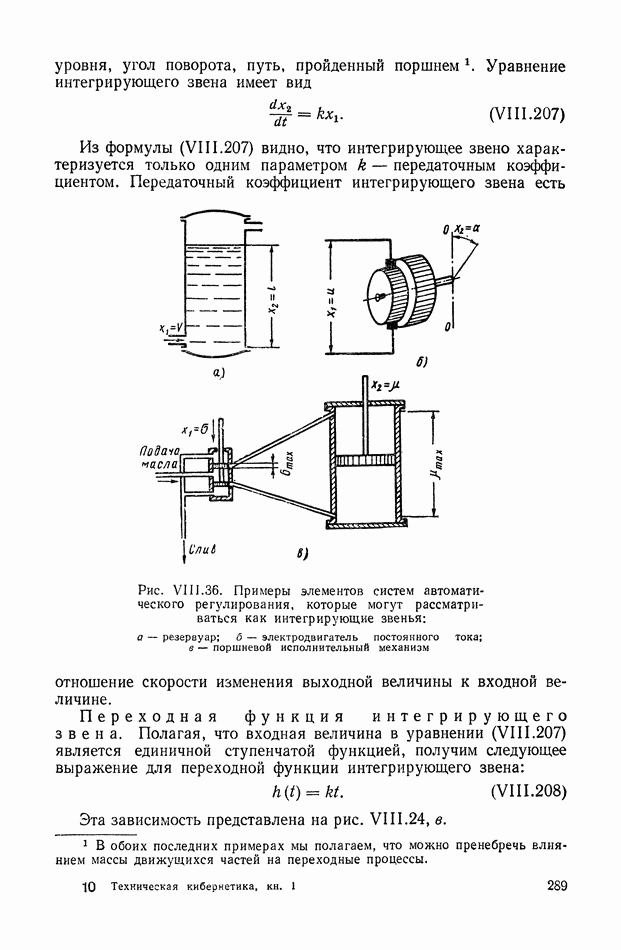
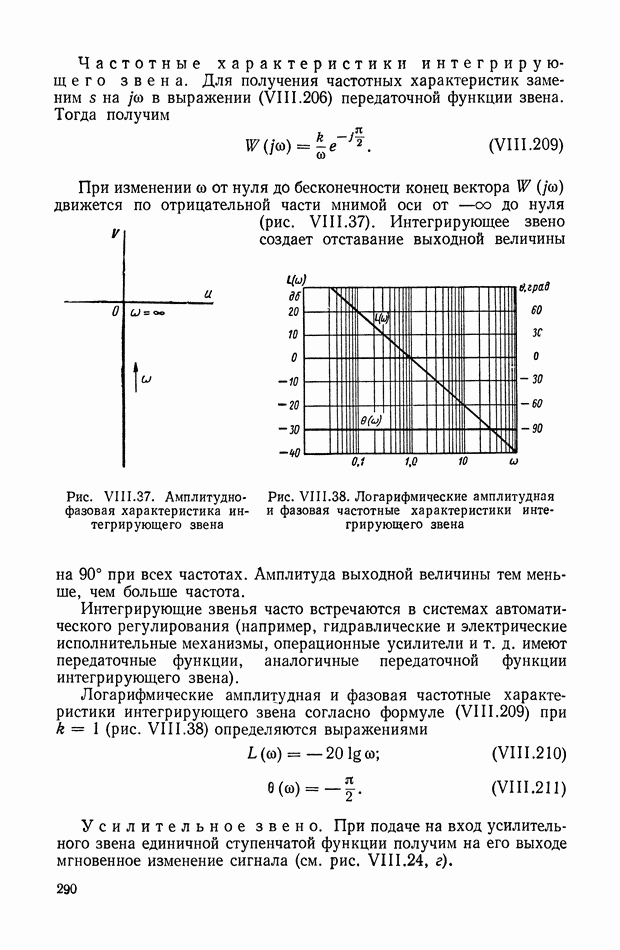
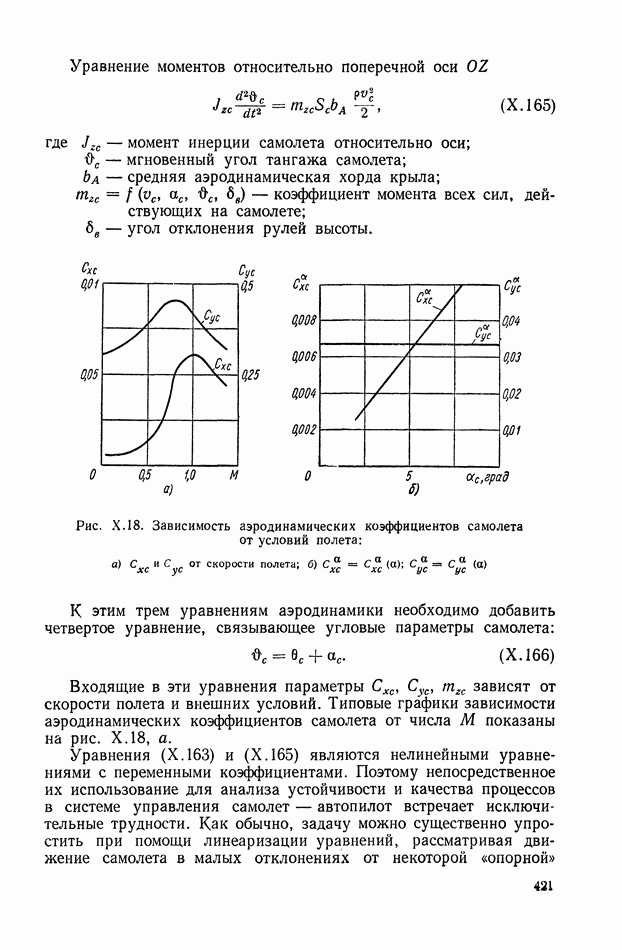
- 16. ИНТЕГРИРУЮЩЕЕ ЗВЕНО
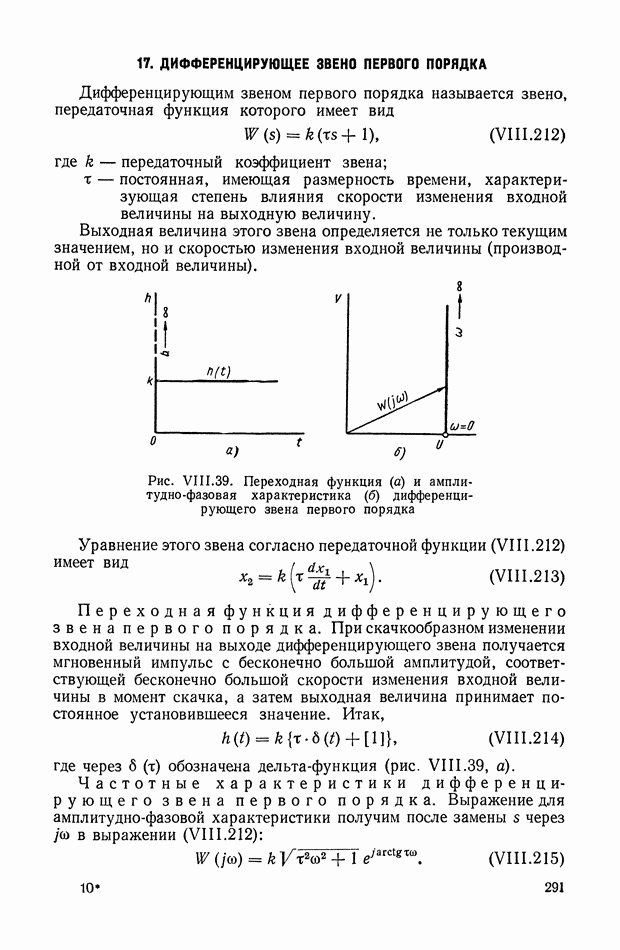
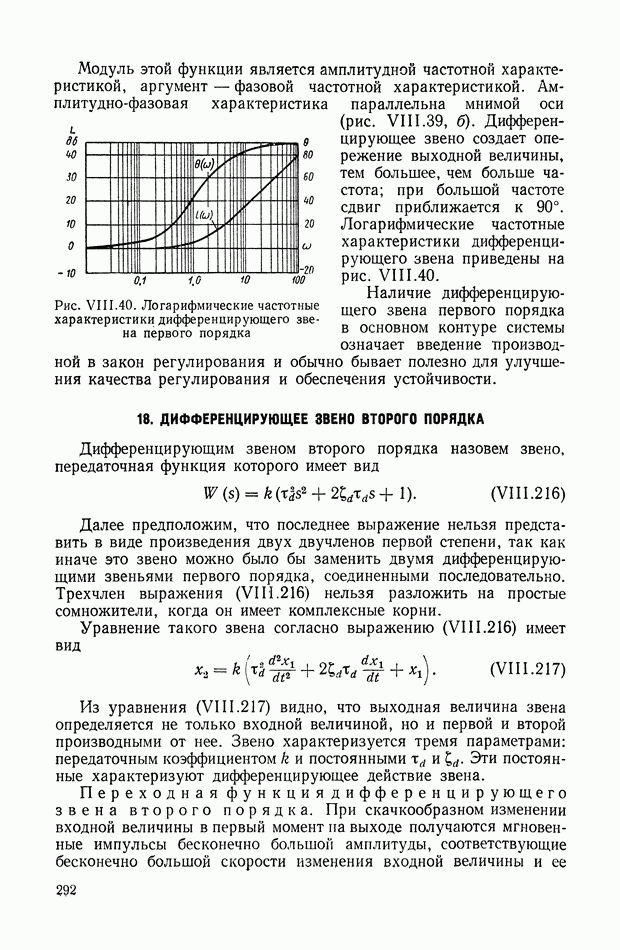
- 17. ДИФФЕРЕНЦИРУЮЩЕЕ ЗВЕНО ПЕРВОГО ПОРЯДКА
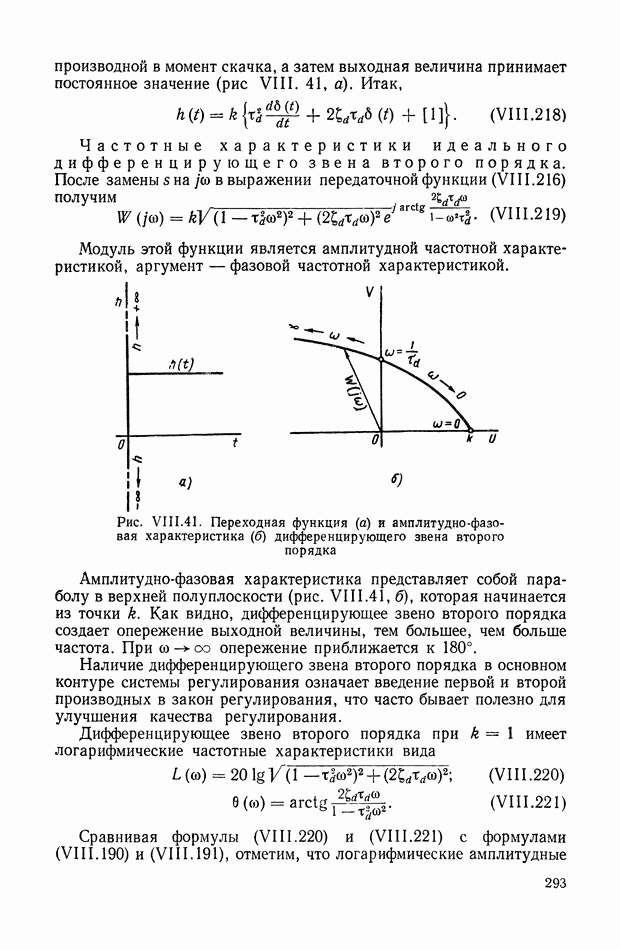
- 18. ДИФФЕРЕНЦИРУЮЩЕЕ ЗВЕНО ВТОРОГО ПОРЯДКА
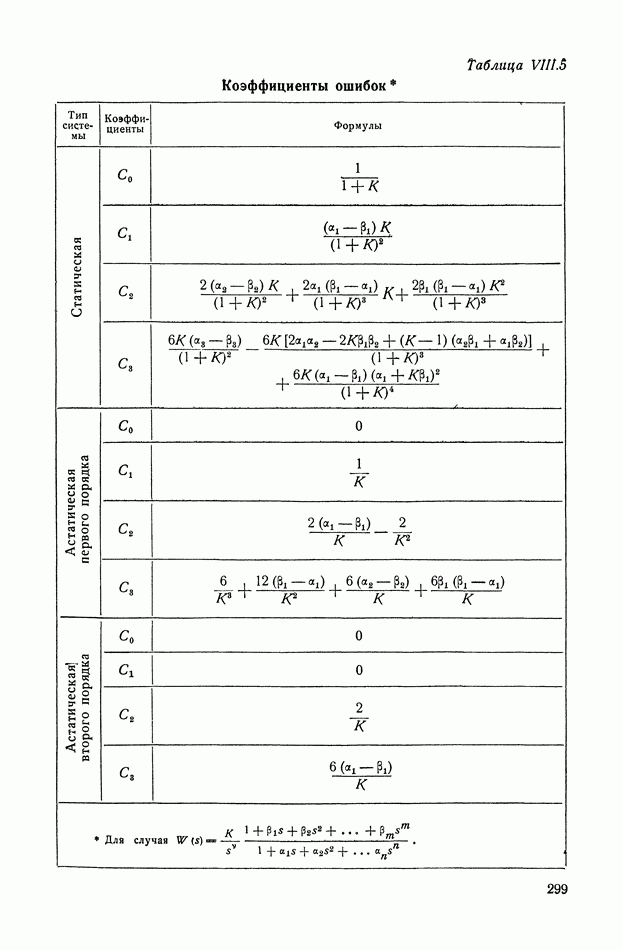
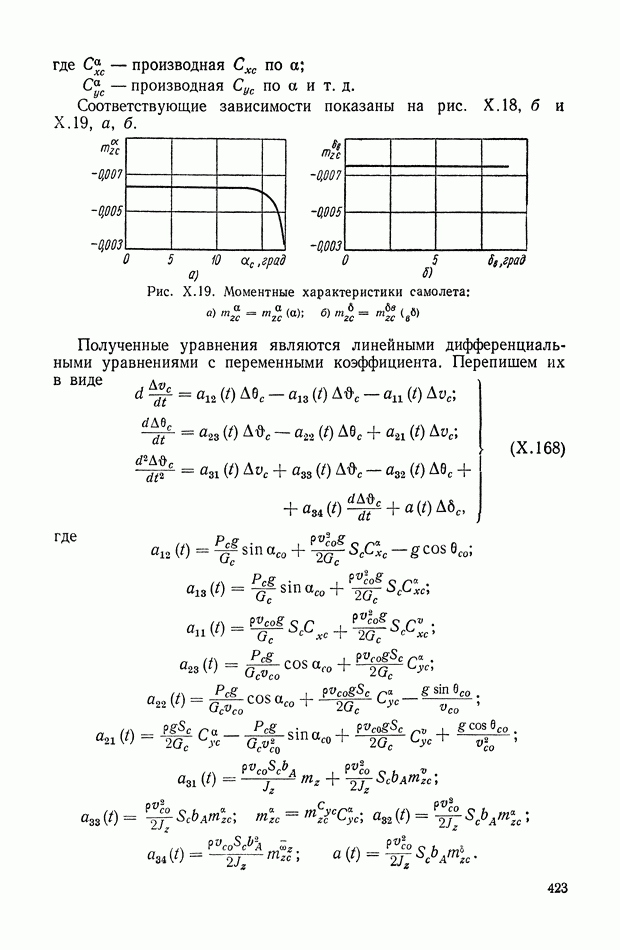
- 19. КОЭФФИЦИЕНТЫ ОШИБКИ
- ГЛАВА IX. МЕТОДЫ СТРУКТУРНЫХ ПРЕОБРАЗОВАНИЙ В СИСТЕМАХ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
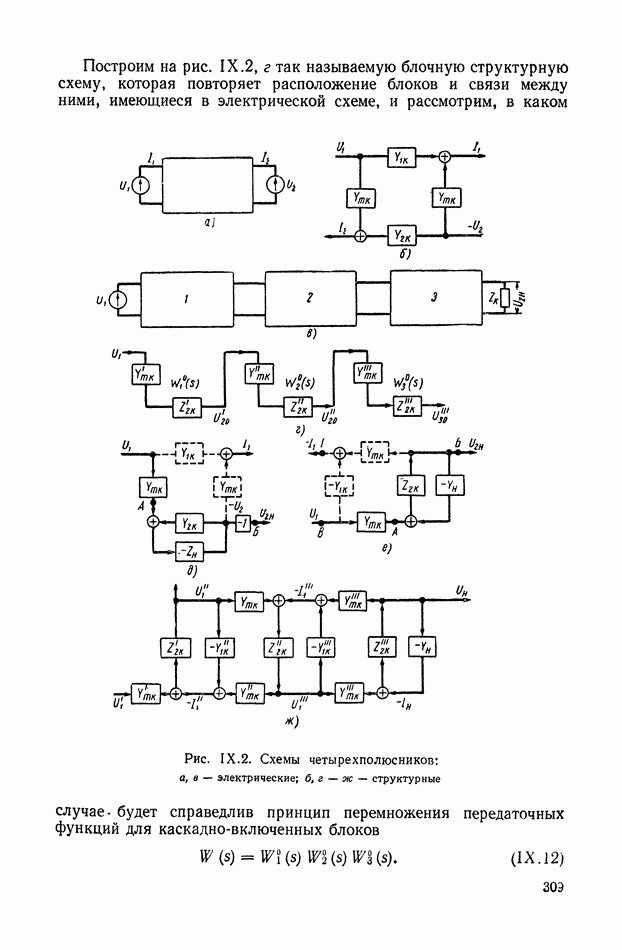
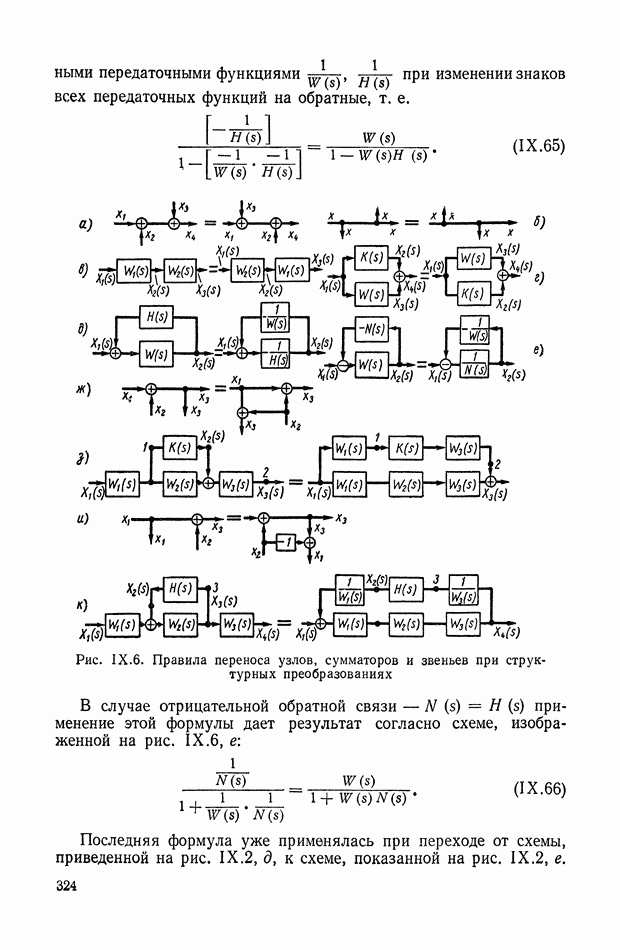
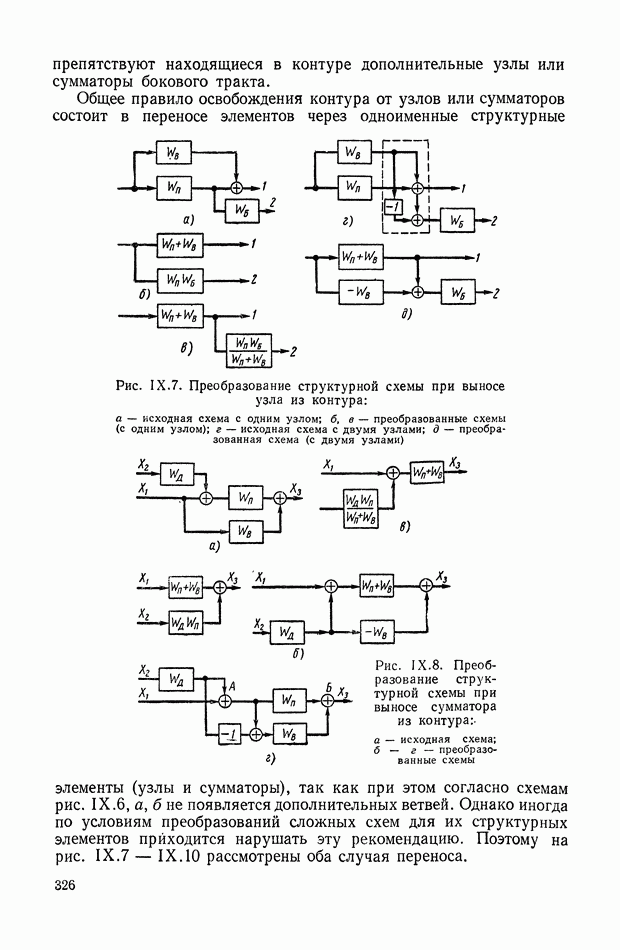
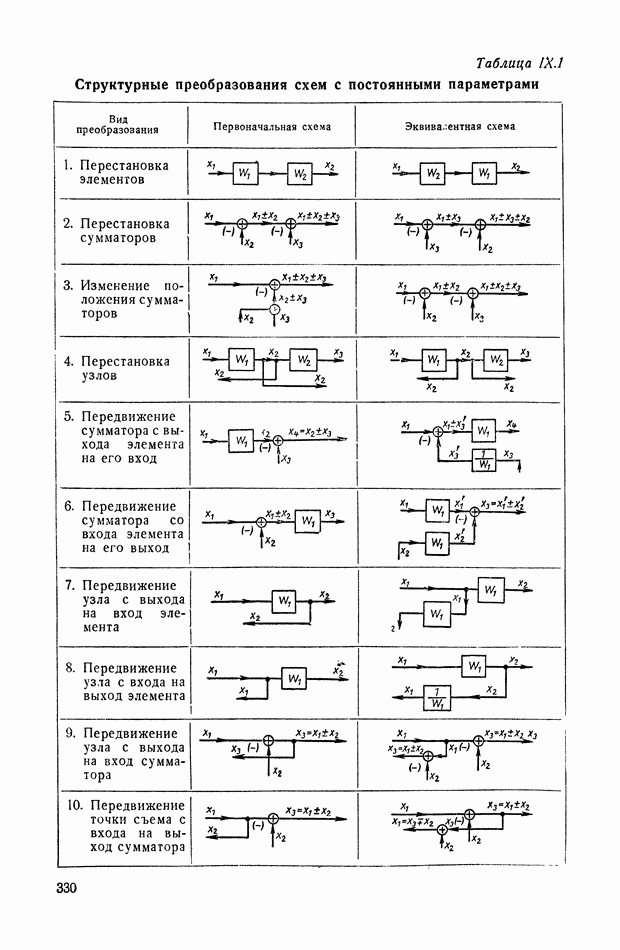
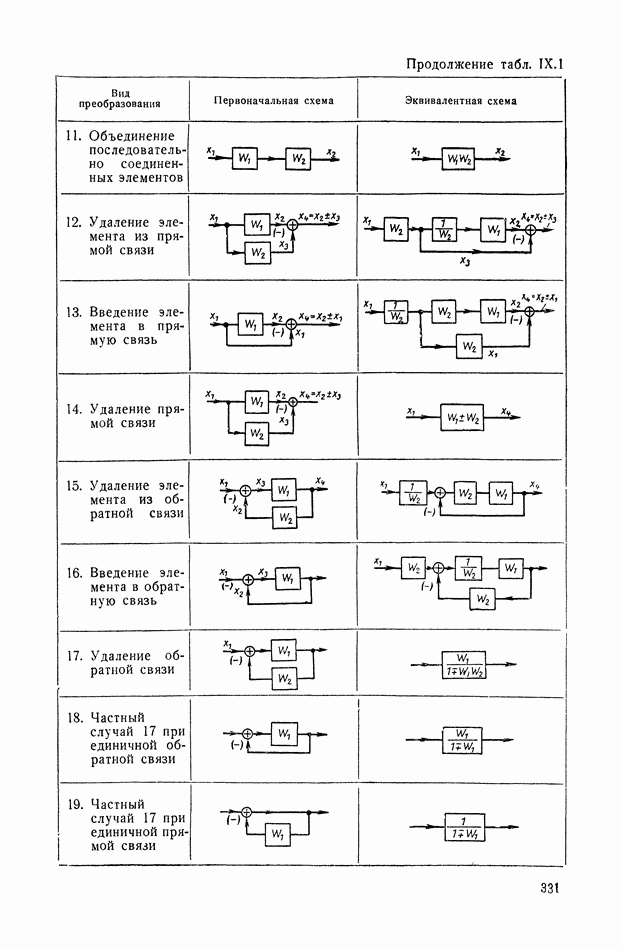
- 1. ГРАФИЧЕСКИЕ ИЗОБРАЖЕНИЯ УСЛОВИЙ ПРЕОБРАЗОВАНИЯ СИГНАЛОВ
- 2. СХЕМЫ С ЭЛЕМЕНТАМИ, ОБЛАДАЮЩИМИ И НЕ ОБЛАДАЮЩИМИ СВОЙСТВОМ НАПРАВЛЕННОСТИ ДЕЙСТВИЯ
- 3. ДЕТАЛИЗИРОВАННЫЕ СТРУКТУРЫ
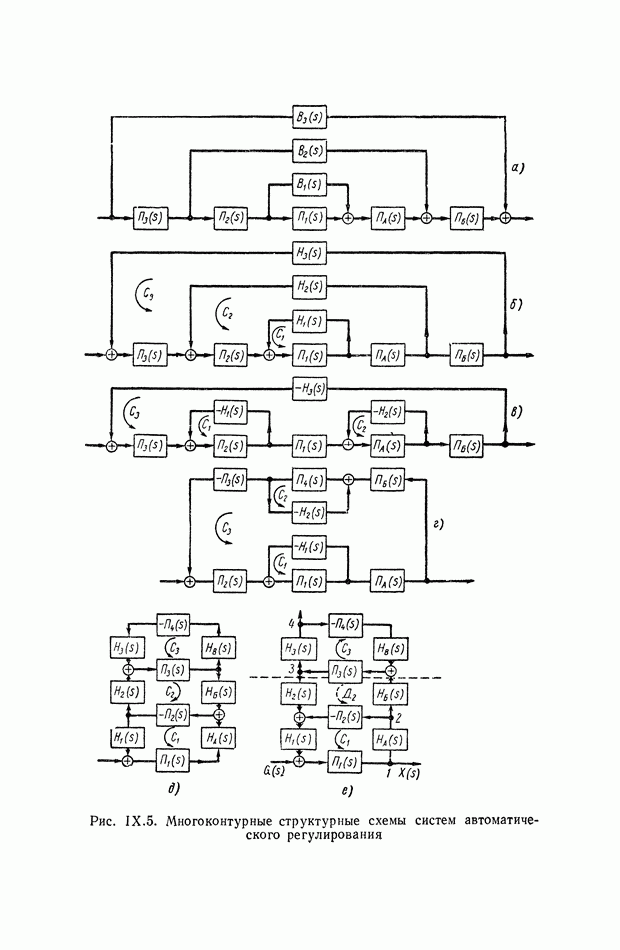
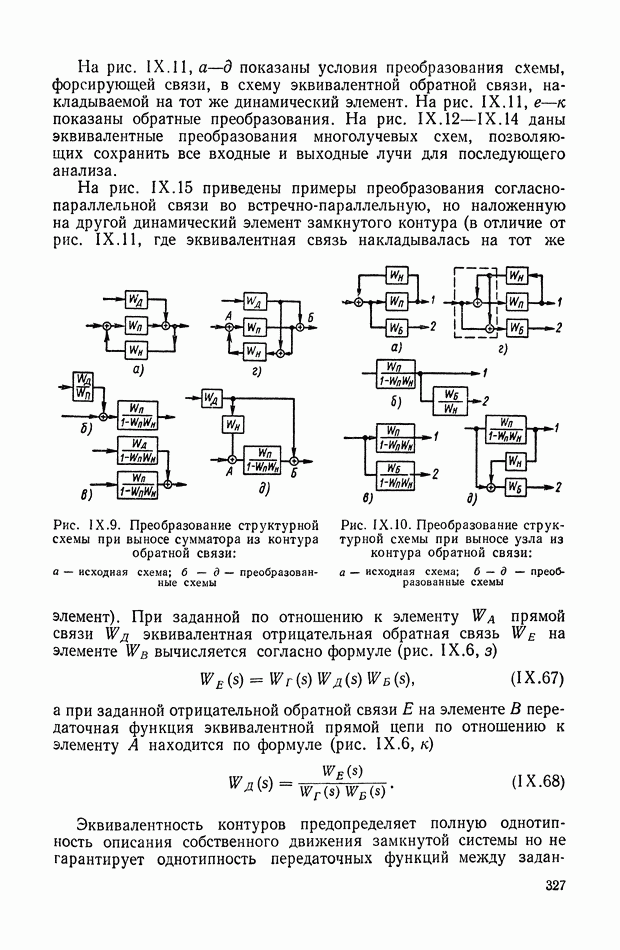
- 4. ПРЕОБРАЗОВАНИЯ МНОГОКОНТУРНЫХ СТРУКТУРНЫХ СХЕМ, ДОПУСКАЮЩИХ ПОСЛЕДОВАТЕЛЬНОЕ ПРИМЕНЕНИЕ ПРАВИЛ СВЕРТЫВАНИЯ КОНТУРОВ, И НЕКОТОРЫЕ ЭКВИВАЛЕНТНЫЕ ПРЕОБРАЗОВАНИЯ
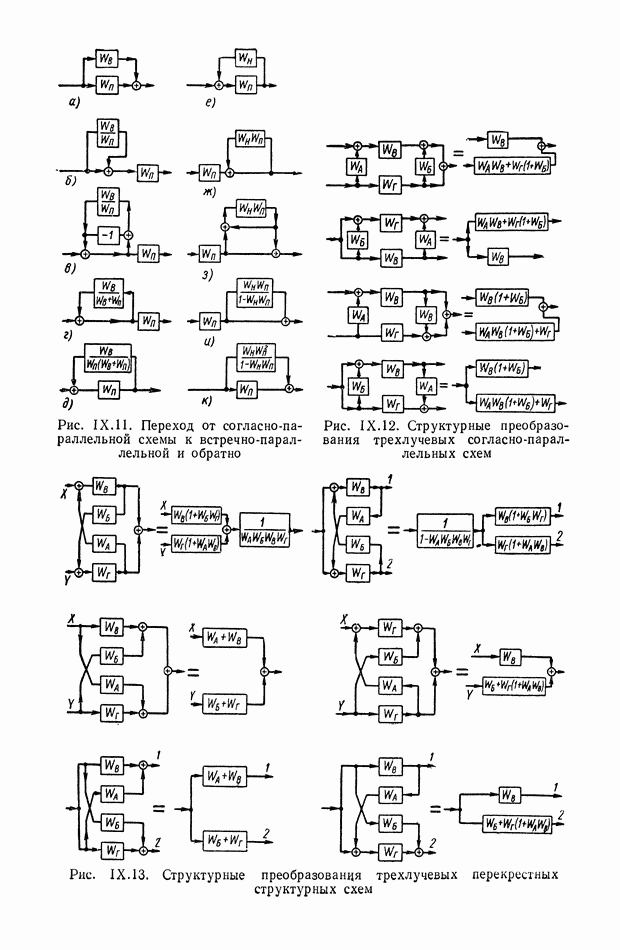
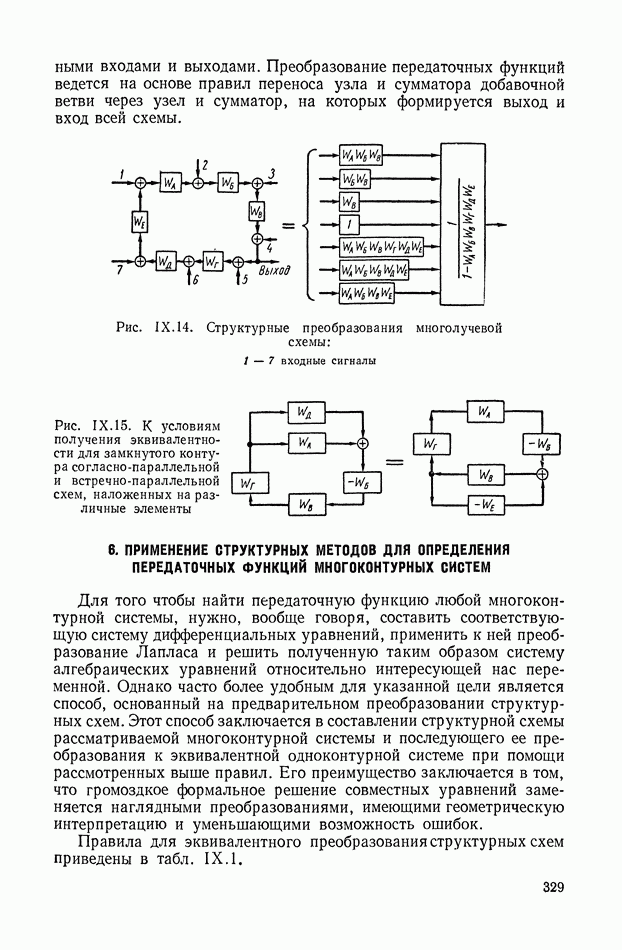
- 5. ПРЕОБРАЗОВАНИЯ ПЕРЕКРЕСТНЫХ СТРУКТУРНЫХ СХЕМ МЕТОДОМ РАЗВЯЗКИ КОНТУРОВ И НЕКОТОРЫЕ ЭКВИВАЛЕНТНЫЕ ПРЕОБРАЗОВАНИЯ
- 6. ПРИМЕНЕНИЕ СТРУКТУРНЫХ МЕТОДОВ ДЛЯ ОПРЕДЕЛЕНИЯ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ МНОГОКОНТУРНЫХ СИСТЕМ
- 7. СОСТАВЛЕНИЕ И ПРЕОБРАЗОВАНИЕ СТРУКТУРНОЙ СХЕМЫ НА ПРИМЕРЕ ЭЛЕКТРОДВИГАТЕЛЯ ПОСТОЯННОГО ТОКА ДВОЙНОГО ПИТАНИЯ
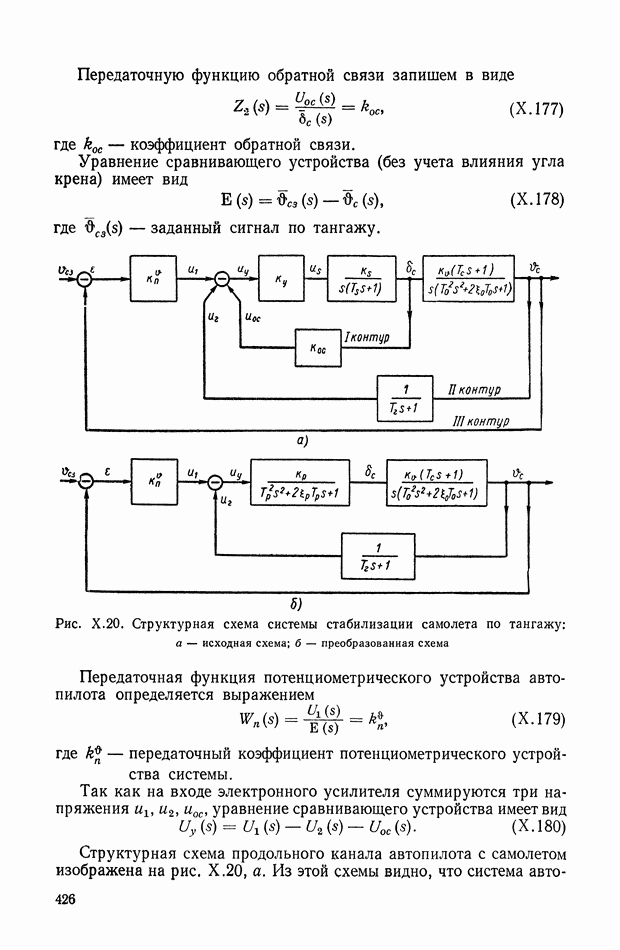
- Учет зависимости момента нагрузки от угла поворота вала и его производных по времени.
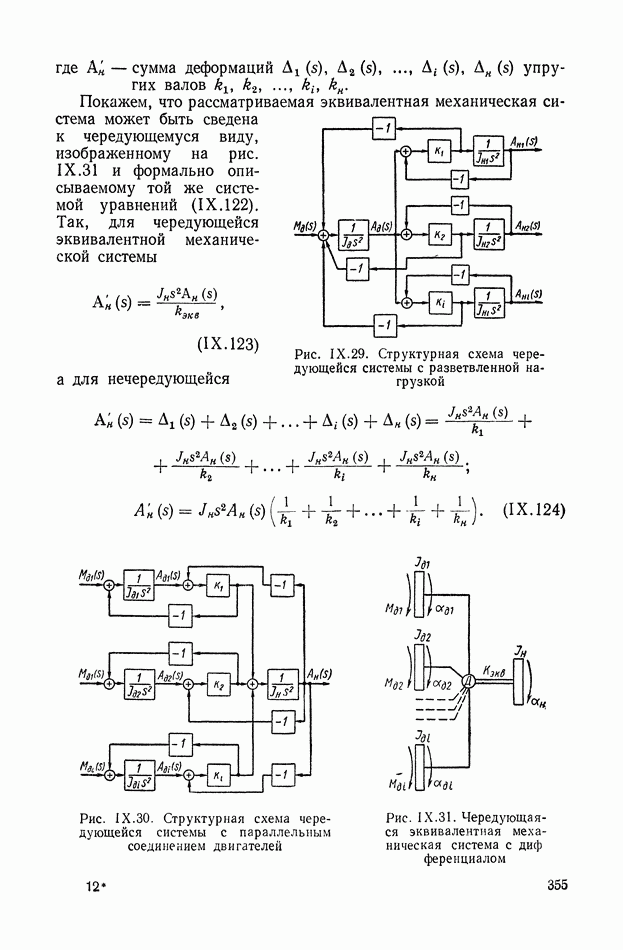
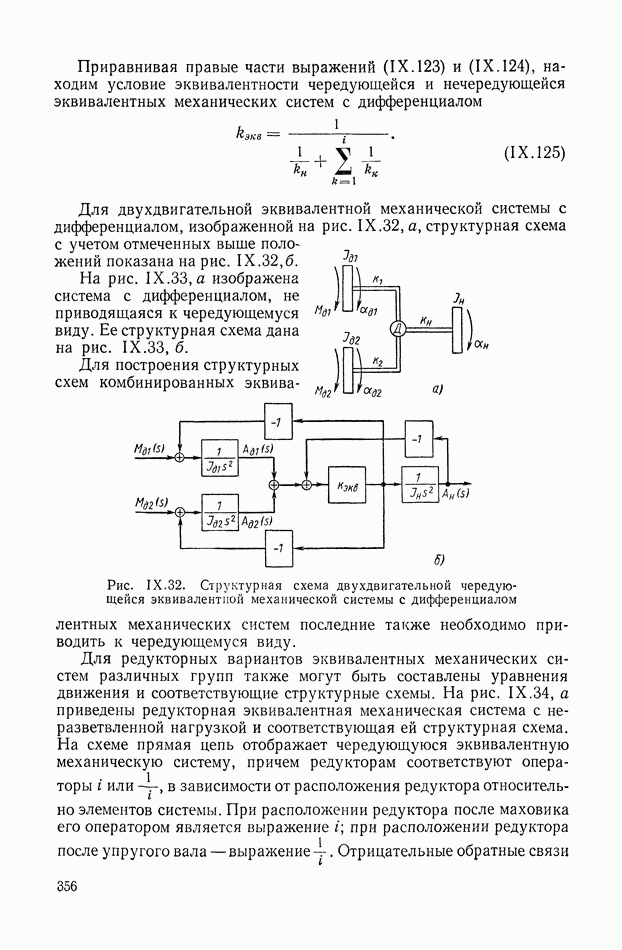
- 8. СТРУКТУРНЫЕ СХЕМЫ МЕХАНИЧЕСКИХ ОБЪЕКТОВ РЕГУЛИРОВАНИЯ С РЕДУКТОРАМИ, ДИФФЕРЕНЦИАЛАМИ И УПРУГИМИ ЭЛЕМЕНТАМИ В СИЛОВЫХ ПЕРЕДАЧАХ
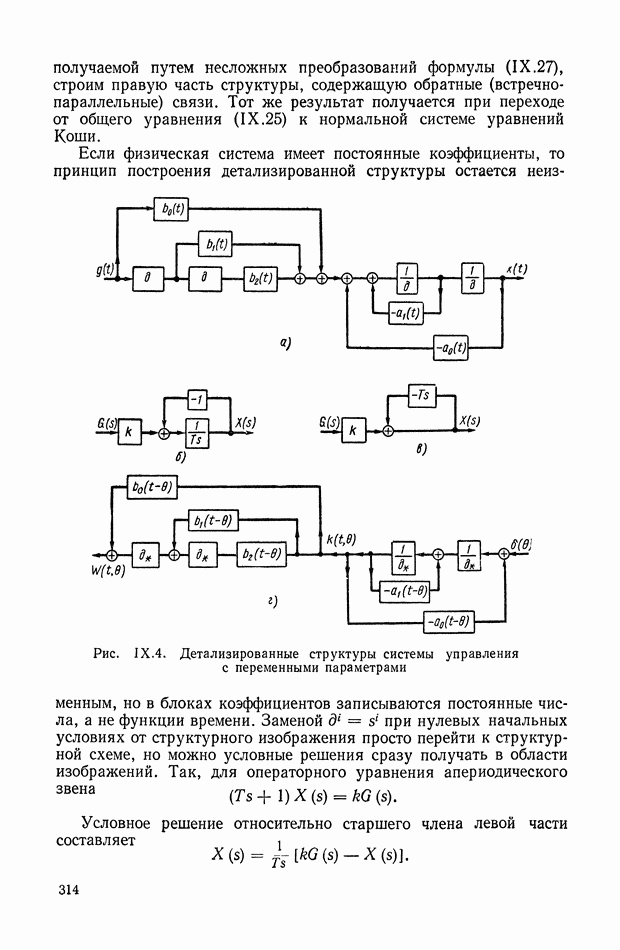
- 9. ПРАВИЛА СТРУКТУРНЫХ ПРЕОБРАЗОВАНИЙ ДЛЯ СИСТЕМ С ПЕРЕМЕННЫМИ ПАРАМЕТРАМИ
- 10. ФУНКЦИОНАЛЬНЫЕ СТРУКТУРНЫЕ СХЕМЫ ДЛЯ АНАЛИЗА СОВМЕСТНЫХ СТАТИЧЕСКИХ ХАРАКТЕРИСТИК НЕЛИНЕЙНЫХ ЗВЕНЬЕВ
- ГЛАВА X. ПРИМЕРЫ СОСТАВЛЕНИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ, СТРУКТУРНЫХ СХЕМ И ПЕРЕДАТОЧНЫХ ФУНКЦИЙ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
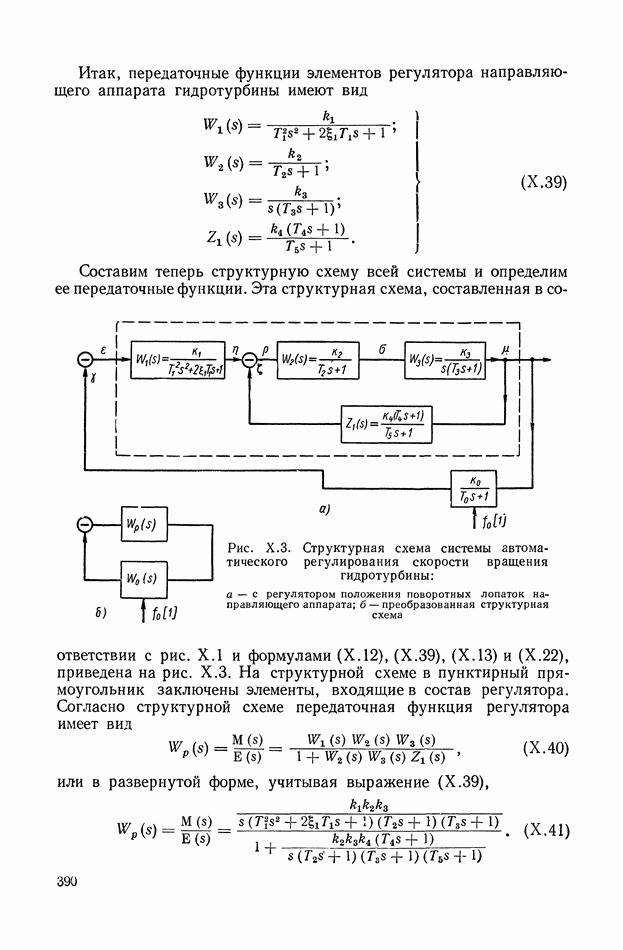
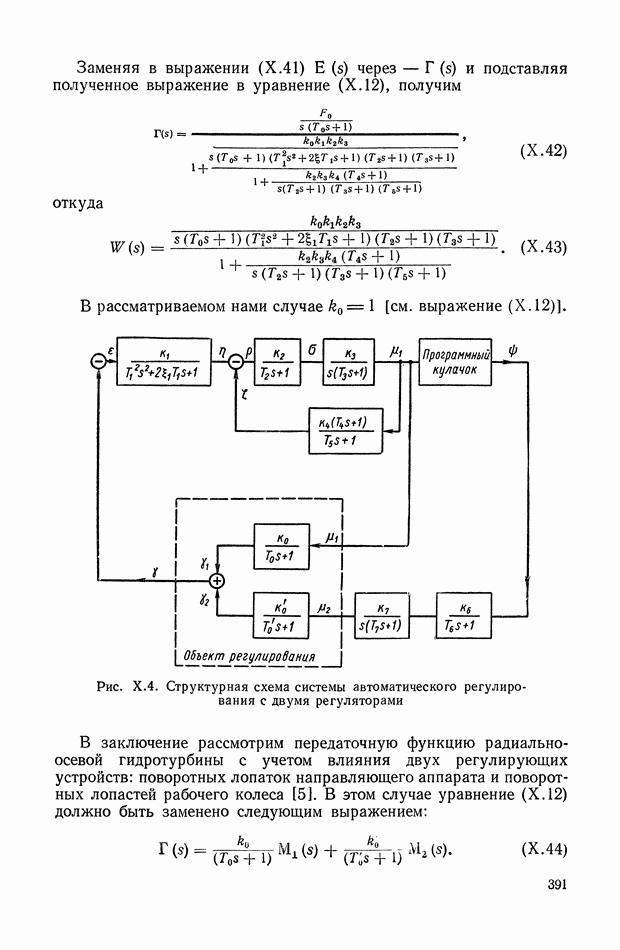
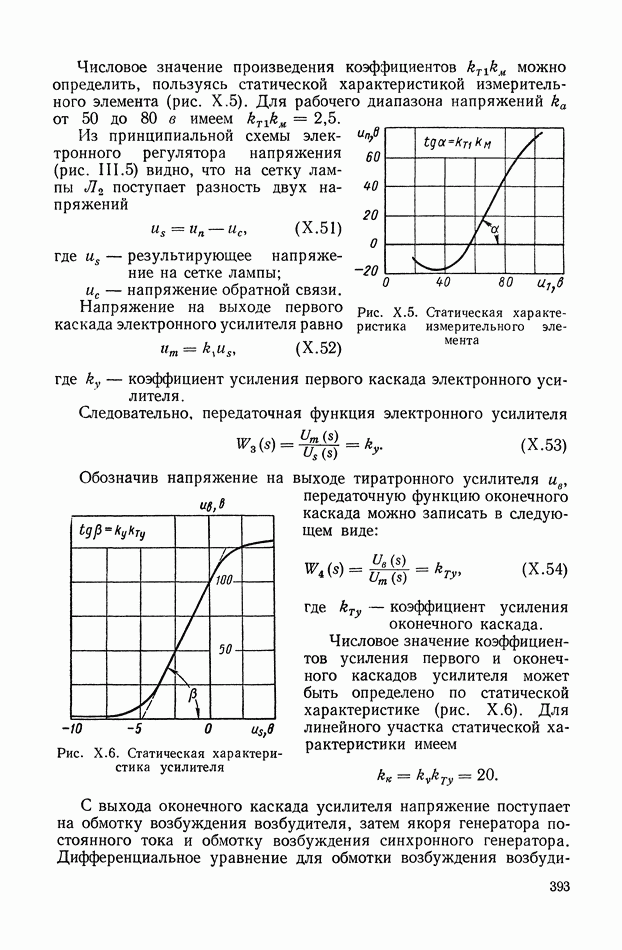
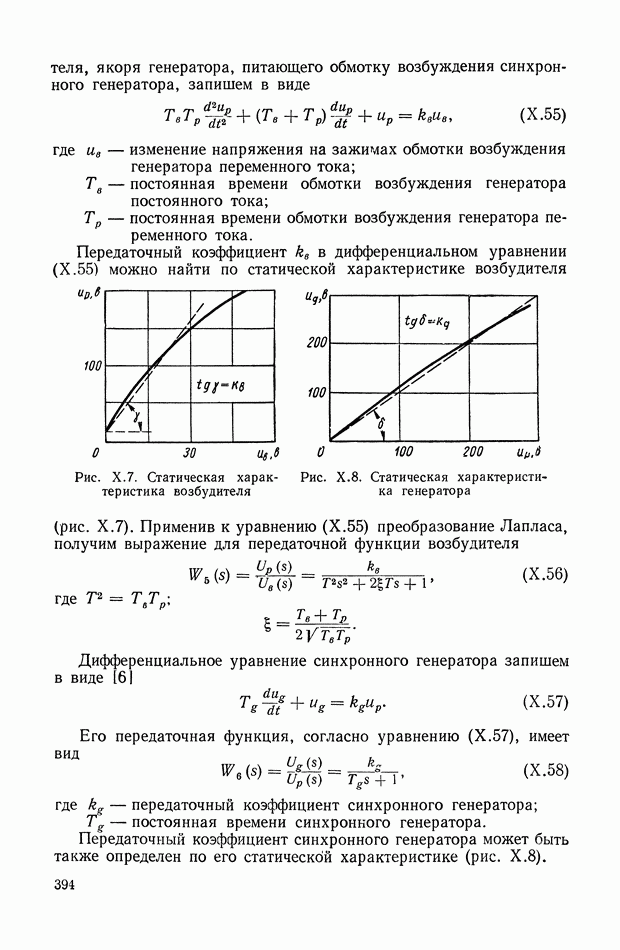
- 1. СИСТЕМА АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ СКОРОСТИ ВРАЩЕНИЯ ГИДРОТУРБИНЫ
- 2. ЭЛЕКТРОННЫЙ РЕГУЛЯТОР НАПРЯЖЕНИЯ ВЭИ
- 3. СИСТЕМА АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ МОЩНОСТИ ЯДЕРНОГО ЭНЕРГЕТИЧЕСКОГО РЕАКТОРА НА ТЕПЛОВЫХ НЕЙТРОНАХ
- 4. СЛЕДЯЩАЯ СИСТЕМА РАДИОЛОКАЦИОННОЙ СТАНЦИИ
- 5. СИСТЕМА АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ УНИВЕРСАЛЬНЫХ ЛЕТУЧИХ НОЖНИЦ
- 6. САМОЛЕТ С АВТОПИЛОТОМ
- 7. СЛЕДЯЩАЯ СИСТЕМА КОПИРОВАЛЬНО-ФРЕЗЕРНОГО СТАНКА
- РАЗДЕЛ II. АНАЛИЗ УСТОЙЧИВОСТИ НЕПРЕРЫВНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- ГЛАВА XI. ОБЩАЯ ПОСТАНОВКА ЗАДАЧИ УСТОЙЧИВОСТИ ПО ЛЯПУНОВУ И АНАЛИЗ УСТОЙЧИВОСТИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. ПОСТАНОВКА ЗАДАЧИ ОБ УСТОЙЧИВОСТИ В ТЕОРИИ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 2. ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ УСТАНОВИВШИХСЯ ДВИЖЕНИЙ ПО УРАВНЕНИЮ ПЕРВОГО ПРИБЛИЖЕНИЯ
- 3. О ПРЯМОМ МЕТОДЕ ЛЯПУНОВА
- 4. О ПРИМЕНЕНИИ ПРЯМОГО МЕТОДА ЛЯПУНОВА К АНАЛИЗУ УСТОЙЧИВОСТИ ОДНОГО КЛАССА СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- ГЛАВА XII. КРИТЕРИИ И МЕТОДЫ АНАЛИЗА УСТОЙЧИВОСТИ ЛИНЕАРИЗОВАННЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЙ
- 1. УСТОЙЧИВОСТЬ И ПРИНЦИП АРГУМЕНТА
- 2. КРИТЕРИЙ УСТОЙЧИВОСТИ МИХАЙЛОВА
- 3. КРИТЕРИЙ УСТОЙЧИВОСТИ РАУСА И ГУРВИЦА
- 4. ЧАСТОТНЫЙ КРИТЕРИЙ УСТОЙЧИВОСТИ
- 5. ОБОБЩЕНИЕ ЧАСТОТНОГО КРИТЕРИЯ НА АСТАТИЧЕСКИЕ СИСТЕМЫ
- 6. ОБОБЩЕНИЕ ЧАСТОТНОГО КРИТЕРИЯ НА СЛУЧАЙ, КОГДА РАЗОМКНУТАЯ СИСТЕМА НЕУСТОЙЧИВА
- 7. ЧАСТОТНЫЙ КРИТЕРИЙ УСТОЙЧИВОСТИ ДЛЯ ОБРАТНОЙ АМПЛИТУДНО-ФАЗОВОЙ ХАРАКТЕРИСТИКИ
- 8. АНАЛИЗ УСТОЙЧИВОСТИ ОДНОКОНТУРНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ПО ИХ ЛОГАРИФМИЧЕСКИМ ЧАСТОТНЫМ ХАРАКТЕРИСТИКАМ
- 9. ПРИБЛИЖЕННЫЙ СПОСОБ ПОСТРОЕНИЯ ЛОГАРИФМИЧЕСКИХ ЧАСТОТНЫХ ХАРАКТЕРИСТИК ОДНОКОНТУРНЫХ СИСТЕМ
- 10. ОБОБЩЕНИЕ ЧАСТОТНОГО КРИТЕРИЯ УСТОЙЧИВОСТИ НА МНОГОКОНТУРНЫЕ СИСТЕМЫ
- 11. АНАЛИЗ УСТОЙЧИВОСТИ МНОГОКОНТУРНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ПРИ ПОМОЩИ ЛОГАРИФМИЧЕСКИХ ЧАСТОТНЫХ ХАРАКТЕРИСТИК
- ГЛАВА XIII. ВЫДЕЛЕНИЕ ОБЛАСТЕЙ УСТОЙЧИВОСТИ
- 1. ПОНЯТИЕ О Д-РАЗБИЕНИИ ПРОСТРАНСТВА КОЭФФИЦИЕНТОВ ХАРАКТЕРИСТИЧЕСКОГО УРАВНЕНИЯ И ПРОСТРАНСТВА ПАРАМЕТРОВ
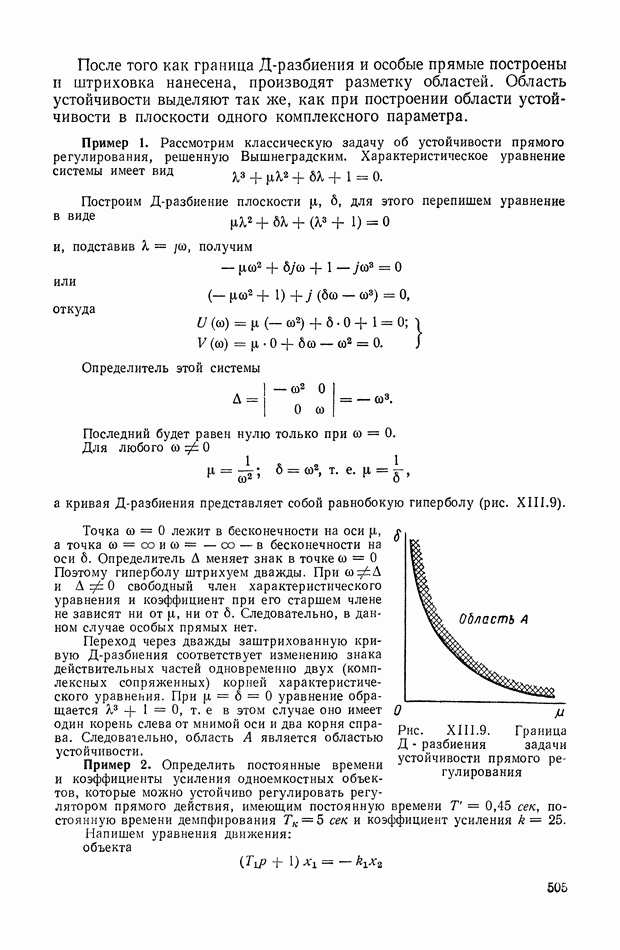
- 2. Д-РАЗБИЕНИЕ ПЛОСКОСТИ ОДНОГО КОМПЛЕКСНОГО ПАРАМЕТРА
- 3. СВЯЗЬ Д-РАЗБИЕНИЯ С КРИТЕРИЯМИ УСТОЙЧИВОСТИ
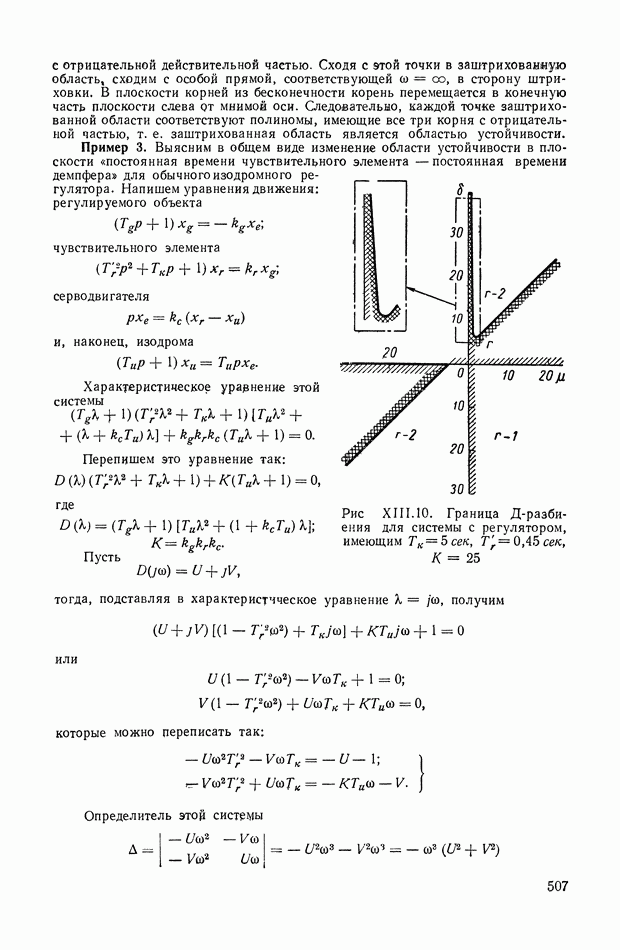
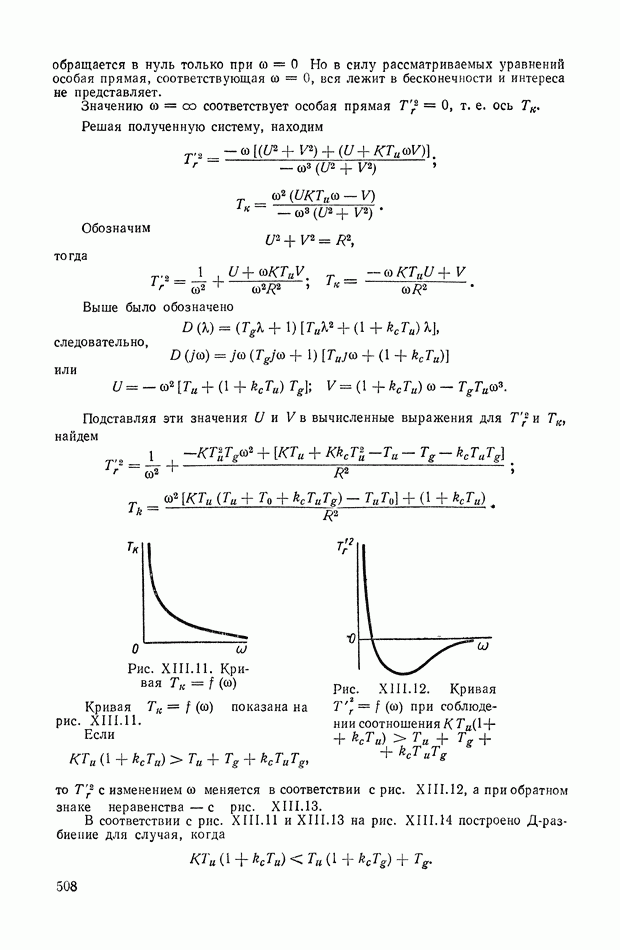
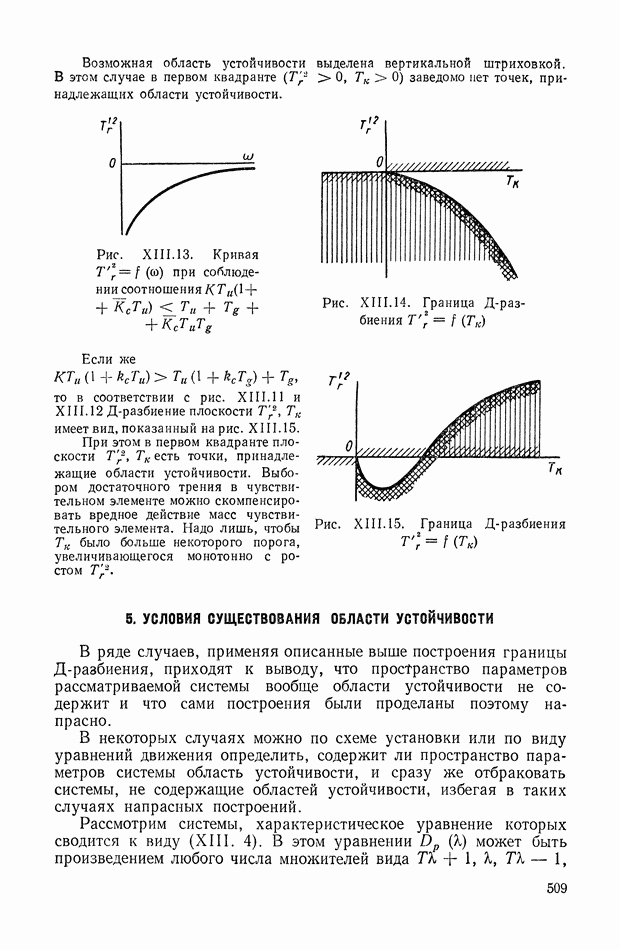
- 4. Д-РАЗБИЕНИЕ ПЛОСКОСТИ ДВУХ ДЕЙСТВИТЕЛЬНЫХ ПАРАМЕТРОВ (ДИАГРАММА ВЫШНЕГРАДСКОГО)
- 5. УСЛОВИЯ СУЩЕСТВОВАНИЯ ОБЛАСТИ УСТОЙЧИВОСТИ
- ГЛАВА XIV. ПРИМЕРЫ АНАЛИЗА УСТОЙЧИВОСТИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
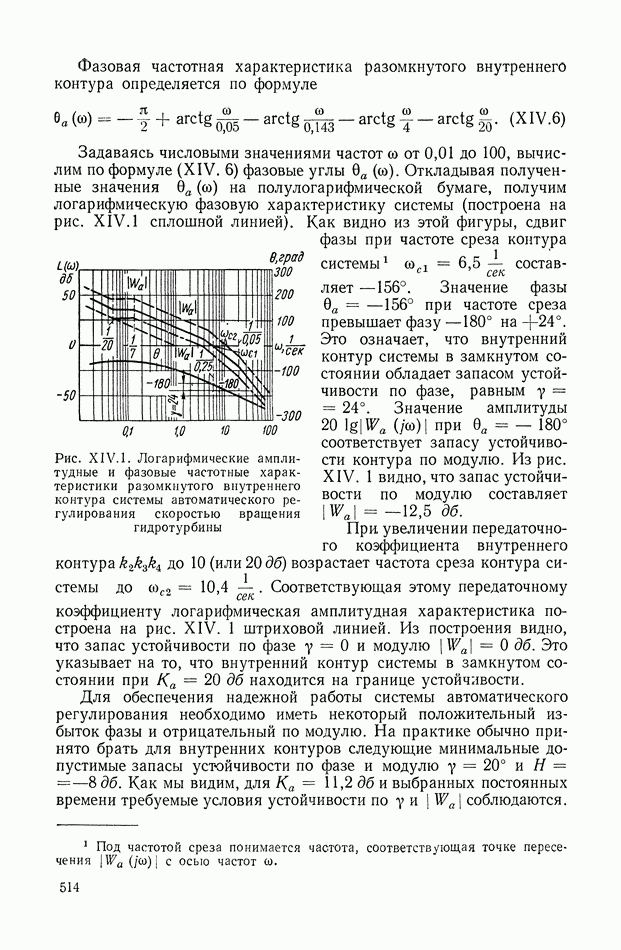
- 1. СИСТЕМА АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ СКОРОСТИ ВРАЩЕНИЯ ГИДРОТУРБИНЫ
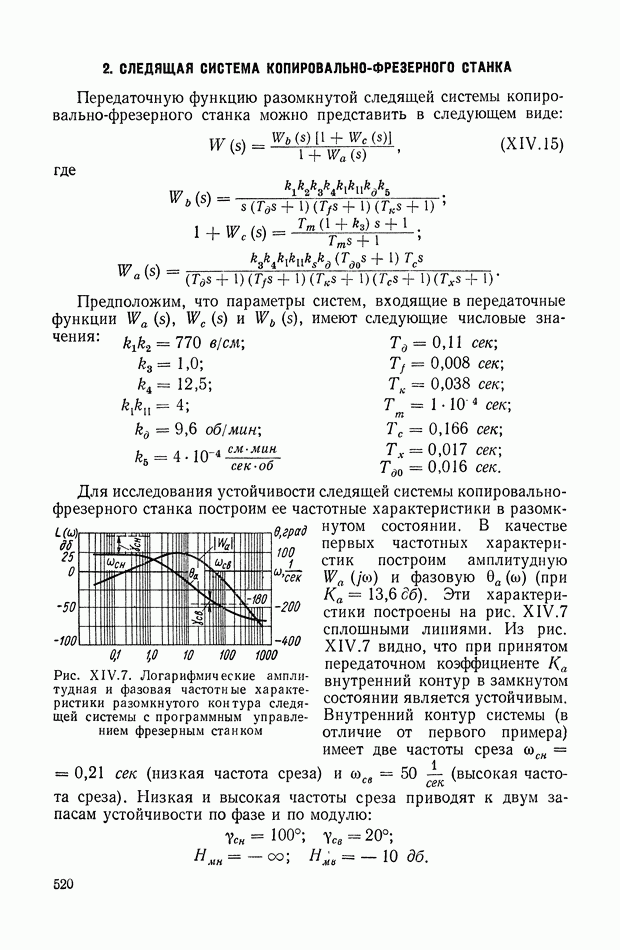
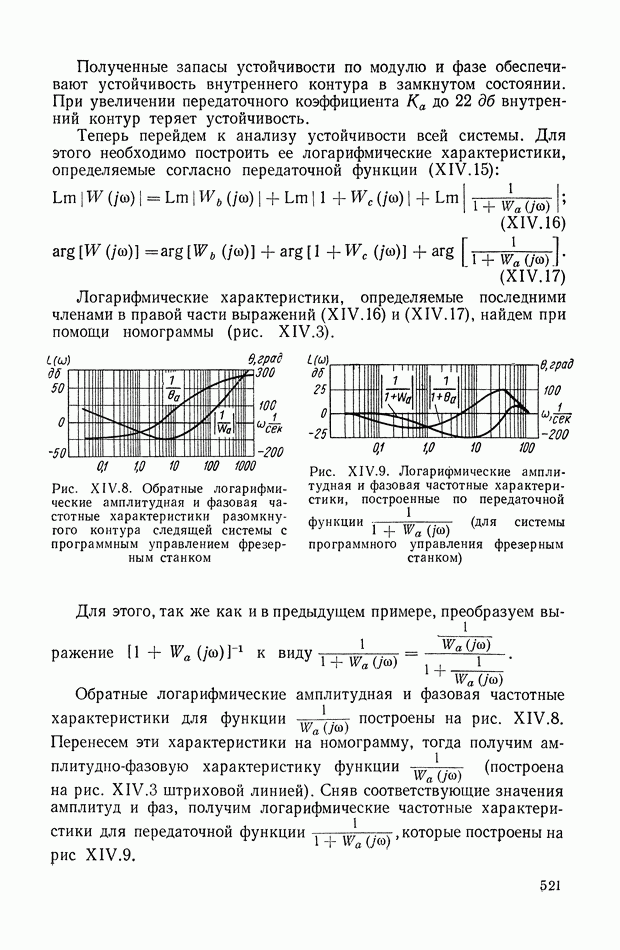
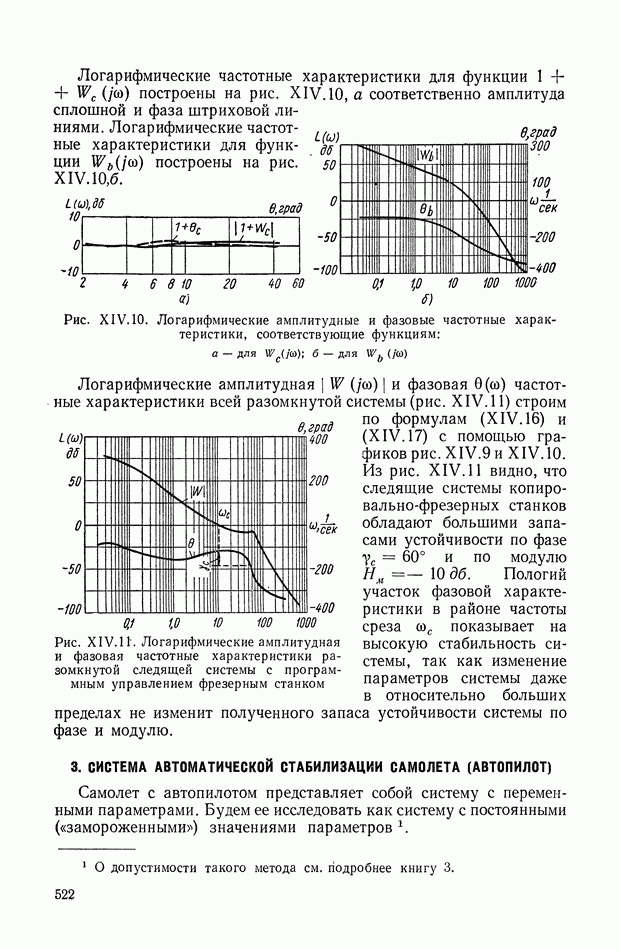
- 2. СЛЕДЯЩАЯ СИСТЕМА КОПИРОВАЛЬНО-ФРЕЗЕРНОГО СТАНКА
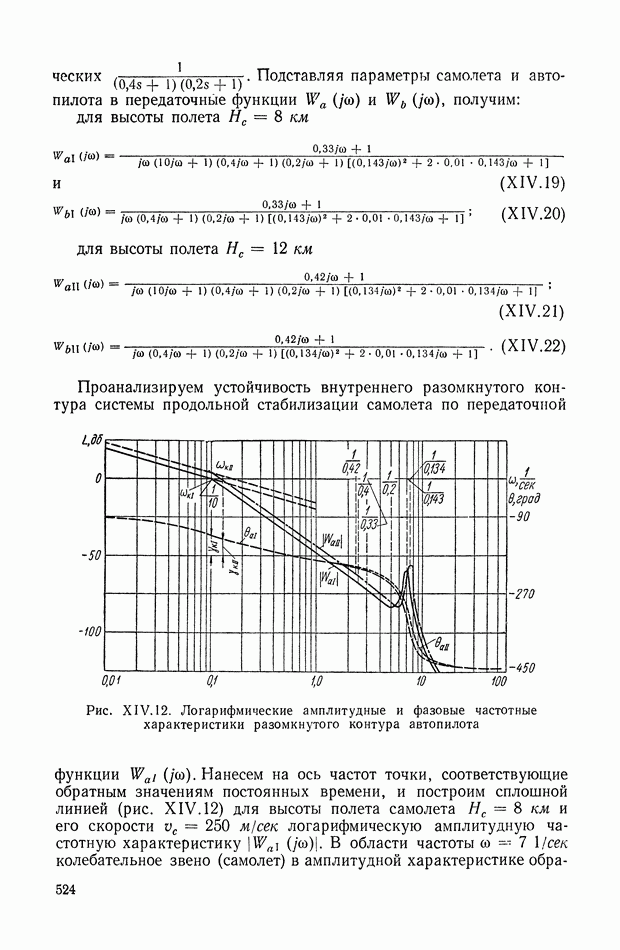
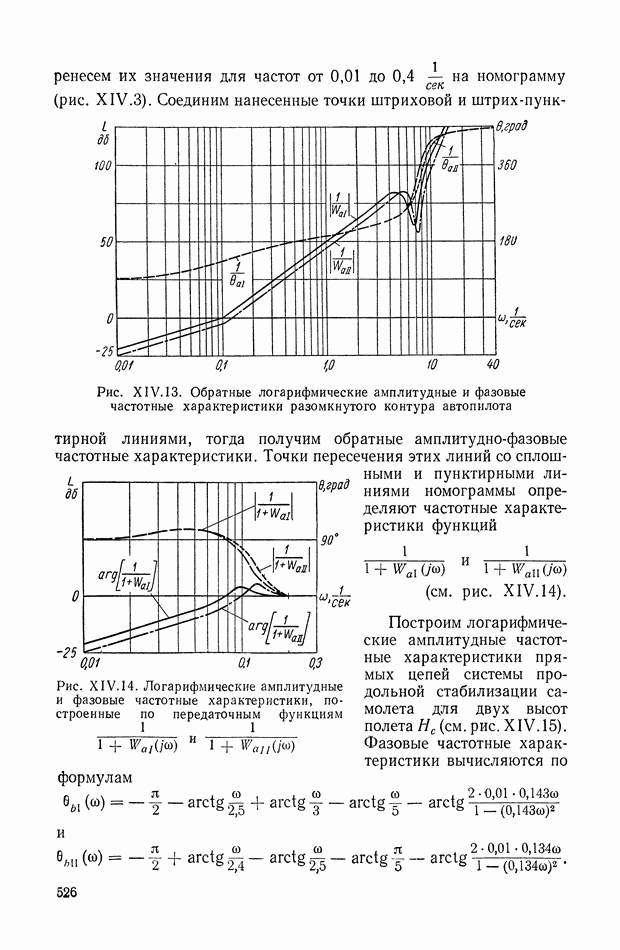
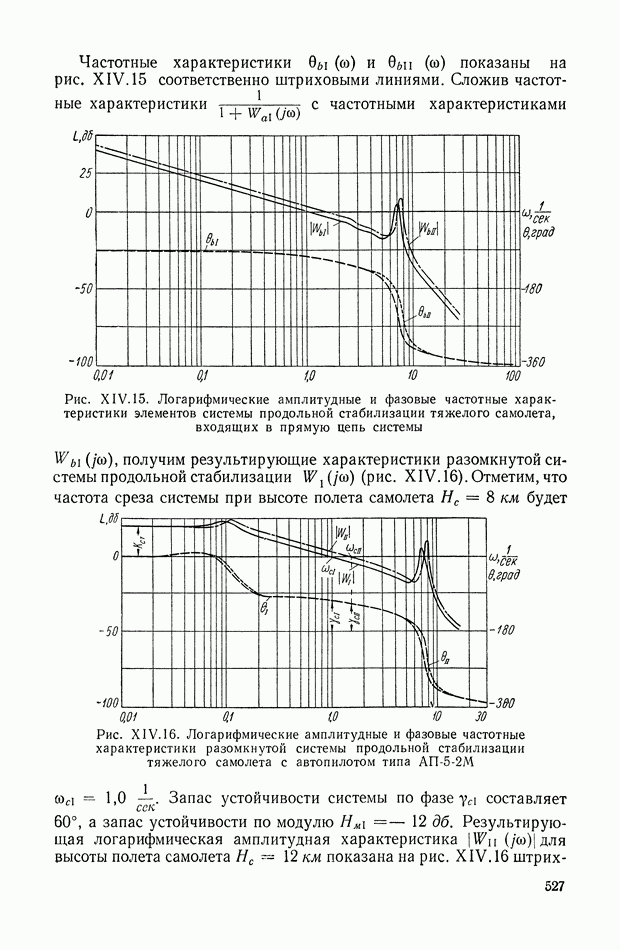
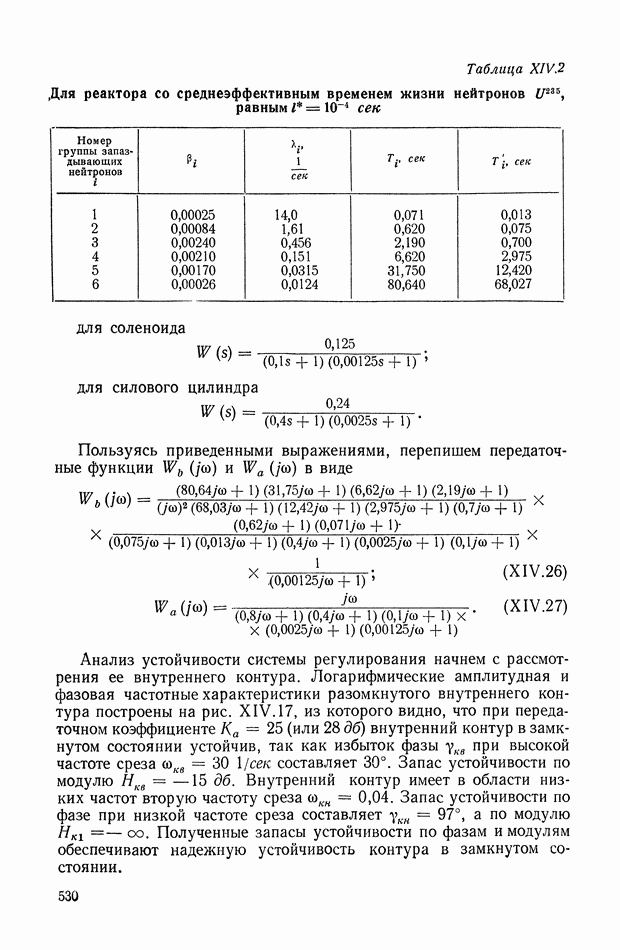
- 3. СИСТЕМА АВТОМАТИЧЕСКОЙ СТАБИЛИЗАЦИИ САМОЛЕТА (АВТОПИЛОТ)
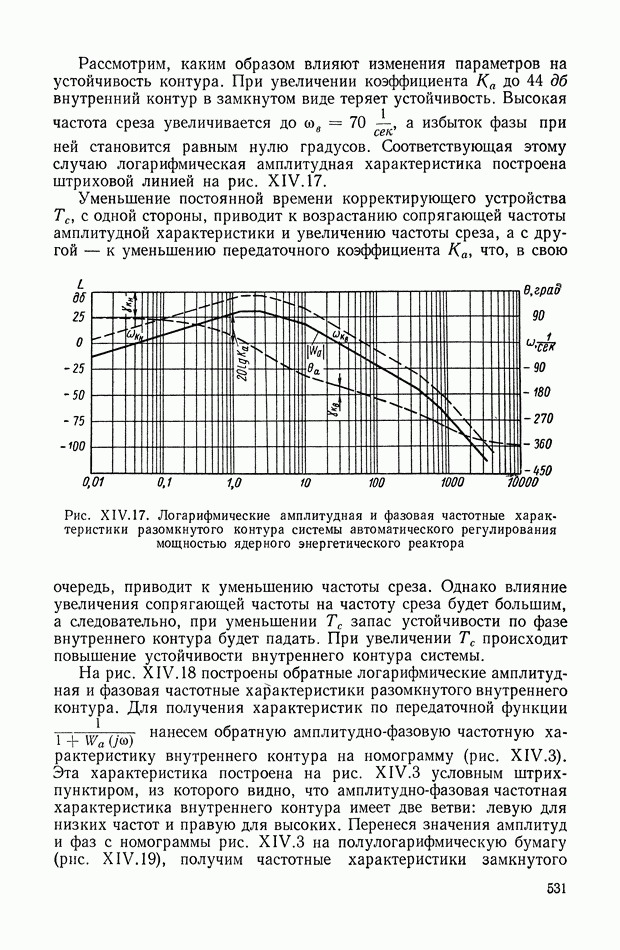
- 4. СИСТЕМА АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ МОЩНОСТИ ЯДЕРНОГО ЭНЕРГЕТИЧЕСКОГО РЕАКТОРА
- РАЗДЕЛ III. АНАЛИЗ ПЕРЕХОДНЫХ ПРОЦЕССОВ И КАЧЕСТВА ЛИНЕЙНЫХ НЕПРЕРЫВНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- ГЛАВА XV. ЧАСТОТНЫЙ МЕТОД АНАЛИЗА ПЕРЕХОДНЫХ ПРОЦЕССОВ
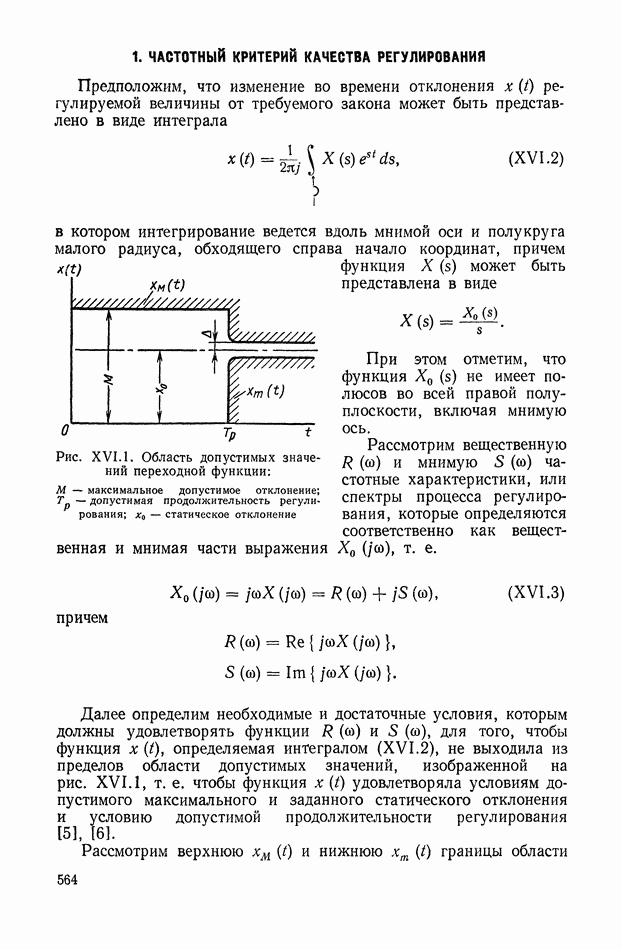
- 1. ОБОБЩЕННЫЕ ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ И ИХ СВЯЗЬ С ПЕРЕХОДНЫМИ ПРОЦЕССАМИ
- 2. ОПРЕДЕЛЕНИЕ ОБОБЩЕННЫХ ЧАСТОТНЫХ ХАРАКТЕРИСТИК В ОБЩЕМ СЛУЧАЕ
- 3. СЛУЧАЙ, КОГДА ФУНКЦИЯ X(s) НЕ СОДЕРЖИТ ОСОБЕННОСТЕЙ ВО ВСЕЙ ПРАВОЙ ПОЛУПЛОСКОСТИ И НА МНИМОЙ ОСИ
- 4. СВЯЗЬ МЕЖДУ ЧАСТОТНЫМИ ХАРАКТЕРИСТИКАМИ P(w), Q(w) И ИМПУЛЬСНОЙ ПЕРЕХОДНОЙ ФУНКЦИЕЙ k(t)
- 5. СЛУЧАЙ, КОГДА ВСЕ ПОЛЮСА ФУНКЦИИ X(s) РАСПОЛОЖЕНЫ В ЛЕВОЙ ПОЛУПЛОСКОСТИ, ЗА ИСКЛЮЧЕНИЕМ ПОЛЮСА В НАЧАЛЕ КООРДИНАТ
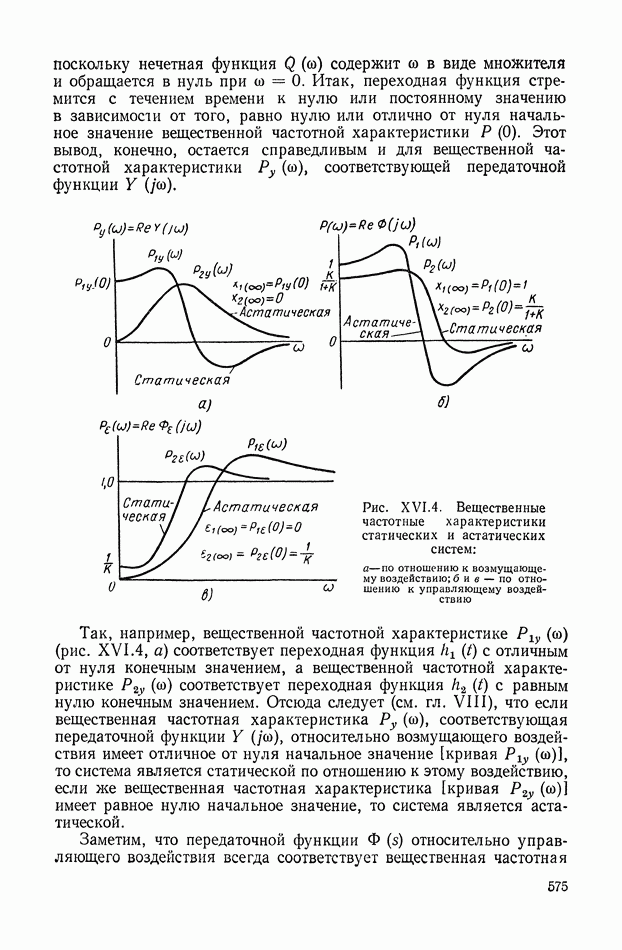
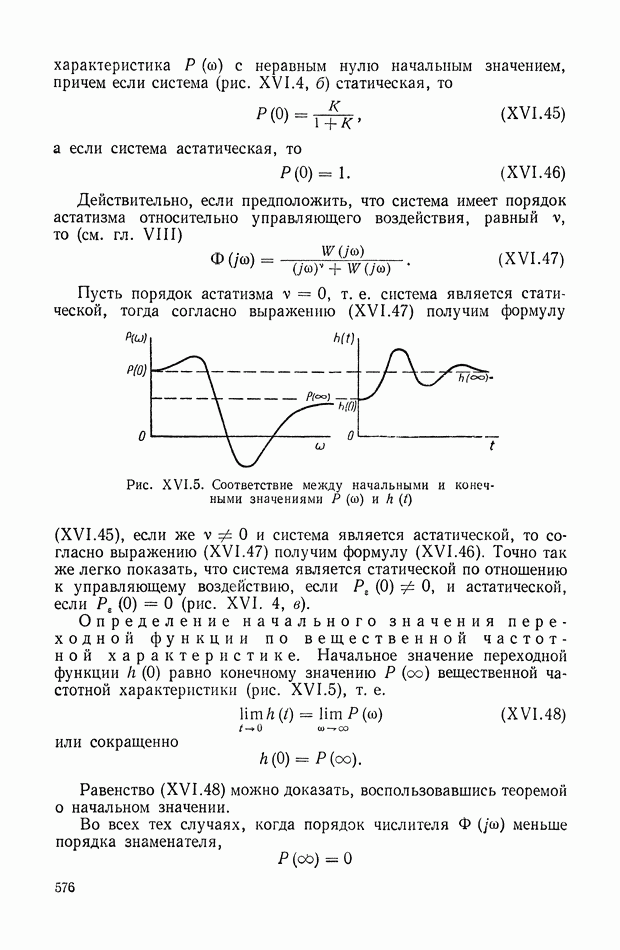
- 6. СВЯЗЬ МЕЖДУ ЧАСТОТНЫМИ ХАРАКТЕРИСТИКАМИ И ПЕРЕХОДНОЙ ФУНКЦИЕЙ h(t)
- 7. СЛУЧАЙ, КОГДА ФУНКЦИЯ X(s) ИМЕЕТ ДВА СОПРЯЖЕННЫХ ПОЛЮСА НА МНИМОЙ ОСИ
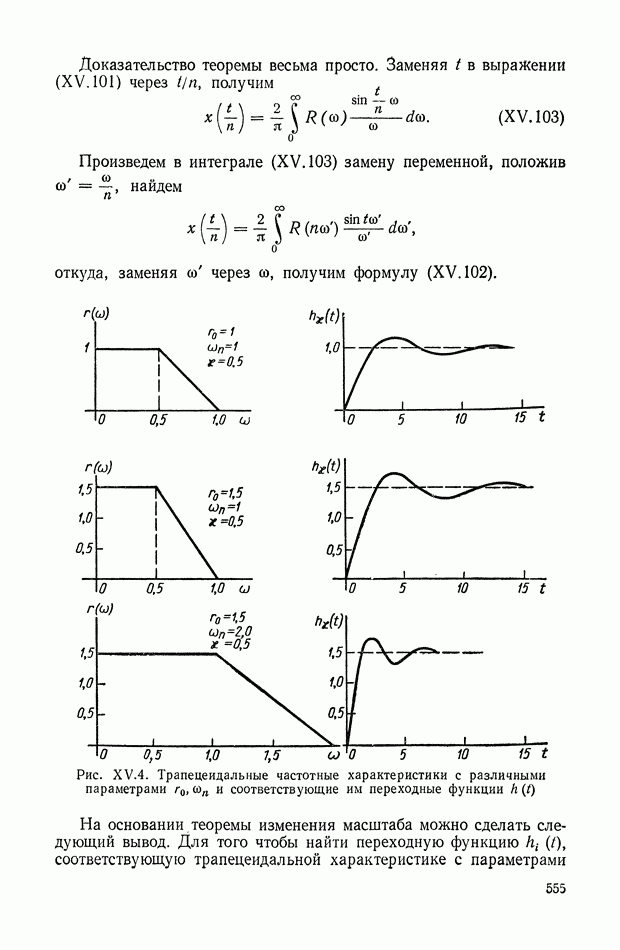
- 8. АНАЛИЗ ПЕРЕХОДНЫХ ПРОЦЕССОВ МЕТОДОМ ТРАПЕЦЕИДАЛЬНЫХ ЧАСТОТНЫХ ХАРАКТЕРИСТИК
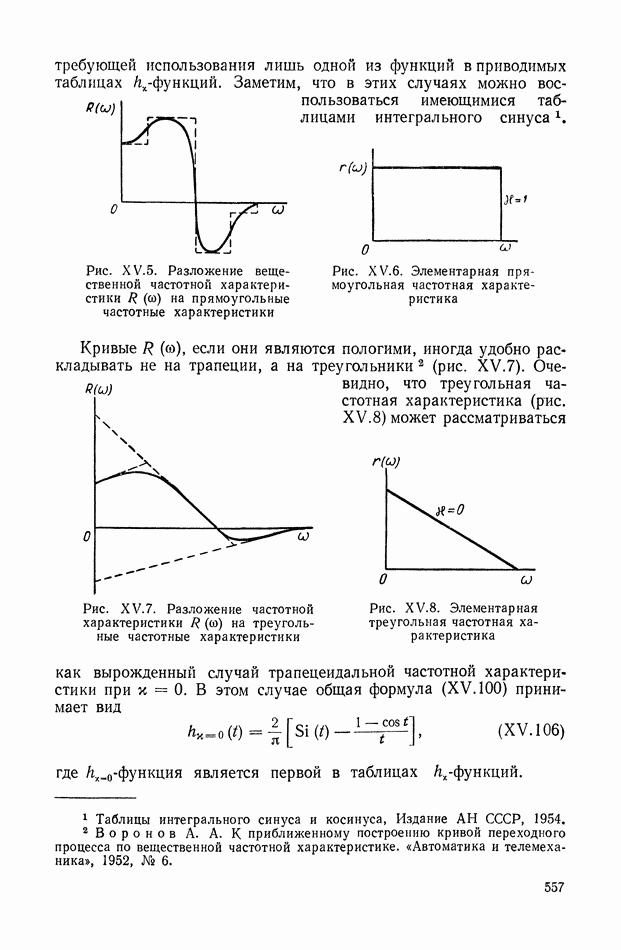
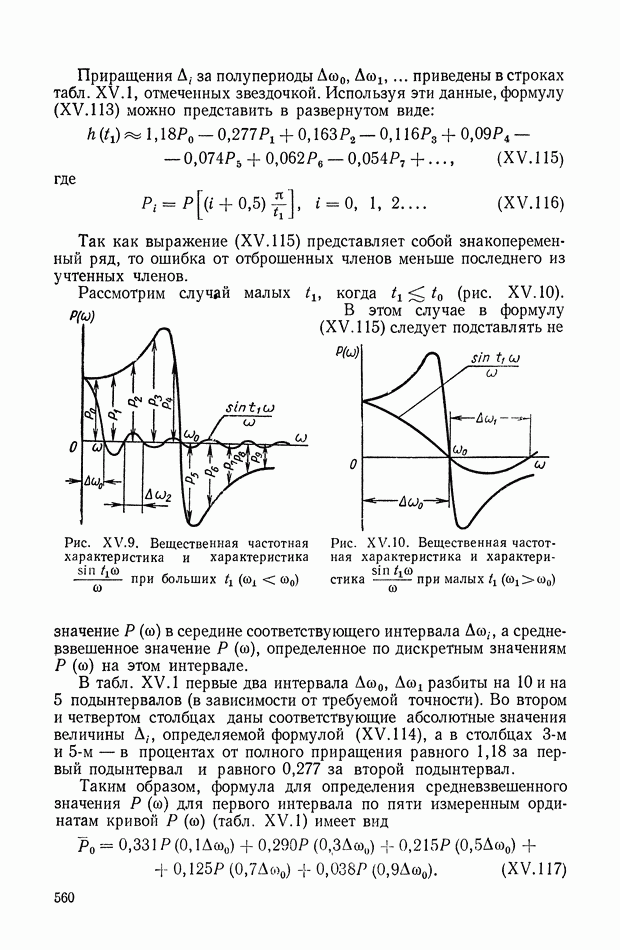
- 9. О НЕКОТОРЫХ ЧАСТНЫХ СЛУЧАЯХ МЕТОДА ТРАПЕЦЕИДАЛЬНЫХ ЧАСТОТНЫХ ХАРАКТЕРИСТИК
- 10. ОБ УСЛОВИЯХ ПРИМЕНИМОСТИ ЧАСТОТНОГО МЕТОДА АНАЛИЗА ПЕРЕХОДНЫХ ПРОЦЕССОВ
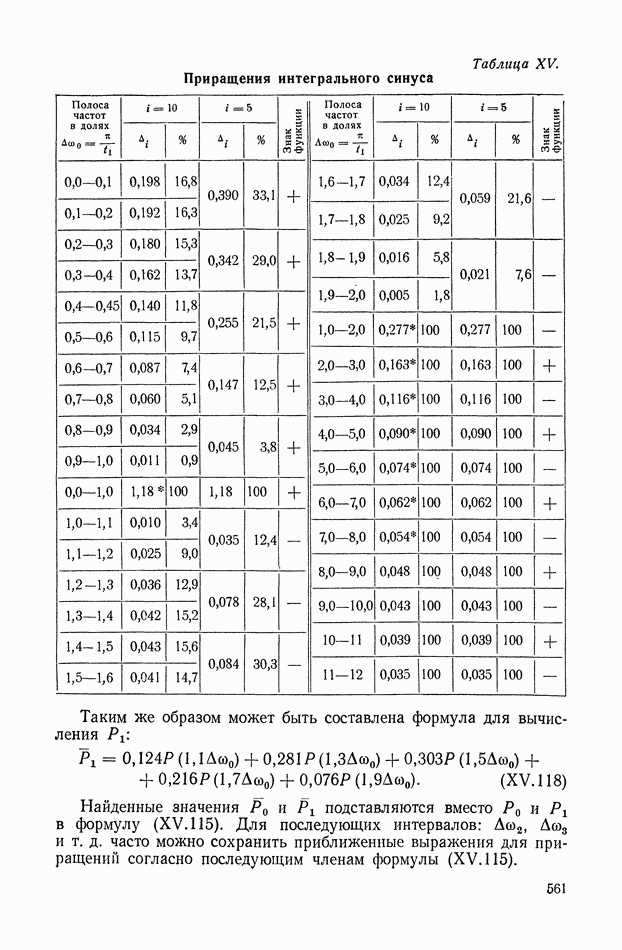
- 11. ОПРЕДЕЛЕНИЕ ДИСКРЕТНЫХ ЗНАЧЕНИЙ ПЕРЕХОДНОЙ ФУНКЦИИ
- ГЛАВА XVI. ЧАСТОТНЫЙ МЕТОД АНАЛИЗА КАЧЕСТВА
- 1. ЧАСТОТНЫЙ КРИТЕРИЙ КАЧЕСТВА РЕГУЛИРОВАНИЯ
- 2. ЧАСТОТНЫЙ КРИТЕРИЙ ОТСУТСТВИЯ ПЕРЕРЕГУЛИРОВАНИЙ И ЧАСТОТНЫЙ КРИТЕРИЙ МОНОТОННОСТИ
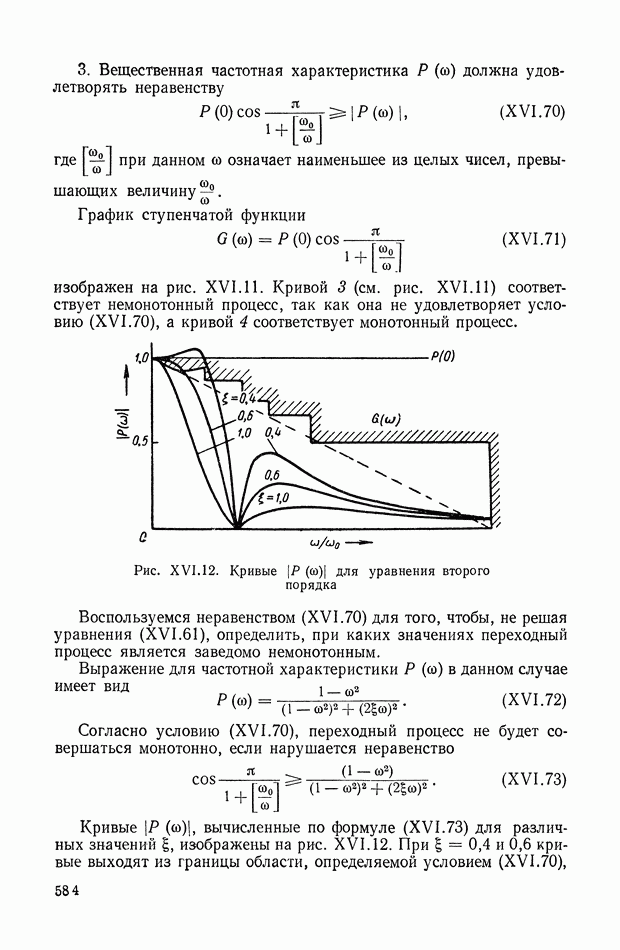
- 3. О ПРОВЕРКЕ ВЫПОЛНЕНИЯ СФОРМУЛИРОВАННЫХ КРИТЕРИЕВ
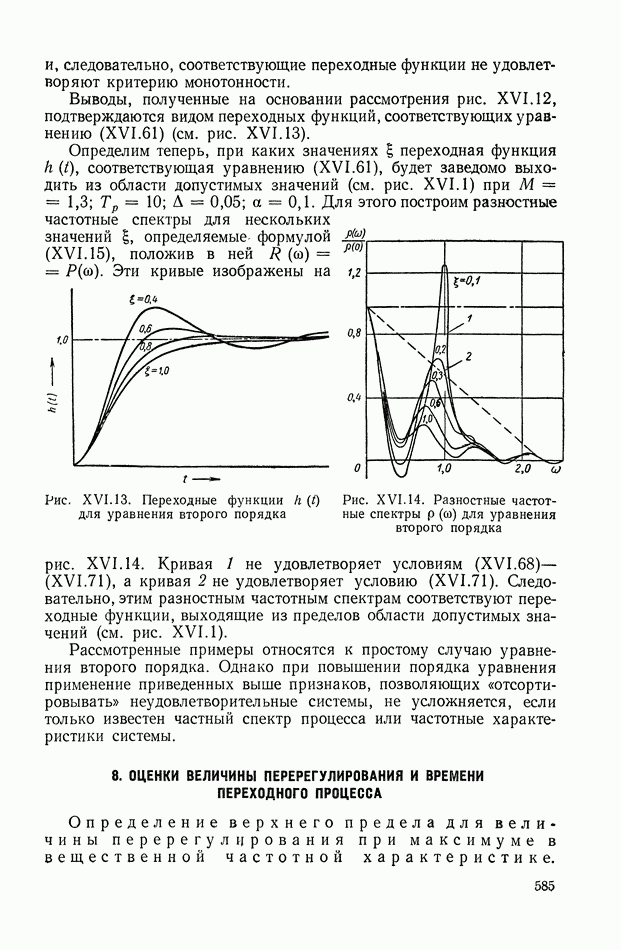
- 4. НЕКОТОРЫЕ ПРИЗНАКИ НЕУДОВЛЕТВОРЕНИЯ КРИТЕРИЕВ КАЧЕСТВА И КРИТЕРИЕВ ОТСУТСТВИЯ ПЕРЕРЕГУЛИРОВАНИЙ И МОНОТОННОСТИ
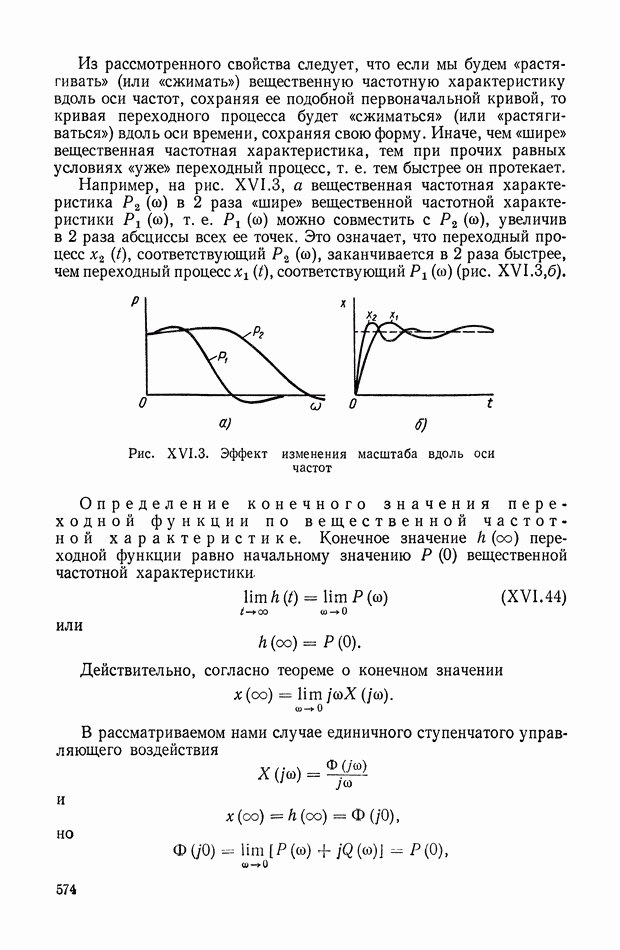
- 5. НЕКОТОРЫЕ ЭЛЕМЕНТАРНЫЕ СВОЙСТВА ЧАСТОТНЫХ ХАРАКТЕРИСТИК
- 6. ДОСТАТОЧНЫЕ УСЛОВИЯ ДЛЯ МАЛЫХ ПЕРЕРЕГУЛИРОВАНИЙ И НЕОБХОДИМЫЕ УСЛОВИЯ ДЛЯ ОТСУТСТВИЯ ПЕРЕРЕГУЛИРОВАНИЙ
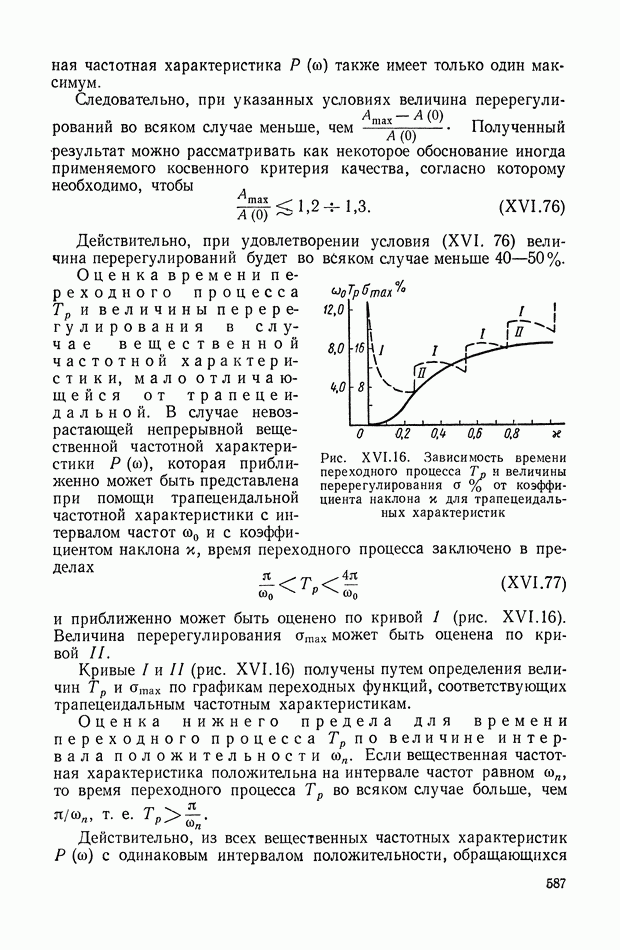
- 7. КРИТЕРИЙ, ОПРЕДЕЛЯЮЩИЙ ДОСТАТОЧНЫЕ УСЛОВИЯ ДЛЯ МОНОТОННОСТИ
- 8. ОЦЕНКИ ВЕЛИЧИНЫ ПЕРЕРЕГУЛИРОВАНИЯ И ВРЕМЕНИ ПЕРЕХОДНОГО ПРОЦЕССА
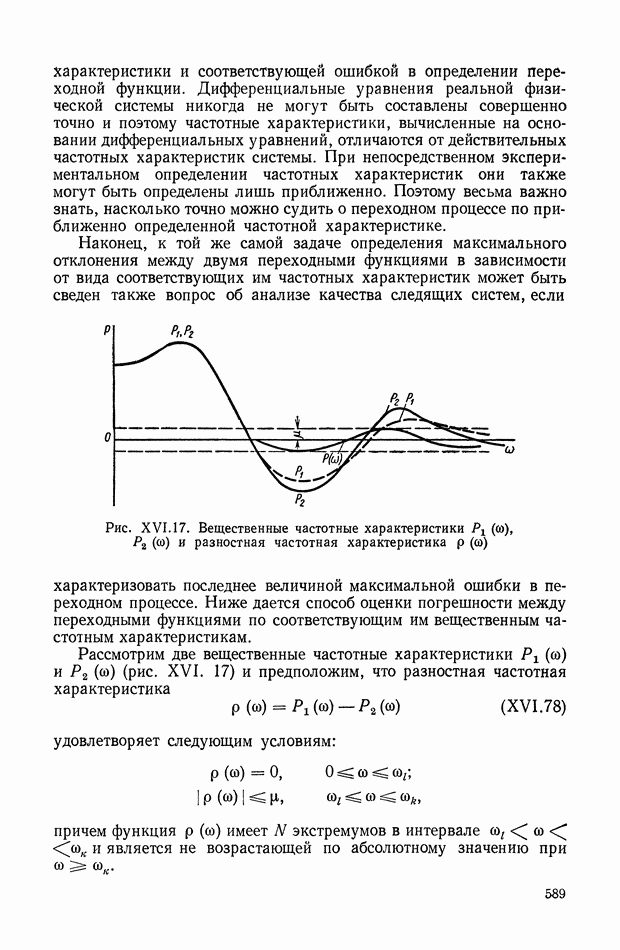
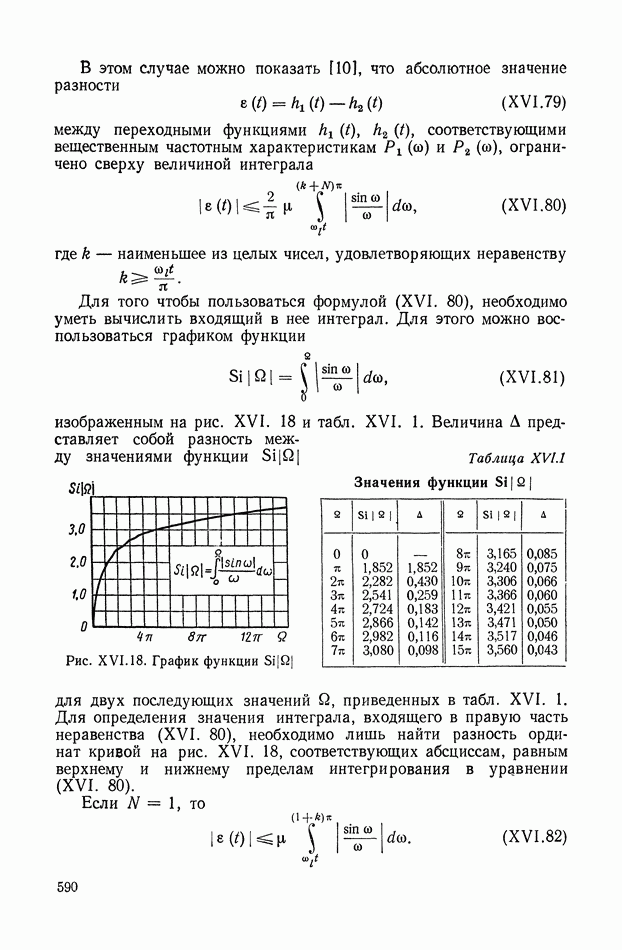
- 9. ОЦЕНКА АБСОЛЮТНОГО ЗНАЧЕНИЯ РАЗНОСТИ МЕЖДУ ПЕРЕХОДНЫМИ ФУНКЦИЯМИ ПО СООТВЕТСТВУЮЩИМ ИМ ЧАСТОТНЫМ ХАРАКТЕРИСТИКАМ
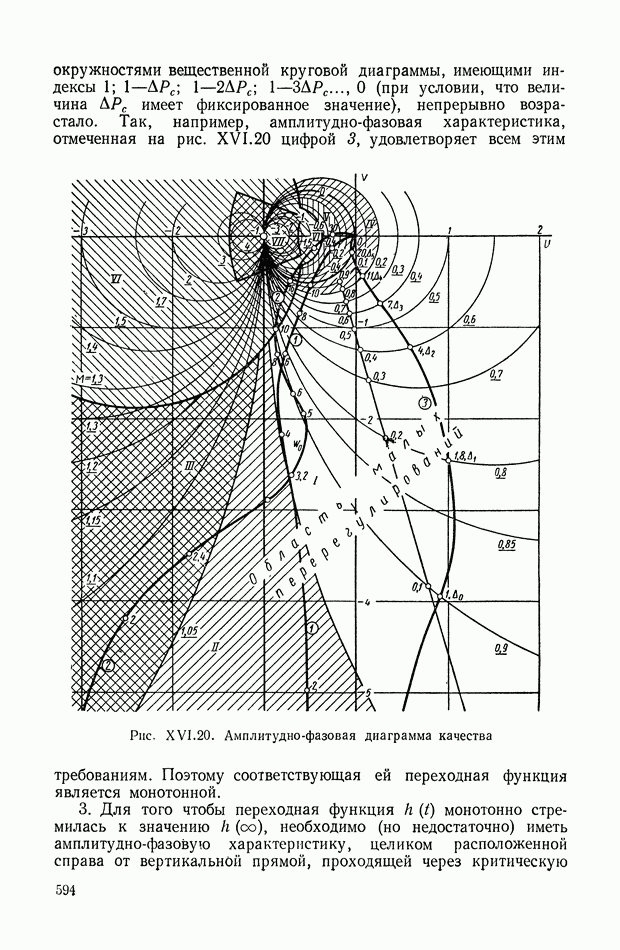
- 10. СВЯЗЬ МЕЖДУ СВОЙСТВАМИ АМПЛИТУДНО-ФАЗОВОЙ ХАРАКТЕРИСТИКИ РАЗОМКНУТОЙ СИСТЕМЫ И КАЧЕСТВОМ
- 11. ТРЕБОВАНИЯ К ЧАСТОТНЫМ ХАРАКТЕРИСТИКАМ, ОБЕСПЕЧИВАЮЩИЕ ВЫСОКУЮ ТОЧНОСТЬ В СЛЕДЯЩИХ СИСТЕМАХ
- 12. СВЯЗЬ МЕЖДУ СВОЙСТВАМИ ЛОГАРИФМИЧЕСКОЙ АМПЛИТУДНОЙ ХАРАКТЕРИСТИКИ И КАЧЕСТВОМ
- 13. ОПРЕДЕЛЕНИЕ ВЕЛИЧИНЫ ПЕРЕДАТОЧНОГО КОЭФФИЦИЕНТА ИЛИ ДОБРОТНОСТИ ПО ЛОГАРИФМИЧЕСКОЙ АМПЛИТУДНОЙ ХАРАКТЕРИСТИКЕ
- 14. ОПРЕДЕЛЕНИЕ УСТАНОВИВШЕЙСЯ ОШИБКИ ПРИ ГАРМОНИЧЕСКОМ УПРАВЛЯЮЩЕМ ВОЗДЕЙСТВИИ ПО ЛОГАРИФМИЧЕСКОЙ АМПЛИТУДНОЙ ХАРАКТЕРИСТИКЕ
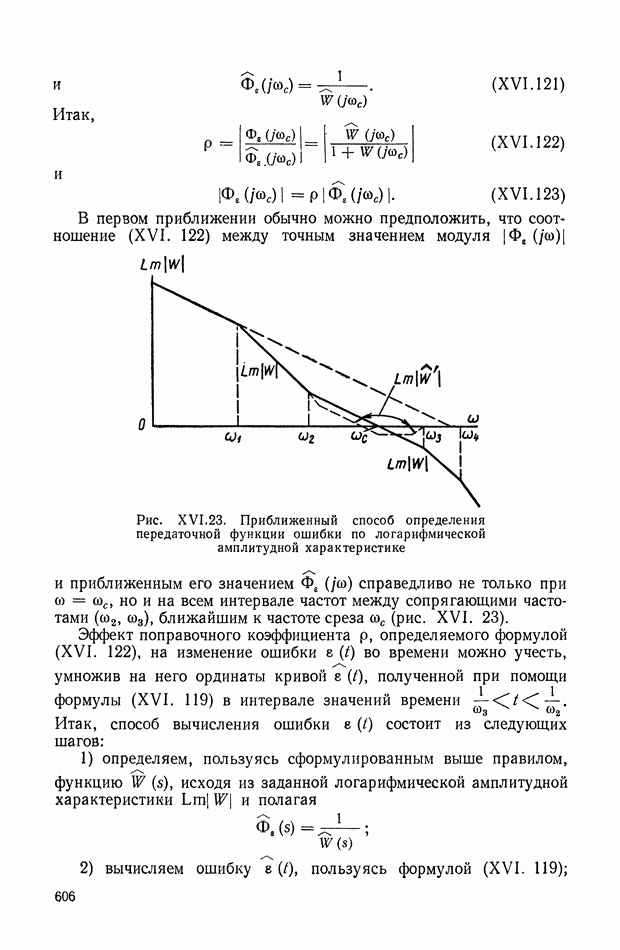
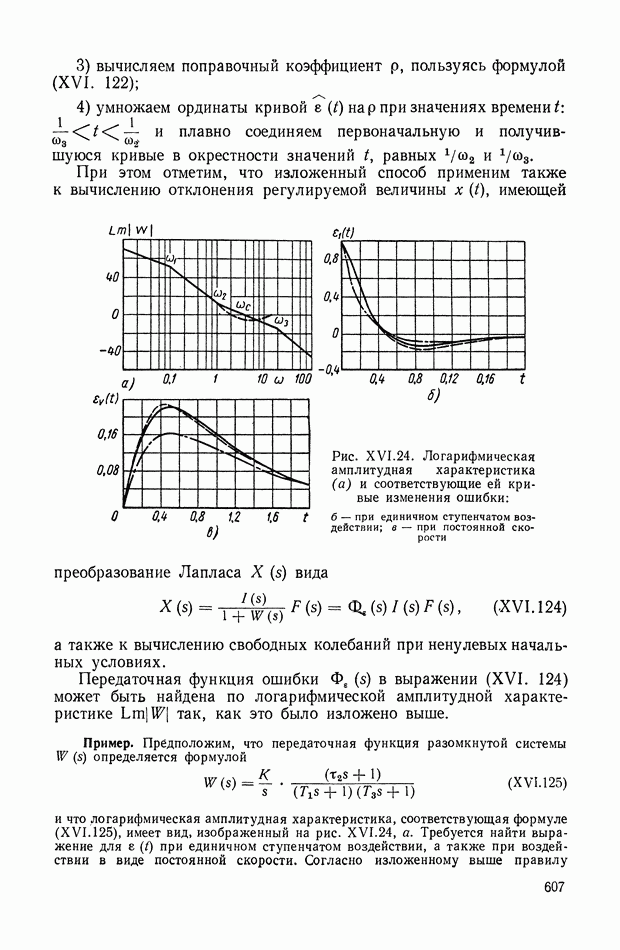
- 15. ПРИБЛИЖЕННЫЙ СПОСОБ ВЫЧИСЛЕНИЯ ПЕРЕХОДНОГО ПРОЦЕССА ПО СОПРЯГАЮЩИМ ЧАСТОТАМ ЛОГАРИФМИЧЕСКОЙ АМПЛИТУДНОЙ ЧАСТОТНОЙ ХАРАКТЕРИСТИКИ
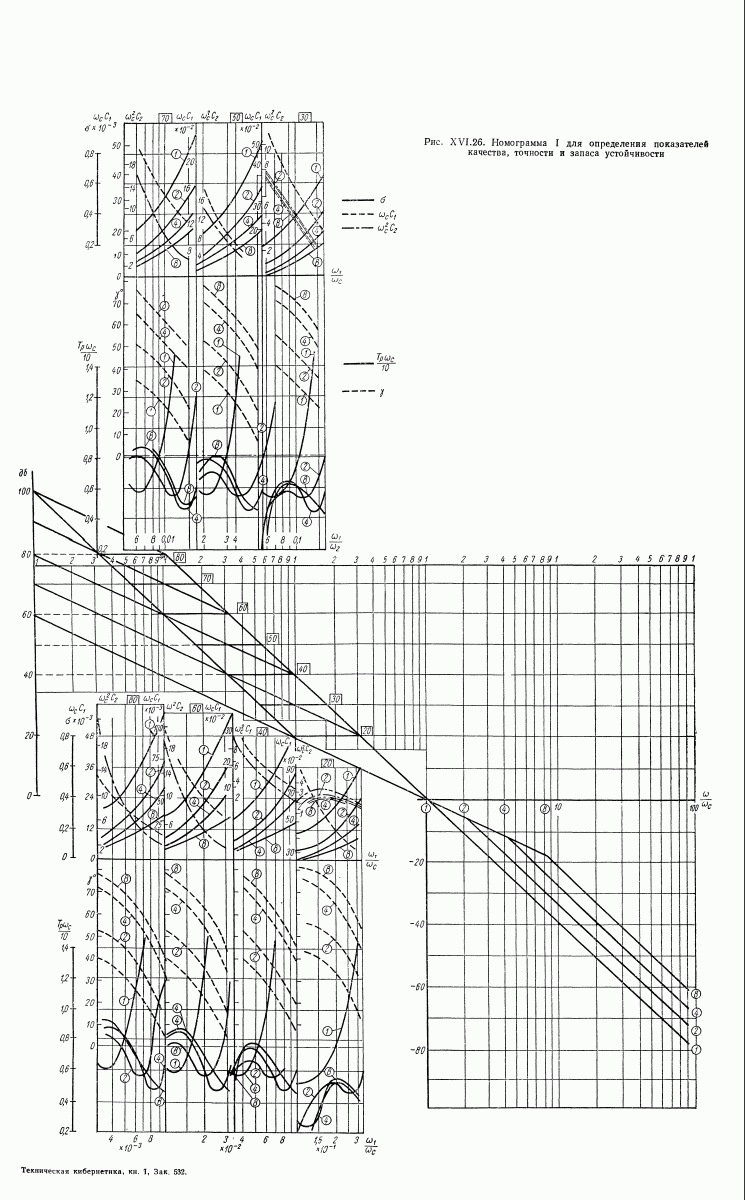
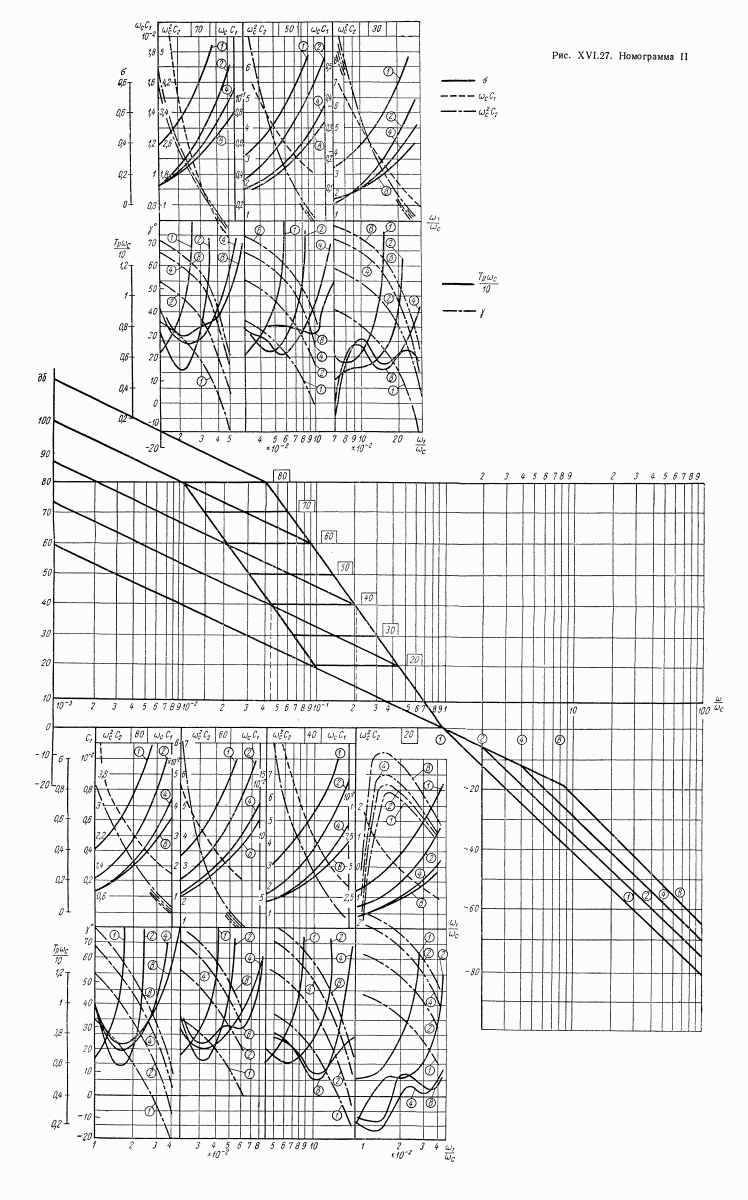
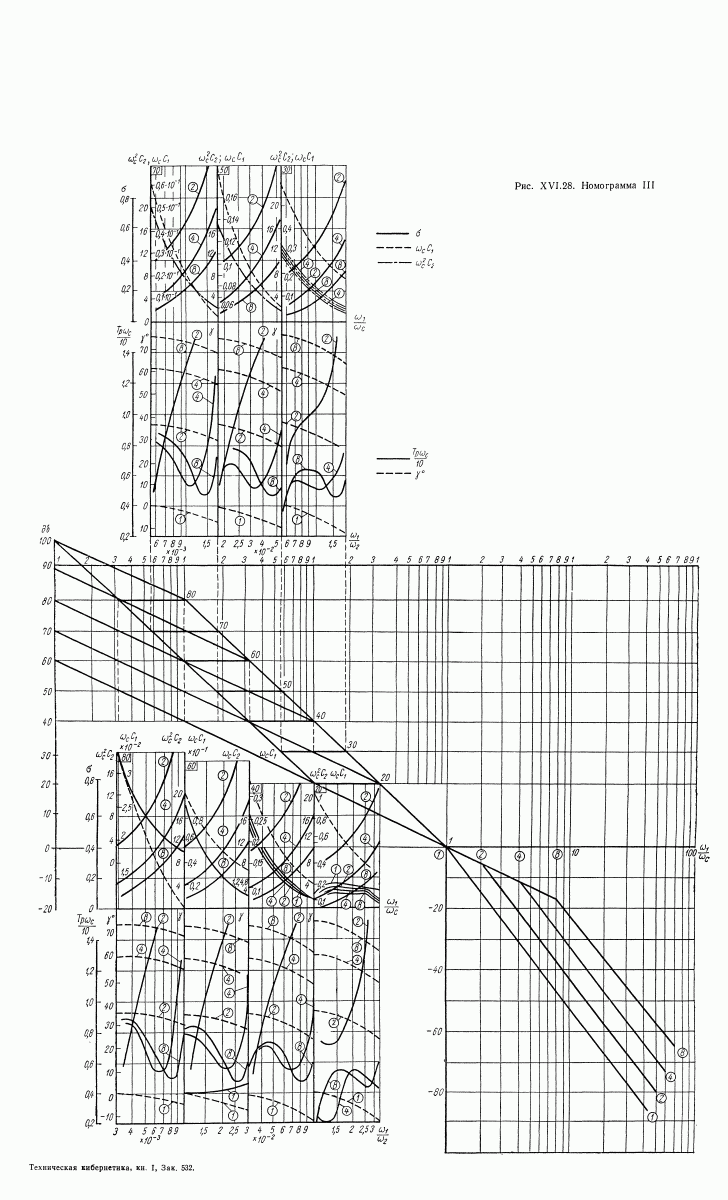
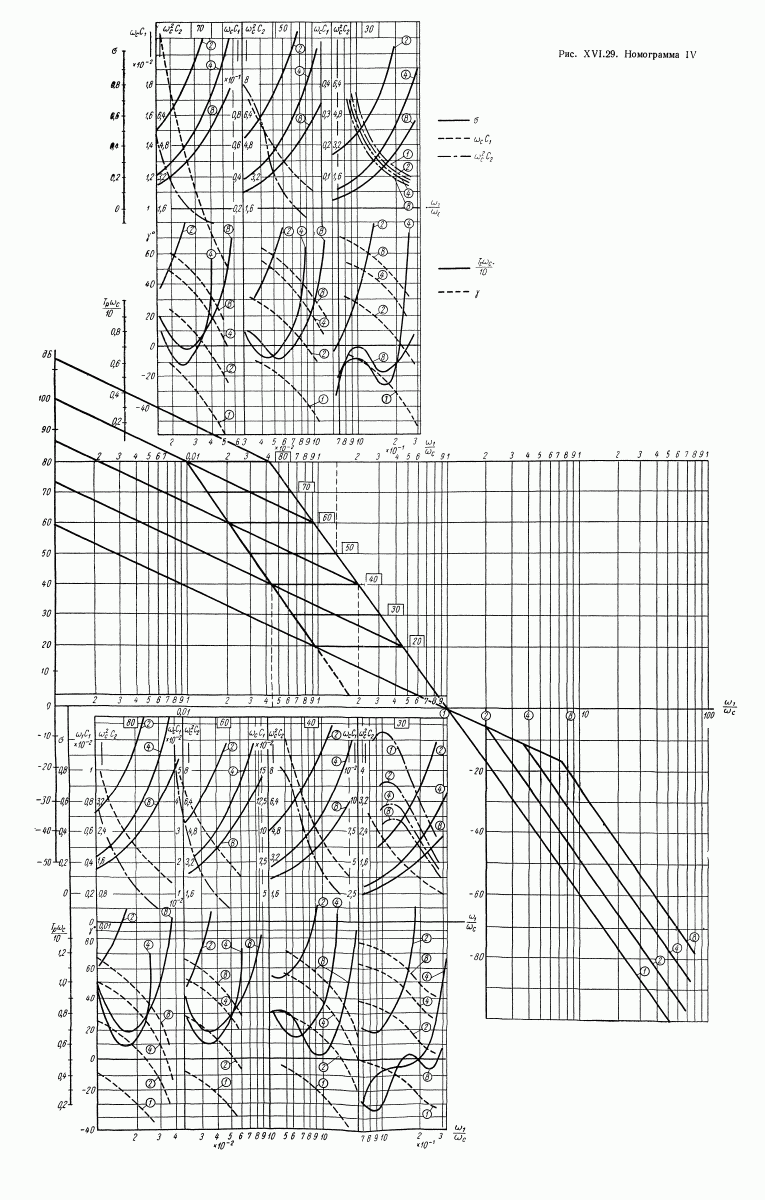
- 16. НОМОГРАММА ДЛЯ ОПРЕДЕЛЕНИЯ ЗАПАСА УСТОЙЧИВОСТИ, ПОКАЗАТЕЛЕЙ КАЧЕСТВА И КОЭФФИЦИЕНТОВ ОШИБОК ПО ВИДУ ЛОГАРИФМИЧЕСКОЙ АМПЛИТУДНОЙ ХАРАКТЕРИСТИКИ
- ГЛАВА XVII. СВЯЗЬ МЕЖДУ КАЧЕСТВОМ ПЕРЕХОДНОГО ПРОЦЕССА И РАСПРЕДЕЛЕНИЕМ НУЛЕЙ И ПОЛЮСОВ ПЕРЕДАТОЧНОЙ ФУНКЦИИ. МЕТОД КОРНЕВЫХ ГОДОГРАФОВ
- 2. АНАЛИЗ РАСПРЕДЕЛЕНИЯ КОРНЕЙ ХАРАКТЕРИСТИЧЕСКОГО УРАВНЕНИЯ СИСТЕМЫ И ОЦЕНКА КАЧЕСТВА ПЕРЕХОДНОГО ПРОЦЕССА
- 3. ГЕОМЕТРИЧЕСКИЙ МЕТОД ПОСТРОЕНИЯ КОРНЕВОГО ГОДОГРАФА
- 4. АНАЛИТИЧЕСКОЕ ПОСТРОЕНИЕ ГЕОМЕТРИЧЕСКОГО МЕСТА КОРНЕЙ
- 5. ОПРЕДЕЛЕНИЕ ОБЛАСТЕЙ УСТОЙЧИВОСТИ ЛИНЕЙНЫХ СИСТЕМ МЕТОДОМ КОРНЕВОГО ГОДОГРАФА
- 6. ОЦЕНКИ ПАРАМЕТРОВ ПЕРЕХОДНОЙ И ЧАСТОТНОЙ ХАРАКТЕРИСТИК ПО КОРНЕВОМУ ГОДОГРАФУ
- 7. ВЛИЯНИЕ РАСПОЛОЖЕНИЯ НУЛЕЙ И ПОЛЮСОВ ЗАМКНУТОЙ СИСТЕМЫ НА ПЕРЕХОДНУЮ ХАРАКТЕРИСТИКУ h(t)
- 8. ВЛИЯНИЕ РАСПОЛОЖЕНИЯ НУЛЕЙ И ПОЛЮСОВ ЗАМКНУТОЙ СИСТЕМЫ НА ЕЕ ПОЛОСУ ЧАСТОТ
- 9. КОРНЕВОЙ ГОДОГРАФ И ПЕРЕХОДНАЯ ХАРАКТЕРИСТИКА СИСТЕМЫ ПРИ ВОЗМУЩЕНИЯХ, ПРИЛОЖЕННЫХ НЕ К ОСНОВНОМУ ВХОДУ СИСТЕМЫ
- 10. ВЛИЯНИЕ РАСПРЕДЕЛЕНИЯ НУЛЕЙ И ПОЛЮСОВ ПЕРЕДАТОЧНОЙ ФУНКЦИИ НА КАЧЕСТВО ПЕРЕХОДНОГО ПРОЦЕССА ПРИ НАЛИЧИИ ВНЕШНЕГО ВОЗДЕЙСТВИЯ
- ГЛАВА XVIII. МЕТОД ЛОГАРИФМИЧЕСКИХ КОРНЕВЫХ ГОДОГРАФОВ
- 2. ОПРЕДЕЛЕНИЕ КОРНЕЙ ЗАМКНУТОЙ СИСТЕМЫ ПО ЛОГАРИФМИЧЕСКОЙ АМПЛИТУДНОЙ КОМПЛЕКСНО-ЧАСТОТНОЙ ХАРАКТЕРИСТИКЕ РАЗОМКНУТОЙ СИСТЕМЫ
- 3. ЛОГАРИФМИЧЕСКИЕ КОРНЕВЫЕ ГОДОГРАФЫ
- 4. ЛОГАРИФМИЧЕСКИЕ КОМПЛЕКСНО-ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЗВЕНЬЕВ ВТОРОГО ПОРЯДКА
- 5. ПРИМЕР ПОСТРОЕНИЯ ЛОГАРИФМИЧЕСКОГО КОРНЕВОГО ГОДОГРАФА
- ГЛАВА XIX. ИНТЕГРАЛЬНЫЕ ОЦЕНКИ И КРИТЕРИИ КАЧЕСТВА РЕГУЛИРОВАНИЯ
- 2. МЕТОДИКА ПРИМЕНЕНИЯ ИНТЕГРАЛЬНЫХ КВАДРАТИЧНЫХ ОЦЕНОК
- 3. ЛИНЕЙНЫЕ ИНТЕГРАЛЬНЫЕ ОЦЕНКИ
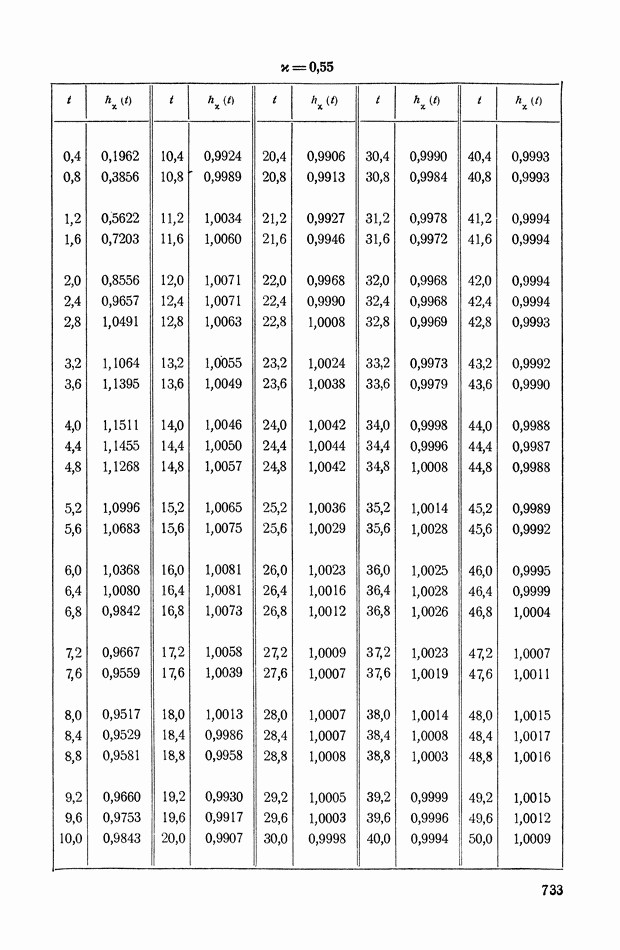
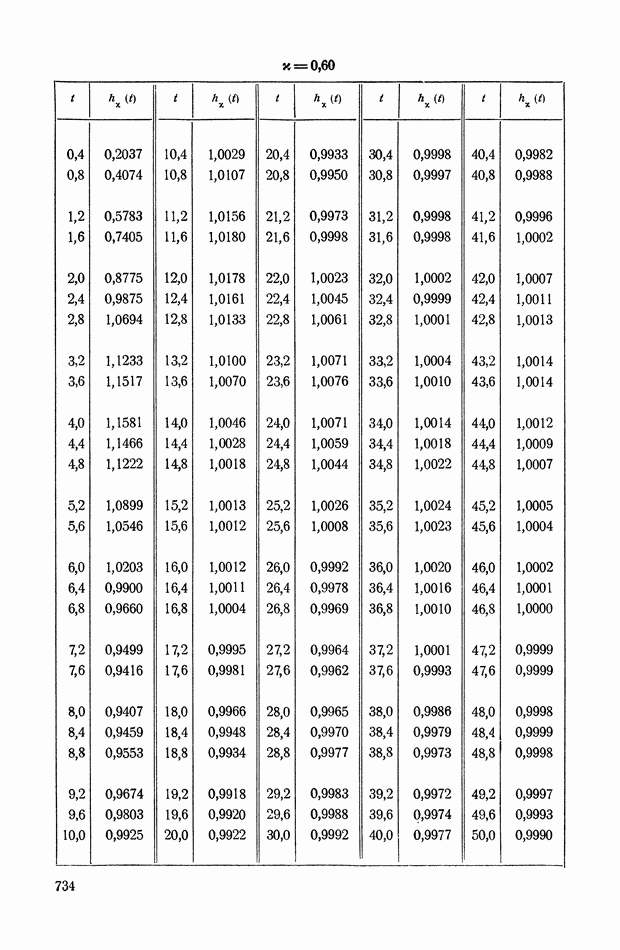
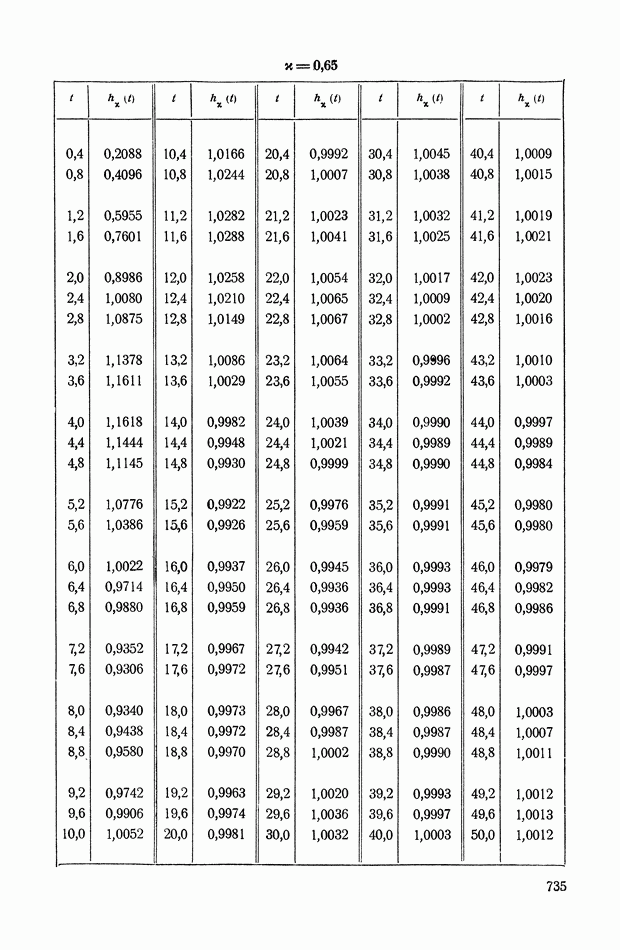
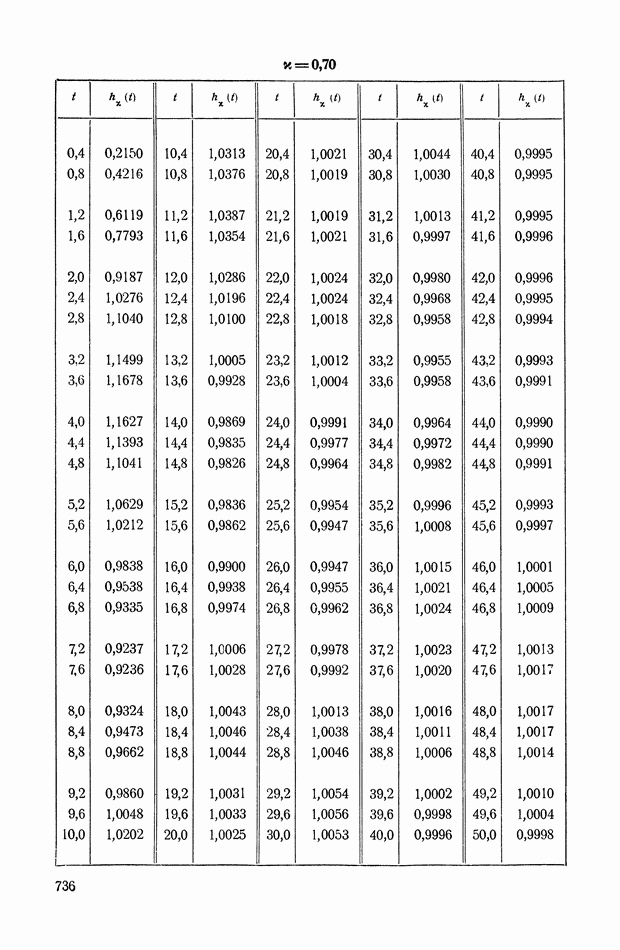
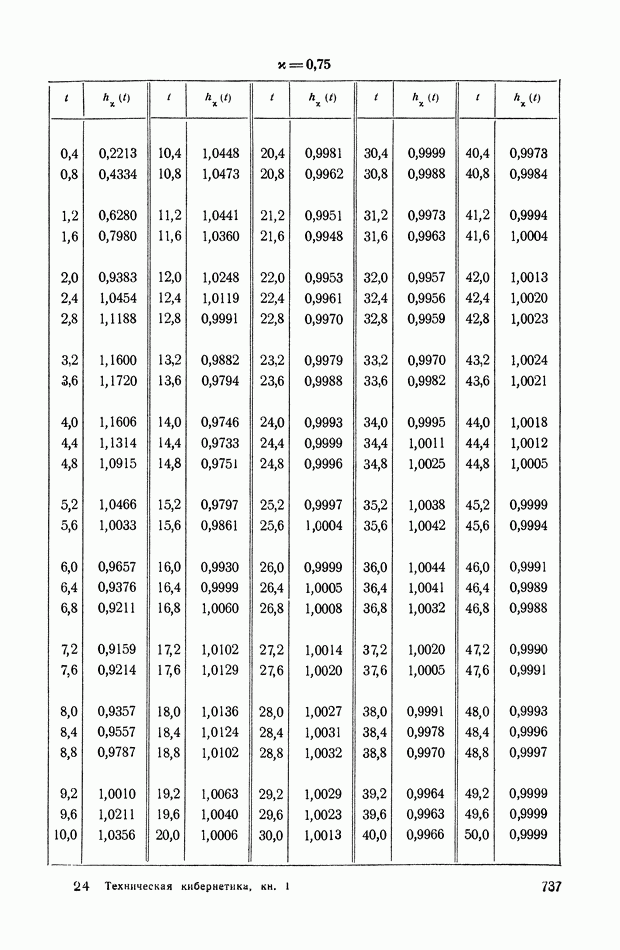
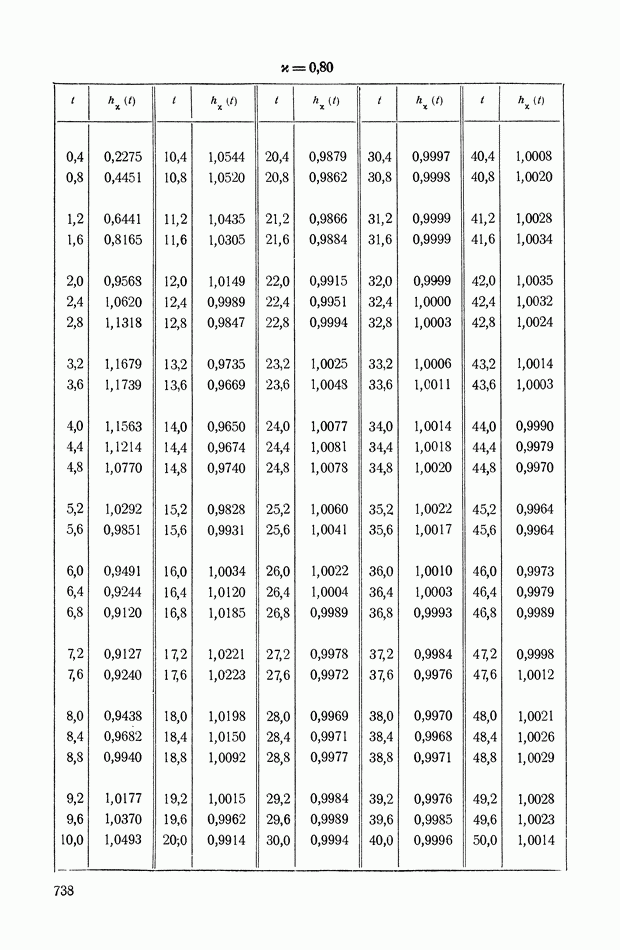
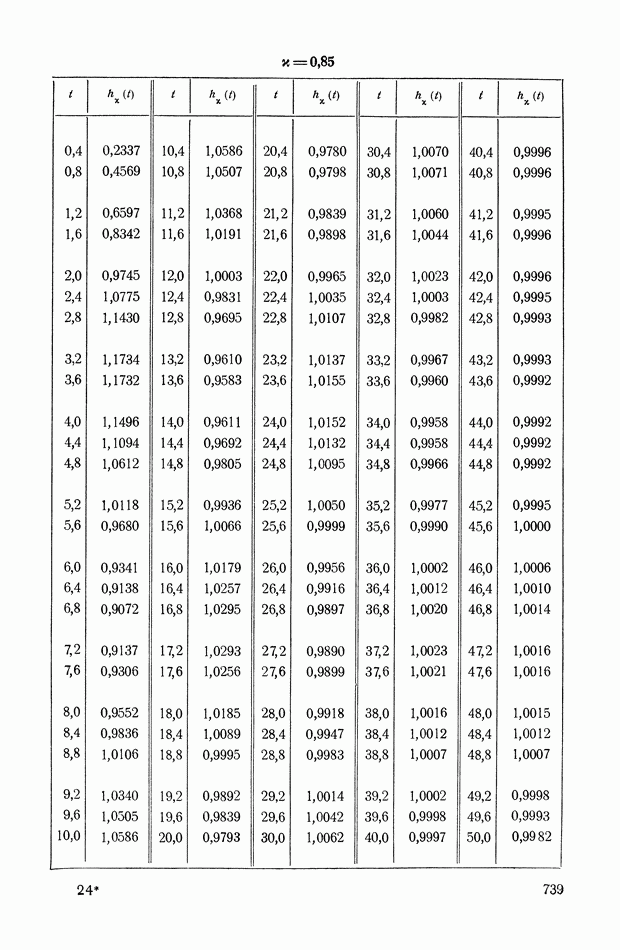
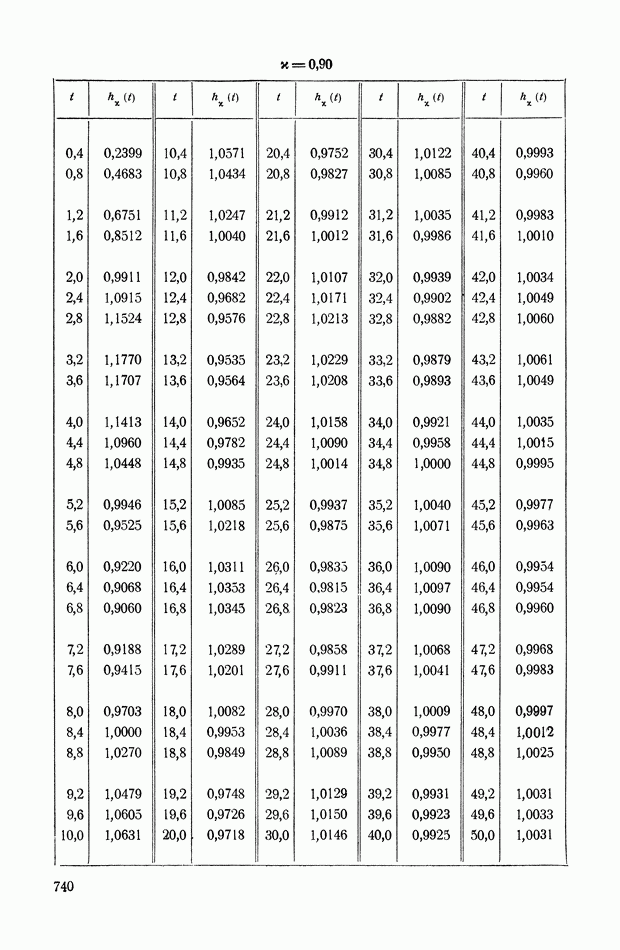
- ПРИЛОЖЕНИЕ
- БИБЛИОГРАФИЯ ПО РАЗДЕЛАМ КНИГИ