| Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ПРЕДИСЛОВИЕ К РУССКОМУ ИЗДАНИЮ
Книга Фавара представляет собой курс лекций, посвященный основным вопросам дифференциальной геометрии. От большинства сочинений этого рода она отличается тем, что автор поставил себе задачу включить классическую локальную, дифференциальную геометрию в круг идей, сыгравших значительную роль в развитии математики за последнее полустолетие. Мы имеем в виду в первую очередь идеи, связанные с теоретико-множественной и групповой точками зрения на вопросы математики. В дифференциальную геометрию эти идеи вошли, как известно, прежде всего через теорию римановых пространств и принцип относительности, затем через теорию непрерывных групп и метод Картана.
Все это и отражено в настоящей книге, представляющей собой вместе с тем и учебник, в котором систематически излагаются вопросы локальной дифференциальной геометрии.
Замысел книги оригинален, и его можно приветствовать. Следует отметить интересное и ясное изложение вводной части, особенно теории групп, как абстрактных, так и непрерывных. Однако не всегда автору удается сделать убедительной необходимость введения тех или иных понятий. Так, например, некоторые понятия топологии — размерность, канторово и обычное многообразие — в сущности остаются почти без приложений.. Не вполне удались автору и некоторые главы, например глава о преобразованиях касания и глава о параметризации. Тяжеловато изложение методом Картана начал теории кривых и поверхностей как в эвклидовом, так и в аффинном случае, но зато сам метод на этом простом материале становится очень ясным и выпуклым. Оригинально написана глава об огибающих.
Несмотря на указанные недостатки, книга написана очень интересно не только по замыслу, но и по выполнению. По ней можно научиться методу Картана и другим методам современной дифференциальной геометрии, она побуждает читателя к размышлениям об основах этой науки.
Главы I и II введения, часть I, главы I и II первого раздела и главы I и II второго раздела части II, а также часть III перевела Ю. А. Рожанская; остальные главы перевел С. П. Фиников.
С. П. Фиников
ПРЕДИСЛОВИЕ АВТОРА
«Дифференциальная геометрия готова утонуть в океане выкладок», — сказал мне один из моих товарищей. «Когда открываешь книгу по математическому анализу, - сказал другой, — видишь много рисунков и не так уж много выкладок, когда же открываешь книгу по геометрии, наоборот, рисунков почти не находишь, бросаются в глаза выкладки, поселяющие ужас среди наиболее усердных учащихся и приводящие в уныние профессиональных метематиков с не слишком акцентированными научными интересами. Не находится ли дифференциальная геометрия в состоянии упадка и не обязано ли нерасположение, которое некоторые к ней проявляют, тому, что она состарилась и что ее можно приукрасить лишь с помощью средств, столь же банальных, как румяна и драгоценности кокетки?»
Лично я этого не думаю; скорее я вижу в геометрии кризис роста, вызванный слишком быстрым ее развитием после успехов теории относительности. Теперь, когда усиленное производство работ приостановилось, можно выбрать время, чтобы подумать об основаниях и довести до совершенства методы, перед тем как отправиться дальше по новым путям.
Не говоря о глобальной дифференциальной геометрии, которая в части, соприкасающейся с алгебраической геометрией, сейчас находится в полном расцвете, в локальной дифференциальной геометрии в ее современном состоянии также имеется немало важных проблем, требующих решения; в ней имеются и курьезные пробелы — например, обычная кинематическая геометрия с числом параметров более двух до сих пор не получила своего развития, хотя, казалось бы, уже давно надо было заполнить этот пробел. Что же касается оснований дифференциальной геометрии, то о них едва-едва начали думать; я делаю здесь свой вклад в разработку этого вопроса, но он далеко еще недостаточный (например, с моей точки зрения, основания теории огибающих все еще неудовлетворительны).
Как, скажут мне, в книге, претендующей на модернизацию преподавания, вы считаете нужным еще говорить о теории касания, об огибающих, о преобразованиях касания — словом, о таких старых вопросах? Да! Я излагаю здесь эти теории и имею слабость находить их важными даже сегодня; что касается первой из них, то я считаю ее даже основной, ибо что такое локальная дифференциальная
геометрия, как не учение об элементах касания? Я не откажусь от моей точки зрения, пока мне не покажут, как можно преподавать анализ, не излагая или не предполагая известной "старую теорию действительных чисел.
Хотя во многих вопросах я решительно порвал с традициями, я все же старался сохранить переходный характер изложения, чтобы облегчить понимание многочисленных книг и работ, написанных в другом стиле.
К сожалению, сейчас в дифференциальной геометрии нет единого, всеми принятого метода, необходимо выбирать один из многих; и я остановился на методе Эли Картана, который мне кажется наилучшим; я думаю, что этот метод позволит без большого труда объединить в более обширном трактате наиболее трудоемкие результаты дифференциальной геометрии, получаемые теперь ценою изнурительных выкладок, причем эти выкладки в большинстве случаев значительно сократятся.
Мои намерения здесь более скромны — на пороге мирового кризиса, который готов охватить преподавание основ математики, я хотел бы внести свой вклад в дело сближения преподавания и научных исследований, и я полагаю, что прежде всего можно попытаться это сделать в дифференциальной геометрии, где отставание преподавания, пожалуй, менее велико, чем в анализе.
Всегда опасно писать книги для преподавания, ибо критика таких книг особенно легка: обучать — значит выбирать, направлять, а это трудные искусства. Как сказано выше, я решил написать книгу переходного характера, которая, я надеюсь, может принести пользу. Кое-кто мне поставит в упрек, что я придаю слишком много значения классической геометрии; я мог бы перенести всю ее в упражнения после общей теории вложенных многообразий, которой заканчивается введение, но я решил, что это было бы преждевременно и даже чрезмерно. Другие, напротив, будут сожалеть о прекрасных страницах, которые некогда посвящались теории асимптотических линий и линий кривизны; я рассудил, что это — уже прошлое, но некоторые результаты в этом направлении включил в упражнения.
Книга содержит введение, где первая глава (ее можно пропустить при первом чтении) посвящена основаниям; мне казалось, что требовательность в отношении аксиоматики, характерная для современных курсов анализа, должна в какой-то мере найти отзвук и в дифференциальной геометрии.
Первая часть содержит, наряду с изложением классических вопросов прямой геометрии, существенные указания по проблемам параметризации.
Во второй части, посвященной изложению эвклидовой, аффинной унимодулярной и проективной геометрий, я должен был, естественно, ограничивать себя, и, быть может, кое-кто найдет, что я отвел слишком много места метрической эвклидовой геометрии.
В третьей части я излагаю теорию параллельного переноса в пространствах аффинной связности и римановых пространствах.
Желая сделать книгу, для пользы учащихся, не очень объемистой, я должен был отказаться от мысли поместить в ней изложение теории гексагональной конфигурации (которая представляет интерес хотя бы для демонстрации того, что прямая геометрия не окаменела, как слишком часто думают), аффинной и проективной линейчатой геометрии, а также теории пространств Финслера и Кавагучи. Наоборот, повторения казались мне необходимыми, поэтому понятия параллельного переноса и ковариантной производной излагаются сначала при изучении линейного элемента  поверхности, а потом повторяются с общей точки зрения в третьей части.
поверхности, а потом повторяются с общей точки зрения в третьей части.
Моя цель будет достигнута, если мне удастся зародить у читателя чувство неудовлетворенности, создать впечатление незаконченности, одновременно возбуждая интерес и любопытство.
Я благодарю Декомба, ныне читающего университетский курс в Лилле, за помощь при редактировании старого литографированного издания этого курса, благодарю Деама и Хаддада, воспитанников Высшей Нормальной Школы, которые просмотрели рукопись курса, аббата Мирге и Гальвани, профессора университета в Гренобле, которые пожелали прочесть корректуры.
Г. Жюлиа включил эту книгу в серию "Cahiers Scientifiques", которой он руководит, — я приношу ему здесь свою благодарность.
Я признателен также издательству Готье-Вийар, которое осуществило издание и проявило обычное внимание к набору книги.
ПРЕДУПРЕЖДЕНИЕ
Книга содержит введение и три части; вторая часть делится на три раздела. Ссылки даются следующим образом: введение обозначается знаком 0, части — римскими цифрами I, II и III; разделы второй части обозначаются индексами наверху: II1, II2, II3; номера глав обозначаются после этого римскими цифрами, номера параграфов — арабскими цифрами; наконец, вторая арабская цифра указывает номер соотношения в данном параграфе, к которому относится ссылка.
Например, (О, III, 9.7) — ссылка на формулу (9.7), которая находится в параграфе 9 главы III введения.
Когда идет речь о ссылке на ту же часть, номер этой части в ссылке не обозначается; например, (III, 9.7) означает, что надо искать формулу (9.7) в главе III той же части. Если речь идет о ссылке на ту же главу, то и номер главы опускается.
Чтобы облегчить розыски, номер параграфа всегда повторяется перед номером формулы.
| Следующий параграф >> |
- ПРЕДИСЛОВИЕ К РУССКОМУ ИЗДАНИЮ
- ВВЕДЕНИЕ
- Глава I. ОБЩИЕ ПОНЯТИЯ. ОСНОВАНИЯ
- 2. Топологические пространства.
- 3. Подпространства.
- 4. Непрерывные функции.
- 5. Гомеоморфизм.
- 6. Метрические пространства.
- 7. Полные пространства. Компактные пространства и множества.
- 8. Связные пространства и множества.
- 9. Эвклидово аморфное пространство.
- 10. Симплексы. Комплексы.
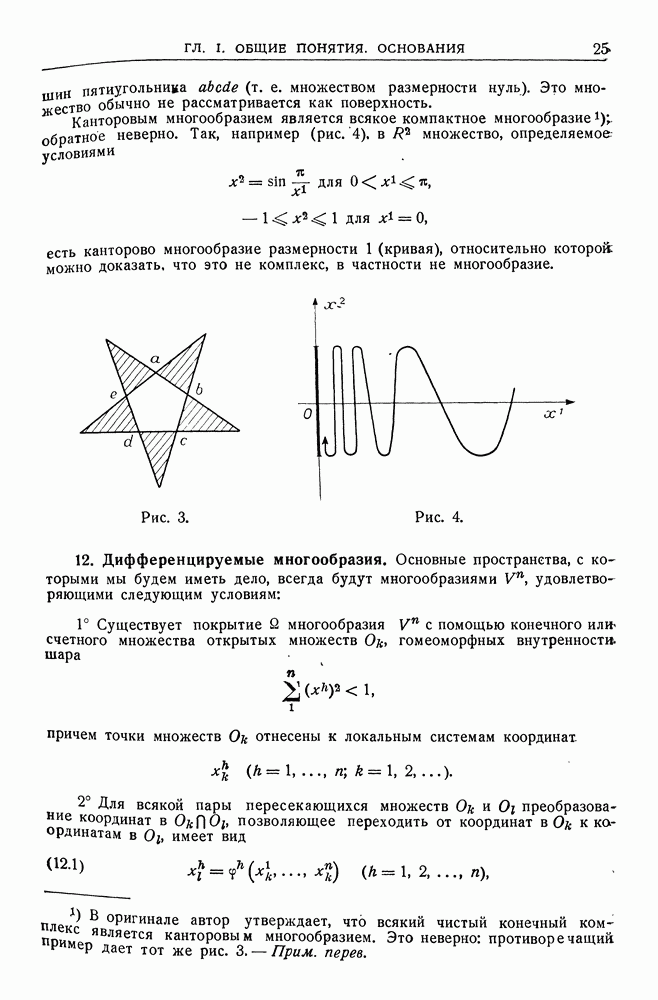
- 11. Размерность. Кривые и поверхности. Канторовы многообразия.
- 12. Дифференцируемые многообразия.
- 13. Общие свойства групп.
- 14. Преобразования. Группы преобразований.
- 15. Топологические группы.
- 16. Группы Ли.
- 17. Геометрические объекты. Транзитивность и интранзитивность. Ориентация.
- 18. Группы Ли классических геометрий.
- 19. Группа движений.
- 20. Аффинная группа.
- 21. Проективная группа.
- 22. Группы дифференциальной геометрии.
- 23. Дополнение о коллинеациях.
- Глава II. ДОПОЛНЕНИЕ К АЛГЕБРЕ. ТЕНЗОРЫ
- 1. Векторное центро-аффинное пространство Сn.
- 2. Тензорные произведения центро-аффинных пространств. Тензоры.
- 3. Аффинные тензоры.
- 4. Соглашение об обозначениях.
- 5. Операции над аффинными тензорами.
- 6. Симметричные и антисимметричные тензоры.
- 7. Антисимметричные контравариантные тензоры. Мультивекторы.
- 8. Антисимметричные ковариантные векторы. Внешние формы.
- 9. Внешние квадратичные формы. Теорема Картана.
- 10. Эвклидовы тензоры.
- 11. Элементарный тензорный анализ.
- Глава III. ДОПОЛНЕНИЯ К АНАЛИЗУ: ВНЕШНЕЕ ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ; ПРИЛОЖЕНИЯ К ГРУППАМ ЛИ И К ОБЩЕЙ ТЕОРИИ ПОГРУЖЕННЫХ МНОГООБРАЗИЙ
- 1. Внешние дифференциальные формы.
- 2. Система Пфаффа. Теорема Фробениуса.
- 3. Группы Ли. Инфинитезимальные преобразования. Относительные и абсолютные компоненты.
- 4. Первая теорема Ли.
- 5. Группа параметров.
- 6. Уравнения структуры Эли Картана.
- 7. Уравнения структуры классических групп.
- 8. Элементы касания, погруженные в многообразие. Продолжение группы преобразований.
- 9. Общая теория погруженных многообразий.
- 10. Метод подвижного репера Эли Картана.
- ПЕРВАЯ ЧАСТЬ. ПРЯМАЯ ИНФИНИТЕЗИМАЛЬНАЯ ГЕОМЕТРИЯ
- Глава I. ВЛОЖЕННЫЕ МНОГООБРАЗИЯ. ПАРАМЕТРИЗАЦИЯ
- 2. Вложенные многообразия. Основной локальный инвариант. Обыкновенные точки.
- 3. Контингенция. Паратингенция.
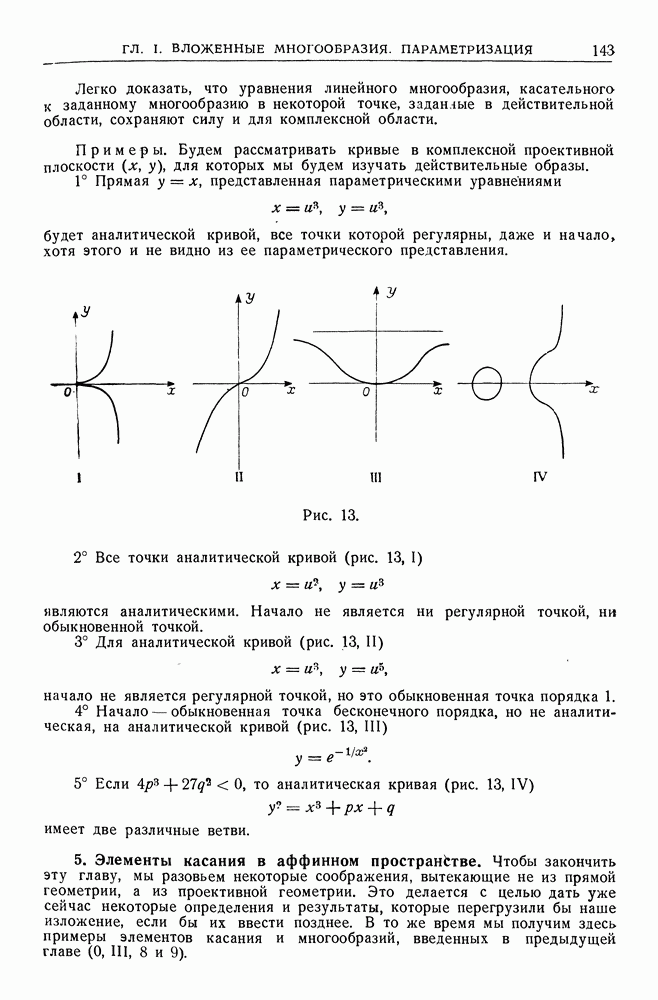
- 4. Аналитические многообразия. Регулярные точки.
- 5. Элементы касания в аффинном пространстве.
- 6. Соприкасающаяся плоскость и соприкасающаяся полуплоскость кривой в пространстве E3. Вогнутость.
- Глава II. ТЕОРИЯ КАСАНИЯ
- 2. Касание двух кривых.
- 3. Касание кривой и поверхности.
- 4. Касание двух поверхностей.
- Глава III. ОГИБАЮЩИЕ
- 2. Огибающие плоских кривых.
- 3. Огибающие поверхностей, зависящих от одного параметра.
- 4. Огибающие поверхностей, зависящих от двух параметров.
- 5. Огибающие пространственных кривых, зависящих от одного параметра.
- 6. Конгруэнции кривых.
- Глава IV. ПРЕОБРАЗОВАНИЯ КАСАНИЯ
- 1. Примыкающие элементы касания.
- 2. Преобразования касания.
- 3. Примеры.
- ВТОРАЯ ЧАСТЬ. КЛАССИЧЕСКИЕ ГЕОМЕТРИИ
- Глава I. ТЕОРИЯ ПРОСТРАНСТВЕННЫХ КРИВЫХ
- 2. Формулы Серре-Френе.
- 3. Триэдр Френе.
- 4. Кривизна и кручение.
- 5. Положение кривой в окрестности точки по отношению к триэдру Серре — Френе. Знак кручения.
- 6. Определение кривой ее натуральными уравнениями.
- 7. Винтовые линии.
- 8. Конгруэнция нормалей к пространственной кривой.
- 9. Замечания.
- 10. Изотропные кривые (или минимальные линии).
- Глава II. ТЕОРИЯ ПОВЕРХНОСТЕЙ; ТРИЭДР ФРЕНЕ
- 1. Триэдр Френе.
- 2. Особые случаи.
- 3. Поверхности, инвариантные относительно группы движений.
- 4. Теоремы равенства и существования.
- 5. Вычисление инвариантных линейных форм и кривизн.
- 6. Геодезические свойства. Внешние свойства.
- Глава III. ТЕОРИЯ ПОВЕРХНОСТЕЙ; ПЕРВАЯ ОСНОВНАЯ КВАДРАТИЧНАЯ ФОРМА
- 2. Минимальные линии (линии нулевой длины).
- 3. Конформное отображение одной поверхности на другую. Изотермические координаты.
- 4. Изометрия. Полная кривизна.
- 5. Изометричные поверхности.
- 6. Группа изометрии линейных элементов ds2 постоянной кривизны.
- 7. Поверхности, изометричные плоскости.
- 8. Вопросы анализа на поверхности.
- 9. Геодезические линии («внешняя» теория).
- 10. Геодезическая кривизна.
- 11. Поле векторов. Ковариантные частные производные Параллельный перенос.
- 12. Формула Оссиана Бонне.
- 13. Поле тензоров. Ковариантная производная.
- Глава IV. ТЕОРИЯ ПОВЕРХНОСТЕЙ, ВТОРАЯ ОСНОВНАЯ КВАДРАТИЧНАЯ ФОРМА
- 2. Расположение поверхности по отношению к касательной плоскости. Обыкновенные точки второго порядка.
- 3. Асимптотические линии.
- 4. Сопряженные направления. Сопряженные семейства кривых.
- 5. Триэдр Френе для кривой, проведенной на поверхности. Теоремы Менье и Оссиана Бонне.
- 6. Кривизна нормальных сечений. Индикатриса Дюпена.
- 7. Главные направления. Главные кривизны.
- 8. Линия кривизны. Эволюты, или поверхности центров кривизны поверхности.
- 9. Конгруэнции нормалей.
- 10. Примеры.
- 11. Сферическое изображение. Третья квадратичная форма поверхности.
- 12. Относительное кручение. Четвертая квадратичная форма.
- 13. Точечные преобразования и преобразования касания, сохраняющие асимптотические линии.
- 14. Точечные преобразования, сохраняющие линии кривизны.
- 15. Преобразование Ли. Преобразования касания, сохраняющие линии кривизны.
- 16. Возвращение к условиям интегрируемости.
- Глава V. ЛИНЕЙЧАТАЯ ЭВКЛИДОВА ГЕОМЕТРИЯ
- 1. Плюккеровы координаты.
- 2. Линейчатые поверхности.
- 3. Конгруэнции прямых.
- 4. Линейчатые поверхности конгруэнции.
- 5. Вычисление инвариантов. Квадратичные формы.
- 6. Формула Эли Картана. Конгруэнции нормалей.
- 7. Изотропные конгруэнции.
- 8. Комплексы прямых.
- 9. Срединные линии. Кривые, касательные к которым принадлежат комплексу. Линейные комплексы.
- 10. Подсчет инвариантных линейных форм и инвариантов. Конгруэнции и линейчатые поверхности комплекса.
- ВТОРОЙ РАЗДЕЛ. АФФИННАЯ УНИМОДУЛЯРНАЯ ГЕОМЕТРИЯ
- 2. Теория плоских кривых.
- 3. Геометрическая интерпретация. Конические сечения.
- 4. Теория пространственных кривых. Репер Френе.
- 5. Вычисление аффинной дуги и инвариантов. Пространственные кривые третьего порядка.
- Глава II. ТЕОРИЯ ПОВЕРХНОСТЕЙ
- 1. Репер Френе. Общие случаи.
- 2. Поверхности второго порядка (не развертывающиеся). Линейчатые поверхности.
- 3. Развертывающиеся поверхности.
- 4. Приведенные уравнения.
- 5. Соприкасающиеся квадрики. Касательные Дарбу.
- 6. Квадрика Ли.
- 7. Поверхности, инвариантные относительно транзитивной группы.
- 8. Кривые, лежащие на поверхности.
- 9. Алгебраические дифференциальные инвариантные формы.
- 10. Условия интегрируемости в терминах форм …
- ТРЕТИЙ РАЗДЕЛ. ПРОЕКТИВНАЯ ГЕОМЕТРИЯ
- 1. Формулы перемещений репера. Перемещения коррелятивного репера.
- 2. Теория плоских кривых. Репер Френе.
- 3. Конические сечения.
- 4. Вычисление проективной дуги и проективной кривизны. Приведенное уравнение. Секстактические точки.
- 5. Ангармоническое отношение четырех точек.
- 6. Огибающие прямых.
- 7. Теория пространственных кривых.
- 8. Теория поверхностей. Репер Френе.
- 9. Уравнение, приведенное в окрестности точки.
- 10. Коррелятивная точка зрения. Огибающие плоскостей.
- 11. Проективная наложимость.
- ТРЕТЬЯ ЧАСТЬ. ТЕОРИЯ ПЕРЕНЕСЕНИЯ
- Глава I. ПЕРЕНЕСЕНИЕ И СВЯЗНОСТЬ. ПРОСТРАНСТВА АФФИННОЙ СВЯЗНОСТИ
- 2. Группа голономий.
- 3. Линейные аффинные связности. Эквивалентность.
- 4. Тензоры кривизны и кручения.
- 5. Ковариантная производная тензора.
- 6. Тождества Бианки.
- 7. Вычисление компонент тензоров кривизны и кручения.
- 8. Параллельный перенос. Геодезические.
- 9. Основная теорема.
- 10. Изучение связности в окрестности точки.
- 11. Геодезические наложения.
- 12. Поля параллельных контравариантные векторов.
- 13. Разложимые пространства.
- 14. Эквиаффинная связность.
- 15. Метрические связности. Пространства Эддингтона, Вейля и Эйнштейна.
- 16. Проективные связности.
- 17. Проективные тензоры.
- Глава II. РИМАНОВЫ ПРОСТРАНСТВА
- 2. Геодезические. Экстремальное свойство. Аналитические римановы пространства.
- 3. Кривизна пространства в направлении площадки. Пространства постоянной кривизны
- 4. Тензор конформной кривизны.
- 5. Движения.
- 6. Разложимые пространства.
- 7. Теория кривых.
- 8. Вложенные многообразия.