| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
19. Группа движений.
Это группа определяемая в пространстве  уравнениями
уравнениями

где и  параметры, причем
параметры, причем  таковы, что матрица ортогональна и нормирована, т. е.
таковы, что матрица ортогональна и нормирована, т. е.

и, кроме того,

Мы видим, что матрица, обратная матрице  скажем матрица Дудет транспонированной из нее матрицей:
скажем матрица Дудет транспонированной из нее матрицей:  это позволяет
это позволяет
выписать преобразование, обратное к преобразованию (19.1) в виде:

Другое следствие из соотношений (19.2) состоит в том, что  условие (19.3) сводится к исключению из преобразований (19.1) тех, для которых
условие (19.3) сводится к исключению из преобразований (19.1) тех, для которых  и которые вместе с движениями образуют новую группу (с двумя связными компонентами), а именно группу движений и движений с преобразованиями симметрии. Число параметров
и которые вместе с движениями образуют новую группу (с двумя связными компонентами), а именно группу движений и движений с преобразованиями симметрии. Число параметров  равно
равно  соотношений (19.2) имеется
соотношений (19.2) имеется  Следовательно, группа зависит от
Следовательно, группа зависит от  параметров.
параметров.
Всякое движение является гомеоморфизмом пространства  пространство
пространство  в котором мы воздержимся от других преобразований, кроме движений, или, как говорят, пространство
в котором мы воздержимся от других преобразований, кроме движений, или, как говорят, пространство  снабженное структурой группы движений, называется эвклидовым метрическим пространством
снабженное структурой группы движений, называется эвклидовым метрическим пространством  Группа действует транзитивно на точках, а также на линейных подпространствах одной и той же размерности.
Группа действует транзитивно на точках, а также на линейных подпространствах одной и той же размерности.
Два геометрических объекта, таких, что можно перейти от одного к другому с помощью преобразования этой группы, называются равными.
На множестве геометрических объектов, состоящих из  точек, группа не действует транзитивно; существует, следовательно, по крайней мере один инвариант пары точек (с точностью до функции); легко показать, что такой инвариант только один и что для пары точек
точек, группа не действует транзитивно; существует, следовательно, по крайней мере один инвариант пары точек (с точностью до функции); легко показать, что такой инвариант только один и что для пары точек  он является функцией от
он является функцией от

Величина  является расстоянием между двумя точками. Как мы видели, расстояние дает возможность определить топологию в
является расстоянием между двумя точками. Как мы видели, расстояние дает возможность определить топологию в  (для произвольно фиксированного
(для произвольно фиксированного  множество сфер радиуса
множество сфер радиуса  образует класс объектов, эквивалентных точкам). Множество движений, оставляющих одну точку неподвижной, образует группу
образует класс объектов, эквивалентных точкам). Множество движений, оставляющих одну точку неподвижной, образует группу  называемую группой вращений вокруг этой точки; для вращений вокруг начала координат эта группа состоит из преобразований (19.1) с
называемую группой вращений вокруг этой точки; для вращений вокруг начала координат эта группа состоит из преобразований (19.1) с  эта группа непрерывна.
эта группа непрерывна.
Определим подгруппу, оставляющую неподвижной прямую. Мы можем выбрать в качестве этой прямой ось  последнее из уравнений (19.1) сводится в этом случае, в силу условий (19.2), к
последнее из уравнений (19.1) сводится в этом случае, в силу условий (19.2), к

а  первых уравнений (19.1) определяют ортогональное и нормированное, преобразование в пространстве
первых уравнений (19.1) определяют ортогональное и нормированное, преобразование в пространстве  Множество этих преобразований будет в
Множество этих преобразований будет в  группой движений и движений вместе с симметрией; оно не связно. Мы приходим к определению нового геометрического объекта: ориентированной прямой, или оси, причем каждая прямая является носителем двух осей, из которых каждая остается инвариантной относительно группы, изоморфной
группой движений и движений вместе с симметрией; оно не связно. Мы приходим к определению нового геометрического объекта: ориентированной прямой, или оси, причем каждая прямая является носителем двух осей, из которых каждая остается инвариантной относительно группы, изоморфной  Семейство реперов, присоединенных к оси, которую мы будем называть положительной (другая будет называться отрицательной), — это семейство, получаемое из основного репера ространства
Семейство реперов, присоединенных к оси, которую мы будем называть положительной (другая будет называться отрицательной), — это семейство, получаемое из основного репера ространства  операциями предыдущей группы. Множество реперов,
операциями предыдущей группы. Множество реперов,
симметричных к предыдущим (получаемых преобразованием  будет семейством реперов, присоединенных к отрицательной оси. Положительная ось называется осью
будет семейством реперов, присоединенных к отрицательной оси. Положительная ось называется осью  она может быть определена также с помощью двух точек
она может быть определена также с помощью двух точек  с заданным
с заданным  взятых именно в этом порядке; первая из них называется началом, вторая концом. Множество преобразований рассматриваемой группы преобразует их в новый объект:
взятых именно в этом порядке; первая из них называется началом, вторая концом. Множество преобразований рассматриваемой группы преобразует их в новый объект:  произвольно). Мы получаем таким образом новый объект, который назовем скользящим вектором длины
произвольно). Мы получаем таким образом новый объект, который назовем скользящим вектором длины  и той же ориентации, что и ось.
и той же ориентации, что и ось.
Рассмотрим теперь две точки, взятые в порядке  где
где  на этот раз отрицательно; мы скажем, что они определяют скользящий вектор на прямой
на этот раз отрицательно; мы скажем, что они определяют скользящий вектор на прямой  длины
длины  и ориентации, противоположной, ориентации оси
и ориентации, противоположной, ориентации оси 
Преобразования  сохраняющие скользящие векторы на прямой
сохраняющие скользящие векторы на прямой  образуют группу с одним параметром
образуют группу с одним параметром  группу переносов параллельно прямой
группу переносов параллельно прямой 
Рассмотрим теперь множество прямых

Движения, сохраняющие это множество, образуют группу, являющуюся произведением группы преобразований (19.4) на Геометрический объект (19.5) называется направлением прямой (в частности, направлением прямой  Прямые (19.5) называются параллельными. Связная группа — произведение группы преобразований
Прямые (19.5) называются параллельными. Связная группа — произведение группы преобразований  на — преобразует ось, лежащую на прямой
на — преобразует ось, лежащую на прямой  (например, положительную ось), в ось, лежащую на прямой (19.5), причем мы говорим, что эта ось имеет ту же ориентацию, что и ось, выбранная нами на прямой
(например, положительную ось), в ось, лежащую на прямой (19.5), причем мы говорим, что эта ось имеет ту же ориентацию, что и ось, выбранная нами на прямой 
Рассмотрим также скользящий вектор на прямой  предыдущая группа преобразует его в скользящий вектор той же длины и той же ориентации на произвольной прямой (19.5). Геометрическое понятие, определенное таким образом, называется свободным вектором. Он определяется своей ориентацией и своей длиной; аналитически он определяется разностями координат его конца
предыдущая группа преобразует его в скользящий вектор той же длины и той же ориентации на произвольной прямой (19.5). Геометрическое понятие, определенное таким образом, называется свободным вектором. Он определяется своей ориентацией и своей длиной; аналитически он определяется разностями координат его конца  и начала
и начала 

которые называются его компонентами. Совокупность движений, сохраняющих множество всех свободных векторов, есть группа

называемая группой переносов (операция группы называется параллельным переносом).
Совокупность двух точек  взятых в этом порядке, например
взятых в этом порядке, например

сохраняется группой, изоморфной группе Это геометрическое понятие называется связанным вектором с началом х и концом х. Связанный вектор определяет свободный вектор. Два связанных вектора, принадлежащих одному и тому же свободному вектору, называются эквивалентными.
Движения, оставляющие неподвижной плоскость, например плоскость  состоят из движений группы и движений группы комбинируемых с симметрией
состоят из движений группы и движений группы комбинируемых с симметрией  Они образуют группу, которая не
Они образуют группу, которая не
будет связной. Следовательно, можно рассматривать плоскость как носитель двух ориентированных плоскостей.
Множество плоскостей  где
где  произвольная постоянная, инвариантно относительно произведения преобразований предыдущей группы на переносы
произвольная постоянная, инвариантно относительно произведения преобразований предыдущей группы на переносы  Эти плоскости называются параллельными, а объект, который этим определяется, называется направлением плоскости
Эти плоскости называются параллельными, а объект, который этим определяется, называется направлением плоскости 
Мы не будем больше останавливаться на преобразованиях, сохраняющих линейные многообразия.
Рассмотрим теперь множество пар пересекающихся прямых. Так как группа не действует транзитивно на этом множестве, то существует инвариант пары пересекающихся прямых (наиболее обычный — квадрат тангенса их угла, определяемого с точностью до знака и с точностью до  для
для  ).
).
В случае двух пересекающихся осей положение вещей такое же, и существует инвариант двух осей, обычно — косинус угла между ними.
Используя понятия параллельных прямых или параллельных осей, можно обобщить предыдущие понятия и говорить об угле между двумя осями (заключенном между нулем и  при этом порядок, в котором задаются эти оси, не имеет значения.
при этом порядок, в котором задаются эти оси, не имеет значения.
Пусть  свободный вектор с компонентами
свободный вектор с компонентами  свободный вектор с компонентами
свободный вектор с компонентами  будет обозначаться
будет обозначаться  и эта операция называется умножением на скаляр
и эта операция называется умножением на скаляр  Вектор
Вектор  называется противоположным к
называется противоположным к  Это понятие лишено смысла для
Это понятие лишено смысла для  ; мы придадим ему смысл, условившись, что две совпадающие точки также определяют свободный вектор, а именно нулевой вектор
; мы придадим ему смысл, условившись, что две совпадающие точки также определяют свободный вектор, а именно нулевой вектор  (или просто 0), и будем писать
(или просто 0), и будем писать  Нулевой вектор не имеет ориентации. Тем не менее в некоторых случаях приходится приписывать ему некоторую ориентацию, которую можно выбрать произвольно.
Нулевой вектор не имеет ориентации. Тем не менее в некоторых случаях приходится приписывать ему некоторую ориентацию, которую можно выбрать произвольно.
Если заданы два свободных вектора  то свободный вектор
то свободный вектор  где
где  называют их геометрической суммой и пишут
называют их геометрической суммой и пишут  Эта операция называется сложением векторов. Сложение коммутативно и ассоциативно; умножение на скаляр дистрибутивно относительно сложения. Для вектора
Эта операция называется сложением векторов. Сложение коммутативно и ассоциативно; умножение на скаляр дистрибутивно относительно сложения. Для вектора  решения уравнения
решения уравнения  имеем, как это непосредственно видно,
имеем, как это непосредственно видно,  равенство, которое записывается в виде
равенство, которое записывается в виде  Таким образом определяется вычитание — операция, обратная сложению.
Таким образом определяется вычитание — операция, обратная сложению.
Если  вектор длины 1, лежащий на оси
вектор длины 1, лежащий на оси  то, как легко видеть,
то, как легко видеть,

Квадрат длины вектора  равен
равен

Для произвольно заданных  эта величина инвариантна относительно всех преобразований из
эта величина инвариантна относительно всех преобразований из  так как 2 и 2 также инвариантны, то отсюда следует, что величина
так как 2 и 2 также инвариантны, то отсюда следует, что величина

есть инвариант совокупности двух векторов  Его называют скалярным произведением этих векторов и пишут
Его называют скалярным произведением этих векторов и пишут

Это выражение показывает, что скалярное умножение коммутативно,

Поскольку оно билинейно по  оно дистрибутивно относительно сложения:
оно дистрибутивно относительно сложения:

и если  означает скаляр, то
означает скаляр, то

Если произведение  равно нулю, векторы
равно нулю, векторы  называются ортогональными, или перпендикулярными, друг другу. Из (19.8) следует, что в этом случае два любых вектора, направления которых совпадают с направлениями
называются ортогональными, или перпендикулярными, друг другу. Из (19.8) следует, что в этом случае два любых вектора, направления которых совпадают с направлениями  также ортогональны. Направления прямой или определяющие их ориентации осей будут тогда также называться ортогональными (или перпендикулярными).
также ортогональны. Направления прямой или определяющие их ориентации осей будут тогда также называться ортогональными (или перпендикулярными).
Репер  составленный из осей
составленный из осей  образован попарно ортогональными осями; то же самое справедливо относительно реперов
образован попарно ортогональными осями; то же самое справедливо относительно реперов  полученных из
полученных из  преобразованием из группы Кроме указанных, реперами с попарно ортогональными осями будут только те реперы, которые получаются из реперов
преобразованием из группы Кроме указанных, реперами с попарно ортогональными осями будут только те реперы, которые получаются из реперов  о симметрией.
о симметрией.
Заметим также, что если обозначить через  длину вектора
длину вектора  то скалярное произведение
то скалярное произведение  которое записывается в виде
которое записывается в виде  равно
равно  Наконец, в силу (19.8), величина
Наконец, в силу (19.8), величина

не меняется, если заменить  на
на  соответственно, где
соответственно, где  Эта величина будет, таким образом, инвариантом совокупности двух направлений осей, определяемых векторами
Эта величина будет, таким образом, инвариантом совокупности двух направлений осей, определяемых векторами  Это — косинус угла между ними
Это — косинус угла между ними

В заключение рассмотрим пример другого рода.
Пусть  неприводимый многочлен. Тогда уравнение
неприводимый многочлен. Тогда уравнение

определяет, вообще говоря, многообразие, и легко показать, что степень этого многочлена остается неизменной при любом преобразовании группы  Это первый инвариант, связанный с многообразием. Что касается отыскания других инвариантов, то мы ограничимся случаем, когда степень
Это первый инвариант, связанный с многообразием. Что касается отыскания других инвариантов, то мы ограничимся случаем, когда степень  равна 2; многообразие называется тогда многообразием второго порядка, или квадрикой. Мы знаем, что в этом случае можно записать
равна 2; многообразие называется тогда многообразием второго порядка, или квадрикой. Мы знаем, что в этом случае можно записать  в форме суммы
в форме суммы
не более  квадратов линейно независимых многочленов первого порядка (при этом число также рассматривается как линейный многочлен), из которых
квадратов линейно независимых многочленов первого порядка (при этом число также рассматривается как линейный многочлен), из которых  взято со знаком
взято со знаком  а остальные
а остальные  со знаком
со знаком  Два числа
Два числа  суть инварианты, которые геометрически интерпретируют как инварианты квадрики (род квадрики). В том частном случае, когда уравнение квадрики можно привести к виду
суть инварианты, которые геометрически интерпретируют как инварианты квадрики (род квадрики). В том частном случае, когда уравнение квадрики можно привести к виду

где  форма, имеющая вид суммы
форма, имеющая вид суммы  взятых со знаком
взятых со знаком  квадратов линейно независимых форм, квадрика будет эллипсоидом. В этом случае можно показать, что существует по крайней мере один репер, в котором уравнение эллипсоида имеет вид
квадратов линейно независимых форм, квадрика будет эллипсоидом. В этом случае можно показать, что существует по крайней мере один репер, в котором уравнение эллипсоида имеет вид

где  положительные константы, образующие систему инвариантов эллипсоида (длины полуосей).
положительные константы, образующие систему инвариантов эллипсоида (длины полуосей).
Группа подобий. Комбинируя операции группы с преобразованиями  где
где  означает параметр, отличный от нуля
означает параметр, отличный от нуля  мы получаем новую группу, называемую группой подобий (для
мы получаем новую группу, называемую группой подобий (для  это группа элементарной геометрии).
это группа элементарной геометрии).
Два объекта, такие, что можно перейти от одного к другому преобразованием этой группы, называются подобными. При таком преобразовании две точки, лежащие на расстоянии  друг от друга, переходят в две точки, лежащие на расстоянии
друг от друга, переходят в две точки, лежащие на расстоянии  друг от друга, а углы не меняются
друг от друга, а углы не меняются 
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К РУССКОМУ ИЗДАНИЮ
- ВВЕДЕНИЕ
- Глава I. ОБЩИЕ ПОНЯТИЯ. ОСНОВАНИЯ
- 2. Топологические пространства.
- 3. Подпространства.
- 4. Непрерывные функции.
- 5. Гомеоморфизм.
- 6. Метрические пространства.
- 7. Полные пространства. Компактные пространства и множества.
- 8. Связные пространства и множества.
- 9. Эвклидово аморфное пространство.
- 10. Симплексы. Комплексы.
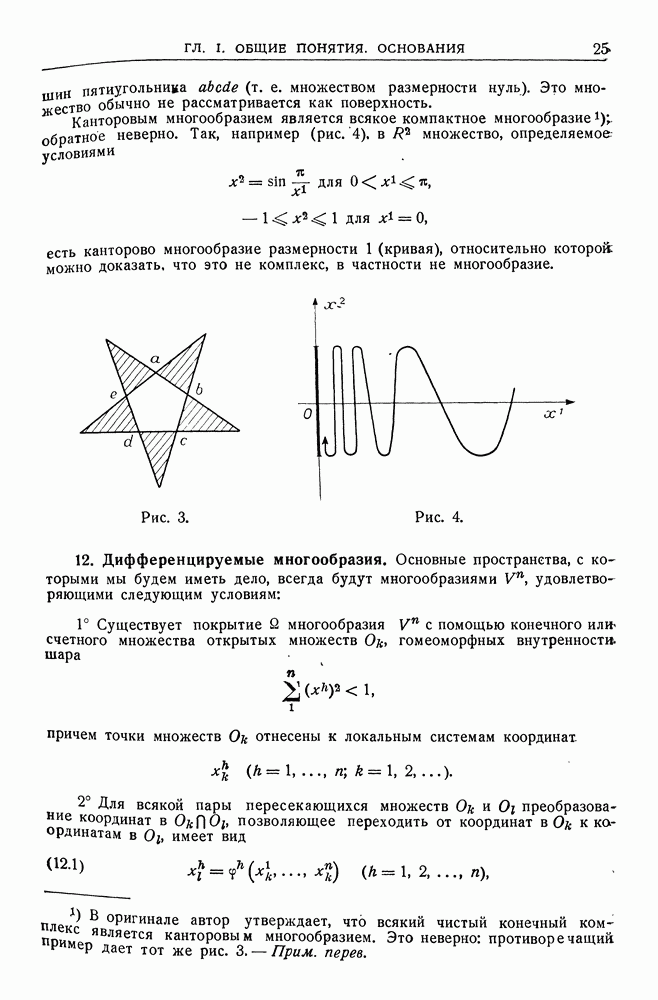
- 11. Размерность. Кривые и поверхности. Канторовы многообразия.
- 12. Дифференцируемые многообразия.
- 13. Общие свойства групп.
- 14. Преобразования. Группы преобразований.
- 15. Топологические группы.
- 16. Группы Ли.
- 17. Геометрические объекты. Транзитивность и интранзитивность. Ориентация.
- 18. Группы Ли классических геометрий.
- 19. Группа движений.
- 20. Аффинная группа.
- 21. Проективная группа.
- 22. Группы дифференциальной геометрии.
- 23. Дополнение о коллинеациях.
- Глава II. ДОПОЛНЕНИЕ К АЛГЕБРЕ. ТЕНЗОРЫ
- 1. Векторное центро-аффинное пространство Сn.
- 2. Тензорные произведения центро-аффинных пространств. Тензоры.
- 3. Аффинные тензоры.
- 4. Соглашение об обозначениях.
- 5. Операции над аффинными тензорами.
- 6. Симметричные и антисимметричные тензоры.
- 7. Антисимметричные контравариантные тензоры. Мультивекторы.
- 8. Антисимметричные ковариантные векторы. Внешние формы.
- 9. Внешние квадратичные формы. Теорема Картана.
- 10. Эвклидовы тензоры.
- 11. Элементарный тензорный анализ.
- Глава III. ДОПОЛНЕНИЯ К АНАЛИЗУ: ВНЕШНЕЕ ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ; ПРИЛОЖЕНИЯ К ГРУППАМ ЛИ И К ОБЩЕЙ ТЕОРИИ ПОГРУЖЕННЫХ МНОГООБРАЗИЙ
- 1. Внешние дифференциальные формы.
- 2. Система Пфаффа. Теорема Фробениуса.
- 3. Группы Ли. Инфинитезимальные преобразования. Относительные и абсолютные компоненты.
- 4. Первая теорема Ли.
- 5. Группа параметров.
- 6. Уравнения структуры Эли Картана.
- 7. Уравнения структуры классических групп.
- 8. Элементы касания, погруженные в многообразие. Продолжение группы преобразований.
- 9. Общая теория погруженных многообразий.
- 10. Метод подвижного репера Эли Картана.
- ПЕРВАЯ ЧАСТЬ. ПРЯМАЯ ИНФИНИТЕЗИМАЛЬНАЯ ГЕОМЕТРИЯ
- Глава I. ВЛОЖЕННЫЕ МНОГООБРАЗИЯ. ПАРАМЕТРИЗАЦИЯ
- 2. Вложенные многообразия. Основной локальный инвариант. Обыкновенные точки.
- 3. Контингенция. Паратингенция.
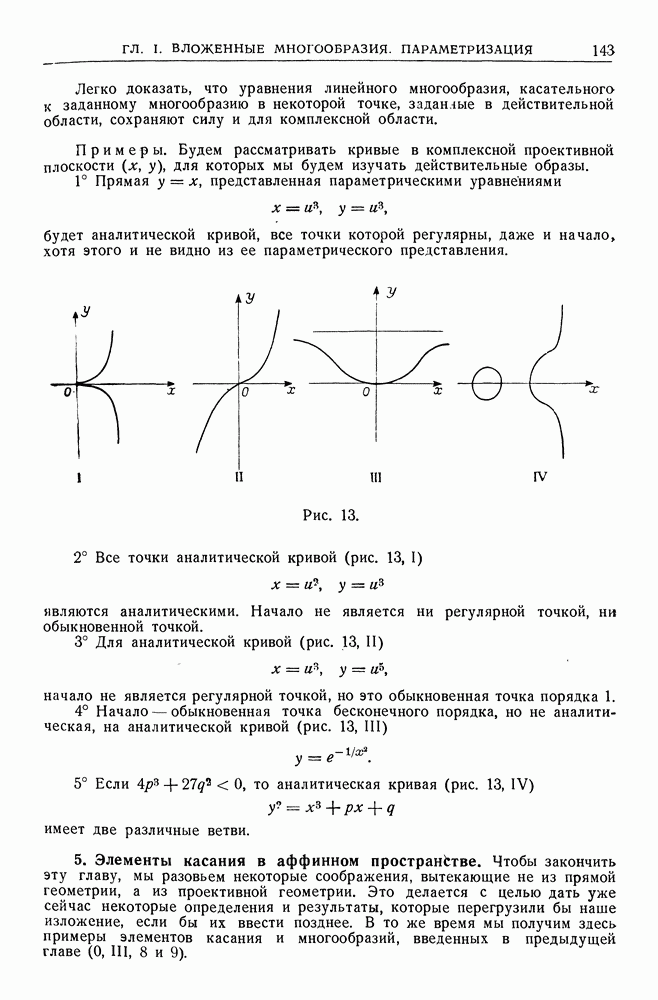
- 4. Аналитические многообразия. Регулярные точки.
- 5. Элементы касания в аффинном пространстве.
- 6. Соприкасающаяся плоскость и соприкасающаяся полуплоскость кривой в пространстве E3. Вогнутость.
- Глава II. ТЕОРИЯ КАСАНИЯ
- 2. Касание двух кривых.
- 3. Касание кривой и поверхности.
- 4. Касание двух поверхностей.
- Глава III. ОГИБАЮЩИЕ
- 2. Огибающие плоских кривых.
- 3. Огибающие поверхностей, зависящих от одного параметра.
- 4. Огибающие поверхностей, зависящих от двух параметров.
- 5. Огибающие пространственных кривых, зависящих от одного параметра.
- 6. Конгруэнции кривых.
- Глава IV. ПРЕОБРАЗОВАНИЯ КАСАНИЯ
- 1. Примыкающие элементы касания.
- 2. Преобразования касания.
- 3. Примеры.
- ВТОРАЯ ЧАСТЬ. КЛАССИЧЕСКИЕ ГЕОМЕТРИИ
- Глава I. ТЕОРИЯ ПРОСТРАНСТВЕННЫХ КРИВЫХ
- 2. Формулы Серре-Френе.
- 3. Триэдр Френе.
- 4. Кривизна и кручение.
- 5. Положение кривой в окрестности точки по отношению к триэдру Серре — Френе. Знак кручения.
- 6. Определение кривой ее натуральными уравнениями.
- 7. Винтовые линии.
- 8. Конгруэнция нормалей к пространственной кривой.
- 9. Замечания.
- 10. Изотропные кривые (или минимальные линии).
- Глава II. ТЕОРИЯ ПОВЕРХНОСТЕЙ; ТРИЭДР ФРЕНЕ
- 1. Триэдр Френе.
- 2. Особые случаи.
- 3. Поверхности, инвариантные относительно группы движений.
- 4. Теоремы равенства и существования.
- 5. Вычисление инвариантных линейных форм и кривизн.
- 6. Геодезические свойства. Внешние свойства.
- Глава III. ТЕОРИЯ ПОВЕРХНОСТЕЙ; ПЕРВАЯ ОСНОВНАЯ КВАДРАТИЧНАЯ ФОРМА
- 2. Минимальные линии (линии нулевой длины).
- 3. Конформное отображение одной поверхности на другую. Изотермические координаты.
- 4. Изометрия. Полная кривизна.
- 5. Изометричные поверхности.
- 6. Группа изометрии линейных элементов ds2 постоянной кривизны.
- 7. Поверхности, изометричные плоскости.
- 8. Вопросы анализа на поверхности.
- 9. Геодезические линии («внешняя» теория).
- 10. Геодезическая кривизна.
- 11. Поле векторов. Ковариантные частные производные Параллельный перенос.
- 12. Формула Оссиана Бонне.
- 13. Поле тензоров. Ковариантная производная.
- Глава IV. ТЕОРИЯ ПОВЕРХНОСТЕЙ, ВТОРАЯ ОСНОВНАЯ КВАДРАТИЧНАЯ ФОРМА
- 2. Расположение поверхности по отношению к касательной плоскости. Обыкновенные точки второго порядка.
- 3. Асимптотические линии.
- 4. Сопряженные направления. Сопряженные семейства кривых.
- 5. Триэдр Френе для кривой, проведенной на поверхности. Теоремы Менье и Оссиана Бонне.
- 6. Кривизна нормальных сечений. Индикатриса Дюпена.
- 7. Главные направления. Главные кривизны.
- 8. Линия кривизны. Эволюты, или поверхности центров кривизны поверхности.
- 9. Конгруэнции нормалей.
- 10. Примеры.
- 11. Сферическое изображение. Третья квадратичная форма поверхности.
- 12. Относительное кручение. Четвертая квадратичная форма.
- 13. Точечные преобразования и преобразования касания, сохраняющие асимптотические линии.
- 14. Точечные преобразования, сохраняющие линии кривизны.
- 15. Преобразование Ли. Преобразования касания, сохраняющие линии кривизны.
- 16. Возвращение к условиям интегрируемости.
- Глава V. ЛИНЕЙЧАТАЯ ЭВКЛИДОВА ГЕОМЕТРИЯ
- 1. Плюккеровы координаты.
- 2. Линейчатые поверхности.
- 3. Конгруэнции прямых.
- 4. Линейчатые поверхности конгруэнции.
- 5. Вычисление инвариантов. Квадратичные формы.
- 6. Формула Эли Картана. Конгруэнции нормалей.
- 7. Изотропные конгруэнции.
- 8. Комплексы прямых.
- 9. Срединные линии. Кривые, касательные к которым принадлежат комплексу. Линейные комплексы.
- 10. Подсчет инвариантных линейных форм и инвариантов. Конгруэнции и линейчатые поверхности комплекса.
- ВТОРОЙ РАЗДЕЛ. АФФИННАЯ УНИМОДУЛЯРНАЯ ГЕОМЕТРИЯ
- 2. Теория плоских кривых.
- 3. Геометрическая интерпретация. Конические сечения.
- 4. Теория пространственных кривых. Репер Френе.
- 5. Вычисление аффинной дуги и инвариантов. Пространственные кривые третьего порядка.
- Глава II. ТЕОРИЯ ПОВЕРХНОСТЕЙ
- 1. Репер Френе. Общие случаи.
- 2. Поверхности второго порядка (не развертывающиеся). Линейчатые поверхности.
- 3. Развертывающиеся поверхности.
- 4. Приведенные уравнения.
- 5. Соприкасающиеся квадрики. Касательные Дарбу.
- 6. Квадрика Ли.
- 7. Поверхности, инвариантные относительно транзитивной группы.
- 8. Кривые, лежащие на поверхности.
- 9. Алгебраические дифференциальные инвариантные формы.
- 10. Условия интегрируемости в терминах форм …
- ТРЕТИЙ РАЗДЕЛ. ПРОЕКТИВНАЯ ГЕОМЕТРИЯ
- 1. Формулы перемещений репера. Перемещения коррелятивного репера.
- 2. Теория плоских кривых. Репер Френе.
- 3. Конические сечения.
- 4. Вычисление проективной дуги и проективной кривизны. Приведенное уравнение. Секстактические точки.
- 5. Ангармоническое отношение четырех точек.
- 6. Огибающие прямых.
- 7. Теория пространственных кривых.
- 8. Теория поверхностей. Репер Френе.
- 9. Уравнение, приведенное в окрестности точки.
- 10. Коррелятивная точка зрения. Огибающие плоскостей.
- 11. Проективная наложимость.
- ТРЕТЬЯ ЧАСТЬ. ТЕОРИЯ ПЕРЕНЕСЕНИЯ
- Глава I. ПЕРЕНЕСЕНИЕ И СВЯЗНОСТЬ. ПРОСТРАНСТВА АФФИННОЙ СВЯЗНОСТИ
- 2. Группа голономий.
- 3. Линейные аффинные связности. Эквивалентность.
- 4. Тензоры кривизны и кручения.
- 5. Ковариантная производная тензора.
- 6. Тождества Бианки.
- 7. Вычисление компонент тензоров кривизны и кручения.
- 8. Параллельный перенос. Геодезические.
- 9. Основная теорема.
- 10. Изучение связности в окрестности точки.
- 11. Геодезические наложения.
- 12. Поля параллельных контравариантные векторов.
- 13. Разложимые пространства.
- 14. Эквиаффинная связность.
- 15. Метрические связности. Пространства Эддингтона, Вейля и Эйнштейна.
- 16. Проективные связности.
- 17. Проективные тензоры.
- Глава II. РИМАНОВЫ ПРОСТРАНСТВА
- 2. Геодезические. Экстремальное свойство. Аналитические римановы пространства.
- 3. Кривизна пространства в направлении площадки. Пространства постоянной кривизны
- 4. Тензор конформной кривизны.
- 5. Движения.
- 6. Разложимые пространства.
- 7. Теория кривых.
- 8. Вложенные многообразия.