| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
10. Эвклидовы тензоры.
Если в пространстве  введена структура группы вращений вокруг начала [формулы (I, 19.1) с
введена структура группы вращений вокруг начала [формулы (I, 19.1) с  ], то вместо
], то вместо  мы получаем пространство
мы получаем пространство  центро-эвклидово пространство. Это — пространство свободных (контравариантных) векторов пространства
центро-эвклидово пространство. Это — пространство свободных (контравариантных) векторов пространства  всякой точке пространства
всякой точке пространства  соответствует свободный вектор в пространстве
соответствует свободный вектор в пространстве  и обратно.
и обратно.
Во многих вопросах интересно заставить действовать на  общее преобразование центро-аффинной группы
общее преобразование центро-аффинной группы  но тогда, вообще
но тогда, вообще
говоря, оси, составляющие основной  -эдр, теряют свойство ортогональности.
-эдр, теряют свойство ортогональности.
Пусть в некотором ортогональном репере  компоненты двух векторов х и у. После преобразования
компоненты двух векторов х и у. После преобразования

скалярное произведение  записывается в виде
записывается в виде

где  -константы
-константы  нетрудно видеть, что
нетрудно видеть, что

и что форма  положительно определенная.
положительно определенная.
Возвращаясь к исходным обозначениям  (вместо
(вместо  ), мы назовем центро-эвклидовым пространством
), мы назовем центро-эвклидовым пространством  пространство
пространство  в котором задана квадратичная форма
в котором задана квадратичная форма

у которой

представляющая собой инвариант; здесь  координаты произвольного вектора х.
координаты произвольного вектора х.
Ввиду (10.2) эта форма есть сумма квадратов  линейно независимых форм, снабженных знаком
линейно независимых форм, снабженных знаком  или
или  Нам следовало бы прибавить, что все квадраты снабжены знаком
Нам следовало бы прибавить, что все квадраты снабжены знаком  но это требование оказывается излишним для того, о чем мы будем говорить; поэтому мы не будем его накладывать.
но это требование оказывается излишним для того, о чем мы будем говорить; поэтому мы не будем его накладывать.
Значение формы (10.1) для вектора х будет называться скалярным квадратом или просто квадратом вектора х и обозначаться  Мы будем называтьдлиной вектора х и обозначать через
Мы будем называтьдлиной вектора х и обозначать через  величину
величину

Пусть  координаты двух векторов х и у; квадрат длины вектора
координаты двух векторов х и у; квадрат длины вектора  где
где  произвольные константы, равен
произвольные константы, равен

Так как первый и последний члены правой части инвариантны, то отсюда следует, поскольку  произвольны, что билинейная форма
произвольны, что билинейная форма

также инвариантна. Она называется скалярным произведением двух векторов. Когда оно равно нулю, векторы называются ортогональными. Скалярное произведение вектора самого на себя есть квадрат этого вектора.
Из этой инвариантности следует (§ 3), что  компоненты симметричного тензора (2) называемого основным тензором.
компоненты симметричного тензора (2) называемого основным тензором.
Непосредственно видно, что  . Базис называется ортогональным, или прямоугольным, если
. Базис называется ортогональным, или прямоугольным, если  для
для  и ортонормированным, если, кроме
и ортонормированным, если, кроме  . Если форма (10.1) положительно определенная (истинное центро-эвклидово пространство), то мы имеем
. Если форма (10.1) положительно определенная (истинное центро-эвклидово пространство), то мы имеем

Рассмотрим ковариантный вектор, определенный равенством

Всякому контравариантному вектору х мы ставим таким образом в соответствие ковариантный вектор х с координатами  и это соответствие взаимно однозначно, поскольку
и это соответствие взаимно однозначно, поскольку  Это соответствие, будучи, очевидно, линейным, сохраняет умножение на скаляр и сумму. Так как вектор х, с другой стороны, может быть так же хорошо определен посредством чисел
Это соответствие, будучи, очевидно, линейным, сохраняет умножение на скаляр и сумму. Так как вектор х, с другой стороны, может быть так же хорошо определен посредством чисел  как и посредством чисел
как и посредством чисел  то мы условимся отождествлять два объекта тихи говорить, что
то мы условимся отождествлять два объекта тихи говорить, что  ковариантные координаты вектора
ковариантные координаты вектора  его контравариантные координаты.
его контравариантные координаты.
В пространстве  таким образом, не будет ковариантных или контравариантных векторов, а будут только векторы, определенные его ковариантными или контравариантными координатами.
таким образом, не будет ковариантных или контравариантных векторов, а будут только векторы, определенные его ковариантными или контравариантными координатами.
Равенство (10.4) показывает, что  есть величина ортогональной проекции вектора х на ось
есть величина ортогональной проекции вектора х на ось  нормированных равенствами
нормированных равенствами  прямоугольных координатах ковариантные координаты вектора равны контравариантным координатам с соответствующими номерами. Полагая
прямоугольных координатах ковариантные координаты вектора равны контравариантным координатам с соответствующими номерами. Полагая

где  алгебраическое дополнение элемента
алгебраическое дополнение элемента  в определителе
в определителе  так что
так что

мы получаем решение системы (10.4) в виде

будут компонентами тензора  Формулы (10.4) и (10.40) позволяют переходить от контравариантных координат вектора к его ковариантным координатам и обратно. При этом соглашении формула (10.3) принимает простой вид
Формулы (10.4) и (10.40) позволяют переходить от контравариантных координат вектора к его ковариантным координатам и обратно. При этом соглашении формула (10.3) принимает простой вид

Наше соглашение сводится к тому, что мы отождествляем элемент  базиса дуального пространства
базиса дуального пространства  с элементом
с элементом  пространства
пространства  [формула (10.40]. Вообще, условимся отождествлять элемент
[формула (10.40]. Вообще, условимся отождествлять элемент  пространства
пространства  с элементом
с элементом  пространства
пространства  и аналогично для тензорных произведений с большим числом множителей, так что всякий контравариантный вектор пространства
и аналогично для тензорных произведений с большим числом множителей, так что всякий контравариантный вектор пространства  будет отождествляться с контравариантным вектором пространства
будет отождествляться с контравариантным вектором пространства  Это все равно, что сказать, что всякий тензор пространства
Это все равно, что сказать, что всякий тензор пространства  будет отождествляться с тензором
будет отождествляться с тензором  Множество всех тензоров, тождественных одному тензору, называется эвклидовым тензором.
Множество всех тензоров, тождественных одному тензору, называется эвклидовым тензором.

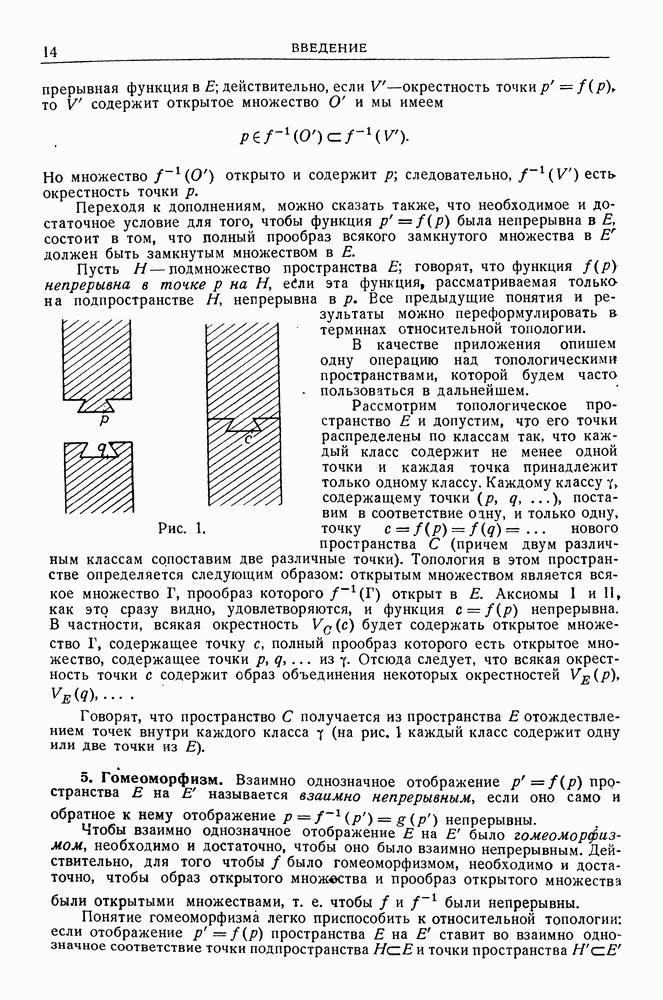
Рис. 10.
Эвклидов тензор не имеет специфического характера ковариантного или контравариантного тензора, он может быть охарактеризован его порядком  суммой порядков контравариантности и ковариантности одного из его представителей. Его различные представления (в числе
суммой порядков контравариантности и ковариантности одного из его представителей. Его различные представления (в числе  координат каждое), напротив, имеют
координат каждое), напротив, имеют
каждое специфический характер контравариантности или ковариантности. Так, например, тензор  третьего порядка имеет восемь представлений:
третьего порядка имеет восемь представлений:

Для аффинных тензоров нам нужно было только точно знать названия и места ковариантных индексов в последовательности этих индексов и названия и места контравариантных индексов в последовательности этих индексов. В случае же эвклидовых тензоров, напротив, нужно заботиться о том, чтобы все индексы сохраняли свои места. Так, например, исходя из представления  предыдущего тензора, мы получаем представление
предыдущего тензора, мы получаем представление  опуская индекс
опуская индекс  , а представление
, а представление  также
также  получаем, опуская индекс k.
получаем, опуская индекс k.
Переходя от одного представления к другому, мы уточняем  нашей записи места индексов, которые были опущены или подняты, т. е. которые перешли из состояния контравариантности в состояние ковариантности, или наоборот.
нашей записи места индексов, которые были опущены или подняты, т. е. которые перешли из состояния контравариантности в состояние ковариантности, или наоборот.
Основная задача, с которой мы эдесь сталкиваемся, — это задача перехода от одного представления к другому, т. е. задача опускания или поднятия индексов.
Эта задача разрешена формулами (10.4) и (10.4) и соотношениями между базисами  которые мы дали. Пусть, например, надо опустить второй индекс в тензоре
которые мы дали. Пусть, например, надо опустить второй индекс в тензоре  записанном в контравариантной форме
записанном в контравариантной форме  Имеем
Имеем

откуда после замены обозначений

Для поднятия индекса можно получить таким же образом формулу

Вообще, мы имеем формулы следующего типа:

Эти формулы показывают, в частности, что контравариантное представление основного тензора  дается в виде
дается в виде  [формула (10.5)]; что касается его смешанных представлений:
[формула (10.5)]; что касается его смешанных представлений:  и то в силу (10.50
и то в силу (10.50
имеем

т. е. тензор  будет единичным тензором валентности 2.
будет единичным тензором валентности 2.
Заметим также, что в силу симметрии  если тензор: является симметричным или антисимметричным по отношению к некоторым индексам, записанным на контравариантных местах, то же самое будет справедливо и для его представления, в котором эти индексы стоят на ковариантных местах, и наоборот.
если тензор: является симметричным или антисимметричным по отношению к некоторым индексам, записанным на контравариантных местах, то же самое будет справедливо и для его представления, в котором эти индексы стоят на ковариантных местах, и наоборот.
Относительно операций над эвклидовыми тензорами можно сделать следующие замечания:
1° Можно складывать два тензора одного порядка: берем два подобных представления этих тензоров, например контравариантные представления, и контравариантное представление суммы получаем, складывая соответственные контравариантные компоненты этих тензоров.
2° Пусть заданы два тензора  для определенности порядка 3 и 2 своими представлениями, скажем
для определенности порядка 3 и 2 своими представлениями, скажем  и
и  тогда тензор
тогда тензор

называется произведением тензоров  взятых в этом порядке; он не зависит от представлений, выбранных для множителей.
взятых в этом порядке; он не зависит от представлений, выбранных для множителей.
3° Пусть задан тензор  порядка
порядка  выбрав произвольна два его индекса, приведем один из них в ковариантное, другой в контравариантное положение и свернем полученный тензор по этим двум индексам. Мы получим новый тензор валентности
выбрав произвольна два его индекса, приведем один из них в ковариантное, другой в контравариантное положение и свернем полученный тензор по этим двум индексам. Мы получим новый тензор валентности  называемый тензором, полученным из
называемый тензором, полученным из  свертыванием по двум выбранным индексам.
свертыванием по двум выбранным индексам.
Пусть, например, нужно свернуть тензор  по индексам
по индексам  Начинаем с того, что образуем представление
Начинаем с того, что образуем представление  тогда свертывание дает нам тензор
тогда свертывание дает нам тензор

Исходя из другого представления тензора  мы получили бы другое представление тензора
мы получили бы другое представление тензора 
Эти результаты легко доказать, исходя из соотношений (10.6) и (10.60 и принимая во внимание симметрию основного тензора.
В заключение рассмотрим одно приложение.
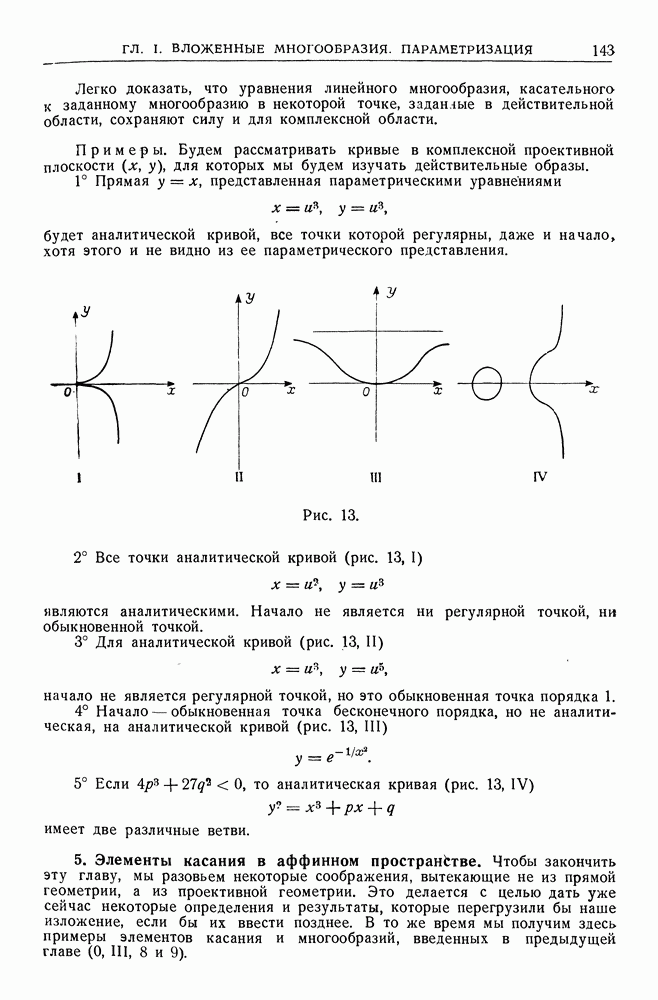
При замене базиса имеем

полагая  выводим отсюда, что
выводим отсюда, что

Допустим теперь, что  и ограничимся преобразованиями, которые сохраняют ориентацию базиса
и ограничимся преобразованиями, которые сохраняют ориентацию базиса  Имеем
Имеем

Следовательно, в силу формул (7.1) величины

[ или 1 в зависимости от четности перестановки
или 1 в зависимости от четности перестановки  ] будут контравариантными компонентами антисимметричного тензора валентности
] будут контравариантными компонентами антисимметричного тензора валентности  Проверяется без труда, что его ковариантные компоненты равны
Проверяется без труда, что его ковариантные компоненты равны

Рассмотрим теперь антисимметричный тензор  валентности
валентности  Пусть
Пусть  одно из его представлений. Тензор
одно из его представлений. Тензор  валентности
валентности  получаемый умножением со свертыванием тензора
получаемый умножением со свертыванием тензора  на предыдущий тензор, называется присоединенным к
на предыдущий тензор, называется присоединенным к  Имеем
Имеем

Тензором, присоединенным к  будет
будет  Тензор, присоединенный к вектору, есть антисимметричный тензор валентности
Тензор, присоединенный к вектору, есть антисимметричный тензор валентности  и наоборот.
и наоборот.
В обычном трехмерном эвклидовом пространстве всякому антисимметричному тензору валентности 2 можно, таким образом, поставить в соответствие вектор. Рассмотрим, в частности, случай бивектора  и предположим, что базис ортонормированный:
и предположим, что базис ортонормированный:

Ненулевые компоненты бивектора выражаются следующими формулами, в которых  обозначают компоненты векторов х и у:
обозначают компоненты векторов х и у:

Присоединенный вектор  имеет компоненты
имеет компоненты

Он называется векторным произведением двух векторов х и у. Путаница в обозначениях, которая теперь приобрела силу привычки, привела к тому, что этот вектор обозначают 
Вектор  таков, что три направления х, у, z образуют правый триэдр. Длина вектора
таков, что три направления х, у, z образуют правый триэдр. Длина вектора  равна
равна

Если перейти к случаю антисимметричного тензора валентности  имеющего только одну главную компоненту
имеющего только одну главную компоненту  то присоединенный к нему тензор будет скаляром
то присоединенный к нему тензор будет скаляром  . В случае если тензор будет внешним произведением
. В случае если тензор будет внешним произведением  векторов
векторов  этот скаляр называется смешанным произведением
этот скаляр называется смешанным произведением  векторов и обозначается через
векторов и обозначается через  Обозначая через
Обозначая через  координаты вектора
координаты вектора  мы имеем
мы имеем

Смешанное произведение обладает всеми свойствами линейности и антикоммутативности внешнего произведения. Когда оно равно нулю,  векторов определяют линейное многообразие размерности
векторов определяют линейное многообразие размерности  Оно представляет ориентированный объем параллелепипеда, построенного на
Оно представляет ориентированный объем параллелепипеда, построенного на  векторах.
векторах.
Для  также пишут (из-за путаницы в обозначениях)
также пишут (из-за путаницы в обозначениях)

| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К РУССКОМУ ИЗДАНИЮ
- ВВЕДЕНИЕ
- Глава I. ОБЩИЕ ПОНЯТИЯ. ОСНОВАНИЯ
- 2. Топологические пространства.
- 3. Подпространства.
- 4. Непрерывные функции.
- 5. Гомеоморфизм.
- 6. Метрические пространства.
- 7. Полные пространства. Компактные пространства и множества.
- 8. Связные пространства и множества.
- 9. Эвклидово аморфное пространство.
- 10. Симплексы. Комплексы.
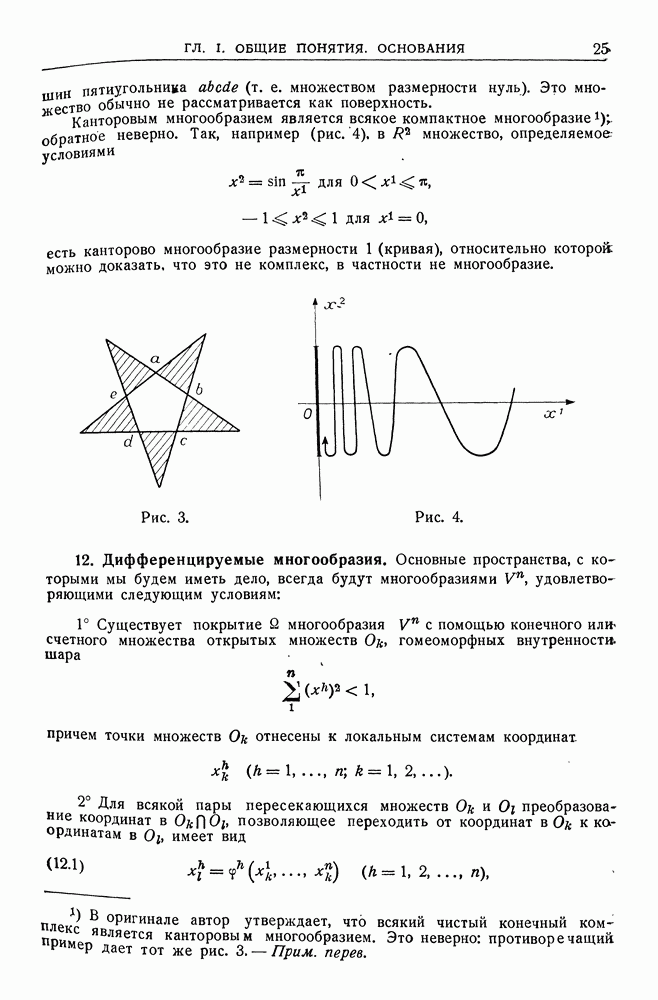
- 11. Размерность. Кривые и поверхности. Канторовы многообразия.
- 12. Дифференцируемые многообразия.
- 13. Общие свойства групп.
- 14. Преобразования. Группы преобразований.
- 15. Топологические группы.
- 16. Группы Ли.
- 17. Геометрические объекты. Транзитивность и интранзитивность. Ориентация.
- 18. Группы Ли классических геометрий.
- 19. Группа движений.
- 20. Аффинная группа.
- 21. Проективная группа.
- 22. Группы дифференциальной геометрии.
- 23. Дополнение о коллинеациях.
- Глава II. ДОПОЛНЕНИЕ К АЛГЕБРЕ. ТЕНЗОРЫ
- 1. Векторное центро-аффинное пространство Сn.
- 2. Тензорные произведения центро-аффинных пространств. Тензоры.
- 3. Аффинные тензоры.
- 4. Соглашение об обозначениях.
- 5. Операции над аффинными тензорами.
- 6. Симметричные и антисимметричные тензоры.
- 7. Антисимметричные контравариантные тензоры. Мультивекторы.
- 8. Антисимметричные ковариантные векторы. Внешние формы.
- 9. Внешние квадратичные формы. Теорема Картана.
- 10. Эвклидовы тензоры.
- 11. Элементарный тензорный анализ.
- Глава III. ДОПОЛНЕНИЯ К АНАЛИЗУ: ВНЕШНЕЕ ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ; ПРИЛОЖЕНИЯ К ГРУППАМ ЛИ И К ОБЩЕЙ ТЕОРИИ ПОГРУЖЕННЫХ МНОГООБРАЗИЙ
- 1. Внешние дифференциальные формы.
- 2. Система Пфаффа. Теорема Фробениуса.
- 3. Группы Ли. Инфинитезимальные преобразования. Относительные и абсолютные компоненты.
- 4. Первая теорема Ли.
- 5. Группа параметров.
- 6. Уравнения структуры Эли Картана.
- 7. Уравнения структуры классических групп.
- 8. Элементы касания, погруженные в многообразие. Продолжение группы преобразований.
- 9. Общая теория погруженных многообразий.
- 10. Метод подвижного репера Эли Картана.
- ПЕРВАЯ ЧАСТЬ. ПРЯМАЯ ИНФИНИТЕЗИМАЛЬНАЯ ГЕОМЕТРИЯ
- Глава I. ВЛОЖЕННЫЕ МНОГООБРАЗИЯ. ПАРАМЕТРИЗАЦИЯ
- 2. Вложенные многообразия. Основной локальный инвариант. Обыкновенные точки.
- 3. Контингенция. Паратингенция.
- 4. Аналитические многообразия. Регулярные точки.
- 5. Элементы касания в аффинном пространстве.
- 6. Соприкасающаяся плоскость и соприкасающаяся полуплоскость кривой в пространстве E3. Вогнутость.
- Глава II. ТЕОРИЯ КАСАНИЯ
- 2. Касание двух кривых.
- 3. Касание кривой и поверхности.
- 4. Касание двух поверхностей.
- Глава III. ОГИБАЮЩИЕ
- 2. Огибающие плоских кривых.
- 3. Огибающие поверхностей, зависящих от одного параметра.
- 4. Огибающие поверхностей, зависящих от двух параметров.
- 5. Огибающие пространственных кривых, зависящих от одного параметра.
- 6. Конгруэнции кривых.
- Глава IV. ПРЕОБРАЗОВАНИЯ КАСАНИЯ
- 1. Примыкающие элементы касания.
- 2. Преобразования касания.
- 3. Примеры.
- ВТОРАЯ ЧАСТЬ. КЛАССИЧЕСКИЕ ГЕОМЕТРИИ
- Глава I. ТЕОРИЯ ПРОСТРАНСТВЕННЫХ КРИВЫХ
- 2. Формулы Серре-Френе.
- 3. Триэдр Френе.
- 4. Кривизна и кручение.
- 5. Положение кривой в окрестности точки по отношению к триэдру Серре — Френе. Знак кручения.
- 6. Определение кривой ее натуральными уравнениями.
- 7. Винтовые линии.
- 8. Конгруэнция нормалей к пространственной кривой.
- 9. Замечания.
- 10. Изотропные кривые (или минимальные линии).
- Глава II. ТЕОРИЯ ПОВЕРХНОСТЕЙ; ТРИЭДР ФРЕНЕ
- 1. Триэдр Френе.
- 2. Особые случаи.
- 3. Поверхности, инвариантные относительно группы движений.
- 4. Теоремы равенства и существования.
- 5. Вычисление инвариантных линейных форм и кривизн.
- 6. Геодезические свойства. Внешние свойства.
- Глава III. ТЕОРИЯ ПОВЕРХНОСТЕЙ; ПЕРВАЯ ОСНОВНАЯ КВАДРАТИЧНАЯ ФОРМА
- 2. Минимальные линии (линии нулевой длины).
- 3. Конформное отображение одной поверхности на другую. Изотермические координаты.
- 4. Изометрия. Полная кривизна.
- 5. Изометричные поверхности.
- 6. Группа изометрии линейных элементов ds2 постоянной кривизны.
- 7. Поверхности, изометричные плоскости.
- 8. Вопросы анализа на поверхности.
- 9. Геодезические линии («внешняя» теория).
- 10. Геодезическая кривизна.
- 11. Поле векторов. Ковариантные частные производные Параллельный перенос.
- 12. Формула Оссиана Бонне.
- 13. Поле тензоров. Ковариантная производная.
- Глава IV. ТЕОРИЯ ПОВЕРХНОСТЕЙ, ВТОРАЯ ОСНОВНАЯ КВАДРАТИЧНАЯ ФОРМА
- 2. Расположение поверхности по отношению к касательной плоскости. Обыкновенные точки второго порядка.
- 3. Асимптотические линии.
- 4. Сопряженные направления. Сопряженные семейства кривых.
- 5. Триэдр Френе для кривой, проведенной на поверхности. Теоремы Менье и Оссиана Бонне.
- 6. Кривизна нормальных сечений. Индикатриса Дюпена.
- 7. Главные направления. Главные кривизны.
- 8. Линия кривизны. Эволюты, или поверхности центров кривизны поверхности.
- 9. Конгруэнции нормалей.
- 10. Примеры.
- 11. Сферическое изображение. Третья квадратичная форма поверхности.
- 12. Относительное кручение. Четвертая квадратичная форма.
- 13. Точечные преобразования и преобразования касания, сохраняющие асимптотические линии.
- 14. Точечные преобразования, сохраняющие линии кривизны.
- 15. Преобразование Ли. Преобразования касания, сохраняющие линии кривизны.
- 16. Возвращение к условиям интегрируемости.
- Глава V. ЛИНЕЙЧАТАЯ ЭВКЛИДОВА ГЕОМЕТРИЯ
- 1. Плюккеровы координаты.
- 2. Линейчатые поверхности.
- 3. Конгруэнции прямых.
- 4. Линейчатые поверхности конгруэнции.
- 5. Вычисление инвариантов. Квадратичные формы.
- 6. Формула Эли Картана. Конгруэнции нормалей.
- 7. Изотропные конгруэнции.
- 8. Комплексы прямых.
- 9. Срединные линии. Кривые, касательные к которым принадлежат комплексу. Линейные комплексы.
- 10. Подсчет инвариантных линейных форм и инвариантов. Конгруэнции и линейчатые поверхности комплекса.
- ВТОРОЙ РАЗДЕЛ. АФФИННАЯ УНИМОДУЛЯРНАЯ ГЕОМЕТРИЯ
- 2. Теория плоских кривых.
- 3. Геометрическая интерпретация. Конические сечения.
- 4. Теория пространственных кривых. Репер Френе.
- 5. Вычисление аффинной дуги и инвариантов. Пространственные кривые третьего порядка.
- Глава II. ТЕОРИЯ ПОВЕРХНОСТЕЙ
- 1. Репер Френе. Общие случаи.
- 2. Поверхности второго порядка (не развертывающиеся). Линейчатые поверхности.
- 3. Развертывающиеся поверхности.
- 4. Приведенные уравнения.
- 5. Соприкасающиеся квадрики. Касательные Дарбу.
- 6. Квадрика Ли.
- 7. Поверхности, инвариантные относительно транзитивной группы.
- 8. Кривые, лежащие на поверхности.
- 9. Алгебраические дифференциальные инвариантные формы.
- 10. Условия интегрируемости в терминах форм …
- ТРЕТИЙ РАЗДЕЛ. ПРОЕКТИВНАЯ ГЕОМЕТРИЯ
- 1. Формулы перемещений репера. Перемещения коррелятивного репера.
- 2. Теория плоских кривых. Репер Френе.
- 3. Конические сечения.
- 4. Вычисление проективной дуги и проективной кривизны. Приведенное уравнение. Секстактические точки.
- 5. Ангармоническое отношение четырех точек.
- 6. Огибающие прямых.
- 7. Теория пространственных кривых.
- 8. Теория поверхностей. Репер Френе.
- 9. Уравнение, приведенное в окрестности точки.
- 10. Коррелятивная точка зрения. Огибающие плоскостей.
- 11. Проективная наложимость.
- ТРЕТЬЯ ЧАСТЬ. ТЕОРИЯ ПЕРЕНЕСЕНИЯ
- Глава I. ПЕРЕНЕСЕНИЕ И СВЯЗНОСТЬ. ПРОСТРАНСТВА АФФИННОЙ СВЯЗНОСТИ
- 2. Группа голономий.
- 3. Линейные аффинные связности. Эквивалентность.
- 4. Тензоры кривизны и кручения.
- 5. Ковариантная производная тензора.
- 6. Тождества Бианки.
- 7. Вычисление компонент тензоров кривизны и кручения.
- 8. Параллельный перенос. Геодезические.
- 9. Основная теорема.
- 10. Изучение связности в окрестности точки.
- 11. Геодезические наложения.
- 12. Поля параллельных контравариантные векторов.
- 13. Разложимые пространства.
- 14. Эквиаффинная связность.
- 15. Метрические связности. Пространства Эддингтона, Вейля и Эйнштейна.
- 16. Проективные связности.
- 17. Проективные тензоры.
- Глава II. РИМАНОВЫ ПРОСТРАНСТВА
- 2. Геодезические. Экстремальное свойство. Аналитические римановы пространства.
- 3. Кривизна пространства в направлении площадки. Пространства постоянной кривизны
- 4. Тензор конформной кривизны.
- 5. Движения.
- 6. Разложимые пространства.
- 7. Теория кривых.
- 8. Вложенные многообразия.