| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2. Расположение поверхности по отношению к касательной плоскости. Обыкновенные точки второго порядка.
Если форма II не равна тождественно нулю в точке  поверхности
поверхности  то положение точки
то положение точки  по отношению к касательной плоскости в точке
по отношению к касательной плоскости в точке  определяется знаком выражения
определяется знаком выражения

при этом вторые частные производные функции  предполагаются непрерывными,
предполагаются непрерывными,  обозначают скаляры, стремящиеся к нулю вместе с приращениями
обозначают скаляры, стремящиеся к нулю вместе с приращениями  Выражение (2.1) можно также записать в форме
Выражение (2.1) можно также записать в форме

где  также стремится к нулю вместе с
также стремится к нулю вместе с  чтобы изучить его знак, нам надо будет рассмотреть три случая.
чтобы изучить его знак, нам надо будет рассмотреть три случая.
Первый случай. Эллиптическая точка. Форма II или форма  знакоопределенная, т. е.
знакоопределенная, т. е.

Если  будет достаточно малым, то можно найти такое число
будет достаточно малым, то можно найти такое число  что неравенство
что неравенство

будет иметь место, если

при этих условиях  сохраняет постоянный знак и обращается в нуль только для
сохраняет постоянный знак и обращается в нуль только для  Это означает, что точка
Это означает, что точка
 остается все время по одну сторону от касательной плоскости в точке
остается все время по одну сторону от касательной плоскости в точке  если
если  и ко будут достаточно малы; поверхность не пересекает свою касательную плоскость и имеет с ней в некоторой окрестности только одну общую точку — точку касания. Для определенности будем говорить, что поверхность лежит выше своей касательной плоскости в точке
и ко будут достаточно малы; поверхность не пересекает свою касательную плоскость и имеет с ней в некоторой окрестности только одну общую точку — точку касания. Для определенности будем говорить, что поверхность лежит выше своей касательной плоскости в точке 
Пусть заданы две точки  с координатами соответственно
с координатами соответственно  с точностью до бесконечно малых высшего порядка проекция точки
с точностью до бесконечно малых высшего порядка проекция точки  с координатами
с координатами

на касательную плоскость совпадает с серединой отрезка между проекциями точек  и разность
и разность

с точностью до бесконечно малых высшего порядка может быть представлена в виде

она имеет знак формы II. Между тем  представляет собой отметку высоты точки
представляет собой отметку высоты точки  по отношению к касательной плоскости; замечание, которое мы только что сделали, показывает, что точка
по отношению к касательной плоскости; замечание, которое мы только что сделали, показывает, что точка  лежит в плоскости, проектирующей отрезок, соединяющий точки
лежит в плоскости, проектирующей отрезок, соединяющий точки  и
и  ниже середины этого отрезка.
ниже середины этого отрезка.

Рис. 35.
Поэтому говорят, что поверхность  выпукла в окрестности рассматриваемой точки, которая называется эллиптической точкой поверхности
выпукла в окрестности рассматриваемой точки, которая называется эллиптической точкой поверхности 
Второй случай. Гиперболическая точка, или точка с кривизнами противоположных знаков. Форма II или форма  не
не
является определенной, т. е.

Возвращаемся к выражению  ; аналогичные рассуждения показывают нам, что уравнение
; аналогичные рассуждения показывают нам, что уравнение

определяет в окрестности точки  и в касательной плоскости в точке
и в касательной плоскости в точке  две ветви кривых
две ветви кривых  которые представляют собой сечения поверхности
которые представляют собой сечения поверхности  касательной плоскостью в точке
касательной плоскостью в точке  и соответственно касаются направлений
и соответственно касаются направлений  обращающих в нуль форму II
обращающих в нуль форму II

эти направления называются асимптотическими направлениями поверхности в точке 
Более того,  изменяет знак при пересечении кривой
изменяет знак при пересечении кривой  или кривой
или кривой  следовательно, поверхность пересекает свою касательную плоскость.
следовательно, поверхность пересекает свою касательную плоскость.
Рассечем поверхность плоскостью, проходящей через точку  и нормаль к поверхности
и нормаль к поверхности  в точке
в точке  пусть это сечение имеет направление
пусть это сечение имеет направление  отличное от асимптотических направлений.
отличное от асимптотических направлений.

Рис. 36.
Примем теперь  достаточно малыми, чтобы
достаточно малыми, чтобы  сохраняло один и тот же знак в точках
сохраняло один и тот же знак в точках

С точностью до бесконечно малых высшего порядка эти точки проектируются на касательную плоскость на направление  имеем
имеем

это показывает, что сечение поверхности рассматриваемой плоскостью будет кривой, которая в окрестности точки  обращена своей вогнутостью к положительному направлению нормали или к ее отрицательному направлению, смотря по знаку формы II для направления
обращена своей вогнутостью к положительному направлению нормали или к ее отрицательному направлению, смотря по знаку формы II для направления 
Если же мы примем за направление  асимптотическое направление, то, предполагая существование непрерывных частных производных третьего порядка для функции
асимптотическое направление, то, предполагая существование непрерывных частных производных третьего порядка для функции  мы видим, что выражение
мы видим, что выражение  будет по крайней мере третьего порядка малости: следовательно, асимптотическое направление имеет с поверхностью
будет по крайней мере третьего порядка малости: следовательно, асимптотическое направление имеет с поверхностью  касание не ниже второго порядка, оно будет направлением, соприкасающимся к поверхности в точке
касание не ниже второго порядка, оно будет направлением, соприкасающимся к поверхности в точке 
Главные кривизны поверхности в такой точке имеют противоположные знаки. Такая точка называется гиперболической точкой поверхности 
Третий случай. Параболическая точка. Развертывающиеся поверхности. Форма II или форма  сохраняет постоянный знак, но не является знакоопределенной: это случай, когда
сохраняет постоянный знак, но не является знакоопределенной: это случай, когда

Имеется одно двойное асимптотическое направление  задаваемое уравнением
задаваемое уравнением

и точка называется параболической.
Такие же соображения показывают теперь, что нормальные сечения, проходящие по направлению, отличному от асимптотического, имеют вогнутость в одну и ту же сторону. Однако поверхность может пересекать касательную плоскость или же оставлять ее с одной стороны в зависимости от рассматриваемого случая; так, поверхность  пересекает свою касательную плоскость в начале, между тем как поверхность
пересекает свою касательную плоскость в начале, между тем как поверхность  не пересекает ее.
не пересекает ее.
В силу (1.2) соотношение (2.3) напишется так:

оно показывает, что два вектора и коллинеарны, например,

в точке  существует направление, определяемое равенством
существует направление, определяемое равенством  вдоль которого
вдоль которого  и это условие достаточно для того, чтобы точка
и это условие достаточно для того, чтобы точка  была параболической.
была параболической.
На поверхности существует, вообще говоря, линия параболических точек, определяемая уравнением (2.3); например, на торе экстремальные параллели, вдоль которых касательная плоскость перпендикулярна к оси, будут линиями параболических точек; они отделяют множество эллиптических точек от множества гиперболических точек. Впрочем, вообще, если поверхность касается плоскости вдоль некоторой линии, то эта линия будет линией параболических точек, ибо мы имеем  вдоль всей этой, линии.
вдоль всей этой, линии.
Если поверхность состоит только из параболических точек, то через каждую точку проходит линия, вдоль которой  Пусть
Пусть  определяет это семейство линий; равенство
определяет это семейство линий; равенство  должно иметь следствием
должно иметь следствием  соотношения (II, 1.2) показывают теперь, что
соотношения (II, 1.2) показывают теперь, что  отсюда
отсюда  Поверхность, следовательно, будет развертывающейся (III, 7). Кроме того, вдоль прямолинейной образующей развертывающейся поверхности мы имеем
Поверхность, следовательно, будет развертывающейся (III, 7). Кроме того, вдоль прямолинейной образующей развертывающейся поверхности мы имеем  Таким образом,
Таким образом,
Поверхность, все точки которой параболические, является развертывающейся, и обратно.
Точки уплощения. Если форма II обращается в нуль тождественно, то для изучения расположения поверхности по отношению к ее касательной плоскости нужно рассматривать производные высших порядков. Уравнения

не что иное, как уравнения  ; такая точка, следовательно, будет точкой уплощения, согласно введенному там определению. Предыдущие три уравнения относительно
; такая точка, следовательно, будет точкой уплощения, согласно введенному там определению. Предыдущие три уравнения относительно  вообще говоря, будут несовместны, следовательно, на поверхности в общем случае не имеется точек уплощения.
вообще говоря, будут несовместны, следовательно, на поверхности в общем случае не имеется точек уплощения.
В силу того, что мы видели в (I, 1.5), поверхность, целиком состоящая из точек уплощения, является плоскостью, и обратно.
Обыкновенные точки второго порядка. На поверхности  не являющейся развертывающейся, эллиптические точки и гиперболические точки образуют открытые множества; параболические точки представляют собой особенные точки.
не являющейся развертывающейся, эллиптические точки и гиперболические точки образуют открытые множества; параболические точки представляют собой особенные точки.
Мы будем называть обыкновенной точкой второго порядка на поверхности  такую точку, в окрестности которой может быть введена такая допустимая параметризация
такую точку, в окрестности которой может быть введена такая допустимая параметризация  что функция
что функция  будет иметь в этой окрестности непрерывные частные производные второго порядка; точка тогда представляет собой или эллиптическую или гиперболическую точку. Можно показать, как и в первой части, что это свойство можно обнаружить, принимая в качестве параметров подходящим образом выбранную пару декартовых координат.
будет иметь в этой окрестности непрерывные частные производные второго порядка; точка тогда представляет собой или эллиптическую или гиперболическую точку. Можно показать, как и в первой части, что это свойство можно обнаружить, принимая в качестве параметров подходящим образом выбранную пару декартовых координат.
На развертывающейся поверхности  все точки будут параболическими; мы будем называть на ней обыкновенной точкой второго порядка любую точку, не являющуюся точкой уплощения. Легко видеть, оставляя в стороне особые точки ребра, возврата, что из обыкновенных точек второго порядка будут состоять те прямолинейные образующие, которые выходят из обыкновенных точек третьего порядка на ребре возврата.
все точки будут параболическими; мы будем называть на ней обыкновенной точкой второго порядка любую точку, не являющуюся точкой уплощения. Легко видеть, оставляя в стороне особые точки ребра, возврата, что из обыкновенных точек второго порядка будут состоять те прямолинейные образующие, которые выходят из обыкновенных точек третьего порядка на ребре возврата.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К РУССКОМУ ИЗДАНИЮ
- ВВЕДЕНИЕ
- Глава I. ОБЩИЕ ПОНЯТИЯ. ОСНОВАНИЯ
- 2. Топологические пространства.
- 3. Подпространства.
- 4. Непрерывные функции.
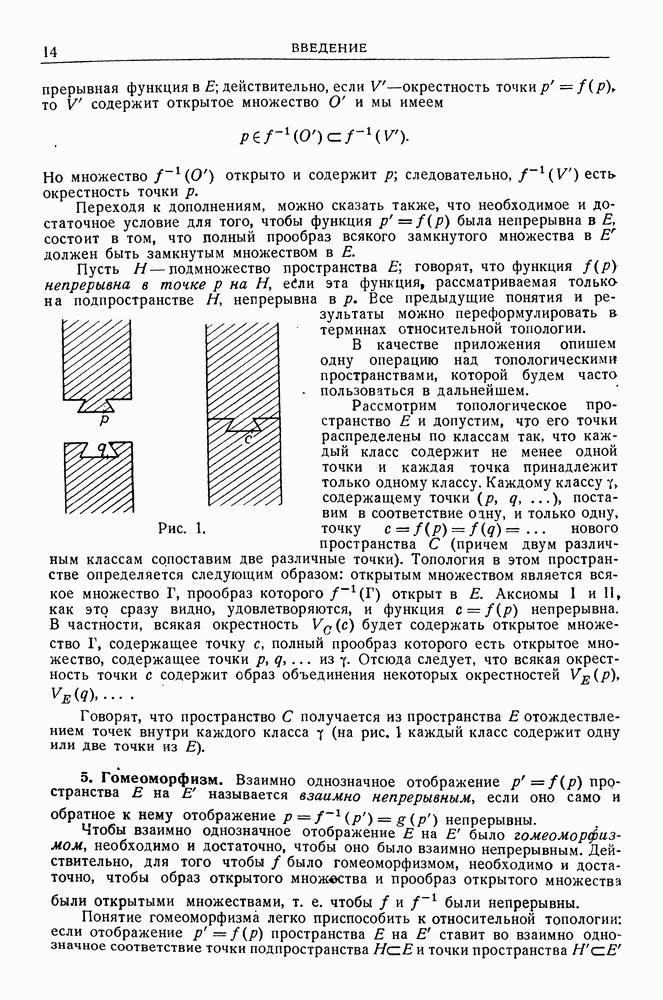
- 5. Гомеоморфизм.
- 6. Метрические пространства.
- 7. Полные пространства. Компактные пространства и множества.
- 8. Связные пространства и множества.
- 9. Эвклидово аморфное пространство.
- 10. Симплексы. Комплексы.
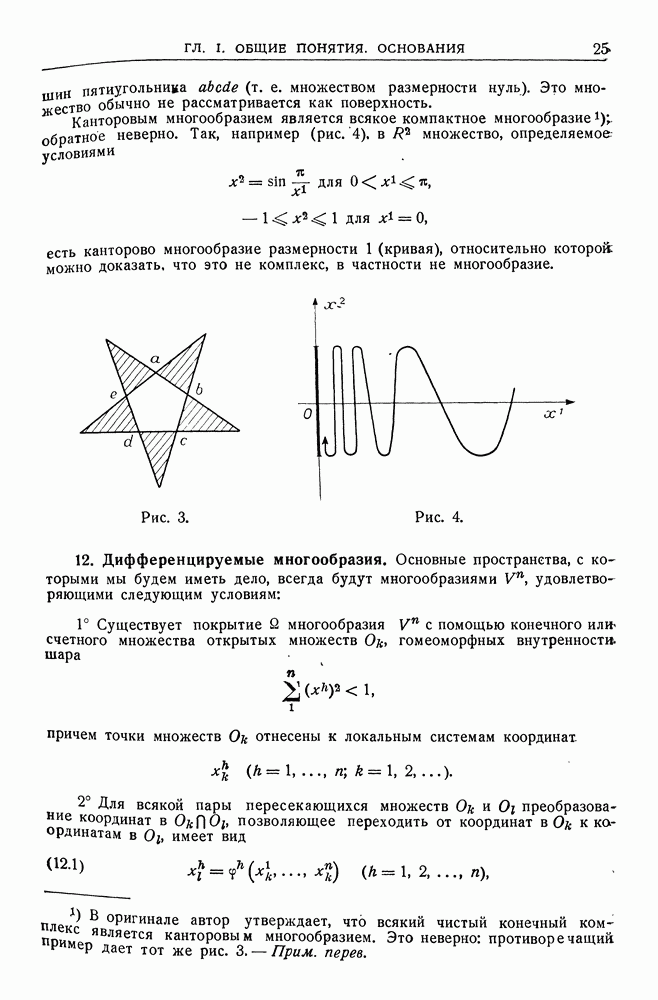
- 11. Размерность. Кривые и поверхности. Канторовы многообразия.
- 12. Дифференцируемые многообразия.
- 13. Общие свойства групп.
- 14. Преобразования. Группы преобразований.
- 15. Топологические группы.
- 16. Группы Ли.
- 17. Геометрические объекты. Транзитивность и интранзитивность. Ориентация.
- 18. Группы Ли классических геометрий.
- 19. Группа движений.
- 20. Аффинная группа.
- 21. Проективная группа.
- 22. Группы дифференциальной геометрии.
- 23. Дополнение о коллинеациях.
- Глава II. ДОПОЛНЕНИЕ К АЛГЕБРЕ. ТЕНЗОРЫ
- 1. Векторное центро-аффинное пространство Сn.
- 2. Тензорные произведения центро-аффинных пространств. Тензоры.
- 3. Аффинные тензоры.
- 4. Соглашение об обозначениях.
- 5. Операции над аффинными тензорами.
- 6. Симметричные и антисимметричные тензоры.
- 7. Антисимметричные контравариантные тензоры. Мультивекторы.
- 8. Антисимметричные ковариантные векторы. Внешние формы.
- 9. Внешние квадратичные формы. Теорема Картана.
- 10. Эвклидовы тензоры.
- 11. Элементарный тензорный анализ.
- Глава III. ДОПОЛНЕНИЯ К АНАЛИЗУ: ВНЕШНЕЕ ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ; ПРИЛОЖЕНИЯ К ГРУППАМ ЛИ И К ОБЩЕЙ ТЕОРИИ ПОГРУЖЕННЫХ МНОГООБРАЗИЙ
- 1. Внешние дифференциальные формы.
- 2. Система Пфаффа. Теорема Фробениуса.
- 3. Группы Ли. Инфинитезимальные преобразования. Относительные и абсолютные компоненты.
- 4. Первая теорема Ли.
- 5. Группа параметров.
- 6. Уравнения структуры Эли Картана.
- 7. Уравнения структуры классических групп.
- 8. Элементы касания, погруженные в многообразие. Продолжение группы преобразований.
- 9. Общая теория погруженных многообразий.
- 10. Метод подвижного репера Эли Картана.
- ПЕРВАЯ ЧАСТЬ. ПРЯМАЯ ИНФИНИТЕЗИМАЛЬНАЯ ГЕОМЕТРИЯ
- Глава I. ВЛОЖЕННЫЕ МНОГООБРАЗИЯ. ПАРАМЕТРИЗАЦИЯ
- 2. Вложенные многообразия. Основной локальный инвариант. Обыкновенные точки.
- 3. Контингенция. Паратингенция.
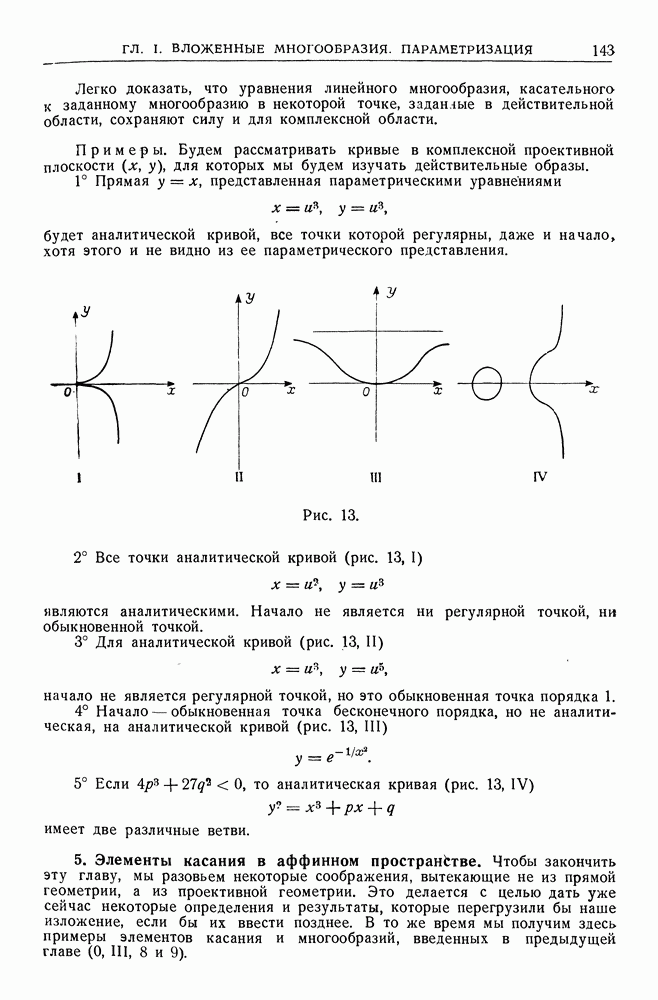
- 4. Аналитические многообразия. Регулярные точки.
- 5. Элементы касания в аффинном пространстве.
- 6. Соприкасающаяся плоскость и соприкасающаяся полуплоскость кривой в пространстве E3. Вогнутость.
- Глава II. ТЕОРИЯ КАСАНИЯ
- 2. Касание двух кривых.
- 3. Касание кривой и поверхности.
- 4. Касание двух поверхностей.
- Глава III. ОГИБАЮЩИЕ
- 2. Огибающие плоских кривых.
- 3. Огибающие поверхностей, зависящих от одного параметра.
- 4. Огибающие поверхностей, зависящих от двух параметров.
- 5. Огибающие пространственных кривых, зависящих от одного параметра.
- 6. Конгруэнции кривых.
- Глава IV. ПРЕОБРАЗОВАНИЯ КАСАНИЯ
- 1. Примыкающие элементы касания.
- 2. Преобразования касания.
- 3. Примеры.
- ВТОРАЯ ЧАСТЬ. КЛАССИЧЕСКИЕ ГЕОМЕТРИИ
- Глава I. ТЕОРИЯ ПРОСТРАНСТВЕННЫХ КРИВЫХ
- 2. Формулы Серре-Френе.
- 3. Триэдр Френе.
- 4. Кривизна и кручение.
- 5. Положение кривой в окрестности точки по отношению к триэдру Серре — Френе. Знак кручения.
- 6. Определение кривой ее натуральными уравнениями.
- 7. Винтовые линии.
- 8. Конгруэнция нормалей к пространственной кривой.
- 9. Замечания.
- 10. Изотропные кривые (или минимальные линии).
- Глава II. ТЕОРИЯ ПОВЕРХНОСТЕЙ; ТРИЭДР ФРЕНЕ
- 1. Триэдр Френе.
- 2. Особые случаи.
- 3. Поверхности, инвариантные относительно группы движений.
- 4. Теоремы равенства и существования.
- 5. Вычисление инвариантных линейных форм и кривизн.
- 6. Геодезические свойства. Внешние свойства.
- Глава III. ТЕОРИЯ ПОВЕРХНОСТЕЙ; ПЕРВАЯ ОСНОВНАЯ КВАДРАТИЧНАЯ ФОРМА
- 2. Минимальные линии (линии нулевой длины).
- 3. Конформное отображение одной поверхности на другую. Изотермические координаты.
- 4. Изометрия. Полная кривизна.
- 5. Изометричные поверхности.
- 6. Группа изометрии линейных элементов ds2 постоянной кривизны.
- 7. Поверхности, изометричные плоскости.
- 8. Вопросы анализа на поверхности.
- 9. Геодезические линии («внешняя» теория).
- 10. Геодезическая кривизна.
- 11. Поле векторов. Ковариантные частные производные Параллельный перенос.
- 12. Формула Оссиана Бонне.
- 13. Поле тензоров. Ковариантная производная.
- Глава IV. ТЕОРИЯ ПОВЕРХНОСТЕЙ, ВТОРАЯ ОСНОВНАЯ КВАДРАТИЧНАЯ ФОРМА
- 2. Расположение поверхности по отношению к касательной плоскости. Обыкновенные точки второго порядка.
- 3. Асимптотические линии.
- 4. Сопряженные направления. Сопряженные семейства кривых.
- 5. Триэдр Френе для кривой, проведенной на поверхности. Теоремы Менье и Оссиана Бонне.
- 6. Кривизна нормальных сечений. Индикатриса Дюпена.
- 7. Главные направления. Главные кривизны.
- 8. Линия кривизны. Эволюты, или поверхности центров кривизны поверхности.
- 9. Конгруэнции нормалей.
- 10. Примеры.
- 11. Сферическое изображение. Третья квадратичная форма поверхности.
- 12. Относительное кручение. Четвертая квадратичная форма.
- 13. Точечные преобразования и преобразования касания, сохраняющие асимптотические линии.
- 14. Точечные преобразования, сохраняющие линии кривизны.
- 15. Преобразование Ли. Преобразования касания, сохраняющие линии кривизны.
- 16. Возвращение к условиям интегрируемости.
- Глава V. ЛИНЕЙЧАТАЯ ЭВКЛИДОВА ГЕОМЕТРИЯ
- 1. Плюккеровы координаты.
- 2. Линейчатые поверхности.
- 3. Конгруэнции прямых.
- 4. Линейчатые поверхности конгруэнции.
- 5. Вычисление инвариантов. Квадратичные формы.
- 6. Формула Эли Картана. Конгруэнции нормалей.
- 7. Изотропные конгруэнции.
- 8. Комплексы прямых.
- 9. Срединные линии. Кривые, касательные к которым принадлежат комплексу. Линейные комплексы.
- 10. Подсчет инвариантных линейных форм и инвариантов. Конгруэнции и линейчатые поверхности комплекса.
- ВТОРОЙ РАЗДЕЛ. АФФИННАЯ УНИМОДУЛЯРНАЯ ГЕОМЕТРИЯ
- 2. Теория плоских кривых.
- 3. Геометрическая интерпретация. Конические сечения.
- 4. Теория пространственных кривых. Репер Френе.
- 5. Вычисление аффинной дуги и инвариантов. Пространственные кривые третьего порядка.
- Глава II. ТЕОРИЯ ПОВЕРХНОСТЕЙ
- 1. Репер Френе. Общие случаи.
- 2. Поверхности второго порядка (не развертывающиеся). Линейчатые поверхности.
- 3. Развертывающиеся поверхности.
- 4. Приведенные уравнения.
- 5. Соприкасающиеся квадрики. Касательные Дарбу.
- 6. Квадрика Ли.
- 7. Поверхности, инвариантные относительно транзитивной группы.
- 8. Кривые, лежащие на поверхности.
- 9. Алгебраические дифференциальные инвариантные формы.
- 10. Условия интегрируемости в терминах форм …
- ТРЕТИЙ РАЗДЕЛ. ПРОЕКТИВНАЯ ГЕОМЕТРИЯ
- 1. Формулы перемещений репера. Перемещения коррелятивного репера.
- 2. Теория плоских кривых. Репер Френе.
- 3. Конические сечения.
- 4. Вычисление проективной дуги и проективной кривизны. Приведенное уравнение. Секстактические точки.
- 5. Ангармоническое отношение четырех точек.
- 6. Огибающие прямых.
- 7. Теория пространственных кривых.
- 8. Теория поверхностей. Репер Френе.
- 9. Уравнение, приведенное в окрестности точки.
- 10. Коррелятивная точка зрения. Огибающие плоскостей.
- 11. Проективная наложимость.
- ТРЕТЬЯ ЧАСТЬ. ТЕОРИЯ ПЕРЕНЕСЕНИЯ
- Глава I. ПЕРЕНЕСЕНИЕ И СВЯЗНОСТЬ. ПРОСТРАНСТВА АФФИННОЙ СВЯЗНОСТИ
- 2. Группа голономий.
- 3. Линейные аффинные связности. Эквивалентность.
- 4. Тензоры кривизны и кручения.
- 5. Ковариантная производная тензора.
- 6. Тождества Бианки.
- 7. Вычисление компонент тензоров кривизны и кручения.
- 8. Параллельный перенос. Геодезические.
- 9. Основная теорема.
- 10. Изучение связности в окрестности точки.
- 11. Геодезические наложения.
- 12. Поля параллельных контравариантные векторов.
- 13. Разложимые пространства.
- 14. Эквиаффинная связность.
- 15. Метрические связности. Пространства Эддингтона, Вейля и Эйнштейна.
- 16. Проективные связности.
- 17. Проективные тензоры.
- Глава II. РИМАНОВЫ ПРОСТРАНСТВА
- 2. Геодезические. Экстремальное свойство. Аналитические римановы пространства.
- 3. Кривизна пространства в направлении площадки. Пространства постоянной кривизны
- 4. Тензор конформной кривизны.
- 5. Движения.
- 6. Разложимые пространства.
- 7. Теория кривых.
- 8. Вложенные многообразия.