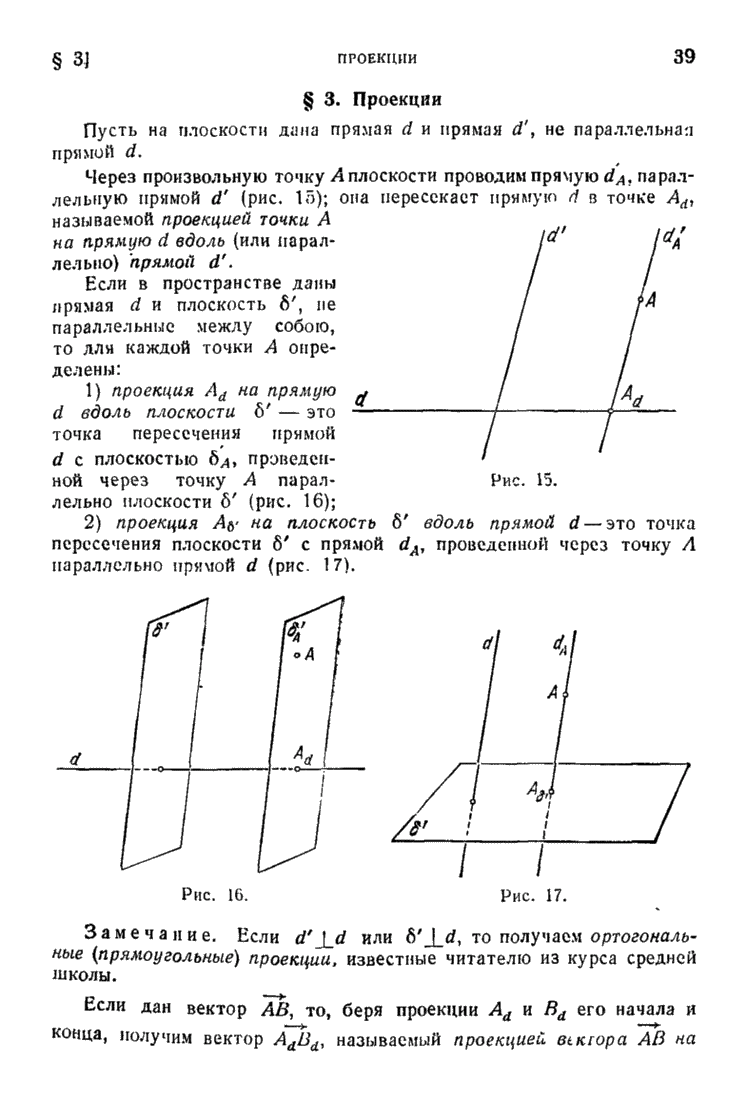
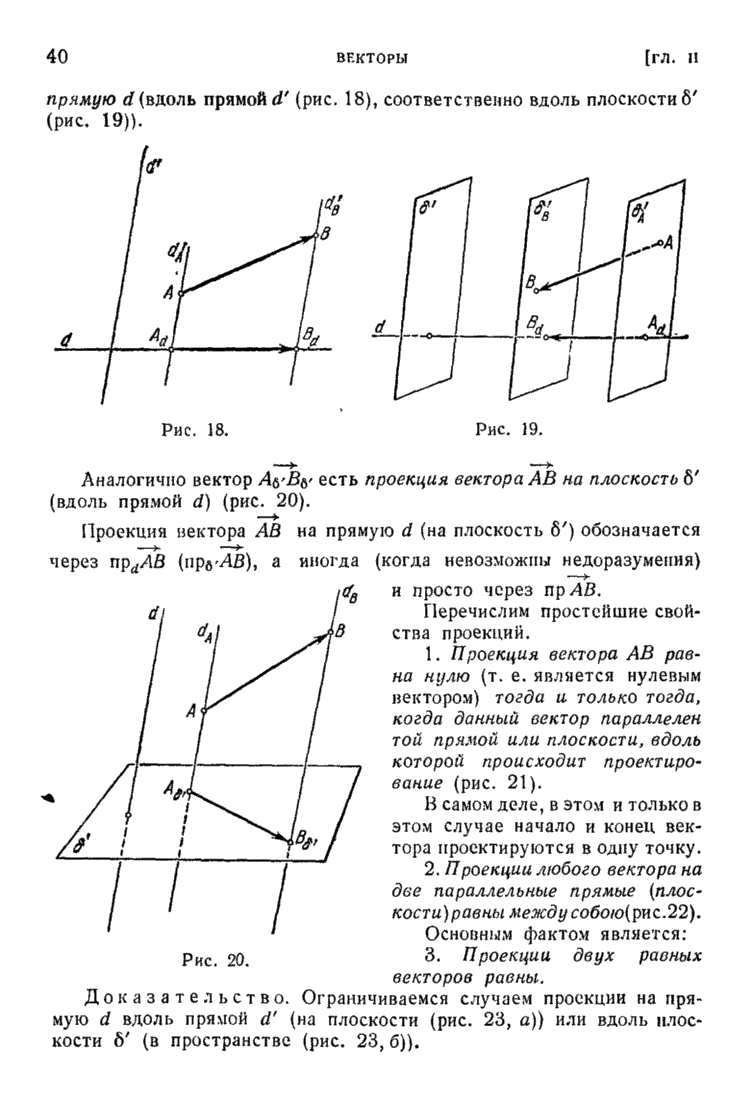
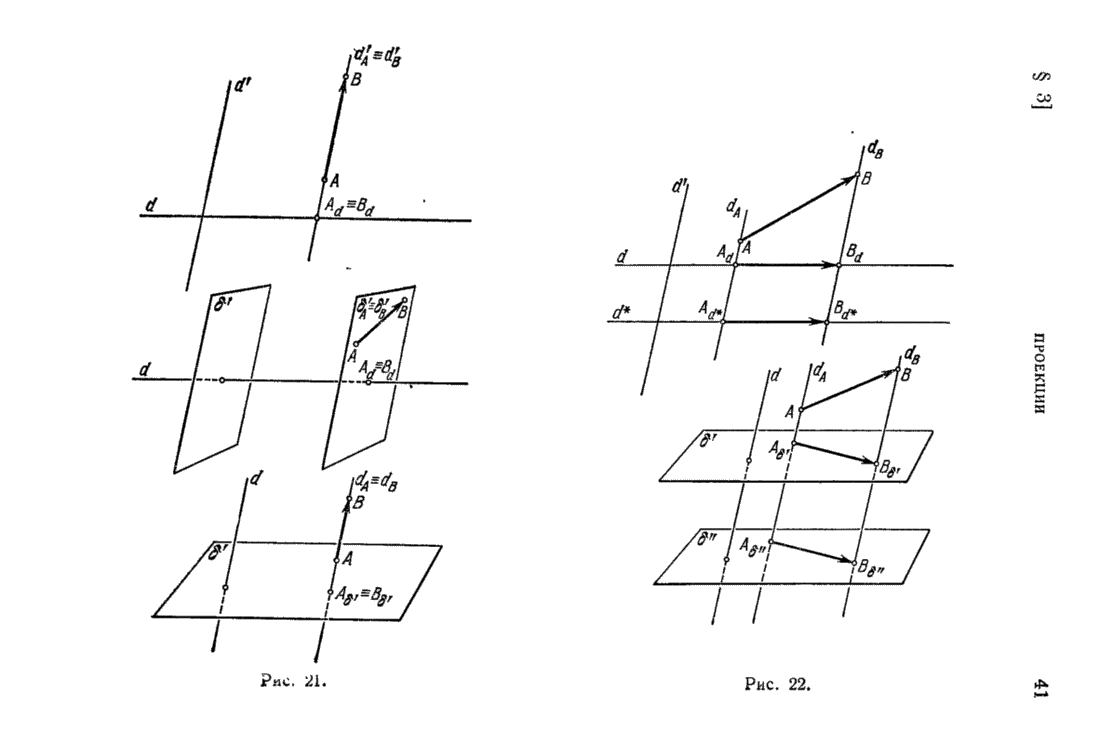
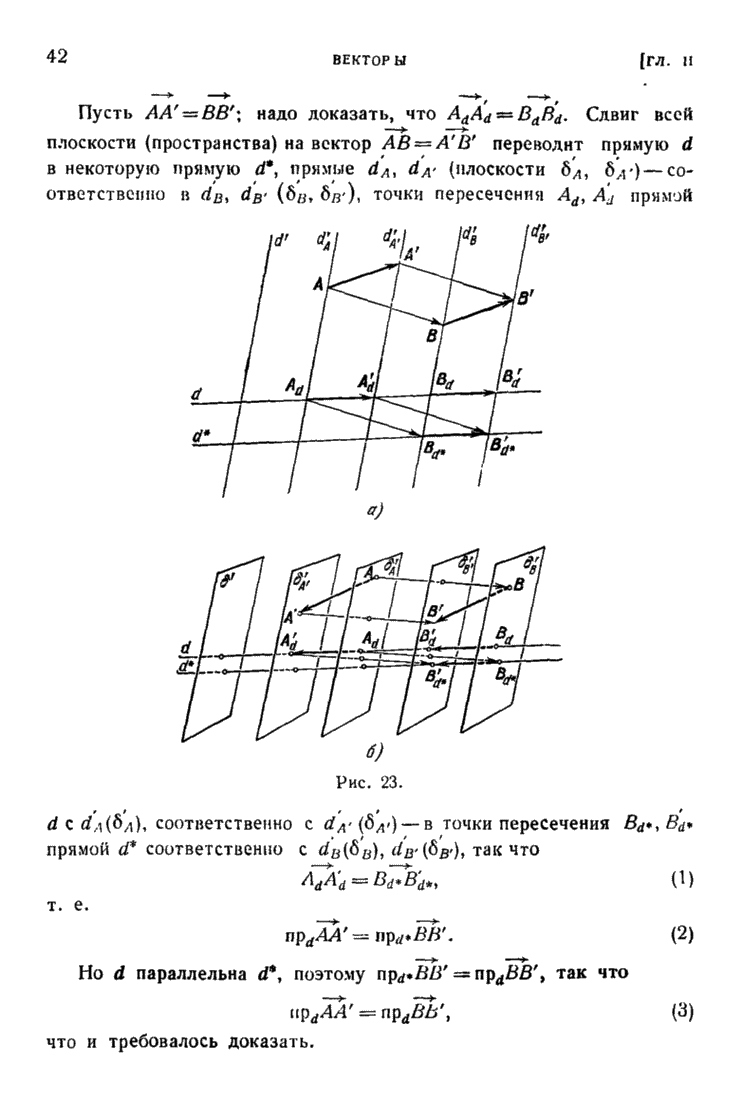
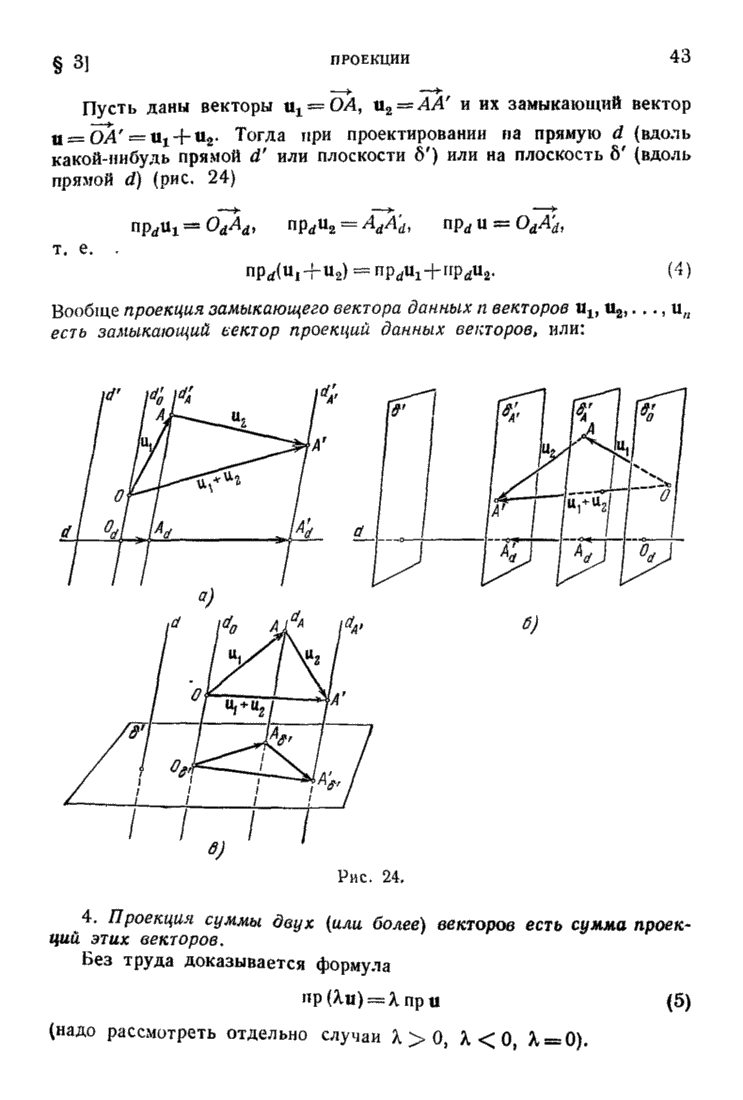
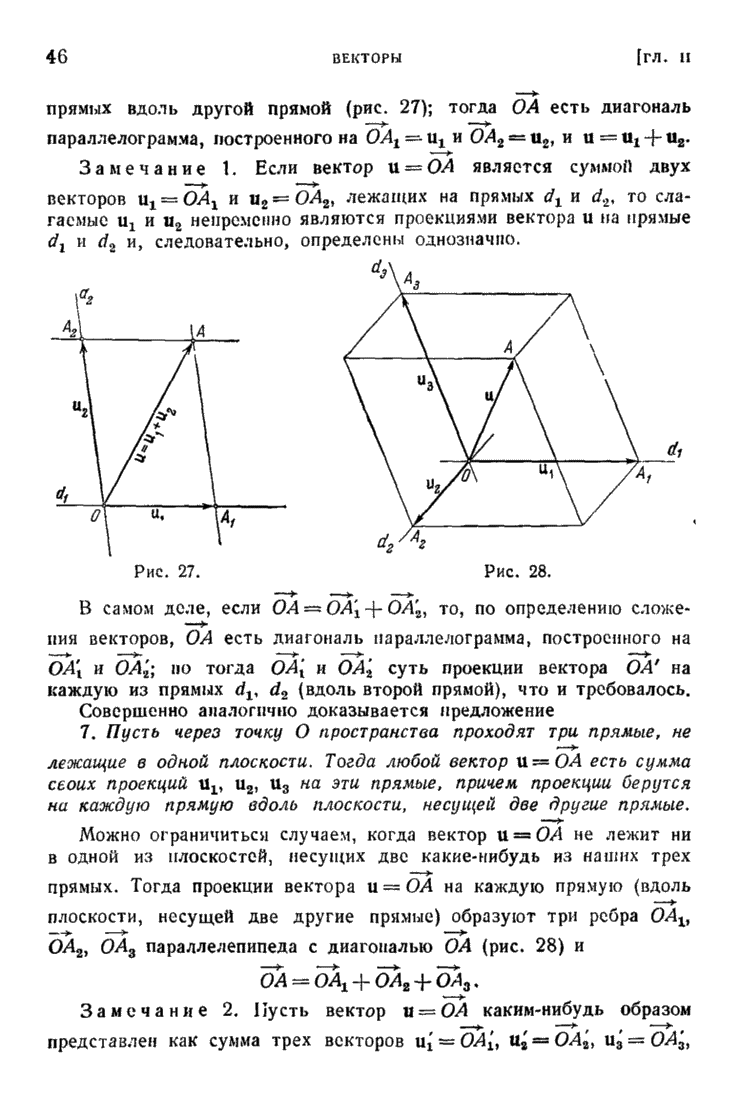
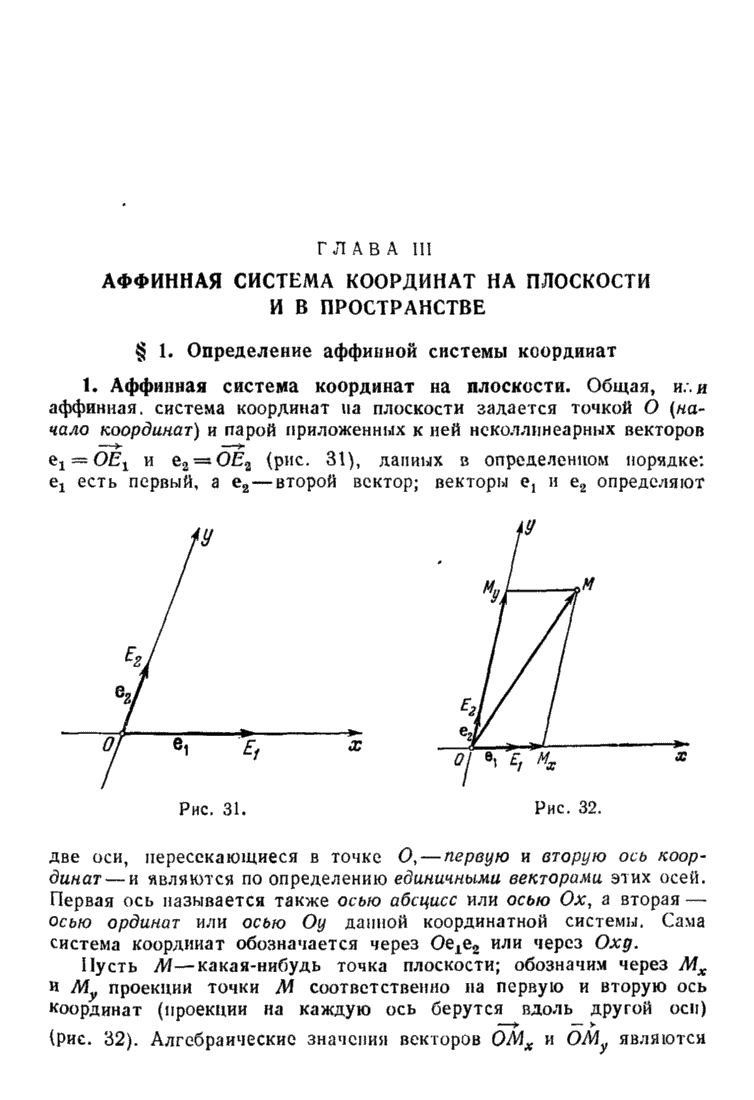
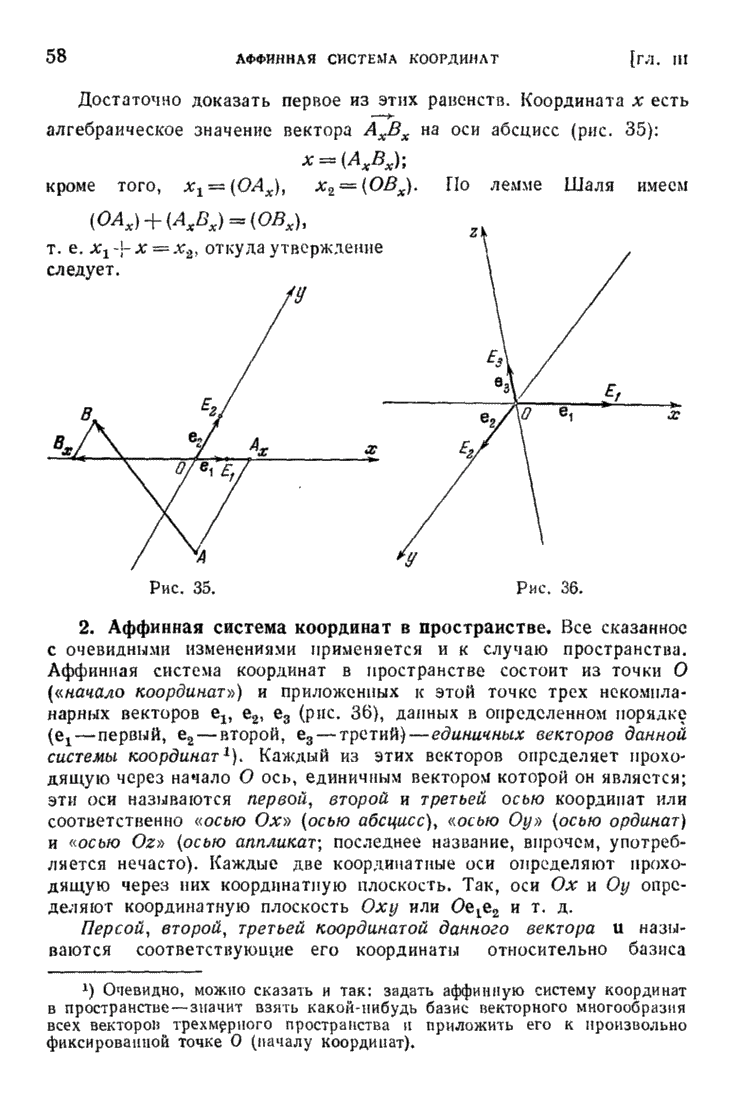
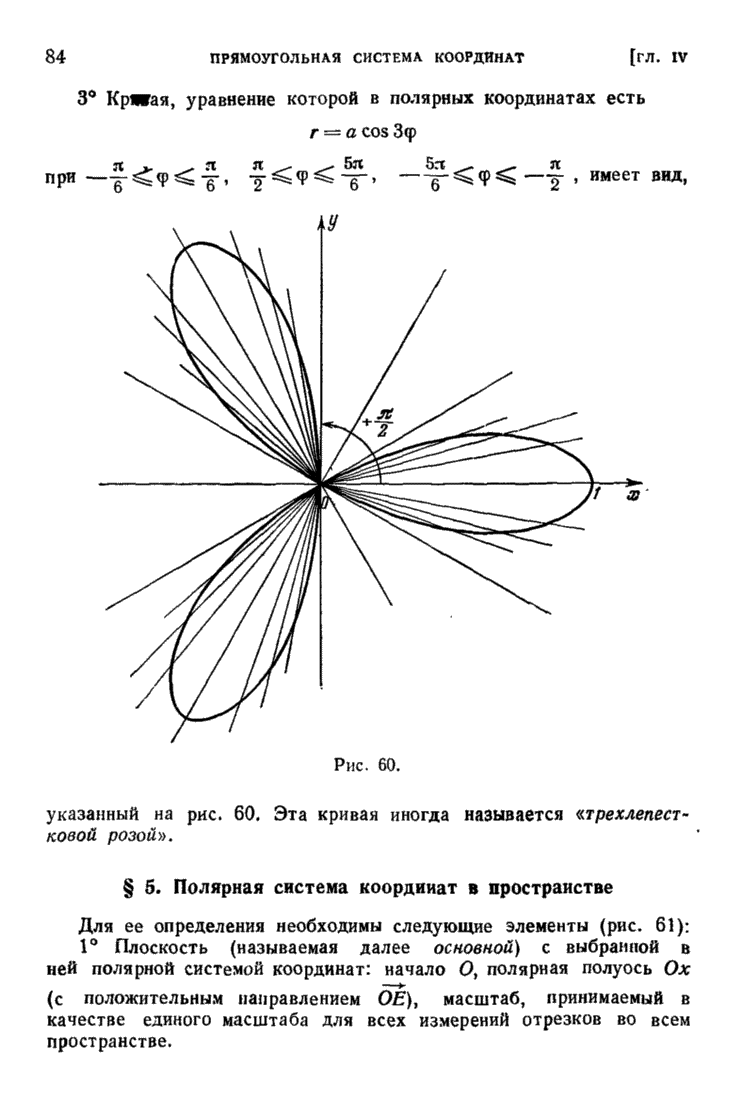
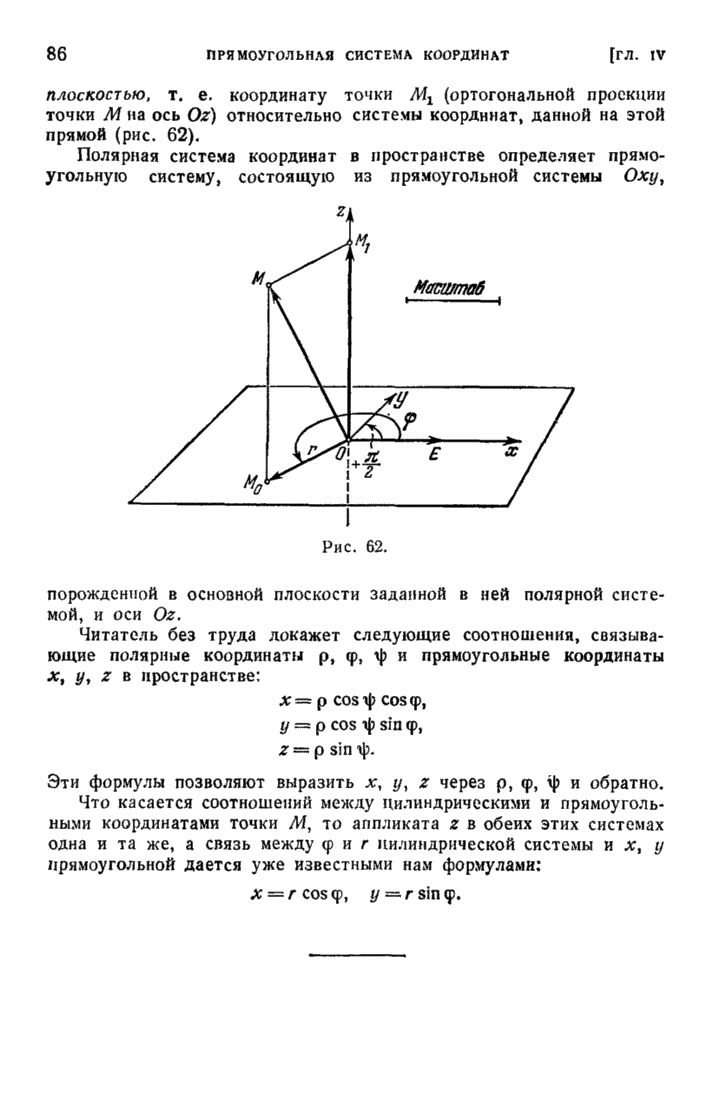
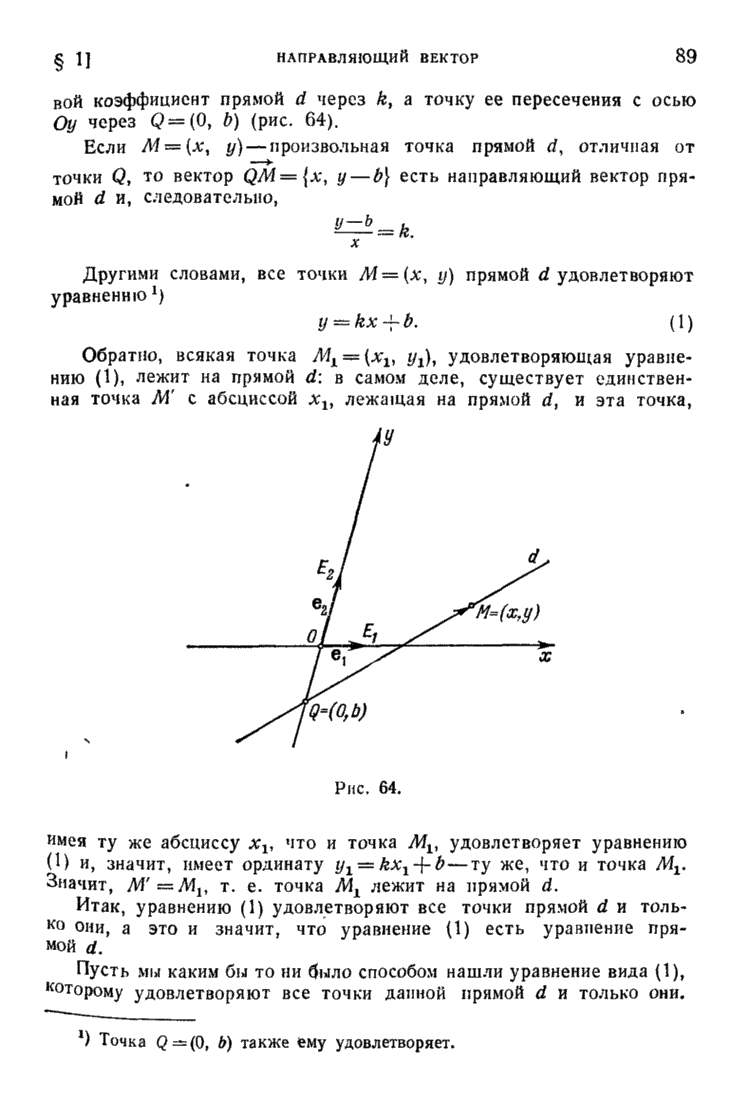
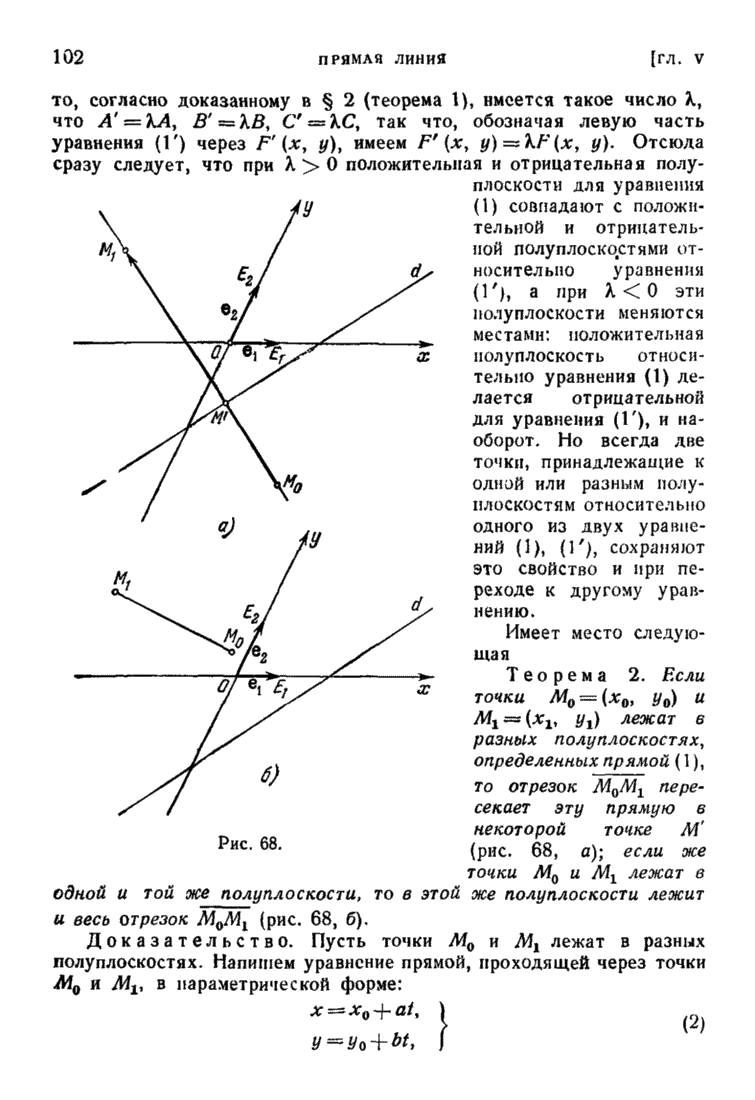
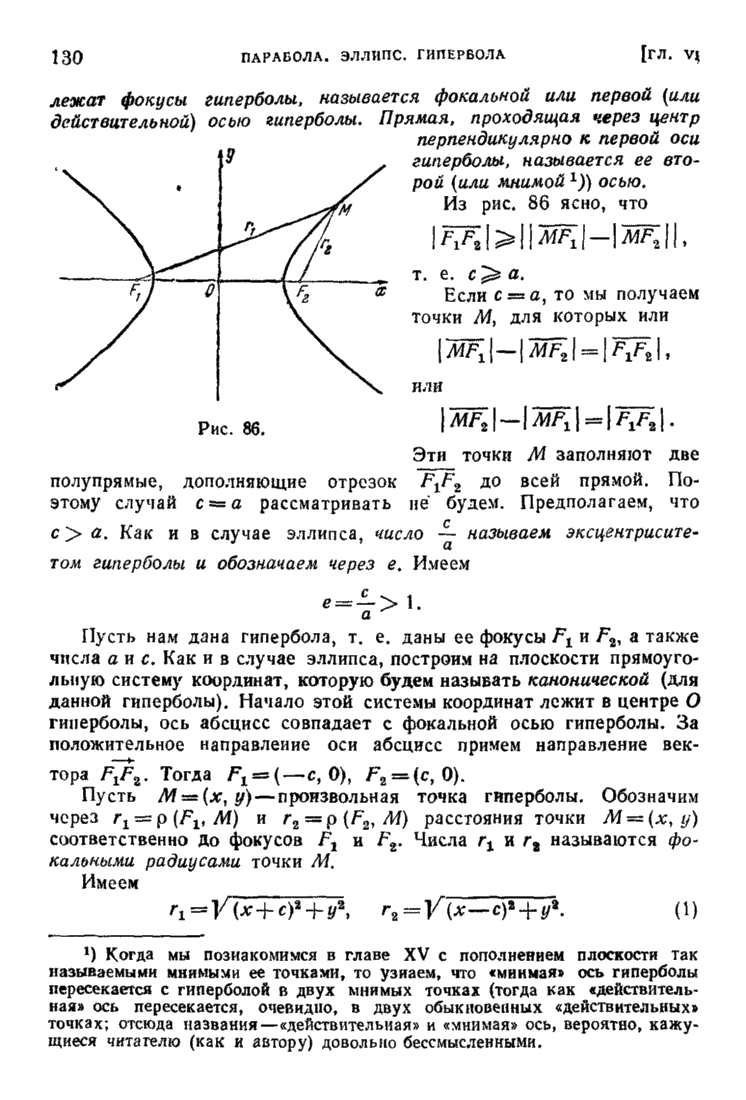
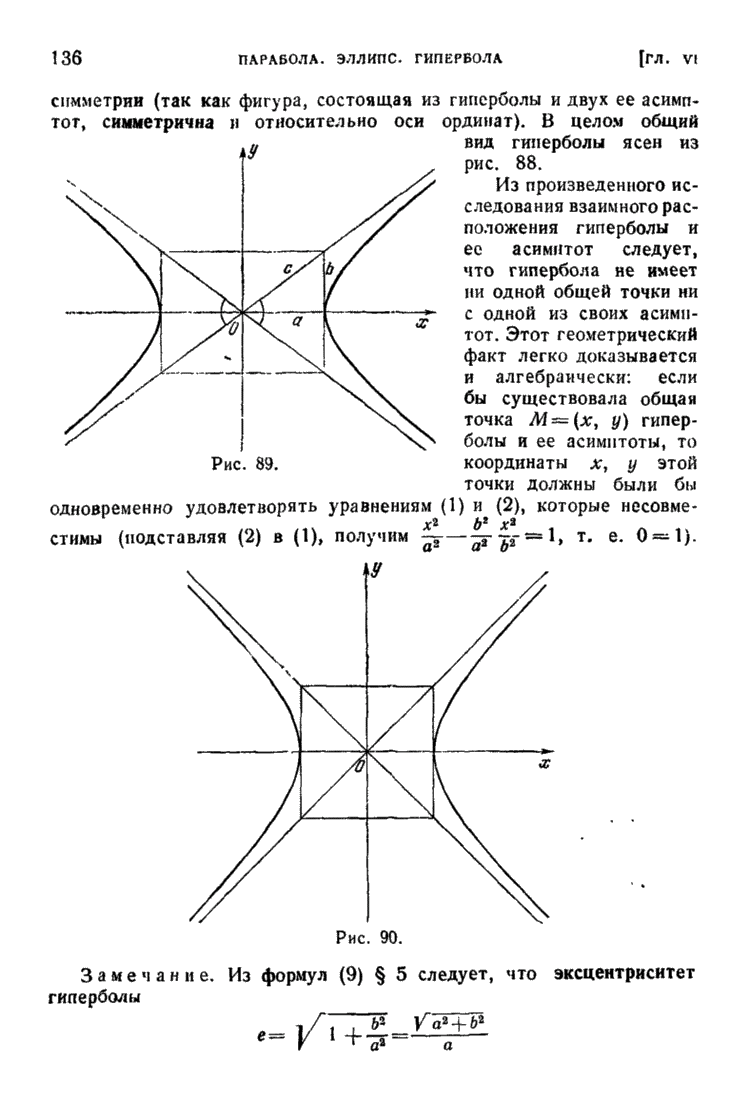
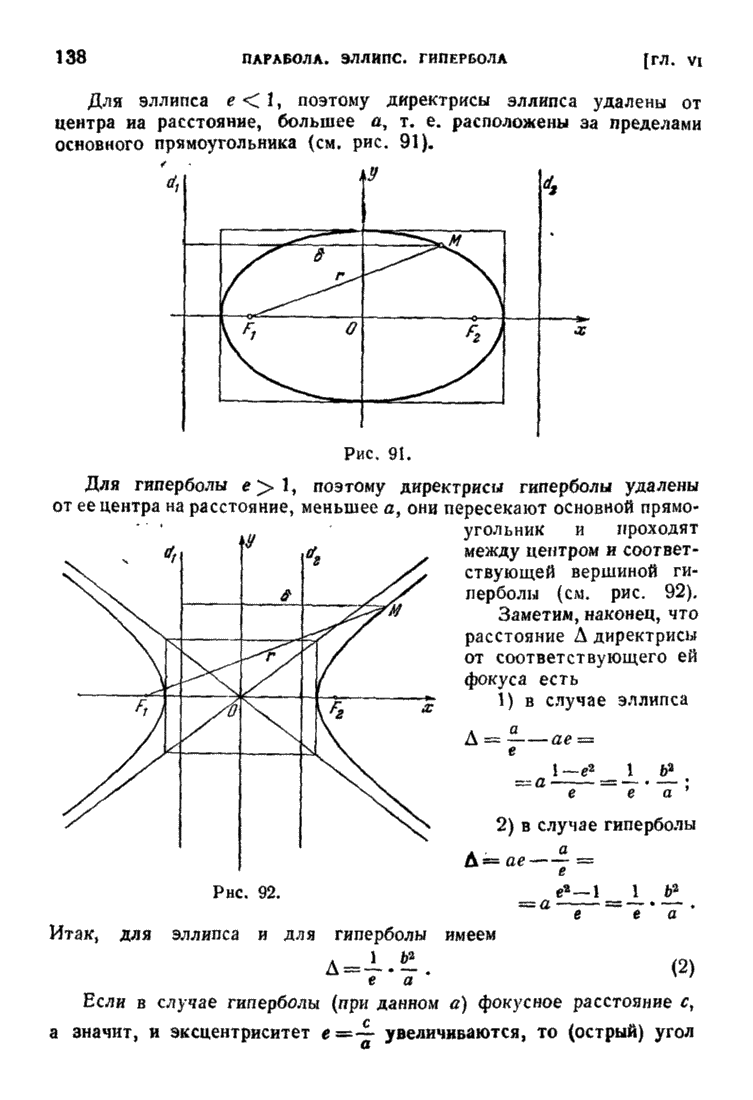
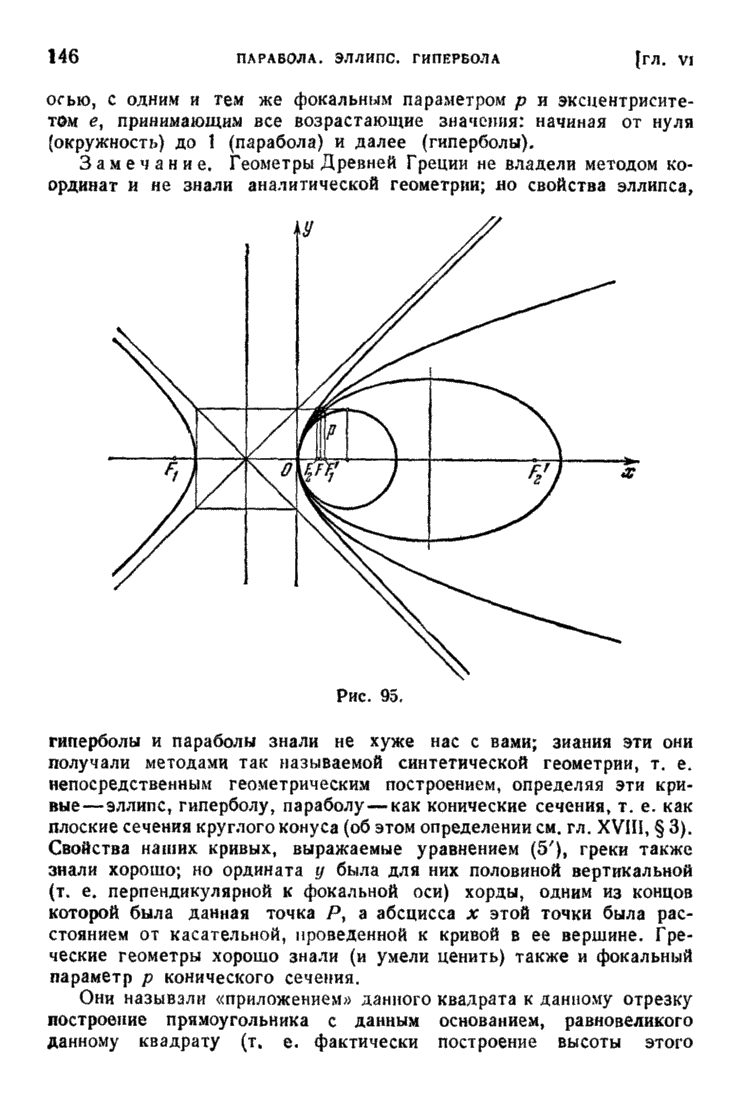
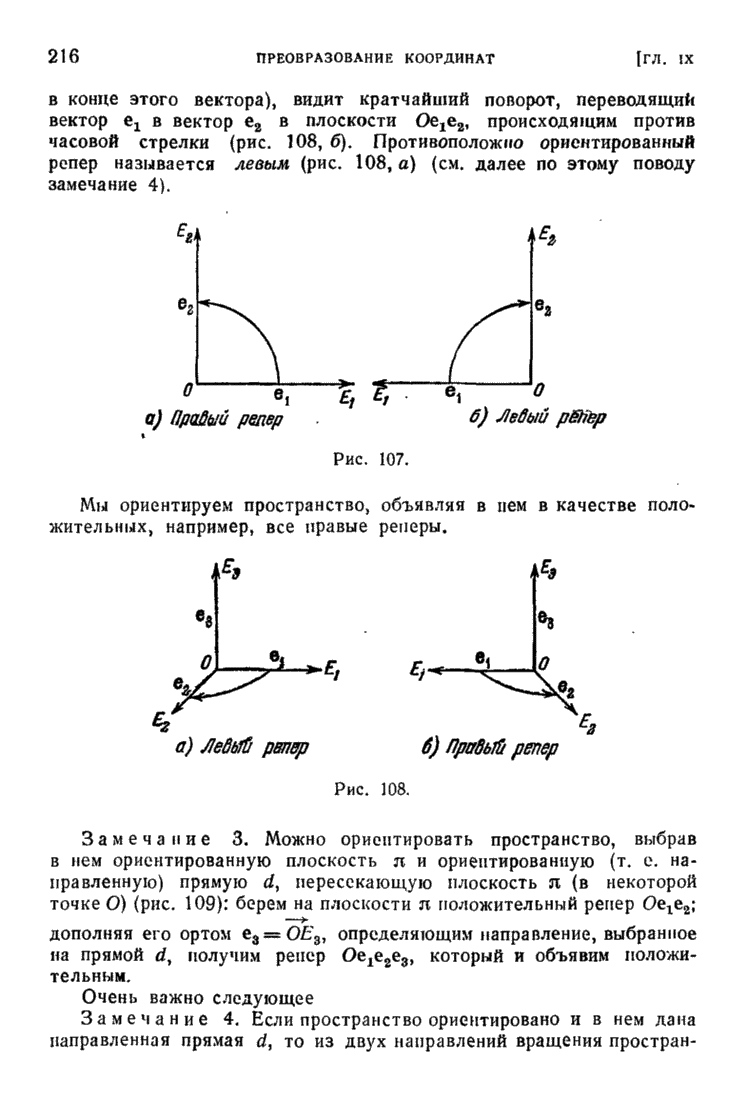
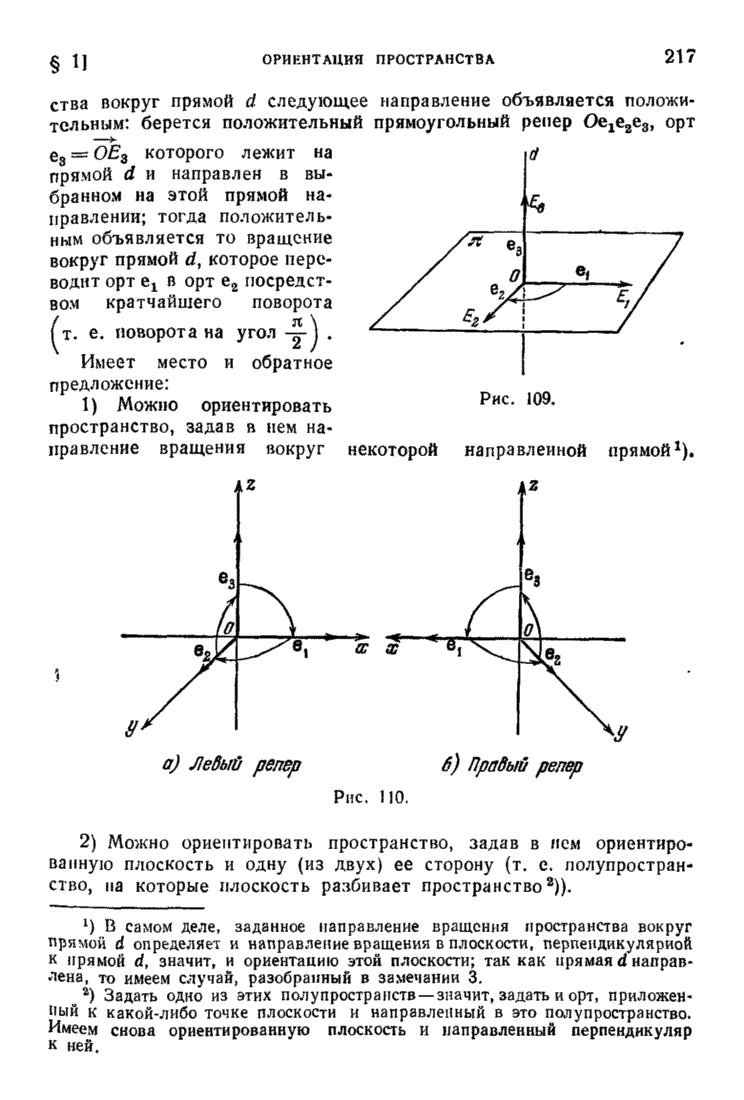
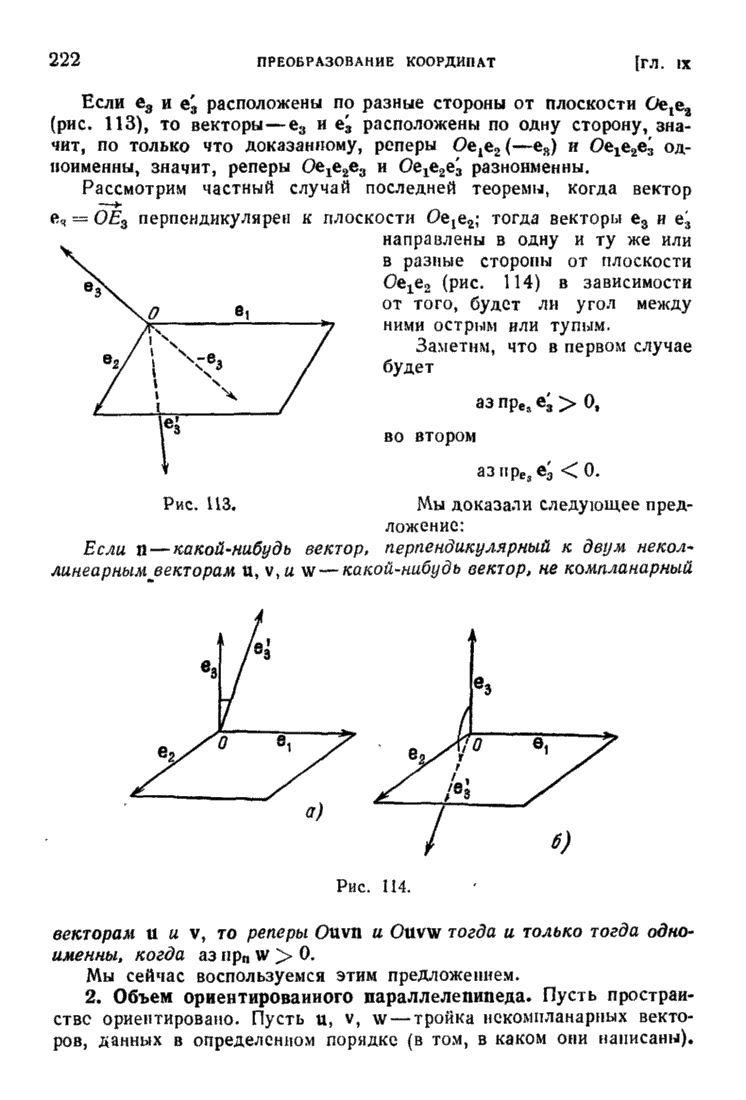
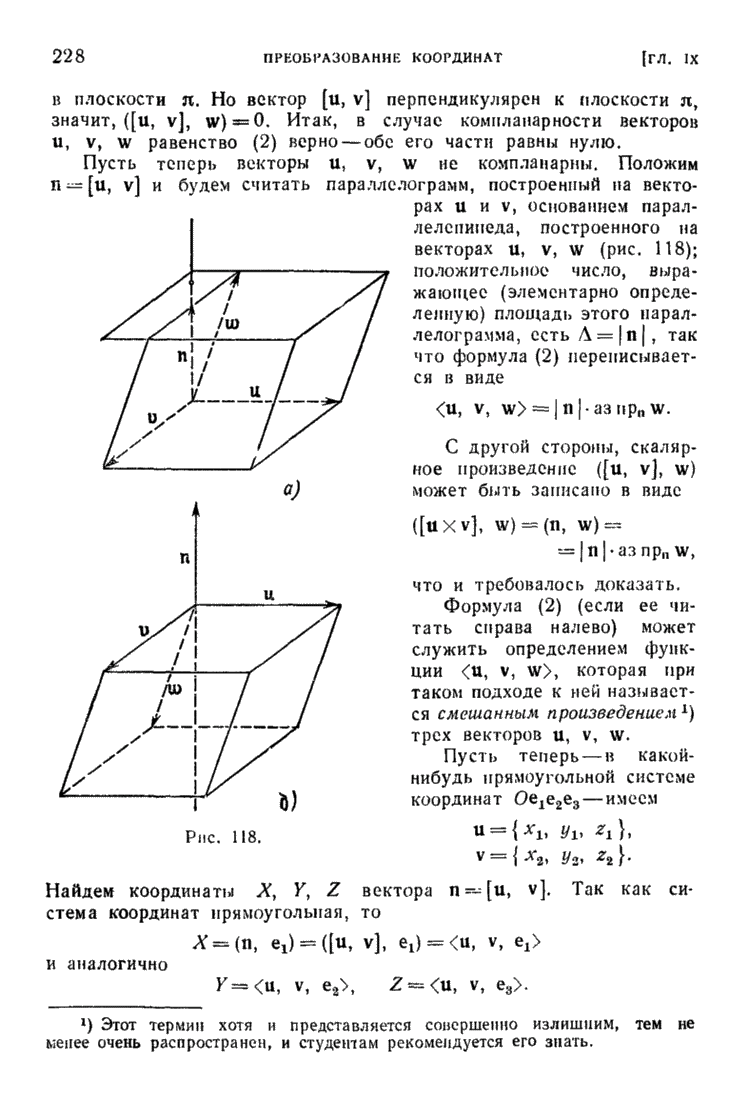
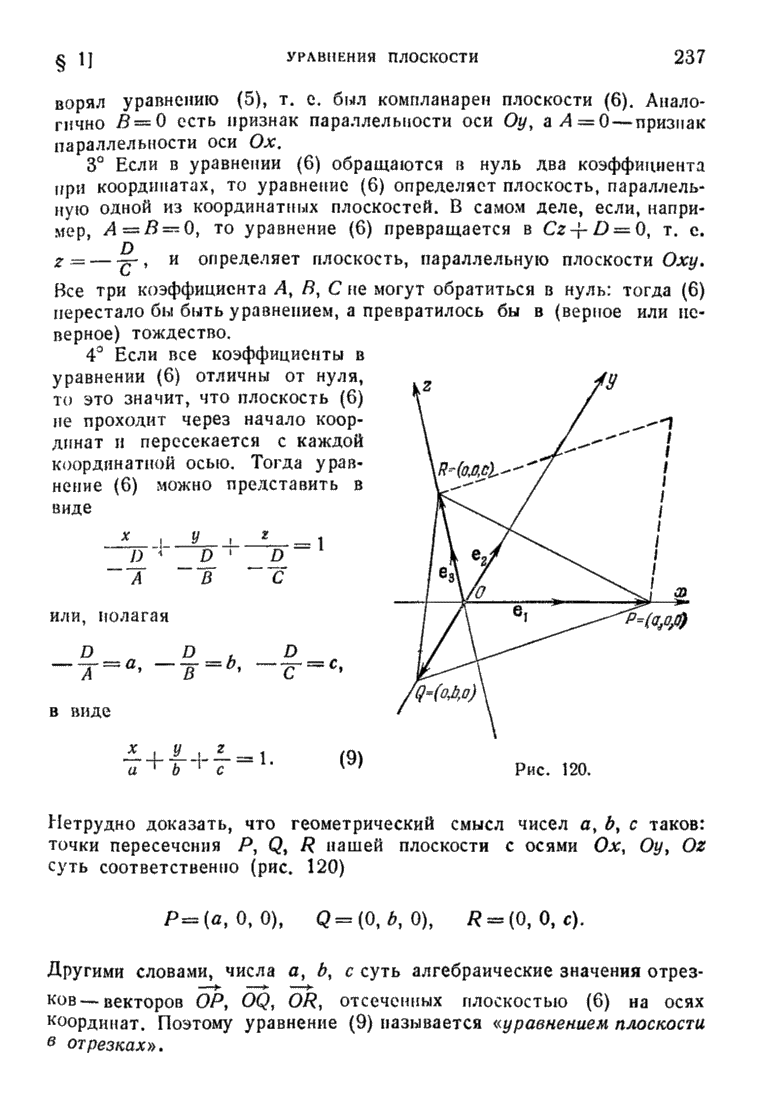
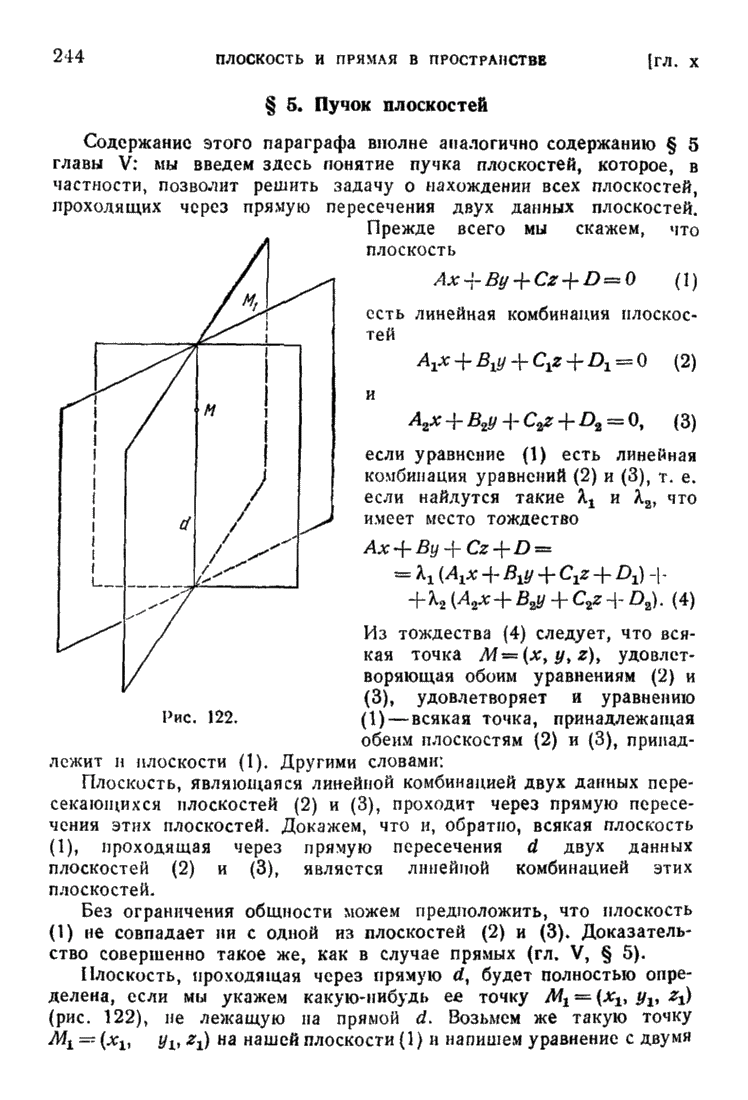
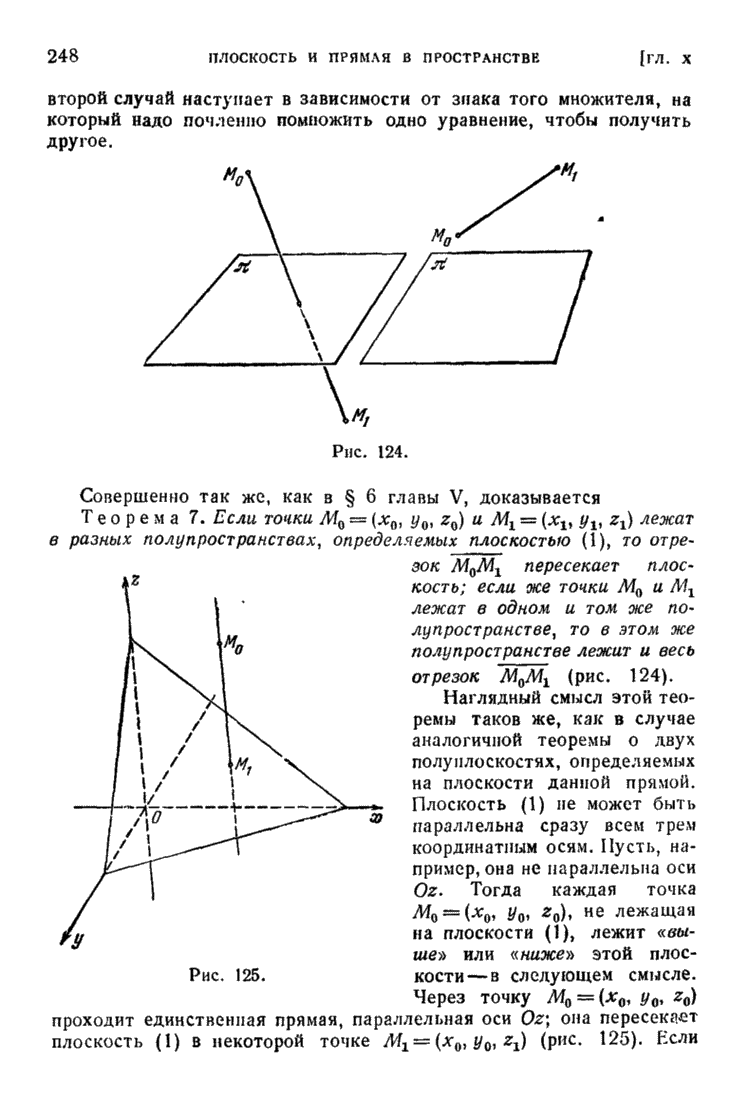
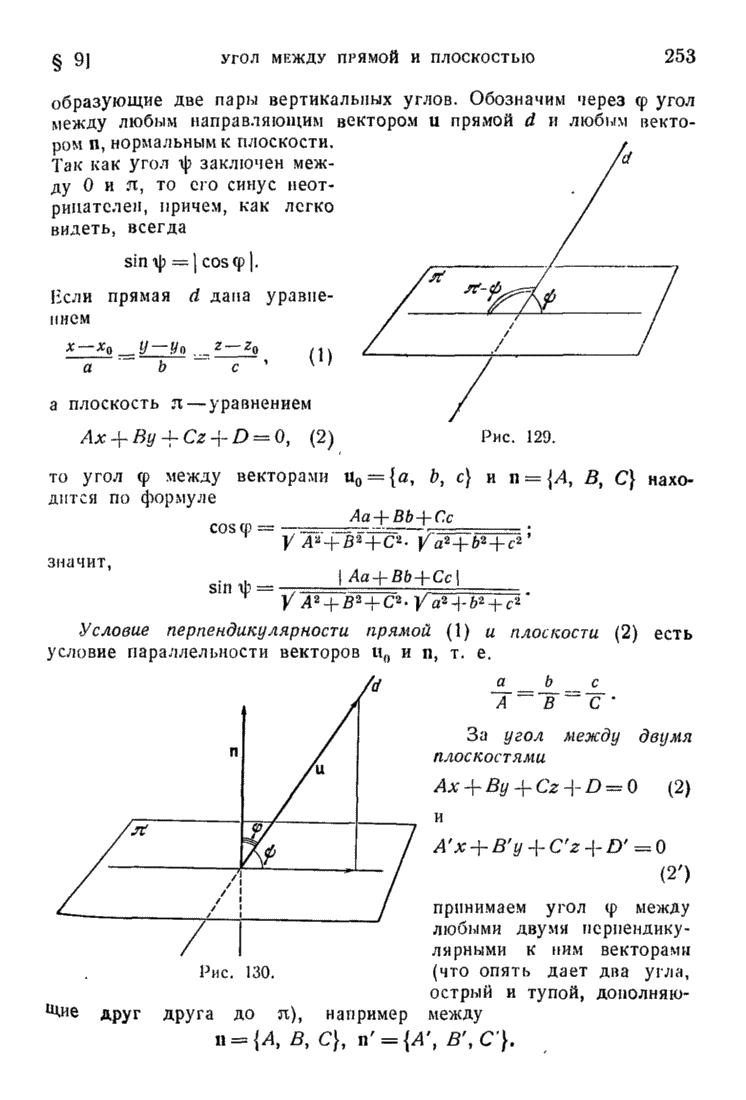
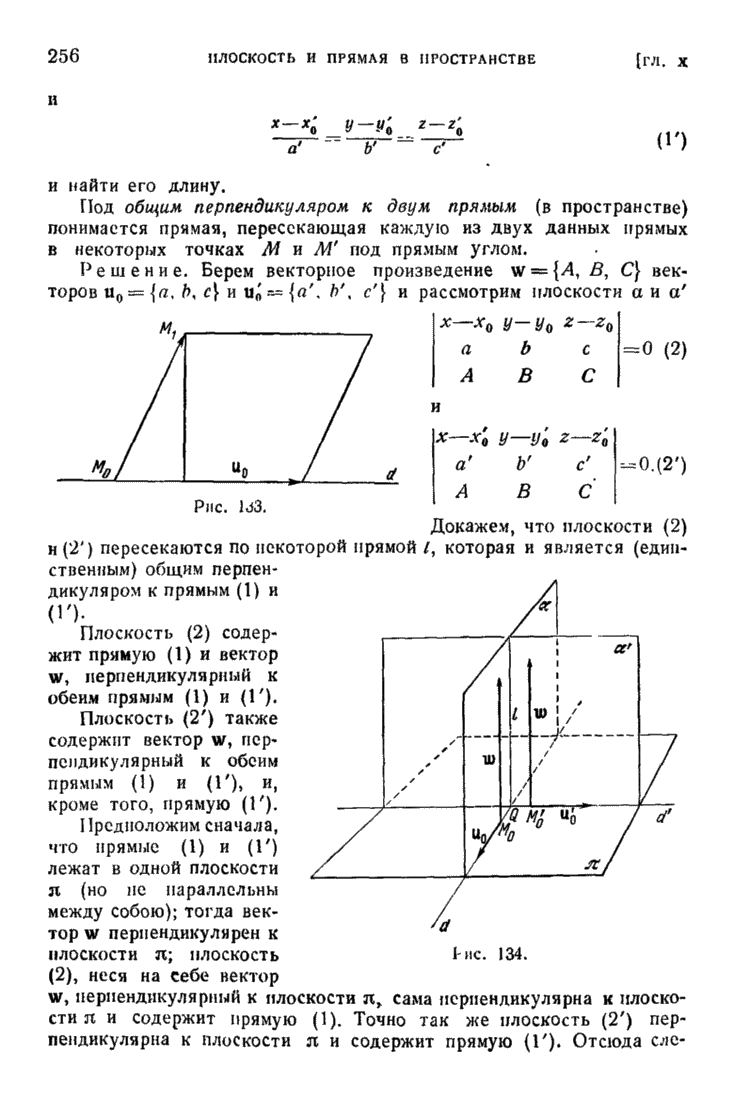
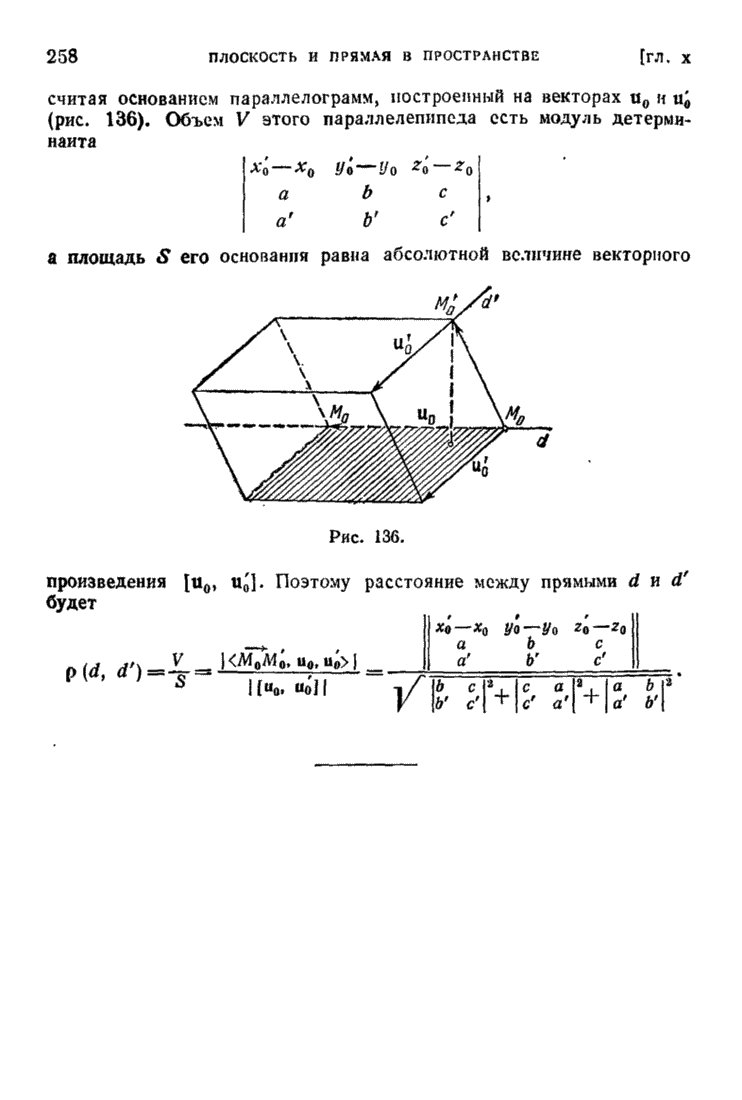
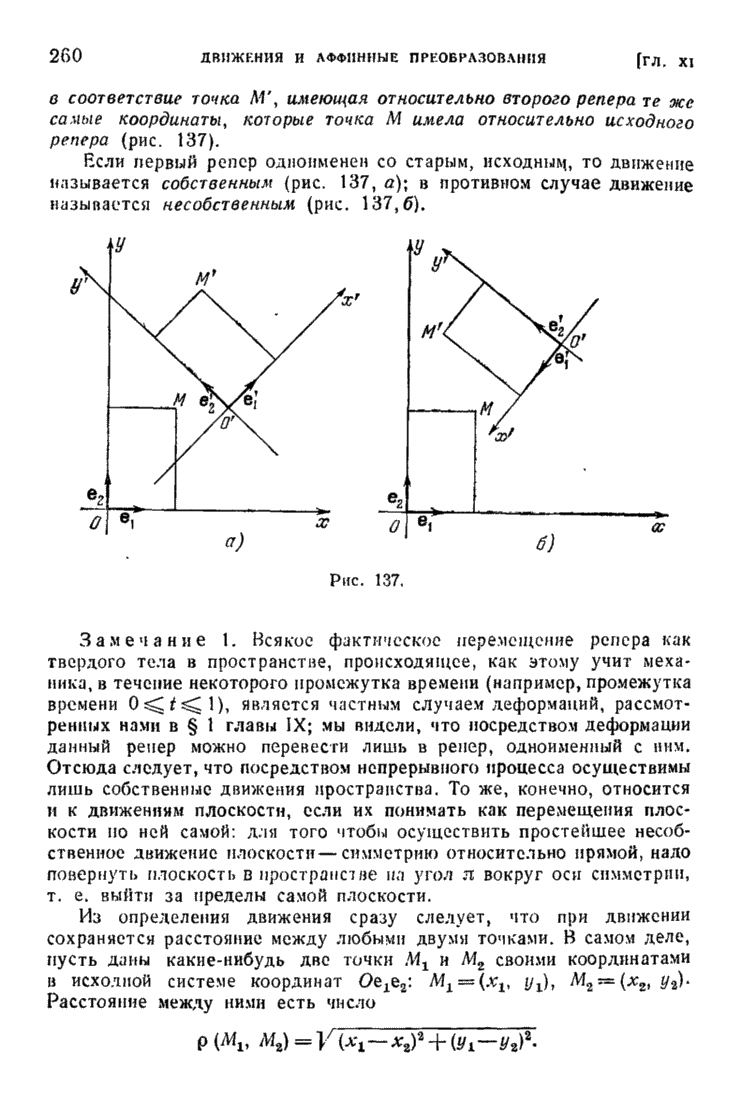
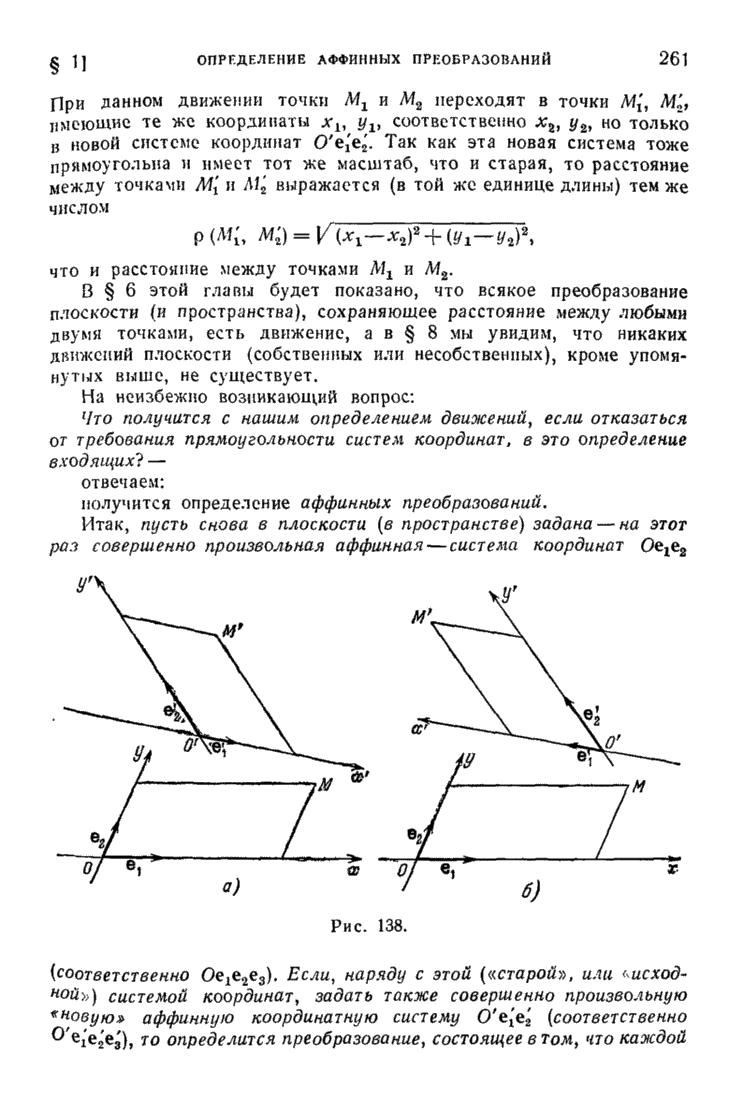
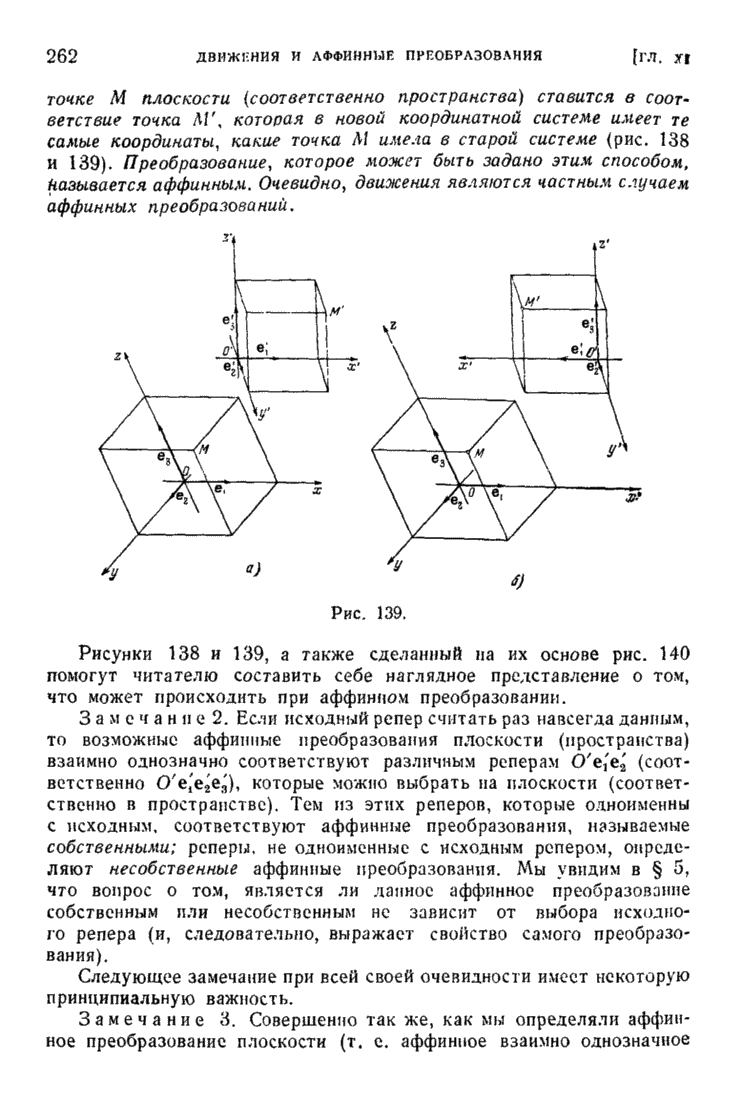
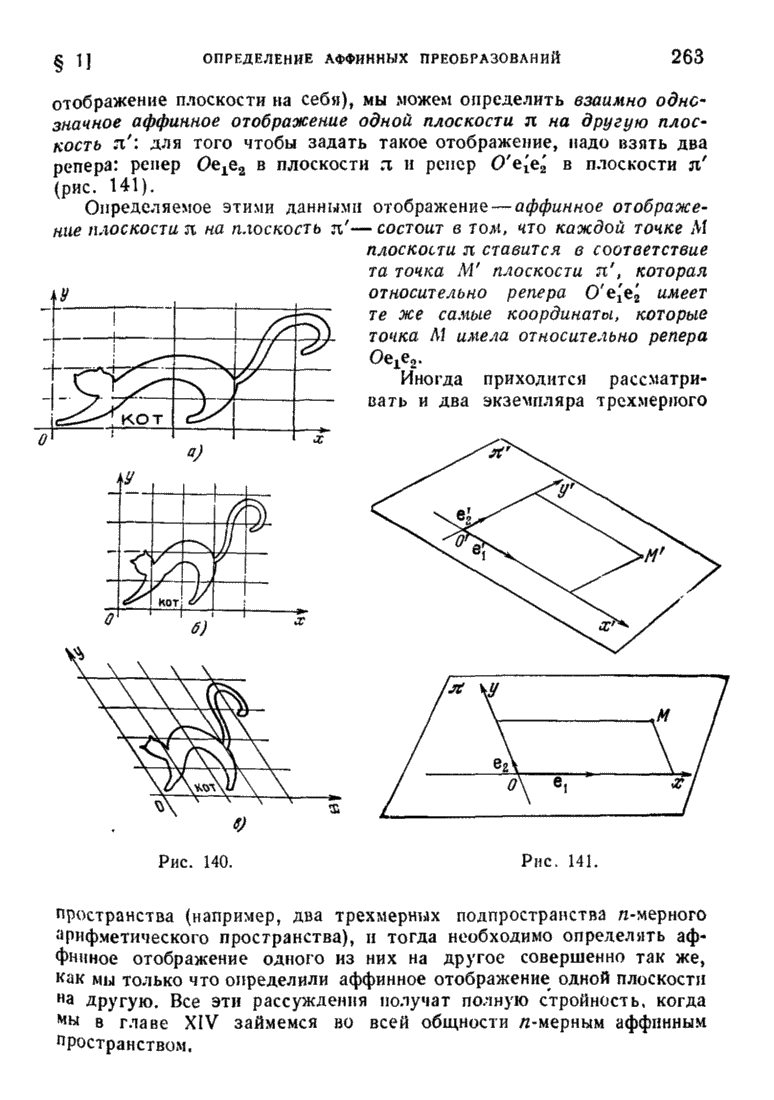
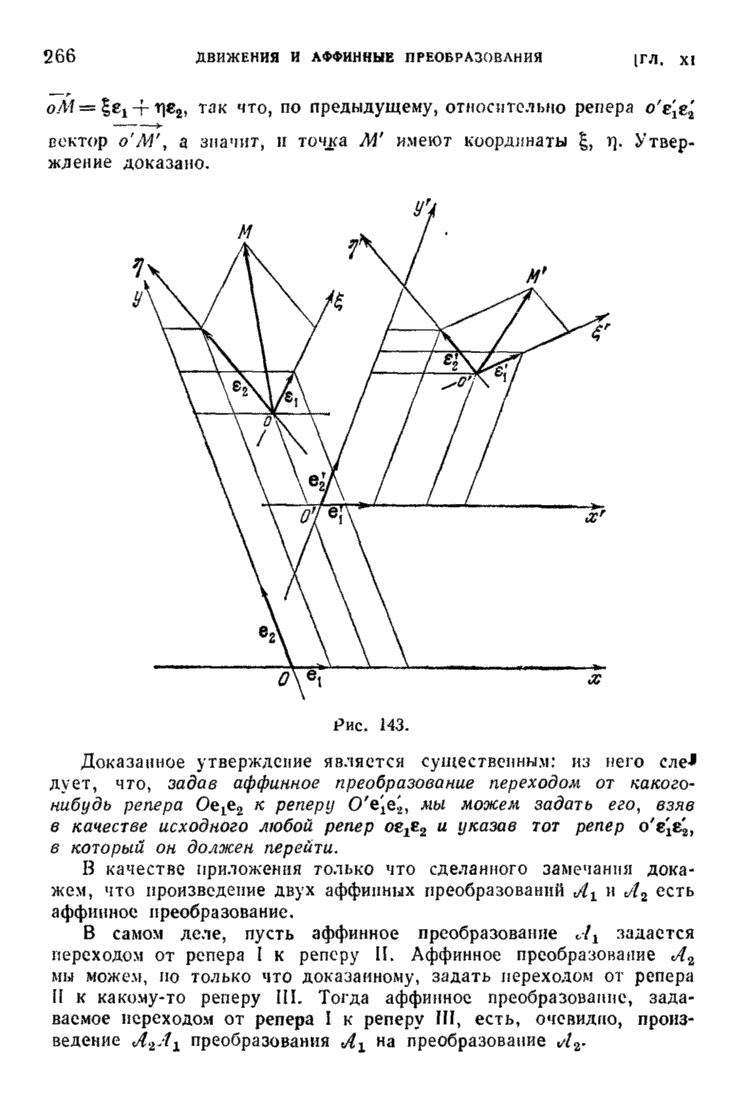
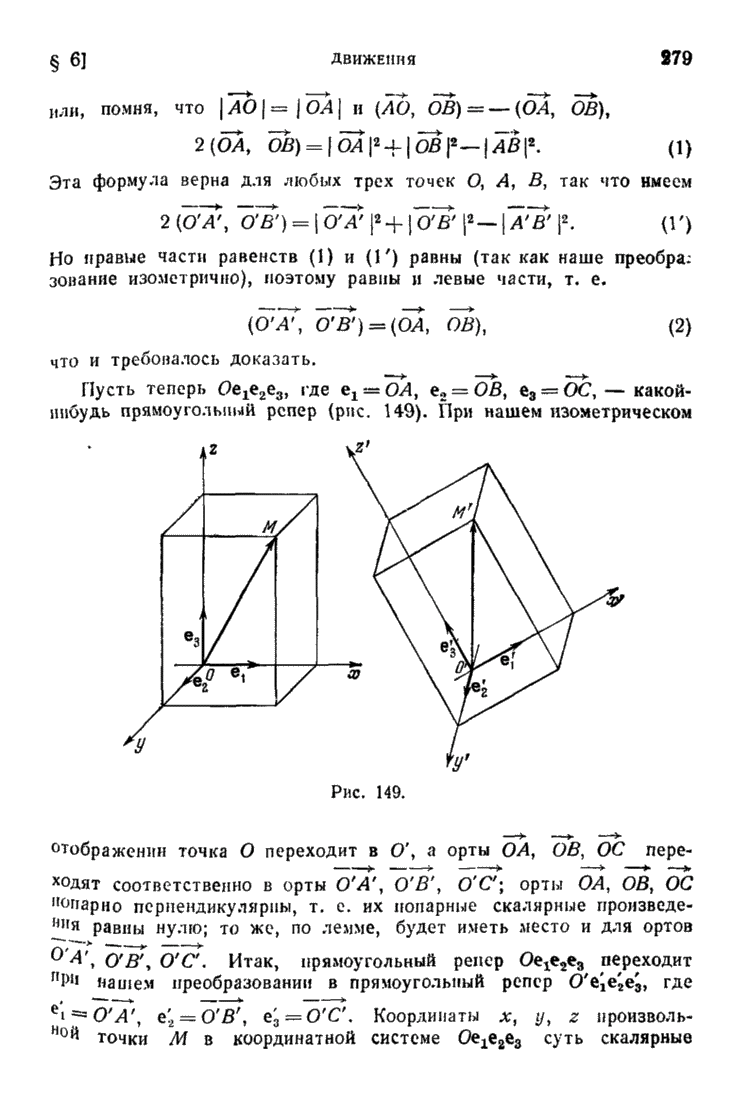
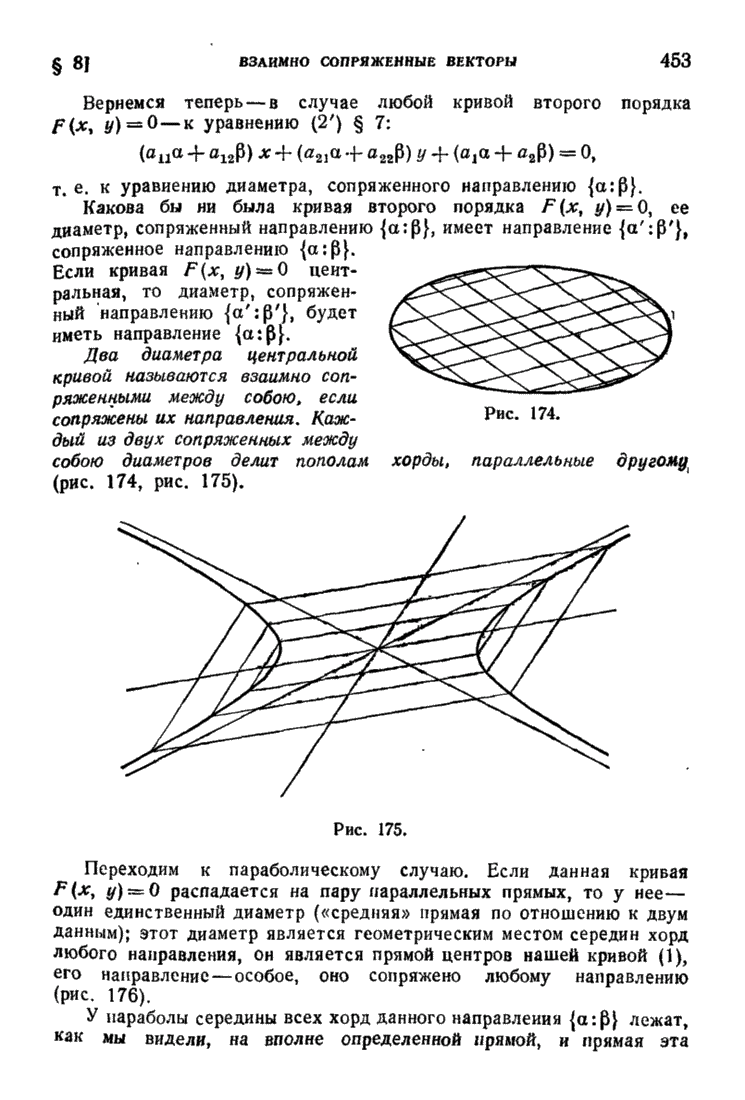
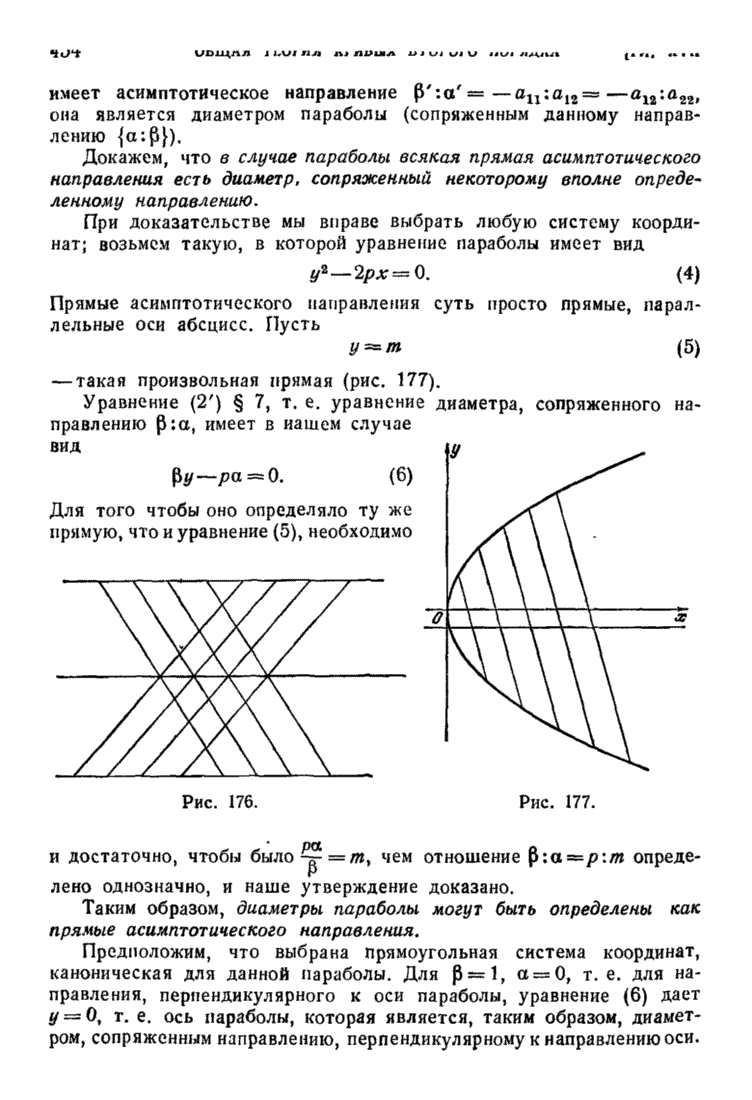
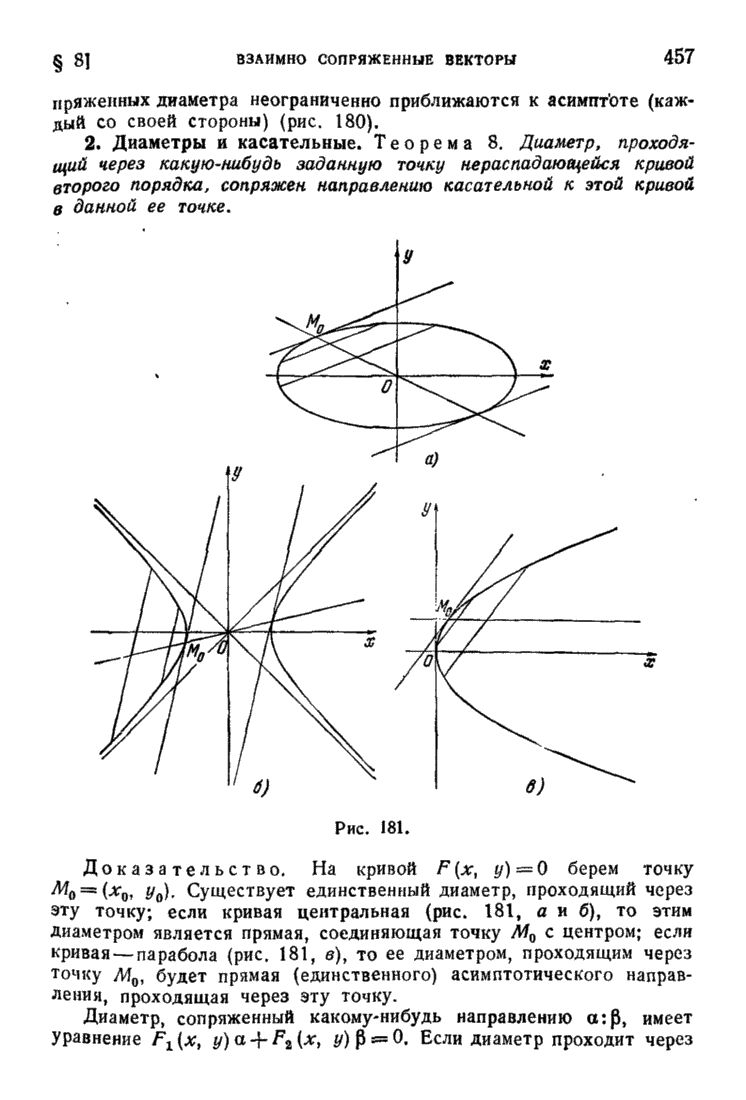
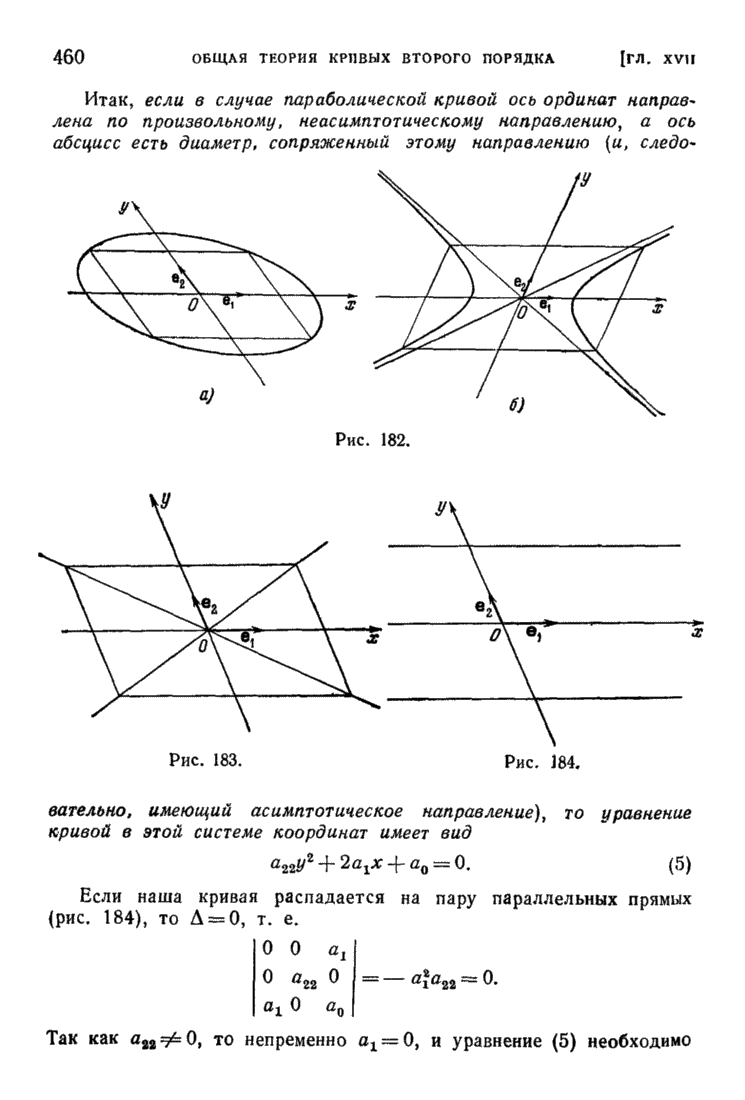
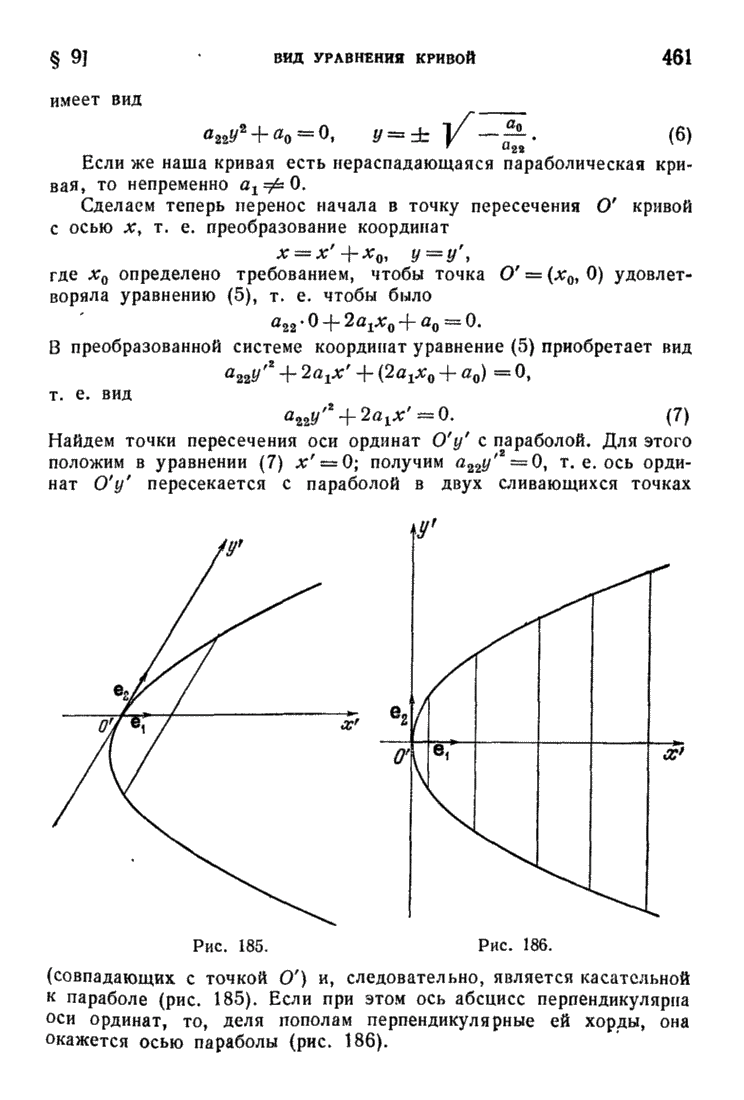
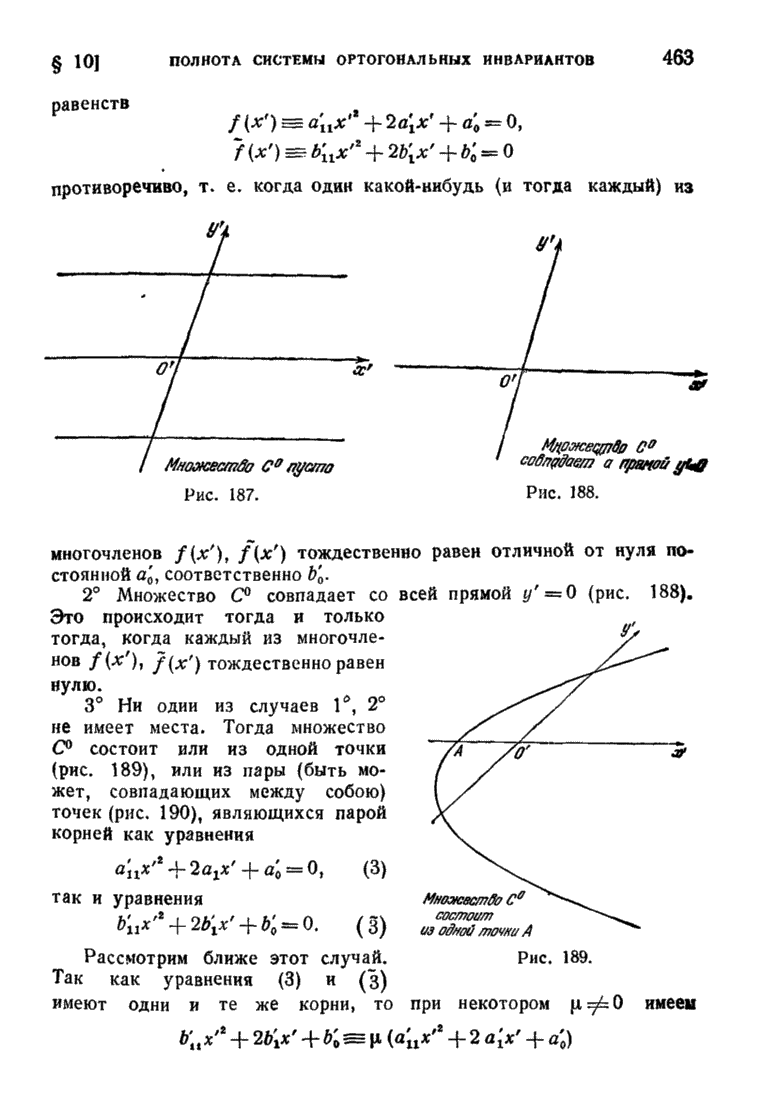
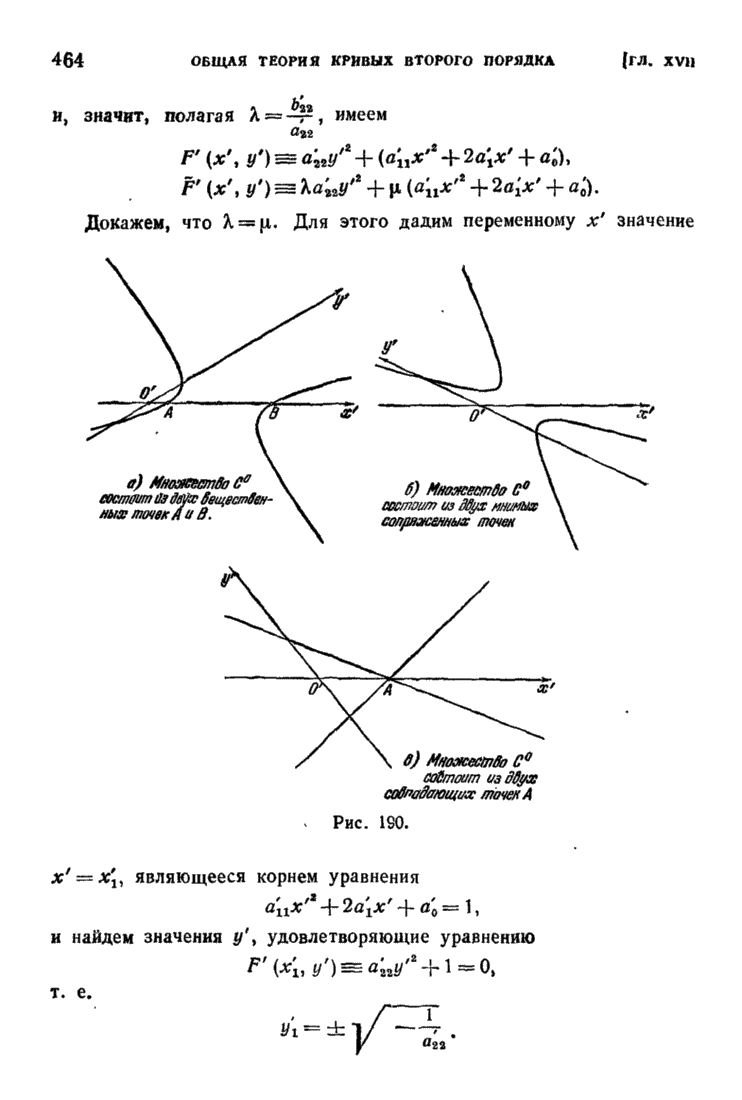
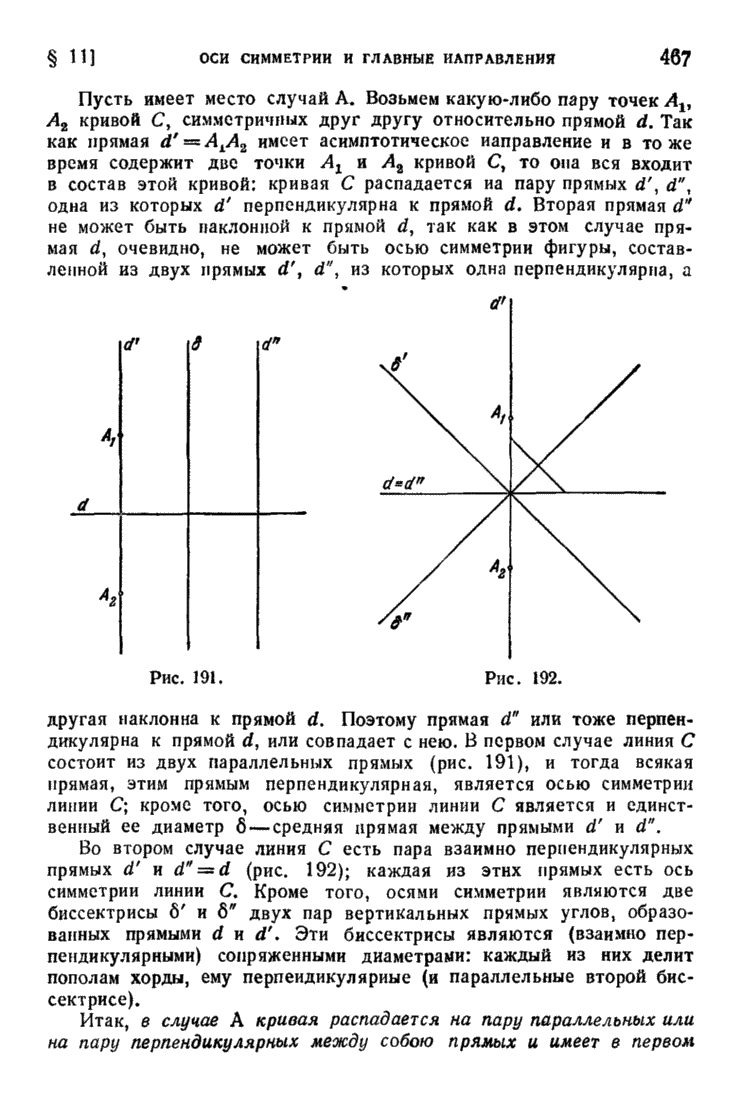
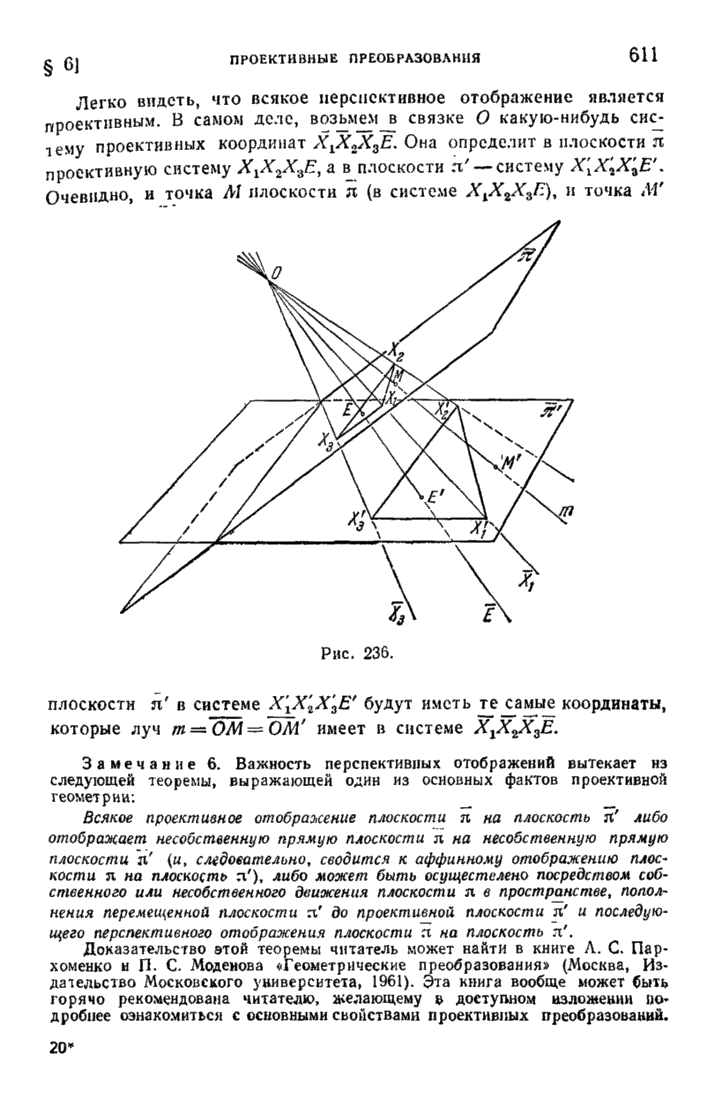
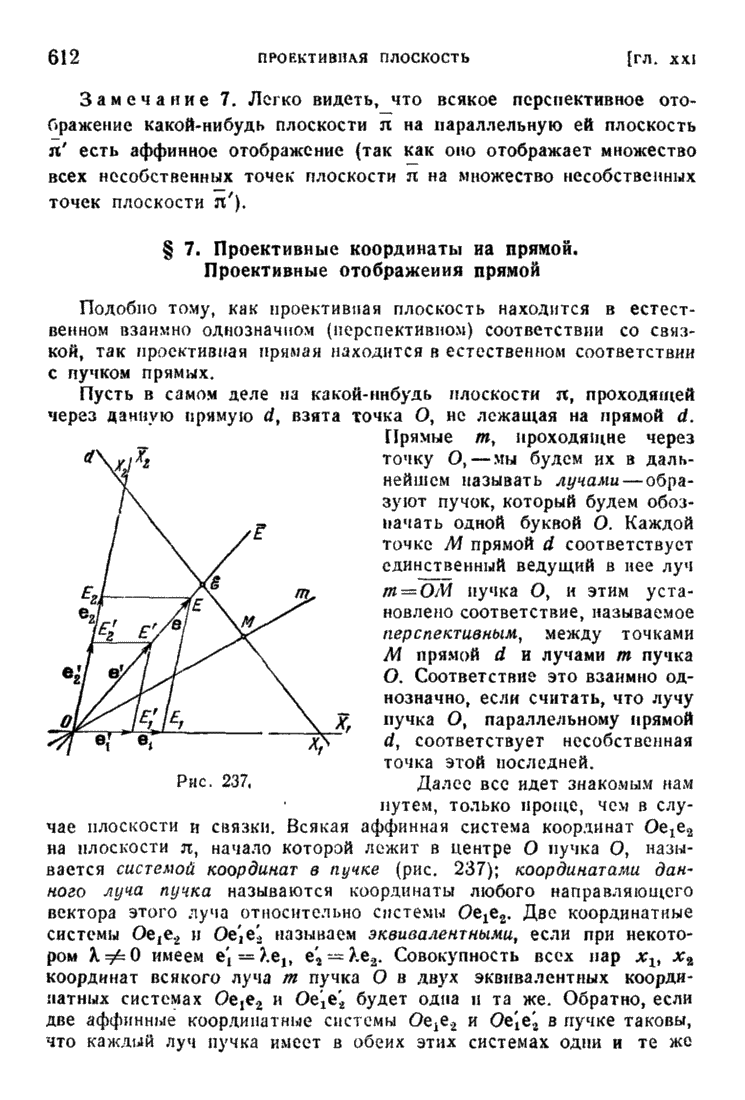
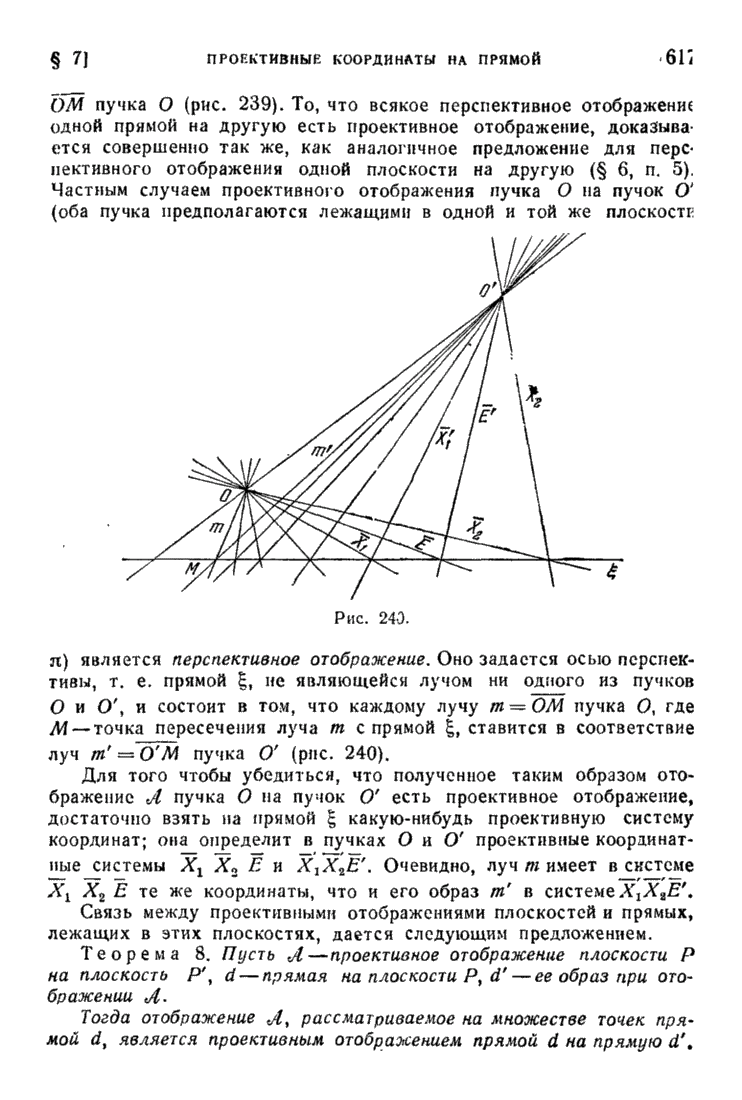
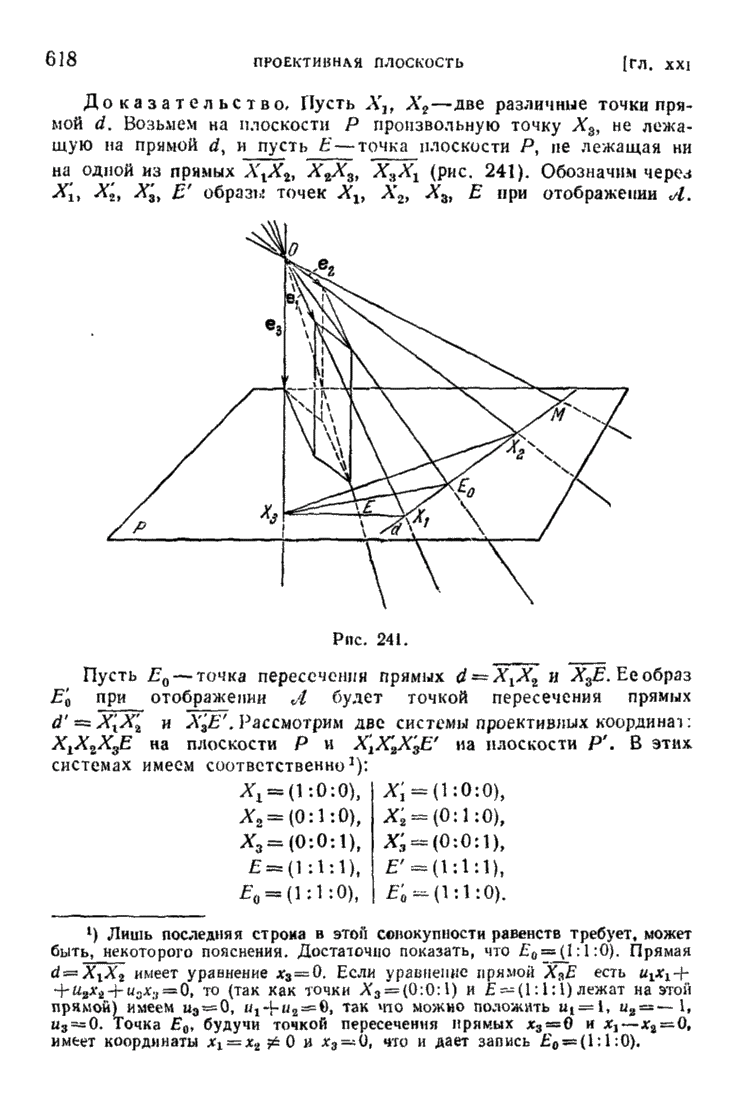
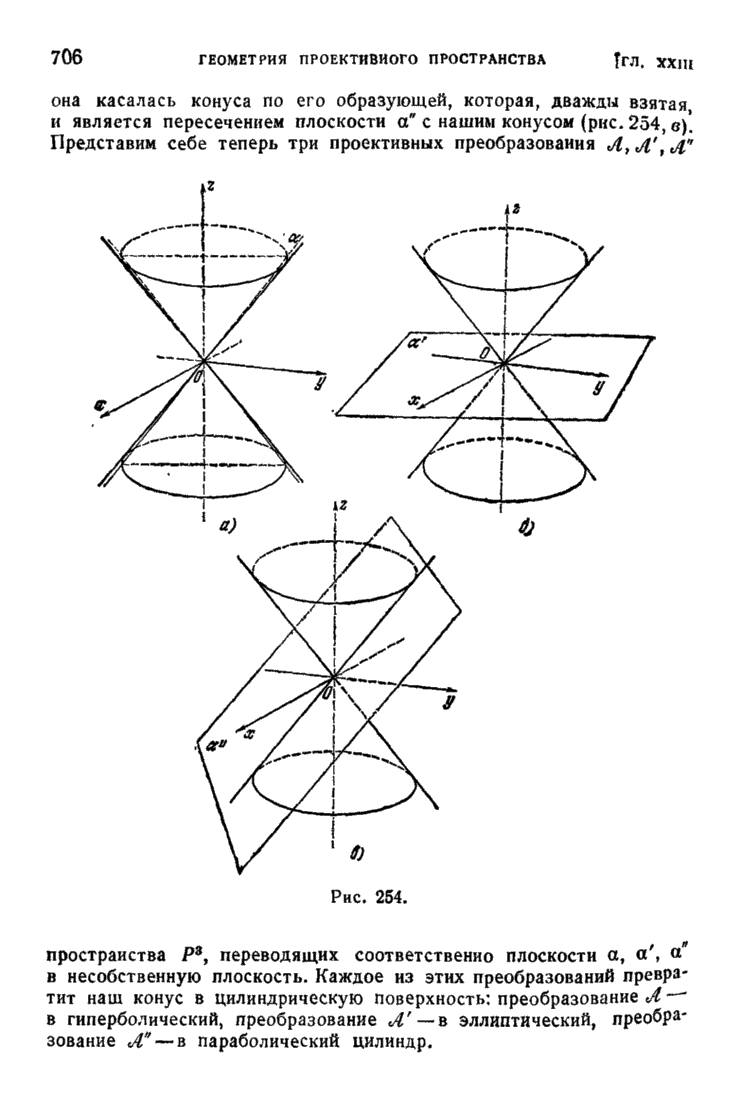
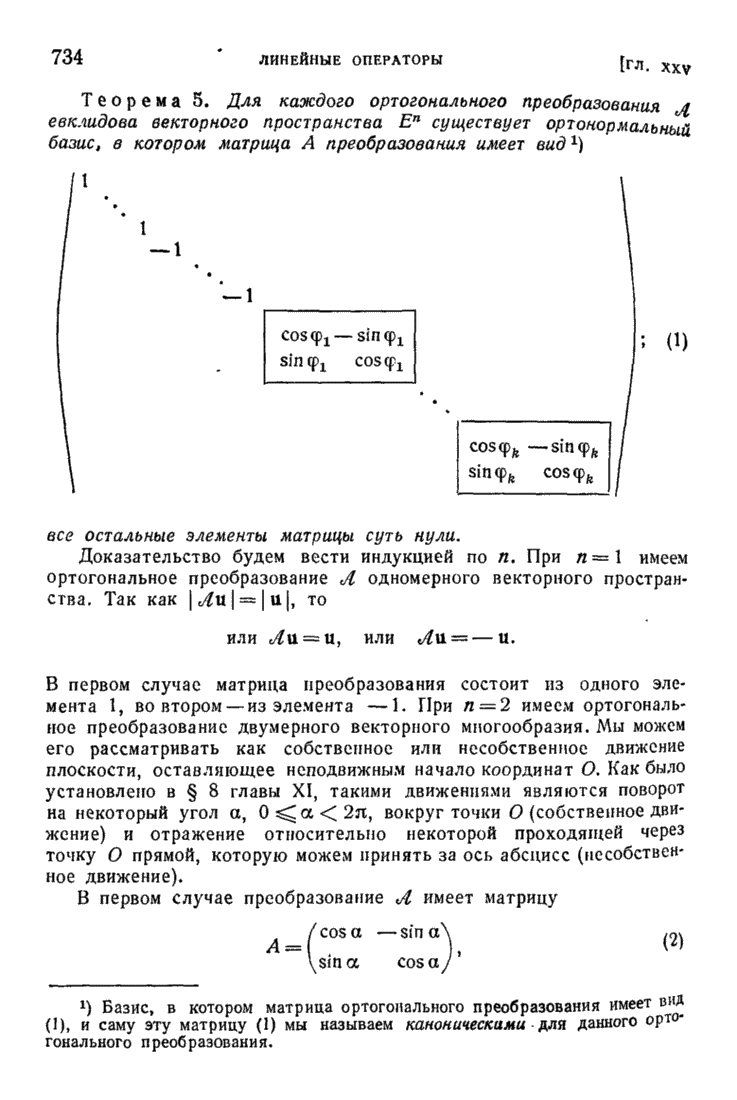
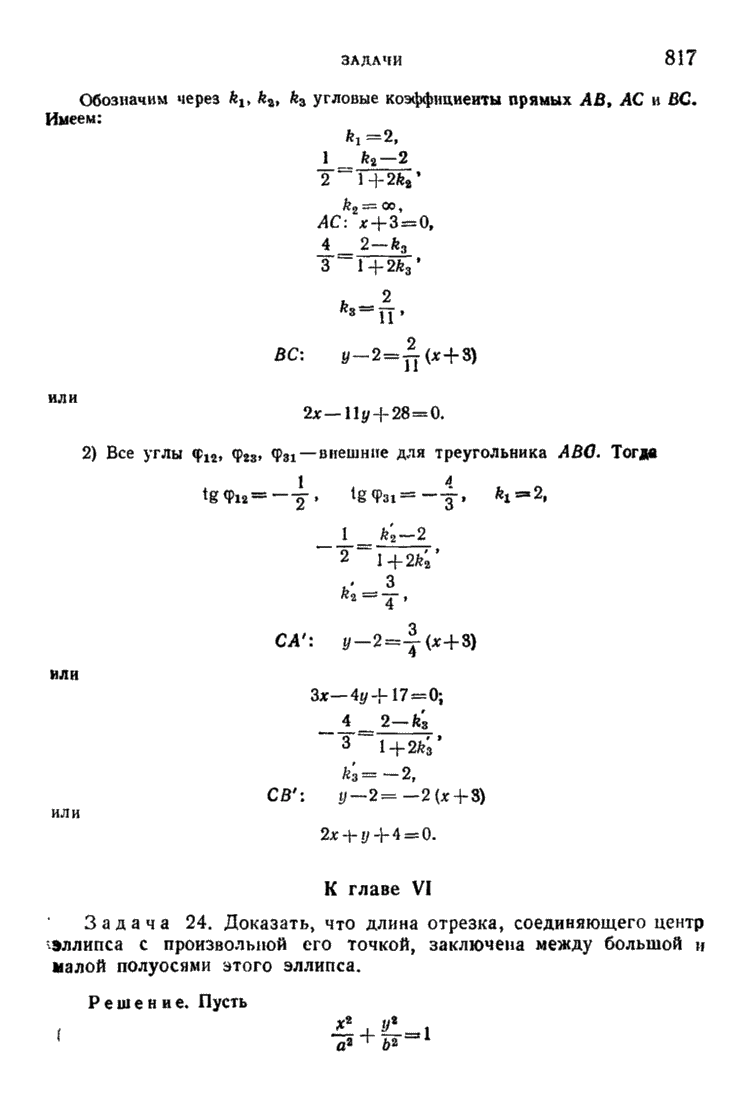
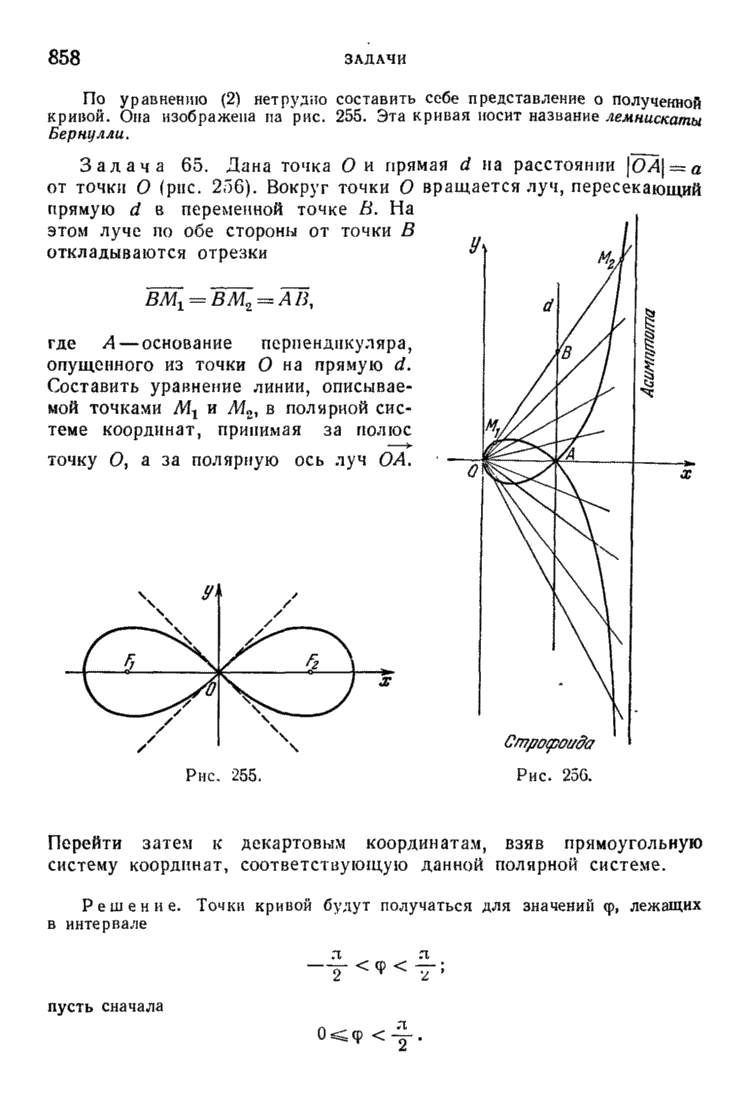
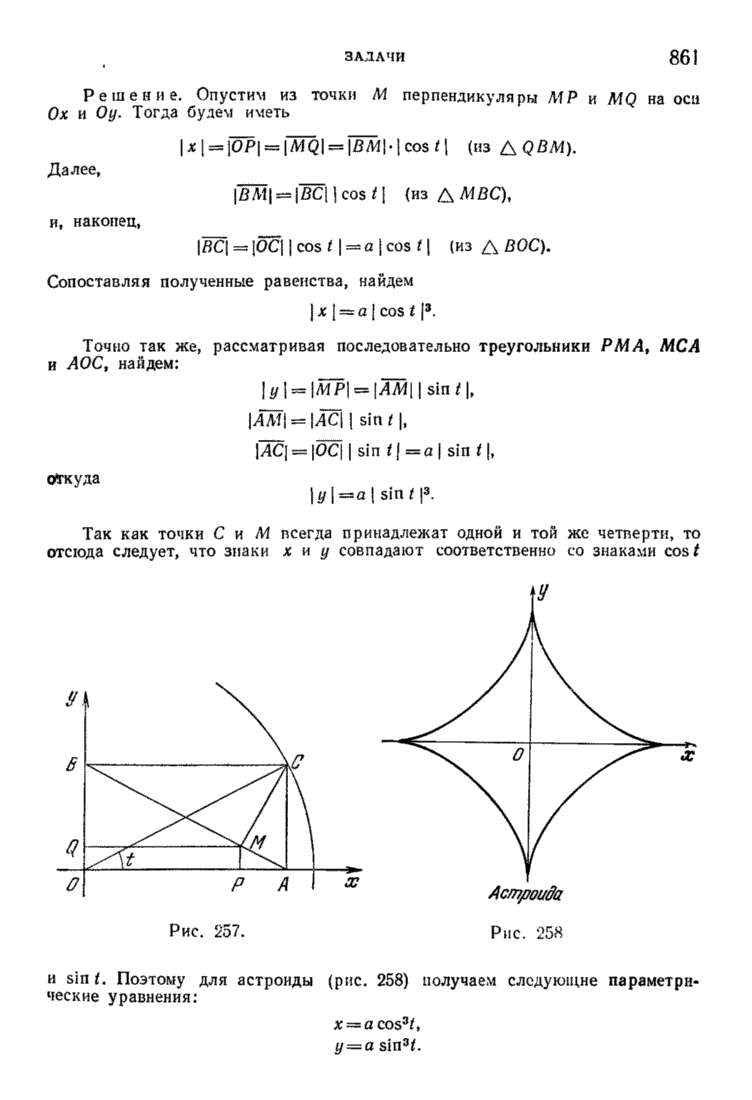
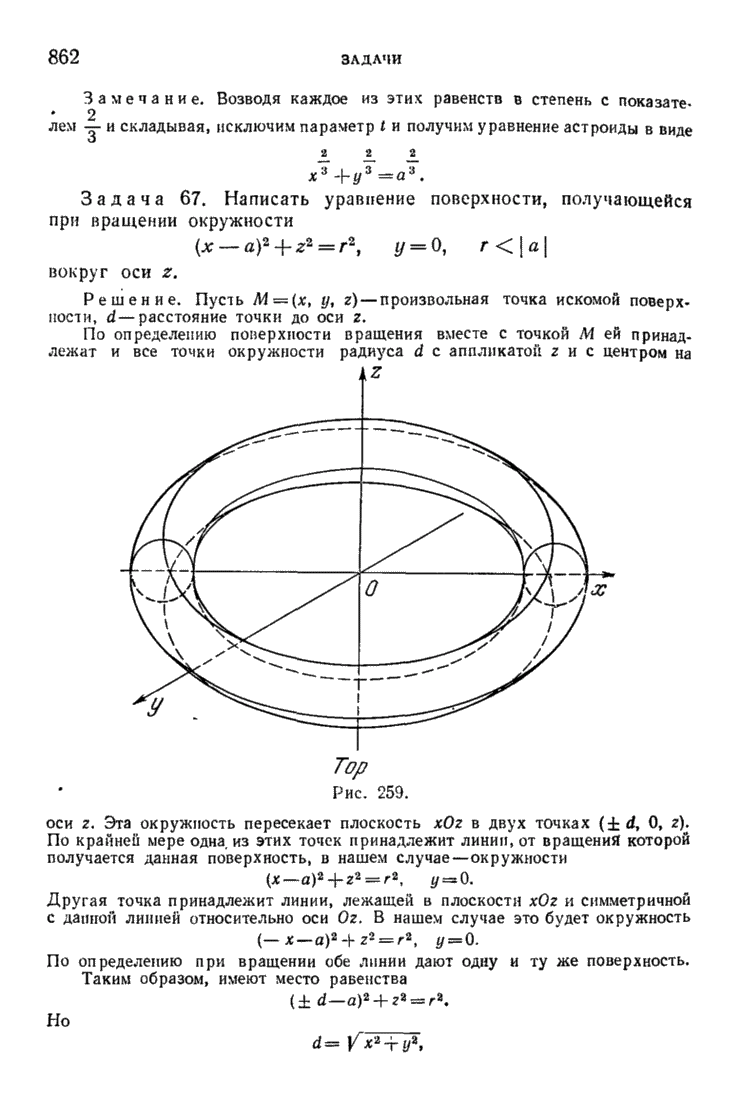
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 5. Прямая линия на комплексной плоскости
Прямую линию на комплексной плоскости естественно определять как линию первого порядка, т. е. задавать ее уравнением первой степени

(«общее уравнение прямой»). При этом весьма частным случаем общих теорем об уравнениях первой степени, доказанных в главе XIV, § 5, является следующее предложение.
Теорема 1. Два уравнения (1) и

тогда и только тогда имеют одно и то же множество решений («определяют одну и ту же прямую»), когда их коэффициенты пропорциональны, т. е. когда при некотором  имеем
имеем

Уравнения (1) и ( ) тогда и только тогда несовместны (задаваемые ими прямые параллельны в собственном смысле), когда
) тогда и только тогда несовместны (задаваемые ими прямые параллельны в собственном смысле), когда

Доказываем элементарно. Если уравнения (1) и (1) эквиралентны, то при некотором  имеют место соотношения (2). В самом деле, из предположения следует, что система двух уравнений (1), (1) имеет бесконечное множество решений, значит, детерминант системы равен нулю:
имеют место соотношения (2). В самом деле, из предположения следует, что система двух уравнений (1), (1) имеет бесконечное множество решений, значит, детерминант системы равен нулю:

т. е. при некотором k имеем  .
.
Если при этом  то, как легко убедиться, уравнения (1), (1') были бы несовместны. Итак, из эквивалентности уравнений (1) и (1') следует пропорциональность их коэффициентов. Обратное утверждение очевидно. Остается доказать: из несовместности уравнений (1) и (1') вытекает условие (3). Но из несовместности уравнений (1) и (1') вытекает прежде всего равенство (4), т. е. пропорция
то, как легко убедиться, уравнения (1), (1') были бы несовместны. Итак, из эквивалентности уравнений (1) и (1') следует пропорциональность их коэффициентов. Обратное утверждение очевидно. Остается доказать: из несовместности уравнений (1) и (1') вытекает условие (3). Но из несовместности уравнений (1) и (1') вытекает прежде всего равенство (4), т. е. пропорция

Если бы она продолжалась до пропорции

то уравнения (1) и (1') были бы эквивалентны и, значит, совместны, поэтому имеет место  все доказано.
все доказано.
Замечание. Из теоремы 1 вытекает, что те трудности, которые возникают при определении алгебраической линии как множества решений алгебраического уравнения  , не возникают, когда степень этого уравнения равна
, не возникают, когда степень этого уравнения равна  -прямую линию мы сейчас уже в праве определить как множество всех точек
-прямую линию мы сейчас уже в праве определить как множество всех точек  плоскости, удовлетворяющих уравнению (1). Это было законно на обыкновенной, вещественной плоскости и продолжает быть законным на комплексной плоскости.
плоскости, удовлетворяющих уравнению (1). Это было законно на обыкновенной, вещественной плоскости и продолжает быть законным на комплексной плоскости.
Во многих случаях, однако, прямую на комплексной плоскости удобнее задавать не ее «общим» уравнением (1), а параметрически, т. е. как множество точек  комплексной плоскости, определяемых равенствами
комплексной плоскости, определяемых равенствами

когда t пробегает все комплексные числовые значения  любые данные комплексные числа, лишь случай
любые данные комплексные числа, лишь случай  исключен).
исключен).
Докажем, что оба способа определения прямой эквивалентны между собою.
1° Пусть прямая задана уравнением (1). Как и на вещественной плоскости, назовем направляющим вектором прямой (1) вектор  и всякий ему коллинеарный ненулевой вектор
и всякий ему коллинеарный ненулевой вектор  Другими словами, направляющим вектором прямой (1) называется всякий вектор
Другими словами, направляющим вектором прямой (1) называется всякий вектор  удовлетворяющий уравнению
удовлетворяющий уравнению

Докажем следующее предложение:
Если  — какая-нибудь точка прямой (1), а
— какая-нибудь точка прямой (1), а  — какой-нибудь направляющий вектор этой прямой, то точками прямой (1) являются те и только те точки
— какой-нибудь направляющий вектор этой прямой, то точками прямой (1) являются те и только те точки  , координаты которых могут быть записаны в виде (5).
, координаты которых могут быть записаны в виде (5).
В самом деле, если точка  при некотором t записывается в виде (5), то
при некотором t записывается в виде (5), то

т. е. точка М лежит на прямой (1).
Обратно, пусть  — какая-нибудь точка, лежащая на прямой (1). Так как
— какая-нибудь точка, лежащая на прямой (1). Так как  тоже лежит на этой прямой, то имеем множество
тоже лежит на этой прямой, то имеем множество

и, значит,

Так как  — направляющий вектор прямой (1), т. е.
— направляющий вектор прямой (1), т. е.

то из (6) и (7) вытекает

или

что и означает, что при некотором t имеем

2° Рассмотрим множество всех точек  , которые при каких-нибудь постоянных
, которые при каких-нибудь постоянных  (исключен лишь случай
(исключен лишь случай  допускают запись (5). Эта запись означает, что имеет место пропорция (8), т. е. что точка
допускают запись (5). Эта запись означает, что имеет место пропорция (8), т. е. что точка  лежит на прямой
лежит на прямой

Тогда  тоже лежит на прямой (9), а вектор
тоже лежит на прямой (9), а вектор  является ее направляющим вектором. Следовательно, данная с самого начала система уравнений (5) является системой параметрических уравнений именно этой прямой.
является ее направляющим вектором. Следовательно, данная с самого начала система уравнений (5) является системой параметрических уравнений именно этой прямой.
Эквивалентность двух способов задавать прямую — общим уравнением (1) или системой параметрических уравнений (5) - доказана.
Как и раньше, будем разрешать себе вместо «система параметрических уравнений прямой» говорить просто «параметрическое уравнение прямой».
Прямая, проходящая через две данные точки. Пусть прямая дана своим уравнением (1) и, значит, эквивалентным ему параметрическим уравнением (5).
Если  точка, лежащая на нашей прямой (5) и отличная от точки
точка, лежащая на нашей прямой (5) и отличная от точки  то, полагая
то, полагая  получим направляющий вектор
получим направляющий вектор  прямой
прямой  следовательно, ее параметрическое уравнение (5) может быть записано в виде
следовательно, ее параметрическое уравнение (5) может быть записано в виде

Уравнение (8) при этом принимает вид

или

или, наконец,

— получаем уравнение прямой, проходящей через точки 
По аналогии со случаем вещественной плоскости говорят, что точка  делит отрезок
делит отрезок  в отношении
в отношении  если
если  , откуда
, откуда

В частности, при  получаем точку
получаем точку  называемую серединой отрезка
называемую серединой отрезка 
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ГЛАВА I. КООРДИНАТЫ НА ПРЯМОЙ
- § 1. Отношение отрезков
- § 2. Направленные отрезки (векторы); их отношение
- § 3. Ось. Алгебраическое значение (координата) вектора на оси
- § 4. Сложение векторов на прямой
- § 5. Система координат на прямой
- § 6. Деление отрезка в данном отношении
- § 7. Пропорциональность пар чисел
- § 8. Бесконечно удаленная точка прямой
- § 9. Пропорциональность двух последовательностей, состоящих из и чисел
- ГЛАВА II. ВЕКТОРЫ
- § 1. Равенство векторов. Свободный вектор
- § 2. Линейные операции над векторами (сложение и умножение на число)
- § 3. Проекции
- § 4. Коллинеарные и компланарные векторы; координаты вектора относительного данного базиса
- § 5. Линейная зависимость и независимость векторов
- § 6. Геометрический смысл линейной зависимости векторов
- § 7. Векторные многообразия
- ГЛАВА III. АФФИННАЯ СИСТЕМА КООРДИНАТ НА ПЛОСКОСТИ И В ПРОСТРАНСТВЕ
- § 1. Определение аффинной системы координат
- § 2. Перенос начала координат
- § 3. Деление отрезка в данном отношении
- ГЛАВА IV. ПРЯМОУГОЛЬНАЯ СИСТЕМА КООРДИНАТ. ПОЛЯРНЫЕ КООРДИНАТЫ
- § 1. Прямоугольная система координат на плоскости и в пространстве. Расстояние между двумя точками. Уравнение окружности и сферы
- § 2. Скалярное произведение векторов; угол между двумя векторами
- § 3. Угол от одного вектора до другого на плоскости
- § 4. Полярная система координат на плоскости
- § 5. Полярная система координат в пространстве
- ГЛАВА V. ПРЯМАЯ ЛИНИЯ
- § 1. Направляющий вектор и угловой коэффициент прямой (в произвольной аффинной системе координат). Уравнение прямой
- § 2. Расположение двух прямых на плоскости
- § 3. Частные случаи общего уравнения прямой
- § 4. Векторная и параметрическая форма уравнения прямой. Уравнение прямой, проходящей через две заданные точки
- § 5. Задача: когда прямая Ax+By+C=0 на плоскости проходит через точку пересечения двух заданных прямых A1x+B1y+C1=0 и A2x+B2y+C2=0?
- § 6. Две полуплоскости, определяемые данной прямой на плоскости
- § 7. Прямая на плоскости в прямоугольной системе координат. Нормальное уравнение прямой на плоскости
- § 8. Расстояние от точки до прямой (на плоскости)
- § 9. Углы, образуемые двумя прямыми на плоскости
- § 10. Прямая в пространстве, снабженном прямоугольной системой координат
- ГЛАВА VI. ПАРАБОЛА. ЭЛЛИПС. ГИПЕРБОЛА
- § 1. Парабола
- § 2. Определение и каноническое уравнение эллипса
- § 3. Параметрическая запись уравнения эллипса; построение эллипса по точкам. Эллипс как результат сжатия окружности к одному из ее диаметров
- § 4. Эллипс как проекция окружности и как сечение круглого цилиндра
- § 5. Определение гиперболы. Каноническое уравнение гиперболы
- § 6. Основной прямоугольник и асимптоты гиперболы
- § 7. Директрисы эллипса и гиперболы
- § 8. Фокальный параметр эллипса и гиперболы. Уравнение при вершине
- § 9. Уравнение эллипса, гиперболы и параболы в полярных координатах
- ГЛАВА VII. ДЕТЕРМИНАНТЫ
- § 1. Плошадь ориентированного параллелограмма и треугольника
- § 2. Детерминант второго порядка. Матрицы
- § 4. Разложение детерминанта третьего порядка по элементам какой-либо строки. Приложение к системе трех уравнений с тремя неизвестными (правило Крамера)
- § 5. Системы трех уравнений с тремя неизвестными с детерминантом системы, равным нулю
- § 6. Арифметическое n-мерное векторное многообразие (пространство). Общее определение матрицы. Детерминанты любого порядка
- § 7. Разложение детерминанта n-го порядка по элементам данной строки (данного столбца)
- § 8. Правило Крамера для решений систем и уравнений с n неизвестными
- § 9. Общее определение миноров матрицы. Теорема Лапласа
- § 10. Умножение детерминантов
- § 11. Детерминант n-го порядка как линейная нечетная нормированная функция от n векторов
- ГЛАВА VIII. ПРЕОБРАЗОВАНИЕ КООРДИНАТ. МАТРИЦЫ
- § 1. Переход от одной аффинной системы координат к другой
- § 2. Перемножение матриц. Новое определение обратной матрицы
- § 3. Переход от одной прямоугольной системы координат к другой
- § 4. Действия над матрицами в общем случае
- ГЛАВА IX. ПРЕОБРАЗОВАНИЕ КООРДИНАТ (ПРОДОЛЖЕНИЕ): ОРИЕНТАЦИЯ ПЛОСКОСТИ И ПРОСТРАНСТВА; УГЛЫ ЭЙЛЕРА; ОБЪЕМ ОРИЕНТИРОВАННОГО ПАРАЛЛЕЛЕПИПЕДА; ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ ДВУХ ВЕКТОРОВ
- § 1. Ориентация пространства (плоскости)
- § 2. Углы Эйлера
- § 3. Объем ориентированного параллелепипеда
- § 4. Векторное произведение двух векторов
- ГЛАВА X. ПЛОСКОСТЬ И ПРЯМАЯ В ПРОСТРАНСТВЕ
- § 1. Уравнения плоскости
- § 2. Множество решений системы двух однородных линейных уравнений с тремя неизвестными
- § 3. Взаимное расположение двух плоскостей
- § 4. Прямая как пересечение двух плоскостей
- § 5. Пучок плоскостей
- § 6. Взаимное расположение двух прямых в пространстве
- § 7. О двух полупространствах, определяемых данной плоскостью
- § 8. Плоскость в прямоугольной системе координат; нормальное уравнение плоскости; расстояние от точки до плоскости
- § 9. Угол между прямой и плоскостью; угол между двумя плоскостями
- § 10. Две задачи
- ГЛАВА XI. ДВИЖЕНИЯ И АФФИННЫЕ ПРЕОБРАЗОВАНИЯ
- § 1. Определение движений и аффинных преобразований
- § 2. Преобразование векторов при аффинном преобразовании плоскости и пространства. Основные свойства аффинных преобразований
- § 3. Аналитическое выражение аффинных преобразований
- § 4. Сохранение отношений площадей и объемов при аффинных преобразованиях
- § 5. Получение собственных аффинных преобразований посредством деформации тождественного преобразования. Следствия
- § 6. Движения как изометрические преобразования
- § 7. Преобразования подобия
- § 8. Классификация движений прямой и плоскости
- ГЛАВА XII. ВЕКТОРНЫЕ ПРОСТРАНСТВА (МНОГООБРАЗИЯ) ЛЮБОГО КОНЕЧНОГО ЧИСЛА ИЗМЕРЕНИЙ. СИСТЕМЫ ЛИНЕЙНЫХ ОДНОРОДНЫХ УРАВНЕНИЙ
- § 1. Определение векторного пространства
- § 2. Размерность. Базис. Координаты
- § 3. Теорема об изоморфизме между любыми двумя векторными пространствами одной и той же конечной размерности n
- § 4. Подпространства векторного пространства. Дальнейшие теоремы о линейной зависимости векторов и о базисе векторного пространства
- § 5. Алгебраическая (в частности, прямая) сумма подпространств
- § 6. Линейные отображения векторных пространств
- § 7. Теорема о ранге матрицы
- § 8. Системы линейных однородных уравнения
- ГЛАВА XIII. ЛИНЕЙНЫЕ, БИЛИНЕЙНЫЕ И КВАДРАТИЧНЫЕ ФУНКЦИИ НА ВЕКТОРНЫХ ПРОСТРАНСТВАХ
- § 1. Линейные функции
- § 2. Билинейные функции и билинейные формы
- § 3. Матрица билинейной и квадратичной формы и ее преобразование при переходе к новому базису (при преобразовании переменных)
- § 4. Ранг билинейной и квадратичной формы (билинейной и квадратичной функции)
- § 5. Существование канонического базиса для всякой квадратичной и всякой билинейной функции («приведение квадратичных форм к каноническому виду»)
- ГЛАВА XIV. ТОЧЕЧНО-ВЕКТОРНОЕ АФФИННОЕ n-МЕРНОЕ ПРОСТРАНСТВО
- § 1. Определение n-мерного аффинного пространства
- § 2. Системы координат. Арифметическое пространство. Изоморфизм всех n-мерных пространств между собою
- § 3. r-мерные плоскости n-мерного аффинного пространства; r-мерные параллелепипеды
- § 4. Геометрически независимые системы точек. Барицентрические координаты. Симплексы
- § 5. Системы линейных уравнений
- § 6. Аффинные преобразования n-мерного аффинного пространства
- ГЛАВА XV. АЛГЕБРАИЧЕСКИЕ ЛИНИИ И ПОВЕРХНОСТИ. КОМПЛЕКСНАЯ ПЛОСКОСТЬ И КОМПЛЕКСНОЕ ПРОСТРАНСТВО
- § 1. Определение алгебраических линий и поверхностей
- § 2. Преобразование многочлена второй степени при преобразовании координат
- § 3. Аффинная эквивалентность линий и поверхностей
- § 4. Комплексная плоскость
- § 5. Прямая линия на комплексной плоскости
- § 6. Замечание о действительных и мнимых линиях
- § 7. Комплексное пространство
- § 8. Распадающиеся линии и поверхности. Цилиндрические и конические поверхности. Поверхности вращения
- § 9. Несколько заключительных замечаний о линиях и поверхностях
- ГЛАВА XVI. Различные виды кривых второго порядка
- § 1. О линиях, определяемых уравнениями второй степени с двумя неизвестными
- § 2. Инварианты многочлена второй степени
- § 3. Центральный случай
- § 4. Параболический случай
- § 5. Аффинная классификация кривых второго порядка
- § 6. Несколько заключительных замечаний
- ГЛАВА XVII. ОБЩАЯ ТЕОРИЯ КРИВЫХ ВТОРОГО ПОРЯДКА
- § 1. Пересечение алгебраической кривой с прямой. Асимптотические направления и асимптоты алгебраической кривой
- § 2. Теорема единственности для кривых второго порядка. Пучок кривых второго порядка
- § 3. Асимптотические направления кривых второго порядка
- § 4. Пересечение кривой второго порядка с прямой иеасимптотического направления. Касательные
- § 5. Пересечение кривой второго порядка с прямой асимптотического направления. Геометрическая характеристика асимптотических и неасимптотических направлений
- § 6. Центр кривой второго порядка
- § 7. Диаметры кривой второго порядка
- § 8. Взаимно сопряженные векторы (направления). Диаметры и касательные
- § 9. Вид уравнения кривой, если оси координат имеют сопряженные направления
- § 10. Второе доказательство теоремы единственности. О полноте системы ортогональных инвариантов
- § 11. Оси симметрии и главные направления кривой второго порядка
- § 12. Основная теорема об аффинных преобразованиях
- ГЛАВА XVIII. КРАТКОЕ ОПИСАНИЕ РАЗЛИЧНЫХ ВИДОВ ПОВЕРХНОСТЕЙ ВТОРОГО ПОРЯДКА
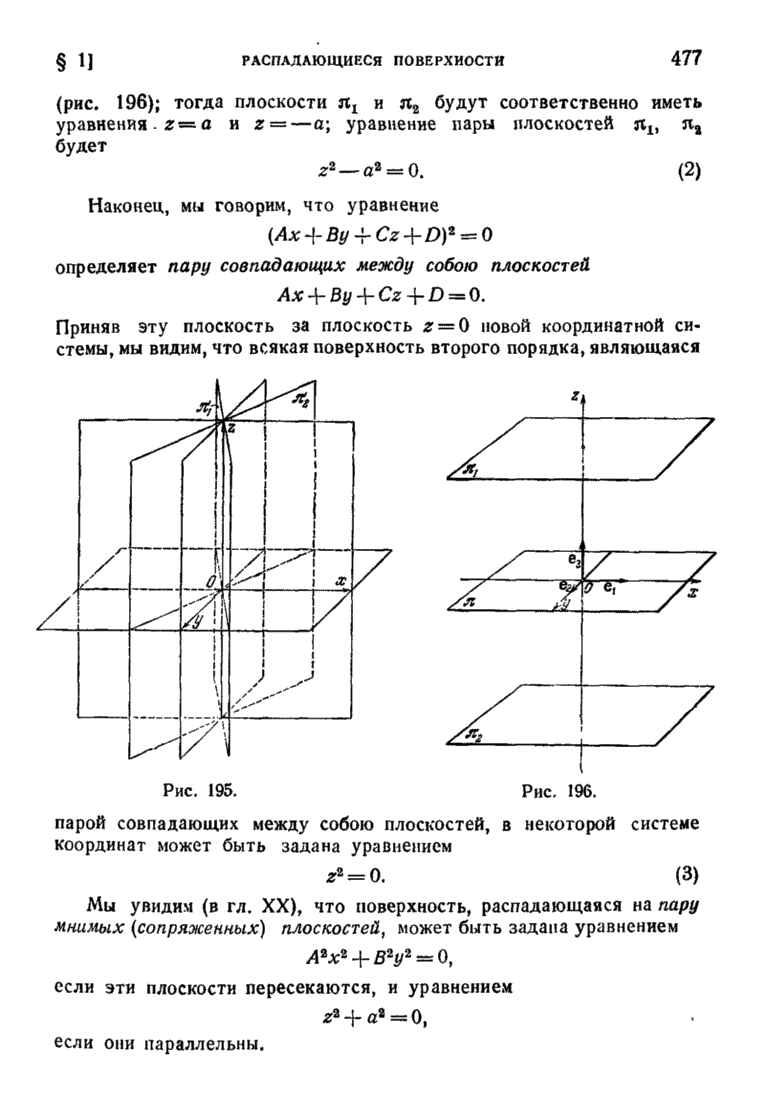
- § 1. Распадающиеся поверхности
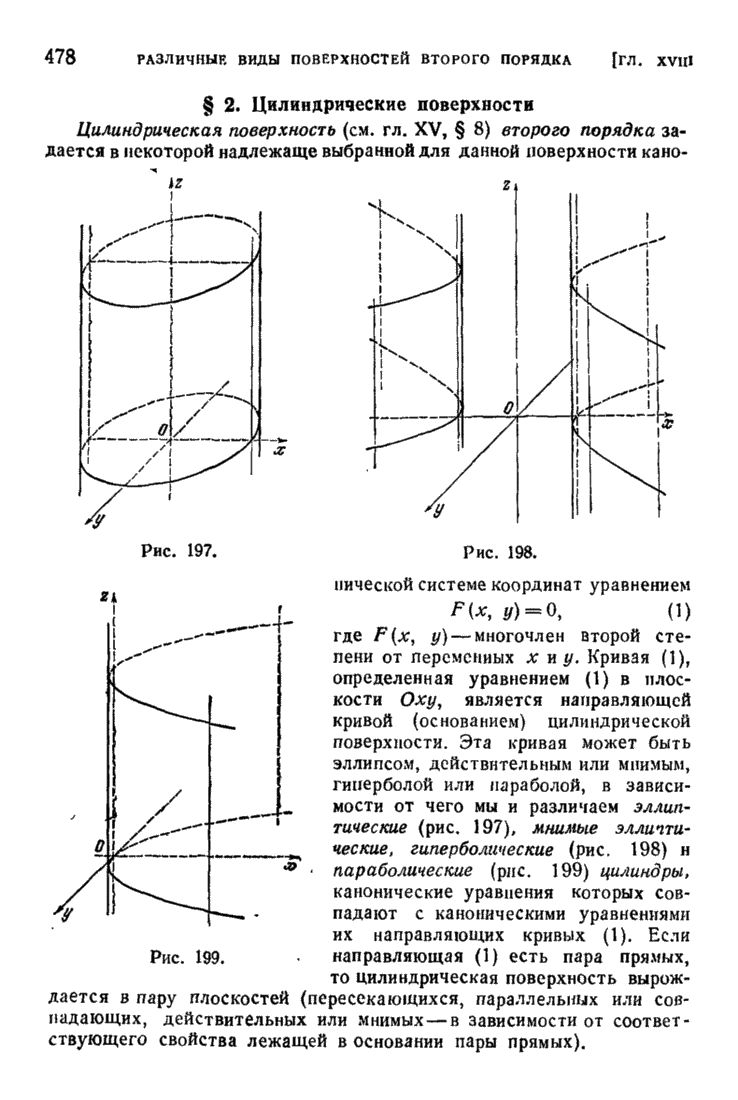
- § 2. Цилиндрические поверхности
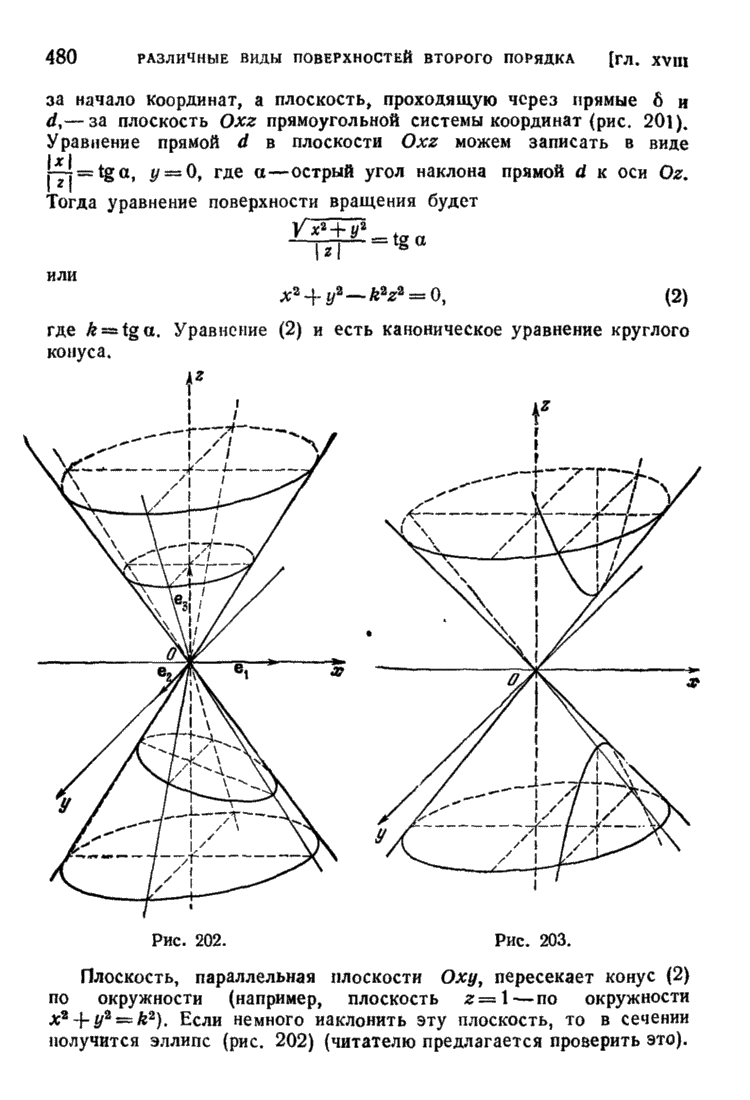
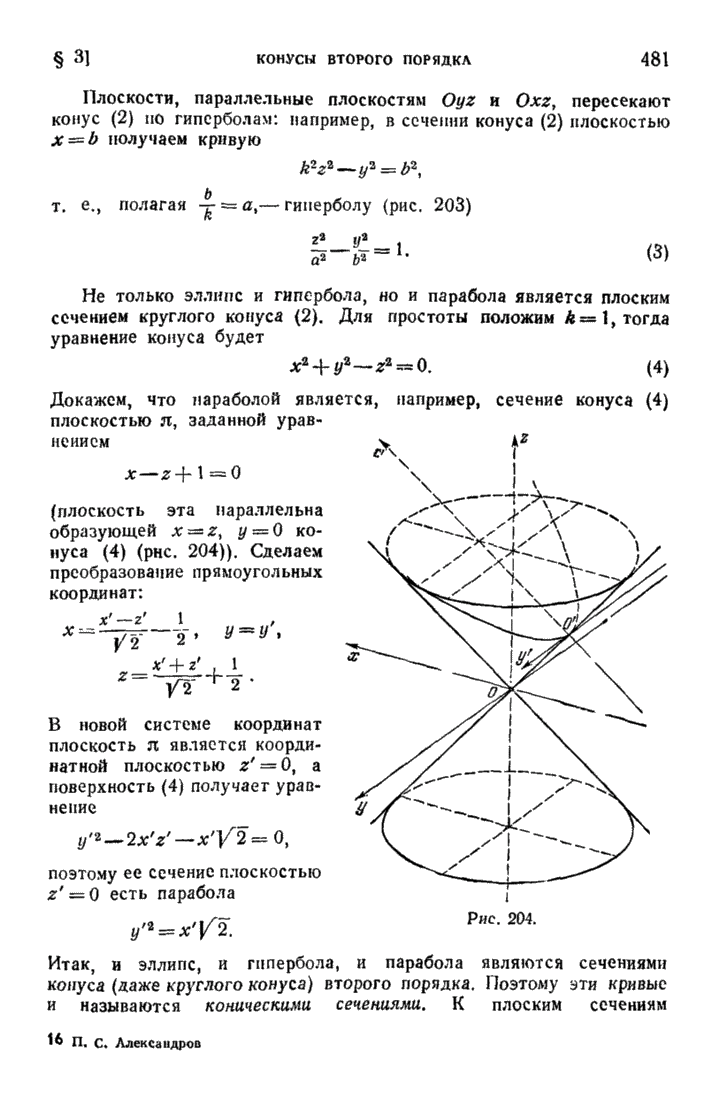
- § 3. Конусы второго порядка
- § 4. Эллипсоиды и гиперболоиды
- § 5. Параболоиды
- § 6. Прямолинейные образующие
- ГЛАВА XIX. ОБЩАЯ ТЕОРИЯ ПОВЕРХНОСТЕЙ ВТОРОГО ПОРЯДКА. I (ПЕРЕСЕЧЕНИЕ С ПЛОСКОСТЬЮ И С ПРЯМОЙ; АСИМПТОТИЧЕСКИЕ НАПРАВЛЕНИЯ; КАСАТЕЛЬНАЯ ПЛОСКОСТЬ; ЦЕНТР)
- § 1. Ранг и детерминант малой и большой матрицы многочлена второй степени
- § 2. Пересечение поверхности второго порядка с плоскостью
- § 3. Пересечение поверхности второго порядка с прямой. Асимптотические направления. Касательные прямые и касательная плоскость. Особые точки поверхности второго порядка
- § 4. Асимптотические направления, конус асимптотических направлений, прямолинейные образующие поверхностей второго порядка
- § 5. Центр поверхности второго порядка
- ГЛАВА XX. ОБЩАЯ ТЕОРИЯ ПОВЕРХНОСТЕЙ ВТОРОГО ПОРЯДКА. II (ДИАМЕТРАЛЬНЫЕ ПЛОСКОСТИ; ОСОБЫЕ И ГЛАВНЫЕ НАПРАВЛЕНИЯ; АФФИННАЯ КЛАССИФИКАЦИЯ)
- § 1. Диаметральные плоскости. Особые направления
- § 2. Диаметральные плоскости поверхностей различных видов
- § 3. Сопряженные направления
- § 4. Уравнение поверхности второго порядка относительно координатной системы с сопряженными направлениями осей
- § 5. Теорема единственности
- § 6. Главные направления
- § 7. Приведение к каноническому виду уравнения поверхности второго порядка
- § 8. Аффинная классификация поверхностей второго порядка
- ГЛАВА XXI. ПРОЕКТИВНАЯ ПЛОСКОСТЬ
- § 1. Перспективное соответствие между плоскостью и связкой
- § 2. Однородные координаты точек на плоскости и лучел в связке
- § 3. Координаты прямой; арифметическая проективная плоскость; общее определение проективной плоскости
- § 4. Принцип двойственности для проективной плоскости
- § 5. Проективная система координат в связке и на проективной плоскости
- § 6. Проективные преобразования и отображения проективной плоскости
- § 7. Проективные координаты на прямой. Проективные отображения прямой
- § 8. Двойное отношение
- ГЛАВА XXII. КРИВЫЕ ВТОРОГО ПОРЯДКА НА ПРОЕКТИВНОЙ ПЛОСКОСТИ
- § 1. Определение. Теорема единственности
- § 2. Пересечение кривой второго порядка с прямой. Касательные; асимптоты
- § 3. Пучок кривых второго порядка. Второе доказательство теоремы единственности. Теорема Паскаля. Теорема Штейнера
- § 4. Поляры и полюсы
- § 5. Коррелятивное, в частности полярное, соответствие. Тангенциальное уравнение кривой
- § 6. Диаметры как поляры несобственных точек
- § 7. Автополярный треугольник
- § 8. Проективная классификация кривых второго порядка
- ГЛАВА XXIII. НАЧАЛЬНЫЕ СВЕДЕНИЯ ИЗ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ ПРОЕКТИВНОГО ПРОСТРАНСТВА
- § 1. Проективное пространство; его плоскости и прямые
- § 2. Проективные координаты. Проективные преобразования.
- § 3. Понятие об n-мерном проективном пространстве
- § 4. Поверхности второго порядка в проективном пространстве. Теорема единственности
- § 5. Пересечение поверхности второго порядка с плоскостью и с прямой. Касательные прямые. Касательная плоскость. Прямолинейные образующие
- § 6. Полюсы и полярные плоскости
- § 7. Проективная классификация поверхностей второго порядка
- § 8. Распределение по проективным классам поверхностей различных аффинных классов. Проективно-аффинная классификация поверхностей второго порядка
- ГЛАВА XXIV. ЕВКЛИДОВО n-МЕРНОЕ ПРОСТРАНСТВО
- § 1. Введение. Ортогональные матрицы
- § 2. Положительно определенные симметричные билинейные функции в векторном пространстве
- § 3. Определение евклидовых пространств и простейших относящихся к ним понятий
- § 4. Неравенство Коши—Буняковского и его следствия. Углы
- § 5. Подпространства евклидовых пространств. Ортогональное дополнение к данному подпространству
- ГЛАВА XXV. ЛИНЕЙНЫЕ ОПЕРАТОРЫ, БИЛИНЕЙНЫЕ И КВАДРАТИЧНЫЕ ФУНКЦИИ В ЕВКЛИДОВЫХ ПРОСТРАНСТВАХ. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
- § 1. Инвариантные подпространства и собственные векторы линейного оператора в любом векторном пространстве
- § 2. Ортогональные преобразования n-мерного евклидова пространства
- § 3. Движения трехмерного евклидова пространства
- § 4. Преобразования подобия. Дальнейшие проблемы
- § 5. Самосопряженные операторы
- § 6. Теорема о структуре произвольного линейного преобразования евклидова пространства
- § 7. Билинейные и квадратичные формы в евклидовых пространствах
- § 8. (n-1)-мерные многообразия (поверхности) второго поряд] в -мерном аффинном и евклидовом пространствах
- ПРИБАВЛЕНИЕ. ПЕРЕСТАНОВКИ, МНОЖЕСТВА И ИХ ОТОБРАЖЕНИЯ; ГРУППЫ
- § 1. Перестановки
- § 2. Множества
- § 3. Отображения или функции
- § 4. Разбиение множества на подмножества. Отношение эквивалентности
- § 5. Определение группы
- § 6. Простейшие теоремы о группах
- § 7. Эквивалентность подмножеств данного множества по отношению к дайной группе его преобразований
- ЗАДАЧИ
- Задачи к главе IV
- Задачи к главе V
- Задачи к главе VI
- Задачи к главе VIII
- Задачи к главе IX
- Задачи к главе X
- Задачи к главе XI
- Задачи к главе XII
- Задачи к главе XIII
- Задачи к главе XIV
- Задачи к главе XV
- Задачи к главам XVI и XVII
- Задачи к главе XVIII
- Задачи к главам XIX и XX
- Задачи к главе XXI
- Задачи к главе XXII