| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ГЛАВА IX. ПРЕОБРАЗОВАНИЕ КООРДИНАТ (ПРОДОЛЖЕНИЕ): ОРИЕНТАЦИЯ ПЛОСКОСТИ И ПРОСТРАНСТВА; УГЛЫ ЭЙЛЕРА; ОБЪЕМ ОРИЕНТИРОВАННОГО ПАРАЛЛЕЛЕПИПЕДА; ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ ДВУХ ВЕКТОРОВ
§ 1. Ориентация пространства (плоскости)
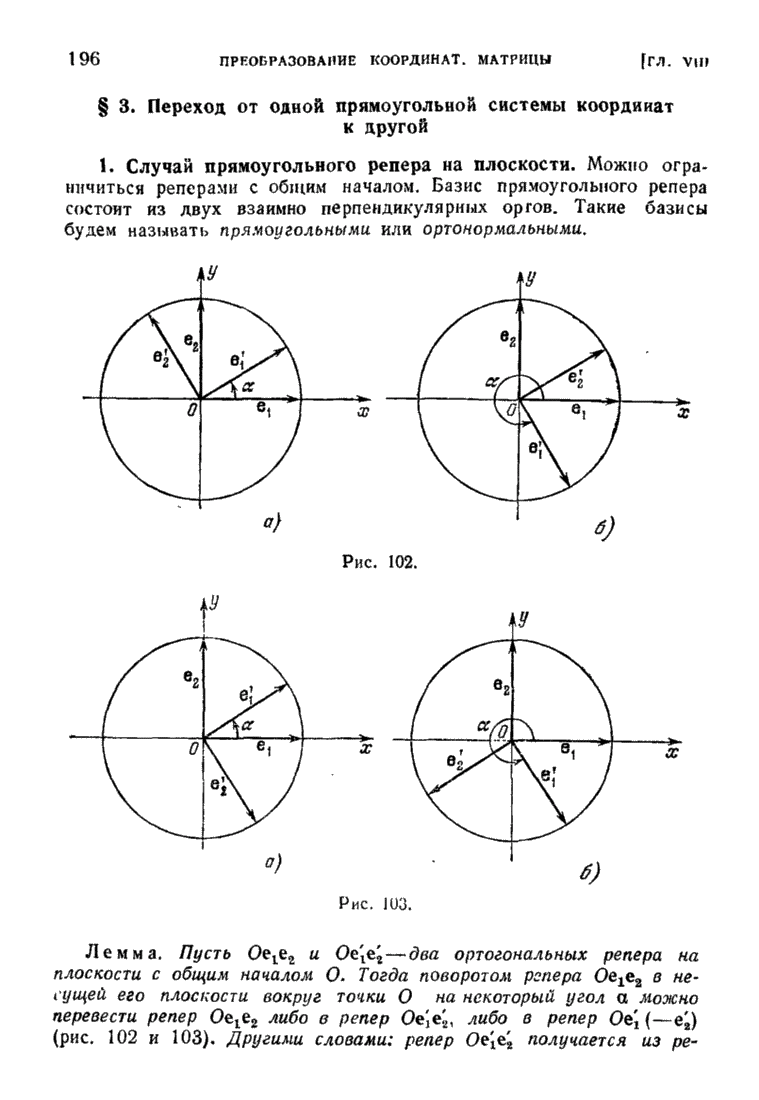
Назовем в пространстве (или на плоскости) два координатных базиса (два репера) одноименными, если матрица перехода от одного из них к другому имеет положительный детерминант; в противном случае (т. е. если детерминант матрицы перехода отрицателен) назовем базисы разноименными. В случае ортогональных базисов на плоскости это определение и его геометрический смысл нам уже известны из § 3 главы VIII. Одноименность двух базисов  будем иногда записывать так:
будем иногда записывать так:  .
.
Покажем, что данное определение одноименности удовлетворяет так называемым аксиомам равенства, т. е. требованиям рефлексивности  , симметрии (из
, симметрии (из  следует
следует  ) и транзитивности (из
) и транзитивности (из  следует
следует  ).
).
Рефлексивность вытекает из того, что матрица перехода от базиса  к нему самому (т. е. матрица тождественного преобразования) есть единичная матрица, имеющая детерминант 1.
к нему самому (т. е. матрица тождественного преобразования) есть единичная матрица, имеющая детерминант 1.
Симметрия вытекает из того, что детерминанты матрицы С и обратной к ней матрицы  имеют один и тот же знак. Для того чтобы убедиться в транзитивности, рассмотрим три базиса:
имеют один и тот же знак. Для того чтобы убедиться в транзитивности, рассмотрим три базиса:

Если обозначить матрицы перехода от I к II, от II к III и от I к III соответственно через  , то
, то  , значит, и
, значит, и  , откуда утверждение следует.
, откуда утверждение следует.
Из сказанного следует:
Множество всех базисов пространства (плоскости) распадается на попарно не пересекающиеся классы, обладающие тем свойством, что все базисы, принадлежащие одному какому-нибудь классу, одноименны, а всякие два базиса, принадлежащие различным классам, разноименны между собою.
Докажем, что число этих классов равно двум.
Для того чтобы убедиться, что имеется по крайней мере два класса, возьмем какой-нибудь базис  и заметим, что матрица перехода от
и заметим, что матрица перехода от  есть
есть

ее детерминант равен —1, значит, базисы  разноименны, они принадлежат к различным классам.
разноименны, они принадлежат к различным классам.
Теперь мы покажем, что всякий базис  принадлежит к одному из двух классов: либо к классу, содержащему базис
принадлежит к одному из двух классов: либо к классу, содержащему базис  , либо к классу, содержащему базис
, либо к классу, содержащему базис  . Другими словами, докажем, что всякий базис
. Другими словами, докажем, что всякий базис  , не одноименный базису
, не одноименный базису  , одноименен базису
, одноименен базису  .
.
В самом деле, матрица перехода от  имеет (в силу разноименности этих базисов) отрицательный детерминант; матрица перехода от
имеет (в силу разноименности этих базисов) отрицательный детерминант; матрица перехода от  имеет детерминант —1; значит, матрица перехода от
имеет детерминант —1; значит, матрица перехода от  (будучи произведением двух названных матриц) имеет положительный детерминант. Утверждение доказано.
(будучи произведением двух названных матриц) имеет положительный детерминант. Утверждение доказано.
В каждом из двух классов базисов имеются ортогональные базисы. В самом деле, берем какой-нибудь ортогональный базис  . Он содержится в одном из наших двух классов; ортогональный базис
. Он содержится в одном из наших двух классов; ортогональный базис  содержится тогда во втором классе.
содержится тогда во втором классе.
Два базиса, получающиеся один из другого одной транспозицией (т. е. перестановкой двух каких-либо из трех векторов, образующих данный базис), всегда разноименны. В самом деле, пусть базис  получается из базиса
получается из базиса  перестановкой двух каких-нибудь векторов этого последнего, например векторов
перестановкой двух каких-нибудь векторов этого последнего, например векторов  , так что
, так что

Тогда соответствующая матрица перехода

имеет детерминант —1.
Поэтому два базиса, получающиеся один из другого произвольной перестановкой их векторов, одноименны, если эта перестановка четная, и разноименны, если перестановка нечетная: базисы

входят в один класс, а базисы

— в другой.
Введем теперь следующее весьма важное определение.
Скажем, что базис  переходит в базис
переходит в базис  посредством непрерывной деформации, если для каждого числа t, принадлежащего некоторому отрезку
посредством непрерывной деформации, если для каждого числа t, принадлежащего некоторому отрезку  , дай базис
, дай базис  , а именно:
, а именно:

так что все координаты  и т. д. являются непрерывными функциями от t на отрезке
и т. д. являются непрерывными функциями от t на отрезке  , причем при
, причем при  мы получаем исходный базис
мы получаем исходный базис  , т. е.
, т. е.

а при  получаем базис
получаем базис  :
:

Теперь предположим, кроме того, что базис  приложен к точке
приложен к точке  , где
, где  , суть также непрерывные на отрезке
, суть также непрерывные на отрезке  функции от t, причем
функции от t, причем  Тогда мы говорим, что репер
Тогда мы говорим, что репер  переходит в репер
переходит в репер  посредством непрерывной деформации. Наглядный смысл этих определений таков.
посредством непрерывной деформации. Наглядный смысл этих определений таков.
Считая параметр t временем, изменяющимся от начального момента  до конечного
до конечного  , мы имеем непрерывно меняющийся («деформирующийся») во времени репер
, мы имеем непрерывно меняющийся («деформирующийся») во времени репер  , начальное состояние которого (при
, начальное состояние которого (при  есть наш исходный репер
есть наш исходный репер  , а конечное — репер
, а конечное — репер  (в который превратился репер
(в который превратился репер  в результате процесса деформации, длившегося отрезок времени
в результате процесса деформации, длившегося отрезок времени  ).
).
Имеет место следующее очевидное предложение.
Если базис  переходит в базис
переходит в базис  посредством деформации, которая длится, положим, отрезок времени
посредством деформации, которая длится, положим, отрезок времени  , а базис
, а базис  , переходит в базис
, переходит в базис  посредством деформации, которая длится в течение отрезка времени
посредством деформации, которая длится в течение отрезка времени  , то базис
, то базис  переходит в
переходит в  посредством деформации, которая длится в течение отрезка времени
посредством деформации, которая длится в течение отрезка времени
Далее, если базис  переходит посредством непрерывной деформации
переходит посредством непрерывной деформации  в базис
в базис  , то и базис
, то и базис  переходит посредством непрерывной деформации в базис
переходит посредством непрерывной деформации в базис  , достаточно положить
, достаточно положить  и
и

при  получаем
получаем  и, следовательно,
и, следовательно,  и т. д., при
и т. д., при  имеем
имеем  , значит,
, значит,  и т. д.
и т. д.
Аналогичные предложения, разумеется, верны и для деформации реперов.
Замечание. Обычно за отрезок  берут единичный отрезок
берут единичный отрезок  .
.
Если рассматривать (как это привычно читателю из элементарного курса механики) движение твердого тела в пространстве как непрерывный процесс, происходящий в течение некоторого промежутка времени (положим, от  до
до  ), то становится очевидным, что частным случаем непрерывной деформации репера
), то становится очевидным, что частным случаем непрерывной деформации репера  является движение (перемещение) этого репера (рассматриваемого как твердое тело): в начальный момент времени
является движение (перемещение) этого репера (рассматриваемого как твердое тело): в начальный момент времени  наш репер занимает положение
наш репер занимает положение  (которое будем обозначать также через
(которое будем обозначать также через  ), в конечный момент
), в конечный момент  репер займет положение а в
репер займет положение а в  промежуточный момент t репер (перемещаясь в пространстве как твердое тело) будет находиться в положении Сеевз. Обозначим координаты вектора
промежуточный момент t репер (перемещаясь в пространстве как твердое тело) будет находиться в положении Сеевз. Обозначим координаты вектора  (относительно начального репера
(относительно начального репера  ) через
) через  , так что
, так что

и аналогично

Тогда непрерывность процесса перемещения и находит свое математическое выражение в том, что координаты  суть непрерывные функции времени
суть непрерывные функции времени  .
.

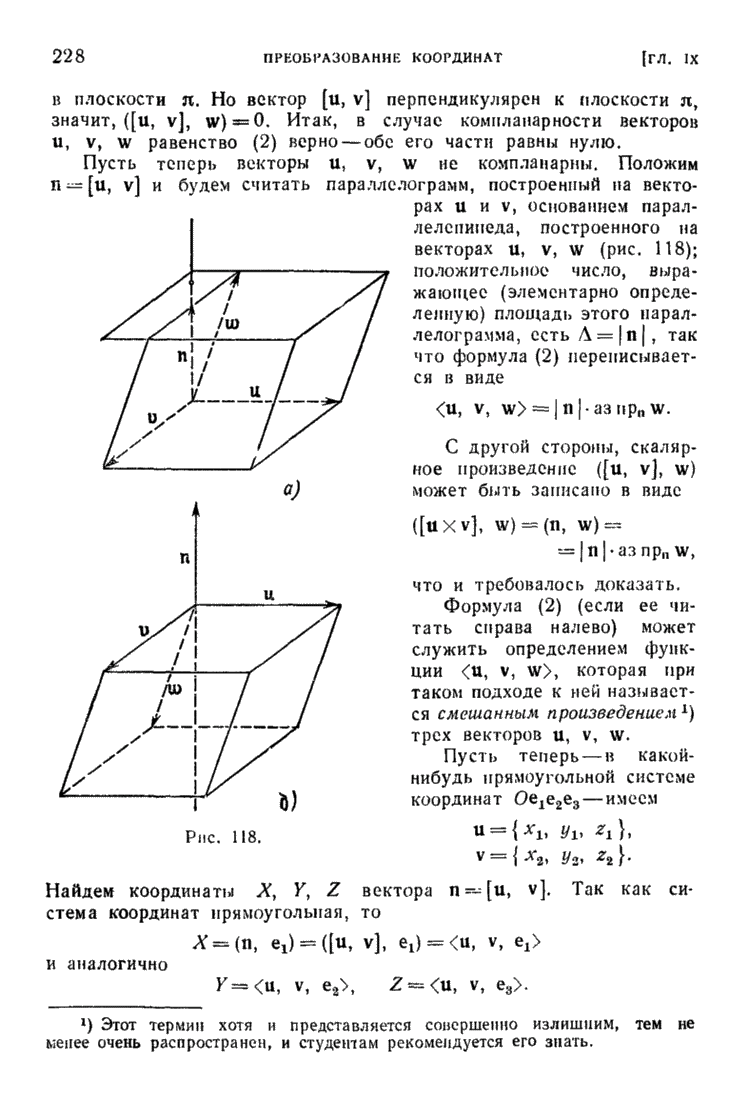
Докажем следующее основное предложение:
1а. Если базис  переходит в базис
переходит в базис  посредством непрерывной деформации, то оба базиса одноименны.
посредством непрерывной деформации, то оба базиса одноименны.
В самом деле, положим

надо доказать, что числа  и
и  - одного и того же знака. Но детерминант
- одного и того же знака. Но детерминант  , будучи многочленом от своих элементов
, будучи многочленом от своих элементов  , являющихся непрерывными функциями от t, есть непрерывная функция от t на всем отрезке
, являющихся непрерывными функциями от t, есть непрерывная функция от t на всем отрезке  . Если бы ее значения в концах этого отрезка имели разные знаки, то существовало бы промежуточное значение
. Если бы ее значения в концах этого отрезка имели разные знаки, то существовало бы промежуточное значение  , для которого
, для которого  . Но этого не может быть, так как
. Но этого не может быть, так как  , как детерминант матрицы перехода от базиса
, как детерминант матрицы перехода от базиса  к базису
к базису  , всегда отличен от нуля.
, всегда отличен от нуля.
Теперь мы докажем обратное предложение:
16. Всякие два одноименных базиса (репера) могут быть переведены друг в друга непрерывной деформацией.
План доказательства таков. Мы сначала доказываем, что всякий репер может быть непрерывной деформацией переведен в прямоугольный. После этого доказываем, что всякие два одноименных прямоугольных репера могут быть переведены друг в друга движением в пространстве, т. е. специальным видом непрерывной деформации.
Предположим, что мы доказали оба эти факта. Пусть  и Оееез — два произвольных одноименных репера,
и Оееез — два произвольных одноименных репера,  переводим их непрерывной деформацией соответственно в прямоугольные реперы
переводим их непрерывной деформацией соответственно в прямоугольные реперы  . Тогда
. Тогда  , следовательно (по свойству
, следовательно (по свойству  . Но одноименные реперы
. Но одноименные реперы  , Огортогональны; значит, по сделанному предположению они могут быть переведены друг в друга непрерывной деформацией.
, Огортогональны; значит, по сделанному предположению они могут быть переведены друг в друга непрерывной деформацией.
Переводим теперь непрерывными деформациями последовательно

(последнее возможно: раз существует деформация, переводящая  , то существует, как мы видели, и деформация, переводящая
, то существует, как мы видели, и деформация, переводящая  ). В результате трех последовательных деформаций (А), (Б), (В) получаем искомую деформацию, переводящую
). В результате трех последовательных деформаций (А), (Б), (В) получаем искомую деформацию, переводящую  в
в  . Основное предложение доказано.
. Основное предложение доказано.

Рис. 104.
Переходим к выполнению намеченного плана.
Доказываем первое утверждение: всякий репер может быть непрерывной деформацией переведен в ортогональный.
Докажем это утверждение сначала для плоскости. Пусть  данный репер,
данный репер,  . Построим ортогональный репер
. Построим ортогональный репер  так, чтобы орт
так, чтобы орт  лежал на оси, несущей вектор
лежал на оси, несущей вектор  , а орт
, а орт  (перпендикулярный к
(перпендикулярный к  лежал в той же полуплоскости (из двух полуплоскостей, определяемых прямой
лежал в той же полуплоскости (из двух полуплоскостей, определяемых прямой  ), в которой лежит вектор
), в которой лежит вектор  . Тогда, если угол
. Тогда, если угол  , между векторами
, между векторами  и
и  острый (рис. 104, а), то он весь лежит внутри прямого угла между
острый (рис. 104, а), то он весь лежит внутри прямого угла между  , а если угол
, а если угол  туггой (рис. 104, б), то он, наоборот, содержит прямой угол между
туггой (рис. 104, б), то он, наоборот, содержит прямой угол между  . Для каждого
. Для каждого  , обозначим через
, обозначим через  , соответственно через
, соответственно через  , точку отрезка
, точку отрезка  , соответственно
, соответственно  , делящую этот отрезок в отношении
, делящую этот отрезок в отношении  . При любом t,
. При любом t,  , вектор
, вектор  лежит на полупрямой
лежит на полупрямой  , несущей вектор
, несущей вектор  , а вектор
, а вектор  лежит внутри треугольника
лежит внутри треугольника  , имеющего с полупрямой
, имеющего с полупрямой  , единственную общую точку О.
, единственную общую точку О.
Поэтому векторы  при любом t не коллинеарны, т. е. образуют репер
при любом t не коллинеарны, т. е. образуют репер  , непрерывно меняющийся при изменении t от 0 до 1 и осуществляющий непрерывный переход (деформацию) от репера
, непрерывно меняющийся при изменении t от 0 до 1 и осуществляющий непрерывный переход (деформацию) от репера  к реперу
к реперу  .
.
Переходим к случаю пространства. В плоскости  произведем те же построения, как и выше. Обозначим через
произведем те же построения, как и выше. Обозначим через  орт, перпендикулярный к плоскости
орт, перпендикулярный к плоскости  и направленный в ту же сторону от этой плоскости, что и вектор
и направленный в ту же сторону от этой плоскости, что и вектор  (рис. 105).
(рис. 105).

Рис. 105.
В полной аналогии с предыдущим случаем обозначаем через  , точку отрезка
, точку отрезка  , делящую этот отрезок в отношении
, делящую этот отрезок в отношении  любом i,
любом i,  , определен, таким образом, вектор
, определен, таким образом, вектор  и репер
и репер  , непрерывно зависящий от
, непрерывно зависящий от  и осуществляющий при изменении
и осуществляющий при изменении  от 0 до 1 непрерывный переход от данного репера
от 0 до 1 непрерывный переход от данного репера  к прямоугольному реперу
к прямоугольному реперу  . Первое утверждение доказано.
. Первое утверждение доказано.
Переходим к доказательству второго утверждения. Всякий прямоугольный репер  может быть посредством непрерывного движения, являющегося, как было сказано выше, частным случаем непрерывной деформации, переведен во всякий другой одноименный с ним прямоугольный репер
может быть посредством непрерывного движения, являющегося, как было сказано выше, частным случаем непрерывной деформации, переведен во всякий другой одноименный с ним прямоугольный репер  .
.
Посредством сдвига на вектор ОО можно прежде всего совместить начала О и  обоих реперов; поэтому можно ограничиться случаем, когда оба репера имеют общее начало О. Теперь начинаем с того, что совмещаем орты
обоих реперов; поэтому можно ограничиться случаем, когда оба репера имеют общее начало О. Теперь начинаем с того, что совмещаем орты  . Для этого проведем через эти орты (имеющие общее начало О) плоскость
. Для этого проведем через эти орты (имеющие общее начало О) плоскость  (рис. 106) и восставим к этой плоскости в точке О перпендикуляр d. Совершим теперь поворот репера
(рис. 106) и восставим к этой плоскости в точке О перпендикуляр d. Совершим теперь поворот репера  (как твердого тела) вокруг прямой d на угол
(как твердого тела) вокруг прямой d на угол  , между ортами
, между ортами  , в таком направлении, чтобы орт
, в таком направлении, чтобы орт  совместился с ортом
совместился с ортом  .
.
Этот поворот переведет орты  в какие-то взаимно перпендикулярные орты
в какие-то взаимно перпендикулярные орты  , лежащие в плоскости, перпендикулярной к орту
, лежащие в плоскости, перпендикулярной к орту  (и проходящей через точку О), т. е. в плоскости
(и проходящей через точку О), т. е. в плоскости  . Теперь остается поворотом репера вокруг прямой, несущей орт
. Теперь остается поворотом репера вокруг прямой, несущей орт  , совместить орт
, совместить орт  с ортом ОЕ. Этот поворот, оставляя пару ортов
с ортом ОЕ. Этот поворот, оставляя пару ортов  в их плоскости (которая есть плоскость
в их плоскости (которая есть плоскость  ) и совместив орт
) и совместив орт  с ортом
с ортом  , переведет орт
, переведет орт  (с которым еще ранее был совмещен орт
(с которым еще ранее был совмещен орт  ) в орт, перпендикулярный к
) в орт, перпендикулярный к  , т. е. либо в
, т. е. либо в  , либо в
, либо в  . Но вторая возможность исключена, так как реперы
. Но вторая возможность исключена, так как реперы  и
и  , разноименны и поэтому не могут быть совмещены движением в пространстве. Утверждение доказано.
, разноименны и поэтому не могут быть совмещены движением в пространстве. Утверждение доказано.

Рис. 106.
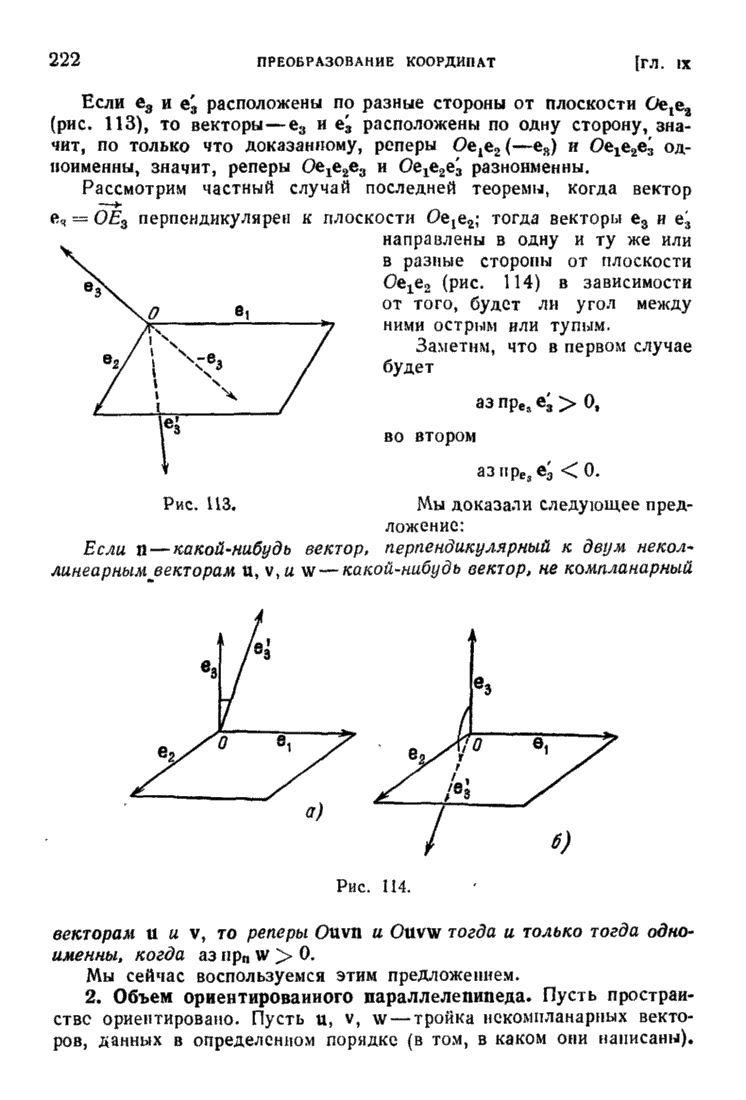
Вместе с ним завершено доказательство и следующего результата (верного как для плоскости, так и для пространства).
Теорема 1. Для того чтобы два репера (два базиса) были одноименны, необходимо и достаточно, чтобы один из них можно было непрерывной деформацией перевести в другой. Если данные реперы прямоугольны, то их можно перевести друг в друга даже движением в пространстве. Если реперы разноименны, то их нельзя перевести друг в друга даже никакой деформацией, значит, и подавно никаким движением.
Поэтому
Теорема 1. Два прямоугольных репера (на плоскости или в пространстве) тогда и только тогда одноименны, когда один из них может быть переведен в другой непрерывным движением (в плоскости, соответственно в пространстве).
Пусть  — два прямоугольных разноименных репера. Тогда реперы
— два прямоугольных разноименных репера. Тогда реперы  одноименны и, например, первый из них может быть движением переведен во второй. Но репер
одноименны и, например, первый из них может быть движением переведен во второй. Но репер  является зеркальным отражением репера
является зеркальным отражением репера  относительно плоскости
относительно плоскости  . Поэтому имеет место
. Поэтому имеет место
Теорема 2. Если ортогональные реперы и  разноименны, то один из них может быть переведен в другой посредством движения со следующим за ним (или предшествующим ему) зеркальным отражением.
разноименны, то один из них может быть переведен в другой посредством движения со следующим за ним (или предшествующим ему) зеркальным отражением.
Доказательство следующего замечания можно в качестве упражнения предоставить читателю.
Замечание. 1. Беря зеркальные отражения етносительно произвольной плоскости всех базисов (реперов) одного какого-нибудь класса в пространстве, получим все базисы (реперы) другого класса. Аналогичный результат, разумеется, имеет место и в плоскости.
Определение. Ориентировать плоскость или пространство — значит один из двух классов базисов (реперов) объявить положительным (а другой — отрицательным). Тогда и всякий базис (репер) называется положительным или отрицательным в зависимости от того, к какому классу он принадлежит.
Для того чтобы ориентировать (плоскость или пространство), достаточно задать один какой-нибудь базис и объявить положительными все с ним одноименные базисы.
Замечание 2. Если плоскость ориентирована, то в пей определяется и положительное направление вращения: это направление кратчайшего вращения т. е. вращения на угол из тех двух вращений (на  и на
и на  , посредством которых можно первый орт (т. е. орт
, посредством которых можно первый орт (т. е. орт  ) положительного прямоугольного репера
) положительного прямоугольного репера  перевести во второй (т. е. в орт
перевести во второй (т. е. в орт  ).
).
Обратно, если на плоскости задано положительное направление вращения, то определена и ориентация плоскости: репер  положителен, если кратчайший поворот на угол (т. е. поворот на угол
положителен, если кратчайший поворот на угол (т. е. поворот на угол 
переводящий орт  в орт
в орт  , происходит в положительном направлении.
, происходит в положительном направлении.
Таким образом, ориентация плоскости фактически совпадает с выбором положительного направления вращения.
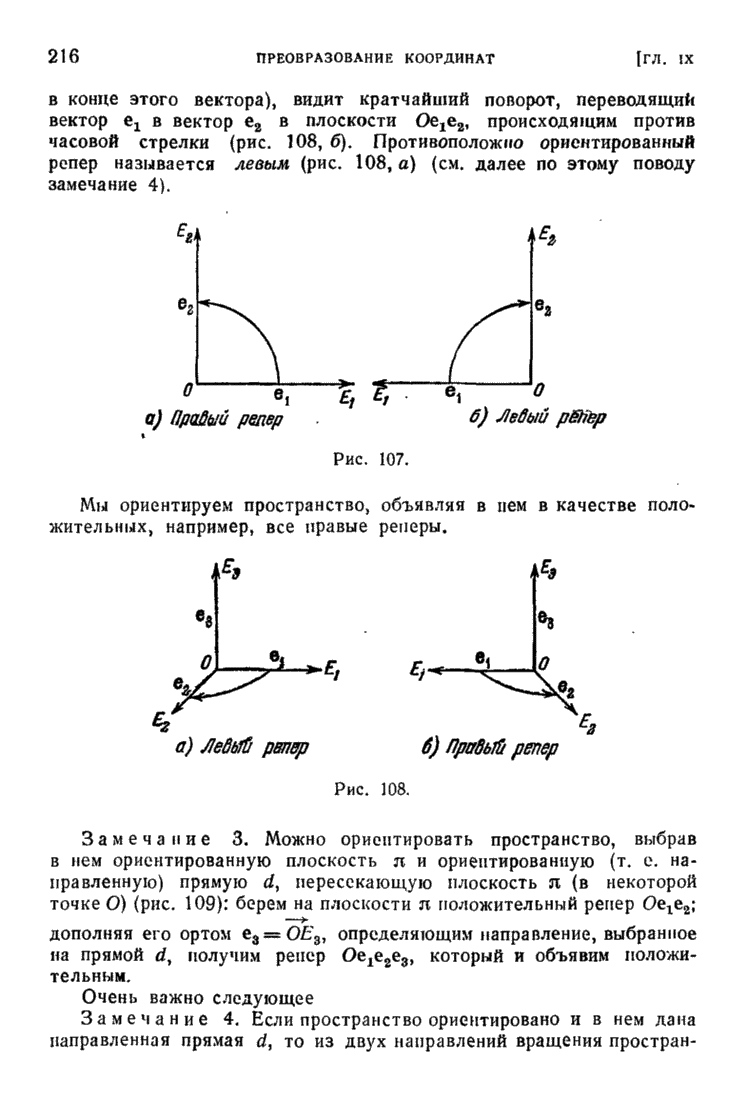
«Физическое», если так можно выразиться, осмысливание двух классов реперов на плоскости общеизвестно: назовем правым такой репер  , где кратчайший поворот, переводящий орт
, где кратчайший поворот, переводящий орт  в орт
в орт  , происходит против часовой стрелки (рис. 107, а), т. е. где
, происходит против часовой стрелки (рис. 107, а), т. е. где  расположены, как большой и указательный пальцы правой руки, если смотреть на ее ладонь.
расположены, как большой и указательный пальцы правой руки, если смотреть на ее ладонь.
Левым назовем противоположно ориентированный репер (рис. 107, б) (в нем аналогичный поворот происходит по часовой стрелке).
В пространстве репер  называется правым, если наблюдатель, стоящий вдоль вектора
называется правым, если наблюдатель, стоящий вдоль вектора  (ногами — в начале, головой — в конце этого вектора), видит кратчайший поворот, переводящий вектор
(ногами — в начале, головой — в конце этого вектора), видит кратчайший поворот, переводящий вектор  в вектор
в вектор  в плоскости
в плоскости  , происходящим против часовой стрелки (рис. 108, б). Противоположно ориентированный репер называется левым (рис. 108, а) (см. далее по этому поводу замечание 4).
, происходящим против часовой стрелки (рис. 108, б). Противоположно ориентированный репер называется левым (рис. 108, а) (см. далее по этому поводу замечание 4).

Рис. 107.
Мы ориентируем пространство, объявляя в нем в качестве положительных, например, все правые реперы.

Рис. 108.
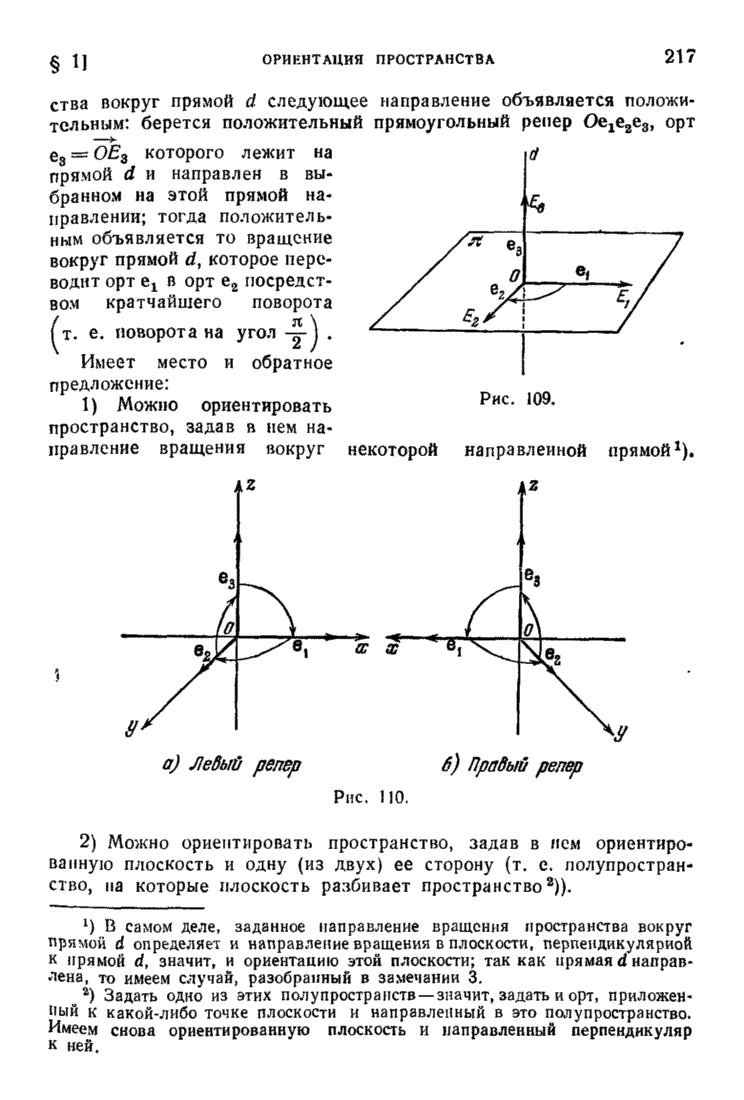
Замечание 3. Можно ориентировать пространство, выбрав в нем ориентированную плоскость  и ориентированную (т. е. направленную) прямую d, пересекающую плоскость 31 (в некоторой точке О) (рис. 109): берем на плоскости
и ориентированную (т. е. направленную) прямую d, пересекающую плоскость 31 (в некоторой точке О) (рис. 109): берем на плоскости  положительный репер
положительный репер  ; дополняя его ортом
; дополняя его ортом  , определяющим направление, выбранное на прямой d, получим репер
, определяющим направление, выбранное на прямой d, получим репер  , который и объявим положительным.
, который и объявим положительным.
Очень важно следующее
Замечание 4.
Если пространство ориентировано и в нем дана направленная прямая d, то из двух направлений вращения пространства вокруг прямой d следующее направление объявляется положительным: берется положительный прямоугольный репер  , орт
, орт  которого лежит на прямой d и направлен в выбранном на этой прямой направлении; тогда положительным объявляется то вращение вокруг прямой d, которое переводит орт
которого лежит на прямой d и направлен в выбранном на этой прямой направлении; тогда положительным объявляется то вращение вокруг прямой d, которое переводит орт  в орт
в орт  посредством кратчайшего поворота т. е. поворота на угол
посредством кратчайшего поворота т. е. поворота на угол  .
.
Имеет место и обратное предложение:
1) Можно ориентировать пространство, задав в нем направление вращения вокруг некоторой направленной прямой.

Рис. 109.

Рис. 110.
2) Можно ориентировать пространство, задав в нем ориентированную плоскость и одну (из двух) ее сторону (т. е. полупространство, на которые плоскость разбивает пространство).
Замечание 5. Пусть в пространстве дан прямоугольный репер  этим задана и ориентация пространства. Тогда определяется и соответствующее этой ориентации («положительное») направление вращения вокруг каждой из координатных осей; это направления кратчайших вращений на угол —
этим задана и ориентация пространства. Тогда определяется и соответствующее этой ориентации («положительное») направление вращения вокруг каждой из координатных осей; это направления кратчайших вращений на угол —  осей
осей  , (рис. 110) (несущих соответственно орты
, (рис. 110) (несущих соответственно орты  ), переводящих
), переводящих

Если выбранный репер правый, то каждое из названных вращений есть вращение против часовой стрелки (для зрителя, расположенного вдоль соответствующей оси ногами в начале, головой в конце орта этой оси).
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ГЛАВА I. КООРДИНАТЫ НА ПРЯМОЙ
- § 1. Отношение отрезков
- § 2. Направленные отрезки (векторы); их отношение
- § 3. Ось. Алгебраическое значение (координата) вектора на оси
- § 4. Сложение векторов на прямой
- § 5. Система координат на прямой
- § 6. Деление отрезка в данном отношении
- § 7. Пропорциональность пар чисел
- § 8. Бесконечно удаленная точка прямой
- § 9. Пропорциональность двух последовательностей, состоящих из и чисел
- ГЛАВА II. ВЕКТОРЫ
- § 1. Равенство векторов. Свободный вектор
- § 2. Линейные операции над векторами (сложение и умножение на число)
- § 3. Проекции
- § 4. Коллинеарные и компланарные векторы; координаты вектора относительного данного базиса
- § 5. Линейная зависимость и независимость векторов
- § 6. Геометрический смысл линейной зависимости векторов
- § 7. Векторные многообразия
- ГЛАВА III. АФФИННАЯ СИСТЕМА КООРДИНАТ НА ПЛОСКОСТИ И В ПРОСТРАНСТВЕ
- § 1. Определение аффинной системы координат
- § 2. Перенос начала координат
- § 3. Деление отрезка в данном отношении
- ГЛАВА IV. ПРЯМОУГОЛЬНАЯ СИСТЕМА КООРДИНАТ. ПОЛЯРНЫЕ КООРДИНАТЫ
- § 1. Прямоугольная система координат на плоскости и в пространстве. Расстояние между двумя точками. Уравнение окружности и сферы
- § 2. Скалярное произведение векторов; угол между двумя векторами
- § 3. Угол от одного вектора до другого на плоскости
- § 4. Полярная система координат на плоскости
- § 5. Полярная система координат в пространстве
- ГЛАВА V. ПРЯМАЯ ЛИНИЯ
- § 1. Направляющий вектор и угловой коэффициент прямой (в произвольной аффинной системе координат). Уравнение прямой
- § 2. Расположение двух прямых на плоскости
- § 3. Частные случаи общего уравнения прямой
- § 4. Векторная и параметрическая форма уравнения прямой. Уравнение прямой, проходящей через две заданные точки
- § 5. Задача: когда прямая Ax+By+C=0 на плоскости проходит через точку пересечения двух заданных прямых A1x+B1y+C1=0 и A2x+B2y+C2=0?
- § 6. Две полуплоскости, определяемые данной прямой на плоскости
- § 7. Прямая на плоскости в прямоугольной системе координат. Нормальное уравнение прямой на плоскости
- § 8. Расстояние от точки до прямой (на плоскости)
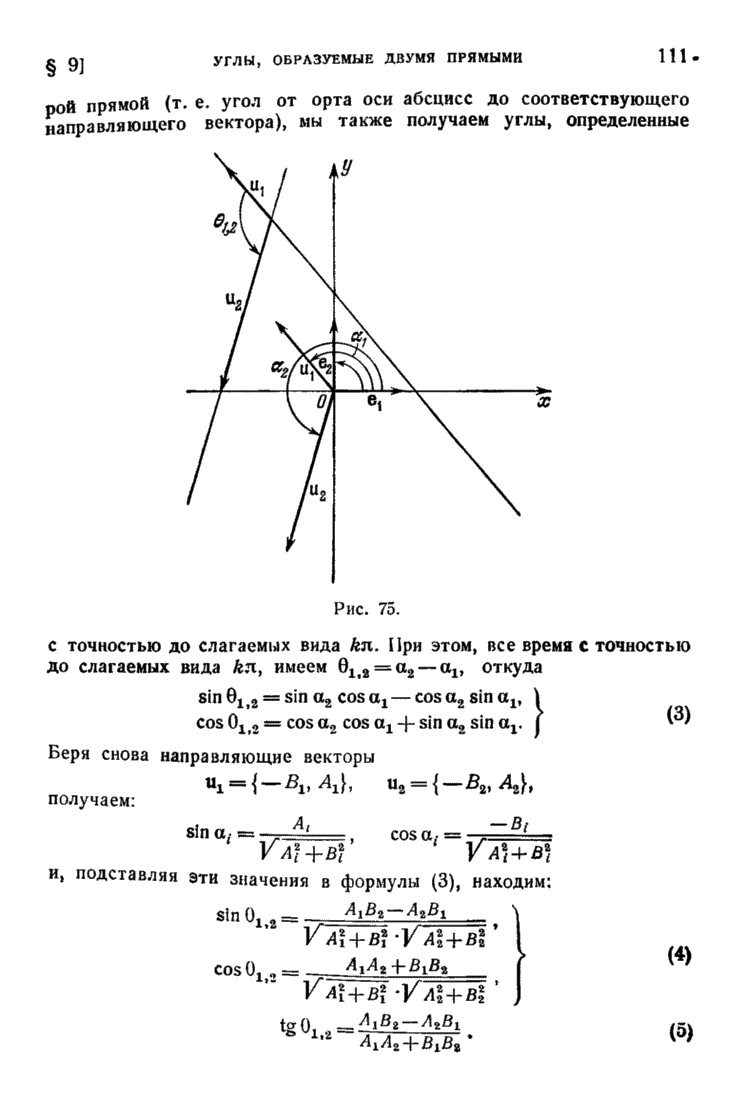
- § 9. Углы, образуемые двумя прямыми на плоскости
- § 10. Прямая в пространстве, снабженном прямоугольной системой координат
- ГЛАВА VI. ПАРАБОЛА. ЭЛЛИПС. ГИПЕРБОЛА
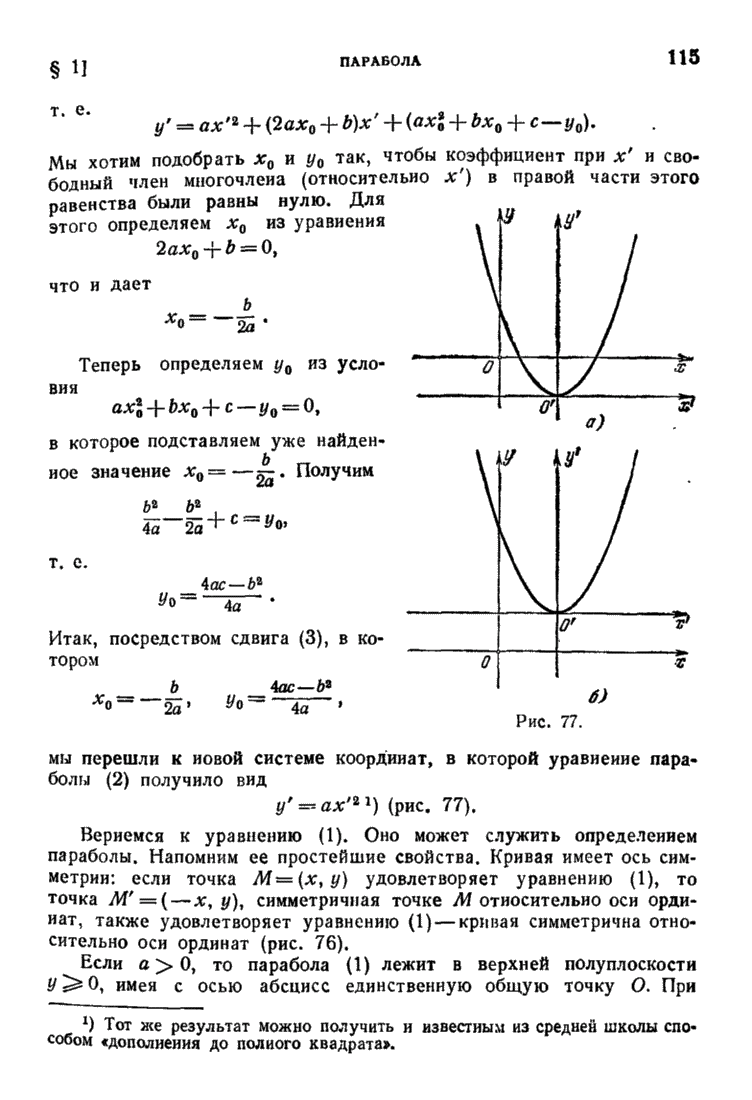
- § 1. Парабола
- § 2. Определение и каноническое уравнение эллипса
- § 3. Параметрическая запись уравнения эллипса; построение эллипса по точкам. Эллипс как результат сжатия окружности к одному из ее диаметров
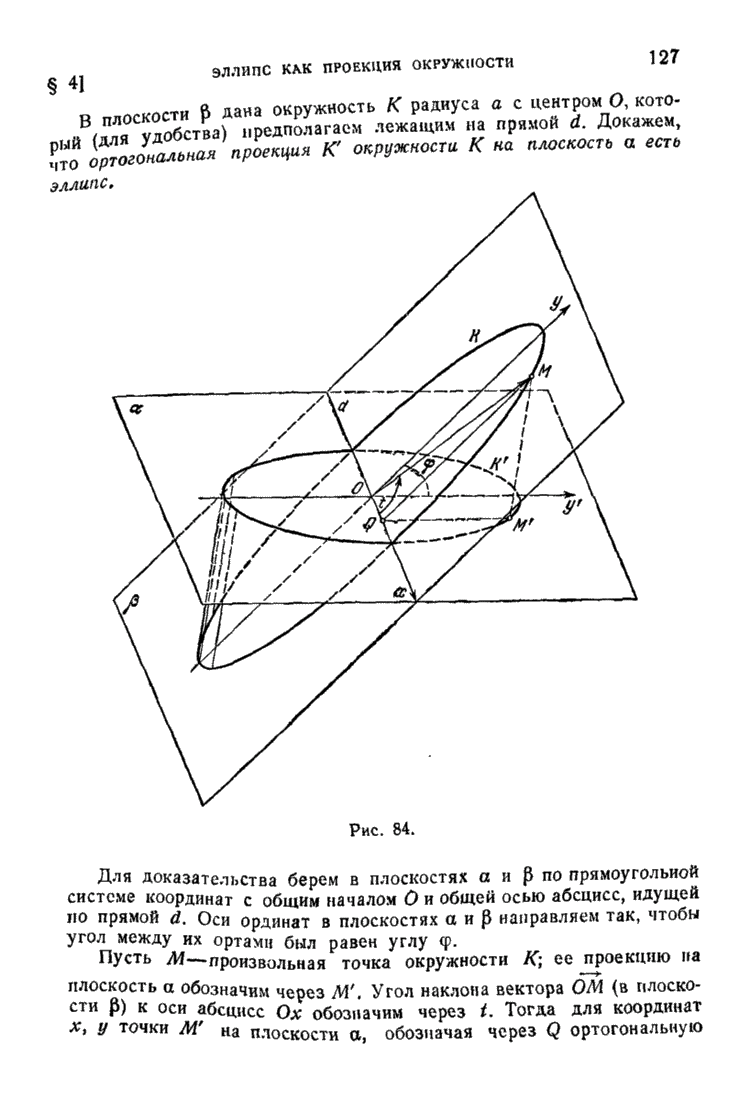
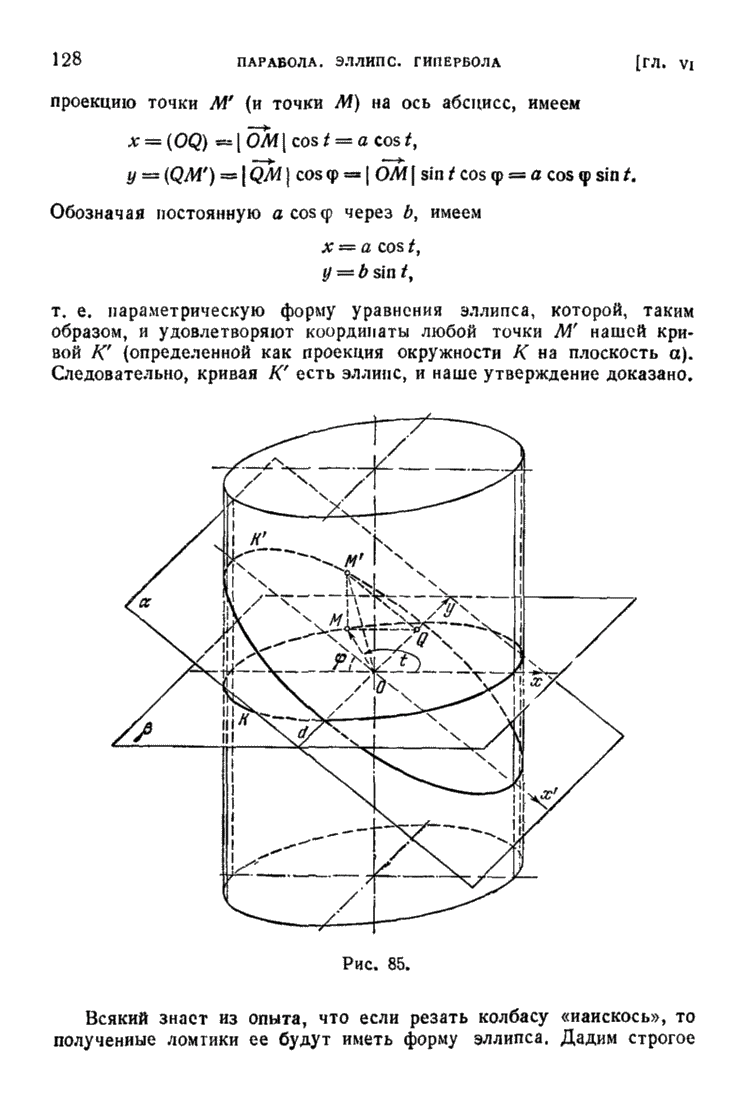
- § 4. Эллипс как проекция окружности и как сечение круглого цилиндра
- § 5. Определение гиперболы. Каноническое уравнение гиперболы
- § 6. Основной прямоугольник и асимптоты гиперболы
- § 7. Директрисы эллипса и гиперболы
- § 8. Фокальный параметр эллипса и гиперболы. Уравнение при вершине
- § 9. Уравнение эллипса, гиперболы и параболы в полярных координатах
- ГЛАВА VII. ДЕТЕРМИНАНТЫ
- § 1. Плошадь ориентированного параллелограмма и треугольника
- § 2. Детерминант второго порядка. Матрицы
- § 4. Разложение детерминанта третьего порядка по элементам какой-либо строки. Приложение к системе трех уравнений с тремя неизвестными (правило Крамера)
- § 5. Системы трех уравнений с тремя неизвестными с детерминантом системы, равным нулю
- § 6. Арифметическое n-мерное векторное многообразие (пространство). Общее определение матрицы. Детерминанты любого порядка
- § 7. Разложение детерминанта n-го порядка по элементам данной строки (данного столбца)
- § 8. Правило Крамера для решений систем и уравнений с n неизвестными
- § 9. Общее определение миноров матрицы. Теорема Лапласа
- § 10. Умножение детерминантов
- § 11. Детерминант n-го порядка как линейная нечетная нормированная функция от n векторов
- ГЛАВА VIII. ПРЕОБРАЗОВАНИЕ КООРДИНАТ. МАТРИЦЫ
- § 1. Переход от одной аффинной системы координат к другой
- § 2. Перемножение матриц. Новое определение обратной матрицы
- § 3. Переход от одной прямоугольной системы координат к другой
- § 4. Действия над матрицами в общем случае
- ГЛАВА IX. ПРЕОБРАЗОВАНИЕ КООРДИНАТ (ПРОДОЛЖЕНИЕ): ОРИЕНТАЦИЯ ПЛОСКОСТИ И ПРОСТРАНСТВА; УГЛЫ ЭЙЛЕРА; ОБЪЕМ ОРИЕНТИРОВАННОГО ПАРАЛЛЕЛЕПИПЕДА; ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ ДВУХ ВЕКТОРОВ
- § 1. Ориентация пространства (плоскости)
- § 2. Углы Эйлера
- § 3. Объем ориентированного параллелепипеда
- § 4. Векторное произведение двух векторов
- ГЛАВА X. ПЛОСКОСТЬ И ПРЯМАЯ В ПРОСТРАНСТВЕ
- § 1. Уравнения плоскости
- § 2. Множество решений системы двух однородных линейных уравнений с тремя неизвестными
- § 3. Взаимное расположение двух плоскостей
- § 4. Прямая как пересечение двух плоскостей
- § 5. Пучок плоскостей
- § 6. Взаимное расположение двух прямых в пространстве
- § 7. О двух полупространствах, определяемых данной плоскостью
- § 8. Плоскость в прямоугольной системе координат; нормальное уравнение плоскости; расстояние от точки до плоскости
- § 9. Угол между прямой и плоскостью; угол между двумя плоскостями
- § 10. Две задачи
- ГЛАВА XI. ДВИЖЕНИЯ И АФФИННЫЕ ПРЕОБРАЗОВАНИЯ
- § 1. Определение движений и аффинных преобразований
- § 2. Преобразование векторов при аффинном преобразовании плоскости и пространства. Основные свойства аффинных преобразований
- § 3. Аналитическое выражение аффинных преобразований
- § 4. Сохранение отношений площадей и объемов при аффинных преобразованиях
- § 5. Получение собственных аффинных преобразований посредством деформации тождественного преобразования. Следствия
- § 6. Движения как изометрические преобразования
- § 7. Преобразования подобия
- § 8. Классификация движений прямой и плоскости
- ГЛАВА XII. ВЕКТОРНЫЕ ПРОСТРАНСТВА (МНОГООБРАЗИЯ) ЛЮБОГО КОНЕЧНОГО ЧИСЛА ИЗМЕРЕНИЙ. СИСТЕМЫ ЛИНЕЙНЫХ ОДНОРОДНЫХ УРАВНЕНИЙ
- § 1. Определение векторного пространства
- § 2. Размерность. Базис. Координаты
- § 3. Теорема об изоморфизме между любыми двумя векторными пространствами одной и той же конечной размерности n
- § 4. Подпространства векторного пространства. Дальнейшие теоремы о линейной зависимости векторов и о базисе векторного пространства
- § 5. Алгебраическая (в частности, прямая) сумма подпространств
- § 6. Линейные отображения векторных пространств
- § 7. Теорема о ранге матрицы
- § 8. Системы линейных однородных уравнения
- ГЛАВА XIII. ЛИНЕЙНЫЕ, БИЛИНЕЙНЫЕ И КВАДРАТИЧНЫЕ ФУНКЦИИ НА ВЕКТОРНЫХ ПРОСТРАНСТВАХ
- § 1. Линейные функции
- § 2. Билинейные функции и билинейные формы
- § 3. Матрица билинейной и квадратичной формы и ее преобразование при переходе к новому базису (при преобразовании переменных)
- § 4. Ранг билинейной и квадратичной формы (билинейной и квадратичной функции)
- § 5. Существование канонического базиса для всякой квадратичной и всякой билинейной функции («приведение квадратичных форм к каноническому виду»)
- ГЛАВА XIV. ТОЧЕЧНО-ВЕКТОРНОЕ АФФИННОЕ n-МЕРНОЕ ПРОСТРАНСТВО
- § 1. Определение n-мерного аффинного пространства
- § 2. Системы координат. Арифметическое пространство. Изоморфизм всех n-мерных пространств между собою
- § 3. r-мерные плоскости n-мерного аффинного пространства; r-мерные параллелепипеды
- § 4. Геометрически независимые системы точек. Барицентрические координаты. Симплексы
- § 5. Системы линейных уравнений
- § 6. Аффинные преобразования n-мерного аффинного пространства
- ГЛАВА XV. АЛГЕБРАИЧЕСКИЕ ЛИНИИ И ПОВЕРХНОСТИ. КОМПЛЕКСНАЯ ПЛОСКОСТЬ И КОМПЛЕКСНОЕ ПРОСТРАНСТВО
- § 1. Определение алгебраических линий и поверхностей
- § 2. Преобразование многочлена второй степени при преобразовании координат
- § 3. Аффинная эквивалентность линий и поверхностей
- § 4. Комплексная плоскость
- § 5. Прямая линия на комплексной плоскости
- § 6. Замечание о действительных и мнимых линиях
- § 7. Комплексное пространство
- § 8. Распадающиеся линии и поверхности. Цилиндрические и конические поверхности. Поверхности вращения
- § 9. Несколько заключительных замечаний о линиях и поверхностях
- ГЛАВА XVI. Различные виды кривых второго порядка
- § 1. О линиях, определяемых уравнениями второй степени с двумя неизвестными
- § 2. Инварианты многочлена второй степени
- § 3. Центральный случай
- § 4. Параболический случай
- § 5. Аффинная классификация кривых второго порядка
- § 6. Несколько заключительных замечаний
- ГЛАВА XVII. ОБЩАЯ ТЕОРИЯ КРИВЫХ ВТОРОГО ПОРЯДКА
- § 1. Пересечение алгебраической кривой с прямой. Асимптотические направления и асимптоты алгебраической кривой
- § 2. Теорема единственности для кривых второго порядка. Пучок кривых второго порядка
- § 3. Асимптотические направления кривых второго порядка
- § 4. Пересечение кривой второго порядка с прямой иеасимптотического направления. Касательные
- § 5. Пересечение кривой второго порядка с прямой асимптотического направления. Геометрическая характеристика асимптотических и неасимптотических направлений
- § 6. Центр кривой второго порядка
- § 7. Диаметры кривой второго порядка
- § 8. Взаимно сопряженные векторы (направления). Диаметры и касательные
- § 9. Вид уравнения кривой, если оси координат имеют сопряженные направления
- § 10. Второе доказательство теоремы единственности. О полноте системы ортогональных инвариантов
- § 11. Оси симметрии и главные направления кривой второго порядка
- § 12. Основная теорема об аффинных преобразованиях
- ГЛАВА XVIII. КРАТКОЕ ОПИСАНИЕ РАЗЛИЧНЫХ ВИДОВ ПОВЕРХНОСТЕЙ ВТОРОГО ПОРЯДКА
- § 1. Распадающиеся поверхности
- § 2. Цилиндрические поверхности
- § 3. Конусы второго порядка
- § 4. Эллипсоиды и гиперболоиды
- § 5. Параболоиды
- § 6. Прямолинейные образующие
- ГЛАВА XIX. ОБЩАЯ ТЕОРИЯ ПОВЕРХНОСТЕЙ ВТОРОГО ПОРЯДКА. I (ПЕРЕСЕЧЕНИЕ С ПЛОСКОСТЬЮ И С ПРЯМОЙ; АСИМПТОТИЧЕСКИЕ НАПРАВЛЕНИЯ; КАСАТЕЛЬНАЯ ПЛОСКОСТЬ; ЦЕНТР)
- § 1. Ранг и детерминант малой и большой матрицы многочлена второй степени
- § 2. Пересечение поверхности второго порядка с плоскостью
- § 3. Пересечение поверхности второго порядка с прямой. Асимптотические направления. Касательные прямые и касательная плоскость. Особые точки поверхности второго порядка
- § 4. Асимптотические направления, конус асимптотических направлений, прямолинейные образующие поверхностей второго порядка
- § 5. Центр поверхности второго порядка
- ГЛАВА XX. ОБЩАЯ ТЕОРИЯ ПОВЕРХНОСТЕЙ ВТОРОГО ПОРЯДКА. II (ДИАМЕТРАЛЬНЫЕ ПЛОСКОСТИ; ОСОБЫЕ И ГЛАВНЫЕ НАПРАВЛЕНИЯ; АФФИННАЯ КЛАССИФИКАЦИЯ)
- § 1. Диаметральные плоскости. Особые направления
- § 2. Диаметральные плоскости поверхностей различных видов
- § 3. Сопряженные направления
- § 4. Уравнение поверхности второго порядка относительно координатной системы с сопряженными направлениями осей
- § 5. Теорема единственности
- § 6. Главные направления
- § 7. Приведение к каноническому виду уравнения поверхности второго порядка
- § 8. Аффинная классификация поверхностей второго порядка
- ГЛАВА XXI. ПРОЕКТИВНАЯ ПЛОСКОСТЬ
- § 1. Перспективное соответствие между плоскостью и связкой
- § 2. Однородные координаты точек на плоскости и лучел в связке
- § 3. Координаты прямой; арифметическая проективная плоскость; общее определение проективной плоскости
- § 4. Принцип двойственности для проективной плоскости
- § 5. Проективная система координат в связке и на проективной плоскости
- § 6. Проективные преобразования и отображения проективной плоскости
- § 7. Проективные координаты на прямой. Проективные отображения прямой
- § 8. Двойное отношение
- ГЛАВА XXII. КРИВЫЕ ВТОРОГО ПОРЯДКА НА ПРОЕКТИВНОЙ ПЛОСКОСТИ
- § 1. Определение. Теорема единственности
- § 2. Пересечение кривой второго порядка с прямой. Касательные; асимптоты
- § 3. Пучок кривых второго порядка. Второе доказательство теоремы единственности. Теорема Паскаля. Теорема Штейнера
- § 4. Поляры и полюсы
- § 5. Коррелятивное, в частности полярное, соответствие. Тангенциальное уравнение кривой
- § 6. Диаметры как поляры несобственных точек
- § 7. Автополярный треугольник
- § 8. Проективная классификация кривых второго порядка
- ГЛАВА XXIII. НАЧАЛЬНЫЕ СВЕДЕНИЯ ИЗ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ ПРОЕКТИВНОГО ПРОСТРАНСТВА
- § 1. Проективное пространство; его плоскости и прямые
- § 2. Проективные координаты. Проективные преобразования.
- § 3. Понятие об n-мерном проективном пространстве
- § 4. Поверхности второго порядка в проективном пространстве. Теорема единственности
- § 5. Пересечение поверхности второго порядка с плоскостью и с прямой. Касательные прямые. Касательная плоскость. Прямолинейные образующие
- § 6. Полюсы и полярные плоскости
- § 7. Проективная классификация поверхностей второго порядка
- § 8. Распределение по проективным классам поверхностей различных аффинных классов. Проективно-аффинная классификация поверхностей второго порядка
- ГЛАВА XXIV. ЕВКЛИДОВО n-МЕРНОЕ ПРОСТРАНСТВО
- § 1. Введение. Ортогональные матрицы
- § 2. Положительно определенные симметричные билинейные функции в векторном пространстве
- § 3. Определение евклидовых пространств и простейших относящихся к ним понятий
- § 4. Неравенство Коши—Буняковского и его следствия. Углы
- § 5. Подпространства евклидовых пространств. Ортогональное дополнение к данному подпространству
- ГЛАВА XXV. ЛИНЕЙНЫЕ ОПЕРАТОРЫ, БИЛИНЕЙНЫЕ И КВАДРАТИЧНЫЕ ФУНКЦИИ В ЕВКЛИДОВЫХ ПРОСТРАНСТВАХ. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
- § 1. Инвариантные подпространства и собственные векторы линейного оператора в любом векторном пространстве
- § 2. Ортогональные преобразования n-мерного евклидова пространства
- § 3. Движения трехмерного евклидова пространства
- § 4. Преобразования подобия. Дальнейшие проблемы
- § 5. Самосопряженные операторы
- § 6. Теорема о структуре произвольного линейного преобразования евклидова пространства
- § 7. Билинейные и квадратичные формы в евклидовых пространствах
- § 8. (n-1)-мерные многообразия (поверхности) второго поряд] в -мерном аффинном и евклидовом пространствах
- ПРИБАВЛЕНИЕ. ПЕРЕСТАНОВКИ, МНОЖЕСТВА И ИХ ОТОБРАЖЕНИЯ; ГРУППЫ
- § 1. Перестановки
- § 2. Множества
- § 3. Отображения или функции
- § 4. Разбиение множества на подмножества. Отношение эквивалентности
- § 5. Определение группы
- § 6. Простейшие теоремы о группах
- § 7. Эквивалентность подмножеств данного множества по отношению к дайной группе его преобразований
- ЗАДАЧИ
- Задачи к главе IV
- Задачи к главе V
- Задачи к главе VI
- Задачи к главе VIII
- Задачи к главе IX
- Задачи к главе X
- Задачи к главе XI
- Задачи к главе XII
- Задачи к главе XIII
- Задачи к главе XIV
- Задачи к главе XV
- Задачи к главам XVI и XVII
- Задачи к главе XVIII
- Задачи к главам XIX и XX
- Задачи к главе XXI
- Задачи к главе XXII