| << Предыдущий параграф | Следующий параграф >> |
Пред.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
333
334
335
336
337
338
339
340
341
342
343
344
345
346
347
348
349
350
351
352
353
354
355
356
357
358
359
360
361
362
363
364
365
366
367
368
369
370
371
372
373
374
375
376
377
378
379
380
381
382
383
384
385
386
387
388
389
390
391
392
393
394
395
396
397
398
399
400
401
402
403
404
405
406
407
408
409
410
411
412
413
414
415
416
417
418
419
420
421
422
423
424
425
426
427
428
429
430
431
432
433
434
435
436
437
438
439
440
441
442
443
444
445
446
447
448
449
450
451
452
453
454
455
456
457
458
459
460
461
462
463
464
465
466
467
468
469
470
471
472
473
474
475
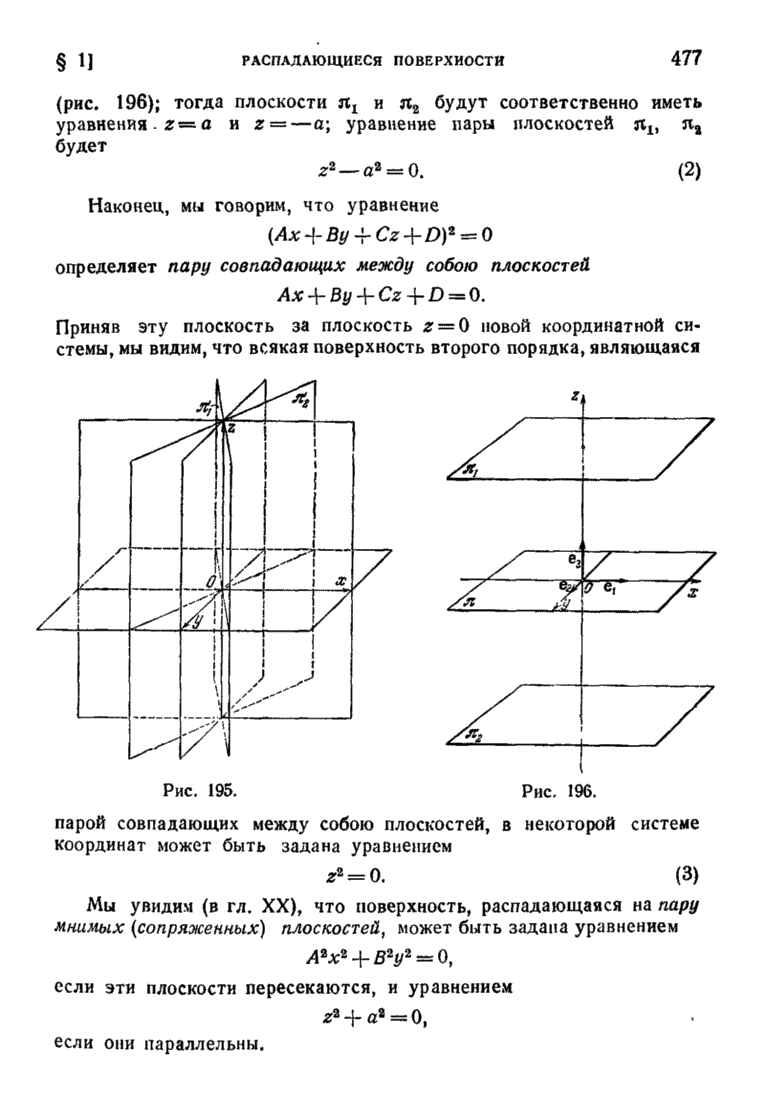
476
477
478
479
480
481
482
483
484
485
486
487
488
489
490
491
492
493
494
495
496
497
498
499
500
501
502
503
504
505
506
507
508
509
510
511
512
513
514
515
516
517
518
519
520
521
522
523
524
525
526
527
528
529
530
531
532
533
534
535
536
537
538
539
540
541
542
543
544
545
546
547
548
549
550
551
552
553
554
555
556
557
558
559
560
561
562
563
564
565
566
567
568
569
570
571
572
573
574
575
576
577
578
579
580
581
582
583
584
585
586
587
588
589
590
591
592
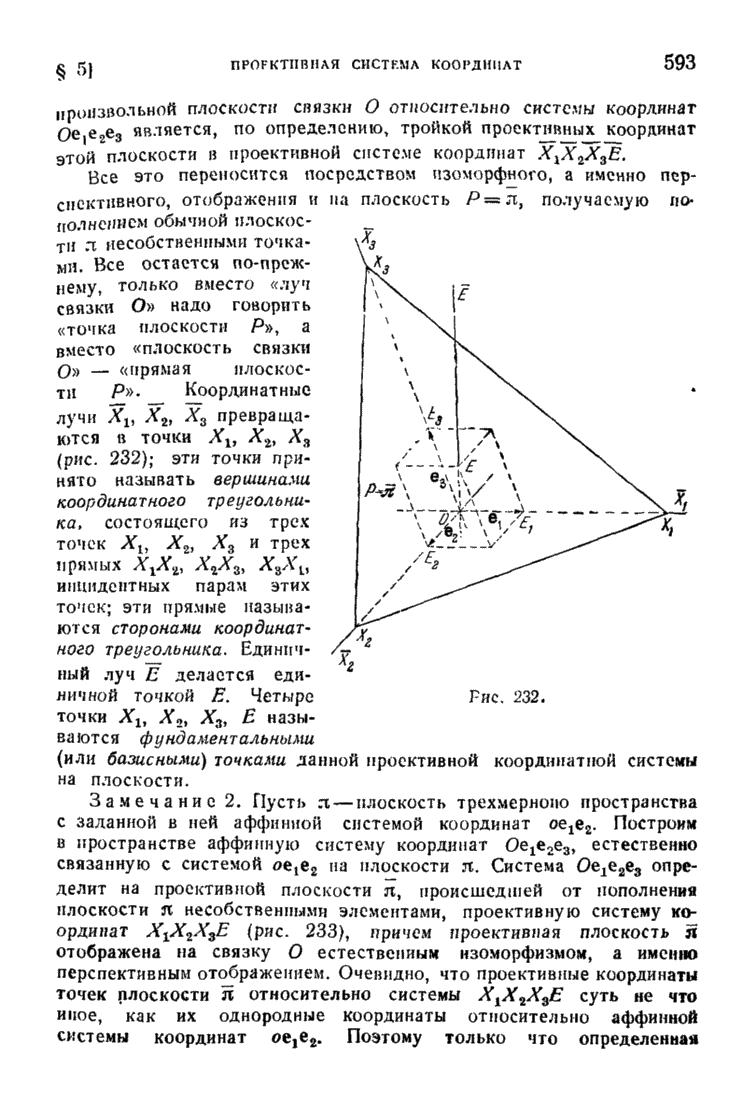
593
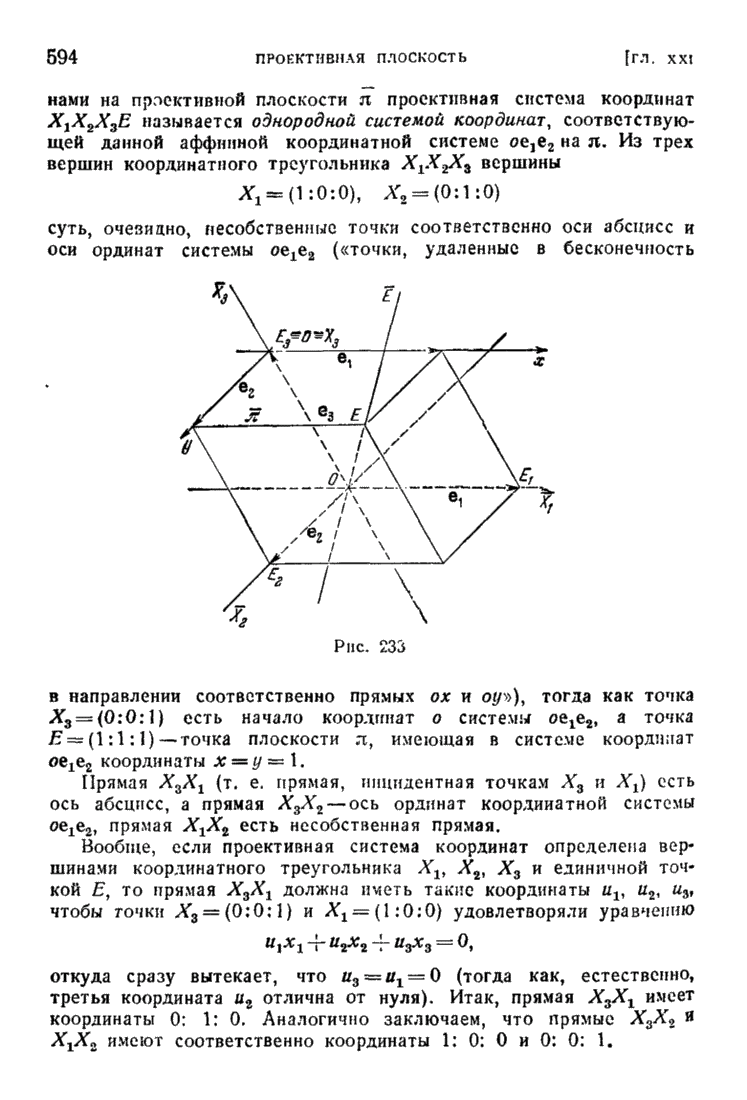
594
595
596
597
598
599
600
601
602
603
604
605
606
607
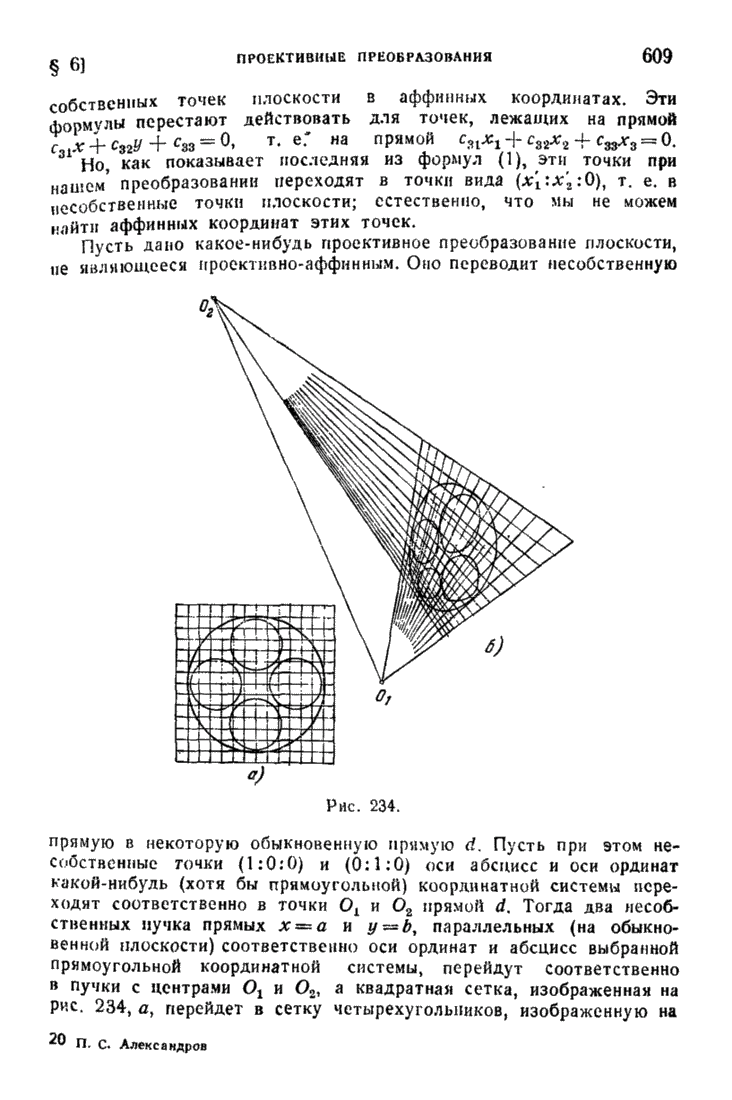
608
609
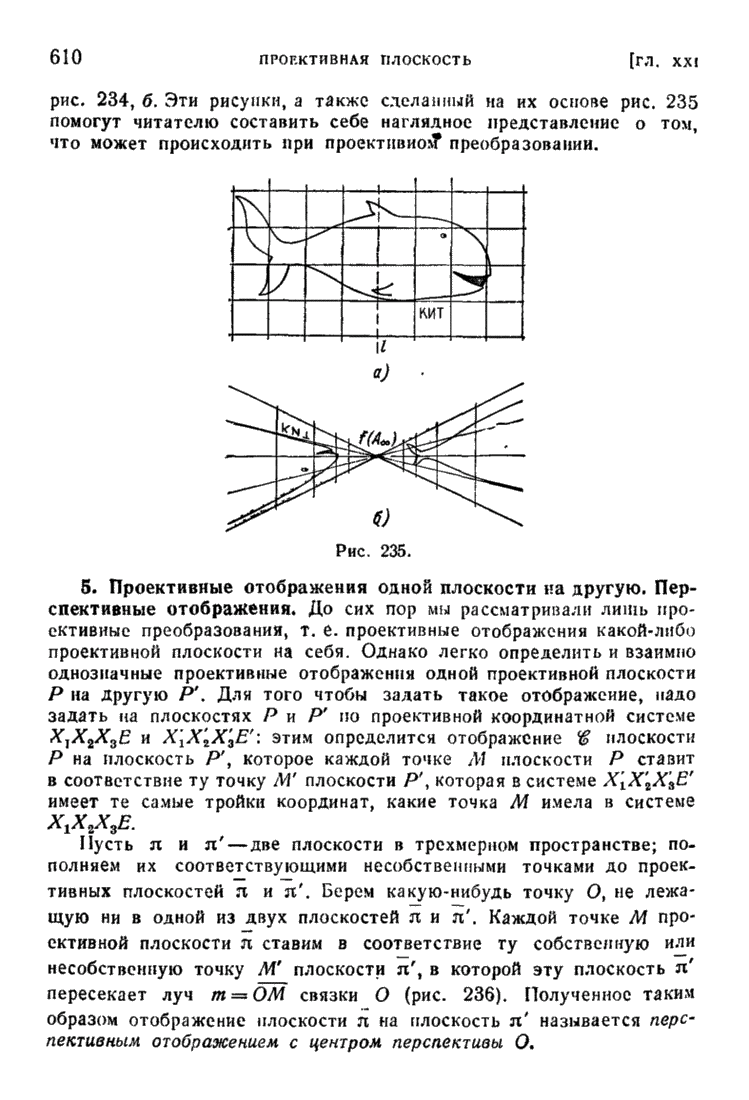
610
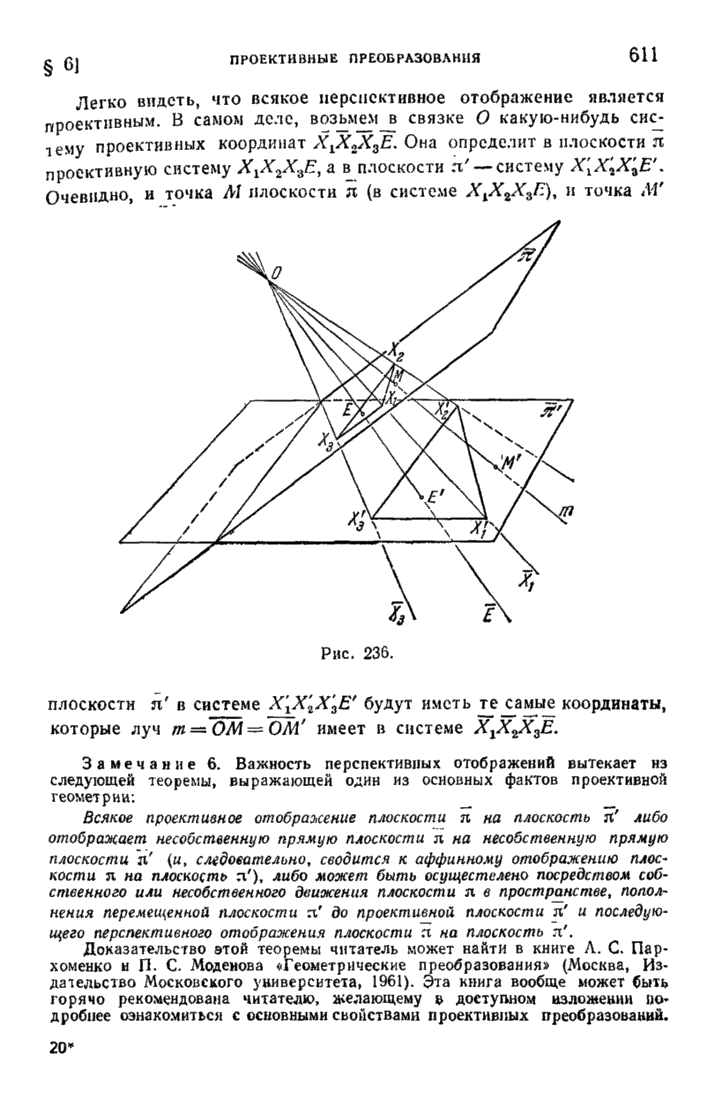
611
612
613
614
615
616
617
618
619
620
621
622
623
624
625
626
627
628
629
630
631
632
633
634
635
636
637
638
639
640
641
642
643
644
645
646
647
648
649
650
651
652
653
654
655
656
657
658
659
660
661
662
663
664
665
666
667
668
669
670
671
672
673
674
675
676
677
678
679
680
681
682
683
684
685
686
687
688
689
690
691
692
693
694
695
696
697
698
699
700
701
702
703
704
705
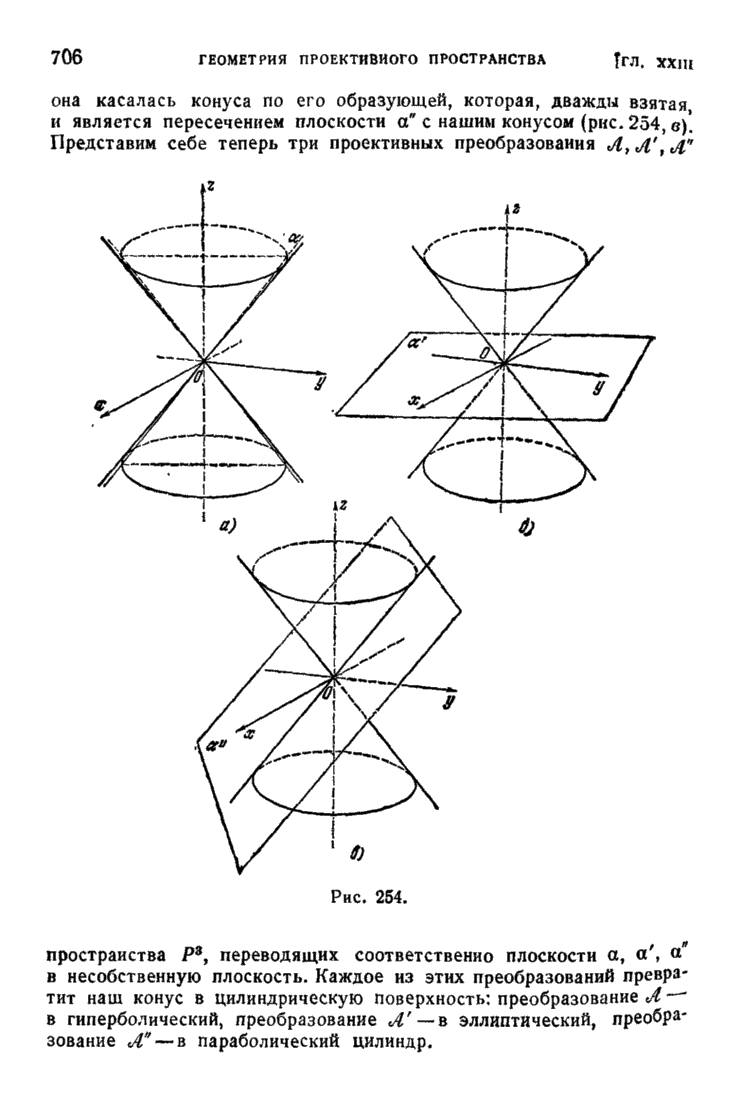
706
707
708
709
710
711
712
713
714
715
716
717
718
719
720
721
722
723
724
725
726
727
728
729
730
731
732
733
734
735
736
737
738
739
740
741
742
743
744
745
746
747
748
749
750
751
752
753
754
755
756
757
758
759
760
761
762
763
764
765
766
767
768
769
770
771
772
773
774
775
776
777
778
779
780
781
782
783
784
785
786
787
788
789
790
791
792
793
794
795
796
797
798
799
800
801
802
803
804
805
806
807
808
809
810
811
812
813
814
815
816
817
818
819
820
821
822
823
824
825
826
827
828
829
830
831
832
833
834
835
836
837
838
839
840
841
842
843
844
845
846
847
848
849
850
851
852
853
854
855
856
857
858
859
860
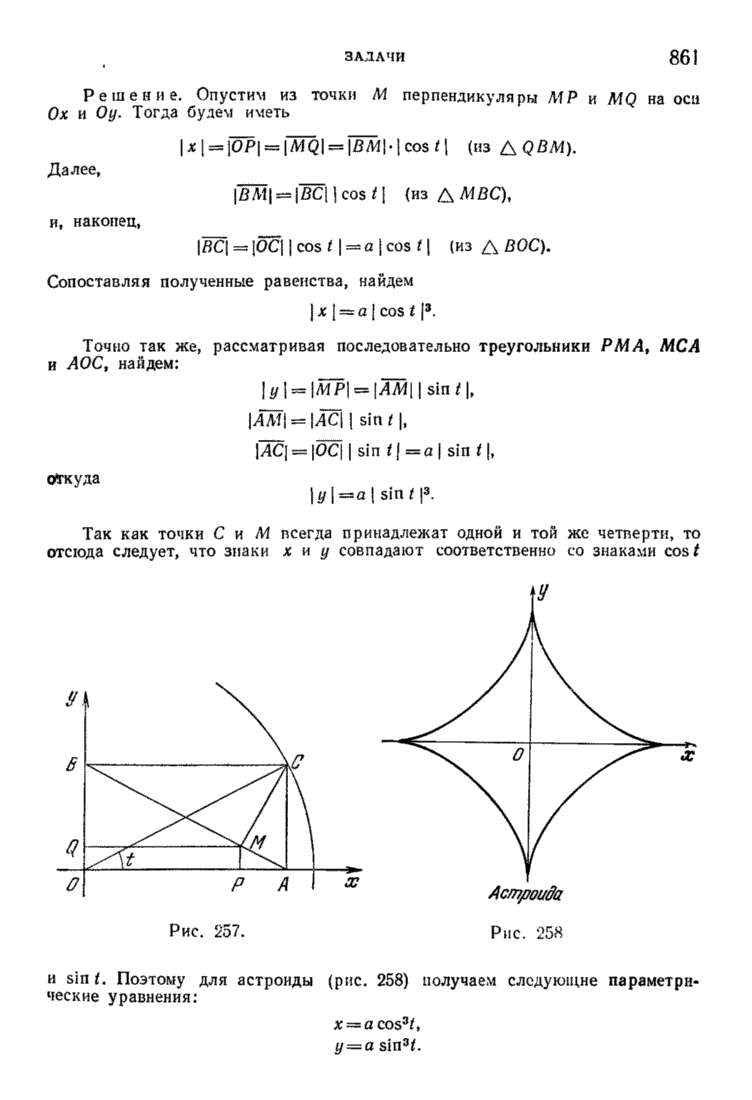
861
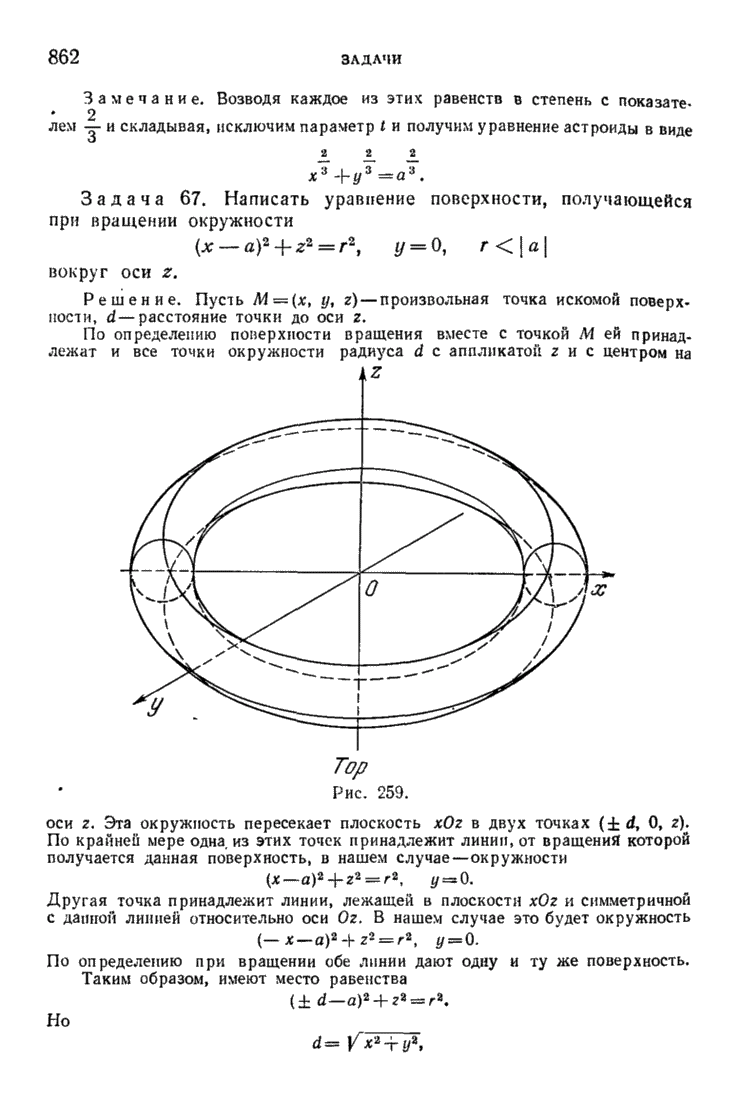
862
863
864
865
866
867
868
869
870
871
872
873
874
875
876
877
878
879
880
881
882
883
884
885
886
887
888
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 4. Полярная система координат на плоскости
1. Определение полярных координат. Понятие угла наклона вектора к данной оси находит постоянные применения в геометрии плоскости. Одним из важнейших среди них является определение полярных координат.
Для определения системы полярных координат на плоскости надо задать:
1° Масштаб (т. е. единицу измерения длины).
2° Направление вращения в плоскости, считаемое положительным.
3° Точку О (называемую «началом» или полюсом системы координат).
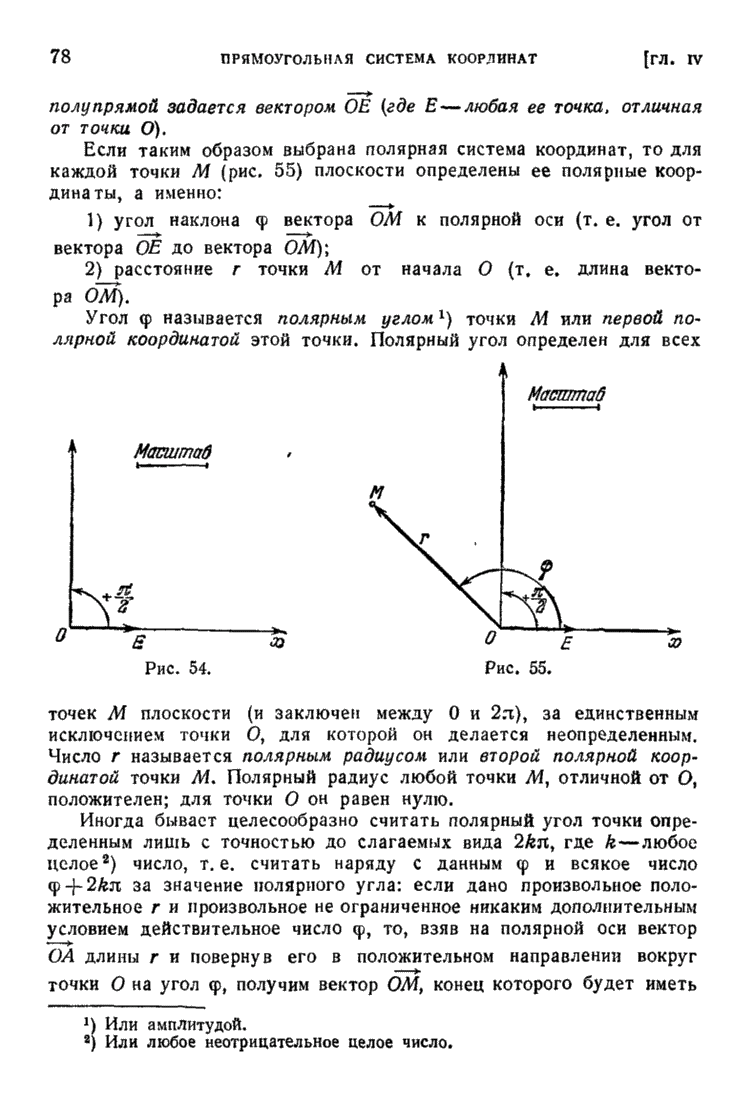
4° Полупрямую  , исходящую из точки О (рис. 54) (эта полупрямая называется полярной осью).
, исходящую из точки О (рис. 54) (эта полупрямая называется полярной осью).
Положительное направление на полупрямой задается вектором ОЕ (где Е — любая ее точка, отличная от точки О).
Если таким образом выбрана полярная система координат, то для каждой точки М (рис. 55) плоскости определены ее полярные координаты, а именно:
1) угол наклона  вектора ОМ к полярной оси (т. е. угол от вектора ОЕ до вектора СМ);
вектора ОМ к полярной оси (т. е. угол от вектора ОЕ до вектора СМ);
2) расстояние  точки М от начала О (т. е. длина вектора ОМ).
точки М от начала О (т. е. длина вектора ОМ).
Угол  называется полярным углом точки М или первой полярной координатой этой точки. Полярный угол определен для всех
называется полярным углом точки М или первой полярной координатой этой точки. Полярный угол определен для всех

Рис. 54.

Рис. 55.
точек М плоскости (и заключен между 0 и  ), за единственным исключением точки О, для которой он делается неопределенным. Число
), за единственным исключением точки О, для которой он делается неопределенным. Число  называется полярным радиусом или второй полярной координатой точки М. Полярный радиус любой точки М, отличной от О, положителен; для точки О он равен нулю.
называется полярным радиусом или второй полярной координатой точки М. Полярный радиус любой точки М, отличной от О, положителен; для точки О он равен нулю.
Иногда бывает целесообразно считать полярный угол точки определенным лишь с точностью до слагаемых вида  , где k — любое целое число, т. е. считать наряду с данным
, где k — любое целое число, т. е. считать наряду с данным  и всякое число
и всякое число  за значение полярного угла: если дано произвольное положительное
за значение полярного угла: если дано произвольное положительное  и произвольное не ограниченное никаким дополнительным условием действительное число
и произвольное не ограниченное никаким дополнительным условием действительное число  , то, взяв на полярной оси вектор ОА длины
, то, взяв на полярной оси вектор ОА длины  и повернув его в положительном направлении вокруг точки О на угол
и повернув его в положительном направлении вокруг точки О на угол  , получим вектор ОМ, конец которого будет иметь полярные координаты
, получим вектор ОМ, конец которого будет иметь полярные координаты  .
.
Точку М, полярные координаты которой равны данным  , будем обозначать так:
, будем обозначать так:  .
.
Пример. Пусть  . Будем давать углу всевозможные значения
. Будем давать углу всевозможные значения  . Множество всех точек с полярными координатами
. Множество всех точек с полярными координатами  (т. е. множество всех точек
(т. е. множество всех точек  , где
, где  пробегает все значения
пробегает все значения  (рис.
(рис.  ) образует кривую, называемую спиралью Архимеда.
) образует кривую, называемую спиралью Архимеда.

Рис. 56.
Уравнение

которому удовлетворяют полярные координаты любой точки М спирали Архимеда, называется уравнением, этой кривой в полярных координатах.
2. Связь прямоугольных координат с полярными. Если на плоскости дана полярная система координат, то этим определена и некоторая прямоугольная система координат: за масштаб и начало координат в этой прямоугольной системе берем масштаб и начало полярной системы; полярную полуось объявляем положительной полуосью абсцисс. Таким образом определена ось абсцисс (вместе с ее направлением).
Так как в определение полярной системы входит и направление положительного вращения плоскости, то мы можем определить  ординат как ту ось, в которую перейдет ось абсцисс при повороте ее на угол
ординат как ту ось, в которую перейдет ось абсцисс при повороте ее на угол  в положительном направлении.
в положительном направлении.
Полученную таким образом прямоугольную систему координат будем называть системой, определенной данной полярной системой (рис. 57).
Обратно, если дана какая-нибудь прямоугольная система координат, то однозначно определяем полярную систему, сохраняя в ней масштаб и начало данной прямоугольной системы и  полярная полуось созпадала с положительной полуосью абсцисс, а положительное направление вращения было тем вращением, которое переводит ось абсцисс в ось ординат поворотом на угол
полярная полуось созпадала с положительной полуосью абсцисс, а положительное направление вращения было тем вращением, которое переводит ось абсцисс в ось ординат поворотом на угол  . Очевидно, если мы для полученной таким образом полярной системы координат построим определенную ею прямоугольную, то вернемся к исходной прямоугольной системе.
. Очевидно, если мы для полученной таким образом полярной системы координат построим определенную ею прямоугольную, то вернемся к исходной прямоугольной системе.

Рис..
Итак, каждой полярной системе координат соответствует вполне определенная прямоугольная система, и обратно.
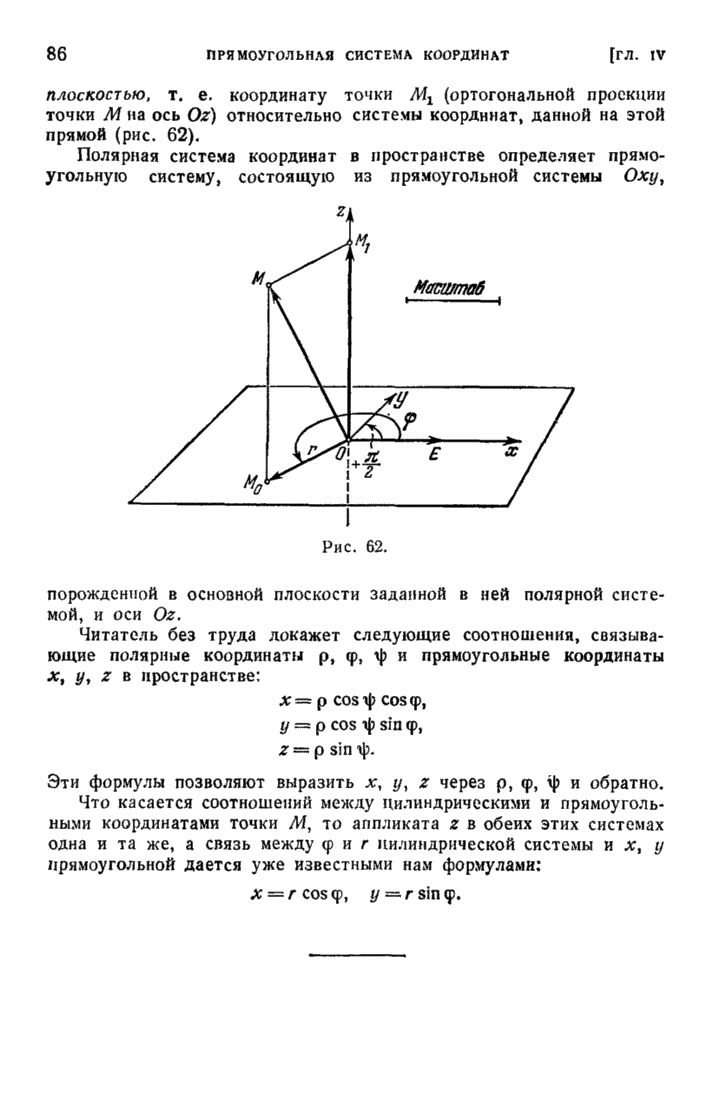
Посмотрим, как связаны между собою координаты х, у и  какой-нибудь точки М плоскости в обеих системах.
какой-нибудь точки М плоскости в обеих системах.
Имеем очевидные формулы:

Они позволяют перейти от полярных координат точки М к прямоугольным. Но они же позволяют произвести и обратный переход по формулам:

Из двух последних равенств (2) вытекает

Но формула (3) позволяет определить угол  лишь с точностью до слагаемых вида
лишь с точностью до слагаемых вида  при целом
при целом  .
.
3. Примеры. Дадим еще несколько примеров кривых, заданных их уравнениями в полярных координатах.
1° Гиперболическая спираль определяется как множество всех точек М, полярные координаты которых связаны между собою уравнением

где  — положительная постоянная, а полярный угол
— положительная постоянная, а полярный угол  пробегает все положительные значения. Начав исследование уравнения (4) с какого-нибудь положительного значения
пробегает все положительные значения. Начав исследование уравнения (4) с какого-нибудь положительного значения  и заставляя
и заставляя  возрастать, видим, что полярный радиус точки
возрастать, видим, что полярный радиус точки  , монотонно уменьшаясь, стремится к нулю при неограниченном возрастании
, монотонно уменьшаясь, стремится к нулю при неограниченном возрастании  , так что кривая, совершая бесконечное число оборотов, неограниченно приближается к началу О, никогда его, однако, не достигая.
, так что кривая, совершая бесконечное число оборотов, неограниченно приближается к началу О, никогда его, однако, не достигая.

Рис. 58.
Если мы теперь, начиная с данного  , будем давать углу
, будем давать углу  монотонно Убывающие значения,
монотонно Убывающие значения,  то
то  будет неограниченно возрастать. Для того чтобы понять, как при этом убывании
будет неограниченно возрастать. Для того чтобы понять, как при этом убывании  и возрастании будет изменяться положение точки
и возрастании будет изменяться положение точки  , воспользуемся второй из формул (1), а именно:
, воспользуемся второй из формул (1), а именно:

Подставляя сюда значение  получаем
получаем

откуда видно, что при  , стремящемся к нулю, ордината точки у стремится к а, так что кривая при возрастании
, стремящемся к нулю, ордината точки у стремится к а, так что кривая при возрастании  уходит в бесконечность, неограниченно приближаясь к прямой
уходит в бесконечность, неограниченно приближаясь к прямой  . Это обстоятельство выражают, говоря, что прямая
. Это обстоятельство выражают, говоря, что прямая  является асимптотой гиперболической спирали (4).
является асимптотой гиперболической спирали (4).
Произведенное исследование показывает, что гиперболическая спираль имеет  , указанный на рис. 58.
, указанный на рис. 58.
2° Логарифмическая спираль. Она определяется как совокупность точек  , полярные координаты которых удовлетворяют уравнению
, полярные координаты которых удовлетворяют уравнению

Примем за положительное направление вращения направление против часовой стрелки. При  получаем точку
получаем точку  . При возрастании
. При возрастании  возрастает и
возрастает и  (в частности, когда
(в частности, когда  возрастает на
возрастает на  , то полярный радиус умножается на
, то полярный радиус умножается на  , спираль быстро
, спираль быстро
«раскручивается» против часовой стрелки). Если же  , начиная со значения
, начиная со значения  , принимает неограниченно возрастающие по абсолютной величине отрицательные значения, то
, принимает неограниченно возрастающие по абсолютной величине отрицательные значения, то  стремится к нулю — спираль закручивается по часовой стрелке, неограниченно приближаясь к точке О.
стремится к нулю — спираль закручивается по часовой стрелке, неограниченно приближаясь к точке О.
Общий вид логарифмической спирали дан на рис. 59.
Среди многочисленных замечательных свойств логарифмических спиралей отметим следующее: две подобные между собою логарифмические спирали конгруэнтны (т. е. могут быть совмещены посредством движения). Мы докажем важнейший частный случай этой теоремы, а именно следующий.

Рис. 59.
Пусть логарифмическая спираль дана своим уравнением

в определенной полярной системе координат. При растяжении (гомотетии) плоскости с центром в начале координат О и коэффициентом растяжения  эта спираль переходит в ту же спираль, но повернутую на угол —с, где
эта спираль переходит в ту же спираль, но повернутую на угол —с, где

В самом деле, при нашем растяжении каждая точка

переходит в точку

В частности, точка  перейдет в точку
перейдет в точку  . Значит, множество точек, удовлетворяющих уравнению
. Значит, множество точек, удовлетворяющих уравнению

переходит в множество точек, удовлетворяющих уравнению

Другими словами, растянутая с коэффициентом растяжения k логарифмическая спираль имеет своим уравнением в полярных координатах уравнение

При повороте на угол —с точка  переходит в точку
переходит в точку  . Значит, если точка
. Значит, если точка  удовлетворяла уравнению (5), то после поворота она перейдет в точку
удовлетворяла уравнению (5), то после поворота она перейдет в точку  , удовлетворяющую уравнению
, удовлетворяющую уравнению

Это и будет уравнение нашей спирали, повернутой на угол —с; мы видим, что она совпадает с уравнением спирали, растянутой с коэффициентом растяжения k. Теорема доказана.
Замечание. Мы рассмотрели лишь случай  читателю предлагается разобрать логарифмическую спираль при положительном
читателю предлагается разобрать логарифмическую спираль при положительном  При
При  логарифмическая спираль, очевидно, превращается в окружность.
логарифмическая спираль, очевидно, превращается в окружность.
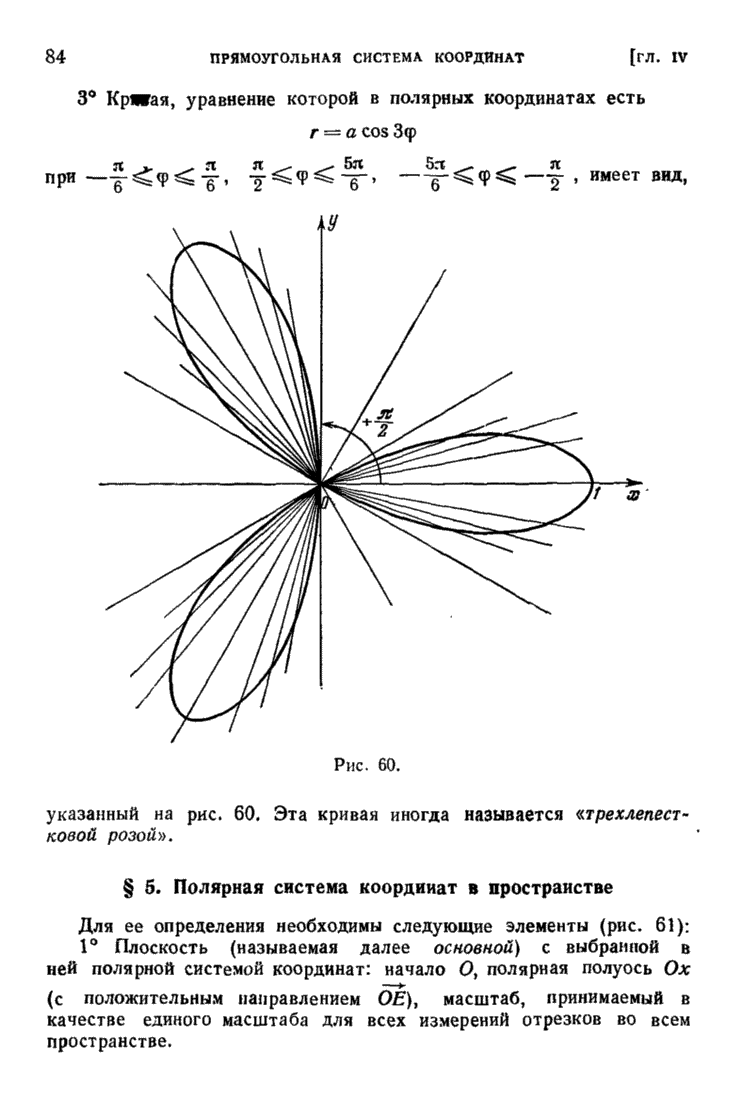
3° Кривая, уравнение которой в полярных координатах есть

при  , имеет вид, указанный на рис. 60. Эта кривая иногда называется «трехлепестковой розой».
, имеет вид, указанный на рис. 60. Эта кривая иногда называется «трехлепестковой розой».

Рис. 60.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ГЛАВА I. КООРДИНАТЫ НА ПРЯМОЙ
- § 1. Отношение отрезков
- § 2. Направленные отрезки (векторы); их отношение
- § 3. Ось. Алгебраическое значение (координата) вектора на оси
- § 4. Сложение векторов на прямой
- § 5. Система координат на прямой
- § 6. Деление отрезка в данном отношении
- § 7. Пропорциональность пар чисел
- § 8. Бесконечно удаленная точка прямой
- § 9. Пропорциональность двух последовательностей, состоящих из и чисел
- ГЛАВА II. ВЕКТОРЫ
- § 1. Равенство векторов. Свободный вектор
- § 2. Линейные операции над векторами (сложение и умножение на число)
- § 3. Проекции
- § 4. Коллинеарные и компланарные векторы; координаты вектора относительного данного базиса
- § 5. Линейная зависимость и независимость векторов
- § 6. Геометрический смысл линейной зависимости векторов
- § 7. Векторные многообразия
- ГЛАВА III. АФФИННАЯ СИСТЕМА КООРДИНАТ НА ПЛОСКОСТИ И В ПРОСТРАНСТВЕ
- § 1. Определение аффинной системы координат
- § 2. Перенос начала координат
- § 3. Деление отрезка в данном отношении
- ГЛАВА IV. ПРЯМОУГОЛЬНАЯ СИСТЕМА КООРДИНАТ. ПОЛЯРНЫЕ КООРДИНАТЫ
- § 1. Прямоугольная система координат на плоскости и в пространстве. Расстояние между двумя точками. Уравнение окружности и сферы
- § 2. Скалярное произведение векторов; угол между двумя векторами
- § 3. Угол от одного вектора до другого на плоскости
- § 4. Полярная система координат на плоскости
- § 5. Полярная система координат в пространстве
- ГЛАВА V. ПРЯМАЯ ЛИНИЯ
- § 1. Направляющий вектор и угловой коэффициент прямой (в произвольной аффинной системе координат). Уравнение прямой
- § 2. Расположение двух прямых на плоскости
- § 3. Частные случаи общего уравнения прямой
- § 4. Векторная и параметрическая форма уравнения прямой. Уравнение прямой, проходящей через две заданные точки
- § 5. Задача: когда прямая Ax+By+C=0 на плоскости проходит через точку пересечения двух заданных прямых A1x+B1y+C1=0 и A2x+B2y+C2=0?
- § 6. Две полуплоскости, определяемые данной прямой на плоскости
- § 7. Прямая на плоскости в прямоугольной системе координат. Нормальное уравнение прямой на плоскости
- § 8. Расстояние от точки до прямой (на плоскости)
- § 9. Углы, образуемые двумя прямыми на плоскости
- § 10. Прямая в пространстве, снабженном прямоугольной системой координат
- ГЛАВА VI. ПАРАБОЛА. ЭЛЛИПС. ГИПЕРБОЛА
- § 1. Парабола
- § 2. Определение и каноническое уравнение эллипса
- § 3. Параметрическая запись уравнения эллипса; построение эллипса по точкам. Эллипс как результат сжатия окружности к одному из ее диаметров
- § 4. Эллипс как проекция окружности и как сечение круглого цилиндра
- § 5. Определение гиперболы. Каноническое уравнение гиперболы
- § 6. Основной прямоугольник и асимптоты гиперболы
- § 7. Директрисы эллипса и гиперболы
- § 8. Фокальный параметр эллипса и гиперболы. Уравнение при вершине
- § 9. Уравнение эллипса, гиперболы и параболы в полярных координатах
- ГЛАВА VII. ДЕТЕРМИНАНТЫ
- § 1. Плошадь ориентированного параллелограмма и треугольника
- § 2. Детерминант второго порядка. Матрицы
- § 4. Разложение детерминанта третьего порядка по элементам какой-либо строки. Приложение к системе трех уравнений с тремя неизвестными (правило Крамера)
- § 5. Системы трех уравнений с тремя неизвестными с детерминантом системы, равным нулю
- § 6. Арифметическое n-мерное векторное многообразие (пространство). Общее определение матрицы. Детерминанты любого порядка
- § 7. Разложение детерминанта n-го порядка по элементам данной строки (данного столбца)
- § 8. Правило Крамера для решений систем и уравнений с n неизвестными
- § 9. Общее определение миноров матрицы. Теорема Лапласа
- § 10. Умножение детерминантов
- § 11. Детерминант n-го порядка как линейная нечетная нормированная функция от n векторов
- ГЛАВА VIII. ПРЕОБРАЗОВАНИЕ КООРДИНАТ. МАТРИЦЫ
- § 1. Переход от одной аффинной системы координат к другой
- § 2. Перемножение матриц. Новое определение обратной матрицы
- § 3. Переход от одной прямоугольной системы координат к другой
- § 4. Действия над матрицами в общем случае
- ГЛАВА IX. ПРЕОБРАЗОВАНИЕ КООРДИНАТ (ПРОДОЛЖЕНИЕ): ОРИЕНТАЦИЯ ПЛОСКОСТИ И ПРОСТРАНСТВА; УГЛЫ ЭЙЛЕРА; ОБЪЕМ ОРИЕНТИРОВАННОГО ПАРАЛЛЕЛЕПИПЕДА; ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ ДВУХ ВЕКТОРОВ
- § 1. Ориентация пространства (плоскости)
- § 2. Углы Эйлера
- § 3. Объем ориентированного параллелепипеда
- § 4. Векторное произведение двух векторов
- ГЛАВА X. ПЛОСКОСТЬ И ПРЯМАЯ В ПРОСТРАНСТВЕ
- § 1. Уравнения плоскости
- § 2. Множество решений системы двух однородных линейных уравнений с тремя неизвестными
- § 3. Взаимное расположение двух плоскостей
- § 4. Прямая как пересечение двух плоскостей
- § 5. Пучок плоскостей
- § 6. Взаимное расположение двух прямых в пространстве
- § 7. О двух полупространствах, определяемых данной плоскостью
- § 8. Плоскость в прямоугольной системе координат; нормальное уравнение плоскости; расстояние от точки до плоскости
- § 9. Угол между прямой и плоскостью; угол между двумя плоскостями
- § 10. Две задачи
- ГЛАВА XI. ДВИЖЕНИЯ И АФФИННЫЕ ПРЕОБРАЗОВАНИЯ
- § 1. Определение движений и аффинных преобразований
- § 2. Преобразование векторов при аффинном преобразовании плоскости и пространства. Основные свойства аффинных преобразований
- § 3. Аналитическое выражение аффинных преобразований
- § 4. Сохранение отношений площадей и объемов при аффинных преобразованиях
- § 5. Получение собственных аффинных преобразований посредством деформации тождественного преобразования. Следствия
- § 6. Движения как изометрические преобразования
- § 7. Преобразования подобия
- § 8. Классификация движений прямой и плоскости
- ГЛАВА XII. ВЕКТОРНЫЕ ПРОСТРАНСТВА (МНОГООБРАЗИЯ) ЛЮБОГО КОНЕЧНОГО ЧИСЛА ИЗМЕРЕНИЙ. СИСТЕМЫ ЛИНЕЙНЫХ ОДНОРОДНЫХ УРАВНЕНИЙ
- § 1. Определение векторного пространства
- § 2. Размерность. Базис. Координаты
- § 3. Теорема об изоморфизме между любыми двумя векторными пространствами одной и той же конечной размерности n
- § 4. Подпространства векторного пространства. Дальнейшие теоремы о линейной зависимости векторов и о базисе векторного пространства
- § 5. Алгебраическая (в частности, прямая) сумма подпространств
- § 6. Линейные отображения векторных пространств
- § 7. Теорема о ранге матрицы
- § 8. Системы линейных однородных уравнения
- ГЛАВА XIII. ЛИНЕЙНЫЕ, БИЛИНЕЙНЫЕ И КВАДРАТИЧНЫЕ ФУНКЦИИ НА ВЕКТОРНЫХ ПРОСТРАНСТВАХ
- § 1. Линейные функции
- § 2. Билинейные функции и билинейные формы
- § 3. Матрица билинейной и квадратичной формы и ее преобразование при переходе к новому базису (при преобразовании переменных)
- § 4. Ранг билинейной и квадратичной формы (билинейной и квадратичной функции)
- § 5. Существование канонического базиса для всякой квадратичной и всякой билинейной функции («приведение квадратичных форм к каноническому виду»)
- ГЛАВА XIV. ТОЧЕЧНО-ВЕКТОРНОЕ АФФИННОЕ n-МЕРНОЕ ПРОСТРАНСТВО
- § 1. Определение n-мерного аффинного пространства
- § 2. Системы координат. Арифметическое пространство. Изоморфизм всех n-мерных пространств между собою
- § 3. r-мерные плоскости n-мерного аффинного пространства; r-мерные параллелепипеды
- § 4. Геометрически независимые системы точек. Барицентрические координаты. Симплексы
- § 5. Системы линейных уравнений
- § 6. Аффинные преобразования n-мерного аффинного пространства
- ГЛАВА XV. АЛГЕБРАИЧЕСКИЕ ЛИНИИ И ПОВЕРХНОСТИ. КОМПЛЕКСНАЯ ПЛОСКОСТЬ И КОМПЛЕКСНОЕ ПРОСТРАНСТВО
- § 1. Определение алгебраических линий и поверхностей
- § 2. Преобразование многочлена второй степени при преобразовании координат
- § 3. Аффинная эквивалентность линий и поверхностей
- § 4. Комплексная плоскость
- § 5. Прямая линия на комплексной плоскости
- § 6. Замечание о действительных и мнимых линиях
- § 7. Комплексное пространство
- § 8. Распадающиеся линии и поверхности. Цилиндрические и конические поверхности. Поверхности вращения
- § 9. Несколько заключительных замечаний о линиях и поверхностях
- ГЛАВА XVI. Различные виды кривых второго порядка
- § 1. О линиях, определяемых уравнениями второй степени с двумя неизвестными
- § 2. Инварианты многочлена второй степени
- § 3. Центральный случай
- § 4. Параболический случай
- § 5. Аффинная классификация кривых второго порядка
- § 6. Несколько заключительных замечаний
- ГЛАВА XVII. ОБЩАЯ ТЕОРИЯ КРИВЫХ ВТОРОГО ПОРЯДКА
- § 1. Пересечение алгебраической кривой с прямой. Асимптотические направления и асимптоты алгебраической кривой
- § 2. Теорема единственности для кривых второго порядка. Пучок кривых второго порядка
- § 3. Асимптотические направления кривых второго порядка
- § 4. Пересечение кривой второго порядка с прямой иеасимптотического направления. Касательные
- § 5. Пересечение кривой второго порядка с прямой асимптотического направления. Геометрическая характеристика асимптотических и неасимптотических направлений
- § 6. Центр кривой второго порядка
- § 7. Диаметры кривой второго порядка
- § 8. Взаимно сопряженные векторы (направления). Диаметры и касательные
- § 9. Вид уравнения кривой, если оси координат имеют сопряженные направления
- § 10. Второе доказательство теоремы единственности. О полноте системы ортогональных инвариантов
- § 11. Оси симметрии и главные направления кривой второго порядка
- § 12. Основная теорема об аффинных преобразованиях
- ГЛАВА XVIII. КРАТКОЕ ОПИСАНИЕ РАЗЛИЧНЫХ ВИДОВ ПОВЕРХНОСТЕЙ ВТОРОГО ПОРЯДКА
- § 1. Распадающиеся поверхности
- § 2. Цилиндрические поверхности
- § 3. Конусы второго порядка
- § 4. Эллипсоиды и гиперболоиды
- § 5. Параболоиды
- § 6. Прямолинейные образующие
- ГЛАВА XIX. ОБЩАЯ ТЕОРИЯ ПОВЕРХНОСТЕЙ ВТОРОГО ПОРЯДКА. I (ПЕРЕСЕЧЕНИЕ С ПЛОСКОСТЬЮ И С ПРЯМОЙ; АСИМПТОТИЧЕСКИЕ НАПРАВЛЕНИЯ; КАСАТЕЛЬНАЯ ПЛОСКОСТЬ; ЦЕНТР)
- § 1. Ранг и детерминант малой и большой матрицы многочлена второй степени
- § 2. Пересечение поверхности второго порядка с плоскостью
- § 3. Пересечение поверхности второго порядка с прямой. Асимптотические направления. Касательные прямые и касательная плоскость. Особые точки поверхности второго порядка
- § 4. Асимптотические направления, конус асимптотических направлений, прямолинейные образующие поверхностей второго порядка
- § 5. Центр поверхности второго порядка
- ГЛАВА XX. ОБЩАЯ ТЕОРИЯ ПОВЕРХНОСТЕЙ ВТОРОГО ПОРЯДКА. II (ДИАМЕТРАЛЬНЫЕ ПЛОСКОСТИ; ОСОБЫЕ И ГЛАВНЫЕ НАПРАВЛЕНИЯ; АФФИННАЯ КЛАССИФИКАЦИЯ)
- § 1. Диаметральные плоскости. Особые направления
- § 2. Диаметральные плоскости поверхностей различных видов
- § 3. Сопряженные направления
- § 4. Уравнение поверхности второго порядка относительно координатной системы с сопряженными направлениями осей
- § 5. Теорема единственности
- § 6. Главные направления
- § 7. Приведение к каноническому виду уравнения поверхности второго порядка
- § 8. Аффинная классификация поверхностей второго порядка
- ГЛАВА XXI. ПРОЕКТИВНАЯ ПЛОСКОСТЬ
- § 1. Перспективное соответствие между плоскостью и связкой
- § 2. Однородные координаты точек на плоскости и лучел в связке
- § 3. Координаты прямой; арифметическая проективная плоскость; общее определение проективной плоскости
- § 4. Принцип двойственности для проективной плоскости
- § 5. Проективная система координат в связке и на проективной плоскости
- § 6. Проективные преобразования и отображения проективной плоскости
- § 7. Проективные координаты на прямой. Проективные отображения прямой
- § 8. Двойное отношение
- ГЛАВА XXII. КРИВЫЕ ВТОРОГО ПОРЯДКА НА ПРОЕКТИВНОЙ ПЛОСКОСТИ
- § 1. Определение. Теорема единственности
- § 2. Пересечение кривой второго порядка с прямой. Касательные; асимптоты
- § 3. Пучок кривых второго порядка. Второе доказательство теоремы единственности. Теорема Паскаля. Теорема Штейнера
- § 4. Поляры и полюсы
- § 5. Коррелятивное, в частности полярное, соответствие. Тангенциальное уравнение кривой
- § 6. Диаметры как поляры несобственных точек
- § 7. Автополярный треугольник
- § 8. Проективная классификация кривых второго порядка
- ГЛАВА XXIII. НАЧАЛЬНЫЕ СВЕДЕНИЯ ИЗ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ ПРОЕКТИВНОГО ПРОСТРАНСТВА
- § 1. Проективное пространство; его плоскости и прямые
- § 2. Проективные координаты. Проективные преобразования.
- § 3. Понятие об n-мерном проективном пространстве
- § 4. Поверхности второго порядка в проективном пространстве. Теорема единственности
- § 5. Пересечение поверхности второго порядка с плоскостью и с прямой. Касательные прямые. Касательная плоскость. Прямолинейные образующие
- § 6. Полюсы и полярные плоскости
- § 7. Проективная классификация поверхностей второго порядка
- § 8. Распределение по проективным классам поверхностей различных аффинных классов. Проективно-аффинная классификация поверхностей второго порядка
- ГЛАВА XXIV. ЕВКЛИДОВО n-МЕРНОЕ ПРОСТРАНСТВО
- § 1. Введение. Ортогональные матрицы
- § 2. Положительно определенные симметричные билинейные функции в векторном пространстве
- § 3. Определение евклидовых пространств и простейших относящихся к ним понятий
- § 4. Неравенство Коши—Буняковского и его следствия. Углы
- § 5. Подпространства евклидовых пространств. Ортогональное дополнение к данному подпространству
- ГЛАВА XXV. ЛИНЕЙНЫЕ ОПЕРАТОРЫ, БИЛИНЕЙНЫЕ И КВАДРАТИЧНЫЕ ФУНКЦИИ В ЕВКЛИДОВЫХ ПРОСТРАНСТВАХ. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
- § 1. Инвариантные подпространства и собственные векторы линейного оператора в любом векторном пространстве
- § 2. Ортогональные преобразования n-мерного евклидова пространства
- § 3. Движения трехмерного евклидова пространства
- § 4. Преобразования подобия. Дальнейшие проблемы
- § 5. Самосопряженные операторы
- § 6. Теорема о структуре произвольного линейного преобразования евклидова пространства
- § 7. Билинейные и квадратичные формы в евклидовых пространствах
- § 8. (n-1)-мерные многообразия (поверхности) второго поряд] в -мерном аффинном и евклидовом пространствах
- ПРИБАВЛЕНИЕ. ПЕРЕСТАНОВКИ, МНОЖЕСТВА И ИХ ОТОБРАЖЕНИЯ; ГРУППЫ
- § 1. Перестановки
- § 2. Множества
- § 3. Отображения или функции
- § 4. Разбиение множества на подмножества. Отношение эквивалентности
- § 5. Определение группы
- § 6. Простейшие теоремы о группах
- § 7. Эквивалентность подмножеств данного множества по отношению к дайной группе его преобразований
- ЗАДАЧИ
- Задачи к главе IV
- Задачи к главе V
- Задачи к главе VI
- Задачи к главе VIII
- Задачи к главе IX
- Задачи к главе X
- Задачи к главе XI
- Задачи к главе XII
- Задачи к главе XIII
- Задачи к главе XIV
- Задачи к главе XV
- Задачи к главам XVI и XVII
- Задачи к главе XVIII
- Задачи к главам XIX и XX
- Задачи к главе XXI
- Задачи к главе XXII