| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
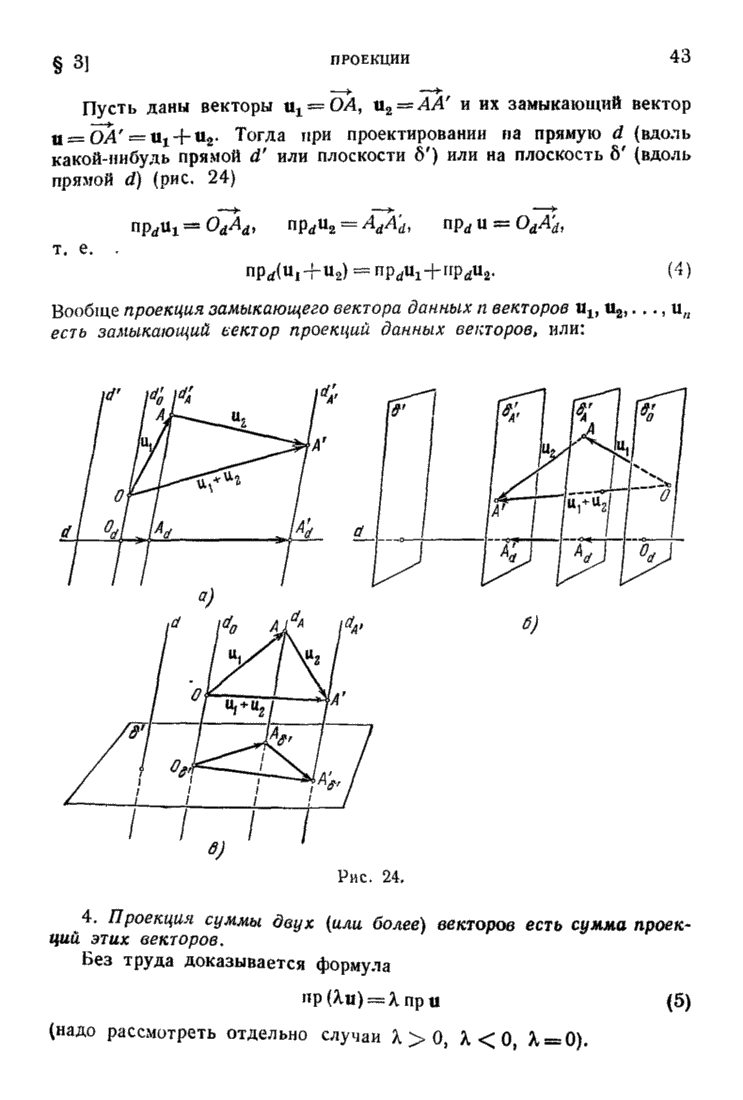
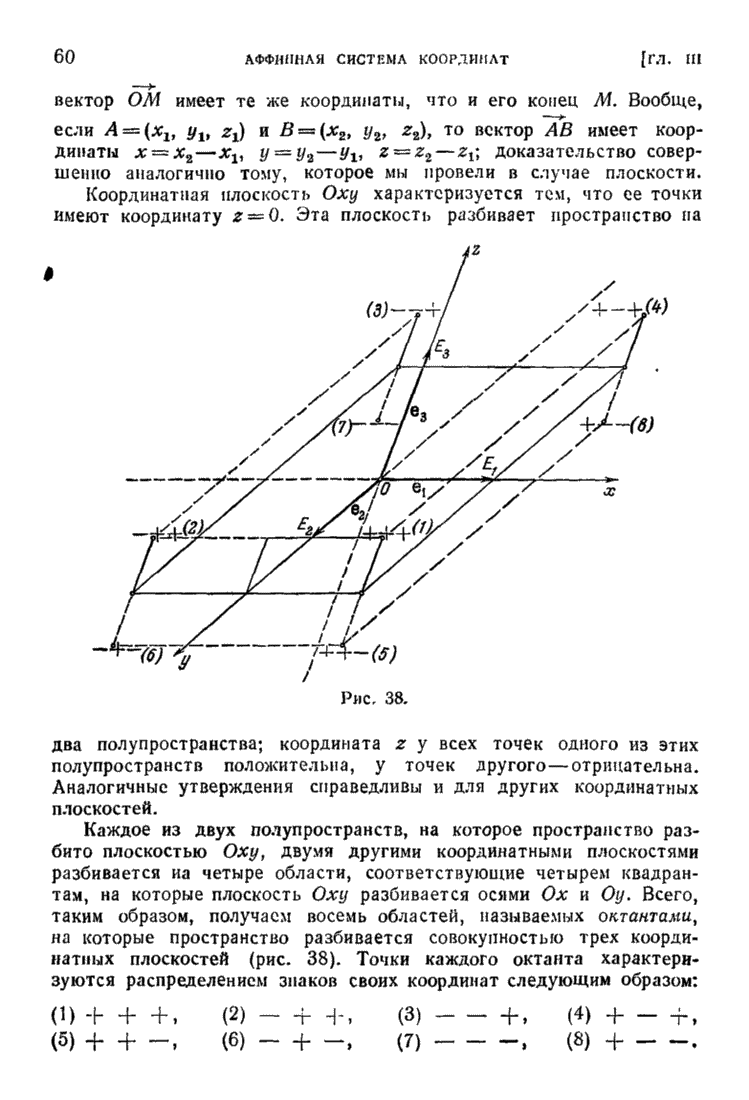
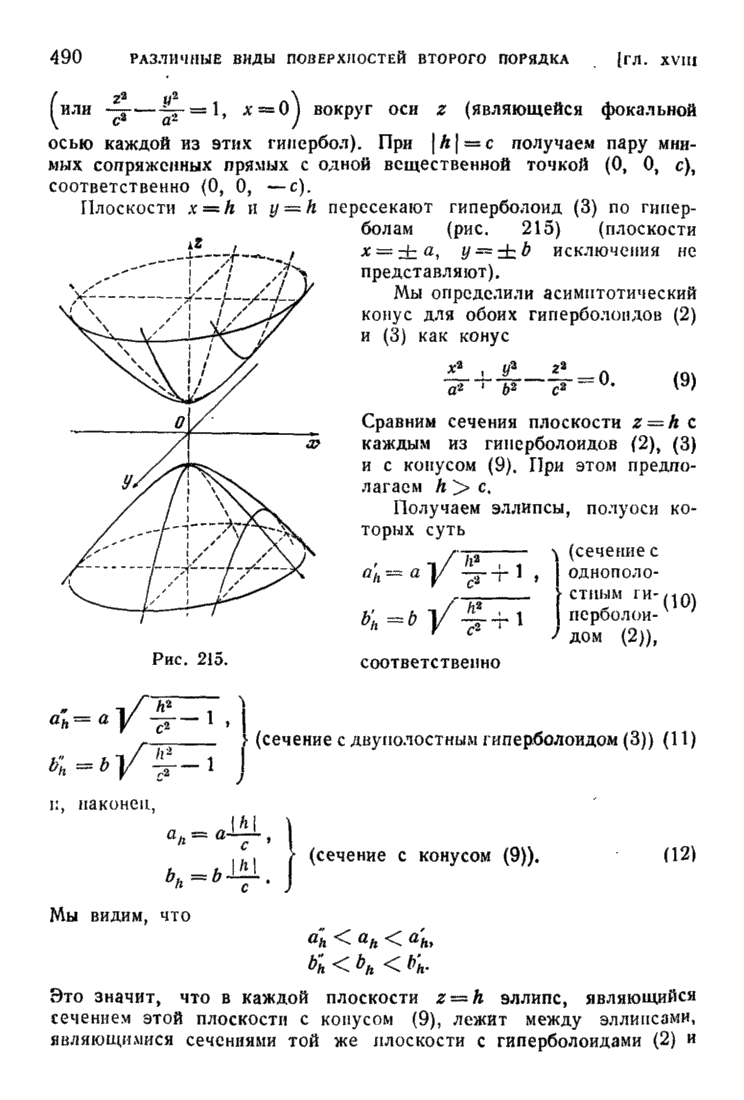
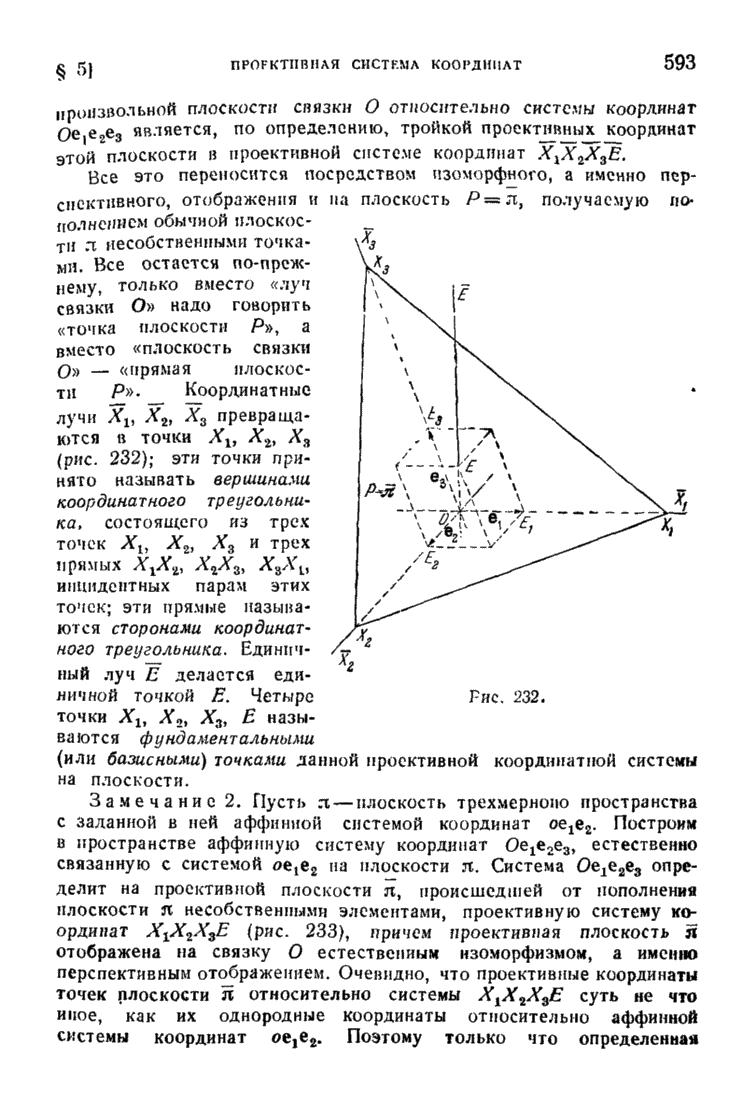
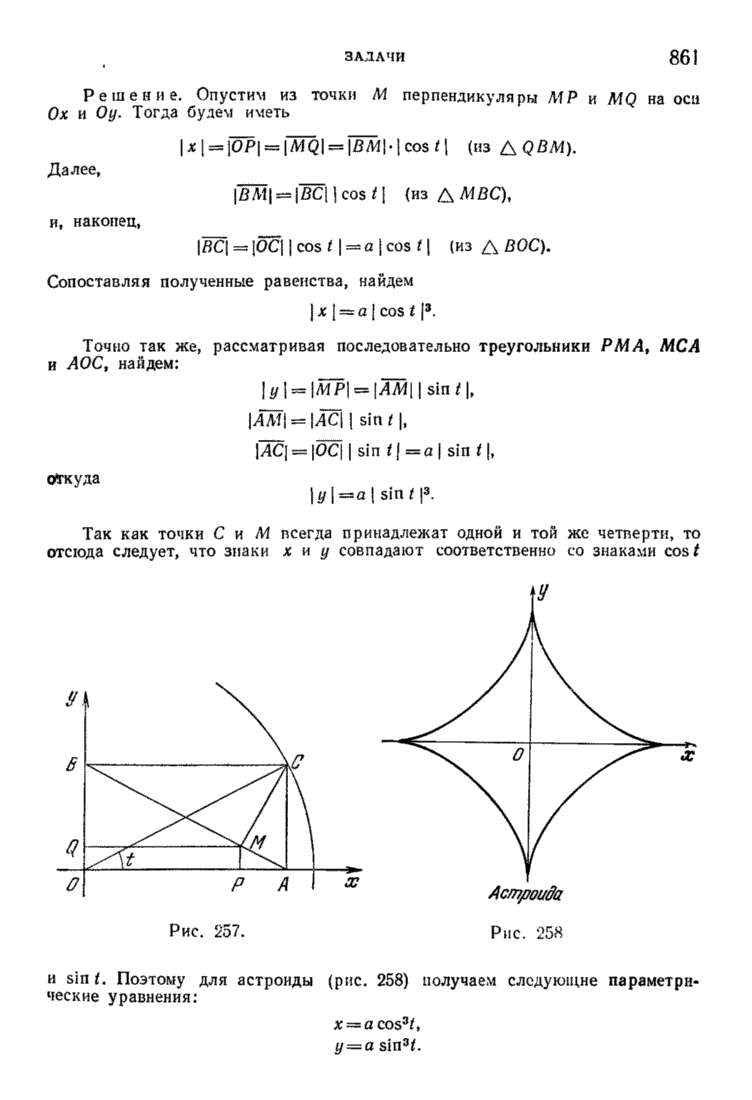
§ 6. Взаимное расположение двух прямых в пространстве
Две прямые

и

могут лежать или не лежать в одной плоскости (быть или не быть компланарными).
Положим

Для компланарности прямых (1) и (1') необходимым и достаточным условием является компланарность трех векторов (рис. 123):

т. е. равенство
 (2)
(2)
Следовательно, прямые скрещиваются (т. е. не лежат в одной плоскости) тогда и только тогда, когда равенство (2) не имеет места.

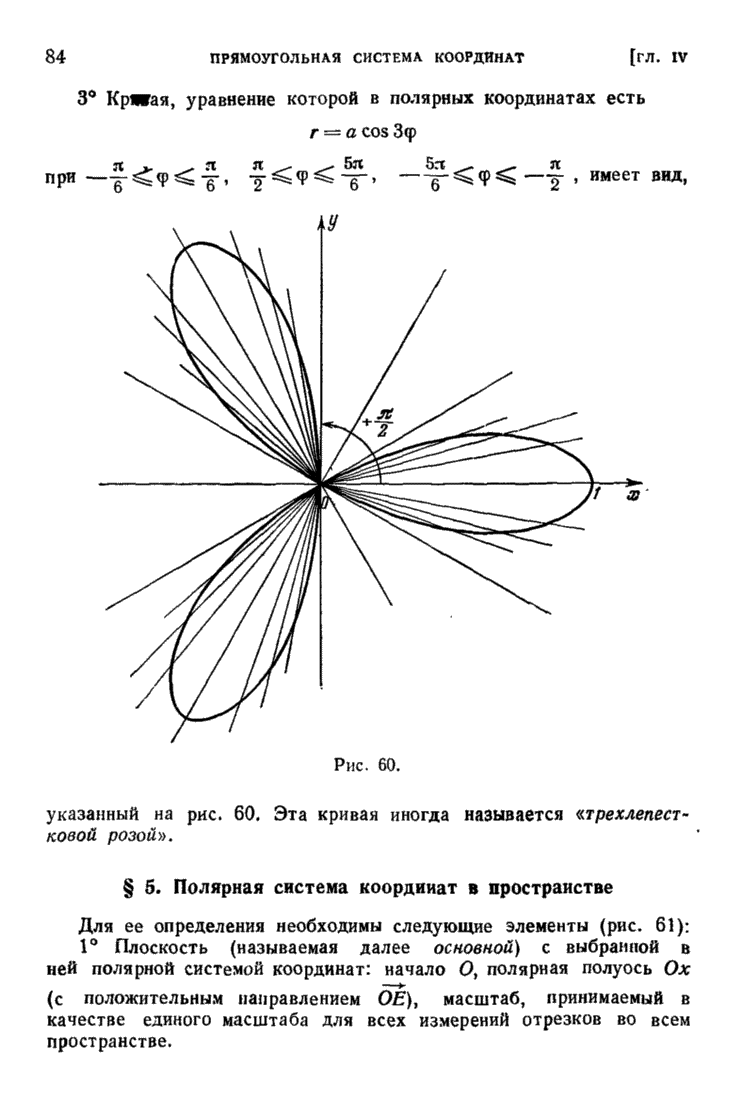
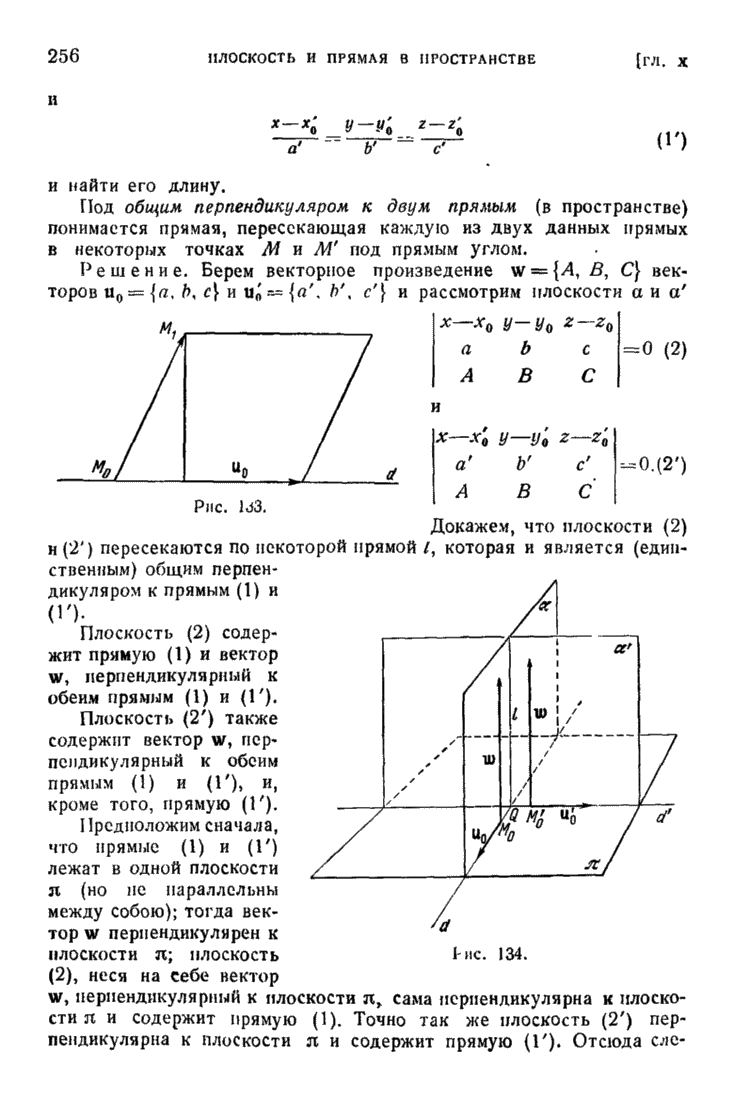
Рис. 123.
Найдем уравнение плоскости, содержащей две компланарные прямые (1) и (1'). Предположим сначала, что прямые (1) и (1') пересекаются и что  — их точка пересечения. Тогда плоскость, в которой лежат обе наши прямые, есть плоскость, проходящая через точку
— их точка пересечения. Тогда плоскость, в которой лежат обе наши прямые, есть плоскость, проходящая через точку  и два приложенных к ней неколлинеарных вектора
и два приложенных к ней неколлинеарных вектора  .
.
Уравнением этой плоскости  вляется, как мы знаем (§ 1), уравнение
вляется, как мы знаем (§ 1), уравнение
 (3)
(3)
оно и дает ответ на поставленный вопрос.
Пусть теперь прямые (1) и (1') параллельны. Тогда векторы  коллинеарны, следовательно, уравнение (3) обращается в тождество и ничего нам не дает. Чтобы определить уравнение плоскости, содержащей две данные параллельные прямые (1) и (1'), заметим, что эта плоскость содержит точку
коллинеарны, следовательно, уравнение (3) обращается в тождество и ничего нам не дает. Чтобы определить уравнение плоскости, содержащей две данные параллельные прямые (1) и (1'), заметим, что эта плоскость содержит точку  одной из наших прямых, ее направляющий вектор
одной из наших прямых, ее направляющий вектор  и вектор
и вектор  .
.
Поэтому уравнение искомой плоскости есть 

Замечание. Если прямые (1) и ( ) скрещиваются, то уравнение (3) есть уравнение плоскости, проходящей через прямую (1) параллельно прямой (1). Доказательство предоставляется читателю.
) скрещиваются, то уравнение (3) есть уравнение плоскости, проходящей через прямую (1) параллельно прямой (1). Доказательство предоставляется читателю.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ГЛАВА I. КООРДИНАТЫ НА ПРЯМОЙ
- § 1. Отношение отрезков
- § 2. Направленные отрезки (векторы); их отношение
- § 3. Ось. Алгебраическое значение (координата) вектора на оси
- § 4. Сложение векторов на прямой
- § 5. Система координат на прямой
- § 6. Деление отрезка в данном отношении
- § 7. Пропорциональность пар чисел
- § 8. Бесконечно удаленная точка прямой
- § 9. Пропорциональность двух последовательностей, состоящих из и чисел
- ГЛАВА II. ВЕКТОРЫ
- § 1. Равенство векторов. Свободный вектор
- § 2. Линейные операции над векторами (сложение и умножение на число)
- § 3. Проекции
- § 4. Коллинеарные и компланарные векторы; координаты вектора относительного данного базиса
- § 5. Линейная зависимость и независимость векторов
- § 6. Геометрический смысл линейной зависимости векторов
- § 7. Векторные многообразия
- ГЛАВА III. АФФИННАЯ СИСТЕМА КООРДИНАТ НА ПЛОСКОСТИ И В ПРОСТРАНСТВЕ
- § 1. Определение аффинной системы координат
- § 2. Перенос начала координат
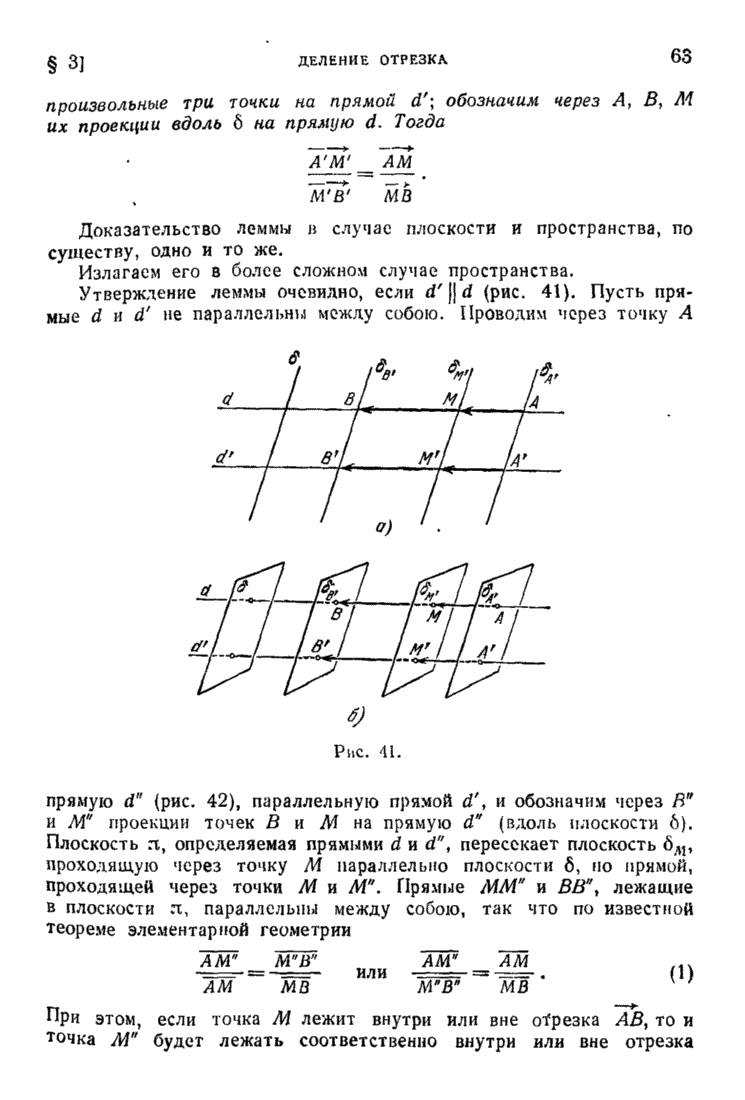
- § 3. Деление отрезка в данном отношении
- ГЛАВА IV. ПРЯМОУГОЛЬНАЯ СИСТЕМА КООРДИНАТ. ПОЛЯРНЫЕ КООРДИНАТЫ
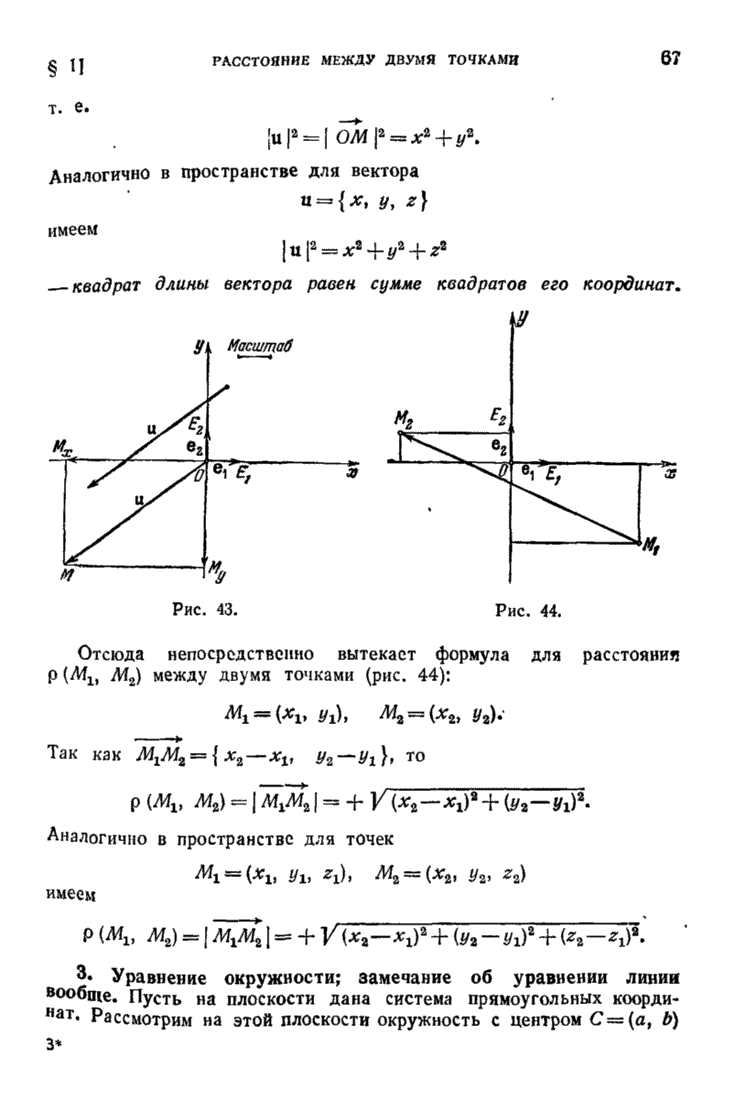
- § 1. Прямоугольная система координат на плоскости и в пространстве. Расстояние между двумя точками. Уравнение окружности и сферы
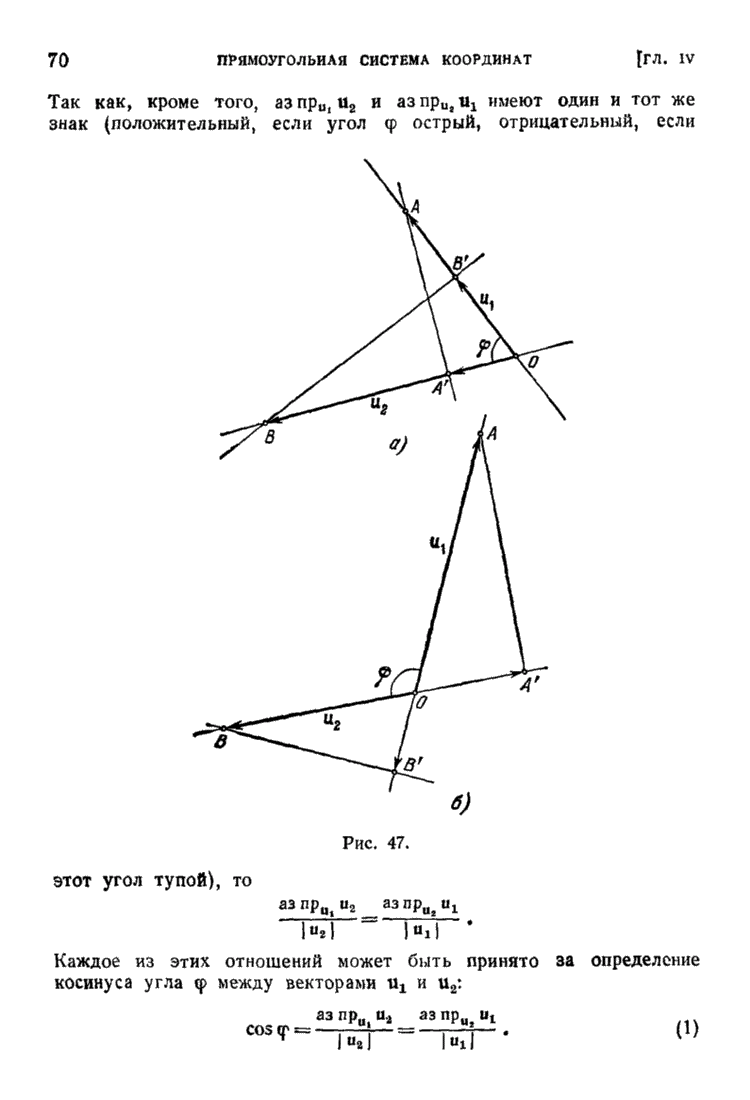
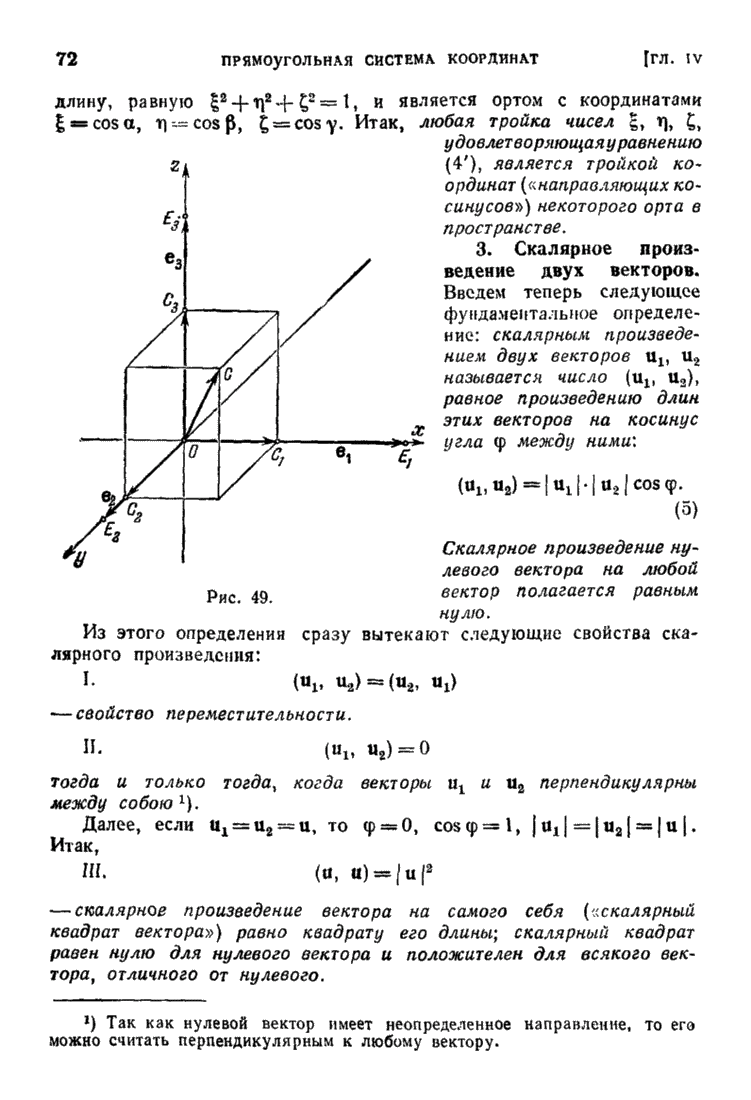
- § 2. Скалярное произведение векторов; угол между двумя векторами
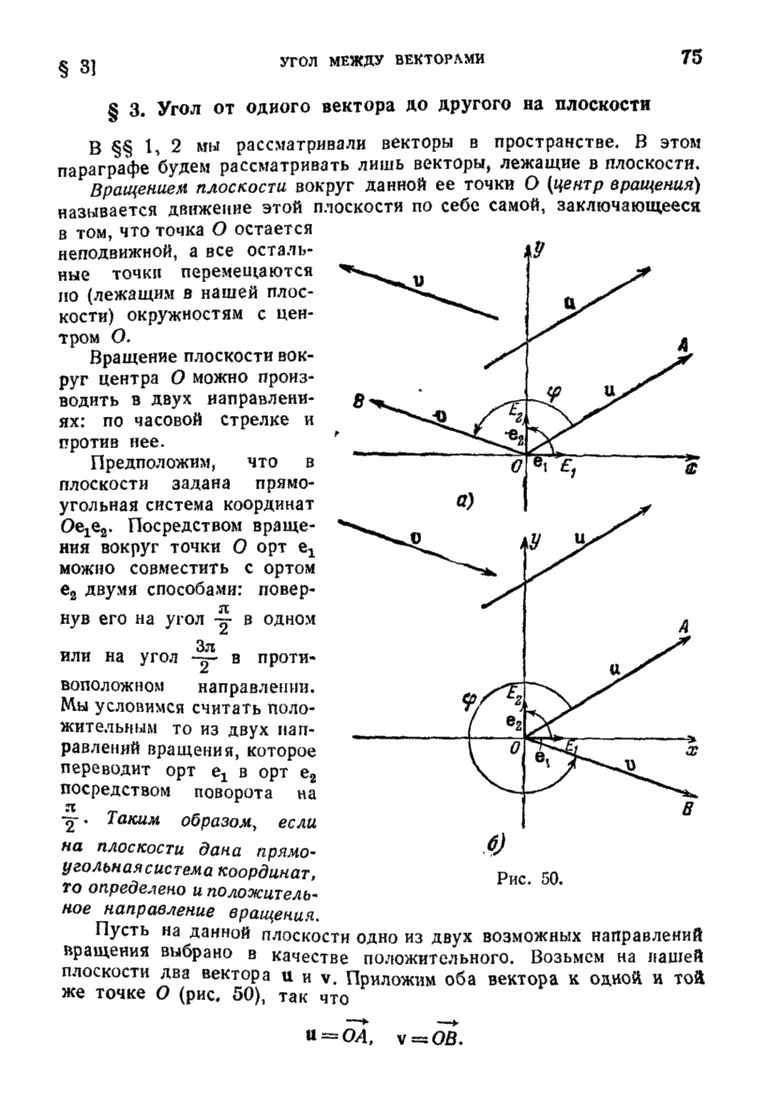
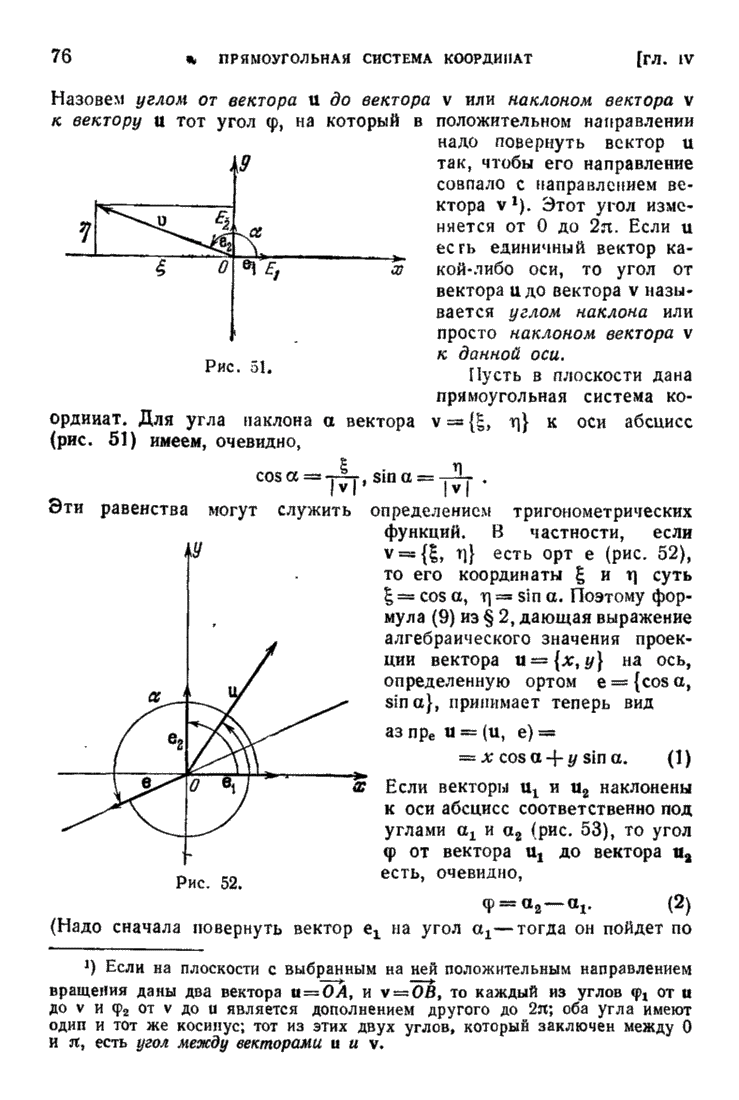
- § 3. Угол от одного вектора до другого на плоскости
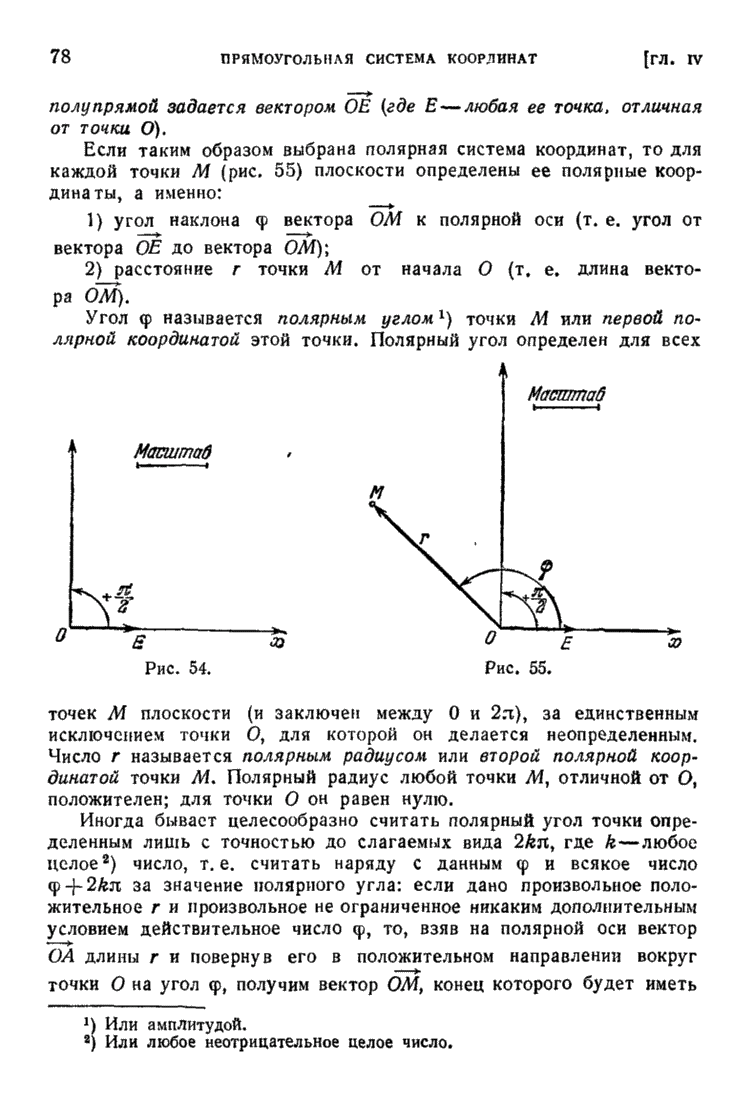
- § 4. Полярная система координат на плоскости
- § 5. Полярная система координат в пространстве
- ГЛАВА V. ПРЯМАЯ ЛИНИЯ
- § 1. Направляющий вектор и угловой коэффициент прямой (в произвольной аффинной системе координат). Уравнение прямой
- § 2. Расположение двух прямых на плоскости
- § 3. Частные случаи общего уравнения прямой
- § 4. Векторная и параметрическая форма уравнения прямой. Уравнение прямой, проходящей через две заданные точки
- § 5. Задача: когда прямая Ax+By+C=0 на плоскости проходит через точку пересечения двух заданных прямых A1x+B1y+C1=0 и A2x+B2y+C2=0?
- § 6. Две полуплоскости, определяемые данной прямой на плоскости
- § 7. Прямая на плоскости в прямоугольной системе координат. Нормальное уравнение прямой на плоскости
- § 8. Расстояние от точки до прямой (на плоскости)
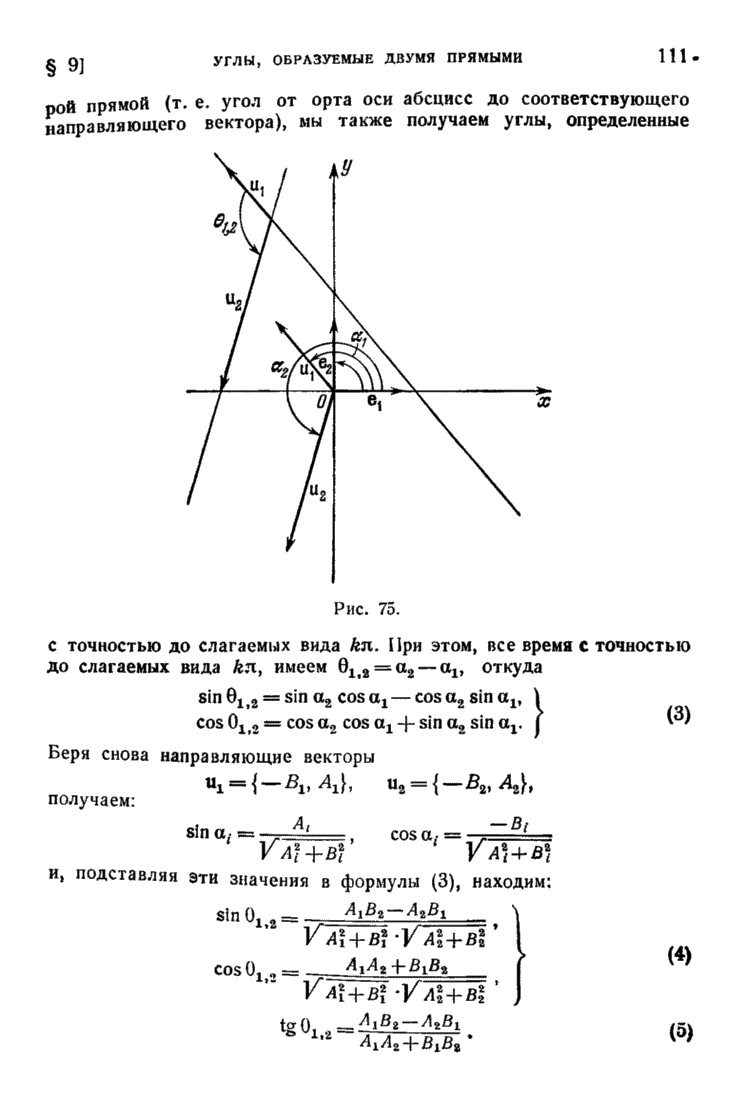
- § 9. Углы, образуемые двумя прямыми на плоскости
- § 10. Прямая в пространстве, снабженном прямоугольной системой координат
- ГЛАВА VI. ПАРАБОЛА. ЭЛЛИПС. ГИПЕРБОЛА
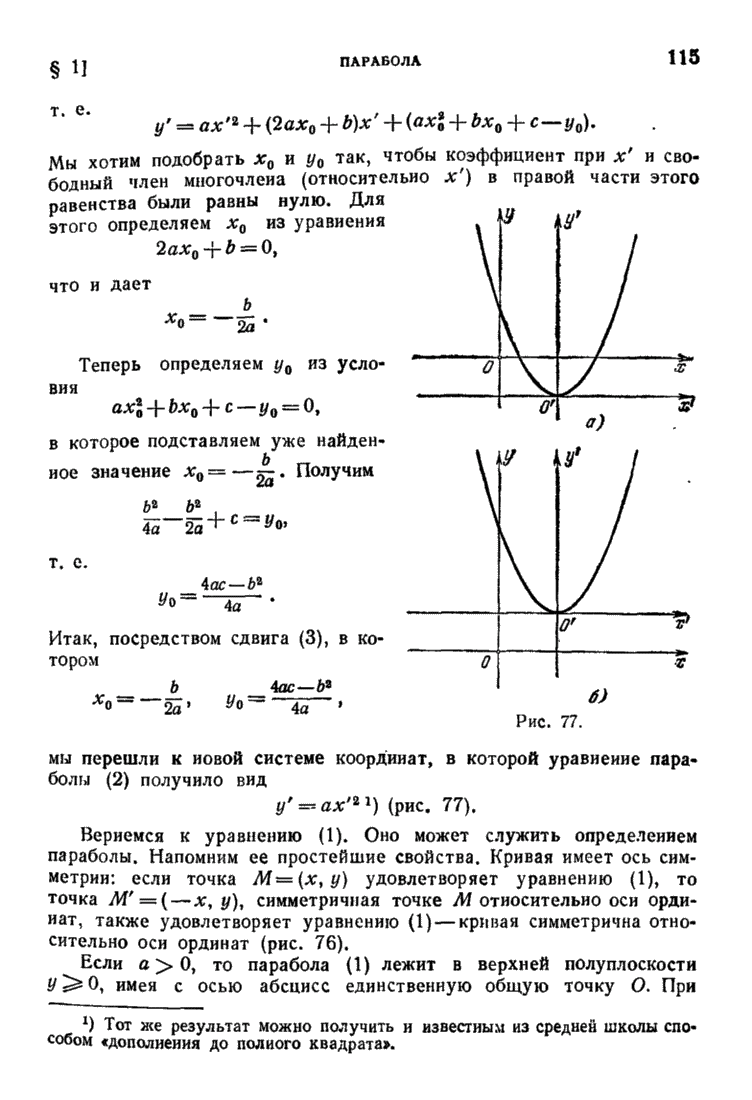
- § 1. Парабола
- § 2. Определение и каноническое уравнение эллипса
- § 3. Параметрическая запись уравнения эллипса; построение эллипса по точкам. Эллипс как результат сжатия окружности к одному из ее диаметров
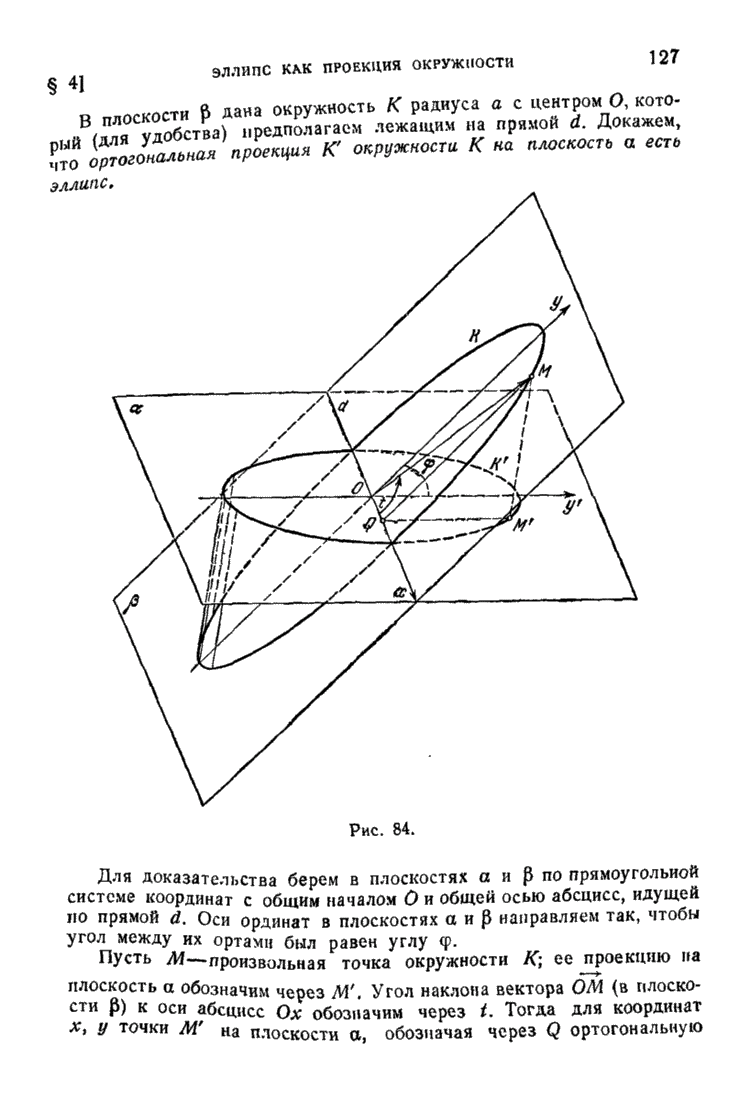
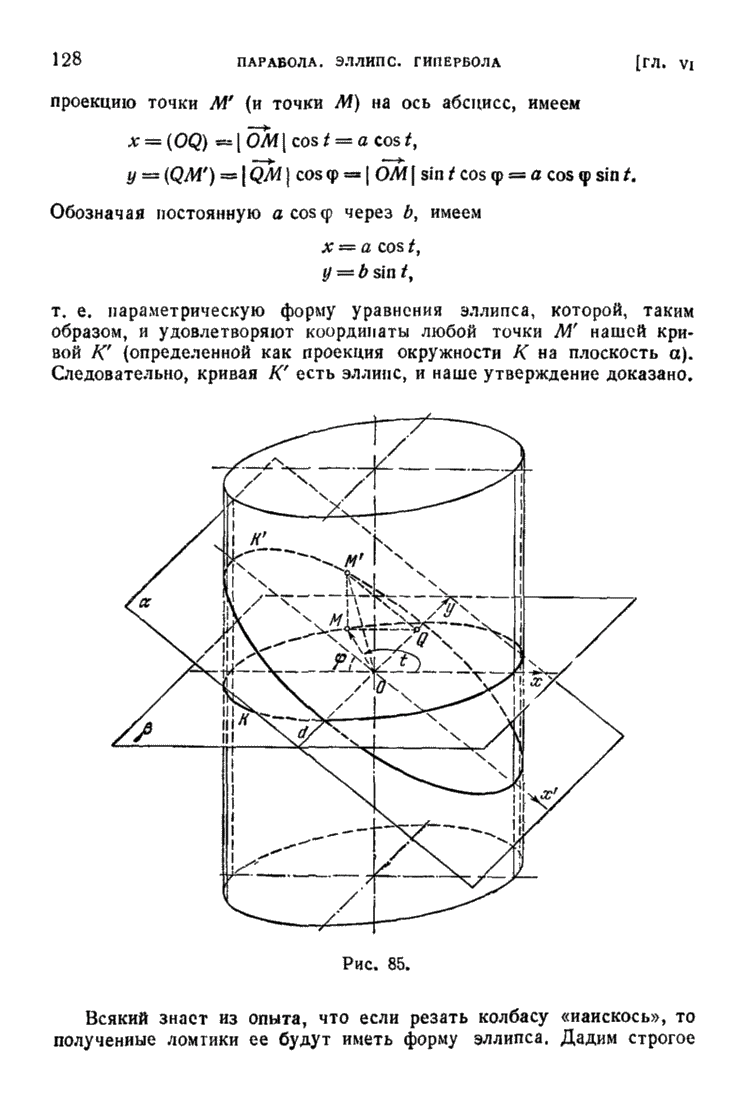
- § 4. Эллипс как проекция окружности и как сечение круглого цилиндра
- § 5. Определение гиперболы. Каноническое уравнение гиперболы
- § 6. Основной прямоугольник и асимптоты гиперболы
- § 7. Директрисы эллипса и гиперболы
- § 8. Фокальный параметр эллипса и гиперболы. Уравнение при вершине
- § 9. Уравнение эллипса, гиперболы и параболы в полярных координатах
- ГЛАВА VII. ДЕТЕРМИНАНТЫ
- § 1. Плошадь ориентированного параллелограмма и треугольника
- § 2. Детерминант второго порядка. Матрицы
- § 4. Разложение детерминанта третьего порядка по элементам какой-либо строки. Приложение к системе трех уравнений с тремя неизвестными (правило Крамера)
- § 5. Системы трех уравнений с тремя неизвестными с детерминантом системы, равным нулю
- § 6. Арифметическое n-мерное векторное многообразие (пространство). Общее определение матрицы. Детерминанты любого порядка
- § 7. Разложение детерминанта n-го порядка по элементам данной строки (данного столбца)
- § 8. Правило Крамера для решений систем и уравнений с n неизвестными
- § 9. Общее определение миноров матрицы. Теорема Лапласа
- § 10. Умножение детерминантов
- § 11. Детерминант n-го порядка как линейная нечетная нормированная функция от n векторов
- ГЛАВА VIII. ПРЕОБРАЗОВАНИЕ КООРДИНАТ. МАТРИЦЫ
- § 1. Переход от одной аффинной системы координат к другой
- § 2. Перемножение матриц. Новое определение обратной матрицы
- § 3. Переход от одной прямоугольной системы координат к другой
- § 4. Действия над матрицами в общем случае
- ГЛАВА IX. ПРЕОБРАЗОВАНИЕ КООРДИНАТ (ПРОДОЛЖЕНИЕ): ОРИЕНТАЦИЯ ПЛОСКОСТИ И ПРОСТРАНСТВА; УГЛЫ ЭЙЛЕРА; ОБЪЕМ ОРИЕНТИРОВАННОГО ПАРАЛЛЕЛЕПИПЕДА; ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ ДВУХ ВЕКТОРОВ
- § 1. Ориентация пространства (плоскости)
- § 2. Углы Эйлера
- § 3. Объем ориентированного параллелепипеда
- § 4. Векторное произведение двух векторов
- ГЛАВА X. ПЛОСКОСТЬ И ПРЯМАЯ В ПРОСТРАНСТВЕ
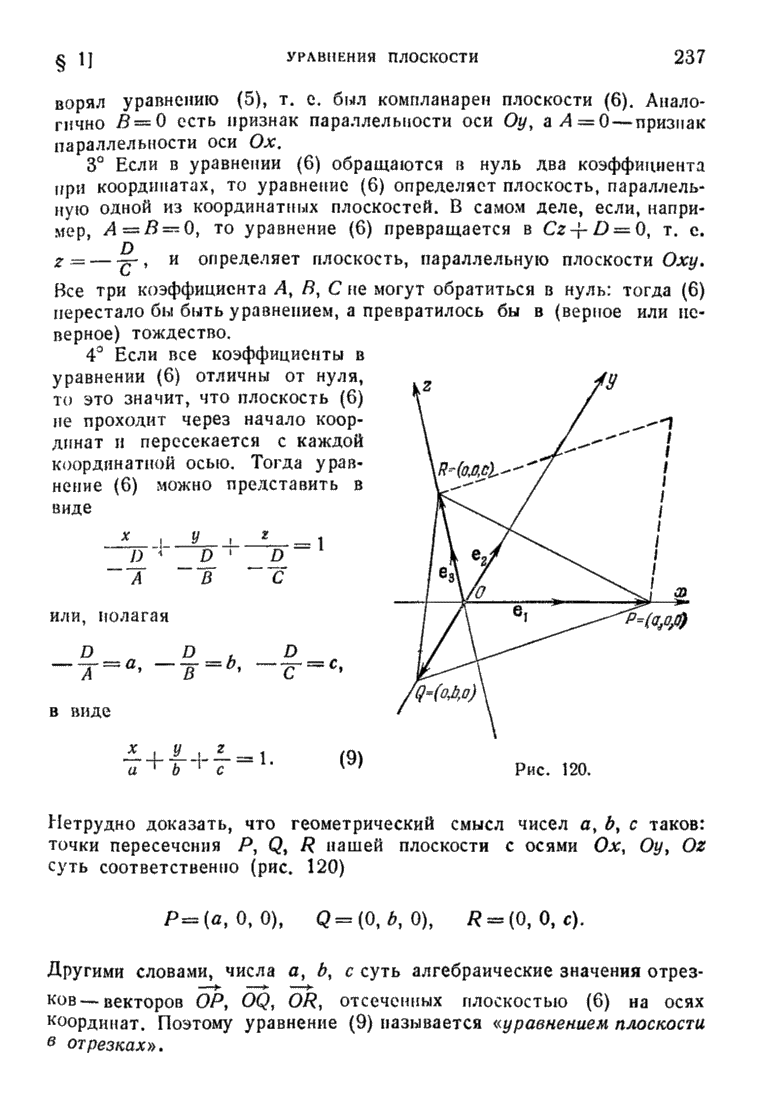
- § 1. Уравнения плоскости
- § 2. Множество решений системы двух однородных линейных уравнений с тремя неизвестными
- § 3. Взаимное расположение двух плоскостей
- § 4. Прямая как пересечение двух плоскостей
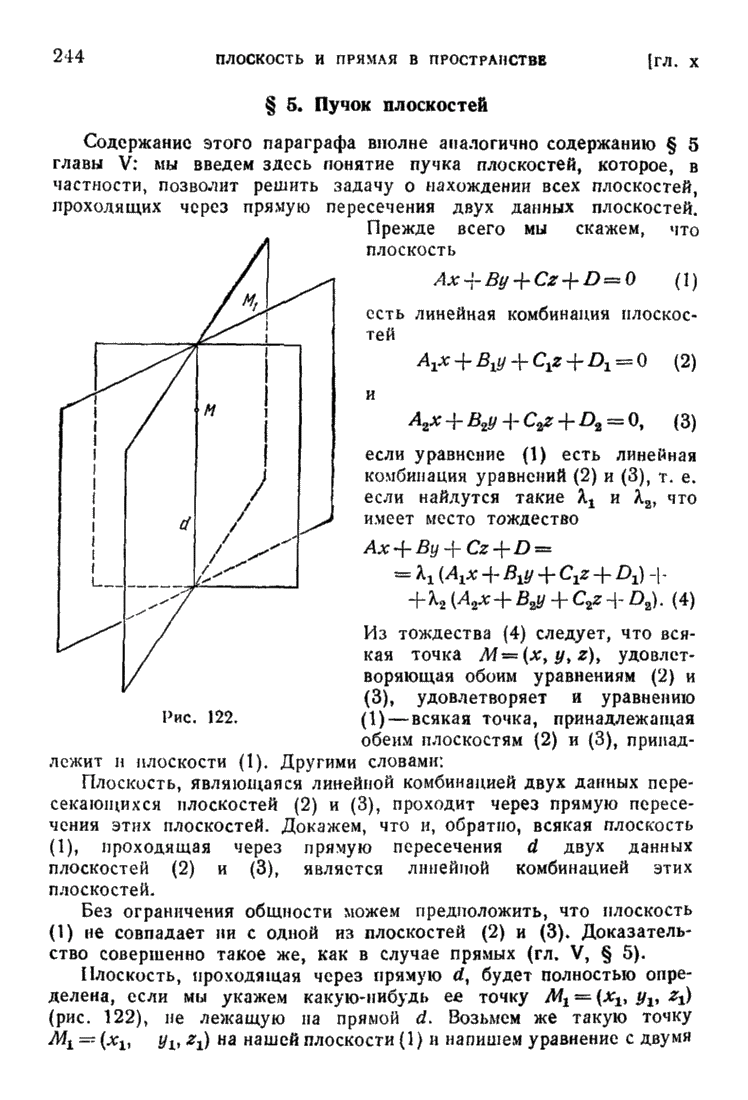
- § 5. Пучок плоскостей
- § 6. Взаимное расположение двух прямых в пространстве
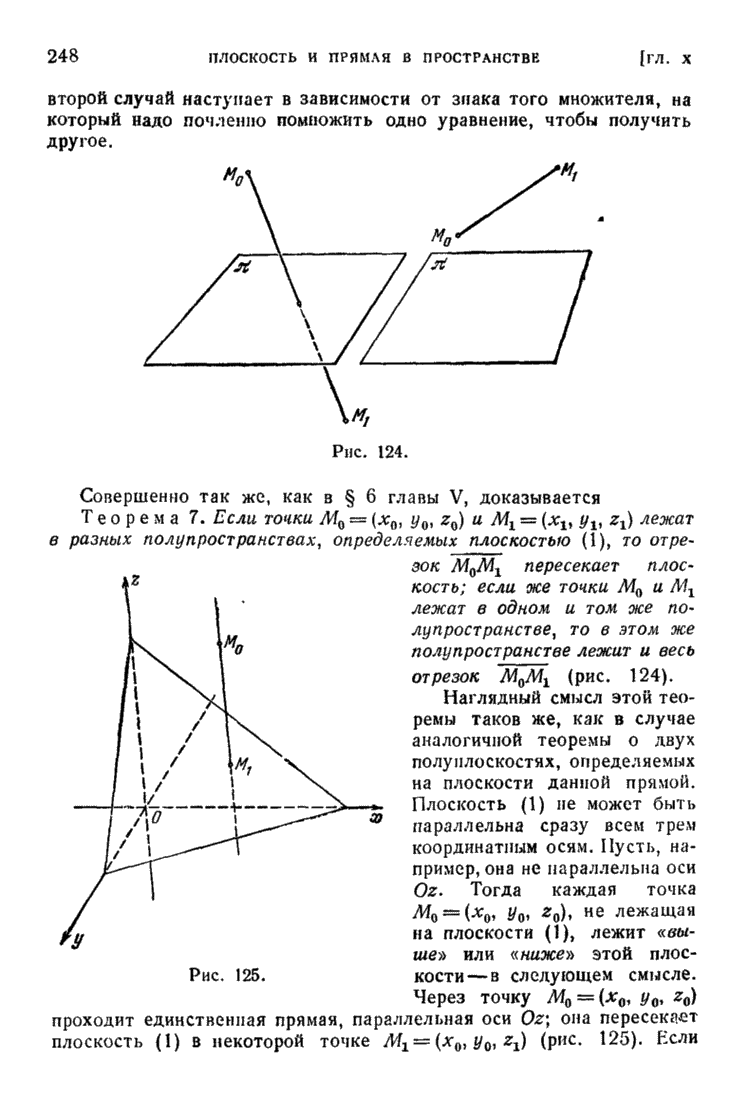
- § 7. О двух полупространствах, определяемых данной плоскостью
- § 8. Плоскость в прямоугольной системе координат; нормальное уравнение плоскости; расстояние от точки до плоскости
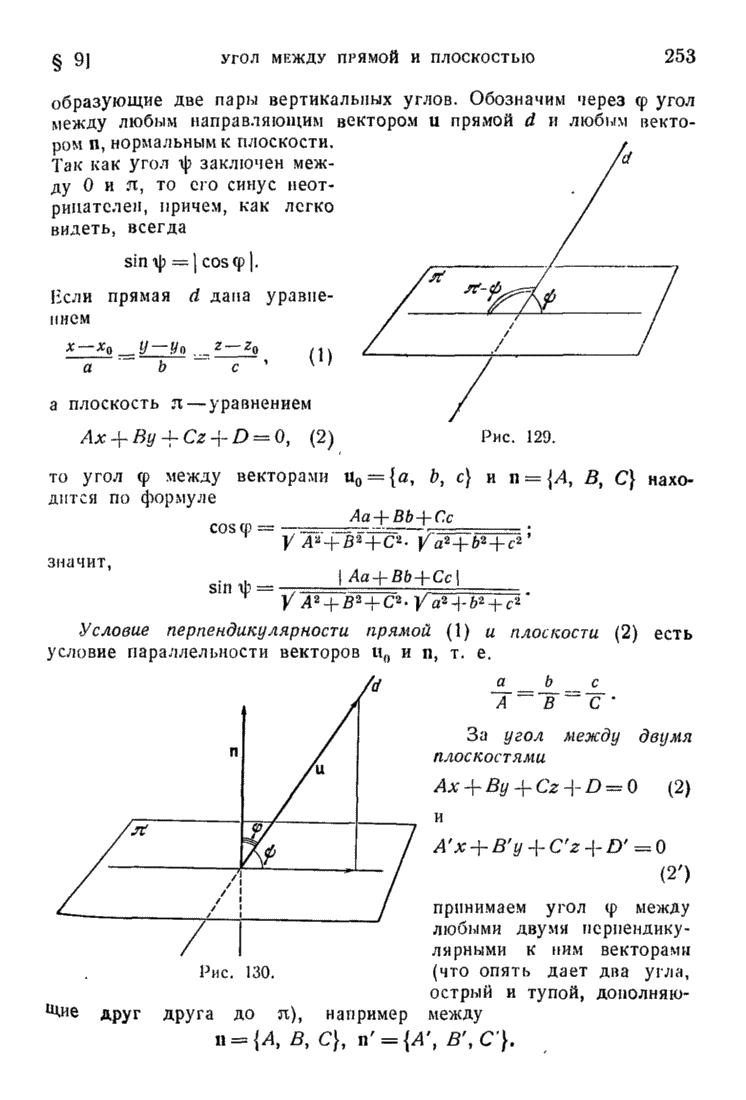
- § 9. Угол между прямой и плоскостью; угол между двумя плоскостями
- § 10. Две задачи
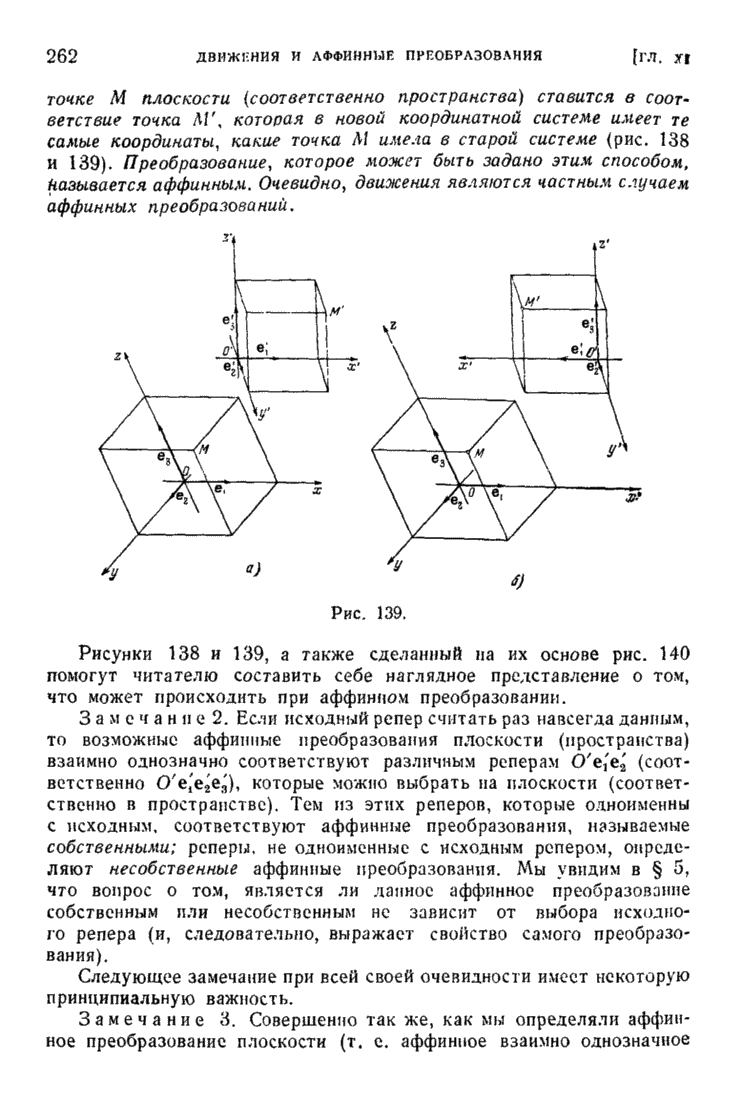
- ГЛАВА XI. ДВИЖЕНИЯ И АФФИННЫЕ ПРЕОБРАЗОВАНИЯ
- § 1. Определение движений и аффинных преобразований
- § 2. Преобразование векторов при аффинном преобразовании плоскости и пространства. Основные свойства аффинных преобразований
- § 3. Аналитическое выражение аффинных преобразований
- § 4. Сохранение отношений площадей и объемов при аффинных преобразованиях
- § 5. Получение собственных аффинных преобразований посредством деформации тождественного преобразования. Следствия
- § 6. Движения как изометрические преобразования
- § 7. Преобразования подобия
- § 8. Классификация движений прямой и плоскости
- ГЛАВА XII. ВЕКТОРНЫЕ ПРОСТРАНСТВА (МНОГООБРАЗИЯ) ЛЮБОГО КОНЕЧНОГО ЧИСЛА ИЗМЕРЕНИЙ. СИСТЕМЫ ЛИНЕЙНЫХ ОДНОРОДНЫХ УРАВНЕНИЙ
- § 1. Определение векторного пространства
- § 2. Размерность. Базис. Координаты
- § 3. Теорема об изоморфизме между любыми двумя векторными пространствами одной и той же конечной размерности n
- § 4. Подпространства векторного пространства. Дальнейшие теоремы о линейной зависимости векторов и о базисе векторного пространства
- § 5. Алгебраическая (в частности, прямая) сумма подпространств
- § 6. Линейные отображения векторных пространств
- § 7. Теорема о ранге матрицы
- § 8. Системы линейных однородных уравнения
- ГЛАВА XIII. ЛИНЕЙНЫЕ, БИЛИНЕЙНЫЕ И КВАДРАТИЧНЫЕ ФУНКЦИИ НА ВЕКТОРНЫХ ПРОСТРАНСТВАХ
- § 1. Линейные функции
- § 2. Билинейные функции и билинейные формы
- § 3. Матрица билинейной и квадратичной формы и ее преобразование при переходе к новому базису (при преобразовании переменных)
- § 4. Ранг билинейной и квадратичной формы (билинейной и квадратичной функции)
- § 5. Существование канонического базиса для всякой квадратичной и всякой билинейной функции («приведение квадратичных форм к каноническому виду»)
- ГЛАВА XIV. ТОЧЕЧНО-ВЕКТОРНОЕ АФФИННОЕ n-МЕРНОЕ ПРОСТРАНСТВО
- § 1. Определение n-мерного аффинного пространства
- § 2. Системы координат. Арифметическое пространство. Изоморфизм всех n-мерных пространств между собою
- § 3. r-мерные плоскости n-мерного аффинного пространства; r-мерные параллелепипеды
- § 4. Геометрически независимые системы точек. Барицентрические координаты. Симплексы
- § 5. Системы линейных уравнений
- § 6. Аффинные преобразования n-мерного аффинного пространства
- ГЛАВА XV. АЛГЕБРАИЧЕСКИЕ ЛИНИИ И ПОВЕРХНОСТИ. КОМПЛЕКСНАЯ ПЛОСКОСТЬ И КОМПЛЕКСНОЕ ПРОСТРАНСТВО
- § 1. Определение алгебраических линий и поверхностей
- § 2. Преобразование многочлена второй степени при преобразовании координат
- § 3. Аффинная эквивалентность линий и поверхностей
- § 4. Комплексная плоскость
- § 5. Прямая линия на комплексной плоскости
- § 6. Замечание о действительных и мнимых линиях
- § 7. Комплексное пространство
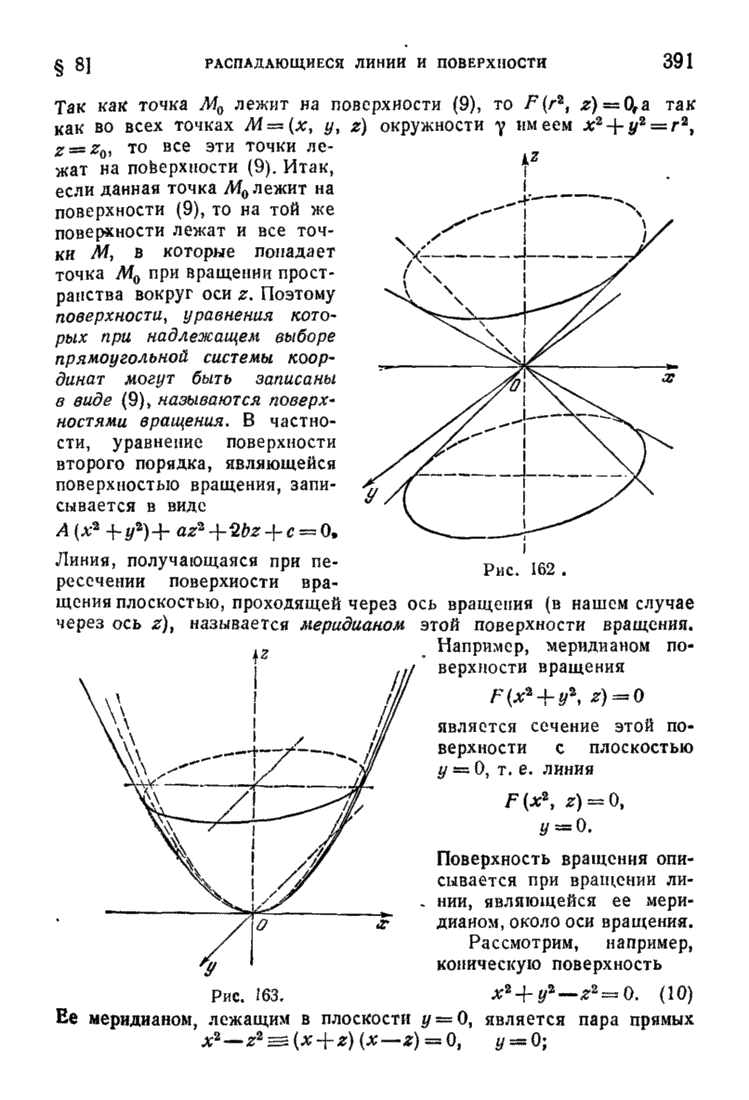
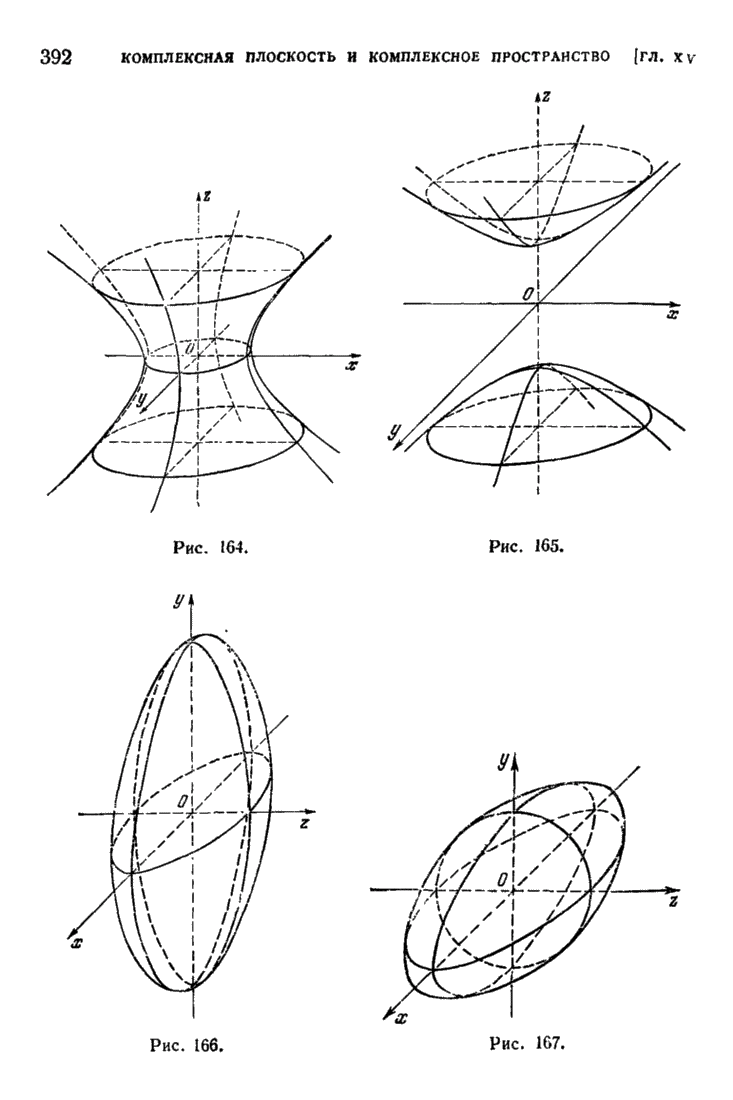
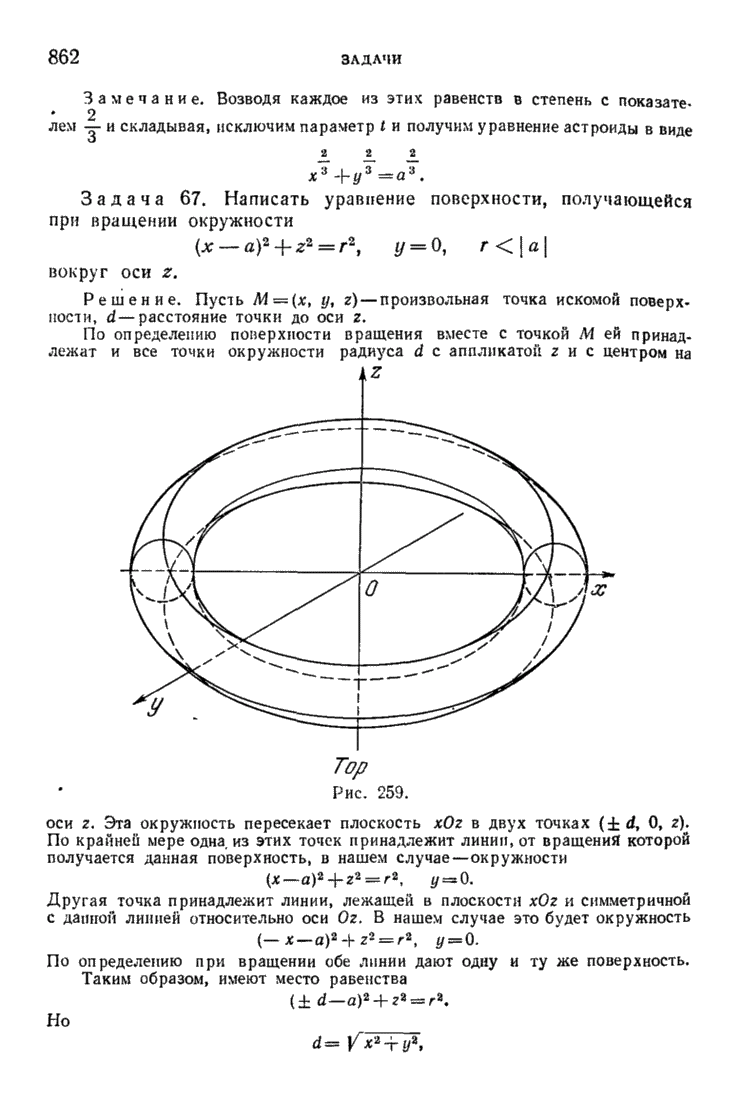
- § 8. Распадающиеся линии и поверхности. Цилиндрические и конические поверхности. Поверхности вращения
- § 9. Несколько заключительных замечаний о линиях и поверхностях
- ГЛАВА XVI. Различные виды кривых второго порядка
- § 1. О линиях, определяемых уравнениями второй степени с двумя неизвестными
- § 2. Инварианты многочлена второй степени
- § 3. Центральный случай
- § 4. Параболический случай
- § 5. Аффинная классификация кривых второго порядка
- § 6. Несколько заключительных замечаний
- ГЛАВА XVII. ОБЩАЯ ТЕОРИЯ КРИВЫХ ВТОРОГО ПОРЯДКА
- § 1. Пересечение алгебраической кривой с прямой. Асимптотические направления и асимптоты алгебраической кривой
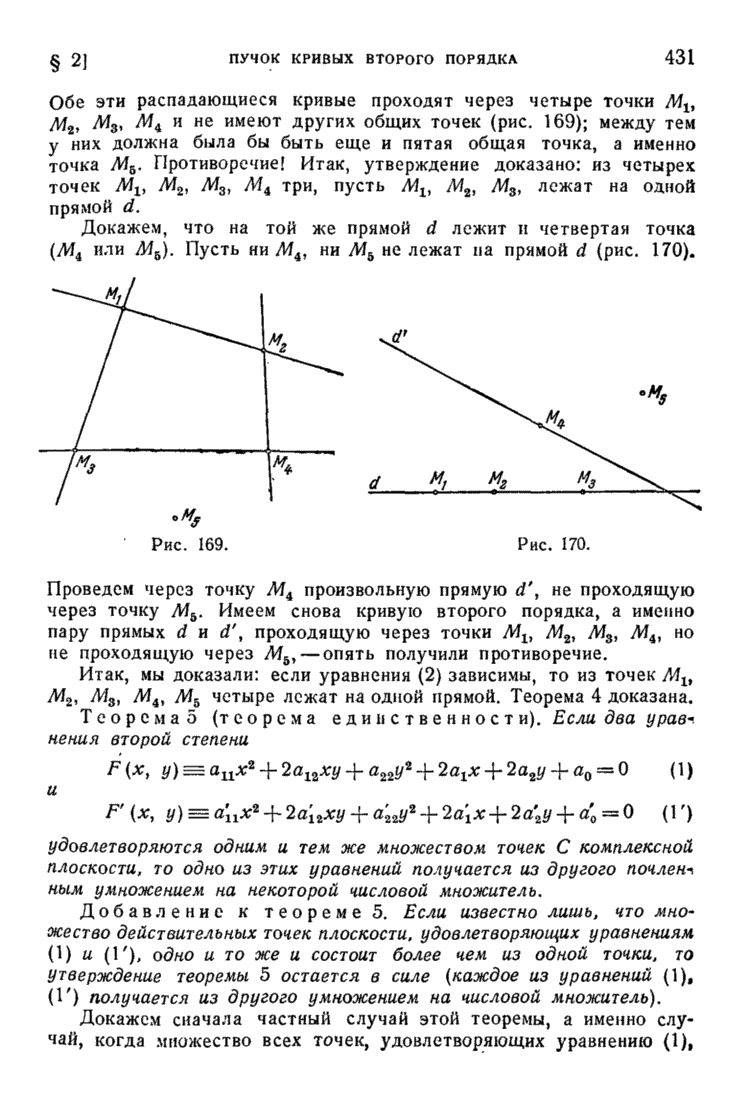
- § 2. Теорема единственности для кривых второго порядка. Пучок кривых второго порядка
- § 3. Асимптотические направления кривых второго порядка
- § 4. Пересечение кривой второго порядка с прямой иеасимптотического направления. Касательные
- § 5. Пересечение кривой второго порядка с прямой асимптотического направления. Геометрическая характеристика асимптотических и неасимптотических направлений
- § 6. Центр кривой второго порядка
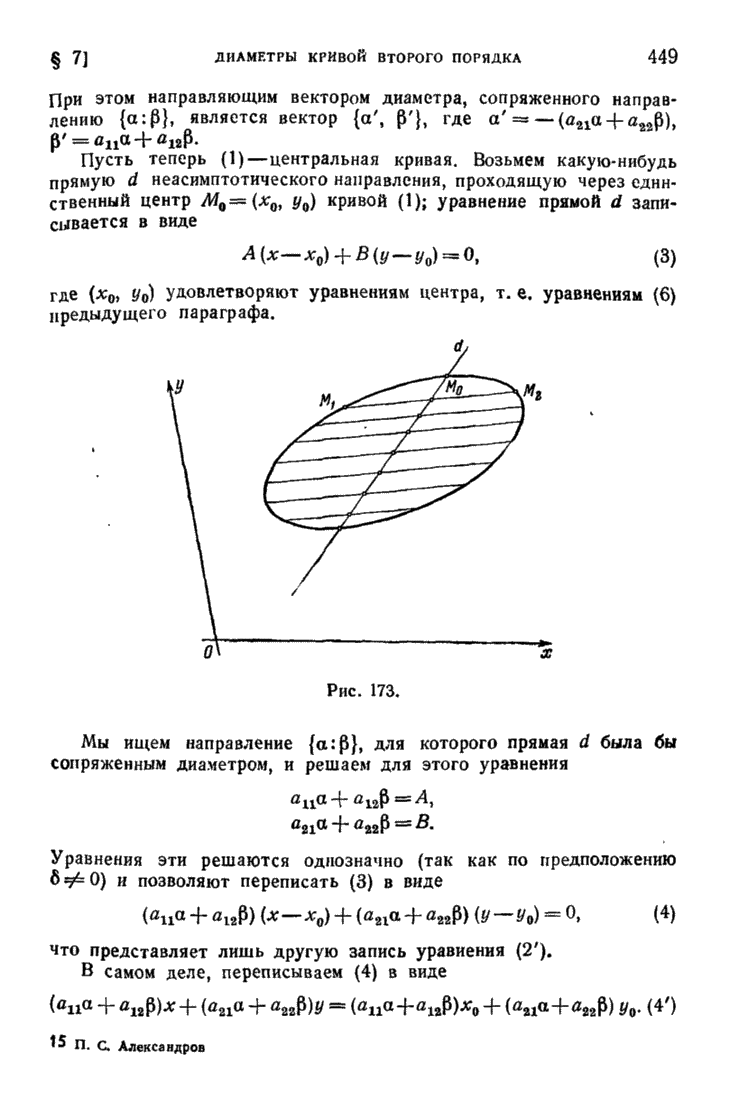
- § 7. Диаметры кривой второго порядка
- § 8. Взаимно сопряженные векторы (направления). Диаметры и касательные
- § 9. Вид уравнения кривой, если оси координат имеют сопряженные направления
- § 10. Второе доказательство теоремы единственности. О полноте системы ортогональных инвариантов
- § 11. Оси симметрии и главные направления кривой второго порядка
- § 12. Основная теорема об аффинных преобразованиях
- ГЛАВА XVIII. КРАТКОЕ ОПИСАНИЕ РАЗЛИЧНЫХ ВИДОВ ПОВЕРХНОСТЕЙ ВТОРОГО ПОРЯДКА
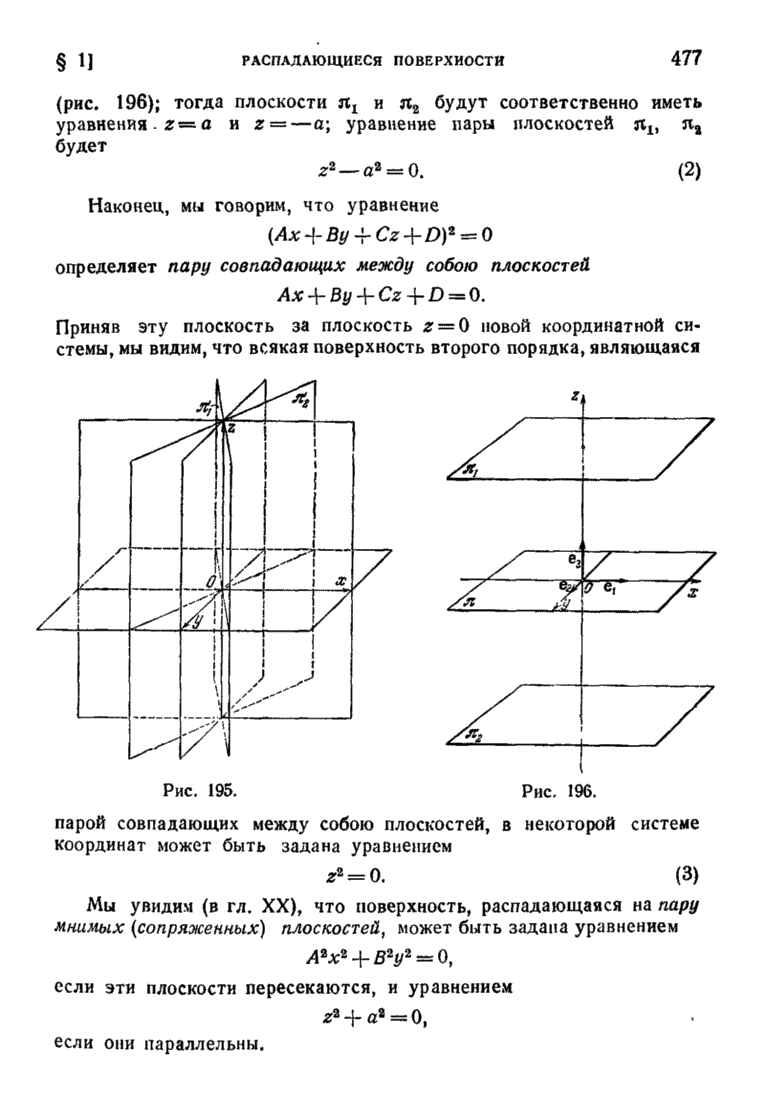
- § 1. Распадающиеся поверхности
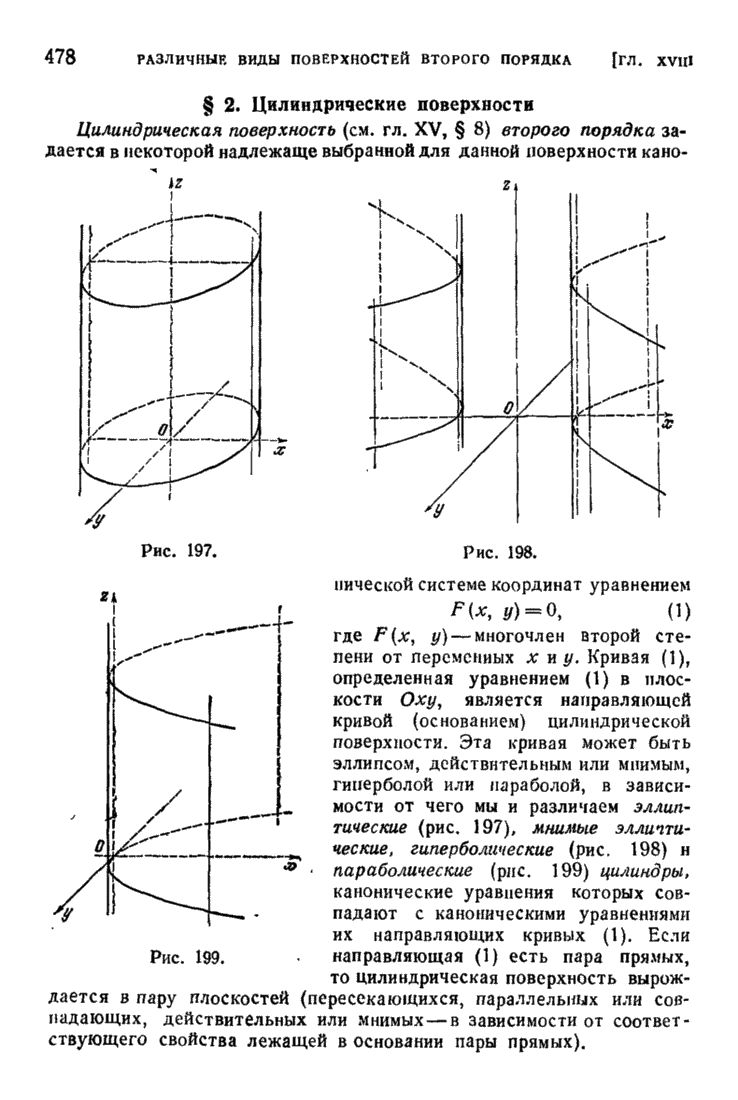
- § 2. Цилиндрические поверхности
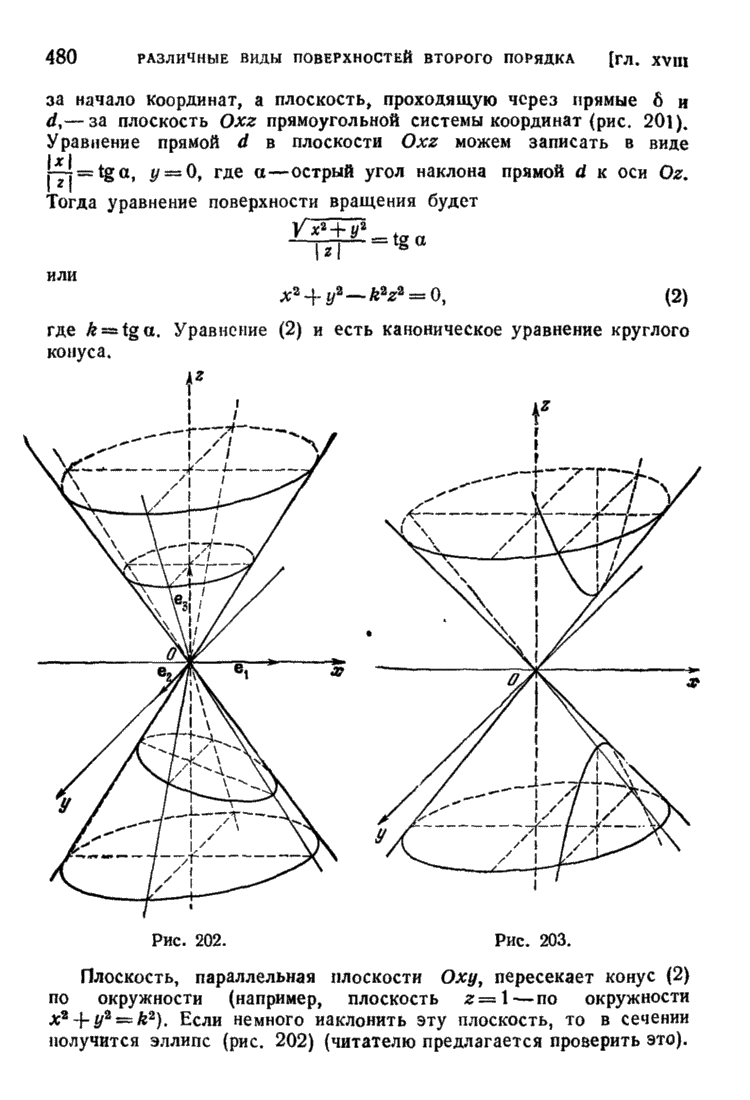
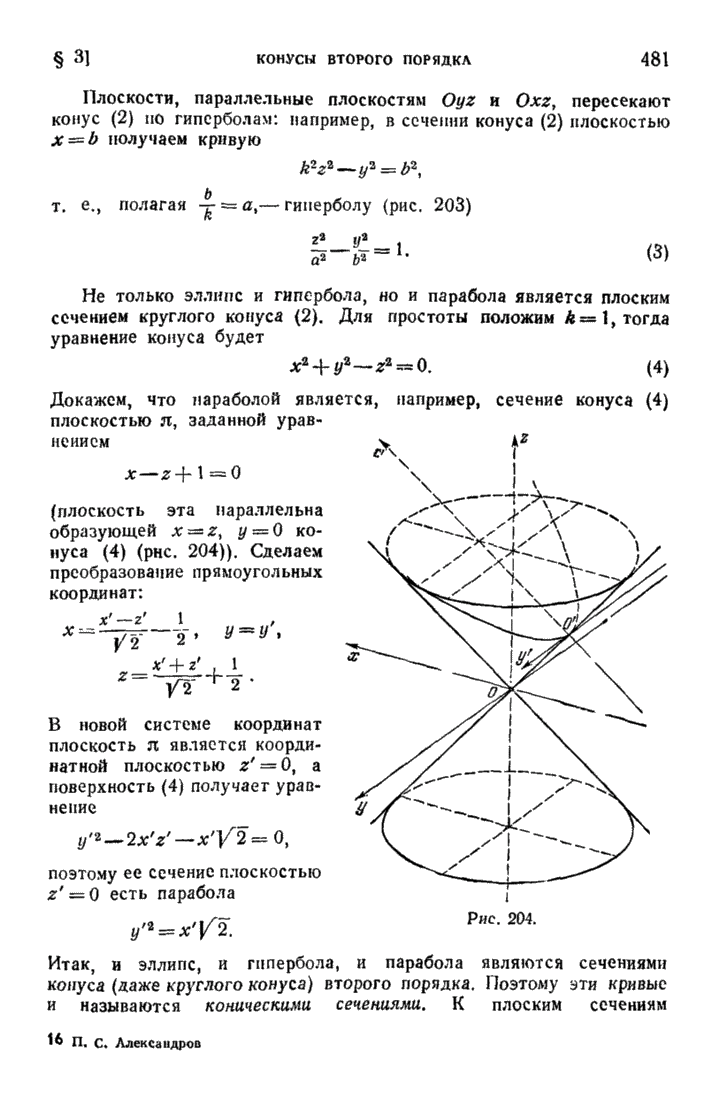
- § 3. Конусы второго порядка
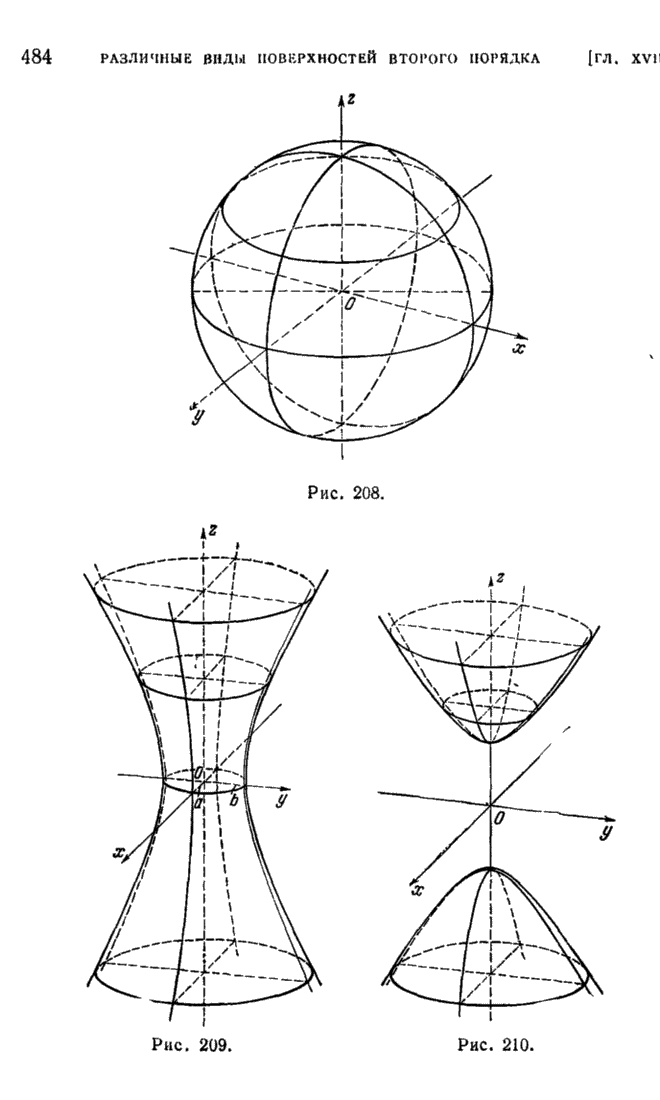
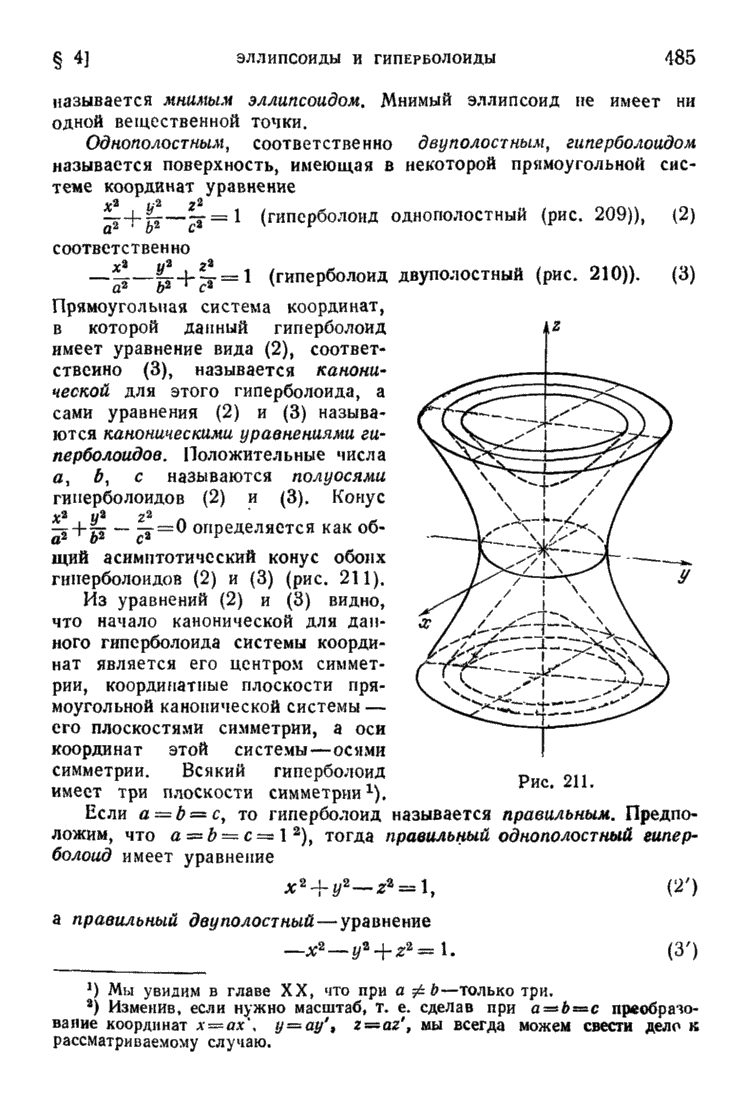
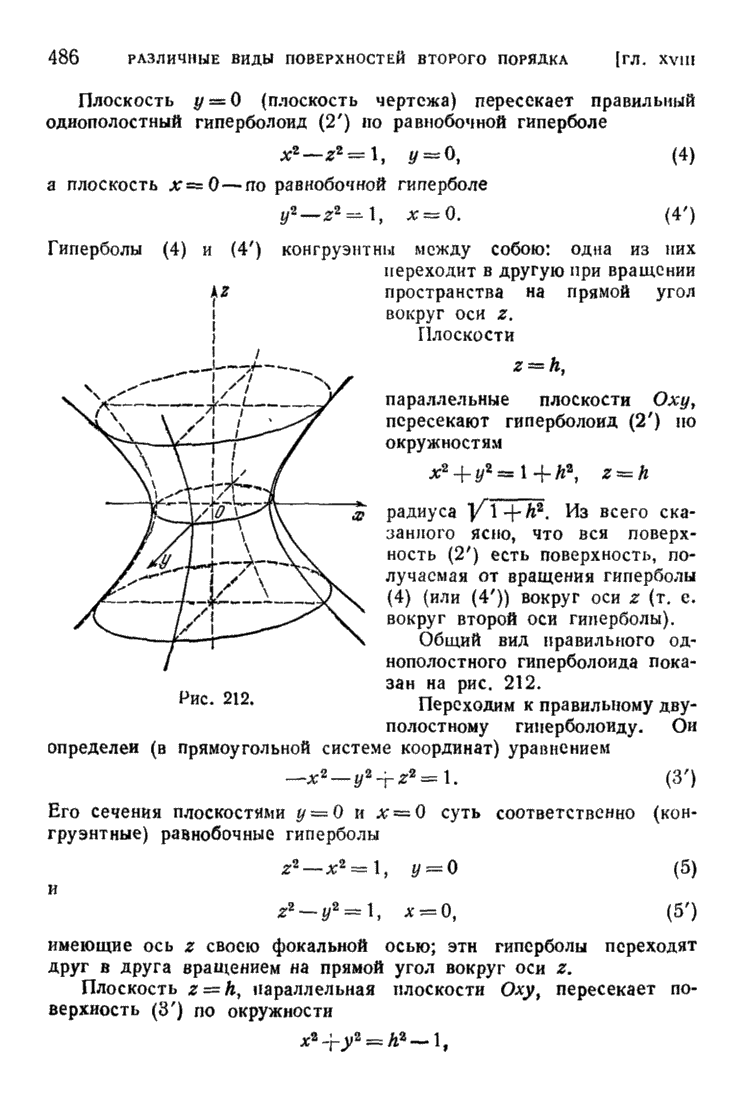
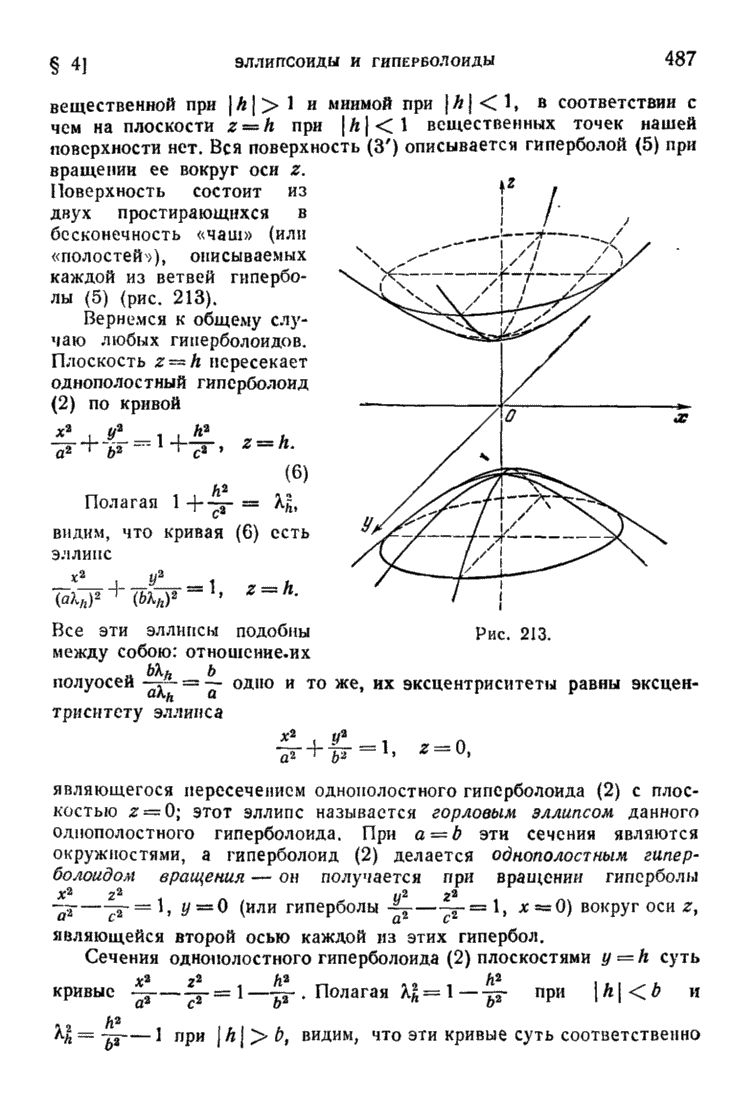
- § 4. Эллипсоиды и гиперболоиды
- § 5. Параболоиды
- § 6. Прямолинейные образующие
- ГЛАВА XIX. ОБЩАЯ ТЕОРИЯ ПОВЕРХНОСТЕЙ ВТОРОГО ПОРЯДКА. I (ПЕРЕСЕЧЕНИЕ С ПЛОСКОСТЬЮ И С ПРЯМОЙ; АСИМПТОТИЧЕСКИЕ НАПРАВЛЕНИЯ; КАСАТЕЛЬНАЯ ПЛОСКОСТЬ; ЦЕНТР)
- § 1. Ранг и детерминант малой и большой матрицы многочлена второй степени
- § 2. Пересечение поверхности второго порядка с плоскостью
- § 3. Пересечение поверхности второго порядка с прямой. Асимптотические направления. Касательные прямые и касательная плоскость. Особые точки поверхности второго порядка
- § 4. Асимптотические направления, конус асимптотических направлений, прямолинейные образующие поверхностей второго порядка
- § 5. Центр поверхности второго порядка
- ГЛАВА XX. ОБЩАЯ ТЕОРИЯ ПОВЕРХНОСТЕЙ ВТОРОГО ПОРЯДКА. II (ДИАМЕТРАЛЬНЫЕ ПЛОСКОСТИ; ОСОБЫЕ И ГЛАВНЫЕ НАПРАВЛЕНИЯ; АФФИННАЯ КЛАССИФИКАЦИЯ)
- § 1. Диаметральные плоскости. Особые направления
- § 2. Диаметральные плоскости поверхностей различных видов
- § 3. Сопряженные направления
- § 4. Уравнение поверхности второго порядка относительно координатной системы с сопряженными направлениями осей
- § 5. Теорема единственности
- § 6. Главные направления
- § 7. Приведение к каноническому виду уравнения поверхности второго порядка
- § 8. Аффинная классификация поверхностей второго порядка
- ГЛАВА XXI. ПРОЕКТИВНАЯ ПЛОСКОСТЬ
- § 1. Перспективное соответствие между плоскостью и связкой
- § 2. Однородные координаты точек на плоскости и лучел в связке
- § 3. Координаты прямой; арифметическая проективная плоскость; общее определение проективной плоскости
- § 4. Принцип двойственности для проективной плоскости
- § 5. Проективная система координат в связке и на проективной плоскости
- § 6. Проективные преобразования и отображения проективной плоскости
- § 7. Проективные координаты на прямой. Проективные отображения прямой
- § 8. Двойное отношение
- ГЛАВА XXII. КРИВЫЕ ВТОРОГО ПОРЯДКА НА ПРОЕКТИВНОЙ ПЛОСКОСТИ
- § 1. Определение. Теорема единственности
- § 2. Пересечение кривой второго порядка с прямой. Касательные; асимптоты
- § 3. Пучок кривых второго порядка. Второе доказательство теоремы единственности. Теорема Паскаля. Теорема Штейнера
- § 4. Поляры и полюсы
- § 5. Коррелятивное, в частности полярное, соответствие. Тангенциальное уравнение кривой
- § 6. Диаметры как поляры несобственных точек
- § 7. Автополярный треугольник
- § 8. Проективная классификация кривых второго порядка
- ГЛАВА XXIII. НАЧАЛЬНЫЕ СВЕДЕНИЯ ИЗ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ ПРОЕКТИВНОГО ПРОСТРАНСТВА
- § 1. Проективное пространство; его плоскости и прямые
- § 2. Проективные координаты. Проективные преобразования.
- § 3. Понятие об n-мерном проективном пространстве
- § 4. Поверхности второго порядка в проективном пространстве. Теорема единственности
- § 5. Пересечение поверхности второго порядка с плоскостью и с прямой. Касательные прямые. Касательная плоскость. Прямолинейные образующие
- § 6. Полюсы и полярные плоскости
- § 7. Проективная классификация поверхностей второго порядка
- § 8. Распределение по проективным классам поверхностей различных аффинных классов. Проективно-аффинная классификация поверхностей второго порядка
- ГЛАВА XXIV. ЕВКЛИДОВО n-МЕРНОЕ ПРОСТРАНСТВО
- § 1. Введение. Ортогональные матрицы
- § 2. Положительно определенные симметричные билинейные функции в векторном пространстве
- § 3. Определение евклидовых пространств и простейших относящихся к ним понятий
- § 4. Неравенство Коши—Буняковского и его следствия. Углы
- § 5. Подпространства евклидовых пространств. Ортогональное дополнение к данному подпространству
- ГЛАВА XXV. ЛИНЕЙНЫЕ ОПЕРАТОРЫ, БИЛИНЕЙНЫЕ И КВАДРАТИЧНЫЕ ФУНКЦИИ В ЕВКЛИДОВЫХ ПРОСТРАНСТВАХ. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
- § 1. Инвариантные подпространства и собственные векторы линейного оператора в любом векторном пространстве
- § 2. Ортогональные преобразования n-мерного евклидова пространства
- § 3. Движения трехмерного евклидова пространства
- § 4. Преобразования подобия. Дальнейшие проблемы
- § 5. Самосопряженные операторы
- § 6. Теорема о структуре произвольного линейного преобразования евклидова пространства
- § 7. Билинейные и квадратичные формы в евклидовых пространствах
- § 8. (n-1)-мерные многообразия (поверхности) второго поряд] в -мерном аффинном и евклидовом пространствах
- ПРИБАВЛЕНИЕ. ПЕРЕСТАНОВКИ, МНОЖЕСТВА И ИХ ОТОБРАЖЕНИЯ; ГРУППЫ
- § 1. Перестановки
- § 2. Множества
- § 3. Отображения или функции
- § 4. Разбиение множества на подмножества. Отношение эквивалентности
- § 5. Определение группы
- § 6. Простейшие теоремы о группах
- § 7. Эквивалентность подмножеств данного множества по отношению к дайной группе его преобразований
- ЗАДАЧИ
- Задачи к главе IV
- Задачи к главе V
- Задачи к главе VI
- Задачи к главе VIII
- Задачи к главе IX
- Задачи к главе X
- Задачи к главе XI
- Задачи к главе XII
- Задачи к главе XIII
- Задачи к главе XIV
- Задачи к главе XV
- Задачи к главам XVI и XVII
- Задачи к главе XVIII
- Задачи к главам XIX и XX
- Задачи к главе XXI
- Задачи к главе XXII