| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
3.14. Электромагнитная индукция
Закон электромагнитной индукции. При перемещении или деформации контура с током в постоянном магнитном поле силы Ампера, направленные на каждом участке перпендикулярно току, согласно (62) совершают механическую работу  Так как полная работа силы Лоренца над любой движущейся частицей равна нулю, то такая же по величине, но обратная по знаку работа совершается магнитным полем (тангенциальной компонентой силы Лоренца) над движущимися по контуру свободными зарядами, что приводит к возникновению в контуре дополнительной ЭДС индукции:
Так как полная работа силы Лоренца над любой движущейся частицей равна нулю, то такая же по величине, но обратная по знаку работа совершается магнитным полем (тангенциальной компонентой силы Лоренца) над движущимися по контуру свободными зарядами, что приводит к возникновению в контуре дополнительной ЭДС индукции:

Из принципа относительности Эйнштейна следует, что ЭДС индукции должна возникать и при помещении неподвижного контура в изменяющееся со временем магнитное поле. Рассмотрим, например, сближение с постоянной скоростью замкнутого контура и постоянного магнита. В инерциальной системе отсчета (ИСО), связанной с магнитом, создаваемое им поле не зависит от времени, и возникновение ЭДС в контуре объясняется действием силы Лоренца. В другой ИСО, связанной с контуром, наблюдается такая же ЭДС, но в неподвижном проводнике она не может быть вызвана магнитными силами. Следовательно, в изменяющемся со временем магнитном поле должно возникать электрическое поле. Так как работа этого поля при обходе контура должна быть отлична от нуля, то это поле не является электростатическим: его называют вихревым электрическим полем. Итак, независимо от причины, по которой меняется пронизывающий контур магнитный поток, в нем возникает ЭДС индукции, равная

(закон Фарадея). Средняя ЭДС индукции за конечное время  равна
равна  Прошедший по контуру за это время заряд равен
Прошедший по контуру за это время заряд равен  где
где  — сопротивление контура.
— сопротивление контура.
Правило Ленца. Направление ЭДС определяется ее знаком; напомним (см. разд. 3.12), что контур должен быть ориентир о ванным: положительное направление нормали к поверхности при вычислении Ф и положительное направление обхода контура для определения знака ЭДС должны быть связаны правилом буравчика. Знак в формуле (76) соответствует правилу Ленца, которое утверждает, что ЭДС индукции должна иметь такое направление, чтобы магнитное поле текущего в этом направлении тока создавало магнитный поток противоположного знака по сравнению с тем изменением потока, которое является причиной возникновения ЭДС. Правило Ленца тесно связано с законом сохранения энергии.
Движение участка контура. При движении элемента контура  со скоростью
со скоростью  работа силы Лоренца по переносу, пробного заряда
работа силы Лоренца по переносу, пробного заряда  вдоль
вдоль  равна
равна  наводимые при
наводимые при

Рис. 44.
произвольном движении участка и при поступательном движении в однородном поле, равны соответственно:

где  — вектор, соединяющий начало и конец участка. Если концы движущегося проводника разомкнуты, то между ними возникает разность потенциалов, равная ЭДС (в каждой точке проводника электростатическая сила уравновешивается силой Лоренца).
— вектор, соединяющий начало и конец участка. Если концы движущегося проводника разомкнуты, то между ними возникает разность потенциалов, равная ЭДС (в каждой точке проводника электростатическая сила уравновешивается силой Лоренца).
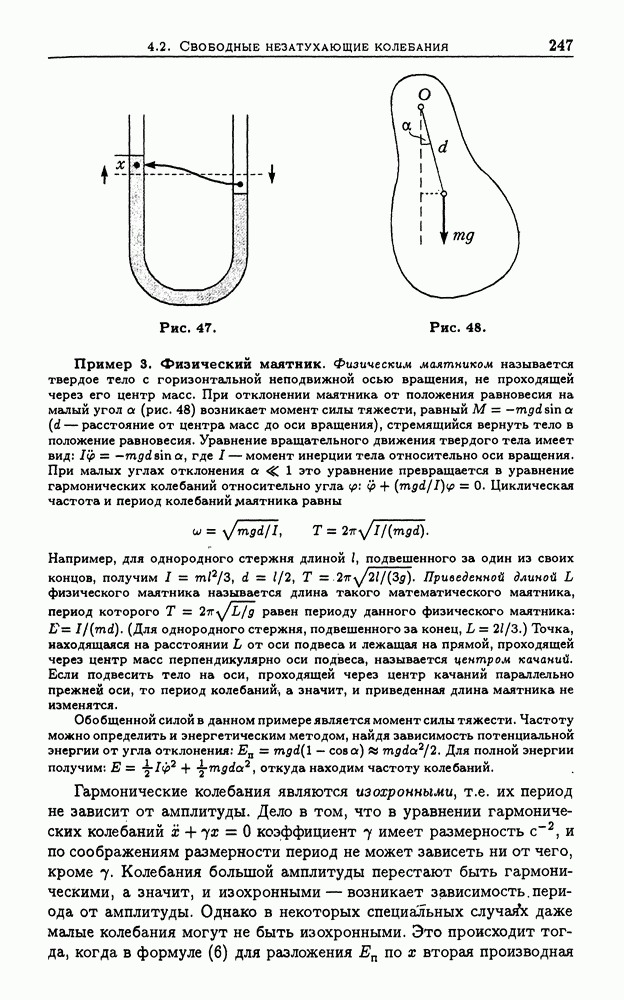
Пример 1. Рассмотрим движение перемычки сопротивлением  в вертикальном магнитном поле (рис. 44) по двум горизонтальным рельсам, расстояние между которыми равно I. Предположим, что рельсы замкнуты с одной стороны от перемычки сопротивлением
в вертикальном магнитном поле (рис. 44) по двум горизонтальным рельсам, расстояние между которыми равно I. Предположим, что рельсы замкнуты с одной стороны от перемычки сопротивлением  а с другой — сопротивлением
а с другой — сопротивлением  Чтобы найти ток через перемычку при ее движении со скоростью
Чтобы найти ток через перемычку при ее движении со скоростью  используя (77), вычислим ЭДС в перемычке:
используя (77), вычислим ЭДС в перемычке:  Тот факт, что ЭДС локализована в движущейся перемычке, позволяет изобразить эквивалентную схему и найти силу тока:
Тот факт, что ЭДС локализована в движущейся перемычке, позволяет изобразить эквивалентную схему и найти силу тока:  , где
, где 
Уравнения вихревого электрического поля. Уравнение для вихревого поля в интегральной форме получается при записи закона Фарадея (76) для неподвижного контура в переменном магнитном поле:

Так как циркуляция напряженности электростатического поля по замкнутому контуру равна нулю, то такому же уравнению удовлетворяет полное электрическое поле. Дифференциальная форма этого уравнения имеет вид

Уравнения (78), (79) представляют собой одно из уравнений Максвелла (в интегральной и дифференциальной формах).
Квазистационарное приближение. Если токи и поля меняются не очень быстро, то можно пренебречь запаздыванием процессов по времени. Сказанное означает, что переменное магнитное поле в любой точке системы определяется (по формулам Био — Савара — Лапласа) токами в этот же момент времени; электростатическое поле определяется распределением зарядов в этот же момент времени,
а вихревое электрическое поле вычисляется по изменяющемуся магнитному полю с помощью (78), (79). Именно в этом приближении рассчитываются цепи переменного тока. Для выполнения этого приближения надо, чтобы характерное время изменения токов  было велико по сравнению, во-первых, с временами локальных релаксационных процессов (например, временем установления равновесного распределения заряда на проводнике
было велико по сравнению, во-первых, с временами локальных релаксационных процессов (например, временем установления равновесного распределения заряда на проводнике  и во-вторых, со временем запаздывания
и во-вторых, со временем запаздывания  характерный размер системы). Последнее условие означает, что мы пренебрегаем током смещения в уравнениях Максвелла.
характерный размер системы). Последнее условие означает, что мы пренебрегаем током смещения в уравнениях Максвелла.
Пример 2. Оценим время перераспределения заряда на проводнике. Будем считать, что где-то в проводнике образовался объемный заряд. Убывание заряда внутри произвольного объема подчиняется уравнению

Самоиндукция и взаимная индукция. Рассмотрим неподвижный контур с током. Предположим, что ток I в этом контуре равномерно изменяется со временем. Создаваемая этим током магнитная индукция будет меняться со скоростью, пропорциональной  Следовательно, возникающее в каждой точке пространства вихревое поле тоже пропорционально
Следовательно, возникающее в каждой точке пространства вихревое поле тоже пропорционально  Это поле создает в контуре ЭДС самоиндукции:
Это поле создает в контуре ЭДС самоиндукции:

где L называется коэффициентом самоиндукции или индуктивностью контура. Индуктивность измеряется в генри (в СГС — в см). Величину  в
в  называют потокосцеплением самоиндукции контура. С учетом (80) получим:
называют потокосцеплением самоиндукции контура. С учетом (80) получим:

Эта формула оказывается верной и в том случае, когда изменяется не только  но и
но и 
Заметим, что определение  как коэффициента пропорциональности между потоком и током встречается с трудностями: в случае линейного провода собственный поток бесконечен, а для провода конечной толщины обычное определение потока не годится.
как коэффициента пропорциональности между потоком и током встречается с трудностями: в случае линейного провода собственный поток бесконечен, а для провода конечной толщины обычное определение потока не годится.
Пример 3. Индуктивность соленоида. Рассмотрим соленоид длиной  и площадью
и площадью  по которому течет ток с поверхностной плотностью
по которому течет ток с поверхностной плотностью  где
где  — число витков, I — ток в обмотке. Магнитное поле в соленоиде однородно, его индукция (в приближении идеального соленоида) согласно формуле (61) равна
— число витков, I — ток в обмотке. Магнитное поле в соленоиде однородно, его индукция (в приближении идеального соленоида) согласно формуле (61) равна  При изменении тока циркуляция вихревого поля вычисляется так:
При изменении тока циркуляция вихревого поля вычисляется так:  а ЭДС на всей длине обмотки равна
а ЭДС на всей длине обмотки равна  Для индуктивности и потокосцепления
Для индуктивности и потокосцепления
получим:

Пример 4. Так как ЭДС самоиндукции пропорциональна скорости изменения тока, то наличие в контуре индуктивности препятствует слишком быстрым изменениям тока. Предположим, что последовательно соединенные сопротивление  и катушку индуктивностью
и катушку индуктивностью  замкнули на источник с постоянной ЭДС, равной Нарастание тока от нуля до
замкнули на источник с постоянной ЭДС, равной Нарастание тока от нуля до  происходит за конечное время и подчиняется уравнению
происходит за конечное время и подчиняется уравнению  решение которого имеет вид
решение которого имеет вид  . Характерное время нарастания тока равно
. Характерное время нарастания тока равно 
Если имеется два неподвижных контура, то изменение тока одного контура вызовет в другом пропорциональную  взаимной индукции:
взаимной индукции:

где  называются коэффициентами взаимной индукции; для них оказывается верна теорема взаимности:
называются коэффициентами взаимной индукции; для них оказывается верна теорема взаимности:  (в неферромагнитной среде). Потокосцепление взаимной индукции определяется как
(в неферромагнитной среде). Потокосцепление взаимной индукции определяется как  Эта величина оказывается определенной и для двух линейных токов (в этом случае
Эта величина оказывается определенной и для двух линейных токов (в этом случае 
Энергия контура. Энергией контура с током называется работа внешних сил и источников при создании тока (или работа вихревого поля при его уничтожении). Работа источника против ЭДС самоиндукции контура вычисляется так:

При последовательно полевом подходе энергия должна быть связана не с током в контуре, а с магнитным полем. Зависимость плотности энергии от магнитной индукции проще всего установить в случае длинного соленоида, в котором поле однородно:

В случае нелинейной зависимости  от
от  для плотности энергии получается выражение:
для плотности энергии получается выражение:

Используя теорему взаимности  можно получить обобщение выражения (84) для нескольких контуров:
можно получить обобщение выражения (84) для нескольких контуров:

Здесь  полное потокосцепление для
полное потокосцепление для  контура. Видно, что энергия токов включает в себя энергию каждого тока и энергию их взаимодействия. С помощью уравнений магнитного поля можно показать, что это выражение всегда преобразуется к виду:
контура. Видно, что энергия токов включает в себя энергию каждого тока и энергию их взаимодействия. С помощью уравнений магнитного поля можно показать, что это выражение всегда преобразуется к виду:

Закон сохранения энергии и вычисление сил. При медленном изотермическом изменении расположения тел и контуров с током суммарная работа внешних сил и источников тока идет на изменение энергии магнитного поля и на выделение джоулевой теплоты. При этом работа внешних сил над каждым телом равна работе сил, действующих на тело со стороны магнитного поля. Если токи поддерживаются постоянными, то надо учитывать только дополнительную работу источников против ЭДС индукции, а работа исходной ЭДС равна выделяющейся теплоте, и в законе сохранения энергии они сокращаются.
Пример 5. Рассмотрим два контура с токами  которые поддерживаются постоянными. Запишем закон сохранения энергии при медленном смещении первого контура. Согласно (86) изменяется только энергия взаимодействия токов, равная
которые поддерживаются постоянными. Запишем закон сохранения энергии при медленном смещении первого контура. Согласно (86) изменяется только энергия взаимодействия токов, равная  где
где  — поток в первом контуре, создаваемый вторым током. В то же время потенциальная функция контура с током во внешнем поле равна
— поток в первом контуре, создаваемый вторым током. В то же время потенциальная функция контура с током во внешнем поле равна  см. (63). Кажущееся противоречие объясняется, если учесть дополнительную работу источников против ЭДС индукции в каждом контуре. Эта работа равна
см. (63). Кажущееся противоречие объясняется, если учесть дополнительную работу источников против ЭДС индукции в каждом контуре. Эта работа равна  что в два раза больше, чем изменение энергии поля
что в два раза больше, чем изменение энергии поля 
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- 1. Аналитическая геометрия на плоскости
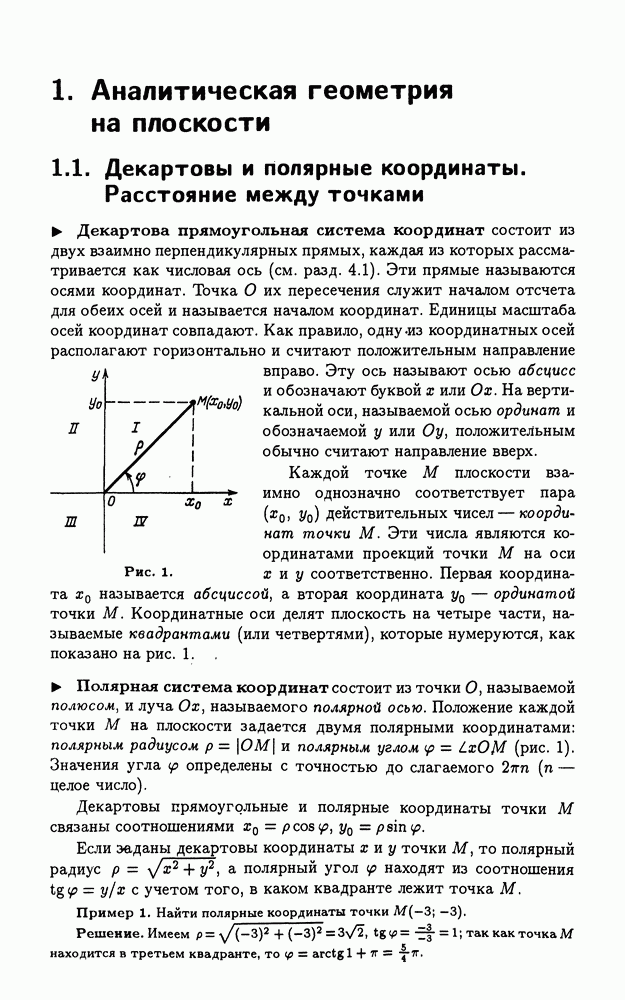
- 1.1. Декартовы и полярные координаты. Расстояние между точками
- 1.2. Деление отрезка в данном отношении. Площадь многоугольника
- 1.3. Различные виды уравнения прямой
- 1.4. Угол между прямыми. Расстояние от точки до прямой
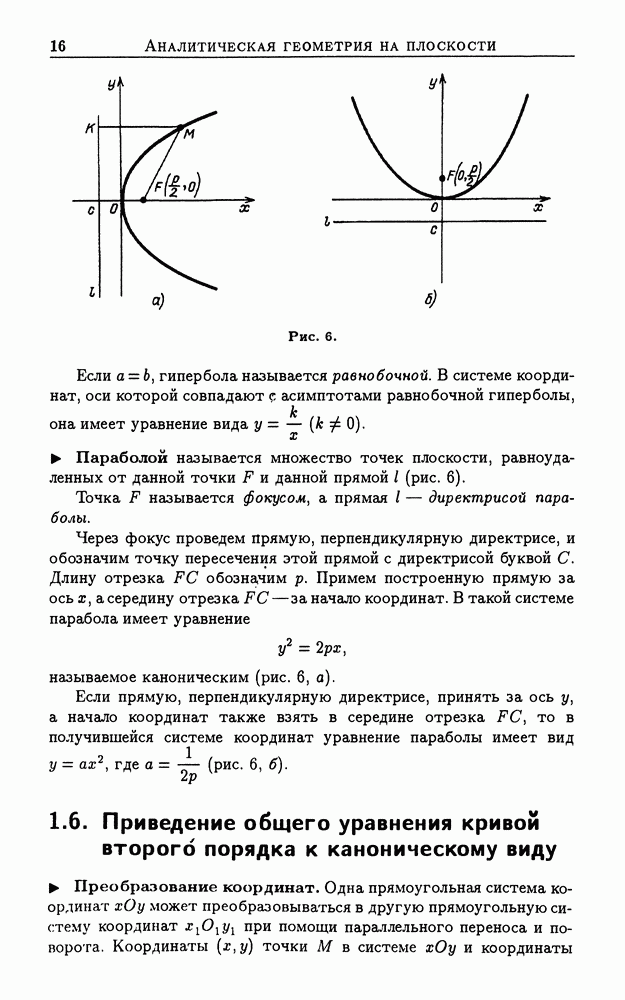
- 1.5. Окружность, эллипс, гипербола и парабола
- 1.6. Приведение общего уравнения кривой второго порядка к каноническому виду
- 2. Аналитическая геометрия в пространстве
- 2.2. Векторы
- 2.3. Действия над векторами. Скалярное произведение
- 2.4. Векторное и смешанное произведения
- 2.5. Плоскость в пространстве
- 2.6. Прямая в пространстве
- 2.7. Прямая и плоскость в пространстве
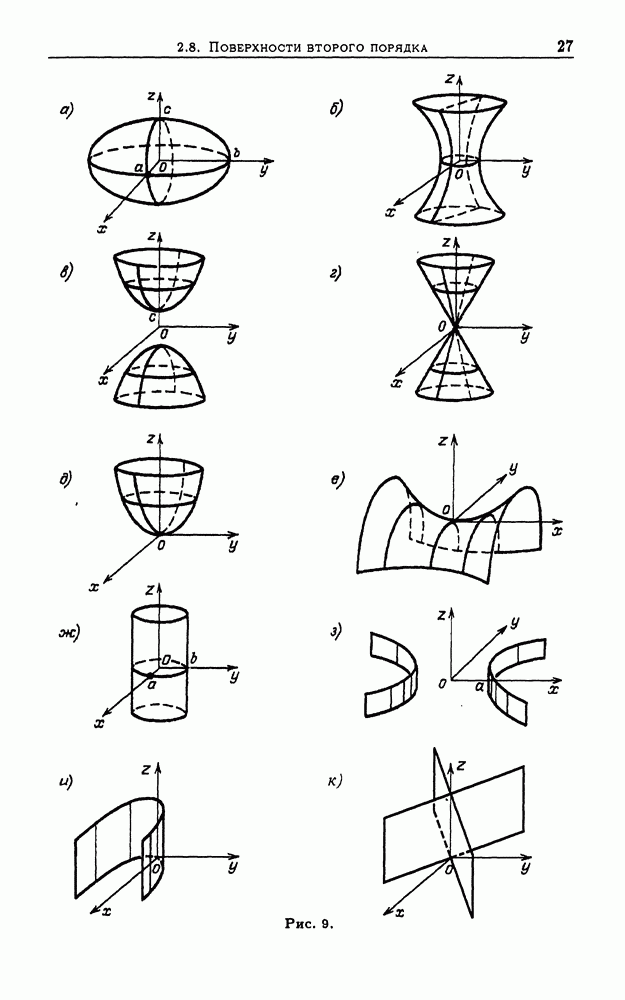
- 2.8. Поверхности второго порядка
- 3. Линейная алгебра
- 3.2. Матрицы
- 3.3. Системы линейных уравнений
- 3.4. Системы n-мерных векторов. Собственные значения и собственные векторы матрицы
- 4. Основные понятия математического анализа
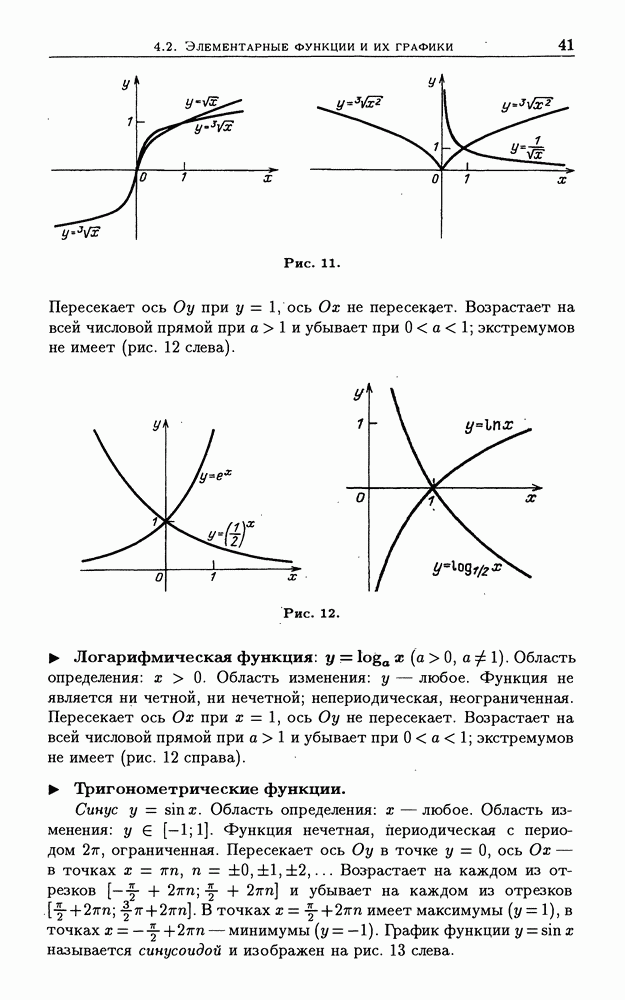
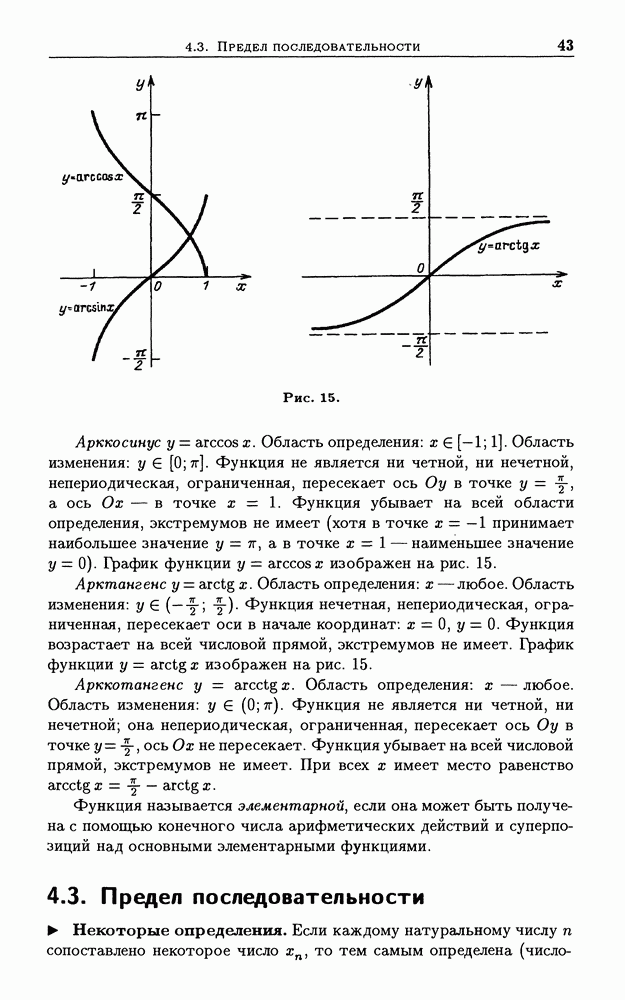
- 4.2. Элементарные функции и их графики
- 4.3. Предел последовательности
- 4.4. Предел функции
- 4.5. Бесконечно малые и бесконечно большие функции
- 4.6. Непрерывность
- 4.7. Асимптоты графика функции
- 5. Дифференциальное исчисление функций одной переменной
- 5.2. Таблица производных и правила дифференцирования
- 5.3. Теоремы о дифференцируемых функциях. Правило Лопиталя
- 5.4. Производные и дифференциалы высших порядков. Формула Тейлора
- 5.5. Экстремумы. Точки перегиба
- 5.6. Общая схема исследования функции и построение графика
- 6. Функции нескольких переменных
- 6.1. Точечные множества. Функции. Предел и непрерывность
- 6.2. Дифференцирование функций нескольких переменных
- 6.3. Производная по направлению. Геометрические приложения
- 6.4. Экстремумы функций нескольких переменных
- 7. Неопределенный интеграл
- 7.1. Первообразная. Неопределенный интеграл и его свойства
- 7.2. Таблица основных интегралов. Примеры интегрирования
- 7.3. Интегрирование по частям. Метод замены переменной
- 7.4. Интегрирование рациональных функций
- 7.5. Интегрирование иррациональных функций
- 7.6. Интегрирование показательных и тригонометрических функций
- 8. Определенный интеграл
- 8.1. Основные определения. Геометрический смысл определенного интеграла
- 8.2. Свойства определенного интеграла
- 8.3. Геометрические и физические приложения определенного интеграла
- 8.4. Несобственные интегралы
- 9. Двойные и тройные интегралы
- 9.1. Определение и свойства двойного интеграла
- 9.2. Вычисление двойного интеграла
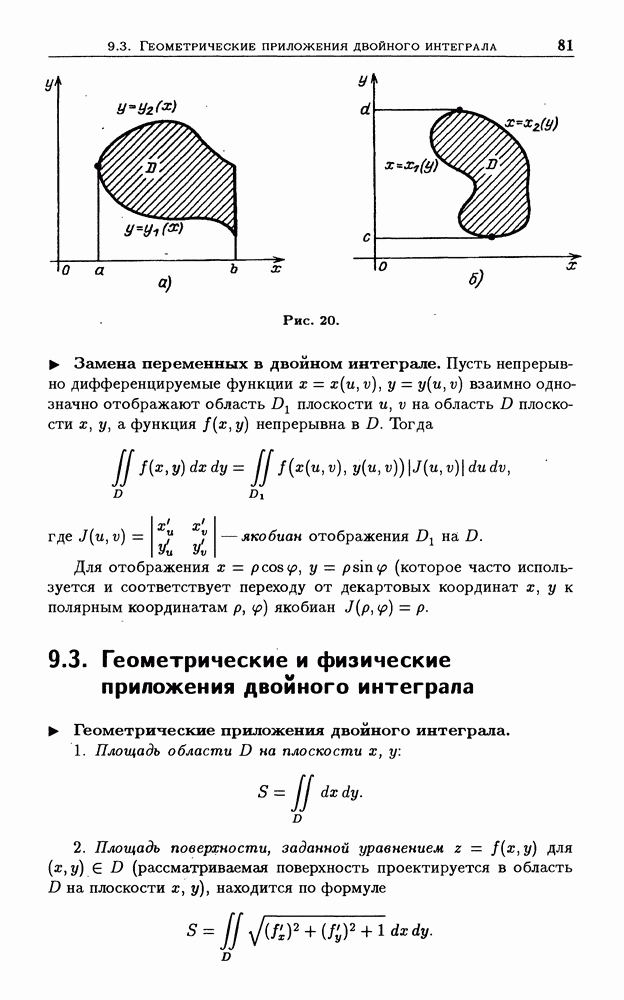
- 9.3. Геометрические и физические приложения двойного интеграла
- 9.4. Определение и свойства тройного интеграла
- 9.5. Вычисление тройного интеграла. Некоторые приложения
- 10. Криволинейные и поверхностные интегралы
- 10.2. Криволинейный интеграл второго рода
- 10.3. Поверхностный интеграл первого рода
- 10.4. Поверхностный интеграл второго рода
- 10.5. Дифференциальные операции и интегральные формулы теории поля
- 11. Ряды
- 11.1. Числовые ряды
- 11.2. Функциональные ряды
- 11.3. Степенные ряды
- 11.4. Ряд Фурье
- 11.5. Интеграл Фурье. Преобразование Фурье
- 12. Обыкновенные дифференциальные уравнения
- 12.2. Дифференциальные уравнения высших порядков
- 12.3. Линейные уравнения n-го порядка
- 12.4. Решение линейных однородных уравнений n-го порядка с постоянными коэффициентами
- 12.5. Линейные неоднородные уравнения n-го порядка
- 12.6. Системы обыкновенных дифференциальных уравнений
- 13. Приближенные вычисления
- 13.1. Метод наименьших квадратов
- 13.2. Приближенное решение алгебраических уравнений
- 13.3. Вычисление определенного интеграла
- 13.4. Численное интегрирование дифференциальных уравнений
- 14. Теория вероятностей
- 14.1. Правила и формулы комбинаторики
- 14.2. Основные понятия теории вероятностей
- 14.3. Условная вероятность. Теоремы и формулы теории вероятностей
- 14.4. Математическое ожидание и дисперсия
- 14.5. Закон больших чисел
- 1. Физические основы механики
- 1.1. Кинематика точки
- 1.2. Кинематика твердого тела
- 1.3. Динамика
- 1.4. Закон сохранения импульса
- 1.5. Закон сохранения энергии
- 1.6. Закон сохранения момента импульса
- 1.7. Задана двух тел и движение в центральном поле
- 1.8. Поле тяготения
- 1.9. Неинерциальные системы отсчета
- 1.10. Динамика твердого тела
- 1.11. Специальная теория относительности
- 2. Молекулярная физика и термодинамика
- 2.2. Первое начало термодинамики
- 2.3. Второе начало термодинамики
- 2.4. Энтропия. Свободная энергия
- 2.5. Кинетическая теория идеального газа
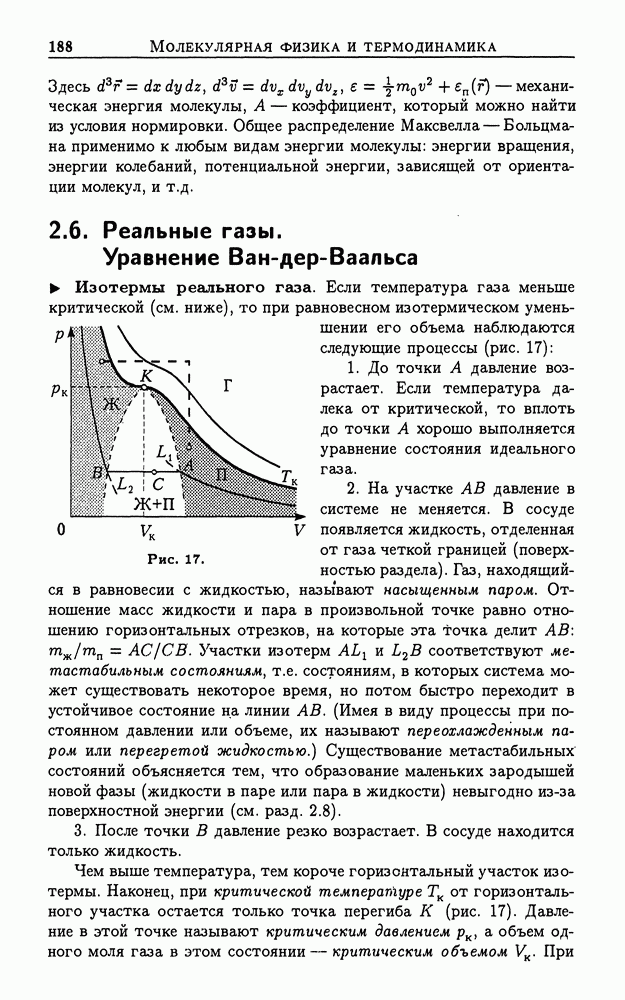
- 2.6. Реальные газы. Уравнение Ван-дер-Ваальса
- 2.7. Равновесие фаз. Фазовые переходы
- 2.8. Поверхностное натяжение
- 2.9. Явления переноса в газах
- 3. Электродинамика
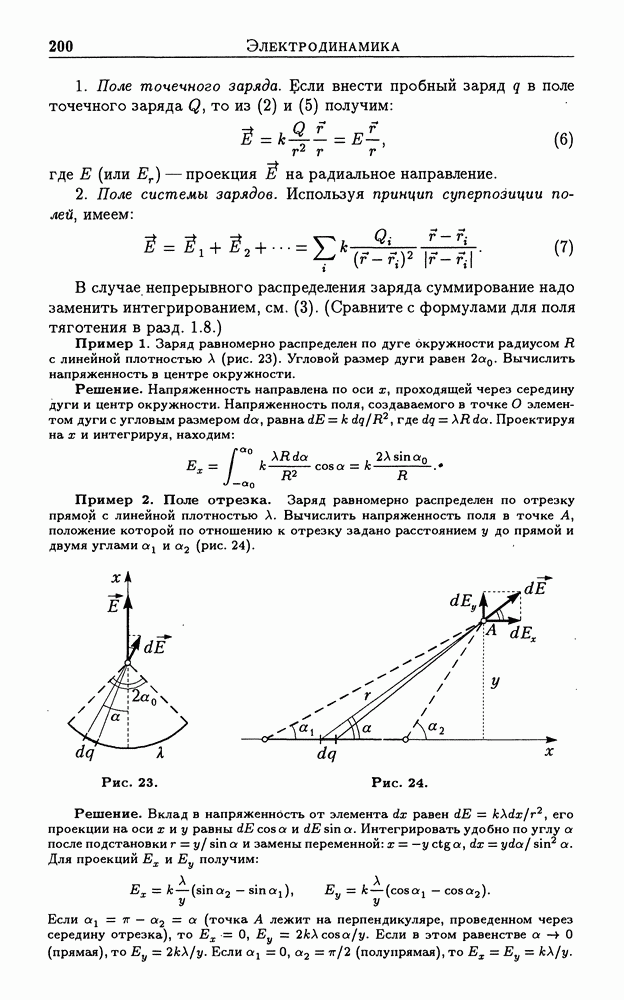
- 3.1. Электрический заряд. Закон Кулона
- 3.2. Электрическое поле. Напряженность поля
- 3.3. Электростатическое поле. Принцип суперпозиции для напряженности и потенциала
- 3.4. Теорема Гаусса
- 3.5. Электростатика проводников
- 3.6. Электростатика диэлектриков
- 3.7. Конденсаторы
- 3.8. Энергия электростатического поля
- 3.9. Постоянный ток
- 3.10. Магнитное поле. Сила Лоренца и закон Ампера
- 3.11. Вычисление магнитной индукции
- 3.12. Циркуляция и поток вектора магнитной индукции
- 3.13. Магнитное поле в веществе
- 3.14. Электромагнитная индукция
- 3.15. Уравнения Максвелла
- 4. Колебания и волны
- 4.1. Гармонические колебания. Сложение колебаний
- 4.2. Свободные незатухающие колебания
- 4.3. Затухающие и вынужденные колебания
- 4.4. Упругие волны
- 4.5. Электромагнитные волны
- 5. Оптика
- 5.1. Геометрическая оптика. Фотометрия
- 5.2. Интерференция света
- 5.3. Дифракция
- 5.4. Поляризация света. Формулы Френеля
- 5.5. Дисперсия и поглощение света
- 5.6. Тепловое излучение
- 5.7. Световые кванты
- Список литературы
- 1. Кинематика
- 1.1. Кинематика точки
- 1.2. Кинематика твердого тела
- 1.3. Плоскопараллельное движение твердого тела
- 1.4. Произвольное движение твердого тела
- 1.5. Сложное движение точки
- 2. Основные понятия и аксиомы механики
- 2.2. Аксиомы механики
- 3. Статика
- 3.2. Условия уравновешенности систем сил, приложенных к твердому телу
- 3.3. Решение задан статики
- 3.4. Центр параллельных сил. Центр тяжести твердого тела
- 3.5. Распределенные силы
- 3.6. Законы трения (законы Кулона)
- 4. Динамика материальной точки
- 4.2. Первая и вторая задачи динамики
- 5. Общие теоремы динамики механической системы
- 5.2. Теорема о движении центра масс
- 5.3. Теорема об изменении количества движения
- 5.4. Теорема об изменении кинетического момента
- 5.5. Теорема об изменении кинетической энергии
- 6. Принцип Даламбера. Элементы аналитической механики
- 6.2. Классификация механических связей. Обобщенные координаты
- 6.3. Принцип возможных перемещений
- 6.4. Общее уравнение динамики (принцип Даламбера — Лагранжа)
- 6.5. Уравнения Лагранжа второго рода
- 1. Основные понятия
- 1.1. Введение. Внешние и внутренние силы
- 1.2. Напряжения и деформации в точке
- 1.3. Основные понятия и допущения
- 2. Напряженно-деформированное состояние в точке
- 2.2. Одноосное растяжение и сжатие
- 2.3. Чистый сдвиг
- 3. Центральное растяжение и сжатие
- 3.2. Напряжения и деформации при растяжении или сжатии
- 3.3. Расчеты на прочность при растяжении и сжатии
- 4. Кручение
- 4.2. Напряжения и деформации при кручении
- 4.3. Расчеты на прочность при кручении
- 5. Прямой изгиб
- 5.2. Напряжения и деформации при прямом чистом изгибе
- 5.3. Напряжения и деформации при прямом поперечном изгибе
- 5.4. Расчет на прочность при прямом изгибе
- 6. Сложное сопротивление
- 6.2. Внецентренное растяжение или сжатие
- 6.3. Изгиб с кручением
- 7. Устойчивость сжатых стержней
- 7.2. Формула Эйлера
- 7.3. Влияние способов закрепления концов стержня на величину критической силы
- 7.4. Пределы применимости формулы Эйлера
- 7.5. Расчеты сжатых стержней на устойчивость
- ПРИЛОЖЕНИЯ
- 1. Элементарные функции и их свойства
- 2. Таблица неопределенных интегралов
- 3. Решения обыкновенных дифференциальных уравнений
- 4. Ортогональные криволинейные системы координат
- 5. Некоторые физические постоянные