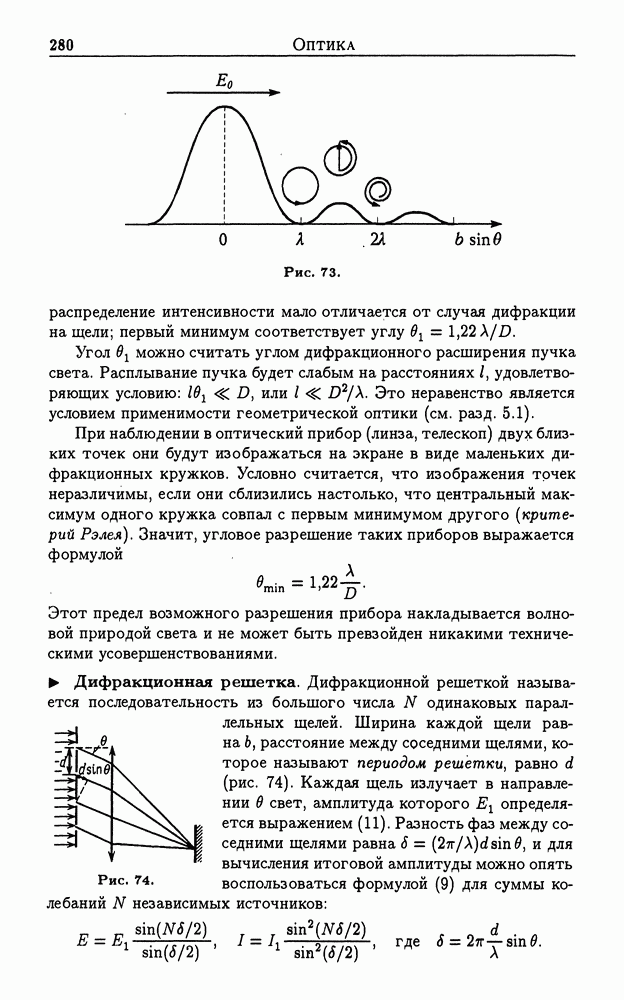
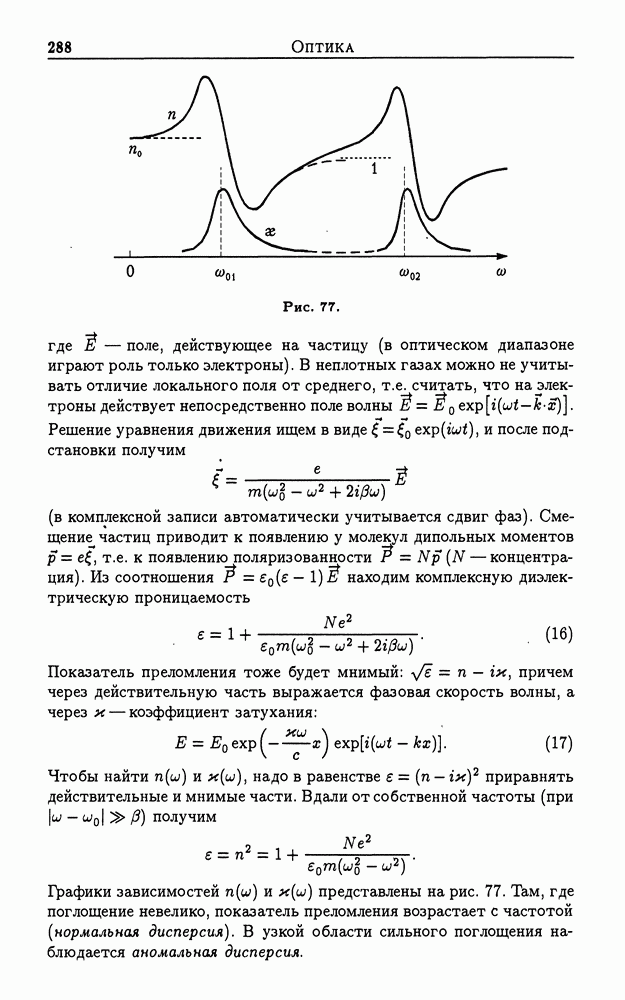
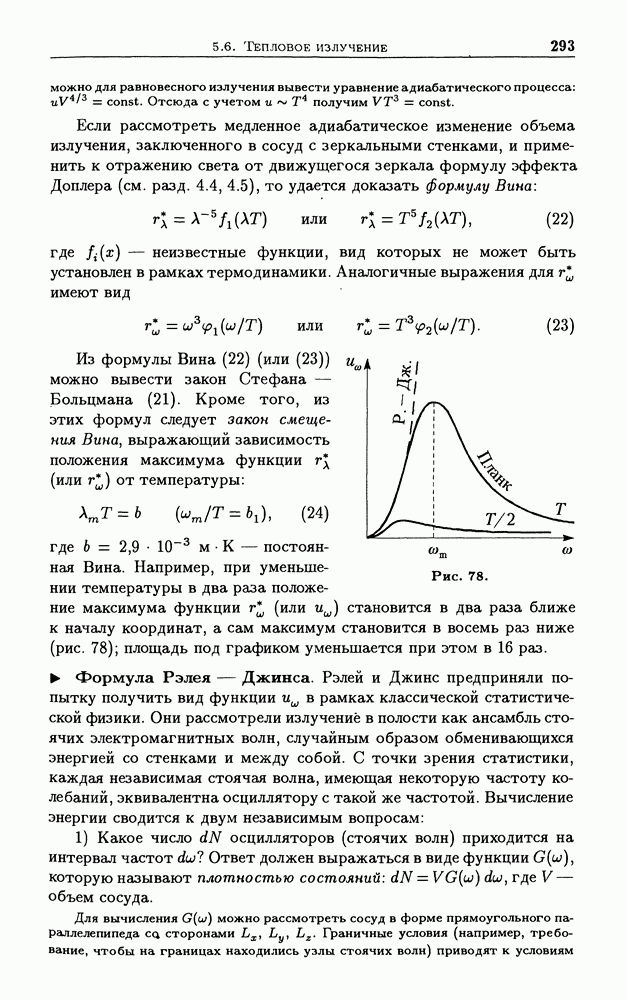
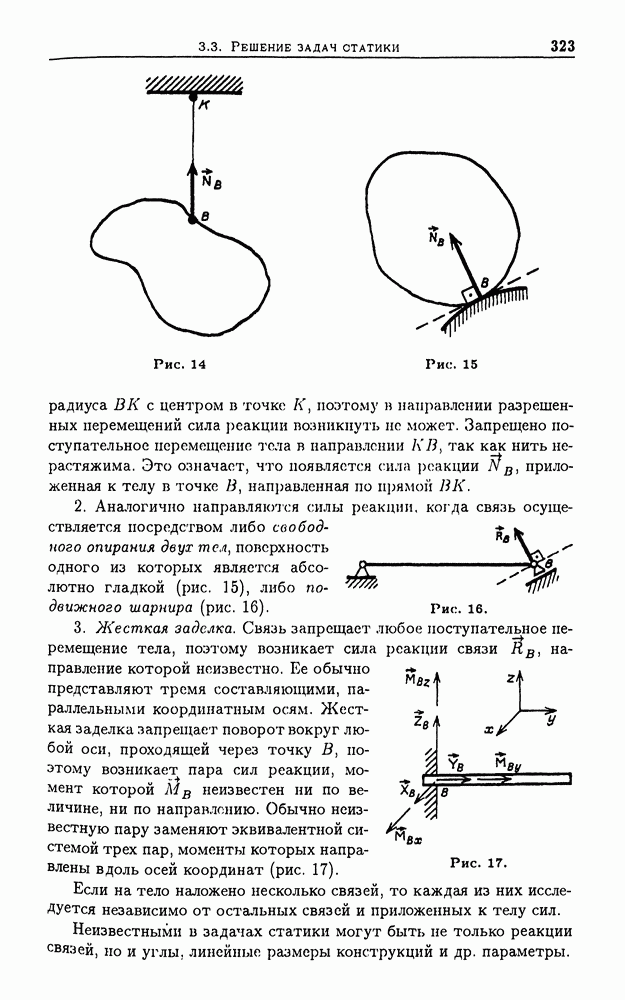
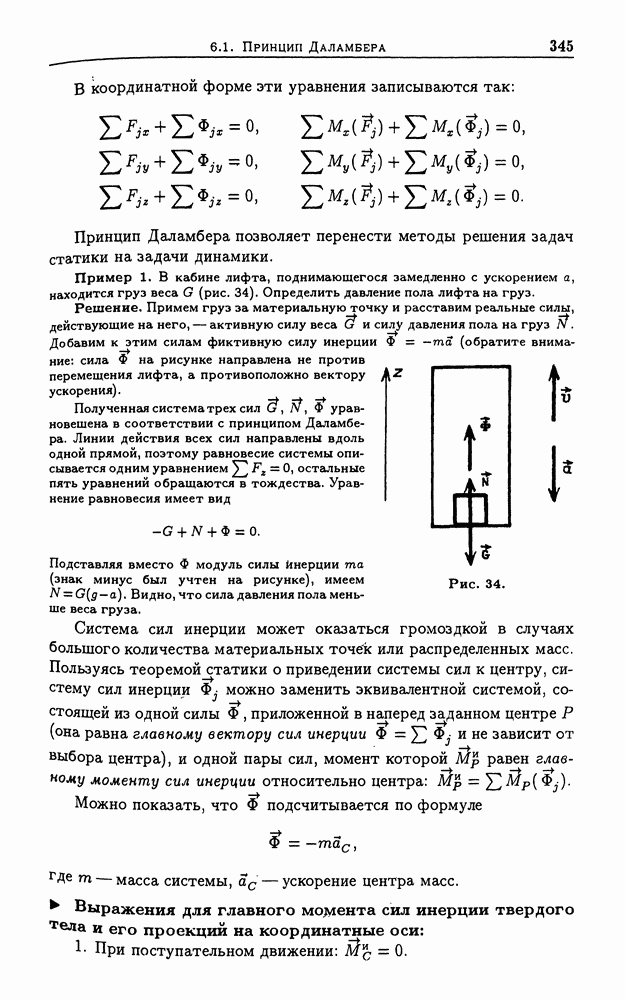
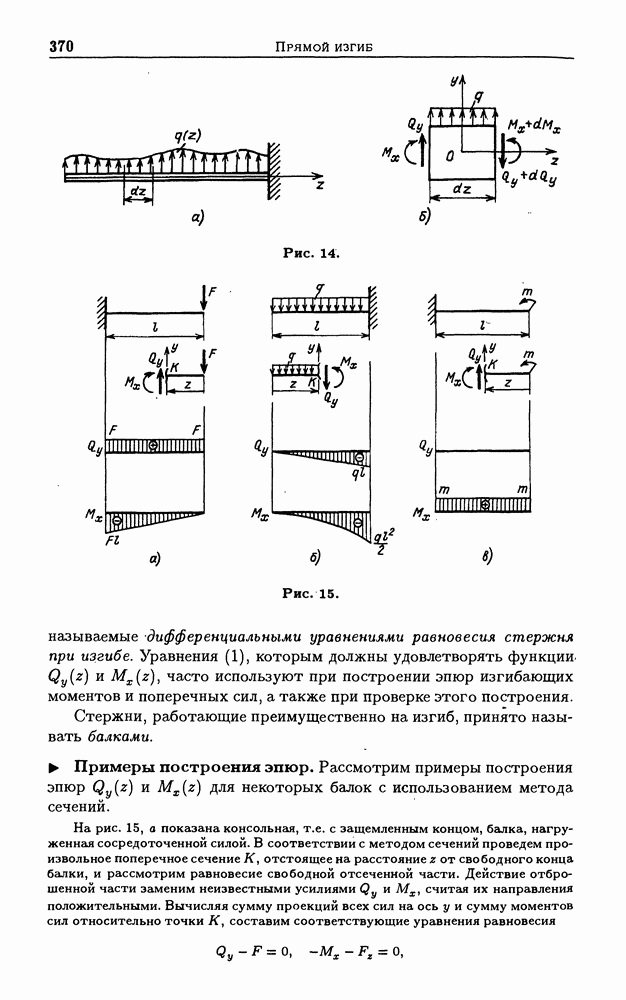
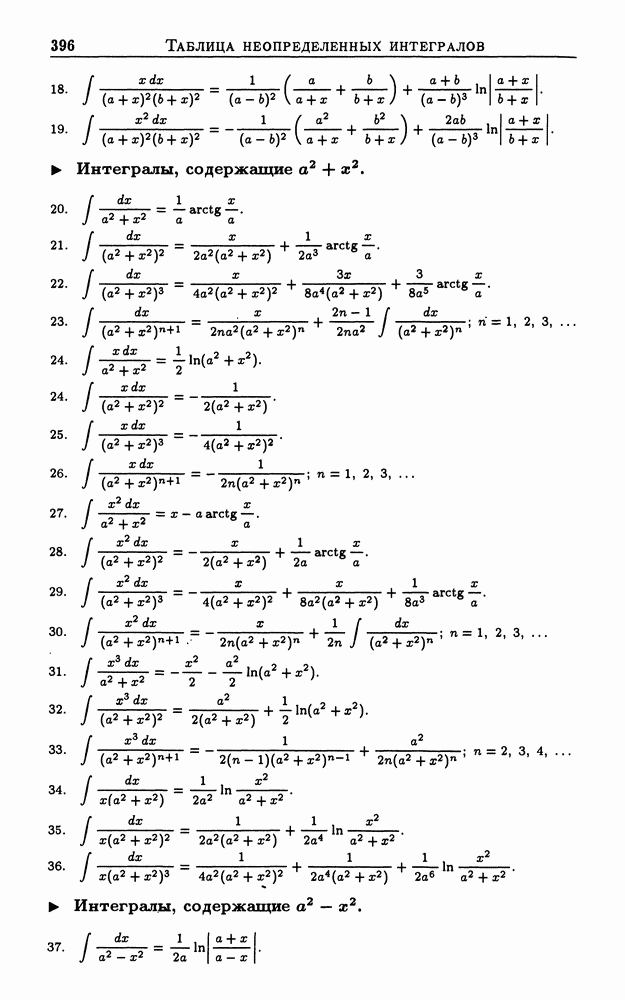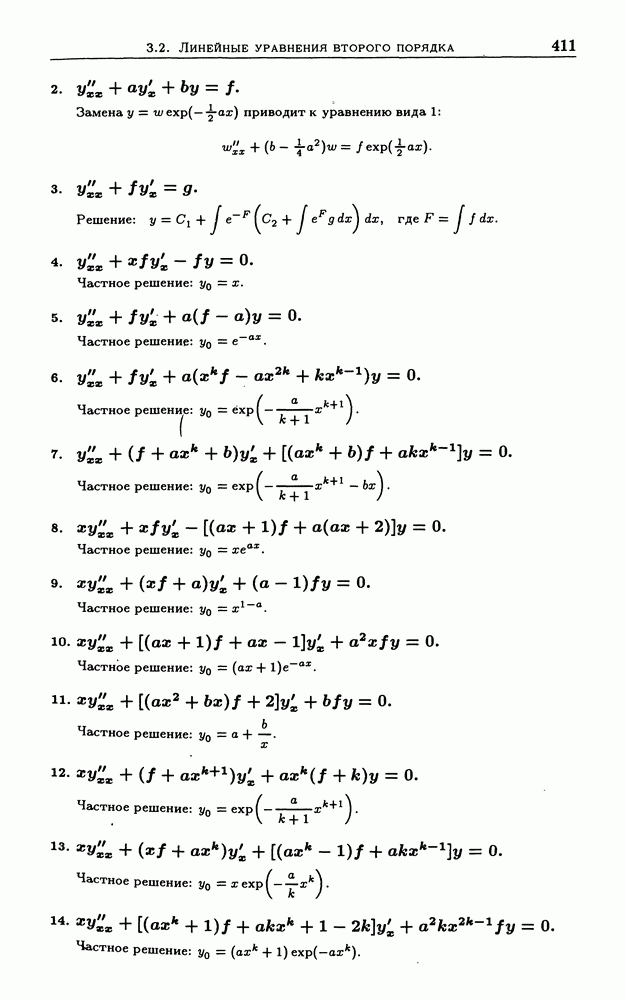| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
5.2. Интерференция света
Когерентность световых волн. При наложении световых волн, обладающих очень высокой частотой колебаний, можно наблюдать только усредненную по времени энергию колебаний, которую характеризуют интенсивностью колебаний  При сложении двух колебаний
При сложении двух колебаний  получим
получим  где
где  называют интерференционным членом. Если
называют интерференционным членом. Если  то пучки света называют некогерентными. Волны, поляризованные во взаимно перпендикулярных направлениях, всегда некогерентны. Монохроматические волны являются когерентными только в том случае, если остается постоянной их разность фаз (т.е. их частоты совпадают) и если они параллельно (или почти параллельно) поляризованы. При наложении таких волн
то пучки света называют некогерентными. Волны, поляризованные во взаимно перпендикулярных направлениях, всегда некогерентны. Монохроматические волны являются когерентными только в том случае, если остается постоянной их разность фаз (т.е. их частоты совпадают) и если они параллельно (или почти параллельно) поляризованы. При наложении таких волн

где  — разность фаз колебаний в данной точке. В частном случае при
— разность фаз колебаний в данной точке. В частном случае при  имеем
имеем  Для синфазных колебаний:
Для синфазных колебаний:  Для колебаний
Для колебаний  противофазе:
противофазе: 
Интерференция двух волн. При наложении двух плоских волн  получим
получим  Поверхности постоянной разности фаз представляют собой плоскости, перпендикулярные вектору
Поверхности постоянной разности фаз представляют собой плоскости, перпендикулярные вектору  Расстояние между соседними плоскостями с максимальной интенсивностью равно
Расстояние между соседними плоскостями с максимальной интенсивностью равно

где а — угол между векторами  При малых а получим
При малых а получим  Если в области перекрытия волн поставить плоский экран, параллельный
Если в области перекрытия волн поставить плоский экран, параллельный  то на нем будут наблюдаться параллельные чередующиеся темные и светлые полосы.
то на нем будут наблюдаться параллельные чередующиеся темные и светлые полосы.
При наложении сферических волн от двух синфазных точечных источников условие максимума интенсивности  порядка имеет вид
порядка имеет вид  (это уравнение гиперболоида вращения с осью, проходящей через источники). При размещении экрана параллельно этой оси получим светлые и темные полосы в виде гипербол. Если расстояние до экрана
(это уравнение гиперболоида вращения с осью, проходящей через источники). При размещении экрана параллельно этой оси получим светлые и темные полосы в виде гипербол. Если расстояние до экрана  велико по сравнению с расстоянием
велико по сравнению с расстоянием  между источниками, то в центре экрана получим равноотстоящие почти параллельные полосы. Расстояние между полосами будет такое же, как в опыте Юнга, где интерференция создается двумя параллельными линейными источниками когерентного света. Если х — расстояние от некоторой точки экрана до его центра (рис. 64), то
между источниками, то в центре экрана получим равноотстоящие почти параллельные полосы. Расстояние между полосами будет такое же, как в опыте Юнга, где интерференция создается двумя параллельными линейными источниками когерентного света. Если х — расстояние от некоторой точки экрана до его центра (рис. 64), то  и при
и при  получим для разности хода
получим для разности хода  где а
где а  — угол, под которым источник виден из центра экрана. Интенсивность меняется от
— угол, под которым источник виден из центра экрана. Интенсивность меняется от  при
при  до нуля при
до нуля при  Расстояние между полосами равно
Расстояние между полосами равно 

Рис. 64.
На большом расстоянии от двух синфазных линейных источников  можно написать
можно написать  где в — угол между нормалью к плоскости источников и направлением наблюдения интерференции (приближение Фраунгофера). Амплитуды колебаний в интерферирующих волнах можно считать одинаковыми, т.е.
где в — угол между нормалью к плоскости источников и направлением наблюдения интерференции (приближение Фраунгофера). Амплитуды колебаний в интерферирующих волнах можно считать одинаковыми, т.е.  Максимумы интерференции наблюдаются под углами, удовлетворяющими соотношению
Максимумы интерференции наблюдаются под углами, удовлетворяющими соотношению 

Рис. 65.
Интерференция большого числа волн.
Рассмотрим интерференцию от  одинаковых синфазных источников, расположенных на одной прямой на расстоянии
одинаковых синфазных источников, расположенных на одной прямой на расстоянии  друг от друга. На большом расстоянии от источников
друг от друга. На большом расстоянии от источников  в направлении в происходит сложение
в направлении в происходит сложение  колебаний одинаковой амплитуды
колебаний одинаковой амплитуды  причем разность фаз между соседними колебаниями равна
причем разность фаз между соседними колебаниями равна  Результирующую амплитуду А найдем из уравнений (см. векторную диаграмму на рис. 65):
Результирующую амплитуду А найдем из уравнений (см. векторную диаграмму на рис. 65):  Исключая радиус описанной окружности
Исключая радиус описанной окружности  , получим:
, получим:

Интерференция от естественных источников света. Излучение естественный (тепловых) источников света состоит из множества цугов волн) спонтанно испущенных возбужденными атомами при их высвечивании, т.е. при возвращении в нормальное состояние. Длительность цуга  , он содержит
, он содержит  колебаний. Значит, два разных естественных источника некогерентны даже при выделении в их излучении узкой спектральной полосы, поскольку разность фаз колебаний очень быстро и хаотически меняется в каждой точке наблюдения. Для наблюдения интерференции надо излучение от одного источника расщепить на два или несколько пучков и заставить их попадать в точку наблюдения различными путями. При этом будет происходить интерференция каждого из цугов с самим собой, и условие максимума или минимума будет одновременно выполняться для всех цугов одной частоты, испущенных из одной и той же точки источника. Удобно ввести оптическую разность хода пучков
колебаний. Значит, два разных естественных источника некогерентны даже при выделении в их излучении узкой спектральной полосы, поскольку разность фаз колебаний очень быстро и хаотически меняется в каждой точке наблюдения. Для наблюдения интерференции надо излучение от одного источника расщепить на два или несколько пучков и заставить их попадать в точку наблюдения различными путями. При этом будет происходить интерференция каждого из цугов с самим собой, и условие максимума или минимума будет одновременно выполняться для всех цугов одной частоты, испущенных из одной и той же точки источника. Удобно ввести оптическую разность хода пучков

где интегрирование ведется вдоль линии, которую данный пучок проходит от точки излучения до точки интерференции. Условие максимума:  условие минимума:
условие минимума:  где
где  называется порядком интерференции.
называется порядком интерференции.
Приведем классические примеры получения двух когерентных источников.
1. Опыт Юнга (упоминался выше). Солнечный свет падает на очень узкую щель в первом экране, вследствие дифракции расходится и падает на две узкие щели во втором экране. Опять же из-за дифракции после этих щелей свет расходится и образует перекрывающиеся когерентные пучки.
2. Зеркала Френеля. Свет от ярко светящейся щели падает на два зеркала, скрещенных под углом почти 180°. Близко расположенные мнимые изображения щели образуют два когерентных источника.
3. Бипризма Френеля. Свет от ярко освещенной щели преломляется в двух стеклянных призмах с малыми преломляющими углами, сложенных своими основаниями. В результате преломления образуются два близко расположенных мнимых изображения щели.
4. Билинза Бийе. Собирающая линза разрезается пополам и половинки слегка раздвигаются. Билинза освещается узкой щелью, параллельной линии разреза. Каждая половинка линзы формирует свое действительное изображение щели.
5. Зеркало Ллойда. Свет от узкой щели отражается от зеркальной плоскости, образуя мнимое изображение щели. Интерферируют свет от самой щели и от ее изображения.
Влияние размеров источника. Пространственная когерентность. Разность хода лучей в данной точке экрана имеет определенное значение только в случае точечного источника. При переходе от одной точки протяженного источника к другой разность хода меняется. Если разность хода изменится на  то условие максимума превратится в условие минимума, т. е. наложение интерференционных картин от разных участков протяженного источника приводит к смазыванию общей интерференционной картины.
то условие максимума превратится в условие минимума, т. е. наложение интерференционных картин от разных участков протяженного источника приводит к смазыванию общей интерференционной картины.
Рассмотрим, например, плоский источник. Предположим, что первый из интерферирующих лучей исходит от источника под углом  к его нормали, а второй — под углом
к его нормали, а второй — под углом  Пусть эти лучи лежат в одной плоскости с нормалью, а углы излучения почти одинаковы для всех точек источника (рис. 66). При переходе от одного конца источника к другому длина пути первого луча изменится на
Пусть эти лучи лежат в одной плоскости с нормалью, а углы излучения почти одинаковы для всех точек источника (рис. 66). При переходе от одного конца источника к другому длина пути первого луча изменится на  второго — на
второго — на  — размеры Источника в плоскости лучей), а разность хода изменится на
— размеры Источника в плоскости лучей), а разность хода изменится на 

Рис. 66.
Условие сохранения интерференционной картины (условие пространственной когерентности) принимает вид

Пример 1. В опыте Юнга  — ширина щели в первом экране,
— ширина щели в первом экране,  где
где  — расстояние между щелями во втором экране,
— расстояние между щелями во втором экране,  — расстояние между экранами; получим:
— расстояние между экранами; получим:  т.е.
т.е.  Перепишем эту формулу в виде:
Перепишем эту формулу в виде:  где
где  — угловые размеры источника, или угол расхождения падающих на две щели лучей. Например, при прямом освещении щелей Солнцем
— угловые размеры источника, или угол расхождения падающих на две щели лучей. Например, при прямом освещении щелей Солнцем  рад,
рад,  нм, т.е. расстояние между щелями должно быть меньше 0,06 мм. Именно поэтому надо сначала солнечный свет пропускать через узкую щель.
нм, т.е. расстояние между щелями должно быть меньше 0,06 мм. Именно поэтому надо сначала солнечный свет пропускать через узкую щель. 
Влияние немонохроматичности света. Временная когерентность. Нарушение монохроматичности складывающихся волн может привести к смазыванию картины интерференции. Предположим, что частоты излучаемых волн лежат в узком спектральном интервале  Сильное искажение картины интерференции происходит в том случае, если разность хода
Сильное искажение картины интерференции происходит в том случае, если разность хода  превышает некоторое критическое значение
превышает некоторое критическое значение  которое называют длиной когерентности;
которое называют длиной когерентности;  имеет смысл длины цуга волн) испускаемого атомом в одном акте излучения (напомним, что устойчивая интерференция происходит при сложении цугов в одном из разделенных пучков с соответствующими им цугами в другом пучке). Время
имеет смысл длины цуга волн) испускаемого атомом в одном акте излучения (напомним, что устойчивая интерференция происходит при сложении цугов в одном из разделенных пучков с соответствующими им цугами в другом пучке). Время  которое называют временем когерентности, имеет смысл длительности цуга волн. В соответствии с общими свойствами преобразования Фурье, спектральная ширина волнового пакета связана с его длительностью соотношением
которое называют временем когерентности, имеет смысл длительности цуга волн. В соответствии с общими свойствами преобразования Фурье, спектральная ширина волнового пакета связана с его длительностью соотношением  (Пример: «оборванная» синусоида
(Пример: «оборванная» синусоида  , где
, где
 в интервале
в интервале  вне этого интервала, имеет разложение Фурье
вне этого интервала, имеет разложение Фурье  ширина которого равна
ширина которого равна  Максимальный порядок спектра, в котором можно наблюдать интерференцию, можно оценить как
Максимальный порядок спектра, в котором можно наблюдать интерференцию, можно оценить как  .
.
Интерференция в тонких пленках. Рассмотрим интерференцию лучей, отраженных от передней и задней поверхностей тонкой пленки (рис. 67). Будем считать фронт волны плоским, т.е. источник достаточно удаленными. Так как фронт преломленной волны перпендикулярен лучу, то луч 1 в точке D и луч 2 в точке  имеют одинаковые фазы. Значит, оптическая разность хода лучей в точке
имеют одинаковые фазы. Значит, оптическая разность хода лучей в точке  равна
равна 

Рис. 67.
Кроме того, к разности хода надо добавить  что позволит учесть изменение фазы на
что позволит учесть изменение фазы на  при отражении от среды с большим показателем преломления (на границе воздух — пленка в точке
при отражении от среды с большим показателем преломления (на границе воздух — пленка в точке  После преобразований получим:
После преобразований получим:

где  — толщина пленки,
— толщина пленки,  — ее показатель преломления. Условие максимума для наблюдения в отраженном свете
— ее показатель преломления. Условие максимума для наблюдения в отраженном свете  выполняется для определенных длин волн. Для очень тонких пленок условию максимума удовлетворяют одна или две длины волны из видимого диапазона, и пленка оказывается окрашенной. Условию максимума для наблюдения в отраженном свете соответствует для той же длины волны условие минимума для наблюдения в проходящем свете (отражений на границе воздух — пленка не происходит). Как всегда при интерференции, энергия не увеличивается, а перераспределяется.
выполняется для определенных длин волн. Для очень тонких пленок условию максимума удовлетворяют одна или две длины волны из видимого диапазона, и пленка оказывается окрашенной. Условию максимума для наблюдения в отраженном свете соответствует для той же длины волны условие минимума для наблюдения в проходящем свете (отражений на границе воздух — пленка не происходит). Как всегда при интерференции, энергия не увеличивается, а перераспределяется.
Рассмотрим теперь два важных случая.
1) Полосы равной толщины. Если лучи падают под почти постоянным углом, например нормально, а толщина пленки меняется, то линии постоянной толщины есть линии постоянной разности хода. При освещении монохроматическим светом эти линии будут видны в виде темных или светлых полос. При наблюдении в белом свете (при условии малой толщины пленки) линии будут цветными. Интерференция происходит вблизи поверхности пленки (интерференционная картина локализована на поверхности).
2) Полосы равного наклона. Толщина пленки постоянна, освещение ведется рассеянным светом от удаленного источника. Меняя угол наблюдения, мы будем получать то условие максимума, то минимума.
Интерференционная картина локализована на бесконечности (или в фокальной плоскости линзы). Для очень тонких пленок свет может быть не монохроматичным, наблюдение под данным углом выделяет ту длину волны, для которой выполнено условие максимума.
Пример 2. Кольца Ньютона. Бели плосковыпуклую линзу положить на поверхность стеклянной пластинки и освещать монохроматическим светом, падающим нормально, то на воздушном промежутке будут наблюдаться полосы равной толщины, имеющие форму окружностей. Толщина промежутка равна  где
где  — радиус окружности (рис. 68). Условие минимума имеет вид
— радиус окружности (рис. 68). Условие минимума имеет вид  или
или  . В центре картины будет темное пятно.
. В центре картины будет темное пятно.
Принципы голографии. Голография используется для записи объемного изображения предмета. Предмет освещается светом лазера, обладающим очень высокой степенью когерентности, и попадает на фотопластинку. Информацию о форме предмета несет зависимость фазы предметной волны от положения на пластинке. Если на пластинку одновременно со светом, отраженным от предмета, послать отраженный от зеркала опорный лазерный луч, которым освещается предмет, то в результате интерференции образуется волна, амплитуда и интенсивность которой будут зависеть от фазы предметной волны. Так как почернение фотопластинки пропорционально интенсивности, то на ней сохранится информация о фазе волны. Освещая проявленную пластинку светом того же лазера, можно восстановить исходный сигнал.

Рис. 68.
При записи интерференционного сигнала в объеме толстой прозрачной фотопластинки возникает объемная голограмма, которая несет информацию как о форме предмета, так и о длине волны лазерного сигнала. При освещении голограммы белым светом волны других частот гасят друг друга за счет интерференции, и возникает изображение предмета, освещенного монохроматическим лазерным светом. Если в одной пластинке записать три голограммы от лазеров с различными длинами волн, то при освещении белым светом возникает объемное цветное изображение.
Излучение Вавилова — Черенкова. При движении частицы в среде со скоростью V, превышающей фазовую скорость  света в этой среде, возникает излучение электромагнитных волн под определенным углом к направлению движения частицы. Элементарное объяснение этого явления совершенно аналогично объяснению возникновения ударной волны при движении со сверхзвуковой скоростью. При прохождении частицы возникает излучение возбужденных ею атомов среды. Разность хода волн, излученных возбужденными
света в этой среде, возникает излучение электромагнитных волн под определенным углом к направлению движения частицы. Элементарное объяснение этого явления совершенно аналогично объяснению возникновения ударной волны при движении со сверхзвуковой скоростью. При прохождении частицы возникает излучение возбужденных ею атомов среды. Разность хода волн, излученных возбужденными
атомами в направлении в из положений А и В (рис. 69), равна

Если  то для любого угла в можно подобрать такое
то для любого угла в можно подобрать такое  что излучение точек А и В гасит друг друга
что излучение точек А и В гасит друг друга  При
При  то же самое относится к любому углу, не равному
то же самое относится к любому углу, не равному  (можно добиться
(можно добиться  Однако в направлении 60 все точки излучают волны с одной и той же фазой, т.е. происходит взаимное усиление излучения.
Однако в направлении 60 все точки излучают волны с одной и той же фазой, т.е. происходит взаимное усиление излучения.

Рис. 69.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- 1. Аналитическая геометрия на плоскости
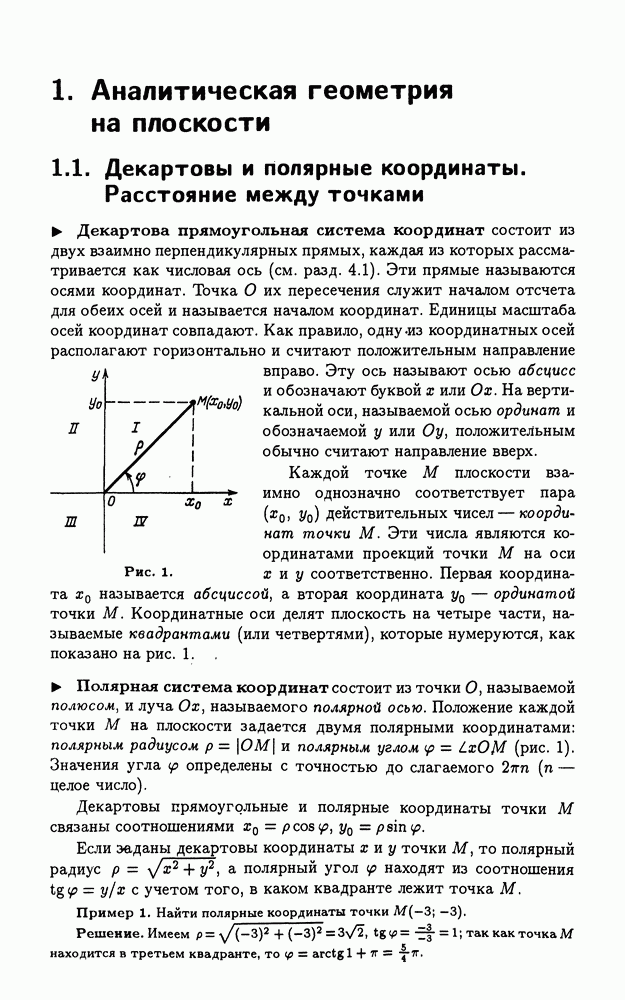
- 1.1. Декартовы и полярные координаты. Расстояние между точками
- 1.2. Деление отрезка в данном отношении. Площадь многоугольника
- 1.3. Различные виды уравнения прямой
- 1.4. Угол между прямыми. Расстояние от точки до прямой
- 1.5. Окружность, эллипс, гипербола и парабола
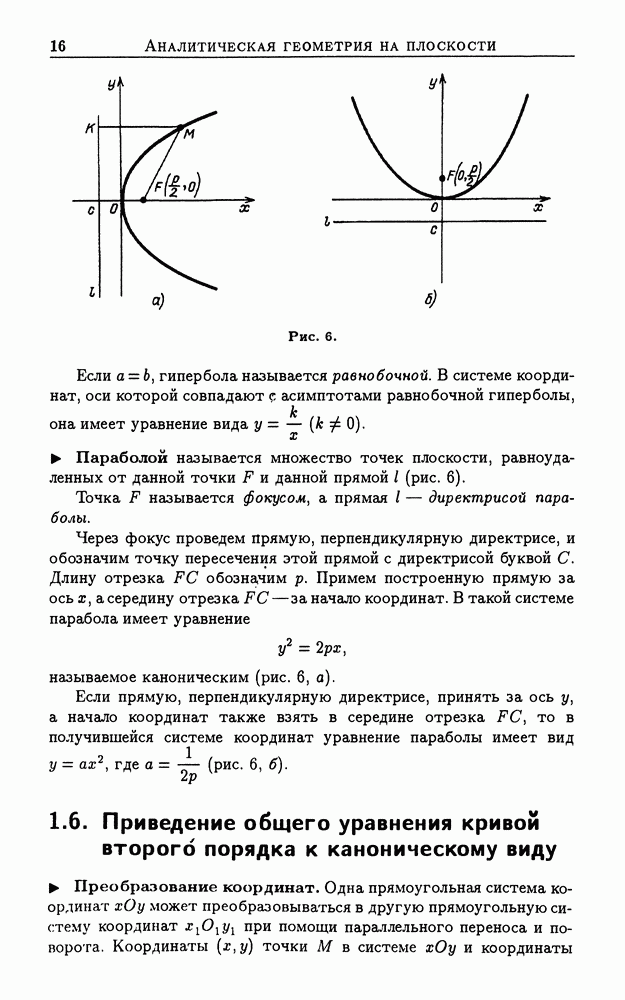
- 1.6. Приведение общего уравнения кривой второго порядка к каноническому виду
- 2. Аналитическая геометрия в пространстве
- 2.2. Векторы
- 2.3. Действия над векторами. Скалярное произведение
- 2.4. Векторное и смешанное произведения
- 2.5. Плоскость в пространстве
- 2.6. Прямая в пространстве
- 2.7. Прямая и плоскость в пространстве
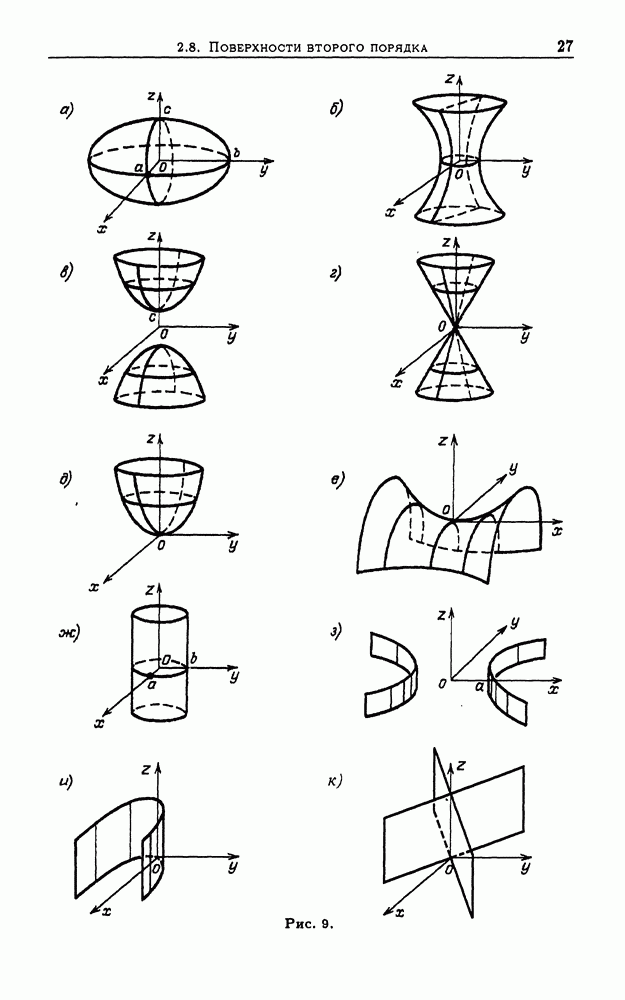
- 2.8. Поверхности второго порядка
- 3. Линейная алгебра
- 3.2. Матрицы
- 3.3. Системы линейных уравнений
- 3.4. Системы n-мерных векторов. Собственные значения и собственные векторы матрицы
- 4. Основные понятия математического анализа
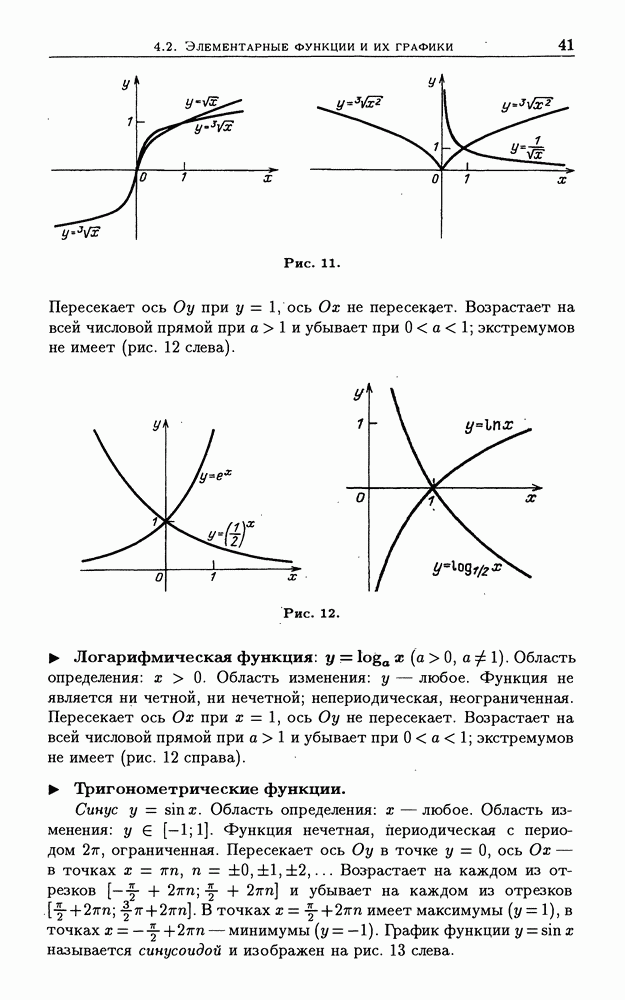
- 4.2. Элементарные функции и их графики
- 4.3. Предел последовательности
- 4.4. Предел функции
- 4.5. Бесконечно малые и бесконечно большие функции
- 4.6. Непрерывность
- 4.7. Асимптоты графика функции
- 5. Дифференциальное исчисление функций одной переменной
- 5.2. Таблица производных и правила дифференцирования
- 5.3. Теоремы о дифференцируемых функциях. Правило Лопиталя
- 5.4. Производные и дифференциалы высших порядков. Формула Тейлора
- 5.5. Экстремумы. Точки перегиба
- 5.6. Общая схема исследования функции и построение графика
- 6. Функции нескольких переменных
- 6.1. Точечные множества. Функции. Предел и непрерывность
- 6.2. Дифференцирование функций нескольких переменных
- 6.3. Производная по направлению. Геометрические приложения
- 6.4. Экстремумы функций нескольких переменных
- 7. Неопределенный интеграл
- 7.1. Первообразная. Неопределенный интеграл и его свойства
- 7.2. Таблица основных интегралов. Примеры интегрирования
- 7.3. Интегрирование по частям. Метод замены переменной
- 7.4. Интегрирование рациональных функций
- 7.5. Интегрирование иррациональных функций
- 7.6. Интегрирование показательных и тригонометрических функций
- 8. Определенный интеграл
- 8.1. Основные определения. Геометрический смысл определенного интеграла
- 8.2. Свойства определенного интеграла
- 8.3. Геометрические и физические приложения определенного интеграла
- 8.4. Несобственные интегралы
- 9. Двойные и тройные интегралы
- 9.1. Определение и свойства двойного интеграла
- 9.2. Вычисление двойного интеграла
- 9.3. Геометрические и физические приложения двойного интеграла
- 9.4. Определение и свойства тройного интеграла
- 9.5. Вычисление тройного интеграла. Некоторые приложения
- 10. Криволинейные и поверхностные интегралы
- 10.2. Криволинейный интеграл второго рода
- 10.3. Поверхностный интеграл первого рода
- 10.4. Поверхностный интеграл второго рода
- 10.5. Дифференциальные операции и интегральные формулы теории поля
- 11. Ряды
- 11.1. Числовые ряды
- 11.2. Функциональные ряды
- 11.3. Степенные ряды
- 11.4. Ряд Фурье
- 11.5. Интеграл Фурье. Преобразование Фурье
- 12. Обыкновенные дифференциальные уравнения
- 12.2. Дифференциальные уравнения высших порядков
- 12.3. Линейные уравнения n-го порядка
- 12.4. Решение линейных однородных уравнений n-го порядка с постоянными коэффициентами
- 12.5. Линейные неоднородные уравнения n-го порядка
- 12.6. Системы обыкновенных дифференциальных уравнений
- 13. Приближенные вычисления
- 13.1. Метод наименьших квадратов
- 13.2. Приближенное решение алгебраических уравнений
- 13.3. Вычисление определенного интеграла
- 13.4. Численное интегрирование дифференциальных уравнений
- 14. Теория вероятностей
- 14.1. Правила и формулы комбинаторики
- 14.2. Основные понятия теории вероятностей
- 14.3. Условная вероятность. Теоремы и формулы теории вероятностей
- 14.4. Математическое ожидание и дисперсия
- 14.5. Закон больших чисел
- 1. Физические основы механики
- 1.1. Кинематика точки
- 1.2. Кинематика твердого тела
- 1.3. Динамика
- 1.4. Закон сохранения импульса
- 1.5. Закон сохранения энергии
- 1.6. Закон сохранения момента импульса
- 1.7. Задана двух тел и движение в центральном поле
- 1.8. Поле тяготения
- 1.9. Неинерциальные системы отсчета
- 1.10. Динамика твердого тела
- 1.11. Специальная теория относительности
- 2. Молекулярная физика и термодинамика
- 2.2. Первое начало термодинамики
- 2.3. Второе начало термодинамики
- 2.4. Энтропия. Свободная энергия
- 2.5. Кинетическая теория идеального газа
- 2.6. Реальные газы. Уравнение Ван-дер-Ваальса
- 2.7. Равновесие фаз. Фазовые переходы
- 2.8. Поверхностное натяжение
- 2.9. Явления переноса в газах
- 3. Электродинамика
- 3.1. Электрический заряд. Закон Кулона
- 3.2. Электрическое поле. Напряженность поля
- 3.3. Электростатическое поле. Принцип суперпозиции для напряженности и потенциала
- 3.4. Теорема Гаусса
- 3.5. Электростатика проводников
- 3.6. Электростатика диэлектриков
- 3.7. Конденсаторы
- 3.8. Энергия электростатического поля
- 3.9. Постоянный ток
- 3.10. Магнитное поле. Сила Лоренца и закон Ампера
- 3.11. Вычисление магнитной индукции
- 3.12. Циркуляция и поток вектора магнитной индукции
- 3.13. Магнитное поле в веществе
- 3.14. Электромагнитная индукция
- 3.15. Уравнения Максвелла
- 4. Колебания и волны
- 4.1. Гармонические колебания. Сложение колебаний
- 4.2. Свободные незатухающие колебания
- 4.3. Затухающие и вынужденные колебания
- 4.4. Упругие волны
- 4.5. Электромагнитные волны
- 5. Оптика
- 5.1. Геометрическая оптика. Фотометрия
- 5.2. Интерференция света
- 5.3. Дифракция
- 5.4. Поляризация света. Формулы Френеля
- 5.5. Дисперсия и поглощение света
- 5.6. Тепловое излучение
- 5.7. Световые кванты
- Список литературы
- 1. Кинематика
- 1.1. Кинематика точки
- 1.2. Кинематика твердого тела
- 1.3. Плоскопараллельное движение твердого тела
- 1.4. Произвольное движение твердого тела
- 1.5. Сложное движение точки
- 2. Основные понятия и аксиомы механики
- 2.2. Аксиомы механики
- 3. Статика
- 3.2. Условия уравновешенности систем сил, приложенных к твердому телу
- 3.3. Решение задан статики
- 3.4. Центр параллельных сил. Центр тяжести твердого тела
- 3.5. Распределенные силы
- 3.6. Законы трения (законы Кулона)
- 4. Динамика материальной точки
- 4.2. Первая и вторая задачи динамики
- 5. Общие теоремы динамики механической системы
- 5.2. Теорема о движении центра масс
- 5.3. Теорема об изменении количества движения
- 5.4. Теорема об изменении кинетического момента
- 5.5. Теорема об изменении кинетической энергии
- 6. Принцип Даламбера. Элементы аналитической механики
- 6.2. Классификация механических связей. Обобщенные координаты
- 6.3. Принцип возможных перемещений
- 6.4. Общее уравнение динамики (принцип Даламбера — Лагранжа)
- 6.5. Уравнения Лагранжа второго рода
- 1. Основные понятия
- 1.1. Введение. Внешние и внутренние силы
- 1.2. Напряжения и деформации в точке
- 1.3. Основные понятия и допущения
- 2. Напряженно-деформированное состояние в точке
- 2.2. Одноосное растяжение и сжатие
- 2.3. Чистый сдвиг
- 3. Центральное растяжение и сжатие
- 3.2. Напряжения и деформации при растяжении или сжатии
- 3.3. Расчеты на прочность при растяжении и сжатии
- 4. Кручение
- 4.2. Напряжения и деформации при кручении
- 4.3. Расчеты на прочность при кручении
- 5. Прямой изгиб
- 5.2. Напряжения и деформации при прямом чистом изгибе
- 5.3. Напряжения и деформации при прямом поперечном изгибе
- 5.4. Расчет на прочность при прямом изгибе
- 6. Сложное сопротивление
- 6.2. Внецентренное растяжение или сжатие
- 6.3. Изгиб с кручением
- 7. Устойчивость сжатых стержней
- 7.2. Формула Эйлера
- 7.3. Влияние способов закрепления концов стержня на величину критической силы
- 7.4. Пределы применимости формулы Эйлера
- 7.5. Расчеты сжатых стержней на устойчивость
- ПРИЛОЖЕНИЯ
- 1. Элементарные функции и их свойства
- 2. Таблица неопределенных интегралов
- 3. Решения обыкновенных дифференциальных уравнений
- 4. Ортогональные криволинейные системы координат
- 5. Некоторые физические постоянные