| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
5.6. Тепловое излучение
Равновесное тепловое излучение. Излучение электромагнитной (лучистой) энергии телом за счет энергии хаотического (теплового) движения его молекул называется тепловым излучением. Свойства теплового излучения определяются материалом тела и его температурой. Если из любого материала сделать замкнутую полость и поддерживать температуру ее стенок постоянной, то система
(стенка  излучение) придет в состояние термодинамического равновесия, и в объеме полости установится равновесное тепловое излучение. Важнейшая особенность равновесного излучения состоит в том, что его свойства полностью определяются температурой стенок и не зависят от их материала. Это утверждение является следствием второго начала термодинамики. Кроме того, равновесное излучение однородно и изотропно.
излучение) придет в состояние термодинамического равновесия, и в объеме полости установится равновесное тепловое излучение. Важнейшая особенность равновесного излучения состоит в том, что его свойства полностью определяются температурой стенок и не зависят от их материала. Это утверждение является следствием второго начала термодинамики. Кроме того, равновесное излучение однородно и изотропно.
Основные характеристики как излучения с поверхности тела, так и излучения в объеме были введены в разд. 5.1. Излучение с поверхности характеризуется энергетической яркостью В и энергетической светимостью  равной количеству лучистой энергии, излученной с единицы поверхности за единицу времени по всем направлениям (т.е. в телесный угол
равной количеству лучистой энергии, излученной с единицы поверхности за единицу времени по всем направлениям (т.е. в телесный угол  Вводятся также спектральные разложения энергетической светимости
Вводятся также спектральные разложения энергетической светимости  например,
например,  величины
величины  называются излучательными способностями тела. Излучение в объеме характеризуется интенсивностью лучистого потока I и объемной плотностью лучистой энергии и, а также их спектральными разложениями. В случае изотропного излучения они связаны соотношением
называются излучательными способностями тела. Излучение в объеме характеризуется интенсивностью лучистого потока I и объемной плотностью лучистой энергии и, а также их спектральными разложениями. В случае изотропного излучения они связаны соотношением  Освещенность Е определяется как полный лучистый поток через единичную площадку со всех направлений (из телесного угла
Освещенность Е определяется как полный лучистый поток через единичную площадку со всех направлений (из телесного угла  ); в случае изотропного излучения выполняются соотношения
); в случае изотропного излучения выполняются соотношения

Спектральные плотности освещенности Е обозначим  Пересчет от одной спектральной характеристики к другой обсуждается в разд. 5.1.
Пересчет от одной спектральной характеристики к другой обсуждается в разд. 5.1.
Поглощательная способность. Закон Кирхгофа. Поглощательной способностью тела называется доля падающей лучистой энергии, поглощенная телом (для узкого интервала длин волн или частот):

Тело, для которого  во всем спектральном интервале, называется абсолютно черным телом. Моделью черного тела может служить замкнутая полость с небольшим отверстием; почти все лучи, попадающие в полость через отверстие, в результате многократных отражений от внутренних стенок оказываются поглощенными. Тело, У которого
во всем спектральном интервале, называется абсолютно черным телом. Моделью черного тела может служить замкнутая полость с небольшим отверстием; почти все лучи, попадающие в полость через отверстие, в результате многократных отражений от внутренних стенок оказываются поглощенными. Тело, У которого  называют серым.
называют серым.
Так как равновесное излучение находится в равновесии с поверхностью, то для любого спектрального интервала количество поглощенной лучистой энергии, равное ехах  должно быть равно количеству излученной энергии, равному
должно быть равно количеству излученной энергии, равному  Поскольку характеристики
Поскольку характеристики
равновесного объемного излучения не зависят от свойств конкретного тела, то отношение излучательной способности любого тела к его поглощательной способности оказывается универсальной функцией длины волны и температуры (закон Кирхгофа):

Поскольку для абсолютно черного тела поглощательная способность равна единице, то стоящая справа функция есть не что иное, как излучательная способность абсолютно черного тела, которую обозначим 

Видно, что излучательная способность абсолютно черного тела и его энергетическая светимость не зависят от способа его изготовления; они связаны с объемной плотностью энергии соотношениями

При одной и той же температуре абсолютно черное тело обладает самой большой излучательной способностью и энергетической светимостью. Например, для серого тела  . Отметим, что поскольку равновесное излучение изотропно, черное тела является ламбертовским источником (см. разд. 5.1).
. Отметим, что поскольку равновесное излучение изотропно, черное тела является ламбертовским источником (см. разд. 5.1).
Законы Стефана — Больцмана и Вина. Излучательная способность абсолютно черного тела при данной температуре стремится к нулю при малых и больших А и достигает максимального значения при некоторой длине волны  которая зависит от температуры. Площадь под кривой
которая зависит от температуры. Площадь под кривой  равна энергетической светимости
равна энергетической светимости  Применение к равновесному излучению в полости общих соотношений термодинамики позволило получить для него ряд общих соотношений. (Температура равновесного теплового излучения считается равной температуре стенок.) Закон Стефана — Больцмана утверждает, что энергетическая светимость абсолютно черного тела пропорциональна четвертой степени температуры:
Применение к равновесному излучению в полости общих соотношений термодинамики позволило получить для него ряд общих соотношений. (Температура равновесного теплового излучения считается равной температуре стенок.) Закон Стефана — Больцмана утверждает, что энергетическая светимость абсолютно черного тела пропорциональна четвертой степени температуры:

где  — постоянная Стефана — Больцмана.
— постоянная Стефана — Больцмана.
Для вывода (21) надо воспользоваться выражением для давления изотропного излучения  (см. разд. 2.5) и формулой
(см. разд. 2.5) и формулой  которая является следствием второго начала термодинамики (разд. 2.3). Подставляя
которая является следствием второго начала термодинамики (разд. 2.3). Подставляя  придем к уравнению
придем к уравнению  откуда получим
откуда получим  Кроме того, из формулы для давления и из первого начала термодинамики
Кроме того, из формулы для давления и из первого начала термодинамики 
можно для равновесного излучения вывести уравнение адиабатического процесса:  Отсюда с учетом и
Отсюда с учетом и  получим
получим 
Если рассмотреть медленное адиабатическое изменение объема излучения, заключенного в сосуд с зеркальными стенками, и применить к отражению света от движущегося зеркала формулу эффекта Доплера (см. разд. 4.4, 4.5), то удается доказать формулу Вина:

где  — неизвестные функции, вид которых не может быть установлен в рамках термодинамики. Аналогичные выражения для
— неизвестные функции, вид которых не может быть установлен в рамках термодинамики. Аналогичные выражения для  имеют вид
имеют вид

Из формулы Вина (22) (или  можно вывести закон Стефана —
можно вывести закон Стефана —
Больцмана (21). Кроме того, из этих формул следует закон смещения Вина, выражающий зависимость положения максимума функции  от температуры:
от температуры:

где  — постоянная Вина. Например, при уменьшении температуры в два раза положение максимума функции
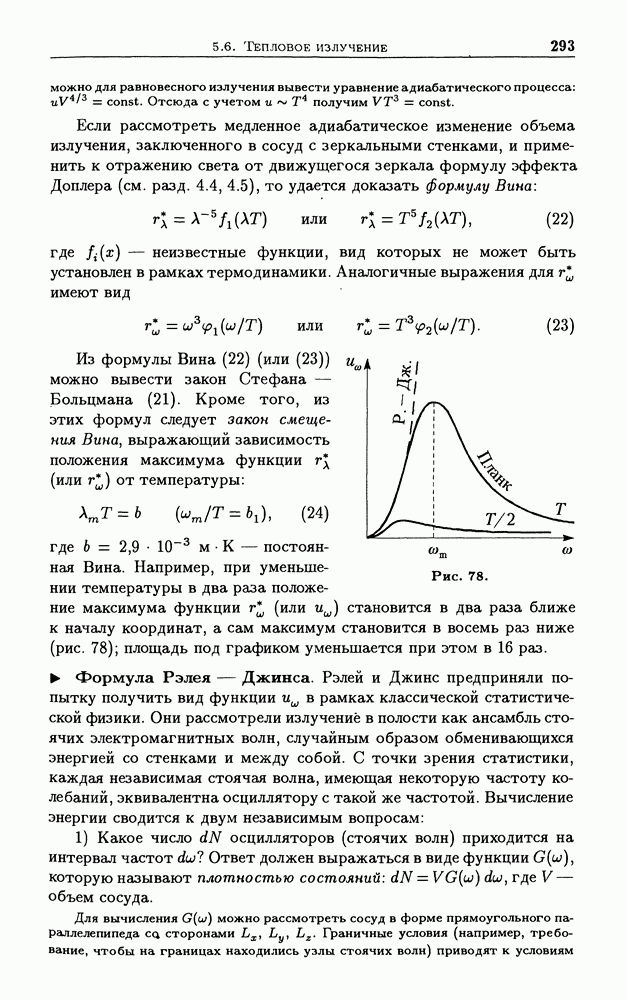
— постоянная Вина. Например, при уменьшении температуры в два раза положение максимума функции  становится в два раза ближе к началу координат, а сам максимум становится в восемь раз ниже (рис. 78); площадь под графиком уменьшается при этом в 16 раз.
становится в два раза ближе к началу координат, а сам максимум становится в восемь раз ниже (рис. 78); площадь под графиком уменьшается при этом в 16 раз.

Рис. 78.
Формула Рэлея — Джинса. Рэлей и Джинс предприняли попытку получить вид функции  в рамках классической статистической физики. Они рассмотрели излучение в полости как ансамбль стоячих электромагнитных волн, случайным образом обменивающихся энергией со стенками и между собой. С точки зрения статистики, каждая независимая стоячая волна, имеющая некоторую частоту колебаний, эквивалентна осциллятору с такой же частотой. Вычисление энергии сводится к двум независимым вопросам:
в рамках классической статистической физики. Они рассмотрели излучение в полости как ансамбль стоячих электромагнитных волн, случайным образом обменивающихся энергией со стенками и между собой. С точки зрения статистики, каждая независимая стоячая волна, имеющая некоторую частоту колебаний, эквивалентна осциллятору с такой же частотой. Вычисление энергии сводится к двум независимым вопросам:
1) Какое число  осцилляторов (стоячих волн) приходится на интервал частот
осцилляторов (стоячих волн) приходится на интервал частот  Ответ должен выражаться в виде функции
Ответ должен выражаться в виде функции  которую называют плотностью состояний:
которую называют плотностью состояний:  где V — объем сосуда.
где V — объем сосуда.
Для вычисления  можно рассмотреть сосуд в форме прямоугольного параллелепипеда
можно рассмотреть сосуд в форме прямоугольного параллелепипеда  сторонами
сторонами  Граничные условия (например, требование, чтобы на границах находились узлы стоячих волн) приводят к условиям
Граничные условия (например, требование, чтобы на границах находились узлы стоячих волн) приводят к условиям
 Значит, в пространстве волновых векторов допустимые состояния соответствуют узлам решетки со сторонами
Значит, в пространстве волновых векторов допустимые состояния соответствуют узлам решетки со сторонами  и объемом ячейки
и объемом ячейки  Объем
Объем  -пространства, соответствующий изменению величины волнового вектора от к до к
-пространства, соответствующий изменению величины волнового вектора от к до к  равен,
равен,  сферического слоя, отсекаемый первым квадрантом). Разделив на объем ячейки, получим число пространственно различных колебаний в интервале
сферического слоя, отсекаемый первым квадрантом). Разделив на объем ячейки, получим число пространственно различных колебаний в интервале  Необходимо также учесть дополнительные степени свободы (в случае электромагнитных волн — два возможных состояния поляризации), которые для общности учтем дополнительным множителем
Необходимо также учесть дополнительные степени свободы (в случае электромагнитных волн — два возможных состояния поляризации), которые для общности учтем дополнительным множителем 
Найдем число состояний на единицу объема:

Эта формула получена из граничных условий и имеет очень общий характер и многочисленные применения. Для перехода к и надо учесть соотношение  Окончательно получим
Окончательно получим

2) Чему равна средняя энергия одного осциллятора? Классическая физика дает следующий ответ (см. разд. 2.2): каждому осциллятору, независимо от его частоты, надо приписать две степени свободы, и в соответствии с теоремой о равнораспределении энергии, средняя энергия каждого осциллятора должна быть равна  , где k — постоянная Больцмана.
, где k — постоянная Больцмана.
В результате таких рассуждений классическая физика приводит к формуле Рэлея—Джинса:

Опыт показывает, что формула Рэлея — Джинса хорошо выполняется на малых частотах (при и  но абсолютно неверна на больших (рис. 78). Действительно, хотя (27) удовлетворяет требованиям, налагаемым на любую возможную функцию формулой Вина (23), но сразу видно, что полученная функция не имеет максимума; она монотонно возрастает, и интеграл
но абсолютно неверна на больших (рис. 78). Действительно, хотя (27) удовлетворяет требованиям, налагаемым на любую возможную функцию формулой Вина (23), но сразу видно, что полученная функция не имеет максимума; она монотонно возрастает, и интеграл  т.е. полная энергия излучения, равен бесконечности! Эта ситуация стала одним из признаков глубокого кризиса классической физики и была названа современниками ультрафиолетовой катастрофой.
т.е. полная энергия излучения, равен бесконечности! Эта ситуация стала одним из признаков глубокого кризиса классической физики и была названа современниками ультрафиолетовой катастрофой.
Формула Планка. Теорема о равнораспределении энергии является следствием того, что классическая энергия осциллятора, пропорциональная квадрату его амплитуды, может принимать любые, в
том числе очень маленькие значения. Согласно квантовой гипотезе Планка энергия осциллятора (отсчитываемая от минимального значения) может принимать только дискретные значения, кратные некоторой величине, зависящей от частоты осциллятора:

Для вычисления средней энергии можно использовать формулу Максвелла—Больцмана (см. разд. 2.5), согласно которой вероятность состояния с энергией  пропорциональна
пропорциональна  . Получаем
. Получаем

Ряд в знаменателе есть просто сумма геометрической прогрессии, а числитель получается из знаменателя дифференцированием по  Проведя вычисления, имеем
Проведя вычисления, имеем

Сравнение с формулой Вина (23) показывает, что  должна быть пропорциональна и:
должна быть пропорциональна и:

где  — универсальная постоянная, называемая постоянной Планка. Так как энергия кванта пропорциональна частоте осциллятора, то при данной температуре колебания высоких частот возбуждаются с очень малой вероятностью и их вклад в энергию излучения оказывается ничтожно малым. Это разрешает проблему ультрафиолетовой катастрофы.
— универсальная постоянная, называемая постоянной Планка. Так как энергия кванта пропорциональна частоте осциллятора, то при данной температуре колебания высоких частот возбуждаются с очень малой вероятностью и их вклад в энергию излучения оказывается ничтожно малым. Это разрешает проблему ультрафиолетовой катастрофы.
После подстановки (30) в формулу для средней энергии получим формулу Планка для спектральной плотности энергии:

График этой функции приведен на рис. 78. Запишем формулу Планка также в переменных  :
:

При  формула Планка переходит в формулу Рэлея — Джинса (27). Из формулы Планка можно получить выражения для постоянных Стефана — Больцмана и Вина через универсальные постоянные:
формула Планка переходит в формулу Рэлея — Джинса (27). Из формулы Планка можно получить выражения для постоянных Стефана — Больцмана и Вина через универсальные постоянные:

Формула Планка очень хорошо согласуется с экспериментом во всем диапазоне частот.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- 1. Аналитическая геометрия на плоскости
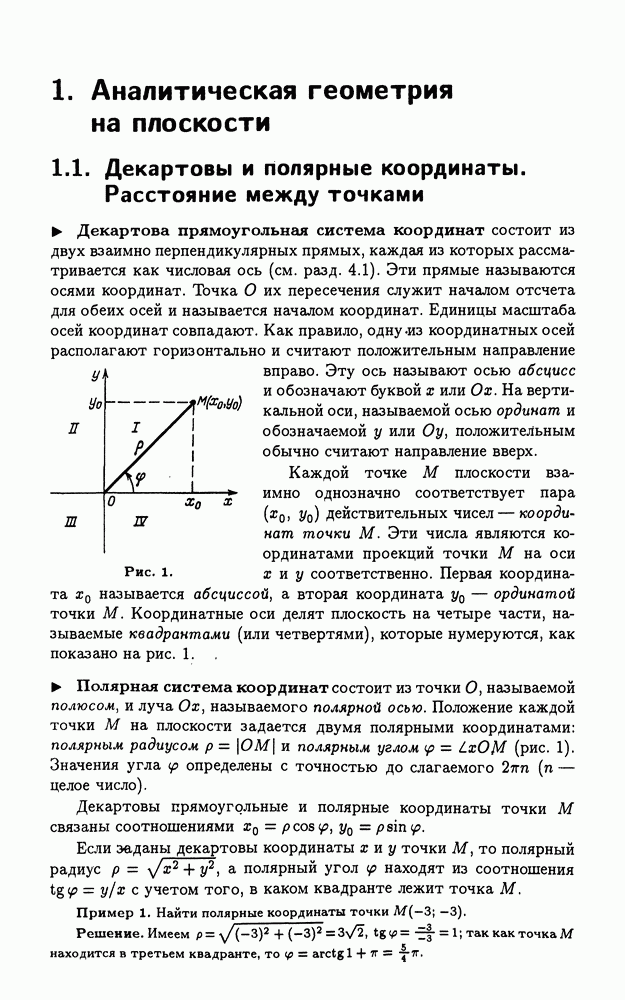
- 1.1. Декартовы и полярные координаты. Расстояние между точками
- 1.2. Деление отрезка в данном отношении. Площадь многоугольника
- 1.3. Различные виды уравнения прямой
- 1.4. Угол между прямыми. Расстояние от точки до прямой
- 1.5. Окружность, эллипс, гипербола и парабола
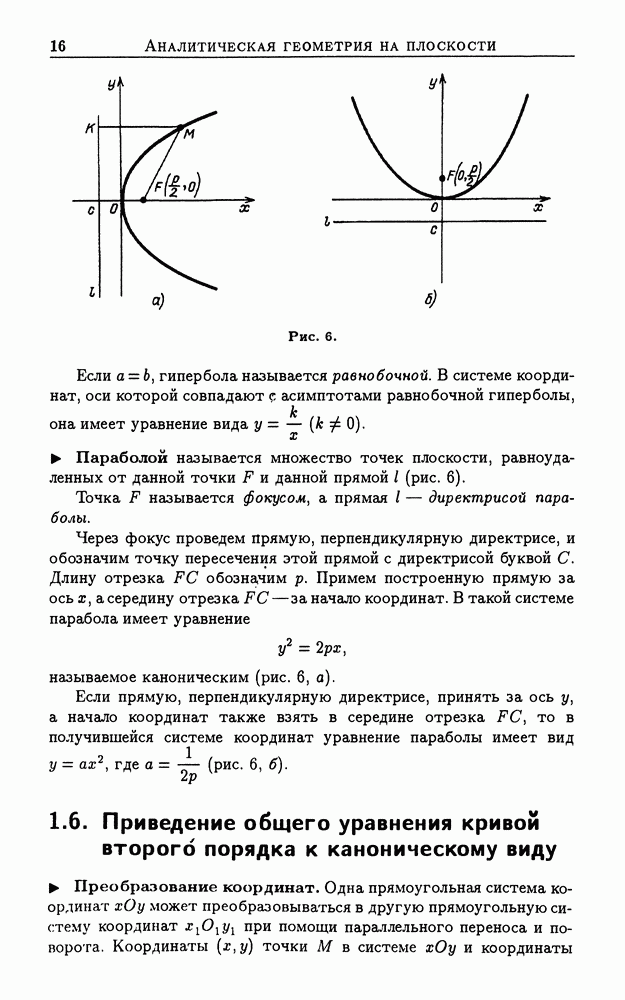
- 1.6. Приведение общего уравнения кривой второго порядка к каноническому виду
- 2. Аналитическая геометрия в пространстве
- 2.2. Векторы
- 2.3. Действия над векторами. Скалярное произведение
- 2.4. Векторное и смешанное произведения
- 2.5. Плоскость в пространстве
- 2.6. Прямая в пространстве
- 2.7. Прямая и плоскость в пространстве
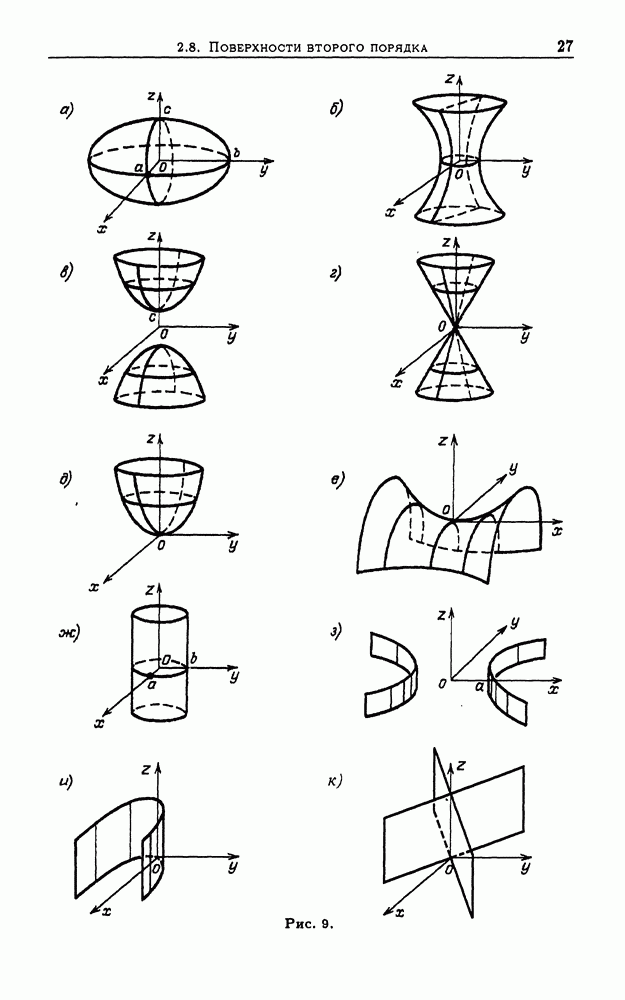
- 2.8. Поверхности второго порядка
- 3. Линейная алгебра
- 3.2. Матрицы
- 3.3. Системы линейных уравнений
- 3.4. Системы n-мерных векторов. Собственные значения и собственные векторы матрицы
- 4. Основные понятия математического анализа
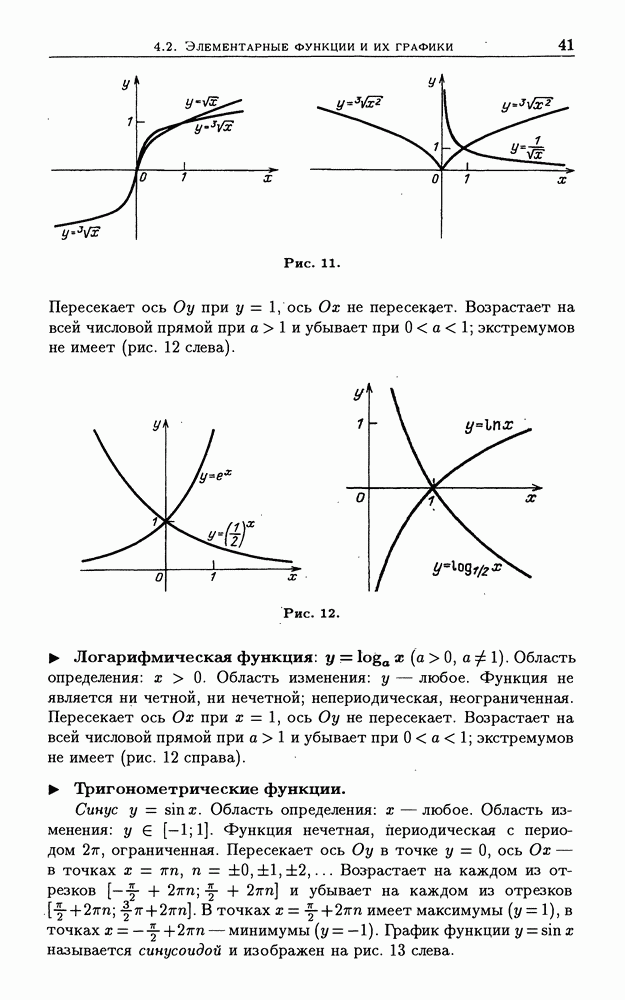
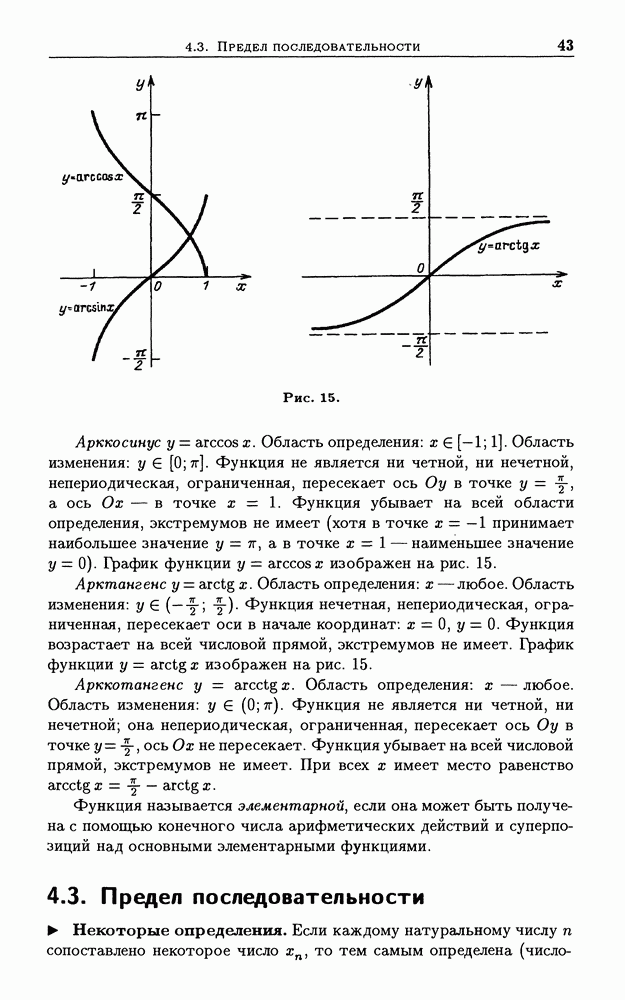
- 4.2. Элементарные функции и их графики
- 4.3. Предел последовательности
- 4.4. Предел функции
- 4.5. Бесконечно малые и бесконечно большие функции
- 4.6. Непрерывность
- 4.7. Асимптоты графика функции
- 5. Дифференциальное исчисление функций одной переменной
- 5.2. Таблица производных и правила дифференцирования
- 5.3. Теоремы о дифференцируемых функциях. Правило Лопиталя
- 5.4. Производные и дифференциалы высших порядков. Формула Тейлора
- 5.5. Экстремумы. Точки перегиба
- 5.6. Общая схема исследования функции и построение графика
- 6. Функции нескольких переменных
- 6.1. Точечные множества. Функции. Предел и непрерывность
- 6.2. Дифференцирование функций нескольких переменных
- 6.3. Производная по направлению. Геометрические приложения
- 6.4. Экстремумы функций нескольких переменных
- 7. Неопределенный интеграл
- 7.1. Первообразная. Неопределенный интеграл и его свойства
- 7.2. Таблица основных интегралов. Примеры интегрирования
- 7.3. Интегрирование по частям. Метод замены переменной
- 7.4. Интегрирование рациональных функций
- 7.5. Интегрирование иррациональных функций
- 7.6. Интегрирование показательных и тригонометрических функций
- 8. Определенный интеграл
- 8.1. Основные определения. Геометрический смысл определенного интеграла
- 8.2. Свойства определенного интеграла
- 8.3. Геометрические и физические приложения определенного интеграла
- 8.4. Несобственные интегралы
- 9. Двойные и тройные интегралы
- 9.1. Определение и свойства двойного интеграла
- 9.2. Вычисление двойного интеграла
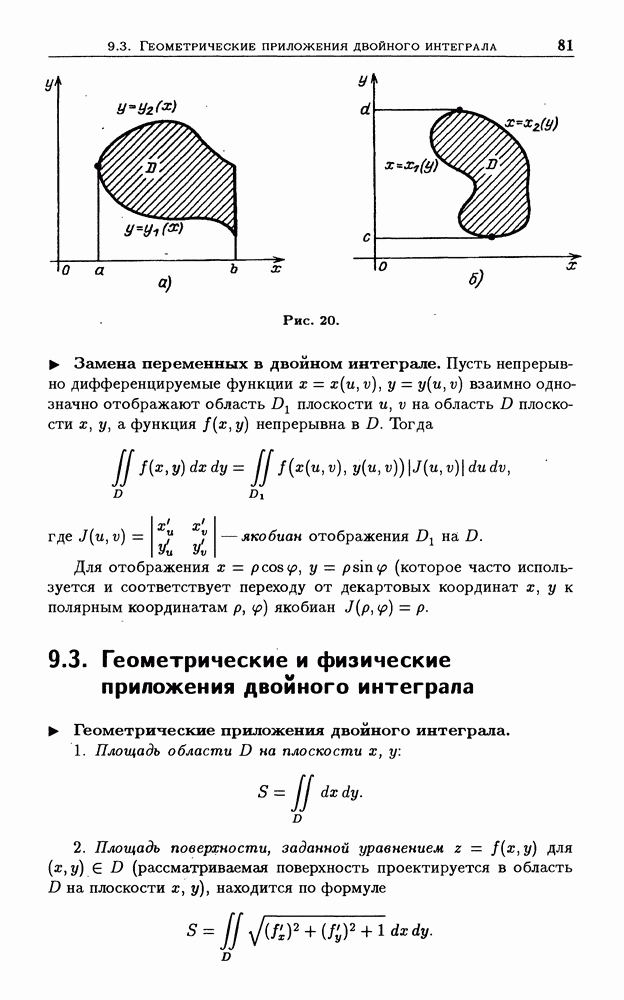
- 9.3. Геометрические и физические приложения двойного интеграла
- 9.4. Определение и свойства тройного интеграла
- 9.5. Вычисление тройного интеграла. Некоторые приложения
- 10. Криволинейные и поверхностные интегралы
- 10.2. Криволинейный интеграл второго рода
- 10.3. Поверхностный интеграл первого рода
- 10.4. Поверхностный интеграл второго рода
- 10.5. Дифференциальные операции и интегральные формулы теории поля
- 11. Ряды
- 11.1. Числовые ряды
- 11.2. Функциональные ряды
- 11.3. Степенные ряды
- 11.4. Ряд Фурье
- 11.5. Интеграл Фурье. Преобразование Фурье
- 12. Обыкновенные дифференциальные уравнения
- 12.2. Дифференциальные уравнения высших порядков
- 12.3. Линейные уравнения n-го порядка
- 12.4. Решение линейных однородных уравнений n-го порядка с постоянными коэффициентами
- 12.5. Линейные неоднородные уравнения n-го порядка
- 12.6. Системы обыкновенных дифференциальных уравнений
- 13. Приближенные вычисления
- 13.1. Метод наименьших квадратов
- 13.2. Приближенное решение алгебраических уравнений
- 13.3. Вычисление определенного интеграла
- 13.4. Численное интегрирование дифференциальных уравнений
- 14. Теория вероятностей
- 14.1. Правила и формулы комбинаторики
- 14.2. Основные понятия теории вероятностей
- 14.3. Условная вероятность. Теоремы и формулы теории вероятностей
- 14.4. Математическое ожидание и дисперсия
- 14.5. Закон больших чисел
- 1. Физические основы механики
- 1.1. Кинематика точки
- 1.2. Кинематика твердого тела
- 1.3. Динамика
- 1.4. Закон сохранения импульса
- 1.5. Закон сохранения энергии
- 1.6. Закон сохранения момента импульса
- 1.7. Задана двух тел и движение в центральном поле
- 1.8. Поле тяготения
- 1.9. Неинерциальные системы отсчета
- 1.10. Динамика твердого тела
- 1.11. Специальная теория относительности
- 2. Молекулярная физика и термодинамика
- 2.2. Первое начало термодинамики
- 2.3. Второе начало термодинамики
- 2.4. Энтропия. Свободная энергия
- 2.5. Кинетическая теория идеального газа
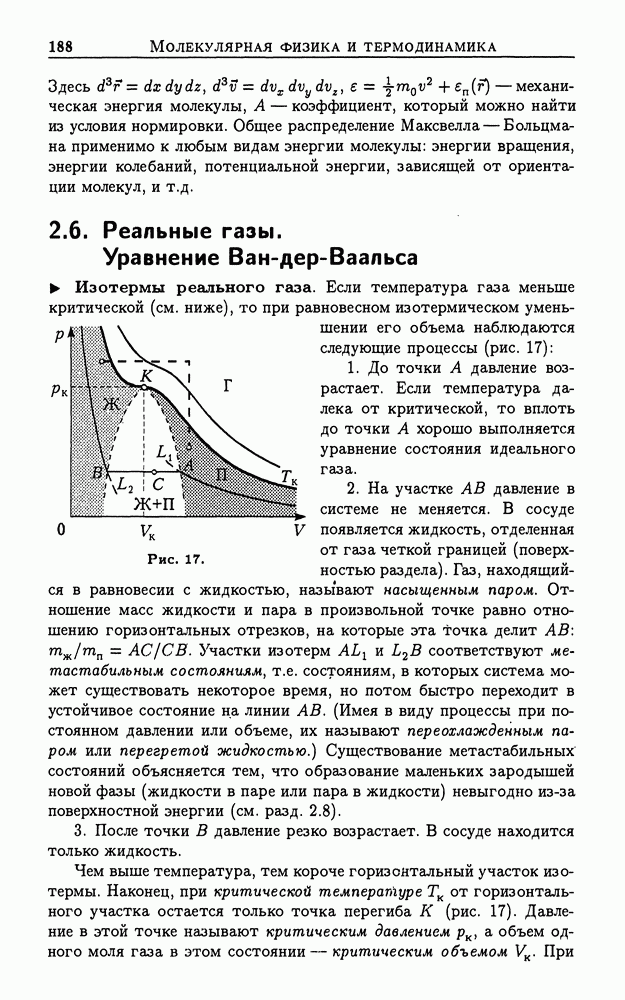
- 2.6. Реальные газы. Уравнение Ван-дер-Ваальса
- 2.7. Равновесие фаз. Фазовые переходы
- 2.8. Поверхностное натяжение
- 2.9. Явления переноса в газах
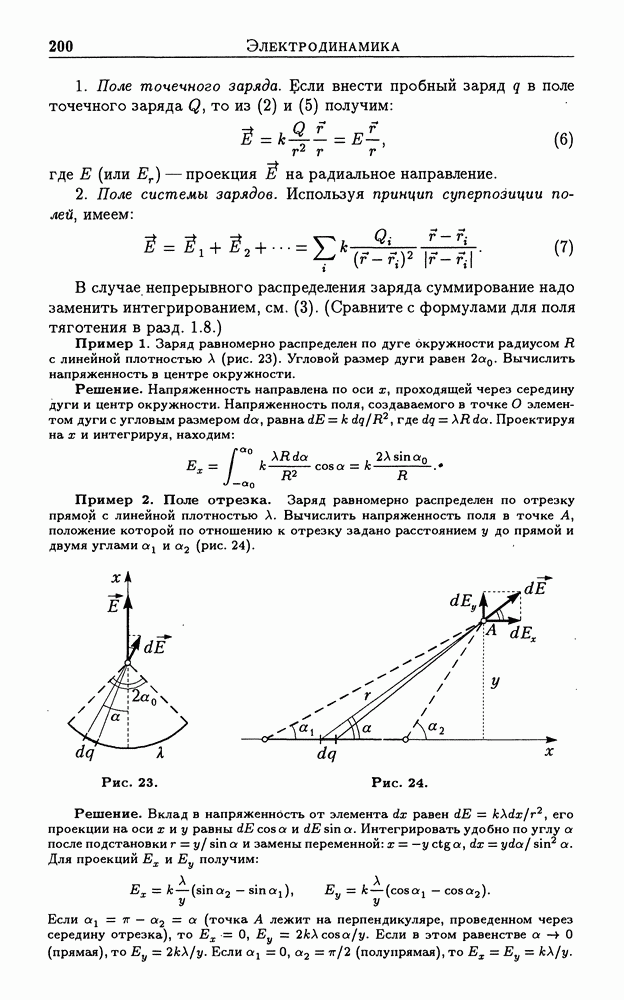
- 3. Электродинамика
- 3.1. Электрический заряд. Закон Кулона
- 3.2. Электрическое поле. Напряженность поля
- 3.3. Электростатическое поле. Принцип суперпозиции для напряженности и потенциала
- 3.4. Теорема Гаусса
- 3.5. Электростатика проводников
- 3.6. Электростатика диэлектриков
- 3.7. Конденсаторы
- 3.8. Энергия электростатического поля
- 3.9. Постоянный ток
- 3.10. Магнитное поле. Сила Лоренца и закон Ампера
- 3.11. Вычисление магнитной индукции
- 3.12. Циркуляция и поток вектора магнитной индукции
- 3.13. Магнитное поле в веществе
- 3.14. Электромагнитная индукция
- 3.15. Уравнения Максвелла
- 4. Колебания и волны
- 4.1. Гармонические колебания. Сложение колебаний
- 4.2. Свободные незатухающие колебания
- 4.3. Затухающие и вынужденные колебания
- 4.4. Упругие волны
- 4.5. Электромагнитные волны
- 5. Оптика
- 5.1. Геометрическая оптика. Фотометрия
- 5.2. Интерференция света
- 5.3. Дифракция
- 5.4. Поляризация света. Формулы Френеля
- 5.5. Дисперсия и поглощение света
- 5.6. Тепловое излучение
- 5.7. Световые кванты
- Список литературы
- 1. Кинематика
- 1.1. Кинематика точки
- 1.2. Кинематика твердого тела
- 1.3. Плоскопараллельное движение твердого тела
- 1.4. Произвольное движение твердого тела
- 1.5. Сложное движение точки
- 2. Основные понятия и аксиомы механики
- 2.2. Аксиомы механики
- 3. Статика
- 3.2. Условия уравновешенности систем сил, приложенных к твердому телу
- 3.3. Решение задан статики
- 3.4. Центр параллельных сил. Центр тяжести твердого тела
- 3.5. Распределенные силы
- 3.6. Законы трения (законы Кулона)
- 4. Динамика материальной точки
- 4.2. Первая и вторая задачи динамики
- 5. Общие теоремы динамики механической системы
- 5.2. Теорема о движении центра масс
- 5.3. Теорема об изменении количества движения
- 5.4. Теорема об изменении кинетического момента
- 5.5. Теорема об изменении кинетической энергии
- 6. Принцип Даламбера. Элементы аналитической механики
- 6.2. Классификация механических связей. Обобщенные координаты
- 6.3. Принцип возможных перемещений
- 6.4. Общее уравнение динамики (принцип Даламбера — Лагранжа)
- 6.5. Уравнения Лагранжа второго рода
- 1. Основные понятия
- 1.1. Введение. Внешние и внутренние силы
- 1.2. Напряжения и деформации в точке
- 1.3. Основные понятия и допущения
- 2. Напряженно-деформированное состояние в точке
- 2.2. Одноосное растяжение и сжатие
- 2.3. Чистый сдвиг
- 3. Центральное растяжение и сжатие
- 3.2. Напряжения и деформации при растяжении или сжатии
- 3.3. Расчеты на прочность при растяжении и сжатии
- 4. Кручение
- 4.2. Напряжения и деформации при кручении
- 4.3. Расчеты на прочность при кручении
- 5. Прямой изгиб
- 5.2. Напряжения и деформации при прямом чистом изгибе
- 5.3. Напряжения и деформации при прямом поперечном изгибе
- 5.4. Расчет на прочность при прямом изгибе
- 6. Сложное сопротивление
- 6.2. Внецентренное растяжение или сжатие
- 6.3. Изгиб с кручением
- 7. Устойчивость сжатых стержней
- 7.2. Формула Эйлера
- 7.3. Влияние способов закрепления концов стержня на величину критической силы
- 7.4. Пределы применимости формулы Эйлера
- 7.5. Расчеты сжатых стержней на устойчивость
- ПРИЛОЖЕНИЯ
- 1. Элементарные функции и их свойства
- 2. Таблица неопределенных интегралов
- 3. Решения обыкновенных дифференциальных уравнений
- 4. Ортогональные криволинейные системы координат
- 5. Некоторые физические постоянные